Poly. - Javapakke til behandling af polynomier
|
|
|
- Eva Thomsen
- 8 år siden
- Visninger:
Transkript
1 Poly - Javapakke til behandling af polynomier z 3 x y x 2 3 x -3 Skrevet af Susanne Nykjær Knudsen, John Thystrup Jensen, Jens Lykke Brandt, Troels C. Damgaard, Jacob W. Winther og Mikkel Bundgaard Vejleder: Jørgen Larsen Naturvidenskabelig Basisuddannelse 4. semester Forår 2 Roskilde UniversitetsCenter
2 Abstract Formålet med dette projekt er at udvikle en Javapakke, der udfører aritmetiske funktioner på polynomier og undersøger forholdet mellem datastruktur og problemløsning. Javapakken baserer sin interne repræsentation på en datastruktur foreslået af Donald E. Knuth. Denne træstruktur er blevet anvendt, selvom vi fandt visse begrænsninger under programudviklingen. Disse begrænsninger har vi analyseret, og i perspektiveringen har vi foreslået en forbedret datastruktur til repræsentation af polynomier. De aritmetiske funktioner, der er implementeret i pakken er addition, subtraktion, multiplikation, division, integration, differentiation, eksponentialisering og negering. Desuden er der lavet en parser for at tilbyde en bruger af pakken et enkelt brugerinterface, hvori der anvendes tekststrenge til repræsentation af polynomier. Derudover har vi inkluderet en grafisk udskrift af datastrukturen via HTML. Konklusionen er, at det er muligt at lave en korrekt fungerende Javapakke, som kan anvendes til polynomieregning. Ydermere konkluderes det, at udformningen af datastrukturen har en stor effekt på problemløsningen, da det i høj grad er datastrukturen, som sætter rammerne for disse løsninger. English Title: Java-package for polynomial handling. - -
3 Indholdsfortegnelse. Indledning Definition på et polynomium Polynomium Led i polynomium Brugervejledning Beskrivelse af metoderne Datastruktur Beskrivelse af træstrukturen Variable og konstanter Konstant Variable Traversering i strukturen Isolering af ét led Design af programpakke Implementering af design i Java Problemstillinger under implementering af brøker Beskrivelse af enkelte klasser Klassen SuperToNode Klassen Node Klassen Konstant Klassen Variabel Klassen InternPolynomim Klassen Polynomium Parsing Problemstilling Overvejelser Krav til syntaks Hvad skal vores algoritme kunne gøre Parsing af simple udtryk Parsing af mere avancerede udtryk Matematiske udtryk, der indeholder parenteser Matematiske udtryk, der indeholder multiplikation Syntaksdiagrammer Fejlfinding Opsamling på parsing Fremtidige udvidelser af parsing Vigtige ikke-matematiske metoder i pakken Metoden checkchars() Formål Algoritmebeskrivelse Metoden copy() Formål Algoritmebeskrivelse Metoden genererled() Formål Algoritmebeskrivelse Anvendelsen af genererled() tostring() Formål Algoritmebeskrivelse printtohtml() Formål Algoritmebeskrivelse Matematiske Metoder Metoden Addition() Formål
4 9..2. Algoritmebeskrivelse Knuths additionsalgoritme Metoden multiply() Formål Algoritmebeskrivelse Division Formål Forbehold Algoritmebeskrivelse Integration Formål Algoritmebeskrivelse Differentiation Formål Algoritmebeskrivelse Negate Formål Algoritmebeskrivelse Subtract Formål Algoritmebeskrivelse polyexp Formål Algoritmebeskrivelse Afprøvning Opstilling af ækvivalensklasser for ét polynomium Afprøvning af matematiske metoder Opsummering af afprøvningsresultater Diskussion af afprøvning Analyse af datastrukturen Datastrukturens begrænsninger Undersøgelse af problemstillingerne Konklusion på analysen af datastrukturen Konklusion Perspektivering Et udtømt videnskabeligt område? Idé til ændret datastruktur Litteraturliste: Bilag printtohtml eksempler Bilag 2 Afprøvningsresultat
5 Forord Udgangspunktet for dette projekt er en fælles interesse for repræsentation og løsning af problemstillinger ved datalogiske metoder. Ideen stammer fra et af mange projektforslag stillet af Keld Helsgaun på datalogis hjemmeside. Forslaget omhandler en implementering af en Java-pakke til behandling af polynomier. Keld Helsgaun nævner samtidig en reference til The Art of Computer Programming, Vol. skrevet af Donald E. Knuth. På et par sider præsenterer Knuth en datastruktur til repræsentation af et flerleddet polynomium med et vilkårligt antal variable og angiver desuden i pseudokode en algoritme, der kan addere to sådant repræsenterede polynomier. Vi fik indledende en håndsrækning af Keld Helsgaun, der trak et gammelt projekt, skrevet over netop denne ide, frem af gemmerne. Dette projekt En Simula-klasse til Polynomium manipulation (Langberg, Finn og Peter Nielsen, 983) gav os først og fremmest et overblik over de mange muligheder, der var for funktionaliteter i en sådan Java-pakke. Det primære fokus har gennem hele processen været rettet mod den strukturerede udvikling og implementering af selve algoritmerne på den valgte datastruktur. Dette fokus ses også tydeligt i den færdige rapport. Vi har desuden forsøgt, igennem hele forløbet at forholde os kritiske og analyserende i forhold til både datastruktur og algoritmedesign. Det har resulteret i et langt udviklingsforløb, men har også bidraget til større forståelse for de valg og begrænsninger, man kan støde ind i, i forbindelse med datalogisk analyse og modellering. Vi vil gerne takke følgende personer: Vores vejleder Jørgen Larsen for at hjælpe os på vej, selv om han ikke fik meget fra os at arbejde med i starten af forløbet. Henrik Legind Larsen for hjælp og ideer på flere kritiske tidspunkter i forløbet. Vores opponentgruppe for kritisk gennemlæsning og gode diskussioner. Keld Helsgaun for at inspirere til et lærerigt og udfordrende projekt. Sidst, men ikke mindst Finn Langberg og Peter Nielsen, hvis rapport også har givet os et indblik i, hvordan man kan dokumentere et datalogisk udviklingsprojekt. Se
6 . Indledning Dette projekt handler først og fremmest om datalogisk modellering og samspillet mellem datastrukturer og de algoritmer, der virker på dem. Vi har valgt at undersøge dette eksemplarisk i forhold til en konkret matematisk problemstilling. Dvs. idéen er, via udviklingen af funktionelt program, at lade dette understøtte en undersøgelse og analyse af en række datalogiske problemstillinger. Vi har i projektforløbet bl.a. stødt ind i en konkret problemstilling, der satte fokus på specielt de afgrænsninger, en defineret datastruktur kan give på problemløsning i forhold til den konkrete situation. Anvendelsen af datalogiske metoder til løsning af en problemstilling kræver i første omgang en datalogisk repræsentation af problemstillingen. Dvs. valg af en datastruktur, der kan repræsentere de kritiske data. Dernæst følger udviklingen og implementeringen af algoritmer, der løser problemerne på den valgte datastruktur. Sidst kræves en oversættelse og en fortolkning af de løsninger, algoritmerne udformer, så en løsning på den oprindelige ( virkelige ) problemstilling opnås. Dvs. den løsning, der ligger i datastrukturen(e) efter programkørsel, skal præsenteres for brugeren - selvfølgelig på en form, der er umiddelbart forståelig i forhold til den referenceramme, problemstillingen udstikker. Vi har valgt et velkendt og umiddelbart enkelt matematisk problem; beregning af resultater af aritmetiske operationer med polynomier. Dette stemmer overens med vores ønsker om at fokusere på problemerne i det datalogiske domæne. For at en computer skal kunne arbejde med et polynomium, skal det oversættes til en repræsentation, som er nem for computeren at arbejde med. En tekststreng er i princippet den enkleste entydige repræsentation af et polynomium. Det er den repræsentation, vi mennesker normalt sætter lig med et polynomium (selv om man ikke kan sige, at en notation er lig det matematiske udtryk, den beskriver) Vi har set meget enkle løsninger baseret direkte på tekststrengs-formen. I første omgang mener vi simpelthen ikke, at denne repræsentation er datalogisk pæn, og den er dermed heller ikke hensigtsmæssig i forhold til vores overordnede formål at lære noget om datalogisk modellering og samspillet mellem datastrukturer og algoritmer! For os mennesker er det let at overskue og finde f.eks. to ens led, hvis koefficienter skal adderes i en polynomieaddition, hvilket ikke er tilfældet for en computer. En fornuftig repræsentation vil derfor forsøge, at skabe det overblik over polynomiet, der gør det muligt for den hurtigere at finde og fortolke de rette elementer. I en tekststreng vil det være nødvendigt at gennemløbe hele strukturen før man med sikkerhed kan sige noget om forekomsten af ensartede led. En repræsentation, som ofte er hensigtsmæssig for en computer, er et træ eller en hægtet liste. Begge disse repræsentationer har den fordel, at de er dynamiske. De har den fordel, fremfor f.eks. et statisk array, at hvis man har brug for at indsætte et element midt i datastrukturen under programkørsel, behøver man blot at ændre i et par referencer i stedet for at skulle flytte alle de resterende elementer et felt frem. Vi har også set et eksempel på anvendelsen af en cirkulær enkelt-hægtet liste som datastruktur. Denne datastruktur havde det problem, at nok var den dynamisk mht. tilføjelsen af flere led, men den var ikke dynamisk i forhold til tilføjelsen af nye variable. Den krævede en eksplicit angivelse af de benyttede variable. Vi har i dette projekt valgt en datastruktur skitseret af Donald E. Knuth fra Stanford University. Denne datastruktur er beskrevet i hans bog The Art of Computer Programming (knuth 973), og tilføjer denne fleksibilitet mht. antallet af variable. Denne datastruktur er, som vi vil komme nærmere ind på i afsnittet Datastruktur, på en måde en sammenbygning af de to ovennævnte repræsentationsformer træer og hægtede lister. Den datastruktur, vi har valgt til repræsentation af et polynomium er rig i den forstand, at den er specialiseret til problemet, og vi mener, at den fanger de essentielle træk i forhold til problemstillingen. Vi har med andre ord valgt denne fremfor en række mere simple, der for det første kunne være for simple i forhold til vores overordnede mål om, at løse problemstillingen datalogisk smukt, og for det andet kunne lægge begrænsninger på datastrukturens dynamik. Vi har valgt, at arbejde med sproget Java, der er det sprog vi primært kommer til at anvende på overbygningen på Datalogi på RUC. Desuden tilbyder det en enkel måde, at distribuere kode på - som en Javapakke, der i princippet er en samling metoder, der kan anvendes i andre programmer med det interface, der tilbydes, uden at skulle bekymre sig om, hvordan funktionaliteten inden i pakken er. For at indpakke den datalogiske problemløsning i forhold til en programmør, der ønsker at bruge pakken (og i tråd med god objektorienteret tankegang), har vi desuden valgt, at lade den interne repræsentation være skjult inde i en pakke, der tilbyder et letforståeligt interface at arbejde med. Helt enkelt har vi valgt, at input og output skal være i form af tekststrenge. - 5-
7 Vi vil løbende forsøge at dokumentere og begrunde de valg, vi tager i design og implementering, og vi har valgt i et separat analyse-afsnit, med udgangspunkt i ønsket om at udvide problemstillingen til også at medtage negative eksponenter, at diskutere Knuths datastruktur og de begrænsninger selv denne rige datastruktur medfører. Dette leder frem til en problemformulering, som lyder - Problemformulering Med udgangspunkt i den valgte datastruktur, ønsker vi at udvikle en Java pakke til matematiske manipulationer med polynomier. Dermed ønskes følgende problemstillinger løst: - Implementering af datastrukturen - Udvikling/implementering af algoritmer, som udfører aritmetiske operationer baseret på denne datastruktur Endvidere ønskes pakken anvendt med tekststrenge og til dette formål skal følgende problemer løses - Udvikling af en algoritme, som parser en tekststreng til datastrukturen - Udvikling af en algoritme, som udskriver et polynomium som tekststreng. Vi vil desuden udfra en konkret problemstilling, der som nævnt gav fokus til de afgrænsninger en defineret datastruktur kan give på problemløsning, vurdere den valgte datastruktur som repræsentationsform for polynomier og give et bud på, hvordan den opståede problemstilling kunne afhjælpes ved at modificere datastrukturen. Målgruppe Projektets målgruppe er i første omgang dataloger og matematikere med interesse for samspillet mellem datastrukturer og algoritmer. Projektet anvender i udstrakt grad datalogisk terminologi specielt indenfor softwareudvikling. Det er en fordel at have programmeringserfaring i objektorienterede sprog. Rapportens opbygning Vi starter i rapporten med give en matematisk definition på et polynomium. I den efterfølgende brugervejledning gives et overblik over pakkens funktionaliteter. Dette afsnit håber vi både kan fungere som en hjælp til en programmør, der ønsker at anvende vores pakke, og derudover som et indledende overblik over de metoder, der senere vil blive gennemgået grundigere i metodebeskrivelserne. Inden metodebeskrivelserne er der en grundig gennemgang af den datastruktur, som vi anvender til intern repræsentation af et polynomium. Herefter følger afsnit om designet af Javapakken og den senere implementering af denne datastruktur i Java. I metodebeskrivelserne starter vi med at beskrive parsingen af tekststrenge til polynomier efterfulgt af de ikkematematiske metoder i pakken. Vi anvender både i dette afsnit og i det følgende om de matematiske metoder flowcharts og kodeudsnit som forklarende værktøjer. I det efterfølgende afprøvningsafsnit forsøger vi med systematiske tests (der er vedlagt i Bilag 2 Afprøvningsresultat at afprøve pakkens funktionalitet, og i afsnittet Analyse af datastrukturen præsenterer vi en række overvejelser omkring datastrukturen og dens begrænsninger. Vi viser i perspektiveringen et alternativt forslag til en datastruktur, som kan repræsentere polynomier. Vi har valgt, at vedlægge hele koden i en separat bilagsrapport så man har mulighed for at referere til denne under læsning af rapporten. Vi forestiller os, at det kan være hjælpsomt i at følge med i koden, ved læsning af flowcharts. Desuden er koden tilgængelig i digital form på
8 2. Definition på et polynomium I dette afsnit vil vi give en kort matematisk definition på et polynomium. Denne definition er anvendt af Donald E. Knuth 2, og vi anvender den direkte som grundlag for vores program. Det skal dog bemærkes, at vi arbejder med rationelle koefficienter og heltalseksponenter > (det første er en udvidelse fra Knuth). 2.. Polynomium Vi definerer et polynomium af flere variable, som en sum af flere delpolynomier. Dette kan angives: g j j n x e j j Definition hvor x j er en variabel for j>. For j= er x j =. Det gælder ligeledes, at =e <e < <e n og at g j er et polynomium, der kun indeholder variable x,,x j- (g er altså en konstant). Desuden gælder det, at g,,g n er forskellig fra nul. De sidstnævnte regler "bøjes" lidt, da vi tillader, at man indtaster matematiske udtryk, der skal beregnes, som input til oprettelsen af et polynomium. Den ovennævnte definition angiver dermed den reducerede form, vi ønsker at vores Javapakke skal give som output til brugeren. Se Bilag 2 Afprøvningsresultat for eksempler på polynomier generet med denne definition Led i polynomium Som det fremgår af Definition kan man betragte et polynomium som summen af ét eller flere polynomier. Analogt til dette kan det enkelte led i et polynomium siges at være produktet af et eller flere polynomier bestående af enten en konstant eller en variabel opløftet i en potens. kx e e 2 2 x... x n e n Definition 2 Et led kan dermed have et af følgende formater: En konstant. En endelig række af variable, der alle er opløftet i en potens. En konstant ganget med en endelig række af variable, der alle er opløftet i en potens. 2 Knuth The Art of computer programming s
9 3. Brugervejledning Følgende afsnit har til formål at give en bruger en oversigt over vores Java-pakke. Dette afsnit omhandler altså kun pakkens interface og brugen heraf. Når brugeren skal bruge vores javapakke er der to ting, som han skal gøre. Importere pakken med import-sætningen for at få adgang til pakkens faciliteter og erklære de enkelte polynomier med new-sætningen. Når dette er sket har brugeren adgang til polynomierne og alle deres tilhørende metoder. De enkelte metoder er: add(), multiply(), subtract(), integrate(), diff(), copy(), iscorrect(), negate(), polydiv(), polyexp(), polymod(), tostring(), printtohtml(). Alle metoder, der modtager et polynomium kan kaldes men enten en reference til et polynomium, eller en tekststreng der angiver et polynomium. Et eksempel på brug af pakken kan ses nedenstående: import Poly.*; public class TestAfPoly { public static void main ( String args [] ){ Polynomium poly = new Polynomium( "2x^2+4" ); System.out.println( "poly: " + poly ); poly2.add( poly ); System.out.println( "poly2+poly: " + poly2 ); poly2.multiply("2xy^2+4x" ); System.out.println( "poly2*poly: " + poly2 ); Her er det brugeren, der selv opretter polynomierne. Her har han ikke brug for den fejlfinding, der ligger i pakken ved oprettelse af nye polynomier. Hvis brugeren derimod skulle lave en applikation, der tillod andre brugere at indtaste tekststrenge, der skulle laves om til polynomier, skulle disse jo testes om de overholdt syntaksen. Til dette bruges metoden iscorrect. Det skal her yderligere bemærkes, at bogstaverne æ,ø,å ikke er understøttet af pakken (dette er både som variabelnavn og som argument til integrate og diff) og at alle bogstaver bliver parset som små bogstaver. import Poly.*; import javax.swing.joptionpane; public class testafopretpolynomium { public static void main ( String args[] ) { String polyindtekst = JOptionPane.showInputDialog( "Indtast polynomium: " ); Polynomium indpoly = new Polynomium( polyindtekst ); // Bliver ved med at spørge efter et polynomium // indtil et korrekt er indtastet while (!( indpoly.iscorrect() ) ) { JOptionPane.showMessageDialog( null, "Polynomiet kan ikke oprettes med: " + polyindtekst ); polyindtekst = JOptionPane.showInputDialog( "Indtast polynomium: " ); indpoly = new Polynomium( polyindtekst ); JOptionPane.showMessageDialog( null, "Polynomiet er :" + indpoly ); Pakken er implementeret til at kunne tolke hele matematiske udtryk. Dette kunne f.eks. være udtryk som "((2.5xy^2+.6)*.5xy)^2", som den beregner under parsingen. Her ses det, at koefficienter også kan være negative og positive decimaltal. Som eksponenter modtages Integer-værdier. - 8-
10 Overholder et polynomium ikke den angivne syntaks, vil det under parsingen bliver sat til null. I pakken er der derfor indbygget en ekstra sikkerhed, der opdager metodekald med null som argument. Opdager en metode, at den bliver forsøgt kaldt med null udskriver den en fejlbesked og afsluttes. Ved et metodekald er det også muligt at det kaldende polynomium peger på null. Et metodekald med en reference, der peger på null, resulterer i, at Java kaster en NullPointerException, som kan fanges under programkørslen på følgende måde. import Poly.*; public class TestAfPolyVedFejl { public static void main ( String args [] ){ // poly overholder ikke syntaks og bliver under parsing sat til null Polynomium poly = new Polynomium( "2x^-2" ); Polynomium poly2 = new Polynomium( "2xy^2+4x" ); //forsøg addition til en refence, der peger på null try { poly.add( poly2 ); // fang NullPointerException og udskriv fejlbesked catch ( NullPointerException NPE ) { System.out.println( "Relevant fejlbesked" ); 3.. Beskrivelse af metoderne Vi vil i det følgende afsnit give en kort beskrivelse af de forskellige metoder, hvordan de kaldes og hvad de gør. Fælles for alle de metoder, der modtager et Polynomium 3 som argument, er at de også kan modtage en tekststreng, der så bliver parset til et Polynomium. Vi vil i eksemplerne bruge to polynomier: poly.add( poly2 ); poly.multiply( poly2 ); poly.subtract( poly2 ); poly.integrate('x'); poly.diff('x'); poly.copy( poly2 ); poly.iscorrect(); poly = 3x-2y^2 poly2 = 2x Metoden adderer de to polynomier og gemmer summen i poly. poly = 5x-2y^2 Metoden multiplicerer de to polynomier og gemmer produktet i poly. poly = 6x^2-4xy^2 Metoden subtraherer poly2 fra poly og gemmer differencen i poly. poly = x-2y^2 Metoden integrerer poly med hensyn til x, dvs. at den finder en stamfunktion til poly. Metoden tager som argument en char i intervallet [a;z], og gemmer resultatet i poly. poly =,5x^2-2xy^2 Metoden differentierer poly med hensyn til x, der som argument skal komme i form af en char i intervallet [a;z], og gemmer resultatet i poly. poly = 3 Metoden kopierer indholdet af poly2, hvis denne ikke er null, over i poly, der skal være oprettet på forhånd. Metoden returnerer true, hvis polynomiet er oprettet korrekt og false, hvis der opstod problemer under parsingen. 3 Her refereres der til klassen Polynomium - 9-
11 poly.negate(); poly.polydiv( poly2 ); poly.polymod( poly2 ); poly.polyexp(2); poly.tostring(); poly.printtohtml("c:\\test.html"); Metoden negerer poly. poly = -3x+2y^2 Metoden dividerer poly2 op i poly. poly indeholder derefter resultatet uden resten. poly2 må dog kun indeholde variable af en type i intervallet [a;z], men gerne flere led. Poly =. Metoden returnerer resten af divisionen af poly2 op i poly og gemmer resultatet i poly. poly2 må dog kun indeholde variable af en type i intervallet [a;z], men gerne flere led. poly = 3x-2y^2 Metoden opløfter poly i den potens angivet i argumentet som positivt heltal. poly = 9x^2+4y^4-2xy^2 Metoden udskriver poly som tekststreng. Metoden udskriver poly, som det ser ud på vores datastruktur. Den tager stien til udskriftsfilen som argument. I denne tekststreng skal det huskes at backslash i stien skal komme dobbelt pga. Javas måde at implementere specialtegn. - -
12 4. Datastruktur Dette afsnit redegør for, hvorledes et polynomium repræsenteres på den foreslåede datastruktur. Vi vil her give en dybtgående forklaring af dens opbygning, da den er udgangspunktet for resten af vores projekt. Da vi mange gange gennem rapporten anvender betegnelser omkring datastrukturen og dens egenskaber, vil vi nedenfor ligeledes forsøge at indføre den vigtigste nomenklatur. Man kan diskutere, hvordan datastrukturen skal betegnes. Knuth selv kalder den for et træ, og den har også mange ligheder med f.eks. et binært træ. Begge har de en rod, hvorunder der sidder noder, der så igen kan betragtes som en rødder i forhold til de underliggende noder. Den umiddelbare forskel på datastrukturen og klassiske træer er de cirkulære referencer, som træer normalt ikke indeholder. Strukturen er en kompleks hægtet liste. Den kunne nærmere opfattes som en quadro-hægtet liste, som måske ville være den betegnelse, der passer bedst. Men vi vil i det følgende afsnit bruge Knuths egen betegnelse og kalde strukturen for et træ. Bagerst i dette afsnit er en ordliste, hvor ord og begreber brugt i dette afsnit er opsummeret til hurtig reference. 4.. Beskrivelse af træstrukturen Grundbyggeklodsen i træstrukturen er noder, som vist i Fejl! Henvisningskilde ikke fundet.. Hver node indeholder seks felter. Up, Down, Left og Right er referencer til andre noder. EXP indeholder en heltalsværdi for eksponenten og CV værdien kan enten indeholde et tal eller en variabel (ét bogstav). Up EXP Right Left CV Down Figur : Node i datastruktur z 3 x y x 2 3 x -3 Figur 2 : Træ, der repræsenterer polynomiet : 3 + x 2 + xyz + z 3-3xz 3. Det indrammede område viser delpolynomiet 3 + x 2. Roden, den øverste node i træet, indeholder altid den alfabetisk største variabel i polynomiet, i dette tilfælde z. Roden er den eneste node i strukturen, hvis Left- og Right-referencer peger på sig selv. Desuden er eksponenten altid i roden (den bruges ikke!). - -
13 Som det fremgår af definitionen af et polynomium [Definition ], kan man betragte et polynomium, som summen af et antal mindre polynomier. De adderede polynomier kan på mindste plan bestå af produktet af en evt. konstant og et endeligt antal variable opløftet i en eksponent. I datastrukturen er dette afspejlet ved måden noderne er hægtet sammen på. En Up- eller Down-reference angiver, at to noder skal multipliceres sammen, mens en Right- eller Left-reference angiver, at de skal adderes. Et led bestående af multiplicerede noder kan derfor i strukturen aflæses ved at starte fra en node, hvis Down-reference peger på null, og følge Up-referencerne indtil denne peger på null, hvilket Up-referencen kun gør i roden af træet. Hver node, hvis Down-reference peger på null, angiver altså starten på et led, der skal adderes til resten af leddene. Eksponenterne for en CV-variabel kan læses af EXP-værdierne i det underlæggende niveaus noder. Eksponenterne er stigende, når man bevæger sig fra venstre mod højre i samme niveau i træet, og de må ikke være ens. Det er her vigtigt, at pointere at et niveau i træet refererer til noder hæftet cirkulært sammen og ikke nødvendigvis til grafisk sidestillede noder. Eksponenten er altid i noden, som en Down reference peger på, dvs. den node, som er placeret længst til venstre i et niveau. z x 3 2 Figur 3 : Udsnit af polynomiet i Figur 2 Polynomier kan betragtes som bestående af en række mindre polynomier. Figur 3, som er et udsnit af Figur 2, viser de to delpolynomier 3 og x 2. Dette læses ved at starte fra alle bundnoder (dvs. noder hvor Down-referencen er lig null) og følge Up-referencerne til roden. På Figur 3 starter konstant-polynomiet 3 i noden nederst, længst til venstre (på figuren markeret med gråt). I strukturen skal dette læses som 3. x. z. eksponenterne angiver jf. ovenstående eksponenterne for de ovenstående variable. Dette ses tydeligere i det andet delpolynomium x 2, der skal læses i strukturen som. x 2. z Variable og konstanter Et polynomium er, som tidligere beskrevet, defineret som summen af polynomier. Disse polynomier kan på mindste plan bestå af produktet af en evt. konstant og et endeligt antal variable opløftet i en eksponent. Dette betyder, at vi blot behøver at definere de to typer af træer, som repræsenterer henholdsvis en konstant og en variabel. Når vi kan oprette disse to typer, kan vi ved addition og multiplikation oprette alle andre polynomier Konstant Som det fremgår af Figur 4, består en konstant af en node, hvis CV-værdi indeholder den talværdi, som den skal repræsentere og en Down-reference, som altid peger på null. - 2-
14 k Figur 4 : Konstant, repræsenteret ved en træstruktur I det tilfælde, hvor en konstant alene repræsenterer et polynomium, vil denne ligeledes være rod, og dens referencer sat i henhold til definitionen for denne, hvilket er angivet i Figur 5. En node, der indeholder en konstant, vil ofte blive refereret til som en konstantnode. De grå felter i figurerne er irrelevante i sammenhængen. Figur 5viser en konstant, der er rod. k Figur 5 : En konstant som rod Variable Hvis polynomiet består af en variabel, skal der derimod altid være mindst 3 noder. Argumentationen for eksistensen af hver af disse tre noder kan findes i definitionen på træet. Som angivet i det ovenstående skal EXP-værdien for noden længst til venstre altid have værdien. Da opbygningen af datastrukturen ligeledes dikterer, at eksponenten for en variabel skal angives i det underlæggende niveau, er der behov for to noder på dette niveau, én med eksponenten nul og en, som indeholder eksponenten for variablen. x EXP Figur 6 : Variablen x EXP Da en variabel både kan have en eksponent og en koefficient, skal koefficienten naturligvis også kunne angives i træet. En koefficient kan betragtes som et konstantpolynomium, der er multipliceret på et variabelpolynomium. Som beskrevet tidligere er multiplikationer angivet ved Up- og Down-referencer samt, at de eneste betingelser en konstant skal opfylde er, at den indeholder en talværdi i CV, samt at dens Down reference peger på null. Grundet dette kan vi indsætte talværdien i den node under variablen, der indeholder eksponenten for variablen. - 3-
15 x EXP K Figur 7 : Variabel med koefficient Analogt til ovenstående kan vi udnytte, at Right- og Left-referencer angiver additionen af to led, når vi ønsker at addere en konstant til en variabel. Konstanten kan placeres i CV-værdien i noden længst til venstre, da den multiplikation som denne nodes Up-reference angiver, resulterer i konstanten selv. Vi har nu det mest komplekse polynomium som kan repræsenteres med tre noder. Følgende figur viser eksemplet : k x EXP2 + k 2. x EXP 2 K 2 K Figur 8 : Variabel med koefficient og adderet konstant Hvis k 2 faktisk er, refererer vi ofte til denne type noder som en nulnode eller en -node (refererer til, at både EXP og CV er ). Denne type node forekommer, jf. ovennævnte nomenklatur, kun længst til venstre i en række. En generel definitionen på repræsentation af en variabel med flere eksponenter, som er i overensstemmelse med definitionen, kan opskrives på følgende måde. x e e n... g g g n Figur 9 : Generel figur af udsnit af træstruktur, som repræsenterer en række i polynomium( Knuth, 973) Figur 9 viser et polynomium: g + g x e + g 2 x e g n x en, hvor <e <e 2 <...<e n og g,., g n er polynomier med alfabetisk mindre variable end x. g, g n må ikke være nul, dermed følges den matematiske definition angivet ovenfor. Relevante observationer om datastrukturens definition er opsummeret her: - Den øverste node, kaldet træets rod, indeholder altid den alfabetisk største CV-værdi i polynomiet, og som den eneste node i strukturen peger dens Up-reference på null, mens Right og Left referencerne peger på noden selv. - Eksponenterne for en variabel er angivet af EXP-værdierne i det underlæggende niveau. - Eksponenterne er stigende, når man bevæger sig fra venstre mod højre på et niveau i træet. - 4-
16 - Eksponenten er altid i noden som en Down reference peger på, dvs. den node som er placeret længst til venstre på et niveau i en forgrening. - To eksponenter på samme niveau kan ikke være ens. - Polynomier kan betragtes som bestående af en række mindre polynomier. - Koefficienten i ét led af et polynomium er angivet i noden, findes ved at følge roots Down-referencer til bunden Traversering i strukturen For at kunne traversere rundt i strukturen er det nødvendigt med nogle stopbetingelser, der fortæller, hvor vi befinder os i strukturen. Udgangspunktet for en traversering af træstrukturen er givet ved opbygningen af strukturen og vil blive forklaret følgende. EXP-værdien i noden længst til venstre på et givent niveau er altid. Dette bliver anvendt som stopbetingelse i den vandrette traversering i et niveau i træet. Traversering foregår ved, at man går ned og til venstre - derved står man så langt til højre i et niveau som muligt. Ved derefter at traversere til venstre i niveauet vides det, at man har været hele niveauet igennem, når en node med EXP-værdien nås. En anden måde at kontrollere, om man står længst til venstre, er ved at gå Up og derefter Down. Da en Down-reference altid peger på noden længst til venstre i niveauet, kan vi ved en forespørgsel på, om noden vi står ved, bliver peget på af en Down-reference, konkludere om traverseringen skal afsluttes. Vi kan ved vandret traversering i strukturen finde relevante led ved at undersøge størrelsen af EXP-værdier, da det vides at EXP-værdierne er stigende fra venstre mod højre. Lodret traversering i strukturen benytter tre relevante stopbetingelser. Rodens Up-reference peger på null. Den alfanumeriske værdi bliver mindre når vi traverserer ned i niveauerne i et delpolynomium, og den nederste nodes Down-reference peger på null. Den fuldstændige traversering foregår naturligvis ved en kombination af lodret og vandret traversering, hvilket følgende vil forklare Isolering af ét led I de algoritmer 4, der manipulerer træet, benyttes en metode, der har til formål at isolere et led. Da definitionen på en variabel dikterer, at dens Down-reference skal pege på en node med eksponent =, og et leds koefficient er angivet i den nederste node, kan man traversere ét led ved at gå ned og til venstre indtil en konstant nås. Fra denne node følges Upreferencerne indtil man står i roden. De fundne noder på vejen op i træet vil udgøre de multiplicerede dele af leddet (én konstant og antal variable). Ønskes det at finde det næste led i polynomiet, rykkes blot til venstre fra den sidst fundne konstantnode. Konstateres det, at man allerede står længst til venstre i et niveau (EXP = ), går man et niveau op og rykker til venstre og forsøger den nedadvendte traversering igen. På denne måde når man ned til alle konstantnoder og derved alle led i polynomiet. Et led kan derfor betragtes som værende på en slags trappestruktur, da de noder, som måtte være placeret til venstre for en node i leddet, kan betragtes som irrelevant, men for at bibeholde den strukturelle integritet skal en nulnode være placeret i hvert niveau. Dette princip vil blive anvendt i metoden genererled(), som er beskrevet i [8.3 Metoden genererled()] Afslutningsvis vil vi kort opsummere de mest relevante betegnelser præsenteret i afsnittet: Begreb Fuldt (repræsenteret) polynomium adderede led. "Længst til venstre" i en række i strukturen -node eller -led Forklaring Polynomium, der kan indeholde et vilkårligt antal Node, som en Down-reference peger på. Node, hvor både CV= og EXP= - forekommer kun længst til venstre i strukturen. 4 Additionen undtaget, da denne er udviklet af Knuth. - 5-
17 Rod Konstant polynomium Variabel polynomium Led Node øverst i strukturen Polynomium, der blot indeholder en konstantnode, der er rod. Polynomium, der indeholder tre noder, der tilsammen kun repræsenterer en variabel. En del af et fuldt repræsenteret polynomium. 5. Design af programpakke Følgende afsnit har til formål at beskrive den overordnede ide i programpakkens design. Udgangspunktet for denne beskrivelse vil være en række krav til programmet, som kan opstilles på baggrund af repræsentationen af polynomier, samt de krav, som skal opfyldes for at opnå den ønskede funktionalitet.. Træstrukturen skal bestå af noder som angivet i afsnit 4 Datastruktur 2. Der skal være mulighed for at oprette konstanter og variable. 3. Programmets funktionalitet skal implementeres, så den virker på både konstanter og variable, samt mere komplekse træer bestående af flere led. 4. Brugeren af programpakken skal ikke have adgang til den interne repræsentationsform, men blot anvende programpakken med tekststrenge. Designet, der opfylder disse krav, er angivet i følgende klassediagram (variable er angivet øverst, metoder nederst). - 6-
18 - 7-
19 - Node Up, Down, Left, Right - int EXP SuperToNode Node getup(), Node getdown() Node getleft(), Node getright() setup( Node U ), setdown( Node D ) setleft( Node L ), setright( Node R ) getexp() setexp( int EXP ), void abriviate() - Object CV - Integer CVNaevner, CVTaeller Node void setcv( Object cv ) Object getcv() void setcvnaevner( String BigIntInd) void setcvtaeller( String BigIntInd ) BigInteger getcvnaevner() BigInteger getcvtaeller() 3 Konstant - Node root Variabel void chainnode() void chainnodes() Node getroot().. *.. * - Node root - StringBuffer name InternPolynomium void add( InternPolynomium toadd ) void subtract( InternPolynomium tosubtract ) void multiply( InternPolynomium tomultiply ) void polydiv( InternPolynomium todivide ) void polymod( InternPolynomium todivide ) void copy( InternPolynomium tocopy ) void polyexp( int toexp ), void integrate ( char parttoint ) void diff( char parttodiff ) void negate() void printtohtml (String filnavn) String tostring() Node getroot() vigtige hjælpemetoder int checkchars( Node q, Node p ) genererled( InternPolynomium indpoly ) - InternPolynomium - Boolean iscorrect Polynomium void add( Polynomium toadd ) void subtract( Polynomium tosubtract ) void multiply( InternPolynomium tomultiply ) void polydiv( Polynomium todivide ) void polymod( Polynomium todivide ) void copy( Polynomium tocopy ) InternPolynomium pars( String strforste ) void polyexp( int toexp ) void integrate( char parttoint ) void diff( char parttodiff ) void negate() void printtohtml (String filnavn) String tostring() InternPolynomium getpoly() Boolean iscorrect() Figur : Klassediagram for javapakke Forklaringen vil tage sit udgangspunkt i den fundamentale enhed i træet - noden. Et polynomium er, som angivet i definitionen af denne Figur : Node i datastruktur, repræsenteret ved én eller flere af disse noder. Betragter vi - 8-
20 definitionen for noden, indeholder den fire variable med referencer til andre noder : Up, Down, Left, Right. Ligeledes indeholder den en variabel EXP, som ifølge definitionen indeholder et positivt heltal. Den sidste variabel, CV, kan enten indeholde et tal eller et bogstav. Grundet en bedre overskuelighed blev det besluttet, at eftersom CV er den eneste variabel som kræver typecheck, gav det god mening at oprette de metoder, som behandlede CV-variablen i en separat klasse. Dette gav et design, hvor en abstrakt superklasse SuperToNode indeholdt alle metoder, der ikke behandlede CVvariablen, mens subklassen Node indeholdt de metoder, som behandlede CV-variablen, som illustreret i ovenstående klassediagram. For at imødekomme computeres dårlige evne til at behandle rationelle tal, blev det besluttet, at når CV værdien bliver initialiseret som en talværdi, bliver to variable (CVNaevner og CVTaeller) tildelt heltalsværdier således, at de tilsammen repræsenterede CV ved en brøk. På denne må kunne vi anvende heltal, når vi ønskede at udføre aritmetiske operationer. Vi har nu det grundlæggende design, som muliggør sammenhægtning af noder, og det første krav er opfyldt. Det næste krav angiver muligheden for at oprette konstanter og variable. Som det fremgår af Figur er Konstant en subklasse af Node, hvilket giver god mening, da en konstant kan betragtes som et særtilfælde af denne. Konstant indeholder blot en metode chainnode(), som sætter referencerne som angivet i definitionen på en konstant når denne er rod. Som det fremgår af definitionen, indeholder Variabel tre noder. [4.2 Variable og konstanter]. Disse bliver oprettet, når en instans af Variabel bliver erklæret. Ligesom Konstant indeholder Variabel en metode chainnodes(), som sætter referencerne i noderne som angivet i definitionen for en variabel. Da en instans af Variabel indeholder flere Noder, benyttes en reference root, som peger på roden i træet. Denne variabel fungerer som indgang til den oprettede datastruktur. Vi har nu redegjort for, hvorledes designet opfylder de første to krav. Da både Konstant og Variabel består af noder, er det hensigtsmæssigt at anvende en klasse, der samler og anvender disse to klasser til at definere et helt polynomium. Når en instans af InternPolynomium bliver oprettet, undersøger den hvilken parameter, den er blevet erklæret med, og opretter enten en instans af Konstant eller af Variabel. Klassen InternPolynomium indeholder en variabel root, der sættes til at referere til enten Konstant-noden eller til roden i Variabel en, og der er nu adgang til træet igennem root variablen. Vi har nu et lag i designet, der gør det muligt at betragte både instanser af Konstant og Variabel som InternPolynomier. Vi har adgang til den underliggende træstruktur, hvilket muliggør implementeringen af algoritmer, der udfører matematiske metoder på strukturen. Disse metoder er derfor ligeledes implementeret i klassen InternPolynomium, hvilket opfylder det tredje krav. Det fjerde og sidste krav var, at brugeren af pakken ikke skal have adgang til den underliggende træstruktur, men blot anvende tekststrenge til at angive polynomier. Dette kræver, at endnu et lag bliver lagt på programpakken, som udgør pakkens interface udadtil. Klassen Polynomium indeholder ét InternPolynomium samt alle de metoder, der skal kunne udføres på et polynomium. Forskellen ligger i, at adgangen til metoderne i InternPolynomium er begrænset til programpakken, mens metoderne i Polynomium er offentligt tilgængelige for en bruger af pakken. Når disse metoder bliver kaldt på en instans af Polynomium, kalder Polynomium den tilsvarende metode for sit InternPolynomium. Polynomium indeholder ligeledes de metoder, som udfører parsingen af tekststrenge. Når Polynomium bliver erklæret med en tekststreng, kalder den parsingmetoden og gemmer resultatet i sit InternPolynomium. - 9-
Skriftlig eksamen i Datalogi
 Roskilde Universitetscenter side 1 af 11 sider Skriftlig eksamen i Datalogi Modul 1 Sommer 2000 Opgavesættet består af 6 opgaver, der ved bedømmelsen tillægges følgende vægte: Opgave 1 10% Opgave 2 10%
Roskilde Universitetscenter side 1 af 11 sider Skriftlig eksamen i Datalogi Modul 1 Sommer 2000 Opgavesættet består af 6 opgaver, der ved bedømmelsen tillægges følgende vægte: Opgave 1 10% Opgave 2 10%
Skriftlig eksamen i Datalogi
 Roskilde Universitetscenter side 1 af 9 sider Skriftlig eksamen i Datalogi Modul 1 Vinter 1999/2000 Opgavesættet består af 6 opgaver, der ved bedømmelsen tillægges følgende vægte: Opgave 1 5% Opgave 2
Roskilde Universitetscenter side 1 af 9 sider Skriftlig eksamen i Datalogi Modul 1 Vinter 1999/2000 Opgavesættet består af 6 opgaver, der ved bedømmelsen tillægges følgende vægte: Opgave 1 5% Opgave 2
University of Southern Denmark Syddansk Universitet. DM502 Forelæsning 2
 DM502 Forelæsning 2 Repetition Kompilere og køre Java program javac HelloWorld.java java HeloWorld.java Debugge Java program javac -g HelloWorld.java jswat Det basale Java program public class HelloWorld
DM502 Forelæsning 2 Repetition Kompilere og køre Java program javac HelloWorld.java java HeloWorld.java Debugge Java program javac -g HelloWorld.java jswat Det basale Java program public class HelloWorld
Eksempel: Skat i år 2000
 Kursus 02199: Programmering afsnit 2.1-2.7 Anne Haxthausen IMM, DTU 1. Værdier og typer (bl.a. char, boolean, int, double) (afsnit 2.4) 2. Variable og konstanter (afsnit 2.3) 3. Sætninger (bl.a. assignments)
Kursus 02199: Programmering afsnit 2.1-2.7 Anne Haxthausen IMM, DTU 1. Værdier og typer (bl.a. char, boolean, int, double) (afsnit 2.4) 2. Variable og konstanter (afsnit 2.3) 3. Sætninger (bl.a. assignments)
Skriftlig eksamen i Datalogi
 Roskilde Universitetscenter Skriftlig eksamen i Datalogi Modul 1 Sommer 1999 Opgavesættet består af 5 opgaver, der ved bedømmelsen tillægges følgende vægte: Opgave 1 15% Opgave 2 15% Opgave 3 8% Opgave
Roskilde Universitetscenter Skriftlig eksamen i Datalogi Modul 1 Sommer 1999 Opgavesættet består af 5 opgaver, der ved bedømmelsen tillægges følgende vægte: Opgave 1 15% Opgave 2 15% Opgave 3 8% Opgave
University of Southern Denmark Syddansk Universitet. DM502 Forelæsning 3
 DM502 Forelæsning 3 Indlæsning fra tastatur Udskrift til skærm Repetition Beregning af middelværdi Gentagelse med stop-betingelse (while) Heltalsdivision Division med nul Type-casting ( (double) ) Betinget
DM502 Forelæsning 3 Indlæsning fra tastatur Udskrift til skærm Repetition Beregning af middelværdi Gentagelse med stop-betingelse (while) Heltalsdivision Division med nul Type-casting ( (double) ) Betinget
BRP Tal. Om computer-repræsentation og -manipulation. Logaritmer
 BRP 13.9.2006 Tal. Om computer-repræsentation og -manipulation. Logaritmer 1. Opgaverne til i dag dækker det meste af stoffet 2. Resten af stoffet logaritmer binære træer 3. Øvelse ny programmeringsopgave
BRP 13.9.2006 Tal. Om computer-repræsentation og -manipulation. Logaritmer 1. Opgaverne til i dag dækker det meste af stoffet 2. Resten af stoffet logaritmer binære træer 3. Øvelse ny programmeringsopgave
AAU, Programmering i Java Intern skriftlig prøve 18. maj 2007
 AAU, Programmering i Java Intern skriftlig prøve 18. maj 2007 Opgavebesvarelsen skal afleveres som enten en printerudskrift eller som et passende dokument sendt via email til fjj@noea.dk. Besvarelsen skal
AAU, Programmering i Java Intern skriftlig prøve 18. maj 2007 Opgavebesvarelsen skal afleveres som enten en printerudskrift eller som et passende dokument sendt via email til fjj@noea.dk. Besvarelsen skal
Skriftlig eksamen i Datalogi
 Roskilde Universitetscenter Skriftlig eksamen i Datalogi Modul 1 Vinter 1998/99 Opgavesættet består af 5 opgaver, der ved bedømmelsen tillægges følgende vægte: Opgave 1 16% Opgave 2 12% Opgave 3 10% Opgave
Roskilde Universitetscenter Skriftlig eksamen i Datalogi Modul 1 Vinter 1998/99 Opgavesættet består af 5 opgaver, der ved bedømmelsen tillægges følgende vægte: Opgave 1 16% Opgave 2 12% Opgave 3 10% Opgave
Vejledende løsninger
 Roskilde Universitetscenter side 1 af 8 sider Vejledende løsninger Opgave 1 Spørgsmål 1.1 a = b - a; b = b - a; a = b + a; Opgaven har flere løsninger. En anden løsning er: a = b + a; b = a - b; a = a
Roskilde Universitetscenter side 1 af 8 sider Vejledende løsninger Opgave 1 Spørgsmål 1.1 a = b - a; b = b - a; a = b + a; Opgaven har flere løsninger. En anden løsning er: a = b + a; b = a - b; a = a
ALMINDELIGT ANVENDTE FUNKTIONER
 ALMINDELIGT ANVENDTE FUNKTIONER I dette kapitel gennemgås de almindelige regnefunktioner, samt en række af de mest nødvendige redigerings- og formateringsfunktioner. De øvrige redigerings- og formateringsfunktioner
ALMINDELIGT ANVENDTE FUNKTIONER I dette kapitel gennemgås de almindelige regnefunktioner, samt en række af de mest nødvendige redigerings- og formateringsfunktioner. De øvrige redigerings- og formateringsfunktioner
DM507 Algoritmer og datastrukturer
 DM507 Algoritmer og datastrukturer Forår 2012 Projekt, del II Institut for matematik og datalogi Syddansk Universitet 15. marts, 2012 Dette projekt udleveres i tre dele. Hver del har sin deadline, således
DM507 Algoritmer og datastrukturer Forår 2012 Projekt, del II Institut for matematik og datalogi Syddansk Universitet 15. marts, 2012 Dette projekt udleveres i tre dele. Hver del har sin deadline, således
Ugeseddel 4 1. marts - 8. marts
 Ugeseddel 4 1. marts - 8. marts Læs følgende sider i kapitel 6 i lærebogen: s. 233 258 og s. 291 317 (afsnit 6.3 overspringes). Begynd at overveje, hvad afleveringsopgaven skal omhandle. Læs vejledningen,
Ugeseddel 4 1. marts - 8. marts Læs følgende sider i kapitel 6 i lærebogen: s. 233 258 og s. 291 317 (afsnit 6.3 overspringes). Begynd at overveje, hvad afleveringsopgaven skal omhandle. Læs vejledningen,
DM507 Algoritmer og datastrukturer
 DM507 Algoritmer og datastrukturer Forår 2013 Projekt, del I Institut for matematik og datalogi Syddansk Universitet 5. marts, 2013 Dette projekt udleveres i to dele. Hver del har sin deadline, således
DM507 Algoritmer og datastrukturer Forår 2013 Projekt, del I Institut for matematik og datalogi Syddansk Universitet 5. marts, 2013 Dette projekt udleveres i to dele. Hver del har sin deadline, således
DM507 Algoritmer og datastrukturer
 DM507 Algoritmer og datastrukturer Forår 2018 Projekt, del II Institut for matematik og datalogi Syddansk Universitet 13. marts, 2018 Dette projekt udleveres i tre dele. Hver del har sin deadline, således
DM507 Algoritmer og datastrukturer Forår 2018 Projekt, del II Institut for matematik og datalogi Syddansk Universitet 13. marts, 2018 Dette projekt udleveres i tre dele. Hver del har sin deadline, således
Kursus i OOP og Java. Kursus i Objektorienteret programmering i Java
 Kursus i OOP og Java Kursus i Objektorienteret programmering i Java Åben Dokumentlicens Dette foredragsmateriale er under Åben Dokumentlicens (ÅDL) Du har derfor lov til frit at kopiere dette værk Bruger
Kursus i OOP og Java Kursus i Objektorienteret programmering i Java Åben Dokumentlicens Dette foredragsmateriale er under Åben Dokumentlicens (ÅDL) Du har derfor lov til frit at kopiere dette værk Bruger
π er irrationel Frank Nasser 10. december 2011
 π er irrationel Frank Nasser 10. december 2011 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold 1 Introduktion
π er irrationel Frank Nasser 10. december 2011 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold 1 Introduktion
DM507 Algoritmer og datastrukturer
 DM507 Algoritmer og datastrukturer Forår 2018 Projekt, del II Institut for matematik og datalogi Syddansk Universitet 20. marts, 2019 Dette projekt udleveres i tre dele. Hver del har sin deadline, således
DM507 Algoritmer og datastrukturer Forår 2018 Projekt, del II Institut for matematik og datalogi Syddansk Universitet 20. marts, 2019 Dette projekt udleveres i tre dele. Hver del har sin deadline, således
SWC eksamens-spørgsmål. Oversigt
 SWC eksamens-spørgsmål Oversigt #1 Typer og variable #2 Aritmetik og logik #3 Klasser (definition, objekter) #4 Klasser (metoder) #5 Klasser (nedarvning, polymorfi) #6 Conditional statements #7 Repetition
SWC eksamens-spørgsmål Oversigt #1 Typer og variable #2 Aritmetik og logik #3 Klasser (definition, objekter) #4 Klasser (metoder) #5 Klasser (nedarvning, polymorfi) #6 Conditional statements #7 Repetition
Forelæsning Uge 4 Mandag
 Forelæsning Uge 4 Mandag Algoritmeskabeloner Kan (ved simple tilretningerne) bruges til at implementere metoder, der gennemsøger en arrayliste (eller anden objektsamling) og finder objekter, der opfylder
Forelæsning Uge 4 Mandag Algoritmeskabeloner Kan (ved simple tilretningerne) bruges til at implementere metoder, der gennemsøger en arrayliste (eller anden objektsamling) og finder objekter, der opfylder
class Time { int hours, min; } } Time t1; // Erklær variabel af type Time class Time1 { public static void main(string[] args) { Time t1; t1.
![class Time { int hours, min; } } Time t1; // Erklær variabel af type Time class Time1 { public static void main(string[] args) { Time t1; t1. class Time { int hours, min; } } Time t1; // Erklær variabel af type Time class Time1 { public static void main(string[] args) { Time t1; t1.](/thumbs/82/86996609.jpg) Programmering 1999 Forelæsning 4, fredag 10. september 1999 Klasser og objekter Felter, konstruktorer, this Eksempler på klasser: Time, Appointment Eksempler på metoder i Time og Appointment Klassefelter:
Programmering 1999 Forelæsning 4, fredag 10. september 1999 Klasser og objekter Felter, konstruktorer, this Eksempler på klasser: Time, Appointment Eksempler på metoder i Time og Appointment Klassefelter:
dcomnet-nr. 8 Simpel aritmetik på maskinniveau Computere og Netværk (dcomnet)
 dcomnet-nr. 8 Simpel aritmetik på maskinniveau Computere og Netværk (dcomnet) Efterår 2009 1 Simpel aritmetik på maskinniveau I SCO, appendix A, er det beskrevet, hvordan man adderer ikke-negative heltal
dcomnet-nr. 8 Simpel aritmetik på maskinniveau Computere og Netværk (dcomnet) Efterår 2009 1 Simpel aritmetik på maskinniveau I SCO, appendix A, er det beskrevet, hvordan man adderer ikke-negative heltal
Forelæsning Uge 2 Torsdag
 Forelæsning Uge 2 Torsdag Java syntax og style guide Sætninger Simple sætninger (assignment, interne og eksterne metodekald) Sammensatte sætninger (blok, selektion, gentagelse) Udtryk og operatorer Brug
Forelæsning Uge 2 Torsdag Java syntax og style guide Sætninger Simple sætninger (assignment, interne og eksterne metodekald) Sammensatte sætninger (blok, selektion, gentagelse) Udtryk og operatorer Brug
DM507 Algoritmer og datastrukturer
 DM507 Algoritmer og datastrukturer Forår 2016 Projekt, del III Institut for matematik og datalogi Syddansk Universitet 20. april, 2016 Dette projekt udleveres i tre dele. Hver del har sin deadline, således
DM507 Algoritmer og datastrukturer Forår 2016 Projekt, del III Institut for matematik og datalogi Syddansk Universitet 20. april, 2016 Dette projekt udleveres i tre dele. Hver del har sin deadline, således
Indhold. Maskinstruktur... 3. Kapitel 1. Assemblersprog...3. 1.1 Indledning...3 1.2 Hop-instruktioner... 7 1.3 Input og output...
 Indhold Maskinstruktur... 3 Kapitel 1. Assemblersprog...3 1.1 Indledning...3 1.2 Hop-instruktioner... 7 1.3 Input og output... 9 Kapitel 2. Maskinkode... 13 2.1 Den fysiske maskine... 13 2.2 Assemblerens
Indhold Maskinstruktur... 3 Kapitel 1. Assemblersprog...3 1.1 Indledning...3 1.2 Hop-instruktioner... 7 1.3 Input og output... 9 Kapitel 2. Maskinkode... 13 2.1 Den fysiske maskine... 13 2.2 Assemblerens
Repræsentation af tal
 Repræsentation af tal DM534 Rolf Fagerberg 1 / 18 Mål Målet for disse slides er at beskrive, hvordan tal repræsenteres som bitmønstre i computere. Dette emne er et uddrag af kurset DM548 Computerarkitektur
Repræsentation af tal DM534 Rolf Fagerberg 1 / 18 Mål Målet for disse slides er at beskrive, hvordan tal repræsenteres som bitmønstre i computere. Dette emne er et uddrag af kurset DM548 Computerarkitektur
Kapitel 4 Løkker i C#
 Kapitel 4 Løkker i C# Løkker en vigtig del af alle programmeringssprog, og C# er ikke andeles. En løkke er en måde at udføre en del af koden gentagne gange. Ideen er at du fortsætter med at udføre en opgave
Kapitel 4 Løkker i C# Løkker en vigtig del af alle programmeringssprog, og C# er ikke andeles. En løkke er en måde at udføre en del af koden gentagne gange. Ideen er at du fortsætter med at udføre en opgave
Om binære søgetræer i Java
 Om binære søgetræer i Java Mads Rosendahl 7. november 2002 Resumé En fix måde at gemme data på er i en træstruktur. Måden er nyttig hvis man får noget data ind og man gerne vil have at det gemt i en sorteret
Om binære søgetræer i Java Mads Rosendahl 7. november 2002 Resumé En fix måde at gemme data på er i en træstruktur. Måden er nyttig hvis man får noget data ind og man gerne vil have at det gemt i en sorteret
DM507 Algoritmer og datastrukturer
 DM507 Algoritmer og datastrukturer Forår 2016 Projekt, del I Institut for matematik og datalogi Syddansk Universitet 29. februar, 2016 Dette projekt udleveres i tre dele. Hver del har sin deadline, således
DM507 Algoritmer og datastrukturer Forår 2016 Projekt, del I Institut for matematik og datalogi Syddansk Universitet 29. februar, 2016 Dette projekt udleveres i tre dele. Hver del har sin deadline, således
3 Algebra. Faglige mål. Variable og brøker. Den distributive lov. Potenser og rødder
 3 Algebra Faglige mål Kapitlet Algebra tager udgangspunkt i følgende faglige mål: Variable og brøker: kende enkle algebraiske udtryk med brøker og kunne behandle disse ved at finde fællesnævner. Den distributive
3 Algebra Faglige mål Kapitlet Algebra tager udgangspunkt i følgende faglige mål: Variable og brøker: kende enkle algebraiske udtryk med brøker og kunne behandle disse ved at finde fællesnævner. Den distributive
JavaScript. nedarvning.
 JavaScript er et sprog, der kan give en hjemmeside mere funktionalitet og gøre den interaktiv, så den reagerer på læsernes handlinger. CGI (Common Gateway Interface) har hidtil været de protokoller, man
JavaScript er et sprog, der kan give en hjemmeside mere funktionalitet og gøre den interaktiv, så den reagerer på læsernes handlinger. CGI (Common Gateway Interface) har hidtil været de protokoller, man
DM507 Algoritmer og datastrukturer
 DM507 Algoritmer og datastrukturer Forår 2019 Projekt, del III Institut for matematik og datalogi Syddansk Universitet 10. april, 2019 Dette projekt udleveres i tre dele. Hver del har sin deadline, således
DM507 Algoritmer og datastrukturer Forår 2019 Projekt, del III Institut for matematik og datalogi Syddansk Universitet 10. april, 2019 Dette projekt udleveres i tre dele. Hver del har sin deadline, således
DM01 DM01. 3. Obl. Afl. Jacob Christiansen, 130282, jacob.ch@mail.tdcadsl.dk. D12, Elias 18/3-2003. Side 1 af 11
 DM01 DM01 3. Obl. Afl. Jacob Christiansen, 130282, jacob.ch@mail.tdcadsl.dk D12, Elias 18/3-2003 Side 1 af 11 DM01 Indholdsfortegnelse: BILAG:...2 1 FORMÅL:...3 2 KLASSER:...4 2.1 DILEMMA:...4 2.1.1 METODER:...4
DM01 DM01 3. Obl. Afl. Jacob Christiansen, 130282, jacob.ch@mail.tdcadsl.dk D12, Elias 18/3-2003 Side 1 af 11 DM01 Indholdsfortegnelse: BILAG:...2 1 FORMÅL:...3 2 KLASSER:...4 2.1 DILEMMA:...4 2.1.1 METODER:...4
Forelæsning Uge 4 Torsdag
 Forelæsning Uge 4 Torsdag Algoritmeskabeloner findone, findall, findnoof, findsumof (i mandags) findbest Levetid for variabler og parametre Virkefeltsregler Hvor kan man bruge de forskellige variabler?
Forelæsning Uge 4 Torsdag Algoritmeskabeloner findone, findall, findnoof, findsumof (i mandags) findbest Levetid for variabler og parametre Virkefeltsregler Hvor kan man bruge de forskellige variabler?
Maple. Skærmbilledet. Vi starter med at se lidt nærmere på opstartsbilledet i Maple. Værktøjslinje til indtastningsområdet. Menulinje.
 Maple Dette kapitel giver en kort introduktion til hvordan Maple 12 kan benyttes til at løse mange af de opgaver, som man bliver mødt med i matematiktimerne på HHX. Skærmbilledet Vi starter med at se lidt
Maple Dette kapitel giver en kort introduktion til hvordan Maple 12 kan benyttes til at løse mange af de opgaver, som man bliver mødt med i matematiktimerne på HHX. Skærmbilledet Vi starter med at se lidt
Studiepraktik. Thomas Bøgholm Mikkel Hansen Jacob Elefsen
 Studiepraktik Thomas Bøgholm boegholm@cs.aau.dk Mikkel Hansen mhan@cs.aau.dk Jacob Elefsen jelefs12@student.aau.dk 1 Studiepraktik -- program Program onsdag 10.00 10.15 Registrering af fremmøde og gennemgang
Studiepraktik Thomas Bøgholm boegholm@cs.aau.dk Mikkel Hansen mhan@cs.aau.dk Jacob Elefsen jelefs12@student.aau.dk 1 Studiepraktik -- program Program onsdag 10.00 10.15 Registrering af fremmøde og gennemgang
Programmering for begyndere Lektion 2. Opsamling mm
 Lektion 2 Opsamling mm God tone Der er indlagt spørge sessioner Lektion 2 - Agenda Programmering for Lidt ændringer til teknikken, herunder hvordan du genser en lektion Lidt generelle tilbagemeldinger
Lektion 2 Opsamling mm God tone Der er indlagt spørge sessioner Lektion 2 - Agenda Programmering for Lidt ændringer til teknikken, herunder hvordan du genser en lektion Lidt generelle tilbagemeldinger
DM507 Algoritmer og datastrukturer
 DM507 Algoritmer og datastrukturer Forår 2017 Projekt, del III Institut for matematik og datalogi Syddansk Universitet 6. april, 2017 Dette projekt udleveres i tre dele. Hver del har sin deadline, således
DM507 Algoritmer og datastrukturer Forår 2017 Projekt, del III Institut for matematik og datalogi Syddansk Universitet 6. april, 2017 Dette projekt udleveres i tre dele. Hver del har sin deadline, således
Klasse 1.4 Michael Jokil 03-05-2010
 HTX I ROSKILDE Afsluttende opgave Kommunikation og IT Klasse 1.4 Michael Jokil 03-05-2010 Indholdsfortegnelse Indledning... 3 Formål... 3 Planlægning... 4 Kommunikationsplan... 4 Kanylemodellen... 4 Teknisk
HTX I ROSKILDE Afsluttende opgave Kommunikation og IT Klasse 1.4 Michael Jokil 03-05-2010 Indholdsfortegnelse Indledning... 3 Formål... 3 Planlægning... 4 Kommunikationsplan... 4 Kanylemodellen... 4 Teknisk
Forelæsning Uge 2 Mandag
 Forelæsning Uge 2 Mandag Sætninger Simple sætninger (assignment, interne og eksterne metodekald) Sammensatte sætninger (blok, selektion, gentagelse) Udtryk og operatorer Java syntax og style guide Afleveringsopgave:
Forelæsning Uge 2 Mandag Sætninger Simple sætninger (assignment, interne og eksterne metodekald) Sammensatte sætninger (blok, selektion, gentagelse) Udtryk og operatorer Java syntax og style guide Afleveringsopgave:
Algoritmedesign med internetanvendelser ved Keld Helsgaun
 Algoritmedesign med internetanvendelser ved Keld Helsgaun 1 Analyse af algoritmer Input Algoritme Output En algoritme er en trinvis metode til løsning af et problem i endelig tid 2 Algoritmebegrebet D.
Algoritmedesign med internetanvendelser ved Keld Helsgaun 1 Analyse af algoritmer Input Algoritme Output En algoritme er en trinvis metode til løsning af et problem i endelig tid 2 Algoritmebegrebet D.
Python programmering. Per Tøfting. MacFest
 Python programmering MacFest 2005 Per Tøfting http://pertoefting.dk/macfest/ Indhold Måder at afvikle Python program på Variabler Data typer Tal Sekvenser Strenge Tupler Lister Dictionaries Kontrolstrukturer
Python programmering MacFest 2005 Per Tøfting http://pertoefting.dk/macfest/ Indhold Måder at afvikle Python program på Variabler Data typer Tal Sekvenser Strenge Tupler Lister Dictionaries Kontrolstrukturer
Sproget Six. Til brug i rapportopgaven på kurset Oversættere. Vinter 2006. Abstract
 Sproget Six Til brug i rapportopgaven på kurset Oversættere Vinter 2006 Abstract Six er baseret på det sprog, der vises i figur 6.2 og 6.4 i Basics of Compiler Design. Den herværende tekst beskriver basissproget
Sproget Six Til brug i rapportopgaven på kurset Oversættere Vinter 2006 Abstract Six er baseret på det sprog, der vises i figur 6.2 og 6.4 i Basics of Compiler Design. Den herværende tekst beskriver basissproget
Oprids over grundforløbet i matematik
 Oprids over grundforløbet i matematik Dette oprids er tænkt som en meget kort gennemgang af de vigtigste hovedpointer vi har gennemgået i grundforløbet i matematik. Det er en kombination af at repetere
Oprids over grundforløbet i matematik Dette oprids er tænkt som en meget kort gennemgang af de vigtigste hovedpointer vi har gennemgået i grundforløbet i matematik. Det er en kombination af at repetere
Løsning af møntproblemet
 Løsning af møntproblemet Keld Helsgaun RUC, oktober 1999 Antag at tilstandene i problemet (stillingerne) er repræsenteret ved objekter af klassen State. Vi kan da finde en kortest mulig løsning af problemet
Løsning af møntproblemet Keld Helsgaun RUC, oktober 1999 Antag at tilstandene i problemet (stillingerne) er repræsenteret ved objekter af klassen State. Vi kan da finde en kortest mulig løsning af problemet
DM507 Algoritmer og datastrukturer
 DM507 Algoritmer og datastrukturer Forår 2019 Projekt, del I Institut for matematik og datalogi Syddansk Universitet 27. februar, 2019 Dette projekt udleveres i tre dele. Hver del har sin deadline, således
DM507 Algoritmer og datastrukturer Forår 2019 Projekt, del I Institut for matematik og datalogi Syddansk Universitet 27. februar, 2019 Dette projekt udleveres i tre dele. Hver del har sin deadline, således
Løsning af simple Ligninger
 Løsning af simple Ligninger Frank Nasser 19. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk:
Løsning af simple Ligninger Frank Nasser 19. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk:
DANMARKS TEKNISKE UNIVERSITET
 DANMARKS TEKNISKE UNIVERSITET Skriftlig prøve, 14. december 2018, 4 timer Side 1 af 18 Kursus navn: 02101 Indledende Programmering Kursus : 02101 Tilladte hjælpemidler: Ikke-digitale skriftlige hjælpemidler
DANMARKS TEKNISKE UNIVERSITET Skriftlig prøve, 14. december 2018, 4 timer Side 1 af 18 Kursus navn: 02101 Indledende Programmering Kursus : 02101 Tilladte hjælpemidler: Ikke-digitale skriftlige hjælpemidler
Andreas Lauge V. Hansen klasse 3.3t Roskilde HTX
 IT -Eksamen Andreas Lauge V. Hansen klasse 3.3t Roskilde HTX [Vælg en dato] Indhold Indledning... 2 Teori... 3 Hvorfor dette design... 4 Produktet... 4 Test og afprøvning... 9 Konklusion... 10 Indledning
IT -Eksamen Andreas Lauge V. Hansen klasse 3.3t Roskilde HTX [Vælg en dato] Indhold Indledning... 2 Teori... 3 Hvorfor dette design... 4 Produktet... 4 Test og afprøvning... 9 Konklusion... 10 Indledning
Datalogi OB, Efterår 2002 OH er, forelæsning 10/ Klasser og nedarvning
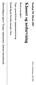 Datalogi OB, Efterår 2002 OH er, forelæsning 10/9-2002 Klasser og nedarvning Hvad er formålet? Typer, generisk kode, typeparameterisering Kritisk kig på, hvordan man gør i Java. Eftermiddagens opgave:
Datalogi OB, Efterår 2002 OH er, forelæsning 10/9-2002 Klasser og nedarvning Hvad er formålet? Typer, generisk kode, typeparameterisering Kritisk kig på, hvordan man gør i Java. Eftermiddagens opgave:
Forelæsning Uge 4 Mandag
 Forelæsning Uge 4 Mandag Algoritmeskabeloner findone, findall, findnoof, findsumof Primitive typer (forfremmelse og begrænsning) Identitet versus lighed (for objekter, herunder strenge) Opfølgning på Skildpadde
Forelæsning Uge 4 Mandag Algoritmeskabeloner findone, findall, findnoof, findsumof Primitive typer (forfremmelse og begrænsning) Identitet versus lighed (for objekter, herunder strenge) Opfølgning på Skildpadde
Skriftlig Eksamen Algoritmer og Datastrukturer (dads)
 Skriftlig Eksamen Algoritmer og Datastrukturer (dads) Datalogisk Institut Aarhus Universitet Mandag den 27. maj 2002, kl. 9.00 13.00 Opgave 1 (25%) Denne opgave handler om multiplikation af positive heltal.
Skriftlig Eksamen Algoritmer og Datastrukturer (dads) Datalogisk Institut Aarhus Universitet Mandag den 27. maj 2002, kl. 9.00 13.00 Opgave 1 (25%) Denne opgave handler om multiplikation af positive heltal.
Hvad er Objekter - Programmering
 Denne guide er oprindeligt udgivet på Eksperten.dk Hvad er Objekter - Programmering En rigtig god gennemgang af hvad objekter er! Hvordan de oprettes og anvendes! Det er helt klart til nybegyndere, som
Denne guide er oprindeligt udgivet på Eksperten.dk Hvad er Objekter - Programmering En rigtig god gennemgang af hvad objekter er! Hvordan de oprettes og anvendes! Det er helt klart til nybegyndere, som
University of Southern Denmark Syddansk Universitet. DM502 Forelæsning 4
 DM502 Forelæsning 4 Flere kontrolstrukturer for-løkke switch-case Metoder Indhold Arrays og sortering af arrays String-funktioner for-løkke Ofte har man brug for at udføre det samme kode, for en sekvens
DM502 Forelæsning 4 Flere kontrolstrukturer for-løkke switch-case Metoder Indhold Arrays og sortering af arrays String-funktioner for-løkke Ofte har man brug for at udføre det samme kode, for en sekvens
class subklasse-navn extends superklasse-navn { } NorwaySpruce har superklassen Spruce, som igen har superklassen Tree.
 Programmering 1999 Forelæsning 11, tirsdag 5. oktober 1999 Oversigt Klasse-hierarkier: superklasser og subklasser Nedarvning Polymorfi Programmering 1999 KVL Side 11-1 Hierarkier En klasse repræsenterer
Programmering 1999 Forelæsning 11, tirsdag 5. oktober 1999 Oversigt Klasse-hierarkier: superklasser og subklasser Nedarvning Polymorfi Programmering 1999 KVL Side 11-1 Hierarkier En klasse repræsenterer
APPENDIX A INTRODUKTION TIL DERIVE
 APPENDIX A INTRODUKTION TIL DERIVE z x y z=exp( x^2 0.5y^2) CAS er en fællesbetegnelse for matematikprogrammer, som foruden numeriske beregninger også kan regne med symboler og formler. Det betyder: Computer
APPENDIX A INTRODUKTION TIL DERIVE z x y z=exp( x^2 0.5y^2) CAS er en fællesbetegnelse for matematikprogrammer, som foruden numeriske beregninger også kan regne med symboler og formler. Det betyder: Computer
Grundlæggende Matematik
 Grundlæggende Matematik Hayati Balo, AAMS August 2012 1. Matematiske symboler For at udtrykke de verbale udsagn matematisk korrekt, så det bliver lettere og hurtigere at skrive, indføres en række matematiske
Grundlæggende Matematik Hayati Balo, AAMS August 2012 1. Matematiske symboler For at udtrykke de verbale udsagn matematisk korrekt, så det bliver lettere og hurtigere at skrive, indføres en række matematiske
DRONNINGER (QUEENS) Opgave 1
 DRONNINGER (QUEENS) I denne opgave vil vi beskæftige os med det såkaldte 8-dronningeproblem, hvor man skal placerede 8 dronninger på et 8 x 8 skakbræt, således at ingen af dronningerne kan slå hinanden.
DRONNINGER (QUEENS) I denne opgave vil vi beskæftige os med det såkaldte 8-dronningeproblem, hvor man skal placerede 8 dronninger på et 8 x 8 skakbræt, således at ingen af dronningerne kan slå hinanden.
IT opgave. Informationsteknologi B. Vejleder: Karl. Navn: Devran Kücükyildiz. Klasse: 2,4
 IT opgave Informationsteknologi B Vejleder: Karl Navn: Devran Kücükyildiz Klasse: 2,4 Dato:03-03-2009 1 Indholdsfortegnelse 1. Indledning... 3 2. Planlægning... 3 Kommunikationsplanlægning... 3 Problemstillingen...
IT opgave Informationsteknologi B Vejleder: Karl Navn: Devran Kücükyildiz Klasse: 2,4 Dato:03-03-2009 1 Indholdsfortegnelse 1. Indledning... 3 2. Planlægning... 3 Kommunikationsplanlægning... 3 Problemstillingen...
Talregning. Aktivitet Emne Klassetrin Side. Indledning til VisiRegn ideer 1-7 2 Oversigt over VisiRegn ideer 1-7 3
 VisiRegn ideer 1 Talregning Inge B. Larsen ibl@dpu.dk INFA juli 2001 Indhold: Aktivitet Emne Klassetrin Side Indledning til VisiRegn ideer 1-7 2 Oversigt over VisiRegn ideer 1-7 3 Vejledning til Talregning
VisiRegn ideer 1 Talregning Inge B. Larsen ibl@dpu.dk INFA juli 2001 Indhold: Aktivitet Emne Klassetrin Side Indledning til VisiRegn ideer 1-7 2 Oversigt over VisiRegn ideer 1-7 3 Vejledning til Talregning
Tree klassen fra sidste forelæsning
 Programmering 1999 Forelæsning 12, fredag 8. oktober 1999 Oversigt Abstrakte klasser. Grænseflader. Programmering 1999 KVL Side 12-1 Tree klassen fra sidste forelæsning class Tree { int age; // in years
Programmering 1999 Forelæsning 12, fredag 8. oktober 1999 Oversigt Abstrakte klasser. Grænseflader. Programmering 1999 KVL Side 12-1 Tree klassen fra sidste forelæsning class Tree { int age; // in years
Sproget Rascal (v. 2)
 Sproget Rascal (v. 2) Til brug i K1 på kurset Oversættere Opdateret 29/11 2004 Abstract Rascal er et simpelt Pascal-lignende imperativt sprog. Dette dokument beskriver uformelt Rascals syntaks og semantik
Sproget Rascal (v. 2) Til brug i K1 på kurset Oversættere Opdateret 29/11 2004 Abstract Rascal er et simpelt Pascal-lignende imperativt sprog. Dette dokument beskriver uformelt Rascals syntaks og semantik
Fejlkorligerende køder Fejlkorrigerende koder
 Fejlkorligerende køder Fejlkorrigerende koder Olav Geil Skal man sende en fødselsdagsgave til fætter Børge, så pakker man den godt ind i håb om, at kun indpakningen er beskadiget ved modtagelsen. Noget
Fejlkorligerende køder Fejlkorrigerende koder Olav Geil Skal man sende en fødselsdagsgave til fætter Børge, så pakker man den godt ind i håb om, at kun indpakningen er beskadiget ved modtagelsen. Noget
Matematiske kompetencer - hvad og hvorfor? DLF-Kursus Frederikshavn 24.-25.9 2015 Eva Rønn UCC
 Matematiske kompetencer - hvad og hvorfor? DLF-Kursus Frederikshavn 24.-25.9 2015 Eva Rønn UCC Komrapporten Kompetencer og matematiklæring. Ideer og inspiration til udvikling af matematikundervisningen
Matematiske kompetencer - hvad og hvorfor? DLF-Kursus Frederikshavn 24.-25.9 2015 Eva Rønn UCC Komrapporten Kompetencer og matematiklæring. Ideer og inspiration til udvikling af matematikundervisningen
Repræsentation af tal
 Repræsentation af tal DM534 Rolf Fagerberg Mål Målet for disse slides er at beskrive, hvordan tal repræsenteres som bitmønstre i computere. Dette emne er et uddrag af kurset DM548 Computerarkitektur og
Repræsentation af tal DM534 Rolf Fagerberg Mål Målet for disse slides er at beskrive, hvordan tal repræsenteres som bitmønstre i computere. Dette emne er et uddrag af kurset DM548 Computerarkitektur og
//Udskriver System.out.println("Hej " + ditfornavn + " " + ditefternavn + "."); System.out.println("Du er " + dinalder + " aar gammel!
 Denne guide er oprindeligt udgivet på Eksperten.dk Brugerinput i Java Denne her artikel gennemgår diverse ting ved brug af brugerinput i Java. Den starter med det simple og fortæller derefter skridt for
Denne guide er oprindeligt udgivet på Eksperten.dk Brugerinput i Java Denne her artikel gennemgår diverse ting ved brug af brugerinput i Java. Den starter med det simple og fortæller derefter skridt for
Med TI-89 / TI-92 Plus kan du også sammenligne eller manipulere binære tal bit for bit.
 Kapitel 20: Talsystemer 20 Resumé af talsystemer... 344 Indtastning og omregning af talsystemer... 345 Udførelse af matematiske beregninger med hexadecimale og binære tal... 346 Sammenligning eller manipulation
Kapitel 20: Talsystemer 20 Resumé af talsystemer... 344 Indtastning og omregning af talsystemer... 345 Udførelse af matematiske beregninger med hexadecimale og binære tal... 346 Sammenligning eller manipulation
Abstrakte datatyper C#-version
 Note til Programmeringsteknologi Akademiuddannelsen i Informationsteknologi Abstrakte datatyper C#-version Finn Nordbjerg 1/9 Abstrakte Datatyper Denne note introducerer kort begrebet abstrakt datatype
Note til Programmeringsteknologi Akademiuddannelsen i Informationsteknologi Abstrakte datatyper C#-version Finn Nordbjerg 1/9 Abstrakte Datatyper Denne note introducerer kort begrebet abstrakt datatype
DM507 Algoritmer og datastrukturer
 DM507 Algoritmer og datastrukturer Forår 2010 Projekt, del III Institut for matematik og datalogi Syddansk Universitet 24. april, 2010 (let justeret 10. maj og 21. maj 2010) Dette projekt udleveres i tre
DM507 Algoritmer og datastrukturer Forår 2010 Projekt, del III Institut for matematik og datalogi Syddansk Universitet 24. april, 2010 (let justeret 10. maj og 21. maj 2010) Dette projekt udleveres i tre
Programmering C Eksamensprojekt. Lavet af Suayb Köse & Nikolaj Egholk Jakobsen
 Programmering C Eksamensprojekt Lavet af Suayb Köse & Nikolaj Egholk Jakobsen Indledning Analyse Læring er en svær størrelse. Der er hele tiden fokus fra politikerne på, hvordan de danske skoleelever kan
Programmering C Eksamensprojekt Lavet af Suayb Köse & Nikolaj Egholk Jakobsen Indledning Analyse Læring er en svær størrelse. Der er hele tiden fokus fra politikerne på, hvordan de danske skoleelever kan
DM507 Algoritmer og datastrukturer
 DM507 Algoritmer og datastrukturer Forår 2015 Projekt, del I Institut for matematik og datalogi Syddansk Universitet 3. marts, 2015 Dette projekt udleveres i to dele. Hver del har sin deadline, således
DM507 Algoritmer og datastrukturer Forår 2015 Projekt, del I Institut for matematik og datalogi Syddansk Universitet 3. marts, 2015 Dette projekt udleveres i to dele. Hver del har sin deadline, således
Algoritmeskabeloner: Sweep- og søgealgoritmer C#-version
 Note til Programmeringsteknologi Akademiuddannelsen i Informationsteknologi Algoritmeskabeloner: Sweep- og søgealgoritmer C#-version Finn Nordbjerg 1/9 Indledning I det følgende introduceres et par abstrakte
Note til Programmeringsteknologi Akademiuddannelsen i Informationsteknologi Algoritmeskabeloner: Sweep- og søgealgoritmer C#-version Finn Nordbjerg 1/9 Indledning I det følgende introduceres et par abstrakte
Repræsentation af tal
 Repræsentation af tal DM534 Rolf Fagerberg Bitmønstre 01101011 0001100101011011... Bitmønstre skal fortolkes for at have en betydning: Tal (heltal, decimaltal (kommatal)) Bogstaver Computerinstruktion
Repræsentation af tal DM534 Rolf Fagerberg Bitmønstre 01101011 0001100101011011... Bitmønstre skal fortolkes for at have en betydning: Tal (heltal, decimaltal (kommatal)) Bogstaver Computerinstruktion
Grundlæggende Programmering ITU, Efterår 1999. Skriftlig eksamen i Grundlæggende Programmering
 Skriftlig eksamen i Grundlæggende Programmering ITU, 20. januar 2000 Alle hjælpemidler tilladt, dog ikke datamat. Eksamen er skriftlig, fire timer, og bedømmes efter 13-skalaen. Opgavesættet består af
Skriftlig eksamen i Grundlæggende Programmering ITU, 20. januar 2000 Alle hjælpemidler tilladt, dog ikke datamat. Eksamen er skriftlig, fire timer, og bedømmes efter 13-skalaen. Opgavesættet består af
Forelæsning Uge 4 Torsdag
 Forelæsning Uge 4 Torsdag Algoritmeskabeloner findone, findall, findnoof, findsumof (sidste mandag) findbest Levetid for variabler og parametre Virkefeltsregler Hvor kan man bruge de forskellige variabler?
Forelæsning Uge 4 Torsdag Algoritmeskabeloner findone, findall, findnoof, findsumof (sidste mandag) findbest Levetid for variabler og parametre Virkefeltsregler Hvor kan man bruge de forskellige variabler?
Forelæsning Uge 2 Torsdag
 Forelæsning Uge 2 Torsdag Niveauer af programbeskrivelser Statiske / dynamiske beskrivelser Klassevariabler og klassemetoder Variabler og metoder der et tilknyttet klassen (i stedet for at være tilknyttet
Forelæsning Uge 2 Torsdag Niveauer af programbeskrivelser Statiske / dynamiske beskrivelser Klassevariabler og klassemetoder Variabler og metoder der et tilknyttet klassen (i stedet for at være tilknyttet
Første del af rapporten består af et diagram, der viser, hvor mange point eleverne på landsplan fik i de enkelte opgaver.
 Til matematiklæreren Dette er en rapport omtaler prøven med hjælpemidler maj 2016. Rapporten kan bruges til at evaluere dit arbejde med klassen og få ideer til dit arbejde med kommende klasser i overbygningen.
Til matematiklæreren Dette er en rapport omtaler prøven med hjælpemidler maj 2016. Rapporten kan bruges til at evaluere dit arbejde med klassen og få ideer til dit arbejde med kommende klasser i overbygningen.
Forelæsning Uge 4 Mandag
 Forelæsning Uge 4 Mandag Algoritmeskabeloner Kan (ved simple tilretningerne) bruges til at implementere metoder, der gennemsøger en arrayliste (eller anden objektsamling) og finder objekter, der opfylder
Forelæsning Uge 4 Mandag Algoritmeskabeloner Kan (ved simple tilretningerne) bruges til at implementere metoder, der gennemsøger en arrayliste (eller anden objektsamling) og finder objekter, der opfylder
Dokumentation af programmering i Python 2.75
 Dokumentation af programmering i Python 2.75 Af: Alexander Bergendorff Jeg vil i dette dokument, dokumentere det arbejde jeg har lavet i løbet opstarts forløbet i Programmering C. Jeg vil forsøge, så vidt
Dokumentation af programmering i Python 2.75 Af: Alexander Bergendorff Jeg vil i dette dokument, dokumentere det arbejde jeg har lavet i løbet opstarts forløbet i Programmering C. Jeg vil forsøge, så vidt
Software Construction 1 semester (SWC) Spørgsmål 1
 Spørgsmål 1 Objekter #1 Giv en kort præsentation af begrebet objekt, samt hvorledes du erklærer(declare), opretter(create) og bruger objekter Du kan beskrive o Datatyper o Variable / Instans variable /
Spørgsmål 1 Objekter #1 Giv en kort præsentation af begrebet objekt, samt hvorledes du erklærer(declare), opretter(create) og bruger objekter Du kan beskrive o Datatyper o Variable / Instans variable /
Forelæsning Uge 2 Mandag
 Forelæsning Uge 2 Mandag Sætninger Simple sætninger (assignment, interne og eksterne metodekald) Sammensatte sætninger (blok, selektion, gentagelse) Udtryk og operatorer Java syntax og style guide Afleveringsopgaver
Forelæsning Uge 2 Mandag Sætninger Simple sætninger (assignment, interne og eksterne metodekald) Sammensatte sætninger (blok, selektion, gentagelse) Udtryk og operatorer Java syntax og style guide Afleveringsopgaver
Aritmetiske Forelæsning Pr ogrammering operatorer tir 1999 sda præcedens september 1999 Logiske Sammenligningsoperatorer operatorer præcedens
 Programmering 1999 Forelæsning 3, tirsdag 7. september 1999 Aritmetiske og logiske operatorer, præcedens Den indbyggede klasse String: tegnstrenge Metoder i klasser Metoder: returtype eller void Metoder:
Programmering 1999 Forelæsning 3, tirsdag 7. september 1999 Aritmetiske og logiske operatorer, præcedens Den indbyggede klasse String: tegnstrenge Metoder i klasser Metoder: returtype eller void Metoder:
Danmarks Tekniske Universitet
 side af sider Danmarks Tekniske Universitet Skriftlig prøve, den. maj 00. Kursusnavn Algoritmer og datastrukturer Kursus nr. 06. Tilladte hjælpemidler: Alle hjælpemidler. Vægtning af opgaverne: Opgave
side af sider Danmarks Tekniske Universitet Skriftlig prøve, den. maj 00. Kursusnavn Algoritmer og datastrukturer Kursus nr. 06. Tilladte hjælpemidler: Alle hjælpemidler. Vægtning af opgaverne: Opgave
Skriftlig Eksamen Algoritmer og Datastrukturer (dads)
 Skriftlig Eksamen Algoritmer og Datastrukturer (dads) Datalogisk Institut Aarhus Universitet Tirsdag den 27. maj 2003, kl. 9.00 3.00 Opgave (25%) For konstanten π = 3.4592... gælder identiteten π 2 6 =
Skriftlig Eksamen Algoritmer og Datastrukturer (dads) Datalogisk Institut Aarhus Universitet Tirsdag den 27. maj 2003, kl. 9.00 3.00 Opgave (25%) For konstanten π = 3.4592... gælder identiteten π 2 6 =
DM507 Algoritmer og datastrukturer
 DM507 Algoritmer og datastrukturer Forår 2012 Projekt, del III Institut for matematik og datalogi Syddansk Universitet 29. april, 2012 Dette projekt udleveres i tre dele. Hver del har sin deadline, således
DM507 Algoritmer og datastrukturer Forår 2012 Projekt, del III Institut for matematik og datalogi Syddansk Universitet 29. april, 2012 Dette projekt udleveres i tre dele. Hver del har sin deadline, således
22 Hobe. Noter. PS1 -- Hobe. Binære hobe. Minimum-hob og maximum-hob. Den abstrakte datatype minimum-hob. Opbygning af hobe. Operationen siv-ned.
 22 Hobe. Binære hobe. Minimum-hob og maximum-hob. Den abstrakte datatype minimum-hob. Opbygning af hobe. Operationen siv-ned. Indsættelse i hobe. Sletning af minimalt element i hobe. Repræsentation. 327
22 Hobe. Binære hobe. Minimum-hob og maximum-hob. Den abstrakte datatype minimum-hob. Opbygning af hobe. Operationen siv-ned. Indsættelse i hobe. Sletning af minimalt element i hobe. Repræsentation. 327
Forslag til løsning af Opgaver til afsnittet om de naturlige tal (side 80)
 Forslag til løsning af Opgaver til afsnittet om de naturlige tal (side 80) Opgave 1 Vi skal tegne alle de linjestykker, der forbinder vilkårligt valgte punkter blandt de 4 punkter. Gennem forsøg finder
Forslag til løsning af Opgaver til afsnittet om de naturlige tal (side 80) Opgave 1 Vi skal tegne alle de linjestykker, der forbinder vilkårligt valgte punkter blandt de 4 punkter. Gennem forsøg finder
1 monotoni & funktionsanalyse
 1 monotoni & funktionsanalyse I dag har vi grafregnere (TI89+) og programmer på computer (ex.vis Derive og Graph), hvorfor det ikke er så svært at se hvordan grafen for en matematisk funktion opfører sig
1 monotoni & funktionsanalyse I dag har vi grafregnere (TI89+) og programmer på computer (ex.vis Derive og Graph), hvorfor det ikke er så svært at se hvordan grafen for en matematisk funktion opfører sig
Sortering. Eksempel: De n tal i sorteret orden
 Sortering 1 / 34 Sortering Input: Output: Eksempel: n tal De n tal i sorteret orden 6, 2, 9, 4, 5, 1, 4, 3 1, 2, 3, 4, 4, 5, 9 2 / 34 Sortering Input: Output: Eksempel: n tal De n tal i sorteret orden
Sortering 1 / 34 Sortering Input: Output: Eksempel: n tal De n tal i sorteret orden 6, 2, 9, 4, 5, 1, 4, 3 1, 2, 3, 4, 4, 5, 9 2 / 34 Sortering Input: Output: Eksempel: n tal De n tal i sorteret orden
Programmering 1999 KVL Side 5-4. Klassen Time: metoder. Metoder i objektet giver mulighed for at ændre tilstanden, eller kigge på tilstanden.
 Programmering 1999 Forelæsning 5, tirsdag 14. september 1999 Oversigt Mere om klasser og objekter Klassefelter: static Konstante felter: final Indkapsling og synlighed: private og public Overlæsning af
Programmering 1999 Forelæsning 5, tirsdag 14. september 1999 Oversigt Mere om klasser og objekter Klassefelter: static Konstante felter: final Indkapsling og synlighed: private og public Overlæsning af
Test af It-komponent
 Test af It-komponent I programmeringssproget Java Programmet Login service Elev: Mads Funch Klasse 2.4 Mat, It, Programmering Skole: Roskilde Tekniske Gymnasium HTX Underviser: Karl Dato: 31-08-2016 Side
Test af It-komponent I programmeringssproget Java Programmet Login service Elev: Mads Funch Klasse 2.4 Mat, It, Programmering Skole: Roskilde Tekniske Gymnasium HTX Underviser: Karl Dato: 31-08-2016 Side
Træer. Datastrukturer & Algoritmer, Datalogi C Forelæsning 9/
 Datastrukturer & Algoritmer, Datalogi C Forelæsning 9/11-2004 Træer En meget vigtig datastruktur Repræsentation af sprog (i meget generel betydning), syntakstræer: Java (i en compiler), SQL (i et databasesystem),
Datastrukturer & Algoritmer, Datalogi C Forelæsning 9/11-2004 Træer En meget vigtig datastruktur Repræsentation af sprog (i meget generel betydning), syntakstræer: Java (i en compiler), SQL (i et databasesystem),
Søgetræer: Generel repræsentation af (sorterede) mængder og funktioner Databasesystemer...
 Datastrukturer & Algoritmer, Datalogi C Forelæsning 11/11-2003 Træer En meget vigtig datastruktur Repræsentation af sprog (i meget generel betydning), syntakstræer: Java (i en compiler), SQL (i et databasesystem),
Datastrukturer & Algoritmer, Datalogi C Forelæsning 11/11-2003 Træer En meget vigtig datastruktur Repræsentation af sprog (i meget generel betydning), syntakstræer: Java (i en compiler), SQL (i et databasesystem),
DM502. Peter Schneider-Kamp (petersk@imada.sdu.dk) http://imada.sdu.dk/~petersk/dm502/
 DM502 Peter Schneider-Kamp (petersk@imada.sdu.dk) http://imada.sdu.dk/~petersk/dm502/ 1 DM502 Bog, ugesedler og noter De første øvelser Let for nogen, svært for andre Kom til øvelserne! Lav opgaverne!
DM502 Peter Schneider-Kamp (petersk@imada.sdu.dk) http://imada.sdu.dk/~petersk/dm502/ 1 DM502 Bog, ugesedler og noter De første øvelser Let for nogen, svært for andre Kom til øvelserne! Lav opgaverne!
4. Snittets kædebrøksfremstilling og dets konvergenter
 Dette er den fjerde af fem artikler under den fælles overskrift Studier på grundlag af programmet SKALAGENERATOREN (forfatter: Jørgen Erichsen) 4. Snittets kædebrøksfremstilling og dets konvergenter Vi
Dette er den fjerde af fem artikler under den fælles overskrift Studier på grundlag af programmet SKALAGENERATOREN (forfatter: Jørgen Erichsen) 4. Snittets kædebrøksfremstilling og dets konvergenter Vi
Introduktion til differentialregning 1. Jens Siegstad og Annegrethe Bak
 Introduktion til differentialregning 1 Jens Siegstad og Annegrete Bak 16. juli 2008 1 Indledning I denne note vil vi kort introduktion til differentilregning, idet vi skal bruge teorien i et emne, Matematisk
Introduktion til differentialregning 1 Jens Siegstad og Annegrete Bak 16. juli 2008 1 Indledning I denne note vil vi kort introduktion til differentilregning, idet vi skal bruge teorien i et emne, Matematisk
Danmarks Tekniske Universitet
 side af sider Danmarks Tekniske Universitet Skriftlig prøve, den. maj 00. Kursusnavn Algoritmer og datastrukturer I Kursus nr. 005. Tilladte hjælpemidler: Alle skriftlige hjælpemidler. Vægtning af opgaverne:
side af sider Danmarks Tekniske Universitet Skriftlig prøve, den. maj 00. Kursusnavn Algoritmer og datastrukturer I Kursus nr. 005. Tilladte hjælpemidler: Alle skriftlige hjælpemidler. Vægtning af opgaverne:
Polynomiumsbrøker og asymptoter
 Polynomiumsbrøker og asymptoter Frank Villa 9. marts 2012 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold
Polynomiumsbrøker og asymptoter Frank Villa 9. marts 2012 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold
