Den homogene ligning. Vi betragter den n te ordens, homogene, lineære differentialligning. d n y dt n. an 1 + any = 0 (1.2) dt. + a1 d n 1 y dt n 1
|
|
|
- Knud Ludvigsen
- 5 år siden
- Visninger:
Transkript
1 1/7 Den homogene ligning Vi betragter den n te ordens, homogene, lineære differentialligning a 0 d n y dt n + a1 d n 1 y dt n 1 hvor a 0,..., a n R og a 0 0. Vi skriver ligningen på kort form som + + dy an 1 + any = 0 (1.2) dt D n(y) = 0 (1.6)
2 2/7 Karakterligningen og løsninger Karakterligningen hørende til ligningen D n(y) = 0 er P (λ) = a 0λ n + a 1λ n a n 1λ + a n = 0. Man er ofte interesseret i den fuldstændige reelle løsning. I den forbindelse er der to problemstillinger: Sætning 1.6 giver kun en basis for løsningsrummet, hvis karakterligningen har n forskellige rødder. Karakterligningen kan have komplekse rødder, der leder til komplekse løsninger.
3 Multiple rødder 3/7
4 Reelle løsninger 4/7
5 Den fuldstændige reelle løsning 5/7
6 6/7 Den inhomogene ligning Vi betragter nu den inhomogene ligning D n(y) = u (1.14) En partikulær løsning findes ved hjælp af gættemetoden. Betragt en ligning på formen D n(y) = c 1u 1 + c 2u 2
7 7/7 Overføringsfunktioner Til en differentialligning på formen a 0y (n) + a 1y (n 1) + + a ny = b 0u (m) + b 1u (m 1) + + b mu (1.16) knyttes overføringsfunktionen H(s) = b0sm + b 1s m b m 1s + b m a 0s n + a 1s n a n 1s + a n, (1.20) defineret på mængden {s C P (s) 0}.
8 1/9 Det homogene system Vi betragter det homogene system ẋ = Ax. (2.10) Vi definerer det karakteristiske polynomium som P (λ) = det (A λi)
9 Reelle løsninger 2/9
10 Geometrisk multiplicitet og løsninger 3/9
11 4/9 Geometrisk multiplicitet og løsninger Se Eksempel 2.12 i bogen.
12 Fuldstændig løsning 5/9
13 6/9 Det inhomogene system Vi betragter det inhomogene system ẋ = Ax + u. (2.21) Sætning (Analog til Sætning 1.20) Lad y 0 betegne en løsning til ligningen (2.21) og lad y HOM betegne samtlige løsninger til den tilsvarende homogene ligning. Da er samtlige løsninger til (2.21). y = y 0 + y HOM En partikulær løsning kan ofte findes via gættemetoden. Superpositionsprincippet gælder for lineære systemer af differentialligninger.
14 7/9 Fundamentalmatricen Vi giver her samme definition med et lidt andet ordvalg: Definition (Fundamentalmatrix) Antag at x 1(t), x 2(t),..., x n(t) er n lineært uafhængige løsninger til det homogene system ẋ = Ax. Vi definerer fundamentalmatricen Φ ved Φ(t) = (x 1(t), x 2(t),..., x n(t)), t I. (2.17) Dvs. Φ(t) er matricen med funktionerne x 1(t),..., x n(t) som søjler. Det bemærkes at fundamentalmatricen ikke er entydigt bestemt. F.eks. kan søjlerne ombyttes frit.
15 Fundamentalmatricens egenskaber 8/9
16 9/9 Den generelle løsningsformel Den generelle løsningsformel er meget regnetung og bør derfor kun anvendes, hvis gættemetoden ikke virker.
17 1/7 Overføringsfunktioner for systemer Vi betragter et system på den specielle form { ẋ = Ax + bu, y = d x (2.32) Vi definerer overføringsfunktionen hørende til systemet (2.32) ved for de s C for hvilke det(a si) 0. H(s) = d (A si)b (2.36)
18 2/7 Begrænsede funktioner Definition (Begrænset funktion) Lad I R. En funktion f : I C siges at være begrænset, hvis der findes en konstant K > 0 således at f(t) K for alle t I. En vektorfunktion x: I C n, x(t) = x 1(t). x n(t) er begrænset, hvis alle dens koordinatfunktioner x 1,..., x n hver især er begrænsede. Dette er ensbetydende med at der findes en konstant K > 0 så x(t) := x 1(t) x n(t) 2 K for alle t I.
19 3/7 Stabilitet Vi betragter de homogene system ẋ(t) = Ax(t), t [t 0, [. (2.41)
20 4/7 Resultater vedrørende stabilitet Vi betragter de homogene system ẋ(t) = Ax(t), t [t 0, [. (2.41)
21 Routh-Hurwitz kriterium Det er muligt at afgøre om et system er asymptotisk stabilt uden at udregne egenværdierne. 5/7
22 Korollarer Routh-Hurwitz kriterium 6/7
23 7/7 Stabilitet for inhomogene systemer Vi betragter det inhomogene system ẋ(t) = Ax(t) + u(t), t [t 0, [. (2.51)
24 1/4 Uegentlige integraler Nyttigt resultat: Lad p R. Det uegentlige integral 1 1 x p dx er konvergent for p > 1 og divergent for p 1.
25 2/4 Talfølger For en uendelige talfølge anvendes notationen {x n} n=1 = {x 1, x 2,...}.
26 3/4 Taylorpolynomier Definition (Taylorpolynomiet) Lad I R være et interval og lad f : I R være en (uendeligt ofte) differentiabel funktion. Lad x 0 I og N N. Det N te Taylorpolynomium for f i punktet x 0 defineres som P N (x) = f(x 0) + f (x 0) 1! N = n=0 f (n) (x 0) (x x 0) n. n! (x x 0) + f (x 0) 2! (x x 0) f (N) (x 0) (x x 0) N N!
27 Taylors sætning 4/4
28 1/5 Uendelige rækker En uendelig række er et udtryk på formen hvor a n R (eller C) for alle n N. a n n=1 For en given uendelige række defineres den N te afsnitssum som tallet N S N = a a N = a n (4.20) n=1 Den N te afsnitssum er altså summen af rækkens N første led.
29 2/5 Uendelige rækker Bemærk: n te-ledskriteriet kan aldrig bruges til at slutte at en række er konvergent.
30 Konvergenskriterier 3/5
31 4/5 Absolut konvergens Bemærk at (4.27) er en generalisering af trekantsuligheden.
32 5/5 Kvotientkriteriet Bemærk at hvis C = 1 giver kvotientkriteriet ingen konklusion. Man må i så fald finde en anden metode til at afgøre om rækken er konvergent eller divergent.
33 1/5 Integralkriteriet Betragt en uendelig række n=1 a n. I visse tilfælde kan det være en fordel at betragte rækkens led som funktionsværdier. Man skal altså finde en funktion f : [1, [ C, så a n = f(n) for alle n N (eller i hvert fald fra et vist n og opefter).
34 Integralkriteriet 2/5
35 3/5 Vurdering af summen af en uendelig række Lad os antage at vi ønsker at bestemme summen f(n) med en fejl der ikke overstiger et givet tal ε > 0. Metode (i): Vælg N N således at Så vil den endelige sum uendelige sum. N+1 N n=1 n=1 f(x)dx + f(n + 1) ε. f(n) højst afvige med ε fra den ønskede Metode (ii): Vælg N N således at f(n + 1) ε. Da vil tallet N n=1 f(n) + f(x)dx N+1 højst afvige med ε fra den ønskede uendelige sum.
36 4/5 Alternerende rækker Rækker med skiftevis positive og negative led kaldes alternerende rækker.
37 Alternerende rækker 5/5
38 Kvotientrækker 1/5
39 Taylorrækker / potensrækker 2/5
40 3/5 Potensrækker Tallet ρ kaldes for rækkens konvergensradius. I tilfældene (i) og (ii) sættes ρ til henholdsvis 0 og. Bemærk at tilfældet (iii) ikke udtaler sig om konvergens hvis x = ρ.
41 Potensrækker 4/5
42 Differentiation og integration af potensrækker 5/5
43 Uniform konvergens 1/3
44 Majorantrække og uniform konvergens 2/3
45 Ledvis integration og differentiation 3/3
46 1/4 Fourierrækker En funktion f : R C kaldes 2π-periodisk hvis f(x + 2π) = f(x) for alle x R. Se også Appendix C i lærebogen om funktioner med andre perioder.
47 Lige og ulige funktioner 2/4
48 Fourierrækker for lige og ulige funktioner 3/4
49 Fouriers sætning 4/4
50 Vurdering af sum for Fourierrækker 1/5
51 Fourierrækker på kompleks form 2/5
52 Reel form kompleks form 3/5
53 4/5 Reel form og kompleks form Det bemærkes at den reelle form og den komplekse form af en Fourierrække blot er to forskellige notationer for præcis den samme række. Der gælder altså 1 2 a0 + (a n cos(nx) + b n sin(nx)) = c ne inx n=1 n= Fouriers sætning (Sætning 6.12) kan derfor også skrives med den komplekse notation:
54 5/5 Parsevals sætning For visse uendelige rækker kan summen findes ved brug af Parsevals sætning - nemlig hvis rækken kan skrives som en sum af Fourierkoefficienter for en funktion f.
55 Fourierrækkemetoden 1/2
56 2/2 Fourierrækkemetoden Procedure for brug af Sætning 7.8: 1. Tjek at differentialligningssystemet (2.32) er asymptotisk stabilt. 2. Beregn overføringsfunktionen H(s) (husk at angive definitionsmængden). 3. Opstil Fourierrækken for påvirkningen u, u n= c ne int. 4. Tjek at u er 2π-periodisk, stykkevis differentiabel og kontinuert, så u(t) = n= c ne int. 5. Opstil løsningen y(t) = n= cnh(in)eint. 6. (Ofte:) Find N N så y(t) N n= N c nh(in)e int ɛ for alle t R.
57 1/4 Ligninger med variable koefficienter Vi betragter den inhomogene 2. ordensligning d 2 y dt 2 dy + a1(t) + a2(t)y = u(t), t I, (1.36) dt hvor a 1, a 2 og u er givne funktioner, og y = y(t) er den søgte løsning. Den tilsvarende homogene ligning er d 2 y dt 2 dy + a1(t) + a2(t)y = 0, t I. (1.37) dt Sætning 1.31 (se næste slide) fortæller at hvis vi kan finde en løsning y 1 til den homogene ligning (1.37), som opfylder at y 1(t) 0 for alle t I, så kan vi også finde den fuldstændige løsning både til den homogene ligning (1.37) og til den inhomogene ligning (1.36).
58 Ligninger med variable koefficienter 2/4
59 3/4 Potensrækkemetoden Vi betragter en differentialligning på formen a 0(t) dn y dt n + a1(t) dn 1 y dt n 1 dy + + an 1(t) + an(t)y = 0, t I (7.1) dt Oftest vil vi have n = 2 og a 0(t) = 1, så ligningen får formen d 2 y dt 2 dy + a1(t) + a2(t)y = 0, t I. (1.37) dt Potensrækkemetoden: 1. Gæt på en potensrækkeløsning y(t) = n=0 cntn. 2. Indsæt i den homogene ligning (7.1) eller (1.37) og bestem koefficienterne c n, så vi får en løsning. 2.1 Start med (om nødvendigt) at ændre summationsindex, så alle summer får t (eller x) i samme potens, 2.2 Træk dernæst (om nødvendigt) led ud af nogle summer, så der summes over de samme n i alle summer. 3. Find konvergensradius for den fundne potensrække. 4. Evt. find N så y(t) N n=0 cnxn ɛ for t i et passende interval.
60 4/4 Potensrækkemetoden Er der nogen garanti for at potensrækkemetoden virker? Ja, hvis a 1 og a 2 er analytiske funktioner (se sætning nedenfor).
61 1/4 Ulineære systemer Vi betragter et system på formen ẋ 1(t) = f 1 (x 1(t),..., x n(t)),. ẋ n(t) = f n (x 1(t),..., x n(t)), (3.1) hvor f 1,..., f n er funktioner R n R. På vektorform kan systemet skrives som ẋ(t) = f (x(t)). (3.2) Systemet kaldes et ulineært autonomt differentialligningssystem.
62 Stationære punkter og stabilitet 2/4
63 3/4 Stationære punkter og stabilitet For en vektorfunktion f : R n R n defineres funktionalmatricen Df i et punkt x R n ved f 1 f x 1 (x) 1 x n (x) Df(x) = f n f x 1 (x) n x n (x)
64 4/4 Faseportræt i Maple Eksempel: Vi vil tegne et faseportræt for systemet { ẋ1 = x 2, x 2 = x 1 + x 1x 2. Nedenfor defineres systemet som ligningerne eqn1 og eqn2. Dernæst beder vi Maple om et faseportræt på området x 1 [ 2, 2], x 2 [ 2, 2] og vi lader t [ 1, 1]. Se mere i lærebogens appendix D.3.2.
65 1/7 Vurdering af sum for uendelige rækker Matematik 2 August 2016
66 Rækker med positive led Lad f : [1, [ [0, [ være en kontinuert og aftagende funktion. Vi ønsker at bestemme summen a n = f(n) med en fejl der ikke overstiger et givet tal ε > 0. n=1 n=1 Metode (i): Vælg N N således at N+1 N f(x)dx + f(n + 1) ε. Så vil den endelige sum f(n) højst afvige med ε fra den ønskede n=1 uendelige sum, dvs. f(n) N f(n) ɛ. n=1 n=1 Metode (ii): Vælg N N således at f(n + 1) ε. Da vil tallet N f(n) + f(x)dx N+1 n=1 højst afvige ( med ε fra den ønskede uendelige sum, dvs. N f(n) f(n) + ) f(x)dx ɛ. N+1 n=1 n=1 2/7
67 3/7 Rækker med positive led Bemærk: Både metode (i) og metode (ii) giver en tilnærmet værdi for rækken f(n), men det er forskelligt, hvordan det tilnærmende udtryk n=1 ser ud. I metode (i) er det afsnitssummen n=1 f(n) + f(x)dx. N+1 N n=1 f(n), i metode (ii) er det Dette betyder at hvis opgaven lyder på at bestemme N så afsnitssummen kommer tæt på den uendelige række, dvs. så N a n a n ɛ n=1 er man nødt til at benytte metode (i). n=1
68 Alternerende rækker Rækker med skiftevis positive og negative led kaldes alternerende rækker, se Definition 4.37 i lærebogen. Til at vurdere summen for en alternerende række benyttes Leibniz kriterium (hvis forudsætningerne for dette er opfyldt). 4/7
69 5/7 Generelle rækker For en absolut konvergent række a n bemærkes at (ifølge sætning 4.27) n=0 n=0 N a n a n = n=0 n=n+1 a n n=n+1 a n. Rækken til højre har positive led, så hvis vi kan finde en kontinuert, aftagende funktion f : [1, [ [0, [, således at har vi ifølge korollar 4.35 at n=n+1 f(n) = a n for alle n N a n N+1 f(x)dx + f(n + 1). Vi skal nu blot finde et N, så f(x)dx + f(n + 1) ɛ, og dette vil så N+1 sikre at N a n a n ɛ. n=0 n=0
70 6/7 Forierrækker Hvis f er en kontinuert, stykkevis differentiabel og 2π-periodisk funktion (og derfor ifølge Korollar 6.13 lig med sin egen Fourierrække) kan vi bruge korollar 6.16 til at finde N. Dette kan dog kun bruges hvis vi kender funktionen f, så vi kan finde dens afledede f. Hvis vi kun kender f udtrykt som en række, kan vi ikke bruge korollar I stedet kan vi bruge sætning 6.17 (se næste slide).
71 7/7 Forierrækker Hvis vi har en funktion f som er givet ved (altså lig med) sin Fourierrække, dvs. f(x) = 1 2 a0 + (a n cos(nx) + b n sin(nx)) n=0 kan vi benytte sætning 6.17, som giver f(x) S N (x) n=n+1 ( a n + b n ), for all x R. Rækken til højre har positive led, så hvis vi kan finde en kontinuert, aftagende funktion g : [1, [ [0, [, således at har vi ifølge korollar 4.35 at n=n+1 g(n) = a n + b n for alle n N ( a n + b n ) N+1 g(x)dx + g(n + 1). Vi skal nu blot finde et N, så g(x)dx + g(n + 1) ɛ, og dette vil så N+1 sikre at f(x) S N (x) ɛ.
Analyse 1, Prøve 2 Besvarelse
 Københavns Universitet Prøve ved Det naturvidenskabelige Fakultet maj Analyse, Prøve Besvarelse Opgave (3%) (a) (%) Bestem mængden af x R for hvilke rækken ( + (x) n ) er konvergent og angiv sumfunktionen
Københavns Universitet Prøve ved Det naturvidenskabelige Fakultet maj Analyse, Prøve Besvarelse Opgave (3%) (a) (%) Bestem mængden af x R for hvilke rækken ( + (x) n ) er konvergent og angiv sumfunktionen
DESIGNMAT FORÅR 2012: UGESEDDEL Forberedelse Læs alle opgaverne fra tidligere ugesedler, og læg særlig mærke til dem du har spørgsmål til.
 DESIGNMAT FORÅR 2012: UGESEDDEL 13 INSTITUT FOR MATEMATIK 1. Forberedelse Læs alle opgaverne fra tidligere ugesedler, og læg særlig mærke til dem du har spørgsmål til. 2. Aktiviteter mandag 13 17 2.1.
DESIGNMAT FORÅR 2012: UGESEDDEL 13 INSTITUT FOR MATEMATIK 1. Forberedelse Læs alle opgaverne fra tidligere ugesedler, og læg særlig mærke til dem du har spørgsmål til. 2. Aktiviteter mandag 13 17 2.1.
MM502+4 forelæsningsslides
 MM502+4 forelæsningsslides uge 11+12 1, 2009 Produceret af Hans J. Munkholm, delvis på baggrund af lignende materiale udarbejdet af Mikael Rørdam 1 I nærværende forbindelse er 11 + 12 23 1 Egenskaber for
MM502+4 forelæsningsslides uge 11+12 1, 2009 Produceret af Hans J. Munkholm, delvis på baggrund af lignende materiale udarbejdet af Mikael Rørdam 1 I nærværende forbindelse er 11 + 12 23 1 Egenskaber for
Oversigt [S] 7.3, 7.4, 7.5, 7.6; [LA] 15, 16, 17
![Oversigt [S] 7.3, 7.4, 7.5, 7.6; [LA] 15, 16, 17 Oversigt [S] 7.3, 7.4, 7.5, 7.6; [LA] 15, 16, 17](/thumbs/62/47131431.jpg) Oversigt [S] 7.3, 7.4, 7.5, 7.6; [LA] 15, 16, 17 Nøgleord og begreber 1. ordens lineær ligning Løsningsmetode August 2002, opgave 7 1. ordens lineært system Løsning ved egenvektor Lille opgave Stor opgave
Oversigt [S] 7.3, 7.4, 7.5, 7.6; [LA] 15, 16, 17 Nøgleord og begreber 1. ordens lineær ligning Løsningsmetode August 2002, opgave 7 1. ordens lineært system Løsning ved egenvektor Lille opgave Stor opgave
MATEMATIK 11 Eksamensopgaver Juni 1995 Juni 2001, 3. fjerdedel
 MATEMATIK Eksamensopgaver Juni 995 Juni 200, 3. fjerdedel August 998 Opgave. Lad f : R \ {0} R betegne funktionen givet ved f(x) = ex x for x 0. (a) Find eventuelle lokale maksimums- og minimumspunkter
MATEMATIK Eksamensopgaver Juni 995 Juni 200, 3. fjerdedel August 998 Opgave. Lad f : R \ {0} R betegne funktionen givet ved f(x) = ex x for x 0. (a) Find eventuelle lokale maksimums- og minimumspunkter
Afgør for hver af følgende rækker om den er divergent, betinget konvergent eller absolut konvergent. 2 n. n=1 2n (n + 1)2 1 = 2(n + n+1
 Analyse Reeksamen 00 Rasmus Sylvester Bryder 5. august 0 Opgave Afgør for hver af følgende rækker om den er divergent, betinget konvergent eller absolut konvergent. ( ) n n +3n+7 n= n + For alle n N vil
Analyse Reeksamen 00 Rasmus Sylvester Bryder 5. august 0 Opgave Afgør for hver af følgende rækker om den er divergent, betinget konvergent eller absolut konvergent. ( ) n n +3n+7 n= n + For alle n N vil
Nøgleord og begreber. Definition 15.1 Den lineære 1. ordens differentialligning er
 Oversigt [S] 7.3, 7.4, 7.5, 7.6; [LA] 15, 16, 17 Nøgleord og begreber 1. ordens lineær ligning Løsningsmetode August 2002, opgave 7 1. ordens lineært system Løsning ved egenvektor Lille opgave Stor opgave
Oversigt [S] 7.3, 7.4, 7.5, 7.6; [LA] 15, 16, 17 Nøgleord og begreber 1. ordens lineær ligning Løsningsmetode August 2002, opgave 7 1. ordens lineært system Løsning ved egenvektor Lille opgave Stor opgave
Nøgleord og begreber Separable ligninger 1. ordens lineær ligning August 2002, opgave 7 Rovdyr-Byttedyr system 1. ordens lineært system Opgave
 Oversigt [S] 7.3, 7.4, 7.5, 7.6; [LA] 14, 15 Nøgleord og begreber Separable ligninger 1. ordens lineær ligning August 2002, opgave 7 Rovdyr-Byttedyr system 1. ordens lineært system Opgave Calculus 2-2005
Oversigt [S] 7.3, 7.4, 7.5, 7.6; [LA] 14, 15 Nøgleord og begreber Separable ligninger 1. ordens lineær ligning August 2002, opgave 7 Rovdyr-Byttedyr system 1. ordens lineært system Opgave Calculus 2-2005
Modulpakke 3: Lineære Ligningssystemer
 Chapter 4 Modulpakke 3: Lineære Ligningssystemer 4. Homogene systemer I teknikken møder man meget ofte modeller der leder til systemer af koblede differentialligninger. Et eksempel på et sådant system
Chapter 4 Modulpakke 3: Lineære Ligningssystemer 4. Homogene systemer I teknikken møder man meget ofte modeller der leder til systemer af koblede differentialligninger. Et eksempel på et sådant system
Indhold. Litteratur 11
 Indhold Forord ii 00-sættet 1 Opgave 1....................................... 1 Spørgsmål (a).................................. 1 Spørgsmål (b).................................. 1 Spørgsmål (c)..................................
Indhold Forord ii 00-sættet 1 Opgave 1....................................... 1 Spørgsmål (a).................................. 1 Spørgsmål (b).................................. 1 Spørgsmål (c)..................................
DesignMat Lineære differentialligninger I
 DesignMat Lineære differentialligninger I Preben Alsholm Uge Forår 0 1 Lineære differentialligninger af første orden 1.1 Normeret lineær differentialligning Normeret lineær differentialligning En differentialligning,
DesignMat Lineære differentialligninger I Preben Alsholm Uge Forår 0 1 Lineære differentialligninger af første orden 1.1 Normeret lineær differentialligning Normeret lineær differentialligning En differentialligning,
DesignMat Uge 1 Gensyn med forårets stof
 DesignMat Uge 1 Gensyn med forårets stof Preben Alsholm Efterår 2010 1 Hovedpunkter fra forårets pensum 11 Taylorpolynomium Taylorpolynomium Det n te Taylorpolynomium for f med udviklingspunkt x 0 : P
DesignMat Uge 1 Gensyn med forårets stof Preben Alsholm Efterår 2010 1 Hovedpunkter fra forårets pensum 11 Taylorpolynomium Taylorpolynomium Det n te Taylorpolynomium for f med udviklingspunkt x 0 : P
Besvarelse, Eksamen Analyse 1, 2013
 Københavns Universitet Prøve ved Det naturvidenskabelige Fakultet juni 23 Besvarelse, Eksamen Analyse, 23 Opgave Lad, for n N, funktionen f n : [, ) R være givet ved NB. Trykfejl. Burde være x. f n (x)
Københavns Universitet Prøve ved Det naturvidenskabelige Fakultet juni 23 Besvarelse, Eksamen Analyse, 23 Opgave Lad, for n N, funktionen f n : [, ) R være givet ved NB. Trykfejl. Burde være x. f n (x)
Oversigt [S] 7.3, 7.4, 7.5, 7.6; [DL] 1, 2
![Oversigt [S] 7.3, 7.4, 7.5, 7.6; [DL] 1, 2 Oversigt [S] 7.3, 7.4, 7.5, 7.6; [DL] 1, 2](/thumbs/82/86922880.jpg) Oversigt [S] 7.3, 7.4, 7.5, 7.6; [DL] 1, 2 Her skal du lære om Separable ligninger Logistisk ligning og eksponentiel vækst 1. ordens lineær ligning August 2002, opgave 7 Rovdyr-Byttedyr system 1. ordens
Oversigt [S] 7.3, 7.4, 7.5, 7.6; [DL] 1, 2 Her skal du lære om Separable ligninger Logistisk ligning og eksponentiel vækst 1. ordens lineær ligning August 2002, opgave 7 Rovdyr-Byttedyr system 1. ordens
Lineære 2. ordens differentialligninger med konstante koefficienter
 enote 13 1 enote 13 Lineære 2. ordens differentialligninger med konstante koefficienter I forlængelse af enote 11 og enote 12 om differentialligninger, kommer nu denne enote omkring 2. ordens differentialligninger.
enote 13 1 enote 13 Lineære 2. ordens differentialligninger med konstante koefficienter I forlængelse af enote 11 og enote 12 om differentialligninger, kommer nu denne enote omkring 2. ordens differentialligninger.
DesignMat Lineære differentialligninger I
 DesignMat Lineære differentialligninger I Preben Alsholm Uge 9 Forår 2010 1 Lineære differentialligninger af første orden 1.1 Normeret lineær differentialligning Normeret lineær differentialligning En
DesignMat Lineære differentialligninger I Preben Alsholm Uge 9 Forår 2010 1 Lineære differentialligninger af første orden 1.1 Normeret lineær differentialligning Normeret lineær differentialligning En
MATEMATIK 11 Eksamensopgaver Juni 1995 Juni 2001, 4. fjerdedel
 Juni 2000 MATEMATIK 11 Eksamensopgaver Juni 1995 Juni 2001, 4. fjerdedel Opgave 1. (a) Find den fuldstændige løsning til differentialligningen y 8y + 16y = 0. (b) Find den fuldstændige løsning til differentialligningen
Juni 2000 MATEMATIK 11 Eksamensopgaver Juni 1995 Juni 2001, 4. fjerdedel Opgave 1. (a) Find den fuldstændige løsning til differentialligningen y 8y + 16y = 0. (b) Find den fuldstændige løsning til differentialligningen
DesignMat Uge 4 Systemer af lineære differentialligninger I
 DesignMat Uge Systemer af lineære differentialligninger I Preben Alsholm Efterår 008 1 Lineære differentialligningssystemer 11 Lineært differentialligningssystem af første orden I Lineært differentialligningssystem
DesignMat Uge Systemer af lineære differentialligninger I Preben Alsholm Efterår 008 1 Lineære differentialligningssystemer 11 Lineært differentialligningssystem af første orden I Lineært differentialligningssystem
Analyse 1, Prøve 4 Besvarelse
 Københavns Universitet Prøve ved Det naturvidenskabelige Fakultet juni 2011 1 Analyse 1, Prøve 4 Besvarelse Lad Opgave 1 (50%) M = {T R 2 T er en åben trekant} og lad A : M R være arealfunktionen, dvs.
Københavns Universitet Prøve ved Det naturvidenskabelige Fakultet juni 2011 1 Analyse 1, Prøve 4 Besvarelse Lad Opgave 1 (50%) M = {T R 2 T er en åben trekant} og lad A : M R være arealfunktionen, dvs.
Matematisk modellering og numeriske metoder. Lektion 8
 Matematisk modellering og numeriske metoder Lektion 8 Morten Grud Rasmussen 18. oktober 216 1 Fourierrækker 1.1 Periodiske funktioner Definition 1.1 (Periodiske funktioner). En periodisk funktion f er
Matematisk modellering og numeriske metoder Lektion 8 Morten Grud Rasmussen 18. oktober 216 1 Fourierrækker 1.1 Periodiske funktioner Definition 1.1 (Periodiske funktioner). En periodisk funktion f er
DesignMat Uge 5 Systemer af lineære differentialligninger II
 DesignMat Uge 5 Systemer af lineære differentialligninger II Preben Alsholm Efterår 21 1 Lineære differentialligningssystemer 11 Lineært differentialligningssystem af første orden Lineært differentialligningssystem
DesignMat Uge 5 Systemer af lineære differentialligninger II Preben Alsholm Efterår 21 1 Lineære differentialligningssystemer 11 Lineært differentialligningssystem af første orden Lineært differentialligningssystem
Noter om Komplekse Vektorrum, Funktionsrum og Differentialligninger LinAlg 2004/05-Version af 16. Dec.
 Noter om Komplekse Vektorrum, Funktionsrum og Differentialligninger LinAlg 2004/05-Version af 16. Dec. 1 Komplekse vektorrum I defininitionen af vektorrum i Afsnit 4.1 i Niels Vigand Pedersen Lineær Algebra
Noter om Komplekse Vektorrum, Funktionsrum og Differentialligninger LinAlg 2004/05-Version af 16. Dec. 1 Komplekse vektorrum I defininitionen af vektorrum i Afsnit 4.1 i Niels Vigand Pedersen Lineær Algebra
Førsteordens lineære differentialligninger
 enote 16 1 enote 16 Førsteordens lineære differentialligninger I denne enote gives først en kort introduktion til differentialligninger i almindelighed, hvorefter hovedemnet er en særlig type af differentialligninger,
enote 16 1 enote 16 Førsteordens lineære differentialligninger I denne enote gives først en kort introduktion til differentialligninger i almindelighed, hvorefter hovedemnet er en særlig type af differentialligninger,
Besvarelser til de to blokke opgaver på Ugeseddel 7
 Besvarelser til de to blokke opgaver på Ugeseddel 7 De anførte besvarelser er til dels mere summariske end en god eksamensbesvarelse bør være. Der kan godt være fejl i - jeg vil meget gerne informeres,
Besvarelser til de to blokke opgaver på Ugeseddel 7 De anførte besvarelser er til dels mere summariske end en god eksamensbesvarelse bør være. Der kan godt være fejl i - jeg vil meget gerne informeres,
Chapter 3. Modulpakke 3: Egenværdier. 3.1 Indledning
 Chapter 3 Modulpakke 3: Egenværdier 3.1 Indledning En vektor v har som bekendt både størrelse og retning. Hvis man ganger vektoren fra højre på en kvadratisk matrix A bliver resultatet en ny vektor. Hvis
Chapter 3 Modulpakke 3: Egenværdier 3.1 Indledning En vektor v har som bekendt både størrelse og retning. Hvis man ganger vektoren fra højre på en kvadratisk matrix A bliver resultatet en ny vektor. Hvis
Lineære 1. ordens differentialligningssystemer
 enote enote Lineære ordens differentialligningssystemer Denne enote beskriver ordens differentialligningssystemer og viser, hvordan de kan løses enoten er i forlængelse af enote, der beskriver lineære
enote enote Lineære ordens differentialligningssystemer Denne enote beskriver ordens differentialligningssystemer og viser, hvordan de kan løses enoten er i forlængelse af enote, der beskriver lineære
af koblede differentialligninger (se Apostol Bind II, s 229ff) 3. En n te ordens differentialligning
 EKSISTENS- OG ENTYDIGHEDSSÆTNINGEN Vi vil nu bevise eksistens- og entydighedssætningen for ordinære differentialligninger. For overskuelighedens skyld vil vi indskrænke os til at undersøge een 1. ordens
EKSISTENS- OG ENTYDIGHEDSSÆTNINGEN Vi vil nu bevise eksistens- og entydighedssætningen for ordinære differentialligninger. For overskuelighedens skyld vil vi indskrænke os til at undersøge een 1. ordens
(c) Opskriv den reelle Fourierrække for funktionen y(t) fra (b), og afgør dernæst om y(t) er en lige eller ulige funktion eller ingen af delene.
 MATEMATIK 3 EN,MP 4. februar 2016 Eksamenopgaver fra 2011 2016 (jan. 2016) Givet at 0 for 0 < t < 1 mens e (t 1) cos(7(t 1)) for t 1, betragt da begyndelsesværdiproblemet for t > 0: y (t) + 2y (t) + 50y(t)
MATEMATIK 3 EN,MP 4. februar 2016 Eksamenopgaver fra 2011 2016 (jan. 2016) Givet at 0 for 0 < t < 1 mens e (t 1) cos(7(t 1)) for t 1, betragt da begyndelsesværdiproblemet for t > 0: y (t) + 2y (t) + 50y(t)
Gamle eksamensopgaver (DOK)
 EO 1 Gamle eksamensopgaver ) Opgave 1. sommer 1994, opgave 1) a) Find den fuldstændige løsning til differentialligningen x 6x + 9x =. b) Find den fuldstændige løsning til differentialligningen Opgave 2.
EO 1 Gamle eksamensopgaver ) Opgave 1. sommer 1994, opgave 1) a) Find den fuldstændige løsning til differentialligningen x 6x + 9x =. b) Find den fuldstændige løsning til differentialligningen Opgave 2.
Lineære 1. ordens differentialligningssystemer
 enote 7 enote 7 Lineære ordens differentialligningssystemer Denne enote beskriver ordens differentialligningssystemer og viser, hvordan de kan løses Der bruges egenværdier og egenvektorer i løsningsproceduren,
enote 7 enote 7 Lineære ordens differentialligningssystemer Denne enote beskriver ordens differentialligningssystemer og viser, hvordan de kan løses Der bruges egenværdier og egenvektorer i løsningsproceduren,
MATEMATIK 3 EN,MP 30. august 2013 Oversigt nr. 1
 EN,MP 30. august 2013 Oversigt nr. 1 Litteratur: I Matematik 3 bruger vi (igen) i efteråret 2013 E. Kreyzig: Advanced engineering mathematics, 10. udg., Wiley, 2011. Beskrivelse: Kurset vil handle om matematiske
EN,MP 30. august 2013 Oversigt nr. 1 Litteratur: I Matematik 3 bruger vi (igen) i efteråret 2013 E. Kreyzig: Advanced engineering mathematics, 10. udg., Wiley, 2011. Beskrivelse: Kurset vil handle om matematiske
Lineære differentialligningers karakter og lineære 1. ordens differentialligninger
 enote 11 1 enote 11 Lineære differentialligningers karakter og lineære 1. ordens differentialligninger I denne note introduceres lineære differentialligninger, som er en speciel (og bekvem) form for differentialligninger.
enote 11 1 enote 11 Lineære differentialligningers karakter og lineære 1. ordens differentialligninger I denne note introduceres lineære differentialligninger, som er en speciel (og bekvem) form for differentialligninger.
ANALYSE 1, 2014, Uge 5
 ANALYSE, 204, Uge 5 Afleveringsfrist for Prøve 2 er Tirsdag den 20/5 kl 0:5. Forelæsninger Tirsdag Vi går videre med Afsnit 4 om uniform konvergens af Fourierrækker, hvor hovedsætningen er Sætning 4.3.
ANALYSE, 204, Uge 5 Afleveringsfrist for Prøve 2 er Tirsdag den 20/5 kl 0:5. Forelæsninger Tirsdag Vi går videre med Afsnit 4 om uniform konvergens af Fourierrækker, hvor hovedsætningen er Sætning 4.3.
Mat H 2 Øvelsesopgaver
 Mat H 2 Øvelsesopgaver 18. marts 1998 1) dx dt + 2t 1+t x = 1 2 1+t, fuldstændig løsning. 2 2) ẋ + t 2 x = t 2, fuldstændig løsning. 3) ẋ 2tx = t, x() = 1. 4) ẋ + 1 t x = 1 t 2, t >, undersøg løsningen
Mat H 2 Øvelsesopgaver 18. marts 1998 1) dx dt + 2t 1+t x = 1 2 1+t, fuldstændig løsning. 2 2) ẋ + t 2 x = t 2, fuldstændig løsning. 3) ẋ 2tx = t, x() = 1. 4) ẋ + 1 t x = 1 t 2, t >, undersøg løsningen
Oversigt [S] 8.7, 8.8, 8.9
![Oversigt [S] 8.7, 8.8, 8.9 Oversigt [S] 8.7, 8.8, 8.9](/thumbs/62/47922248.jpg) Oversigt [S] 8.7, 8.8, 8.9 Nøgleord og begreber Potensrækker og opgaver Binomialformlen Binomialkoefficienter Binomialrækken Taylor polynomier Vurdering af Taylor s restled Eksponentialrækken konvereger
Oversigt [S] 8.7, 8.8, 8.9 Nøgleord og begreber Potensrækker og opgaver Binomialformlen Binomialkoefficienter Binomialrækken Taylor polynomier Vurdering af Taylor s restled Eksponentialrækken konvereger
Hilbert rum. Chapter 3. 3.1 Indre produkt rum
 Chapter 3 Hilbert rum 3.1 Indre produkt rum I det følgende skal vi gøre brug af komplekse såvel som reelle vektorrum. Idet L betegner enten R eller C minder vi om, at et vektorrum over L er en mængde E
Chapter 3 Hilbert rum 3.1 Indre produkt rum I det følgende skal vi gøre brug af komplekse såvel som reelle vektorrum. Idet L betegner enten R eller C minder vi om, at et vektorrum over L er en mængde E
Her skal du lære om 1. Talfølge og talrække 2. Afsnitssum 3. Konvergens 4. Konvergente rækker har små led 5. Regneregler
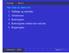 Oversigt [S] 8.2 Her skal du lære om. Talfølge og talrække 2. Afsnitssum 3. Konvergens 4. Konvergente rækker har små led 5. Regneregler Calculus - 2003 Uge 4. - Uendelig række Definition Givet en talfølge
Oversigt [S] 8.2 Her skal du lære om. Talfølge og talrække 2. Afsnitssum 3. Konvergens 4. Konvergente rækker har små led 5. Regneregler Calculus - 2003 Uge 4. - Uendelig række Definition Givet en talfølge
Taylorudvikling I. 1 Taylorpolynomier. Preben Alsholm 3. november Definition af Taylorpolynomium
 Taylorudvikling I Preben Alsholm 3. november 008 Taylorpolynomier. Definition af Taylorpolynomium Definition af Taylorpolynomium Givet en funktion f : I R! R og et udviklingspunkt x 0 I. Find et polynomium
Taylorudvikling I Preben Alsholm 3. november 008 Taylorpolynomier. Definition af Taylorpolynomium Definition af Taylorpolynomium Givet en funktion f : I R! R og et udviklingspunkt x 0 I. Find et polynomium
DOK-facitliste DOK. DOK-facitliste 1
 -facitliste 1 -facitliste Listens numre refererer til samlingen af supplerede -opgaver (de gamle eksamensopgaver. På listen står næsten kun facitter, og ikke tilstrækkelige svar på opgaverne. [Korrigeret
-facitliste 1 -facitliste Listens numre refererer til samlingen af supplerede -opgaver (de gamle eksamensopgaver. På listen står næsten kun facitter, og ikke tilstrækkelige svar på opgaverne. [Korrigeret
Fordybelsesprojekt Matematik 2, forår 2005 Potensrækker
 Fordybelsesprojekt Matematik 2, forår 2005 Potensrækker Arne Jensen 7. 11. marts 2005 1 Indledning I forbindelse med kurset i Reelle og Komplekse Funktioner afholdes et fordybelsesprojekt med et omfang
Fordybelsesprojekt Matematik 2, forår 2005 Potensrækker Arne Jensen 7. 11. marts 2005 1 Indledning I forbindelse med kurset i Reelle og Komplekse Funktioner afholdes et fordybelsesprojekt med et omfang
2. Fourierrækker i en variabel
 .1. Fourierrækker i en variabel I Kapitel II 7 blev der indført, dels funktionsrummene L p (X, µ) (mere udførligt skrevet L p (X, E, µ)), dels rummene L p (X, µ), der fås af L p (X, µ) ved at funktioner
.1. Fourierrækker i en variabel I Kapitel II 7 blev der indført, dels funktionsrummene L p (X, µ) (mere udførligt skrevet L p (X, E, µ)), dels rummene L p (X, µ), der fås af L p (X, µ) ved at funktioner
12.1 Cayley-Hamilton-Sætningen
 SEKTION 12.1 CAYLEY-HAMILTON-SÆTNINGEN 12.1 Cayley-Hamilton-Sætningen Sætning 12.1.1 (Cayley-Hamilton) Lad A Mat n,n (C). Så gælder p A (A) =. Sætningen gælder faktisk over et vilkårligt legeme, men vi
SEKTION 12.1 CAYLEY-HAMILTON-SÆTNINGEN 12.1 Cayley-Hamilton-Sætningen Sætning 12.1.1 (Cayley-Hamilton) Lad A Mat n,n (C). Så gælder p A (A) =. Sætningen gælder faktisk over et vilkårligt legeme, men vi
n=1 er veldefineret for alle følger for hvilke højresiden er endelig. F.eks. tilhører følgen
 2 Hilbert rum 2. Eksempler på Hilbert rum Vi skal nu først forsøge at begrunde, at de indre produkt rum af funktioner eller følger, som blev indført i Kapitel, ikke er omfattende nok til vores formål.
2 Hilbert rum 2. Eksempler på Hilbert rum Vi skal nu først forsøge at begrunde, at de indre produkt rum af funktioner eller følger, som blev indført i Kapitel, ikke er omfattende nok til vores formål.
Eksamen i Calculus. Onsdag den 1. juni Første Studieår ved Det Teknisk-Naturvidenskabelige Fakultet og Det Sundhedsvidenskabelige Fakultet
 Eksamen i Calculus Onsdag den 1. juni 211 Første Studieår ved Det Teknisk-Naturvidenskabelige Fakultet og Det Sundhedsvidenskabelige Fakultet Nærværende eksamenssæt består af 7 nummererede sider med ialt
Eksamen i Calculus Onsdag den 1. juni 211 Første Studieår ved Det Teknisk-Naturvidenskabelige Fakultet og Det Sundhedsvidenskabelige Fakultet Nærværende eksamenssæt består af 7 nummererede sider med ialt
Egenværdier og egenvektorer
 1 Egenværdier og egenvektorer 2 Definition Lad A være en n n matrix. En vektor v R n, v 0, kaldes en egenvektor for A, hvis der findes en skalar λ således Av = λv Skalaren λ kaldes en tilhørende egenværdi.
1 Egenværdier og egenvektorer 2 Definition Lad A være en n n matrix. En vektor v R n, v 0, kaldes en egenvektor for A, hvis der findes en skalar λ således Av = λv Skalaren λ kaldes en tilhørende egenværdi.
DesignMat Uge 1 Repetition af forårets stof
 DesignMat Uge 1 Repetition af forårets stof Preben Alsholm Efterår 008 01 Lineært ligningssystem Lineært ligningssystem Et lineært ligningssystem: a 11 x 1 + a 1 x + + a 1n x n = b 1 a 1 x 1 + a x + +
DesignMat Uge 1 Repetition af forårets stof Preben Alsholm Efterår 008 01 Lineært ligningssystem Lineært ligningssystem Et lineært ligningssystem: a 11 x 1 + a 1 x + + a 1n x n = b 1 a 1 x 1 + a x + +
Lineære 1. ordens differentialligningssystemer
 enote enote Lineære ordens differentialligningssystemer Denne enote beskriver ordens differentialligningssystemer og viser, hvordan de kan løses enoten er i forlængelse af enote, der beskriver lineære
enote enote Lineære ordens differentialligningssystemer Denne enote beskriver ordens differentialligningssystemer og viser, hvordan de kan løses enoten er i forlængelse af enote, der beskriver lineære
Nøgleord og begreber Eksistens og entydighed Retningsfelt Eulers metode Hastighedsfelt Stabilitet
 Oversigt [S] 7.2, 7.5, 7.6; [LA] 17, 18 Nøgleord og begreber Eksistens og entydighed Retningsfelt Eulers metode Hastighedsfelt Stabilitet Calculus 2-2004 Uge 49.2-1 Ligning og løsning [LA] 17 Generel ligning
Oversigt [S] 7.2, 7.5, 7.6; [LA] 17, 18 Nøgleord og begreber Eksistens og entydighed Retningsfelt Eulers metode Hastighedsfelt Stabilitet Calculus 2-2004 Uge 49.2-1 Ligning og løsning [LA] 17 Generel ligning
DesignMat Uge 2. Preben Alsholm. Efterår Lineære afbildninger. Preben Alsholm. Lineære afbildninger. Eksempel 2 på lineær.
 er DesignMat Uge 2 er er lineær lineær lineær lineære er I smatrix lineære er II smatrix I smatrix II Efterår 2010 Lad V og W være vektorrum over samme skalarlegeme L (altså enten R eller C for begge).
er DesignMat Uge 2 er er lineær lineær lineær lineære er I smatrix lineære er II smatrix I smatrix II Efterår 2010 Lad V og W være vektorrum over samme skalarlegeme L (altså enten R eller C for begge).
Noter til An0 DIFFERENTIALLIGNINGER MED KONSTANTE KOEFFICIENTER
 UDKAST 7122009 Noter til An0 Inst f Matematiske Fag Gerd Grubb December 2009 DIFFERENTIALLIGNINGER MED KONSTANTE KOEFFICIENTER 1 Generelle resultater 11 Introduktion I tidligere kurser er der gennemgået
UDKAST 7122009 Noter til An0 Inst f Matematiske Fag Gerd Grubb December 2009 DIFFERENTIALLIGNINGER MED KONSTANTE KOEFFICIENTER 1 Generelle resultater 11 Introduktion I tidligere kurser er der gennemgået
Vejledende besvarelse på august 2009-sættet 2. december 2009
 Vejledende besvarelse på august 29-sættet 2. december 29 Det følgende er en vejledende besvarelse på eksamenssættet i kurset Calculus, som det så ud i august 29. Den tjener primært til illustration af,
Vejledende besvarelse på august 29-sættet 2. december 29 Det følgende er en vejledende besvarelse på eksamenssættet i kurset Calculus, som det så ud i august 29. Den tjener primært til illustration af,
z + w z + w z w = z 2 w z w = z w z 2 = z z = a 2 + b 2 z w
 Komplekse tal Hvis z = a + ib og w = c + id gælder z + w = (a + c) + i(b + d) z w = (a c) + i(b d) z w = (ac bd) + i(ad bc) z w = a+ib c+id = ac+bd + i bc ad, w 0 c +d c +d z a b = i a +b a +b Konjugation
Komplekse tal Hvis z = a + ib og w = c + id gælder z + w = (a + c) + i(b + d) z w = (a c) + i(b d) z w = (ac bd) + i(ad bc) z w = a+ib c+id = ac+bd + i bc ad, w 0 c +d c +d z a b = i a +b a +b Konjugation
Eksamen i Calculus. 14. juni f (x, y, z) = 1 + x 2 + y 2. x 2 + y 2 1 Hele rummet uden z aksen
 Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 14. juni 019 Opgave 1 (6 point) En
Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 14. juni 019 Opgave 1 (6 point) En
Matematisk modellering og numeriske metoder. Lektion 6
 Matematisk modellering og numeriske metoder Lektion 6 Morten Grud Rasmussen 24. september, 2013 1 Forcerede oscillationer [Bogens afsnit 2.8, side 85] 1.1 Et forstyrret masse-fjeder-system I udledningen
Matematisk modellering og numeriske metoder Lektion 6 Morten Grud Rasmussen 24. september, 2013 1 Forcerede oscillationer [Bogens afsnit 2.8, side 85] 1.1 Et forstyrret masse-fjeder-system I udledningen
Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 2016
 Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
ANALYSE 1. Uge 7, 4. juni juni, 2007
 ANALYSE 1 Uge 7, 4. juni - 10. juni, 2007 Forelæsninger Mandag 4. juni Formålet med denne dags forelæsninger er at etablere en overgang til emnet metriske rum, hvis hovedformål er at udvide begreber som
ANALYSE 1 Uge 7, 4. juni - 10. juni, 2007 Forelæsninger Mandag 4. juni Formålet med denne dags forelæsninger er at etablere en overgang til emnet metriske rum, hvis hovedformål er at udvide begreber som
DIFFERENTIALLIGNINGER NOTER TIL CALCULUS 2003 AARHUS UNIVERSITET
 DIFFERENTIALLIGNINGER NOTER TIL CALCULUS 2003 AARHUS UNIVERSITET H.A. NIELSEN INDHOLD. Lineær ligning 2 2. Lineært system 8 3. Generel ligning 6 4. Stabilitet 8 Litteratur 2 Noterne er til 4 timers forelæsninger
DIFFERENTIALLIGNINGER NOTER TIL CALCULUS 2003 AARHUS UNIVERSITET H.A. NIELSEN INDHOLD. Lineær ligning 2 2. Lineært system 8 3. Generel ligning 6 4. Stabilitet 8 Litteratur 2 Noterne er til 4 timers forelæsninger
Taylor s approksimationsformler for funktioner af én variabel
 enote 4 1 enote 4 Taylor s approksimationsformler for funktioner af én variabel I enote 19 og enote 21 er det vist hvordan funktioner af én og to variable kan approksimeres med førstegradspolynomier i
enote 4 1 enote 4 Taylor s approksimationsformler for funktioner af én variabel I enote 19 og enote 21 er det vist hvordan funktioner af én og to variable kan approksimeres med førstegradspolynomier i
Eksamen i Mat F, april 2006
 Eksamen i Mat F, april 26 Opgave Lad F være et vektorfelt, givet i retvinklede koordinater som: Udregn F og F: F x F = F x i + F y j + F z k = F y = z 2 F z xz y 2 F = F x + F y + F z = + + x. F = F z
Eksamen i Mat F, april 26 Opgave Lad F være et vektorfelt, givet i retvinklede koordinater som: Udregn F og F: F x F = F x i + F y j + F z k = F y = z 2 F z xz y 2 F = F x + F y + F z = + + x. F = F z
MATEMATIK 3 ET,MP, FYS, NANO 29. august 2012 Oversigt nr. 1
 ET,MP, FYS, NANO 29. august 202 Oversigt nr. Litteratur: I Matematik 3 bruger vi i efteråret 202 følgende bog: E. Kreyzig: Advanced engineering mathematics, 0. udg., Wiley, 20. Beskrivelse: Kurset vil
ET,MP, FYS, NANO 29. august 202 Oversigt nr. Litteratur: I Matematik 3 bruger vi i efteråret 202 følgende bog: E. Kreyzig: Advanced engineering mathematics, 0. udg., Wiley, 20. Beskrivelse: Kurset vil
Fordybelsesprojekt Analyse 2, forår 2012 Potensrækker
 Fordybelsesprojekt Analyse 2, forår 2012 Potensrækker Udarbejdet af Arne Jensen 1 Indledning I forbindelse med kurset Matematisk Analyse 2 på Mat 2 afholdes et fordybelsesprojekt med et omfang af 3 ECTS.
Fordybelsesprojekt Analyse 2, forår 2012 Potensrækker Udarbejdet af Arne Jensen 1 Indledning I forbindelse med kurset Matematisk Analyse 2 på Mat 2 afholdes et fordybelsesprojekt med et omfang af 3 ECTS.
Københavns Universitet, Det naturvidenskabelige Fakultet. Forelæsningsnote 8. (NB: Noten er ikke en del af pensum)
 Københavns Universitet, Det naturvidenskabelige Fakultet Lineær Algebra LinAlg Forelæsningsnote 8 NB: Noten er ikke en del af pensum Eksempel på brug af egenværdier og egenvektorer Måske er det stadig
Københavns Universitet, Det naturvidenskabelige Fakultet Lineær Algebra LinAlg Forelæsningsnote 8 NB: Noten er ikke en del af pensum Eksempel på brug af egenværdier og egenvektorer Måske er det stadig
Lotka-Volterra modellen
 Lotka-Volterra modellen G4-105 Matematik Aalborg Universitet 20. december 2016 School of Engineering and Science Fredrik Bajers Vej 7G 9220 Aalborg Øst www.ses.aau.dk Titel: Lotka-Volterra modellen Tema:
Lotka-Volterra modellen G4-105 Matematik Aalborg Universitet 20. december 2016 School of Engineering and Science Fredrik Bajers Vej 7G 9220 Aalborg Øst www.ses.aau.dk Titel: Lotka-Volterra modellen Tema:
Lektion 12. højere ordens lineære differentiallininger. homogene. inhomogene. eksempler
 Lektion 12 2. ordens lineære differentialligninger homogene inhomogene eksempler højere ordens lineære differentiallininger 1 Anden ordens lineære differentialligninger med konstante koefficienter A. Homogene
Lektion 12 2. ordens lineære differentialligninger homogene inhomogene eksempler højere ordens lineære differentiallininger 1 Anden ordens lineære differentialligninger med konstante koefficienter A. Homogene
Taylor-polynomier. John V Petersen
 Taylor-polynomier John V Petersen Taylor-polynomier 2018 John V Petersen art-science-soul Indhold 1. Indledning... 4 2. Udledning af Sætning om Taylor polynomiet... 4 3. Sætning og Definition af Taylor
Taylor-polynomier John V Petersen Taylor-polynomier 2018 John V Petersen art-science-soul Indhold 1. Indledning... 4 2. Udledning af Sætning om Taylor polynomiet... 4 3. Sætning og Definition af Taylor
Matematisk modellering og numeriske metoder. Lektion 5
 Matematisk modellering og numeriske metoder Lektion 5 Morten Grud Rasmussen 19. september, 2013 1 Euler-Cauchy-ligninger [Bogens afsnit 2.5, side 71] 1.1 De tre typer af Euler-Cauchy-ligninger Efter at
Matematisk modellering og numeriske metoder Lektion 5 Morten Grud Rasmussen 19. september, 2013 1 Euler-Cauchy-ligninger [Bogens afsnit 2.5, side 71] 1.1 De tre typer af Euler-Cauchy-ligninger Efter at
MATEMATIK 3 EN,MP 28. august 2014 Oversigt nr. 1
 EN,MP 28. august 2014 Oversigt nr. 1 Litteratur: I Matematik 3 bruger vi (igen) i efteråret 2014 [K] E. Kreyzig: Advanced engineering mathematics, 10. udg., Wiley, 2011. Beskrivelse: Kurset vil handle
EN,MP 28. august 2014 Oversigt nr. 1 Litteratur: I Matematik 3 bruger vi (igen) i efteråret 2014 [K] E. Kreyzig: Advanced engineering mathematics, 10. udg., Wiley, 2011. Beskrivelse: Kurset vil handle
Fundamentale begreber fra Analysen. Introduktion. De reelle tal. Carsten Lunde Petersen
 IMFUFA Carsten Lunde Petersen Fundamentale begreber fra Analysen Introduktion Disse noter udgør et meget ltreret udkik over de grundlæggende begreber i reel analyse. Noten indeholder meget lidt om det
IMFUFA Carsten Lunde Petersen Fundamentale begreber fra Analysen Introduktion Disse noter udgør et meget ltreret udkik over de grundlæggende begreber i reel analyse. Noten indeholder meget lidt om det
Introduktion til Laplace transformen (Noter skrevet af Nikolaj Hess-Nielsen sidst revideret marts 2013)
 Introduktion til Laplace transformen (oter skrevet af ikolaj Hess-ielsen sidst revideret marts 23) Integration handler ikke kun om arealer. Tværtimod er integration basis for mange af de vigtigste værktøjer
Introduktion til Laplace transformen (oter skrevet af ikolaj Hess-ielsen sidst revideret marts 23) Integration handler ikke kun om arealer. Tværtimod er integration basis for mange af de vigtigste værktøjer
Besvarelse af Eksamensopgaver Juni 2005 i Matematik H1
 Besvarelse af Eksamensopgaver Juni 5 i Matematik H Opgave De fire vektorer stilles op i en matrix som reduceres: 4 4 4 8 4 4 (a) Der er ledende et-taller så dim U =. Som basis kan f.eks. bruges a a jfr.
Besvarelse af Eksamensopgaver Juni 5 i Matematik H Opgave De fire vektorer stilles op i en matrix som reduceres: 4 4 4 8 4 4 (a) Der er ledende et-taller så dim U =. Som basis kan f.eks. bruges a a jfr.
Taylor s approksimationsformler for funktioner af én variabel
 enote 17 1 enote 17 Taylor s approksimationsformler for funktioner af én variabel I enote 14 og enote 16 er det vist hvordan funktioner af én og to variable kan approksimeres med førstegradspolynomier
enote 17 1 enote 17 Taylor s approksimationsformler for funktioner af én variabel I enote 14 og enote 16 er det vist hvordan funktioner af én og to variable kan approksimeres med førstegradspolynomier
EKSAMENSOPGAVELØSNINGER CALCULUS 2 (2005) JANUAR 2006 AARHUS UNIVERSITET.. Beregn den retningsafledede D u f(0, 0).
 EKSAMENSOPGAVELØSNINGER CALCULUS 2 (2005) JANUAR 2006 AARHUS UNIVERSITET H.A. NIELSEN & H.A. SALOMONSEN Opgave. Lad f betegne funktionen f(x, y) = x cos(y) + y sin(x). ) Angiv gradienten f. 2) Lad u betegne
EKSAMENSOPGAVELØSNINGER CALCULUS 2 (2005) JANUAR 2006 AARHUS UNIVERSITET H.A. NIELSEN & H.A. SALOMONSEN Opgave. Lad f betegne funktionen f(x, y) = x cos(y) + y sin(x). ) Angiv gradienten f. 2) Lad u betegne
DesignMat Uge 11 Lineære afbildninger
 DesignMat Uge Lineære afbildninger Preben Alsholm Forår 008 Lineære afbildninger. Definition Definition Lad V og W være vektorrum over samme skalarlegeme L (altså enten R eller C for begge). Afbildningen
DesignMat Uge Lineære afbildninger Preben Alsholm Forår 008 Lineære afbildninger. Definition Definition Lad V og W være vektorrum over samme skalarlegeme L (altså enten R eller C for begge). Afbildningen
Modulpakke 3: Uendelige Rækker
 Chapter 5 Modulpakke 3: Uendelige Rækker 5. Indledning. Summer. En meget benyttet notation til at udtrykke gentagen addition benytter det græske store sigma (Σ) på følgende måde: de enkelte led man summer
Chapter 5 Modulpakke 3: Uendelige Rækker 5. Indledning. Summer. En meget benyttet notation til at udtrykke gentagen addition benytter det græske store sigma (Σ) på følgende måde: de enkelte led man summer
Oversigt [S] 7.2, 7.5, 7.6; [LA] 18, 19
![Oversigt [S] 7.2, 7.5, 7.6; [LA] 18, 19 Oversigt [S] 7.2, 7.5, 7.6; [LA] 18, 19](/thumbs/63/49989105.jpg) Oversigt [S] 7.2, 7.5, 7.6; [LA] 18, 19 Nøgleord og begreber Eksistens og entydighed Elementære funktioner Eksponential af matrix Retningsfelt Eulers metode Hastighedsfelt for system Eulers metode for
Oversigt [S] 7.2, 7.5, 7.6; [LA] 18, 19 Nøgleord og begreber Eksistens og entydighed Elementære funktioner Eksponential af matrix Retningsfelt Eulers metode Hastighedsfelt for system Eulers metode for
MATEMATIK 3 EN,MP 17. september 2014 Oversigt nr. 1
 MATEMATIK 3 EN,MP 7. september 204 Oversigt nr. Her bringes en samling af de gamle eksamensopgaver: (jan. 204) Betragt begyndelsesværdiproblemet y (t) + 7y (t) + 2y(t) = e t sin(2t) for t > 0, y(0) = 2,
MATEMATIK 3 EN,MP 7. september 204 Oversigt nr. Her bringes en samling af de gamle eksamensopgaver: (jan. 204) Betragt begyndelsesværdiproblemet y (t) + 7y (t) + 2y(t) = e t sin(2t) for t > 0, y(0) = 2,
Oversigt [S] 4.5, 5.10
![Oversigt [S] 4.5, 5.10 Oversigt [S] 4.5, 5.10](/thumbs/20/426063.jpg) Oversigt [S] 4.5, 5.0 Nøgleord og begreber Ubestemte udtryk l Hospitals regel l Hospitals regel 2 Test l Hospitals regel Uegentlige integraler Test uegentlige integraler Uegentlige integraler 2 Test uegentlige
Oversigt [S] 4.5, 5.0 Nøgleord og begreber Ubestemte udtryk l Hospitals regel l Hospitals regel 2 Test l Hospitals regel Uegentlige integraler Test uegentlige integraler Uegentlige integraler 2 Test uegentlige
9.1 Egenværdier og egenvektorer
 SEKTION 9.1 EGENVÆRDIER OG EGENVEKTORER 9.1 Egenværdier og egenvektorer Definition 9.1.1 1. Lad V være et F-vektorrum; og lad T : V V være en lineær transformation. λ F er en egenværdi for T, hvis der
SEKTION 9.1 EGENVÆRDIER OG EGENVEKTORER 9.1 Egenværdier og egenvektorer Definition 9.1.1 1. Lad V være et F-vektorrum; og lad T : V V være en lineær transformation. λ F er en egenværdi for T, hvis der
Eksamen i Calculus Tirsdag den 3. juni 2014
 Eksamen i Calculus Tirsdag den 3. juni 2014 Første Studieår ved Det Teknisk-Naturvidenskabelige Fakultet og Det Sundhedsvidenskabelige Fakultet Nærværende eksamenssæt består af 7 nummererede sider med
Eksamen i Calculus Tirsdag den 3. juni 2014 Første Studieår ved Det Teknisk-Naturvidenskabelige Fakultet og Det Sundhedsvidenskabelige Fakultet Nærværende eksamenssæt består af 7 nummererede sider med
Besvarelser til Calculus Ordinær Eksamen Juni 2018
 Besvarelser til Calculus Ordinær Eksamen - 5. Juni 08 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 5. Juni 08 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
(Prøve)Eksamen i Calculus
 (Prøve)Eksamen i Calculus Sæt 1, april 2011 Første Studieår ved Det Teknisk-Naturvidenskabelige Fakultet og Det Sundhedsvidenskabelige Fakultet Nærværende (prøve)eksamenssæt består af 7 nummererede sider
(Prøve)Eksamen i Calculus Sæt 1, april 2011 Første Studieår ved Det Teknisk-Naturvidenskabelige Fakultet og Det Sundhedsvidenskabelige Fakultet Nærværende (prøve)eksamenssæt består af 7 nummererede sider
Eksamen i Mat F, april 2006
 Eksamen i Mat F, april 26 Opgave 1 Lad F være et vektorfelt, givet i retvinklede koordinater som: F x x F = F x i + F y j + F z k = F y = 2z F z y Udregn F og F: F = F x + F y + F z = 1 + +. F = F z F
Eksamen i Mat F, april 26 Opgave 1 Lad F være et vektorfelt, givet i retvinklede koordinater som: F x x F = F x i + F y j + F z k = F y = 2z F z y Udregn F og F: F = F x + F y + F z = 1 + +. F = F z F
Eksamen 2014/2015 Mål- og integralteori
 Eksamen 4/5 Mål- og integralteori Københavns Universitet Institut for Matematiske Fag Formalia Eksamensopgaven består af 4 opgaver med ialt spørgsmål Ved bedømmelsen indgår de spørgsmål med samme vægt
Eksamen 4/5 Mål- og integralteori Københavns Universitet Institut for Matematiske Fag Formalia Eksamensopgaven består af 4 opgaver med ialt spørgsmål Ved bedømmelsen indgår de spørgsmål med samme vægt
Mini-formelsamling. Matematik 1
 Indholdsfortegnelse 1 Diverse nyttige regneregler... 1 1.1 Regneregler for brøker... 1 1.2 Potensregneregler... 1 1.3 Kvadratsætninger... 2 1.4 (Nogle) Rod-regneregler... 2 1.5 Den naturlige logaritme...
Indholdsfortegnelse 1 Diverse nyttige regneregler... 1 1.1 Regneregler for brøker... 1 1.2 Potensregneregler... 1 1.3 Kvadratsætninger... 2 1.4 (Nogle) Rod-regneregler... 2 1.5 Den naturlige logaritme...
Eksamen i Calculus. 14. juni f (x, y, z) = 1 + x 2 + y 2. Hele rummet uden z aksen
 Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 14. juni 019 Opgave 1 (6 point) En
Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 14. juni 019 Opgave 1 (6 point) En
Eksamen i Calculus. 14. juni f (x, y, z) = 1 + x 2 + y 2. x 2 + y 2 1 Hele rummet uden z aksen
 Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 14. juni 19 Opgave 1 (6 point) En funktion
Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 14. juni 19 Opgave 1 (6 point) En funktion
Nøgleord og begreber Eksistens og entydighed Retningsfelt Eulers metode Hastighedsfelt Stabilitet
 Oversigt [S] 7.2, 7.5, 7.6; [LA] 17, 18 Nøgleord og begreber Eksistens og entydighed Retningsfelt Eulers metode Hastighedsfelt Stabilitet Calculus 2-2005 Uge 49.2-1 Ligning og løsning [LA] 17 Generel ligning
Oversigt [S] 7.2, 7.5, 7.6; [LA] 17, 18 Nøgleord og begreber Eksistens og entydighed Retningsfelt Eulers metode Hastighedsfelt Stabilitet Calculus 2-2005 Uge 49.2-1 Ligning og løsning [LA] 17 Generel ligning
Reaktionskinetik - 1 Baggrund. lineære og ikke-lineære differentialligninger. Køreplan
 Reaktionskinetik - lineære og ikke-lineære differentialligninger Køreplan 1 Baggrund På 2. eller 4. semester møder kemi/bioteknologi studerende faget Indledende Fysisk Kemi (26201/26202). Her behandles
Reaktionskinetik - lineære og ikke-lineære differentialligninger Køreplan 1 Baggrund På 2. eller 4. semester møder kemi/bioteknologi studerende faget Indledende Fysisk Kemi (26201/26202). Her behandles
MATEMATIK 3 EN3,MP3 28. august 2015 Oversigt nr. 1
 EN3,MP3 28. august 205 Oversigt nr. Litteratur: I Matematik 3 bruger vi (igen) i efteråret 205 [K] E. Kreyzig: Advanced engineering mathematics, 0. udg., Wiley, 20. Beskrivelse: Kurset vil handle om matematiske
EN3,MP3 28. august 205 Oversigt nr. Litteratur: I Matematik 3 bruger vi (igen) i efteråret 205 [K] E. Kreyzig: Advanced engineering mathematics, 0. udg., Wiley, 20. Beskrivelse: Kurset vil handle om matematiske
x 2 + y 2 dx dy. f(x, y) = ln(x 2 + y 2 ) + 2 1) Angiv en ligning for tangentplanen til fladen z = f(x, y) i punktet
 Eksamensopgaver fra Matematik Alfa 1 Naturvidenskabelig Kandidateksamen August 1999. Matematik Alfa 1 Opgave 1. Udregn integralet 1 1 y 2 (Vink: skift til polære koordinater.) Opgave 2. Betragt funktionen
Eksamensopgaver fra Matematik Alfa 1 Naturvidenskabelig Kandidateksamen August 1999. Matematik Alfa 1 Opgave 1. Udregn integralet 1 1 y 2 (Vink: skift til polære koordinater.) Opgave 2. Betragt funktionen
Supplerende opgaver. S1.3.1 Lad A, B og C være delmængder af X. Vis at
 Supplerende opgaver Analyse Jørgen Vesterstrøm Forår 2004 S.3. Lad A, B og C være delmængder af X. Vis at (A B C) (A B C) (A B) C og find en nødvendig og tilstrækkelig betingelse for at der gælder lighedstegn
Supplerende opgaver Analyse Jørgen Vesterstrøm Forår 2004 S.3. Lad A, B og C være delmængder af X. Vis at (A B C) (A B C) (A B) C og find en nødvendig og tilstrækkelig betingelse for at der gælder lighedstegn
DesignMat. Preben Alsholm. September Egenværdier og Egenvektorer. Preben Alsholm. Egenværdier og Egenvektorer
 DesignMat September 2008 fortsat Eksempel : et Eksempel 4 () af I II uden I Lad V være et vektorrum over L (enten R eller C). fortsat Eksempel : et Eksempel 4 () af I II uden I Lad V være et vektorrum
DesignMat September 2008 fortsat Eksempel : et Eksempel 4 () af I II uden I Lad V være et vektorrum over L (enten R eller C). fortsat Eksempel : et Eksempel 4 () af I II uden I Lad V være et vektorrum
Eksamen i Calculus Mandag den 4. juni 2012
 Eksamen i Calculus Mandag den 4. juni 212 Første Studieår ved Det Teknisk-Naturvidenskabelige Fakultet og Det Sundhedsvidenskabelige Fakultet Nærværende eksamenssæt består af 7 nummererede sider med ialt
Eksamen i Calculus Mandag den 4. juni 212 Første Studieår ved Det Teknisk-Naturvidenskabelige Fakultet og Det Sundhedsvidenskabelige Fakultet Nærværende eksamenssæt består af 7 nummererede sider med ialt
Taylorpolynomier og -rækker samt lokale ekstrema for funktioner af flere variable
 Taylorpolynomier og -rækker samt lokale ekstrema for funktioner af flere variable Morten Grud Rasmussen 1. marts 2016 1 Taylors Sætning for funktioner af én variabel Sætning 1.1 (Taylors Sætning med restled).
Taylorpolynomier og -rækker samt lokale ekstrema for funktioner af flere variable Morten Grud Rasmussen 1. marts 2016 1 Taylors Sætning for funktioner af én variabel Sætning 1.1 (Taylors Sætning med restled).
Matematik F2 Opgavesæt 2
 Opgaver uge 2 I denne uge kigger vi nærmere på Cauchy-Riemann betingelserne, potensrækker, konvergenskriterier og flertydige funktioner. Vi skal også se på integration langs en ve i den komplekse plan.
Opgaver uge 2 I denne uge kigger vi nærmere på Cauchy-Riemann betingelserne, potensrækker, konvergenskriterier og flertydige funktioner. Vi skal også se på integration langs en ve i den komplekse plan.
Reeksamen i Calculus
 Reeksamen i Calculus Torsdag den 11. august 2011 Første Studieår ved Det Teknisk-Naturvidenskabelige Fakultet og Det Sundhedsvidenskabelige Fakultet Nærværende eksamenssæt består af 8 nummererede sider
Reeksamen i Calculus Torsdag den 11. august 2011 Første Studieår ved Det Teknisk-Naturvidenskabelige Fakultet og Det Sundhedsvidenskabelige Fakultet Nærværende eksamenssæt består af 8 nummererede sider
EKSAMENSOPGAVELØSNINGER CALCULUS 2 (2005) AUGUST 2006 AARHUS UNIVERSITET
 EKSAMENSOPGAVELØSNINGER CALCULUS 2 (2005) AUGUST 2006 AARHUS UNIVERSITET H.A. NIELSEN & H.A. SALOMONSEN Opgave. Lad f betegne funktionen f(x,y) = x 3 + x 2 y + xy 2 + y 3. ) Angiv gradienten f. 2) Angiv
EKSAMENSOPGAVELØSNINGER CALCULUS 2 (2005) AUGUST 2006 AARHUS UNIVERSITET H.A. NIELSEN & H.A. SALOMONSEN Opgave. Lad f betegne funktionen f(x,y) = x 3 + x 2 y + xy 2 + y 3. ) Angiv gradienten f. 2) Angiv
Eksamen Analyse 1, Juni 2015, Besvarelse 1. Opgave 1. ( ln x) q x p dx =
 Eksmen Anlyse, Juni 25, Besvrelse Ld p >, q, og r. Opgve () Vis t integrlet ( ln x)r x p dx konvergerer. [Vink: Smmenlign med x s for pssende vlgt s.] ( ln x)q x p dx. [Vink: Anvend (b) Bevis formlen (
Eksmen Anlyse, Juni 25, Besvrelse Ld p >, q, og r. Opgve () Vis t integrlet ( ln x)r x p dx konvergerer. [Vink: Smmenlign med x s for pssende vlgt s.] ( ln x)q x p dx. [Vink: Anvend (b) Bevis formlen (
Det teknisk-naturvidenskabelige basisår Matematik 1A, Efterår 2005, Hold 3 Prøveopgave C
 Det teknisk-naturvidenskabelige basisår Matematik 1A, Efterår 2005, Hold 3 Prøveopgave C Opgaven består af tre dele, hver med en række spørgsmål, efterfulgt af en liste af teorispørgsmål. I alle opgavespørgsmålene
Det teknisk-naturvidenskabelige basisår Matematik 1A, Efterår 2005, Hold 3 Prøveopgave C Opgaven består af tre dele, hver med en række spørgsmål, efterfulgt af en liste af teorispørgsmål. I alle opgavespørgsmålene
