Ligningsløsning som det at løse gåder
|
|
|
- Rebecca Iversen
- 8 år siden
- Visninger:
Transkript
1 Ligningsløsning som det at løse gåder Nedenstående er et skærmklip fra en TI-Nspirefil. Vi ser at tre kræmmerhuse og fem bolsjer balancerer med to kræmmerhuse og 10 bolsjer. Spørgsmålet er hvor mange bolsjer, der er i kræmmerhusene (der er lige mange i dem hver). Du kan trække bolsjer og kræmmerhusene helt fri af vægen ved at trække til siden (henholdsvis til højre og venstre) idet kræmmerhusene trækkes i punktet i midten. Sørg for hele tiden at bringe vægten i balance. Så hvis du fjerner et bolsje i skålen til venstre skal du også fjerne et til højre! Tilsvarende gælder for kræmmerhuse! Antallet er bolsjer i kræmmerhusene er: Bemærk at for at få vægten til fungere kan det være nødvendigt at evaluere formlen nederst til venstre i tns-filen ved at klikke på formlen og trykke ENTER: Øvelse 1 Bestem antallet af bolsjer i kræmmerhusene i de følgende opgaver i tns-filen, hvor kræmmerhusene i hver opgave er pakket forskelligt: Fra ligevægt til ligning 1
2 En ligning er udtryk for at to størrelser er i balance. Man kan som ovenfor forestille sig en gammeldags vægt med to vægtskåle. Vi ser at fem poser balancerer med to poser og 12 terninger men spørgsmålet er hvor mange terninger, der er i hver pose idet der er lige mange terninger i hver. Denne oplysning kan også udtrykkes ved en ligning: 5 pose = 2 pose + 12 Ved at fjerne to poser fra hver vægtskål bevarer vi ligevægten. Altså gælder der: 5 pose 2 pose = 2 pose pose som giver at 3 pose = 12 En tredjedel af det der er på venstre vægtskål, må veje det samme som en tredjedel af det der er på den højre vægtskål. Altså kan vi skalere ned med 3: 3 pose = som giver at pose = 4 Altså er der 4 terninger i hver pose da en pose balancerer med 4 terninger Ovenfor har vi løst en ligning. Lad x være udtryk for antal af terninger i en pose så ligner det en mere traditionel ligning : 5 pose = 2 pose + 12 svarer dermed til ligningen 5 x = 2 x + 12 Dermed er en ligning en formel, der udtrykker at to størrelser (udtryk) er i balance. Hvis vi skal løse ovenstående ligning skal vi altså bestemme den værdi x kan være for at ligningen er sand (stadig i balance). Metoden til at bestemme x-værdien går ud på at isolere x på den ene side at lighedstegnet vi skal altså have x til at stå alene på enten venstre eller højre side af lighedstegnet som vi netop gjorde ved at lade pose stå alene. 2
3 Øvelse 2 På venstre skål ligger tre poser med et ukendt antal terninger sammen med en terning. På højre skål ligger en pose og syv terninger. 1) Ud fra ovenstående oplysninger skal du på den første vægt herunder indtegne antallet af poser og terninger, der er i balance. Bestem herefter antallet af terninger i en pose ved hjælp af nedenstående vægte ved at fjerne poser og terninger mens der bevares ligevægt på vægten. 2) I rækken under vægtene skal du ovenfor skrive de tilsvarende ligninger idet x står for antal af terninger i en pose. Sammenfatter vi ovenstående øvelser ser vi altså at der gælder et balanceprincip: Fjerner vi noget, eller tilføjer vi noget på den ene skål, bliver der ubalance, hvis ikke vi gør præcis det samme på den anden skål. Men foretager vi de samme operationer på begge sider gælder lighedstegnet stadig. Det gælder følgende regler for ligningsløsning: Nr. Regel 1 I en ligning må samme led lægges til eller trækkes fra på hver side af lighedstegnet 2 I en ligning må man gange eller dividere med samme tal på begge sider af lighedstegnet (bare ikke med tallet 0) Øvelse 3 Prøv at forklare følgende billedserie ud fra balanceprincippet og ovenstående regler. Altså skal du forklare hvad der sker billede for billede for at sikre balance: Hvordan forstås lignigen i forhold til poser og terninger Hvad er der trukket fra? 3
4 Lær at løse ligninger med TI-Nspire CAS Trin 1 TI-Nspire CAS kan hjælpe os med at lære at løse ligninger efter balanceprincippet idet målet er at isolere en ukendt størrelse, der indgår i ligningen. Åben TI-Nspire CAS og inddel siden i to ved at vælge det andet layouttype fra ikonen Sidelayout. Indsæt en Beregner-applikation til venstre og en Noter-applikation vil højre: Skriv følgende ligning i Beregner værkstedet og tryk ENTER: Til venstre står vores indtastning og til højre står det evaluerede resultat af vores indtastning som her er det samme! Det er nu en god idé at samle x erne på den ene side af lighedstegnet. Så for at forenkle ligningen kan vi trække 2 x fra på begge sider af lighedstegnet. I anden linje starter vi med at lave en parentes. Placer herefter cursoren inde i parentesen og brug PIL OP tasten på tastaturet en gang for at markere ligningen ovenfor til højre. Tryk herefter på ENTER på tastaturet en gang for at indsætte ligningen i parentesen: Efter parentesen skriver vi nu 2 x for at trække 2 x fra på begge sider af lighedstegnet: VOILA! Vores ligning er blevet forenklet idet vi har samlet x erne på den ene side af lighedstegnet. Bemærk at du i Noter-værkstedet kan skrive hvad du har gjort! Det er nu en god idé at få x erne til at stå alene på den ene side af lighedstegnet. Så for at forenkle ligningen kan vi lægge 3 fra på begge sider af lighedstegnet. I tredje linje laver vi en parentes og henter den evaluerede ligning ovenfor til højre. Efter ligningen skriver vi +3, trykker ENTER for at evaluere ligningen og skriver note til hvad vi har gjort: 4
5 Vi kunne nu godt gætte på et x der løser ligningen 4 x = 10. Men lad os anvende TI-Nspire CAS til at få x til at stå HELT alene på venstre side således at det bliver klart hvad løsningen til ligningen er. For at forenkle ligningen skal vi skalere begge sider passende ned for at få x til at stå alene på højre side af ligningen. Det gør vi ved at dividere med 4 på begge sider af lighedstegnet. Den evaluerede ligning ovenfor divideres med 4 ved at skrive /4 efter parentesen: HURRA, vi har løst ligningen! Eller vi har i hvert fald et bud på et x der løser ligningen. For at sikre os at vi har løst ligningen korrekt skal vi nu lave en kontrol. Erstat 2.5 i den oprindelige ligning i stedet for x og tryk Enter: True betyder sandt hvilket betyder at 2.5 er løsning til ligningen! Øvelse 4 Løs nedenstående ligninger ved hjælp af TI-Nspire CAS som ovenfor: Opgave Ligning Løsning a) 2.5 x + 4 = x b) x = x c) x = 12 x + 10 d) x = 2.3 x + 11 e) f) 6.4 = 4.3 x = x x 5
6 Lær at løse ligninger med TI-Nspire CAS Trin 2 Vi skal nu gerne have indset at ligningsløsning kan betragtes som en dynamisk proces efter ligevægtsprincippet, hvor vi hele tiden anvender modsatte eller omvendte funktioner (operationer) for at forenkle ligningerne for til sidst at have isoleret en ukendt størrelse: 3 ophæves af det modsatte tal +3 2x ophæves af det modsatte led 2x Gange med 4 ophæves af den omvendte operation: division med 4. Dette gælder generelt, også for trigonometriske, eksponentielle og logaritmiske ligninger eller ligninger med potenser og rødder: En bestemt operation ophæves at anvende den omvendte operation på begge sider af lighedstegnet. Øvelse 5 Åben TI-Nspire CAS. Vælg Tastatur som tredje faneblad i venstre sidepanel og vælg herefter TI-Nspire TM CAS med Clickpad med Normal visning. Ud fra tastaturet kan du identificere omvendte regneoperationer idet + tasten ligger under tasten og kvadratrods tegnet ligger på samme tast som kvadratet på x. Udfyld nedenstående tabel over omvendte operationer: Operation Omvendte operation Operation Omvendte operation + - sin(..) - + cos(..) tan(..) : (eller /) e x (..) 2 ln(x).. 10 x (.. ) n Log(x) n.. Vi vil nu med et eksempel vise anvendelse af omvendte operationer. Vi ved fra Pythagoras læresætning af arealerne på kvadraterne på kateterne balancerer med arealet af kvadratet på hypotenusen. Vi får oplyst at en katete er 5 og hypotenusen er 8. Altså har vi følgende balance: x 2 = 8 2 6
7 Hvis vi løser ligningen med hensyn til x bestemmer vi altså længden af den sidste katete. Åben TI-Nspire CAS og inddel siden i tre med hhv. en Beregner, Noter og Geometri applikation. Tegn en skitse af en retvinklet trekant i Geometri værkstedet hvor de oplyste størrelse sættes ind og i Beregner værkstedet opskrives ligningen: For at isolere x 2 på venstre side trækker vi 25 fra på begge sider: At løse ligningen x 2 = 39 svarer til at bestemme det (de) tal der ganget med sig selv giver 39. Den omvendte operation til at kvadrere er at uddrage kvadratroden. Dermed skal vi tage kvadratroden på begge sider af lighedstegnet. Brug lommeregner tastaturet i 3. faneblad i sidepanelet for at indsætte kvadratrodstegnet idet du skal benytte CTRL tasten. Indsæt ligningen ovenfor til højre og skriv eventuelt et decimalpunktum efter tallet 39. Afslut med ENTER for at gennemføre udregningen: De lodrette streger omkring x betyder at den numeriske værdi af x er lig Det svarer til at både x = og x = er løsning til ligningen x 2 = 39. I denne opgave giver det ikke mening at x er negativ idet længden af en katete ikke kan være negativ. Altså er x = løsning til ligningen. Øvelse 6 Brug de omvendte operationer/funktioner til at løse følgende ligninger i en Beregner applikation via lommeregner tastaturet: a) cos(v) = 0.83 b) log(m) = 2.9 c) x 3 = 68 d) e 3 x = 200 7
Regneoperationerne plus og minus er hinandens omvendte regneoperation og at gange og dividere er hinandens omvendte regneoperation.
 Ligninger Eksempel 1. Et eksempel på en ligning er 2x 4 = 10 En ligning er et matematisk udtryk hvor der indgår et lighedstegn. I en ligning indgår der et bogstav, en ukendt størrelse/variabel. Dette bogstav
Ligninger Eksempel 1. Et eksempel på en ligning er 2x 4 = 10 En ligning er et matematisk udtryk hvor der indgår et lighedstegn. I en ligning indgår der et bogstav, en ukendt størrelse/variabel. Dette bogstav
ØVEHÆFTE FOR MATEMATIK C FORMLER OG LIGNINGER
 ØVEHÆFTE FOR MATEMATIK C FORMLER OG LIGNINGER INDHOLDSFORTEGNELSE 0. FORMELSAMLING TIL FORMLER OG LIGNINGER... 2 Tal, regneoperationer og ligninger... 2 Isolere en ubekendt... 3 Hvis x står i første brilleglas...
ØVEHÆFTE FOR MATEMATIK C FORMLER OG LIGNINGER INDHOLDSFORTEGNELSE 0. FORMELSAMLING TIL FORMLER OG LIGNINGER... 2 Tal, regneoperationer og ligninger... 2 Isolere en ubekendt... 3 Hvis x står i første brilleglas...
Øvelser til Eksamensopgaver i matematik
 Øvelser til Eksamensopgaver i matematik med TI-Nspire CAS ver. 2.0 Udarbejdet af: Brian M.V. Olesen Marts 2010 Indholdsfortegnelse TI-Nspire CAS version 2.0...2 Generelle TIPS & TRICKS (T&T)...3 Eksempel
Øvelser til Eksamensopgaver i matematik med TI-Nspire CAS ver. 2.0 Udarbejdet af: Brian M.V. Olesen Marts 2010 Indholdsfortegnelse TI-Nspire CAS version 2.0...2 Generelle TIPS & TRICKS (T&T)...3 Eksempel
Trekants- beregning for hf
 Trekants- beregning for hf C C 5 l 5 A 34 8 B 018 Karsten Juul Indhold 1. Vinkler... 1 1.1 Regler for vinkler.... 1. Omkreds, areal, højde....1 Omkreds..... Rektangel....3 Kvadrat....4 Højde....5 Højde-grundlinje-formel
Trekants- beregning for hf C C 5 l 5 A 34 8 B 018 Karsten Juul Indhold 1. Vinkler... 1 1.1 Regler for vinkler.... 1. Omkreds, areal, højde....1 Omkreds..... Rektangel....3 Kvadrat....4 Højde....5 Højde-grundlinje-formel
Vejledning til Excel 2010
 Vejledning til Excel 2010 Indhold Eksempel på problemregning i Excel... 2 Vejledning til skabelon og opstilling... 3 Indskrivning... 5 Tips til problemregninger... 6 Brøker... 6 Når du skal bruge pi...
Vejledning til Excel 2010 Indhold Eksempel på problemregning i Excel... 2 Vejledning til skabelon og opstilling... 3 Indskrivning... 5 Tips til problemregninger... 6 Brøker... 6 Når du skal bruge pi...
Simple udtryk og ligninger
 Simple udtryk og ligninger 009 Karsten Juul Til eleven Brug blyant og viskelæder når du skriver og tegner i hæftet, så du får et hæfte der er egenet til jævnligt at slå op i under dit videre arbejde med
Simple udtryk og ligninger 009 Karsten Juul Til eleven Brug blyant og viskelæder når du skriver og tegner i hæftet, så du får et hæfte der er egenet til jævnligt at slå op i under dit videre arbejde med
TREKANTER. Indledning. Typer af trekanter. Side 1 af 7. (Der har været tre kursister om at skrive denne projektrapport)
 Side 1 af 7 (Der har været tre kursister om at skrive denne projektrapport) TREKANTER Indledning Vi har valgt at bruge denne projektrapport til at udarbejde en oversigt over det mest grundlæggende materiale
Side 1 af 7 (Der har været tre kursister om at skrive denne projektrapport) TREKANTER Indledning Vi har valgt at bruge denne projektrapport til at udarbejde en oversigt over det mest grundlæggende materiale
Problemløsning i retvinklede trekanter
 Problemløsning i retvinklede trekanter Frank Villa 14. februar 2012 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug
Problemløsning i retvinklede trekanter Frank Villa 14. februar 2012 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug
Løsning af simple Ligninger
 Løsning af simple Ligninger Frank Nasser 19. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk:
Løsning af simple Ligninger Frank Nasser 19. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk:
Matematik projekt. Klasse: Sh-mab05. Fag: Matematik B. Projekt: Trigonometri
 Matematik projekt Klasse: Sh-mab05 Fag: Matematik B Projekt: Trigonometri Kursister: Anders Jørgensen, Kirstine Irming, Mark Petersen, Tobias Winberg & Zehra Köse Underviser: Vibeke Wulff Side 1 af 11
Matematik projekt Klasse: Sh-mab05 Fag: Matematik B Projekt: Trigonometri Kursister: Anders Jørgensen, Kirstine Irming, Mark Petersen, Tobias Winberg & Zehra Köse Underviser: Vibeke Wulff Side 1 af 11
Bogstavregning. En indledning for stx og hf. 2008 Karsten Juul
 Bogstavregning En indledning for stx og hf 2008 Karsten Juul Dette hæfte træner elever i den mest grundlæggende bogstavregning (som omtrent springes over i lærebøger for stx og hf). Når elever har lært
Bogstavregning En indledning for stx og hf 2008 Karsten Juul Dette hæfte træner elever i den mest grundlæggende bogstavregning (som omtrent springes over i lærebøger for stx og hf). Når elever har lært
Beregning til brug for opmåling, udfoldning og konstruktion
 VVS-branchens efteruddannelse Beregning til brug for opmåling, udfoldning og konstruktion Beregning til brug for opmåling, udfoldning og konstruktion Med de trigonometriske funktioner, kan der foretages
VVS-branchens efteruddannelse Beregning til brug for opmåling, udfoldning og konstruktion Beregning til brug for opmåling, udfoldning og konstruktion Med de trigonometriske funktioner, kan der foretages
Funktioner generelt. for matematik pä B- og A-niveau i stx og hf. 2014 Karsten Juul
 Funktioner generelt for matematik pä B- og A-niveau i st og hf f f ( ),8 014 Karsten Juul 1 Funktion og dens graf, forskrift og definitionsmängde 11 Koordinatsystem I koordinatsystemer (se Figur 1): -akse
Funktioner generelt for matematik pä B- og A-niveau i st og hf f f ( ),8 014 Karsten Juul 1 Funktion og dens graf, forskrift og definitionsmängde 11 Koordinatsystem I koordinatsystemer (se Figur 1): -akse
Brug af Word til matematik
 Flex på KVUC, matematik C Brug af Word til matematik Word er et af de gængse tekstbehandlingssystemer der slipper bedst fra det at skrive matematiske formler. Selvfølgelig findes der andre systemer der
Flex på KVUC, matematik C Brug af Word til matematik Word er et af de gængse tekstbehandlingssystemer der slipper bedst fra det at skrive matematiske formler. Selvfølgelig findes der andre systemer der
VUC Vestsjælland Syd, Slagelse Nr. 1 Institution: Projekt Trigonometri
 VUC Vestsjælland Syd, Slagelse Nr. 1 Institution: 333247 2015 Anders Jørgensen, Mark Kddafi, David Jensen, Kourosh Abady og Nikolaj Eriksen 1. Indledning I dette projekt, vil man kunne se definitioner
VUC Vestsjælland Syd, Slagelse Nr. 1 Institution: 333247 2015 Anders Jørgensen, Mark Kddafi, David Jensen, Kourosh Abady og Nikolaj Eriksen 1. Indledning I dette projekt, vil man kunne se definitioner
Uafhængig og afhængig variabel
 Uddrag fra http://www.emu.dk/gym/fag/ma/undervisningsforloeb/hf-mat-c/introduktion.doc ved Hans Vestergaard, Morten Overgaard Nielsen, Peter Trautner Brander Variable og sammenhænge... 1 Uafhængig og afhængig
Uddrag fra http://www.emu.dk/gym/fag/ma/undervisningsforloeb/hf-mat-c/introduktion.doc ved Hans Vestergaard, Morten Overgaard Nielsen, Peter Trautner Brander Variable og sammenhænge... 1 Uafhængig og afhængig
Oprids over grundforløbet i matematik
 Oprids over grundforløbet i matematik Dette oprids er tænkt som en meget kort gennemgang af de vigtigste hovedpointer vi har gennemgået i grundforløbet i matematik. Det er en kombination af at repetere
Oprids over grundforløbet i matematik Dette oprids er tænkt som en meget kort gennemgang af de vigtigste hovedpointer vi har gennemgået i grundforløbet i matematik. Det er en kombination af at repetere
Matematik. 1 Matematiske symboler. Hayati Balo,AAMS. August, 2014
 Matematik Hayati Balo,AAMS August, 2014 1 Matematiske symboler For at udtrykke de verbale udsagn matematisk korrekt, så det bliver lettere og hurtigere at skrive, indføres en række matematiske symboler.
Matematik Hayati Balo,AAMS August, 2014 1 Matematiske symboler For at udtrykke de verbale udsagn matematisk korrekt, så det bliver lettere og hurtigere at skrive, indføres en række matematiske symboler.
Indhold. Kontrol af resultater, skrivemåder osv.
 Indhold Kontrol af resultater, skrivemåder osv.... 1 Om materialer:... 2 Om opgaverne... 2 1.0 Om regningsarternes hierarki og talforståelse... Opgave 1.1... 4 Opgave 1.2... 4 Opgave 1.... 4 R1 Kortfattet
Indhold Kontrol af resultater, skrivemåder osv.... 1 Om materialer:... 2 Om opgaverne... 2 1.0 Om regningsarternes hierarki og talforståelse... Opgave 1.1... 4 Opgave 1.2... 4 Opgave 1.... 4 R1 Kortfattet
Matematik B Klasse 1.4 Hjemmeopaver
 Matematik B Klasse 1.4 Hjemmeopaver 1) opgave 336, side 23 Opgaven går ud på at jeg skal finde ud af hvor gamle børnene højst kan være, når forældrene tilsammen er 65 år og de skal være 40 år ældre end
Matematik B Klasse 1.4 Hjemmeopaver 1) opgave 336, side 23 Opgaven går ud på at jeg skal finde ud af hvor gamle børnene højst kan være, når forældrene tilsammen er 65 år og de skal være 40 år ældre end
ØVEHÆFTE FOR MATEMATIK C GEOMETRI
 ØVEHÆFTE FOR MATEMATIK C GEOMETRI Indhold Begreber i klassisk geometri + formelsamling... 2 Pythagoras Sætning... 8 Retvinklede trekanter. Beregn den ukendte side markeret med et bogstav.... 9 Øve vinkler
ØVEHÆFTE FOR MATEMATIK C GEOMETRI Indhold Begreber i klassisk geometri + formelsamling... 2 Pythagoras Sætning... 8 Retvinklede trekanter. Beregn den ukendte side markeret med et bogstav.... 9 Øve vinkler
06 Formler i retvinklede trekanter del 2
 06 Formler i retvinklede trekanter del 2 I del 2 udledes (nogle af) de generelle formler, der gælder for sinus, cosinus og tangens i retvinklede trekanter. Sætning 1 For enhver vinkel v gælder der BEVIS
06 Formler i retvinklede trekanter del 2 I del 2 udledes (nogle af) de generelle formler, der gælder for sinus, cosinus og tangens i retvinklede trekanter. Sætning 1 For enhver vinkel v gælder der BEVIS
ØVEHÆFTE FOR MATEMATIK C FORMLER OG LIGNINGER
 ØVEHÆFTE FOR MATEMATIK C FORMLER OG LIGNINGER INDHOLDSFORTEGNELSE 0. FORMELSAMLING TIL FORMLER OG LIGNINGER... 2 Tal, regneoperationer og ligninger... 2 Ligning med + - / hvor x optræder 1 gang... 3 IT-programmer
ØVEHÆFTE FOR MATEMATIK C FORMLER OG LIGNINGER INDHOLDSFORTEGNELSE 0. FORMELSAMLING TIL FORMLER OG LIGNINGER... 2 Tal, regneoperationer og ligninger... 2 Ligning med + - / hvor x optræder 1 gang... 3 IT-programmer
Funktioner. 1. del Karsten Juul
 Funktioner 1. del 0,6 5, 9 2018 Karsten Juul 1. Koordinater 1.1 Koordinatsystem... 1 1.2 Kvadranter... 1 1.3 Koordinater... 2 1.4 Aflæs x-koordinat... 2 1.5 Aflæs y-koordinat... 2 1.6 Koordinatsæt... 2
Funktioner 1. del 0,6 5, 9 2018 Karsten Juul 1. Koordinater 1.1 Koordinatsystem... 1 1.2 Kvadranter... 1 1.3 Koordinater... 2 1.4 Aflæs x-koordinat... 2 1.5 Aflæs y-koordinat... 2 1.6 Koordinatsæt... 2
Geometri, (E-opgaver 9d)
 Geometri, (E-opgaver 9d) GEOMETRI, (E-OPGAVER 9D)... 1 Vinkler... 1 Trekanter... 2 Ensvinklede trekanter... 2 Retvinklede trekanter... 3 Pythagoras sætning... 3 Sinus, Cosinus og Tangens... 4 Vilkårlige
Geometri, (E-opgaver 9d) GEOMETRI, (E-OPGAVER 9D)... 1 Vinkler... 1 Trekanter... 2 Ensvinklede trekanter... 2 Retvinklede trekanter... 3 Pythagoras sætning... 3 Sinus, Cosinus og Tangens... 4 Vilkårlige
Introduktion til TI-Nspire 1. Dokumentformat
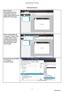 1 Dokumentformat Åbn TI-Nspire. Første gang man åbner programmet vises som regel et skærmbillede fra en håndholdt lommeregner. Denne visning skiftes til Computer i menuen eller ved ALT-Shift-C. Denne indstilling
1 Dokumentformat Åbn TI-Nspire. Første gang man åbner programmet vises som regel et skærmbillede fra en håndholdt lommeregner. Denne visning skiftes til Computer i menuen eller ved ALT-Shift-C. Denne indstilling
Louise F Jensen MATEMATIK. VUC Roskilde
 Louise F Jensen VUC Roskilde 1 INDHOLD Potensregneregler... 2 Kvadratrod... 3 Algebra... 3 Ligninger... 3 Ulighedstegn i ligning... 4 Brøker... 4 Procent... 5 Indextal... 6 Rentesregning... 6 Geometri...
Louise F Jensen VUC Roskilde 1 INDHOLD Potensregneregler... 2 Kvadratrod... 3 Algebra... 3 Ligninger... 3 Ulighedstegn i ligning... 4 Brøker... 4 Procent... 5 Indextal... 6 Rentesregning... 6 Geometri...
RENTES REGNING SIMULATION LANDMÅLING MÅLSCORE I HÅNDBO . K R I S T I A N S E N KUGLE G Y L D E N D A L
 SIMULATION 4 2 RENTES REGNING F I NMED N H REGNEARK. K R I S T I A N S E N KUGLE 5 LANDMÅLING 3 MÅLSCORE I HÅNDBO G Y L D E N D A L Faglige mål: Anvende simple geometriske modeller og løse simple geometriske
SIMULATION 4 2 RENTES REGNING F I NMED N H REGNEARK. K R I S T I A N S E N KUGLE 5 LANDMÅLING 3 MÅLSCORE I HÅNDBO G Y L D E N D A L Faglige mål: Anvende simple geometriske modeller og løse simple geometriske
5 Ligninger og uligheder
 5 Ligninger og uligheder Faglige mål Kapitlet Ligninger og uligheder tager udgangspunkt i følgende faglige mål: Regler for løsning af ligninger og uligheder: kende reglerne for ligningsløsning og uligheder
5 Ligninger og uligheder Faglige mål Kapitlet Ligninger og uligheder tager udgangspunkt i følgende faglige mål: Regler for løsning af ligninger og uligheder: kende reglerne for ligningsløsning og uligheder
Cosinusrelationen. Frank Nasser. 11. juli 2011
 Cosinusrelationen Frank Nasser 11. juli 2011 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold 1 Introduktion
Cosinusrelationen Frank Nasser 11. juli 2011 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold 1 Introduktion
Kompendium i faget. Matematik. Tømrerafdelingen. 2. Hovedforløb. Y = ax 2 + bx + c. (x,y) Svendborg Erhvervsskole Tømrerafdelingen Niels Mark Aagaard
 Kompendium i faget Matematik Tømrerafdelingen 2. Hovedforløb. Y Y = ax 2 + bx + c (x,y) X Svendborg Erhvervsskole Tømrerafdelingen Niels Mark Aagaard Indholdsfortegnelse for H2: Undervisningens indhold...
Kompendium i faget Matematik Tømrerafdelingen 2. Hovedforløb. Y Y = ax 2 + bx + c (x,y) X Svendborg Erhvervsskole Tømrerafdelingen Niels Mark Aagaard Indholdsfortegnelse for H2: Undervisningens indhold...
Lektion 3 Sammensætning af regnearterne
 Lektion Sammensætning af regnearterne Indholdsfortegnelse Indholdsfortegnelse... Plus, minus, gange og division... Negative tal... Parenteser og brøkstreger... Potenser og rødder... Lektion Side 1 Plus,
Lektion Sammensætning af regnearterne Indholdsfortegnelse Indholdsfortegnelse... Plus, minus, gange og division... Negative tal... Parenteser og brøkstreger... Potenser og rødder... Lektion Side 1 Plus,
ØVEHÆFTE FOR MATEMATIK C GEOMETRI
 ØVEHÆFTE FOR MATEMATIK C GEOMETRI Indhold Begreber i klassisk geometri + formelsamling... 2 Ensvinklede trekanter... 7 Pythagoras Sætning... 10 Øve vinkler i retvinklede trekanter... 15 Sammensatte opgaver....
ØVEHÆFTE FOR MATEMATIK C GEOMETRI Indhold Begreber i klassisk geometri + formelsamling... 2 Ensvinklede trekanter... 7 Pythagoras Sætning... 10 Øve vinkler i retvinklede trekanter... 15 Sammensatte opgaver....
Hvad er matematik? C, i-bog ISBN 978 87 7066 499 8
 Et af de helt store videnskabelige projekter i 1700-tallets Danmark var kortlægningen af Danmark. Projektet blev varetaget af Det Kongelige Danske Videnskabernes Selskab og løb over en periode på et halvt
Et af de helt store videnskabelige projekter i 1700-tallets Danmark var kortlægningen af Danmark. Projektet blev varetaget af Det Kongelige Danske Videnskabernes Selskab og løb over en periode på et halvt
Mini AT-forløb om kommunalvalg: Mandatfordeling og Retfærdighed 1.x og 1.y 2009 ved Ringsted Gymnasium MANDATFORDELING
 MANDATFORDELING Dette materiale er lavet som supplement til Erik Vestergaards hjemmeside om samme emne. 1 http://www.matematiksider.dk/mandatfordelinger.html I dette materiale er en række øvelser der knytter
MANDATFORDELING Dette materiale er lavet som supplement til Erik Vestergaards hjemmeside om samme emne. 1 http://www.matematiksider.dk/mandatfordelinger.html I dette materiale er en række øvelser der knytter
Eksamensspørgsmål: Trekantberegning
 Eksamensspørgsmål: Trekantberegning Indhold Definition af Sinus og Cosinus... 1 Bevis for Sinus- og Cosinusformlerne... 3 Tangens... 4 Pythagoras s sætning... 4 Arealet af en trekant... 7 Vinkler... 8
Eksamensspørgsmål: Trekantberegning Indhold Definition af Sinus og Cosinus... 1 Bevis for Sinus- og Cosinusformlerne... 3 Tangens... 4 Pythagoras s sætning... 4 Arealet af en trekant... 7 Vinkler... 8
Maple. Skærmbilledet. Vi starter med at se lidt nærmere på opstartsbilledet i Maple. Værktøjslinje til indtastningsområdet. Menulinje.
 Maple Dette kapitel giver en kort introduktion til hvordan Maple 12 kan benyttes til at løse mange af de opgaver, som man bliver mødt med i matematiktimerne på HHX. Skærmbilledet Vi starter med at se lidt
Maple Dette kapitel giver en kort introduktion til hvordan Maple 12 kan benyttes til at løse mange af de opgaver, som man bliver mødt med i matematiktimerne på HHX. Skærmbilledet Vi starter med at se lidt
Matricer og lineære ligningssystemer
 Matricer og lineære ligningssystemer Grete Ridder Ebbesen Virum Gymnasium Indhold 1 Matricer 11 Grundlæggende begreber 1 Regning med matricer 3 13 Kvadratiske matricer og determinant 9 14 Invers matrix
Matricer og lineære ligningssystemer Grete Ridder Ebbesen Virum Gymnasium Indhold 1 Matricer 11 Grundlæggende begreber 1 Regning med matricer 3 13 Kvadratiske matricer og determinant 9 14 Invers matrix
-9-8 -7-6 -5-4 -3-2 -1 1 2 3 4 5 6 7 8 9. f(x)=2x-1 Serie 1
 En funktion beskriver en sammenhæng mellem elementer fra to mængder - en definitionsmængde = Dm(f) består af -værdier og en værdimængde = Vm(f) består af -værdier. Til hvert element i Dm(f) knttes netop
En funktion beskriver en sammenhæng mellem elementer fra to mængder - en definitionsmængde = Dm(f) består af -værdier og en værdimængde = Vm(f) består af -værdier. Til hvert element i Dm(f) knttes netop
Pythagoras Ensvinklede trekanter Trigonometri. Helle Fjord Morten Graae Kim Lorentzen Kristine Møller-Nielsen
 MATEMATIKBANKENS P.E.T. KOMPENDIUM Pythagoras Ensvinklede trekanter Trigonometri Helle Fjord Morten Graae Kim Lorentzen Kristine Møller-Nielsen FORENKLEDE FÆLLES MÅL FOR PYTHAGORAS, ENSVINKLEDE TREKANTER
MATEMATIKBANKENS P.E.T. KOMPENDIUM Pythagoras Ensvinklede trekanter Trigonometri Helle Fjord Morten Graae Kim Lorentzen Kristine Møller-Nielsen FORENKLEDE FÆLLES MÅL FOR PYTHAGORAS, ENSVINKLEDE TREKANTER
Formelsamling C-niveau
 Formelsamling C-niveau Maj 2017 Indhold C-niveau 1 Tal og Regnearter 3 1.1 Regnearternes hierarki................................... 3 1.1.1 Regneregler..................................... 3 1.2 Parenteser..........................................
Formelsamling C-niveau Maj 2017 Indhold C-niveau 1 Tal og Regnearter 3 1.1 Regnearternes hierarki................................... 3 1.1.1 Regneregler..................................... 3 1.2 Parenteser..........................................
Eksponentielle sammenhænge
 Eksponentielle sammenhænge 0 1 2 3 4 5 6 7 8 9 10 11 12 13 Indholdsfortegnelse Variabel-sammenhænge... 1 1. Hvad er en eksponentiel sammenhæng?... 2 2. Forklaring med ord af eksponentiel vækst... 2, 6
Eksponentielle sammenhænge 0 1 2 3 4 5 6 7 8 9 10 11 12 13 Indholdsfortegnelse Variabel-sammenhænge... 1 1. Hvad er en eksponentiel sammenhæng?... 2 2. Forklaring med ord af eksponentiel vækst... 2, 6
I kapitlet arbejdes med følgende centrale matematiske objekter og begreber:
 INTRO Efter mange års pause er trigonometri med Fælles Mål 2009 tilbage som fagligt emne i grundskolens matematikundervisning. Som det fremgår af den følgende sides udpluk fra faghæftets trinmål, er en
INTRO Efter mange års pause er trigonometri med Fælles Mål 2009 tilbage som fagligt emne i grundskolens matematikundervisning. Som det fremgår af den følgende sides udpluk fra faghæftets trinmål, er en
User s guide til cosinus og sinusrelationen
 User s guide til cosinus og sinusrelationen Frank Nasser 20. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for
User s guide til cosinus og sinusrelationen Frank Nasser 20. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for
Matematik A August 2016 Delprøve 1
 Anvendelse af løsningerne læses på hjemmesiden www.matematikhfsvar.page.tl Sættet løses med begrænset tekst og konklusion. Formålet er jo, at man kan se metoden, og ikke skrive af! Opgave 1 - Vektorer,
Anvendelse af løsningerne læses på hjemmesiden www.matematikhfsvar.page.tl Sættet løses med begrænset tekst og konklusion. Formålet er jo, at man kan se metoden, og ikke skrive af! Opgave 1 - Vektorer,
Vektorer og lineær regression
 Vektorer og lineær regression Peter Harremoës Niels Brock April 03 Planproduktet Vi har set, at man kan gange en vektor med et tal Et oplagt spørgsmål er, om man også kan gange to vektorer med hinanden
Vektorer og lineær regression Peter Harremoës Niels Brock April 03 Planproduktet Vi har set, at man kan gange en vektor med et tal Et oplagt spørgsmål er, om man også kan gange to vektorer med hinanden
FlexMatematik B. Introduktion
 Introduktion TI-89 er fra start indstillet til at åbne skrivebordet med de forskellige applikationer, når man taster. Almindelige regneoperationer foregår på hovedskærmen som fås ved at vælge applikationen
Introduktion TI-89 er fra start indstillet til at åbne skrivebordet med de forskellige applikationer, når man taster. Almindelige regneoperationer foregår på hovedskærmen som fås ved at vælge applikationen
Geometri, (E-opgaver 9b & 9c)
 Geometri, (E-opgaver 9b & 9c) Indhold GEOMETRI, (E-OPGAVER 9B)... 1 Arealet af en er ½ højde grundlinje... 1 Vinkelsummen i en er altid 180... 1 Ensvinklede er... 1 Retvinklede er... Sinus,... FORMLER...
Geometri, (E-opgaver 9b & 9c) Indhold GEOMETRI, (E-OPGAVER 9B)... 1 Arealet af en er ½ højde grundlinje... 1 Vinkelsummen i en er altid 180... 1 Ensvinklede er... 1 Retvinklede er... Sinus,... FORMLER...
Vektorer og lineær regression. Peter Harremoës Niels Brock
 Vektorer og lineær regression Peter Harremoës Niels Brock April 2013 1 Planproduktet Vi har set, at man kan gange en vektor med et tal. Et oplagt spørgsmål er, om man også kan gange to vektorer med hinanden.
Vektorer og lineær regression Peter Harremoës Niels Brock April 2013 1 Planproduktet Vi har set, at man kan gange en vektor med et tal. Et oplagt spørgsmål er, om man også kan gange to vektorer med hinanden.
Løsningsforslag Mat B August 2012
 Løsningsforslag Mat B August 2012 Opgave 1 (5 %) a) Løs uligheden: 2x + 11 x 1 Løsning: 2x + 11 x 1 2x x + 1 0 3x + 12 0 3x 12 Divideres begge sider med -3 (og husk at vende ulighedstegnet!) x 4 Opgave
Løsningsforslag Mat B August 2012 Opgave 1 (5 %) a) Løs uligheden: 2x + 11 x 1 Løsning: 2x + 11 x 1 2x x + 1 0 3x + 12 0 3x 12 Divideres begge sider med -3 (og husk at vende ulighedstegnet!) x 4 Opgave
Tekst, tal og formler I et regneark kan man indtaste tekst, tal og formler:
 Tekst, tal og formler I et regneark kan man indtaste tekst, tal og formler: I cellerne A1, A2 og A3 er der indtastet tekst. Tekst bliver venstrestillet. I cellerne B1 og B2 er der indtastet tal. Tal bliver
Tekst, tal og formler I et regneark kan man indtaste tekst, tal og formler: I cellerne A1, A2 og A3 er der indtastet tekst. Tekst bliver venstrestillet. I cellerne B1 og B2 er der indtastet tal. Tal bliver
GrundlÄggende variabelsammenhänge
 GrundlÄggende variabelsammenhänge for C-niveau i hf 2014 Karsten Juul LineÄr sammenhäng 1. OplÄg om lineäre sammenhänge... 1 2. Ligning for lineär sammenhäng... 1 3. Graf for lineär sammenhäng... 2 4.
GrundlÄggende variabelsammenhänge for C-niveau i hf 2014 Karsten Juul LineÄr sammenhäng 1. OplÄg om lineäre sammenhänge... 1 2. Ligning for lineär sammenhäng... 1 3. Graf for lineär sammenhäng... 2 4.
Differential- regning
 Differential- regning del () f () m l () 6 Karsten Juul Indhold Tretrinsreglen 59 Formler for differentialkvotienter64 Regneregler for differentialkvotienter67 Differentialkvotient af sammensat funktion7
Differential- regning del () f () m l () 6 Karsten Juul Indhold Tretrinsreglen 59 Formler for differentialkvotienter64 Regneregler for differentialkvotienter67 Differentialkvotient af sammensat funktion7
Vejledning til WordMat på Mac
 Installation: WordMat på MAC Vejledning til WordMat på Mac Hent WordMat for MAC på www.eduap.com Installationen er først slut når du har gjort følgende 1. Åben Word 2. I menuen vælges: Word > Indstillinger
Installation: WordMat på MAC Vejledning til WordMat på Mac Hent WordMat for MAC på www.eduap.com Installationen er først slut når du har gjort følgende 1. Åben Word 2. I menuen vælges: Word > Indstillinger
Nspire 4.2 kom godt i gang
 Nspire 4.2 kom godt i gang Disse 3 knapper åbner nyt dokument, henter eksisterende dokument og gemmer det åbne dokument Her kan dokumentet lukkes Indstillinger Indstillinger 1. Først skal vi have den rigtige
Nspire 4.2 kom godt i gang Disse 3 knapper åbner nyt dokument, henter eksisterende dokument og gemmer det åbne dokument Her kan dokumentet lukkes Indstillinger Indstillinger 1. Først skal vi have den rigtige
Integralregning med TI-Interactive! Stamfunktioner Integraler Arealer Jan Leffers (2005)
 Integralregning med TI-Interactive! Stamfunktioner Integraler Arealer Jan Leffers (005) Indholdsfortegnelse Indholdsfortegnelse... Stamfunktion og integralregning...3 Numerisk integration...3 Areal under
Integralregning med TI-Interactive! Stamfunktioner Integraler Arealer Jan Leffers (005) Indholdsfortegnelse Indholdsfortegnelse... Stamfunktion og integralregning...3 Numerisk integration...3 Areal under
Regning. Mike Vandal Auerbach ( 7) 4x 2 y 2xy 5. 2x + 4 = 3. (x + 3)(2x 1) = 0. (a + b)(a b) a 2 + b 2 2ab.
 Mike Vandal Auerbach Regning + 6 ( 7) (x + )(x 1) = 0 x + = 7 + x y xy 5 7 + 5 (a + (a a + b ab www.mathematicus.dk Regning 1. udgave, 018 Disse noter er en opsamling på generelle regne- og algebraiske
Mike Vandal Auerbach Regning + 6 ( 7) (x + )(x 1) = 0 x + = 7 + x y xy 5 7 + 5 (a + (a a + b ab www.mathematicus.dk Regning 1. udgave, 018 Disse noter er en opsamling på generelle regne- og algebraiske
Mathcad Survival Guide
 Mathcad Survival Guide Mathcad er en blanding mellem et tekstbehandlingsprogram (Word), et regneark (Ecel) og en grafisk CAS-lommeregner. Programmet er velegnet til matematikopgaver, fysikrapporter og
Mathcad Survival Guide Mathcad er en blanding mellem et tekstbehandlingsprogram (Word), et regneark (Ecel) og en grafisk CAS-lommeregner. Programmet er velegnet til matematikopgaver, fysikrapporter og
Variabel- sammenhænge
 Variabel- sammenhænge 2008 Karsten Juul Dette hæfte kan bruges som start på undervisningen i variabelsammenhænge for st og hf. Indhold 1. Hvordan viser en tabel sammenhængen mellem to variable?... 1 2.
Variabel- sammenhænge 2008 Karsten Juul Dette hæfte kan bruges som start på undervisningen i variabelsammenhænge for st og hf. Indhold 1. Hvordan viser en tabel sammenhængen mellem to variable?... 1 2.
Eksponentielle sammenhænge
 Eksponentielle sammenhænge Udgave 009 Karsten Juul Dette hæfte er en fortsættelse af hæftet "Lineære sammenhænge, udgave 009" Indhold 1 Eksponentielle sammenhænge, ligning og graf 1 Procent 7 3 Hvad fortæller
Eksponentielle sammenhænge Udgave 009 Karsten Juul Dette hæfte er en fortsættelse af hæftet "Lineære sammenhænge, udgave 009" Indhold 1 Eksponentielle sammenhænge, ligning og graf 1 Procent 7 3 Hvad fortæller
Aktivitet 1b: Regnehistorie
 Aktivitet 1b: Regnehistorie Vi tager igen udgangspunkt i en eksamensopgave fra sommeren 014: En regneopskrift består af nogle linjer med en ordre i hver linje. Det tal, du får, når du følger en ordre i
Aktivitet 1b: Regnehistorie Vi tager igen udgangspunkt i en eksamensopgave fra sommeren 014: En regneopskrift består af nogle linjer med en ordre i hver linje. Det tal, du får, når du følger en ordre i
VEJLEDNING TIL WORD INDHOLDSFORTEGNELSE. 1. Linjeafstand. side 3. 2. Margener.. side 3. 3. Sidehoved og sidefod... side 4. 4. Sidetal..
 VEJLEDNING TIL WORD VEJLEDNING TIL WORD INDHOLDSFORTEGNELSE 1. Linjeafstand. side 3 2. Margener.. side 3 3. Sidehoved og sidefod... side 4 4. Sidetal.. side 5 5. Spalter.... side 5 6. Skifte ordbog.. side
VEJLEDNING TIL WORD VEJLEDNING TIL WORD INDHOLDSFORTEGNELSE 1. Linjeafstand. side 3 2. Margener.. side 3 3. Sidehoved og sidefod... side 4 4. Sidetal.. side 5 5. Spalter.... side 5 6. Skifte ordbog.. side
APPENDIX A INTRODUKTION TIL DERIVE
 APPENDIX A INTRODUKTION TIL DERIVE z x y z=exp( x^2 0.5y^2) CAS er en fællesbetegnelse for matematikprogrammer, som foruden numeriske beregninger også kan regne med symboler og formler. Det betyder: Computer
APPENDIX A INTRODUKTION TIL DERIVE z x y z=exp( x^2 0.5y^2) CAS er en fællesbetegnelse for matematikprogrammer, som foruden numeriske beregninger også kan regne med symboler og formler. Det betyder: Computer
Start-mat. for stx og hf Karsten Juul
 Start-mat for stx og hf 0,6 5, 9 2017 Karsten Juul Start-mat for stx og hf 2017 Karsten Juul 1/8-2017 (7/8-2017) Nyeste version af dette hæfte kan downloades fra http://mat1.dk/noter.htm. Hæftet må benyttes
Start-mat for stx og hf 0,6 5, 9 2017 Karsten Juul Start-mat for stx og hf 2017 Karsten Juul 1/8-2017 (7/8-2017) Nyeste version af dette hæfte kan downloades fra http://mat1.dk/noter.htm. Hæftet må benyttes
Lineære sammenhænge. Udgave 2. 2009 Karsten Juul
 Lineære sammenhænge Udgave 2 y = 0,5x 2,5 2009 Karsten Juul Dette hæfte er en fortsættelse af hæftet "Variabelsammenhænge, 2. udgave 2009". Indhold 1. Lineære sammenhænge, ligning og graf... 1 2. Lineær
Lineære sammenhænge Udgave 2 y = 0,5x 2,5 2009 Karsten Juul Dette hæfte er en fortsættelse af hæftet "Variabelsammenhænge, 2. udgave 2009". Indhold 1. Lineære sammenhænge, ligning og graf... 1 2. Lineær
Introduktion til cosinus, sinus og tangens
 Introduktion til cosinus, sinus og tangens Jes Toft Kristensen 24. maj 2010 1 Forord Her er en lille introduktion til cosinus, sinus og tangens. Det var et af de emner jeg selv havde svært ved at forstå,
Introduktion til cosinus, sinus og tangens Jes Toft Kristensen 24. maj 2010 1 Forord Her er en lille introduktion til cosinus, sinus og tangens. Det var et af de emner jeg selv havde svært ved at forstå,
Studieretningsopgave
 Virum Gymnasium Studieretningsopgave Harmoniske svingninger i matematik og fysik Vejledere: Christian Holst Hansen (matematik) og Bodil Dam Heiselberg (fysik) 30-01-2014 Indholdsfortegnelse Indledning...
Virum Gymnasium Studieretningsopgave Harmoniske svingninger i matematik og fysik Vejledere: Christian Holst Hansen (matematik) og Bodil Dam Heiselberg (fysik) 30-01-2014 Indholdsfortegnelse Indledning...
H Å N D B O G M A T E M A T I K 2. U D G A V E
 H Å N D B O G M A T E M A T I K C 2. U D G A V E ÁÒ ÓÐ Indhold 1 1 Procentregning 3 1.1 Delingsprocent.............................. 3 1.2 Vækstprocent.............................. 4 1.3 Renteformlen..............................
H Å N D B O G M A T E M A T I K C 2. U D G A V E ÁÒ ÓÐ Indhold 1 1 Procentregning 3 1.1 Delingsprocent.............................. 3 1.2 Vækstprocent.............................. 4 1.3 Renteformlen..............................
Undersøgelser af trekanter
 En rød tråd igennem kapitlet er en søgen efter svar på spørgsmålet: Hvordan kan vi beregne os frem til længder, vi ikke kan komme til at måle?. Hvordan kan vi fx beregne højden på et træ eller et hus,
En rød tråd igennem kapitlet er en søgen efter svar på spørgsmålet: Hvordan kan vi beregne os frem til længder, vi ikke kan komme til at måle?. Hvordan kan vi fx beregne højden på et træ eller et hus,
Bedste rette linje ved mindste kvadraters metode
 1/9 Bedste rette linje ved mindste kvadraters metode - fra www.borgeleo.dk Figur 1: Tre datapunkter og den bedste rette linje bestemt af A, B og C Målepunkter og bedste rette linje I ovenstående koordinatsystem
1/9 Bedste rette linje ved mindste kvadraters metode - fra www.borgeleo.dk Figur 1: Tre datapunkter og den bedste rette linje bestemt af A, B og C Målepunkter og bedste rette linje I ovenstående koordinatsystem
Mattip om. Ligninger 1. Du skal lære: Kan ikke Kan næsten Kan. Hvad en ligning er. Hvordan du kan genkende en ligning
 Mattip om Ligninger 1 Du skal lære: Hvad en ligning er Kan ikke Kan næsten Kan Hvordan du kan genkende en ligning Ligningsløsning ved gæt og kontrol Reducering og løsning af ligninger 2016 mattip.dk 1
Mattip om Ligninger 1 Du skal lære: Hvad en ligning er Kan ikke Kan næsten Kan Hvordan du kan genkende en ligning Ligningsløsning ved gæt og kontrol Reducering og løsning af ligninger 2016 mattip.dk 1
Afstandsformlen og Cirklens Ligning
 Afstandsformlen og Cirklens Ligning Frank Villa 19. august 2012 2008-2012. IT Teaching Tools. ISBN-13: 978-87-92775-00-9. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk.
Afstandsformlen og Cirklens Ligning Frank Villa 19. august 2012 2008-2012. IT Teaching Tools. ISBN-13: 978-87-92775-00-9. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk.
5: Trigonometri Den del af matematik, der beskæftiger sig med figurer og deres egenskaber, kaldes for geometri. Selve
 5: Trigonometri Den del af matematik, der beskæftiger sig med figurer og deres egenskaber, kaldes for geometri. Selve ordet geometri er græsk og betyder jord(=geo)måling(=metri). Interessen for figurer
5: Trigonometri Den del af matematik, der beskæftiger sig med figurer og deres egenskaber, kaldes for geometri. Selve ordet geometri er græsk og betyder jord(=geo)måling(=metri). Interessen for figurer
Måling - Fase 3 Bestemme afstande med beregning
 Navn: Klasse: Måling - Fase 3 Bestemme afstande med beregning Vurdering fra 1 til 5 (hvor 5 er højst) Læringsmål Selv Lærer Beviser og forslag til forbedring 1. Jeg kan anvende forholdet mellem sider i
Navn: Klasse: Måling - Fase 3 Bestemme afstande med beregning Vurdering fra 1 til 5 (hvor 5 er højst) Læringsmål Selv Lærer Beviser og forslag til forbedring 1. Jeg kan anvende forholdet mellem sider i
Måling - Fase 3 Bestemme afstande med beregning
 Navn: Klasse: Måling - Fase 3 Bestemme afstande med beregning Vurdering fra 1 til 5 (hvor 5 er højst) Læringsmål Selv Lærer Beviser og forslag til forbedring 1. Jeg kan anvende forholdet mellem sider i
Navn: Klasse: Måling - Fase 3 Bestemme afstande med beregning Vurdering fra 1 til 5 (hvor 5 er højst) Læringsmål Selv Lærer Beviser og forslag til forbedring 1. Jeg kan anvende forholdet mellem sider i
Sammensætning af regnearterne
 Sammensætning af regnearterne Plus, minus, gange og division... 19 Negative tal... 0 Parenteser og brøkstreger... Potenser og rødder... 4 Sammensætning af regnearterne Side 18 Plus, minus, gange og division
Sammensætning af regnearterne Plus, minus, gange og division... 19 Negative tal... 0 Parenteser og brøkstreger... Potenser og rødder... 4 Sammensætning af regnearterne Side 18 Plus, minus, gange og division
Forslag til løsning af Opgaver til afsnittet om de naturlige tal (side 80)
 Forslag til løsning af Opgaver til afsnittet om de naturlige tal (side 80) Opgave 1 Vi skal tegne alle de linjestykker, der forbinder vilkårligt valgte punkter blandt de 4 punkter. Gennem forsøg finder
Forslag til løsning af Opgaver til afsnittet om de naturlige tal (side 80) Opgave 1 Vi skal tegne alle de linjestykker, der forbinder vilkårligt valgte punkter blandt de 4 punkter. Gennem forsøg finder
Velkommen til TI-Nspire CAS 2.0 (Lærerversion)
 Velkommen til TI-Nspire CAS 2.0 (Lærerversion) Når du åbner for TI-Nspire CAS i en standardopsætning ser brugerfladen således ud (hvis ikke, så vælg Dialogboks > Indlæs standardområdet): I midterpanelet
Velkommen til TI-Nspire CAS 2.0 (Lærerversion) Når du åbner for TI-Nspire CAS i en standardopsætning ser brugerfladen således ud (hvis ikke, så vælg Dialogboks > Indlæs standardområdet): I midterpanelet
Introduktion til Calc Open Office med øvelser
 Side 1 af 8 Introduktion til Calc Open Office med øvelser Introduktion til Calc Open Office... 2 Indtastning i celler... 2 Formler... 3 Decimaler... 4 Skrifttype... 5 Skrifteffekter... 6 Justering... 6
Side 1 af 8 Introduktion til Calc Open Office med øvelser Introduktion til Calc Open Office... 2 Indtastning i celler... 2 Formler... 3 Decimaler... 4 Skrifttype... 5 Skrifteffekter... 6 Justering... 6
Kapitel 4. Trigonometri. Matematik C (må anvendes på Ørestad Gymnasium) Kapitel 4
 Matematik C (må anvendes på Ørestad Gymnasium) Trigonometri Den del af matematik, der beskæftiger sig med figurer og deres egenskaber, kaldes for geometri. Selve ordet geometri er græsk og betyder jord(=geo)måling(=metri).
Matematik C (må anvendes på Ørestad Gymnasium) Trigonometri Den del af matematik, der beskæftiger sig med figurer og deres egenskaber, kaldes for geometri. Selve ordet geometri er græsk og betyder jord(=geo)måling(=metri).
matx.dk Enkle modeller
 matx.dk Enkle modeller Dennis Pipenbring 28. juni 2011 Indhold 1 Indledning 4 2 Funktionsbegrebet 4 3 Lineære funktioner 8 3.1 Bestemmelse af funktionsværdien................. 9 3.2 Grafen for en lineær
matx.dk Enkle modeller Dennis Pipenbring 28. juni 2011 Indhold 1 Indledning 4 2 Funktionsbegrebet 4 3 Lineære funktioner 8 3.1 Bestemmelse af funktionsværdien................. 9 3.2 Grafen for en lineær
Trigonometri. Store konstruktioner. Måling af højde
 Trigonometri Ordet trigonometri er sammensat af de to ord trigon og metri, hvor trigon betyder trekant og metri kommer af det græske ord metros, som kan oversættes til måling. Så ordet trigonometri er
Trigonometri Ordet trigonometri er sammensat af de to ord trigon og metri, hvor trigon betyder trekant og metri kommer af det græske ord metros, som kan oversættes til måling. Så ordet trigonometri er
Modellering af elektroniske komponenter
 Modellering af elektroniske komponenter Formålet er at give studerende indblik i hvordan matematik som fag kan bruges i forbindelse med at modellere fysiske fænomener. Herunder anvendelse af Grafregner(TI-89)
Modellering af elektroniske komponenter Formålet er at give studerende indblik i hvordan matematik som fag kan bruges i forbindelse med at modellere fysiske fænomener. Herunder anvendelse af Grafregner(TI-89)
t a l e n t c a m p d k Matematik Intro Mads Friis, stud.scient 7. november 2015 Slide 1/25
 Slide 1/25 Indhold 1 2 3 4 5 6 7 8 Slide 2/25 Om undervisningen Hvorfor er vi her? Slide 3/25 Om undervisningen Hvorfor er vi her? Hvad kommer der til at ske? 1) Teoretisk gennemgang ved tavlen. 2) Instruktion
Slide 1/25 Indhold 1 2 3 4 5 6 7 8 Slide 2/25 Om undervisningen Hvorfor er vi her? Slide 3/25 Om undervisningen Hvorfor er vi her? Hvad kommer der til at ske? 1) Teoretisk gennemgang ved tavlen. 2) Instruktion
Mike Vandal Auerbach. Geometri i planen. # b. # a. # a # b.
 Mike Vandal Auerbach Geometri i planen # a # a www.mathematicus.dk Geometri i planen 1. udgave, 2018 Disse noter dækker kernestoffet i plangeometri på stx A- og B-niveau efter gymnasiereformen 2017. Al
Mike Vandal Auerbach Geometri i planen # a # a www.mathematicus.dk Geometri i planen 1. udgave, 2018 Disse noter dækker kernestoffet i plangeometri på stx A- og B-niveau efter gymnasiereformen 2017. Al
potenstal og rodtal trin 2 brikkerne til regning & matematik preben bernitt
 brikkerne til regning & matematik potenstal og rodtal trin 2 preben bernitt brikkerne til regning & matematik potenstal og rodtal, trin 2 ISBN: 978-87-92488-06-0 1. Udgave som E-bog 2003 by bernitt-matematik.dk
brikkerne til regning & matematik potenstal og rodtal trin 2 preben bernitt brikkerne til regning & matematik potenstal og rodtal, trin 2 ISBN: 978-87-92488-06-0 1. Udgave som E-bog 2003 by bernitt-matematik.dk
fx 8 Sandsynligheden for at slå en 4 er med en 6-sidet 1 terning 2
 Logik Udsagn Reduktion Ligninger Uligheder Regnehistorier I en trekant er den største vinkel 0 større end den næststørste og denne igen 0 større end den mindste. Find vinklernes gradtal. = og Lig med og
Logik Udsagn Reduktion Ligninger Uligheder Regnehistorier I en trekant er den største vinkel 0 større end den næststørste og denne igen 0 større end den mindste. Find vinklernes gradtal. = og Lig med og
Forløb om undervisnings- differentiering. Elevark
 Program for løft af de fagligt svageste elever Intensivt læringsforløb Lærervejledning Forløb om undervisnings- differentiering Elevark Dato September 2018 Udviklet for Undervisningsministeriet Udviklet
Program for løft af de fagligt svageste elever Intensivt læringsforløb Lærervejledning Forløb om undervisnings- differentiering Elevark Dato September 2018 Udviklet for Undervisningsministeriet Udviklet
formler og ligninger trin 2 brikkerne til regning & matematik preben bernitt
 brikkerne til regning & matematik formler og ligninger trin 2 preben bernitt brikkerne til regning & matematik formler og ligninger, trin 2 ISBN: 978-87-92488-09-1 1. Udgave som E-bog 2003 by bernitt-matematik.dk
brikkerne til regning & matematik formler og ligninger trin 2 preben bernitt brikkerne til regning & matematik formler og ligninger, trin 2 ISBN: 978-87-92488-09-1 1. Udgave som E-bog 2003 by bernitt-matematik.dk
1 Geometri & trigonometri
 1 Geometri & trigonometri 1.0.1 Generelle forhold Trigonometri tager sit udgangspunkt i trekanter, hvor der er visse generelle regler: vinkelsum areal A trekant = 1 2 h G A B C = 180 o retvinklet trekant
1 Geometri & trigonometri 1.0.1 Generelle forhold Trigonometri tager sit udgangspunkt i trekanter, hvor der er visse generelle regler: vinkelsum areal A trekant = 1 2 h G A B C = 180 o retvinklet trekant
Grundlæggende færdigheder
 Regnetest A: Grundlæggende færdigheder Træn og Test Niveau: 7. klasse Uden brug af lommeregner 1 INFA-Matematik: Informatik i matematikundervisningen Et delprojekt under INFA: Informatik i skolens fag
Regnetest A: Grundlæggende færdigheder Træn og Test Niveau: 7. klasse Uden brug af lommeregner 1 INFA-Matematik: Informatik i matematikundervisningen Et delprojekt under INFA: Informatik i skolens fag
A U T O F I G U R E R T I L E X C E L S i d e 1. ISBN GeGe Jørn Blok
 A U T O F I G U R E R T I L E X C E L 2 0 1 0 S i d e 1 A U T O F I G U R E R T I L E X C E L 2 0 1 0 S i d e 2 Inden du går i gang Inden du går i gang, skal du have en gemmemappe til dine øvelser. På
A U T O F I G U R E R T I L E X C E L 2 0 1 0 S i d e 1 A U T O F I G U R E R T I L E X C E L 2 0 1 0 S i d e 2 Inden du går i gang Inden du går i gang, skal du have en gemmemappe til dine øvelser. På
Kapital- og rentesregning
 Rentesregning Rettet den 28-12-11 Kapital- og rentesregning Kapital- og rentesregning Navngivning ved rentesregning I eksempler som Niels Oles, hvor man indskyder en kapital i en bank (én gang), og banken
Rentesregning Rettet den 28-12-11 Kapital- og rentesregning Kapital- og rentesregning Navngivning ved rentesregning I eksempler som Niels Oles, hvor man indskyder en kapital i en bank (én gang), og banken
Lærervejledning Matematik 1-2-3 på Smartboard
 Lærervejledning Matematik 1-2-3 på Smartboard Lærervejledning til Matematik 1-2-3 på Smartboard Materialet består af 33 færdige undervisningsforløb til brug i matematikundervisningen i overbygningen. Undervisningsforløbene
Lærervejledning Matematik 1-2-3 på Smartboard Lærervejledning til Matematik 1-2-3 på Smartboard Materialet består af 33 færdige undervisningsforløb til brug i matematikundervisningen i overbygningen. Undervisningsforløbene
Differentialregning med TI-Interactive! Indledende differentialregning Tangenter Monotoniforhold og ekstremum Optimering Jan Leffers (2009)
 Differentialregning med TI-Interactive! Indledende differentialregning Tangenter Monotoniforhold og ekstremum Optimering Jan Leffers (2009) Indholdsfortegnelse Indholdsfortegnelse...2 Indledende differentialregning...3
Differentialregning med TI-Interactive! Indledende differentialregning Tangenter Monotoniforhold og ekstremum Optimering Jan Leffers (2009) Indholdsfortegnelse Indholdsfortegnelse...2 Indledende differentialregning...3
Trigonometri at beregne Trekanter
 Trigonometri at beregne Trekanter Pythagoras, en stor matematiker fandt ud af, at der i en retvinklet trekant summen af kvadraterne på kateterne er lig med kvadratet på hypotenusen. ( a 2 + b 2 = c 2 )
Trigonometri at beregne Trekanter Pythagoras, en stor matematiker fandt ud af, at der i en retvinklet trekant summen af kvadraterne på kateterne er lig med kvadratet på hypotenusen. ( a 2 + b 2 = c 2 )
Matematik B1. Mike Auerbach. c h A H
 Matematik B1 Mike Auerbach B c h a A b x H x C Matematik B1 2. udgave, 2015 Disse noter er skrevet til matematikundervisning på stx og kan frit anvendes til ikke-kommercielle formål. Noterne er skrevet
Matematik B1 Mike Auerbach B c h a A b x H x C Matematik B1 2. udgave, 2015 Disse noter er skrevet til matematikundervisning på stx og kan frit anvendes til ikke-kommercielle formål. Noterne er skrevet
Matematik - et grundlæggende kursus. Dennis Cordsen Pipenbring
 Matematik - et grundlæggende kursus Dennis Cordsen Pipenbring 22. april 2006 2 Indhold I Matematik C 9 1 Grundlæggende algebra 11 1.1 Sprog................................ 11 1.2 Tal.................................
Matematik - et grundlæggende kursus Dennis Cordsen Pipenbring 22. april 2006 2 Indhold I Matematik C 9 1 Grundlæggende algebra 11 1.1 Sprog................................ 11 1.2 Tal.................................
Potensfunktioner samt proportional og omvent proportional. for hf Karsten Juul
 Potensfunktioner samt proportional og omvent proportional for hf 2018 Karsten Juul Potensfunktion 1. Oplæg til forskrift for potensfunktion...1 2. Forskrift for potensfunktion...2 3. Udregn x eller y i
Potensfunktioner samt proportional og omvent proportional for hf 2018 Karsten Juul Potensfunktion 1. Oplæg til forskrift for potensfunktion...1 2. Forskrift for potensfunktion...2 3. Udregn x eller y i
