Prøver Evaluering Undervisning. Matematik. Maj-juni 2008
|
|
|
- Birgit Thomsen
- 8 år siden
- Visninger:
Transkript
1 Prøver Evaluering Undervisning Matematik Maj-juni 2008 Ved fagkonsulent Klaus Fink
2 Indhold Indledning...3 Fælles for faget...4 Fagets identitet...5 De skriftlige prøver i matematik...8 Den nye karakterskala...8 Den nye bedømmelsesprocedure...8 Vurdering af især problemløsning...8 Hjælpemidler Elevens aflevering af besvarelse Hvordan fremkommer der en karakter i skriftlig matematik? FSA Matematiske færdigheder Landsresultatet Kommentarer til enkelte opgaver FSA Matematisk problemløsning Landsresultatet Kommentarer til enkelte opgaver FS10, skriftlig matematik Landsresultatet Kommentarer til enkelte opgaver FS10, mundtlig matematik Den nye karakterskala Prøveoplæg Anvendelse af computer Prøvens afholdelse Tekstopgivelser Landsresultatet
3 Indledning PEU 2008 er skrevet ud fra en række vurderinger af årets prøvesæt. Alle ministerielt beskikkede censorer har bidraget med en evalueringsrapport, og der har været afholdt et evalueringsmøde i forbindelse med forcensuren. Desuden har der kunnet trækkes mange oplysninger om elevernes arbejde med prøveopgaverne ud af Skolestyrelsens retteprogram, som blev anvendt i forbindelse med vurderingen af mere end 10 % af alle elevbesvarelser. Der skal lyde en stor tak til alle, der på disse måder har givet værdifulde informationer til årets prøveevaluering. 3
4 Fælles for faget Der er tre hjemmesider, hvor man som matematiklærer kan hente information om og inspiration til sit daglige arbejde med undervisningen og til arbejdet med afgangsprøverne. Det kan anbefales regelmæssigt at besøge disse hjemmesider. Her kan matematiklæreren hente inspiration til den løbende evaluering i sit fag. Der er både generelle artikler om evaluering og fagspecifikke inspirationsartikler. Hjemmesiden giver desuden adgang til de nationale test. Endelig er der også inspiration til arbejdet med elevplaner. Her ligger alle bekendtgørelser og vejledninger om prøverne samt de årlige PEU-hæfter. Nyhedsbreve og informationsbreve til skolerne vil også kunne findes på denne side. Her er alt om karakterskalaen, blandt andet karakterbekendtgørelsen og karakterbeskrivelser, og der er et link til Fælles Mål. Desuden er der mange andre oplysninger om folkeskolen og de frie grundskoler. 4
5 Fagets identitet Faget matematik er et af de centrale fag i grundskolen. Der er tale om verdens største fag, da det blandt andet er det eneste fag, der er på skemaet i alle verdens skoler. Faget er et sprogligt fag, hvor anvendelse af både mundtligt og skriftligt sprog er afgørende for elevernes begrebsudvikling, præcisering af tankegange og læring i matematik. Matematik er også et af de vigtigste faglige redskaber i en lang række andre fag og funktioner i dagligdagen. Således har matematik en stadig stigende betydning i de videregående uddannelser, i den teknologiske udvikling og i samfundet i øvrigt. Men samtidig er meget af matematikkens anvendelse skjult for mennesket i dagligdagen. Dette skisma har også betydning for arbejdet i skolen, hvor ikke al matematik kan gøres umiddelbart motiverende med eksempler fra elevernes nære hverdag. Alligevel er det lykkedes lærerne at være med til at gøre faget til det mest populære fag for eleverne (Gallupundersøgelse offentliggjort i Berlingske Tidende august 2007). Der er da også til stadighed mange diskussioner om fagets indhold, undervisningens tilrettelæggelse og fagets målsætning. Disse diskussioner sker ofte på baggrund af Fælles Mål og indimellem med inddragelse af ny didaktisk forskning. Disse diskussioner er med til at udvikle faget matematik i folkeskolen. Det drejer sig om såvel den mere overordnede fastlæggelse af undervisningsmål ud fra slut- og trinmål i Fælles Mål som den mere individuelle fastsættelse af læringsmål for den enkelte elev. Naturligt nok er undervisningsmålene, som de fremtræder i faghæftet, af en overordnet karakter, der skal dække flere klassetrin og større grupper af elever. Arbejdet for skolerne (lærerne) består så i at fastlægge læringsmålene og de dertil hørende mere specificerede faglige beskrivelser for de enkelte elever. Disse læringsmål er således forskellige for den enkelte elev eller grupper af elever. Hvis klassen arbejder med for eksempel ligningsløsning har nogle elever en målsætning, der handler om inspektion og helt enkle ligninger, hvor andre arbejder hen mod at kunne løse mere komplicerede 5
6 ligninger i en formaliseret løsningsproces. Et eksempel fra begyndertrinnet kan være addition, hvor nogle elever er klar til en formaliseret opstilling, og andre slet ikke er kommet så langt og derfor arbejder med at udvikle algoritmer ud fra konkrete materialer og andre repræsentationer. Her er læringsmålene således af forskellig karakter, og det er nødvendigt at anskue disse mål gennem det overliggende hierarki, som består af fagets formål, centrale kundskaber og færdigheder (slutmål) og trinmålene og dernæst forholde sig til den enkelte elev. For den enkelte elev vil der således være tale om afvejning og fokusering på nogle mål mere end på andre. Grundlaget for denne modeltænkning er, at CKF erne og de tilhørende trinmål er et kompliceret system, hvor det næppe er muligt at arbejde med matematik og kun opfylde et enkelt trinmål. Målene og CKF erne har en indbyrdes sammenhæng. Matrixmodellen, som blev omtalt i PEUhæftet 2003, er en anskuelsesmodel, der kan tydeliggøre, hvilke delmål den enkelte elev skal eller kan tage udgangspunkt i og efterfølgende forsøge at opfylde gennem sit arbejde med matematikken. Det har også den konsekvens, at en helhedsvurdering af elevens præstationer bygger på flere veje til målet og dermed (måske) forskellige kvaliteter i såvel arbejde som resultater. Med KOM-rapportens (Kompetencer og matematiklæring) offentliggørelse i 2001 kom der en ny dimension ind i diskussionerne om matematikundervisningen i form af definition af otte matematiske kompetencer, der kan beskrives for hele uddannelsesforløbet. Kompetencerne er omtalt i kortfattet form i Fælles Mål fra Kompetencetænkningen og flere af elementerne i de otte matematiske kompetencer er allerede med i Fælles Mål. Med de obligatoriske nationale test og indførelse af obligatoriske afgangsprøver er der nu tre nationale evalueringer i faget matematik. Det er vigtigt at gøre sig klart, at de to nationale test i 3. og 6. klasse er tænkt som formative test, der kan hjælpe læreren i evalueringen og planlægningen af sin undervisning. Desuden betyder testformen og den tid, der er afsat til den, at kun en mindre del af fagets mål kan evalueres i disse test. For at kunne evaluere alle mål og på alle klassetrin skal der flere evalueringsredskaber i brug. Til dette arbejde er der meget inspiration at hente på den ovenover omtalte evalueringsportal. 6
7 Afgangsprøven er til gengæld en summativ evaluering som afslutning på grundskoleforløbet. Prøven i matematik kommer dybere i evalueringen af fagets mål end de nationale test. Men heller ikke afgangsprøven evaluerer alle mål, idet det mundtlige arbejde med matematik ikke prøves ved FSA. Da dette også skal evalueres, blandt andet fordi det er med i målene, og fordi det skal bedømmes med standpunktskarakterer, er det både nødvendigt at arbejde med den mundtlige dimension og evaluering af dette arbejde i den daglige undervisning. 7
8 De skriftlige prøver i matematik Den nye karakterskala Overgangen til ny karakterskala ser ikke ud til at have givet problemer. Tilbagemeldinger fra de beskikkede censorer både i de skriftlige prøver og ved den mundtlige prøve i FS10 viser klart, at overgangen til 7-trins-skalaen er foregået stort set problemfrit. Det kan skyldes, at der er blevet gennemført et omfattende arbejde med informationsmøder, skriftlige materialer og møder i fagteam og klasseteam på de enkelte skoler. Det spiller også en rolle, at 7-trins-skalaen med de færre trin, den tydeligere trindifferentiering og den mere præcise beskrivelse af de enkelte karakterer i skalaen er lettere at arbejde med, end 13-skalaen var. Den nye bedømmelsesprocedure De uhensigtsmæssigheder, der har været med den nye bedømmelsesprocedure, er blevet løst med den procedure, der gælder fra decemberprøven Den giver en nærmere beskrivelse af, hvordan den ministerielle og den kommunale censor drøfter karaktergivningen inden karakterlisterne sendes til skolen. Tilbagemeldingen fra de ministerielle censorer ved decemberprøven udtrykker stor tilfredshed med denne ordning. Derimod melder mange kommunale censorer, at de ikke er uddannet i censorarbejdet, som for eksempel de ministerielle censorer, der deltager i de årlige censormøder. Flere kommunale censorer har oplyst, at arbejdet er blevet brugt som skemakit med den konsekvens, at der nogle steder er kommunale censorer, der ikke før har vurderet folkeskolens afgangsprøver, og endda enkelte steder, hvor den kommunale censor aldrig har undervist i matematik. Vurdering af især problemløsning Det er vigtigt at slå fast, at vurdering af matematisk problemløsning ikke kun kan være en kontrol af antallet af rigtige facitter. Der er mange andre forhold i elevbesvarelserne, der skal indgå i bedømmelsen. Det kan man læse om i prøvevejledningen. Her skal blot gengives en del af bekendtgørelse nummer 863 af 5. juli 2007: 2.9. I bedømmelsen vil der blive lagt vægt på elevens 8
9 brug af faglige begrundelser, herunder anvendelse af matematiske modeller, samt elevens anvendelse af forklarende tekst, algebraiske udtryk, tegninger og grafer. Ligeledes indgår det i bedømmelsen, hvorledes eleven på grundlag af de foreliggende oplysninger og data kan vurdere problemer, beskrive løsningsstrategier og udarbejde løsninger ved hjælp af matematikken. Det er vigtigt, at eleverne forholder deres matematiske løsninger til det praktiske problem, der skal løses, blandt andet ved at angive den endelige løsning med et passende antal betydende cifre og decimaler. Jeg vil her citere en af historiens mest fremtrædende matematikere, Carl Friederich Gauss, : Der er intet, som i højere grad er udtryk for en mangel på matematisk uddannelse som en umådelig nøjagtighed ved regning med tal. To forhold skal nærmere kommenteres: Skal der altid være en begrundelse i form af tekst, tegning, regneudtryk mv.? Ja, principielt kan der højst gives et point for et rigtigt facit helt uden begrundelse eller ledsagende tekst. Der forekommer dog opgaver, hvor en begrundelse kan være undladt, for eksempel ved simple aflæsninger i et skema eller diagram. Kan en begrundelse være udelukkende i dagligsprog uden regneudtryk eller lignende matematiksprog? Ja, men det forekommer sjældent, da det for langt de fleste elever er lettere at opstille et regneudtryk. Derimod bør sammenblanding af dagligsprog og et regneudtryk medføre et fratræk i point. Her er et par eksempler: Eksempel 1 FSA, opgave 1.3 Den procentvise stigning fra sommeren 07 til sommeren 08 er (75-70 som er priserne fra 08 og 07 = 5 som er stigningen / 70 = 0,071 x 100) = 7,1 % Eksempel 2 FSA, opgave 3.3 9
10 Menuen som Peter spiser dækker (4000 som er det menuen indeholder / som er det maksimum indtag bør være x 100) = 37,73 % af hans daglige forbrug. Hjælpemidler Der er forsat en vis usikkerhed på skolerne om reglerne for tilladte hjælpemidler i matematisk problemløsning til FSA og skriftlig matematik til FS10. Til FSA er alle hjælpemidler, der er anvendt i den daglige undervisning tilladte ifølge bekendtgørelse nummer 863 af 5. juli Desuden er der nævnt nogle eksempler på, hvad disse hjælpemidler kan være: lommeregner, skrive- og tegneredskaber, elevens egne udførte noter og opgaver samt den af ministeriet udgivne formel- og tabelsamling eller lignende. Men andre eksempler kan tænkes i denne sammenhæng: grafregner, computer med alle de programmer, eleven er fortrolig med gennem det daglige arbejde med matematik, elevens lærebog, opslagsværker, matematiske leksika, rettede opgaver, lærerfremstillede kompendier, matematikrapporter og kladdehæfter. Flere eksempler kan sikkert findes. Men der er tre forhold at holde sig for øje: Alle hjælpemidler, som eleven har anvendt i sit daglige arbejde med matematik, er tilladte at medbringe til prøven. Elektronisk udstyr, som kan sætte eleven i stand til at kommunikere med andre under prøven, er derimod ikke tilladt. Det er vigtig at diskutere omfanget af hjælpemidler med eleverne forud for prøven at der kun medbringes de hjælpemidler, den enkelte elev er fortrolig med og kan have glæde af i den tre timer lange prøve. For prøven FS10 er formuleringen af tilladte hjælpemidler lidt anderledes: Ved den skriftlige prøve må anvendes en godkendt formel- og tabelsamling, egne optegnelser og opslagsværker samt andre hjælpemidler, herunder lommeregner og computer (bekendtgørelse nummer 737 af 14. juli 2005). I praksis betyder det næsten det samme, idet en formel- og tabelsamling, egne noter og et opslagsværk (for eksempel lærebogen eller et leksikon), lommeregner og eventuelt en compu- 10
11 ter er de hjælpemidler, langt de fleste elever vil vælge at medbringe og kunne have glæde af ved prøven. Elevens aflevering af besvarelse Nogle censorer bemærker, at der stadig er enkelte klasser, hvor de fleste elever er usikre på reglerne i forbindelse med afleveringen af deres besvarelser. Eleven skal selv vælge de ark, vedkommende ønsker at aflevere til bedømmelse. Hvert ark nummereres fortløbende og forsynes med antal afleverede ark i alt samt elevens underskrift. Ved ark forstås også et foldet A3-ark, som altså kun tæller som ét ark. Mange elever afleverer to svarark, selvom der kun er arbejdet på det ene. Enkelte elever afleverer nogle opgaver i to versioner (kladde og indskrivning?), hvilket sætter censoren i en vanskelig situation. I sådanne tilfælde er censor ikke forpligtet til at vurdere pågældende opgaver. Den tilsynsførende er ansvarlig for, at eleven har opfyldt reglerne for aflevering og attesterer med sin underskrift. Hvordan fremkommer der en karakter i skriftlig matematik? Forud for prøvens afholdelse har opgavekommissionen givet hver enkelt opgave et antal point. Pointene fordeles til en vis grad lige til hver delopgave. Der tages for eksempel hensyn til, at særligt arbejdskrævende opgaver tildeles lidt flere point. Begrundelsen for at tilstræbe ligelig fordeling af point på de enkelte opgaver er, at svære og lette opgaver ikke nødvendigvis er de samme for alle elever, og at der ikke er noget matematik, der er finere, fordi det er svært. Opgaverne skal afspejle Fælles Mål. Stærkt svingende antal point vil betyde store problemer med omsætningstabellen, hvilket blandt andet vil gå ud over elever i midterområdet. Desuden vil det være svært for en meget stor gruppe elever at opnå point til karakteren 02 efter den gængse omsætningstabel. Alle spørgsmål kan vurderes ensartet: 3 point for den fuldendte besvarelse 2 point for en besvarelse, der i princippet kan være rigtig, men med en regne-/aflæsning- /skrivefejl undervejs eller uklar kommunikation til en ellers rigtig besvarelse 11
12 1 point til de elever, der har skrevet rigtig facit uden tekst/mellemregning, eller til besvarelser med elementer af rigtige tanker 0 point, hvis der ikke er arbejdet med opgaven, eller hvis det skrevne er uden mening. Pointfordelingen offentliggøres på Skolestyrelsens hjemmeside dagen efter prøvens afholdelse. Et antal beskikkede censorer deltager i en forcensur, hvori der skal være vurderinger af mindst elevbesvarelser. Disse bearbejdes statistisk, og opgavekommissionen vurderer, om der skal ske justeringer i omsætningstabellen for at tage højde for eventuelle fejl eller lignende. 12
13 FSA Matematiske færdigheder Prøven i matematiske færdigheder er en selvstændig prøve og består af 50 opgaver. De fleste er de traditionelle opgavetyper, som vi kender dem fra tidligere opgavesæt. Der er således opgaver inden for et bredt udvalg af de færdigheder, der må forventes at være kendt af eleverne. Dette fremgår da også af censorernes tilbagemeldinger, som bekræfter, at opgavetyperne i vidt omfang er de samme som tidligere år, og at opgaverne er bredt sammensat fra fagets stofområder. Arbejdsmængden har været passende, selvom flere censorer påpeger, at en stor del af eleverne klarer opgaverne på cirka minutter. Landsresultatet Nedenfor er karakterfordelingen for de elever, der aflagde prøve i matematiske færdigheder. Ud over karakterfordelingen er der fremstillet en procentvis fordeling af karaktererne 2-12, for at man kan sammenligne med den fordeling, der over tid tilstræbes: ECTS F Fx E D C B A 7-trins-skalaen Andel over tid 10 % 25 % 30 % 25 % 10 % 40,0% 35,0% 32,9% 40,0% 35,0% 34,9% 30,0% 25,0% 20,0% 17,9% 23,7% 30,0% 25,0% 20,0% 19,0% 25,1% 15,0% 10,0% 5,0% 0,0% 9,0% 10,8% 5,6% 0,0% ,0% 10,0% 5,0% 0,0% 9,5% 11,5%
14 I forcensuren deltog vurderinger af elevbesvarelser, og de danner grundlaget for de følgende betragtninger og de nedenstående diagrammer. Næsten halvdelen af opgaverne er besvaret af mere end 90 % af eleverne, og kun tre opgaver har en besvarelsesfrekvens på lidt under 80 %. Ser vi på, hvor mange korrekte svar der er afgivet, ser billedet således ud: 70 % af opgaverne er besvaret korrekt af mere end 50 % af eleverne. Seks af opgaverne skiller sig ud ved kun at være korrekt besvaret af mellem 18 og 29 % af eleverne. Det er ikke overraskende de opgaver, der stiller krav til elevernes symbolbehandling på det mere abstrakte plan. Desuden er der en del elever, der ikke har styr på de matematiske begreber. Nogle censorer har bemærket, at der i enkelte klasser er en eller flere fejl, som ofte forekommer hos eleverne, hvilket ofte vil pege på mangler i undervisningen i de pågældende klasser. Kommentarer til enkelte opgaver Ved læsningen af dette afsnit er det godt at have årets prøve i matematiske færdigheder ved siden af. Opgave
15 100% 90% 80% 70% 60% 50% 40% 30% 20% 10% 0% Opgave 2-4 Det er overraskende, at disse tre opgaver kun besvares rigtigt af lidt over 70 % af eleverne. Det er mindre end opgaver med omsætning mellem procenttal og decimaltal og beregninger af rumfang og areal. Der henvises til bemærkningerne i PEU Opgave 6-7 Det er positivt, at mere end 80 % af eleverne kan omsætte fra procenttal til decimaltal. Opgave Der er positivt, at langt flere elever kan give korrekte svar på disse opgaver i forhold til de tilsvarende opgaver sidste år. Opgave 13 Overraskende kender kun lidt over 30 % af eleverne begrebet produkt. Opgave 17 15
16 Årsagen til de få rigtige besvarelser kan skyldes, at der i den daglige undervisning bruges andre ord for begrebet hældningstal. Opgave 18 Den typiske fejl er, at eleven ikke angiver en ligning. Opgave 19 Der forventes et resultat skrevet som brøk, men da der ikke er forlangt dette, må et resultat som 0,5333 accepteres. Opgave 23 Resultater, som er fremkommet ved målinger og beregninger, er i orden inden for en vis måleusikkerhed. Opgave % 90% 80% 70% 60% 50% 40% 30% 20% 10% 0% Opgave
17 Den typiske fejl er, at eleverne skriver tallet helt ud. Opgave 30 Mange elever har afsat medianen i stedet for vinkelhalveringslinjen. Opgave 43 Denne opgavetype volder ofte eleverne problemer. Derfor er det positivt overraskende, at næsten halvdelen er besvaret korrekt. 17
18 FSA Matematisk problemløsning Vurderingen af en elevbesvarelse i problemløsning er meget mere end en kontrol af rigtigt svar. I bekendtgørelse nummer 863 af 5. juli 2007 står der: 2.9. I bedømmelsen vil der blive lagt vægt på elevens brug af faglige begrundelser, herunder anvendelse af matematiske modeller, samt elevens anvendelse af forklarende tekst, algebraiske udtryk, tegninger og grafer. Ligeledes indgår det i bedømmelsen, hvorledes eleven på grundlag af de foreliggende oplysninger og data kan vurdere problemer, beskrive løsningsstrategier og udarbejde løsninger ved hjælp af matematikken. Forventningen er altså, at eleven i sin besvarelse redegør for sin proces for at komme frem til sit løsningsforslag. Denne redegørelse skal indgå i bedømmelsen og stiller krav til de to censorers arbejde med vurderingen af elevbesvarelserne. Med overgangen til 7-trins-skalaen blev prøvevejledningen ændret således, at det afsluttende skøn kun kan ændre karakteren, hvis pointtallet er i nærheden af det pointtal, der betyder en højere eller lavere karakter. De ministerielle censorer er blevet bedt om at angive antal tilfælde, hvor det afsluttende skøn har bevirket en ændring af karakteren. På baggrund af censorernes tilbagemeldinger kan man konkludere, at gennemsnitligt ændrer det afsluttende skøn karakteren hos cirka 5 % af eleverne. Årsagen til disse relativt få tilfælde kan være den nye skalas færre karakterer med deraf følgende større pointintervaller. Det er ikke alle fejltyper, der nødvendigvis skal trækkes point fra, hver gang de optræder. Eksempler på disse fejltyper kan være for mange/få decimaler, forkert afrunding, forkert brug af benævnelser og lignende. Optræder disse flere gange gennem en besvarelse, bør det overvejes kun at trække point en gang for den samme fejltype. Der er en hel del elever, der anvender computer ved prøven, men det spænder lige fra skoler, hvor ikke en eneste elev anvender computer, til skoler, hvor alle elever har arbejdet på en computer. Der er desværre ikke tal på det, men det er ambitionen at bruge ministeriets censor- 18
19 retteprogram til at få et indtryk af udviklingen. Det er de fleste censorers vurdering, at eleverne bruger computeren som skrivemaskine og kun i enkelte tilfælde, som for eksempel fremstilling af cirkeldiagram, anvender computerens programmer matematisk. Dog vurderer flere censorer, at anvendelsen af computer, også hvis det udelukkende er som skriveredskab, fremmer kommunikationen, ikke mindst fordi en del censorer klager over en faldende læsbarhed i håndskrift. I forcensuren deltog elevbesvarelser, der var vurderet af mere end 50 erfarne ministerielle censorer. Landsresultatet Nedenfor er karakterfordelingen for de elever, der aflagde prøve i matematisk problemløsning. Ud over karakterfordelingen er der fremstillet en procentvis fordeling af karaktererne 2-12, for at man kan sammenligne med den fordeling, der over tid tilstræbes: ECTS F Fx E D C B A 7-trins-skalaen Andel over tid 10 % 25 % 30 % 25 % 10 % 40,0% 35,0% 30,0% 25,0% 20,0% 15,0% 10,0% 7,7% 13,6% 22,7% 30,4% 16,8% 8,5% 40,0% 35,0% 30,0% 25,0% 20,0% 15,0% 10,0% 5,0% 14,8% 24,7% 33,0% 18,3% 9,2% 5,0% 0,0% 0,2% ,0% Karakterfordeling Fordeling af karaktererne
20 Der har deltaget elevbesvarelser i forcensuren, og de danner grundlaget for de nedenstående diagrammer. Der er registreret fire forhold for hver enkelt delopgave: Andelen af elever, der har opnået maksimumpoint for deres besvarelse. Andelen af elever, der har fået point for deres besvarelse. Andelen af elever, der har arbejdet med en opgave uden at få point. Andelen af elever, der ikke har arbejdet med opgaven. Kommentarer til enkelte opgaver Ved læsningen af dette afsnit er det godt at have årets prøve i matematisk problemløsning ved siden af. Opgave 1: Indgang Opgaven indledes med nogle relativt lette spørgsmål og fortsætter med nogle noget sværere spørgsmål, der kræver procentregning og valutaberegninger. Det er positivt, at den overvejende del af eleverne har arbejdet med langt de fleste spørgsmål, men overraskende få er nået frem til en korrekt løsning i procentregning. Opgave 1 80% 70% 60% Max point Delvist løst 0 point Sprunget over 50% 40% 30% 20% 10% 0%
21 1.1 og 1.2 Fokus er faglig læsning af åbningstider og prisskilte. Oplysningerne er de originale fra det tidspunkt, hvor opgaven blev fremstillet. I 1.1 er det i orden at nøjes med at skrive resultatet 8 timer. Men eleverne bør lære at skrive ved aflæsning eller lignende, når de aflæser i en tabel, en graf osv. Det er overraskende, at under halvdelen af eleverne ikke har kunnet beregne den samlede entre. I opgave 1.2 vil en løsning som 70 kr. 24 give point, da det ene tal er læst rigtigt i pristabellen. De typiske misforståelser er: 75 kr. Formuleringen i det felt i skemaet, der skal bruges, narrer eleven, ved at teksten i netop dette felt står i flertal, mens resten af teksterne står i ental. 475 kr. Eleven har lagt alle beløbene sammen. Eleven regner med 26 personer. Eleven bruger tallene fra og 1.4 Procentregning er traditionelt svært for en del elever. Det kan give anledning til overvejelser om, hvordan procentbegrebet introduceres og udvikles i undervisningen. Den typiske fejl er, at eleven argumenterer med lineær vækst på 5 kr. per år: Den stiger 5 kr. fra sommer 2007 til sommer Derfor vil den også stige med 5 kr. næste år. Entreen bliver altså 80 kr. 1.5 Opgaven kræver en begrundelse, for eksempel i en omsætning fra euro til kr., så et svar uden begrundelse giver 0 point. I denne type opgaver forventes der en konklusion ud fra beregningerne. Det er positivt overraskende, at langt over halvdelen af eleverne har kunnet gennemføre undersøgelsen
22 Det faglige indhold af opgaven er beregning af valutakurser. Forventningen er, at eleverne beregner de tre kurser og konkluderer ud fra disse. Mange elever har det korrekte svar uden begrundelse. Det kan ikke give point, da svaret tilfældigvis er det højeste beløb i euro. En almindelig misforståelse: Der regnes med den opgivne kurs, og den største forskel i priserne findes, det vil sige, at eleven bruger metoden fra forrige opgave. En anden type misforståelse er: Voksenbillettens pris i danske kr. bliver det største beløb. 21,5 x 7,45 = 160,18 kr., altså er voksenbillettens pris udregnet efter den højeste kurs. Opgave 2: Den blå kube Generelt har eleverne besvaret opgave 2 s delopgaver som forventet. Opgave 2 80% 70% 60% Max point Delvist løst 0 point Sprunget over 50% 40% 30% 20% 10% 0% Den typiske misforståelse i dette spørgsmål er, at eleven har blandet dagligsprogets terning sammen med matematikkens begreb terning. Det kan give anledning til at overveje, hvordan man introducerer og arbejder videre med faglige begreber i undervisningen, og hvordan man ar- 22
23 bejder med sammenhænge og forskelle mellem dagligdagens sprog og matematikkens sprog. En elevfremstillet opslagsbog, hvor der også er definitioner af faglige begreber, kan være en fordel. 2.2 Denne opgave er kompleks for mange elever, hvilket også kan ses af, at en tredjedel af eleverne har opgaven delvis rigtig. De typiske fejl er: Eleven udregner rumfang i stedet for overfladeareal. Eleven beregner kun en enkelt af siderne og ganger med fem. Eleven beregner den samlede overflade og ikke de fem, der er nævnt i opgaven. 2.3 Næsten halvdelen af eleverne har denne procentberegning rigtig, hvorimod den tilsvarende i opgave 1.4. kun er beregnet korrekt af en tredjedel af eleverne. En elevbesvarelse som denne: %=2223,05 cm 2 viser (ud over at der regnes videre pået forkert resultat) manglende hjælpemiddelkompetence. 2.4 og 2.5 Den typiske mangel i disse opgaver er, at eleven kun har arbejdet med et forsvindingspunkt og derfor tegnet i frontperspektiv. Opgave 3: Cafeen Opgaven er den af sættes fem opgaver, eleverne har klaret bedst. Det kan skyldes, at emnet sund kost er i fokus i disse år, også i faget matematik. 23
24 Opgave 3 70% 60% 50% Max point Delvist løst 0 point Sprunget over 40% 30% 20% 10% 0% Opgaven lægger op til angivelse af de seks forskellige muligheder eller en besvarelse som denne: 3.2 I denne opgave er nedenstående korrekte besvarelse ikke et krav. En beregning er tilstrækkelig begrundelse. 24
25 3.3 Der forventes en beregning, men ikke nødvendigvis et præcist resultat, der i dette tilfælde vil være mindre sigende. Derfor må resultater som ca. 40 % eller ca. 5 2 på baggrund af afrun ding af en beregning anses for korrekte. Derimod kan et svar som højst give 1 point Den typiske misforståelse i denne opgave er, at eleven finder forskellen i stedet for forholdet. 3.4 Omkring bedømmelse af cirkeldiagrammer henvises til prøvevejledningen og PEU Der forventes nogle beregninger på baggrund af målinger på prøveoplæggets figur. En del elever bruger øjemål til at fastsætte den anbefalede energifordeling i procent. I disse tilfælde kan der ikke gives fuldt point for opgaven. Eksempler på elevbesvarelser: Der mangler lidt fedt. Der skal være flere proteiner og lidt mindre kulhydrater. 25
26 I den anbefalede cirkeldiagram er der mere fedt i end den anden. Der er mindre kulhydrat i den anbefalede end den anden. Han har for meget kulhydrat og for lidt protein. Fedt er det samme. De passer hinanden. Den anbefalede energifordeling passer meget godt med måltidets energifordeling. Der er lige meget kulhydrat, fedt og protein. Hvis man kigger på måltidets energifordeling og sammenligner det med det daglige, kan man se, at der er store ligheder mellem dem. Proteinerne måtte gerne have været lidt højere, og kulhydraterne lidt lavere, men ellers ser det fornuftigt ud. 26
27 3.7 Der bliver bedt om en beregning og et resultat angivet i minutter. Derfor kan et resultat som klippe hæk i cirka 60 minutter ikke give fuldt pointtal. Opgave 4: Kædepumpe Opgaven er sættets sværeste, selvom der er spørgsmål, der er relativt lette. 27
28 Opgave 4 90% 80% 70% 60% Max point Delvist løst 0 point Sprunget over 50% 40% 30% 20% 10% 0% og 4.2 De to opgaver giver ikke de store problemer for eleverne. 4.3 Kun få elever kan gennemføre denne opgave fuldt ud. Det skyldes både det forhold at skulle forestille sig en rumlig figur ud fra en todimensional tegning og den usædvanlige figur. Mange elever vælger at beregne rumfanget af en cylinder, hvilket selvfølgelig skal give point. Dette er den opgave i sættet, som lægger mest op til problemløsning. Der er flere steder, hvor eleverne kunne have angivet et forbehold, som for eksempel at kædens rumfang ikke medregnes. 4.4 Denne opgave er tilsvarende opgave 1.3 og besvares korrekt af cirka lige så mange elever
Prøver Evaluering Undervisning. Matematik. Maj-juni 2008
 Prøver Evaluering Undervisning Matematik Maj-juni 2008 Ved fagkonsulent Klaus Fink Indhold Indledning 3 Fælles for faget 3 Fagets identitet 3 De skriftlige prøver i matematik 5 FSA 9 Matematiske færdigheder
Prøver Evaluering Undervisning Matematik Maj-juni 2008 Ved fagkonsulent Klaus Fink Indhold Indledning 3 Fælles for faget 3 Fagets identitet 3 De skriftlige prøver i matematik 5 FSA 9 Matematiske færdigheder
Formativ brug af folkeskolens prøver årets resultater på landsplan Den skriftlige prøve i matematik med hjælpemidler, FP9 maj 2019
 Formativ brug af folkeskolens prøver årets resultater på landsplan Den skriftlige prøve i matematik med hjælpemidler, FP9 maj 2019 Skrevet af Klaus Fink på baggrund af oplysninger fra opgavekommissionen
Formativ brug af folkeskolens prøver årets resultater på landsplan Den skriftlige prøve i matematik med hjælpemidler, FP9 maj 2019 Skrevet af Klaus Fink på baggrund af oplysninger fra opgavekommissionen
Første del af rapporten består af et diagram, der viser, hvor mange point eleverne på landsplan fik i de enkelte opgaver.
 Til matematiklæreren Dette er en rapport omtaler prøven med hjælpemidler maj 2016. Rapporten kan bruges til at evaluere dit arbejde med klassen og få ideer til dit arbejde med kommende klasser i overbygningen.
Til matematiklæreren Dette er en rapport omtaler prøven med hjælpemidler maj 2016. Rapporten kan bruges til at evaluere dit arbejde med klassen og få ideer til dit arbejde med kommende klasser i overbygningen.
Formativ brug af folkeskolens prøver. Den skriftlige prøve i matematik i 10. klasse, FP10, maj 2018
 Formativ brug af folkeskolens prøver Den skriftlige prøve i matematik i 10. klasse, FP10, maj 2018 1 Til matematiklæreren i 10. klasse Dette er en rapport om den skriftlige prøve i matematik maj 2018.
Formativ brug af folkeskolens prøver Den skriftlige prøve i matematik i 10. klasse, FP10, maj 2018 1 Til matematiklæreren i 10. klasse Dette er en rapport om den skriftlige prøve i matematik maj 2018.
Prøver Evaluering Undervisning Matematik maj-juni 2009
 Ved fagkonsulent Klaus Fink Styrelsen for Evaluering og Kvalitetsudvikling af Grundskolen Kontor for Afgangsprøver, Test og Evalueringer Indhold INDLEDNING... 3 FÆLLES FOR FAGET... 3 FAGETS IDENTITET OG
Ved fagkonsulent Klaus Fink Styrelsen for Evaluering og Kvalitetsudvikling af Grundskolen Kontor for Afgangsprøver, Test og Evalueringer Indhold INDLEDNING... 3 FÆLLES FOR FAGET... 3 FAGETS IDENTITET OG
Vejledende karakterbeskrivelser for matematik
 Vejledende karakterbeskrivelser for matematik Folkeskolens Afgangsprøve efter 9. klasse Karakterbeskrivelse for matematiske færdigheder. Der prøves i tal og algebra geometriske begreber og fremgangsmåder
Vejledende karakterbeskrivelser for matematik Folkeskolens Afgangsprøve efter 9. klasse Karakterbeskrivelse for matematiske færdigheder. Der prøves i tal og algebra geometriske begreber og fremgangsmåder
Formativ brug af folkeskolens prøver. Den skriftlige prøve i matematik med hjælpemidler, FP9 maj 2018
 Formativ brug af folkeskolens prøver Den skriftlige prøve i matematik med hjælpemidler, FP9 maj 2018 1 Til matematiklæreren i 9. klasse Dette er en rapport om den skriftlige prøve i matematik med hjælpemidler
Formativ brug af folkeskolens prøver Den skriftlige prøve i matematik med hjælpemidler, FP9 maj 2018 1 Til matematiklæreren i 9. klasse Dette er en rapport om den skriftlige prøve i matematik med hjælpemidler
Matematik. Evaluering, orientering og vejledning
 Folkeskolens afsluttende prøver Matematik 2011 Evaluering, orientering og vejledning Udarbejdet på grundlag af censorers faglige feedback ved prøverne Institut for Læring Udarbejdet af: Konsulent Erik
Folkeskolens afsluttende prøver Matematik 2011 Evaluering, orientering og vejledning Udarbejdet på grundlag af censorers faglige feedback ved prøverne Institut for Læring Udarbejdet af: Konsulent Erik
Formativ brug af folkeskolens prøver årets resultater på landsplan Den skriftlige prøve i matematik FP10 maj 2019
 Formativ brug af folkeskolens prøver årets resultater på landsplan Den skriftlige prøve i matematik FP10 maj 2019 Skrevet af Klaus Fink på baggrund af oplysninger fra opgavekommissionen 1 Til matematiklæreren
Formativ brug af folkeskolens prøver årets resultater på landsplan Den skriftlige prøve i matematik FP10 maj 2019 Skrevet af Klaus Fink på baggrund af oplysninger fra opgavekommissionen 1 Til matematiklæreren
Undervisningsplan: Matematik Skoleåret 2014/2015 Strib Skole: 5B Ugenumre: Hovedområder: Emner og temaer: Side 1 af 5
 Ugenumre: Hovedområder: Emner og temaer: 33 Addition og subtraktion Anvendelse af regningsarter 34 Multiplikation og division Anvendelse af regningsarter 35 Multiplikation med decimaltal Anvendelse af
Ugenumre: Hovedområder: Emner og temaer: 33 Addition og subtraktion Anvendelse af regningsarter 34 Multiplikation og division Anvendelse af regningsarter 35 Multiplikation med decimaltal Anvendelse af
Matematik. Evaluering, orientering og vejledning
 Folkeskolens afsluttende prøver Matematik 2015 Evaluering, orientering og vejledning Institut for Læring Evaluering af årets matematikprøver 2015 Færdighedsprøven På landsbasis gik 593 folkeskoleelever
Folkeskolens afsluttende prøver Matematik 2015 Evaluering, orientering og vejledning Institut for Læring Evaluering af årets matematikprøver 2015 Færdighedsprøven På landsbasis gik 593 folkeskoleelever
Vejledning til prøverne i faget matematik
 Vejledning til prøverne i faget matematik Kvalitets- og Tilsynsstyrelsen Evaluerings- og prøvekontor Januar 2012 Indhold Forord... 3 1. Generelt om de skriftlige afgangsprøver i matematik... 4 2. Folkeskolens
Vejledning til prøverne i faget matematik Kvalitets- og Tilsynsstyrelsen Evaluerings- og prøvekontor Januar 2012 Indhold Forord... 3 1. Generelt om de skriftlige afgangsprøver i matematik... 4 2. Folkeskolens
Evaluering af matematik undervisning
 Evaluering af matematik undervisning Udarbejdet af Khaled Zaher, matematiklærer 6-9 klasse og Boushra Chami, matematiklærer 2-5 klasse Matematiske kompetencer. Fællesmål efter 3.klasse indgå i dialog om
Evaluering af matematik undervisning Udarbejdet af Khaled Zaher, matematiklærer 6-9 klasse og Boushra Chami, matematiklærer 2-5 klasse Matematiske kompetencer. Fællesmål efter 3.klasse indgå i dialog om
Opgavesættets tema er KRAM (Kost, Rygning, Alkohol og Motion).
 Sammendrag af censorrapporter for matematik D maj 2013 Opgavesættets tema er KRAM (Kost, Rygning, Alkohol og Motion). Opgave 1: Kost Opgaven inddrager de 4 regningsarter, brug af regneark, fremstilling
Sammendrag af censorrapporter for matematik D maj 2013 Opgavesættets tema er KRAM (Kost, Rygning, Alkohol og Motion). Opgave 1: Kost Opgaven inddrager de 4 regningsarter, brug af regneark, fremstilling
Kemi 2015. Evaluering af skriftlig eksamen kemi A, htx Maj juni 2015
 Kemi 2015 Evaluering af skriftlig eksamen kemi A, htx Maj juni 2015 Ministeriet for Børn, Undervisning og Ligestilling Styrelsen for Undervisning og Kvalitet August 2015 Hermed udsendes evalueringsrapporten
Kemi 2015 Evaluering af skriftlig eksamen kemi A, htx Maj juni 2015 Ministeriet for Børn, Undervisning og Ligestilling Styrelsen for Undervisning og Kvalitet August 2015 Hermed udsendes evalueringsrapporten
Matematik. Evaluering, orientering og vejledning
 Folkeskolens afsluttende prøver Matematik 2014 Evaluering, orientering og vejledning Institut for Læring Evaluering af årets matematikprøver Følgende rapport er udformet således, at resultater fra karakterdatabasen
Folkeskolens afsluttende prøver Matematik 2014 Evaluering, orientering og vejledning Institut for Læring Evaluering af årets matematikprøver Følgende rapport er udformet således, at resultater fra karakterdatabasen
Årsplan for 5. klasse, matematik
 Årsplan for 5. klasse, matematik I matematik bruger vi bogsystemet Sigma som grundmateriale. I systemet er der, ud over også kopiark og tests tilknyttet de enkelte kapitler. Systemet er udarbejdet så det
Årsplan for 5. klasse, matematik I matematik bruger vi bogsystemet Sigma som grundmateriale. I systemet er der, ud over også kopiark og tests tilknyttet de enkelte kapitler. Systemet er udarbejdet så det
Skolens formål med faget matematik følger beskrivelsen af formål i folkeskolens Fælles Mål:
 Formål: Skolens formål med faget matematik følger beskrivelsen af formål i folkeskolens Fælles Mål: Formålet med undervisningen i matematik er, at eleverne bliver i forstå og anvende matematik i sammenhænge,
Formål: Skolens formål med faget matematik følger beskrivelsen af formål i folkeskolens Fælles Mål: Formålet med undervisningen i matematik er, at eleverne bliver i forstå og anvende matematik i sammenhænge,
Nyt i faget Matematik
 Almen voksenuddannelse Nyt i faget Matematik Juli 2012 Indhold Bekendtgørelsesændringer Ændringer af undervisningsvejledningen Den nye opgavetype ved den skriftlige prøve efter D Ændringer af rettevejledningen
Almen voksenuddannelse Nyt i faget Matematik Juli 2012 Indhold Bekendtgørelsesændringer Ændringer af undervisningsvejledningen Den nye opgavetype ved den skriftlige prøve efter D Ændringer af rettevejledningen
Klassen er sammenlæst, altså 5 og 6 klasse på en og samme tid. Samtidig er klassen pt på ca 11 elever ialt.
 Introduktion til mat i 5/6 klasse Vejle Privatskole 13/14: Klassen er sammenlæst, altså 5 og 6 klasse på en og samme tid. Samtidig er klassen pt på ca 11 elever ialt. Udgangspunktet bliver en blød screening,
Introduktion til mat i 5/6 klasse Vejle Privatskole 13/14: Klassen er sammenlæst, altså 5 og 6 klasse på en og samme tid. Samtidig er klassen pt på ca 11 elever ialt. Udgangspunktet bliver en blød screening,
Prøver Evaluering - Undervisning
 Prøver Evaluering - Undervisning Matematik Maj juni 2011 Fagkonsulent Klaus Fink Kvalitets- og Tilsynsstyrelsen Evaluerings- og Prøvekontor Indhold Indledning... 4 Læsevejledning... 4 Generelt om prøverne...
Prøver Evaluering - Undervisning Matematik Maj juni 2011 Fagkonsulent Klaus Fink Kvalitets- og Tilsynsstyrelsen Evaluerings- og Prøvekontor Indhold Indledning... 4 Læsevejledning... 4 Generelt om prøverne...
Fagårsplan 10/11 Fag: Matematik Klasse: 7.ABC Lærer: Henrik Stillits. Fagområde/ emne
 Fagårsplan 10/11 Fag: Matematik Klasse: 7.ABC Lærer: Henrik Stillits. Fagområde/ emne Matematiske færdigheder Grundlæggende færdigheder - plus, minus, gange, division (hele tal, decimaltal og brøker) Identificer
Fagårsplan 10/11 Fag: Matematik Klasse: 7.ABC Lærer: Henrik Stillits. Fagområde/ emne Matematiske færdigheder Grundlæggende færdigheder - plus, minus, gange, division (hele tal, decimaltal og brøker) Identificer
Selam Friskole Fagplan for Matematik
 Selam Friskole Fagplan for Matematik Formål Formålet med undervisningen er, at eleverne udvikler matematiske kompetencer og opnår viden og kunnen således, at de bliver i stand til at begå sig hensigtsmæssigt
Selam Friskole Fagplan for Matematik Formål Formålet med undervisningen er, at eleverne udvikler matematiske kompetencer og opnår viden og kunnen således, at de bliver i stand til at begå sig hensigtsmæssigt
Matematik. Matematiske kompetencer
 Matematiske kompetencer formulere sig skriftligt og mundtligt om matematiske påstande og spørgsmål og have blik for hvilke typer af svar, der kan forventes (tankegangskompetence) løse matematiske problemer
Matematiske kompetencer formulere sig skriftligt og mundtligt om matematiske påstande og spørgsmål og have blik for hvilke typer af svar, der kan forventes (tankegangskompetence) løse matematiske problemer
Vejledning til matematik A htx Maj 2018
 Vejledning til matematik A htx Maj 2018 Censorkorpset skriftlig matematik, htx Denne skrivelse skal tjene til almindelig orientering og vejledning for censorerne om forhold vedrørende skriftlig eksamen,
Vejledning til matematik A htx Maj 2018 Censorkorpset skriftlig matematik, htx Denne skrivelse skal tjene til almindelig orientering og vejledning for censorerne om forhold vedrørende skriftlig eksamen,
3. klasse 6. klasse 9. klasse
 Børne- og Undervisningsudvalget 2012-13 BUU Alm.del Bilag 326 Offentligt Elevplan 3. klasse 6. klasse 9. klasse Matematiske kompetencer Status tal og algebra sikker i, er usikker i de naturlige tals opbygning
Børne- og Undervisningsudvalget 2012-13 BUU Alm.del Bilag 326 Offentligt Elevplan 3. klasse 6. klasse 9. klasse Matematiske kompetencer Status tal og algebra sikker i, er usikker i de naturlige tals opbygning
Emne Tema Materiale r - - - - - aktiviteter
 Fag: Matematik Hold: 24 Lærer: TON Undervisningsmål Læringsmål 9 klasse 32-34 Introforløb: række tests, som viser eleverne faglighed og læringsstil. Faglige aktiviteter Emne Tema Materiale r IT-inddragelse
Fag: Matematik Hold: 24 Lærer: TON Undervisningsmål Læringsmål 9 klasse 32-34 Introforløb: række tests, som viser eleverne faglighed og læringsstil. Faglige aktiviteter Emne Tema Materiale r IT-inddragelse
Mundtlighed i matematikundervisningen
 Mundtlighed i matematikundervisningen 1 Mundtlighed Annette Lilholt Side 2 Udsagn! Det er nemt at give karakter i færdighedsregning. Mine elever får generelt højere standpunktskarakter i færdighedsregning
Mundtlighed i matematikundervisningen 1 Mundtlighed Annette Lilholt Side 2 Udsagn! Det er nemt at give karakter i færdighedsregning. Mine elever får generelt højere standpunktskarakter i færdighedsregning
Årsplan for 7. klasse, matematik
 Årsplan for 7. klasse, matematik I matematik bruger vi bogsystemet Sigma som grundmateriale. I systemet er der, ud over grundbogen, også kopiark og tests tilknyttet de enkelte kapitler. Systemet er udarbejdet
Årsplan for 7. klasse, matematik I matematik bruger vi bogsystemet Sigma som grundmateriale. I systemet er der, ud over grundbogen, også kopiark og tests tilknyttet de enkelte kapitler. Systemet er udarbejdet
Fagplan for faget matematik
 Fagplan for faget matematik Der undervises i matematik på alle klassetrin (0. - 7. klasse). De centrale kundskabs- og færdighedsområder er: I matematik skal de grundlæggende kundskaber og færdigheder i
Fagplan for faget matematik Der undervises i matematik på alle klassetrin (0. - 7. klasse). De centrale kundskabs- og færdighedsområder er: I matematik skal de grundlæggende kundskaber og færdigheder i
Indledning. Fælles for faget. Matematik. Prøver - Evaluering Undervisning. Maj-juni 2007
 Prøver - Evaluering Undervisning Matematik Maj-juni 2007 Indledning Der har ikke været fremstillet PEU-hæfter for matematik i 2005 og 2006. De ministerielle censorer har begge disse år som sædvanligt ydet
Prøver - Evaluering Undervisning Matematik Maj-juni 2007 Indledning Der har ikke været fremstillet PEU-hæfter for matematik i 2005 og 2006. De ministerielle censorer har begge disse år som sædvanligt ydet
Årsplan for matematik 4. klasse 14/15
 Årsplan for matematik 4. klasse 14/15 Status: 4.b er en klasse der består af ca. 20 elever. Der er en god fordeling mellem piger og drenge i klasser. Klassen har 5 matematiktimer om ugen. Vi fortsætter
Årsplan for matematik 4. klasse 14/15 Status: 4.b er en klasse der består af ca. 20 elever. Der er en god fordeling mellem piger og drenge i klasser. Klassen har 5 matematiktimer om ugen. Vi fortsætter
Årsplan matematik 7.klasse 2014/2015
 Årsplan matematik 7.klasse 2014/2015 Emne Indhold Mål Tal og størrelser Arbejde med brøktal som repræsentationsform på omverdenssituationer. Fx i undersøgelser. Arbejde med forskellige typer af diagrammer.
Årsplan matematik 7.klasse 2014/2015 Emne Indhold Mål Tal og størrelser Arbejde med brøktal som repræsentationsform på omverdenssituationer. Fx i undersøgelser. Arbejde med forskellige typer af diagrammer.
Afholdelse. Folkeskolens skriftlige og mundtlige. afgangsprøver. Skolen ved Søerne
 Afholdelse af Folkeskolens skriftlige og mundtlige afgangsprøver på Skolen ved Søerne 2014 De skriftlige afgangsprøver Fra onsdag den 05. maj 2014 til onsdag den 14. maj 2014 afholdes folkeskolens skriftlige
Afholdelse af Folkeskolens skriftlige og mundtlige afgangsprøver på Skolen ved Søerne 2014 De skriftlige afgangsprøver Fra onsdag den 05. maj 2014 til onsdag den 14. maj 2014 afholdes folkeskolens skriftlige
Når vi forbereder et nyt emne eller område vælger vi de metoder, materialer og evalueringsformer, der egner sig bedst til forløbet.
 MATEMATIK Delmål for fagene generelt. Al vores undervisning hviler på de i Principper for skole & undervisning beskrevne områder (- metoder, materialevalg, evaluering og elevens personlige alsidige udvikling),
MATEMATIK Delmål for fagene generelt. Al vores undervisning hviler på de i Principper for skole & undervisning beskrevne områder (- metoder, materialevalg, evaluering og elevens personlige alsidige udvikling),
LÆRINGSMÅL PÅ NIF MATEMATIK 2014-15
 LÆRINGSMÅL PÅ NIF MATEMATIK 2014-15 Mål for undervisningen i Matematik på NIF Følgende er baseret på de grønlandske læringsmål, tilføjelser fra de danske læringsmål står med rød skrift. Læringsmål Yngstetrin
LÆRINGSMÅL PÅ NIF MATEMATIK 2014-15 Mål for undervisningen i Matematik på NIF Følgende er baseret på de grønlandske læringsmål, tilføjelser fra de danske læringsmål står med rød skrift. Læringsmål Yngstetrin
Matematik samlet evaluering for Ahi Internationale Skole
 efter 3.klasse. e efter 6.klasse. e Skole efter 9.klasse. e indgå i dialog om spørgsmål og svar, som er karakteristiske i arbejdet med matematik (tankegangskompetence formulere sig skriftligt og mundtligt
efter 3.klasse. e efter 6.klasse. e Skole efter 9.klasse. e indgå i dialog om spørgsmål og svar, som er karakteristiske i arbejdet med matematik (tankegangskompetence formulere sig skriftligt og mundtligt
Årsplan 2012/2013. 9. årgang: Matematik. Lyreskovskolen. FORMÅL OG FAGLIGHEDSPLANER - Fælles Mål II 2009
 Årsplan 2012/2013 9. årgang: Matematik FORMÅL OG FAGLIGHEDSPLANER - Fælles Mål II 2009 Formålet med undervisningen i matematik er, at eleverne udvikler matematiske r og opnår viden og kunnen således, at
Årsplan 2012/2013 9. årgang: Matematik FORMÅL OG FAGLIGHEDSPLANER - Fælles Mål II 2009 Formålet med undervisningen i matematik er, at eleverne udvikler matematiske r og opnår viden og kunnen således, at
Matematik på Humlebæk lille Skole
 Matematik på Humlebæk lille Skole Matematikundervisningen på HLS er i overensstemmelse med Undervisningsministeriets Fælles Mål, dog med få justeringer som passer til vores skoles struktur. Det betyder
Matematik på Humlebæk lille Skole Matematikundervisningen på HLS er i overensstemmelse med Undervisningsministeriets Fælles Mål, dog med få justeringer som passer til vores skoles struktur. Det betyder
Års- og aktivitetsplan i matematik hold 4 2014/2015
 Års- og aktivitetsplan i matematik hold 4 2014/2015 Der arbejdes hen mod slutmålene i matematik efter 10. klassetrin. www.uvm.dk => Fælles Mål 2009 => Faghæfter alfabetisk => Matematik => Slutmål for faget
Års- og aktivitetsplan i matematik hold 4 2014/2015 Der arbejdes hen mod slutmålene i matematik efter 10. klassetrin. www.uvm.dk => Fælles Mål 2009 => Faghæfter alfabetisk => Matematik => Slutmål for faget
Læseplan for faget matematik. 1. 9. klassetrin
 Læseplan for faget matematik 1. 9. klassetrin Matematikundervisningen bygger på elevernes mange forudsætninger, som de har med når de starter i skolen. Der bygges videre på elevernes forskellige faglige
Læseplan for faget matematik 1. 9. klassetrin Matematikundervisningen bygger på elevernes mange forudsætninger, som de har med når de starter i skolen. Der bygges videre på elevernes forskellige faglige
Årsplan 8. klasse matematik 2013-2014 Uge Emne Faglige mål Trinmål Materialer/ systemer 33 og løbende
 Årsplan 8. klasse matematik 2013-2014 33 løbende 33-34 løbende Løbende Problemregning ( faglig læsning) Mundtlig matematik (forberede oplæg til 6. klasse) - flere forskellige trinmål Ben, formelsamlingen,
Årsplan 8. klasse matematik 2013-2014 33 løbende 33-34 løbende Løbende Problemregning ( faglig læsning) Mundtlig matematik (forberede oplæg til 6. klasse) - flere forskellige trinmål Ben, formelsamlingen,
Årsplan 9. klasse matematik 2013-2014 Uge Emne Faglige mål Trinmål Materialer/ systemer 33 Årsprøven i matematik
 Årsplan 9. klasse matematik 2013-2014 33 Årsprøven i matematik Årsprøve og rettevejledledning 34-35 36 og løbe nde Talmængder og regnemetoder Mundtlig matematik 37 Fordybelses uge 38-39 Procent - Gennemgå
Årsplan 9. klasse matematik 2013-2014 33 Årsprøven i matematik Årsprøve og rettevejledledning 34-35 36 og løbe nde Talmængder og regnemetoder Mundtlig matematik 37 Fordybelses uge 38-39 Procent - Gennemgå
Afholdelse. Folkeskolens skriftlige og mundtlige. afgangsprøver. Skolen ved Søerne
 Afholdelse af Folkeskolens skriftlige og mundtlige afgangsprøver på Skolen ved Søerne 2013 De skriftlige afgangsprøver Fra onsdag den 13. maj 2013 til onsdag den 17. maj 2013 afholdes folkeskolens skriftlige
Afholdelse af Folkeskolens skriftlige og mundtlige afgangsprøver på Skolen ved Søerne 2013 De skriftlige afgangsprøver Fra onsdag den 13. maj 2013 til onsdag den 17. maj 2013 afholdes folkeskolens skriftlige
Samfundsfag. Maj-juni 2008
 Prøver Evaluering Undervisning Samfundsfag Maj-juni 2008 Ved fagkonsulent Niels Lysholm Indhold Forord 2 Evalueringen 3 Hovedkonklusioner 8 Afrunding 9 Forord Det er blevet en fast tradition, at der udarbejdes
Prøver Evaluering Undervisning Samfundsfag Maj-juni 2008 Ved fagkonsulent Niels Lysholm Indhold Forord 2 Evalueringen 3 Hovedkonklusioner 8 Afrunding 9 Forord Det er blevet en fast tradition, at der udarbejdes
Kemi Evaluering af skriftlig eksamen kemi A, htx Maj juni 2016
 Kemi 2016 Evaluering af skriftlig eksamen kemi A, htx Maj juni 2016 Ministeriet for Børn, Undervisning og Ligestilling Styrelsen for Undervisning og Kvalitet Juli 2016 Hermed udsendes evalueringsrapporten
Kemi 2016 Evaluering af skriftlig eksamen kemi A, htx Maj juni 2016 Ministeriet for Børn, Undervisning og Ligestilling Styrelsen for Undervisning og Kvalitet Juli 2016 Hermed udsendes evalueringsrapporten
Matematik Delmål og slutmål
 Matematik Delmål og slutmål Ferritslev friskole 2006 SLUTMÅL efter 9. Klasse: Regning med de rationale tal, såvel som de reelle tal skal beherskes. Der skal kunne benyttes og beherskes formler i forbindelse
Matematik Delmål og slutmål Ferritslev friskole 2006 SLUTMÅL efter 9. Klasse: Regning med de rationale tal, såvel som de reelle tal skal beherskes. Der skal kunne benyttes og beherskes formler i forbindelse
Undervisningsplan for matematik
 Undervisningsplan for matematik Formål for faget Formålet med undervisningen i matematik er, at eleverne udvikler kompetencer og opnår viden og kunnen således, at de bliver i stand til at begå sig hensigtsmæssigt
Undervisningsplan for matematik Formål for faget Formålet med undervisningen i matematik er, at eleverne udvikler kompetencer og opnår viden og kunnen således, at de bliver i stand til at begå sig hensigtsmæssigt
Matematika rsplan for 8. kl
 Matematika rsplan for 8. kl 2015-2016 Årsplanen tager udgangspunkt i fællesmål (færdigheds- og vidensmål) efter 9. klassetrin. Desuden tilrettelægges undervisningen efter læseplanen for matematik. Formålet
Matematika rsplan for 8. kl 2015-2016 Årsplanen tager udgangspunkt i fællesmål (færdigheds- og vidensmål) efter 9. klassetrin. Desuden tilrettelægges undervisningen efter læseplanen for matematik. Formålet
Space Challenge og Undervisningsminsteriets Fælles Mål for folkeskolen
 Space Challenge og Undervisningsminsteriets Fælles Mål for folkeskolen I dette kapitel beskrives det, hvilke Fælles Mål man kan nå inden for udvalgte fag, når man i skolen laver aktiviteter med Space Challenge.
Space Challenge og Undervisningsminsteriets Fælles Mål for folkeskolen I dette kapitel beskrives det, hvilke Fælles Mål man kan nå inden for udvalgte fag, når man i skolen laver aktiviteter med Space Challenge.
Matematik. Evaluering, orientering og vejledning
 Folkeskolens afsluttende evaluering Matematik 2016 Evaluering, orientering og vejledning Uddannelsesstyrelsen 1. Konklusion Denne evaluering bygger på prøveresultaterne for skriftlige og mundtlige prøver
Folkeskolens afsluttende evaluering Matematik 2016 Evaluering, orientering og vejledning Uddannelsesstyrelsen 1. Konklusion Denne evaluering bygger på prøveresultaterne for skriftlige og mundtlige prøver
Colofon. Udgivet af Inerisaavik 2009 Udarbejdet af fagkonsulent Erik Christiansen Redigeret af specialkonsulent Louise Richter Elektronisk udgave
 Colofon Udgivet af Inerisaavik 2009 Udarbejdet af fagkonsulent Erik Christiansen Redigeret af specialkonsulent Louise Richter Elektronisk udgave Indhold Evaluering af matematik 2008 2 Tekstopgivelser 2
Colofon Udgivet af Inerisaavik 2009 Udarbejdet af fagkonsulent Erik Christiansen Redigeret af specialkonsulent Louise Richter Elektronisk udgave Indhold Evaluering af matematik 2008 2 Tekstopgivelser 2
Prøver Evaluering Undervisning. Hjemkundskab. maj-juni 2009
 Af fagkonsulent Bo Ditlev Pedersen Styrelsen for Evaluering og Kvalitetsudvikling af Grundskolen Kontor for Afgangsprøver, Test og Evalueringer Indhold INDLEDNING...3 PRØVEOPLÆGGENE...4 UNDERVISNINGSBESKRIVELSERNE...4
Af fagkonsulent Bo Ditlev Pedersen Styrelsen for Evaluering og Kvalitetsudvikling af Grundskolen Kontor for Afgangsprøver, Test og Evalueringer Indhold INDLEDNING...3 PRØVEOPLÆGGENE...4 UNDERVISNINGSBESKRIVELSERNE...4
Foreløbig udgave af læringsmål til: Kapitel 1 Regn med store tal Fælles Mål Læringsmål Forslag til tegn på læring
 Foreløbig udgave af læringsmål til: Kapitel 1 Regn med store tal Fælles Mål Læringsmål Forslag til tegn på læring udføre beregninger med de fire regningsarter inden for naturlige tal, herunder beregninger
Foreløbig udgave af læringsmål til: Kapitel 1 Regn med store tal Fælles Mål Læringsmål Forslag til tegn på læring udføre beregninger med de fire regningsarter inden for naturlige tal, herunder beregninger
Bedømmelse af den skriftlige prøve efter matematik D
 Bedømmelse af den skriftlige prøve efter matematik D Bedømmelseskriterierne til den skriftlige prøve efter D findes i læreplanen (Bilag 28 til avu-bekendtgørelsen) som punkt 4.3 Der lægges vægt på, at
Bedømmelse af den skriftlige prøve efter matematik D Bedømmelseskriterierne til den skriftlige prøve efter D findes i læreplanen (Bilag 28 til avu-bekendtgørelsen) som punkt 4.3 Der lægges vægt på, at
I kapitlet arbejdes med følgende centrale matematiske objekter og begreber:
 INTRO Efter mange års pause er trigonometri med Fælles Mål 2009 tilbage som fagligt emne i grundskolens matematikundervisning. Som det fremgår af den følgende sides udpluk fra faghæftets trinmål, er en
INTRO Efter mange års pause er trigonometri med Fælles Mål 2009 tilbage som fagligt emne i grundskolens matematikundervisning. Som det fremgår af den følgende sides udpluk fra faghæftets trinmål, er en
Matematik. Evaluering, orientering og vejledning
 Folkeskolens afsluttende prøver Matematik 2013 Evaluering, orientering og vejledning Institut for Læring Evaluering af årets matematikprøver Rapporten er skrevet på baggrund af det data, som forefindes
Folkeskolens afsluttende prøver Matematik 2013 Evaluering, orientering og vejledning Institut for Læring Evaluering af årets matematikprøver Rapporten er skrevet på baggrund af det data, som forefindes
Årsplan i matematik for 9. klasse 2018/2019
 Årsplan i matematik for 9. klasse 2018/2019 Undervisningen generelt: Undervisningen tilrettelægges ud fra fagets CKF er og forenklede fællesmål for faget. Undervisning bygges primært op ud fra emnerne
Årsplan i matematik for 9. klasse 2018/2019 Undervisningen generelt: Undervisningen tilrettelægges ud fra fagets CKF er og forenklede fællesmål for faget. Undervisning bygges primært op ud fra emnerne
Introduktion til mat i 4 klasse Vejle Privatskole 2013/14:
 Introduktion til mat i 4 klasse Vejle Privatskole 2013/14: Udgangspunktet bliver en blød screening, der skal synliggøre summen af elevernes standpunkt. Det betyder i realiteten, at der uddeles 4 klasses
Introduktion til mat i 4 klasse Vejle Privatskole 2013/14: Udgangspunktet bliver en blød screening, der skal synliggøre summen af elevernes standpunkt. Det betyder i realiteten, at der uddeles 4 klasses
Årsplan 8. Klasse Matematik Skoleåret 2016/17
 Hovedformål Der arbejdes med følgende 3 matematiske emner: 1. tal og algebra, 2. geometri samt 3. statistik og sandsynlighed. Derudover skal der arbejdes med matematik i anvendelse samt de matematiske
Hovedformål Der arbejdes med følgende 3 matematiske emner: 1. tal og algebra, 2. geometri samt 3. statistik og sandsynlighed. Derudover skal der arbejdes med matematik i anvendelse samt de matematiske
Emmas og Frederiks nye værelser - maling eller tapet?
 Emmas og Frederiks nye værelser - maling eller tapet? Emmas og Frederiks familie skal flytte til et nyt hus. De har fået lov til at bestemme, hvordan væggene på deres værelser skal se ud. Emma og Frederik
Emmas og Frederiks nye værelser - maling eller tapet? Emmas og Frederiks familie skal flytte til et nyt hus. De har fået lov til at bestemme, hvordan væggene på deres værelser skal se ud. Emma og Frederik
Prøver Evaluering Undervisning. Biologi og geografi. Maj-juni 2008
 Prøver Evaluering Undervisning Biologi og geografi Maj-juni 2008 Ved fagkonsulent Henrik Nørregaard 1 Indhold Indledning 1 Formålet med de digitale afgangsprøver i geografi og i biologi 1 Det testpædagogiske
Prøver Evaluering Undervisning Biologi og geografi Maj-juni 2008 Ved fagkonsulent Henrik Nørregaard 1 Indhold Indledning 1 Formålet med de digitale afgangsprøver i geografi og i biologi 1 Det testpædagogiske
Årsplan for 5. klasse, matematik
 Ringsted Lilleskole, Uffe Skak Årsplan for 5. klasse, matematik Som det fremgår af nedenstående uddrag af undervisningsministeriets publikation om fælles trinmål til matematik efter 6. klasse, bliver faget
Ringsted Lilleskole, Uffe Skak Årsplan for 5. klasse, matematik Som det fremgår af nedenstående uddrag af undervisningsministeriets publikation om fælles trinmål til matematik efter 6. klasse, bliver faget
Matematika rsplan for 9. kl
 Matematika rsplan for 9. kl. 2019-2020 Årsplanen tager udgangspunkt i fællesmål (færdigheds- og vidensmål) efter 9. klassetrin. Desuden tilrettelægges undervisningen efter læseplanen for matematik. Formålet
Matematika rsplan for 9. kl. 2019-2020 Årsplanen tager udgangspunkt i fællesmål (færdigheds- og vidensmål) efter 9. klassetrin. Desuden tilrettelægges undervisningen efter læseplanen for matematik. Formålet
Matematik. Matematikundervisningen tager udgangspunkt i Folkeskolens Fælles Mål
 Matematik Matematikundervisningen tager udgangspunkt i Folkeskolens Fælles Mål Formålet med undervisningen i matematik er, at eleverne bliver i stand til at forstå og anvende matematik i sammenhænge, der
Matematik Matematikundervisningen tager udgangspunkt i Folkeskolens Fælles Mål Formålet med undervisningen i matematik er, at eleverne bliver i stand til at forstå og anvende matematik i sammenhænge, der
Vejledning til prøverne i faget fysik/kemi
 Vejledning til prøverne i faget fysik/kemi Kvalitets- og Tilsynsstyrelsen Februar 2014 1 Indhold Forord... 3 Generelt... 4 Tekstopgivelser... 5 Prøveoplæg... 5 Eksempler på prøveoplæg... 6 Prøven... 7
Vejledning til prøverne i faget fysik/kemi Kvalitets- og Tilsynsstyrelsen Februar 2014 1 Indhold Forord... 3 Generelt... 4 Tekstopgivelser... 5 Prøveoplæg... 5 Eksempler på prøveoplæg... 6 Prøven... 7
I alt 321 elever var til mundtlig prøve. Gennemsnitskarakteren var 6,96.
 Den mundtlige prøve Ved prøveterminen 2009 blev engelsk udtrukket som mundtligt prøvefag på 8 skoler. Herudover har elever fra yderligere 10 skoler valgt at gå til den mundtlige prøve i engelsk. I alt
Den mundtlige prøve Ved prøveterminen 2009 blev engelsk udtrukket som mundtligt prøvefag på 8 skoler. Herudover har elever fra yderligere 10 skoler valgt at gå til den mundtlige prøve i engelsk. I alt
Vejledning til prøverne i faget fysik/kemi
 Vejledning til prøverne i faget fysik/kemi Kvalitets- og Tilsynsstyrelsen Evaluerings- og Prøvekontor Januar 2012 1 Indhold Forord... 3 Generelt... 4 Tekstopgivelser og prøveoplæg... 5 Eksempel på forløbet
Vejledning til prøverne i faget fysik/kemi Kvalitets- og Tilsynsstyrelsen Evaluerings- og Prøvekontor Januar 2012 1 Indhold Forord... 3 Generelt... 4 Tekstopgivelser og prøveoplæg... 5 Eksempel på forløbet
MATEMATIK. GIDEONSKOLENS UNDERVISNINGSPLAN Oversigt over undervisning i forhold til trinmål og slutmål
 MATEMATIK GIDEONSKOLENS UNDERVISNINGSPLAN Oversigt over undervisning i forhold til trinmål og slutmål KOMMENTAR Vi har i det følgende foretaget en analyse og en sammenstilling af vore materialer til skriftlig
MATEMATIK GIDEONSKOLENS UNDERVISNINGSPLAN Oversigt over undervisning i forhold til trinmål og slutmål KOMMENTAR Vi har i det følgende foretaget en analyse og en sammenstilling af vore materialer til skriftlig
Faglige delmål og slutmål i faget Matematik. Trin 1
 Faglige delmål og slutmål i faget Matematik. Trin 1 Faglige delmål for matematik i 1. og 2. klasse. Undervisningen skal lede frem mod, at eleverne efter 2. klasse har tilegnet sig kundskaber og færdigheder,
Faglige delmål og slutmål i faget Matematik. Trin 1 Faglige delmål for matematik i 1. og 2. klasse. Undervisningen skal lede frem mod, at eleverne efter 2. klasse har tilegnet sig kundskaber og færdigheder,
http://us.uvm.dk/gymnasie/almen/eksamen/opgaver/sommer04/vurderingsgrundlag-b-niveau2004-8- 2og2004-8-2-sf.pdf?menuid=150560
 http://us.uvm.dk/gymnasie/almen/eksamen/opgaver/sommer04/vurderingsgrundlag-b-niveau2004-8- 2og2004-8-2-sf.pdf?menuid=150560 Vurderingsgrundlag ved Skriftlig studentereksamen i matematik 2004. Det betyder
http://us.uvm.dk/gymnasie/almen/eksamen/opgaver/sommer04/vurderingsgrundlag-b-niveau2004-8- 2og2004-8-2-sf.pdf?menuid=150560 Vurderingsgrundlag ved Skriftlig studentereksamen i matematik 2004. Det betyder
Årsplan 2013/2014 6. ÅRGANG: MATEMATIK. Lyreskovskolen. FORMÅL OG FAGLIGHEDSPLANER - Fælles Mål II 2009
 Årsplan 2013/2014 6. ÅRGANG: MATEMATIK FORMÅL OG FAGLIGHEDSPLANER - Fælles Mål II 2009 Formålet med undervisningen i matematik er, at eleverne udvikler matematiske r og opnår viden og kunnen således, at
Årsplan 2013/2014 6. ÅRGANG: MATEMATIK FORMÅL OG FAGLIGHEDSPLANER - Fælles Mål II 2009 Formålet med undervisningen i matematik er, at eleverne udvikler matematiske r og opnår viden og kunnen således, at
Fagårsplan 10/11 Fag: Matematik Klasse: 8.A Lærer: Henrik Stillits Fagområde/ emne Færdighedsregning - Typer af opgaver - Systematik
 Fagårsplan 10/11 Fag: Matematik Klasse: 8.A Lærer: Henrik Stillits Fagområde/ emne Færdighedsregning - Typer af opgaver - Systematik Periode Mål Eleverne skal: 32/33 Få kendskab til opgavetypen og få rutine.
Fagårsplan 10/11 Fag: Matematik Klasse: 8.A Lærer: Henrik Stillits Fagområde/ emne Færdighedsregning - Typer af opgaver - Systematik Periode Mål Eleverne skal: 32/33 Få kendskab til opgavetypen og få rutine.
ÅRSPLAN Matematik 9.klasse SKOLEÅRET 2017/2018
 ÅRSPLAN Matematik 9.klasse SKOLEÅRET 2017/2018 UGE 35-40 44-47 Matematiske Fokuspunkter Tal, talsystemer regneregler, herunder: - Potens kvadratregner egler Økonomi, herunder: - Decimaltal - Brøktal -
ÅRSPLAN Matematik 9.klasse SKOLEÅRET 2017/2018 UGE 35-40 44-47 Matematiske Fokuspunkter Tal, talsystemer regneregler, herunder: - Potens kvadratregner egler Økonomi, herunder: - Decimaltal - Brøktal -
Vejledende årsplan for matematik 4.v 2008/09
 Vejledende årsplan for matematik 4.v 2008/09 Uge Emne Formål Opgaver samt arbejdsområder 33-35 Kendskab og skriftligt arbejde At finde elevernes individuelle niveau samt tilegne mig kendskab til deres
Vejledende årsplan for matematik 4.v 2008/09 Uge Emne Formål Opgaver samt arbejdsområder 33-35 Kendskab og skriftligt arbejde At finde elevernes individuelle niveau samt tilegne mig kendskab til deres
Årsplan i matematik 8 klasse. 2018/2019 Abdiaziz Farah
 Årsplan i matematik 8 klasse. 2018/2019 Abdiaziz Farah Materialer: arbejdsbog, /9 begrebsbog Uger Indhold Videns eller færdigheds mål Materialer Evaluering 34-38 kende de reelle tal og En Negative tal
Årsplan i matematik 8 klasse. 2018/2019 Abdiaziz Farah Materialer: arbejdsbog, /9 begrebsbog Uger Indhold Videns eller færdigheds mål Materialer Evaluering 34-38 kende de reelle tal og En Negative tal
Terminsprøver 10. klasse Marts 2017
 Terminsprøver 10. klasse Marts 2017 Dato Fag Ordinær tid Forlænget tid 08.03.17 Dansk 09.00-13.00 13.00-14.20 09.03.17 Matematik 09.00-13.00 13.00-14.20 10.03.17 Engelsk 09.00-12.00 12.00-13.00 Alle terminsprøver
Terminsprøver 10. klasse Marts 2017 Dato Fag Ordinær tid Forlænget tid 08.03.17 Dansk 09.00-13.00 13.00-14.20 09.03.17 Matematik 09.00-13.00 13.00-14.20 10.03.17 Engelsk 09.00-12.00 12.00-13.00 Alle terminsprøver
Fag- og indholdsplan 9. kl.:
 Fag- og indholdsplan 9. kl.: Indholdsområder: Tal og algebra: Tal - regneregler og formler Størrelser måling, beregning og sammenligning. Matematiske udtryk Algebra - teoretiske sammenhænge absolut og
Fag- og indholdsplan 9. kl.: Indholdsområder: Tal og algebra: Tal - regneregler og formler Størrelser måling, beregning og sammenligning. Matematiske udtryk Algebra - teoretiske sammenhænge absolut og
Årsplan matematik 4.klasse - skoleår 11/12- Ida Skov Andersen Med ret til ændringer og justeringer
 Basis: Klassen består af 22 elever og der er afsat 4 ugentlige timer. Grundbog: Vi vil arbejde ud fra Matematrix 4, arbejds- og grundbog, kopisider, Rema, ekstraopgaver og ugentlige afleveringsopgaver
Basis: Klassen består af 22 elever og der er afsat 4 ugentlige timer. Grundbog: Vi vil arbejde ud fra Matematrix 4, arbejds- og grundbog, kopisider, Rema, ekstraopgaver og ugentlige afleveringsopgaver
Bioteknologi Evaluering af skriftlig eksamen bioteknologi A htx og stx. Maj juni 2017
 Bioteknologi 217 Evaluering af skriftlig eksamen bioteknologi A htx og stx Maj juni 217 Undervisningsministeriet Styrelsen for Undervisning og Kvalitet Juni 217 Evalueringsrapport Bioteknologi A skriftlig
Bioteknologi 217 Evaluering af skriftlig eksamen bioteknologi A htx og stx Maj juni 217 Undervisningsministeriet Styrelsen for Undervisning og Kvalitet Juni 217 Evalueringsrapport Bioteknologi A skriftlig
Årsplan i matematik for 9. klasse 2017/2018
 Årsplan i matematik for 9. klasse 2017/2018 Undervisningen generelt: Undervisningen tilrettelægges ud fra fagets CKF er og forenklede fællesmål for faget. Undervisning bygges primært op ud fra emnerne
Årsplan i matematik for 9. klasse 2017/2018 Undervisningen generelt: Undervisningen tilrettelægges ud fra fagets CKF er og forenklede fællesmål for faget. Undervisning bygges primært op ud fra emnerne
Vejledning til prøverne i faget matematik
 Vejledning til prøverne i faget matematik Kvalitets- og Tilsynsstyrelsen Center for Kvalitetsudvikling, Prøver og Eksamen Marts 2013 Indhold Forord...4 1. Indledning...5 Prøvernes forskellige dele...5
Vejledning til prøverne i faget matematik Kvalitets- og Tilsynsstyrelsen Center for Kvalitetsudvikling, Prøver og Eksamen Marts 2013 Indhold Forord...4 1. Indledning...5 Prøvernes forskellige dele...5
Bioteknologi Evaluering af skriftlig eksamen bioteknologi A htx og stx. Maj juni 2016
 Bioteknologi 216 Evaluering af skriftlig eksamen bioteknologi A htx og stx Maj juni 216 Ministeriet for Børn, Undervisning og Ligestilling Styrelsen for Undervisning og Kvalitet Juli 216 Hermed udsendes
Bioteknologi 216 Evaluering af skriftlig eksamen bioteknologi A htx og stx Maj juni 216 Ministeriet for Børn, Undervisning og Ligestilling Styrelsen for Undervisning og Kvalitet Juli 216 Hermed udsendes
Vejledning til prøverne i faget matematik
 Vejledning til prøverne i faget matematik Kvalitets- og Tilsynsstyrelsen Center for Prøver, Eksamen og Test Marts 2014 Indhold Forord... 4 1. Indledning... 5 Prøvernes forskellige dele... 5 2. FSA... 9
Vejledning til prøverne i faget matematik Kvalitets- og Tilsynsstyrelsen Center for Prøver, Eksamen og Test Marts 2014 Indhold Forord... 4 1. Indledning... 5 Prøvernes forskellige dele... 5 2. FSA... 9
Samfundsfag. Evaluering, orientering og vejledning
 Folkeskolens afsluttende prøver Samfundsfag 2015 Evaluering, orientering og vejledning Institut for Læring De afsluttende prøver i samfundsfag Ifølge folkeskoleloven skal der undervises i samfundsfag i
Folkeskolens afsluttende prøver Samfundsfag 2015 Evaluering, orientering og vejledning Institut for Læring De afsluttende prøver i samfundsfag Ifølge folkeskoleloven skal der undervises i samfundsfag i
Årsplan 9. klasse matematik 2014-2015 Uge Emne Faglige mål Trinmål Materialer/ systemer 33-34
 Årsplan 9. klasse matematik 2014-2015 33-34 Årsprøve og rettevejledledning 34-36 Årsprøven i matematik Talmængder og regnemetoder 37 Fordybelses uge 38-39 40 Termins-prøve 41 Studieturen 42 Efterårsferie
Årsplan 9. klasse matematik 2014-2015 33-34 Årsprøve og rettevejledledning 34-36 Årsprøven i matematik Talmængder og regnemetoder 37 Fordybelses uge 38-39 40 Termins-prøve 41 Studieturen 42 Efterårsferie
Målsætning. Se hovedmål for scenariet og hovedmål for færdighedslæring her. Økonomi
 Målsætning Økonomiske beregninger som baggrund for vurdering af konkrete problemstillinger. Målsætningen for temaet Hvordan får jeg råd? er, at eleverne gennem arbejde med scenariet udvikler matematiske
Målsætning Økonomiske beregninger som baggrund for vurdering af konkrete problemstillinger. Målsætningen for temaet Hvordan får jeg råd? er, at eleverne gennem arbejde med scenariet udvikler matematiske
Kemi Evaluering af skriftlig eksamen kemi A, stx Maj juni 2016
 Kemi 2016 Evaluering af skriftlig eksamen kemi A, stx Maj juni 2016 Ministeriet for Børn, Undervisning og Ligestilling Styrelsen for Undervisning og Kvalitet Juli 2016 Hermed udsendes evalueringsrapporten
Kemi 2016 Evaluering af skriftlig eksamen kemi A, stx Maj juni 2016 Ministeriet for Børn, Undervisning og Ligestilling Styrelsen for Undervisning og Kvalitet Juli 2016 Hermed udsendes evalueringsrapporten
Matematik. Læseplan og formål:
 Matematik Læseplan og formål: Formålet med undervisningen i matematik er, at eleverne bliver i stand til at forstå og anvende matematik i sammenhænge, der vedrører dagligliv, samfundsliv og naturforhold.
Matematik Læseplan og formål: Formålet med undervisningen i matematik er, at eleverne bliver i stand til at forstå og anvende matematik i sammenhænge, der vedrører dagligliv, samfundsliv og naturforhold.
Tal og algebra. I kapitlet arbejdes med følgende centrale matematiske begreber: algebra variable. Huskeliste: Tændstikker (til side 146) FRA FAGHÆFTET
 I kapitlet skal eleverne arbejde med fire forskellige vinkler på algebra de præsenteres på kapitlets første mundtlige opslag. De fire vinkler er algebra som et redskab til at løse matematiske problemer.
I kapitlet skal eleverne arbejde med fire forskellige vinkler på algebra de præsenteres på kapitlets første mundtlige opslag. De fire vinkler er algebra som et redskab til at løse matematiske problemer.
Undersøgende opgaver Opgave 6 er i begge prøvesæt med som sidste opgave en undersøgende opgave af en ny type, som var lidt udfordrende for eleverne.
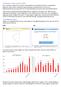 Tendenser i årets prøver 2019 Der er tendenser i prøverne, som kræver matematiklærernes opmærksomhed helst i et samarbejde i fagteamet. Og det kræver skolelederes og forvaltningers opmærksomhed for at
Tendenser i årets prøver 2019 Der er tendenser i prøverne, som kræver matematiklærernes opmærksomhed helst i et samarbejde i fagteamet. Og det kræver skolelederes og forvaltningers opmærksomhed for at
Emne Tema Materialer
 32 36 Uge 35 Fag: Matematik Hold: 20 Lærer: Trine Koustrup Undervisningsmål 9. klasse Læringsmål Faglige aktiviteter Emne Tema Materialer Målsætningen med undervisningen er at eleverne udvikler deres kunnen,opnår
32 36 Uge 35 Fag: Matematik Hold: 20 Lærer: Trine Koustrup Undervisningsmål 9. klasse Læringsmål Faglige aktiviteter Emne Tema Materialer Målsætningen med undervisningen er at eleverne udvikler deres kunnen,opnår
Vejledning til prøverne i matematik
 Vejledning til prøverne i matematik Styrelsen for Undervisning og Kvalitet Februar 2016 1 af 78 Indholdsfortegnelse 1. Indledning... 5 2. FP9... 9 2.1 Prøve i matematik uden hjælpemidler... 9 2.2 Prøve
Vejledning til prøverne i matematik Styrelsen for Undervisning og Kvalitet Februar 2016 1 af 78 Indholdsfortegnelse 1. Indledning... 5 2. FP9... 9 2.1 Prøve i matematik uden hjælpemidler... 9 2.2 Prøve
TW 2011/12. Fag: Matematik Klasse: 9. Mandag, Tirsdag, fredag. Formål for faget matematik:
 TW 2011/12 Fag: Matematik Klasse: 9. Mandag, Tirsdag, fredag Formål for faget matematik: Formålet med undervisningen er, at eleverne udvikler matematiske kompetencer og opnår viden og kunnen således, at
TW 2011/12 Fag: Matematik Klasse: 9. Mandag, Tirsdag, fredag Formål for faget matematik: Formålet med undervisningen er, at eleverne udvikler matematiske kompetencer og opnår viden og kunnen således, at
Kemi Evaluering af skriftlig eksamen kemi A, htx Maj juni Undervisningsministeriet Kvalitets- og Tilsynsstyrelsen
 Kemi 2014 Evaluering af skriftlig eksamen kemi A, htx Maj juni 2014 Undervisningsministeriet Kvalitets- og Tilsynsstyrelsen August 2014 Hermed udsendes evalueringsrapporten fra den skriftlige eksamen i
Kemi 2014 Evaluering af skriftlig eksamen kemi A, htx Maj juni 2014 Undervisningsministeriet Kvalitets- og Tilsynsstyrelsen August 2014 Hermed udsendes evalueringsrapporten fra den skriftlige eksamen i
Matematik - undervisningsplan
 I 4. klasse starter man på andet forløb i matematik, der skal lede frem mod at eleverne kan opfylde fagets trinmål efter 6. klasse. Det er dermed det som undervisningen tilrettelægges ud fra og målsættes
I 4. klasse starter man på andet forløb i matematik, der skal lede frem mod at eleverne kan opfylde fagets trinmål efter 6. klasse. Det er dermed det som undervisningen tilrettelægges ud fra og målsættes
Fælles Mål 2009. Matematik. Faghæfte 12
 Fælles Mål 2009 Matematik Faghæfte 12 Undervisningsministeriets håndbogsserie nr. 14 2009 Fælles Mål 2009 Matematik Faghæfte 12 Undervisningsministeriets håndbogsserie nr. 14 2009 Indhold Formål for faget
Fælles Mål 2009 Matematik Faghæfte 12 Undervisningsministeriets håndbogsserie nr. 14 2009 Fælles Mål 2009 Matematik Faghæfte 12 Undervisningsministeriets håndbogsserie nr. 14 2009 Indhold Formål for faget
Fælles Mål 2009. Matematik. Faghæfte 12
 Fælles Mål 2009 Matematik Faghæfte 12 Undervisningsministeriets håndbogsserie nr. 14 2009 Fælles Mål 2009 Matematik Faghæfte 12 Undervisningsministeriets håndbogsserie nr. 14 2009 Indhold Formål for faget
Fælles Mål 2009 Matematik Faghæfte 12 Undervisningsministeriets håndbogsserie nr. 14 2009 Fælles Mål 2009 Matematik Faghæfte 12 Undervisningsministeriets håndbogsserie nr. 14 2009 Indhold Formål for faget
Årsplan matematik, RE 2018/2019
 Uge Område Ugeinfo. / Indhold er 33 Tal & Størrelser Introuge - Kun Undervisning fredag 34 Tal & Størrelser Introuge - ikke undervisning fredag Decimaltal & Brøker 35 Tal & Størrelser Procentregning 36
Uge Område Ugeinfo. / Indhold er 33 Tal & Størrelser Introuge - Kun Undervisning fredag 34 Tal & Størrelser Introuge - ikke undervisning fredag Decimaltal & Brøker 35 Tal & Størrelser Procentregning 36
Funktioner og ligninger
 Eleverne har både i Kolorit på mellemtrinnet og i Kolorit 7 matematik grundbog arbejdet med funktioner. I 7. klasse blev funktionsbegrebet defineret, og eleverne arbejdede med forskellige måder at beskrive
Eleverne har både i Kolorit på mellemtrinnet og i Kolorit 7 matematik grundbog arbejdet med funktioner. I 7. klasse blev funktionsbegrebet defineret, og eleverne arbejdede med forskellige måder at beskrive
