Navneregning. Aktivitet Emne Klassetrin Side
|
|
|
- Ivar Andersen
- 7 år siden
- Visninger:
Transkript
1 VisiRegn ideer 2 Navneregning Inge B. Larsen ibl@dpu.dk INFA juli 2001 Indhold: Aktivitet Emne Klassetrin Side Vejledning til Navneregning 2-5 Elevaktiviteter til Navneregning 2.1 Værdifulde navne M-Æ Indkøb M-Æ Ugepenge M-Æ Temperatur M-Æ 16 Angivelsen af klassetrin må naturligvis tages med en del forbehold. B: Begyndertrinnet klasse M: Mellemtrinnet klasse Æ: Ældste klassetrin klasse
2 Navneregning (Modeller) VisiRegn Vejledning Her tages det vigtige skridt fra at bruge VisiRegn blot som lommeregner og til at anvende navne (variable), der giver mulighed for at opbygge modeller med inddata og uddata, og med mulighed for at opsamle data fra modellen og afbilde data grafisk. Dette åbner for enkel løsning (ved hjælp af gættemetoden) af problemer, der før har været uden for rækkevidde. I aktivitet 2.1 Værdifulde navne gives en introduktion til opbygning af modeller og til opsamling i tabel af data fra modellen. I de tre sidste aktiviteter arbejdes med situationer, der beskrives ved lineære modeller/funktioner, og med hvordan tabeldata fra disse kan afbildes som xy-punkter. Kendskab til VisiRegn Aktiviteterne forudsætter, at eleverne har/får kendskab til følgende i VisiRegn: 1. At navne anbragt i Navne kolonnen har den værdi, som findes i samme linies Værdi kolonne. (Klik i VisiRegns indbyggede vejledning på Navn under overskriften Arkets fire kolonner ). 1. At man selv bestemmer, hvor mange decimaler værdierne skal vises med. (Klik i VisiRegns indbyggede vejledning på Værdi under overskriften Arkets fire kolonner ). 2. At man kan T-mærke navne og dermed få deres værdier opsamlet i en tabel. At man ikke selv kan skrive i tabelområdet, men at dette styres fra modellen, men at man dog kan slette linier i tabellen og også helt rense tabellen væk. (Klik i VisiRegns indbyggede vejledning på overskriften Tabel.) NB! Bemærk, at de punkter, der afsættes som xy-punkter, er afsat ud fra de tal, man ser i tabellen. Det er derfor vigtigt at overveje, hvor mange decimaler de T-mærkede værdier i modellen skal vises med. (Dette vil forhåbentlig henad vejen blive rettet i VisiRegn). 3. At man kan afbilde data fra tabellen i xy-punkter og eventuelt få punkterne forbundet med rette linier. (Klik i VisiRegns indbyggede vejledning på overskriften Grafik ud fra værdier i tabel under overskriften Grafik.) Værdifulde navne Aktivitet 2.1 Opgaverne 1)-3) beskæftiger sig med omsætning af timer til minutter og sekunder. Der lægges op til, at det er en god ide at bygge sig en model, hvis man skal foretage de samme udregninger mange gange blot med forskellige tal. I opgave 1 tænkes VisiRegn kun anvendt som lommeregner. Bygningen af modellen beskrives i detaljer i opgave 2, og modellen skal så udbygges i opgave 3. Navne Det springende punkt her er navnenes rolle. Navnene er ikke blot værdifulde, fordi de minder os om, hvad det er for et problem, vi beskæftiger os med. De er også i en anden forstand værdifulde, idet de er tillagt den værdi, som står i deres linie. Indsætter man et sådant navn i et 2
3 udtryk, så vil det ved beregningen blive erstattet med sin værdi. Navnene i et udtryk er altså pladsholdere for tal, eller om man vil dynamiske variable. Dynamiske, fordi beregninger foretages automatisk, når der ændres i inddata eller i modellens opbygning. Opgaverne 4)-5) forudsætter kendskab til omkreds og areal af henholdsvis rektangel og cirkel. I opgave 4 har man to inddata: siderne a og b, og to uddata: omkreds og areal. Altså en model, der strukturmæssigt går ud over skolens gængse funktioner af en variabel. I opgave 5 introduceres opsamling i tabel af tal fra modellen, og denne skal så anvendes i forbindelse med gættemetoden til løsning af det sidste spørgsmål. Der bliver kun bedt om svaret (5,6 m) angivet med 1 decimal, men det ville være oplagt at bede de hurtigste om at bestemme resultatet mere nøjagtigt fx med 2 decimaler (5,64 m). Man kan også løse spørgsmålet ved selv at regne baglæns eller løse ligning. Der vil jo gælde, at 100=ð*r 2, så VisiRegn kan finde radius vha. udtrykket: kvr(100/pi). Men gættemetoden er ulige meget nemmere at anvende, når man har opbygget sin VisiRegn model. Med disse opgaver kunne eleverne starte opbygningen af deres egen dynamiske formelsamling. Dynamisk, fordi man ikke blot har formlerne stående i arket, men man kan også umiddelbart få beregnet værdier ved hjælp af formlerne. Opbygningen af en dynamisk formelsamling kræver så, at man ved, hvordan man gemmer og åbner VisiRegn-ark. Gættemetoden I opgave 5 introduceres gættemetoden, hvor man ved hjælp af en opbygget model gætter sig frem til løsningen på et problem, der ellers ville have krævet tilbageregning eller opstilling og løsning af ligninger. Opgaver, der kræver, at man regner baglæns, volder som regel besvær. Dette kan man undgå med et regneprogram til rådighed. Her opstiller man blot en model, der regner fremad og bruger så gættemetoden. Dette betyder også, at problemstillinger, der førhen lå uden for, hvad man kunne beskæftige sig med i folkeskolens matematikundervisning, nu er kommet inden for rækkevidde. Bemærk, at gættemetoden forudsætter en intuitiv form for forståelse af den sammenhæng, der er i modellen er ens gæt helt tilfældige, er metoden ikke anvendelig. De indhøstede resultater i tabellen skulle gerne lede en stadig nærmere til en løsning. Bemærk endvidere, at man ved gættemetoden selv fastsætter, hvor nøjagtigt (antallet af decimaler) svaret skal være. Opgave 6) giver endnu et eksempel på en situation, hvor det kan være nyttigt at opbygge en model - her for en opskrift. Ved hjælp af modellen er det hurtigt at få opskriften tilpasset til det antal boller, man ønsker, og ligeledes lader problemer som det sidste sig enkelt løse ved hjælp af gættemetoden. Indkøb Aktivitet 2.2 Opgave 1) Forståelsen af, at en model opbygges med navne (variable), er vigtig. Det kan eventuelt tydeliggøres ved i opgave 1) først at give betal udtrykket 3.75*7 og dernæst overveje, hvad der nu skal gøres ved dette udtryk, hvis man ændrer udtryksværdien for antal til fx 8. Det er jo besværligt, hvis man skal ned og rette i udtrykket for betal, hver gang man har et nyt antal, men det kan heldigvis undgås, ved at man lader udtrykket for betal være 3.75*antal. Når dette skal beregnes erstatter VisiRegn navnet antal med den værdi, man har givet det ovenfor. 3
4 Inddata og uddata for en model En model skal kunne fodres med inddata og så automatisk levere os uddata. Sagt på en anden måde: inddata er de tal, vi kender, og uddata er de tal, vi ønsker at kende og som afhænger af inddata. Modellen beskriver den sammenhæng/afhængighed, der er mellem inddata og uddata. Opgaverne 2)-4) giver en blid indgang til at opsamle inddata og uddata i en tabel og at afbilde tabellens data i xy-punkter. Her er det vigtigt at bemærke korrespondancen mellem modellen i arket og tabellen og grafen. Brug af modellen afspejles straks i tabellen og grafen. Ligeledes vil fjernelse af linier i tabellen straks blive reflekteret i grafen. Opgave 5) lægger op til brug af gættemetoden: man prøver med forskellige antal, indtil man har det største antal, man kan have uden at skulle betale mere end 31,25 kr. Af tabellen ses let at 8 pærer giver under kr., mens 9 pærer giver mere end dette beløb. Bemærk i øvrigt, at dersom man i stedet for at bruge modellen og gættemetoden regner baglæns og finder antallet som 31.25/3.75, så bliver resultatet hvilket må give anledning til yderligere overvejelser, da man jo ikke kan købe pærer. Bruger man gættemetoden, vil man naturligvis ikke gætte på brøkdele af en pære. Opgave 6) retter opmærksomheden mod at xy-punkterne ligger på en kurve, og at denne som i så mange andre tilfælde er en ret linie. Opgave 9) skal modellen udbygges med betal2 som fx kan få udtrykket betal+12 eller udtrykket 3.75*antal+12. Det første udtryk er den enkleste viderebygning på modellen. Til gengæld er det måske nemmere at se den lineære model i det andet udtryk. Opgaverne 15)-16) forudsætter kendskab til hældningstallet for en ret linie. Ugepenge Aktivitet 2.3 Her arbejdes videre med to lineære modeller og sammenligning af disse ved hjælp af deres afbildning i et koordinatsystem. Temperatur Aktivitet 2.4 Endnu et eksempel på en lineær model. Om temperaturmåling: I første halvdel af 1700-tallet var der tre forsøg af henholdsvis svenskeren Celsius, polakken Fahrenheit og franskmanden Réamur på at frembringe en standardskala for temperaturmåling. På det tidspunkt var det ca. 100 år siden, at det første primitive termometer blev konstrueret, men man havde endnu ikke en almindeligt anerkendt skala, der kunne gøre det muligt for videnskabsmænd at sammenligne deres temperaturmålinger. Ved fastlæggelsen af de 3 skalaer gik man ud fra afstanden mellem vandets frysepunkt og vandets kogepunkt. Denne afstand delte Celsius i 100, Fahrenheit i 180 og Réamur i 80 lige store afsnit (grader). Både Celsius og Réamur satte vandets frysepunkt til 0 grader, mens Fahrenheit satte det til 32 grader, således at vandets kogepunkt på hans skala er 212 grader. 4
5 Ved omregning mellem de 3 temperaturskalaer kan således benyttes følgende: x grader Celsius = (4/5) x grader Réamur = (9/5) x + 32 grader Fahrenheit x grader Réamur = (5/4) x grader Celsius = (9/4) x + 32 grader Fahrenheit x grader Fahrenheit = (5/9) (x- 32) grader Celsius = (4/9) (x - 32) grader Réamur I Danmark måler man i Celsius-grader, men i de fleste engelsktalende lande måler man i Fahrenheit-grader. Rejser man til et sådant land kan det være nyttigt at have en tabel over omsætningen mellem de to skalaer. 5
6 Værdifulde navne VisiRegn Aktivitet 2.1 1) Brug VisiRegn til at bestemme følgende: (a) 17 timer har min. (b) 24 timer har min. (c) 33 timer har min. 2) Hvis man, som i opgave 1), har brug for mange gange at foretage de samme beregninger blot med forskellige tal, så er det en god idé, at udforme en model i VisiRegn. Det vi kender i opgave 1) er et antal timer, og det vi ønsker at finde er det tilsvarende antal minutter. Vi kan sætte følgende VisiRegn model op: Bemærk, at i udtrykket i linie A2 er der brugt navnet timer, som er givet i linie A1. Vi ville naturligvis have fået samme resultat, hvis vi havde skrevet udtrykket som 17*60, men fidusen er, at for at løse spørgsmål (b) i opgave 1) behøver vi nu blot i linie A1 at erstatte 17 med 24 og så aflæse resultatet i linie A2. Antallet af timer, som vi fodrer modellen med, kaldes for modellens inddata, og det tilsvarende antal minutter, som modellen automatisk leverer os, kaldes modellens uddata. Når man skal opbygge en model til at løse et problem, skal man gøre sig klart: (a) Hvad er inddata? (m.a.o. hvilke størrelser kender jeg) (b) Hvad er uddata? (m.a.o. hvad er det jeg ønsker at finde) (c) Hvilke beregninger skal jeg foretage på inddata for at få uddata? 3) Udbyg modellen med en linie mere, så man som uddata får ikke blot, hvor mange minutter, der er, men også hvor mange sekunder. (Hvad skal man gøre ved minutterne for at få dem i sekunder?) (a) 17 timer har sek. (b) 24 timer har sek. (c) 33 timer har sek.
7 Værdifulde navne VisiRegn Aktivitet 2.1 a=4 b=9 4) De to sider a og b i rektanglet ovenfor er henholdsvis 4 cm og 9 cm. Man skal bestemme rektanglets omkreds og dets areal. Vi vil opbygge en model, sådan at vi hurtigt kan finde svarene ikke blot for rektanglet ovenfor, men for ethvert rektangel, hvis sider vi kender. Hvad er modellens inddata: Hvad er modellens uddata: Udform modellen i VisiRegn. Dette kan bruges som start på modellen: Fyld skemaet nedenfor ud ved brug af modellen: a (i cm) b (i cm) Omkreds (i cm) Areal (i cm 2 ) 5) En cirkel med radius r har Omkreds = 2 p r og Areal = p r 2 Udform i VisiRegn en model, der for enhver cirkel givet ved dens radius finder cirklens omkreds og areal. 7
8 Værdifulde navne VisiRegn Aktivitet 2.1 Tallet p (pi) er indbygget i VisiRegn, med så stor nøjagtighed som VisiRegn kan klare. Brug VisiRegns pi i udtrykkene for omkreds og areal. Med modellen kan man nu nemt finde omkreds og areal for forskellige størrelser af radius, og man behøver ikke selv at huske resultaterne. VisiRegn kan sættes til at opsamle resultaterne i en tabel. Det sker ved at T- mærke de navne, man vil have med i tabellen: T-mærk de 3 navne: r, omkreds og areal ved at klikke i T- kolonnen helt ude til venstre for navnet. Find omkreds og areal for cirkler med radius 3 m, 16 m, 7.45 m og m: Hvad skal radius (angivet med 1 decimal) være for at arealet kommer så tæt på 100 m 2 som muligt uden at overstige 100 m 2? (Prøv dig frem!) 6) Henrik bager grovboller til en fødselsdag. Opskriften siger, at til 12 grovboller skal der bruges: 180 g hvedemel 90 g fuldkornsrugmel 90 g sigtemel 30 g gær 20 g honning 10 g sesamfrø 2 dl lunkent vand lidt salt Henrik vil lave 18 grovboller, så han må omregne alle mængderne ovenfor. Vil han en anden dag bage 25 grovboller, så han skal han igen til at omregne alle mængderne. 8
9 Værdifulde navne VisiRegn Aktivitet 2.1 Henrik beslutter sig til at lægge opskriften ind som en model i VisiRegn, sådan at han blot behøver at angive, hvor mange grovboller der skal bages, så vil han straks nedenfor kunne se den omregnede opskrift. Her er nedenfor vist begyndelsen til modellen. Hvordan vil du forklare udtrykket i linie A3? Indsæt de manglende udtryk. (Kontrollér værdierne) (a) Hvad er modellens inddata: (b) Hvad er modellens uddata: Find opskriften for 18 grovboller. (d) En dag vil Henrik bage rigtig mange grovboller. Af sigtemel har han kun 250 g, men af alt det øvrige har han rigeligt. Hvor mange grovboller kan han bage? (Prøv dig frem!) 9
10 Indkøb VisiRegn Aktivitet 2.2 Jens køber pærer. En pære koster 3,75 kr. 1) Udform en VisiRegn model, der som inddata har antal pærer, som Jens køber, og som uddata har, hvad han så skal betale. (Vis kr. med 2 decimaler) 2) Lav en tabel, der fra modellen samler værdierne for antal og betal op. (T-mærk antal og betal, og prøv så i arket at sætte antal til fx 0, 1, 2, 3 og 4) 3) Afbild tabellens værdier i et koordinatsystem. (Vælg Grafik/Fra tabel/xy-punkter (eller skyd genvej med F5-tasten), så vil antal afsættes ud ad den vandrette akse og betal ud ad den lodrette akse). 4) Prøv nu at øge tabellen ved i arket at taste flere værdier for antal ind, og se hvordan også koordinatsystemet ændres. Prøv også at afmærke nogle linier i tabellen og fjerne dem med Delete tasten. 5) Jens har 31,25 kr. med. Hvor mange pærer kan han købe? pærer 6) Hvilken slags kurve ligger xy-punkterne på? Man kan få punkterne forbundet med rette liniestykker ved at højreklikke på grafen og så klikke på Forbind punkterne. På tilsvarende måde kan liniestykkerne fjernes igen. 7) Prøv at forbinde punkterne med rette liniestykker. 10
11 Indkøb VisiRegn Aktivitet 2.2 8) Man taler om xy-punkter. Hvilket navn har vi i modellen givet til x: Hvilket navn har vi i modellen givet til y: 9) Klik på T i øverste venstre hjørne. Derved fjernes alle T-mærkninger af navne og tabel og graf renses. Næste dag bliver Jens sendt ned for at købe flere af de gode pærer (prisen er ikke ændret), men desuden skal han købe et vaskepulver til 12 kr. Føj en linje til modellen, sådan at den også kan angive, hvad Jens skal betale i alt den næste dag, når han køber et antal pærer. Husk også at vise værdien for betal2 med 2 decimaler. 10) Lav en tabel, der fra modellen samler værdierne for antal, betal og betal2 op, og prøv så i arket at sætte antal til fx 0, 1, 2, 3 og 4. 11) Afbild tabellens værdier i et koordinatsystem. (Vælg Grafik/Fra tabel/xy-punkter (eller skyd genvej med F5-tasten), så vil antal afsættes ud ad den vandrette akse og betal og betal2 ud ad den lodrette akse). 12) Hvilken kurve ligger punkterne for betal2 på? 13) Hvordan ligger kurven for betal2 i forhold til kurven for betal? 11
12 Indkøb VisiRegn Aktivitet ) Hvor mange pærer kan Jens købe den anden dag, hvis han har 40 kr. med? pærer 15) Bestem for den rette linie for betal: hældningstal: og skæring med den lodrette akse: 16) Bestem for den rette linie for betal2: hældningstal: og skæring med den lodrette akse: 12
13 Ugepenge VisiRegn Aktivitet 2.3 Pia har 500 kr. og Per har 900 kr. Pia beslutter at lade sit beløb vokse med 15 kr. hver uge. 1) Hvor mange kr. har Pia efter 2 uger? kr. 2) Udform VisiRegn modellen nedenfor. Inddata er antallet af uger, der er gået. Hver gang der indtastes et antal uger i linie A3, skal udtrykket i linie A4 udregne, hvor mange kroner Pia har. 3) Hvor mange kroner har Pia efter 37 uger? kr. 4) Efter hvor mange uger har Pia nået 1000 kr.? uger 5) Hvor mange kroner har Pia efter 0 uger? kr. 6) Lav en tabel over uger og Piahar. Prøv fx værdierne 0, 1, 2, 3 og 4 for uger. 7) Afbild tabellens værdier som xy-punkter. 8) Hvilket navn er afsat ud ad den vandrette akse: Hvilket navn er afsat ud ad den lodrette akse: 9) Prøv nu at øge tabellen ved at taste flere værdier for uger ind, og se hvordan koordinatsystemet ændres, så også disse punkter kan afsættes. 13
14 Ugepenge VisiRegn Aktivitet ) Hvilken slags kurve ligger xy-punkterne på? 11) Klik på T i øverste venstre hjørne, derved renses tabellen og dens tilhørende graf. Per beslutter modsat. Han vil af sine 900 kr. hver uge bruge 7 kr. til slik. 12) Hvor mange kr. har Per efter 2 uger? kr. 13) Føj en linie til modellen, sådan at man også får beregnet, hvor mange kroner Per har efter det angivne antal uger. 14) Hvor mange kroner har Per efter 12 uger? kr. 15) Efter hvor mange uger har Per under 500 kr.? uger 16) Hvor mange kroner har Per efter 0 uger? kr. 17) Lav tabel over uger og Perhar med ugeværdierne 0, 1, 2, 3 og 4. 18) Afbild tabellens værdier som xy-punkter. 19) Hvilken slags kurve ligger xy-punkterne på? 14
15 Ugepenge VisiRegn Aktivitet ) Klik nu også T ud for Piahar, så der gøres klar til ny tabel med uger og både Piahar og Perhar, og prøv med værdierne 0, 1, 2, 3, og 4 for uger. 21) Afbild tabellens værdier som xy-punkter. 22) Hvor mange uger skal der gå, før Pia har flere kroner end Per? uger (Prøv med forskellige værdier for uger og kig på tabel og graf) 23) Bestem for den rette linie for Piahar: hældningstal: skæring med den lodrette akse: og 24) Bestem for den rette linie for Perhar: hældningstal: og skæring med den lodrette akse: 15
16 Fra Fahrenheit til Celsius VisiRegn Aktivitet 2.4 I USA angiver man temperaturen i Fahrenheit grader. Hvis man får at vide, at temperaturen er 50 grader Fahrenheit, så kan man omsætte dette til vores egne Celsius grader på denne måde: Træk først 32 fra (så har man 50-32=18) Gang dernæst med 5 og del med 9 (så har man 18*5/9=10) Altså er 50 F-grader lig med 10 C-grader. 1) Udform en VisiRegn model, der som inddata har en temperatur givet i Fahrenheit grader og som uddata har temperaturen angivet i Celsius grader. 2) Lav en tabel over Fgrad og Cgrad. 3) Afbild tabellens værdier som xy-punkter. 4) Hvilken slags kurve ligger xy-punkterne på? 5) Hvor mange C-grader er 61 F-grader? C-grader 6) Hvad er vandets kogepunkt angivet i Fahrenheit grader? F-grader 7) Bestem for den rette linie for Cgrad: hældningstal: skæring med den lodrette akse: og 16
Variabel- sammenhænge
 Variabel- sammenhænge Udgave 2 2009 Karsten Juul Dette hæfte kan bruges som start på undervisningen i variabelsammenhænge for stx og hf. Hæftet er en introduktion til at kunne behandle to sammenhængende
Variabel- sammenhænge Udgave 2 2009 Karsten Juul Dette hæfte kan bruges som start på undervisningen i variabelsammenhænge for stx og hf. Hæftet er en introduktion til at kunne behandle to sammenhængende
Talrækker. Aktivitet Emne Klassetrin Side
 VisiRegn ideer 3 Talrækker Inge B. Larsen ibl@dpu.dk INFA juli 2001 Indhold: Aktivitet Emne Klassetrin Side Vejledning til Talrækker 2-4 Elevaktiviteter til Talrækker 3.1 Talrækker (1) M-Æ 5-9 3.2 Hanoi-spillet
VisiRegn ideer 3 Talrækker Inge B. Larsen ibl@dpu.dk INFA juli 2001 Indhold: Aktivitet Emne Klassetrin Side Vejledning til Talrækker 2-4 Elevaktiviteter til Talrækker 3.1 Talrækker (1) M-Æ 5-9 3.2 Hanoi-spillet
Den bedste dåse, en optimeringsopgave
 bksp-20-15e Side 1 af 7 Den bedste dåse, en optimeringsopgave Mange praktiske anvendelser af matematik drejer sig om at optimere en variabel ved at vælge en passende kombination af andre variable. Det
bksp-20-15e Side 1 af 7 Den bedste dåse, en optimeringsopgave Mange praktiske anvendelser af matematik drejer sig om at optimere en variabel ved at vælge en passende kombination af andre variable. Det
VIA læreruddannelsen Silkeborg. WordMat kompendium
 VIA læreruddannelsen Silkeborg WordMat kompendium Bolette Fisker Olesen 25-11-2015 Indholdsfortegnelse Ligning... 2 Løs ligning... 2 WordMat som lommeregner... 4 Geometri... 4 Trekanter... 4 Funktioner...
VIA læreruddannelsen Silkeborg WordMat kompendium Bolette Fisker Olesen 25-11-2015 Indholdsfortegnelse Ligning... 2 Løs ligning... 2 WordMat som lommeregner... 4 Geometri... 4 Trekanter... 4 Funktioner...
Bogstavregning. Formler... 46 Reduktion... 47 Ligninger... 48. Bogstavregning Side 45
 Bogstavregning Formler... 6 Reduktion... 7 Ligninger... 8 Bogstavregning Side I bogstavregning skal du kunne regne med bogstaver og skifte bogstaver ud med tal. Formler En formel er en slags regne-opskrift,
Bogstavregning Formler... 6 Reduktion... 7 Ligninger... 8 Bogstavregning Side I bogstavregning skal du kunne regne med bogstaver og skifte bogstaver ud med tal. Formler En formel er en slags regne-opskrift,
Formler, ligninger, funktioner og grafer
 Formler, ligninger, funktioner og grafer Omskrivning af ligninger og formler... 39 To ligninger med to ubekendte... 44 Formler, ligninger, funktioner og grafer Side 38 Omskrivning af ligninger og formler
Formler, ligninger, funktioner og grafer Omskrivning af ligninger og formler... 39 To ligninger med to ubekendte... 44 Formler, ligninger, funktioner og grafer Side 38 Omskrivning af ligninger og formler
Inverse funktioner. John V Petersen
 Inverse funktioner John V Petersen Indhold Indledning: Indledende eksempel. Grafen for en funktion. Og grafen for den inverse funktion.... 3 Afbildning, funktion og inverse funktion: forklaringer og definitioner...
Inverse funktioner John V Petersen Indhold Indledning: Indledende eksempel. Grafen for en funktion. Og grafen for den inverse funktion.... 3 Afbildning, funktion og inverse funktion: forklaringer og definitioner...
Ligeværdige udtryk. Aktivitet Emne Klassetrin Side. Vejledning til Ligeværdige udtryk 2
 VisiRegn ideer 4 Ligeværdige udtryk Inge B. Larsen ibl@dpu.dk INFA juli 2001 Indhold: Aktivitet Emne Klassetrin Side Vejledning til Ligeværdige udtryk 2 Elevaktiviteter til Ligeværdige udtryk 4.1 Ligeværdige
VisiRegn ideer 4 Ligeværdige udtryk Inge B. Larsen ibl@dpu.dk INFA juli 2001 Indhold: Aktivitet Emne Klassetrin Side Vejledning til Ligeværdige udtryk 2 Elevaktiviteter til Ligeværdige udtryk 4.1 Ligeværdige
Forslag til løsning af Opgaver til analytisk geometri (side 338)
 Forslag til løsning af Opgaver til analytisk geometri (side 8) Opgave Linjerne har ligningerne: a : y x 9 b : x y 0 y x 8 c : x y 8 0 y x Der må gælde: a b, da Skæringspunkt mellem a og b:. Det betyder,
Forslag til løsning af Opgaver til analytisk geometri (side 8) Opgave Linjerne har ligningerne: a : y x 9 b : x y 0 y x 8 c : x y 8 0 y x Der må gælde: a b, da Skæringspunkt mellem a og b:. Det betyder,
Teknologi & Kommunikation
 Side 1 af 6 Indledning Denne note omhandler den lineære funktion, hvis graf i et koordinatsystem er en ret linie. Funktionsbegrebet knytter to størrelser (x og y) sammen, disse to størrelser er afhængige
Side 1 af 6 Indledning Denne note omhandler den lineære funktion, hvis graf i et koordinatsystem er en ret linie. Funktionsbegrebet knytter to størrelser (x og y) sammen, disse to størrelser er afhængige
Tal, funktioner og grænseværdi
 Tal, funktioner og grænseværdi Skriv færdig-eksempler der kan udgøre en væsentlig del af et forløb der skal give indsigt vedrørende begrebet grænseværdi og nogle nødvendige forudsætninger om tal og funktioner
Tal, funktioner og grænseværdi Skriv færdig-eksempler der kan udgøre en væsentlig del af et forløb der skal give indsigt vedrørende begrebet grænseværdi og nogle nødvendige forudsætninger om tal og funktioner
Lineære modeller. Taxakørsel: Et taxa selskab tager 15 kr. pr. km man kører i deres taxa. Hvis vi kører 2 km i taxaen koster turen altså
 Lineære modeller Opg.1 Taxakørsel: Et taxa selskab tager 15 kr. pr. km man kører i deres taxa. Hvis vi kører 2 km i taxaen koster turen altså Hvor meget koster det at køre så at køre 10 km i Taxaen? Sammenhængen
Lineære modeller Opg.1 Taxakørsel: Et taxa selskab tager 15 kr. pr. km man kører i deres taxa. Hvis vi kører 2 km i taxaen koster turen altså Hvor meget koster det at køre så at køre 10 km i Taxaen? Sammenhængen
Statistikkompendium. Statistik
 Statistik INTRODUKTION TIL STATISTIK Statistik er analyse af indsamlet data. Det vil sige, at man bearbejder et datamateriale, som i matematik næsten altid er tal. Derved får man et samlet overblik over
Statistik INTRODUKTION TIL STATISTIK Statistik er analyse af indsamlet data. Det vil sige, at man bearbejder et datamateriale, som i matematik næsten altid er tal. Derved får man et samlet overblik over
Arealer under grafer
 HJ/marts 2013 1 Arealer under grafer 1 Arealer og bestemt integral Som bekendt kan vi bruge integralregning til at beregne arealer under grafer. Helt præcist har vi denne sætning. Sætning 1 (Analysens
HJ/marts 2013 1 Arealer under grafer 1 Arealer og bestemt integral Som bekendt kan vi bruge integralregning til at beregne arealer under grafer. Helt præcist har vi denne sætning. Sætning 1 (Analysens
Start med at vælge hvilken afdeling der skal laves ændringer i f.eks. fodbold.
 Start med at vælge hvilken afdeling der skal laves ændringer i f.eks. fodbold. Her ses da alle sider og undersider som siden fodbold indeholder. Nu kan du gå i gang med f.eks. at tilføje nye sider. Klik
Start med at vælge hvilken afdeling der skal laves ændringer i f.eks. fodbold. Her ses da alle sider og undersider som siden fodbold indeholder. Nu kan du gå i gang med f.eks. at tilføje nye sider. Klik
Afstand fra et punkt til en linje
 Afstand fra et punkt til en linje Frank Villa 6. oktober 2014 Dette dokument er en del af MatBog.dk 2008-2012. IT Teaching Tools. ISBN-13: 978-87-92775-00-9. Se yderligere betingelser for brug her. Indhold
Afstand fra et punkt til en linje Frank Villa 6. oktober 2014 Dette dokument er en del af MatBog.dk 2008-2012. IT Teaching Tools. ISBN-13: 978-87-92775-00-9. Se yderligere betingelser for brug her. Indhold
Opgave 1 Alle tallene er reelle tal, så opgaven er at finde den mindste talmængde, som resultaterne tilhører.
 Opgave 1 Alle tallene er reelle tal, så opgaven er at finde den mindste talmængde, som resultaterne tilhører. A. Q B. R (sidelængden er 5, som er irrational) C. Q Opgave 2 A. 19 = 1 19 24 = 2 3 3 36 =
Opgave 1 Alle tallene er reelle tal, så opgaven er at finde den mindste talmængde, som resultaterne tilhører. A. Q B. R (sidelængden er 5, som er irrational) C. Q Opgave 2 A. 19 = 1 19 24 = 2 3 3 36 =
Reelle tal. Symbolbehandlingskompetencen er central gennem arbejdet med hele kapitlet i elevernes arbejde med tal og regneregler.
 Det første kapitel i grundbogen til Kolorit i 9. klasse handler om de reelle tal. Første halvdel af kapitlet har karakter af at være opsamlende i forhold til, hvad eleverne har arbejdet med på tidligere
Det første kapitel i grundbogen til Kolorit i 9. klasse handler om de reelle tal. Første halvdel af kapitlet har karakter af at være opsamlende i forhold til, hvad eleverne har arbejdet med på tidligere
Om hvordan Google ordner websider
 Om hvordan Google ordner websider Hans Anton Salomonsen March 14, 2008 Man oplever ofte at man efter at have givet Google et par søgeord lynhurtigt får oplysning om at der er fundet et stort antal - måske
Om hvordan Google ordner websider Hans Anton Salomonsen March 14, 2008 Man oplever ofte at man efter at have givet Google et par søgeord lynhurtigt får oplysning om at der er fundet et stort antal - måske
Funktionalligninger - løsningsstrategier og opgaver
 Funktionalligninger - løsningsstrategier og opgaver Altså er f (f (1)) = 1. På den måde fortsætter vi med at samle oplysninger om f og kombinerer dem også med tidligere oplysninger. Hvis vi indsætter =
Funktionalligninger - løsningsstrategier og opgaver Altså er f (f (1)) = 1. På den måde fortsætter vi med at samle oplysninger om f og kombinerer dem også med tidligere oplysninger. Hvis vi indsætter =
Polynomier et introforløb til TII
 Polynomier et introforløb til TII Formål At introducere polynomier af grad 0, 1, 2 samt højere, herunder grafer og rødder At behandle andengradspolynomiet og dets graf, parablen, med fokus på bl.a. toppunkt,
Polynomier et introforløb til TII Formål At introducere polynomier af grad 0, 1, 2 samt højere, herunder grafer og rødder At behandle andengradspolynomiet og dets graf, parablen, med fokus på bl.a. toppunkt,
brikkerne til regning & matematik potenstal og rodtal F+E+D preben bernitt
 brikkerne til regning & matematik potenstal og rodtal F+E+D preben bernitt brikkerne til regning & matematik potenstal og rodtal F ISBN: 978-87-92488-06-0 2. Udgave som E-bog 2010 by bernitt-matematik.dk
brikkerne til regning & matematik potenstal og rodtal F+E+D preben bernitt brikkerne til regning & matematik potenstal og rodtal F ISBN: 978-87-92488-06-0 2. Udgave som E-bog 2010 by bernitt-matematik.dk
Areal. Et af de ældste skrifter om matematik, der findes, hedder Rhind Papyrus. NTRO
 Areal Et af de ældste skrifter om matematik, der findes, hedder Rhind Papyrus. NTRO Det stammer fra Egypten og er ca. 3650 år gammelt. I Rhind Papyrus findes optegnelser, der viser, hvordan egypterne beregnede
Areal Et af de ældste skrifter om matematik, der findes, hedder Rhind Papyrus. NTRO Det stammer fra Egypten og er ca. 3650 år gammelt. I Rhind Papyrus findes optegnelser, der viser, hvordan egypterne beregnede
Secret Sharing. Olav Geil Institut for Matematiske Fag Aalborg Universitet email: olav@math.aau.dk URL: http://www.math.aau.dk/ olav.
 1 Læsevejledning Secret Sharing Olav Geil Institut for Matematiske Fag Aalborg Universitet email: olav@math.aau.dk URL: http://www.math.aau.dk/ olav September 2006 Nærværende note er tænkt som et oplæg
1 Læsevejledning Secret Sharing Olav Geil Institut for Matematiske Fag Aalborg Universitet email: olav@math.aau.dk URL: http://www.math.aau.dk/ olav September 2006 Nærværende note er tænkt som et oplæg
Temaopgave: Parameterkurver Form: 6 timer med vejledning Januar 2010
 Temaopgave: Parameterkurver Form: 6 timer med vejledning Januar 1 Parameterkurver Vi har tidligere set på en linjes parameterfremstilling, feks af typen: 1 OP = t +, hvor t R, og hvor OP er stedvektor
Temaopgave: Parameterkurver Form: 6 timer med vejledning Januar 1 Parameterkurver Vi har tidligere set på en linjes parameterfremstilling, feks af typen: 1 OP = t +, hvor t R, og hvor OP er stedvektor
Det er altså muligt at dele lige på to kvalitativt forskellige måder: Deling uden forståelse af helheden Deling med forståelse af helheden
 DELE 1 Vejledning Division Allerede i børnehaven oplever man børn travlt optaget af at dele legetøj, mad eller andet af interesse ud fra devisen en til dig og en til mig. Når der ikke er flere tilbage
DELE 1 Vejledning Division Allerede i børnehaven oplever man børn travlt optaget af at dele legetøj, mad eller andet af interesse ud fra devisen en til dig og en til mig. Når der ikke er flere tilbage
Pendulbevægelse. Måling af svingningstid: Jacob Nielsen 1
 Pendulbevægelse Jacob Nielsen 1 Figuren viser svingningstiden af et pendul i sekunder som funktion af udsvinget i grader. For udsving mindre end 20 grader er svingningstiden med god tilnærmelse konstant.
Pendulbevægelse Jacob Nielsen 1 Figuren viser svingningstiden af et pendul i sekunder som funktion af udsvinget i grader. For udsving mindre end 20 grader er svingningstiden med god tilnærmelse konstant.
Lektion 9 Statistik enkeltobservationer
 Lektion 9 Statistik enkeltobservationer Middelværdi med mere Hyppigheds- og frekvens-tabeller Diagrammer Hvilket diagram er bedst? Boxplot Lektion 9 Side 1 Når man skal holde styr på mange oplysninger,
Lektion 9 Statistik enkeltobservationer Middelværdi med mere Hyppigheds- og frekvens-tabeller Diagrammer Hvilket diagram er bedst? Boxplot Lektion 9 Side 1 Når man skal holde styr på mange oplysninger,
Potens & Kvadratrod. Navn: Klasse: Matematik Opgave Kompendium. Opgaver: 22 Ekstra: 4 Point: Matematik / Potens & Kvadratrod
 Navn: Klasse: Matematik Opgave Kompendium Potens & Kvadratrod Opgaver: Ekstra: Point: http://madsmatik.dk/ d.0-0-01 1/1 Potenser: Du har måske set udtrykket før eller måske 10 1. Begge to er det vi kalder
Navn: Klasse: Matematik Opgave Kompendium Potens & Kvadratrod Opgaver: Ekstra: Point: http://madsmatik.dk/ d.0-0-01 1/1 Potenser: Du har måske set udtrykket før eller måske 10 1. Begge to er det vi kalder
Bogstavregning. Formler...74 Reduktion...78 Ligninger...81 Ligninger som løsningsmetode...86. Bogstavregning Side 73
 Bogstavregning Formler...7 Reduktion...78 Ligninger...81 Ligninger som løsningsmetode...86 Bogstavregning Side 7 Formler 1: Regn disse opgaver med formler: a: Beregn: y = 5 + når: = b: Beregn: b = 15 a
Bogstavregning Formler...7 Reduktion...78 Ligninger...81 Ligninger som løsningsmetode...86 Bogstavregning Side 7 Formler 1: Regn disse opgaver med formler: a: Beregn: y = 5 + når: = b: Beregn: b = 15 a
Succesfuld start på dine processer. En e-bog om at åbne processer succesfuldt
 Succesfuld start på dine processer En e-bog om at åbne processer succesfuldt I denne e-bog får du fire øvelser, der kan bruges til at skabe kontakt, fælles forståelser og indblik. Øvelserne kan bruges
Succesfuld start på dine processer En e-bog om at åbne processer succesfuldt I denne e-bog får du fire øvelser, der kan bruges til at skabe kontakt, fælles forståelser og indblik. Øvelserne kan bruges
https://www.uvm.dk/~/media/uvm/filer/udd/folke/pdf14/nov/141127_initiativer_til_videreudvikling _af_folkeskolens_proever.pdf
 Digitalt prøvesæt Dette er et opgavesæt, som jeg har forsøgt at forestille mig, det kan se ud, hvis det skal leve op til ordene i det der er initiativ 3 i rækken af initiativer til videreudvikling af folkeskolens
Digitalt prøvesæt Dette er et opgavesæt, som jeg har forsøgt at forestille mig, det kan se ud, hvis det skal leve op til ordene i det der er initiativ 3 i rækken af initiativer til videreudvikling af folkeskolens
Forslag til løsning af Opgaver til ligningsløsning (side172)
 Forslag til løsning af Opgaver til ligningsløsning (side17) Opgave 1 Hvis sønnens alder er x år, så er faderens alder x år. Der går x år, før sønnen når op på x år. Om x år har faderen en alder på: x x
Forslag til løsning af Opgaver til ligningsløsning (side17) Opgave 1 Hvis sønnens alder er x år, så er faderens alder x år. Der går x år, før sønnen når op på x år. Om x år har faderen en alder på: x x
Vejledning til Photofiltre nr.166 Side 1 Lave små grafik knapper i Photofiltre
 Side 1 Photofiltre er jo først og fremmest et fotoredigeringsprogram. MEN det er også udmærket til at lave grafik med. F.eks. disse knapper er hurtig og nemme at lave. Her er der sat en hvid trekant med
Side 1 Photofiltre er jo først og fremmest et fotoredigeringsprogram. MEN det er også udmærket til at lave grafik med. F.eks. disse knapper er hurtig og nemme at lave. Her er der sat en hvid trekant med
Finde invers funktion til en 2-gradsfunktion - ved parallelforskydning. John V Petersen
 Finde invers funktion til en 2-gradsfunktion - ved parallelforskydning John V Petersen Finde invers funktion til en 2-gradsfunktion - ved parallelforskydning 2015 John V Petersen art-science-soul Indhold
Finde invers funktion til en 2-gradsfunktion - ved parallelforskydning John V Petersen Finde invers funktion til en 2-gradsfunktion - ved parallelforskydning 2015 John V Petersen art-science-soul Indhold
FÅ OVERBLIK OVER LØNNEN EXCEL FOR TILLIDSREPRÆSENTANTER DEL 4: FORMATERING AF REGNEARKET INFORMATIONSBOKS
 FÅ OVERBLIK OVER LØNNEN Få overblik over lønnen Excel for tillidsrepræsentanter Del 4: Formatering af regnearket Trin 8: Justér visningen af tallene Nu er vi færdige med selve tal-beregningerne i Excel.
FÅ OVERBLIK OVER LØNNEN Få overblik over lønnen Excel for tillidsrepræsentanter Del 4: Formatering af regnearket Trin 8: Justér visningen af tallene Nu er vi færdige med selve tal-beregningerne i Excel.
Statistik med GeoGebra
 Statistik med GeoGebra Hayati Balo, AAMS, marts 2012 1 Observationssæt Det talmateriale, som man gerne vil undersøge, kaldes et observationssæt. Det talsæt som fremgår i tabel 5.1 kan indsættes i GeoGebra
Statistik med GeoGebra Hayati Balo, AAMS, marts 2012 1 Observationssæt Det talmateriale, som man gerne vil undersøge, kaldes et observationssæt. Det talsæt som fremgår i tabel 5.1 kan indsættes i GeoGebra
Matematik projekt 4. Eksponentiel udvikling. Casper Wandrup Andresen 2.F 16-01-2009. Underskrift:
 Matematik projekt 4 Eksponentiel udvikling Casper Wandrup Andresen 2.F 16-01-2009 Underskrift: Teorien bag eksponentiel udvikling er som sådan meget enkel. Den har forskriften: B er vores begndelsesværdi
Matematik projekt 4 Eksponentiel udvikling Casper Wandrup Andresen 2.F 16-01-2009 Underskrift: Teorien bag eksponentiel udvikling er som sådan meget enkel. Den har forskriften: B er vores begndelsesværdi
Sådan benytter du HOTLINEs ServiceDesk (SD)
 Sådan benytter du HOTLINEs ServiceDesk (SD) Hvor finder jeg ServiceDesk?...2 Fanebladet Start Startside...3 Hvordan opretter jeg en ny opgave?...4 Hvordan laver jeg et skærmdump og får lagt det ind i min
Sådan benytter du HOTLINEs ServiceDesk (SD) Hvor finder jeg ServiceDesk?...2 Fanebladet Start Startside...3 Hvordan opretter jeg en ny opgave?...4 Hvordan laver jeg et skærmdump og får lagt det ind i min
Få mere synlighed! Vejledningshæfte
 Få mere synlighed! Vejledningshæfte Vejledning Sådan kommer dit arrangement på OplevRudersdal.dk Dit arrangement kommer nemt og enkelt på www.oplevrudersdal.dk ved at du opretter dit arrangement på hjemmesiden.
Få mere synlighed! Vejledningshæfte Vejledning Sådan kommer dit arrangement på OplevRudersdal.dk Dit arrangement kommer nemt og enkelt på www.oplevrudersdal.dk ved at du opretter dit arrangement på hjemmesiden.
Ikke-lineære funktioner
 I elevernes arbejde med funktioner på tidligere klassetrin har hovedvægten ligget på sammenhænge, der kan beskrives med lineære funktioner. Dette kapitel berører ligefrem proportionalitet og stykkevist
I elevernes arbejde med funktioner på tidligere klassetrin har hovedvægten ligget på sammenhænge, der kan beskrives med lineære funktioner. Dette kapitel berører ligefrem proportionalitet og stykkevist
Arbejdsmiljøgruppens problemløsning
 Arbejdsmiljøgruppens problemløsning En systematisk fremgangsmåde for en arbejdsmiljøgruppe til løsning af arbejdsmiljøproblemer Indledning Fase 1. Problemformulering Fase 2. Konsekvenser af problemet Fase
Arbejdsmiljøgruppens problemløsning En systematisk fremgangsmåde for en arbejdsmiljøgruppe til løsning af arbejdsmiljøproblemer Indledning Fase 1. Problemformulering Fase 2. Konsekvenser af problemet Fase
Opg. 1. Cylinder. Opg. 1 spm. a løses i hånden. Cylinderens radius er 10 cm og keglen er 20 cm høj. Paraboloidens profil kan beskrives med ligningen
 Opg. 1 spm. a løses i hånden. Cylinderens radius er 10 cm og keglen er 20 cm høj. Paraboloidens profil kan beskrives med ligningen Opg. 1 a) Bestem de funktioner h(t), der beskriver vandhøjden i beholderen,
Opg. 1 spm. a løses i hånden. Cylinderens radius er 10 cm og keglen er 20 cm høj. Paraboloidens profil kan beskrives med ligningen Opg. 1 a) Bestem de funktioner h(t), der beskriver vandhøjden i beholderen,
VisiRegn: En e-bro mellem regning og algebra
 Artikel i Matematik nr. 2 marts 2001 VisiRegn: En e-bro mellem regning og algebra Inge B. Larsen Siden midten af 80 erne har vi i INFA-projektet arbejdet med at udvikle regne(arks)programmer til skolens
Artikel i Matematik nr. 2 marts 2001 VisiRegn: En e-bro mellem regning og algebra Inge B. Larsen Siden midten af 80 erne har vi i INFA-projektet arbejdet med at udvikle regne(arks)programmer til skolens
Vejledning til Photofiltre nr.129 Side 1
 Side 1 Til denne vejledning laver vi lidt ekstra ved hvert billede. Vi skal bruge det der hedder Image Curl. Vi skal altså bruge en fil der kan hentes på min hjemmeside under Photofiltre 7 og nederst på
Side 1 Til denne vejledning laver vi lidt ekstra ved hvert billede. Vi skal bruge det der hedder Image Curl. Vi skal altså bruge en fil der kan hentes på min hjemmeside under Photofiltre 7 og nederst på
Programmering C. Casper Hermansen Klasse 2.7 Programmering C. Navn: Casper Hermansen. Klasse: 2.7. Fag: Programmering C
 Navn: Casper Hermansen Klasse: 2.7 Fag: Skole: Roskilde tekniske gymnasium Side 1 af 16 Indhold Indledende aktivitet... 3 Projektbeskrivelse:... 3 Krav:... 3 Målgrupper:... 3 Problemformulering:... 3 Diskussion
Navn: Casper Hermansen Klasse: 2.7 Fag: Skole: Roskilde tekniske gymnasium Side 1 af 16 Indhold Indledende aktivitet... 3 Projektbeskrivelse:... 3 Krav:... 3 Målgrupper:... 3 Problemformulering:... 3 Diskussion
Brugervejledning. til. Landsforeningen Danske Folkedanseres. Medlemssystem (For dansere)
 Brugervejledning til Landsforeningen Danske Folkedanseres Medlemssystem (For dansere) 1 Indhold Første gang systemet skal have at vide, hvem du er.... 3 Log Ud - VIGTIGT!... 4 Log ind når du har oprettet
Brugervejledning til Landsforeningen Danske Folkedanseres Medlemssystem (For dansere) 1 Indhold Første gang systemet skal have at vide, hvem du er.... 3 Log Ud - VIGTIGT!... 4 Log ind når du har oprettet
Læsevejledning til resultater på regionsplan
 Læsevejledning til resultater på regionsplan Indhold 1. Overblik... 2 2. Sammenligninger... 2 3. Hvad viser figuren?... 3 4. Hvad viser tabellerne?... 5 5. Eksempler på typiske spørgsmål til tabellerne...
Læsevejledning til resultater på regionsplan Indhold 1. Overblik... 2 2. Sammenligninger... 2 3. Hvad viser figuren?... 3 4. Hvad viser tabellerne?... 5 5. Eksempler på typiske spørgsmål til tabellerne...
Ligninger med reelle løsninger
 Ligninger med reelle løsninger, marts 2008, Kirsten Rosenkilde 1 Ligninger med reelle løsninger Når man løser ligninger, er der nogle standardmetoder som er vigtige at kende. Vurdering af antallet af løsninger
Ligninger med reelle løsninger, marts 2008, Kirsten Rosenkilde 1 Ligninger med reelle løsninger Når man løser ligninger, er der nogle standardmetoder som er vigtige at kende. Vurdering af antallet af løsninger
Opgavesæt 12 21/01-2009. Laura Pettrine Madsen Uden hjælpemidler. skitse af grafen for f(x).
 Uden hjælpemidler Opgave 8.00 Funktionen f(x) er bestemt ved skitse af grafen for f(x). f ( x) = x 3 4x. På figuren ses en Grafen skærer førsteaksen i punkterne P(,0), O(0,0) og Q(,0). Sammen med førsteaksen
Uden hjælpemidler Opgave 8.00 Funktionen f(x) er bestemt ved skitse af grafen for f(x). f ( x) = x 3 4x. På figuren ses en Grafen skærer førsteaksen i punkterne P(,0), O(0,0) og Q(,0). Sammen med førsteaksen
Geometriopgaver. Pladeudfoldning Geometriopgaver - 1 -
 2009 Geometriopgaver Pladeudfoldning Geometriopgaver Teknisk Isolering AMUSYD 06 02 2009-1 - Indholdsfortegnelse OPGAVE 1 - A, B, C, D.... 3 OPGAVE 1 A REKTANGEL DEL VED FORSØG... 3 OPGAVE 1 B PARALLELOGRAM...
2009 Geometriopgaver Pladeudfoldning Geometriopgaver Teknisk Isolering AMUSYD 06 02 2009-1 - Indholdsfortegnelse OPGAVE 1 - A, B, C, D.... 3 OPGAVE 1 A REKTANGEL DEL VED FORSØG... 3 OPGAVE 1 B PARALLELOGRAM...
Renteregning.notebook Hjemly 09/10. Rentesregning. Bank og sparekasse
 Rentesregning Lån og långivning Kapital, rentefod og rentedage Hvordan regnes med simpel rente? Andre former for rentesregning Bank og sparekasse Banker og sparekasser har to hovedopgaver: de låner penge
Rentesregning Lån og långivning Kapital, rentefod og rentedage Hvordan regnes med simpel rente? Andre former for rentesregning Bank og sparekasse Banker og sparekasser har to hovedopgaver: de låner penge
Spørgeskema på HVAL.DK
 Skive, d. 24-05-2006 Journal nr. 7.5.286 Spørgeskema på HVAL.DK Et webbaseret værktøj udviklet af Programdatateket i Viborg amt i forbindelse med Videndeling. Indholdsfortegnelse INDHOLDSFORTEGNELSE 2
Skive, d. 24-05-2006 Journal nr. 7.5.286 Spørgeskema på HVAL.DK Et webbaseret værktøj udviklet af Programdatateket i Viborg amt i forbindelse med Videndeling. Indholdsfortegnelse INDHOLDSFORTEGNELSE 2
1. Læsestærke børn i Vores Skole
 1. Læsestærke børn i Vores Skole Vores forældre kan lære at styrke børnenes læsefærdigheder Forældre kan bruges endnu mere til at fremme børnenes læsefærdigheder. Vi kan give dem gode råd og brugbare redskaber
1. Læsestærke børn i Vores Skole Vores forældre kan lære at styrke børnenes læsefærdigheder Forældre kan bruges endnu mere til at fremme børnenes læsefærdigheder. Vi kan give dem gode råd og brugbare redskaber
Løsningsforslag 7. januar 2011
 Løsningsforslag 7. januar 2011 May 9, 2012 Opgave 1 (5%) Funktionen f er givet ved forskriften f(x) = ln(x 2) + x 2. a) Bestem definitionsmængden for f. b) Beregn f (x). a) Definitionsmængden Logaritmen
Løsningsforslag 7. januar 2011 May 9, 2012 Opgave 1 (5%) Funktionen f er givet ved forskriften f(x) = ln(x 2) + x 2. a) Bestem definitionsmængden for f. b) Beregn f (x). a) Definitionsmængden Logaritmen
Matematik A Vejledende opgaver 5 timers prøven
 Højere Teknisk Eksamen 007 Matematik A Vejledende opgaver 5 timers prøven Undervisningsministeriet Prøvens varighed er 5 timer. Opgavebesvarelsen skal dokumenteres/begrundes. Opgavebesvarelsen skal udformes
Højere Teknisk Eksamen 007 Matematik A Vejledende opgaver 5 timers prøven Undervisningsministeriet Prøvens varighed er 5 timer. Opgavebesvarelsen skal dokumenteres/begrundes. Opgavebesvarelsen skal udformes
Projekt 4.8. Kerners henfald (Excel)
 Projekt.8. Kerners henfald (Excel) Når radioaktive kerner henfalder under udsendelse af stråling, sker henfaldet I følge kvantemekanikken helt spontant, dvs. rent tilfældigt uden nogen påviselig årsag.
Projekt.8. Kerners henfald (Excel) Når radioaktive kerner henfalder under udsendelse af stråling, sker henfaldet I følge kvantemekanikken helt spontant, dvs. rent tilfældigt uden nogen påviselig årsag.
sammenhänge for C-niveau i stx 2013 Karsten Juul
 LineÄre sammenhänge for C-niveau i stx y 0,5x 2,5 203 Karsten Juul : OplÄg om lineäre sammenhänge 2 Ligning for lineär sammenhäng 2 3 Graf for lineär sammenhäng 2 4 Bestem y når vi kender x 3 5 Bestem
LineÄre sammenhänge for C-niveau i stx y 0,5x 2,5 203 Karsten Juul : OplÄg om lineäre sammenhänge 2 Ligning for lineär sammenhäng 2 3 Graf for lineär sammenhäng 2 4 Bestem y når vi kender x 3 5 Bestem
Videopoint. Vejledning til simpelt brug
 Videopoint Vejledning til simpelt brug 0. Indledning Videopoint er et smart værktøj, der gør fysikstuderende i stand til, nærmest legende let, at analysere bevægelser af forskellige objekter. Eksempelvis
Videopoint Vejledning til simpelt brug 0. Indledning Videopoint er et smart værktøj, der gør fysikstuderende i stand til, nærmest legende let, at analysere bevægelser af forskellige objekter. Eksempelvis
Lektion 6 Logaritmefunktioner
 Lektion 6 Logaritmefunktioner Den naturlige logaritmefunktion Andre logaritmefunktioner log() Regneregler Integration ln() =, ln(e) = ln(a b) = ln(a) + ln(b) ln(a r ) = r ln(a) d = ln + C En berømt grænseværdi
Lektion 6 Logaritmefunktioner Den naturlige logaritmefunktion Andre logaritmefunktioner log() Regneregler Integration ln() =, ln(e) = ln(a b) = ln(a) + ln(b) ln(a r ) = r ln(a) d = ln + C En berømt grænseværdi
penge, rente og valuta
 brikkerne til regning & matematik penge, rente og valuta F+E+D preben bernitt brikkerne til regning & matematik penge, rente og valuta D ISBN: 978-87-92488-14-5 2. udgave som E-bog 2012 by bernitt-matematik.dk
brikkerne til regning & matematik penge, rente og valuta F+E+D preben bernitt brikkerne til regning & matematik penge, rente og valuta D ISBN: 978-87-92488-14-5 2. udgave som E-bog 2012 by bernitt-matematik.dk
Manual til skinnelayoutprogram
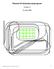 Manual til skinnelayoutprogram Version 1.1 13. marts 2005 Skinnelayoutmanual af 13. marts 2005, version 1.1 1 Indholdsfortegnelse 1. Indledning... 3 2. Oversigt over startbillede... 3 3 Menulinie... 4
Manual til skinnelayoutprogram Version 1.1 13. marts 2005 Skinnelayoutmanual af 13. marts 2005, version 1.1 1 Indholdsfortegnelse 1. Indledning... 3 2. Oversigt over startbillede... 3 3 Menulinie... 4
Gennemførelse. Lektionsplan til Let s Speak! Lektion 1-2
 Gennemførelse Lektionsplan til Let s Speak! Lektion 1-2 Start: Læreren introducerer læringsmålene for undervisningsforløbet og sikrer sig elevernes forståelse af disse måske skal nogle af dem yderligere
Gennemførelse Lektionsplan til Let s Speak! Lektion 1-2 Start: Læreren introducerer læringsmålene for undervisningsforløbet og sikrer sig elevernes forståelse af disse måske skal nogle af dem yderligere
Velkommen til 2. omgang af IT for let øvede
 Velkommen til 2. omgang af IT for let øvede I dag Hjemmeopgave 1 Næste hjemmeopgave Eventuelt vinduer igen Mapper og filer på USB-stik Vi skal hertil grundet opgave 2 Internet Pause (og det bliver nok
Velkommen til 2. omgang af IT for let øvede I dag Hjemmeopgave 1 Næste hjemmeopgave Eventuelt vinduer igen Mapper og filer på USB-stik Vi skal hertil grundet opgave 2 Internet Pause (og det bliver nok
Fakturering kan foretages som en massefakturering eller for en enkelt ordre.
 Fakturering Fakturering kan foretages som en massefakturering eller for en enkelt ordre. Massefakturering. På fanen Dagligt findes mappen Faktura. Herunder kan man vælge mellem Dagligt, Ugentligt, 14 dage
Fakturering Fakturering kan foretages som en massefakturering eller for en enkelt ordre. Massefakturering. På fanen Dagligt findes mappen Faktura. Herunder kan man vælge mellem Dagligt, Ugentligt, 14 dage
Talregning. Aktivitet Emne Klassetrin Side. Indledning til VisiRegn ideer 1-7 2 Oversigt over VisiRegn ideer 1-7 3
 VisiRegn ideer 1 Talregning Inge B. Larsen ibl@dpu.dk INFA juli 2001 Indhold: Aktivitet Emne Klassetrin Side Indledning til VisiRegn ideer 1-7 2 Oversigt over VisiRegn ideer 1-7 3 Vejledning til Talregning
VisiRegn ideer 1 Talregning Inge B. Larsen ibl@dpu.dk INFA juli 2001 Indhold: Aktivitet Emne Klassetrin Side Indledning til VisiRegn ideer 1-7 2 Oversigt over VisiRegn ideer 1-7 3 Vejledning til Talregning
Geometri med Geometer I
 f Frans Kappel Øvre, Morsø Gymnasium Geometri med Geometer I Markeringspil: Klik på et objekt (punkt, linje, cirkel) for at markere det. Hvis du trykker Shift samtidig kan du markere flere objekter eller
f Frans Kappel Øvre, Morsø Gymnasium Geometri med Geometer I Markeringspil: Klik på et objekt (punkt, linje, cirkel) for at markere det. Hvis du trykker Shift samtidig kan du markere flere objekter eller
brøker basis+g brikkerne til regning & matematik preben bernitt
 brikkerne til regning & matematik brøker basis+g preben bernitt brikkerne til regning & matematik brøker G ISBN: 978-87-92488-04 06 2. udgave som E-bog 202 by bernitt-matematik.dk Denne bog er beskyttet
brikkerne til regning & matematik brøker basis+g preben bernitt brikkerne til regning & matematik brøker G ISBN: 978-87-92488-04 06 2. udgave som E-bog 202 by bernitt-matematik.dk Denne bog er beskyttet
starten på rådgivningen
 p l a n f o r 2.1 starten på rådgivningen Ved det første møde bør der som minimum afsættes 40 minutter. Denne vejledning retter sig mod den første indledende del af dette møde. Her er målet at skabe en
p l a n f o r 2.1 starten på rådgivningen Ved det første møde bør der som minimum afsættes 40 minutter. Denne vejledning retter sig mod den første indledende del af dette møde. Her er målet at skabe en
LUP læsevejledning til regionsrapporter
 Indhold 1. Overblik... 2 2. Sammenligninger... 2 3. Hvad viser figuren?... 3 4. Hvad viser tabellerne?... 5 5. Eksempler på typiske spørgsmål til tabellerne... 6 Øvrigt materiale Baggrund og metode for
Indhold 1. Overblik... 2 2. Sammenligninger... 2 3. Hvad viser figuren?... 3 4. Hvad viser tabellerne?... 5 5. Eksempler på typiske spørgsmål til tabellerne... 6 Øvrigt materiale Baggrund og metode for
APV og trivsel 2015. APV og trivsel 2015 1
 APV og trivsel 2015 APV og trivsel 2015 1 APV og trivsel 2015 I efteråret 2015 skal alle arbejdspladser i Frederiksberg Kommune udarbejde en ny grundlæggende APV og gennemføre en trivselsundersøgelse.
APV og trivsel 2015 APV og trivsel 2015 1 APV og trivsel 2015 I efteråret 2015 skal alle arbejdspladser i Frederiksberg Kommune udarbejde en ny grundlæggende APV og gennemføre en trivselsundersøgelse.
Picasa Web. En ressource i SkoleIntra. Version: August 2012
 Picasa Web En ressource i SkoleIntra Version: August 2012 Indholdsfortegnelse Hvad er PicasaWeb?...4 Kom på!...5 Google-konto...5 Når du er logget ind: Indstillinger...5 Når du er logget ind: Upload...6
Picasa Web En ressource i SkoleIntra Version: August 2012 Indholdsfortegnelse Hvad er PicasaWeb?...4 Kom på!...5 Google-konto...5 Når du er logget ind: Indstillinger...5 Når du er logget ind: Upload...6
Opgave 1: Log ind og skift password m.m.
 Opgaver i Typo3 Opgave 1: Log ind og skift password m.m.... 2 Opgave 2: Opret flere filmapper og upload diverse filer... 3 Opgave 3: Opret en ny side som denne her... 4 Opgave 4: Opret fotogallerier med
Opgaver i Typo3 Opgave 1: Log ind og skift password m.m.... 2 Opgave 2: Opret flere filmapper og upload diverse filer... 3 Opgave 3: Opret en ny side som denne her... 4 Opgave 4: Opret fotogallerier med
MATEMATIK C. Videooversigt
 MATEMATIK C Videooversigt Deskriptiv statistik... 2 Eksamensrelevant... 2 Eksponentiel sammenhæng... 2 Ligninger... 3 Lineær sammenhæng... 3 Potenssammenhæng... 4 Proportionalitet... 4 Rentesregning...
MATEMATIK C Videooversigt Deskriptiv statistik... 2 Eksamensrelevant... 2 Eksponentiel sammenhæng... 2 Ligninger... 3 Lineær sammenhæng... 3 Potenssammenhæng... 4 Proportionalitet... 4 Rentesregning...
Differential- regning
 Differential- regning 1 del () (1) 006 Karsten Juul Indhold 1 Funktionsværdi, graf og tilvækst1 Differentialkvotient og tangent8 3 Formler for differentialkvotient16 4 Opgaver med tangent 5 Væksthastighed5
Differential- regning 1 del () (1) 006 Karsten Juul Indhold 1 Funktionsværdi, graf og tilvækst1 Differentialkvotient og tangent8 3 Formler for differentialkvotient16 4 Opgaver med tangent 5 Væksthastighed5
Projekt 10.1 Er der huller i Euklids argumentation? Et moderne aksiomsystem (især for A)
 Projekt 10.1 Er der huller i Euklids argumentation? Et moderne aksiomsystem (især for A) Indhold Introduktion... 2 Hilberts 16 aksiomer Et moderne, konsistent og fuldstændigt aksiomsystem for geometri...
Projekt 10.1 Er der huller i Euklids argumentation? Et moderne aksiomsystem (især for A) Indhold Introduktion... 2 Hilberts 16 aksiomer Et moderne, konsistent og fuldstændigt aksiomsystem for geometri...
Delmængder af Rummet
 Delmængder af Rummet Frank Nasser 11. juli 2011 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold 1 Introduktion
Delmængder af Rummet Frank Nasser 11. juli 2011 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold 1 Introduktion
KL S EFFEKTMÅLINGS- REDSKAB TIL KONTROLOMRÅDET
 KL FEBRUAR 2016 TEKNISK VEJLEDNING KL S EFFEKTMÅLINGS- REDSKAB TIL KONTROLOMRÅDET OFFICE VERSION 2010 OG 2013 2 VEJLEDNING I ANVENDELSE AF VÆRKTØJ TIL EFFEKTMÅLING INDHOLD INDHOLD INDLEDNING A. TEKNISKE
KL FEBRUAR 2016 TEKNISK VEJLEDNING KL S EFFEKTMÅLINGS- REDSKAB TIL KONTROLOMRÅDET OFFICE VERSION 2010 OG 2013 2 VEJLEDNING I ANVENDELSE AF VÆRKTØJ TIL EFFEKTMÅLING INDHOLD INDHOLD INDLEDNING A. TEKNISKE
PERSONALE- OG LEDELSESPOLITIKKEN SAT I SPIL
 114659_Manual_250x250 17/10/03 13:38 Side 1 Kunde & Co. Frederiksholms Kanal 6 1220 København K Tlf: 33 92 40 49 perst@perst.dk www.perst.dk Løngangstræde 25, 4. 1468 København K Tlf: 38 17 81 00 cfu@cfu-net.dk
114659_Manual_250x250 17/10/03 13:38 Side 1 Kunde & Co. Frederiksholms Kanal 6 1220 København K Tlf: 33 92 40 49 perst@perst.dk www.perst.dk Løngangstræde 25, 4. 1468 København K Tlf: 38 17 81 00 cfu@cfu-net.dk
Årsafslutning i SummaSummarum 4
 Årsafslutning i SummaSummarum 4 Som noget helt nyt kan du i SummaSummarum 4 oprette et nyt regnskabsår uden, at det gamle (eksisterende) først skal afsluttes. Dette betyder, at det nu er muligt at bogføre
Årsafslutning i SummaSummarum 4 Som noget helt nyt kan du i SummaSummarum 4 oprette et nyt regnskabsår uden, at det gamle (eksisterende) først skal afsluttes. Dette betyder, at det nu er muligt at bogføre
FRA INDKØB TIL SALG...
 Fra indkøb til salg Kalkulere betyder beregne. Dette hæfte handler om at beregne - kalkulere - Hvor meget der skal bruges til en bestemt opskrift - Hvor meget svind der er på råvarerne - Hvad varerne koster
Fra indkøb til salg Kalkulere betyder beregne. Dette hæfte handler om at beregne - kalkulere - Hvor meget der skal bruges til en bestemt opskrift - Hvor meget svind der er på råvarerne - Hvad varerne koster
Module 2: Beskrivende Statistik
 Forskningsenheden for Statistik ST01: Elementær Statistik Bent Jørgensen og Hans Chr. Petersen Module 2: Beskrivende Statistik 2.1 Histogrammer og søjlediagrammer......................... 1 2.2 Sammenfatning
Forskningsenheden for Statistik ST01: Elementær Statistik Bent Jørgensen og Hans Chr. Petersen Module 2: Beskrivende Statistik 2.1 Histogrammer og søjlediagrammer......................... 1 2.2 Sammenfatning
Sorteringsmaskinen. Hej med dig!
 Sorteringsmaskinen Hej med dig! Jeg er Thomas Tandstærk, og jeg ved en masse om teknik og natur. Jeg skal lære dig noget om at lave forsøg og undersøgelser. Når klassen er færdig får I et flot diplom!
Sorteringsmaskinen Hej med dig! Jeg er Thomas Tandstærk, og jeg ved en masse om teknik og natur. Jeg skal lære dig noget om at lave forsøg og undersøgelser. Når klassen er færdig får I et flot diplom!
Rumfangs. umfangsberegning. Rumfang af en cylinder. På illustrationen til højre er indtegnet en lineær funktion indenfor et afgrænset interval, hvor
 Rumfang af en cylinder På illustrationen til øjre er indtegnet en lineær funktion indenfor et afgrænset interval, vor 0;. Funktionen () kan skrives på formen: = (vor a er en konstant) Det markerede grå
Rumfang af en cylinder På illustrationen til øjre er indtegnet en lineær funktion indenfor et afgrænset interval, vor 0;. Funktionen () kan skrives på formen: = (vor a er en konstant) Det markerede grå
L: Præsenterer og spørger om han har nogle spørgsmål inden de går i gang. Det har han ikke.
 Bilag 4 Transskription af Per Interviewere: Louise og Katariina L: Louise K: Katariina L: Præsenterer og spørger om han har nogle spørgsmål inden de går i gang. Det har han ikke. L: Vi vil gerne høre lidt
Bilag 4 Transskription af Per Interviewere: Louise og Katariina L: Louise K: Katariina L: Præsenterer og spørger om han har nogle spørgsmål inden de går i gang. Det har han ikke. L: Vi vil gerne høre lidt
Vejledning til personlige funktioner på MIT DANSKE ARK ( eksklusive profil og cv) Indholdsfortegnelse:
 Vejledning til personlige funktioner på MIT DANSKE ARK ( eksklusive profil og cv) Indholdsfortegnelse: Side 2: Nyheder valg til personligt nyhedsbrev, Mine Nyheder og visning på enkeltsider Side 3: Funktionen
Vejledning til personlige funktioner på MIT DANSKE ARK ( eksklusive profil og cv) Indholdsfortegnelse: Side 2: Nyheder valg til personligt nyhedsbrev, Mine Nyheder og visning på enkeltsider Side 3: Funktionen
d Kopier formlen fra celle A3 ned i kolonne A. Kopier formlen fra celle C3 ned i kolonne C. Undersøg, hvad der sker med formlen, når den kopieres.
 KOPIARK 17 # ligninger og formler i excel 2007, 1 1 Du skal lave et regneark, som kan bruges til at løse ligningen 5 x 11 = 7 + 3 x. a Lav et regneark som vist. HUSK: Gør en kolonne bredere Man kan gøre
KOPIARK 17 # ligninger og formler i excel 2007, 1 1 Du skal lave et regneark, som kan bruges til at løse ligningen 5 x 11 = 7 + 3 x. a Lav et regneark som vist. HUSK: Gør en kolonne bredere Man kan gøre
Grafteori, Kirsten Rosenkilde, september 2007 1. Grafteori
 Grafteori, Kirsten Rosenkilde, september 007 1 1 Grafteori Grafteori Dette er en kort introduktion til de vigtigste begreber i grafteori samt eksempler på opgavetyper inden for emnet. 1.1 Definition af
Grafteori, Kirsten Rosenkilde, september 007 1 1 Grafteori Grafteori Dette er en kort introduktion til de vigtigste begreber i grafteori samt eksempler på opgavetyper inden for emnet. 1.1 Definition af
Matematik. på Åbent VUC. Trin 2 Xtra eksempler. Trigonometri, boksplot, potensfunktioner, to ligninger med to ubekendte
 Matematik på Åbent VUC Trin Xtra eksempler Trigonometri, boksplot, potensfunktioner, to ligninger med to ubekendte Trigonometri Sinus og cosinus Til alle vinkler hører der to tal, som kaldes cosinus og
Matematik på Åbent VUC Trin Xtra eksempler Trigonometri, boksplot, potensfunktioner, to ligninger med to ubekendte Trigonometri Sinus og cosinus Til alle vinkler hører der to tal, som kaldes cosinus og
Annemette Søgaard Hansen/www.dinwebvejleder.dk
 Google Docs Præsentationer Indholdsfortegnelse Værktøjer... Side 3 Menuer... Side 8 Opgave... Side 13 Få adgang til filerne fra din computer... Side 21 Vejledende løsning... Side 22 GoogleDocs Præsentationer
Google Docs Præsentationer Indholdsfortegnelse Værktøjer... Side 3 Menuer... Side 8 Opgave... Side 13 Få adgang til filerne fra din computer... Side 21 Vejledende løsning... Side 22 GoogleDocs Præsentationer
Differentiation af Logaritmer
 Differentiation af Logaritmer Frank Nasser 11. juli 2011 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold
Differentiation af Logaritmer Frank Nasser 11. juli 2011 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold
Vejledning i brug af Finale NotePad 2008 Pædagogisk konsulent Niels Rebsdorf, CFU i Vejle, UCL
 Vejledning i brug af Finale NotePad 2008 Pædagogisk konsulent Niels Rebsdorf, CFU i Vejle, UCL Når programmet er pakket ud og installeret, er du klar. Når du åbner programmet, hjælper Document Setup Wizard
Vejledning i brug af Finale NotePad 2008 Pædagogisk konsulent Niels Rebsdorf, CFU i Vejle, UCL Når programmet er pakket ud og installeret, er du klar. Når du åbner programmet, hjælper Document Setup Wizard
Til underviseren. I slutningen af hver skrivelse er der plads til, at du selv kan udfylde med konkrete eksempler fra undervisningen.
 Til underviseren Her er nogle små skrivelser med information til forældrene om Perspekt 3. Du kan bruge dem til løbende at lægge på Forældreintra eller lignende efterhånden som undervisningen skrider frem.
Til underviseren Her er nogle små skrivelser med information til forældrene om Perspekt 3. Du kan bruge dem til løbende at lægge på Forældreintra eller lignende efterhånden som undervisningen skrider frem.
Målstyret undervisning og tegn på læring
 Målstyret undervisning og tegn på læring Målstyret undervisning Læringsmål er mål for, hvad eleverne skal kunne - altså mål for elevernes læringsudbytte. I målstyret undervisning skal du som lærer altid
Målstyret undervisning og tegn på læring Målstyret undervisning Læringsmål er mål for, hvad eleverne skal kunne - altså mål for elevernes læringsudbytte. I målstyret undervisning skal du som lærer altid
Bordkort nr. 1 & 7. Sværhedsgrad 1 Ingen kendskab. Bordkort nr. 2 & 3. Sværhedsgrad 2 Lidt kenskab. Bordkort nr. 4 & 6
 SVÆRHEDSGRAD Der er i denne e-bog 8 bordopsætninger, som indeholder 4 sværhedsgrader. Sværhedsgrad 1 er den letteste, og 4 den sværeste. Dog skal det siges, at alle, som er let øvede inden for kort og
SVÆRHEDSGRAD Der er i denne e-bog 8 bordopsætninger, som indeholder 4 sværhedsgrader. Sværhedsgrad 1 er den letteste, og 4 den sværeste. Dog skal det siges, at alle, som er let øvede inden for kort og
Vejret Lærervejledning og opgaver 5.-6. klasse
 Vejret Introduktion De to af delemnerne til vejret - Luftfugtighed og Nedbør skal laves på skolen. Luftfugtighed fordi opgaverne kræver en fryser i nærheden for at kunne laves. Nedbør skal laves på skolen,
Vejret Introduktion De to af delemnerne til vejret - Luftfugtighed og Nedbør skal laves på skolen. Luftfugtighed fordi opgaverne kræver en fryser i nærheden for at kunne laves. Nedbør skal laves på skolen,
Matematisk modellering og numeriske metoder. Lektion 18
 Matematisk modellering numeriske metoder Lektion 18 Morten Grud Rasmussen 12. november, 2013 1 Numeriske metoder til førsteordens ODE er [Bens afsnit 21.1 side 898] 1.1 Euler-metoden Vi stiftede allerede
Matematisk modellering numeriske metoder Lektion 18 Morten Grud Rasmussen 12. november, 2013 1 Numeriske metoder til førsteordens ODE er [Bens afsnit 21.1 side 898] 1.1 Euler-metoden Vi stiftede allerede
KOM/IT DESIGN MANUAL AF SAF
 10/28/2015 KOM/IT DESIGN MANUAL AF SAF Af Nichlas, Lizette, Jake og jonas indholdsfortegnelse Inledning... 3 Problemformulering... 3 Om SAF.... 3 Brainstorming for SAF... 3 Valg af idé.... 4 Færdige produkt...
10/28/2015 KOM/IT DESIGN MANUAL AF SAF Af Nichlas, Lizette, Jake og jonas indholdsfortegnelse Inledning... 3 Problemformulering... 3 Om SAF.... 3 Brainstorming for SAF... 3 Valg af idé.... 4 Færdige produkt...
Alf og Alfabetet. - lær bogstaver, ord og begreber. Vejledning
 Alf og Alfabetet - lær bogstaver, ord og begreber Vejledning Indholdsfortegnelse Forord 3 Sådan navigerer du rundt i Alf og Alfabetet 4 A - Lær bogstaverne 4 L - Stav ordet 5 F - Skriv ordet 5 E - Kombiner
Alf og Alfabetet - lær bogstaver, ord og begreber Vejledning Indholdsfortegnelse Forord 3 Sådan navigerer du rundt i Alf og Alfabetet 4 A - Lær bogstaverne 4 L - Stav ordet 5 F - Skriv ordet 5 E - Kombiner
IKON BETEGNELSE INDLAGT SKAL TILFØJES
 Projekt Sketchbook Tænk på Sketchbook, som en skitsebog eller mappe, på dit skrivebord. Forestil dig at du vil designe en ny quilt. Når du navngiver dit nye projekt, startes der med en tom skitsebog. Mens
Projekt Sketchbook Tænk på Sketchbook, som en skitsebog eller mappe, på dit skrivebord. Forestil dig at du vil designe en ny quilt. Når du navngiver dit nye projekt, startes der med en tom skitsebog. Mens
