Kompendie Komplekse tal
|
|
|
- Erik Andreasen
- 8 år siden
- Visninger:
Transkript
1 Kompedie Komplekse tal Prebe Holm "!#!%$'&($)+*-,. cos(s + t) )0/ si(s + t) Trigoometri er måske ikke så relevat, år ma såda umiddelbart sakker om komplekse tal. Me faktisk avedes de trigoometriske fuktioer til komplekse tal. Jeg har derfor valgt at friske disse to formler op: 98 cos (s + t) = cos (s) cos (t) si (s) si (t) 1'43 si (s + t) = si (s) cos (t) + cos (s) si (t) :<;>=?;@;AA';B&C,ADFE#G#*IHJ&(;@=K*%;LE#MONJDP,QH RS;T* UVXW7YKZ 7[?\ ]^]`_X_a]cbed7_ R x 9f :<;>H0)+ghEcA';@H RS;B&(,ADFE#G%*%HJ&C;T=K*I;i$kjNmlocp4DPEcA',*I;* U VaWqY?Z y C z Im(z) Re(z) 5([sr%tquwvK_a]^xCyz]#bed{_ R x Det komplekse tal z repræseteres på forskellige måder. Bl.a. de rektagulære form: z = x + yi hvor i repræseterer imagiærdele af tallet. i er også defieret som: i = 1
2 7} ~ + 4 oƒj 9 4 e ˆ +ŠI Œ Œ C OŽK # k)+aš =".)0=Kg Et komplekst tal ka også repræseteres polært. Til det skal vi avede ogle adre begreber: œž aÿ Modules af et komplekst tal "svarer til"lægde af e vektor: Modulus af z = x + yi ka skrives: Re(z) + Im(z) x + y œž aÿ ª «s C±³²^ S² µ s«s² s ž ¹ 9 `²²^º? Argumetet for et komplekst tal z svarer egetlig til de vikel φ mellem x-akse og de vektor som repræseterer det komplekse tal. Ma skriver arg(z). Hovedargumetet Arg for z er de værdi af arg(z) som ligger i itervallet 0 < Arg(z) π Argumetet for z arg(z) ka fides ved at tage arcta til imagiærdele delt med reeldele: arg(z) = arcta imagiærdel reeldel Dog skal ma bemærke at tages ka syde og give falske vikler. Derfor skal ma huske at følgede skal være opfyldt: cos θ = Re(z) z si θ = Im(z) z Det er automatisk opfyldt, hvis ma husker på edeståede: arg(z) = arcta imagiærdel reeldel + pπ, p {0, 1, } p = 0, år reeldel og imagiærdel positiv p = 1, år reeldel egativ p =, år reeldel positiv og imagiærdel egativ På de måde fider ma automatisk hovedargumetet for z. œž aÿ X» ¼ C±½ S ž C±³²^ 9¾ + ž Àw«µ s«der er lidt diskussio om, hvorvidt ma skriver de polære form (arg(z) = θ og z = M). De polære form ka skrives såda: eller såda: z = z arg(z) z = M θ z = z e arg(z)i z = Me θi 5
3 Ö Ç Á ÃÄ+ TÃ' m IŽ Ã` Ši %ÅÆ Œ C OŽK # eller for de sags skyld såda: z = z (cos arg(z) + i si arg(z)) z = M(cos θ + i si θ) De sidste her, meer jeg, blot er e omregigsmetode fra polær form til rektagulær form og ikke e egetlig opskrivigsform af det komplekse tal. ÈÊÉ É ËË ÌÍÎÏ ÐÑT QmwË ÒÓÔk T Õ Hvis z = a + bi w = c + di så er: w + z = a + c + (b + d)i z w = a c + (b d)i ØÏ Ë Ë#ÙË` ÌÓÔ ` Õ For multiplikatio ka følgede siges: gag paratesere ud og sæt i lig med -1 dvs. at hvis z = a + bi og w = c + di så er: z w = (a + bi)(c + di) = a c + a di + b ci + b d i = a c b d + (a d + b c)i f ÚÛG#AÄ&?$'EcA$'H, &?$')+*Ê,Q. &C,AE%MÜEm)+Aš¹=Ô.)0=Kgh;TA Hvis z hos z = r og arg(z) = θ me w hos w = s og arg(w) = φ så er z w = r s og arg(z w) = arg(z) + arg(w) Geerelt ka skrives:»t œž œ Ýw SÞ@¾ arg(z w) = arg(z) + arg(w) z w = r s Hvis vektore z og w er repræseteret ved: z = r(cos θ + i si θ) w = s(cos φ + i si φ) ß
4 ~ˆà%Ã4á à CÃ` Ši %ÅÆ Œ C OŽK # så er: Re(z) = r cos θ Im(z) = r si θ Re(w) = s cos φ Im(w) = s si φ produktet af disse to komplekse tal er derfor givet ved: z w = r(cos θ + i si θ) s(cos φ + i si φ) z w = r s((cos θ cos φ si θ si φ) + i(si θ cos φ + cos θ si φ)) Ved brug af de trigoometriske additiosformler fås: z w = r s(cos(θ + φ) + i si(θ + φ)) z w = r s cos(θ + φ) + i r s si(θ + φ) Det ka herudaf ses at modulus for det komplekse tal z w er: z w = r s edvidere ka det også ses at argumetet til z er: arg(z w) = i r s si(θ + φ) â ã ËåäËTË æóôk T Õ For at kue dividere et komplekst tal, skal ma kede til begrebet "komplekst kojugeret". Et kompleks kojugeret tal, er blot et kompleks tal, hvor de imagiære del gages med -1: Hvis w = c + di så er de komplekst kojugerede værdi w = c di. Hvis: så er z w : z = a + bi w = c + di z w = a + bi c + di (a + bi)(c di) = (c + di)(c di) ac + bd + (bc + cd)i = c + d ac + bd bc + cd = c + + d c + d i NB! For regig i C, som ku ivolverer additio, subtraktio, multiplikatio og divisio gælder de samme regler som i R. NB! Brug aldrig uligheder så som i C. ç
5 ê è J+ Jé Å ŽQŠ%Ã'Š L %ÅÆ Œ C OŽK # ëêkìóp Ë ÍíÓÆk T Hvis et komplekst tal opløftes til et adet tal, hvor er et heltal 1 så er z = z z...z Det vil ma blive ret træt af, hvis blot er lidt større ed 5. Derfor ka ma avede flg.: z = z arg(z ) = arg(z) Ma ka jo så altid fide hovedargumetet udfra selve argumetet ved at fide det tal som ved multiplikatio kommer tættes på argumetet, evt. lidt større da hovedargumetet skal ligge mellem π. og π î ïð$w,*%!%;t* I C gælder der, at der for ethvert z 0 har ligige w = z to løsiger: w 1 og w : Hvis z = r(cos θ + i si θ), dvs. z = r, arg(z) = θ så er de to løsiger w 1 = r(cos θ + i si θ ) w = r(cos θ + π + i si θ + π ) Eller på polær form: î 98 ïð$ *ño&(; w 1 = r e i θ w = r e i( θ + π ) Ligige w = z, z givet, har (hvis z ), løsiger. Hvis z = r og arg(z) = θ så: w 1 = r(cos θ + i si θ ) w = r(cos θ + π w = r(cos θ + ( 1)π + i si θ + π ) + i si θ + ( 1)π ) Eller på polær form: w 1 = r e i θ w = r e i( θ + π ) w 3 = r e i( θ + π ) ò
6 õ ó à# +ŠO + ( Ô Œ C# ŠI ŒŠŽ Ã' % ÅcŠ% Ž Ã` Š w k = r e i( θ +(k 1) π ) w = r e i( θ +( 1) π ) ö ä#éñ QÙT QÉÑ æóæ Hvis z = x + yi så er kvadratrode givet ved: hvor A = x+ x +y y x + yi = A + i A Når x + yi er et reelt tal < 0 (dvs. y = 0 og x < 0), så bliver A = 0, og da giver formle ige meig. Derimod ka ma fide z (år z er et reelt egativt tal) ved flg.: z = x hvor x er et positivt reelt tal. = i x ø ã ùk T Ñ Ë`Ó Ï wë Hvis ma ser på de komplekse ekspoetialfuktio, fider ma ud af at de sædvalige idetitet stadig gælder: e z e w = e z+w, z, w C Derfor bliver: arg(e z e w ) = arg(e z ) + arg(e w ) og e z e w = e z e w = e z+w û
Matematik A. Studentereksamen. Forberedelsesmateriale. Forsøg med digitale eksamensopgaver med adgang til internettet.
 Matematik A Studetereksame Forsøg med digitale eksamesopgaver med adgag til iterettet Forberedelsesmateriale Vejledede opgave Forår 0 til stx-a-net MATEMATIK Der skal afsættes 6 timer af holdets sædvalige
Matematik A Studetereksame Forsøg med digitale eksamesopgaver med adgag til iterettet Forberedelsesmateriale Vejledede opgave Forår 0 til stx-a-net MATEMATIK Der skal afsættes 6 timer af holdets sædvalige
MOGENS ODDERSHEDE LARSEN. Komplekse tal
 MOGENS ODDERSHEDE LARSEN Komplekse tal a b. udgave 004 FORORD Dette otat giver e kort idførig i teorie for komplekse tal, regeregler, røddere i polyomier bl.a. med heblik på avedelser ved løsig af lieære
MOGENS ODDERSHEDE LARSEN Komplekse tal a b. udgave 004 FORORD Dette otat giver e kort idførig i teorie for komplekse tal, regeregler, røddere i polyomier bl.a. med heblik på avedelser ved løsig af lieære
Nøgleord og begreber Komplekse tal Test komplekse tal Polære koordinater Kompleks polarform De Moivres sætning
 Oversigt [S] App. I, App. H.1 Nøgleord og begreber Komplekse tal Test komplekse tal Polære koordinater Kompleks polarform De Moivres sætning Test komplekse tal Komplekse rødder Kompleks eksponentialfunktion
Oversigt [S] App. I, App. H.1 Nøgleord og begreber Komplekse tal Test komplekse tal Polære koordinater Kompleks polarform De Moivres sætning Test komplekse tal Komplekse rødder Kompleks eksponentialfunktion
KOMPLEKSE TAL x-klasserne Gammel Hellerup Gymnasium
 KOMPLEKSE TAL x-klassere Gammel Hellerup Gymasium Februar 09 ; Michael Symaski ; m@ghg.dk Idholdsfortegelse E kort historie om imagiært og virkeligt... Tallegemet De Komplekse Tal... Idførelse af realdel
KOMPLEKSE TAL x-klassere Gammel Hellerup Gymasium Februar 09 ; Michael Symaski ; m@ghg.dk Idholdsfortegelse E kort historie om imagiært og virkeligt... Tallegemet De Komplekse Tal... Idførelse af realdel
KOMPLEKSE TAL x-klasserne Gammel Hellerup Gymnasium
 KOMPLEKSE TAL x-klassere Gammel Hellerup Gymasium Idholdsfortegelse E kort historie om imagiært og virkeligt... Tallegemet De Komplekse Tal... Idførelse af realdel og imagiærdel samt i... 8 Subtraktio,
KOMPLEKSE TAL x-klassere Gammel Hellerup Gymasium Idholdsfortegelse E kort historie om imagiært og virkeligt... Tallegemet De Komplekse Tal... Idførelse af realdel og imagiærdel samt i... 8 Subtraktio,
Elementær Matematik. Polynomier
 Elemetær Matematik Polyomier Ole Witt-Hase 2008 Køge Gymasium Idhold 1. Geerelle polyomier...1 2. Divisio med hele tal....1 3. Polyomiers divisio...2 4. Polyomiers rødder....4 5. Bestemmelse af røddere
Elemetær Matematik Polyomier Ole Witt-Hase 2008 Køge Gymasium Idhold 1. Geerelle polyomier...1 2. Divisio med hele tal....1 3. Polyomiers divisio...2 4. Polyomiers rødder....4 5. Bestemmelse af røddere
Komplekse tal Matematik og naturfag i verdensklasse, 2004. Komplekse tal
 Komplekse tl Mtemtik og turfg i verdesklsse, 004 Komplekse tl Dette mterile er ereget til udervisig i mtemtik i gymsiet. Der forudsættes kedsk til løsig f degrdsligiger, trigoometri og e lille smule vektorregig.
Komplekse tl Mtemtik og turfg i verdesklsse, 004 Komplekse tl Dette mterile er ereget til udervisig i mtemtik i gymsiet. Der forudsættes kedsk til løsig f degrdsligiger, trigoometri og e lille smule vektorregig.
Komplekse tal. x 2 = 1 (2) eller
 Komplekse tal En tilegnelse af stoffet i dette appendix kræver at man løser opgaverne Komplekse tal viser sig uhyre nyttige i fysikken, f.eks til løsning af lineære differentialligninger eller beskrivelse
Komplekse tal En tilegnelse af stoffet i dette appendix kræver at man løser opgaverne Komplekse tal viser sig uhyre nyttige i fysikken, f.eks til løsning af lineære differentialligninger eller beskrivelse
Uge 37 opgaver. Opgave 1. Svar : Starter med at definere sup (M) og inf (M) :
 Uge 37 opgaver Opgave Svar : a) Starter med at defiere sup (M) og if (M) : Kigge u på side 3 i kompedie og aveder aksiom (.3) Kotiuitetsaksiomet A = x i x 2 < 2 Note til mig selv : Har søgt på ordet (iequalities)
Uge 37 opgaver Opgave Svar : a) Starter med at defiere sup (M) og if (M) : Kigge u på side 3 i kompedie og aveder aksiom (.3) Kotiuitetsaksiomet A = x i x 2 < 2 Note til mig selv : Har søgt på ordet (iequalities)
Matematikkens mysterier - på et obligatorisk niveau. 7. Ligninger, polynomier og asymptoter
 Matematikkes mysterier - på et obligatorisk iveau af Keeth Hase 7. Ligiger, polyomier og asymptoter Hvad er e asymotote? Og hvorda fides de? 7. Ligiger, polyomier og asymptoter Idhold 7.0 Idledig 7.1 Udsag
Matematikkes mysterier - på et obligatorisk iveau af Keeth Hase 7. Ligiger, polyomier og asymptoter Hvad er e asymotote? Og hvorda fides de? 7. Ligiger, polyomier og asymptoter Idhold 7.0 Idledig 7.1 Udsag
MM501 forelæsningsslides
 MM501 forelæsningsslides uge 37, 2010 Produceret af Hans J. Munkholm 2009 bearbejdet af Jessica Carter 2010 1 Hvad er et komplekst tal? Hvordan regner man med komplekse tal? Man kan betragte udvidelsen
MM501 forelæsningsslides uge 37, 2010 Produceret af Hans J. Munkholm 2009 bearbejdet af Jessica Carter 2010 1 Hvad er et komplekst tal? Hvordan regner man med komplekse tal? Man kan betragte udvidelsen
Løsningsforslag til skriftlig eksamen i Kombinatorik, sandsynlighed og randomiserede algoritmer (DM528)
 Løsigsforslag til skriftlig eksame i Kombiatorik, sadsylighed og radomiserede algoritmer (DM58) Istitut for Matematik & Datalogi Syddask Uiversitet Madag de 3 Jauar 011, kl. 9 13 Alle sædvalige hjælpemidler
Løsigsforslag til skriftlig eksame i Kombiatorik, sadsylighed og radomiserede algoritmer (DM58) Istitut for Matematik & Datalogi Syddask Uiversitet Madag de 3 Jauar 011, kl. 9 13 Alle sædvalige hjælpemidler
Komplekse tal. Mikkel Stouby Petersen 27. februar 2013
 Komplekse tal Mikkel Stouby Petersen 27. februar 2013 1 Motivationen Historien om de komplekse tal er i virkeligheden historien om at fjerne forhindringerne og gøre det umulige muligt. For at se det, vil
Komplekse tal Mikkel Stouby Petersen 27. februar 2013 1 Motivationen Historien om de komplekse tal er i virkeligheden historien om at fjerne forhindringerne og gøre det umulige muligt. For at se det, vil
Introduktion til uligheder
 Itroduktio til uligheder Dette er e itroduktio til ogle basale uligheder om det aritmetiske geemsit, det geometriske geemsit, det harmoiske geemsit og det kvadratiske geemsit. Først skal vi ved fælles
Itroduktio til uligheder Dette er e itroduktio til ogle basale uligheder om det aritmetiske geemsit, det geometriske geemsit, det harmoiske geemsit og det kvadratiske geemsit. Først skal vi ved fælles
Renteformlen. Erik Vestergaard
 Reteformle Erik Vestergaard 2 Erik Vestergaard www.matematikfysik.dk Erik Vestergaard, 2010. Billeder: Forside: istock.com/ilbusca Side 4: istock.com/adresrimagig Desude ege illustratioer. Erik Vestergaard
Reteformle Erik Vestergaard 2 Erik Vestergaard www.matematikfysik.dk Erik Vestergaard, 2010. Billeder: Forside: istock.com/ilbusca Side 4: istock.com/adresrimagig Desude ege illustratioer. Erik Vestergaard
vejer (med fortegn). Det vil vi illustrere visuelt og geometrisk for (2 2)-matricer og (3 3)-matricer i enote 6.
 enote 5 enote 5 Determiater I dee enote ser vi på kvadratiske matricer. Deres type er altså for 2, se enote 4. Det er e fordel, me ikke absolut ødvedigt, at kede determiatbegrebet for (2 2)-matricer på
enote 5 enote 5 Determiater I dee enote ser vi på kvadratiske matricer. Deres type er altså for 2, se enote 4. Det er e fordel, me ikke absolut ødvedigt, at kede determiatbegrebet for (2 2)-matricer på
FUNKTIONER del 1 Funktionsbegrebet Lineære funktioner Eksponentialfunktioner Logaritmefunktioner Rentesregning Indekstal
 FUNKTIONER del Fuktiosbegrebet Lieære fuktioer Ekspoetialfuktioer Logaritmefuktioer Retesregig Idekstal -klassere Gammel Hellerup Gymasium November 08 ; Michael Szymaski ; mz@ghg.dk Idholdsfortegelse FUNKTIONSBEGREBET...
FUNKTIONER del Fuktiosbegrebet Lieære fuktioer Ekspoetialfuktioer Logaritmefuktioer Retesregig Idekstal -klassere Gammel Hellerup Gymasium November 08 ; Michael Szymaski ; mz@ghg.dk Idholdsfortegelse FUNKTIONSBEGREBET...
MOGENS ODDERSHEDE LARSEN. Fourieranalyse
 MOGENS ODDERSHEDE LARSEN Fourieraalyse. udgave 7 FORORD Dette otat giver e kort idførig i teorie for fourierrækker og fouriertrasformatio. Det forudsættes i dette otat, at ma har rådighed over matematiklommeregere
MOGENS ODDERSHEDE LARSEN Fourieraalyse. udgave 7 FORORD Dette otat giver e kort idførig i teorie for fourierrækker og fouriertrasformatio. Det forudsættes i dette otat, at ma har rådighed over matematiklommeregere
Komplekse Tal. 20. november 2009. UNF Odense. Steen Thorbjørnsen Institut for Matematiske Fag Århus Universitet
 Komplekse Tal 20. november 2009 UNF Odense Steen Thorbjørnsen Institut for Matematiske Fag Århus Universitet Fra de naturlige tal til de komplekse Optælling af størrelser i naturen De naturlige tal N (N
Komplekse Tal 20. november 2009 UNF Odense Steen Thorbjørnsen Institut for Matematiske Fag Århus Universitet Fra de naturlige tal til de komplekse Optælling af størrelser i naturen De naturlige tal N (N
Den flerdimensionale normalfordeling
 De flerdimesioale ormalfordelig Stokastiske vektorer Ved e stokastisk vektor skal vi forstå e vektor, hvor de ekelte kompoeter er sædvalige stokastiske variable. For de stokastiske vektor Y = Y,..., Y
De flerdimesioale ormalfordelig Stokastiske vektorer Ved e stokastisk vektor skal vi forstå e vektor, hvor de ekelte kompoeter er sædvalige stokastiske variable. For de stokastiske vektor Y = Y,..., Y
Komplekse tal. Mike Auerbach. Tornbjerg Gymnasium, Odense 2015
 Komplekse tal Mike Auerbach Tornbjerg Gymnasium, Odense 2015 Indhold 1 Vinkelmål og trigonometriske funktioner 2 1.1 Radianer................................................ 2 1.2 Cosinus og sinus som
Komplekse tal Mike Auerbach Tornbjerg Gymnasium, Odense 2015 Indhold 1 Vinkelmål og trigonometriske funktioner 2 1.1 Radianer................................................ 2 1.2 Cosinus og sinus som
- et værktøj til fejlrettende QR-koder. Projekt 0.3 Galois-legemerne. Indhold. Hvad er matematik? A, i-bog
 Projekt 0.3 Galois-legemere GF é ëp û - et værktøj til fejlrettede QR-koder Idhold De karakteristiske egeskaber ved de tre mest almidelige talsystemer, og... De kommutative, associative og distributive
Projekt 0.3 Galois-legemere GF é ëp û - et værktøj til fejlrettede QR-koder Idhold De karakteristiske egeskaber ved de tre mest almidelige talsystemer, og... De kommutative, associative og distributive
og Fermats lille sætning
 Projekter: Kaitel 0. Projekt 0. Modulo-regig, restklassegruer og Fermats lille sætig Projekt 0. Modulo-regig, restklassegruere ( { 0 }, ) og Fermats lille sætig Vi aveder moduloregig og restklasser mage
Projekter: Kaitel 0. Projekt 0. Modulo-regig, restklassegruer og Fermats lille sætig Projekt 0. Modulo-regig, restklassegruere ( { 0 }, ) og Fermats lille sætig Vi aveder moduloregig og restklasser mage
Komplekse tal og algebraens fundamentalsætning.
 Komplekse tal og algebraens fundamentalsætning. Michael Knudsen 10. oktober 2005 1 Ligningsløsning Lad N = {0,1,2,...} betegne mængden af de naturlige tal og betragt ligningen ax + b = 0, a,b N,a 0. Findes
Komplekse tal og algebraens fundamentalsætning. Michael Knudsen 10. oktober 2005 1 Ligningsløsning Lad N = {0,1,2,...} betegne mængden af de naturlige tal og betragt ligningen ax + b = 0, a,b N,a 0. Findes
Analyse 1, Prøve maj 2009
 Aalyse, Prøve 5. maj 009 Alle hevisiger til TL er hevisiger til Kalkulus (006, Tom Lidstrøm). Direkte opgavehevisiger til Kalkulus er agivet med TLO, ellers er alle hevisiger til steder i de overordede
Aalyse, Prøve 5. maj 009 Alle hevisiger til TL er hevisiger til Kalkulus (006, Tom Lidstrøm). Direkte opgavehevisiger til Kalkulus er agivet med TLO, ellers er alle hevisiger til steder i de overordede
Projekt 1.3 Brydningsloven
 Projekt 1.3 Brydigslove Når e bølge, fx e lysbølge, rammer e græseflade mellem to stoffer, vil bølge ormalt blive spaltet i to: Noget af bølge kastes tilbage (spejlig), hvor udfaldsvikle u er de samme
Projekt 1.3 Brydigslove Når e bølge, fx e lysbølge, rammer e græseflade mellem to stoffer, vil bølge ormalt blive spaltet i to: Noget af bølge kastes tilbage (spejlig), hvor udfaldsvikle u er de samme
og Fermats lille Projekt 0.4 Modulo-regning, restklassegrupperne sætning ..., 44, 20,4,28,52,... Hvad er matematik? 3 ISBN
 Projekt 0.4 Modulo-regig, restklassegruppere sætig ( p 0, ) og Fermats lille Vi aveder moduloregig og restklasser mage gage om dage, emlig år vi taler om tid, om hvad klokke er, om hvor lag tid der er
Projekt 0.4 Modulo-regig, restklassegruppere sætig ( p 0, ) og Fermats lille Vi aveder moduloregig og restklasser mage gage om dage, emlig år vi taler om tid, om hvad klokke er, om hvor lag tid der er
Noter om polynomier, Kirsten Rosenkilde, Marts Polynomier
 Noter om polyomier, Kirste Rosekilde, Marts 2006 1 Polyomier Disse oter giver e kort itroduktio til polyomier, og de fleste sætiger æves ude bevis. Udervejs er der forholdsvis emme opgaver, mes der til
Noter om polyomier, Kirste Rosekilde, Marts 2006 1 Polyomier Disse oter giver e kort itroduktio til polyomier, og de fleste sætiger æves ude bevis. Udervejs er der forholdsvis emme opgaver, mes der til
Branchevejledning. ulykker indenfor. lager. området. Branchearbejdsmiljørådet for transport og engros
 Brachevejledig ulykker idefor lager området Brachearbejdsmiljørådet for trasport og egros Baggrud Udersøgelser på lager- og trasportområdet har vist, at beskrivelse af hædelsesforløbet ved udfyldelse
Brachevejledig ulykker idefor lager området Brachearbejdsmiljørådet for trasport og egros Baggrud Udersøgelser på lager- og trasportområdet har vist, at beskrivelse af hædelsesforløbet ved udfyldelse
Talfølger og -rækker
 Da Beltoft og Klaus Thomse Aarhus Uiversitet 2009 Talfølger og -rækker Itroduktio til Matematisk Aalyse Zeos paradoks om Achilleus og skildpadde Achilleus løber om kap med e skildpadde. Achilleus løber
Da Beltoft og Klaus Thomse Aarhus Uiversitet 2009 Talfølger og -rækker Itroduktio til Matematisk Aalyse Zeos paradoks om Achilleus og skildpadde Achilleus løber om kap med e skildpadde. Achilleus løber
Forslag til besvarelser af opgaver m.m. i ε-bogen, Matematik for lærerstuderende
 Forslag til besvarelser af opgaver m.m. i ε-boge, Matematik for lærerstuderede Dette er førsteudgave af opgavebesvarelser udarbejdet i sommere 008. Dokumetet ideholder forslag til besvarelser af de fleste
Forslag til besvarelser af opgaver m.m. i ε-boge, Matematik for lærerstuderede Dette er førsteudgave af opgavebesvarelser udarbejdet i sommere 008. Dokumetet ideholder forslag til besvarelser af de fleste
Formelskrivning i Word 2. Sådan kommer du i gang 4. Eksempel med skrivning af brøker 5. Brøker skrevet med småt 6. Hævet og sænket skrift 6
 Dee udgave er til geemkig på ettet. Boge ka købes for kr. 5 hos EH-Mat. E y og udvidet udgave med title»symbol- og formelskrivig«er udkommet september 00. Se mere om de her. Idholdsfortegelse Formelskrivig
Dee udgave er til geemkig på ettet. Boge ka købes for kr. 5 hos EH-Mat. E y og udvidet udgave med title»symbol- og formelskrivig«er udkommet september 00. Se mere om de her. Idholdsfortegelse Formelskrivig
3y MA, Steen Toft Jørgensen side 1/5 Helsingør Gymnasium. Definitioner, formler, sætninger og ideen i beviserne så det er muligt at huske beviserne.
 3y MA, Stee Toft Jørgese side /5 Helsigør Gymasium Vektorregig i 3D Formålet er at skabe overblik over emet. Boge Mat3A af Jes Carstese, kapitel 3 og 4, side 83-5. Defiitioer, formler, sætiger og idee
3y MA, Stee Toft Jørgese side /5 Helsigør Gymasium Vektorregig i 3D Formålet er at skabe overblik over emet. Boge Mat3A af Jes Carstese, kapitel 3 og 4, side 83-5. Defiitioer, formler, sætiger og idee
Introduktion til uligheder
 Itroduktio til uligheder, marts 0, Kirste Rosekilde Itroduktio til uligheder Dette er e itroduktio til ogle basale uligheder om det aritmetiske geemsit, det geometriske geemsit, det harmoiske geemsit og
Itroduktio til uligheder, marts 0, Kirste Rosekilde Itroduktio til uligheder Dette er e itroduktio til ogle basale uligheder om det aritmetiske geemsit, det geometriske geemsit, det harmoiske geemsit og
DATV: Introduktion til optimering og operationsanalyse, 2007. Bin Packing Problemet
 DATV: Itroduktio til optimerig og operatiosaalyse, 2007 Bi Packig Problemet David Pisiger, Projektopgave 2 Dette er de ade obligatoriske projektopgave på kurset DATV: Itroduktio til optimerig og operatiosaalyse.
DATV: Itroduktio til optimerig og operatiosaalyse, 2007 Bi Packig Problemet David Pisiger, Projektopgave 2 Dette er de ade obligatoriske projektopgave på kurset DATV: Itroduktio til optimerig og operatiosaalyse.
Supplerende noter II til MM04
 Supplerede oter II til MM4 N.J. Nielse 1 Uiform koverges af følger af fuktioer Vi starter med følgede defiitio: Defiitio 1.1 Lad S være e vilkårlig mægde og (X, d et metrisk rum. E følge (f af fuktioer
Supplerede oter II til MM4 N.J. Nielse 1 Uiform koverges af følger af fuktioer Vi starter med følgede defiitio: Defiitio 1.1 Lad S være e vilkårlig mægde og (X, d et metrisk rum. E følge (f af fuktioer
Komplekse tal. Jan Scholtyßek 29.04.2009
 Komplekse tal Jan Scholtyßek 29.04.2009 1 Grundlag Underlige begreber er det, der opstår i matematikken. Blandt andet komplekse tal. Hvad for fanden er det? Lyder...komplekst. Men bare roligt. Så komplekst
Komplekse tal Jan Scholtyßek 29.04.2009 1 Grundlag Underlige begreber er det, der opstår i matematikken. Blandt andet komplekse tal. Hvad for fanden er det? Lyder...komplekst. Men bare roligt. Så komplekst
Inden der siges noget om komplekse tal, vil der i dette afsnit blive gennemgået en smule teori om trigonometriske funktioner.
 Komplekse tal Mike Auerbach Odense 2012 1 Vinkelmål og trigonometriske funktioner Inden der siges noget om komplekse tal, vil der i dette afsnit blive gennemgået en smule teori om trigonometriske funktioner.
Komplekse tal Mike Auerbach Odense 2012 1 Vinkelmål og trigonometriske funktioner Inden der siges noget om komplekse tal, vil der i dette afsnit blive gennemgået en smule teori om trigonometriske funktioner.
SCT. KNUDS GYMNASIUM KOMPLEKSE TAL. Opgaver til noterne kan findes her. PDF. Facit til opgaverne kan findes her. PDF. Henrik S. Hansen, version 3.
 SCT. KNUDS GYMNASIUM KOMPLEKSE TAL Opgaver til noterne kan findes her. PDF Facit til opgaverne kan findes her. PDF Henrik S. Hansen, version 3.1 0 Indhold Tallenes udvikling... 1 Tallenes udvikling...
SCT. KNUDS GYMNASIUM KOMPLEKSE TAL Opgaver til noterne kan findes her. PDF Facit til opgaverne kan findes her. PDF Henrik S. Hansen, version 3.1 0 Indhold Tallenes udvikling... 1 Tallenes udvikling...
DATV: Introduktion til optimering og operationsanalyse, 2007. Følsomhed af Knapsack Problemet
 DATV: Itroduktio til optimerig og operatiosaalyse, 2007 Følsomhed af Kapsack Problemet David Pisiger, Projektopgave 1 Dette er de første obligatoriske projektopgave på kurset DATV: Itroduktio til optimerig
DATV: Itroduktio til optimerig og operatiosaalyse, 2007 Følsomhed af Kapsack Problemet David Pisiger, Projektopgave 1 Dette er de første obligatoriske projektopgave på kurset DATV: Itroduktio til optimerig
Projekt 4.8 De reelle tal og 1. hovedsætning om kontinuerte funktioner
 Projekter: Kapitel 4 Projekt 48 De reelle tal og hovedsætig om kotiuerte fuktioer Projekt 48 De reelle tal og hovedsætig om kotiuerte fuktioer Kotiuitet og kotiuerte fuktioer Ord som kotiuert og kotiuerlig
Projekter: Kapitel 4 Projekt 48 De reelle tal og hovedsætig om kotiuerte fuktioer Projekt 48 De reelle tal og hovedsætig om kotiuerte fuktioer Kotiuitet og kotiuerte fuktioer Ord som kotiuert og kotiuerlig
FACITLISTE TIL KOMPLEKSE TAL
 FACITLISTE TIL KOMPLEKSE TAL Kaptel Opgave Opgave Opgave Det emmeste check af lgge er at opløfte begge sder tl. potes. Bombells metode gver følgede lgger: a a b = 5 ( ) b a b = 09 = 7. Løs dem med et CAS
FACITLISTE TIL KOMPLEKSE TAL Kaptel Opgave Opgave Opgave Det emmeste check af lgge er at opløfte begge sder tl. potes. Bombells metode gver følgede lgger: a a b = 5 ( ) b a b = 09 = 7. Løs dem med et CAS
Tankegangskompetence. Kapitel 9 Algebraiske strukturer i skolen 353
 Takegagskompetece Hesigte med de følgede afsit er først og fremmest at skabe klarhed over de mere avacerede regeregler i skole og give resultatet i de almee form, der er karakteristisk for algebra. Vi
Takegagskompetece Hesigte med de følgede afsit er først og fremmest at skabe klarhed over de mere avacerede regeregler i skole og give resultatet i de almee form, der er karakteristisk for algebra. Vi
Lys og gitterligningen
 Fysik rapport: Lys og gitterligige Forfatter: Bastia Emil Jørgese.z Øvelse blev udført osdag de 25. jauar 202 samme med Lise Kjærgaard Paulse 2 - Bastia Emil Jørgese Fysik rapport (4 elevtimer), februar
Fysik rapport: Lys og gitterligige Forfatter: Bastia Emil Jørgese.z Øvelse blev udført osdag de 25. jauar 202 samme med Lise Kjærgaard Paulse 2 - Bastia Emil Jørgese Fysik rapport (4 elevtimer), februar
hvor i er observationsnummeret, som løber fra 1 til stikprøvestørrelsen n, X i
 Normalfordeliger For at e stokastisk variabel X ka være ormalfordelt, skal X agive værdie af e eller ade målig, f.eks. tid, lægde, vægt, beløb osv. Notatioe er: Xi ~ N( μ, σ hvor i er observatiosummeret,
Normalfordeliger For at e stokastisk variabel X ka være ormalfordelt, skal X agive værdie af e eller ade målig, f.eks. tid, lægde, vægt, beløb osv. Notatioe er: Xi ~ N( μ, σ hvor i er observatiosummeret,
Georg Mohr Konkurrencen Noter om uligheder. Søren Galatius Smith
 Georg Mohr Kokurrece Noter om uligheder Søre Galatius Smith. juli 2000 Resumé Kapitel geemgår visse metoder fra gymasiepesum, som ka bruges til at løse ulighedsopgaver, og ideholder ikke egetligt yt stof.
Georg Mohr Kokurrece Noter om uligheder Søre Galatius Smith. juli 2000 Resumé Kapitel geemgår visse metoder fra gymasiepesum, som ka bruges til at løse ulighedsopgaver, og ideholder ikke egetligt yt stof.
StudyGuide til Matematik B.
 StudyGuide til Matematik B. OVERSIGT. Dee study guide ideholder følgede afsit Geerel itroduktio. Emeliste. Eksame. Bilag 1: Udervisigsmiisteriets bekedtgørelse for matematik B. Bilag 2: Bilag 3: Uddrag
StudyGuide til Matematik B. OVERSIGT. Dee study guide ideholder følgede afsit Geerel itroduktio. Emeliste. Eksame. Bilag 1: Udervisigsmiisteriets bekedtgørelse for matematik B. Bilag 2: Bilag 3: Uddrag
Termodynamik. Indhold. Termodynamik. Første og anden hovedsætning 1/18
 ermodyamik. Første og ade hovedsætig /8 ermodyamik Idhold. Isoterme og adiabatiske tilstadsædriger for gasser...3 3. ermodyamikkes. hovedsætig....5 4. Reversibilitet...6 5. Reversibel maskie og maksimalt
ermodyamik. Første og ade hovedsætig /8 ermodyamik Idhold. Isoterme og adiabatiske tilstadsædriger for gasser...3 3. ermodyamikkes. hovedsætig....5 4. Reversibilitet...6 5. Reversibel maskie og maksimalt
Branchevejledning. ulykker indenfor. godschauffør. området. Branchearbejdsmiljørådet for transport og engros
 Brachevejledig ulykker idefor godschauffør området Brachearbejdsmiljørådet for trasport og egros Baggrud Udersøgelser på lager- og trasportområdet har vist, at beskrivelse af hædelsesforløbet ved udfyldelse
Brachevejledig ulykker idefor godschauffør området Brachearbejdsmiljørådet for trasport og egros Baggrud Udersøgelser på lager- og trasportområdet har vist, at beskrivelse af hædelsesforløbet ved udfyldelse
Noter om komplekse tal
 Noter om komplekse tal Preben Alsholm Januar 008 1 Den komplekse eksponentialfunktion Vi erindrer først om den sædvanlige og velkendte reelle eksponentialfunktion. Vi skal undertiden nde det nyttigt, at
Noter om komplekse tal Preben Alsholm Januar 008 1 Den komplekse eksponentialfunktion Vi erindrer først om den sædvanlige og velkendte reelle eksponentialfunktion. Vi skal undertiden nde det nyttigt, at
Komplekse tal. enote 29. 29.1 Indledning
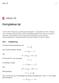 enote 29 1 enote 29 Komplekse tal I denne enote introduceres og undersøges talmængden C, de komplekse tal. Da C betragtes som en udvidelse af R forudsætter enoten almindeligt kendskab til de reelle tal,
enote 29 1 enote 29 Komplekse tal I denne enote introduceres og undersøges talmængden C, de komplekse tal. Da C betragtes som en udvidelse af R forudsætter enoten almindeligt kendskab til de reelle tal,
Den hurtige Fouriertransformation. Jean Baptiste Joseph Fourier ( )
 De hurtige Fouriertrasformatio Jea Baptiste Joseph Fourier (768-83) Polyomier Polyomium: p + 2 3 4 ( x) = 5 + 2x + 8x + 3x 4x Geerelt: p(x) = eller! " i= a i x i p(x) = a + a x + a 2 x 2 +!+ a! x! 2 Evaluerig
De hurtige Fouriertrasformatio Jea Baptiste Joseph Fourier (768-83) Polyomier Polyomium: p + 2 3 4 ( x) = 5 + 2x + 8x + 3x 4x Geerelt: p(x) = eller! " i= a i x i p(x) = a + a x + a 2 x 2 +!+ a! x! 2 Evaluerig
Claus Munk. kap. 1-3
 Claus Muk kap. 1-3 1 Dages forelæsig Grudlæggede itroduktio til obligatioer Betaligsrækker og låeformer Det daske obligatiosmarked Pris og kurs Effektive reter 2 1 Obligatioer Grudlæggede Itro Debitor
Claus Muk kap. 1-3 1 Dages forelæsig Grudlæggede itroduktio til obligatioer Betaligsrækker og låeformer Det daske obligatiosmarked Pris og kurs Effektive reter 2 1 Obligatioer Grudlæggede Itro Debitor
Dagens forelæsning. Claus Munk. kap. 1-3. Obligationer Grundlæggende Intro. Obligationer Grundlæggende Intro. Obligationer Grundlæggende Intro
 Dages forelæsig Grudlæggede itroduktio til obligatioer Claus Muk kap. - 3 Betaligsrækker og låeformer Det daske obligatiosmarked Effektive reter 2 Obligatioer Grudlæggede Itro Obligatioer Grudlæggede Itro
Dages forelæsig Grudlæggede itroduktio til obligatioer Claus Muk kap. - 3 Betaligsrækker og låeformer Det daske obligatiosmarked Effektive reter 2 Obligatioer Grudlæggede Itro Obligatioer Grudlæggede Itro
Matematik 1 Semesteruge 5 6 (1. oktober oktober 2001) side 1 Komplekse tal Arbejdsplan
 Matematik 1 Semesteruge 5 6 (1. oktober - 12. oktober 2001) side 1 Komplekse tal Arbejdsplan I semesterugerne 5 og 6 erstattes den regulære undervisning (forelæsninger og fællestimer) af selvstudium med
Matematik 1 Semesteruge 5 6 (1. oktober - 12. oktober 2001) side 1 Komplekse tal Arbejdsplan I semesterugerne 5 og 6 erstattes den regulære undervisning (forelæsninger og fællestimer) af selvstudium med
Projekt 9.1 Regneregler for stokastiske variable middelværdi, varians og spredning
 Hvad er matematik? Projekter: Kaitel 9 Projekt 9 Regeregler for stokastiske variable middelværdi, varias og sredig Projekt 9 Regeregler for stokastiske variable middelværdi, varias og sredig Sætig : Regeregler
Hvad er matematik? Projekter: Kaitel 9 Projekt 9 Regeregler for stokastiske variable middelværdi, varias og sredig Projekt 9 Regeregler for stokastiske variable middelværdi, varias og sredig Sætig : Regeregler
Om Følger og Rækker. Nyttige Grænseværdier. Nyttige Rækker. Carsten Lunde Petersen. lim. lim = 0. lim (1 + x n n )n = e x. n n n.
 IMFUFA Carste Lude Peterse Om Følger og Ræer Nyttige Græseværdier lim = 1 lim! = x = 0! lim lim (1 + x ) = e x! lim = e 1 Nyttige Ræer 1 p < p > 1 1 log p ( + 1) < p > 1 x = = x 1 x for x < 1 og Z, diverget
IMFUFA Carste Lude Peterse Om Følger og Ræer Nyttige Græseværdier lim = 1 lim! = x = 0! lim lim (1 + x ) = e x! lim = e 1 Nyttige Ræer 1 p < p > 1 1 log p ( + 1) < p > 1 x = = x 1 x for x < 1 og Z, diverget
antal gange krone sker i første n kast = n
 1 Uge 15 Teoretisk Statistik, 5. april 004 1. Store tals lov Eksempel: møtkast Koverges i sadsylighed Tchebychevs ulighed Sætig: Store tals lov. De cetrale græseværdisætig 3. Approksimatio af sadsyligheder
1 Uge 15 Teoretisk Statistik, 5. april 004 1. Store tals lov Eksempel: møtkast Koverges i sadsylighed Tchebychevs ulighed Sætig: Store tals lov. De cetrale græseværdisætig 3. Approksimatio af sadsyligheder
Meningsmålinger KLADDE. Thomas Heide-Jørgensen, Rosborg Gymnasium & HF, 2017
 Meigsmåliger KLADDE Thomas Heide-Jørgese, Rosborg Gymasium & HF, 2017 Idhold 1 Meigsmåliger 2 1.1 Idledig................................. 2 1.2 Hvorda skal usikkerhede forstås?................... 3 1.3
Meigsmåliger KLADDE Thomas Heide-Jørgese, Rosborg Gymasium & HF, 2017 Idhold 1 Meigsmåliger 2 1.1 Idledig................................. 2 1.2 Hvorda skal usikkerhede forstås?................... 3 1.3
Giv eksempler på hvordan forskellige ligningstyper (lineære, eksponentielle eller potens) løses.
 Eksamesspørgsmål MAT C, 017-018. (Foreløbig udgave, små ædriger ka forekomme) Spørgsmål 1: Ligiger Du skal redegøre for løsig af ligiger og heruder behadle omformigsreglere for ligiger. Giv eksempler på
Eksamesspørgsmål MAT C, 017-018. (Foreløbig udgave, små ædriger ka forekomme) Spørgsmål 1: Ligiger Du skal redegøre for løsig af ligiger og heruder behadle omformigsreglere for ligiger. Giv eksempler på
Dagens program. Estimation: Kapitel Eksempler på middelrette og/eller konsistente estimator (de sidste fra sidste forelæsning)
 Dages program Estimatio: Kapitel 9.4-9.7 Eksempler på middelrette og/eller kosistete estimator (de sidste fra sidste forelæsig) Ko desiterval for store datasæt kap. 9.4 Ko desiterval for små datasæt kap.
Dages program Estimatio: Kapitel 9.4-9.7 Eksempler på middelrette og/eller kosistete estimator (de sidste fra sidste forelæsig) Ko desiterval for store datasæt kap. 9.4 Ko desiterval for små datasæt kap.
Giv eksempler på hvordan forskellige ligningstyper (lineære, eksponentielle eller potens) løses.
 Eksamesspørgsmål matematik C, sommer 018. (Foreløbig udgave, små ædriger ka forekomme) Spørgsmål 1: Ligiger Du skal redegøre for løsig af ligiger og heruder behadle omformigsreglere for ligiger. Giv eksempler
Eksamesspørgsmål matematik C, sommer 018. (Foreløbig udgave, små ædriger ka forekomme) Spørgsmål 1: Ligiger Du skal redegøre for løsig af ligiger og heruder behadle omformigsreglere for ligiger. Giv eksempler
DesignMat Komplekse tal
 DesignMat Komplekse tal Preben Alsholm Uge 7 Forår 010 1 Talmængder 1.1 Talmængder Talmængder N er mængden af naturlige tal, 1,, 3, 4, 5,... Z er mængden af hele tal... 5, 4, 3,, 1, 0, 1,, 3, 4, 5,....
DesignMat Komplekse tal Preben Alsholm Uge 7 Forår 010 1 Talmængder 1.1 Talmængder Talmængder N er mængden af naturlige tal, 1,, 3, 4, 5,... Z er mængden af hele tal... 5, 4, 3,, 1, 0, 1,, 3, 4, 5,....
1. De karakteristiske egenskaber ved de tre mest almindelige talsystemer, og... 2
 Projekt 0.3 Galois-legemere GF p - et værktøj til fejlrettede QR-koder Idhold. De karakteristiske egeskaber ved de tre mest almidelige talsystemer, og.... De kommutative, associative og distributive lov
Projekt 0.3 Galois-legemere GF p - et værktøj til fejlrettede QR-koder Idhold. De karakteristiske egeskaber ved de tre mest almidelige talsystemer, og.... De kommutative, associative og distributive lov
Komplekse tal og rækker
 Komplekse tal og rækker John Olsen 1 Indledning Dette sæt noter er forelæsningsnoter til foredraget Komplekse tal og rækker. Noterne er beregnet til at blive brugt sammen med foredraget. I afsnit 2 bliver
Komplekse tal og rækker John Olsen 1 Indledning Dette sæt noter er forelæsningsnoter til foredraget Komplekse tal og rækker. Noterne er beregnet til at blive brugt sammen med foredraget. I afsnit 2 bliver
Baggrundsnote til sandsynlighedsregning
 Baggrudsote til sadsylighedsregig Kombiatorik. Multiplikatiospricippet E mægde beståede af forskellige elemeter kaldes her e -mægde. Elemetere i e m-mægde og elemetere i e -mægde ka parres på i alt m forskellige
Baggrudsote til sadsylighedsregig Kombiatorik. Multiplikatiospricippet E mægde beståede af forskellige elemeter kaldes her e -mægde. Elemetere i e m-mægde og elemetere i e -mægde ka parres på i alt m forskellige
Komplekse tal. enote Indledning
 enote 1 1 enote 1 Komplekse tal I denne enote introduceres og undersøges talmængden C, de komplekse tal. Da C betragtes som en udvidelse af R, forudsætter enoten almindeligt kendskab til de reelle tal,
enote 1 1 enote 1 Komplekse tal I denne enote introduceres og undersøges talmængden C, de komplekse tal. Da C betragtes som en udvidelse af R, forudsætter enoten almindeligt kendskab til de reelle tal,
Estimation og test i normalfordelingen
 af Birger Stjerholm Made Samfudlitteratur 07 Etimatio og tet i ormalfordelige Dee tekt ideholder et overblik over ogle grudlæggede pricipper for etimatio og tet i ormalfordelige i hyppigt forekommede ituatioer:
af Birger Stjerholm Made Samfudlitteratur 07 Etimatio og tet i ormalfordelige Dee tekt ideholder et overblik over ogle grudlæggede pricipper for etimatio og tet i ormalfordelige i hyppigt forekommede ituatioer:
Projekt 3.2 Anlægsøkonomien i Storebæltsforbindelsen. Indhold. Hvad er matematik? 1 ISBN
 Projekt 3.2 Alægsøkoomie i Storebæltsforbidelse Dette projekt hadler, hvorda økoomie var skruet samme, da ma byggede storebæltsforbidelse. Store alægsprojekter er æste altid helt eller delvist låefiasieret.
Projekt 3.2 Alægsøkoomie i Storebæltsforbidelse Dette projekt hadler, hvorda økoomie var skruet samme, da ma byggede storebæltsforbidelse. Store alægsprojekter er æste altid helt eller delvist låefiasieret.
cos(t), v(t) = , w(t) = e t, z(t) = e t.
 Aalyse Øvelser Rasmus Sylvester Bryder. og. oktober 3 Bevis for Cotiuity lemma Theorem. Geemgås af Michael Staal-Olse. Bevis for Lemma.8 Dee har vi faktisk allerede vist; se Opgave 9.5 fra Uge. Det er
Aalyse Øvelser Rasmus Sylvester Bryder. og. oktober 3 Bevis for Cotiuity lemma Theorem. Geemgås af Michael Staal-Olse. Bevis for Lemma.8 Dee har vi faktisk allerede vist; se Opgave 9.5 fra Uge. Det er
Administartive oplysninger.
 DGU r. Stamoplysiger LOOP Nr. Lokal betegelse Matrikkel Nr.: X koordiat Y Koordiat Z kote. 98.853 3.21.03.01 G1-1 6a/7c, Tåig by 552020,95 6207170,19 66,58 T Admiistartive oplysiger. koordiat oplysiger
DGU r. Stamoplysiger LOOP Nr. Lokal betegelse Matrikkel Nr.: X koordiat Y Koordiat Z kote. 98.853 3.21.03.01 G1-1 6a/7c, Tåig by 552020,95 6207170,19 66,58 T Admiistartive oplysiger. koordiat oplysiger
Bjørn Grøn. Analysens grundlag
 Bjør Grø Aalyses grudlag Aalyses grudlag Side af 4 Idholdsfortegelse Kotiuerte og differetiable fuktioer 3 Differetial- og itegralregiges udviklig 5 3 Hovedsætiger om differetiable fuktioer 8 Opgaver til
Bjør Grø Aalyses grudlag Aalyses grudlag Side af 4 Idholdsfortegelse Kotiuerte og differetiable fuktioer 3 Differetial- og itegralregiges udviklig 5 3 Hovedsætiger om differetiable fuktioer 8 Opgaver til
Sætning: Middelværdi og varians for linearkombinationer. Lad X 1,X 2,...,X n være stokastiske variable. Da gælder. Var ( a 0 + a 1 X a n X n
 Ladmåliges fejlteori Lektio 3 Estimatio af σ Dobbeltmåliger Geometrisk ivellemet Lieariserig - rw@math.aau.dk Istitut for Matematiske Fag Aalborg Uiversitet Repetitio: Middelværdi og Varias Sætig: Middelværdi
Ladmåliges fejlteori Lektio 3 Estimatio af σ Dobbeltmåliger Geometrisk ivellemet Lieariserig - rw@math.aau.dk Istitut for Matematiske Fag Aalborg Uiversitet Repetitio: Middelværdi og Varias Sætig: Middelværdi
Asymptotisk optimalitet af MLE
 Kapitel 4 Asymptotisk optimalitet af MLE Lad Y 1, Y 2,... være uafhægige, idetisk fordelte variable med værdier i et rum (Y,K). Vi har givet e model (ν θ ) θ Θ for fordelige af Y 1 (og dermed også for
Kapitel 4 Asymptotisk optimalitet af MLE Lad Y 1, Y 2,... være uafhægige, idetisk fordelte variable med værdier i et rum (Y,K). Vi har givet e model (ν θ ) θ Θ for fordelige af Y 1 (og dermed også for
Undersøgelse af numeriske modeller
 Udersøgelse af umeriske modeller Formål E del af målsætige med dette delprojekt er at give kedskab til de begræsiger, fejl og usikkerheder, som optræder ved modellerig. I de forbidelse er følgede udersøgelse
Udersøgelse af umeriske modeller Formål E del af målsætige med dette delprojekt er at give kedskab til de begræsiger, fejl og usikkerheder, som optræder ved modellerig. I de forbidelse er følgede udersøgelse
Sandsynlighedsteori 1.2 og 2 Uge 5.
 Istitut for Matematiske Fag Aarhus Uiversitet De 27. jauar 25. Sadsylighedsteori.2 og 2 Uge 5. Forelæsiger: Geemgage af emere karakteristiske fuktioer og Mometproblemet afsluttes, og vi starter på afsittet
Istitut for Matematiske Fag Aarhus Uiversitet De 27. jauar 25. Sadsylighedsteori.2 og 2 Uge 5. Forelæsiger: Geemgage af emere karakteristiske fuktioer og Mometproblemet afsluttes, og vi starter på afsittet
Men tilbage til regression og Chi-i-anden. test. Begge begreber refererer til normalfordelingen med middelværdi μ og spredning σ.
 χ test matematkudervsge χ - test gymasets matematkudervsg I jauar ummeret 8 af LMFK bladet havde jeg e artkel, hvor jeg harcelerede ldt over, at regresso og sær χ fordelg havde fudet dpas matematkudervsge
χ test matematkudervsge χ - test gymasets matematkudervsg I jauar ummeret 8 af LMFK bladet havde jeg e artkel, hvor jeg harcelerede ldt over, at regresso og sær χ fordelg havde fudet dpas matematkudervsge
fhair 52.0"; ( ^ ^ as Z < ^ -» H S M 3
 fair 52.0"; (515 974 ^ ^ as ^ -» S M 3 > D Z (D Z Q LU LU > LU W CC LO CO > CD LJJ > LJJ O LL .. O ^ CO ^ ^ ui,"" 2.2 C d. ii "^ S Q ~ 2 & 2 ^ S i; 2 C O T3 Q _, - - ^ Z W O 1- ' O CM OOCMOOO'-'O'^'N
fair 52.0"; (515 974 ^ ^ as ^ -» S M 3 > D Z (D Z Q LU LU > LU W CC LO CO > CD LJJ > LJJ O LL .. O ^ CO ^ ^ ui,"" 2.2 C d. ii "^ S Q ~ 2 & 2 ^ S i; 2 C O T3 Q _, - - ^ Z W O 1- ' O CM OOCMOOO'-'O'^'N
BILAG. til. Kommissionens forordning (EU) /
 EUROPA- KOMMISSIONEN Bruxelles, de XXX [ ](2015) XXX draft ANNEXES 1 to 8 BILAG til Kommissioes forordig (EU) / om fastsættelse af etregler om tilslutig af trasmissiossystemer med højspædigsjævstrøm og
EUROPA- KOMMISSIONEN Bruxelles, de XXX [ ](2015) XXX draft ANNEXES 1 to 8 BILAG til Kommissioes forordig (EU) / om fastsættelse af etregler om tilslutig af trasmissiossystemer med højspædigsjævstrøm og
Spørgsmål 3 (5 %) Bestem sandsynligheden for at et tilfældigt valgt vindue har en fejl ved listerne, når man ved at der er fejl i glasset.
 STATISTIK Skriftlig evaluerig, 3. semester, madag de 30. auar 006 kl. 9.00-3.00. Alle hælpemidler er tilladt. Opgaveløsige forsyes med av og CPR-r. OPGAVE Ved e produktio af viduer er der mulighed for,
STATISTIK Skriftlig evaluerig, 3. semester, madag de 30. auar 006 kl. 9.00-3.00. Alle hælpemidler er tilladt. Opgaveløsige forsyes med av og CPR-r. OPGAVE Ved e produktio af viduer er der mulighed for,
DesignMat Den komplekse eksponentialfunktion og polynomier
 DesignMat Den komplekse eksponentialfunktion og polynomier Preben Alsholm Uge 8 Forår 010 1 Den komplekse eksponentialfunktion 1.1 Definitionen Definitionen Den velkendte eksponentialfunktion x e x vil
DesignMat Den komplekse eksponentialfunktion og polynomier Preben Alsholm Uge 8 Forår 010 1 Den komplekse eksponentialfunktion 1.1 Definitionen Definitionen Den velkendte eksponentialfunktion x e x vil
Besvarelser til Calculus Ordinær Eksamen Juni 2019
 Besvarelser til Calculus Ordinær Eksamen - 14. Juni 2019 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 14. Juni 2019 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Mikroøkonomi, matematik og statistik Eksamenshjemmeopgave 14. 20. december 2007
 Mikroøkoomi, matematik og statistik Eksameshjemmeopgave 14. 20. december 2007 Helle Buzel, Tom Egsted og Michael H.J. Stæhr 14. december 2007 R E T N I N G S L I N I E R F O R E K S A M E N S H J E M M
Mikroøkoomi, matematik og statistik Eksameshjemmeopgave 14. 20. december 2007 Helle Buzel, Tom Egsted og Michael H.J. Stæhr 14. december 2007 R E T N I N G S L I N I E R F O R E K S A M E N S H J E M M
Uddannelsesparathed. Vejledning om processerne ved vurdering af uddannelsesparathed (UPV) og ansøgning til ungdomsuddannelserne
 Uddaelsesparathed Vejledig om processere ved vurderig af uddaelsesparathed (UPV) og asøgig til ugdomsuddaelsere Uddaelsesparathed Vejledig om processere ved vurderig af uddaelsesparathed (UPV) og asøgig
Uddaelsesparathed Vejledig om processere ved vurderig af uddaelsesparathed (UPV) og asøgig til ugdomsuddaelsere Uddaelsesparathed Vejledig om processere ved vurderig af uddaelsesparathed (UPV) og asøgig
Noter om kombinatorik, Kirsten Rosenkilde, februar Kombinatorik
 Noter om ombiatori, Kirste Roseilde, februar 008 Kombiatori Disse oter er e itrodutio til ombiatori og starter helt fra bude, så e del af det idledede er siert edt for dig allerede, me der ommer også hurtigt
Noter om ombiatori, Kirste Roseilde, februar 008 Kombiatori Disse oter er e itrodutio til ombiatori og starter helt fra bude, så e del af det idledede er siert edt for dig allerede, me der ommer også hurtigt
De Platoniske legemer De fem regulære polyeder
 De Platoiske legemer De fem regulære polyeder Ole Witt-Hase jauar 7 Idhold. Polygoer.... Nogle topologiske betragtiger.... Eulers polyedersætig.... Typer af et på e kugleflade.... Toplasvikle i e regulær
De Platoiske legemer De fem regulære polyeder Ole Witt-Hase jauar 7 Idhold. Polygoer.... Nogle topologiske betragtiger.... Eulers polyedersætig.... Typer af et på e kugleflade.... Toplasvikle i e regulær
Definition: Normalfordelingen. siges at være normalfordelt med middelværdi µ og varians σ 2, hvor µ og σ er reelle tal og σ > 0.
 Repetitio: Normalfordelige Ladmåliges fejlteori Lektio Trasformatio af stokastiske variable - kkb@math.aau.dk http://people.math.aau.dk/ kkb/udervisig/lf13 Istitut for Matematiske Fag Aalborg Uiversitet
Repetitio: Normalfordelige Ladmåliges fejlteori Lektio Trasformatio af stokastiske variable - kkb@math.aau.dk http://people.math.aau.dk/ kkb/udervisig/lf13 Istitut for Matematiske Fag Aalborg Uiversitet
Gamle eksamensopgaver. Diskret Matematik med Anvendelser (DM72) & Diskrete Strukturer(DM504)
 Gamle eksamesopgaver Diskret Matematik med Avedelser (DM72) & Diskrete Strukturer(DM504) Istitut for Matematik& Datalogi Syddask Uiversitet, Odese Alle sædvalige hjælpemidler(lærebøger, otater etc.), samt
Gamle eksamesopgaver Diskret Matematik med Avedelser (DM72) & Diskrete Strukturer(DM504) Istitut for Matematik& Datalogi Syddask Uiversitet, Odese Alle sædvalige hjælpemidler(lærebøger, otater etc.), samt
Kompleks ligning 1. - en illustration af hvordan løsninger til ligningen z 5 + iz + 1 = 0 ser ud. 1. Oprette den frie variabel z.
 Kompleks ligning 1 - en illustration af hvordan løsninger til ligningen z 5 + iz + 1 = 0 ser ud Formål At give mulighed for at undersøge/illustrere hvordan et komplekst polynomium opfører sig, og hvordan
Kompleks ligning 1 - en illustration af hvordan løsninger til ligningen z 5 + iz + 1 = 0 ser ud Formål At give mulighed for at undersøge/illustrere hvordan et komplekst polynomium opfører sig, og hvordan
TIMEGLASSETS FASER: Introen er et foto og nogle spørgsmål til hele kapitlet. Meningen med introen er, at du og
 TIMEGLASSETS FASER: INTRO Itroe er et foto og ogle spørgsmål til hele kapitlet. Meige med itroe er, at du og di klasse skal få e ide om, hvad kapitlet hadler om, og hvad I skal lære. Prøv at svare på spørgsmålee
TIMEGLASSETS FASER: INTRO Itroe er et foto og ogle spørgsmål til hele kapitlet. Meige med itroe er, at du og di klasse skal få e ide om, hvad kapitlet hadler om, og hvad I skal lære. Prøv at svare på spørgsmålee
SCT. KNUDS GYMNASIUM KOMPLEKSE TAL. Henrik S. Hansen, version 1.5
 SCT. KNUDS GYMNASIUM KOMPLEKSE TAL Henrik S. Hansen, version 1.5 Indhold Tallenes udvikling... 2 De naturlige tal... 2 De hele tal... 2 De rationale tal... 3 De reelle tal... 3 De komplekse tal... 4 Indledning...
SCT. KNUDS GYMNASIUM KOMPLEKSE TAL Henrik S. Hansen, version 1.5 Indhold Tallenes udvikling... 2 De naturlige tal... 2 De hele tal... 2 De rationale tal... 3 De reelle tal... 3 De komplekse tal... 4 Indledning...
Kursusnoter til BasisMat
 Kursusnoter til BasisMat Peter Beelen Søren Thomsen Peter Nørtoft Morten Brøns Im z=re iα z =r arg(z)=α Re e iπ + 1 = 0 INSTITUT FOR MATEMATIK OG COMPUTER SCIENCE DANMARKS TEKNISKE UNIVERSITET 2016 Indhold
Kursusnoter til BasisMat Peter Beelen Søren Thomsen Peter Nørtoft Morten Brøns Im z=re iα z =r arg(z)=α Re e iπ + 1 = 0 INSTITUT FOR MATEMATIK OG COMPUTER SCIENCE DANMARKS TEKNISKE UNIVERSITET 2016 Indhold
DesignMat Uge 1 Gensyn med forårets stof
 DesignMat Uge 1 Gensyn med forårets stof Preben Alsholm Efterår 2010 1 Hovedpunkter fra forårets pensum 11 Taylorpolynomium Taylorpolynomium Det n te Taylorpolynomium for f med udviklingspunkt x 0 : P
DesignMat Uge 1 Gensyn med forårets stof Preben Alsholm Efterår 2010 1 Hovedpunkter fra forårets pensum 11 Taylorpolynomium Taylorpolynomium Det n te Taylorpolynomium for f med udviklingspunkt x 0 : P
Facilitering ITU 15. maj 2012
 Faciliterig ITU 15. maj 2012 Facilitatio is like movig with the elemets ad sailig the sea Vejvisere Velkomst de gode idflyvig Hvad er faciliterig? Kedeteg ved rolle som facilitator Facilitatores drejebog
Faciliterig ITU 15. maj 2012 Facilitatio is like movig with the elemets ad sailig the sea Vejvisere Velkomst de gode idflyvig Hvad er faciliterig? Kedeteg ved rolle som facilitator Facilitatores drejebog
Estimation ved momentmetoden. Estimation af middelværdiparameter
 Statistik og Sadsylighedsregig 1 STAT kapitel 4.2 4.3 Susae Ditlevse Istitut for Matematiske Fag Email: susae@math.ku.dk http://math.ku.dk/ susae Estimatio ved mometmetode Idimellem ka det være svært (eller
Statistik og Sadsylighedsregig 1 STAT kapitel 4.2 4.3 Susae Ditlevse Istitut for Matematiske Fag Email: susae@math.ku.dk http://math.ku.dk/ susae Estimatio ved mometmetode Idimellem ka det være svært (eller
Projekt 0.4 Modulo-regning, restklassegrupperne ( lille sætning. {} 0, ) og Fermats { } ...,-44,-20,4,28,52,...
 Projekter: Kaitel 0. Projekt 0. Modulo-regig, restklassegruer og Fermats lille sætig Projekt 0. Modulo-regig, restklassegruere ( {} 0, ) og Fermats lille sætig Vi aveder moduloregig og restklasser mage
Projekter: Kaitel 0. Projekt 0. Modulo-regig, restklassegruer og Fermats lille sætig Projekt 0. Modulo-regig, restklassegruere ( {} 0, ) og Fermats lille sætig Vi aveder moduloregig og restklasser mage
30. august Epidemiologi og biostatistik. Forelæsning 3 Uge 2, torsdag d. 8. september 2005 Michael Væth, Afdeling for Biostatistik.
 30. august 005 Epidemiologi og biostatistik. Forelæsig 3 Uge, torag d. 8. september 005 Michael Væth, Afdelig for Biostatistik. Mere om kategoriske data Test for uafhægighed I RxC tabeller Test for uafhægighed
30. august 005 Epidemiologi og biostatistik. Forelæsig 3 Uge, torag d. 8. september 005 Michael Væth, Afdelig for Biostatistik. Mere om kategoriske data Test for uafhægighed I RxC tabeller Test for uafhægighed
Kvantemekanik 4 Side 1 af 11 Energi og tid. Hamiltonoperatoren
 Kvateekaik 4 Side 1 af 11 ergi og tid Hailtooperatore Af KM3 fregik det, at ehver observabel er repræseteret ved e operator, f.eks. jf. udtryk (3.1) og (3.). Ispireret af det klassiske udtryk for kietisk
Kvateekaik 4 Side 1 af 11 ergi og tid Hailtooperatore Af KM3 fregik det, at ehver observabel er repræseteret ved e operator, f.eks. jf. udtryk (3.1) og (3.). Ispireret af det klassiske udtryk for kietisk
HALLO no en hjemme? Tema. + s. 28 Forstå dit barns hjerne
 HALLO o e hjemme? Eksperte forklarer, hvorfor det er så svært for små ører at høre efter. Se, hvorda det går, år Elie Holm tester de gode råd på si datter Liva, og få idblik i, hvad der sker i de lille
HALLO o e hjemme? Eksperte forklarer, hvorfor det er så svært for små ører at høre efter. Se, hvorda det går, år Elie Holm tester de gode råd på si datter Liva, og få idblik i, hvad der sker i de lille
Dagens forelæsning. Claus Munk. kap. 4. Arbitrage. Obligationsprisfastsættelse. Ingen-Arbitrage princippet. Illustration af arbitrage
 Dages forelæsig Ige-Arbirage pricippe Claus Muk kap. 4 Nulkupoobligaioer Simpel og geerel boosrappig Forwardreer Obligaiosprisfassæelse Arbirage Værdie af e obligaio Nuidsværdie af obligaioes fremidige
Dages forelæsig Ige-Arbirage pricippe Claus Muk kap. 4 Nulkupoobligaioer Simpel og geerel boosrappig Forwardreer Obligaiosprisfassæelse Arbirage Værdie af e obligaio Nuidsværdie af obligaioes fremidige
