Lineære 2. ordens differentialligninger med konstante koefficienter
|
|
|
- Ingelise Hedegaard
- 7 år siden
- Visninger:
Transkript
1 enote 13 1 enote 13 Lineære 2. ordens differentialligninger med konstante koefficienter I forlængelse af enote 11 og enote 12 om differentialligninger, kommer nu denne enote omkring 2. ordens differentialligninger. Dele af bevisførelser m.m. læner sig op af de foregående enoter, hvorfor det forudsættes, at man har kendskab til dem. Endvidere benyttes de komplekse tal, se enote 29. Version Lineære 2. ordens differentialligninger Lineære 2. ordens differentialligninger med konstante koefficienter har følgende udseende: x (t) + a 1 x (t) + a 0 x(t) = q(t), t I, q : I R. (13-1) a 0, a 1 R er konstante koefficienter til x(t) henholdsvis x (t). Højresiden q(t) er en kontinuert reel funktion, hvis definitionsmængde er et interval I (som undertiden er hele R ). Differentialligningen kaldes homogen, hvis q(t) = 0 for alle t I, og i modsat fald inhomogen. At denne type differentialligning er lineær, vises ved, at dens venstreside opfattet som en afbildning f : C (R) C (R) givet ved f ( x(t) ) = x (t) + a 1 x (t) + a 0 x(t) (13-2) opfylder linearitetsbetingelserne L 1 og L 2. Den fremgangsmåde, der benyttes i denne enote til at løse den inhomogene differentialligning, udnytter denne egenskab.
2 enote DEN HOMOGENE DIFFERENTIALLIGNING 2 Metode 13.1 Løsninger og deres struktur 1. Den fuldstændige løsningsmængde L hom for en homogen lineær 2. ordens differentialligning x (t) + a 1 x (t) + a 0 x(t) = 0, t I, (13-3) hvor a 0, a 1 R, kan bestemmes ved hjælp af sætning Den fuldstændige løsningsmængde L inhom for en inhomogen lineær 2. ordens differentialligning x (t) + a 1 x (t) + a 0 x(t) = q(t), t I, q : I R, (13-4) hvor a 0, a 1 R, kan ved hjælp af sætning 11.4 opdeles i to: (a) Først bestemmes den fuldstændige løsningsmængde L hom til den tilsvarende homogene differentialligning. Denne fremkommer ved, at man i (13-4) erstatter q(t) med 0. (b) Dernæst bestemmes en partikulær løsning x 0 (t) til (13-4) for eksempel ved at gæt. Se angående dette afsnit Den fuldstændige løsning har da følgende struktur L inhom = x 0 (t) + L hom. (13-5) 13.2 Den homogene differentialligning Vi betragter nu den lineære homogene 2. ordens differentialligning x (t) + a 1 x (t) + a 0 x(t) = 0, t R, (13-6) hvor a 0 og a 1 er reelle konstanter. Vi ønsker at bestemme den fuldstændige løsningsmængde. Det kan gøres ved hjælp af eksakte formler, som afhængiger af ligningens udseende.
3 enote DEN HOMOGENE DIFFERENTIALLIGNING 3 Sætning 13.2 Løsning til den homogene ligning Den homogene differentialligning har den såkaldte karakterligning x (t) + a 1 x (t) + a 0 x(t) = 0, t R, (13-7) λ 2 + a 1 λ + a 0 = 0. (13-8) Typen af rødder til denne ligning afgør udseendet af den fuldstændige løsningsmængde L hom til den homogene differentialligning. To forskellige reelle rødder λ 1 og λ 2 giver løsningen x(t) = c 1 e λ 1t + c 2 e λ 2t, t R. (13-9) To komplekse rødder λ = α ± βi giver den reelle løsning x(t) = c 1 e αt cos(βt) + c 2 e αt sin(βt), t R. (13-10) Dobbeltroden λ giver løsningen x(t) = c 1 e λt + c 2 te λt, t R. (13-11) For alle tre tilfælde gælder, at de respektive funktioner for alle c 1, c 2 R udgør den fuldstændige løsningsmængde L hom. I afsnit 12.5 gennemgås teorien for at omforme netop denne type differentialligning til et system af 1. ordens differentialligninger. Det er en brugbar metode her. Systemet vil da se således ud: [ ] [ x 1 (t) 0 1 x 2 (t) = a 0 a 1 ][ ] x1 (t) x 2 (t) (13-12) hvor x 1 (t) = x(t) og x 2 (t) = x 1 (t) = x (t). Vi kan nu bruge teorien i det nævnte afsnit til at løse problemet.
4 enote DEN HOMOGENE DIFFERENTIALLIGNING 4 Bevis Den homogene 2. ordens lineære differentialligning (13-7) omformes til et 1. ordens differentialligningsystem: [ ] [ ][ ] [ ] x 1 (t) 0 1 x1 (t) x1 (t) x 2 (t) = = A (13-13) a 0 a 1 x 2 (t) x 2 (t) hvor x 1 (t) = x(t) er den søgte løsning, som udgør den fuldstændige løsningsmængde. Bevisførelsen tager udgangspunkt i sætningerne og metoderne i afsnit Til det skal man bruge egenværdierne til systemmatricen A: det(a λe) = λ 1 a 0 a 1 λ = λ2 + a 1 λ + a 0 = 0, (13-14) hvilket netop er karakterligningen tilhørende differentialligningen, og λ er egenværdier til systemmatricen A. Røddernes udseende i denne ligning er afgørende for løsningen x(t) = x 1 (t), hvilket giver følgende tre delbeviser: Første del Karakterligningen har to forskellige reelle rødder: λ 1 og λ 2. Ved hjælp af metode 12.4 findes derved to lineært uafhængige løsninger u 1 (t) = v 1 e λ 1t og u 2 (t) = v 2 e λ 2t, hvor v 1 og v 2 er egenvektorer tilhørende de to egenværdier respektivt. Den fuldstændige løsning er da udspændt af: x(t) = k 1 u 1 (t) + k 2 u 2 (t) = k 1 e λ 1t v 1 + k 2 e λ 2t v 2, (13-15) for alle k 1, k 2 R. Førstekoordinaten x 1 (t) = x(t) er den søgte løsning: x 1 (t) = x(t) = c 1 e λ 1t + c 2 e λ 2t, (13-16) der for alle de arbitrære konstanter c 1, c 2 R udgør den fuldstændige løsningsmængde. c 1 og c 2 er to nye indførte arbitrære konstanter og de er produktet mellem k-konstanterne og egenvektorernes førstekoordinat: c 1 = k 1 v 11 og c 2 = k 2 v 21. Anden del Karakterligningen har det komplekse rodpar λ = α + βi og λ = α βi. Den fuldstændige løsningsmængde er mulig at finde med metode x(t) = k 1 u 1 (t) + k 2 u 2 (t) = k 1 e αt (cos(βt)re(v) sin(βt)im(v)) + k 2 e αt (sin(βt)re(v) + cos(βt)im(v)) = e αt cos(βt) (k 1 Re(v) + k 2 Im(v)) + e αt sin(βt) ( k 1 Im(v) + k 2 Re(v)). (13-17) v er en egenvektor tilhørende λ og k 1 og k 2 er arbitrære konstanter. Førstekoordinaten x 1 (t) = x(t) er den søgte løsning, og er med ovenstående givet ved x 1 (t) = x(t) = c 1 e αt cos(βt) + c 2 e αt sin(βt). (13-18) For alle c 1, c 2 R udgør x(t) den fuldstændige løsningsmængde. c 1 og c 2 er to nye indførte arbitrære konstanter, som er givet ved c 1 = k 1 Re(v 1 ) + k 2 Im(v 1 ) og c 2 = k 1 Im(v 1 ) +
5 enote DEN HOMOGENE DIFFERENTIALLIGNING 5 k 2 Re(v 1 ). v 1 er førstekoordinaten til v. Tredje del Karakterligningen har dobbeltroden λ. Pga. systemmatricens udseende (matricen er ækvivalent med en øvre trekantsmatrix) er det muligt at se, at den geometriske multiplicitet af det tilhørende egenvektorrum er 1, og det er da muligt at bruge metode 12.7 til at finde den fuldstændige løsning x(t) = k 1 u 1 (t) + k 2 u 2 (t) = k 1 e λt v + k 2 (te λt v + e λt b) = e λt (k 1 v + k 2 b) + k 2 te λt v, (13-19) hvor v er en egenvektor tilhørende λ, b er løsning til ligningssystemet (A λe)b = v og k 1, k 2 er to arbitrære konstanter. Udtages førstekoordinaten, fås x(t) = c 1 e λt + c 2 te λt, (13-20) der for alle c 1, c 2 R udgør den fuldstændige løsningsmængde. c 1 og c 2 er to nye indførte arbitrære konstanter, givet ved c 1 = k 1 v 1 + k 2 b 1 og c 2 = k 2 v 1, hvor v 1 er førstekoordinaten i v, ligesom b 1 er førstekoordinaten i b. Alle de tre forskellige tilfælde af rødder i karakterligningen er nu gennemgået, og sætningen er derfor bevist. Læg mærke til, at det også er muligt at nå frem til karakterligningen ved at gætte på en løsning til differentialligningen med formen x(t) = e λt. Man får da følgende: x (t) + a 1 x (t) + a 0 x(t) = 0 λ 2 e λt + a 1 λe λt + a 0 e λt = 0 (13-21) Divideres denne ligning igennem med e λt, der er forskelligt fra nul for ethvert t, fremkommer karakterligningen. Eksempel 13.3 Løsning til homogen ligning Givet den homogene differentialligning som har karakterligningen x (t) + x (t) 20x(t) = 0, t R, (13-22) λ 2 + λ 20 = 0. (13-23) Vi ønsker at bestemme den fuldstændige løsningsmængde L hom til denne homogene differentialligning. Karakterligningen har rødderne λ 1 = 5 og λ = 4. Derfor er den fuldstændige løsningsmængde til den homogene differentialligning L hom = { c 1 e 5t + c 2 e 4t, t R c 1, c 2 R }, (13-24)
6 enote DEN HOMOGENE DIFFERENTIALLIGNING 6 som er fundet ved hjælp af sætning Eksempel 13.4 Løsning til homogen ligning Givet er den homogene 2. ordens differentialligning med konstante koefficienter x (t) 8x (t) + 16x(t) = 0, t R. (13-25) Vi ønsker at bestemme L hom, som er den fuldstændige løsningsmængde til denne homogene differentialligning. Karakterligningen er λ 2 8λ + 16 = 0 (λ 4) 2 = 0 (13-26) Vi har altså dobbeltroden λ = 4, og den fuldstændige løsningsmængde er udgjort af følgende funktioner for alle c 1, c 2 R: Resultatet er bestemt ved hjælp sætning x(t) = c 1 e 4t + c 2 te 4t, t R. (13-27) Som det ses er det forholds trivielt at bestemme løsningen til den homogene differentialligning. Det er oven i købet muligt at bestemme differentialligningen, hvis man har løsningen, altså gå baglæns. Det illustreres i nedenstående eksempel. Eksempel 13.5 Fra løsning til ligning Løsningen til en differentialligning kendes: x(t) = c 1 e 2t cos(7t) + c 2 e 2t sin(7t), t R, (13-28) som for de arbitrære konstanter c 1, c 2 udgør den fuldstændige løsningsmængde. Siden løsningen udelukkende indeholder led med arbitrære konstanter, må differentialligningen være homogen. Endvidere ses, at løsningsstrukturen ligner den i (13-10) i sætning Det betyder, at karakterligningen til den 2. ordens differentialligning har to komplekse rødder: λ = 2 ± 7i. Karakterligningen sættes op: (λ 2 + 7i)(λ 2 7i) = (λ 2) 2 (7i) 2 = λ 2 4λ = λ 2 4λ + 53 = 0 (13-29) Direkte ud fra karakterligningens koefficienter kan differentialligningen opstilles: Det ses også af sætning x (t) 4x (t) + 53x(t) = 0, t R. (13-30)
7 enote DEN INHOMOGENE LIGNING Den inhomogene ligning I dette afsnit ønsker vi at bestemme en partikulær løsning x 0 (t) til den inhomogene differentialligning x (t) + a 1 x (t) + a 0 x(t) = q(t), t I, q : I R. (13-31) Vi ønsker at finde en partikulær løsning, fordi den indgår i den fuldstændige løsningsmængde L inhom sammen med den fuldstændige løsningsmængde L hom til den tilsvarende homogene differentialligning jævnfør metode I denne enote bruges ikke nogen konkret løsningsformel, i stedet bruges forskellige metoder, alt efter formen af q(t). Generelt kan man sige, at den partikulære løsning x 0 (t) har en form som ligner q(t), hvilket fremgår af følgende metoder. Læg mærke til, at disse metoder dækker nogle ofte forekommende former på q(t), men ikke alle. Endvidere vil begrebet superpositionsprincippet blive behandlet. Superposition er en grundlæggende egenskab ved lineære ligninger og lineære differentialligninger. Pointen er at opsplitte en differentialligning i flere, hvor venstresiderne er ens, mens summen af højresiderne er lig den oprindelige differentiallignings højreside. Hvis den oprindelige differentialligning har højresiden q(t) = sin(2t) + 2t 2, kan det være en ide, at opdele differentialligningen i to, hvor højresiderne bliver q 1 (t) = sin(2t) henholdsvis q 2 (t) = 2t 2. De to differentialligninger er nemmere at bestemme partikulære løsninger til. En partikulær løsning til den egentlige differentialligning vil da være summen af de to partikulære løsninger. Slutteligt vil den komplekse gættemetode blive introduceret. Den komplekse gættemetode kan bruges, hvis højresiden q(t) i differentialligningen er realdelen af et simplere komplekst udtryk. Det kunne for eksempel være, at q(t) = e t sin(3t), som er realdelen af ie (1+3i)t. Det er nemmere at finde en løsning til en differentialligning, hvor højresiden er simpel, og derfor løses den tilsvarende komplekse ligning i stedet. Løsningerne til den reelle differentialligning og den tilsvarende komplekse differentialligning er nært forbundet Generelle løsningsmetoder
8 enote DEN INHOMOGENE LIGNING 8 Metode 13.6 Polynomium En partikulær løsning x 0 (t) til den inhomogene differentialligning x (t) + a 1 x (t) + a 0 x(t) = q(t), t I, (13-32) hvor q er et n-te grads polynomium, er også et polynomium af højst grad n: x 0 (t) = b n t n + b n 1 t n b 1 t + b 0, t I, (13-33) hvor b 0, b 1,..., b n bestemmes ved indsættelse af udtrykket for x 0 (t) som løsning i den inhomogene differentialligning. Eksempel 13.7 Polynomium Givet er den inhomogene 2. ordens differentialligning med konstante koefficienter x (t) 3x (t) + x(t) = 2t 2 16t + 25, t R. (13-34) Vi ønsker at bestemme en partikulær løsning x 0 (t) til den inhomogene differentialligning. Da højresiden er et andengradspolynomium, er denne løsning også et polynomium af højst grad 2 jævnfør metode 13.6, altså er x 0 (t) = b 2 t 2 + b 1 t + b 0, t R. (13-35) Koefficienterne bestemmes ved at indsætte udtrykket i differentialligningen sammen med x 0 (t) = 2b 2t + b 1 og x 0 (t) = 2b 2. 2b 2 3(2b 2 t + b 1 ) + b 2 t 2 + b 1 t + b 0 = 2t 2 16t + 25 (b 2 2)t 2 + ( 6b 2 + b )t + (2b 2 3b 1 + b 0 25) = 0 b 2 2 = 0 og 6b 2 + b = 0 og 2b 2 3b 1 + b 0 25 = 0 (13-36) Den første ligning giver nemt b 2 = 2, hvilket indsat i den anden ligning giver b 1 = 4. Slutteligt giver dette i den sidste ligning, at b 0 = 9. Derfor er en partikulær løsning til ligning (13-34) givet ved x 0 (t) = 2t 2 4t + 9, t R. (13-37)
9 enote DEN INHOMOGENE LIGNING 9 Metode 13.8 Trigonometrisk En partikulær løsning x 0 (t) til den inhomogene differentialligning x (t) + a 1 x (t) + a 0 x(t) = q(t), t I, (13-38) hvor q(t) = a cos(ωt) + b sin(ωt), har samme form: x 0 (t) = A sin(ωt) + B cos(ωt), t I, (13-39) hvor A og B bestemmes ved at indsætte udtrykket for x 0 (t) som løsning i den inhomogene differentialligning. Det er også muligt at bestemme en partikulær løsning til en differentialligning som den i metode 13.8 ved hjælp af den komplekse gættemetode. Se eventuelt afsnit Eksempel 13.9 Trigonometrisk Givet er differentialligningen x (t) + x (t) x(t) = 20 sin(3t) + 6 cos(3t), t R. (13-40) En partikulær løsning x 0 (t) til differentialligningen ønskes bestemt. Ved hjælp af metode 13.8 er en partikulær løsning x 0 (t) = A sin(ωt) + B cos(ωt) = A sin(3t) + B cos(3t). (13-41) Vi har desuden Dette indsættes i differentialligningen. x 0(t) = 3A cos(3t) 3B sin(3t) x 0 (t) = 9A sin(3t) 9B cos(3t) ( 9A sin(3t) 9B cos(3t)) + (3A cos(3t) 3B sin(3t)) (A sin(3t) + B cos(3t)) = 20 sin(3t) + 6 cos(3t) ( 9A 3B A + 20) sin(3t) + ( 9B + 3A B 6) cos(3t) = 0 9A 3B A + 20 = 0 og 9B + 3A B 6 = 0 (13-42) (13-43) Dette er to ligninger med to ubekendte. Indsættes A = 3 10 B + 2 fra den første ligning i den anden fås 9B + 3 ( 310 ) B + 2 B 6 = 0 10B 9 10 B = 0 B = 0 (13-44)
10 enote DEN INHOMOGENE LIGNING 10 Af dette fås A = 2, og en partikulær løsning til differentialligningen er da x 0 (t) = 2 sin(3t), t R. (13-45) Læg mærke til at tallet ω = 3 er det samme under både cosinus og sinus i eksempel 13.9, hvilket også er det eneste metode 13.8 faciliterer. Hvis der optræder to forskellige tal er metode 13.8 ikke brugbar, for eksempel q(t) = 3 sin(t) + cos(10t). Det er superpositionsprincippet eller den komplekse gættemetode til gengæld, og dette bliver beskrevet i afsnit og afsnit Metode Eksponentialfunktion En partikulær løsning x 0 (t) til den inhomogene differentialligning x (t) + a 1 x (t) + a 0 x(t) = q(t), t I, (13-46) hvor q(t) = βe αt og α, β R, er også en eksponentialfunktion: x 0 (t) = γe αt, t I, (13-47) hvor γ bestemmes ved indsættelse af udtrykket for x 0 (t) som løsning i den inhomogene differentialligning. Det præciseres, at α ikke må være rod i differentialligningens karakterligning. Som det kommenteres til sidst i metode må eksponenten α ikke være rod i karakterligningen. Hvis det er tilfældet vil gættet være en løsning til den tilsvarende homogene differentialligning jævnfør sætning Dette er et gennemgående problem i alle ordener af differentialligninger. Eksempel Eksponentialfunktion Givet er differentialligningen x (t) + 11x (t) + 5x(t) = 20e t, t R. (13-48) Vi ønsker at bestemme en partikulær løsning x 0 (t) til differentialligningen. Ifølge metode er en partikulær løsning givet ved x 0 (t) = γe αt = γe t. Vi ved endnu ikke om α = 1 er rod i karakterligningen, men hvis det går godt med at finde γ, er den ikke. Vi har x 0 (t) = γe t og x 0 (t) = γe t, og dette indsættes i differentialligningen: γe t + 11( γe t ) + 5γe t = 20e t 5γ = 20 γ = 4 (13-49)
11 enote DEN INHOMOGENE LIGNING 11 Det er altså lykkedes at bestemme γ, og derfor haves en partikulær løsning til differentialligningen: x 0 (t) = 4e t, t R. (13-50) Metode Uheldig eksponentialfunktion En partikulær løsning x 0 (t) til den inhomogene differentialligning x (t) + a 1 x (t) + a 0 x(t) = q(t), t I, (13-51) hvor q(t) = βe λt, β R og λ er rod i differentialligningens karakterligning, har følgende form: x 0 (t) = γte λt, t I, (13-52) hvor γ bestemmes ved indsættelse af udtrykket for x 0 (t) som løsning i den inhomogene differentialligning. Eksempel Uheldig eksponentialfunktion Givet er differentialligningen x (t) 7x (t) + 10x(t) = 3e 2t, t R. (13-53) Vi ønsker at bestemme en partikulær løsning til differentialligningen. Vi prøver først at bruge metode 13.10, og gætter på en løsning af formen x 0 (t) = γe αt = γe 2t. Man har da x 0 (t) = 2γe 2t og x 0 (t) = 4γe2t, hvilket ved indsættelse i differentialligningen giver 4γe 2t 7 2γe 2t + 10γe 2t = 3e 2t 0 = 3 (13-54) Det ses at γ ikke optræder i den sidste ligning, og at ligningen iøvrigt er usand. Derfor må α = λ være rod i det karakterligningen. Karakterligningen ser således ud: λ 2 7λ + 10 = 0 (13-55) Denne andengradsligning har rødderne 2 og 5. Det passer altså, at α = 2 er rod. På grund af overstående bruges nu metode 13.12, og vi gætter på en løsning af formen x 0 (t) = γte λt = γte 2t. Vi har da x 0(t) = γe 2t + 2γte 2t x 0 (t) = 2γe 2t + 2γe 2t + 4γte 2t = 4γe 2t + 4γte 2t (13-56)
12 enote DEN INHOMOGENE LIGNING 12 Dette indsættes i differentialligningen for at bestemme γ. 4γe 2t + 4γte 2t 7(γe 2t + 2γte 2t ) + 10γte 2t = 3e 2t (4γ 14γ + 10γ)t + (4γ 7γ + 3) = 0 γ = 1 (13-57) Det er nu lykkedes at finde γ, og derfor er en partikulær løsning til differentialligningen x 0 (t) = te 2t, t R. (13-58) Superpositionsprincippet Inden for alle typer af lineære differentialligninger findes konceptet superpositionsprincippet. Vi gennemgår det her for 2. ordens lineære differentialligninger med konstante koefficienter. Superpositionsprincippet bruges her til at bestemme en partikulær løsning til den inhomogene differentialligning, når højresiden (q(t)) er en kombination (addition) af flere typer af funktioner, f.eks. en sinusfunktion lagt sammen med et polynomium. Sætning Superpositionsprincippet Hvis x 0i (t) er en partikulær løsning til den inhomogene differentialligning x (t) + a 1 x (t) + a 0 x(t) = q i (t) (13-59) for ethvert i = 1,..., n, er x 0 (t) = x 01 (t) + x 02 (t) x 0n (t) (13-60) en partikulær løsning til x (t) + a 1 x (t) + a 0 x(t) = q(t) = q 1 (t) + q 2 (t) q n (t), (13-61) hvor højresiderne q og q 1, q 2,..., q n er kontinuerte funktioner i et interval I.
13 enote DEN INHOMOGENE LIGNING 13 Bevis Superposition er en følge af at differentialligningerne er lineære. Vi gennemfører her et generelt bevis for alle typer af lineære differentialligninger. Venstresiden af en differentialligning kaldes f (x(t)). Vi opstiller nu n differentialligninger: f (x 01 (t)) = q 1 (t), f (x 02 (t)) = q 2 (t),..., f (x 0n (t)) = q n (t) (13-62) hvor x 01, x 02,..., x 0n er partikulære løsninger til de respektive inhomogene differentialligninger. Vi definerer nu x 0 = x 01 + x x 0n og indsætter denne i venstresiden: f (x 0 (t)) = f (x 01 (t) + x 02 (t) x 0n (t)) = f (x 01 (t)) + f (x 02 (t)) f (x 0n (t)) = q 1 (t) + q 2 (t) q n (t) (13-63) På højresiden fås en sum af funktionerne q 1, q 2,..., q n, som kaldes for q. Sætningen er da bevist. Eksempel Superposition Givet er den inhomogene differentialligning x (t) x (t) 3x(t) = 9e 4t + 3t 14, t R. (13-64) Vi ønsker at bestemme en partikulær løsning x 0 (t) til differentialligningen. Det ses, at højresiden er en kombination af en eksponentialfunktion (q 1 (t) = 9e 4t ) og et polynomium (q 2 (t) = 3t 14). Derfor bruges superpositionsprincippet fra sætning og differentialligningen opsplittes i to dele. x (t) x (t) 3x(t) = 9e 4t = q 1 (t) (13-65) x (t) x (t) 3x(t) = 3t 14 = q 2 (t) (13-66) Først behandles ligning (13-65), hvortil vi skal bruge metode En partikulær løsning er da af formen x 01 (t) = γe αt = γe 4t. Vi har x 0 1 (t) = 4γe 4t og x 0 1 (t) = 16γe 4t. Dette indsættes i ligningen. 16γe 4t 4γe 4t 3γe 4t = 9e 4t γ = 1 (13-67) Derfor er x 01 (t) = e 4t. Nu behandles ligning (13-66), hvor en partikulær løsning er et polynomium af højst grad 1, jævnfør metode 13.6, altså er x 02 (t) = b 1 t + b 0. Derfor er x 0 2 (t) = b 1 og x 0 2 (t) = 0. Dette indsættes i differentialligningen. 0 b 1 3(b 1 t + b 0 ) = 3t 14 ( 3b 1 3)t + ( b 1 3b ) = 0 (13-68)
14 enote DEN INHOMOGENE LIGNING 14 Vi har således to ligninger med to ubekendte, og vi finder, at b 1 = 1, og derfor er b 0 = 5. Altså er en partikulær løsning x 02 (t) = t + 5. Den samlede partikulære løsning til (13-64) findes da som summen af de to allerede fundne partikulære løsninger til de to opsplittede ligninger: x 0 (t) = x 01 (t) + x 02 (t) = e 4t t + 5, t R. (13-69) Den komplekse gættemetode Den komplekse gættemetode benyttes når det er bekvemt at omskrive differentialligningens højreside til en kompleks højreside, således at den givne reelle højreside er realdelen af den komplekse. Er højresiden for eksempel 2e 2t cos(3t), og man til denne lægger i( 2e 2t sin(3t)), fås 2e 2t (cos(3t) i sin(3t)) = 2e (2 3i)t. (13-70) Her gælder der klart nok at Re(2e (2 3i)t ) = 2e 2t cos(3t). Man finder nu en kompleks partikulær løsning til differentialligningen med den komplekse højreside. Den ønskede reelle partikulære løsning til den oprindelige differentialligning er da realdelen af den fundne komplekse løsning. Bemærk at denne metode kan kun benyttes fordi differentialligningen er lineær. Det er netop lineariteten der sikrer at realdelen af den fundne komplekse løsning er den ønskede reelle løsning. Dette vises ved at vi opfatter differentialligningens venstreside som en lineær afbildning f (z(t)) i mængden af komplekse funktioner af en reel variabel og bruger følgende generelle sætning: Sætning Der er givet en lineær afbildning f : (C (R), C) (C (R), C) og ligningen f (z(t)) = s(t). (13-71) Hvis vi sætter z(t) og s(t) på rektangulær form ved z(t) = x(t) + i y(t) og s(t) = q(t) + i r(t), så gælder der at (13-71) sand hvis og kun hvis f (x(t)) = q(t) og f (y(t)) = r(t). (13-72)
15 enote DEN INHOMOGENE LIGNING 15 Bevis Givet er funktionen z(t) og Lad den lineære afbildning f og funktionerne z(t) og s(t) være givet som i sætning Som følge af egenskaberne ved lineære afbildninger, se definition 11.2, gælder der følgende: f (z(t)) = s(t) f (x(t) + i y(t)) = q(t) + i r(t) f (x(t)) + i f (y(t)) = q(t) + i r(t) f (x(t)) = q(t) og f (y(t)) = r(t). (13-73) Sætningen er dermed bevist. Metode Den komplekse gættemetode En partikulær løsning x 0 (t) til den reelle inhomogene differentialligning x (t) + a 1 x (t) + a 0 x(t) = q(t), t R, (13-74) hvor a 0 og a 1 er reelle koefficienter og ( q(t) = Re (a + bi)e (α+ωi)t) = ae αt cos(ωt) be αt sin(ωt), (13-75) bestemmes i første omgang ved at finde den tilsvarende komplekse partikulære løsning til følgende komplekse differentialligning z (t) + a 1 z (t) + a 0 z(t) = (a + bi)e (α+ωi)t, t R, (13-76) Den komplekse partikulære løsning har formen z 0 (t) = (c + di)e (α+ωi)t, hvor c og d bestemmes ved indsættelse af z 0 (t) i differentialligningen (13-76). Efterfølgende er en partikulær løsning til differentialligningen (13-74) givet ved x 0 (t) = Re(z 0 (t)). (13-77) En afgørende grund til, at man benytter den komplekse gættemetode, er, at det er så enkelt at differentiere eksponentialfunktionen, selv når den er kompleks.
16 enote DEN INHOMOGENE LIGNING 16 Eksempel Den komplekse gættemetode Givet er en 2. ordens inhomogene differentialligning: x (t) 2x (t) 2x(t) = 19e 4t cos(t) 35e 4t sin(t), t R. (13-78) Bestem en partikulær løsning til denne differentialligning. Det er oplagt at bruge den komplekse gættemetode fra metode til denne opgave. Det ses nemlig i første omgang, at højresiden svarer til reeldelen af et kompleks tal: q(t) = 19e 4t cos(t) 35e 4t sin(t) ( ) = Re 19e 4t (cos(t) + i sin(t)) + 35ie 4t (cos(t) + i sin(t)) = Re (19e 4t e it + 35ie 4t e it) = Re (19e 4t+it + 35ie 4t+it) ( = Re ( i)e (4+i)t). (13-79) Bemærk brugen af Eulers formel fra enote 29 for at opnå omskrivningen fra cos og sin til eksponentiel form, e iv = cos(v) + sin(v). Det kan være en anelse kringlet at gennemskue leddenes komplekse form. Leddet 19e 4t cos(t) er nemt; det udvides let til 19e 4t (cos(t) + i sin(t)), hvor sin-leddet som imaginærdelen er tilføjet. Men leddet 35e 4t sin(t) kræver lidt mere; det får tilføjet et cos-led som imaginærdel, og derfor skal i et flyttes fra cos til sin ved, at udtrykket ganges med i. Vi udvider differentialligningen, så vi har det nye tilsvarende komplekse tal ( i)e (4+i)t på højresiden i stedet. Vi skal så i stedet finde en kompleks partikulær løsning til denne differentialligning: z (t) 2z (t) 2z(t) = ( i)e (4+i)t, t R. (13-80) hvor vi har erstattet x(t) med z(t) for tydeligt at markere, at den løsning, vi nu finder, netop ikke er en løsning til den originale ligning, men kun en løsning til denne udvidede komplekse form af ligningen. Vi gætter nu på, at z 0 (t) = (c + di)e (4+i)t er en løsning, hvor c og d er reelle konstanter. Vi har z 0(t) = (c + di)(4 + i)e (4+i)t = (4c d + (c + 4d)i) e (4+i)t z 0 (t) = (4c d + (c + 4d)i)(4 + i)e (4+i)t = (15c 8d + (8c + 15d)i)e (4+i)t. og (13-81) Disse udtryk samt z 0 (t) indsættes i den komplekse differentialligning for at bestemme c og
17 enote EKSISTENS OG ENTYDIGHED 17 d: (15c 8d + (8c + 15d)i)e (4+i)t 2(4c d + (c + 4d)i)e (4+i)t 2(c + di)e (4+i)t = ( i)e (4+i)t 15c 8d + (8c + 15d)i 2(4c d + (c + 4d)i) 2(c + di) = i 5c 6d + (6c + 5d)i = i 5c 6d = 19 6c + 5d = 35 (13-82) Dette er to ligninger med to ubekendte. Ligningssystemets totalmatrix opskrives: [ ] [ ] [ ] (13-83) Vi har altså, at c = 5 og d = 1, hvilket giver z 0 (t) = (5 + i)e (4+i)t. Dette er som sagt løsningen til den komplekse udvidelse af differentialligningen. En partikulær løsning til den originale differentialligning (13-78) er derfor reeldelen af z 0 (t), ( x 0 (t) = Re(z 0 (t)) = Re (5 + i)e (4+i)t) = 5e 4t cos(t) e 4t sin(t), t R. (13-84) 13.4 Eksistens og entydighed Vi formulerer her en sætning om eksistens og entydighed for differentialligninger af 2. orden med konstante koefficienter. Vi har behov for to begyndelsesværdibetingelser, nemlig funktionens værdi og den afledtes værdi for en værdi af variablen. Sætning Eksistens og entydighed Til ethvert talsæt (t 0, x 0, v 0 ) (dobbelt begyndelsesværdibetingelse) findes netop én løsning x(t) til differentialligningen således, at hvor t 0 I, x 0 R og v 0 R. x (t) + a 1 x (t) + a 0 x(t) = q(t), t I, q : I R (13-85) x(t 0 ) = x 0 og x (t 0 ) = v 0, (13-86)
18 enote EKSISTENS OG ENTYDIGHED 18 Eksempel Eksistens og entydighed Givet differentialligningen x (t) 5x (t) 36x(t) = 0, t R. (13-87) Bestem en funktion x(t), som er løsning til differentialligningen og har begyndelsesværdibetingelsen (t 0, x 0, v 0 ) = (0, 5, 6). Det ses, at differentialligningen er homogen. Den har karakterligningen λ 2 5λ 36 = 0. (13-88) Karakterligningen har rødderne λ 1 = 4 og λ 2 = 9. Derfor er den fuldstændige løsningsmængde til den homogene differentialligning (ved hjælp af sætning 13.2) udspændt af følgende funktioner for alle c 1, c 2 R: Man har da x(t) = c 1 e 4t + c 2 e 9t, t R. (13-89) x (t) = 4c 1 e 4t + 9c 2 e 9t. (13-90) Indsættes begyndelsesværdibetingelserne x(0) = 5 og x (0) = 6 i de to ligninger, kan det løses for (c 1, c 2 ), 5 = c 1 + c 2 (13-91) 6 = 4c 1 + 9c 2. Ligningerne er blevet meget simple, da e 0 = 1. Indsættes c 2 = 5 c 1 i den anden ligning, fås 6 = 4c 1 + 9(5 c 1 ) = 13c c 1 = = 3. (13-92) Derfor er c 2 = 5 3 = 2, og den betingede løsning er x(t) = 3e 4t + 2e 9t, t R. (13-93) Herunder er et eksempel, som gennemgår hele løsningsproceduren for en inhomogen differentialligning med en dobbelt begyndelsesværdibetingelse. Efter det kommer et eksempel, hvor formålet er at finde en differentialligning, hvor den fuldstændige løsningsmængde er opgivet. Den falder derfor i tråd med eksempel 13.5, og nu er der også en højreside forskellig fra nul.
19 enote EKSISTENS OG ENTYDIGHED 19 Eksempel Opsamlende eksempel Givet differentialligningen x (t) + 6x (t) + 5x(t) = 20t t + 13, t R. (13-94) Bestem den fuldstændige løsningsmængde L inhom samt den betingede løsning x(t), som opfylder begyndelsesværdibetingelserne (t 0, x 0, v 0 ) = (0, 5, 8). Først løses den tilsvarende homogene differentialligning, og karakterligningen ser således ud: λ 2 + 6λ + 5 = 0. (13-95) Denne har rødderne λ 1 = 5 og λ 2 = 1. Da disse rødder er reelle og forskellige, er den fuldstændige homogene løsningsmængde ifølge sætning 13.2 givet ved L hom = { c 1 e 5t + c 2 e t, t R c 1, c 2 R }. (13-96) Nu bestemmes en partikulær løsning til den inhomogene ligning. Da højresiden er et andengradspolynomium, gætter vi ved hjælp af metode 13.6 på, at x 0 (t) = b 2 t 2 + b 1 t + b 0 er en løsning. Vi har da, at x 0 (t) = 2b 2t + b 1 og x 0 (t) = 2b 2. Dette indsættes i differentialligningen: 2b 2 + 6(2b 2 t + b 1 ) + 5(b 2 t 2 + b 1 t + b 0 ) = 20t t + 13 (5b 2 20)t 2 + (12b 2 + 5b 1 48)t + (2b 2 + 6b 1 + 5b 0 13) = 0 5b 2 20 = 0 12b 2 + 5b 1 48 = 0 2b 2 + 6b 1 + 5b 0 13 = 0. (13-97) Den første ligning giver nemt b 2 = 4. Indsættes det i den anden ligning, fås ved lidt hovedregning b 1 = 0. Til sidst i den tredje ligning får man b 0 = 1. En partikulær løsning til den inhomogene differentialligning er derfor x 0 (t) = 4t 2 + 1, t R. (13-98) Ifølge struktursætningen, for eksempel metode 13.1, er den fuldstændige løsningsmængde til den inhomogene differentialligning givet ved L inhom = x 0 (t) + L hom = { 4t c 1 e 5t + c 2 e t, t R c 1, c 2 R }. (13-99) Vi bestemmer nu den løsning, der opfylder de givne begyndelsesværdibetingelser. En vilkårlig løsning har formen Den afledede er x(t) = 4t c 1 e 5t + c 2 e t, t R. (13-100) Indsættes x(0) = 5 og x (0) = 8, fås de to ligninger x (t) = 8t 5c 1 e 5t c 2 e t, t R. (13-101) 5 = c 1 + c = 5c 1 c 2. (13-102)
20 enote EKSISTENS OG ENTYDIGHED 20 Indsættes c 1 = 4 c 2 fra den første ligning i den anden, fås 8 = 5(4 c 2 ) c = 4c 2 c 2 = 3. (13-103) Det giver c 1 = 1, og den betingede løsning er derfor x(t) = e 5t + 3e t + 4t 2 + 1, t R. (13-104) Eksempel Fra løsning til ligning Givet den fuldstændige løsning til en lineær 2. ordens differentialligning med konstante koefficienter L inhom = { c 1 e 2t + c 2 e 2t 1 2 sin(2t), t R c 1, c 2 R }. (13-105) Opstil differentialligningen, som generelt har dette udseende: a 1, a 0 og q(t) skal altså bestemmes. x (t) + a 1 x (t) + a 0 x(t) = q(t). (13-106) I første omgang splittes løsningen op i en partikulær løsning og den fuldstændige homogene løsningsmængde: x 0 (t) = 1 2 sin(2t), t R og L hom = { c 1 e 2t + c 2 e 2t t R c 1, c 2 R }. (13-107) Nu betragtes den fuldstændige homogene løsning. Udseendet på denne stemmer overens med den første situation i sætning Karakterligningen har altså to forskellige reelle rødder, og de er λ 1 = 2 og λ 2 = 2. Karakterligningen er derfor (λ + 2)(λ 2) = λ 2 4 = 0. (13-108) Dette afgør koefficienterne på venstresiden af differentialligningen: a 1 = 0 og a 0 = 4. Differentialligningen ser altså indtil videre således ud: x (t) 4x(t) = q(t), t R. (13-109) Da x 0 (t) er en partikulær løsning til den inhomogene differentialligning kan højresiden q(t) bestemmes ved at indsætte x 0 (t). Vi har, at x 0 (t) = 2 sin(2t), og x 0 (t) 4x 0 (t) = q(t) 2 sin(2t) 4( 1 2 sin(2t)) = q(t) 4 sin(2t) = q(t). Nu er samtlige ukendte i differentialligningen bestemt, og den endelige ligning er (13-110) x (t) 4x(t) = 4 sin(2t), t R. (13-111)
21 enote EKSISTENS OG ENTYDIGHED 21 I denne enote beskæftiger vi os ikke med systemer af 2. ordens homogene lineære differentialligninger med konstante koefficienter. Det skal dog tilføjes, at vi allerede med den gennemgåede teori og lidt snilde kan løse sådanne problemer. Hvis vi har et system af 2. ordens homogene differentialligninger, kan vi betragte hver differentialligning for sig. Ved hjælp af afsnit 12.5 kan en sådan ligning omformes til 2 ligninger af 1. orden. Gøres det med alle differentialligningerne i systemet, ender vi med dobbelt så mange differentialligninger, nu af 1. orden. Dette nye system kan vi løse med den gennemgåede teori i enote 12. Systemer af 2. ordens homogene lineære differentialligninger findes mange steder i mekanisk fysik, kemi, elektromagnetisme m.fl.
Lineære 1. ordens differentialligningssystemer
 enote enote Lineære ordens differentialligningssystemer Denne enote beskriver ordens differentialligningssystemer og viser, hvordan de kan løses enoten er i forlængelse af enote, der beskriver lineære
enote enote Lineære ordens differentialligningssystemer Denne enote beskriver ordens differentialligningssystemer og viser, hvordan de kan løses enoten er i forlængelse af enote, der beskriver lineære
Lineære 1. ordens differentialligningssystemer
 enote 7 enote 7 Lineære ordens differentialligningssystemer Denne enote beskriver ordens differentialligningssystemer og viser, hvordan de kan løses Der bruges egenværdier og egenvektorer i løsningsproceduren,
enote 7 enote 7 Lineære ordens differentialligningssystemer Denne enote beskriver ordens differentialligningssystemer og viser, hvordan de kan løses Der bruges egenværdier og egenvektorer i løsningsproceduren,
Lineære 1. ordens differentialligningssystemer
 enote enote Lineære ordens differentialligningssystemer Denne enote beskriver ordens differentialligningssystemer og viser, hvordan de kan løses enoten er i forlængelse af enote, der beskriver lineære
enote enote Lineære ordens differentialligningssystemer Denne enote beskriver ordens differentialligningssystemer og viser, hvordan de kan løses enoten er i forlængelse af enote, der beskriver lineære
Lineære differentialligningers karakter og lineære 1. ordens differentialligninger
 enote 11 1 enote 11 Lineære differentialligningers karakter og lineære 1. ordens differentialligninger I denne note introduceres lineære differentialligninger, som er en speciel (og bekvem) form for differentialligninger.
enote 11 1 enote 11 Lineære differentialligningers karakter og lineære 1. ordens differentialligninger I denne note introduceres lineære differentialligninger, som er en speciel (og bekvem) form for differentialligninger.
Modulpakke 3: Lineære Ligningssystemer
 Chapter 4 Modulpakke 3: Lineære Ligningssystemer 4. Homogene systemer I teknikken møder man meget ofte modeller der leder til systemer af koblede differentialligninger. Et eksempel på et sådant system
Chapter 4 Modulpakke 3: Lineære Ligningssystemer 4. Homogene systemer I teknikken møder man meget ofte modeller der leder til systemer af koblede differentialligninger. Et eksempel på et sådant system
Førsteordens lineære differentialligninger
 enote 16 1 enote 16 Førsteordens lineære differentialligninger I denne enote gives først en kort introduktion til differentialligninger i almindelighed, hvorefter hovedemnet er en særlig type af differentialligninger,
enote 16 1 enote 16 Førsteordens lineære differentialligninger I denne enote gives først en kort introduktion til differentialligninger i almindelighed, hvorefter hovedemnet er en særlig type af differentialligninger,
DesignMat Uge 1 Gensyn med forårets stof
 DesignMat Uge 1 Gensyn med forårets stof Preben Alsholm Efterår 2010 1 Hovedpunkter fra forårets pensum 11 Taylorpolynomium Taylorpolynomium Det n te Taylorpolynomium for f med udviklingspunkt x 0 : P
DesignMat Uge 1 Gensyn med forårets stof Preben Alsholm Efterår 2010 1 Hovedpunkter fra forårets pensum 11 Taylorpolynomium Taylorpolynomium Det n te Taylorpolynomium for f med udviklingspunkt x 0 : P
DesignMat Lineære differentialligninger I
 DesignMat Lineære differentialligninger I Preben Alsholm Uge Forår 0 1 Lineære differentialligninger af første orden 1.1 Normeret lineær differentialligning Normeret lineær differentialligning En differentialligning,
DesignMat Lineære differentialligninger I Preben Alsholm Uge Forår 0 1 Lineære differentialligninger af første orden 1.1 Normeret lineær differentialligning Normeret lineær differentialligning En differentialligning,
DesignMat Lineære differentialligninger I
 DesignMat Lineære differentialligninger I Preben Alsholm Uge 9 Forår 2010 1 Lineære differentialligninger af første orden 1.1 Normeret lineær differentialligning Normeret lineær differentialligning En
DesignMat Lineære differentialligninger I Preben Alsholm Uge 9 Forår 2010 1 Lineære differentialligninger af første orden 1.1 Normeret lineær differentialligning Normeret lineær differentialligning En
DesignMat Uge 1 Repetition af forårets stof
 DesignMat Uge 1 Repetition af forårets stof Preben Alsholm Efterår 008 01 Lineært ligningssystem Lineært ligningssystem Et lineært ligningssystem: a 11 x 1 + a 1 x + + a 1n x n = b 1 a 1 x 1 + a x + +
DesignMat Uge 1 Repetition af forårets stof Preben Alsholm Efterår 008 01 Lineært ligningssystem Lineært ligningssystem Et lineært ligningssystem: a 11 x 1 + a 1 x + + a 1n x n = b 1 a 1 x 1 + a x + +
Noter om Komplekse Vektorrum, Funktionsrum og Differentialligninger LinAlg 2004/05-Version af 16. Dec.
 Noter om Komplekse Vektorrum, Funktionsrum og Differentialligninger LinAlg 2004/05-Version af 16. Dec. 1 Komplekse vektorrum I defininitionen af vektorrum i Afsnit 4.1 i Niels Vigand Pedersen Lineær Algebra
Noter om Komplekse Vektorrum, Funktionsrum og Differentialligninger LinAlg 2004/05-Version af 16. Dec. 1 Komplekse vektorrum I defininitionen af vektorrum i Afsnit 4.1 i Niels Vigand Pedersen Lineær Algebra
Den homogene ligning. Vi betragter den n te ordens, homogene, lineære differentialligning. d n y dt n. an 1 + any = 0 (1.2) dt. + a1 d n 1 y dt n 1
 1/7 Den homogene ligning Vi betragter den n te ordens, homogene, lineære differentialligning a 0 d n y dt n + a1 d n 1 y dt n 1 hvor a 0,..., a n R og a 0 0. Vi skriver ligningen på kort form som + + dy
1/7 Den homogene ligning Vi betragter den n te ordens, homogene, lineære differentialligning a 0 d n y dt n + a1 d n 1 y dt n 1 hvor a 0,..., a n R og a 0 0. Vi skriver ligningen på kort form som + + dy
Chapter 3. Modulpakke 3: Egenværdier. 3.1 Indledning
 Chapter 3 Modulpakke 3: Egenværdier 3.1 Indledning En vektor v har som bekendt både størrelse og retning. Hvis man ganger vektoren fra højre på en kvadratisk matrix A bliver resultatet en ny vektor. Hvis
Chapter 3 Modulpakke 3: Egenværdier 3.1 Indledning En vektor v har som bekendt både størrelse og retning. Hvis man ganger vektoren fra højre på en kvadratisk matrix A bliver resultatet en ny vektor. Hvis
Hans J. Munkholm: En besvarelse af
 Hans J. Munkholm: En besvarelse af Projekt for MM501, Lineære differentialligninger November-december 2009 Nummererede formler fra opgaveformuleringen Her samles alle opgavens differentialligninger og
Hans J. Munkholm: En besvarelse af Projekt for MM501, Lineære differentialligninger November-december 2009 Nummererede formler fra opgaveformuleringen Her samles alle opgavens differentialligninger og
MM501 forelæsningsslides
 MM501 forelæsningsslides uge 37, 2010 Produceret af Hans J. Munkholm 2009 bearbejdet af Jessica Carter 2010 1 Hvad er et komplekst tal? Hvordan regner man med komplekse tal? Man kan betragte udvidelsen
MM501 forelæsningsslides uge 37, 2010 Produceret af Hans J. Munkholm 2009 bearbejdet af Jessica Carter 2010 1 Hvad er et komplekst tal? Hvordan regner man med komplekse tal? Man kan betragte udvidelsen
DESIGNMAT FORÅR 2012: UGESEDDEL Forberedelse Læs alle opgaverne fra tidligere ugesedler, og læg særlig mærke til dem du har spørgsmål til.
 DESIGNMAT FORÅR 2012: UGESEDDEL 13 INSTITUT FOR MATEMATIK 1. Forberedelse Læs alle opgaverne fra tidligere ugesedler, og læg særlig mærke til dem du har spørgsmål til. 2. Aktiviteter mandag 13 17 2.1.
DESIGNMAT FORÅR 2012: UGESEDDEL 13 INSTITUT FOR MATEMATIK 1. Forberedelse Læs alle opgaverne fra tidligere ugesedler, og læg særlig mærke til dem du har spørgsmål til. 2. Aktiviteter mandag 13 17 2.1.
Komplekse tal. Mikkel Stouby Petersen 27. februar 2013
 Komplekse tal Mikkel Stouby Petersen 27. februar 2013 1 Motivationen Historien om de komplekse tal er i virkeligheden historien om at fjerne forhindringerne og gøre det umulige muligt. For at se det, vil
Komplekse tal Mikkel Stouby Petersen 27. februar 2013 1 Motivationen Historien om de komplekse tal er i virkeligheden historien om at fjerne forhindringerne og gøre det umulige muligt. For at se det, vil
Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 2016
 Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær eksamen - Efterår - 8. Januar 2016
 Besvarelser til Calculus Ordinær eksamen - Efterår - 8. Januar 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har
Besvarelser til Calculus Ordinær eksamen - Efterår - 8. Januar 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har
Polynomier af én variabel
 enote 30 1 enote 30 Polynomier af én variabel I denne enote introduceres komplekse polynomier af én variabel. Der forudsættes elementært kendskab til komplekse tal, og kendskab til reelle polynomier af
enote 30 1 enote 30 Polynomier af én variabel I denne enote introduceres komplekse polynomier af én variabel. Der forudsættes elementært kendskab til komplekse tal, og kendskab til reelle polynomier af
Egenværdier og egenvektorer
 enote 9 enote 9 Egenværdier og egenvektorer Denne note indfører begreberne egenværdier og egenvektorer for lineære afbildninger i vilkårlige generelle vektorrum og går derefter i dybden med egenværdier
enote 9 enote 9 Egenværdier og egenvektorer Denne note indfører begreberne egenværdier og egenvektorer for lineære afbildninger i vilkårlige generelle vektorrum og går derefter i dybden med egenværdier
Algebra - Teori og problemløsning
 Algebra - Teori og problemløsning, januar 05, Kirsten Rosenkilde. Algebra - Teori og problemløsning Kapitel -3 giver en grundlæggende introduktion til at omskrive udtryk, faktorisere og løse ligningssystemer.
Algebra - Teori og problemløsning, januar 05, Kirsten Rosenkilde. Algebra - Teori og problemløsning Kapitel -3 giver en grundlæggende introduktion til at omskrive udtryk, faktorisere og løse ligningssystemer.
Nøgleord og begreber. Definition 15.1 Den lineære 1. ordens differentialligning er
 Oversigt [S] 7.3, 7.4, 7.5, 7.6; [LA] 15, 16, 17 Nøgleord og begreber 1. ordens lineær ligning Løsningsmetode August 2002, opgave 7 1. ordens lineært system Løsning ved egenvektor Lille opgave Stor opgave
Oversigt [S] 7.3, 7.4, 7.5, 7.6; [LA] 15, 16, 17 Nøgleord og begreber 1. ordens lineær ligning Løsningsmetode August 2002, opgave 7 1. ordens lineært system Løsning ved egenvektor Lille opgave Stor opgave
Oversigt [S] 7.3, 7.4, 7.5, 7.6; [LA] 15, 16, 17
![Oversigt [S] 7.3, 7.4, 7.5, 7.6; [LA] 15, 16, 17 Oversigt [S] 7.3, 7.4, 7.5, 7.6; [LA] 15, 16, 17](/thumbs/62/47131431.jpg) Oversigt [S] 7.3, 7.4, 7.5, 7.6; [LA] 15, 16, 17 Nøgleord og begreber 1. ordens lineær ligning Løsningsmetode August 2002, opgave 7 1. ordens lineært system Løsning ved egenvektor Lille opgave Stor opgave
Oversigt [S] 7.3, 7.4, 7.5, 7.6; [LA] 15, 16, 17 Nøgleord og begreber 1. ordens lineær ligning Løsningsmetode August 2002, opgave 7 1. ordens lineært system Løsning ved egenvektor Lille opgave Stor opgave
Komplekse Tal. 20. november 2009. UNF Odense. Steen Thorbjørnsen Institut for Matematiske Fag Århus Universitet
 Komplekse Tal 20. november 2009 UNF Odense Steen Thorbjørnsen Institut for Matematiske Fag Århus Universitet Fra de naturlige tal til de komplekse Optælling af størrelser i naturen De naturlige tal N (N
Komplekse Tal 20. november 2009 UNF Odense Steen Thorbjørnsen Institut for Matematiske Fag Århus Universitet Fra de naturlige tal til de komplekse Optælling af størrelser i naturen De naturlige tal N (N
Matematisk modellering og numeriske metoder. Lektion 5
 Matematisk modellering og numeriske metoder Lektion 5 Morten Grud Rasmussen 19. september, 2013 1 Euler-Cauchy-ligninger [Bogens afsnit 2.5, side 71] 1.1 De tre typer af Euler-Cauchy-ligninger Efter at
Matematisk modellering og numeriske metoder Lektion 5 Morten Grud Rasmussen 19. september, 2013 1 Euler-Cauchy-ligninger [Bogens afsnit 2.5, side 71] 1.1 De tre typer af Euler-Cauchy-ligninger Efter at
Eulers equidimensionale differentialligning
 Eulers equidimensionale differentialligning Projektbesvarelse for MM501, udformet af Hans J. Munkholm Differentialligningen September-oktober 2009 For at kunne referere let og elegant gentages differentialligningen
Eulers equidimensionale differentialligning Projektbesvarelse for MM501, udformet af Hans J. Munkholm Differentialligningen September-oktober 2009 For at kunne referere let og elegant gentages differentialligningen
Matematisk modellering og numeriske metoder. Lektion 6
 Matematisk modellering og numeriske metoder Lektion 6 Morten Grud Rasmussen 24. september, 2013 1 Forcerede oscillationer [Bogens afsnit 2.8, side 85] 1.1 Et forstyrret masse-fjeder-system I udledningen
Matematisk modellering og numeriske metoder Lektion 6 Morten Grud Rasmussen 24. september, 2013 1 Forcerede oscillationer [Bogens afsnit 2.8, side 85] 1.1 Et forstyrret masse-fjeder-system I udledningen
Lineære ligningssystemer
 enote 6 1 enote 6 Lineære ligningssystemer Denne enote handler om lineære ligningssystemer, om metoder til at beskrive dem og løse dem, og om hvordan man kan få overblik over løsningsmængdernes struktur.
enote 6 1 enote 6 Lineære ligningssystemer Denne enote handler om lineære ligningssystemer, om metoder til at beskrive dem og løse dem, og om hvordan man kan få overblik over løsningsmængdernes struktur.
Matematisk modellering og numeriske metoder. Lektion 1
 Matematisk modellering og numeriske metoder Lektion 1 Morten Grud Rasmussen 4. september, 2013 1 Ordinære differentialligninger ODE er 1.1 ODE er helt grundlæggende Definition 1.1 (Ordinære differentialligninger).
Matematisk modellering og numeriske metoder Lektion 1 Morten Grud Rasmussen 4. september, 2013 1 Ordinære differentialligninger ODE er 1.1 ODE er helt grundlæggende Definition 1.1 (Ordinære differentialligninger).
Lotka-Volterra modellen
 Lotka-Volterra modellen G4-105 Matematik Aalborg Universitet 20. december 2016 School of Engineering and Science Fredrik Bajers Vej 7G 9220 Aalborg Øst www.ses.aau.dk Titel: Lotka-Volterra modellen Tema:
Lotka-Volterra modellen G4-105 Matematik Aalborg Universitet 20. december 2016 School of Engineering and Science Fredrik Bajers Vej 7G 9220 Aalborg Øst www.ses.aau.dk Titel: Lotka-Volterra modellen Tema:
DesignMat Uge 5 Systemer af lineære differentialligninger II
 DesignMat Uge 5 Systemer af lineære differentialligninger II Preben Alsholm Efterår 21 1 Lineære differentialligningssystemer 11 Lineært differentialligningssystem af første orden Lineært differentialligningssystem
DesignMat Uge 5 Systemer af lineære differentialligninger II Preben Alsholm Efterår 21 1 Lineære differentialligningssystemer 11 Lineært differentialligningssystem af første orden Lineært differentialligningssystem
Affine rum. a 1 u 1 + a 2 u 2 + a 3 u 3 = a 1 u 1 + (1 a 1 )( u 2 + a 3. + a 3. u 3 ) 1 a 1. Da a 2
 Affine rum I denne note behandles kun rum over R. Alt kan imidlertid gennemføres på samme måde over C eller ethvert andet legeme. Et underrum U R n er karakteriseret ved at det er en delmængde som er lukket
Affine rum I denne note behandles kun rum over R. Alt kan imidlertid gennemføres på samme måde over C eller ethvert andet legeme. Et underrum U R n er karakteriseret ved at det er en delmængde som er lukket
Matematik A. Højere teknisk eksamen. Forberedelsesmateriale. htx112-mat/a-26082011
 Matematik A Højere teknisk eksamen Forberedelsesmateriale htx112-mat/a-26082011 Fredag den 26. august 2011 Forord Forberedelsesmateriale til prøverne i matematik A Der er afsat 10 timer på 2 dage til
Matematik A Højere teknisk eksamen Forberedelsesmateriale htx112-mat/a-26082011 Fredag den 26. august 2011 Forord Forberedelsesmateriale til prøverne i matematik A Der er afsat 10 timer på 2 dage til
Polynomier af én variabel
 enote 30 1 enote 30 Polynomier af én variabel I denne enote introduceres komplekse polynomier af én variabel. Der forudsættes elementært kendskab til komplekse tal og kendskab til reelle polynomier af
enote 30 1 enote 30 Polynomier af én variabel I denne enote introduceres komplekse polynomier af én variabel. Der forudsættes elementært kendskab til komplekse tal og kendskab til reelle polynomier af
Ligninger med reelle løsninger
 Ligninger med reelle løsninger Når man løser ligninger, er der nogle standardmetoder som er vigtige at kende. Her er der en kort introduktion til forskellige teknikker efterfulgt af opgaver hvor man kan
Ligninger med reelle løsninger Når man løser ligninger, er der nogle standardmetoder som er vigtige at kende. Her er der en kort introduktion til forskellige teknikker efterfulgt af opgaver hvor man kan
Projekt 4.6 Løsning af differentialligninger ved separation af de variable
 Projekt 4.6 Løsning af differentialligninger ved separation af de variable Differentialligninger af tpen d hx () hvor hx ()er en kontinuert funktion, er som nævnt blot et stamfunktionsproblem. De løses
Projekt 4.6 Løsning af differentialligninger ved separation af de variable Differentialligninger af tpen d hx () hvor hx ()er en kontinuert funktion, er som nævnt blot et stamfunktionsproblem. De løses
12.1 Cayley-Hamilton-Sætningen
 SEKTION 12.1 CAYLEY-HAMILTON-SÆTNINGEN 12.1 Cayley-Hamilton-Sætningen Sætning 12.1.1 (Cayley-Hamilton) Lad A Mat n,n (C). Så gælder p A (A) =. Sætningen gælder faktisk over et vilkårligt legeme, men vi
SEKTION 12.1 CAYLEY-HAMILTON-SÆTNINGEN 12.1 Cayley-Hamilton-Sætningen Sætning 12.1.1 (Cayley-Hamilton) Lad A Mat n,n (C). Så gælder p A (A) =. Sætningen gælder faktisk over et vilkårligt legeme, men vi
DesignMat Lineære ligningssystemer og Gauss-elimination
 DesignMat Lineære ligningssystemer og Gauss-elimination Preben Alsholm Uge Forår 010 1 Lineære ligningssystemer og Gauss-elimination 11 Om talrummet R n Om talsæt bestående af n tal R n er blot mængden
DesignMat Lineære ligningssystemer og Gauss-elimination Preben Alsholm Uge Forår 010 1 Lineære ligningssystemer og Gauss-elimination 11 Om talrummet R n Om talsæt bestående af n tal R n er blot mængden
Introduktion til Laplace transformen (Noter skrevet af Nikolaj Hess-Nielsen sidst revideret marts 2013)
 Introduktion til Laplace transformen (oter skrevet af ikolaj Hess-ielsen sidst revideret marts 23) Integration handler ikke kun om arealer. Tværtimod er integration basis for mange af de vigtigste værktøjer
Introduktion til Laplace transformen (oter skrevet af ikolaj Hess-ielsen sidst revideret marts 23) Integration handler ikke kun om arealer. Tværtimod er integration basis for mange af de vigtigste værktøjer
Om første og anden fundamentalform
 Geometri, foråret 2005 Jørgen Larsen 9. marts 2005 Om første og anden fundamentalform 1 Tangentrummet; første fundamentalform Vi betragter en flade S parametriseret med σ. Lad P = σu 0, v 0 være et punkt
Geometri, foråret 2005 Jørgen Larsen 9. marts 2005 Om første og anden fundamentalform 1 Tangentrummet; første fundamentalform Vi betragter en flade S parametriseret med σ. Lad P = σu 0, v 0 være et punkt
Lektion 12. højere ordens lineære differentiallininger. homogene. inhomogene. eksempler
 Lektion 12 2. ordens lineære differentialligninger homogene inhomogene eksempler højere ordens lineære differentiallininger 1 Anden ordens lineære differentialligninger med konstante koefficienter A. Homogene
Lektion 12 2. ordens lineære differentialligninger homogene inhomogene eksempler højere ordens lineære differentiallininger 1 Anden ordens lineære differentialligninger med konstante koefficienter A. Homogene
Noter til An0 DIFFERENTIALLIGNINGER MED KONSTANTE KOEFFICIENTER
 UDKAST 7122009 Noter til An0 Inst f Matematiske Fag Gerd Grubb December 2009 DIFFERENTIALLIGNINGER MED KONSTANTE KOEFFICIENTER 1 Generelle resultater 11 Introduktion I tidligere kurser er der gennemgået
UDKAST 7122009 Noter til An0 Inst f Matematiske Fag Gerd Grubb December 2009 DIFFERENTIALLIGNINGER MED KONSTANTE KOEFFICIENTER 1 Generelle resultater 11 Introduktion I tidligere kurser er der gennemgået
Polynomier. Indhold. Georg Mohr-Konkurrencen. 1 Polynomier 2. 2 Polynomiumsdivision 4. 3 Algebraens fundamentalsætning og rødder 6
 Indhold 1 Polynomier 2 Polynomier 2 Polynomiumsdivision 4 3 Algebraens fundamentalsætning og rødder 6 4 Koefficienter 8 5 Polynomier med heltallige koefficienter 9 6 Mere om polynomier med heltallige koefficienter
Indhold 1 Polynomier 2 Polynomier 2 Polynomiumsdivision 4 3 Algebraens fundamentalsætning og rødder 6 4 Koefficienter 8 5 Polynomier med heltallige koefficienter 9 6 Mere om polynomier med heltallige koefficienter
Matricer og lineære ligningssystemer
 Matricer og lineære ligningssystemer Grete Ridder Ebbesen Virum Gymnasium Indhold 1 Matricer 11 Grundlæggende begreber 1 Regning med matricer 3 13 Kvadratiske matricer og determinant 9 14 Invers matrix
Matricer og lineære ligningssystemer Grete Ridder Ebbesen Virum Gymnasium Indhold 1 Matricer 11 Grundlæggende begreber 1 Regning med matricer 3 13 Kvadratiske matricer og determinant 9 14 Invers matrix
Det teknisk-naturvidenskabelige basisår Matematik 1A, Efterår 2005, Hold 3 Prøveopgave C
 Det teknisk-naturvidenskabelige basisår Matematik 1A, Efterår 2005, Hold 3 Prøveopgave C Opgaven består af tre dele, hver med en række spørgsmål, efterfulgt af en liste af teorispørgsmål. I alle opgavespørgsmålene
Det teknisk-naturvidenskabelige basisår Matematik 1A, Efterår 2005, Hold 3 Prøveopgave C Opgaven består af tre dele, hver med en række spørgsmål, efterfulgt af en liste af teorispørgsmål. I alle opgavespørgsmålene
MATEMATIK 1A MATEMATISK ANALYSE 12. november 2009 Oversigt nr. 1
 MATEMATISK ANALYSE 12. november 2009 Oversigt nr. 1 På hold 3 fortsætter vi med integration i flere variable i uge 47. Man kan med fordel repetere kapitel 13.4 og 13.5 og deri regne sandt/falsk opgaverne
MATEMATISK ANALYSE 12. november 2009 Oversigt nr. 1 På hold 3 fortsætter vi med integration i flere variable i uge 47. Man kan med fordel repetere kapitel 13.4 og 13.5 og deri regne sandt/falsk opgaverne
Matematisk modellering og numeriske metoder
 Matematisk modellering og numeriske metoder Morten Grud Rasmussen 5. september 2016 1 Ordinære differentialligninger ODE er 1.1 ODE er helt grundlæggende Definition 1.1 (Ordinære differentialligninger).
Matematisk modellering og numeriske metoder Morten Grud Rasmussen 5. september 2016 1 Ordinære differentialligninger ODE er 1.1 ODE er helt grundlæggende Definition 1.1 (Ordinære differentialligninger).
Eksamen i Calculus. 14. juni f (x, y, z) = 1 + x 2 + y 2. x 2 + y 2 1 Hele rummet uden z aksen
 Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 14. juni 019 Opgave 1 (6 point) En
Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 14. juni 019 Opgave 1 (6 point) En
Komplekse tal. enote 29. 29.1 Indledning
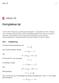 enote 29 1 enote 29 Komplekse tal I denne enote introduceres og undersøges talmængden C, de komplekse tal. Da C betragtes som en udvidelse af R forudsætter enoten almindeligt kendskab til de reelle tal,
enote 29 1 enote 29 Komplekse tal I denne enote introduceres og undersøges talmængden C, de komplekse tal. Da C betragtes som en udvidelse af R forudsætter enoten almindeligt kendskab til de reelle tal,
Oversigt [S] 7.3, 7.4, 7.5, 7.6; [DL] 1, 2
![Oversigt [S] 7.3, 7.4, 7.5, 7.6; [DL] 1, 2 Oversigt [S] 7.3, 7.4, 7.5, 7.6; [DL] 1, 2](/thumbs/82/86922880.jpg) Oversigt [S] 7.3, 7.4, 7.5, 7.6; [DL] 1, 2 Her skal du lære om Separable ligninger Logistisk ligning og eksponentiel vækst 1. ordens lineær ligning August 2002, opgave 7 Rovdyr-Byttedyr system 1. ordens
Oversigt [S] 7.3, 7.4, 7.5, 7.6; [DL] 1, 2 Her skal du lære om Separable ligninger Logistisk ligning og eksponentiel vækst 1. ordens lineær ligning August 2002, opgave 7 Rovdyr-Byttedyr system 1. ordens
Nøgleord og begreber Separable ligninger 1. ordens lineær ligning August 2002, opgave 7 Rovdyr-Byttedyr system 1. ordens lineært system Opgave
 Oversigt [S] 7.3, 7.4, 7.5, 7.6; [LA] 14, 15 Nøgleord og begreber Separable ligninger 1. ordens lineær ligning August 2002, opgave 7 Rovdyr-Byttedyr system 1. ordens lineært system Opgave Calculus 2-2005
Oversigt [S] 7.3, 7.4, 7.5, 7.6; [LA] 14, 15 Nøgleord og begreber Separable ligninger 1. ordens lineær ligning August 2002, opgave 7 Rovdyr-Byttedyr system 1. ordens lineært system Opgave Calculus 2-2005
DesignMat Den komplekse eksponentialfunktion og polynomier
 DesignMat Den komplekse eksponentialfunktion og polynomier Preben Alsholm Uge 8 Forår 010 1 Den komplekse eksponentialfunktion 1.1 Definitionen Definitionen Den velkendte eksponentialfunktion x e x vil
DesignMat Den komplekse eksponentialfunktion og polynomier Preben Alsholm Uge 8 Forår 010 1 Den komplekse eksponentialfunktion 1.1 Definitionen Definitionen Den velkendte eksponentialfunktion x e x vil
Matematik 1 Semesteruge 5 6 (30. september oktober 2002) side 1. Komplekse tal Arbejdsplan
 Matematik Semesteruge 5 6 (30. september -. oktober 2002) side Komplekse tal Arbejdsplan I semesterugerne 5 og 6 erstattes den regulære undervisning (forelæsninger og fællestimer) af selvstudium med opgaveregning
Matematik Semesteruge 5 6 (30. september -. oktober 2002) side Komplekse tal Arbejdsplan I semesterugerne 5 og 6 erstattes den regulære undervisning (forelæsninger og fællestimer) af selvstudium med opgaveregning
DesignMat Uge 4 Systemer af lineære differentialligninger I
 DesignMat Uge Systemer af lineære differentialligninger I Preben Alsholm Efterår 008 1 Lineære differentialligningssystemer 11 Lineært differentialligningssystem af første orden I Lineært differentialligningssystem
DesignMat Uge Systemer af lineære differentialligninger I Preben Alsholm Efterår 008 1 Lineære differentialligningssystemer 11 Lineært differentialligningssystem af første orden I Lineært differentialligningssystem
Besvarelse af Eksamensopgaver Juni 2005 i Matematik H1
 Besvarelse af Eksamensopgaver Juni 5 i Matematik H Opgave De fire vektorer stilles op i en matrix som reduceres: 4 4 4 8 4 4 (a) Der er ledende et-taller så dim U =. Som basis kan f.eks. bruges a a jfr.
Besvarelse af Eksamensopgaver Juni 5 i Matematik H Opgave De fire vektorer stilles op i en matrix som reduceres: 4 4 4 8 4 4 (a) Der er ledende et-taller så dim U =. Som basis kan f.eks. bruges a a jfr.
Eksempel på 2-timersprøve 2 Løsninger
 Eksempel på -timersprøve Løsninger Preben lsholm Februar 4 Opgave Maplekommandoerne expand( (z-*exp(i*pi/))*(z-*exp(-i*pi/))*(z-exp(i*pi/))*(z-exp(-i*pi/))): sort(%); resulterer i polynomiet z 4 z + z
Eksempel på -timersprøve Løsninger Preben lsholm Februar 4 Opgave Maplekommandoerne expand( (z-*exp(i*pi/))*(z-*exp(-i*pi/))*(z-exp(i*pi/))*(z-exp(-i*pi/))): sort(%); resulterer i polynomiet z 4 z + z
Noter om komplekse tal
 Noter om komplekse tal Preben Alsholm Januar 008 1 Den komplekse eksponentialfunktion Vi erindrer først om den sædvanlige og velkendte reelle eksponentialfunktion. Vi skal undertiden nde det nyttigt, at
Noter om komplekse tal Preben Alsholm Januar 008 1 Den komplekse eksponentialfunktion Vi erindrer først om den sædvanlige og velkendte reelle eksponentialfunktion. Vi skal undertiden nde det nyttigt, at
Fordybelsesprojekt Matematik 2, forår 2005 Potensrækker
 Fordybelsesprojekt Matematik 2, forår 2005 Potensrækker Arne Jensen 7. 11. marts 2005 1 Indledning I forbindelse med kurset i Reelle og Komplekse Funktioner afholdes et fordybelsesprojekt med et omfang
Fordybelsesprojekt Matematik 2, forår 2005 Potensrækker Arne Jensen 7. 11. marts 2005 1 Indledning I forbindelse med kurset i Reelle og Komplekse Funktioner afholdes et fordybelsesprojekt med et omfang
Lineære ligningssystemer
 enote 2 1 enote 2 Lineære ligningssystemer Denne enote handler om lineære ligningssystemer, om metoder til at beskrive dem og løse dem, og om hvordan man kan få overblik over løsningsmængdernes struktur.
enote 2 1 enote 2 Lineære ligningssystemer Denne enote handler om lineære ligningssystemer, om metoder til at beskrive dem og løse dem, og om hvordan man kan få overblik over løsningsmængdernes struktur.
Matematik 1 Semesteruge 5 6 (1. oktober oktober 2001) side 1 Komplekse tal Arbejdsplan
 Matematik 1 Semesteruge 5 6 (1. oktober - 12. oktober 2001) side 1 Komplekse tal Arbejdsplan I semesterugerne 5 og 6 erstattes den regulære undervisning (forelæsninger og fællestimer) af selvstudium med
Matematik 1 Semesteruge 5 6 (1. oktober - 12. oktober 2001) side 1 Komplekse tal Arbejdsplan I semesterugerne 5 og 6 erstattes den regulære undervisning (forelæsninger og fællestimer) af selvstudium med
Eksempel på 2-timersprøve 1 Løsninger
 Eksempel på -timersprøve Løsninger Preben lsholm Marts 4 Opgave Vi skal løse ligningen () z (8 + i) e i 6 = Løsningen ønskes angivet på rektangulær form, dvs. på formen x + iy, hvor x; y R. Vi nder umiddelbart
Eksempel på -timersprøve Løsninger Preben lsholm Marts 4 Opgave Vi skal løse ligningen () z (8 + i) e i 6 = Løsningen ønskes angivet på rektangulær form, dvs. på formen x + iy, hvor x; y R. Vi nder umiddelbart
Komplekse tal og algebraens fundamentalsætning.
 Komplekse tal og algebraens fundamentalsætning. Michael Knudsen 10. oktober 2005 1 Ligningsløsning Lad N = {0,1,2,...} betegne mængden af de naturlige tal og betragt ligningen ax + b = 0, a,b N,a 0. Findes
Komplekse tal og algebraens fundamentalsætning. Michael Knudsen 10. oktober 2005 1 Ligningsløsning Lad N = {0,1,2,...} betegne mængden af de naturlige tal og betragt ligningen ax + b = 0, a,b N,a 0. Findes
Besvarelser til de to blokke opgaver på Ugeseddel 7
 Besvarelser til de to blokke opgaver på Ugeseddel 7 De anførte besvarelser er til dels mere summariske end en god eksamensbesvarelse bør være. Der kan godt være fejl i - jeg vil meget gerne informeres,
Besvarelser til de to blokke opgaver på Ugeseddel 7 De anførte besvarelser er til dels mere summariske end en god eksamensbesvarelse bør være. Der kan godt være fejl i - jeg vil meget gerne informeres,
DesignMat Uge 11 Lineære afbildninger
 DesignMat Uge Lineære afbildninger Preben Alsholm Forår 008 Lineære afbildninger. Definition Definition Lad V og W være vektorrum over samme skalarlegeme L (altså enten R eller C for begge). Afbildningen
DesignMat Uge Lineære afbildninger Preben Alsholm Forår 008 Lineære afbildninger. Definition Definition Lad V og W være vektorrum over samme skalarlegeme L (altså enten R eller C for begge). Afbildningen
Eksamen i Calculus. 14. juni f (x, y, z) = 1 + x 2 + y 2. Hele rummet uden z aksen
 Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 14. juni 019 Opgave 1 (6 point) En
Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 14. juni 019 Opgave 1 (6 point) En
Eksamen i Calculus. 14. juni f (x, y, z) = 1 + x 2 + y 2. x 2 + y 2 1 Hele rummet uden z aksen
 Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 14. juni 19 Opgave 1 (6 point) En funktion
Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 14. juni 19 Opgave 1 (6 point) En funktion
Differentialligninger Hvad beskriver en differentialligning? Hvordan noget ændrer sig (oftest over tid). Tangenthældninger langs en kurve.
 Differentialligninger Hvad beskriver en differentialligning? Hvordan noget ændrer sig (oftest over tid) Tangenthældninger langs en kurve x Retningsfelter x x(t) sin(π t) + x / π cos(π t) Jeppe Revall Frisvad
Differentialligninger Hvad beskriver en differentialligning? Hvordan noget ændrer sig (oftest over tid) Tangenthældninger langs en kurve x Retningsfelter x x(t) sin(π t) + x / π cos(π t) Jeppe Revall Frisvad
Taylors formel. Kapitel Klassiske sætninger i en dimension
 Kapitel 3 Taylors formel 3.1 Klassiske sætninger i en dimension Sætning 3.1 (Rolles sætning) Lad f : [a, b] R være kontinuert, og antag at f er differentiabel i det åbne interval (a, b). Hvis f (a) = f
Kapitel 3 Taylors formel 3.1 Klassiske sætninger i en dimension Sætning 3.1 (Rolles sætning) Lad f : [a, b] R være kontinuert, og antag at f er differentiabel i det åbne interval (a, b). Hvis f (a) = f
D = 0. Hvis rører parablen x- aksen i et enkelt punkt, dvs. den tilhørende andengradsligning
 Projekt 55 Andengradspolynomier af to variable Kvadratiske funktioner i to variable - de tre typer paraboloider f() = A + B + C, hvor A 0 Et andengradspolynomium i en variabel har en forskrift på formen
Projekt 55 Andengradspolynomier af to variable Kvadratiske funktioner i to variable - de tre typer paraboloider f() = A + B + C, hvor A 0 Et andengradspolynomium i en variabel har en forskrift på formen
Egenskaber ved Krydsproduktet
 Egenskaber ved Krydsproduktet Frank Nasser 23. december 2011 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold
Egenskaber ved Krydsproduktet Frank Nasser 23. december 2011 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold
Matematisk modellering og numeriske metoder. Lektion 8
 Matematisk modellering og numeriske metoder Lektion 8 Morten Grud Rasmussen 18. oktober 216 1 Fourierrækker 1.1 Periodiske funktioner Definition 1.1 (Periodiske funktioner). En periodisk funktion f er
Matematisk modellering og numeriske metoder Lektion 8 Morten Grud Rasmussen 18. oktober 216 1 Fourierrækker 1.1 Periodiske funktioner Definition 1.1 (Periodiske funktioner). En periodisk funktion f er
Matematisk modellering og numeriske metoder
 Matematisk modellering og numeriske metoder Morten Grud Rasmussen September 0, 016 1 Lineære ODE er af første orden 1.1 De grundlæggende definitioner Definition 1.1. Lineære ODE er af første orden er ODE
Matematisk modellering og numeriske metoder Morten Grud Rasmussen September 0, 016 1 Lineære ODE er af første orden 1.1 De grundlæggende definitioner Definition 1.1. Lineære ODE er af første orden er ODE
Besvarelser til Calculus Ordinær Eksamen Juni 2019
 Besvarelser til Calculus Ordinær Eksamen - 14. Juni 2019 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 14. Juni 2019 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Projekt 2.2 Omvendt funktion og differentiation af omvendt funktion
 ISBN 978877664974 Projekter: Kapitel. Projekt. Omvendt funktion og differentiation af omvendt funktion Projekt. Omvendt funktion og differentiation af omvendt funktion Vi har i Bbogens kapitel 4 afsnit
ISBN 978877664974 Projekter: Kapitel. Projekt. Omvendt funktion og differentiation af omvendt funktion Projekt. Omvendt funktion og differentiation af omvendt funktion Vi har i Bbogens kapitel 4 afsnit
Besvarelser til Calculus Ordinær Eksamen Januar 2019
 Besvarelser til Calculus Ordinær Eksamen - 14. Januar 19 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 14. Januar 19 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Lineær Algebra - Beviser
 Lineær Algebra - Beviser Mads Friis 8 oktober 213 1 Lineære afbildninger Jeg vil i denne note forsøge at give et indblik i, hvor kraftfuldt et værktøj matrix-algebra kan være i analyse af lineære funktioner
Lineær Algebra - Beviser Mads Friis 8 oktober 213 1 Lineære afbildninger Jeg vil i denne note forsøge at give et indblik i, hvor kraftfuldt et værktøj matrix-algebra kan være i analyse af lineære funktioner
Taylor s approksimationsformler for funktioner af én variabel
 enote 17 1 enote 17 Taylor s approksimationsformler for funktioner af én variabel I enote 14 og enote 16 er det vist hvordan funktioner af én og to variable kan approksimeres med førstegradspolynomier
enote 17 1 enote 17 Taylor s approksimationsformler for funktioner af én variabel I enote 14 og enote 16 er det vist hvordan funktioner af én og to variable kan approksimeres med førstegradspolynomier
Komplekse tal. enote Indledning
 enote 1 1 enote 1 Komplekse tal I denne enote introduceres og undersøges talmængden C, de komplekse tal. Da C betragtes som en udvidelse af R, forudsætter enoten almindeligt kendskab til de reelle tal,
enote 1 1 enote 1 Komplekse tal I denne enote introduceres og undersøges talmængden C, de komplekse tal. Da C betragtes som en udvidelse af R, forudsætter enoten almindeligt kendskab til de reelle tal,
Bedste rette linje ved mindste kvadraters metode
 1/9 Bedste rette linje ved mindste kvadraters metode - fra www.borgeleo.dk Figur 1: Tre datapunkter og den bedste rette linje bestemt af A, B og C Målepunkter og bedste rette linje I ovenstående koordinatsystem
1/9 Bedste rette linje ved mindste kvadraters metode - fra www.borgeleo.dk Figur 1: Tre datapunkter og den bedste rette linje bestemt af A, B og C Målepunkter og bedste rette linje I ovenstående koordinatsystem
Temaøvelse i differentialligninger Biokemiske Svingninger
 Temaøvelse i differentialligninger Biokemiske Svingninger Rev. 12. november 2009 I denne temaøvelse studerer vi en simpel model for gærglykolyse. Vi starter i Del 1 med at beskrive modellen. Denne model
Temaøvelse i differentialligninger Biokemiske Svingninger Rev. 12. november 2009 I denne temaøvelse studerer vi en simpel model for gærglykolyse. Vi starter i Del 1 med at beskrive modellen. Denne model
Besvarelser til Lineær Algebra Ordinær Eksamen Juni 2018
 Besvarelser til Lineær Algebra Ordinær Eksamen - 5. Juni 28 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Lineær Algebra Ordinær Eksamen - 5. Juni 28 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Egenværdier og egenvektorer
 1 Egenværdier og egenvektorer 2 Definition Lad A være en n n matrix. En vektor v R n, v 0, kaldes en egenvektor for A, hvis der findes en skalar λ således Av = λv Skalaren λ kaldes en tilhørende egenværdi.
1 Egenværdier og egenvektorer 2 Definition Lad A være en n n matrix. En vektor v R n, v 0, kaldes en egenvektor for A, hvis der findes en skalar λ således Av = λv Skalaren λ kaldes en tilhørende egenværdi.
Tidligere Eksamensopgaver MM505 Lineær Algebra
 Institut for Matematik og Datalogi Syddansk Universitet Tidligere Eksamensopgaver MM55 Lineær Algebra Indhold Typisk forside.................. 2 Juni 27.................... 3 Oktober 27..................
Institut for Matematik og Datalogi Syddansk Universitet Tidligere Eksamensopgaver MM55 Lineær Algebra Indhold Typisk forside.................. 2 Juni 27.................... 3 Oktober 27..................
Matematik F2 Opgavesæt 2
 Opgaver uge 2 I denne uge kigger vi nærmere på Cauchy-Riemann betingelserne, potensrækker, konvergenskriterier og flertydige funktioner. Vi skal også se på integration langs en ve i den komplekse plan.
Opgaver uge 2 I denne uge kigger vi nærmere på Cauchy-Riemann betingelserne, potensrækker, konvergenskriterier og flertydige funktioner. Vi skal også se på integration langs en ve i den komplekse plan.
DesignMat Uge 2. Preben Alsholm. Efterår Lineære afbildninger. Preben Alsholm. Lineære afbildninger. Eksempel 2 på lineær.
 er DesignMat Uge 2 er er lineær lineær lineær lineære er I smatrix lineære er II smatrix I smatrix II Efterår 2010 Lad V og W være vektorrum over samme skalarlegeme L (altså enten R eller C for begge).
er DesignMat Uge 2 er er lineær lineær lineær lineære er I smatrix lineære er II smatrix I smatrix II Efterår 2010 Lad V og W være vektorrum over samme skalarlegeme L (altså enten R eller C for begge).
Afstande, skæringer og vinkler i rummet
 Afstande, skæringer og vinkler i rummet Frank Nasser 9. april 20 c 2008-20. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her.
Afstande, skæringer og vinkler i rummet Frank Nasser 9. april 20 c 2008-20. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her.
i x-aksens retning, så fås ). Forskriften for g fås altså ved i forskriften for f at udskifte alle forekomster af x med x x 0
 BAndengradspolynomier Et polynomium er en funktion på formen f ( ) = an + an + a+ a, hvor ai R kaldes polynomiets koefficienter. Graden af et polynomium er lig med den højeste potens af, for hvilket den
BAndengradspolynomier Et polynomium er en funktion på formen f ( ) = an + an + a+ a, hvor ai R kaldes polynomiets koefficienter. Graden af et polynomium er lig med den højeste potens af, for hvilket den
(c) Opskriv den reelle Fourierrække for funktionen y(t) fra (b), og afgør dernæst om y(t) er en lige eller ulige funktion eller ingen af delene.
 MATEMATIK 3 EN,MP 4. februar 2016 Eksamenopgaver fra 2011 2016 (jan. 2016) Givet at 0 for 0 < t < 1 mens e (t 1) cos(7(t 1)) for t 1, betragt da begyndelsesværdiproblemet for t > 0: y (t) + 2y (t) + 50y(t)
MATEMATIK 3 EN,MP 4. februar 2016 Eksamenopgaver fra 2011 2016 (jan. 2016) Givet at 0 for 0 < t < 1 mens e (t 1) cos(7(t 1)) for t 1, betragt da begyndelsesværdiproblemet for t > 0: y (t) + 2y (t) + 50y(t)
Københavns Universitet, Det naturvidenskabelige Fakultet. Forelæsningsnote 8. (NB: Noten er ikke en del af pensum)
 Københavns Universitet, Det naturvidenskabelige Fakultet Lineær Algebra LinAlg Forelæsningsnote 8 NB: Noten er ikke en del af pensum Eksempel på brug af egenværdier og egenvektorer Måske er det stadig
Københavns Universitet, Det naturvidenskabelige Fakultet Lineær Algebra LinAlg Forelæsningsnote 8 NB: Noten er ikke en del af pensum Eksempel på brug af egenværdier og egenvektorer Måske er det stadig
Differentiation af Trigonometriske Funktioner
 Differentiation af Trigonometriske Funktioner Frank Villa 15. oktober 01 Dette dokument er en del af MatBog.dk 008-01. IT Teaching Tools. ISBN-13: 978-87-9775-00-9. Se yderligere betingelser for brug her.
Differentiation af Trigonometriske Funktioner Frank Villa 15. oktober 01 Dette dokument er en del af MatBog.dk 008-01. IT Teaching Tools. ISBN-13: 978-87-9775-00-9. Se yderligere betingelser for brug her.
Differentialligninger af første orden
 Differentialligninger af første orden Preben Alsholm Februar 2006 Basale begreber. Eksistens og entydighed. En differentialligning af første orden er en ligning, der sammenknytter differentialkvotienten
Differentialligninger af første orden Preben Alsholm Februar 2006 Basale begreber. Eksistens og entydighed. En differentialligning af første orden er en ligning, der sammenknytter differentialkvotienten
Fononiske Båndgab. Køreplan Matematik 1 - FORÅR 2005
 Fononiske Båndgab Køreplan 01005 Matematik 1 - FORÅR 2005 1 Baggrund Bølgeudbredelse i materialer og medier (som f.eks. luft) er et fænomen, der kendes af alle og som observeres i forskellige former i
Fononiske Båndgab Køreplan 01005 Matematik 1 - FORÅR 2005 1 Baggrund Bølgeudbredelse i materialer og medier (som f.eks. luft) er et fænomen, der kendes af alle og som observeres i forskellige former i
DiMS 2010 Uge 7,
 DiMS 2010 Uge 7, 18.10.10 24.10.10 Læsevejledning Emnerne i denne uge er polynomier og komplekse tal. De kan ikke siges at henhøre under diskret matematik som sådan og er ikke dækket af KBR, så vi skal
DiMS 2010 Uge 7, 18.10.10 24.10.10 Læsevejledning Emnerne i denne uge er polynomier og komplekse tal. De kan ikke siges at henhøre under diskret matematik som sådan og er ikke dækket af KBR, så vi skal
Taylor s approksimationsformler for funktioner af én variabel
 enote 4 1 enote 4 Taylor s approksimationsformler for funktioner af én variabel I enote 19 og enote 21 er det vist hvordan funktioner af én og to variable kan approksimeres med førstegradspolynomier i
enote 4 1 enote 4 Taylor s approksimationsformler for funktioner af én variabel I enote 19 og enote 21 er det vist hvordan funktioner af én og to variable kan approksimeres med førstegradspolynomier i
Kvadratiske matricer. enote Kvadratiske matricer
 enote enote Kvadratiske matricer I denne enote undersøges grundlæggende egenskaber ved mængden af kvadratiske matricer herunder indførelse af en invers matrix for visse kvadratiske matricer. Det forudsættes,
enote enote Kvadratiske matricer I denne enote undersøges grundlæggende egenskaber ved mængden af kvadratiske matricer herunder indførelse af en invers matrix for visse kvadratiske matricer. Det forudsættes,
Eksponentielle sammenhænge
 Eksponentielle sammenhænge 0 1 2 3 4 5 6 7 8 9 10 11 12 13 Indholdsfortegnelse Variabel-sammenhænge... 1 1. Hvad er en eksponentiel sammenhæng?... 2 2. Forklaring med ord af eksponentiel vækst... 2, 6
Eksponentielle sammenhænge 0 1 2 3 4 5 6 7 8 9 10 11 12 13 Indholdsfortegnelse Variabel-sammenhænge... 1 1. Hvad er en eksponentiel sammenhæng?... 2 2. Forklaring med ord af eksponentiel vækst... 2, 6
Matematisk modellering og numeriske metoder. Lektion 4
 Matematisk modellering og numeriske metoder Lektion 4 Morten Grud Rasmussen 17. september, 013 1 Homogene andenordens lineære ODE er [Bogens afsnit.1] 1.1 Linearitetsprincippet Vi så sidste gang, at førsteordens
Matematisk modellering og numeriske metoder Lektion 4 Morten Grud Rasmussen 17. september, 013 1 Homogene andenordens lineære ODE er [Bogens afsnit.1] 1.1 Linearitetsprincippet Vi så sidste gang, at førsteordens
INFINITESIMALREGNING del 3 Differentialligninger Funktioner af flere variable Differentialligningssystemer x-klasserne Gammel Hellerup Gymnasium
 INFINITESIMALREGNING del 3 Differentialligninger Funktioner af flere variable Differentialligningssystemer x-klasserne Gammel Hellerup Gymnasium Februar 09 ; Michael Szymanski ; mz@ghg.dk Indholdsfortegnelse
INFINITESIMALREGNING del 3 Differentialligninger Funktioner af flere variable Differentialligningssystemer x-klasserne Gammel Hellerup Gymnasium Februar 09 ; Michael Szymanski ; mz@ghg.dk Indholdsfortegnelse
Eksamen i Calculus. Første Studieår ved Det Tekniske Fakultet for IT og Design samt Det Ingeniør- og Naturvidenskabelige Fakultet. 3.
 Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design samt Det Ingeniør- og Naturvidenskabelige Fakultet. januar 7 Dette eksamenssæt består af 9 nummererede sider med afkrydsningsopgaver.
Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design samt Det Ingeniør- og Naturvidenskabelige Fakultet. januar 7 Dette eksamenssæt består af 9 nummererede sider med afkrydsningsopgaver.
