på følgende måde: Fra den ene ende af kurven til den anden afsættes punkter z 0 således at er dens begyndelsespunkt og z N
|
|
|
- Knud Kjær
- 7 år siden
- Visninger:
Transkript
1 1 Integration af komplekse funktioner For at kunne udlede Riemanns formel for π N og Sylvesters formel for ν N får vi brug for et større apparatur af kompleks funktionsteori, så derfor må sætte os mere ind i denne teori: definere hvad et komplekst integral er og vise nogle sætninger - eller blot kontrollere dem med computeren. Den funktion med komplekse værdier som vi har integreret i definitionen af Li(z), dvs. f(x) = z x /x, hvor z er et komplekst tal, er kun defineret for reelle tal x og integrationen er foregået langs et interval på den reelle tallinie. En egentlig kompleks funktion f(z) derimod er defineret på et område O i den komplekse talplan, og hvis vi skal udvide vores forestilling om integration - som jo er en "uendelig" sum af formen f(x) x taget langs et interval - så den kommer til at indbefatte komplekse funktioner, er det mest nærliggende at lade dette interval være et kurvestykke indenfor O og erstatte x-erne med zer langs dette kurvestykke. Altså: Hvis L er et kurvestykke beliggende i O, danner vi for et (lille) positivt tal ε et komplekst tal S ε på følgende måde: Fra den ene ende af kurven til den anden afsættes punkter z 0, z 1,..., z N således at z 0 er dens begyndelsespunkt og z N er dens endepunkt og således at afstanden imellem to på hinanden følgende punkter er mindre end ε. Imellem z k og z k+1 vælges et punkt z' k på kurven og vi sætter N-1 S ε = f(z' k ) (z k+1 -z k ). k=0 Hvis disse komplekse tal S ε, uafhængigt af vores valg, konvergerer imod et tal S for ε 0, kaldes f(z) integrabel langs kurven L og tallet S kaldes integralet af f(z) langs L og betegnes I computersammenhæng har vi altså: N-1 f(z) dz. L f(z) dz = f(z' k ) (z k+1 -z k ), L k=0
2 2 for N tilstrækkeligt stort og ε tilstrækkeligt lille. Kurven kan selvfølgelig godt være uendelig lang, i så fald må integralet defineres som grænseværdien når en endelig del af kurven gøres længere og længere. Og kurven kan selvfølgelig også være lukket, således at dens begyndelsespunkt og endepunkt falder sammen. De kurver vi vil integrere over i det følgende er altid enten cirkler eller rette linier parallelle med y-aksen. Hvis C er en cirkel med centrum i origo og n er et helt tal er: z n dz = 2πi hvis n = -1 og = 0 hvis n -1. C Thi hvis cirklens radius er r, har den parameterfremstillingen z = re θi, hvor θ går fra 0 til 2π, og da dz/dθ = iz, er 2π z n dz = r n+1 i e (n+1)θi dθ, C 0 og det sidste (reelle) integral er = 2π hvis n = -1 og = 0 hvis n -1 (fordi i så fald bidragene fra θ og θ+π/2 k ophæver hinanden, hvis k er givet ved n+1 = 2 k m hvor m er ulige). Integralet er altså uafhængigt af cirklens størrelse, men det er også uafhængigt af om den lukkede kurve er en cirkel - den skal blot omslutte nulpunktet (én gang). Så hvis en lukket kurve L omslutter punktet z 0 (én gang) gælder: (z - z 0 ) n dz = 2πi hvis n = -1 og = 0 hvis n -1 L (bemærk at integralet kun er 0 når integranden (z - z 0 ) n ikke er defineret i punktet z 0, og det kun er for n = -1 at integralet er 0). Men dette betyder, at hvis funktionen f(z) indenfor et område omkring punktet z 0 kan skrives på formen f(z) = a n (z - z 0 ) n, n=-
3 og hvis L er en lukket kurve indenfor dette område som omslutter z 0 (én gang), da gælder: 3 f(z) dz = 2πi a -1. L En kompleks funktion f(z) kaldes meromorf indenfor det åbne område O, hvis det for ethvert punkt z 0 i dette gælder at f(z) indenfor en (lille) omegn af z 0 kan skrives på formen f(z) = a n (z - z 0 ) n. n=- f(z) er kun defineret i selve punktet z 0 hvis a n = 0 for n < 0, dvs. hvis rækken er en potensrække, i så fald siges f(z) at være analytisk i punktet z 0. En kompleks funktion f(z) som er holomorf indenfor det åbne område O, dvs. kompleks-differentiabel overalt i O (side 58), er analytisk overalt i O, derfor kaldes en holomorf funktion også for en analytisk funktion. For en reel funktion gælder ikke at differentiabilitet i en omegn af x 0 (end ikke vilkårlig ofte differentiabilitet) medfører at den er analytisk i x 0, dvs. at den kan udvikles i en potensrække omkring x 0. Hvis f(z) er meromorf i O og rækkeudvikles ud fra punktet z 0, gælder, at hvis a n = 0 for n < r og a r 0 har vi f(z) = (z - z 0 ) r g(z), hvor g(z) er analytisk i punktet z 0 og g(z 0 ) = a r 0. Hvis r > 0 siges f(z) at have nulpunkt af orden r i punktet z 0, og hvis r < 0 siges f(z) at have pol af orden -r i punktet z 0. Et nulpunkt eller en pol af orden 1 kaldes simpel. Hvis f(z) har simpel pol i z 0, kaldes tallet a -1, som er 0, for denne pols residuum. I så fald gælder at hvor g(z) er analytisk i z 0, og at f(z) = a -1 /(z-z 0 ) + g(z),
4 4 a -1 = lim (z - z 0 ) f(z). z z 0 f(z) har netop simpel pol i z 0, når denne grænseværdi eksisterer og 0. Af det ovenstående følger at vi har denne sætning: hvis f(z) er meromorf i området O og L er en lukket kurve indenfor dette, da er: f(z) dz = 2πi gange summen af f(z)'s residuer indenfor L. L Riemanns zetafunktion ζ(z) er meromorf i hele den komplekse plan, dens eneste pol er z = 1, og denne er simpel med residuum 1: lim (z - 1) ζ(z) = 1 z 1 (dette kan f.eks. ses af formlen for ζ(z) som vi vil udlede i næste kapitel). Det formodes at alle nulpunkterne for ζ(z) er simple. Eksempler på ikke-meromorfe funktioner er logaritmefunktionen log z og funktionen Li(x z ), hvor x er et positivt reelt tal (side...): disse har ikke nogen rækkeudvikling omkring punktet z 0 = 0. Da dli(x z )/dz = x z /z og x z 1 for z 0, og da dlog z/dz = 1/z opfører Li(x z ) sig som log z omkring singulariteten z 0 = 0. Disse funktioner siges at have logaritmisk pol i punktet z = 0. Et eksempel på en meromorf funktion som har pol af orden (i punktet z = 0) er f(z) = exp(1/z). Hvis området O er ubegrænset (f.eks. en halvplan) og hvis den lukkede kurve L (indenfor O) er uendelig lang, er f(z) (en meromorf funktion indenfor O) selvfølgelig kun integrabel langs L, hvis L kun omslutter endelig mange simple poler eller hvis, i tilfælde af at der er uendelig mange, den uendelige række af residuer er konvergent. Et eksempel på en sådan funktion er gammafunktionen Γ(z), som blev indført af Euler og Gauss og som spiller en stor rolle i den højere analyse - og i resten af denne bog. Euler definerede den ved integralet:
5 5 Γ(z) = t z /e t dt/t 0 som er konvergent for Re(z) > 1, og Gauss definerede den ved det uendelige produkt (Gauss' produktfremstilling): Γ(z) = (1/z) ((1+1/k) z /(1+z/k)) k=1 som er konvergent for z 0, -1, -2, -3,... Γ(z) er meromorf i hele den komplekse plan, og dens poler er netop disse punkter: z = -m, m = 0, 1, 2,... De er alle simple, og polen -m har residuum (-1) m /m!. Γ(z) har ingen nulpunkter. Da en ret linie som er parallel med y-aksen og som skærer den positive x-akse kan opfattes som en (uendelig lang) kurve der omslutter alle disse poler (idet den kan opfattes en cirkel med uendelig radius), har vi: a+i Γ(z) dz = 2πi (-1) m /m! = 2πe -1 i, a-i m=0 hvor a > 0. Hvis vi vil kontrollere denne formel på computeren, kan vi omforme det komplekse integral til et reelt integral, da Γ(z) = Γ(z): a+i Γ(z) dz = 2i Re(Γ(a+yi)) dy. a-i 0 Men vi behøver en formel som effektivt kan udregne Γ(z), og en sådan viser vi i næste kapitel. Γ(z) tilfredsstiller funktionalligningen Γ(z + 1) = z Γ(z), og dette betyder at Γ(n+1) = n! for et naturligt tal n (da Γ(1) = 1), og at (for et naturligt tal N): og Γ(z) = Γ(z+N)/(z(z+1)...(z+N-1))
6 6 Γ(z) = Γ(z-N) (z-1)...(z-n), hvilket betyder at Γ(z) let kan udregnes når man blot kender Γ(z) for de z for hvilke 1 Re(z) < 2 (f.eks.). Γ(z) tilfredsstiller desuden funktionalligningerne hvoraf følger at Γ(½) = π, og Γ(z)Γ(-z) = -π/(z sin(πz)), Γ(2z) = (2 2z-1 / π) Γ(z)Γ(½ + z). De følger begge af Gauss' produktfremstilling. Den første ved at benytte denne produktfremstilling for sinus (gældende for alle z): sin z = z (1 - z/(πk)). k=-, k 0 Den anden ved at vise at Γ(2z) = K 2 2z Γ(z)Γ(½ + z), hvor K er en konstant, og derefter finde K ved at sætte z = 1: Γ(2) = 1 = K 4 1 ½ Γ(½), dvs. K = 1/(2 π). Af produktfremstillingen for sin z fås ved anvendelse af formlen for differentation af et produkt (brugt på et uendeligt produkt) og af sin' z = cos z at: cos(z)/sin(z) = 1/(z + πk) k=- (gældende for z kπ, k hel). Indsætter vi her cos z = (e zi + e -zi )/2 og sin z = (e zi - e -zi )/(2i) (de kan udledes af formlen e x+iy = e x (cos y + i sin y) ved at sætte x = 0 og lade y være kompleks) og erstatter vi z med -iz/2 har vi (til senere brug): 1/(e z - 1) + ½ = ½(e z/2 + e -z/2 )/(e z/2 - e -z/2 ) = 1/(z + k2πi). k=- En sådan sum af tal a k fra k = - til skal opfattes som a 0 + summen af tallene a k +a -k fra k = 1 til, og tilsvarende for et produkt.
7 7 Euler-Maclaurins sumformel Fortidens matematikere har skabt mægtige teorier om sære funktioner som Γ (z) og ζ(z) uden at vide ret meget om hvordan disse funktioner egentlig ser ud. Man kendte selvfølgelig udseendet af deres graf for reelle z, fordi man havde tilnærmelsesformler og udtryk for deres præcise værdier for særlige z- værdier. Men for komplekse z kunne kendskabet være beskedent. Hvad beregningen angår kunne man af og til betjene sig af funktionalligninger, så man kunne begrænse det store regnearbejde til et vist interval. 10-tals-logaritmen log 10 x skal man som bekendt kun kende i intervallet 1 x < 10, da log 10 (10 n x) = n + log 10 x, og gammafunktionen Γ(z) behøver man som vi har set kun at kende i intervallet 1 Re(z) < 2. I sådanne intervaller udarbejdede man tabeller som generation efter generation kunne gøre større. Og hertil brugte man oftest en rækkeudvikling af funktionen. Hvis funktionen f(z) er analytisk i punktet z 0 (side...), gælder i en omegn af z 0 at f(z) = a n (z - z 0 ) n, n=0 og her kan man af og til finde koefficienterne a n. Ved succesivt at differentiere begge sider og i hver af de fremkomne rækker sætte z = z 0, ses at a n = f (n) (z 0 )/n!, så koefficienterne kendes altså hvis alle de højere afledede af f(z) kendes i z 0. Dette er Taylors formel: f(z 0 +h) = f (n) (z 0 )h n /n! n=0 En sådan rækkeudvikling gælder kun for h numerisk mindre end et vist tal som kaldes rækkeudviklingens konvergensradius. At konvergensradius er større end 0 betyder netop at f(z) er analytisk i punktet z 0. Hvis konvergensradius er, dvs. hvis rækken er konvergent for alle h, kaldes f(z) en hel funktion - en hel funktion er en funktion der er holomorf i hele den komplekse plan. En rækkeudvikling kan have gode eller dårlige konvergensegenskaber. Funk-
8 8 tionerne e z, sin z og cos z er hele, og deres Taylorrækker ud fra punktet z 0 = 0 (side...) konvergerer rimelig hurtigt. Funktionen log z er ikke defineret for z = 0, men er dog analytisk i resten af planen, men dens Taylorrække ud fra punktet z = 1 (side...), som har konvergensradius 1, er ubrugelig til noget praktisk, selv om den er unægteligt er smuk. Det er ofte ikke Taylors formel man skal bruge. Desuden er det jo heller ikke sikkert at man kan finde brugbare udtryk for tallene f (n) (z 0 ): de første to koefficienter i en sådan rækkeudvikling for ζ(2+h) er henh. 1/n 2 og - log n/n 2, og den første er π 2 /6, men hvad er den anden? Heldigvis kan man ved at teoretisere over Taylors formel få en sumformel frem, som i de tilfælde hvor den kan anvendes kan være uhyre effektiv. Men den skal bruges med forsigtighed, for den uendelige række som den giver anledning til er nemlig ofte divergent: tallene kan nærme sig mere og mere til det ønskede, men kun indtil et vist trin, herefter begynder det at gå den modsatte vej. Når formlen virker, kan dens parametre justeres således at dette trin kan rykkes ligeså langt ud det skal være, men denne justering er bestemt af den konkrete udregning. Så hvis man ikke gør sig teoretiske overvejelser, og det gør man ikke i vor tid med mindre det har betydning at estimere fejlen, så vil man hyppigt opleve at programmet går ned. Formlen som vi skal udlede kaldes Euler-Maclaurins sumformel. Den har udgangspunkt i følgende betragtning: For en funktion f(x) som er differentiabel i punktet a, er differentialkvotienten f'(a) defineret som grænseværdien af tallene (f(a+h) - f(a))/h for h 0. Dvs, hvis vi sætter b = a+h, er h f'(a) = f(b) - f(a) + R, hvor R er et restled som er af mindre størrelsesorden end h. Lad os nu antage at b = a+nh, hvor N er et naturligt tal, så kan vi addere disse formler hvor a succesivt erstattes med a+kh for k = 0, 1,..., N-1, og b med a+(k+1)h, og så får vi (fordi tallene f(a+kh) på højresiderne parvis ophæver hinanden) at
9 N-1 9 h f'(a + kh) = f(b) - f(a) + R. k=1 Men nu kan restleddet R selvsagt være af større betydning. Det viser sig at "den vigtigste" del af R er -h(f'(b) - f'(a))/2, og det gælder om succesivt og rent formelt at subtrahere led af denne form (indeholdende de højere afledede af f(x)) fra R, og så håbe på et det der er tilbage enten går imod 0 eller i det mindste kan estimeres. I den formel man herved får frem, kan man f.eks. sætte h = 1 og lade N og dermed b gå imod, og hvis det gælder at f(x) og dens afledede af enhver orden går imod 0 for x, vil man få en formel hvis begyndelse ser således ud: f'(a + n) = -f(a) + f'(a)/ Og hvis man her f.eks. kan få venstre side til at ligne 1/n z, så har man måske en brugbar formel for Riemanns zetafunktion. Det viser sig, når man følger denne tankegang, at de led som succesivt skal subtraheres fra R - og hvoraf det første er -h(f'(b) - f'(a))/2 - har formen (B n /n!) h n (f (n) (b) - f (n) (a)), hvor B n -erne er rationale tal som er uafhængige af f(x). Dvs. den formel som vi ad denne vej er nået frem til, ser således ud: N-1 M h f'(a + kh) = (B n /n!) h n (f (n) (b) - f (n) (a)) + R M. k=1 n=0 Dette er Euler-Maclaurins sumformel, og da vi intet véd på forhånd om restleddet R M, kan den være helt værdiløs. Ofte er det tydeligt at den ikke virker, i så fald kan den måske bringes til at virke ved at ændre a eller b, således at det kun er en del af summen på venstre side man finder en formel for. Når man fremsætter en anvendelse af denne formel, må den altid være ledsaget af
10 10 en estimation af R M - f.eks. i forhold til det sidste led som er bortkastet, dvs. leddet for n = M+1. Det altsammen afhænger af de rationale tal B n, som er universelle konstanter og som kaldes Bernoullitallene. Bortset fra B 1 = -½ er de 0 for n ulige, og de første B n -er for n lige er: B 0 = 1, B 2 = 1/6, B 4 = -1/30 og B 6 = 1/42. Denne korte følge er numerisk aftagende, men herfra begynder tallene at vokse, og f.eks. er B 32 = /510 (dette er det sidste Bernoullital der er med i mine programmer). Vi kan finde Bernoullitallene ved at anvende Euler-Maclaurins sumformel på en funktion hvor vi let kan udregne summen på venstre side. Vi kan f.eks. sætte f(x) = e -x, a = 0 og h = y, så får vi, da e -y + e -2y +... = 1/(e y - 1) at: y/(e y - 1) = B n /n! y n. n=0 Og her kan Taylors formel anvendes på venstre side: denne meromorfe funktion er analytisk i punktet y = 0 (bemærk at både tæller og nævner er 0 for y = 0), og da dens poler er punkterne y = m2πi, m hel 0, kan vi gå ud fra at dens rækkeudvikling ud fra y = 0, nemlig rækken på højre side, har konvergensradius 2π. Dette betyder at B n simpelthen er den n-te afledede af funktionen y/ (e y - 1) i punktet 0. Det kan vises at det for ethvert n gælder at 1 + ( n 1 )B 1 + (n 2 )B (n n-1 )B n-1 = 0, hvor ( n ) = n!/((n-k)!k!) (binomialkoefficienterne). Og denne ligning betyder k at Bernoullitallene kan udregnes rekursivt ud fra B 0 = 1. Dette gøres i programmet "Rekursion" (i mappen "Diverse") som kører indtil de første 16 Bernoullital (forskellige fra 0) er udregnet. Disse tal er derefter indlagt i unit-en "Bernoullital". Og nu til hvordan man kan bruge Euler-Maclaurins sumformel til at finde en praktisk formel for Riemanns zetafunktion ζ(z). Tilsyneladende er det blot at vælge f(x) = x 1-z /(1-z), fordi f'(x) i så fald er 1/x z, og så vælge a = 0, b = og h = 1, for så har vi
11 11 1/n z = f'(a + k), k=1 og så giver Euler-Maclaurins sumformel os et udtryk for den højre side. Men det går ikke at vælge a = 0, for så aftager restleddet R slet ikke. Hvis vi derimod lader a være et tilstrækkeligt stort naturligt tal N, kan vi opnå at restleddet kan gøres lige så lille som det skal være. I så fald er det vi finder en formel for N-1 1/n z = ζ(z) - 1/n z. n=n Hvis vi differentierer f(x) = x 1-z /(1-z) succesivt mht. x og sætter x = N, giver Euler-Maclaurins sumformel os alt ialt: N-1 M ζ(z)= 1/n z + N 1-z /(z-1) + N -z /2 + (B 2n /(2n)!) z(z+1)...(z+2n-2)/n z+2n-1 +R, og her er det klart at hvis blot N er tilstrækkelig stor, kan det sidste led i den sidste sum (leddet for n = M) gøres ligeså lille det skal være (for Re(z) 0). Det kan vises at restleddet R er numerisk mindre end (z+2m+1)/(re(z) +2M+1) gange det første led der bortkastes (leddet for n = M+1). I programmet har jeg sat M = 16 og N = Im(z)/ Formlen gælder i et vist område tilvenstre for y-aksen, men for Re(z) < ½ findes ζ(z) ud fra ζ(1-z) ved hjælp af Riemanns funktionalligning som sammenknytter ζ(z) og ζ(1-z) og som vi kommer til senere (side...). Programmet "MacZeta" (i mappen "Riemann") viser størrelsen af de forskellige led (undtagen restledet) i Euler-Maclaurins formel for ζ(z) (indtast z således at Re(z) 0). Formlen for potensrækken ovenfor indeholdende B n -erne kan ved anvendelse af formlen for 1/(e y -1) på side... skrives: y ( 1/(y+m2πi) - ½) = B n /n! y n m=- n=0
12 12 (den gælder for y < 2π). Og da venstre side er 1 - y/2 + 2 (y/(m2π)) 2 /(1+(y/(m2π)) 2 ) = 1 - y/2-2 (-(y/(m2π)) 2 ) n m=1 m=1 = 1 - y/2-2 (-1) n (y/(2π)) 2n (1/m) 2n, m=1 ser vi at ζ(2n) = -(-1) n (2π) 2n B 2n /(2(2n)!). Specielt er ζ(2) = π 2 /6. Da ζ(2n) 1 for n, har vi B 2n -(-1) n 2(2n)!/(2π) 2n - denne formel for B 2n er faktisk god allerede fra n = 3. Der findes ingen formel for ζ(n) for n ulige. Da gammafunktionen Γ(z) optræder i Riemanns funktionalligning, må vi også have en effektiv formel for Γ(z), og den kan vi også få ved hjælp af Euler- Maclaurins sumformel. Det er dog en formel for logγ(z) vi vil finde. Ifølge Gauss' definition har vi: og derfor Γ(z) = (1/z) ((1+1/k) z /(1+z/k)), k=1 logγ(z) = -log z + (z log(1+1/k) - log(1+z/k)). k=1 Og hvis vi anvender Euler-Maclaurins sumformel på funktionerne xlogx-x og (z+x)log(z+x)-(z+x) (hvis afledede er henh. logx og log(z+x)), kan vi nå frem til denne formel gældende for Re(z) > 0 (Stirlings formel): logγ(z) = (z-½)logz - z + log(2π)/2 + B 2n /((2n)(2n-1) z 2n-1 ) + R, hvor restleddet R kan vises at være numerisk mindre end (2 z /( z + Re(z))) M gange det første led der bortkastes. Jo større z er, jo færre led behøves at medtages, men for ethvert z vil rækken divergere. I mit program har M
13 13 jeg valgt M = 16, og rækken benyttes for z > 7. Ud fra denne formel for logγ(z) og ud fra Γ(z) = exp(logγ(z)) og Γ(z) = Γ(z+N)/(z(z+1)...(z+N-1)) eller Γ(z) = Γ(z-N)(z-1)...(z-N) (N naturligt tal) kan man udregne Γ(z) med stor præcision, idet N vælges således at (f.eks.) 7 < Re(z±N) < 8. Programmerne der udregner ζ(z) og Γ(z) er indlagt i unit-en "GammaZeta". Fourier-inversion Som bekendt kan enhver svingning - altså en funktion f(x) som er periodisk med en vis periode T: f(x+t) = f(x) - opløses i rene svingninger, dvs. sinuskurver, idet den nemlig (ligesom savtakfunktionen på side...) kan udtrykkes som en uendelig sum af rene svingninger der bliver hurtigere og hurtigere: f(x) = a 0 /2 + (a n cos(nλx) + b n sin(nλx)), hvor λ = 2π/T. At rækken virkelig fremstiller funktionen kan vi dog først være sikre på når denne er stykkevis differentiabel, i så fald er rækkens sum i et diskontinuitetspunkt lig middelværdien af funktionens grænseværdi fra venstre og højre. Tallene a n og b n - Fourierkoefficienterne til f(x) - findes ved T a n = 2/T f(y) cos(nλy) dy og b n = 2/T f(y) sin(nλy) dy 0 0 (disse tal eksisterer når f(x) blot er integrabel), og det gælder at T T a 0 2 /2 + (a n 2 + b n 2 ) = 2/T f(x) 2 dx 0 (Parsevals sætning, den gælder når f(x) blot er stykkevis kontinuert). Til en periodisk funktion svarer der altså en sådan følge af tal a 0, a 1, b 1, a 2, b 2,..., og omvendt (koefficienterne skal være således at rækken konvergerer og er differentiabel undtagen i højst endelig mange punkter indenfor en periode). Vi kan formulere disse formler mere elegant ved at regne med komplekse tal: hvis de komplekse tal c n (n hel) defineres ved
14 14 π Τ/2 c n = 1/(2π) f(y/λ) e -nyi dy = 1/T f(y) e -nλyi dy, er og -π -Τ/2 f(x) = c n e nxλi - π 1/(2π) f(x/λ) 2 dx = c n 2 -π - (idet c n = (a n -ib n )/2 og c -n = (a n +ib n )/2 - vi har benyttet at e xi = cos x + i sin x, og b 0 sættes lig 0). Hvis f.eks. f(x) er savtakfunktionen S(x) (side...), finder vi at a 0 = 0 og b n = 1/n, og også at ζ(2) = 1 + 1/ /n = π 2 /6 (= , jvf. Side...). Ved at forestille os at perioden T kan vi for en funktion f(x) på hele intervallet - < x < (som er stykkevis differentiabel og således at f(x) er integrabel) definere en funktion F(y) - den Fouriertransformerede af f(x) - ved så kommer vi tilbage til f(x) ved F(y) = f(x) e -xyi dx, - f(x) = 1/(2π) F(y) e xyi dy. - Vi får nemlig en tilnærmelse til disse integraler ved i integralet og summen ovenfor at erstatte nλ med y og λ med dy, idet λ = 2π/T er "infinitesimal" for T "uendelig".
15 15 Hvis f(x) 2 er integrabel er F(y) 2 det også, og omvendt, og i så fald gælder: f(x) 2 dx = 1/(2π) F(y) 2 dy. - - Og hvis f(m) (m hel) er summabel er F(n) det også, og omvendt, og i så fald gælder Poissons summationsformel: f(2πm) = 1/(2π) F(n), m=- n=- som vi vil bruge til at udlede Riemanns funktionalligning for ζ(z). Hvis f.eks. f(x) = e - x er (ifølge infinitesimalregningens fundamentalsætning): F(y) = (e -x(1+yi) + e -x(1-yi) ) dx 0 x = = [(-e -x(1+yi) /(1+yi)) + (-e -x(1-yi) /(1-yi))] = 1/(1+yi) + 1/(1-yi) = 2/(1+y 2 ). x = 0 Derfor får vi af Poissons summationsformel (idet e -2πm (sum fra m=1 til ) = 1/(e 2π -1)) at 1/2 + 1/ /(n 2 +1) +... = (π(e 2π +1)/(e 2π -1) - 1)/2 (= ) Vi har iøvrigt helt elementært at 1/3 + 1/ /(n 2-1) +... = 3/4. I det følgende vil vi imidlertid mere få brug for en beslægtet transformation, Fourier-Mellin-transformationen: Hvis f(u) er en funktion defineret for de positive reelle tal, og den komplekse funktion F(z) defineres ved F(z) = f(u)/u z du/u 0
16 16 er a+i f(u) = 1/(2πi) F(z) u z dz a-i - det første integral konvergerer kun når Re(z) er større end et vist tal, og i det anden integral skal a vælges større end dette tal. Denne inversionsformel fås af den foregående (Fourier-transformationen) ved at erstatte f(x) med f(e t )e -xt, idet vi så har de reciproke formler og F(x+iy) = f(e t ) e -(x+iy)t dt - f(e t ) = 1/(2π) F(x+iy) e (x+iy)t dy, - og disse bliver til Fourier-Mellin-transformationen når vi indfører substitutionen t = log u og sætter z = x+iy. Gammafunktionen Γ(z) = t z /e t dt/t 0 er altså således at Γ(-z) er den Fourier-Mellin-transformerede af funktionen f(t) = e -t, så derfor har vi a+i e -t = 1/(2πi) Γ(z) t -z dz for a > 0. Vi har allerede set denne formel for t = 1 (side...), og i det sidste kapitel skal vi se hvorfor den har en særlig interesse. Programmet "Fourier-inversion" (i mappen "Möbius- og Fourier-inversion") viser grafen for den Fourier-Mellin-transformerede af sin(x) (for linier paral- a-i
17 17 lelle med y-aksen) og grafen for sin(x) gendannet ved inversionsformlen. Tre grader af præcision kan vælges. Mertens formodning I næste kapitel vil vi udlede Riemanns formel for π N, men som forberedelse hertil vil vi vende tilbage til en sag som vi ikke har fået gjort færdig, nemlig summen (side...) N µ(n). Möbius funktion µ(n) kan antage værdierne 0, 1 og -1, idet µ(n) er 0 når n indeholder en primfaktor mere end én gang og 1 eller -1 når n har henh. et lige eller ulige antal primfaktorer. Og da der i denne sum, når N er stor, nok er nogenlunde lige mange af hvert fortegn, må den svinge omkring 0, men da vi kørte programmet "Mertens formodning", så vi at udsvingne er større end vi forventede, og dette må sige noget om primtallenes fordeling. Thi dér hvor primtallene ligger tæt, vil summen falde, og dér hvor de sammensatte tal ligger tæt, vil bidragene fra dem der netop har to forskellige primfaktorer få summen til at stige. Hvis vi i definitionen af Riemanns zetafunktion ζ(z) = 1/n z, erstatter 1-tallerne i tællerne med talrækken µ(n), får vi en ny zetafunktion η(z) givet ved η(z) = µ(n)/n z for Re(z) > 1. Og ved hjælp af egenskaben hos µ(n) (side...) som vi brugte til at vise Möbius' inversionsformel, får vi (for Re(z) > 1) at
18 18 ( 1/m z )( µ(n)/n z ) = 1. m=1 Derfor kan funktionen η(z) ligesom Riemanns zetafunktion udvides meromorft til hele den komplekse plan, og udvidelsen er sammenknyttet med Riemanns zetafunktion ved η(z) = 1/ζ(z). Da ethvert naturligt tal n kan skrives entydigt på formen n = km 2, hvor k ikke indeholder primfaktorer i en højere potens, har vi også (for Re(z) > 1) at ( µ(k) /k z )( 1/m 2z ) = ( 1/n z ). k=1 m=1 Dvs. for zetafunktionen defineret på samme måde ud fra µ(n) har vi: µ(n) /n z = ζ(z)/ζ(2z). Sætter vi her z = 1 + 1/N og multiplicerer vi på begge sider med 1/N = z - 1 og lader N, følger af at ζ(z) har pol i z = 1 med residuum 1 (side...), hvilket betyder at ( 1/n 1+1/N )/N 1 for N, og hvilket kan generaliseres til at vi har: N ( µ(n) /n 1+1/N )/( µ(n) ) 1 for N, ( µ(n) )/N 1/ζ(2) for N,
19 19 og dette betyder at sandsynligheden for at et tal ikke indeholder en primfaktor mere end én gang er 1/ζ(2) = 6/π 2 = Den uendelige sum der definerer η(z) er umiddelbart kun konvergent for Re(z) > 1, men hvis det gælder at alle nulpunkterne z for ζ(z) har Re(z) α, hvor ½ α < 1, er den konvergent for Re(z) > α, og omvendt. Dette betyder at Riemanns hypotese er ensbetydende med den påstand, at summen der definerer η(z) er konvergent for Re(z) > ½. Bemærk at det at 1/ζ(1) = 0, betyder at den uendelige række µ(n)/n er konvergent med summen 0. Vi vil finde en formel for µ(n) (sum fra til n=n-1), og hertil udvider vi denne funktion af det naturlige tal N til funktionen Σµ(x) af det positive reelle tal x givet ved: n<x Σµ(x) = µ(n). Og denne funktion er vi istand til at finde den Fourier-Mellin-transformerede af, så derfor har vi ved at benytte Fourier-Mellins inversionsformel, en formel for Σµ(x) og dermed for µ(n). Vi skal altså udregne integralet (den Fourier-Mellin-transformerede af Σµ(x)) n<x ( µ(n))/x z dx/x 0 (for Re(z) > 1), og dette integral kan udregnes ved partiel integration: hvis funktionerne f(x) og g(x) er således at f(x)g(x) = 0 i integrationsintervallets endepunkter a og b, da gælder at b g'(x) f(x) dx = - g(x) f'(x) dx a (formlen beror på at d(f(x)g(x))/dx = f'(x)g(x) + f(x)g'(x) og at vi i dette tilfælde har (d(f(x)g(x))/dx) dx = f(b)g(b) - f(a)g(a) = 0). Denne formel gælder også selv om der er punkter hvor f(x) (f.eks.) er diskontinuert, idet f'(x)dx i så fald skal tolkes som dens spring: hvis f(x) i x 0 har springet k, er dette punkts a b
20 bidrag til integralet g(x 0 )k (integralet g(x) f'(x) dx skal derfor opfattes som 20 Stieltjes-integralet g(x) df(x), se side...). Hvis vi anvender formlen for partiel integration på g(x) = -x -z /z og f(x) = Σµ (x) og med a = 0 og b =, har vi, idet g'(x) = 1/x z+1 og idet springet af Σµ(x) i x = n er µ(n), at det søgte integral har værdien (1/z) µ(n)/n z, og dette er som vi har set funktionen 1/(zζ(z)). Vi får nu af Fourier-Mellins inversionsformel at N-1 a+i µ(n) = 1/(2πi) N z /ζ(z) dz/z a-i (hvor a > 1). Integralet her kan vi enten udregne direkte, eller vi kan benytte residueregning, idet integranden N z /(zζ(z)) er meromorf og dens simple poler er z = 0 samt i alle nulpunkterne for ζ(z). For da man formoder at ethvert nulpunkt ρ for ζ(z) er simpelt (dvs. ζ'(ρ) 0), er enhver pol ρ for 1/ζ(z) simpel og har residuum 1/ζ'(ρ) (at nulpunktet z 0 for en funktion f(z) er simpelt er ensbetydende med at f'(z 0 ) 0, og i så fald har 1/f(z) simpel pol i z 0 med residuum 1/f'(z 0 ), og omvendt, se side...), så derfor har vi: N-1 µ(n) = Ν ρ /(ρζ'(ρ)) + 1/ζ(0). hvor summen går over alle nulpunkterne for ζ(z). Vi vil prøvekøre disse to formler for µ(n) (programmet "Mertens formodning"). I integralet sætter vi a = 3/4 (dvs. vi integrerer langs linien midt imellem linierne x = ½ og x = 1) og = 5000, og i summen summerer vi ud til en radius af 200, nemlig over nulpunkterne -2k, for k = 1 til 100, og over de første 79 nulpunkter (over x-aksen) på linien x = ½. For ζ'(ρ) bruger vi tilnærmelsen ζ'(ρ) ζ(ρ+ε)/ε, hvor ε er et lille tal (10-4 i programmet). Desuden be-
21 21 nytter vi at ζ(0) = -½. Formlerne giver nogenlunde det samme og det rigtige, men de er ikke ekstremt gode, det hænger sammen med at de er langsomt konvergerende, og dette hænger igen sammen med at funktionen µ(n) springer hid og did. Men læg nu mærke til, at i sumformlen kan vi sætte N udenfor en parentes, således at det der er inde i parentesen bliver begrænset, hvis Riemanns hypotese altså er sand, idet vi i så fald har N ρ = ( N)N ti når Re(ρ) > 0 (da ρ har formen ½+it). Og dette betyder at talfølgen N-1 (1/ N) µ(n) må formodes at være begrænset. Mertens formodning (1897) siger at tallene numerisk er begrænset af tallet 1, det er dog blevet bevist (1983) at dette ikke er rigtigt, dvs. tallet 1 skal erstattes med et større tal (hvilket der er det mindste der kan vælges er vist stadig ukendt). Mertens formodning (med det større tal) er stærkere end Riemanns hypotese, idet Riemanns hypotese følger af Mertens formodning. Og ved at bevise Mertens formodning havde Stieltjes i 1885 givet et bevis for Riemanns hypotese. Stieltjes var dog ikke tilfreds med dette bevis, da det byggede på aritmetiske egenskaber ved µ(n) og da han ønskede et simplere bevis som byggede på teorien for zetafunktionen ζ(z), men inden det var lykkedes for ham at finde et sådant, havde han glemt sit oprindelige bevis. Riemanns hypotese er mildere end Mertens formodning på den måde, at af Mertens formodning følger umiddelbart at det for ethvert (lille) positivt tal ε gælder at N-1 1/N ½+ε µ(n) 0 for N, og af denne påstand følger Riemanns hypotese, idet den medfører at funktionen 1/ζ(z) ikke har poler i halvplanen Re(z) > ½. I 1912 beviste Littlewood at det omvendte også gælder, således at det at denne talfølge konvergerer imod 0 for ethvert ε, er ensbetydende med Riemanns hypotese. Ud fra denne måde at formulere Riemanns hypotese på, kan man opstille et statistisk bevis for at Riemanns hypotese: man kan bevise at sandsynligheden
22 22 for at Riemanns hypotese er sand er lig 1. Da der jo tilsyneladende ikke er nogen orden i µ(n)'s værdier, kan vi antage, at for et n for hvilket µ(n) 0 (dvs. et n som er et produkt af forskellige primtal) kommer værdien af µ(n), dvs. et af de to tal 1 og -1, ganske som når man slår plat og krone. Og når man slår plat og krone et stort antal gange N, gælder det, at sandsynligheden for at udfaldet plat (eller udfaldet krone) afviger mindre end m (et givet tal) fra det forventede antal (nemlig N/2) er: (m/ N) (2/π) exp(-x 2 π) dx -(m/ N) (2/π) (funktionen x exp(-x 2 /(2σ 2 ))/(σ (2π)) er tætheden af den såkaldte normalfordeling med spredning σ: sandsynligheden for at et tilfældigt tal ud af en stor talmængde med middelværdi 0 og spredning σ falder i intervallet [a, b] er integralet af denne funktion fra a til b, hos os er σ = 1/ (2π)). Og dette betyder, at sandsynligheden for at differencen imellem antallet af plat og antallet af krone er numerisk mindre end 2m er dette integral. Og anvender vi dette argument på de "tilfældige" tal µ(n), idet vi sætter m = N ½+ε, får vi at: N-1 1/N ½+ε µ(n) 0 for N, for ethvert ε > 0, da N ε for N og da integralet af exp(-x 2 π) fra - til er 1. Hermed har vi fået bekræftet af µ(n)'s vekslen i fortegn virkelig er "tilfældig", og at den kurve man ville få ved i programmet "Mertens formodning" at erstatte µ(n) med en funktion der fik tildelt værdierne ±1 som når man slår plat og krone, ville variere ligeså vildt: kurven afspejler således blot tilfældighedens natur. Mertens formodning er lige på kanten af Riemanns hypotese, og den er vist den måde at formulere noget der minder om Riemanns hypotese på, som lettest kan begribes af almindelige mennesker. Mertens formodning siger jo, at hvis vi betragter de tal mindre end N som er et produkt af primtal der alle er forskellige, så er forskellen imellem antallet af dem der består af henh. lige og ulige mange primtal numerisk begrænset af tallet N (gange en konstant).
23 23 En anden måde at formulere Riemanns hypotese på som handler mere direkte om primtallenes fordeling, er følgende: Primtalssætningen (som Gauss fremsatte) siger at Li(N) er en tilnærmelse til π N (idet π N /Li(N) 1 for N ), men hvor god er denne tilnærmelse? Det er det Riemanns hypotese udtaler sig om. For det kan bevises (von Koch, 1901), at Riemanns hypotese er ensbetydende med den påstand at talfølgen er begrænset. (π N - Li(N))/( N logn) Men det kan også bevises (Littlewood, 1914), at der er uendelig mange af tallene i denne talfølge som er større end 1/(2(log N) 2 ) og uendelig mange som er mindre end -1/(2(log N) 2 ) (jvf. bemærkningen på side...). Man kan udlede et utal af formler der minder om formlen for µ(n). I næste kapitel skal vi udlede den allervigtigste, men inden da vil jeg vise en anden formel af denne slags, nemlig en tilnærmelsesformel for summen N 1/N σ(n), hvor σ(n) er summen af primfaktorerne i n (regnet med multiplicitet, se side...). Dette tal er gennemsnittet af de første N naturlig tals sum af primfaktorer, og da gennemsnittet af de første N naturlige tal er (N+1)/2 N/2, må tallet selvsagt være meget mindre end N/2. En god tilnærmelsesformel lyder: N N 1/N σ(n) ζ(2 log t/log N) t dt/log t. 0 Højresiden er tilnærmelsesvist lig tallet (ζ(2)/2) N/log N (ζ(2)/2) π N = (π 2 /12) π N π N. Så af formlen følger at forholdet imellem gennemsnittet af de første N naturlig tals sum af primfaktorer og antallet af primtal mindre end N konvergerer imod ζ(2)/2 for N. Da σ(n) har logaritmeegenskaben σ(mn) = σ(m)+σ(n), ser vi at summen af primfaktorerne i tallet N! omtrent er givet ved N gange integralet. Bemærk at integranden ζ(2 log t/log N) t/log t har 3 singulariteter i integra-
24 24 tionsintervallet [0, N]: i t = 0 hvor log t ikke er defineret, i t = 1 hvor log t = 0 og i t = N hvor zetafunktionen ikke er defineret. Integrandens graf ser således ud for N = 16: For et sådant integral fra a til b hvor der imellem a og b er en singularitet c for integranden, er værdien defineret som grænseværdien for ε 0 (ε > 0) af integralet fra a til c-ε plus integralet fra c+ε til b (jvf. Side... At integranden ikke er defineret i c betyder normalt at det mest betydningsfylde sker her, så derfor bør man i udregningen udgå herfra, idet man vælger et lille tal d (f.eks ) og går fra c+ε til b og fra c-ε til a igennem intervaller der gøres større og større (ved f.eks. succesivt at gange d med ). Hvis vi i det aktuelle integral vælger tal imellem de tre singulariteter, f.eks. 0.5 og 2, er integralet givet ved: N ε 2 N-ε N... = lim ε 0 ( ). 0 ε ε 2 N+ε De tre første integraler har øjensynlig hver især grænseværdi for ε 0, og de to første er af ganske ringe betydning i forhold til de øvrige, så dem vil vi se bort fra. Vi vil også se bort fra det tredie integral. De to sidste integraler synes hver især at divergere for ε 0, og dette kan vi få bekræftet ved erstatte funktionen med dens absolutværdi, så opdager vi at summen af de to sidste integraler kan gøres ligeså stor det skal være når ε gøres lille. I programmet "SumPrim" udregnes 1/N σ(n) dels ved optælling og dels ved udregning af de to sidste integraler. Hvad selve computerudregningen af integraler angår, har jeg i de fleste af programmerne anvendt trapezformlen - der er ingen grund til at være mere nøjagtig, når der er andre fejlkilder inde i billedet. Trapezformlen vil sige, at
25 25 integrationsintervallet deles op i små bidder hvis bidrag til integralet er deres længde gange middelværdien af funktionsværdierne i deres endepunkter. Hvis intervallet fra a til b deles af punkterne a = x 0, x 1, x 2,..., x N+1 = b, lyder trapezformlen: b N f(x)dx ½(f(a)d 0 + f(x i )(d i-1 +d i ) + f(b)d N ), a i=1 hvor d i = x i+1 -x i. I de fleste af programmerne forøges eller formindskes tallene d i, og i så fald udgør de altid en kvotientrække, dvs. d i+1 =kd i, hvor k er et fast tal lige omkring 1 (og så er d i-1 +d i = (1+k)d i-1 ). Det første eller sidste led udelades oftest, da a eller b enten er henh. - eller eller en singularitet for f(x). Trapezformlen er anvendt i alle de komplekse integrationer. I nogle af de reelle integrationer, nemlig de ovennævnte integraler og funktionen Li(x) for reelle x, har jeg anvendt den mere nøjagtige Simpsons formel (Simpson, ). Denne bygger på at integrationsintervallet deles op i små bidder indenfor hvilke funktionen erstattes med parabler der har samme værdier som funktionen i biddernes endepunkter og i et punkt imellem disse. Følger alle disse punkter en kvotientrække med kvotient k, lyder Simpsons formel: b N f(x)dx k 0 (f(a)k(2-k)d 0 + (k 1 f(x i +d i )+k 2 f(x i +(k+1)d i )d i a i=0 + (-k 2 +2k-1)f(b)d N ), idet x i+1 -x i = (1+k)d i og d i+1 = k 2 d i, og k 0 = (1+1/k)/6, k 1 = (1+k) 2 og k 2 = (2- k)k 3 +2k-1. Her er N og k således at b = a+d 0 (1+k)(k N+1-1)/(k-1), men det sidste led ikke er medtaget i mine programmer. Programmet kan f.eks. se således ud (det sidste led er indrammet af en {}-parentes): k := ; k1 := sqr(1 + k); k2 := (2 - k) * k * k * k + 2 * k 1; d := ; t := a; s := d * (2 - k) * k * f(t);
26 26 while t < b do begin d1 := (1 + k) * d; s := s + d * (k1 * f(t + d) + k2 * f(t + d1)); t := t + d1; d := sqr(k) * d; end; {s := s + d * (2 * k k2) * f(t - d1) / sqr(k);} s := s * (1 + 1 / k) / 6; For k = 1 har vi den oprindelige Simpsons formel: b N-1 f(x)dx (d/3)(f(a) + (4f(x i +d)+2f(x i +2d)) + 4f(b-d) + f(b)), a i=0 idet x i+1 -x i = 2d og d = (b-a)/(2n+2). Disse tilnærmelsesformler er selvfølgelig helt eksakte når f(x) er et andengradspolynomium.
Kompleks Funktionsteori
 Kompleks Funktionsteori Formelræs Holomorfe funktioner Sætning. (Caucy-Riemans ligninger). Funktionen f : G C, f = u+iv er holomorf i z 0 = x 0 + iy 0 hvis og kun hvis i punktet (x 0, y 0 ). du dx = dv
Kompleks Funktionsteori Formelræs Holomorfe funktioner Sætning. (Caucy-Riemans ligninger). Funktionen f : G C, f = u+iv er holomorf i z 0 = x 0 + iy 0 hvis og kun hvis i punktet (x 0, y 0 ). du dx = dv
Omvendingsformler for potensrækker Asymptotiske og svingende asymptotiske potensrækker Riemanns metode og cirkelmetoden
 1 Omvendingsformler for potensrækker Asymptotiske og svingende asymptotiske potensrækker Riemanns metode og cirkelmetoden Af Niels-Henrik Aphel Indledning 1 De talteoretiske funktioner (n) og (n) 2 Euler-Maclaurins
1 Omvendingsformler for potensrækker Asymptotiske og svingende asymptotiske potensrækker Riemanns metode og cirkelmetoden Af Niels-Henrik Aphel Indledning 1 De talteoretiske funktioner (n) og (n) 2 Euler-Maclaurins
Den homogene ligning. Vi betragter den n te ordens, homogene, lineære differentialligning. d n y dt n. an 1 + any = 0 (1.2) dt. + a1 d n 1 y dt n 1
 1/7 Den homogene ligning Vi betragter den n te ordens, homogene, lineære differentialligning a 0 d n y dt n + a1 d n 1 y dt n 1 hvor a 0,..., a n R og a 0 0. Vi skriver ligningen på kort form som + + dy
1/7 Den homogene ligning Vi betragter den n te ordens, homogene, lineære differentialligning a 0 d n y dt n + a1 d n 1 y dt n 1 hvor a 0,..., a n R og a 0 0. Vi skriver ligningen på kort form som + + dy
z j 2. Cauchy s formel er værd at tænke lidt nærmere over. Se på specialtilfældet 1 dz = 2πi z
 Matematik F2 - sæt 3 af 7 blok 4 f(z)dz = 0 Hovedemnet i denne uge er Cauchys sætning (den der står i denne sides hoved) og Cauchys formel. Desuden introduceres nulpunkter og singulariteter: simple poler,
Matematik F2 - sæt 3 af 7 blok 4 f(z)dz = 0 Hovedemnet i denne uge er Cauchys sætning (den der står i denne sides hoved) og Cauchys formel. Desuden introduceres nulpunkter og singulariteter: simple poler,
(c) Opskriv den reelle Fourierrække for funktionen y(t) fra (b), og afgør dernæst om y(t) er en lige eller ulige funktion eller ingen af delene.
 MATEMATIK 3 EN,MP 4. februar 2016 Eksamenopgaver fra 2011 2016 (jan. 2016) Givet at 0 for 0 < t < 1 mens e (t 1) cos(7(t 1)) for t 1, betragt da begyndelsesværdiproblemet for t > 0: y (t) + 2y (t) + 50y(t)
MATEMATIK 3 EN,MP 4. februar 2016 Eksamenopgaver fra 2011 2016 (jan. 2016) Givet at 0 for 0 < t < 1 mens e (t 1) cos(7(t 1)) for t 1, betragt da begyndelsesværdiproblemet for t > 0: y (t) + 2y (t) + 50y(t)
MM502+4 forelæsningsslides
 MM502+4 forelæsningsslides uge 11+12 1, 2009 Produceret af Hans J. Munkholm, delvis på baggrund af lignende materiale udarbejdet af Mikael Rørdam 1 I nærværende forbindelse er 11 + 12 23 1 Egenskaber for
MM502+4 forelæsningsslides uge 11+12 1, 2009 Produceret af Hans J. Munkholm, delvis på baggrund af lignende materiale udarbejdet af Mikael Rørdam 1 I nærværende forbindelse er 11 + 12 23 1 Egenskaber for
. Nemlig ved først at danne zetafunktionen (fra side...): Ζ(z) = 1/p z. p primtal
 1 Udledning af Riemanns formel for π N På samme måde som vi ovenfor har fundet en formel for summen µ(n) for tallene n = 1, 2, 3,... op til N-1, kan vi finde en formel for summen 1 for primtallene p =
1 Udledning af Riemanns formel for π N På samme måde som vi ovenfor har fundet en formel for summen µ(n) for tallene n = 1, 2, 3,... op til N-1, kan vi finde en formel for summen 1 for primtallene p =
Matematisk modellering og numeriske metoder. Lektion 8
 Matematisk modellering og numeriske metoder Lektion 8 Morten Grud Rasmussen 18. oktober 216 1 Fourierrækker 1.1 Periodiske funktioner Definition 1.1 (Periodiske funktioner). En periodisk funktion f er
Matematisk modellering og numeriske metoder Lektion 8 Morten Grud Rasmussen 18. oktober 216 1 Fourierrækker 1.1 Periodiske funktioner Definition 1.1 (Periodiske funktioner). En periodisk funktion f er
Matematik F2 Opgavesæt 2
 Opgaver uge 2 I denne uge kigger vi nærmere på Cauchy-Riemann betingelserne, potensrækker, konvergenskriterier og flertydige funktioner. Vi skal også se på integration langs en ve i den komplekse plan.
Opgaver uge 2 I denne uge kigger vi nærmere på Cauchy-Riemann betingelserne, potensrækker, konvergenskriterier og flertydige funktioner. Vi skal også se på integration langs en ve i den komplekse plan.
Formelsamling - MatF2. Therkel Zøllner og Amalie Christensen 27. juni 2009
 Formelsamling - MatF2 Therkel Zøllner og Amalie Christensen 27. juni 2009 1 Indhold 1 Kompleks variabel teori 3 1.1 Komplekse funktioner 825-830........................... 3 1.2 Powerserier af komplekse
Formelsamling - MatF2 Therkel Zøllner og Amalie Christensen 27. juni 2009 1 Indhold 1 Kompleks variabel teori 3 1.1 Komplekse funktioner 825-830........................... 3 1.2 Powerserier af komplekse
Opspaltning i primfaktorer
 1 Opspaltning i primfaktorer Et program som kan undersøge om et tal er et primtal, eller finde hvilke primtal det er sammensat af, er det allerførste program enhver talentusiast laver. For den tid jo er
1 Opspaltning i primfaktorer Et program som kan undersøge om et tal er et primtal, eller finde hvilke primtal det er sammensat af, er det allerførste program enhver talentusiast laver. For den tid jo er
MATEMATIK 3 EN,MP 17. september 2014 Oversigt nr. 1
 MATEMATIK 3 EN,MP 7. september 204 Oversigt nr. Her bringes en samling af de gamle eksamensopgaver: (jan. 204) Betragt begyndelsesværdiproblemet y (t) + 7y (t) + 2y(t) = e t sin(2t) for t > 0, y(0) = 2,
MATEMATIK 3 EN,MP 7. september 204 Oversigt nr. Her bringes en samling af de gamle eksamensopgaver: (jan. 204) Betragt begyndelsesværdiproblemet y (t) + 7y (t) + 2y(t) = e t sin(2t) for t > 0, y(0) = 2,
Differentiation af sammensatte funktioner
 1/7 Differentiation af sammensatte funktioner - Fra www.borgeleo.dk En sammensat funktion af den variable x er en funktion, vor x først indsættes i den såkaldte indre funktion. Resultatet fra den indre
1/7 Differentiation af sammensatte funktioner - Fra www.borgeleo.dk En sammensat funktion af den variable x er en funktion, vor x først indsættes i den såkaldte indre funktion. Resultatet fra den indre
Besvarelses forslag til Tag-hjemeksamen Vinteren 02 03
 IMFUFA Carsten Lunde Petersen Besvarelses forslag til Tag-hjemeksamen Vinteren 02 0 Hvor ikke andet er angivet er henvisninger til W.R.Wade An Introduction to analysis. Opgave a) Idet udtrykket e x2 cos
IMFUFA Carsten Lunde Petersen Besvarelses forslag til Tag-hjemeksamen Vinteren 02 0 Hvor ikke andet er angivet er henvisninger til W.R.Wade An Introduction to analysis. Opgave a) Idet udtrykket e x2 cos
MATEMATIK 11 Eksamensopgaver Juni 1995 Juni 2001, 4. fjerdedel
 Juni 2000 MATEMATIK 11 Eksamensopgaver Juni 1995 Juni 2001, 4. fjerdedel Opgave 1. (a) Find den fuldstændige løsning til differentialligningen y 8y + 16y = 0. (b) Find den fuldstændige løsning til differentialligningen
Juni 2000 MATEMATIK 11 Eksamensopgaver Juni 1995 Juni 2001, 4. fjerdedel Opgave 1. (a) Find den fuldstændige løsning til differentialligningen y 8y + 16y = 0. (b) Find den fuldstændige løsning til differentialligningen
Kalkulus 2 - Grænseovergange, Kontinuitet og Følger
 Kalkulus - Grænseovergange, Kontinuitet og Følger Mads Friis 8. januar 05 Indhold Grundlæggende uligheder Grænseovergange 3 3 Kontinuitet 9 4 Følger 0 5 Perspektivering 4 Grundlæggende uligheder Sætning
Kalkulus - Grænseovergange, Kontinuitet og Følger Mads Friis 8. januar 05 Indhold Grundlæggende uligheder Grænseovergange 3 3 Kontinuitet 9 4 Følger 0 5 Perspektivering 4 Grundlæggende uligheder Sætning
Eksamen i Matematik F2 d. 19. juni Opgave 2. Svar. Korte svar (ikke fuldstændige)
 Eksamen i Matematik F2 d. 9. juni 28 Korte svar (ikke fuldstændige Opgave Find realdelen, Re z, og imaginærdelen, Im z, for følgende værdier af z, a z = 2 i b z = i i c z = ln( + i Find realdelen, Re z,
Eksamen i Matematik F2 d. 9. juni 28 Korte svar (ikke fuldstændige Opgave Find realdelen, Re z, og imaginærdelen, Im z, for følgende værdier af z, a z = 2 i b z = i i c z = ln( + i Find realdelen, Re z,
Svar til eksamen i Matematik F2 d. 23. juni 2016
 Svar til eksamen i Matematik F d. 3. juni 06 FORBEHOLD FOR FEJL! Bemærk, i modsætning til herunder, så skal det i besvarelsen fremgå tydeligt, hvordan polerne ndes og hvordan de enkelte residuer udregnes.
Svar til eksamen i Matematik F d. 3. juni 06 FORBEHOLD FOR FEJL! Bemærk, i modsætning til herunder, så skal det i besvarelsen fremgå tydeligt, hvordan polerne ndes og hvordan de enkelte residuer udregnes.
π er irrationel Frank Nasser 10. december 2011
 π er irrationel Frank Nasser 10. december 2011 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold 1 Introduktion
π er irrationel Frank Nasser 10. december 2011 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold 1 Introduktion
MATEMATIK 11 Eksamensopgaver Juni 1995 Juni 2001, 3. fjerdedel
 MATEMATIK Eksamensopgaver Juni 995 Juni 200, 3. fjerdedel August 998 Opgave. Lad f : R \ {0} R betegne funktionen givet ved f(x) = ex x for x 0. (a) Find eventuelle lokale maksimums- og minimumspunkter
MATEMATIK Eksamensopgaver Juni 995 Juni 200, 3. fjerdedel August 998 Opgave. Lad f : R \ {0} R betegne funktionen givet ved f(x) = ex x for x 0. (a) Find eventuelle lokale maksimums- og minimumspunkter
Oversigt [S] 8.7, 8.8, 8.9
![Oversigt [S] 8.7, 8.8, 8.9 Oversigt [S] 8.7, 8.8, 8.9](/thumbs/62/47922248.jpg) Oversigt [S] 8.7, 8.8, 8.9 Nøgleord og begreber Potensrækker og opgaver Binomialformlen Binomialkoefficienter Binomialrækken Taylor polynomier Vurdering af Taylor s restled Eksponentialrækken konvereger
Oversigt [S] 8.7, 8.8, 8.9 Nøgleord og begreber Potensrækker og opgaver Binomialformlen Binomialkoefficienter Binomialrækken Taylor polynomier Vurdering af Taylor s restled Eksponentialrækken konvereger
Indhold. Litteratur 11
 Indhold Forord ii 00-sættet 1 Opgave 1....................................... 1 Spørgsmål (a).................................. 1 Spørgsmål (b).................................. 1 Spørgsmål (c)..................................
Indhold Forord ii 00-sættet 1 Opgave 1....................................... 1 Spørgsmål (a).................................. 1 Spørgsmål (b).................................. 1 Spørgsmål (c)..................................
En differentiabel funktion hvis afledte ikke er kontinuert Søren Knudby
 24 En differentiabel funktion hvis afledte ikke er kontinuert Søren Knudby Det er velkendt for de fleste, at differentiabilitet af en reel funktion f medfører kontinuitet af f, mens det modsatte ikke gælder
24 En differentiabel funktion hvis afledte ikke er kontinuert Søren Knudby Det er velkendt for de fleste, at differentiabilitet af en reel funktion f medfører kontinuitet af f, mens det modsatte ikke gælder
SUPPLERENDE OPGAVER TIL KOMPLEKS FUNKTIONSTEORI F2005
 SUPPLERENDE OPGAVER TIL KOMPLEKS FUNKTIONSTEORI F2005 0. maj, 2005 version nr. 8 JØRGEN VESTERSTRØM Indledende bemærkninger De foreliggende opgaver udgør et supplement til lærebogens opgaver. Afsnitsnummereringerne
SUPPLERENDE OPGAVER TIL KOMPLEKS FUNKTIONSTEORI F2005 0. maj, 2005 version nr. 8 JØRGEN VESTERSTRØM Indledende bemærkninger De foreliggende opgaver udgør et supplement til lærebogens opgaver. Afsnitsnummereringerne
Afgør for hver af følgende rækker om den er divergent, betinget konvergent eller absolut konvergent. 2 n. n=1 2n (n + 1)2 1 = 2(n + n+1
 Analyse Reeksamen 00 Rasmus Sylvester Bryder 5. august 0 Opgave Afgør for hver af følgende rækker om den er divergent, betinget konvergent eller absolut konvergent. ( ) n n +3n+7 n= n + For alle n N vil
Analyse Reeksamen 00 Rasmus Sylvester Bryder 5. august 0 Opgave Afgør for hver af følgende rækker om den er divergent, betinget konvergent eller absolut konvergent. ( ) n n +3n+7 n= n + For alle n N vil
ElmTal Primtallene 1.1
 Primtallene.. Primtallene. (.) Setup. Et tal p kaldes som bekendt et primtal, hvis p 2 og p kun har trivielle divisorer, dvs hvis de eneste (positive) divisorer i p er og p. De første primtal er tallene
Primtallene.. Primtallene. (.) Setup. Et tal p kaldes som bekendt et primtal, hvis p 2 og p kun har trivielle divisorer, dvs hvis de eneste (positive) divisorer i p er og p. De første primtal er tallene
Mat H /05 Note 2 10/11-04 Gerd Grubb
 Mat H 1 2004/05 Note 2 10/11-04 Gerd Grubb Nødvendige og tilstrækkelige betingelser for ekstremum, konkave og konvekse funktioner. Fremstillingen i Kapitel 13.1 2 af Sydsæters bog [MA1] suppleres her med
Mat H 1 2004/05 Note 2 10/11-04 Gerd Grubb Nødvendige og tilstrækkelige betingelser for ekstremum, konkave og konvekse funktioner. Fremstillingen i Kapitel 13.1 2 af Sydsæters bog [MA1] suppleres her med
Kortfattet svar til eksamen i Matematik F2 d. 21. juni 2017
 Kortfattet svar til eksamen i Matematik F2 d. 2. juni 27 Opgave Bestem for følgende tilfælde om en funktion f(z) af z = x + iy er analytisk i dele af den komplekse plan, hvis den har real del u(x, y) og
Kortfattet svar til eksamen i Matematik F2 d. 2. juni 27 Opgave Bestem for følgende tilfælde om en funktion f(z) af z = x + iy er analytisk i dele af den komplekse plan, hvis den har real del u(x, y) og
Taylor s approksimationsformler for funktioner af én variabel
 enote 17 1 enote 17 Taylor s approksimationsformler for funktioner af én variabel I enote 14 og enote 16 er det vist hvordan funktioner af én og to variable kan approksimeres med førstegradspolynomier
enote 17 1 enote 17 Taylor s approksimationsformler for funktioner af én variabel I enote 14 og enote 16 er det vist hvordan funktioner af én og to variable kan approksimeres med førstegradspolynomier
Eksamen i Mat F, april 2006
 Eksamen i Mat F, april 26 Opgave 1 Lad F være et vektorfelt, givet i retvinklede koordinater som: F x x F = F x i + F y j + F z k = F y = 2z F z y Udregn F og F: F = F x + F y + F z = 1 + +. F = F z F
Eksamen i Mat F, april 26 Opgave 1 Lad F være et vektorfelt, givet i retvinklede koordinater som: F x x F = F x i + F y j + F z k = F y = 2z F z y Udregn F og F: F = F x + F y + F z = 1 + +. F = F z F
Mere om differentiabilitet
 Mere om differentiabilitet En uddybning af side 57 i Spor - Komplekse tal Kompleks funktionsteori er et af de vigtigste emner i matematikken og samtidig et af de smukkeste I bogen har vi primært beskæftiget
Mere om differentiabilitet En uddybning af side 57 i Spor - Komplekse tal Kompleks funktionsteori er et af de vigtigste emner i matematikken og samtidig et af de smukkeste I bogen har vi primært beskæftiget
Karakteristiske funktioner og Den Centrale Grænseværdisætning
 E6 efterår 1999 Notat 10 Jørgen Larsen 20. oktober 1999 Karakteristiske funktioner og Den Centrale Grænseværdisætning Karakteristiske funktioner som er nære slægtninge til Fourier-transformationen) er
E6 efterår 1999 Notat 10 Jørgen Larsen 20. oktober 1999 Karakteristiske funktioner og Den Centrale Grænseværdisætning Karakteristiske funktioner som er nære slægtninge til Fourier-transformationen) er
Integralregning Infinitesimalregning
 Udgave 2.1 Integralregning Infinitesimalregning Noterne gennemgår begreberne integral og stamfunktion, og anskuer dette som et redskab til bestemmelse af arealer under funktioner. Noterne er supplement
Udgave 2.1 Integralregning Infinitesimalregning Noterne gennemgår begreberne integral og stamfunktion, og anskuer dette som et redskab til bestemmelse af arealer under funktioner. Noterne er supplement
Tal. Vi mener, vi kender og kan bruge følgende talmængder: N : de positive hele tal, Z : de hele tal, Q: de rationale tal.
 1 Tal Tal kan forekomme os nærmest at være selvfølgelige, umiddelbare og naturgivne. Men det er kun, fordi vi har vænnet os til dem. Som det vil fremgå af vores timer, har de mange overraskende egenskaber
1 Tal Tal kan forekomme os nærmest at være selvfølgelige, umiddelbare og naturgivne. Men det er kun, fordi vi har vænnet os til dem. Som det vil fremgå af vores timer, har de mange overraskende egenskaber
Supplerende opgaver. S1.3.1 Lad A, B og C være delmængder af X. Vis at
 Supplerende opgaver Analyse Jørgen Vesterstrøm Forår 2004 S.3. Lad A, B og C være delmængder af X. Vis at (A B C) (A B C) (A B) C og find en nødvendig og tilstrækkelig betingelse for at der gælder lighedstegn
Supplerende opgaver Analyse Jørgen Vesterstrøm Forår 2004 S.3. Lad A, B og C være delmængder af X. Vis at (A B C) (A B C) (A B) C og find en nødvendig og tilstrækkelig betingelse for at der gælder lighedstegn
Epistel E2 Partiel differentiation
 Epistel E2 Partiel differentiation Benny Lautrup 19 februar 24 Funktioner af flere variable kan differentieres efter hver enkelt, med de øvrige variable fasthol Definitionen er f(x, y) x f(x, y) f(x +
Epistel E2 Partiel differentiation Benny Lautrup 19 februar 24 Funktioner af flere variable kan differentieres efter hver enkelt, med de øvrige variable fasthol Definitionen er f(x, y) x f(x, y) f(x +
n=1 er veldefineret for alle følger for hvilke højresiden er endelig. F.eks. tilhører følgen
 2 Hilbert rum 2. Eksempler på Hilbert rum Vi skal nu først forsøge at begrunde, at de indre produkt rum af funktioner eller følger, som blev indført i Kapitel, ikke er omfattende nok til vores formål.
2 Hilbert rum 2. Eksempler på Hilbert rum Vi skal nu først forsøge at begrunde, at de indre produkt rum af funktioner eller følger, som blev indført i Kapitel, ikke er omfattende nok til vores formål.
ANALYSE 1. Uge 7, 4. juni juni, 2007
 ANALYSE 1 Uge 7, 4. juni - 10. juni, 2007 Forelæsninger Mandag 4. juni Formålet med denne dags forelæsninger er at etablere en overgang til emnet metriske rum, hvis hovedformål er at udvide begreber som
ANALYSE 1 Uge 7, 4. juni - 10. juni, 2007 Forelæsninger Mandag 4. juni Formålet med denne dags forelæsninger er at etablere en overgang til emnet metriske rum, hvis hovedformål er at udvide begreber som
Taylor s approksimationsformler for funktioner af én variabel
 enote 4 1 enote 4 Taylor s approksimationsformler for funktioner af én variabel I enote 19 og enote 21 er det vist hvordan funktioner af én og to variable kan approksimeres med førstegradspolynomier i
enote 4 1 enote 4 Taylor s approksimationsformler for funktioner af én variabel I enote 19 og enote 21 er det vist hvordan funktioner af én og to variable kan approksimeres med førstegradspolynomier i
Københavns Universitet, Det naturvidenskabelige Fakultet. Afleveringsopgave 1
 Københavns Universitet, Det naturvidenskabelige Fakultet 1 Lineær Algebra (LinAlg) Afleveringsopgave 1 Eventuelle besvarelser laves i grupper af - 3 personer og afleveres i to eksemplarer med 3 udfyldte
Københavns Universitet, Det naturvidenskabelige Fakultet 1 Lineær Algebra (LinAlg) Afleveringsopgave 1 Eventuelle besvarelser laves i grupper af - 3 personer og afleveres i to eksemplarer med 3 udfyldte
2. Fourierrækker i en variabel
 .1. Fourierrækker i en variabel I Kapitel II 7 blev der indført, dels funktionsrummene L p (X, µ) (mere udførligt skrevet L p (X, E, µ)), dels rummene L p (X, µ), der fås af L p (X, µ) ved at funktioner
.1. Fourierrækker i en variabel I Kapitel II 7 blev der indført, dels funktionsrummene L p (X, µ) (mere udførligt skrevet L p (X, E, µ)), dels rummene L p (X, µ), der fås af L p (X, µ) ved at funktioner
Noter til Perspektiver i Matematikken
 Noter til Perspektiver i Matematikken Henrik Stetkær 25. august 2003 1 Indledning I dette kursus (Perspektiver i Matematikken) skal vi studere de hele tal og deres egenskaber. Vi lader Z betegne mængden
Noter til Perspektiver i Matematikken Henrik Stetkær 25. august 2003 1 Indledning I dette kursus (Perspektiver i Matematikken) skal vi studere de hele tal og deres egenskaber. Vi lader Z betegne mængden
Besvarelse til eksamen i Matematik F2, 2012
 Besvarelse til eksamen i Matematik F2, 202 Partiel besvarelse - har ikke inkluderet alle detaljer! Med forbehold for tastefejl. Opgave Find og bestem typen af alle singulariteter for følgende funktioner:
Besvarelse til eksamen i Matematik F2, 202 Partiel besvarelse - har ikke inkluderet alle detaljer! Med forbehold for tastefejl. Opgave Find og bestem typen af alle singulariteter for følgende funktioner:
Eksamen 2014/2015 Mål- og integralteori
 Eksamen 4/5 Mål- og integralteori Københavns Universitet Institut for Matematiske Fag Formalia Eksamensopgaven består af 4 opgaver med ialt spørgsmål Ved bedømmelsen indgår de spørgsmål med samme vægt
Eksamen 4/5 Mål- og integralteori Københavns Universitet Institut for Matematiske Fag Formalia Eksamensopgaven består af 4 opgaver med ialt spørgsmål Ved bedømmelsen indgår de spørgsmål med samme vægt
Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 2016
 Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Komplekse Tal. 20. november 2009. UNF Odense. Steen Thorbjørnsen Institut for Matematiske Fag Århus Universitet
 Komplekse Tal 20. november 2009 UNF Odense Steen Thorbjørnsen Institut for Matematiske Fag Århus Universitet Fra de naturlige tal til de komplekse Optælling af størrelser i naturen De naturlige tal N (N
Komplekse Tal 20. november 2009 UNF Odense Steen Thorbjørnsen Institut for Matematiske Fag Århus Universitet Fra de naturlige tal til de komplekse Optælling af størrelser i naturen De naturlige tal N (N
z + w z + w z w = z 2 w z w = z w z 2 = z z = a 2 + b 2 z w
 Komplekse tal Hvis z = a + ib og w = c + id gælder z + w = (a + c) + i(b + d) z w = (a c) + i(b d) z w = (ac bd) + i(ad bc) z w = a+ib c+id = ac+bd + i bc ad, w 0 c +d c +d z a b = i a +b a +b Konjugation
Komplekse tal Hvis z = a + ib og w = c + id gælder z + w = (a + c) + i(b + d) z w = (a c) + i(b d) z w = (ac bd) + i(ad bc) z w = a+ib c+id = ac+bd + i bc ad, w 0 c +d c +d z a b = i a +b a +b Konjugation
Analyse 1, Prøve 2 Besvarelse
 Københavns Universitet Prøve ved Det naturvidenskabelige Fakultet maj Analyse, Prøve Besvarelse Opgave (3%) (a) (%) Bestem mængden af x R for hvilke rækken ( + (x) n ) er konvergent og angiv sumfunktionen
Københavns Universitet Prøve ved Det naturvidenskabelige Fakultet maj Analyse, Prøve Besvarelse Opgave (3%) (a) (%) Bestem mængden af x R for hvilke rækken ( + (x) n ) er konvergent og angiv sumfunktionen
Opgaver til f(z) = 1 z 4 1, g(z) = 1
 1.17 Opgaver til 1. 1 1.1. Vis, at f(z) = er vilkårligt ofte differentiabel i C \ {, 1}, og z(1 z) find et udtryk for f (n) (z) for alle n. (Vink. Skriv f(z) = 1 z + 1 1 z ). 1.2. Beskriv billedkurverne
1.17 Opgaver til 1. 1 1.1. Vis, at f(z) = er vilkårligt ofte differentiabel i C \ {, 1}, og z(1 z) find et udtryk for f (n) (z) for alle n. (Vink. Skriv f(z) = 1 z + 1 1 z ). 1.2. Beskriv billedkurverne
Løsningsforslag til opgavesæt 5
 Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
VUC Vestsjælland Syd, Slagelse Nr. 1 Institution: Projekt Trigonometri
 VUC Vestsjælland Syd, Slagelse Nr. 1 Institution: 333247 2015 Anders Jørgensen, Mark Kddafi, David Jensen, Kourosh Abady og Nikolaj Eriksen 1. Indledning I dette projekt, vil man kunne se definitioner
VUC Vestsjælland Syd, Slagelse Nr. 1 Institution: 333247 2015 Anders Jørgensen, Mark Kddafi, David Jensen, Kourosh Abady og Nikolaj Eriksen 1. Indledning I dette projekt, vil man kunne se definitioner
Mujtaba og Farid Integralregning 06-08-2011
 Indholdsfortegnelse Integral regning:... 2 Ubestemt integral:... 2 Integrationsprøven:... 3 1) Integration af potensfunktioner:... 3 2) Integration af sum og Differens:... 3 3) Integration ved Multiplikation
Indholdsfortegnelse Integral regning:... 2 Ubestemt integral:... 2 Integrationsprøven:... 3 1) Integration af potensfunktioner:... 3 2) Integration af sum og Differens:... 3 3) Integration ved Multiplikation
Besvarelser til Calculus Ordinær Eksamen Januar 2019
 Besvarelser til Calculus Ordinær Eksamen - 14. Januar 19 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 14. Januar 19 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Analyse 1, Prøve 4 Besvarelse
 Københavns Universitet Prøve ved Det naturvidenskabelige Fakultet juni 2011 1 Analyse 1, Prøve 4 Besvarelse Lad Opgave 1 (50%) M = {T R 2 T er en åben trekant} og lad A : M R være arealfunktionen, dvs.
Københavns Universitet Prøve ved Det naturvidenskabelige Fakultet juni 2011 1 Analyse 1, Prøve 4 Besvarelse Lad Opgave 1 (50%) M = {T R 2 T er en åben trekant} og lad A : M R være arealfunktionen, dvs.
MM501 forelæsningsslides
 MM50 forelæsningsslides uge 36, 2009 Produceret af Hans J. Munkholm Nogle talmængder s. 3 N = {, 2, 3, } omtales som de naturlige tal eller de positive heltal. Z = {0, ±, ±2, ±3, } omtales som de hele
MM50 forelæsningsslides uge 36, 2009 Produceret af Hans J. Munkholm Nogle talmængder s. 3 N = {, 2, 3, } omtales som de naturlige tal eller de positive heltal. Z = {0, ±, ±2, ±3, } omtales som de hele
MATEMATIK 3 EN,MP 30. august 2013 Oversigt nr. 1
 EN,MP 30. august 2013 Oversigt nr. 1 Litteratur: I Matematik 3 bruger vi (igen) i efteråret 2013 E. Kreyzig: Advanced engineering mathematics, 10. udg., Wiley, 2011. Beskrivelse: Kurset vil handle om matematiske
EN,MP 30. august 2013 Oversigt nr. 1 Litteratur: I Matematik 3 bruger vi (igen) i efteråret 2013 E. Kreyzig: Advanced engineering mathematics, 10. udg., Wiley, 2011. Beskrivelse: Kurset vil handle om matematiske
Algebra - Teori og problemløsning
 Algebra - Teori og problemløsning, januar 05, Kirsten Rosenkilde. Algebra - Teori og problemløsning Kapitel -3 giver en grundlæggende introduktion til at omskrive udtryk, faktorisere og løse ligningssystemer.
Algebra - Teori og problemløsning, januar 05, Kirsten Rosenkilde. Algebra - Teori og problemløsning Kapitel -3 giver en grundlæggende introduktion til at omskrive udtryk, faktorisere og løse ligningssystemer.
Elementær Matematik. Trigonometriske Funktioner
 Elementær Matematik Trigonometriske Funktioner Ole Witt-Hansen Indhold. Gradtal og radiantal.... sin x, cos x og tan x... 3. Trigonometriske ligninger...3 4. Trigonometriske uligheder...5 5. Harmoniske
Elementær Matematik Trigonometriske Funktioner Ole Witt-Hansen Indhold. Gradtal og radiantal.... sin x, cos x og tan x... 3. Trigonometriske ligninger...3 4. Trigonometriske uligheder...5 5. Harmoniske
Noter om komplekse tal
 Noter om komplekse tal Preben Alsholm Januar 008 1 Den komplekse eksponentialfunktion Vi erindrer først om den sædvanlige og velkendte reelle eksponentialfunktion. Vi skal undertiden nde det nyttigt, at
Noter om komplekse tal Preben Alsholm Januar 008 1 Den komplekse eksponentialfunktion Vi erindrer først om den sædvanlige og velkendte reelle eksponentialfunktion. Vi skal undertiden nde det nyttigt, at
Opgaveløsninger til eksamensopgaver. Opgavesæt 46
 EIT3+ITC3/2018 H. Ebert BEREGNINGSTEKNIK INDENFOR ELEKTRONIKOMRÅDET Opgaveløsninger til eksamensopgaver Opgavesæt 46 Beregningsteknik i elektronik for EIT3+ITC3/18 Opgavesæt 46 181229HEb Skriftlig prøve
EIT3+ITC3/2018 H. Ebert BEREGNINGSTEKNIK INDENFOR ELEKTRONIKOMRÅDET Opgaveløsninger til eksamensopgaver Opgavesæt 46 Beregningsteknik i elektronik for EIT3+ITC3/18 Opgavesæt 46 181229HEb Skriftlig prøve
Taylorudvikling I. 1 Taylorpolynomier. Preben Alsholm 3. november Definition af Taylorpolynomium
 Taylorudvikling I Preben Alsholm 3. november 008 Taylorpolynomier. Definition af Taylorpolynomium Definition af Taylorpolynomium Givet en funktion f : I R! R og et udviklingspunkt x 0 I. Find et polynomium
Taylorudvikling I Preben Alsholm 3. november 008 Taylorpolynomier. Definition af Taylorpolynomium Definition af Taylorpolynomium Givet en funktion f : I R! R og et udviklingspunkt x 0 I. Find et polynomium
Heisenbergs usikkerhedsrelationer. Abstrakt. Hvorfor? Funktionsrum. Nils Byrial Andersen Institut for Matematik. Matematiklærerdag 2013
 Heisenbergs usikkerhedsrelationer Nils Byrial Andersen Institut for Matematik Matematiklærerdag 013 1 / 17 Abstrakt Heisenbergs usikkerhedsrelationer udtrykker at man ikke på samme tid både kan bestemme
Heisenbergs usikkerhedsrelationer Nils Byrial Andersen Institut for Matematik Matematiklærerdag 013 1 / 17 Abstrakt Heisenbergs usikkerhedsrelationer udtrykker at man ikke på samme tid både kan bestemme
ANALYSE 1, 2014, Uge 5
 ANALYSE, 204, Uge 5 Afleveringsfrist for Prøve 2 er Tirsdag den 20/5 kl 0:5. Forelæsninger Tirsdag Vi går videre med Afsnit 4 om uniform konvergens af Fourierrækker, hvor hovedsætningen er Sætning 4.3.
ANALYSE, 204, Uge 5 Afleveringsfrist for Prøve 2 er Tirsdag den 20/5 kl 0:5. Forelæsninger Tirsdag Vi går videre med Afsnit 4 om uniform konvergens af Fourierrækker, hvor hovedsætningen er Sætning 4.3.
Løsningsforslag til opgavesæt 5
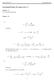 Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
matx.dk Differentialregning Dennis Pipenbring
 mat.dk Differentialregning Dennis Pipenbring 0. december 00 Indold Differentialregning 3. Grænseværdi............................. 3. Kontinuitet.............................. 8 Differentialkvotienten
mat.dk Differentialregning Dennis Pipenbring 0. december 00 Indold Differentialregning 3. Grænseværdi............................. 3. Kontinuitet.............................. 8 Differentialkvotienten
Primtal - hvor mange, hvordan og hvorfor?
 Johan P. Hansen 1 1 Institut for Matematiske Fag, Aarhus Universitet Gult foredrag, EULERs Venner, oktober 2009 Disposition 1 EUKLIDs sætning. Der er uendelig mange primtal! EUKLIDs bevis Bevis baseret
Johan P. Hansen 1 1 Institut for Matematiske Fag, Aarhus Universitet Gult foredrag, EULERs Venner, oktober 2009 Disposition 1 EUKLIDs sætning. Der er uendelig mange primtal! EUKLIDs bevis Bevis baseret
Hilbert rum. Chapter 3. 3.1 Indre produkt rum
 Chapter 3 Hilbert rum 3.1 Indre produkt rum I det følgende skal vi gøre brug af komplekse såvel som reelle vektorrum. Idet L betegner enten R eller C minder vi om, at et vektorrum over L er en mængde E
Chapter 3 Hilbert rum 3.1 Indre produkt rum I det følgende skal vi gøre brug af komplekse såvel som reelle vektorrum. Idet L betegner enten R eller C minder vi om, at et vektorrum over L er en mængde E
MATEMATIK 3 ET,MP, FYS, NANO 29. august 2012 Oversigt nr. 1
 ET,MP, FYS, NANO 29. august 202 Oversigt nr. Litteratur: I Matematik 3 bruger vi i efteråret 202 følgende bog: E. Kreyzig: Advanced engineering mathematics, 0. udg., Wiley, 20. Beskrivelse: Kurset vil
ET,MP, FYS, NANO 29. august 202 Oversigt nr. Litteratur: I Matematik 3 bruger vi i efteråret 202 følgende bog: E. Kreyzig: Advanced engineering mathematics, 0. udg., Wiley, 20. Beskrivelse: Kurset vil
Matematisk modellering og numeriske metoder. Lektion 16
 Matematisk modellering og numeriske metoder Lektion 16 Morten Grud Rasmussen 6. november, 2013 1 Interpolation [Bogens afsnit 19.3 side 805] 1.1 Interpolationspolynomier Enhver kontinuert funktion f på
Matematisk modellering og numeriske metoder Lektion 16 Morten Grud Rasmussen 6. november, 2013 1 Interpolation [Bogens afsnit 19.3 side 805] 1.1 Interpolationspolynomier Enhver kontinuert funktion f på
Besvarelser til Calculus Ordinær Eksamen Juni 2019
 Besvarelser til Calculus Ordinær Eksamen - 14. Juni 2019 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 14. Juni 2019 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Matematisk modellering og numeriske metoder. Lektion 17
 Matematisk modellering og numeriske metoder Lektion 1 Morten Grud Rasmussen. december 16 1 Numerisk integration og differentiation 1.1 Simpsons regel Antag, at vi har en funktion f på intervallet I = [a,
Matematisk modellering og numeriske metoder Lektion 1 Morten Grud Rasmussen. december 16 1 Numerisk integration og differentiation 1.1 Simpsons regel Antag, at vi har en funktion f på intervallet I = [a,
Besvarelser til Calculus Ordinær Eksamen - 3. Januar 2017
 Besvarelser til Calculus Ordinær Eksamen - 3. Januar 17 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 3. Januar 17 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
A. Appendix: Løse ender.
 Løse ender A.1 A. Appendix: Løse ender. (A.1). I dette appendix giver vi et bevis for Bertrand s Postulat, nævnt i Kapitel 1. Som nævnt følger Postulatet af en tilstræelig nøjagtig vurdering af primtalsfuntionen
Løse ender A.1 A. Appendix: Løse ender. (A.1). I dette appendix giver vi et bevis for Bertrand s Postulat, nævnt i Kapitel 1. Som nævnt følger Postulatet af en tilstræelig nøjagtig vurdering af primtalsfuntionen
Noter til Computerstøttet Beregning Taylors formel
 Noter til Computerstøttet Beregning Taylors formel Arne Jensen c 23 1 Introduktion I disse noter formulerer og beviser vi Taylors formel. Den spiller en vigtig rolle ved teoretiske overvejelser, og også
Noter til Computerstøttet Beregning Taylors formel Arne Jensen c 23 1 Introduktion I disse noter formulerer og beviser vi Taylors formel. Den spiller en vigtig rolle ved teoretiske overvejelser, og også
Introduktion til Laplace transformen (Noter skrevet af Nikolaj Hess-Nielsen sidst revideret marts 2013)
 Introduktion til Laplace transformen (oter skrevet af ikolaj Hess-ielsen sidst revideret marts 23) Integration handler ikke kun om arealer. Tværtimod er integration basis for mange af de vigtigste værktøjer
Introduktion til Laplace transformen (oter skrevet af ikolaj Hess-ielsen sidst revideret marts 23) Integration handler ikke kun om arealer. Tværtimod er integration basis for mange af de vigtigste værktøjer
Billeder af Julia-mængder
 1 Billeder af Julia-mængder af Gert Buschmann Vi identificerer planen med de komplekse tal og lader f(z) være en afbildning af planen på sig selv som er defineret og kontinuert-differentiabel næsten overalt.
1 Billeder af Julia-mængder af Gert Buschmann Vi identificerer planen med de komplekse tal og lader f(z) være en afbildning af planen på sig selv som er defineret og kontinuert-differentiabel næsten overalt.
Komplekse tal og rækker
 Komplekse tal og rækker John Olsen 1 Indledning Dette sæt noter er forelæsningsnoter til foredraget Komplekse tal og rækker. Noterne er beregnet til at blive brugt sammen med foredraget. I afsnit 2 bliver
Komplekse tal og rækker John Olsen 1 Indledning Dette sæt noter er forelæsningsnoter til foredraget Komplekse tal og rækker. Noterne er beregnet til at blive brugt sammen med foredraget. I afsnit 2 bliver
Momenter som deskriptive størrelser. Hvad vi mangler fra onsdag. Momenter for sandsynlighedsmål
 Hvad vi mangler fra onsdag Momenter som deskriptive størrelser Sandsynlighedsmål er komplicerede objekter de tildeler numeriske værdier til alle hændelser i en σ-algebra. Vi har behov for simplere, deskriptive
Hvad vi mangler fra onsdag Momenter som deskriptive størrelser Sandsynlighedsmål er komplicerede objekter de tildeler numeriske værdier til alle hændelser i en σ-algebra. Vi har behov for simplere, deskriptive
Hvad vi mangler fra onsdag. Vi starter med at gennemgå slides fra onsdag.
 Hvad vi mangler fra onsdag Vi starter med at gennemgå slides 34-38 fra onsdag. Slide 1/17 Niels Richard Hansen MI forelæsninger 6. December, 2013 Momenter som deskriptive størrelser Sandsynlighedsmål er
Hvad vi mangler fra onsdag Vi starter med at gennemgå slides 34-38 fra onsdag. Slide 1/17 Niels Richard Hansen MI forelæsninger 6. December, 2013 Momenter som deskriptive størrelser Sandsynlighedsmål er
Newton-Raphsons metode
 Newton-Raphsons metode af John V. Petersen Indhold Indledning: Numerisk analyse og Newton-Raphsons metode... 2 Udlede Newtons iterations formel... 2 Sætning 1 Newtons metode... 4 Eksempel 1 konvergens...
Newton-Raphsons metode af John V. Petersen Indhold Indledning: Numerisk analyse og Newton-Raphsons metode... 2 Udlede Newtons iterations formel... 2 Sætning 1 Newtons metode... 4 Eksempel 1 konvergens...
NATURVIDENSKABELIG KANDIDATEKSAMEN VED KØBENHAVNS UNIVERSITET. MI 2007 Obligatorisk opgave 4
 NATURVIDENSKABELIG KANDIDATEKSAMEN VED KØBENHAVNS UNIVERSITET. MI 2007 Obligatorisk opgave 4 Sættet består af 3 opgaver med ialt 15 delopgaver. Besvarelsen vil blive forkastet, medmindre der er gjort et
NATURVIDENSKABELIG KANDIDATEKSAMEN VED KØBENHAVNS UNIVERSITET. MI 2007 Obligatorisk opgave 4 Sættet består af 3 opgaver med ialt 15 delopgaver. Besvarelsen vil blive forkastet, medmindre der er gjort et
Reeksamen 2014/2015 Mål- og integralteori
 Reeksamen 4/5 Mål- og integralteori Københavns Universitet Institut for Matematiske Fag Formalia Eksamensopgaven består af 4 opgaver med ialt spørgsmål. Ved bedømmelsen indgår de spørgsmål med samme vægt.
Reeksamen 4/5 Mål- og integralteori Københavns Universitet Institut for Matematiske Fag Formalia Eksamensopgaven består af 4 opgaver med ialt spørgsmål. Ved bedømmelsen indgår de spørgsmål med samme vægt.
Gamle eksamensopgaver (MASO)
 EO 1 Gamle eksamensopgaver (MASO) Opgave 1. (Vinteren 1990 91, opgave 1) a) Vis, at rækken er divergent. b) Vis, at rækken er konvergent. Opgave 2. (Vinteren 1990 91, opgave 2) Gør rede for at ligningssystemet
EO 1 Gamle eksamensopgaver (MASO) Opgave 1. (Vinteren 1990 91, opgave 1) a) Vis, at rækken er divergent. b) Vis, at rækken er konvergent. Opgave 2. (Vinteren 1990 91, opgave 2) Gør rede for at ligningssystemet
Besvarelse, Eksamen Analyse 1, 2013
 Københavns Universitet Prøve ved Det naturvidenskabelige Fakultet juni 23 Besvarelse, Eksamen Analyse, 23 Opgave Lad, for n N, funktionen f n : [, ) R være givet ved NB. Trykfejl. Burde være x. f n (x)
Københavns Universitet Prøve ved Det naturvidenskabelige Fakultet juni 23 Besvarelse, Eksamen Analyse, 23 Opgave Lad, for n N, funktionen f n : [, ) R være givet ved NB. Trykfejl. Burde være x. f n (x)
Polynomier. Indhold. Georg Mohr-Konkurrencen. 1 Polynomier 2. 2 Polynomiumsdivision 4. 3 Algebraens fundamentalsætning og rødder 6
 Indhold 1 Polynomier 2 Polynomier 2 Polynomiumsdivision 4 3 Algebraens fundamentalsætning og rødder 6 4 Koefficienter 8 5 Polynomier med heltallige koefficienter 9 6 Mere om polynomier med heltallige koefficienter
Indhold 1 Polynomier 2 Polynomier 2 Polynomiumsdivision 4 3 Algebraens fundamentalsætning og rødder 6 4 Koefficienter 8 5 Polynomier med heltallige koefficienter 9 6 Mere om polynomier med heltallige koefficienter
10. Differentialregning
 10. Differentialregning Hayati Balo,AAMS Følgende fremstilling er baseret på 1. Nils Victor-Jensen, Matematik for adgangskursus, B-niveau 2, 2. udg. 10.1 Grænseværdibegrebet I afsnit 7. Funktioner på side
10. Differentialregning Hayati Balo,AAMS Følgende fremstilling er baseret på 1. Nils Victor-Jensen, Matematik for adgangskursus, B-niveau 2, 2. udg. 10.1 Grænseværdibegrebet I afsnit 7. Funktioner på side
3. Differentialregning
 3. Differentialregning 3.1. Differentiabilitet Lad os for en lille stund se lidt på det velkendte, klassiske tangentbegreb, som allerede var kendt i antikkens græske geometri. Tangenter var kun knyttet
3. Differentialregning 3.1. Differentiabilitet Lad os for en lille stund se lidt på det velkendte, klassiske tangentbegreb, som allerede var kendt i antikkens græske geometri. Tangenter var kun knyttet
Komplekse tal og algebraens fundamentalsætning.
 Komplekse tal og algebraens fundamentalsætning. Michael Knudsen 10. oktober 2005 1 Ligningsløsning Lad N = {0,1,2,...} betegne mængden af de naturlige tal og betragt ligningen ax + b = 0, a,b N,a 0. Findes
Komplekse tal og algebraens fundamentalsætning. Michael Knudsen 10. oktober 2005 1 Ligningsløsning Lad N = {0,1,2,...} betegne mængden af de naturlige tal og betragt ligningen ax + b = 0, a,b N,a 0. Findes
Integration m.h.t. mål med tæthed
 Integration m.h.t. mål med tæthed Sætning (EH 11.7) Lad ν = f µ på (X, E). For alle g M + (X, E) gælder at gdν = g f dµ. Bevis: Standardbeviset: 1) indikatorfunktioner 2) simple funktioner 3) M + -funktioner.
Integration m.h.t. mål med tæthed Sætning (EH 11.7) Lad ν = f µ på (X, E). For alle g M + (X, E) gælder at gdν = g f dµ. Bevis: Standardbeviset: 1) indikatorfunktioner 2) simple funktioner 3) M + -funktioner.
t x 1 e t dt. Man kan let vise, at dette integral er endeligt for positive x- værdier (se f.eks. [EA, s ]).
![t x 1 e t dt. Man kan let vise, at dette integral er endeligt for positive x- værdier (se f.eks. [EA, s ]). t x 1 e t dt. Man kan let vise, at dette integral er endeligt for positive x- værdier (se f.eks. [EA, s ]).](/thumbs/56/38252371.jpg) Artikel 35 Gammafunktionen En introduktion Jacob Stevne Jørgensen I 1700-tallet var interolation en vigtig discilin blandt matematikere. Det handler om ud fra et givet datasæt at finde en funktion, hvis
Artikel 35 Gammafunktionen En introduktion Jacob Stevne Jørgensen I 1700-tallet var interolation en vigtig discilin blandt matematikere. Det handler om ud fra et givet datasæt at finde en funktion, hvis
Matematik F2 Opgavesæt 6
 Opgave 4: Udtryk funktionen f(θ) = sin θ ved hjælp af Legendre-polynomierne på formen P l (cos θ). Dvs. find koefficienterne a l i ekspansionen f(θ) = a l P l (cos θ) l= Svar: Bemærk, at funktionen er
Opgave 4: Udtryk funktionen f(θ) = sin θ ved hjælp af Legendre-polynomierne på formen P l (cos θ). Dvs. find koefficienterne a l i ekspansionen f(θ) = a l P l (cos θ) l= Svar: Bemærk, at funktionen er
Vektorfelter langs kurver
 enote 25 1 enote 25 Vektorfelter langs kurver I enote 24 dyrkes de indledende overvejelser om vektorfelter. I denne enote vil vi se på vektorfelternes værdier langs kurver og benytte metoder fra enote
enote 25 1 enote 25 Vektorfelter langs kurver I enote 24 dyrkes de indledende overvejelser om vektorfelter. I denne enote vil vi se på vektorfelternes værdier langs kurver og benytte metoder fra enote
PeterSørensen.dk : Differentiation
 PeterSørensen.dk : Differentiation Betydningen af ordet differentialkvotient...2 Sekant...2 Differentiable funktioner...3 Bestemmelse af differentialkvotient i praksis ved opgaveløsning...3 Regneregler:...3
PeterSørensen.dk : Differentiation Betydningen af ordet differentialkvotient...2 Sekant...2 Differentiable funktioner...3 Bestemmelse af differentialkvotient i praksis ved opgaveløsning...3 Regneregler:...3
Differentialregning. Ib Michelsen
 Differentialregning Ib Michelsen Ikast 2012 Forsidebilledet Tredjegradspolynomium i blåt med rød tangent Version: 0.02 (18-09-12) Denne side er (~ 2) Indholdsfortegnelse Introduktion...5 Definition af
Differentialregning Ib Michelsen Ikast 2012 Forsidebilledet Tredjegradspolynomium i blåt med rød tangent Version: 0.02 (18-09-12) Denne side er (~ 2) Indholdsfortegnelse Introduktion...5 Definition af
Indledning. 1 Martingalerepræsentationssætningen
 Indledning I disse noter vil uddybe nogle af Øksendals resultater i afsnittene 4 og 7 samt give andre beviser for dem. Disse resultater er gennemgået til forelæsningerne. 1 Martingalerepræsentationssætningen
Indledning I disse noter vil uddybe nogle af Øksendals resultater i afsnittene 4 og 7 samt give andre beviser for dem. Disse resultater er gennemgået til forelæsningerne. 1 Martingalerepræsentationssætningen
DesignMat Den komplekse eksponentialfunktion og polynomier
 DesignMat Den komplekse eksponentialfunktion og polynomier Preben Alsholm Uge 8 Forår 010 1 Den komplekse eksponentialfunktion 1.1 Definitionen Definitionen Den velkendte eksponentialfunktion x e x vil
DesignMat Den komplekse eksponentialfunktion og polynomier Preben Alsholm Uge 8 Forår 010 1 Den komplekse eksponentialfunktion 1.1 Definitionen Definitionen Den velkendte eksponentialfunktion x e x vil
Gruppeteori. Michael Knudsen. 8. marts For at motivere indførelsen af gruppebegrebet begynder vi med et eksempel.
 Gruppeteori Michael Knudsen 8. marts 2005 1 Motivation For at motivere indførelsen af gruppebegrebet begynder vi med et eksempel. Eksempel 1.1. Lad Z betegne mængden af de hele tal, Z = {..., 2, 1, 0,
Gruppeteori Michael Knudsen 8. marts 2005 1 Motivation For at motivere indførelsen af gruppebegrebet begynder vi med et eksempel. Eksempel 1.1. Lad Z betegne mængden af de hele tal, Z = {..., 2, 1, 0,
Besvarelser til Calculus Ordinær eksamen - Efterår - 8. Januar 2016
 Besvarelser til Calculus Ordinær eksamen - Efterår - 8. Januar 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har
Besvarelser til Calculus Ordinær eksamen - Efterår - 8. Januar 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har
Eksamen i Mat F, april 2006
 Eksamen i Mat F, april 26 Opgave Lad F være et vektorfelt, givet i retvinklede koordinater som: Udregn F og F: F x F = F x i + F y j + F z k = F y = z 2 F z xz y 2 F = F x + F y + F z = + + x. F = F z
Eksamen i Mat F, april 26 Opgave Lad F være et vektorfelt, givet i retvinklede koordinater som: Udregn F og F: F x F = F x i + F y j + F z k = F y = z 2 F z xz y 2 F = F x + F y + F z = + + x. F = F z
Analytisk geometri. Et simpelt eksempel på dette er en ret linje. Som bekendt kan en ret linje skrives på formen
 Analtisk geometri Mike Auerbach Odense 2015 Den klassiske geometri beskæftiger sig med alle mulige former for figurer: Linjer, trekanter, cirkler, parabler, ellipser osv. I den analtiske geometri lægger
Analtisk geometri Mike Auerbach Odense 2015 Den klassiske geometri beskæftiger sig med alle mulige former for figurer: Linjer, trekanter, cirkler, parabler, ellipser osv. I den analtiske geometri lægger
