Taylorpolynomier og Taylors sætning
|
|
|
- Ludvig Bagge
- 7 år siden
- Visninger:
Transkript
1 og Taylors sætning 10. november 2008
2 I Givet en funktion f og et udviklingspunkt x 0. Find et polynomium P n af grad højst n, så f og P n har samme nulte, første, anden, tredie,..., n te a edede i punktet x 0.
3 I Givet en funktion f og et udviklingspunkt x 0. Find et polynomium P n af grad højst n, så f og P n har samme nulte, første, anden, tredie,..., n te a edede i punktet x 0. I P n skal så opfylde ligningerne P n (x 0 ) = f (x 0 ) Pn 0 (x 0 ) = f 0 (x 0 ) Pn 00 (x 0 ) = f 00 (x 0 ). P n (n) (x 0 ) = f (n) (x 0 )
4 I Givet en funktion f og et udviklingspunkt x 0. Find et polynomium P n af grad højst n, så f og P n har samme nulte, første, anden, tredie,..., n te a edede i punktet x 0. I P n skal så opfylde ligningerne I Skriver vi P n på formen P n (x 0 ) = f (x 0 ) Pn 0 (x 0 ) = f 0 (x 0 ) Pn 00 (x 0 ) = f 00 (x 0 ). P n (n) (x 0 ) = f (n) (x 0 ) P n (x) = a 0 + a 1 (x x 0 ) + a 2 (x x 0 ) 2 + a 3 (x x 0 ) 3 +a 4 (x x 0 ) a n (x x 0 ) n søger vi nu a 0, a 1, a 2,..., a n.
5 I Vi ser med det samme, at a 0 = f (x 0 ). Da Pn 0 (x) = a 1 + 2a 2 (x x 0 ) + 3a 3 (x x 0 ) 2 +4a 4 (x x 0 ) na n (x x 0 ) n 1
6 I Vi ser med det samme, at a 0 = f (x 0 ). Da P 0 n (x) = a 1 + 2a 2 (x x 0 ) + 3a 3 (x x 0 ) 2 I fås, at a 1 = f 0 (x 0 ). Da +4a 4 (x x 0 ) na n (x x 0 ) n 1 P 00 n (x) = 2a a 3 (x x 0 ) a 4 (x x 0 ) n (n 1) a n (x x 0 ) n 2
7 I Vi ser med det samme, at a 0 = f (x 0 ). Da P 0 n (x) = a 1 + 2a 2 (x x 0 ) + 3a 3 (x x 0 ) 2 I fås, at a 1 = f 0 (x 0 ). Da +4a 4 (x x 0 ) na n (x x 0 ) n 1 P 00 n (x) = 2a a 3 (x x 0 ) a 4 (x x 0 ) n (n 1) a n (x x 0 ) n 2 I fås a 2 = 1 2 f 00 (x 0 ). Da P 000 n (x) = 3 2 a a 4 (x x 0 ) n (n 1) (n 2) a n (x x 0 ) n 3 fås, at a 3 = 1 23 f 000 (x 0 ).
8 Formlen I Generelt fås altså således at a k = 1 k! f (k) (x 0 ) P n (x) = f (x 0 ) + f 0 (x 0 ) (x x 0 ) f 00 (x 0 ) (x x 0 ) ! f 000 (x 0 ) (x x 0 ) n! f (n) (x 0 ) (x x 0 ) n
9 Formlen I Generelt fås altså således at a k = 1 k! f (k) (x 0 ) P n (x) = f (x 0 ) + f 0 (x 0 ) (x x 0 ) f 00 (x 0 ) (x x 0 ) ! f 000 (x 0 ) (x x 0 ) n! f (n) (x 0 ) (x x 0 ) n I Dette kan også skrives P n (x) = n k=0 1 k! f (k) (x 0 ) (x x 0 ) k idet vi de nerer 0! = 1 og f (0) = f.
10 I f (x) = e x med udviklingspunkt 0, orden n. Vi har jo f 0 (x) = f 00 (x) = f 000 (x) =... = f (n) (x) = e x.
11 I f (x) = e x med udviklingspunkt 0, orden n. Vi har jo f 0 (x) = f 00 (x) = f 000 (x) =... = f (n) (x) = e x. I Så f (k) (0) = e 0 = 1 for alle k 0.
12 I f (x) = e x med udviklingspunkt 0, orden n. Vi har jo f 0 (x) = f 00 (x) = f 000 (x) =... = f (n) (x) = e x. I Så f (k) (0) = e 0 = 1 for alle k 0. I Hermed fås P n (x) = f (0) + f 0 (0) x f 00 (0) x ! f 000 (0) x n! f (n) (0) x n
13 I f (x) = e x med udviklingspunkt 0, orden n. Vi har jo f 0 (x) = f 00 (x) = f 000 (x) =... = f (n) (x) = e x. I Så f (k) (0) = e 0 = 1 for alle k 0. I Hermed fås P n (x) = f (0) + f 0 (0) x f 00 (0) x ! f 000 (0) x 3 I Altså n! f (n) (0) x n P n (x) = 1 + x x ! x n! x n
14 I f (x) = e x med udviklingspunkt 0, orden n. Vi har jo f 0 (x) = f 00 (x) = f 000 (x) =... = f (n) (x) = e x. I Så f (k) (0) = e 0 = 1 for alle k 0. I Hermed fås P n (x) = f (0) + f 0 (0) x f 00 (0) x ! f 000 (0) x 3 I Altså n! f (n) (0) x n P n (x) = 1 + x x ! x n! x n I Dette kan også skrives P n (x) = n k=0 1 k! x k
15 I f (x) = x arctan x med udviklingspunkt 1, orden 2.
16 I f (x) = x arctan x med udviklingspunkt 1, orden 2. I Vi har f 0 (x) = arctan x + x 1 + x 2 f x (x) = x 2 (1 + x 2 ) 2
17 I f (x) = x arctan x med udviklingspunkt 1, orden 2. I Vi har f 0 (x) = arctan x + x 1 + x 2 f x (x) = x 2 (1 + x 2 ) 2 I Så f (1) = π 4, f 0 (1) = π , f 00 (1) = 1 2.
18 I f (x) = x arctan x med udviklingspunkt 1, orden 2. I Vi har f 0 (x) = arctan x + x 1 + x 2 f x (x) = x 2 (1 + x 2 ) 2 I Så f (1) = π 4, f 0 (1) = π , f 00 (1) = 1 2. I Hermed fås P 2 (x) = f (1) + f 0 (1) (x 1) f 00 (1) (x 1) 2 = π π (x 1) (x 1)2 2 = π π (x 1) + 1 (x 1)2 2 4
19 I f (x) = x arctan x med udviklingspunkt 1, orden 2. I Vi har f 0 (x) = arctan x + x 1 + x 2 f x (x) = x 2 (1 + x 2 ) 2 I Så f (1) = π 4, f 0 (1) = π , f 00 (1) = 1 2. I Hermed fås P 2 (x) = f (1) + f 0 (1) (x 1) f 00 (1) (x 1) 2 = π π (x 1) (x 1)2 2 = π π (x 1) + 1 (x 1)2 2 4 I Maple
20 I Find det 2. med udviklingspunkt 0 for løsningen til en x 0 (t) = t + sin (x (t)) med x (0) = π 2
21 I Find det 2. med udviklingspunkt 0 for løsningen til en x 0 (t) = t + sin (x (t)) med x (0) = π 2 I Vi skal nde P 2 (t) = x (0) + x 0 (0) t x 00 (0) t 2.
22 I Find det 2. med udviklingspunkt 0 for løsningen til en x 0 (t) = t + sin (x (t)) med x (0) = π 2 I Vi skal nde P 2 (t) = x (0) + x 0 (0) t x 00 (0) t 2. I Ved indsættelse af t = 0 i en fås x 0 (0) = 0 + sin (x (0)) = sin π 2 = 1.
23 I Find det 2. med udviklingspunkt 0 for løsningen til en x 0 (t) = t + sin (x (t)) med x (0) = π 2 I Vi skal nde P 2 (t) = x (0) + x 0 (0) t x 00 (0) t 2. I Ved indsættelse af t = 0 i en fås x 0 (0) = 0 + sin (x (0)) = sin π 2 = 1. I Ved di erentiation af en fås x 00 (t) = 1 + cos (x (t)) x 0 (t).
24 I Find det 2. med udviklingspunkt 0 for løsningen til en x 0 (t) = t + sin (x (t)) med x (0) = π 2 I Vi skal nde P 2 (t) = x (0) + x 0 (0) t x 00 (0) t 2. I Ved indsættelse af t = 0 i en fås x 0 (0) = 0 + sin (x (0)) = sin π 2 = 1. I Ved di erentiation af en fås x 00 (t) = 1 + cos (x (t)) x 0 (t). I Ved indsættelse af t = 0 heri fås x 00 (0) = 1 + cos (x (0)) x 0 (0) = 1.
25 I Find det 2. med udviklingspunkt 0 for løsningen til en x 0 (t) = t + sin (x (t)) med x (0) = π 2 I Vi skal nde P 2 (t) = x (0) + x 0 (0) t x 00 (0) t 2. I Ved indsættelse af t = 0 i en fås x 0 (0) = 0 + sin (x (0)) = sin π 2 = 1. I Ved di erentiation af en fås x 00 (t) = 1 + cos (x (t)) x 0 (t). I Ved indsættelse af t = 0 heri fås x 00 (0) = 1 + cos (x (0)) x 0 (0) = 1. I Altså fås P 2 (t) = π 2 + t t = π 2 + t t2.
26 I Find det 2. med udviklingspunkt 0 for løsningen til en x 0 (t) = t + sin (x (t)) med x (0) = π 2 I Vi skal nde P 2 (t) = x (0) + x 0 (0) t x 00 (0) t 2. I Ved indsættelse af t = 0 i en fås x 0 (0) = 0 + sin (x (0)) = sin π 2 = 1. I Ved di erentiation af en fås x 00 (t) = 1 + cos (x (t)) x 0 (t). I Ved indsættelse af t = 0 heri fås x 00 (0) = 1 + cos (x (0)) x 0 (0) = 1. I Altså fås P 2 (t) = π 2 + t t = π 2 + t t2. I Se også Maple.
27 I Hvad er den fejl man begår ved at erstatte en funktion f med dens P n?
28 I Hvad er den fejl man begår ved at erstatte en funktion f med dens P n? I Taylors formel: For givet x ndes et tal ξ mellem x 0 og x, så f (x) = f (x 0 ) + f 0 (x 0 ) (x x 0 ) f 00 (x 0 ) (x x 0 ) n! f (n) (x 0 ) (x x 0 ) n + 1 (n + 1)! f (n+1) (ξ) (x x 0 ) n+1
29 I Hvad er den fejl man begår ved at erstatte en funktion f med dens P n? I Taylors formel: For givet x ndes et tal ξ mellem x 0 og x, så f (x) = f (x 0 ) + f 0 (x 0 ) (x x 0 ) f 00 (x 0 ) (x x 0 ) n! f (n) (x 0 ) (x x 0 ) n + 1 (n + 1)! f (n+1) (ξ) (x x 0 ) n+1 I Altså f (x) = P n (x) + 1 (n+1)! f (n+1) (ξ) (x x 0 ) n+1 = P n (x) + R n (x).
30 I Hvad er den fejl man begår ved at erstatte en funktion f med dens P n? I Taylors formel: For givet x ndes et tal ξ mellem x 0 og x, så f (x) = f (x 0 ) + f 0 (x 0 ) (x x 0 ) f 00 (x 0 ) (x x 0 ) n! f (n) (x 0 ) (x x 0 ) n + 1 (n + 1)! f (n+1) (ξ) (x x 0 ) n+1 I Altså f (x) = P n (x) + 1 (n+1)! f (n+1) (ξ) (x x 0 ) n+1 = P n (x) + R n (x). I Beviset bruger en udvidet udgave af middelværdisætningen.
31 I. f (x) = e x, udviklingspunkt 0. Vi har P n (x) = 1 + x x ! x n! x n.
32 I. f (x) = e x, udviklingspunkt 0. Vi har P n (x) = 1 + x x ! x n! x n. I f (n+1) (x) = e x. Så je x P n (x)j = 1 (n + 1)! eξ x n+1 = e ξ (n + 1)! jxjn+1
33 I. f (x) = e x, udviklingspunkt 0. Vi har P n (x) = 1 + x x ! x n! x n. I f (n+1) (x) = e x. Så je x P n (x)j = 1 (n + 1)! eξ x n+1 = I Bestem n, så je x x 2 [ 0.1, 0.1]. P n (x)j 10 5 for alle e ξ (n + 1)! jxjn+1
34 I. f (x) = e x, udviklingspunkt 0. Vi har P n (x) = 1 + x x ! x n! x n. I f (n+1) (x) = e x. Så je x P n (x)j = 1 (n + 1)! eξ x n+1 = I Bestem n, så je x x 2 [ 0.1, 0.1]. P n (x)j 10 5 for alle e ξ (n + 1)! jxjn+1 I I Taylors formel gælder så jξj 0.1 og dermed je x P n (x)j = e ξ (n + 1)! jxjn+1 e0.1 (n + 1)! (0.1)n+1 2 (n + 1)! (0.1)n+1
35 I. f (x) = e x, udviklingspunkt 0. Vi har P n (x) = 1 + x x ! x n! x n. I f (n+1) (x) = e x. Så je x P n (x)j = 1 (n + 1)! eξ x n+1 = I Bestem n, så je x x 2 [ 0.1, 0.1]. P n (x)j 10 5 for alle e ξ (n + 1)! jxjn+1 I I Taylors formel gælder så jξj 0.1 og dermed je x P n (x)j = e ξ (n + 1)! jxjn+1 e0.1 (n + 1)! (0.1)n+1 2 (n + 1)! (0.1)n+1 I Vi vælger nu n, så 2 (n+1)! (0.1)n n = 3 er nok, idet 2 4! 10 4 = < 10 5.
36 I Lad f (x) for alle x være givet ved f (x) = Z x 0 (1 + t) cos t 3 dt
37 I Lad f (x) for alle x være givet ved f (x) = Z x 0 (1 + t) cos t 3 dt I Vurdér den fejl, der begås ved at erstatte f (x) med dets 2. P 2 (x) med udviklingspunkt 0, når x 2 1 2, 1 2.
38 I Lad f (x) for alle x være givet ved f (x) = Z x 0 (1 + t) cos t 3 dt I Vurdér den fejl, der begås ved at erstatte f (x) med dets 2. P 2 (x) med udviklingspunkt 0, når x 2 1 2, 1 2. I Vi nder f 0 (x) = (1 + x) cos x 3 f 00 (x) = cos x 3 (1 + x) 3x 2 sin x 3 f 000 (x) = 6x (1 + 2x) sin x 3 9x 4 (1 + x) cos x 3
39 I Lad f (x) for alle x være givet ved f (x) = Z x 0 (1 + t) cos t 3 dt I Vurdér den fejl, der begås ved at erstatte f (x) med dets 2. P 2 (x) med udviklingspunkt 0, når x 2 1 2, 1 2. I Vi nder f 0 (x) = (1 + x) cos x 3 f 00 (x) = cos x 3 (1 + x) 3x 2 sin x 3 f 000 (x) = 6x (1 + 2x) sin x 3 9x 4 (1 + x) cos x 3 I Heraf ndes P 2 (x) = x x 2.
40 I Lad f (x) for alle x være givet ved f (x) = Z x 0 (1 + t) cos t 3 dt I Vurdér den fejl, der begås ved at erstatte f (x) med dets 2. P 2 (x) med udviklingspunkt 0, når x 2 1 2, 1 2. I Vi nder f 0 (x) = (1 + x) cos x 3 f 00 (x) = cos x 3 (1 + x) 3x 2 sin x 3 f 000 (x) = 6x (1 + 2x) sin x 3 9x 4 (1 + x) cos x 3 I Heraf ndes P 2 (x) = x x 2. I Vha. Maple ndes, at jf 000 (x)j 1.59 for x 2 1 2, 1 2. Altså fås jf (x) P 2 (x)j jxj ' Den faktiske maksimale fejl kan ndes gra sk til
41 I Når Maplekommandoen taylor(sin(x),x=0,4); som resultat giver x 1 6 x 3 + O x 4, betyder der følgende:
42 I Når Maplekommandoen taylor(sin(x),x=0,4); som 1 resultat giver x 6 x 3 + O x 4, betyder der følgende: I Der ndes en konstant K, så x sin x 1 6 x 3 Kx 4 for alle x i et interval med 0 som indre punkt.
43 I Når Maplekommandoen taylor(sin(x),x=0,4); som 1 resultat giver x 6 x 3 + O x 4, betyder der følgende: I Der ndes en konstant K, så x sin x 1 6 x 3 Kx 4 for alle x i et interval med 0 som indre punkt. I Generelt betyder f (x) = O (u (x)) for x! a, at der ndes en konstant K, så jf (x)j K ju (x)j for alle x i et interval med a som indre punkt.
44 I Når Maplekommandoen taylor(sin(x),x=0,4); som 1 resultat giver x 6 x 3 + O x 4, betyder der følgende: I Der ndes en konstant K, så x sin x 1 6 x 3 Kx 4 for alle x i et interval med 0 som indre punkt. I Generelt betyder f (x) = O (u (x)) for x! a, at der ndes en konstant K, så jf (x)j K ju (x)j for alle x i et interval med a som indre punkt. I Vi har eksempelvis: sin x = O (x), sin x = x + O x 2, men også sin x = x + O x 3 og den allerede viste.
45 I Når Maplekommandoen taylor(sin(x),x=0,4); som 1 resultat giver x 6 x 3 + O x 4, betyder der følgende: I Der ndes en konstant K, så x sin x 1 6 x 3 Kx 4 for alle x i et interval med 0 som indre punkt. I Generelt betyder f (x) = O (u (x)) for x! a, at der ndes en konstant K, så jf (x)j K ju (x)j for alle x i et interval med a som indre punkt. I Vi har eksempelvis: sin x = O (x), sin x = x + O x 2, men også sin x = x + O x 3 og den allerede viste. I I Taylor-sammenhæng kan O ((x x 0 ) n ) tolkes som led af orden n og højere.
Taylorpolynomier. Preben Alsholm. 17. april 2008. Taylorpolynomier. Funktion af ere variable. Preben Alsholm. Taylorpolynomier
. 17. april 008 for I Givet en funktion f og et udviklingspunkt x 0. Find et polynomium P n af grad højst n, så f og P n har samme nulte, første, anden, tredie,..., n te a edede i punktet x 0.. for I Givet
Taylorudvikling I. 1 Taylorpolynomier. Preben Alsholm 3. november Definition af Taylorpolynomium
Taylorudvikling I Preben Alsholm 3. november 008 Taylorpolynomier. Definition af Taylorpolynomium Definition af Taylorpolynomium Givet en funktion f : I R! R og et udviklingspunkt x 0 I. Find et polynomium
DiploMat. Eksempel på 4-timersprøve.
DiloMat. Eksemel å 4-timersrøve. Preben lsholm Maj 4 Ogave Vi skal løse ligningen e i 4 z 3 i = Løsningen skal angives å olær form, dvs. å formen re i, hvor r > og R. Først nder vi e i 4 z = 3 Heraf fås
Noter om komplekse tal
Noter om komplekse tal Preben Alsholm Januar 008 1 Den komplekse eksponentialfunktion Vi erindrer først om den sædvanlige og velkendte reelle eksponentialfunktion. Vi skal undertiden nde det nyttigt, at
Eksempel på 2-timersprøve 2 Løsninger
Eksempel på -timersprøve Løsninger Preben lsholm Februar 4 Opgave Maplekommandoerne expand( (z-*exp(i*pi/))*(z-*exp(-i*pi/))*(z-exp(i*pi/))*(z-exp(-i*pi/))): sort(%); resulterer i polynomiet z 4 z + z
Taylors formel. Kapitel Klassiske sætninger i en dimension
Kapitel 3 Taylors formel 3.1 Klassiske sætninger i en dimension Sætning 3.1 (Rolles sætning) Lad f : [a, b] R være kontinuert, og antag at f er differentiabel i det åbne interval (a, b). Hvis f (a) = f
Lokalt ekstremum DiploMat 01905
Lokalt ekstremum DiploMat 0905 Preben Alsholm Institut for Matematik, DTU 6. oktober 00 De nition Et stationært punkt for en funktion af ere variable f vil i disse noter blive kaldt et egentligt saddelpunkt,
OPGAVER 1. Approksimerende polynomier. Håndregning
OPGAVER 1 Opgaver til Uge 4 Store Dag Opgave 1 Approksimerende polynomier. Håndregning a) Find for hver af de følgende funktioner deres approksimerende polynomiumer af første og anden grad med udviklingspunkt
Noter til Computerstøttet Beregning Taylors formel
Noter til Computerstøttet Beregning Taylors formel Arne Jensen c 23 1 Introduktion I disse noter formulerer og beviser vi Taylors formel. Den spiller en vigtig rolle ved teoretiske overvejelser, og også
Besvarelser til Calculus Ordinær Eksamen Juni 2018
Besvarelser til Calculus Ordinær Eksamen - 5. Juni 08 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
DesignMat Den komplekse eksponentialfunktion og polynomier
DesignMat Den komplekse eksponentialfunktion og polynomier Preben Alsholm Uge 8 Forår 010 1 Den komplekse eksponentialfunktion 1.1 Definitionen Definitionen Den velkendte eksponentialfunktion x e x vil
Besvarelser til Calculus Ordinær Eksamen Juni 2019
Besvarelser til Calculus Ordinær Eksamen - 14. Juni 2019 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Mat 1. 2-timersprøve den 17. maj 2016.
Mat -timersprøve den 7 maj 6 JE 6 Opgave restart; Givet funktionen f:=x-sqrt(*x-); Spørgsmål f := x/ x K Funktionen er defineret for x K R x R Dvs Dm f er intervallet [ ;N[ Spørgsmål Med udviklingspunktet
Taylor s approksimationsformler for funktioner af én variabel
enote 4 1 enote 4 Taylor s approksimationsformler for funktioner af én variabel I enote 19 og enote 21 er det vist hvordan funktioner af én og to variable kan approksimeres med førstegradspolynomier i
Taylor s approksimationsformler for funktioner af én variabel
enote 17 1 enote 17 Taylor s approksimationsformler for funktioner af én variabel I enote 14 og enote 16 er det vist hvordan funktioner af én og to variable kan approksimeres med førstegradspolynomier
Besvarelser til Calculus Ordinær Eksamen - 5. Januar 2018
Besvarelser til Calculus Ordinær Eksamen - 5. Januar 18 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Vejledende besvarelse på august 2009-sættet 2. december 2009
Vejledende besvarelse på august 29-sættet 2. december 29 Det følgende er en vejledende besvarelse på eksamenssættet i kurset Calculus, som det så ud i august 29. Den tjener primært til illustration af,
Funktionsundersøgelse. Rasmus Sylvester Bryder
Funktionsundersøgelse Rasmus Sylvester Bryder 7. november 2008 Dette projekt aeveres i forbindelse med LA T EX 2ε-kurset vejledningsuge 2, 2008-09 på KU; til projektet benyttes noter givet til opgaveløsning.
DesignMat Uge 5 Systemer af lineære differentialligninger II
DesignMat Uge 5 Systemer af lineære differentialligninger II Preben Alsholm Efterår 21 1 Lineære differentialligningssystemer 11 Lineært differentialligningssystem af første orden Lineært differentialligningssystem
Besvarelser til Calculus Ordinær eksamen - Efterår - 8. Januar 2016
Besvarelser til Calculus Ordinær eksamen - Efterår - 8. Januar 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har
Besvarelser til Calculus Ordinær Eksamen - 3. Januar 2017
Besvarelser til Calculus Ordinær Eksamen - 3. Januar 17 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Differentialkvotient af cosinus og sinus
Differentialkvotient af cosinus og sinus Overgangsformler cos( + p ) = cos sin( + p ) = sin cos( -) = cos sin( -) = -sin cos( p - ) = - cos sin( p - ) = sin cos( p + ) = -cos sin( p + ) = -sin (bevises
Det teknisk-naturvidenskabelige basisår Matematik 1A, Efterår 2005, Hold 3 Prøveopgave A
Det teknisk-naturvidenskabelige basisår Matematik 1A, Efterår 2005, Hold 3 Prøveopgave A Opgaven består af tre dele, hver med en række spørgsmål, efterfulgt af en liste af teorispørgsmål. I alle opgavespørgsmålene
DesignMat Uge 1 Gensyn med forårets stof
DesignMat Uge 1 Gensyn med forårets stof Preben Alsholm Efterår 2010 1 Hovedpunkter fra forårets pensum 11 Taylorpolynomium Taylorpolynomium Det n te Taylorpolynomium for f med udviklingspunkt x 0 : P
Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 2016
Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Notesæt - Eksempler på polær integration
Notesæt - Eksempler på polær integration Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument forsøger blot at forklare,
DiploMat Løsninger til 4-timersprøven 4/6 2004
DiploMa Løsninger il -imersprøven / Preben Alsholm / Opgave Polynomie p er give ved p (z) = z 8 z + z + z 8z + De oplyses, a polynomie også kan skrives således p (z) = z + z z + Vi skal nde polynomies
Komplekse tal. Preben Alsholm Juli 2006
Komplekse tal Preben Alsholm Juli 006 Talmængder og regneregler for tal. Talmængder Indenfor matematikken optræder der forskellige klasser af tal: Naturlige tal. N er mængden af naturlige tal, ; ; 3; 4;
Eksempel på 2-timersprøve 1 Løsninger
Eksempel på -timersprøve Løsninger Preben lsholm Marts 4 Opgave Vi skal løse ligningen () z (8 + i) e i 6 = Løsningen ønskes angivet på rektangulær form, dvs. på formen x + iy, hvor x; y R. Vi nder umiddelbart
Oversigt [S] 8.7, 8.8, 8.9
![Oversigt [S] 8.7, 8.8, 8.9](/thumbs/63/48531538.jpg "Oversigt [S] 8.7, 8.8, 8.9")
Oversigt [S] 8.7, 8.8, 8.9 Nøgleord og begreber Binomialformlen Binomialkoefficienter Binomialrækken Taylor polynomier Vurdering af Taylor s restled Eksponentialrækken konvereger mod eksponentialfunktionen
DesignMat Lineære differentialligninger I
DesignMat Lineære differentialligninger I Preben Alsholm Uge 9 Forår 2010 1 Lineære differentialligninger af første orden 1.1 Normeret lineær differentialligning Normeret lineær differentialligning En
Preben Alsholm. 13. marts 2008
Arcus, I 13. marts 2008 I Funktionen f kaldes enentydig (1-1), hvis for alle x 1, x 2 : x 1 6= x 2 =) f (x 1 ) 6= f (x 2 ) Arcus, I I Funktionen f kaldes enentydig (1-1), hvis for alle x 1, x 2 : Arcus,
Partielle afledede og retningsafledede
Partielle afledede og retningsafledede 1 Partielle afledede, definitioner og notationer Bertragt en funktion af to reelle variable f : D R, hvor D R 2 er et åbent område Med benyttelse af tilvækstfunktionen
af koblede differentialligninger (se Apostol Bind II, s 229ff) 3. En n te ordens differentialligning
EKSISTENS- OG ENTYDIGHEDSSÆTNINGEN Vi vil nu bevise eksistens- og entydighedssætningen for ordinære differentialligninger. For overskuelighedens skyld vil vi indskrænke os til at undersøge een 1. ordens
Taylor-polynomier. John V Petersen
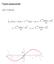Taylor-polynomier John V Petersen Taylor-polynomier 2018 John V Petersen art-science-soul Indhold 1. Indledning... 4 2. Udledning af Sætning om Taylor polynomiet... 4 3. Sætning og Definition af Taylor
MATEMATIK A-NIVEAU. Anders Jørgensen & Mark Kddafi. Vejledende eksempler på eksamensopgaver og eksamensopgaver i matematik, 2012.
MATEMATIK A-NIVEAU Vejledende eksempler på eksamensopgaver og eksamensopgaver i matematik, 2012 Kapitel 6 Differentialregning og modellering med f 2016 MATEMATIK A-NIVEAU Vejledende eksempler på eksamensopgaver
Heisenbergs usikkerhedsrelationer. Abstrakt. Hvorfor? Funktionsrum. Nils Byrial Andersen Institut for Matematik. Matematiklærerdag 2013
Heisenbergs usikkerhedsrelationer Nils Byrial Andersen Institut for Matematik Matematiklærerdag 013 1 / 17 Abstrakt Heisenbergs usikkerhedsrelationer udtrykker at man ikke på samme tid både kan bestemme
Oversigt [S] 8.7, 8.8, 8.9
![Oversigt [S] 8.7, 8.8, 8.9](/thumbs/62/47922248.jpg "Oversigt [S] 8.7, 8.8, 8.9")
Oversigt [S] 8.7, 8.8, 8.9 Nøgleord og begreber Potensrækker og opgaver Binomialformlen Binomialkoefficienter Binomialrækken Taylor polynomier Vurdering af Taylor s restled Eksponentialrækken konvereger
DesignMat Lineære differentialligninger I
DesignMat Lineære differentialligninger I Preben Alsholm Uge Forår 0 1 Lineære differentialligninger af første orden 1.1 Normeret lineær differentialligning Normeret lineær differentialligning En differentialligning,
Andengradspolynomier - Gymnasienoter
- Gymnasienoter http://findinge.com/ Tag forbehold for eventuelle fejl/typos. Indhold Forord 3 Toppunktsformlen - Bevismetode 1 4 Toppunktsformlen - Bevismetode 6 Andengradspolynomiets symmetri 7 Rodfaktorisering
MATEMATIK A-NIVEAU. Anders Jørgensen & Mark Kddafi. Vejledende eksempler på eksamensopgaver og eksamensopgaver i matematik, 2012
MATEMATIK A-NIVEAU Vejledende eksempler på eksamensopgaver og eksamensopgaver i matematik, 01 Kapitel 3 Ligninger & formler 016 MATEMATIK A-NIVEAU Vejledende eksempler på eksamensopgaver og eksamensopgaver
Besvarelser til Calculus Ordinær Eksamen Juni 2017
Besvarelser til Calculus Ordinær Eksamen - 12. Juni 2017 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Funktion af flere variable
Funktion af flere variable Preben Alsholm 6. oktober 2008 1 Funktion af flere variable 1.1 Punktmængder i R k : Definitioner Punktmængder i flerdimensionale rum: Definitioner q Normen af x 2 R k er kxk
Matematik A-niveau - bestemmelse af monotoniforhold (EKSEMPEL 1): Side 94 opgave 11:
Matematik A-niveau - bestemmelse af monotoniforhold (EKSEMPEL 1): Side 94 opgave 11: Opgave a) Ligningen for tangenten bestemmes. Dog defineres funktionen. Tangent-formlen er pr. definition. (1) Altså
Reeksamen i Calculus
Reeksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 0. februar 019 Dette eksamenssæt
Grafisk bestemmelse - fortsat Støttepunkter. Grafisk bestemmelse y. giver grafen. Niveaukurver og retning u = ( 1
Oversigt [S]. Nøgleord og begreber Retningsafledt Gradientvektor Gradient i flere variable Fortolkning af gradientvektoren Agst, opgave 5 Delvis afledt [S]. Directional derivatives and te... Definition
Analyse 1, Prøve 2 Besvarelse
Københavns Universitet Prøve ved Det naturvidenskabelige Fakultet maj Analyse, Prøve Besvarelse Opgave (3%) (a) (%) Bestem mængden af x R for hvilke rækken ( + (x) n ) er konvergent og angiv sumfunktionen
MM501 forelæsningsslides
MM501 forelæsningsslides uge 35-del 1, 2010 Redigeret af Jessica Carter efter udgave af Hans J. Munkholm 1 Nogle talmængder s. 4 N = {1,2,3, } omtales som de naturlige tal eller de positive heltal. Z =
Hvis man ønsker mere udfordring, kan man springe de første 7 opgaver over. Skitser det omdrejningslegeme, der fremkommer, når grafen for f ( x)
Integralregning 3 Hvis man ønsker mere udfordring, kan man springe de første 7 opgaver over. Opgave Skitser det omdrejningslegeme, der fremkommer, når grafen for f ( x) x i [,] drejes 36 om x-aksen. Vis,
Førsteordens lineære differentialligninger
enote 16 1 enote 16 Førsteordens lineære differentialligninger I denne enote gives først en kort introduktion til differentialligninger i almindelighed, hvorefter hovedemnet er en særlig type af differentialligninger,
VUC Vestsjælland Syd, Slagelse Nr. 1 Institution: Projekt Trigonometri
VUC Vestsjælland Syd, Slagelse Nr. 1 Institution: 333247 2015 Anders Jørgensen, Mark Kddafi, David Jensen, Kourosh Abady og Nikolaj Eriksen 1. Indledning I dette projekt, vil man kunne se definitioner
DesignMat Uge 8 Integration og elementære funktioner
DesignMat Uge 8 Integration og elementære funktioner Preben Alsholm Forår 008 Hyperbolske funktioner. sinh og cosh sinh og cosh Sinus hyperbolsk efineres sålees for alle x R sinh x = ex e x Cosinus hyperbolsk
Besvarelser til Calculus Reeksamen August 2017
Besvarelser til Calculus Reeksamen -. August 7 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende til opgave
Hvis man ønsker mere udfordring, kan man springe de første 7 opgaver over. Skitser det omdrejningslegeme, der fremkommer, når grafen for f ( x)
Integralregning 3 Hvis man ønsker mere udfordring, kan man springe de første 7 opgaver over. Opgave 1 1 Skitser det omdrejningslegeme, der fremkommer, når grafen for f ( x) x 1 i [ 1,] drejes 360 om x-aksen.
Matematik 1 Semesteruge 5 6 (1. oktober oktober 2001) side 1 Komplekse tal Arbejdsplan
Matematik 1 Semesteruge 5 6 (1. oktober - 12. oktober 2001) side 1 Komplekse tal Arbejdsplan I semesterugerne 5 og 6 erstattes den regulære undervisning (forelæsninger og fællestimer) af selvstudium med
Eksamen i Calculus. 14. juni f (x, y, z) = 1 + x 2 + y 2. x 2 + y 2 1 Hele rummet uden z aksen
Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 14. juni 019 Opgave 1 (6 point) En
Besvarelser til Calculus Ordinær Eksamen Juni 2017
Besvarelser til Calculus Ordinær Eksamen - 12. Juni 217 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Matematik A-niveau 22. maj 2015 Delprøve 2. Løst af Anders Jørgensen og Saeid Jafari
Matematik A-niveau 22. maj 2015 Delprøve 2 Løst af Anders Jørgensen og Saeid Jafari Opgave 7 - Analytisk Plangeometri Delopgave a) Vi starter ud med at undersøge afstanden fra punktet P(5,4) til linjen
Analytisk geometri. Et simpelt eksempel på dette er en ret linje. Som bekendt kan en ret linje skrives på formen
Analtisk geometri Mike Auerbach Odense 2015 Den klassiske geometri beskæftiger sig med alle mulige former for figurer: Linjer, trekanter, cirkler, parabler, ellipser osv. I den analtiske geometri lægger
Matematik 1 Semesteruge 5 6 (30. september oktober 2002) side 1. Komplekse tal Arbejdsplan
Matematik Semesteruge 5 6 (30. september -. oktober 2002) side Komplekse tal Arbejdsplan I semesterugerne 5 og 6 erstattes den regulære undervisning (forelæsninger og fællestimer) af selvstudium med opgaveregning
Arealer som summer Numerisk integration
Arealer som summer Numerisk integration http://www.zweigmedia2.com/realworld/integral/numint.html Her kan ses formlerne, som er implementeret nedenfor med en effektiv kode. Antag, at funktionen er positiv,
Eksamen i Calculus. Første Studieår ved Det Tekniske Fakultet for IT og Design samt Det Ingeniør- og Naturvidenskabelige Fakultet. 3.
Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design samt Det Ingeniør- og Naturvidenskabelige Fakultet. januar 7 Dette eksamenssæt består af 9 nummererede sider med afkrydsningsopgaver.
MASO Uge 7. Differentiable funktioner. Jesper Michael Møller. Uge 7. Formålet med MASO. Department of Mathematics University of Copenhagen
MASO Uge 7 Differentiable funktioner Jesper Michael Møller Department of Mathematics University of Copenhagen Uge 7 Formålet med MASO Oversigt Differentiable funktioner R n R m Differentiable funktioner
MATEMATIK A-NIVEAU Vejledende eksempler på eksamensopgaver og eksamensopgaver i matematik, 2012 Differentialligninger
MATEMATIK A-NIVEAU Vejledende eksempler på eksamensopgaver og eksamensopgaver i matematik, 2012 Differentialligninger 2016 MATEMATIK A-NIVEAU Vejledende eksempler på eksamensopgaver og eksamensopgaver
Eksamen i Mat F, april 2006
Eksamen i Mat F, april 26 Opgave 1 Lad F være et vektorfelt, givet i retvinklede koordinater som: F x x F = F x i + F y j + F z k = F y = 2z F z y Udregn F og F: F = F x + F y + F z = 1 + +. F = F z F
MM501 forelæsningsslides
MM501 forelæsningsslides uge 37, 2010 Produceret af Hans J. Munkholm 2009 bearbejdet af Jessica Carter 2010 1 Hvad er et komplekst tal? Hvordan regner man med komplekse tal? Man kan betragte udvidelsen
Den homogene ligning. Vi betragter den n te ordens, homogene, lineære differentialligning. d n y dt n. an 1 + any = 0 (1.2) dt. + a1 d n 1 y dt n 1
1/7 Den homogene ligning Vi betragter den n te ordens, homogene, lineære differentialligning a 0 d n y dt n + a1 d n 1 y dt n 1 hvor a 0,..., a n R og a 0 0. Vi skriver ligningen på kort form som + + dy
Besvarelses forslag til Tag-hjemeksamen Vinteren 02 03
IMFUFA Carsten Lunde Petersen Besvarelses forslag til Tag-hjemeksamen Vinteren 02 0 Hvor ikke andet er angivet er henvisninger til W.R.Wade An Introduction to analysis. Opgave a) Idet udtrykket e x2 cos
DesignMat Uge 1 Repetition af forårets stof
DesignMat Uge 1 Repetition af forårets stof Preben Alsholm Efterår 008 01 Lineært ligningssystem Lineært ligningssystem Et lineært ligningssystem: a 11 x 1 + a 1 x + + a 1n x n = b 1 a 1 x 1 + a x + +
Q (0, 1,0) MF(161): y a( x) y b( x) har løsningen: y e b( x) bx ( ) e dx e e dx e dx e. y e 8e. Delprøve uden hjælpemidler: kl
MatA Juni 7 Kr. Bahr Side af 5 Delprøve uden hjælpemidler: kl. 9.. Opgave ( %) To planer er givet ved ligningerne: : z og : z5. a) Gør rede for, at de to planer er parallelle. De to planer er parallelle,
Funktioner. 3. del Karsten Juul
Funktioner 3. del 019 Karsten Juul Funktioner 3. del, 019 Karsten Juul 1/9-019 Nyeste version af dette hæfte kan downloades fra http://mat1.dk/noter.htm. Hæftet må benyttes i undervisningen hvis læreren
Besvarelser til Calculus og Lineær Algebra Globale Forretningssystemer Eksamen - 3. Juni 2014
Besvarelser til Calculus og Lineær Algebra Globale Forretningssystemer Eksamen - 3. Juni 204 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over
DesignMat Komplekse tal
DesignMat Komplekse tal Preben Alsholm Uge 7 Forår 010 1 Talmængder 1.1 Talmængder Talmængder N er mængden af naturlige tal, 1,, 3, 4, 5,... Z er mængden af hele tal... 5, 4, 3,, 1, 0, 1,, 3, 4, 5,....
Kvantitative Metoder 1 - Forår 2007. Dagens program
Dagens program Kapitel 7 Introduktion til statistik Organisering af data Diskrete variabler Kontinuerte variabler Beskrivende statistik Fraktiler Gennemsnit Empirisk varians og spredning Empirisk korrelationkoe
Numerisk. differentiation. Erik Vestergaard
Numerisk differentiation Erik Vestergaard 2 Erik Vestergaard www.matematikfysik.dk Erik Vestergaard, 25. Billeder: Forside: istock.com/iunewind Side 5: istock.com/cienpies Desuden egne illustrationer Erik
Kompleks Funktionsteori
Kompleks Funktionsteori Formelræs Holomorfe funktioner Sætning. (Caucy-Riemans ligninger). Funktionen f : G C, f = u+iv er holomorf i z 0 = x 0 + iy 0 hvis og kun hvis i punktet (x 0, y 0 ). du dx = dv
UGESEDDEL 9 LØSNINGER. Sydsæter Theorem 1. Sætning om implicitte funktioner for ligningen f(x, y) = 0.
UGESEDDEL 9 LØSNINGER Sydsæter 531 Theorem 1 Sætning om implicitte funktioner for ligningen f(x, y) = 0 Lad f(x, y) være C 1 i mængden A R n og lad (x 0, y 0 ) være et indre punkt i A hvor f(x 0, y 0 )
DiploMat 1 Inhomogene lineære differentialligninger
DiploMat 1 Inhomogene lineære differentialligninger Preben Alsholm Uge Efterår 2008 1 Lineære Differentialligninger af anden orden 1.1 Den inhomogene ligning I Den inhomogene ligning I Vi betragter nu
Newton-Raphsons metode
Newton-Raphsons metode af John V. Petersen Indhold Indledning: Numerisk analyse og Newton-Raphsons metode... 2 Udlede Newtons iterations formel... 2 Sætning 1 Newtons metode... 4 Eksempel 1 konvergens...
Om første og anden fundamentalform
Geometri, foråret 2005 Jørgen Larsen 9. marts 2005 Om første og anden fundamentalform 1 Tangentrummet; første fundamentalform Vi betragter en flade S parametriseret med σ. Lad P = σu 0, v 0 være et punkt
Prøveeksamen i Calculus
Prøveeksamen i Calculus Første Studieår ved Det Teknisk-Naturvidenskabelige Fakultet og Det Sundhedsvidenskabelige Fakultet Marts 6 Dette eksamenssæt består af 9 nummererede sider med 4 afkrydsningsopgaver.
Noter om Komplekse Vektorrum, Funktionsrum og Differentialligninger LinAlg 2004/05-Version af 16. Dec.
Noter om Komplekse Vektorrum, Funktionsrum og Differentialligninger LinAlg 2004/05-Version af 16. Dec. 1 Komplekse vektorrum I defininitionen af vektorrum i Afsnit 4.1 i Niels Vigand Pedersen Lineær Algebra
Eksamen i Calculus. Første Studieår ved Det Teknisk-Naturvidenskabelige Fakultet og Det Sundhedsvidenskabelige Fakultet. 6.
Eksamen i Calculus Første Studieår ved Det Teknisk-Naturvidenskabelige Fakultet og Det Sundhedsvidenskabelige Fakultet 6. juni 16 Dette eksamenssæt består af 1 nummererede sider med 14 afkrydsningsopgaver.
Besvarelser til Calculus Ordinær Eksamen Januar 2019
Besvarelser til Calculus Ordinær Eksamen - 14. Januar 19 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
π can never be expressed in numbers. William Jones og John Machins algoritme til beregning af π
can never be expressed in numbers. William Jones og John Machins algoritme til beregning af. Oprindelsen til symbolet Første gang vi møder symbolet som betegnelse for forholdet mellem en cirkels omkreds
To find the English version of the exam, please read from the other end! Eksamen i Calculus
To find the English version of the exam, please read from the other end! Se venligst bort fra den engelske version på bagsiden hvis du følger denne danske version af prøven. Eksamen i Calculus Første Studieår
Figur 1: Kraftpåvirkning af vingeprol
0.. AERODYNAMIK 0. Aerodynamik I dette afsnit opstilles en matematisk model for de kræfter, der virker på en vingeprol. Disse kræfter kan få rotoren til at rotere og kan anvendes til at krøje nacellen,
Eksamen i Calculus. 14. juni f (x, y, z) = 1 + x 2 + y 2. Hele rummet uden z aksen
Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 14. juni 019 Opgave 1 (6 point) En
Eksamen i Calculus. 14. juni f (x, y, z) = 1 + x 2 + y 2. x 2 + y 2 1 Hele rummet uden z aksen
Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 14. juni 19 Opgave 1 (6 point) En funktion
Geometri, (E-opgaver 9d)
Geometri, (E-opgaver 9d) GEOMETRI, (E-OPGAVER 9D)... 1 Vinkler... 1 Trekanter... 2 Ensvinklede trekanter... 2 Retvinklede trekanter... 3 Pythagoras sætning... 3 Sinus, Cosinus og Tangens... 4 Vilkårlige
Eksamen i Calculus. Første Studieår ved Det Tekniske Fakultet for IT og Design samt Det Ingeniør- og Naturvidenskabelige Fakultet. 5.
Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design samt Det Ingeniør- og Naturvidenskabelige Fakultet 5. januar 08 Dette eksamenssæt består af 8 nummererede sider med afkrydsningsopgaver.
Københavns Universitet, Det naturvidenskabelige Fakultet. Afleveringsopgave 1
Københavns Universitet, Det naturvidenskabelige Fakultet 1 Lineær Algebra (LinAlg) Afleveringsopgave 1 Eventuelle besvarelser laves i grupper af - 3 personer og afleveres i to eksemplarer med 3 udfyldte
MM501 forelæsningsslides
MM50 forelæsningsslides uge 36, 2009 Produceret af Hans J. Munkholm Nogle talmængder s. 3 N = {, 2, 3, } omtales som de naturlige tal eller de positive heltal. Z = {0, ±, ±2, ±3, } omtales som de hele
Undervisningsbeskrivelse
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Som 2015 Institution VUC Vest Uddannelse Fag og niveau Lærer(e) Hold Hf/hfe Mat B Niels Johansson 14MACB11E14
Klassisk Taylors formel
p. 1/17 Klassisk Taylors formel Sætning Lad f : (a, b) R være n gange differentiabel. For x 0, x (a, b) findes et ξ mellem x 0 og x der opfylder at f(x) = f(x 0 )+ f (x 0 ) 1! (x x 0 )+...+ f(n 1) (x 0
Reeksamen i Calculus
Reeksamen i Calculus Første Studieår ved Det Teknisk-Naturvidenskabelige Fakultet og Det Sundhedsvidenskabelige Fakultet 9. august 6 Dette eksamenssæt består af nummererede sider med 4 afkrydsningsopgaver.
Opgave 1 - Lineær Funktioner. Opgave 2 - Funktioner. Opgave 3 - Tredjegradsligning
Sh*maa03 1508 Matematik B->A, STX Anders Jørgensen, delprøve 1 - Uden hjælpemidler Følgende opgaver er regnet i hånden, hvorefter de er skrevet ind på PC. Opgave 1 - Lineær Funktioner Vi ved, at år 2001
Matematisk modellering og numeriske metoder. Lektion 5
Matematisk modellering og numeriske metoder Lektion 5 Morten Grud Rasmussen 19. september, 2013 1 Euler-Cauchy-ligninger [Bogens afsnit 2.5, side 71] 1.1 De tre typer af Euler-Cauchy-ligninger Efter at
MASO Uge 7. Differentiable funktioner. Jesper Michael Møller. Uge 7. Formålet med MASO. Department of Mathematics University of Copenhagen
MASO Uge 7 Differentiable funktioner Jesper Michael Møller Department of Mathematics University of Copenhagen Uge 7 Formålet med MASO Oversigt Differentiable funktioner f : R R En funktion f : R R er differentiabel
i x-aksens retning, så fås ). Forskriften for g fås altså ved i forskriften for f at udskifte alle forekomster af x med x x 0
BAndengradspolynomier Et polynomium er en funktion på formen f ( ) = an + an + a+ a, hvor ai R kaldes polynomiets koefficienter. Graden af et polynomium er lig med den højeste potens af, for hvilket den