Fysik 12. Sebastian B. Simonsen. June 13, 2004
|
|
|
- Ella Jeppesen
- 7 år siden
- Visninger:
Transkript
1 Fysik 12 Sebastian B. Simonsen June 13, 2004 Contents 1 Vigtige formler til Fysik Relativitets teori Einsteins postulater Fomler Konstanter Termodynamik Termodynamikens hovedsætninger Udtryk Formler Konstanter Disposition Relativitets teori Det specielle relativitetsprincip, lorentz-transformation og dens følger.(side 1-29) Relativistisk kinematik og Doppler effekten(side 36-52) Rumtiden og fire-vektorer(side 61-73) Etablering af den relativistiske mekanink (side 74-82) Relativistisk energi og impuls og anvendelse (side 78-91) Fire-kraften, tre-kraften og den relativistiske bevægelsesligning (side 91-96) Termodynamik Varme, arbejde og energi Termodynamikkens første hovedsætning Carnot processer og absolut temperatur Termodynamikkens anden hovedsætning
2 Entropiens egenskaber Termodynamisk ligevægt Entropi og anden hovedsætning i den statistiske mekanik Eksempler pa beregning af entropi i den statistiske mekanik Det kanoniske ensemble Termodynamiske størrelser og termodynamisk ligevægt i den statistiske mekanik
3 1 Vigtige formler til Fysik Relativitets teori Einsteins postulater 1. Alle inertialsystemer er ligeværdige for udførelse af alle fysiske eksperimenter. 2. I det tomme rum udbreder lys sig retlinet med hastigheden c i enhver retning og i ethvert inertialsystem Fomler GT LT og den omvendte LT hvor γ = 1 1 v2 c 2 x = x vt y = y z = z t = t x = γ(x vt) y = y z = z t = γ(t vx c 2 ) x = γ(x + vt ) y = y z = z t = γ(t + vx c 2 ) 3
4 Længdeforkortelse Tidsforlængelse L = L 0 γ T = T 0 γ Doppler-effekten For klassisk: ν kl ν 0 = 1 v c 1+ w c 1 u2 c 2 1+ u c For rela: ν rel ν 0 = Denne fremkommer vha. af det klassiske udtryk for doppler-effekten og tidsforlængelsen. Afstanden fra origo til et et punkt i den fire-dim rumtid. Transformation af fire-vektore ds 2 c 2 dt t dx 2 dy 2 dz 2 A 0 = γ(a 0 βa 1 ) A 1 = γ(a 1 βa 0 ) A 2 = A 2 A 3 = A 3 Egentiden Fire-impulsen er givet ved dτ 2 ds2 c 2 og dt dτ = γ P = mu den relativistiske impuls p = γ(u)mu Energien er givet ved E = γmc 2 Den kinetiske energi er givet ved T = E E 0, hvor E 0 = mc 2 4
5 Fire-kraften F d dτ P f dp dt de = f u dt F = γ(u) ( ) f u c, f Den relativistiske bevarelsesligning Konstanter 1.2 Termodynamik f = γm du dt + f u c u 2 1eV = 1, J m e = 0, 511 MeV c Termodynamikens hovedsætninger 0. Hvis to systemer A og B er ad skilt. Hvis A er i ligevægt med et andet system C, og hvis B er i ligevægt med C, så er A og B også i ligevægt. (Det princippet bag et termometer) 1. Energien er altid bevaret, hvis man tager varmen med i betragtning. U = U efter U før = W + Q, hvor W er arbejdet og Q varmen 2. Der er en del udgaver af den anden hovedsætning Planck: Det er umuligt for en maskine, at have en cyklus, hvor der bliver taget varme fra et enkelt reservoir, producer en lige mængde arbejde og ikke have anden effekt. Clausius: Det er umuligt for en maskine, at have en cyklus, hvor der bliver taget varme fra en kloder legeme til et varmer. sæt.: Entropien vokser i et isoleret system. 3. Hvis entropien til ethvert stof i dets stabile form ved T = 0 er nul, så må ethvert stof have en positiv entropi for T > 0. 5
6 1.2.2 Udtryk Tilstands funktion: Funktionen afhænger ikke af systemets historie. Varme: Man kan se på varme på to måder, mikroskopisk og makroskopisk. På det mikroskopiske plan er varme et udtryk for hvor stor bevægelse der er molekylerne er i. På det makroskopiske plan er det et mål for hvor stor energien er i den enkelte system. Arbejde: En måde at tilføre energi til et system. Tryk: Et udtryk for tætheden af partikler i et rum. (En impuls overførelse fra partiklerne til vægen) Reversible: Er en proces som kan modvirkes ved at gøre det nøjagtigt modsatte. Dvs. at dens vej i et (P,V)-diagram er kan gå både fra A til B og omvendt. Irreversible: Er det modsatte af en reversible proces, denne proces kan kun gå en vej i (P,V)-diagrammet. Det er heller ikke muligt at følge processen igennem vejen, denne proces hopper fra et punkt til et andet i diagrammet. Adiabatisk: Er en ændring af et system, hvor der ikke kommer noget varme ind i systemet når dets tyk og volumen ændres. Ekstensive variable: Størrelser det er med systemets antal af partikler, F.eks. U C = U A + U B og entorpien. Alle disse størrelser forekommer lineært i ligninger. Intensive variable: Er kort og godt, størrelser der ikke er ekstensive, F.eks. terperaturen. Mikrotilstande: Den mest detaljeret beskrivelse af et system på et givet tidspunkt. De ændre sig under tiden, pga. indre dynamik eller vekselvirkning med omgivelserne. Makrotilstande: Systemer bestående af meget store antal partikler. Makroskopiske størrelser er oftest en beskrivelse af summer eller gennemsnit af størrelser. Ensemble: Samling af system kopier, hvis antallet er M og der er m i systemer i mikrotilstanden i er sandsynligheden p i = m i M 6
7 1.2.3 Formler Tilstandsfunktioner: En tilstandsfunktion kan skrives som G = g(x, y) En lille ændring i G må være givet ved ( ) ( ) g(x, y) g(x, y) dg = dx + dy x y y x det kan skrives på formen dg = A(x, y)dx + B(x, y)dy Af regler for anden ordens diff. ved vi at ( ( ) ) g(x, y) = ( ) g(x, y) x y y x x y y x dvs. ( ) B = x y ( ) A y x Hermed er det er total differentiale. Nu skal vi vise at den ikke er vejafhæning. Vi bruger Stokes therem ( B G(x, y) = Adx + Bdy = C A x A ) y Temperaturen for en ideal gas er θ G = P V nr Indre energi: U = U 0 + U, hvor U = U efter U før = W + Q Ved en reversibel ændring af massen af stemplet i en cylinder, kan det vises at dw = (m + δm)gdz = (m+δm)g ( Adz) = (m+δm)gdv = A A P dv gælder kun for reversible processer. Enthalpi, Hvis vi ændre volumen reversibelt men fastholdt tryk. du = dq rev P dv dq rev = d(u + P V ), dermed bliver enthalpien def. som H = U + P V og H er en tilstandsfunktion. Varmekapacitet: dq = Cdθ For konstant V: C V = ( ) U θ V For konstant P: dq P = dh C P = ( ) H = ( U θ P θ 7 ) + ( (P V ) P θ ) P
8 Energien af en ideal gas U = 3 2 nrθ G, pga. en ideal gas s frihedsgrader. Varmekapaciteten for ideal gas C P = ( ) H θ P = ( ) (U + P V ) θ C V = 3 2 nr Adiabatisk proces i en ideal gas Dvs. at der er ingen varme tilførsel P og ( ) (P V ) = C V + = C V +R C P = 5 θ 2 R P V = Rθ P dv + V dp = Rdθ Det medføre vha.du = 3 2 Rdθ = C V dθ = R C V du og så ved du = P dv da der ikke er nogle varme tilførsel. = R C V P dv (1 + R CV ) P dv + V dp = 0 ( CV + R C V ) P dv + V dp = 0 C P C V P dv + V dp = 0 P dv + C V C P V dp = 0 dv V + C V dp C P P = ln(v ) + C V C P ln(p ) = 0 ln(p V C P C V ) = 0 P V γ = konstant θv γ 1 = konstant 8
9 Effektiviteten η W Q 1, hvor W = Q 1 Q 2 det medføer at η = 1 Q 2 Q 1. For virkelige maskiner er η < 1 det er kun reversible maskiner der har en η = 1 Den absolutte temperatur. Da Q 1 Q 2 er en funktion af θ, må Q 1 Q 2 = Φ(θ 1) Φ(θ 2 ) og vi definer Φ(θ) til at være den absolutte temperatur T Q 1 Q 2 = T 1 T 2. Det kan så vises at θ G = T Entropi for en ideal gas. du = 3nRdT og P = nrt 2 V Def. Af entropi S = dq rev T Da ds = dqrev T må du = T ds P dv Måling af entropi Ved konstant tryg er dq rev = C p dt S = C P ln ( ) T efter T før Helmholtz frie energi F = U T S Det giver os nu mulighed for af sige noget om Gibbs frie energi S = ( ) F T V og ( ) F P = V G = H T S dg = SdT + V dp Entropiens vækst kan vises udfra effektiviteten. Boltzmann s hypotese S = k B ln(w ) Sterlings approksimation ln(m!) = M ln(m) M T 9
10 Gummibånd W er, ved en forlængelse af gummibåndet på dl, F dl. Derved bliver du = T ds + F dl som medføre at F = k ) T b Det kanoniske ensemble ( ln(w ) l v Boltzmann fordelingen, E i e k b T Z Z = i Entropi S = k b p i ln(p i ) Konstanter Avogadro s tal N A = mol 1 i p i = e Ei k b T Z Boltzmann s konstant k B = J K Gas konstant R = J K mol elektronladning e = C 2 Disposition 2.1 Relativitets teori Det specielle relativitetsprincip, lorentz-transformation og dens følger.(side 1-29) Galilei-transformation Lige snakke hurtigt om den gamle form for transformation mellem to inetialsystemer. Einsteins to postulater. samtidighed, længde og varighed. 10
11 udledning af lorentz-transformationen. vi kræver at der er en lineær transformation,og vi siger at y = y og z = z. At den skal være lineær må betyde at x = γx ρt og t = κx + σt hvor konstanterne afhænger af tiden. x = 0 v = ρ/γ og x = 0 σ = γ hvis vi nu sætter κ = γαv fås transformationen. for at finde γ skal vi bruge sfæriske koordinater i de to systemer i forhold til et lys glimt. Og de mærket koordinater sættes ind. c som max rumtids diagram. Transformationen giver hyperbolske baner Relativistisk kinematik og Doppler effekten(side 36-52) Snak om Einstein og LT husk også det omvendte trans def. af samtidighed og længde Længdeforkortelse. Stang i hvile i S og ved samtidighed ( t = 0) bliver L = L 0 γ Tidsforlængelse. på samme måde som med længden men denne gang er det bare med et lysglimt og ( x = 0), bliver T = γt 0 Hastigheds transformation. Ved LT transformeres u x = dx dt udtryk i u x. om til et Doppler: Det tre tilfælde for den klassiske doppler effekt, 1) ν 0 = 1/T 0, 2) T = (1 + w/c) og 3) T = T 0. Hvor man derefter bruger bruger 1 v/c tilsforlængelsen til at finde det relativistiske tilfælde. Tilsidst siger man at tilfælde 2 og 3 skal det være det samme for rela pga. Einsteins første postulat Rumtiden og fire-vektorer(side 61-73) Intro til rumtiden (t, x, y, z) og dens geometri ds = c 2 dt 2 dr 2 Lyskeglen 11
12 Fire-vektoren, her under transformation af en fire-vektor Egentiden. Da tiden ikke længer er en invariant størrelse vil vi gerne have en ny invariant størrelse dτ 2 ds2 c 2, når vi arbejder i origo er dr = 0 dvs. dτ 2 dt 2 = 1 u2 c dt 2 dτ = 1 1 u2 c 2 = γ(u) Fire-hastigheden U dx dτ så ved brug af kædereglen og egentiden kan den skrives om til U = γ(u)(c, u) Fire-Acc. A d2 X dτ Etablering af den relativistiske mekanink (side 74-82) Krav til den relativistiske mekanik Fire-impulsen. P = mu Vi kan regne lidt vidre på dette udtryk U = γ(u)(c, u) P = mu } P = (γ(u)mc, p) hvor p = γ(u)mu og denne kaldes den relativistiske impuls. vi kan genfinde den klassiske impuls ved at sætte γ = 1 Fire-impuls bevarelse Energi. ved at rækkeudvikle størrelsen γ(u)m = m + mu giver at enhver 2c 2 energiform må bidrage på samme måde til γm Det føre til E 0 mc 2 og energien E = γmc 2. Den kinetiske energi bliver dermed til T E E 0 og ved rækkeudvikling kan vi genfinde det klassiske udtryk. Udfra definitionen på energi kan vi finde et nyt udtryk for P = ( E, p) c 12
13 Sammenhængen mellem energi og impuls. } P 2 = E2 p 2 c 2 P 2 = m 2 c 2, ved p = 0ogE = mc 2 E 2 = p 2 c 2 + m 2 c 4 Denne beregning kan lade sig gøre da P 2 er en invariant størrelse Relativistisk energi og impuls og anvendelse (side 78-91) Energi. ved at rækkeudvikle størrelsen γ(u)m = m + mu giver at enhver 2c 2 energiform må bidrage på samme måde til γm Det føre til E 0 mc 2 og energien E = γmc 2. Den kinetiske energi bliver dermed til T E E 0 og ved rækkeudvikling kan vi genfinde det klassiske udtryk. Udfra definitionen på energi kan vi finde et nyt udtryk for P = ( E, p) c Sammenhængen mellem energi og impuls. } P 2 = E2 p 2 c 2 P 2 = m 2 c 2, ved p = 0ogE = mc 2 E 2 = p 2 c 2 + m 2 c 4 Denne beregning kan lade sig gøre da P 2 er en invariant størrelse Masseløse partikler. E 2 = p 2 c 2 + m 2 c 4 E = pc, det giver partiklerne en impuls P = (1, n), hvor n er en retningsvektor. E c udfra vores viden om frie-impulsen er det også muligt at regne os frem til det relativistiske udtryk for doppler. Men vi skal lige låne lidt fra kvantemekanikken E = hν og så ser vi på en på P = E (1, 1, 0, 0). Hvis c vi kun ser på energien og transformer den fås 1 β E = γ(e βe) = E 1 + β, da E ν giver det stød-processer ν 1 β ν = 1 + β Tærskel-energien Bindings energi Reaktions energi 13
14 Fire-kraften, tre-kraften og den relativistiske bevægelsesligning (side 91-96) Definition af Fire-kraften. F d dτ P = d (mu) = ma dτ, det skal lige nævnes at der må ikke ske en ændring af massen for partiklen dvs. dm = 0 dτ Der kan regnes videre på dette ved frie-impulsen F = d dτ (E c, p) = γ(u) d dt (E c, p) = γ(u)(1 de c dt, f) hvor vi definere f dp dt kaldes for tre-kraften. Udfra prik-produkterne kan man finde = d (γ(u)mu) og det er denne størrelse der dt F = γ(u) ( f u c, f Transformation af krafterne vi tager udgangspunkt i F = γ(u) ( f u c, f ), i S systemet er u = 0 og det giver F = (0, f x, f y, f z), men udfra tranfomationen af 4-vektore finer vi F 1 = γ(v)f x, F 2 = f y og F 3 = f z. Nu kan vi bruge den vi tog udgangs punkt i og finder f x = f x, f y = f y/γ og f z = f z/γ Den relativistiske bevægelsesligning. den er bare tre-kraften der en diff. f = γm du dt + mudγ dt = γmdu dt + u de c 2 dt = γma + f u c u Termodynamik Varme, arbejde og energi Hvad er varme, mikroskopisk og makroskopisk. Temperatur. Hvad er arbejde. Tryk og volumen. Mekanisk ligevægt. Tilstandsfunktion. Energibevarelse. ) Varme på de to planer, Temperatur (her under 0.hovedsætning), Arbejde, Tryk, volumen og mekanisk ligevægt Tilstandsfunktionen Energibeverelse og første hovedsætning 14
15 Termodynamikkens første hovedsætning Indre energi. Reversible og irreversible processer. Entalpi. Varmekapacitet. Adiabatisk proces i en idealgas. Indre energi Tale om joules forsøg der føre til hvordan energien må være bevaret, som føre til første hovedsætning U = W + Q Reversible og irreversible processer Ved en reversibel ændring af massen af stemplet i en cylinder, kan det vises at dw = (m + δm)gdz = (m+δm)g ( Adz) = (m+δm)gdv = A A P dv gælder kun for reversible processer. dvs. at første hovedsætning, kan skrives som du = dq rev pdv enthalpi Hvis volumet indres reversiblet med konstant P. Kan enthalpien defineres som H U + P V det medføre at dq rev = dh Da den består af tilstandsfunktioner er den også selv en tilstandsfunktion. Varmekapacitet er den mængde varme der skal til for at et legeme stiger en grad. dq = Cdθ Man ser så på to tilfælde, konstant tryg go ved konstant volume Adiabatisk proces i en ideal gas Dvs. at der er ingen varme tilførsel P V = Rθ P dv + V dp = Rdθ Det medføre vha.du = 3 2 Rdθ = C V dθ = R C V du 15
16 og så ved du = P dv da der ikke er nogle varme tilførsel. = R C V P dv (1 + R CV ) P dv + V dp = 0 ( CV + R C V ) P dv + V dp = 0 C P C V P dv + V dp = 0 P dv + C V C P V dp = 0 dv V + C V dp C P P = ln(v ) + C V C P ln(p ) = 0 ln(p V C P C V ) = 0 P V γ = konstant θv γ 1 = konstant Carnot processer og absolut temperatur Den basale Carnot-cyklus. Cylinder med stempel. Effektivitet af reversible og irreversible maskiner. Gastemperatur og absolut temperatur. Carnot-cyklus Den er lavet af fire reversible trin, og arealet under den er arbejdet. } U = 0 = Q W W = Q Q = Q 1 Q 1 Q 2 2 Forklar hele processen med et stempel Effektiviteten η W Q 1 = 1 Q 2 Q 1 Ved at sætte en irrev og en rev maskine til at køre sammen imellem to temperature, kan det vises at at η irrev < η rev, da men ikke kan føre varm fra et koldt til et varmt. Det kan også vises på sammen måde at to rev har samme η 16
17 Absolut temp. Ved at sætte to reversible maskiner serie mellem tre temperature. Der må så gælde at Q 1 = Q 1 Q 2 Q 3 Q 2 Q 3 da Q 1 Q 2 = f(θ 1, θ 2 ) og f(θ 2, θ 2 ) = φ(θ 1) φ(θ 2 ) absolut temperatur T = φ(θ) Dette for kelvin til at forslå en Sammenhængen mellem T og θ G Q 1 = B A P dv = nrθ 1 ( ) V B VA og Q1 = C D P dv = nrθ 1 ( ) V C VD Vha. kan det vises at θ 1 V (γ 1) B = θ 2 V (γ 1) C T 1 T 2 = θ 1 θ Termodynamikkens anden hovedsætning Entropi i en idealgas. Totalt differentiale. Formuleringer af anden hovedsaetning. Skal beregne et udtryk for entropien i en idealgas Vi bruger første hovedsætning, men da dq rev er et ineksakt differentiale, skal vi finde en funktion der skal ligges til for at vi kan kalde det et eksakt differentiale. Vi ved at du = 3nRdT og P = nrt for en 2 V idealgas. Ved indsættelse i første hovedsætning får vi dq rev = du + P dv = 3nRdT 2 + nrt dv V for at kunne integrere skal vi lige dividere med T i hele beregningen. Nu kan vi integrere efter før dq rev T = Vi kalder dq rev T efter før dq rev T 3nRdT 2T = 3nRdT 2T + nrdv V efter nrdv + før V for entropien S, det giver S = 3nR 2 ln ( ) Te T f 17 + nr ln = 3nR 2 ln ( ) Ve V f + S 0 ( ) Te T f +nr ln ( ) Ve V f +K
18 Tale om Total differentiale (Det samme som tilstandsfunktioner man skal bare ikke tale om at en er vej uafhængig) Formuleringer af første hovedsætning Entropiens egenskaber Definition af entropi. Maling af entropi. Entropiens væskst. Eksempler herpå. Definition af entropi Vi siger Q 2 Q 1 = T 2 T 1 Dette medføre at vi kan skrive Q 1 T 1 + Q 2 T 2 = 0 for en carnot-cyklus. En enhver reversibel cyklus kan laves ved at sammensætte en masse små cykler, og hver må bidrage med dq, det bliver så T tiol dq i dq i T = 0 T i i Hvis vi så tager to vej fra A til B må de være det samme da det er et lukket integral. Derved kan kan vi def. S som en tilstandsfunktion. Vi kan også skrive første hovedsætning som du = T ds P dv Og udfra def. af entropien kan vi også tale om varmekapaciteten. Måling af entropi Man skal holde trykket konstant, dvs. dq rev = C P dt S(T efter ) = S(T før ) + C P (T ) ln ( ) Tefter T før Det siger bare ikke noget om entropien for fase overgange. I sådanne sitautioner er entropien S = Q P T nu = H T nu da der er konstant tryk entropiens vækst Man bruger at η R > η I Q 2 Q 1 > T 2 T 1 18
19 dvs. dqirrev < 0 T og da man altid kan finde en reversible vej til bage er b a dq irrev T < dq rev T og ved meget små er δq irrev = 0 0 < δs Eksempel på entropiens vækst Termodynamisk ligevægt Mekanisk ligevægt. Termisk ligevægt. Ekstensive og intensive variable for et sammensat system. Tilnærmelse til ligevægt. Mekanisk ligevægt, snakke om cylender og stempel Termisk ligevægt Bruge de to foregående eksempler til at tale om både Ekstensive (U, S, V ) og intensive variable (T, P ) Tilnærmet ligevægt Energi: Vi ser på to systemer A og B, og vi sætter en termisk leder ind mellem dem for at få energien til at flyde fra den ene til den anden. Det betyder at der kan opstå en termisk ligevægt mellem de to. U total dt Systemet af de to systemer er isoleret fra omverden så = du A dt = 0 du B dt Vi kædereglen er S(U A ) = S A (U A ) + S B (U T U A ) ds dt = du A S A + du B S B dt U A dt U B da U total dt = 0 du B dt = du A dt er ds dt = du { A SA S B dt U A U B } = { 1 1 } 0 T A T B 19
20 Volumen: Partikler: ds dt = dv { A SA S } { B PB = P } B 0 dt V A V B T A T B ds dt = dn { A SA S } B dt N A N B Man definere det kemiske potentiale til µ T ( S N { ds dt = dn A µa µ } B 0 dt T A T B ) det giver Entropi og anden hovedsætning i den statistiske mekanik Mikrotilstande og makrotilstande Boltzmann s hypotese. Eksempel med ikke-vekselvirkende molekyler. Energifluktuationer. Varme og arbejde udtrykt ved mikrotilstandenes energier. Mikrotilstande og makrotilstande Boltzmann s hypotese siger S(U, V, N) = φ(w (U, V, N)) Hvis vi ser på S, Som jo som bekendt er en ekstensiv størrelse. Vi ser på to systemer A og B med entropien S A = φ(w A ) og S B = φ(w B ). Det samlet system mellem A og B har entropien S AB = S A + S B det giver en funktion i φ φ(w AB ) = φ(w A W B ) = φ(w A ) + φ(w B ) Den eneste funktion der kan opfylde dette er den logaritmiske funktion, dvs. φ(w ) = k B ln(w ) S = k B ln(w ) ikke-vekselvirkende molekyler Hvis vi har et volumen V med en inddeling δv, et molekyle kan fordeles dvs. at W for N molekyler er på V δv W = ( ) V 2 ( ) V S = Nk B ln V V 20
21 Det giver P = T ( ) S V U P = Nk BT V Energifluktuationer. Fra Boltzmann s hypotese har vi at W = e fracsk B hvis max. entropien af et system A er nåt U A = UA og vi så taylor udvikler ( ) S S(U A ) = S(UA) + (U A UA) For max. vi det ( ) S U A U A =UA udtrykket for W, som bliver U A ( = 0 og U A =U A + (U A U A) 2 2 ) 2 S UA 2 U A =UA W (U A ) = e S(U A )/k B e (U A U A )S /k B ( 2 ) S U 2 A U A =U A < 0 det sættes ind i Dette er den gauss iske fordeling af U A er standart afvigelsen U A = k B S da S < 0 For sammensatte systemer det giver p(ua) = W (U A) i W (U i ) p(u A ) p(u A) = W (U A) W (U A) = e (U A U A )2 /2 U 2 A lad os se på S og huske S = S A + S B ( ) S = 1 U A V T A 1 ( ) T B S = 2 S UA 2 1 T 2 A ( ) V TA U A 1 T 2 B ( S = ( ) ( ) TB U B = 1 1 T 2 C A + 1 C B og hvis C A << C B U 2 A = k B T 2 C A ) ( T 1 A U A + T 1 B U B ) = Eksempler pa beregning af entropi i den statistiske mekanik Spin-kæde. Krystalvakancer. Gummibandsmodel. 21
22 Beregning af W Ved Striling fås W = N! n 1!n 2! = N! n 1!(N n 1 )! S = ln(w ) k B = ln(n!) ln(n 1!) ln((n n 1 )!) N ln(n) N n 1 ln(n 1 ) + n 1 (N n 1 ) ln((n n 1 ) + N n 1!) = {( ) ( ) ( n1 n1 N ln + 1 n ) ( 1 ln 1 n )} 1 N N N N Gummibånd Led i et gummibånd kan enten have en værdi på z (n 2 ) eller z (n 1 ). Hvis det bliver forlænget dl er abejder F dl dvs. at første hovedsætning er du = T ds + F dl Som vist i det forgående er W = N! n 1!(N n 1 )! Længden af båndet må være l = (n 1 n 2 )d = (n 1 (N n 2 ))d = (2n 1 N)d, hvor d er længden af hvert led. Hvis vi sætter x = l = ( 2n 1 Nd N 1) {( ) ( ) ( 1 + x 1 + x ln(w ) = N ln x ) ( ln 1 1 x )} Hvis vi nu ser på første hovedsætning og fastholder U ( ) F ln(w ) T = k dx B x dl Det giver hvis man sætter dx dl = 1 Nd Det kanoniske ensemble F k BT l Nd 2 System i varmebad. Entropi i del kanoniske ensemble. Partitionsfunktion og Helmholtz fri energi. 22 U
23 Termodynamiske størrelser og termodynamisk ligevægt i den statistiske mekanik Termisk ligevægt. Mikrotilstandenes energier og sandsynlighed. Termodynamiske størrelser fra partitionsfunktionen. To-niveau systemer. 23
Fysik 12 Minilex. Henrik Dahl. 11. juni Termodynamik og statistisk mekanik
 Fysik 12 Minilex Henrik Dahl 11. juni 2003 Indhold 1 ermodynamik og statistisk mekanik 1 1.1 igtige størrelser........................... 1 1.2 arme, arbejde og energi....................... 2 1.3 ermodynamikkens
Fysik 12 Minilex Henrik Dahl 11. juni 2003 Indhold 1 ermodynamik og statistisk mekanik 1 1.1 igtige størrelser........................... 1 1.2 arme, arbejde og energi....................... 2 1.3 ermodynamikkens
Termodynamikkens første hovedsætning
 Statistisk mekanik 2 Side 1 af 13 Termodynamikkens første hovedsætning Inden for termodynamikken kan energi overføres på to måder: I form af varme Q: Overførsel af atomar/molekylær bevægelsesenergi på
Statistisk mekanik 2 Side 1 af 13 Termodynamikkens første hovedsætning Inden for termodynamikken kan energi overføres på to måder: I form af varme Q: Overførsel af atomar/molekylær bevægelsesenergi på
Benyttede bøger: Statistisk fysik 1, uredigerede noter, Per Hedegård, 2007.
 Formelsamling Noter til Fysik 3 You can know the name of a bird in all the languages of the world, but when you re finished, you ll know absolutely nothing whatever about the bird... So let s look at the
Formelsamling Noter til Fysik 3 You can know the name of a bird in all the languages of the world, but when you re finished, you ll know absolutely nothing whatever about the bird... So let s look at the
Statistisk mekanik 2 Side 1 af 10 Entropi, Helmholtz- og Gibbs-funktionen og enthalpi. Entropi
 Statistisk mekanik 2 Side 1 af 10 Entropi Entropi er en tilstandsvariabel 1, der løst formuleret udtrykker graden af uorden i et system. Da der er mange flere uordnede (tilfældigt ordnede) mikrotilstande
Statistisk mekanik 2 Side 1 af 10 Entropi Entropi er en tilstandsvariabel 1, der løst formuleret udtrykker graden af uorden i et system. Da der er mange flere uordnede (tilfældigt ordnede) mikrotilstande
Termodynamik. Esben Mølgaard. 5. april N! (N t)!t! Når to systemer sættes sammen bliver fordelingsfunktionen for det samlede system
 Termodynamik Esben Mølgaard 5. april 2006 1 Statistik Hvis man har N elementer hvoraf t er defekte, eller N elementer i to grupper hvor forskydningen fra 50/50 (spin excess) er 2s, vil antallet af mulige
Termodynamik Esben Mølgaard 5. april 2006 1 Statistik Hvis man har N elementer hvoraf t er defekte, eller N elementer i to grupper hvor forskydningen fra 50/50 (spin excess) er 2s, vil antallet af mulige
Statistisk mekanik 2 Side 1 af 10 Entropi, Helmholtz- og Gibbs-funktionen og enthalpi. Entropi
 Statistisk mekanik 2 Side 1 af 10 Entropi Entropi er en tilstandsvariabel 1, der løst formuleret udtrykker graden af uorden. Entropien er det centrale begreb i termodynamikkens anden hovedsætning (TII):
Statistisk mekanik 2 Side 1 af 10 Entropi Entropi er en tilstandsvariabel 1, der løst formuleret udtrykker graden af uorden. Entropien er det centrale begreb i termodynamikkens anden hovedsætning (TII):
Første og anden hovedsætning kombineret
 Statistisk mekanik 3 Side 1 af 12 Første og anden hovedsætning kombineret I dette afsnit udledes ved kombination af I og II en række udtryk, som senere skal vise sig nyttige. Ved at kombinere udtryk (2.27)
Statistisk mekanik 3 Side 1 af 12 Første og anden hovedsætning kombineret I dette afsnit udledes ved kombination af I og II en række udtryk, som senere skal vise sig nyttige. Ved at kombinere udtryk (2.27)
Formelsamling til Mekanik 1 kurset på Københavns Universitet
 Formelsamling til Mekanik 1 kurset på Københavns Universitet af Michael Flemming Hansen Version 1.2b 26. januar 2012 Indhold 2 Bevægelse langs en ret linie 4 2.1 Gennemsnitlig hastighed og fart.................
Formelsamling til Mekanik 1 kurset på Københavns Universitet af Michael Flemming Hansen Version 1.2b 26. januar 2012 Indhold 2 Bevægelse langs en ret linie 4 2.1 Gennemsnitlig hastighed og fart.................
Formler til den specielle relativitetsteori
 Formler til den specielle relativitetsteori Jeppe Willads Petersen 25. oktober 2009 Jeg har i dette dokument forsøgt at samle de fleste af de formler, vi har brugt i forbindelse med den specielle relativitetsteori,
Formler til den specielle relativitetsteori Jeppe Willads Petersen 25. oktober 2009 Jeg har i dette dokument forsøgt at samle de fleste af de formler, vi har brugt i forbindelse med den specielle relativitetsteori,
KOMPENDIUM TIL STATISTISK FYSIK
 KOMPENDIUM TIL STATISTISK FYSIK 3. UDGAVE REVIDERET: 18. APRIL 2011 UDARBEJDET AF SØREN RIIS AARHUS SCHOOL OF ENGINEERING Ö Ô Ý º Ùº DETTE VÆRK ER TRYKT MED ADOBE UTOPIA 10PT LAYOUT OG TYPOGRAFI AF FORFATTEREN
KOMPENDIUM TIL STATISTISK FYSIK 3. UDGAVE REVIDERET: 18. APRIL 2011 UDARBEJDET AF SØREN RIIS AARHUS SCHOOL OF ENGINEERING Ö Ô Ý º Ùº DETTE VÆRK ER TRYKT MED ADOBE UTOPIA 10PT LAYOUT OG TYPOGRAFI AF FORFATTEREN
Nanotermodynamik formelsamling
 Nanotermodynamik formelsamling Af Asmus Ougaard Dohn & Sune Klamer Jørgensen 2. november 2005 ndhold 1 Kombinatorik 2 2 Termodynamik 3 3 deal gasser: 5 4 Entropi og temp.: 7 5 Kemisk potential: 7 6 Gibbs
Nanotermodynamik formelsamling Af Asmus Ougaard Dohn & Sune Klamer Jørgensen 2. november 2005 ndhold 1 Kombinatorik 2 2 Termodynamik 3 3 deal gasser: 5 4 Entropi og temp.: 7 5 Kemisk potential: 7 6 Gibbs
Tilstandssummen. Ifølge udtryk (4.28) kan MB-fordelingen skrives , (5.1) og da = N, (5.2) . (5.3) Indføres tilstandssummen 1 , (5.
 Statistisk mekanik 5 Side 1 af 10 ilstandssummen Ifølge udtryk (4.28) kan M-fordelingen skrives og da er μ N e e k = N g ε k, (5.1) N = N, (5.2) μ k N Ne g = e ε k. (5.3) Indføres tilstandssummen 1 Z g
Statistisk mekanik 5 Side 1 af 10 ilstandssummen Ifølge udtryk (4.28) kan M-fordelingen skrives og da er μ N e e k = N g ε k, (5.1) N = N, (5.2) μ k N Ne g = e ε k. (5.3) Indføres tilstandssummen 1 Z g
1. Beregn sandsynligheden for at samtlige 9 klatter lander i felter med lige numre.
 NATURVIDENSKABELIG GRUNDUDDANNELSE Københavns Universitet, 6. april, 2011, Skriftlig prøve Fysik 3 / Termodynamik Benyttelse af medbragt litteratur, noter, lommeregner og computer uden internetadgang er
NATURVIDENSKABELIG GRUNDUDDANNELSE Københavns Universitet, 6. april, 2011, Skriftlig prøve Fysik 3 / Termodynamik Benyttelse af medbragt litteratur, noter, lommeregner og computer uden internetadgang er
Aalborg Universitet. Skriftlig eksamen i Grundlæggende Mekanik og Termodynamik. Tirsdag d. 31. maj 2016 kl
 Aalborg Universitet Skriftlig eksamen i Grundlæggende Mekanik og Termodynamik Tirsdag d. 31. maj 2016 kl. 9 00-13 00 Ved bedømmelsen vil der blive lagt vægt på argumentationen (som bør være kort og præcis),
Aalborg Universitet Skriftlig eksamen i Grundlæggende Mekanik og Termodynamik Tirsdag d. 31. maj 2016 kl. 9 00-13 00 Ved bedømmelsen vil der blive lagt vægt på argumentationen (som bør være kort og præcis),
Moderne Fysik 1 Side 1 af 7 Speciel Relativitetsteori
 Moderne Fysik 1 Side 1 af 7 Hvad sker der, hvis man kører i en Mazda med nærlysfart og tænder forlygterne?! Kan man se lyset snegle sig afsted foran sig...? Klassisk Relativitet Betragt to observatører
Moderne Fysik 1 Side 1 af 7 Hvad sker der, hvis man kører i en Mazda med nærlysfart og tænder forlygterne?! Kan man se lyset snegle sig afsted foran sig...? Klassisk Relativitet Betragt to observatører
Aalborg Universitet. Skriftlig eksamen i Grundlæggende Mekanik og Termodynamik. Fredag d. 2. juni 2017 kl
 Aalborg Universitet Skriftlig eksamen i Grundlæggende Mekanik og Termodynamik Fredag d. 2. juni 2017 kl. 9 00-13 00 Ved bedømmelsen vil der blive lagt vægt på argumentationen (som bør være kort og præcis),
Aalborg Universitet Skriftlig eksamen i Grundlæggende Mekanik og Termodynamik Fredag d. 2. juni 2017 kl. 9 00-13 00 Ved bedømmelsen vil der blive lagt vægt på argumentationen (som bør være kort og præcis),
AALBORG UNIVERSITET DET INGENIØR-, NATUR- OG SUNDHEDSVIDENSKABELIGE BASISÅR SE - KURSUS TERMODYNAMIK 2. SEMESTER NANOTEKNOLOGI
 AALBORG UNIVERSITET DET INGENIØR-, NATUR- OG SUNDHEDSVIDENSKABELIGE BASISÅR SE - KURSUS TERMODYNAMIK 2. SEMESTER NANOTEKNOLOGI FORÅR 2008 Indholdsfortegnelse TERMODYNAMIK LEK. 1...4 VARMELÆRER...4 Hvorfor
AALBORG UNIVERSITET DET INGENIØR-, NATUR- OG SUNDHEDSVIDENSKABELIGE BASISÅR SE - KURSUS TERMODYNAMIK 2. SEMESTER NANOTEKNOLOGI FORÅR 2008 Indholdsfortegnelse TERMODYNAMIK LEK. 1...4 VARMELÆRER...4 Hvorfor
Tillæg til partikelfysik (foreløbig)
 Tillæg til partikelfysik (foreløbig) Vekselvirkninger Hvordan afgør man, hvilken vekselvirkning, som gør sig gældende i en given reaktion? Gravitationsvekselvirkningen ser vi bort fra. Reaktionen Der skabes
Tillæg til partikelfysik (foreløbig) Vekselvirkninger Hvordan afgør man, hvilken vekselvirkning, som gør sig gældende i en given reaktion? Gravitationsvekselvirkningen ser vi bort fra. Reaktionen Der skabes
Rela2vitetsteori (iii)
 Rela2vitetsteori (iii) Einstein roder rundt med rum og.d Mogens Dam Niels Bohr Ins2tutet Udgangspunktet: Einsteins rela2vitetsprincip Einsteins postulater: 1. Alle iner*alsystemer er ligeværdige for udførelse
Rela2vitetsteori (iii) Einstein roder rundt med rum og.d Mogens Dam Niels Bohr Ins2tutet Udgangspunktet: Einsteins rela2vitetsprincip Einsteins postulater: 1. Alle iner*alsystemer er ligeværdige for udførelse
Aalborg Universitet. Skriftlig eksamen i Grundlæggende Mekanik og Termodynamik. Torsdag d. 23. august 2012 kl
 Aalborg Universitet Skriftlig eksamen i Grundlæggende Mekanik og Termodynamik Torsdag d. 23. august 2012 kl. 9 00-13 00 Ved bedømmelsen vil der blive lagt vægt på argumentationen (som bør være kort og
Aalborg Universitet Skriftlig eksamen i Grundlæggende Mekanik og Termodynamik Torsdag d. 23. august 2012 kl. 9 00-13 00 Ved bedømmelsen vil der blive lagt vægt på argumentationen (som bør være kort og
Aalborg Universitet. Skriftlig eksamen i Grundlæggende Mekanik og Termodynamik. Torsdag d. 8. august 2013 kl
 Aalborg Universitet Skriftlig eksamen i Grundlæggende Mekanik og Termodynamik Torsdag d. 8. august 2013 kl. 9 00 13 00 Ved bedømmelsen vil der blive lagt vægt på argumentationen (som bør være kort og præcis),
Aalborg Universitet Skriftlig eksamen i Grundlæggende Mekanik og Termodynamik Torsdag d. 8. august 2013 kl. 9 00 13 00 Ved bedømmelsen vil der blive lagt vægt på argumentationen (som bør være kort og præcis),
Danmarks Tekniske Universitet
 Danmarks Tekniske Universitet Side 1 af 11 Skriftlig prøve, torsdag den 8 maj, 009, kl 9:00-13:00 Kursus navn: Fysik 1 Kursus nr 100 Tilladte hjælpemidler: Alle hjælpemidler er tilladt "Vægtning": Besvarelsen
Danmarks Tekniske Universitet Side 1 af 11 Skriftlig prøve, torsdag den 8 maj, 009, kl 9:00-13:00 Kursus navn: Fysik 1 Kursus nr 100 Tilladte hjælpemidler: Alle hjælpemidler er tilladt "Vægtning": Besvarelsen
Aalborg Universitet. Skriftlig eksamen i Grundlæggende Mekanik og Termodynamik. Torsdag d. 9. juni 2011 kl
 Aalborg Universitet Skriftlig eksamen i Grundlæggende Mekanik og Termodynamik Torsdag d. 9. juni 2011 kl. 9 00-13 00 Ved bedømmelsen vil der blive lagt vægt på argumentationen (som bør være kort og præcis),
Aalborg Universitet Skriftlig eksamen i Grundlæggende Mekanik og Termodynamik Torsdag d. 9. juni 2011 kl. 9 00-13 00 Ved bedømmelsen vil der blive lagt vægt på argumentationen (som bør være kort og præcis),
Aalborg Universitet. Skriftlig eksamen i Grundlæggende Mekanik og Termodynamik. Mandag d. 11. juni 2012 kl. 9 00-13 00
 Aalborg Universitet Skriftlig eksamen i Grundlæggende Mekanik og Termodynamik Mandag d. 11. juni 2012 kl. 9 00-13 00 Ved bedømmelsen vil der blive lagt vægt på argumentationen (som bør være kort og præcis),
Aalborg Universitet Skriftlig eksamen i Grundlæggende Mekanik og Termodynamik Mandag d. 11. juni 2012 kl. 9 00-13 00 Ved bedømmelsen vil der blive lagt vægt på argumentationen (som bør være kort og præcis),
Aalborg Universitet. Skriftlig eksamen i Grundlæggende Mekanik og Termodynamik. Tirsdag d. 27. maj 2014 kl
 Aalborg Universitet Skriftlig eksamen i Grundlæggende Mekanik og Termodynamik Tirsdag d. 27. maj 2014 kl. 9 00-13 00 Ved bedømmelsen vil der blive lagt vægt på argumentationen (som bør være kort og præcis),
Aalborg Universitet Skriftlig eksamen i Grundlæggende Mekanik og Termodynamik Tirsdag d. 27. maj 2014 kl. 9 00-13 00 Ved bedømmelsen vil der blive lagt vægt på argumentationen (som bør være kort og præcis),
Statistisk mekanik 10 Side 1 af 7 Sortlegemestråling og paramagnetisme. Sortlegemestråling
 Statistisk mekanik 0 Side af 7 Sortlegemestråling I SM9 blev vibrationerne i et krystalgitter beskrevet som fononer. I en helt tilsvarende model beskrives de EM svingninger i en sortlegeme-kavitet som
Statistisk mekanik 0 Side af 7 Sortlegemestråling I SM9 blev vibrationerne i et krystalgitter beskrevet som fononer. I en helt tilsvarende model beskrives de EM svingninger i en sortlegeme-kavitet som
Entropibegrebet Jacob Nielsen 1
 Entropibegrebet Jacob Nielsen 1 I 1871 introducerede Maxwell dæmonen, der ved hjælp af molekylær information tilsyneladende kan krænke termodynamikkens 2. hovedsætning. Centralt i termodynamikken står
Entropibegrebet Jacob Nielsen 1 I 1871 introducerede Maxwell dæmonen, der ved hjælp af molekylær information tilsyneladende kan krænke termodynamikkens 2. hovedsætning. Centralt i termodynamikken står
Anvendt BioKemi: MM2. Anvendt BioKemi: Struktur. 1) MM2- Opsummering. Aminosyrer og proteiner som buffere
 Anvendt BioKemi: Struktur 1) MM1 Intro: Terminologi, Enheder Math/ biokemi : Kemiske ligninger, syre, baser, buffer Små / Store molekyler: Aminosyre, proteiner 2) MM2 Anvendelse: blod som et kemisk system
Anvendt BioKemi: Struktur 1) MM1 Intro: Terminologi, Enheder Math/ biokemi : Kemiske ligninger, syre, baser, buffer Små / Store molekyler: Aminosyre, proteiner 2) MM2 Anvendelse: blod som et kemisk system
Aalborg Universitet. Skriftlig eksamen i Grundlæggende Mekanik og Termodynamik. Tirsdag d. 11. august 2015 kl
 Aalborg Universitet Skriftlig eksamen i Grundlæggende Mekanik og Termodynamik Tirsdag d. 11. august 2015 kl. 9 00-13 00 Ved bedømmelsen vil der blive lagt vægt på argumentationen (som bør være kort og
Aalborg Universitet Skriftlig eksamen i Grundlæggende Mekanik og Termodynamik Tirsdag d. 11. august 2015 kl. 9 00-13 00 Ved bedømmelsen vil der blive lagt vægt på argumentationen (som bør være kort og
Relativitetsteori. Henrik I. Andreasen Foredrag afholdt i matematikklubben Eksponenten Thisted Gymnasium 2015
 Relativitetsteori Henrik I. Andreasen Foredrag afholdt i matematikklubben Eksponenten Thisted Gymnasium 2015 Koordinattransformation i den klassiske fysik Hvis en fodgænger, der står stille i et lyskryds,
Relativitetsteori Henrik I. Andreasen Foredrag afholdt i matematikklubben Eksponenten Thisted Gymnasium 2015 Koordinattransformation i den klassiske fysik Hvis en fodgænger, der står stille i et lyskryds,
Statistisk mekanik 10 Side 1 af 7 Sortlegemestråling og paramagnetisme. Sortlegemestråling
 Statistisk mekanik 0 Side af 7 Sortlegemestråling I SM9 blev vibrationerne i et krystalgitter beskrevet som fononer. I en helt tilsvarende model beskrives de M svingninger i en sortlegeme-kavitet som fotoner.
Statistisk mekanik 0 Side af 7 Sortlegemestråling I SM9 blev vibrationerne i et krystalgitter beskrevet som fononer. I en helt tilsvarende model beskrives de M svingninger i en sortlegeme-kavitet som fotoner.
Større Skriftlig Opgave
 Større Skriftlig Opgave Den specielle relativitetsteori Martin Sparre, 03u24 December 2005 Elev: Martin Sparre Klasse: 3.u Elev Nr.: 03u24 Institution: Frederiksborg Gymnasium Vejleder: Lasse Storr-Hansen
Større Skriftlig Opgave Den specielle relativitetsteori Martin Sparre, 03u24 December 2005 Elev: Martin Sparre Klasse: 3.u Elev Nr.: 03u24 Institution: Frederiksborg Gymnasium Vejleder: Lasse Storr-Hansen
2.1 Den specielle relativitetsteoris grundlag
 Kapitel 2 Lorentz-transformationen 2.1 Den specielle relativitetsteoris grundlag Ligesom den Newtonske mekanik er den specielle relativitetsteori afgørende forbundet med begrebet inertialsystemer. Et inertialsystem
Kapitel 2 Lorentz-transformationen 2.1 Den specielle relativitetsteoris grundlag Ligesom den Newtonske mekanik er den specielle relativitetsteori afgørende forbundet med begrebet inertialsystemer. Et inertialsystem
Skriftlig eksamen i Statistisk Mekanik den fra 9.00 til Alle hjælpemidler er tilladte. Undtaget er dog net-opkoblede computere.
 Skriftlig eksamen i Statistisk Mekanik den 18-01-2007 fra 900 til 1300 lle hjælpemidler er tilladte Undtaget er dog net-opkoblede computere Opgave 1: I en beholder med volumen V er der rgon-atomer i gasfasen,
Skriftlig eksamen i Statistisk Mekanik den 18-01-2007 fra 900 til 1300 lle hjælpemidler er tilladte Undtaget er dog net-opkoblede computere Opgave 1: I en beholder med volumen V er der rgon-atomer i gasfasen,
Den levende kraft energi og varme
 Den levende kraft energi og varme Hvad vil det sige, at noget har energi, og hvordan opstod begrebet? Og hvad er sammenhængen mellem energi og varme? Forståelsen af dette hang i 1800-tallet tæt sammen
Den levende kraft energi og varme Hvad vil det sige, at noget har energi, og hvordan opstod begrebet? Og hvad er sammenhængen mellem energi og varme? Forståelsen af dette hang i 1800-tallet tæt sammen
Statitisk fysik Minilex
 Statitisk fysik Minilex Henrik Dahl 15. januar 006 Indhold 1 Sandsynlighedsteori Fordelinger 3 Eksperimentelle usikkerheder 3 4 Parameterbestemmelse 3 5 Priors, entropi 3 6 Termodynamik 4 6.1 Kanonisk
Statitisk fysik Minilex Henrik Dahl 15. januar 006 Indhold 1 Sandsynlighedsteori Fordelinger 3 Eksperimentelle usikkerheder 3 4 Parameterbestemmelse 3 5 Priors, entropi 3 6 Termodynamik 4 6.1 Kanonisk
Besvarelser til Calculus Ordinær Eksamen - 5. Januar 2018
 Besvarelser til Calculus Ordinær Eksamen - 5. Januar 18 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 5. Januar 18 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Heisenbergs usikkerhedsrelationer. Abstrakt. Hvorfor? Funktionsrum. Nils Byrial Andersen Institut for Matematik. Matematiklærerdag 2013
 Heisenbergs usikkerhedsrelationer Nils Byrial Andersen Institut for Matematik Matematiklærerdag 013 1 / 17 Abstrakt Heisenbergs usikkerhedsrelationer udtrykker at man ikke på samme tid både kan bestemme
Heisenbergs usikkerhedsrelationer Nils Byrial Andersen Institut for Matematik Matematiklærerdag 013 1 / 17 Abstrakt Heisenbergs usikkerhedsrelationer udtrykker at man ikke på samme tid både kan bestemme
Danmarks Tekniske Universitet
 Danmarks Tekniske Universitet Side 1 af 8 sider Skriftlig prøve, den 24. maj 2005 Kursus navn: Fysik 1 Kursus nr.: 10022 Tilladte hjælpemidler: Alle hjælpemidler tilladt. "Vægtning": Besvarelsen vægtes
Danmarks Tekniske Universitet Side 1 af 8 sider Skriftlig prøve, den 24. maj 2005 Kursus navn: Fysik 1 Kursus nr.: 10022 Tilladte hjælpemidler: Alle hjælpemidler tilladt. "Vægtning": Besvarelsen vægtes
PARTIELT MOLÆRT VOLUMEN
 KemiF1 laboratorieøvelser 2008 ØvelseF1-2 PARTIELT MOLÆRT VOLUMEN Indledning I en binær blanding vil blandingens masse være summen af komponenternes masse; men blandingens volumen vil ikke være summen
KemiF1 laboratorieøvelser 2008 ØvelseF1-2 PARTIELT MOLÆRT VOLUMEN Indledning I en binær blanding vil blandingens masse være summen af komponenternes masse; men blandingens volumen vil ikke være summen
INDHOLD. 5 Lektion Opgave a b Opgave K Lynge opgave
 . Indhold 1 Lektion 1 1 1.1 Opgave A............................... 1 1.1.1 A.a............................... 1 1.1. A.b.............................. 1.1.3 A.c............................... 1. Lynge
. Indhold 1 Lektion 1 1 1.1 Opgave A............................... 1 1.1.1 A.a............................... 1 1.1. A.b.............................. 1.1.3 A.c............................... 1. Lynge
Integration m.h.t. mål med tæthed
 Integration m.h.t. mål med tæthed Sætning (EH 11.7) Lad ν = f µ på (X, E). For alle g M + (X, E) gælder at gdν = g f dµ. Bevis: Standardbeviset: 1) indikatorfunktioner 2) simple funktioner 3) M + -funktioner.
Integration m.h.t. mål med tæthed Sætning (EH 11.7) Lad ν = f µ på (X, E). For alle g M + (X, E) gælder at gdν = g f dµ. Bevis: Standardbeviset: 1) indikatorfunktioner 2) simple funktioner 3) M + -funktioner.
Udledning af Keplers love
 Udledning af Keplers love Kristian Jerslev 8. december 009 Resumé Her præsenteres en udledning af Keplers tre love ud fra Newtonsk tyngdekraft. Begyndende med en analyse af et to-legeme problem vil jeg
Udledning af Keplers love Kristian Jerslev 8. december 009 Resumé Her præsenteres en udledning af Keplers tre love ud fra Newtonsk tyngdekraft. Begyndende med en analyse af et to-legeme problem vil jeg
Eksamen i Mat F, april 2006
 Eksamen i Mat F, april 26 Opgave 1 Lad F være et vektorfelt, givet i retvinklede koordinater som: F x x F = F x i + F y j + F z k = F y = 2z F z y Udregn F og F: F = F x + F y + F z = 1 + +. F = F z F
Eksamen i Mat F, april 26 Opgave 1 Lad F være et vektorfelt, givet i retvinklede koordinater som: F x x F = F x i + F y j + F z k = F y = 2z F z y Udregn F og F: F = F x + F y + F z = 1 + +. F = F z F
Epistel E2 Partiel differentiation
 Epistel E2 Partiel differentiation Benny Lautrup 19 februar 24 Funktioner af flere variable kan differentieres efter hver enkelt, med de øvrige variable fasthol Definitionen er f(x, y) x f(x, y) f(x +
Epistel E2 Partiel differentiation Benny Lautrup 19 februar 24 Funktioner af flere variable kan differentieres efter hver enkelt, med de øvrige variable fasthol Definitionen er f(x, y) x f(x, y) f(x +
Besvarelser til Calculus Ordinær Eksamen - 3. Januar 2017
 Besvarelser til Calculus Ordinær Eksamen - 3. Januar 17 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 3. Januar 17 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Fra Absolut Rum til Minkowski Rum
 Fra Absolut Rum til Minkowski Rum R e l a t i v i t e t s t e o r i e n 1 6 3 0-1 9 0 5 Folkeuniversitetet 27. november 2007 Poul Hjorth Institut for Matematik Danmarke Tekniske Universitet 1 Johannes
Fra Absolut Rum til Minkowski Rum R e l a t i v i t e t s t e o r i e n 1 6 3 0-1 9 0 5 Folkeuniversitetet 27. november 2007 Poul Hjorth Institut for Matematik Danmarke Tekniske Universitet 1 Johannes
Statistisk mekanik 6 Side 1 af 11 Hastighedsfordeling for ideal gas. Enatomig ideal gas
 Statistisk ekanik 6 Side 1 af 11 Enatoig ideal gas etragt en enatoig ideal gas bestående af N uskelnelige olekyler ed asse, der befinder sig i en beholder ed rufang V. For at kunne bestee tilstandssuen
Statistisk ekanik 6 Side 1 af 11 Enatoig ideal gas etragt en enatoig ideal gas bestående af N uskelnelige olekyler ed asse, der befinder sig i en beholder ed rufang V. For at kunne bestee tilstandssuen
Dampmaskinen. 2-3) Opvarmning I tanken tilføres varme, hvorved vandet varmes op til kogepunktet, fordamper og forlader tanken ved samme tryk.
 Dampmaskinen I en dampmaskine udnyttes energi i vanddamp til mekanisk arbejde. For at fordampe vand inden det føres ind i dampmaskinen tilføres der energi f.eks. ved forbrænding af kul. Vanddampen kan
Dampmaskinen I en dampmaskine udnyttes energi i vanddamp til mekanisk arbejde. For at fordampe vand inden det føres ind i dampmaskinen tilføres der energi f.eks. ved forbrænding af kul. Vanddampen kan
Formelsamling til Fysik B
 Formelsamling til Fysik B Af Dann Olesen og Søren Andersen Hastighed(velocity) Densitet Tryk Arbejde Definitioner og lignende Hastighed, [ ] Strækning, [ ] Volumen(rumfang), [ ] Tryk, [ ] : Pascal Kraft,
Formelsamling til Fysik B Af Dann Olesen og Søren Andersen Hastighed(velocity) Densitet Tryk Arbejde Definitioner og lignende Hastighed, [ ] Strækning, [ ] Volumen(rumfang), [ ] Tryk, [ ] : Pascal Kraft,
Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 2016
 Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
MATEMATIK A-NIVEAU Vejledende eksempler på eksamensopgaver og eksamensopgaver i matematik, 2012 Differentialligninger
 MATEMATIK A-NIVEAU Vejledende eksempler på eksamensopgaver og eksamensopgaver i matematik, 2012 Differentialligninger 2016 MATEMATIK A-NIVEAU Vejledende eksempler på eksamensopgaver og eksamensopgaver
MATEMATIK A-NIVEAU Vejledende eksempler på eksamensopgaver og eksamensopgaver i matematik, 2012 Differentialligninger 2016 MATEMATIK A-NIVEAU Vejledende eksempler på eksamensopgaver og eksamensopgaver
Aalborg Universitet. Skriftlig eksamen i Grundlæggende Mekanik og Termodynamik. Tirsdag d. 2. juni 2015 kl
 Aalborg Universitet Skriftlig eksamen i Grundlæggende Mekanik og Termodynamik Tirsdag d. 2. juni 2015 kl. 9 00-13 00 Ved bedømmelsen vil der blive lagt vægt på argumentationen (som bør være kort og præcis),
Aalborg Universitet Skriftlig eksamen i Grundlæggende Mekanik og Termodynamik Tirsdag d. 2. juni 2015 kl. 9 00-13 00 Ved bedømmelsen vil der blive lagt vægt på argumentationen (som bør være kort og præcis),
Aalborg Universitet. Skriftlig eksamen i Grundlæggende Mekanik og Termodynamik. Fredag d. 8. juni 2018 kl
 Aalborg Universitet Skriftlig eksamen i Grundlæggende Mekanik og Termodynamik Fredag d. 8. juni 2018 kl. 9 00-13 00 Ved bedømmelsen vil der blive lagt vægt på argumentationen (som bør være kort og præcis),
Aalborg Universitet Skriftlig eksamen i Grundlæggende Mekanik og Termodynamik Fredag d. 8. juni 2018 kl. 9 00-13 00 Ved bedømmelsen vil der blive lagt vægt på argumentationen (som bør være kort og præcis),
Danmarks Tekniske Universitet
 Danmarks Tekniske Universitet Side 1 af 4 sider Skriftlig prøve, den 29. maj 2006 Kursus navn: Fysik 1 Kursus nr. 10022 Tilladte hjælpemidler: Alle "Vægtning": Eksamenssættet vurderes samlet. Alle svar
Danmarks Tekniske Universitet Side 1 af 4 sider Skriftlig prøve, den 29. maj 2006 Kursus navn: Fysik 1 Kursus nr. 10022 Tilladte hjælpemidler: Alle "Vægtning": Eksamenssættet vurderes samlet. Alle svar
Teoretiske Øvelser Mandag den 13. september 2010
 Hans Kjeldsen hans@phys.au.dk 6. september 00 eoretiske Øvelser Mandag den 3. september 00 Computerøvelse nr. 3 Ligning (6.8) og (6.9) på side 83 i Lecture Notes angiver betingelserne for at konvektion
Hans Kjeldsen hans@phys.au.dk 6. september 00 eoretiske Øvelser Mandag den 3. september 00 Computerøvelse nr. 3 Ligning (6.8) og (6.9) på side 83 i Lecture Notes angiver betingelserne for at konvektion
Om første og anden fundamentalform
 Geometri, foråret 2005 Jørgen Larsen 9. marts 2005 Om første og anden fundamentalform 1 Tangentrummet; første fundamentalform Vi betragter en flade S parametriseret med σ. Lad P = σu 0, v 0 være et punkt
Geometri, foråret 2005 Jørgen Larsen 9. marts 2005 Om første og anden fundamentalform 1 Tangentrummet; første fundamentalform Vi betragter en flade S parametriseret med σ. Lad P = σu 0, v 0 være et punkt
Statistisk mekanik 5 Side 1 af 11 Hastighedsfordeling for ideal gas. Enatomig ideal gas
 Statistisk ekanik 5 Side 1 af 11 Enatoig ideal gas etragt en enatoig ideal gas bestående af N uskelnelige olekyler ed asse, der befinder sig i en beholder ed rufang V. For at kunne bestee tilstandssuen
Statistisk ekanik 5 Side 1 af 11 Enatoig ideal gas etragt en enatoig ideal gas bestående af N uskelnelige olekyler ed asse, der befinder sig i en beholder ed rufang V. For at kunne bestee tilstandssuen
Matematik F2 Opgavesæt 6
 Opgave 4: Udtryk funktionen f(θ) = sin θ ved hjælp af Legendre-polynomierne på formen P l (cos θ). Dvs. find koefficienterne a l i ekspansionen f(θ) = a l P l (cos θ) l= Svar: Bemærk, at funktionen er
Opgave 4: Udtryk funktionen f(θ) = sin θ ved hjælp af Legendre-polynomierne på formen P l (cos θ). Dvs. find koefficienterne a l i ekspansionen f(θ) = a l P l (cos θ) l= Svar: Bemærk, at funktionen er
Dynamik. 1. Kræfter i ligevægt. Overvejelser over kræfter i ligevægt er meget vigtige i den moderne fysik.
 M4 Dynamik 1. Kræfter i ligevægt Overvejelser over kræfter i ligevægt er meget vigtige i den moderne fysik. Fx har nøglen til forståelsen af hvad der foregår i det indre af en stjerne været betragtninger
M4 Dynamik 1. Kræfter i ligevægt Overvejelser over kræfter i ligevægt er meget vigtige i den moderne fysik. Fx har nøglen til forståelsen af hvad der foregår i det indre af en stjerne været betragtninger
Elektromagnetisme 13 Side 1 af 8 Maxwells ligninger. Forskydningsstrømme I S 1
 Elektromagnetisme 13 Side 1 af 8 Betragt Amperes lov fra udtryk (1.1) anvendt på en kapacitor der er ved at blive ladet op. For de to flader og S der begge S1 afgrænses af C fås H dl = J ˆ C S n da = I
Elektromagnetisme 13 Side 1 af 8 Betragt Amperes lov fra udtryk (1.1) anvendt på en kapacitor der er ved at blive ladet op. For de to flader og S der begge S1 afgrænses af C fås H dl = J ˆ C S n da = I
FYSIK 3 / TERMODYNAMIK Københavns Universitet, 13. april, 2016, Skriftlig prøve
 FYSIK 3 / TERMODYNAMIK Københavns Universitet, 13. april, 2016, Skriftlig prøve Benyttelse af medbragt litteratur, noter, lommeregner og computer uden internetadgang er tilladt. Der må skrives med blyant.
FYSIK 3 / TERMODYNAMIK Københavns Universitet, 13. april, 2016, Skriftlig prøve Benyttelse af medbragt litteratur, noter, lommeregner og computer uden internetadgang er tilladt. Der må skrives med blyant.
Klassisk relativitet
 Stoffers opbygning og egenskaber 1 Side 1 af 12 Hvad sker der, hvis man kører i sin gamle Mazda med nærlysfart og tænder forlygterne; vil man så se lyset snegle sig af sted foran sig...?! Klassisk relativitet
Stoffers opbygning og egenskaber 1 Side 1 af 12 Hvad sker der, hvis man kører i sin gamle Mazda med nærlysfart og tænder forlygterne; vil man så se lyset snegle sig af sted foran sig...?! Klassisk relativitet
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin August 2011 - Juni 2013 Institution Gymnasiet HTX Skjern 21-02-2012 Uddannelse Fag og niveau Lærer(e) HTX
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin August 2011 - Juni 2013 Institution Gymnasiet HTX Skjern 21-02-2012 Uddannelse Fag og niveau Lærer(e) HTX
Løsningsforslag til opgavesæt 5
 Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
MATEMATIK A-NIVEAU. Kapitel 1
 MATEMATIK A-NIVEAU Vejledende eksempler på eksamensopgaver og eksamensopgaver i matematik, 01 Kapitel 1 016 MATEMATIK A-NIVEAU Vejledende eksempler på eksamensopgaver og eksamensopgaver i matematik 01
MATEMATIK A-NIVEAU Vejledende eksempler på eksamensopgaver og eksamensopgaver i matematik, 01 Kapitel 1 016 MATEMATIK A-NIVEAU Vejledende eksempler på eksamensopgaver og eksamensopgaver i matematik 01
Log - Mikro og makroskopiske tilstande, det mikrokanoniske ensemble, multiplicitet og entropi
 Log - Mikro og makroskopiske tilstande, det mikrokanoniske ensemble, multiplicitet og entropi Amalie Christensen 26. februar 2009 Indhold 1 Om spillet 2 2 Multipliciteten af makroskopiske tilstande 3 3
Log - Mikro og makroskopiske tilstande, det mikrokanoniske ensemble, multiplicitet og entropi Amalie Christensen 26. februar 2009 Indhold 1 Om spillet 2 2 Multipliciteten af makroskopiske tilstande 3 3
Differentialregning i R k
 Differentialregning i R k Lad U R k være åben, og lad h : U R m være differentiabel. Den afledte i et punkt x U er Dh(x) = h 1 (x) x 1 h 2 (x) x 1. h m (x) x 1 h 1 (x) x 2... h 2 (x) x 2.... h m (x) x
Differentialregning i R k Lad U R k være åben, og lad h : U R m være differentiabel. Den afledte i et punkt x U er Dh(x) = h 1 (x) x 1 h 2 (x) x 1. h m (x) x 1 h 1 (x) x 2... h 2 (x) x 2.... h m (x) x
Antag at. 1) f : R k R m er differentiabel i x, 2) g : R m R p er differentiabel i y = f(x), . p.1/18
 Differentialregning i R k Kæderegel Lad U R k være åben, og lad h : U R m være differentiabel Antag at Den afledte i et punkt x U er Dh(x) = 1) f : R k R m er differentiabel i x, 2) g : R m R p er differentiabel
Differentialregning i R k Kæderegel Lad U R k være åben, og lad h : U R m være differentiabel Antag at Den afledte i et punkt x U er Dh(x) = 1) f : R k R m er differentiabel i x, 2) g : R m R p er differentiabel
Indhold. Noter til statistisk fysik II. 3. januar 2012. Jens Egebjerg Bækhøj & Christian Kraglund Andersen
 Noter til statistisk fysik II 3. januar 2012 Jens Egebjerg Bækhøj & Christian Kraglund Andersen Institut for Fysik og Astronomi Aarhus Universitet, Denmark Indhold Indhold i 1 Termodynamik 1 1.1 Systemet
Noter til statistisk fysik II 3. januar 2012 Jens Egebjerg Bækhøj & Christian Kraglund Andersen Institut for Fysik og Astronomi Aarhus Universitet, Denmark Indhold Indhold i 1 Termodynamik 1 1.1 Systemet
Danmarks Tekniske Universitet
 Danmarks Tekniske Universitet Side af 7 Skriftlig prøve, tirsdag den 6. december, 008, kl. 9:00-3:00 Kursus navn: ysik Kursus nr. 00 Tilladte hjælpemidler: Alle hjælpemidler er tilladt. "Vægtning": Besvarelsen
Danmarks Tekniske Universitet Side af 7 Skriftlig prøve, tirsdag den 6. december, 008, kl. 9:00-3:00 Kursus navn: ysik Kursus nr. 00 Tilladte hjælpemidler: Alle hjælpemidler er tilladt. "Vægtning": Besvarelsen
Elementær termodynamik og kalorimetri
 Elementær termodynamik og kalorimetri 1/14 Elementær termodynamik og kalorimetri Indhold 1. Indre og ydre energi...2 2. Varmeteoriens (termodynamikkens) 1. hovedsætning...2 3. Stempelarbejde...4 4. Isoterm
Elementær termodynamik og kalorimetri 1/14 Elementær termodynamik og kalorimetri Indhold 1. Indre og ydre energi...2 2. Varmeteoriens (termodynamikkens) 1. hovedsætning...2 3. Stempelarbejde...4 4. Isoterm
Den klassiske oscillatormodel
 Kvantemekanik 6 Side af 8 n meget central model inden for KM er den såkaldte harmoniske oscillatormodel, som historisk set spillede en afgørende rolle i de banebrydende beskrivelser af bla. sortlegemestråling
Kvantemekanik 6 Side af 8 n meget central model inden for KM er den såkaldte harmoniske oscillatormodel, som historisk set spillede en afgørende rolle i de banebrydende beskrivelser af bla. sortlegemestråling
Elektromagnetisme 13 Side 1 af 8 Maxwells ligninger. Forskydningsstrømme I S 1
 Elektromagnetisme 13 Side 1 af 8 Betragt Amperes lov fra udtryk (1.1) anvendt på en kapacitor der er ved at blive ladet op. For de to flader og S der begge S1 afgrænses af C fås H dl = J ˆ C S n da = I
Elektromagnetisme 13 Side 1 af 8 Betragt Amperes lov fra udtryk (1.1) anvendt på en kapacitor der er ved at blive ladet op. For de to flader og S der begge S1 afgrænses af C fås H dl = J ˆ C S n da = I
Undervisningsbeskrivelse Fysik B - 2.g
 Undervisningsbeskrivelse Fysik B - 2.g Termin August 2014 Juni 2016 Institution Uddannelse Fag og niveau Lærer Rybners HTX Htx Fysik B Tom Løgstrup (TL) Hold 2.b Oversigt over planlagte undervisningsforløb
Undervisningsbeskrivelse Fysik B - 2.g Termin August 2014 Juni 2016 Institution Uddannelse Fag og niveau Lærer Rybners HTX Htx Fysik B Tom Løgstrup (TL) Hold 2.b Oversigt over planlagte undervisningsforløb
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Institution Termin hvori undervisningen afsluttes: Maj-juni 2012 HTX Vibenhus - Københavns Tekniske Gymnasium
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Institution Termin hvori undervisningen afsluttes: Maj-juni 2012 HTX Vibenhus - Københavns Tekniske Gymnasium
Fysik 2 - Den Harmoniske Oscillator
 Fysik 2 - Den Harmoniske Oscillator Esben Bork Hansen, Amanda Larssen, Martin Qvistgaard Christensen, Maria Cavallius 5. januar 2009 Indhold 1 Formål 1 2 Forsøget 2 3 Resultater 3 4 Teori 4 4.1 simpel
Fysik 2 - Den Harmoniske Oscillator Esben Bork Hansen, Amanda Larssen, Martin Qvistgaard Christensen, Maria Cavallius 5. januar 2009 Indhold 1 Formål 1 2 Forsøget 2 3 Resultater 3 4 Teori 4 4.1 simpel
Løsningsforslag til opgavesæt 5
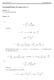 Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
Oversigt [S] 2.7, 2.9, 11.4
![Oversigt [S] 2.7, 2.9, 11.4 Oversigt [S] 2.7, 2.9, 11.4](/thumbs/48/24213798.jpg) Oversigt [S] 2.7, 2.9, 11.4 Nøgleord og begreber Tangentlinje for graf Tangentplan for graf Test tangentplan Lineær approximation i en og flere variable Test approximation Differentiabilitet i flere variable
Oversigt [S] 2.7, 2.9, 11.4 Nøgleord og begreber Tangentlinje for graf Tangentplan for graf Test tangentplan Lineær approximation i en og flere variable Test approximation Differentiabilitet i flere variable
Forklaring. Størrelsesforhold i biologien DIFFUSION. Biofysik forelæsning 8 Kapitel 1 (8) Mindste organisme: 0.3 :m = m (mycoplasma)
 Størrelsesforhold i biologien Forklaring Mindste organisme: 0.3 :m = 3 10-7 m (mycoplasma) Største organisme: 3 10 1 m (blåhval) Største Organismer : 10 Mindste = Enkelte celler: 0.3 :m - 3 :m Største
Størrelsesforhold i biologien Forklaring Mindste organisme: 0.3 :m = 3 10-7 m (mycoplasma) Største organisme: 3 10 1 m (blåhval) Største Organismer : 10 Mindste = Enkelte celler: 0.3 :m - 3 :m Største
MM501 forelæsningsslides
 MM50 forelæsningsslides uge 36, 2009 Produceret af Hans J. Munkholm Nogle talmængder s. 3 N = {, 2, 3, } omtales som de naturlige tal eller de positive heltal. Z = {0, ±, ±2, ±3, } omtales som de hele
MM50 forelæsningsslides uge 36, 2009 Produceret af Hans J. Munkholm Nogle talmængder s. 3 N = {, 2, 3, } omtales som de naturlige tal eller de positive heltal. Z = {0, ±, ±2, ±3, } omtales som de hele
Besvarelser til Calculus Ordinær Eksamen Juni 2018
 Besvarelser til Calculus Ordinær Eksamen - 5. Juni 08 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 5. Juni 08 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Bølgeligningen. Indhold. Udbredelseshastighed for bølger i forskellige stoffer 1
 Udbredelseshastighed for bølger i forskellige stoffer 1 Bølgeligningen Indhold 1. Bølgeligningen.... Udbredelseshastigheden for bølger på en elastisk streng...3 3. Udbredelseshastigheden for longitudinalbølger
Udbredelseshastighed for bølger i forskellige stoffer 1 Bølgeligningen Indhold 1. Bølgeligningen.... Udbredelseshastigheden for bølger på en elastisk streng...3 3. Udbredelseshastigheden for longitudinalbølger
Bevægelsens Geometri
 Bevægelsens Geometri Vi vil betragte bevægelsen af et punkt. Dette punkt kan f.eks. være tyngdepunktet af en flue, et menneske, et molekyle, en galakse eller hvad man nu ellers har lyst til at beskrive.
Bevægelsens Geometri Vi vil betragte bevægelsen af et punkt. Dette punkt kan f.eks. være tyngdepunktet af en flue, et menneske, et molekyle, en galakse eller hvad man nu ellers har lyst til at beskrive.
Undervisningsbeskrivelse. Fysik A - 2.A
 Undervisningsbeskrivelse. Fysik A - 2.A Termin August 2014 Juni 2017 Institution Uddannelse Fag og niveau Lærer Rybners HTX HTX Fysik A Jesper Pedersen (JEPE) Hold 2.A Oversigt over planlagte undervisningsforløb
Undervisningsbeskrivelse. Fysik A - 2.A Termin August 2014 Juni 2017 Institution Uddannelse Fag og niveau Lærer Rybners HTX HTX Fysik A Jesper Pedersen (JEPE) Hold 2.A Oversigt over planlagte undervisningsforløb
Teoretisk Statistik, 16. februar Generel teori,repetition
 1 Uge 8 Teoretisk Statistik, 16. februar 2004 1. Generel teori, repetition 2. Diskret udfaldsrum punktssh. 3. Fordelingsfunktionen 4. Tæthed 5. Transformationer 6. Diskrete vs. Kontinuerte stokastiske
1 Uge 8 Teoretisk Statistik, 16. februar 2004 1. Generel teori, repetition 2. Diskret udfaldsrum punktssh. 3. Fordelingsfunktionen 4. Tæthed 5. Transformationer 6. Diskrete vs. Kontinuerte stokastiske
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin August 2014 Institution Uddannelse Fag og niveau Lærer(e) Hold VUF - Voksenuddannelsescenter Frederiksberg
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin August 2014 Institution Uddannelse Fag og niveau Lærer(e) Hold VUF - Voksenuddannelsescenter Frederiksberg
Momenter som deskriptive størrelser. Hvad vi mangler fra onsdag. Momenter for sandsynlighedsmål
 Hvad vi mangler fra onsdag Momenter som deskriptive størrelser Sandsynlighedsmål er komplicerede objekter de tildeler numeriske værdier til alle hændelser i en σ-algebra. Vi har behov for simplere, deskriptive
Hvad vi mangler fra onsdag Momenter som deskriptive størrelser Sandsynlighedsmål er komplicerede objekter de tildeler numeriske værdier til alle hændelser i en σ-algebra. Vi har behov for simplere, deskriptive
Hvad vi mangler fra onsdag. Vi starter med at gennemgå slides fra onsdag.
 Hvad vi mangler fra onsdag Vi starter med at gennemgå slides 34-38 fra onsdag. Slide 1/17 Niels Richard Hansen MI forelæsninger 6. December, 2013 Momenter som deskriptive størrelser Sandsynlighedsmål er
Hvad vi mangler fra onsdag Vi starter med at gennemgå slides 34-38 fra onsdag. Slide 1/17 Niels Richard Hansen MI forelæsninger 6. December, 2013 Momenter som deskriptive størrelser Sandsynlighedsmål er
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Institution Uddannelse Fag og niveau Lærer(e) Termin hvori undervisningen afsluttes: Maj-juni 2014 Uddannelsescenter
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Institution Uddannelse Fag og niveau Lærer(e) Termin hvori undervisningen afsluttes: Maj-juni 2014 Uddannelsescenter
Debatten om tidens pil
 Debatten om tidens pil - Stemt ved den naturvidenskabelige kammertone Debating the arrow of time -Tuned by the scientific pilottone. Udarbejdet af Steffen Dreyer Andersen Lars Hervig Jacobsen Kim Olsson
Debatten om tidens pil - Stemt ved den naturvidenskabelige kammertone Debating the arrow of time -Tuned by the scientific pilottone. Udarbejdet af Steffen Dreyer Andersen Lars Hervig Jacobsen Kim Olsson
Antag X 1, X 2,..., X n er n uafhængige stokastiske variable, hvor Var(X 1 )=σ 2 1,..., Var(X n )=σ 2 n.
 Simple fejlforplantningslov Landmålingens fejlteori Lektion 6 Den generelle fejlforplantningslov Antag X, X,, X n er n uafhængige stokastiske variable, hvor Var(X )σ,, Var(X n )σ n Lad Y g(x, X,, X n ),
Simple fejlforplantningslov Landmålingens fejlteori Lektion 6 Den generelle fejlforplantningslov Antag X, X,, X n er n uafhængige stokastiske variable, hvor Var(X )σ,, Var(X n )σ n Lad Y g(x, X,, X n ),
Undervisningsbeskrivelse. Fysik B - 2.E
 Undervisningsbeskrivelse. Fysik B - 2.E Termin August 2016 Juni 2018 Institution Uddannelse Fag og niveau Lærer Rybners HTX HTX Fysik B Jesper Pedersen (JEPE) Hold 2.E Oversigt over undervisningsforløb
Undervisningsbeskrivelse. Fysik B - 2.E Termin August 2016 Juni 2018 Institution Uddannelse Fag og niveau Lærer Rybners HTX HTX Fysik B Jesper Pedersen (JEPE) Hold 2.E Oversigt over undervisningsforløb
Matematisk modellering og numeriske metoder. Lektion 11
 Matematisk modellering og numeriske metoder Lektion 11 Morten Grud Rasmussen 17. oktober, 2013 1 Partielle differentialligninger 1.1 D Alemberts løsning af bølgeligningen [Bogens sektion 12.4 på side 553]
Matematisk modellering og numeriske metoder Lektion 11 Morten Grud Rasmussen 17. oktober, 2013 1 Partielle differentialligninger 1.1 D Alemberts løsning af bølgeligningen [Bogens sektion 12.4 på side 553]
Elektrokemisk potential, membranpotential og. Donnanligevægt
 Elektrokemisk potential, membranpotential og Donnanligevægt Elektrokemisk potential: µ Når en elektrisk ladning, q, transporteres i et ydre elektrisk felt fra potentialet φ 1 til φ 2, er det tilhørende
Elektrokemisk potential, membranpotential og Donnanligevægt Elektrokemisk potential: µ Når en elektrisk ladning, q, transporteres i et ydre elektrisk felt fra potentialet φ 1 til φ 2, er det tilhørende
Impuls og kinetisk energi
 Impuls og kinetisk energi Peter Hoberg, Anton Bundgård, and Peter Kongstad Hold Mix 1 (Dated: 7. oktober 2015) 201405192@post.au.dk 201407987@post.au.dk 201407911@post.au.dk 2 I. INDLEDNING I denne øvelse
Impuls og kinetisk energi Peter Hoberg, Anton Bundgård, and Peter Kongstad Hold Mix 1 (Dated: 7. oktober 2015) 201405192@post.au.dk 201407987@post.au.dk 201407911@post.au.dk 2 I. INDLEDNING I denne øvelse
Stabilitet af kølet tankreaktor
 Stabilitet af kølet tankreaktor Vi betragter en velomrørt tankreaktor, i hvilken den exoterme reaktion B skal gennemføres. Tankreaktorens volumen er V m 3 ), og reaktanten tilføres i en opløsning med den
Stabilitet af kølet tankreaktor Vi betragter en velomrørt tankreaktor, i hvilken den exoterme reaktion B skal gennemføres. Tankreaktorens volumen er V m 3 ), og reaktanten tilføres i en opløsning med den
Biofysik forelæsning 8 Kapitel 1 (8)
 Størrelsesforhold i biologien Forklaring Mindste organisme:.3 :m = 3-7 m (mycoplasma) Største organisme: 3 m (blåhval) Største Organismer : Mindste = Enkelte celler:.3 :m - 3 :m Største Celler : Mindste
Størrelsesforhold i biologien Forklaring Mindste organisme:.3 :m = 3-7 m (mycoplasma) Største organisme: 3 m (blåhval) Største Organismer : Mindste = Enkelte celler:.3 :m - 3 :m Største Celler : Mindste
Journalark. Varmekapacitet
 Journalark Varmekapacitet 1 Formål Formålet med dette eksperiment er at undersøge ændringer i temperatur og energimængder ved opvarmning af vand med en elkedel og med varme metalklodser. Til at opfylde
Journalark Varmekapacitet 1 Formål Formålet med dette eksperiment er at undersøge ændringer i temperatur og energimængder ved opvarmning af vand med en elkedel og med varme metalklodser. Til at opfylde
Løsningsforslag Mat B August 2012
 Løsningsforslag Mat B August 2012 Opgave 1 (5 %) a) Løs uligheden: 2x + 11 x 1 Løsning: 2x + 11 x 1 2x x + 1 0 3x + 12 0 3x 12 Divideres begge sider med -3 (og husk at vende ulighedstegnet!) x 4 Opgave
Løsningsforslag Mat B August 2012 Opgave 1 (5 %) a) Løs uligheden: 2x + 11 x 1 Løsning: 2x + 11 x 1 2x x + 1 0 3x + 12 0 3x 12 Divideres begge sider med -3 (og husk at vende ulighedstegnet!) x 4 Opgave
