MOGENS ODDERSHEDE LARSEN. Komplekse tal

Transkript

1 MOGENS ODDERSHEDE LARSEN Komplekse tal a b. udgave 004

2 FORORD Dette otat giver e kort idførig i teorie for komplekse tal, regeregler, røddere i polyomier bl.a. med heblik på avedelser ved løsig af lieære differetialligiger, og i svigigsteorie. Avacerede lommeregere som Ti89 og matematkprogrammer som Maple ka let foretage beregiger med komplekse tal, fide rødder i polyomier osv. Der vil derfor blive givet eksempler på hvorledes ma ka foretage beregigere med etop disse to regemidler, me det må dog betoes, at hvis ma ikke er i stad til at maipulere med simpe udtryk, bliver det æste umuligt at læse e tekisk tekst eller forstå et foredrag, hvori der idgår oge matematik. Det er derfor vigtigt. at ma mauelt foretager beregigere af ekle problemer samtidig med, at ma er i stad til at kue få e avaceret lommereger til at foretager mere komplicerede beregiger, og aturligvis også ka fortolke disse. Det forudsættes derfor, at ma har rådighed over e matematiklommereger som eksempelvis Ti 89. Som eksempel på hvorledes ma ka avede et egetligt matematikprogram, agives også ogle af ordrere i programmet Maple Adre oter i samme serie er Matematiske grudbegreber Giver e kort geemgag af defiitioer og regeregler for de mest almidelige reelle fuktioer af. variabel, disses differetiatio og itegratio, Vektorer Idhold: ) Vektorer i pla og rum, ) Rumgeometri (relatioer mellem pukt, liie og pla) ) Kurver i pla givet ved e parameterfremstillig Matricer og lieære ligiger Idhold: ) Regeregler for matricer, ) Lieære ligigssystemer, heruder løsig af overbestemt ligigssystem Differetialligiger Idhold: ). orde (seperable, lieære, umerisk løsig), ). og højere orde med kostate koefficieter, ) Laplacetrasformetio til løsig af differetialligigssystemer og differetialligiger med forsikelse Fourieraalyse Idhold: ) Reelle Fourierrækker, ) Fourierrækker på kompleks form, ) Fouriertrasformatio 4) Diskret Fouriertrasformatio Alle de ævte otater ka i pdf-format fides på adresse december 004 Moges Oddershede Larse ii

3 Idhold INDHOLD Talmægder... Defiitio af komplekse tal.... Additio af komplekse tal.... Multiplikatio og divisio... Rektagulær form Polær form Ekspoetialfuktioe Polyomier De biome ligig z = a Adegradsligige Polyomier af højere grad ed Dekompoerig af polyomiers brøker... 4 Opgaver... 6 Stikord... 7 iii

4 Talmægder. Talmægder Geem si tilværelse har ma ofte måttet udvide sit talbegreb. Ma starter før skolealdere med med de aturlige tal N:,,,... Hurtigt derefter udvider ma med tallet 0. På et tidspukt møder ma problemer, hvor det er ødvedigt, at udvide talbegrebet til de hele tal Z :...., -, -, -, 0,,,.... Mmatematisk skyldes det, at ma øsker, at ligiger som x + 4 = skal have e løsig. Det bliver også ødvedigt at idføre brøker, dvs. de ratioale tal Q:...,,,,,,,... matematisk fordi ma øsker, at ligiger som 0 x = 5 skal have e løsig. De ratioale tal udgør et såkaldt tallegeme, hvor de 4 regigsarter additio, subtraktio, multiplikatio og divisio af ratioale tal ige giver ratioale tal. Det er derfor ikke mærkeligt, at ma i si dagligdag ikke føler oget behov for et mere omfattede talbegreb. Matematisk betyder det, at Q er et tallegeme, dvs opgylder følgede regler: ) a + b = b + a, a b = b a kommutative love ) (a + b) + c = a + (b + c), (a b) c = a (b c) associative love ) 0 + a = a + 0 = a, a = a = a 0 og er eutrale elemeter 4) a + (-a) = (-a) + a =0, a a = a a = (a 0) modsat og iverst elemet eksisterer 5) ( a+ b) c= a c+ b c distributive lov De reelle tal R. Allerede oldtides grækere opdagede dog, at lægde af hypoteuse i e retviklet ligebeet trekat hvor katedere havde lægde, ikke ka udtrykkes ved ratioalt tal, eller med adre ord så ka ikke skrives som e brøk. Bevis: Lad os atage, at = p p p p, hvor p og q er hele tal og er uforkortelig. Vi har da = = p = q. q q q q Heraf følger, at p er et lige tal. Nu gælder det jo, at produktet af ulige tal ige er ulige, så p ka ikke være ulige. p må følgelig være lige, dvs. kue skrives p =, hvor er et helt tal.vi har u p = q ( ) = q = q. Heraf følger p ige at q er et lige tal. At både p og q er lige tal strider imidlertid mod at brøke er uforkortelig. ka følgelig ikke skrives q siom e brøk. For at kue løse ligiger som x = må vi derfor udvide vort talbegreb til de relle tal R. Ma ka vise, at der til ethvert pukt på e talliie svarer et reelt tal, og omvedt. De reelle tal udgår også et tallegeme, og lagt de fleste matematiske problemer, løses idefor de reelle tal Komplekse tal C: Imidlertid fadt ma allerede ca. år 550, at for at berege sædvalige reelle løsiger til trediegradsligiger ville det være praktisk at idføre ogle ye tal, svarede til, at ligige x = har e løsig. Som vi vil se, vil disse tal med fordel kue askueliggøres som pukter i e talpla. Mægde af komplekse tal C vil også udgøre et tallegeme. I dag betyder de komplekse tal e begrebsmæssig og arbejdsmæssig foreklig af mage problemstilliger og løsigsmetoder, især år der idgår svigiger.

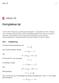
5 Komplekse tal Defiitio af komplekse tal På samme måde som vi kytter de reelle tal til e talliie de reelle tals akse, kyttes de komplekse tal til puktere i e pla. De kaldes de "komplekse talpla". Rektagulære koordiater. I de komplekse talpla idlægges et retviklet koordiatsystem, hvor førsteakse er de reelle tals akse, og adeakse kaldes de imagiære tals akse. Lad et pukt P have koordiatere ( a, a). Ma siger da, at det der til puktet svarer et komplekst tal a, som har realdele og imagiærdele a. Ma skriver kort Re(a) = a og Im(a)= a (se figur.). a Fig... Rektagulære koordiater Polære koordiater. Et pukt P's placerig i et koordiatsystem ka agives i såkaldte polære koordiater (r,v) (se figur.), hvor r = lægde OP af stedvektore til P og v = vikle fra første- akse til stedvektore OP.Vikle måles i plaes positive omløbsretig (mod uret) og er aturligvis ku bestemt på ær et multiplum af. Hvis P = O er vikle ude betydig og ka gives e vilkårlig værdi. Fig. De polære koordiater r,v. Lad det til puktet P svarede komplekse tal være a. De polære koordiater til a beteges a og arg(a) (se figur.4), hvor a kaldes modulus af a eller de umeriske værdi af a, mes arg(a) kaldes argumetet af a. De værdi for arg(a), som tilhører itervallet ; kaldes hovedværdie af arg(a). ] [ E kort skrivemåde er a = () r v, eksempelvis = (). Som det vil blive vist i et seere Fig... Et komplekst tals polære koordiater afsit, er e ade skrivemåde mere hesigtsmæssig. Det komplekse tal med realdel 0 og imagiærdel kaldes de "imagiære ehed" og beteges med bogstavet i (eller med bogstavet j ). Vi har altså i = () (se figur.)

6 Defiitio af komplekse tal Ma ka aturligvis ikke tale om tal, ude at defiere additio og multiplikatio, og de omvedte regigsarter subtraktio og diviso, samt idse at de sædvalige regeregler gælder. Additio og subtraktio Defiitio af additio. To komplekse tal a og b adderes ved at addere deres stedvektorer (Re(a), Im(a)) og (Re(b), Im(b)), dvs. summe a+b har realdele Re(a)+Re(b) og imagiærdele Im(a)+Im(b), (se figur.4). Fig.4. Additio a + b Fig..5. Subtraktio a - b Subtraktio af to komplekse tal a b udføres som vektorsubtraktio (figur.5), dvs. a b får realdel Re(a) - Re(b) og imagiærdel Im(a) - Im(b). Subtraktioe a - b plejer ma at defiere ved additioe a+(- b), hvor det "modsatte tal" - b er givet ved, at der skal gælde b+(- b) = 0, dvs. - b må have realdel - Re(b) og imagiærdel - Im(b) og altså stedvektor modsat b's. Additioe og subtraktio af to reelle tal efter dee regel giver åbebart samme resultat som sædvalig, f.eks. + = 5, +(- ) = - og (- )+(- ) = - 5. Tallet 0 er eutralt elemet ved additio, da a + 0 = 0 + a = a.. Multiplikatio og divisio Defiitio af multiplikatio. To komplekse tal a og b multipliceres ved at multiplicere deres modulus'er og addere deres argumeter, dvs. stedvektore til produktet ab fås, ved at stedvektore til a drejes e vikel på arg(b) og derpå multipliceres med b (se figur.6). a b Fig.6. Multiplikatio ab

7 Komplekse tal Divisio a udføres grafisk ved at stedvektore til a drejes - arg(b) og multipliceres med b ( b 0) b a Divisioe plejer ma at defiere ved multiplikatioe a b hvor det "reciprokke tal" b er givet ved, at der b skal gælde b b = dvs. b må have modulus b og argumet - arg(b). Ligesom de ratioale tal Q og de reelle tal R udgør de komplekse tal C et tallegeme Bevis: Vi skal vise, at der gælder følgede regler: ) a + b = b + a, a b = b a kommutative love ) (a + b) + c = a + (b + c), (a b) c = a (b c) associative love ) 0 + a = a + 0 = a, a = a = a 0 og er eutrale elemeter 4) a + (-a) = (-a) + a =0, a a = a a = (a 0) modsat og iverst elemet eksisterer 5) ( a+ b) c= a c+ b c distributive lov Af afsittee om additio og multiplikatio følger umiddelbart, at puktere -4 er opfyldt. De distributive lov bevises lettest grafisk. ( a+ b) c= ac+ bc Multipliceres a, b og a + b med c, betyder det grafisk, at stedvektorere til a, b og a + b først drejes vikle arg(c) og derefter multipliceres deres lægder med c Da et parallelogram ved e såda drejig efterfulgt af e multiplikatio ige afbildes i et parallelogram, er love bevist. Multiplikatio af to reelle tal efter dee regel giver åbebart samme resultat som sædvalig, f.eks. fås 4 = idet 4 = og arg()+arg() = 0+0 = 0 = arg (6). Aalogt fås ( ) ( ) 4 =, idet 4 = og arg(- ) + arg(- 4) = + = = arg(). Det ses, at ai fås ved at tallet a drejes 90 0, dvs. ai er bestemt ved tværvektore af stedvektore til a. Specielt gælder, at ii = i = da i i = = og arg(i ) = + = Ved regig med komplekse tal vil vi meget ofte skulle beytte at i =. 4

8 . Rektagulær form Rektagulær form Lad et vilkårligt komplekst tal have realdele og imagiærdele. a a Sætig.. (Tal på rektagulær form) Lad et vilkårligt komplekst tal have realdele a og imagiærdele a. Der gælder da a = a + a i. Bevis. Tallet a i fides, ved at stedvektore til det reelle tal a drejes (så vi får tværvektore). Additio med stedvektore for a giver derfor stedvektore til tallet med x - værdie a og y - værdie a dvs. a. (se figur.) Fig.. Rektagulær form De rektagulære forms store fordel ligger i, at regeoperatioere + / ka udføres efter de samme vaer (algebraiske love) som for reelle tal, med de tilføjelse, at tallet i har egeskabe i =. Eksempel.. Regig med komplekse tal. Skriv følgede udtryk på rektagulær form. 5+ i ) ( + i) ( 4+ i) + 6 i ) + 4i Løsig: ) ( + i) ( 4 i) + 6 i = 8+ i 4i 6i + 6 i = 0+ 6i (idet i =.) ) 5 + i + 4i ( 5+ i)( 4i) = = i i i ( + 4i)( 4i) ( ) ( 4i) 5 56i = = i 5 5 Bemærk, at ma ved divisio forlæger med 4i i brøkes tæller og æver, således at ævere bliver et reelt tal. a ibkaldes det kojugerede af a+ ib Ti 89: Idtast udtrykket som det står (beyt d i, tast ligger over Catalog ) Maple: (5+*I)*(-+4*I) 5

9 Komplekse tal 4. Polær form Ved tallet e iθ forstås et komplekst tal med modulus og argumet θ (se figur 4.). e iθ ae iθ θ Fig 4.. Ekspoetialfuktioe θ Fig 4.. Tal på polær form a Sætig 4.. (komplekst tal på polær form). Det komplekse tal a med modulus a og argumetet θ ka skrives a ae i θ =. Bevis. Ved multiplikatio af a med e iα bliver stedvektore til det reelle tal a multipliceret med og drejet vikle α, så vi etop får a (figur 4.). Omregig mellem polære og rektagulære koordiater. Af defiitioe på cos og si fås følgede formler til omregige fra polær form rektagulær form a = a + ia (se figur 4.): a = a cos θ, a = a siθ og omvedt a = a + a a ta θ = ( a 0). a a = ae i θ til a = a + ia = ae i θ θ a = a siθ a = a cosθ Fig 4.. Omregig mellem polær og rektagulær form Bemærk: Ved bestemmelse af θ tilrådes det øje at bemærke, i hvilke kvadrat a ligger. 6

10 Eksempel 4.. Omregig mellem rektagulær og polær form. ) Omskriv tallet a = + i til polær form. e i ) Omskriv tallet b = 4 til rektagulær form. Løsig. ) a = ( ) + = + = taθ = θ = + p 6 5 Da puktet ligger i kvadrat må θ = + = 6 6 a i ) b = e = i 4 4cos 4 si = 4 + i i + 5. Ekspoetialfuktioe = e i Ti89: ) Idtast udtrykket som det står (beyt d i, tast ligger over Catalog ) Da resultatet øskes i polære koordiater skal vælges MODE, COMPLEX FORMAT= Polar Normalt vises beregigere i radiaer. Vælges MODE, ANGLE, Degree fås resultatet i grader: 50 ) Vælg MODE, ANGLE = Radia, COMPLEX FORMAT=Rektagulær Idtast 4*e^(-i* /) Maple: ) covert(-sqrt()+i,polar); Resultat: ) covert(4*exp(-i*pi/),exp); Resultat: Ekspoetialfuktioe. Defiitio af kompleks ekspoetialfuktio.lad x og y være reelle tal. Ved e x+ iy x iy forstås e e, dvs e x+ iy er det komplekse tal, der fås ved, at stedvektore til det reelle tal e x drejes vikle y. Tallet + har åbebart de rektagulære form e cos y+ ie si y e x iy e x+ iy At de ekspoetielle skriveform er rimelig, fremgår af de følgede sætig, der siger, at de sædvalige regeregler for reelle ekspoetialfuktioer også gælder for komplekse ekspoetialfuktioer. x x 7

11 Komplekse tal Sætig 5.. Regler for ekspoetialfuktioe. Lad zz,, z, avære komplekse tal, lad t være et reelt tal og lad være et helt tal. Der gælder da følgede regler z z z + z z e z z z = z ( e ) ) e e = e, ) = e ) e 4) z z e e at de ( ) 5) = at ae 5) e at dt dt a e at = ( a 0) Bevis: ) Når e z = [stedvektore til e x drejet y ] multipliceres med e z = [stedvektore til e x drejet y ] fås e z = [stedvektore til e x + x x drejet y + y ] = + x + i( y e + y ) z = e + z ) Fremkommer af ) ved at erstatte z med z z og dividere igeem med e z ) Fremkommer af ) for z = 0 og z = z. 4) Fremkommer ved getage avedelse af ) for z = z = z og suppleret med ) for < 0 5) Lad a = a+ ia Vi får da at de d dt dt e at iat d at at = + = e cos( a t + ie a t dt ) si( ) at = ae at at at cos( at ) ae si( at ) + iae si( at ) + iae cos( at ) = at = + + a e at at at at iat a t ie a t ia e a t ie a t a ia e at cos( = ae ) si( ) cos( ) si( ) ( ) 6) Ved differetiatio af fås etop a eat e at = e z iu iu iu iu Eulers formler. cosu e + e si e e = og u = i iu iu Bevis: Af e = cosu+ i si u og e = cosu i siu fås ved at lægge ligigere samme og trække dem fra hiade. iu iu iu iu e + e e e iu iu iu iu e + e = cosu og e e = i si u og dermed cosu = og siu = i Eulers formler beyttes til eksempelvis i itegraler at erstatte de trigoometriske fuktioer med ekspoetialfuktioer, som er emmere at itegrere. 8

12 5. Ekspoetialfuktioe Eksempel 5.. Avedelse på vekselstrøm. Lad e elektromotorisk kraft U = U0cos( ωt) være serieforbudet med e modstad på R, e spole med e selviduktio på L og e kodesator med kapacitete C. Der gælder da følgede skema: Nav Symbol Notatio Ehed Spædigsforskel Kompleks Imperdas Ohms modstad R Ohm Ri R Iduktor, spole L H (hery) L di dt iωl Kodesator, Kapacitor C F (Farad) Q t = C C itdt () t 0 ωc Idet (spædigsforskelle over R) +( spædigsforskelle over L) + (spædigsforskelle over C ) = U = U0cos( ωt) fås fra elektricitetslære RI L di Idt + + = U0 cos( ωt) dt C ) Kompleks impedas Z. Der gælder ohms lov U = Z I, hvor Z = R+ iωl+ i ω C ) Seriekoblig. To serieforbude komplekse impedaser Z og Z ka erstattes med e ekelt Zserie = Z + Z 4) Parallelkoblig. To parallelforbude komplekse impedaser Z og Z ka erstattes med e ekelt Z parallel = dvs. = + Zparallel Z Z Z ZZ + Z 9

13 Komplekse tal 6. Polyomier. Ved et polyomium af te grad ( helt positivt tal) forstås fuktioe P () x = a x + a x a x+ a, a 0 0 Ved polyomiets rødder forstås løsigere til ligige P ( x) = 0. I afsit.4 i Matematiske grudbegreber forudsatte vi at såvel koefficieter som rødder var reelle tal, og da idså vi, at et sådat polyomium af te grad højst har rødder. Tillader vi u både koefficieter og rødder at være komplekse tal gælder følgede sætig: Sætig 6. Algebraes fudametalsætig, Polyomiet P z az () = + a z az + a0 hvor er et helt positivt tal a 0 har etop rødder α, α,..., α (hvoraf ogel ka være es). Polyomiet derfor på ku é måde ka opløses i førstegradsfaktorer P z az ( ) = + a z az + a0 = a( z α) ( z α),,, ( z α) Et geerelt bevis for sætige ka fides i matematik for Igeiører Bid supplemet 5A. Vi vil i det følgede betragte ogle af de polyomier, som er af særlig iteresse, og her idse, at sætige er korrekt. 6. De biome ligig z = a Lad være er et helt positivt tal, og a er et vilkårligt komplekst tal forskelligt fra 0. For at fide e rod z til de biome ligig z = a omskrives såvel a som z på polær form, dvs. a ae i θ = og z ze iu iu iθ =. Vi har da z = a z e = ae At de to komplekse tal er es betyder, at θ z = a u = θ + p z = a u= + p, p er et helt tal. Geometrisk ligger røddere altså på e cirkel med radius a og vikle mellem stedvektorere til to på hiade følgede rødder er. Røddere er derfor vikelspidser i e regulær - kat. Eksempelvis vil ligige z 4 = aligge som vikelspidser i et kvadrat (se figur i eksempel 6.) Vi har følgelig, at de biome ligig z = ae ( a 0) har etop forskellige rødder. z = a e θ i + p, iθ hvor p = 0,,,,...., - Eksempel 6. Biom ligig. 4 Løs ligige z = + i. Røddere øskes agivet på såvel polær som rektagulær form. Edvidere øskes de afsat i e kompleks talpla. Avedelse. Fire es systemer, hver med kompleks forstærkig z, serieforbides, og ma måler, at de samlede komplekse forstærkig er + i Hvilke værdier ka z have? 0

14 Løsig: a = + i a = + =, taθ = θ = (da a ligger i. kvadrat) 4 4 i + p i p z = + i z = e z= e i i i i 5, p = 0,,, z= e z= e z= e z= e Ved omskrivig fra polær form til rektagulær form fås: 4 z = cos + isi = ( + i) Da viklere ligger i et kvadrat fås de øvrige rødder lettest ved at tage tværvektore z = ( + i) z = z = ( + i ) z = ( + i) z = z = ( i ) Ti89:MATH, ALGEBRA, csolve(z^4=-+i (),z) 6. Polyomier Hvis ma har sat MODE til polær fås resultatere ovefor (dog med visse egative vikler) Tilsvarede hvis ma har sat MODE til Rektagular Maple: > solve(z^4=-+sqt()*i); Resultat: På figure er afsat de fire rødder )vikelspidser i kvadrat) 6 4

15 Komplekse tal 6. Adegradsligige Az + Bz + C = 0, A 0 Sætig 6.. Adegradsligig Adegradsligige Az Bz C 0, med komplekse koefficieter, B og C og + + = A 0 B D diskrimiate D= B 4 AC har røddere z = ±, hvor α = D bestemmes som e rod A i de biome ligig α = D. Bevis: Vi foretager omskrivige B Az Bz C z A z C B B C B B + + = = 0 z + 0 z A A A + A = + = A 4 A B B 4 AC B D z + = z + = A 4 A A 4 A Idet α er e rod i de biome ligig α = D fås B B B B D z + = z + = α z z A A A α α + =± = ± 4 A A A A C A Problemet er derfor u reduceret til at løse de biome ligig α = D. Tilfælde I: A, B og C reelle tal: Diskrimiate er da et reelt tal, så for D 0 er løsige de kedte fra reelle tal. Er D < 0 beyttes blot, at i =, idet f.eks ± 9 = ± i 9 = ± i (jævfør eksempel 6.) Eksempel 6.. Adegradsligig med reelle koefficieter Løs ligige 4z 8z + = 0 Løsig: i 8 i 4z 8z+ = 0 z = ± z = ± z = ± z = ± z = ± i Tilfælde II: A, B. C er komplekse tal. I dette tilfælde ka formle omskrives til D + Re( D) D Re( D) + i B z = ±α α =, hvor A D + Re( D) D Re( D) i for for Im( D) 0 Im( D) < 0

16 6. Polyomier Eksempel 6.. Adegradsligig med komplekse koefficieter. Løs ligige z + iz 4+ 4i = 0 Løsig: i z + iz 4+ 4i = 0 z = ±α Diskrimiate er D= ( i) 4 ( 4+ 4i) = i = 6i Da Im(D)=-6 < 0 og D = + 6 = 400 = 0 fås α = i Vi har derfor z iz i z i 4 i = 0 = ± ( ) z = z = i = 4 i 6. Polyomier af højere grad ed I forbidelse med eksempelvis løsig af visse typer differetialligiger, ka ma få brug for at studere polyomer af højere grad ed. Lagt de fleste avedelser vil dog være polyomier med reelle koefficieter, så vi vil i det følgede begræse os til sådae. For adegradspolyomier med reelle koefficieter fadt vi, at hvis a = a + ia var e rod, så var også a = a iae rod. Ma kalder a = a ia for det kojugerede tal til a = a + ia (se figure) Geerelt gælder det for alle polyomier med reelle koeficieter, at er a e rod vil også a være e rod. Sætig 6., Rødder i polyomier med reelle koefficieter Lad Pz () = az + a z az+ a, hvor er et positivt helt tal, 0 koefficietere a, a,,..., a, a0 er reelle tal og a 0. Hvis α er e kompleks (ikke-reel) rod i så vil det kojugerede tal α også være e rod. Bevis: Af defiitioe på kojugeret følger a + b = a + b (da a + b = ( a ia) + ( b ib = a + b i( a + b) = a+ b ) a b = a b (da a b = ( a ia) ( b ib = a b ab i( a b + a b) = a b) Hvis α = a+ ia er e "kompleks rod" er P a ( α) = 0 α + a α aα + a0 = 0 Ved kojugerig fås uder brug af de oveævte regler for kojugerig P( α ) = 0 aα + a α aα + a0 = 0 Da koefficietere er reelle tal og dermed a = a osv.fås aα + a α aα + a0 = 0. Heraf ses, at α er e rod i Pz ()

17 Komplekse tal Sætig 6.4. Opløsig af polyomium i faktorer. Lad P() z = az + a z az+ a0, hvor er et positivt helt tal, koefficietere a, a,,..., a, a0 er reelle tal og a 0. P () z ka opløses i et produkt af førstegradsfaktorer med reelle koefficieter og adegradsfaktorer med reelle koefficieter. Bevis: Ifølge sætig 6. (algebraes fudametalsætig har et te grads polyomium P( z) rødder. Det betyder, at P( z) ka opløses i et produkt af førstegradsfaktorer P () z = a z + a z a z+ a = a ( z α )( z α )...( z α ) 0 Nogle af disse er førstegradsfaktorer med reelle koefficieter. Er e rod α ikke reel ved vi fra sætig 6. at så er de kojugerede α også rod. ( z α)( z α) = z ( α + α) z+ α α. Da α + α = ( α + iα ) + ( α iα ) = α er et reelt tal og a a = ( a + ia ) ( a ia ) = a + a også er et reelt tal, ses, at adegradspolyomiet Hermed er sætige bevist. z ( α + α) z+ α α er et polyomium med reelle koefficieter. Er specielt α p gage rod, vil P () z ideholder adegradsfaktore p gage. Eksempel 6.4. Opløsig af polyomium i faktorer 5 4 Opløs polyomiet Pz ()= z 0z + 0z 50z + 48z 0 iet produkt af førstegradsfaktorer med reellle koefficieter og adegradsfaktorer med reellle koefficieter. Løsig: Ti89: MATH, ALGEBRA, FACTOR(z^5-0z^4+0z^-50z^+48z-0,x) Resultat: ( z )( z z+ )( z z+ 5) Maple: factor(*z^5-0*z^4+0*z^-50*z^+48*z-0); Resultat: 6.4 Dekompoerig af polyomiums brøker Px ( ) Vi betragter i dette afsit brøker hvor tæller og æver er polyomier med reelle Qx ( ) x + 7 koefficieter.et eksempel herpå er brøke x x x + Ved ogle avedelser, bl.a, år ma skal løse visse typer differetialligiger, får ma brug for at opløse sådae brøker i e sum af simple stambrøker x + 7 Skal ma eksempelvis itegrere f ( x) = vil dette være ødvedigt, da ma så ka x x x + itegrere hver af disse simplere stambrøker hver for sig. Ver dekompoerige faktoriserer ma ævere som beskrevet i sætig 6.4, og derefter spaltes op i e sum af brøker med disse faktorer som ævere.stambrøkere er brøker, hvor tælleres grad er mider ed æveres, og hvor ævere ete er ( x α ), eller ( ax + bx + c), hvor α, abc,, er reelle tal og er et helt positivt tal. E såda dekompoerig af e brøk og ka opfattes som det modsatte af at sætte på fælles brøkstreg. 4

18 6. Polyomier Beregigere ka hurtig blive omfattede, så ma vil sædvaligvis vælge at lade eksempelvis Ti89 eller Maple foretage beregigere: Eksempel 6.5. Dekompoerig. 8 4 x + 7 x 4x + x + 9 Dekompoer ) f ( x) = ) gx ( ) = x x x + x x + x x x + x x + Løsig: ) Ti 89: MATH ALGEBRA expad((x^+7)/(x^-x^-x+),x) 7 Resultat: f ( x) = + + x + x 4( x ) Maple: covert((x^+7)/(x^-*x^-x+), parfrac, x); Resultat: ) Ti 89: MATH ALGEBRA expad(udtryk),x) x + 7x Resultat: gx ( ) = x ( x + ) ( x + ) ( x + ) 8( x+ ) 8( x ) ( x ) Maple: Giver samme resultat. 5

19 Komplekse tal Opgaver.. Reducér ( i) ( 6+ 5i)( + i) + ( 4+ 7i)( i).. Skriv følgede brøker på rektagulær form ) + 4i 4i + 5i i 5 4, ) ) 4) i i 4i i + + i i i + i.. Bereg ( 5 i) ( 5i) + ( i) ( + i) 4.. Omskriv følgede tal til polær form ) -5 ) 4i ) + i 4) - i 5) i 4.. Omskriv følgede tal til rektagulær form ) e i ) e i ) e i 4 4) Omskriv følgede tal til rektagulær form i i i 5 e i 6 e 6 e ) ) 4e 6 ) 4) i i e i i e e 5.. ) Omskriv +i til polær form og bereg ( + i) 4. Facit skal skrives på rektagulær form ) Skriv ( i) 7 på rektagulær form. ( ) ( ) 6 i ) Skriv på rektagulær form. 6 i 6.. Løs ligigere ) z = ) z = i ) z 4 = i 4) z 6 = i 5) z 6 = Fid alle røddere i ligige z = 7 i Løs ligigere ) z z + = 0. ) z 4z + = Løs ligigere ) z ( + i) z+ ( i) = 0 ) z ( + i) z+ ( + i) = ) Opløs polyomiet Pz ()= z + z + 7z + 6i faktorer af første og ade grad. ) Løs ligige P(z) = ) Opløs polyomiet Pz ()= z + 4z + 6z+ 50i faktorer af første og ade grad. ) Løs ligige P(z) = ) Opløs polyomiet Pz ()= z + z + 7z + 6i faktorer af første og ade grad. ) Løs ligige P(z) = ) Opløs polyomiet Pz ()= z + z + z i faktorer af første og ade grad. ) Løs ligige P(z) = 0 4 x x x Dekompoer fuktioe f ( x) = 5 4 x x + x 5 4 x + x + 9x 4x 6x 6.. Dekompoer fuktioe f ( x) = 4 x + x x + x x + x + 5x 6.. Dekompoer fuktioe f ( x) = x 7x + 6 e i 4 6

20 Stikord STIKORD A additio af komplekse tal algebraes fudametalsætig 0 adegrasdligig argumet B biom ligig 0 C D dekompoerig af polyomiumsbrøk 4 divisio af komplekse tal E ekspoetialfuktio 7 elektromotorisk kraft 9 F faktoriserig af polyomium 4 P polyomier 0, polær form 6 polære koordiater R ratioale tal Q reelle tal R rektagulær form 5 rektagulære koordiater rødder i polyomium 0 S subtraktio af komplekse tal T U V G H I K kojugeret tal kompleks talmægde C kodesator 9 kodesator 9 L M modulus multiplikatio af komplekse tal N aturlige tal N umerisk værdi af kompleks tal O opløsig af polyomium i faktorer 4 opgaver 6 7