Minikvant Fysik 22 - nu også med fysik 312 for os aber
|
|
|
- Bjørn Bech
- 7 år siden
- Visninger:
Transkript
1 Minikvant Fysik - nu også med fysik 31 for os aber. enrik Dahl hdahl@tdc-broadband.dḳ. Resumé ADVARSEL - dette er et total underground-dokument!. Det er livsfarligt at bruge ukritisk. Der er næsten sikkert graverende fejl. Jeg påtager mig intet ansvar overhovedet for noget som helst. Faktisk vil jeg for en sikkerheds skyld fraråde brug af det følgende... Jeg har brugt flere kilder til det følgende. Selvfølgelig Liboff, men også Zettili,N: Quantum Mechanics, Concepts and Aplications Wiley, 001, Woan, G: The Cambridge Handbook of Physics Formulas Cambridge, 000 og Phillips, A.C.: Introduction to Quantum Mechanics Wiley, 003. Desuden også Sakurai og en note om Sjov med tensorer af m og m. Hvis du finder fejl - og der er med garanti næsten lige så mange som i Liboff - eller har andre kommentarer hører jeg meget gerne om det. Send mig en mail, så det kan blive forbedret. På forhånd tak! - og tak til Michael B for at finde fejl og komme med forslag til forbedringer!
2 INDHOLD Indhold 1 Operatorer Definition Operatoralgebra Vigtige operatorer Cartesiske koordinater Sfæriske koordinater Kommutatorer 7.1 Definition Kommutatoralgebra Vigtige kommutatorer Usikkerhedsrelation Egenskaber Diracnotation Definitioner Algebra Sandsynlighed mm Usikkerhedsrelationer Sandsynlighed Middelværdi og spredning Postulaterne 11 6 Schrödinger og stationære tilstande 11 7 Spektrumtyper dimension Specifikke problemer dimension Potentialtrin Potentialbarriere Uendelig brønd Endelig brønd Harmonisk oscillator dimensioner Impulsmoment, spherical harmonics Kartesiske koordinater Sfæriske koordinater Fri partikel
3 INDHOLD Sfærisk æske Hydrogenlignende atomer Spin Specielle funktioner Hermitiske polynomier Legendrepolynomier Sfæriske Besselfunktioner Fra Fysik31 for os aber 1.1 Tensorer Udtrykt ved stedkoordinater Stedkoordinater udtrykt ved tensorer Udvalgsregler Perturbationsteori Statisk, ikke degenereret Statisk, degenereret Tidsafhængig
4 1 OPERATORER 4 1 Operatorer 1.1 Definition Matematisk regel, der transformerer en ket til en anden ket fra samme rum ditto for bra:  ψ = ψ, φ  = φ 1. Operatoralgebra Generelt gælder  ˆB ˆB  ˆBĈ =  ˆBĈ =  ˆBĈ Ân  m = Ân+m  ˆB ψ =  ˆB ψ Hvis  er lineær gælder Âa 1 ψ 1 +a ψ = a 1  ψ 1 +a  ψ og ψ 1 a 1 + ψ a  = a 1 ψ 1  + a ψ  Middelværdien af en operator med hensyn til en tilstand ψ er givet ved ψ  ψ φ ψ er en lineær operator ψ  og  ψ er forbudte udtryk Der gælder ψ  φ = φ  ψ aâ = a   =   + ˆB =  + ˆB  ˆB = ˆB  Ân =  n  ˆB ψ = ψ ˆB   er hermitisk hvis  =  dvs. ψ  φ = φ  ψ  er antihermitisk skævhermitisk hvis  =   er en projektionsoperator hvis  =  hermitisk og  = Â. Produktet af to projektionsoperatorer er en projektionsoperator men det samme gælder normalt ikke for summen
5 1 OPERATORER 5 Enhedsoperator Position Impuls Kinetisk energi Hamilton Impulsmoment 1.3 Vigtige operatorer Cartesiske koordinater Î : Î ψ = ψ ˆX n = x n 1 dimension, ˆR = r i 3 dimensioner ˆP n x = i n n x n ˆT = m x Ĥ = m + ˆV r = m 1 dimension, ˆP = i i 3 dimensioner ˆV r x y z For harmonisk oscillator i 1 dimension: Ĥ = 1 ˆP + m ω m ˆX = ω ˆp + ˆq = ω ˆN + 1 ˆ L = i ˆR ˆL x = Ŷ ˆP z Ẑ ˆP y = i Ŷ Ẑ z y ˆL y = Ẑ ˆP x ˆX ˆP z = i Ẑ ˆX x z ˆL z = ˆX ˆP y Ŷ ˆP x = i ˆX Ŷ y x ˆL = ˆL x + ˆL y + ˆL z Paritet Gradient Laplace Dimensionsfri ˆPψ r = ψ r ˆP r = r ψ r = ψ x i + ψ y j + ψ z k ψ = ψ = ψ x ˆp = ˆP m ω + ψ y + ψ z ˆq = ˆX mω/ Stigeoperatorer â = 1 ˆq + iˆp â = 1 ˆq iˆp ikke-hermitiske â n = n n 1 â n = n + 1 n + 1
6 1 OPERATORER 6 ˆX = â+â β ˆP = mω 0 i â â β Tal-operator Sænke- og hæveoperator occupation number operator: ˆN = â â ˆN n = n n Ĵ ± = Ĵx ± iĵy Ĵ x = 1 Ĵ+ + Ĵ Ĵ y = 1 i Ĵ+ Ĵ Ĵ = Ĵ+ 1 Ĵ + Ĵ Ĵ+ + Ĵ z Ĵ j, m = jj + 1 j, m Ĵ z j, m = m j, m, j m j Ĵ ± j, m = j mj ± m + 1 j, m ± Sfæriske koordinater Laplace Impulsmoment Hæve- og sænkeoperatorer = 1 r r r 1 r ˆL ˆL = [ ˆP r = i 1 r ˆL z = i ϕ 1 sin θ r r θ sin θ θ + 1 sin θ ˆL ± = e ±iϕ i cot θ ϕ ± θ ] ϕ ˆL± Y m l l = [ll + 1 m l m l ± 1] 1/ Y m l±1 l
7 KOMMUTATORER 7 Kommutatorer Kommutator Antikommutator.1 Definition [Â, ˆB] = Â ˆB ˆBÂ {Â, ˆB} = Â ˆB + ˆBÂ. Kommutatoralgebra [Â, Â] = 0 [Â, c] = 0 [Â, ˆB] = [ ˆB, Â] [Â, ˆB + Ĉ] = [Â, ˆB] + [Â, Ĉ] [Â, ˆBĈ] = [Â, ˆB]Ĉ + ˆB[Â, Ĉ] [Â ˆB, Ĉ] = Â[ ˆB, Ĉ] + [Â, Ĉ] ˆB [Â, ˆB] = [ ˆB, Â ] [Â, [ ˆB, Ĉ]] + [ ˆB, [Ĉ, Â]] + [Ĉ, [Â, ˆB]] = 0 [Â, ˆB n ] = n 1 j=0 ˆB j [Â, ˆB]Ân j 1 [Ân, ˆB] = n 1 j j=0 Ân j 1 [Â, ˆB] ˆB Sted og impuls.3 Vigtige kommutatorer [ ˆX, ˆP x ] = i [ ˆX n, ˆP x ] = i n [ ˆX, ˆP x n ] = i n x [f ˆX, ˆP x ] = i n 1 ˆX n 1 ˆP df ˆX d ˆX Sæt j, k = x, y, z - så gælder: [ ˆR j, ˆP k ] = i δ jk [ ˆR j, ˆR k ] = 0 [ ˆP j, ˆP k ] = 0
8 KOMMUTATORER 8 [ ˆ P, f ˆ R ] = i f ˆ R Impulsmoment [ˆL x, ˆL y ] = i ˆL z [ˆL y, ˆL z ] = i ˆL x [ˆL z, ˆL x ] = i ˆL y [ ˆX, ˆL x ] = 0 [ ˆX, ˆL y ] = i Ẑ [ ˆX, ˆL z ] = i Ŷ [ ˆP x, ˆL x ] = 0 [ ˆP x, ˆL y ] = i ˆP z [ ˆP x, ˆL z ] = i ˆP y [ ˆX, ˆL ] = i ˆL y Ẑ + Ẑ ˆL y ˆL z Ŷ Ŷ ˆL y [ ˆP x, ˆL ] = i ˆL y ˆPz + ˆP z ˆLy ˆL z ˆPy ˆP y ˆLy [Ĵx, Ĵy] = i Ĵz [Ĵy, Ĵz] = i Ĵx [Ĵz, Ĵx] = i Ĵy [Ĵ, Ĵk] = 0 [Ĵ, Ĵ±] = 0 [Ĵ+, Ĵ ] = Ĵz [Ĵz, Ĵ±] = ± Ĵ± Andre [ˆq, ˆp] = i [â, â ] = 1 For harmonisk oscillator i 1 dimension: [â, Ĥ] = ωâ [â, Ĥ] = ωâ [ ˆN, â] = â [ ˆN, â ] = â
9 3 DIRACNOTATION 9.4 Usikkerhedsrelation A B 1 [Â, ˆB].5 Egenskaber To observerbare er kompatible, hvis deres operatorer kommuterer, [Â, ˆB] = 0 Hvis to observerbare er kompatible, har deres operatorer et sæt fælles egentilstande Kompatible observerbare kan måles samtidig med vilkårlig præcision det kan inkompatible ikke 3 Diracnotation Ket Bra Skalarprodukt Braket Fortolkning 3.1 Definitioner m n n m = ψnψ m dx n â m = ψ n â ψ m = ψnâψ m dx φ ψ kan fortolkes som sandsynligheden for, at hvis systemet først er i tilstand ψ og der foretages en måling, så er systemet i tilstand φ. 3. Algebra ψ = ψ a ψ = a ψ aψ = a ψ aψ = a ψ φ ψ = ψ φ ψ a 1 ψ 1 + a ψ = a 1 ψ ψ 1 + a ψ ψ a 1 ψ 1 + a ψ ψ = a 1 ψ 1 ψ + a ψ ψ
10 4 SANDSYNLIGHED MM. 10 a 1 φ 1 + a φ b 1 ψ 1 + b ψ = a 1b 1 φ 1 ψ 1 + a 1b φ 1 ψ + a b 1 φ ψ 1 + a b φ ψ ψ ψ 0 = 0 for ψ = 0 Hvis tilstanden er normaliseret er ψ ψ = 1 Schwarz: ψ φ ψ ψ φ φ Trekantsulighed: ψ + φ ψ + φ ψ ψ + φ φ Ortogonalitet: Hvis ψ φ = 0 Ortonormalitet: ψ φ = 0, ψ ψ = φ φ = 1 4 Sandsynlighed mm. Generelt Heissenberg 4.1 Usikkerhedsrelationer a b 1 i[â, ˆb] 4 p x 4. Sandsynlighed P x, tdx = ψx, t dx jx = m ψ ψ ψ ψ x x Middelværdi Tidsudvikling Superposition Ehrenfest 4.3 Middelværdi og spredning a = â = ψ â ψ = ψ âψdx Hvis ikke normaliseret gælder â = ψ â ψ ψ ψ d â = i â [Ĥ, â] + dt t Hvis âψ n = a n ψ n og Ψ = c n ψ n er a = c n a n m d dt d dt r = p p = V
11 5 POSTULATERNE 11 Varians a = a a Ĵ x = Ĵ y = 1 Ĵ Ĵ z = [jj + 1 m ] 5 Postulaterne Tilstand Observerbare Måling Spektre Tidsudvikling Et fysisk system er til enhver tid t specificeret ved en tilstandsvektor ψt. En superposition af sådanne er også en tilstand Til enhver observerbar A svarer en lineær hermitisk operator Â, hvis egenvektorer udgør en komplet basis Måling kan repræsenteres ved at en operator  virker på en tilstand ψt. Hvis målingen giver a n er tilstanden umiddelbart efter givet ved en projektion på egenvektoren ψ n, der svarer til a n : ψ efter = ψ n ψ n ψt Sandsynligheden for et bestemt måleresultat er for diskrete spekre givet ved P n a n = ψn ψ ψ ψ og for kontinuerte spektre ved dp a = ψa = ψa da ψ ψ ψa da Tidsudviklingen er givet ved den tidsafhængige Schrödingerligning = Ĥ ψt i ψt t 6 Schrödinger og stationære tilstande Den tidsafhængige Schrödingerligning kan skrives i Ψ r, t t = m Ψ r, t + ˆV r, tψ r, t Antag tidsuafhængigt potential, ˆV r, t = ˆV r. Da fås den tidsuafhængige Schrödingerligning: [ m + ˆV ] r ψ r = Eψ r Løsningerne til den tidsafhængige ligning bliver Ψ r, t = ψ r e iet/ = ψ r e iωt E = ω
12 7 SPEKTRUMTYPER 1 Denne løsning er en stationær tilstand. Den generelle løsning bliver Ψ r, t = c n ψ n r exp ie nt n 7 Spektrumtyper Bundne tilstande Ubundne tilstande Blandede tilstande Paritet dimension Partiklen kan ikke gå til ±. I så fald er spektret diskret Partiklen kan gå mod eller eller begge. Ikke begge: Spektret er kontinuert, ingen egenværdier er degenererede Begge: Spektret er kontinuert, alle egenværdier er dobbelt degenererede For nogle energiniveauer er partiklen bundet, for andre ubundet. Symmetrisk potential: V x = V x Bundne egentilstande har enten lige eller ulige paritet: ψ x = ±ψx Degenereret spektrum: Egentilstande har ikke nogen given paritet 8 Specifikke problemer dimension Potentialtrin Partiklen kommer fra venstre. Potential For E > V 0 { 0 x < 0 V x = V 0 x > 0 { ψ1 xe Ψx, t = iωt = Ae ik1x ωt + Be ik 1x+ωt x < 0 ψ xe iωt = Ce ik x ωt x > 0 B = k 1 k C = k 1 k 1 +k A k 1 +k A R = k 1 k k 1 +k = 1 κ 1+κ T = 4k 1k k 1 +k = 4κ 1+κ κ = k /k 1 = 1 V 0 /E
13 8 SPECIFIKKE PROBLEMER 13 For E < V 0 Ψx, t = B = k 1 ik k 1 +ik A C = k 1 k 1 +ik A { Ae ik 1 x ωt + Be ik 1x+ωt x < 0 Ce k x e iωt x > 0 R = 1 P x = C e k x 8.1. Potentialbarriere Potential For E > V 0 > 0 Partiklen kommer fra venstre. 0 x < 0 V = V 0 0 x a 0 x > a ψ 1 x = Ae ik1x + Be ik 1x x 0 ψx = ψ x = Ce ikx + De ik x 0 < x < a ψ 3 x = Ee ik 1x x a k 1 = me/ k = me V 0 / Randbetingelser: ψ 1 0 = ψ 0 dψ 1 0 = dψ 0 dx dx ψ a = ψ 3 a dψ a dx = dψ 3a dx For E > V 0 < 0 E = 4k 1 k Ae ik 1a [4k 1 k cosk a ik 1 + k sink a] 1 [ T = E = A 4εε 1 sin λ ] 1 ε 1 λ = a mv 0 / ε = E/V 0 [ ] 1 R = 1 + 4εε 1 sin λ ε 1 [ T = εε+1 sin λ ] 1 ε + 1 λ = a m V 0 /
14 8 SPECIFIKKE PROBLEMER 14 For E < V 0 ε = E/ V 0 ψ 1 x = Ae ik1x + Be ik 1x x 0 ψx = ψ x = Ce kx + De k x 0 < x < a ψ 3 x = Ee ik 1x x a k 1 = me/ k = me V 0 / [ T = ε1 ε sinh λ 1 ε λ = a mv 0 / ε = E/V 0 ] 1 R = T 4ε1 ε sinh λ 1 ε Asymmetrisk potential Symmetrisk potential Potential For E > V 0 For 0 < E < V Uendelig brønd x < 0 V x = 0 0 x a x > a E n = m k n = π ψ n x = ψ n = ma n, n = 1,, 3,... sin nπ x, n = 1,, 3,... a a Ψx, t = n=1 ψ nxe ient/ = x < a/ V x = 0 a/ x a/ x > a/ a sin [ nπ a x + a/] = Endelig brønd V 0 x < a/ V x = 0 a/ x a/ V 0 x > a/ a n=1 sin nπ x e in E 1 t/ a cosnπx/a a n = 1, 3, 5,... sinnπx/a n =, 4, 6... Endelig reflektionskoefficient, oscillation i alle tre områder k 1 = mv 0 E/ a
15 8 SPECIFIKKE PROBLEMER 15 k = me/ d k dx 1 ψ 1 x = 0, x < a/ d + k dx ψ x = 0, a/ x a/ d k dx 1 ψ 1 x = 0, x > a/ ψ 1 x = Ae k1x, x < a/ { B cosk x symmetrisk ψ x = C sink x antisymmetrisk ψ 3 x = De k 1x, x > a/ Harmonisk oscillator Potential V = 1 mω x Ĥ = ˆP + 1 m mω ˆX = ω ˆN = â â ˆN + 1 E n = n + 1 ω ψ 0 x = 1 πx0 exp ψ n x = 1 1 π n n! x n+1/ 0 x, x x 0 = /mω 0 x x 0 d dx n exp x x 0 = 1 mω n ˆX n = 1 n ˆP n = 1 n Ĥ n virialsætningen m x = p = mω n + 1 m ωn + 1 x p = n + 1/ / De første 6 egenenergier og -tilstande π n n!x 0 e x /x 0 Hn x x 0
16 8 SPECIFIKKE PROBLEMER 16 n E n ψ n 0 ω/ A 0 e ξ / 1 3 ω/ A 1 ξe ξ / 5 ω/ A 4ξ e ξ / 3 7 ω/ A 3 8ξ 3 1ξe ξ / 4 9 ω/ A 4 16ξ 4 48ξ + 1e ξ / 5 11 ω/ A 5 3ξ 5 160ξ ξe ξ / A n = n n! π ξ = mω x 8. 3 dimensioner 8..1 Impulsmoment, spherical harmonics ˆL l, m = ll + 1 l, m ˆL z l, m = m l, m θ, ϕ l, m = Y lm θ, ϕ ˆL Y lm θ, ϕ = ll + 1Y lm θ, ϕ ˆL z Y lm θ, ϕ = m Y lm θ, ϕ ˆL ± Y lm θ, ϕ = ll + 1 mm ± 1Y lm±1 θ, ϕ Y lm θ, ϕ = 1 m l+1 l m! P m 4π l+m! l cos θe imϕ m 0 Y lm θ, ϕ = 1l l l! l+1 l+m! 4π l m! eimϕ 1 sin m θ [Y lm θ, ϕ] = 1 m Y l, m θ, ϕ d l m dcos θ l m sin θ l m 0 Y lm θ, ϕ Y lm x, y, z Y 00 θ, ϕ = 1 4π Y 00 x, y, z = 1 4π 3 Y 10 θ, ϕ = cos θ Y 3 z 4π 10x, y, z = 4π r 3 Y 1,±1 θ, ϕ = 8π e±iϕ sin θ Y 1,±1 x, y, z = 5 Y,0 θ, ϕ = 3 16π cos 5 θ 1 Y,0 x, y, z = 16π 15 Y,±1 θ, ϕ = 8π e±iϕ sin θ cos θ Y,±1 x, y, z = 15 Y,± θ, ϕ = 3π e±iϕ sin θ Y,± x, y, z = 3 8π x±iy r 3z r r 15 8π 15 3π x±iyz r x y ±ixy r
17 8 SPECIFIKKE PROBLEMER 17 Schrödinger Antag tidsuafhængigt potential Separation Fri partikel Kassepotential Kubisk kasse Anisotropisk harmonisk oscillator Isotropisk harmonisk oscillator 8.. Kartesiske koordinater m Ψx, y, z, t + ˆV x, y, z, tψx, y, z, t = i Ψx,y,z,t t Ψx, y, z, t = ψx, y, ze iet/ Hvis V x, y, z = V x x + V y y + V z z fås separation ψx, y, z = π 3/ e ikxx e ikyy e ikzz = π 3/ e i k r kx = me x / E = E x + E y + E z = m k { 0 0 < x < a, 0 < y < b, 0 < z < c V x, y, z = ellers ψ nx,ny,n z x, y, z = E nx,n y,n z = π m n x a 8 sinn abc xπx/a sinn y πy/b sinn z πz/c + n z c + n y b a = b = c = A E nx,ny,n z = π n ma x + n y + n z E nx,ny,n z /E 1 x n, n y, n z Degenerering, g n ,11, ,1, ,131, ,31,31,13,13,13 6 ˆV ˆx, ŷ, ẑ = 1 mω ˆX x + 1 mω yŷ + 1 mω zẑ E nx,ny,n z = E nx + E ny + E nz = n x + 1/ ω x + n y + 1/ ω y + n z + 1/ ω z ψ er produktet af de tre en-dimensionale harmoniske oscillatorer ω x = ω y = ω z = ω E nx,ny,n z = n x + n y + n z + 3/ ω Degenerering g n = n + 1n + / n E n / ω n x, n y, n z g n ,010, ,00,00,110,101, ,030,003,10,01, ,10,01,111
18 9 HYDROGENLIGNENDE ATOMER Sfæriske koordinater Fri partikel Se også Liboff, s.44 Fri partikel ˆp r = i 1 r Ĥ = m r r Schrödinger: 1 m = ˆp r m + ˆL mr ϕ klm r, θ, φ = j l kry m l θ, φ E k = k m ˆp r + ˆL r ϕ klm = E klm ϕ klm Centralt potential 8.3. Sfærisk æske V { 0 r < a r = V r = r > a ϕ nlm = j xln r l a Y m l θ, φ E nl = x ln ma 9 Hydrogenlignende atomer Schrödinger Reduceret masse Egenfunktioner Energi Middelværdier Tilladte kvantetal µ Ψ nlm Ze 4πε 0 r Ψ nlm = E n Ψ nlm µ = mem kerne m e+m kerne Ψ nlm = a = me µ n l 1! nn+l! a 0 Z a 0 = ε 0h πm ee x = r an L l+1 n l 1 = n l 1 k=0 E n = µe4 Z 8ε 0 h n 1/ 3/ an x l e x/ L l+1 n l 1 Y l m θ, φ l+n! x k l+1+k!n l 1 k!k! r = a 3n ll + 1 r = a n 5n + 1 3ll + 1 1/r = 1 an 1/r = l+1n 3 a n = 1,, 3,...
19 10 SPIN 19 l = 0, 1,,..., n 1 m = 0, ±1, ±,..., ±l Udvalgsregler Bølgefunktioner n 0 l = ±1 m { 1, 0, 1} Ψ 100 = a 3/ π 1/ e r/a Ψ 00 = a 3/ 4π r 1/ a e r/a Ψ 10 = a 3/ r 4π 1/ a e r/a cos θ Ψ 1±1 = a 3/ r 8π 1/ a e r/a sin θe ±iφ Ψ 300 = a 3/ 813π 1/ Ψ 310 = 1/ a 3/ 81π 1/ Ψ 31±1 = a 3/ 81π 6 r 1/ a Ψ 30 = 7 18 r + r e r/3a a 6 r r a a e r/3a cos θ r a e r/3a sin θe ±iφ a a 3/ r e r/3a 3 cos θ 1 816π 1/ a Ψ 3±1 = a 3/ r e r/3a sin θ cos θe ±iφ 81π 1/ a Ψ 3± = a 3/ r e r/3a sin θe ±iφ 16π 1/ a 10 Spin 0 1 Paulimatricer σ 1 = i σ = i σ 3 = I = 0 1 Antikommutation{σ i, σ j } = σ i σ j + σ j σ i = δ ij I Cyklisk permutation Spinmatricer σ i σ j = iσ k σi = I 0 1 Ŝ x = i Ŝ y = i 0
20 10 SPIN 0 Ŝ z = Egenværdier Egenvektorer λ = ± α x = 1 1 spin op i x-retningen 1 β x = 1 1 spin ned i x-retningen 1 α y = 1 1 spin op i y-retningen i β y = 1 1 spin ned i y-retningen i α z = 1 1 spin op i z-retningen 0 β z = 0 1 spin ned i z-retningen 1 ˆ Sammensætning J i j i, m i = j i j i + 1 j i, m i Ĵiz j i, m i = m i j i, m i Ŝ tot = Ŝ1 + Ŝ Ŝ tot,z = S 1z + S z Antal tilstande = s + 1, s m s s = Hvem og hvad? Bosoner heltalligt spin, fermioner halvtalligt spin. Liboff tabel 11.3 Spinbølgefunktioner for to elektroner i koblet repræsentation: Spinkombination Bølgefunktion s 1 s s m ξ = s 1 s sm 1 ξ = α 1 α ξ 0 1 = α 1 β + β 1 α ξ = β 1 β ξ 0 0 = α 1 β β 1 α 0 0
21 11 SPECIELLE FUNKTIONER 1 11 Specielle funktioner 11.1 Hermitiske polynomier H 0 y = 1 H 1 y = y H y = 4y H 3 y = 8y 3 1y H 4 y = 16y 4 48y + 1 H n+1 y = yh n y nh n 1 y 11. Legendrepolynomier Løsning til Får 1 sin θ d dθ sin θ dθ ] lmθ + [ll + 1 m dθ sin Θ lm θ = 0 θ Θ lm θ = C lm P m l cos θ Pl m x = 1 x m / d m dx P lx m P l x = 1 d l l l! dx l x 1 l C lm = 1 m l + 1 l m! l + m! Se Liboff, s.373 for stor tabel. Her en lille tabel. Legendrepolynomium Associeret Legendrepolynomium P 0 cos θ = 1 P 1 cos θ = cos θ P1 1 cos θ = sin θ P 1 cos θ = 3 cos θ sin θ P cos θ = 3 cos θ 1/ P cos θ = 3 sin θ P 3 cos θ = 5 cos 3 θ 3 cos θ/ P3 1 cos θ = 3 sin θ5 cos 3 θ 1/ P 4 cos θ = 35 cos 4 θ 30 cos θ + 3/8 P3 cos θ = 15 sin θ cos θ P 5 cos θ = 63 cos 5 θ 70 cos 3 θ + 15 cos θ/8 P3 3 cos θ = 15 sin 3 θ 11.3 Sfæriske Besselfunktioner j 0 x = sin x x j 1 x = sin x cos x x x j x = 3 1 x 3 x sin x 3 cos x x
22 1 FRA FYSIK31 FOR OS ABER 1 Fra Fysik31 for os aber 1.1 Tensorer Udtrykt ved stedkoordinater T 0 0 = 1 3 x + y + z = 1 3 r T 1 0 = z T 1 1 = 1 x + iy T 1 1 = 1 x iy T = 1 x + iy T = 1 x iy T 1 = 1 zx iy hvis [x, y] = [y, z] = 0 T 1 = 1 zx iy hvis [x, y] = [y, z] = 0 T 0 = 1 6 z x y = 1 6 3z r 1.1. Stedkoordinater udtrykt ved tensorer x = 1 T 1 1 T 1 1 y = i T T 1 1 z = T 1 0 x = 1 T + T 1 6 T 0 T 0 y = 1 T + T 1 6 T 0 T 0 z = 6 T 0 T 0 0 hvis [x, y] = 0 xy = 1 T i T hvis [x, y] = 0 zy = i T 1 + T 1 hvis [z, y] = 0 zx = 1 T 1 T 1 hvis [z, x] = 0 x y = T + T 0 hvis [x, y] = [y, z] = 0 0 hvis [x, y] = [y, z] = 0 1. Udvalgsregler Sfærisk potential V r giver egentilstande nlm. Vi skal afgøre, hvornår n l m nlm nødvendigvis er = 0 når systemet perturberes med en operator W. Regel 1: Paritet. l lige hvis W er lige har positiv paritet. l ulige hvis W er ulige har negativ paritet. NB - nogle operatorer er hverken lige eller ulige.
23 1 FRA FYSIK31 FOR OS ABER 3 Regel : Oversæt operator W til tensor: W T q k. m = q ved Wigner- Eckhart Regel 3: l k ved Wigner-Eckhart Sammenfat resultaterne fra de tre regler. Overtrædelse betyder, at n l m nlm = Perturbationsteori Statisk, ikke degenereret H 0 H 0 + V Til H 0 svarer egenværdier En 0 og egentilstande ψn 0 Problem: Find første ordens korrektion til En. 0 Løsning gen 1 = ψn gv 0 ψn 0 note 18. Problem: Find første ordens korrektion til ψn. 0 Løsning: Definer V mn = ψm V 0 ψn. 0 Første ordens korrektion er da ψ 1 n = m n V mn E 0 n E 0 m ψ 0 m note 1. Problem: Find anden ordens korrektion til En. 0 Løsning: En = m n Statisk, degenereret V mn E 0 n E 0 m note H 0 er degenereret med degeneracy d n for egenværdi n: H 0 n 0 i = E n 0 n 0 i, i = 1,..., d n H 0 H = H 0 + V, giver splitting af disse degenerationer: H n i = E n,i n i, i = 1,..., d n Problem: Find første ordens korrektion til E 0 i. Løsning: Nedskriv matricen A = n 0 i V n 0 j den er d n d n. Find egenværdier for A. Disse udgør E 1 i, altså første ordens korrektionerne. Problem: Find nulte ordens korrektion til egentilstande n 0 i. Løsning: Nedskriv A som ovenfor og find egenvektorer for A. Nulte ordens korrektion er da l 0 i = d n j=1 c ij n 0 j Tidsafhængig H 0 H 0 + V t Antag, at ψt 0 = e ie kt 0 / k Definer ω lk = E0 k Definer V lk t = E 0 l V t E 0 k Da er ψt I = l c lt l i Interaction picture, hvor c l fås fra TDP: l E 0
24 1 FRA FYSIK31 FOR OS ABER 4 c lk = t t 0 e iω lks t 0 V lk sds I Schrödinger picture fås ψt S = e ih 0t/ ψt I = l c lkte ie lt/ l P k l,k l t, t 0 = 1 c lk NB bemærk ovenfor, at l k. Husk at være opmærksom på singulariteter. TDP er kun gyldig for små perturbationer og muligvis også kun for kort tid.
Formelsamling til. Kvantemekanik. 27. marts Dennis Hansen 1
 Formelsamling til Kvantemekanik 7. marts 1 Dennis Hansen 1 Indhold 1 Grundlæggende ligninger 4 1.1 Generelt...................................... 4 1. Postulater i kvantemekanik............................
Formelsamling til Kvantemekanik 7. marts 1 Dennis Hansen 1 Indhold 1 Grundlæggende ligninger 4 1.1 Generelt...................................... 4 1. Postulater i kvantemekanik............................
Kvant 2. Notesamling....Of doom!
 Kvant 2 Notesamling...Of doom! Indhold 1 To-partikelsystemer 1 2 Brint 1 3 Perturbation 2 3.1 Udartet perturbationsteori...................... 3 3.2 Zeeman-effekt............................. 4 3.3 Tidsafhængig
Kvant 2 Notesamling...Of doom! Indhold 1 To-partikelsystemer 1 2 Brint 1 3 Perturbation 2 3.1 Udartet perturbationsteori...................... 3 3.2 Zeeman-effekt............................. 4 3.3 Tidsafhængig
Noter til KM1 og KM2 på KU (Kvantemekanik 1 og 2)
 Noter til KM1 og KM2 på KU (Kvantemekanik 1 og 2) Nikolai Plambech Nielsen, LPK331. Version 1.1 Indhold I Kvant 1 4 1 Bølgefunktionen 4 1.1 Schrödingerligningen....................................... 4
Noter til KM1 og KM2 på KU (Kvantemekanik 1 og 2) Nikolai Plambech Nielsen, LPK331. Version 1.1 Indhold I Kvant 1 4 1 Bølgefunktionen 4 1.1 Schrödingerligningen....................................... 4
Kvantemekanik 8 Side 2 af 10 Observable og operatorer. Grundlæggende egenskaber ved operatorrepræsentanter ( ) O= O. (8.4)
 Kvantemekanik 8 Side 1 af 10 Opsummering Egenskaber ved operatorrepræsentanter Det blev i KM3-4 vist, at enhver målbar bevægelsesegenskab (observabel) er repræsenteret ved en operator, som for position,
Kvantemekanik 8 Side 1 af 10 Opsummering Egenskaber ved operatorrepræsentanter Det blev i KM3-4 vist, at enhver målbar bevægelsesegenskab (observabel) er repræsenteret ved en operator, som for position,
Den klassiske oscillatormodel
 Kvantemekanik 6 Side af 8 n meget central model inden for KM er den såkaldte harmoniske oscillatormodel, som historisk set spillede en afgørende rolle i de banebrydende beskrivelser af bla. sortlegemestråling
Kvantemekanik 6 Side af 8 n meget central model inden for KM er den såkaldte harmoniske oscillatormodel, som historisk set spillede en afgørende rolle i de banebrydende beskrivelser af bla. sortlegemestråling
Chapter 6. Hydrogen Atom. 6.1 Schrödinger Equation. The Hamiltonian for a hydrogen atom is. Recall that. 1 r 2 sin 2 θ + 1. and.
 Chapter 6 Hydrogen Atom 6. Schrödinger Equation The Hamiltonian for a hydrogen atom is Recall that Ĥ = h e m e 4πɛ o r = r ) + r r r r sin θ sin θ ) + θ θ r sin θ φ and [ ˆL = h sin θ ) + )] sin θ θ θ
Chapter 6 Hydrogen Atom 6. Schrödinger Equation The Hamiltonian for a hydrogen atom is Recall that Ĥ = h e m e 4πɛ o r = r ) + r r r r sin θ sin θ ) + θ θ r sin θ φ and [ ˆL = h sin θ ) + )] sin θ θ θ
Rektangulær potentialbarriere
 Kvantemekanik 5 Side 1 af 8 ektangulær potentialbarriere Med udgangspunkt i det KM begrebsapparat udviklet i KM1-4 beskrives i denne lektion flg. to systemer, idet system gennemgås, og system behandles
Kvantemekanik 5 Side 1 af 8 ektangulær potentialbarriere Med udgangspunkt i det KM begrebsapparat udviklet i KM1-4 beskrives i denne lektion flg. to systemer, idet system gennemgås, og system behandles
2 Lektion Opgave C Opgave Opgave Opgave Opgave a b...
 . Indhold 1 Lektion 1 1 1.1 Opgave A............................... 1 1. Opgave 1............................... 1 1..1 1.a.............................. 1 1.. 1.b.............................. 1.3 Opgave
. Indhold 1 Lektion 1 1 1.1 Opgave A............................... 1 1. Opgave 1............................... 1 1..1 1.a.............................. 1 1.. 1.b.............................. 1.3 Opgave
Heisenbergs usikkerhedsrelationer. Abstrakt. Hvorfor? Funktionsrum. Nils Byrial Andersen Institut for Matematik. Matematiklærerdag 2013
 Heisenbergs usikkerhedsrelationer Nils Byrial Andersen Institut for Matematik Matematiklærerdag 013 1 / 17 Abstrakt Heisenbergs usikkerhedsrelationer udtrykker at man ikke på samme tid både kan bestemme
Heisenbergs usikkerhedsrelationer Nils Byrial Andersen Institut for Matematik Matematiklærerdag 013 1 / 17 Abstrakt Heisenbergs usikkerhedsrelationer udtrykker at man ikke på samme tid både kan bestemme
Hans Harhoff Andersen juni 2010 Projekt i numeriske metoder. Resumé
 Hans Harhoff Andersen 20072394 25. juni 2010 Projekt i numeriske metoder Resumé Ved hjælp af en finite difference approksimation og dertilhørende diskretisering af akserne konstrueres matricer for Schrödingerligningen.
Hans Harhoff Andersen 20072394 25. juni 2010 Projekt i numeriske metoder Resumé Ved hjælp af en finite difference approksimation og dertilhørende diskretisering af akserne konstrueres matricer for Schrödingerligningen.
Anvendelser af den kvantemekaniske bølgemekanik
 Syddansk Universitet, Teknisk Fakultet Anvendelser af den kvantemekaniske bølgemekanik FY529, projekt nr. 2 Skrevet af: Simon Holst Traberg-Larsen;Søren Emil Wegner Petersen d. 24. marts 2013 Resumé el.
Syddansk Universitet, Teknisk Fakultet Anvendelser af den kvantemekaniske bølgemekanik FY529, projekt nr. 2 Skrevet af: Simon Holst Traberg-Larsen;Søren Emil Wegner Petersen d. 24. marts 2013 Resumé el.
Niels Wessel Larsen MOLEKYLSPEKTROSKOPI. En kvantitativ beskrivelse af vibrations- og rotations-spektroskopi. Noter til Gasfasespektroskopi
 Niels Wessel Larsen MOLEKYLSPEKTROSKOPI En kvantitativ beskrivelse af vibrations- og rotations-spektroskopi Noter til Gasfasespektroskopi KEMISK INSTITUT KØBENHAVNS UNIVERSITET 007 ii Indhold KVANTEMEKANISK
Niels Wessel Larsen MOLEKYLSPEKTROSKOPI En kvantitativ beskrivelse af vibrations- og rotations-spektroskopi Noter til Gasfasespektroskopi KEMISK INSTITUT KØBENHAVNS UNIVERSITET 007 ii Indhold KVANTEMEKANISK
Note om Laplace-transformationen
 Note om Laplace-transformationen Den harmoniske oscillator omskrevet til et ligningssystem I dette opgavesæt benyttes laplacetransformationen til at løse koblede differentialligninger. Fordelen ved at
Note om Laplace-transformationen Den harmoniske oscillator omskrevet til et ligningssystem I dette opgavesæt benyttes laplacetransformationen til at løse koblede differentialligninger. Fordelen ved at
SINGULÆR PERTURBATIONSTEORI
 SINGULÆR PERTURBATIONSTEORI FOR DISKRETE LINEÆRE OPERATORER AALBORG UNIVERSITET Institut for Matematiske Fag Niels Lund 0. semester på matematik Foråret 04 AALBORG UNIVERSITET INSTITUT FOR MATEMATISKE
SINGULÆR PERTURBATIONSTEORI FOR DISKRETE LINEÆRE OPERATORER AALBORG UNIVERSITET Institut for Matematiske Fag Niels Lund 0. semester på matematik Foråret 04 AALBORG UNIVERSITET INSTITUT FOR MATEMATISKE
1 Eksamen Spin Spin-halv-operatorer Spin-orbitaler... 3
 . Indhold 1 Eksamen 1 1 1.1 Spin.................................. 1 1.1.1 Spin-halv-operatorer..................... 3 1.1.2 Spin-orbitaler......................... 3 2 Eksamen 2 5 2.1 Atomer................................
. Indhold 1 Eksamen 1 1 1.1 Spin.................................. 1 1.1.1 Spin-halv-operatorer..................... 3 1.1.2 Spin-orbitaler......................... 3 2 Eksamen 2 5 2.1 Atomer................................
Eksamen i Mat F, april 2006
 Eksamen i Mat F, april 26 Opgave 1 Lad F være et vektorfelt, givet i retvinklede koordinater som: F x x F = F x i + F y j + F z k = F y = 2z F z y Udregn F og F: F = F x + F y + F z = 1 + +. F = F z F
Eksamen i Mat F, april 26 Opgave 1 Lad F være et vektorfelt, givet i retvinklede koordinater som: F x x F = F x i + F y j + F z k = F y = 2z F z y Udregn F og F: F = F x + F y + F z = 1 + +. F = F z F
Svar til eksamen i Matematik F2 d. 23. juni 2016
 Svar til eksamen i Matematik F d. 3. juni 06 FORBEHOLD FOR FEJL! Bemærk, i modsætning til herunder, så skal det i besvarelsen fremgå tydeligt, hvordan polerne ndes og hvordan de enkelte residuer udregnes.
Svar til eksamen i Matematik F d. 3. juni 06 FORBEHOLD FOR FEJL! Bemærk, i modsætning til herunder, så skal det i besvarelsen fremgå tydeligt, hvordan polerne ndes og hvordan de enkelte residuer udregnes.
Uskelnelige kvantepartikler
 Kvantemekanik 3 Side af 4 Inden for den klassiske determinisme kan man med kendskab til de kræfter, der virker på et partikelsystem, samt begyndelsesbetingelserne for position og hastighed, vha. Newtons
Kvantemekanik 3 Side af 4 Inden for den klassiske determinisme kan man med kendskab til de kræfter, der virker på et partikelsystem, samt begyndelsesbetingelserne for position og hastighed, vha. Newtons
Løsningsforslag til opgavesæt 5
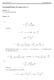 Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
Module 1: Lineære modeller og lineær algebra
 Module : Lineære modeller og lineær algebra. Lineære normale modeller og lineær algebra......2 Lineær algebra...................... 6.2. Vektorer i R n................... 6.2.2 Regneregler for vektorrum...........
Module : Lineære modeller og lineær algebra. Lineære normale modeller og lineær algebra......2 Lineær algebra...................... 6.2. Vektorer i R n................... 6.2.2 Regneregler for vektorrum...........
Youngs dobbeltspalteforsøg 1
 Kvantemekanik Side af Youngs dobbeltspalteforsøg Klassisk beskrivelse Inden for den klassiske fysik kan man forklare forekomsten af et interferensmønster ud fra flg. bølgemodel. x Før spalterne beskrives
Kvantemekanik Side af Youngs dobbeltspalteforsøg Klassisk beskrivelse Inden for den klassiske fysik kan man forklare forekomsten af et interferensmønster ud fra flg. bølgemodel. x Før spalterne beskrives
standard normalfordelingen på R 2.
 Standard normalfordelingen på R 2 Lad f (x, y) = 1 x 2 +y 2 2π e 2. Vi har så f (x, y) = 1 2π e x2 2 1 2π e y2 2, og ved Tonelli f dm 2 = 1. Ved µ(a) = A f dm 2 defineres et sandsynlighedsmål på R 2 målet
Standard normalfordelingen på R 2 Lad f (x, y) = 1 x 2 +y 2 2π e 2. Vi har så f (x, y) = 1 2π e x2 2 1 2π e y2 2, og ved Tonelli f dm 2 = 1. Ved µ(a) = A f dm 2 defineres et sandsynlighedsmål på R 2 målet
Wigner s semi-cirkel lov
 Wigner s semi-cirkel lov 12. december 2009 Eulers Venner Steen Thorbjørnsen Institut for Matematiske Fag Århus Universitet Diagonalisering af selvadjungeret matrix Lad H være en n n matrix med komplekse
Wigner s semi-cirkel lov 12. december 2009 Eulers Venner Steen Thorbjørnsen Institut for Matematiske Fag Århus Universitet Diagonalisering af selvadjungeret matrix Lad H være en n n matrix med komplekse
Momenter som deskriptive størrelser. Hvad vi mangler fra onsdag. Momenter for sandsynlighedsmål
 Hvad vi mangler fra onsdag Momenter som deskriptive størrelser Sandsynlighedsmål er komplicerede objekter de tildeler numeriske værdier til alle hændelser i en σ-algebra. Vi har behov for simplere, deskriptive
Hvad vi mangler fra onsdag Momenter som deskriptive størrelser Sandsynlighedsmål er komplicerede objekter de tildeler numeriske værdier til alle hændelser i en σ-algebra. Vi har behov for simplere, deskriptive
Hvad vi mangler fra onsdag. Vi starter med at gennemgå slides fra onsdag.
 Hvad vi mangler fra onsdag Vi starter med at gennemgå slides 34-38 fra onsdag. Slide 1/17 Niels Richard Hansen MI forelæsninger 6. December, 2013 Momenter som deskriptive størrelser Sandsynlighedsmål er
Hvad vi mangler fra onsdag Vi starter med at gennemgå slides 34-38 fra onsdag. Slide 1/17 Niels Richard Hansen MI forelæsninger 6. December, 2013 Momenter som deskriptive størrelser Sandsynlighedsmål er
Anvendt Lineær Algebra
 Anvendt Lineær Algebra Kursusgang 3 Anita Abildgaard Sillasen Institut for Matematiske Fag AAS (I17) Anvendt Lineær Algebra 1 / 38 Vi betragter et lineært ligningssystem (af m ligninger med n ubekendte)
Anvendt Lineær Algebra Kursusgang 3 Anita Abildgaard Sillasen Institut for Matematiske Fag AAS (I17) Anvendt Lineær Algebra 1 / 38 Vi betragter et lineært ligningssystem (af m ligninger med n ubekendte)
DOK-facitliste DOK. DOK-facitliste 1
 -facitliste 1 -facitliste Listens numre refererer til samlingen af supplerede -opgaver (de gamle eksamensopgaver. På listen står næsten kun facitter, og ikke tilstrækkelige svar på opgaverne. [Korrigeret
-facitliste 1 -facitliste Listens numre refererer til samlingen af supplerede -opgaver (de gamle eksamensopgaver. På listen står næsten kun facitter, og ikke tilstrækkelige svar på opgaverne. [Korrigeret
Løsningsforslag til opgavesæt 5
 Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
Stochastic Variational Method -Used on Small Atoms. 14. september 2011
 Stochastic Variational Method -Used on Small Atoms 14. september 2011 Jens Egebjerg Bækhøj Årskortnummer: 20082846 Institut for Fysik og Astronomi Aarhus Universitet, Denmark j j j Abstract j In this paper
Stochastic Variational Method -Used on Small Atoms 14. september 2011 Jens Egebjerg Bækhøj Årskortnummer: 20082846 Institut for Fysik og Astronomi Aarhus Universitet, Denmark j j j Abstract j In this paper
DesignMat Uge 1 Repetition af forårets stof
 DesignMat Uge 1 Repetition af forårets stof Preben Alsholm Efterår 008 01 Lineært ligningssystem Lineært ligningssystem Et lineært ligningssystem: a 11 x 1 + a 1 x + + a 1n x n = b 1 a 1 x 1 + a x + +
DesignMat Uge 1 Repetition af forårets stof Preben Alsholm Efterår 008 01 Lineært ligningssystem Lineært ligningssystem Et lineært ligningssystem: a 11 x 1 + a 1 x + + a 1n x n = b 1 a 1 x 1 + a x + +
Magnetisk dipolmoment
 Kvantemekanik 9 Side 1 af 8 Magnetisk dipolmoment Klassisk Ifølge EM udtyk (8.16) e det magnetiske dipolmoment af en ladning q i en cikulæ bane med adius givet ved μ = IA (9.1) v q > 0 μ L hvo A = π og
Kvantemekanik 9 Side 1 af 8 Magnetisk dipolmoment Klassisk Ifølge EM udtyk (8.16) e det magnetiske dipolmoment af en ladning q i en cikulæ bane med adius givet ved μ = IA (9.1) v q > 0 μ L hvo A = π og
Indhold En statistisk beskrivelse... 3 Bølgefunktionen... 4 Eksempel... 4 Opgave 1... 5 Tidsafhængig og tidsuafhængig... 5 Opgave 2...
 Introduktion til kvantemekanik Indhold En statistisk beskrivelse... 3 Bølgefunktionen... 4 Eksempel... 4 Opgave 1... 5 Tidsafhængig og tidsuafhængig... 5 Opgave 2... 6 Hvordan må bølgefunktionen se ud...
Introduktion til kvantemekanik Indhold En statistisk beskrivelse... 3 Bølgefunktionen... 4 Eksempel... 4 Opgave 1... 5 Tidsafhængig og tidsuafhængig... 5 Opgave 2... 6 Hvordan må bølgefunktionen se ud...
DesignMat Uge 1 Gensyn med forårets stof
 DesignMat Uge 1 Gensyn med forårets stof Preben Alsholm Efterår 2010 1 Hovedpunkter fra forårets pensum 11 Taylorpolynomium Taylorpolynomium Det n te Taylorpolynomium for f med udviklingspunkt x 0 : P
DesignMat Uge 1 Gensyn med forårets stof Preben Alsholm Efterår 2010 1 Hovedpunkter fra forårets pensum 11 Taylorpolynomium Taylorpolynomium Det n te Taylorpolynomium for f med udviklingspunkt x 0 : P
Kvantemekanik postulater, notation, polarisationstilstande, entanglement, Bells ulighed,...
 Kvantemekanik postulater, notation, polarisationstilstande, entanglement, Bells ulighed,... Ulrich B. Hoff DTU Fysik, Danmarks Tekniske Universitet, Fysikvej bld. 309, 800 Kgs. Lyngby, Denmark (Dated:
Kvantemekanik postulater, notation, polarisationstilstande, entanglement, Bells ulighed,... Ulrich B. Hoff DTU Fysik, Danmarks Tekniske Universitet, Fysikvej bld. 309, 800 Kgs. Lyngby, Denmark (Dated:
Outline. Chapter 6: (cont d) Qijin Chen. November 21, 2013 NH = =6 CH = 15 4
 Chapter 6: Qjn Chen Department of Physcs, Zhejang Unversty November 1, 013 Copyrght c 013 by Qjn Chen; all rghts reserved. ω 3 4 1. (cont d) 1 3 n3n3n 3n (x 1, y 1, z 1 )(x, y, z ) (x 1 x ) + (y 1 y )
Chapter 6: Qjn Chen Department of Physcs, Zhejang Unversty November 1, 013 Copyrght c 013 by Qjn Chen; all rghts reserved. ω 3 4 1. (cont d) 1 3 n3n3n 3n (x 1, y 1, z 1 )(x, y, z ) (x 1 x ) + (y 1 y )
Besvarelse til eksamen i Matematik F2, 2012
 Besvarelse til eksamen i Matematik F2, 202 Partiel besvarelse - har ikke inkluderet alle detaljer! Med forbehold for tastefejl. Opgave Find og bestem typen af alle singulariteter for følgende funktioner:
Besvarelse til eksamen i Matematik F2, 202 Partiel besvarelse - har ikke inkluderet alle detaljer! Med forbehold for tastefejl. Opgave Find og bestem typen af alle singulariteter for følgende funktioner:
ˆ Š ˆ ˆ É ÉÊ, ± Ö, ²μ Ö.. ƒ μ ±μ
 ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2009.. 40.. 5 ˆ Š ˆ ˆ ˆ Š ˆ ˆ É ÉÊ, ± Ö, ²μ Ö.. ƒ μ ±μ Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê ˆ 1273 ˆ ˆŸ ˆ Œ Ÿ ˆ 1279 Œ ƒˆ ˆ Šˆ ƒ Œ ˆŠ 1286 Š -Œ ˆ Š Ÿ Œ œ ˆ Š ˆ ˆ 1290 Œμ ²Ó ÉμÎ ±μ³. 1291 ² Ò Î Ò Ê ²μ
ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2009.. 40.. 5 ˆ Š ˆ ˆ ˆ Š ˆ ˆ É ÉÊ, ± Ö, ²μ Ö.. ƒ μ ±μ Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê ˆ 1273 ˆ ˆŸ ˆ Œ Ÿ ˆ 1279 Œ ƒˆ ˆ Šˆ ƒ Œ ˆŠ 1286 Š -Œ ˆ Š Ÿ Œ œ ˆ Š ˆ ˆ 1290 Œμ ²Ó ÉμÎ ±μ³. 1291 ² Ò Î Ò Ê ²μ
Magnetisk dipolmoment
 Kvantemekanik 9 Side 1 af 9 Magnetisk dipolmoment Klassisk Ifølge EM udtyk (8.16) e det magnetiske dipolmoment af en ladning q i en cikulæ bane med adius givet ved μ = IA (9.1) v q > 0 μ L hvo A = π I
Kvantemekanik 9 Side 1 af 9 Magnetisk dipolmoment Klassisk Ifølge EM udtyk (8.16) e det magnetiske dipolmoment af en ladning q i en cikulæ bane med adius givet ved μ = IA (9.1) v q > 0 μ L hvo A = π I
Analyse 1, Prøve 4 Besvarelse
 Københavns Universitet Prøve ved Det naturvidenskabelige Fakultet juni 2011 1 Analyse 1, Prøve 4 Besvarelse Lad Opgave 1 (50%) M = {T R 2 T er en åben trekant} og lad A : M R være arealfunktionen, dvs.
Københavns Universitet Prøve ved Det naturvidenskabelige Fakultet juni 2011 1 Analyse 1, Prøve 4 Besvarelse Lad Opgave 1 (50%) M = {T R 2 T er en åben trekant} og lad A : M R være arealfunktionen, dvs.
6.1 Reelle Indre Produkter
 SEKTION 6.1 REELLE INDRE PRODUKTER 6.1 Reelle Indre Produkter Definition 6.1.1 Et indre produkt på et reelt vektorrum V er en funktion, : V V R således at, for alle x, y V, I x, x 0 med lighed x = 0, II
SEKTION 6.1 REELLE INDRE PRODUKTER 6.1 Reelle Indre Produkter Definition 6.1.1 Et indre produkt på et reelt vektorrum V er en funktion, : V V R således at, for alle x, y V, I x, x 0 med lighed x = 0, II
Elementær sandsynlighedsregning
 Elementær sandsynlighedsregning Sandsynlighedsbegrebet Et udfaldsrum S er mængden af alle de mulige udfald af et eksperiment. En hændelse A er en delmængde af udfaldsrummet S. Den hændelse, der ikke indeholder
Elementær sandsynlighedsregning Sandsynlighedsbegrebet Et udfaldsrum S er mængden af alle de mulige udfald af et eksperiment. En hændelse A er en delmængde af udfaldsrummet S. Den hændelse, der ikke indeholder
Statitisk fysik Minilex
 Statitisk fysik Minilex Henrik Dahl 15. januar 006 Indhold 1 Sandsynlighedsteori Fordelinger 3 Eksperimentelle usikkerheder 3 4 Parameterbestemmelse 3 5 Priors, entropi 3 6 Termodynamik 4 6.1 Kanonisk
Statitisk fysik Minilex Henrik Dahl 15. januar 006 Indhold 1 Sandsynlighedsteori Fordelinger 3 Eksperimentelle usikkerheder 3 4 Parameterbestemmelse 3 5 Priors, entropi 3 6 Termodynamik 4 6.1 Kanonisk
Kortfattet svar til eksamen i Matematik F2 d. 21. juni 2017
 Kortfattet svar til eksamen i Matematik F2 d. 2. juni 27 Opgave Bestem for følgende tilfælde om en funktion f(z) af z = x + iy er analytisk i dele af den komplekse plan, hvis den har real del u(x, y) og
Kortfattet svar til eksamen i Matematik F2 d. 2. juni 27 Opgave Bestem for følgende tilfælde om en funktion f(z) af z = x + iy er analytisk i dele af den komplekse plan, hvis den har real del u(x, y) og
Course on Continuum Mechanics - academic year Màster en Enginyeria de Camins, Canals i Ports. Màster en Enginyeria Geològica i de Mines.
 Official Fom Chapte. Desciption of Motion (, t) (, t) + (, t) (, t) t t Chapte. Defomation an Stain s S X E X e i ij j i ij j F X X U F J E F F JJ J J T T T e F F jj j j T T T T s JJ T a JJ T E T t t ij
Official Fom Chapte. Desciption of Motion (, t) (, t) + (, t) (, t) t t Chapte. Defomation an Stain s S X E X e i ij j i ij j F X X U F J E F F JJ J J T T T e F F jj j j T T T T s JJ T a JJ T E T t t ij
Anvendt Lineær Algebra
 Anvendt Lineær Algebra Kursusgang 4 Anita Abildgaard Sillasen Institut for Matematiske Fag AAS (I17) Anvendt Lineær Algebra 1 / 32 Vægtet mindste kvadraters metode For et lineært ligningssystem (af m ligninger
Anvendt Lineær Algebra Kursusgang 4 Anita Abildgaard Sillasen Institut for Matematiske Fag AAS (I17) Anvendt Lineær Algebra 1 / 32 Vægtet mindste kvadraters metode For et lineært ligningssystem (af m ligninger
Skriftlig eksamen i Statistisk Mekanik den fra 9.00 til Alle hjælpemidler er tilladte. Undtaget er dog net-opkoblede computere.
 Skriftlig eksamen i Statistisk Mekanik den 18-01-2007 fra 900 til 1300 lle hjælpemidler er tilladte Undtaget er dog net-opkoblede computere Opgave 1: I en beholder med volumen V er der rgon-atomer i gasfasen,
Skriftlig eksamen i Statistisk Mekanik den 18-01-2007 fra 900 til 1300 lle hjælpemidler er tilladte Undtaget er dog net-opkoblede computere Opgave 1: I en beholder med volumen V er der rgon-atomer i gasfasen,
Elementær sandsynlighedsregning
 Elementær sandsynlighedsregning Sandsynlighedsbegrebet Et udfaldsrum S er mængden af alle de mulige udfald af et eksperiment. En hændelse A er en delmængde af udfaldsrummet S. Et sandsynlighedsmål er en
Elementær sandsynlighedsregning Sandsynlighedsbegrebet Et udfaldsrum S er mængden af alle de mulige udfald af et eksperiment. En hændelse A er en delmængde af udfaldsrummet S. Et sandsynlighedsmål er en
Lambforskydning i en elektrisk ledende mesoskopisk ring
 Lambforskydning i en elektrisk ledende mesoskopisk ring AALBORG UNIVERSITET e Institut for Fysik og Nanoteknologi Skjernvej 4A DK-922 Aalborg Ø Aalborg Universitet Institut for Fysik og Nanoteknologi
Lambforskydning i en elektrisk ledende mesoskopisk ring AALBORG UNIVERSITET e Institut for Fysik og Nanoteknologi Skjernvej 4A DK-922 Aalborg Ø Aalborg Universitet Institut for Fysik og Nanoteknologi
nr. 495c (2. udgave)
 - I, OM OG MED MATEMATIK OG FYSIK Opgavesamling til Kvantemekanik Eksamensopgaver stillet i perioden januar 1978 til august 2016 Redigeret af Bo Jakobsen marts 2017 nr. 495c - 2017 (2. udgave) Roskilde
- I, OM OG MED MATEMATIK OG FYSIK Opgavesamling til Kvantemekanik Eksamensopgaver stillet i perioden januar 1978 til august 2016 Redigeret af Bo Jakobsen marts 2017 nr. 495c - 2017 (2. udgave) Roskilde
Oversigt Matematik Alfa 1, August 2002
 Oversigt [S], [LA] Nøgleord og begreber Egenvektorer, egenværdier og diagonalisering Dobbelt integral og polært koordinatskift Ortogonal projektion og mindste afstand Retningsafledt og gradient Maksimum/minimums
Oversigt [S], [LA] Nøgleord og begreber Egenvektorer, egenværdier og diagonalisering Dobbelt integral og polært koordinatskift Ortogonal projektion og mindste afstand Retningsafledt og gradient Maksimum/minimums
GEOMETRI-TØ, UGE 6. . x 1 x 1. = x 1 x 2. x 2. k f
 GEOMETRI-TØ, UGE 6 Hvis I falder over tryk- eller regne-fejl i nedenstående, må I meget gerne sende rettelser til fuglede@imfaudk Opvarmningsopgave 1 Lad f : R 2 R være tre gange kontinuert differentierbar
GEOMETRI-TØ, UGE 6 Hvis I falder over tryk- eller regne-fejl i nedenstående, må I meget gerne sende rettelser til fuglede@imfaudk Opvarmningsopgave 1 Lad f : R 2 R være tre gange kontinuert differentierbar
Overheads til forelæsninger, mandag 5. uge På E har vi en mængde af mulige sandsynlighedsfordelinger for X, (P θ ) θ Θ.
 Statistiske modeller (Definitioner) Statistik og Sandsynlighedsregning 2 IH kapitel 0 og En observation er en vektor af tal x (x,..., x n ) E, der repræsenterer udfaldet af et (eller flere) eksperimenter.
Statistiske modeller (Definitioner) Statistik og Sandsynlighedsregning 2 IH kapitel 0 og En observation er en vektor af tal x (x,..., x n ) E, der repræsenterer udfaldet af et (eller flere) eksperimenter.
Bachelor opgaven. Vincent Appel ( )
 Bachelor opgaven Vincent Appel (3088-94). oktober 00 Vejleder: Jens Paaske Indhold Abstract Grundlæggende Gruppeteori. Grupper.................................. Klasser............................ 3. Repræsentationer...........................
Bachelor opgaven Vincent Appel (3088-94). oktober 00 Vejleder: Jens Paaske Indhold Abstract Grundlæggende Gruppeteori. Grupper.................................. Klasser............................ 3. Repræsentationer...........................
Lineær Algebra F08, MØ
 Lineær Algebra F08, MØ Vejledende besvarelser af udvalgte opgaver fra Ugeseddel 3 og 4 Ansvarsfraskrivelse: Den følgende vejledning er kun vejledende. Opgaverne kommer i vilkårlig rækkefølge. Visse steder
Lineær Algebra F08, MØ Vejledende besvarelser af udvalgte opgaver fra Ugeseddel 3 og 4 Ansvarsfraskrivelse: Den følgende vejledning er kun vejledende. Opgaverne kommer i vilkårlig rækkefølge. Visse steder
Formelsamling - MatF2. Therkel Zøllner og Amalie Christensen 27. juni 2009
 Formelsamling - MatF2 Therkel Zøllner og Amalie Christensen 27. juni 2009 1 Indhold 1 Kompleks variabel teori 3 1.1 Komplekse funktioner 825-830........................... 3 1.2 Powerserier af komplekse
Formelsamling - MatF2 Therkel Zøllner og Amalie Christensen 27. juni 2009 1 Indhold 1 Kompleks variabel teori 3 1.1 Komplekse funktioner 825-830........................... 3 1.2 Powerserier af komplekse
Eksamen i Mat F, april 2006
 Eksamen i Mat F, april 26 Opgave Lad F være et vektorfelt, givet i retvinklede koordinater som: Udregn F og F: F x F = F x i + F y j + F z k = F y = z 2 F z xz y 2 F = F x + F y + F z = + + x. F = F z
Eksamen i Mat F, april 26 Opgave Lad F være et vektorfelt, givet i retvinklede koordinater som: Udregn F og F: F x F = F x i + F y j + F z k = F y = z 2 F z xz y 2 F = F x + F y + F z = + + x. F = F z
Oversigt [S] 7.3, 7.4, 7.5, 7.6; [DL] 1, 2
![Oversigt [S] 7.3, 7.4, 7.5, 7.6; [DL] 1, 2 Oversigt [S] 7.3, 7.4, 7.5, 7.6; [DL] 1, 2](/thumbs/82/86922880.jpg) Oversigt [S] 7.3, 7.4, 7.5, 7.6; [DL] 1, 2 Her skal du lære om Separable ligninger Logistisk ligning og eksponentiel vækst 1. ordens lineær ligning August 2002, opgave 7 Rovdyr-Byttedyr system 1. ordens
Oversigt [S] 7.3, 7.4, 7.5, 7.6; [DL] 1, 2 Her skal du lære om Separable ligninger Logistisk ligning og eksponentiel vækst 1. ordens lineær ligning August 2002, opgave 7 Rovdyr-Byttedyr system 1. ordens
Atomare kvantegasser. Michael Budde. Institut for Fysik og Astronomi og QUANTOP: Danmarks Grundforskningsfonds Center for Kvanteoptik
 Atomare kvantegasser Når ultrakoldt bliver hot Michael Budde Institut for Fysik og Astronomi og QUANTOP: Danmarks Grundforskningsfonds Center for Kvanteoptik Aarhus Universitet Plan for foredraget Hvad
Atomare kvantegasser Når ultrakoldt bliver hot Michael Budde Institut for Fysik og Astronomi og QUANTOP: Danmarks Grundforskningsfonds Center for Kvanteoptik Aarhus Universitet Plan for foredraget Hvad
Calculus Uge
 Oversigt [S], [LA] Nøgleord og begreber Egenvektorer, egenværdier og diagonalisering Dobbelt integral og polært koordinatskift Ortogonal projektion og mindste afstand Retningsafledt og gradient Maksimum/minimums
Oversigt [S], [LA] Nøgleord og begreber Egenvektorer, egenværdier og diagonalisering Dobbelt integral og polært koordinatskift Ortogonal projektion og mindste afstand Retningsafledt og gradient Maksimum/minimums
Kvantitative Metoder 1 - Forår Dagens program
 Dagens program Kontinuerte fordelinger Ventetider i en Poissonproces Beskrivelse af kontinuerte fordelinger: - Median og kvartiler - Middelværdi - Varians Simultane fordelinger 1 Ventetider i en Poissonproces
Dagens program Kontinuerte fordelinger Ventetider i en Poissonproces Beskrivelse af kontinuerte fordelinger: - Median og kvartiler - Middelværdi - Varians Simultane fordelinger 1 Ventetider i en Poissonproces
Matematisk modellering og numeriske metoder. Lektion 10
 Matematisk modellering og numeriske metoder Lektion 10 Morten Grud Rasmussen 2. november 2016 1 Partielle differentialligninger 1.1 Det grundlæggende om PDE er Definition 1.1 Partielle differentialligninger
Matematisk modellering og numeriske metoder Lektion 10 Morten Grud Rasmussen 2. november 2016 1 Partielle differentialligninger 1.1 Det grundlæggende om PDE er Definition 1.1 Partielle differentialligninger
by antisymmetry of ɛ s
 PHY 396 K. Solutions for homework set #6. Problem 2a: Ĵi, Ĵj] 1 4 ɛikl ɛ jmn Ĵ kl, Ĵmn] = by eq. 1 = 1 4 ɛikl ɛ jmn ig km Ĵ ln + ig kn Ĵ lm + ig lm Ĵ kn g ln Ĵ km by antisymmetry of ɛ s = ɛ ikl ɛ jmn ig
PHY 396 K. Solutions for homework set #6. Problem 2a: Ĵi, Ĵj] 1 4 ɛikl ɛ jmn Ĵ kl, Ĵmn] = by eq. 1 = 1 4 ɛikl ɛ jmn ig km Ĵ ln + ig kn Ĵ lm + ig lm Ĵ kn g ln Ĵ km by antisymmetry of ɛ s = ɛ ikl ɛ jmn ig
Ganganalyse. Modellering og estimation. Klaus Kähler Holst. 5. Januar 2006
 Ganganalyse Modellering og estimation Klaus Kähler Holst 5. Januar 2006 Oversigt 1 Introduktion 2 Model for ledvinkelsrotation 3 PCA 4 Perspektivering Ganganalyse er studiet af hvordan et menneske bevæger
Ganganalyse Modellering og estimation Klaus Kähler Holst 5. Januar 2006 Oversigt 1 Introduktion 2 Model for ledvinkelsrotation 3 PCA 4 Perspektivering Ganganalyse er studiet af hvordan et menneske bevæger
Moderne acceleratorers fysik og anvendelse
 Moderne acceleratorers fysik og anvendelse Forelæsning 4b, uge 6/08, mandag d. 4/2 16:15-17:00 Kapitel 6 i Wilson: Imperfections and multipoles. Cirkeldiagrammet Closed-orbit distortions Orbitkorrektion
Moderne acceleratorers fysik og anvendelse Forelæsning 4b, uge 6/08, mandag d. 4/2 16:15-17:00 Kapitel 6 i Wilson: Imperfections and multipoles. Cirkeldiagrammet Closed-orbit distortions Orbitkorrektion
Analytisk perturbationsteori
 master 2009/6/2 23:09 page # f Analytisk perturbationsteori for lineære operatorer JUNI 2009 Speciale af Mette Kristensen AALBORG UNIVERSITET INSTITUT FOR MATEMATISKE FAG FREDRIK BAYERS VEJ 7 G, 9220 AALBORG
master 2009/6/2 23:09 page # f Analytisk perturbationsteori for lineære operatorer JUNI 2009 Speciale af Mette Kristensen AALBORG UNIVERSITET INSTITUT FOR MATEMATISKE FAG FREDRIK BAYERS VEJ 7 G, 9220 AALBORG
Uge 10 Teoretisk Statistik 1. marts 2004
 1 Uge 10 Teoretisk Statistik 1. marts 004 1. u-fordelingen. Normalfordelingen 3. Middelværdi og varians 4. Mere normalfordelingsteori 5. Grafisk kontrol af normalfordelingsantagelse 6. Eksempler 7. Oversigt
1 Uge 10 Teoretisk Statistik 1. marts 004 1. u-fordelingen. Normalfordelingen 3. Middelværdi og varians 4. Mere normalfordelingsteori 5. Grafisk kontrol af normalfordelingsantagelse 6. Eksempler 7. Oversigt
Sandsynlighed og Statistik
 36 Sandsynlighed og Statistik 6.1 Indledning Denne note beskriver de statistiske begreber og formler som man med rimelig sandsynlighed kan komme ud for i eksperimentelle øvelser. Alt er yderst korfattet,
36 Sandsynlighed og Statistik 6.1 Indledning Denne note beskriver de statistiske begreber og formler som man med rimelig sandsynlighed kan komme ud for i eksperimentelle øvelser. Alt er yderst korfattet,
n=1 er veldefineret for alle følger for hvilke højresiden er endelig. F.eks. tilhører følgen
 2 Hilbert rum 2. Eksempler på Hilbert rum Vi skal nu først forsøge at begrunde, at de indre produkt rum af funktioner eller følger, som blev indført i Kapitel, ikke er omfattende nok til vores formål.
2 Hilbert rum 2. Eksempler på Hilbert rum Vi skal nu først forsøge at begrunde, at de indre produkt rum af funktioner eller følger, som blev indført i Kapitel, ikke er omfattende nok til vores formål.
Lys på (kvante-)spring: fra paradox til præcision
 Lys på (kvante-)spring: fra paradox til præcision Metrologidag, 18. maj, 2015, Industriens Hus Lys og Bohrs atomteori, 1913 Kvantemekanikken, 1925-26 Tilfældigheder, usikkerhedsprincippet Kampen mellem
Lys på (kvante-)spring: fra paradox til præcision Metrologidag, 18. maj, 2015, Industriens Hus Lys og Bohrs atomteori, 1913 Kvantemekanikken, 1925-26 Tilfældigheder, usikkerhedsprincippet Kampen mellem
Abstract. This paper examines the symmetries in particle physics and the mathematics behind. It investigates
 Abstract This paper examines the symmetries in particle physics and the mathematics behind. It investigates the algebraic structures and uses them to describe a vector space as it derives the Hilbert space
Abstract This paper examines the symmetries in particle physics and the mathematics behind. It investigates the algebraic structures and uses them to describe a vector space as it derives the Hilbert space
Sandsynlighedsregning
 Mogens Bladt www2.imm.dtu.dk/courses/02405 21. September, 2007 Lidt om binomialkoefficienter n størrelsen af en mængde/population. Vi ønsker at udtage en sub population af størrelse r. To sub populationer
Mogens Bladt www2.imm.dtu.dk/courses/02405 21. September, 2007 Lidt om binomialkoefficienter n størrelsen af en mængde/population. Vi ønsker at udtage en sub population af størrelse r. To sub populationer
4. Differentialligninger i højere dimension, Dirichlet problemet
 4.1 4. Differentialligninger i højere dimension, Dirichlet problemet 4.1. Indledning, de forskellige typer. Der er tre hovedeksempler på partielle differentialligninger, som har særlig betydning i fysik:
4.1 4. Differentialligninger i højere dimension, Dirichlet problemet 4.1. Indledning, de forskellige typer. Der er tre hovedeksempler på partielle differentialligninger, som har særlig betydning i fysik:
8 Regulære flader i R 3
 8 Regulære flader i R 3 Vi skal betragte særligt pæne delmængder S R 3 kaldet flader. I det følgende opfattes S som et topologisk rum i sportopologien, se Definition 5.9. En åben omegn U af p S er således
8 Regulære flader i R 3 Vi skal betragte særligt pæne delmængder S R 3 kaldet flader. I det følgende opfattes S som et topologisk rum i sportopologien, se Definition 5.9. En åben omegn U af p S er således
Resonant Tunneling Diodes
 Resonant Tunneling Diodes Af studerer nanoteknologi på 8. semester ved Institut for Fysik og Nanoteknologi på Aalborg Universitet. Hans primære interesser er teori og modellering af fysiske fænomener indenfor
Resonant Tunneling Diodes Af studerer nanoteknologi på 8. semester ved Institut for Fysik og Nanoteknologi på Aalborg Universitet. Hans primære interesser er teori og modellering af fysiske fænomener indenfor
Landmålingens fejlteori Lektion 1 Det matematiske fundament Kontinuerte stokastiske variable
 Landmålingens fejlteori Lektion 1 Det matematiske fundament Kontinuerte stokastiske variable - rw@math.aau.dk Institut for Matematiske Fag Aalborg Universitet 1/41 Landmålingens fejlteori - lidt om kurset
Landmålingens fejlteori Lektion 1 Det matematiske fundament Kontinuerte stokastiske variable - rw@math.aau.dk Institut for Matematiske Fag Aalborg Universitet 1/41 Landmålingens fejlteori - lidt om kurset
EKSAMENSOPGAVELØSNINGER CALCULUS 2 (2005) JANUAR 2006 AARHUS UNIVERSITET.. Beregn den retningsafledede D u f(0, 0).
 EKSAMENSOPGAVELØSNINGER CALCULUS 2 (2005) JANUAR 2006 AARHUS UNIVERSITET H.A. NIELSEN & H.A. SALOMONSEN Opgave. Lad f betegne funktionen f(x, y) = x cos(y) + y sin(x). ) Angiv gradienten f. 2) Lad u betegne
EKSAMENSOPGAVELØSNINGER CALCULUS 2 (2005) JANUAR 2006 AARHUS UNIVERSITET H.A. NIELSEN & H.A. SALOMONSEN Opgave. Lad f betegne funktionen f(x, y) = x cos(y) + y sin(x). ) Angiv gradienten f. 2) Lad u betegne
A4: Introduction to Cosmology. Forelæsning 2 (kap. 4-5): Kosmisk Dynamik
 A4: Introduction to Cosmology Forelæsning (kap. 4-5): Kosmisk Dynamik 1-komponent modeller Robertson-Walker metrikken ds = c dt² a t [ Metrik med medfølgende koordinater (x,θ,φ), x= S κ (r) i den rumlige
A4: Introduction to Cosmology Forelæsning (kap. 4-5): Kosmisk Dynamik 1-komponent modeller Robertson-Walker metrikken ds = c dt² a t [ Metrik med medfølgende koordinater (x,θ,φ), x= S κ (r) i den rumlige
Selv-absorberende C*-algebraer
 Selv-absorberende C*-algebraer Speciale af Randi Rohde 5. marts 006 Vejleder: Mikael Rørdam Indhold Indledning Tensorprodukter 3. Indledende resultater................................. 3. Fuldstændigt
Selv-absorberende C*-algebraer Speciale af Randi Rohde 5. marts 006 Vejleder: Mikael Rørdam Indhold Indledning Tensorprodukter 3. Indledende resultater................................. 3. Fuldstændigt
Klassisk kaos. Kaotiske systemer. Visse regulariteter universalitet
 Klassisk kaos Deterministiske bevægelsesligninger kan under visse omstændigheder udvise løsninger som er uforudsigelige, dvs. løsninger der opfører sig kaotisk: Faserum Forudsigelige Integrable systemer
Klassisk kaos Deterministiske bevægelsesligninger kan under visse omstændigheder udvise løsninger som er uforudsigelige, dvs. løsninger der opfører sig kaotisk: Faserum Forudsigelige Integrable systemer
1/41. 2/41 Landmålingens fejlteori - Lektion 1 - Kontinuerte stokastiske variable
 Landmålingens fejlteori - lidt om kurset Landmålingens fejlteori Lektion 1 Det matematiske fundament Kontinuerte stokastiske variable - rw@math.aau.dk Institut for Matematiske Fag Aalborg Universitet Kursusholder
Landmålingens fejlteori - lidt om kurset Landmålingens fejlteori Lektion 1 Det matematiske fundament Kontinuerte stokastiske variable - rw@math.aau.dk Institut for Matematiske Fag Aalborg Universitet Kursusholder
Moderne acceleratorers fysik og anvendelse Forelæsning 2 Transverse motion, Lattices
 Moderne acceleratorers fysik og anvendelse Forelæsning 2 Transverse motion, Lattices Optiske elementer: Styring og fokusering. Bevægelsesligningen og dens løsning. Stabilitet. Typiske latticekonfigurationer.
Moderne acceleratorers fysik og anvendelse Forelæsning 2 Transverse motion, Lattices Optiske elementer: Styring og fokusering. Bevægelsesligningen og dens løsning. Stabilitet. Typiske latticekonfigurationer.
Integration m.h.t. mål med tæthed
 Integration m.h.t. mål med tæthed Sætning (EH 11.7) Lad ν = f µ på (X, E). For alle g M + (X, E) gælder at gdν = g f dµ. Bevis: Standardbeviset: 1) indikatorfunktioner 2) simple funktioner 3) M + -funktioner.
Integration m.h.t. mål med tæthed Sætning (EH 11.7) Lad ν = f µ på (X, E). For alle g M + (X, E) gælder at gdν = g f dµ. Bevis: Standardbeviset: 1) indikatorfunktioner 2) simple funktioner 3) M + -funktioner.
Den todimensionale normalfordeling
 Den todimensionale normalfordeling Definition En todimensional stokastisk variabel X Y siges at være todimensional normalfordelt med parametrene µ µ og når den simultane tæthedsfunktion for X Y kan skrives
Den todimensionale normalfordeling Definition En todimensional stokastisk variabel X Y siges at være todimensional normalfordelt med parametrene µ µ og når den simultane tæthedsfunktion for X Y kan skrives
StatDataN: Plot af data
 StatDataN: Plot af data JLJ StatDataN: Plot af data p. 1/39 Repetition binomial(n,p): P(X = k) = ( n) k p k (1 p) n k n uafhængige kast med en mønt, X= antal krone X binomial(n, p), Y binomial(m, p), uafhængige
StatDataN: Plot af data JLJ StatDataN: Plot af data p. 1/39 Repetition binomial(n,p): P(X = k) = ( n) k p k (1 p) n k n uafhængige kast med en mønt, X= antal krone X binomial(n, p), Y binomial(m, p), uafhængige
Trykfejlsliste - alle fejl Asymptotisk teori
 9. januar 2005 Stat 2A / EH Trykfejlsliste - alle fejl Asymptotisk teori Denne liste indeholder alle de regulære fejl, slåfejl og stavefejl der er fundet i 2A-noterne indtil nu. 9 1 Forkert: x C x ro alle
9. januar 2005 Stat 2A / EH Trykfejlsliste - alle fejl Asymptotisk teori Denne liste indeholder alle de regulære fejl, slåfejl og stavefejl der er fundet i 2A-noterne indtil nu. 9 1 Forkert: x C x ro alle
Eksamen 2014/2015 Mål- og integralteori
 Eksamen 4/5 Mål- og integralteori Københavns Universitet Institut for Matematiske Fag Formalia Eksamensopgaven består af 4 opgaver med ialt spørgsmål Ved bedømmelsen indgår de spørgsmål med samme vægt
Eksamen 4/5 Mål- og integralteori Københavns Universitet Institut for Matematiske Fag Formalia Eksamensopgaven består af 4 opgaver med ialt spørgsmål Ved bedømmelsen indgår de spørgsmål med samme vægt
Nøgleord og begreber. Definition 15.1 Den lineære 1. ordens differentialligning er
 Oversigt [S] 7.3, 7.4, 7.5, 7.6; [LA] 15, 16, 17 Nøgleord og begreber 1. ordens lineær ligning Løsningsmetode August 2002, opgave 7 1. ordens lineært system Løsning ved egenvektor Lille opgave Stor opgave
Oversigt [S] 7.3, 7.4, 7.5, 7.6; [LA] 15, 16, 17 Nøgleord og begreber 1. ordens lineær ligning Løsningsmetode August 2002, opgave 7 1. ordens lineært system Løsning ved egenvektor Lille opgave Stor opgave
Oversigt [S] 7.3, 7.4, 7.5, 7.6; [LA] 15, 16, 17
![Oversigt [S] 7.3, 7.4, 7.5, 7.6; [LA] 15, 16, 17 Oversigt [S] 7.3, 7.4, 7.5, 7.6; [LA] 15, 16, 17](/thumbs/62/47131431.jpg) Oversigt [S] 7.3, 7.4, 7.5, 7.6; [LA] 15, 16, 17 Nøgleord og begreber 1. ordens lineær ligning Løsningsmetode August 2002, opgave 7 1. ordens lineært system Løsning ved egenvektor Lille opgave Stor opgave
Oversigt [S] 7.3, 7.4, 7.5, 7.6; [LA] 15, 16, 17 Nøgleord og begreber 1. ordens lineær ligning Løsningsmetode August 2002, opgave 7 1. ordens lineært system Løsning ved egenvektor Lille opgave Stor opgave
Den Brownske Bevægelse
 Den Brownske Bevægelse N.J. Nielsen 1 Notation I dette notesæt vil vi generelt benytte samme notation som i det øvrige undervisningsmateriale i MM23. For ethvert n N betegner B n Borelalgebraen på R, og
Den Brownske Bevægelse N.J. Nielsen 1 Notation I dette notesæt vil vi generelt benytte samme notation som i det øvrige undervisningsmateriale i MM23. For ethvert n N betegner B n Borelalgebraen på R, og
af koblede differentialligninger (se Apostol Bind II, s 229ff) 3. En n te ordens differentialligning
 EKSISTENS- OG ENTYDIGHEDSSÆTNINGEN Vi vil nu bevise eksistens- og entydighedssætningen for ordinære differentialligninger. For overskuelighedens skyld vil vi indskrænke os til at undersøge een 1. ordens
EKSISTENS- OG ENTYDIGHEDSSÆTNINGEN Vi vil nu bevise eksistens- og entydighedssætningen for ordinære differentialligninger. For overskuelighedens skyld vil vi indskrænke os til at undersøge een 1. ordens
Udledning af Keplers love
 Udledning af Keplers love Kristian Jerslev 8. december 009 Resumé Her præsenteres en udledning af Keplers tre love ud fra Newtonsk tyngdekraft. Begyndende med en analyse af et to-legeme problem vil jeg
Udledning af Keplers love Kristian Jerslev 8. december 009 Resumé Her præsenteres en udledning af Keplers tre love ud fra Newtonsk tyngdekraft. Begyndende med en analyse af et to-legeme problem vil jeg
Lineær algebra 4. kursusgang
 Lineær algebra 4. kursusgang Vi betragter et lineært ligningssystem (af m ligninger med n ubekendte) Ax = b. Ligningssystemet antages at være inkonsistent (ingen løsninger) fordi tallene er fremkommet
Lineær algebra 4. kursusgang Vi betragter et lineært ligningssystem (af m ligninger med n ubekendte) Ax = b. Ligningssystemet antages at være inkonsistent (ingen løsninger) fordi tallene er fremkommet
Signalbehandling og matematik 1 (Tidsdiskrete signaler og systemer)
 Signalbehandling og matematik 1 (Tidsdiskrete signaler og systemer) Session 1. Sekvenser, diskrete systemer, Lineære systemer, foldning og lineære tidsinvariante systemer Ved Samuel Schmidt sschmidt@hst.aau.dk
Signalbehandling og matematik 1 (Tidsdiskrete signaler og systemer) Session 1. Sekvenser, diskrete systemer, Lineære systemer, foldning og lineære tidsinvariante systemer Ved Samuel Schmidt sschmidt@hst.aau.dk
Besvarelse, Eksamen Analyse 1, 2013
 Københavns Universitet Prøve ved Det naturvidenskabelige Fakultet juni 23 Besvarelse, Eksamen Analyse, 23 Opgave Lad, for n N, funktionen f n : [, ) R være givet ved NB. Trykfejl. Burde være x. f n (x)
Københavns Universitet Prøve ved Det naturvidenskabelige Fakultet juni 23 Besvarelse, Eksamen Analyse, 23 Opgave Lad, for n N, funktionen f n : [, ) R være givet ved NB. Trykfejl. Burde være x. f n (x)
Minikaos - må ikke bruges til noget. Henrik Dahl
 Minikaos - må ikke bruges til noget. Henrik Dahl hdahl@tdc-broadband.dḳ. 1 DEFINITIONER 2 1 Definitioner Aperiodisk adfærd Attraktor Der findes baner, der ikke lander i FP eller i periodiske baner eller
Minikaos - må ikke bruges til noget. Henrik Dahl hdahl@tdc-broadband.dḳ. 1 DEFINITIONER 2 1 Definitioner Aperiodisk adfærd Attraktor Der findes baner, der ikke lander i FP eller i periodiske baner eller
Elektromagnetisme 14 Side 1 af 9 Elektromagnetiske bølger. Bølgeligningen
 Elektromagnetisme 14 Side 1 af 9 Bølgeligningen Maxwells ligninger udtrykker den indbyrdes sammenhæng mellem de elektromagnetiske felter. I det flg. udledes en ligning, der opfyldes af hvert enkelt felt.
Elektromagnetisme 14 Side 1 af 9 Bølgeligningen Maxwells ligninger udtrykker den indbyrdes sammenhæng mellem de elektromagnetiske felter. I det flg. udledes en ligning, der opfyldes af hvert enkelt felt.
Diffusionsligningen. Fællesprojekt for FY520 og MM502. Marts Hans J. Munkholm og Paolo Sibani. Besvarelse fra Hans J.
 Diffusionsligningen Fællesprojekt for FY50 og MM50 Marts 009 Hans J. Munkholm og Paolo Sibani Besvarelse fra Hans J. Munkholm 1 (a) Lad [x, x + x] være et lille delinterval af [a, b]. Den masse, der er
Diffusionsligningen Fællesprojekt for FY50 og MM50 Marts 009 Hans J. Munkholm og Paolo Sibani Besvarelse fra Hans J. Munkholm 1 (a) Lad [x, x + x] være et lille delinterval af [a, b]. Den masse, der er
Matematik F2 Opgavesæt 6
 Opgave 4: Udtryk funktionen f(θ) = sin θ ved hjælp af Legendre-polynomierne på formen P l (cos θ). Dvs. find koefficienterne a l i ekspansionen f(θ) = a l P l (cos θ) l= Svar: Bemærk, at funktionen er
Opgave 4: Udtryk funktionen f(θ) = sin θ ved hjælp af Legendre-polynomierne på formen P l (cos θ). Dvs. find koefficienterne a l i ekspansionen f(θ) = a l P l (cos θ) l= Svar: Bemærk, at funktionen er
DesignMat Den komplekse eksponentialfunktion og polynomier
 DesignMat Den komplekse eksponentialfunktion og polynomier Preben Alsholm Uge 8 Forår 010 1 Den komplekse eksponentialfunktion 1.1 Definitionen Definitionen Den velkendte eksponentialfunktion x e x vil
DesignMat Den komplekse eksponentialfunktion og polynomier Preben Alsholm Uge 8 Forår 010 1 Den komplekse eksponentialfunktion 1.1 Definitionen Definitionen Den velkendte eksponentialfunktion x e x vil
Statistisk mekanik 10 Side 1 af 7 Sortlegemestråling og paramagnetisme. Sortlegemestråling
 Statistisk mekanik 0 Side af 7 Sortlegemestråling I SM9 blev vibrationerne i et krystalgitter beskrevet som fononer. I en helt tilsvarende model beskrives de EM svingninger i en sortlegeme-kavitet som
Statistisk mekanik 0 Side af 7 Sortlegemestråling I SM9 blev vibrationerne i et krystalgitter beskrevet som fononer. I en helt tilsvarende model beskrives de EM svingninger i en sortlegeme-kavitet som
