Skolemateriale til udstillingen. Det Aktive UNIVERS
|
|
|
- Daniel Ibsen
- 9 år siden
- Visninger:
Transkript
1 Skolemateriale til udstillingen Det Aktive UNIVERS Skolematerialet Skolematerialet til Det Aktive Univers er inddelt i emner, der relaterer sig til zonerne i udstillingen. Til indskolingen (bh-2. klasse) er der udarbejdet materiale, der koncentrerer sig om Solen og Månen samt planeterne i Solsystemet og om de kendte stjernebilleder. Det kalder vi niveau I. Til hver af udstillingens emner er der desuden lavet opgaver i to niveauer. Niveau II kan bruges i skolernes klasser, mens niveau III kræver forudsætninger fra 8. klasse og opefter (visse opgaver på gymnasieniveau). Mange af opgaverne kan dog tilpasses flere niveauer. Nogle af opgaverne kan med fordel løses hjemme, mens andre løses i udstillingen. God fornøjelse! Produceret af SKOLESERVICE, Tycho Brahe Planetarium & Omnimaxteater Tlf.: (man. - fre. kl , dog ikke i skolernes ferieperioder) skoleservice@tycho.dk Forfattere: Niels Elbrønd Hansen Michael Linden-Vørnle Bjørn Franck Jørgensen Kit Søndergaard Grafisk tilrettelæggelse: Susanne Armand Andersen
2 Indhold Det Aktive Univers Tycho Brahe Planetariums nye permanente udstilling Det Aktive Univers er opdelt i zoner med hvert sit astronomiske eller rumfartsrelaterede emne. Historisk astronomi Den astronomiske baggrund for vores egen kulturs succes. Tidlig arabisk og ægyptisk astronomi har bidraget til udviklingen af den græske naturvidenskab og den europæiske renæssance. Afstande og dimensioner Her anskueliggøres rummets dimensioner og de forskellige metoder til afstandsmåling. Solsystemet Foruden Solen og planeterne hører også måner, asteroider og kometer til her. Sammenstød mellem dem er en del af Solsystemets historie. Månen Månens betydning for Jorden. Månens aktuelle fase og afstand. Månens tilblivelse og udvikling samt formørkelser. Solen Solen indeholder mere end 99 % af alt stof i Solsystemet. Livebillede af Solen, aktuelle op- og nedgange samt kommende formørkelser. Stjernerne Stjerner gennemfører en livscyklus en dannelsesfase, et langt liv og en afslutning. De danner konstellationer, som vi giver navne. Kosmologi Om store spørgsmål som universets struktur, Big Bang og rummets udvidelse. Har fx rummets usynlige stråling betydning for livet? Astrobiologi Forskningsområde på grænsefladen mellem astronomi og livets opståen. Opstod livet i rummet eller på Jorden, og er der liv på Mars? Mennesket i rummet Det sovjetrussiske forspring blev overhalet af amerikanernes landinger på Månen. Opbygningen af Den Internationale Rumstation. Astronomernes værktøj Hvordan aflurer man universets hemmeligheder.
3 Historisk astronomi Side 1 Til læreren Verdensbilleder Historisk astronomi verdensbilleder Alle kulturer har til enhver tid forsøgt at forstå indretningen af deres omgivelser. Hvor lurer farerne, og hvor uddeler naturen gaver. Nogle gange skal man selv yde en indsats, før naturen viser sig fra sin gavmilde side. Udviklingen i verdensbilledet sker ofte i ryk og er som regel et resultat af enkelte markante erkendelser, som medfører, at flere tænkere eller filosoffer får et nyt grundlag at udvikle beskrivelsen på. Det kræver imidlertid et materielt og åndeligt overskud, for at en sådan udvikling sættes i gang. Og det er tankevækkende, at udviklingen i vores del af verden er sket i ryk omkring tre tidsafgrænsede perioder: 1. Måske uafhængigt af hinanden udvikler to store antikke kulturer (sumererne langs Eufrat og Tigris, og ægypterne langs Nilen) et effektivt agerbrug baseret på flodernes skiftende vandstand. Inden for samme årtusinde udvikler de ved astronomisk hjælp hver for sig et kalendersystem, der gør det muligt for dem at forudsige, hvornår floderne vil gå over deres bredder, oversvømme markerne og aflejre de sedimenter og næringssalte, der er ført med vandet fra de to flodsystemers bjergrige udspring. 2. Begge kulturer har udspillet deres rolle, da den græske kultur overtager dominansen i det østlige Middelhav. Her udvikler en lang række naturfilosoffer verdensbilledet i en ny dimension. Fra at være praktiske og brugbare erkendelser i den arabiske og ægyptiske kultur bliver anskuelserne nu mere filosofiske og nærmer sig så småt det, vi i dag ville kalde et naturvidenskabeligt verdensbillede. Det er bemærkelsesværdigt, at det afsæt, grækerne tager på dét, som de dengang kaldte de to antikke kulturer, udvikler en filosofisk metode, hvor det rationelle, det logiske og det argumenterende hele tiden sætter påstande på en prøve. Det har i sig en grundlæggende dynamik en automatik, der fremtvinger en udvikling. I modsætning til de tidligere mytiske forestillinger er det nu logikken, der bærer grundlaget for den fremtidige udvikling. Det er måske den grundlæggende årsag til den vesterlandske kulturs succes. Dette træsnit viser en missionær fra middelalderen, der har fundet det punkt, hvor himlen og Jorden rører hinanden. Manden kigger ud gennem himlen og studerer Guds domæne udenfor. Træsnittet er udført af en ukendt kunstner i 1888 til en populær astronomibog af Camille Flammarion. Det er en typisk karikatur fra oplysningstiden, hvor man latterliggjorde tidligere opfattelser af verdens indretning.
4 Historisk astronomi Side 2 Til læreren 3. Da romerne overtager magten efter den græske dominans, stopper denne udvikling. Alt, hvad den græske kultur havde bidraget med, står nu som gammel visdom en visdom, som romerne værdsætter, nyder godt af, men som de ikke formår at udvikle yderligere. De koncentrerer sig om bygningskunst, hærledelse og administration af deres imperium. Da imperiet splittes i de østromerske og vestromerske riger, flytter videnskaben østpå og overvintrer i mere end et årtusinde i den arabiske kulturkreds. I Vesteuropa sker der i denne periode stort set ingen nye erkendelser. Perioden er præget af ressourcekrævende krige og folkevandringer, indtil den arabiske kultur i renæssancen giver Europa tilbage, hvad kontinentet har mistet i initiativ ved opløsningen af den græske kultur. I begyndelsen må de europæiske lærde selv lære sig arabisk for at studere astronomi på universitetsniveau. Den polske astronom Nikolaus Kopernikus genfremsætter tanker om Solsystemets indretning tanker, som allerede har været diskuteret, før den store stilstand indledtes. Tycho Brahe udvikler teknikker og metoder, kikkerten bliver opfundet, og Galilei ser som én af de første himmellegemer kredse omkring et andet himmellegeme og opdager, at Tycho Brahe planeter ikke bare er vandrende stjerner, men kuglerunde kloder. Dermed er vejen banet for forståelsen af, at planeter ikke er mystiske, guddommelige symboler, men reelle fysiske kloder som Jorden og Månen. Nikolaus Kopernikus Den industrielle udvikling og den tekniske revolution bygger naturligvis på den seneste bølge af erkendelser, men den er også et resultat af en stigende internationalisering med deraf følgende udveksling af forskningsresultater. Galileo Galilei Verdensbilleder
5 Historisk astronomi Side 3 På Planetariet Niveau II Verdensbillede i udvikling 1. Prøv på computerskærmen at finde frem til de tre verdensbilleder: det ptolemæiske det tychoniske og det kopernikanske. Hvilket af dem vises på den store model i loftet? (sæt kryds) 2. Prøv at dreje håndsvinget på væggen, og læg mærke til, hvad der sker i loftet. Jorden er den lille grønne kugle. Hvilken af de to næste sætninger er rigtig? Alle de andre himmellegemer (Solen og planeterne) drejer om Jorden: ja nej Solen drejer om Jorden, men alle de andre planeter drejer om Solen: ja nej 3. Har det ptolemæiske verdensbillede Jorden eller Solen i centrum? Jorden Solen 4. Har det kopernikanske verdensbillede Jorden eller Solen i centrum? Jorden Solen 5. Hvor havde Tycho Brahe sit observatorium, Uraniborg? 6. Hvad er Stjerneborg? 7. Hvorfor byggede Tycho Brahe Stjerneborg? 8. Hvad hed den italienske astronom, der i renæssancen opdagede, at Jupiter har måner? 9. Johannes Kepler, en tysk astronom og matematiker, brugte Tycho Brahes præcise målinger til at forklare, hvorfor planeterne bevæger sig uregelmæssigt. Han skrev tre love, som kaldes Keplers love. Hvad indeholder Keplers første lov? 10. Hvad er det for en kraft, den engelske fysiker Isaac Newton beskrev, og som holder planeter, kometer og asteroider fast i et kredsløb om Solen, og måner i kredsløb om planeterne?
6 Historisk astronomi Side 4 På Planetariet + i klassen Niveau II + III Historisk astronomi tidslinie Svar på nogle af spørgsmålene kan findes i udstillingen. Marker på tidsaksen nogle af de store, betydningsfulde opdagelser og personer i astronomi gennem tiderne, fx Apollo 11 (første mennesker på Månen, Neil Armstrong og Edwin Aldrin) Aristarchos (heliocentrisk verdensbillede) Aristoteles (geocentrisk verdensbillede) Christiaan Huygens (opdager Titan Saturns måne, forklarer Saturns ringe) Edmund Halley (bestemmer omløbstiden for Halleys komet) Edwin Hubble (observerer, at Andromedatågen er en selvstændig galakse, universets udvidelse) Eratosthenes (måler Jordens omkreds) Galileo Galilei (observerer, at Jupiter med sine måner udgør et system i og svarende til Solsystemet) Hipparchos (opdager bl.a. Jordens præcession) Hubble Space Telescope (astronomisk observatorium i jordomkredsning) Isaac Newton (beskriver bl.a. tyngdeloven) Johannes Kepler (udarbejder 3 love på baggrund af Tycho Brahes observationer) Julius Cæsar (indfører den ægyptiske solkalender) Juri Gagarin (første bemandede rumflyvning) New Grange (Irland) Nikolaus Kopernikus (heliocentrisk verdensbillede) Ole Rømer (bestemmer lysets tøven vha. Jupiters måner) Ptolemæus (bibliotekar i Alexandria, samlede beskrivelser af kendte astronomiske fænomener) Sputnik I (første rumsonde i kredsløb omkring Jorden) Stonehenge (England) Sumerisk kalender Thales fra Milet (første forudsigelse af solformørkelse) Tycho Brahe (bryder med Middelalderens verdensopfattelse og indfører den naturvidenskabelige metode) Very Large Telescope (VLT). Det Europæiske Sydobservatorium (ESO) tager ny kæmpekikkert i brug på Cerro Paranal i Chile William Herschel (opdager planeten Uranus samt Mælkevejssystemets diskosform) Ægyptisk kalender Efter vor tidsregning Før vor tidsregning Tidsaksen
7 Historisk astronomi Side 5 I klassen Niveau III Verdensbilledets udvikling tænkt som oplæg til klassediskussion eller skriftlig projektopgave På forrige side ses et udvalg af højdepunkter inden for astronomi. Sæt årstal på begivenhederne, og marker årstallet med et lille x på tidsaksen. Punkterne fordeler sig i 3-4 grupper. I hvilke geografiske områder sker udviklingen hovedsagelig i hver af grupperne? Hvorfor var det nødvendigt for de sumeriske og ægyptiske kulturer at kende noget til astronomi? Hvordan adskiller den sumeriske og den ægyptiske kalender sig fra hinanden? Brug hjælpemidler, fx kan følgende kilder anbefales: Danmarks Nationalleksikon. Flemming Claussen m.fl., Skabt til at skabe Renaissancens kultur i Europa, Aschehoug Johs. Fabricius, Verdensbilleder, Undervisningsafdelingen, DR, Hvilket billede havde Aristoteles af himmellegemernes indbyrdes placering? Hvorfor kaldes Aristoteles og Ptolemæus verdensopfattelser for geocentriske? Find en skitse over Ptolemæus verdensbillede. Hvordan forklares planeternes bevægelse i denne model? Og hvad med Solens bevægelse? Hvor lang tid har man vidst, at Jorden er rund? Hvilke argumenter har ligget til grund for denne viden? Videnskabens Verden, bd. 8 Store Videnskabsmænd, Politikens Forlag Olaf Pedersen og Helge Kragh, Fra Kaos til Kosmos, Gyldendal Henry Nørgaard m.fl., Universets Melodi, Gyldendal Uddannelse, Specielt fire personer har foruden Isaac Newton været med til at gennemføre den naturvidenskabelige revolution. Hvad hed de, og hvad bidrog de hovedsagelig med? Find en skitse over Kopernikus verdensbillede. Hvordan forklares planeternes og Solens bevægelse i denne model? Hvad var den største svaghed ved hans model? Hvordan var Kopernikus forhold til kirken?
8 Historisk astronomi Side 6 I klassen Niveau III Tycho Brahes største bedrift bestod dels i udvikling af meget nøjagtigt observationsudstyr, dels i at sammenholde teori med observationer det, vi i dag kalder den naturvidenskabelige metode. Tycho Brahe havde en lidt anden opfattelse af verdensbilledet end Kopernikus. Hvorfor holdt Tycho fast i, at Jorden er centrum for Solsystemet? Dvs., hvorfor anså han sin model for at være bedre end Kopernikus model? Hvad bidrog Kepler med i udviklingen af verdensbilledet og på hvilket grundlag opstillede han sine love? Hvilket nyt instrument fik stor indflydelse på Galileis observationer og hvad iagttog han med dette instrument? Hvilken opfattelse havde man af kloder før 1610? Hvorfor blev ideen om Jordens bevægelse omkring Solen opfattet som kættersk? 1687 er et vigtigt årstal, da Newton her giver den første beskrivelse af den fysiske årsag til himmellegemernes bevægelse. Hvad hedder Newtons hovedværk, som han udgav dette år? Newton sammenlignede selv et æbles fald mod Jorden med Månens omløb om Jorden. Hvori består ligheden? I 1929 gjorde Hubble en betydningsfuld opdagelse om den måde, hvorpå galakser bevæger sig i forhold til hinanden. Hvad iagttog han, og hvordan blev det fortolket? Hubble målte i 1923 afstanden til Andromedagalaksen til at være lidt under en mio. lysår. Hvor langt tror vi i dag, at der er til denne vores nærmeste nabogalakse? Universet består i alt væsentlig af to forskellige grundstoffer. Hvilke to grundstoffer er der tale om, og hvordan er deres indbyrdes mængdeforhold? Hvilken temperatur er der ude i rummet, den såkaldte baggrundstemperatur? I dag er den fremherskende teori for universets dannelse Big Bang. Hvor gammel er universet ifølge Big Bang? Astronomi Historisk
9 Afstande Side 1 Til læreren Afstande Afstande i universet Her får man en fornemmelse af rummeligheden i universet at stjernerne ikke, som antaget i Middelalderen, sidder på indersiden af en kugleflade, men i stedet er spredt i rummet med forskellige afstande. Afstandene i universet er så enorme, at vores abstraktionsevne bliver sat på en hård prøve. Alligevel er vi optaget af at få klarhed over disse relationer, fordi det er vigtige elementer i forståelsen af rummets opbygning. Ud over at præsentere dette perspektiv vil vi på de følgende sider forsøge at få en fornemmelse af mere eksakte afstande i universet. Måleenheder som astronomisk enhed, lysår og parsec er umiddelbart uforståelige begreber, men hvis vi starter med at arbejde med mindre afstande på Jorden, som vi umiddelbart kan forholde os til, og derpå arbejder os udad i rummet til større og større afstande, så kan disse begreber forholdsvis nemt illustreres og forstås. Afstande i universet beskrives ofte ved den såkaldte afstandsstige, se figur på næste side. Afstandene grupperes i forskellige trin, der er karakteriseret ved hver sin målemetode til afstandsbestemmelse. Hele fidusen består så i, at der for hvert trin er et vist overlap med både det foregående og det efterfølgende trin, så der kan laves en sammenhængende absolut afstandsskala startende med vores velkendte længdeenhed meteren. I vores dagligdag anvender vi med stor fortrolighed både mm, cm og km. Mere problematisk bliver det med enheden Mm, som vi ikke er vant til at anvende. Afstanden mellem København og San Francisco er omkring km. Hvis vores dagligdag bestod i at bevæge os langt omkring på Jordens overflade, ville det være naturligt at skifte enhed og angive denne afstand som 8,7 Mm (8,7 mio. m) og hele Jordens omkreds som 40 Mm i stedet for km.
10 Afstande Til læreren Side 2 Det første trin på afstandsstigen er afstandene i Solsystemet, hvor det i dag er muligt at bestemme afstandene ved radarmåling. Tidligere har man måttet klare sig med trekantsberegninger. Længder i Solsystemet måles mest praktisk i astronomiske enheder. Til de allernærmeste stjerner på andet trin bestemmer man afstanden ved parallaksemåling, dvs. bestemmelse af, hvor stor en vinkel stjernen flytter sig i forhold til baggrundsstjernerne set fra to forskellige steder i rummet med et halvt års mellemrum. Den naturlige enhed er her parsec, men ofte bruges også enheden lysår. Stjernerne i Mælkevejssystemet udgør tredje trin, hvor man bruger spektroskopiske metoder til at klassificere stjernerne. Når man så ved, hvilken type stjerne der er tale om, ved man også, hvor meget lys den udsender. Svækkelsen af lysintensiteten fra stjernen, som vi kan måle, er da et udtryk for afstanden (sammen med absorption i det mellemliggende område, som der skal korrigeres for). På det fjerde trin bygges der bro til de nærmeste galakser med de variable stjerner, de såkaldte cepheider. Deres svingningstid hænger nøje sammen med lysudsendelsen, hvorfor vi som ovenfor kan bestemme afstanden. Fjernere galakser på femte trin afstandsbestemmes ved såkaldte standardlys. Når en mindre stjerne på slutstadiet er blevet til en hvid dværg, og den derefter modtager stof fx fra en nabostjerne, vil der dannes en bestemt type supernova, når massen af den hvide dværg når op på 1,4 solmasser. Lysstyrken i en sådan supernovaeksplosion menes at være ens hver gang, hvorfor en måling hos os igen siger noget om afstanden. Endelig har man på det sidste trin i form af Hubbles lov fundet en sammenhæng mellem galaksens afstand til os og den hastighed, som den fjerner sig fra os med. Hastigheden kan bestemmes ud fra forskydningen af spektrallinjer i galaksernes spektre. Afstande til de fjerneste galakser måles i mia. lysår eller Mpc (megaparsec). Afstande
11 Afstande Side 3 På Planetariet Niveau II Rummets 3. dimension Selv om vi taler om en stjernehimmel, er det jo ikke en himmelkugle, hvorpå alle stjernerne sidder. De befinder sig i vidt forskellig afstand fra os. Alle de stjerner, du ser på himlen, hører til vores egen galakse, Mælkevejssystemet. Der findes andre galakser, der er millioner af lysår fra os, dvs. de er så langt væk, at det tager lyset fra dem millioner af år om at nå os. Vi ved derfor ikke, om den galakse, der ses i rummet bag stjernerne, stadig ser sådan ud. Også de stjerner, der danner stjernebillederne, har meget forskellig afstand. På computerskærmen kan du finde fire stjernebilleder: Karlsvognen, Svanen, Cassiopeia og Orion. Her ser du de fire stjernebilleder tegnet på papiret. Tegn en lille ring om den stjerne, du mener er nærmest. Karlsvognen ses bedst om foråret Svanen ses bedst om sommeren Afstande Orion er vinterens tydeligste stjernebillede Cassiopeia ses lige over vores hoveder om efteråret
12 Afstande Side 4 På Planetariet Niveau II + III Afstanden til Jorden og Månen Afstande på Jorden Afstande her på Jorden kan forholdsvis nemt bestemmes ved hjælp af en meterstok (eller en hvilken som helst anden måleenhed). Jordens radius blev bestemt allerede af Eratosthenes (ca f.kr.). Han observerede, at man ved sommersolhverv ikke så nogen skygge, når man kiggede ned i en dyb brønd i Syene (det nuværende Aswan i Ægypten). Det må betyde, at Solen står lodret over stedet, Solen er altså i zenit. I Alexandria, der ligger ca. 800 km længere nordpå, målte Eratosthenes samtidigt, at en lodret søjle kaster en skygge, så vinklen mellem solstrålerne og søjlen er 7,2. Astronomiens længdeenheder Bestem Jordens omkreds, idet en cirkel udgør 360. Bestem Jordens radius r, idet du bruger sammenhængen mellem en cirkels omkreds og radius. Standardenheden En meter blev oprindeligt i tiden omkring den franske revolution fastsat til at være 1/ af afstanden fra Nordpolen til ækvator. I dag er denne længdeenhed defineret ud fra lysets hastighed og tiden, som er fastlagt ud fra en ganske bestemt svingning i et cæsium-133 atom. Afstanden til Månen Under Apollo-ekspeditionerne til Månen blev der anbragt et spejl på måneoverfladen. Hvis vi sender lys fra Jorden mod dette spejl, vil vi modtage lyset retur med en vis tidsforsinkelse, da det bevæger sig med en hastighed på km/s. Bestem afstanden til Månen, idet det reflekterede lys modtages retur fra Månen 2,5 s efter afsendelsen.
13 Afstande Side 5 Afstande Afstande i Solsystemet Afstanden til Solen Aristarchos fra Samos (ca f.kr.) forsøgte at finde ud af, hvor mange gange afstanden til Solen er større end afstanden til Månen. Midt mellem fuldmåne og nymåne ses den ene halvdel af Månen belyst, mens den anden halvdel ligger i skygge. Stråleretningen fra Solen mod Månen danner derfor en ret vinkel med vores synsretning fra Jorden mod Månen, se figur. Aristarchos bestemte vinklen v mellem retningen til Solen og retningen til Månen til 87. Lav en model, hvor du afsætter Jorden og Månen i kanten af et stort stykke papir, fx 1 cm mellem Jord og Måne, hvis du bruger et stykke A4 (2 cm, hvis du bruger A3). Tegn fra Månen en linje vinkelret på forbindelseslinjen mellem Jorden og Månen. Ved Jorden afsætter du omhyggeligt med en vinkelmåler en vinkel på 87. Der, hvor de to linjer mødes, befinder Solen sig. Mål, hvor mange gange længere der er til Solen sammenlignet med afstanden til Månen. I klassen Niveau II + III Du får et resultat, der er alt for lille (fordi vinklen på 87 er alt for lille). I dag ved vi, at forholdet er ca. 390, og at vinklen er ca. 89,85. Bestem afstanden til Solen, idet du bruger den afstand til Månen, som blev bestemt ovenfor. Afstanden til planeterne Her kan man anvende Keplers 3. lov, der giver en sammenhæng mellem en planets omløbstid T og afstanden til Solen a: a 3 T 2 = 1 (hvis tiden måles i år og afstanden i AE) Astronomisk længdeenhed Længdeenheden meter bliver hurtigt upraktisk, når afstandene bliver store. Derfor har man indført en astronomisk enhed, der svarer til den gennemsnitlige afstand mellem Jorden og Solen. 1 AE = 149,6 mio. km Omløbstiden for Venus er bestemt til 224,7 døgn (= 0,615 år). Hvor stor er afstanden mellem Solen og Venus? Omløbstiden for Jupiter er bestemt til 11,86 år. Hvor stor er afstanden mellem Jupiter og Venus, når den er størst? Når den er mindst?
14 Afstande Side 6 Afstande Afstanden til stjernerne I klassen Niveau II + III Afstanden et lysår Beregn et lysår i meter, idet lysets hastighed er km/s. Hvor mange lyssekunder er der til Månen? Hvor mange lysminutter er der til Solen? Ny astronomisk længdeenhed Ofte bruges længdeenheden lysår (ly), der svarer til den afstand, som lyset tilbagelægger på et år. Afstanden til stjernerne parallaksemetoden 1 ly = 9, m Prøv at finde afstanden til en flagstang eller et nedløbsrør, som findes på den anden side af gaden lige overfor det vindue, du står og kigger igennem.» Anbring en blød plade vandret i vinduets venstre side.» Lad pladens kant flugte præcist med vindueskarmen.» Anbring en knappenål (1) midt på pladen langs kanten længst væk fra dig selv.» Anbring endnu en knappenål (2) nær kanten tæt ved dig selv, således at de to knappenåle og flagstangen kommer til at ligge på linje.» Marker i vinduet, hvor den første knappenål er placeret (A).» Flyt pladen til vinduets højre side (bedst i et stort vindue), hvor pladen igen anbringes, så den flugter med vindueskarmen. Marker i vinduet, hvor den første knappenål nu er placeret (B).» Anbring derpå en tredje knappenål (3) nær kanten tæt ved dig selv, så den sammen med den første knappenål ligger på linje med flagstangen.» De tre nåle på pladen danner nu en vinkel, der sammen med pladens kant udgør en trekant. Mål afstanden D i vindueskarmen mellem de to placeringer af den første knappenål. Mål også afstanden d på pladen mellem knappenål 2 og 3. Hvor mange gange er D større end d? Mål højden h i trekanten på pladen, og find til sidst den ukendte afstand x til flagstangen.
15 Afstande Side 7 I klassen Niveau III Afstande i hele universet Hvis vi tænker os, at vi står på en stjerne og kigger mod vort eget Solsystem, så vil synsretningen mod Solen danne en vinkel med synsretningen mod Jorden. Denne vinkel kaldes stjernens parallakse. Vinklerne er meget små, og de måles derfor i buesekunder ( 1 = 1/60 bueminut = 1/3.600 grad). Vores nærmeste nabo, Alpha Proxima, har en parallakse på 0,742. Bestem afstanden til denne stjerne i parsec og i lysår. Parallaksemetoden kan kun benyttes for stjerner, der ikke befinder sig længere væk end ca. 300 ly. Ved større afstande anvendes der forskellige andre metoder. Større afstande Der findes forskellige metoder til bestemmelse af meget store afstande. Nogle af dem er nævnt nedenfor, dog uden at vi vil komme nærmere ind på dem her. Spektroskopisk parallakse Metoden bygger på en vurdering af stjernernes absolutte størrelsesklasse ved hjælp af et HR-diagram. Herefter kan afstanden bestemmes ud fra afstandsmodulet. Metoden kan anvendes ud til en afstand på ca pc. Cepheidemetoden Metoden bygger bro til fjernere galakser. Denne type stjerner har regelmæssige variationer i lysstyrken, da stjernerne skiftevis puster sig op og falder sammen igen. Perioden for denne variation hænger nøje sammen med cepheidens absolutte størrelsesklasse. Afstanden bestemmes derpå vha. afstandsmodulet, se næste side. Standardlys Et eksempel herpå er fx type I supernovaer, der opstår, når en hvid dværg i et dobbeltstjernesystem ved at modtage stof fra nabostjernen når op på en kritisk grænse på 1,4 solmasser. Herved sker der en kraftig kulstof-detonation med en enorm lysudsendelse til følge. Da man formoder, at denne type supernovaeksplosioner altid er ens, vil forskelle i de tilsyneladende størrelsesklasser udelukkende kunne forklares vha. afstandskvadratloven. Endnu en ny astronomisk længdeenhed Hvis parallaksen p for en stjerne er 1 siges afstanden til stjernen at være 1 parsec (pc). 1 pc = AE = 3,26 ly Sammenhængen mellem afstand d og parallakse p er 1 d = p hvor d måles i pc og p i buesekunder. Rødforskydning De allerstørste afstande i universet bestemmes ved hjælp af kosmologisk rødforskydning, der opstår, fordi universet udvider sig. Jo længere væk galaksen er, desto større hastighed bort fra os har den, og dermed også en større rødforskydning.
16 Afstande Side 8 I klassen Niveau III Afstande Afstandskvadratloven fortæller os, at intensiteten fra en lyskilde som fx en stjerne aftager med kvadratet på afstanden. Hvis ikke lyset svækkes undervejs er det den samme mængde lys, der hele tiden passerer udad i området mellem de fire stiplede linjer. Da lyset i den dobbelte afstand er fordelt på et fire gange så stort areal, vil intensiteten derfor kun være en fjerdedel. I den tredobbelte afstand er intensiteten faldet til en niendedel osv. Afstandsmodulet er udtrykt ved m M = 5 log(d) 5 m, den tilsyneladende størrelsesklasse, er et udtryk for den lysstyrke, som vi måler her på Jorden. M, den absolutte størrelsesklasse, er et udtryk for den lysstyrke, som vi ville måle her på Jorden, hvis stjernen var anbragt i afstanden 10 parsec. Størrelsen bestemmes ved at typebestemme stjernen vha. spektre. d er afstanden til stjernen i parsec. For en uddybning af begreberne, se fx Henry Nørgaard m.fl., Universets Melodi, side 77 ff, Gyldendal Uddannelse, 2001.
17 Solsystemet Side 1 Til læreren Solsystemet Solsystemet Solsystemet er dannet ved sammentrækning af en stor interstellar sky af støv og gas. Skyen bestod hovedsagelig af grundstofferne brint og helium de to simpleste grundstoffer men var tillige beriget med tungere grundstoffer, tilført skyen fra udbrændte stjerner i det kosmiske nabolag. Forløbet Skyens temperatur er et udtryk for, at dens enkeltpartikler bevæger sig tilfældigt mellem hinanden med en vis hastighed. Alligevel er der indlejret en rotationsretning, som er en sum af alle enkeltpartiklernes bevægelser. Den kommer dog først til udtryk, når sammentrækningen for alvor tager fat, hvorved skyen får en endnu mere markant rotationsretning med akse og ækvatorplan. Under den fortsatte sammentrækning øges rotationshastigheden. Situationen kan sammenlignes med den forøgelse af rotationshastigheden, som en skøjteløber eller en balletdanser opnår med at trække arme og ben tæt sammen omkring rotationsaksen. Imidlertid er den interstellare sky af støv og gas ikke nær så fast i kødet som balletdansere, og materialet over og under rotationsplanet samler sig mere og mere i skyens ækvatoriale plan, som det pga. rotationshastigheden breder sig ud i. Denne udstrakte flade skive roterer differentielt (dvs. at de nærmeste dele roterer hurtigst og langsommere, desto længere fra centrum materialet er). Visse steder kondenserer stoffet til planetoider, som senere danner grundlag for de store planeter. Asteroider og kometer er det materiale, der blev tilovers. Alle planeterne bevæger sig derfor samme vej rundt om centrum, ligesom i den oprindelige flade skive af støv og gas. Rotationsretningen er mod uret, hvis man betragter den fra Solsystemets nordpol. Langt hovedparten af planeterne roterer samme vej ligesom planeternes måner samt asteroider og kometer også bevæger sig denne vej rundt i deres omløb. Det er helt naturligt, da det hele er blevet dannet af den samme roterende sky. Solsystemet består af: Solen, der er en almindelig stjerne. Ni planeter, Merkur, Venus, Jorden, Mars, Jupiter, Saturn, Uranus, Neptun og Pluto, der kredser i voksende afstande omkring Solen i den nævnte rækkefølge med Merkur som den inderste planet. Et stort antal asteroider (måske af størrelsesordenen ). Et stort antal kometer (frosne gasser, der svæver om Solsystemet i stor afstand). Store støvmængder, der hovedsagelig ligger i planetbaneplanet. Derimod er den kemiske sammensætning af de enkelte planeter forskellig. Der er en generel udvikling ud gennem planetsystemet, således at de letfordampelige gasser hører til i planetsystemets ydre regioner, fordi der først herude er koldt nok til, at de kan kondensere. De tungere grundstoffer og kemiske forbindelser med højere temperaturer for smeltning og fordampning findes i Solsystemets indre regioner.
18 Solsystemet På Planetariet Side 2 Niveau II Solsystemet Solsystemets planeter Hvad hedder den største planet i Solsystemet? Hvor mange planeter findes der i Solsystemet? Hvor mange af planeterne har en fast overflade? En planet med en fast overflade kan man stå på, mens planeter, der for det meste består af luftarter eller forskellige gasser, kaldes gasplaneter, og dem synker man ind i. Hvor mange gasplaneter er der i Solsystemet? Hvilke andre kategorier af himmellegemer findes der i Solsystemet? (nævn mindst 3 typer) I den blå bane i gulvet ses en række metalskiver med planeternes navne på. Skriv ud for hver planet, hvor langt de er fra Solen. Solen Afstand fra Solen i millioner km Modelafstand fra Solen Merkur Venus Jorden Mars Jupiter Saturn Uranus Neptun Pluto I loftet hænger der en række planetmodeller. De er 100 millioner gange mindre end de virkelige. Den store rødlige planet Jupiter er 140 cm i diameter. Ganger du dette tal med 100 millioner (8 nuller), får du cm. Det er det samme som km. I skemaet mangler du nu bare at skrive, hvor store afstandene ville være i en model af Solsystemet, hvis planeterne havde den størrelse, de har i loftet. Afstandene skal så være 100 millioner gange mindre end de virkelige.
19 Solsystemet Side 3 På Planetariet + i klassen Niveau III Solsystemet Sammenstød i rummet I udstillingen præsenteres forskellige animationer på en stor skærm. Der vises tre forskellige store nedslag i Solsystemet, hvilke? Desuden er der udstillet to store meteoritter. I begge tilfælde er der tale om jernmeteoritter. Den lille jernmeteorit, der vejer ca. 12 kg, er en flække, der røg af, inden en ca. 40 meter i diameter stor jernmeteorit ramte busksteppen nær ved Flagstaff i Arizona for år siden. Et himmellegeme med en diameter på nær ved 40 meter kan godt have et rumfang på kubikmeter. En enkelt kubikcentimeter jern vejer 7,8 gram. Hvad vejer en jernmeteorit på én kubikdecimeter (10x10x10 cm)? Hvad vejer en jernmeteorit på én kubikmeter? Hvad vejer en jernmeteorit på kubikmeter?
20 Solsystemet Side 4 I klassen Niveau III Stjerneskud er i virkeligheden glødende spor i atmosfæren efter sammenstød med små partikler. Når de sand- eller gruskorn store partikler rammer vores atmosfære, får det luften til at gløde langs den bane, som de følger ned gennem atmosfæren under opbremsningen. Det sker i højder på mellem 110 og 80 km over Jordens overflade. Det er måske mærkeligt, at disse små partikler kan få luften til at gløde så meget, at vi kan se det på den store afstand. Men de kommer med meget stor fart omkring 40 km i sekundet. Jorden selv har en fart på 30 km i sekundet i sin bane omkring Solen. Farten ved sammenstødet kan derfor være meget forskellig. Den er høj, hvis vi støder frontalt sammen med partiklen, men meget lavere, hvis partiklen indhenter Jorden bagfra. Hvor stor vil sammenstødsfarten være hvis. Partiklen støder frontalt sammen med Jorden? km/s Partiklen indhenter Jorden bagfra? km/s Nogle gange støder Jorden sammen med rester fra kometer, hvis bane skærer Jordens bane. Komethaler er fyldt med gas og støv, og når Jorden maser sig vej gennem disse kometrester, kommer der mange stjerneskud. Da kometens bane ligger nogenlunde fast i rummet, vil det være på de samme tidspunkter hvert år, at disse meteorsværme optræder. Notér i skemaet herunder de fire mest aktive meteorsværme, hvornår de er aktive, og hvor mange stjerneskud du kan forvente at se under maksimum. meteorsværm dato antal
21 Solsystemet Side 5 I klassen Niveau II + III Kometer Hvad er en komet? Tycho Brahe observerede i 1577 en komet og beregnede, at afstanden til den var større end afstanden til Månen. Hvad havde man tidligere troet om kometer? Hvor stor er risikoen for at omkomme pga. et meteornedslag sammenlignet med risikoen for at omkomme ved en flyulykke? For 65 mio. år siden uddøde de store øgler. Hvad mener man, årsagen var til det? Hvor ofte regner man med, at der sker et nedslag på størrelse med det, der dannede krateret på Yucatán-halvøen? Omfanget af ødelæggelserne ved et nedslag afhænger i høj grad af himmellegemets størrelse. Hvor ofte rammes Jorden i gennemsnit af himmellegemer» i 10-m-klassen?» i 100-m-klassen?» i km-klassen? og hvilken skadevirkning forvolder de? Hvorfor er Jupiter en større kometfanger end Jorden? Nævn nogle historiske og geografiske eksempler på komet- og meteornedslag. Meteorer og stjerneskud Stenblokke, der flyver rundt omkring os i rummet, kaldes meteoroider eller, hvis de er store nok, asteroider. Når de rammer Jordens atmosfære og efterlader sig et lysende spor, taler man om meteorer eller i daglig tale om stjerneskud. Hvis stenene er store nok og undgår at brænde fuldstændigt op under nedturen, kaldes resterne meteoritter. Afhængig af størrelsen kan de have fra slet ingen til en enorm skadevirkning. Der findes forskellige eksempler på meteorkratere overalt i Solsystemet. Hvor stammer meteorerne hovedsagelig fra? Hvor stammer kometerne fra? Nævn nogle kendte kometer hvorfor er de kendte? Tegn en kometbane en ellipse.» Det kan gøres ved, at du anbringer to knappenåle (brændpunkter) fx 10 cm fra hinanden på en plade.» Tag et stykke kraftigt sytråd på ca. 20 cm, og lav en lille løkke i hver ende.» De to løkker fastholdes af hver sin knappenål, og du kan nu tegne en ellipse ved at holde snoren strakt ud, mens du trækker en blyant hele vejen rundt. Hold blyanten lodret hele tiden. Prøv at ændre lidt på snorlængden og afstanden mellem brændpunkterne.
22 Solsystemet Side 6 Hvad vejer jeg på Månen eller på Mars? I udstillingen finder du et 5-kg-lod placeret på Jorden, Månen og Jupiter. Prøv at løfte lodderne for at mærke, hvor meget 5-kg-loddet vejer de forskellige steder. Beskriv dine iagttagelser. På Planetariet + i klassen Niveau II + III Solsystemet I daglig tale siger vi, at loddet vejer 5 kg. Det korrekte er egentlig at sige, at loddet har massen 5 kg, og det vil loddet også have, hvis det flyttes til Månen, Mars osv. Massen er et udtryk for stofindholdet, altså en egenskab, der er knyttet til de enkelte atomer, som loddet består af. Loddets vægt er derimod et udtryk for den tyngdekraft, som fx Jorden, Månen eller Mars trækker i loddet med. Loddets vægt afhænger derfor af Jordens, Månens eller Mars sammensætning og størrelse. Sammenhængen mellem vægten F (i N Newton), og massen m (i kg) er givet ved: F = m g hvor g kaldes tyngdeaccelerationen. Her på Jorden er g = 9,82 N/kg (København). Hvor meget vejer 5-kg-loddet på: Jorden? Månen? Mars? Jupiter? Hvor stor er din egen masse (m i kg)? Hvor meget vejer du selv (F i N) på: Jorden? Månen? Mars? Jupiter? Massetiltrækning eller tyngdekraft er en fundamental vekselvirkning mellem stofmængder, og den eksisterer overalt i universet. I 1687 gjorde Isaac Newton i sit hovedværk Principia rede for den matematiske sammenhæng, der generelt kan beskrives ved F = G M m r 2 Her betyder: F tyngdekraften (= vægten) i enheden Newton (N) Nm G = 6, kg 2 er en naturkonstant M er planetens masse m er loddets eller din masse r er afstanden fra planetens centrum til overfladen Tyngdeaccelerationen ved overfladen Solen 275 N/kg Mars 3,7 N/kg Månen 1,67 N/kg Jupiter 25 N/kg Merkur 3,8 N/kg Saturn 10,8 N/kg Venus 8,9 N/kg Uranus 8,8 N/kg Jorden 9,8 N/kg Neptun 10,8 N/kg Pluto 0,69 N/kg Indsætter vi fx de kendte værdier ved Jordens overflade, kan Newtons formel for massetiltrækning som et specialtilfælde her skrives som M F = (G ) m r 2 = (6, Nm 2 5, kg ) m kg 2 (6, m) 2 = 9,82 N/kg m = g m hvor g = 9,82 N/kg er tyngdeaccelerationen.
23 Månen Side 1 Til læreren Månen Månen Der er en række forskellige teorier for Månens dannelse. Månen kunne være et fremmed himmellegeme, der af Jordens tyngdefelt er indfanget i et kredsløb om Jorden. Der er også fremsat teorier om, at Månen blot er et stykke af Jorden, der har revet sig løs. Endnu en teori er sammenstødsteorien, som er en kombination af de to første. Månen kan også være et himmellegeme, der er blevet til i samme afstand som Jorden, sådan at Jorden og Månen udgør en dobbeltplanet. Undersøgelse af mineralsammensætningen i de stenprøver, som astronauterne hjembragte fra Månen, godtgør, at de meget minder om de tilsvarende jordiske bjergarter. Men selv om bjergarterne er de samme, kan der i nogle tilfælde godt være en forskellig isotopbalance. Det kunne tyde på, at Månen både består af mineraler, der stammer fra Jorden eller som i det mindste er dannet i samme afstand fra Solen og at der tillige findes materiale, som er kommet til udefra, dvs. fra et andet sted i Solsystemet. Det understøtter den såkaldte sammenstødsteori, hvor et større himmellegeme i fortiden har ramt Jorden, revet noget af jordskorpen løs, hvorefter det knuste materiale efter nogen tid atter har samlet sig til den klode, vi kender som Månen. Imidlertid kan det fremmede materiale også være tilført Månen ved meteornedslag. Men uanset hvilken teori der er den rigtige, har Månen med sikkerhed været i kredsløb om Jorden i hele den periode, hvorunder livet har udviklet sig. Månens tilstedeværelse har derfor haft en afgørende indflydelse på, hvordan livet har udviklet sig på Jorden. Og der er stadig en del afhængigheder, primært i havet, i forbindelse med tidevandet. Her drejer det sig om forskellige livsformer i havet, hvis livsrytme (som regel gydning, æglægning osv.) er afhængig af de ekstraordinære udsving i vandstanden ved høj- og lavvande, der optræder ved nymåne og fuldmåne. Når det gælder dyr på landjorden, drejer det sig mere om styrken af lyset fra specielt fuldmånen, dvs. at faserne spiller en vis rolle. Men at Månen skulle påvirke mennesker vha. sin tyngdekraft er at gå for vidt. Den opfattelse bunder i flere misforståelser. Se om påstande og argumenter på Særark vedr. Månen. Månens faser Når Månen ser forskellig ud, er det, fordi Solen skinner på Månen fra én retning, og vi ser den her fra Jorden i en anden retning.
24 Månen Særark Side 2 Månen Almindelige påstande 1. Månen skaber tidevand (nogle steder op til mere end 10 meters højdeforskel mellem ebbe og flod), så hvorfor skulle Månen ikke på samme måde tiltrække vandet i kroppen og lave tidevand i os vi består jo af 65 % vand når den kan tiltrække vandet i havet? De fleste mener, at det hænger sammen med fuldmånen. 2. Når det er fuldmåne, er det næsten altid skyfrit! 3. Der sker flest ulykker i trafikken ved fuldmåne. 4. Der bliver født flere børn ved fuldmåne. Ad 1 Ja, Månen skaber et markant tidevand på Jorden og endda tidejord, idet også jordskorpen hæver og sænker sig nogle cm op og ned. Når vandstanden ved højvande nogle steder kan blive så markant, er det, fordi vandet løber til områderne fra meget store havarealer. Virkningens størrelse hænger sammen med kystformerne og de muligheder, havvandet har for at passere. Vandet i kroppen kan ikke flytte sig på denne måde. Det sidder for det meste fastlåst i kroppens celler. Tyngdekraften fra Månen har intet med Månens faser at gøre. Det er Månens tilstedeværelse på himlen, der kan udøve en tyngdekraft. Månen kan sagtens være på himlen i dagtimerne, uden at nogen føler sig generet af det. I øvrigt er kraften så svag, at det svarer til den variation i Jordens tyngdekraft, man oplever ved at bevæge sig fra fortovsniveau til 3. sals højde over jordoverfladen og effekten har kun denne størrelse, hvis Månen kunne stå lodret over hovedet på os. Derimod kan man ikke se bort fra, at det reflekterede sollys fra Månen især i dagene omkring fuldmåne kan have en vis indflydelse. Ad 2 Det er en anden misforståelse. Når man først én gang har hørt det, er der en tilbøjelighed til, at man ser efter og oplever derved kun, at påstanden er rigtig hver gang det passer. Men det er tilstrækkeligt til, at mange får oplevelsen af, at der er noget om snakken. Alle forbierne ignorerer man måske fordi man ikke ser dem, og så trækker de ikke fra i regnskabet. Faktisk er det skyfrit i langt under halvdelen af tilfældene ved fuldmåne. Man kunne spørge, hvor skulle de mange skyer have forvildet sig hen? For det er fuldmåne overalt på Jorden samtidig. Ad 3 Denne påstand har været fremsat mange gange og har givet anledning til flere interviews i radioen. Selv om nogle personer mener at kunne spore en højere ulykkesfrekvens, er der intet videnskabeligt bevis på, at det er rigtigt. Uvidenskabelige undersøgelser lider ofte under den kendsgerning, at den adspurgte selv lader sig påvirke af påstanden og således bevidst går efter at bevise sin antagelse. Risikoen for at få et farvet resultat er meget stor. Hverken hospitaler eller forsikringsselskaber kan bekræfte en overrepræsentation af ulykker omkring fuldmåne. Ad 4 Den samme effekt er gældende som omtalt under 3.
25 Månen Side 3 I klassen Niveau II Månen Månen kredser om Jorden én gang i løbet af en måned. Navnet måned stammer herfra. En sådan naturlig måned, der varer fra nymåne til nymåne, er blevet brugt i en lang række lande i Mellemøsten gennem 5000 år og bruges stadig. Desværre er længden af en sådan naturlig måned kun 29,5 døgn og ikke 30,5, så 12 af dem passer ikke ind i et år på 365 dage. Derfor lavede den romerske kejser Julius Cæsar en ny kalender med en kunstig inddeling af året i 12 måneder. I den gamle kalender var en måned på 29 eller 30 døgn, og den begyndte, når præsten/astronomen havde observeret det smalle månesegl lavt over den vestlige horisont efter solnedgang. Derefter kunne alle (uden at kunne læse og skrive) følge med i, hvordan måneden udviklede sig ved at se på Månens form. Hvor mange døgn skal Månen bruge til 12 omløb om Jorden? Månen Hvor mange døgn er et år? Hvor stor er fejlen? Hvor mange år skal der så gå, før man kan indskyde en ekstra måned? Året varer ikke præcis 365 døgn, men 365,25 døgn. Derfor laver vi også en fejl på ca. 6 timer hvert år. Hvor mange år skal der gå, før denne fejl løber op i et helt døgn? Hvad kalder vi det år, hvor vi har indskudt en ekstra dag?
26 Månen Side 4 På Planetariet + i klassen Niveau II + III Opgave Svarene på de fleste spørgsmål kan findes i udstillingen Gruppeopgave. Luk øjnene et lille stykke tid, og tænk på, hvordan Månen ser ud for dig. Lav en tegning af din opfattelse på et blankt stykke papir. Sammenlign derefter dit billede med nogle af dine kammeraters billeder, og snak om, hvad der er forskelligt, og hvad der er ens på billederne og hvorfor. Der er fem fremherskende teorier for, hvordan Månen er dannet. Hvad går de fem teorier ud på? Lav en tegning, der illustrerer, hvordan en måneformørkelse opstår. Lav en tegning, der illustrerer, hvordan en solformørkelse opstår. Lav en tegning, der illustrerer Månens faser fuldmåne, halvmåne (både aftagende og tiltagende) og nymåne. Hvornår var der første gang mennesker på Månen? Hvornår har der sidst været mennesker på Månen? Både amerikanerne og russerne har haft bemandede rumstationer i længere tid. Hvad hedder de? Hvorfor kan man ofte svagt se måneoverfladen ved nymåne? Observer Månen Du skal følge Månens udseende og bevægelse gennem lang tid (helst en hel måned). Start fx ved nymåne, og lav hver dag (eller så tit som muligt) på kopier af månekortet en skitse over grænsen mellem lys og skygge på Månens overflade. Prøv at indtegne skyggen rigtigt i forhold til konturerne på kortet. Foretag observationerne nogenlunde på samme tid hver dag, og noter også, i hvilken retning Månen befinder sig (fx i forhold til syd). Når du har alle skitserne, lægges de op i en cirkel anbragt dag for dag mod uret (ca grader mellem billederne pr. dags forskel). Forestil dig, at du befinder dig i cirklens centrum hvor befinder Solen sig så?
27 Solen I klassen Side 1 Niveau II Solen Vi har lært, at Solen står op i øst, er højest på himlen i syd og går ned i vest. I hvilken retning står Solen midt om natten? (Sæt kryds) Under horisonten i vest: Under horisonten i nord: Under horisonten i øst: Solens bane på himlen Midsommer Solen står dog ikke altid op i øst. Midt om sommeren står den tidligt op ikke i øst, men til venstre for øst, nemlig i nordøst. Sent om aftenen går Solen ned i nordvest. Det giver en meget lang dag, fordi Solens dagbue er lang, og Solen er derfor over horisonten i mange timer. Solen Midvinter Midt om vinteren står Solen sent op ikke i øst, men til højre for øst, dvs. i sydøst. Sidst på eftermiddagen går Solen ned i sydvest. Det giver en meget kort dag, fordi Solens dagbue er kort, og Solen er over horisonten i få timer. Efterår og forår (jævndøgn) Præcist i hvilket verdenshjørne står Solen op ved jævndøgn? Præcist i hvilket verdenshjørne går Solen ned ved jævndøgn? Hvor mange gange om året er det jævndøgn? Ved midsommer er dagen godt 17 timer lang, hvor lang er natten? Ved midvinter er dagen kun ca. 7 timer lang, hvor lang er natten?
28 Solen Side 2 I klassen Solen Niveau III Hvor kommer Solens energi fra? Solen er ca. 5 mia. år gammel, og man regner med, at den vil eksistere i endnu 5-7 mia. år. Hvis hele Solens lysudsendelse skyldtes afbrænding af kul, så kan en simpel beregning vise, at Solen i løbet af kun nogle få tusinde år ville have afbrændt hele sin egen masse. I dag ved vi, at det er kerneprocesser (fusion), der leverer den nødvendige energi. Fire brintkerner (protoner) sammensmeltes gennem en række processer til grundstoffet helium. Ved denne proces forsvinder der lidt masse. Benyt tabellen til at bestemme dette massetab i enheden u. Omregn massetabet til energi, idet 1 u svarer til 1, J. Hvert sekund udsender Solen en energimængde på 3, J. Hvor mange processer foregår der hvert sekund på Solen? Hvor stort et massetab er der på Solen hvert sekund i u? i kg? Hvor mange sekunder går der, inden der er sket et massetab på Solen, der svarer til hele Jordens masse (6, kg)? Hvor mange år svarer det til? I kernefysik arbejder man med en speciel atommasseenhed, der kaldes en unit (u). 1 u = 1, kg Einsteins ligning E = m c 2 beskriver omdannelsen af masse m til energi E. c = 3, m/s er lysets hastighed. Hvis massen 1 u omdannes fuldstændigt, frigøres der derfor energimængden E = 1 u c 2 = 1, kg (3, m/s) 2 = 1, J = 931,5 MeV hvor der er brugt sammenhængen 1 MeV = 1, J. Et brintatom og et heliumatom har masserne m H = 1, u m He = 4, u Hvis Solen fortsætter med at skinne i endnu 5 mia. år, hvor stor er Solens samlede massetab da i denne periode? Hvor stor en brøkdel udgør dette massetab af Solens nuværende masse (2, kg)? Jorden modtager hvert år en energimængde i form af solstråling på 5, J. Ved fusion smelter 4 brintkerner sammen og danner helium. Samtidig hermed sker der et massetab, der omdannes til energi. Hvilken massetilførsel svarer det til hvert år i u? i kg? Hvorfor vokser Jordens masse så ikke med 22 mio. kg hvert år?
29 Stjernerne Til læreren Side 1 Stjernerne Stjernebilleder Vi mennesker har til alle tider dannet figurer af stjernehimlens stjerner. Vi gør det for lettere at kunne navigere, dvs. finde rundt på himlen, og for lettere at kunne identificere de enkelte stjerner, som vi giver navne osv. Alt sammen med det formål at lære stjernehimlens indretning at kende. I en tid, hvor man forestillede sig, at stjernerne var placeret på indersiden af en himmelhvælving, og hvor øjet var det eneste instrument, man kunne se med, var der ingen vanskeligheder med at acceptere stjernebillederne som egentlige konstellationer, hvori de enkelte stjerner hørte sammen. Men med erkendelsen af at stjernerne var mere eller mindre frit distribueret i rummet, blev det sværere at fastholde illusionen om, at stjernerne i et stjernebillede hørte sammen. Afstandene mellem os og de enkelte stjerner er meget forskellige. Nogle stjerner ligger få lysår herfra, mens andre ligger tusinder af lysår borte. Faktisk kan en klar stjerne i ét stjernebillede i rummet sagtens ligge nærmere en anden klar stjerne i et andet stjernebillede, end de hver for sig gør i forhold til resten af stjernerne i de stjernebilleder, de ellers menes at høre til. Eksempelvis sidder Vega i Lyren og Altair i Ørnen kun lysår fra hinanden i rummet, mens alle andre klare stjerner i hvert af de to stjernebilleder er meget længere væk. Stjerner og navne Stjernebilledernes navne afspejler de tankebaner, man har haft i forskellige kulturer. I nogle tilfælde har indsigten og observationsevnen været af meget høj kvalitet. F.eks. har det længe været kendt, at visse stjerner varierer i lysstyrke. For os i dag kan det virke overraskende, at man allerede noterede sig dette for flere tusinde år siden. Måske er det blot, fordi vi som fortravlede byboere ikke længere har tid til og mulighed for at iagttage stjernehimlens detaljer. Et interessant eksempel er stjernen Algol i stjernebilledet Perseus. Vi ved i dag, at der er tale om en formørkelsesvariabel stjerne, hvor to stjerner kredser omkring hinanden i et plan, som får dem til gensidigt at dække for hinanden. Det kunne man ikke vide, før spektroskopets opfindelse, fordi de to stjerner, der kredser omkring hinanden, er så langt væk, at de end ikke i store kikkerter kan ses som to adskilte stjerner. Alligevel kunne den døvstumme engelske amatørastronom John Goodridge i 1782 ud fra sine observationer af formørkelsesmønstret fastslå, at variationerne måtte skyldes gensidige formørkelser. De to stjerner er ikke lige lysstærke. Når den lyssvage stjerne dækker for den lysstærke, vil den samlede lysstyrke fra stjerneparret falde markant for efter nogle timer at stige igen. Når lyset fra begge stjerner når frem til vores øjne, fremstår Algol lysstærkest. Når den lysstærkere stjerne dækker for den lyssvagere er faldet i lysstyrken noget mindre. Formørkelsesmønstret fortæller ikke alene om årsagen, men også om de to stjerners lysstyrker, deres baner, størrelser og masser. Astronomi er en slags detektivarbejde, hvor forskeren forsøger at finde alle de informationer, lyset bringer med sig ude fra verdensrummet.
30 Stjernerne Side 2 Til læreren Navnet Algol er stjernens nutidige navn og er en sammentrækning af det gamle arabiske navn for denne stjerne: Al Ra s al Ghul (Dæmonens hoved) en fin betegnelse for en stjerne, der er utilregnelig. Navnet fortæller samtidig om, hvilke observationer araberne har gjort, og hvordan opdagelserne har spillet en rolle for de historier og myter, der senere er blevet til. Et godt eksempel er den græske kulturs myte om Perseus, der med list hugger hovedet af Medusa den ene af Gorgosøstrene, som Gaia havde skabt for at hjælpe giganterne i kampen mod de olympiske guder. På gamle stjernekort kan man se Perseus holde Medusas hoved præcis dér, hvor stjernen Algol sidder i stjernebilledet. Perseus var den tids agent 007, og han er hovedpersonen i de fantastiske historier, der inddrager mange af de figurer, som er synlige på efterårets nattehimmel. Faktisk kan man læse mange informationer om datidens opfattelse af aktiviteterne i himlen ved at studere stjernernes og stjernebilledernes navne. Det vil være en rigtig god idé at højtlæse de græske myter om disse figurer, f.eks. Nattens eventyr af Sys Matthiesen og Anne Værnholt Olesen for mindre børn (Borgen) og Græske Guder og Helte af Leo Hjortsø for de lidt større børn og voksne (Gyldendal). Stjerner og farver Ved første øjekast synes stjernerne at være hvide, at danne mere eller mindre genkendelige mønstre og at lyse med forskellig styrke. Hvis man giver sig selv lidt tid og prøver at sammenligne de enkelte klare stjerner med hinanden, kan man faktisk godt se, at de har forskellig teint svage pastelfarver. Det bliver tydeligere, desto nærmere de stjerner, man sammenligner, er på hinanden. Det, man kalder visuelle dobbeltstjerner, er oplagte mål for at få stjernernes farve at se. Rundt om på himlen findes talrige eksempler på sådanne dobbeltstjerner, og bedst er det at betragte dem gennem en kikkert gerne en god håndkikkert. Stjernernes overfladetemperatur bærer direkte ansvaret for, hvilken farvenuance i det synlige spektrum stjernen udsender mest af. Jo koldere stjernens overflade er, desto mere rødlig fremstår den. Jo varmere overfladen er, desto mere blålig synes stjernen at være. En rødlig stjerne som Betelgeuse i Orion eller Antares i Skorpionen har overfladetemperaturer på omkring 3000 grader. Solen fremstår hvidgul og har en temperatur på omkring 6000 grader, mens en stjerne som Vega i Lyren eller Rigel i Orion er meget varme (omkring 9000 grader) og næsten blåhvide. Læs i øvrigt artiklen i Planetariets tidsskrift aktuel ASTRONOMI 2002 nr. 3 om stjernernes farver. Stjernerne
31 Stjernerne Side 3 Til læreren Stjernernes lysstyrke Når en stjerne fremstår lysstærk på himlen, er det, enten fordi den er tæt på os, eller fordi den faktisk er lysstærk. Måske endda en kombination af begge dele. Himlens klareste stjerne, Sirius i Store Hund, er ikke en specielt lysstærk stjerne den er faktisk med 8,7 lysår bare tæt på os. Når en stjerne udsender lys, spredes det i alle retninger i rummet. Derfor udtyndes intensiteten med kvadratet på afstanden, således at en fordobling af afstanden formindsker intensiteten med en faktor fire. Ved en tredobling af afstanden nedsættes intensiteten af lyset fra stjernen ni gange. Omvendt kan afstanden til en stjerne så beregnes som et forhold mellem en stjernes tilsyneladende lysstyrke (som vi ser den) og dens absolutte lysstyrke (den faktiske derude i rummet). Disse tre faktorer hænger således sammen, og kender man to af dem, kan man finde den tredje. Stjernernes liv Stjerner dannes ved en sammentrækning af interstellare støv- og gasskyer. Hvor meget stof, der trækker sig sammen, er afgørende for, hvor tung og varm stjernen bliver, når dens sammentrækning er tilendebragt, og hvor lang levetid stjernen får i den stabile fase. Når en del af brændstoffet er omsat, bliver stjernen ustabil og afslutter sin eksistens på en mere eller mindre voldsom måde. Også denne afsluttende fase af en stjernes liv er bestemt af, hvor stor og tung stjernen oprindeligt var. Stjernerne
32 Stjernerne I klassen Side 4 Niveau II Stjerner og stjernebilleder Hvornår er stjernehimlen bedst at iagttage: Om sommeren eller om vinteren? Når man er i byen eller på landet? Hvorfor? I august og september er nattehimlen igen ved at blive mørk efter de lyse sommernætter i juni og juli. Men der er stadig noget varme tilbage fra sommeren, så de første efterårsmåneder er gode at se på stjerner i. Når man kommer længere hen på efteråret og vinteren, kan stjernehimlen blive endnu flottere, men det bliver samtidig mere koldt, og man skal sørge for at være godt klædt på. Hvilke årstider skal man helst vælge, hvis man vil ud at se følgende stjernebilleder (dvs. hvornår de bedst ses i syd om natten): Orion Løven Stjernerne Lyren Cassiopeia Tyren Herkules Svanen Perseus Tvillingerne Store Bjørn Ørnen Andromeda
33 Stjernerne I klassen Side 5 Niveau II Stjernernes farver Hvilken farve tænker du på, når du hører om ild? Hvilken farve tænker du på, når du hører om noget koldt? På badeværelser kan man ofte se små farvemærker på vandhanerne. Hvilken farve sidder på den varme vandhane? Hvilken farve sidder på den kolde vandhane? Når du varmer f.eks. jern op, bliver det efterhånden så varmt, at det begynder at gløde. Hvilken farve er det? Hvilken farve tror du jernet vil få, hvis du varmer det mere op? Jo mere man varmer jernet op, desto længere kommer farven væk fra den røde farve i spektret. Stjernerne Sådan er det også med andre ting i naturen, f.eks. stjerner. Jo varmere de er, desto mere blå er de at se på, og jo koldere de er, desto mere røde er de at se på. Prøv at give en forklaring på, hvorfor man på badeværelser har valgt at bruge farverne omvendt af, hvordan det ellers er i naturen:
34 Stjernerne I klassen Side 6 Niveau II Stjernernes lysstyrker et eksperiment Når nogle stjerner er lysstærke, er det, enten fordi det faktisk er store lysstærke stjerner eller også er det, fordi de ikke er så langt væk fra os i universet. Lyset fra en stjerne bliver svagere og svagere, efterhånden som det spredes ud i alle retninger i rummet. Hvor meget svagere lyset bliver, kan du selv regne ud. Men først skal der laves et simpelt forsøg: For at demonstrere, hvorledes lyset fra en lysgiver aftager med kvadratet på afstanden, kan man lave følgende simple eksperiment. Lån en almindelig dværgpære (evt. 4,5 volt) og en tilhørende fatning fra fysiklokalet. Tilslut et fladt 4,5-volt batteri for at sikre, at pæren lyser, som den skal. Fremstil af kraftigt karton en boks, der har en længde på 21 cm samt en bredde og højde på hver 9,9 cm. Endestykkerne er derfor på 9,9 x 9,9 cm (de skæve mål passer med to A4-ark). Der skal også bruges en lineal eller et målebånd. Klip et kvadratisk hul på 3 x 3 cm i midten af frontstykket. Montér pære og fatning med ledninger på bunden af den lille boks, og lad ledningerne slippe ud gennem bagenden. Sørg for, at pæren er placeret nogenlunde ud for det kvadratiske hul. Frontpladen med hul i skal bruges til at afgrænse den lysmængde, der skal måles på. Placér boksen med pæren tæt ved kanten af et bord. Tilslut batteriet, og lad lyset, der slipper igennem hullet, skinne nogenlunde vinkelret ind på midten af et stort stykke hvidt karton, der bruges som lærred så afstanden fra pæren til lærredet er 30 cm. Der frem-
35 Stjernerne I klassen Side 7 Niveau II kommer nu et belyst firkantet felt. Markér hjørnerne, og giv dem bogstaverne a-b-c-d, som markeres på kartonen. Tegn firkanten op. Flyt nu bordet tilbage, så afstanden mellem det hvide lærred og pæren er dobbelt så stor, dvs. 60 cm. Den belyste firkant vokser, mens lyset bliver svagere. Den større belyste firkant har også fire hjørner, som markeres med bogstaverne A-B-C-D. Tegn den store firkant op. Pæren, som lyser med samme lysstyrke, kan sammenlignes med en stjerne, der har en bestemt lysstyrke. I første forsøg kunne man sige, at afstanden til stjernen var 30 lysår, og i andet forsøg var den samme stjerne flyttet ud i en afstand på 60 lysår. Man behøver ikke at måle på lysintensiteten for at registrere, at den er faldet til ¼ man kan let regne det ud. Først beregnes arealet af den lille firkant, a-b-c-d (længde gange bredde), og derefter arealet af den store firkant, A-B-C-D. Arealet af den lille firkant (a-b-c-d): cm² Arealet af den store firkant (A-B-C-D): cm² Hvor mange gange er det store areal større end det lille areal? Det er ca. gange så stort. Arealet eller feltet, som lyset skulle dække på lærredet, er ca. så stort, når du flytter pæren dobbelt så langt væk. Sagt på en anden måde, så er lysstyrken på ethvert punkt på kartonen faldet til ¼, fordi den samme lysmængde nu skulle dække et fire gange så stort areal. Helt på samme måde er det med stjerner. Hvis en stjerne blev flyttet dobbelt så langt væk, så ville stjernen kun synes at lyse med ¼ lysstyrke. Det er vigtigt, når man skal bedømme, hvad stjernens rigtige lysstyrke er derude i rummet. Den lysstyrke, vi ser stjernerne har, er afhængig af den afstand, de befinder sig i. Stjernerne Hvad tror du, der sker med størrelsen af det belyste felt og med lysstyrken, hvis du placerer pæren tre gange så langt væk fra lærredet som ved første opmåling? Feltet er gange større. Så vil lysstyrken også være gange så svag. Det samme gælder for stjerner. Hvis en stjerne flyttes 10 gange så langt væk, hvor meget tror du så, den lysstyrke, vi ser stjernen med her på Jorden, ville falde? Den ville være gange så lyssvag.
36 Stjernerne Side 8 I klassen Niveau III Eksempel fra virkeligheden Lad os tage et praktisk eksempel og regne lidt på, hvilken af de tre stjerner i Sommertrekanten der i virkeligheden er den lysstærkeste. Her fra Jorden er stjernen Vega i Lyren 3 gange så lysstærk som Deneb i Svanen og 2 gange så lysstærk som Altair i Ørnen. Så Vega ser ud til at være er den lysstærkeste. Men de tre stjerner i Sommertrekanten befinder sig i meget forskellig afstand fra Jorden. Afstanden til Vega er 25 lysår, til Deneb 3200 lysår og til Altair 16 lysår, så det må betyde noget. For at sammenligne dem må vi flytte stjernerne, så de har nogenlunde samme afstand fra os. Men når afstanden til en stjerne øges, vil den også blive lyssvagere. Det letteste er at flytte de to nærmeste stjerner, Altair og Vega, ud til 3200 lysår, så de befinder sig i samme afstand som Deneb. Vega flyttes fra 25 lysår til 3200 lysår. Hvor mange gange er det længere væk? Hvor mange gange bliver Vegas lys derved svagere? Altair flyttes fra 16 lysår til 3200 lysår. Hvor mange gange er det længere væk? Hvor mange gange bliver Altairs lys derved svagere? Vi får nu en helt anden opfattelse af stjernen Deneb. Selv om det var den lyssvageste af de tre stjerner (1/3 af Vegas lysstyrke, når vi ser det her fra Jorden), så er den i virkeligheden meget lysstærk faktisk mere end 5000 gange så lysstærk som Vega. Stjernen Altair i Ørnen kan heller ikke måle sig med Deneb (selvom Altair synes dobbelt så lysstærk her fra Jorden), for Altair vil svinde ca gange i lysstyrke, og dermed er Deneb i virkeligheden hele gange lysstærkere end Altair. Både Vega og Altair ville være for svage til, at de overhovedet kunne ses, hvis de blev anbragt i den afstand, som Deneb befinder sig i. Også vores egen stjerne, Solen, ville være usynlig på den afstand. Stjernerne
37 Stjernerne Side 9 I klassen Niveau III Hvor hurtigt bevæger en stjerne sig? Stjernernes hastigheder i vores synsretning, dvs. imod os eller væk fra os, kan bestemmes vha. den såkaldte dopplereffekt. Det er det samme princip, der får lyden fra en sirene på en ambulance til at skifte tonehøjde, idet ambulancen passerer forbi os. En lydkilde, der ikke bevæger sig i forhold til dig som lytter, vil hele tiden udsende et system af ringformede bølgedale og bølgetoppe, alle med centrum i selve kilden. Men hvis lydkilden samtidig bevæger sig, så vil dette centrum for udsendelse af ringbølgerne hele tiden flytte sig i takt med lydkildens bevægelse. Afstanden mellem bølgetoppene også kaldet bølgelængden vil blive presset sammen i retningen mod iagttageren, mens afstanden mellem toppene tilsvarende vil blive større i retningen væk fra iagttageren. Stillestående lydgiver. Der høres den samme bølgelængde (eller tone) i alle retninger. Dopplereffekt Det kan vises, at den relative forskel mellem den bølgelængde λ, som man iagttager, og den rigtige bølgelængde λ o, når lydkilden ikke bevæger sig, er lig med forholdet mellem bølgegiverens hastighed v og lysets (eller lydens) hastighed c: (λ- λ o ) λ o = v c Et regneeksempel En sirene udsender en tone med frekvensen 440 Hz, der ved en lydhastighed på 340 m/s svarer til en bølgelængde på 340m/s λ o = = 0,773 m. 440 Hz Sirenen bevæger sig nu bort fra os, og vi måler frekvensen til 405 Hz, svarende til bølgelængen λ = 0,840 m Den relative forskel er (λ λ o ) λ o (0,840 m 0,773 m) = 0,773 m = 0,087 = 8,7 % Lydkilden bevæger sig mod højre. Bølgelængden bliver mindst (tonen højest) for en iagttager ved B, og bølgelængden bliver størst (dybeste tone) ved A. Ambulancens hastighed er derfor 8,7 % af 340 m/s = 0, m/s = 29,6 m/s = 106 km/h Opgave Beregn bølgelængden, da sirenen bevægede sig imod os med den fundne hastighed, se regneeksemplet. Find derefter den tilsvarende frekvens. Prøv fx med en tonegenerator at skifte mellem de to frekvenser. Lyder det velkendt?
38 Stjernerne Side 10 I klassen Niveau III Stjernerne For lys gælder der noget helt tilsvarende, som det vi lige har omtalt for lyd. Vi kan fx vælge at undersøge det bestemte rødlige lys, der absorberes af brintatomerne på en stjernes overflade. Det er den ene af de fire synlige linjer i brintspektret. Hvis dette røde lys, den såkaldte Hαlinje, udsendes eller absorberes af en stjerne, der ikke bevæger sig i forhold til os, vil vi se linjen ved en bølgelængde λ o på 656,285 nm. Hvis stjernen i stedet for bevæger sig, vil der ske en forskydning af bølgelængden, dvs. at lysets farve ændres en lille smule. Der gælder den samme sammenhæng som ovenfor, blot skal vi i stedet for lydens hastighed nu bruge lysets hastighed, der er c = km/s. Opgave Vi ser på et system bestående af to stjerner, der kredser omkring hinanden. Den ene stjerne (A) er så svag, at vi næsten ikke kan se den, hvorimod den anden (B) er så kraftig, at vi kan undersøge spektret fra stjernen, dvs. at vi kan spalte lyset op i regnbuens farver og bestemme bølgelængderne. Der er vist tre spektre (forenklede) fra stjernen. Det første spektrum (I), når stjernen B bevæger sig med størst hastighed bort fra os, det midterste spektrum (II), når bevægelsen er vinkelret på vores synslinje, og det tredje spektrum (III), når stjernen bevæger sig direkte imod os. Bølgelængderne for den forskudte røde Hα-linje er angivet nedenunder spektrene. Bestem stjernens hastighed bort fra os eller imod os i hvert af de tre tilfælde. Hvor hurtigt bevæger hele dobbeltstjernesystemet sig bort fra os? Hvor hurtigt bevæger den synlige stjerne sig rundt omkring den anden stjerne?
Afstande Afstande i universet
 Side 1 Til læreren i universet Her får man en fornemmelse af rummeligheden i universet at stjernerne ikke, som antaget i Middelalderen, sidder på indersiden af en kugleflade, men i stedet er spredt i rummet
Side 1 Til læreren i universet Her får man en fornemmelse af rummeligheden i universet at stjernerne ikke, som antaget i Middelalderen, sidder på indersiden af en kugleflade, men i stedet er spredt i rummet
EKSPERIMENTELLE BEVISER
 kapitel 4 EKSPERIMENTELLE BEVISER Der er et væld af, hvad man kunne kalde eksperimentelle beviser for, at relativitetsteorien er korrekt. Når jeg skriver beviser i anførelsestegn, er det i tråd med den
kapitel 4 EKSPERIMENTELLE BEVISER Der er et væld af, hvad man kunne kalde eksperimentelle beviser for, at relativitetsteorien er korrekt. Når jeg skriver beviser i anførelsestegn, er det i tråd med den
Fra Støv til Liv. Af Lektor Anja C. Andersen Dark Cosmology Center, Niels Bohr Institutet, Københavns Universitet
 Fra Støv til Liv Af Lektor Anja C. Andersen Dark Cosmology Center, Niels Bohr Institutet, Københavns Universitet Observationer af universet peger på, at det er i konstant forandring. Alle galakserne fjerner
Fra Støv til Liv Af Lektor Anja C. Andersen Dark Cosmology Center, Niels Bohr Institutet, Københavns Universitet Observationer af universet peger på, at det er i konstant forandring. Alle galakserne fjerner
NÅR DU SER ET STJERNESKUD? GUIDE TIL IDENTIFICERING AF HIMLENS FÆNOMENER
 NÅR DU SER ET STJERNESKUD? GUIDE TIL IDENTIFICERING AF HIMLENS FÆNOMENER NÅR DU SER ET STJERNESKUD? - guide til identificering af himlens fænomener NAT Skandinavisk UFO Information (SUFOI) 2. udgave 2005.
NÅR DU SER ET STJERNESKUD? GUIDE TIL IDENTIFICERING AF HIMLENS FÆNOMENER NÅR DU SER ET STJERNESKUD? - guide til identificering af himlens fænomener NAT Skandinavisk UFO Information (SUFOI) 2. udgave 2005.
Mekanik. Notecentralen. - Indledende niveau - Uden differentialregning. Ole Trinhammer
 Notecentralen Mekanik - Indledende niveau - Uden differentialregning Ole Trinhammer. udgave af første 3 kapitler af Amtrup og Trinhammer Obligatorisk Fysik, Gyldendal Indhold Forord 1 Gode råd til eleven
Notecentralen Mekanik - Indledende niveau - Uden differentialregning Ole Trinhammer. udgave af første 3 kapitler af Amtrup og Trinhammer Obligatorisk Fysik, Gyldendal Indhold Forord 1 Gode råd til eleven
Fra Aristoteles til Newton Træk af den naturvidenskabelige tænkemådes historie
 Fra Aristoteles til Newton Træk af den naturvidenskabelige tænkemådes historie Af Carl Henrik Koch, Institut for Medier, Erkendelse og Formidling, Københavns Universitet Der foregik ikke en naturvidenskabelig
Fra Aristoteles til Newton Træk af den naturvidenskabelige tænkemådes historie Af Carl Henrik Koch, Institut for Medier, Erkendelse og Formidling, Københavns Universitet Der foregik ikke en naturvidenskabelig
Introduktion til den specielle relativitetsteori
 Introduktion til den specielle relativitetsteori Mogens Dam Niels Bohr Institutet 18. september 2007 7. udgave Denne tekst søger for at dokumentet printer som tiltænkt Forord Denne indføring i den specielle
Introduktion til den specielle relativitetsteori Mogens Dam Niels Bohr Institutet 18. september 2007 7. udgave Denne tekst søger for at dokumentet printer som tiltænkt Forord Denne indføring i den specielle
Hvad er matematik? Grundbog. Bjørn Grøn Bjørn Felsager Bodil Bruun Olav Lyndrup. L&R Uddannelse
 0. Hvad er matematik? Hvad er matematik? C Grundbog Bjørn Grøn Bjørn Felsager Bodil Bruun Olav Lyndrup L&R Uddannelse 1 Indholdsfortegnelse Indholdsfortegnelse Forord.........................................................
0. Hvad er matematik? Hvad er matematik? C Grundbog Bjørn Grøn Bjørn Felsager Bodil Bruun Olav Lyndrup L&R Uddannelse 1 Indholdsfortegnelse Indholdsfortegnelse Forord.........................................................
Tillæg til partikelfysik
 Tillæg til partikelfysik Erik Vestergaard Erik Vestergaard www.matematikfysik.dk Erik Vestergaard, 015 Forsidebillede er fra CERN s Photo Service og viser CMS detektoren hos CERN. CMS står for Compact
Tillæg til partikelfysik Erik Vestergaard Erik Vestergaard www.matematikfysik.dk Erik Vestergaard, 015 Forsidebillede er fra CERN s Photo Service og viser CMS detektoren hos CERN. CMS står for Compact
DE MENTALE LOVE MÅDEN SINDET FUNGERER PÅ
 1 DE MENTALE LOVE MÅDEN SINDET FUNGERER PÅ af Barbara Berger (Copyright Barbara Berger 2000/2009) 2 Indhold Introduktion 3 De Mentale Love / Måden sindet fungerer på - Loven om at tanker opstår 4 - Loven
1 DE MENTALE LOVE MÅDEN SINDET FUNGERER PÅ af Barbara Berger (Copyright Barbara Berger 2000/2009) 2 Indhold Introduktion 3 De Mentale Love / Måden sindet fungerer på - Loven om at tanker opstår 4 - Loven
Mellem stjerner og planeter
 Mellem stjerner og planeter Et undervisningmateriale for gymnasieklasser om begrebet parallakse og statistik. Titelbladet fra Tycho Brahes bog De Nova Stella, udgivet i 1573. Oversat fra latin står der
Mellem stjerner og planeter Et undervisningmateriale for gymnasieklasser om begrebet parallakse og statistik. Titelbladet fra Tycho Brahes bog De Nova Stella, udgivet i 1573. Oversat fra latin står der
Bjørn Grøn: Fra græsk geometri til moderne algebra Side 1 af 29. Bjørn Grøn. (bearbejdet af Thomas Jensen og Morten Overgård Nielsen)
 Bjørn Grøn: Fra græsk geometri til moderne algebra Side 1 af 29 Bjørn Grøn Fra græsk geometri til moderne algebra (bearbejdet af Thomas Jensen og Morten Overgård Nielsen) INDHOLD Oprindelsen... 2 Påvirkninger
Bjørn Grøn: Fra græsk geometri til moderne algebra Side 1 af 29 Bjørn Grøn Fra græsk geometri til moderne algebra (bearbejdet af Thomas Jensen og Morten Overgård Nielsen) INDHOLD Oprindelsen... 2 Påvirkninger
Figur 1.1. Solsystemet befinder sig i udkanten af Mælkevejen 27.000 lysår fra centret. Jorden er den tredje af solsystemets otte planeter.
 Figur 1.1. Solsystemet befinder sig i udkanten af Mælkevejen 27.000 lysår fra centret. Jorden er den tredje af solsystemets otte planeter. Figur 1.2. Solens omløbstid i sin bane (vist som en røde cirkel)
Figur 1.1. Solsystemet befinder sig i udkanten af Mælkevejen 27.000 lysår fra centret. Jorden er den tredje af solsystemets otte planeter. Figur 1.2. Solens omløbstid i sin bane (vist som en røde cirkel)
Den digitale revolution
 datalogisk institut københavns universitet Den digitale revolution fortællinger fra datalogiens verden DIKU 1970 2010 Den digitale revolution fortællinger fra datalogiens verden Datalogisk Institut, Københavns
datalogisk institut københavns universitet Den digitale revolution fortællinger fra datalogiens verden DIKU 1970 2010 Den digitale revolution fortællinger fra datalogiens verden Datalogisk Institut, Københavns
CO 2 Hvorfra, hvorfor, hvor meget?
 Hvorfra, hvorfor, hvor meget? Jes Fenger Afdeling for Atmosfærisk Miljø Miljø- og Energiministeriet Danmarks Miljøundersøgelser 2000 TEMA-rapport fra DMU, 31/2000 - Hvorfra, hvorfor, hvor meget? Forfatter:
Hvorfra, hvorfor, hvor meget? Jes Fenger Afdeling for Atmosfærisk Miljø Miljø- og Energiministeriet Danmarks Miljøundersøgelser 2000 TEMA-rapport fra DMU, 31/2000 - Hvorfra, hvorfor, hvor meget? Forfatter:
Abstract. Forskel på naturfag og andre fag i skolen. Af Gert Wahlgren
 Af Gert Wahlgren Abstract I artiklen beskrives den historiske udvikling i kvalitet og kvantitet med hensyn til erkendelse af vores omverden, og at den udvikling har ført til en undervisning i naturfag,
Af Gert Wahlgren Abstract I artiklen beskrives den historiske udvikling i kvalitet og kvantitet med hensyn til erkendelse af vores omverden, og at den udvikling har ført til en undervisning i naturfag,
Den Kreative Platform
 Den Kreative Platform Søren Hansen & Christian Byrge Kreativitetslaboratoriet, Aalborg Universitet 2. udgave 2 Indholdsfortegnelse Indholdsfortegnelse........................................................................................................................................................
Den Kreative Platform Søren Hansen & Christian Byrge Kreativitetslaboratoriet, Aalborg Universitet 2. udgave 2 Indholdsfortegnelse Indholdsfortegnelse........................................................................................................................................................
50 år med ufoer - erfaringer fra halvtreds års rapportarbejde. Toke Haunstrup
 50 år med ufoer - erfaringer fra halvtreds års rapportarbejde Toke Haunstrup Toke Haunstrup 50 år med ufoer - erfaringer fra halvtreds års rapportarbejde Skandinavisk UFO Information 50 år med ufoer -
50 år med ufoer - erfaringer fra halvtreds års rapportarbejde Toke Haunstrup Toke Haunstrup 50 år med ufoer - erfaringer fra halvtreds års rapportarbejde Skandinavisk UFO Information 50 år med ufoer -
Matematisk modellering: Hvor tidligt står Venus op?
 Matematisk modellering: Hvor tidligt står Venus op? Kasper Bjering Søby Jensen, ph.d. studerende i matematikkens didaktik ved Roskilde Universitet I LMFK bladet 2/2012 bragtes artiklen Anvendelse og modellering
Matematisk modellering: Hvor tidligt står Venus op? Kasper Bjering Søby Jensen, ph.d. studerende i matematikkens didaktik ved Roskilde Universitet I LMFK bladet 2/2012 bragtes artiklen Anvendelse og modellering
Introduktion til teknikken bag MR-skanning
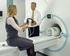 Introduktion til teknikken bag MR-skanning Lars G. Hanson, larsh@drcmr.dk MR-afdelingen, Hvidovre Hospital, DRCMR For seneste dokumentversion, se http://www.drcmr.dk/ English version: An introduction to
Introduktion til teknikken bag MR-skanning Lars G. Hanson, larsh@drcmr.dk MR-afdelingen, Hvidovre Hospital, DRCMR For seneste dokumentversion, se http://www.drcmr.dk/ English version: An introduction to
MATINTRO FUNKTIONER AF FLERE VARIABLE
 MATINTRO FUNKTIONER AF FLERE VARIABLE Tore August Kro Matematisk Institutt Universitetet i Oslo 5.kapitel skrevet af: Jan Philip Solovej Institut for de Matematiske Fag Københavns Universitet Forår 3 På
MATINTRO FUNKTIONER AF FLERE VARIABLE Tore August Kro Matematisk Institutt Universitetet i Oslo 5.kapitel skrevet af: Jan Philip Solovej Institut for de Matematiske Fag Københavns Universitet Forår 3 På
Statistik. Erik Vestergaard
 Statistik Erik Vestergaard 2 Erik Vestergaard www.matematiksider.dk Erik Vestergaard www.matematiksider.dk 3 1. Grupperede observationer I statistik beskæftiger man sig med indsamling, bearbejdelse og
Statistik Erik Vestergaard 2 Erik Vestergaard www.matematiksider.dk Erik Vestergaard www.matematiksider.dk 3 1. Grupperede observationer I statistik beskæftiger man sig med indsamling, bearbejdelse og
Unge på kanten af livet. Spørgsmål og svar om selvmord. Bente Hjorth Madsen Center for Selvmordsforebyggelse, Risskov
 Unge på kanten af livet Spørgsmål og svar om selvmord Bente Hjorth Madsen Center for Selvmordsforebyggelse, Risskov 1 Indhold Brugervejledning 3 Hvad er problemet? Fup eller fakta 5 Metode 9 Piger/Drenge
Unge på kanten af livet Spørgsmål og svar om selvmord Bente Hjorth Madsen Center for Selvmordsforebyggelse, Risskov 1 Indhold Brugervejledning 3 Hvad er problemet? Fup eller fakta 5 Metode 9 Piger/Drenge
Begreberne om evighed og tid indenfor hedensk og kristen nyplatonisme, med hovedfokus på Plotin som hedenskabets repræsentant
 Begreberne om evighed og tid indenfor hedensk og kristen nyplatonisme, med hovedfokus på Plotin som hedenskabets repræsentant af Maria Pontoppidan Københavns Universitet Abstract Artiklen giver en redegørelse
Begreberne om evighed og tid indenfor hedensk og kristen nyplatonisme, med hovedfokus på Plotin som hedenskabets repræsentant af Maria Pontoppidan Københavns Universitet Abstract Artiklen giver en redegørelse
En læreplads som keglebillardspiller.
 En læreplads som keglebillardspiller. En total uddannelse der følger dig hele vejen til succes. Forfatter: Kjeld Reby Løren Side 2 af 140 Side 3 af 140 Indhold Forord... 7 Hvorfor har jeg skrevet denne
En læreplads som keglebillardspiller. En total uddannelse der følger dig hele vejen til succes. Forfatter: Kjeld Reby Løren Side 2 af 140 Side 3 af 140 Indhold Forord... 7 Hvorfor har jeg skrevet denne
Regler og medbestemmelse i børnehaven
 Regler og medbestemmelse i børnehaven En undersøgelse i Børnerådets Minibørnepanel BØRNERÅDETS Minibørnepanel Regler og medbestemmelse i børnehaven 1 2 Børnerådets Minibørnepanel Indhold Indledning / 3
Regler og medbestemmelse i børnehaven En undersøgelse i Børnerådets Minibørnepanel BØRNERÅDETS Minibørnepanel Regler og medbestemmelse i børnehaven 1 2 Børnerådets Minibørnepanel Indhold Indledning / 3
