Laplace transformationen
|
|
|
- Karl Juhl
- 8 år siden
- Visninger:
Transkript
1 MODUL 6 Laplace transformationen Forfattere: Michael ELMEGÅRD & Øistein WIND-WILLASSEN 24. juni 214
2 2
3 Indhold 1 Laplace transformationen En lineær transformation Lidt krav til f (t), funktionsklassen L Translation, differentiation, integration og partialbrøker Translation i t-domænet, f (t a) Afledte i t-domænet, f (n) (t) Integraler i t-domænet, t f (τ)dτ Translation i s-domænet Periodiske funktioner Teaser: en lineær partielle differentialligning Tabel: operationer for Laplace transformationen
4 4 INDHOLD
5 Kapitel 1 Laplace transformationen I det følgende skal vi stifte bekendtskab med et matematisk værktøj Laplace transformationen der finder anvendelse indenfor en lang række ingeniørtekniske udfordringer, eksempelvis elektriske kredsløb, varmetransmission, mekaniske svingninger og reguleringsteknik. Mere generelt er det et formidabelt værktøj til at simplificere løsningsprocessen forbundet med differentialligninger. En af de smarte ting ved Laplace transformationen er, at den blandt andet kan transformere differentialligninger til algebraiske problemer som man så løser med simple regneregler og transformerer tilbage, dette er visualiseret i Figur 1.1. Rent formelt er Laplace transformationen, L, af en funktion f (t) defineret ved Definition 1.1. L { f (t)} = F(s) = f (t)e st dt. (1.1) Vi antager desuden at t. Den inverse Laplace transformation noteret som L 1 {F(s)} = f (t). Der findes en inversionsformel, men den er, overraskende nok, praktisk talt unødvendiggjort af f.eks. matematiske programmer som Maple og Mathematica og opslag i lister over Laplace transformationer, se Tabel 1.1. For eksemplets skyld viser vi hvordan transformationen udregnes for to simple funktioner. Først ser vi hvorledes man transformerer en konstant funktion f (t) = 1. 5
6 6 KAPITEL 1. LAPLACE TRANSFORMATIONEN L Differentialligning (DL) Algebraisk Ligning (AL) Andre metoder Simpel Algebra Løsning til Differentialligningen Løs den Algebraiske Ligning L 1 Figur 1.1: Fremgangsmåden til løsning af differentialligninger med Laplace transformationen. Algoritmen udføres i tre trin: 1) Laplace transformer differentialligningen (dette gøres ved at anvende alle de sætninger som vi har gennemgået i det foregående); 2) Løs den algebraiske ligning (dette gøres ved at isolere den variabel/funktion som man vil bestemme); 3) bestem den inverse Laplace transformation til den nyligt isolerede ubekendte funktion (dette gøres ved at benytte matematikprogrammer som Matlab, Maple, Mathematica eller tabelopslag eller kompleks integration). Herved er differentialligningen løst. Eksempel 1.1. Givet f (t) = 1 for alle t, find F(s). Vi benytter Ligning (1.1) fra definitionen på Laplace transformationen, altså F(s) = L ( f (t)) = = = = 1 s 1 e st dt, [ 1 s e st ], (s > ). f (t)e st dt, Bemærk at integralet ikke er defineret for s. (Overbevis lige dig selv om dette!)
7 1.1. EN LINEÆR TRANSFORMATION 7 I det næste eksempel finder vi Laplace transformationen F(s) af den rette linie f (t) = ax med hældning a = 1. Eksempel 1.2. Givet f (t) = t for alle t, find F(s). Vi benytter Ligning (1.1) fra definitionen på Laplace transformationen, altså F(s) = L ( f (t)) = = = t e st dt, [( t s 1 ) ] s 2 e st, = 1 s 2 (s > ). f (t)e st dt, Bemærk at integralet ikke er defineret for s. (Overbevis lige dig selv om dette!) Vi skal i det følgende gennemgå de mest essentielle matematiske omstændigheder og udlede en række vigtige regneregler. Ydermere, skal vi undersøge Laplace transformationer for nogle af de ofte anvendte funktioner, f.eks., e λt,cos(ωt),sin(ωt) og Heavisides trinfunktion. Desuden skal vi også vise hvordan man kan behandle en bred vifte af differentialligninger med denne metode. Tanken med modulets opbygning er at det opbygger det matematiske fundament for anvendelsen af Laplace transformationen samtidig med at man lærer at anvende den på relevante ingeniørtekniske problemer. Man vil erfare at man kan håndtere avancerede anvendelser, og inden længe kan man f.eks. løse en lang række lineære differentialligninger! 1.1 En lineær transformation Lad os allerførst overveje betydningen af Ligning (1.1). Vi forestiller os, at f (t) er en vilkårlig funktion af tid, altså f.eks. et elektrisk signal eller udbøjningen af tippen på en bjælke; i dette tilfælde overfører Laplace transformationen f (t) til en ny funktion F(s), altså L : f (t) F(s). (1.2) Transformationen identificerer funktionen f af variablen t med en ny funktion F i en ny variabel s (se figur 1.2). L er en såkaldt lineær operator og dette er kendetegnet ved egenskaberne L ( f 1 (t) + f 2 (t)) = L ( f 1 (t)) + L ( f 2 (t)), (1.3) L (c f (t)) = cl ( f (t)), (1.4)
8 8 KAPITEL 1. LAPLACE TRANSFORMATIONEN L f (t) F(s) L 1 Figur 1.2: Laplace transformationen, L afbilder funktioner i den uafhængige variabel t til funktioner i den uafhængige variabel s. Omvendt afbilder den inverse Laplace transformation funktioner i den uafhængige variabel s til funktioner i den uafhængige variabel t. hvor c er en vilkårlig konstant. Vi kalder de to egenskaber additivitet og homogenitet. Begge egenskaber følger direkte af definitionen, L ( f 1 (t) + f 2 (t)) = = ( f 1 (t) + f 2 (t))e st dt, f 1 (t)e st dt + = L ( f 1 (t)) + L ( f 2 (t)). f 2 (t)e st dt, Tilsvarende kan man vise homogenitetsegenskaben. (Gør det lige, for at overbevise dig selv, det tager kun et øjeblik). Desuden er den inverse Laplace transformation også en lineær operator. Bemærk, at disse egenskaber er enormt vigtige. Den ene medfører, at vi kan transformere hvert enkelt led i en ligning hver for sig, og den anden at amplituderne af funktionerne overføres uændret. Se nu hvordan vi f.eks. kan bestemme Laplace transformationen til den lineær funktion f (t) = at + b hvor a, b er vilkårlige konstanter. Eksempel 1.3. (Linearitet af Laplace transformationen). f (t) = at + b. Laplace transformationen kan opslittes på følgende måde, L ( f (t)) = F(s) = L (at + b), = L (at) + L (b), = al (t) + bl (1), hvor vi først har gjort brug af Ligning (1.3) til at splitte ledene fra hinanden og dernæst Ligning (1.4) til at flytte konstanterne udenfor transformationen. Den endelige transformation
9 1.1. EN LINEÆR TRANSFORMATION 9 findes nu ved at anvende resultaterne fra Eksempel 1.1 og Eksempel 1.2 for at opnå, F(s) = a s 2 + b s. Det betyder altså at f (t) = 5t + 6 f.eks. har Laplace transformationen F(s) = s 2 s. Netop pga. disse egenskaber kan vi altså klare os med at kende transformationer for nogle få funktioner hver for sig og i Tabel 1.1 har vi opskrevet de hyppigst forekommende. Tabel over Laplace transformationer F(s) f (t) 1 s 1 1 s 2 1 s n, n = 1,2,... 1 s a ω s 2 +ω 2 s s 2 +ω 2 ω (s a) 2 +ω 2 s a (s a) 2 +ω 2 t t n 1 (n 1)! e at sinωt cosωt e at sinωt e at cosωt e as s, a > u a (t) Tabel 1.1: Laplace transformationer af kendte funktioner (Joel Schiff: The Laplace Transform Theory and Applications ). Vi har foreløbig undgået diskussionen om for hvilke funktioner integralet giver mening heldigvis kan en stor klasse af funktioner anvendes og det vil vi forklare i den følgende sektion.
10 1 KAPITEL 1. LAPLACE TRANSFORMATIONEN 1.2 Lidt krav til f (t), funktionsklassen L Vi skal nu beskrive en klasse af funktioner som vi vil holde os indenfor i dette modul. Helt generelt kan man tale om funktionsklassen af alle de funktioner for hvilke Laplace transformationen er meningsfuld, altså de f (t) hvor integralet i Ligning (1.1) kan beregnes. Af praktiske årsager og med tanke på den tekniske anvendelse som vi har for øje, kan vi med fordel begrænse os til en marginalt mindre klasse af funktioner og derved spare os selv for en enorm mængde matematiske spidsfindigheder. Lad os benævne denne klasse af funktioner ved L og definere den på følgende måde, Definition 1.2. Klassen L består af funktionerne f som er stykkevis kontinuerte på [, [, af eksponentiel orden α f (t) Me αt. Intuitivt kan man sige, at de stykkevis kontinuerte funktioner dækker over dem som vi kan tegne med en blyant hvor vi kun må løfte blyanten et endeligt antal gange i ethvert interval [,b]. Geomtrisk set kan man også huske på, at den eksponentielle orden betyder, at f (t) bare skal kunne holdes under kurven for en eksponential funktion Me αt. I praksis dækker disse funktioner over de fleste ingeniørtekniske udfordringer hvor man måler eller beregner en proces hvor input og output ikke eksploderer. I Figur 1.2 giver vi to grafiske eksempler. Vi nævner uden bevis denne meget vigtige sætning vedrørende funktionerne i klassen L, Sætning 1.1. Hvis f (t) L så eksisterer Laplace transformationen F(s) = L ( f (t)) for s > α og integralet er absolut konvergent. Med Sætning 1.1 er vi nu på sikker grund og godt udrustet til at anvende Laplace transformationen. Vi ser nu nærmere på de meget velkendte trigonometriske funktioner og eksponentialfunktionen. Lad os i det følgende eksempel beregne Laplace transformationen for eksponentialfunktionen e λt hvor λ C, altså Eksempel 1.4. Givet f (t) = e λt for alle t, find F(s). Bemærk at f (t) tilhører funktionsklassen L. Dette følger direkte fordi eksponentialfunktionen er af eksponentiel orden α(> Re(λ)) og ydermere kontinuert på intervallet.
11 1.2. LIDT KRAV TIL F(T ), FUNKTIONSKLASSEN L 11 f(t) f(t).5 t.5 t f(t) f(t) M e αt M t t Figur 1.3: Øverst: f (t) = 1/(t.5). Denne funktion har en lodret asymptote og hører ikke til klassen L. Nederst: en stykkevis kontinuert funktion som er begrænset og tilhører klassen L. Dernæst benytter vi Ligning (1.1) fra definitionen på Laplace transformationen, altså F(s) = L ( f (t)) = = e λt e st dt, [ 1 = λ s e(λ s)t = 1 s λ ] f (t)e st dt,, (s > Re(λ)). Bemærk igen, at ligningen kun er gældende når s er større end real-delen af λ fordi dette forbehold sikrer at e (λ s)t når t. Fra det foregående eksempel og ved at gøre brug af superpositionsprincippet fra tidligere og Eulers formel 1 kan man lynhurtigt vise de tilsvarende transformationer for cos(ωt) og sin(ωt). 1 Eulers formel: e iθ = cos(θ) + isin(θ) hvor θ er et reelt tal.
12 12 KAPITEL 1. LAPLACE TRANSFORMATIONEN Eksempel 1.5. Givet f (t) = cos(ωt) for alle t, find F(s). Indse først at f (t) tilhører funktionsklassen L. I stedet for at indsætte f (t) i definitionen som i de foregående eksempler, bemærker vi at man vha. Eulers formel kan skrive cos(ωt) = e iωt +e iωt 2. Dermed bliver F(s) = L (cos(ωt)), ( e iωt + e iωt ) = L = L (eiωt ) L (e iωt ), = 1 ( 1 2 s iω + 1 ), (s > ), s + iω s = s 2, (s > ), + ω2 Vis på samme måde resultatet for sin(ωt), nemlig L (sin(ωt)) = ω s 2 +ω 2. Vi nævner uden bevis en sætning som vedrører Laplace transformationers asymptotiske opførsel. Sætning 1.2. Hvis f (t) L så gælder F(s) for s. Dette er et ganske praktisk resultat, fordi det giver os en nødvendig betingelse for at F(s) overhovedet kan være en Laplace transformation af f (t) L. F.eks. kan F(s) = e s ikke være en Laplace transformation af f (t) L. Vi tjekker et par af vores tidligere resultater fra eksemplerne. Eksempel 1.6. Laplace transformationerne for f (t) = 1, f (t) = t og f (t) = e λt. F(s) = L (1) = 1 s, s, F(s) = L (t) = 1, s. s2 Vi ser altså at vores transformationer i det mindste overholder det nødvendige krav. Bemærk, at når et krav en nødvendig betingelse er det ikke tilstrækkeligt til at vise hvorvidt vi har regnet rigtigt!
13 1.3. TRANSLATION, DIFFERENTIATION, INTEGRATION OG PARTIALBRØKER 13 k x m f(t) c Figur 1.4: Mass, spring and damper system diagram. Dette er værd at huske når man regner! I den næste sektion ser vi nærmere på hvordan Laplace transformationen hjælper os med at håndtere f.eks. f (t) og t f (τ)dτ. 1.3 Translation, differentiation, integration og partialbrøker En af de helt store styrker ved Laplace transformationen er som nævnt tidligere at vi kan håndtere differentialligninger på en relativt simpel måde. Det bliver let som en leg at løse såkaldte begyndelsesværdiproblemer 2. Disse kunne f.eks. være det velkendte mekaniske system Masse/fjeder/dæmper system (se figur 1.4): mẍ + cẋ + kx = f (t), (1.5) x() = a og ẋ() = b. (1.6) Hvor m er massekonstanten, c er dæmpningskonstanten og k er fjederkonstanten. Det mekaniske system er under påvirkning af en kraft f (t). Et andet eksempel er det ækvivalente elektriske kredsløb 2 Det er dem hvor man har betingelser der skal opfyldes til tiden t = t.
14 14 KAPITEL 1. LAPLACE TRANSFORMATIONEN R E L C Figur 1.5: RLC kredsløb. RLC kredsløb (se figur 1.5): LÏ + Rİ + 1 I = E(t), (1.7) C I() = a og İ() = b. (1.8) Hvor L er induktansen, R er modstanden og c er kapacitansen. Det elektriske kredsløb er drevet af den elektromotoriske kraft E(t). Bemærk, at vi nøjes med at kræve, at hvert led skal tilhøre L. Det betyder, at påvirkningerne f (t) og E(t) kan være meget generelle funktioner. Inden vi er helt klar til at håndtere differentialligninger skal vi først udvide vores repetoire af regneregler Translation i t-domænet, f (t a) Før vi udleder regnereglerne for translation introducerer vi Heavisides trin-funktion, Heavisides trin-funktion (se figur 1.6): 1, t a u a (t) =, t < a. (1.9) Lad os beregne Laplace transformationen af trin-funktionen.
15 1.3. TRANSLATION, DIFFERENTIATION, INTEGRATION OG PARTIALBRØKER 15 f(t) 1 a t Figur 1.6: Heavisides trin-funktion. Eksempel 1.7. Laplace transformationen af trin-funktionen: F(s) = L (u a (t)), = = a u a (t)e st dt, e st dt, = e as, (s > ). s Sammenlign dette resultat med Eksempel 1.1 når a =. Bemærk at trin-funktionen giver os en mere kompakt måde at skrive stykkevis kontinuerte funktioner på. F.eks. kan man på en simpel måde skrive boks-funktionen som en kombination af to trin-funktioner ( f boks (t) = u a (t) u b (t) hvor a < b, skitser funktionen og overvej hvorledes man kan bruge dette til at skrive en stykkevis defineret funktion). Lad os nu vise det følgende resultat. Sætning 1.3. (Translation i t-domænet). Hvis F(s) = L ( f (t)), så gælder L (u a (t) f (t a)) = e as F(s), (a ). (1.1) Bevis. Resultatet følger umiddelbart direkte ved anvendelse af definitionen på Laplace transfor-
16 16 KAPITEL 1. LAPLACE TRANSFORMATIONEN mationen. L (u a (t) f (t a)) = Benyt koordinatskiftet τ = t a for at opnå = L (u a (t) f (t a)) = Vi har hermed kommet frem til Ligning (1.1). a e st u a (t) f (t a)dt, e st f (t a)dt. e s(τ+a) f (τ)dτ, = e as e sτ f (τ)dτ, = e as L ( f (τ)), = e as F(s). Sætning 1.3 er enormt praktisk i systemer hvor man tænder og slukker for påvirkninger, f.eks. i et elektrisk kredsløb. En praktisk fortolkning af translation er at man forsinker et signal eller en påvirkning fra t = til t = a Afledte i t-domænet, f (n) (t) Når vi skal håndtere differentialligninger får vi brug for at kunne transformere afledte af f (t), f.eks. f, f, f. Dette er formuleret i de følgende sætninger. Sætning 1.4. (Transformation af afledte). Lad f være kontinuert på [, [ og af eksponentiel orden α og lad f være stykkevis kontinuert på [, [. Så L ( f (t)) = sl ( f (t)) f (), (R(s) > α). (1.11) Bevis. Dette viser vi ved at anvende partiel integration b u(t)v (t)dt = [u(t)v(t)] b a a b a u (t)v(t)dt hvor vi fra definitionen på Laplace transformationen L ( f (t)) = e st f (t)dt vælger u(t) = e st og v(t) = f (t). Ved direkte indsættelse giver det, e st f (t)dt = [e st f (t)] + s e st f (t)dt, = lim e sτ f (τ) f () + s e st f (t)dt, τ = f () + sl ( f (t)), (R(s) > α).
17 1.3. TRANSLATION, DIFFERENTIATION, INTEGRATION OG PARTIALBRØKER 17 Vi har hermed vist sætningen. Det er fornuftigt at bemærke detaljerne i det ovenstående bevis, altså hvor opstår antagelserne som står i Sætning 1.4. F.eks. er den eksponentielle orden α nødvendig for at vi kan gå fra den næstsidste ligning til den sidste. Det er nærliggende at tænke over hvorledes dette forsætter til højere ordens afledte. Dette er formuleret i følgende generalisering (uden bevis): Sætning 1.5. (Transformation af n te ordens afledte). Lad f (t), f (t),..., f (n 1) (t) være kontinuert på [, [ og af eksponentiel orden α og lad f (n) (t) være stykkevis kontinuert. Så L ( f (n) (t)) = s n L ( f (t)) s n 1 f () s n 2 f () f (n 1) (). (1.12) Det medfører f.eks. resultatet for andenordens afledte, L ( f (t)) = s 2 L ( f (t)) s f () f (). (1.13) (Opskriv tilsvarende udtrykket for L ( f (t)) ved hjælp af Ligning 1.12). Inden vi begiver os ud i at løse vores første differentialligning med Laplace transformationen giver vi et kort overblik over de enkelte trin der er forbundet med denne udfordring. Betragt igen Figur 1.1 som forklarer hvordan Laplace transformationen benyttes til løsning af differentialligninger. Det er vigtigt at nævne at der findes andre løsningsmetoder til lineære differentialligninger og derfor er det nærliggende at undre sig over hvorfor vi finder et behov for at introducere endnu en metode. Det fordelagtige ved denne metode er blandt andre ting at man kan behandle diskontinuerte påvirkninger, f.eks. en elektromotorisk kraft som tænder og slukker på en relativt simpel måde. Desuden fremhæver metoden hvordan enkelte elementer i et system påvirker den komplette løsning og dette kan man med fordel udnytte i f.eks. reguleringsteknik hvor man er interesseret i at regulere et givet systems opførsel. Lad os nu teste vores regneregler for de afledte på den simpleste differentialligning vi kan finde på. Eksempel 1.8. (Bevægelse med konstant hastighed.) Lad x(t) være positionen af en partikel/bil/person/bold der bevæger sig på en linie. Vi kræver, at partiklen bevæger sig med konstant hastighed v. Dette formulerer en ordinær differentialligning dx dt = v.
18 18 KAPITEL 1. LAPLACE TRANSFORMATIONEN Vi ved på forhånd at løsningen til denne ligning er x(t) = x() + vt, men lad os alligevel anvende Laplace transformationen: L (x (t)) = L (v), sx(s) x() = v, (s > α), s X(s) = x() + v s s 2. Vi genkender denne transformation fra Eksempel 1.3, og finder x(t), x(t) = L 1 (X(s)), = x() + vt. Det ovenstående eksempel kunne også løses ved direkte integration. For træningens skyld forsætter vi med endnu et simpelt eksempel. Eksempel 1.9. (Frit fald uden friktion). Inden Galileo Galilei udførte sit eksperiment som påviste at legemer falder lige hurtigt i frit fald uanset vægt var det en udbredt misforståelse at tunge legemer faldt hurtigst. Galileo påviste netop, at alle legemerne i frit fald har den samme accelleration nemlig tyngdeacceleration g. Vi lader x(t) angive den vertikale position og specificerer to begyndelsesbetingelser, positionen og hastigheden vi lader x() = x og vælger x () = v. Systemet som vi skal løse er altså x = g, x() = x, x () = v. Vi anvender nu Laplace transformationen på differentialligningen, L (x (t)) = L (g), s 2 X(s) sx() x () = g s, X(s) = x() s + x () s 2 + g s 3. Vi finder nu x(t) ved at transformere hvert led, f.eks. benytter vi at L (t 2 ) = 2/s 3. Hermed finder vi x(t) og indsætter samtidig begyndelsesbetingelserne, x(t) = L 1 (X(s)) = x + v t gt2.
19 1.3. TRANSLATION, DIFFERENTIATION, INTEGRATION OG PARTIALBRØKER 19 I det faktiske eksperiment slap Galileo to legemer af samme materiale fra det skæve tårn i Pisa og viste at det tog den samme tid for legemerne at nå jorden. Vi kan se at han havde ret ifølge vores formel fordi bevægelsesligningen for x(t) er uafhængig af legemets masse. Hvorvidt Galileo rent faktisk udførte det omtalte eksperiment fra det skæve tårn i Pisa er tvivlsomt, men det er en god historie! Lad os nu forsætte med et mere generelt eksempel, nemlig en inhomogen anden-ordens lineær differentialligning med konstante koefficienter og begyndelsesbetingelser - det ser således ud ax + bx + cx = f (t), (1.14) x() = x, x () = v. (1.15) Bemærk, at a,b,c og f (t) kan vælges så man har et RLC kredsløb eller et masse/fjeder/dæmper system. Rent formelt, tager vi nu Laplace transformationen af Ligning (1.14), altså a [ s 2 X(s) sx() x () ] + b[sx(s) x()] + cx(s) = F(s), X(s) = (as + b)x() + ax () as 2 + bs + c + F(s) as 2 + bs + c. I en mere overskuelig form kan det skrives som hvor X(s) = P(s) Q(s) + F(s) Q(s), (1.16) Q(s) = as 2 + bs + c, P(s) = (as + b)x() + ax (). Man finder nu x(t) ved at anvende den inverse Laplace transformation, altså x(t) = L 1 (X(s)), men dette kræver behandling af flere specialtilfælde. Bemærk, at der findes matematiske programmer som kan håndtere standard Laplace transformationer (også den inverse) direkte, f.eks. Maple, Mathematica og Matlab. Inden man havde programmer der kunne håndtere disse transformationer symbolsk, var man nødsaget til at manipulere udtrykkene P(s)/Q(s) og F(s)/Q(s) ved at splitte dem op i mindre komplicerede dele som man kendte den inverse transformation til. Denne fremgangsmåde er baseret på en opsplitning af en polynomiumsbrøk i dens såkaldte stambrøker (engelsk: partial fraction expansion/decomposition). Lad os give et eksempel på opsplitning i stambrøker,
20 2 KAPITEL 1. LAPLACE TRANSFORMATIONEN Eksempel 1.1. (Opsplitning i stambrøker). Bestem den inverse Laplace transformation af F(s) = 5s (s 2 + 1)(s 2 + 2s + 2). Vi kender ikke umiddelbart f (t) = L 1 (F(s)), men det er muligt at splitte F(s) op i dens såkaldte stambrøker. Således kan man opnå, F(s) = 1/2 + i s + i + 1/2 i s i + 1/2 3/2i s + 1 i + 1/2 + 3/2i, s i og til disse kender vi de inverse Laplace transformationer (anvend linearitetsegenskaberne Ligning (1.3) og (1.4) og se Eksempel 1.4 eller en Tabel 1.1). Vi viser hvordan man kan gøre med det første led, ( ) ( ) 1/2 + i 1 L 1 = (1/2 + i) L 1, s + i s + i = (1/2 + i) e it. På samme måde kan man finde de resterende transformationer og ved at anvende Eulers formel på det samlede resultat kan udtrykket reduceres til, f (t) = L 1 (F(s)) = cos(t) + 2sin(t) e t (cos(t) + 3sin(t)) (1.17) Vi skal i dette modul ikke komme ind på hvorledes man systematisk udfører opsplitning til stambrøker, men blot nævne at dette også kan udføres i diverse matematikprogrammer, f.eks. umiddelbart via funktioner som residue() i Matlab eller convert() i Maple eller Apart() i Mathematica. Som nævnt tidligere findes der i Tabel 1.1 en række praktiske transformationer til opslag. Alternativt kan man finde den inverse transformation vha. kompleks integration, men dette forudsætter, som nævnt tidligere, en del kendskab til kompleks funktionsteori som vi ikke skal ind på i dette modul - desuden er konklusionen dog også, at matematik-programmer er meget brugbare i denne sammenhæng. Lad os undersøge det følgende generelle system Eksempel (Anden-ordens differentialligning under harmonisk påvirkning). I dette eksempel tager vi fat på et specialtilfælde af differentiallignings-systemet (1.14) med begyndelsesbetingelserne (1.15). (Systemet er også et specialtilfælde af de tidligere nævnte praktiske systemer givet ved differentialligningerne (1.5) og (1.7)). ẍ + 2ẋ + 2x = 5cos(t), (1.18) x() = 1, ẋ() = 1. (1.19)
21 1.3. TRANSLATION, DIFFERENTIATION, INTEGRATION OG PARTIALBRØKER 21 Ved anvendelse af Ligning (1.16), altså ved at tage Laplace transformationen på systemet, kan vi skrive hvor X(s) ved indsættelse findes som, X(s) = P(s)/Q(s) + F(s)/Q(s), X(s) = s + 1 s 2 + 2s s (s 2 + 1)(s 2 + 2s + 2). Vi finder x(t) ved at bestemme den inverse Laplace transformation, x(t) = L 1 (X(s)), ( ) s + 1 = L 1 s 2 + 2s s (s 2 + 1)(s s + 2) For at bestemme den inverse Laplace transformation til dette udtryk kan vi enten gøre det direkte ved brug af f.eks. invlaplace() i Maple eller ilaplace() i Matlab eller vha. opslitning i stambrøker hvor vi i Eksempel 1.1 håndterede den ene af brøkerne. Vi får således direkte x(t) = cos(t) + (2 3e t )sin(t). Vi tjekker om løsningen er korrekt ved at verificere at den overholder startbetingelserne (til tiden t = ) og differentialligningen (for alle t > ). På den måde er vi helt sikre på at vi har regnet rigtigt. Bemærk, at vi ikke har redegjort for hvorvidt det var meningsfuldt at anvende Laplace transformationen på alle de afledte, altså om antagelserne i Sætning 1.5 er overholdt. Generelt gælder det for n te ordens lineære differentialligninger med konstante koefficienter, at Laplace transformationen er veldefineret for påvirkninger f (t) som er kontinuerte og af eksponentiel orden Integraler i t-domænet, t f (τ)dτ I adskillige anvendelser opstår der naturligt integraler i differentialligningerne og så kalder man dem integro-differentialligninger. Et typisk eksempel på en sådan er det elektriske kredsløb fra Figur 1.7. Integro-differentialligningen for dette kredsløb er, Lİ + 1 C t I(τ)dτ = E(t), hvor L er induktansen, C er kapacitansen og E(t) er den elektromotoriske kraft. Vi skal nu vise, at Laplace transformationen også kan håndtere integralled uden de store kvaler. Lad os vise følgende sætning,
22 22 KAPITEL 1. LAPLACE TRANSFORMATIONEN Sætning 1.6. Hvis f er stykkevis kontinuert og af eksponentiel orden α, og så gælder g(t) = t f (τ)dτ, (1.2) L (g(t)) = 1 L ( f (t)), R(s) > α. (1.21) s Bevis. I det første trin skal vi omskrive integralet L(g(t)) til noget mere bekvemt fordi vi gerne vil finde en relation til f (t). Vi beviser dette vha. partiel integration som vi også anvendte i beviset for Sætning 1.4. Lad os gentage formlen, b a b u(t)v (t)dt = [u(t)v(t)] b a u (t)v(t)dt. a Nu sætter vi a =, b =, u(t) = g(t) og v(t) = 1 s e st. Bemærk, at det følger af integralregningens hovedsætning, at f (t) = g (t) når g(t) = t f (τ)dτ. Vi kan således opnå [ e st g(t)dt = 1 ] s e st g(t) + 1 e st f (t)dt, s [ L (g(t)) = 1 ] s e st g(t) + 1 s L ( f (t)). Vi indser dernæst, at det følger af definitionen 3 af g(t) at g() = og at lim t e st g(t) = fordi R(s) > α. Tilsammen medfører dette, at vi har opnået den ønskede identitet, L (g(t)) = 1 s L ( f (t)). Lad os afslutte med en eksemplarisk anvendelse inden vi forsætter med reglerne for differentiation og integration i s-domænet. Faktisk skal vi nu løse en såkaldt integro-differentialligning! Eksempel Integro-differentialligning LC-circuit (se figur 1.7). Betragt det elektriske kredsløb givet ved 3 Husk at lim t + t f (t)dt = Lİ + 1 C t I(τ)dτ = E. (1.22)
23 1.3. TRANSLATION, DIFFERENTIATION, INTEGRATION OG PARTIALBRØKER 23 E L C Figur 1.7: LC kredsløb. Se Figur 1.7 for et systemdiagram. De tre led repræsenterer henholdsvis induktans, kapacitans og elektromotorisk kraft og L,C og E er positive konstanter. Lad endvidere strømmen I(t) være givet som I() = fra start. Vi Laplace transformerer nu Ligning (1.22) og anvender Sætning 1.4 og Sætning 1.6, for således at opnå L(sL (I) I()) + L (I) = E Cs s, E L (I) = L(s 2 + 1/LC). Man kan, som nævnt tidligere, finde den inverse Laplace transformation ved brug computerprogrammer. Alternativt så kan man også gøre dette ved at anvende Tabel 1.1 man skal blot indse at udtrykket for L (I) minder om inversionen for sinus og så ændre lidt på udtrykket. Vi finder løsningen, ( C 1/ ) LC I(t) = E, L L 1 C = E L sin s 2 + 1/LC ). ( 1 LC t Bemærk, at vi benyttede os af tabelopslaget L (sin(ωt)) = ω, hvor vi havde ω = 1 s 2 +ω 2 LC Translation i s-domænet I dette korte afsnit skal vi se nærmere på hvorledes translation i s-domænet opfører sig i forhold til Laplace transformationen.
24 24 KAPITEL 1. LAPLACE TRANSFORMATIONEN Sætning 1.7. Hvis F(s) = L ( f (t)) når R(s) >, så F(s a) = L (e at f (t)), (a R,R(s) > a). (1.23) Bevis. Under forudsætningen af at Laplace transformationen er veldefineret for F(s) = L ( f (t)) når R(s) > følger det af definitionen at F(s a) er veldefineret når R(s) > a. Derfor, F(s a) = = e (s a)t f (t)dt, e st e at f (t)dt, = L (e at f (t)). Lad os give et eksempel på hvordan man kan anvende dette resultat. Eksempel Vi ved fra tidligere, at L (sin(ωt)) = ω s 2 + ω 2. Det betyder, at hvis vi translaterer funktionen fra s til s a og benytter Sætning 1.7 får vi, at L (e at sin(ωt)) = ω (s a) 2 + ω 2. Dette kan være brugbart til at bestemme inverse transformationer direkte. (Bemærk, at dette også er forskellen på en harmonisk svinging og dæmpet svingning). Sætninger vedrørende operationer i s-domænet har umiddelbart lidt mere begrænset anvendelse i forbindelse med f.eks. differentialligninger, og alene derfor skal vi ikke tærske langhalm på disse egenskaber. Vi noterer blot at der findes tilsvarende resultater for differentation og integration i s-domænet (se evt. Tabel 1.2 for flere af disse egenskaber) Periodiske funktioner Vi skal give et resultat for periodiske funktioner. Vi kalder en funktion f (t) T-periodisk hvis f (t) = f (t + T ) for et T > og alle t. (T er den mindste periode for funktionen). Velkendte eksempler på periodiske funktioner er cos(ωt) og sin(ωt) der begge er T-periodiske med T = 2π/ω.
25 1.3. TRANSLATION, DIFFERENTIATION, INTEGRATION OG PARTIALBRØKER 25 Sætning 1.8. Hvis F(s) = L ( f (t)) og f (t) er T-periodisk, så er hvor F(s) = 1 1 e st F 1(s), (1.24) F 1 (s) = T e st f (t)dt (1.25) Bevis. Dette bevis udføres ved et enkelt koordinatskifte - en translation i integrationsvariablen, F(s) = L ( f (t)), = = T = F 1 (s) + e st f (t)dt, e st f (t)dt + T T e st f (t)dt. e st f (t)dt, Observer dernæst, at man ved et koordinatskifte τ = t T i det sidste integral i ovenstående ligning kan opnå hvorved vi har, T e st f (t)dt = e s(τ+t ) f (τ + T )dτ, = e st e sτ f (τ)dτ, = e st F(s), Den ønskede identitet følger straks ved at isolere F(s). F(s) = F 1 (s) + e st F(s). (1.26) Sætning 1.8 giver os en god mulighed for at simplificere udregningen af Laplace funktionen for forskellige periodiske funktioner f (t). Betragt det følgende eksempel på en square-wave funktion. Eksempel Square-wave funktionen er plottet på Figur 1.8 og det ses, at foreskriften på den 2a-periodiske funktion kan gives vha. en trin-funktion på intervallet [,2a[. f 1 (t) = u a (t), for t < 2a.
26 26 KAPITEL 1. LAPLACE TRANSFORMATIONEN f(t) 1 a 2a 3a 4a 5a t Figur 1.8: En såkaldt square-wave funktion med periode 2a. Ved anvendelse af Sætning 1.8 finder vi, F(s) findes nu trivielt som F 1 (s) = 2a 2a e st u a (t)dt, = e st dt, a = [ 1s ] 2a e st, = 1 s (e as e 2as ). 1 F(s) = 1 e 2as F 1(s), 1 = s(1 + e as ). Husk at transformationen kun er meningsfuld for R(s) >. a 1.4 Teaser: en lineær partielle differentialligning Lad os afslutningsvist se på et lidt mere indviklet ingeniørteknisk problem - nemlig varmeledning. (Dette eksempel er taget fra Joel L. Schiff The Laplace Transform - Theory and Applications. og er ikke en del af pensum).
27 1.4. TEASER: EN LINEÆR PARTIELLE DIFFERENTIALLIGNING 27 Eksempel T = 2 T, t x2 t >, x l, (1.27) T (x,) = T, (begyndelsesbetingelsen), (1.28) T (,t) =, x (den ene ende er isoleret!), (1.29) T (l,t) = T 1, (den anden ende har konstant temperatur T 1 ). (1.3) Vi anvender nu Laplace transformationen på denne partielle differentialligning i tidsvariablen t. Det betyder at vi forestiller os at T (x,s) = L (T (x,t)). Vi får således, s T T (x,) = 2 T x 2, s T T = 2 T x 2. Husk at man kan opfatte s som en konstant i denne differentialligning. Faktisk kræver vi at s >. Den generelle løsning til ligningen kan skrives som (tjek dette, enten ved selv at finde løsningen eller ved at indsætte den!) T (x,s) = c 1 cosh( sx) + c 2 sinh( sx) + u s. (1.31) Vi har kun brugt begyndelsesbetingelsen T, vi bestemmer c 1 og c 2 ved at bruge de to randbetingelser. Vi transformerer vores randbetingelser, ( ) T L x (,t) = L () =, (1.32) L (T (l,t)) = L (T 1 ) = T 1 s. (1.33) (1.34) Isolerings-randbetingelsen ved x = medfører direkte at c 2 =. I den anden ende, dvs. x = l, er randbetingelsen med konstant temperatur og denne giver os følgende sammenhæng, T 1 s = c 1 cosh( sl) + T 1 s, (1.35) c 1 = (T 1 T ) scosh( sl). (1.36)
28 28 KAPITEL 1. LAPLACE TRANSFORMATIONEN Løsningen i s-domænet er altså givet ved, T (x,s) = (T 1 T )cosh( sx) scosh( sl) + T s. (1.37) Vi finder ved den inverse Laplace transformation løsningen i t-domænet til, T (x,t) = T 1 + 4(T 1 T ) ( 1) π n ( ) n=1 2n 1 e(2n 1)2 π 2 t/(4l 2) 2n 1 cos πx. (1.38) 2l Hvor vi har benyttet os af ( ) cosh( sx) L 1 scosh( sl) = π ( 1) n n=1 2n 1 e(2n 1)2 π 2 t/(4l 2) cos ( 2n 1 2l ) πx. Det generelle løsningsudtryk indikerer at vi har sluppet let ved at arbejde i s-domænet! Der findes en lang række andre partielle differentialligninger osv. hvor Laplace transformationen virker formidabelt, dette var bare en smagsprøve!
29 1.5. TABEL: OPERATIONER FOR LAPLACE TRANSFORMATIONEN Tabel: operationer for Laplace transformationen
30 3 KAPITEL 1. LAPLACE TRANSFORMATIONEN Tabel over operationer for Laplace transformationer F(s) f (t) c 1 F 1 (s) + c 2 F 2 (s) c 1 f 1 (t) + c 2 f 2 (t) F(as), a > 1 a f ( ) t a F(s a) e at f (t a) e as F(s), a u a (t) f (t a) sf(s) f ( + ) s 2 F(s) s f ( + ) f ( + ) f (t) f (t) s n F(s) s n 1 f ( + ) s n 2 f ( + )... f (n 1) ( + ) F(s) s F (s) F (n) (s) f (n) (t) t f (τ)dτ t f (t) ( 1) n t n f (t) s F(ξ )dξ 1 t f (t) F(s)G(s) lim sf(s) s lim sf(s) s t f (τ)g(t τ)dτ lim f (t) = f t (+ ) + lim f (t) t Tabel 1.2: Relevante operationer for Laplace transformationen (Joel Schiff: The Laplace Transform Theory and Applications ).
Introduktion til Laplace transformen (Noter skrevet af Nikolaj Hess-Nielsen sidst revideret marts 2013)
 Introduktion til Laplace transformen (oter skrevet af ikolaj Hess-ielsen sidst revideret marts 23) Integration handler ikke kun om arealer. Tværtimod er integration basis for mange af de vigtigste værktøjer
Introduktion til Laplace transformen (oter skrevet af ikolaj Hess-ielsen sidst revideret marts 23) Integration handler ikke kun om arealer. Tværtimod er integration basis for mange af de vigtigste værktøjer
Note om Laplace-transformationen
 Note om Laplace-transformationen Den harmoniske oscillator omskrevet til et ligningssystem I dette opgavesæt benyttes laplacetransformationen til at løse koblede differentialligninger. Fordelen ved at
Note om Laplace-transformationen Den harmoniske oscillator omskrevet til et ligningssystem I dette opgavesæt benyttes laplacetransformationen til at løse koblede differentialligninger. Fordelen ved at
Fourier transformationen
 MODUL 6 Fourier transformationen Forfattere: Øistein WIND-WILLASSEN & Michael ELMEGÅRD 4. juni 4 Indhold Fourier transformationen 5. Definition og oprindelse.............................. 5.. Funktioner
MODUL 6 Fourier transformationen Forfattere: Øistein WIND-WILLASSEN & Michael ELMEGÅRD 4. juni 4 Indhold Fourier transformationen 5. Definition og oprindelse.............................. 5.. Funktioner
DesignMat Lineære differentialligninger I
 DesignMat Lineære differentialligninger I Preben Alsholm Uge Forår 0 1 Lineære differentialligninger af første orden 1.1 Normeret lineær differentialligning Normeret lineær differentialligning En differentialligning,
DesignMat Lineære differentialligninger I Preben Alsholm Uge Forår 0 1 Lineære differentialligninger af første orden 1.1 Normeret lineær differentialligning Normeret lineær differentialligning En differentialligning,
Noter om Komplekse Vektorrum, Funktionsrum og Differentialligninger LinAlg 2004/05-Version af 16. Dec.
 Noter om Komplekse Vektorrum, Funktionsrum og Differentialligninger LinAlg 2004/05-Version af 16. Dec. 1 Komplekse vektorrum I defininitionen af vektorrum i Afsnit 4.1 i Niels Vigand Pedersen Lineær Algebra
Noter om Komplekse Vektorrum, Funktionsrum og Differentialligninger LinAlg 2004/05-Version af 16. Dec. 1 Komplekse vektorrum I defininitionen af vektorrum i Afsnit 4.1 i Niels Vigand Pedersen Lineær Algebra
DesignMat Lineære differentialligninger I
 DesignMat Lineære differentialligninger I Preben Alsholm Uge 9 Forår 2010 1 Lineære differentialligninger af første orden 1.1 Normeret lineær differentialligning Normeret lineær differentialligning En
DesignMat Lineære differentialligninger I Preben Alsholm Uge 9 Forår 2010 1 Lineære differentialligninger af første orden 1.1 Normeret lineær differentialligning Normeret lineær differentialligning En
Modulpakke 3: Lineære Ligningssystemer
 Chapter 4 Modulpakke 3: Lineære Ligningssystemer 4. Homogene systemer I teknikken møder man meget ofte modeller der leder til systemer af koblede differentialligninger. Et eksempel på et sådant system
Chapter 4 Modulpakke 3: Lineære Ligningssystemer 4. Homogene systemer I teknikken møder man meget ofte modeller der leder til systemer af koblede differentialligninger. Et eksempel på et sådant system
Førsteordens lineære differentialligninger
 enote 16 1 enote 16 Førsteordens lineære differentialligninger I denne enote gives først en kort introduktion til differentialligninger i almindelighed, hvorefter hovedemnet er en særlig type af differentialligninger,
enote 16 1 enote 16 Førsteordens lineære differentialligninger I denne enote gives først en kort introduktion til differentialligninger i almindelighed, hvorefter hovedemnet er en særlig type af differentialligninger,
Lineære 2. ordens differentialligninger med konstante koefficienter
 enote 13 1 enote 13 Lineære 2. ordens differentialligninger med konstante koefficienter I forlængelse af enote 11 og enote 12 om differentialligninger, kommer nu denne enote omkring 2. ordens differentialligninger.
enote 13 1 enote 13 Lineære 2. ordens differentialligninger med konstante koefficienter I forlængelse af enote 11 og enote 12 om differentialligninger, kommer nu denne enote omkring 2. ordens differentialligninger.
Københavns Universitet, Det naturvidenskabelige Fakultet. Afleveringsopgave 1
 Københavns Universitet, Det naturvidenskabelige Fakultet 1 Lineær Algebra (LinAlg) Afleveringsopgave 1 Eventuelle besvarelser laves i grupper af - 3 personer og afleveres i to eksemplarer med 3 udfyldte
Københavns Universitet, Det naturvidenskabelige Fakultet 1 Lineær Algebra (LinAlg) Afleveringsopgave 1 Eventuelle besvarelser laves i grupper af - 3 personer og afleveres i to eksemplarer med 3 udfyldte
Fysik 2 - Den Harmoniske Oscillator
 Fysik 2 - Den Harmoniske Oscillator Esben Bork Hansen, Amanda Larssen, Martin Qvistgaard Christensen, Maria Cavallius 5. januar 2009 Indhold 1 Formål 1 2 Forsøget 2 3 Resultater 3 4 Teori 4 4.1 simpel
Fysik 2 - Den Harmoniske Oscillator Esben Bork Hansen, Amanda Larssen, Martin Qvistgaard Christensen, Maria Cavallius 5. januar 2009 Indhold 1 Formål 1 2 Forsøget 2 3 Resultater 3 4 Teori 4 4.1 simpel
Lineære differentialligningers karakter og lineære 1. ordens differentialligninger
 enote 11 1 enote 11 Lineære differentialligningers karakter og lineære 1. ordens differentialligninger I denne note introduceres lineære differentialligninger, som er en speciel (og bekvem) form for differentialligninger.
enote 11 1 enote 11 Lineære differentialligningers karakter og lineære 1. ordens differentialligninger I denne note introduceres lineære differentialligninger, som er en speciel (og bekvem) form for differentialligninger.
Komplekse Tal. 20. november 2009. UNF Odense. Steen Thorbjørnsen Institut for Matematiske Fag Århus Universitet
 Komplekse Tal 20. november 2009 UNF Odense Steen Thorbjørnsen Institut for Matematiske Fag Århus Universitet Fra de naturlige tal til de komplekse Optælling af størrelser i naturen De naturlige tal N (N
Komplekse Tal 20. november 2009 UNF Odense Steen Thorbjørnsen Institut for Matematiske Fag Århus Universitet Fra de naturlige tal til de komplekse Optælling af størrelser i naturen De naturlige tal N (N
Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 2016
 Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Løsningsforslag til opgavesæt 5
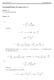 Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
Komplekse tal. Mikkel Stouby Petersen 27. februar 2013
 Komplekse tal Mikkel Stouby Petersen 27. februar 2013 1 Motivationen Historien om de komplekse tal er i virkeligheden historien om at fjerne forhindringerne og gøre det umulige muligt. For at se det, vil
Komplekse tal Mikkel Stouby Petersen 27. februar 2013 1 Motivationen Historien om de komplekse tal er i virkeligheden historien om at fjerne forhindringerne og gøre det umulige muligt. For at se det, vil
Fononiske Båndgab. Køreplan Matematik 1 - FORÅR 2004
 Fononiske Båndgab Køreplan 01005 Matematik 1 - FORÅR 2004 1 Baggrund Bølgeudbredelse i materialer og medier (som f.eks. luft) er et fænomen, der kendes af alle og som observeres i forskellige former i
Fononiske Båndgab Køreplan 01005 Matematik 1 - FORÅR 2004 1 Baggrund Bølgeudbredelse i materialer og medier (som f.eks. luft) er et fænomen, der kendes af alle og som observeres i forskellige former i
DesignMat Uge 1 Repetition af forårets stof
 DesignMat Uge 1 Repetition af forårets stof Preben Alsholm Efterår 008 01 Lineært ligningssystem Lineært ligningssystem Et lineært ligningssystem: a 11 x 1 + a 1 x + + a 1n x n = b 1 a 1 x 1 + a x + +
DesignMat Uge 1 Repetition af forårets stof Preben Alsholm Efterår 008 01 Lineært ligningssystem Lineært ligningssystem Et lineært ligningssystem: a 11 x 1 + a 1 x + + a 1n x n = b 1 a 1 x 1 + a x + +
Den homogene ligning. Vi betragter den n te ordens, homogene, lineære differentialligning. d n y dt n. an 1 + any = 0 (1.2) dt. + a1 d n 1 y dt n 1
 1/7 Den homogene ligning Vi betragter den n te ordens, homogene, lineære differentialligning a 0 d n y dt n + a1 d n 1 y dt n 1 hvor a 0,..., a n R og a 0 0. Vi skriver ligningen på kort form som + + dy
1/7 Den homogene ligning Vi betragter den n te ordens, homogene, lineære differentialligning a 0 d n y dt n + a1 d n 1 y dt n 1 hvor a 0,..., a n R og a 0 0. Vi skriver ligningen på kort form som + + dy
af koblede differentialligninger (se Apostol Bind II, s 229ff) 3. En n te ordens differentialligning
 EKSISTENS- OG ENTYDIGHEDSSÆTNINGEN Vi vil nu bevise eksistens- og entydighedssætningen for ordinære differentialligninger. For overskuelighedens skyld vil vi indskrænke os til at undersøge een 1. ordens
EKSISTENS- OG ENTYDIGHEDSSÆTNINGEN Vi vil nu bevise eksistens- og entydighedssætningen for ordinære differentialligninger. For overskuelighedens skyld vil vi indskrænke os til at undersøge een 1. ordens
I kurset Samhørende og partielle differentialligninger vil vi i foråret 2006 benytte bogen
 S.&P. DIFFERENTIALLIGNINGER 2. februar 2006 Oversigt nr. 1 I kurset Samhørende og partielle differentialligninger vil vi i foråret 2006 benytte bogen [EP] Elementary differential equations with boundary
S.&P. DIFFERENTIALLIGNINGER 2. februar 2006 Oversigt nr. 1 I kurset Samhørende og partielle differentialligninger vil vi i foråret 2006 benytte bogen [EP] Elementary differential equations with boundary
Projekt 2.2 Omvendt funktion og differentiation af omvendt funktion
 ISBN 978877664974 Projekter: Kapitel. Projekt. Omvendt funktion og differentiation af omvendt funktion Projekt. Omvendt funktion og differentiation af omvendt funktion Vi har i Bbogens kapitel 4 afsnit
ISBN 978877664974 Projekter: Kapitel. Projekt. Omvendt funktion og differentiation af omvendt funktion Projekt. Omvendt funktion og differentiation af omvendt funktion Vi har i Bbogens kapitel 4 afsnit
MM501 forelæsningsslides
 MM501 forelæsningsslides uge 37, 2010 Produceret af Hans J. Munkholm 2009 bearbejdet af Jessica Carter 2010 1 Hvad er et komplekst tal? Hvordan regner man med komplekse tal? Man kan betragte udvidelsen
MM501 forelæsningsslides uge 37, 2010 Produceret af Hans J. Munkholm 2009 bearbejdet af Jessica Carter 2010 1 Hvad er et komplekst tal? Hvordan regner man med komplekse tal? Man kan betragte udvidelsen
Fononiske Båndgab. Køreplan Matematik 1 - FORÅR 2005
 Fononiske Båndgab Køreplan 01005 Matematik 1 - FORÅR 2005 1 Baggrund Bølgeudbredelse i materialer og medier (som f.eks. luft) er et fænomen, der kendes af alle og som observeres i forskellige former i
Fononiske Båndgab Køreplan 01005 Matematik 1 - FORÅR 2005 1 Baggrund Bølgeudbredelse i materialer og medier (som f.eks. luft) er et fænomen, der kendes af alle og som observeres i forskellige former i
DesignMat Uge 1 Gensyn med forårets stof
 DesignMat Uge 1 Gensyn med forårets stof Preben Alsholm Efterår 2010 1 Hovedpunkter fra forårets pensum 11 Taylorpolynomium Taylorpolynomium Det n te Taylorpolynomium for f med udviklingspunkt x 0 : P
DesignMat Uge 1 Gensyn med forårets stof Preben Alsholm Efterår 2010 1 Hovedpunkter fra forårets pensum 11 Taylorpolynomium Taylorpolynomium Det n te Taylorpolynomium for f med udviklingspunkt x 0 : P
Introduktion til differentialregning 1. Jens Siegstad og Annegrethe Bak
 Introduktion til differentialregning 1 Jens Siegstad og Annegrete Bak 16. juli 2008 1 Indledning I denne note vil vi kort introduktion til differentilregning, idet vi skal bruge teorien i et emne, Matematisk
Introduktion til differentialregning 1 Jens Siegstad og Annegrete Bak 16. juli 2008 1 Indledning I denne note vil vi kort introduktion til differentilregning, idet vi skal bruge teorien i et emne, Matematisk
Matematisk modellering og numeriske metoder. Lektion 6
 Matematisk modellering og numeriske metoder Lektion 6 Morten Grud Rasmussen 24. september, 2013 1 Forcerede oscillationer [Bogens afsnit 2.8, side 85] 1.1 Et forstyrret masse-fjeder-system I udledningen
Matematisk modellering og numeriske metoder Lektion 6 Morten Grud Rasmussen 24. september, 2013 1 Forcerede oscillationer [Bogens afsnit 2.8, side 85] 1.1 Et forstyrret masse-fjeder-system I udledningen
Projekt 4.6 Løsning af differentialligninger ved separation af de variable
 Projekt 4.6 Løsning af differentialligninger ved separation af de variable Differentialligninger af tpen d hx () hvor hx ()er en kontinuert funktion, er som nævnt blot et stamfunktionsproblem. De løses
Projekt 4.6 Løsning af differentialligninger ved separation af de variable Differentialligninger af tpen d hx () hvor hx ()er en kontinuert funktion, er som nævnt blot et stamfunktionsproblem. De løses
Besvarelser til Calculus Ordinær Eksamen Juni 2019
 Besvarelser til Calculus Ordinær Eksamen - 14. Juni 2019 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 14. Juni 2019 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
C R. Figur 1 Figur 2. er eksempler på kredsløbsfunktioner. Derimod er f.eks. indgangsimpedansen
 Kredsløbsfunktioner Lad os i det følgende betragte kredsløb, der er i hvile til t = 0. Det vil sige, at alle selvinduktionsstrømme og alle kondensatorspændinger er nul til t = 0. I de Laplace-transformerede
Kredsløbsfunktioner Lad os i det følgende betragte kredsløb, der er i hvile til t = 0. Det vil sige, at alle selvinduktionsstrømme og alle kondensatorspændinger er nul til t = 0. I de Laplace-transformerede
Matematisk modellering og numeriske metoder. Lektion 5
 Matematisk modellering og numeriske metoder Lektion 5 Morten Grud Rasmussen 19. september, 2013 1 Euler-Cauchy-ligninger [Bogens afsnit 2.5, side 71] 1.1 De tre typer af Euler-Cauchy-ligninger Efter at
Matematisk modellering og numeriske metoder Lektion 5 Morten Grud Rasmussen 19. september, 2013 1 Euler-Cauchy-ligninger [Bogens afsnit 2.5, side 71] 1.1 De tre typer af Euler-Cauchy-ligninger Efter at
Løsningsforslag til opgavesæt 5
 Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
Bevægelsens Geometri
 Bevægelsens Geometri Vi vil betragte bevægelsen af et punkt. Dette punkt kan f.eks. være tyngdepunktet af en flue, et menneske, et molekyle, en galakse eller hvad man nu ellers har lyst til at beskrive.
Bevægelsens Geometri Vi vil betragte bevægelsen af et punkt. Dette punkt kan f.eks. være tyngdepunktet af en flue, et menneske, et molekyle, en galakse eller hvad man nu ellers har lyst til at beskrive.
Matematisk modellering og numeriske metoder
 Matematisk modellering og numeriske metoder Morten Grud Rasmussen 5. september 2016 1 Ordinære differentialligninger ODE er 1.1 ODE er helt grundlæggende Definition 1.1 (Ordinære differentialligninger).
Matematisk modellering og numeriske metoder Morten Grud Rasmussen 5. september 2016 1 Ordinære differentialligninger ODE er 1.1 ODE er helt grundlæggende Definition 1.1 (Ordinære differentialligninger).
π er irrationel Frank Nasser 10. december 2011
 π er irrationel Frank Nasser 10. december 2011 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold 1 Introduktion
π er irrationel Frank Nasser 10. december 2011 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold 1 Introduktion
Temaøvelse i differentialligninger Biokemiske Svingninger
 Temaøvelse i differentialligninger Biokemiske Svingninger Rev. 12. november 2009 I denne temaøvelse studerer vi en simpel model for gærglykolyse. Vi starter i Del 1 med at beskrive modellen. Denne model
Temaøvelse i differentialligninger Biokemiske Svingninger Rev. 12. november 2009 I denne temaøvelse studerer vi en simpel model for gærglykolyse. Vi starter i Del 1 med at beskrive modellen. Denne model
Besvarelser til Calculus Ordinær Eksamen Juni 2018
 Besvarelser til Calculus Ordinær Eksamen - 5. Juni 08 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 5. Juni 08 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
MM502+4 forelæsningsslides
 MM502+4 forelæsningsslides uge 11+12 1, 2009 Produceret af Hans J. Munkholm, delvis på baggrund af lignende materiale udarbejdet af Mikael Rørdam 1 I nærværende forbindelse er 11 + 12 23 1 Egenskaber for
MM502+4 forelæsningsslides uge 11+12 1, 2009 Produceret af Hans J. Munkholm, delvis på baggrund af lignende materiale udarbejdet af Mikael Rørdam 1 I nærværende forbindelse er 11 + 12 23 1 Egenskaber for
Komplekse tal og algebraens fundamentalsætning.
 Komplekse tal og algebraens fundamentalsætning. Michael Knudsen 10. oktober 2005 1 Ligningsløsning Lad N = {0,1,2,...} betegne mængden af de naturlige tal og betragt ligningen ax + b = 0, a,b N,a 0. Findes
Komplekse tal og algebraens fundamentalsætning. Michael Knudsen 10. oktober 2005 1 Ligningsløsning Lad N = {0,1,2,...} betegne mængden af de naturlige tal og betragt ligningen ax + b = 0, a,b N,a 0. Findes
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Maj/Juni 2018 Institution HF & VUC Nordsjælland Hillerød afdeling Uddannelse Fag og niveau Lærer(e) Hold stx
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Maj/Juni 2018 Institution HF & VUC Nordsjælland Hillerød afdeling Uddannelse Fag og niveau Lærer(e) Hold stx
Det teknisk-naturvidenskabelige basisår Matematik 1A, Efterår 2005, Hold 3 Prøveopgave C
 Det teknisk-naturvidenskabelige basisår Matematik 1A, Efterår 2005, Hold 3 Prøveopgave C Opgaven består af tre dele, hver med en række spørgsmål, efterfulgt af en liste af teorispørgsmål. I alle opgavespørgsmålene
Det teknisk-naturvidenskabelige basisår Matematik 1A, Efterår 2005, Hold 3 Prøveopgave C Opgaven består af tre dele, hver med en række spørgsmål, efterfulgt af en liste af teorispørgsmål. I alle opgavespørgsmålene
MM501 forelæsningsslides
 MM50 forelæsningsslides uge 36, 2009 Produceret af Hans J. Munkholm Nogle talmængder s. 3 N = {, 2, 3, } omtales som de naturlige tal eller de positive heltal. Z = {0, ±, ±2, ±3, } omtales som de hele
MM50 forelæsningsslides uge 36, 2009 Produceret af Hans J. Munkholm Nogle talmængder s. 3 N = {, 2, 3, } omtales som de naturlige tal eller de positive heltal. Z = {0, ±, ±2, ±3, } omtales som de hele
Besvarelser til Calculus Ordinær Eksamen Januar 2019
 Besvarelser til Calculus Ordinær Eksamen - 14. Januar 19 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 14. Januar 19 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Differentiation af Trigonometriske Funktioner
 Differentiation af Trigonometriske Funktioner Frank Villa 15. oktober 01 Dette dokument er en del af MatBog.dk 008-01. IT Teaching Tools. ISBN-13: 978-87-9775-00-9. Se yderligere betingelser for brug her.
Differentiation af Trigonometriske Funktioner Frank Villa 15. oktober 01 Dette dokument er en del af MatBog.dk 008-01. IT Teaching Tools. ISBN-13: 978-87-9775-00-9. Se yderligere betingelser for brug her.
DESIGNMAT FORÅR 2012: UGESEDDEL Forberedelse Læs alle opgaverne fra tidligere ugesedler, og læg særlig mærke til dem du har spørgsmål til.
 DESIGNMAT FORÅR 2012: UGESEDDEL 13 INSTITUT FOR MATEMATIK 1. Forberedelse Læs alle opgaverne fra tidligere ugesedler, og læg særlig mærke til dem du har spørgsmål til. 2. Aktiviteter mandag 13 17 2.1.
DESIGNMAT FORÅR 2012: UGESEDDEL 13 INSTITUT FOR MATEMATIK 1. Forberedelse Læs alle opgaverne fra tidligere ugesedler, og læg særlig mærke til dem du har spørgsmål til. 2. Aktiviteter mandag 13 17 2.1.
(c) Opskriv den reelle Fourierrække for funktionen y(t) fra (b), og afgør dernæst om y(t) er en lige eller ulige funktion eller ingen af delene.
 MATEMATIK 3 EN,MP 4. februar 2016 Eksamenopgaver fra 2011 2016 (jan. 2016) Givet at 0 for 0 < t < 1 mens e (t 1) cos(7(t 1)) for t 1, betragt da begyndelsesværdiproblemet for t > 0: y (t) + 2y (t) + 50y(t)
MATEMATIK 3 EN,MP 4. februar 2016 Eksamenopgaver fra 2011 2016 (jan. 2016) Givet at 0 for 0 < t < 1 mens e (t 1) cos(7(t 1)) for t 1, betragt da begyndelsesværdiproblemet for t > 0: y (t) + 2y (t) + 50y(t)
Matematik A. Højere teknisk eksamen. Forberedelsesmateriale. htx112-mat/a-26082011
 Matematik A Højere teknisk eksamen Forberedelsesmateriale htx112-mat/a-26082011 Fredag den 26. august 2011 Forord Forberedelsesmateriale til prøverne i matematik A Der er afsat 10 timer på 2 dage til
Matematik A Højere teknisk eksamen Forberedelsesmateriale htx112-mat/a-26082011 Fredag den 26. august 2011 Forord Forberedelsesmateriale til prøverne i matematik A Der er afsat 10 timer på 2 dage til
MATEMATIK A. Indhold. 92 videoer.
 MATEMATIK A Indhold Differentialligninger... 2 Differentialregning... 3 Eksamen... 3 Hvorfor Matematik?... 3 Integralregning... 3 Regression... 4 Statistik... 5 Trigonometriske funktioner... 5 Vektorer
MATEMATIK A Indhold Differentialligninger... 2 Differentialregning... 3 Eksamen... 3 Hvorfor Matematik?... 3 Integralregning... 3 Regression... 4 Statistik... 5 Trigonometriske funktioner... 5 Vektorer
Matematik 1 Semesteruge 5 6 (30. september oktober 2002) side 1. Komplekse tal Arbejdsplan
 Matematik Semesteruge 5 6 (30. september -. oktober 2002) side Komplekse tal Arbejdsplan I semesterugerne 5 og 6 erstattes den regulære undervisning (forelæsninger og fællestimer) af selvstudium med opgaveregning
Matematik Semesteruge 5 6 (30. september -. oktober 2002) side Komplekse tal Arbejdsplan I semesterugerne 5 og 6 erstattes den regulære undervisning (forelæsninger og fællestimer) af selvstudium med opgaveregning
Noter til Computerstøttet Beregning Taylors formel
 Noter til Computerstøttet Beregning Taylors formel Arne Jensen c 23 1 Introduktion I disse noter formulerer og beviser vi Taylors formel. Den spiller en vigtig rolle ved teoretiske overvejelser, og også
Noter til Computerstøttet Beregning Taylors formel Arne Jensen c 23 1 Introduktion I disse noter formulerer og beviser vi Taylors formel. Den spiller en vigtig rolle ved teoretiske overvejelser, og også
Test grafisk afledede Højere partielle afledede Differentiationsordenen er ligegyldig Partielle differentialligninger Test Laplaces ligning
 Oversigt [S] 2.7, 3.1, 3.4, 11.3 Nøgleord og begreber Differentiabel funktion i en variabel Partielle afledede i flere variable Notation og regneregler for partielle afledede Test partielle afledede Grafisk
Oversigt [S] 2.7, 3.1, 3.4, 11.3 Nøgleord og begreber Differentiabel funktion i en variabel Partielle afledede i flere variable Notation og regneregler for partielle afledede Test partielle afledede Grafisk
Mere om differentiabilitet
 Mere om differentiabilitet En uddybning af side 57 i Spor - Komplekse tal Kompleks funktionsteori er et af de vigtigste emner i matematikken og samtidig et af de smukkeste I bogen har vi primært beskæftiget
Mere om differentiabilitet En uddybning af side 57 i Spor - Komplekse tal Kompleks funktionsteori er et af de vigtigste emner i matematikken og samtidig et af de smukkeste I bogen har vi primært beskæftiget
ANALYSE 1, 2014, Uge 5
 ANALYSE, 204, Uge 5 Afleveringsfrist for Prøve 2 er Tirsdag den 20/5 kl 0:5. Forelæsninger Tirsdag Vi går videre med Afsnit 4 om uniform konvergens af Fourierrækker, hvor hovedsætningen er Sætning 4.3.
ANALYSE, 204, Uge 5 Afleveringsfrist for Prøve 2 er Tirsdag den 20/5 kl 0:5. Forelæsninger Tirsdag Vi går videre med Afsnit 4 om uniform konvergens af Fourierrækker, hvor hovedsætningen er Sætning 4.3.
Lineære systemer med hukommelse.
 Lineær Response Teori. I responseteorien interesserer man sig for, hvad der kan siges generelt om sammenhængen mellem input φ(t) og output γ(t) for et system. Valg af variable. Det betragtede systems forskellige
Lineær Response Teori. I responseteorien interesserer man sig for, hvad der kan siges generelt om sammenhængen mellem input φ(t) og output γ(t) for et system. Valg af variable. Det betragtede systems forskellige
MATEMATIK 3 EN,MP 30. august 2013 Oversigt nr. 1
 EN,MP 30. august 2013 Oversigt nr. 1 Litteratur: I Matematik 3 bruger vi (igen) i efteråret 2013 E. Kreyzig: Advanced engineering mathematics, 10. udg., Wiley, 2011. Beskrivelse: Kurset vil handle om matematiske
EN,MP 30. august 2013 Oversigt nr. 1 Litteratur: I Matematik 3 bruger vi (igen) i efteråret 2013 E. Kreyzig: Advanced engineering mathematics, 10. udg., Wiley, 2011. Beskrivelse: Kurset vil handle om matematiske
Matematisk modellering og numeriske metoder. Lektion 1
 Matematisk modellering og numeriske metoder Lektion 1 Morten Grud Rasmussen 4. september, 2013 1 Ordinære differentialligninger ODE er 1.1 ODE er helt grundlæggende Definition 1.1 (Ordinære differentialligninger).
Matematisk modellering og numeriske metoder Lektion 1 Morten Grud Rasmussen 4. september, 2013 1 Ordinære differentialligninger ODE er 1.1 ODE er helt grundlæggende Definition 1.1 (Ordinære differentialligninger).
Projekt 4.9 Bernouillis differentialligning
 Projekt 4.9 Bernouillis differentialligning (Dette projekt dækker læreplanens krav om supplerende stof vedr. differentialligningsmodeller. Projektet hænger godt sammen med projekt 4.0: Fiskerimodeller,
Projekt 4.9 Bernouillis differentialligning (Dette projekt dækker læreplanens krav om supplerende stof vedr. differentialligningsmodeller. Projektet hænger godt sammen med projekt 4.0: Fiskerimodeller,
Opgaver til Maple kursus 2012
 Opgaver til Maple kursus 2012 Jonas Camillus Jeppesen, jojep07@student.sdu.dk Martin Gyde Poulsen, gyde@nqrd.dk October 7, 2012 1 1 Indledende opgaver Opgave 1 Udregn følgende regnestykker: (a) 2342 +
Opgaver til Maple kursus 2012 Jonas Camillus Jeppesen, jojep07@student.sdu.dk Martin Gyde Poulsen, gyde@nqrd.dk October 7, 2012 1 1 Indledende opgaver Opgave 1 Udregn følgende regnestykker: (a) 2342 +
Komplekse tal. x 2 = 1 (2) eller
 Komplekse tal En tilegnelse af stoffet i dette appendix kræver at man løser opgaverne Komplekse tal viser sig uhyre nyttige i fysikken, f.eks til løsning af lineære differentialligninger eller beskrivelse
Komplekse tal En tilegnelse af stoffet i dette appendix kræver at man løser opgaverne Komplekse tal viser sig uhyre nyttige i fysikken, f.eks til løsning af lineære differentialligninger eller beskrivelse
Matematik F2 Opgavesæt 6
 Opgave 4: Udtryk funktionen f(θ) = sin θ ved hjælp af Legendre-polynomierne på formen P l (cos θ). Dvs. find koefficienterne a l i ekspansionen f(θ) = a l P l (cos θ) l= Svar: Bemærk, at funktionen er
Opgave 4: Udtryk funktionen f(θ) = sin θ ved hjælp af Legendre-polynomierne på formen P l (cos θ). Dvs. find koefficienterne a l i ekspansionen f(θ) = a l P l (cos θ) l= Svar: Bemærk, at funktionen er
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin 5. 6. semester efterår 2017-forår 2018 Institution Videndjurs, Grenaa Uddannelse Fag og niveau Lærer(e) Hold
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin 5. 6. semester efterår 2017-forår 2018 Institution Videndjurs, Grenaa Uddannelse Fag og niveau Lærer(e) Hold
Bedste rette linje ved mindste kvadraters metode
 1/9 Bedste rette linje ved mindste kvadraters metode - fra www.borgeleo.dk Figur 1: Tre datapunkter og den bedste rette linje bestemt af A, B og C Målepunkter og bedste rette linje I ovenstående koordinatsystem
1/9 Bedste rette linje ved mindste kvadraters metode - fra www.borgeleo.dk Figur 1: Tre datapunkter og den bedste rette linje bestemt af A, B og C Målepunkter og bedste rette linje I ovenstående koordinatsystem
Gamle eksamensopgaver (DOK)
 EO 1 Gamle eksamensopgaver ) Opgave 1. sommer 1994, opgave 1) a) Find den fuldstændige løsning til differentialligningen x 6x + 9x =. b) Find den fuldstændige løsning til differentialligningen Opgave 2.
EO 1 Gamle eksamensopgaver ) Opgave 1. sommer 1994, opgave 1) a) Find den fuldstændige løsning til differentialligningen x 6x + 9x =. b) Find den fuldstændige løsning til differentialligningen Opgave 2.
Eksaminationsgrundlag for selvstuderende Skolens eksaminationsgrundlag:
 Eksaminationsgrundlag for selvstuderende Skolens eksaminationsgrundlag: Jeg ønsker at gå til eksamen i nedennævnte eksaminationsgrundlag (pensum), som skolen har lavet. Du skal ikke foretage dig yderligere
Eksaminationsgrundlag for selvstuderende Skolens eksaminationsgrundlag: Jeg ønsker at gå til eksamen i nedennævnte eksaminationsgrundlag (pensum), som skolen har lavet. Du skal ikke foretage dig yderligere
Matematik 1 Semesteruge 5 6 (1. oktober oktober 2001) side 1 Komplekse tal Arbejdsplan
 Matematik 1 Semesteruge 5 6 (1. oktober - 12. oktober 2001) side 1 Komplekse tal Arbejdsplan I semesterugerne 5 og 6 erstattes den regulære undervisning (forelæsninger og fællestimer) af selvstudium med
Matematik 1 Semesteruge 5 6 (1. oktober - 12. oktober 2001) side 1 Komplekse tal Arbejdsplan I semesterugerne 5 og 6 erstattes den regulære undervisning (forelæsninger og fællestimer) af selvstudium med
Impedans. I = C du dt (1) og en spole med selvinduktionen L
 Impedans I et kredsløb, der består af andre netværkselementer end blot lække (modstande) og kilder vil der ikke i almindelighed være en simpel proportional, tidslig sammenhæng mellem strøm og spænding,
Impedans I et kredsløb, der består af andre netværkselementer end blot lække (modstande) og kilder vil der ikke i almindelighed være en simpel proportional, tidslig sammenhæng mellem strøm og spænding,
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Institution Uddannelse Fag og niveau Lærer(e) Hold December 2015 vinter VUC Vestegnen stx Mat A Gert Friis
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Institution Uddannelse Fag og niveau Lærer(e) Hold December 2015 vinter VUC Vestegnen stx Mat A Gert Friis
Lineære 1. ordens differentialligningssystemer
 enote enote Lineære ordens differentialligningssystemer Denne enote beskriver ordens differentialligningssystemer og viser, hvordan de kan løses enoten er i forlængelse af enote, der beskriver lineære
enote enote Lineære ordens differentialligningssystemer Denne enote beskriver ordens differentialligningssystemer og viser, hvordan de kan løses enoten er i forlængelse af enote, der beskriver lineære
Matematisk modellering og numeriske metoder. Lektion 13
 Matematisk modellering og numeriske metoder Lektion 3 Morten Grud Rasmussen 9. november 25 Divergens af et vektorfelt [Sektion 9.8 og.7 i bogen, s. 43]. Definition af og og egenskaber for divergens Lad
Matematisk modellering og numeriske metoder Lektion 3 Morten Grud Rasmussen 9. november 25 Divergens af et vektorfelt [Sektion 9.8 og.7 i bogen, s. 43]. Definition af og og egenskaber for divergens Lad
Differentiation af sammensatte funktioner
 1/7 Differentiation af sammensatte funktioner - Fra www.borgeleo.dk En sammensat funktion af den variable x er en funktion, vor x først indsættes i den såkaldte indre funktion. Resultatet fra den indre
1/7 Differentiation af sammensatte funktioner - Fra www.borgeleo.dk En sammensat funktion af den variable x er en funktion, vor x først indsættes i den såkaldte indre funktion. Resultatet fra den indre
Vektorfunktioner. (Parameterkurver) x-klasserne Gammel Hellerup Gymnasium
 Vektorfunktioner (Parameterkurver) x-klasserne Gammel Hellerup Gymnasium Indholdsfortegnelse VEKTORFUNKTIONER... Centrale begreber... Cirkler... 5 Epicykler... 7 Snurretoppen... 9 Ellipser... 1 Parabler...
Vektorfunktioner (Parameterkurver) x-klasserne Gammel Hellerup Gymnasium Indholdsfortegnelse VEKTORFUNKTIONER... Centrale begreber... Cirkler... 5 Epicykler... 7 Snurretoppen... 9 Ellipser... 1 Parabler...
MODUL 8. Differensligninger. Forfattere: Michael ELMEGÅRD & Øistein WIND-WILLASSEN. Modulet er baseret på noter af Peter BEELEN.
 MODUL 8 Differensligninger Forfattere: Michael ELMEGÅRD & Øistein WIND-WILLASSEN Modulet er baseret på noter af Peter BEELEN. 26. august 2014 2 Indhold 1 Introduktion 5 1.1 Rekursioner og differensligninger.........................
MODUL 8 Differensligninger Forfattere: Michael ELMEGÅRD & Øistein WIND-WILLASSEN Modulet er baseret på noter af Peter BEELEN. 26. august 2014 2 Indhold 1 Introduktion 5 1.1 Rekursioner og differensligninger.........................
MATEMATIK B. Videooversigt
 MATEMATIK B Videooversigt 2. grads ligninger.... 2 CAS værktøj... 3 Differentialregning... 3 Eksamen... 5 Funktionsbegrebet... 5 Integralregning... 5 Statistik... 6 Vilkårlige trekanter... 7 71 videoer.
MATEMATIK B Videooversigt 2. grads ligninger.... 2 CAS værktøj... 3 Differentialregning... 3 Eksamen... 5 Funktionsbegrebet... 5 Integralregning... 5 Statistik... 6 Vilkårlige trekanter... 7 71 videoer.
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin December/januar 14/15 Institution VUC Vestegnen Uddannelse Fag og niveau Lærer(e) Hold stx Mat A Karin Hansen
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin December/januar 14/15 Institution VUC Vestegnen Uddannelse Fag og niveau Lærer(e) Hold stx Mat A Karin Hansen
Differentialligninger af første orden
 Differentialligninger af første orden Preben Alsholm Februar 2006 Basale begreber. Eksistens og entydighed. En differentialligning af første orden er en ligning, der sammenknytter differentialkvotienten
Differentialligninger af første orden Preben Alsholm Februar 2006 Basale begreber. Eksistens og entydighed. En differentialligning af første orden er en ligning, der sammenknytter differentialkvotienten
Numeriske metoder - til løsning af differentialligninger - fra borgeleo.dk
 Numeriske metoder - til løsning af differentialligninger - fra borgeleo.dk Eksakte løsninger: fuldstændig løsning og partikulær løsning Mange differentialligninger kan løses eksakt. Fx kan differentialligningen
Numeriske metoder - til løsning af differentialligninger - fra borgeleo.dk Eksakte løsninger: fuldstændig løsning og partikulær løsning Mange differentialligninger kan løses eksakt. Fx kan differentialligningen
Introduktion til cosinus, sinus og tangens
 Introduktion til cosinus, sinus og tangens Jes Toft Kristensen 24. maj 2010 1 Forord Her er en lille introduktion til cosinus, sinus og tangens. Det var et af de emner jeg selv havde svært ved at forstå,
Introduktion til cosinus, sinus og tangens Jes Toft Kristensen 24. maj 2010 1 Forord Her er en lille introduktion til cosinus, sinus og tangens. Det var et af de emner jeg selv havde svært ved at forstå,
Differentialligninger. Ib Michelsen
 Differentialligninger Ib Michelsen Ikast 203 2 Indholdsfortegnelse Indholdsfortegnelse Indholdsfortegnelse...2 Ligninger og løsninger...3 Indledning...3 Lineære differentialligninger af første orden...3
Differentialligninger Ib Michelsen Ikast 203 2 Indholdsfortegnelse Indholdsfortegnelse Indholdsfortegnelse...2 Ligninger og løsninger...3 Indledning...3 Lineære differentialligninger af første orden...3
Sætning (Kædereglen) For f(u), u = g(x) differentiable er den sammensatte funktion F = f g differentiabel med
 Oversigt [S] 3.5, 11.5 Nøgleord og begreber Kædereglen i en variabel Kædereglen to variable Test kædereglen Kædereglen i tre eller flere variable Jacobimatricen Kædereglen på matrixform Test matrixform
Oversigt [S] 3.5, 11.5 Nøgleord og begreber Kædereglen i en variabel Kædereglen to variable Test kædereglen Kædereglen i tre eller flere variable Jacobimatricen Kædereglen på matrixform Test matrixform
Affine rum. a 1 u 1 + a 2 u 2 + a 3 u 3 = a 1 u 1 + (1 a 1 )( u 2 + a 3. + a 3. u 3 ) 1 a 1. Da a 2
 Affine rum I denne note behandles kun rum over R. Alt kan imidlertid gennemføres på samme måde over C eller ethvert andet legeme. Et underrum U R n er karakteriseret ved at det er en delmængde som er lukket
Affine rum I denne note behandles kun rum over R. Alt kan imidlertid gennemføres på samme måde over C eller ethvert andet legeme. Et underrum U R n er karakteriseret ved at det er en delmængde som er lukket
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Som 2015 Institution VUC Vest Uddannelse Fag og niveau Lærer(e) Hold Hf/hfe Mat B Niels Johansson 14MACB11E14
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Som 2015 Institution VUC Vest Uddannelse Fag og niveau Lærer(e) Hold Hf/hfe Mat B Niels Johansson 14MACB11E14
Matematisk modellering og numeriske metoder. Lektion 8
 Matematisk modellering og numeriske metoder Lektion 8 Morten Grud Rasmussen 18. oktober 216 1 Fourierrækker 1.1 Periodiske funktioner Definition 1.1 (Periodiske funktioner). En periodisk funktion f er
Matematisk modellering og numeriske metoder Lektion 8 Morten Grud Rasmussen 18. oktober 216 1 Fourierrækker 1.1 Periodiske funktioner Definition 1.1 (Periodiske funktioner). En periodisk funktion f er
Idenne note giver vi et eksempel på, hvorledes det er vigtigt at holde sig
 Analyse : Eulers formel Sebastian rsted 9. maj 015 Idenne note giver vi et eksempel på, hvorledes det er vigtigt at holde sig for øje, hvor de matematiske resultater kommer fra, og hvad de baseres på;
Analyse : Eulers formel Sebastian rsted 9. maj 015 Idenne note giver vi et eksempel på, hvorledes det er vigtigt at holde sig for øje, hvor de matematiske resultater kommer fra, og hvad de baseres på;
Matematisk modellering og numeriske metoder. Lektion 11
 Matematisk modellering og numeriske metoder Lektion 11 Morten Grud Rasmussen 5. november 2016 1 Partielle differentialligninger 1.1 Udledning af varmeligningen Vi vil nu på samme måde som med bølgeligningen
Matematisk modellering og numeriske metoder Lektion 11 Morten Grud Rasmussen 5. november 2016 1 Partielle differentialligninger 1.1 Udledning af varmeligningen Vi vil nu på samme måde som med bølgeligningen
i x-aksens retning, så fås ). Forskriften for g fås altså ved i forskriften for f at udskifte alle forekomster af x med x x 0
 BAndengradspolynomier Et polynomium er en funktion på formen f ( ) = an + an + a+ a, hvor ai R kaldes polynomiets koefficienter. Graden af et polynomium er lig med den højeste potens af, for hvilket den
BAndengradspolynomier Et polynomium er en funktion på formen f ( ) = an + an + a+ a, hvor ai R kaldes polynomiets koefficienter. Graden af et polynomium er lig med den højeste potens af, for hvilket den
1/41. 2/41 Landmålingens fejlteori - Lektion 1 - Kontinuerte stokastiske variable
 Landmålingens fejlteori - lidt om kurset Landmålingens fejlteori Lektion 1 Det matematiske fundament Kontinuerte stokastiske variable - rw@math.aau.dk Institut for Matematiske Fag Aalborg Universitet Kursusholder
Landmålingens fejlteori - lidt om kurset Landmålingens fejlteori Lektion 1 Det matematiske fundament Kontinuerte stokastiske variable - rw@math.aau.dk Institut for Matematiske Fag Aalborg Universitet Kursusholder
Mini-formelsamling. Matematik 1
 Indholdsfortegnelse 1 Diverse nyttige regneregler... 1 1.1 Regneregler for brøker... 1 1.2 Potensregneregler... 1 1.3 Kvadratsætninger... 2 1.4 (Nogle) Rod-regneregler... 2 1.5 Den naturlige logaritme...
Indholdsfortegnelse 1 Diverse nyttige regneregler... 1 1.1 Regneregler for brøker... 1 1.2 Potensregneregler... 1 1.3 Kvadratsætninger... 2 1.4 (Nogle) Rod-regneregler... 2 1.5 Den naturlige logaritme...
DesignMat Uge 8 Integration og elementære funktioner
 DesignMat Uge 8 Integration og elementære funktioner Preben Alsholm Forår 008 Hyperbolske funktioner. sinh og cosh sinh og cosh Sinus hyperbolsk efineres sålees for alle x R sinh x = ex e x Cosinus hyperbolsk
DesignMat Uge 8 Integration og elementære funktioner Preben Alsholm Forår 008 Hyperbolske funktioner. sinh og cosh sinh og cosh Sinus hyperbolsk efineres sålees for alle x R sinh x = ex e x Cosinus hyperbolsk
Hans J. Munkholm: En besvarelse af
 Hans J. Munkholm: En besvarelse af Projekt for MM501, Lineære differentialligninger November-december 2009 Nummererede formler fra opgaveformuleringen Her samles alle opgavens differentialligninger og
Hans J. Munkholm: En besvarelse af Projekt for MM501, Lineære differentialligninger November-december 2009 Nummererede formler fra opgaveformuleringen Her samles alle opgavens differentialligninger og
Emneopgave: Lineær- og kvadratisk programmering:
 Emneopgave: Lineær- og kvadratisk programmering: LINEÆR PROGRAMMERING I lineær programmering løser man problemer hvor man for en bestemt funktion ønsker at finde enten en maksimering eller en minimering
Emneopgave: Lineær- og kvadratisk programmering: LINEÆR PROGRAMMERING I lineær programmering løser man problemer hvor man for en bestemt funktion ønsker at finde enten en maksimering eller en minimering
Studieplan. Stamoplysninger. Oversigt over planlagte undervisningsforløb. Periode August 2015 Maj 2016 Institution Vejen Business College.
 Studieplan Stamoplysninger Periode August 2015 Maj 2016 Institution Vejen Business College Uddannelse Fag og niveau Lærer(e) Hold Hhx Matematik-A Ole Gentz Nørager MatematikAhh1313-VØ Oversigt over planlagte
Studieplan Stamoplysninger Periode August 2015 Maj 2016 Institution Vejen Business College Uddannelse Fag og niveau Lærer(e) Hold Hhx Matematik-A Ole Gentz Nørager MatematikAhh1313-VØ Oversigt over planlagte
Maple. Skærmbilledet. Vi starter med at se lidt nærmere på opstartsbilledet i Maple. Værktøjslinje til indtastningsområdet. Menulinje.
 Maple Dette kapitel giver en kort introduktion til hvordan Maple 12 kan benyttes til at løse mange af de opgaver, som man bliver mødt med i matematiktimerne på HHX. Skærmbilledet Vi starter med at se lidt
Maple Dette kapitel giver en kort introduktion til hvordan Maple 12 kan benyttes til at løse mange af de opgaver, som man bliver mødt med i matematiktimerne på HHX. Skærmbilledet Vi starter med at se lidt
Matematik F2 Opgavesæt 2
 Opgaver uge 2 I denne uge kigger vi nærmere på Cauchy-Riemann betingelserne, potensrækker, konvergenskriterier og flertydige funktioner. Vi skal også se på integration langs en ve i den komplekse plan.
Opgaver uge 2 I denne uge kigger vi nærmere på Cauchy-Riemann betingelserne, potensrækker, konvergenskriterier og flertydige funktioner. Vi skal også se på integration langs en ve i den komplekse plan.
Eksaminationsgrundlag for selvstuderende
 Eksaminationsgrundlag for selvstuderende Jeg ønsker at aflægge prøve på nedenstående eksaminationsgrundlag. Jeg har foretaget ændringer i vejlederens fortrykte forslag: nej ja Dato: Underskrift HUSK at
Eksaminationsgrundlag for selvstuderende Jeg ønsker at aflægge prøve på nedenstående eksaminationsgrundlag. Jeg har foretaget ændringer i vejlederens fortrykte forslag: nej ja Dato: Underskrift HUSK at
Besvarelser til Calculus Ordinær eksamen - Efterår - 8. Januar 2016
 Besvarelser til Calculus Ordinær eksamen - Efterår - 8. Januar 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har
Besvarelser til Calculus Ordinær eksamen - Efterår - 8. Januar 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har
BEVISER TIL KAPITEL 3
 BEVISER TIL KAPITEL 3 Alle beviserne i dette afsnit bruger følgende algoritme fra side 88 i bogen. Algoritme: Fremgangsmåde til udledning af forskellige regneregler for differentiation af forskellige funktionstyper
BEVISER TIL KAPITEL 3 Alle beviserne i dette afsnit bruger følgende algoritme fra side 88 i bogen. Algoritme: Fremgangsmåde til udledning af forskellige regneregler for differentiation af forskellige funktionstyper
Foredrag i Eulers Venner 30. nov. 2004
 BSD-prosper.tex Birch og Swinnerton-Dyer formodningen Johan P. Hansen 26/11/2004 13:34 p. 1/20 Birch og Swinnerton-Dyer formodningen Foredrag i Eulers Venner 30. nov. 2004 Johan P. Hansen matjph@imf.au.dk
BSD-prosper.tex Birch og Swinnerton-Dyer formodningen Johan P. Hansen 26/11/2004 13:34 p. 1/20 Birch og Swinnerton-Dyer formodningen Foredrag i Eulers Venner 30. nov. 2004 Johan P. Hansen matjph@imf.au.dk
Differential- ligninger
 Differential- ligninger Et oplæg 2007 Karsten Juul Dette hæfte er tænkt brugt som et oplæg der kan gennemgås før man går i gang med en lærebogs fremstilling af emnet differentialligninger Læreren skal
Differential- ligninger Et oplæg 2007 Karsten Juul Dette hæfte er tænkt brugt som et oplæg der kan gennemgås før man går i gang med en lærebogs fremstilling af emnet differentialligninger Læreren skal
Besvarelser til Calculus Ordinær Eksamen Juni 2017
 Besvarelser til Calculus Ordinær Eksamen - 12. Juni 2017 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 12. Juni 2017 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
