Youngs dobbeltspalteforsøg 1

Transkript

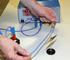
1 Kvantemekanik Side af Youngs dobbeltspalteforsøg Klassisk beskrivelse Inden for den klassiske fysik kan man forklare forekomsten af et interferensmønster ud fra flg. bølgemodel. x Før spalterne beskrives den indkommende bølge som flg. plane, monokromatiske bølge: ( ( ω u x, t A'cos kx t, A'. Pga. diffraktionen fra de smalle spalter, udsender hver spalte en cylinderbølge, der tilsammen danner et interferensmønster, sådan at bølgeudsvinget ved punktet P er A'' A'' up cos kr t + kr R R Acos kr t + Acos kr ωt, ( ω cos( ωt ( ω ( R R P Fotografisk plade (. hvor tilnærmelsen er baseret på den antagelse, at afstanden mellem spalterne og den fotografiske plade er meget større end afstanden d mellem spalterne. Da energitætheden er proportional med kvadratet på udsvinget, og da u v u+ v cosu+ cosv cos cos, er P R R R+ R ρe up cos k cos ( ωt+ φ, φ k. (. Thomas Young, 805. Thomas B. Lynge, Institut for Fysik og Nanoteknologi, AAU 9/0/007

2 Kvantemekanik Side af De sværtede striber med konstruktiv interferens (maksimal energitæthed er således kendetegnet ved π R λ R som forventet. nπ, n : R R n n, (. λ, Kvantemekanisk beskrivelse I det flg. beskrives en strøm af kvantepartiklers passage af de to spalter. Eftersom den klassiske bølgemodel er i stand til at give en korrekt beskrivelse af fænomenet, skal der være korrespondens /overensstemmelse mellem den KM og den klassiske model i beskrivelsen af dette fænomen. Betragt derfor en fri kvantepartikel, som før passagen af spalterne er kendetegnet ved den planbølgeformede bølgefunktion fra udtryk (.9: ikx, ' ( ωt ψ xt Ae, A'. (.4 ( Ved punktet P fås analogt til den klassiske beskrivelse jf. udtryk (.: ikr ( ωt ikr ( ωt ψ P Ae + Ae ψ+ ψ. (.5 Ved den fotografiske plade finder der en sværtning og dermed en observation af position sted, som jf. diskussionen i KM vil få kvantepartiklen til at materialisere sig, idet man siger, at dens bølgefunktion kollapser. En KM beskrivelse af interferensmønstret indebærer således en beregning af sandsynligheden for, at kvantepartiklen materialiserer sig i et givet punkt P. Thomas B. Lynge, Institut for Fysik og Nanoteknologi, AAU 9/0/007

3 Kvantemekanik Side af Pr. analogi med udtryk (. må P ψ være et udtryk for denne sandsynlighed: ψ R R. (.6 P cos k Ved sammenligning med udtryk (. ses således, at sandsynligheden for materialisering af kvantepartikler ved den fotografiske plade følger samme interferensmønster som den klassiske bølgemodel. Så hvis der er tale om en lysstråle, der jo består af mange kvantepartikler, vil der være overensstemmelse mellem KM og den klassiske model, hvilket som nævnt er en nødvendighed, i og med at den klassiske model giver en korrekt beskrivelse af fænomenet. Hvis der blot passerer få kvantepartikler ad gangen, f.eks. kun en enkelt, vil interferensmønstret blive opbygget løbende, svarende til at den enkelte kvantepartikels position ikke kan forudsiges, men at mange kvantepartiklers positioner vil fordele sig i henhold til den forudsigelige sandsynlighedsfordeling. Så i kraft af sine bølgeegenskaber passerer kvante- partiklen således igennem begge spalter, interfererer med sig selv, og materialiserer sig et sted på den fotografiske plade i henhold til det viste interferensmønster Bølgefunktionen ψ beskriver kvantepartiklens kvantetilstand, så jf. udtryk (.5 er den efter passage af spalterne i en superponeret tilstand af at have passeret begge spalter. Thomas B. Lynge, Institut for Fysik og Nanoteknologi, AAU 9/0/007

4 Kvantemekanik Side 4 af Hvad ville der ske, hvis det på en eller anden måde var muligt at afgøre, hvilken spalte kvantepartiklen havde valgt? Ja så forsvinder interferensmønstret, og kvantepartiklen sætter sig bag den spalte, den er blevet målt til at have passeret I dette tilfælde har vi nemlig muliggjort bestemmelse af position allerede ved spalterne og ikke som før først ved den fotografiske plade, og så kollapser bølgefunktionen allerede ved spalterne og mister derved sine bølgeegenskaber, og så er der ingen interferens. Som det fremgår af udtryk (.6 svarer observationen/kollapset til uddragelsen af absolutkvadratet af bølgefunktionen. Hvis man ikke har mulighed for at afgøre kvantepartiklens valg af spalte, og observationen dermed finder sted ved den fotografiske plade, er sandsynligheden for at finde kvantepartiklen i punktet P givet ved ψ ψ +, (.7 hvorimod den afgørende størrelse, hvis der finder en observation sted ved spalterne, er ψ + ψ. (.8 Interferensen opstår, fordi ψ og ψ har en fase og dermed kan udslukke og forstærke hinanden 4. Ved uddragelsen af absolutkvadratet forsvinder denne fase og dermed også interferensen, og det er dermed helt afgørende, om dette sker før eller efter overlejringen af ψ og ψ. Dette lader sig faktisk gøre i praksis; eks. ved at anvende elektroner med et bestemt spin, lade den ene spalte flippe spinnet, og vælge en detektor (her den fotografiske plade, der er spinafhængig. Det er nemlig ikke afgørende, om vi rent faktisk bestemmer kvantepartiklens valg af spalte, men om det er muligt i princippet at afgøre kvantepartiklens valg. Thomas B. Lynge, Institut for Fysik og Nanoteknologi, AAU 9/0/007

5 Kvantemekanik Side 5 af Bølgefunktionens sandsynlighedsfortolkning ψ rt, Inspireret af ovenstående fastslog tyskeren Max Born 5 i 96, at ( skulle fortolkes som sandsynlighedstætheden for positionen af kvantepartiklen kendetegnet ved ( rt, ψ. Sandsynligheden for til tiden t at finde kvantepartiklen i volumenelementet omkring punktet er således givet ved r ( dv ψ rt, dv, (.9 og den tilsvarende sandsynlighed for rumfanget V dermed givet ved udtryk (.. Selve bølgefunktionen ψ ( rt, omtales indimellem som sandsynlighedsamplituden. I dobbeltspalteforsøget opstår der således interferens, når der overlejres komplekse sandsynlighedsamplituder med en fase, hvorimod interferensen forsvinder, når der overlejres reelle sandsynlighedstætheder uden en fase. En bølgefunktion er normeret, når sandsynligheden for at finde den et eller andet sted i rummet er lig : jf. udtryk (.9. ψ dv, (.0 ( rt, 4 Dette viser således, at bølgefunktionen er kompleks (har en fase af fysisk nødvendighed. 5 Nobelpris i 954 for sit bidrag til KM. Thomas B. Lynge, Institut for Fysik og Nanoteknologi, AAU 9/0/007

6 Kvantemekanik Side 6 af Bølgefunktioner i p-rum Som nævnt i KM kan enhver bølgefunktion skrives som bølgepakken i udtryk (.4, hvori A( k er den vægt, hvormed planbølge-bølgefunktionen med den veldefinerede bevægelsesmængde 6 p k (. indgår. Hvis man måler den pågældende kvantepartikels bevægelsesmængde, vil sandsynligheden for at måle en værdi p p således afhænge af A, idet det viser sig, at sandsynlighedstætheden for bevægelsesmængden er givet ved Dette er analogt til ( rt, p A i t e ω Indføres φ ( og ψ A p i t e ω, som jo er sandsynlighedstætheden for positionen, så må således kunne fortolkes som en bølgefunktion i p -rum. π p i t p, t A e ω fås således ψ i pr rt, φ ( pte, d p ( ( π φ,, ( p t i pr ψ ( r t e d r ( π. (., (. sådan at bølgefunktionen i det ligefremme r -rum og bølgefunktionen i det reciprokke p -rum er hinandens (unitære Fouriertransforme. 6 Denne sammenhæng blev udledt KM s.. Thomas B. Lynge, Institut for Fysik og Nanoteknologi, AAU 9/0/007

7 Kvantemekanik Side 7 af En kvantepartikel er således kendetegnet ved en bølgefunktion ψ ( rt, i r - repræsentationen og en bølgefunktion ( p, t φ ene, kan den anden findes vha. udtryk (.-(.. Da ( rt, i p -repræsentationen, og givet den ψ indeholder alle oplysninger om kvantepartiklens bevægelse, gør ( p, t det således også, så begge bølgefunktioner giver det fulde billede, og hvilken repræsentation, det er mest praktisk at bringe i anvendelse, vil afhænge af den givne sammenhæng. φ Der er fuldstændig analogi mellem de to beskrivelser; f.eks. er sandsynligheden for at finde kvantepartiklen inden for det ligefremme rumfang V givet ved udtryk (., og sandsynligheden for at finde, at kvantepartiklens bevægelsesmængde er inden for det reciprokke rumfang V p, er helt tilsvarende givet ved svarende til at ( p, t φ P t p t d p, (.4 Vp ( ( φ, Vp er sandsynlighedstætheden for bevægelsesmængden. Thomas B. Lynge, Institut for Fysik og Nanoteknologi, AAU 9/0/007

8 Kvantemekanik Side 8 af Da ( rt, ψ Forventningsværdier er sandsynlighedstætheden for positionen, er forventningsværdien af positionen ifølge udtryk (.0 givet ved r rψ r t (, d r, (.5 som i øvrigt ses generelt at afhænge af tiden. Tilsvarende for bevægelsesmængden, for hvilken ( p, t φ er sandsynlighedstætheden: p p φ p t d (, p. (.6 I det flg. vises, hvordan p beregnes ud fra bølgefunktionen i r -repræsentationen. Ifølge udtryk (. er i i pr pr ψ ( rt, φ ( pte, d p φ ( pt, pe d p i i, ( π ( π sådan at i pr ψ rt, ψ rtdr, ψ rt, φ( pt, pe d p dr * * ( ( ( i ( π p * ψ (, φ(, ( π * ( pt, pφ( pt, d p : φ p φ p t d p (, i pr rte dr p ptd p * p ψ ( rt, ψ ( rtdr,. (.7 i Thomas B. Lynge, Institut for Fysik og Nanoteknologi, AAU 9/0/007

9 Kvantemekanik Side 9 af Det kan vises 7, at der mellem sådanne forventningsværdier gælder de velkendte klassiske relationer, eks. d p r v, (.8 dt m d p F, (.9 dt hvilket illustrerer betydningen af forventningsværdierne som de KM pendanter til de tilsvarende klassiske begreber. Da bølgefunktionen er deterministisk fremskrivelig, så længe der ikke ved observation fremkaldes et kollaps, er forventningsværdierne således også deterministisk fremskrivelige, ligesom de klassiske begreber. 7 Se opg. til KM8. Thomas B. Lynge, Institut for Fysik og Nanoteknologi, AAU 9/0/007

10 Kvantemekanik Side 0 af Operatorrepræsentanter Bølgefunktionen for en kvantepartikel indeholder alle oplysninger om den pågældende kvantepartikels bevægelse, og som det fremgår af udtryk (.7 afkodes informationen om forventningsværdien for p vha. differentialoperatoren. i En målbar bevægelsesegenskab, såsom r, p, E,, kaldes en observabel, og til 8 enhver sådan observabel O hører en operatorrepræsentant Ô, sådan at * ˆ O ψ r, t Oψ r,. (.0 ( ( t d r Ved sammenligning med udtryk (.5 og (.7 ses således, at ˆr r, (. ˆp. i (. 8 Jf. udtryk (.0 er Ô underforstået operatorrepræsentanten i r -repræsentationen, og i kraft af analogien til p - repræsentationen har alle observable tilsvarende operatorrepræsentanter i p -rum. Som det fremgår af udtryk (.6 er operatorrepræsentanten for bevægelsesmængden i p -rum således p selv, hvilket nok engang understreger analogien mellem r og p. Thomas B. Lynge, Institut for Fysik og Nanoteknologi, AAU 9/0/007

11 Kvantemekanik Side af Dirac-notationen Som alternativ til den mere ligefremme notation anvendt i lærebogen indføres i det flg. den såkaldte Dirac-notation, som er mere kompakt, mere anvendt i den videnskabelige litteratur og endvidere mere generel, idet den kan anvendes til at beskrive egenskaber, der ikke kan udtrykkes ved r og p, såsom f.eks. spin 9. I Dirac-notationen erstattes bølgefunktionen og dens kompleks konjugerede med tilstandsvektorer kaldet hhv. en ket og en bra 0 : ψ ( rt, ψ "Ket", (. ψ rt, ψ "Bra". * ( En sammenstilling af en bra med en ket svarer således til det indre produkt mellem de to tilstandsvektorer eller bølgefunktioner. Normeringsbetingelsen kan således skrives ( rt, (, * ψ ψ rtdr ψ ψ. (.4 Forventningsværdien for observablen O kan tilsvarende skrives som det indre produkt mellem ψ og Ôψ : ˆ O ψ Oψ. (.5 F.eks. ˆ r ψ r ψ ψ r ψ, p ψ pˆ ψ ψ ψ. i (.6 9 Se KM0. 0 Efter det engelske udtryk bracket, som betyder (knækkede parenteser. Udtryk (.5 kaldes i øvrigt matrixelementet af O mellem tilstandene ψ og ψ. Thomas B. Lynge, Institut for Fysik og Nanoteknologi, AAU 9/0/007