Regneark i undervisningen
|
|
|
- Andreas Juhl
- 8 år siden
- Visninger:
Transkript
1 Regneark i undervisningen den regner selv Indledning... 3 Computeren som regnemaskine... 4 Den procesorienterede, eksperimenterende arbejdsmetode med regneark... 5 Optællinger med regnearksprogrammet... 6 Et redskab i mange fag... 8 Modeller og simulering Dynamiske modeller Spil som modeller Om øvelserne til modulet Læsning til modulet Regneark i undervisningen Side 1 af 14
2 Regneark i undervisningen Side 2 af 14
3 Indledning Eleverne møder som oftest op med en mere eller mindre veludviklet forhåndsviden om tal. Denne viden baserer sig både på: Tal i talesproget, hvor de første talnavne udgør en integreret del af førskolebarnets sprog Tal som ordningsredskab, hvor barnet kan sætte tal i rækkefølge Tal som mængdebetegnelse, hvor barnet kan vurdere to talangivelser ift. hinanden. Ved skolestarten er børnenes talbegreb imidlertid meget forskelligt udviklet. Nogle børn har brugt meget tid på at lege med tal. Store tal, små tal, talsystemer osv. fascinerer mange børn. Andre børn har af forskellige grunde et mindre veludviklet talbegreb og en mindre interesse for tal. Gennem de første skoleår er det skolens opgave at udvikle talbegrebet hos alle eleverne, så de senere hen har mulighed for at beskæftige sig med mere abstrakte, matematiske emner og begreber. Her anvendes som regel mange forskellige materialer: konkrete materialer, øvehæfter osv. Der findes også en del gode computerprogrammer, der kan anvendes. Det er karakteristisk for en del af regneundervisningen i de første år, at den ofte har legens og eksperimentets karakter, og at børnene arbejder interesseret og motiveret med opgaverne. Senere i skoleforløbet fortoner det undersøgende aspekt sig imidlertid let, fordi opgaverne bliver sværere, talområdet og kravene til regnefærdigheden øges, og fokus rettes mod formelle metoder. Samtidig kan nogle børn savne anvendelsesperspektivet. Det ville nok være en overdrivelse at påstå, at regnearksprogrammer er matematikundervisningens svar på tekstbehandlingsprogrammet. Hertil er anvendelsesområdet for regneark trods alt mere snævert. Selv om regnearket må suppleres med fx programmer til modeller og simulering mv., er det alligevel det mest generelle program til undervisningen i regning og matematik. Brugt rigtigt i matematikundervisningen kan regnearksprogrammet være et af de redskaber, der gør det muligt at anvende den undersøgende, eksperimenterende og anvendelsesorienterede arbejdsform gennem hele skoleforløbet. Elevernes talbegreb Udvikling af talbegrebet gennem undervisningen Det undersøgende aspekt i undervisningen Regnearkets rolle i undervisningen Regneark i undervisningen Side 3 af 14
4 Computeren som regnemaskine Et regnearksprogram er et værktøj som ethvert andet. Før man kan have nytte af redskabet, er man nødt til at lære det nærmere at kende. Hvad er et regneark? Regnearksprogrammet går som type flere årtier tilbage i computerens historie. Det opstod oprindeligt som et administrativt værktøj: en dynamisk side i en kolonnebog, hvor programmet kunne foretage de rutinemæssige sammentællinger og andre beregninger. Det har siden vist sig, at regnearksprogrammets muligheder gik langt ud over det simple bogholderi. Med introduktionen af de traditionelle matematiske funktioner i regnearket blev det muligt at bruge det som redskab for afprøvning af modeller, der kunne simulere fremskrivninger og andre regneprocesser. Regnearket er et dynamisk redskab, der umiddelbart giver resultaterne fra sig på skærmen. Det er derfor muligt at lade regnearket være et hjælperedskab ved den meget vigtige proces, hvor forhold i den praktiske virkelighed skal oversættes til matematikkens mere abstrakte sprog. Derved bliver det abstrakte begreb en matematisk model pludselig noget konkret og manipulerbart. Et dynamisk redskab Matematik Styr på pengene Klassen skulle afholde en klassefest, og matematiklæreren greb muligheden for at anvende regnearket til opstilling af et budget for arrangementet. Umiddelbart var det svært for klassen at overskue økonomien i et sådant arrangement for ikke at tale om at tage beslutninger vedr. priser og indkøb. I en klassesamtale blev den matematiske model bag budgettet fastlagt ud fra en diskussion af de indtægter og udgifter, der kunne indgå i det, fx: Klassekassens beholdning Indtægter fra salg fra nogle boder Udgifter til forskellige materialer Tilmeldingsgebyr. Modellen voksede langsomt frem på tavlen. Modellen fra tavlen blev overført til et regneark. Derefter kunne læreren og eleverne i fællesskab ændre på regnearket og de talværdier, der indgik i det. Eksperimenterne med budgetmodellen gjorde det muligt at tage realistiske beslutninger om, hvilke varer der skulle sælges ved arrangementet og til hvilke priser, hvad det skulle koste at tilmelde sig, hvad og hvor meget der skulle købes ind i forvejen osv. Regneark i undervisningen Side 4 af 14
5 Som ved mange andre undervisningsprocesser i skolen er det vigtigt, at der er et reelt og konkret formål med elevernes eksperimenter med regnearket, og her er et arrangement som klassefesten (se ovenfor) på mellemtrinnet et glimrende udgangspunkt. Men anvendelse af regneark er lige så relevant i overbygningen, fx i forbindelse med: Planlægning af studietur Beregning af mandatfordeling ved prøvevalg på skolen Beregninger på data indsamlet med pulsure i idrætsundervisningen. Et muligt og særdeles relevant forløb på såvel mellemtrinnet som i overbygningen er en sammenligning af mobiltelefonpriser, hvor forbrug, abonnement, SMSpriser mv. sammenlignes de forskellige teleudbydere imellem. Her benyttes naturligt et regneark til beregning af omkostningerne ved de forskellige mobilløsninger. For inspiration se: På Skats websted findes et undervisningsmateriale til brug i de ældste klasser om skatteforhold, selvangivelse, indtægter og udgifter. Regneark anvendes helt naturligt i arbejdet med forløbet: unge.toldskat.dk/introduktion.asp. Et konkret formål med arbejdet Hvad betaler du for din mobiltelefon? Skat Den procesorienterede, eksperimenterende arbejdsmetode med regneark Den mest almindelige måde at anvende et regneark på er til regnskaber. En af fordelene ved regnearket sammenlignet med et regnskab på papir er den store fleksibilitet: det er meget lettere at rette i tallene. En karakteristisk egenskab ved regnearket er, at regnearket automatisk gennemregnes, når en ændring af en talcelle finder sted. E stor fordel, når man arbejder med fx et budget, hvor tallet på bundlinjen ikke må overskrides. Ved gradvis at ændre på forudsætningerne priser, antal mv. kan man eksperimentere sig frem til et budget, der balancerer. Eleverne skal opleve regnearkets fleksibilitet. Det betyder, at det nok er nødvendigt men slet ikke tilstrækkeligt at lade eleverne møde opgaver, hvor parametre som fx antal kg og pris pr. kg er givet, og hvor regnearket blot benyttes til at lave en pæn opstilling og automatisk udregning. Noget man næsten lige så nemt kunne have gjort i et kladdehæfte med hjælp fra lommeregneren. Det er vigtigt, at eleverne også møder opgaver, hvor Regnskaber Automatisk gennemregning Regnearkets fleksibilitet Baglæns Regneark i undervisningen Side 5 af 14
6 de bruger regnearket til at regne baglæns. Et godt eksempel kunne være et lejrskolebudget eller et budget for en klassefest, hvor man på forhånd ved, hvor mange penge man råder over. Her kan man bruge regnearket til at afprøve mange forskellige muligheder. udregning Julen koster mange penge Klassen skal undersøge omkostningerne ved at holde jul. For at have et materiale at arbejde med indsamlede eleverne gennem en periode på ca. tre uger tilbudsaviser fra de lokale handlende. Undervisningsforløbet blev opdelt i flere faser. Da eleverne ikke havde arbejdet med regnearksprogrammet for nylig, skulle de grundlæggende funktioner først repeteres. Derefter arbejdede eleverne med flere udgaver af regnearket. Den første udgave var meget simpel: her angav eleverne blot varens navn og pris. Hvis der skulle købes flere enheder af samme vare, blev den samlede pris blot udregnet i en celle. Det viste sig snart, at det var bedre at have stykprisen for alle varerne placeret i celler for sig, således at man blot kunne angive varens navn og antal stk. i det egentlige budget. Rigtig spændende blev det, da der blev sat begrænsning på dele af budgettet for juleaften. Nu kunne man ikke længere bare købe den længe ønskede knallert til storebror! I stedet blev det nødvendigt at eksperimentere med, hvor mange forskellige ting der kunne købes, hvor meget der kunne købes og hvad tingene kostede hos forskellige handlende. Enden på det hele blev, at der måtte skæres ned på omfanget af grupperne Gaver og Hygge. Til sidst fremlagde eleverne deres budget for resten af klassen. Her skulle de begrunde deres valg. Læreren fortalte bagefter, at eleverne havde fået øget deres forståelse for, hvordan de kan udnytte regnearket til at eksperimentere med tallene for at opnå, at deres regnskab kom til at holde sig inden for de givne rammer. Optællinger med regnearksprogrammet Der findes programmer, der er fremstillet specielt til spørgeskemaundersøgelser, men til enkle undersøgelser kan et regneark sagtens anvendes i stedet. Der er bl.a. den fordel ved regnearket, at programmet i forvejen er tilgængeligt på skolens computere, og at eleverne kender programmet. Hertil kommer, at det er let at lave diagrammer på grundlag af de tal, regnearket indeholder. Talmaterialet kan stamme fra elevernes egne indsamlinger; men der er også en række muligheder for at skaffe data fra eksterne kilder. Skolebussen, skolebussen.emu.dk, er en tjeneste under EMU, hvor klasser kan opstille spørgsmål til opinionsundersøgelser. Man har også mulighed for at hente data fra arkivet og således arbejde med talmateriale fra tidligere undersøgelser. Tallene kan importeres direkte i Regnearket som redskab ved spørgeskemaundersøgelser Skolebussen Regneark i undervisningen Side 6 af 14
7 regnearksprogrammet. På Danmarks Statistik findes desuden en skatkiste af gratis talmateriale til download, se dst.dk og statistikbanken.dk Danmarks Statistik og Statistikbanken Matematik, de små klasser Trafik i søjler Eleverne i klassen er sure over, at de ikke kan få en gangbro hen over Centervejen, der går fra ringvejen ned til indkøbscentret. Hvem er det egentlig, der bestemmer sådan noget? Efter en ophidset diskussion bliver man enige om, at man vil skrive til kommunens trafikudvalg om problemet. Men læreren har indvendinger: De siger bare, at der ikke er trafik nok på vejen; og der er vist heller ikke så mange af jer, der skal over den vej for at komme i skole? Slutningen på det hele bliver naturligvis, at der skal foretages nogle optællinger som bilag til brevet: Hvor mange elever fra hvert enkelt klassetrin skal krydse Centervejen for at komme i skole? Hvor meget trafik af forskellige typer cykler, knallerter, motorcykler, biler, lastbiler og busser er der på det tidspunkt, hvor eleverne møder om morgenen? Noget af arbejdet kan laves i løbet af skoledagen, og en gruppe elever går derfor rundt i klasserne og tæller op, hvor mange der skal krydse Centervejen til og fra skole. Andre grupper mødes med læreren om morgenen og om eftermiddagen for at tælle trafikken i nogle intervaller på ti minutter. Der bliver mange tal ud af gruppernes arbejde, så læreren beslutter, at der skal laves diagrammer. Og det er jo nemt med et regneark. Læreren laver først et regneark, hvor antallet af elever, der skal krydse vejen, kan skrives ind for hvert klassetrin. Tallene omsættes til et illustrativt søjlediagram: det er tydeligt, at det faktisk er eleverne fra 3. og 4. klasse, der topper her! Læreren laver også et regneark, hvor eleverne kan skrive ind, hvor mange biler, cykler, busser osv. de har talt i tidsintervallet mellem kl og Regnearket lægger tallene sammen, så man kan se både den samlede trafikmængde og trafikkens størrelse omkring tidspunktet, hvor eleverne møder. Desuden fremstilles et diagram, der viser trafiktætheden. Klassen skriver til kommunen og vedlægger resultaterne af undersøgelsen. De skriver også til den lokale avis. Regneark i undervisningen Side 7 af 14
8 Regneark egner sig godt til at opgøre resultater af spørgeskemaundersøgelser af multiple-choice-typen. Her drejer det sig nemlig om enkle spørgsmål med få svarmuligheder, der er lette at registrere og tælle op. Begyndelsen af spørgeskemaet kunne fx se således ud: Få svarmuligheder er nemmest at arbejde med Sæt kryds Køn Pige Dreng Alder Under 10 år 10 til 20 år Over 20 år Kender du eventyret Fyrtøjet? Ja Nej Når man arbejder med resultaterne af en større undersøgelse, kan man let løbe ind i praktiske problemer, når data skal tastes ind i regnearket. Eleverne er ofte meget længe om indtastningen længere end man som lærer havde forestillet sig i planlægningsfasen. Her kan man med fordel lade eleverne dele arbejdet imellem sig. Det kan man lettest gøre ved at fremstille et basisregneark, kopiere dette til de enkelte computere og så lade eleverne arbejde ved flere computere på samme tid. Til sidst kan man samle de enkelte delindtastninger i et fælles regneark, som man igen kan kopiere ud til de enkelte elevgrupper. Eleverne kan så arbejde videre med diagrammer, opgørelser mv. Hvis man skal lave en mere dybgående analyse af datamaterialet, vil man dog blive nødt til at tage et egentligt spørgeskemaprogram i anvendelse. Organisering af indtastningsarbejdet Arbejde i grupper med resultaterne Regnearkets begrænsninger Et redskab i mange fag Et samarbejde mellem to eller flere fag kan have forskellige udgangspunkter. Når man i fællesskab planlægger et samarbejde om et emne eller tema, er det fagene, der er i centrum. Samarbejdet indledes måske med en bemærkning a la: Kan vi ikke lave et eller andet projekt sammen i dansk og matematik?. Fagene som udgangspunkt eller som redskaber Hvis man derimod fra starten vælger projektarbejdsformen, optræder fagene som hjælpeværktøjer. Her er det problemformuleringen og arbejdsprocessen, der bestemmer, hvilke fag og faglige discipliner der skal inddrages. Det er ikke usædvanligt, at man som matematiklærer i et tværfagligt projekt har fornemmelsen af at levere timer til projektet, uden at eleverne får et rimeligt ma- Matematikken i tværfaglige Regneark i undervisningen Side 8 af 14
9 tematikfagligt udbytte af den investerede tid. Synspunktet er imidlertid ikke særlig konstruktivt. Pointen i det tværfaglige samarbejde kunne netop bestå i, at eleverne oplever nytten af den matematik, de allerede har lært, og derved møder med en større interesse for faget, når det tværfaglige projektforløb er overstået. Det kan være en dårlig idé at bruge et tværfagligt projektforløb som basis for at introducere eleverne til et regnearksprogram. I stedet kan det tværfaglige forløb bruges til at indarbejde nogle it-faglige arbejdsvaner, fx: Brug af udklipsholder ved kopiering mellem programmer Opsætning af tekster og regneark på en overskuelig måde Systematik i håndtering af store datamængder. Introduktionen til regneark behøver ikke nødvendigvis at finde sted i matematiktimerne, idet behandling af taldata og opstilling af grafer forekommer i mange af skolens fag: Geografi, fx grafisk sammenligning af produktionsdata, indbyggertal eller erhvervsstruktur Fysik/kemi, fx beregninger og grafisk opstilling af måleresultater Natur/teknik, fx beregning og sammenligning af vandforbrug og registrering af vejrdata Dansk, fx undersøgelser af læsevaner og litteraturkendskab Idræt, fx registrering og grafisk opstilling af præstationer gennem en periode Sprogfagene, fx alfabetisk sorterede gloselister vha. regneark, som er en født tabel. Hvis digte indsættes i regneark, er det let at tilføje gloser til hver linje. Gennem undervisningen bør eleverne møde opgavetyper, der lægger op til selvstændig analyse og eksperimenterende holdning. Det giver dem forudsætningerne for at kunne arbejde med regnearket på den måde, der forventes i et fagligt eller et tværfagligt forløb. projekter Arbejdsvaner omkring it Nogle eksempler Elevernes forudsætninger Regneark i undervisningen Side 9 af 14
10 Modeller og simulering De fleste kender historien om den indiske fyrste, der spurgte opfinderen af skakspillet, hvad han ønskede i belønning for sin opfindelse. Svaret lød som bekendt således: Jeg vil blot have et enkelt riskorn på det første felt, det dobbelte på det næste og således videre på alle felterne. Fyrsten var derefter overbevist om, at han nemt kunne betale honoraret for opfindelsen. En opstilling af et regneark til beregning af denne udgift ville nok havde fået fyrsten på andre tanker. Beregningen i et regneark er enkel, idet udtrykket i den anden linje blot er to gange det forrige tal. Når man kopierer denne formel til de følgende 62 linjer i regnearket, kan programmet lynhurtigt gennemføre beregningen. Regnearket med riskorn kan betragtes som en model af virkeligheden. Når man lærer regnearkets indbyggede matematiske funktioner at kende, får man mulighed for at anvende programmet til at eksperimentere med forskellige modeltyper. Med de såkaldte dynamiske modeller kan man beskrive, hvordan forskellige elementer påvirker hinanden i fx et kompliceret økologisk system, eller man kan opstille økonomiske modeller, hvor man bl.a. kan simulere budgetter. Med andre matematiske modeller simulerer man meget simple fænomener som terningkast, kast med mønter mv. Et af de nye store temaer i skolen efter Globaliseringsrådets rapport bliver iværksætteri, se globalisering.dk/page.dsp?page=131. I forbindelse med projekter, hvor eleverne fx simulerer igangsættelse af ny virksomhed, er arbejdet med regneark helt centralt. Se fx iværksætteri som tema i undervisningen på EMU: ivaerksaetter.emu.dk Jeg vil blot have et enkelt riskorn på det første felt Modeller af virkeligheden Iværksætter Dynamiske modeller Regnearkets anvendelse til budgetsimulering er omtalt tidligere, men regnearket kan anvendes til andre typer af fremskrivninger. Dette afsnit vil især omhandle modeller for: Vækst Opsparing Finansiering Andre dynamiske modeller. Dynamiske modeller beskriver sammenhængen mellem flere forskellige faktorer. Et klassisk eksempel handler Dynamiske modeller i regnearket Regneark i undervisningen Side 10 af 14
11 således om, hvordan størrelsen af en bestand af kaniner og ræve på en ø vil variere over tid. Arbejdet med almindelige vækstmodeller i skolens ældste klasser kan indledes med spørgsmål af typen: Hvad kan bedst betale sig: at låne 5000 kr. til 1.5 % i rente pr. måned eller til 4 % i rente pr. kvartal med 150 kr. i kvartalsadministrationsgebyr?. Dette spørgsmål kan næppe besvares umiddelbart af eleverne, og situationen lægger derfor op til formulering af en model og fremskrivning i et regneark. Ved opgaver med fx vækstmodeller vil man have nogle startbetingelser: de værdier, der skal indgå i beregningerne. Derefter vil man opstille formlen for den første beregning det første kvartal og derefter bruge regnearksprogrammets indbyggede mulighed for at gentage en formel et vilkårligt antal gange. Der findes flere forskellige typer af dynamiske modeller. Ved de mest simple er der tale om en vækst uden grænser. Her kan man i princippet lade en bestand af rotter vokse uden grænse. Mere realistiske er dog de modeller, der tager hensyn til begrænsninger i fx føde eller plads. Disse modeller lader en bestand vokse mod en øvre grænse, som ikke kan overskrides. Et eksempel kunne være en flok kameler, der er afhængige af vandmængden i det samme vandhul. Deres antal kan kun vokse, indtil det begrænses naturligt af mængden af drikkevand. De mest komplicerede modeller beskriver samspillet mellem flere forskellige faktorer. Det kunne fx dreje sig om en model, der beskrev antallet af kaniner og ræve på en ø; kaninerne formerer sig i teorien uden nogen grænse, men derved bliver der mere mad til rævene. Når bestanden af ræve vokser, falder antallet af kaniner og omvendt. Nogle af de store modelsystemer, der anvendes til simulering af forhold i den virkelige verden, bygger på disse principper. Det drejer sig fx om den såkaldte Nordsømodel, der beskriver udviklingen i fiskebestanden i Nordsøen. Vækstmodeller Modellens startbetingelser Vækst med og uden grænser Modeller af virkeligheden Regneark i undervisningen Side 11 af 14
12 Spil som modeller De matematiske modeller giver for alvor lærer og elever mulighed for at arbejde eksperimenterende og procesorienteret. Med anvendelse af regnearkets indbyggede matematiske funktioner kan man opbygge egentlige matematiske modeller til simulering af tilfældige begivenheder som kast med en terning. Erfaringen viser, at eleverne let bliver fascineret af de spillignende scenarier, der kan opbygges på grundlag af arbejdet med tilfældige tal. Med forholdsvis simple regneark kan man simulere kast med en terning eller en mønt, og med lidt mere komplicerede regneark kan man endda lave sit eget kasino. En eksperimenterende og procesorienteret arbejdsform Spil i matematiktimen Lad os sprænge banken! To klasser arbejdede i fire uger med et emne om sandsynligheder. Forløbet bestod af en række faser, hvor eleverne nogle gange selv kastede med terninger og i andre faser lod computeren både kaste terninger og beregne resultaterne. Eleverne skulle i den første fase gøre iagttagelser med kast med en almindelig terning. Hver elev kastede en terning 50 gange og noterede resultaterne. På baggrund af resultaterne lavede eleverne en hyppighedstabel og beregnede middeltallet for kastene. Efter en samtale om resultaterne og deres forskellighed blev resultatet for hver klasse beregnet. Hver elev sammenlignede derefter sine resultater med klassens. Den første fase i undervisningsforløbet blev afsluttet med, at eleverne benyttede en computer til at udføre beregninger, som de tidligere havde udført i hånden. Computerens resultater blev derefter sammenlignet med de håndregnede. I den følgende fase benyttede eleverne en computer til at simulere terningkast. Eleverne lod computeren udføre 5000 kast og sammenlignede derefter resultaterne med de tidligere. I den næste fase kastede eleverne med to terninger ad gangen. De skulle forsøge at udarbejde et beskrivelsesmiddel, så de kunne notere resultaterne. Skulle dette være summen af øjnene eller blå terning viser og rød terning viser? Efterhånden fandt klassens frem til en notationsform, der var anvendelig. I forløbets næstsidste fase skulle eleverne først afprøve forskellige spilmuligheder, fx: Det koster 10 kroner pr. spil at spille. Kast en terning og udbetal tre gange øjentallet. Eleverne skulle her først prøve både at være spiller og bankør. Hvem gav dette spil overskud for? Efter at have afprøvet forskellige spil, skulle eleverne selv opstille et spil med betaling for hvert kast og udbetaling for flere forskellige hændelser. Disse spil blev afprøvet både i hånden og på computer. Forløbets sidste fase foregik på en forældredag, hvor en del af de elevfremstillede spil blev afprøvet i forskellige spilleboder. Inden denne aften blev spillene gennemgået i klassen, således at det ikke lykkedes for nogen forælder at sprænge banken på selve aftenen. Regneark i undervisningen Side 12 af 14
13 De fleste elevers umiddelbare sandsynlighedsbegreb er forholdsvis svagt udviklet, og de har derfor svært ved at forudsige resultaterne af forskellige væddemål og chancesituationer. Hvad er fx lettest at få med to terninger, 2 eller 6 øjne? Bliver der overskud i et spil med to terninger, hvor man betaler 4 kr. pr. kast og får det tilbage, som øjnene viser? De regneark, der har været anvendt indtil nu, har altid benyttet sig af den såkaldte automatiske gennemregning. Det betyder ganske enkelt, at regnearket foretager en opdatering af samtlige formelceller, hver gang indholdet af en celle ændres. Dette er praktisk, når man retter tal i et budget og øjeblikkeligt ser resultatet på bundlinjen. Denne funktion kan imidlertid slås fra, således at man selv kan bestemme, hvornår der skal regnes. Det er nyttigt i spillignende situationer, hvor man skal indtaste indsatser mv., inden man kører modellen i regnearket og får resultatet af et spil. Ved modeller af den type, der anvendes til spillignende regneark, anvender man en indbygget, matematisk funktion, der på kommando kan give et tilfældigt tal fra sig. Dette tal ligger altid i intervallet fra og med 0 til men ikke med værdien 1. Derfor skal der regnes på tallet, hvis man fx ønsker at få tallene 1, 2, 3 osv., svarende til en ternings øjne. Ved at bruge den manuelle gennemregning kan man få regnearket til at gennemregne alle formelceller ved et tryk på en tast, men uden at man har ændret indholdet af en celle i regnearket. Herved kan man langsomt fremskrive en model i et tempo, hvor man kan følge med i, hvad der sker. Netop ved efterligning af mange terningkast er det vigtigt, at man selv kan styre den hastighed, som regnearbejdet foregår i. På den måde kan man fx se, hvordan sandsynlighederne efterhånden nærmer sig den forventede teoretiske værdi. Elevernes sandsynlighedsbegreb Automatisk eller manuel gennemregning Tilfældige tal som grundlag for modellerne Trinvis fremskrivning af modellen Regneark i undervisningen Side 13 af 14
14 Om øvelserne til modulet I valgmodulet Den regner selv introduceres de grundlæggende funktioner i et regnearksprogram: Opstilling af diagrammer på basis af tallene i regnearket Gennemførelse af små undersøgelser, hvor regnearket anvendes ved opgørelse og analyse af resultaterne Eksempler på, hvordan man kan arbejde med regnearket i en tværfaglig undervisning Arbejde med forskellige modeller, hvor et regneark er velegnet: Rentemodeller med opsparing Modeller for talrækker Modeller, hvor computeren anvendes til at simulere kast med en eller flere terninger. Se øvelser til modulet i IT-værktøjskassen Læsning til modulet Arne Mogensen: Regneark hvorfor nu det? En indledningsartikel om regneark. Artiklen indledes med en beskrivelse af, hvad et regneark er. Desuden omtales tre forskellige måder, elever kan arbejde med regneark på. Inge B. Larsen: Regneprogrammer en analyse af faglige og pædagogiske muligheder En artikel, hvor forfatteren undersøger regneprogrammers anvendelighed i matematikundervisningen, herunder brug ved afgangsprøver. Se link til læsning på kursuswebben Regneark i undervisningen Side 14 af 14
Regneark hvorfor nu det?
 Regneark hvorfor nu det? Af seminarielektor, cand. pæd. Arne Mogensen Et åbent program et værktøj... 2 Sådan ser det ud... 3 Type 1 Beregning... 3 Type 2 Præsentation... 4 Type 3 Gæt... 5 Type 4 Eksperiment...
Regneark hvorfor nu det? Af seminarielektor, cand. pæd. Arne Mogensen Et åbent program et værktøj... 2 Sådan ser det ud... 3 Type 1 Beregning... 3 Type 2 Præsentation... 4 Type 3 Gæt... 5 Type 4 Eksperiment...
Simulering af stokastiske fænomener med Excel
 Simulering af stokastiske fænomener med Excel John Andersen, Læreruddannelsen i Aarhus, VIA Det kan være en ret krævende læreproces at udvikle fornemmelse for mange begreber fra sandsynlighedsregningen
Simulering af stokastiske fænomener med Excel John Andersen, Læreruddannelsen i Aarhus, VIA Det kan være en ret krævende læreproces at udvikle fornemmelse for mange begreber fra sandsynlighedsregningen
Målsætning. Se hovedmål for scenariet og hovedmål for færdighedslæring her. Økonomi
 Målsætning Økonomiske beregninger som baggrund for vurdering af konkrete problemstillinger. Målsætningen for temaet Hvordan får jeg råd? er, at eleverne gennem arbejde med scenariet udvikler matematiske
Målsætning Økonomiske beregninger som baggrund for vurdering af konkrete problemstillinger. Målsætningen for temaet Hvordan får jeg råd? er, at eleverne gennem arbejde med scenariet udvikler matematiske
Gennemsnit og normalfordeling illustreret med terningkast, simulering og SLUMP()
 Gennemsnit og normalfordeling illustreret med terningkast, simulering og SLUMP() John Andersen, Læreruddannelsen i Aarhus, VIA Et kast med 10 terninger gav følgende udfald Fig. 1 Result of rolling 10 dices
Gennemsnit og normalfordeling illustreret med terningkast, simulering og SLUMP() John Andersen, Læreruddannelsen i Aarhus, VIA Et kast med 10 terninger gav følgende udfald Fig. 1 Result of rolling 10 dices
VisiRegn: En e-bro mellem regning og algebra
 Artikel i Matematik nr. 2 marts 2001 VisiRegn: En e-bro mellem regning og algebra Inge B. Larsen Siden midten af 80 erne har vi i INFA-projektet arbejdet med at udvikle regne(arks)programmer til skolens
Artikel i Matematik nr. 2 marts 2001 VisiRegn: En e-bro mellem regning og algebra Inge B. Larsen Siden midten af 80 erne har vi i INFA-projektet arbejdet med at udvikle regne(arks)programmer til skolens
Mobiltelefoner og matematik
 Mobiltelefoner og matematik Forord og lærervejledning Mobiltelefonen er blevet et meget vigtigt kommunikationsredskab i de sidste år. Mange af skolens elever har i dag en mobiltelefon, som de ofte bruger.
Mobiltelefoner og matematik Forord og lærervejledning Mobiltelefonen er blevet et meget vigtigt kommunikationsredskab i de sidste år. Mange af skolens elever har i dag en mobiltelefon, som de ofte bruger.
Simulering af stokastiske fænomener med Excel
 Simulering af stokastiske fænomener med Excel John Andersen, Læreruddannelsen i Aarhus, VIA Det kan være en ret krævende læreproces at udvikle fornemmelse for mange begreber fra sandsynlighedsregningen
Simulering af stokastiske fænomener med Excel John Andersen, Læreruddannelsen i Aarhus, VIA Det kan være en ret krævende læreproces at udvikle fornemmelse for mange begreber fra sandsynlighedsregningen
Skolens formål med faget matematik følger beskrivelsen af formål i folkeskolens Fælles Mål:
 Formål: Skolens formål med faget matematik følger beskrivelsen af formål i folkeskolens Fælles Mål: Formålet med undervisningen i matematik er, at eleverne bliver i forstå og anvende matematik i sammenhænge,
Formål: Skolens formål med faget matematik følger beskrivelsen af formål i folkeskolens Fælles Mål: Formålet med undervisningen i matematik er, at eleverne bliver i forstå og anvende matematik i sammenhænge,
Læseplan for faget matematik. 1. 9. klassetrin
 Læseplan for faget matematik 1. 9. klassetrin Matematikundervisningen bygger på elevernes mange forudsætninger, som de har med når de starter i skolen. Der bygges videre på elevernes forskellige faglige
Læseplan for faget matematik 1. 9. klassetrin Matematikundervisningen bygger på elevernes mange forudsætninger, som de har med når de starter i skolen. Der bygges videre på elevernes forskellige faglige
LÆRINGSMÅL PÅ NIF MATEMATIK 2014-15
 LÆRINGSMÅL PÅ NIF MATEMATIK 2014-15 Mål for undervisningen i Matematik på NIF Følgende er baseret på de grønlandske læringsmål, tilføjelser fra de danske læringsmål står med rød skrift. Læringsmål Yngstetrin
LÆRINGSMÅL PÅ NIF MATEMATIK 2014-15 Mål for undervisningen i Matematik på NIF Følgende er baseret på de grønlandske læringsmål, tilføjelser fra de danske læringsmål står med rød skrift. Læringsmål Yngstetrin
Matematik på Humlebæk lille Skole
 Matematik på Humlebæk lille Skole Matematikundervisningen på HLS er i overensstemmelse med Undervisningsministeriets Fælles Mål, dog med få justeringer som passer til vores skoles struktur. Det betyder
Matematik på Humlebæk lille Skole Matematikundervisningen på HLS er i overensstemmelse med Undervisningsministeriets Fælles Mål, dog med få justeringer som passer til vores skoles struktur. Det betyder
Statistik og sandsynlighed
 Statistik og sandsynlighed Statistik handler om at beskrive og analysere en stor mængde data. som I eller andre har indsamlet. Det kan fx være tal, der fortæller om, hvor mange lynnedslag der er i Danmark
Statistik og sandsynlighed Statistik handler om at beskrive og analysere en stor mængde data. som I eller andre har indsamlet. Det kan fx være tal, der fortæller om, hvor mange lynnedslag der er i Danmark
AT-forløb Jordskælv i Chile 1.u
 Kapitel 1 AT-forløb Jordskælv i Chile 1.u 1.1 Indgående fag I forløbet indgår fagene naturgeografi v. Mikkel Røjle Bruun (BR), samfundsfag v. Ann Britt Wolsing (AW) og matematik v. Flemming Pedersen (FP).
Kapitel 1 AT-forløb Jordskælv i Chile 1.u 1.1 Indgående fag I forløbet indgår fagene naturgeografi v. Mikkel Røjle Bruun (BR), samfundsfag v. Ann Britt Wolsing (AW) og matematik v. Flemming Pedersen (FP).
Årsplan for 2.kl i Matematik
 Årsplan for 2.kl i Matematik Vi følger matematiksystemet "Matematrix". Her skal vi i år arbejde med bøgerne 2A og 2B. Eleverne i 2. klasse skal i 2. klasse gennemgå de fire regningsarter. Specielt skal
Årsplan for 2.kl i Matematik Vi følger matematiksystemet "Matematrix". Her skal vi i år arbejde med bøgerne 2A og 2B. Eleverne i 2. klasse skal i 2. klasse gennemgå de fire regningsarter. Specielt skal
Fagårsplan 10/11 Fag: Matematik Klasse: 7.ABC Lærer: Henrik Stillits. Fagområde/ emne
 Fagårsplan 10/11 Fag: Matematik Klasse: 7.ABC Lærer: Henrik Stillits. Fagområde/ emne Matematiske færdigheder Grundlæggende færdigheder - plus, minus, gange, division (hele tal, decimaltal og brøker) Identificer
Fagårsplan 10/11 Fag: Matematik Klasse: 7.ABC Lærer: Henrik Stillits. Fagområde/ emne Matematiske færdigheder Grundlæggende færdigheder - plus, minus, gange, division (hele tal, decimaltal og brøker) Identificer
Kapital- og rentesregning
 Rentesregning Rettet den 28-12-11 Kapital- og rentesregning Kapital- og rentesregning Navngivning ved rentesregning I eksempler som Niels Oles, hvor man indskyder en kapital i en bank (én gang), og banken
Rentesregning Rettet den 28-12-11 Kapital- og rentesregning Kapital- og rentesregning Navngivning ved rentesregning I eksempler som Niels Oles, hvor man indskyder en kapital i en bank (én gang), og banken
Talregning. Aktivitet Emne Klassetrin Side. Indledning til VisiRegn ideer 1-7 2 Oversigt over VisiRegn ideer 1-7 3
 VisiRegn ideer 1 Talregning Inge B. Larsen ibl@dpu.dk INFA juli 2001 Indhold: Aktivitet Emne Klassetrin Side Indledning til VisiRegn ideer 1-7 2 Oversigt over VisiRegn ideer 1-7 3 Vejledning til Talregning
VisiRegn ideer 1 Talregning Inge B. Larsen ibl@dpu.dk INFA juli 2001 Indhold: Aktivitet Emne Klassetrin Side Indledning til VisiRegn ideer 1-7 2 Oversigt over VisiRegn ideer 1-7 3 Vejledning til Talregning
Når vi forbereder et nyt emne eller område vælger vi de metoder, materialer og evalueringsformer, der egner sig bedst til forløbet.
 MATEMATIK Delmål for fagene generelt. Al vores undervisning hviler på de i Principper for skole & undervisning beskrevne områder (- metoder, materialevalg, evaluering og elevens personlige alsidige udvikling),
MATEMATIK Delmål for fagene generelt. Al vores undervisning hviler på de i Principper for skole & undervisning beskrevne områder (- metoder, materialevalg, evaluering og elevens personlige alsidige udvikling),
statistik og sandsynlighed
 brikkerne til regning & matematik statistik og sandsynlighed trin 1 preben bernitt brikkerne statistik og sandsynlighed 1 1. udgave som E-bog ISBN: 978-87-92488-19-0 2004 by bernitt-matematik.dk Kopiering
brikkerne til regning & matematik statistik og sandsynlighed trin 1 preben bernitt brikkerne statistik og sandsynlighed 1 1. udgave som E-bog ISBN: 978-87-92488-19-0 2004 by bernitt-matematik.dk Kopiering
Fortsættelse af Regneark II. Indhold. Side 1 af 14. Regneark EXCEL
 Side 1 af 14 Fortsættelse af Regneark II Indhold Telefonliste...2 Budget...4 Diagram...7 Regning...9 Underskrift...9 Rundt om Jorden...11 Matematisk problem...13 Et sidste eksempel...14 Side 2 af 14 Telefonliste
Side 1 af 14 Fortsættelse af Regneark II Indhold Telefonliste...2 Budget...4 Diagram...7 Regning...9 Underskrift...9 Rundt om Jorden...11 Matematisk problem...13 Et sidste eksempel...14 Side 2 af 14 Telefonliste
Matematik. Matematikundervisningen tager udgangspunkt i Folkeskolens Fælles Mål
 Matematik Matematikundervisningen tager udgangspunkt i Folkeskolens Fælles Mål Formålet med undervisningen i matematik er, at eleverne bliver i stand til at forstå og anvende matematik i sammenhænge, der
Matematik Matematikundervisningen tager udgangspunkt i Folkeskolens Fælles Mål Formålet med undervisningen i matematik er, at eleverne bliver i stand til at forstå og anvende matematik i sammenhænge, der
Modellering med Målskytten
 Modellering med Målskytten - Et undervisningsforløb i WeDo med udgangspunkt i matematiske emner og kompetencer Af Ralf Jøker Dohn Henrik Dagsberg Målskytten - et modelleringsprojekt i matematik ved hjælp
Modellering med Målskytten - Et undervisningsforløb i WeDo med udgangspunkt i matematiske emner og kompetencer Af Ralf Jøker Dohn Henrik Dagsberg Målskytten - et modelleringsprojekt i matematik ved hjælp
Kom i gang med regneark:
 Kendte og nye værktøjs ikoner på værktøjslinien. Det er de samme værktøjs ikoner der går igen i mange af programmerne, men der er dog også nogle nye. Autosum Formel regner Sortering Diagrammer Flet og
Kendte og nye værktøjs ikoner på værktøjslinien. Det er de samme værktøjs ikoner der går igen i mange af programmerne, men der er dog også nogle nye. Autosum Formel regner Sortering Diagrammer Flet og
Talrækker. Aktivitet Emne Klassetrin Side
 VisiRegn ideer 3 Talrækker Inge B. Larsen ibl@dpu.dk INFA juli 2001 Indhold: Aktivitet Emne Klassetrin Side Vejledning til Talrækker 2-4 Elevaktiviteter til Talrækker 3.1 Talrækker (1) M-Æ 5-9 3.2 Hanoi-spillet
VisiRegn ideer 3 Talrækker Inge B. Larsen ibl@dpu.dk INFA juli 2001 Indhold: Aktivitet Emne Klassetrin Side Vejledning til Talrækker 2-4 Elevaktiviteter til Talrækker 3.1 Talrækker (1) M-Æ 5-9 3.2 Hanoi-spillet
Allan C. Malmberg. Terningkast
 Allan C. Malmberg Terningkast INFA 2008 Programmet Terning Terning er et INFA-program tilrettelagt med henblik på elever i 8. - 10. klasse som har særlig interesse i at arbejde med situationer af chancemæssig
Allan C. Malmberg Terningkast INFA 2008 Programmet Terning Terning er et INFA-program tilrettelagt med henblik på elever i 8. - 10. klasse som har særlig interesse i at arbejde med situationer af chancemæssig
Faglige delmål og slutmål i faget Matematik. Trin 1
 Faglige delmål og slutmål i faget Matematik. Trin 1 Faglige delmål for matematik i 1. og 2. klasse. Undervisningen skal lede frem mod, at eleverne efter 2. klasse har tilegnet sig kundskaber og færdigheder,
Faglige delmål og slutmål i faget Matematik. Trin 1 Faglige delmål for matematik i 1. og 2. klasse. Undervisningen skal lede frem mod, at eleverne efter 2. klasse har tilegnet sig kundskaber og færdigheder,
Hvad er meningen? Et forløb om opinionsundersøgelser
 Hvad er meningen? Et forløb om opinionsundersøgelser Jette Rygaard Poulsen, Frederikshavn Gymnasium og HF-kursus Hans Vestergaard, Frederikshavn Gymnasium og HF-kursus Søren Lundbye-Christensen, AAU 17-10-2004
Hvad er meningen? Et forløb om opinionsundersøgelser Jette Rygaard Poulsen, Frederikshavn Gymnasium og HF-kursus Hans Vestergaard, Frederikshavn Gymnasium og HF-kursus Søren Lundbye-Christensen, AAU 17-10-2004
Lidt historisk om chancelære i grundskolen
 Lidt historisk om chancelære i grundskolen 1976 1.-2.klassetrin Vejledende forslag til læseplan:.det tilstræbes endvidere at eleverne i et passende talmaterialer kan bestemme for eksempel det største tal,
Lidt historisk om chancelære i grundskolen 1976 1.-2.klassetrin Vejledende forslag til læseplan:.det tilstræbes endvidere at eleverne i et passende talmaterialer kan bestemme for eksempel det største tal,
Formativ brug af folkeskolens prøver. Den skriftlige prøve i matematik i 10. klasse, FP10, maj 2018
 Formativ brug af folkeskolens prøver Den skriftlige prøve i matematik i 10. klasse, FP10, maj 2018 1 Til matematiklæreren i 10. klasse Dette er en rapport om den skriftlige prøve i matematik maj 2018.
Formativ brug af folkeskolens prøver Den skriftlige prøve i matematik i 10. klasse, FP10, maj 2018 1 Til matematiklæreren i 10. klasse Dette er en rapport om den skriftlige prøve i matematik maj 2018.
Matematik - undervisningsplan
 I 4. klasse starter man på andet forløb i matematik, der skal lede frem mod at eleverne kan opfylde fagets trinmål efter 6. klasse. Det er dermed det som undervisningen tilrettelægges ud fra og målsættes
I 4. klasse starter man på andet forløb i matematik, der skal lede frem mod at eleverne kan opfylde fagets trinmål efter 6. klasse. Det er dermed det som undervisningen tilrettelægges ud fra og målsættes
Eksponentielle funktioner for C-niveau i hf
 Eksponentielle funktioner for C-niveau i hf 2017 Karsten Juul Procent 1. Procenter på en ny måde... 1 2. Bestem procentvis ændring... 2 3. Bestem begyndelsesværdi... 2 4. Bestem slutværdi... 3 5. Vækstrate...
Eksponentielle funktioner for C-niveau i hf 2017 Karsten Juul Procent 1. Procenter på en ny måde... 1 2. Bestem procentvis ændring... 2 3. Bestem begyndelsesværdi... 2 4. Bestem slutværdi... 3 5. Vækstrate...
Lærervejledning Matematik 1-2-3 på Smartboard
 Lærervejledning Matematik 1-2-3 på Smartboard Lærervejledning til Matematik 1-2-3 på Smartboard Materialet består af 33 færdige undervisningsforløb til brug i matematikundervisningen i overbygningen. Undervisningsforløbene
Lærervejledning Matematik 1-2-3 på Smartboard Lærervejledning til Matematik 1-2-3 på Smartboard Materialet består af 33 færdige undervisningsforløb til brug i matematikundervisningen i overbygningen. Undervisningsforløbene
Årsplan 8. Klasse Matematik Skoleåret 2016/17
 Hovedformål Der arbejdes med følgende 3 matematiske emner: 1. tal og algebra, 2. geometri samt 3. statistik og sandsynlighed. Derudover skal der arbejdes med matematik i anvendelse samt de matematiske
Hovedformål Der arbejdes med følgende 3 matematiske emner: 1. tal og algebra, 2. geometri samt 3. statistik og sandsynlighed. Derudover skal der arbejdes med matematik i anvendelse samt de matematiske
Årsplan for matematik 4. klasse 14/15
 Årsplan for matematik 4. klasse 14/15 Status: 4.b er en klasse der består af ca. 20 elever. Der er en god fordeling mellem piger og drenge i klasser. Klassen har 5 matematiktimer om ugen. Vi fortsætter
Årsplan for matematik 4. klasse 14/15 Status: 4.b er en klasse der består af ca. 20 elever. Der er en god fordeling mellem piger og drenge i klasser. Klassen har 5 matematiktimer om ugen. Vi fortsætter
Lineære sammenhænge, residualplot og regression
 Lineære sammenhænge, residualplot og regression Opgave 1: Er der en bagvedliggende lineær sammenhæng? I mange sammenhænge indsamler man data som man ønsker at undersøge og afdække eventuelle sammenhænge
Lineære sammenhænge, residualplot og regression Opgave 1: Er der en bagvedliggende lineær sammenhæng? I mange sammenhænge indsamler man data som man ønsker at undersøge og afdække eventuelle sammenhænge
Regneark III Calc Open Office
 Side 1 af 10 Fortsættelse af Calc II Indhold Indhold... 1 Telefonliste... 2 Sortering... 2 Budget... 3 Diagram... 5 Regning... 6 Underskrift... 7 Rundt om Jorden... 8 Matematisk problem... 9 Et sidste
Side 1 af 10 Fortsættelse af Calc II Indhold Indhold... 1 Telefonliste... 2 Sortering... 2 Budget... 3 Diagram... 5 Regning... 6 Underskrift... 7 Rundt om Jorden... 8 Matematisk problem... 9 Et sidste
Klassen er sammenlæst, altså 5 og 6 klasse på en og samme tid. Samtidig er klassen pt på ca 11 elever ialt.
 Introduktion til mat i 5/6 klasse Vejle Privatskole 13/14: Klassen er sammenlæst, altså 5 og 6 klasse på en og samme tid. Samtidig er klassen pt på ca 11 elever ialt. Udgangspunktet bliver en blød screening,
Introduktion til mat i 5/6 klasse Vejle Privatskole 13/14: Klassen er sammenlæst, altså 5 og 6 klasse på en og samme tid. Samtidig er klassen pt på ca 11 elever ialt. Udgangspunktet bliver en blød screening,
Andengradsligninger. Frank Nasser. 12. april 2011
 Andengradsligninger Frank Nasser 12. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk: Dette
Andengradsligninger Frank Nasser 12. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk: Dette
Kapitlet indledes med en beskrivelse af - og opgaver med - de tre former for sandsynlighed, som er omtalt i læseplanen for 7.- 9.
 Kapitlet indledes med en beskrivelse af - og opgaver med - de tre former for sandsynlighed, som er omtalt i læseplanen for 7.- 9. klassetrin: statistisk sandsynlighed, kombinatorisk sandsynlighed og personlig
Kapitlet indledes med en beskrivelse af - og opgaver med - de tre former for sandsynlighed, som er omtalt i læseplanen for 7.- 9. klassetrin: statistisk sandsynlighed, kombinatorisk sandsynlighed og personlig
How to do in rows and columns 8
 INTRODUKTION TIL REGNEARK Denne artikel handler generelt om, hvad regneark egentlig er, og hvordan det bruges på et principielt plan. Indholdet bør derfor kunne anvendes uden hensyn til, hvilken version
INTRODUKTION TIL REGNEARK Denne artikel handler generelt om, hvad regneark egentlig er, og hvordan det bruges på et principielt plan. Indholdet bør derfor kunne anvendes uden hensyn til, hvilken version
Asbjørn Madsen Årsplan for 8. klasse Matematik Jakobskolen
 Årsplan for matematik i 8. klasse Årsplanen er opbygget ud fra kapitlerne i kernebogen Kontext+ 8. De forskellige kapitler tager udgangspunkt i matematikholdige kontekster, som eleverne på den ene eller
Årsplan for matematik i 8. klasse Årsplanen er opbygget ud fra kapitlerne i kernebogen Kontext+ 8. De forskellige kapitler tager udgangspunkt i matematikholdige kontekster, som eleverne på den ene eller
Fagplan for faget matematik
 Fagplan for faget matematik Der undervises i matematik på alle klassetrin (0. - 7. klasse). De centrale kundskabs- og færdighedsområder er: I matematik skal de grundlæggende kundskaber og færdigheder i
Fagplan for faget matematik Der undervises i matematik på alle klassetrin (0. - 7. klasse). De centrale kundskabs- og færdighedsområder er: I matematik skal de grundlæggende kundskaber og færdigheder i
forstå, arbejde med og analysere problemstillinger af matematisk art i sammenhænge, der vedrører dagligliv, samfundsliv og naturforhold
 Årsplan for undervisningen i matematik på 4. klassetrin 2006/2007 Retningslinjer for undervisningen i matematik: Da Billesborgskolen ikke har egne læseplaner for faget matematik, udgør folkeskolens formål
Årsplan for undervisningen i matematik på 4. klassetrin 2006/2007 Retningslinjer for undervisningen i matematik: Da Billesborgskolen ikke har egne læseplaner for faget matematik, udgør folkeskolens formål
Årsplan Matematrix 3. kl. Kapitel 1: Jubii
 Årsplan Matematrix. kl. A Første halvår Kapitel : Jubii I bogens første kapitel får eleverne mulighed for at repetere det faglige stof, som de arbejdede med i. klasse. Dette er samtidig et redskab for
Årsplan Matematrix. kl. A Første halvår Kapitel : Jubii I bogens første kapitel får eleverne mulighed for at repetere det faglige stof, som de arbejdede med i. klasse. Dette er samtidig et redskab for
Matematik. Læseplan og formål:
 Matematik Læseplan og formål: Formålet med undervisningen i matematik er, at eleverne bliver i stand til at forstå og anvende matematik i sammenhænge, der vedrører dagligliv, samfundsliv og naturforhold.
Matematik Læseplan og formål: Formålet med undervisningen i matematik er, at eleverne bliver i stand til at forstå og anvende matematik i sammenhænge, der vedrører dagligliv, samfundsliv og naturforhold.
Det er svært at komme på ældste trin. Der er mange helt nye ord, fx provokation og oplevelsesfase.
 Overgang fra mellemtrin til ældste trin samtale med 6. kl. Det er svært at komme på ældste trin. Der er mange helt nye ord, fx provokation og oplevelsesfase. Det er en meget anderledes arbejdsform, men
Overgang fra mellemtrin til ældste trin samtale med 6. kl. Det er svært at komme på ældste trin. Der er mange helt nye ord, fx provokation og oplevelsesfase. Det er en meget anderledes arbejdsform, men
MatematiKan Et matematisk skriveværktøj for hele skoleforløbet
 MatematiKan Et matematisk skriveværktøj for hele skoleforløbet Tænk, hvis alle elever kunne arbejde med procesorienteret matematik. En arbejdsform, hvor du forsøger at arbejde med matematiske problemstillinger
MatematiKan Et matematisk skriveværktøj for hele skoleforløbet Tænk, hvis alle elever kunne arbejde med procesorienteret matematik. En arbejdsform, hvor du forsøger at arbejde med matematiske problemstillinger
Gør det selv-øvelser udi regneark for begyndere! - en manual fra Skolekonsulenterne.dk
 Gør det selv-øvelser udi regneark for begyndere! - en manual fra Skolekonsulenterne.dk Versionsdato: August 2009 Indholdsfortegnelse Generelt om manualer fra Skolekonsulenterne.dk...3 Hvad er et regneark?...4
Gør det selv-øvelser udi regneark for begyndere! - en manual fra Skolekonsulenterne.dk Versionsdato: August 2009 Indholdsfortegnelse Generelt om manualer fra Skolekonsulenterne.dk...3 Hvad er et regneark?...4
Regneark for begyndere
 Regneark for begyndere Regneark i Open- og LibreOffice Version: August 2012 Indholdsfortegnelse Hvad er et regneark?...4 Grundlæggende opbygning...4 Kast dig ud i det!...5 Du arbejder med: Din første
Regneark for begyndere Regneark i Open- og LibreOffice Version: August 2012 Indholdsfortegnelse Hvad er et regneark?...4 Grundlæggende opbygning...4 Kast dig ud i det!...5 Du arbejder med: Din første
Årsplan for matematik i 1. klasse 2010-11
 Årsplan for matematik i 1. klasse 2010-11 Vanløse den 6. juli 2010 af Musa Kronholt Formål for faget matematik Formålet med undervisningen er, at eleverne udvikler matematiske kompetencer og opnår viden
Årsplan for matematik i 1. klasse 2010-11 Vanløse den 6. juli 2010 af Musa Kronholt Formål for faget matematik Formålet med undervisningen er, at eleverne udvikler matematiske kompetencer og opnår viden
WORKSHOP 2C, DLF-kursus, Krogerup, 26. november 2015
 WORKSHOP 2C, DLF-kursus, Krogerup, 26. november 2015 At I får overblik over statistik og sandsynlighed som fagområde i folkeskolen indblik i didaktiske forskeres anbefalinger til undervisningen i statistik
WORKSHOP 2C, DLF-kursus, Krogerup, 26. november 2015 At I får overblik over statistik og sandsynlighed som fagområde i folkeskolen indblik i didaktiske forskeres anbefalinger til undervisningen i statistik
Spørgeskemaer i SkoleIntra
 Spørgeskemaer i SkoleIntra Brug det indbyggede værktøj, når du vil vide mere! Version: August 2012 Indholdsfortegnelse Spørgeskema kun for skoler med ElevIntra!...4 Spørgeskemaer i SkoleIntra...4 Hvor
Spørgeskemaer i SkoleIntra Brug det indbyggede værktøj, når du vil vide mere! Version: August 2012 Indholdsfortegnelse Spørgeskema kun for skoler med ElevIntra!...4 Spørgeskemaer i SkoleIntra...4 Hvor
Vejledende årsplan for matematik 4.v 2008/09
 Vejledende årsplan for matematik 4.v 2008/09 Uge Emne Formål Opgaver samt arbejdsområder 33-35 Kendskab og skriftligt arbejde At finde elevernes individuelle niveau samt tilegne mig kendskab til deres
Vejledende årsplan for matematik 4.v 2008/09 Uge Emne Formål Opgaver samt arbejdsområder 33-35 Kendskab og skriftligt arbejde At finde elevernes individuelle niveau samt tilegne mig kendskab til deres
Dette kapitel tager især udgangspunkt i det centrale kundskabs- og færdighedsområde: Matematik i anvendelse med økonomi som omdrejningspunktet.
 Dette kapitel tager især udgangspunkt i det centrale kundskabs- og færdighedsområde: Matematik i anvendelse med økonomi som omdrejningspunktet. Kapitlet indledes med fokus på løn og skat og lægger op til,
Dette kapitel tager især udgangspunkt i det centrale kundskabs- og færdighedsområde: Matematik i anvendelse med økonomi som omdrejningspunktet. Kapitlet indledes med fokus på løn og skat og lægger op til,
Formativ brug af folkeskolens prøver årets resultater på landsplan Den skriftlige prøve i matematik med hjælpemidler, FP9 maj 2019
 Formativ brug af folkeskolens prøver årets resultater på landsplan Den skriftlige prøve i matematik med hjælpemidler, FP9 maj 2019 Skrevet af Klaus Fink på baggrund af oplysninger fra opgavekommissionen
Formativ brug af folkeskolens prøver årets resultater på landsplan Den skriftlige prøve i matematik med hjælpemidler, FP9 maj 2019 Skrevet af Klaus Fink på baggrund af oplysninger fra opgavekommissionen
Andengradsligninger. Frank Nasser. 11. juli 2011
 Andengradsligninger Frank Nasser 11. juli 2011 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold 1 Introduktion
Andengradsligninger Frank Nasser 11. juli 2011 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold 1 Introduktion
Excel regneark. I dette kapitel skal I arbejde med noget af det, Excel regneark kan bruges til. INTRO EXCEL REGNEARK
 Excel regneark Et regneark er et computerprogram, der bl.a. kan regne, tegne grafer og lave diagrammer. Regnearket kan bruges i mange forskellige sammenhænge, når I arbejder med matematik. Det kan gøre
Excel regneark Et regneark er et computerprogram, der bl.a. kan regne, tegne grafer og lave diagrammer. Regnearket kan bruges i mange forskellige sammenhænge, når I arbejder med matematik. Det kan gøre
Introduktion til Calc Open Office med øvelser
 Side 1 af 8 Introduktion til Calc Open Office med øvelser Introduktion til Calc Open Office... 2 Indtastning i celler... 2 Formler... 3 Decimaler... 4 Skrifttype... 5 Skrifteffekter... 6 Justering... 6
Side 1 af 8 Introduktion til Calc Open Office med øvelser Introduktion til Calc Open Office... 2 Indtastning i celler... 2 Formler... 3 Decimaler... 4 Skrifttype... 5 Skrifteffekter... 6 Justering... 6
Undersøgende opgaver Opgave 6 er i begge prøvesæt med som sidste opgave en undersøgende opgave af en ny type, som var lidt udfordrende for eleverne.
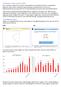 Tendenser i årets prøver 2019 Der er tendenser i prøverne, som kræver matematiklærernes opmærksomhed helst i et samarbejde i fagteamet. Og det kræver skolelederes og forvaltningers opmærksomhed for at
Tendenser i årets prøver 2019 Der er tendenser i prøverne, som kræver matematiklærernes opmærksomhed helst i et samarbejde i fagteamet. Og det kræver skolelederes og forvaltningers opmærksomhed for at
ÅRSPLAN MATEMATIK 3.KLASSE
 ÅRSPLAN MATEMATIK 3.KLASSE Matematiklærerens tænkebobler illustrerer, at matematikundervisning ikke udelukkende handler om opgaver, men om en (lige!) blanding af: Kompetencer Indhold Arbejdsmåder CENTRALE
ÅRSPLAN MATEMATIK 3.KLASSE Matematiklærerens tænkebobler illustrerer, at matematikundervisning ikke udelukkende handler om opgaver, men om en (lige!) blanding af: Kompetencer Indhold Arbejdsmåder CENTRALE
Årsplan 2018/19 Matematik 3. årgang. Kapitel 1: Jubii
 Årsplan 08/9 Matematik. årgang TriX A Kapitel : Jubii I bogens første kapitel får eleverne mulighed for at repetere det faglige stof, som de arbejdede med i. klasse. Kapitlet har især fokus på kerneområderne
Årsplan 08/9 Matematik. årgang TriX A Kapitel : Jubii I bogens første kapitel får eleverne mulighed for at repetere det faglige stof, som de arbejdede med i. klasse. Kapitlet har især fokus på kerneområderne
Matematik, basis. Undervisningen på basisniveau skal udvikle kursisternes matematikkompetencer til at følge undervisningen
 avu-bekendtgørelsen, august 2009 Matematik Basis, G-FED Matematik, basis 1. Identitet og formål 1.1 Identitet I matematik basis er arbejdet med forståelsen af de faglige begreber i centrum. Den opnåede
avu-bekendtgørelsen, august 2009 Matematik Basis, G-FED Matematik, basis 1. Identitet og formål 1.1 Identitet I matematik basis er arbejdet med forståelsen af de faglige begreber i centrum. Den opnåede
OM KAPITLET DIGITALE VÆRKTØJER. egne svar eller Elevernes egne forklaringer. I disse
 OM KPITLET I dette kapitel om digitale værktøjer skal eleverne arbejde med anvendelse og vurdering af forskellige digitale værktøjer, som kan bruges til at løse opgaver og matematiske problemstillinger.
OM KPITLET I dette kapitel om digitale værktøjer skal eleverne arbejde med anvendelse og vurdering af forskellige digitale værktøjer, som kan bruges til at løse opgaver og matematiske problemstillinger.
3 Algebra. Faglige mål. Variable og brøker. Den distributive lov. Potenser og rødder
 3 Algebra Faglige mål Kapitlet Algebra tager udgangspunkt i følgende faglige mål: Variable og brøker: kende enkle algebraiske udtryk med brøker og kunne behandle disse ved at finde fællesnævner. Den distributive
3 Algebra Faglige mål Kapitlet Algebra tager udgangspunkt i følgende faglige mål: Variable og brøker: kende enkle algebraiske udtryk med brøker og kunne behandle disse ved at finde fællesnævner. Den distributive
Fagplan for matematik på Bakkelandets Friskole
 Fagplan for matematik på Bakkelandets Friskole Formål for faget matematik: Formålet med undervisningen i matematik er, at eleverne bliver i stand til at forstå og anvende matematik i sammenhænge, der vedrører
Fagplan for matematik på Bakkelandets Friskole Formål for faget matematik: Formålet med undervisningen i matematik er, at eleverne bliver i stand til at forstå og anvende matematik i sammenhænge, der vedrører
Denne vejledning er kun til introperioden, det anbefales at du også læser lærervejledningen til hele forløbet!
 Vejledning til introperioden Denne vejledning er kun til introperioden, det anbefales at du også læser lærervejledningen til hele forløbet! Indholdsfortegnelse Vejledning til introperioden... 1 Indledning...
Vejledning til introperioden Denne vejledning er kun til introperioden, det anbefales at du også læser lærervejledningen til hele forløbet! Indholdsfortegnelse Vejledning til introperioden... 1 Indledning...
M A T E M A T I K FAGBESKRIVELSE FOR UNDERVISNING I MATEMATIK PÅ HARESKOVENS LILLESKOLE:
 M A T E M A T I K FAGBESKRIVELSE FOR UNDERVISNING I MATEMATIK PÅ HARESKOVENS LILLESKOLE: Udgangspunktet for Hareskovens Lilleskoles matematikundervisning er vores menneskesyn: det hele menneske. Der lægges
M A T E M A T I K FAGBESKRIVELSE FOR UNDERVISNING I MATEMATIK PÅ HARESKOVENS LILLESKOLE: Udgangspunktet for Hareskovens Lilleskoles matematikundervisning er vores menneskesyn: det hele menneske. Der lægges
Elevforudsætninger I forløbet indgår aktiviteter, der forudsætter, at eleverne kan læse enkle ord og kan samarbejde i grupper om en fælles opgave.
 Undersøgelse af de voksnes job Uddannelse og job; eksemplarisk forløb 0-3.klasse Faktaboks Kompetenceområde: Fra uddannelse til job Kompetencemål: Eleven kan beskrive forskellige uddannelser og job Færdigheds-
Undersøgelse af de voksnes job Uddannelse og job; eksemplarisk forløb 0-3.klasse Faktaboks Kompetenceområde: Fra uddannelse til job Kompetencemål: Eleven kan beskrive forskellige uddannelser og job Færdigheds-
Mål Kompetencer Matematiske arbejdsmåder. Problembehandling. Ræsonnement
 Forslag til årsplan for 9. klasse, matematik Udarbejdet af Susanne Nielson og Pernille Peiter revideret august 2011 af pædagogisk konsulent Rikke Teglskov 33-38 Rumgeometri Kende og anvende forskellige
Forslag til årsplan for 9. klasse, matematik Udarbejdet af Susanne Nielson og Pernille Peiter revideret august 2011 af pædagogisk konsulent Rikke Teglskov 33-38 Rumgeometri Kende og anvende forskellige
Årsplan 9. klasse matematik 2013-2014 Uge Emne Faglige mål Trinmål Materialer/ systemer 33 Årsprøven i matematik
 Årsplan 9. klasse matematik 2013-2014 33 Årsprøven i matematik Årsprøve og rettevejledledning 34-35 36 og løbe nde Talmængder og regnemetoder Mundtlig matematik 37 Fordybelses uge 38-39 Procent - Gennemgå
Årsplan 9. klasse matematik 2013-2014 33 Årsprøven i matematik Årsprøve og rettevejledledning 34-35 36 og løbe nde Talmængder og regnemetoder Mundtlig matematik 37 Fordybelses uge 38-39 Procent - Gennemgå
VisiRegn og folkeskolens skriftlige afgangsprøve i matematik, maj-juni 2000 Inge B. Larsen (ibl@dpu.dk)
 VisiRegn og folkeskolens skriftlige afgangsprøve i matematik, maj-juni 2000 Inge B. Larsen (ibl@dpu.dk) I det følgende gives et forslag til, hvordan en elev i 9. klasse med programmet VisiRegn til rådighed
VisiRegn og folkeskolens skriftlige afgangsprøve i matematik, maj-juni 2000 Inge B. Larsen (ibl@dpu.dk) I det følgende gives et forslag til, hvordan en elev i 9. klasse med programmet VisiRegn til rådighed
Jeg ville udfordre eleverne med en opgave, som ikke umiddelbar var målbar; Hvor høj er skolens flagstang?.
 Hvor høj er skolens flagstang? Undersøgelsesbaseret matematik 8.a på Ankermedets Skole i Skagen Marts 2012 Klassen deltog for anden gang i Fibonacci Projektet, og der var afsat ca. 8 lektioner, fordelt
Hvor høj er skolens flagstang? Undersøgelsesbaseret matematik 8.a på Ankermedets Skole i Skagen Marts 2012 Klassen deltog for anden gang i Fibonacci Projektet, og der var afsat ca. 8 lektioner, fordelt
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Institution Uddannelse Fag og niveau Lærer(e) Hold Termin hvori undervisningen afsluttes: Maj-juni, 11. Denne
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Institution Uddannelse Fag og niveau Lærer(e) Hold Termin hvori undervisningen afsluttes: Maj-juni, 11. Denne
Indhold. Indledning 7 Læsevejledning 9
 Indhold Indledning 7 Læsevejledning 9 1 Hvad er åbne opgaver? 13 2 Hvorfor arbejde med åbne opgaver? 17 3 Udfordringer i arbejdet med åbne opgaver 19 4 En ny didaktisk kontrakt 21 5 Et par eksempler 23
Indhold Indledning 7 Læsevejledning 9 1 Hvad er åbne opgaver? 13 2 Hvorfor arbejde med åbne opgaver? 17 3 Udfordringer i arbejdet med åbne opgaver 19 4 En ny didaktisk kontrakt 21 5 Et par eksempler 23
Dagens program. Velkommen og præsentation.
 Dagens program Velkommen og præsentation. Evt. udveksling af mailadresser. Forenklede Fælles Mål om geometri og dynamiske programmer. Screencast, hvordan og hvorfor? Opgave om polygoner i GeoGebra, løst
Dagens program Velkommen og præsentation. Evt. udveksling af mailadresser. Forenklede Fælles Mål om geometri og dynamiske programmer. Screencast, hvordan og hvorfor? Opgave om polygoner i GeoGebra, løst
Excel - begynderkursus
 Excel - begynderkursus 1. Skriv dit navn som undertekst på et Excel-ark Det er vigtigt når man arbejder med PC er på skolen at man kan få skrevet sit navn på hver eneste side som undertekst.gå ind under
Excel - begynderkursus 1. Skriv dit navn som undertekst på et Excel-ark Det er vigtigt når man arbejder med PC er på skolen at man kan få skrevet sit navn på hver eneste side som undertekst.gå ind under
MATEMATIK. GIDEONSKOLENS UNDERVISNINGSPLAN Oversigt over undervisning i forhold til trinmål og slutmål
 MATEMATIK GIDEONSKOLENS UNDERVISNINGSPLAN Oversigt over undervisning i forhold til trinmål og slutmål KOMMENTAR Vi har i det følgende foretaget en analyse og en sammenstilling af vore materialer til skriftlig
MATEMATIK GIDEONSKOLENS UNDERVISNINGSPLAN Oversigt over undervisning i forhold til trinmål og slutmål KOMMENTAR Vi har i det følgende foretaget en analyse og en sammenstilling af vore materialer til skriftlig
Spil og svar. Journal nr. 13.12.599. Et webbaseret værktøj udviklet af Programdatateket i Skive
 Journal nr. 13.12.599 Spil og svar Et webbaseret værktøj udviklet af Programdatateket i Skive E-mail: programdatateket@viauc.dk Web: http://www.programdatateket.dk Kolofon HVAL-vejledning Spil og svar
Journal nr. 13.12.599 Spil og svar Et webbaseret værktøj udviklet af Programdatateket i Skive E-mail: programdatateket@viauc.dk Web: http://www.programdatateket.dk Kolofon HVAL-vejledning Spil og svar
Tal og algebra Eleverne kan anvende rationelle tal og variable i beskrivelser og beregninger
 ÅRSPLAN MATEMATIK 4. KLASSE 2016/17 I de enkelte undervisningsforløb indgår der mål fra både de matematiske kompetencer og fra de 3 stofområder: Matematiske kompetencer handle med overblik i sammensatte
ÅRSPLAN MATEMATIK 4. KLASSE 2016/17 I de enkelte undervisningsforløb indgår der mål fra både de matematiske kompetencer og fra de 3 stofområder: Matematiske kompetencer handle med overblik i sammensatte
SÅDAN BRUGER DU REGNEARK INTRODUKTION
 SÅDAN BRUGER DU REGNEARK INTRODUKTION I vejledningen bruger vi det gratis program Calc fra OpenOffice som eksempel til at vise, hvordan man bruger nogle helt grundlæggende funktioner i regneark. De øvrige
SÅDAN BRUGER DU REGNEARK INTRODUKTION I vejledningen bruger vi det gratis program Calc fra OpenOffice som eksempel til at vise, hvordan man bruger nogle helt grundlæggende funktioner i regneark. De øvrige
Selam Friskole Fagplan for Matematik
 Selam Friskole Fagplan for Matematik Formål Formålet med undervisningen er, at eleverne udvikler matematiske kompetencer og opnår viden og kunnen således, at de bliver i stand til at begå sig hensigtsmæssigt
Selam Friskole Fagplan for Matematik Formål Formålet med undervisningen er, at eleverne udvikler matematiske kompetencer og opnår viden og kunnen således, at de bliver i stand til at begå sig hensigtsmæssigt
Arbejdsrum - hva' nyt er der egentlig i det?
 Arbejdsrum - hva' nyt er der egentlig i det? Et arbejdsrum har vel til alle tider været en form for installation, som kunne omkranse en undervisning? Et rum indeholder muligheder - f.eks. døre, som kan
Arbejdsrum - hva' nyt er der egentlig i det? Et arbejdsrum har vel til alle tider været en form for installation, som kunne omkranse en undervisning? Et rum indeholder muligheder - f.eks. døre, som kan
4. Snittets kædebrøksfremstilling og dets konvergenter
 Dette er den fjerde af fem artikler under den fælles overskrift Studier på grundlag af programmet SKALAGENERATOREN (forfatter: Jørgen Erichsen) 4. Snittets kædebrøksfremstilling og dets konvergenter Vi
Dette er den fjerde af fem artikler under den fælles overskrift Studier på grundlag af programmet SKALAGENERATOREN (forfatter: Jørgen Erichsen) 4. Snittets kædebrøksfremstilling og dets konvergenter Vi
Projekt 6.1 Rygtespredning - modellering af logistisk vækst
 Projekt 6.1 Rygtespredning - modellering af logistisk vækst (Projektet anvender værktøjsprogrammet TI Nspire) Alle de tilstedeværende i klassen tildeles et nummer, så med 28 elever i klassen uddeles numrene
Projekt 6.1 Rygtespredning - modellering af logistisk vækst (Projektet anvender værktøjsprogrammet TI Nspire) Alle de tilstedeværende i klassen tildeles et nummer, så med 28 elever i klassen uddeles numrene
Årsplan matematik 7.klasse 2014/2015
 Årsplan matematik 7.klasse 2014/2015 Emne Indhold Mål Tal og størrelser Arbejde med brøktal som repræsentationsform på omverdenssituationer. Fx i undersøgelser. Arbejde med forskellige typer af diagrammer.
Årsplan matematik 7.klasse 2014/2015 Emne Indhold Mål Tal og størrelser Arbejde med brøktal som repræsentationsform på omverdenssituationer. Fx i undersøgelser. Arbejde med forskellige typer af diagrammer.
Matematik A og Informationsteknologi B
 Matematik A og Informationsteknologi B Projektopgave 2 Eksponentielle modeller Benjamin Andreas Olander Christiansen Jens Werner Nielsen Klasse 2.4 6. december 2010 Vejledere: Jørn Christian Bendtsen og
Matematik A og Informationsteknologi B Projektopgave 2 Eksponentielle modeller Benjamin Andreas Olander Christiansen Jens Werner Nielsen Klasse 2.4 6. december 2010 Vejledere: Jørn Christian Bendtsen og
Mattip om. Statistik 2. Tilhørende kopier: Statistik 3, 4 og 5. Du skal lære om: Faglig læsning. Chance og risiko. Sandsynlighed
 Mattip om Statistik Du skal lære om: Faglig læsning Kan ikke Kan næsten Kan Chance og risiko Sandsynlighed Observationer, hyppighed og frekvens Gennemsnit Tilhørende kopier: Statistik, og mattip.dk Statistik
Mattip om Statistik Du skal lære om: Faglig læsning Kan ikke Kan næsten Kan Chance og risiko Sandsynlighed Observationer, hyppighed og frekvens Gennemsnit Tilhørende kopier: Statistik, og mattip.dk Statistik
Sprog billeder kortlink.dk/rudd
 Sprog billeder kortlink.dk/rudd Workshop beskrivelse I denne workshop vil vi kigge på strategier for ordblinde elever i matematikvanskeligheder samt vigtigheden af, at eleverne laver visuelle repræsentationer
Sprog billeder kortlink.dk/rudd Workshop beskrivelse I denne workshop vil vi kigge på strategier for ordblinde elever i matematikvanskeligheder samt vigtigheden af, at eleverne laver visuelle repræsentationer
Introduktion til EXCEL med øvelser
 Side 1 af 10 Introduktion til EXCEL med øvelser Du kender en almindelig regnemaskine, som kan være til stort hjælp, når man skal beregne resultater med store tal. Et regneark er en anden form for regnemaskine,
Side 1 af 10 Introduktion til EXCEL med øvelser Du kender en almindelig regnemaskine, som kan være til stort hjælp, når man skal beregne resultater med store tal. Et regneark er en anden form for regnemaskine,
Uddybning Undervisning form IT Færdigheds- og vidensmål
 Årsplan 2016/17 Fag Matematik 9.kl Gymnastikefterskolen Stevns Lærer Christina Permin Caspersen Årgang 2016/17 Undervisningen opbygges således, at eleverne igennem deres daglige arbejde med matematikken
Årsplan 2016/17 Fag Matematik 9.kl Gymnastikefterskolen Stevns Lærer Christina Permin Caspersen Årgang 2016/17 Undervisningen opbygges således, at eleverne igennem deres daglige arbejde med matematikken
Introduktion til mat i 4 klasse Vejle Privatskole 2013/14:
 Introduktion til mat i 4 klasse Vejle Privatskole 2013/14: Udgangspunktet bliver en blød screening, der skal synliggøre summen af elevernes standpunkt. Det betyder i realiteten, at der uddeles 4 klasses
Introduktion til mat i 4 klasse Vejle Privatskole 2013/14: Udgangspunktet bliver en blød screening, der skal synliggøre summen af elevernes standpunkt. Det betyder i realiteten, at der uddeles 4 klasses
Michael Jokil 11-05-2012
 HTX, RTG Det skrå kast Informationsteknologi B Michael Jokil 11-05-2012 Indholdsfortegnelse Indledning... 3 Teori... 3 Kravspecifikationer... 4 Design... 4 Funktionalitet... 4 Brugerflade... 4 Implementering...
HTX, RTG Det skrå kast Informationsteknologi B Michael Jokil 11-05-2012 Indholdsfortegnelse Indledning... 3 Teori... 3 Kravspecifikationer... 4 Design... 4 Funktionalitet... 4 Brugerflade... 4 Implementering...
statistik og sandsynlighed
 brikkerne til regning & matematik statistik og sandsynlighed trin 1 preben bernitt brikkerne statistik og sandsynlighed 1 1. udgave som E-bog ISBN: 978-87-92488-19-0 2004 by bernitt-matematik.dk Kopiering
brikkerne til regning & matematik statistik og sandsynlighed trin 1 preben bernitt brikkerne statistik og sandsynlighed 1 1. udgave som E-bog ISBN: 978-87-92488-19-0 2004 by bernitt-matematik.dk Kopiering
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Termin maj-juni 10/11 Institution Favrskov Gymnasium Uddannelse Fag og niveau Lærer Hold stx Matematik C Trille Hertz Quist 1.c mac Oversigt over gennemførte undervisningsforløb
Undervisningsbeskrivelse Termin maj-juni 10/11 Institution Favrskov Gymnasium Uddannelse Fag og niveau Lærer Hold stx Matematik C Trille Hertz Quist 1.c mac Oversigt over gennemførte undervisningsforløb
Årsplan matematik 1.klasse - skoleår 12/13- Ida Skov Andersen Med ret til ændringer og justeringer
 BASIS: Klassen består af 26 elever og der er afsat 5 ugentlige timer. Grundbog: Vi vil arbejde ud fra Matematrix 1A og 1B, de tilhørende kopisider + CD-rom, Rema samt evt. ekstraopgaver. Derudover vil
BASIS: Klassen består af 26 elever og der er afsat 5 ugentlige timer. Grundbog: Vi vil arbejde ud fra Matematrix 1A og 1B, de tilhørende kopisider + CD-rom, Rema samt evt. ekstraopgaver. Derudover vil
Vejledning til forløbet: Hvad er chancen?
 Vejledning til forløbet: Hvad er chancen? Denne lærervejledning beskriver i detaljer forløbets gennemførelse med fokus på lærerstilladsering og modellering. Beskrivelserne er blevet til på baggrund af
Vejledning til forløbet: Hvad er chancen? Denne lærervejledning beskriver i detaljer forløbets gennemførelse med fokus på lærerstilladsering og modellering. Beskrivelserne er blevet til på baggrund af
Rente, lån og opsparing
 Rente, lån og opsparing Simpel rente og sammensat rente... 107 Nogle vigtige begreber omkring lån og opsparing... 109 Serielån... 110 Annuitetslån... 111 Opsparing... 115 Rente, lån og opsparing Side 106
Rente, lån og opsparing Simpel rente og sammensat rente... 107 Nogle vigtige begreber omkring lån og opsparing... 109 Serielån... 110 Annuitetslån... 111 Opsparing... 115 Rente, lån og opsparing Side 106
Regnetest B: Praktisk regning. Træn og Test. Niveau: 9. klasse. Med brug af lommeregner
 Regnetest B: Praktisk regning Træn og Test Niveau: 9. klasse Med brug af lommeregner 1 INFA-Matematik: Informatik i matematikundervisningen Et delprojekt under INFA: Informatik i skolens fag Et forskningsprogram
Regnetest B: Praktisk regning Træn og Test Niveau: 9. klasse Med brug af lommeregner 1 INFA-Matematik: Informatik i matematikundervisningen Et delprojekt under INFA: Informatik i skolens fag Et forskningsprogram
Matematik i 5. klasse
 Matematik i 5. klasse Igen i år benytter vi os af Faktor i femte. Systemet indeholder en grundbog, hvortil der er supplerende materiale i form af kopiark, som er tilpasset de gennemgåede emner. Grundbogen
Matematik i 5. klasse Igen i år benytter vi os af Faktor i femte. Systemet indeholder en grundbog, hvortil der er supplerende materiale i form af kopiark, som er tilpasset de gennemgåede emner. Grundbogen
