Teoretiske Øvelser Mandag den 13. september 2010
|
|
|
- Adam Brodersen
- 7 år siden
- Visninger:
Transkript
1 Hans Kjeldsen 6. september 00 eoretiske Øvelser Mandag den 3. september 00 Computerøvelse nr. 3 Ligning (6.8) og (6.9) på side 83 i Lecture Notes angiver betingelserne for at konvektion finder sted i det indre af en stjerne. I nærværende computerøvelse skal vi undersøge denne betingelse for en simpel model af Solen. Det er tanken at øvelsen skal bruges som optakt til øvelse Ø-0. I det følgende ser vi på en simpel model af Solen, hvor ligningen for en ideal gas antages at gælde: k B μ m Vi antager at gassen i Solens indre er fuldstændigt ioniseret og at værdien af middel molekylvægten overalt i Solen er: μ 0,60 Vi antager desuden at opaciteten kan beskrives ved Kramers approksimation. I denne øvelse benyttes følgende udtryk: κ κ 4 0,4 0 cm / u g il undersøgelsen af (6.8) og (6.9) benytter vi nu følgende approksimation for temperaturen i Solens indre (som funktion af radius): 7 (,33 0 K , ( r / R) + 0,54 hvor r er afstanden fra Solen centrum og R er Solens radius. Side
2 For tætheden benyttes følgende approksimation (som er mindre præcis end den vi benytter for temperaturen): ( 0,77g / cm ( r / R) + 0,0 0, / + 0 (,44,0 ( r / R) ) g / cm C-3..: lot (eller log()) som funktion af r/r (vi benytter ovenstående approksimation for (). C-3.: Antag at L(/m( er konstant ud gennem Solen. Beregn og plot ud fra denne antagelse værdien af strålings-temperaturgradienten som funktion af r (benyt ligning 6.8). Hvor i Solen er der konvektion? Bestem dybden af den ydre konvektions zone. Sammenlign med figur 6.3. C-3.3.: Benyt nu approksimationen for ( til at beregne m( ved numerisk integration (benyt ligning 4.5). C-3.4.: Beregn massen af konvektionszonen i forhold til hele Solens masse, ved at benytte m( (fra C-3.3) og dybden af konvektionszonen som blev fundet i C-3.. Side
3 eoretiske Øvelser nr. 0 Fagpakke i Astronomi: Stjerner Vi skal i denne øvelse (som i computerøvelsen ovenfo regne på ligning (6.8) og via (6.9) undersøge betingelsen for konvektion i Solen. I C-3 benyttede vi MatLab til generelt at plotte strålings-temperaturgradienten som funktion af r, mens vi i denne opgave skal undersøge den samme problemstilling analytisk. I områder med adiabatisk konvektion er temperaturgradienten givet ved ad 0,4 Ø-0.: Vi antager at Solen består af en atmosfære og under dette ligger et område med adiabatisk konvektion, som vi antager begynder lige under atmosfæren. Vi antager at atmosfæren når % ind i Solen (til r/r 0,99) og at værdierne for temperatur og tryk (i cgs-enhede ved bunden af atmosfæren (og toppen af konvektionszonen) er: 4 4,0 0 K og 9,5 0 dyn / cm Vi antager at stoffet er fuldstændigt ioniseret (og at strålingstrykket negligeres). Bestem sammenhængen mellem og i konvektionszonen. Ø-0.: Vi antager nu (i lighed med computerøvelse C-3) at ligningen for en ideal gas gælder for stoffet i Solen: k B μ m Vi antager samtidigt at værdien af middel molekylvægten overalt i Solen er: μ 0,60 Desuden antages at opaciteten kan beskrives ved Kramers approksimation. I denne øvelse benyttes (som i C-3) følgende udtryk: κ κ 4 0,4 0 cm / u g Vi ønsker nu at bestemme værdierne for temperaturen, trykket og tætheden ved bunden af konvektionszonen i Solen, idet vi antager at værdien for L/m er konstant i konvektionszonen og er lig med L(sol)/M(sol). Side 3
4 Hint: Opskriv sammenhængen mellem og, og samt og i konvektionszonen. Indsæt nu værdierne for middel molekylvægten, opaciteten (som funktion af og ) og L/m i ligning (6.8) og bestem det sted hvor (6.9) går fra at være opfyldt til ikke længere at gælde. Dette sted udgør bunden af konvektionszonen. Ved indsættelse af () i (6.8) er den eneste ubekendte som derfor kan bestemmes under antagelse af (6.9). Bestem herefter og ud fra. Ø-0.3: Det er nu muligt at bestemme den brøkdel af Solens radius som konvektionszonen strækker sig over. Idéen er at benytte relationen mellem tætheden () og trykket () i konvektionszonen i sammenhæng med ligningen for hydrostatisk ligevægt. Herved er det muligt at opstille følgende ligning, hvor konstanten (k) er bestem ud fra værdierne i Ø-0. og Ø-0.: d dr k r Vis (ved at kombinere () med ligningen for hydrostatisk ligevægt) at ovenstående ligning er korrekt i konvektionszonen og bestem værdien af k. Vis nu at denne ligning har følgende løsning: 3/5 5 / 5 c + k r hvor c er en ny konstant. Benyt værdien for trykket i toppen af konvektionszonen (ved r/r 0,99) til at bestemme c. Indsæt herefter værdien for trykket i bunden af konvektionszonen og find r/r for konvektionszonens bund. Sammenlign resultatet med det vi fandt i øvelse C-3 og det vi finder ved aflæsning på figur 6.3. Side 4
5 eoretiske Øvelser nr. Fagpakke i Astronomi: Stjerner Den dynamiske tidsskala for Solen er omkring 30 millioner år og udtrykker bl.a. den tid energien er om at bevæge sig fra centrum af Solen til overfladen. Det er i forlængelse af dette, naturligvis interessant at undersøge om energistrømmen ud gennem Solen sker med konstant hastighed, eller om der er steder i Solen hvor energien transporteres væsentligt hurtigere. Dette vil vi undersøge i denne øvelse. Ø-.: Den termiske tidsskala (Kelvin-Helmholtz tiden) er givet ved: t KH GM RL S U L tot S Vis at vi kan opstille et lignende udtryk for den tid det tager energien at strømme gennem kugleskallen dr i afstanden r fra stjernens centrum, hvor u( er den indre energi pr. enhedsvolumen og L( er total luminositeten dt 4 r u( dr π L( Benyt sammenhængen mellem u og til at opstille et udtryk for hastigheden dr/dt som funktion af r, ( og L( og vis at for Solen bliver denne energistrømningshastighed (i cgs-enhede: v Energi dyn cm s L / L 0 S 4, 0 ( r / R) Ø-.: Benyt tabellen herunder til at beregne hastigheden i forskellige dybder af Solen. Værdierne i tabellen er hentet fra tabel. (side 47 i Lecture Notes). r/r L/LS log( cm²/dyn) 0,0 0,938 6,637 0,30 0,999 6,04 0,40,000 5,433 0,50,000 4,86 0,60,000 4,33 0,70,000 3,80 0,80,000 3,3 0,90,000,38 0,99,000 9,37 0,999,000 6,063 Side 5
6 eoretiske Øvelser nr. I følgende opgave skal en sollignende stjerne undersøges. å de to figurer herunder ses Solens temperatur og tryk som funktion af afstanden fra centrum. De afsatte værdier er identiske med værdierne i tabel. i Lecture Notes on Stellar Structure and Evolution. Den fuldtoptrukne kurve er en analytisk beskrivelse af temperatur- og trykprofilen, som i store dele af Solens indre stemmer godt overens med den model, der er vist i figurerne. Nær centrum af den stjernemodel, som er vist ovenfor, kan den analytiske beskrivelse opskrives som ( ( C C e e r / R 8r / R Hvor C og C er hhv. den centrale temperatur og det central tryk. R er stjernens radius, og r er afstanden fra centrum. Ø-. Bestem værdien for temperaturgradienten d ln d ln d dr d dr nær stjernens centrum. og undersøg om energien nær den pågældende stjernes centrum transporteres ved stråling eller ved konvektion. Side 6
7 Det antages, at idealgasligningen kan benyttes til at beskrive sammenhængen mellem tryk, tæthed og temperatur i stjernens indre. Ø-. Vis, at der i centrum af denne stjerne (hvis vi ser bort fra variationen i middelmolekylvægten (μ)) gælder ( hvor C er den centrale densitet. r e 7r / R ) C eoretiske Øvelser nr. 3 Middel vejlængden for en foton i det indre af en stjerne er givet ved ligning (5.3): λ n σ R κ Beregn hvor langt en foton bevæger sig (i middel) i forskellige afstande fra Solens centrum. Benyt værdierne i tabellen herunder (fra tabel.) til beregningen af middel vejlængden. r/r log( cm³/g) κ g/cm² 0,00,88,4 0,0,94,54 0,0,543, 0,40 0,595 5,0 0,60-0,95,54 0,70-0,68 9,6 0,80 -,038 50,9 0,90 -, ,95 -,0 00 0,98 -, ,99-3, ,996-4, ,999-5, Side 7
Teoretiske Øvelser Mandag den 30. august 2010
 Hans Kjeldsen hans@phys.au.dk 3. august 010 Teoretiske Øvelser Mandag den 30. august 010 Computerøvelse (brug MatLab) Det er tanken at I - i forbindelse med hver øvelsesgang - får en opgave som kræver
Hans Kjeldsen hans@phys.au.dk 3. august 010 Teoretiske Øvelser Mandag den 30. august 010 Computerøvelse (brug MatLab) Det er tanken at I - i forbindelse med hver øvelsesgang - får en opgave som kræver
Kvalifikationsbeskrivelse
 Astrofysik II Kvalifikationsbeskrivelse Kursets formål er at give deltagerne indsigt i centrale aspekter af astrofysikken. Der lægges vægt på en detaljeret beskrivelse af en række specifikke egenskaber
Astrofysik II Kvalifikationsbeskrivelse Kursets formål er at give deltagerne indsigt i centrale aspekter af astrofysikken. Der lægges vægt på en detaljeret beskrivelse af en række specifikke egenskaber
Teoretiske Øvelser Mandag den 28. september 2009
 Hans Kjeldsen hans@phys.au.dk 21. september 2009 Teoretiske Øvelser Mandag den 28. september 2009 Øvelse nr. 10: Solen vor nærmeste stjerne Solens masse-lysstyrkeforhold meget stort. Det vil sige, at der
Hans Kjeldsen hans@phys.au.dk 21. september 2009 Teoretiske Øvelser Mandag den 28. september 2009 Øvelse nr. 10: Solen vor nærmeste stjerne Solens masse-lysstyrkeforhold meget stort. Det vil sige, at der
Teoretiske Øvelser Mandag den 31. august 2009
 agpakke i Astronomi: Introduktion til Astronomi Hans Kjeldsen hans@phys.au.dk 3. august 009 Teoretiske Øvelser Mandag den 31. august 009 Øvelse nr. 1: Keplers og Newtons love Keplers 3. lov giver en sammenhæng
agpakke i Astronomi: Introduktion til Astronomi Hans Kjeldsen hans@phys.au.dk 3. august 009 Teoretiske Øvelser Mandag den 31. august 009 Øvelse nr. 1: Keplers og Newtons love Keplers 3. lov giver en sammenhæng
1. Beregn sandsynligheden for at samtlige 9 klatter lander i felter med lige numre.
 NATURVIDENSKABELIG GRUNDUDDANNELSE Københavns Universitet, 6. april, 2011, Skriftlig prøve Fysik 3 / Termodynamik Benyttelse af medbragt litteratur, noter, lommeregner og computer uden internetadgang er
NATURVIDENSKABELIG GRUNDUDDANNELSE Københavns Universitet, 6. april, 2011, Skriftlig prøve Fysik 3 / Termodynamik Benyttelse af medbragt litteratur, noter, lommeregner og computer uden internetadgang er
MODUL 1-2: ELEKTROMAGNETISK STRÅLING
 MODUL 1-2: ELEKTROMAGNETISK STRÅLING MODUL 1 - ELEKTROMAGNETISKE BØLGER I 1. modul skal I lære noget omkring elektromagnetisk stråling (EM- stråling). I skal lære noget om synligt lys, IR- stråling, UV-
MODUL 1-2: ELEKTROMAGNETISK STRÅLING MODUL 1 - ELEKTROMAGNETISKE BØLGER I 1. modul skal I lære noget omkring elektromagnetisk stråling (EM- stråling). I skal lære noget om synligt lys, IR- stråling, UV-
Bitten Gullberg. Solen. Niels Bohr Institutet
 Solen Niels Bohr Institutet 1 Sol data Gennemsnits afstanden til Jorden Lysets rejse tid til Jorden 1 AU = 149 598 000 km 8.32 min Radius 696 000 km = 109 Jord-radier Masse 1.9891 10 30 kg = 3.33 10 5
Solen Niels Bohr Institutet 1 Sol data Gennemsnits afstanden til Jorden Lysets rejse tid til Jorden 1 AU = 149 598 000 km 8.32 min Radius 696 000 km = 109 Jord-radier Masse 1.9891 10 30 kg = 3.33 10 5
Projektopgave Observationer af stjerneskælv
 Projektopgave Observationer af stjerneskælv Af: Mathias Brønd Christensen (20073504), Kristian Jerslev (20072494), Kristian Mads Egeris Nielsen (20072868) Indhold Formål...3 Teori...3 Hvorfor opstår der
Projektopgave Observationer af stjerneskælv Af: Mathias Brønd Christensen (20073504), Kristian Jerslev (20072494), Kristian Mads Egeris Nielsen (20072868) Indhold Formål...3 Teori...3 Hvorfor opstår der
STJERNER OG STJERNEMODELLER
 STJERNER OG STJERNEMODELLER JAKOB RØRSTED MOSUMGAARD, PHD STUDERENDE SILKEBORG HØJSKOLE, AUGUST HVAD ER STJERNER? Kilde: https://dk.pinterest.com/unforgettable28/night-sky/ HVAD ER STJERNER? OG HVORFOR
STJERNER OG STJERNEMODELLER JAKOB RØRSTED MOSUMGAARD, PHD STUDERENDE SILKEBORG HØJSKOLE, AUGUST HVAD ER STJERNER? Kilde: https://dk.pinterest.com/unforgettable28/night-sky/ HVAD ER STJERNER? OG HVORFOR
Udledning af den barometriske højdeformel. - Beregning af højde vha. trykmåling. af Jens Lindballe, Silkeborg Gymnasium
 s.1/5 For at kunne bestemme cansatsondens højde må vi se på, hvorledes tryk og højde hænger sammen, når vi bevæger os opad i vores atmosfære. I flere fysikbøger kan man læse om den Barometriske højdeformel,
s.1/5 For at kunne bestemme cansatsondens højde må vi se på, hvorledes tryk og højde hænger sammen, når vi bevæger os opad i vores atmosfære. I flere fysikbøger kan man læse om den Barometriske højdeformel,
Formelsamling i astronomi. Februar 2016
 Formelsamling i astronomi. Februar 016 Formelsamlingen er ikke komplet det bliver den nok aldrig. Men måske kan alligevel være til en smule gavn. Sammenhæng mellem forskellige tidsenheder Jordens sideriske
Formelsamling i astronomi. Februar 016 Formelsamlingen er ikke komplet det bliver den nok aldrig. Men måske kan alligevel være til en smule gavn. Sammenhæng mellem forskellige tidsenheder Jordens sideriske
DETTE OPGAVESÆT INDEHOLDER 5 OPGAVER MED IALT 11 SPØRGSMÅL. VED BEDØMMELSEN VÆGTES DE ENKELTE
 DETTE OPGAVESÆT INDEHOLDER 5 OPGAVER MED IALT 11 SPØRGSMÅL. VED BEDØMMELSEN VÆGTES DE ENKELTE SPØRGSMÅL ENS. SPØRGSMÅLENE I DE ENKELTE OPGAVER KAN LØSES UAFHÆNGIGT AF HINANDEN. 1 Opgave 1 En massiv metalkugle
DETTE OPGAVESÆT INDEHOLDER 5 OPGAVER MED IALT 11 SPØRGSMÅL. VED BEDØMMELSEN VÆGTES DE ENKELTE SPØRGSMÅL ENS. SPØRGSMÅLENE I DE ENKELTE OPGAVER KAN LØSES UAFHÆNGIGT AF HINANDEN. 1 Opgave 1 En massiv metalkugle
Reaktionskinetik - 1 Baggrund. lineære og ikke-lineære differentialligninger. Køreplan
 Reaktionskinetik - lineære og ikke-lineære differentialligninger Køreplan 1 Baggrund På 2. eller 4. semester møder kemi/bioteknologi studerende faget Indledende Fysisk Kemi (26201/26202). Her behandles
Reaktionskinetik - lineære og ikke-lineære differentialligninger Køreplan 1 Baggrund På 2. eller 4. semester møder kemi/bioteknologi studerende faget Indledende Fysisk Kemi (26201/26202). Her behandles
Differentiation af sammensatte funktioner
 1/7 Differentiation af sammensatte funktioner - Fra www.borgeleo.dk En sammensat funktion af den variable x er en funktion, vor x først indsættes i den såkaldte indre funktion. Resultatet fra den indre
1/7 Differentiation af sammensatte funktioner - Fra www.borgeleo.dk En sammensat funktion af den variable x er en funktion, vor x først indsættes i den såkaldte indre funktion. Resultatet fra den indre
Stjerneudvikling, grundstofsyntese og supernovaer. Jørgen Christensen-Dalsgaard Dansk AsteroSeismologi Center Institut for Fysik og Astronomi
 Stjerneudvikling, grundstofsyntese og supernovaer Jørgen Christensen-Dalsgaard Dansk AsteroSeismologi Center Institut for Fysik og Astronomi SN 1994D Starmodels ifølge GOOGLE Tromsø Astronomiforening Stjernebrettingskomiteen
Stjerneudvikling, grundstofsyntese og supernovaer Jørgen Christensen-Dalsgaard Dansk AsteroSeismologi Center Institut for Fysik og Astronomi SN 1994D Starmodels ifølge GOOGLE Tromsø Astronomiforening Stjernebrettingskomiteen
Skråplan. Esben Bork Hansen Amanda Larssen Martin Sven Qvistgaard Christensen. 2. december 2008
 Skråplan Esben Bork Hansen Amanda Larssen Martin Sven Qvistgaard Christensen 2. december 2008 1 Indhold 1 Formål 3 2 Forsøg 3 2.1 materialer............................... 3 2.2 Opstilling...............................
Skråplan Esben Bork Hansen Amanda Larssen Martin Sven Qvistgaard Christensen 2. december 2008 1 Indhold 1 Formål 3 2 Forsøg 3 2.1 materialer............................... 3 2.2 Opstilling...............................
Formelsamling i astronomi. November 2015.
 Formelsamling i astronomi. November 015. Formelsamlingen er ikke komplet det bliver den nok aldrig. Men måske kan alligevel være til en smule gavn. Sammenhæng mellem forskellige tidsenheder: Jordens sideriske
Formelsamling i astronomi. November 015. Formelsamlingen er ikke komplet det bliver den nok aldrig. Men måske kan alligevel være til en smule gavn. Sammenhæng mellem forskellige tidsenheder: Jordens sideriske
MODERNE KOSMOLOGI STEEN HANNESTAD, INSTITUT FOR FYSIK OG ASTRONOMI
 MODERNE KOSMOLOGI STEEN HANNESTAD, INSTITUT FOR FYSIK OG ASTRONOMI T (K) t (år) 10 30 10-44 sekunder 1 mia. 10 sekunder 3000 300.000 50 1 mia. He, D, Li Planck tiden Dannelse af grundstoffer Baggrundsstråling
MODERNE KOSMOLOGI STEEN HANNESTAD, INSTITUT FOR FYSIK OG ASTRONOMI T (K) t (år) 10 30 10-44 sekunder 1 mia. 10 sekunder 3000 300.000 50 1 mia. He, D, Li Planck tiden Dannelse af grundstoffer Baggrundsstråling
Udledning af Keplers love
 Udledning af Keplers love Kristian Jerslev 8. december 009 Resumé Her præsenteres en udledning af Keplers tre love ud fra Newtonsk tyngdekraft. Begyndende med en analyse af et to-legeme problem vil jeg
Udledning af Keplers love Kristian Jerslev 8. december 009 Resumé Her præsenteres en udledning af Keplers tre love ud fra Newtonsk tyngdekraft. Begyndende med en analyse af et to-legeme problem vil jeg
Resumé fra sidst. Stjernerne i bulen er mere metalrige end i skiven
 Galakser 2014 F3 1 Resumé fra sidst Mælkevejen består grundlæggende af en skive, en bule og en halo. Solen befinder sig sammen med spiralarmene i skiven i en afstand af ca. 8.0 kpc fra centrum af galaksen.
Galakser 2014 F3 1 Resumé fra sidst Mælkevejen består grundlæggende af en skive, en bule og en halo. Solen befinder sig sammen med spiralarmene i skiven i en afstand af ca. 8.0 kpc fra centrum af galaksen.
Termodynamik. Esben Mølgaard. 5. april N! (N t)!t! Når to systemer sættes sammen bliver fordelingsfunktionen for det samlede system
 Termodynamik Esben Mølgaard 5. april 2006 1 Statistik Hvis man har N elementer hvoraf t er defekte, eller N elementer i to grupper hvor forskydningen fra 50/50 (spin excess) er 2s, vil antallet af mulige
Termodynamik Esben Mølgaard 5. april 2006 1 Statistik Hvis man har N elementer hvoraf t er defekte, eller N elementer i to grupper hvor forskydningen fra 50/50 (spin excess) er 2s, vil antallet af mulige
Differential- ligninger
 Differential- ligninger Et oplæg 2007 Karsten Juul Dette hæfte er tænkt brugt som et oplæg der kan gennemgås før man går i gang med en lærebogs fremstilling af emnet differentialligninger Læreren skal
Differential- ligninger Et oplæg 2007 Karsten Juul Dette hæfte er tænkt brugt som et oplæg der kan gennemgås før man går i gang med en lærebogs fremstilling af emnet differentialligninger Læreren skal
DETTE OPGAVESÆT INDEHOLDER 6 OPGAVER MED IALT 11 SPØRGSMÅL. VED BEDØMMELSEN VÆGTES DE ENKELTE
 DETTE OPGAVESÆT INDEHOLDER 6 OPGAVER MED IALT 11 SPØRGSMÅL. VED BEDØMMELSEN VÆGTES DE ENKELTE SPØRGSMÅL ENS. SPØRGSMÅLENE I DE ENKELTE OPGAVER KAN LØSES UAFHÆNGIGT AF HINANDEN. 1 Opgave 1 En cylinderkapacitor
DETTE OPGAVESÆT INDEHOLDER 6 OPGAVER MED IALT 11 SPØRGSMÅL. VED BEDØMMELSEN VÆGTES DE ENKELTE SPØRGSMÅL ENS. SPØRGSMÅLENE I DE ENKELTE OPGAVER KAN LØSES UAFHÆNGIGT AF HINANDEN. 1 Opgave 1 En cylinderkapacitor
MATEMATIK A-NIVEAU. Anders Jørgensen & Mark Kddafi. Vejledende eksempler på eksamensopgaver og eksamensopgaver i matematik, 2012.
 MATEMATIK A-NIVEAU Vejledende eksempler på eksamensopgaver og eksamensopgaver i matematik, 2012 Kapitel 6 Differentialregning og modellering med f 2016 MATEMATIK A-NIVEAU Vejledende eksempler på eksamensopgaver
MATEMATIK A-NIVEAU Vejledende eksempler på eksamensopgaver og eksamensopgaver i matematik, 2012 Kapitel 6 Differentialregning og modellering med f 2016 MATEMATIK A-NIVEAU Vejledende eksempler på eksamensopgaver
Solindstråling på vandret flade Beregningsmodel
 Solindstråling på vandret flade Beregningsmodel Formål Når solens stråler rammer en vandret flade på en klar dag, består indstrålingen af diffus stråling fra himlen og skyer såvel som solens direkte stråler.
Solindstråling på vandret flade Beregningsmodel Formål Når solens stråler rammer en vandret flade på en klar dag, består indstrålingen af diffus stråling fra himlen og skyer såvel som solens direkte stråler.
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin December 2016. Institution KØBENHAVN SYD HF & VUC Uddannelse Fag og niveau Lærer(e) Hold GSK-hold Fysik B
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin December 2016. Institution KØBENHAVN SYD HF & VUC Uddannelse Fag og niveau Lærer(e) Hold GSK-hold Fysik B
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin December-januar 2015-2016 Institution VUC Hvidovre-Amager Uddannelse Fag og niveau Lærer(e) Hold GSK-hold
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin December-januar 2015-2016 Institution VUC Hvidovre-Amager Uddannelse Fag og niveau Lærer(e) Hold GSK-hold
Drivhuseffekten. Hvordan styres Jordens klima?
 Drivhuseffekten Hvordan styres Jordens klima? Jordens atmosfære og lyset Drivhusgasser Et molekyle skal indeholde mindst 3 atomer for at være en drivhusgas. Eksempler: CO2 (Kuldioxid.) H2O (Vanddamp.)
Drivhuseffekten Hvordan styres Jordens klima? Jordens atmosfære og lyset Drivhusgasser Et molekyle skal indeholde mindst 3 atomer for at være en drivhusgas. Eksempler: CO2 (Kuldioxid.) H2O (Vanddamp.)
Newtons love - bevægelsesligninger - øvelser. John V Petersen
 Newtons love - bevægelsesligninger - øvelser John V Petersen Newtons love 2016 John V Petersen art-science-soul Indhold 1. Indledning og Newtons love... 4 2. Integration af Newtons 2. lov og bevægelsesligningerne...
Newtons love - bevægelsesligninger - øvelser John V Petersen Newtons love 2016 John V Petersen art-science-soul Indhold 1. Indledning og Newtons love... 4 2. Integration af Newtons 2. lov og bevægelsesligningerne...
Mini SRP. Afkøling. Klasse 2.4. Navn: Jacob Pihlkjær Hjortshøj, Jonatan Geysner Hvidberg og Kevin Høst Husted
 Mini SRP Afkøling Klasse 2.4 Navn: Jacob Pihlkjær Lærere: Jørn Christian Bendtsen og Karl G Bjarnason Roskilde Tekniske Gymnasium SO Matematik A og Informations teknologi B Dato 31/3/2014 Forord Under
Mini SRP Afkøling Klasse 2.4 Navn: Jacob Pihlkjær Lærere: Jørn Christian Bendtsen og Karl G Bjarnason Roskilde Tekniske Gymnasium SO Matematik A og Informations teknologi B Dato 31/3/2014 Forord Under
SONG Stellar Observations Network Group
 SONG Stellar Observations Network Group Frank Grundahl, IFA, 23. Januar - 2009 SONG gruppen: Jørgen Christensen Dalsgaard (PI), IFA Per Kjærgaard Rasmussen (PM), NBI Frank Grundahl (PS), IFA Hans Kjeldsen,
SONG Stellar Observations Network Group Frank Grundahl, IFA, 23. Januar - 2009 SONG gruppen: Jørgen Christensen Dalsgaard (PI), IFA Per Kjærgaard Rasmussen (PM), NBI Frank Grundahl (PS), IFA Hans Kjeldsen,
Fysik 2 - Den Harmoniske Oscillator
 Fysik 2 - Den Harmoniske Oscillator Esben Bork Hansen, Amanda Larssen, Martin Qvistgaard Christensen, Maria Cavallius 5. januar 2009 Indhold 1 Formål 1 2 Forsøget 2 3 Resultater 3 4 Teori 4 4.1 simpel
Fysik 2 - Den Harmoniske Oscillator Esben Bork Hansen, Amanda Larssen, Martin Qvistgaard Christensen, Maria Cavallius 5. januar 2009 Indhold 1 Formål 1 2 Forsøget 2 3 Resultater 3 4 Teori 4 4.1 simpel
Impuls og kinetisk energi
 Impuls og kinetisk energi Peter Hoberg, Anton Bundgård, and Peter Kongstad Hold Mix 1 (Dated: 7. oktober 2015) 201405192@post.au.dk 201407987@post.au.dk 201407911@post.au.dk 2 I. INDLEDNING I denne øvelse
Impuls og kinetisk energi Peter Hoberg, Anton Bundgård, and Peter Kongstad Hold Mix 1 (Dated: 7. oktober 2015) 201405192@post.au.dk 201407987@post.au.dk 201407911@post.au.dk 2 I. INDLEDNING I denne øvelse
Danmarks Tekniske Universitet
 Danmarks Tekniske Universitet Side af 7 Skriftlig prøve, tirsdag den 6. december, 008, kl. 9:00-3:00 Kursus navn: ysik Kursus nr. 00 Tilladte hjælpemidler: Alle hjælpemidler er tilladt. "Vægtning": Besvarelsen
Danmarks Tekniske Universitet Side af 7 Skriftlig prøve, tirsdag den 6. december, 008, kl. 9:00-3:00 Kursus navn: ysik Kursus nr. 00 Tilladte hjælpemidler: Alle hjælpemidler er tilladt. "Vægtning": Besvarelsen
Eksamen i Matematik F2 d. 19. juni Opgave 2. Svar. Korte svar (ikke fuldstændige)
 Eksamen i Matematik F2 d. 9. juni 28 Korte svar (ikke fuldstændige Opgave Find realdelen, Re z, og imaginærdelen, Im z, for følgende værdier af z, a z = 2 i b z = i i c z = ln( + i Find realdelen, Re z,
Eksamen i Matematik F2 d. 9. juni 28 Korte svar (ikke fuldstændige Opgave Find realdelen, Re z, og imaginærdelen, Im z, for følgende værdier af z, a z = 2 i b z = i i c z = ln( + i Find realdelen, Re z,
Dronninglund Gymnasium Fysik skriftlig eksamen 27. maj 2011
 Opgave 1. Solfanger Det viste anlæg er et ventilationssystem, som opvarmer luft udefra og blæser den ind i huset. Luften opvarmes idet, den strømmer langs en sort metalplade, der er opvarmet af solstrålingen.
Opgave 1. Solfanger Det viste anlæg er et ventilationssystem, som opvarmer luft udefra og blæser den ind i huset. Luften opvarmes idet, den strømmer langs en sort metalplade, der er opvarmet af solstrålingen.
Besvarelser til Calculus Ordinær Eksamen - 5. Januar 2018
 Besvarelser til Calculus Ordinær Eksamen - 5. Januar 18 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 5. Januar 18 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
1. Bevægelse med luftmodstand
 Programmering i TI nspire. Michael A. D. Møller. Marts 2018. side 1/7 1. Bevægelse med luftmodstand Formål a) At lære at programmere i Basic. b) At bestemme stedbevægelsen for et legeme, der bevæger sig
Programmering i TI nspire. Michael A. D. Møller. Marts 2018. side 1/7 1. Bevægelse med luftmodstand Formål a) At lære at programmere i Basic. b) At bestemme stedbevægelsen for et legeme, der bevæger sig
Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 2016
 Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Eksamen i fysik 2016
 Eksamen i fysik 2016 NB: Jeg gør brug af DATABOG fysik kemi, 11. udgave, 4. oplag & Fysik i overblik, 1. oplag. Opgave 1 Proptrækker Vi kender vinens volumen og masse. Enheden liter omregnes til kubikmeter.
Eksamen i fysik 2016 NB: Jeg gør brug af DATABOG fysik kemi, 11. udgave, 4. oplag & Fysik i overblik, 1. oplag. Opgave 1 Proptrækker Vi kender vinens volumen og masse. Enheden liter omregnes til kubikmeter.
Strålingsintensitet I = Hvor I = intensiteten PS = effekten hvormed strålingen rammer en given flade S AS = arealet af fladen
 Strålingsintensitet Skal det fx afgøres hvor skadelig en given radioaktiv stråling er, er det ikke i sig selv relevant at kende aktiviteten af kilden til strålingen. Kilden kan være langt væk eller indkapslet,
Strålingsintensitet Skal det fx afgøres hvor skadelig en given radioaktiv stråling er, er det ikke i sig selv relevant at kende aktiviteten af kilden til strålingen. Kilden kan være langt væk eller indkapslet,
Aalborg Universitet. Skriftlig eksamen i Grundlæggende Mekanik og Termodynamik. Torsdag d. 7. august 2014 kl
 Aalborg Universitet Skriftlig eksamen i Grundlæggende Mekanik og Termodynamik Torsdag d. 7. august 2014 kl. 9 00-13 00 Ved bedømmelsen vil der blive lagt vægt på argumentationen (som bør være kort og præcis),
Aalborg Universitet Skriftlig eksamen i Grundlæggende Mekanik og Termodynamik Torsdag d. 7. august 2014 kl. 9 00-13 00 Ved bedømmelsen vil der blive lagt vægt på argumentationen (som bør være kort og præcis),
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Maj-juni 2015 Institution VUC Hvidovre-Amager Uddannelse Fag og niveau Lærer(e) Hold GSK-hold Fysik 0-B efter
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Maj-juni 2015 Institution VUC Hvidovre-Amager Uddannelse Fag og niveau Lærer(e) Hold GSK-hold Fysik 0-B efter
Danmarks Tekniske Universitet
 Danmarks Tekniske Universitet Side 1 af 8 sider Skriftlig prøve, den 24. maj 2005 Kursus navn: Fysik 1 Kursus nr.: 10022 Tilladte hjælpemidler: Alle hjælpemidler tilladt. "Vægtning": Besvarelsen vægtes
Danmarks Tekniske Universitet Side 1 af 8 sider Skriftlig prøve, den 24. maj 2005 Kursus navn: Fysik 1 Kursus nr.: 10022 Tilladte hjælpemidler: Alle hjælpemidler tilladt. "Vægtning": Besvarelsen vægtes
Introduktion til Astronomi
 Introduktion til Astronomi Hans Kjeldsen Kontor: 1520-230 Email: hans@phys.au.dk Tlf.: 8942 3779 Introduktion til Astronomi 1 Introduktion til Astronomi Studieretning Astronomi 3. år Valgfag Relativistisk
Introduktion til Astronomi Hans Kjeldsen Kontor: 1520-230 Email: hans@phys.au.dk Tlf.: 8942 3779 Introduktion til Astronomi 1 Introduktion til Astronomi Studieretning Astronomi 3. år Valgfag Relativistisk
Røntgenspektrum fra anode
 Røntgenspektrum fra anode Elisabeth Ulrikkeholm June 24, 2016 1 Formål I denne øvelse skal I karakterisere et røntgenpektrum fra en wolframanode eller en molybdænanode, og herunder bestemme energien af
Røntgenspektrum fra anode Elisabeth Ulrikkeholm June 24, 2016 1 Formål I denne øvelse skal I karakterisere et røntgenpektrum fra en wolframanode eller en molybdænanode, og herunder bestemme energien af
Aalborg Universitet. Skriftlig eksamen i Grundlæggende Mekanik og Termodynamik. Torsdag d. 9. juni 2011 kl
 Aalborg Universitet Skriftlig eksamen i Grundlæggende Mekanik og Termodynamik Torsdag d. 9. juni 2011 kl. 9 00-13 00 Ved bedømmelsen vil der blive lagt vægt på argumentationen (som bør være kort og præcis),
Aalborg Universitet Skriftlig eksamen i Grundlæggende Mekanik og Termodynamik Torsdag d. 9. juni 2011 kl. 9 00-13 00 Ved bedømmelsen vil der blive lagt vægt på argumentationen (som bør være kort og præcis),
Bernoulli s lov. Med eksempler fra Hydrodynamik og aerodynamik. Indhold
 Bernoulli s lov Med eksempler fra Indhold 1. Indledning...1 2. Strømning i væsker...1 3. Bernoulli s lov...2 4. Tømning af en beholder via en hane i bunden...4 Ole Witt-Hansen Køge Gymnasium 2008 Bernoulli
Bernoulli s lov Med eksempler fra Indhold 1. Indledning...1 2. Strømning i væsker...1 3. Bernoulli s lov...2 4. Tømning af en beholder via en hane i bunden...4 Ole Witt-Hansen Køge Gymnasium 2008 Bernoulli
Aalborg Universitet. Skriftlig eksamen i Grundlæggende Mekanik og Termodynamik. Tirsdag d. 11. august 2015 kl
 Aalborg Universitet Skriftlig eksamen i Grundlæggende Mekanik og Termodynamik Tirsdag d. 11. august 2015 kl. 9 00-13 00 Ved bedømmelsen vil der blive lagt vægt på argumentationen (som bør være kort og
Aalborg Universitet Skriftlig eksamen i Grundlæggende Mekanik og Termodynamik Tirsdag d. 11. august 2015 kl. 9 00-13 00 Ved bedømmelsen vil der blive lagt vægt på argumentationen (som bør være kort og
Lineære sammenhænge. Udgave 2. 2009 Karsten Juul
 Lineære sammenhænge Udgave 2 y = 0,5x 2,5 2009 Karsten Juul Dette hæfte er en fortsættelse af hæftet "Variabelsammenhænge, 2. udgave 2009". Indhold 1. Lineære sammenhænge, ligning og graf... 1 2. Lineær
Lineære sammenhænge Udgave 2 y = 0,5x 2,5 2009 Karsten Juul Dette hæfte er en fortsættelse af hæftet "Variabelsammenhænge, 2. udgave 2009". Indhold 1. Lineære sammenhænge, ligning og graf... 1 2. Lineær
Opgave 1. (a) Bestem de to kapacitorers kapacitanser C 1 og C 2.
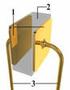 2 Opgave 1 I første del af denne opgave skal kapacitansen af to kapacitorer bestemmes. Den ene kapacitor er konstrueret af to tynde koaksiale cylinderskaller af metal. Den inderste skal har radius r a
2 Opgave 1 I første del af denne opgave skal kapacitansen af to kapacitorer bestemmes. Den ene kapacitor er konstrueret af to tynde koaksiale cylinderskaller af metal. Den inderste skal har radius r a
Matematisk modellering og numeriske metoder. Lektion 11
 Matematisk modellering og numeriske metoder Lektion 11 Morten Grud Rasmussen 5. november 2016 1 Partielle differentialligninger 1.1 Udledning af varmeligningen Vi vil nu på samme måde som med bølgeligningen
Matematisk modellering og numeriske metoder Lektion 11 Morten Grud Rasmussen 5. november 2016 1 Partielle differentialligninger 1.1 Udledning af varmeligningen Vi vil nu på samme måde som med bølgeligningen
Matematik A. Studentereksamen. Fredag den 5. december 2014 kl. 9.00-14.00. stx143-mat/a-05122014
 Matematik A Studentereksamen stx143-mat/a-05122014 Fredag den 5. december 2014 kl. 9.00-14.00 Opgavesættet er delt i to dele. Delprøven uden hjælpemidler består af opgave 1-6 med i alt 6 spørgsmål. Delprøven
Matematik A Studentereksamen stx143-mat/a-05122014 Fredag den 5. december 2014 kl. 9.00-14.00 Opgavesættet er delt i to dele. Delprøven uden hjælpemidler består af opgave 1-6 med i alt 6 spørgsmål. Delprøven
Aalborg Universitet. Skriftlig eksamen i Grundlæggende Mekanik og Termodynamik. Fredag d. 2. juni 2017 kl
 Aalborg Universitet Skriftlig eksamen i Grundlæggende Mekanik og Termodynamik Fredag d. 2. juni 2017 kl. 9 00-13 00 Ved bedømmelsen vil der blive lagt vægt på argumentationen (som bør være kort og præcis),
Aalborg Universitet Skriftlig eksamen i Grundlæggende Mekanik og Termodynamik Fredag d. 2. juni 2017 kl. 9 00-13 00 Ved bedømmelsen vil der blive lagt vægt på argumentationen (som bør være kort og præcis),
Hvorfor bevæger lyset sig langsommere i fx glas og vand end i det tomme rum?
 Hvorfor bevæger lyset sig langsommere i fx glas og vand end i det tomme rum? - om fysikken bag til brydningsindekset Artiklen er udarbejdet/oversat ud fra især ref. 1 - fra borgeleo.dk Det korte svar:
Hvorfor bevæger lyset sig langsommere i fx glas og vand end i det tomme rum? - om fysikken bag til brydningsindekset Artiklen er udarbejdet/oversat ud fra især ref. 1 - fra borgeleo.dk Det korte svar:
Log - Mikro og makroskopiske tilstande, det mikrokanoniske ensemble, multiplicitet og entropi
 Log - Mikro og makroskopiske tilstande, det mikrokanoniske ensemble, multiplicitet og entropi Amalie Christensen 26. februar 2009 Indhold 1 Om spillet 2 2 Multipliciteten af makroskopiske tilstande 3 3
Log - Mikro og makroskopiske tilstande, det mikrokanoniske ensemble, multiplicitet og entropi Amalie Christensen 26. februar 2009 Indhold 1 Om spillet 2 2 Multipliciteten af makroskopiske tilstande 3 3
Begge bølgetyper er transport af energi.
 I 1. modul skal I lære noget omkring elektromagnetisk stråling(em-stråling). Herunder synligt lys, IR-stråling, Uv-stråling, radiobølger samt gamma og røntgen stråling. I skal stifte bekendtskab med EM-strålings
I 1. modul skal I lære noget omkring elektromagnetisk stråling(em-stråling). Herunder synligt lys, IR-stråling, Uv-stråling, radiobølger samt gamma og røntgen stråling. I skal stifte bekendtskab med EM-strålings
MATEMATIK A-NIVEAU. Kapitel 1
 MATEMATIK A-NIVEAU Vejledende eksempler på eksamensopgaver og eksamensopgaver i matematik, 01 Kapitel 1 016 MATEMATIK A-NIVEAU Vejledende eksempler på eksamensopgaver og eksamensopgaver i matematik 01
MATEMATIK A-NIVEAU Vejledende eksempler på eksamensopgaver og eksamensopgaver i matematik, 01 Kapitel 1 016 MATEMATIK A-NIVEAU Vejledende eksempler på eksamensopgaver og eksamensopgaver i matematik 01
Skriftlig eksamen BioMatI (MM503)
 INSTITUT FOR MATEMATIK OG DATALOGI SYDDANSK UNIVERSITET, ODENSE Skriftlig eksamen BioMatI (MM503) 14. januar 2009 2 timer med alle sædvanlige hjælpemidler, inklusive brug af lommeregner/computer. OPGAVESÆTTET
INSTITUT FOR MATEMATIK OG DATALOGI SYDDANSK UNIVERSITET, ODENSE Skriftlig eksamen BioMatI (MM503) 14. januar 2009 2 timer med alle sædvanlige hjælpemidler, inklusive brug af lommeregner/computer. OPGAVESÆTTET
GUX. Matematik. A-Niveau. Torsdag den 31. maj Kl Prøveform a GUX181 - MAA
 GUX Matematik A-Niveau Torsdag den 31. maj 018 Kl. 09.00-14.00 Prøveform a GUX181 - MAA 1 Matematik A Prøvens varighed er 5 timer. Prøven består af opgaverne 1 til 11 med i alt 5 spørgsmål. De 5 spørgsmål
GUX Matematik A-Niveau Torsdag den 31. maj 018 Kl. 09.00-14.00 Prøveform a GUX181 - MAA 1 Matematik A Prøvens varighed er 5 timer. Prøven består af opgaverne 1 til 11 med i alt 5 spørgsmål. De 5 spørgsmål
Måling og modellering af partikelspredning
 Måling og modellering af partikelspredning Formålet med partikeltransporten er at bestemme partikelspredningen ud fra målinger i strømrenden, og herefter modellere partikelspredningen i en af projektgruppen
Måling og modellering af partikelspredning Formålet med partikeltransporten er at bestemme partikelspredningen ud fra målinger i strømrenden, og herefter modellere partikelspredningen i en af projektgruppen
Cirkulær hyperboloide (snoet trætårn i Camp Adventure ved Gisselfeld Kloster v/ Haslev)
 Cirkulær hyperboloide (snoet trætårn i Camp Adventure ved Gisselfeld Kloster v/ Haslev) https://en.wikipedia.org/wiki/quadric#euclidean_space Ligning og parametrisering https://en.wikipedia.org/wiki/hyperboloid
Cirkulær hyperboloide (snoet trætårn i Camp Adventure ved Gisselfeld Kloster v/ Haslev) https://en.wikipedia.org/wiki/quadric#euclidean_space Ligning og parametrisering https://en.wikipedia.org/wiki/hyperboloid
Danmarks Tekniske Universitet
 Danmarks Tekniske Universitet Side 1 af 11 sider Skriftlig prøve, lørdag den 22. august, 2015 Kursus navn Fysik 1 Kursus nr. 10916 Varighed: 4 timer Tilladte hjælpemidler: Alle hjælpemidler tilladt "Vægtning":
Danmarks Tekniske Universitet Side 1 af 11 sider Skriftlig prøve, lørdag den 22. august, 2015 Kursus navn Fysik 1 Kursus nr. 10916 Varighed: 4 timer Tilladte hjælpemidler: Alle hjælpemidler tilladt "Vægtning":
Dosering af anæstesistoffer
 Dosering af anæstesistoffer Køreplan 01005 Matematik 1 - FORÅR 2005 1 Formål Formålet med opgaven er at undersøge hvordan man kan opnå kendskab til koncentrationen af anæstesistoffer i vævet på en person
Dosering af anæstesistoffer Køreplan 01005 Matematik 1 - FORÅR 2005 1 Formål Formålet med opgaven er at undersøge hvordan man kan opnå kendskab til koncentrationen af anæstesistoffer i vævet på en person
Matematik A. Studentereksamen
 Matematik A Studentereksamen 1stx131-MAT/A-24052013 Fredag den 24. maj 2013 kl. 9.00-14.00 Opgavesættet er delt i to dele. Delprøven uden hjælpemidler består af opgave 1-6 med i alt 6 spørgsmål. Delprøven
Matematik A Studentereksamen 1stx131-MAT/A-24052013 Fredag den 24. maj 2013 kl. 9.00-14.00 Opgavesættet er delt i to dele. Delprøven uden hjælpemidler består af opgave 1-6 med i alt 6 spørgsmål. Delprøven
Modeldannelse og simulering
 Modeldannelse og simulering Tom S. Pedersen, Palle Andersen tom@es.aau.dk pa@es.aau.dk Aalborg Universitet, Institut for Elektroniske Systemer Automation and Control Modeldannelse og simulering p. 1/21
Modeldannelse og simulering Tom S. Pedersen, Palle Andersen tom@es.aau.dk pa@es.aau.dk Aalborg Universitet, Institut for Elektroniske Systemer Automation and Control Modeldannelse og simulering p. 1/21
Aalborg Universitet. Skriftlig eksamen i Grundlæggende Mekanik og Termodynamik. Tirsdag d. 27. maj 2014 kl
 Aalborg Universitet Skriftlig eksamen i Grundlæggende Mekanik og Termodynamik Tirsdag d. 27. maj 2014 kl. 9 00-13 00 Ved bedømmelsen vil der blive lagt vægt på argumentationen (som bør være kort og præcis),
Aalborg Universitet Skriftlig eksamen i Grundlæggende Mekanik og Termodynamik Tirsdag d. 27. maj 2014 kl. 9 00-13 00 Ved bedømmelsen vil der blive lagt vægt på argumentationen (som bør være kort og præcis),
a og b. Den magnetiske kraftlov Og måling af B ved hjælp af Tangensboussole
 3.1.2. a og b Den magnetiske kraftlov Og måling af B ved hjælp af Tangensboussole Udført d. 15.04.08 Deltagere Kåre Stokvad Hansen Max Berg Michael Ole Olsen 1 Formål: Formålet med øvelsen er at måle/beregne
3.1.2. a og b Den magnetiske kraftlov Og måling af B ved hjælp af Tangensboussole Udført d. 15.04.08 Deltagere Kåre Stokvad Hansen Max Berg Michael Ole Olsen 1 Formål: Formålet med øvelsen er at måle/beregne
gl. Matematik A Studentereksamen
 gl. Matematik A Studentereksamen gl-1stx131-mat/a-24052013 Fredag den 24. maj 2013 kl. 9.00-14.00 Opgavesættet er delt i to dele. Delprøven uden hjælpemidler består af opgave 1-6 med i alt 6 spørgsmål.
gl. Matematik A Studentereksamen gl-1stx131-mat/a-24052013 Fredag den 24. maj 2013 kl. 9.00-14.00 Opgavesættet er delt i to dele. Delprøven uden hjælpemidler består af opgave 1-6 med i alt 6 spørgsmål.
1 Løsningsforslag til årsprøve 2009
 1 Løsningsforslag til årsprøve 009 Opgave 1 Figur 1 viser en tegning af en person der står på en skrænt og smider en sten ud over vandet. Vandet har overflade i t-aksen. Stenen følger grafen for funktionen
1 Løsningsforslag til årsprøve 009 Opgave 1 Figur 1 viser en tegning af en person der står på en skrænt og smider en sten ud over vandet. Vandet har overflade i t-aksen. Stenen følger grafen for funktionen
Solen - Vores Stjerne
 Solen - Vores Stjerne af Christoffer Karoff, Aarhus Universitet På et sekund udstråler Solen mere energi end vi har brugt i hele menneskehedens historie. Uden Solen ville der ikke findes liv på Jorden.
Solen - Vores Stjerne af Christoffer Karoff, Aarhus Universitet På et sekund udstråler Solen mere energi end vi har brugt i hele menneskehedens historie. Uden Solen ville der ikke findes liv på Jorden.
Rektangulær potentialbarriere
 Kvantemekanik 5 Side 1 af 8 ektangulær potentialbarriere Med udgangspunkt i det KM begrebsapparat udviklet i KM1-4 beskrives i denne lektion flg. to systemer, idet system gennemgås, og system behandles
Kvantemekanik 5 Side 1 af 8 ektangulær potentialbarriere Med udgangspunkt i det KM begrebsapparat udviklet i KM1-4 beskrives i denne lektion flg. to systemer, idet system gennemgås, og system behandles
Simuleringsresultater
 Alfred Heller Solvarmeanlæg ved biomassefyrede fjernvarmecentraler m.m. Simuleringsresultater DANMARKS TEKNISKE UNIVERSITET Sagsrapport BYG DTU SR-01-16 001 ISSN 1396-40x Solvarmeanlæg ved biomassefyrede
Alfred Heller Solvarmeanlæg ved biomassefyrede fjernvarmecentraler m.m. Simuleringsresultater DANMARKS TEKNISKE UNIVERSITET Sagsrapport BYG DTU SR-01-16 001 ISSN 1396-40x Solvarmeanlæg ved biomassefyrede
Øvre rand ilt. Den målte variation, er antaget at være gældende på randen i en given periode før og efter målingerne er foretaget.
 MIKE 11 model til beskrivelse af iltvariation i Østerå Formål Formålet med denne model er at blive i stand til at beskrive den naturlige iltvariation over døgnet i Østerå. Til beskrivelse af denne er der
MIKE 11 model til beskrivelse af iltvariation i Østerå Formål Formålet med denne model er at blive i stand til at beskrive den naturlige iltvariation over døgnet i Østerå. Til beskrivelse af denne er der
Note om Laplace-transformationen
 Note om Laplace-transformationen Den harmoniske oscillator omskrevet til et ligningssystem I dette opgavesæt benyttes laplacetransformationen til at løse koblede differentialligninger. Fordelen ved at
Note om Laplace-transformationen Den harmoniske oscillator omskrevet til et ligningssystem I dette opgavesæt benyttes laplacetransformationen til at løse koblede differentialligninger. Fordelen ved at
Nanotermodynamik formelsamling
 Nanotermodynamik formelsamling Af Asmus Ougaard Dohn & Sune Klamer Jørgensen 2. november 2005 ndhold 1 Kombinatorik 2 2 Termodynamik 3 3 deal gasser: 5 4 Entropi og temp.: 7 5 Kemisk potential: 7 6 Gibbs
Nanotermodynamik formelsamling Af Asmus Ougaard Dohn & Sune Klamer Jørgensen 2. november 2005 ndhold 1 Kombinatorik 2 2 Termodynamik 3 3 deal gasser: 5 4 Entropi og temp.: 7 5 Kemisk potential: 7 6 Gibbs
Første og anden hovedsætning kombineret
 Statistisk mekanik 3 Side 1 af 12 Første og anden hovedsætning kombineret I dette afsnit udledes ved kombination af I og II en række udtryk, som senere skal vise sig nyttige. Ved at kombinere udtryk (2.27)
Statistisk mekanik 3 Side 1 af 12 Første og anden hovedsætning kombineret I dette afsnit udledes ved kombination af I og II en række udtryk, som senere skal vise sig nyttige. Ved at kombinere udtryk (2.27)
Gaslovene. SH ver. 1.2. 1 Hvad er en gas? 2 1.1 Fysiske størrelser... 2 1.2 Gasligninger... 3
 Gaslovene SH ver. 1.2 Indhold 1 Hvad er en gas? 2 1.1 Fysiske størrelser................... 2 1.2 Gasligninger...................... 3 2 Forsøgene 3 2.1 Boyle Mariottes lov.................. 4 2.1.1 Konklusioner.................
Gaslovene SH ver. 1.2 Indhold 1 Hvad er en gas? 2 1.1 Fysiske størrelser................... 2 1.2 Gasligninger...................... 3 2 Forsøgene 3 2.1 Boyle Mariottes lov.................. 4 2.1.1 Konklusioner.................
Cepheider. Af Michael A. D. Møller. Oktober side 1/12. Cepheider
 Cepheider. Af Michael A. D. Møller. Oktober 2017. side 1/12 Cepheider Af Michael Andrew Dolan Møller Rosborg Gymnasium og Hf Oktober 2017 Cepheider. Af Michael A. D. Møller. Oktober 2017. side 2/12 Indholdsfortegnelse
Cepheider. Af Michael A. D. Møller. Oktober 2017. side 1/12 Cepheider Af Michael Andrew Dolan Møller Rosborg Gymnasium og Hf Oktober 2017 Cepheider. Af Michael A. D. Møller. Oktober 2017. side 2/12 Indholdsfortegnelse
1, c. 52% af er ca , så der skulle bortskaffes m 3 moræneler.
 Kapitel 3 Øvelse 3.1 b. Vi dividerer arealet af tre sten på,336 m 2 op i det samlede areal på tre for at få det samlede antal sten. Dette giver 8 1,4 1 6 1,16 1 eller 14 millioner mursten. m 2 og ganger
Kapitel 3 Øvelse 3.1 b. Vi dividerer arealet af tre sten på,336 m 2 op i det samlede areal på tre for at få det samlede antal sten. Dette giver 8 1,4 1 6 1,16 1 eller 14 millioner mursten. m 2 og ganger
Figur 1 Energetisk vekselvirkning mellem to systemer.
 Energibånd Fysiske fænomener er i reglen forbundet med udveksling af energi mellem forskellige systemer. Udvekslingen af energi mellem to systemer A og B kan vi illustrere grafisk som på figur 1 med en
Energibånd Fysiske fænomener er i reglen forbundet med udveksling af energi mellem forskellige systemer. Udvekslingen af energi mellem to systemer A og B kan vi illustrere grafisk som på figur 1 med en
FYSIK 3 / TERMODYNAMIK Københavns Universitet, 13. april, 2016, Skriftlig prøve
 FYSIK 3 / TERMODYNAMIK Københavns Universitet, 13. april, 2016, Skriftlig prøve Benyttelse af medbragt litteratur, noter, lommeregner og computer uden internetadgang er tilladt. Der må skrives med blyant.
FYSIK 3 / TERMODYNAMIK Københavns Universitet, 13. april, 2016, Skriftlig prøve Benyttelse af medbragt litteratur, noter, lommeregner og computer uden internetadgang er tilladt. Der må skrives med blyant.
Kalkulus 1 - Opgaver. Anne Ryelund, Anders Friis og Mads Friis. 20. januar 2015
 Kalkulus 1 - Opgaver Anne Ryelund, Anders Friis og Mads Friis 20. januar 2015 Mængder Opgave 1 Opskriv følgende mængder med korrekt mængdenotation. a) En mængde A indeholder alle hele tal fra og med 1
Kalkulus 1 - Opgaver Anne Ryelund, Anders Friis og Mads Friis 20. januar 2015 Mængder Opgave 1 Opskriv følgende mængder med korrekt mængdenotation. a) En mængde A indeholder alle hele tal fra og med 1
Danmarks Tekniske Universitet
 Danmarks Tekniske Universitet Side 1 af 11 Skriftlig prøve, torsdag den 8 maj, 009, kl 9:00-13:00 Kursus navn: Fysik 1 Kursus nr 100 Tilladte hjælpemidler: Alle hjælpemidler er tilladt "Vægtning": Besvarelsen
Danmarks Tekniske Universitet Side 1 af 11 Skriftlig prøve, torsdag den 8 maj, 009, kl 9:00-13:00 Kursus navn: Fysik 1 Kursus nr 100 Tilladte hjælpemidler: Alle hjælpemidler er tilladt "Vægtning": Besvarelsen
Løsningsforslag til fysik A eksamenssæt, 23. maj 2008
 Løsningsforslag til fysik A eksamenssæt, 23. maj 2008 Kristian Jerslev 22. marts 2009 Geotermisk anlæg Det geotermiske anlæg Nesjavellir leverer varme til forbrugerne med effekten 300MW og elektrisk energi
Løsningsforslag til fysik A eksamenssæt, 23. maj 2008 Kristian Jerslev 22. marts 2009 Geotermisk anlæg Det geotermiske anlæg Nesjavellir leverer varme til forbrugerne med effekten 300MW og elektrisk energi
Kernefysik og dannelse af grundstoffer. Fysik A - Note. Kerneprocesser. Gunnar Gunnarsson, april 2012 Side 1 af 14
 Kerneprocesser Side 1 af 14 1. Kerneprocesser Radioaktivitet Fission Kerneproces Fusion Kollisioner Radioaktivitet: Spontant henfald ( af en ustabil kerne. Fission: Sønderdeling af en meget tung kerne.
Kerneprocesser Side 1 af 14 1. Kerneprocesser Radioaktivitet Fission Kerneproces Fusion Kollisioner Radioaktivitet: Spontant henfald ( af en ustabil kerne. Fission: Sønderdeling af en meget tung kerne.
Danmarks Tekniske Universitet
 Danmarks Tekniske Universitet Side 1 af 4 sider Skriftlig prøve, den 29. maj 2006 Kursus navn: Fysik 1 Kursus nr. 10022 Tilladte hjælpemidler: Alle "Vægtning": Eksamenssættet vurderes samlet. Alle svar
Danmarks Tekniske Universitet Side 1 af 4 sider Skriftlig prøve, den 29. maj 2006 Kursus navn: Fysik 1 Kursus nr. 10022 Tilladte hjælpemidler: Alle "Vægtning": Eksamenssættet vurderes samlet. Alle svar
Matematik A. Studentereksamen
 Matematik A Studentereksamen stx103-mat/a-101010 Fredag den 10. december 010 kl. 9.00-14.00 Opgavesættet er delt i to dele. Delprøven uden hjælpemidler består af opgave 1-6 med i alt 6 spørgsmål. Delprøven
Matematik A Studentereksamen stx103-mat/a-101010 Fredag den 10. december 010 kl. 9.00-14.00 Opgavesættet er delt i to dele. Delprøven uden hjælpemidler består af opgave 1-6 med i alt 6 spørgsmål. Delprøven
Eksperimentelle øvelser, øvelse nummer 3 : Røntgenstråling målt med Ge-detektor
 Modtaget dato: (forbeholdt instruktor) Godkendt: Dato: Underskrift: Eksperimentelle øvelser, øvelse nummer 3 : Røntgenstråling målt med Ge-detektor Kristian Jerslev, Kristian Mads Egeris Nielsen, Mathias
Modtaget dato: (forbeholdt instruktor) Godkendt: Dato: Underskrift: Eksperimentelle øvelser, øvelse nummer 3 : Røntgenstråling målt med Ge-detektor Kristian Jerslev, Kristian Mads Egeris Nielsen, Mathias
a og b Den magnetiske kraftlov Og måling af B ved hjælp af Tangensboussole
 3.1.2. a og b Den magnetiske kraftlov Og måling af B ved hjælp af Tangensboussole Udført d. 15.04.08 Deltagere Kåre Stokvad Hansen Max Berg Michael Ole Olsen 1 Formål: Formålet med øvelsen er at måle/beregne
3.1.2. a og b Den magnetiske kraftlov Og måling af B ved hjælp af Tangensboussole Udført d. 15.04.08 Deltagere Kåre Stokvad Hansen Max Berg Michael Ole Olsen 1 Formål: Formålet med øvelsen er at måle/beregne
Skriftlig eksamen i Statistisk Mekanik den fra 9.00 til Alle hjælpemidler er tilladte. Undtaget er dog net-opkoblede computere.
 Skriftlig eksamen i Statistisk Mekanik den 18-01-2007 fra 900 til 1300 lle hjælpemidler er tilladte Undtaget er dog net-opkoblede computere Opgave 1: I en beholder med volumen V er der rgon-atomer i gasfasen,
Skriftlig eksamen i Statistisk Mekanik den 18-01-2007 fra 900 til 1300 lle hjælpemidler er tilladte Undtaget er dog net-opkoblede computere Opgave 1: I en beholder med volumen V er der rgon-atomer i gasfasen,
SOLOBSERVATION Version
 SOLOBSERVATION Version 3-2012 Jørgen Valentin Enkelund JVE januar 2012 1 SOLOBSERVATION INDHOLDSFORTEGNELSE 1. Solen Vores nærmeste stjerne 2. Elektromagnetisk emission fra brint 3. Egne observationer
SOLOBSERVATION Version 3-2012 Jørgen Valentin Enkelund JVE januar 2012 1 SOLOBSERVATION INDHOLDSFORTEGNELSE 1. Solen Vores nærmeste stjerne 2. Elektromagnetisk emission fra brint 3. Egne observationer
Måling af turbulent strømning
 Måling af turbulent strømning Formål Formålet med at måle hastighedsprofiler og fluktuationer i en turbulent strømning er at opnå et tilstrækkeligt kalibreringsgrundlag til modellering af turbulent strømning
Måling af turbulent strømning Formål Formålet med at måle hastighedsprofiler og fluktuationer i en turbulent strømning er at opnå et tilstrækkeligt kalibreringsgrundlag til modellering af turbulent strømning
Besvarelser til Calculus Ordinær Eksamen - 3. Januar 2017
 Besvarelser til Calculus Ordinær Eksamen - 3. Januar 17 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 3. Januar 17 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
AARHUS UNIVERSITET. Det naturvidenskabelige fakultet 3. kvarter forår OPGAVESTILLER: Allan H. Sørensen
 AARHUS UNIVERSITET Det naturvidenskabelige fakultet 3. kvarter forår 2006 FAG: Elektromagnetisme OPGAVESTILLER: Allan H. Sørensen Antal sider i opgavesættet (inkl. forsiden): 5 Eksamensdag: fredag dato:
AARHUS UNIVERSITET Det naturvidenskabelige fakultet 3. kvarter forår 2006 FAG: Elektromagnetisme OPGAVESTILLER: Allan H. Sørensen Antal sider i opgavesættet (inkl. forsiden): 5 Eksamensdag: fredag dato:
EKSAMENSOPGAVELØSNINGER CALCULUS 2 (2005) JANUAR 2006 AARHUS UNIVERSITET.. Beregn den retningsafledede D u f(0, 0).
 EKSAMENSOPGAVELØSNINGER CALCULUS 2 (2005) JANUAR 2006 AARHUS UNIVERSITET H.A. NIELSEN & H.A. SALOMONSEN Opgave. Lad f betegne funktionen f(x, y) = x cos(y) + y sin(x). ) Angiv gradienten f. 2) Lad u betegne
EKSAMENSOPGAVELØSNINGER CALCULUS 2 (2005) JANUAR 2006 AARHUS UNIVERSITET H.A. NIELSEN & H.A. SALOMONSEN Opgave. Lad f betegne funktionen f(x, y) = x cos(y) + y sin(x). ) Angiv gradienten f. 2) Lad u betegne
DET USYNLIGE UNIVERS. STEEN HANNESTAD 24. januar 2014
 DET USYNLIGE UNIVERS STEEN HANNESTAD 24. januar 2014 GANSKE KORT OM KOSMOLOGIENS UDVIKLING FØR 1920: HELE UNIVERSET FORMODES AT VÆRE NOGENLUNDE AF SAMME STØRRELSE SOM MÆLKEVEJEN OMKRING 30,000 LYSÅR GANSKE
DET USYNLIGE UNIVERS STEEN HANNESTAD 24. januar 2014 GANSKE KORT OM KOSMOLOGIENS UDVIKLING FØR 1920: HELE UNIVERSET FORMODES AT VÆRE NOGENLUNDE AF SAMME STØRRELSE SOM MÆLKEVEJEN OMKRING 30,000 LYSÅR GANSKE
Tallene angivet i rapporten som kronologiske punkter refererer til de i opgaven stillede spørgsmål.
 Labøvelse 2, fysik 2 Uge 47, Kalle, Max og Henriette Tallene angivet i rapporten som kronologiske punkter refererer til de i opgaven stillede spørgsmål. 1. Vi har to forskellige størrelser: a: en skive
Labøvelse 2, fysik 2 Uge 47, Kalle, Max og Henriette Tallene angivet i rapporten som kronologiske punkter refererer til de i opgaven stillede spørgsmål. 1. Vi har to forskellige størrelser: a: en skive
Matematik A. Højere teknisk eksamen
 Matematik A Højere teknisk eksamen Matematik A 215 Prøvens varighed er 5 timer. Alle hjælpemidler er tilladte. Opgavebesvarelsen skal afleveres renskrevet, det er tilladt at skrive med blyant. Notatpapir
Matematik A Højere teknisk eksamen Matematik A 215 Prøvens varighed er 5 timer. Alle hjælpemidler er tilladte. Opgavebesvarelsen skal afleveres renskrevet, det er tilladt at skrive med blyant. Notatpapir
Erik Vestergaard 1. Opgaver. i Lineære. funktioner. og modeller
 Erik Vestergaard www.matematikfsik.dk Opgaver i Lineære funktioner og modeller Erik Vestergaard www.matematikfsik.dk Erik Vestergaard, Haderslev. www.matematikfsik.dk Teknik. Aflæse forskrift fra graf...
Erik Vestergaard www.matematikfsik.dk Opgaver i Lineære funktioner og modeller Erik Vestergaard www.matematikfsik.dk Erik Vestergaard, Haderslev. www.matematikfsik.dk Teknik. Aflæse forskrift fra graf...
