Fourier transformationen
|
|
|
- Freja Frederikke Bro
- 6 år siden
- Visninger:
Transkript
1 MODUL 6 Fourier transformationen Forfattere: Øistein WIND-WILLASSEN & Michael ELMEGÅRD 4. juni 4
2
3 Indhold Fourier transformationen 5. Definition og oprindelse Funktioner der kan transformeres Tabel over Fourier transformationer Egenskaber af F Linearitet Modulering af frekvens Translation i tid Skalering af tid Dualitet og specielle funktioner Dualitet Delta funktionen Cosinus og sinus Differentialligninger
4 4 INDHOLD
5 Kapitel Fourier transformationen Fourier transformeringen er et matematisk værktøj der anvendes til at studere frekvensindholdet i funktioner. Som eksempel kan man Fourier transformere digitaliseret musik og få information om hvilke frekvenser (eller toner) der indgår. Vi er interesserede i at analysere funktioner der ikke nødvendigvis er periodiske i tid, men blot definerede for de reelle tal, R. Vi starter med at definere Fourier transformationen i afsnit.. I afsnit.3 ser vi på nogle vigtige egenskaber af transformationen, og viser nogle regneeksempler. Vi har i afsnit. inkluderet en liste over kendte funktioner samt deres Fourier transformation.. Definition og oprindelse Fourier transformationen F er opkaldt efter den franske matematiker og fysiker Joseph Fourier (767 83), og bliver som nævnt hyppigt anvendt til at transformere signaler fra det tidslige eller rumlige domæne til frekvens domænet. Hvis funktionerne der betragtes er periodiske med periode T, kan Fourier rækker anvendes. Periodiske funktioner kan således repræsenteres ved en linearkombination af cosinus og sinus funktioner med forskellige frekvenser og amplituder. Vi vil i det følgende betragte funktioner, f (t), der ikke længere er periodiske, og til det formål anvendes Fourier transformationen; F { f (t)} F(ω) f (t)e iωt dt. (.) Eksempel.. Vi vil finde Fourier transformationen af Boks-funktionen, der har følgende forskrift,, < t < f (t) /, t ± (.), ellers. 5
6 6 KAPITEL. FOURIER TRANSFORMATIONEN Vi udregner dens Fourier transformation: F { f (t)} F(ω) f (t)e iωt dt e iωt dt [ e iωt ] iω iω ( i)sin(ω) sin(ω) ω. Denne funktion kan også udtrykkes ved sinc funktionen, der er defineret som sin(x) x, x sinc(x), x. (.3) Vi har altså, at F(ω) sinc(ω). I figur. og. er boks-funktionen samt dens Fourier tranformation vist. Signal styrke Fourier transformation Tid [s] Frekvens [/s] Figur.: Boks-funktionen beskrevet i ligning (..) Figur.: Fourier transformationen af ligning (.). Vi kan desuden skrive den inverse Fourier transformation, F, som F {F(ω)} f (t) F(ω)e iωt dω. (.4) π Denne størrelse kaldes også integral-repræsentationen af f (t). Bemærk, at t ikke nødvendigvis er et udtryk for tid, men også kunne være udtryk for en rumlig position.
7 .. DEFINITION OG OPRINDELSE 7 Eksempel.. Vi fortsætter det forrige eksempel og vil finde den inverse transformation af F(ω) sin(ω) ω. Uden tøven anvender vi definitionen, F {F(ω)} sin(ω) π ω eiωt dω. (.5) Umiddelbart ser dette udtryk lidt vanskeligt ud, men vi kan udnytte Eulers formel, hvorved følgende opnås, F {F(ω)} π π e iωt cos(ωt) + isin(ωt), sin(ω) [cos(ωt) + isin(ωt)]dω (.6) ω ω sin(ω)cos(ωt)dω + i sin(ω)sin(ωt)dω. (.7) π ω For at komme videre skal vi anvende, at cos(t) er en lige funktion, og at sin(t) er en ulige funktion. For en lige funktion, f, gælder følgende egenskaber, A A og for en ulige funktion, g, tilsvarende A f (x) f ( x) (.8) f (x)dx A A f (x)dx. (.9) g(x) g( x) (.) g(x)dx. (.) I ligning (.7) ser vi, at /ω er en ulige funktion, at sin(ω)cos(ωt) er en ulige funktion, samt at sin(ω) sin(ωt) er en lige funktion. Produktet af en ulige funktion med en ulige funktion giver en lige funktion, og produktet af en ulige funktion med en lige funktion giver en ulige funktion. De to integraler bliver derfor F {F(ω)} π π ω sin(ω)cos(ωt)dω + i sin(ω)sin(ωt)dω. (.) π ω sin(ω)cos(ωt)dω +. (.3) ω
8 8 KAPITEL. FOURIER TRANSFORMATIONEN Ved hjælp af den trigonometriske identitet, bliver integralet nu F {F(ω)} π sin(α)cos(β) sin(α + β) + sin(α β), ω sin(ω)cos(ωt)dω [ sin(ω + ωt) + π ω ] sin(ω ωt) dω. ω (.4) Dette integrale kan vi ikke umiddelbart evaluere, men ved slå op i en tabel over kendte integraler kan man finde, at sin(ax) dx x π/ a > π/ a < a I sidste ende får vi følgende udtryk for f (t),, < t < f (t) /, t ±, ellers (.5) hvilket er identisk med funktionen vi startede med... Funktioner der kan transformeres Umiddelbart ser det ud til, at de funktioner der kan Fourier transformeres er dem der kan integreres fra til. Hvis ikke dette er tilfældet giver integralet i definitionen, ligning (.) ikke mening, da dets værdi vil gå imod uendelig. For anvendelige funktioner vil man typisk observere, at de går imod i grænserne, altså f (t) når t ±. Selvom denne betingelse måske virker meget begrænsende, har de fleste signaler/funktioner i praksis både en begyndelse og en start. Man kan umiddelbart Fourier transformere signaler/funktioner der er begrænsede, i den forstand at de har en begyndelse og en afslutning. Der er dog en undtagelse til enhver regel, og der findes derfor funktioner der ikke har som grænseværdi for t ±, men som vi stadig ønsker at Fourier transformere; i afsnit.4 vil vi se på hvordan vi behandler de vigtigste og mest anvendte af sådanne funktioner. Det er desuden et krav, at de anvendte funktioner er stykkevis kontinuerte; se figur.3. Funktionerne må altså kun være diskontinuerte i et endeligt antal punkter. Dette betyder også, at en funktion kan deles op i mindre stykker i mellem diskontinuiteterne. Mellem diskontinuiteterne er det altså et krav, at funktionen er kontinuert. Et eksempel på et signal hvor man gerne vil
9 .. DEFINITION OG OPRINDELSE 9 f(t) t Figur.3: Et eksempel på en funktion med diskontinuiteter i enkelte punkter. Cirklerne indikerer funktionsværdien i et givent punkt: de fyldte cirkler betyder at værdien er med, hvorimod en åben cirkel betyder at værdien ikke er med. undersøge frekvensindholdet er vist til venstre på figur.4. Signalet i dette tilfælde er cos(3t) + cos(t) + cos(5t) t π f (t), ellers og den tilhørende Fourier transformation er vist til højre i figur.4; bemærk her, at transformationen er symmetrisk omkring ω /s, og at der tydeligt ses tre peaks ved de frekvenser der er anvendt i input signalet. Læg desuden mærke til, at den anvendte funktion, f (t), var begrænset, idet den kun var forskellig fra nul i intervallet t π. Dette sikrede os, at dens Fourier transformation kunne beregnes. Eksempel.3. Vi vil finde Fourier transformationen af funktionen f (t) u(t)e t, hvor t u(t) t <, er Heavisides stepfunktion. Problemet løses igen ved at bruge definitionen på Fourier trans-
10 KAPITEL. FOURIER TRANSFORMATIONEN Signal styrke 3 Fouriertransformation Tid [s] Frekvens [/s] Figur.4: Venstre: Et eksempel på et input signal som består af summen af tre cosinus funktioner med frekvenser på 3, og 5 Hz. Højre: Fourier transformationen af signalet til venstre; løsningen er symmetrisk omkring, og der ses tre tydelige peaks omkring 3, og 5 Hz. formationen, F { f (t)} F(ω) f (t)e iωt dt e t e iωt dt e (+iω)t dt [ ] e (+iω)t ( + iω) + iω. Sidste lighedstegn opnåede vi ved at betragte grænsen t, for hvilken e (+iω)t. Det er god regnetræning at udregne integralet hver gang man skal lave en Fourier transformation, men det er også tidskrævende. Det vil derfor tit være en god ide at benytte en tabel over funktioner samt deres transformerede, og vi har derfor inkluderet en række kendte funktioner i tabel. samt deres Fourier transformerede (inkluderet til sidst i dette dokument). Opgave.. Find Fourier transformationen af de følgende funktioner /4 t 3 a) f (t) t > 3
11 .. DEFINITION OG OPRINDELSE t/ t b) f (t) +t/ t ellers e αt t c) f (t), hvor α > e αt t < e t t d) f (t) t < e) f (t) u(t)e t/τ, hvor τ er en konstant og u(t) er Heavisides stepfunktion.
12 KAPITEL. FOURIER TRANSFORMATIONEN. Tabel over Fourier transformationer Fourier transformationer f (t) F(ω) f (t) Au(t)e αt, α > F(ω) α+iω A α t α f (t) F(ω) sin(ωα) ω ellers f (t) A, hvor A er en konstant f (t) u(t)a F(ω) πaδ(ω) F(ω) A ( πδ(ω) i ω ) f (t) δ(t) F(ω) f (t) δ(t a) f (t) cos(at) F(ω) e iωa F(ω) π [δ(ω + a) + δ(ω a)] f (t) sin(at) f (t) e α t, α > F(ω) α t > f (t) sgn(t) F(ω) iω t < f (t) t F(ω) π i [δ(ω + a) δ(ω a)] α +ω F(ω) iπsgn(ω) f (t) e at F(ω) πa e ω /(4a) Tabel.: Fourier transformationen af kendte funktioner, hentet fra A. Croft et al.: Engineering mathematics: A Foundation for Electronic, Electrical, Communications and Systems Engineers..3 Egenskaber af F Man kommer langt med definitionen af Fourier transformationen samt listen over funktioner i tabel.. Dog kan man vise en række meget anvendelige egenskaber, og i det følgende vil vi fremhæve de vigtigste. Der eksisterer flere end dem vi viser, og hvis man er interesseret må man konsultere en mere uddybende tekst om Fourier transformationen.
13 .3. EGENSKABER AF F 3.3. Linearitet Fourier transformationen opfylder F { f (t) + g(t)} F { f (t)} + F {g(t)} (.6) F {c f (t)} cf { f (t)}. (.7) Man siger, at transformationen er en lineær operation, netop på grund af disse to egenskaber. Bevis. Vi undersøger det første krav, F { f (t) + g(t)}: F { f (t) + g(t)} Det andet krav er, at F {c f (t)} cf { f (t)}: ( f (t) + g(t))e iωt dt f (t)e iωt dt + F { f (t)} + F {g(t)}. F {c f (t)} c c f (t)e iωt dt cf { f (t)}, f (t)e iωt dt g(t)e iωt dt hvor sidste lighed gælder fordi c ikke er afhængig af t. Vi har nu vist at Fourier transformationen er en lineær operation. Opgave.. Vis, at den inverse transformation, ligning (.4), også er en lineær operation. Eksempel.4. Betragt funktionen f (t) u(t)e 7t + u(t)e 3t ; vi vil finde F { f (t)}. Ud fra lineariteten af F samt tabel., får vi, F { f (t)} F { u(t)e 7t + u(t)e 3t} F { u(t)e 7t} + F { u(t)e 3t} 7 + iω iω + iω ω + iω + ω ( ω) + ω + i 58ω ω 3 ( ω) + ω
14 4 KAPITEL. FOURIER TRANSFORMATIONEN.3. Modulering af frekvens Denne egenskab kaldes på engelsk First shift theorem og på dansk siger man, at frekvensen moduleres, F { e iω t f (t) } F(ω ω ). (.8) Bevis. Denne egenskab vises også ved at betragte definitionen på Fourier transformationen, F { e iω t f (t) } F(ω ω ). e iω t f (t)e iωt dt f (t)e i(ω ω )t dt Eksempel.5. Ligning (.8) kan fx. bruges til at finde ud af hvilken funktion en bestemt transformation tilhører. Lad os først beregne F af funktionen e 3t t f (t) e 3t t <. Vi finder Fourier transformationen på den sædvanlige måde, F { f (t)} F(ω) Antag nu, at vi har givet en transformation, [ e 3t e iωt dt + e (3 iω)t dt + [ e (3 iω)t 3 iω F {g(t)} G(ω) ] + 3 iω iω ω. 6 + ω + ω. e 3t e iωt dt e (3+iω)t dt e (3+iω)t (3 + iω) Vi vil gerne finde funktionen g(t) og undersøger derfor om der skulle være en sammenhæng ]
15 .3. EGENSKABER AF F 5 mellem F(ω) og G(ω). Vi ser nu, at G(ω) og vi kan derfor benytte os af ligning (.8); 6 (ω + ) F(ω + ), + 9 F(ω + ) e it f (t), og derfor er e ( 3 i)t t g(t) e (3 i)t t <. Vi tager endnu et eksempel. Eksempel.6. Lad os betragte en lidt simplere udgave af funktionen der var anvendt til at producere figur.4, nemlig cos(3t) π t π f (t) (.9) ellers Denne funktion er plottet til venstre i figur.5. Vi ønsker at finde dens Fourier transformerede, og anvender til dette ligning.8 samt følgende identitet, cos(ω t) eiωt + e iω t. (.) Bemærk, at funktionen f (t) kan skrives som f (t) cos(3t)g(t), hvor g(t) er boks-funktionen nævnt i eksempel.. I ligning (.) ganger vi med netop g(t) samt e iωt, og tager derefter integralet, cos(3t) ei3t + e i3t g(t)cos(3t) [ g(t)e i3t + g(t)e i3t] e iωt g(t)cos(3t) [g(t)e i(ω 3)t + g(t)e i(ω+3)t] e iωt g(t)cos(3t)dt [ ] g(t)e i(ω 3)t dt + g(t)e i(ω+3)t dt.
16 6 KAPITEL. FOURIER TRANSFORMATIONEN Vi ser nu, at venstre-siden er lig med F {g(t)cos(3t)} F { f (t)}. Hvis vi samtidig anvender ligning (.8) får vi, F {g(t)cos(3t)} [G(ω 3) + G(ω + 3)], hvor G(ω) sin(ωπ) ω blev fundet i eksempel.. Resultatet kan ses til højre i figur.5. 8 Signal styrke Tid [s] Fourier transformation Frekvens [/s] Figur.5: Venstre: Funktionen f (t). Højre: F { f (t)}..3.3 Translation i tid Hvis vi laver en translation eller et skift i tid, t a, får vi dét der på engelsk kaldes Second shift theorem, Bevis. Vi anvender definitionen af Fourier transformationen, F { f (t a)} e iωa F(ω). (.) F { f (t a)} og benytter nu substitutionen s t a, F { f (t a)} e iωa f (t a)e iωt dt, f (s)e iω(s+a) ds e iωa F(ω). f (s)e iωs ds
17 .3. EGENSKABER AF F 7 Ved et skift i tid får man altså en løsning der er proportional med løsningen til det originale problem men med et skift i fasen. En forsinkelse i tiden ændrer altså ikke indholdet i frekvenssignalet, hvilket også giver intuitiv mening, da det oprindelige signal blot er forskudt i tid, men ikke i amplitude. Eksempel.7. En anvendelse af tidsskiftet kan findes ved fx. at betragte funktionen t 3 g(t) ellers. For at finde F {g(t)} ser vi hurtigt, at g(t) f (t ), hvor t f (t) ellers Vi kender Fourier transformationen af f (t) fra tabel., og derfor er.3.4 Skalering af tid F {g(t)} F { f (t )} e iω iω sin(ω) F(ω) e ω I det tilfælde hvor tiden er skaleret med en faktor b, opnås følgende resultat, F { f (bt)} b F ( ω b ). (.) Bevis. Udledningen af denne egenskab fås ved at tage Fourier transformationen af f (bt) og anvende substitutionen s bt i de efterfølgende integraler. Dette betyder samtidig, at ds bdt. I det følgende bruger vi også den numeriske værdi af b, da grænserne skiftes i det tilfælde at b er negativ. Her vil man, ved at skifte grænserne tilbage til det oprindelige, opnå en faktor b, hvilket er ækvivalent med at skrive b : F { f (bt)} b b f (bt)e iωt dt. b F ( ω b f (s)e iωs/b ds. f (s)e i ω b s ds. ).
18 8 KAPITEL. FOURIER TRANSFORMATIONEN Et eksempel på betydningen af en skalering af tiden, får man ved at betragte et lydklip der afspilles ved en anderledes hastighed end normalt. Funktionen f (t) repræsenterer i det følgende lydklippet afspillet ved normal hastighed. Funktionen g(t) f (bt), hvor b > er en konstant, repræsenterer således lydklippet afspillet ved en anden hastighed. Hvis < b < afspilles lyden langsommere end normalt, og hvis b > afspilles lyden hurtigere. f(t) g(t)f(t/3) h(t)f(3t) 6 5 F(ω) G(ω) 3F(3ω) H(ω)/3F(/3ω) Signalstyrke Fourier transformering t 5 5 ω Figur.6: Venstre: De tre funktioner f (t) e t, g(t) f (t/3) og h(t) f (3t). Højre: De tilhørende Fourier transformationer. Den venstre del af figur.6 viser et eksempel på funktionen f (t) e (bt) plottet for b, b /3 og b 3..4 Dualitet og specielle funktioner I tabel. præsenterede vi en liste over Fourier transformationen af nogle kendte funktioner. Vi diskuterede også i indledningen hvilke krav der skulle stilles til funktionerne for at det gav mening at tage den transformerede. Et af kravene var bl.a. at f (t) for t ±. Fourier transformationen giver os information om frekvens indholdet af et signal, så hvis vi fx. valgte at betragte funktionen med en enkelt frekvens, f (t) cos(t) hvor t (, ), ville vi forvente, at det transformerede signal bestod udelukkende af den ene frekvens. Fourier transformationen af f (t) cos(t), F { f (t)} cos(t)e ωt dt, kan dog ikke umiddelbart evalueres da cos oscillerer i tid, hvilket resulterer i, at integralet ikke kan beregnes. Det viser sig, at vi har brug for at indføre en ny funktion kaldet delta funktionen for at kunne beregne Fourier transformationen af cosinus og sinus. Først introducerer vi dog begrebet om dualitet, og derefter kigger vi på delta funktionen og dens egenskaber.
19 .4. DUALITET OG SPECIELLE FUNKTIONER 9.4. Dualitet Integral repræsentationen af en funktion f (t) blev defineret i ligning (.4), F {F(ω)} f (t) π Variablen ω kan uden problemer omdøbes til fx. z, hvilket giver F {F(z)} f (t) π Samtidig kan vi omdøbe variablen t til ω, for at opnå hvilket jo er π f ( ω) π F(z)e iωz dz π F(ω)e iωt dω. F(z)e izt dz. gange Fourier transformationen af F(t), altså F(t)e iωt dt,, f ( ω) F {F(t)}. (.3) π Dette resultat kaldes dualitetsprincippet, og kan bruges til at finde Fourier transformationer af funktioner der ellers ville være svære at beregne. Eksempel.8. Vi betragter igen funktionen f (t) u(t)e t, der har Fourier transformationen F(ω) +iω. Hvis vi nu ønsker at finde F af F(t) +it, kan vi benytte dualitetsprincippet; F {F(t)} π f ( ω) πu( ω)e ω..4. Delta funktionen For at kunne analysere Fourier transformationen af funktioner som fx. cosinus og sinus, skal vi også introducere delta funktionen (også kaldet Dirac s delta funktion). Denne funktion støder man på mange steder indenfor matematik og fysik, så det er en god ide at bruge noget tid på at forstå den. Det specielle ved delta funktionen er, at den kun er forskellig fra nul i et enkelt punkt, a. I dette punkt er dens værdi uendelig stor. Dette kan virke en smule mærkeligt, og delta funktionen er som sådan heller ikke en helt normal funktion. Forskriften for den er, t a δ(t a) (.4), ellers og den opfylder samtidig Desuden har den følgende meget anvendelige egenskab δ(t a)dt. (.5)
20 KAPITEL. FOURIER TRANSFORMATIONEN δ(t a) f (t)dt f (a), (.6) for alle pæne funktioner f, fx. de kontinuerte og differentiable funktioner. Lad os finde Fourier transformationen af delta funktionen, F {δ(t a)} δ(t a)e iωt dt, hvilket sammen med egenskaben i ligning (.6) giver F {δ(t a)} e iωa. (.7) Eksempel.9. Lad os finde Fourier transformationen af g(t) e ita. Vi ved, at for f (t) δ(t a) bliver F(ω) e iωa, ud fra ligning (.7). Dualitetsprincippet giver os nu, Altså er f ( ω) δ( ω a) π F { e ita}. F {g(t)} F { e ita} πδ( ω a) πδ( (ω + a)) πδ(ω + a), (.8) hvor det sidste lighedstegn gælder fordi δ(t) er en lige funktion..4.3 Cosinus og sinus Funktionerne cosinus og sinus er så hyppigt anvendte, at vi her viser udledningen af deres Fourier transformation. Disse funktioner er periodiske med en enkelt specifik frekvens, så vi forventer som sagt, at frekvensindholdet afspejler dette. Cosinus kan udtrykkes via Eulers formel som cos(at) eiat + e iat. (.9) Vi fandt i ligning (.8), at F { e ita} πδ(ω + a), og samtidig (ved at udskifte a med a), F { e ita} πδ(ω a). Kombineres disse to resultater med Eulers formel samt lineariteten af Fourier transformationen, får vi F { e ita} + F { e ita} πδ(ω + a) + πδ(ω a) F { e ita + e ita} πδ(ω + a) + πδ(ω a) { e ita + e ita } F {cos(at)} F πδ(ω + a) + πδ(ω a). Som forventet ser vi, at transformationen udelukkende består af en enkelt frekvens komponent, lokaliseret ved ±a. I figur.7 har vi til venstre vist input signalet, f (t) cos(t), og den tilhørende fourier transformation er vist til højre.
21 .5. DIFFERENTIALLIGNINGER Signal styrke Tid [/s] Fourier transformation Frekvens [/s] Figur.7: Venstre: Funktionen f (t). Højre: F { f (t)}. Opgave.3. Find F {sin(at)}. Det er en god ide at tage udgangspunkt i ovenstående udledning af F {cos(at)}.5 Differentialligninger For at illustrere hvorledes vi kan løse differentialligninger med Fourier transformationen vælger vi at betragte et konkret eksempel. Vi skal kigge på en partiel differentialligning, og det kan måske virke som et svært eksempel. Der er dog ikke noget i eksemplet der ikke er gennemgået i denne note; man kan tænke på funktionen u i det følgende som en funktion der er afhængig af de to variable x og t, og når vi skriver u(x,t) menes der den anden afledte af u med hensyn til t variablen t. Princippet i det følgende eksempel er, at Fourier transformere en partiel differentialligning i flere variable til en ordinær differentialligning i en af variablene. Herfra kan man så få information om løsninger og opførsel. Den ligning vi vil kigge på er bølgeligningen, der beskriver en bølges afhængighed af tid t og sted x. I dens simpleste form er den u(x,t) t c u(x,t) x, (.3) hvor u(x,t) er bølgens amplitude og c er dens udbredelseshastighed. Vi antager, at < x < og t >. For at kunne løse problemet skal vi også finde randbetingelserne. Vi beskriver amplituden til tiden t ved funktionen g(x), og antager desuden, at hastigheden af amplituden til tiden t er nul; u(x, ) g(x) (.3) u(x,) t. (.3)
22 KAPITEL. FOURIER TRANSFORMATIONEN Vi vil lave en transformation af ligning (.3) med hensyn til stedet, x (og ikke tiden t). Dette betyder også, at hvor vi tidligere har transformeret fra det tidslige domæne med t over til frekvensdomænet med ω, skal vi nu transformere fra domænet med x over til domænet med λ. Dimensionen af ω var s, og i dette eksempel er dimensionen af λ således m. Vi får nu { } { u(x,t) c } u(x,t) F t F x. (.33) I det følgende lader vi F {u(x,t)} U(λ,t). Ved at indsætte i definitionen af Fourier transformationen får vi u(x,t) t e iωx dx c u(x,t) x e iωx dx. (.34) For at lette arbejdet vil vi nu benytte os af følgende egenskab til at udregne højresiden af ligning (.34), { d n } F dx n f (x) (iλ) n F(λ). (.35) Højresiden bliver nu { } u(x,t) F x c λ U(λ,t). (.36) Til at udregne venstresiden af ligning (.34) skal vi indse, at den variabel der integreres med hensyn til er x, mens differentiationen er med hensyn til t. Dette betyder, at vi kan flytte differentiationen ud foran integralet (dette kaldes også Leibniz regel), { } u(x,t) F t t F {u(x,t)} tu(λ,t). (.37) Nu samler vi ligning (.36) og (.37), t U(λ,t) c ω U(λ,t), (.38) hvilket er en ordinær differentialligning i tid, hvis løsning er givet ved U(λ,t) A(λ)cos(cλt) + B(ω)sin(cλt). (.39) Koefficienterne A og B finder vi ved at anvende vores randbetingelser, der dog også skal transformeres til frekvensdomænet: U(λ, ) G(λ) (.4) U(λ,) t, (.4) hvor vi har antaget at funktionen g(x) har en Fourier transformation der eksisterer, så G(λ) F {g(x)}. Fra de to ovenstående randbetingelser får vi, at U(λ,t) G(λ)cos(λt). (.4)
23 .5. DIFFERENTIALLIGNINGER 3 Sidste skridt er nu, at benytte den inverse transformation til at finde u(x,t), u(x,t) F {U(λ,t)} F {G(λ)cos(cλt)}. (.43) Ved at anvende Eulers relation, ligning (.9), samt ligning (.) får vi u(x,t) [g(x + ct) + g(x ct)], (.44) hvilket betyder, at løsningerne u(x,t) er vandrende bølger (travelling waves) der bevæger sig til højre og venstre med hastigheden c. Dette problem blev oprindeligt undersøgt af Jean le Rond d Alembert og senere af Leonhard Euler. Opgave.4. Udregn resultatet i ligning (.44) med udgangspunkt i ligning (.4) samt de skridt der beskrives i teksten.
Introduktion til Laplace transformen (Noter skrevet af Nikolaj Hess-Nielsen sidst revideret marts 2013)
 Introduktion til Laplace transformen (oter skrevet af ikolaj Hess-ielsen sidst revideret marts 23) Integration handler ikke kun om arealer. Tværtimod er integration basis for mange af de vigtigste værktøjer
Introduktion til Laplace transformen (oter skrevet af ikolaj Hess-ielsen sidst revideret marts 23) Integration handler ikke kun om arealer. Tværtimod er integration basis for mange af de vigtigste værktøjer
Heisenbergs usikkerhedsrelationer. Abstrakt. Hvorfor? Funktionsrum. Nils Byrial Andersen Institut for Matematik. Matematiklærerdag 2013
 Heisenbergs usikkerhedsrelationer Nils Byrial Andersen Institut for Matematik Matematiklærerdag 013 1 / 17 Abstrakt Heisenbergs usikkerhedsrelationer udtrykker at man ikke på samme tid både kan bestemme
Heisenbergs usikkerhedsrelationer Nils Byrial Andersen Institut for Matematik Matematiklærerdag 013 1 / 17 Abstrakt Heisenbergs usikkerhedsrelationer udtrykker at man ikke på samme tid både kan bestemme
Det teknisk-naturvidenskabelige basisår Matematik 1A, Efterår 2005, Hold 3 Prøveopgave C
 Det teknisk-naturvidenskabelige basisår Matematik 1A, Efterår 2005, Hold 3 Prøveopgave C Opgaven består af tre dele, hver med en række spørgsmål, efterfulgt af en liste af teorispørgsmål. I alle opgavespørgsmålene
Det teknisk-naturvidenskabelige basisår Matematik 1A, Efterår 2005, Hold 3 Prøveopgave C Opgaven består af tre dele, hver med en række spørgsmål, efterfulgt af en liste af teorispørgsmål. I alle opgavespørgsmålene
Besvarelse til eksamen i Matematik F2, 2012
 Besvarelse til eksamen i Matematik F2, 202 Partiel besvarelse - har ikke inkluderet alle detaljer! Med forbehold for tastefejl. Opgave Find og bestem typen af alle singulariteter for følgende funktioner:
Besvarelse til eksamen i Matematik F2, 202 Partiel besvarelse - har ikke inkluderet alle detaljer! Med forbehold for tastefejl. Opgave Find og bestem typen af alle singulariteter for følgende funktioner:
Matematisk modellering og numeriske metoder. Lektion 6
 Matematisk modellering og numeriske metoder Lektion 6 Morten Grud Rasmussen 24. september, 2013 1 Forcerede oscillationer [Bogens afsnit 2.8, side 85] 1.1 Et forstyrret masse-fjeder-system I udledningen
Matematisk modellering og numeriske metoder Lektion 6 Morten Grud Rasmussen 24. september, 2013 1 Forcerede oscillationer [Bogens afsnit 2.8, side 85] 1.1 Et forstyrret masse-fjeder-system I udledningen
Lineære systemer med hukommelse.
 Lineær Response Teori. I responseteorien interesserer man sig for, hvad der kan siges generelt om sammenhængen mellem input φ(t) og output γ(t) for et system. Valg af variable. Det betragtede systems forskellige
Lineær Response Teori. I responseteorien interesserer man sig for, hvad der kan siges generelt om sammenhængen mellem input φ(t) og output γ(t) for et system. Valg af variable. Det betragtede systems forskellige
Laplace transformationen
 MODUL 6 Laplace transformationen Forfattere: Michael ELMEGÅRD & Øistein WIND-WILLASSEN 24. juni 214 2 Indhold 1 Laplace transformationen 5 1.1 En lineær transformation.............................. 7 1.2
MODUL 6 Laplace transformationen Forfattere: Michael ELMEGÅRD & Øistein WIND-WILLASSEN 24. juni 214 2 Indhold 1 Laplace transformationen 5 1.1 En lineær transformation.............................. 7 1.2
Svingninger. Erik Vestergaard
 Svingninger Erik Vestergaard 2 Erik Vestergaard www.matematikfysik.dk Erik Vestergaard, 2009. Billeder: Forside: Bearbejdet billede af istock.com/-m-i-s-h-a- Desuden egne illustrationer. Erik Vestergaard
Svingninger Erik Vestergaard 2 Erik Vestergaard www.matematikfysik.dk Erik Vestergaard, 2009. Billeder: Forside: Bearbejdet billede af istock.com/-m-i-s-h-a- Desuden egne illustrationer. Erik Vestergaard
Besvarelser til Calculus Ordinær Eksamen Juni 2019
 Besvarelser til Calculus Ordinær Eksamen - 14. Juni 2019 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 14. Juni 2019 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Eksamen i Mat F, april 2006
 Eksamen i Mat F, april 26 Opgave 1 Lad F være et vektorfelt, givet i retvinklede koordinater som: F x x F = F x i + F y j + F z k = F y = 2z F z y Udregn F og F: F = F x + F y + F z = 1 + +. F = F z F
Eksamen i Mat F, april 26 Opgave 1 Lad F være et vektorfelt, givet i retvinklede koordinater som: F x x F = F x i + F y j + F z k = F y = 2z F z y Udregn F og F: F = F x + F y + F z = 1 + +. F = F z F
Matematisk modellering og numeriske metoder. Lektion 10
 Matematisk modellering og numeriske metoder Lektion 10 Morten Grud Rasmussen 2. november 2016 1 Partielle differentialligninger 1.1 Det grundlæggende om PDE er Definition 1.1 Partielle differentialligninger
Matematisk modellering og numeriske metoder Lektion 10 Morten Grud Rasmussen 2. november 2016 1 Partielle differentialligninger 1.1 Det grundlæggende om PDE er Definition 1.1 Partielle differentialligninger
Bevægelsens Geometri
 Bevægelsens Geometri Vi vil betragte bevægelsen af et punkt. Dette punkt kan f.eks. være tyngdepunktet af en flue, et menneske, et molekyle, en galakse eller hvad man nu ellers har lyst til at beskrive.
Bevægelsens Geometri Vi vil betragte bevægelsen af et punkt. Dette punkt kan f.eks. være tyngdepunktet af en flue, et menneske, et molekyle, en galakse eller hvad man nu ellers har lyst til at beskrive.
Formelsamling - MatF2. Therkel Zøllner og Amalie Christensen 27. juni 2009
 Formelsamling - MatF2 Therkel Zøllner og Amalie Christensen 27. juni 2009 1 Indhold 1 Kompleks variabel teori 3 1.1 Komplekse funktioner 825-830........................... 3 1.2 Powerserier af komplekse
Formelsamling - MatF2 Therkel Zøllner og Amalie Christensen 27. juni 2009 1 Indhold 1 Kompleks variabel teori 3 1.1 Komplekse funktioner 825-830........................... 3 1.2 Powerserier af komplekse
Eksamen i Mat F, april 2006
 Eksamen i Mat F, april 26 Opgave Lad F være et vektorfelt, givet i retvinklede koordinater som: Udregn F og F: F x F = F x i + F y j + F z k = F y = z 2 F z xz y 2 F = F x + F y + F z = + + x. F = F z
Eksamen i Mat F, april 26 Opgave Lad F være et vektorfelt, givet i retvinklede koordinater som: Udregn F og F: F x F = F x i + F y j + F z k = F y = z 2 F z xz y 2 F = F x + F y + F z = + + x. F = F z
Lineære differentialligningers karakter og lineære 1. ordens differentialligninger
 enote 11 1 enote 11 Lineære differentialligningers karakter og lineære 1. ordens differentialligninger I denne note introduceres lineære differentialligninger, som er en speciel (og bekvem) form for differentialligninger.
enote 11 1 enote 11 Lineære differentialligningers karakter og lineære 1. ordens differentialligninger I denne note introduceres lineære differentialligninger, som er en speciel (og bekvem) form for differentialligninger.
Matematisk modellering og numeriske metoder. Lektion 8
 Matematisk modellering og numeriske metoder Lektion 8 Morten Grud Rasmussen 18. oktober 216 1 Fourierrækker 1.1 Periodiske funktioner Definition 1.1 (Periodiske funktioner). En periodisk funktion f er
Matematisk modellering og numeriske metoder Lektion 8 Morten Grud Rasmussen 18. oktober 216 1 Fourierrækker 1.1 Periodiske funktioner Definition 1.1 (Periodiske funktioner). En periodisk funktion f er
Lineære 2. ordens differentialligninger med konstante koefficienter
 enote 13 1 enote 13 Lineære 2. ordens differentialligninger med konstante koefficienter I forlængelse af enote 11 og enote 12 om differentialligninger, kommer nu denne enote omkring 2. ordens differentialligninger.
enote 13 1 enote 13 Lineære 2. ordens differentialligninger med konstante koefficienter I forlængelse af enote 11 og enote 12 om differentialligninger, kommer nu denne enote omkring 2. ordens differentialligninger.
Københavns Universitet, Det naturvidenskabelige Fakultet. Afleveringsopgave 1
 Københavns Universitet, Det naturvidenskabelige Fakultet 1 Lineær Algebra (LinAlg) Afleveringsopgave 1 Eventuelle besvarelser laves i grupper af - 3 personer og afleveres i to eksemplarer med 3 udfyldte
Københavns Universitet, Det naturvidenskabelige Fakultet 1 Lineær Algebra (LinAlg) Afleveringsopgave 1 Eventuelle besvarelser laves i grupper af - 3 personer og afleveres i to eksemplarer med 3 udfyldte
Note om Laplace-transformationen
 Note om Laplace-transformationen Den harmoniske oscillator omskrevet til et ligningssystem I dette opgavesæt benyttes laplacetransformationen til at løse koblede differentialligninger. Fordelen ved at
Note om Laplace-transformationen Den harmoniske oscillator omskrevet til et ligningssystem I dette opgavesæt benyttes laplacetransformationen til at løse koblede differentialligninger. Fordelen ved at
Eulers equidimensionale differentialligning
 Eulers equidimensionale differentialligning Projektbesvarelse for MM501, udformet af Hans J. Munkholm Differentialligningen September-oktober 2009 For at kunne referere let og elegant gentages differentialligningen
Eulers equidimensionale differentialligning Projektbesvarelse for MM501, udformet af Hans J. Munkholm Differentialligningen September-oktober 2009 For at kunne referere let og elegant gentages differentialligningen
Pointen med Differentiation
 Pointen med Differentiation Frank Nasser 20. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk:
Pointen med Differentiation Frank Nasser 20. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk:
Indhold. Litteratur 11
 Indhold Forord ii 00-sættet 1 Opgave 1....................................... 1 Spørgsmål (a).................................. 1 Spørgsmål (b).................................. 1 Spørgsmål (c)..................................
Indhold Forord ii 00-sættet 1 Opgave 1....................................... 1 Spørgsmål (a).................................. 1 Spørgsmål (b).................................. 1 Spørgsmål (c)..................................
Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 2016
 Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Matematisk modellering og numeriske metoder. Lektion 11
 Matematisk modellering og numeriske metoder Lektion 11 Morten Grud Rasmussen 5. november 2016 1 Partielle differentialligninger 1.1 Udledning af varmeligningen Vi vil nu på samme måde som med bølgeligningen
Matematisk modellering og numeriske metoder Lektion 11 Morten Grud Rasmussen 5. november 2016 1 Partielle differentialligninger 1.1 Udledning af varmeligningen Vi vil nu på samme måde som med bølgeligningen
Laplace- og Fouriertransformationer med anvendelser. Karin Lentfer Kristiansen og Thomas Hecksher
 Laplace- og Fouriertransformationer med anvendelser Karin Lentfer Kristiansen og Thomas Hecksher EVU master i matematikuddannelsen på Aalborg Universitet 6. september 4 Resumé The following report is a
Laplace- og Fouriertransformationer med anvendelser Karin Lentfer Kristiansen og Thomas Hecksher EVU master i matematikuddannelsen på Aalborg Universitet 6. september 4 Resumé The following report is a
ANALYSE 1, 2014, Uge 5
 ANALYSE, 204, Uge 5 Afleveringsfrist for Prøve 2 er Tirsdag den 20/5 kl 0:5. Forelæsninger Tirsdag Vi går videre med Afsnit 4 om uniform konvergens af Fourierrækker, hvor hovedsætningen er Sætning 4.3.
ANALYSE, 204, Uge 5 Afleveringsfrist for Prøve 2 er Tirsdag den 20/5 kl 0:5. Forelæsninger Tirsdag Vi går videre med Afsnit 4 om uniform konvergens af Fourierrækker, hvor hovedsætningen er Sætning 4.3.
MM501 forelæsningsslides
 MM501 forelæsningsslides uge 37, 2010 Produceret af Hans J. Munkholm 2009 bearbejdet af Jessica Carter 2010 1 Hvad er et komplekst tal? Hvordan regner man med komplekse tal? Man kan betragte udvidelsen
MM501 forelæsningsslides uge 37, 2010 Produceret af Hans J. Munkholm 2009 bearbejdet af Jessica Carter 2010 1 Hvad er et komplekst tal? Hvordan regner man med komplekse tal? Man kan betragte udvidelsen
(c) Opskriv den reelle Fourierrække for funktionen y(t) fra (b), og afgør dernæst om y(t) er en lige eller ulige funktion eller ingen af delene.
 MATEMATIK 3 EN,MP 4. februar 2016 Eksamenopgaver fra 2011 2016 (jan. 2016) Givet at 0 for 0 < t < 1 mens e (t 1) cos(7(t 1)) for t 1, betragt da begyndelsesværdiproblemet for t > 0: y (t) + 2y (t) + 50y(t)
MATEMATIK 3 EN,MP 4. februar 2016 Eksamenopgaver fra 2011 2016 (jan. 2016) Givet at 0 for 0 < t < 1 mens e (t 1) cos(7(t 1)) for t 1, betragt da begyndelsesværdiproblemet for t > 0: y (t) + 2y (t) + 50y(t)
Hans J. Munkholm: En besvarelse af
 Hans J. Munkholm: En besvarelse af Projekt for MM501, Lineære differentialligninger November-december 2009 Nummererede formler fra opgaveformuleringen Her samles alle opgavens differentialligninger og
Hans J. Munkholm: En besvarelse af Projekt for MM501, Lineære differentialligninger November-december 2009 Nummererede formler fra opgaveformuleringen Her samles alle opgavens differentialligninger og
Projektopgave 1. Navn: Jonas Pedersen Klasse: 3.4 Skole: Roskilde Tekniske Gymnasium Dato: 5/ Vejleder: Jørn Christian Bendtsen Fag: Matematik
 Projektopgave 1 Navn: Jonas Pedersen Klasse:.4 Skole: Roskilde Tekniske Gymnasium Dato: 5/9-011 Vejleder: Jørn Christian Bendtsen Fag: Matematik Indledning Jeg har i denne opgave fået følgende opstilling.
Projektopgave 1 Navn: Jonas Pedersen Klasse:.4 Skole: Roskilde Tekniske Gymnasium Dato: 5/9-011 Vejleder: Jørn Christian Bendtsen Fag: Matematik Indledning Jeg har i denne opgave fået følgende opstilling.
Varmeligningen og cosinuspolynomier.
 Varmeligningen og cosinuspolynomier. Projekt for MM50 Marts 009 Hans J. Munkholm 0. Praktiske oplysninger Dette projekt besvares af de studerende, som er tilmeldt eksamen i MM50 uden at være tilmeldt eksamen
Varmeligningen og cosinuspolynomier. Projekt for MM50 Marts 009 Hans J. Munkholm 0. Praktiske oplysninger Dette projekt besvares af de studerende, som er tilmeldt eksamen i MM50 uden at være tilmeldt eksamen
Diffusionsligningen. Fællesprojekt for FY520 og MM502. Marts Hans J. Munkholm og Paolo Sibani. Besvarelse fra Hans J.
 Diffusionsligningen Fællesprojekt for FY50 og MM50 Marts 009 Hans J. Munkholm og Paolo Sibani Besvarelse fra Hans J. Munkholm 1 (a) Lad [x, x + x] være et lille delinterval af [a, b]. Den masse, der er
Diffusionsligningen Fællesprojekt for FY50 og MM50 Marts 009 Hans J. Munkholm og Paolo Sibani Besvarelse fra Hans J. Munkholm 1 (a) Lad [x, x + x] være et lille delinterval af [a, b]. Den masse, der er
Den homogene ligning. Vi betragter den n te ordens, homogene, lineære differentialligning. d n y dt n. an 1 + any = 0 (1.2) dt. + a1 d n 1 y dt n 1
 1/7 Den homogene ligning Vi betragter den n te ordens, homogene, lineære differentialligning a 0 d n y dt n + a1 d n 1 y dt n 1 hvor a 0,..., a n R og a 0 0. Vi skriver ligningen på kort form som + + dy
1/7 Den homogene ligning Vi betragter den n te ordens, homogene, lineære differentialligning a 0 d n y dt n + a1 d n 1 y dt n 1 hvor a 0,..., a n R og a 0 0. Vi skriver ligningen på kort form som + + dy
Integralregning Infinitesimalregning
 Udgave 2.1 Integralregning Infinitesimalregning Noterne gennemgår begreberne integral og stamfunktion, og anskuer dette som et redskab til bestemmelse af arealer under funktioner. Noterne er supplement
Udgave 2.1 Integralregning Infinitesimalregning Noterne gennemgår begreberne integral og stamfunktion, og anskuer dette som et redskab til bestemmelse af arealer under funktioner. Noterne er supplement
MM501 forelæsningsslides
 MM50 forelæsningsslides uge 36, 2009 Produceret af Hans J. Munkholm Nogle talmængder s. 3 N = {, 2, 3, } omtales som de naturlige tal eller de positive heltal. Z = {0, ±, ±2, ±3, } omtales som de hele
MM50 forelæsningsslides uge 36, 2009 Produceret af Hans J. Munkholm Nogle talmængder s. 3 N = {, 2, 3, } omtales som de naturlige tal eller de positive heltal. Z = {0, ±, ±2, ±3, } omtales som de hele
Spektrumrepræsentation
 Spektrumrepræsentation (Kapitel 3) Jens D. Andersen Datalogisk Institut Københavns Universitet p.1/35 $ $ $ Spektrumrepræsentation Matematisk repræsentation af en sinusoide: hvor "! er en fasor. Mere komplicerede
Spektrumrepræsentation (Kapitel 3) Jens D. Andersen Datalogisk Institut Københavns Universitet p.1/35 $ $ $ Spektrumrepræsentation Matematisk repræsentation af en sinusoide: hvor "! er en fasor. Mere komplicerede
Differentialligninger. Ib Michelsen
 Differentialligninger Ib Michelsen Ikast 203 2 Indholdsfortegnelse Indholdsfortegnelse Indholdsfortegnelse...2 Ligninger og løsninger...3 Indledning...3 Lineære differentialligninger af første orden...3
Differentialligninger Ib Michelsen Ikast 203 2 Indholdsfortegnelse Indholdsfortegnelse Indholdsfortegnelse...2 Ligninger og løsninger...3 Indledning...3 Lineære differentialligninger af første orden...3
Løsningsforslag til opgavesæt 5
 Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
π er irrationel Frank Nasser 10. december 2011
 π er irrationel Frank Nasser 10. december 2011 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold 1 Introduktion
π er irrationel Frank Nasser 10. december 2011 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold 1 Introduktion
Kortfattet svar til eksamen i Matematik F2 d. 21. juni 2017
 Kortfattet svar til eksamen i Matematik F2 d. 2. juni 27 Opgave Bestem for følgende tilfælde om en funktion f(z) af z = x + iy er analytisk i dele af den komplekse plan, hvis den har real del u(x, y) og
Kortfattet svar til eksamen i Matematik F2 d. 2. juni 27 Opgave Bestem for følgende tilfælde om en funktion f(z) af z = x + iy er analytisk i dele af den komplekse plan, hvis den har real del u(x, y) og
Løsningsforslag til opgavesæt 5
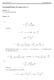 Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
Matematisk modellering og numeriske metoder. Lektion 11
 Matematisk modellering og numeriske metoder Lektion 11 Morten Grud Rasmussen 17. oktober, 2013 1 Partielle differentialligninger 1.1 D Alemberts løsning af bølgeligningen [Bogens sektion 12.4 på side 553]
Matematisk modellering og numeriske metoder Lektion 11 Morten Grud Rasmussen 17. oktober, 2013 1 Partielle differentialligninger 1.1 D Alemberts løsning af bølgeligningen [Bogens sektion 12.4 på side 553]
Reaktionskinetik - 1 Baggrund. lineære og ikke-lineære differentialligninger. Køreplan
 Reaktionskinetik - lineære og ikke-lineære differentialligninger Køreplan 1 Baggrund På 2. eller 4. semester møder kemi/bioteknologi studerende faget Indledende Fysisk Kemi (26201/26202). Her behandles
Reaktionskinetik - lineære og ikke-lineære differentialligninger Køreplan 1 Baggrund På 2. eller 4. semester møder kemi/bioteknologi studerende faget Indledende Fysisk Kemi (26201/26202). Her behandles
Analyse 1, Prøve 4 Besvarelse
 Københavns Universitet Prøve ved Det naturvidenskabelige Fakultet juni 2011 1 Analyse 1, Prøve 4 Besvarelse Lad Opgave 1 (50%) M = {T R 2 T er en åben trekant} og lad A : M R være arealfunktionen, dvs.
Københavns Universitet Prøve ved Det naturvidenskabelige Fakultet juni 2011 1 Analyse 1, Prøve 4 Besvarelse Lad Opgave 1 (50%) M = {T R 2 T er en åben trekant} og lad A : M R være arealfunktionen, dvs.
Kalkulus 2 - Grænseovergange, Kontinuitet og Følger
 Kalkulus - Grænseovergange, Kontinuitet og Følger Mads Friis 8. januar 05 Indhold Grundlæggende uligheder Grænseovergange 3 3 Kontinuitet 9 4 Følger 0 5 Perspektivering 4 Grundlæggende uligheder Sætning
Kalkulus - Grænseovergange, Kontinuitet og Følger Mads Friis 8. januar 05 Indhold Grundlæggende uligheder Grænseovergange 3 3 Kontinuitet 9 4 Følger 0 5 Perspektivering 4 Grundlæggende uligheder Sætning
Mujtaba og Farid Integralregning 06-08-2011
 Indholdsfortegnelse Integral regning:... 2 Ubestemt integral:... 2 Integrationsprøven:... 3 1) Integration af potensfunktioner:... 3 2) Integration af sum og Differens:... 3 3) Integration ved Multiplikation
Indholdsfortegnelse Integral regning:... 2 Ubestemt integral:... 2 Integrationsprøven:... 3 1) Integration af potensfunktioner:... 3 2) Integration af sum og Differens:... 3 3) Integration ved Multiplikation
Impedans. I = C du dt (1) og en spole med selvinduktionen L
 Impedans I et kredsløb, der består af andre netværkselementer end blot lække (modstande) og kilder vil der ikke i almindelighed være en simpel proportional, tidslig sammenhæng mellem strøm og spænding,
Impedans I et kredsløb, der består af andre netværkselementer end blot lække (modstande) og kilder vil der ikke i almindelighed være en simpel proportional, tidslig sammenhæng mellem strøm og spænding,
Projekt 4.6 Løsning af differentialligninger ved separation af de variable
 Projekt 4.6 Løsning af differentialligninger ved separation af de variable Differentialligninger af tpen d hx () hvor hx ()er en kontinuert funktion, er som nævnt blot et stamfunktionsproblem. De løses
Projekt 4.6 Løsning af differentialligninger ved separation af de variable Differentialligninger af tpen d hx () hvor hx ()er en kontinuert funktion, er som nævnt blot et stamfunktionsproblem. De løses
C R. Figur 1 Figur 2. er eksempler på kredsløbsfunktioner. Derimod er f.eks. indgangsimpedansen
 Kredsløbsfunktioner Lad os i det følgende betragte kredsløb, der er i hvile til t = 0. Det vil sige, at alle selvinduktionsstrømme og alle kondensatorspændinger er nul til t = 0. I de Laplace-transformerede
Kredsløbsfunktioner Lad os i det følgende betragte kredsløb, der er i hvile til t = 0. Det vil sige, at alle selvinduktionsstrømme og alle kondensatorspændinger er nul til t = 0. I de Laplace-transformerede
Grafmanipulation. Frank Nasser. 14. april 2011
 Grafmanipulation Frank Nasser 14. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk: Dette er
Grafmanipulation Frank Nasser 14. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk: Dette er
Matematisk modellering og numeriske metoder. Overskrifter
 Matematisk modellering og numeriske metoder Overskrifter Morten Grud Rasmussen 25. november, 2013 Lektion 1 Ordinære differentialligninger ODE er helt grundlæggende Løsninger Begyndelsesværdiproblemer
Matematisk modellering og numeriske metoder Overskrifter Morten Grud Rasmussen 25. november, 2013 Lektion 1 Ordinære differentialligninger ODE er helt grundlæggende Løsninger Begyndelsesværdiproblemer
Mere om differentiabilitet
 Mere om differentiabilitet En uddybning af side 57 i Spor - Komplekse tal Kompleks funktionsteori er et af de vigtigste emner i matematikken og samtidig et af de smukkeste I bogen har vi primært beskæftiget
Mere om differentiabilitet En uddybning af side 57 i Spor - Komplekse tal Kompleks funktionsteori er et af de vigtigste emner i matematikken og samtidig et af de smukkeste I bogen har vi primært beskæftiget
n=1 er veldefineret for alle følger for hvilke højresiden er endelig. F.eks. tilhører følgen
 2 Hilbert rum 2. Eksempler på Hilbert rum Vi skal nu først forsøge at begrunde, at de indre produkt rum af funktioner eller følger, som blev indført i Kapitel, ikke er omfattende nok til vores formål.
2 Hilbert rum 2. Eksempler på Hilbert rum Vi skal nu først forsøge at begrunde, at de indre produkt rum af funktioner eller følger, som blev indført i Kapitel, ikke er omfattende nok til vores formål.
Matematik F2 Opgavesæt 6
 Opgave 4: Udtryk funktionen f(θ) = sin θ ved hjælp af Legendre-polynomierne på formen P l (cos θ). Dvs. find koefficienterne a l i ekspansionen f(θ) = a l P l (cos θ) l= Svar: Bemærk, at funktionen er
Opgave 4: Udtryk funktionen f(θ) = sin θ ved hjælp af Legendre-polynomierne på formen P l (cos θ). Dvs. find koefficienterne a l i ekspansionen f(θ) = a l P l (cos θ) l= Svar: Bemærk, at funktionen er
DesignMat Lineære differentialligninger I
 DesignMat Lineære differentialligninger I Preben Alsholm Uge Forår 0 1 Lineære differentialligninger af første orden 1.1 Normeret lineær differentialligning Normeret lineær differentialligning En differentialligning,
DesignMat Lineære differentialligninger I Preben Alsholm Uge Forår 0 1 Lineære differentialligninger af første orden 1.1 Normeret lineær differentialligning Normeret lineær differentialligning En differentialligning,
Besvarelser til Calculus Ordinær Eksamen - 3. Januar 2017
 Besvarelser til Calculus Ordinær Eksamen - 3. Januar 17 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 3. Januar 17 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Førsteordens lineære differentialligninger
 enote 16 1 enote 16 Førsteordens lineære differentialligninger I denne enote gives først en kort introduktion til differentialligninger i almindelighed, hvorefter hovedemnet er en særlig type af differentialligninger,
enote 16 1 enote 16 Førsteordens lineære differentialligninger I denne enote gives først en kort introduktion til differentialligninger i almindelighed, hvorefter hovedemnet er en særlig type af differentialligninger,
Ting man gør med Vektorfunktioner
 Ting man gør med Vektorfunktioner Frank Nasser. april 11 c 8-11. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk: Dette
Ting man gør med Vektorfunktioner Frank Nasser. april 11 c 8-11. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk: Dette
Signalbehandling og matematik 1 (Tidsdiskrete signaler og systemer)
 Signalbehandling og matematik 1 (Tidsdiskrete signaler og systemer) Session 1. Sekvenser, diskrete systemer, Lineære systemer, foldning og lineære tidsinvariante systemer Ved Samuel Schmidt sschmidt@hst.aau.dk
Signalbehandling og matematik 1 (Tidsdiskrete signaler og systemer) Session 1. Sekvenser, diskrete systemer, Lineære systemer, foldning og lineære tidsinvariante systemer Ved Samuel Schmidt sschmidt@hst.aau.dk
Matematisk modellering og numeriske metoder. Lektion 17
 Matematisk modellering og numeriske metoder Lektion 1 Morten Grud Rasmussen. december 16 1 Numerisk integration og differentiation 1.1 Simpsons regel Antag, at vi har en funktion f på intervallet I = [a,
Matematisk modellering og numeriske metoder Lektion 1 Morten Grud Rasmussen. december 16 1 Numerisk integration og differentiation 1.1 Simpsons regel Antag, at vi har en funktion f på intervallet I = [a,
Idenne note giver vi et eksempel på, hvorledes det er vigtigt at holde sig
 Analyse : Eulers formel Sebastian rsted 9. maj 015 Idenne note giver vi et eksempel på, hvorledes det er vigtigt at holde sig for øje, hvor de matematiske resultater kommer fra, og hvad de baseres på;
Analyse : Eulers formel Sebastian rsted 9. maj 015 Idenne note giver vi et eksempel på, hvorledes det er vigtigt at holde sig for øje, hvor de matematiske resultater kommer fra, og hvad de baseres på;
VUC Vestsjælland Syd, Slagelse Nr. 1 Institution: Projekt Trigonometri
 VUC Vestsjælland Syd, Slagelse Nr. 1 Institution: 333247 2015 Anders Jørgensen, Mark Kddafi, David Jensen, Kourosh Abady og Nikolaj Eriksen 1. Indledning I dette projekt, vil man kunne se definitioner
VUC Vestsjælland Syd, Slagelse Nr. 1 Institution: 333247 2015 Anders Jørgensen, Mark Kddafi, David Jensen, Kourosh Abady og Nikolaj Eriksen 1. Indledning I dette projekt, vil man kunne se definitioner
DesignMat Lineære differentialligninger I
 DesignMat Lineære differentialligninger I Preben Alsholm Uge 9 Forår 2010 1 Lineære differentialligninger af første orden 1.1 Normeret lineær differentialligning Normeret lineær differentialligning En
DesignMat Lineære differentialligninger I Preben Alsholm Uge 9 Forår 2010 1 Lineære differentialligninger af første orden 1.1 Normeret lineær differentialligning Normeret lineær differentialligning En
MATEMATIK 3 EN,MP 17. september 2014 Oversigt nr. 1
 MATEMATIK 3 EN,MP 7. september 204 Oversigt nr. Her bringes en samling af de gamle eksamensopgaver: (jan. 204) Betragt begyndelsesværdiproblemet y (t) + 7y (t) + 2y(t) = e t sin(2t) for t > 0, y(0) = 2,
MATEMATIK 3 EN,MP 7. september 204 Oversigt nr. Her bringes en samling af de gamle eksamensopgaver: (jan. 204) Betragt begyndelsesværdiproblemet y (t) + 7y (t) + 2y(t) = e t sin(2t) for t > 0, y(0) = 2,
Eksamen i Matematik F2 d. 19. juni Opgave 2. Svar. Korte svar (ikke fuldstændige)
 Eksamen i Matematik F2 d. 9. juni 28 Korte svar (ikke fuldstændige Opgave Find realdelen, Re z, og imaginærdelen, Im z, for følgende værdier af z, a z = 2 i b z = i i c z = ln( + i Find realdelen, Re z,
Eksamen i Matematik F2 d. 9. juni 28 Korte svar (ikke fuldstændige Opgave Find realdelen, Re z, og imaginærdelen, Im z, for følgende værdier af z, a z = 2 i b z = i i c z = ln( + i Find realdelen, Re z,
VEKSELSPÆNDINGENS VÆRDIER. Frekvens Middelværdi & peak værdi (max) Effektiv værdi (RMS) Mere om effektiv værdi!
 AC VEKSELSPÆNDINGENS VÆRDIER Frekvens Middelværdi & peak værdi (max) Effektiv værdi (RMS) Mere om effektiv værdi! Frekvens: Frekvensen (f) af et system er antallet af svingninger eller rotationer pr. sekund:
AC VEKSELSPÆNDINGENS VÆRDIER Frekvens Middelværdi & peak værdi (max) Effektiv værdi (RMS) Mere om effektiv værdi! Frekvens: Frekvensen (f) af et system er antallet af svingninger eller rotationer pr. sekund:
Matematisk modellering og numeriske metoder
 Matematisk modellering og numeriske metoder Morten Grud Rasmussen 5. september 2016 1 Ordinære differentialligninger ODE er 1.1 ODE er helt grundlæggende Definition 1.1 (Ordinære differentialligninger).
Matematisk modellering og numeriske metoder Morten Grud Rasmussen 5. september 2016 1 Ordinære differentialligninger ODE er 1.1 ODE er helt grundlæggende Definition 1.1 (Ordinære differentialligninger).
Formelsamling til Fourieranalyse 10. udgave
 Formelsmling til Fouriernlyse. udgve Kristin Jerslev og Steven Hyden 3. oktober 9 Her følger en formelsmling lvet til kurset Fouriernlyse på Arhus Universitet. Bemærk venligst, t smlingen indeholder sætninger
Formelsmling til Fouriernlyse. udgve Kristin Jerslev og Steven Hyden 3. oktober 9 Her følger en formelsmling lvet til kurset Fouriernlyse på Arhus Universitet. Bemærk venligst, t smlingen indeholder sætninger
Ting man gør med Vektorfunktioner
 Ting man gør med Vektorfunktioner Frank Villa 3. august 13 Dette dokument er en del af MatBog.dk 8-1. IT Teaching Tools. ISBN-13: 978-87-9775--9. Se yderligere betingelser for brug her. Indhold 1 Introduktion
Ting man gør med Vektorfunktioner Frank Villa 3. august 13 Dette dokument er en del af MatBog.dk 8-1. IT Teaching Tools. ISBN-13: 978-87-9775--9. Se yderligere betingelser for brug her. Indhold 1 Introduktion
Wavelet Analyse. Arne Jensen Institut for Matematiske Fag Aalborg Universitet
 Wavelet Analyse Arne Jensen Institut for Matematiske Fag Aalborg Universitet 1 Introduktion Numb3rs episoden on pengeforfalskning brugte wavelet analyse. Wavelet analyse er en relativt ny opdagelse, som
Wavelet Analyse Arne Jensen Institut for Matematiske Fag Aalborg Universitet 1 Introduktion Numb3rs episoden on pengeforfalskning brugte wavelet analyse. Wavelet analyse er en relativt ny opdagelse, som
Elementær Matematik. Trigonometriske Funktioner
 Elementær Matematik Trigonometriske Funktioner Ole Witt-Hansen Indhold. Gradtal og radiantal.... sin x, cos x og tan x... 3. Trigonometriske ligninger...3 4. Trigonometriske uligheder...5 5. Harmoniske
Elementær Matematik Trigonometriske Funktioner Ole Witt-Hansen Indhold. Gradtal og radiantal.... sin x, cos x og tan x... 3. Trigonometriske ligninger...3 4. Trigonometriske uligheder...5 5. Harmoniske
DESIGNMAT FORÅR 2012: UGESEDDEL Forberedelse Læs alle opgaverne fra tidligere ugesedler, og læg særlig mærke til dem du har spørgsmål til.
 DESIGNMAT FORÅR 2012: UGESEDDEL 13 INSTITUT FOR MATEMATIK 1. Forberedelse Læs alle opgaverne fra tidligere ugesedler, og læg særlig mærke til dem du har spørgsmål til. 2. Aktiviteter mandag 13 17 2.1.
DESIGNMAT FORÅR 2012: UGESEDDEL 13 INSTITUT FOR MATEMATIK 1. Forberedelse Læs alle opgaverne fra tidligere ugesedler, og læg særlig mærke til dem du har spørgsmål til. 2. Aktiviteter mandag 13 17 2.1.
Komplekse Tal. 20. november 2009. UNF Odense. Steen Thorbjørnsen Institut for Matematiske Fag Århus Universitet
 Komplekse Tal 20. november 2009 UNF Odense Steen Thorbjørnsen Institut for Matematiske Fag Århus Universitet Fra de naturlige tal til de komplekse Optælling af størrelser i naturen De naturlige tal N (N
Komplekse Tal 20. november 2009 UNF Odense Steen Thorbjørnsen Institut for Matematiske Fag Århus Universitet Fra de naturlige tal til de komplekse Optælling af størrelser i naturen De naturlige tal N (N
Besvarelser til Calculus Ordinær Eksamen - 5. Januar 2018
 Besvarelser til Calculus Ordinær Eksamen - 5. Januar 18 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 5. Januar 18 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Matematisk modellering og numeriske metoder. Lektion 4
 Matematisk modellering og numeriske metoder Lektion 4 Morten Grud Rasmussen 17. september, 013 1 Homogene andenordens lineære ODE er [Bogens afsnit.1] 1.1 Linearitetsprincippet Vi så sidste gang, at førsteordens
Matematisk modellering og numeriske metoder Lektion 4 Morten Grud Rasmussen 17. september, 013 1 Homogene andenordens lineære ODE er [Bogens afsnit.1] 1.1 Linearitetsprincippet Vi så sidste gang, at førsteordens
Introduktion til cosinus, sinus og tangens
 Introduktion til cosinus, sinus og tangens Jes Toft Kristensen 24. maj 2010 1 Forord Her er en lille introduktion til cosinus, sinus og tangens. Det var et af de emner jeg selv havde svært ved at forstå,
Introduktion til cosinus, sinus og tangens Jes Toft Kristensen 24. maj 2010 1 Forord Her er en lille introduktion til cosinus, sinus og tangens. Det var et af de emner jeg selv havde svært ved at forstå,
MM501 forelæsningsslides
 MM501 forelæsningsslides uge 35-del 1, 2010 Redigeret af Jessica Carter efter udgave af Hans J. Munkholm 1 Nogle talmængder s. 4 N = {1,2,3, } omtales som de naturlige tal eller de positive heltal. Z =
MM501 forelæsningsslides uge 35-del 1, 2010 Redigeret af Jessica Carter efter udgave af Hans J. Munkholm 1 Nogle talmængder s. 4 N = {1,2,3, } omtales som de naturlige tal eller de positive heltal. Z =
Differentialligninger af første orden
 Differentialligninger af første orden Preben Alsholm Februar 2006 Basale begreber. Eksistens og entydighed. En differentialligning af første orden er en ligning, der sammenknytter differentialkvotienten
Differentialligninger af første orden Preben Alsholm Februar 2006 Basale begreber. Eksistens og entydighed. En differentialligning af første orden er en ligning, der sammenknytter differentialkvotienten
Fordybelsesprojekt Matematik 2, forår 2005 Potensrækker
 Fordybelsesprojekt Matematik 2, forår 2005 Potensrækker Arne Jensen 7. 11. marts 2005 1 Indledning I forbindelse med kurset i Reelle og Komplekse Funktioner afholdes et fordybelsesprojekt med et omfang
Fordybelsesprojekt Matematik 2, forår 2005 Potensrækker Arne Jensen 7. 11. marts 2005 1 Indledning I forbindelse med kurset i Reelle og Komplekse Funktioner afholdes et fordybelsesprojekt med et omfang
En differentiabel funktion hvis afledte ikke er kontinuert Søren Knudby
 24 En differentiabel funktion hvis afledte ikke er kontinuert Søren Knudby Det er velkendt for de fleste, at differentiabilitet af en reel funktion f medfører kontinuitet af f, mens det modsatte ikke gælder
24 En differentiabel funktion hvis afledte ikke er kontinuert Søren Knudby Det er velkendt for de fleste, at differentiabilitet af en reel funktion f medfører kontinuitet af f, mens det modsatte ikke gælder
En sumformel eller to - om interferens
 En sumformel eller to - om interferens - fra borgeleo.dk Vi ønsker - af en eller anden grund - at beregne summen og A x = cos(0) + cos(φ) + cos(φ) + + cos ((n 1)φ) A y = sin (0) + sin(φ) + sin(φ) + + sin
En sumformel eller to - om interferens - fra borgeleo.dk Vi ønsker - af en eller anden grund - at beregne summen og A x = cos(0) + cos(φ) + cos(φ) + + cos ((n 1)φ) A y = sin (0) + sin(φ) + sin(φ) + + sin
MATEMATIK 11 Eksamensopgaver Juni 1995 Juni 2001, 4. fjerdedel
 Juni 2000 MATEMATIK 11 Eksamensopgaver Juni 1995 Juni 2001, 4. fjerdedel Opgave 1. (a) Find den fuldstændige løsning til differentialligningen y 8y + 16y = 0. (b) Find den fuldstændige løsning til differentialligningen
Juni 2000 MATEMATIK 11 Eksamensopgaver Juni 1995 Juni 2001, 4. fjerdedel Opgave 1. (a) Find den fuldstændige løsning til differentialligningen y 8y + 16y = 0. (b) Find den fuldstændige løsning til differentialligningen
Momenter som deskriptive størrelser. Hvad vi mangler fra onsdag. Momenter for sandsynlighedsmål
 Hvad vi mangler fra onsdag Momenter som deskriptive størrelser Sandsynlighedsmål er komplicerede objekter de tildeler numeriske værdier til alle hændelser i en σ-algebra. Vi har behov for simplere, deskriptive
Hvad vi mangler fra onsdag Momenter som deskriptive størrelser Sandsynlighedsmål er komplicerede objekter de tildeler numeriske værdier til alle hændelser i en σ-algebra. Vi har behov for simplere, deskriptive
Hvad vi mangler fra onsdag. Vi starter med at gennemgå slides fra onsdag.
 Hvad vi mangler fra onsdag Vi starter med at gennemgå slides 34-38 fra onsdag. Slide 1/17 Niels Richard Hansen MI forelæsninger 6. December, 2013 Momenter som deskriptive størrelser Sandsynlighedsmål er
Hvad vi mangler fra onsdag Vi starter med at gennemgå slides 34-38 fra onsdag. Slide 1/17 Niels Richard Hansen MI forelæsninger 6. December, 2013 Momenter som deskriptive størrelser Sandsynlighedsmål er
Additionsformlerne. Frank Villa. 19. august 2012
 Additionsformlerne Frank Villa 19. august 2012 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold 1 Introduktion
Additionsformlerne Frank Villa 19. august 2012 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold 1 Introduktion
Matematisk modellering og numeriske metoder
 Matematisk modellering og numeriske metoder Morten Grud Rasmussen September 0, 016 1 Lineære ODE er af første orden 1.1 De grundlæggende definitioner Definition 1.1. Lineære ODE er af første orden er ODE
Matematisk modellering og numeriske metoder Morten Grud Rasmussen September 0, 016 1 Lineære ODE er af første orden 1.1 De grundlæggende definitioner Definition 1.1. Lineære ODE er af første orden er ODE
Eksamen i Calculus. 14. juni f (x, y, z) = 1 + x 2 + y 2. x 2 + y 2 1 Hele rummet uden z aksen
 Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 14. juni 019 Opgave 1 (6 point) En
Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 14. juni 019 Opgave 1 (6 point) En
Fejlforplantning. Landmålingens fejlteori - Lektion 5 - Fejlforplantning. Repetition: Varians af linear kombination. Eksempel: Vinkelberegning
 Fejlforplantning Landmålingens fejlteori Lektion 5 Fejlforplantning - kkb@math.aau.dk http://people.math.aau.dk/ kkb/undervisning/lf13 Landmåling involverer ofte bestemmelse af størrelser som ikke kan
Fejlforplantning Landmålingens fejlteori Lektion 5 Fejlforplantning - kkb@math.aau.dk http://people.math.aau.dk/ kkb/undervisning/lf13 Landmåling involverer ofte bestemmelse af størrelser som ikke kan
Noter om Komplekse Vektorrum, Funktionsrum og Differentialligninger LinAlg 2004/05-Version af 16. Dec.
 Noter om Komplekse Vektorrum, Funktionsrum og Differentialligninger LinAlg 2004/05-Version af 16. Dec. 1 Komplekse vektorrum I defininitionen af vektorrum i Afsnit 4.1 i Niels Vigand Pedersen Lineær Algebra
Noter om Komplekse Vektorrum, Funktionsrum og Differentialligninger LinAlg 2004/05-Version af 16. Dec. 1 Komplekse vektorrum I defininitionen af vektorrum i Afsnit 4.1 i Niels Vigand Pedersen Lineær Algebra
Mat H /05 Note 2 10/11-04 Gerd Grubb
 Mat H 1 2004/05 Note 2 10/11-04 Gerd Grubb Nødvendige og tilstrækkelige betingelser for ekstremum, konkave og konvekse funktioner. Fremstillingen i Kapitel 13.1 2 af Sydsæters bog [MA1] suppleres her med
Mat H 1 2004/05 Note 2 10/11-04 Gerd Grubb Nødvendige og tilstrækkelige betingelser for ekstremum, konkave og konvekse funktioner. Fremstillingen i Kapitel 13.1 2 af Sydsæters bog [MA1] suppleres her med
Teoretisk Statistik, 16. februar Generel teori,repetition
 1 Uge 8 Teoretisk Statistik, 16. februar 2004 1. Generel teori, repetition 2. Diskret udfaldsrum punktssh. 3. Fordelingsfunktionen 4. Tæthed 5. Transformationer 6. Diskrete vs. Kontinuerte stokastiske
1 Uge 8 Teoretisk Statistik, 16. februar 2004 1. Generel teori, repetition 2. Diskret udfaldsrum punktssh. 3. Fordelingsfunktionen 4. Tæthed 5. Transformationer 6. Diskrete vs. Kontinuerte stokastiske
Matematik A. Højere teknisk eksamen. Forberedelsesmateriale. htx112-mat/a-26082011
 Matematik A Højere teknisk eksamen Forberedelsesmateriale htx112-mat/a-26082011 Fredag den 26. august 2011 Forord Forberedelsesmateriale til prøverne i matematik A Der er afsat 10 timer på 2 dage til
Matematik A Højere teknisk eksamen Forberedelsesmateriale htx112-mat/a-26082011 Fredag den 26. august 2011 Forord Forberedelsesmateriale til prøverne i matematik A Der er afsat 10 timer på 2 dage til
Nedenfor er tegnet svingningsmønsteret for to sinus-toner med frekvensen 440 og 443 Hz:
 Appendiks 1: Om svævning: Hvis to toner ligger meget tæt på hinanden opstår et interessant akustisk og matematisk fænomen, der kaldes svævning. Det er dette fænomen, der ligger bag alle de steder, hvor
Appendiks 1: Om svævning: Hvis to toner ligger meget tæt på hinanden opstår et interessant akustisk og matematisk fænomen, der kaldes svævning. Det er dette fænomen, der ligger bag alle de steder, hvor
Afgør for hver af følgende rækker om den er divergent, betinget konvergent eller absolut konvergent. 2 n. n=1 2n (n + 1)2 1 = 2(n + n+1
 Analyse Reeksamen 00 Rasmus Sylvester Bryder 5. august 0 Opgave Afgør for hver af følgende rækker om den er divergent, betinget konvergent eller absolut konvergent. ( ) n n +3n+7 n= n + For alle n N vil
Analyse Reeksamen 00 Rasmus Sylvester Bryder 5. august 0 Opgave Afgør for hver af følgende rækker om den er divergent, betinget konvergent eller absolut konvergent. ( ) n n +3n+7 n= n + For alle n N vil
MM501 forelæsningsslides
 MM501 forelæsningsslides uge 40, 2010 Produceret af Hans J. Munkholm bearbejdet af JC 1 Separabel 1. ordens differentialligning En generel 1. ordens differentialligning har formen s.445-8 dx Eksempler
MM501 forelæsningsslides uge 40, 2010 Produceret af Hans J. Munkholm bearbejdet af JC 1 Separabel 1. ordens differentialligning En generel 1. ordens differentialligning har formen s.445-8 dx Eksempler
Besvarelser til Calculus Ordinær Eksamen Januar 2019
 Besvarelser til Calculus Ordinær Eksamen - 14. Januar 19 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 14. Januar 19 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Matematisk modellering og numeriske metoder. Lektion 5
 Matematisk modellering og numeriske metoder Lektion 5 Morten Grud Rasmussen 19. september, 2013 1 Euler-Cauchy-ligninger [Bogens afsnit 2.5, side 71] 1.1 De tre typer af Euler-Cauchy-ligninger Efter at
Matematisk modellering og numeriske metoder Lektion 5 Morten Grud Rasmussen 19. september, 2013 1 Euler-Cauchy-ligninger [Bogens afsnit 2.5, side 71] 1.1 De tre typer af Euler-Cauchy-ligninger Efter at
Differentiation af Trigonometriske Funktioner
 Differentiation af Trigonometriske Funktioner Frank Villa 15. oktober 01 Dette dokument er en del af MatBog.dk 008-01. IT Teaching Tools. ISBN-13: 978-87-9775-00-9. Se yderligere betingelser for brug her.
Differentiation af Trigonometriske Funktioner Frank Villa 15. oktober 01 Dette dokument er en del af MatBog.dk 008-01. IT Teaching Tools. ISBN-13: 978-87-9775-00-9. Se yderligere betingelser for brug her.
DesignMat Uge 1 Gensyn med forårets stof
 DesignMat Uge 1 Gensyn med forårets stof Preben Alsholm Efterår 2010 1 Hovedpunkter fra forårets pensum 11 Taylorpolynomium Taylorpolynomium Det n te Taylorpolynomium for f med udviklingspunkt x 0 : P
DesignMat Uge 1 Gensyn med forårets stof Preben Alsholm Efterår 2010 1 Hovedpunkter fra forårets pensum 11 Taylorpolynomium Taylorpolynomium Det n te Taylorpolynomium for f med udviklingspunkt x 0 : P
Hvorfor bevæger lyset sig langsommere i fx glas og vand end i det tomme rum?
 Hvorfor bevæger lyset sig langsommere i fx glas og vand end i det tomme rum? - om fysikken bag til brydningsindekset Artiklen er udarbejdet/oversat ud fra især ref. 1 - fra borgeleo.dk Det korte svar:
Hvorfor bevæger lyset sig langsommere i fx glas og vand end i det tomme rum? - om fysikken bag til brydningsindekset Artiklen er udarbejdet/oversat ud fra især ref. 1 - fra borgeleo.dk Det korte svar:
