Noter til Fysik 6 - Elektrodynamik og bølger
|
|
|
- Bertha Gregersen
- 6 år siden
- Visninger:
Transkript
1 Noter til Fysik 6 - Elektrodynamik og bølger Anders S. Sørensen Niels Bohr Institutet, Københavns Universitet 22. oktober 2009
2 2 Om disse noter Disse noter udgør en del af pensum til kurset Fysik 6 - elektrondynamik og bølger og er et supplement til lærebogen D.J. Griffiths, Introduction to electrodynamics. Der laves derfor engang imellem henvisning til Griffiths. I disse henvisninger referer sidenumre mm. til den 3. udgave (af den internationale udgave). Det er så vidt jeg ved den udgave I også har. Kapitlerne i disse noter er sammensat af forskellige noter fra tidligere. Hvert kapitel er derfor et separat afsnit som kan læses uden sammenhæng med resten (og der refereres ikke til tidligere kapitler). Desuden er der nogle af kapitlerne hvor jeg referer til appendiks. Disse appendiks kommer sidst i hver af kapitlerne i modsætning til alm. bøger hvor appendiks typisk kommer til aller sidst. De forskellige kapitler er derfor ikke helt så sammenhængende som man normalt ville se i en bog. Mest tydeligt er det at sproget varierer mellem dansk og engelsk, og notationen kan variere en anelse fra kapitel til kapitel. Jeg tror dog ikke dette burde volde de store problemer.
3 Indhold 1 About complex numbers Fundamentals Magnitude and argument The complex exponential function Purely real exponent Purely imaginary exponent Writing complex numbers in terms of magnitude and argument Multiplying complex numbers General complex exponent Time evolution Problems Grundlæggende elektronik Passive komponenter Modstand Kapacitor Induktans Batterier og spændingsforsyninger Kirchhoff s love Kirchhoffs 1. lov Kirchhoffs 2. lov Eksempler Jævnstrømskredse Transienter Vekselstrøm Arbejde og energi Svingningskredsen Aktive komponenter Forstærkning - transistoren Ensretning - dioden Opgaver
4 4 INDHOLD 3 Fourier Transformation A physical example Fourier transformation Fourier series Fourier integrals Applications in physics Appendices x and p in quantum mechanics Proof of Fourier transformation Fourier Series from Fourier integrals Fourier integrals from Fourier series Why is Fourier transformation so useful in physics? Problems More on waves Standing waves Waves in three dimensions Plane waves Spherical waves Interference Spatial interference Interference in time Electromagnetic waves in wires Appendix: Sound waves Sound in one dimension Sound in three dimensions Appendix: Water waves Problems Flere Opgaver 109
5 Chapter 1 About complex numbers In this course we shall use complex numbers a lot. You are supposed to have learned about complex numbers before, but experience tells me that you have not used them so much, and that you are therefore not very comfortable using them. During the course you will develop the required experience in working with complex numbers, but to help you a little bit along the way, these notes refresh what you are supposed to know about complex numbers. Since the purpose of these notes is only to refresh what you are supposed to know, the explanations given here are very brief. If you feel that the explanations are not sufficient for you to understand it, I STRONGLY advice you to reread your old mathematics book on this subject. 1.1 Fundamentals The starting point of complex numbers is that we introduce the number i, which has the property i 2 = 1. (1.1) A general complex number can now be written as z = x + iy, (1.2) where x and y are two ordinary (real) numbers. z now has both a real part and an imaginary part Re(z) = x, (1.3) Im(z) = y. (1.4) Furthermore we shall need the complex conjugate of z, which we call z. The complex conjugate of z is obtained by simply changing the sign of the imaginary component z = x iy. (1.5) 5
6 6 CHAPTER 1. ABOUT COMPLEX NUMBERS That is, we just change the sign of all the is. Ex: As a particular example we could take the complex number z = 3 + 4i. This has a real part Re(z) = 3 and an imaginary part Im(z) = 4. The complex conjugate is then z = 3 4i Any complex number can be represented as a point in the complex plane with coordinates (x,y), as shown in Fig In this plane the complex conjugate is obtained by taking the mirror image in the horizontal axis. y=im(z) y z=x+iy z θ x x=re(z) z * =x-iy Figure 1.1: Representation of complex numbers in the complex plane. The complex number z can be thought of as either an x and a y coordinate, or as a length z and an angle θ. 1.2 Magnitude and argument Instead of writing a complex number as z = x + iy, it is often convenient to think about the number as having a length z and an angle θ, as it is also shown in Fig By looking at the right angle triangle we can use Pythagoras to find the magnitude z = x 2 + y 2, (1.6)
7 1.2. MAGNITUDE AND ARGUMENT 7 and the angle can be found from the definition of the trignometric functions tan θ = y x cos θ = x z (1.7) (1.8) sin θ = y z. (1.9) Instead of talking about length and angle of a complex number, one typically refers to z as the magnitude of z and the angle θ is the phase or argument of z θ = Arg(z). (1.10) Note, that the use of the word argument here should not be confused with the argument of a function f(x), which is x. Ex: if we again take z = 3 + 4i we have the magnitude z = = 5 and the tangent of the angle is tan θ = 3/4. To find the magnitude of a complex number a convenient trick is to multiply the number by its complex conjugate We thus see that z z = (x iy)(x + iy) = x 2 + y 2. (1.11) z = z z. (1.12) Ex: to see how this is useful, let us try to calculate the magnitude of the complex number z = 3 + 4i 5 + 6i. (1.13) We can now find the magnitude from z z: z z = ( 3 + 4i 5 + 6i The magnitude is therefore ) 3 + 4i 5 + 6i = 3 4i 3 + 4i 5 6i 5 + 6i = (3 4i)(3 + 4i) (5 6i)(5 + 6i) = (1.14) z = (1.15) While the above arguments finds the magnitude of a complex number we will also sometimes need to find the argument of a fraction like the one in (1.13). To do this we multiply by the complex conjugate of the denominator z = We can now see that tan θ = 2/39. (5 6i)(3 + 4i) (5 6i)(5 + 6i) i =. (1.16) 61
8 8 CHAPTER 1. ABOUT COMPLEX NUMBERS 1.3 The complex exponential function We shall use the complex exponential function e z a lot in this course, so it it very important that you know how it works Purely real exponent If we take the exponential of a real number z = x there is nothing new e z = e x. (1.17) We just use the ordinary exponential function that we are used to Purely imaginary exponent If the exponent is purely imaginary z = iy, the exponential function works as follows e iy = cos(y) + i sin(y). (1.18) We can calculate the magnitude of the complex number e iy in two different ways: using z 2 = Re(z) 2 + Im(z) 2 we find e iy = cos 2 (y) + sin 2 (y) = 1, (1.19) or using z = z z we again find e iy = (e iy ) e iy = e iy e iy = e (iy iy) = 1 (1.20) The argument θ can be found from (1.7): tan θ = sin(y) cos(y) = tan(y). (1.21) y is thus the same as the angle θ 1. In the complex plane, the function e iy therefore simply runs around on the unit circle as shown in Fig Strictly speaking this equation imply θ = y + nπ, where n is an integer, but if you also look at the expressions for sine and cosine you realise that θ = y + n2π, and the change of the angle by 2π is irrelevant.
9 1.3. THE COMPLEX EXPONENTIAL FUNCTION 9 Im(e iy ) y 1 Re(e iy ) Figure 1.2: The complex exponential function e iy in the complex plane Writing complex numbers in terms of magnitude and argument The complex exponential function allows us to write complex numbers in terms of their magnitude and argument. If we have the complex number z = x + iy we see from Eqs. (1.8) and (1.9) that This form will be very convenient for us in this course. z = z e iθ. (1.22) Multiplying complex numbers If you have two complex numbers z 1 = x 1 +iy 1 and z 2 = x 2 +iy 2 you can of course just multiply them together in the ordinary fashion z 1 z 2 = x 1 x 2 y 1 y 2 + i(x 1 y 2 + y 1 x 2 ), but it is often more convenient to use the representation in terms of the magnitudes and arguments z 1 z 2 = z 1 e iθ 1 z 2 e iθ 2 = z 1 z 2 e i(θ 1+θ 2 ). (1.23) The new length z 1 z 2 is just the product of the two lengths and new argument is just the sum of the two arguments θ 1 + θ 2.
10 10 CHAPTER 1. ABOUT COMPLEX NUMBERS General complex exponent If the exponential function has a general complex argument e z, where z = x + iy, we use the property of the exponential function that e a+b = e a e b. We can therefore write e x+iy = e x e iy. (1.24) The magnitude is thus e x+iy = e x, (1.25) since e iy has magnitude 1. The argument is since e x has argument 0. θ = Arg(e x+iy ) = y, (1.26) 1.4 Time evolution We shall mainly use the complex exponential function to describe time evolution. Specifically we shall write real physical quantities like an oscillating electromotive force E = E 0 cos(ωt) as the real part of a complex function E = Re ( E 0 e iωt). (1.27) Note the the minus sign in the exponent is an arbitrary choice. The minus used here is the convention ordinarily used for time evolution in physics. Compare for instance with quantum mechanics where the time evolution is e iet/. Throughout this course we shall use the minus, but be aware that the plus is sometimes used in the literature. In general we shall be dealing with expressions, which have both a real and an imaginary part in the exponent. Like f(t) = e (γ+iω)t (1.28) This can be rewritten as f(t) = e γt e iωt. (1.29) Here the first factor will lead to an exponential damping in time, whereas the last factor give oscillations. In Fig. 1.3 we show an example of the real part of f(t). Also shown in the figure are the so called envelope functions ±e γt, which the curve is oscillating between.
11 1.5. PROBLEMS Problems 1. What is (1 + i) ( 1 + i)? Do it both by direct multiplication, and using the magnitudes and arguments (in this case the direct multiplication is the simplest, but do the magnitude and argument as an exercise). For the magnitude and argument part, it is an advantage to plot the two numbers in the complex plane. 2. What is the magnitude and argument of a) z = 8 + 6i b) z = 8 + 6i c) i z = 8 7i. (1.30) 3. How would Fig. 1.3 have looked if instead one had used γ = 0.01, γ = 1, or γ = 10? You don t have to make a detailed drawing, just sketch how it will roughly look. How would it look if you instead changed ω? 4. Sketch how the imaginary part of the function f(t) in Eq. (1.29) will look. Also sketch the real part of the function for different values of φ. f(t) = e γt i(ωt+φ) (1.31)
12 12 CHAPTER 1. ABOUT COMPLEX NUMBERS Re[f(t)] t Figure 1.3: The full curve is the real part of f(t) = e (γ+iω)t, with ω = 1 and γ = 0.1. The dotted lines are the envelope functions ±e γt
13 Kapitel 2 Grundlæggende elektronik Dette kapitel er oprindeligt skrevet af Per Hedegård, men er blevet omskrevet til dette kursus. Tusind tak til Per for at lade mig overtage teksten! OK, lad os bygge et farvefjernsyn! Inden vi kan gå i gang med detaljerne i dette projekt, må vi lige få de grundlæggende principper i elektronik på plads. Et elektronisk kredsløb, består af en række kanaler ofte ledninger, men i dag er det meget mere almindeligt, at kanalerne er lavet af meget små metalstriber, der er pådampet fx. en silicium krystal. Disse kanaler fører elektroner rundt til og igennem en antal komponenter, som ændrer på disses bevægelse, afhængig af opladningen af, feltet over, eller magnetfeltet igennem komponenten. Dette koncept er meget kraftfuldt og al moderne civilisation med dens fjernsyn, radio, computere, internet, mikrobølgeovne, telefoner, etc. bygger teknisk set herpå. I dette kapitel vil vi gennemgå de mest basale love for sådanne elektroniske kredsløb, som de blev formuleret i anden halvdel af 1800 tallet. 2.1 Passive komponenter Passive komponenter er elementer i et kredsløb, som ikke er i stand til at forstærke strømmen, dvs. ikke er i stand til at tilføre kredsløbet energi. De mest almindelige passive komponenter er modstande, kapacitorer (kondensatorer) og induktorer (spoler). 13
14 14 KAPITEL 2. GRUNDLÆGGENDE ELEKTRONIK Modstand Grunden til at elektroner i et materiale bevæger sig og laver en elektrisk strøm er til syvende og sidst at de er udsat for en elektrisk kraft, som er beskrevet ved et elektrisk felt E. Hvis materialet var helt perfekt, dvs. hvis alle atomerne sad fuldstændigt stille på deres plads i det gitter, som alle krystallinske materialer er opbygget af, og hvis der ikke er fremmedatomer til stede, så vil elektronerne falde frit ned gennem ledningen i en accelereret bevægelse jvf. Newtons love. I praksis har vi aldrig en sådan idealiseret situation. Atomerne foretager små termiske vibrationer og selv i det reneste stof er der et vist antal fremmedatomer. Disse forstyrrelser bevirker, at elektronerne ikke falder frit men snarere falder som en faldskærmsudspringer: Uden faldskærm ville han hele tiden blive accelereret ned mod jorden, med faldskærm vil han kun i starten blive accelereret, men på grund af faldskærmens mange stød med luftmolekylerne ophører accelerationen og han opnår en konstant sluthastighed, der på kontrolleret vis fører ham ned mod jordoverfladen. Denne sluthastighed er faktisk proportional med tyngdekraften v = αg, (2.1) hvor proportionalitetskonstanten (mobiliteten) α afhænger af skærmens størrelse, tætheden af luftmolekyler etc. For elektroner i en ledning sker noget tilsvarende. Deres sluthastighed i et elektrisk felt vil også være proportional med feltets styrke v = µ E. (2.2) Ved nu at multiplicere med elektrontætheden og elektronladningen resulterer ovenstående i Ohms lov J = σ E. (2.3) Den tyske fysiker Paul Drude skrev en simpel formel ned for værdien af konduktiviteten, σ: σ = ne2 τ m, (2.4) hvor n er elektrontætheden (eller snarere ladningsbærertætheden, idet mange af elektronerne i stoffet er bundet til de enkelte atomer og kan ikke bevæge sig frit), e er elektronens ladning, og m er elektronens masse. Endelig er τ den gennemsnitlige tid der går mellem at en elektron støder ind i et vibrererende atom eller i et fremmedatom. På samme måde som i Griffiths kapitel 7 er det nu muligt at relatere den samlede strøm igennem en ledning, I = S J d a, hvor S er et tværsnit af ledningen, til spændingsfaldet V = E d l, over et stykke af ledningen via den mere kendte version af Ohms lov V = RI, (2.5)
15 2.1. PASSIVE KOMPONENTER 15 hvor R = L/(σA) (L er stykkets længde, og A er ledningens tværsnitsareal). Den vigtigste fysiske egenskab ved elektrisk modstand, er at der heri overføres energi fra det strømmende elektronsystem til de vibrerende atomer, dvs. til varme i ledningen. Denne energioverførsel sker med en hastighed (Griffiths formel (8.6)) dw dt = V J E dτ, (2.6) hvor der her integreres over hele ledningens volumen. Strengt taget udtrykker denne formel den energi pr. tid, dvs. det arbejde pr. tid, som det elektriske felt udfører på elektronerne. Denne ekstra energi, som tilføres elektronerne, vil så til syvende og sidst overføres til varme i ledningen gennem stød mellem elektroner og atomer. Den tidslige forsinkelse mellem at elektronen modtager energien fra feltet og til den afleveres til atomerne er så kort sek. at vi kan se bort fra den. Ligningen (2.6) har også en version i termer af V og I, nemlig dw dt = V I = RI 2. (2.7) Som det fremgår af Griffiths tabel 7.1 varierer konduktiviteten (eller dens reciprokke, resistiviteten) med mange størrelsesordener. Det mest ledende materiale bortset fra superledere er sølv, og det leder en faktor bedre end den bedste isolator! I et kredsløb, hvor ledningerne mellem komponenterne er lavet af kobber eller sølv, kan man derfor ofte se bort fra modstanden i disse ledninger og kun inkludere modstanden i komponenter, der med vilje er anbragt i kredsløbet med det formål at skabe et spændingsfald og derfor er lavet af et mindre ledende materiale Kapacitor I et kredsløb kan der ofte være områder, hvor der sker en vis ladningsophobning, og der vil som følge heraf opstå et elektrisk felt med feltlinier, der ender andre steder i kredsløbet, hvor den modsvarende negative ladning befinder sig. Der er med andre ord opstået en spændingsforskel mellem disse ladede områder. Som regel sker sådanne opladninger på kontrollerede steder, ofte i form af en komponent, kondensatoren. Fra den generelle teori i Griffiths kapitel ved vi, at der er en lineær sammenhæng mellem mængden af ophobet ladning, Q, og spændingsforskellen, V Q = CV. (2.8) Kapacitansen, C, afhænger af den geometriske udformning af komponenten, og den har typisk en værdi på C ɛ 0 a, hvor a er en typisk længde i komponenten. Umiddelbart vil man sige, at der ikke kan passere strøm igennem en kondensator den består jo af to metalplader adskilt af en meget god isolator, og der kan ikke
16 16 KAPITEL 2. GRUNDLÆGGENDE ELEKTRONIK passere elektroner gennem en isolator. I et kort tidsrum kan man godt sige, at der bevæger sig strøm gennem kondensatoren: mens den oplades løber der ladning til den ene plade og ladning væk fra den anden, så set udefra er det som om, der bevæger sig ladning gennem komponenten. Prisen er dog at den lades op og det koster energi W = Q2 2C, (2.9) så der er grænser for hvor længe strømmen kan have samme retning. Ud fra (2.8) og sammenhængen mellem strøm og ladning, dq/dt = I, kan vi få Ohms lov for en kapacitor I = C dv dt, eller V = 1 Idt. (2.10) C For en kapacitor er sammenhængen mellem strøm og spænding altså en differentialligning! Som regel er kapacitorer indført i et kredsløb med vilje for at de skal tjene et bestemt formål, men man skal være opmærksom på, at der kan opstå uønskede ladningsophobninger og dertil hørende kapacitanser og spændingsforskelle imellem forskellige dele af kredsløbet Induktans Når vi har at gøre med tidsligt varierende strømme, vil der ifølge Amperes lov opstå varierende magnetfelter, som på sin side ifølge Faradays lov vil resultere i varierende elektriske felter med dertil hørende varierende elektromotoriske kræfter. Sådanne elektromotoriske kræfter er man ofte interesseret i at udnytte i et kredsløb. Man får de kraftigste magnetfelter, hvis man lader strømmen løbe igennem en spole, der eventuelt kan have en kerne lavet af et magnetisk materiale. En sådan komponent kaldes en induktor, eller blot en spole. Dens symbol er en idealiseret spole. Den samlede elektromotoriske kraft i sådan en komponent er jvf. Faradays lov, Griffiths ligning (7.14) E = E d l = dφ dt. (2.11) Her er det vigtigt at indse, at integralet der definerer E er et lukket kurve- integral, dvs. det inkluderer også dele af kredsen, som er uden for spolen. På den anden side har vi den samlede flux igennem den lukkede kurve. Her vil det dominerende bidrag komme fra spolen og det er derfor muligt at tale om at spolen opfylder en slags Ohms lov. Vi har nemlig, at fluxen Φ er linieært relateret til strømmen gennem spolen, via Φ = LI, hvor L er spolens induktans. Den ønskede sammenhæng mellem elektromotorisk kraft og strøm bliver så E = L di dt, (2.12)
17 2.1. PASSIVE KOMPONENTER 17 dvs. en differentialligning. Vi bemærker her, at der ikke er nogen elektromotorisk kraft, hvis der løber en konstant strøm gennem spolen, da vi så har di/dt = 0. Hvis vi derimod vil ændre strømmen kommer der en elektromotorisk kraft. Grunden til dette er, at når der løber strøm i en spole, opstår der et magnetfelt. Et sådant magnetfelt koster energi at lave, og i en spole er der derfor oplagret en energi W = 1 2 LI2. (2.13) At ændre på strømmen kræver derfor, at vi ændrer energien. Der skal altså udføres et (positivt eller negativt) arbejde for at ændre strømmen i en spole, og der induceres derfor en elektromotorisk kraft som vil modvirke enhver ændring i strømmen (vi vil se på dette i mere detalje nedenfor). I enhver kreds vil der altid være en vis induktans. For en kreds uden nogen spole er induktansen en geometrisk størrelse der har en approximativ værdi L µ 0 a, hvor a er en typisk længde. Indsætter man derimod en spole med mange vindinger kan man forøge induktansen betydeligt L µ 0 an 2, hvor N er antallet af vindinger. Induktansen vil derfor typisk være domineret af spolen hvis N 1. Udover tilsigtede induktanser fra spoler kan der i et kredsløb være utilsigtede induktanser, idet det er fluxen igennem den samlede kreds der bestemmer kredsens samlede induktans. Denne opdeles ofte i gensidige induktanser mellem forskellige dele af kredsløbet (magnetisk flux fra strømme i en del af kredsen, der inducerer strømme i andre dele af kredsen) Batterier og spændingsforsyninger For at få strømme til at løbe i en kreds er det naturligvis nødvendigt at have komponenter, der kan skabe elektromotoriske kræfter, dvs. pumpe energi ind i systemet selv i jævnstrømstilfældet. Disse komponenter er strengt taget ikke passive, men de er nødvendige at omtale på dette sted. Et batteri eller en spændingsforsyning kan bedst karakteriseres som en elektronelevator. Det er en indretning, der kan løfte ladninger fra et spændingsniveau til et højere, dvs. mod den retning som det elektriske felt trækker i ladningen. Kraften og den energi som dens arbejde repræsenterer kan være af kemisk natur, som det ofte er i et batteri. Det kan dog også være en bogstavelig elevator, som det er i en såkaldt van de Graaf generator. Det vigtige ved en sådan spændingsforsyning er, at den repræsenterer en kraft per ladning, f, der ikke er knyttet til det elektriske felt E. Kraften udfører et arbejde på en enhedsladning den såkaldte elektromotoriske kraft: E 0 = f d l, (2.14)
18 18 KAPITEL 2. GRUNDLÆGGENDE ELEKTRONIK hvor integralet strengt taget er over en lukket kreds, men bidraget fra f er naturligvis koncentreret til batteriets område. Den samlede energi som en sådan spændingsforsyning pumper ind i systemet pr. sekund er givet som dw = d dt dt (QE 0) = IE 0. (2.15) 2.2 Kirchhoff s love Gustav Kirchhoff formulerede i midten af 1800 tallet to love som ethvert elektrisk kredsløb opfylder. Den almene gyldighed af lovene er sikret derved, at lovene er direkte konsekvenser af to fundamentale love i hele fysikken, nemlig lovene om ladningsbevarelse og energibevarelse. En yderligere antagelse indgår, nemlig, at elektriske signaler forplanter sig uendelig hurtigt. Når eksempelvis ladningstætheden eller strømmen ændrer sig et sted i kredsen, så vil de dertil hørende elektriske og magnetiske felter være ændrede overalt i resten af kredsen. Dette er naturligvis principielt umuligt. Enhver forandring vil højst kunne forplante sig med lysets hastig rundt i kredsen. Dette har kun praktisk relevans, hvis vi har at gøre med meget hurtige forandringer, dvs. med variationer, der har en meget høj frekvens (se nøjere diskussion af frekvens i næste afsnit). Et krav må være, at alle forandringer er kommunikeret rundt i kredsen inden yderligere forandringer sker. Matematisk kan det udtrykkes at Varighed af forandring 1 ν L c varighed af kommunikation, (2.16) hvor L er kredsens geometriske størrelse og ν er en typisk frekvens for systemet. Med andre ord bølgelængden λ = c/ν af et lyssignal med frekvensen ν skal være meget længere end kredsens udstrækning λ = c ν L. (2.17) I praksis betyder det, for centimeter store kredse, at de anvendte frekvenser må være mindre end 10 GHz Kirchhoffs 1. lov Tilbage til Kirchhoffs love. En typisk elektrisk kreds kan være som vist i Fig Den består af en række såkaldte knuder hvor 3 eller flere kanaler mødes. Ladningsbevarelse siger, at ladninger, der strømmer ind mod sådan en knude må forlade knuden igen. Hvis vi regner strømmene, I i, i de forskellige kanaler med fortegn, fx. som positiv, hvis ladningerne strømmer ind mod knuden og negativ hvis de strømmer bort,
19 2.2. KIRCHHOFF S LOVE 19 så kan Kirchhoffs 1. lov skrives I i = 0. (2.18) i Bemærk, at en knude er et lille metallisk område, hvor der ikke sker ladningsophobning. Hvis der kunne ske ladningsophobning, så ville området ikke være kvalificeret som knude, men snarere som del af en kapacitor-komponent. Figur 2.1: Elektrisk kredsløb (simpel spændingsforstærker) Kirchhoffs 2. lov Betragter vi igen kredsen i Fig. 2.1, så kan vi opfatte den som et antal mindre delkredse, fx. ABCD. En sådan delkreds kaldes en maske. Det samlede arbejde per ladning udført af elektriske og andre kræfter pr. tid er givet som ( f + E) Jdτ, (2.19) hvor integralet er et volumenintegral over den strømførende del af kredsen. I en enkelt gren benævnt i af kredsen vil dette arbejde blive afsat som varme, som allerede beskrevet i forrige afsnit. Vi har altså en lokal form for energibevarelse: ( f + E) Jdτ = R i Ii 2. (2.20) i
20 20 KAPITEL 2. GRUNDLÆGGENDE ELEKTRONIK Venstresiden omskrives nu, idet vi antager at kraftfelterne er konstante hen over et tværsnit af ledningen: I i (E i + E d l), (2.21) hvor E i er den elektromotoriske kraft fra eventuelle batterier og generatorer i den i te gren. Divideres nu med I i fås følgende identitet for hver gren af masken: E i + E d l = R i I i. (2.22) i Hvis en gren indeholder en kapacitor, så vil kurveintegralet over E ikke inkludere stykket mellem kapacitorens plader. Vi kan addere og subtrahere et sådant bidrag og få E i + E d l V Ci = R i I i, (2.23) hele i hvor V Ci er spændingen over kapacitoren V Ci = b E d l. Vi vil nu addere disse a ligninger for samtlige grene i en maske og ende med E + E d l V C = R i I i. (2.24) batterier i kapacitorer modstande Sidste skridt består nu i at anvende Faradays lov. Den siger, at det lukkede kurveintegral af E er lig med minus den samlede fluxændring omsluttet af masken E d l = Φ t = spoler L i di i dt, (2.25) hvor vi til slut har set bort fra gensidige induktanser fra andre dele af kredsløbet og mellem spoler indenfor masken 1. Efter denne lidt besværlige omgang er vi omsider nået frem til Kirchhoffs 2. lov, eller maskeligningen, som den også kaldes: batterier E i = spoler L i di i dt + kapacitorer V Ci + modstande R i I i. (2.26) Når man skal anvende disse ligninger skal man erstatte V Ci med C 1 t I(t )dt, der således bliver integro-differentialligninger med strømmene som ubekendte. Spændinger kan så indføres som matematiske hjælpestørrelser. 1 Strengt taget er V Ci ikke veldefineret, da den vil afhænge af integrationsvejen fra den ene kapacitorplade til den anden. Det samlede resultat er dog entydigt, idet et skift i vej (og dermed i V Ci ) vil være kompenseret af et skift i fluxen Φ. Det er naturligvis mest praktisk, at vælge integrationsvejen som den korteste vej mellem kapacitorpladerne, hvorved også Φ vil være domineret af fluxen gennem kredsens spoler.
21 2.3. EKSEMPLER 21 Er man uddannet som elektroingeniør eller elektriker har man en meget nem huskeregel for Kirchhoffs 2. lov. Man siger ganske enkelt, at hver komponent i kredsen bidrager med et for komponenten karakteristisk spændingsfald: R i I i for en den ite modstand, V Ci for den ite kapacitor og L i di i /dt for den ite spole. Dette spændingsfald vil i langt de flest tilfælde være det man måler, hvis man tilslutter et voltmeter på hver side af en komponent (se dog Griffiths opgave 7.50 for et eksempel, hvor det ikke er tilfældet, fordi der går et varierende magnetfelt gennem kredsen). Når man går rundt i en kreds siger ligning (2.26) at summen af alle spændingsfaldene modsvares af spændingsforsyningens spænding, E (eller summen af dem hvis der er flere). Bemærk her, at når man går rundt i en kreds med mange knuder vil stømmen ikke være den samme i alle grene. I det tilfælde er det vigtigt at spændingsfaldet over en komponent er bestemt af strømmen gennem den gren som komponenten sidder i. Til dagligt brug er spændingsfald en overordentlig nyttig tænkemåde, men der kan opstå situationer, hvor det er vigtigt at forstå, at det egentlige fysiske indhold i loven er energibevarelse samt, at spændinger ikke er veldefinerede fysiske størrelser det er kun strømme og elektromotoriske kræfter (se igen Griffiths opg. 7.50). 2.3 Eksempler Jævnstrømskredse Når strømmene i en kreds er tidsuafhængige vil hverken kapacitorer eller induktorer spille nogen rolle og de kan droppes fra ligningerne. Kapacitoren fordi der ikke kan løbe en konstant strøm igennem en kapacitor uden at der vil blive opbygget ufysiske store ladningsophobninger. Induktorer forsvinder ganske enkelt fordi di/dt = 0. Tilbage er kun batterier og modstande. Vores første eksempel er den simpleste kreds med kun ét batteri og én modstand (Fig. 2.2). Figur 2.2: Simpel kreds med batteri og modstand Den ene maskeligning siger så det velkendte, at der løber en strøm i kredsen, og
22 22 KAPITEL 2. GRUNDLÆGGENDE ELEKTRONIK denne har en styrke, der er givet ved: E = RI. (2.27) Lidt mere udfordrende er spændingsdeleren (Fig. 2.3). E R 1 I 1 R B I B I 2 R 2 Figur 2.3: Spændingsdeleren For at løse dette problem, skal vi først indføre nogle størrelser som beskriver det vi vil regne ud. Vi kalder strømmen gennem modstand 1 for I 1, strømmen gennem modstand 2 for I 2, og strømmen gennem belastningsmodstanden I B. Strømmene bliver regnet positivt som vist med pilene i figuren. Vi har 2 knuder og 2 masker. De to knudeligninger siger det samme nemlig Maskeligningerne er I 2 = I 1 + I B. (2.28) E = R 1 I 1 + R 2 I 2 0 = R B I B R 1 I 1. (2.29) Bemærk at der kommer er minus i den sidste fordi vi går i modsat regning af I 1 når vi går med uret rundt i masken. Vi har altså 3 ligninger med 3 ubekendte strømme. Løsningen er I B = E R 1 R B R 1 + R 2 + R 1 R 2 /R B E I 1 = R 1 + R 2 + R 1 R 2 /R B I 2 = I 1 + I B. (2.30)
23 2.3. EKSEMPLER 23 Strømmen gennem belastningsmodstanden er E eff /R B, hvor den effektive spænding er R 1 E eff = E, (2.31) R 1 + R 2 + R 1 R 2 /R B dvs. en spænding som i grænsen, hvor belastningsmodstanden er meget stor (R B R 1, R 2 ) blot er en bestemt brøkdel af batterispændingen: R 1 E eff = E, (2.32) R 1 + R 2 heraf navnet spændingsdeler. Det er vigtigt at huske, at for at få den ønskede deling må man kunne se bort fra strømmen i belastningsmodstanden, dvs. have en stor sådan belastningsmodstand Transienter I det første eksempel i dette afsnit betragtede vi en simpel kreds med en modstand og et batteri, hvori der løber en konstant strøm. Man kan nu spørge, hvordan denne stationære situation egentlig er kommet i stand. Det virker ufysisk at strømstyrken skulle være sprunget direkte fra nul til E/R i det øjeblik batteriet blev sluttet til. Det er det da også. Enhver kreds selv uden spoler vil have en induktans, idet den naturligvis vil omslutte den variable magnetiske flux genereret af strømmen. En mere fysisk korrekt repræsentation af kredsen er derfor som vist i Fig 2.4. Figur 2.4: Realistisk kreds med batteri, induktans, og modstand Den ny maskeligning er nu E 0 = L di dt + RI, (2.33)
24 24 KAPITEL 2. GRUNDLÆGGENDE ELEKTRONIK med den randbetingelse, at klokken t = 0 (netop da batteriet sluttes til) er strømmen lig nul. Ligningen er en inhomogen, lineær, første ordens differentialligning, hvis fuldstændige løsning som bekendt er en partikulær løsning til ligningen plus en fuldstændig løsning til den homogene ligning. Det er nemt at gætte en partikulær løsning, vi kan nemlig blot tage løsningen fra jævnstrømstilfældet, som vi allerede har diskuteret. Løsningen til den homogene ligning er en exponentialfunktion, således at den samlede løsning bliver I(t) = E R + ke Rt/L, (2.34) hvor konstanten k bestemmes af begyndelsesbetingelsen I(0) = 0. Vi får I(t) = E R (1 e Rt/L ). (2.35) Vi ser at det faktisk tager en endelig tid τ L/R for strømmen at vokse op til sin stationære værdi. Dette kan også ses af selve maskeligningen evalueret klokken t = 0, hvor der da står, at di/dt = E/L. For L µ 0 a (med a = 1 cm) og R = 10 Ω bliver τ 10 9 sekunder meget hurtigt. Vi har flere gange argumenteret, at man ikke i det lange løb kan have en jævnstrøm løbende igennem en kapacitor. Hvor langt er det lange løb? Det kan vi finde ud af ved at sætte et batteri på kapacitoren. Kredsen bliver så, idet man aldrig kan undgå at have en modstand i kredsen. Se Fig Figur 2.5: Opladning af kapacitor Maskeligningen bliver i dette tilfælde E = RI(t) + 1 C t 0 I(t )dt. (2.36)
25 2.3. EKSEMPLER 25 Ligningen løses lettest ved i stedet for strømmen, I, at bruge ladningen Q(t) på kapacitoren som variabel: E = R dq dt + Q C. (2.37) Denne ligning har samme form, som ligning (2.33), og ovenikøbet med samme begyndelsesbetingelse, nemlig at ladningen på kapacitoren er nul til t = 0. Vi kan derfor uden videre skrive løsningen ned: Q(t) = EC(1 e t/rc ). (2.38) Vi ser at ladningen vokser til sin slutværdi Q = EC med en karakteristisk tidskonstant τ RC. Med en typisk modstand på R= 1 kω og en kapacitet C = ɛ 0 a, hvor a = 10 cm, fås τ 10 9 sek. I dette sidste tilfælde burde vi egentlig også tilføje en induktans til kredsen, for også her springer strømmen fra en værdi 0 før t = 0 til en værdi I = E/R umiddelbart efter at batteriet er sluttet til. Dette kan synes som en uskyldig lille korrektion men der introduceres herved en ny fysisk effekt, hvis omfang og rækkevidde næppe kan overvurderes. Først den fysiske effekt. Den realistiske kreds ser nu ud som vist i Fig. 2.6 og kaldes ofte for svingningskredsen af grunde som vi skal se nedenfor. Figur 2.6: RCL-kreds Maskeligningen har nu formen E = L di dt + 1 C t 0 I(t )dt + RI. (2.39) Lad os differentiere én gang mht tiden, flytte lidt om på leddene og få L d2 I dt 2 = 1 C I RdI dt. (2.40)
26 26 KAPITEL 2. GRUNDLÆGGENDE ELEKTRONIK Denne ligning minder om Newtons 2. lov for en partikel med koordinat x = I og massse m = L udsat for en fjederkraft (med fjederkonstant k = C 1 ) samt en g- nidningskraft (gnidningskoefficient γ = R). Løsningen til en sådan be- vægelse er (dæmpede) svingninger med en svingningsfrekvens ω 0 = k/m = LC 1. Fysisk er det ladning, der oscillerer ind og ud af kapacitoren. Når kapacitoren er fuldt opladet findes al energien i systemet i form af et elektrisk felt mellem kapacitorpladerne. En kvart periode senere er ladningen på kapacitoren lig med 0; til gengæld er strømmen maximal og al energien er nu til stede i form af det med strømmen forbundne magnetfelt. Dette er meget generelt for elektromagnetiske bølger lys og anden elektromagnetisk stråling er et andet vigtigt eksempel. Svingningen kan ikke fortsætte i det uendelige gnidningen vil med tiden standse den og overføre energien til Ohmsk varme i ledningerne. Den matematiske analyse af problemet forløber således. Vi har at gøre med en lineær, 2. ordens differentialligning. En sådan har generelt to lineært uafhængige løsninger. Disse løsninger findes ved at gætte på en løsning af formen I(t) = e λt, sætte ind i ligningen og løse den resulterende andengradsligning for λ den såkaldte karakterligning. Vi får Lλ 2 Rλ + 1 C = 0, (2.41) der har løsningerne λ ± = R 2L ± i ω 2 0 ( ) 2 R, (2.42) 2L hvor ω 0 = 1/ LC er den ovenfor nævnte svingningsfrekvens. Der er nu tre muligheder. 1) ω 0 > R/(2L), 2) ω 0 = R/(2L) samt 3) ω 0 < R/(2L). I tilfældet 1) er begge løsninger komplekse og en generel reel løsning til strømligningen (2.40) er I(t) = (A cos(ωt) + B sin(ωt))e Rt/(2L), (2.43) hvor ω = ω 2 0 (R/(2L)) 2 og A og B er konstanter, der skal bestemmes af begyndelsesbetingelser. En sådan svingning kaldes underdæmpet. Som det ses svinger strømmen frem og tilbage med en frekvens ω som er ca. lig det simple udtryk ω 0 = 1/ LC hvis modstanden er lille - deraf navnet svingningskredsen. Svingningen har dog en endelig levetid og henfalder i løbet af en tid τ = 2L/R, som er længere jo mindre modstanden R er. Forholdet mellem dæmpningstiden τ og svingningstiden T = 2π/ω 0 kaldes kredsens godhed og benævnes med bogstavet Q Q = π τ T = Lω 0 (2.44) R (bemærk at dette Q ikke må forveksles med ladningen Q. Man bruger desværre bogstavet Q for begge).
27 2.3. EKSEMPLER 27 I tilfældet 2) er λ + = λ og vi har kun fundet en løsning til (2.40). Det er dog nemt at se at i dette tilfælde er også I(t) = te λ +t en løsning. En generel reel løsning bliver så: I(t) = (A + Bt)e Rt/(2L). (2.45) Det strømforløb kaldes kritisk dæmpet. I det sidste tilfælde 3) er både λ + og λ reelle, positive tal. Den generelle løsning er i dette overdæmpede tilfælde så I(t) = Ae λ +t + Be λ t. (2.46) For at løse det fysiske problem, hvor vi klokken t = 0 spænder batteriet på kredsen, må vi løse ligningen (2.39), som i termer af ladningen Q i stedet for strømmen I har formen E = L d2 Q dt C Q + RdQ dt, (2.47) med begyndelsesbetingelserne Q(0) = 0 og I(0) = 0. En partikulær løsning er den statisk opladede kapacitor Q = CE. Den homogene ligning har præcis samme form som strømligningen (2.40) og derfor samme type løsninger. Det er nu ligetil at finde løsningerne i de tre tilfælde. Her skal vi nøjes med at vise det tidslige forløb grafisk, se Fig Q/EC ILω 0 /E ω 0 t ω 0 t Figur 2.7: Transienter for svingningskredsen. Figuren viser tidsudviklingen i ladningen Q (venstre) og strømmen I (højre) efter der tændes. Kurverne viser forløbet for tilfældene 1) underdæmpet R/2L = 0.3ω 0 eller godhed Q 1.7 (fuld kurve), 2) kritisk dæmpet R/2L = ω 0 eller godhed Q = 0.5 (stiplet kurve) og 3) underdæmpet R/2L = 3ω 0 eller godhed Q 0.17 (prikket kurve).
28 28 KAPITEL 2. GRUNDLÆGGENDE ELEKTRONIK 2.4 Vekselstrøm Den simple såkaldte RCL-kreds vi diskuterede i sidste afsnit danner grundlaget for al radiokommunikation. Hjertet i enhver (gammel) radio er sådan en svingningskreds. Forskellen fra det vi allerede har studeret er, at nu vil spændingskilden være en tidsligt varierende funktion, nemlig signalet som kommer ind på radioens antenne. Vi vil derfor se på tilfældet, hvor den elektromotoriske kraft er tidsafhængig, E(t). I praksis bliver radiosignaler sendt som en elektromotorisk kraft, der varierer harmonisk i tiden, d.v.s. Es tidsafhængighed er E(t) = E 0 cos(ωt + θ), (2.48) hvor ω er den såkaldte vinkelfrekvens, der relaterer sig til den almindelige frekvens ν = 1/T, hvor T er peiodetiden, ved ω = 2πν. θ kaldes fasen af E, og E 0 er amplituden af svingningen. Samme tidsafhængighed har også den elektromotoriske kraft, som findes i vores stikkontakter. Det er derfor yderst relevant at se lidt nærmere på kredse med en sådan en tidsafhængighed. Faktisk spiller denne type tidsafhængig også en helt speciel rolle, når man skal betragte mere generelle tidafhængigheder, men dette vender vi tilbage til senere i kurset, når vi skal snakke om Fourier transformation. For simpelheds skyld vil vi i regningerne nedenfor se bort fra transiente effekter. D.v.s. vi vil ikke kigge på, hvad der sker når men f.eks. tænder en kontakt, men kun kigge på situationen uendeligt lang tid efter der blev tændt på kontakten. Hvad der sker lige når man tænder, overlader vi til en af opgaverne. I de ligninger vi fandt tidligere indgik ting som di/dt og dt I(t ). En meget rar ting ved tidsafhængigheden (2.48) er, at den er simpel både at differentiere og integrere d cos(x)/dx = sin(x), dx cos(x) = sin(x). Endnu lettere bliver det dog, hvis vi kigger på en funktion som 2 exp( iωt), der differentieret og integreret giver sig selv: d exp( iωt)/dt = iω exp( iωt) og dt exp( iωt ) = exp( iωt)/( iω). Denne egenskab er meget nyttig som vi skal se nedenfor. Den generelle udledning kan nemt blive uoverskuelig, selvom regningerne dybest set er ret simple. Lad os derfor starte med at give et lille eksempel på, hvordan vi vil behandle vekselstrøm, og så generaliserer vi det bagefter. Vi betrager et simpelt kredsløb med en spole, en modstand og en elektromotorisk kraft E = E 0 cos(ωt), d.v.s. som i Fig. 2.4, men uden kontakten og med jævnstrømsspændingen erstatter med vekselstrøm. Vi vælger nu at skrive den elektromotriske kraft som real delen af en kompleks funktion E(t) = Re[Ẽ(t)] = Re[ E 0 e iωt] ] = Re [Ẽ0 e iωt, 2 At vi i eksponenten bruger i og ikke bare i er et fuldstændigt tilfældigt valg, men fortegnet her er det man normalt bruger i fysikken. F.eks. bruger man i kvantemekanikken også exp( iet/ ). Der er dog mange, f.eks. ingeniører, som bruger det modsatte fortegn eller indfører j = i, når de skal regne på elektronik, så pas derfor meget på, når du tager en formel fra en anden bog!
29 2.4. VEKSELSTRØM 29 hvor den komplekse amplitude er Ẽ0 = E 0 (det kan måske virke lidt forvirrende, at jeg her indfører en ny størrelse, der er det samme som en anden, men jeg gør dette for at være konsistent med de regninger som kommer senere). Dette har vi selvfølgelig lov til, men hvorfor gør vi det? Jo, det smarte kommer, når vi kigger på Kirchhoffs 2. lov (2.26). Lad os prøve også at skrive strømmen som real delen af en kompleks funktion 3 ] ] I(t) = Re[Ĩ(t) = Re [Ĩ0 e iωt. Kirchhoffs 2. lov (2.26) lyder da Re[Ẽ(t)] = ( L d dt Re[Ĩ(t)] + R Re[Ĩ(t)] ). (2.49) Da vi ved, at Re[x + y]=re[x]+re[y], kunne vi i stedet for at tage real delen på hvert enkelt led, lige så godt tage real delen af hele højre siden til sidst. Lad os nu prøve helt at lade være med at tage real værdien Ẽ(t) = (L ddtĩ(t) ) + RĨ(t). (2.50) Real værdien af denne ligninger giver Kirchhoffs 2. lov (2.49) for de reelle fysiske størrelser vi er interesserede i, mens vi er ligeglade med imaginær delen. Hvis den komplekse ligning (2.50) er opfyldt, vil real værdierne altså opfylde Kirchhoffs 2. lov (2.26). Som vi skal se om lidt er den komplekse ligning meget nemmere at løse end den reelle ligning. Den nemmeste måde at løse Kirchoffs 2. lov for de reelle størrelser, er derfor først at løse den komplekse hjælpeligninger (2.50) og derefter tage real delen af den komplekse strøm. (Læs lige dette afsnit igennem en gang til for at være sikker på du forstår det. Dette er det springende punkt i udledningen.) Lad os nu løse (2.50). Fordi differentation af en eksponential funktion er det nemmeste i verden, får vi med det samme Ẽ 0 e iωt = ( iωl + R)Ĩ0e iωt. Her kan vi forkorte eksponential funktionen på begge sider og ender med Ẽ 0 = ( iωl + R)Ĩ0. (2.51) Denne ligning minder om Ohms lov. Den eneste forskel er, at den omhandler de komplekse størrelser, og at i stedet for modstanden R har vi nu parentesen, som vi kalder for impedansen Z = R iωl. Når vi regner med de komplekse strømme, skal 3 Vi antager her, at tidsudviklingen af strømmen har en helt bestemt form. Denne antagelse bliver bekræftet af, at vi nedenfor rent faktisk finder løsninger til Kirchhoffs love ved at bruge denne form.
30 30 KAPITEL 2. GRUNDLÆGGENDE ELEKTRONIK vi således aldrig løse differential ligninger, men kan nøjes med at løse simplere algebraiske ligninger. Det bliver derfor ikke sværere at regne med spoler (og kapacitorer, som vi skal se nedenfor), end det var at regne med modstande for jævnstrøm. Fra resultatet ovenfor kan vi hurtigt finde amplituden af den komplekse strøm Ĩ 0 = Ẽ0 Z = E 0 R iωl. (2.52) Hermed har vi løst problemer for de komplekse strømme, men mangler stadig at komme tilbage til den reelle fysiske strøm vi er interesseret i. Dette gøres nemmest ved at skrive impedansen på polær form Z = Z exp(iφ), hvor 4 Z = R 2 + (ωl) 2 tan φ = ωl R. Den komplekse amplitude kan nu omskrive til Ĩ0 = Ĩ0 exp( iφ), hvor Ĩ0 = E 0 Z = E 0 R2 + (ωl) 2. Hvorefter den reelle fysiske strøm fåes ved at tage real delen af den komplekse strøm ] I(t) = Re [ Ĩ0 e i(ωt+φ) = Ĩ0 cos(ωt + φ). Ovenstående udledning kan måske synes lidt kompliceret, men da vi først havde udledt den komplekse Ohms lov (2.51) var resten af regningen faktisk ret hurtig. Lad os derfor prøve at generalisere regningerne ovenfor til et generelt kredsløb med mange komponenter og grene: I den jte gren er der en elektromotorisk kraft givet ved E j (t) = E 0,j cos(ωt + θ j ). Denne vælger vi nu at skrive som E j (t) = Re[Ẽj(t)] = Re [ E 0,j e ] ] i(ωt+θ j) = Re [Ẽ0,j e iωt, (2.53) 4 Der skal dog her gives en lille advarsel: Udtrykket for tan φ er altid rigtigt, men nogle gange er det ikke helt nok. Hvis man tager den inverse tangens får man altid et resultat mellem π/2 og π/2, men dette er jo forkert hvis vinklen ikke ligger i dette interval. For situationen her er R altid større end nul og fasen ligger derfor i intervallet fra π/2 til π/2, så der er ikke noget problem. Hvis man derimod beregner strømmen i en lille gren i et kompliceret kredsløb, kan man komme i problemer, hvis man udelukkende kigger på tan φ.
31 2.4. VEKSELSTRØM 31 hvor den komplekse amplitude er givet ved Ẽ0,j = E 0 exp( iθ j ). Tilsvarende indfører vi også den komplekse ladning på den jte kapacitor og den komplekse strøm i den jte gren ] Q j (t) = Re[ Qj (t) ] I j (t) = Re[Ĩj (t) Kirchhoffs love (2.18) og (2.26) lyder så Re[Ĩj] = 0 alle kanaler der løber til en knude batterier spoler [ ] = Re Q0,j e iωt ] [Ĩ0,j e iωt = Re ] Re [Ẽj = [ ] dĩj Re L j + dt kapacitorer [ ] Qj Re + C j (2.54). (2.55) modstande ] Re [R j Ĩ j. Igen vælger vi helt at udelade real værdien fra denne ligning, fordi vi ved at når de komplekse ligninger er opfyldt, vil real værdierne opfylde Kirchhoffs love. Vi får derfor de komplekse ligninger Ĩ j = 0 (2.56) alle kanaler der løber til en knude batterier Ẽ j = spoler L j dĩj dt + kapacitorer Q j C j + modstande R j Ĩ j. (2.57) Vores mål er af finde strømmene som løser (2.56) og (2.57). Problemet er dog, at for at gøre dette, skal vi komme af med ladningen Q j. Vi bruger nu, at strømmen er Ĩj = d Q j /dt. Derved får vi Ĩ j = Ĩ0,je iωt = d Q j dt = iω Q 0,j e iωt eller Q 0,j = Ĩ0,j iω. (2.58) Indsættes dette i (2.56) og (2.57) samtidig med at vi differentierer strømmen giver det Ĩ 0,j e iωt = 0 alle kanaler der løber til en knude batterier Ẽ 0,j e iωt = iωl j Ĩ 0,j e iωt + spoler kapacitorer Ĩ 0,j iωc j e iωt + modstande R j Ĩ 0,j e iωt.
32 32 KAPITEL 2. GRUNDLÆGGENDE ELEKTRONIK Som det ses indeholder alle led en faktor exp( iωt), som vi kan forkorte væk. Vi får derfor endelig Ĩ 0,j = 0 (2.59) alle kanaler der løber til en knude batterier Ẽ 0,j = iωl j Ĩ 0,j + spoler kapacitorer 1 iωc j Ĩ 0,j + modstande RĨ0,j. (2.60) Dette er vores endelige form af Kirchhoffs love for vekselstrøm. Bemærk, at de minder meget om de rigtige Kirchhoffs love for de reelle størrelser. Dog er der den store forskel at Kirchhoffs 2. lov (2.60) ikke længere er en differential ligning, men en helt almindelig algebraisk ligning, som er meget lettere at løse. For vekselstrøm er det således ikke meget sværere at løse et kredsløb med både spoler og kapacitorer, end det er at beskrive et jævnstrømskredsløb med en masse modstande. Den eneste forskel fra jævnstrøm og modstande er, at der i stedet for modstande står en komplekse impedans. Impedanserne opfører sig præcist som elektriske modstande gør i et jævnstrømskredsløb, blot skal man huske, at de er komplekse tal. En kapacitor har impedansen 1/( iωc) og har således høj impedans for lave frekvenser. Bemærk specielt, at man ikke kan sende jævnstrøm, som svarer til ω = 0, gennem en kapacitor, og en kapacitor har derfor uendelig impedans for ω = 0. En spole har impedansen iωl, der er størst for høje frekvenser. Hvis der i en gren optræder flere komponenter lægger man blot deres impedanser sammen, ligesom man gør med modstade. Inden vi går videre med nogle lidt mere komplicerede eksempler, må vi hellere lige sikre os at vi forstår de generelle udtryk ovenfor. Vi betragter derfor igen det samme kresløb som ovenfor. D.v.s. et kredsløb med en spole, en modstand og en elektromotorisk kraft E = E 0 cos(ωt) (som i Fig. 2.4 uden kontakten og med jævnstrømsspændingen erstatter med vekselstrøm). Kredsløbet har ingen knuder. Der er således kun en kompleks strøm Ĩ og vi behøver ikke bekymre os om (2.59). Fordi fasen er nul er den komplekse amplitude Ẽ0 = E 0. På højre siden af (2.60) står der bare iωlĩ0 + RĨ0, og vi får derfor med det samme svaret i (2.52) - det var meget hurtigere end at løse en differentialligning. Eksempel: Høj-pas filter Denne kreds består af en variabel spændingsforsyning E in samt en uspecificeret kreds med impedans Z. Imellem de to er anbragt et såkaldt høj-pas filter. Det består af en modstand, R, anbragt parallelt med Z, samt en kapacitor, C, i serie. Se Fig For at beregne hvilken strøm, der løber gennem den ukendte impedans Z, opstiller vi nu knudeligningen Ĩ 0,C = Ĩ0,R + Ĩ0,Z
33 2.4. VEKSELSTRØM 33 I Z Z I R R I C C E Figur 2.8: Høj-pas filter samt maskeligningerne Ẽ 0,in = Ĩ 0,Z Z Ĩ0,RR = 0 Ĩ0,C iωc + RĨ0,R. Vi har nu opstillet de fysiske love som beskriver systemet og mangler kun at løse ligningerne. Dette kan man gøre ved at bruge den første maskeligning til at komme af med Ĩ0,R = Ĩ0,ZZ/R. Indsætter vi nu dette i knudeligningen kommer vi også af med Ĩ0,C = (1 + Z/R)Ĩ0,Z. Den sidste maskeligning bliver så ( ) 1 + Z R Ẽ 0,in = iωc + Z Ĩ 0,Z. Vi kun nu endelig finde strømmen Ĩ0,Z ved at dividere med parantesen. Frem for at kigge på strømmen er det interessant at kigge på spændingen over den uspecificerede komponent Ẽ0,out = ZĨ0,Z. Efter lidt omskrivninger får vi Ẽ 0,out = iωrc 1 + R Ẽ0,in iωrc Z iωrc 1 iωrc Ẽ0,in, (2.61) hvor vi i den sidste ligning har antaget, at Z er meget større end R. Dette er en ofte anvendt approksimation, men man skal naturligvis checke, at den gælder i hvert enkelt tilfælde. Vi kan nu se, hvorfor konfigurationen kaldes et høj-pas filter. For små frekvenser ωrc 1 vil out-spændingen være meget mindre end in-spændingen, hvorimod vi i den modsatte grænse har at de to spændinger er ens.
Impedans. I = C du dt (1) og en spole med selvinduktionen L
 Impedans I et kredsløb, der består af andre netværkselementer end blot lække (modstande) og kilder vil der ikke i almindelighed være en simpel proportional, tidslig sammenhæng mellem strøm og spænding,
Impedans I et kredsløb, der består af andre netværkselementer end blot lække (modstande) og kilder vil der ikke i almindelighed være en simpel proportional, tidslig sammenhæng mellem strøm og spænding,
MODUL 5 ELLÆRE: INTRONOTE. 1 Basisbegreber
 1 Basisbegreber ellæren er de mest grundlæggende størrelser strøm, spænding og resistans Strøm er ladningsbevægelse, og som det fremgår af bogen, er strømmens retning modsat de bevægende elektroners retning
1 Basisbegreber ellæren er de mest grundlæggende størrelser strøm, spænding og resistans Strøm er ladningsbevægelse, og som det fremgår af bogen, er strømmens retning modsat de bevægende elektroners retning
Lineære differentialligningers karakter og lineære 1. ordens differentialligninger
 enote 11 1 enote 11 Lineære differentialligningers karakter og lineære 1. ordens differentialligninger I denne note introduceres lineære differentialligninger, som er en speciel (og bekvem) form for differentialligninger.
enote 11 1 enote 11 Lineære differentialligningers karakter og lineære 1. ordens differentialligninger I denne note introduceres lineære differentialligninger, som er en speciel (og bekvem) form for differentialligninger.
Elektromagnetisme 7 Side 1 af 12 Elektrisk strøm. Elektrisk strøm
 Elektromagnetisme 7 Side 1 af 12 Med dette emne overgås fra elektrostatikken, som beskriver stationære ladninger, til elektrodynamikken, som beskriver ladninger i bevægelse (elektriske strømme, magnetfelter,
Elektromagnetisme 7 Side 1 af 12 Med dette emne overgås fra elektrostatikken, som beskriver stationære ladninger, til elektrodynamikken, som beskriver ladninger i bevægelse (elektriske strømme, magnetfelter,
Matematik 1 Semesteruge 5 6 (30. september oktober 2002) side 1. Komplekse tal Arbejdsplan
 Matematik Semesteruge 5 6 (30. september -. oktober 2002) side Komplekse tal Arbejdsplan I semesterugerne 5 og 6 erstattes den regulære undervisning (forelæsninger og fællestimer) af selvstudium med opgaveregning
Matematik Semesteruge 5 6 (30. september -. oktober 2002) side Komplekse tal Arbejdsplan I semesterugerne 5 og 6 erstattes den regulære undervisning (forelæsninger og fællestimer) af selvstudium med opgaveregning
Note om Laplace-transformationen
 Note om Laplace-transformationen Den harmoniske oscillator omskrevet til et ligningssystem I dette opgavesæt benyttes laplacetransformationen til at løse koblede differentialligninger. Fordelen ved at
Note om Laplace-transformationen Den harmoniske oscillator omskrevet til et ligningssystem I dette opgavesæt benyttes laplacetransformationen til at løse koblede differentialligninger. Fordelen ved at
Theory Danish (Denmark) Ikke-lineær dynamik i elektriske kredsløb (10 point)
 Q2-1 Ikke-lineær dynamik i elektriske kredsløb (10 point) Læs venligst de generelle instruktioner i den separate konvolut før du starter på opgaven. Introduktion Bi-stabile ikke-lineære halvlederkomponenter
Q2-1 Ikke-lineær dynamik i elektriske kredsløb (10 point) Læs venligst de generelle instruktioner i den separate konvolut før du starter på opgaven. Introduktion Bi-stabile ikke-lineære halvlederkomponenter
Elektromagnetisme 7 Side 1 af 12 Elektrisk strøm. Elektrisk strøm
 Elektromagnetisme 7 Side 1 af 1 Med dette emne overgås fra elektrostatikken, som beskriver stationære ladninger, til elektrodynamikken, som beskriver ladninger i bevægelse (elektriske strømme, magnetfelter,
Elektromagnetisme 7 Side 1 af 1 Med dette emne overgås fra elektrostatikken, som beskriver stationære ladninger, til elektrodynamikken, som beskriver ladninger i bevægelse (elektriske strømme, magnetfelter,
ELEKTRISKE KREDSLØB (DC)
 ELEKTRISKE KREDSLØB (DC) Kredsløbstyper: Serieforbindelser Parallelforbindelser Blandede forbindelser Central lovmæssigheder Ohms lov, effektformel, Kirchhoffs 1. & 2. lov DC kredsløb DC står for direct
ELEKTRISKE KREDSLØB (DC) Kredsløbstyper: Serieforbindelser Parallelforbindelser Blandede forbindelser Central lovmæssigheder Ohms lov, effektformel, Kirchhoffs 1. & 2. lov DC kredsløb DC står for direct
Benjamin Franklin Prøv ikke at gentage forsøget! hvor er den passerede ladning i tiden, og enheden 1A =
 E3 Elektricitet 1. Grundlæggende Benjamin Franklin Prøv ikke at gentage forsøget! I E1 og E2 har vi set på ladning (som måles i Coulomb C), strømstyrke I (som måles i Ampere A), energien pr. ladning, også
E3 Elektricitet 1. Grundlæggende Benjamin Franklin Prøv ikke at gentage forsøget! I E1 og E2 har vi set på ladning (som måles i Coulomb C), strømstyrke I (som måles i Ampere A), energien pr. ladning, også
DESIGNMAT FORÅR 2012: UGESEDDEL Forberedelse Læs alle opgaverne fra tidligere ugesedler, og læg særlig mærke til dem du har spørgsmål til.
 DESIGNMAT FORÅR 2012: UGESEDDEL 13 INSTITUT FOR MATEMATIK 1. Forberedelse Læs alle opgaverne fra tidligere ugesedler, og læg særlig mærke til dem du har spørgsmål til. 2. Aktiviteter mandag 13 17 2.1.
DESIGNMAT FORÅR 2012: UGESEDDEL 13 INSTITUT FOR MATEMATIK 1. Forberedelse Læs alle opgaverne fra tidligere ugesedler, og læg særlig mærke til dem du har spørgsmål til. 2. Aktiviteter mandag 13 17 2.1.
Frequency Dispersion: Dielectrics, Conductors, and Plasmas
 1/23 Frequency Dispersion: Dielectrics, Conductors, and Plasmas Carlos Felipe Espinoza Hernández Professor: Jorge Alfaro Instituto de Física Pontificia Universidad Católica de Chile 2/23 Contents 1 Simple
1/23 Frequency Dispersion: Dielectrics, Conductors, and Plasmas Carlos Felipe Espinoza Hernández Professor: Jorge Alfaro Instituto de Física Pontificia Universidad Católica de Chile 2/23 Contents 1 Simple
Lineære systemer med hukommelse.
 Lineær Response Teori. I responseteorien interesserer man sig for, hvad der kan siges generelt om sammenhængen mellem input φ(t) og output γ(t) for et system. Valg af variable. Det betragtede systems forskellige
Lineær Response Teori. I responseteorien interesserer man sig for, hvad der kan siges generelt om sammenhængen mellem input φ(t) og output γ(t) for et system. Valg af variable. Det betragtede systems forskellige
Matematik 1 Semesteruge 5 6 (1. oktober oktober 2001) side 1 Komplekse tal Arbejdsplan
 Matematik 1 Semesteruge 5 6 (1. oktober - 12. oktober 2001) side 1 Komplekse tal Arbejdsplan I semesterugerne 5 og 6 erstattes den regulære undervisning (forelæsninger og fællestimer) af selvstudium med
Matematik 1 Semesteruge 5 6 (1. oktober - 12. oktober 2001) side 1 Komplekse tal Arbejdsplan I semesterugerne 5 og 6 erstattes den regulære undervisning (forelæsninger og fællestimer) af selvstudium med
KREDSLØBSTEORI 10 FORELÆSNINGER OM ELEKTRISKEKREDSLØB
 EE Basis, foråret 2010 KREDSLØBSTEORI 10 FORELÆSNINGER OM ELEKTRISKEKREDSLØB Jan H. Mikkelsen EE- Basis, Kredsløbsteori, F10, KRT4 1 Emner for idag Kondensatorer Spoler TidsaGængige kredsløb Universalformlen
EE Basis, foråret 2010 KREDSLØBSTEORI 10 FORELÆSNINGER OM ELEKTRISKEKREDSLØB Jan H. Mikkelsen EE- Basis, Kredsløbsteori, F10, KRT4 1 Emner for idag Kondensatorer Spoler TidsaGængige kredsløb Universalformlen
Vina Nguyen HSSP July 13, 2008
 Vina Nguyen HSSP July 13, 2008 1 What does it mean if sets A, B, C are a partition of set D? 2 How do you calculate P(A B) using the formula for conditional probability? 3 What is the difference between
Vina Nguyen HSSP July 13, 2008 1 What does it mean if sets A, B, C are a partition of set D? 2 How do you calculate P(A B) using the formula for conditional probability? 3 What is the difference between
Hvorfor bevæger lyset sig langsommere i fx glas og vand end i det tomme rum?
 Hvorfor bevæger lyset sig langsommere i fx glas og vand end i det tomme rum? - om fysikken bag til brydningsindekset Artiklen er udarbejdet/oversat ud fra især ref. 1 - fra borgeleo.dk Det korte svar:
Hvorfor bevæger lyset sig langsommere i fx glas og vand end i det tomme rum? - om fysikken bag til brydningsindekset Artiklen er udarbejdet/oversat ud fra især ref. 1 - fra borgeleo.dk Det korte svar:
Den klassiske oscillatormodel
 Kvantemekanik 6 Side af 8 n meget central model inden for KM er den såkaldte harmoniske oscillatormodel, som historisk set spillede en afgørende rolle i de banebrydende beskrivelser af bla. sortlegemestråling
Kvantemekanik 6 Side af 8 n meget central model inden for KM er den såkaldte harmoniske oscillatormodel, som historisk set spillede en afgørende rolle i de banebrydende beskrivelser af bla. sortlegemestråling
Velkommen til. EDR Frederikssund Afdelings Almen elektronik kursus. Joakim Soya OZ1DUG Formand. EDR Frederikssund afdeling Almen elektronik kursus
 Velkommen til EDR Frederikssund Afdelings Joakim Soya OZ1DUG Formand 2012-09-01 OZ1DUG 1 Kursus målsætning Praksisorienteret teoretisk gennemgang af elektronik Forberedelse til Certifikatprøve A som radioamatør
Velkommen til EDR Frederikssund Afdelings Joakim Soya OZ1DUG Formand 2012-09-01 OZ1DUG 1 Kursus målsætning Praksisorienteret teoretisk gennemgang af elektronik Forberedelse til Certifikatprøve A som radioamatør
ELEKTRISKE KREDSLØB OG DYNAMISKE SYSTEMER
 EE Basis, foråret 2009 ELEKTRISKE KREDSLØB OG DYNAMISKE SYSTEMER Jan H. Mikkelsen EKDS6, F09 1 Emner for idag Komplekse tal sådan helt fra bunden DefiniHoner og regneregler Lidt flere definihoner og lidt
EE Basis, foråret 2009 ELEKTRISKE KREDSLØB OG DYNAMISKE SYSTEMER Jan H. Mikkelsen EKDS6, F09 1 Emner for idag Komplekse tal sådan helt fra bunden DefiniHoner og regneregler Lidt flere definihoner og lidt
KØBENHAVNS UNIVERSITET NATURVIDENSKABELIG BACHELORUDDANNELSE Skriftlig prøve i Fysik 4 (Elektromagnetisme) 27. juni 2008
 KØBENHAVNS UNIVERSITET NATURVIDENSKABELIG BACHELORUDDANNELSE Skriftlig prøve i Fysik 4 (Elektromagnetisme) 27. juni 2008 Tilladte hjælpemidler: Medbragt litteratur, noter og lommeregner. Der må besvares
KØBENHAVNS UNIVERSITET NATURVIDENSKABELIG BACHELORUDDANNELSE Skriftlig prøve i Fysik 4 (Elektromagnetisme) 27. juni 2008 Tilladte hjælpemidler: Medbragt litteratur, noter og lommeregner. Der må besvares
Når enderne af en kobbertråd forbindes til en strømforsyning, bevæger elektronerne i kobbertråden sig (fortrinsvis) i samme retning.
 E2 Elektrodynamik 1. Strømstyrke Det meste af vores moderne teknologi bygger på virkningerne af elektriske ladninger, som bevæger sig. Elektriske ladninger i bevægelse kalder vi elektrisk strøm. Når enderne
E2 Elektrodynamik 1. Strømstyrke Det meste af vores moderne teknologi bygger på virkningerne af elektriske ladninger, som bevæger sig. Elektriske ladninger i bevægelse kalder vi elektrisk strøm. Når enderne
The X Factor. Målgruppe. Læringsmål. Introduktion til læreren klasse & ungdomsuddannelser Engelskundervisningen
 The X Factor Målgruppe 7-10 klasse & ungdomsuddannelser Engelskundervisningen Læringsmål Eleven kan give sammenhængende fremstillinger på basis af indhentede informationer Eleven har viden om at søge og
The X Factor Målgruppe 7-10 klasse & ungdomsuddannelser Engelskundervisningen Læringsmål Eleven kan give sammenhængende fremstillinger på basis af indhentede informationer Eleven har viden om at søge og
Udledning af Keplers love
 Udledning af Keplers love Kristian Jerslev 8. december 009 Resumé Her præsenteres en udledning af Keplers tre love ud fra Newtonsk tyngdekraft. Begyndende med en analyse af et to-legeme problem vil jeg
Udledning af Keplers love Kristian Jerslev 8. december 009 Resumé Her præsenteres en udledning af Keplers tre love ud fra Newtonsk tyngdekraft. Begyndende med en analyse af et to-legeme problem vil jeg
DETTE OPGAVESÆT INDEHOLDER 6 OPGAVER MED IALT 11 SPØRGSMÅL. VED BEDØMMELSEN VÆGTES DE ENKELTE
 DETTE OPGAVESÆT INDEHOLDER 6 OPGAVER MED IALT 11 SPØRGSMÅL. VED BEDØMMELSEN VÆGTES DE ENKELTE SPØRGSMÅL ENS. SPØRGSMÅLENE I DE ENKELTE OPGAVER KAN LØSES UAFHÆNGIGT AF HINANDEN. 1 Opgave 1 En cylinderkapacitor
DETTE OPGAVESÆT INDEHOLDER 6 OPGAVER MED IALT 11 SPØRGSMÅL. VED BEDØMMELSEN VÆGTES DE ENKELTE SPØRGSMÅL ENS. SPØRGSMÅLENE I DE ENKELTE OPGAVER KAN LØSES UAFHÆNGIGT AF HINANDEN. 1 Opgave 1 En cylinderkapacitor
Studieretningsopgave
 Virum Gymnasium Studieretningsopgave Harmoniske svingninger i matematik og fysik Vejledere: Christian Holst Hansen (matematik) og Bodil Dam Heiselberg (fysik) 30-01-2014 Indholdsfortegnelse Indledning...
Virum Gymnasium Studieretningsopgave Harmoniske svingninger i matematik og fysik Vejledere: Christian Holst Hansen (matematik) og Bodil Dam Heiselberg (fysik) 30-01-2014 Indholdsfortegnelse Indledning...
University of Copenhagen Faculty of Science Written Exam - 3. April Algebra 3
 University of Copenhagen Faculty of Science Written Exam - 3. April 2009 Algebra 3 This exam contains 5 exercises which are to be solved in 3 hours. The exercises are posed in an English and in a Danish
University of Copenhagen Faculty of Science Written Exam - 3. April 2009 Algebra 3 This exam contains 5 exercises which are to be solved in 3 hours. The exercises are posed in an English and in a Danish
Teknologi & kommunikation
 Grundlæggende Side af NV Elektrotekniske grundbegreber Version.0 Spænding, strøm og modstand Elektricitet: dannet af det græske ord elektron, hvilket betyder rav, idet man tidligere iagttog gnidningselektricitet
Grundlæggende Side af NV Elektrotekniske grundbegreber Version.0 Spænding, strøm og modstand Elektricitet: dannet af det græske ord elektron, hvilket betyder rav, idet man tidligere iagttog gnidningselektricitet
Komplekse tal. x 2 = 1 (2) eller
 Komplekse tal En tilegnelse af stoffet i dette appendix kræver at man løser opgaverne Komplekse tal viser sig uhyre nyttige i fysikken, f.eks til løsning af lineære differentialligninger eller beskrivelse
Komplekse tal En tilegnelse af stoffet i dette appendix kræver at man løser opgaverne Komplekse tal viser sig uhyre nyttige i fysikken, f.eks til løsning af lineære differentialligninger eller beskrivelse
Algebra - Teori og problemløsning
 Algebra - Teori og problemløsning, januar 05, Kirsten Rosenkilde. Algebra - Teori og problemløsning Kapitel -3 giver en grundlæggende introduktion til at omskrive udtryk, faktorisere og løse ligningssystemer.
Algebra - Teori og problemløsning, januar 05, Kirsten Rosenkilde. Algebra - Teori og problemløsning Kapitel -3 giver en grundlæggende introduktion til at omskrive udtryk, faktorisere og løse ligningssystemer.
Elektronikkens grundbegreber 1
 Elektronikkens grundbegreber 1 B/D certifikatkursus 2016 Efterår 2016 OZ7SKB EDR Skanderborg afdeling Lektions overblik 1. Det mest basale stof 2. Både B- og D-stof 3. VTS side 21-28 4. Det meste B-stof
Elektronikkens grundbegreber 1 B/D certifikatkursus 2016 Efterår 2016 OZ7SKB EDR Skanderborg afdeling Lektions overblik 1. Det mest basale stof 2. Både B- og D-stof 3. VTS side 21-28 4. Det meste B-stof
Elektromagnetisme 14 Side 1 af 10 Elektromagnetiske bølger. Bølgeligningen
 Elektromagnetisme 14 Side 1 af 1 Bølgeligningen Maxwells ligninger udtrykker den indbyrdes sammenhæng mellem de elektromagnetiske felter samt sammenhængen mellem disse felter og de feltskabende ladninger
Elektromagnetisme 14 Side 1 af 1 Bølgeligningen Maxwells ligninger udtrykker den indbyrdes sammenhæng mellem de elektromagnetiske felter samt sammenhængen mellem disse felter og de feltskabende ladninger
Fysik 2 - Den Harmoniske Oscillator
 Fysik 2 - Den Harmoniske Oscillator Esben Bork Hansen, Amanda Larssen, Martin Qvistgaard Christensen, Maria Cavallius 5. januar 2009 Indhold 1 Formål 1 2 Forsøget 2 3 Resultater 3 4 Teori 4 4.1 simpel
Fysik 2 - Den Harmoniske Oscillator Esben Bork Hansen, Amanda Larssen, Martin Qvistgaard Christensen, Maria Cavallius 5. januar 2009 Indhold 1 Formål 1 2 Forsøget 2 3 Resultater 3 4 Teori 4 4.1 simpel
Basic statistics for experimental medical researchers
 Basic statistics for experimental medical researchers Sample size calculations September 15th 2016 Christian Pipper Department of public health (IFSV) Faculty of Health and Medicinal Science (SUND) E-mail:
Basic statistics for experimental medical researchers Sample size calculations September 15th 2016 Christian Pipper Department of public health (IFSV) Faculty of Health and Medicinal Science (SUND) E-mail:
Elektromagnetisme 14 Side 1 af 9 Elektromagnetiske bølger. Bølgeligningen
 Elektromagnetisme 14 Side 1 af 9 Bølgeligningen Maxwells ligninger udtrykker den indbyrdes sammenhæng mellem de elektromagnetiske felter. I det flg. udledes en ligning, der opfyldes af hvert enkelt felt.
Elektromagnetisme 14 Side 1 af 9 Bølgeligningen Maxwells ligninger udtrykker den indbyrdes sammenhæng mellem de elektromagnetiske felter. I det flg. udledes en ligning, der opfyldes af hvert enkelt felt.
Lineære 2. ordens differentialligninger med konstante koefficienter
 enote 13 1 enote 13 Lineære 2. ordens differentialligninger med konstante koefficienter I forlængelse af enote 11 og enote 12 om differentialligninger, kommer nu denne enote omkring 2. ordens differentialligninger.
enote 13 1 enote 13 Lineære 2. ordens differentialligninger med konstante koefficienter I forlængelse af enote 11 og enote 12 om differentialligninger, kommer nu denne enote omkring 2. ordens differentialligninger.
Lineære 1. ordens differentialligningssystemer
 enote enote Lineære ordens differentialligningssystemer Denne enote beskriver ordens differentialligningssystemer og viser, hvordan de kan løses enoten er i forlængelse af enote, der beskriver lineære
enote enote Lineære ordens differentialligningssystemer Denne enote beskriver ordens differentialligningssystemer og viser, hvordan de kan løses enoten er i forlængelse af enote, der beskriver lineære
University of Copenhagen Faculty of Science Written Exam April Algebra 3
 University of Copenhagen Faculty of Science Written Exam - 16. April 2010 Algebra This exam contains 5 exercises which are to be solved in hours. The exercises are posed in an English and in a Danish version.
University of Copenhagen Faculty of Science Written Exam - 16. April 2010 Algebra This exam contains 5 exercises which are to be solved in hours. The exercises are posed in an English and in a Danish version.
Eksamen i Signalbehandling og matematik
 Opgave. (%).a. Figur og afbilleder et diskret tid signal [n ] og dets DTFT. [n] bruges som input til et LTI filter med en frekvens amplitude respons som vist på figur. Hvilket af de 4 output signaler (y
Opgave. (%).a. Figur og afbilleder et diskret tid signal [n ] og dets DTFT. [n] bruges som input til et LTI filter med en frekvens amplitude respons som vist på figur. Hvilket af de 4 output signaler (y
MASKELIGNINGER - KIRCHHOFFS LOVE (DC) Eksempel
 MASKELIGNINGER - KIRCHHOFFS LOVE (DC) Eksempel Ved beregning af kredsløb med flere masker og flere elektromotoriske kræfter (E), er det ofte ret besværligt at løse for ubekendte uden hjælpeværktøjer. Side
MASKELIGNINGER - KIRCHHOFFS LOVE (DC) Eksempel Ved beregning af kredsløb med flere masker og flere elektromotoriske kræfter (E), er det ofte ret besværligt at løse for ubekendte uden hjælpeværktøjer. Side
Andengradsligninger. Frank Nasser. 12. april 2011
 Andengradsligninger Frank Nasser 12. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk: Dette
Andengradsligninger Frank Nasser 12. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk: Dette
Project Step 7. Behavioral modeling of a dual ported register set. 1/8/ L11 Project Step 5 Copyright Joanne DeGroat, ECE, OSU 1
 Project Step 7 Behavioral modeling of a dual ported register set. Copyright 2006 - Joanne DeGroat, ECE, OSU 1 The register set Register set specifications 16 dual ported registers each with 16- bit words
Project Step 7 Behavioral modeling of a dual ported register set. Copyright 2006 - Joanne DeGroat, ECE, OSU 1 The register set Register set specifications 16 dual ported registers each with 16- bit words
Noter til EM2 på KU (Elektrodynamik og Bølger)
 Noter til EM2 på KU (Elektrodynamik og Bølger) af Nikolai Plambech Nielsen, LPK331. Version 1.0 Indhold I Kredsløbsregning 6 1 Grundlæggende elektronik (Noter kapitel 2) 7 1.1 Passive komponenter.......................................
Noter til EM2 på KU (Elektrodynamik og Bølger) af Nikolai Plambech Nielsen, LPK331. Version 1.0 Indhold I Kredsløbsregning 6 1 Grundlæggende elektronik (Noter kapitel 2) 7 1.1 Passive komponenter.......................................
Opgave 1. (a) Bestem de to kapacitorers kapacitanser C 1 og C 2.
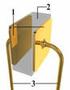 2 Opgave 1 I første del af denne opgave skal kapacitansen af to kapacitorer bestemmes. Den ene kapacitor er konstrueret af to tynde koaksiale cylinderskaller af metal. Den inderste skal har radius r a
2 Opgave 1 I første del af denne opgave skal kapacitansen af to kapacitorer bestemmes. Den ene kapacitor er konstrueret af to tynde koaksiale cylinderskaller af metal. Den inderste skal har radius r a
Diffusionsligningen. Fællesprojekt for FY520 og MM502. Marts Hans J. Munkholm og Paolo Sibani. Besvarelse fra Hans J.
 Diffusionsligningen Fællesprojekt for FY50 og MM50 Marts 009 Hans J. Munkholm og Paolo Sibani Besvarelse fra Hans J. Munkholm 1 (a) Lad [x, x + x] være et lille delinterval af [a, b]. Den masse, der er
Diffusionsligningen Fællesprojekt for FY50 og MM50 Marts 009 Hans J. Munkholm og Paolo Sibani Besvarelse fra Hans J. Munkholm 1 (a) Lad [x, x + x] være et lille delinterval af [a, b]. Den masse, der er
GUIDE TIL BREVSKRIVNING
 GUIDE TIL BREVSKRIVNING APPELBREVE Formålet med at skrive et appelbrev er at få modtageren til at overholde menneskerettighederne. Det er en god idé at lægge vægt på modtagerens forpligtelser over for
GUIDE TIL BREVSKRIVNING APPELBREVE Formålet med at skrive et appelbrev er at få modtageren til at overholde menneskerettighederne. Det er en god idé at lægge vægt på modtagerens forpligtelser over for
En sumformel eller to - om interferens
 En sumformel eller to - om interferens - fra borgeleo.dk Vi ønsker - af en eller anden grund - at beregne summen og A x = cos(0) + cos(φ) + cos(φ) + + cos ((n 1)φ) A y = sin (0) + sin(φ) + sin(φ) + + sin
En sumformel eller to - om interferens - fra borgeleo.dk Vi ønsker - af en eller anden grund - at beregne summen og A x = cos(0) + cos(φ) + cos(φ) + + cos ((n 1)φ) A y = sin (0) + sin(φ) + sin(φ) + + sin
Matematik A. Højere teknisk eksamen. Forberedelsesmateriale. htx112-mat/a-26082011
 Matematik A Højere teknisk eksamen Forberedelsesmateriale htx112-mat/a-26082011 Fredag den 26. august 2011 Forord Forberedelsesmateriale til prøverne i matematik A Der er afsat 10 timer på 2 dage til
Matematik A Højere teknisk eksamen Forberedelsesmateriale htx112-mat/a-26082011 Fredag den 26. august 2011 Forord Forberedelsesmateriale til prøverne i matematik A Der er afsat 10 timer på 2 dage til
Andengradsligninger. Frank Nasser. 11. juli 2011
 Andengradsligninger Frank Nasser 11. juli 2011 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold 1 Introduktion
Andengradsligninger Frank Nasser 11. juli 2011 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold 1 Introduktion
ELLÆRENS KERNE- BEGREBER (DC) Hvad er elektrisk: Ladning Strømstyrke Spændingsforskel Resistans Energi og effekt
 ELLÆRENS KERNE- BEGREBER (DC) Hvad er elektrisk: Ladning Strømstyrke Spændingsforskel Resistans Energi og effekt Atomets partikler: Elektrisk ladning Lad os se på et fysisk stof som kobber: Side 1 Atomets
ELLÆRENS KERNE- BEGREBER (DC) Hvad er elektrisk: Ladning Strømstyrke Spændingsforskel Resistans Energi og effekt Atomets partikler: Elektrisk ladning Lad os se på et fysisk stof som kobber: Side 1 Atomets
Antennens udstrålingsmodstand hvad er det for en størrelse?
 Antennens udstrålingsmodstand hvad er det for en størrelse? Det faktum, at lyset har en endelig hastighed er en forudsætning for at en antenne udstråler, og at den har en ohmsk udstrålingsmodstand. Den
Antennens udstrålingsmodstand hvad er det for en størrelse? Det faktum, at lyset har en endelig hastighed er en forudsætning for at en antenne udstråler, og at den har en ohmsk udstrålingsmodstand. Den
IMPEDANSBEGREBET - SPOLEN. Faseforskydning mellem I og U Eksempel: R, X og Z I og U P, Q og S. Diagrammer
 AC IMPEDANSBEGREBET - SPOLEN Faseforskydning mellem I og U Eksempel: R, X og Z I og U P, Q og S Diagrammer Spolens faseforskydning: En spole består egentlig af en resistiv del (R) og en ideel reaktiv del
AC IMPEDANSBEGREBET - SPOLEN Faseforskydning mellem I og U Eksempel: R, X og Z I og U P, Q og S Diagrammer Spolens faseforskydning: En spole består egentlig af en resistiv del (R) og en ideel reaktiv del
what is this all about? Introduction three-phase diode bridge rectifier input voltages input voltages, waveforms normalization of voltages voltages?
 what is this all about? v A Introduction three-phase diode bridge rectifier D1 D D D4 D5 D6 i OUT + v OUT v B i 1 i i + + + v 1 v v input voltages input voltages, waveforms v 1 = V m cos ω 0 t v = V m
what is this all about? v A Introduction three-phase diode bridge rectifier D1 D D D4 D5 D6 i OUT + v OUT v B i 1 i i + + + v 1 v v input voltages input voltages, waveforms v 1 = V m cos ω 0 t v = V m
Dato: 24. oktober 2013 Side 1 af 7. Teknologisk singularitet. 24. oktober 2013
 Side 1 af 7 Teknologisk singularitet 24. oktober 2013 Side 2 af 7 Begreberne teknologisk singularitet og accelereret udvikling dukker ofte op i transhumanistiske sammenhænge, idet de beskriver en udvikling,
Side 1 af 7 Teknologisk singularitet 24. oktober 2013 Side 2 af 7 Begreberne teknologisk singularitet og accelereret udvikling dukker ofte op i transhumanistiske sammenhænge, idet de beskriver en udvikling,
Engelsk. Niveau C. De Merkantile Erhvervsuddannelser September 2005. Casebaseret eksamen. www.jysk.dk og www.jysk.com.
 052430_EngelskC 08/09/05 13:29 Side 1 De Merkantile Erhvervsuddannelser September 2005 Side 1 af 4 sider Casebaseret eksamen Engelsk Niveau C www.jysk.dk og www.jysk.com Indhold: Opgave 1 Presentation
052430_EngelskC 08/09/05 13:29 Side 1 De Merkantile Erhvervsuddannelser September 2005 Side 1 af 4 sider Casebaseret eksamen Engelsk Niveau C www.jysk.dk og www.jysk.com Indhold: Opgave 1 Presentation
AARHUS UNIVERSITET. Det naturvidenskabelige fakultet 3. kvarter forår OPGAVESTILLER: Allan H. Sørensen
 AARHUS UNIVERSITET Det naturvidenskabelige fakultet 3. kvarter forår 2006 FAG: Elektromagnetisme OPGAVESTILLER: Allan H. Sørensen Antal sider i opgavesættet (inkl. forsiden): 5 Eksamensdag: fredag dato:
AARHUS UNIVERSITET Det naturvidenskabelige fakultet 3. kvarter forår 2006 FAG: Elektromagnetisme OPGAVESTILLER: Allan H. Sørensen Antal sider i opgavesættet (inkl. forsiden): 5 Eksamensdag: fredag dato:
Elektromagnetisme 13 Side 1 af 8 Maxwells ligninger. Forskydningsstrømme I S 1
 Elektromagnetisme 13 Side 1 af 8 Betragt Amperes lov fra udtryk (1.1) anvendt på en kapacitor der er ved at blive ladet op. For de to flader og S der begge S1 afgrænses af C fås H dl = J ˆ C S n da = I
Elektromagnetisme 13 Side 1 af 8 Betragt Amperes lov fra udtryk (1.1) anvendt på en kapacitor der er ved at blive ladet op. For de to flader og S der begge S1 afgrænses af C fås H dl = J ˆ C S n da = I
Komplekse Tal. 20. november 2009. UNF Odense. Steen Thorbjørnsen Institut for Matematiske Fag Århus Universitet
 Komplekse Tal 20. november 2009 UNF Odense Steen Thorbjørnsen Institut for Matematiske Fag Århus Universitet Fra de naturlige tal til de komplekse Optælling af størrelser i naturen De naturlige tal N (N
Komplekse Tal 20. november 2009 UNF Odense Steen Thorbjørnsen Institut for Matematiske Fag Århus Universitet Fra de naturlige tal til de komplekse Optælling af størrelser i naturen De naturlige tal N (N
Ohms Lov Ohms lov beskriver sammenhæng mellem spænding, strømstyrke og modstand.
 Ellære Ohms Lov Ohms lov beskriver sammenhæng mellem spænding, strømstyrke og modstand. Spænding [V] Strømstyrke [A] Modstand [W] kan bruge følgende måde til at huske hvordan i regner de forskellige værdier.
Ellære Ohms Lov Ohms lov beskriver sammenhæng mellem spænding, strømstyrke og modstand. Spænding [V] Strømstyrke [A] Modstand [W] kan bruge følgende måde til at huske hvordan i regner de forskellige værdier.
Engelsk. Niveau D. De Merkantile Erhvervsuddannelser September Casebaseret eksamen. og
 052431_EngelskD 08/09/05 13:29 Side 1 De Merkantile Erhvervsuddannelser September 2005 Side 1 af 4 sider Casebaseret eksamen Engelsk Niveau D www.jysk.dk og www.jysk.com Indhold: Opgave 1 Presentation
052431_EngelskD 08/09/05 13:29 Side 1 De Merkantile Erhvervsuddannelser September 2005 Side 1 af 4 sider Casebaseret eksamen Engelsk Niveau D www.jysk.dk og www.jysk.com Indhold: Opgave 1 Presentation
Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 2016
 Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Fononiske Båndgab. Køreplan Matematik 1 - FORÅR 2005
 Fononiske Båndgab Køreplan 01005 Matematik 1 - FORÅR 2005 1 Baggrund Bølgeudbredelse i materialer og medier (som f.eks. luft) er et fænomen, der kendes af alle og som observeres i forskellige former i
Fononiske Båndgab Køreplan 01005 Matematik 1 - FORÅR 2005 1 Baggrund Bølgeudbredelse i materialer og medier (som f.eks. luft) er et fænomen, der kendes af alle og som observeres i forskellige former i
Fononiske Båndgab. Køreplan Matematik 1 - FORÅR 2004
 Fononiske Båndgab Køreplan 01005 Matematik 1 - FORÅR 2004 1 Baggrund Bølgeudbredelse i materialer og medier (som f.eks. luft) er et fænomen, der kendes af alle og som observeres i forskellige former i
Fononiske Båndgab Køreplan 01005 Matematik 1 - FORÅR 2004 1 Baggrund Bølgeudbredelse i materialer og medier (som f.eks. luft) er et fænomen, der kendes af alle og som observeres i forskellige former i
Matematisk modellering og numeriske metoder
 Matematisk modellering og numeriske metoder Morten Grud Rasmussen 5. september 2016 1 Ordinære differentialligninger ODE er 1.1 ODE er helt grundlæggende Definition 1.1 (Ordinære differentialligninger).
Matematisk modellering og numeriske metoder Morten Grud Rasmussen 5. september 2016 1 Ordinære differentialligninger ODE er 1.1 ODE er helt grundlæggende Definition 1.1 (Ordinære differentialligninger).
E-PAD Bluetooth hængelås E-PAD Bluetooth padlock E-PAD Bluetooth Vorhängeschloss
 E-PAD Bluetooth hængelås E-PAD Bluetooth padlock E-PAD Bluetooth Vorhängeschloss Brugervejledning (side 2-6) Userguide (page 7-11) Bedienungsanleitung 1 - Hvordan forbinder du din E-PAD hængelås med din
E-PAD Bluetooth hængelås E-PAD Bluetooth padlock E-PAD Bluetooth Vorhängeschloss Brugervejledning (side 2-6) Userguide (page 7-11) Bedienungsanleitung 1 - Hvordan forbinder du din E-PAD hængelås med din
Elektromagnetisme 13 Side 1 af 8 Maxwells ligninger. Forskydningsstrømme I S 1
 Elektromagnetisme 13 Side 1 af 8 Betragt Amperes lov fra udtryk (1.1) anvendt på en kapacitor der er ved at blive ladet op. For de to flader og S der begge S1 afgrænses af C fås H dl = J ˆ C S n da = I
Elektromagnetisme 13 Side 1 af 8 Betragt Amperes lov fra udtryk (1.1) anvendt på en kapacitor der er ved at blive ladet op. For de to flader og S der begge S1 afgrænses af C fås H dl = J ˆ C S n da = I
Heisenbergs usikkerhedsrelationer. Abstrakt. Hvorfor? Funktionsrum. Nils Byrial Andersen Institut for Matematik. Matematiklærerdag 2013
 Heisenbergs usikkerhedsrelationer Nils Byrial Andersen Institut for Matematik Matematiklærerdag 013 1 / 17 Abstrakt Heisenbergs usikkerhedsrelationer udtrykker at man ikke på samme tid både kan bestemme
Heisenbergs usikkerhedsrelationer Nils Byrial Andersen Institut for Matematik Matematiklærerdag 013 1 / 17 Abstrakt Heisenbergs usikkerhedsrelationer udtrykker at man ikke på samme tid både kan bestemme
C R. Figur 1 Figur 2. er eksempler på kredsløbsfunktioner. Derimod er f.eks. indgangsimpedansen
 Kredsløbsfunktioner Lad os i det følgende betragte kredsløb, der er i hvile til t = 0. Det vil sige, at alle selvinduktionsstrømme og alle kondensatorspændinger er nul til t = 0. I de Laplace-transformerede
Kredsløbsfunktioner Lad os i det følgende betragte kredsløb, der er i hvile til t = 0. Det vil sige, at alle selvinduktionsstrømme og alle kondensatorspændinger er nul til t = 0. I de Laplace-transformerede
Privat-, statslig- eller regional institution m.v. Andet Added Bekaempelsesudfoerende: string No Label: Bekæmpelsesudførende
 Changes for Rottedatabasen Web Service The coming version of Rottedatabasen Web Service will have several changes some of them breaking for the exposed methods. These changes and the business logic behind
Changes for Rottedatabasen Web Service The coming version of Rottedatabasen Web Service will have several changes some of them breaking for the exposed methods. These changes and the business logic behind
Lineære 1. ordens differentialligningssystemer
 enote 7 enote 7 Lineære ordens differentialligningssystemer Denne enote beskriver ordens differentialligningssystemer og viser, hvordan de kan løses Der bruges egenværdier og egenvektorer i løsningsproceduren,
enote 7 enote 7 Lineære ordens differentialligningssystemer Denne enote beskriver ordens differentialligningssystemer og viser, hvordan de kan løses Der bruges egenværdier og egenvektorer i løsningsproceduren,
Eksamen i fysik 2016
 Eksamen i fysik 2016 NB: Jeg gør brug af DATABOG fysik kemi, 11. udgave, 4. oplag & Fysik i overblik, 1. oplag. Opgave 1 Proptrækker Vi kender vinens volumen og masse. Enheden liter omregnes til kubikmeter.
Eksamen i fysik 2016 NB: Jeg gør brug af DATABOG fysik kemi, 11. udgave, 4. oplag & Fysik i overblik, 1. oplag. Opgave 1 Proptrækker Vi kender vinens volumen og masse. Enheden liter omregnes til kubikmeter.
DesignMat Den komplekse eksponentialfunktion og polynomier
 DesignMat Den komplekse eksponentialfunktion og polynomier Preben Alsholm Uge 8 Forår 010 1 Den komplekse eksponentialfunktion 1.1 Definitionen Definitionen Den velkendte eksponentialfunktion x e x vil
DesignMat Den komplekse eksponentialfunktion og polynomier Preben Alsholm Uge 8 Forår 010 1 Den komplekse eksponentialfunktion 1.1 Definitionen Definitionen Den velkendte eksponentialfunktion x e x vil
Skriftlig Eksamen Kombinatorik, Sandsynlighed og Randomiserede Algoritmer (DM528)
 Skriftlig Eksamen Kombinatorik, Sandsynlighed og Randomiserede Algoritmer (DM58) Institut for Matematik og Datalogi Syddansk Universitet, Odense Torsdag den 1. januar 01 kl. 9 13 Alle sædvanlige hjælpemidler
Skriftlig Eksamen Kombinatorik, Sandsynlighed og Randomiserede Algoritmer (DM58) Institut for Matematik og Datalogi Syddansk Universitet, Odense Torsdag den 1. januar 01 kl. 9 13 Alle sædvanlige hjælpemidler
U = φ. R = ρ l A. Figur 1 Sammenhængen mellem potential, φ og spændingsfald, U: U = φ = φ 1 φ 2.
 Ohms lov Vi vil samle os en række byggestene, som kan bruges i modelleringen af fysiske systemer. De første to var hhv. en spændingskilde og en strømkilde. Disse elementer (sources) er aktive og kan tilføre
Ohms lov Vi vil samle os en række byggestene, som kan bruges i modelleringen af fysiske systemer. De første to var hhv. en spændingskilde og en strømkilde. Disse elementer (sources) er aktive og kan tilføre
LESSON NOTES Extensive Reading in Danish for Intermediate Learners #8 How to Interview
 LESSON NOTES Extensive Reading in Danish for Intermediate Learners #8 How to Interview CONTENTS 2 Danish 5 English # 8 COPYRIGHT 2019 INNOVATIVE LANGUAGE LEARNING. ALL RIGHTS RESERVED. DANISH 1. SÅDAN
LESSON NOTES Extensive Reading in Danish for Intermediate Learners #8 How to Interview CONTENTS 2 Danish 5 English # 8 COPYRIGHT 2019 INNOVATIVE LANGUAGE LEARNING. ALL RIGHTS RESERVED. DANISH 1. SÅDAN
Kurver og flader Aktivitet 15 Geodætiske kurver, Isometri, Mainardi-Codazzi, Teorema Egregium
 Kurver og flader Aktivitet 15 Geodætiske kurver, Isometri, Mainardi-Codazzi, Teorema Egregium Lisbeth Fajstrup Institut for Matematiske Fag Aalborg Universitet Kurver og Flader 2013 Lisbeth Fajstrup (AAU)
Kurver og flader Aktivitet 15 Geodætiske kurver, Isometri, Mainardi-Codazzi, Teorema Egregium Lisbeth Fajstrup Institut for Matematiske Fag Aalborg Universitet Kurver og Flader 2013 Lisbeth Fajstrup (AAU)
Vores mange brugere på musskema.dk er rigtig gode til at komme med kvalificerede ønsker og behov.
 På dansk/in Danish: Aarhus d. 10. januar 2013/ the 10 th of January 2013 Kære alle Chefer i MUS-regi! Vores mange brugere på musskema.dk er rigtig gode til at komme med kvalificerede ønsker og behov. Og
På dansk/in Danish: Aarhus d. 10. januar 2013/ the 10 th of January 2013 Kære alle Chefer i MUS-regi! Vores mange brugere på musskema.dk er rigtig gode til at komme med kvalificerede ønsker og behov. Og
Københavns Universitet, Det naturvidenskabelige Fakultet. Afleveringsopgave 1
 Københavns Universitet, Det naturvidenskabelige Fakultet 1 Lineær Algebra (LinAlg) Afleveringsopgave 1 Eventuelle besvarelser laves i grupper af - 3 personer og afleveres i to eksemplarer med 3 udfyldte
Københavns Universitet, Det naturvidenskabelige Fakultet 1 Lineær Algebra (LinAlg) Afleveringsopgave 1 Eventuelle besvarelser laves i grupper af - 3 personer og afleveres i to eksemplarer med 3 udfyldte
Skriftlig Eksamen Diskret matematik med anvendelser (DM72)
 Skriftlig Eksamen Diskret matematik med anvendelser (DM72) Institut for Matematik & Datalogi Syddansk Universitet, Odense Onsdag den 18. januar 2006 Alle sædvanlige hjælpemidler (lærebøger, notater etc.),
Skriftlig Eksamen Diskret matematik med anvendelser (DM72) Institut for Matematik & Datalogi Syddansk Universitet, Odense Onsdag den 18. januar 2006 Alle sædvanlige hjælpemidler (lærebøger, notater etc.),
Lineære 1. ordens differentialligningssystemer
 enote enote Lineære ordens differentialligningssystemer Denne enote beskriver ordens differentialligningssystemer og viser, hvordan de kan løses enoten er i forlængelse af enote, der beskriver lineære
enote enote Lineære ordens differentialligningssystemer Denne enote beskriver ordens differentialligningssystemer og viser, hvordan de kan løses enoten er i forlængelse af enote, der beskriver lineære
Angle Ini/al side Terminal side Vertex Standard posi/on Posi/ve angles Nega/ve angles. Quadrantal angle
 Mrs. Valentine AFM Objective: I will be able to identify angle types, convert between degrees and radians for angle measures, identify coterminal angles, find the length of an intercepted arc, and find
Mrs. Valentine AFM Objective: I will be able to identify angle types, convert between degrees and radians for angle measures, identify coterminal angles, find the length of an intercepted arc, and find
PARALLELIZATION OF ATTILA SIMULATOR WITH OPENMP MIGUEL ÁNGEL MARTÍNEZ DEL AMOR MINIPROJECT OF TDT24 NTNU
 PARALLELIZATION OF ATTILA SIMULATOR WITH OPENMP MIGUEL ÁNGEL MARTÍNEZ DEL AMOR MINIPROJECT OF TDT24 NTNU OUTLINE INEFFICIENCY OF ATTILA WAYS TO PARALLELIZE LOW COMPATIBILITY IN THE COMPILATION A SOLUTION
PARALLELIZATION OF ATTILA SIMULATOR WITH OPENMP MIGUEL ÁNGEL MARTÍNEZ DEL AMOR MINIPROJECT OF TDT24 NTNU OUTLINE INEFFICIENCY OF ATTILA WAYS TO PARALLELIZE LOW COMPATIBILITY IN THE COMPILATION A SOLUTION
AARHUS UNIVERSITET. Det Naturvidenskabelige Fakultet Augusteksamen OPGAVESTILLER: Allan H. Sørensen
 AARHUS UNIVERSITET Det Naturvidenskabelige Fakultet Augusteksamen 2006 FAG: Elektromagnetisme OPGAVESTILLER: Allan H. Sørensen Antal sider i opgavesættet (inkl. forsiden): 6 Eksamensdag: fredag dato: 11.
AARHUS UNIVERSITET Det Naturvidenskabelige Fakultet Augusteksamen 2006 FAG: Elektromagnetisme OPGAVESTILLER: Allan H. Sørensen Antal sider i opgavesættet (inkl. forsiden): 6 Eksamensdag: fredag dato: 11.
Materialer: Strømforsyningen Ledninger. 2 fatninger med pære. 1 multimeter. Forsøg del 1: Serieforbindelsen. Serie forbindelse
 Formål: Vi skal undersøge de egenskaber de 2 former for elektriske forbindelser har specielt med hensyn til strømstyrken (Ampere) og spændingen (Volt). Forsøg del 1: Serieforbindelsen Materialer: Strømforsyningen
Formål: Vi skal undersøge de egenskaber de 2 former for elektriske forbindelser har specielt med hensyn til strømstyrken (Ampere) og spændingen (Volt). Forsøg del 1: Serieforbindelsen Materialer: Strømforsyningen
MM501 forelæsningsslides
 MM501 forelæsningsslides uge 37, 2010 Produceret af Hans J. Munkholm 2009 bearbejdet af Jessica Carter 2010 1 Hvad er et komplekst tal? Hvordan regner man med komplekse tal? Man kan betragte udvidelsen
MM501 forelæsningsslides uge 37, 2010 Produceret af Hans J. Munkholm 2009 bearbejdet af Jessica Carter 2010 1 Hvad er et komplekst tal? Hvordan regner man med komplekse tal? Man kan betragte udvidelsen
Besvarelser til Calculus Ordinær Eksamen Juni 2019
 Besvarelser til Calculus Ordinær Eksamen - 14. Juni 2019 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 14. Juni 2019 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
DesignMat Uge 1 Gensyn med forårets stof
 DesignMat Uge 1 Gensyn med forårets stof Preben Alsholm Efterår 2010 1 Hovedpunkter fra forårets pensum 11 Taylorpolynomium Taylorpolynomium Det n te Taylorpolynomium for f med udviklingspunkt x 0 : P
DesignMat Uge 1 Gensyn med forårets stof Preben Alsholm Efterår 2010 1 Hovedpunkter fra forårets pensum 11 Taylorpolynomium Taylorpolynomium Det n te Taylorpolynomium for f med udviklingspunkt x 0 : P
Elektrodynamik Lab 1 Rapport
 Elektrodynamik Lab 1 Rapport Indhold Fysik 6, EL Bo Frederiksen (bo@fys.ku.dk) Stanislav V. Landa (stas@fys.ku.dk) John Niclasen (niclasen@fys.ku.dk) 1. Transienter og RC-kredsløb 1.1 Formål 1. Teori 1.3
Elektrodynamik Lab 1 Rapport Indhold Fysik 6, EL Bo Frederiksen (bo@fys.ku.dk) Stanislav V. Landa (stas@fys.ku.dk) John Niclasen (niclasen@fys.ku.dk) 1. Transienter og RC-kredsløb 1.1 Formål 1. Teori 1.3
Besvarelser til Calculus Ordinær Eksamen - 3. Januar 2017
 Besvarelser til Calculus Ordinær Eksamen - 3. Januar 17 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 3. Januar 17 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
19.3. Second Order ODEs. Introduction. Prerequisites. Learning Outcomes
 Second Order ODEs 19.3 Introduction In this Section we start to learn how to solve second-order differential equations of a particular type: those that are linear and that have constant coefficients. Such
Second Order ODEs 19.3 Introduction In this Section we start to learn how to solve second-order differential equations of a particular type: those that are linear and that have constant coefficients. Such
Hvor er mine runde hjørner?
 Hvor er mine runde hjørner? Ofte møder vi fortvivlelse blandt kunder, når de ser deres nye flotte site i deres browser og indser, at det ser anderledes ud, i forhold til det design, de godkendte i starten
Hvor er mine runde hjørner? Ofte møder vi fortvivlelse blandt kunder, når de ser deres nye flotte site i deres browser og indser, at det ser anderledes ud, i forhold til det design, de godkendte i starten
Skriftlig Eksamen Beregnelighed (DM517)
 Skriftlig Eksamen Beregnelighed (DM517) Institut for Matematik & Datalogi Syddansk Universitet Mandag den 31 Oktober 2011, kl. 9 13 Alle sædvanlige hjælpemidler (lærebøger, notater etc.) samt brug af lommeregner
Skriftlig Eksamen Beregnelighed (DM517) Institut for Matematik & Datalogi Syddansk Universitet Mandag den 31 Oktober 2011, kl. 9 13 Alle sædvanlige hjælpemidler (lærebøger, notater etc.) samt brug af lommeregner
Trolling Master Bornholm 2015
 Trolling Master Bornholm 2015 (English version further down) Panorama billede fra starten den første dag i 2014 Michael Koldtoft fra Trolling Centrum har brugt lidt tid på at arbejde med billederne fra
Trolling Master Bornholm 2015 (English version further down) Panorama billede fra starten den første dag i 2014 Michael Koldtoft fra Trolling Centrum har brugt lidt tid på at arbejde med billederne fra
Det er muligt at chekce følgende opg. i CodeJudge: og
 Det er muligt at chekce følgende opg. i CodeJudge:.1.7 og.1.14 Exercise 1: Skriv en forløkke, som producerer følgende output: 1 4 9 16 5 36 Bonusopgave: Modificer dit program, så det ikke benytter multiplikation.
Det er muligt at chekce følgende opg. i CodeJudge:.1.7 og.1.14 Exercise 1: Skriv en forløkke, som producerer følgende output: 1 4 9 16 5 36 Bonusopgave: Modificer dit program, så det ikke benytter multiplikation.
Om lyn. RF-ID & Radio control. Og transienter i elektronik. Lynnedslag, hvordan genereres ødelæggende spændinger i elektronik
 Senest redigeret 1. april 2014 Om lyn Og transienter i elektronik Lynnedslag, hvordan genereres ødelæggende spændinger i elektronik Materialet er meget foreløbigt. Derfor modtages rettelser og forslag
Senest redigeret 1. april 2014 Om lyn Og transienter i elektronik Lynnedslag, hvordan genereres ødelæggende spændinger i elektronik Materialet er meget foreløbigt. Derfor modtages rettelser og forslag
Formelsamling og noter. Elektrodynamik og bølger
 Formelsamling og noter. Elektrodynamik og bølger 26. oktober 212 Dennis Hansen E = ρ ɛ B = E = B B = µ J + µ ɛ E E da = Q enc ɛ E dl = Φ B Ei = L i di i dt + Q i C i + R i Ẽ i = iωl i Ĩ i + i ωc i Ĩ i
Formelsamling og noter. Elektrodynamik og bølger 26. oktober 212 Dennis Hansen E = ρ ɛ B = E = B B = µ J + µ ɛ E E da = Q enc ɛ E dl = Φ B Ei = L i di i dt + Q i C i + R i Ẽ i = iωl i Ĩ i + i ωc i Ĩ i
Titel: Hungry - Fedtbjerget
 Titel: Hungry - Fedtbjerget Tema: fedme, kærlighed, relationer Fag: Engelsk Målgruppe: 8.-10.kl. Data om læremidlet: Tv-udsendelse: TV0000006275 25 min. DR Undervisning 29-01-2001 Denne pædagogiske vejledning
Titel: Hungry - Fedtbjerget Tema: fedme, kærlighed, relationer Fag: Engelsk Målgruppe: 8.-10.kl. Data om læremidlet: Tv-udsendelse: TV0000006275 25 min. DR Undervisning 29-01-2001 Denne pædagogiske vejledning
Elementær Matematik. Trigonometriske Funktioner
 Elementær Matematik Trigonometriske Funktioner Ole Witt-Hansen Indhold. Gradtal og radiantal.... sin x, cos x og tan x... 3. Trigonometriske ligninger...3 4. Trigonometriske uligheder...5 5. Harmoniske
Elementær Matematik Trigonometriske Funktioner Ole Witt-Hansen Indhold. Gradtal og radiantal.... sin x, cos x og tan x... 3. Trigonometriske ligninger...3 4. Trigonometriske uligheder...5 5. Harmoniske
Noter om komplekse tal
 Noter om komplekse tal Preben Alsholm Januar 008 1 Den komplekse eksponentialfunktion Vi erindrer først om den sædvanlige og velkendte reelle eksponentialfunktion. Vi skal undertiden nde det nyttigt, at
Noter om komplekse tal Preben Alsholm Januar 008 1 Den komplekse eksponentialfunktion Vi erindrer først om den sædvanlige og velkendte reelle eksponentialfunktion. Vi skal undertiden nde det nyttigt, at
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Juni 2012 Institution Københavns tekniske Gymnasium/Sukkertoppen Uddannelse Fag og niveau Lærer Hold Htx Fysik
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Juni 2012 Institution Københavns tekniske Gymnasium/Sukkertoppen Uddannelse Fag og niveau Lærer Hold Htx Fysik
