Lineære systemer med hukommelse.
|
|
|
- Martin Steffensen
- 7 år siden
- Visninger:
Transkript
1 Lineær Response Teori. I responseteorien interesserer man sig for, hvad der kan siges generelt om sammenhængen mellem input φ(t) og output γ(t) for et system. Valg af variable. Det betragtede systems forskellige vekselvirkninger med omgivelserne kaldes for energibånd. Til hvert energibånd vil der være knyttet to såkaldte konjugerede variable, den generaliserede spænding, effort, e og den generaliserede strøm, flow, f. Produktet e f skal angive en art overført energimængde pr. tid. Strøm-variablen genkendes på, at den vil skifte fortegn ved tidsvending, mens spændings-variablen ikke vil gøre det. Herudover defineres to ekstra variable: forskydningen q, der er tidsintegralet af strømmen, og impulsen p, der er tidsintegralet af spændingen. Ved at fastlægge vor beskrivelse af systemer i disse termer bliver det let at angive analogier mellem forskellige fysiske systemer. Som eksempler kan nævnes, at de konjugerede variable i et termisk energibånd kunne være Carnotfaktoren 1 T /T 1 og varmestrømmen J Q. I et mekanisk energibånd kunne det være normalspændingen σ og volumenstrømmen J V. I elektriske energibånd svarer e til spændingsforskel U, f til strøm I, q til ladning Q og p til magnetisk fluks Φ B. Lineære systemer med hukommelse. I den lineære responseteori antager vi, at for tilstrækkeligt små påvirkninger vil der være en lineær sammenhæng mellem input, φ og output, γ; men der kan godt være en after effect. Ændringen dφ(t ) i φ til tiden t giver således et bidrag til ændringen dγ(t) i γ til tiden t: dγ(t) = R(t, t )dφ(t ) = R(t t )dφ(t ), (1) hvor vi yderligere har antaget, at denne ændring kun afhænger af tidsforskellen (tidshomogenitet). Da response må komme efter stimuli må R være for t < t, altså R(t) =, for t < (kausalitet) (2) 1 Hvilket blot er den relative temperaturvariation (T T )/T for små temperaturændringer 1
2 Opsummering af alle bidragene fra t = til t = t giver γ(t) = = t R(t t )dφ(t ) = t R(t t ) φ(t )dt R(t ) φ(t t )dt. (3) Her er φ den afledede af φ. Hvis vi indfører kompositionen som kort skrivemåde for den lineære operation foldning med den tidsafledede så kan ligning (3) skrives γ = R φ. (4) Bemærk, at dimensionen af R bliver dim(output)/dim(input). Responsefunktionernes navne. Afhængigt af typen af input og output giver vi responsefunktionen R forskellige navne. γ og φ kan hver især være f, q, e, p; men de må tilhøre hver sin kausale klasse. Hvis således φ er e eller p skal γ være f eller q og vice versa. Dette giver otte mulige responsefunktioner, hvoraf dog to er identiske med to andre således, at der kun er 6: Med input fra spændingsklassen: Krybefunktionen (compliance) J, q = J e, Admittansen Y, f = Y e, Letheden F, f = F p. Med input fra strømklassen: Stivheden (modulus) G, e = G q, Impedansen Z, e = Z f, Inertansen M, p = M f. Een af responsefunktionerne er nok til at karakterisere et system, idet de seks funktioner hænger matematisk sammen. Når man alligevel ikke blot nøjes med en af dem, er det fordi, det eksperimentelt kan være praktisk at kunne bestemme, hvilke variable (input), der styres, og hvilke (output), der måles. I en teori vil det også være forskelligt hvilken r.f.,det er mest naturlig at betragte. Skemaet giver et overblik over definitionen af de forskellige responsefunktioner 2
3 γ q f e p ladning strøm spænding magn. fluks φ forskydning hastighed kraft impuls q ladning forskydning G modulus stivhed f Z M strøm impedans inertans hastighed modstand masse e J Y spænding compliance admittans kraft krybefunktion bevægelighed p magn. fluks impuls F lethed Tabel 1 Skema over response-funktionerne, R og de mulige relationer, γ = R φ mellem input, φ og output, γ. Operatoren er "foldning med den tidsafledede" i tidsbilledet, men simpel multiplikation i frekvensbilledet. 3
4 Tidsbilledet. Lad stimuli (input) være en en pludselig ændring i φ fra til φ til tiden t = (en stepfunktion). Det kan vi udtrykke ved hjælp af Heaviside funktionen {, t < E(t) = (5) 1, t > idet vi da har φ(t) = φ E(t). Differentierer vi Heaviside funktionen får vi deltafunktionen δ(t), der er overalt undtagen for t =, hvor den til gengæld er så uendelig, at integralet af den er 1 2. Da er γ(t) = R(t )φ δ(t t )dt = φ R(t) (6) Responsefunktionen R(t) er altså simpelthen svaret γ(t) på et enhedsstep i stimuli til tiden t =, og kan derfor måles ved et såkaldt stepresponse forsøg. Frekvensbilledet. Formel (3) udtrykker, at output er givet ved at folde den tidsafledede af input med responsefunktionen. Ved en Fouriertransformation overgår foldning til produkt, differentiation til multiplikation med iω og integration til division med iω. Derfor vil diskussionen ofte være lettere i frekvensbilledet. Betragt derfor et periodisk input φ(t) = φ ω e iωt Da ligningerne er lineære, kan vi gerne regne med det komplekse input og tage realdel til sidst. Vi får γ(t) = R(t )(iω)φ ω e iω(t t ) dt = (iω)φ ω e iωt R(t )e iωt dt (7) 2 Det lyder selvfølgelig matematisk forkert; men de matematiske indvendinger kan man komme til livs ved blot at bruge en differentiabel funktion, der ligner Heavisidefunktionen undtagen i et tidsinterval, τ efter, der er meget kort i forhold til nogen relevant fysisk tid. Deltafunktionen er opfundet af Dirac og meget benyttet i fysikken. Den er normalt defineret symmetrisk omkring ; men i responseteorien skal approksimationerne til Heaviside og deltafunktionen kun leve for t > af hensyn til kausalitet. Mere præcist burde vi derfor skrive E(t + ) og δ(t + ), da Heaviside-funktionen skal være forskudt et infinitesimalt stykke væk fra, så dens afledede, deltafunktionen kun lever inden for integrationsområdet i (6). Man integrerer altså først med δ(t ǫ) og foretager grænseovergangen ǫ bagefter. En realisering af Heaviside funktionen, der er kausal, kunne være grænsen for τ af funktionerne H τ (t) = { for t, e τ/t for t > }. 4
5 Udregningen viser, at et harmonisk input resulterer i et harmonisk output. Skriver vi γ(t) = γ ω e iωt, ser vi hvor og F{R, ω} er den Fouriertransformerede af R(t), γ ω = ˆR(ω)φ ω, (8) ˆR(ω) = iωf{r, ω}, (9) F{R, ω} = R(t)e iωt dt. (1) Her kunne nedre grænse føres til t =, som normalt i en Fouriertransformation pga. kausalitetsbetingelsen (2). Læg mærke til, at der udover Fouriertransformation skal ganges med iω. Frekvensresponsefunktionen ˆR(ω) bliver derved den funktion, som man naturligt ville måle og definere ved (8) i et forsøg med harmonisk varierende input. ˆR(ω) har således samme dimension som R(t), og grænseopførslerne ˆR(ω) for ω eller vil svare til henholdsvis R(t) for t eller. Skrives frekvensresponsefunktionen på modulusargument form: ˆR(ω) = ˆR(ω) e iθω bliver γ(t) = ˆR(ω) e i(ωt+θω), så θ ω angiver, hvor mange radianer γ(t) er fasedrejet forud i forhold til φ(t), mens = ˆR(ω) angiver amplitudeforholdet γ ω / φ ω. Tilbagevenden til R(t) sker ved invers Fouriertransformation R(t) = 1 2π ˆR(ω) iω eiωt dω (11) Laplace-Stieltjes transformation. Fouriertransformationen kan analytisk udvides til at gælde for komplekse frekvenser ω = ω +iω. I den nedre halvplan, hvor ω < kan dette stadig findes ved (1) idet faktoren e ω t får integralet til at konvergere for t >, mens denne faktor ikke skaber problemer for t <, fordi R(t) = her. Man indfører ofte Laplace-frekvensen s = iω og definerer s-frekvensresponsefunktionen R(s) ved R(s) = s R(t)e st dt = sl{r, s} (12) altså s gange den Laplacetransformerede af R(t). Frekvensresponsefunktionen kan nu fås ved ˆR(ω) = lim s iω,s > R(s) (13) 5
6 Relationer mellem responsefunktionerne. I frekvensbilledet bliver sammenhængene mellem responsefunktionerne meget simple: Inden for de to klasser: Mellem de to klasser: M = 1 s Z = 1 s 2 G, J = 1 sỹ = 1 s 2 F (14) J = 1 G, Ỹ = 1 Z, F = 1 M (15) I tidsbilledet er det derimod kun inden for samme kausalitetsklasse, at det er enkelt at omregne (ved integration eller differentiation). Skift fra den ene klasse til den anden kræver løsning af en integralligning, som i praksis lettest løses ved netop at gå til frekvensbilledet. Sammensatte systemer. Det er let at indse at, hvis to systemer sammensættes med en Kirchhoff strømsamler (maske), dvs. så de har fælles strøm, mens den resulterende spænding er summen af delspændingerne, så er sammensætningen additivt i strømklasse responsefunktionerne (G, Z, M). Omvendt, hvis to systemer sammensættes med en Kirchhoff spændingssamler (knude), dvs så de har fælles spænding, mens den resulterende strøm er summen af delstrømmene, så er sammensætningen additiv i spændingsklasse responsefunktionerne (J, Y, F). Ved brug af dette samt skift mellem klasserne kan man opstille responsefunktioner for meget komplicerede fysiske netværk. 6
Impedans. I = C du dt (1) og en spole med selvinduktionen L
 Impedans I et kredsløb, der består af andre netværkselementer end blot lække (modstande) og kilder vil der ikke i almindelighed være en simpel proportional, tidslig sammenhæng mellem strøm og spænding,
Impedans I et kredsløb, der består af andre netværkselementer end blot lække (modstande) og kilder vil der ikke i almindelighed være en simpel proportional, tidslig sammenhæng mellem strøm og spænding,
Figur 1 Energetisk vekselvirkning mellem to systemer.
 Energibånd Fysiske fænomener er i reglen forbundet med udveksling af energi mellem forskellige systemer. Udvekslingen af energi mellem to systemer A og B kan vi illustrere grafisk som på figur 1 med en
Energibånd Fysiske fænomener er i reglen forbundet med udveksling af energi mellem forskellige systemer. Udvekslingen af energi mellem to systemer A og B kan vi illustrere grafisk som på figur 1 med en
Introduktion til Laplace transformen (Noter skrevet af Nikolaj Hess-Nielsen sidst revideret marts 2013)
 Introduktion til Laplace transformen (oter skrevet af ikolaj Hess-ielsen sidst revideret marts 23) Integration handler ikke kun om arealer. Tværtimod er integration basis for mange af de vigtigste værktøjer
Introduktion til Laplace transformen (oter skrevet af ikolaj Hess-ielsen sidst revideret marts 23) Integration handler ikke kun om arealer. Tværtimod er integration basis for mange af de vigtigste værktøjer
Note om Laplace-transformationen
 Note om Laplace-transformationen Den harmoniske oscillator omskrevet til et ligningssystem I dette opgavesæt benyttes laplacetransformationen til at løse koblede differentialligninger. Fordelen ved at
Note om Laplace-transformationen Den harmoniske oscillator omskrevet til et ligningssystem I dette opgavesæt benyttes laplacetransformationen til at løse koblede differentialligninger. Fordelen ved at
C R. Figur 1 Figur 2. er eksempler på kredsløbsfunktioner. Derimod er f.eks. indgangsimpedansen
 Kredsløbsfunktioner Lad os i det følgende betragte kredsløb, der er i hvile til t = 0. Det vil sige, at alle selvinduktionsstrømme og alle kondensatorspændinger er nul til t = 0. I de Laplace-transformerede
Kredsløbsfunktioner Lad os i det følgende betragte kredsløb, der er i hvile til t = 0. Det vil sige, at alle selvinduktionsstrømme og alle kondensatorspændinger er nul til t = 0. I de Laplace-transformerede
GEOMETRI-TØ, UGE 3. og resultatet følger fra [P] Proposition 2.3.1, der siger, at
![GEOMETRI-TØ, UGE 3. og resultatet følger fra [P] Proposition 2.3.1, der siger, at GEOMETRI-TØ, UGE 3. og resultatet følger fra [P] Proposition 2.3.1, der siger, at](/thumbs/50/26870860.jpg) GEOMETRI-TØ, UGE 3 Hvis I falder over tryk- eller regne-fejl i nedenstående, må I meget gerne sende rettelser til fuglede@imf.au.dk. Opvarmningsopgave 1. Lad γ : (α, β) R 2 være en regulær kurve i planen.
GEOMETRI-TØ, UGE 3 Hvis I falder over tryk- eller regne-fejl i nedenstående, må I meget gerne sende rettelser til fuglede@imf.au.dk. Opvarmningsopgave 1. Lad γ : (α, β) R 2 være en regulær kurve i planen.
Fourier transformationen
 MODUL 6 Fourier transformationen Forfattere: Øistein WIND-WILLASSEN & Michael ELMEGÅRD 4. juni 4 Indhold Fourier transformationen 5. Definition og oprindelse.............................. 5.. Funktioner
MODUL 6 Fourier transformationen Forfattere: Øistein WIND-WILLASSEN & Michael ELMEGÅRD 4. juni 4 Indhold Fourier transformationen 5. Definition og oprindelse.............................. 5.. Funktioner
Københavns Universitet, Det naturvidenskabelige Fakultet. Afleveringsopgave 1
 Københavns Universitet, Det naturvidenskabelige Fakultet 1 Lineær Algebra (LinAlg) Afleveringsopgave 1 Eventuelle besvarelser laves i grupper af - 3 personer og afleveres i to eksemplarer med 3 udfyldte
Københavns Universitet, Det naturvidenskabelige Fakultet 1 Lineær Algebra (LinAlg) Afleveringsopgave 1 Eventuelle besvarelser laves i grupper af - 3 personer og afleveres i to eksemplarer med 3 udfyldte
MATEMATIK 3 EN,MP 17. september 2014 Oversigt nr. 1
 MATEMATIK 3 EN,MP 7. september 204 Oversigt nr. Her bringes en samling af de gamle eksamensopgaver: (jan. 204) Betragt begyndelsesværdiproblemet y (t) + 7y (t) + 2y(t) = e t sin(2t) for t > 0, y(0) = 2,
MATEMATIK 3 EN,MP 7. september 204 Oversigt nr. Her bringes en samling af de gamle eksamensopgaver: (jan. 204) Betragt begyndelsesværdiproblemet y (t) + 7y (t) + 2y(t) = e t sin(2t) for t > 0, y(0) = 2,
Matematik 1 Semesteruge 5 6 (30. september oktober 2002) side 1. Komplekse tal Arbejdsplan
 Matematik Semesteruge 5 6 (30. september -. oktober 2002) side Komplekse tal Arbejdsplan I semesterugerne 5 og 6 erstattes den regulære undervisning (forelæsninger og fællestimer) af selvstudium med opgaveregning
Matematik Semesteruge 5 6 (30. september -. oktober 2002) side Komplekse tal Arbejdsplan I semesterugerne 5 og 6 erstattes den regulære undervisning (forelæsninger og fællestimer) af selvstudium med opgaveregning
Diffusionsligningen. Fællesprojekt for FY520 og MM502. Marts Hans J. Munkholm og Paolo Sibani. Besvarelse fra Hans J.
 Diffusionsligningen Fællesprojekt for FY50 og MM50 Marts 009 Hans J. Munkholm og Paolo Sibani Besvarelse fra Hans J. Munkholm 1 (a) Lad [x, x + x] være et lille delinterval af [a, b]. Den masse, der er
Diffusionsligningen Fællesprojekt for FY50 og MM50 Marts 009 Hans J. Munkholm og Paolo Sibani Besvarelse fra Hans J. Munkholm 1 (a) Lad [x, x + x] være et lille delinterval af [a, b]. Den masse, der er
(c) Opskriv den reelle Fourierrække for funktionen y(t) fra (b), og afgør dernæst om y(t) er en lige eller ulige funktion eller ingen af delene.
 MATEMATIK 3 EN,MP 4. februar 2016 Eksamenopgaver fra 2011 2016 (jan. 2016) Givet at 0 for 0 < t < 1 mens e (t 1) cos(7(t 1)) for t 1, betragt da begyndelsesværdiproblemet for t > 0: y (t) + 2y (t) + 50y(t)
MATEMATIK 3 EN,MP 4. februar 2016 Eksamenopgaver fra 2011 2016 (jan. 2016) Givet at 0 for 0 < t < 1 mens e (t 1) cos(7(t 1)) for t 1, betragt da begyndelsesværdiproblemet for t > 0: y (t) + 2y (t) + 50y(t)
Elektromagnetisme 14 Side 1 af 10 Elektromagnetiske bølger. Bølgeligningen
 Elektromagnetisme 14 Side 1 af 1 Bølgeligningen Maxwells ligninger udtrykker den indbyrdes sammenhæng mellem de elektromagnetiske felter samt sammenhængen mellem disse felter og de feltskabende ladninger
Elektromagnetisme 14 Side 1 af 1 Bølgeligningen Maxwells ligninger udtrykker den indbyrdes sammenhæng mellem de elektromagnetiske felter samt sammenhængen mellem disse felter og de feltskabende ladninger
Matematik F2 Opgavesæt 6
 Opgave 4: Udtryk funktionen f(θ) = sin θ ved hjælp af Legendre-polynomierne på formen P l (cos θ). Dvs. find koefficienterne a l i ekspansionen f(θ) = a l P l (cos θ) l= Svar: Bemærk, at funktionen er
Opgave 4: Udtryk funktionen f(θ) = sin θ ved hjælp af Legendre-polynomierne på formen P l (cos θ). Dvs. find koefficienterne a l i ekspansionen f(θ) = a l P l (cos θ) l= Svar: Bemærk, at funktionen er
Karakteristiske funktioner og Den Centrale Grænseværdisætning
 E6 efterår 1999 Notat 10 Jørgen Larsen 20. oktober 1999 Karakteristiske funktioner og Den Centrale Grænseværdisætning Karakteristiske funktioner som er nære slægtninge til Fourier-transformationen) er
E6 efterår 1999 Notat 10 Jørgen Larsen 20. oktober 1999 Karakteristiske funktioner og Den Centrale Grænseværdisætning Karakteristiske funktioner som er nære slægtninge til Fourier-transformationen) er
Løsningsforslag til opgavesæt 5
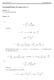 Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
π er irrationel Frank Nasser 10. december 2011
 π er irrationel Frank Nasser 10. december 2011 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold 1 Introduktion
π er irrationel Frank Nasser 10. december 2011 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold 1 Introduktion
Fysik 2 - Den Harmoniske Oscillator
 Fysik 2 - Den Harmoniske Oscillator Esben Bork Hansen, Amanda Larssen, Martin Qvistgaard Christensen, Maria Cavallius 5. januar 2009 Indhold 1 Formål 1 2 Forsøget 2 3 Resultater 3 4 Teori 4 4.1 simpel
Fysik 2 - Den Harmoniske Oscillator Esben Bork Hansen, Amanda Larssen, Martin Qvistgaard Christensen, Maria Cavallius 5. januar 2009 Indhold 1 Formål 1 2 Forsøget 2 3 Resultater 3 4 Teori 4 4.1 simpel
Elektromagnetisme 14 Side 1 af 9 Elektromagnetiske bølger. Bølgeligningen
 Elektromagnetisme 14 Side 1 af 9 Bølgeligningen Maxwells ligninger udtrykker den indbyrdes sammenhæng mellem de elektromagnetiske felter. I det flg. udledes en ligning, der opfyldes af hvert enkelt felt.
Elektromagnetisme 14 Side 1 af 9 Bølgeligningen Maxwells ligninger udtrykker den indbyrdes sammenhæng mellem de elektromagnetiske felter. I det flg. udledes en ligning, der opfyldes af hvert enkelt felt.
Løsningsforslag til opgavesæt 5
 Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
Harmonisk oscillator. Thorbjørn Serritslev Nieslen Erik Warren Tindall
 Harmonisk oscillator Thorbjørn Serritslev Nieslen Erik Warren Tindall November 27, 2007 Formål At studere den harmoniske oscillator, som indgår i mange fysiske sammenhænge. Den harmoniske oscillator illustreres
Harmonisk oscillator Thorbjørn Serritslev Nieslen Erik Warren Tindall November 27, 2007 Formål At studere den harmoniske oscillator, som indgår i mange fysiske sammenhænge. Den harmoniske oscillator illustreres
Matematik 1 Semesteruge 5 6 (1. oktober oktober 2001) side 1 Komplekse tal Arbejdsplan
 Matematik 1 Semesteruge 5 6 (1. oktober - 12. oktober 2001) side 1 Komplekse tal Arbejdsplan I semesterugerne 5 og 6 erstattes den regulære undervisning (forelæsninger og fællestimer) af selvstudium med
Matematik 1 Semesteruge 5 6 (1. oktober - 12. oktober 2001) side 1 Komplekse tal Arbejdsplan I semesterugerne 5 og 6 erstattes den regulære undervisning (forelæsninger og fællestimer) af selvstudium med
Integralregning Infinitesimalregning
 Udgave 2.1 Integralregning Infinitesimalregning Noterne gennemgår begreberne integral og stamfunktion, og anskuer dette som et redskab til bestemmelse af arealer under funktioner. Noterne er supplement
Udgave 2.1 Integralregning Infinitesimalregning Noterne gennemgår begreberne integral og stamfunktion, og anskuer dette som et redskab til bestemmelse af arealer under funktioner. Noterne er supplement
Wigner s semi-cirkel lov
 Wigner s semi-cirkel lov 12. december 2009 Eulers Venner Steen Thorbjørnsen Institut for Matematiske Fag Århus Universitet Diagonalisering af selvadjungeret matrix Lad H være en n n matrix med komplekse
Wigner s semi-cirkel lov 12. december 2009 Eulers Venner Steen Thorbjørnsen Institut for Matematiske Fag Århus Universitet Diagonalisering af selvadjungeret matrix Lad H være en n n matrix med komplekse
Mekaniske og dielektriske målinger på 1,2-propandiol og methyl m-toluate
 Mekaniske og dielektriske målinger på 1,2-propandiol og methyl m-toluate En undersøgelse af sammenhængen mellem væskernes shearmodul og permittivitet Dielectric and mechanical measurements on 1,2-propanediol
Mekaniske og dielektriske målinger på 1,2-propandiol og methyl m-toluate En undersøgelse af sammenhængen mellem væskernes shearmodul og permittivitet Dielectric and mechanical measurements on 1,2-propanediol
- I, OM OG MED MATEMATIK OG FYSIK
 - I, OM OG MED MATEMATIK OG FYSIK Mekaniske og dielektriske målinger på 1,2-propandiol og methyl m-toluate En undersøgelse af sammenhængen mellem væskernes shearmodul og permittivitet af Louise Schnegell,
- I, OM OG MED MATEMATIK OG FYSIK Mekaniske og dielektriske målinger på 1,2-propandiol og methyl m-toluate En undersøgelse af sammenhængen mellem væskernes shearmodul og permittivitet af Louise Schnegell,
Eksamen i Matematik F2 d. 19. juni Opgave 2. Svar. Korte svar (ikke fuldstændige)
 Eksamen i Matematik F2 d. 9. juni 28 Korte svar (ikke fuldstændige Opgave Find realdelen, Re z, og imaginærdelen, Im z, for følgende værdier af z, a z = 2 i b z = i i c z = ln( + i Find realdelen, Re z,
Eksamen i Matematik F2 d. 9. juni 28 Korte svar (ikke fuldstændige Opgave Find realdelen, Re z, og imaginærdelen, Im z, for følgende værdier af z, a z = 2 i b z = i i c z = ln( + i Find realdelen, Re z,
Formelsamling - MatF2. Therkel Zøllner og Amalie Christensen 27. juni 2009
 Formelsamling - MatF2 Therkel Zøllner og Amalie Christensen 27. juni 2009 1 Indhold 1 Kompleks variabel teori 3 1.1 Komplekse funktioner 825-830........................... 3 1.2 Powerserier af komplekse
Formelsamling - MatF2 Therkel Zøllner og Amalie Christensen 27. juni 2009 1 Indhold 1 Kompleks variabel teori 3 1.1 Komplekse funktioner 825-830........................... 3 1.2 Powerserier af komplekse
Signalbehandling og matematik 1 (Tidsdiskrete signaler og systemer)
 Signalbehandling og matematik 1 (Tidsdiskrete signaler og systemer) Session 1. Sekvenser, diskrete systemer, Lineære systemer, foldning og lineære tidsinvariante systemer Ved Samuel Schmidt sschmidt@hst.aau.dk
Signalbehandling og matematik 1 (Tidsdiskrete signaler og systemer) Session 1. Sekvenser, diskrete systemer, Lineære systemer, foldning og lineære tidsinvariante systemer Ved Samuel Schmidt sschmidt@hst.aau.dk
Heisenbergs usikkerhedsrelationer. Abstrakt. Hvorfor? Funktionsrum. Nils Byrial Andersen Institut for Matematik. Matematiklærerdag 2013
 Heisenbergs usikkerhedsrelationer Nils Byrial Andersen Institut for Matematik Matematiklærerdag 013 1 / 17 Abstrakt Heisenbergs usikkerhedsrelationer udtrykker at man ikke på samme tid både kan bestemme
Heisenbergs usikkerhedsrelationer Nils Byrial Andersen Institut for Matematik Matematiklærerdag 013 1 / 17 Abstrakt Heisenbergs usikkerhedsrelationer udtrykker at man ikke på samme tid både kan bestemme
Taylors formel. Kapitel Klassiske sætninger i en dimension
 Kapitel 3 Taylors formel 3.1 Klassiske sætninger i en dimension Sætning 3.1 (Rolles sætning) Lad f : [a, b] R være kontinuert, og antag at f er differentiabel i det åbne interval (a, b). Hvis f (a) = f
Kapitel 3 Taylors formel 3.1 Klassiske sætninger i en dimension Sætning 3.1 (Rolles sætning) Lad f : [a, b] R være kontinuert, og antag at f er differentiabel i det åbne interval (a, b). Hvis f (a) = f
U = φ. R = ρ l A. Figur 1 Sammenhængen mellem potential, φ og spændingsfald, U: U = φ = φ 1 φ 2.
 Ohms lov Vi vil samle os en række byggestene, som kan bruges i modelleringen af fysiske systemer. De første to var hhv. en spændingskilde og en strømkilde. Disse elementer (sources) er aktive og kan tilføre
Ohms lov Vi vil samle os en række byggestene, som kan bruges i modelleringen af fysiske systemer. De første to var hhv. en spændingskilde og en strømkilde. Disse elementer (sources) er aktive og kan tilføre
Matematik F2 Opgavesæt 2
 Opgaver uge 2 I denne uge kigger vi nærmere på Cauchy-Riemann betingelserne, potensrækker, konvergenskriterier og flertydige funktioner. Vi skal også se på integration langs en ve i den komplekse plan.
Opgaver uge 2 I denne uge kigger vi nærmere på Cauchy-Riemann betingelserne, potensrækker, konvergenskriterier og flertydige funktioner. Vi skal også se på integration langs en ve i den komplekse plan.
MATEMATIK 11 Eksamensopgaver Juni 1995 Juni 2001, 4. fjerdedel
 Juni 2000 MATEMATIK 11 Eksamensopgaver Juni 1995 Juni 2001, 4. fjerdedel Opgave 1. (a) Find den fuldstændige løsning til differentialligningen y 8y + 16y = 0. (b) Find den fuldstændige løsning til differentialligningen
Juni 2000 MATEMATIK 11 Eksamensopgaver Juni 1995 Juni 2001, 4. fjerdedel Opgave 1. (a) Find den fuldstændige løsning til differentialligningen y 8y + 16y = 0. (b) Find den fuldstændige løsning til differentialligningen
MATEMATIK 3 ET,MP, FYS, NANO 29. august 2012 Oversigt nr. 1
 ET,MP, FYS, NANO 29. august 202 Oversigt nr. Litteratur: I Matematik 3 bruger vi i efteråret 202 følgende bog: E. Kreyzig: Advanced engineering mathematics, 0. udg., Wiley, 20. Beskrivelse: Kurset vil
ET,MP, FYS, NANO 29. august 202 Oversigt nr. Litteratur: I Matematik 3 bruger vi i efteråret 202 følgende bog: E. Kreyzig: Advanced engineering mathematics, 0. udg., Wiley, 20. Beskrivelse: Kurset vil
Grafmanipulation. Frank Nasser. 14. april 2011
 Grafmanipulation Frank Nasser 14. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk: Dette er
Grafmanipulation Frank Nasser 14. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk: Dette er
Digitale periodiske signaler
 KAPITEL FEM Digitale periodiske signaler For digitale signaler, som er periodiske, gælder det, at for alle n vil hvor det hele tal er perioden. g(n + ) = g(n), (5.) Af udtrykkene ses det, at periodiske
KAPITEL FEM Digitale periodiske signaler For digitale signaler, som er periodiske, gælder det, at for alle n vil hvor det hele tal er perioden. g(n + ) = g(n), (5.) Af udtrykkene ses det, at periodiske
VEKSELSPÆNDINGENS VÆRDIER. Frekvens Middelværdi & peak værdi (max) Effektiv værdi (RMS) Mere om effektiv værdi!
 AC VEKSELSPÆNDINGENS VÆRDIER Frekvens Middelværdi & peak værdi (max) Effektiv værdi (RMS) Mere om effektiv værdi! Frekvens: Frekvensen (f) af et system er antallet af svingninger eller rotationer pr. sekund:
AC VEKSELSPÆNDINGENS VÆRDIER Frekvens Middelværdi & peak værdi (max) Effektiv værdi (RMS) Mere om effektiv værdi! Frekvens: Frekvensen (f) af et system er antallet af svingninger eller rotationer pr. sekund:
Kortfattet svar til eksamen i Matematik F2 d. 21. juni 2017
 Kortfattet svar til eksamen i Matematik F2 d. 2. juni 27 Opgave Bestem for følgende tilfælde om en funktion f(z) af z = x + iy er analytisk i dele af den komplekse plan, hvis den har real del u(x, y) og
Kortfattet svar til eksamen i Matematik F2 d. 2. juni 27 Opgave Bestem for følgende tilfælde om en funktion f(z) af z = x + iy er analytisk i dele af den komplekse plan, hvis den har real del u(x, y) og
Projektopgave Observationer af stjerneskælv
 Projektopgave Observationer af stjerneskælv Af: Mathias Brønd Christensen (20073504), Kristian Jerslev (20072494), Kristian Mads Egeris Nielsen (20072868) Indhold Formål...3 Teori...3 Hvorfor opstår der
Projektopgave Observationer af stjerneskælv Af: Mathias Brønd Christensen (20073504), Kristian Jerslev (20072494), Kristian Mads Egeris Nielsen (20072868) Indhold Formål...3 Teori...3 Hvorfor opstår der
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin 5. 6. semester efterår 2013-forår 2014 Institution Grenaa Tekniske Gymnasium Uddannelse Fag og niveau Lærer(e)
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin 5. 6. semester efterår 2013-forår 2014 Institution Grenaa Tekniske Gymnasium Uddannelse Fag og niveau Lærer(e)
Appendiks 6: Universet som en matematisk struktur
 Appendiks 6: Universet som en matematisk struktur En matematisk struktur er et meget abstrakt dyr, der kan defineres på følgende måde: En mængde, S, af elementer {s 1, s 2,,s n }, mellem hvilke der findes
Appendiks 6: Universet som en matematisk struktur En matematisk struktur er et meget abstrakt dyr, der kan defineres på følgende måde: En mængde, S, af elementer {s 1, s 2,,s n }, mellem hvilke der findes
DesignMat Komplekse tal
 DesignMat Komplekse tal Preben Alsholm Uge 7 Forår 010 1 Talmængder 1.1 Talmængder Talmængder N er mængden af naturlige tal, 1,, 3, 4, 5,... Z er mængden af hele tal... 5, 4, 3,, 1, 0, 1,, 3, 4, 5,....
DesignMat Komplekse tal Preben Alsholm Uge 7 Forår 010 1 Talmængder 1.1 Talmængder Talmængder N er mængden af naturlige tal, 1,, 3, 4, 5,... Z er mængden af hele tal... 5, 4, 3,, 1, 0, 1,, 3, 4, 5,....
Den homogene ligning. Vi betragter den n te ordens, homogene, lineære differentialligning. d n y dt n. an 1 + any = 0 (1.2) dt. + a1 d n 1 y dt n 1
 1/7 Den homogene ligning Vi betragter den n te ordens, homogene, lineære differentialligning a 0 d n y dt n + a1 d n 1 y dt n 1 hvor a 0,..., a n R og a 0 0. Vi skriver ligningen på kort form som + + dy
1/7 Den homogene ligning Vi betragter den n te ordens, homogene, lineære differentialligning a 0 d n y dt n + a1 d n 1 y dt n 1 hvor a 0,..., a n R og a 0 0. Vi skriver ligningen på kort form som + + dy
Mujtaba og Farid Integralregning 06-08-2011
 Indholdsfortegnelse Integral regning:... 2 Ubestemt integral:... 2 Integrationsprøven:... 3 1) Integration af potensfunktioner:... 3 2) Integration af sum og Differens:... 3 3) Integration ved Multiplikation
Indholdsfortegnelse Integral regning:... 2 Ubestemt integral:... 2 Integrationsprøven:... 3 1) Integration af potensfunktioner:... 3 2) Integration af sum og Differens:... 3 3) Integration ved Multiplikation
Idenne note giver vi et eksempel på, hvorledes det er vigtigt at holde sig
 Analyse : Eulers formel Sebastian rsted 9. maj 015 Idenne note giver vi et eksempel på, hvorledes det er vigtigt at holde sig for øje, hvor de matematiske resultater kommer fra, og hvad de baseres på;
Analyse : Eulers formel Sebastian rsted 9. maj 015 Idenne note giver vi et eksempel på, hvorledes det er vigtigt at holde sig for øje, hvor de matematiske resultater kommer fra, og hvad de baseres på;
KREDSLØBSTEORI 10 FORELÆSNINGER OM ELEKTRISKEKREDSLØB
 EE Basis, foråret 2010 KREDSLØBSTEORI 10 FORELÆSNINGER OM ELEKTRISKEKREDSLØB Jan H. Mikkelsen EE- Basis, Kredsløbsteori, F10, KRT4 1 Emner for idag Kondensatorer Spoler TidsaGængige kredsløb Universalformlen
EE Basis, foråret 2010 KREDSLØBSTEORI 10 FORELÆSNINGER OM ELEKTRISKEKREDSLØB Jan H. Mikkelsen EE- Basis, Kredsløbsteori, F10, KRT4 1 Emner for idag Kondensatorer Spoler TidsaGængige kredsløb Universalformlen
Matematisk modellering og numeriske metoder. Lektion 8
 Matematisk modellering og numeriske metoder Lektion 8 Morten Grud Rasmussen 18. oktober 216 1 Fourierrækker 1.1 Periodiske funktioner Definition 1.1 (Periodiske funktioner). En periodisk funktion f er
Matematisk modellering og numeriske metoder Lektion 8 Morten Grud Rasmussen 18. oktober 216 1 Fourierrækker 1.1 Periodiske funktioner Definition 1.1 (Periodiske funktioner). En periodisk funktion f er
Komplekse tal. Mikkel Stouby Petersen 27. februar 2013
 Komplekse tal Mikkel Stouby Petersen 27. februar 2013 1 Motivationen Historien om de komplekse tal er i virkeligheden historien om at fjerne forhindringerne og gøre det umulige muligt. For at se det, vil
Komplekse tal Mikkel Stouby Petersen 27. februar 2013 1 Motivationen Historien om de komplekse tal er i virkeligheden historien om at fjerne forhindringerne og gøre det umulige muligt. For at se det, vil
Gruppeteori. Michael Knudsen. 8. marts For at motivere indførelsen af gruppebegrebet begynder vi med et eksempel.
 Gruppeteori Michael Knudsen 8. marts 2005 1 Motivation For at motivere indførelsen af gruppebegrebet begynder vi med et eksempel. Eksempel 1.1. Lad Z betegne mængden af de hele tal, Z = {..., 2, 1, 0,
Gruppeteori Michael Knudsen 8. marts 2005 1 Motivation For at motivere indførelsen af gruppebegrebet begynder vi med et eksempel. Eksempel 1.1. Lad Z betegne mængden af de hele tal, Z = {..., 2, 1, 0,
Bevægelsens Geometri
 Bevægelsens Geometri Vi vil betragte bevægelsen af et punkt. Dette punkt kan f.eks. være tyngdepunktet af en flue, et menneske, et molekyle, en galakse eller hvad man nu ellers har lyst til at beskrive.
Bevægelsens Geometri Vi vil betragte bevægelsen af et punkt. Dette punkt kan f.eks. være tyngdepunktet af en flue, et menneske, et molekyle, en galakse eller hvad man nu ellers har lyst til at beskrive.
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin 5. 6. semester efterår 2017-forår 2018 Institution Videndjurs, Grenaa Uddannelse Fag og niveau Lærer(e) Hold
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin 5. 6. semester efterår 2017-forår 2018 Institution Videndjurs, Grenaa Uddannelse Fag og niveau Lærer(e) Hold
Bilag I. ~ i ~ Oversigt BILAG II MATEMATISK APPENDIKS. The Prisoner s Dilemma THE PRISONER S DILEMMA INTRODUKTION I RELATION TIL SAMORDNET PRAKSIS
 Oversigt BILAG I I THE PRISONER S DILEMMA INTRODUKTION I RELATION TIL SAMORDNET PRAKSIS I I II BILAG II III GENNEMSIGTIGHEDENS BETYDNING III MATEMATISK APPENDIKS V GENERELT TILBAGEDISKONTERINGSFAKTOREN
Oversigt BILAG I I THE PRISONER S DILEMMA INTRODUKTION I RELATION TIL SAMORDNET PRAKSIS I I II BILAG II III GENNEMSIGTIGHEDENS BETYDNING III MATEMATISK APPENDIKS V GENERELT TILBAGEDISKONTERINGSFAKTOREN
Introduktion til differentialregning 1. Jens Siegstad og Annegrethe Bak
 Introduktion til differentialregning 1 Jens Siegstad og Annegrete Bak 16. juli 2008 1 Indledning I denne note vil vi kort introduktion til differentilregning, idet vi skal bruge teorien i et emne, Matematisk
Introduktion til differentialregning 1 Jens Siegstad og Annegrete Bak 16. juli 2008 1 Indledning I denne note vil vi kort introduktion til differentilregning, idet vi skal bruge teorien i et emne, Matematisk
Besvarelse, Eksamen Analyse 1, 2013
 Københavns Universitet Prøve ved Det naturvidenskabelige Fakultet juni 23 Besvarelse, Eksamen Analyse, 23 Opgave Lad, for n N, funktionen f n : [, ) R være givet ved NB. Trykfejl. Burde være x. f n (x)
Københavns Universitet Prøve ved Det naturvidenskabelige Fakultet juni 23 Besvarelse, Eksamen Analyse, 23 Opgave Lad, for n N, funktionen f n : [, ) R være givet ved NB. Trykfejl. Burde være x. f n (x)
MM501 forelæsningsslides
 MM501 forelæsningsslides uge 37, 2010 Produceret af Hans J. Munkholm 2009 bearbejdet af Jessica Carter 2010 1 Hvad er et komplekst tal? Hvordan regner man med komplekse tal? Man kan betragte udvidelsen
MM501 forelæsningsslides uge 37, 2010 Produceret af Hans J. Munkholm 2009 bearbejdet af Jessica Carter 2010 1 Hvad er et komplekst tal? Hvordan regner man med komplekse tal? Man kan betragte udvidelsen
Fysik 2, Foreslåede løsninger til prøveeksamenssæt, januar 2007
 Fysik 2 Foresåede øsninger ti prøveeksamenssæt januar 2007 Opgave a) Størresen af kraften i cirkebevægesen er Totaenergien er da F = m r 2 v = E = m r = m v2 r r + 2 mv2 = m 2r b) umskibets totaenergi
Fysik 2 Foresåede øsninger ti prøveeksamenssæt januar 2007 Opgave a) Størresen af kraften i cirkebevægesen er Totaenergien er da F = m r 2 v = E = m r = m v2 r r + 2 mv2 = m 2r b) umskibets totaenergi
Fysik 2 - Oscillator. Amalie Christensen 7. januar 2009
 Fysik 2 - Oscillator Amalie Christensen 7. januar 2009 1 Indhold 1 Forsøgsopstilling 3 2 Forsøgsdata 3 3 Teori 4 3.1 Den udæmpede svingning.................... 4 3.2 Dæmpning vha. luftmodstand..................
Fysik 2 - Oscillator Amalie Christensen 7. januar 2009 1 Indhold 1 Forsøgsopstilling 3 2 Forsøgsdata 3 3 Teori 4 3.1 Den udæmpede svingning.................... 4 3.2 Dæmpning vha. luftmodstand..................
Differentiation af sammensatte funktioner
 1/7 Differentiation af sammensatte funktioner - Fra www.borgeleo.dk En sammensat funktion af den variable x er en funktion, vor x først indsættes i den såkaldte indre funktion. Resultatet fra den indre
1/7 Differentiation af sammensatte funktioner - Fra www.borgeleo.dk En sammensat funktion af den variable x er en funktion, vor x først indsættes i den såkaldte indre funktion. Resultatet fra den indre
Mini-formelsamling. Matematik 1
 Indholdsfortegnelse 1 Diverse nyttige regneregler... 1 1.1 Regneregler for brøker... 1 1.2 Potensregneregler... 1 1.3 Kvadratsætninger... 2 1.4 (Nogle) Rod-regneregler... 2 1.5 Den naturlige logaritme...
Indholdsfortegnelse 1 Diverse nyttige regneregler... 1 1.1 Regneregler for brøker... 1 1.2 Potensregneregler... 1 1.3 Kvadratsætninger... 2 1.4 (Nogle) Rod-regneregler... 2 1.5 Den naturlige logaritme...
Projekt 4.9 Bernouillis differentialligning
 Projekt 4.9 Bernouillis differentialligning (Dette projekt dækker læreplanens krav om supplerende stof vedr. differentialligningsmodeller. Projektet hænger godt sammen med projekt 4.0: Fiskerimodeller,
Projekt 4.9 Bernouillis differentialligning (Dette projekt dækker læreplanens krav om supplerende stof vedr. differentialligningsmodeller. Projektet hænger godt sammen med projekt 4.0: Fiskerimodeller,
Hvorfor bevæger lyset sig langsommere i fx glas og vand end i det tomme rum?
 Hvorfor bevæger lyset sig langsommere i fx glas og vand end i det tomme rum? - om fysikken bag til brydningsindekset Artiklen er udarbejdet/oversat ud fra især ref. 1 - fra borgeleo.dk Det korte svar:
Hvorfor bevæger lyset sig langsommere i fx glas og vand end i det tomme rum? - om fysikken bag til brydningsindekset Artiklen er udarbejdet/oversat ud fra især ref. 1 - fra borgeleo.dk Det korte svar:
Svar til eksamen i Matematik F2 d. 23. juni 2016
 Svar til eksamen i Matematik F d. 3. juni 06 FORBEHOLD FOR FEJL! Bemærk, i modsætning til herunder, så skal det i besvarelsen fremgå tydeligt, hvordan polerne ndes og hvordan de enkelte residuer udregnes.
Svar til eksamen i Matematik F d. 3. juni 06 FORBEHOLD FOR FEJL! Bemærk, i modsætning til herunder, så skal det i besvarelsen fremgå tydeligt, hvordan polerne ndes og hvordan de enkelte residuer udregnes.
MATEMATIK 3 EN,MP 30. august 2013 Oversigt nr. 1
 EN,MP 30. august 2013 Oversigt nr. 1 Litteratur: I Matematik 3 bruger vi (igen) i efteråret 2013 E. Kreyzig: Advanced engineering mathematics, 10. udg., Wiley, 2011. Beskrivelse: Kurset vil handle om matematiske
EN,MP 30. august 2013 Oversigt nr. 1 Litteratur: I Matematik 3 bruger vi (igen) i efteråret 2013 E. Kreyzig: Advanced engineering mathematics, 10. udg., Wiley, 2011. Beskrivelse: Kurset vil handle om matematiske
Fejlforplantning. Landmålingens fejlteori - Lektion 5 - Fejlforplantning. Repetition: Varians af linear kombination. Eksempel: Vinkelberegning
 Fejlforplantning Landmålingens fejlteori Lektion 5 Fejlforplantning - kkb@math.aau.dk http://people.math.aau.dk/ kkb/undervisning/lf13 Landmåling involverer ofte bestemmelse af størrelser som ikke kan
Fejlforplantning Landmålingens fejlteori Lektion 5 Fejlforplantning - kkb@math.aau.dk http://people.math.aau.dk/ kkb/undervisning/lf13 Landmåling involverer ofte bestemmelse af størrelser som ikke kan
Projekt 7.4 Kvadratisk programmering anvendt til optimering af elektriske kredsløb
 Projekt 7.4 Kvadratisk programmering anvendt til optimering af elektriske kredsløb Indledning: I B-bogen har vi i studieretningskapitlet i B-bogen om matematik-fsik set på parallelkoblinger af resistanser
Projekt 7.4 Kvadratisk programmering anvendt til optimering af elektriske kredsløb Indledning: I B-bogen har vi i studieretningskapitlet i B-bogen om matematik-fsik set på parallelkoblinger af resistanser
Differentialregning i R k
 Differentialregning i R k Lad U R k være åben, og lad h : U R m være differentiabel. Den afledte i et punkt x U er Dh(x) = h 1 (x) x 1 h 2 (x) x 1. h m (x) x 1 h 1 (x) x 2... h 2 (x) x 2.... h m (x) x
Differentialregning i R k Lad U R k være åben, og lad h : U R m være differentiabel. Den afledte i et punkt x U er Dh(x) = h 1 (x) x 1 h 2 (x) x 1. h m (x) x 1 h 1 (x) x 2... h 2 (x) x 2.... h m (x) x
Antag at. 1) f : R k R m er differentiabel i x, 2) g : R m R p er differentiabel i y = f(x), . p.1/18
 Differentialregning i R k Kæderegel Lad U R k være åben, og lad h : U R m være differentiabel Antag at Den afledte i et punkt x U er Dh(x) = 1) f : R k R m er differentiabel i x, 2) g : R m R p er differentiabel
Differentialregning i R k Kæderegel Lad U R k være åben, og lad h : U R m være differentiabel Antag at Den afledte i et punkt x U er Dh(x) = 1) f : R k R m er differentiabel i x, 2) g : R m R p er differentiabel
Noter om Komplekse Vektorrum, Funktionsrum og Differentialligninger LinAlg 2004/05-Version af 16. Dec.
 Noter om Komplekse Vektorrum, Funktionsrum og Differentialligninger LinAlg 2004/05-Version af 16. Dec. 1 Komplekse vektorrum I defininitionen af vektorrum i Afsnit 4.1 i Niels Vigand Pedersen Lineær Algebra
Noter om Komplekse Vektorrum, Funktionsrum og Differentialligninger LinAlg 2004/05-Version af 16. Dec. 1 Komplekse vektorrum I defininitionen af vektorrum i Afsnit 4.1 i Niels Vigand Pedersen Lineær Algebra
Besvarelser til Calculus Ordinær Eksamen Januar 2019
 Besvarelser til Calculus Ordinær Eksamen - 14. Januar 19 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 14. Januar 19 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
MATEMATIK 11 Eksamensopgaver Juni 1995 Juni 2001, 3. fjerdedel
 MATEMATIK Eksamensopgaver Juni 995 Juni 200, 3. fjerdedel August 998 Opgave. Lad f : R \ {0} R betegne funktionen givet ved f(x) = ex x for x 0. (a) Find eventuelle lokale maksimums- og minimumspunkter
MATEMATIK Eksamensopgaver Juni 995 Juni 200, 3. fjerdedel August 998 Opgave. Lad f : R \ {0} R betegne funktionen givet ved f(x) = ex x for x 0. (a) Find eventuelle lokale maksimums- og minimumspunkter
Kompleks Funktionsteori
 Kompleks Funktionsteori Formelræs Holomorfe funktioner Sætning. (Caucy-Riemans ligninger). Funktionen f : G C, f = u+iv er holomorf i z 0 = x 0 + iy 0 hvis og kun hvis i punktet (x 0, y 0 ). du dx = dv
Kompleks Funktionsteori Formelræs Holomorfe funktioner Sætning. (Caucy-Riemans ligninger). Funktionen f : G C, f = u+iv er holomorf i z 0 = x 0 + iy 0 hvis og kun hvis i punktet (x 0, y 0 ). du dx = dv
En sumformel eller to - om interferens
 En sumformel eller to - om interferens - fra borgeleo.dk Vi ønsker - af en eller anden grund - at beregne summen og A x = cos(0) + cos(φ) + cos(φ) + + cos ((n 1)φ) A y = sin (0) + sin(φ) + sin(φ) + + sin
En sumformel eller to - om interferens - fra borgeleo.dk Vi ønsker - af en eller anden grund - at beregne summen og A x = cos(0) + cos(φ) + cos(φ) + + cos ((n 1)φ) A y = sin (0) + sin(φ) + sin(φ) + + sin
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin 5. 6. semester efterår 2015-forår 2016 Institution Grenaa Tekniske Gymnasium Uddannelse Fag og niveau Lærer(e)
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin 5. 6. semester efterår 2015-forår 2016 Institution Grenaa Tekniske Gymnasium Uddannelse Fag og niveau Lærer(e)
Tilstandssummen. Ifølge udtryk (4.28) kan MB-fordelingen skrives , (5.1) og da = N, (5.2) . (5.3) Indføres tilstandssummen 1 , (5.
 Statistisk mekanik 5 Side 1 af 10 ilstandssummen Ifølge udtryk (4.28) kan M-fordelingen skrives og da er μ N e e k = N g ε k, (5.1) N = N, (5.2) μ k N Ne g = e ε k. (5.3) Indføres tilstandssummen 1 Z g
Statistisk mekanik 5 Side 1 af 10 ilstandssummen Ifølge udtryk (4.28) kan M-fordelingen skrives og da er μ N e e k = N g ε k, (5.1) N = N, (5.2) μ k N Ne g = e ε k. (5.3) Indføres tilstandssummen 1 Z g
MATEMATIK 3 EN,MP 28. august 2014 Oversigt nr. 1
 EN,MP 28. august 2014 Oversigt nr. 1 Litteratur: I Matematik 3 bruger vi (igen) i efteråret 2014 [K] E. Kreyzig: Advanced engineering mathematics, 10. udg., Wiley, 2011. Beskrivelse: Kurset vil handle
EN,MP 28. august 2014 Oversigt nr. 1 Litteratur: I Matematik 3 bruger vi (igen) i efteråret 2014 [K] E. Kreyzig: Advanced engineering mathematics, 10. udg., Wiley, 2011. Beskrivelse: Kurset vil handle
Figur 1.1: Blokdiagram over regulatorprincip
 Indhold 1 Design af regulator til DC-motor 2 1.1 Besrivelse af regulatorer............................. 2 1.2 Krav til regulator................................. 3 1.2.1 Integrator anti-windup..........................
Indhold 1 Design af regulator til DC-motor 2 1.1 Besrivelse af regulatorer............................. 2 1.2 Krav til regulator................................. 3 1.2.1 Integrator anti-windup..........................
Komplekse tal. Jan Scholtyßek 29.04.2009
 Komplekse tal Jan Scholtyßek 29.04.2009 1 Grundlag Underlige begreber er det, der opstår i matematikken. Blandt andet komplekse tal. Hvad for fanden er det? Lyder...komplekst. Men bare roligt. Så komplekst
Komplekse tal Jan Scholtyßek 29.04.2009 1 Grundlag Underlige begreber er det, der opstår i matematikken. Blandt andet komplekse tal. Hvad for fanden er det? Lyder...komplekst. Men bare roligt. Så komplekst
De rigtige reelle tal
 De rigtige reelle tal Frank Villa 17. januar 2014 Dette dokument er en del af MatBog.dk 2008-2012. IT Teaching Tools. ISBN-13: 978-87-92775-00-9. Se yderligere betingelser for brug her. Indhold 1 Introduktion
De rigtige reelle tal Frank Villa 17. januar 2014 Dette dokument er en del af MatBog.dk 2008-2012. IT Teaching Tools. ISBN-13: 978-87-92775-00-9. Se yderligere betingelser for brug her. Indhold 1 Introduktion
DESIGNMAT FORÅR 2012: UGESEDDEL Forberedelse Læs alle opgaverne fra tidligere ugesedler, og læg særlig mærke til dem du har spørgsmål til.
 DESIGNMAT FORÅR 2012: UGESEDDEL 13 INSTITUT FOR MATEMATIK 1. Forberedelse Læs alle opgaverne fra tidligere ugesedler, og læg særlig mærke til dem du har spørgsmål til. 2. Aktiviteter mandag 13 17 2.1.
DESIGNMAT FORÅR 2012: UGESEDDEL 13 INSTITUT FOR MATEMATIK 1. Forberedelse Læs alle opgaverne fra tidligere ugesedler, og læg særlig mærke til dem du har spørgsmål til. 2. Aktiviteter mandag 13 17 2.1.
Besvarelse til eksamen i Matematik F2, 2012
 Besvarelse til eksamen i Matematik F2, 202 Partiel besvarelse - har ikke inkluderet alle detaljer! Med forbehold for tastefejl. Opgave Find og bestem typen af alle singulariteter for følgende funktioner:
Besvarelse til eksamen i Matematik F2, 202 Partiel besvarelse - har ikke inkluderet alle detaljer! Med forbehold for tastefejl. Opgave Find og bestem typen af alle singulariteter for følgende funktioner:
NATURVIDENSKABELIG KANDIDATEKSAMEN VED KØBENHAVNS UNIVERSITET. MI 2007 Obligatorisk opgave 4
 NATURVIDENSKABELIG KANDIDATEKSAMEN VED KØBENHAVNS UNIVERSITET. MI 2007 Obligatorisk opgave 4 Sættet består af 3 opgaver med ialt 15 delopgaver. Besvarelsen vil blive forkastet, medmindre der er gjort et
NATURVIDENSKABELIG KANDIDATEKSAMEN VED KØBENHAVNS UNIVERSITET. MI 2007 Obligatorisk opgave 4 Sættet består af 3 opgaver med ialt 15 delopgaver. Besvarelsen vil blive forkastet, medmindre der er gjort et
MM502+4 forelæsningsslides
 MM502+4 forelæsningsslides uge 11+12 1, 2009 Produceret af Hans J. Munkholm, delvis på baggrund af lignende materiale udarbejdet af Mikael Rørdam 1 I nærværende forbindelse er 11 + 12 23 1 Egenskaber for
MM502+4 forelæsningsslides uge 11+12 1, 2009 Produceret af Hans J. Munkholm, delvis på baggrund af lignende materiale udarbejdet af Mikael Rørdam 1 I nærværende forbindelse er 11 + 12 23 1 Egenskaber for
Epistel E2 Partiel differentiation
 Epistel E2 Partiel differentiation Benny Lautrup 19 februar 24 Funktioner af flere variable kan differentieres efter hver enkelt, med de øvrige variable fasthol Definitionen er f(x, y) x f(x, y) f(x +
Epistel E2 Partiel differentiation Benny Lautrup 19 februar 24 Funktioner af flere variable kan differentieres efter hver enkelt, med de øvrige variable fasthol Definitionen er f(x, y) x f(x, y) f(x +
Vektorfunktioner. (Parameterkurver) x-klasserne Gammel Hellerup Gymnasium
 Vektorfunktioner (Parameterkurver) x-klasserne Gammel Hellerup Gymnasium Indholdsfortegnelse VEKTORFUNKTIONER... Centrale begreber... Cirkler... 5 Epicykler... 7 Snurretoppen... 9 Ellipser... 1 Parabler...
Vektorfunktioner (Parameterkurver) x-klasserne Gammel Hellerup Gymnasium Indholdsfortegnelse VEKTORFUNKTIONER... Centrale begreber... Cirkler... 5 Epicykler... 7 Snurretoppen... 9 Ellipser... 1 Parabler...
Kræfter og Arbejde. Frank Nasser. 21. april 2011
 Kræfter og Arbejde Frank Nasser 21. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk: Dette er
Kræfter og Arbejde Frank Nasser 21. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk: Dette er
Rapport uge 48: Skråplan
 Rapport uge 48: Skråplan Morten A. Medici, Jonatan Selsing og Filip Bojanowski 2. december 2008 Indhold 1 Formål 2 2 Teori 2 2.1 Rullebetingelsen.......................... 2 2.2 Konstant kraftmoment......................
Rapport uge 48: Skråplan Morten A. Medici, Jonatan Selsing og Filip Bojanowski 2. december 2008 Indhold 1 Formål 2 2 Teori 2 2.1 Rullebetingelsen.......................... 2 2.2 Konstant kraftmoment......................
Impuls og kinetisk energi
 Impuls og kinetisk energi Peter Hoberg, Anton Bundgård, and Peter Kongstad Hold Mix 1 (Dated: 7. oktober 2015) 201405192@post.au.dk 201407987@post.au.dk 201407911@post.au.dk 2 I. INDLEDNING I denne øvelse
Impuls og kinetisk energi Peter Hoberg, Anton Bundgård, and Peter Kongstad Hold Mix 1 (Dated: 7. oktober 2015) 201405192@post.au.dk 201407987@post.au.dk 201407911@post.au.dk 2 I. INDLEDNING I denne øvelse
Pointen med Differentiation
 Pointen med Differentiation Frank Nasser 20. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk:
Pointen med Differentiation Frank Nasser 20. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk:
Øvelse i termisk analyse
 Øvelse i termisk analyse Fysisk teknik ved Bo Jakobsen http://dirac.ruc.dk/~boj/teaching Efterår 2011 1 Baggrund Øvelsenhartilformålatsættejerindienmetodetilatbestemmeetmateriales frekvensafhængige varmekapacitet.
Øvelse i termisk analyse Fysisk teknik ved Bo Jakobsen http://dirac.ruc.dk/~boj/teaching Efterår 2011 1 Baggrund Øvelsenhartilformålatsættejerindienmetodetilatbestemmeetmateriales frekvensafhængige varmekapacitet.
Antennens udstrålingsmodstand hvad er det for en størrelse?
 Antennens udstrålingsmodstand hvad er det for en størrelse? Det faktum, at lyset har en endelig hastighed er en forudsætning for at en antenne udstråler, og at den har en ohmsk udstrålingsmodstand. Den
Antennens udstrålingsmodstand hvad er det for en størrelse? Det faktum, at lyset har en endelig hastighed er en forudsætning for at en antenne udstråler, og at den har en ohmsk udstrålingsmodstand. Den
Resonans 'modes' på en streng
 Resonans 'modes' på en streng Indhold Elektrodynamik Lab 2 Rapport Fysik 6, EL Bo Frederiksen (bo@fys.ku.dk) Stanislav V. Landa (stas@fys.ku.dk) John Niclasen (niclasen@fys.ku.dk) 1. Formål 2. Teori 3.
Resonans 'modes' på en streng Indhold Elektrodynamik Lab 2 Rapport Fysik 6, EL Bo Frederiksen (bo@fys.ku.dk) Stanislav V. Landa (stas@fys.ku.dk) John Niclasen (niclasen@fys.ku.dk) 1. Formål 2. Teori 3.
Om hypoteseprøvning (1)
 E6 efterår 1999 Notat 16 Jørgen Larsen 11. november 1999 Om hypoteseprøvning 1) Det grundlæggende problem kan generelt formuleres sådan: Man har en statistisk model parametriseret med en parameter θ Ω;
E6 efterår 1999 Notat 16 Jørgen Larsen 11. november 1999 Om hypoteseprøvning 1) Det grundlæggende problem kan generelt formuleres sådan: Man har en statistisk model parametriseret med en parameter θ Ω;
Projekt 4.6 Løsning af differentialligninger ved separation af de variable
 Projekt 4.6 Løsning af differentialligninger ved separation af de variable Differentialligninger af tpen d hx () hvor hx ()er en kontinuert funktion, er som nævnt blot et stamfunktionsproblem. De løses
Projekt 4.6 Løsning af differentialligninger ved separation af de variable Differentialligninger af tpen d hx () hvor hx ()er en kontinuert funktion, er som nævnt blot et stamfunktionsproblem. De løses
Bevægelse i (lineære) magnetfelter
 Moderne acceleratorers fysik og anvendelse Forelæsning 3 Lineær Beam Optik - betafunktion Wille kapitel 3.7 til og med 3.13 Repetition Betafunktion og betatron bevægelse Faserum Beam størrelse og emmitans
Moderne acceleratorers fysik og anvendelse Forelæsning 3 Lineær Beam Optik - betafunktion Wille kapitel 3.7 til og med 3.13 Repetition Betafunktion og betatron bevægelse Faserum Beam størrelse og emmitans
Lineære differentialligningers karakter og lineære 1. ordens differentialligninger
 enote 11 1 enote 11 Lineære differentialligningers karakter og lineære 1. ordens differentialligninger I denne note introduceres lineære differentialligninger, som er en speciel (og bekvem) form for differentialligninger.
enote 11 1 enote 11 Lineære differentialligningers karakter og lineære 1. ordens differentialligninger I denne note introduceres lineære differentialligninger, som er en speciel (og bekvem) form for differentialligninger.
Integration m.h.t. mål med tæthed
 Integration m.h.t. mål med tæthed Sætning (EH 11.7) Lad ν = f µ på (X, E). For alle g M + (X, E) gælder at gdν = g f dµ. Bevis: Standardbeviset: 1) indikatorfunktioner 2) simple funktioner 3) M + -funktioner.
Integration m.h.t. mål med tæthed Sætning (EH 11.7) Lad ν = f µ på (X, E). For alle g M + (X, E) gælder at gdν = g f dµ. Bevis: Standardbeviset: 1) indikatorfunktioner 2) simple funktioner 3) M + -funktioner.
Laplace- og Fouriertransformationer med anvendelser. Karin Lentfer Kristiansen og Thomas Hecksher
 Laplace- og Fouriertransformationer med anvendelser Karin Lentfer Kristiansen og Thomas Hecksher EVU master i matematikuddannelsen på Aalborg Universitet 6. september 4 Resumé The following report is a
Laplace- og Fouriertransformationer med anvendelser Karin Lentfer Kristiansen og Thomas Hecksher EVU master i matematikuddannelsen på Aalborg Universitet 6. september 4 Resumé The following report is a
Komplekse tal og algebraens fundamentalsætning.
 Komplekse tal og algebraens fundamentalsætning. Michael Knudsen 10. oktober 2005 1 Ligningsløsning Lad N = {0,1,2,...} betegne mængden af de naturlige tal og betragt ligningen ax + b = 0, a,b N,a 0. Findes
Komplekse tal og algebraens fundamentalsætning. Michael Knudsen 10. oktober 2005 1 Ligningsløsning Lad N = {0,1,2,...} betegne mængden af de naturlige tal og betragt ligningen ax + b = 0, a,b N,a 0. Findes
