Andres Lahe. Ehitusmehaanika. Varrassüsteemi mehaanika. b x k l/2 l. Tallinn 2003
|
|
|
- Vibeke Fischer
- 6 år siden
- Visninger:
Transkript
1 Andres Lahe Ehitusmehaanika Varrassüsteemi mehaanika F k c p f a b x k l/2 l Tallinn 2003
2 2 Dokumendi koostas: Andres Lahe, Tallinna Tehnikaülikool Mehaanikainstituut Käesolev dokument on vaba. Te võite seda edasi levitada ja/või muuta vastavalt GNU Üldise Avaliku Litsentsi tingimustele, nagu need on Vaba Tarkvara Fondi poolt; kas Litsentsi versioon number 2 või (vastavalt Teie valikule) ükskõik milline hilisem versioon. Seda dokumenti levitatakse lootuses, et see on kasulik, kuid ILMA IGASUGUSE GA- RANTIITA; isegi KESKMISE/TAVALISE KVALITEEDI GARANTIITA või SOBIVUSELE TEATUD KINDLAKS EESMÄRGIKS. Üksikasjade suhtes vaata GNU Üldist Avalikku Litsentsi. Te peaks olema saanud GNU Üldise Avaliku Litsentsi koopia koos selle dokumendiga, kui ei, siis kontakteeruge Free Software Foundation iga, 59 Temple Place - Suite 330, Boston, MA , USA GNU Üldise Avaliku Litsentsi koopia: Lisa D lk 305 ehk Õppevahend on vormindatud tekstitöötlusprogrammiga LATEX (loe: lateh). Tekstitöötlusprogramm LATEX on programmi TEX (loe: teh) makropakett. TEX erineb kirjastuste süsteemidest VENTURA ja PageMaker selle poolest, et ta on public domain i produkt. LATEX-is kirjutatud teksti on võimalik töödelda msdos, UNIX (Linux) ja teistel arvutitel. LATEX disainib aruandeid, artikleid, raamatuid. Vastavad stiilifailid (*.sty failid) valivad pealkirjade suuruse, numeratsiooni, jooniste ja valemite paigutuse, aitavad koostada sisukorda, panevad indekseid, kirjandusviiteid jne. LATEX i kohta loe kodulehelt: c 2003 Tallinna Tehnikaülikool ISBN
3 3 Mente et manu (TTÜ moto) Elektronraamat ehitusmehaanika kursuse EME AP E S ; EME AP E S ja Ehitusmehaanika I EME ,0 AP 3,5 1,5-0-2 E S ; Ehitusmehaanika II EME ,0 AP 3,5 1,5-0-2 E K kuulajatele Tallinna Tehnikaülikoolis. Ülesannete lahendamiseks on vaja installeerida numbriliste arvutuste programm GNU Octave (vt C.1 lk 205). Õppeaine tööprogrammi saab aadressilt 3. Internetis oleva tööprogrammi 4 kirjanduse viidetega saab vormistada raamatukogu nõudesedelid. Klõpsates esitamisele tuleva iseseisva ülesande numbri järel olevale kastikesele, satute selle ülesande tekstile ja joonisele. Ülesanded iseseisvaks lahendamiseks on saadaval ka elektronraamatuna 5. Õppevahendis on kasutatud õpiku [Rää75] 6 määranguid, liigitusi ja näiteid. Käesolevat e-raamatut saab lugeda aadressil: Õppevahendid, konspektid Tänan oma abikaasat Lilja Lahe t mõistva suhtumise eest e-raamatu kirjutamisse. Kulutasin selleks palju oma vaba aega. Suur aitäh keeletoimetaja Juhan Nurme le teksti silumise eest. Andres Lahe
4 4
5 Sisukord Sisukord 5 Joonised 9 Tabelid 13 I Staatiliselt määratud süsteemid 15 1 Sissejuhatus Varrassüsteemide koht mehaanikas Lõikemeetod Sisejõud ja rajajõud Sise- ja rajasiirded Koormused ja koondatud jõud Aproksimatsioonitasemed. Mudelid Lihtsustused varda paindeteoorias Epüürid ja diferentsiaalseosed Põikjõud vardas Tala mõjujooned Mõjujoone mõiste Toereaktsioonide mõjujooned Põikjõu mõjujooned Paindemomendi mõjujooned Konsooli mõjujooned Põikjõu mõjujoon Paindemomendi mõjujoon Mõjujoonte kasutamine Varrassüsteemide liigitus Varrassüsteemide liigituse alused Toed ja toereaktsioonid Kontaktjõud ja liigendid
6 6 SISUKORD 3.4 Rajajõud ja sõlmpunktid Arvutusskeem Staatikaga määratav mitmesildeline tala Staatikaga määratav mitmesildeline tala Põhiosad ja lisaosad Sisejõudude arvutus Gerberi tala mõjujooned Kolme liigendiga kaar ja raam Üldised mõisted Toereaktsioonide ja sisejõudude arvutus Vertikaalne koormus Kaare telgjoone võrrandid Kaare sisejõud Kolme liigendiga raam Kolme liigeendiga raami arvutusnäide Sõrestikskeemid Sõrestikskeemide liigitus Staatiliselt määratud sõrestike arvutus Sõlmede eraldamise võte Momendipunkti võte Projektsioonide võte J. C. Maxwelli L. Cremona diagramm Talasõrestike mõjujooned Mõjujoonte leidmine arvutiga Sõrestiku arvutamise näited Siirete arvutus Märgikokkulepped Sise- ja rajajõudude töö Töö ja energia Tööde vastastikkuse teoreem Siirete vastastikkuse teoreem Reaktsioonide vastastikkuse teoreem Siirete arvutamine Siirded temperatuuri muutusest Numbriline integreerimine Simpsoni valem Simpsoni 3/8 valem Vereštšagini võte Siirete arvutamise näited
7 SISUKORD 7 II Staatiliselt määramatud süsteemid Staatikaga määramatute konstruktsioonide arvutus Staatikaga määramatu konstruktsioon Staatikaga määramatute konstruktsioonide omadused Jõumeetod Raamid Staatikalise määramatuse aste Põhiskeem ja lisatundmatud Võrrandid lisatundmatute arvutamiseks Raami arvutamise näited Jätkuvtalad Põhiskeem ja lisatundmatud Kanoonilised võrrandid Kolme momendi võrrandiga arvutamise näited Jätkuvtalade arvutus fookussuhtega Fookussuhted Koormatud silde toemomendid Fookussuhetega arvutamise näited Deformatsioonimeetod Geomeetrilise määratuse aste Kinnitusmomendid Deformatsioonimeetodiga arvutamise näited Kaared ja võlvid Kaarkonstruktsioonid Kaheliigendiga kaar Kaheliigendiga kaare arvutamise näited Liigendita sümmeetriline kaar Liigendita kaare arvutamise näited III Lisad 185 A Mõisteid varda teooriast 187 A.1 Kohalik ja üldteljestik A.2 Koordinaatide teisendus A.3 Varda tööd A.3.1 Varda töö pikkel A.3.2 Varda töö paindel
8 8 SISUKORD B Maatriksid 195 B.1 Maatriksi mõiste B.2 Rea- ja veeruvektor B.3 Maatriksite liitmine ja lahutamine B.4 Vektorite ja maatriksite korrutamine B.5 Maatriksite element-element korrutamine B.6 Osamaatriksid B.7 Maatriksite Transponeerimine B.8 Pöördmaatriksid C Arvutiprogrammid 203 C.1 Programmist Octave C.2 Arvutiprogramme tala arvutamiseks C.2.1 Arvutifunktsioonid tala arvutamiseks C.3 Arvutiprogramme kaare arvutamiseks C.3.1 Arvutifunktsioonid kaare arvutamiseks C.4 Arvutiprogramme sõrestiku arvutamiseks C.5 Arvutiprogramme siirete arvutamiseks C.6 Arvutiprogramme raami arvutamiseks. Jõumeetod C.7 Arvutiprogramme jätkuvtala arvutamiseks C.7.1 Arvutifunktsioonid jätkuvtala arvutamiseks C.8 Arvutiprogramme deformatsioonimeetodiga arvutamiseks C.8.1 Arvutifunktsioonid deformatsioonimeetodiga arvutamiseks C.9 Arvutiprogramme staatiliselt määramatu kaare arvutamiseks C.9.1 Arvutifunktsioonid staatiliselt määramatu kaare arvutamiseks C.10 Arvutiprogramme kriitilise koormuse arvutamiseks D GNU Üldine Avalik Litsents 303 Kirjandus 309 Aineregister 311
9 Joonised 1.1 Varrassüsteemi koht mehaanikas Sisejõud ja kontaktjõud Varda tööseisundid Löök kõrguselt h = Koondjõud Deltafunktsioon Aproksimatsiooni tasemed Varda fenomenoloogilise mudeli strukruuriskeem Joone kõverus Tala deformatsioon Ekstsentriline surve Ekstsentriline surve II järku teoorias Põikjõu märgi määramine Põikjõud horisontaalses vardas Põikjõud kaldu vardas Liikuv koormus Epüürid ja mõjujooned Toereaktsioonide A ja B mõjujooned Konsoolidega tala toereaktsioonide mõjujooned Põikjõu mõjujoone vasak pool Põikjõu Q k mõjujoon Paindemomendi vasak pool Paindemomendi M k mõjujoon Konsooli mõjujooned Momendi ja põikjõu mõjujooned Mõjujoonte kasutamine Sisejõu leidmine mõjujoonte abil Toed ja toereaktsioonid Kontaktjõud ja liigendid Gerberi tala 1. Lisaosad ja põhiosad Gerberi tala
10 10 JOONISED 4.3 Gerberi tala Gerberi tala 3 epüürid Gerberi tala 2 mõjujooned Kolme liigendiga kaar Kaare telgjoon Kolme liigendiga kaare sisejõud Kaar A. Koormused Kaar A. Tabelarvutus Kaar A. Paindemomendi epüür Kaar A. Põikjõu epüür Kaar A. Normaaljõu epüür Kaar B. Koormused Kaar B Kaar B. Paindemomendi epüür Kaar B. Põikjõu epüür Kaar B. Normaaljõu epüür Kaar B. Paindemomendi epüür kolmekümne jaotusega Kolme liigendiga raam Kolme liigendiga raami sisejõud Sõrestikskeemide liigitus Sõlmede eraldamise võte Varda suunakoosinused Varraste eraldamise võte Sõrestiku topoloogia Võrrandisüsteemi vasak pool Võrrandisüsteemi koostamine Jõud sõlmedes Vasaku poole pöördmaatriks G Lõige I-I Momendipunkti võte Maxwelli-Cremona diagramm Jõuhulknurgad Sõrestiku sisejõud Sõrestiku vasakpoolne osa Sõrestiku parempoolne osa Sõlme 7 tasakaal Sõlme 4 tasakaal Sõrestik. Ühikjõud paremal Sõrestik. Ühikjõud vasakul Sõlm Sõlm Sõrestiku mõjujooned
11 JOONISED Märgikokkulepped Passiivtöö Aktiivtöö Täiendtöö Vastastikune töö Prinkused temperatuuri muutusest Märgikokkulepped Vereštšagini võte Epüüride pindalad Siirete arvutus Tundmatud ja võrrandid Tundmatute üldarv Kinnised kontuurid ja lihtliigendid Geomeetriliselt ja hetkmuutuvad skeemid Raam ja põhiskeemi Põhiskeemi epüürid Paindemomendi epüür Octave ga Jätkuvtala põhiskeem Jätkuvtala ühikepüürid Jätkuvtala tähised Jätkuvtala. Kolme momendi võrrand Fiktiivsete koormuste leidmine Kolme momendi võrrandisüsteemi lahendamine Jätkuvtala. Toereaktsioonid Jätkuvtala fookused Jätkuvtala fookussuhted Jätkuvtala toemomendid Jätkuvtala. Fookussuhted Fookussuhete arvutamine Toemomentide arvutamine Fookussuhted. Koormus kolmandal sildel Fookussuhted. Koormus teisel sildel Fookussuhted. Koormus konsoolil Fookussuhted. Koormus esimesel sildel Alaline koormus Alalise koormuse fiktiivsed reaktsioonid Poolusplaan ja varraste pöörded Varda deformatsioon Raam Geomeetriliselt määratud põhiskeem Varrasahel
12 12 JOONISED 11.6 Kinnitusmomendid Reaktsioonimomendid sõlme 1 pöördest Reaktsioonimomendid sõlme 2 pöördest Reaktsioonimomendid varda pöördest Pöördenurkade arvutamine Momendid varda otstes Momendid varda otstes ja paindemomendi epüür Raami põikjõu märk ja epüür Sõlme 1 tasakaal Sõlme 2 tasakaal Raami normaaljõu epüür Raam II Raami varrasahel II Geomeetriliselt määratud põhiskeem II Sõlme a pööre ϕ a Sõlme b pööre ϕ b Varda ad pööre ψ Varda kinnitusmomendid koormusest II Deformatsioonimeetod Octave iga Momendid varraste otstes Põikjõu epüür Kaared Kahe liigendiga kaar Kahe liigendiga kaar Kahe liigendiga kaare paindemomendi epüür Liigendita sümmeetriline kaar Liigendita kaar. Tundmatu X Liigendita kaar. Tundmatu X Liigendita kaar. Tundmatu X Liigenditeta kaar A.1 Vasaku ja parema käe teljestik A.2 Koordinaatide teisendus B.1 Maatriksi sisestamine Octave iga B.2 Maatriksite ja vektorite element-element korrutamine
13 Tabelid 1.1 Koormused Sõrestiku arvutustabel I Sõrestiku arvutustabel II Varraste sisejõudude võrdlus Valemid vabaliikmete arvutamiseks Kinnitusmomendid ja põikjõud
14 14 TABELID
15 Osa I Staatiliselt määratud süsteemid 15
16
17 Peatükk 1 Sissejuhatus 1.1 Varrassüsteemide koht mehaanikas Mehaanika on teadus, mis käsitleb vedelike, tahkete kehade ja gaaside liikumist (paigalseisu) neile rakendatud jõudude mõjul. Klassikaline mehaanika uurib makrokehade Omadus Objekt Meetod Arvutusmehaanika (meetodite järgi) MEHAANIKA Arvutusmatemaatika Informaatika Geomeetriline Omadus Füüsikaline Hüdromehaanika Tahke deformeeruva keha mehaanika Aero ja gaasimehaanika Geomeetriliste omaduste järgi Füüsikaliste omaduste järgi Vardamehaanika Varrassüsteemi mehaakia Plaadi ja koorikumehaanika Massiivimehaanika Elastsusteooria Viskoelastsusteooria Termoelastsusteooria Plastsusteooria Masspunkti mehaanika Masspunktide süsteemi mehaanika Jäiga keha mehaanika Joonis 1.1. Varrassüsteemi koht mehaanikas paigalseisu ja liikumist valguse kiirusest tunduvalt väiksemate kiiruste juures. Valguse kiirusele lähedaste kiiruste ja mikroosakeste puhul rakendatakse relativistlikku mehaanikat ja kvantmehaanikat. 17
18 18 PEATÜKK 1. SISSEJUHATUS Vaatleme klassikalist mehaanikat ja nimetame seda lühiduse mõttes mehaanikaks. Varrassüsteemide mehaanika koha määramiseks võtame aluseks mõisted objekt, omadus ja meetod (vt joonis 1.1). Mehaanika üheks objektiks on tahked kehad. Tahkeid kehi võib liigitada nende geomeetriliste ja füüsikaliste omaduste järgi. Üheks geomeetriliseks omaduseks on kuju. Geomeetrilise kuju (omaduse) järgi on tahked kehad vardad, plaadid ja koorikud ning massiivid. Füüsikaliste omaduste põhjal räägitakse elastsetest, plastsetest, viskoelastsetest jne kehadest. Abstraktsioonina loetakse tahket keha vahel jäigaks, vahel vaadeldakse jäika keha masspunktina. Mehaanika objektide liikumise kirjeldamiseks ja nende omaduste uurimiseks kasutatakse teooriaid, mida võib liigitada selle järgi, missuguse omaduse nad seavad esikohale (fookusesse). Füüsikaliste omaduste uurimisega tegelevad elastsusteooria, plastsusteooria, viskoelastsusteooria (vt joonis 1.1). Abstraktse jäiga keha liikumist uurib teoreetiline mehaanika. Tahke keha geomeetriliste omaduste alt loeme vardamehaanika, varrassüsteemi mehaanika, plaadi- ja koorikumehaanika ning massiivimehaanika (joonis 1.1). Vardamehaanikas on kasutusel järgmised teooriad: Bernoulli 1 vardateooria, Navier 2 vardateooria, elastsusteooria, viskoelastsusteooria jne. Edaspidi vaatleme põhiliselt Bernoulli vardateooriat, mida käsitleti tehnilises mehaanikas. Iga teooria kasutab objektide (kehade) liikumise ja nende omaduste uurimiseks kindlapiirilisi uurimisviise ehk meetodeid. Näiteks kasutatakse vardateoorias varda tasakaaluvõrrandite koostamiseks lõikemeetodit, tasakaaluvõrrandite lahendamiseks võib aga kasutada Gaussi meetodit. Varda deformatsioonide pidevusvõrrandi koostamisel kasutatakse toe eemaldamise võtet. Pingete ja deformatsioonide vaheline seos leitakse katseliselt. Näeme, et üks teooria vajab erinevaid meetodeid. Igale meetodile on võimalik koostada algoritm. 1.2 Lõikemeetod Lõikemeetodi eesmärk on keha (süsteemi) jaotamisega osadeks muuta sisejõud vaadeldava osa suhtes välisjõududeks, et nende määramiseks rakendada tasakaalutingimusi ( [Jür85] lk 12). Vaatleme õpikutes [Jür85] [MR96] [Rää75] leiduvaid lõikemeetodi erinevaid määranguid. Lõikemeetodi määranguid: ([Jür85] lk 12) Tasakaalus kehast mõtteliselt väljalõigatud osa on ka tasakaalus. Vaadeldavale kehast väljalõigatud osale mõjub jõudude süsteem, milles tuntud välisjõudude kõrval rakendatakse tundmatuid jõude lõikepindadel, asendamaks lahtilõikamata keha vastavaid sisejõudusid. Lõikepindadel mõjuvad tundmatud jõud, mis on võrdsed sisejõududega, määratakse vaadeldava osa tasakaalutingimustest. 1 Jakob Bernoulli, sveitsi matemaatik, Louis Marie Navier, prantsuse insener ja füüsik,
19 1.2. LÕIKEMEETOD 19 ([MR96] lk 15) Kohas, kus soovitakse leida sisejõude, sooritatakse läbi varda kujuteldav lõige, mis jaotab varda kaheks. Et kogu varras on tasakaalus, siis peab tasakaalus olema ka kumbki tema mõtteline osa. Ükskõik kummale osale rakendatud sisejõude saab arvutada osa tasakaakutingimustest. ([Rää75] lk 316) Sisejõudude töö arvutamiseks eraldatakse vardast, varda teljega kahe perpendikulaarse lõikega lõpmatult lühike element pikkusega ds. Kahe naaberosa mõju sellele eraldatud elemendile asendatakse jõududega, mis arvuliselt on võrdsed terve varda nendes lõigetes esinevate sisejõududega. Eraldatud elemendi suhtes mõjuvad need jõud välisjõududena. ([Rää75] lk 369)... kui läbilõigatud kohtades on rakendatud nendes ristlõigetes esinevate sisejõududega arvuliselt võrdsed jõud, mida edaspidi lihtsuse pärast nimetatakse ka sisejõududeks. Välja arvatud tehnilise mehaanika õpikus ([MR96] lk 15), kus lõikepinnale rakendatakse sisejõudu) ei ole õpikutes [Jür85] lk 12 ja [Rää75] lk 316 lõikepinnale rakendatud jõud sisejõud (vt Eraldatud elemendi suhtes mõjuvad need jõud välisjõududena ). Rajajõudude mõiste selgitamiseks kirjutame pikijõu diferentsiaalseose dn x dx = q x (x) (1.1) ehk ( d EA du ) = q x (x) (1.2) dx dx Korrutame avaldise (1.2) suvalise siirdega û ja integreerime üle tala pikkuse l b a ( d EA du ) b ûdx = q x (x) ûdx (1.3) dx dx a Võrrandi (1.3) parempoolne liige väljendab väliskoormuse q x tööd W v siirdel û. On võimalik näidata, et koondkoormuse F xi töö varda telje punkti i siirdel û i on F xi û i. Seega W v = Võrrandi (1.3) vasakpoolset avaldist integreerime ositi valemi b a q x (x) ûdx + F xi û i (1.4) b a b udv = uv b a vdu a (1.5)
20 20 PEATÜKK 1. SISSEJUHATUS järgi, võttes u ja dv järgmiselt: b saame avaldise b a a }{{} û u ( d EA du ) dx dx dx }{{} dv ( ûd EA du ) ( = EA du ) ( b û b a EA du ) dx dx a dx }{{}}{{} N x N x dû dx }{{} ˆλ dx (1.6) Võrrandi (1.6) parema poole esimene liige väljendab rajajõudude N x tööd W r rajasiiretel û. Võrrandi (1.6) parema poole teine liige kirjeldab sisejõudude tööd W s. Võttes arvesse välisjõudude töö avaldise (1.4) ja rajajõudude töö avaldise (1.6), võib integraali (1.3) kirjutada kujul N x û }{{} W r b b b a N xˆλdx = ( q x (x) ûdx + F xi û i ) (1.7) a a }{{}}{{} W s W v Rajajõudu N x b avaldises (1.6) tähistatakse N xb (joonis 1.2). Kui rajajõudu tähistatakse N x -ga, siis on see mugavusest, kusjuures peab aru saama, et see ei ole sisejõud N x. Rajajõu väärtus punktis b on võrdne sisejõu väärtusega selles punktis. Nende suunad punktis b on vastupidised (joonis 1.2). Nagu selgub avaldisest (1.6), on rajajõudude mõiste üldisem kui toereaktsioonide (joonis 3.1) ja kontaktjõudude mõiste. Välisjõud avaldises (1.4) on kui joon- ja punktallikas. Rajajõude võib vaadelda kui vooge läbi pinna (punkti) (1.6). Rajajõudude ja välisjõudude olemused on erinevad. Rajajõudude mõistet vaatlevad W.B. Krätzig ja U. Wittek [KW90]. F. Hartmanni Ehitumehaanika matemaatilistes alustes [Har85] käsitletakse neid mõisteid põhjalikult. Vaadeldud lõikemeetodi määrangutest selguvad järgmised lõikemeetodi sammud: Vaadeldava varda (joonis 1.2a) sisepindadel n +, n (kontaktpindadel [MR96] lk 9) mõjuvad sisejõud on paarisjõud, mis koosnevad kahest võrdvastupidisest jõust või momendist. Vardast eraldatakse mõttelise lõikega üks osa ja edasi vaadeldakse seda osa (teine osa jääb vaatlusest välja). Selle osa pinnanormaal n + määrab vaadeldava osa välispinna (joonis 1.2b). Vardast mõttelise lõikega eraldatud osa tasakaalustamiseks rakendame selle välispinnale n + rajajõudu (kontaktjõudu) Nb (joonis 1.2c) (vaadeldavale osale ei rakendata sisejõude ega ka äravisatud osa sisejõude, sest need ei ole vaatluse all), mis on võimelised tasakalustama vaadeldavat osa. Arvuliselt on see rajajõud võrdne vastava sisejõuga, kuid vastupidise suunaga.
21 1.3. SISEJÕUD JA RAJAJÕUD 21 a) F b) F c) F n N n n + N Välispind n n + N (kontaktpind) N x F n + Rajajõud N b (kontaktjõud) x = b Joonis 1.2. Sisejõud ja kontaktjõud Koostame vardast mõttelise lõikega eraldatud osale tasakaalutingimused. Leitud rajajõud (kontaktjõud) Nb (joonis 1.2c) on arvuliselt võrdsed vastavate sisejõududega. 1.3 Sisejõud ja rajajõud Tehnilises mehaanikas [MR96] kasutusel olevad sisejõudude mõisted on joonisel 1.3. Tahke keha sisejõududena mõistame jõudusid keha osade vahel, mis säilitavad keha terviklikkuse ja annavad talle iseloomuliku mahu- ja kujukindluse mõõdukate välisjõudude mõju all [Jür85]. Varda toereaktsioonid on joonisel Sise- ja rajasiirded Sisesiireteks on pikkuse muut [MR95] Λ, paindenurk Ψ, lihe, lihke [MR95] B z, väändenurk Θ (joonis 1.3). Terminit sisesiire kasutavad W.B. Krätzig ja U. Wittek [KW90]. Tehnilises mehaanikas [MR95] nimetatakse neid põhideformatsioonideks. Rajasiirded u b a avaldises (1.6) on varda siirded punktides a ja b. Rajasiirete ja rajajõudude arv on vastavuses. Kui üks nendest on ette antud, siis teine tuleb leida. Rajasiirete ja rajajõudude üheks osaks on toesiirded ja toereaktsioonid. Vaata etteantud ja tundmatuid toetingimusi (joonis 3.1).
22 22 PEATÜKK 1. SISSEJUHATUS Tööseisund Prinkus [MR95] Sisejõud [MR96] Ristlõike jäikus Elastsusseosed Deformatsioonienergia [MR96] N Pike dx N du Pikkeprinkus λ = du dx λ = Λ L siin Λ = u Pikkejõud N Pikkejäikus EA N = EAλ du N = 1 2 Nλdx M y Paine ϕ d y M y dx Paindeprinkus ψ = dϕy dx ψ = Ψ L siin Ψ = ϕ y Paindemoment M y Paindejäikus EI y M y = EI y ψ y du M = 1 2 M yψ y dx Q z Lõige dx β x Q z dw Q Lõikeprinkus β z = dw Q dx βz = Bz L siin B z = w Q Põikjõud Q z Lõikejäikus GA red Q Z = GA red β z du Q = 1 2 Q zβ z dx M x Vääne dx dϕ x M x Väändeprinkus ϑ = dϕx dx ϑ = Θ L siin Θ = ϕ x Väändemoment M x Väändejäikus x = M GI GI x ϑ x du γ = 1 2 M xϑdx Joonis 1.3. Varda tööseisundid 1.5 Koormused ja koondatud jõud Koormusi liigitatakse ajas muutumise järgi dünaamilisteks ja staatilisteks. Kui koormus muutub ajas nii aeglaselt, et konstruktsiooni deformeerumisel võib inertsjõu hüljata, siis nimetatakse koormust staatiliseks. Suuruselt, sihilt, suunalt või asukohalt muutuvat koormust nimetatakse dünaamiliseks. Edaspidi piirdume ainult staatiliste koormuste vaatlemisega. Koormused esinevad alati kas kogu konstruktsiooni või selle osa ulatuses hajutatult lauskoormustena, mida võib jaotada ruum-, pind- ja joonkoormusteks. Ruumkoormus rakendub tavaliselt massi kaudu (raskusjõud, inertsjõud jne) ja on ruumis hajutatud. Ruumkoormust mõõdetakse selle intensiivsusega q (x, y, z), mis näitab vaadeldava punkti vahetus läheduses ruumiühikule mõjuvat jõudu N/m 3, kn/m 3 jne. Pindkoormus rakendub konstruktsiooni kogu pinnale või selle osadele ja väljendab teiste kehade vahetut kontaktmõju. Pindkoormuse intensiivsus q (x, y) näitab pinna-
23 1.5. KOORMUSED JA KOONDATUD JÕUD 23 G h Joonisel 1.4 on tehnilise mehaanika näide, kus raskuse G kukkumine (löök) kõrguselt h = 0 kutsub esile kaks korda suuremad sisejõud ja siirded kui staatiline koormus. Joonis 1.4. Löök kõrguselt h = 0 ühikule mõjuvat jõudu vaadeldavas punktis N/m 2, kn/m 2. Joonkoormus on nii taandatud ruum- kui ka pindkoormus intensiivsusega q (x), mille mõõtühikuks on N/m, kn/m, vt tabelit 1.1. Tabel 1.1. Koormused Indeksid Koormus Tähis Mõõtühik Mõõde F z v j põhjus koht siht Koondkoormus F z, F x N, kn, MN [F ] Moment M y, M x Nm, knm, MNm [F L] Joonkoormus q z, q x N/m, kn/m, MN/m [F/L] Lausmoment m x, m y, m z N, kn, MN [F L/L] Sageli mõjub pind- ja joonkoormus konstruktsiooni üldmõõtmetega võrreldes väikesele pinnale (joonele). Sellist koormust loetakse ühte punkti koondatud punkt- ehk koondkoormuseks, mille tähiseks on F ja mõõtühikuks N/m, kn/m. Koondkoormus esitatakse enamasti projektsioonidena F x, F y, F z, (tabel 1.1). Vahel taandub koormus jõupaariks, mille toimet hinnatakse momendiga. Momendi tähisena kasutatakse tähti M x, M y ja M z, mis väljendavad momendi mõju telje x, y, z suhtes. Suhteliselt harva esineb hajutatud moment m ehk lausmoment. Lausmomendi projektsioonid on m x, m y ja m z ning mõõtühikud N, kn (tabel 1.1). Vaatleme joonkoormuse q z koondamist koondkoormuseks F z (joonis 1.5). Olgu koondkoormuse F z rakenduspunkti koordinaat x i. Koondjõu väärtus avaldub joonkoormuse kaudu järgmiselt: F zi = q z 2ε (1.8)
24 24 PEATÜKK 1. SISSEJUHATUS a) b) F zi Q zv q z Q zp x i l x i ε + ε ehk Joonis 1.5. Koondjõud xi +ε F zi = lim q z (x) dx (1.9) ε 0 x i ε Varda ristlõiget, kus mõjub koondatud koormus, nimetame iseäraseks ehk singulaarseks ristlõikeks. Vaatleme varda elementi (joonis 1.5) pikkusega 2ε. Parempoolses ristlõikes mõjub põikjõud Q zp ja vasakpoolses ristlõikes põikjõud Q zv. Need põikjõud erinevad üksteisest q z ε võrra. Kui nüüd vähendada varda elemendi pikkust (lim ε 0 ), siis saab ühes ristlõikes kaks erinevat põikjõudu Q zp ja Q zv. Selline ristlõige on iseärane ristlõige. Võtame kasutusele deltafunktsiooni δ i (joonis 1.6). Lisaks avaldisele (1.11) võib kirjutada järgmise seose: l xi +ε F zi δ (x x i ) dx = F zi δ (x x i ) dx = F zi (1.10) 0 x i ε Joonisel 1.6 on deltafunktsioon δ i = δ (x x i ). See funktsioon on aproksimeeritud ristkülikulise kujuga, mille pindala D ε = 1, kui ε 0 ning D D x i D*2 ε = 1 ε + ε x = l 0 xi +ε x i ε δ (x x i ) dx = δ (x x i ) dx = 1 (1.11) δ i kus ε on meelevaldselt väike positiivne arv. Joonis 1.6. Deltafunktsioon 1.6 Aproksimatsiooni tasemed. Mudelid Tegeliku konstruktsiooni aproksimeerimine 3 on inseneripraktikas üheks raskemaks ülesandeks (joonis 1.7). Tegelikku konstruktsiooni pole alati võimalik otseselt uurida kui 3 Aproksimeerimine, lähendamine objekti asendamine mingi teise, temast teatavas mõttes vähe erineva objektiga.
25 1.6. APROKSIMATSIOONI TASEMED. MUDELID 25 tervikut, sest konstruktsiooni olekuparameetrite arv on suur. Olekuparameetrite all mõistame füüsikalisi suurusi, mis iseloomustavad süsteemi olekut. Välisteks olekuparameetriteks on välisjõud ja väliste väljade tugevus. Sisemisteks olekuparameetriteks on sisejõud, siseenergia, temperatuur jne. Erinevate olekuparameetrite kirjeldamiseks on olemas erinevaid teooriaid: Bernoulli 4 vardateooria, Navier i 5 vardateooria, elastsus teooria, viskoelastsusteooria jne. Parameetrite hulga vähendamiseks peab tegema lihtsustavaid hüpoteese. Nende hüpoteeside aluseks on kas vaatlus (katsetused), teoreetilised kaalutlused või tehakse need intuitiivselt [Krä91a]. Kaasaliikuvate Lagrange i 6 koordinaatide abil on võimalik kirjeldada suuri deformatsioone ja stabiilsuse kadu. Varraste asukohti kirjeldatakse topoloogiaga. Absoluutselt sirgeid vardaid tegelikkuses ei esine, seega jälle aproksimatsioon. Konstruktsioonis on vardad omavahel ühendatud kas jäigalt või liigenditega. Vaadeldav teooria koosneb fenomenoloogilisest 7 ja matemaatilisest mudelist. Siin tehakse teise taseme aproksimatsioonid. Fenomenoloogilise mudeli 8 struktuuriskeem on joonisel 1.8. Matemaatiline mudel kirjeldab fenomenoloogilise mudeli kvalitatiivseid liikmeid. Kolmanda taseme aproksimatsioonid tehakse arvutusmeetodi valikul. Üldiselt ei ole arvutusmeetodis võimalik kõiki arvutusmudeli muutujaid arvestada. Võib osutuda, et osa muutujaid tuleb elimineerida. Tavaliselt on selle taseme aproksimatsioonide üle hea kontroll, sest on võimalik anda vea hinnang. 4 Jakob Bernoulli, šveitsi matemaatik, Louis Marie Henri Navier, prantsuse insener ja füüsik, Joseph Louis de Lagrange, prantsuse matemaatik ja mehaanikateadlane, Fenomen (< kr phainomenos nähtavale ilmuv ) juhtum, meeltega tajutav olukord või fakt. 8 Mudel süsteemi, teooria või fenomeni kirjeldus, mis arvestab nende tuntud omadusi ja mida võib kasutada nende omaduste uurimiseks. Tegelik konstruktsioon Arvulised tulemused I taseme aproksimatsioon Koordinaadid Teooria Topoloogia Kõrvaltingimused Koordinaadid Lagrange i koordinaadid Parandatud Lagrange i koordinaadid Kaasaliikuvad Lagrange i koordinaadid Euleri koordinaadid II taseme aproksimatsioon Fenomenoloogiline mudel Matemaatiline mudel Teooria Bernoulli vardateooria Navi er i vardateooria Õhukeseseinalise varda teooria Elastsusteooria Plastsusteooria Viskoelastsusteooria III taseme aproksimatsioon Arvutusmeetod Arvutusmeetod Newton Raphsoni meetod Kvaasi Newtoni meetod Joonis 1.7. Aproksimatsiooni tasemed
26 26 PEATÜKK 1. SISSEJUHATUS Välisjõud ] Välisjõudude töö S = [F, q z, q x, m y W v = S V Välissiirded ] V = [u, w, ϕ y dn dx Tasakaaluvõrrandid dq dmy = qx, = qx, dx dx = Qz Rajajõud ja rajasiirded 1.3 Sisejõud ja rajajõud 1.4 Sise- ja rajasiirded 7.2 Sise- ja rajajõudude töö Siirete pidevusvõrrandid λ = du dw dϕy, βz =, ψy = dx dx dx Rajajõud [ ] Rajajõudude töö N, Q z, My W r = N u + Q z w + M y ϕ y Rajasiirded ] [u, w, ϕ y Sisejõud ] [N, Q z, M y Sisejõudude töö W s = ( Nλ + Q zβ z + M y ψ y Seosed sisejõudude ja siirete vahel ) dx Sisesiirded [KW90] Λ, B z, Ψ y [MR95] λ = dλ dbz dψy, βz =, ψy = dx dx dx Joonis 1.8. Varda fenomenoloogilise mudeli strukruuriskeem Varrassüsteemide mehaanikas on fookuses geomeetriline omadus kuju, mille füüsikaliste omaduste kirjeldamiseks valitakse sobiv teooria ja seejärel sobivad meetodid. Kõikides teooriates, mida varrassüsteemid kasutavad, esinevad järgmised mõisted (joonis 1.8): välisjõud (F ), välissiirded (V ), sisejõud (N, Q, M; σ xx, σ yy, τ xy ), sisesiirded My ), rajasiirded ( u, w, ϕ y ), (+Lambda, B, Ψ, Θ; ɛ xx, ɛ yy, ɛ xy ), rajajõud ( N, Q z, tasakaaluvõrrandid, siirete pidevusvõrrandid, olekuvõrrandid, rajatingimused. Rajajõudude mõiste üldistab toereaktsioone ja varraste vahel mõjuvaid kontaktjõude. Rajasiirded on tugede vajumised ja varraste siirded ning pöörded ühendustes (liigendites). Joonisel 1.8 toodud mõisteid on käsitletud tehnilises mehaanikas varda teoorias. Taskaaluvõrrandid seostavad sisejõud välisjõududega. Siirete pidevuse võrrandid loovad seosed sisesiirete (tehnilises mehaanikas varda pikkuse muut) ja välissiirete vahel. Geomeetriliselt mittelineaarses teoorias on sisesiirete ja välissiirete vahelised seosed mittelineaarsed. Rajajõud ristlõike välispinnal on võrdsed ja suunatud vastupidi vastavate sisejõududega ristlõike sisepinnal. Rajasiireteks on toe siirded ja varraste ühenduspunktides (sõlmedes) varraste vastastikused siirded ja pöörded. Füüsikaliselt lineaarse vardateooria olekuvõrrandid (elastsusseosed) väljenduvad Hooke i 9 seaduse kaudu. 9 Robert Hooke, inglise füüsik,
27 1.7. LIHTSUSTUSED VARDA PAINDETEOORIAS Lihtsustused varda paindeteoorias Vaatleme joone kõverust diferentsiaalgeomeetrias ja elastse joone kõverust tehnilises mehaanikas a) dx b) dx z z, w ϕ ds dϕ z = f(x) x z + dz ϕ + dϕ 1 ρ = w ψ w = ϕ w = f(x) z, w dϕ x w + dw Joonis 1.9. Joone kõverus Tähistame joone z = f (x) kõveruse ψ j -ga ja elastse joone w = f (x) kõveruse ψ p -ga. Joone element ds (joonis 1.9) kus Elastse joone element ds siin Joone kõverus ψ j ds = dx 2 + dz 2 = dx 1 + (z ) 2 (1.12) z = dz dx = tan ϕ, ds = ϱdϕ, dz ϕ = arctan dx 1 ϱ = ψ = dϕ ds (1.13) (1.14) dϕ ds = d (arctan z ) dx dx ds = z dx 1 + (z ) 2 (1.15) dx 1 + (z ) 2 ψ j = 1 ϱ = dϕ ds = z [ 1 + (z ) 2] 3 2 (1.16) siin on ϱ joone kõverusraadius. Teeme lihtsustused lihtsustus tan ϕ ϕ, millest järeldub 1 ϱ = dϕ ds = z 1 + (z ) 2 (1.17)
28 28 PEATÜKK 1. SISSEJUHATUS l I järku teooria II järku teooria l Joonis Tala deformatsioon lihtsustus tan ϕ ϕ, ds dx, millest järeldub Kuna elastse joone kõverus ψ p = ψ j, siis Avaldis (1.19) on lineaarne diferentsiaalvõrrand. ψ j = 1 ϱ = dϕ ds = z (1.18) ψ ψ p = w (1.19) Lineaarses ehk esimest järku teoorias (I järku teoorias) kasutatakse seost (1.19) ψ = w dw, ds dx, dx = w = ϕ, tan ϕ sin ϕ ϕ, cos ϕ 1 (1.20) Diferentsiaalseoste (tasakaalutingimuste) koostamisel lähtutakse deformeerumata kujust (algmõõtmete printsiibist) (joonis 1.10). Joonisel 1.11 on ekstsentrilise surve paindemomendi epüür I järku teoorias, kus ei e F Fe h M x Joonis Ekstsentriline surve arvestata varda deformatsiooni. Üldistatud Hooke i seadus I järku teoorias M y = EI y w (1.21)
29 1.8. EPÜÜRID JA DIFERENTSIAALSEOSED 29 Teist järku teoorias (II järku teoorias) arvestatakse varda deformeerunud kuju diferentsiaalseoste (tasakaalutingimuste) koostamisel. Joonisel 1.12 on esitatud jõu ja momendi vaheline seos. Kui esimest järku teoorias on seos lineaarne, siis teist järku teoorias mittelineaarne. kus M (x) = I }{{} F e järku teooria w 1 (x, F ) = f + F [w 1 (x) + w 2 (, F )] }{{} lisa liikmed ( 1 x ) h (1.22) (1.23) Kolmandat järku teooriat (III järku teooriat) kasutatakse eriti saledate konstruktsioonide ja ka vedrude arvutamiseks. Arvestatakse deformeerunud kuju ja kõveruse täpset avaldist 1 ϱ = z [ 1 + (z ) 2] 3 2 (1.24) ehk 1 ϱ = z 1 + (z ) 2 (1.25) Ehituskonstruktsioonide arvutamisel III järku teooriat peaaegu ei kasutata. 1.8 Epüürid ja diferentsiaalseosed Varraste põikjõu märgi määramiseks vaatleme joonist Paindemomendi tuletise geomeetriliseks tõlgenduseks punktis on selles punktis paindemomendi epüüri puutuja x w 2 w 1 f e F a b c h Fw 1 Fw 2 Ff Fe maxm Fkr e II järku teooria I järku teooria F F kr Joonis Ekstsentriline surve II järku teoorias
30 30 PEATÜKK 1. SISSEJUHATUS t 1 (t 2 ) tõusunurga tangens (tan α). Põikjõu märk oleneb puutuja (joonis 1.13) pööramise suunast (puutujat pöörame nii, et ta ühtiks varda teljega, seejuures α < π ): vastupäeva 2 pöörates on põikjõud positiivne ja päripäeva pöörates negatiivne. q l t 1 α M dm dx t 2 α = Q = tan α + Q Joonis Põikjõu märgi määramine Põikjõud horisontaalses vardas leiame epüüride liitmisena (joonis 1.14). Joonisel c M o + _ h o Q a d M x f + s M x a M _ s h Q c d f h + o Q = Q + M x Joonis Põikjõud horisontaalses vardas 1.14 on näidatud paindemomendid ja nendele vastavad põikjõud. Lineaarselt muutuva paindemonendi korral võime diferentsiaalseose (1.26) asendada diferentsseosega (1.27). Q = dm dx Q = M x Q = Q (0) + M x siin on Q (0) vastava lihttala põikjõud. (1.26) (1.27) (1.28)
31 1.9. PÕIKJÕUD VARDAS Põikjõud vardas Põikjõu leidmiseks kaldu olevas vardas (joonist 1.15) koostame tasakaaluvõrrandi varda lõpu b kohta q N ba Q ab b N ab a α l * Q ba M ba M ab l Joonis Põikjõud kaldu vardas ΣM b = 0 : ning tasakaaluvõrrandi varda alguse a kohta Q ab l M ab + M ba (q l) l 2 = 0 (1.29) (q l) Q ab = l 2 l + M ab M ba l (1.30) Q ab = Q (0) ab cos α + M ab M ba cos α (1.31) l ΣM a = 0 : Q ba l M ab + M ba + (q l) l 2 = 0 (1.32) (q l) Q ba = l 2 l + M ab M ba l (1.33) Q ba = Q (0) ba cos α + M ab M ba cos α (1.34) l kus l = l cos α
32 32 PEATÜKK 1. SISSEJUHATUS
33 Peatükk 2 Tala mõjujooned 2.1 Mõjujoone mõiste Liikuvat koormust tuleb arvestada sildade, kraanatalade ja teiste tehnoehitiste projekteerimisel. Paigalseisva koormuse puhul kujutati varraste sisejõude epüüridel. Koormus oli fikseeritud ja sisejõud olid varda telje (x-koordinaadi) funktsioonid. Liikuva koormuse puhul fikseeritakse ristlõige ja leitakse selles sisejõud või toereaktsioon sõltuvalt koormuse asukohast. Ristlõigete jaoks koostatakse graafikud (mõjujooned). Mõjujoon on graafik, mis kujutab konstruktsioonil liikuvast ja suunda säilitavast ühikjõust tingitud toereaktsiooni, sisejõu, siirde vms suurust arvutusskeemi kindlas ristlõikes. Mõjujoone ja epüüri erinevust selgitame mõjufunktsiooni M (x, ξ) abil. Mõjufunktsiooni üheks muutujaks on ristlõike asukoht x (joonis 2.1) ja teiseks muutujaks jõu asukoht ξ. Tala elastse joone diferentsiaalvõrrandi d4 w dx 4 z x ξ F = 1 ξ a b i m k x x C 1 C 2 l = d2 M dx 2 = 0 lahendina Joonis 2.1. Liikuv koormus järgmistel rajatingimustel M (0) = 0, M (l) = 0 saab leida mõjufunktsiooni (Greeni 1 funktsiooni) M (x, ξ) = { x(l ξ) l, kui x ξ ξ(l x) l, kui x ξ (2.1) 1 Georg Green, inglise füüsik ja matemaatik,
34 34 PEATÜKK 2. TALA MÕJUJOONED Epüüride ja mõjujoonte võrdlemiseks vaatleme mõjufunktsiooni (2.1). Epüüride saamiseks fikseerime muutuja ξ (ξ = a m ) ja mõjujoonte saamiseks muutuja x (x = a i ). a) F = 1 b) ξ ξ ξ F = 1 ξ a b i m k x x C 1 C 2 l a b i m k x x C 1 C 2 l M ep M mj Q ep Q mj Joonis 2.2. Epüürid ja mõjujooned Epüüride puhul fikseerime muutuja ξ (ξ = a m ) { x(l am), kui x a M (x, ξ) = l m a m(l x) (2.2), kui x a l m Mõjujoonte puhul fikseerime muutuja x (x = a i ) M (x, ξ) = { ai (l ξ) l, kui a i ξ ξ(l a i ) l, kui a i ξ (2.3) Avaldistega (2.2) ja (2.3) leitud graafikud on joonisel 2.2. Põikjõudude epüüride ja mõjujoonte saamiseks tuleb võtta vastavad tuletised, mida me tegema ei hakka. Mõjujoonte leidmist vaatleme eraldi. 2.2 Toereaktsioonide mõjujooned Staatiline meetod Tala avas liigub koondatud koormus F = 1, mille kaugus toest a on ξ ja toest b ξ = l ξ. Tasakaalutingimusest ΣM b = 0 Mb = 0; Al + F (1 ξ) = 0 (2.4) saame A = F l ξ l = ξ l (2.5)
35 2.2. TOEREAKTSIOONIDE MÕJUJOONED 35 Toereaktsioon A on muutuja ξ lineaarne funktsioon (joonisel 2.3 sirgjoon). Sarnaselt leiame tasakaalutingimusest M a = 0 1 a b ξ ξ, A B l η a =1 ξ, η = 1 l l k A mj Mõjujoon A η = 1 l ξ η = 1 B mj Mõjujoon B Joonis 2.3. Toereaktsioonide A ja B mõjujooned Ma = 0; Bl + F ξ = 0 (2.6) toereaktsiooni B B = F ξ l = ξ l on joonisel 2.3 näidatud sirgjoon. Konsoolidega tala toereaktsioonide mõjujooned on joonisel 2.4. (2.7) a b k l A B r 1 Mõjujoon A 1 Mõjujoon B Joonis 2.4. Konsoolidega tala toereaktsioonide mõjujooned
36 36 PEATÜKK 2. TALA MÕJUJOONED 2.3 Põikjõu mõjujooned Staatiline meetod Vaatleme kahte juhtu. Liikuv koormus asub ristlõike k ja toe b vahel (joonis 2.5). Tasakaalutingimusest ΣY = 0 saame Q k A = 0; Q k = A. Vahemikus x k ξ l on mõjujoon sarnane toereaktsiooni A mõjujoonega (avaldis 2.5). ξ 1 ξ, a k b A x k x k l B a Q k A x k l A Joonis 2.5. Põikjõu mõjujoone vasak pool Liikuv koormus asub toe a ja ristlõike k vahel (joonis 2.6). Tasakaalutingimusest ΣY = 0 saame Q k + B = 0; Q k = B. Vahemikus 0 ξ x k on mõjujoon sarnane toereaktsiooni -B mõjujoonega (2.7). Põikjõu Q k mõjujoon Q k = { A = (l ξ) l, kui a k ξ l B = ξ l, kui 0 ξ a k (2.8)
37 2.3. PÕIKJÕU MÕJUJOONED 37 1 a k b A x k x k l B Q k b B x k l B x k l 1 Q k mj 1 x k l Joonis 2.6. Põikjõu Q k mõjujoon
38 38 PEATÜKK 2. TALA MÕJUJOONED 2.4 Paindemomendi mõjujooned Staatiline meetod Vaatleme kahte juhtu. Liikuv koormus asub ristlõike k ja toe b vahel (joonis 2.7). Tasakaalutingimusest ΣM k = 0 saame M k A x k = 0; M k = A x k. Vahemikus x k ξ l on mõjujoon sarnane toereaktsiooni A mõjujoonega, mis on korrutatud x k. Liikuv koormus asub toe a ja ristlõike k vahel (joonis 2.8). Tasakaalutingimusest ΣM k = 0 saame M k B x k = 0; M k = B x k. Vahemikus 0 ξ x k on mõjujoon sarnane toereaktsiooni B mõjujoonega, mis on korrutatud x k. ξ 1 ξ, a k b A x k x k l B a Q k M k A 1* x k x k x k l A x k Joonis 2.7. Paindemomendi vasak pool Paindemomendi M k mõjujoon { a M k = k A = a k (l ξ), kui a l k ξ l (l a k ) B = (l a k ) ξ, kui 0 ξ a l k (2.9) kus a k on ristlõike k kaugus vasakust toest (x k ). Konsoolidega tala paindemomendi ja põikjõu mõjujooned õpikust [DK62] on toodud joonisel 2.10.
39 2.4. PAINDEMOMENDI MÕJUJOONED 39 1 a k b A x k x k l B M k Q k x k x k l b B B * x k 1* x k x k x k x k l x k M k mj Joonis 2.8. Paindemomendi M k mõjujoon
40 40 PEATÜKK 2. TALA MÕJUJOONED 2.5 Konsooli mõjujooned Põikjõu mõjujoon Konsooli (joonis 2.9 a) põikjõu mõjujoon lõike k jaoks koosneb kahest sirgest. Kui ühikjõud asetseb lõikest k paremal, on põikjõud lõikes k null. Kui ühikjõud asetseb a) ξ F = 1 b) ξ F = 1 a a k k l 1 1 b a a k k l b k b Q mj Q mj 1 1 a k M mj b k M mj Joonis 2.9. Konsooli mõjujooned. lõikest k vasakul, on lõikes k põikjõud Q k = 1. Põikjõu Q k mõjujoon on joonisel 2.9 a). Joonisel 2.9 b on toodud parempoolse konsooli ristlõike k põikjõu Q k mõjujoon. Erinevus vaskpoolsest on põikjõu märgis Paindemomendi mõjujoon Konsooli lõike k paindemomendi mõjujoon M k on joonisel 2.9 a. Kui ühikjõud on lõike k ja toe vahel, siis M k = 0. Kui ühikjõud asetseb vasakul pool lõiget k (joonis 2.9 a), siis M k = F (a k ξ) (2.10)
41 2.6. MÕJUJOONTE KASUTAMINE 41 c k I II III IV V VI VII k l/2 l/2 r l Mõjujoon M I Mõjujoon M II Mõjujoon M III!!!!!!!! " " " " " " " "!!!!!!!! " " " " " " " " a Mõjujoon M IV l/2 b Mõjujoon M V Mõjujoon M VI Mõjujoon M VII r d 1 1 & & & & & & & & & & # # # # # # # # # $ $ $ $ $ $ $ $ $ # # # # # # # # # $ $ $ $ $ $ $ $ $ I IIa IIb III IV V VIaVIb VII c a b d k l r Mõjujoon Q VII Mõjujoon Q I Mõjujoon Q IIa,,,,,,,,, ) ) ) ) ) ) ) ) ) * * * * * * * * *' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ( ( ( ( ( ( ( ( ( ( ( ( ( ( ( ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ( ( ( ( ( ( ( ( ( ( ( ( ( ( ( Mõjujoon Q IIb / / / / / / / / / Mõjujoon = = = = Q > > > III ; ; ; ; ; ; ; ; ; < < < < < < < < < : : : : : : : : : 1 1 Mõjujoon I I I I Q J J J IV B B B B B B B B B B B E E E E E E E E E F F F F F F F @A A A A A A A A A A A A G G G H H C C C C C D D D D Mõjujoon Q v 1 1 K K K K K K K K K L L L L L L L L LO O O O O O O O O O O O O O O P P P P P P P P P P P P P P P M M M M M M M M M N N N N N N N N N K K K K K K K K K L L L L L L L L LO O O O O O O O O O O O O O O P P P P P P P P P P P P P P P 1 1 Mõjujoon Q VIa R R R R R R R R R Q Q Q Q Q Q Q Q Q R R R R R R R R R Mõjujoon Q VIb Q Q Q Q Q Q Q Q Q S S S S S T T T T S S S S S T T T T 1 1 Joonis Momendi ja põikjõu mõjujooned 2.6 Mõjujoonte kasutamine Tuleb teada, kuidas kasutada mõjujooni toereaktsioonide, sisejõudude ja siirete leidmiseks. Mõjujoone iga ordinaat η i näitab otsitavat suurust ühikulisest koormusest Fi = 1 (vt joonis 2.11). Kui talale mõjub koormus F i, siis leime otsitava suuruse Z k avaldisest Z k = F i η i. Mitme koondatud jõu olemasolul summeerime need (vt avaldist 2.11). Z k = F 1 η 1 + F 2 η F i η i (2.11) siin on F 1, F i koondatud jõud ja η 1, η i vastavate jõudude all olevad ordinaadid mõjujoonel (joonis 2.11). Ühtlaselt jaotatud koormusest (q = konst) põhjustatud sisejõu Z k (joonis 2.11) saame avaldisest (2.12) Z k = c a q (ξ) η (ξ) dξ = q Ω (2.12)
42 42 PEATÜKK 2. TALA MÕJUJOONED kus Z k on sisejõud ning Ω mõjujoone pindala (vt joonisel 2.11 viirutatud osa) ja kogu koormusest (vt joonist 2.11) avaldisega (2.13). Z k = F 1 η 1 + F i η i + q c a η (ξ) dξ = F 1 η 1 + F i η i + q Ω (2.13) siin on F 1, F i koondatud jõud ja η 1, η i vastavate jõudude all olevad ordinaadid mõjujoonel (joonis 2.11). q( ξ) k d ξ 1 i a b ξ Z K mj η η i Ω 1 η ( ξ) Joonis Mõjujoonte kasutamine F 1 F i Näide 2.1 Arvutada joonisel 2.12 kujutatud konsoolidega tala toereaktsioon A, põikjõud Q p a toest a paremal, põikjõud Q v a toest a vasakul, paindemoment M k, põikjõud Q k lõikes k. Talale mõjuv koormus ja vajalikud mõjujooned on joonisel Kasutades avaldist (2.13), saame toereaktsiooni A väärtuseks A = Põikjõud Q p a toest a paremal leiame avaldisega Q p a = Põikjõud Q v a toest a vasakul arvutame avaldisega Paindemomendi M b väärtuseks toel b saame M b = Paindemoment M k ristlõikes k on = 7.4 kn (2.14) = 3.4 kn (2.15) Q v a = = 4.0 kn (2.16) M k = = 1.0 knm (2.17) = 6.2 knm (2.18) Ristlõikes k on põikjõul kaks väärtust. Parempoolse põikjõu väärtuse Q p k (2.19) saab, kui kasutada mõjujoone vasakpoolset väärtust Q p k Vasakpoolse põikjõu väärtuse Q v k = Q v k = = 1.6 knm (2.19) (2.20) saab, kui kasutada mõjujoone parempoolset väärtust = 3.4 knm (2.20)
43 2.6. MÕJUJOONTE KASUTAMINE 43 F 1 = 4 kn F 2 = 5 kn q = 2 kn/m a k 3 m 2 m 1 m 5 m 1 m b A mj v Q a M b 1.0 M k Q a p mj mj mj 1.2 mj k 0.2 Q mj Joonis Sisejõu leidmine mõjujoonte abil
44 44 PEATÜKK 2. TALA MÕJUJOONED
45 Peatükk 3 Varrassüsteemide liigitus 3.1 Varrassüsteemide liigituse alused Varrassüsteemiks nimetatakse varraste kogumit, milles iga varda asend ja asendi muutus on määratud ülejäänud varraste asendi muutusega. Varraskonstruktsiooni liigitamisel võetakse arvesse järgmisi varrassüsteemi omadusi: varda telgjoone kuju varda tööseisundit (joonis 1.3) varraskonstruktsiooni toesidemete arvu liigendite arvu. Esmalt vaatleme, kas konstruktsioon on valmistatud sirgetest või kõveratest varrastest või kasutatakse mõlemaid, s.t tegemist on segasüsteemiga. Järgnevalt uurime, milline on varraste tööseisund (joonis 1.3). Näiteks sirgetest varrastest valmistatud varrassüsteemi, mille vardad töötavad pikkele, nimetatakse talaskeemiks. Sirgetest varrastest valmistatud varrassüsteemi, mille vardad töötavad liittööseisundis, nimetatakse raamskeemiks. Edaspidi vaatleme liigendite arvu ja räägime kolme liigendiga, kahe liigendiga ja liigenditeta raamskeemist. Kõvera telgjoonega varrast, mis töötab ainult tõmbele, nimetame vandiks (kasutatakse ka nimetust niit, niidivõrrand) ja nendest moodustatud varrassüsteemi vantskeemiks. Kõvera telgjoonega varrastest valmistatud varrassüsteemi, mille vardad töötavad liittööseisundis (võimalik on valida selline varraste telgjoone kuju, et varrassüsteem töötab ainult survele), nimetatakse kaarskeemiks. Liigendite arvu alusel eristatakse kolme liigendiga, kahe liigendiga ja liigenditeta kaarskeemi. Tuleb vahet teha sõrestikkonstruktsiooni ja sõrestikskeemi vahel, sest sõrestikkonstruktsioone on võimalik arvutada nii sõrestikskeemi kui ka raamskeemi järgi. Sõrestikskeemi, talaskeemi, raamskeemi, kaarskeemi, vantskeemi ja segaskeemi üldnimetuseks on arvutusskeem. Ühel konstruktsioonil võib olla mitu arvutusskeemi. See sõltub tehtud aproksimatsioonidest. 45
46 46 PEATÜKK 3. VARRASSÜSTEEMIDE LIIGITUS Jäik tugi Paigalseisev liigendtugi Liikuv liigendtugi Vaba ots Liikuv pöördumatu tugi Tugede sümbolid X, u M y, ϕ y Z, w Toetingimused: ette antud ja tundmatud Fx =?, u = 0 Fz =?, w = 0 My =?, ϕy = 0 Fx =?, u = 0 Fz =?, w = 0 My = 0, ϕy =? Fx = 0, u =? Fz =?, w = 0 My = 0, ϕy =? Fx =?, u = 0 Fz = 0, w =? My = 0, ϕy =? Fx = 0, u =? Fz = 0, w =? My = 0, ϕy =? Fx =?, u = 0 Fz = 0, w =? My =?, ϕy = 0 Toe siirde tähis ja arv 0 ϕ y 1 u, ϕ y 2 w, ϕ y 2 u, w, ϕ y 3 w 1 Toereaktsioonid ja nende arv F x M y F z 3 F x 2 F z 1 F z F x 1 0 F x M y 2 Joonis 3.1. Toed ja toereaktsioonid 3.2 Toed ja toereaktsioonid Lihtsuse mõttes vaatleme tasapinnalist konstruktsiooni. Kirjeldame toereaktsioonide F x, F z ja M y tööd W t tugede siiretel u, w ja ϕ y W t = F x u + F z w + M y ϕ y (3.1) Toereaktsioonid kuuluvad rajajõudude hulka, tugede siirded ja pöörded rajasiirete hulka. Rajatingimustest antakse ette kas toereaktsioon või toe siire (pööre). Kui toed ei vaju, siis on tugede siire (pööre) null. Arvutusskeemil kasutatavate tugede sümbolid on joonisel 3.1. Joonisel 3.1 on järgmised toed:
47 3.3. KONTAKTJÕUD JA LIIGENDID 47 Jäik tugi ei võimalda siirdeid ega pööret, tema vabadusastmete arv on null. Tundmatuid toereaktsioone on kolm. Tundmatute toereaktsioonide ja vabadusastmete summa on kolm; Paigalseisev liigendtugi võimaldab ainult pööret. Vabadusastmete arv on üks. Tundmatuteks on horisontaalne ja vertikaalne toereaktsioon ning pööre. Tundmatute toereaktsioonide ja vabadusastmete summa on kolm; Liikuv liigendtugi võimaldab pööret ja ühes sihis siiret. Vabadusastmete arv on kaks. Tundmatuteks on üks toereaktsioon, pööre ja siire; Vaba ots võimaldab siirdeid ja pöördeid. Vabadusastmete arv on kolm, need on ka tundmatuteks. Toereaktsioonid puuduvad; Liikuv pöördumatu tugi võimaldab siiret ühes sihis. Vabadusastmete arv on üks. Tundmatuteks on toemoment, üks toereaktsioon (joonisel 3.1 on selleks horisontaalne toereaktsioon) ja siire. 3.3 Kontaktjõud ja liigendid Liigendite sümbolid arvutusskeemi jaoks ja kontaktjõudude tähised on joonisel 3.2. Nii nagu tugede ja toereaktsioonide vaatlemisel kasutame töö mõistet ka kontaktjõudude ja liigendite vaatlemisel. Vaatleme hõõrdevabu liigendeid, mille kontaktjõudude töö on null nii nagu toereaktsioonidel M y tööd W k kontaktpindade vastastikustel sii- siin vaatleme kontaktjõudude N x, Q z, retel ja pööretel u, w, ϕ y, kus W k = N x u + Q z w + M y ϕ y (3.2) u = u p u v, w = w p w v, ϕ y = ϕ yp ϕ yv quad (3.3) Avaldises (3.3) tähistavad indeksid p ja v siirdeid ja pöördeid liigendist paremal ja vasakul. Varda otsa ristlõikepinda kirjeldame tema pinnanormaaliga. Varda ristlõikepinda, mille pinnanormaal on suunatud varraste ühenduse poole, nimetatakse kontaktpinnaks, kontaktpindadel mõjuvaid jõude kontaktjõududeks. Varda otsa ristlõikepind, mille pinnanormaal on suunatud varda sisse, on sisepind. Sisepinnal mõjuvad jõud on sisejõud. Kontaktjõud ja sisejõud varda otsa ristlõikes on võrdsed, kuid suunalt erinevad. Sisejõud leitakse kontaktjõudude kaudu. 3.4 Rajajõud ja sõlmpunktid Arvutite kasutamise tõttu tuleb vaatluse alla võtta nii konstruktsioonielemendid (vardad) kui ka nende ühenduspunktid, nn sõlmpunktid. Varrassüsteemide uurimise põhiliseks probleemiks on rajatingimuste kirjeldamine. Täpsemalt käsitletakse seda probleemi tala-, sõrestik-, raam- ja kaarskeemide juures.
48 48 PEATÜKK 3. VARRASSÜSTEEMIDE LIIGITUS Jäik ühendus Paindemomendi liigend Normaaljõu liigend Põikjõu liigend Vabad otsad Ühenduste sümbolid. Vastastikused siirded M y, ϕ y z, w v p x, u u = u p u v w = w p w v ϕ y = ϕ p ϕ v v vasakul p paremal v p v p v p Kontaktitingimused sõlmedes: ette antud ja tundmatud N x =?, u = 0 Q z =?, w = 0 M y =?, ϕy = 0 N x =?, u = 0 Q z =?, w = 0 M y = 0, ϕy =? N x = 0, u =? Q z =?, w = 0 M y = 0, ϕy =? N x =?, u = 0 Q z = 0, w =? M y =?, ϕy = 0 N x = 0, u =? Q z = 0, w =? M y = 0, ϕy =? Vastastikuste siirete tähis ja vabadusastmete arv 0 ϕ y 1 u 1 w 1 u, w, ϕ y 3 Kontaktjõud ja nende arv M y M y N Q z 3 N Q z N Q z 2 N Q z Q z M y 2 M y Q z N M y 2 M y N Arvutusskeem Joonis 3.2. Kontaktjõud ja liigendid Arvutusskeem on ehituskonstruktsiooni, masina vms kujutis, mille alusel tehakse arvutusi. Valitud arvutusskeemist oleneb arvutuse täpsus ja keerukus. Alati on võimalik valida täpsem arvutusskeem ja täpsem teooria, kuid siis muutuvad arvutused keerulisemaks. Täpsemaid teooriaid on vaja selleks, et kindlaks teha lihtsamate teooriate kehtivuse piirid. Arvutusskeem sisaldab vähemalt järgmist informatsiooni [KW90]: kõigi sõlmpunktide asukohti koos mõõtmetega
49 3.5. ARVUTUSSKEEM 49 varraste telgjooni tugede ja liigendite asukohti kõigi varraste ristlõikejäikusi koormusi kohalike telgede positiivseid suundi. Arvutis tuleb arvutusskeemi toetada arvutustabeliga [KW90]. Arvutusskeem ja arvutustabel sõltuvad vaadeldavast konstruktsioonist.
50 50 PEATÜKK 3. VARRASSÜSTEEMIDE LIIGITUS
51 Peatükk 4 Staatikaga määratav mitmesildeline tala 4.1 Staatikaga määratav mitmesildeline tala Liigenditeta mitmesildeline tala on toeraktsioonide suhtes staatikaga määramatu. Staatilise määramatuse aste leitakse valemiga (10.1) n = t 3 (4.1) kus t on toesidemete arv. Mitmesildeline tala on staatikaga määratav, kui lihtliigendite arv l on võrdne ilma liigenditeta tala staatikaga määramatuse astmega (10.1) l = t 3 (4.2) kus t on toesidemete arv. Liigendite asetus peab olema niisugune, mis tagab mitmesildelise tala geomeetrilise muutumatuse. Geomeetriliselt muutumatus staatikaga määratavas mitmesildelises talas ei ole ühes sildes rohkem kui kaks ja kahes naabersildes rohkem kui kolm liigendit. Kahes naabersildes peab olema vähemalt üks liigend [Rää75]. 4.2 Põhiosad ja lisaosad Staatikaga määratavad mitmesildelised talad koosnevad põhi- ja lisaosadest. Põhiosa on geomeetriliselt muutumatu ka siis, kui naaberosad on eemaldatud. Lisaosad muutuvad naaberosade eemaldamisel mehanismideks. Joonisel 4.1 on põhiosad a f 1 ja f 3 g. Lisaosadeks on f 1 f 2 ja f 2 f 3. Joonisel 4.2 on põhiosad a f 1 ja f 2 f 3. Lisaosadeks on f 1 f 2 ja f 3 e. Joonisel 4.3 on põhiosad a f 1 ja f 3 d. Lisaosadeks on f 1 f 2 ja f 2 f 3. Korrusskeemide joonistamisel (joonised ) võib ette kujutada, et niisugune on montaaži järjekord. Põhiosad saab monteerida ilma naabertaladeta. 51
52 52 PEATÜKK 4. STAATIKAGA MÄÄRATAV MITMESILDELINE TALA q = 8 kn/m a b f 1 c f 2 f d 3 e g A B C D E f 2 f 3 F 2 F 3 F 2 F 3 f 1 F 1 c f 2 f 3 d e g a b F 1 f 1 C D E A B Joonis 4.1. Gerberi tala 1. Lisaosad ja põhiosad q = 1.6 kn/m a b f 1 f 2 c d f 3 e A B C D 10 m 2 6 m 2 10 m m E f 1 f 2 f 3 F 1 F 2 F e 3 F 1 F F 2 3 f 1 f a 2 f b c d 3 E A B C D Joonis 4.2. Gerberi tala 2 a q = 2 kn/m b f 1 f 2 c f 3 d M d A B C 6.0 m m m f 1 f 2 F 1 F 2 D a b F 1 f 1 f 2 F 2 c f 3 F 3 A B C f 3 F 3 d M d D Joonis 4.3. Gerberi tala 3
53 4.3. SISEJÕUDUDE ARVUTUS Sisejõudude arvutus Sisejõudude arvutust alustatakse lisaosadest (vt joonist 4.4). Lisaosade liigendites määratavad jõud rakendatake allpool olevale talale vastupidiste suundadega (vt joonist 4.4). a q = 2 kn/m!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! b f 1 f 2 c f 3 d M d A B C 6.0 m m m f 1 f 2 F 1 F 2 D a b F 1 f 1 f 2 F 2 c f 3 F 3 A B C f 3 F 3 d M d D iv 6.50 I 4.00 II III M ep [knm] m 3.0 m 2.0 m iv II I III Q ep [kn] Joonis 4.4. Gerberi tala 3 epüürid 4.4 Gerberi tala mõjujooned Staatiliselt määratud mitmesildelise tala (joonis 4.5) mõjujoonte leidmisel kasutame joonisel 2.10 toodud konsoolidega tala paindemomendi ja põikjõu mõjujooni. Gerberi tala (joonis 4.5) toereaktsioonide A ja C mõjujoonte leidmisel joonistame vastava konsoolidega tala (joonis 2.4) toereaktsioonide mõjujooned joonisele 4.5.
54 54 PEATÜKK 4. STAATIKAGA MÄÄRATAV MITMESILDELINE TALA a i b f 1 f 2 c k d f 3 e A 4 m 3 m B C D 10 m 2 6 m 2 10 m m E a f 1 F 1 F 1 F 2 b f 1 f 2 f 2 F 2 c f 3 F 3 d F 3 e f 3 E A "A" B C D B mj "C" " Q i " "M i " M i mj " Q k " Q k mj "M k " M k mj v " Q d" v Q d mj p Q d mj C mj Q i mj "Q p d " Joonis 4.5. Gerberi tala 2 mõjujooned Kui vaadeldava tala toereaktsioon sõltub naabertalal liikuvast ühikkoormusest, siis jätkame seda mõjujoont. Ühikjõu liikumisel sõlme f 2, on jõud F 1 = 0 (joonis 4.5) ja
55 4.4. GERBERI TALA MÕJUJOONED 55 sellest tulenevalt B = 0. Selle väärtuse kanname joonisel 4.5 ühikjõu alla. Jätkame toereaktsiooni C mõjujoont sõlmest f 2 vasakule. Ühikjõu liikumisel sõlme f 1, on reaktsioon F 2 = 0 ja sellest tulenevalt C = 0. Selle väärtuse kanname joonisel 4.5 ühikjõu alla. Põikjõu Q i ja paindemomendi M i mõjujoonte leidmisel joonestame vastavad mõjujooned jooniselt 2.10 joonisele 4.5 ringi. Ühikkoormuse liikumisel naaberosale jälgime reaktsiooni F 1 muutumist. Kui ühikjõud on sõlmes f 2 on F 1 = 0. Selle väärtuse kanname ühikjõu alla (st sõlme f 2 alla).
56 56 PEATÜKK 4. STAATIKAGA MÄÄRATAV MITMESILDELINE TALA
57 Peatükk 5 Kolme liigendiga kaar ja raam 5.1 Üldmõisted Kahele toele toetuvast ühest või mitmest surutud kõverast vardast moodustatud konstruktsiooni, milles vertikaalne koormus põhjustab nii vertikaalseid kui ka horisontaalseid toereaktsioone, nimetatakse kaareks. Kolme liigendiga kaare toeliigendeid a ja b (joonis 5.1) nimetatakse kannaliigenditeks a ) H a a F a i i k y k q c ϕk f b H b x k V a l/2 V b l b ) i F i k q c V o a V o b M o o M c Q o Joonis 5.1. Kolme liigendiga kaar ja keskmist liigendit c lukuliigendiks. Lukuliigendi vertikaalset kaugust toeliigendeid 57
58 58 PEATÜKK 5. KOLME LIIGENDIGA KAAR JA RAAM ühendavast sirgest nimetatakse kaare kõrguseks ja tähistatakse tähega f (vt joonist 5.1). Kaare kõrguse ja silde l suhet f l nimetatakse kaare tõusuks. 5.2 Toereaktsioonide ja sisejõudude arvutus Vertikaalne koormus Toereaktsioonide vertikaalsed komponendid tähistame V a ja V b (joonis 5.1) ja leiame tugede a ja b kohta kirjutatud tasakaaluvõrranditest (5.2). ΣM b = 0; V a l + F i (l a i ) + q l2 2 = 0 (5.1) ΣM a = 0; V b l + F i a i + q l ( l l ) = 0 (5.2) 4 Horisontaalsed toereaktsioonid H a ja H b leiame lukuliigendi c kohta kirjutatud tasakaaluvõrrandist (5.3). ΣM v c = 0; H a f + V a l ( ) l 2 + F i 2 a i = 0 (5.3) H a = H b = M o c f (5.4) 5.3 Kaare telgjoone võrrandid Kaare telgjooneks on ruutparabool, mille võrrand on y = 4f x (l x) l 2 (5.5) Kaare sille l, tõus f ja kaare telje puutuja kaldenurk ϕ on näidatud joonisel 5.2. Kaare x k α c F y f H a x V a a l/2 l/2 l b V b H b y Joonis 5.2. Kaare telgjoon
59 5.4. KAARE SISEJÕUD 59 telje puutuja kaldenurga siinuse ja koosinuse leiame valemitega ( ) 1 2 x sin ϕ = cos ϕ = ( l 4f 1 + ( 4f l ) 2 ( x l 1 l ) 2 ( 1 2 x l ) 2 (5.6) ) 2 (5.7) Tähistades saame ξ = x l, ξ = (l x) l (5.8) y = 4fξξ (5.9) (1 2ξ) sin ϕ = ( ) 2 l 4f + (1 2ξ) 2 1 cos ϕ = 1 + ( ) 4f 2 l (1 2ξ) 2 (5.10) (5.11) Kaare telgjooneks on ringi kaar, mille võrrand on ( ) 2 l y = R2 2 x (R f) (5.12) Avaldises (5.12) on R kaare telje kõverusraadius, mille arvutame järgmise valemiga: R = (l2 + 4f 2 ) 8f Kaare telje puutuja kaldenurga siinuse ja koosinuse leiame valemitega 5.4 Kaare sisejõud (5.13) sin ϕ = l ( 1 R 2 x ) (5.14) l ( ) 2 (1 l cos ϕ = 1 R 2 x ) 2 (5.15) l Kaare sisejõudude arvutamise valemite kirjutamiseks vaatame joonist 5.1. Teeme mõttelises ristlõikes k mõttelise lõike ja vaatleme vaskule poole jäävat osa (joonis 5.3). Ristlõikes k koostatud momentide tasakaaluvõrrand
60 60 PEATÜKK 5. KOLME LIIGENDIGA KAAR JA RAAM a ) H a a a i F i ϕ k k M k N k y Q k k ϕ k b ) V o a i F i k Q k o M k o x k V a l Joonis 5.3. Kolme liigendiga kaare sisejõud M k = V a x k F i a i H y (5.16) ehk M k = Mk o H y (5.17) Jõudude projektsioonide tasakaaluvõrrand Q k suunale Q k = (V a F i ) cos ϕ k H sin ϕ k (5.18) ehk Q k = Q o k cos ϕ k H sin ϕ k (5.19) Jõudude projektsioonide tasakaaluvõrrand N k suunale N k = (V a F i ) sin ϕ k + H cos ϕ k (5.20) ehk Q k = Q o k sin ϕ k + H cos ϕ k (5.21) Sisejõud kaare lõikes x arvutame järgmiste valemitega: M x = Mx o H y (5.22) Q x = Q o x cos ϕ H sin ϕ (5.23) N x = Q o x sin ϕ + H cos ϕ (5.24)
61 5.4. KAARE SISEJÕUD 61 Näide 5.1 Arvutada joonisel 5.4 toodud kaare sisejõud. Kaare telgjooneks on parabool. x c 6 F = 4 kn H a a f = 4 m 9 b 10 H b y V a a = 11.2 m 4.8 m V b l = 16 m Joonis 5.4. Kaar A. Koormused Kaare horisontaalsed toereaktsioonid leiame avaldisega (5.4). Kaare telgjoone võrrandi (5.9), sin ϕ ja cos ϕ (5.11) ja sisejõudude (5.24) avaldised kanname tabelarvutusse 5.5. See tabelarvutus on arvutivõrgus KaarA.sdc 1. Tabelarvutusega leitud sisejõud on joonisel 5.5. Joonis 5.5. Kaar A. Tabelarvutus Järgnevalt teisendame tabelarvutusega saadud tabeli, mis on joonisel 5.5, andmed programmide Octave 2 (matlab) andmeteks. Selleks avame StarOffice ga (OpenOffice 3 ) uue teksti dokumendi; avame StarCalc iga tabeli KaarA.sdc;
62 62 PEATÜKK 5. KOLME LIIGENDIGA KAAR JA RAAM kopeerime tabeli ja asetame ( Paste Special ), kui formateerimata teksti ( unformatted text ) uude teksti documenti ja salvestame (.sdw); salvestame veel kord kui teksti (.txt) faili; teksti redaktoriga avame selle (.txt) faili ja salvestame octave failina (.m); töötleme seda faili (vt Programm C.5 KaarA1.m). Lisades [, ]; asendades korrutusmärgi * vektori nimetustes märgiga. ja plot( ) käsud ja Programmi C.5 KaarA1.m (lk 213) abil leiame paindemomendi (5.6), põikjõu (5.7) ja normaaljõu (12.3) epüürid. Joonistel (5.6, (5.7), (5.8) on epüürid joonistatud, kui kaar oli Joonis 5.6. Kaar A. Paindemomendi epüür Joonis 5.7. Kaar A. Põikjõu epüür jaotatud 10-neks. Antud epüüride puhul suurema jaotusega (30 punkti) epüürid langevad hästi kokku 10-ne punktise jaotusega. Mitte alati ei ole see nii (vt joonist 5.14). Näide 5.2 Arvutada joonisel 5.9 toodud kaare sisejõud. Kaare telgjooneks on ringjoon. Kaare horisontaalsed toereaktsioonid leiame avaldisega (5.4). Kaare telgjoone võrrandi (5.12), (5.13), sin ϕ ja cos ϕ (5.15), sisejõudude (5.24) avaldised kanname tabelarvutusse See tabelarvutus on arvutivõrgus KaarB.sdc 4. Tabelarvutusega leitud sisejõud on joonisel Tabelarvutusega saadud tabeli, mis on joonisel 5.10, andmed teisendame nagu programmi C.5 (lk 213) andmed. 4
63 5.4. KAARE SISEJÕUD 63 Joonis 5.8. Kaar A. Normaaljõu epüür q = 2 kn/m F = 4 kn x c H a a f = 4 m 9 b 10 H b y V a m V b l = 16 m Joonis 5.9. Kaar B. Koormused Programmi C.6 KaarB1.m (lk 215) abil leiame paindemomendi (5.13), põikjõu (5.12) ja normaaljõu (5.13) epüürid. Joonistel (5.11, (5.12), (5.13) on epüürid joonistatud, kui kaar oli jaotatud kümneks. Täpsemate epüüride saamiseks oleks vaja rohkem punkte (suuremat jaotust). Vaata joonist 5.14, kus on toodud graafikud kümnene ja kolmekümne jaotuse puhul.
64 64 PEATÜKK 5. KOLME LIIGENDIGA KAAR JA RAAM Joonis Kaar B Joonis Kaar B. Paindemomendi epüür Joonis Kaar B. Põikjõu epüür
65 5.4. KAARE SISEJÕUD 65 Joonis Kaar B. Normaaljõu epüür Joonis Kaar B. Paindemomendi epüür kolmekümne jaotusega
66 66 PEATÜKK 5. KOLME LIIGENDIGA KAAR JA RAAM 5.5 Kolme liigendiga raam Kolme liigendiga raami arvutamisel kehtivad kolme liigendiga kaare jaoks tuletatud valemid. Raamil võetakse tõmme positiivsena ja surve negatiivsena Kolme liigendiga raami arvutus Näide 5.3 Koostada joonisel 5.15 kuiutatud kolme liigendiga raami sisejõudude epüürid (näide on võetud näidisülesannetest [ER83] lk 47) cos α = , sin α = a) q = 2 kn/m c F xd = 1 kn d m α i 2 m H a V a F = 3 kn j e 1.6 m 2 m 2 m a b 4 m 4 m k h = 4 m 1 m H b V b b) 6.4 c m i d 10.4 e a M [knm] b Joonis Kolme liigendiga raam Vertikaalsete toereaktsioonide arvutus Mb = 0; V a = 0 V a = 6.25 kn (5.25) Ma = 0; V b = 0 V b = 4.75 kn Vertikaalsete toereaktsioonide arvutuse kontroll Y = 0; = 0 0 = 0 Horisontaalsete toereaktsioonide arvutus M v c = 0; H a = 0 H a = 1.6 kn (5.26) (5.27) (5.28) M p c = 0; H b = 0 H b = 2.6 kn Horisontaalsete toereaktsioonide arvutuse kontroll X = 0; = 0 0 = 0 (5.29) (5.30)
67 5.5. KOLME LIIGENDIGA RAAM 67 Paindemomendi epüüri (vt joonis 5.15 b) ordinaatide arvutus M d = = 6.4 knm (5.31) M m = = 0.8 knm (5.32) M m = = 0.8 knm (5.33) M i = = 2.2 knm (5.34) M i = = 2.2 knm 2 (5.35) M e = = 10.4 knm (5.36) a) b) d c i m a 1.6 b Q [kn] e c m i d e a b N [kn] Joonis Kolme liigendiga raami sisejõud Põikjõu epüüri (vt joonis 5.16 a) ordinaatide arvutus Q ad = 1.6 kn (5.37) Q dc = ( ) = kn (5.38) Q cd = ( ) = kn (5.39) Q ci = ( ) = kn (5.40) Q ie = = kn (5.41) Pikijõu epüüri (vt joonis 5.16 b) ordinaatide arvutus N ad = 6.25 kn (5.42) N dc = ( ) = kn (5.43) N cd = ( ) = kn (5.44) N ci = ( ) = kn (5.45) N ie = = kn (5.46)
68 68 PEATÜKK 5. KOLME LIIGENDIGA KAAR JA RAAM
69 Peatükk 6 Sõrestikskeemid 6.1 Sõrestikskeemide liigitus Varrassüsteemide mehaanikas võetakse arvutusskeemide liigitamise aluseks varda telgjoone kuju, varda tööseisund (joonis 1.3), toesidemete arv, liigendite arv. Otstes hõõrdevabade liigenditega ühendatud sirgetest varrastest geomeetriliselt muutumatut konstruktsiooni, mis on koormatud vaid hõõrdevabades liigendites, nimetatakse sõrestikskeemiks. Sõrestikskeemi vardad töötavad ainult pikkele. Sõrestiku ülemised vardad (joonis 6.1) a) b) c) d) Joonis 6.1. Sõrestikskeemide liigitus moodustavad ülemise vöö, alumised vardad alumise vöö. Vöödevahelised vardad moodustavad sõrestikuvõrgu. Võrgu vertikaalseid vardaid nimetatakse postideks ja kaldvardaid diagonaalideks. Horisontaalse vöö kahe naabersõlme vahekaugust nimetatakse paneeli pikkuseks. Sõrestikke liigitatakse ülesande järgi katusesõrestikud, sillasõrestikud, kraanasõrestikud jne 69
70 70 PEATÜKK 6. SÕRESTIKSKEEMID toereaktsioonide järgi talasõrestikud, konsoolsõrestikud, konsoolidega talasõrestikud; kaar-, raam- ja rippsõrestikud; kombineeritud sõrestikud kuju järgi paralleelvöödega sõrestikud (joonis 6.1 a); kolmnurksõrestikud (joonis 6.1 b); kõvera vööga sõrestikud (joonis 6.1 d) võrgu järgi diagonaalvõrguga sõrestikud (joonis 6.1 a); post-diagonaalvõrguga sõrestikud (joonis 6.1 c). 6.2 Staatiliselt määratud sõrestike arvutus Staatiliselt määratud sõrestike sisejõudude leidmiseks koostatakse tasakaaluvõrrandid. Tasakaaluvõrrandite koostamiseks kasutatakse lõikemeetodit. Sõrestiku arvutusskeemist eraldatakse üks sõlm või osa sõrestikust ja teiste osade mõju asendatakse läbilõigatud varraste kontaktjõududega (rajajõududega). Eraldatud sõlme või sõrestikuosa tasakaalutingimustest leitakse läbilõigatud varraste kontaktjõud. Kontaktjõud on läbilõigatud varda välispinnal. Läbilõigatud varda ristlõike sisepinnal on kontaktjõuga võrdne sisejõud. Esimese märgikokkuleppe puhul loetakse kontaktjõud positiivseks, kui tema suund ühtib kohaliku telje positiivse suunaga. Teise märgikokkuleppe puhul loetakse kontaktjõud positiivseks, kui tema suund ühtib kohaliku telje positiivse suunaga. Arvutuse tulemusena saadud miinusmärk näitab, et oletus oli vale ja kontaktjõud on vastupidise suunaga. Staatiliselt määratud tasandsõrestikus ei ole liigseid sidemeid. Liigsidemete arv on null. n = n v + n t 2 n s (6.1) kus n v on sõrestikuvarraste arv, n t toesidemete arv, n s sõrestikusõlmede arv. Sõrestikuvarraste kontaktjõudude arvutamisel kasutatakse sõlmede eraldamise võtet momendipunkti võtet projektsioonide võtet Nende võtete abil koostatakse tasakaaluvõrrandid. Kui tasakaaluvõrrandid koostatakse ja lahendatakse käsitsi, siis on otstarbekas koostada võrrandid nii, et seal oleks ainult üks tundmatu Sõlmede eraldamise võte Eraldame lõikega sõrestikskeemist sõlmed (joonis 6.2) ja koostame nende jaoks tasakaalutingimused. Tasandil võib iga sõlme jaoks koostada kaks teineteisest sõltumatut tasakaaluvõrrandit 2 n s. Toereaktsioonide määramiseks kasutatakse n t (staatiliselt määratud tasandraami puhul n t = 3) võrrandit. Sõltumatute tasakaaluvõrrandite üldarv on 2 n s n t.
71 6.2. STAATILISELT MÄÄRATUD SÕRESTIKE ARVUTUS 71 z a) x 2 F=15 kn N 4 F=15 kn F=15 kn 4 N 6 8 b) 2 F=15 kn N 4 1 N 1 N 2 N 5 N 6 N 9 N 10 h=1.732 m N 1 N 2 C 1 C 2 1 N 3 3 N 7 d=2 m l = 12 m 5 N 11 7 C 3 c) C 1 2 N N 3 C 2 13 Joonis 6.2. Sõlmede eraldamise võte Näide 6.1 Vaatleme joonisel 6.2 toodud sõrestikskeemi. Eraldame lõikega sõlmed. Arvutame sõrestikuvarraste suunakoosinused (vt joonis 6.3). cos α = x l (6.2) kus l on varda pikkus l = cos β = z l (6.3) ( x) 2 + ( z) 2 (6.4) siin x = x L x A (6.5) z = z L z A (6.6) x a x l x z l z a z Algus β α x Lõpp z Joonis 6.3. Varda suunakoosinused
72 72 PEATÜKK 6. SÕRESTIKSKEEMID 2 1 F=15 kn 2 N 4 4 N F=15 kn 4 N F=15 kn 10 N 8 6 N 1 N 2 N 5 N 6 N 9 N C 1 1 N 1 N 3 3 N 3 N 2 3 N 5 N 7 7 N N 6 9 N N 7 N 11 N C C 3 Joonis 6.4. Varraste eraldamise võte ja x A, z A, x L, z L on varda alguse ning lõpu koordinaadid. Sõrestiku (joonis 6.2) sõlmede koordinaadid on toodud joonisel 6.5 tabelina Sõlmed. Valime varraste algused ja lõpud nii, nagu on näidatud joonisel 6.5 tabelis Topoloogia. Arvutusprogrammiga C.11 (vt lisa C.4 lk 228) leiame varraste koosinused. Varraste koosinuste väärtused on joonisel 6.6 tabelis Varraste suunakoosinused ridades Algus cosa ja Algus cosb. Joonis 6.5. Sõrestiku topoloogia Joonisel 6.6 on tabelisse Varraste suunakoosinused kantud varraste (joonis 6.4) suuna-
73 6.2. STAATILISELT MÄÄRATUD SÕRESTIKE ARVUTUS 73 koosinused joonisel 6.2 näidatud sisejõudude suundade alusel. Joonis 6.6. Võrrandisüsteemi vasak pool Sõlmede vabadusastmete suunad nummerdame nii, nagu on näidatud joonisel 6.5 tabelis Vabadusastmete numbrid sõlmedes. Nii koostame sõlme 2 tasakaaluvõrrandid suundadele 1 ja 2. Suunas1 = 0; N 1 cos α N 2 cos α N 4 cos α 2 4 = 0 (6.7) Suunas2 = 0; N 1 cos β N 2 cos β N 4 cos β 2 4 = 0 (6.8) Sõlmes 1 on tasakaaluvõrrandid suundadele 12 ja 13. Suunas12 = 0; N 1 cos α N 3 cos α C1 = 0 (6.9) Suunas13 = 0; N 1 cos β N 3 cos β C2 = 0 (6.10) Nii nagu võrrandid (6.7), (6.8), (6.9) ja (6.10) koostatakse võrrandid igas sõlmes. Saame võrrandisüsteemi (6.11). GX = S (6.11)
74 74 PEATÜKK 6. SÕRESTIKSKEEMID Joonis 6.7. Võrrandisüsteemi koostamine kus X koosneb sõrestikuvarraste sisejõudude vektorist N ja toereaktsioonide vektorist C, S on koormusvektor. Tasakaaluvõrrandite süsteemi vasak pool on joonisel 6.6. Koormusvektor S ehk võrrandisüsteemi parem pool on joonisel 6.8. Koormusvektori saame jõu väärtuste, vt tabel Jõud sõlmedes, kandmisel tabelisse Võrrandisüsteemi parem pool vastavalt tabelile Vabadusastmete numbrid sõlmedes. Võrrandisüsteemi saame koostada ka kõigi varraste (joonis 6.4) vabadusastmete ja nende suunakoosinuste abil (vt joonis 6.7). Arvutusprogramm C.11 kasutab moodust, kus sõlmede tasakaaluvõrrandid saadakse kõigi varraste suunakoosinuste võrrandisüsteemi kandmisega. Toereaktsioonide leidmiseks lisatakse võrrandisüsteemi (joonis 6.6) negatiivne ühikmaatriks. Mõjujoonte ordinaatide leidmiseks kasutame võrrandisüsteemi (6.11) vasaku poole G pöördmaatriksit G (joonis 6.9), mmõjujoonte vajalike ordinaatide väljatoomiseks pöördmaatriksist G X = G S (6.12) vaatleme joonist 6.2 ja teeme kindlaks, milliseid sõlmi läbib ühikjõud. Nii näiteks sõdutee all puhul läbib ühikjõud sõlmi 1, 3, 5 ja 7. Need sõlmed ja nendele vastavad vabadusastmed on joonisel 6.8. Vabadusastmete järgi valitakse pöördmaatriksist G veerud (vt joonis 6.9).
75 6.2. STAATILISELT MÄÄRATUD SÕRESTIKE ARVUTUS 75 Joonis 6.8. Jõud sõlmedes Joonis 6.9. Vasaku poole pöördmaatriks G
76 76 PEATÜKK 6. SÕRESTIKSKEEMID Momendipunkti võte Momendipunkti võtte eeliseks on, et ta võimaldab leida sisejõu ühes sõrestikuvardas sõltumata teiste sõrestikuvarraste sisejõududest. Momendipunkti võtet nimetatakse ka Ritteri 1 lõikemeetodiks. x F=15 kn F=15 kn F=15 kn z 2 I h=1.732 m C 1 C I d=2 m l = 12 m C 3 Joonis Lõige I-I Momendipunkti võtte puhul jagatakse sõrestiku arvutusskeem lõikega kaheks osaks (joonis 6.10). Lõigatakse läbi varras, mille sisejõudu otsitakse (näiteks varras 7) ja veel kaks varrast (vardad 4 ja 5, vt lõiget I-I). Nende kahe läbilõigatud varda sihtide lõikepunkti nimetatakse momendipunktiks ehk Ritteri punktiks. Varda 4 ja 5 sihtide lõikepunktiks on 4, mis on varda 7 sisejõu N 7 leidmise momendipunkt. Varda 4 ja 5 sisejõu (N 4, N 5 ) moment momendipunkti (sõlmpunkt 4) suhtes on null. Vaatleme lõikest I-I vasakule (paremale) jäävat sõrestikuosa (joonis 6.11). x F=15 kn F=15 kn F=15 kn z 2 I N N h=1.732 m C 1 1 N C 2 = 22.5 kn I d=2 m l = 12 m C 3 Joonis Momendipunkti võte Koostame selle sõrestikuosa kohta momentide tasakaalu tingimuse momendipunkti 4 suhtes (6.13) ΣM 4 = 0; N 7 h + F d + C2 1.5d = 0 (6.13) Toereaktsioon C1 = 0 ja sisejõu N 4 ning N 5 õlg momendipunkti 4 suhtes on null. Toereaktsiooni C2 väärtuseks on -22.5, sest toereaktsiooni suund on vastupidi joonisel 1 August Ritter, insener ja mehaanikaprofessor Hannoveris ja Aachenis
77 6.2. STAATILISELT MÄÄRATUD SÕRESTIKE ARVUTUS 77 oletatuga. Tingimusest (6.13) avaldame sisejõu N 7 F d + C2 1.5d N 7 = h = M o 4 h (6.14) kus M o 4 on sõrestikule vastava lihttala moment punkti 4 suhtes. Sõrestikuvarda sisejõu N 4 leidmiseks on momentpunktiks sõlmpunkt 3. Selle punkti suhtes on momentide tasakaalu tingimus ΣM 3 = 0; N 4 h + F 0.5d + C2 d = 0 (6.15) Tingimusest (6.15) avaldame sisejõu N 4 F 0.5d + C2 d N 4 = h = M o 3 h (6.16) kus M o 3 on sõrestikule vastava lihttala moment punkti 3 suhtes. Sõrestikuvarda sisejõu N 5 leidmiseks momendipunkti võte ei kõlba, sest kahe ülejäänud varda (varras 4 ja 7) sihid ei lõiku (om ) Projektsioonide võte Paralleelvöödega sõrestiku diagonaali sisejõudu (N 5 ) (joonis 6.10) ei saa leida momentide tasakaalu tingimusest, kuna momendipunkt on lõpmatuses. Kahe läbilõigatud paralleelse vöö risttelje kohta kirjutatud jõudude projektsioonide tasakaalu tingimus (6.17), (joonis 6.11) ΣZ = 0; N 5 cos (n, z) + F + C2 = 0 (6.17) kus cos (n, z) väärtuse saab joonise 6.6 tabelist Varraste suunakoosinused. Kantud varraste (joonis 6.4) suunakoosinuste väärtused on toodud joonisel 6.6 tabelis Varraste suunakoosinused ridades Algus cosa ja Algus cosb. Sisejõu N 5 suund ühtib varda 5 suunaga 3 4. Nii saab cos (n, z) = Võrrandist (6.17) saame avaldada sisejõu N 5 N 5 = F + C2 cos (n, z) = Qo 3 4 cos (n, z) (6.18) kus Q o 3 4 on sõrestikule vastava lihttala põikjõud sõlmede 3 ja 4 vahel Maxwelli-Cremona diagramm Sõrestikuvarraste sisejõudude graafilisel leidmisel konstrueeritskse Maxwelli-Cremona diagramm (sisejõudude diagramm). Sisejõudude diagrammi võib koostada käsitsi või arvutiprogrammiga DesignView. Sisejõudude diagrammi koostamist selgitame joonise 6.12 abil. Sõrestiku väliskontuuril kahe naabervälisjõuga ja vööga piiratud pinda tähistatakse tähega (või numbriga).
78 78 PEATÜKK 6. SÕRESTIKSKEEMID a) F=15 kn F=15 kn F=15 kn c d b) b C 2 b f g a k n p e C 3 k g n f p c a d e Joonis Maxwelli-Cremona diagramm Need pinnad ja varrastega ümbritsetud pinnad on väljad. Joonisel 6.12 a on sõrestikku ümbritsevad väljad a, b, c, d, e ning sõrestikuvarrastega ümbritsetud väljad f, g, k, n, p. Välis- ja sisejõud märgitakse kahe tähega, mis näitavad, milliste väljade vahel jõud asub. Toereaktsiooni C2 tähistatakse a b ja sõlmes 2 rakendatud jõudu F b c. Välisjõudude hulknurk koostatakse järjekorras, nagu neid kohatakse päripäeva liikumisel ümber sõrestiku. Joonisel 6.12 b) on välisjõud b c, c d, d e, e a ja a b. Sisejõudude määramine põhineb vaadeldava jõu tasakaalustamisel jõududega, mil- a) b b) b c) N 1 f N 3 C2 a g N 2 N 1 N 4 f F c b N 5 k g N 2 f N 3 N 7 p a d) g c k f p a n d e Joonis Jõuhulknurgad
79 6.3. TALASÕRESTIKE MÕJUJOONED 79 le sihid ühtivad sõrestikuvarraste telgjoonte sihtidega (joonis 6.13). Sisejõudude diagrammi koostamist alustatakse sõlmest, mis on moodustatud kahest vardast (sõlm 1, joonis 6.12 a). Toereaktsiooni C2 tasakaalustame varraste 1 ja 3 sisejõududega (joonis 6.13). Nende varraste sihid lõikuvad punktis f (joonis 6.12 b). Leitud sisejõudude märgi määramiseks liigume ümber sõlme 1 päripäeva (joonis 6.12 a). Liikudes väljalt b väljale f, näeme diagrammilt (joonis 6.12 b), et jõud mõjub sõlme 1 suunas, s.t varras b-f on surutud. Liikudes väljalt f väljale a, näeme diagrammilt, et varras f-a on tõmmatud. Joonisel 6.13 b ja c on näidatud sõlmi 2 ja 3 tasakaalustavate jõudude hulknurgad. Varda sisejõud esineb diagrammi kahe naabersõlme jõuhulknurgas vastupidiste suundadega (sisejõud N 1, joonis 6.13 a ja b). sisjõudude diagrammis (joonis 6.12 b) jõudude suundi ei märgita. 6.3 Talasõrestike mõjujooned Mõjujoonte leidmine arvutiga Sõrestiku sõlmede eraldamisel saadud tasakaaluvõrrandid (vt näide 6.1 joonis 6.6) esitame võrrandiga G s = S (6.19) kus G on tasakaalumaatriks ja s sisejõudude ja toereaktsioonide vektor, S sõlmkoormuste vektor (tähistused on võetud õpikust [KW90]). G = [ G (N, N) G (N, C) G (C, N) G (C, C) ] ; s = N 1 N 2 N 3. N i. C1 C2 C3 ; S = F x, 1 F z, 1 F x, 2 F z, 3. F x, i F z, i. F C1 F C2 F C3 (6.20) kus G (C, C) on negatiivne ühikmaatriks G (C, C) = Lahendades võrrandisüsteemi (6.19), saame (6.21) s = G 1 S = b S (6.22)
80 80 PEATÜKK 6. SÕRESTIKSKEEMID kus b on pööratud tasakaalumaatriks, mille struktuur on (vt näide 6.1 joonis 6.9) b = [ b (N, F ) b (N, C) b (C, F ) b (C, C) ] (6.23) Maatriksit b võiksime nimetada ka mõjumaatriksiks, sest tema elemendid määravad kõikide mõjujoonte ordinaadid. Maatriksiga b (N, F ) saame määrata sisejõud N i sõluvalt väliskoormusest F j. Valides väliskoormuse F j = 1, saame mõjujoone ordinaadid. 6.4 Sõrestiku arvutamise näited Näide 6.2 Leida joonisel esitatud sõrestikuvarraste sisejõud arvutiprogrammiga C.12 lk 238. Kontrollida sõrestiku kolmanda paneeli varraste sisejõude ja konstrueerida nende mõjujooned. Sõrestikule mõjub koormus F 3 = 5 kn, F 5 = 10 kn, F 7 = 4 kn, F 9 = 8 kn, F 13 = 4 kn, F 15 = 8 kn. Sõrestiku mõõtmed on arvutusskeemil II I α α β C1 1 β C2 F 3 I II F 5 F 7 F 9 F 13 d = 3 m F 15 C3 L = 24 m z Joonis Sõrestiku sisejõud Sõrestikuvarraste sisejõudude leidmiseks arvutil lisame arvutustabelid (tabel 6.1 ja 6.2). Sõrestikusõlmede kirjeldamiseks valime x-telje sõrestiku alumisse vöösse ja z-telje vertikaalselt sõlmest 1 alla (joonis 6.14). Sõlmpunktide koordinaadid ja sõlmedes mõjuvad koormused on esitatud tabelina 6.1. Sõrestikuvardaid kirjeldame sõlmede abil, andes varda alguse ja lõpu sõlme numbri. Varraste kirjeldus (topoloogia) on tabelis 6.2. Sõrestiku sisejõud arvutame programmiga srstkn2.m C.12 lk 238. Arvutiprogrammis langevad toereaktsioonide ja koormuste positiivsed suunad kokku koordinaattelgede positiivsete suundadega. Tulemused kirjutame päevikusse 6.1. Päevik 6.1 srstkn2.out octave:2> diary srstkn2.out octave:3> diary on octave:4> srstkn2 SolmedeArv = 16 ElementideArv = x
81 6.4. SÕRESTIKU ARVUTAMISE NÄITED 81 Tabel 6.1. Sõrestiku arvutustabel I Sõlm X Z F z Sõlm X Z F z Tabel 6.2. Sõrestiku arvutustabel II Varras Algus Lõpp Varras Algus Lõpp ans = S~olmpunktide ja Elementide arv on 16,29 Kui SolmedeArv ja ElementideArv on ~oiged vajuta klahvile Enter =============================== S~olmede koordinaadid X Z
82 82 PEATÜKK 6. SÕRESTIKSKEEMID ============================= Elementide topoloogia Algus L~opp =============================== Toes~olmed X-suunas Z-suunas
83 6.4. SÕRESTIKU ARVUTAMISE NÄITED ================================ S~olmede vabadusastmete numbrid X-suunas Z-suunas ============================== Elementide suunakoosinused cosalpha cosbeta
84 84 PEATÜKK 6. SÕRESTIKSKEEMID ============================= J~oud s~olmedes X-suunas Z-suunas ============================= Varraste sisej~oud N
85 6.4. SÕRESTIKU ARVUTAMISE NÄITED ============================= Ühikj~oud s~olmedes X-suunas Z-suunas ============================= M~ojujooned N(i)-le s~olmedes. Viimased kaks on toereaktsioonide m~ojujooned Columns 1 through 8:
86 86 PEATÜKK 6. SÕRESTIKSKEEMID Column 9:
87 6.4. SÕRESTIKU ARVUTAMISE NÄITED ============================= M~ojujoone x koordinaadid octave:5> diary off Päevikust 6.1 saame kontrollida sisestatud sõlmede koordinaate ja varraste topoloogiat. Varda 4 ja 8 suunakoosinused saame päevikust cos α 4 = , cos β 4 = , cos α 8 = , cos β 8 = Kontrollime leitud toereaktsioonide väärtusi C2 = kn, C3 = kn, koostades tasakaalutingimuse Z-teljele Z = = 0 kn (6.24) K 3 α 8 Sisejõudude leidmiseks eraldame lõikega II II sõrestiku vasakpoolse osa ja vaatleme selle tasakaalu (joonis 6.15). Varda 10 momendipunktiks on sõlm 6 (joonis 6.15). Varda momena 3 = 21 m r 5 6 = 21.6 m C1 C2 r z 1 I 4 N α 8 α β β = m II N 10 7 I II F 3 F 5 L = 24 m N 9 Joonis Sõrestiku vasakpoolne osa dipunkti otsimiseks teeme lõike II II läbi kolme varda. Fikseerime varda, mille sisejõudu otsime. Selle varda momendipunkt on seal, kus kaks ülejäänud varrast lõikuvad. Sisejõu N 10 sihi kaugus sõlmest 6 r 5 7 = 4.0 m. Momendipunkti kohta koostatud tasakaalutingimusest M6 = 0 : N 10 r 5 7 F 5 d F 3 2d C2 3d = 0 (6.25) saame N 10 = M 5 o = = kn (6.26) r 5 7 4
88 88 PEATÜKK 6. SÕRESTIKSKEEMID siin tähistab M o 5 vastava lihttala paindemomenti punkti 5 suhtes antud koormusest. Varda 8 1 II N N N 9 16 a 3 II F 7 F 9 F 13 F 15 d = 3 m L = 24 m C3 z Joonis Sõrestiku parempoolne osa momendipunktiks on sõlm 5. Varda momendipunkti otsimiseks teeme lõike II II läbi kolme varda. Fikseerime varda, mille sisejõudu otsime. Selle varda momendipunkt on seal, kus kaks ülejäänud varrast lõikuvad. Sisejõu N 8 sihi kaugus sõlmest 5 on r 4 6 = h 2 cos α 8 = m. Siin h 2 = 3.6 m. Momendipunkti 5 kohta koostatud tasakaalutingimusest M5 = 0 : N 8 r 4 6 F 3 d C2 2d = 0 (6.27) tuleneb N 8 = M 5 o = = kn (6.28) r kus M5 o tähistab vastava lihttala paindemomenti punkti 5 suhtes antud koormusest. Märk - näitab, et ülemised kiud on surutud. Sõrestikuvarda 8 momendipunktiks on sõlm 5. Varda momendipunkti otsimiseks teeme lõike I I (joonis 6.15) läbi kolme varda. Fikseerime varda, mille sisejõudu otsime. Selle varda momendipunkt on seal, kus kaks ülejäänud varrast lõikuvad. Koostame lõikega I I eraldatud osa kohta tasakaalutingimuse, millest saame analoogiliselt varda 8 sisejõuga N 4 = M 5 o = = kn (6.29) r siin on sisejõu N 4 sihi kaugus sõlmest 5 r 2 4 = h 2 cos α 4 = m, kus h 2 = 3.6 m. Varda 9 momendipunkti otsimiseks teeme lõike II II (joonis 6.15) läbi kolme varda. Fikseerime varda 9, milles otsime sisejõudu. Selle varda momendipunkt on seal, kus kaks ülejäänud varrast (vardad 10 ja 8) lõikuvad. Joonisel 6.15 on see punkt tähistatud K 3 -ga. Koostame selle punkti kohta tasakaaluvõrrandi MK3 = 0 : N 9 r F 5 (a 3 + 2d) + F 3 (a 3 + d) + C2 a 3 = 0 (6.30) kus r 5 6 = 21.6 m ja a 3 = 21 m (joonis 6.15). Tasakaaluvõrrandist (6.30) saame N 9 = = 1.75 kn (6.31)
89 6.4. SÕRESTIKU ARVUTAMISE NÄITED 89 Sõlme 7 tasakaalutingimusest Z-teljele Z = 0 : N11 + F 7 = 0 (6.32) N 10 N11 N 7 14 saame N 11 = 4 kn (6.33) F 7 Joonis Sõlme 7 tasakaal N N α β 4 N7 α 8 β 8 Sõlme 4 tasakaalutingimusest Z-teljele Z = 0 : N7 N 8 cos β 8 + N 4 cos β 4 = 0 (6.34) saame avaldisi (6.28) ja (6.29) kasutades N 7 = M o 5 r 4 6 cos β 8 M o 5 r 2 4 cos β 4 (6.35) Joonis Sõlme 4 tasakaal Varraste 11 ja 7 sisejõu leidmiseks lõikame sõlmed 7 ja 4 välja (joonis 6.17 ja 6.18). Võttes arvesse seosed r 4 6 = h 2 cos α 8 ja r 2 4 = h 2 cos α 4, saame N 7 = M o 5 h 2 ( cos β8 cos β ) 4 cos α 8 cos α 4 (6.36) ehk arvestades seoseid (6.2) ja (6.3) saame N 7 = M 5 o (tan α 4 tan α 8 ) = ( 1.2 h ) = 7.94 kn (6.37) 3 Sõrestiku sisejõude võib leida ka lõikest II II paremale jääva osa (joonis 6.16) vaatlemisega. Mõjujoonte konstrueerimiseks jagame lõikega II II sõrestiku kaheks osaks (joonis 6.23). Kui ühikjõud liigub läbilõigatud paneelist paremal, siis vaatleme vasakpoolse osa tasakaalu (joonis 6.19) ja kui ühikjõud liigub läbilõigatud paneelist vasakul, siis vaatleme parempoolse osa tasakaalu (joonis 6.20). Varda 10 momendipunktiks on sõlm 6 (joonis 6.19). Sisejõu N 10 sihi kaugus sõlmest 6 h 3 = 4.0 m. Momendipunkti kohta koostatud tasakaalutingimusest M6 = 0 : N 10 h 3 C2 3d = 0 (6.38) saame N 10 = M 5 o C2 3d = = 9 r 5 7 h 3 4 (6.39)
90 90 PEATÜKK 6. SÕRESTIKSKEEMID 6 r = m I 4 N α 8 α β K 3 α 2 β C N 10 7 a 3 = 21 m r 5 6 = 21.6 m C2 z I L = 24 m N 9 II II "1" Joonis Sõrestik. Ühikjõud paremal Varda 10 mõjujoon (joonis 6.23) on sarnane lihttala mõjujoonega M5 o ristlõike 5 jaoks, mille ordinaadid on jagatud h 3 = 4 m-ega. Varda 10 mõjujoone iseloomuliku ordinaadi saame, kui korrutame toereaktsiooni C2 mõjujoone ordinaadid 9 4 -ga. Varda 8 momendipunktiks on sõlm 5. Sisejõu N 8 sihi kaugus sõlmest 5 on r 4 6 = h 2 cos α 8 = m. Siin h 2 = 3.6 m. Momendipunkti 5 kohta koostatud tasakaalutingimusest M5 = 0 : N 8 r C2 2d = 0 (6.40) saame N 8 = M 5 o C2 2d = = 6 r 4 6 r (6.41) kus M5 o on sõrestikule vastava lihttala paindemomendi mõjujoon punkti 5 suhtes. Varda 8 mõjujoon on joonisel Varda 8 mõjujoon sarnaneb lihttala mõjujoonega M5 o, mille ordinaadid on jagatud r 4 6 -ga. 1 II N N 10 N a 3 "1" II L = 24 m d = 3 m C3 z Joonis Sõrestik. Ühikjõud vasakul
91 6.4. SÕRESTIKU ARVUTAMISE NÄITED 91 Sõrestikuvarda 4 momendipunktiks on sõlmpunkt 5. Koostame lõikega I I eraldatud sõrestikuosa (joonis 6.15) kohta tasakaalutingimuse, millest saame varda 8 sisejõu N 4 = M 5 o C2 2d = = 6 r 2 4 r (6.42) kus sisejõu N 4 sihi kaugus sõlmest 5 on r 2 4 = h 2 cos α 4 = m. Varda 9 momendipunktiks on varraste 8 ja 10 sihtide lõikepunkt K 3. Sisejõu N 9 sihi kaugus punktist K 3 on r 4 6 = 21.6 m. Momendipunkti K 3 kohta koostatud tasakaalutingimusest MK3 = 0 : N 9 r C2 a 3 = 0 (6.43) kus a 3 = 21 m (joonis 6.19), saame N 9 = C2 a 3 r 5 6 = (6.44) Liikuva koormuse all (läbilõigatud paneelist paremal) sarnaneb varda N 9 mõjujoon toereaktsiooni C2 mõjujoonega, mille ordinaadid on korrutatud a 3 /r 5 6 -ga. Kui koormus liigub vasakul pool läbilõigatud paneeli, siis vaatleme sõrestiku parempoolse osa tasakaalu (joonis 6.20). Varda 9 momendipunkti K 3 kohta koostatud tasakaalutingimusest MK3 = 0 : N 9 r C3 (a 3 + L) = 0 (6.45) kus a 3 = 21 m (joonis 6.19), saame N 9 = C3 (a 3 + L) = = 45 r (6.46) Liikuva koormuse all (läbilõigatud paneelist vasakul) sarnaneb varda N 9 mõjujoon toereaktsiooni C3 mõjujoonega, mille ordinaadid on korrutatud (a 3 + L) /r 5 6 -ga (joonis 6.23). Varda 11 mõjujoone leidmiseks lõikame sõrestikust (joonis 6.23) välja sõlme 7 (joonis 6.21). Varda 7 mõjujoone leidmiseks lõikame sõrestikust (joonis 6.23) välja sõlme 4 (joonis 6.22).
92 92 PEATÜKK 6. SÕRESTIKSKEEMID Sõlme 7 tasakaalutingimusest Z-teljele Z = 0 : N = 0 (6.47) N 10 N11 N 7 "1" 14 saame N 11 = 1 (6.48) Joonis Sõlm 7 Sõlme 4 tasakaalutingimusest Z-teljele "1" N N α β 4 N7 α 8 β 8 Z = 0 : N7 N 8 cos β 8 + N 4 cos β 4 = 0 (6.49) saame avaldisi (6.28) ja (6.29) kasutades N 7 = M o 5 r 4 6 cos β 8 + M o 5 r 2 4 cos β 4 (6.50) Joonis Sõlm 4 Võttes arvesse seosed r 4 6 = h 2 cos α 8 ja r 2 4 = h 2 cos α 4, (6.2), (6.3), saame N 7 = M 5 o (tan α 4 tan α 8 ) = M o ( h ) (6.51) 3 Varda ( N 7 mõjujoon ) sarnaneb lihttala mõjujoonega M5 o, mille ordinaadid on korrutatud (joonis 6.23). Mõjujoonte abil arvutame sisejõud valemiga N i = F j η ij = F j η ij (6.52) kus η ij on sisejõu N i mõjujoone ordinaat sõlmes j ja F j on koormus sõlmes j. N 10 = ( ) + +8 ( ) = kn N 8 = [ ( ) + +8 ( )] = kn N 9 = ( ) + +8 ( ) = 1.75 kn N 11 = = 4.00 kn N 7 = ( ) + +8 ( ) = 7.94 kn Tabelis 6.3 on otseselt ja mõjujoonte abil leitud sisejõudude võrdlus.
93 6.4. SÕRESTIKU ARVUTAMISE NÄITED 93 II I α α β C1 1 β I II "1" d = 3 m C2 C3 L = 24 m z x 9 4 N 10 mj N 8 mj N 9 mj ( ) 3 N mj N 11 mj 1.0 Joonis Sõrestiku mõjujooned Tabel 6.3. Varraste sisejõudude võrdlus Varras N i otseselt [kn] N i mõjujoontega [kn]
94 94 PEATÜKK 6. SÕRESTIKSKEEMID
95 Peatükk 7 Siirete arvutus 7.1 Märgikokkulepped Rajajõudude (kontaktjõudude) positiivse suuna määramisel on kasutusel kaks märgikokkulepet (joonis 7.1, kus on kasutusel parema käe teljestik, vt joonis A.1). Esimene M L a) b) x* x* M L N A α Q L N L x M A Q A α Q L N L x Q A N A M A II märgikokkulepe I märgikokkulepe z z* z z* Joonis 7.1. Märgikokkulepped märgikokkulepe (joonis 7.1 b) on tuttav tehnilisest mehaanikast. Teine märgikokkulepe (joonis 7.1 a) on vajalik varrassüsteemide tasakaaluvõrrandite algoritmide koostamiseks. Võrreldes I märgikokkulepet II märgikokkuleppega, näeme, et varda lõpus olevad rajajõudude (kontaktjõudude) suunad langevad kokku. Varda alguses on rajajõudude suunad vastasmärgilised. Sisejõude leitakse rajajõudude kaudu. Sisejõudude märgid ei tohi sõltuda rajajõudude märgikokkuleppest. Sisejõudude märgireeglid on raamatus [MR96] lk 35 Tõmbejõu loeme positiivseks, Survejõu loeme negatiivseks ; lk 45 Põikjõu range märgireegel: positiivseks loeme põikjõudu, mis positiivset sisepinda nihutab koordinaattelje positiivses suunas või negatiivset sisepinda koordinaattelje negatiivses suunas, Põikjõu märgi tööreegel: positiivseks loeme põikjõudu, mis nihutab positiivset sisepinda päripäeva ; lk 43 Painde- momendi loeme positiivseks, kui varda positiivsed kiud on tõmmatud. 95
96 96 PEATÜKK 7. SIIRETE ARVUTUS Tehnilises mehaanikas (tugevusõpetuses) langevad sisejõudude märgireeglid ja rajajõudude (kontaktjõudude) märgireeglid (I märgikokkulepe) kokku. Kasutades II märgikokkulepet, tuleb sisejõudude märgi määramisel rajajõudude (kontaktjõudude) kaudu varda alguses arvestada nende erinevaid märke. Rõhutame, et sisejõud on varda sisepinnal ja rajajõud (kontaktjõud) mõjuvad varda välispinnal. 7.2 Sise- ja rajajõudude töö Tööde avaldise (1.7) pikkel kirjutame kujule N x û }{{} W r b b a N xˆλdx + ( q x (x) ûdx + F xi û i ) = 0 (7.1) W s W v a } {{ } a }{{} b Kui vaadelda avaldises (7.1) û-d kui virtuaalset siiret, siis väljendab see avaldis virtuaalsiirete printsiipi. Kirjutame võrrandi (7.1) ringi järgmiselt: kus W (p) = W (p) r + W (p) s + W (p) v = 0 (7.2) W (p) r = N x û b a (7.3) W (p) s b = N xˆλdx (7.4) a b W v (p) = a q x (x) ûdx + F xi û i (7.5) Avaldist (7.2) nimetatakse energiateoreemiks pikkel: rajajõudude, sisejõudude ja välisjõudude tööde summa on null. Avaldises (7.2) esinevat tööd W (p) on passiivtööd, kuna vaadeldavad jõud ei kutsunud esile virtuaalsiirdeid û. Kui vaadeldav jõud sõltub siiretest ja pööretest, siis tööd, mida need jõud teevad nendel siiretel ja pööretel, nimetatakse aktiivtööks (joonis 7.3). Aktiivtööde energiateoreem [KW90] kus W (a) = W (a) r + W (a) s W (a) r = W (p) v = 0 (7.6) N x û b a (7.7) W s (a) = 1 b N xˆλdx (7.8) 2 a
97 7.3. TÖÖ JA ENERGIA 97 F W (p) u^ F F = f(u) (a) W u F W (t) u = f(f) u Joonis 7.2. Passiivtöö Joonis 7.3. Aktiivtöö Joonis 7.4. Täiendtöö W v (a) = 1 b q x (x) ûdx + F xi û i (7.9) 2 a Sisejõudude töö avaldisel (7.8) on miinusmärk. Sisejõudude potentsiaalne energia Π s ehk deformatsioonienergia (joonis 1.3) U on arvuliselt võrdne sisejõudude tööga, kuid vastupidise märgiga Π s = U = W s (a) = 1 b N xˆλdx (7.10) 2 a 7.3 Töö ja energia Vaatleme vedrut (joonis 7.5 a) kui lihtsaimat elementi, et selgitada vardamehaanika printsiipe. Rakendame vedrule jõu F ja ˆF (joonis 7.5 a, b). Vedru jäikusega c siirded δ, ˆδ on jõududega proportsionaalsed F = kδ, ˆF = kˆδ (7.11) a b c δ δ F F Joonis 7.5. Vastastikune töö
98 98 PEATÜKK 7. SIIRETE ARVUTUS siin on k vedru jäikus. Siirete δ, ˆδ erinevate arvuliste väärtuste korral kirjutame samasuse Kui asendame avaldise (7.12) δk jõuga F, saame }{{} δk ˆδ δkˆδ = 0 (7.12) F F ˆδ δkˆδ = 0 (7.13) Seda triviaalset samasust nimetatakse vedru esimeseks samasuseks [Har85] G ( δ, ˆδ ) F ˆδ δkˆδ = 0, δ, ˆδ (7.14) siin tuleb tähistust δ, ˆδ lugeda kõigi δ, ˆδ puhul. Avaldis (7.14) väljendab energiateoreemi, s.t välisjõudude ja sisejõudude tööde summa on null. Samasus (7.14) jääb kehtima, kui vahetame δ ja ˆδ ning F ja ˆF ära G (ˆδ, δ ) ˆF δ ˆδkδ = 0, δ, ˆδ (7.15) Vedru teise samasuse saame, kui lahutame avaldisest (7.14) avaldise (7.15) B ( δ, ˆδ ) G ( δ, ˆδ ) G (ˆδ, δ ) = F ˆδ ˆF δ (7.16) Avaldis (7.16) väljendab Betti 1 teoreemi (tööde vastastikkuse teoreemi): esimese koormusolukorra välisjõudude võimalik töö teise koormusolukorra jõudude poolt põhjustatud siiretel on võrdne teise koormusolukorra välisjõudude võimaliku tööga esimese koormusolukorra jõudude poolt põhjustatud siiretel. Vaatleme vedru aktiivtööd W (a) (joonis 7.3). Elastse vedru deformatsioonienergia U (vedru sisejõudude potentsiaalne energia Π s ) on võrdne vedru aktiivtööga W s (a), kuid vastupidise märgiga Energiateoreem (7.14) aktiivtöö korral U (δ) = Π s (δ) = W (a) s (δ) = 1 2 δkˆδ (7.17) 1 2 G (δ, δ) 1 2 F δ 1 δkδ = 0 (7.18) 2 Vedru potentsiaalne energia Π (δ) koosneb sisejõudude potentsiaalsest energiast Π (a) s välisjõudude potentsiaalsest energiast Π (a) v siin Π (δ) = Π (a) v + Π (a) s = 1 2 δkδ 1 2 F δ (7.19) Π v = W v (7.20) ja W v on välisjõudude töö. Vedru potentsiaalse energia (7.19) esimene variatsioon on funktsionaal Π (δ) 1 Enrico Betti, itaalia ehitusinsener, ja
99 7.4. TÖÖDE VASTASTIKKUSE TEOREEM Tööde vastastikkuse teoreem Tööde vastastikkuse teoreem (Betti teoreemi): esimese koormusolukorra välisjõudude võimalik töö teise koormusolukorra jõudude poolt põhjustatud siiretel on võrdne teise koormusolukorra välisjõudude võimaliku tööga esimese koormusolukorra jõudude poolt põhjustatud siiretel. Sisejõudude tööde vastastikkuse teoreem pikkel on toodud avaldisega (A.26) lk 193. l N x 0 ˆNx l EA dx = 0 N x ˆN x dx (7.21) EA ja paindel avaldisega (A.41) l ˆMy M y dx 0 EI y }{{} Ws I) = l M y ˆM y dx 0 EI y }{{} Ws II) (7.22) Raja- ja välisjõudude töö vastastikkuse teoreem pikkel on toodud avaldisega (A.22) lk 193. N x û }{{} W I r l l 0 + ja paindel avaldisega (A.39) [ Qz ŵ+ M y ˆϕ y ] l 0 } {{ } Wr I q x (x) ûdx + F xi û i = 0 } {{ } Wv I = l + 0 ˆN x u }{{} Ŵ II r l l 0 + q z (x) ŵdx + F zi ŵ i = } {{ } Wv I ] ˆM y ϕ y [ ˆQz w+ l 0 } {{ } Wr II l + 0 ˆq x (x) udx + ˆF xi u i 0 }{{} Ŵ II v ˆq z (x) wdx + F zi ŵ i } {{ } Wv II (7.23) (7.24) siin on Q z, M y, p z, w ja ϕ y esimese koormusolukorra jõud ja siirded, ning ˆQ z, ˆMy, ˆp z, ŵ ja ˆϕ y teise koormusolukorra jõud ja siirded. 7.5 Siirete vastastikkuse teoreem Siirete vastastikkuse teoreem on tööde vastastikkuse teoreemi erijuht. Siirete vastastikkuse teoreem (J. Maxwell 2 ):kohas k mõjuvale jõule 1 k vastav üldistatud siire, mis on põhjustatud ühikjõust kohas i, võrdub jõule 1 i vastava üldistatud siirdega, mis on põhjustatud ühikjõust kohas k. 2 James Clerk Maxwell, inglise füüsik,
100 100 PEATÜKK 7. SIIRETE ARVUTUS 7.6 Reaktsioonide vastastikkuse teoreem Reaktsioonide vastastikkuse teoreem (J. Rayleigh 3 ): sideme j ühiksiirdest põhjustatud reaktsioon sidemes i võrdub sideme i ühiksiirdest põhjustatud reaktsiooniga sidemes j. 7.7 Siirete arvutamine Konstruktsiooni mingi punkti siirde arvutamisel vaadeldakse konstruktsiooni arvutusskeemi kahte tasakaaluolukorda. Ühe olukorrana vaadeldakse koormuse põhjustatud tasakaaluolukorda p ja arvutusskeemis tekkivaid sisejõude tähistatakse sel juhul N p, Q p, M p. Teise olukorrana vaadeldakse tasakaaluolukorda, kus arvutusskeemile mõjub ainult üks otsitavale siirdele vastav üldistatud ühikjõud 1 i. Selles tasakaaluolukorras i sisejõud ja reaktsioonid tähistatakse väikeste tähtedega n i, q i, m i ja c i. Võimaliku töö avaldised pikkel (A.18) ja paindel (A.37) on W p = F xi û i + l 0 q x (x) ûdx + N l x û l 0 N xˆλdx = 0 (7.25) 0 W p = F zi ŵ i + l 0 [ Qz q z (x) ŵdx + ŵ+ M ] y ˆϕ y Kirjutagem lahti avaldistes (7.25) ja (7.26) esinevad rajaväärtused l l 0 M y ˆψy dx = 0 (7.26) 0 N x û b a= N xb û b N xa û a (7.27) [ Qz ŵ+ M ] y ˆϕ y b a= Q zb ŵ b + M yb ˆϕ yb Q za ŵ a M ya ˆϕ ya (7.28) Tugede siirete mõju arvestamisel võetakse kasutusele II märgikokkulepe. See kokkulepe avaldub toe siirde ja toereaktsiooni korrutises, vt R. Räämet [Rää75] lk 335: Korrutis c j r jk on positiivne, kui paigutise ja reaktsiooni suunad ühtivad, ja negatiivne, kui nad on vastassuunalised. Võtame kasutusele parema käe teljestiku (joonis A.1). Seome x-telje varda teljega nii, et x-telg on suunatud varda algusest A lõppu B. Võtame kasutusele II märgikokkuleppe, mille puhul varda lõpus olevate rajajõudude suunad langevad kokku I märgikokkulepes kasutusel olevate suundadega. Varda alguses olevate rajajõudude suunad on vastupidised I märgikokkulepes kasutusel olevate suundadega. Seega langevad varda alguses olevad rajajõudude suunad kokku varda lõpus olevate rajajõudude suundadega. Selgituse kohaselt võtame avaldistes (7.25) ja (7.26) kasutusele 3 John William Rayleigh, inglise füüsik, , a Nobeli preemia.
101 7.8. SIIRDED TEMPERATUURI MUUTUSEST 101 järgmised tähised: F xi û i,, 1 i u i N x ˆλ n i Np EA N x û a C a (N) u a N x û b C (N) b u b F zi ŵ i,, 1 i w i M y ˆψ y m i Mp EI M y ˆϕ y a C a (My) ϕ a M y ˆϕ y b C (My) ϕ b Q z ŵ a C a (Qz) w a Q z ŵ b C (Q Z) b w b b (7.29) Üldistatud ühikjõu,, 1 i rakendamisel q x (x) = 0 ja q z (x) = 0. Koormuse põhjustatud tasakaaluolukorra,, p arvutusskeemis tekkivad sisejõud N p, Q p, M p ja siire leitakse üldistatud ühikjõu,, 1 i sihis järgmiste avaldistega: b,, 1 N p i u i = n i dx C(N) b u b C a (N) u a (7.30) a EA b,, 1 i w i = a M p m i dx C(Qz) b w b C a (Qz) w a C (My) b ϕ b C a (My) ϕ a (7.31) EI Siin on ühikjõust,, 1 i põhjustatud rajajõudude (kontaktjõudude,, C contact force [KW90]) C a (N), C (N) b, C a (Qz), C (Qz) b, C a (My) ϕ a, C a (My) ϕ b ja toe siirete u a, u b, w a, w b, ϕ a, ϕ b korrutised positiivsed siis, kui nende suunad ühtivad. 7.8 Siirded temperatuuri muutusest Joonisel 7.6 on vardast eraldatud elementaarlõik pikkusega dx. Temperatuuri muutust z-telje positiivsel poolel tähistame T (+) ja z-telje negatiivsel poolel T ( ). Temperatuuri tõusmisel varda elementaarlõigu ülemised ja alumised kiud pikenevad α T T (+) dx ja α T T ( ) dx. Varda elementaarlõigu pikenemine λ = α T T 0 (7.32) kus α T on materjali joonpaisumistegur. Näiteks ehitusterasel (St 37) α T = K 1. Kui ristlõige on mõlema peatelje suhtes sümmeetriline, siis arvutatakse temperatuuri muut telgjoonel valemiga T 0 = 1 2 ( T(+) + T ( ) ) (7.33)
102 102 PEATÜKK 7. SIIRETE ARVUTUS z x h dx T o soojem Ψ y dx T külmem soojem Pikkeprinkus λ = d Λ = α T dx T o Paindeprinkus d Ψ dx y T Ψ y = = α T h Joonis 7.6. Prinkused temperatuuri muutusest Kui aga ristlõige ei ole peatelje suhtes sümmeetriline, siis arvutatakse temperatuuri muut telgjoonel järgmise avaldisega: T 0 = 1 ( ) hülemine T (+) + h alumine T ( ) (7.34) h kus hülemine ja h alumine on tala ristlõike ülemiste ja alumiste kiudude kaugused varda telgjoonest. Ülemiste ja alumiste kiudude erinevast temperatuuri muutusest tingitud varda kõverdumist nimetatakse temperatuuri mitteühtlasest muutusest põhjustatud prinkuseks ψ y siin 1 ψ y = α T T (7.35) h T = ( T (+) T (+) ) (7.36) Temperatuuri muutusest põhjustatud siirete arvutamiseks asendame valemites (7.25), (7.26) ˆλ ja ˆψ y avaldistega (7.32), (7.35). Koormusest põhjustatud siirete arvutamiseks valemitest (7.30), (7.31) saab järgmised temperatuuri muutusest põhjustatud siirete arvutamise avaldised: b,, 1 i w i = a,, 1 i u i = b a n i α T T 0 dx C (N) b u b C (N) a u a (7.37) 1 m i α T T dx C(Qz) b w b C a (Qz) w a C (My) b h Avaldises (7.37) esineva integraali märk sõltub sisejõu n i ja temperatuurist põhjustatud pikkeprinkuse α T T 0 märkidest. Kui sisejõud n i ja α T T 0 on ühemärgilised, siis on integraali märk positiivne. Avaldises (7.38) esineva integraali märgi võib määrata ka varda deformeerunud kuju ϕ b C (My) a ϕ a (7.38) järgi: kui ühikjõust põhjustatud kõverus mn i ja temperatuuri mitteühtlasest muutusest EI 1 põhjustatud kõverus α T T on ühesuunalised, siis on korrutis positiivne vastupidisel h juhul negatiivne. Viimase kõveruse hindamisel arvestame, missugused kiud pikenevad ja missugused lühenevad.
103 7.9. NUMBRILINE INTEGREERIMINE Numbriline integreerimine Paljude varraskonstruktsiooni ülesannete lahendamisel tuleb arvutada siirdeid. Sirgetest varrastest koosneva konstruktsiooni elementide siirded leitakse valemitega (7.30) ja (7.31), milles on piki- ja paindemomentide integraalid. Vaatleme nende integraalide M numbrilist integreerimist. Kasutame lühiduse mõttes järgmist tähistust m p i f (x). EI Seega vaatleme integraali b a f (x) dx numbrilist integreerimist. a) b) a c b a c M a M b M a M c l/2 l/2 l M c l/2 l/2 l M b b a m a c m c b m b m a a m c c b m b Joonis 7.7. Märgikokkulepped Simpsoni valem Simpsoni 4 valemi puhul jagame pideva funktsiooni f (x) integreerimisel lõigu [a, b] pikkusega l poolels (l/2 ja l/2 ) ja saame b f (x) dx = l [f (a) + 4 f (c) + f (b)] (7.39) a 6 kus f (a) funktsiooni väärtus lõigu alguses, f (c) funktsiooni väärtus lõigu keskel, f (b) funktsiooni väärtus lõigu lõpus. Simpsoni valem (7.39) annab täpse tulemuse kuni kuuppolünoomini. Simpsoni valemi (7.39) kuju integreerimisvahemiku a-b paarisarvuliseks n võrdseks osaks jagamisel s = l/n b f (s) ds s a 3 [f f f f f f n f n 1 + f n ] (7.40) Joonisel 7.7 a on koormusest põhjustatud epüüri M p ja ühikjõust põhjustatud epüüri m i ordinaadid ühesuguste märkidega. Joonisel 7.7 b on epüüridel M p ja m i otstes erinevad märgid. Siirete arvutamiseks rakendame Simpsoni valemit (7.39) b a m i Mp EI dx = l 6 4 T. Simpson sai selle valemi aastal. [ m a M a M c ] M b EI + 4 m c EI + m b EI (7.41)
104 104 PEATÜKK 7. SIIRETE ARVUTUS M Valemis (7.41) on korrutised m a a, m EI c Mc ja m EI b M b positiivsed, kui ühikjõust ja koormusest põhjustatud epüüride ordinaadid on varda samal poolel, ja negatiivsed, kui epüüride EI ordinaadid on vastupidiste märkidega. Näiteks joonisel 7.7 b on lõigu algul (punktis a) ja lõpus (punktis b) epüüride ordinaatide korrutis negatiivne, kuna ordinaadid on suunatud eri poole. Lõigu keskel (punktis c) on epüüride ordinaatide korrutis positiivne. Simpsoni valemiga (7.41) saab täpse tulemuse lineaarsete epüüride korrutise, lineaarsete ja ruutparaboolse epüüri korrutise korral. Kõrgemat järku epüüride korrutise puhul tuleb kasutada 3/8 valemit (7.47). Numbrilisel integreerimisel Simpsoni valemiga (7.41) kasutame arvutusprogrammi Octave. Vekrorite a (7.42) ja b (7.43) korrutamiseks kasutame elememt-element korrutamist (vt paragrahvi B.5 avaldist (B.24) lk 201). Korrutamise tulemus on näidatud avaldisega (7.44) a = [m a m c m b ] (7.42) b = [M a M c M b ] (7.43) a. b = [m a M a m c M c m b M b ] (7.44) Võtame kasutusele Simpsoni valemi kordajaid sisaldava vektori smps, mille transponeeritud kuju on toodod avaldisega (7.45) smps = 1 6 [ l EI 4 l EI ] l EI (7.45) Element-element korrutamisega saadud tulemuse (7.44) korrutame skalaarselt (vt avaldist B.14 lk 199) vektoriga (7.45). Tulemuseks on Simpsoni valem (7.41). a. b smps = 1 6 [m a M a m c M c m b M b ] Simpsoni 3/8 valem = l [ ] M a m a 6 EI + 4 m M c c EI + m M b b EI l EI 4 l EI l EI = (7.46) Simpsoni 3/8 valemit kasutades jagame pideva funktsiooni f (x) integreerimisel lõigu [a, b] pikkusega l kolmeks (l/3, l/3 ja l/3 ) ja saame b a f (x) dx = l [f (a) + 3 f (c) + 3 f (d) + f (b)] (7.47) 8 kus f (a) funktsiooni väärtus lõigu alguses, f (c) funktsiooni väärtus 1 lõigul [a, b], 3 f (d) funktsiooni väärtus 2 lõigul [a, b], 3 f (b) funktsiooni väärtus lõigu lõpus.
105 7.9. NUMBRILINE INTEGREERIMINE Vereštšagini võte Vereštšagini 5 võte integraali arvutamisel, kui EI = konst ja üks epüüridest on lineaarne. Joonisel 7.8 on ühikjõust põhjustatud paindemomendi epüür lineaarne ja tema ordinaadi O* z c raskuskeskme kohal olev ordinaat (lineaarses epüüris) Ω epüüri pindala x dx a b Ω M p x c O z c x c z = = tan x α α a b z z c m i Joonis 7.8. Vereštšagini võte m i saab avaldada m i = z = x tanα. Siirde valemi integraali teisendame kujule ip = b Epüüri M p staatiline moment telje OO suhtes a M p tanα b m i dx = x M p dx (7.48) EI EI a Ω x c = b a x M p dx (7.49) Siirde valemi integraalis (7.48) asendame b a x M pdx avaldisega (7.49). Jooniselt 7.8 näeme, et x c tanα = z c, kus viimane on koormusest põhjustatud paindemomendi epüüri pindala Ω raskuskeskme kohal olev ordinaat z c teises lineaarselt muutuvas epüüris. Eelnenut arvesse võttes avaldub siirde valemi integraal (7.48) järgmiselt: ip = Ω x c 1 EI (7.50) Seega on paindemomendi epüüride m i, M p ordinaatide korrutise integraal lõigul [a, b] võrdne korrutisega, mille üheks teguriks on epüüri pindala ja teiseks teguriks epüüri pindala raskuskeskme kohal olev ordinaat teises lineaarselt muutuvas epüüris. Korrutis Ω z c on positiivne, kui koormusest põhjustatud paindemomendi epüür M p ja ordinaat z c on sama märgiga. Joonisel 7.9 on näidatud lihtsate epüüride pindalad ja nende raskuskeskmete kaugused. Epüüri raskuskeskme arvutamise asemel on lihtsam kasutada Simpsoni valemit. 5 A. N. Vereštšagin, Moskva Raudteetranspordi Inseneride Instituudi üliõpilane, esitas selle valemi aastal.
106 106 PEATÜKK 7. SIIRETE ARVUTUS Siirete arvutamise näited Näide 7.1 Vaatleme siirete arvutust 1) koormusest, 2) temperatuuri muutusest, 3) tugede siiretest (näide on võetud raamatust [Rää75] lk 346). Arvutada joonisel 7.10 a) kujutatud murtud varda arvutusskeemi ristlõike c vertikaalsiire, toeristlõike a horisontaalsiire ja toeristlõike b pööre 1) koormusest, 2) temperatuuri muutusest, 3) tugede siiretest. Temperatuur tõuseb sisepoolel 10 o C ja välispool vasakul ning üleval 20 o C ja paremal 10 o C võrra. Varraste ristlõiked on sümmeetrilised, ristlõigete inertsimomendid I 1 = I 3 = I ja I 2 = 2I ning ristlõigete kõrgused h 1 = h 3 = 50 cm ja h 2 = 60 cm. Joonpaisumistegur α = Tugi a vajub a z = 2 cm ja tugi b b z = 1 cm ning nihkub vasakult paremale b x = 0.5 cm võrra. Koormusest põhjustatud paindemomendi epüür on joonisel 7.10 b. Ristlõike c vertikaalsiirde arvutamiseks rakendatakse sinna ühikjõudu. Ühikjõust põhjustatud paindemomendi epüür on joonisel 7.10 c. Vertikaalsiirde w cp arvutamiseks vaatleme epüüri M p (joonis 7.10 b) ja epüüri m c (joonis 7.10 c). Määrame integreerimisrajad (korrutisel m c M p ei tohi vaadeldaval lõigul olla murdepunkte). w cp = d c M c p m c E2I dx + e M p m c dx (7.51) E2I Avaldise (7.51) mõlemad integraalid arvutame Simpsoni valemi (7.41) järgi w cp = 3.0 [ ] + 6E2I [ ] = 6E2I = cm (7.52) EI EI Ristlõikesse a rakendatud horisontaalsest ühikjõust põhjustatud paindemomendi epüür on joonisel 7.10 d). Toeristlõike a horisontaalsiirde arvutamiseks vaatleme epüüri M p (joonis 7.10 b) Epüüri kuju Epüüri pindala Raskuskeskme kaugus l l/2 h l*h 1/2 l l l/3 h 1/2 l*h 1/3 l l l/4 h 1/3 l*h 1/4 l 5/8 l l h 2/3 l*h 5/8 l Joonis 7.9. Epüüride pindalad
107 & & & & & & & & & & & & & & & D D ' ' ' ' ' ' ' ' ' ' ' ' ' ' ( ( ( ( ( ( ( ( ( ( ( ( ( ( ( S S > 8 ) ) ) ) ) ) ) ) ) ) ) ) ) ) * * * * * * * * * * * * * * * J J 3 H 7.9. NUMBRILINE INTEGREERIMINE 107 a) 4 m 20 kn/m o C 20 o C d 2 c 2I I 10 kn k 10 o C 1 a 3 m 3 m 2 m e I 3 b 10 o C b) c d e k 20.0 a M p [kn/m] b H = 10 kn b V a = kn V b = kn f) 0.5 c) 1 d) 4 4 e) c 4 4 d e d c e d NNN k k PP 2 k m c [m] m d [m] m b [ ] a b B B C C 1 6 a b 7 1!!!!!!!!!!!!!!! """"""""""""""" 1 c e $$$$$$$$$$$$$$$$$$$$$$$ /6 1/6 g) ####################### $$$$$$$$$$$$$$$$$$$$$$$ j) d c e 0.5 d c e 1/6 d c e k a : : k k n c [ ] n d [ ] n b [1/m] b a b 1.0 a F F b G a 1 1/6 b /6 1/6 Joonis Siirete arvutus ja epüüri m d (joonis 7.10 d. Määrame integreerimisrajad (korrutisel m d M p ei tohi vaadeldaval lõigul olla murdepunkte). u ap = k d M d p m d EI dx + M c p m d E2I dx + M e p m d E2I dx + c e b M p m d dx (7.53) E2I Avaldise (7.53) esimesed kaks integraali arvutame Simpsoni valemi (7.41) järgi. Viimase kahe integraali arvutamiseks kasutame Vereštšagini võtet (7.50). u ap = 2.0 [ ] + 6EI E2I [ ] + ( ) ( ) (12.5 3) 4 + E2I EI = EI m (7.54) Toeristlõikesse b rakendatud ühikmomendist põhjustatud paindemomendi epüür on joonisel 7.10 e. Määrame integreerimisrajad (korrutisel m e M p ei tohi vaadeldaval lõigul olla murdepunkte). ϕ bp = c d M e p m e EI dx + M d p m e E2I dx + c e M p m e dx (7.55) E2I
108 108 PEATÜKK 7. SIIRETE ARVUTUS Avaldise (7.55) esimesed kaks integraali arvutame Simpsoni valemi (7.41) järgi. Viimase integraali arvutamiseks kasutame Vereštšagini võtet (7.50). ϕ bp = 3.0 [ ] + 6E2I [ ] + 6E2I ( ) = EI = rad 90.6 rad (7.56) EI EI Sümmeetriliste ristlõigetega varraste puhul arvutatakse temperatuuri muutus varda telgjoonel valemiga (7.33) T 01 = 1 ) (T 2 (+) + T ( ) = 1 2 ( ) = 15 o C (7.57) T 02 = T 01 = 15 o C (7.58) T 03 = 1 2 ( ) = 10 o C (7.59) Temperatuuri muutused varraste alumiste ja ülemiste kiudude vahel on järgmised (7.36): ) T 1 = T 2 = (T (+) T (+) = = 10 o C (7.60) T 3 = = 0 o C (7.61) Siirded temperatuuri muutusest arvutatakse valemitega (7.37), (7.38) it = b a n i α T T 0 dx + b Ristlõike c vertikaalsiire temperatuuri muutusest w ct = [15 ( 5 1 ) 2 4 [ a 1 m i α T T dx (7.62) h ( 1 )] 2 4 ] = m = 1.5 mm (7.63) Toeristlõike a horisontaalsiire temperatuuri muutusest u at = [15 (0 4) + 15 ( 1 6) + 10 (0 4)] + [ ( ) + 10 ] 0 ( 4 6.0) (4 4.0) = = m = 5.64 mm (7.64) Toeristlõike b pööre temperatuuri muutusest ( ) 1 ϕ bt = [ [ ( 0.6 = + ] + 15 (0 6) + 10 (0 4) ) ( 1 4.0) ] = = rad = rad (7.65)
109 7.9. NUMBRILINE INTEGREERIMINE 109 Siirded tugede nihkumisest arvutatakse valemitega (7.30), (7.31) ic = C (N) b C (Qz) b u b C (N) a w b C (Qz) a u a w a C (My) b ϕ b C (My) a ϕ a (7.66) w cr = ( ) = 1.5 cm (7.67) u ar = ( 0.5 1) = 0.5 cm (7.68) ( ϕ cr = ) = 1 rad (7.69) Näide 7.2 Vaatleme eelmist näidet 7.1. Teostame arvutused arvutiprogrammiga Octave (vt lõik C.5 programm C.13 lk 251). Numbrilisel integreerimisel kasutame Simpsoni valemit (7.46 lk 104). Moodustame ühikepüüridest (vt joonist 7.10 c, d ja e) maatriksi Mx ja koormusest põhjustatud paindemomendi epüürist maatriksi Mp Mx = ; post 1 (pool postist 1)... post 1 (pool postist 1)... riiv (pool riivist)... riiv (pool riivist)... post 2 Mp = (7.70) Võtame kasutusele Simpsoni valemi kordajaid sisaldava vektori smps ja varda telgjoonel tem-
110 110 PEATÜKK 7. SIIRETE ARVUTUS peratuuri kirjeldava vektori T o, mille transponeeritud kuju on toodod avaldisega (7.71) smps = 1 6 h2/i2 4 h2/i2 h2/i2... h2/i2 4 h2/i2 h2/i2... L05/I1 4 L05/I1 L05/I1... L05/I1 4 L05/I1 L05/I1... h2/i2 4 h2/i2 h2/i2 post 1 (pool postist 1)... post 1 (pool postist 1)... riiv (pool riivist)... riiv (pool riivist)... post 2 ; T o = (7.71) siin h = 4; h2 = h/2; L = 6; L05 = L/2; I1 = 2; I2 = 1; Simpsoni valemi abil pindalat integreerides ei ole vaja ristlõike inertsimomente I1, I2. Järgnevalt avaldame simpsoni valemi kordajaid sisaldava vektori smps0 (7.72) smps0 = 1 6 h2 } 4 {{ h2 h2} pool posti 1 } L05 4 {{ L05 L05} pool riivi h2 } 4 {{ h2 h2} pool posti 1 L05 } 4 {{ L05 L05} pool riivi h} 4{{ h h} post 2 (7.72) Ühikjõust põhjustatud normaaljõu epüüridest (vt joonis 7.10 f, g ja j) moodustame maatriksi Nx ja temperatuuri muutusi alumiste ja ülemiste kiudude vahel kirjeldava vektori Tp (7.73)
111 7.9. NUMBRILINE INTEGREERIMINE 111 (paine temperatuurist) / / / / / / Nx = ; / / /6 post 1 (pool postist 1)... post 1 (pool postist 1)... riiv (pool riivist)... riiv (pool riivist)... post 2 Tp = 10 \ Hpost 10 \ Hpost 10 \ Hpost \ Hpost 10 \ Hpost 10 \ Hpost \ Hriiv 10 \ Hriiv 10 \ Hriiv \ Hriiv 10 \ Hriiv 10 \ Hriiv... 0 \ Hpost 0 \ Hpost 0 \ Hpost (7.73) siin Hpost posti ristlõike kõrgus, Hriiv riivi ristlõike kõrgus. Vekrorite Mx (7.70) ja Mp (7.70) korrutamiseks kasutame element-element korrutamist (vt paragrahvi B.5 avaldist (B.24) lk 201). Tulemuse korrutame veel vektoriga smps (7.71) W = Mx. [ Mp ; Mp ; Mp ] smps = (7.74) Saadud tulemus langeb kokku avaldistega (7.52), (7.54) ja (7.56). Siirete arvutamiseks temperatuurist transponeerime ning korrutame Tp ja To avaldised (7.73) ja (7.71) joonpaisumisteguriga (talpha = ) läbi. Korrutame epüürid temperatuuri ja temperatuuri erinevustega Leiame siirded temperatuurist TpT = talpha Tp (7.75) ToT = talpha To (7.76) MxTTp = Mx. [TpT; TpT; TpT] (7.77) NxTTo = Nx. [ToT; ToT; ToT] (7.78) WT = MxTTp smps0 + NxTTo smps0 = Leitud tulemus (7.79) ühtib tulemustega (7.63), (7.64) ja (7.65) e e e 04 (7.79)
112 112 PEATÜKK 7. SIIRETE ARVUTUS
113 Osa II Staatiliselt määramatud süsteemid 113
114
115 Peatükk 8 Staatikaga määramatute konstruktsioonide arvutus 8.1 Staatikaga määramatu konstruktsioon Konstruktsiooni arvutusskeem on staatikaga määramatu, kui kõik sisejõud ja toereaktsioonid ei ole arvutatavad ainult tasakaaluvõrranditest. Staatikaga määramatu konstruktsiooni arvutamisel esineb kahte liiki tundmatuid. a ) b ) c ) d ) Φ 1 C 4 W 1 w ϕ 1 1 ϕ 1 F = 3 kn q = 1 kn/m M1 M2v M2p M3 Q Q Q Q 1 1 e ) 1 1 ϕ 2v wv2 2v ϕ 2v w2p w 3 M1 M2v Qv2 M2p M3 Q Q 1 2p 3 1 C C C3 1 2 wv2 w 2p ϕ 2p w 3 W Joonis 8.1. Tundmatud ja võrrandid 2 ϕ 2p 2p ϕ 3 3 ϕ 3 3 W 3 Joonisel 8.1 a on näidatud tala, mille sisejõudude ja toereaktsioonide leidmiseks ei piisa staatika tasakaaluvõrranditest. Tundmatute arv n n = 8 n varras + n tugi ; (8 = 4 jõudu + 4 siiret ) kus n varras varraste arv; n tugi toereaktsioonide arv. Tasakaalu- ja siirdevõrrandid n varda tasakaalu = 2 n varras n varda siire = 2 n varras n sõlme tasakaalu = 2 n sõlm n sõlme siire = 2 n sõlm Toetingimused on võrrandites: n sõlme tasakaalu sisaldab võrrandit M 3 = 0; n sõlme siire sisaldab nelja võrrandit ϕ 1 = 0, w 1 = 0, w 2 = 0, w 3 = 0. Ülejäänud kaks n sõlme siire siirdevõrrandit seovad sõlmes 2 siirded ja pöörded. Varraste otstes esinevaid rajajõude ehk kontaktjõude (vahel lihtsuse mõttes nime- 115
116 116PEATÜKK 8. STAATIKAGA MÄÄRAMATUTE KONSTRUKTSIOONIDE ARVUTUS tatakse neid ka sisejõududeks vt [Rää75] lk 369) ja toereaktsioone nimetatakse staatikalisteks tundmatuteks (staatikalisteks rajatingimusteks). Varraste otstes esinevaid rajasiirdeid nimetatakse kinemaatilisteks tundmatuteks (kinemaatilisteks rajatingimusteks). Nüüdisaegne arvutustehnika võimaldab neid tundmatuid arvutada ühel ajal. Üheks selliseks meetodiks on rajaelementide meetod (REM) [Har87]. Täpse lahendi rajajõududele ja rajasiiretele saab EST meetodiga [Lah97a], [Lah97b], [Lah98a], [Lah98b]. Suurte hõredate mittesümmeetriliste võrrandisüsteemide lahendamiseks on loodud häid meetodeid. Kui kõiki tundmatuid ei arvutata ühel ajal, koostatakse võrrandisüsteem esialgu leitavatele tundmatutele ehk lisatundmatutele. Ülejäänud teised tundmatud arvutatakse koormuse ja lisatundmatute funktsioonidena. Sõltuvalt sellest, missugused tundmatud võetakse lisatundmatuteks, jagatakse arvutusmeetodid järgmiselt: Jõumeetodi puhul valitakse lisatundmatuteks varraste otstes olevad rajajõud. Lisatundmatute leidmiseks koostatakse võrrandisüsteem geomeetriliste pidevustingimuste alusel. Siirde- ehk deformatsioonimeetodi puhul valitakse lisatundmatuteks raami sõlmede siirded. Kinemaatiliste lisatundmatute leidmiseks koostatakse võrrandisüsteem sõlmede tasakaalutingimuste alusel. Segameetodi puhul võetakse lisatundmatuteks osalt siirded ja osalt jõud. Tervikmeetodi (ingl Integrity Method) puhul koostatakse võrrandisüsteem kõigi tundmatute kohta (ei tehta vahet lisatundmatute ja ülejäänud tundmatute vahel) korraga. Staatiliselt määramatute konstruktsioonide üheks iseloomulikumaks iseärasuseks on see, et nende sisejõudude jaotus oleneb varraste ristlõike jäikusest. Tugede siirded ja ka temperatuuri muutus kutsuvad esile sisejõude. 8.2 Staatikaga määramatute konstruktsioonide omadused Loetelu on võetud raamatust [Rää75]. 1. Staatikaga määramatul konstruktsioonil on lõpmata palju lahendeid, mis rahuldavad tasakaalutingimusi, kuid ainult üks neist rahuldab ka deformatsioonide pidevuse tingimusi. 2. Staatikaga määramatul konstruktsioonil on liigsidemeid. Liigside on niisugune element, mille eemaldamisel ülejäänud konstruktsiooniosa on ikka geomeetriliselt muutumatu.
117 8.2. STAATIKAGA MÄÄRAMATUTE KONSTRUKTSIOONIDE OMADUSED Tingimata vajalikes sidemetes on sisejõud leitavad tasakaalutingimustega. Tingimata vajaliku sideme eemaldamisel muutub osa konstruktsioonist geomeetriliselt muutuvaks. 4. Temperatuuri muutus, tugede siirded ja konstruktsiooni elementide mõõtmete ebatäpsus võib põhjustada staatikaga määramatus konstruktsioonis sisejõudusid. Tingimata vajalikes sidemetes need mõjud sisejõudusid ei põhjusta. 5. Staatikaga määramatu konstruktsiooni sisejõud olenevad varraste jäikusest. 6. Staatikaga määramatus konstruktsioonis võivad esineda pinged ka ilma koormuseta. Neid pingeid nimetatakse eelpingeteks.
118 118PEATÜKK 8. STAATIKAGA MÄÄRAMATUTE KONSTRUKTSIOONIDE ARVUTUS
119 Peatükk 9 Jõumeetod Konstruktsiooni varraste arv v (vt joonis 9.1) koosneb kolmest osast. v = v 6 + v 5 + v 4 (9.1) kus v 6 on mõlemast otsast jäigalt kinnitatud varraste arv, v 5 ühest otsast jäigalt ja teises otsas liigendiga kinnitatud varraste arv, v 4 mõlemast otsast liigendiga kinnitatud varras. Varraste otstes olevad rajajõud koos toereaktsioonidega on a ) d e f b ) d s s 3 2 s2 e f k a b c a t = 2 b c c ) a v 5 v 5 d e e f e v 4 k v 6 v 5 b c vardaid v 4 = 1 v 5 = 3 v 6 = 1 v = 5 sõlmi (jäikade sõlmede arv ei sisalda toesõlmi) s 2 = 3 s 3 = 1 s = 4 sõlmede tundmatud 3s 3 + 2s 2 t varraste tundmatud 6v 6 + 5v 5 +4v + t 4 Joonis 9.1. Tundmatute üldarv siin on t liigendtugede toesidemete arv. Konstruktsiooni sõlmede arv s 6 v v v 4 + t (9.2) s = s 3 + s 2 (9.3) 119
120 120 PEATÜKK 9. JÕUMEETOD kus s 2 on liigendsõlmede arv ja s 3 jäikade sõlmede arv, mis ei sisalda jäikasid toesõlmi. Varraste ja sõlmede kohta saab kirjutada 3 v + 3 s s 2 (9.4) tasakaaluvõrrandit. Lisatundmatute arv n on võrdne staatikaliste tundmatute üldarvu (9.2) ja tasakaaluvõrrandite (9.4) arvu vahega n = 6 v v v 4 + t 3 v 3 s 3 2 s 2 (9.5) mida nimetatakse staatilise määramatuse astmeks. Kui asetada avaldisse (9.5) varraste üldarv v (9.1), saab n = 3 v v 5 + v 4 + t 3 s 3 2 s 2 (9.6) Valemis (9.6) tähistab t ainult liigendtugede toesidemete arvu. Ülesannet nimetatakse n-kordselt staatikaga määramatuks. 9.1 Raamid Staatikalise määramatuse aste Avaldis (9.6) kehtib kõigi varrastest moodustatud konstruktsioonide kohta. Raamide staatikalise määramatuse astet saab arvutada lihtsamate valemitega. Kui konstruktsioonis on nii liigendita kui ka liigenditega suletud kontuure, siis saab staatikalise määramatuse astet arvutada valemiga (9.7) n = 3 m 1 l 1 (9.7) siin on m 1 suletud (nii liigendita kui ka liigenditega) kontuuride arv, l 1 lihtliigendite arv. Näiteks raamil (joonis 9.1 a) on suletud kontuuride arv m 1 = 2 ja lihtliigendeid l 1 = 3. Seega on staatilise määramatuse aste n n = 3 m 1 l 1 = = 3 (9.8) kolm. Joonisel 9.2 näidatud raamil on 8 kinnist kontuuri ja 20 lihtliigendit. n = 3 m 1 l 1 = = 4 (9.9) Lihtliigendite arv on ühe võrra väiksem selles liigendis kinnitatud kehade arvust. Näiteks on joonisel 9.2 all vasakus nurgas üks lihtliigend (kinnitatud üks jäik nurk ja toe varras). Samal joonisel üleval keskel olevas liigendis on ühendatud neli keha (varrast) ja lihtliigendite arv on kolm.
121 9.1. RAAMID lihtliigendit II III 8 kinnist kontuuri 3 I kontuur 3 20 lihtliigendit n = 3*8 20 = 4 IV V VI VII lihtliigend VIII Joonis 9.2. Kinnised kontuurid ja lihtliigendid Põhiskeem ja lisatundmatud Staatikaga määramatust raamist saadakse liigsidemete eemaldamisel staatikaga määratav raam. Selliselt saadud uut staatikaga määratavat skeemi nimetatakse põhiskeemiks. Jõumeetodi puhul on eemaldatud sidemete asemel rakendatud jõud lisatundmatuteks. Liigsidemeteks võib valida sidemed, mille eemaldamisel skeem ei ole geomeetriliselt muutuv (vt joonis 9.3 a ja b) või hetkmuutuv (joonis 9.3 c). a) d e f b) d e f c) d e f a b c a b c a b c Joonis 9.3. Geomeetriliselt ja hetkmuutuvad skeemid Võrrandid lisatundmatute arvutamiseks Lisatundmatute X i leidmiseks koostatakse võrrandid staatikaga määramatu skeemi siirete pidevustingimuste alusel. Arvutusskeemi suvalise punkti siire arvutatakse jõudude sõltumatuse printsiibi alusel. k = δ k1 X 1 + δ k2 X δ kn X n + k0 (9.10) kus k0 on ristlõike k siire koormusest, temperatuurist ja tugede vajumisest põhjustatud siire põhiskeemis; δ ki on ristlõike k siire lisatundmatust X i = 1. Kui arvutusskeem on n korda staatikaga määramatu, siis koostatakse n võrrandit: 1 = δ 11 X 1 + δ 12 X δ 1n X n = δ 21 X 1 + δ 22 X δ 2n X n k = δ k1 X 1 + δ k2 X δ kn X n + k n = δ n1 X 1 + δ n2 X δ nn X n + n0 (9.11)
122 122 PEATÜKK 9. JÕUMEETOD ehk k = δ ki X i + k0 (k, i = 1, 2,..., n) (9.12) Võrrandisüsteemi (9.12) nimetatakse jõumeetodi kanooniliseks võrrandisüsteemiks. Võrrandisüsteemi (9.11),(9.12) kordajad δ ij ja i0 leitakse valemitega δ ij = l j 0 ip = l j 0 ( mi m j ( EI mi Mp 0 EI + n in j EA + n in 0 p EA + k j q ) iq j dx EA + k q i Q 0 p j EA it = ( ) l j 0 α tj j h j m i + t 0j n i dx ir = c j r ji i0 = ip + it + ir ) dx (9.13) kus α j varda j materjali temperatuuri-joonpaisumistegur; k j tegur, mis arvestab nihkepindete ebaühtlast jaotumist varda j ristlõikes, näiteks ristkülikulise ristlõike puhul k j = 1.2. Võrrandisüsteemi (9.11),(9.12) kordajad δ ij ja i0 leidmiseks kasutame numbrilist integreerimist (vt näidet (9.1) ja programmi C.14 lk 255) Raami arvutamise näited Näide 9.1 Koostada joonisel 9.4 a näidatud raamile paindemomendi epüür, kasutades arvutusprogrammi Octave (programm C.14 lk 255). Raami kõrgus h = 4 m ja avad l = 6 m. Raami riivile d-e on rakendatud ühtlaselt jaotatud koormus q = 8 kn/m ja posti b-e keskele koondatud jõud F = 10 kn. Raami postide ristlõike jäikus I 2 = I ja riivide ristlõike jäikus I 1 = 2I. a) d 8 kn/m e 2I I 2I f b) d X 1 e X 3 f I 10 kn k I h = 4 m X 3 X 1 a b 2 m 6 m 6 m c a b Põhiskeem X 2 c Joonis 9.4. Raam ja põhiskeemi Joonisel 9.4 b on näidatud valitud põhiskeem. Selle põhiskeemile vastavad ühikjõududest ja koormusest põhjustatud momendid on näidatud joonisel 9.5. Jõumeetodi kanoonilise võrrandisüsteemi koostamiseks ja lahendamiseks arvutusprogrammiga Octave (programm C.14 lk 255) esitame ühikjõududest ja koormusest põhjustatud momendid maatriksitena Mx ja M p (vt avaldised (9.14) ja (9.15)). Nendes sõltub avaldistes elementide arv integreerimispiirkondade arvust (kasutame Simpsoni valemit (7.41), kus on momendi väärtused alguses, keskel ja lõpus). Raami varras, millel on koondatud jõud, on jagatud punktis k kaheks. Vaatleme põhiskeemi epüüre joonisel 9.5. Iga varda otsas ja lõpus ning varda d e
123 & & ' ' 9.1. RAAMID 123 d 1 e f d e 1 f 1 a b c a b c m 1 m d e f a b c & & m )* )* '( '( 2 )* )* 1 1 ( ( d e f 36 a b!! c!!!! # $ # $ " " 20 # $ # $ M o p " " Joonis 9.5. Põhiskeemi epüürid keskel tähistame momendid järgmiselt: Momentide märgi võtame kokkuleppeliselt. Jooniselt 9.19 võtame positiivse märgiga väärtused, mis asetsevad punktiirjoonega tähistatud poolel ja kanname maatriksisse (9.15) (vt programm C.14). M = M ad M adk M da... M de M dek M ed... M ek M ekk M ke... M kb M kbk M bk... M fe M fek M ef... M fc M fck M cf ; Mx = m 1 ad m 2 ad m 3 ad m 1 adk m 2 adk m 3 adk m 1 da m 2 da m 3 da m 1 de m 2 de m 3 de m 1 dek m 2 dek m 3 dek m 1 ed m 2 ed m 3 ed m 1 ek m 2 ek m 3 ek m 1 ekk m 2 ekk m 3 ekk m 1 ke m 2 ke m 3 ke m 1 kb m 2 kb m 3 kb m 1 kbk m 2 kbk m 3 kbk m 1 bk m 2 bk m 3 bk m 1 ef m 2 ef m 3 ef m 1 efk m 2 efk m 3 efk m 1 fe m 2 fe m 3 fe m 1 fc m 2 cfc m 3 fc m 1 fck m 2 fck m 3 fck m 1 cf m 2 cf m 3 cf post 1... riiv 1... pool postist 2... ; Mp = pool postist 2... riiv 2... post 3 M o ad M o adk M o da... M o ed M o edk M o de... M o ek M o ekk M o ke... M o kb M o kbk M o bk... M o ef M o efk M o fe... M o fc M o fck M o cf (9.14) Raami varras, millel on koondatud jõud, on jagatud kaheks. Nii tuleb kokku 6 integreerimispiirkonda.
124 124 PEATÜKK 9. JÕUMEETOD Igas piirkonnas on kirjeldatud 3 ordinaati (alguses, keskel, lõpus). Kokku 3x6=18 väärtust igalt epüürilt (ühikepüüridelt => Mx ja Mp0 epüüürilt => Mp). Paremaks jälgimiseks on maatriksites (9.15) integreerimispiirkonnad eraldatud punktiiriga. Mx = ; post 1... riiv 1... pool postist 2... pool postist 2... riiv 2... post 3 Mp = post 1... riiv 1... pool postist 2... pool postist 2... riiv 2... post 3 (9.15) Ühikepüüride korrutamiseks kasutame element-element korrutamist (vt paragrahvi B.5 avaldist (B.24) lk 201). Integreerime numbriliselt Simpsoni valemi (7.41) järgi. Selleks korrutame element-element korrutamisega saadud tulemuse skalaarselt (vt avaldist B.14 lk 199)
125 9.1. RAAMID 125 vektoriga (9.16). smps T = 1 6 siin h = 4; h2 = h/2; L = 6; L05 = L/2; I1 = 2; I2 = 1; Jõumeetodi kanoonilise võrrandisüsteemi ehk h/i2 4 h/i2 h/i2... L/I1 4 L/I1 L/I1... h2/i2 4 h2/i2 h2/i2... h2/i2 4 h2/i2 h2/i2... L/I1 4 L/I1 L/I1... h2/i2 4 h2/i2 h2/i2 δ 11 x 1 δ 12 x 2 δ 13 x 3 δ 21 x 1 δ 22 x 2 δ 23 x 3 δ 31 x 1 δ 32 x 2 δ 33 x 3 = post 1... riiv 1... pool postist 2... pool postist 2... riiv 2... post 3 1p 2p 3p (9.16) (9.17) δ ij x i = ip (i, j = 1, 2, 3) (9.18) koostab ja lahendab arvutiprogramm Octave ise. Saadud lahendit x i (i=1,2,3) kasutame paindemomentide arvutamiseks. Paindemomendid arvutatakse ühikepüüride m 1, m 2, m 3 (joonis 9.5) korrutamisega vastavate x i -dega Võrrandi (9.19) kirjutame maatrikskujule M p = m 1 x 1 + m 2 x 2 + m 3 x 3 + M 0 p (9.19) M = Mx x + Mp (9.20) Saadud tulemuste põhjal koostame (programm C.14) epüüri (joonis 9.6).
126 126 PEATÜKK 9. JÕUMEETOD d e f a b M c [knm] Joonis 9.6. Paindemomendi epüür Octave ga
127 Peatükk 10 Jätkuvtalad Jätkuvtalaks nimetatakse liigenditeta mitmesildelist tala. Tasapinnalise geomeetriliselt muutumatu kujundi kinnitamiseks on vaja kolme toesidet. Jätkuvtalal on toesidemeid rohkem kui kolm, seepärast on ta staatikaga määramatu. Staatilise määramatuse aste leitakse valemiga (10.1) kus t on toesidemete arv 10.1 Põhiskeem ja lisatundmatud n = t 3 (10.1) Põhiskeem ja lisatundmatud tuleb valida nii, et kanoonilise võrrandisüsteemi (10.2) kordajaid oleks lihtne arvutada. δ ij X j + ip = 0, (i, j = 1, 2, 3,..., n) (10.2) Joonisel 10.1 on lisatundmatuteks valitud toemomendid. a) b) X X X X X 1 1 X 2 2 X X Joonis Jätkuvtala põhiskeem 10.2 Kanoonilised võrrandid Valime jätkuvtala (joonis 10.2 a) põhiskeemi nii, et tundmatuteks on toemomendid X i (joonis 10.2 b). Võrrandisüsteemi (10.2) kordajad leiame avaldisega 127
128 ` L V. 8 T T 128 PEATÜKK 10. JÄTKUVTALAD a) i 2 i 1$$$$$$$$$$$$$$$$$ i i+1 """"""""" i+2 X X Z Z \ ^ ^ b) X i 2 X i 2 X i 1 X i 1 X X X X X X i i i+1 i+1 i+2 i+2 c) X i 1 X i 1 d) e) f) D D F F H J J N N OP OP QR S S 1 X i X i 1 X i+1 X i+1 i 2 i 1 i i+1 i+2 & & '( '( )* +, +, 1 m i 1 m i m i+1 M o p g) a i+1 b a b i+1 i i i 2 Ω i 1 i i+1 i 1 Ω i Ω i+1 Ω i+2 i Af i 1 Bf Af i Bf i 1 Af B f i i+1 i+1 Ai+2 f Bf i+2 Joonis Jätkuvtala ühikepüürid δ i j = n l i=1 siin on n varraste arv ja EI ristlõike jäikus. 0 m i m j ds (10.3) EI i p = n l i=1 0 m i M o p EI ds (10.4) Ühikepüüride (joonis 10.2 c, d,e) korrutamisel ja integreerimisel saame järgmised nullist erinevad kordajad δ i j EI o δ i i 1 = 1 1 l ii o 6I i (10.5) EI o δ i i = 1 1 l ii o 3I i l i+1 3I i+1 (10.6)
129 10.3. KOLME MOMENDI VÕRRANDIGA ARVUTAMISE NÄITED 129 EI o δ i i+1 = 1 1 l i+1i o 6I i+1 (10.7) Koormusliikme i p integreerimisel kasutame Vereštšagini võtet lk 105. EI o i p = Ω i 1 a i I o l i I i Toe i kohta koostatud pidevusvõrrand on + Ω i+1 1 b i+1 I o l i+1 I i+1 (10.8)... + δ i i 1 X i 1 + δ i i X i + δ i i+1 X i i p = 0 (10.9) Avaldistes (10.5), (10.6), (10.7) ja (10.8) võtame kasutusele järgmised tähistused l i = l i I 0 I i (10.10) B f i = Ω i a i l i (10.11) A f i+1 = Ω i+1 b i+1 l i+1 (10.12) ning asetame võrrandisse (10.9). Saame kolme momendi võrrandi (10.13) l ix i ( l i + l i+1) Xi + l i+1x i+1 = 6B f i I 0 I 0 6A f i+1 (10.13) I i I i+1 kus l i = l i I 0 Ii, ning A f i+1, B f i on fiktiivsed koormused. Fiktiivsed koormused A f i, B f i on toodud tabelis 10.1 [Rää75]. Ühtlaselt jaotatud koormuse q, ühtlase ristlõike jäikuse (I i = I 0 ) puhul on avaldis (10.14) ning koondatud jõu F k puhul avaldised (10.15) ja (10.16). 6A f i = 6B f i = ql3 i 4 (10.14) 6A f i = F k li 2 ξ k ξ k (1 + ξ k) (10.15) 6B f i = F k l 2 i ξ k ξ k (1 + ξk) (10.16) Siin ξ k = a k li ja ξ k = b k li (vt joonis 10.3) Kolme momendi võrrandiga arvutamise näited Näide 10.1 Arvutada joonisel 10.4 a) esitatud jätkuvtala toemomendid kolme momendi võrrandiga ning kujutada paindemomendi ja põikjõu epüürid. Andmed: l 1 = 8 m, l 2 = 10 m, l 3 = 9 m; F 1 = 20 kn, F 2 = 20 kn, F 3 = 50 kn, F 4 = 40 kn, q = 10 kn/m; EI = konst. Staatikaga määramatuse aste n = 3. Lisatundmatuteks on toemomendid X 1, X 2 ja X 3 (joonis 10.4 b). Näide on võetud raamatust [ERL85]. Kolme momendi võrrandi (10.13) vabaliikmed koondatud jõu puhul leiame avaldistega (10.15) ja (10.16).
130 130 PEATÜKK 10. JÄTKUVTALAD F i 2 i 1 k i i+1 a k ξ k = l i ξ k = bl i k l i 1 l i l i+1 Af i a k ξ k b k ξ k f B i Joonis Jätkuvtala tähised F 1 = 20 kn q = 10 kn/m F 2 = 20 kn F 3 = 50 kn F 4 = 40 kn " " 0 a 1 b c #$ 2 d 2 4 m 4 m 3 m 3 m 4 m 4.5 m 4.5 m 2 l 1 = 8 m l 2 = 10 m l 3 = 9 m X 1 X 2 X l 4 = ,, ' (( ' ( '' ((( '' (( )) ** ((((((((((( ''''''''''' )))) **** ))) *** '''''''' (((((((( ***** )))) ''' ((( M [knm] Q [kn] Joonis Jätkuvtala. Kolme momendi võrrand Ühtlasest koormusest põhjustatud vabaliikmed leiame avaldisega (10.14). Tugede 1, 2 ja 3 kohta koostatud kolme momendi võrrandid on järgmised: l 1 X o + 2 (l 1 + l 2 ) X 1 + l 2 X 2 = 6B f 1 6Af 2 l 2 X (l 2 + l 3 ) X 2 + l 3 X 3 = 6B f 2 6Af 3 + l 3 X 2 + 2l 3 X 3 = 6B f 3 (10.17) kus toemoment X o ja koormusliikmed 6A f i, 6Bf i on X o = F 1 2 = 20 2 = 40 knm
131 10.3. KOLME MOMENDI VÕRRANDIGA ARVUTAMISE NÄITED 131 6B f 1 = ql3 1 4 = = 1280 knm 2 4 6A f 2 = F 2 l2 ξ 2 2 ξ 2 ( 1 + ξ ) 2 + F3 l2 ξ 2 3 ξ 3 ( 1 + ξ ) 3 = = ( ) ( ) = = 2394 knm 2 6B f 2 = F 2 l 2 2 ξ 2 ξ 2 (1 + ξ 2 ) + F 3 l 2 2 ξ 3 ξ 3 (1 + ξ 3 ) = = ( ) ( ) = = 2466 knm 2 6A f 3 = 6B f 3 = ( ) = 1215 knm 2 (10.18) Vabaliikmete arvutamiseks võib kasutada Octave i funktsiooni C.15 lk 258. Funktsiooni afbfikt1.m kasutamist jälgi joonisel Joonis Fiktiivsete koormuste leidmine Pärast toemomendi X o ja vabaliikmete 6A f i, 6Bf i arvväärtuste (10.18) asetamist võrrandisse (10.13) saame järgmise võrrandisüsteemi: ehk X 1 X 2 X 3 = (10.19) A X = B (10.20)
132 132 PEATÜKK 10. JÄTKUVTALAD Joonis Kolme momendi võrrandisüsteemi lahendamine kus A = ; X = X 1 X 2 X 3 ; B = (10.21) Võrrandisüsteemi lahendame arvutiprogrammiga Octave (vt lõik C.1 lk 205). Võrrandisüsteemi (10.19) lahend on X 1 = knm; X 2 = knm; X 3 = knm (10.22) Paindemomendi ja põikjõu epüüri (joonis 10.4) lõigetes a, b, c ja d leiame järgmise avaldistega: M k = Mk o + X i 1 ξ k + X i ξ k (10.23) Q k = Q o k + M (10.24) x kus ξ k ja ξ k on ristlõike k mõõduta kaugused vasakust ja paremast toest (vt joonis 10.3 lk 130). Põikjõu Q k ja M/ x kohta on selgitus joonisel 1.14 (vt lk 30). M a = = knm 8 M b = ( ) = = knm M c = ( ) = = knm M d = = knm (10.25)
133 10.3. KOLME MOMENDI VÕRRANDIGA ARVUTAMISE NÄITED 133 F 1 = 20 kn F 2 = 20 kn F 3 = 50 kn F 4 = 40 kn q = 10 kn/m a m 4 m 3 m 3 m 4 m 4.5 m 4.5 m 2 l 1 = 8 m l 2 = 10 m l 3 = 9 m b c d Q [kn] " " Q = + V 0 = kn V 1 = kn V 2 = kn V 3 = kn Joonis Jätkuvtala. Toereaktsioonid Q 0 1 = 40 + = kn 8 Q 1 0 = = kn 8 Q 1 2 = = kn 10 Q 2 1 = = kn 10 Q 2 3 = = kn 9 Q 3 2 = = kn 9 (10.26) Konsoolis on põikjõud Q (v) a = 20 kn. Jätkuvtala vertikaalsed toereaktsioonid V i (vt joonis 10.7) leiame põikjõu epüüri abil. V 0 = = kn V 1 = = kn V 2 = = kn V 3 = kn (10.27) Kontrollime tasakaalu ΣY = 0; = = 0 (10.28)
134 134 PEATÜKK 10. JÄTKUVTALAD Tabel Valemid vabaliikmete arvutamiseks Jrk. nr Skeem 6 I 0 Ii A f i 6 I 0 Ii B f i 1 F i 1 i ξl ξ l A f i B f i F l i l i ξξ (1 + ξ ) F l i l i ξξ (1 + ξ) q i 1 i 1 A f l i B f i q i 1 5 i A f l/2 l/2 i B f i q i 1 i 7 A f l B f i i 4 ql2 i l i 32 ql2 i l i 60 ql2 i l i 1 4 ql2 i l i 5 32 ql2 i l i 2 15 ql2 i l i 5 q i 1 i 1 ξl ξ l f A i f B i 4 ql2 i l i ξ 2 ( 2 ξ 2) 1 4 ql2 i l i ξ 2 (2 ξ ) 2 6 M i 1 i A f i ξl ξ l B f i Ml i ( 1 3ξ 2 ) Ml i ( 1 3ξ 2 ) 10.4 Jätkuvtalade arvutus fookussuhtega Fookussuhted Jätkuvtala arvutamisel fookussuhtega koormatakse ainult ühte sillet (joonis 10.8). Koormatud sildest kaugemal asetseval toel on toemoment väiksem kui koormatud sildele lähemal asetseval toel. Kuna koormamata silde paindemomendid on erinevate märkidega, siis on igas koormamata sildes paindemomendi epüüris üks nullpunkt. Seda nullpunkti nimetatakse fookuseks. Fookus asub koormatud sildest kaugemal asetsevale toele lähemal. Koormatud sildest vasakul asetsevaid nullpunkte (joonisel 10.8 f 1, f 2 ja f 3 ) nimetatakse vasakpoolseteks fookusteks. Koormatud sildest paremal asetsevaid nullpunkte (joonisel 10.8 f 5, f 6 ja f 7) nimetatakse parempoolseteks fookusteks. Fookuste asukohad ei olene koormusest. Koormatud silde paindemomendi epüüri nullpunktid olenevad koormusest ega ole seepärast fookused. Sildes on kaks fookust: vasakpoolne fookus f i ja parempoolne fookus f i. Vasakpoolseks fookussuhteks nimetatakse vasakpoolse fookuse kauguste suhet parem- ja vasakpoolsest toest (vt joonis 10.9 d), kus vasakpoolne kaugus on c i 1 ja parempoolne
135 10.4. JÄTKUVTALADE ARVUTUS FOOKUSSUHTEGA 135 f 1 f 2 2 f 3 f 5 5 f 6 f l 1 l 2 l 3 l 4 l 5 l 6 l 7 kaugus (l i 1 c i 1 )). Joonis Jätkuvtala fookused k i 1 = (l i 1 c i 1 ) c i 1 (10.29) Parempoolseks fookussuhteks nimetatakse parempoolse fookuse kauguste suhet vasakja parempoolsest toest (vt joonist 10.9 d), kus vasakpoolne kaugus on ( l i+1 c i+1) ja parempoolne kaugus c i+1). ( li+1 c i+1) k i+1 = c i+1 (10.30) Kuna koormatud sildest kaugemal asetseval toel on toemoment väiksem kui koormatud sildele lähemal asetseval toel, siis vasak- ja parempoolse fookussuhte k i 1 ja k i+1 arvväärtus on suurem kui üks. Joonisel 10.9 sarnastest kolmnurkadest X i 1 o i 1 f i 1 ja X i 2 o i 2 f i 1 saame X i 1 = (l i 1 c i 1 ) = k i 1 (10.31) X i 2 c i 1 ja kolmnurkadest X i1 o i f i 1 ja X i+1 o i+1 f i 1 ( X li+1 i c i+1) = X i+1 c i+1 = k i+1 (10.32) a) i 2 i 1 i i+1 i+2 l 1 l 2 l 3 l i 1 l i l i+1 l i+2 b) c) c 2 X 1 f 2 X 2 X 2 c 3 f2 f 3 X 1 X 3 d) c i 1 f i 1 X i 1 Xi c c i+1 i+2 o f f i+1 i+2 oi 2 i+1 o o i 1 i X i 2 Xi+1 X i+2 Joonis Jätkuvtala fookussuhted
136 136 PEATÜKK 10. JÄTKUVTALAD Fookussuhete avaldiste saamiseks vaatleme joonist 10.9 b ja sõlme1 kohta kirjutame välja kolme momendi võrrandi (10.13), arvestades, et avad on koormamata. siin X 0 = 0 ja ning l 1X (l 1 + l 2) X 1 + l 2X 2 = 0 (10.33) 2 (l 1 + l 2) X 1 + l 2X 2 = 0 (10.34) X 2 = 2 (l 1 + l 2) X 1 l 2 Sõlme 2 kohta on kolme momendi võrrand = k 2 (10.35) l 2X (l 2 + l 3) X 2 + l 3X 3 = 0 (10.36) Võrrandist (10.35) avaldame X 1 = X 2 k 2 ja astame võrrandisse (10.36) Siit saame Sõlme 3 kohta saame l 2 X (l 2 + l k 3) X 2 + l 3X 3 = 0 (10.37) 2 [ ( X 3 = 2 + l ) ] = k X 2 l 3 3 (10.38) k 2 l 3X (l 3 + l 4) X 3 + l 4X 4 = 0 (10.39) Võrrandist (10.38) avaldame X 2 = X 3 k 3 ja astame võrrandisse (10.39) Siit saame l 3 X (l 3 + l k 4) X 3 + l 4X 4 = 0 (10.40) 3 [ ( X 4 = 2 + l ) ] = k X 3 l 4 4 (10.41) k 3 Üldistame saadud avaldised (10.35), (10.38) ja (10.41). Vasakpoolseteks fookussuheteks on avaldis (10.42) ( k j = 2 + l j ), X l j j 1 = X j (10.42) k j 1 k j Samamoodi saadakse valem ka parempoolsete fookussuhete arvutamiseks ( k j = 2 + l j ), X l j k j+1 j = X j 1 k j (10.43)
137 10.4. JÄTKUVTALADE ARVUTUS FOOKUSSUHTEGA 137 i 3 l i 2 i 2 i 1 i i+1 i+2 l i 1 l i l i+1 l i+2 X i 3 f i 2 X i 1 X i f i 1 f f i+1 i+2 X i 2 Xi+1 X i+2 Ω i A i f a i b i B i f Joonis Jätkuvtala toemomendid Koormatud silde toemomendid Joonisel esitatud tala tugede i-1 ja i kohta kirjutame kolme momendi võrrandi (10.13) l i 1X i ( l i 1 + l i) Xi 1 + l ix i = 6A f i l ix i ( l i + l i+1) Xi + l i+1x i+1 = 6B f i I 0 I i I 0 I i (10.44) Võrranditest (10.44) elimineerime momendid valemite (10.42) ja (10.43) abil momendid X i 2 ja X i+1 X i 2 = X i 1 k i 1, X i+1 = X i k i+1 (10.45) Arvestades seoseid (10.45), esitame võrrandisüsteemi (10.44) järgmisel kujul: 2 + l i 1 l i ( 2 1 k i 1 ) l i+1 l i [ 1 ( ) Xi X i k i+1 ] = 6Af i 6B f i I 0 I i l i I 0 I i l i (10.46)
138 138 PEATÜKK 10. JÄTKUVTALAD ehk [ ki 1 1 k i ] [ Xi 1 X i ] = 6A f i l i 6B f i l i (10.47) siin 1 l i = I 0 I i l i (10.48) st koormusliikmetes ei ole redutseeritud pikkused. Võrrandisüsteemi (10.47) lahend ja toemomendid on X i 1 = 6Af i k i 6B f i l i (k i k i 1) X i = 6Bf i k i 6A f i l i (k i k i 1) (10.49) (10.50) Kui äärmised toed on liigendtoed (s.t k i =, k i = ), siis avaldiste (10.49), (10.50) kasutamisel tekib määramatus ning see tuleb avada k n = ; X n = 0; X n 1 = 6Af nk n 6Bn f 1 l n (k n k n 1) k n 1 f n = 6Af n 6B k n ( l n kn 1 k n k 1 = ; X 0 = 0; X 1 = 6Bf 1 k 1 6A f 1 1 l 1 (k 1 k 1 1) k 1 f 1 k n = ) = 6Af n l n k n (10.51) 1 k 1 = = 6Bf 1 6A k ( 1 ) = 6B f 1 l 1 k 1 1 l 1 k k 1 1 (10.52) 10.5 Fookussuhetega arvutamise näited Näide 10.2 Arvutada joonisel c esitatud jätkuvtala toemomendid fookussuhetega ning kujutada paindemomendi ja põikjõu epüürid. Andmed: l 1 = 8 m, l 2 = 10 m, l 3 = 9 m. Tala on koormatud ajutise koormusega sillete kaupa: 1. koormusvariant: koormatud on kolmas sille F 4 = 40 kn (joonis a); 2. koormusvariant: koormatud on teine sille F 2 = 20 kn ja F 3 = 50 kn (joonis b); 3. koormusvariant: koormatud on konsool F 1 = 20 kn (joonis c); 4. koormusvariant: koormatud on esimene sille q = 10 kn/m (joonis d).
139 10.5. FOOKUSSUHETEGA ARVUTAMISE NÄITED 139 Sillete ristlõikejäikused EI = konst. Näide on järg näitele 10.1 lk 129. Fookussuhted joonisel c esitatud tala jaoks arvutame valemitega (10.42) ja (10.43) k 1 = k 2 = 2 + l 1 l 2 k 3 = 2 + l 2 l 3 Samamoodit arvutame ka parempoolsed fookussuheted k 3 = 2 k 2 = 2 + l 3 l 2 k 1 = 2 + l 2 l 1 (2 1 ) = ( 2 1 ) = 3.6 k1 10 (2 1 ) = ( 2 1 ) = (10.53) k ( 2 1 ) k 3 = ( 2 1 ) = ( 2 1 ) k 2 = ( 2 1 ) = (10.54) Fookussuheid võib arvutada Octave i funktsiooni C.16 (vt 260) abil. Arvutamise näide on joonisel Kus esimese ava fookussuhe k 1 = 1 eps. Siin on eps arvutil lõpmatult väike suurus (arvuti null). Tema pöördväärtus on lõpmatult suur arv (arvuti lõpmatus). Tulemused näitame joonisel d. Fookussuhetega leiame toemomendid eraldi iga silde koormusest. Alustame kolmandast sildest (vt joonis a ja 10.14). Kolmanda silde koormamisel tekkinud toemomendid arvutame valemitega (10.49) ja (10.50). Nendes esinevad koormusliikmed 6A f i, 6Bf i on juba leitud näites a) F 4 = 40 kn b) F 2 = 20 kn F 3 = 50 kn c) F 1 = 20 kn d) c) d) 0 a 1 b c 2 d m 4 m 3 m 3 m 4 m 4.5 m 4.5 m 2 q = 10 kn/m l 1 = 8 m l 2 = 10 m l 3 = 9 m k 1 = oo k 2 = 3.6 k 3 = k = k = 3.35 k = Joonis Jätkuvtala. Fookussuhted
140 140 PEATÜKK 10. JÄTKUVTALAD Joonis Fookussuhete arvutamine 10.1 lk 129 (vt avaldis lk 131) X 2 3 = 6Af 3 k 3 6Bf l 3 (k 3 k 3 = = knm (10.55) 1) 9 ( ) X 3 3 = 6Bf 3 k 3 6A f l 3 (k 3 k 3 = 1215 = knm (10.56) 1) 9 ( ) Toemomente võib arvutada Octave i funktsiooni C.17 (vt 261) abil. Arvutamise näide on joonisel 10.13, kus esimese ava fookussuhe k 1 = 1 eps. Siin on eps arvutil lõpmatult väike suurus (arvuti null). Tema pöördväärtus on lõpmatult suur arv (arvuti lõpmatus). Toemomendi X 1 3 leiame vasakpoolse fookussuhtega (10.42) X 1 3 = X 2 3 = = kn m (10.57) k Leitud toemomendid X i 3 kanname epüürile (joonis 10.14). Kolmanda ava keskel oleva paindemomendi epüüri ordinaadi arvutamiseks kasutame valemit (10.23). M d = M o d + X 2 ξ d + X 3 ξ d = = = kn m (10.58) Teise silde koormamisel tekkinud toemomendid arvutame valemitega (10.49) ja (10.50). Nendes esinevad koormusliikmed 6A f i, 6Bf i on juba leitud näites 10.1 lk 129 (vt avaldis lk 131) X 1 2 = 6Af 2 k 2 6Bf l 2 (k 2 k 2 = = knm (10.59) 1) 10 ( ) X 2 2 = 6Bf 2 k 2 6A f l 2 (k 2 k 2 = = knm (10.60) 1) 10 ( )
141 10.5. FOOKUSSUHETEGA ARVUTAMISE NÄITED 141 Joonis Toemomentide arvutamine F 4 = 40 kn a m 4 m 3 m 3 m 4 m 4.5 m 4.5 m 2 l 1 = 8 m l 2 = 10 m l 3 = 9 m b c d Toe number X 1 3 X 2 3 Koormatud silde number X X 3 3 M [knm] Q [kn] Joonis Fookussuhted. Koormus kolmandal sildel
142 142 PEATÜKK 10. JÄTKUVTALAD F 2 = 20 kn F 3 = 50 kn a 2 l 1 = 8 m l 2 = 10 m l 3 = 9 m b m 4 m 3 m 3 m 4 m 4.5 m 4.5 m c d X 3 2 Toe number Koormatud silde number X 12 X 2 2 X M [knm] Q [kn] Joonis Fookussuhted. Koormus teisel sildel Parempoolse toemomendi X 3 2 leiame parempoolse fookussuhtega (10.43) X 3 2 = X 2 2 k 3 = = kn m (10.61) Arvutame teise ava lihttala toereaktsioonid V 1 ja V 2 koormusest F 2 ja F 3. Kasutame toereaktsioonide mõjujooni (vt avaldist (2.11), siin on toeraktsiooni A i jaoks η i = ξ i ja toeraktsiooni B i jaoks η i = ξ i ). V 1 = F 2 ξ b + F 3 ξ c = = 34 kn V 2 = F 2 ξ b + F 3 ξ c = = 36 kn (10.62) Teise ava ristlõigetes b ja c olevate paindemomendi epüüri ordinaatide arvutamiseks kasutame valemit (10.23). M b = M o b + X 1 ξ b + X 2 ξ b = = = knm M c = M o s + X 1 ξ b + X 2 ξ b = = = kn m (10.63)
143 10.5. FOOKUSSUHETEGA ARVUTAMISE NÄITED 143 Konsoolil mõjuv koormus tekitab toel 0 momendi X 0 k = 40 knm (joonis 10.16). Parempoolsed toemomendid X i k leiame parempoolse fookussuhtega (10.43) F 1 = 20 kn a m 4 m 3 m 3 m 4 m 4.5 m 4.5 m 2 l 1 = 8 m l 2 = 10 m l 3 = 9 m b c d Toe number X 3 k Koormatud silde number X 0 k X 1 k X 2 k M [knm] X 3 k Q [kn] Joonis Fookussuhted. Koormus konsoolil X 1 k = X 0 k k 1 X 2 k = X 1 k k 2 X 3 k = X 2 k k 3 = 40.0 = knm = = knm 3.35 = = kn m (10.64) 2 Esimese ava koormamisel leiame momendi toel 1 X 1 1. Toel 0 on moment X 0 1 = 0 ja vasakpoolne fookussuhe k 1 =. Toereaktsiooni X 1 1 määramiseks kasutame valemit (10.52). Fiktiivne toereaktsioon 6B f 1 = 1280 knm2 on leitud varem (vt avaldisi (10.18) lk 131). X 1 1 = 6Bf 1 l 1 k 1 = 1280 = knm (10.65) Parempoolsed toemomendid leiame parempoolsete fookussuhetega (10.43) X 2 1 = X 1 1 k 2 X 3 1 = X 2 1 k 3 = = knm 3.35 = = kn m (10.66) 2
144 144 PEATÜKK 10. JÄTKUVTALAD q = 10 kn/m 0 a 1 b c 2 d m 4 m 3 m 3 m 4 m 4.5 m 4.5 m 2 l 1 = 8 m l 2 = 10 m l 3 = 9 m X 3 1 Toe number Koormatud silde number X 1 1 X X X M [knm] Q [kn] Joonis Fookussuhted. Koormus esimesel sildel Esimese ava ristlõikes a oleva paindemomendi epüüri ordinaadi leidmiseks kasutame valemit (10.23). M a = Ma o + X 0 ξ a X 1 ξ a = = 8 = kn m (10.67) Saadud tulemused kanname joonisele Talale (joonis 10.18) mõjub alaline koormus q = 8 kn/m. Toemomendid leiame kolme momendi võrrandiga (10.13). Tugede 1, 2 ja 3 kohta koostatud kolme momendi võrrandid (10.68) on sarnased võrranditega (10.17) l 1 X o + 2 (l 1 + l 2 ) X 1 + l 2 X 2 = 6B f 1 6Af 2 l 2 X (l 2 + l 3 ) X 2 + l 3 X 3 = 6B f 2 6Af 3 + l 3 X 2 + 2l 3 X 3 = 6B f 3 (10.68) kus toemoment X o ja koormusliikmed 6A f i, 6Bf i on X o = q B f 1 = ql3 1 4 = = = 16 knm = 1024 knm 2
145 10.5. FOOKUSSUHETEGA ARVUTAMISE NÄITED 145 a q = 8 kn/m m 4 m 3 m 3 m 4 m 4.5 m 4.5 m 2 l 1 = 8 m l 2 = 10 m l 3 = 9 m b c d X 1 X 0 X 2 X M [knm] Q [kn] Joonis Alaline koormus 6A f 2 = ql3 2 4 = = 2000 knm 2 8 6B f 2 = 6A f 2 = 2000 knm2 6A f 3 = 6B f 3 = ql3 3 4 = = 1458 knm 2 (10.69) Vabaliikmete arvutamiseks võib kasutada Octave i funktsiooni C.15 lk 258. Funktsiooni afbfikt1.m kasutamist jälgi joonisel Pärast toemomendi X o ja vabaliikmete 6A f i, 6Bf i arvväärtuste (10.69) asetamist võrrandisse (10.68) saame järgmise võrrandisüsteemi: X X 2 = 3458 (10.70) X ehk A X = B (10.71) kus A = ; X = X 1 X 2 X 3 ; B = (10.72) Võrrandisüsteemi lahendame arvutiprogrammiga Octave (vt lõik C.1 lk 205). Võrrandisüsteemi (10.70) lahend on X 1 = knm; X 2 = knm; X 3 = knm (10.73)
146 146 PEATÜKK 10. JÄTKUVTALAD Joonis Alalise koormuse fiktiivsed reaktsioonid Leitud toemomendid (10.73) kanname joonisele
147 Peatükk 11 Deformatsioonimeetod 11.1 Geomeetrilise määratuse aste Sirgetest varrastest moodustatud raami geomeetrilise määramatuse aste, s.t lisatundmatute arv, leitakse valemiga (11.1) kus w n = s 3 + w (11.1) w = 2s v t (11.2) on raami vabadusaste ja tähistab varraste pöördenurki määravate sõltumatute geomeetriliste parameetrite arvu. Geomeetrilise määramatuse aste (11.1) võrdub jäikade sõlmede (ilma toesõlmedeta) arvuga, kui raami vabadusaste (11.2) on null või negatiivne n = s 3, w 0 (11.3) Viltu olevate postidega raamide varrasahela pöörded leitakse poolusplaanist (joonis 11.1). Varrasahela ühele vardale antakse ühikpööre ja teiste varraste pöörded leitakse selle varda pöörde funktsioonina. Joonisel 11.1 kujutatud varrasahela paigutusolukorras ψ 1 pöörduvad vardad ca ja db ümber toesõlme c ja d. Nende varraste peapoolusteks on toesõlmed c O ac,1 ja d O bd,1. Liigend a ühendab vardaid ac ja ab ning on nende varraste liikumise hetkpoolus. Varda ab peapoolus asub vektoriga aa risti oleval sirgel. Liigend b ühendab vardaid ab ja db ning on nende varraste liikumise hetkpoolus. Varda ab peapoolus asub ka vektoriga bb risti oleval sirgel. Nende risti olevate sirgete lõikepunktiks on O ab,1. See punkt O ab,1 on varda ab peapoolus. Varras ab pöördub ümber peapooluse O ab,1 uude asendisse a b. Paigutusolukorras ψ 1 antakse vardale ab pöördenurk ϑ ac,1 = 1 (vt joonist 11.1). Kolmnurkadel aa O ab,1 ja aa c on ühine külg aa. Sellest tingimusest saame H ϑ ac,1 = H ϑ ab,1 ϑ ab,1 = H H ϑ ac,1 (11.4) 147
148 148 PEATÜKK 11. DEFORMATSIOONIMEETOD b) O ab,1 peapoolus ϑ = ϑ ab,1 ϑ = ϑ ab,1 a) a c d b H H* hetkpoolus a a ϑ ab,1 b a b hetkpoolus b ϑ ac,1 ϑ bd,1 ψ 1 c c = Oac,1 d d = Obd,1 peapoolus peapoolus L L* Joonis Poolusplaan ja varraste pöörded Kolmnurkadel bb O ab,1 ja bb d on ühine külg bb. Siit saame bo ab,1 ϑ ab,1 = bd ϑ bd,1 ϑ bd,1 = bo ab,1 bd Seoses (11.5) avaldame pöörde ϑ ab,1 pöörde ϑ ac,1 kaudu. ϑ ab,1 (11.5) ϑ bd,1 = H H bo ab,1 bd ϑ ac,1 = ϑ ac,1 (11.6) 11.2 Kinnitusmomendid Vaatleme konstruktsiooni varrast AB (joonis 11.2 a). Temale mõjuvate jõudude mõjul liigub varras uude asendisse A B. Varda asendi A B saame järgmiste sõltumatute liikumiste tulemusena: varda mõlemad otsad siirduvad ühe ja sama suuruse võrra A (joonis 11.2 b); ühe varda otsa siire on risti varda teljega, näiteks varda otsa B siirdumine punkti B (joonis 11.2 e). Varda otsa siire on B A ja pööre ϑ AB ; varda otsa A pööre nurga ϕ A võrra. Varda elastse joone kuju on joonisel (joonis 11.2 c); varda otsa B pööre nurga ϕ B võrra. Varda elastse joone kuju on joonisel (joonis 11.2 d);
149 11.2. KINNITUSMOMENDID 149 a) b) B A A A B BA A L A B A e) BA = L ϑ AB = ϑ BA B BA c) A B A B d) ϕ A ϕ B B f) A B A Joonis Varda deformatsioon varda telje punktide siirded. Varda otsad ei siirdu ega pöördu (joonis 11.2 f)). Paindemomendid M jk ja M kj arvutatakse varda otste ristlõigetes koormusest tekkiva paindemomendi M (p) jk, M (p) kj ja sõlmede j, k pöörete ϕ j, ϕ k ning varda pöördest ϑ jk tekkivate paindemomentide summeerimisega M jk = M (p) jk + 4 i jk ϕ j + 2 i jk ϕ k 6 i jk ϑ jk M kj = M (p) (11.7) kj + 2 i jk ϕ j + 4 i jk ϕ k 6 i jk ϑ jk Siin on varda mõlemad otsad jäigalt kinnitatud ega ole summeerimist indeksite j ja k järgi. Varda ots j on jäigalt kinnitatud. Varda otsas k on liigend M jk = M (p) jk + 3 i jk ϕ j 3 i jk ϑ jk M kj = 0 (11.8) Siin ei ole summeerimist indeksite j ja k järgi. Kinnitusmomendid on toodud tabelis 11.1 leheküljel 150.
150 150 PEATÜKK 11. DEFORMATSIOONIMEETOD Tabel Kinnitusmomendid ja põikjõud Jrk.nr Skeem M JK M KJ Q JK Q KJ A ϕ y =1 J l K 4i 2i 6i l B J l ϕ y =1 K 2i 4i 6i l 1 J ϑ l K 6iϑ 1 6iϑ 1 12iϑ 1 l C J ϕ =1 y l K 3i 3i l 2 J l ϑ 2 K 3iϑ 2 3iϑ 2 l 3 J q K ql2 12 ql 2 12 ql 2 ql 2 4 J a F b K ξη 2 F l ξ 2 ηf l (1 + 2ξ) η 2 F ξ 2 (1 + 2η) F 5 J M K a b 6 J q K l J F K 7 a b η (2 3η) M ξ (2 3ξ) M ql2 8 η ( 1 η 2) F l 2 ( 1 ξ 2 η 2) 3M l 5ql 8 3ql 8 η ( 2 3 η 2 ) F ξ2 2 (3 ξ) F J M K ( 1 3η 2 ) M 8 a b J q K 9 l ql ( 1 η 2 ) M l 3ql 8 5ql 8 10 J a F b K ξ ( 1 ξ 2) F l 2 η 2 2 (3 η) F ξ ( 2 3 ξ 2 ) F M 11 b J a K ( 1 3ξ 2 ) M 2 ( ξ 2 ) M l ξ = a l η = b l
151 11.3. DEFORMATSIOONIMEETODIGA ARVUTAMISE NÄITED Deformatsioonimeetodiga arvutamise näited Näide 11.1 Leiame joonisel 11.3 näidatud raami sisejõudude jaotuse deformatsioonimeetodiga. Raam on koormatud ühtlaselt jaotatud koormusega q z = 15 kn m ning horisontaalse jõuga H = 90 kn. Raami posti ristlõike jäikus EI P = knm 2 ja raami riivi ristlõike jäikus EI R = 1.5EI P. Raami ava on 6 m, postide pikkused 5 m ja 2.5 m. Sarnast raami, kus vaadeldud koormusele on lisaks veel postidele rakendatud kaks vertikaalset jõudu F = 750 kn, on vaadeldud deformeerunud olukorra järgi [Bor79a]. 5 m q = 15 kn/m 1 2 EI P 4 EI R 6 m EI P m H = 90 kn EI P = 2*!0 knm EI EI R = 1.5 P Joonis Raam Raami geomeetriliselt määratud põhiskeem ja siirdeolukorda määravad sõlmede pöörded ξ 1, ξ 2 ja varda pööre ξ 3 (ϕ 1, ϕ 2 ja ψ 1 ) on näidatud joonisel 11.4 a. Joonisel 11.4 b on takistatud varda pöörde asemel sõlme takistatud siire. a) b) 1 2 ξ 1 ξ ξ 1 ξ 2 ξ 3 3 ξ Joonis Geomeetriliselt määratud põhiskeem Raami virtuaalsed siirded (varrasahel) on joonisel Deformatsioonimeetodi koormusliikmete arvutamiseks vaatleme joonist 11.6 ja kasutame tabelit 11.1 lk 150. M 0 12 = M 0 21 = q z l = 15 = 45 knm (11.9) 12 M 0 14 = M 0 41 = M 0 23 = 0 (11.10)
152 152 PEATÜKK 11. DEFORMATSIOONIMEETOD l 14 ϑ 14 l 23 ϑ l 23 ϑ 14 = 2 ξ 3 l 14 ϑ 14 = = 1 ξ Joonis Varrasahel Esitame varraste kinnitusmomendid veeruvektorina M M 0 M = M 0 14 = 0 M M kn m (11.11) Veeruvektori sisestamine arvutiprogrammiga Octave on näidatud (B.7) lk 198. a) Z M 2 q = 15 kn/m M 0 Z H = 90 kn M M Z M 41 3 Z b) Z Z M M 0 2 q = 15 kn/m Z H = 90 kn M 14 0 M M 23 Joonis Kinnitusmomendid Koormusliikme Z 0 1 leiame sõlme 1 tasakaalust Z 0 1 = M M 0 14 = = 45 knm (11.12) Koormusliikme Z 0 2 leiame sõlme 2 tasakaalust Z 0 2 = M M 0 23 = = 45 knm (11.13) Koormusliikme Z3 0 leidmiseks vaatleme jõudude ja momentide võimalikku tööd varrasahela (joonis 11.5) siiretel. Posti pööret ξ 3 takistavas sidemes tekkiva reaktsioonimomendi Z3 0 esitame jõupaarina. Jõud on rakendatud varda mõlemas otsas risti varda teljega ja jõudude suurusteks on reaktsioonimoment Z3 0 jagatud varda pikkusega 5 (joonis 11.6). Varrasahela võimalik töö Z 0 3δϑ 14 Hδ (l 23 ϑ 23 ) = 0 (11.14)
153 11.3. DEFORMATSIOONIMEETODIGA ARVUTAMISE NÄITED 153 Kinnitusmomentide M12 0, M 21 0 võimalik töö on null, sest varras 1 2 ei pöördu. Virtuaalpööre δϑ 14 ja siire δ (l 23 ϑ 23 ) avalduvad virtuaalpöörde δξ 23 kaudu δϑ 14 = δξ 3, δ (l 23 ϑ 23 ) = 2.5 2δξ 3 (11.15) Arvestades virtuaalsiirete avaldisi (11.15), saame varrasahela võimaliku töö [ ] Z3 0 H 5 δξ 3 = 0 (11.16) millest avaldame koormusliikme Z 0 3 Z 0 3 = H 5 = 90 5 = 450 knm (11.17) Koormusliikmed esitame veeruvektorina Z 0. Vastupidiseid märke kasutame eesmärgina viia koormusliikmed võrrandisüsteemi paremale poole. Z = Z 0 1 Z 0 2 Z 0 3 = kn m (11.18) Veeruvektori sisestamist arvutiprogrammiga Octave on näidatud (B.7) lk 198. Varraste reaktsioonimomendid sõlme 1 pöördest (joonis 11.7) ξ 1 = 1 a) 1 Z 1 1 M M 21 Z 2 b) Z M 12 M 21 Z M 14 Z M M 23 Z Z M 14 1 M M 23 Joonis Reaktsioonimomendid sõlme 1 pöördest M 1 12 = 4 EI R l 12, 1 M12 1 = = 1.0 (11.19) EI P 6 M 1 21 = 2 EI R l 12, 1 M21 1 = = 0.5 (11.20) EI P 6 M 1 14 = 4 EI P l 14, 1 M14 1 = = 0.8 (11.21) EI P 5
154 154 PEATÜKK 11. DEFORMATSIOONIMEETOD M 1 41 = 2 EI P l 14, 1 M41 1 = = 0.4 (11.22) EI P 5 M 1 23 = 0 (11.23) Esitame varraste reaktsioonimomendid sõlme 1 pöördest ξ maartiksi M 123 veeruna M 123 = M M M M M ξ 1 ξ 2 ξ 3 EI P ξ 1 ξ 2 ξ 3 (11.24) Maatriksi sisestamist arvutiprogrammis Octave vaatleme pärast pöördest ξ 2 ja ξ 2 varraste reaktsioonimomentide leidmist. Sõlmede reaktsioonimomendid sõlme 1 pöördest (joonis 11.7) saame vastava sõlme tasakaalust. Sõlme 1 tasakaalust (joonis 11.7) saame Sõlme 2 tasakaalust Z 1 1 = M M 1 14 = EI P ( ) = 1.8EI P (11.25) Z 1 2 = M M 1 23 = EI P ( ) = 0.5EI P (11.26) Reaktsioonimomendi Z3 2 leidmiseks vaatleme varraste reaktsioonimomentide võimalikku tööd varrasahela (joonis 11.5) siiretel. Posti pööret ξ 3 takistavas sidemes tekkiva reaktsioonimomendi Z3 2 esitame jõupaarina. Jõud on rakendatud varda mõlemas otsas risti varda teljega ja jõudude suurusteks on reaktsioonimoment Z3 2 jagatud varda pikkusega 5 (joonis 11.7). Varraste reaktsioonimomentide võimalik töö sõlme 1 pöördest Võrrandist (11.27) saame ( ) [ ( )] Z3δϑ M M41 1 δϑ 14 = Z3 1 + M M41 1 δϑ 14 = 0 (11.27) ( ) Z3 1 = M M41 1 = EI P ( ) = 1.2EI P (11.28) Sõlmede ja varraste pöörete leidmiseks alustame võrrandisüsteemi koostamist. Võrrandisüsteemi tundmatute ees olevatest kordajatest moodustame 3 3 maartiksi A, mille esimene veerg on A = Z1 1.. Z2 1.. Z3 1.. ξ 1 ξ 2 ξ 3 = EI P Varraste reaktsioonimomendid sõlme 2 pöördest (joonis 11.8) ξ 1 ξ 2 ξ 3 (11.29) M 2 12 = 2 EI R l 12, 1 M12 2 = = 0.5 (11.30) EI P 6
155 11.3. DEFORMATSIOONIMEETODIGA ARVUTAMISE NÄITED 155 M 2 21 = 4 EI R l 12, 1 M21 2 = = 1.0 (11.31) EI P 6 M 2 14 = M 2 41 = 0 (11.32) M 2 23 = 3 EI P l 23, 1 M23 2 = = 1.2 (11.33) EI P 2.5 Esitame varraste reaktsioonimomendid sõlme 2 pöördest ξ maatriksi M 123 teise veeruna M12 1 M M M M ξ ξ 1 = M 1 14 M14 2. ξ 2 = EI M41 1 M41 2 P ξ 2 (11.34). ξ ξ 3 M23 1 M Maatriksi sisestamist arvutiprogrammis Octave vaatleme pärast pöördest ξ 3 varraste reaktsioonimomentide leidmist. Sõlmede reaktsioonimomendid sõlme 2 pöördest (joonis 11.8) saame vastava sõlme ta- a) 2 Z 1 2 M M 21 Z 2 ξ 2 = 1 b) Z M 12 M 21 Z M 14 Z M M 23 Z Z M 14 2 M M 23 Joonis Reaktsioonimomendid sõlme 2 pöördest sakaalust. Sõlme 1 tasakaalust (joonis 11.8) saame ja sõlme 2 tasakaalust Z 2 1 = M M 2 14 = EI P ( ) = 0.5EI P (11.35) Z 2 2 = M M 2 23 = EI P ( ) = 2.2EI P (11.36) Reaktsioonimomendi Z2 2 leidmiseks vaatleme varraste reaktsioonimomentide võimalikku tööd varrasahela (joonis 11.5) siiretel. Posti pööret ξ 3 takistavas sidemes tekkiva reaktsioonimomendi Z3 1 esitame jõupaarina. Jõud on rakendatud varda mõlemas otsas risti varda teljega ja jõudude suurusteks on reaktsioonimoment Z2 2 jagatud varda pikkusega 5 (joonis 11.5). Varraste reaktsioonimomentide võimalik töö sõlme 2 pöördest (ϑ 23 = 2ϑ 14 ) (joonis 11.5) [ ] Z3δϑ M23δϑ 2 23 = Z M23 2 δϑ 14 = 0 (11.37)
156 156 PEATÜKK 11. DEFORMATSIOONIMEETOD Võrrandist(11.27) saame Z 2 3 = M 2 23 = EI P = 2.4EI P (11.38) Lisame võrrandisüsteemi tundmatute ees olevate kordajate maatriksile A (11.29) teise veeru A = Z 1 1 Z 2 1. Z 1 2 Z 2 2. Z 1 3 Z 2 3. ξ 1 ξ 2 ξ 3 = EI P Varraste reaktsioonimomendid varda 1 2 siirdest (joonis 11.9) ξ 1 ξ 2 ξ 3 (11.39) a) 4 Z M 41 3 M 12 ξ 3 = 1 M 21 Z b) 3 Z 1 M 21 Z M Z 3 M M 14 M M Z Z M 41 2 Joonis Reaktsioonimomendid varda pöördest M 3 12 = M 3 21 = 0 (11.40) M 3 14 = 6 EI P l 14, 1 M14 3 = 6 1 = 1.2 (11.41) EI P 5 M 3 41 = M 3 14 = 1.2 (11.42) M 3 23 = 3 EI P l 23, 1 M23 3 = 3 1 = 2.4 (11.43) EI P 2.5 Esitame varraste reaktsioonimomendid varda pöördest ξ maatriksi M 123 kolmanda veeruna M 123 = M12 1 M12 2 M12 3 M21 1 M21 2 M21 3 M14 1 M14 2 M14 3 M41 1 M41 2 M41 3 M23 1 M23 2 M23 3 ξ 1 ξ 2 ξ 3 = EI P ξ 1 ξ 2 ξ 3 (11.44)
157 11.3. DEFORMATSIOONIMEETODIGA ARVUTAMISE NÄITED 157 Maatriksi sisestamist arvutiprogrammis Octave on näidatud (B.3) lk 197. Sõlmede reaktsioonimomendid varda 1 2 siirdest (joonis 11.9) saame vastava sõlme tasakaalust. Sõlme 1 tasakaalust (joonis 11.9) saame ja sõlme 2 tasakaalust Z 3 1 = M M 3 14 = EI P (0 1.2) = 1.2EI P (11.45) Z 3 2 = M M 3 23 = EI P (0 2.4) = 2.4EI P (11.46) Reaktsioonimomendi Z2 3 leidmiseks vaatleme varraste reaktsioonimomentide võimalikku tööd varrasahela (joonis 11.5) siiretel. Posti pööret ξ 3 takistavas sidemes tekkiva reaktsioonimomendi Z2 3 esitame jõupaarina. Jõud on rakendatud varda mõlemas otsas risti varda teljega ja jõudude suuruseks on reaktsioonimoment Z2 3 jagatud varda pikkusega 5 (joonis 11.9). Varraste reaktsioonimomentide võimalik töö varda 3 pöördest (ϑ 23 = 2ϑ 14 = ξ 3 ) j(oonis 11.5) ( ) [ ] Z3δϑ M M14 3 δϑ 14 + M23δϑ 3 23 = Z3 3 + M M M23 3 δϑ 14 = 0 (11.47) Võrrandist (11.47) saame ( ) Z3 3 = M M41 3 2M23 3 = EI P [ ] = 7.2EI P (11.48) Lisme võrrandisüsteemi tundmatute ees olevate kordajate maatriksile A (11.27) kolmanda veeru Z1 1 Z1 2 Z 3 1 ξ ξ 1 A = Z2 1 Z2 2 Z2 3 ξ 2 = EI P ξ 2 (11.49) Z3 1 Z3 2 Z3 3 ξ ξ 3 Maatriksi sisestamist arvutiprogrammiga Octave on näidatud (B.3) lk 197. Sõlmede ja varraste pöörete leidmiseks koostasime võrrandisüsteemi Aξ = Z (11.50) kus maatriks A on leitud avaldisega (11.49) ja vektor Z (11.18) ning vektor ξ ξ = ξ 1 ξ 2 ξ 3 (11.51) Võtame kasutusele uue muutuja A = EI P ξ ja maartiksi a = EI P A ning esitame võrrandisüsteemi (11.50) järgmisel kujul: ax = Z (11.52) ehk ξ 1 ξ 2 ξ 3 = (11.53)
158 158 PEATÜKK 11. DEFORMATSIOONIMEETOD Joonis Pöördenurkade arvutamine Võrrandisüsteemi (11.52) võib lahendada maatriksi a pöördmaatriksi a 1 abil X = a 1 Z (11.54) Arvutiprogrammiga Octave lahendame võrrandisüsteemi (11.53) Gaussi elimineerimismeetodiga (vt avaldist (11.55) ja joonist 11.10). kus z = Z. Võrrandisüsteemi (11.52) lahend X 1 X 2 X 3 = EI P X = a \ z (11.55) Momendid varraste otstes leiame avaldisega ξ 1 ξ 2 ξ 3 = (11.56) M = M 0 + M 123 ξ (11.57) ehk M 12 M 21 M 14 M 41 M 23 = M 0 12 M 0 21 M 0 14 M 0 41 M M12 1 M12 2 M12 3 M21 1 M21 2 M21 3 M14 1 M14 2 M14 3 M41 1 M41 2 M41 3 M23 1 M23 2 M23 3 ξ 1 ξ 2 ξ 3 (11.58)
159 11.3. DEFORMATSIOONIMEETODIGA ARVUTAMISE NÄITED 159 kus maatriks M 0 on toodud avaldisega (11.11) ja maatriks M 123 avaldisega (11.44). Momentide avaldise (11.57), (11.58) esitame leitud X kaudu M = M EI P M 123 X (11.59) M 12 M 21 M 14 M 41 M 23 = = (11.60) Momentide väärtused varraste otstes arvutame arvutiprogrammiga Octave (joonis 11.11). Joonis Momendid varda otstes M 12 M 21 M 14 M 41 M 23 = (11.61) Leitud momendid varraste otstes (11.61) kanname joonisele b. Momendi positiivne ja negatiivne suund on näidatud joonisel c. Joonisel a on varda 1 2 lihttala pain-
160 160 PEATÜKK 11. DEFORMATSIOONIMEETOD a) ql 2 8 = b) } M [knm] c) M Joonis Momendid varda otstes ja paindemomendi epüür demomendi epüür jaotatud koormusest q z. Joonisel b on raami paindemomendi epüür. Joonisel c on paindemomendi positiivne ja negatiivne suund. Raami varraste põikjõu märgi määramiseks vaatleme esmalt joonist 1.13 lk 30. Paindemomendi tuletise geomeetriliseks tõlgenduseks punktis on selles punktis paindemomendi epüüri puutuja tõusunurga tangens (tan α). Põikjõu märk oleneb puutuja (joonis 1.13) pööramise suunast (puutujat pöörame nii, et ta ühtiks varda teljega, seejuures α < π 2 ): vastupäeva pöörates on põikjõud positiivne ja päripäeva pöörates negatiivne. Raami varda 1 4 paindemomendi epüüri (joonis 11.12) puutuja ühtimiseks varda teljega tuleb teda pöörata päripäeva, s.t põikjõu märk on miinus (joonis 1.13 lk 30). Kanname põikjõu märgi joonisele a. Raami varda 2 3 paindemomendi epüüri (joonis 11.12) puutuja ühtimiseks varda teljega tuleb teda pöörata päripäeva, s.t põikjõu märk on miinus (joonis 1.13). Raami varda 1 2 paindemomendi epüüri alguses (joonis 11.12) puutuja ühtimiseks varda teljega tuleb teda pöörata vastupäeva, s.t põikjõu märk on pluss (joonis 1.13). Põikjõu arvutamiseks vaatleme joonist ja Varda 1 4 põikjõud, mille märk peab a) b) Q [kn] Q [kn] 50.6 Joonis Raami põikjõu märk ja epüür tulema miinus
161 11.3. DEFORMATSIOONIMEETODIGA ARVUTAMISE NÄITED 161 Q 14 = Q 41 = M x = Varda 2 3 põikjõud, mille märk peab tulema miinus = 50.6 kn (11.62) Q 23 = Q 32 = M x = = 39.4 kn (11.63) 2.5 Varda 1 2 põikjõu arvutamisel leiame vastava lihttala põikjõu Q o ja põikjõu momentidest Q M = M x Q 12 = Q o + M x = = = 82.2 kn (11.64) Q 21 = Q o + M x = = = 7.8 kn (11.65) Leitud põikjõud on kantud joonisele b N 12 Joonisel on näidatud sõlmele 1 mõjuvad jõud X = 0, N12 = 50.6 kn (11.66) 50.6 N 14 Q Z = 0, Joonis Sõlme 1 tasakaal N 14 = 82.2 kn (11.67) Joonisel on näidatud sõlmele 2 mõjuvad jõud N X = 0, N 21 = = 50.6 kn (11.68) Q N 23 Z = 0, Joonis Sõlme 2 tasakaal N 23 = 7.8 kn (11.69) Raami varrastes mõjuva normaaljõu leidmiseks lõikame välja sõlmed 1 ja 2 (joonis ja 11.15). Kanname joonisele kõik sõlmele mõjuvad jõud. Normaaljõud N 12, N 14, N 21, N 23, mida me otsime, näitame positiivses suunas. Põikjõud kanname joonisele nende mõjumise suunas. Positiivne põikjõud pöörab vaadeldavat elementi päripäeva (joonised ja 11.15). Leitud normaaljõud kanname joonisele
162 162 PEATÜKK 11. DEFORMATSIOONIMEETOD N [kn] Joonis Raami normaaljõu epüür
163 11.3. DEFORMATSIOONIMEETODIGA ARVUTAMISE NÄITED 163 Näide 11.2 Leiame joonisel näidatud raami sisejõudude jaotuse deformatsioonimeetodiga. Raami riivide ristlõike jäikus EI R on kolm korda suurem kui postidel EI R = 3 EI P. Raami vertikaalne koormus q = 8 kn/m ja horisontaalne koormus keskmisele postile F = 30 kn. Joonisel on näidatud vaadeldava raami varrasahel. Raami kõigi varraste pöörded ϑ ij a I q = 8 kn/m 3 I F = 30 kn b 3 I k I 1.8 m d e f 1 6 m 6 m c 1 I 3 m Joonis Raam II a i ad = 1 H* = 18 m H H* = 3 18 = ϑ i ab = 1.5 bc = a b c b i bc = 1.5 c i ϑ be = 1 ad = 1 ϑ ϑ cf be = 1 = 1 i cf = d e f Joonis Raami varrasahel II avaldame esimese varda ad pöörde ϑ ad kaudu. Varda bc pöörde leidmisel kasutame avaldist (11.6). ϑ bc = H H ϑ ad = (11.70) Raami varraste jäikuste i = EI l baasjäikuseks. arvutamisel võtame varda ad jäikuse i ad = EI ad l ad aluseks, s.t i o = EI ad i ad = i ab = i bc = i be = i cf = l ad = 1 3 EI ad l ad i o = = 1 EI ab l ab i o = EI bc l bc i o = EI be l be i o = = 1 EI cf l cf i o = = = = (11.71)
164 164 PEATÜKK 11. DEFORMATSIOONIMEETOD Raami geomeetriliselt määratud põhiskeem on joonisel ϕ a i= 1 a b c i = 1.5 i = 1.5 ψ 1 ϕ b i= 1 i = d e f Joonis Geomeetriliselt määratud põhiskeem II Raami sõlme a pööramisel ühikulise nurga võrra ϕ a = 1 tekkivad momendid on arvutatud tabelis 11.1 toodud valemite alusel. Tulemused on kantud joonisele Joonistel kasutatakse järgmisi tähistusi m k mn momentide märkimiseks: indeks k kirjeldab deformeerunud olukorda (k = 1, 2, 3); m ja n tähistavad varda algust ja lõppu. Raami sõlme b r aa ϕ a = 1 ϕ a = 1 m 1 ab = 4i m 1 ba = 2i m 1 bc = 0 a m 1 = 3i b m 1 be = 0 ad r ba c d e m 1 = 0 eb m 1 = 0 f fc Joonis Sõlme a pööre ϕ a pööramisel ühikulise nurga võrra ϕ b = 1 tekkivad momendid on arvutatud tabelis 11.1 toodud valemitega. Tulemused on kantud joonisele Raami varda ad pööramisel ühikulise nurga r ab a 2 2 ϕ m ab = 2i m ba = 4i b= 1 m 2 bc = 3i m ad 2 = 0 ϕ = 1 b b 2 m be = 4i r bb c d e m eb = 2i f 2 m 1 fc = 0 Joonis Sõlme b pööre ϕ b võrra ψ 1 = 1 tekkivad momendid on arvutatud tabelis 11.1 toodud valemitega. Tulemused on kantud joonisele Momentide m k mn avaldised, mis on joonistel , kanname
165 11.3. DEFORMATSIOONIMEETODIGA ARVUTAMISE NÄITED 165 r a1 ψ 1 = 1 r b1 3 m ab m 3 3 = 0 ba = 0 m bc= 3iϑ bc a 3 m b ad = 3iϑ ad m be = 6iϑ be c ψ 1 = d e m eb = 6iϑ m eb f fc = 3iϑ fc r Σ12iϑ 2 Σ 3iϑ 2 11 = + Joonis Varda ad pööre ψ 1 maatriksisse mx. M = M da M ad... M ab M ba... M be M eb... M bc M cb... M cf M fc ; mx = m 1 da m 2 da m 3 da m 1 ad m 2 ad m 3 ad m 1 ab m 2 ab m 3 ab m 1 ba m 2 ba m 3 ba m 1 be m 2 be m 3 be m 1 eb m 2 eb m 3 eb m 1 bc m 2 bc m 3 bc m 1 cb m 2 cb m 3 cb m 1 cf m 2 cf m 3 cf m 1 fc m 2 fc m 3 fc varras 1 post... varras 2 riiv... varras 3 post mp =... ; varras 4 riiv... varras 5 post m o da m o ad... m o ab m o ba... m o be m o eb... m o bc m o cb... m o cf m o fc (11.72) ehk mx = 0 eli (1) 0 eli (1) 0 eli (1) deta (1) 3 eli (1) 0 eli (1) 3 eli (1) deta (1) eli (2) 2 eli (2) 0 eli (2) deta (2) 2 eli (2) 4 eli (2) 0 eli (2) deta (2) eli (3) 4 eli (3) 6 eli (3) deta (1) 0 eli (3) 2 eli (3) 6 eli (3) deta (1) eli (4) 3 eli (4) 3 eli (4) deta (4) 0 eli (4) 0 eli (4) 0 eli (4) deta (4) eli (5) 0 eli (5) 0 eli (5) deta (5) ; 0 eli (5) 0 eli (5) 3 eli (5) deta (5) varras 1 post... varras 2 riiv... varras 3 post mp =... ; varras 4 riiv... varras 5 post Mab Mba... Mbe Meb (11.73) Jaotatud ja koondatud koormusest tekkivad kinnitusmomendid on arvutatud funktsiooni kinnmom1.m C.19 lk 265 abil tabelis 11.1 toodud valemitega. Tulemused on kantud joonisele
166 166 PEATÜKK 11. DEFORMATSIOONIMEETOD r ap m o o k m ab a mo ad = 0 m o r bp m o ba m o bc = 0 b mo be m o eb d e f c m o fc = 0 r 1p o = Σ ( m alguses + m lõpus + S ) ϑ o Joonis Varda kinnitusmomendid koormusest II Võrrandisüsteemi vasku poole kordajad arvutame Octave iga järgmiselt: r (1, 1) = 3 eli (1) + 4 eli (2) r (1, 2) = 2 eli (2) r (2, 1) = r (1, 2) r (2, 2) = 4 eli (2) + 4 eli (3) + 3 eli (4) r (1, 3) = 3 eli (1) deta (1) r (3, 1) = r (1, 3) (11.74) r (2, 3) = 6 eli (6) deta (6) 3 eli (4) deta (4) r (3, 2) = r (2, 3) r (3, 3) = 3 eli (1) deta (1) eli (3) deta (3) eli (4) deta (4) eli (5) deta (5) 2 Võrrandisüsteemi parem pool. Kordajate leidmiseks kasutame Octave i funktsiooni kinnmom1.m C.19 lk 265, mis on kirjutatud tabeli 11.1 alusel. r (1p) = Mab + 4 r (2p) = Mba + Mbe r (3p) = (Meb + Mbe ) deta (3) (11.75) Võrrandisüsteemi (11.76) r 11 r 12 r 13 r 21 r 22 r 23 r 31 r 32 r 33 = r 1p r 2p r 3p (11.76) ehk r x = r p (11.77) koostamiseks ja lahendamiseks kasutame Octave i (vt joonis ja programm C.18 lk 263). Lahendamisel saadud tulemuste salvestamiseks avame päeviku diary defnab.out (vt Päevik 11.1). Päevik 11.1 defnab.out octave:2> diary defnab.out octave:3> diary on octave:4> defnab
167 11.3. DEFORMATSIOONIMEETODIGA ARVUTAMISE NÄITED 167 Joonis Deformatsioonimeetod Octave iga varraste_pikkused_l = varraste_ristloigete_jaikused_ei = varraste_poordenurdad_deta = varraste_jaikused_i = mx = Vb = 24 Va = 24 Vb = 18 Va = 12 mp =
168 168 PEATÜKK 11. DEFORMATSIOONIMEETOD r = rp = x = M = octave:5> diary off Arvutusega saadud momendid varraste otstes (vt Päevik 11.1) kanname joonisele a. Joonise a põhjal joonestame momendi epüüri b. Põikjõu epüür on joonisel
169 11.3. DEFORMATSIOONIMEETODIGA ARVUTAMISE NÄITED 169 a) a b c d e f b) a b c d f e M ep [knm] Joonis Momendid varraste otstes a c b d e f Q [kn] ep Joonis Põikjõu epüür 2.974
170 170 PEATÜKK 11. DEFORMATSIOONIMEETOD
171 Peatükk 12 Kaared ja võlvid 12.1 Kaarkonstruktsioonid Olenevalt liigendite arvust nimetatakse neid kolme, kahe, ühe liigendiga või liigenditeta kaarteks (joonis 12.1). Kolme liigendiga kaar on staatikaga määratav, teised kaared on staatikaga määramatud. Staatiliselt määramatu kaare sisejõud olenevad kaare telje a) b) c) d) e) Joonis Kaared kujust ja ka ristlõike mõõtmetest. Kaare ristlõike esialgsed mõõtmed valitakse ligikaudsete valemitega või kogemuste põhjal. Lõplikud ristlõike mõõtmed ja telje kuju peavad vastama arvutuslike sisejõudude jaotusele (insener valib ja siis kontrollib arvutustega). Sümmeetriliste kaarte puhul võib ristlõike inertsimomendi muutuse piki kaare telge valida järgmiste avaldistega [Rää75]: liigenditeta kaare jaoks kahe liigendiga kaare jaoks ( ) I c x r I = 1 (1 n) (12.1) l 1 I c I ( ) x r = 1 + (1 n) (12.2) l1 171
172 172 PEATÜKK 12. KAARED JA VÕLVID I = I c cos ϕ (12.3) n = I c I k cos ϕ k (12.4) kus x kaare telje abstsiss (koordinaatide alguspunkt lukuristlõike raskuskeskmes); ϕ nurk kaare telje puutuja ja horisontaali vahel; I c lukuristlõike inertsimoment; I ristlõike, mille abstsiss on x, inertsimoment; l 1 pool sillet; l k kaare kannaristlõike inertsimoment; ϕ k nurk telje puutuja ja horisontaali vahel kaare kannas; Enamikul juhtudel võetakse valemites (12.1), (12.2), r = 1 ja valemis (12.2) sageli ka n = 1. Väikese kõverusega kaarkonstruktsioonides ( ϱ > 5, milles ϱ on kõverusraadius ja h h kaare ristlõike kõrgus) arvutatakse siirded järgmise avaldisega: ip = lj 0 ( mi M p EI + n in p EA m in p EAϱ n im p EAϱ + k j ) q i Q p ds (12.5) EA Avaldises (12.5) on kolmanda ja neljanda liikme ees miinus, sest kaarskeemis võetakse tõmbejõud negatiivsena Kahe liigendiga kaar Kahe liigendiga kaar (joonis 12.2 a) on staatikaga ühekordselt määramatu. Põhiskeemiks võetakse kõver tala (joonis 12.2 b). Lisatundmatuks võetakse toe b toereaktsiooni horisontaalne komponent X 1 = H. Ühiktundmatust X 1 tekivad sisejõud m 1 = y (12.6) q 1 = sin ϕ (12.7) n 1 = cos ϕ (12.8) mille epüürid on joonistel 12.2 c, 12.2 d, 12.2 e. Vertikaalsest koormusest põhjustatud sisejõud põhiskeemis arvutatakse valemitega M 0 p = M 0 (12.9) Q 0 p = Q 0 cos ϕ (12.10) N 0 p = Q 0 sin ϕ (12.11) kus M 0 ja Q 0 on paindemoment ja põikjõud kaarele vastavas lihttalas. Jõumeetodi kanooniline võrrand δ 1 1 X p = 0 (12.12)
173 12.2. KAHE LIIGENDIGA KAAR 173 a) b) y ϕ lf a b c) f m 1 ep x x d) sin ϕ k y l sin ϕ k X 1 = H q 1 ep e) cos ϕ k 1 cos ϕ k n 1 ep Joonis Kahe liigendiga kaar kus δ 1 1 ja 1 p leidmisel arvestatakse pikijõu mõju. δ 1 1 = 1 p = l 0 l 0 m 1 m 1 ds + EI m 1 Mp 0 ds + EI l 0 l 0 n 1 n l 1 EA ds + k 0 l ds + k n 1 N 0 p EA 0 q 1 q 1 ds GA (12.13) q 1 Q 0 p ds GA (12.14) Avaldistes (12.13) ja (12.14) ei ole arvestatud kõveruse 1 ϱ mõju. Kui avaldiste (12.13), (12.14)) analüütiline integreerimine osutub tülikaks, kasutatakse numbrilist integreerimist. Pärast lisatundmatu X 1 leidmist arvutatakse sisejõud järgmiste avaldistega: koormusest M p = M 0 p y X 1 p (12.15) Q p = Q 0 p sin ϕ X 1 p (12.16) N p = Q 0 p + cos ϕ X 1 p (12.17) temperatuuri muutusest M t = y X 1 t (12.18) Q t = sin ϕ X 1 t (12.19) N t = cos ϕ X 1 t (12.20)
174 174 PEATÜKK 12. KAARED JA VÕLVID tugede siiretest M r = y X 1 r (12.21) Q r = sin ϕ X 1 r (12.22) N r = cos ϕ X 1 r (12.23) Tõmbiga kahe liigendiga kaare (vt joonis 12.2 e) arvutamisel võib võtta tundmatuks tõmbis tekkiva tõmbejõu X 1. Võrreldes kahe liigendiga kaare arvutamisega on erinevus siirete δ 1 1 ja 1 t arvutamisel. Arvesse tuleb võtta temperatuuri muutus. δ 1 1 = l 0 m 1 m l 1 n 1 n l 1 ds + EI 0 EA ds + k q 1 q 1 0 GA ds + 1 l (12.24) E t A t ( ) l y 1 t = (α α t ) t 0 l α t dx (12.25) 0 h cos ϕ Avaldistes (12.24) ja (12.25) ei ole arvestatud kõveruse 1 ϱ mõju Kahe liigendiga kaare arvutamise näited Näide 12.1 Arvutada kahe liigendiga kaare (joonis 12.3), mille pool sillet on koormatud ühtlaselt jaotatud koormusega p, horisontaalreaktsioon H ja sisejõudude M, Q ja N ordinaadid. Andmed: l = 32 m; l 1 = 16 m; f = 4 m; A c = m 2 (h c = 1.3 m; b c = 0.65 m); I c = 0.12 m 4 I ; c I cos ϕ = 1; y = 4fξξ ; ξ = x l ; p = 80 kn m (näide on võetud raamatust [Rää75] lk 521 ja 524). Kaare ristlõike muutus I c I = cos ϕ ; A c A = 3 cos ϕ (12.26) Jõumeetodi kanoonilise võrrandi kordajad EI c δ 1 1 ja EI c 1 p arvutatakse järmiste integraalidega EI c δ 1 1 = = s 0 s EI c 1 p = y 2 I c I ds + I l c I y 2 I c I dx + I c I 0 s ym 0 I c p 0 0 l 0 I ds = s cos 2 ϕ A c A ds = cos ϕ 3 cos ϕ dx (12.27) 0 l ymp 0 cos ϕ ds = 0 ymp 0 dx (12.28) Simpsoni valemiga (7.40 lk 103) numbriliseks integreerimiseks vajalikud suurused on näidatud Octave iga lahendamise päevikus 12.1, kus EI c δ 1 1 = ja EI c 1 p = e H = X 1 = EI c 1 p e + 05 = = kn (12.29) EI c δ Numbriliselt leitud lahend H = kn (vt programm C.25 lk 275) langeb kokku analüütiliselt leitud toereaktsiooniga H = 1259 kn (vt õpik [Rää75] lk 521). Joonisel 12.3 toodud
175 12.3. KAHE LIIGENDIGA KAARE ARVUTAMISE NÄITED 175 p = 80 kn/m c H a f = 4 m b H p = 80 kn/m Va l 1 = 16 m l = 32 m Vb l 1 = 16 m l = 32 m M [knm] M o [knm] Q [kn] N [kn] Q o [kn] Joonis Kahe liigendiga kaar analüütiliselt leitud sisejõudude epüüre on võimalik võrrelda numbriliselt leitutega (vt Päevik 12.1). Lahendamisel saadud tulemused on toodud päevikus diary kaarsjpr1.out (vt Päevik 12.1). Päevik 12.1 kaarsjpr1.out octave:27> diary kaarsjpr1.out octave:28> diary on octave:29> kaarsjpr1 l = 32 f = 4 F1 = 0 F2 = 0 qz = 80 af1 = 32 af2 = 32 aqa = 0 aql = 16 NT = 20 NN = 22 Ic = Ac = Vb = 320 Va = 960 EIcDelta = e+05 EIcdelta = H = Kahe liigendiga kaar
176 176 PEATÜKK 12. KAARED JA VÕLVID x y y^2 cosfi cosfi^(1/3) cosfi*cosfi^(1/3) Lihttala sisej~oud ja kahe liigendiga kaar x y Qo Mo y*mo e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e+00
177 12.3. KAHE LIIGENDIGA KAARE ARVUTAMISE NÄITED Kaare sisej~oud N Q M x e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e e ans = 1 ans = 2 ans = 3 ans = 4 ans = 5 octave:30> diary off Programm C.25 joonistab ka kaare sisejõudude epüürid. Joonisel 12.4 on kahe liigendiga kaare paindemomendi epüür Kahe liigendiga kaare paindemomendi epüür line 1 line 2 M x Joonis Kahe liigendiga kaare paindemomendi epüür
178 178 PEATÜKK 12. KAARED JA VÕLVID 12.4 Liigendita sümmeetriline kaar Liigendita sümmeetriline kaar on kolmekordselt staatikaga määramatu (joonis 12.5). Lisatundmatu valikul on soovitatav, et võrrandisüsteemis (12.30) a) x c b) x 1 ϕ c x 2 x 3 x c y c f a b y x l/2 l/2 a b c) d) c x 1 yc x 1 x 1 x 1 y c x 2 x 2 x 2 x 3 a x 3 x 3 b Joonis Liigendita sümmeetriline kaar δ 11 δ 12 δ 13 δ 21 δ 22 δ 23 δ 31 δ 32 δ 33 X 1 X 2 X 3 + 1p 2p 3p = 0 (12.30) võrduksid kõik kõrvalpaigutised δ 13 = δ 31 = 0 ja δ 23 = δ 32 = 0 nulliga. Kui põhiskeemis on jäikade konsoolide otsad kaare elastsuskeskmes, siis kõrvalpaigutis δ 12 = δ 21 = 0. võrrandisüsteemi lahendid on δ δ δ 33 Võtame kasutusele järgmised tundmatud: X 1 X 2 X 3 + 1p 2p 3p = 0 (12.31) X 1 = 1p δ 11 X 2 = 2p δ 22 (12.32) X 3 = 3p δ 33 kolme liigendiga kaares sümmeetriline tundmatu X 1 = y c (vt joonis 12.6 a), sümmeetriline grupptundmatu X 2 = 1 (vaata joonis 12.7 a)) ja antisümmeetriline grupptundmatu X 3 = x c (vaata joonis 12.8 a));
179 12.4. LIIGENDITA SÜMMEETRILINE KAAR 179 kõvera tala puhul sümmetrilised grupptundmatud X 1 = 1 (vt joonis 12.6 b), X 2 = 1 (vt joonis 12.7 b) ja antisümmeetriline grupptundmatu X 3 = l (vt joonis b); kahe konsooliga põhiskeemis X 1 = 1 (vt joonis 12.6 c), X 2 = 1(vt joonis 12.7 c)), X 3 = 1 (vaata joonis 12.8 c). a) d c e d) y c X 1 = y c a b b) c X 1 = 1 X 1 = 1 a b c) a c X 1 = 1 b e) f yc cos ϕ k f) sin ϕ k 1.00 m 1 ep n 1 ep q 1 ep sin ϕ k cos ϕ k f y c Joonis Liigendita kaar. Tundmatu X 1 X = 1 a) 2 X 2 = 1 X 2 = 1 c d e a b d ) m 2 ep b) e) n 2 ep X 2 = 1 X 2 = 1 a b f) q 2 ep c) c a X 2 = 1 X 2 = 1 b Joonis Liigendita kaar. Tundmatu X 2
180 180 PEATÜKK 12. KAARED JA VÕLVID a) a b X = x c X = x c 3 3 b) X = l/2 X = l/2 a 3 3 b c) d a b X 3 = 1 c c e d) l 2 m 3 ep e) f) cos ϕ k sin ϕ k n ep q 3 ep l 2 sin ϕ k cos ϕ k Joonis Liigendita kaar. Tundmatu X 3 Kõigi kolme põhiskeemi jaoks on nendest tundmatutest põhjustatud sisejõudude avaldised ühesugused [Rää75]: m 1 = y y c ; n 1 = cos ϕ; q 1 = sin ϕ m 2 = 1; n 2 = 0; q 1 = 0 m 3 = x; n 3 = sin ϕ; q 3 = cos ϕ (12.33) Kaare elastsuskeskme ordinaat y c määratakse tingimusest EI c δ 1 2 = 0. Avaldise (12.5) abil saame I c EI c δ 1 2 = m 1 m 2 I ds + I c A c n 1 n 2 A c A ds I c m1 n 2 A c ds I c n1 m 2 A c ds + A c ϱ A c A c ϱ A c +k E G I c A c Arvestades avaldisi (12.33), kirjutame valemi (12.34) ringi EI c δ 1 2 = A c q 1 q 2 ds = 0 (12.34) A (y y c ) I c I ds I c I Võrrandist (12.35) avaldame elastsuskeskme ordinaadi y c y I c y c = I ds Ic cos ϕ A c A c ϱ A c ds Ic I ds cos ϕ A c ds = 0 (12.35) ϱ A c (12.36) Koormusest põhjustatud siirete 1 p, 2 p ja 3 p arvutamiseks on soovitatav lahutada koormus sümmeetriliseks ja antisümmeetriliseks. Sümmeetrilisest koormusest saame
181 12.4. LIIGENDITA SÜMMEETRILINE KAAR 181 siirded 1 p ja 2 p ning antisümmeetrilisest koormusest siirde 3 p. EI c δ i j = I c m i m j I ds + I c A c n i n j A c A ds 2 I c mi n j A c ds + k E I c A c q i q j ds = 0 (12.37) A c ϱ A c G A c A siin i = j, (j = 1, 2, 3) ja joone y = y (x) kõverusraadius ϱ = 1 ψ (joone kõverus ψ j avaldis (1.16)) [ ϱ = (y ψ = ) 2 ] 3 2 y (12.38) EI c ip = m i M 0 p I c A c +k E G I c A c I c I ds + I c mi Np 0 A c A c n i N 0 p ϱ A ds I c A c q i Q 0 p A c A ds ni M 0 p ϱ A c A ds + A c ds (12.39) A kus M 0 p, Q 0 p, N 0 p on paindemoment, põik- ja pikijõud staatikaga määratavas põhiskeemis, mis saadakse liigendita kaarest kolme sideme eemaldamisega. Kui valemites (12.37) ja (12.39) kasutada sisejõudude avaldisi (12.33), saame EI c δ 11 = EI c δ 22 = EI c δ 33 = EI c 1p = (y y c ) 2 I c I ds + I c cos 2 ϕ A c A c A ds 2 I c (y yc ) cos ϕ A c A c ϱ A ds + +k E I c sin 2 ϕ A c ds (12.40) G A c A Ic ds (12.41) I x 2 I c I ds + I c sin 2 ϕ A c A c A ds + +2 I c x sin ϕ A c A c ϱ A ds + +k E I c cos 2 ϕ A c ds (12.42) G A c A (y y c ) Mp 0 I c I ds + I c Np 0 cos ϕ A c A ds I c A c (y yc ) N 0 p ϱ A c A c A ds
182 182 PEATÜKK 12. KAARED JA VÕLVID EI c 2p = I c A c k E G EI c 3p = M 0 p + I c A c +k E G M 0 p cos ϕ A c ϱ A ds Q 0 p sin ϕ A c ds (12.43) A I c I ds I c N 0 p A c ds (12.44) ϱ A I c A c xm 0 p I c A c A c I c I ds + I c xn 0 p ϱ A c A c A ds I c A c Np 0 sin ϕ A c A ds + M 0 p sin ϕ ϱ A c A ds + Q 0 p cos ϕ A c ds (12.45) A Pärast tundmatute leidmist (vt avaldised (12.32)) arvutatakse sisejõud M p = M 0 p + (y y c ) X 1 + X 2 xx 3 N p = N 0 p + X 1 cos ϕ + X 3 sin ϕ (12.46) Q p = Q 0 p X 1 sin ϕ + X 3 cos ϕ 12.5 Liigendita kaare arvutamise näited Näide 12.2 Arvutada liigendita kaare (joonis 12.9), mis on koormatud jaotatud koormusega q (q c = 10 kn m, q k = 50 kn m ) sisejõudude M, Q ja N ordinaadid. Andmed: l = 32 m; l 1 = 16 m; f = 4 m; A c = m 2 (h c = 1.3 m; b c = 0.65 m); I c = 0.12 m 4 ; G = 0.425E; Ic A c = m 2. Kaare telgjooneks on ruutparabool y = 4fx2 l 2 (12.47) Näide on võetud raamatust [Rää75] lk 536. Kaare ristlõige on jääva laiusega ja kõrgus muutub selliselt, et I = A = I c cos ϕ 3 A c (12.48) cos ϕ (12.49) Kaare elastsuskeskme ordinaat y c arvutatakse avaldisega (12.36) kus I c I = cos ϕ, A c A = 3 cos ϕ, ds = dx cos ϕ (12.50) y c = l/2 0 y dx Ic l/2 A c 0 l/2 0 dx 1 ϱ 3 cos ϕ dx (12.51)
183 12.5. LIIGENDITA KAARE ARVUTAMISE NÄITED 183 a) q k q c q k b) x a c 8 lf 6 l y 1 l b d) q k a q c 8 10 c q k b 0 q k q c q k c) ξ ξ = 1 ξ η = 0 ξ = M ep f) e) N ep , , Q ep Joonis Liigenditeta kaar Kaare kõveruse ϱ leiame valemiga (12.38) ϱ = [ 1 + (y ) 2] 3 2 y = ( f 2 x 2 l 4 ) 3 (12.52) 8f l 2 Vastava lihttala paraboolse jaotusega koormuse saame kirjeldada avaldisega q (ξ) = N 1 q k + N 2 q c + N 1 q k = = 1 ( 2 ξ (ξ 1) q k + 1 ξ 2) q c ξ (ξ + 1) q k = = q c + (q k q c ) ξ 2 (12.53) siin on ξ = x l/2 mõõtmeteta koordinaat, mille null on tala keskel, N i on kujufunktsioonid (Lagrange i interpolatsioonipolünoomi kordajad). Lihttala (joonis 12.9 d) paindemomendi ja põikjõu epüüri ordinaadid paraboolsest koormusest M 0 (ξ k ) = V a ( l 2 x k = V a ( l 2 l 2 ξ k ) l/2 ) x k (x x k ) q dx = 1 = V a l 2 (1 ξ k) q c q (ξ) (1 ξ k ) l2 ξ k 4 dξ = ( ) 1 2 ξ k + ξ2 k l (q k q c ) ( 1 4 ξ ) k 3 + ξ4 k l (12.54)
184 184 PEATÜKK 12. KAARED JA VÕLVID l/2 1 Q 0 (ξ k ) = V a q dx = V a x k ξ k q l 2 dξ = = V a q c (1 ξ k ) l 2 (q k q c ) kus V a on lihttala toereaktsioon antud koormusest I c A c ( 1 3 ξ3 k 3 ) l 2 (12.55) l V a = q c 2 + (q k q c ) l2 (12.56) 6 Lihttala paindemomendi ja põikjõu epüüri ordinaatide arvutamiseks paraboolsest koormusest saame kasutada funktsiooni lihttalaprbksj.m (C.4 vt lk 212) ja programmi lihttalaprbksjpr.m (C.2 vt lk 207). Koormusest põhjustatud siirete leidmiseks arvutatakse sisejõudude Mp 0, Np 0, Q 0 p epüüride ordinaadid kolme liigendiga kaare (joonis 12.9 b) jaoks, mille kaks liigendit on kannaristlõigetes. Nende sisejõudude leidmiseks kaares (paraboolse telgjoone kujuga) kasutame Octave i funktsiooni kaarprbstmsj.m (C.28 vt lk 290) ja programmi kaarprbstmsjpr.m (C.26 vt lk 280). Viimasel programm arvutab ka elastsuskeskme ordinaadi (vt avaldist(12.36)), kus y I c I ds m2 (12.57) cos ϕ A c ds m 2 (12.58) ϱ A c ja Ic ds = 16 m (12.59) I 21, y c = = m (12.60) 16 Programmiga kaarprbstmsjpr.m C.26 saab arvutada õpikus [Rää75] lk 538 toodud valemitega. Toereaktsioonid: Vap 0 l = q c (q k q c ) l 16 = = 1120 kn (12.61) [ 3 Hp 0 = ] /4 = 1600 kn (12.62) 3 3 Pikijõud lukuliigendis on N 0 cp = H 0 p. Sisejõud staatikaga määratavas põhiskeemis: M 0 xp = N 0 cpy q c x (q x q c ) = y x2 2 x4 [ 768 N 0 xp = N 0 cp cos ϕ + = Q 0 xp = q c x + 4 (q x q c ) x 4 12 l 2 = ] x3 3 l 2 sin ϕ = (12.63) ( ) cos ϕ + x + x3 sin ϕ (12.64) 192 ( ) sin ϕ + x + x3 cos ϕ (12.65) 192
185 12.5. LIIGENDITA KAARE ARVUTAMISE NÄITED 185 Siirete EI c δ 11 ja EI c δ 22 arvutamisel avaldistega (12.40), (12.41) ja (12.43), (12.44) kasutame seoseid (12.50) 1 2 EI cδ 11 = 1 2 EI cδ 22 = l/2 (y y c ) 2 dx + I c 0 +k E I l/2 c G A c 0 l/2 0 A c l/2 0 cos ϕ 3 cos ϕ dx + sin 2 ϕ tg ϕ 3 cos ϕ dx (12.66) dx = 16 m (12.67) 1 2 EI c 1p = 1 2 EI c 2p = l/2 (y y c ) M 0 p dx + I c 0 k E I l/2 c G A c 0 l/2 0 A c l/2 0 N 0 p 3 cos ϕ dx Q 0 ptg ϕ 3 cos ϕ dx (12.68) M 0 p dx (12.69) Avaldistes (12.66) (12.69) ei ole arvestatud kõveruse 1 ϱ mõju. Programmiga kaarprbstmsjpr.m C.26 arvutatud võrrandisüsteemi kordajad Võrrandisüsteemi lahend 1 2 EI cδ 11 = m 1 2 EI cδ 22 = 16 m 1 2 EI c 1p = knm EI c 2p = knm 2 (12.70) X 1 = knm; X 2 = knm; X 3 = 0 (12.71) Liigenditeta kaare paindemomendi M p, normaaljõu N p ja põikjõu Q p epüüri ordinaadid arvutame järgmiste valemite abil: M p = M 0 p + (y y c ) X 1 + X 2 xx 3 N p = N 0 p + X 1 cos ϕ + X 3 sin ϕ (12.72) Q p = Q 0 p X 1 sin ϕ + X 3 cos ϕ programmiga C.26. Programm C.26 joonestab ka nende sisejõudude epüürid.
186 186 PEATÜKK 12. KAARED JA VÕLVID
187 Osa III Lisad 187
188
189 Lisa A Mõisteid vardateooriast A.1 Kohalik ja üldteljestik Varraskonstruktsiooni iga vardaga seostatakse teljestik nii, et x-telg ühtib varda teljega (vt joonis 7.1, teljed x ja z ). Nimetame neid kohalikeks teljestikeks. Konstruktsiooni varraste asukoha ja nende suuna kirjeldamiseks kasutame üldteljestikku (teljed x ja z). Kasutame ainult parema käe teljestikku (joonis A.1). Vaadates telje positiivsest otsast, loeme pööret positiivseks z-teljest x-telje suunas, x-teljest y-telje suunas ja y-teljest z-telje suunas. Joonisel A.1 on näidatud nii parema käe kui ka vasaku käe teljestik. Tasapinnaliste konstruktsioonide kirjeldamisel vaatame y-telje positiivsest otsast, nii näeme x- ja z-telge. Positiivne pöördenurk on z-teljest x-telje suunas. Parema käe teljestiku puhul on positiivne pööre vastupäeva. Vasaku käe teljestiku korral on positiivne pööre päripäeva. Siirete ja jõuvektorite kirjeldamiseks kohalikes ja üldkoordinaatides on vajalikud koordinaatide teisendused. Joonis A.1. Vasaku ja parema käe teljestik Joonisel A.1 on näidatud positiivse pöördenurga suund. Vaadates telje positiivsest otsast, loeme pööret positiivseks z-teljest x-telje suunas, x-teljest y-telje suunas ja y-teljest z-telje suunas. A.2 Koordinaatide teisendus Koordinaatide teisendusvalemite tuletamiseks vaatleme joonist A.2. Olgu koordinaadid xyz üldkoordinaadid ja x y z kohalikud koordinaadid. Vaatleme veel parema käe 189
190 190 LISA A. MÕISTEID VARDATEOORIAST kolmikuid i, j, k ja i, j, k. Need on ühikvektorite kolmikud, mis määravad ära koordinaattelgede suunad. Joonisel A.2 on ühikvektorid j ja j suunatud vaataja poole. k β k* α zz* α i* α i F β α xx α xz* x* cos α xx = cosα x cos α xz* = cosβ α zx* cos α zx* = cos β z z* cos α zz* = cos α Joonis A.2. Koordinaatide teisendus Vektori F projektsioonid telgedele xz on F x, F z ja telgedele x x on F x, F z. Seega F = F x i + F z k = Fx i + Fz k, i k, i k (A.1) Korrutame avaldise (A.1) vektoriga i ja vektoriga k. Võtame arvesse, et risti olevate vektorite skalaarkorrutis (sisekorrutis) on null. Saame F i = Fx = F x i i + F z k i F k = Fz = F x i k + F z k k (A.2) Pöördseoste leidmiseks korrutame avaldist (A.1) vektoriga i ja vektoriga k. Pöördseosed on F i = F x = Fx i i + Fz k i F k = Fz = Fx i k + Fz k k (A.3) Ühikvektorite skalaarkorrutis võrdub nende positiivsete suundade vahelise nurga koosinusega i i = i i = cos α xx, k k = k k = cos α zz, i k = cos α xz i k = cos α zx (A.4) Telje x suunakoosinused tähistame järgmiselt cos α xx = cos α ja cos α zx = cos β (cos β = cos (90 o + α) = sin α). Jooniselt A.2 näeme, et cos α xx = cos α, cos α zx = cos β cos α zz = cos α, cos α xz = cos β (A.5)
191 A.3. VARDA TÖÖD 191 Varda lõpu ja alguse koordinaatide (joonis 7.1) x L, z L, x A, z A järgi saab need suunakoosinused arvutada cos α = x L x A l (A.6) cos β = z L z A l (A.7) kus l on varda pikkus l = (z L z A ) 2 + (x L x A ) 2 (A.8) Nüüd avaldame koordinaatteisendused järgmiselt: [ F x Fz ] [ cos α cos β = cos β cos α ] [ Fx F z ] (A.9) [ Fx F z ] [ cos α cos β = cos β cos α ] [ F x F z ] (A.10) Võrreldes avaldistes (A.9) ja (A.10) koordinaatide teisendusmaatrikseid, näeme, et nendes on read ja veerud ära vahetatud, s.t ühe saab teisest transponeerimisel. Asendades võrrandis (A.9) F x ja F z nende avaldistega võrrandis (A.10), saame maatrikskorrutise [ ] [ ] cos α cos β cos α cos β = cos β cos α cos β cos α [ ] (A.11) Siin annab maatriksi korrutamine tema transponeeritud kujuga ühikmaatriksi. Selliseid maatrikseid nimetatakse ortogonaalseteks maatriksiteks. Nendel on hea omadus, et pöördmaatriks võrdub tema transponeeritud kujuga (mõlemal juhul on korrutiseks ühikmaatriks). A.3 Varda tööd Varda tööde leidmiseks kasutame ositi integreerimise valemit (A.12) b a b udv = uv b a vdu a (A.12)
192 192 LISA A. MÕISTEID VARDATEOORIAST A.3.1 Varda töö pikkel Kirjutame pikijõu diferentsiaalseose dn x dx = q x (x) (A.13) ehk ( d EA du ) = q x (x) (A.14) dx dx kus N x = EA du dx. Korrutame avaldise (A.14) suvalise siirdega û ja integreerime üle tala pikkuse l b a ( d EA du ) b ûdx = q x (x) ûdx dx dx a (A.15) Võrrandi (A.15) parempoolne liige väljendab väliskoormuse q x tööd W v siirdel û. On võimalik näidata, et koondkoormuse F xi töö varda telje punkti i siirdel û i on F xi û i. Seega W v = b a q x (x) ûdx + F xi û i (A.16) Võrrandi (A.15) vasakpoolset avaldist integreerime ositi valemi (A.12) järgi, võttes u ja dv järgmiselt: b a ( d }{{} û EA du ) dx dx dx u }{{} dv saame avaldise ( b ûd EA du ) ( = EA du ) ( b û b a EA du ) a dx dx a dx }{{}}{{} N x N x dû dx }{{} ˆλ dx (A.17) Võrrandi (A.17) parema poole esimene liige väljendab rajajõudude N x tööd W r rajasiiretel û. Võrrandi (A.17) parema poole teine liige kirjeldab sisejõudude tööd W s. Võttes arvesse välisjõudude töö avaldise (A.16) ja rajajõudude töö avaldise (A.17), võib integraali (A.15) kirjutada kujul N x û }{{} W r b b a N xˆλdx = ( q x (x) ûdx + F xi û i ) (A.18) W s W v a } {{ } a }{{} b
193 A.3. VARDA TÖÖD 193 Kui vaadelda avaldises (A.18) û-d kui virtuaalsiiret, siis väljendab see avaldis virtuaalsiirete printsiipi. Jätkame võrrandi (A.17) viimase liikme ositi integreerimist ( l 0 EA dû ) dx }{{} u du dx }{{} dv ( dx = EA dû ) dx }{{} ˆN x l u l ( d dx EA dû ) udx dx }{{} ˆN x (A.19) Võttes arvesse saadud avaldise (A.19), võime avaldise (A.18) kirjutada kujul N x û }{{} W r l 0 ˆN x u }{{} Ŵ r l 0 + l 0 ( d dx EA dû ) dx }{{} ˆN x l udx = q x (x) ûdx F xi û i 0 } {{ } W v (A.20) Võrrandi (A.20) vasaku poole viimase liikme sisu selgitamiseks võtame vaatluse alla teise (II) koormusolukorra. Võrrandi (A.15), (A.16) eeskujul saame järgmise võrrandi: l Võrranditest (A.20) ja (A.21) saab 0 ( d EA dû ) l udx = ˆq x (x) udx dx dx ˆF xi u i 0 (A.21) N x û }{{} W I r l l 0 + q x (x) ûdx + F xi û i = 0 } {{ } Wv I ˆN x u }{{} Ŵ II r l l 0 + ˆq x (x) udx + ˆF xi u i 0 }{{} Ŵ II v (A.22) tööde vastastikkuse teoreemi tõestuse välis- ja rajajõudude kohta pikkel. Sisejõudude tööde vastastikkuse teoreemi tõestamiseks kirjutame virtuaalsiirete printsiibi (A.18) ringi järgmisele kujule W (p) s = W (p) r + W (p) v (A.23) Kuna avaldise (A.22) põhjal on esimese (I) ja teise (II) koormusolukorra tööd (Wr I + Wv I = Ŵ r II + Ŵ v II ) võrdsed, siis on avaldise (A.23) põhjal ka sisejõudude tööd võrdsed ehk ( l 0 EA du ) dx }{{} N x W (I) s dû dx }{{} ˆλ dx = = W (II) s ( l 0 EA dû ) dx }{{} ˆN x du dx }{{} λ dx (A.24) (A.25) Seega tööde vastastikkuse teoreem pikkel on l N x 0 ˆNx l EA dx = 0 ˆN x N x EA dx (A.26)
194 194 LISA A. MÕISTEID VARDATEOORIAST A.3.2 Varda töö paindel Paindemomendi ja põikjõu tööde avaldise saamisel lähtume diferentsiaalseostest ja Bernoulli hüpoteesist d 2 M y dx 2 = dq z dx = q z (x) ϕ y = dw dx ψ y = d2 w d 2 (A.27) (A.28) (A.29) γ = 0 (A.30) ning seostest M y = EI ydϕ dx, Q z = dm y dx (A.31) d2 dx EI d 2 w 2 y dx = q 2 z (x) (A.32) Nii nagu pikkejõu puhul korrutame võrrandi (A.32) siirdega ŵ ja integreerime üle varda l ( l d d 0 dx dx EI d 2 ) w l y ŵdx = q dx 2 z (x) ŵdx (A.33) 0 Võrrandi (A.33) parempoolne liige väljendab väliskoormuse tööd W v siirdel ŵ. Koondkoormuse F zi töö varda telje punkti i siirdel ŵ i on F zi ŵ i. Seega W v = l 0 q z (x) ŵdx + F zi ŵ i Võrrandi (A.33) vasakpoolset liiget integreerime ositi ( l d d }{{} ŵ 0 dx dx EI d 2 ) ( w d y dx = dx 2 dx EI d 2 ) w y ŵ l dx u }{{}}{{} dv l + 0 d dx Q z ( d 2 ) w dŵ EI y dx dx 2 }{{}}{{} dx M ϕˆ y y Avaldise (A.35) viimast liiget integreerime veel üks kord ( l dŵ d d 2 ) ( w d 2 ) ( w dŵ l l d 2 ) w EI y dx = EI 0 }{{} dx dx dx 2 y dx 2 0 EI y dx }{{}}{{}}{{} 0 dx 2 }{{} u dv M ϕˆ y y M y d 2 ŵ dx 2 }{{} ˆ ψ y dx (A.34) (A.35) (A.36)
195 A.3. VARDA TÖÖD 195 Arvestades saadud avaldisi (A.35) ja (A.36) võime võrrandi (A.33) esitada võimalike tööde (passiivtööde) summana (virtuaalsiirete printsiip paindel) [Q z ŵ + M y ˆϕ y ] }{{} W (p) r l l 0 M y ˆψy dx } 0 {{ } W s (p) l = q z (x) ŵdx F zi ŵ i } 0 {{ } W v (p) (A.37) Paindel tööde vastastikkuse teoreemi tõestamiseks jätkame avaldise (A.37) teise liikme ositi integreerimist ( l 0 d 2 ) ŵ EI y dx 2 }{{} d 2 w dx 2 }{{} ψ y dx = ˆM y ( d 3 ) ŵ = w EI y dx 3 }{{} ˆQ z ( dw d 2 ) ŵ EI y }{{} dx dx 2 }{{} ϕ y ˆM y ( l d 2 ) ŵ dw 0 EI y dx 2 dx }{{}}{{} ˆM y ϕ y l l ( d d 3 ) ŵ EI y dx dx 3 }{{} ˆQ z ( l l d 4 ) ŵ 0 EI y 0 dx 4 }{{} ˆp z wdx dw dx = (A.38) Saadud seosed (A.38) asetame avaldisse (A.37), kust saab tööde vastastikkuse teoreemi paindel [ Qz ŵ+ M y ˆϕ y ] l 0 } {{ } Wr I = l + 0 q z (x) ŵdx + F zi ŵ i = } {{ } Wv I ] ˆM y ϕ y [ ˆQz w+ l 0 } {{ } Wr II l + 0 ˆq z (x) wdx + F zi ŵ i } {{ } Wv II (A.39) siin Q z, M y, p z, w ja ϕ y on esimese koormusolukorra jõud ja siirded ning ˆQ z, ˆMy, ˆp z, ŵ ja ˆϕ y teise koormusolukorra jõud ja siirded. Arvestades saadud avaldisi (A.37), (A.39), saame sisejõudude vastastikuse töö paindel l M y ˆψy dx = 0 } {{ } Ws I) l ˆM y ψ y dx 0 } {{ } Ws II) (A.40) ehk l ˆMy M y dx 0 EI y }{{} Ws I) = l M y ˆM y dx 0 EI y }{{} Ws II) (A.41)
196 196 LISA A. MÕISTEID VARDATEOORIAST
197 Lisa B Maatriksid B.1 Maatriksi mõiste Maatriksiks nimetatakse ridadesse ja veergudesse korrastatud arvude (või nende sümbolite) massiivi a 11 a a 1n a 12 a a 2n A = (B.1).... a m3 a m2... a mn ehk lühidalt A = [a ij ], (i = 1, 2,..., m; j = 1, 2,..., n) (B.2) kus a ij on maatriksi A i-nda rea ja j-nda veeru element. Arvutiprogrammis Octave 1 (vt ka Matlab 2 ) sisestatakse maatriks a = [ ] (B.3) järgmiselt a = [ 1 3 4; ] (vt joonis B.1). Joonis B.1. Maatriksi sisestamine Octave iga
198 198 LISA B. MAATRIKSID B.2 Rea- ja veeruvektor Maatriksit, mis koosneb ainult ühest reast, nimetatakse reavektoriks b = [ b 1 b 2... b n ] (B.4) Arvutiprogrammis Octave (Matlab) sisestatakse reavektor b järgmiselt b=[4 3 5] b = [ ] (B.6) Maatriksit, mis koosneb ainult ühest veerust, nimetatakse veeruvektoriks c = c 1 c 2. c m (B.5) Arvutiprogrammis Octave (Matlab) sisestatakse veeruvektor c 3 c = 8 (B.7) 2 järgmiselt c=[3; 8; 2] Üleminek reavektorilt veeruvektorile ja vastupidi teostatakse Octave is (Matlab is) ülakomaga. Näiteks d=b ja reavektor b (B.6) muudetakse veeruvektoriks d d = B.3 Maatriksite liitmine ja lahutamine (B.8) Maatriksite liitmine (lahutamine) on võimalik siis ja ainult siis, kui nad on üht ja sama järku, s.t kui neil on ühesugune arv veergusid ja ühesugune arv ridu. Näiteks [ ] [ ] [ ] a11 a 12 b11 b + 12 (a11 + b = 11 ) (a 12 + b 12 ) (B.9) a 21 a 22 b 21 b 22 (a 21 + b 21 ) (a 22 + b 22 ) Järgmise näite [ ] + [ ] = [ ] (B.10) puhul tähistame avaldise (B.10) vasakul pool olevad maatriksid a, b ja sisestame nad Octave is (Matlab is) järgmiselt:
199 B.4. VEKTORITE JA MAATRIKSITE KORRUTAMINE 199 a=[1 3 4; 2 1 5] b=[2 0 3; 1 3 2] ning seejärel sisestame järgmise avaldise c=a+b Tulemuseks saame [ c = ] (B.11) B.4 Vektorite ja maatriksite korrutamine Reavektori b (B.4) ja veeruvektori c (B.5) korrutis on vektorite b ja c vastavate elementide korrutiste summa. Sellist korrutist nimetatakse vektorite skalaarkorrutiseks ehk lühidalt [ ] b1 b 2... b n c 1 c 2. c m = b 1c 1 + b 2 c b n c n (B.12) bc = b i c i (i = 1, 2,..., n) (B.13) Veeruvektori c (B.5) ja reavektori b (B.4) korrutis on maatriks, mille elementideks on vektorielementide korrutis. Sellist korrutist nimetatakse vektorite diaad- ehk otsekorrutiseks ehk lühidalt c 1 c 2. c m [ ] b1 b 2... b n = c 1 b 1 c 1 b 2... c 1 b n c 2 b 1 c 2 b 2... c 2 b n.... c m b 1 c m b 2... c m b n (B.14) c b = b i c j, (i = 1, 2,..., m; j = 1, 2,..., n) (B.15) Maatriksi A korrutiseks veeruvektoriga c nimetatakse veeruvektorit d, mille elemendid on maatriksi A ridade elementide ja veeruvektori c vastavate elementide korrutiste summad a 11 a a 1n a 21 a a 2n.... a m1 a m2... a mn c 1 c 2. c m = (a 11 c 1 + a 12 c a 1n c n ) (a 21 c 1 + a 22 c a 2n c n ). (a m1 c 1 + a m2 c a mn c n ) (B.16)
200 200 LISA B. MAATRIKSID ehk lühidalt Ac = a ij c j, (i = 1, 2,..., m; j = 1, 2,..., n) (B.17) Analoogiliselt leitakse reavektori b korrutis maatriksiga A, mis kujutab endast reavektorit r a 11 a a 1m [ ] a 21 a a 2m b1 b 2... b n.... = [ ] r 1 r 2... r m (B.18) a n1 a n2... a nm kus ehk lühidalt r 1 = (b 1 a 11 + b 2 a b n a n1 ) r 2 = (b 1 a 12 + b 2 a b n a n2 ). =. r m = (b 1 a 1m + b 2 a 2m b n a nm ) (B.19) ba = b i a ij, (i = 1, 2,..., n; j = 1, 2,..., m) (B.20) Maatriksite omavahelist korrutamist võime vaadelda kui ühe maatriksi mitmekordset korrutamist vektoritega, milleks on jaotatud teine maatriks. Maatriksite A ja B korrutiseks C nimetatakse maatriksit, mille elemendid on maatriksi A i-nda rea ja maatriksi B j-nda veeru vastavate elementide korrutiste summad b 11 b 12 b 1j... b 1k b 21 b 22 b 2j... b 2k b 31 b 32 b 3j... b 31k = B..... A; b n1 b n2 b nj... b nk a 11 a 12 a a 1n a 21 a 22 a a 2n a i1 a i2 a i3... a in..... a m1 a m2 a m3... a mn kus maatriksi element c ij ehk lühidalt on järgmine: ; c 11 c 12 c 1j... c 1k c 21 c 22 c 2j... c 2k c i1 c i2 c ij... c ik..... c m1 c m2 c mj... c mk c ij = a i1 b 1j + a i2 b 2j + a i3 b 3j a in b nj = C (B.21) AB = a il b lj, (l = 1, 2,..., n; i = 1, 2,..., m; j = 1, 2,..., k) (B.22) Oluline on, et maatriksite veergude ja ridade arvud oleksid omavahel kooskõlas. Sisestame Octave is (Matlab is) järgmised maatriksid a ja b
201 B.5. MAATRIKSITE ELEMENT-ELEMENT KORRUTAMINE 201 a=[1 3; 2 0; 3 1] b=[2 1 0; 3 4 1] ning seejärel teostame korrutamise c=a b Tulemuseks saame c = (B.23) B.5 Maatriksite element-element korrutamine Maatriksite element-element kaupa korrutamine (ingl element-by-element multiplication). A. B = a ij b ij (siin ei ole summeerimist i ja j järgi) (B.24) Vektorite m1 = [ ], M p = [ ] element-elemendi kaupa korrutamine K = m1. M p annab tulemuseks K = [ ] (vt joonis B.2). Seda korruta- Joonis B.2. Maatriksite ja vektorite element-element korrutamine mist saab kasutada Simpsoni valemiga numbrilisel integreerimisel
Analüütiline geomeetria
 Sügissemester 2016 Loengukonspekt Loengukonspektid 1 Aivo Parring, Algebra ja geomeetria, (IV. peatükk, Vektoralgebra, V. peatükk, Sirged ja tasandid, VI. peatükk, Ellips, hüperbool ja parabool), math.ut.ee
Sügissemester 2016 Loengukonspekt Loengukonspektid 1 Aivo Parring, Algebra ja geomeetria, (IV. peatükk, Vektoralgebra, V. peatükk, Sirged ja tasandid, VI. peatükk, Ellips, hüperbool ja parabool), math.ut.ee
ANALÜÜTILISE GEOMEETRIA PRAKTIKUM
 ANALÜÜTILISE GEOMEETRIA PRAKTIKUM 198 5 TARTU RIIKLIK ÜLIKOOL Algebra ja geomeetria kateeder ANALÜÜTILISE GEOMEETRIA PRAKTIKUM II Sirge ja tasand L. Tuulmets Teine parandatud trükk TARTU 1985 Kinnitatud
ANALÜÜTILISE GEOMEETRIA PRAKTIKUM 198 5 TARTU RIIKLIK ÜLIKOOL Algebra ja geomeetria kateeder ANALÜÜTILISE GEOMEETRIA PRAKTIKUM II Sirge ja tasand L. Tuulmets Teine parandatud trükk TARTU 1985 Kinnitatud
PUUDE LOENDAMINE. Teema 7.3 (Lovász: Ch 8) Jaan Penjam, Diskreetne Matemaatika II: Puude loendamine 1 / 55
 PUUDE LOENDAMINE Teema 7.3 (Lovász: Ch 8) Jaan Penjam, email: jaan@cs.ioc.ee Diskreetne Matemaatika II: Puude loendamine 1 / 55 Loengu kava 1 Märgendatud ja märgendamata puud 2 Puude esitamine arvuti mälus
PUUDE LOENDAMINE Teema 7.3 (Lovász: Ch 8) Jaan Penjam, email: jaan@cs.ioc.ee Diskreetne Matemaatika II: Puude loendamine 1 / 55 Loengu kava 1 Märgendatud ja märgendamata puud 2 Puude esitamine arvuti mälus
5. TERMODÜNAAMIKA ALUSED
 KOOLIFÜÜSIKA: SOOJUS (kaugõppele) 5. ERMODÜNAAMIKA ALUSED 5. ermodünaamika I seadus ermodünaamika I seadus annab seose kehale antava soojushulga, keha siseenergia ja paisumistöö vahel = U + A, kus on juurdeantav
KOOLIFÜÜSIKA: SOOJUS (kaugõppele) 5. ERMODÜNAAMIKA ALUSED 5. ermodünaamika I seadus ermodünaamika I seadus annab seose kehale antava soojushulga, keha siseenergia ja paisumistöö vahel = U + A, kus on juurdeantav
Lisakonstruktsioonid geomeetrias
 Lisakonstruktsioonid geomeetrias 1. Tsentraalpunkt Väga sageli piisab geomeetriaülesannete lahendamisel lisakonstruktsioonist, kus tuuakse sisse üksainus sobivalt valitud punkt, mis jagab joonise teatud
Lisakonstruktsioonid geomeetrias 1. Tsentraalpunkt Väga sageli piisab geomeetriaülesannete lahendamisel lisakonstruktsioonist, kus tuuakse sisse üksainus sobivalt valitud punkt, mis jagab joonise teatud
POOLJUHTIDE F00S1KA ALUSED
 TARTU KUKUK C4LIKOOL Ы./МОММ POOLJUHTIDE F00S1KA ALUSED TARTU 1958 TARTU RIIKLIK tflikool U, Nõmm POOLJUHTIDE FtmSIKA ALUSED (Loengukursuse konspekt) Tartu 1968 У.Х. Нымы ОСНОВЫ ФИЗИКИ ПОЛУПРОВОДНИКОВ
TARTU KUKUK C4LIKOOL Ы./МОММ POOLJUHTIDE F00S1KA ALUSED TARTU 1958 TARTU RIIKLIK tflikool U, Nõmm POOLJUHTIDE FtmSIKA ALUSED (Loengukursuse konspekt) Tartu 1968 У.Х. Нымы ОСНОВЫ ФИЗИКИ ПОЛУПРОВОДНИКОВ
TARTU RIIKLIK ÜLIKOOL MATEMAATILISE ANALÜÜSI PRAKTIKUM
 I TARTU RIIKLIK ÜLIKOOL S.Baron, E.Jürimäe, E.Reimers MATEMAATILISE ANALÜÜSI PRAKTIKUM II tartu saa 1972 TARTU RIIKLIK ÜLIKOOL Matemaatilise analüüsi kateeder S.Baron, E.Jürimäe, E.Reimers MATEMAATILISE
I TARTU RIIKLIK ÜLIKOOL S.Baron, E.Jürimäe, E.Reimers MATEMAATILISE ANALÜÜSI PRAKTIKUM II tartu saa 1972 TARTU RIIKLIK ÜLIKOOL Matemaatilise analüüsi kateeder S.Baron, E.Jürimäe, E.Reimers MATEMAATILISE
Wilcoxoni astaksummatest (Wilcoxon Rank-Sum Test )
 Peatükk 3 Wilcoxoni astaksummatest Wilcoxon Rank-Sum Test 3.1 Teststatistiku konstrueerimine Wilcoxoni astaksummatest on mitteparameetriline test kahe sõltumatu populatsiooni võrdlemiseks. Testprotseduuri
Peatükk 3 Wilcoxoni astaksummatest Wilcoxon Rank-Sum Test 3.1 Teststatistiku konstrueerimine Wilcoxoni astaksummatest on mitteparameetriline test kahe sõltumatu populatsiooni võrdlemiseks. Testprotseduuri
MÅLESTOKSFORHOLD HFB 2012 / 13. Målestoksforhold OP SL AG. Byggecentrum
 MÅLESTOKSFORHOLD Målestoksforhold 340 MÅLEENHEDER Måleenheder Omsætning: Gl. dansk mål metermål gl. engelsk mål (= amerikansk mål). Se også: Målesystemer og enheder. Gl. dansk mål Metermål Gl. engelsk
MÅLESTOKSFORHOLD Målestoksforhold 340 MÅLEENHEDER Måleenheder Omsætning: Gl. dansk mål metermål gl. engelsk mål (= amerikansk mål). Se også: Målesystemer og enheder. Gl. dansk mål Metermål Gl. engelsk
FÜÜSIKA AINEKAVA gümnaasiumi 10. klassile
 FÜÜSIKA AINEKAVA gümnaasiumi 10. klassile 1.Õppe-eesmärgid Gümnaasiumi füüsikaõppega taotletakse, et õpilane: 1. Teadvustab füüsikat kui looduse kõige üldisemaid põhjuslikke seoseid uurivat teadust ja
FÜÜSIKA AINEKAVA gümnaasiumi 10. klassile 1.Õppe-eesmärgid Gümnaasiumi füüsikaõppega taotletakse, et õpilane: 1. Teadvustab füüsikat kui looduse kõige üldisemaid põhjuslikke seoseid uurivat teadust ja
Outline. Chapter 6: (cont d) Qijin Chen. November 21, 2013 NH = =6 CH = 15 4
 Chapter 6: Qjn Chen Department of Physcs, Zhejang Unversty November 1, 013 Copyrght c 013 by Qjn Chen; all rghts reserved. ω 3 4 1. (cont d) 1 3 n3n3n 3n (x 1, y 1, z 1 )(x, y, z ) (x 1 x ) + (y 1 y )
Chapter 6: Qjn Chen Department of Physcs, Zhejang Unversty November 1, 013 Copyrght c 013 by Qjn Chen; all rghts reserved. ω 3 4 1. (cont d) 1 3 n3n3n 3n (x 1, y 1, z 1 )(x, y, z ) (x 1 x ) + (y 1 y )
Üldinfo. Me teeme elu kasutajate jaoks lihtsamaks, arendades pidevalt töökindlaid ja pika elueaga süsteeme.
 TOOTEÜLEVAADE 2014 Üldinfo Me teeme elu kasutajate jaoks lihtsamaks, arendades pidevalt töökindlaid ja pika elueaga süsteeme. Meie tooted teevad läbi mitmeastmelise korrosioonikaitsetöötluse*. Kõik tooted
TOOTEÜLEVAADE 2014 Üldinfo Me teeme elu kasutajate jaoks lihtsamaks, arendades pidevalt töökindlaid ja pika elueaga süsteeme. Meie tooted teevad läbi mitmeastmelise korrosioonikaitsetöötluse*. Kõik tooted
PHP II. Ivari Horm Ivari Horm,
 PHP II Ivari Horm ranger@risk.ee Sissejuhatus Failid Massiivid Eriotstarbelised massiivid Abifunktsioonid E-kirjade saatmine PHP-s Failid Ivari Horm ranger@risk.ee Failid Arvutis olevaid faile on võimalik
PHP II Ivari Horm ranger@risk.ee Sissejuhatus Failid Massiivid Eriotstarbelised massiivid Abifunktsioonid E-kirjade saatmine PHP-s Failid Ivari Horm ranger@risk.ee Failid Arvutis olevaid faile on võimalik
Arvu mõiste kujunemise alused
 Peatükk 1 Arvu mõiste kujunemise alused 1.1 Lühiülevaade arvu mõiste kujunemise ajaloolistest aspektidest Tundub, et kõige lihtsam hulkade võrdlemise viis on üksühese vastavuse moodustamine. Hulga elementide
Peatükk 1 Arvu mõiste kujunemise alused 1.1 Lühiülevaade arvu mõiste kujunemise ajaloolistest aspektidest Tundub, et kõige lihtsam hulkade võrdlemise viis on üksühese vastavuse moodustamine. Hulga elementide
Optimeerimine. Pidu, silindrilkäik ja pank. Lauri Tart
 Optimeerimine. Pidu, silindrilkäik ja pank. Lauri Tart Sissejuhatus Peatükk 7 (ja edasi kuni kümnendani) uurib nn optimisatsiooniprobleeme ja püüab nende lahendamiseks mingeid vahendeid anda. Optimisatsiooniprobleemide
Optimeerimine. Pidu, silindrilkäik ja pank. Lauri Tart Sissejuhatus Peatükk 7 (ja edasi kuni kümnendani) uurib nn optimisatsiooniprobleeme ja püüab nende lahendamiseks mingeid vahendeid anda. Optimisatsiooniprobleemide
5. RÕHK JA ÜLESLÜKKEJÕUD
 5. RÕHK JA ÜLESLÜKKEJÕUD 5.1. Rõhumisjõud ja rõhk Jõud ja rõhk on erinevad asjad. Rõhk oleneb peale jõu ka kokkupuutepindalast. Rõhumisjõud on pinnaga risti. Joonis 5.1. Kahe käe nimetissõrme vahel on
5. RÕHK JA ÜLESLÜKKEJÕUD 5.1. Rõhumisjõud ja rõhk Jõud ja rõhk on erinevad asjad. Rõhk oleneb peale jõu ka kokkupuutepindalast. Rõhumisjõud on pinnaga risti. Joonis 5.1. Kahe käe nimetissõrme vahel on
3. ENERGIA JA SOOJUSHULK
 Soojusõpetus 3 1 3. ENERGIA JA SOOJUSHULK 3.1. Termodünaamiline süsteem ja termodünaamilised protsessid Termodünaamilise süsteemina võib vaadelda iga piiritletud keha või kehade hulka. Süsteemi võib liigendada
Soojusõpetus 3 1 3. ENERGIA JA SOOJUSHULK 3.1. Termodünaamiline süsteem ja termodünaamilised protsessid Termodünaamilise süsteemina võib vaadelda iga piiritletud keha või kehade hulka. Süsteemi võib liigendada
PC PSI PT JEAN-MARIE MONIER GUILLAUME HABERER CÉCILE LARDON MÉTHODES ET EXERCICES. Mathématiques. méthodes et exercices. 3 e.
 PC PSI PT MÉTHODES ET EXERCICES JEAN-MARIE MONIER GUILLAUME HABERER CÉCILE LARDON Mathématiques méthodes et exercices 3 e édition Conception et création de couverture : Atelier 3+ Dunod, 201 5 rue Laromiguière,
PC PSI PT MÉTHODES ET EXERCICES JEAN-MARIE MONIER GUILLAUME HABERER CÉCILE LARDON Mathématiques méthodes et exercices 3 e édition Conception et création de couverture : Atelier 3+ Dunod, 201 5 rue Laromiguière,
III ÜLDINE LINEAARNE MUDEL
 VL.09 Loomade aretusväärtuse hindamine ja aretusprogrammid III ÜLDINE LINEAARNE MUDEL 3. PÕHIMÕISED Üldise lineaarse mudeli rakendamiseks jagatakse registreeritud tunnused kahte ossa uuritavateks e sõltuvateks
VL.09 Loomade aretusväärtuse hindamine ja aretusprogrammid III ÜLDINE LINEAARNE MUDEL 3. PÕHIMÕISED Üldise lineaarse mudeli rakendamiseks jagatakse registreeritud tunnused kahte ossa uuritavateks e sõltuvateks
6. Peatükk. KEEMILISE SIDEME OLEMUS. MOLEKULIDE MOODUSTUMINE
 6. Peatükk. KEEMILISE SIDEME OLEMUS. MOLEKULIDE MOODUSTUMINE 6.1. Keemilise sideme olemus Küsimus keemilise sideme olemusest on (bio)keemia põhiküsimus. Mis on molekul? Üldiselt igasugune püsiv aatomite
6. Peatükk. KEEMILISE SIDEME OLEMUS. MOLEKULIDE MOODUSTUMINE 6.1. Keemilise sideme olemus Küsimus keemilise sideme olemusest on (bio)keemia põhiküsimus. Mis on molekul? Üldiselt igasugune püsiv aatomite
Procedure 2(b) (obvious errors in a number of language versions)
 COU CIL OF THE EUROPEA U IO Brussels, 18 April 2012 8693/12 Interinstitutional File: 2005/0191 (COD) JUR 217 AVIATIO 64 CODEC 969 LEGISLATIVE ACTS A D OTHER I STRUME TS: CORRIGE DUM/RECTIFICATIF Subject:
COU CIL OF THE EUROPEA U IO Brussels, 18 April 2012 8693/12 Interinstitutional File: 2005/0191 (COD) JUR 217 AVIATIO 64 CODEC 969 LEGISLATIVE ACTS A D OTHER I STRUME TS: CORRIGE DUM/RECTIFICATIF Subject:
1. VIHIK. Materjalid ja nende omadused ning üldised nõuded müürile ja müüritöödele. AS Columbia-Kivi Vana-Kastre Tartu maakond
 1. VIHIK Materjalid ja nende omadused ning üldised nõuded müürile ja müüritöödele 1998 2 Columbiakivi projekteerimisjuhend 1 Saateks 1.1 Sissejuhatus Käesolevas juhendis antakse juhised AS Columbiakivi
1. VIHIK Materjalid ja nende omadused ning üldised nõuded müürile ja müüritöödele 1998 2 Columbiakivi projekteerimisjuhend 1 Saateks 1.1 Sissejuhatus Käesolevas juhendis antakse juhised AS Columbiakivi
Loodusteaduste alused. PhD Jaanis Priimets
 Loodusteaduste alused PhD Jaanis Priimets Füüsika ja keemia Füüsika ja keemia kui teadus kujutab endast filosoofilist süsteemi, kus reaalsetele loodusnähtustele seatakse vastavusse nende matemaatilised
Loodusteaduste alused PhD Jaanis Priimets Füüsika ja keemia Füüsika ja keemia kui teadus kujutab endast filosoofilist süsteemi, kus reaalsetele loodusnähtustele seatakse vastavusse nende matemaatilised
Peatükk 1. Arvuteooria
 Peatükk 1 Arvuteooria I Täisarvu esitus positsioonilises arvusüsteemis Põhimõisted 1) Arvu esitamisel positsioonilises arvusüsteemis, mille aluseks on valitud ühest suurem positiivne täisarv k, kasutatakse
Peatükk 1 Arvuteooria I Täisarvu esitus positsioonilises arvusüsteemis Põhimõisted 1) Arvu esitamisel positsioonilises arvusüsteemis, mille aluseks on valitud ühest suurem positiivne täisarv k, kasutatakse
8. Peatükk. AINETE AGREGAATOLEKUD. VEDELIKUD
 8. Peatükk. AINETE AGREGAATOLEKUD. VEDELIKUD 8.1. Aine olekufaasid Vedelik on juba teine ainete olekufaas, mida me oma kursuses käsitleme. Eelmise loengu lõpus nägime, et aine võib teatud tingimustel ühest
8. Peatükk. AINETE AGREGAATOLEKUD. VEDELIKUD 8.1. Aine olekufaasid Vedelik on juba teine ainete olekufaas, mida me oma kursuses käsitleme. Eelmise loengu lõpus nägime, et aine võib teatud tingimustel ühest
Mart Kuurme FÜÜSIKA TÖÖVIHIK. 8. klassile. Fyysika TV 8. klassile.indd , 10:59:49
 Mart Kuurme FÜÜSIKA TÖÖVIHIK 8. klassile 1 Fyysika TV 8. klassile.indd 1 19.09.2005, 10:59:49 Mart Kuurme Füüsika töövihik 8. klassile AS BIT, 2005 ISBN 9985-2-1086-7 Retsenseerinud Koit Timpmann ja Toomas
Mart Kuurme FÜÜSIKA TÖÖVIHIK 8. klassile 1 Fyysika TV 8. klassile.indd 1 19.09.2005, 10:59:49 Mart Kuurme Füüsika töövihik 8. klassile AS BIT, 2005 ISBN 9985-2-1086-7 Retsenseerinud Koit Timpmann ja Toomas
Momenter som deskriptive størrelser. Hvad vi mangler fra onsdag. Momenter for sandsynlighedsmål
 Hvad vi mangler fra onsdag Momenter som deskriptive størrelser Sandsynlighedsmål er komplicerede objekter de tildeler numeriske værdier til alle hændelser i en σ-algebra. Vi har behov for simplere, deskriptive
Hvad vi mangler fra onsdag Momenter som deskriptive størrelser Sandsynlighedsmål er komplicerede objekter de tildeler numeriske værdier til alle hændelser i en σ-algebra. Vi har behov for simplere, deskriptive
Hvad vi mangler fra onsdag. Vi starter med at gennemgå slides fra onsdag.
 Hvad vi mangler fra onsdag Vi starter med at gennemgå slides 34-38 fra onsdag. Slide 1/17 Niels Richard Hansen MI forelæsninger 6. December, 2013 Momenter som deskriptive størrelser Sandsynlighedsmål er
Hvad vi mangler fra onsdag Vi starter med at gennemgå slides 34-38 fra onsdag. Slide 1/17 Niels Richard Hansen MI forelæsninger 6. December, 2013 Momenter som deskriptive størrelser Sandsynlighedsmål er
III NÕO RG AINEKAVA LOODUSAINED:FÜÜSIKA
 III NÕO RG AINEKAVA LOODUSAINED:FÜÜSIKA 4.4.1. Õpetamise eesmärgid Füüsikaõppega taotletakse, et õpilane: 1) teadvustab füüsikat kui looduse kõige üldisemaid põhjuslikke seoseid uurivat teadust ja olulist
III NÕO RG AINEKAVA LOODUSAINED:FÜÜSIKA 4.4.1. Õpetamise eesmärgid Füüsikaõppega taotletakse, et õpilane: 1) teadvustab füüsikat kui looduse kõige üldisemaid põhjuslikke seoseid uurivat teadust ja olulist
8. Peatükk. VEDELIKUD
 8. Peatükk. VEDELIKUD 8.1. Aine olekufaas - vedelik Aine läheb vedelasse faasi kui molekulide soojusliikumise kineetiline energia RT on väiksem molekulidevaheliste tõmbejõudude poolt põhjustatud seoste
8. Peatükk. VEDELIKUD 8.1. Aine olekufaas - vedelik Aine läheb vedelasse faasi kui molekulide soojusliikumise kineetiline energia RT on väiksem molekulidevaheliste tõmbejõudude poolt põhjustatud seoste
Huseftersynsordningen plus, minus ti år -
 Huseftersynsordningen plus, minus ti år - ! # # # % & # ( ( #! # ) # ( & # # # # +! #!# %, # # #! %.# / # # 0#( # # # # # # %, # # # 1 # # % 2 # & # # 0#( # # # # # 2 # #! 2 ( # # 3 ( & # # # (#! #, #
Huseftersynsordningen plus, minus ti år - ! # # # % & # ( ( #! # ) # ( & # # # # +! #!# %, # # #! %.# / # # 0#( # # # # # # %, # # # 1 # # % 2 # & # # 0#( # # # # # 2 # #! 2 ( # # 3 ( & # # # (#! #, #
Trykfejlsliste - alle fejl Asymptotisk teori
 9. januar 2005 Stat 2A / EH Trykfejlsliste - alle fejl Asymptotisk teori Denne liste indeholder alle de regulære fejl, slåfejl og stavefejl der er fundet i 2A-noterne indtil nu. 9 1 Forkert: x C x ro alle
9. januar 2005 Stat 2A / EH Trykfejlsliste - alle fejl Asymptotisk teori Denne liste indeholder alle de regulære fejl, slåfejl og stavefejl der er fundet i 2A-noterne indtil nu. 9 1 Forkert: x C x ro alle
VÕLAKIRJA TINGIMUSED. võlakiri nr Aktsiavõlakiri Euroopa 2012
 Käesolevad tingimused on algselt koostatud rootsi keeles. Juhul, kui esinevad erinevused rootsi- ja eestikeelsete tingimuste vahel, loetakse õigeks rootsikeelsed tingimused. VÕLAKIRJA TINGIMUSED võlakiri
Käesolevad tingimused on algselt koostatud rootsi keeles. Juhul, kui esinevad erinevused rootsi- ja eestikeelsete tingimuste vahel, loetakse õigeks rootsikeelsed tingimused. VÕLAKIRJA TINGIMUSED võlakiri
Wigner s semi-cirkel lov
 Wigner s semi-cirkel lov 12. december 2009 Eulers Venner Steen Thorbjørnsen Institut for Matematiske Fag Århus Universitet Diagonalisering af selvadjungeret matrix Lad H være en n n matrix med komplekse
Wigner s semi-cirkel lov 12. december 2009 Eulers Venner Steen Thorbjørnsen Institut for Matematiske Fag Århus Universitet Diagonalisering af selvadjungeret matrix Lad H være en n n matrix med komplekse
11. KONDENSEERITUD AINE
 11. KONDENSEERITUD AINE 11.1. Ainete olekufaasid Vedelik on juba teine ainete olekufaas, mida me oma kursuses käsitleme. Eelmise loengu lõpus nägime, et aine võib teatud tingimustel ühest faasist teise
11. KONDENSEERITUD AINE 11.1. Ainete olekufaasid Vedelik on juba teine ainete olekufaas, mida me oma kursuses käsitleme. Eelmise loengu lõpus nägime, et aine võib teatud tingimustel ühest faasist teise
M45, M60, M80 M45E, M60E, M80E, M90E
 M45, M60, M80 M45E, M60E, M80E, M90E DA Monterings- og brugsanvisning for elektrisk saunaovn Elektrikerise kasutus- ja paigaldusjuhis M (Sound) ME (Sound) M ME 01022006H INHOLDSFORTEGNELSE 1. ANVISNINGER
M45, M60, M80 M45E, M60E, M80E, M90E DA Monterings- og brugsanvisning for elektrisk saunaovn Elektrikerise kasutus- ja paigaldusjuhis M (Sound) ME (Sound) M ME 01022006H INHOLDSFORTEGNELSE 1. ANVISNINGER
Aalborg Universitet Esbjerg 18. december 2009 Spændings- og deformationsanalyse af perforeret RHS stålprofil Appendiks K Analytiske
 18. december 2009 Spændings- og deformationsanalyse af perforeret RHS stålprofil Appendiks K Analytiske overslagsberegninger Appendiks K Analytiske overslagsberegninger... 3 K-1. Airy s spændingsfunktion
18. december 2009 Spændings- og deformationsanalyse af perforeret RHS stålprofil Appendiks K Analytiske overslagsberegninger Appendiks K Analytiske overslagsberegninger... 3 K-1. Airy s spændingsfunktion
Pontryagin Approximations for Optimal Design of Elastic Structures
 Pontryagin Approximations for Optimal Design of Elastic Structures Jesper Carlsson NADA, KTH jesperc@nada.kth.se Collaborators: Anders Szepessy, Mattias Sandberg October 5, 2005 A typical optimal design
Pontryagin Approximations for Optimal Design of Elastic Structures Jesper Carlsson NADA, KTH jesperc@nada.kth.se Collaborators: Anders Szepessy, Mattias Sandberg October 5, 2005 A typical optimal design
ÕPIOBJEKT Binaarsete tunnuste analüüsimeetodid
 ÕPIOBJEKT Binaarsete tunnuste analüüsimeetodid Tanel Kaart http://ph.emu.ee/~ktanel/ bin_tunnuste_analyys/ Tanel Kaart EMÜ VLI 1 Sisukord 1. Sissejuhatus... 3 1.1. Binaarsete tunnuste olemus ja kodeerimine...
ÕPIOBJEKT Binaarsete tunnuste analüüsimeetodid Tanel Kaart http://ph.emu.ee/~ktanel/ bin_tunnuste_analyys/ Tanel Kaart EMÜ VLI 1 Sisukord 1. Sissejuhatus... 3 1.1. Binaarsete tunnuste olemus ja kodeerimine...
Eksamen i Mat F, april 2006
 Eksamen i Mat F, april 26 Opgave 1 Lad F være et vektorfelt, givet i retvinklede koordinater som: F x x F = F x i + F y j + F z k = F y = 2z F z y Udregn F og F: F = F x + F y + F z = 1 + +. F = F z F
Eksamen i Mat F, april 26 Opgave 1 Lad F være et vektorfelt, givet i retvinklede koordinater som: F x x F = F x i + F y j + F z k = F y = 2z F z y Udregn F og F: F = F x + F y + F z = 1 + +. F = F z F
11/3/2002. Statik og bygningskonstruktion Program lektion Tøjninger og spændinger. Introduktion. Tøjninger og spændinger
 Statik og bygningskonstruktion rogram lektion 9 8.30-9.15 Tøjninger og spændinger 9.15 9.30 ause 9.30 10.15 Spændinger i plan bjælke Deformationer i plan bjælke 10.15 10.45 ause 10.45 1.00 Opgaveregning
Statik og bygningskonstruktion rogram lektion 9 8.30-9.15 Tøjninger og spændinger 9.15 9.30 ause 9.30 10.15 Spændinger i plan bjælke Deformationer i plan bjælke 10.15 10.45 ause 10.45 1.00 Opgaveregning
Matthias Beck Gerald Marchesi Dennis Pixton Lucas Sabalka
 Matthias Beck Gerald Marchesi Dennis Pixton Lucas Sabalka Version.53 z 7! z 2 0 + i i x 2 + = 0. i i 2 + = 0 i 2 = i x 3 + px + q q q 2 4 + p3 27 p q C := {(x, y) : x, y 2 R}, (x, y)+(a, b) := (x
Matthias Beck Gerald Marchesi Dennis Pixton Lucas Sabalka Version.53 z 7! z 2 0 + i i x 2 + = 0. i i 2 + = 0 i 2 = i x 3 + px + q q q 2 4 + p3 27 p q C := {(x, y) : x, y 2 R}, (x, y)+(a, b) := (x
! "# "!# +,- ). "%/")" $" 0* '122 *3 14"5"""!! '16) "!! ":",3);/, 13":", <"))"/
 !! $%&'$( ))$*! +,- ). %/) $ 0* '122 *3 145!! '16)!! 1764)3)*83) 019313:,3);/, 13:,
!! $%&'$( ))$*! +,- ). %/) $ 0* '122 *3 145!! '16)!! 1764)3)*83) 019313:,3);/, 13:,
DVD loomise tarkvara võrdlemine
 Tallinna Ülikool Informaatika Instituut DVD loomise tarkvara võrdlemine Seminaritöö Autor: Jevgeni Salnikov Juhendaja: Andrus Rinde Tallinn 2008 Sisukord SISSEJUHATUS... - 3-1. DVD AJALUGU... - 4-2. VÕRDLEMISPROTSESSIST
Tallinna Ülikool Informaatika Instituut DVD loomise tarkvara võrdlemine Seminaritöö Autor: Jevgeni Salnikov Juhendaja: Andrus Rinde Tallinn 2008 Sisukord SISSEJUHATUS... - 3-1. DVD AJALUGU... - 4-2. VÕRDLEMISPROTSESSIST
Estimation. Lad (ν θ ) θ Θ være en statistisk model på (X, E). En estimator af θ er en afbildning t : X Θ. En konkret værdi t(x) kaldes et estimat.
 Estimation Lad (ν θ ) θ Θ være en statistisk model på (X, E). En estimator af θ er en afbildning t : X Θ. En konkret værdi t(x) kaldes et estimat. En estimator er en gætteregel.. p.1/22 Estimation X acements
Estimation Lad (ν θ ) θ Θ være en statistisk model på (X, E). En estimator af θ er en afbildning t : X Θ. En konkret værdi t(x) kaldes et estimat. En estimator er en gætteregel.. p.1/22 Estimation X acements
ELEMENTAARMATEMAATIKA
 T A R TU R IIK LIK Ü L IK O O L J. Reimand, K. Velsker ELEMENTAARMATEMAATIKA I Algpraktikum T A R T U 1 9 7 2 Matemaatika õpetamise metoodika kateeder J. Reimand, K. Velsker ELEMENTAARMATEMAATIKA I Algpraktikum
T A R TU R IIK LIK Ü L IK O O L J. Reimand, K. Velsker ELEMENTAARMATEMAATIKA I Algpraktikum T A R T U 1 9 7 2 Matemaatika õpetamise metoodika kateeder J. Reimand, K. Velsker ELEMENTAARMATEMAATIKA I Algpraktikum
 1 2 3 4 1 2 3 4 (p A ) (p B ) (p C ) 1 2, 3, 4 2, 3, 4 {2, 3, 4} 1 2 (p A ) (p B ) (p C ) d d {1, 2} (p A,p B )=0
1 2 3 4 1 2 3 4 (p A ) (p B ) (p C ) 1 2, 3, 4 2, 3, 4 {2, 3, 4} 1 2 (p A ) (p B ) (p C ) d d {1, 2} (p A,p B )=0
Program lektion Indre kræfter i plane konstruktioner Snitkræfter Indre kræfter i plane konstruktioner Snitkræfter.
 Tektonik Program lektion 4 8.15-9.00 Indre kræfter i plane konstruktioner 9.00 9.15 Pause 9.15 10.00 Indre kræfter i plane konstruktioner. Opgaver 10.00 10.15 Pause 10.15 12.00 Tøjninger og spændinger
Tektonik Program lektion 4 8.15-9.00 Indre kræfter i plane konstruktioner 9.00 9.15 Pause 9.15 10.00 Indre kræfter i plane konstruktioner. Opgaver 10.00 10.15 Pause 10.15 12.00 Tøjninger og spændinger
Füüsika ainekava. 1. Õppe- ja kasvatuseesmärgid. Gümnaasiumi füüsikaõppega taotletakse, et õpilane:
 Füüsika ainekava 1. Õppe- ja kasvatuseesmärgid Gümnaasiumi füüsikaõppega taotletakse, et õpilane: 1) arendab loodusteaduste- ja tehnoloogiaalast kirjaoskust, loovust ning süsteemset mõtlemist loodusnähtusi
Füüsika ainekava 1. Õppe- ja kasvatuseesmärgid Gümnaasiumi füüsikaõppega taotletakse, et õpilane: 1) arendab loodusteaduste- ja tehnoloogiaalast kirjaoskust, loovust ning süsteemset mõtlemist loodusnähtusi
TUNDIDE ARV 70 AINE SISU. I Valgusõpetus. Päikesesüsteem
 AINE KLASS Füüsika 8. klass TUNDIDE ARV 70 AINE SISU I Valgusõpetus Päikesesüsteem Päike. Täht. Päikesesüsteem. Päikesesüsteemi koostisosad planeedid ja nende kaaslased, väikekehad komeedid, meteoorkehad,
AINE KLASS Füüsika 8. klass TUNDIDE ARV 70 AINE SISU I Valgusõpetus Päikesesüsteem Päike. Täht. Päikesesüsteem. Päikesesüsteemi koostisosad planeedid ja nende kaaslased, väikekehad komeedid, meteoorkehad,
Eksamen i Mat F, april 2006
 Eksamen i Mat F, april 26 Opgave Lad F være et vektorfelt, givet i retvinklede koordinater som: Udregn F og F: F x F = F x i + F y j + F z k = F y = z 2 F z xz y 2 F = F x + F y + F z = + + x. F = F z
Eksamen i Mat F, april 26 Opgave Lad F være et vektorfelt, givet i retvinklede koordinater som: Udregn F og F: F x F = F x i + F y j + F z k = F y = z 2 F z xz y 2 F = F x + F y + F z = + + x. F = F z
Betonkonstruktioner - Lektion 3 - opgave 1
 Betonkonstruktioner - Lektion 3 - opgave Data: bredde flange b 50mm Højde 400mm Rumvægt ρ 4 kn m 3 Længde L 4m q 0 kn R 0kN m q egen ρb.44 kn m M Ed 8 q egen q L 4 RL 4.88 kn m Linjelast for egen vægten
Betonkonstruktioner - Lektion 3 - opgave Data: bredde flange b 50mm Højde 400mm Rumvægt ρ 4 kn m 3 Længde L 4m q 0 kn R 0kN m q egen ρb.44 kn m M Ed 8 q egen q L 4 RL 4.88 kn m Linjelast for egen vægten
Partielle afledede og retningsafledede
 Partielle afledede og retningsafledede 1 Partielle afledede, definitioner og notationer Bertragt en funktion af to reelle variable f : D R, hvor D R 2 er et åbent område Med benyttelse af tilvækstfunktionen
Partielle afledede og retningsafledede 1 Partielle afledede, definitioner og notationer Bertragt en funktion af to reelle variable f : D R, hvor D R 2 er et åbent område Med benyttelse af tilvækstfunktionen
Statistisk hypotese. Lad P være en statistisk model på (X, E). (P er altså en familie af sandsynlighedsmål på (X, E).)
 Statistisk hypotese Lad P være en statistisk model på (X, E). (P er altså en familie af sandsynlighedsmål på (X, E).) En statistisk hypotese er en delmængde P 0 P.. p.1/23 Statistisk hypotese PSfrag replacements
Statistisk hypotese Lad P være en statistisk model på (X, E). (P er altså en familie af sandsynlighedsmål på (X, E).) En statistisk hypotese er en delmængde P 0 P.. p.1/23 Statistisk hypotese PSfrag replacements
ELEKTROONIKA KOMPONENDID
 Uudo Usai ELEKTROONIKA KOMPONENDID Elektroonika alused TPT 1998 ELEKTROONIKAKOMPONEND1D lk.1 SISSEJUHATUS Kaasaegsed elektroonikaseadmed koosnevad väga suurest hulgast elementidest, millest on koostatud
Uudo Usai ELEKTROONIKA KOMPONENDID Elektroonika alused TPT 1998 ELEKTROONIKAKOMPONEND1D lk.1 SISSEJUHATUS Kaasaegsed elektroonikaseadmed koosnevad väga suurest hulgast elementidest, millest on koostatud
Numerisk simulering af ikke-lineære fænomener inden for geoteknik
 Numerisk simulering af ikke-lineære fænomener inden for geoteknik Emil Smed Sørensen COWI, Aalborg Geoteknikerdagen - 9. juni 217 Page 1 of 25 Ph.d.-studie i perioden 212-216, AAU Titel: Numerical simulation
Numerisk simulering af ikke-lineære fænomener inden for geoteknik Emil Smed Sørensen COWI, Aalborg Geoteknikerdagen - 9. juni 217 Page 1 of 25 Ph.d.-studie i perioden 212-216, AAU Titel: Numerical simulation
Områdeestimator. X x. P θ. ν θ. Θ C(x) En områdeestimator er en afbildning C : X P(Θ). . p.1/30
 Områdeestimator X (Ω, F) (X, E) x 01 01 P θ ν θ θ Θ 0000 1111 000000 111111 0000 1111 0000 1111 C(x) En områdeestimator er en afbildning C : X P(Θ).. p.1/30 Konfidensområde En områdestimator C : X P(Θ)
Områdeestimator X (Ω, F) (X, E) x 01 01 P θ ν θ θ Θ 0000 1111 000000 111111 0000 1111 0000 1111 C(x) En områdeestimator er en afbildning C : X P(Θ).. p.1/30 Konfidensområde En områdestimator C : X P(Θ)
Egentyngd (+Struc. dead load) Glas Nyttiglast balkong Egentyngd (+Struc. dead load) Glas Nyttiglast balkong
 Eurocode (NA: Swedih) Eurocode (NA: Swedih) Load combination No. Name ype Factor.35*Egentyngd +.35*Gla +.50*0.70*Nyttiglat balong Ultimate.350.350 3 Egentyngd + Gla + 0.30*Nyttiglat balong Ultimate Quaipermanent.050.0.0.500.000.000
Eurocode (NA: Swedih) Eurocode (NA: Swedih) Load combination No. Name ype Factor.35*Egentyngd +.35*Gla +.50*0.70*Nyttiglat balong Ultimate.350.350 3 Egentyngd + Gla + 0.30*Nyttiglat balong Ultimate Quaipermanent.050.0.0.500.000.000
Aristoteles Camillo. To cite this version: HAL Id: hal
 An experimentally-based modeling study of the effect of anti-angiogenic therapies on primary tumor kinetics for data analysis of clinically relevant animal models of metastasis Aristoteles Camillo To cite
An experimentally-based modeling study of the effect of anti-angiogenic therapies on primary tumor kinetics for data analysis of clinically relevant animal models of metastasis Aristoteles Camillo To cite
Benyttede bøger: Introduction to Cosmology, Barbara Ryden, 2003.
 Formelsamling Noter til Astronomi 1 You can know the name of a bird in all the languages of the world, but when you re finished, you ll know absolutely nothing whatever about the bird... So let s look
Formelsamling Noter til Astronomi 1 You can know the name of a bird in all the languages of the world, but when you re finished, you ll know absolutely nothing whatever about the bird... So let s look
Computing the constant in Friedrichs inequality
 Computing the constant in Friedrichs inequality Tomáš Vejchodský vejchod@math.cas.cz Institute of Mathematics, Žitná 25, 115 67 Praha 1 February 8, 212, SIGA 212, Prague Motivation Classical formulation:
Computing the constant in Friedrichs inequality Tomáš Vejchodský vejchod@math.cas.cz Institute of Mathematics, Žitná 25, 115 67 Praha 1 February 8, 212, SIGA 212, Prague Motivation Classical formulation:
DOKUMENT: Dato/løbenummer: TINGLYSNINGSDATO:
 side 1 ================================================================================ DOKUMENTAKTUELHENT ================================================================================ DOKUMENT: Dato/løbenummer:
side 1 ================================================================================ DOKUMENTAKTUELHENT ================================================================================ DOKUMENT: Dato/løbenummer:
EESTI VABARIIGI ÜLEMNÕUKOGU XII KOOSSEISU 78., ERAKORRALINE ISTUNGJÄRK
 EESTI VABARIIGI ÜLEMNÕUKOGU XII KOOSSEISU 78., ERAKORRALINE ISTUNGJÄRK 6. 9. juuli 1992 SISUKORD EESTI VABARIIGI ÜLEMNÕUKOGU XII KOOSSEISU 78., ERAKORRALINE ISTUNGJÄRK ESIMENE ISTUNG 6. juuli 1992... 4
EESTI VABARIIGI ÜLEMNÕUKOGU XII KOOSSEISU 78., ERAKORRALINE ISTUNGJÄRK 6. 9. juuli 1992 SISUKORD EESTI VABARIIGI ÜLEMNÕUKOGU XII KOOSSEISU 78., ERAKORRALINE ISTUNGJÄRK ESIMENE ISTUNG 6. juuli 1992... 4
Course on Continuum Mechanics - academic year Màster en Enginyeria de Camins, Canals i Ports. Màster en Enginyeria Geològica i de Mines.
 Official Fom Chapte. Desciption of Motion (, t) (, t) + (, t) (, t) t t Chapte. Defomation an Stain s S X E X e i ij j i ij j F X X U F J E F F JJ J J T T T e F F jj j j T T T T s JJ T a JJ T E T t t ij
Official Fom Chapte. Desciption of Motion (, t) (, t) + (, t) (, t) t t Chapte. Defomation an Stain s S X E X e i ij j i ij j F X X U F J E F F JJ J J T T T e F F jj j j T T T T s JJ T a JJ T E T t t ij
GEOMETRI-TØ, UGE 6. . x 1 x 1. = x 1 x 2. x 2. k f
 GEOMETRI-TØ, UGE 6 Hvis I falder over tryk- eller regne-fejl i nedenstående, må I meget gerne sende rettelser til fuglede@imfaudk Opvarmningsopgave 1 Lad f : R 2 R være tre gange kontinuert differentierbar
GEOMETRI-TØ, UGE 6 Hvis I falder over tryk- eller regne-fejl i nedenstående, må I meget gerne sende rettelser til fuglede@imfaudk Opvarmningsopgave 1 Lad f : R 2 R være tre gange kontinuert differentierbar
Statistisk hypotese. Lad P være en statistisk model på (X, E). (P er altså en familie af sandsynlighedsmål på (X, E).)
 Statistisk hypotese Lad P være en statistisk model på (X, E). (P er altså en familie af sandsynlighedsmål på (X, E).) En statistisk hypotese er en delmængde P 0 P.. p.1/26 PSfrag replacements Statistisk
Statistisk hypotese Lad P være en statistisk model på (X, E). (P er altså en familie af sandsynlighedsmål på (X, E).) En statistisk hypotese er en delmængde P 0 P.. p.1/26 PSfrag replacements Statistisk
Energy-saving Technology Adoption under Uncertainty in the Residential Sector
 Energy-saving Technology doption under Uncertainty in the esidential Sector Dorothée Charlier, lejandro Mosino, ude Pommeret To cite this version: Dorothée Charlier, lejandro Mosino, ude Pommeret. Energy-saving
Energy-saving Technology doption under Uncertainty in the esidential Sector Dorothée Charlier, lejandro Mosino, ude Pommeret To cite this version: Dorothée Charlier, lejandro Mosino, ude Pommeret. Energy-saving
Moderne acceleratorers fysik og anvendelse Forelæsning 2 Transverse motion, Lattices
 Moderne acceleratorers fysik og anvendelse Forelæsning 2 Transverse motion, Lattices Optiske elementer: Styring og fokusering. Bevægelsesligningen og dens løsning. Stabilitet. Typiske latticekonfigurationer.
Moderne acceleratorers fysik og anvendelse Forelæsning 2 Transverse motion, Lattices Optiske elementer: Styring og fokusering. Bevægelsesligningen og dens løsning. Stabilitet. Typiske latticekonfigurationer.
264.. Cox, Daio Jang (23) Grandell (1976). 1.1 (Ω, F, {F, [, ]}, P). N λ, λ F, 1 2 u R, λ d < a... E{e iu(n 2 N 1 ) F λ 2 } = e {(eiu 1) 2 1 λ d}, F λ
![264.. Cox, Daio Jang (23) Grandell (1976). 1.1 (Ω, F, {F, [, ]}, P). N λ, λ F, 1 2 u R, λ d < a... E{e iu(n 2 N 1 ) F λ 2 } = e {(eiu 1) 2 1 λ d}, F λ 264.. Cox, Daio Jang (23) Grandell (1976). 1.1 (Ω, F, {F, [, ]}, P). N λ, λ F, 1 2 u R, λ d < a... E{e iu(n 2 N 1 ) F λ 2 } = e {(eiu 1) 2 1 λ d}, F λ](/thumbs/92/110314096.jpg) 212 6 Chinee Journal of Applied Probabiliy and Saiic Vol.28 No.3 Jun. 212 Lévy (,, 2156),, Lévy.., (Credi Defaul Swap). :,,,. : O211.6. 1.,.,.,,.,, O Kane urnbull (23), Jamhidian (24), Crepey, Jeanblanc
212 6 Chinee Journal of Applied Probabiliy and Saiic Vol.28 No.3 Jun. 212 Lévy (,, 2156),, Lévy.., (Credi Defaul Swap). :,,,. : O211.6. 1.,.,.,,.,, O Kane urnbull (23), Jamhidian (24), Crepey, Jeanblanc
 Sõnastik / KKK www.monbjergpil.dk --- www.a-b.dk --- www.recycler.dk Google Tõlge on kohandatud õige eestlane. *) OEM = Original Equipment Manufacturer. Ümbertöödeldud OEM ühilduvad. Teema vigu materjali.
Sõnastik / KKK www.monbjergpil.dk --- www.a-b.dk --- www.recycler.dk Google Tõlge on kohandatud õige eestlane. *) OEM = Original Equipment Manufacturer. Ümbertöödeldud OEM ühilduvad. Teema vigu materjali.
GEOMETRI-TØ, UGE 3. og resultatet følger fra [P] Proposition 2.3.1, der siger, at
![GEOMETRI-TØ, UGE 3. og resultatet følger fra [P] Proposition 2.3.1, der siger, at GEOMETRI-TØ, UGE 3. og resultatet følger fra [P] Proposition 2.3.1, der siger, at](/thumbs/50/26870860.jpg) GEOMETRI-TØ, UGE 3 Hvis I falder over tryk- eller regne-fejl i nedenstående, må I meget gerne sende rettelser til fuglede@imf.au.dk. Opvarmningsopgave 1. Lad γ : (α, β) R 2 være en regulær kurve i planen.
GEOMETRI-TØ, UGE 3 Hvis I falder over tryk- eller regne-fejl i nedenstående, må I meget gerne sende rettelser til fuglede@imf.au.dk. Opvarmningsopgave 1. Lad γ : (α, β) R 2 være en regulær kurve i planen.
Analyse 2. Gennemgå bevis for Sætning Supplerende opgave 1. Øvelser. Sætning 1. For alle mængder X gælder #X < #P(X).
 Analyse 2 Øvelser Rasmus Sylvester Bryder 3. og 6. september 2013 Gennemgå bevis for Sætning 2.10 Sætning 1. For alle mængder X gælder #X < #P(X). Bevis. Der findes en injektion X P(X), fx givet ved x
Analyse 2 Øvelser Rasmus Sylvester Bryder 3. og 6. september 2013 Gennemgå bevis for Sætning 2.10 Sætning 1. For alle mængder X gælder #X < #P(X). Bevis. Der findes en injektion X P(X), fx givet ved x
ECL Comfort 210 / 296 / 310
 Kasutusjuhend ECL Comfort 210 / 296 / 310 Eesti www.danfoss.com Ohutusnõue Vajalikke koostamis-, käitamis- ja hooldustöid tohivad teha ainult selleks koolitatud ja volitatud isikud. 2 Danfoss 2016.02 VI.KT.Y2.26
Kasutusjuhend ECL Comfort 210 / 296 / 310 Eesti www.danfoss.com Ohutusnõue Vajalikke koostamis-, käitamis- ja hooldustöid tohivad teha ainult selleks koolitatud ja volitatud isikud. 2 Danfoss 2016.02 VI.KT.Y2.26
SUPPLERENDE OPGAVER TIL KOMPLEKS FUNKTIONSTEORI F2005
 SUPPLERENDE OPGAVER TIL KOMPLEKS FUNKTIONSTEORI F2005 0. maj, 2005 version nr. 8 JØRGEN VESTERSTRØM Indledende bemærkninger De foreliggende opgaver udgør et supplement til lærebogens opgaver. Afsnitsnummereringerne
SUPPLERENDE OPGAVER TIL KOMPLEKS FUNKTIONSTEORI F2005 0. maj, 2005 version nr. 8 JØRGEN VESTERSTRØM Indledende bemærkninger De foreliggende opgaver udgør et supplement til lærebogens opgaver. Afsnitsnummereringerne
FÜÜSIKA AINEKAVA klass
 FÜÜSIKA AINEKAVA 8. - 9. klass Füüsika õppe- ja kasvatuseesmärgid: Põhikooli füüsikaõpetusega taotletakse, et põhikooli lõpuks õpilane: 1) tunneb huvi füüsika ja teiste loodusteaduste vastu ning saab aru
FÜÜSIKA AINEKAVA 8. - 9. klass Füüsika õppe- ja kasvatuseesmärgid: Põhikooli füüsikaõpetusega taotletakse, et põhikooli lõpuks õpilane: 1) tunneb huvi füüsika ja teiste loodusteaduste vastu ning saab aru
DesignMat Uge 1 Repetition af forårets stof
 DesignMat Uge 1 Repetition af forårets stof Preben Alsholm Efterår 008 01 Lineært ligningssystem Lineært ligningssystem Et lineært ligningssystem: a 11 x 1 + a 1 x + + a 1n x n = b 1 a 1 x 1 + a x + +
DesignMat Uge 1 Repetition af forårets stof Preben Alsholm Efterår 008 01 Lineært ligningssystem Lineært ligningssystem Et lineært ligningssystem: a 11 x 1 + a 1 x + + a 1n x n = b 1 a 1 x 1 + a x + +
Integration m.h.t. mål med tæthed
 Integration m.h.t. mål med tæthed Sætning (EH 11.7) Lad ν = f µ på (X, E). For alle g M + (X, E) gælder at gdν = g f dµ. Bevis: Standardbeviset: 1) indikatorfunktioner 2) simple funktioner 3) M + -funktioner.
Integration m.h.t. mål med tæthed Sætning (EH 11.7) Lad ν = f µ på (X, E). For alle g M + (X, E) gælder at gdν = g f dµ. Bevis: Standardbeviset: 1) indikatorfunktioner 2) simple funktioner 3) M + -funktioner.
Õpetaja kui teadmiste edastaja, terapeut ja ämmaemand
 Dr Lotte Rahbek Schou (haridusfilosoofia dotsent) Danish School of Education Aarhusi Ülikool Haridusteaduskond lrs@dpu.dk Detsember 2009 Õpetaja kui teadmiste edastaja, terapeut ja ämmaemand Lühitutvustus
Dr Lotte Rahbek Schou (haridusfilosoofia dotsent) Danish School of Education Aarhusi Ülikool Haridusteaduskond lrs@dpu.dk Detsember 2009 Õpetaja kui teadmiste edastaja, terapeut ja ämmaemand Lühitutvustus
Løsningsforslag til opgavesæt 5
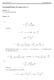 Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
Multi-Split kompaktpaneeliga kassett siseosa kasutusjuhend
 Paigaldus- ja kasutusjuhend Multi-Split kompaktpaneeliga kassett siseosa kasutusjuhend See kasutusjuhend on sobiv järgmistele juhenditele: ACMI-26HPDC1 ACMI-36HPDC1 ACMI-53HPDC1 Palun lugege seda kasutusjuhendit
Paigaldus- ja kasutusjuhend Multi-Split kompaktpaneeliga kassett siseosa kasutusjuhend See kasutusjuhend on sobiv järgmistele juhenditele: ACMI-26HPDC1 ACMI-36HPDC1 ACMI-53HPDC1 Palun lugege seda kasutusjuhendit
DATŠNAJA-DVUŠKA. kärgpolükarbonaadiga kaetud kasvuhoone. Tehniline pass. lk Kokkupanemise juhend. lk kõrgus 2,2 m. pikkus 2,0; 4,0; 6,0 m
 DATŠNAJA-DVUŠKA kärgpolükarbonaadiga kaetud kasvuhoone kõrgus, m laius,0 m pikkus,0; 4,0; 6,0 m Tehniline pass lk. -6 Kokkupanemise juhend lk. 7-01 Tehniline pass Kasvuhoone paigaldamisel ja kasutamisel
DATŠNAJA-DVUŠKA kärgpolükarbonaadiga kaetud kasvuhoone kõrgus, m laius,0 m pikkus,0; 4,0; 6,0 m Tehniline pass lk. -6 Kokkupanemise juhend lk. 7-01 Tehniline pass Kasvuhoone paigaldamisel ja kasutamisel
A B C D E Hjemmeværnmuseet's arkiv/depot Søgaard Distrikter - LMD. Reol/hylde Region/distrikt/m.m. Kasse nr. Indhold 2C3 Flyverhjemmeværne 1
 0 A B C D E Hjemmeværnmuseet's arkiv/depot Søgaard LMK Distrikter - LMD. Reol/hylde Region/distrikt/m.m. Kasse nr. Indhold C Flyverhjemmeværne Flyverhjemmeværnet LMD Odense Nyt fra stabseskadrillen -.
0 A B C D E Hjemmeværnmuseet's arkiv/depot Søgaard LMK Distrikter - LMD. Reol/hylde Region/distrikt/m.m. Kasse nr. Indhold C Flyverhjemmeværne Flyverhjemmeværnet LMD Odense Nyt fra stabseskadrillen -.
8 Regulære flader i R 3
 8 Regulære flader i R 3 Vi skal betragte særligt pæne delmængder S R 3 kaldet flader. I det følgende opfattes S som et topologisk rum i sportopologien, se Definition 5.9. En åben omegn U af p S er således
8 Regulære flader i R 3 Vi skal betragte særligt pæne delmængder S R 3 kaldet flader. I det følgende opfattes S som et topologisk rum i sportopologien, se Definition 5.9. En åben omegn U af p S er således
SISSEJUHATUS ORGAANILISSE KEEMIASSE
 SISSEJUATUS RGAANILISSE KEEMIASSE Kaido Viht Õppematerjal TÜ teaduskooli õpilastele Tartu 2016 1. Aatomiehitus ja keemiline side rgaaniliste ühendite struktuurides on enamlevinud elementideks mittemetallid:,
SISSEJUATUS RGAANILISSE KEEMIASSE Kaido Viht Õppematerjal TÜ teaduskooli õpilastele Tartu 2016 1. Aatomiehitus ja keemiline side rgaaniliste ühendite struktuurides on enamlevinud elementideks mittemetallid:,
UGESEDDEL 10 LØSNINGER. = f
 UGESEDDEL 10 LØSNINGER Theorem 1. Algoritme for løsning af max f(x, y) når g(x, y) c. Dan Lagrange-funktionen: L (x, y) = f(x, y) λ(g(x, y) c). Beregn de partielle afledte af L og kræv at de begge er nul:
UGESEDDEL 10 LØSNINGER Theorem 1. Algoritme for løsning af max f(x, y) når g(x, y) c. Dan Lagrange-funktionen: L (x, y) = f(x, y) λ(g(x, y) c). Beregn de partielle afledte af L og kræv at de begge er nul:
Løsningsforslag til opgavesæt 5
 Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
Oversigt [S] 9.6, 11.1, 11.2, App. H.1
![Oversigt [S] 9.6, 11.1, 11.2, App. H.1 Oversigt [S] 9.6, 11.1, 11.2, App. H.1](/thumbs/62/47252518.jpg) Oversigt [S] 9.6, 11.1, 11.2, App. H.1 Her skal du lære om 1. Funktioner i flere variable 2. Grafen og niveaukurver 3. Grænseovergange og grænseværdier 4. Kontinuitet i flere variable 5. Polære koordinater
Oversigt [S] 9.6, 11.1, 11.2, App. H.1 Her skal du lære om 1. Funktioner i flere variable 2. Grafen og niveaukurver 3. Grænseovergange og grænseværdier 4. Kontinuitet i flere variable 5. Polære koordinater
Overheads til forelæsninger, mandag 5. uge På E har vi en mængde af mulige sandsynlighedsfordelinger for X, (P θ ) θ Θ.
 Statistiske modeller (Definitioner) Statistik og Sandsynlighedsregning 2 IH kapitel 0 og En observation er en vektor af tal x (x,..., x n ) E, der repræsenterer udfaldet af et (eller flere) eksperimenter.
Statistiske modeller (Definitioner) Statistik og Sandsynlighedsregning 2 IH kapitel 0 og En observation er en vektor af tal x (x,..., x n ) E, der repræsenterer udfaldet af et (eller flere) eksperimenter.
Sandsynlighed og Statistik
 36 Sandsynlighed og Statistik 6.1 Indledning Denne note beskriver de statistiske begreber og formler som man med rimelig sandsynlighed kan komme ud for i eksperimentelle øvelser. Alt er yderst korfattet,
36 Sandsynlighed og Statistik 6.1 Indledning Denne note beskriver de statistiske begreber og formler som man med rimelig sandsynlighed kan komme ud for i eksperimentelle øvelser. Alt er yderst korfattet,
18th ICSMGE Paris Earth Pressure from Strip Footings on an Anchored Sheet Pile Wall
 18th ICSMGE Paris 213 Earth Pressure fro Strip Footings on an Anchored Sheet Pile Wall Hans Denver & Lindita Kellezi GEO, Lyngby, Denark 1 DGF 18th ICSMGE Hans Denver & Lindita Kellezi Indhold Forskellige
18th ICSMGE Paris 213 Earth Pressure fro Strip Footings on an Anchored Sheet Pile Wall Hans Denver & Lindita Kellezi GEO, Lyngby, Denark 1 DGF 18th ICSMGE Hans Denver & Lindita Kellezi Indhold Forskellige
Hamiltons princip. Et systems bane (i konfigurationsrummet) fra t 1 til t 2 er bestemt
 Hamtons prncp.1 Konfguratonsrum q 3 Et systems bane ( konfguratonsrummet) fra t t er bestemt af, at aktonsntegraet I = Lt har en statonær vær. t q 1 q () Systemet ska være monogensk, vs. ae kræfter (ekskusvt
Hamtons prncp.1 Konfguratonsrum q 3 Et systems bane ( konfguratonsrummet) fra t t er bestemt af, at aktonsntegraet I = Lt har en statonær vær. t q 1 q () Systemet ska være monogensk, vs. ae kræfter (ekskusvt
(c) Opskriv den reelle Fourierrække for funktionen y(t) fra (b), og afgør dernæst om y(t) er en lige eller ulige funktion eller ingen af delene.
 MATEMATIK 3 EN,MP 4. februar 2016 Eksamenopgaver fra 2011 2016 (jan. 2016) Givet at 0 for 0 < t < 1 mens e (t 1) cos(7(t 1)) for t 1, betragt da begyndelsesværdiproblemet for t > 0: y (t) + 2y (t) + 50y(t)
MATEMATIK 3 EN,MP 4. februar 2016 Eksamenopgaver fra 2011 2016 (jan. 2016) Givet at 0 for 0 < t < 1 mens e (t 1) cos(7(t 1)) for t 1, betragt da begyndelsesværdiproblemet for t > 0: y (t) + 2y (t) + 50y(t)
Fortolkning. Foldning af sandsynlighedsmål. Foldning af tætheder. Foldning af Γ-fordelinger Eksempel: Hvis X og Y er uafhængige og. Sætning (EH 20.
 Foldning af sandsnlighedsmål Lad µ og ν være to sandsnlighedsmål på (R, B). Fortolkning Lad φ : R R være φ(, ) = + for (, ) R. Lad X og Y være to reelle stokastiske variable defineret på (Ω, F, P). Definition
Foldning af sandsnlighedsmål Lad µ og ν være to sandsnlighedsmål på (R, B). Fortolkning Lad φ : R R være φ(, ) = + for (, ) R. Lad X og Y være to reelle stokastiske variable defineret på (Ω, F, P). Definition
Haid puhi! ÜLE VAL LA JÕU LU PI DU. Tõs ta maa rah va ma jas 23. det semb ril
 Nr. 9 (182) / detsember 2011 Haid puhi! Foto: Eve Käär ÜLE VAL LA JÕU LU PI DU Tõs ta maa rah va ma jas 23. det semb ril kell 20 väi ke jõu lu kont sert kell 21 peoõh tu koos an samb li ga OR KES TER Õh
Nr. 9 (182) / detsember 2011 Haid puhi! Foto: Eve Käär ÜLE VAL LA JÕU LU PI DU Tõs ta maa rah va ma jas 23. det semb ril kell 20 väi ke jõu lu kont sert kell 21 peoõh tu koos an samb li ga OR KES TER Õh
Kasutusjuhend NIBE F1226
 Kasutusjuhend Maasoojuspump LEK UHB EE 1127-1 431183 Nuppude funktsioonide üksikasjalikud selgitused on toodud lk 10. Menüüde sirvimise ja erinevate seadistuste määramise kirjeldus on toodud lk 13. Peamenüü
Kasutusjuhend Maasoojuspump LEK UHB EE 1127-1 431183 Nuppude funktsioonide üksikasjalikud selgitused on toodud lk 10. Menüüde sirvimise ja erinevate seadistuste määramise kirjeldus on toodud lk 13. Peamenüü
9 Geodætiske kurver og Gauss-krumning
 9 Geodætiske kurver og Guss-krumning 9. Geodætiske kurver En ret linie i plnen fr punktet p til punktet q hr den egenskb t enhver nden kurve fr p til q hr kurvelængde som er mindst p q. Et stykke f en
9 Geodætiske kurver og Guss-krumning 9. Geodætiske kurver En ret linie i plnen fr punktet p til punktet q hr den egenskb t enhver nden kurve fr p til q hr kurvelængde som er mindst p q. Et stykke f en
For at finde ud af om konstruktionen kan holde, beregnes spændingstilstanden. Her skal det gælde: s 2 C 3 t 2 % f y
 Spændingstilstand For at finde ud af om konstruktionen kan holde, beregnes spændingstilstanden. Her skal det gælde: s 2 C 3 t 2 % f y. For at beregne dette, findes først normalspændinger s ved Naviers
Spændingstilstand For at finde ud af om konstruktionen kan holde, beregnes spændingstilstanden. Her skal det gælde: s 2 C 3 t 2 % f y. For at beregne dette, findes først normalspændinger s ved Naviers
Kompleks Funktionsteori
 Kompleks Funktionsteori Formelræs Holomorfe funktioner Sætning. (Caucy-Riemans ligninger). Funktionen f : G C, f = u+iv er holomorf i z 0 = x 0 + iy 0 hvis og kun hvis i punktet (x 0, y 0 ). du dx = dv
Kompleks Funktionsteori Formelræs Holomorfe funktioner Sætning. (Caucy-Riemans ligninger). Funktionen f : G C, f = u+iv er holomorf i z 0 = x 0 + iy 0 hvis og kun hvis i punktet (x 0, y 0 ). du dx = dv
Vridning, hvælving og kipning
 Vridning, vælving og kipning april 17/LC Vridning vælving og kipning 1 Vridning, vælving og kipning april 17/LC Indold 1 Hvælvingsinertimoment. 1.1 Teoretisk udledning for et U-profil. 1. Taelværdier 1.3
Vridning, vælving og kipning april 17/LC Vridning vælving og kipning 1 Vridning, vælving og kipning april 17/LC Indold 1 Hvælvingsinertimoment. 1.1 Teoretisk udledning for et U-profil. 1. Taelværdier 1.3
Kvantitative Metoder 1 - Efterår Dagens program
 Dagens program Afsnit 6.1. Ligefordelinger, fra sidst Den standardiserede normalfordeling Normalfordelingen Beskrivelse af normalfordelinger: - Tæthed og fordelingsfunktion - Middelværdi, varians og fraktiler
Dagens program Afsnit 6.1. Ligefordelinger, fra sidst Den standardiserede normalfordeling Normalfordelingen Beskrivelse af normalfordelinger: - Tæthed og fordelingsfunktion - Middelværdi, varians og fraktiler
