Henstock-Kurzweil Laplace Transform
|
|
|
- Oscar Clemmensen
- 5 år siden
- Visninger:
Transkript
1 Chper 5 Hensock-Kurzweil Lplce Trnsform 5.1 Inroducion The Lplce rnsform of funcion f : [, ) R, s C, is defined s he inegrl [15] e s f() d. (5.1) Mny uhors, in some previous decdes, showed heir ineres in sudying he Lplce rnsform in clssicl sense; by clssicl mening Lebesgue inegrl nd/or Riemnn inegrl on he rel line. In his chper, we focus on n inegrl rnsform h generlizes he clssicl Lplce rnsform. Here he generlizion is given by he replcemen, in he definiion of Lplce rnsform, i.e., in (5.1), of Lebesgue inegrl wih Hensock-Kurzweil (HK) inegrl. The Hensock-Kurzweil inegrl is defined in erms of Riemnn sums bu wih sligh modificion, ye i includes he Riemnn, improper Riemnn, nd Lebesgue inegrls s specil cses. This inegrl is equivlen o he Denjoy nd Perron inegrls. 117
2 The firs quesion rises is h wheher (or in which condiions) he Lplce rnsform when reed s HK inegrl mke sense. The sufficien condiion for he exisence of Lplce rnsform is h he funcion f is loclly inegrble on [, ), becuse he produc of loclly inegrble funcion nd bounded mesurble funcion is loclly inegrble. Since Hensock- Kurzweil inegrl llows nonbsolue convergence, i mkes n idel seing for he Lplce rnsform. I ws proved [9] h, on compc inervl, he produc of nonbsolue inegrble funcion nd bounded vriion funcion is sill nonbsolue inegrble nd his remins vlid in cse of n unbounded inervl [1]. We observed in (5.1) h he kernel funcion e s, s C, is no bounded vriion funcion on [, ) hence we cnno clim (s in he clssicl sense) h he HK Lplce rnsform exiss for ny HK inegrble funcion. The convoluion plys n imporn role in pure nd pplied mhemics, pproximion heory, differenil nd inegrl equions nd mny oher res. Lplce rnsform hs he propery h i cn inerc wih convoluions so we obin vrious resuls on convoluion. We give necessry nd sufficien condiions so h he convoluion operor s HK inegrl is coninuous. Finlly we solve he problem of inversion by using generlized differeniion. The resuls in his chper re ppered in [, 14]. 5. Exisenil Condiions In his secion, we ckle he problem of exisence of Lplce rnsform s HK inegrl. According o Zyed [16], he clssicl sufficien condiion for he exisence 118
3 of Lplce rnsform is h he funcion f is loclly inegrble on [, ), i.e., f L loc [, ). This is becuse he muliplier for he Lebesgue inegrble funcions is bounded mesurble funcion nd he funcion e s, s C, is bounded mesurble funcion. We know h he mulipliers for HK inegrble funcions re precisely he funcions of bounded vriion [1]. Noe h in (5.1), he funcion e s, s C, is no of bounded vriion on [, ) bu i is of bounded vriion on ny compc inervl J R. Hence we cn no consider (5.1) s HK inegrl direcly. So we cnno ge ny specific condiion for he exisence of Lplce rnsform s HK inegrl. However we do hve he following differen condiions. Theorem Le f : [, ) R be ny coninuous funcion such h F (x) = x f, x <, is bounded on [, ). Then he Lplce rnsform L{f}(s), i.e., L{f}(s) = e s f() d, Re.s > exiss. Proof. Le < x <, s = σ + iω, σ, ω R. We hve (F () e s ) = s F () e s + f() e s. Since e s is of bounded vriion on ny compc inervl, sy [, b] nd F () is bounded on [, ). Then F () e s is HK inegrble on [, b]. Therefore s F () e s is inegrble over I = [, b]. Now (e s ) d = s e s d = = σ + ω e σ d σ + ω [e σ e σb ]. σ Wihou loss of generliy le us ke =. Therefore (e s ) σ + ω d = [1 e σb ] <. σ 119
4 Hence (e s ) is bsoluely inegrble over [, b]. Now by Hke s heorem [1], we cn wrie lim (e s ) σ + ω d = lim [1 e σb ] b b σ σ + ω =, σ > σ σ + ω =, Re.s >. σ This shows h (e s ) is bsoluely inegrble on [, ). Agin lim e s =, Re.s >. Hence he funcion e s : [, ) R is coninuous on [, ) wih lim e s = nd (e s ) is bsoluely inegrble over [, ) nd we hve ssumed h f : [, ) R is coninuous funcion such h F (x) = x f, x <, is bounded on [, ). Therefore by Dedekind s es [1], we cn sy h he inegrl e s f() d exiss for Re.s >. Remrk 5... The bove resul cn lso be proved by using Du-Bois Reymond s es [1] s follows: Tke φ() = e s, s = σ + iω, J = [, ). Then clerly φ() is differenible nd φ L 1 (J). Since F is bounded, we hve lim F () e s =, Re.S >. Hence F (x) = x f, x < is bounded on J, e s is differenible on J, (e s ) L 1 (J) nd F () e s s, Re.s >. Therefore by Du-Bois Reymond s es, f()e s HK(J). Th is, he Lplce rnsform of f(), e s f() d exiss, Re.s >. 1
5 Theorem If he Lplce rnsform of f(), e s f() d exiss for Re.s >, hen he funcion f HK loc. Proof. Suppose he inegrl e s f() d exiss for Re.s >. Noe h he funcion e s, s C, s funcion of rel vrible, is no of bounded vriion on [, ) bu is of bounded vriion on ny compc inervl I = [, b]. By Hke s heorem [1], we cn wrie e s f() d = lim b e s f() d. Since he limis on R.H.S. exis, we cn sy h he HK inegrl e s f()d exiss, Re.s > for some compc inervl [, b]. Hence he funcion f() is HK inegrble necessrily on he compc inervl I = [, b], h is, f HK loc. Theorem Le f HK([, )). Define F (x) = f() d. Then x L{f}(s) exiss if nd only if e s F () d exiss s C. Proof. Le T >. The funcion e s, s C, is of bounded vriion on compc inervl [, T ] nd he funcion f is HK inegrble on [, ). Hence e s f(), s C, is HK inegrble on [, T ] nd by inegring by prs, we ge T T e s f() d = e st F (T ) F () + s e s F () d. Since he funcion f is HK inegrble on [, ), F () is finie, sy A nd by [9.1(), [5]], F is coninuous funcion such h lim F (T ) =. T Therefore by Hke s heorem [1], T { T } lim e s f() d = lim e st F (T ) F () + s e s F () d. T T 11
6 Hence e s f() d = s e s F () d A. This shows h L{f}(s) exiss if nd only if e s F () d exiss s C, Re.s >. Theorem (Uniqueness heorem) Le L{f}(s) = e s f() d nd L{g}(s) = e s g() d. If f() = g().e. on [, ), hen L{f}(s) = L{g}(s). 5.3 Bsic Properies The usul elemenry properies such s lineriy, dilion, modulion, rnslion re remins sme for he HK Lplce rnsform, he proofs of which re quie similr o h of clssicl ones. Also here re some oher resuls h re nlogous o he clssicl one wih some modificion in he hypohesis which we discuss below. Theorem (HK Lplce rnsform of derivive) Le f : [, ) f() R be funcion which is in ACG δ (R) such h lim =. Then for Re.s > e s boh L{f}(s) nd L{f }(s) fil o exis or L{f }(s) = s L{f}(s) f(). Proof. Le T >. Consider he inegrl J = T e s f () d. This inegrl is vlid since he funcion e s, s C, is bounded vriion on ny compc inervl [, T ] nd he funcion f is HK inegrble on R. By inegring by prs, we ge By Hke s heorem [1], T lim T J = e st f(t ) f() + s T e s f() d. T e s f () d = lim T e st f(t ) f() + lim s e s f() d T 1
7 Therefore = s e s f () d = s Th is, L{f }(s) = s L{f}(s) f(). e s f() d f(). e s f() d f(). Remrk The bove resul cn be generlize by imposing he condiions on f s: For k =, 1,,..., (n 1), f (k) f re in ACG δ (R) nd lim (k) =, Re.s >. e s Then L{f (n) }(s) nd L{f}(s) fils o exis or L{f (n) }(s) = s n L{f}(s) s n 1 f() s n f ()... f (n 1) (). Theorem (Differeniion of HK Lplce rnsform) Le f : [, ) R be funcion such h L{f}(s) exiss on compc inervl, sy J = [α, β], α, β R. Define g() = f() nd ssume h g HK(R + ). Then L{g}(s) exiss nd L{g}(s) = (L{f}(s)).e. Here s R. Proof. Suppose L{f}(s) = Define g() = f(). e s f() d exiss on [α, β], α, β R. We know he necessry nd sufficien condiion for differeniing under he HK inegrl is h for ll [, b] [α, β] [1]. Now e s f() ds d = = s= s= = e s f() ds d = = s= = e s f() d ds (5.) (e e b )f() d 13
8 = L{f}() L{f}(b) which exiss. Therefore he double HK inegrl = s= e s f() ds d exiss. Hence by [lemm 5(), [13]], he equliy in (5.) holds nd we cn differenie under he HK inegrl. By (5.), we hve s= = e s f() d ds = L{f}() L{f}(b) = (L{f}(s)) ds. Therefore e s f() d ds = s= = for ll [, b] [α, β]. Which implies h (L{f}(s)) ds e s f() d = (L{f}(s)).e. on [α, β]. Th is, L{ f()}(s) = (L{f}(s)).e. on [α, β]. Hence he derivive of he HK Lplce rnsform of f() exiss.e. on [α, β]. Remrk Le G(s) = L{ f()}(s) nd H(s) = L{f()}(s). Then (H(s)) = G(s).e. on [α, β]. And, we know h [5], A funcion f : [, b] R is HK inegrble on [, b] if nd only if here exiss n ACG δ funcion F on [, b] such h F = f.e. on [, b]. Agin, by fundmenl heorem of clculus [1], (H(s)) is HK inegrble, i.e., every derivive is HK inegrble. Hence G(s) is lso HK inegrble. Consequenly, he funcion H(s) is ACG δ on [α, β]. Coninuing in his wy n-imes, we cn sy h if n f() is HK inegrble, hen ny order of derivive of L{f}(s) exiss.e. So L{f}(s) is nlyic.e. 14
9 Theorem (Muliplicion by 1 ) Le f : [, ) R be funcion { } such h L{f}(s) exiss nd ssume h f() HK(R + ). Then L f() (s) exiss nd Here s R. { } f() L (s) = Proof. Assume h f() HK(R + ). s L{f}(u) du. Since he funcion e s is of bounded vriion on ny compc inervl I = [, b], we hve e s f() HK([, b]). Th is, e s f() d exiss. Wihou loss of generliy, le us ke = so h e s f() d exiss. By Hke s heorem [1], lim } Hence L (s) exiss. { f() Now consider he inegrls I 1 = s b e s f() d exiss. e u f() du d, I = I 1 = = Therefore I 1 exiss on R R. [e s ] f() d s f() e d which exiss. s e u f() d du. Also, noe h he funcion e s is of bounded vriion on ny compc inervl J R. Therefore R V J(e s ) d < M J, for some consn M J >. Hence by [lemm 5(), [13]], I exiss on R R nd I 1 = I on R R. So Th is, L s f() e d = = s { } f() (s) = L{f}(u) du. s s e u f() d du L{f}(u) du. 15
10 Theorem (HK Lplce rnsform of inegrl) Le f : [, ) R { } be HK inegrble funcion such h L{f}(s) exiss. Then L f(u) du (s) { } exiss nd L f(u) du (s) = 1 L{f}(s). s Proof. Define F () = f(u) du, R+. Then F () = f().e. on R + [9.1(b), [5]]. Since f HK(R + ), he inegrl Th is, lim Hence lim F () is bounded on R +. Now for T >, consider T f(u) du exiss on R +. f(u) du exiss on R +. e s f() d = T e s F () d. This inegrl exiss since e s is of bounded vriion on [, T ] nd he funcion f() is HK inegrble on R +. By inegring by prs, we ge T T e s f() d = e st F (T ) + s e s F () d. Since lim F (T ) is bounded on R, se lim F (T ) = A. T T By Hke s heorem [1], we cn wrie T e s f() d = lim e s f() d T = lim T e st F (T ) + s lim = s T T e s F () d Re.s >. e s F () d 16
11 Therefore Th is, e s F () d = 1 s e s f() d, Re.s >. e s f(u) du d = 1 L{f}(s), Re.s >. s { } Hence L f(u) du = 1 L{f}(s), Re.s >. s 5.4 Convoluion In his secion we shll discuss some clssicl resuls of Lplce convoluion in he HK inegrl seing, clled HK-convoluion. Firs we give wo resuls bou he exisence of HK-convoluion. Theorem Le f HK(R + ) nd g BV(R + ). Then we hve f g exiss on R +. Proof. By definiion [4], f g() = f( τ) g(τ) dτ which exiss s HK-inegrl by muliplier heorem [1]. By inegring by prs, we ge Hence f g exiss on R +. f g() A f { } inf g + V R + [,] g(τ). Theorem Le f HK loc nd g BV such h he suppor of g is in he compc inervl I = [, b]. Then } f g() A f [ b, ] {inf g + V [,b] g(τ). [,b] 17
12 Proof. Suppose supp(g) [, b]. Then we hve f g() = f( τ)g(τ) dτ. Inegre by prs, we ge f g() g(τ) b f( τ) dτ + f( τ) dg(τ) inf g(τ) b b τ [,b] f( τ) dτ + f( τ) dτ V [,b] g(τ) { } inf g(τ) + V [,b] g(τ) sup τ [,b] f(u) du. [ b, ] b Therefore } f g() A f [ b, ] {inf g + V [,b] g(τ). [,b] The following resul shows h he HK-convoluion is bounded. Theorem Le f HK(R + ) nd g L 1 (R + ) BV(R + ). Then we hve A f g A f g 1. Proof. For < b, we hve Le f g() d = f( τ)g(τ) dτ d. I 1 = Consider f( τ)g(τ) dτ d nd I = I = f( τ)g(τ) d dτ. Since f HK(R + ), we hve f( τ) d exiss nd finie. Le b f(τ) dτ = M. 18 f( τ)g(τ) d dτ.
13 Therefore I M g(τ) dτ. Since g L 1 (R + ), we hve for some finie K, g(τ) dτ = K. So I MK nd hence I exiss on R + R +. Now s g L 1 (R + ), we hve g 1 K 1 nd lso V R + [,] g M 1. Therefore by [lemm 5, [13]], I 1 = I on R + R +. Hence f g() d sup b f(u) du g(τ) dτ [, b] A f [, b] g 1. Therefore sup [,b] Th is, A f g A f g 1. f g() d A f [, b] g 1. Now we give some bsic elemenry properies of HK-convoluion. Theorem Suppose f HK(R + ) nd g BV(R + ). Then he following holds: I) f g() = g f() for ll R +. II) (λf) g = f (λg) = λ(f g) for some λ C. III) (f g) x () = f x g() = f g x (). IV) h (f + g)() = h f() + h g() for some h HK(R + ). Proof. The proof is similr o h of he clssicl cse. 19
14 The ssociive propery of HK-convoluion is given in he nex heorem. Theorem If f HK(R + ), g BV(R + ) nd h L 1 (R + ), hen (f g) h() = f (g h)(), R +. Proof. Consider (f g) h() = τ By chnging he order of inegrion, we ge Now Consider nd Le (f g) h() = I 1 = I = = ξ= ξ= f(ξ) f(ξ) g(τ ξ) h( τ) dξ dτ. ξ f(ξ) g h( ξ) dξ = f (g h)(). τ=ξ ξ= J = ξ= g(u) h( u ξ) du dξ f(ξ) g(τ ξ) h( τ) dξ dτ f(ξ) g(τ ξ) h( τ) dτ dξ. τ=ξ τ=ξ g(τ ξ) h( τ) dτ. Inegre by prs, we ge J g( ξ) u h( τ) dτ + h( τ) dτ dg(τ ξ) τ=ξ τ=ξ τ=ξ inf g [ξ,] h( τ) dτ + h( τ) dτ V [ξ,] g(τ ξ) inf [ξ,] g τ=ξ τ=ξ h( τ) dτ + τ=ξ τ=ξ inf [ξ,] g h 1 + h 1 V [ξ,] g(τ ξ) 13 h( τ) dτ V [ξ,] g(τ ξ)
15 Therefore } h 1 {inf g + V [ξ,] g(τ ξ). [ξ,] I sup R + f(ξ) dξ { h 1 { inf A f h 1 {inf [ξ,] g + V [ξ,] g(τ ξ) }} g + V [ξ,] g(τ ξ) [ξ,] }. Hence I exiss on R + R +. And, by [lemm 5, [13]] we re hrough. Now we show h he HK-Lplce rnsform of convoluion of wo funcions is he produc of heir HK-Lplce rnsforms. Theorem Le f 1 HK(R + ), f L 1 (R + ) BV(R + ). Then f g exiss nd if L {f 1 ()} nd L {f ()} exis s C, hen L {f 1 f ()} exiss s C nd L {f 1 f ()} (s) = L {f 1 ()} (s) L {f ()} (s). Proof. Consider L {f 1 f ()} (s) = = e s f 1 f () d By inerchnging he iered inegrls, we hve L {f 1 f ()} (s) = τ= Bu by hypohesis boh he inegrls = e sτ f 1 (τ)e s( τ) f ( τ) dτ d. e sτ f 1 (τ) e sτ f 1 (τ) dτ =τ e s( τ) f ( τ) d dτ e su f (u) du. e sτ f 1 (τ) dτ nd e sτ f (τ) dτ exis s C. Therefore L {f 1 f ()} exiss s C nd 131
16 L {f 1 f ()} (s) = L {f 1 ()} (s) L {f ()} (s). Now i remins o show he jusificion for inerchnging he iered inegrls. Since he funcion f L 1 (R + ), K I such h f 1 < K I, where I = [, b] R + is ny compc inervl. Clerly, V [,b] e s( τ) f ( τ) e σu V [ b, ] f (τ) + f (τ) e σr for some rels u nd r nd so V [ b, ] e sτ f (τ) dτ e σu V [ b, ] f (τ) dτ +e σr f (τ) dτ. Therefore V [ b, ] e sτ f (τ) dτ e σu V [ b, ] f (τ) dτ + K I e σr. Since f BV(R + ), here exiss consn M I such h Then V [ b, ] f (τ) dτ < M I. V [ b, ] e sτ f (τ) dτ e σu M I + K I e σr. Thus for ech compc inervl I = [, b] R +, he inegrl is finie nd f 1 K I. Hence he inegrl V [ b, ] e sτ f (τ) dτ τ= =τ e s f 1 (τ) f ( τ) d dτ exiss on R + R +. And, by [lemm 5, [13]], we cn inerchnge he iered inegrls. 13
17 Theorem In ddiion o he hypohesis of he bove heorem if f 1 f () is in HK(R + ) nd f is coninuous, hen f 1 f () is coninuous wih respec o he Alexiewicz norm. Proof. Choose ny δ > such h < δ 1 (The cse for negive δ is nlogous). Define D(, δ) = f 1 f ( + δ) f 1 f () = I 1 + I. Where I 1 = f 1 (τ) [f ( + δ τ) f ( τ)] dτ, I = Since f BV(R + ), f is bounded on R +. +δ So here exiss M such h f (x) M, for ll x R +. Then +δ I M f 1 (τ) dτ. Bu f 1 HK(R + ) implies h lim δ Therefore I s δ. Now consider I 1 = +δ f 1 (τ) dτ. f 1 (τ) [f ( + δ τ) f ( τ)] dτ. f 1 (τ)f (+δ τ) dτ. By inegring by prs, we ge I 1 [f ( + δ τ) f ( τ)] f 1 (τ) dτ u + f 1 (τ) dτ d(f (u + δ τ) f (u τ)) f ( + δ τ) f ( τ) sup f 1 (τ) dτ R + u + sup f 1 (τ) dτ d(f (u + δ τ) f (u τ)) u R + 133
18 = f ( + δ τ) f ( τ) sup f 1 (τ) dτ R + u + sup f 1 (τ) dτ f (u + δ τ) f (u τ). u R + Therefore I 1 f ( + δ τ) f ( τ) sup f 1 (τ) dτ R + u + sup f 1 (τ) dτ f (u + δ τ) f (u τ). u R + Since f is coninuous on R +, for given ɛ > here exiss η > such h I 1 ɛ, δ < η. Therefore D(, δ) I 1 + I < ɛ, δ < η. Th is, for given ɛ > here exiss η > such h D(, δ) < ɛ, δ < η. Hence f 1 f is coninuous R +. Now, le α, β R +. Consider β α [f 1 f ( + δ) f 1 f ()] d = α+δ α f 1 f () d β+δ β f 1 f () d. Wrie F 1, (x) = x f 1 f () d. Then β sup [f 1 f ( + δ) f 1 f ()] d sup F 1, (α + δ) F 1, (α) α, β R + α R + α + sup β R + F 1, (β + δ) F 1, (β). Since F 1, is n indefinie HK inegrl of f 1 f on R +, i is coninuous on R + [5]. Therefore for given ɛ > here exiss η > such h Hence we hve F 1, (ξ + δ) F 1, (ξ) < ɛ, δ < η nd for ll ξ R+. sup α, β R + β α [f 1 f ( + δ) f 1 f ()] d < ɛ, δ < η. 134
19 Thus for given ɛ > here exiss η > such h A f 1 f (+δ) f 1 f () < ɛ, δ < η. This shows h f 1 f () is coninuous R + wih respec o he Alexiewicz norm. The following resul concerns wih necessry nd sufficien condiions on f n nd g n : [, ] R so h he HK-convoluion s n operor is coninuous. I involves eiher uniform boundedness or uniform convergence of he indefinie HK inegrl of f n. Theorem Le {f n } be sequence of HK-inegrble funcions, f n : [, ] R, n such h f n = f s n for some HK-inegrble funcion f : [, ] R. Define F n (x) = x f n, F (x) = x f. Le {g n } be sequence of uniform bounded vriion funcions, g n : [, ] R, n, such h g n g poinwise on [, ], where g : [, ] R. Then f n g n () f g() s n if nd only if i) F n F uniformly on [, ] s n. ii) F n F poinwise on [, ], {F n } is uniformly bounded nd V (g n g). Proof. i) Suppose F n F uniformly on [, ] s n. By ssumpion nd muliplier heorem [1], f n g n () exiss R + nd f n g n () = f n (u) g n ( u) du nd f g() = Consider f n g n () f g() = I 1 + I, where I 1 = [f n (u) f(u)] g n ( u) du, I = f(u) g( u) du. [g n ( u) g( u)] f(u) du. 135
20 By inegring by prs, we ge Then I 1 = g n ( u) [f n (u) f(u)] du = g n ( u)[f n () F ()] I 1 Mx u F n(u) F (u) s n Hence I 1 s n. And by inegring by prs, we ge y [F n (u) F (u)] dg n. [f n (u) f(u)] dg n dg n + M F n () F () (Since F n F uniformly). I = {g n ( u) g( u)} f F dg n + F dg. By ssumpion he firs erm ends o nd since F is coninuous nd ech g n is of bounded vriion wih g n g s n, so we hve F dg n F dg. Hence I s n. Therefore f n g n () f g() s n. Now for he converse pr, suppose h eiher F n F on [, ] or F n F no uniformly on [, ]. Then here is sequence {x i } i Λ in [, ] on which F n F uniformly. So, by Bolzno-Weiersrss heorem [7], we cn find subsequence {y i } i Γ of {x i } i Λ, Γ Λ, such h F n (y i ) F (y i ) for ll i nd y i y s i, i.e., F n (y i ) F (y i ). Le us ssume wihou loss of generliy h < y n y. Le H be Heviside sep funcion. Define H(u y n ), g n ( u) = H(u y), n Γ oherwise 136
21 nd g( u) = H(u y). Then we hve, for n Γ, f n g n () = F n () F n (y n ) nd f g() = F () F (y). Since F n (y n ) F (y n ) s n, y n y s n nd F is coninuous, we hve F n (y n ) F (y). Bu F n () F () s n. Therefore f n g n () f g() s n which is conrdicion. Hence we mus hve F n F uniformly on [, ]. ii) Suppose F n F poinwise on [, ], F n is uniformly bounded nd V (g n g). Consider f n g n () f g() = I 1 + I, where I 1 = f n (u) [g n ( u) g( u)] du, I = By inegring by prs, we ge I 1 = [g n ( u) g( u)] f n = [g n ( u) g( u)] F n () Therefore y [f n (u) f(u)] g( u) du. f n d(g n g) F n (y) d(g n g). I 1 g n ( u) g( u) F n () + F n (y) V (g n g). Since {F n } is uniformly bounded, we hve F n M, n nd for some consn M. Therefore I 1 g n ( u) g( u) M + M V (g n g). By ssumpion g n g s n nd lso V (g n g). Hence I 1 s n. Agin by inegring by prs, we wrie I = g( u) {F n () F ()} 137 (F n F ) dg. (5.3)
22 By ssumpion F n () F (), so he firs erm ends o. And, since F n M, F n F nd g is of bounded vriion, by he domined convergence heorem for Riemnn-Sieljes inegrl [6], we hve F n dg F dg s n. Therefore by (5.3), I s n. Hence f n g n () f g() s n. Now for he converse pr suppose here is c (, b) such h F n (c) F (c) s n. Le g n ( x) = g( x) = H(x c). Then f n (u) g n ( u) du = F n () F n (c), f(u) g( u) du = F () F (c). Since F n () F () nd F n (c) F (c), we hve F n () F n (c) F () F (c) s n. Th is, f n g n () f g() s n which is conrdicion. Hence we mus hve F n F poinwise on [, ]. Now if {F n } is no uniformly bounded, hen here is sequence {x i } i Λ in [, ] on which F n. Therefore by Bolzno-Weiersrss heorem [7], we cn find subsequence {y i } i Γ of {x i } i Λ, Γ Λ, such h F n (y i ) 1 for ll n nd F n (y i ) nd y i y. Wihou loss of generliy le us ke y i y. Define g n ( u) = H(u y i). Fn(yi ) Then V (g n ) 1, g = nd V (g n g) = nd f n (u) g n ( u) du = 138 f n (u) H(u y i) Fn (y i ) du
23 f n (u) = y i Fn (y i ) du = F n() Fn (y i ) F n (y i ). Therefore nd f n (u)g n ( u) du s n f(u)g( u) du =. Hence f n g n f g s n which is conrdicion nd so we mus hve {F n } is uniformly bounded sequence. 5.5 Inversion Since in cse of Hensock-Kurzweil inegrl, he inegrion process nd differeniion process re inverse of ech oher. Here we shll esblish he inverse of Hensock-Kurzweil Lplce rnsform by using Pos s generlized differeniion mehod [8]. For his we shll need following lemms: Lemm Le η be such h < η < b, nd h(x) C ( x + η), h () =, h () <, h(x) is nonincresing on (, b]. Then ( π e k h(x) dx e k h() k h () k. Proof. Since h(x) C ( x + η), h (x) is coninuous. Le ɛ > be such h < ɛ < h (). Choose δ >, δ < η such h h (x) h () < ɛ, x + δ. Th is, h () ɛ < h (x) < h () + ɛ, x + δ. (5.4) 139
24 Consider he inegrl We wrie I k = I k + I k, where I k = +δ I k = e k [h(x) h()] dx. e k [h(x) h()] dx, I k = e k [h(x) h()] dx. +δ Since h is nonincresing on (, b], we hve h(x) h( + δ) for ll x > + δ. Therefore nd Hence I k Now consider s k. I k e k [h(+δ) h()] dx +δ I k e k [h(+δ) h()] (b δ). I k = +δ By Tylor s series wih reminder, we hve Therefore h(x) h() h (ξ) So by (5.4), we cn wrie +δ Th is, I k = e k [h () ɛ] (x ) dx +δ +δ e k [h(x) h()] dx. (x ), ξ + δ. e k h (ξ) (x ) dx. +δ e k h (ξ) (x ) dx e k [h ()+ɛ] (x ) dx. Consider +δ +δ e k [h () ɛ] (x ) dx I k e k [h ()+ɛ] (x ) dx. (5.5) J = +δ e k [h () ɛ] (x ) dx. 14
25 Afer subsiuing x = u, we ge Therefore +δ Similrly, +δ J = = = δ e k [h () ɛ] u du 1 k (h () ɛ) k 1 (h () ɛ) 1 π k (h () ɛ) ( e k [h () ɛ] (x ) dx = ( e k [h ()+ɛ] (x ) dx = δ k (h () ɛ) Therefore (5.5) becomes ( ( π I k (h k () ɛ) Since ɛ > is rbirry, we hve ( π I k h k () Hence So Th is, ( I k π k h () ( e k [h(x) h()] dx e u du e u du s k s k. π k (h () ɛ) π k (h () + ɛ) ( π k h () ( e k h(x) dx e k h() π k h () π k (h () + ɛ) π. k h () s k. s k. s k.. s k. s k. 141
26 Lemm Le η be such h < η < b, nd h(x) C (b η x b), h (b) =, h (b) <, h(x) is nonincresing on [, b). Then ( e k h(x) dx e k h(b) π s k. k h (b) Proof. The proof is similr o h of previous lemm. Lemm Le η be such h < η < b, nd h(x) C ( x + η), h () =, h () <, h(x) is nonincresing on (, b]. Suppose φ(x) HK([, b]). Then ( φ(x) e k h(x) dx φ() e k h() π k h () s k. Proof. Since h(x) C ( x + η), we hve h (x) is coninuous. Le ɛ > be such h < ɛ < h (). Choose δ >, δ < η such h h (x) h () < ɛ, x + δ. Th is, Consider he inegrl h () ɛ < h (x) < h () + ɛ, x + δ. I k = We show h I k s k. Le We clim h g k s k. [φ(x) φ()] e k [h(x) h()] dx. e k [h(x) h()], x [, b] g k (x) =, x =. Since h is nonincresing on (, b], we hve h(x) h() < for ll x (, b]. Therefore g k (x) = e k [h(x) h()] s k. Se g(x) = for ll x [, b]. Then g k (x) = e k [h(x) h()] = g(x) for ll x [, b], s k. 14
27 Since φ(x) HK([, b]), he inegrl [φ(x) φ()] dx exiss. Observe h he sequence {g k (x)} is of uniform bounded vriion on [, b] wih g k (x) s k. Then by [Cor.3., [11]], we hve [φ(x) φ()] e k [h(x) h()] dx [φ(x) φ()] dx s k s k. Therefore Th is, φ(x) e k [h(x) h()] dx = φ() Bu by lemm (5.5.1), we hve Therefore φ(x) e k h(x) dx = φ() ( π e k h(x) dx e k h() k h () e k [h(x) h()] dx. e k h(x) dx. ( π φ(x) e k h(x) dx φ() e k h() k h () s k. s k. Lemm Le η be such h < η < b, nd h(x) C (b η x b), h (b) =, h (b) <, h(x) is nonincresing on [, b) nd suppose φ(x) HK([, b]). Then ( π φ(x) e k h(x) dx φ(b) e k h(b) k h (b) 143 s k.
28 Proof. The proof is similr o h of he previous lemm. Now we re redy o obin he inversion heorem for Hensock-Kurzweil Lplce rnsform. Theorem (Inversion Theorem) If f() HK(R + ) nd if he HK- Lplce rnsform of f(), L{f}(s) exiss, hen lim k 1 k! ( ) k+1 k e ku u k f(u) du = f(). Proof. The inversion heorem follows immediely, if we cn prove he following: I) II) lim k lim k I) We hve he relion 1 k! 1 k! ( ) k+1 k e ku u k f(u) du = f() (5.6) ( ) k+1 k e ku u k f(u) du = f(). (5.7) ( π f(x) e k φ(x) dx f() e k φ() k φ () Tke = nd φ(x) = ln(x) x Therefore Th is, f(x) e k [ln(x) x ] dx f() e k [ln() 1] ( s k. for ll x [, ). Then we hve π k ( 1 ) ( f(x) x k e kx π dx f() k e k k s k. s k. f(x) x k e kx dx f() k+1 e k ( π k s k. 144
29 Therefore s k, we hve 1 k! ( ) k+1 k b f(x) x k e kx dx = 1 k! = ( k e ( ) k+1 k ( π f() k+1 e k k ) k k ( π k! f(). k The Sirling s formul is given by ( ) n n e πn n!, using his we cn wrie 1 k! ( ) k+1 k b f(x) x k e kx dx = k f() πk = f() ( π k s k. s k This is rue for every b R, b >. Therefore by Hke s heorem [1], we hve lim k 1 k! ( ) k+1 k f(x) x k e kx dx = f(). II) Agin we hve he relion ( π f(x) e k φ(x) dx f(b) e k φ(b) k φ (b) s k. Tke b = nd φ(x) = ln(x) x, for ll x (, ]. Then we ge lim k 1 k! By Hke s heorem [1], we hve lim k 1 k! ( ) k+1 k f(x) x k e kx dx = f(). ( ) k+1 k f(x) x k e kx dx = f(). Therefore from (5.6) nd (5.7), we cn wrie lim k 1 k! ( ) k+1 k f(x) x k e kx dx = f(). 145
30 5.6 Exmples Here we shll give some exmples of HK-Lplce rnsformble funcions whose clssicl Lplce rnsform do no exis. However we could no ble o find he exc form of he HK-Lplce rnsform of hese funcions. Exmple Consider he funcion g() = e s sin ln(+), s C. Le f() = e s sin nd φ() = 1 ln(+). Observe h he funcion φ() is differenible on R + nd φ L 1 (R + ) nd if F () = e su sin u du, Re.s >, hen F () M for ll (, ), Re.s > for some consn M >. Now Then { e s (s sin cos ) F () φ() = s } s ln( + ). { e s (s sin cos ) lim F () φ() = lim + 1 } 1 s + 1 s + 1 ln( + ). Therefore lim F () φ() exiss. Hence by Du-Bois-Reymond s es [1], we hve e s sin ln(+) HK(R + ), Re.s >. Th is, e s sin ln( + ) d exiss, Re.s >. Hence he HK-Lplce rnsform of he funcion g() =. Exmple Consider he funcion f() = cos. We hve F () = cos u u du = cos u du. sin ln(+) exiss, Re.s > 146
31 Le φ() = e s, s C. Then φ () = s e s L 1 (R + ), Re.s >. Now Then F () φ() = e s cos u du. lim F () φ() = lim e s = lim e s lim =, Re.s >. cos u du cos u du Therefore by Du-Bois-Reymond s es [1], we hve f() φ() HK(R + ), Re.s >. Hence he HK-Lplce rnsform of he funcion f() = cos exiss for Re.s >. Exmple Le φ() = e σ, R +, σ >. This funcion is coninuous on R + nd φ( + 1) = 1 ( + 1) e < 1 = φ() for ll σ(+1) R+ eσ 1 nd lso lim φ() = lim =, σ >. e σ Therefore φ() is decresing o zero s. Observe h he inegrl diverges. e σ d, σ > Now le n N be such h < (1 + 4n ) π 4ω. For R, we hve sin ω 1 if nd only if ω n=n [(1 + 4n) π 4, (3 + 4n) π 4 ]. 147
32 If n N, hen (3 + 4n) π < (1 + n) π. 4 (1+n)π e σ sin d = n (3+4j) π 4 e σ j=n (1+4j) π 4 n (3+4j) π 4 e σ j=n 1 = 1 (1+4j) π 4 n (3+4j) π 4 j=n n (1+4j) π 4 j=n 4 sin ω d 1 d 1 (3 + 4j) π 4 eσ(3+4j) π 4 (3 + 4j) π e s(3+4j) π 4 π n 1 (1 + j) π e. σ(1+j)π j=n π d On he oher hnd, we hve (1+n)π e σ Bu since e σ d = = = n π e σ n π e σ n π e σ n π e σ HK(R + ), we hve Therefore j=n e σjπ jπ =. So e σ sin ω / L 1 (R + ), σ >. Similrly, e σ cos ω / L 1 (R + ), σ >. Now le f() = sin ω, φ() = e σ, R. d + d + d + (1+n)π e σ d n π n (1+j)π e σ j=n jπ n (1+j)π e σjπ j=n jπ n d + e σjπ jπ π. j=n e σ d =. Observe h φ() is monoone funcion nd φ() s. And sin ωu du, ω for ll ω R+. Th is, F is bounded. Therefore by Chrier-Dirichle s es [1], we hve e σ sin ω HK(R + ). 148 jπ d d
33 Similrly, e σ cos ω HK(R + ). Hence e σ {cos ω i sin ω} HK(R + ). Th is, Thus e s e σ e iω d exiss, σ >. d exiss, Re.s > s HK inegrl, where s = σ + iω. 149
34 References [1] Brle R. G., A Modern Theory of Inegrion, Grd. Sud. Mh. 3, Amer. Mh. Soc. Providence, 1. [] Chudhry M. S., Tikre S. A., On Guge Lplce Trnsform, In. Journl of Mh. Anlysis, Vol. 5, No. 35 (11), [3] Erdelyi A., Tbles of Inegrl rnsforms, Vol. 1, McGrw Hill Book Compny, Inc [4] Gsque C., P. Wiomski P., Fourier nlysis nd pplicions, Springer- Verlg, New York, Inc [5] Gordon R. A., The Inegrls of Lebesgue, Denjoy, Perron, nd Hensock, Grd. Sud. Mh. 4, Amer. Mh. Soc. Providence, [6] McLeod R. M., The Generlized Riemnn Inegrl, Crus Mh. Monogrphs, No., The Mhemicl Associion of Americ, Wshingon DC, 198. [7] Nnson I. P., Theory of funcions of rel vrible, Vol. 1, Frederick Unger Publishing Co. New York, [8] Pos E. L., Generlized differeniion, Trns. Amer. Mh. Soc. Vol. 3 (193),
35 [9] Sks S., Theory of he Inegrl, Dover Publicions, New York, [1] Swrz C., Inroducion o Guge Inegrls, World Scienific Publishing Co. Singpore, 1. [11] Tlvil E., Limis nd Hensock inegrls of producs, Rel Anl. Exchnge 5 (1999-), [1] Tlvil E., Necessry nd sufficien condiions for differeniing under he inegrl sign, Amer. Mh. Monhly, 18 (1), [13] Tlvil E., Hensock-Kurzweil Fourier rnsforms, Ill. Jour. Mh. Vol. 46, No. 4(), [14] Tikre S. A., Chudhry M. S., On some resuls of HK-convoluion, In. Elecron. J. Pure Appl. Mh. Vol., No. (1), [15] Widder D. V., The Lplce rnsform, Princeon Universiy Press, Princeon, [16] Zyed A. I., The Hndbook of Funcion nd Generlized Funcion rnsformions, CRC Press, Inc
Hermite-Hadamard-Fejer Type Inequalities for s Convex Function in the Second Sense via Fractional Integrals
 Filom 30: 06), 33 338 DOI 0.98/FIL63S Published by Fculy o Sciences nd Mhemics, Universiy o Niš, Serbi Avilble : hp://www.pm.ni.c.rs/ilom Hermie-Hdmrd-Fejer Type Ineuliies or s Convex Funcion in he Second
Filom 30: 06), 33 338 DOI 0.98/FIL63S Published by Fculy o Sciences nd Mhemics, Universiy o Niš, Serbi Avilble : hp://www.pm.ni.c.rs/ilom Hermie-Hdmrd-Fejer Type Ineuliies or s Convex Funcion in he Second
Fractional Wavelet Transform in Terms of Fractional Convolution
 Progr. Frc. Differ. Appl., No. 3, 20-20 205 20 Progress in Frcionl Differeniion nd Applicions An Inernionl Journl hp://dx.doi.org/0.2785/pfd/00305 Frcionl Wvele Trnsform in Terms of Frcionl Convoluion
Progr. Frc. Differ. Appl., No. 3, 20-20 205 20 Progress in Frcionl Differeniion nd Applicions An Inernionl Journl hp://dx.doi.org/0.2785/pfd/00305 Frcionl Wvele Trnsform in Terms of Frcionl Convoluion
Exercise 6.14 Linearly independent vectors are also affinely independent.
 Affine sets Linear Inequality Systems Definition 6.12 The vectors v 1, v 2,..., v k are affinely independent if v 2 v 1,..., v k v 1 is linearly independent; affinely dependent, otherwise. We first check
Affine sets Linear Inequality Systems Definition 6.12 The vectors v 1, v 2,..., v k are affinely independent if v 2 v 1,..., v k v 1 is linearly independent; affinely dependent, otherwise. We first check
A known plaintext attack on the ISAAC keystream generator
 A known plinex ck on he ISAAC keysrem generor Mrin Pudovkin mrip@online.ru Moscow Engineering Physics Insiue (Technicl Universiy) Deprmen of Crypology nd Discree Mhemics Absrc. Srem ciphers re ofen used
A known plinex ck on he ISAAC keysrem generor Mrin Pudovkin mrip@online.ru Moscow Engineering Physics Insiue (Technicl Universiy) Deprmen of Crypology nd Discree Mhemics Absrc. Srem ciphers re ofen used
Pontryagin Approximations for Optimal Design of Elastic Structures
 Pontryagin Approximations for Optimal Design of Elastic Structures Jesper Carlsson NADA, KTH jesperc@nada.kth.se Collaborators: Anders Szepessy, Mattias Sandberg October 5, 2005 A typical optimal design
Pontryagin Approximations for Optimal Design of Elastic Structures Jesper Carlsson NADA, KTH jesperc@nada.kth.se Collaborators: Anders Szepessy, Mattias Sandberg October 5, 2005 A typical optimal design
On Hermite-Hadamard-Fejér type inequalities for convex functions via fractional integrals
 Mthemtic Morvic Vol. 1, No. 1 (017), 105 13 On Hermite-Hdmrd-Fejér type inequlities for convex functions vi frctionl integrls Adullh Akkurt nd Hüsey ın Yıldırım Astrct. In this pper, we hve estlished some
Mthemtic Morvic Vol. 1, No. 1 (017), 105 13 On Hermite-Hdmrd-Fejér type inequlities for convex functions vi frctionl integrls Adullh Akkurt nd Hüsey ın Yıldırım Astrct. In this pper, we hve estlished some
Large time behavior of solutions for a complex-valued quadratic heat equation
 Nonlinear Differ. Equ. Appl. 5, 5 45 c 5 Springer Basel -97/5/55-4 published online March 5, 5 DOI.7/s3-5-3-7 Nonlinear Differenial Equaions and Applicaions NoDEA Large ime behavior of soluions for a complex-valued
Nonlinear Differ. Equ. Appl. 5, 5 45 c 5 Springer Basel -97/5/55-4 published online March 5, 5 DOI.7/s3-5-3-7 Nonlinear Differenial Equaions and Applicaions NoDEA Large ime behavior of soluions for a complex-valued
AALBORG UNIVERSITY. Spectral Analysis of a δ-interaction in One Dimension Defined as a Quadratic Form
 AALBOG UNIVESITY Specral Analysis of a δ-ineracion in One Dimension Defined as a Quadraic Form by Peer Jensen February 9h, 008 Maser Thesis Deparmen of Mahemaical Sciences Aalborg Universiy Fredrik Bajers
AALBOG UNIVESITY Specral Analysis of a δ-ineracion in One Dimension Defined as a Quadraic Form by Peer Jensen February 9h, 008 Maser Thesis Deparmen of Mahemaical Sciences Aalborg Universiy Fredrik Bajers
SKRIFTLIG EKSAMEN I NUMERISK DYNAMIK Bygge- og Anlægskonstruktion, 7. semester Torsdag den 19. juni 2003 kl Alle hjælpemidler er tilladt
 SKRIFTLIG EKSAMEN I NUMERISK DYNAMIK Bygge- og Anlægskonstruktion, 7. semester Torsdag den 9. juni 23 kl. 9.-3. Alle hjælpemidler er tilladt OPGAVE f(x) x Givet funktionen f(x) x, x [, ] Spørgsmål (%)
SKRIFTLIG EKSAMEN I NUMERISK DYNAMIK Bygge- og Anlægskonstruktion, 7. semester Torsdag den 9. juni 23 kl. 9.-3. Alle hjælpemidler er tilladt OPGAVE f(x) x Givet funktionen f(x) x, x [, ] Spørgsmål (%)
MONOTONE POSITIVE SOLUTIONS FOR p-laplacian EQUATIONS WITH SIGN CHANGING COEFFICIENTS AND MULTI-POINT BOUNDARY CONDITIONS
 Electronic Journal of Differential Equations, Vol. 22, No. 22, pp. 2. ISSN: 72-669. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu ftp ejde.math.txstate.edu MONOTONE POSITIVE SOLUTIONS FOR
Electronic Journal of Differential Equations, Vol. 22, No. 22, pp. 2. ISSN: 72-669. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu ftp ejde.math.txstate.edu MONOTONE POSITIVE SOLUTIONS FOR
Critical exponent for semilinear wave equation with critical potential
 Nonlinear Differ. Equ. Appl. (13), 1379 1391 c 1 Springer Basel 11-97/13/31379-13 published online December 16, 1 DOI 1.17/s3-1-14-x Nonlinear Differential Equations and Applications NoDEA Critical exponent
Nonlinear Differ. Equ. Appl. (13), 1379 1391 c 1 Springer Basel 11-97/13/31379-13 published online December 16, 1 DOI 1.17/s3-1-14-x Nonlinear Differential Equations and Applications NoDEA Critical exponent
Kurver og flader Aktivitet 15 Geodætiske kurver, Isometri, Mainardi-Codazzi, Teorema Egregium
 Kurver og flader Aktivitet 15 Geodætiske kurver, Isometri, Mainardi-Codazzi, Teorema Egregium Lisbeth Fajstrup Institut for Matematiske Fag Aalborg Universitet Kurver og Flader 2013 Lisbeth Fajstrup (AAU)
Kurver og flader Aktivitet 15 Geodætiske kurver, Isometri, Mainardi-Codazzi, Teorema Egregium Lisbeth Fajstrup Institut for Matematiske Fag Aalborg Universitet Kurver og Flader 2013 Lisbeth Fajstrup (AAU)
Sign variation, the Grassmannian, and total positivity
 Sign variation, the Grassmannian, and total positivity arxiv:1503.05622 Slides available at math.berkeley.edu/~skarp Steven N. Karp, UC Berkeley FPSAC 2015 KAIST, Daejeon Steven N. Karp (UC Berkeley) Sign
Sign variation, the Grassmannian, and total positivity arxiv:1503.05622 Slides available at math.berkeley.edu/~skarp Steven N. Karp, UC Berkeley FPSAC 2015 KAIST, Daejeon Steven N. Karp (UC Berkeley) Sign
Basic statistics for experimental medical researchers
 Basic statistics for experimental medical researchers Sample size calculations September 15th 2016 Christian Pipper Department of public health (IFSV) Faculty of Health and Medicinal Science (SUND) E-mail:
Basic statistics for experimental medical researchers Sample size calculations September 15th 2016 Christian Pipper Department of public health (IFSV) Faculty of Health and Medicinal Science (SUND) E-mail:
Computing the constant in Friedrichs inequality
 Computing the constant in Friedrichs inequality Tomáš Vejchodský vejchod@math.cas.cz Institute of Mathematics, Žitná 25, 115 67 Praha 1 February 8, 212, SIGA 212, Prague Motivation Classical formulation:
Computing the constant in Friedrichs inequality Tomáš Vejchodský vejchod@math.cas.cz Institute of Mathematics, Žitná 25, 115 67 Praha 1 February 8, 212, SIGA 212, Prague Motivation Classical formulation:
Chapter 6. Hydrogen Atom. 6.1 Schrödinger Equation. The Hamiltonian for a hydrogen atom is. Recall that. 1 r 2 sin 2 θ + 1. and.
 Chapter 6 Hydrogen Atom 6. Schrödinger Equation The Hamiltonian for a hydrogen atom is Recall that Ĥ = h e m e 4πɛ o r = r ) + r r r r sin θ sin θ ) + θ θ r sin θ φ and [ ˆL = h sin θ ) + )] sin θ θ θ
Chapter 6 Hydrogen Atom 6. Schrödinger Equation The Hamiltonian for a hydrogen atom is Recall that Ĥ = h e m e 4πɛ o r = r ) + r r r r sin θ sin θ ) + θ θ r sin θ φ and [ ˆL = h sin θ ) + )] sin θ θ θ
INTERVAL VALUED FUZZY IDEALS OF GAMMA NEAR-RINGS
 BULLETIN OF THE INTERNATIONAL MATHEMATICAL VIRTUAL INSTITUTE ISSN (p) 2303-4874, ISSN (o) 2303-4955 www.imvibl.org /JOURNALS / BULLETIN Vol. 8(2018), 301-314 DOI: 10.7251/BIMVI1802301C Former BULLETIN
BULLETIN OF THE INTERNATIONAL MATHEMATICAL VIRTUAL INSTITUTE ISSN (p) 2303-4874, ISSN (o) 2303-4955 www.imvibl.org /JOURNALS / BULLETIN Vol. 8(2018), 301-314 DOI: 10.7251/BIMVI1802301C Former BULLETIN
University of Copenhagen Faculty of Science Written Exam - 3. April Algebra 3
 University of Copenhagen Faculty of Science Written Exam - 3. April 2009 Algebra 3 This exam contains 5 exercises which are to be solved in 3 hours. The exercises are posed in an English and in a Danish
University of Copenhagen Faculty of Science Written Exam - 3. April 2009 Algebra 3 This exam contains 5 exercises which are to be solved in 3 hours. The exercises are posed in an English and in a Danish
264.. Cox, Daio Jang (23) Grandell (1976). 1.1 (Ω, F, {F, [, ]}, P). N λ, λ F, 1 2 u R, λ d < a... E{e iu(n 2 N 1 ) F λ 2 } = e {(eiu 1) 2 1 λ d}, F λ
![264.. Cox, Daio Jang (23) Grandell (1976). 1.1 (Ω, F, {F, [, ]}, P). N λ, λ F, 1 2 u R, λ d < a... E{e iu(n 2 N 1 ) F λ 2 } = e {(eiu 1) 2 1 λ d}, F λ 264.. Cox, Daio Jang (23) Grandell (1976). 1.1 (Ω, F, {F, [, ]}, P). N λ, λ F, 1 2 u R, λ d < a... E{e iu(n 2 N 1 ) F λ 2 } = e {(eiu 1) 2 1 λ d}, F λ](/thumbs/92/110314096.jpg) 212 6 Chinee Journal of Applied Probabiliy and Saiic Vol.28 No.3 Jun. 212 Lévy (,, 2156),, Lévy.., (Credi Defaul Swap). :,,,. : O211.6. 1.,.,.,,.,, O Kane urnbull (23), Jamhidian (24), Crepey, Jeanblanc
212 6 Chinee Journal of Applied Probabiliy and Saiic Vol.28 No.3 Jun. 212 Lévy (,, 2156),, Lévy.., (Credi Defaul Swap). :,,,. : O211.6. 1.,.,.,,.,, O Kane urnbull (23), Jamhidian (24), Crepey, Jeanblanc
Nøgleord og begreber. l Hospitals regel 2. Test l Hospitals regel. Uegentlige integraler 2. Test uegentlige integraler. Sammenligning.
 Oversig [S] 4.5, 5. Nøgleord og begreber Ubeseme udryk l Hospils regel l Hospils regel 2 Tes l Hospils regel Uegenlige inegrler Tes uegenlige inegrler Uegenlige inegrler 2 Tes uegenlige inegrler Smmenligning
Oversig [S] 4.5, 5. Nøgleord og begreber Ubeseme udryk l Hospils regel l Hospils regel 2 Tes l Hospils regel Uegenlige inegrler Tes uegenlige inegrler Uegenlige inegrler 2 Tes uegenlige inegrler Smmenligning
University of Copenhagen Faculty of Science Written Exam April Algebra 3
 University of Copenhagen Faculty of Science Written Exam - 16. April 2010 Algebra This exam contains 5 exercises which are to be solved in hours. The exercises are posed in an English and in a Danish version.
University of Copenhagen Faculty of Science Written Exam - 16. April 2010 Algebra This exam contains 5 exercises which are to be solved in hours. The exercises are posed in an English and in a Danish version.
Eric Nordenstam 1 Benjamin Young 2. FPSAC 12, Nagoya, Japan
 Eric 1 Benjamin 2 1 Fakultät für Matematik Universität Wien 2 Institutionen för Matematik Royal Institute of Technology (KTH) Stockholm FPSAC 12, Nagoya, Japan The Aztec Diamond Aztec diamonds of orders
Eric 1 Benjamin 2 1 Fakultät für Matematik Universität Wien 2 Institutionen för Matematik Royal Institute of Technology (KTH) Stockholm FPSAC 12, Nagoya, Japan The Aztec Diamond Aztec diamonds of orders
The LWR Model in Lagrangian coordinates
 The LWR Model in Lagrangian coordinaes ACI-NIM: Mah Models on Traffic Flow Ludovic Leclercq, LICIT (ENTPE/INRETS) Jorge Laval, Georgiaech Universiy 31 ocober 2007 INRETS Ouline Lagrangian resoluion of
The LWR Model in Lagrangian coordinaes ACI-NIM: Mah Models on Traffic Flow Ludovic Leclercq, LICIT (ENTPE/INRETS) Jorge Laval, Georgiaech Universiy 31 ocober 2007 INRETS Ouline Lagrangian resoluion of
One-dimensional chemotaxis kinetic model
 Nonlinear Differ. Equ. Appl. 18 (211), 139 172 c 21 Springer Basel AG 121-9722/11/2139-34 published online November 11, 21 DOI 1.17/s3-1-88-8 Nonlinear Differential Equations and Applications NoDEA One-dimensional
Nonlinear Differ. Equ. Appl. 18 (211), 139 172 c 21 Springer Basel AG 121-9722/11/2139-34 published online November 11, 21 DOI 1.17/s3-1-88-8 Nonlinear Differential Equations and Applications NoDEA One-dimensional
x t X t, t 1 τ =0 A t,τ (ξ t )x t τ = h t (ξ t )
 POLYHEDRAL RISK MEASURES IN SOCHASIC PROGRAMMING A. EICHHORN AND W. RÖMISCH Absrac. Sochasic programs ha do no only minimize expeced cos bu also ake ino accoun risk are of grea ineres in many applicaion
POLYHEDRAL RISK MEASURES IN SOCHASIC PROGRAMMING A. EICHHORN AND W. RÖMISCH Absrac. Sochasic programs ha do no only minimize expeced cos bu also ake ino accoun risk are of grea ineres in many applicaion
Aktivering af Survey funktionalitet
 Surveys i REDCap REDCap gør det muligt at eksponere ét eller flere instrumenter som et survey (spørgeskema) som derefter kan udfyldes direkte af patienten eller forsøgspersonen over internettet. Dette
Surveys i REDCap REDCap gør det muligt at eksponere ét eller flere instrumenter som et survey (spørgeskema) som derefter kan udfyldes direkte af patienten eller forsøgspersonen over internettet. Dette
Deepak Kumar Dubey, V. K. Jain RATE OF APPROXIMATION FOR INTEGRATED SZASZ-MIRAKYAN OPERATORS
 DEMONSTRATIO MATHEMATICA Vol. XLI No 4 8 Deepak Kumar Dubey, V. K. Jai RATE OF APPROXIMATION FOR INTEGRATED SZASZ-MIRAKYAN OPERATORS Absrac. Recely Jai e al. [3] proposed a iegral modificaio of Szasz-Mirakya
DEMONSTRATIO MATHEMATICA Vol. XLI No 4 8 Deepak Kumar Dubey, V. K. Jai RATE OF APPROXIMATION FOR INTEGRATED SZASZ-MIRAKYAN OPERATORS Absrac. Recely Jai e al. [3] proposed a iegral modificaio of Szasz-Mirakya
Outline. Chapter 6: (cont d) Qijin Chen. November 21, 2013 NH = =6 CH = 15 4
 Chapter 6: Qjn Chen Department of Physcs, Zhejang Unversty November 1, 013 Copyrght c 013 by Qjn Chen; all rghts reserved. ω 3 4 1. (cont d) 1 3 n3n3n 3n (x 1, y 1, z 1 )(x, y, z ) (x 1 x ) + (y 1 y )
Chapter 6: Qjn Chen Department of Physcs, Zhejang Unversty November 1, 013 Copyrght c 013 by Qjn Chen; all rghts reserved. ω 3 4 1. (cont d) 1 3 n3n3n 3n (x 1, y 1, z 1 )(x, y, z ) (x 1 x ) + (y 1 y )
SKRIFTLIG EKSAMEN I NUMERISK DYNAMIK Bygge- og Anlægskonstruktion, 8. semester Fredag den 30. juni 2005, kl Alle hjælpemidler er tilladt
 SKRIFTLIG EKSAMEN I NUMERISK DYNAMIK Bygge- og Anlægskonstruktion, 8. semester Fredag den 3. juni 5, kl. 8.3-.3 Alle hjælpemidler er tilladt OPGAVE u = y B u = u C A x c u = D u = Figuren viser en homogen
SKRIFTLIG EKSAMEN I NUMERISK DYNAMIK Bygge- og Anlægskonstruktion, 8. semester Fredag den 3. juni 5, kl. 8.3-.3 Alle hjælpemidler er tilladt OPGAVE u = y B u = u C A x c u = D u = Figuren viser en homogen
= λ([ x, y)) + λ((y, x]) = ( y ( x)) + (x y) = 2(x y).
![= λ([ x, y)) + λ((y, x]) = ( y ( x)) + (x y) = 2(x y). = λ([ x, y)) + λ((y, x]) = ( y ( x)) + (x y) = 2(x y).](/thumbs/58/42581589.jpg) Analyse 2 Øvelser Rasmus Sylvester Bryder 17. og 20. september 2013 Supplerende opgave 1 Lad λ være Lebesgue-målet på R og lad A B(R). Definér en funktion f : [0, ) R ved f(x) = λ(a [ x, x]). Vis, at f(x)
Analyse 2 Øvelser Rasmus Sylvester Bryder 17. og 20. september 2013 Supplerende opgave 1 Lad λ være Lebesgue-målet på R og lad A B(R). Definér en funktion f : [0, ) R ved f(x) = λ(a [ x, x]). Vis, at f(x)
Nodal set of strongly competition systems with fractional Laplacian
 Nonlinear Differ. Equ. Appl. 22 (2015), 1483 1513 c 2015 Springer Basel 1021-9722/15/051483-31 published online June 2, 2015 DOI 10.1007/s00030-015-0332-3 Nonlinear Differential Equations and Applications
Nonlinear Differ. Equ. Appl. 22 (2015), 1483 1513 c 2015 Springer Basel 1021-9722/15/051483-31 published online June 2, 2015 DOI 10.1007/s00030-015-0332-3 Nonlinear Differential Equations and Applications
what is this all about? Introduction three-phase diode bridge rectifier input voltages input voltages, waveforms normalization of voltages voltages?
 what is this all about? v A Introduction three-phase diode bridge rectifier D1 D D D4 D5 D6 i OUT + v OUT v B i 1 i i + + + v 1 v v input voltages input voltages, waveforms v 1 = V m cos ω 0 t v = V m
what is this all about? v A Introduction three-phase diode bridge rectifier D1 D D D4 D5 D6 i OUT + v OUT v B i 1 i i + + + v 1 v v input voltages input voltages, waveforms v 1 = V m cos ω 0 t v = V m
yt () p0 cos( t) OPGAVE 1
 SKRIFTLIG EKSAMEN I SVINGNINGSTEORI Bygge- og Anlægskonstruktion, 8.semester Fredag den 22. juni 2 kl. 9.-3. Alle hjælpemidler er tilladt OPGAVE B yt ) p cos t) l x A Konstruktionen på figuren er lodret
SKRIFTLIG EKSAMEN I SVINGNINGSTEORI Bygge- og Anlægskonstruktion, 8.semester Fredag den 22. juni 2 kl. 9.-3. Alle hjælpemidler er tilladt OPGAVE B yt ) p cos t) l x A Konstruktionen på figuren er lodret
Danish and English. Standard Field Analysis (Diderichsen) Standard Field Analysis (Diderichsen)
 Danish and English Some major poins of synacic conrass [Righ click for speaker s noes] Sandard Field nalysis (Diderichsen) Main clause able fel Forfel (Fundamenfel) Nexusfel ndholdsfel og Hvorfor Søren
Danish and English Some major poins of synacic conrass [Righ click for speaker s noes] Sandard Field nalysis (Diderichsen) Main clause able fel Forfel (Fundamenfel) Nexusfel ndholdsfel og Hvorfor Søren
Multivariate Extremes and Dependence in Elliptical Distributions
 Multivariate Extremes and Dependence in Elliptical Distributions Filip Lindskog, RiskLab, ETH Zürich joint work with Henrik Hult, KTH Stockholm I II III IV V Motivation Elliptical distributions A class
Multivariate Extremes and Dependence in Elliptical Distributions Filip Lindskog, RiskLab, ETH Zürich joint work with Henrik Hult, KTH Stockholm I II III IV V Motivation Elliptical distributions A class
CHAPTER 6 Derive differential Continuity, Momentum and Energy equations form Integral equations for control volumes.
 CHAPER 6 Derie differenil Conini, Momenm nd Energ eions form Inegrl eions for onrol olmes. imlif hese eions for -D sed, isenroi flo ih rible densi CHAPER 8 Wrie he D eions in erms of eloi oenil reding
CHAPER 6 Derie differenil Conini, Momenm nd Energ eions form Inegrl eions for onrol olmes. imlif hese eions for -D sed, isenroi flo ih rible densi CHAPER 8 Wrie he D eions in erms of eloi oenil reding
Probabilistic properties of modular addition. Victoria Vysotskaya
 Probabilistic properties of modular addition Victoria Vysotskaya JSC InfoTeCS, NPK Kryptonite CTCrypt 19 / June 4, 2019 vysotskaya.victory@gmail.com Victoria Vysotskaya (Infotecs, Kryptonite) Probabilistic
Probabilistic properties of modular addition Victoria Vysotskaya JSC InfoTeCS, NPK Kryptonite CTCrypt 19 / June 4, 2019 vysotskaya.victory@gmail.com Victoria Vysotskaya (Infotecs, Kryptonite) Probabilistic
A C 1,α partial regularity result for non-autonomous convex integrals with discontinuous coefficients
 Nonlinear Differ. Equ. Appl. (015), 1319 1343 c 015 Springer Basel 101-97/15/051319-5 published online April 9, 015 DOI 10.1007/s00030-015-034-3 Nonlinear Differential Equations and Applications NoDEA
Nonlinear Differ. Equ. Appl. (015), 1319 1343 c 015 Springer Basel 101-97/15/051319-5 published online April 9, 015 DOI 10.1007/s00030-015-034-3 Nonlinear Differential Equations and Applications NoDEA
Positive solutions of Kirchhoff type elliptic equations involving a critical Sobolev exponent
 Nonlinear Differ. Equ. Appl. 1 (014, 885 914 c 014 Springer Basel 101-97/14/060885-30 published online April 18, 014 DOI 10.1007/s00030-014-071-4 Nonlinear Differential Equations and Applications NoDEA
Nonlinear Differ. Equ. Appl. 1 (014, 885 914 c 014 Springer Basel 101-97/14/060885-30 published online April 18, 014 DOI 10.1007/s00030-014-071-4 Nonlinear Differential Equations and Applications NoDEA
University of Copenhagen Faculty of Science Written Exam - 8. April 2008. Algebra 3
 University of Copenhagen Faculty of Science Written Exam - 8. April 2008 Algebra 3 This exam contains 5 exercises which are to be solved in 3 hours. The exercises are posed in an English and in a Danish
University of Copenhagen Faculty of Science Written Exam - 8. April 2008 Algebra 3 This exam contains 5 exercises which are to be solved in 3 hours. The exercises are posed in an English and in a Danish
DoodleBUGS (Hands-on)
 DoodleBUGS (Hands-on) Simple example: Program: bino_ave_sim_doodle.odc A simulation example Generate a sample from F=(r1+r2)/2 where r1~bin(0.5,200) and r2~bin(0.25,100) Note that E(F)=(100+25)/2=62.5
DoodleBUGS (Hands-on) Simple example: Program: bino_ave_sim_doodle.odc A simulation example Generate a sample from F=(r1+r2)/2 where r1~bin(0.5,200) and r2~bin(0.25,100) Note that E(F)=(100+25)/2=62.5
Global attractor for the Navier Stokes equations with fractional deconvolution
 Nonlinear Differ. Equ. Appl. 5), 8 848 c 4 Springer Basel -97/5/48-38 published online December 5, 4 DOI.7/s3-4-35-y Nonlinear Differential Equations and Applications NoDEA Global attractor for the Navier
Nonlinear Differ. Equ. Appl. 5), 8 848 c 4 Springer Basel -97/5/48-38 published online December 5, 4 DOI.7/s3-4-35-y Nonlinear Differential Equations and Applications NoDEA Global attractor for the Navier
since a p 1 1 (mod p). x = 0 1 ( 1) p 1 (p 1)! (mod p) (p 1)! 1 (mod p) for p odd and for p = 2, (2 1)! = 1! = 1 1 (mod 2).
 5 Sice φ = ϕ is multiplicative, if = m j= pα j j is the stadard factorisatio, m φ() = φ(p α j j ). j= Theorem so ( φ(p α ) = p α ) p φ() = ( ). p p Proof. Cosider the atural umbers i the iterval j p α.
5 Sice φ = ϕ is multiplicative, if = m j= pα j j is the stadard factorisatio, m φ() = φ(p α j j ). j= Theorem so ( φ(p α ) = p α ) p φ() = ( ). p p Proof. Cosider the atural umbers i the iterval j p α.
Eksamen i Signalbehandling og matematik
 Opgave. (%).a. Figur og afbilleder et diskret tid signal [n ] og dets DTFT. [n] bruges som input til et LTI filter med en frekvens amplitude respons som vist på figur. Hvilket af de 4 output signaler (y
Opgave. (%).a. Figur og afbilleder et diskret tid signal [n ] og dets DTFT. [n] bruges som input til et LTI filter med en frekvens amplitude respons som vist på figur. Hvilket af de 4 output signaler (y
Løsningsforslag til opgavesæt 5
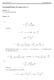 Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
Fremkomsten af mængdelæren. Stig Andur Pedersen
 Fremkomsten f mængdelæren Stig Andur Pedersen 1 Fourier række for f(x)=x x n 1 ( 1) 2 sin( nx) n n= 1 sin(2 x) sin(3 x) sin(4 x) = 2 sin( x) + + 2 3 4 De første 15 led er tget med på kurven. 2 Fourierrække
Fremkomsten f mængdelæren Stig Andur Pedersen 1 Fourier række for f(x)=x x n 1 ( 1) 2 sin( nx) n n= 1 sin(2 x) sin(3 x) sin(4 x) = 2 sin( x) + + 2 3 4 De første 15 led er tget med på kurven. 2 Fourierrække
Gribskov kommune Tisvilde By, Tibirke
 Birkevænget 1 10 cx 2036 2 Birkevænget 2 10 cp 2836 2 Birkevænget 3 10 cz 2010 2 Birkevænget 5 10 cy 2085 2 Birkevænget 6 10 cr 2953 4 Samlet 10 cs 2940 ejendom Birkevænget 7 10 cn 2045 2 Birkevænget 9
Birkevænget 1 10 cx 2036 2 Birkevænget 2 10 cp 2836 2 Birkevænget 3 10 cz 2010 2 Birkevænget 5 10 cy 2085 2 Birkevænget 6 10 cr 2953 4 Samlet 10 cs 2940 ejendom Birkevænget 7 10 cn 2045 2 Birkevænget 9
Uniform central limit theorems for kernel density estimators
 Probab. Theory elat. Fields (2008) 141:333 387 DOI 10.1007/s00440-007-0087-9 Uniform central limit theorems for kernel density estimators Evarist Giné ichard Nickl eceived: 12 December 2006 / evised: 5
Probab. Theory elat. Fields (2008) 141:333 387 DOI 10.1007/s00440-007-0087-9 Uniform central limit theorems for kernel density estimators Evarist Giné ichard Nickl eceived: 12 December 2006 / evised: 5
Løsningsforslag til opgavesæt 5
 Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
Asymptotic analysis of a non-linear non-local integro-differential equation arising from bosonic quantum field dynamics
 Nonlinear Differ. Equ. Appl. 21 (214), 51 61 c 213 Springer Basel 121-9722/14/151-11 published online May 8, 213 DOI 1.17/s3-13-237-y Nonlinear Differenial Equaions and Applicaions NoDEA Asympoic analysis
Nonlinear Differ. Equ. Appl. 21 (214), 51 61 c 213 Springer Basel 121-9722/14/151-11 published online May 8, 213 DOI 1.17/s3-13-237-y Nonlinear Differenial Equaions and Applicaions NoDEA Asympoic analysis
Besvarelser til Lineær Algebra Reeksamen Februar 2017
 Besvarelser til Lineær Algebra Reeksamen - 7. Februar 207 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Lineær Algebra Reeksamen - 7. Februar 207 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Generalized Probit Model in Design of Dose Finding Experiments. Yuehui Wu Valerii V. Fedorov RSU, GlaxoSmithKline, US
 Generalized Probit Model in Design of Dose Finding Experiments Yuehui Wu Valerii V. Fedorov RSU, GlaxoSmithKline, US Outline Motivation Generalized probit model Utility function Locally optimal designs
Generalized Probit Model in Design of Dose Finding Experiments Yuehui Wu Valerii V. Fedorov RSU, GlaxoSmithKline, US Outline Motivation Generalized probit model Utility function Locally optimal designs
OPGAVE 1. Spørgsmål 1 (15%) Opstil bevægelsesligningen med tilhørende begyndelsesbetingelser for massen i punkt D.
 SKRIFTLIG EKSMEN I STRUKTUREL DYNMIK ygge- og nlægskonstruktion, 7. semester Onsdg den 9. jnur 25 kl. 9.-3. lle hjælpemidler er tilldt OPGVE ft) ft) EI, µ = EI, µ = C EI, µ = D m f t Figuren viser en vndret,
SKRIFTLIG EKSMEN I STRUKTUREL DYNMIK ygge- og nlægskonstruktion, 7. semester Onsdg den 9. jnur 25 kl. 9.-3. lle hjælpemidler er tilldt OPGVE ft) ft) EI, µ = EI, µ = C EI, µ = D m f t Figuren viser en vndret,
MATEMATIK 11 Eksamensopgaver Juni 1995 Juni 2001, 3. fjerdedel
 MATEMATIK Eksamensopgaver Juni 995 Juni 200, 3. fjerdedel August 998 Opgave. Lad f : R \ {0} R betegne funktionen givet ved f(x) = ex x for x 0. (a) Find eventuelle lokale maksimums- og minimumspunkter
MATEMATIK Eksamensopgaver Juni 995 Juni 200, 3. fjerdedel August 998 Opgave. Lad f : R \ {0} R betegne funktionen givet ved f(x) = ex x for x 0. (a) Find eventuelle lokale maksimums- og minimumspunkter
Integration m.h.t. mål med tæthed
 Integration m.h.t. mål med tæthed Sætning (EH 11.7) Lad ν = f µ på (X, E). For alle g M + (X, E) gælder at gdν = g f dµ. Bevis: Standardbeviset: 1) indikatorfunktioner 2) simple funktioner 3) M + -funktioner.
Integration m.h.t. mål med tæthed Sætning (EH 11.7) Lad ν = f µ på (X, E). For alle g M + (X, E) gælder at gdν = g f dµ. Bevis: Standardbeviset: 1) indikatorfunktioner 2) simple funktioner 3) M + -funktioner.
Spørgsmål 1 (5%) Forklar med relevant argumentation, at den stationære temperaturfordeling i områdets indre er bestemt ved følgende randværdiproblem
 SKRIFTLIG EKSAMEN I NUMERISK DYNAMIK Bygge- og Anlægskonstruktion, 8. semester Fredag den 9. juni 006, kl. 09.00-3.00 Alle hjælpemidler er tilladt OPGAVE y u = 0 isoleret rand r u = u 0 θ 0 θ c c u = 0
SKRIFTLIG EKSAMEN I NUMERISK DYNAMIK Bygge- og Anlægskonstruktion, 8. semester Fredag den 9. juni 006, kl. 09.00-3.00 Alle hjælpemidler er tilladt OPGAVE y u = 0 isoleret rand r u = u 0 θ 0 θ c c u = 0
Semi-smooth Newton method for Solving Unilateral Problems in Fictitious Domain Formulations
 Semi-smooth Newton method for Solving Unilateral Problems in Fictitious Domain Formulations Jaroslav Haslinger, Charles University, Prague Tomáš Kozubek, VŠB TU Ostrava Radek Kučera, VŠB TU Ostrava SNA
Semi-smooth Newton method for Solving Unilateral Problems in Fictitious Domain Formulations Jaroslav Haslinger, Charles University, Prague Tomáš Kozubek, VŠB TU Ostrava Radek Kučera, VŠB TU Ostrava SNA
UGESEDDEL 9 LØSNINGER. Sydsæter Theorem 1. Sætning om implicitte funktioner for ligningen f(x, y) = 0.
 UGESEDDEL 9 LØSNINGER Sydsæter 531 Theorem 1 Sætning om implicitte funktioner for ligningen f(x, y) = 0 Lad f(x, y) være C 1 i mængden A R n og lad (x 0, y 0 ) være et indre punkt i A hvor f(x 0, y 0 )
UGESEDDEL 9 LØSNINGER Sydsæter 531 Theorem 1 Sætning om implicitte funktioner for ligningen f(x, y) = 0 Lad f(x, y) være C 1 i mængden A R n og lad (x 0, y 0 ) være et indre punkt i A hvor f(x 0, y 0 )
Additive Property of Drazin Invertibility of Elements in a Ring
 Filomat 30:5 (2016), 1185 1193 DOI 10.2298/FIL1605185W Published by Faculty of Sciences and Mathematics, University of Niš, Serbia Available at: http://www.pmf.ni.ac.rs/filomat Additive Property of Drazin
Filomat 30:5 (2016), 1185 1193 DOI 10.2298/FIL1605185W Published by Faculty of Sciences and Mathematics, University of Niš, Serbia Available at: http://www.pmf.ni.ac.rs/filomat Additive Property of Drazin
Hydrogen Burning in Stars-II
 ydrogen Burning in Stars-II ydrogen in induced reaction have lowest oulomb barrier highest reaction rate Reaction chain with lowest Z elements are the -chains -chains limited by weak interaction based
ydrogen Burning in Stars-II ydrogen in induced reaction have lowest oulomb barrier highest reaction rate Reaction chain with lowest Z elements are the -chains -chains limited by weak interaction based
Some results for the weighted Drazin inverse of a modified matrix
 International Journal of Applied Mathematics Computation Journal homepage: www.darbose.in/ijamc ISSN: 0974-4665 (Print) 0974-4673 (Online) Volume 6(1) 2014 1 9 Some results for the weighted Drazin inverse
International Journal of Applied Mathematics Computation Journal homepage: www.darbose.in/ijamc ISSN: 0974-4665 (Print) 0974-4673 (Online) Volume 6(1) 2014 1 9 Some results for the weighted Drazin inverse
BJB 06012-0018 5. T e l: 050-35 4 0 61 - E-m a il: in fo @ n ie u w la n d.b e - W e b s it e : - Fa x :
 D a t a b a n k m r in g R a p p o r t M A a n g e m a a k t o p 17 /09/2007 o m 17 : 4 3 u u r I d e n t if ic a t ie v a n d e m S e c t o r BJB V o lg n r. 06012-0018 5 V o o r z ie n in g N ie u w
D a t a b a n k m r in g R a p p o r t M A a n g e m a a k t o p 17 /09/2007 o m 17 : 4 3 u u r I d e n t if ic a t ie v a n d e m S e c t o r BJB V o lg n r. 06012-0018 5 V o o r z ie n in g N ie u w
Combined concave convex effects in anisotropic elliptic equations with variable exponent
 Nonlinear Differ. Equ. Appl. 22 (205), 39 40 c 204 Springer Basel 02-9722/5/03039-20 published online October 4, 204 DOI 0.007/s00030-04-0288-8 Nonlinear Differential Equations and Applications NoDEA Combined
Nonlinear Differ. Equ. Appl. 22 (205), 39 40 c 204 Springer Basel 02-9722/5/03039-20 published online October 4, 204 DOI 0.007/s00030-04-0288-8 Nonlinear Differential Equations and Applications NoDEA Combined
Engelsk. Niveau D. De Merkantile Erhvervsuddannelser September Casebaseret eksamen. og
 052431_EngelskD 08/09/05 13:29 Side 1 De Merkantile Erhvervsuddannelser September 2005 Side 1 af 4 sider Casebaseret eksamen Engelsk Niveau D www.jysk.dk og www.jysk.com Indhold: Opgave 1 Presentation
052431_EngelskD 08/09/05 13:29 Side 1 De Merkantile Erhvervsuddannelser September 2005 Side 1 af 4 sider Casebaseret eksamen Engelsk Niveau D www.jysk.dk og www.jysk.com Indhold: Opgave 1 Presentation
A B C D E Hjemmeværnmuseet's arkiv/depot Søgaard Distrikter - LMD. Reol/hylde Region/distrikt/m.m. Kasse nr. Indhold 2C3 Flyverhjemmeværne 1
 0 A B C D E Hjemmeværnmuseet's arkiv/depot Søgaard LMK Distrikter - LMD. Reol/hylde Region/distrikt/m.m. Kasse nr. Indhold C Flyverhjemmeværne Flyverhjemmeværnet LMD Odense Nyt fra stabseskadrillen -.
0 A B C D E Hjemmeværnmuseet's arkiv/depot Søgaard LMK Distrikter - LMD. Reol/hylde Region/distrikt/m.m. Kasse nr. Indhold C Flyverhjemmeværne Flyverhjemmeværnet LMD Odense Nyt fra stabseskadrillen -.
On the complexity of drawing trees nicely: corrigendum
 Acta Informatica 40, 603 607 (2004) Digital Object Identifier (DOI) 10.1007/s00236-004-0138-y On the complexity of drawing trees nicely: corrigendum Thorsten Akkerman, Christoph Buchheim, Michael Jünger,
Acta Informatica 40, 603 607 (2004) Digital Object Identifier (DOI) 10.1007/s00236-004-0138-y On the complexity of drawing trees nicely: corrigendum Thorsten Akkerman, Christoph Buchheim, Michael Jünger,
The Size of the Selberg Zeta-Function at Places Symmetric with Respect to the Line Re(s)= 1/2
 Results Math 7 16, 71 81 c 15 Springer Basel 14-6383/16/171-11 published online July, 15 DOI 117/s5-15-486-7 Results in Mathematics The Size of the Selberg Zeta-Function at Places Symmetric with Respect
Results Math 7 16, 71 81 c 15 Springer Basel 14-6383/16/171-11 published online July, 15 DOI 117/s5-15-486-7 Results in Mathematics The Size of the Selberg Zeta-Function at Places Symmetric with Respect
DM549 Diskrete Metoder til Datalogi
 DM549 Diskrete Metoder til Datalogi Spørgsmål 1 (8%) Hvilke udsagn er sande? Husk, at symbolet betyder går op i. Which propositions are true? Recall that the symbol means divides. Svar 1.a: n Z: 2n > n
DM549 Diskrete Metoder til Datalogi Spørgsmål 1 (8%) Hvilke udsagn er sande? Husk, at symbolet betyder går op i. Which propositions are true? Recall that the symbol means divides. Svar 1.a: n Z: 2n > n
8 Regulære flader i R 3
 8 Regulære flader i R 3 Vi skal betragte særligt pæne delmængder S R 3 kaldet flader. I det følgende opfattes S som et topologisk rum i sportopologien, se Definition 5.9. En åben omegn U af p S er således
8 Regulære flader i R 3 Vi skal betragte særligt pæne delmængder S R 3 kaldet flader. I det følgende opfattes S som et topologisk rum i sportopologien, se Definition 5.9. En åben omegn U af p S er således
On the Fučik spectrum of non-local elliptic operators
 Nonlinear Differ. Equ. Appl. 21 (2014), 567 588 c 2014 Springer Basel 1021-9722/14/040567-22 published online January 7, 2014 DOI 10.1007/s00030-013-0258-6 Nonlinear Differential Equations and Applications
Nonlinear Differ. Equ. Appl. 21 (2014), 567 588 c 2014 Springer Basel 1021-9722/14/040567-22 published online January 7, 2014 DOI 10.1007/s00030-013-0258-6 Nonlinear Differential Equations and Applications
Gamle eksamensopgaver (MASO)
 EO 1 Gamle eksamensopgaver (MASO) Opgave 1. (Vinteren 1990 91, opgave 1) a) Vis, at rækken er divergent. b) Vis, at rækken er konvergent. Opgave 2. (Vinteren 1990 91, opgave 2) Gør rede for at ligningssystemet
EO 1 Gamle eksamensopgaver (MASO) Opgave 1. (Vinteren 1990 91, opgave 1) a) Vis, at rækken er divergent. b) Vis, at rækken er konvergent. Opgave 2. (Vinteren 1990 91, opgave 2) Gør rede for at ligningssystemet
Formale Systeme 2 Sommer 2012 Prof. P. H. Schmitt
 Formale Systeme 2 Sommer 2012 Prof. P. H. Schmitt I NSTITUT F U R T HEORETISCHE I NFORMATIK KIT Universita t des Landes Baden-Wu rttemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft
Formale Systeme 2 Sommer 2012 Prof. P. H. Schmitt I NSTITUT F U R T HEORETISCHE I NFORMATIK KIT Universita t des Landes Baden-Wu rttemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft
Nonlinear Nonhomogeneous Dirichlet Equations Involving a Superlinear Nonlinearity
 Results. Math. 70 2016, 31 79 c 2015 Springer Basel 1422-6383/16/010031-49 published online May 19, 2015 DOI 10.1007/s00025-015-0461-3 Results in Mathematics Nonlinear Nonhomogeneous Dirichlet Equations
Results. Math. 70 2016, 31 79 c 2015 Springer Basel 1422-6383/16/010031-49 published online May 19, 2015 DOI 10.1007/s00025-015-0461-3 Results in Mathematics Nonlinear Nonhomogeneous Dirichlet Equations
On the Relations Between Fuzzy Topologies and α Cut Topologies
 S Ü Fen Ed Fak Fen Derg Sayı 23 (2004) 21-27, KONYA On the Relations Between Fuzzy Topologies and α Cut Topologies Zekeriya GÜNEY 1 Abstract: In this study, some relations have been generated between fuzzy
S Ü Fen Ed Fak Fen Derg Sayı 23 (2004) 21-27, KONYA On the Relations Between Fuzzy Topologies and α Cut Topologies Zekeriya GÜNEY 1 Abstract: In this study, some relations have been generated between fuzzy
Rotational Properties of Bose - Einstein Condensates
 Rotational Properties of Bose - Einstein Condensates Stefan Baumgärtner April 30, 2013 1 / 27 Stefan Baumgärtner Rotational Properties of Bose - Einstein Condensates Outline 2 / 27 Stefan Baumgärtner Rotational
Rotational Properties of Bose - Einstein Condensates Stefan Baumgärtner April 30, 2013 1 / 27 Stefan Baumgärtner Rotational Properties of Bose - Einstein Condensates Outline 2 / 27 Stefan Baumgärtner Rotational
Funktionsundersøgelse. Rasmus Sylvester Bryder
 Funktionsundersøgelse Rasmus Sylvester Bryder 7. november 2008 Dette projekt aeveres i forbindelse med LA T EX 2ε-kurset vejledningsuge 2, 2008-09 på KU; til projektet benyttes noter givet til opgaveløsning.
Funktionsundersøgelse Rasmus Sylvester Bryder 7. november 2008 Dette projekt aeveres i forbindelse med LA T EX 2ε-kurset vejledningsuge 2, 2008-09 på KU; til projektet benyttes noter givet til opgaveløsning.
Decomposition theorem for the cd-index of Gorenstein* posets
 J Algebr Comb (2007) 26:225 251 DOI 10.1007/s10801-006-0055-y Decomposition theorem for the cd-index of Gorenstein* posets Richard Ehrenborg Kalle Karu Received: 20 June 2006 / Accepted: 15 December 2006
J Algebr Comb (2007) 26:225 251 DOI 10.1007/s10801-006-0055-y Decomposition theorem for the cd-index of Gorenstein* posets Richard Ehrenborg Kalle Karu Received: 20 June 2006 / Accepted: 15 December 2006
The X Factor. Målgruppe. Læringsmål. Introduktion til læreren klasse & ungdomsuddannelser Engelskundervisningen
 The X Factor Målgruppe 7-10 klasse & ungdomsuddannelser Engelskundervisningen Læringsmål Eleven kan give sammenhængende fremstillinger på basis af indhentede informationer Eleven har viden om at søge og
The X Factor Målgruppe 7-10 klasse & ungdomsuddannelser Engelskundervisningen Læringsmål Eleven kan give sammenhængende fremstillinger på basis af indhentede informationer Eleven har viden om at søge og
Vores mange brugere på musskema.dk er rigtig gode til at komme med kvalificerede ønsker og behov.
 På dansk/in Danish: Aarhus d. 10. januar 2013/ the 10 th of January 2013 Kære alle Chefer i MUS-regi! Vores mange brugere på musskema.dk er rigtig gode til at komme med kvalificerede ønsker og behov. Og
På dansk/in Danish: Aarhus d. 10. januar 2013/ the 10 th of January 2013 Kære alle Chefer i MUS-regi! Vores mange brugere på musskema.dk er rigtig gode til at komme med kvalificerede ønsker og behov. Og
Du kan efter ønske opfatte integralet som et Riemann-integral eller et Lebesgue-integral (idet de to er identiske på C([a, b], C) jf. Theorem 11.8.
![Du kan efter ønske opfatte integralet som et Riemann-integral eller et Lebesgue-integral (idet de to er identiske på C([a, b], C) jf. Theorem 11.8. Du kan efter ønske opfatte integralet som et Riemann-integral eller et Lebesgue-integral (idet de to er identiske på C([a, b], C) jf. Theorem 11.8.](/thumbs/73/68329897.jpg) Anlyse Øvelser Rsmus Sylvester Bryder. og 5. oktober 3 Supplerende opgve Ld C([, b], C) betegne rummet f lle kontinuerte funktioner f : [, b] C, hvor < b, og definér et indre produkt på C([, b], C) ved
Anlyse Øvelser Rsmus Sylvester Bryder. og 5. oktober 3 Supplerende opgve Ld C([, b], C) betegne rummet f lle kontinuerte funktioner f : [, b] C, hvor < b, og definér et indre produkt på C([, b], C) ved
PARALLELIZATION OF ATTILA SIMULATOR WITH OPENMP MIGUEL ÁNGEL MARTÍNEZ DEL AMOR MINIPROJECT OF TDT24 NTNU
 PARALLELIZATION OF ATTILA SIMULATOR WITH OPENMP MIGUEL ÁNGEL MARTÍNEZ DEL AMOR MINIPROJECT OF TDT24 NTNU OUTLINE INEFFICIENCY OF ATTILA WAYS TO PARALLELIZE LOW COMPATIBILITY IN THE COMPILATION A SOLUTION
PARALLELIZATION OF ATTILA SIMULATOR WITH OPENMP MIGUEL ÁNGEL MARTÍNEZ DEL AMOR MINIPROJECT OF TDT24 NTNU OUTLINE INEFFICIENCY OF ATTILA WAYS TO PARALLELIZE LOW COMPATIBILITY IN THE COMPILATION A SOLUTION
Engelsk. Niveau C. De Merkantile Erhvervsuddannelser September 2005. Casebaseret eksamen. www.jysk.dk og www.jysk.com.
 052430_EngelskC 08/09/05 13:29 Side 1 De Merkantile Erhvervsuddannelser September 2005 Side 1 af 4 sider Casebaseret eksamen Engelsk Niveau C www.jysk.dk og www.jysk.com Indhold: Opgave 1 Presentation
052430_EngelskC 08/09/05 13:29 Side 1 De Merkantile Erhvervsuddannelser September 2005 Side 1 af 4 sider Casebaseret eksamen Engelsk Niveau C www.jysk.dk og www.jysk.com Indhold: Opgave 1 Presentation
Symplectic and contact properties of the Mañé critical value of the universal cover
 Nonlinear Differ. Equ. Appl. 21 (214), 679 78 c 214 Springer Basel 121-9722/14/5679-3 published online January 7, 214 DOI 1.17/s3-13-262-x Nonlinear Differential Equations and Applications NoDEA Symplectic
Nonlinear Differ. Equ. Appl. 21 (214), 679 78 c 214 Springer Basel 121-9722/14/5679-3 published online January 7, 214 DOI 1.17/s3-13-262-x Nonlinear Differential Equations and Applications NoDEA Symplectic
Eksamen i Mat F, april 2006
 Eksamen i Mat F, april 26 Opgave 1 Lad F være et vektorfelt, givet i retvinklede koordinater som: F x x F = F x i + F y j + F z k = F y = 2z F z y Udregn F og F: F = F x + F y + F z = 1 + +. F = F z F
Eksamen i Mat F, april 26 Opgave 1 Lad F være et vektorfelt, givet i retvinklede koordinater som: F x x F = F x i + F y j + F z k = F y = 2z F z y Udregn F og F: F = F x + F y + F z = 1 + +. F = F z F
User Manual for LTC IGNOU
 User Manual for LTC IGNOU 1 LTC (Leave Travel Concession) Navigation: Portal Launch HCM Application Self Service LTC Self Service 1. LTC Advance/Intimation Navigation: Launch HCM Application Self Service
User Manual for LTC IGNOU 1 LTC (Leave Travel Concession) Navigation: Portal Launch HCM Application Self Service LTC Self Service 1. LTC Advance/Intimation Navigation: Launch HCM Application Self Service
Frequency Dispersion: Dielectrics, Conductors, and Plasmas
 1/23 Frequency Dispersion: Dielectrics, Conductors, and Plasmas Carlos Felipe Espinoza Hernández Professor: Jorge Alfaro Instituto de Física Pontificia Universidad Católica de Chile 2/23 Contents 1 Simple
1/23 Frequency Dispersion: Dielectrics, Conductors, and Plasmas Carlos Felipe Espinoza Hernández Professor: Jorge Alfaro Instituto de Física Pontificia Universidad Católica de Chile 2/23 Contents 1 Simple
The fundamental solution of compressible and incompressible fluid flow past a rotating obstacle
 The fundamental solution of compressible and incompressible fluid flow past a rotating obstacle JSPS-DFG Japanese-German Graduate Externship Kickoff Meeting Waseda University, Tokyo, June 17-18, 2014 Reinhard
The fundamental solution of compressible and incompressible fluid flow past a rotating obstacle JSPS-DFG Japanese-German Graduate Externship Kickoff Meeting Waseda University, Tokyo, June 17-18, 2014 Reinhard
19.3. Second Order ODEs. Introduction. Prerequisites. Learning Outcomes
 Second Order ODEs 19.3 Introduction In this Section we start to learn how to solve second-order differential equations of a particular type: those that are linear and that have constant coefficients. Such
Second Order ODEs 19.3 Introduction In this Section we start to learn how to solve second-order differential equations of a particular type: those that are linear and that have constant coefficients. Such
Erratum to: Closed-Range Composition Operators on A 2 and the Bloch Space
 Integr. Equ. Oper. Theory 76 (2013), 131 143 DOI 10.1007/s00020-013-2043-7 Published online March 9, 2013 c Springer Basel 2013 Integral Equations and Operator Theory Erratum Erratum to: Closed-Range Composition
Integr. Equ. Oper. Theory 76 (2013), 131 143 DOI 10.1007/s00020-013-2043-7 Published online March 9, 2013 c Springer Basel 2013 Integral Equations and Operator Theory Erratum Erratum to: Closed-Range Composition
Satisability of Boolean Formulas
 SAT exercises 1 March, 2016 slide 1 Satisability of Boolean Formulas Combinatorics and Algorithms Prof. Emo Welzl Assistant: (CAB G36.1, cannamalai@inf.ethz.ch) URL: http://www.ti.inf.ethz.ch/ew/courses/sat16/
SAT exercises 1 March, 2016 slide 1 Satisability of Boolean Formulas Combinatorics and Algorithms Prof. Emo Welzl Assistant: (CAB G36.1, cannamalai@inf.ethz.ch) URL: http://www.ti.inf.ethz.ch/ew/courses/sat16/
Adaptive Algorithms for Blind Separation of Dependent Sources. George V. Moustakides INRIA, Sigma 2
 Adaptive Algorithms for Blind Separation of Dependent Sources George V. Moustakides INRIA, Sigma 2 Problem definition-motivation Existing adaptive scheme-independence General adaptive scheme-dependence
Adaptive Algorithms for Blind Separation of Dependent Sources George V. Moustakides INRIA, Sigma 2 Problem definition-motivation Existing adaptive scheme-independence General adaptive scheme-dependence
p-laplacian problems with nonlinearities interacting with the spectrum
 Nonlinear Differ. Equ. Appl. 20 (2013), 1701 1721 c 2013 Springer Basel 1021-9722/13/051701-21 published online March 24, 2013 DOI 10.1007/s00030-013-0226-1 Nonlinear Differential Equations and Applications
Nonlinear Differ. Equ. Appl. 20 (2013), 1701 1721 c 2013 Springer Basel 1021-9722/13/051701-21 published online March 24, 2013 DOI 10.1007/s00030-013-0226-1 Nonlinear Differential Equations and Applications
On a multidimensional moving boundary problem governed by anomalous diffusion: analytical and numerical study
 Nonlinear Differ. Equ. Appl. 22 (215), 543 577 c 214 Springer Basel 121-9722/15/4543-35 published online December 16, 214 DOI 1.17/s3-14-295-9 Nonlinear Differential Equations and Applications NoDEA On
Nonlinear Differ. Equ. Appl. 22 (215), 543 577 c 214 Springer Basel 121-9722/15/4543-35 published online December 16, 214 DOI 1.17/s3-14-295-9 Nonlinear Differential Equations and Applications NoDEA On
ATEX direktivet. Vedligeholdelse af ATEX certifikater mv. Steen Christensen stec@teknologisk.dk www.atexdirektivet.
 ATEX direktivet Vedligeholdelse af ATEX certifikater mv. Steen Christensen stec@teknologisk.dk www.atexdirektivet.dk tlf: 7220 2693 Vedligeholdelse af Certifikater / tekniske dossier / overensstemmelseserklæringen.
ATEX direktivet Vedligeholdelse af ATEX certifikater mv. Steen Christensen stec@teknologisk.dk www.atexdirektivet.dk tlf: 7220 2693 Vedligeholdelse af Certifikater / tekniske dossier / overensstemmelseserklæringen.
E-PAD Bluetooth hængelås E-PAD Bluetooth padlock E-PAD Bluetooth Vorhängeschloss
 E-PAD Bluetooth hængelås E-PAD Bluetooth padlock E-PAD Bluetooth Vorhängeschloss Brugervejledning (side 2-6) Userguide (page 7-11) Bedienungsanleitung 1 - Hvordan forbinder du din E-PAD hængelås med din
E-PAD Bluetooth hængelås E-PAD Bluetooth padlock E-PAD Bluetooth Vorhängeschloss Brugervejledning (side 2-6) Userguide (page 7-11) Bedienungsanleitung 1 - Hvordan forbinder du din E-PAD hængelås med din
Our activities. Dry sales market. The assortment
 First we like to start to introduce our activities. Kébol B.V., based in the heart of the bulb district since 1989, specialises in importing and exporting bulbs world-wide. Bulbs suitable for dry sale,
First we like to start to introduce our activities. Kébol B.V., based in the heart of the bulb district since 1989, specialises in importing and exporting bulbs world-wide. Bulbs suitable for dry sale,
Integration m.h.t. mål med tæthed
 Integration m.h.t. mål med tæthed Sætning (EH 11.7) Lad ν = f µ på (X, E). For alle g M + (X, E) gælder at gdν = g f dµ. Bevis: Standardbeviset: 1) indikatorfunktioner 2) simple funktioner 3) M + -funktioner.
Integration m.h.t. mål med tæthed Sætning (EH 11.7) Lad ν = f µ på (X, E). For alle g M + (X, E) gælder at gdν = g f dµ. Bevis: Standardbeviset: 1) indikatorfunktioner 2) simple funktioner 3) M + -funktioner.
Strings and Sets: set complement, union, intersection, etc. set concatenation AB, power of set A n, A, A +
 Strings and Sets: A string over Σ is any nite-length sequence of elements of Σ The set of all strings over alphabet Σ is denoted as Σ Operators over set: set complement, union, intersection, etc. set concatenation
Strings and Sets: A string over Σ is any nite-length sequence of elements of Σ The set of all strings over alphabet Σ is denoted as Σ Operators over set: set complement, union, intersection, etc. set concatenation
DM547 Diskret Matematik
 DM547 Diskret Matematik Spørgsmål 1 (11%) Hvilke udsagn er sande? Husk, at symbolet betyder går op i. Which propositions are true? Recall that the symbol means divides. Svar 1.a: n Z: 2n > n + 2 Svar 1.b:
DM547 Diskret Matematik Spørgsmål 1 (11%) Hvilke udsagn er sande? Husk, at symbolet betyder går op i. Which propositions are true? Recall that the symbol means divides. Svar 1.a: n Z: 2n > n + 2 Svar 1.b:
MM537 Introduktion til Matematiske Metoder
 MM537 Introduktion til Matematiske Metoder Spørgsmål 1 (11%) Hvilke udsagn er sande? Husk, at symbolet betyder går op i. Which propositions are true? Recall that the symbol means divides. Svar 1.a: n Z:
MM537 Introduktion til Matematiske Metoder Spørgsmål 1 (11%) Hvilke udsagn er sande? Husk, at symbolet betyder går op i. Which propositions are true? Recall that the symbol means divides. Svar 1.a: n Z:
