Evaluering. Matematik på hhx 1/16
|
|
|
- Jørgen Mathiasen
- 8 år siden
- Visninger:
Transkript
1 Evaluering af Matematik på hhx Sommeren /16
2 Indholdsfortegnelse Forord... 3 Generelle bemærkninger... 4 Omsætningstabeller... 4 A-niveau... 4 B-niveau... 4 Årets prøve i tal... 5 Matematik A... 5 Matematik B... 6 Vurdering af opgavesættet... 7 A-niveau... 7 Kommentarer til sættet... 9 B-niveau...11 Kommentarer til sættet...13 Giv kommentarer til årets opgavesæt /16
3 Forord Hermed en evaluering af de skriftlige prøver i matematik A og B (ny ordning) ved højere handelseksamen, sommeren Materialet er baseret på de kommentarer som censorerne er kommet med. Censorerne blev bedt om at: vurdere opgavesættende vurdere elevernes muligheder for at vise, at de har opnået kernekompetencerne beskrive positive sider ved besvarelserne beskrive typiske fejl og mangler I år blev der opdaget flere tilfælde af snyd ved de skriftlige prøver. Udfaldet af disse sager kendes endnu ikke, men de tages meget alvorligt. Det er mit håb at denne rapport kan være en hjælp og inspiration for matematiklæreren i såvel undervisningen som under retningen af elevbesvarelser. Marit Hvalsøe Schou Fagkonsulent (til 1/8 2008) 3/16
4 Generelle bemærkninger Evalueringsrapporten er opbygget således at årets eksamensresultater først beskrives i tal. Herefter fremlægges nogle af censorernes kommentarer, der så vidt muligt er udvalgt, så de giver et typisk billede at censorernes holdninger og oplevelser under bedømmelsen. Til slut diskuteres nogle af disse kommentarer i forhold til fagets mål. Som afgået fagkonsulent på hhx, vil jeg meget nødig komme med alt for konkrete svar f.eks. på kravet til dokumentation med it. Dér skal den kommende fagkonsulent have lov til at sætte dagsordenen! Mine egne erfaringer fra det tekniske gymnasium viser, at såvel it- som kompetencediskussionen kommer til at foregå løbende det næste lange stykke tid, og her forventer jeg, at de erhvervsgymnasiale uddannelser vil komme til at arbejde sammen og bruge hinandens erfaringer. Omsætningstabeller Censorerne blev bedt om ved hver delopgave at give point i forhold til graden af målopfyldelse, dvs. i hvor høj grad eleven viste at have erhvervet sig de matematiske kernekompetencer. Ved helhedsvurderingen skulle graden af tilstedeværelsen af samtlige kompetencer indgå. Karaktergivningen foregik i et samarbejde mellem de 2 censorer. Følgende vejledende omsætningstabeller blev benyttet: A-niveau Point Karakter B-niveau Point Karakter /16
5 Årets prøve i tal Matematik A I alt 1031 elever gik op til den skriftlige prøve i matematik A. Karaktererne fordelte sig således karakter i alt antal frekvens (%) kum. frekv. (%) Grafisk ser resultaterne således ud: I alt 890 elever bestod og blandt disse fordelte karaktererne sig således: karakter i alt frekvens (%) Sammenfatning: Gennemsnittet var 5,87 Typetallet var 7 Kvartilsættet var 02, 4 og 10 Andelen af elever der fik under 02 var 14 % 5/16
6 Konklusion: Resultatet er yderst fornuftigt, ja faktisk utrolig flot. Det er første gang prøven afholdes, og det er derfor vanskeligt at sammenligne med tidligere års resultater. Måske skyldes det gode resultat at de elever, der vælger matematik A, er elever, som virkelig ønsker at have faget og som prioriterer det. Måske har niveauet ikke helt fundet et passende leje. Et gennemsnit på 6 er absolut tilfredsstillende, mens det må være et fokuspunkt at få flere elever til at bestå. Ser man på de beståede elever, er karaktererne symmetrisk fordelt om karakteren 7. Matematik B I alt 1346 elever gik op til den skriftlige prøve i matematik B. Karaktererne fordelte sig således karakter i alt antal frekvens (%) kum. frekv. (%) Grafisk ser resultaterne således ud: 30,0 25,0 20,0 15,0 10,0 5,0 0, I alt 954 elever bestod og blandt disse fordelte karaktererne sig således: karakter i alt frekvens (%) /16
7 Sammenfatning: Gennemsnittet var 3,47 Typetallet var 00 Kvartilsættet var 00, 4 og 7 Andelen af elever der fik under 02 var 29 % Konklusion: Resultatet er på ingen måde tilfredsstillende. Det er anden gang prøven afholdes, og resultatet er endnu dårligere end sidste år, hvor 1169 elever gik op med et gennemsnit på 4,0, og hvor 27,4% ikke bestod prøven. Der er derfor tale om et resultat, der må arbejdes målrettet på at få ændret. Det er uklart, hvorfor det er gået på denne måde, men mange censorer oplevede sættet som svært og mindre traditionelt. Dette bør undersøges, så man kan få at vide, hvor der skal sættes ind. Ser man på de beståede elever, er karaktererne næsten symmetrisk fordelt om karakteren 4. Vurdering af opgavesættet A-niveau Censorerne blev bedt om at svare på nedenstående spørgsmål. 23 censorer ud af 64 har svaret. Tallene viser den samlede vurdering. Delprøven uden hjælpemidler: Hvordan vurderer du det faglige niveau for højt 0 passende 21 for lavt 2 Hvordan vurderer du opgavens omfang for stort 0 passende 19 for lille 4 Hvordan vurderer du læseligheden (formuleringer, billeder, grafer) fin 4 ok 18 ringe 1 Delprøven med hjælpemidler: Hvordan vurderer du det faglige niveau for højt 0 passende 13 for lavt 10 7/16
8 Hvordan vurderer du opgavens omfang for stort 0 passende 16 for lille 7 Hvordan vurderer du læseligheden (formuleringer, billeder, grafer) fin 3 ok 20 ringe 0 Hvordan vurderer du alsidigheden (dele af kernestoffet, der berøres) fin 3 ok 18 ringe 2 Angiv din helhedsvurdering af sættet fin 1 ok 20 ringe 2 Censorerne nogenlunde enige om, at det har været et udmærket sæt af passende sværhedsgrad og omfang dog mener knap halvdelen af censorerne at det faglige niveau var lidt lavt. I forbindelse med gymnasiereformen er de faglige mål, der skal bedømmes ved prøven, blevet beskrevet vha. de 8 matematiske kernekompetencer. Censorerne har derfor skulle vurdere i hvor høj grad eleverne har opnået disse kompetencer, og derfor blev censorerne bedt om at vurdere hvorvidt det gennem besvarelsen af årets prøve var muligt for eleverne at vise, de havde opnået disse kompetencer. God Rimelig Ringe Tankegang Ræsonnement Problembehandling Modellering Repræsentation Symbol- og formalisme Hjælpemiddel Kommunikation Opgavekommissionen vil ved udfærdigelse af kommende prøver været meget opmærksom på, at alle kompetencer er repræsenteret, og der for er det vigtigt at se, hvorledes årets sæt er blevet bedømt fra denne synsvinkel. Det er primært modelleringskompetencen og hjælpemiddelkompetencen, der skal arbejdes med, når næste års opgaver skal laves. Med hensyn til brug af hjælpemidler skal der arbejdes med lærernes holdning i såvel undervisnings- som bedømmelsessituationen. Her er det vigtigt at få diskuteret krav til dokumentation, når der benyttes IT-værktøjer. Ovenstående svar skal ses i lyset af, at mange lærere stadig er usikre på brugen af kompetencebegrebet. 8/16
9 Kommentarer til sættet Censorerne blev bedt om at kommenterer såvel positive sider som typiske fejl og mangler ved elevernes besvarelser. Mange kommentarer går igen: Om de positive sider: Gode generelle besvarelser...eleverne har været godt rundt i stoffet Da eleverne har haft god tid, har de kunnet gøre det rimelig godt. Selvfølgeligt har der været nogle mangler, men slet ikke som tidligere, hvor mange opgaver var ubesvarede. Eleverne har regnet mere end forventer ved opgaven uden hjælpemidler. Eleverne er generelt gode til at dokumentere deres svar med uddybende tekst. De har i højere grad end tidligere år anvendt IT-programmer som støtte til graftegning...og med held. De fleste vælger de rigtige metoder og gennemfører beregninger uden at der er mange fejl En del elever skriver de nødvendige formler. Funktionsundersøgelser af polynomier (6A) var relativt god Grundig argumentation for valg af metode i f.eks. opg. 3 med hjælpemidler Om typiske fejl eller mangler: Eleverne kan ikke ræsonnere logisk.. For lidt argumentation for opstilling af ligninger f.eks. for ellipsens sammentrækning for voksende t, eller i opg. 1 del 1. Generelt for lidt tekst og for mange regnestykker. For lidt brug af figurer og metodeforklaring Hvor mange er gode til at finde svaret på opgaverne, så er eleverne meget dårlige til at forklare den metode de har brugt. Alt for mange fokuserer for ensidigt på at finde svaret og ikke på at forklare vejen hen til svaret og tolkningen af det matematiske svar. En del elever får resultater, som en åbenbaring. Det er sandsynligvis på baggrund af lommeregner. Eleverne er (stadig) for dårlige til at skrive forklaringer og kommentarer. Der er også problemer med at gennemskue, hvilke typer forklaringer/kommentarer/dokumentation de enkelte opgavetyper kræver. Der mangler præcision visse steder (fx mangler grundmængder til ligninger, definitioner af variable mm.) i den typiske besvarelse. Censorernes oplevelser er tydeligvis meget forskellige, idet mange af de positive sider ved besvarelserne samtidig optræder med modsat fortegn under typiske fejl og mangler! Kommentarerne tyder på, at der skal arbejdes med elevens brug af ræsonnement og matematisk argumentation. Samtidig skal der fokuseres meget mere på dokumentation, dvs. brug at forklarende tekst, tegning af hjælpeskitser samt vurdering/tolkning af resultater. Om elevernes brug af IT-værktøjer: Ingen dokumentation for f.eks. brug af CAS-værktøjer. Men det bruges kan man se, specielt i opgave 3. 9/16
10 Elevernes brug af it / grafiske lommeregnere er ikke særlig udbredt. Mange elever bruger ikke it som et hjælpemiddel Jeg er ikke stødt på elever, der anvender CAS-værktøjer. Elevernes anvendelse af it er hovedsaglig begrænset til skrivning og præsentation. Kun få elever har anvendt it (ud over lommeregneren). Eleverne er alt for dårlige til at "erstatte" gammeldags mellemregninger med forklaringer på, hvorledes it (inkl. lommeregner) anvendes. Det er meget uheldigt, hvis eleverne besvarer opgaven vha. word eller lig. it-værktøj. De får ikke alle mellemregninger med og det koster dem points. Det må anbefales, at man besvarer matematikopgaven med kuglepen eller blyant. Det er tydeligt at brugen af hjælpemidler ikke er slået igennem på hhx endnu. Til forskel for de øvrige gymnasiale uddannelser er de bekendtgørelsesmæssige krav også mindre på hhx. Det er naturligt, at man som lærer er tilbageholdende med at anbefale eleverne at benytte it ved prøven, så længe der ikke hersker nogen form for konsensus på området. Det er derfor vigtigt, at få denne diskussion i gang. Den sidste censorkommentar passer dårligt med ovenstående. Min egen erfaring er, at mange elever skriver både hurtigere og bedre dokumentation på computeren, men det kræver naturligvis træning. Kommentarer om opgavesættet: Generelt har sættet med hjælpemidler været for kort. Alle opgaverne kunne jo sagtens have forekommet i et gammelt mata, hvor der havde været 4 timer til opgaver svarende til 100%, men nu har de 4 timer til 80% (opgaver af samme sværhedsgrad). Det ser ud til, at der er blevet mere tid til opgaverne, uden at man for alvor har ændret på opgavernes indhold. Eleverne har kunnet regne sættet igennem 2 gange. Uden hjælpemidler: Opgave 3: Voldsomt meget for eleven både at skulle tænke på nulregel, løsning af ligning og ligningens grundmængde. Og så kun til 2 point. Med hjælpemiddel:opgave 1: spm. b) Det virker ikke som om at eleverne forstår hvad opgavestilleren har ment med "den praktiske betydning". Jeg synes generelt at sættet har været for let og for kort. Omvendt indeholder de fleste opgaver en finte, der gør at man enten kan løse opgaven eller ikke. Dvs. man kan miste alt eller intet (f.eks. 3.b.). Jeg savner generelt noget om modeller dvs. en opgave med noget potens/eksponentiel vækst eller noget, hvor man skal differentiere sammensatte funktioner m.v. eller noget hvor man skal integrere andet end sumfunktioner. Opgavesættet er meget lidt regnetungt. Det kræver ikke ret mange udregninger i betragtning af at det er en 5-timers prøve. Ellers er der en god vægt mellem de 3 års kernestof fra alle 3 år. Lidt problematisk med åbne opgaver, hvis eleverne tror, at der kun findes ét rigtigt svar med 2 streger under. Opgaven kunne måske signalere, om det var det ene eller det andet? Burde starte med de opgaver, der ligger lige til højrebenet og slutte med de mere komplicerede opgaver - og afpasse points hertil, således at en let opgave giver få points og en svær flere points Et par kommentarer handler om selve vurderingen og karakterfastsættelsen: Jeg synes det ville være en god ide at få en diskussion af vurdering af elevbesvarelser i relation til den vejledning, der er udsendt i år. Hvis vi skal vurdere, om eleverne demonstrerer flest mulige kompetencer i hver opgave, så er vi nødt til at vægte det i højere grad i pointfordelingen, således det ikke kun får indflydelse i helhedsvurderingen. Det vil kræve et stort benarbejde, at indføre vurdering af den enkelte 10/16
11 opgave i forhold til kompetencer, og få det implementeret hos alle matematiklærere. Ja, ingen tvivl om at det kommer til at tage tid at få implementeret kompetencetænkningen i såvel undervisning som ved bedømmelsen. Ved årets censormøde blev det pointeret at opnåelsen af kompetencer (~ opfyldelsen af de faglige mål) indgik i pointgivningen af den enkelte opgave. Derudover indgik elevens evne til at vise opnåelse af samtlige kompetencer i helhedsvurderingen. Det er altså muligt (men nok højst usandsynligt!) at få maximalt pointtal, uden at opnå karakteren 12, nemlig hvis man konsekvent viger uden om en eller flere kompetencer til fordel for andre kompetencer, der til gengæld er opnået fuldt ud. Dette er en ny måde at bedømme på, som man skal vænne sig til. Omsætningstabellen overraskede, idet karakteren 0 gik fra points. Der er MEGET stor forskel på en ogpave med 12 % korrekt og 44 %. Jeg er klar over, der er tale om en helhedsbetragtning, men... Det er trist for en elev, der ikke har afsluttet C eller B at dumpe på A-niveau. Jeg er ked af at dumpe en elev, der har 2/5 korrekt! Jeg er klar over, den nye karakterskala lægger op til denne bedømmelse men det tager nok lidt tid at vænne sig til! Her skal det bemærkes at bekendtgørelsen åbner mulighed for, at en elev, der ikke består et fag på B- eller A-niveau kan bede skolelederen om at få godskrevet faget på et lavere niveau: 113 Stk. 4. En elev, der har afsluttet et fag på B- eller A-niveau med en karakter i faget under bestågrænsen kan, hvis skolens leder på baggrund af tidligere givne standpunktskarakterer finder grundlag herfor, på anmodning få udleveret attestation for, at faget er afsluttet og bestået på et lavere niveau B-niveau Censorerne blev bedt om at svare på nedenstående spørgsmål. 22 censorer ud af 64 har svaret. Tallene viser den samlede vurdering. Delprøven uden hjælpemidler: Hvordan vurderer du det faglige niveau for højt 10 passende 10 for lavt 2 Hvordan vurderer du opgavens omfang for stort 5 passende 17 for lille 0 Hvordan vurderer du læseligheden (formuleringer, billeder, grafer) fin 1 ok 15 ringe 6 Delprøven med hjælpemidler: Hvordan vurderer du det faglige niveau 11/16
12 for højt 12 passende 10 for lavt 0 Hvordan vurderer du opgavens omfang for stort 10 passende 12 for lille 0 Hvordan vurderer du læseligheden (formuleringer, billeder, grafer) fin 0 ok 14 ringe 8 Hvordan vurderer du alsidigheden (dele af kernestoffet, der berøres) fin 2 ok 19 ringe 1 Angiv din helhedsvurdering af sættet fin 2 ok 7 ringe 13 Tilfredsheden med B-sættet er markant mindre end med A-sættet, og der var da også en del problemer med dette opgavesæt. Nogle af problemerne skyldes indførelse af nye opgavetyper, primært de mere åbne opgaver, og dette diskuteres nedenfor. Hvor censorerne deler sig i to lige store grupper, når det handler om opgavernes sværhedsgrad og omfang ( for højt/stort og passende ) er der langt større enighed om, at det ikke var noget særlig godt sæt. Her synes jeg nu, at de problemer, der var med et par af opgaverne, er kommet til at fylde for meget i censorernes bevidsthed. Sættet indeholdt mange fine opgaver, og kunne på mange måder langt bedre teste fagets mål end tidligere opgavesæt. netop derfor var sættet også anderledes, og måske derfor gik det ikke godt. I forbindelse med gymnasiereformen er de faglige mål, der skal bedømmes ved prøven, blevet beskrevet vha. de 8 matematiske kernekompetencer. Censorerne har derfor skulle vurdere i hvor høj grad eleverne har opnået disse kompetencer, og derfor blev censorerne bedt om at vurdere hvorvidt det gennem besvarelsen af årets prøve var muligt for eleverne at vise, de havde opnået disse kompetencer. God Rimelig Ringe Tankegang Ræsonnement Problembehandling Modellering Repræsentation Symbol- og formalisme Hjælpemiddel Kommunikation /16
13 I sættet med hjælpemidler var især opgave 5 og 6 problematiske. Som en censor kommenterer: Opgave 5 med hjælpemidler burde ikke kunne forekomme i et gennemtænkt eksamenssæt for en gymnasial uddannelse. Opgave 6 med hjælpemidler er meningsløs, idet der formentlig kun er ganske få elever (og lærere) som kan gennemskue, at der enten ikke er nogen løsning eller, at det er den effektive rente, som afgør, hvilket lån, der skal foretrækkes. Censorerne var blevet informeret om, hvordan de skulle forholde sig til opgaverne, men dette ændrer ikke ved, at det var yderst uheldigt at opgaverne var formuleret som tilfældet var. Dog ser det ud til at problemerne har været større for lærere end for elever. Ved begge opgaver findes (mindst) 2 løsninger, der begge kunne give fuldt point. Opgave 5 Tanken med opgaven var, at eleven benyttede den omskrevne cirkel til at finde lysestagens diameter. Denne fremgangsmåde gav derfor fuldt point, såfremt besvarelsen er veldokumenteret. Imidlertid får man på denne måde ikke den mindste diameter for en cirkel, der kan dække trekanten. Vælger man nemlig midtpunktet på trekantens længste side, og med dette punkt som centrum tegner en cirkel med radius 4, vil denne cirkel naturligvis gå gennem de to af trekantens hjørner, og langt uden om det sidste. Man kan nemt beregne, at afstanden mellem centrum og dette hjørne er mindre end 4. En cirkel med diameter 8 kan altså dække hullet. Endvidere vil en diameter mindre end 8 ikke kunne bruges, da den største afstand mellem 2 hjørnepunkter er 8. Denne besvarelse skal naturligvis også give fuldt point også selv om den ikke er beregnet med 2 dec. som krævet i opgaveformuleringen. Opgave 6 Resultatet: er bilforhandleren eller banken billigst? afhænger af elevens antagelser om terminslig rentefod og antallet af rentetilskrivninger. Besvarelsen skulle derfor vurderes på baggrund af, hvilke antagelser der var gjort. Der vil blive gjort alt for at ovenstående problemer ikke forekommer igen. Endvidere vil opgavekommissionen ved udfærdigelse af kommende prøver været meget opmærksom på, at alle kompetencer er repræsenteret. Ser man på censorernes kommentarer i relation til kompetencevinklen, er det tydeligt at der også fra lærerside skal arbejdes meget mere med begrebet, som jo er essentielt i forhold til de faglige mål. En del kommentarer afspejler, at der stadig er mange lærere/censorer, der ikke er klar over indholdet af de forskellige kompetencer, og derfor må have meget svært ved at bedømme dem korrekt. Kommentarer til sættet Som eksamensresultaterne antyder, var der ikke mange positive bemærkninger at hente fra censorerne. Hvad der forekom som positivt for nogle, stod som negativt for andre, og det har ikke været muligt at finde nogle gennemgående positive svar. Om de positive sider: Langt de fleste elever er klar over, hvad der forlanges, selvom de jo ikke helt kommer i mål; dog er der nogle opgaver, hvor de på grund af formulering(?) ikke forstår at der kræves argumenter. Men overordnet benyttes virkemidlerne skift mellem tekst, beregning og illustration 13/16
14 Om typiske fejl eller mangler: Eleverne laver ikke meget dokumentation i opgaverne uden hjælpemidler, og giver op overfor mange af opgaverne. 14/16
15 Med hjælpemidler: O1 Mange elever laver forskrift for en lineær funktion. Mange elever giver bare op. O2 Mange elever opfatter C som retvinklet, og laver mange mærkelige ting. Den stumpe vinkel udregnes af mange elever til 55 grader. O3 Mange elever laver noget købmandsregning, og bruger ikke noget, der tilnærmelsesvis ligner LP. Ingen begrænsninger, niveaulinier og tegning. O4 Eleverne forstår generelt ikke opgaven, og får ikke hentet mange points. O5 Eleverne tegner lidt og skriver nogle tilfældige svar, ingen elever bruger den omskrevne cirkel. O6 Det er meget tilfældigt, hvad eleverne finder på. Mange elever beregner blot summen af alle ydelser. Eleverne kan slet ikke bruge deres rentesregning. Mange bruger Kn? O7A Mange elever scorer de billige points, men kan ikke opstille en forskrift. O7B Ikke ret mange elever bruger it til at tegne med, og skitserne er generelt ringe, og ofte er det f' der indtegnes i stedet for f. Nulreglen magter mange ikke. De ganger ind i parentes. Manglende forklaringer - eleverne er for resultatorienterede. Mange elever springer en opgave over uden overhovedet at forsøge at løse den - skrive noget op. En del afleverer noget, der ser forfærdeligt ud... Den kritiske sans er for lille! Overraskende mange kan ikke løse en dobbeltulighed - og meget få skriver løsningen op til sidst /(Finder fællesmængden). Eleverne viser blot, at det kan lade sig gøre at producere de angivne tøjstykker, i stedet for at løse opgaven som LP-problem. Argumenterer for lidt. Viser for lidt metode Eleverne kan ikke forstå spørgsmålene, og svarer ud fra vidt forskellige opfattelser af, hvad der spørges om Der er stadigt mange der springer mellemregninger over eller går direkte fra den formelle formel til facit eller kun henviser til grafregneren. Tegningen i opgave 3 var for manges vedkommende meget ringe som dokumentation, ligesom en tegning i opgave 4 sikkert ville have ryddet en del forkerte svar af vejen. Nogle af ovenstående kommentarer kunne også placeres nedenfor, idet de handler om brug af it. Det er tydeligt, at vi behøver en diskussion af krav til dokumentation, når der anvendes it. Herunder hører naturligvis også, hvad der ikke længere kræves. Det giver ingen mening, at eleverne benytter CAS til beregninger, hvis de stadig skal indføre detaljerede mellemregninger. Her står vi i lidt med et ben i hver lejr, idet nogle opgaver bliver alt for lette (meningsløse), hvis man ikke kræver at mellemregninger medtages. Det er derfor også formuleringen af opgaverne og det matematiske fokus, der ændrer karakter, når vi tillader brug af it. Om elevernes brug af IT-værktøjer: Meget lidt brug af it i opgaverne. Eleverne har ikke været gode til at dokumentere svar. Eleverne anvender stort set ikke IT-værktøjer - ud over tekstbehandling. Mange skitserer grafen fra graf-lommeregneren uden medfølgende forklaring. Ikke et interessant spørgsmål når vi både har graf-lommeregner og it-værktøjer. En del elever bruger grafprogram til grafer. Det er problematisk endnu med it, idet det kræver øvelse for eleverne at forklare hvordan de løser opgaven, når de anvender it. Mange undlader at forklare tankegang og mellemregninger - men kopierer bare en graf ind, som de evt. aflæser på. Brugen af it er ikke systematisk, og der er behov for diskussion og nogle retningslinjer. Som afgået fagkonsulent vil jeg nødig komme med konkrete krav, da den nye konsulent skal have mulighed for selv at lede vejen, men en retningsspil er, at eleverne skal vise, at de forstår og behersker den matematik, der 15/16
16 er i spil, og at de kan viderebringe deres viden i et præcist matematisk sprog og med korrekt matematisk notation. Når man holder sig dette for øje også set i relation til brugen af CAS-værktøjer er man godt på vej! Kommentarer om opgavesættet: Det er lidt ærgerligt, at man vælger at lægge nogle af de sværere opgaver i sættet uden hjælpemidler. Hvis man vil ramme de svage elever, så har man opnået, det man gerne ville. Umiddelbart ser opgavesættet fornuftigt ud, men efter at have set elevernes besvarelser er det tydeligt at opgavesættet er alt for svært for denne gruppe af elever. Opg. 7Bc Det er ikke helt oplagt, at eleverne skal tegne grafen, da de kun kender ekstrema og monotoniforhold. Forventes det at eleverne vil bestemme nulpukter? Det er fint med "åbne" opgaver - men 2 lige efter hinanden en i overkanten, når resten af sættet er formuleret på traditionel vis. Nogle af opgaverne er måske for åbne - eleverne er i hvert ikke helt klar over at de skal dokumentere. Det bør gå meget langsomt med indførslen af åbne opgaver og det må kunne introduceres eventuelt i form af vejledende opgaver eller opgavesæt og vurderingen af sådanne opgaver bør diskuteres. Ikke så heldigt at der blot bedes om statistiske betragtninger uden at konkretisere. Det betyder, nogle elver kan misbruge tiden og bruger alt for mange kræfter på en 5 points opgave. Fælles for rigtig mange kommentarer til sættet er irritation over formuleringer, der ikke er klare, og over de åbne opgaver, hvor eleverne selv skal reflektere over, hvad der vil være relevant at inddrage i svaret. Et eksempel er opgave 2 i prøven uden hjælpemidler, hvor eleverne skal beskrive et statistik materiale, hvor de konkrete deskriptorer ikke er nævnt. Dette er helt bevist idet, det er en kompetence, at kunne identificere, hvilke spørgsmål/opgaver det vil være relevant at stille sig i en given situation. Her skal eleven selv udvælge, hvilke deskriptorer, der bedst beskriver fordelingen. Man må indstille sig på, at der vil komme flere opgaver af denne type, og at opgaverne i det hele taget vil ændre karakter, for at give mulighed for at bedømme om eleverne har opnået de faglige mål. Giv kommentarer til årets opgavesæt Som nævnt i forordet er evalueringen baseret på censorernes gode og konstruktive kommentarer til opgavesættene. Opgavekommissionen er imidlertid også interesseret i tilbagemeldinger fra de øvrige matematiklærere og modtager derfor gerne kommentarer til eksamenssættene Kommentarer sendes til fagkonsulenten, Laila Madsen, Laila.Madsen@uvm.dk, der videregiver dem til opgavekommissionen. 16/16
TANKERNE BAG DE NYE VEJLEDENDE SÆT I MATEMATIK
 TANKERNE BAG DE NYE VEJLEDENDE SÆT I MATEMATIK De foreliggende vejledende sæt i matematik er gældende fra sommeren 2012 på matematik B og sommeren 2013 på matematik A. Der er en del ændringer i forhold
TANKERNE BAG DE NYE VEJLEDENDE SÆT I MATEMATIK De foreliggende vejledende sæt i matematik er gældende fra sommeren 2012 på matematik B og sommeren 2013 på matematik A. Der er en del ændringer i forhold
Evaluering. Matematik A på htx. Undervisningsministeriet Kvalitets- og Tilsynsstyrelsen Center for Prøver, Eksamen og Test September 2014
 Evaluering af Matematik A på htx Undervisningsministeriet Kvalitets- og Tilsynsstyrelsen Center for Prøver, Eksamen og Test September 2014 Indhold Censorernes vurdering af opgavesættene... 3 Forberedelsesmaterialet...
Evaluering af Matematik A på htx Undervisningsministeriet Kvalitets- og Tilsynsstyrelsen Center for Prøver, Eksamen og Test September 2014 Indhold Censorernes vurdering af opgavesættene... 3 Forberedelsesmaterialet...
Evaluering Matematik A på htx
 Evaluering af Matematik A på htx Sommeren 2011 1 Indholdsfortegnelse Forord... 3 Generelle bemærkninger... 4 Omsætningstabel... 6 Årets prøve i tal... 6 Vurdering af opgavesættet... 8 Forberedelsesmaterialet...
Evaluering af Matematik A på htx Sommeren 2011 1 Indholdsfortegnelse Forord... 3 Generelle bemærkninger... 4 Omsætningstabel... 6 Årets prøve i tal... 6 Vurdering af opgavesættet... 8 Forberedelsesmaterialet...
Kommentarer til matematik B-projektet 2015
 Kommentarer til matematik B-projektet 2015 Mandag d. 13/4 udleveres årets eksamensprojekt i matematik B. Dette brev er tænkt som en hjælp til vejledningsprocessen for de lærere, der har elever, som laver
Kommentarer til matematik B-projektet 2015 Mandag d. 13/4 udleveres årets eksamensprojekt i matematik B. Dette brev er tænkt som en hjælp til vejledningsprocessen for de lærere, der har elever, som laver
Vejledning til matematik A htx Maj 2018
 Vejledning til matematik A htx Maj 2018 Censorkorpset skriftlig matematik, htx Denne skrivelse skal tjene til almindelig orientering og vejledning for censorerne om forhold vedrørende skriftlig eksamen,
Vejledning til matematik A htx Maj 2018 Censorkorpset skriftlig matematik, htx Denne skrivelse skal tjene til almindelig orientering og vejledning for censorerne om forhold vedrørende skriftlig eksamen,
Evaluering Matematik på htx
 Evaluering af Matematik på htx Sommeren 2006 1 Indholdsfortegnelse Forord... 3 Eksamensresultaterne i tal... 4 Matematik B... 4 Matematik A (ordinær prøve)... 5 Matematik A (forsøgsprøve)... 6 Vurdering
Evaluering af Matematik på htx Sommeren 2006 1 Indholdsfortegnelse Forord... 3 Eksamensresultaterne i tal... 4 Matematik B... 4 Matematik A (ordinær prøve)... 5 Matematik A (forsøgsprøve)... 6 Vurdering
Eksaminanderne på hf tilvalg forventes ikke at kunne udnytte grafregnerens muligheder for regression.
 Bilag 3: Uddrag af Matematik 1999. Skriftlig eksamen og større skriftlig opgave ved studentereksamen og hf. Kommentarer på baggrund af censorernes tilbagemeldinger HF-tilvalgsfag (opgavesæt HF 99-8-1)
Bilag 3: Uddrag af Matematik 1999. Skriftlig eksamen og større skriftlig opgave ved studentereksamen og hf. Kommentarer på baggrund af censorernes tilbagemeldinger HF-tilvalgsfag (opgavesæt HF 99-8-1)
Evaluering. Matematik A HTX 2018
 Evaluering af Matematik A HTX 2018 Hermed en evaluering af den skriftlige prøve i matematik A ved HTX, sommeren 2018. Opgavesættet kan hentes på Materialeplatformen. Emnet for årets forberedelsesmateriale
Evaluering af Matematik A HTX 2018 Hermed en evaluering af den skriftlige prøve i matematik A ved HTX, sommeren 2018. Opgavesættet kan hentes på Materialeplatformen. Emnet for årets forberedelsesmateriale
Evaluering Matematik på htx
 Evaluering af Matematik på htx Sommeren 2010 1 Indholdsfortegnelse Forord... 3 Generelle bemærkninger... 4 Omsætningstabel... 6 Årets prøve i tal... 6 Vurdering af opgavesættet... 9 Forberedelsesmaterialet...
Evaluering af Matematik på htx Sommeren 2010 1 Indholdsfortegnelse Forord... 3 Generelle bemærkninger... 4 Omsætningstabel... 6 Årets prøve i tal... 6 Vurdering af opgavesættet... 9 Forberedelsesmaterialet...
Formativ brug af folkeskolens prøver. Den skriftlige prøve i matematik i 10. klasse, FP10, maj 2018
 Formativ brug af folkeskolens prøver Den skriftlige prøve i matematik i 10. klasse, FP10, maj 2018 1 Til matematiklæreren i 10. klasse Dette er en rapport om den skriftlige prøve i matematik maj 2018.
Formativ brug af folkeskolens prøver Den skriftlige prøve i matematik i 10. klasse, FP10, maj 2018 1 Til matematiklæreren i 10. klasse Dette er en rapport om den skriftlige prøve i matematik maj 2018.
Første del af rapporten består af et diagram, der viser, hvor mange point eleverne på landsplan fik i de enkelte opgaver.
 Til matematiklæreren Dette er en rapport omtaler prøven med hjælpemidler maj 2016. Rapporten kan bruges til at evaluere dit arbejde med klassen og få ideer til dit arbejde med kommende klasser i overbygningen.
Til matematiklæreren Dette er en rapport omtaler prøven med hjælpemidler maj 2016. Rapporten kan bruges til at evaluere dit arbejde med klassen og få ideer til dit arbejde med kommende klasser i overbygningen.
Formativ brug af folkeskolens prøver. Den skriftlige prøve i matematik med hjælpemidler, FP9 maj 2018
 Formativ brug af folkeskolens prøver Den skriftlige prøve i matematik med hjælpemidler, FP9 maj 2018 1 Til matematiklæreren i 9. klasse Dette er en rapport om den skriftlige prøve i matematik med hjælpemidler
Formativ brug af folkeskolens prøver Den skriftlige prøve i matematik med hjælpemidler, FP9 maj 2018 1 Til matematiklæreren i 9. klasse Dette er en rapport om den skriftlige prøve i matematik med hjælpemidler
Vedlagt følger en beskrivelse af proceduren ved skriftlig censur samt en vejledning i bedømmelse af besvarelserne.
 o Til censor Fagkonsulent Matematik, htx Vedr.: Skriftlig censur i matematik på htx Velkommen som skriftlig censor i matematik på htx. Marit Hvalsøe Schou Oehlenschlægersvej 55 5230 Odense M Tlf: 2565
o Til censor Fagkonsulent Matematik, htx Vedr.: Skriftlig censur i matematik på htx Velkommen som skriftlig censor i matematik på htx. Marit Hvalsøe Schou Oehlenschlægersvej 55 5230 Odense M Tlf: 2565
Opgavesættets tema er KRAM (Kost, Rygning, Alkohol og Motion).
 Sammendrag af censorrapporter for matematik D maj 2013 Opgavesættets tema er KRAM (Kost, Rygning, Alkohol og Motion). Opgave 1: Kost Opgaven inddrager de 4 regningsarter, brug af regneark, fremstilling
Sammendrag af censorrapporter for matematik D maj 2013 Opgavesættets tema er KRAM (Kost, Rygning, Alkohol og Motion). Opgave 1: Kost Opgaven inddrager de 4 regningsarter, brug af regneark, fremstilling
Formativ brug af folkeskolens prøver årets resultater på landsplan Den skriftlige prøve i matematik med hjælpemidler, FP9 maj 2019
 Formativ brug af folkeskolens prøver årets resultater på landsplan Den skriftlige prøve i matematik med hjælpemidler, FP9 maj 2019 Skrevet af Klaus Fink på baggrund af oplysninger fra opgavekommissionen
Formativ brug af folkeskolens prøver årets resultater på landsplan Den skriftlige prøve i matematik med hjælpemidler, FP9 maj 2019 Skrevet af Klaus Fink på baggrund af oplysninger fra opgavekommissionen
Evaluering Matematik A på htx
 Evaluering af Matematik A på htx Sommeren 2013 1 Indholdsfortegnelse Forord... 3 Generelle bemærkninger... 4 Omsætningstabel... 6 Årets prøve i tal... 6 Vurdering af opgavesættet... 9 Forberedelsesmaterialet...
Evaluering af Matematik A på htx Sommeren 2013 1 Indholdsfortegnelse Forord... 3 Generelle bemærkninger... 4 Omsætningstabel... 6 Årets prøve i tal... 6 Vurdering af opgavesættet... 9 Forberedelsesmaterialet...
Formativ brug af folkeskolens prøver årets resultater på landsplan Den skriftlige prøve i matematik FP10 maj 2019
 Formativ brug af folkeskolens prøver årets resultater på landsplan Den skriftlige prøve i matematik FP10 maj 2019 Skrevet af Klaus Fink på baggrund af oplysninger fra opgavekommissionen 1 Til matematiklæreren
Formativ brug af folkeskolens prøver årets resultater på landsplan Den skriftlige prøve i matematik FP10 maj 2019 Skrevet af Klaus Fink på baggrund af oplysninger fra opgavekommissionen 1 Til matematiklæreren
Vedr.: Skriftlig censur i matematik på htx Dato: 25/5 2011
 Til censor Fagkonsulent Matematik, htx Marit Hvalsøe Schou Oehlenschlægersvej 55 5230 Odense M Tlf: 2565 9207 E-mail: Marit.Schou@udst.dk Vedr.: Skriftlig censur i matematik på htx Dato: 25/5 2011 Velkommen
Til censor Fagkonsulent Matematik, htx Marit Hvalsøe Schou Oehlenschlægersvej 55 5230 Odense M Tlf: 2565 9207 E-mail: Marit.Schou@udst.dk Vedr.: Skriftlig censur i matematik på htx Dato: 25/5 2011 Velkommen
Vejledning til matematik A og B hhx Maj 2016
 Vejledning til matematik A og B hhx Maj 2016 Censorkorpset skriftlig matematik, hhx Denne skrivelse skal tjene til almindelig orientering og vejledning for censorerne om forhold vedrørende skriftlig eksamen,
Vejledning til matematik A og B hhx Maj 2016 Censorkorpset skriftlig matematik, hhx Denne skrivelse skal tjene til almindelig orientering og vejledning for censorerne om forhold vedrørende skriftlig eksamen,
Matematik B. Højere handelseksamen. Mandag den 15. december 2014 kl. 9.00-13.00. hhx143-mat/b-15122014
 Matematik B Højere handelseksamen hhx143-mat/b-15122014 Mandag den 15. december 2014 kl. 9.00-13.00 Matematik B Prøven består af to delprøver. Delprøven uden hjælpemidler består af opgave 1 til 5 med i
Matematik B Højere handelseksamen hhx143-mat/b-15122014 Mandag den 15. december 2014 kl. 9.00-13.00 Matematik B Prøven består af to delprøver. Delprøven uden hjælpemidler består af opgave 1 til 5 med i
Matematik B. Højere handelseksamen. 1. Delprøve, uden hjælpemidler kl Mandag den 15. august 2011 kl hhx112-mat/b
 Matematik B Højere handelseksamen 1. Delprøve, uden hjælpemidler kl. 9.00-10.00 hhx112-mat/b-15082011 Mandag den 15. august 2011 kl. 9.00-13.00 Matematik B Prøven uden hjælpemidler Prøvens varighed er
Matematik B Højere handelseksamen 1. Delprøve, uden hjælpemidler kl. 9.00-10.00 hhx112-mat/b-15082011 Mandag den 15. august 2011 kl. 9.00-13.00 Matematik B Prøven uden hjælpemidler Prøvens varighed er
Matematik B. Højere handelseksamen
 Matematik B Højere handelseksamen hh141-mat/b-23052014 Fredag den 23. maj 2014 kl. 9.00-13.00 Matematik B Prøven består af to delprøver. Delprøven uden hjælpemidler består af opgave 1 til 5 med i alt 5
Matematik B Højere handelseksamen hh141-mat/b-23052014 Fredag den 23. maj 2014 kl. 9.00-13.00 Matematik B Prøven består af to delprøver. Delprøven uden hjælpemidler består af opgave 1 til 5 med i alt 5
Matematik A. Højere handelseksamen. 1. Delprøve, uden hjælpemidler. kl. 9.00-14.00
 Matematik A Højere handelseksamen 1. Delprøve, uden hjælpemidler kl. 9.00-10.00 hh101-mat/a-27052010 Torsdag den 27. maj 2010 kl. 9.00-14.00 Matematik A Prøven uden hjælpemidler Prøvens varighed er 1 time.
Matematik A Højere handelseksamen 1. Delprøve, uden hjælpemidler kl. 9.00-10.00 hh101-mat/a-27052010 Torsdag den 27. maj 2010 kl. 9.00-14.00 Matematik A Prøven uden hjælpemidler Prøvens varighed er 1 time.
Matematik B. Højere handelseksamen. 1. Delprøve, uden hjælpemidler. Mandag den 20. december kl
 Matematik B Højere handelseksamen 1. Delprøve, uden hjælpemidler kl. 9.00-10.00 hhx103-mat/b-20122010 Mandag den 20. december 2010 kl. 9.00-13.00 Matematik B Prøven uden hjælpemidler Dette opgavesæt består
Matematik B Højere handelseksamen 1. Delprøve, uden hjælpemidler kl. 9.00-10.00 hhx103-mat/b-20122010 Mandag den 20. december 2010 kl. 9.00-13.00 Matematik B Prøven uden hjælpemidler Dette opgavesæt består
Bioteknologi Evaluering af skriftlig eksamen bioteknologi A htx og stx. Maj juni 2016
 Bioteknologi 216 Evaluering af skriftlig eksamen bioteknologi A htx og stx Maj juni 216 Ministeriet for Børn, Undervisning og Ligestilling Styrelsen for Undervisning og Kvalitet Juli 216 Hermed udsendes
Bioteknologi 216 Evaluering af skriftlig eksamen bioteknologi A htx og stx Maj juni 216 Ministeriet for Børn, Undervisning og Ligestilling Styrelsen for Undervisning og Kvalitet Juli 216 Hermed udsendes
Kemi 2015. Evaluering af skriftlig eksamen kemi A, htx Maj juni 2015
 Kemi 2015 Evaluering af skriftlig eksamen kemi A, htx Maj juni 2015 Ministeriet for Børn, Undervisning og Ligestilling Styrelsen for Undervisning og Kvalitet August 2015 Hermed udsendes evalueringsrapporten
Kemi 2015 Evaluering af skriftlig eksamen kemi A, htx Maj juni 2015 Ministeriet for Børn, Undervisning og Ligestilling Styrelsen for Undervisning og Kvalitet August 2015 Hermed udsendes evalueringsrapporten
Matematik A. Højere handelseksamen. 1. Delprøve, uden hjælpemidler. kl. 9.00-14.00
 Matematik A Højere handelseksamen 1. Delprøve, uden hjælpemidler kl. 9.00-10.00 hhx111-mat/a-305011 Mandag den 3. maj 011 kl. 9.00-14.00 Matematik A Prøven uden hjælpemidler Prøvens varighed er 1 time.
Matematik A Højere handelseksamen 1. Delprøve, uden hjælpemidler kl. 9.00-10.00 hhx111-mat/a-305011 Mandag den 3. maj 011 kl. 9.00-14.00 Matematik A Prøven uden hjælpemidler Prøvens varighed er 1 time.
Matematik B. Højere forberedelseseksamen
 Matematik B Højere forberedelseseksamen hfe102-mat/b-31082010 Tirsdag den 31. august 2010 kl. 9.00-13.00 Opgavesættet er delt i to dele. Delprøven uden hjælpemidler består af opgave 1-6 med i alt 6 spørgsmål.
Matematik B Højere forberedelseseksamen hfe102-mat/b-31082010 Tirsdag den 31. august 2010 kl. 9.00-13.00 Opgavesættet er delt i to dele. Delprøven uden hjælpemidler består af opgave 1-6 med i alt 6 spørgsmål.
Matematik B. Studentereksamen
 Matematik B Studentereksamen 2stx111-MAT/B-24052011 Tirsdag den 24. maj 2011 kl. 9.00-13.00 Opgavesættet er delt i to dele. Delprøven uden hjælpemidler består af opgave 1-6 med i alt 6 spørgsmål. Delprøven
Matematik B Studentereksamen 2stx111-MAT/B-24052011 Tirsdag den 24. maj 2011 kl. 9.00-13.00 Opgavesættet er delt i to dele. Delprøven uden hjælpemidler består af opgave 1-6 med i alt 6 spørgsmål. Delprøven
Matematik A. Højere handelseksamen. 1. Delprøve, uden hjælpemidler. Mandag den 4. juni 2012. kl. 9.00-14.00
 Matematik A Højere handelseksamen 1. Delprøve, uden hjælpemidler kl. 9.00-10.00 hh121-mat/a-04062012 Mandag den 4. juni 2012 kl. 9.00-14.00 Matematik A Prøven uden hjælpemidler Prøvens varighed er 1 time.
Matematik A Højere handelseksamen 1. Delprøve, uden hjælpemidler kl. 9.00-10.00 hh121-mat/a-04062012 Mandag den 4. juni 2012 kl. 9.00-14.00 Matematik A Prøven uden hjælpemidler Prøvens varighed er 1 time.
Kemi Evaluering af skriftlig eksamen kemi A, htx Maj juni 2016
 Kemi 2016 Evaluering af skriftlig eksamen kemi A, htx Maj juni 2016 Ministeriet for Børn, Undervisning og Ligestilling Styrelsen for Undervisning og Kvalitet Juli 2016 Hermed udsendes evalueringsrapporten
Kemi 2016 Evaluering af skriftlig eksamen kemi A, htx Maj juni 2016 Ministeriet for Børn, Undervisning og Ligestilling Styrelsen for Undervisning og Kvalitet Juli 2016 Hermed udsendes evalueringsrapporten
GUX. Matematik. B-Niveau. Torsdag 25. august Kl Prøveform b GUX162 - MAB
 GUX Matematik B-Niveau Torsdag 25. august 2016 Kl. 9.00-13.00 Prøveform b GUX162 - MAB 1 Matematik B Prøvens varighed er 4 timer. Delprøven uden hjælpemidler består af opgaverne 1 til 6 med i alt 6 spørgsmål.
GUX Matematik B-Niveau Torsdag 25. august 2016 Kl. 9.00-13.00 Prøveform b GUX162 - MAB 1 Matematik B Prøvens varighed er 4 timer. Delprøven uden hjælpemidler består af opgaverne 1 til 6 med i alt 6 spørgsmål.
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin maj-juni 2017 Institution Uddannelse Fag og niveau Lærer(e) Hold Skanderborg-Odder Handelsskole Højvangens
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin maj-juni 2017 Institution Uddannelse Fag og niveau Lærer(e) Hold Skanderborg-Odder Handelsskole Højvangens
Matematik B. Højere handelseksamen. Mandag den 16. december 2013 kl hhx133-mat/b
 Matematik B Højere handelseksamen hhx133-mat/b-161013 Mandag den 16. december 013 kl. 9.00-13.00 Matematik B Prøven består af to delprøver. Delprøven uden hjælpemidler består af opgave 1 til 5 med i alt
Matematik B Højere handelseksamen hhx133-mat/b-161013 Mandag den 16. december 013 kl. 9.00-13.00 Matematik B Prøven består af to delprøver. Delprøven uden hjælpemidler består af opgave 1 til 5 med i alt
Nye eksamensformer - mulige scenarier
 Nye eksamensformer - mulige scenarier Matematik på hf Marts 2015 Bodil Bruun, fagkonsulent i matematik stx/hf Nye eksamensformer?? Problemer, der skal løses: Internet er et vilkår mundtligt og skriftligt
Nye eksamensformer - mulige scenarier Matematik på hf Marts 2015 Bodil Bruun, fagkonsulent i matematik stx/hf Nye eksamensformer?? Problemer, der skal løses: Internet er et vilkår mundtligt og skriftligt
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Maj-juni 10/11 Institution Frederikshavn Handelsskole Uddannelse Fag og niveau Lærer(e) Hold HHX Matematik
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Maj-juni 10/11 Institution Frederikshavn Handelsskole Uddannelse Fag og niveau Lærer(e) Hold HHX Matematik
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Maj-juni 10/11 Institution Frederikshavn Handelsskole Uddannelse Fag og niveau Lærer(e) Hold HHX Matematik
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Maj-juni 10/11 Institution Frederikshavn Handelsskole Uddannelse Fag og niveau Lærer(e) Hold HHX Matematik
GUX. Matematik. B-Niveau. August 2015. Kl. 9.00-13.00. Prøveform b GUX152 - MAB
 GUX Matematik B-Niveau August 2015 Kl. 9.00-13.00 Prøveform b GUX152 - MAB 1 Matematik B Prøvens varighed er 4 timer. Delprøven uden hjælpemidler består af opgaverne 1 til 6 med i alt 6 spørgsmål. Besvarelsen
GUX Matematik B-Niveau August 2015 Kl. 9.00-13.00 Prøveform b GUX152 - MAB 1 Matematik B Prøvens varighed er 4 timer. Delprøven uden hjælpemidler består af opgaverne 1 til 6 med i alt 6 spørgsmål. Besvarelsen
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin maj-juni 2018 Institution Uddannelse Fag og niveau Lærer(e) Hold Skanderborg-Odder Handelsskole Højvangens
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin maj-juni 2018 Institution Uddannelse Fag og niveau Lærer(e) Hold Skanderborg-Odder Handelsskole Højvangens
Bioteknologi Evaluering af skriftlig eksamen bioteknologi A htx og stx. Maj juni 2017
 Bioteknologi 217 Evaluering af skriftlig eksamen bioteknologi A htx og stx Maj juni 217 Undervisningsministeriet Styrelsen for Undervisning og Kvalitet Juni 217 Evalueringsrapport Bioteknologi A skriftlig
Bioteknologi 217 Evaluering af skriftlig eksamen bioteknologi A htx og stx Maj juni 217 Undervisningsministeriet Styrelsen for Undervisning og Kvalitet Juni 217 Evalueringsrapport Bioteknologi A skriftlig
Matematik B. Højere handelseksamen
 Matematik B Højere handelseksamen hh11-mat/b-70501 Mandag den 7. maj 01 kl. 9.00-1.00 Matematik B Prøven består af to delprøver. Delprøven uden hjælpemidler består af opgave 1 til 5 med i alt 5 spørgsmål.
Matematik B Højere handelseksamen hh11-mat/b-70501 Mandag den 7. maj 01 kl. 9.00-1.00 Matematik B Prøven består af to delprøver. Delprøven uden hjælpemidler består af opgave 1 til 5 med i alt 5 spørgsmål.
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Juni, 10/11 Institution Grenaa Handelsskole Uddannelse Fag og niveau Lærer(e) Hold hhx Matematik B Hasse Rasmussen
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Juni, 10/11 Institution Grenaa Handelsskole Uddannelse Fag og niveau Lærer(e) Hold hhx Matematik B Hasse Rasmussen
MATEMATIK B. Xxxxdag den xx. måned åååå. Kl. 10.00 15.00 GL083-MAB. GU HHX DECEMBER 2008 Vejledende opgavesæt. Undervisningsministeriet
 GU HHX DECEMBER 2008 Vejledende opgavesæt MATEMATIK B Xxxxdag den xx. måned åååå Kl. 10.00 15.00 Undervisningsministeriet GL083-MAB 574604_GL083-MAB_12s.indd 1 14/01/09 14:40:30 Matematik B Prøvens varighed
GU HHX DECEMBER 2008 Vejledende opgavesæt MATEMATIK B Xxxxdag den xx. måned åååå Kl. 10.00 15.00 Undervisningsministeriet GL083-MAB 574604_GL083-MAB_12s.indd 1 14/01/09 14:40:30 Matematik B Prøvens varighed
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Institution Uddannelse Fag og niveau Lærer(e) Hold Termin hvori undervisningen afsluttes: Maj-juni, 11. Denne
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Institution Uddannelse Fag og niveau Lærer(e) Hold Termin hvori undervisningen afsluttes: Maj-juni, 11. Denne
TERMINSPRØVE APRIL 2018 MATEMATIK. Kl
 TERMINSPRØVE APRIL 2018 1p MATEMATIK tirsdag den 10. april 2018 Kl. 09.00 12.00 Opgavesættet er delt i to dele: Delprøve 1: 1 time kun med den centralt udmeldte formelsamling. Delprøve 2: 2 timer med alle
TERMINSPRØVE APRIL 2018 1p MATEMATIK tirsdag den 10. april 2018 Kl. 09.00 12.00 Opgavesættet er delt i to dele: Delprøve 1: 1 time kun med den centralt udmeldte formelsamling. Delprøve 2: 2 timer med alle
Matematik A. Højere handelseksamen. 1. Delprøve, uden hjælpemidler. Mandag den 15. august 2011 kl. 9.00-14.00. kl. 9.00-10.00. hhx112-mat/a-15082011
 Matematik A Højere handelseksamen 1. Delprøve, uden hjælpemidler kl. 9.00-10.00 hhx11-mat/a-1508011 Mandag den 15. august 011 kl. 9.00-14.00 Matematik A Prøven uden hjælpemidler Prøvens varighed er 1 time.
Matematik A Højere handelseksamen 1. Delprøve, uden hjælpemidler kl. 9.00-10.00 hhx11-mat/a-1508011 Mandag den 15. august 011 kl. 9.00-14.00 Matematik A Prøven uden hjælpemidler Prøvens varighed er 1 time.
GUX Matematik Niveau B prøveform b Vejledende sæt 1
 GUX-013 Matematik Niveau B prøveform b Vejledende sæt 1 Matematik B Prøvens varighed er 4 timer. Delprøven uden hjælpemidler består af opgaverne 1 til 6 med i alt 6 spørgsmål. Besvarelsen af denne delprøve
GUX-013 Matematik Niveau B prøveform b Vejledende sæt 1 Matematik B Prøvens varighed er 4 timer. Delprøven uden hjælpemidler består af opgaverne 1 til 6 med i alt 6 spørgsmål. Besvarelsen af denne delprøve
Højere Handelseksamen Handelsskolernes enkeltfagsprøve August 2008. Matematik Niveau A. Delprøven uden hjælpemidler
 Højere Handelseksamen Handelsskolernes enkeltfagsprøve August 2008 HHX082-MAA Matematik Niveau A Delprøven uden hjælpemidler Dette opgavesæt består af 6 opgaver, der indgår i bedømmelsen af den samlede
Højere Handelseksamen Handelsskolernes enkeltfagsprøve August 2008 HHX082-MAA Matematik Niveau A Delprøven uden hjælpemidler Dette opgavesæt består af 6 opgaver, der indgår i bedømmelsen af den samlede
gl. Matematik A Studentereksamen Torsdag den 22. maj 2014 kl gl-1stx141-mat/a
 gl. Matematik A Studentereksamen gl-1st141-mat/a-05014 Torsdag den. maj 014 kl. 9.00-14.00 Opgavesættet er delt i to dele. Delprøven uden hjælpemidler består af opgave 1-6 med i alt 6 spørgsmål. Delprøven
gl. Matematik A Studentereksamen gl-1st141-mat/a-05014 Torsdag den. maj 014 kl. 9.00-14.00 Opgavesættet er delt i to dele. Delprøven uden hjælpemidler består af opgave 1-6 med i alt 6 spørgsmål. Delprøven
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin aug-juni 11/12 Institution Campus Vejle Handelsgymnasie Uddannelse Fag og niveau Lærer(e) Hold HHX Matematik
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin aug-juni 11/12 Institution Campus Vejle Handelsgymnasie Uddannelse Fag og niveau Lærer(e) Hold HHX Matematik
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Institution Uddannelse Fag og niveau Lærer(e) Hold Termin hvori undervisningen afsluttes: Maj Juni 2011 Roskilde
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Institution Uddannelse Fag og niveau Lærer(e) Hold Termin hvori undervisningen afsluttes: Maj Juni 2011 Roskilde
Læreplansændringer & Nye eksamensformer mulige scenarier
 Læreplansændringer & Nye eksamensformer mulige scenarier Læreplansændringer? Nye kernestofemner? Færre? Flere? Specielt: Trigonometri og statistik hvordan? Eksamensopgaver? Programmering? Bindinger på
Læreplansændringer & Nye eksamensformer mulige scenarier Læreplansændringer? Nye kernestofemner? Færre? Flere? Specielt: Trigonometri og statistik hvordan? Eksamensopgaver? Programmering? Bindinger på
Kemi Evaluering af skriftlig eksamen kemi A, stx Maj juni 2016
 Kemi 2016 Evaluering af skriftlig eksamen kemi A, stx Maj juni 2016 Ministeriet for Børn, Undervisning og Ligestilling Styrelsen for Undervisning og Kvalitet Juli 2016 Hermed udsendes evalueringsrapporten
Kemi 2016 Evaluering af skriftlig eksamen kemi A, stx Maj juni 2016 Ministeriet for Børn, Undervisning og Ligestilling Styrelsen for Undervisning og Kvalitet Juli 2016 Hermed udsendes evalueringsrapporten
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin maj-juni 2017 Institution Uddannelse Fag og niveau Lærer(e) Hold Skanderborg-Odder Handelsskole Højvangens
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin maj-juni 2017 Institution Uddannelse Fag og niveau Lærer(e) Hold Skanderborg-Odder Handelsskole Højvangens
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin maj-juni 2015/2016 Institution Det Blå Gymnasium, hhx Tønder, Martin Hammerichsvej 2, 6270 Tønder. Uddannelse
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin maj-juni 2015/2016 Institution Det Blå Gymnasium, hhx Tønder, Martin Hammerichsvej 2, 6270 Tønder. Uddannelse
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin maj-juni 16/17 Institution Uddannelse Fag og niveau Lærer(e) Haderslev Handelsskole hhx Matematik B Mette
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin maj-juni 16/17 Institution Uddannelse Fag og niveau Lærer(e) Haderslev Handelsskole hhx Matematik B Mette
Kemi Evaluering af skriftlig eksamen kemi A, stx Maj juni Undervisningsministeriet Kvalitets- og Tilsynsstyrelsen
 Kemi 2014 Evaluering af skriftlig eksamen kemi A, stx Maj juni 2014 Undervisningsministeriet Kvalitets- og Tilsynsstyrelsen August 2014 Hermed udsendes evalueringsrapporten fra den skriftlige eksamen i
Kemi 2014 Evaluering af skriftlig eksamen kemi A, stx Maj juni 2014 Undervisningsministeriet Kvalitets- og Tilsynsstyrelsen August 2014 Hermed udsendes evalueringsrapporten fra den skriftlige eksamen i
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Institution Uddannelse Fag og niveau Lærer(e) Hold Termin hvori undervisningen afsluttes: Maj Juni 2011 Roskilde
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Institution Uddannelse Fag og niveau Lærer(e) Hold Termin hvori undervisningen afsluttes: Maj Juni 2011 Roskilde
Matematik B. Studentereksamen. Skriftlig prøve (4 timer)
 Matematik B Studentereksamen Skriftlig prøve (4 timer) STX093-MAB Fredag den 11. december 2009 kl. 9.00-13.00 Opgavesættet er delt i to dele. Delprøven uden hjælpemidler består af opgave 1-5 med i alt
Matematik B Studentereksamen Skriftlig prøve (4 timer) STX093-MAB Fredag den 11. december 2009 kl. 9.00-13.00 Opgavesættet er delt i to dele. Delprøven uden hjælpemidler består af opgave 1-5 med i alt
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin maj-juni 2019 Institution Uddannelse Fag og niveau Lærer(e) Hold Skanderborg-Odder Center for Uddannelse (SCU)
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin maj-juni 2019 Institution Uddannelse Fag og niveau Lærer(e) Hold Skanderborg-Odder Center for Uddannelse (SCU)
Grundfagsbekendtgørelsen Fagbilag juni 2004 MATEMATIK. Formål
 Grundfagsbekendtgørelsen Fagbilag juni 2004 MATEMATIK Formål Formålet med faget er, at eleverne bliver i stand til at identificere matematiske problemstillinger i både erhvervsfaglig og almen sammenhæng,
Grundfagsbekendtgørelsen Fagbilag juni 2004 MATEMATIK Formål Formålet med faget er, at eleverne bliver i stand til at identificere matematiske problemstillinger i både erhvervsfaglig og almen sammenhæng,
24. maj 2013. Kære censor i skriftlig fysik
 24. maj 2013 Kære censor i skriftlig fysik I år afvikles den første skriftlig prøve i fysik den 27. maj, mens den anden prøve først er placeret den 3. juni. Som censor vil du normalt kun få besvarelser
24. maj 2013 Kære censor i skriftlig fysik I år afvikles den første skriftlig prøve i fysik den 27. maj, mens den anden prøve først er placeret den 3. juni. Som censor vil du normalt kun få besvarelser
Matematik A. Højere handelseksamen. 1. Delprøve, uden hjælpemidler. Mandag den 19. december 2011. kl. 9.00-14.00
 Matematik A Højere handelseksamen 1. Delprøve, uden hjælpemidler kl. 9.00-10.00 hhx113-mat/a-19122011 Mandag den 19. december 2011 kl. 9.00-14.00 Matematik A Prøven uden hjælpemidler Prøvens varighed er
Matematik A Højere handelseksamen 1. Delprøve, uden hjælpemidler kl. 9.00-10.00 hhx113-mat/a-19122011 Mandag den 19. december 2011 kl. 9.00-14.00 Matematik A Prøven uden hjælpemidler Prøvens varighed er
Evaluering. Matematik A på htx
 Evaluering af Matematik A på htx Ministeriet for Børn, Undervisning og Ligestilling Styrelsen for Undervisning og Kvalitet Kontor for Prøver, Eksamen og Test August 201 Indhold Censorernes vurdering af
Evaluering af Matematik A på htx Ministeriet for Børn, Undervisning og Ligestilling Styrelsen for Undervisning og Kvalitet Kontor for Prøver, Eksamen og Test August 201 Indhold Censorernes vurdering af
Matematik A. Højere handelseksamen
 Matematik A Højere handelseksamen hhx131-mat/a-705013 Mandag den 7. maj 013 kl. 9.00-14.00 Matematik A Prøven består af to delprøver. Delprøven uden hjælpemidler består af opgave 1 til 5 med i alt 5 spørgsmål.
Matematik A Højere handelseksamen hhx131-mat/a-705013 Mandag den 7. maj 013 kl. 9.00-14.00 Matematik A Prøven består af to delprøver. Delprøven uden hjælpemidler består af opgave 1 til 5 med i alt 5 spørgsmål.
Bedømmelsesplan for Matematik C
 Bedømmelsesplan for Matematik C Matematik C Hovedområder: Fagretningen: Uddannelser i fagretningen indeholder: Varighed: Læringselementer: Læringsmiljø: Kontor handel og forretningsservice Detail, Handel,
Bedømmelsesplan for Matematik C Matematik C Hovedområder: Fagretningen: Uddannelser i fagretningen indeholder: Varighed: Læringselementer: Læringsmiljø: Kontor handel og forretningsservice Detail, Handel,
MATEMATIK A-NIVEAU 2g
 NETADGANGSFORSØGET I MATEMATIK APRIL 2009 MATEMATIK A-NIVEAU 2g Prøve April 2009 1. delprøve: 2 timer med formelsamling samt 2. delprøve: 3 timer med alle hjælpemidler Hver delprøve består af 14 spørgsmål,
NETADGANGSFORSØGET I MATEMATIK APRIL 2009 MATEMATIK A-NIVEAU 2g Prøve April 2009 1. delprøve: 2 timer med formelsamling samt 2. delprøve: 3 timer med alle hjælpemidler Hver delprøve består af 14 spørgsmål,
Højere Handelseksamen Handelsskolernes enkeltfagsprøve 2006. Typeopgave 2. Matematik Niveau B. Delprøven uden hjælpemidler. Prøvens varighed: 1 time.
 Højere Handelseksamen Handelsskolernes enkeltfagsprøve 2006 05-B-2-U Typeopgave 2 Matematik Niveau B Delprøven uden hjælpemidler Prøvens varighed: 1 time. Dette opgavesæt består af 5 opgaver, der indgår
Højere Handelseksamen Handelsskolernes enkeltfagsprøve 2006 05-B-2-U Typeopgave 2 Matematik Niveau B Delprøven uden hjælpemidler Prøvens varighed: 1 time. Dette opgavesæt består af 5 opgaver, der indgår
Anvendt litteratur : Mat C v. Bregendal, Nitschky Schmidt og Vestergård, Systime 2005
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin juni 2011 Institution Campus Bornholm Uddannelse Fag og niveau Lærer Hold Hhx Matematik C Peter Seide 1AB
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin juni 2011 Institution Campus Bornholm Uddannelse Fag og niveau Lærer Hold Hhx Matematik C Peter Seide 1AB
STUDENTEREKSAMEN MATHIT PRØVESÆT MAJ 2007 2010 MATEMATIK A-NIVEAU. MATHIT Prøvesæt 2010. Kl. 09.00 14.00 STXA-MATHIT
 STUDENTEREKSAMEN MATHIT PRØVESÆT MAJ 007 010 MATEMATIK A-NIVEAU MATHIT Prøvesæt 010 Kl. 09.00 14.00 STXA-MATHIT Opgavesættet er delt i to dele. Delprøve 1: timer med autoriseret formelsamling Delprøve
STUDENTEREKSAMEN MATHIT PRØVESÆT MAJ 007 010 MATEMATIK A-NIVEAU MATHIT Prøvesæt 010 Kl. 09.00 14.00 STXA-MATHIT Opgavesættet er delt i to dele. Delprøve 1: timer med autoriseret formelsamling Delprøve
Undersøgende opgaver Opgave 6 er i begge prøvesæt med som sidste opgave en undersøgende opgave af en ny type, som var lidt udfordrende for eleverne.
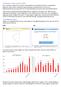 Tendenser i årets prøver 2019 Der er tendenser i prøverne, som kræver matematiklærernes opmærksomhed helst i et samarbejde i fagteamet. Og det kræver skolelederes og forvaltningers opmærksomhed for at
Tendenser i årets prøver 2019 Der er tendenser i prøverne, som kræver matematiklærernes opmærksomhed helst i et samarbejde i fagteamet. Og det kræver skolelederes og forvaltningers opmærksomhed for at
Kemi 2015. Evaluering af skriftlig eksamen kemi A, stx Maj juni 2015
 Kemi 2015 Evaluering af skriftlig eksamen kemi A, stx Maj juni 2015 Ministeriet for Børn, Undervisning og Ligestilling Styrelsen for Undervisning og Kvalitet August 2015 Hermed udsendes evalueringsrapporten
Kemi 2015 Evaluering af skriftlig eksamen kemi A, stx Maj juni 2015 Ministeriet for Børn, Undervisning og Ligestilling Styrelsen for Undervisning og Kvalitet August 2015 Hermed udsendes evalueringsrapporten
Eksamensopgaver i matematik
 Eksamensopgaver i matematik med TI-Nspire CAS ver. 2.0 Udarbejdet af: Brian M.V. Olesen Marts 2010 Indholdsfortegnelse Indledning...1 Bedømmelse af besvarelse...2 Eksempel 1 Lineære sammenhænge...3 Eksempel
Eksamensopgaver i matematik med TI-Nspire CAS ver. 2.0 Udarbejdet af: Brian M.V. Olesen Marts 2010 Indholdsfortegnelse Indledning...1 Bedømmelse af besvarelse...2 Eksempel 1 Lineære sammenhænge...3 Eksempel
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Institution Uddannelse Fag og niveau Lærer(e) Hold Termin hvori undervisningen afsluttes: Maj Juni 2012 Roskilde
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Institution Uddannelse Fag og niveau Lærer(e) Hold Termin hvori undervisningen afsluttes: Maj Juni 2012 Roskilde
Matematik B. Højere handelseksamen. Tirsdag den 26. maj 2015 kl hhx151-mat/b
 Matematik B Højere handelseksamen hhx151-mat/b-26052015 Tirsdag den 26. maj 2015 kl. 9.00-13.00 Matematik B Prøven består af to delprøver. Delprøven uden hjælpemidler består af opgave 1 til 5 med i alt
Matematik B Højere handelseksamen hhx151-mat/b-26052015 Tirsdag den 26. maj 2015 kl. 9.00-13.00 Matematik B Prøven består af to delprøver. Delprøven uden hjælpemidler består af opgave 1 til 5 med i alt
Kemi Evaluering af skriftlig eksamen kemi A, htx Maj juni Undervisningsministeriet Kvalitets- og Tilsynsstyrelsen
 Kemi 2014 Evaluering af skriftlig eksamen kemi A, htx Maj juni 2014 Undervisningsministeriet Kvalitets- og Tilsynsstyrelsen August 2014 Hermed udsendes evalueringsrapporten fra den skriftlige eksamen i
Kemi 2014 Evaluering af skriftlig eksamen kemi A, htx Maj juni 2014 Undervisningsministeriet Kvalitets- og Tilsynsstyrelsen August 2014 Hermed udsendes evalueringsrapporten fra den skriftlige eksamen i
Matematik B. Studentereksamen
 Matematik B Studentereksamen 1stx111-MAT/B-18052011 Onsdag den 18. maj 2011 kl. 9.00-13.00 Opgavesættet er delt i to dele. Delprøven uden hjælpemidler består af opgave 1-6 med i alt 6 spørgsmål. Delprøven
Matematik B Studentereksamen 1stx111-MAT/B-18052011 Onsdag den 18. maj 2011 kl. 9.00-13.00 Opgavesættet er delt i to dele. Delprøven uden hjælpemidler består af opgave 1-6 med i alt 6 spørgsmål. Delprøven
Kemi Evaluering af skriftlig eksamen kemi A, htx Maj juni Undervisningsministeriet Styrelsen for Undervisning og Kvalitet
 Kemi 219 Evaluering af skriftlig eksamen kemi A, htx Maj juni 219 Undervisningsministeriet Styrelsen for Undervisning og Kvalitet Juli 219 Hermed udsendes evalueringsrapporten fra den skriftlige eksamen
Kemi 219 Evaluering af skriftlig eksamen kemi A, htx Maj juni 219 Undervisningsministeriet Styrelsen for Undervisning og Kvalitet Juli 219 Hermed udsendes evalueringsrapporten fra den skriftlige eksamen
Fysik Råd og vink til den skriftlige prøve Fysik htx Maj 2017
 Fysik 2017 Råd og vink til den skriftlige prøve Fysik htx Maj 2017 Undervisningsministeriet Styrelsen for Undervisning og Kvalitet September 2017 Indhold 1. Indledende bemærkninger... 3 2. Censorernes
Fysik 2017 Råd og vink til den skriftlige prøve Fysik htx Maj 2017 Undervisningsministeriet Styrelsen for Undervisning og Kvalitet September 2017 Indhold 1. Indledende bemærkninger... 3 2. Censorernes
Vejledende karakterbeskrivelser for matematik
 Vejledende karakterbeskrivelser for matematik Folkeskolens Afgangsprøve efter 9. klasse Karakterbeskrivelse for matematiske færdigheder. Der prøves i tal og algebra geometriske begreber og fremgangsmåder
Vejledende karakterbeskrivelser for matematik Folkeskolens Afgangsprøve efter 9. klasse Karakterbeskrivelse for matematiske færdigheder. Der prøves i tal og algebra geometriske begreber og fremgangsmåder
Løsning til opgave 7, 9, 10 og 11C Matematik B Sommer 2014
 Vejledning til udvalgte opgave fra Matematik B, sommer 2014 Opgave 7 Størrelsen og udbudsprisen på 100 fritidshuse på Rømø er indsamlet via boligsiden.dk. a) Grafisk præsentation, der beskriver fordelingen
Vejledning til udvalgte opgave fra Matematik B, sommer 2014 Opgave 7 Størrelsen og udbudsprisen på 100 fritidshuse på Rømø er indsamlet via boligsiden.dk. a) Grafisk præsentation, der beskriver fordelingen
GU HHX MAJ 2009 MATEMATIK B. Onsdag den 13. maj 2009. Kl. 9.00 13.00 GL091-MAB. Undervisningsministeriet
 GU HHX MAJ 009 MATEMATIK B Onsdag den 13. maj 009 Kl. 9.00 13.00 Undervisningsministeriet GL091-MAB Matematik B Prøvens varighed er 4 timer. Alle hjælpemidler er tilladt. Af opgaverne 8A, 8B, 8C, 8D og
GU HHX MAJ 009 MATEMATIK B Onsdag den 13. maj 009 Kl. 9.00 13.00 Undervisningsministeriet GL091-MAB Matematik B Prøvens varighed er 4 timer. Alle hjælpemidler er tilladt. Af opgaverne 8A, 8B, 8C, 8D og
http://us.uvm.dk/gymnasie/almen/eksamen/opgaver/sommer04/vurderingsgrundlag-b-niveau2004-8- 2og2004-8-2-sf.pdf?menuid=150560
 http://us.uvm.dk/gymnasie/almen/eksamen/opgaver/sommer04/vurderingsgrundlag-b-niveau2004-8- 2og2004-8-2-sf.pdf?menuid=150560 Vurderingsgrundlag ved Skriftlig studentereksamen i matematik 2004. Det betyder
http://us.uvm.dk/gymnasie/almen/eksamen/opgaver/sommer04/vurderingsgrundlag-b-niveau2004-8- 2og2004-8-2-sf.pdf?menuid=150560 Vurderingsgrundlag ved Skriftlig studentereksamen i matematik 2004. Det betyder
Matematik B. Højere handelseksamen
 Matematik B Højere handelseksamen hh123-mat/b-17122012 Mandag den 17. december 2012 kl. 9.00-13.00 Prøven består af to delprøver. Delprøven uden hjælpemidler består af opgave 1 til 5 med i alt 5 spørgsmål.
Matematik B Højere handelseksamen hh123-mat/b-17122012 Mandag den 17. december 2012 kl. 9.00-13.00 Prøven består af to delprøver. Delprøven uden hjælpemidler består af opgave 1 til 5 med i alt 5 spørgsmål.
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Institution Uddannelse Fag og niveau Lærer Hold Termin hvori undervisningen afsluttes: Juni 2017 HANSENBERG
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Institution Uddannelse Fag og niveau Lærer Hold Termin hvori undervisningen afsluttes: Juni 2017 HANSENBERG
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin 2014/2015 Institution Tønder Handelsskole, Martin Hammerichsvej 2, DK - 6270 Tønder http://www.toha.dk, e-mail:
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin 2014/2015 Institution Tønder Handelsskole, Martin Hammerichsvej 2, DK - 6270 Tønder http://www.toha.dk, e-mail:
Bilag til konference om evaluering Grundforløb Kernestof Faglige mål Fokuspunkter Forslag til løbende evaluering
 Grundforløb Kernestof Faglige mål Fokuspunkter Forslag til løbende evaluering Regningsarternes hierarki At lære at lave lektier og afleveringer Ligningsløsning (lineære) med analytiske metoder og med itværktøjer
Grundforløb Kernestof Faglige mål Fokuspunkter Forslag til løbende evaluering Regningsarternes hierarki At lære at lave lektier og afleveringer Ligningsløsning (lineære) med analytiske metoder og med itværktøjer
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Maj-juni 10/12 Institution Frederikshavn Handelsskole Uddannelse Fag og niveau Lærer(e) Hold HHX Matematik
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Maj-juni 10/12 Institution Frederikshavn Handelsskole Uddannelse Fag og niveau Lærer(e) Hold HHX Matematik
Matematik A. Højere handelseksamen. Mandag den 15. december 2014 kl. 9.00-14.00. hhx143-mat/a-15122014
 Matematik A Højere handelseksamen hh143-mat/a-151014 Mandag den 15. december 014 kl. 9.00-14.00 Matematik A Prøven består af to delprøver. Delprøven uden hjælpemidler består af opgave 1 til 5 med i alt
Matematik A Højere handelseksamen hh143-mat/a-151014 Mandag den 15. december 014 kl. 9.00-14.00 Matematik A Prøven består af to delprøver. Delprøven uden hjælpemidler består af opgave 1 til 5 med i alt
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin aug-juni 13/14 Institution Campus Vejle Handelsgymnasie Uddannelse Fag og niveau Lærer(e) Hold HHX Matematik
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin aug-juni 13/14 Institution Campus Vejle Handelsgymnasie Uddannelse Fag og niveau Lærer(e) Hold HHX Matematik
Matematik A. Studentereksamen. Skriftlig prøve (5 timer) Fredag den. december kl... STX MAA LQGG
 Matematik A Studentereksamen Skriftlig prøve (5 timer) STX MAA 581710_STX093-MAA.indd 1 LQGG Fredag den. december kl... 03/11/09 10:53:00 Opgavesættet er delt i to dele. Delprøven uden hjælpemidler består
Matematik A Studentereksamen Skriftlig prøve (5 timer) STX MAA 581710_STX093-MAA.indd 1 LQGG Fredag den. december kl... 03/11/09 10:53:00 Opgavesættet er delt i to dele. Delprøven uden hjælpemidler består
Kemi Evaluering af skriftlig eksamen kemi A, htx Maj juni Undervisningsministeriet Styrelsen for Undervisning og Kvalitet
 Kemi 18 Evaluering af skriftlig eksamen kemi A, htx Maj juni 18 Undervisningsministeriet Styrelsen for Undervisning og Kvalitet Juli 18 Hermed udsendes evalueringsrapporten fra den skriftlige eksamen i
Kemi 18 Evaluering af skriftlig eksamen kemi A, htx Maj juni 18 Undervisningsministeriet Styrelsen for Undervisning og Kvalitet Juli 18 Hermed udsendes evalueringsrapporten fra den skriftlige eksamen i
Evaluering af skriftlig matematik B og A på hhx. Sommeren 2015
 Evaluering af skriftlig matematik B og A på hhx Sommeren 2015 1 Indholdsfortegnelse Forord... 3 Vejledning til censorerne... 4 Omsætningstabel... 5 Fordeling... 6 Censorernes vurdering af sættene... 7
Evaluering af skriftlig matematik B og A på hhx Sommeren 2015 1 Indholdsfortegnelse Forord... 3 Vejledning til censorerne... 4 Omsætningstabel... 5 Fordeling... 6 Censorernes vurdering af sættene... 7
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Institution Uddannelse Fag og niveau Lærer(e) Hold Termin hvori undervisningen afsluttes: Maj Juni 2014 Roskilde
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Institution Uddannelse Fag og niveau Lærer(e) Hold Termin hvori undervisningen afsluttes: Maj Juni 2014 Roskilde
Matematik B. Studentereksamen
 Matematik B Studentereksamen 2st101-MAT/B-01062010 Tirsdag den 1. juni 2010 kl. 9.00-13.00 Opgavesættet er delt i to dele. Delprøven uden hjælpemidler består af opgave 1-6 med i alt 6 spørgsmål. Delprøven
Matematik B Studentereksamen 2st101-MAT/B-01062010 Tirsdag den 1. juni 2010 kl. 9.00-13.00 Opgavesættet er delt i to dele. Delprøven uden hjælpemidler består af opgave 1-6 med i alt 6 spørgsmål. Delprøven
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin aug-juni 10/11 Institution Campus Vejle Handelsgymnasie Uddannelse Fag og niveau Lærer(e) Hold HHX Matematik
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin aug-juni 10/11 Institution Campus Vejle Handelsgymnasie Uddannelse Fag og niveau Lærer(e) Hold HHX Matematik
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Maj-juni 12/13 Institution Frederikshavn Handelsskole Uddannelse Fag og niveau Lærer(e) Hold HHX Matematik
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Maj-juni 12/13 Institution Frederikshavn Handelsskole Uddannelse Fag og niveau Lærer(e) Hold HHX Matematik
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Juni, 08/09 Institution Grenaa Handelsskole Uddannelse Fag og niveau Lærer(e) Hold hhx Matematik C Sanne Schyum
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Juni, 08/09 Institution Grenaa Handelsskole Uddannelse Fag og niveau Lærer(e) Hold hhx Matematik C Sanne Schyum
FRANSK BEGYNDERSPROG HØJT NIVEAU FORTSÆTTERSPROG TILVALGSFAG HØJERE FORBEREDELSESEKSAMEN AUGUST 2009 HØJERE FORBEREDELSESEKSAMEN AUGUST 2009
 STUDENTEREKSAMEN MAJ 2005 2005-11-2 SPROGLIG OG MATEMATISK LINJE HØJERE FORBEREDELSESEKSAMEN MAJ 2005 HØJERE FORBEREDELSESEKSAMEN AUGUST 2009 HØJERE FORBEREDELSESEKSAMEN AUGUST 2009 FRANSK BEGYNDERSPROG
STUDENTEREKSAMEN MAJ 2005 2005-11-2 SPROGLIG OG MATEMATISK LINJE HØJERE FORBEREDELSESEKSAMEN MAJ 2005 HØJERE FORBEREDELSESEKSAMEN AUGUST 2009 HØJERE FORBEREDELSESEKSAMEN AUGUST 2009 FRANSK BEGYNDERSPROG
