Mundtlig gruppeprøve. Odense 13. maj 2013
|
|
|
- Ludvig Jespersen
- 9 år siden
- Visninger:
Transkript
1 Mundtlig gruppeprøve Odense 13. maj 2013
2 Den store positive nyhed Aldrig før har så mange matematiklærere været på kursus som i til de generelle foredrag Mindst 1500 til workshops med fremstilling af prøveoplæg
3 De 8 matematiske kompetencer 2002 offentliggørelse her i Odense 2003 med i undervisningsvejledningen 2009 selve formålet med undervisningen 2013 Så prøver vi eleverne i deres besiddelse af matematisk kompetence
4 Muligheder - udfordringer Genopdage mundtligheden i matematikundervisningen - og nyde den positive effekt på elevernes læring og præstationer Hvordan bedømmer vi kompetencer problemstilling og åbenhed
5 Den svære problemstilling Åbne spørgsmål betyder ikke frit valg Problemstilling ikke opgaver Eleverne skal kunne arbejde undersøgende Eleverne skal have mulighed for at vise deres matematiske kompetence
6 Et eksempel: Tages kvadrat Den danske matematiker, Tage Werner, fandt på figuren, som ses herunder. Hvordan kan figuren konstrueres i et dynamisk geometriprogram? Tage Werner påstod bl.a., at de otte længste linjestykker i kvadratet er lige lange der er kongruente og ligedannede figurer i kvadratet, og at disse figurers arealer kan beregnes størrelsen på hver vinkel i kvadratets figurer kan findes ved at beregne. Problemstilling Jeres opgave er at undersøge Tage Werners tre påstande om kvadratet. I skal både bruge it-værktøjer, beregninger og matematiske forklaringer.
7 Standby sheet eller ideside Ideer: Konstruer Tages kvadrat ved hjælp af et it-værktøj. I kan fx lade sidelængden være 10. Beskriv, hvordan Tages kvadrat kan konstrueres. Undersøg længderne af de længste linjestykker i Tages kvadrat. Kan I finde resultaterne på flere forskellige måder? Har Tage Werner ret i påstand 1)? Kan I forklare hvorfor/ hvorfor ikke uden at måle? Læg mærke til nogle af figurerne, der gemmer sig i Tages kvadrat: Har disse figurer kongruente og/eller ligedannede makkere? Hvis ja: Hvordan kan I være sikre på, at figurerne er kongruente og/eller ligedannede? Find - på flere forskellige måder - arealet af nogle kongruente og/eller ligedannede figurer. Kan I bruge resultatet fra før til at beregne størrelsen af flere vinkler i Tages kvadrat?
8 Vurdering Vurdering af matematiske kompetencer og arbejdsmåder i prøvesituationen kan foregå på baggrund af følgende spørgsmål: Viser eleven sine matematiske kompetencer ved at handle på en indsigtsfuld måde i forbindelse med problemstillingen? Kan eleven benytte sin viden og sine færdigheder i forhold til problemstillingen? Arbejder eleven undersøgende og systematisk, viser eleven initiativ, indgår i dialog og samarbejder med sin gruppe Kan eleven kommunikere med og om matematik? [email protected] Mobil: Side 8
9 Bedømmelsen Matematiser e Færdigheder /Analyse Fortolkning At bringe det virkelige problem over i matematikkens verden Overvejer valg af: - målemetode - måleredskab - løsningsmuligheder At kunne behandle problemet i matematikkens verden Anvender formler til beregning Måler længde og tid (uden gps) Beregner Oversætter mellem enheder Af matematiske resultater til brug i den virkelige verden Evaluerer ideerne ift. kriterierne Vurderer om resultat er realistisk Sammenligner og forholder sig til resultater
10 Tekstopgivelse Undervisningsforløb, hvor der har været fokus på en matematisk kompetence fx problembehandlings-, modellerings- eller ræsonnementskompetencen. Projekter med rapportskrivning, præsentationer, film eller anden form for fremlæggelse. Kender eleverne kompetencerne som begreber eller kan de alene udøve dem? Anvendte it-værktøjer Arbejds- og organisationsformer.
11 Den daglige undervisning Projektorienteret Kompetencebaseret Med undersøgende arbejdsmåder Med andre skriftlige arbejder end opgaveløsning Med andre kommunikationsformer end skrift Med masser af mundtlighed
12 Hvad sker der til juni 160 tekstopgivelser gennemses 80 mundtlige censorer vil samle prøveoplæg sammen til evaluering Evaluering med gode råd kommer i PEU og andre skrifter Løbende vil der være hjælp at hente fx på SkoleKom
13 Fremtiden Glostrup: Ingen lærer må lades alene tilbage Brug dit fagteam En ny lærerkultur
14 Hvad sker der ellers Folkeskolereform Arbejdsgruppe for matematik 3 årigt udviklingsprojekt
Opgave 1 -Tages kvadrat
 Opgave 1 -Tages kvadrat Den danske matematiker, Tage Werner, fandt på figuren, som ses herunder. Figuren kan laves ved 1) at tegne et kvadrat, 2) markere midtpunkterne på kvadratets sider og 3) tegne linjestykker
Opgave 1 -Tages kvadrat Den danske matematiker, Tage Werner, fandt på figuren, som ses herunder. Figuren kan laves ved 1) at tegne et kvadrat, 2) markere midtpunkterne på kvadratets sider og 3) tegne linjestykker
Mundtlig gruppeprøve i matematik. 17-09-2012 [email protected] Mobil: 2041 0721 Side 1
 Mundtlig gruppeprøve i matematik 2012 [email protected] Mobil: 2041 0721 Side 1 Hvorfor en mundtlig prøve? Der er trinmål, vi ikke kan prøve eleverne i ved en skriftlig prøve Eller kun delvist kan prøve
Mundtlig gruppeprøve i matematik 2012 [email protected] Mobil: 2041 0721 Side 1 Hvorfor en mundtlig prøve? Der er trinmål, vi ikke kan prøve eleverne i ved en skriftlig prøve Eller kun delvist kan prøve
Mundtlig prøve i matematik
 Mundtlig prøve i matematik Onsdag d. 5. december 2012 CFU Sjælland Mari-Ann Skovlund & Mikael Scheby Hvorfor en mundtlig prøve? Der er trinmål, vi ikke kan prøve eleverne i ved en skriftlig prøve, eller
Mundtlig prøve i matematik Onsdag d. 5. december 2012 CFU Sjælland Mari-Ann Skovlund & Mikael Scheby Hvorfor en mundtlig prøve? Der er trinmål, vi ikke kan prøve eleverne i ved en skriftlig prøve, eller
UCC - Matematikdag - 08.04.14
 UCSJ Målstyret + 21 PD - UCC - 25.02.14 www.mikaelskaanstroem.dk Der var engang. Skovshoved Skole Hvad svarer du på elevspørgsmålet: Hvad skal jeg gøre for at få en højere karakter i mundtlig matematik?
UCSJ Målstyret + 21 PD - UCC - 25.02.14 www.mikaelskaanstroem.dk Der var engang. Skovshoved Skole Hvad svarer du på elevspørgsmålet: Hvad skal jeg gøre for at få en højere karakter i mundtlig matematik?
Undersøgelser af trekanter
 En rød tråd igennem kapitlet er en søgen efter svar på spørgsmålet: Hvordan kan vi beregne os frem til længder, vi ikke kan komme til at måle?. Hvordan kan vi fx beregne højden på et træ eller et hus,
En rød tråd igennem kapitlet er en søgen efter svar på spørgsmålet: Hvordan kan vi beregne os frem til længder, vi ikke kan komme til at måle?. Hvordan kan vi fx beregne højden på et træ eller et hus,
PRØV! mundtlig til undervisningen og prøvesituationen
 PRØV! mundtlig til undervisningen og prøvesituationen - Teoretisk grundlag for prøverne - Liste med links - Portalen: PRØV!Mundtlig matematik Niveau 1 vedrører viden om objekter, definitioner, tekniske
PRØV! mundtlig til undervisningen og prøvesituationen - Teoretisk grundlag for prøverne - Liste med links - Portalen: PRØV!Mundtlig matematik Niveau 1 vedrører viden om objekter, definitioner, tekniske
Odense, den 4. marts 2013 Heidi Kristiansen. 04-03-2013 Heidi Kristiansen - Folkeskolens afsluttende prøver i matematik
 Odense, den 4. marts 2013 Heidi Kristiansen Oplæg til mundtlig gruppeprøve, der gør det muligt at evaluere kompetencer hvordan??? indeholde tydelige problemstillinger rene eller anvendte matematiske problemer,
Odense, den 4. marts 2013 Heidi Kristiansen Oplæg til mundtlig gruppeprøve, der gør det muligt at evaluere kompetencer hvordan??? indeholde tydelige problemstillinger rene eller anvendte matematiske problemer,
Mundtlig matematik. - et udviklingsarbejde Startet på Skovshoved Skole fortsætter her. Ikke bare en proces, men i proces..
 Mundtlig matematik - et udviklingsarbejde Startet på Skovshoved Skole fortsætter her. Ikke bare en proces, men i proces.. Hjørring 7. sep. 2012 Line Engsig matematikvejleder på Skovshoved Skole og Mikael
Mundtlig matematik - et udviklingsarbejde Startet på Skovshoved Skole fortsætter her. Ikke bare en proces, men i proces.. Hjørring 7. sep. 2012 Line Engsig matematikvejleder på Skovshoved Skole og Mikael
Mundtlighed i matematikundervisningen
 Mundtlighed i matematikundervisningen 1 Mundtlighed Annette Lilholt Side 2 Udsagn! Det er nemt at give karakter i færdighedsregning. Mine elever får generelt højere standpunktskarakter i færdighedsregning
Mundtlighed i matematikundervisningen 1 Mundtlighed Annette Lilholt Side 2 Udsagn! Det er nemt at give karakter i færdighedsregning. Mine elever får generelt højere standpunktskarakter i færdighedsregning
Inspirationsforløb i faget matematik i 7.- 9. klasse. Trekanter et inspirationsforløb om geometri i 8. klasse
 Inspirationsforløb i faget matematik i 7.- 9. klasse Trekanter et inspirationsforløb om geometri i 8. klasse Indhold Indledning 2 Undervisningsforløbet 3 Mål for forløbet 3 Relationsmodellen 3 Planlægningsfasen
Inspirationsforløb i faget matematik i 7.- 9. klasse Trekanter et inspirationsforløb om geometri i 8. klasse Indhold Indledning 2 Undervisningsforløbet 3 Mål for forløbet 3 Relationsmodellen 3 Planlægningsfasen
Første del af rapporten består af et diagram, der viser, hvor mange point eleverne på landsplan fik i de enkelte opgaver.
 Til matematiklæreren Dette er en rapport omtaler prøven med hjælpemidler maj 2016. Rapporten kan bruges til at evaluere dit arbejde med klassen og få ideer til dit arbejde med kommende klasser i overbygningen.
Til matematiklæreren Dette er en rapport omtaler prøven med hjælpemidler maj 2016. Rapporten kan bruges til at evaluere dit arbejde med klassen og få ideer til dit arbejde med kommende klasser i overbygningen.
Den mundtlige prøve i matematik og forenklede Fælles Mål Odense 20. April 2015
 Den mundtlige prøve i matematik og forenklede Fælles Mål Odense 20. April 2015 153 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 + 13 + 14+ 15 + 16 + 17 153 = 1! + 2! + 3! + 4! + 5! 153 = 1 3 + 5
Den mundtlige prøve i matematik og forenklede Fælles Mål Odense 20. April 2015 153 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 + 13 + 14+ 15 + 16 + 17 153 = 1! + 2! + 3! + 4! + 5! 153 = 1 3 + 5
Kompetencetræning #2 også til prøven. 31. Januar 2019
 Kompetencetræning #2 også til prøven 31. Januar 2019 Bordet rundt Har I prøvet noget af? Var der nogle forhindringer i at prøve noget af? Hvis du har prøvet noget af hvor var udfordringerne så for dig
Kompetencetræning #2 også til prøven 31. Januar 2019 Bordet rundt Har I prøvet noget af? Var der nogle forhindringer i at prøve noget af? Hvis du har prøvet noget af hvor var udfordringerne så for dig
TRIGONOMETRI, 4 UGER, 9.KLASSE.
 TRIGONOMETRI, 4 UGER, 9.KLASSE. FRA FÆLLES MÅL Målsætninger for undervisningsforløbet er opsat efter kompetence, færdigheds og vidensmål samt læringsmål i lærersprog. Geometri og måling Fase 3 Geometriske
TRIGONOMETRI, 4 UGER, 9.KLASSE. FRA FÆLLES MÅL Målsætninger for undervisningsforløbet er opsat efter kompetence, færdigheds og vidensmål samt læringsmål i lærersprog. Geometri og måling Fase 3 Geometriske
Nye Fælles Mål og årsplanen. Thomas Kaas, Lektor og Kirsten Søs Spahn, pæd. konsulent
 Nye Fælles Mål og årsplanen Thomas Kaas, Lektor og Kirsten Søs Spahn, pæd. konsulent Interview Find en makker, som du ikke kender i forvejen Stil spørgsmål, så du kan fortælle os andre om vedkommende ift.:
Nye Fælles Mål og årsplanen Thomas Kaas, Lektor og Kirsten Søs Spahn, pæd. konsulent Interview Find en makker, som du ikke kender i forvejen Stil spørgsmål, så du kan fortælle os andre om vedkommende ift.:
Matematik. Evaluering, orientering og vejledning
 Folkeskolens afsluttende prøver Matematik 2011 Evaluering, orientering og vejledning Udarbejdet på grundlag af censorers faglige feedback ved prøverne Institut for Læring Udarbejdet af: Konsulent Erik
Folkeskolens afsluttende prøver Matematik 2011 Evaluering, orientering og vejledning Udarbejdet på grundlag af censorers faglige feedback ved prøverne Institut for Læring Udarbejdet af: Konsulent Erik
I kapitlet arbejdes med følgende centrale matematiske objekter og begreber:
 INTRO Efter mange års pause er trigonometri med Fælles Mål 2009 tilbage som fagligt emne i grundskolens matematikundervisning. Som det fremgår af den følgende sides udpluk fra faghæftets trinmål, er en
INTRO Efter mange års pause er trigonometri med Fælles Mål 2009 tilbage som fagligt emne i grundskolens matematikundervisning. Som det fremgår af den følgende sides udpluk fra faghæftets trinmål, er en
MaxiMat det digitale matematiksystem
 MaxiMat det digitale matematiksystem 0.-10. klasse 4. og 7. er udkommet 1., 5. og 8. klasse er klar til skolestart 2014 MaxiMat er et fleksibelt digitalt matematiksystem, der fuldt udbygget indeholder
MaxiMat det digitale matematiksystem 0.-10. klasse 4. og 7. er udkommet 1., 5. og 8. klasse er klar til skolestart 2014 MaxiMat er et fleksibelt digitalt matematiksystem, der fuldt udbygget indeholder
Hvad kan de nationale test?
 NYT Hvad kan de nationale test? 24-04-2017 [email protected] 2 http://uvm.dk/folkeskolen/elevplaner-nationale-test-og-trivselsmaaling/nationale-test/vejledninger 24-04-2017 [email protected]
NYT Hvad kan de nationale test? 24-04-2017 [email protected] 2 http://uvm.dk/folkeskolen/elevplaner-nationale-test-og-trivselsmaaling/nationale-test/vejledninger 24-04-2017 [email protected]
Formativ brug af folkeskolens prøver årets resultater på landsplan Den skriftlige prøve i matematik med hjælpemidler, FP9 maj 2019
 Formativ brug af folkeskolens prøver årets resultater på landsplan Den skriftlige prøve i matematik med hjælpemidler, FP9 maj 2019 Skrevet af Klaus Fink på baggrund af oplysninger fra opgavekommissionen
Formativ brug af folkeskolens prøver årets resultater på landsplan Den skriftlige prøve i matematik med hjælpemidler, FP9 maj 2019 Skrevet af Klaus Fink på baggrund af oplysninger fra opgavekommissionen
Vejledning til prøverne i faget matematik
 Vejledning til prøverne i faget matematik Kvalitets- og Tilsynsstyrelsen Center for Prøver, Eksamen og Test Marts 2014 Indhold Forord... 4 1. Indledning... 5 Prøvernes forskellige dele... 5 2. FSA... 9
Vejledning til prøverne i faget matematik Kvalitets- og Tilsynsstyrelsen Center for Prøver, Eksamen og Test Marts 2014 Indhold Forord... 4 1. Indledning... 5 Prøvernes forskellige dele... 5 2. FSA... 9
Emmas og Frederiks nye værelser - maling eller tapet?
 Emmas og Frederiks nye værelser - maling eller tapet? Emmas og Frederiks familie skal flytte til et nyt hus. De har fået lov til at bestemme, hvordan væggene på deres værelser skal se ud. Emma og Frederik
Emmas og Frederiks nye værelser - maling eller tapet? Emmas og Frederiks familie skal flytte til et nyt hus. De har fået lov til at bestemme, hvordan væggene på deres værelser skal se ud. Emma og Frederik
Fag- og indholdsplan 9. kl.:
 Fag- og indholdsplan 9. kl.: Indholdsområder: Tal og algebra: Tal - regneregler og formler Størrelser måling, beregning og sammenligning. Matematiske udtryk Algebra - teoretiske sammenhænge absolut og
Fag- og indholdsplan 9. kl.: Indholdsområder: Tal og algebra: Tal - regneregler og formler Størrelser måling, beregning og sammenligning. Matematiske udtryk Algebra - teoretiske sammenhænge absolut og
MaxiMat og de forenklede Fælles mål
 MaxiMat og de forenklede Fælles mål Dette er en oversigt over hvilke læringsmål de enkelte forløb indeholder. Ikke alle forløb er udarbejdet endnu, men i skemaet kan man se alle læringsmålene også de,
MaxiMat og de forenklede Fælles mål Dette er en oversigt over hvilke læringsmål de enkelte forløb indeholder. Ikke alle forløb er udarbejdet endnu, men i skemaet kan man se alle læringsmålene også de,
Formativ brug af folkeskolens prøver. Den skriftlige prøve i matematik med hjælpemidler, FP9 maj 2018
 Formativ brug af folkeskolens prøver Den skriftlige prøve i matematik med hjælpemidler, FP9 maj 2018 1 Til matematiklæreren i 9. klasse Dette er en rapport om den skriftlige prøve i matematik med hjælpemidler
Formativ brug af folkeskolens prøver Den skriftlige prøve i matematik med hjælpemidler, FP9 maj 2018 1 Til matematiklæreren i 9. klasse Dette er en rapport om den skriftlige prøve i matematik med hjælpemidler
Geometriske eksperimenter
 I kapitlet arbejder eleverne med nogle af de egenskaber, der er knyttet til centrale geometriske figurer og begreber (se listen her under). Set fra en emneorienteret synsvinkel handler kapitlet derfor
I kapitlet arbejder eleverne med nogle af de egenskaber, der er knyttet til centrale geometriske figurer og begreber (se listen her under). Set fra en emneorienteret synsvinkel handler kapitlet derfor
Matematiske kompetencer - hvad og hvorfor? DLF-Kursus Frederikshavn 24.-25.9 2015 Eva Rønn UCC
 Matematiske kompetencer - hvad og hvorfor? DLF-Kursus Frederikshavn 24.-25.9 2015 Eva Rønn UCC Komrapporten Kompetencer og matematiklæring. Ideer og inspiration til udvikling af matematikundervisningen
Matematiske kompetencer - hvad og hvorfor? DLF-Kursus Frederikshavn 24.-25.9 2015 Eva Rønn UCC Komrapporten Kompetencer og matematiklæring. Ideer og inspiration til udvikling af matematikundervisningen
Evaluering af kompetencer
 Evaluering af kompetencer Odense den 13. maj 2013 http://tinyurl.com/cca2glm Montaigne Man burde spørge hvem der ved rigtigst, ikke hvem der ved mest. KOMPIS http://tinyurl.com/d4m295w Målsætning og planlægning
Evaluering af kompetencer Odense den 13. maj 2013 http://tinyurl.com/cca2glm Montaigne Man burde spørge hvem der ved rigtigst, ikke hvem der ved mest. KOMPIS http://tinyurl.com/d4m295w Målsætning og planlægning
Formativ brug af folkeskolens prøver årets resultater på landsplan Den skriftlige prøve i matematik FP10 maj 2019
 Formativ brug af folkeskolens prøver årets resultater på landsplan Den skriftlige prøve i matematik FP10 maj 2019 Skrevet af Klaus Fink på baggrund af oplysninger fra opgavekommissionen 1 Til matematiklæreren
Formativ brug af folkeskolens prøver årets resultater på landsplan Den skriftlige prøve i matematik FP10 maj 2019 Skrevet af Klaus Fink på baggrund af oplysninger fra opgavekommissionen 1 Til matematiklæreren
Konference om mundtlige prøver. PRØV! Et program til de mundtlige prøver (og det daglige arbejde?)
 Konference om mundtlige prøver PRØV! Et program til de mundtlige prøver (og det daglige arbejde?) Faglig læsning for matematiklærere Bekendtgørelse nr. 1824 af 16. december 2015 om folkeskolens prøver
Konference om mundtlige prøver PRØV! Et program til de mundtlige prøver (og det daglige arbejde?) Faglig læsning for matematiklærere Bekendtgørelse nr. 1824 af 16. december 2015 om folkeskolens prøver
Vejledning til prøverne i matematik
 Vejledning til prøverne i matematik Styrelsen for Undervisning og Kvalitet Februar 2016 1 af 78 Indholdsfortegnelse 1. Indledning... 5 2. FP9... 9 2.1 Prøve i matematik uden hjælpemidler... 9 2.2 Prøve
Vejledning til prøverne i matematik Styrelsen for Undervisning og Kvalitet Februar 2016 1 af 78 Indholdsfortegnelse 1. Indledning... 5 2. FP9... 9 2.1 Prøve i matematik uden hjælpemidler... 9 2.2 Prøve
Fælles Mål 2009. Matematik. Faghæfte 12
 Fælles Mål 2009 Matematik Faghæfte 12 Undervisningsministeriets håndbogsserie nr. 14 2009 Fælles Mål 2009 Matematik Faghæfte 12 Undervisningsministeriets håndbogsserie nr. 14 2009 Indhold Formål for faget
Fælles Mål 2009 Matematik Faghæfte 12 Undervisningsministeriets håndbogsserie nr. 14 2009 Fælles Mål 2009 Matematik Faghæfte 12 Undervisningsministeriets håndbogsserie nr. 14 2009 Indhold Formål for faget
Fælles Mål Matematik. Faghæfte 12
 Fælles Mål 2009 Matematik Faghæfte 12 Undervisningsministeriets håndbogsserie nr. 14 2009 Fælles Mål 2009 Matematik Faghæfte 12 Undervisningsministeriets håndbogsserie nr. 14 2009 Indhold Formål for faget
Fælles Mål 2009 Matematik Faghæfte 12 Undervisningsministeriets håndbogsserie nr. 14 2009 Fælles Mål 2009 Matematik Faghæfte 12 Undervisningsministeriets håndbogsserie nr. 14 2009 Indhold Formål for faget
Formativ brug af folkeskolens prøver. Den skriftlige prøve i matematik i 10. klasse, FP10, maj 2018
 Formativ brug af folkeskolens prøver Den skriftlige prøve i matematik i 10. klasse, FP10, maj 2018 1 Til matematiklæreren i 10. klasse Dette er en rapport om den skriftlige prøve i matematik maj 2018.
Formativ brug af folkeskolens prøver Den skriftlige prøve i matematik i 10. klasse, FP10, maj 2018 1 Til matematiklæreren i 10. klasse Dette er en rapport om den skriftlige prøve i matematik maj 2018.
Vejledning til folkeskolens prøver i faget matematik 10. klasse
 Vejledning til folkeskolens prøver i faget matematik 10. klasse Styrelsen for Undervisning og Kvalitet Januar 2018 1 Indhold Indledning... 4 Ændringer i denne prøvevejledning... 4 1 Prøvegrundlag (Fælles
Vejledning til folkeskolens prøver i faget matematik 10. klasse Styrelsen for Undervisning og Kvalitet Januar 2018 1 Indhold Indledning... 4 Ændringer i denne prøvevejledning... 4 1 Prøvegrundlag (Fælles
Kompetencetræning i matematik - også til prøverne. KP 10. januar 2019
 Kompetencetræning i matematik - også til prøverne KP 10. januar 2019 Kompetencetræning i matematik - også til prøven Prøverne i matematik bliver i stadig højere grad kompetencebaseret, så det giver god
Kompetencetræning i matematik - også til prøverne KP 10. januar 2019 Kompetencetræning i matematik - også til prøven Prøverne i matematik bliver i stadig højere grad kompetencebaseret, så det giver god
Klare MÅL. Matematik F/E
 Klare MÅL Matematik F/E 2 Mål for undervisningen Niveau F 1. Eleven kan foretage matematisk modellering til løsning af praktiske opgaver fra erhverv, hverdag eller samfund 2. Eleven kan genkende matematikken
Klare MÅL Matematik F/E 2 Mål for undervisningen Niveau F 1. Eleven kan foretage matematisk modellering til løsning af praktiske opgaver fra erhverv, hverdag eller samfund 2. Eleven kan genkende matematikken
Selam Friskole Fagplan for Matematik
 Selam Friskole Fagplan for Matematik Formål Formålet med undervisningen er, at eleverne udvikler matematiske kompetencer og opnår viden og kunnen således, at de bliver i stand til at begå sig hensigtsmæssigt
Selam Friskole Fagplan for Matematik Formål Formålet med undervisningen er, at eleverne udvikler matematiske kompetencer og opnår viden og kunnen således, at de bliver i stand til at begå sig hensigtsmæssigt
Vejledning til folkeskolens prøver i faget matematik 9. klasse
 Vejledning til folkeskolens prøver i faget matematik 9. klasse Styrelsen for Undervisning og Kvalitet August 2016 Indhold Indledning... 2 1 Prøvegrundlag (Fælles mål)... 3 1.1 Prøvernes forskellige dele...
Vejledning til folkeskolens prøver i faget matematik 9. klasse Styrelsen for Undervisning og Kvalitet August 2016 Indhold Indledning... 2 1 Prøvegrundlag (Fælles mål)... 3 1.1 Prøvernes forskellige dele...
Evaluering af matematik undervisning
 Evaluering af matematik undervisning Udarbejdet af Khaled Zaher, matematiklærer 6-9 klasse og Boushra Chami, matematiklærer 2-5 klasse Matematiske kompetencer. Fællesmål efter 3.klasse indgå i dialog om
Evaluering af matematik undervisning Udarbejdet af Khaled Zaher, matematiklærer 6-9 klasse og Boushra Chami, matematiklærer 2-5 klasse Matematiske kompetencer. Fællesmål efter 3.klasse indgå i dialog om
Matematik Matematik efter Lillegruppen (0-1 kl.)
 Matematik Matematik efter Lillegruppen (0-1 kl.) Undervisningsministeriets forenklede fælles mål: Matematiske kompetencer Eleven kan handle hensigtsmæssigt i situationer med matematik Problembehandling
Matematik Matematik efter Lillegruppen (0-1 kl.) Undervisningsministeriets forenklede fælles mål: Matematiske kompetencer Eleven kan handle hensigtsmæssigt i situationer med matematik Problembehandling
Forenklede Fælles Mål Matematik. Maj 2014
 Forenklede Fælles Mål Matematik Maj 2014 Matematiske kompetencer Tal og algebra Statistik og sandsynlighed Geometri og måling Skrivegruppen Annette Lilholt, lærer Hjørring Line Engsig, lærer Gentofte Bent
Forenklede Fælles Mål Matematik Maj 2014 Matematiske kompetencer Tal og algebra Statistik og sandsynlighed Geometri og måling Skrivegruppen Annette Lilholt, lærer Hjørring Line Engsig, lærer Gentofte Bent
Tal og algebra. I kapitlet arbejdes med følgende centrale matematiske begreber: algebra variable. Huskeliste: Tændstikker (til side 146) FRA FAGHÆFTET
 I kapitlet skal eleverne arbejde med fire forskellige vinkler på algebra de præsenteres på kapitlets første mundtlige opslag. De fire vinkler er algebra som et redskab til at løse matematiske problemer.
I kapitlet skal eleverne arbejde med fire forskellige vinkler på algebra de præsenteres på kapitlets første mundtlige opslag. De fire vinkler er algebra som et redskab til at løse matematiske problemer.
Undervisningsbeskrivelse for Matematik A 2. E 2011/2012
 Undervisningsbeskrivelse for Matematik A 2. E 2011/2012 Termin Undervisningen afsluttes den 16. maj 2012 Skoleåret hvor undervisningen har foregået: 2011-2012 Institution Skive Teknisk Gymnasium Uddannelse
Undervisningsbeskrivelse for Matematik A 2. E 2011/2012 Termin Undervisningen afsluttes den 16. maj 2012 Skoleåret hvor undervisningen har foregået: 2011-2012 Institution Skive Teknisk Gymnasium Uddannelse
Årsplan 9. Klasse Matematik Skoleåret 2015/16
 Årsplan 9 Klasse Matematik Skoleåret 2015/16 Hovedformål Årsplanen for 9 Klasse i Matematik tager udgangspunkt i Forenklede Fællesmål (Undervisningsministeriet) Formålet med undervisningen er, at eleverne
Årsplan 9 Klasse Matematik Skoleåret 2015/16 Hovedformål Årsplanen for 9 Klasse i Matematik tager udgangspunkt i Forenklede Fællesmål (Undervisningsministeriet) Formålet med undervisningen er, at eleverne
HVAD STÅR DER I DE NYE FÆLLES MÅL OM DEN MATEMATISKE KOMPETENCE, KOMMUNIKATION? KØBENHAVN 29. SEPTEMBER 2015
 HVAD STÅR DER I DE NYE FÆLLES MÅL OM DEN MATEMATISKE KOMPETENCE, KOMMUNIKATION? KØBENHAVN 29. SEPTEMBER 2015 BINDENDE/VEJLEDENDE BINDENDE MÅL OG TEKSTER: FAGETS FORMÅL KOMPETENCEMÅL (12 STK.) FÆRDIGHEDS-
HVAD STÅR DER I DE NYE FÆLLES MÅL OM DEN MATEMATISKE KOMPETENCE, KOMMUNIKATION? KØBENHAVN 29. SEPTEMBER 2015 BINDENDE/VEJLEDENDE BINDENDE MÅL OG TEKSTER: FAGETS FORMÅL KOMPETENCEMÅL (12 STK.) FÆRDIGHEDS-
Kompetencemål for Matematik, klassetrin
 Kompetencemål for Matematik, 4.-10. klassetrin Matematik omhandler samspil mellem matematiske emner, matematiske kompetencer, matematikdidaktisk teori samt matematiklærerens praksis i folkeskolen og bidrager
Kompetencemål for Matematik, 4.-10. klassetrin Matematik omhandler samspil mellem matematiske emner, matematiske kompetencer, matematikdidaktisk teori samt matematiklærerens praksis i folkeskolen og bidrager
Evaluering og feedback i matematikundervisningen. Sommeruni, august 2015
 Evaluering og feedback i matematikundervisningen Sommeruni, august 2015 Forskellige hensigter med evaluering Hvad evalueres? Af hvem? Hvorfor? Elevens læringsudbytte Læreren For at kunne give feedback,
Evaluering og feedback i matematikundervisningen Sommeruni, august 2015 Forskellige hensigter med evaluering Hvad evalueres? Af hvem? Hvorfor? Elevens læringsudbytte Læreren For at kunne give feedback,
Eksempler på arbejdsark: Arkitektur og ligedannethed i trigonometri
 : Arkitektur og ligedannethed i trigonometri Eksemplerne indeholder arbejdsark, som kan bruges i forbindelse med gennemførelse af undervisningsforløb. Indholdsfortegnelse Arbejdsark 1: Before action opgave.....2
: Arkitektur og ligedannethed i trigonometri Eksemplerne indeholder arbejdsark, som kan bruges i forbindelse med gennemførelse af undervisningsforløb. Indholdsfortegnelse Arbejdsark 1: Before action opgave.....2
EN SKOLE FOR LIVET ÅRSPLAN 18/19. Lærer: LH Fag: Matematik i 10. klasse Uge Emne Mål Materialer. Eleven kan anvende basisfunktioner i WordMat.
 ÅRSPLAN 18/19 Lærer: LH Fag: Matematik i 10. klasse Uge Emne Mål Materialer Uge 33-37 Intro 15/8-16/8 Fælles Aktivitetsdag 23/8 Uge 36: Iværksætteri WordMat Tal og algebra Eleven kan anvende basisfunktioner
ÅRSPLAN 18/19 Lærer: LH Fag: Matematik i 10. klasse Uge Emne Mål Materialer Uge 33-37 Intro 15/8-16/8 Fælles Aktivitetsdag 23/8 Uge 36: Iværksætteri WordMat Tal og algebra Eleven kan anvende basisfunktioner
Konference om mundtlige prøver PRØV! Et program til de mundtlige prøver (og det daglige arbejde?)
 Konference om mundtlige prøver PRØV! Et program til de mundtlige prøver (og det daglige arbejde?) En tydelig problemstilling, som Mundtlig prøve? giver mulighed for at vise matematiske kompetencer, viden
Konference om mundtlige prøver PRØV! Et program til de mundtlige prøver (og det daglige arbejde?) En tydelig problemstilling, som Mundtlig prøve? giver mulighed for at vise matematiske kompetencer, viden
ÅRSPLAN Matematik 9.klasse SKOLEÅRET 2017/2018
 ÅRSPLAN Matematik 9.klasse SKOLEÅRET 2017/2018 UGE 35-40 44-47 Matematiske Fokuspunkter Tal, talsystemer regneregler, herunder: - Potens kvadratregner egler Økonomi, herunder: - Decimaltal - Brøktal -
ÅRSPLAN Matematik 9.klasse SKOLEÅRET 2017/2018 UGE 35-40 44-47 Matematiske Fokuspunkter Tal, talsystemer regneregler, herunder: - Potens kvadratregner egler Økonomi, herunder: - Decimaltal - Brøktal -
Eleven kan handle med overblik i sammensatte situationer med matematik. Eleven kan anvende rationale tal og variable i beskrivelser og beregninger
 Kompetenceområde Efter klassetrin Efter 6. klassetrin Efter 9. klassetrin Matematiske kompetencer handle hensigtsmæssigt i situationer med handle med overblik i sammensatte situationer med handle med dømmekraft
Kompetenceområde Efter klassetrin Efter 6. klassetrin Efter 9. klassetrin Matematiske kompetencer handle hensigtsmæssigt i situationer med handle med overblik i sammensatte situationer med handle med dømmekraft
Der er ikke væsentlig niveauforskel i opgaverne inden for de fire emner, men der er fokus på forskellige matematiske områder.
 Dette tema lægger forskellige vinkler på temaet biografen. Udgangspunktet er således ikke et bestemt matematisk område, men et stykke virkelighed, der bl.a. kan beskrives ved hjælp af matematik. I dette
Dette tema lægger forskellige vinkler på temaet biografen. Udgangspunktet er således ikke et bestemt matematisk område, men et stykke virkelighed, der bl.a. kan beskrives ved hjælp af matematik. I dette
Undersøgende matematik i prøverne. Odense 26. april 2019
 Undersøgende matematik i prøverne Odense 26. april 2019 Programmet En del af opgaverne i Folkeskolens Prøver handler om, at eleverne skal undersøge et eller andet. Det er ofte opgaver, eleverne har svært
Undersøgende matematik i prøverne Odense 26. april 2019 Programmet En del af opgaverne i Folkeskolens Prøver handler om, at eleverne skal undersøge et eller andet. Det er ofte opgaver, eleverne har svært
Matematik og målfastsættelse
 Matematik og målfastsættelse Målfastsættelse, feedforward og evaluering i matematik, oplæg og drøftelse 1 Problemløsning s e k s + s e k s t o l v 2 Punkter Målfastsættelse af undervisning i matematik
Matematik og målfastsættelse Målfastsættelse, feedforward og evaluering i matematik, oplæg og drøftelse 1 Problemløsning s e k s + s e k s t o l v 2 Punkter Målfastsættelse af undervisning i matematik
MULTI 6 Forenklede Fælles Mål
 MULTI 6 Forenklede Fælles Mål Oversigt over Forenklende Fælles Mål i forbindelse med kapitlerne i MULTI Kapitel 1 Faglig læsning og skrivning Eleverne kan anvende forskellige strategier til matematisk
MULTI 6 Forenklede Fælles Mål Oversigt over Forenklende Fælles Mål i forbindelse med kapitlerne i MULTI Kapitel 1 Faglig læsning og skrivning Eleverne kan anvende forskellige strategier til matematisk
Årsplan for 5. klasse, matematik
 Årsplan for 5. klasse, matematik I matematik bruger vi bogsystemet Sigma som grundmateriale. I systemet er der, ud over også kopiark og tests tilknyttet de enkelte kapitler. Systemet er udarbejdet så det
Årsplan for 5. klasse, matematik I matematik bruger vi bogsystemet Sigma som grundmateriale. I systemet er der, ud over også kopiark og tests tilknyttet de enkelte kapitler. Systemet er udarbejdet så det
SYNLIG LÆRING OG LÆRINGSMÅL I MATEMATIK. Sommeruni 2015. Louise Falkenberg og Eva Rønn
 SYNLIG LÆRING OG LÆRINGSMÅL I MATEMATIK Sommeruni 2015 Louise Falkenberg og Eva Rønn UCC PRÆSENTATION Eva Rønn, UCC, [email protected] Louise Falkenberg, UCC, [email protected] PROGRAM Mandag d. 3/8 Formiddag (kaffepause
SYNLIG LÆRING OG LÆRINGSMÅL I MATEMATIK Sommeruni 2015 Louise Falkenberg og Eva Rønn UCC PRÆSENTATION Eva Rønn, UCC, [email protected] Louise Falkenberg, UCC, [email protected] PROGRAM Mandag d. 3/8 Formiddag (kaffepause
MatematiKan og Fælles Mål
 MatematiKan og Fælles Mål MatematiKan er et digitalt værktøj til matematik. Det hører til gruppen af interaktive CAS værktøjer. Denne type digitale værktøjer er kendetegnet ved, at de har en delvis blank
MatematiKan og Fælles Mål MatematiKan er et digitalt værktøj til matematik. Det hører til gruppen af interaktive CAS værktøjer. Denne type digitale værktøjer er kendetegnet ved, at de har en delvis blank
8:30-14:30 Sproglig udvikling Kort aktivitet Planlægning af undervisningsforløb Fremlæggelse af undervisningsforløb
 8:30-14:30 Sproglig udvikling Kort aktivitet Planlægning af undervisningsforløb Fremlæggelse af undervisningsforløb Kaffepause 10:00-10:15 Frokost 12:15-13:00 Kaffepause 13:45-14:00 SPROGLIG UDVIKLING
8:30-14:30 Sproglig udvikling Kort aktivitet Planlægning af undervisningsforløb Fremlæggelse af undervisningsforløb Kaffepause 10:00-10:15 Frokost 12:15-13:00 Kaffepause 13:45-14:00 SPROGLIG UDVIKLING
KOMPETENCEMÅL OG MUNDTLIG PRØVE I MATEMATIK
 ([email protected]) INSTITUT FOR UDDANNELSE OG PÆDAGOGIK (DPU) KONFERENCE OM MUNDTLIGE PRØVER ODENSE CONGRESS CENTER UNI VERSITET HVAD ER GOD EVALUERING? To klassiske kvalitetskriterier: Validitet: Måler evalueringen
([email protected]) INSTITUT FOR UDDANNELSE OG PÆDAGOGIK (DPU) KONFERENCE OM MUNDTLIGE PRØVER ODENSE CONGRESS CENTER UNI VERSITET HVAD ER GOD EVALUERING? To klassiske kvalitetskriterier: Validitet: Måler evalueringen
Matematik. Matematiske kompetencer
 Matematiske kompetencer stille spørgsmål, som er karakteristiske for matematik og have blik for hvilke typer af svar, som kan forventes(tankegangskompetence) erkende, formulere, afgrænse og løse matematiske
Matematiske kompetencer stille spørgsmål, som er karakteristiske for matematik og have blik for hvilke typer af svar, som kan forventes(tankegangskompetence) erkende, formulere, afgrænse og løse matematiske
Forenklede Fælles Mål. Matematik i marts 27. marts 2014
 Forenklede Fælles Mål Matematik i marts 27. marts 2014 Læringskonsulenter klar med bistand Side 2 Forenklede Fælles Mål hvad ligger der i de nye mål? Hvorfor nye Fælles Mål? Hvorfor? Målene bruges generelt
Forenklede Fælles Mål Matematik i marts 27. marts 2014 Læringskonsulenter klar med bistand Side 2 Forenklede Fælles Mål hvad ligger der i de nye mål? Hvorfor nye Fælles Mål? Hvorfor? Målene bruges generelt
ÅRSPLAN MATEMATIK 3.KLASSE
 ÅRSPLAN MATEMATIK 3.KLASSE Matematiklærerens tænkebobler illustrerer, at matematikundervisning ikke udelukkende handler om opgaver, men om en (lige!) blanding af: Kompetencer Indhold Arbejdsmåder CENTRALE
ÅRSPLAN MATEMATIK 3.KLASSE Matematiklærerens tænkebobler illustrerer, at matematikundervisning ikke udelukkende handler om opgaver, men om en (lige!) blanding af: Kompetencer Indhold Arbejdsmåder CENTRALE
Kompetencemål for Matematik, klassetrin
 Kompetencemål for Matematik, 1.-6. klassetrin Matematik omhandler samspil mellem matematiske emner, matematiske arbejds- og tænkemåder, matematikdidaktik samt matematiklærerens praksis i folkeskolen og
Kompetencemål for Matematik, 1.-6. klassetrin Matematik omhandler samspil mellem matematiske emner, matematiske arbejds- og tænkemåder, matematikdidaktik samt matematiklærerens praksis i folkeskolen og
Klasseundervisning. Makkerpar. Individuelt arbejde. få forståelse for og erfaringer med, hvordan man regner med negative tal
 Fagårsplan 13/14 Fag: Matematik Fagområde/ emne Tal og regning Regneregler Periode Mål Eleverne skal: Klasse: 8.a Lærer: LBJ få indblik i ligheder og forskelle mellem naturlige tal, hele tal, rationale
Fagårsplan 13/14 Fag: Matematik Fagområde/ emne Tal og regning Regneregler Periode Mål Eleverne skal: Klasse: 8.a Lærer: LBJ få indblik i ligheder og forskelle mellem naturlige tal, hele tal, rationale
Matematik - undervisningsplan
 I 4. klasse starter man på andet forløb i matematik, der skal lede frem mod at eleverne kan opfylde fagets trinmål efter 6. klasse. Det er dermed det som undervisningen tilrettelægges ud fra og målsættes
I 4. klasse starter man på andet forløb i matematik, der skal lede frem mod at eleverne kan opfylde fagets trinmål efter 6. klasse. Det er dermed det som undervisningen tilrettelægges ud fra og målsættes
Matematikken og naturens kræfter
 INTRO Omdrejningspunktet for dette tema er matematikkens anvendelse som beskrivelsesmiddel i forbindelse med fysiske love. Temaet er inddelt i følgende fire emner: Pendulure Frit fald Bremselængder og
INTRO Omdrejningspunktet for dette tema er matematikkens anvendelse som beskrivelsesmiddel i forbindelse med fysiske love. Temaet er inddelt i følgende fire emner: Pendulure Frit fald Bremselængder og
Matematik i marts. nu i april
 Matematik i marts nu i april Dagens fødselar 2 127 1 1857 1876 Diofantiske ligninger En løsning for N>1: N = 24 og M = 70 François Édouard Anatole Lucas (4 April 1842 3 October 1891) 2, 1, 3, 4, 7, 11,
Matematik i marts nu i april Dagens fødselar 2 127 1 1857 1876 Diofantiske ligninger En løsning for N>1: N = 24 og M = 70 François Édouard Anatole Lucas (4 April 1842 3 October 1891) 2, 1, 3, 4, 7, 11,
Matematik. Evaluering, orientering og vejledning
 Folkeskolens afsluttende evaluering Matematik 2016 Evaluering, orientering og vejledning Uddannelsesstyrelsen 1. Konklusion Denne evaluering bygger på prøveresultaterne for skriftlige og mundtlige prøver
Folkeskolens afsluttende evaluering Matematik 2016 Evaluering, orientering og vejledning Uddannelsesstyrelsen 1. Konklusion Denne evaluering bygger på prøveresultaterne for skriftlige og mundtlige prøver
Matematik. Matematiske kompetencer
 Matematiske kompetencer formulere sig skriftligt og mundtligt om matematiske påstande og spørgsmål og have blik for hvilke typer af svar, der kan forventes (tankegangskompetence) løse matematiske problemer
Matematiske kompetencer formulere sig skriftligt og mundtligt om matematiske påstande og spørgsmål og have blik for hvilke typer af svar, der kan forventes (tankegangskompetence) løse matematiske problemer
Årsplan for 9 årgang
 Årsplan 9.årgang matematik 09-00: Matematrix grundbog 9.kl Kopiark Færdighedsregning 9.kl Computer Vi skal i løbet af året arbejde med følgende IT værktøjer: Excel Matematikfessor Wordmat Excel, og wordmat
Årsplan 9.årgang matematik 09-00: Matematrix grundbog 9.kl Kopiark Færdighedsregning 9.kl Computer Vi skal i løbet af året arbejde med følgende IT værktøjer: Excel Matematikfessor Wordmat Excel, og wordmat
Bedømmelsesplan for Matematik C
 Bedømmelsesplan for Matematik C Matematik C Hovedområder: Fagretningen: Uddannelser i fagretningen indeholder: Varighed: Læringselementer: Læringsmiljø: Kontor handel og forretningsservice Detail, Handel,
Bedømmelsesplan for Matematik C Matematik C Hovedområder: Fagretningen: Uddannelser i fagretningen indeholder: Varighed: Læringselementer: Læringsmiljø: Kontor handel og forretningsservice Detail, Handel,
Elevbog s. 14-25 Vi opsummerer hvad vi ved i. kendskab til geometriske begreber og figurer.
 Årsplan 5. LH. Matematik Lærer Pernille Holst Overgaard (PHO) Lærebogsmateriale. Format 5 Tid og fagligt Aktivitet område Uge 33-37 Tal Uge 38-41 (efterårsferie uge 42) Figurer Elevbog s. 1-13 Vi opsummerer
Årsplan 5. LH. Matematik Lærer Pernille Holst Overgaard (PHO) Lærebogsmateriale. Format 5 Tid og fagligt Aktivitet område Uge 33-37 Tal Uge 38-41 (efterårsferie uge 42) Figurer Elevbog s. 1-13 Vi opsummerer
Undersøgende opgaver Opgave 6 er i begge prøvesæt med som sidste opgave en undersøgende opgave af en ny type, som var lidt udfordrende for eleverne.
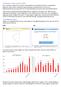 Tendenser i årets prøver 2019 Der er tendenser i prøverne, som kræver matematiklærernes opmærksomhed helst i et samarbejde i fagteamet. Og det kræver skolelederes og forvaltningers opmærksomhed for at
Tendenser i årets prøver 2019 Der er tendenser i prøverne, som kræver matematiklærernes opmærksomhed helst i et samarbejde i fagteamet. Og det kræver skolelederes og forvaltningers opmærksomhed for at
Mindmaps og begrebsudvikling i matematik i 6.kl.
 Mindmaps og begrebsudvikling i matematik i 6.kl. Målsætning: Lærermål: At observere på og udvikle brugen af mindmaps i forbindelse med begrebsudvikling og evaluering af matematiske begreber i matematik
Mindmaps og begrebsudvikling i matematik i 6.kl. Målsætning: Lærermål: At observere på og udvikle brugen af mindmaps i forbindelse med begrebsudvikling og evaluering af matematiske begreber i matematik
Vejledning til folkeskolens prøver i faget matematik 9. klasse
 Vejledning til folkeskolens prøver i faget matematik 9. klasse 1 Styrelsen for Undervisning og Kvalitet Januar 2018 Indholdsfortegnelse Indledning... 4 Ændringer i denne prøvevejledning... 4 1 Prøvegrundlag
Vejledning til folkeskolens prøver i faget matematik 9. klasse 1 Styrelsen for Undervisning og Kvalitet Januar 2018 Indholdsfortegnelse Indledning... 4 Ændringer i denne prøvevejledning... 4 1 Prøvegrundlag
Kompetencemål i undervisningsfaget Matematik yngste klassetrin
 Kompetencemål i undervisningsfaget Matematik yngste klassetrin Kort bestemmelse af faget Faget matematik er i læreruddannelsen karakteriseret ved et samspil mellem matematiske emner, matematiske arbejds-
Kompetencemål i undervisningsfaget Matematik yngste klassetrin Kort bestemmelse af faget Faget matematik er i læreruddannelsen karakteriseret ved et samspil mellem matematiske emner, matematiske arbejds-
FFM Matematik pop-up eftermiddag. CFU, UCC 11. Maj 2015
 FFM Matematik pop-up eftermiddag CFU, UCC 11. Maj 2015 Formål Deltagerne har: Kendskab til Forenklede Fælles Måls opbygning Kendskab til tankegangen bag den målstyrede undervisning i FFM Kendskab til læringsmål
FFM Matematik pop-up eftermiddag CFU, UCC 11. Maj 2015 Formål Deltagerne har: Kendskab til Forenklede Fælles Måls opbygning Kendskab til tankegangen bag den målstyrede undervisning i FFM Kendskab til læringsmål
UCC_KURSUS_261016
 26.10.2016 UCC_KURSUS_261016 UCSJ www.mikaelskaanstroem.dk UCC_KURSUS_261016 09 Intro med diverse Dagens forestilling 25. oktober 2016 It, digitale værktøjer & Fælles Mål Øget anvendelse -> Digitalisering
26.10.2016 UCC_KURSUS_261016 UCSJ www.mikaelskaanstroem.dk UCC_KURSUS_261016 09 Intro med diverse Dagens forestilling 25. oktober 2016 It, digitale værktøjer & Fælles Mål Øget anvendelse -> Digitalisering
Klare MÅL. Matematik D/C
 Klare MÅL Matematik D/C 2 Matematik F/E Mål for undervisningen - Niveau D 1. Eleven kan anvende matematisk modellering til løsning af opgaver og undersøgelse af spørgsmål fra erhverv, hverdag eller samfund,
Klare MÅL Matematik D/C 2 Matematik F/E Mål for undervisningen - Niveau D 1. Eleven kan anvende matematisk modellering til løsning af opgaver og undersøgelse af spørgsmål fra erhverv, hverdag eller samfund,
Årsplan 2018/19 Matematik 3. årgang. Kapitel 1: Jubii
 Årsplan 08/9 Matematik. årgang TriX A Kapitel : Jubii I bogens første kapitel får eleverne mulighed for at repetere det faglige stof, som de arbejdede med i. klasse. Kapitlet har især fokus på kerneområderne
Årsplan 08/9 Matematik. årgang TriX A Kapitel : Jubii I bogens første kapitel får eleverne mulighed for at repetere det faglige stof, som de arbejdede med i. klasse. Kapitlet har især fokus på kerneområderne
Kompetencer, færdigheder og evaluering
 Kompetencer, færdigheder og evaluering Tomas Højgaard ([email protected]) Danmarks Pædagogiske Universitetsskole Foredrag på MONA-konferencen 2010 Fredericia, 27. oktober 2010 Evaluering Tre delprocesser (jf.
Kompetencer, færdigheder og evaluering Tomas Højgaard ([email protected]) Danmarks Pædagogiske Universitetsskole Foredrag på MONA-konferencen 2010 Fredericia, 27. oktober 2010 Evaluering Tre delprocesser (jf.
Årsplan Matematrix 3. kl. Kapitel 1: Jubii
 Årsplan Matematrix. kl. A Første halvår Kapitel : Jubii I bogens første kapitel får eleverne mulighed for at repetere det faglige stof, som de arbejdede med i. klasse. Dette er samtidig et redskab for
Årsplan Matematrix. kl. A Første halvår Kapitel : Jubii I bogens første kapitel får eleverne mulighed for at repetere det faglige stof, som de arbejdede med i. klasse. Dette er samtidig et redskab for
Årsplan matematik 5. klasse 2017/2018
 Årsplan matematik 5. klasse 2017/2018 Årsplanen tager udgangspunkt i fællesmål (færdigheds- og vidensmål) efter 6. klassetrin. Desuden tilrettelægges undervisningen efter læseplanen for matematik. Formålet
Årsplan matematik 5. klasse 2017/2018 Årsplanen tager udgangspunkt i fællesmål (færdigheds- og vidensmål) efter 6. klassetrin. Desuden tilrettelægges undervisningen efter læseplanen for matematik. Formålet
Matematiske konkurrencer i grundskolen
 Matematiske konkurrencer i grundskolen DMUK 10. november 2016 21-11-2016 [email protected] og Søs Spahn, [email protected] 1 Danmarks Matematiklærerforening Forlaget Matematik Samarbejde lokalt og internationalt.
Matematiske konkurrencer i grundskolen DMUK 10. november 2016 21-11-2016 [email protected] og Søs Spahn, [email protected] 1 Danmarks Matematiklærerforening Forlaget Matematik Samarbejde lokalt og internationalt.
Forskellig eller ens? Geometriforløb i 5 klasse.
 Forskellig eller ens? Geometriforløb i 5 klasse. Introduktion til undervisningsforløbet Forløbet behandler forskellige plangeometriske problemstillinger ud fra dagligdagsbegreberne ens og forskellig. Alle
Forskellig eller ens? Geometriforløb i 5 klasse. Introduktion til undervisningsforløbet Forløbet behandler forskellige plangeometriske problemstillinger ud fra dagligdagsbegreberne ens og forskellig. Alle
Matematiske kompetencer
 Matematiske kompetencer I dette kapitel skal du arbejde med forskellige matematiske kompetencer. I matematik skal du kunne andet og mere end blot at gentage paratviden og regne opgaver i kendte situationer.
Matematiske kompetencer I dette kapitel skal du arbejde med forskellige matematiske kompetencer. I matematik skal du kunne andet og mere end blot at gentage paratviden og regne opgaver i kendte situationer.
Ræsonnement og tankegang. DLF-Kursus Frederikshavn 24.-25.9 2015 Eva Rønn UCC
 Ræsonnement og tankegang DLF-Kursus Frederikshavn 24.-25.9 2015 Eva Rønn UCC Mål og indhold for workshoppen Mål At I kan Indhold opstille og synliggøre læringsmål knyttet til ræsonnement og tankegang på
Ræsonnement og tankegang DLF-Kursus Frederikshavn 24.-25.9 2015 Eva Rønn UCC Mål og indhold for workshoppen Mål At I kan Indhold opstille og synliggøre læringsmål knyttet til ræsonnement og tankegang på
