(c) Opskriv den reelle Fourierrække for funktionen y(t) fra (b), og afgør dernæst om y(t) er en lige eller ulige funktion eller ingen af delene.
|
|
|
- Peter Lauritzen
- 4 år siden
- Visninger:
Transkript
1 MATEMATIK 3 EN,MP 4. februar 2016 Eksamenopgaver fra (jan. 2016) Givet at 0 for 0 < t < 1 mens e (t 1) cos(7(t 1)) for t 1, betragt da begyndelsesværdiproblemet for t > 0: y (t) + 2y (t) + 50y(t) = r(t), y(0) = 2, y (0) = 9. (a) Bestem den Laplacetransformerede L(e t cos(7t)) og angiv billedligningen for Y (s) = Ly(s). (b) Opskriv et udtryk for Y (s) og beregn de inverst transformerede af de led, hvori y(0) og y (0) indgår. (Vink: Man kan udnytte at s 2 + 2s + 50 = (s + 1) ) (c) Bestem løsningen y(t). (jan. 2016) (a) Lad f(t) betegne den 2π-periodiske funktion bestemt ved at f(t) = e 3t for 0 t < π mens f(t) = 0 for π t < 0. Udregn ved integration koefficienterne c n i den komplekse Fourierrække f(t) = n= c ne i nt. (b) Bestem den komplekse Fourierrække y(t) = n= K ne i nt for den 2π-periodiske løsning y(t) til y (t) + 5y (t) 3y(t) = r(t), hvorved r(t) har komplekse Fourierkoefficienter c n = 1/(4 + n 2 ) for n 0, mens c 0 = 7. (c) Opskriv den reelle Fourierrække for funktionen y(t) fra (b), og afgør dernæst om y(t) er en lige eller ulige funktion eller ingen af delene. (jan. 2016) (a) Bestem rot F for vektorfeltet F = ( 6x 2 z 4 +2xz 3, 2yz 3, 8(xz) 3 +3(x 2 +y 2 )z 2), og begrund at F har et potential. (b) Bestem en funktion f(x, y, z) sådan at F = grad f. (c) Benyt en hovedsætning til at bestemme kurveintegralet C F d r, idet C med positiv orientering gennemløber de punkter (x, y, z) som opfylder x 2 + y 2 = 4 og z = 0. (jan. 2016) (a) Bestem radius og centrum i konvergenscirklen for potensrækken n=1 2 n (6 + 8 i) n (z i)n. (b) Brug Cauchy-produktet til at bestemme koefficienterne a n for n 0 i potensrækken med z 0 = 0 for f(z) = 1 Ln(1 z). 1 z (c) Brug Cauchy Riemann ligningerne til at afgøre ved hvilke z C, om nogen, funktionen e z er analytisk. 1
2 (jan. 2015) Betragt begyndelsesværdiproblemet for t > 0: y 1 (t) + 3y 1 (t) + 5y 2 (t) = sin(4t), y 1 (0) = 5, y 2(t) 5y 1 (t) 3y 2 (t) = cos(4t), y 2 (0) = 3. (a) Bestem billedligningerne for de Laplacetransformerede funktioner Y 1 (s) = Ly 1 (s), Y 2 (s) = Ly 2 (s). (b) Udregn determinanten D for billedligningerne og brug den til at vise at (c) Bestem funktionen y 2 (t). y 1 (t) = ( t) cos(4t) + (9 8 t 3 32 ) sin(4t). (jan. 2015) Lad r(t) betegne den 2π-periodiske funktion bestemt ved at 0 for 0 t < π, cos t for π t < 0. (a) Vis ved integration at r(t) har en kompleks Fourierrække n= c ne i nt med koefficienter c n = i n for n lige, og med c π n 2 1 n = 0 for ulige n ±1. Udregn også c 1 og c 1. (b) Bestem den komplekse Fourierrække y(t) = n= K ne i nt for den 2π-periodiske løsning y(t) til y (t) + 10y (t) + 21y(t) = r(t). (c) Opskriv den reelle Fourierrække for funktionen y(t) fra (b). (jan. 2015) Her betragtes vektorfeltet F i R 2 givet ved F = ( y x, ) for (x, y) (0, 0). x 2 +y 2 x 2 +y 2 (a) Lad C betegne cirklen hvor x 2 + y 2 = 9, med positiv orientering (dvs. mod uret). Beregn værdien af kurveintegralet C F d r. (b) Bestem et potential for F og angiv, hvor det er defineret. (c) Begrund teoretisk at K F d r har samme værdi som i (a), når K betegner den positivt orienterede rand af kvadratet hvori x 3, y 3. (Vink: Betragt en kvadrant ad gangen.) (jan. 2015) (a) Angiv definitionsmængden D for og begrund at f er analytisk. f(z) = z3 z 5 + z (b) Bestem funktionens nulpunkter og poler, og angiv disses orden. (c) Udregn f s residuer i de poler, som tilhører halvplanen hvor Im z > 0. (d) Brug residueintegration til at udlede at f(x) dx = π 2. (feb. 2015) Betragt begyndelsesværdiproblemet for t > 0: y (t) 10y (t) + 16y(t) = te 5t cos(3t), y(0) = 0, y (0) = 6. 2
3 (a) Bestem billedligningen for den Laplacetransformerede funktion Y (s) = Ly(s) ved hjælp af formlen L(t cos(βt)) = s2 β 2 (s 2 + β 2 ) 2. ( ) (b) Udled formlen ( ). (c) Bestem løsningen y(t). (feb. 2015) Lad r(t) betegne den 2π-periodiske funktion bestemt ved at sinh(t) for π t < π. (a) Vis ved integration at r(t) har en kompleks Fourierrække n= c ne i nt med koefficienter c n = sinh(π) i n( 1) n for alle heltal n. π n 2 +1 (b) Bestem den komplekse Fourierrække y(t) = n= K ne i nt for den 2π-periodiske løsning y(t) til y (t) + 3y (t) 17y(t) = r(t). (c) Opskriv den reelle Fourierrække for løsningen y(t) fra punkt (b), og afgør dernæst om y(t) er en lige eller ulige funktion eller ingen af delene. (feb. 2015) Her betragtes vektorfeltet F i R 3 givet ved F (x, y, z) = 1 1+x 2 +y 2 +z 2 ( y, z 3, x). (a) Lad C betegne cirklen i x, y-planet givet ved x 2 + y 2 = 1, med positiv orientering (dvs. mod uret). Beregn værdien af kurveintegralet C F d r. (b) Afgør om F har et potential f(x, y, z), og angiv i så fald f. (c) Bestem fladeintegralet P (rot F ) n da, idet P betegner paraboloiden givet ved at z = 1 x 2 y 2 og z 0, og enhedsnormalvektoren n er valgt således at n k < 0 f.eks. i punktet (0, 0, 1). (feb. 2015) (a) Angiv definitionsmængden D for og begrund at f er analytisk på D. f(z) = z 2 (z 2 + 1) 2 (b) Bestem funktionens nulpunkter og poler, og angiv disses orden. (c) Udregn f s residuer i de poler, som tilhører halvplanen hvor Im z > 0. (d) Brug residueintegration til at udlede at x 2 dx = π. (x 2 +1) 2 2 (aug. 2015) Betragt begyndelsesværdiproblemet for t > 0: y (t) + 6y (t) + 13y(t) = e 3t cos(2t), y(0) = 1, y (0) = 3. (a) Bestem billedligningen for den Laplacetransformerede funktion Y (s) = Ly(s). (b) Angiv den invers Laplacetransformerede af de led i Y (s), der hidrører fra y(0) eller y (0). 3
4 (c) Bestem løsningen y(t). (aug. 2015) (a) Lad f(t) betegne den 2π-periodiske funktion bestemt ved at f(t) = cosh(3t) for π t < π. Udregn ved integration koefficienterne c n i den komplekse Fourierrække f(t) = n= c ne i nt. (b) Bestem den komplekse Fourierrække y(t) = n= K ne i nt for den 2π-periodiske løsning y(t) til y (t) + 7y (t) 13y(t) = r(t), hvor r(t) er en anden funktion havende komplekse Fourier koefficienter givet ved c n = ( 1) n 3 9+n 2. (c) Opskriv den reelle Fourierrække for løsningen y(t) fra punkt (b), og afgør dernæst om y(t) er en lige eller ulige funktion eller ingen af delene. (aug. 2015) Her betragtes vektorfeltet F i R 3 givet ved F (x, y, z) = ( 4x 2 y + z 3 y, x 3 3z 2 x, (x + y + z) 4 ). (a) Bestem for vektorfeltet F dets rotation rot F og dets divergens div F. (b) Lad C betegne cirklen i x, y-planet givet ved x 2 + y 2 = 1, med positiv orientering. Beregn værdien af kurveintegralet C F d r. (c) Bestem fladeintegralet S (rot F ) n da, idet S betegner kuglesfæren givet ved at x 2 + y 2 + z 2 = 1 og enhedsnormalvektoren n er valgt således at n k > 0 i punktet (0, 0, 1). (aug. 2015) Her betragtes funktionerne af det komplekse tal z givet ved f 1 (z) = 3 sin z z, f 2(z) = 1 z, f 3(z) = sin( 3 z ), f 4(z) = sin(3z) z 4. (a) Angiv hvilken af disse funktioner, der har hævelig singularitet i z = 0, og bestem denne funktions potensrække i udviklingspunktet z 0 = 0, inklusive rækkens konvergensradius. (b) Angiv den af funktionerne, der har pol i z = 0, og bestem såvel ordenen m af polen som funktionens Laurentrække i z 0 = 0. (De første 3 led i rækken vil være tilstrækkeligt.) (c) Udregn C sin(3z) z 4 dz, idet C betegner enhedscirklen med positiv orientering. (jan. 2014) Betragt begyndelsesværdiproblemet y (t) + 7y (t) + 12y(t) = e t sin(2t) for t > 0, y(0) = 2, y (0) = 3. (a) Bestem billedligningen for den Laplacetransformerede funktion Y (s) = Ly(s). (b) Find L 1 af (2s + 17)/((s + 3)(s + 4)) ved først at eftervise formlerne, for a b, 1 (s a)(s b) = L( 1 a b (eat e bt )), 4 s (s a)(s b) = L( 1 a b (aeat be bt )).
5 (c) Bestem løsningen y(t). (jan. 2014) Lad r(t) betegne den 2π-periodiske funktion bestemt ved at cos t for 0 t π, cos t for π t < 0. (a) Afgør om r(t) er lige eller ulige, og udnyt dette til at bestemme Fourierrækken for r(t). (b) Bestem en 2π-periodisk partikulærløsning til differentialligningen y (t) 9y (t) + 14y(t) = r(t). (jan. 2014) Her betragtes vektorfeltet F i R 3 givet ved F = (4x 2 y + sin z, 7y 2 x + tan z, 0). (a) Eftervis at rot F er lig med ( 1 tan 2 z, cos z, 7y 2 4x 2 ). (b) Lad S betegne cirkelskiven bestående af de punkter (x, y, z) R 3 som opfylder x 2 + y 2 4, z = 4. Beregn da fladeintegralet S rot F n da, idet enhedsnormalvektoren n til S er valgt så n k > 0. (c) Bestem fluxen P rot F p da, idet P betegner fladen givet ved P = (x, y, z) R 3 x 2 + y 2 4, z = x 2 y 2 } og p betegner den enhedsnormalvektor til P som opfylder p k < 0. (jan. 2014) (a) Bestem potensrækken med udviklingspunkt z 0 = 0 for funktionen og angiv dens konvergensradius. f(z) = cos(πz) + 5πz (b) Vis ved indsættelse at f(z) løser Cauchy-Riemanns ligninger i ethvert punkt z C. (c) Bestem det område D i C, hvori f(z) er en konform afbildning. (feb. 2014) Betragt differentialligningen y (t) 9y(t) = cosh(2t) for t > 0 med begyndelsesbetingelserne y(0) = 0 og y (0) = 6. (a) Bestem billedligningen for den Laplacetransformerede funktion Y (s) = Ly(s). (b) Udtryk løsningen y(t) ved hjælp af funktionen sinh(3t) og foldningen cosh(2t) sinh(3t). (c) Bestem cosh(2t) sinh(3t) og opskriv løsningen y(t) ved hjælp af eksponentialfunktioner. (feb. 2014) Lad r(t) betegne den 2π-periodiske funktion bestemt ved at t(π 2 t 2 ) for π < t π. (a) Forklar hvorfor der ingen cosinus-led optræder i Fourierrækken for r(t), og bestem denne. 5
6 (b) Bestem en 2π-periodisk partikulærløsning til differentialligningen y (t) + 2y (t) + 3y(t) = r(t). (feb. 2014) (a) Bestem vektorfeltet rot F, idet F = (x + 2yz 2 ) 2 (1, 2z2, 4yz). (feb. 2014) (b) Undersøg om F er et gradientfelt, og bestem i så fald et potential for F. (c) Lad C betegne den kvartcirkel der har centrum i origo og går fra P = (1, 0, 0) til Q = (0, 1, 0) i planen hvor z = 0. Beregn da kurveintegralet F ( r) d r C og sammenlign med værdien af L F ( r) d r, idet L betegner det rette liniestykke fra P til Q. (a) Omskriv rækken n=1 (z i 4) n 3 + i 4 til en potensrække, og bestem dernæst radius og centrum for konvergenscirklen. (b) Diskuter hvilke af de følgende funktioner, der er analytiske for z C: (c) Afgør om forskriften f(z) = z + z 2, g(z) = e sin z, h(z) = G(z) = z 1 z 2 + 3z 4 1 (z i 2) 3. fastlægger en analytisk funktion for z 4, og bestem kurveintegralet G(z) dz, S idet S betegner den cirkel hvor z = 2. (jan. 2013) Betragt begyndelsesværdiproblemet y (t) + 4y (t) 5y(t) = e t for t > 0, y(0) = 1, y (0) = 4. (1) Anvend Laplacetransformationen L til at finde løsningen y(t). Man kan benytte at s 1 s + 5 s + 1 = L( 1 6 sinh t (e 5t e t ) ). ( ) (2) Eftervis at der om foldningen e at e bt, for a b, gælder formlen Bestem L(e at e bt ). e at e bt = 1 a b (eat e bt ). 6
7 (3) Udled formlen ( ). (jan. 2013) Lad r(t) betegne den 2π-periodiske funktion bestemt ved at π t for 0 t π, π t for π t < 0. (1) Vis at r(t) er en ulige funktion. (2) Opskriv Fourierrækken for r(t). (3) Bestem en 2π-periodisk partikulærløsning til differentialligningen y (t) 3y (t) + 28y(t) = r(t). (jan. 2013) Lad S betegne fladen i R 3 med parameterfremstillingen, hvor 0 ρ 1 og 0 φ 2π, r(ρ, φ) = (ρ cos φ, 2ρ sin φ, 1 ρ 2 (cos 2 φ + 4 sin 2 φ)), Desuden betragtes vektorfeltet F = (2xy 3 cos 2 z, 3x 2 y 2 cos 2 z, x 2 y 3 sin(2z)). (1) Angiv ved en ligning sammenhængen mellem x, y og z for hvert punkt (x, y, z) S. (2) Bestem C F d r, når C betegner randkurven af S med parameterfremstillingen r(1, φ). (3) Beregn fluxen ( F ) n da, idet n = r r betegner normalvektorfeltet på S. s ρ φ (jan. 2013) Lad f(z) betegne funktionen givet ved (1) Begrund at den uendelige række f(z) = z 2. ( 1 7 )n z 2n n=0 er konvergent for alle komplekse tal z C for hvilke z < 7. (2) Bestem potensrækken for f(z) med z 0 = 0 som udviklingspunkt, og angiv dens konvergensradius. (3) Lad z 1 = i 7. Vis at f(z) fremstilles (for z z 1 < 2 7) af Laurent-rækken f(z) = i z z 1 n=0 i n (2 7) n+2 (z z 1) n. [Vink: Man kan bruge at z = (z i 7)(z + i 7), hvor man kan omskrive z + i 7 = z z 1 + i 2 7.] Angiv hvilken type singularitet f(z) har i punktet z 1. (4) Udled ved brug af residueregning at 7 f(x) dx = π 7.
8 (feb. 2013) (1) Forklar hvorfor L(u(t 1)e t ) = e1 s s 1, idet L betegner Laplacetransformationen og u(t) står for Heaviside funktionen. (2) Anvend L til at finde løsningen y 1 (t), y 2 (t) til begyndelsesværdiproblemet y 1 (t) = 2y 1 (t) 4y 2 (t) + u(t 1)e t, y 1 (0) = 3, y 2(t) = y 1 (t) 3y 2 (t) + u(t 1)e t, y 2 (0) = 0. (feb. 2013) Lad r(t) betegne den 2π-periodiske funktion bestemt ved at (1) Opskriv Fourierrækken for r(t). t 2, for π t π. (2) Bestem en 2π-periodisk partikulærløsning til differentialligningen y (t) 12y (t) + 5y(t) = r(t). (feb. 2013) Foruden vektorfeltet F (x, y, z) = (3x 2 y 2 tan z, 2x 3 y tan z, x 3 y 2 (cos z) 2 ) betragtes en kurve C med parameterfremstillingen r(φ) = (2, 2 cos φ + 1, π sin φ), 0 φ π. (feb. 2013) (1) Vis at C er en cirkelbue, og karakteriser denne. (2) Udregn divergensen og rotationen af F. (3) Bestem kurveintegralet C F d r. (1) Bestem konvergensradius R for potensrækken ( 1) n 1 (z 1) n. n n=1 Begrund at sumfunktionen g(z) er analytisk i cirkelskiven z 1 < 1. (2) Udled at G(z) er analytisk i halvplanen hvor Re z > 0, idet G(z) = 1 2 ln(x2 + y 2 ) + i arctan( y ), z = x + i y, x, y R. x (3) Vis at G(z) = g(z) når z 1 < 1. (Vink: Man kan bestemme en potensrække for G.) (jan. 2012) Betragt begyndelsesværdiproblemet givet ved y(1) = 0, y (1) = 0 og ligningen y (t) + 9y(t) = r(t), hvor r(t) er defineret ved 0, for t < 2, t 2, for t (5 point) Omskriv begyndelsesværdiproblemet således at begyndelsesbetingelserne ligger ved t = (20 point) Anvend Laplacetransformationen til at finde y(t). 8
9 (jan. 2012) Betragt differentialligningen y (t) + 4y (t) + 8y(t) = r(t), hvor r(t) er den 2πperiodiske funktion defineret ved: π 2 t 2, for π t < 0, π 2 + t 2, for 0 t < π. 1.(5 point) Vis at r(t) kan skrives som en sum af en lige og en ulige funktion. 2.(10 point) Find Fourierrækken for r(t). 3.(15 point) Find den periodiske partikulærløsning til ligningen. (jan. 2012) Betragt vektorfeltet F(x, y, z) = (x 6 z)i + xyzj + (x 5 z 3 + x)k og fladen S med parameterfremstillingen r(ρ, φ) = 2ρ cos φi + ρ sin φk, hvorved 0 ρ 5 og 0 φ 2π. 1.(5 point) Beregn F(x, y, z). 2.(10 point) Beregn F n da. S 3.(10 point) Beregn C γ F dr, når C γ betegner kurven med parameterfremstillingen γ(t) = 10 cos ti + 5 sin tk, 0 t 2π. (jan. 2012) 1. Vis at z n+1 n=0 konvergerer for alle z i det komplekse plan C. n! Lad f(z) = z n+1 n=0. Da potensrækken for konvergerer for alle z C er f(z) analytisk n! i hele C. 2. Lad C 3 (0) betegne cirklen med radius 3 og centrum i z 0 = 0 og orienteret mod uret. Beregn f(z) dz. z C 3 (0) (jan. 2011) Anvend Laplace transformationen til at løse ligningen y (t) + 2y (t) + y(t) = t 2, med begyndelsesbetingelsen y(2) = 0, y (2) = 1. (jan. 2011) Betragt vektorfeltet F (x, y, z) = (0, xz, y 2 x). Lad σ være fladen med parameterfremstillingen r(u, v) = (u + v, u 2, v 2 ), u 2 + v 2 1, og lad C betegne kurven givet ved γ(t) = (cos t + sin t, cos 2 t, sin 2 t), 0 t 2π. (i) Beregn σ rot F n da, idet n betegner σ s normalvektor. (ii) Beregn C F d γ. Hvorfor får man samme resultat? 9
10 (jan. 2011) Betragt ligningen y (t) + 2y (t) + y(t) = r(t), hvor den ydre kraft r(t) er den 2π-periodiske funktion der er defineret ved t + π/2, for π < t < 0, t 2 /π + π/2, for 0 t π. Vis at r(t) hverken er lige eller ulige. Find en 2π-periodisk partikulærløsning til ligningen. (jan. 2011) Betragt funktionen givet ved f(z) = 2z + z 2, hvor z = x + i y for reelle tal x, y. 1. Find to reelle funktioner u og v sådan at f(z) = u(x, y) + i v(x, y) for alle z. Vis at f(z) ikke er analytisk. 2. Lad γ betegne cirklen med radius 2, centrum i z 0 = i og orientering mod uret. Beregn det komplekse kurveintegral f(z) dz. γ Med venlig hilsen Jon Johnsen 10
MATEMATIK 3 EN,MP 17. september 2014 Oversigt nr. 1
 MATEMATIK 3 EN,MP 7. september 204 Oversigt nr. Her bringes en samling af de gamle eksamensopgaver: (jan. 204) Betragt begyndelsesværdiproblemet y (t) + 7y (t) + 2y(t) = e t sin(2t) for t > 0, y(0) = 2,
MATEMATIK 3 EN,MP 7. september 204 Oversigt nr. Her bringes en samling af de gamle eksamensopgaver: (jan. 204) Betragt begyndelsesværdiproblemet y (t) + 7y (t) + 2y(t) = e t sin(2t) for t > 0, y(0) = 2,
MATEMATIK 3 ET,MP, FYS, NANO 29. august 2012 Oversigt nr. 1
 ET,MP, FYS, NANO 29. august 202 Oversigt nr. Litteratur: I Matematik 3 bruger vi i efteråret 202 følgende bog: E. Kreyzig: Advanced engineering mathematics, 0. udg., Wiley, 20. Beskrivelse: Kurset vil
ET,MP, FYS, NANO 29. august 202 Oversigt nr. Litteratur: I Matematik 3 bruger vi i efteråret 202 følgende bog: E. Kreyzig: Advanced engineering mathematics, 0. udg., Wiley, 20. Beskrivelse: Kurset vil
MATEMATIK 3 EN,MP 30. august 2013 Oversigt nr. 1
 EN,MP 30. august 2013 Oversigt nr. 1 Litteratur: I Matematik 3 bruger vi (igen) i efteråret 2013 E. Kreyzig: Advanced engineering mathematics, 10. udg., Wiley, 2011. Beskrivelse: Kurset vil handle om matematiske
EN,MP 30. august 2013 Oversigt nr. 1 Litteratur: I Matematik 3 bruger vi (igen) i efteråret 2013 E. Kreyzig: Advanced engineering mathematics, 10. udg., Wiley, 2011. Beskrivelse: Kurset vil handle om matematiske
MATEMATIK 11 Eksamensopgaver Juni 1995 Juni 2001, 4. fjerdedel
 Juni 2000 MATEMATIK 11 Eksamensopgaver Juni 1995 Juni 2001, 4. fjerdedel Opgave 1. (a) Find den fuldstændige løsning til differentialligningen y 8y + 16y = 0. (b) Find den fuldstændige løsning til differentialligningen
Juni 2000 MATEMATIK 11 Eksamensopgaver Juni 1995 Juni 2001, 4. fjerdedel Opgave 1. (a) Find den fuldstændige løsning til differentialligningen y 8y + 16y = 0. (b) Find den fuldstændige løsning til differentialligningen
Eksamen i Matematik F2 d. 19. juni Opgave 2. Svar. Korte svar (ikke fuldstændige)
 Eksamen i Matematik F2 d. 9. juni 28 Korte svar (ikke fuldstændige Opgave Find realdelen, Re z, og imaginærdelen, Im z, for følgende værdier af z, a z = 2 i b z = i i c z = ln( + i Find realdelen, Re z,
Eksamen i Matematik F2 d. 9. juni 28 Korte svar (ikke fuldstændige Opgave Find realdelen, Re z, og imaginærdelen, Im z, for følgende værdier af z, a z = 2 i b z = i i c z = ln( + i Find realdelen, Re z,
MATEMATIK 3 EN,MP 28. august 2014 Oversigt nr. 1
 EN,MP 28. august 2014 Oversigt nr. 1 Litteratur: I Matematik 3 bruger vi (igen) i efteråret 2014 [K] E. Kreyzig: Advanced engineering mathematics, 10. udg., Wiley, 2011. Beskrivelse: Kurset vil handle
EN,MP 28. august 2014 Oversigt nr. 1 Litteratur: I Matematik 3 bruger vi (igen) i efteråret 2014 [K] E. Kreyzig: Advanced engineering mathematics, 10. udg., Wiley, 2011. Beskrivelse: Kurset vil handle
MATEMATIK 11 Eksamensopgaver Juni 1995 Juni 2001, 3. fjerdedel
 MATEMATIK Eksamensopgaver Juni 995 Juni 200, 3. fjerdedel August 998 Opgave. Lad f : R \ {0} R betegne funktionen givet ved f(x) = ex x for x 0. (a) Find eventuelle lokale maksimums- og minimumspunkter
MATEMATIK Eksamensopgaver Juni 995 Juni 200, 3. fjerdedel August 998 Opgave. Lad f : R \ {0} R betegne funktionen givet ved f(x) = ex x for x 0. (a) Find eventuelle lokale maksimums- og minimumspunkter
Svar til eksamen i Matematik F2 d. 23. juni 2016
 Svar til eksamen i Matematik F d. 3. juni 06 FORBEHOLD FOR FEJL! Bemærk, i modsætning til herunder, så skal det i besvarelsen fremgå tydeligt, hvordan polerne ndes og hvordan de enkelte residuer udregnes.
Svar til eksamen i Matematik F d. 3. juni 06 FORBEHOLD FOR FEJL! Bemærk, i modsætning til herunder, så skal det i besvarelsen fremgå tydeligt, hvordan polerne ndes og hvordan de enkelte residuer udregnes.
Kortfattet svar til eksamen i Matematik F2 d. 21. juni 2017
 Kortfattet svar til eksamen i Matematik F2 d. 2. juni 27 Opgave Bestem for følgende tilfælde om en funktion f(z) af z = x + iy er analytisk i dele af den komplekse plan, hvis den har real del u(x, y) og
Kortfattet svar til eksamen i Matematik F2 d. 2. juni 27 Opgave Bestem for følgende tilfælde om en funktion f(z) af z = x + iy er analytisk i dele af den komplekse plan, hvis den har real del u(x, y) og
MATEMATIK 3 EN3,MP3 28. august 2015 Oversigt nr. 1
 EN3,MP3 28. august 205 Oversigt nr. Litteratur: I Matematik 3 bruger vi (igen) i efteråret 205 [K] E. Kreyzig: Advanced engineering mathematics, 0. udg., Wiley, 20. Beskrivelse: Kurset vil handle om matematiske
EN3,MP3 28. august 205 Oversigt nr. Litteratur: I Matematik 3 bruger vi (igen) i efteråret 205 [K] E. Kreyzig: Advanced engineering mathematics, 0. udg., Wiley, 20. Beskrivelse: Kurset vil handle om matematiske
SUPPLERENDE OPGAVER TIL KOMPLEKS FUNKTIONSTEORI F2005
 SUPPLERENDE OPGAVER TIL KOMPLEKS FUNKTIONSTEORI F2005 0. maj, 2005 version nr. 8 JØRGEN VESTERSTRØM Indledende bemærkninger De foreliggende opgaver udgør et supplement til lærebogens opgaver. Afsnitsnummereringerne
SUPPLERENDE OPGAVER TIL KOMPLEKS FUNKTIONSTEORI F2005 0. maj, 2005 version nr. 8 JØRGEN VESTERSTRØM Indledende bemærkninger De foreliggende opgaver udgør et supplement til lærebogens opgaver. Afsnitsnummereringerne
Besvarelse til eksamen i Matematik F2, 2012
 Besvarelse til eksamen i Matematik F2, 202 Partiel besvarelse - har ikke inkluderet alle detaljer! Med forbehold for tastefejl. Opgave Find og bestem typen af alle singulariteter for følgende funktioner:
Besvarelse til eksamen i Matematik F2, 202 Partiel besvarelse - har ikke inkluderet alle detaljer! Med forbehold for tastefejl. Opgave Find og bestem typen af alle singulariteter for følgende funktioner:
Formelsamling - MatF2. Therkel Zøllner og Amalie Christensen 27. juni 2009
 Formelsamling - MatF2 Therkel Zøllner og Amalie Christensen 27. juni 2009 1 Indhold 1 Kompleks variabel teori 3 1.1 Komplekse funktioner 825-830........................... 3 1.2 Powerserier af komplekse
Formelsamling - MatF2 Therkel Zøllner og Amalie Christensen 27. juni 2009 1 Indhold 1 Kompleks variabel teori 3 1.1 Komplekse funktioner 825-830........................... 3 1.2 Powerserier af komplekse
Eksamen i Calculus. 14. juni f (x, y, z) = 1 + x 2 + y 2. x 2 + y 2 1 Hele rummet uden z aksen
 Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 14. juni 019 Opgave 1 (6 point) En
Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 14. juni 019 Opgave 1 (6 point) En
Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 2016
 Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Matematik F2 Opgavesæt 2
 Opgaver uge 2 I denne uge kigger vi nærmere på Cauchy-Riemann betingelserne, potensrækker, konvergenskriterier og flertydige funktioner. Vi skal også se på integration langs en ve i den komplekse plan.
Opgaver uge 2 I denne uge kigger vi nærmere på Cauchy-Riemann betingelserne, potensrækker, konvergenskriterier og flertydige funktioner. Vi skal også se på integration langs en ve i den komplekse plan.
z j 2. Cauchy s formel er værd at tænke lidt nærmere over. Se på specialtilfældet 1 dz = 2πi z
 Matematik F2 - sæt 3 af 7 blok 4 f(z)dz = 0 Hovedemnet i denne uge er Cauchys sætning (den der står i denne sides hoved) og Cauchys formel. Desuden introduceres nulpunkter og singulariteter: simple poler,
Matematik F2 - sæt 3 af 7 blok 4 f(z)dz = 0 Hovedemnet i denne uge er Cauchys sætning (den der står i denne sides hoved) og Cauchys formel. Desuden introduceres nulpunkter og singulariteter: simple poler,
Eksamen i Calculus. 14. juni f (x, y, z) = 1 + x 2 + y 2. Hele rummet uden z aksen
 Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 14. juni 019 Opgave 1 (6 point) En
Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 14. juni 019 Opgave 1 (6 point) En
Eksamen i Calculus. 14. juni f (x, y, z) = 1 + x 2 + y 2. x 2 + y 2 1 Hele rummet uden z aksen
 Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 14. juni 19 Opgave 1 (6 point) En funktion
Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 14. juni 19 Opgave 1 (6 point) En funktion
To find the English version of the exam, please read from the other end! Eksamen i Calculus
 To find the English version of the exam, please read from the other end! Se venligst bort fra den engelske version på bagsiden hvis du følger denne danske version af prøven. Eksamen i Calculus Første Studieår
To find the English version of the exam, please read from the other end! Se venligst bort fra den engelske version på bagsiden hvis du følger denne danske version af prøven. Eksamen i Calculus Første Studieår
Indhold. Litteratur 11
 Indhold Forord ii 00-sættet 1 Opgave 1....................................... 1 Spørgsmål (a).................................. 1 Spørgsmål (b).................................. 1 Spørgsmål (c)..................................
Indhold Forord ii 00-sættet 1 Opgave 1....................................... 1 Spørgsmål (a).................................. 1 Spørgsmål (b).................................. 1 Spørgsmål (c)..................................
Kompleks Funktionsteori
 Kompleks Funktionsteori Formelræs Holomorfe funktioner Sætning. (Caucy-Riemans ligninger). Funktionen f : G C, f = u+iv er holomorf i z 0 = x 0 + iy 0 hvis og kun hvis i punktet (x 0, y 0 ). du dx = dv
Kompleks Funktionsteori Formelræs Holomorfe funktioner Sætning. (Caucy-Riemans ligninger). Funktionen f : G C, f = u+iv er holomorf i z 0 = x 0 + iy 0 hvis og kun hvis i punktet (x 0, y 0 ). du dx = dv
Eksamen i Mat F, april 2006
 Eksamen i Mat F, april 26 Opgave Lad F være et vektorfelt, givet i retvinklede koordinater som: Udregn F og F: F x F = F x i + F y j + F z k = F y = z 2 F z xz y 2 F = F x + F y + F z = + + x. F = F z
Eksamen i Mat F, april 26 Opgave Lad F være et vektorfelt, givet i retvinklede koordinater som: Udregn F og F: F x F = F x i + F y j + F z k = F y = z 2 F z xz y 2 F = F x + F y + F z = + + x. F = F z
To find the English version of the exam, please read from the other end! Eksamen i Calculus
 To find the English version of the exam, please read from the other end! Se venligst bort fra den engelske version på bagsiden hvis du følger denne danske version af prøven. Eksamen i Calculus Første Studieår
To find the English version of the exam, please read from the other end! Se venligst bort fra den engelske version på bagsiden hvis du følger denne danske version af prøven. Eksamen i Calculus Første Studieår
Eksamen i Mat F, april 2006
 Eksamen i Mat F, april 26 Opgave 1 Lad F være et vektorfelt, givet i retvinklede koordinater som: F x x F = F x i + F y j + F z k = F y = 2z F z y Udregn F og F: F = F x + F y + F z = 1 + +. F = F z F
Eksamen i Mat F, april 26 Opgave 1 Lad F være et vektorfelt, givet i retvinklede koordinater som: F x x F = F x i + F y j + F z k = F y = 2z F z y Udregn F og F: F = F x + F y + F z = 1 + +. F = F z F
Den homogene ligning. Vi betragter den n te ordens, homogene, lineære differentialligning. d n y dt n. an 1 + any = 0 (1.2) dt. + a1 d n 1 y dt n 1
 1/7 Den homogene ligning Vi betragter den n te ordens, homogene, lineære differentialligning a 0 d n y dt n + a1 d n 1 y dt n 1 hvor a 0,..., a n R og a 0 0. Vi skriver ligningen på kort form som + + dy
1/7 Den homogene ligning Vi betragter den n te ordens, homogene, lineære differentialligning a 0 d n y dt n + a1 d n 1 y dt n 1 hvor a 0,..., a n R og a 0 0. Vi skriver ligningen på kort form som + + dy
Vektoranalyse INDLEDNING. Indhold. 1 Integraltricks. Jens Kusk Block Jacobsen 21. januar 2008
 Vektoranalyse Jens Kusk Block Jacobsen 21. januar 2008 INLENING ette er en opsamling af ting, jeg synes er gode at have ifbm vektoranalyse som præsenteret i kurset VEKANAE07 ved IMF på AU. Noten er dels
Vektoranalyse Jens Kusk Block Jacobsen 21. januar 2008 INLENING ette er en opsamling af ting, jeg synes er gode at have ifbm vektoranalyse som præsenteret i kurset VEKANAE07 ved IMF på AU. Noten er dels
Reeksamen i Calculus. Første Studieår ved Det Tekniske Fakultet for IT og Design samt Det Ingeniør- og Naturvidenskabelige Fakultet. 17.
 Reeksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design samt Det Ingeniør- og Naturvidenskabelige Fakultet 17. februar 2017 Dette eksamenssæt består af 11 nummererede sider med
Reeksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design samt Det Ingeniør- og Naturvidenskabelige Fakultet 17. februar 2017 Dette eksamenssæt består af 11 nummererede sider med
Skriftlig prøve i Beregningsteknik indenfor elektronikområdet
 Beregningsteknik i elektronik for EIT3+ITC3/11 Opgavesæt 18 111203HEb Skriftlig prøve i Beregningsteknik indenfor elektronikområdet Prøve d. 3. januar 2012 kl. 09.00-13.00. Ved bedømmelsen vægtes de 6
Beregningsteknik i elektronik for EIT3+ITC3/11 Opgavesæt 18 111203HEb Skriftlig prøve i Beregningsteknik indenfor elektronikområdet Prøve d. 3. januar 2012 kl. 09.00-13.00. Ved bedømmelsen vægtes de 6
INSTITUT FOR MATEMATIK OG DATALOGI. TIDLIGERE EKSAMENSOPGAVER MM01 Juni 1993 marts 2006
 INSTITUT FOR MATEMATIK OG DATALOGI TIDLIGERE EKSAMENSOPGAVER MM01 Juni 1993 marts 2006 i Forord Denne opgavesamling skal bruges med den forståelse, at pensumbeskrivelsen for kurset har undergået en række
INSTITUT FOR MATEMATIK OG DATALOGI TIDLIGERE EKSAMENSOPGAVER MM01 Juni 1993 marts 2006 i Forord Denne opgavesamling skal bruges med den forståelse, at pensumbeskrivelsen for kurset har undergået en række
Reeksamen i Calculus
 Reeksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design samt Det Ingeniør- og Naturvidenskabelige Fakultet. februar 08 Dette eksamenssæt består af 8 nummererede sider med afkrydsningsopgaver.
Reeksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design samt Det Ingeniør- og Naturvidenskabelige Fakultet. februar 08 Dette eksamenssæt består af 8 nummererede sider med afkrydsningsopgaver.
To find the English version of the exam, please read from the other end! Eksamen i Calculus
 To find the English version of the exam, please read from the other end! Se venligst bort fra den engelske version på bagsiden hvis du følger denne danske version af prøven. Eksamen i Calculus Første Studieår
To find the English version of the exam, please read from the other end! Se venligst bort fra den engelske version på bagsiden hvis du følger denne danske version af prøven. Eksamen i Calculus Første Studieår
Opgaveløsninger til eksamensopgaver. Opgavesæt 46
 EIT3+ITC3/2018 H. Ebert BEREGNINGSTEKNIK INDENFOR ELEKTRONIKOMRÅDET Opgaveløsninger til eksamensopgaver Opgavesæt 46 Beregningsteknik i elektronik for EIT3+ITC3/18 Opgavesæt 46 181229HEb Skriftlig prøve
EIT3+ITC3/2018 H. Ebert BEREGNINGSTEKNIK INDENFOR ELEKTRONIKOMRÅDET Opgaveløsninger til eksamensopgaver Opgavesæt 46 Beregningsteknik i elektronik for EIT3+ITC3/18 Opgavesæt 46 181229HEb Skriftlig prøve
INSTITUT FOR MATEMATIK OG DATALOGI. TIDLIGERE EKSAMENSOPGAVER MM501 Calculus I, MM502 Calculus II Januar 2006 juni 2010
 INSTITUT FOR MATEMATIK OG DATALOGI TIDLIGERE EKSAMENSOPGAVER MM501 Calculus I, MM502 Calculus II Januar 2006 juni 2010 Forord Denne opgavesamling indeholder samtlige eksamensopgaver, der har været stillet
INSTITUT FOR MATEMATIK OG DATALOGI TIDLIGERE EKSAMENSOPGAVER MM501 Calculus I, MM502 Calculus II Januar 2006 juni 2010 Forord Denne opgavesamling indeholder samtlige eksamensopgaver, der har været stillet
Besvarelser til Calculus Ordinær Eksamen Juni 2019
 Besvarelser til Calculus Ordinær Eksamen - 14. Juni 2019 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 14. Juni 2019 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Eksamen i Calculus. Første Studieår ved Det Tekniske Fakultet for IT og Design samt Det Ingeniør- og Naturvidenskabelige Fakultet. 3.
 Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design samt Det Ingeniør- og Naturvidenskabelige Fakultet. januar 7 Dette eksamenssæt består af 9 nummererede sider med afkrydsningsopgaver.
Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design samt Det Ingeniør- og Naturvidenskabelige Fakultet. januar 7 Dette eksamenssæt består af 9 nummererede sider med afkrydsningsopgaver.
Note om Laplace-transformationen
 Note om Laplace-transformationen Den harmoniske oscillator omskrevet til et ligningssystem I dette opgavesæt benyttes laplacetransformationen til at løse koblede differentialligninger. Fordelen ved at
Note om Laplace-transformationen Den harmoniske oscillator omskrevet til et ligningssystem I dette opgavesæt benyttes laplacetransformationen til at løse koblede differentialligninger. Fordelen ved at
Besvarelser til Calculus Ordinær Eksamen - 3. Januar 2017
 Besvarelser til Calculus Ordinær Eksamen - 3. Januar 17 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 3. Januar 17 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Matematik F2 Opgavesæt 6
 Opgave 4: Udtryk funktionen f(θ) = sin θ ved hjælp af Legendre-polynomierne på formen P l (cos θ). Dvs. find koefficienterne a l i ekspansionen f(θ) = a l P l (cos θ) l= Svar: Bemærk, at funktionen er
Opgave 4: Udtryk funktionen f(θ) = sin θ ved hjælp af Legendre-polynomierne på formen P l (cos θ). Dvs. find koefficienterne a l i ekspansionen f(θ) = a l P l (cos θ) l= Svar: Bemærk, at funktionen er
Opgaveløsninger til eksamensopgaver. Opgavesæt 22
 EIT3+ITC3/2012 H. Ebert BEREGNINGSTEKNIK INDENFOR ELEKTRONIKOMRÅDET Opgaveløsninger til eksamensopgaver Opgavesæt 22 Beregningsteknik i elektronik for EIT3+ITC3/12 Opgavesæt 22 121201HEb Skriftlig prøve
EIT3+ITC3/2012 H. Ebert BEREGNINGSTEKNIK INDENFOR ELEKTRONIKOMRÅDET Opgaveløsninger til eksamensopgaver Opgavesæt 22 Beregningsteknik i elektronik for EIT3+ITC3/12 Opgavesæt 22 121201HEb Skriftlig prøve
Eksamen i Calculus. Første Studieår ved Det Teknisk-Naturvidenskabelige Fakultet og Det Sundhedsvidenskabelige Fakultet. 6.
 Eksamen i Calculus Første Studieår ved Det Teknisk-Naturvidenskabelige Fakultet og Det Sundhedsvidenskabelige Fakultet 6. juni 16 Dette eksamenssæt består af 1 nummererede sider med 14 afkrydsningsopgaver.
Eksamen i Calculus Første Studieår ved Det Teknisk-Naturvidenskabelige Fakultet og Det Sundhedsvidenskabelige Fakultet 6. juni 16 Dette eksamenssæt består af 1 nummererede sider med 14 afkrydsningsopgaver.
Opgaver til f(z) = 1 z 4 1, g(z) = 1
 1.17 Opgaver til 1. 1 1.1. Vis, at f(z) = er vilkårligt ofte differentiabel i C \ {, 1}, og z(1 z) find et udtryk for f (n) (z) for alle n. (Vink. Skriv f(z) = 1 z + 1 1 z ). 1.2. Beskriv billedkurverne
1.17 Opgaver til 1. 1 1.1. Vis, at f(z) = er vilkårligt ofte differentiabel i C \ {, 1}, og z(1 z) find et udtryk for f (n) (z) for alle n. (Vink. Skriv f(z) = 1 z + 1 1 z ). 1.2. Beskriv billedkurverne
Matematik F Et bud på hvordan eksamenssæt løses
 Matematik F Et bud på hvordan eksamenssæt løses Jeppe Trøst Nielsen 11. april 21 Denne samling af ligninger og løsninger er udarbejdet efter det princip, at eksamenssættene ikke ændrer sig specielt meget
Matematik F Et bud på hvordan eksamenssæt løses Jeppe Trøst Nielsen 11. april 21 Denne samling af ligninger og løsninger er udarbejdet efter det princip, at eksamenssættene ikke ændrer sig specielt meget
To find the English version of the exam, please read from the other end! Eksamen i Calculus
 To find the English version of the exam, please read from the other end! Se venligst bort fra den engelske version på bagsiden hvis du følger denne danske version af prøven. Eksamen i Calculus Første Studieår
To find the English version of the exam, please read from the other end! Se venligst bort fra den engelske version på bagsiden hvis du følger denne danske version af prøven. Eksamen i Calculus Første Studieår
Reeksamen i Calculus
 Reeksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 0. februar 019 Dette eksamenssæt
Reeksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 0. februar 019 Dette eksamenssæt
x 2 + y 2 dx dy. f(x, y) = ln(x 2 + y 2 ) + 2 1) Angiv en ligning for tangentplanen til fladen z = f(x, y) i punktet
 Eksamensopgaver fra Matematik Alfa 1 Naturvidenskabelig Kandidateksamen August 1999. Matematik Alfa 1 Opgave 1. Udregn integralet 1 1 y 2 (Vink: skift til polære koordinater.) Opgave 2. Betragt funktionen
Eksamensopgaver fra Matematik Alfa 1 Naturvidenskabelig Kandidateksamen August 1999. Matematik Alfa 1 Opgave 1. Udregn integralet 1 1 y 2 (Vink: skift til polære koordinater.) Opgave 2. Betragt funktionen
Eksamen i Calculus. Første Studieår ved Det Tekniske Fakultet for IT og Design samt Det Ingeniør- og Naturvidenskabelige Fakultet. 5.
 Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design samt Det Ingeniør- og Naturvidenskabelige Fakultet 5. januar 08 Dette eksamenssæt består af 8 nummererede sider med afkrydsningsopgaver.
Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design samt Det Ingeniør- og Naturvidenskabelige Fakultet 5. januar 08 Dette eksamenssæt består af 8 nummererede sider med afkrydsningsopgaver.
Besvarelser til Calculus Ordinær Eksamen Januar 2019
 Besvarelser til Calculus Ordinær Eksamen - 14. Januar 19 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 14. Januar 19 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Prøveeksamen MR1 januar 2008
 Skriftlig eksamen Matematik 1A Prøveeksamen MR1 januar 2008 Tilladte hjælpemidler Alle sædvanlige hjælpemidler er tilladt (lærebøger, notater, osv.), og også elektroniske hjælpemidler som lommeregner og
Skriftlig eksamen Matematik 1A Prøveeksamen MR1 januar 2008 Tilladte hjælpemidler Alle sædvanlige hjælpemidler er tilladt (lærebøger, notater, osv.), og også elektroniske hjælpemidler som lommeregner og
Prøveeksamen i Calculus
 Prøveeksamen i Calculus Første Studieår ved Det Teknisk-Naturvidenskabelige Fakultet og Det Sundhedsvidenskabelige Fakultet Marts 6 Dette eksamenssæt består af 9 nummererede sider med 4 afkrydsningsopgaver.
Prøveeksamen i Calculus Første Studieår ved Det Teknisk-Naturvidenskabelige Fakultet og Det Sundhedsvidenskabelige Fakultet Marts 6 Dette eksamenssæt består af 9 nummererede sider med 4 afkrydsningsopgaver.
Opgaveløsninger til eksamensopgaver. Opgavesæt 42
 EIT3+ITC3/2017 H. Ebert BEREGNINGSTEKNIK INDENFOR ELEKTRONIKOMRÅDET Opgaveløsninger til eksamensopgaver Opgavesæt 42 Beregningsteknik i elektronik for EIT3+ITC3/17 Opgavesæt 42 171225HEb Skriftlig prøve
EIT3+ITC3/2017 H. Ebert BEREGNINGSTEKNIK INDENFOR ELEKTRONIKOMRÅDET Opgaveløsninger til eksamensopgaver Opgavesæt 42 Beregningsteknik i elektronik for EIT3+ITC3/17 Opgavesæt 42 171225HEb Skriftlig prøve
Opgave 1 Opskriv følgende vinkler i radianer 180, 90, 135, 270, 60, 30.
 Opgaver Polære koordinater Opgave 1 Opskriv følgende vinkler i radianer 180, 90, 15, 70, 60, 0. Opgave Bestem sin π Opgave. Et punkt p i xy-planen er givet ved de kartesiske koordinater,. Bestem p s polære
Opgaver Polære koordinater Opgave 1 Opskriv følgende vinkler i radianer 180, 90, 15, 70, 60, 0. Opgave Bestem sin π Opgave. Et punkt p i xy-planen er givet ved de kartesiske koordinater,. Bestem p s polære
Besvarelser til Calculus Ordinær Eksamen Juni 2018
 Besvarelser til Calculus Ordinær Eksamen - 5. Juni 08 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 5. Juni 08 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
OPGAVE 1 Det nedenstående klip er fra et Maple-ark hvor en reel funktion f (x, y) med definitionsmængden (x,y) x 2 + y 2 < 1 } bliver undersøgt:
 DANMARKS TEKNISKE UNIVERSITET Skriftlig prøve den 7. maj 00. Kursus Navn: Matematik (-timers prøve for forårssemesteret). Kursus nr. 0005 Tilladte hjælpemidler: Alle af DTU tilladte hjælpemidler må medbringes
DANMARKS TEKNISKE UNIVERSITET Skriftlig prøve den 7. maj 00. Kursus Navn: Matematik (-timers prøve for forårssemesteret). Kursus nr. 0005 Tilladte hjælpemidler: Alle af DTU tilladte hjælpemidler må medbringes
Besvarelser til Calculus Ordinær Eksamen - 5. Januar 2018
 Besvarelser til Calculus Ordinær Eksamen - 5. Januar 18 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 5. Januar 18 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
To find the English version of the exam, please read from the other end! Eksamen i Calculus
 To find the English version of the exam, please read from the other end! Se venligst bort fra den engelske version på bagsiden hvis du følger denne danske version af prøven. Eksamen i Calculus Første Studieår
To find the English version of the exam, please read from the other end! Se venligst bort fra den engelske version på bagsiden hvis du følger denne danske version af prøven. Eksamen i Calculus Første Studieår
Det teknisk-naturvidenskabelige basisår Matematik 1A, Efterår 2005, Hold 3 Prøveopgave A
 Det teknisk-naturvidenskabelige basisår Matematik 1A, Efterår 2005, Hold 3 Prøveopgave A Opgaven består af tre dele, hver med en række spørgsmål, efterfulgt af en liste af teorispørgsmål. I alle opgavespørgsmålene
Det teknisk-naturvidenskabelige basisår Matematik 1A, Efterår 2005, Hold 3 Prøveopgave A Opgaven består af tre dele, hver med en række spørgsmål, efterfulgt af en liste af teorispørgsmål. I alle opgavespørgsmålene
MM502+4 forelæsningsslides
 MM502+4 forelæsningsslides uge 11+12 1, 2009 Produceret af Hans J. Munkholm, delvis på baggrund af lignende materiale udarbejdet af Mikael Rørdam 1 I nærværende forbindelse er 11 + 12 23 1 Egenskaber for
MM502+4 forelæsningsslides uge 11+12 1, 2009 Produceret af Hans J. Munkholm, delvis på baggrund af lignende materiale udarbejdet af Mikael Rørdam 1 I nærværende forbindelse er 11 + 12 23 1 Egenskaber for
To find the English version of the exam, please read from the other end! Eksamen i Calculus
 To find the English version of the exam, please read from the other end! Se venligst bort fra den engelske version på bagsiden hvis du følger denne danske version af prøven. Eksamen i Calculus Første Studieår
To find the English version of the exam, please read from the other end! Se venligst bort fra den engelske version på bagsiden hvis du følger denne danske version af prøven. Eksamen i Calculus Første Studieår
2. Fourierrækker i en variabel
 .1. Fourierrækker i en variabel I Kapitel II 7 blev der indført, dels funktionsrummene L p (X, µ) (mere udførligt skrevet L p (X, E, µ)), dels rummene L p (X, µ), der fås af L p (X, µ) ved at funktioner
.1. Fourierrækker i en variabel I Kapitel II 7 blev der indført, dels funktionsrummene L p (X, µ) (mere udførligt skrevet L p (X, E, µ)), dels rummene L p (X, µ), der fås af L p (X, µ) ved at funktioner
Analyse 1, Prøve 2 Besvarelse
 Københavns Universitet Prøve ved Det naturvidenskabelige Fakultet maj Analyse, Prøve Besvarelse Opgave (3%) (a) (%) Bestem mængden af x R for hvilke rækken ( + (x) n ) er konvergent og angiv sumfunktionen
Københavns Universitet Prøve ved Det naturvidenskabelige Fakultet maj Analyse, Prøve Besvarelse Opgave (3%) (a) (%) Bestem mængden af x R for hvilke rækken ( + (x) n ) er konvergent og angiv sumfunktionen
Opgave nr. 1. Find det fjerde Taylorpolynomium. (nul). Opgave nr Lad der være givet et sædvanligt retvinklet koordinatsystem
 \ De reelle tal betegnes i det følgende med m og de komplekse tal med
\ De reelle tal betegnes i det følgende med m og de komplekse tal med
Matematik F2 Opgavesæt 1
 Opgaer uge 1 I denne uge er temaet komplekse tal og komplekse funktioner af en kompleks ariabel. De første opgaer skulle gerne øge jeres fortrolighed med komplekse tal. I kan med fordel repetere de basale
Opgaer uge 1 I denne uge er temaet komplekse tal og komplekse funktioner af en kompleks ariabel. De første opgaer skulle gerne øge jeres fortrolighed med komplekse tal. I kan med fordel repetere de basale
1. Vis, at hvis realdelen af en holomorf (analytisk) funktion er konstant (på et åbent område) er funktionen konstant.
 Matematik F2 - sæt 2 af 7 blok 4 f(z)dz = 0 1 I denne uge vil vi studere Cauchy-Riemann betingelserne, potensrækker, konvergenskriterier og flertydige funktioner. Vi skal også se på integration langs en
Matematik F2 - sæt 2 af 7 blok 4 f(z)dz = 0 1 I denne uge vil vi studere Cauchy-Riemann betingelserne, potensrækker, konvergenskriterier og flertydige funktioner. Vi skal også se på integration langs en
Afgør for hver af følgende rækker om den er divergent, betinget konvergent eller absolut konvergent. 2 n. n=1 2n (n + 1)2 1 = 2(n + n+1
 Analyse Reeksamen 00 Rasmus Sylvester Bryder 5. august 0 Opgave Afgør for hver af følgende rækker om den er divergent, betinget konvergent eller absolut konvergent. ( ) n n +3n+7 n= n + For alle n N vil
Analyse Reeksamen 00 Rasmus Sylvester Bryder 5. august 0 Opgave Afgør for hver af følgende rækker om den er divergent, betinget konvergent eller absolut konvergent. ( ) n n +3n+7 n= n + For alle n N vil
Matematik F2 Opgavesæt 1
 Opgaer uge 1 I denne uge er temaet komplekse tal og komplekse funktioner af en kompleks ariabel. De første opgaer skulle gerne øge jeres fortrolighed med komplekse tal. I kan med fordel repetere de basale
Opgaer uge 1 I denne uge er temaet komplekse tal og komplekse funktioner af en kompleks ariabel. De første opgaer skulle gerne øge jeres fortrolighed med komplekse tal. I kan med fordel repetere de basale
Løsningsforslag til opgavesæt 5
 Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
Løsningsforslag til opgavesæt 5
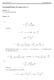 Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
Besvarelser til Calculus Ordinær eksamen - Efterår - 8. Januar 2016
 Besvarelser til Calculus Ordinær eksamen - Efterår - 8. Januar 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har
Besvarelser til Calculus Ordinær eksamen - Efterår - 8. Januar 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har
Højere Teknisk Eksamen maj 2008. Matematik A. Forberedelsesmateriale til 5 timers skriftlig prøve NY ORDNING. Undervisningsministeriet
 Højere Teknisk Eksamen maj 2008 HTX081-MAA Matematik A Forberedelsesmateriale til 5 timers skriftlig prøve NY ORDNING Undervisningsministeriet Fra onsdag den 28. maj til torsdag den 29. maj 2008 Forord
Højere Teknisk Eksamen maj 2008 HTX081-MAA Matematik A Forberedelsesmateriale til 5 timers skriftlig prøve NY ORDNING Undervisningsministeriet Fra onsdag den 28. maj til torsdag den 29. maj 2008 Forord
Noter til MatF2 på KU (Matematik for Fysikere 2)
 Noter til MatF2 på KU (Matematik for Fysikere 2) af Nikolai Plambech Nielsen, LPK33, Version.0 8. juni 206 Resumé Dette notesæt er udarbejdet til kurset Matematik for Fysikere 2 (Forkortet MatF2). Bogen,
Noter til MatF2 på KU (Matematik for Fysikere 2) af Nikolai Plambech Nielsen, LPK33, Version.0 8. juni 206 Resumé Dette notesæt er udarbejdet til kurset Matematik for Fysikere 2 (Forkortet MatF2). Bogen,
ANALYSE 1, 2014, Uge 5
 ANALYSE, 204, Uge 5 Afleveringsfrist for Prøve 2 er Tirsdag den 20/5 kl 0:5. Forelæsninger Tirsdag Vi går videre med Afsnit 4 om uniform konvergens af Fourierrækker, hvor hovedsætningen er Sætning 4.3.
ANALYSE, 204, Uge 5 Afleveringsfrist for Prøve 2 er Tirsdag den 20/5 kl 0:5. Forelæsninger Tirsdag Vi går videre med Afsnit 4 om uniform konvergens af Fourierrækker, hvor hovedsætningen er Sætning 4.3.
Komplekse tal. Mikkel Stouby Petersen 27. februar 2013
 Komplekse tal Mikkel Stouby Petersen 27. februar 2013 1 Motivationen Historien om de komplekse tal er i virkeligheden historien om at fjerne forhindringerne og gøre det umulige muligt. For at se det, vil
Komplekse tal Mikkel Stouby Petersen 27. februar 2013 1 Motivationen Historien om de komplekse tal er i virkeligheden historien om at fjerne forhindringerne og gøre det umulige muligt. For at se det, vil
Vi begynder med at repetere noget af det tidligere gennemgåede som vi skal bruge.
 Cykloider Vi begynder med at repetere noget af det tidligere gennemgåede som vi skal bruge Retningspunkt (repetition) Figur 1 viser enhedscirklen Det viste punkt P er anbragt sådan at den øverste af buerne
Cykloider Vi begynder med at repetere noget af det tidligere gennemgåede som vi skal bruge Retningspunkt (repetition) Figur 1 viser enhedscirklen Det viste punkt P er anbragt sådan at den øverste af buerne
DESIGNMAT FORÅR 2012: UGESEDDEL Forberedelse Læs alle opgaverne fra tidligere ugesedler, og læg særlig mærke til dem du har spørgsmål til.
 DESIGNMAT FORÅR 2012: UGESEDDEL 13 INSTITUT FOR MATEMATIK 1. Forberedelse Læs alle opgaverne fra tidligere ugesedler, og læg særlig mærke til dem du har spørgsmål til. 2. Aktiviteter mandag 13 17 2.1.
DESIGNMAT FORÅR 2012: UGESEDDEL 13 INSTITUT FOR MATEMATIK 1. Forberedelse Læs alle opgaverne fra tidligere ugesedler, og læg særlig mærke til dem du har spørgsmål til. 2. Aktiviteter mandag 13 17 2.1.
af koblede differentialligninger (se Apostol Bind II, s 229ff) 3. En n te ordens differentialligning
 EKSISTENS- OG ENTYDIGHEDSSÆTNINGEN Vi vil nu bevise eksistens- og entydighedssætningen for ordinære differentialligninger. For overskuelighedens skyld vil vi indskrænke os til at undersøge een 1. ordens
EKSISTENS- OG ENTYDIGHEDSSÆTNINGEN Vi vil nu bevise eksistens- og entydighedssætningen for ordinære differentialligninger. For overskuelighedens skyld vil vi indskrænke os til at undersøge een 1. ordens
Besvarelse, Eksamen Analyse 1, 2013
 Københavns Universitet Prøve ved Det naturvidenskabelige Fakultet juni 23 Besvarelse, Eksamen Analyse, 23 Opgave Lad, for n N, funktionen f n : [, ) R være givet ved NB. Trykfejl. Burde være x. f n (x)
Københavns Universitet Prøve ved Det naturvidenskabelige Fakultet juni 23 Besvarelse, Eksamen Analyse, 23 Opgave Lad, for n N, funktionen f n : [, ) R være givet ved NB. Trykfejl. Burde være x. f n (x)
DesignMat Lineære differentialligninger I
 DesignMat Lineære differentialligninger I Preben Alsholm Uge Forår 0 1 Lineære differentialligninger af første orden 1.1 Normeret lineær differentialligning Normeret lineær differentialligning En differentialligning,
DesignMat Lineære differentialligninger I Preben Alsholm Uge Forår 0 1 Lineære differentialligninger af første orden 1.1 Normeret lineær differentialligning Normeret lineær differentialligning En differentialligning,
Vektorfelter langs kurver
 enote 25 1 enote 25 Vektorfelter langs kurver I enote 24 dyrkes de indledende overvejelser om vektorfelter. I denne enote vil vi se på vektorfelternes værdier langs kurver og benytte metoder fra enote
enote 25 1 enote 25 Vektorfelter langs kurver I enote 24 dyrkes de indledende overvejelser om vektorfelter. I denne enote vil vi se på vektorfelternes værdier langs kurver og benytte metoder fra enote
Maj 2015 (alle opgaver og alle spørgsmål)
 Maj 2015 (alle opgaver og alle spørgsmål) Alternativ besvarelse (med brug af Maple til beregninger, incl. pakker til VektorAnalyse2 og Integrator8). Ved eksamen er der ikke tid til f.eks. at lave illustrationer,
Maj 2015 (alle opgaver og alle spørgsmål) Alternativ besvarelse (med brug af Maple til beregninger, incl. pakker til VektorAnalyse2 og Integrator8). Ved eksamen er der ikke tid til f.eks. at lave illustrationer,
Mat H 2 Øvelsesopgaver
 Mat H 2 Øvelsesopgaver 18. marts 1998 1) dx dt + 2t 1+t x = 1 2 1+t, fuldstændig løsning. 2 2) ẋ + t 2 x = t 2, fuldstændig løsning. 3) ẋ 2tx = t, x() = 1. 4) ẋ + 1 t x = 1 t 2, t >, undersøg løsningen
Mat H 2 Øvelsesopgaver 18. marts 1998 1) dx dt + 2t 1+t x = 1 2 1+t, fuldstændig løsning. 2 2) ẋ + t 2 x = t 2, fuldstændig løsning. 3) ẋ 2tx = t, x() = 1. 4) ẋ + 1 t x = 1 t 2, t >, undersøg løsningen
Eksamen maj 2018, Matematik 1, DTU
 Eksamen maj 2018, Matematik 1, DTU NB: Nedenstående udregninger viser flere steder mere end én metode. Det er der IKKE tid til eksamen! Ligeledes er der ikke krav om eller tid til at illustrere med plots!
Eksamen maj 2018, Matematik 1, DTU NB: Nedenstående udregninger viser flere steder mere end én metode. Det er der IKKE tid til eksamen! Ligeledes er der ikke krav om eller tid til at illustrere med plots!
Mat 1. 2-timersprøve den 13. maj 2017.
 Mat. -timersprøve den. maj 7. JE.5.7 Opgave restart:with(plots): En funktion f af to reelle variable er for x, y s, givet ved f:=(x,y)-y/(x^+y^); f d x, y / y x Cy f(x,y); y x Cy Spørgsmål I x, y Kplanen
Mat. -timersprøve den. maj 7. JE.5.7 Opgave restart:with(plots): En funktion f af to reelle variable er for x, y s, givet ved f:=(x,y)-y/(x^+y^); f d x, y / y x Cy f(x,y); y x Cy Spørgsmål I x, y Kplanen
To find the English version of the exam, please read from the other end! Eksamen i Calculus
 To find the English version of the exam, please read from the other end! Se venligst bort fra den engelske version på bagsiden hvis du følger denne danske version af prøven. Eksamen i Calculus Første Studieår
To find the English version of the exam, please read from the other end! Se venligst bort fra den engelske version på bagsiden hvis du følger denne danske version af prøven. Eksamen i Calculus Første Studieår
Lineære 2. ordens differentialligninger med konstante koefficienter
 enote 13 1 enote 13 Lineære 2. ordens differentialligninger med konstante koefficienter I forlængelse af enote 11 og enote 12 om differentialligninger, kommer nu denne enote omkring 2. ordens differentialligninger.
enote 13 1 enote 13 Lineære 2. ordens differentialligninger med konstante koefficienter I forlængelse af enote 11 og enote 12 om differentialligninger, kommer nu denne enote omkring 2. ordens differentialligninger.
Gamle eksamensopgaver (DOK)
 EO 1 Gamle eksamensopgaver ) Opgave 1. sommer 1994, opgave 1) a) Find den fuldstændige løsning til differentialligningen x 6x + 9x =. b) Find den fuldstændige løsning til differentialligningen Opgave 2.
EO 1 Gamle eksamensopgaver ) Opgave 1. sommer 1994, opgave 1) a) Find den fuldstændige løsning til differentialligningen x 6x + 9x =. b) Find den fuldstændige løsning til differentialligningen Opgave 2.
Vektorfelter. enote Vektorfelter
 enote 24 1 enote 24 Vektorfelter I enote 6 indføres og studeres vektorer i plan og rum. I enote 16 ser vi på gradienterne for funktioner f (x, y) af to variable. Et gradientvektorfelt for en funktion af
enote 24 1 enote 24 Vektorfelter I enote 6 indføres og studeres vektorer i plan og rum. I enote 16 ser vi på gradienterne for funktioner f (x, y) af to variable. Et gradientvektorfelt for en funktion af
Hans J. Munkholm: En besvarelse af
 Hans J. Munkholm: En besvarelse af Projekt for MM501, Lineære differentialligninger November-december 2009 Nummererede formler fra opgaveformuleringen Her samles alle opgavens differentialligninger og
Hans J. Munkholm: En besvarelse af Projekt for MM501, Lineære differentialligninger November-december 2009 Nummererede formler fra opgaveformuleringen Her samles alle opgavens differentialligninger og
Oversigt [S] 8.7, 8.8, 8.9
![Oversigt [S] 8.7, 8.8, 8.9 Oversigt [S] 8.7, 8.8, 8.9](/thumbs/62/47922248.jpg) Oversigt [S] 8.7, 8.8, 8.9 Nøgleord og begreber Potensrækker og opgaver Binomialformlen Binomialkoefficienter Binomialrækken Taylor polynomier Vurdering af Taylor s restled Eksponentialrækken konvereger
Oversigt [S] 8.7, 8.8, 8.9 Nøgleord og begreber Potensrækker og opgaver Binomialformlen Binomialkoefficienter Binomialrækken Taylor polynomier Vurdering af Taylor s restled Eksponentialrækken konvereger
Supplement til Matematik 1GB. Jan Philip Solovej
 Supplement til Matematik 1GB Jan Philip Solovej ii c 2001 Jan Philip Solovej, Institut for Matematiske Fag, Københavns Universitet. Alle har tilladelse til at reproducere hele eller dele af dette materiale
Supplement til Matematik 1GB Jan Philip Solovej ii c 2001 Jan Philip Solovej, Institut for Matematiske Fag, Københavns Universitet. Alle har tilladelse til at reproducere hele eller dele af dette materiale
Reeksamen i Calculus
 Reeksamen i Calculus Første Studieår ved Det Teknisk-Naturvidenskabelige Fakultet og Det Sundhedsvidenskabelige Fakultet 9. august 6 Dette eksamenssæt består af nummererede sider med 4 afkrydsningsopgaver.
Reeksamen i Calculus Første Studieår ved Det Teknisk-Naturvidenskabelige Fakultet og Det Sundhedsvidenskabelige Fakultet 9. august 6 Dette eksamenssæt består af nummererede sider med 4 afkrydsningsopgaver.
DesignMat Lineære differentialligninger I
 DesignMat Lineære differentialligninger I Preben Alsholm Uge 9 Forår 2010 1 Lineære differentialligninger af første orden 1.1 Normeret lineær differentialligning Normeret lineær differentialligning En
DesignMat Lineære differentialligninger I Preben Alsholm Uge 9 Forår 2010 1 Lineære differentialligninger af første orden 1.1 Normeret lineær differentialligning Normeret lineær differentialligning En
NATURVIDENSKABELIG KANDIDATEKSAMEN VED KØBENHAVNS UNIVERSITET. MI 2007 Obligatorisk opgave 4
 NATURVIDENSKABELIG KANDIDATEKSAMEN VED KØBENHAVNS UNIVERSITET. MI 2007 Obligatorisk opgave 4 Sættet består af 3 opgaver med ialt 15 delopgaver. Besvarelsen vil blive forkastet, medmindre der er gjort et
NATURVIDENSKABELIG KANDIDATEKSAMEN VED KØBENHAVNS UNIVERSITET. MI 2007 Obligatorisk opgave 4 Sættet består af 3 opgaver med ialt 15 delopgaver. Besvarelsen vil blive forkastet, medmindre der er gjort et
Eksamen i Calculus. Onsdag den 1. juni Første Studieår ved Det Teknisk-Naturvidenskabelige Fakultet og Det Sundhedsvidenskabelige Fakultet
 Eksamen i Calculus Onsdag den 1. juni 211 Første Studieår ved Det Teknisk-Naturvidenskabelige Fakultet og Det Sundhedsvidenskabelige Fakultet Nærværende eksamenssæt består af 7 nummererede sider med ialt
Eksamen i Calculus Onsdag den 1. juni 211 Første Studieår ved Det Teknisk-Naturvidenskabelige Fakultet og Det Sundhedsvidenskabelige Fakultet Nærværende eksamenssæt består af 7 nummererede sider med ialt
Gradienter og tangentplaner
 enote 16 1 enote 16 Gradienter og tangentplaner I denne enote vil vi fokusere lidt nærmere på den geometriske analyse og inspektion af funktioner af to variable. Vi vil især studere sammenhængen mellem
enote 16 1 enote 16 Gradienter og tangentplaner I denne enote vil vi fokusere lidt nærmere på den geometriske analyse og inspektion af funktioner af to variable. Vi vil især studere sammenhængen mellem
Projektopgave 1. Navn: Jonas Pedersen Klasse: 3.4 Skole: Roskilde Tekniske Gymnasium Dato: 5/ Vejleder: Jørn Christian Bendtsen Fag: Matematik
 Projektopgave 1 Navn: Jonas Pedersen Klasse:.4 Skole: Roskilde Tekniske Gymnasium Dato: 5/9-011 Vejleder: Jørn Christian Bendtsen Fag: Matematik Indledning Jeg har i denne opgave fået følgende opstilling.
Projektopgave 1 Navn: Jonas Pedersen Klasse:.4 Skole: Roskilde Tekniske Gymnasium Dato: 5/9-011 Vejleder: Jørn Christian Bendtsen Fag: Matematik Indledning Jeg har i denne opgave fået følgende opstilling.
Besvarelser til Calculus Ordinær Eksamen Juni 2017
 Besvarelser til Calculus Ordinær Eksamen - 12. Juni 2017 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 12. Juni 2017 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Matematiske hjælpemidler. Koordinater. 2.1 De mange bredder.
 2. Matematiske hjælpemidler. Koordinater. 2.1 De mange bredder. 2.1 I Figur 1.1 i kapitel 1 er der vist et ideelt Kartesiske eller Euklidiske koordinatsystem, med koordinater ( X, Y, Z) = ( X 1, X 2, X
2. Matematiske hjælpemidler. Koordinater. 2.1 De mange bredder. 2.1 I Figur 1.1 i kapitel 1 er der vist et ideelt Kartesiske eller Euklidiske koordinatsystem, med koordinater ( X, Y, Z) = ( X 1, X 2, X
MM501 forelæsningsslides
 MM501 forelæsningsslides uge 37, 2010 Produceret af Hans J. Munkholm 2009 bearbejdet af Jessica Carter 2010 1 Hvad er et komplekst tal? Hvordan regner man med komplekse tal? Man kan betragte udvidelsen
MM501 forelæsningsslides uge 37, 2010 Produceret af Hans J. Munkholm 2009 bearbejdet af Jessica Carter 2010 1 Hvad er et komplekst tal? Hvordan regner man med komplekse tal? Man kan betragte udvidelsen
Matematik 1 Semesteruge 5 6 (30. september oktober 2002) side 1. Komplekse tal Arbejdsplan
 Matematik Semesteruge 5 6 (30. september -. oktober 2002) side Komplekse tal Arbejdsplan I semesterugerne 5 og 6 erstattes den regulære undervisning (forelæsninger og fællestimer) af selvstudium med opgaveregning
Matematik Semesteruge 5 6 (30. september -. oktober 2002) side Komplekse tal Arbejdsplan I semesterugerne 5 og 6 erstattes den regulære undervisning (forelæsninger og fællestimer) af selvstudium med opgaveregning
