. Atunci. (a), deci consideraţiile referitoare la derivabilitatea după un vector se pot practic reduce la situaţia în care vectorul este un versor.
|
|
|
- Nicklas Aagaard
- 5 år siden
- Visninger:
Transkript
1 t 0 Observaţie. Fie u R n, u 0 n, v f(a+tv u ) f t u u u dv u f(a+tu) f u. Atunci du, deci consideraţiile referitoare la derivabilitatea după un vector se pot practic reduce la situaţia în care vectorul este un versor. Exemplu. Fie f : R 3 R, f(x, y, z) sin x + y + z şi u (, 1, ). Atunci 5 cos 5. du f(a+tu) f f(t,4+t,3 t) f(0,4,3) sin (0, 4, 3) 4t +(4+t) +(3 t) sin 5 Propoziţie. Dacă e i (0, 0,...1, 0,..., 0), i 1, n sunt versorii bazei canonice, atunci f. de i Într-adevăr, de i f. f(a+te i) f f(a 1,a,...,a i 1,a i+t,a i+1,...,a n) f(a 1,a,...,a i 1,a i,a i+1,...,a n) Observaţie. Funcţiile derivabile într-un punct după orice versor nu sunt neapărat continue în punctul respectiv (vezi probleme propuse). Prezentăm în cele ce urmează următoarea formă în R n a teoremei lui Lagrange: Teoremă (de medie). Fie D R n o mulţime deschisă şi convexă şi fie f : D R, o funcţie derivabilă pe orice direcţie în orice punct din D. Atunci, a, b D, c (a, b) (segmentul deschis din R n de capete a, b) astfel încât f(b) f d(b a) (c). Demonstraţie. Definim, ca şi în precedent, funcţia ϕ : [0, 1] R, ϕ(t) f(a + t(b a)), t [0, 1]. Evident, deoarece mulţimea D este convexă, atunci t [0, 1], a + t(b a) [a, b] D, deci ϕ este bine definită. Observăm că ϕ este derivabilă în orice punct din [0, 1] : t 0 [0, 1], ϕ(t) ϕ(t 0 ) f(a + t(b a)) f(a + t 0 (b a)) t t 0 t t 0 t t0 t t 0 Mai mult, ϕ (t) t t0 f(a + t 0 (b a) + (t t 0 )(b a)) f(a + t 0 (b a)) t t 0 f(a + t 0 (b a) + s(b a)) f(a + t 0 (b a)) s 0 s d(b a) (a + t 0(b a)). d(b a) (a + t(b a)), t [0, 1]. 1
2 Aplicând teorema lui Lagrange funcţiei ϕ, θ (0, 1) astfel încât ϕ(1) ϕ(0) ϕ (θ). Notând c a + θ(b a) (a, b), rezultă că f(b) f d(b a) (c). Consecinţă. Dacă D R n este o mulţime deschisă şi convexă şi f : D R este o funcţie derivabilă cu derivata nulă pe orice direcţie, în orice punct din D, atunci f este constantă pe D. Demonstraţie. Din teorema de medie rezultă că f(b) f, a, b D, de unde concluzia. FUNCŢII DIFERENŢIABILE. Să amintim pentru început următoarea noţiune din cazul funcţiilor reale de o variabilă reală: Fie f : (a, b) R R şi t 0 (a, b). Funcţia f este derivabilă în t 0 dacă există şi este finită ita, care se notează cu f (t 0 ) şi se numeşte f(t) f(t 0) t t0 t t 0 derivata funcţiei f în punctul t 0. De asemenea, se cunoaşte faptul că f este derivabilă în t 0 dacă şi numai dacă f este diferenţiabilă în t 0, adică există o aplicaţie liniară T (t 0 ) : R R (numită diferenţiala lui f în t 0 ), h R T (h) f (t 0 )h R, astfel încât f(t) f(t 0) T (t t 0) t t t t Fie D R n o mulţime deschisă, F : D R m, a D (deci S(a, r) D). Este natural să dăm următoarea definiţie: Definiţie. i) Funcţia F se numeşte diferenţiabilă în punctul a dacă există un operator liniar T : R n R m astfel încât F (x) F T (x a) (D) 0. x a ii) Funcţia F se numeşte diferenţiabilă pe D dacă este diferenţiabilă în orice punct din D. Observaţie. i) Notând x a h, (D) se poate scrie sub forma echivalentă (D F (a + h) F T (h) ) 0. h 0 h { F (x) F T (x a) ii) Notând α(x) x a, x D, x a 0, x a scrie sub forma echivalentă: x D,, atunci (D) se poate (D ) F (x) F + T (x a) + α(x) x a,
3 unde α(x) α 0, sau, echivalent, (D ) F (a + h) F + T (h) + α(a + h) h, h R n, cu a + h D şi h 0 α(a + h) α 0. Definiţie. Numim diferenţiala funcţiei F în punctul a, aplicaţia liniară T : R n R m, T not df, h R n df (h) R m (diferenţiala lui F în punctul a calculată în h). Observaţie. Dacă m 1, n 1, se obţine definiţia diferenţiabilităţii (care echivalează cu definiţia derivabilităţii) pentru funcţii reale de o variabilă reală. Teoremă. Dacă există, diferenţiala unei funcţii într-un punct este unică. Demonstraţie. Presupunem, prin reducere la absurd, că există doi operatori liniari diferiţi T, S : R n R m F (x) F T (x a) astfel încât x a 0 (T S)(x a) şi 0. Atunci x a 0, adică, echivalent, F (x) F S(x a) x a (T S)(h) h 0 ( ). h 0 Pe de altă parte, deoarece T S, există h 0 R n (h 0 0) aşa încât T (h 0 ) S(h 0 ). (T S)(th Din ( ) rezultă în particular că 0) (T S)(h t 0,t>0 th 0 0, deci 0) t 0,t>0 h 0 (T S)(h 0) h 0 0, de unde T (h 0 ) S(h 0 ), contradicţie. Condiţii necesare de diferenţiabilitate. Teoremă (legătura dintre diferenţiabilitate şi continuitate). Orice funcţie F : D R n R m diferenţiabilă într-un punct a D este continuă în a. (Prin urmare, dacă o funcţie nu este continuă într-un punct, nu este nici diferenţiabilă în acel punct). Demonstraţie. Deoarece F este diferenţiabilă în a, există un operator liniar T : R n R m şi o aplicaţie α : D R n R m, cu α(x) α 0, astfel încât x D, F (x) F + T (x a) + α(x) x a, de unde, întrucât operatorul liniar T este continuu, avem F (x) F, adică F este continuă în a. Observaţie. Reciproca teoremei anterioare nu este adevărată: există funcţii continue într-un punct, care nu sunt diferenţiabile în punctul respectiv, după cum se va vedea într-un exemplu următor. 3
4 Teoremă (legătura dintre diferenţiabilitate şi derivabilitatea după o direcţie). Dacă f : D R n R este diferenţiabilă în a D, atunci f este derivabilă în a după orice direcţie u 0 şi (u) du. Demonstraţie. Deoarece a D şi D este mulţime deschisă, S(a, r) D. u R n \{0}, δ r u astfel încât t R, cu t < δ, a + tu S(a, r) D. Prin urmare, deoarece f este diferenţiabilă în a D, f(a + tu) f T (tu) + α(a + tu) tu T (u) (u) (T (u) + t α(a + tu) u ) există şi este finită, deci f este derivabilă în a după u şi (u) du. Observaţie. Reciproca acestui rezultat nu este adevărată (aşa cum am văzut deja, există funcţii derivabile după orice vector nenul, dar care nu sunt continue, deci nici diferenţiabile într-un punct). Consecinţă (legătura dintre diferenţiabilitate şi derivabilitatea parţială). Dacă f : D R n R este diferenţiabilă în a D, atunci f este derivabilă parţial în raport cu orice variabilă în a şi (h) n f h i, h (h 1,..., h n ) R n. i1 Demonstraţie. Conform teoremei precedente, f este derivabilă în a după orice direcţie u 0, deci şi după versorii bazei canonice. Există aşadar f R, i 1, n şi (e i ) de i f. Atunci h (h 1,..., h n ) R n, (h) ( n h i e i ) i1 Observaţie. Prin urmare, n (e i )h i i1 T (x a) (x a) n f h i. i1 n f (x i a i ). Observaţie. Reciproca teoremei anterioare nu { este adevărată: xy Exemplu. Fie funcţia f : R R, f(x, y) x +y 0, (x, y) (0, 0). Vom arăta că deşi funcţia f este continuă şi admite derivate parţiale în (0, 0), nu este diferenţiabilă în (0, 0). Într-adevăr, dacă am presupune prin reducere la absurd că f este diferenţiabilă în (0, 0), aceasta ar însemna că (x,y) (0,0) xy (x,y) (0,0) x +y i1 f(x,y) f(0,0) [ f f x (0,0)(x 0)+ y (0,0)(y 0)] x +y 0, adică (x,y) (0,0) 0, contradicţie, deoarece ultima ită nu există. xy x +y x +y 4
5 Condiţii suficiente de diferenţiabilitate. După cum am remarcat, continuitatea unei funcţii, ca de altfel nici derivabilitatea sa parţială într-un punct nu garanteaza diferenţiabilitatea funcţiei în punctul respectiv. Totuşi, aşa cum vom demonstra în cele ce urmează, existenţa derivatelor parţiale pe o vecinătate a unui punct şi continuitatea acestora în punct antrenează diferenţiabilitatea funcţiei în punctul respectiv: Teoremă (criteriu de diferenţiabilitate). Fie f : D R n R, a D. Dacă f este parţial derivabilă în raport cu toate variabilele pe o vecinătate deschisă V V D şi dacă toate derivatele sale parţiale sunt continue în a, atunci f este diferenţiabilă în a. Demonstraţie. Pentru uşurinţa scrierii, vom presupune că n 3. Deci a (a 1, a, a 3 ). Fără a restrânge generalitatea, presupunem că V S(a, r) D. Considerăm x (x 1, x, x 3 ) S(a, r) oarecare. Avem: f(x 1, x, x 3 ) f(a 1, a, a 3 ) [f(x 1, x, x 3 ) f(a 1, x, x 3 )]+[f(a 1, x, x 3 ) f(a 1, a, x 3 )]+[f(a 1, a, x 3 ) f(a 1, a, a 3 )]. Observăm că (a 1, x, x 3 ), (a 1, a, x 3 ) S(a, r) D, deci scrierea de mai sus este corectă. Fie ϕ(t) f(t, x, x 3 ), t [a 1, x 1 ] (sau [x 1, a 1 ]). Deoarece f este parţial derivabilă în raport cu toate variabilele pe S(a, r), rezultă că funcţia de o variabilă ϕ este derivabilă, deci şi continuă pe [a 1, x 1 ] (sau [x 1, a 1 ]). Aplicând Teorema lui Lagrange funcţiei ϕ, ξ 1 (a 1, x 1 ) (sau (x 1, a 1 )) astfel încât f(x 1, x, x 3 ) f(a 1, x, x 3 ) ϕ(x 1 ) ϕ(a 1 ) ϕ (ξ 1 )(x 1 a 1 ) f (ξ 1, x, x 3 )(x 1 a 1 ). Similar, ξ (a, x ) (sau (x, a )), ξ 3 (a 3, x 3 ) (sau (x 3, a 3 )) astfel încât în final avem 5
6 f(x 1, x, x 3 ) f(a 1, a, a 3 ) f (ξ 1, x, x 3 )(x 1 a 1 ) + f (a 1, ξ, x 3 )(x a ) + + f x 3 (a 1, a, ξ 3 )(x 3 a 3 ) f (a 1, a, a 3 )(x 1 a 1 ) + f (a 1, a, a 3 )(x a ) + + f (a 1, a, a 3 )(x 3 a 3 ) + x 3 +{[ f (ξ 1, x, x 3 ) f (a 1, a, a 3 )] x (x 1 a 1 ) + }{{ 1 } α 1(x) +[ f (a 1, ξ, x 3 ) f (a 1, a, a 3 )] x (x a ) + }{{ } α (x) +[ f (a 1, a, ξ 3 ) f (a 1, a, a 3 )] x 3 x (x 3 a 3 )}. }{{ 3 } α 3(x) Dacă x (x 1, x, x 3 ) a (a 1, a, a 3 ), atunci x 1 a 1, x a, x 3 a 3, de unde ξ 1 a 1, ξ a, ξ 3 a 3. Folosind continuitatea derivatelor parţiale în (a 1, a, a 3 ), rezultă că α i (x) 0, i 1, 3, şi, ţinând seama că xi ai este mărginit, i 1, 3, rezultă că 0. x a f(x 1,x,x 3) f(a 1,a,a 3) [ f x (a 1 1,a,a 3)(x 1 a 1)+ f x (a 1,a,a 3)(x a )+ f x (a 3 1,a,a 3)(x 3 a 3)] (x (x 1,x,x 3) (a 1,a,a 3) 1,x,x 3) (a 1,a,a 3) Prin urmare, f este diferenţiabilă în a. Definiţie. Fie f : D R n R. Spunem că f este de clasă C 1 pe D (şi notăm aceasta prin f C 1 (D)) dacă f este parţial derivabilă în raport cu toate variabilele pe D şi toate derivatele sale parţiale sunt continue pe D. Consecinţă. Dacă f C 1 (D), atunci f este diferenţiabilă pe D. Reciproca acestui rezultat nu este adevărată (vezi probleme propuse). Teoremă (de reducere la componente pentru funcţii vectoriale). O funcţie F (f 1, f,..., f m ) : D deschis R n R m este diferenţiabilă în a D dacă şi numai dacă toate funcţiile componente f 1, f,..., f m : D R n R sunt diferenţiabile în a. Mai mult, diferenţierea se face pe componente: df (h) ( 1 (h), (h),..., m (h)), h R n. Demonstraţie. F (f 1, f,..., f m ) este diferenţiabilă în a dacă şi numai dacă există un operator liniar T (t 1, t,..., t m ) : R n R m şi o aplicaţie 6
7 α (α 1, α,..., α m ) : D R n R m, cu α(x) α 0, astfel încât x D, F (x) F + T (x a) + α(x) x a, adică, echivalent, x D, f 1 (x) f 1 + t 1 (x a) + α 1 (x) x a f (x) f + t (x a) + α (x) x a... f m (x) f m + t m (x a) + α m (x) x a, unde aplicaţiile t 1, t,..., t m : R n R sunt liniare şi α i (x) α i 0, i 1, m. Aceasta înseamnă că, echivalent, i 1, m, f i este diferenţiabilă în a. În plus, T df (t 1, t,..., t m ) ( 1,,..., m ). Exemplu. Fie F : R R 3, F (x, y) (x y, xy + y, x 3 ). Să calculăm df (1, )(h 1, h ), unde (h 1, h ) R este oarecare. Fie f 1, f, f 3 : R R, f 1 (x, y) x y, f (x, y) xy + y, f 3 (x, y) x 3. Evident, f 1, f, f 3 C 1 (R ), deci sunt diferenţiabile pe R şi în consecinţă F este diferenţiabilă pe R. 1 (1, )(h 1, h ) f1 x (1, )h 1 + f1 y (1, )h 4h 1 + h, (1, )(h 1, h ) f x (1, )h 1 + f y (1, )h h 1 + 5h, 3 (1, )(h 1, h ) f3 x (1, )h 1 + f3 y (1, )h 3h 1, de unde df (1, )(h 1, h ) (4h 1 + h, h 1 + 5h, 3h 1 ). Operaţii cu funcţii diferenţiabile. Propoziţie. Fie D R n o mulţime deschisă. i) Dacă F, G : D R m sunt diferenţiabile în a D, atunci: a) F + G este diferenţiabilă în a şi d(f + G) df + dg; b) λ R, λf este diferenţiabilă în a şi d(λf ) λdf ; ii) Dacă F : D R, G : D R m sunt diferenţiabile în a D, atunci F G este diferenţiabilă în a şi d(f G) F dg + G df. h 0 Demonstraţie. i) a) Fie T df şi S dg. Avem: F (a+h) F T (h) h 0 h G(a+h) G S(h) 0 şi h 0 h 0, de unde (F +G)(a+h) (F +G) (T +S)(h) h 0, deci concluzia are loc, deoarece T + S : R n R m este de asemenea operator liniar. b) se raţionează asemănător. ii) Din ipoteză, există α : D R, cu α(x) α 0, astfel încât x D, F (x) F + df (x a) + α(x) x a şi există β : D R m, cu 7
8 β(x) β 0, astfel încât x D, G(x) G + dg(x a) + β(x) x a. T df şi S dg sunt operatori liniari, T : R n R, S : R n R m. Atunci x D\{a}, (F G)(x) F (x) G(x) (F + T (x a) + α(x) x a ) (G + S(x a) + β(x) x a ) (F G) + [F S + G T ](x a) + + x a γ(x), unde γ(x) G α(x) + α(x) S(x a) + x a α(x) β(x) + T (x a) S(x a) +F β(x) + β(x) T (x a) +. x a S T {}}{{}}{ Deoarece F dg+ df G este un operator liniar, rămâne să arătăm că γ(x) 0. Într-adevăr, deoarece orice operator liniar este continuu, avem + T (x a) S(x a) x a γ(x) G α(x) + F + [α(x) S(x a) + β(x) T (x a) + +α(x) β(x) x a ] + S(x a) T (x a) 0, x a deoarece T (x a) T (0) 0, iar S(x a) S(x a) x a x a operator liniar, deci funcţie lipschitziană). L (S fiind Matrice jacobiană Fie acum F (f 1, f,..., f m ) : D deschis R n R m diferenţiabilă în punctul a D. Atunci i 1, m, f i : D R n R este diferenţiabilă, deci derivabilă parţial în raport cu toate variabilele în a D. Introducem matricea asociată diferenţialei T df : R n R m (care este operator liniar) a funcţiei F în punctul a D : ( ) J F fi x j i1,m j1,n f 1 f1... f1 f... f... f m fm... fm 8 M m,n(r)
9 numită matricea jacobiană a funcţiei F în punctul a. (denumirea este dată în onoarea matematicianului german Carl Jacobi). Evident, dacă f : D R R, atunci J f f. În situaţia în care m n, J F este matrice pătratică, iar f 1 f1... f1 det J F D(f1,...fn) D(x 1,...x n) f... f... f n fn... fn se numeşte determinantul jacobian (jacobianul) (determinantul funcţional) al lui F în a. Exemple. 1) Coordonate polare. Fie funcţia vectorială F : R + [0, π) R, F (ρ, θ) (ρ cos θ, ρ sin θ), (ρ, θ) R + [0, π). Observăm că F exprimă { legătura dintre coordonatele carteziene şi coordonatele polare în plan: ρ > 0, θ [0, π). x ρ cos θ y ρ sin θ, F este diferenţiabilă pe D deschis R + [0, π) deoarece f 1, f : R + [0, π) R sunt diferenţiabile pe D (fiind de clasă C 1 ), unde f 1 (ρ, θ) ρ cos θ, f (ρ, θ) ρ sin θ. J F (ρ, θ) ( f1 f 1 ρ θ ρ θ det J F (ρ, θ) D(f1,f) D(ρ,θ) ) Coordonate cilindrice f 1 ρ f 1 θ f 1 z ρ f 3 ρ θ f 3 θ z f 3 z ) ( ) cos θ ρ sin θ, sin θ ρ cos θ cos θ ρ sin θ sin θ ρ cos θ ρ(cos θ + sin θ) ρ. Fie funcţia vectorială F : R + [0, π) R R 3, F (ρ, θ, z) (ρ cos θ, ρ sin θ, z). x ρ cos θ y ρ sin θ, ρ > 0, θ [0, π), z R. z z Observăm că F exprimă legătura dintre coordonatele carteziene şi coordonatele cilindrice în spaţiu. F este diferenţiabilă pe D deschis R + [0, π) R deoarece f 1, f, f 3 : R + [0, π) R R sunt diferenţiabile pe D (fiind de clasă C 1 ), unde f 1 (ρ, θ, z) ρ cos θ, f (ρ, θ, z) ρ sin θ, f 3 (ρ, θ, z) z. cos θ ρ sin θ 0 J F (ρ, θ, z) sin θ ρ cos θ 0,
10 ρ. det J F (ρ, θ, z) D(f1,f,f3) D(ρ,θ,z) cos θ ρ sin θ 0 sin θ ρ cos θ ρ(cos θ + sin θ) Probleme propuse. { xy 1. Fie funcţia f : R R, f(x, y) x +y 0, (x, y) (0, 0). i) Arătaţi că funcţia f este continuă şi admite derivate parţiale în (0, 0), dar nu este diferenţiabilă în (0, 0). ii) Arătaţi că funcţia f este diferenţiabilă pe R \{(0, 0)}. { (x. Fie funcţia f : R + y 1 ) sin R, f(x, y) x +y 0, (x, y) (0, 0). Arătaţi că f este diferenţiabilă pe R, dar nu este de clasă C 1 pe R. 3. Studiaţi diferenţiabilitatea pe R a funcţiilor următoare f : R R: i) f(x, y) xy ; ii) f(x, y) 3 { xy; xy 3 iii) f(x, y) x4 +y4 0, (x, y) (0, 0); { x y iv) f(x, y) x 6 +y 0, (x, y) (0, 0); { x y x v) f(x, y) +y 0, (x, y) (0, 0). 4. Pornind de la definiţie, arătaţi ca funcţia f(x, y) x 3 + xy + y este diferenţiabilă în (1, 1). Cum se poate stabili altfel, mai simplu, acest rezultat? Este funcţia diferenţiabilă şi în rest? 5. Dacă a R n, iar F : R n R m este, pe rând: a) o funcţie constantă; b) un operator liniar, arătaţi că F este diferenţiabilă şi calculaţi df. 6. Fie F : R R 3, F (x, y) (x y, xy + y, x 3 ). Scrieţi J F (1, ). 7. Arătaţi că funcţia f : S((0, 0), r) R R îndeplinind condiţia f(x, y) x + y, (x, y) S((0, { 0), r), este diferenţiabilă în (0, 0). 8. Fie f : R x 3 y R, f(x, y) x 6 +y 0, (x, y) (0, 0). Studiaţi: i) diferenţiabilitatea lui f în (0, 0); ii) continuitatea în (0, 0) pentru funcţia g : R R, g(x, y) ( f x f (x, y), y (x, y)). 9. Fie f : R R, f(x, y) x+y x +y +1. Arătaţi că f este diferenţiabilă pe R. 10
11 10. Cercetaţi dacă f : R R, f(x, y) diferenţiabilă în (0, 0). { x 3 x +y 0, (x, y) (0, 0) 11. Studiaţi dacă derivatele { parţiale mixte de ordin în (0, 0) coincid pentru x 3 funcţia f : R (x y ) R, f(x, y) (x +y ) 0, (x, y) (0, 0). Cercetaţi dacă funcţia este diferenţiabilă pe R. 1. Scrieţi matricea jacobiană şi calculaţi determinantul (dacă este posibil) pentru următoarele funcţii vectoriale: i) F (x, y) (x + y, xy), (x, y) R ; ii) F (x, y) (x + cos y, y sin x), (x, y) R ; iii) F (x, y) (xe y, e xy, y ), (x, y) R ; iv) F (x, y, z) (x + z, y + z ), (x, y, z) R Fie f : R 3 R, f(x, y, z) x cos(y sin z). Motivaţi diferenţiabilitatea funcţiei f şi, în caz afirmativ, calculaţi (0, π, π). este 11
7. Algoritmi divide et impera
 7. Algoritmi divide et impera 7.1 Tehnica divide et impera Divide et impera este o tehnica de elaborare a algoritmilor care consta in: Descompunerea cazului ce trebuie rezolvat intr-un numar de subcazuri
7. Algoritmi divide et impera 7.1 Tehnica divide et impera Divide et impera este o tehnica de elaborare a algoritmilor care consta in: Descompunerea cazului ce trebuie rezolvat intr-un numar de subcazuri
DIDACTICA MATHEMATICA, Vol. 33(2015), pp Andra-Monica Manu
 DIDACTICA MATHEMATICA, Vol. 33(2015), pp. 51 66 REZOLVAREA NUMERICĂ A ECUAŢIILOR NELINIARE CU MAPLE Andra-Monica Manu Abstract. The paper aims to present several iterative methods for solving algebraic
DIDACTICA MATHEMATICA, Vol. 33(2015), pp. 51 66 REZOLVAREA NUMERICĂ A ECUAŢIILOR NELINIARE CU MAPLE Andra-Monica Manu Abstract. The paper aims to present several iterative methods for solving algebraic
PIESE PT SUPRASTRUCTURI FRIGORIFICE SRL
 PIESE PT SUPRASTRUCTURI FRIGORIFICE ARTICULATII PT USI LATERALE 7.1 5101-010-3 5101-010-4 5101-020-4 5101-020-3 5101-030-3 5101-030-4 COD DENUMIRE SUPRAFATA kg/buc 5101-010-4 articulatie usa laterala 135x60
PIESE PT SUPRASTRUCTURI FRIGORIFICE ARTICULATII PT USI LATERALE 7.1 5101-010-3 5101-010-4 5101-020-4 5101-020-3 5101-030-3 5101-030-4 COD DENUMIRE SUPRAFATA kg/buc 5101-010-4 articulatie usa laterala 135x60
Grafică pe calculator. Mihai-Sorin Stupariu
 Grafică pe calculator Mihai-Sorin Stupariu Sem. I, 2015-2016 Cuprins 1 Generalităţi 3 1.1 Exemplu de program OpenGL................... 3 1.2 Despre OpenGL........................... 4 1.3 Biblioteci utilizate
Grafică pe calculator Mihai-Sorin Stupariu Sem. I, 2015-2016 Cuprins 1 Generalităţi 3 1.1 Exemplu de program OpenGL................... 3 1.2 Despre OpenGL........................... 4 1.3 Biblioteci utilizate
Gamle eksamensopgaver (MASO)
 EO 1 Gamle eksamensopgaver (MASO) Opgave 1. (Vinteren 1990 91, opgave 1) a) Vis, at rækken er divergent. b) Vis, at rækken er konvergent. Opgave 2. (Vinteren 1990 91, opgave 2) Gør rede for at ligningssystemet
EO 1 Gamle eksamensopgaver (MASO) Opgave 1. (Vinteren 1990 91, opgave 1) a) Vis, at rækken er divergent. b) Vis, at rækken er konvergent. Opgave 2. (Vinteren 1990 91, opgave 2) Gør rede for at ligningssystemet
DIRECTIVA CONSILIULUI. din 13 decembrie 1976
 31977L0092 DIRECTIVA CONSILIULUI din 13 decembrie 1976 privind măsurile destinate să faciliteze exercitarea efectivă a libertăţii de stabilire şi a libertăţii de a presta servicii în cazul activităţilor
31977L0092 DIRECTIVA CONSILIULUI din 13 decembrie 1976 privind măsurile destinate să faciliteze exercitarea efectivă a libertăţii de stabilire şi a libertăţii de a presta servicii în cazul activităţilor
DOK-facitliste DOK. DOK-facitliste 1
 -facitliste 1 -facitliste Listens numre refererer til samlingen af supplerede -opgaver (de gamle eksamensopgaver. På listen står næsten kun facitter, og ikke tilstrækkelige svar på opgaverne. [Korrigeret
-facitliste 1 -facitliste Listens numre refererer til samlingen af supplerede -opgaver (de gamle eksamensopgaver. På listen står næsten kun facitter, og ikke tilstrækkelige svar på opgaverne. [Korrigeret
Eksamen i Mat F, april 2006
 Eksamen i Mat F, april 26 Opgave 1 Lad F være et vektorfelt, givet i retvinklede koordinater som: F x x F = F x i + F y j + F z k = F y = 2z F z y Udregn F og F: F = F x + F y + F z = 1 + +. F = F z F
Eksamen i Mat F, april 26 Opgave 1 Lad F være et vektorfelt, givet i retvinklede koordinater som: F x x F = F x i + F y j + F z k = F y = 2z F z y Udregn F og F: F = F x + F y + F z = 1 + +. F = F z F
PC PSI PT JEAN-MARIE MONIER GUILLAUME HABERER CÉCILE LARDON MÉTHODES ET EXERCICES. Mathématiques. méthodes et exercices. 3 e.
 PC PSI PT MÉTHODES ET EXERCICES JEAN-MARIE MONIER GUILLAUME HABERER CÉCILE LARDON Mathématiques méthodes et exercices 3 e édition Conception et création de couverture : Atelier 3+ Dunod, 201 5 rue Laromiguière,
PC PSI PT MÉTHODES ET EXERCICES JEAN-MARIE MONIER GUILLAUME HABERER CÉCILE LARDON Mathématiques méthodes et exercices 3 e édition Conception et création de couverture : Atelier 3+ Dunod, 201 5 rue Laromiguière,
Mr. Adam Smith Smith's Plastics 8 Crossfield Road Selly Oak Birmingham West Midlands B29 1WQ
 - Adresse Mr. J. Rhodes Rhodes & Rhodes Corp. 212 Silverback Drive California Springs CA 92926 Amerikansk adresse format: Vejnummer + Vejnavn Bynavn + forkortelse af staten + Postnummer Mr. Adam Smith
- Adresse Mr. J. Rhodes Rhodes & Rhodes Corp. 212 Silverback Drive California Springs CA 92926 Amerikansk adresse format: Vejnummer + Vejnavn Bynavn + forkortelse af staten + Postnummer Mr. Adam Smith
Partielle afledede og retningsafledede
 Partielle afledede og retningsafledede 1 Partielle afledede, definitioner og notationer Bertragt en funktion af to reelle variable f : D R, hvor D R 2 er et åbent område Med benyttelse af tilvækstfunktionen
Partielle afledede og retningsafledede 1 Partielle afledede, definitioner og notationer Bertragt en funktion af to reelle variable f : D R, hvor D R 2 er et åbent område Med benyttelse af tilvækstfunktionen
HOTĂRÂREA CURŢII (Camera a treia) 17 decembrie 1987 * Landsorganisationen i Danmark for Tjenerforbundet i Danmark împotriva Ny Mølle Kro
 HOTĂRÂREA CURŢII (Camera a treia) 17 decembrie 1987 * Landsorganisationen i Danmark for Tjenerforbundet i Danmark împotriva Ny Mølle Kro [cerere de pronunţare a unei hotărâri preliminare formulată de Arbejdsret
HOTĂRÂREA CURŢII (Camera a treia) 17 decembrie 1987 * Landsorganisationen i Danmark for Tjenerforbundet i Danmark împotriva Ny Mølle Kro [cerere de pronunţare a unei hotărâri preliminare formulată de Arbejdsret
Rejse Almen. Almen - Essentielle. Almen - Samtale. At spørge efter hjælp. At spørge efter om en person snakker engelsk
 - Essentielle Kan du hjælpe mig, tak? At spørge efter hjælp Snakker du engelsk? At spørge efter om en person snakker engelsk Mă puteți ajuta, vă rog? Vorbiți în engleză? snakker du _[language]_? At spørge
- Essentielle Kan du hjælpe mig, tak? At spørge efter hjælp Snakker du engelsk? At spørge efter om en person snakker engelsk Mă puteți ajuta, vă rog? Vorbiți în engleză? snakker du _[language]_? At spørge
Integration m.h.t. mål med tæthed
 Integration m.h.t. mål med tæthed Sætning (EH 11.7) Lad ν = f µ på (X, E). For alle g M + (X, E) gælder at gdν = g f dµ. Bevis: Standardbeviset: 1) indikatorfunktioner 2) simple funktioner 3) M + -funktioner.
Integration m.h.t. mål med tæthed Sætning (EH 11.7) Lad ν = f µ på (X, E). For alle g M + (X, E) gælder at gdν = g f dµ. Bevis: Standardbeviset: 1) indikatorfunktioner 2) simple funktioner 3) M + -funktioner.
Integration m.h.t. mål med tæthed
 Integration m.h.t. mål med tæthed Sætning (EH 11.7) Lad ν = f µ på (X, E). For alle g M + (X, E) gælder at gdν = g f dµ. Bevis: Standardbeviset: 1) indikatorfunktioner 2) simple funktioner 3) M + -funktioner.
Integration m.h.t. mål med tæthed Sætning (EH 11.7) Lad ν = f µ på (X, E). For alle g M + (X, E) gælder at gdν = g f dµ. Bevis: Standardbeviset: 1) indikatorfunktioner 2) simple funktioner 3) M + -funktioner.
Immigration Dokumenter
 - Generelt Unde pot găsi un formular pentru? Hvor kan jeg finde formularen til? Spørg efter en formular Când a fost emis [documentul]? Spørg hvornår et dokument blev udstedt Unde a fost emis [documentul]?
- Generelt Unde pot găsi un formular pentru? Hvor kan jeg finde formularen til? Spørg efter en formular Când a fost emis [documentul]? Spørg hvornår et dokument blev udstedt Unde a fost emis [documentul]?
Calculus Uge
 Oversigt [S], [LA] Nøgleord og begreber Egenvektorer, egenværdier og diagonalisering Dobbelt integral og polært koordinatskift Ortogonal projektion og mindste afstand Retningsafledt og gradient Maksimum/minimums
Oversigt [S], [LA] Nøgleord og begreber Egenvektorer, egenværdier og diagonalisering Dobbelt integral og polært koordinatskift Ortogonal projektion og mindste afstand Retningsafledt og gradient Maksimum/minimums
ANCA APĂTEAN. Aspecte de bază în programarea în limbaj de asamblare folosind SIMULATOR DE MICROPROCESOR 8086
 Aspecte de bază în programarea în limbaj de asamblare folosind SIMULATOR DE MICROPROCESOR 8086 2016 ANCA APĂTEAN UT Press Cluj-Napoca, 2016 ISBN 978-606-737-216-8 Editura U.T.PRESS Str. Observatorului
Aspecte de bază în programarea în limbaj de asamblare folosind SIMULATOR DE MICROPROCESOR 8086 2016 ANCA APĂTEAN UT Press Cluj-Napoca, 2016 ISBN 978-606-737-216-8 Editura U.T.PRESS Str. Observatorului
EKSAMENSOPGAVELØSNINGER CALCULUS 2 (2005) JANUAR 2006 AARHUS UNIVERSITET.. Beregn den retningsafledede D u f(0, 0).
 EKSAMENSOPGAVELØSNINGER CALCULUS 2 (2005) JANUAR 2006 AARHUS UNIVERSITET H.A. NIELSEN & H.A. SALOMONSEN Opgave. Lad f betegne funktionen f(x, y) = x cos(y) + y sin(x). ) Angiv gradienten f. 2) Lad u betegne
EKSAMENSOPGAVELØSNINGER CALCULUS 2 (2005) JANUAR 2006 AARHUS UNIVERSITET H.A. NIELSEN & H.A. SALOMONSEN Opgave. Lad f betegne funktionen f(x, y) = x cos(y) + y sin(x). ) Angiv gradienten f. 2) Lad u betegne
Eksamen i Mat F, april 2006
 Eksamen i Mat F, april 26 Opgave Lad F være et vektorfelt, givet i retvinklede koordinater som: Udregn F og F: F x F = F x i + F y j + F z k = F y = z 2 F z xz y 2 F = F x + F y + F z = + + x. F = F z
Eksamen i Mat F, april 26 Opgave Lad F være et vektorfelt, givet i retvinklede koordinater som: Udregn F og F: F x F = F x i + F y j + F z k = F y = z 2 F z xz y 2 F = F x + F y + F z = + + x. F = F z
Outline. Chapter 6: (cont d) Qijin Chen. November 21, 2013 NH = =6 CH = 15 4
 Chapter 6: Qjn Chen Department of Physcs, Zhejang Unversty November 1, 013 Copyrght c 013 by Qjn Chen; all rghts reserved. ω 3 4 1. (cont d) 1 3 n3n3n 3n (x 1, y 1, z 1 )(x, y, z ) (x 1 x ) + (y 1 y )
Chapter 6: Qjn Chen Department of Physcs, Zhejang Unversty November 1, 013 Copyrght c 013 by Qjn Chen; all rghts reserved. ω 3 4 1. (cont d) 1 3 n3n3n 3n (x 1, y 1, z 1 )(x, y, z ) (x 1 x ) + (y 1 y )
Hotărâre din data 18 noiembrie 1999 Cauza
 Hotărâre din data 18 noiembrie 1999 Cauza C-275/98 Obiectul cererii Contracte lucrări publice - Directiva 93/36/CEE - Atribuirea contractelor de lucrări publice de către un organism altul decât autoritatea
Hotărâre din data 18 noiembrie 1999 Cauza C-275/98 Obiectul cererii Contracte lucrări publice - Directiva 93/36/CEE - Atribuirea contractelor de lucrări publice de către un organism altul decât autoritatea
Oversigt Matematik Alfa 1, August 2002
 Oversigt [S], [LA] Nøgleord og begreber Egenvektorer, egenværdier og diagonalisering Dobbelt integral og polært koordinatskift Ortogonal projektion og mindste afstand Retningsafledt og gradient Maksimum/minimums
Oversigt [S], [LA] Nøgleord og begreber Egenvektorer, egenværdier og diagonalisering Dobbelt integral og polært koordinatskift Ortogonal projektion og mindste afstand Retningsafledt og gradient Maksimum/minimums
Momenter som deskriptive størrelser. Hvad vi mangler fra onsdag. Momenter for sandsynlighedsmål
 Hvad vi mangler fra onsdag Momenter som deskriptive størrelser Sandsynlighedsmål er komplicerede objekter de tildeler numeriske værdier til alle hændelser i en σ-algebra. Vi har behov for simplere, deskriptive
Hvad vi mangler fra onsdag Momenter som deskriptive størrelser Sandsynlighedsmål er komplicerede objekter de tildeler numeriske værdier til alle hændelser i en σ-algebra. Vi har behov for simplere, deskriptive
Hvad vi mangler fra onsdag. Vi starter med at gennemgå slides fra onsdag.
 Hvad vi mangler fra onsdag Vi starter med at gennemgå slides 34-38 fra onsdag. Slide 1/17 Niels Richard Hansen MI forelæsninger 6. December, 2013 Momenter som deskriptive størrelser Sandsynlighedsmål er
Hvad vi mangler fra onsdag Vi starter med at gennemgå slides 34-38 fra onsdag. Slide 1/17 Niels Richard Hansen MI forelæsninger 6. December, 2013 Momenter som deskriptive størrelser Sandsynlighedsmål er
Computing the constant in Friedrichs inequality
 Computing the constant in Friedrichs inequality Tomáš Vejchodský vejchod@math.cas.cz Institute of Mathematics, Žitná 25, 115 67 Praha 1 February 8, 212, SIGA 212, Prague Motivation Classical formulation:
Computing the constant in Friedrichs inequality Tomáš Vejchodský vejchod@math.cas.cz Institute of Mathematics, Žitná 25, 115 67 Praha 1 February 8, 212, SIGA 212, Prague Motivation Classical formulation:
MÅLESTOKSFORHOLD HFB 2012 / 13. Målestoksforhold OP SL AG. Byggecentrum
 MÅLESTOKSFORHOLD Målestoksforhold 340 MÅLEENHEDER Måleenheder Omsætning: Gl. dansk mål metermål gl. engelsk mål (= amerikansk mål). Se også: Målesystemer og enheder. Gl. dansk mål Metermål Gl. engelsk
MÅLESTOKSFORHOLD Målestoksforhold 340 MÅLEENHEDER Måleenheder Omsætning: Gl. dansk mål metermål gl. engelsk mål (= amerikansk mål). Se også: Målesystemer og enheder. Gl. dansk mål Metermål Gl. engelsk
4. C05-CAPITOLUL 4: PROCEDEE DE TRATARE A AERULUI [ii]
![4. C05-CAPITOLUL 4: PROCEDEE DE TRATARE A AERULUI [ii] 4. C05-CAPITOLUL 4: PROCEDEE DE TRATARE A AERULUI [ii]](/thumbs/83/87845260.jpg) 4.2. Tratarea aerului cu apă 4. C05-CAPITOLUL 4: PROCEDEE DE TRATARE A AERULUI [ii] 4.1 4.1. Probleme generale Aerul încăperilor din clădirile civile și industriale tinde să-și modifice permanent parametrii
4.2. Tratarea aerului cu apă 4. C05-CAPITOLUL 4: PROCEDEE DE TRATARE A AERULUI [ii] 4.1 4.1. Probleme generale Aerul încăperilor din clădirile civile și industriale tinde să-și modifice permanent parametrii
Aplicaţii ale radiaţiilor electromagnetice în domeniul medical
 J. Neamţu P.G. Anoaica Aplicaţii ale radiaţiilor electromagnetice în domeniul medical 2991,10 1377,59 1053,87 628,69 1763,98 Abs 1239,44 Editura Medicală Universitară Craiova, 2006 Prefaţă Lucrarea de
J. Neamţu P.G. Anoaica Aplicaţii ale radiaţiilor electromagnetice în domeniul medical 2991,10 1377,59 1053,87 628,69 1763,98 Abs 1239,44 Editura Medicală Universitară Craiova, 2006 Prefaţă Lucrarea de
Punktgrupper. Klaus Thomsen
 Punktgrupper Klaus Thomsen 1. Forord Disse noter er skrevet med henblik på et efteruddannelses-kursus for gymnasielærere i matematik og/eller kemi. Formålet er at give en introduktion til matematikken
Punktgrupper Klaus Thomsen 1. Forord Disse noter er skrevet med henblik på et efteruddannelses-kursus for gymnasielærere i matematik og/eller kemi. Formålet er at give en introduktion til matematikken
z + w z + w z w = z 2 w z w = z w z 2 = z z = a 2 + b 2 z w
 Komplekse tal Hvis z = a + ib og w = c + id gælder z + w = (a + c) + i(b + d) z w = (a c) + i(b d) z w = (ac bd) + i(ad bc) z w = a+ib c+id = ac+bd + i bc ad, w 0 c +d c +d z a b = i a +b a +b Konjugation
Komplekse tal Hvis z = a + ib og w = c + id gælder z + w = (a + c) + i(b + d) z w = (a c) + i(b d) z w = (ac bd) + i(ad bc) z w = a+ib c+id = ac+bd + i bc ad, w 0 c +d c +d z a b = i a +b a +b Konjugation
Multivariate Extremes and Dependence in Elliptical Distributions
 Multivariate Extremes and Dependence in Elliptical Distributions Filip Lindskog, RiskLab, ETH Zürich joint work with Henrik Hult, KTH Stockholm I II III IV V Motivation Elliptical distributions A class
Multivariate Extremes and Dependence in Elliptical Distributions Filip Lindskog, RiskLab, ETH Zürich joint work with Henrik Hult, KTH Stockholm I II III IV V Motivation Elliptical distributions A class
8 Regulære flader i R 3
 8 Regulære flader i R 3 Vi skal betragte særligt pæne delmængder S R 3 kaldet flader. I det følgende opfattes S som et topologisk rum i sportopologien, se Definition 5.9. En åben omegn U af p S er således
8 Regulære flader i R 3 Vi skal betragte særligt pæne delmængder S R 3 kaldet flader. I det følgende opfattes S som et topologisk rum i sportopologien, se Definition 5.9. En åben omegn U af p S er således
Heisenbergs usikkerhedsrelationer. Abstrakt. Hvorfor? Funktionsrum. Nils Byrial Andersen Institut for Matematik. Matematiklærerdag 2013
 Heisenbergs usikkerhedsrelationer Nils Byrial Andersen Institut for Matematik Matematiklærerdag 013 1 / 17 Abstrakt Heisenbergs usikkerhedsrelationer udtrykker at man ikke på samme tid både kan bestemme
Heisenbergs usikkerhedsrelationer Nils Byrial Andersen Institut for Matematik Matematiklærerdag 013 1 / 17 Abstrakt Heisenbergs usikkerhedsrelationer udtrykker at man ikke på samme tid både kan bestemme
Vektoranalyse INDLEDNING. Indhold. 1 Integraltricks. Jens Kusk Block Jacobsen 21. januar 2008
 Vektoranalyse Jens Kusk Block Jacobsen 21. januar 2008 INLENING ette er en opsamling af ting, jeg synes er gode at have ifbm vektoranalyse som præsenteret i kurset VEKANAE07 ved IMF på AU. Noten er dels
Vektoranalyse Jens Kusk Block Jacobsen 21. januar 2008 INLENING ette er en opsamling af ting, jeg synes er gode at have ifbm vektoranalyse som præsenteret i kurset VEKANAE07 ved IMF på AU. Noten er dels
Asking whether there are commission fees when you withdraw money in a certain country
 - General Kan jeg hæve penge i [land] uden at betale gebyrer? Pot retrage numerar în [țara] fără a plăti comisioane? Asking whether there are commission fees when you withdraw money in a certain country
- General Kan jeg hæve penge i [land] uden at betale gebyrer? Pot retrage numerar în [țara] fără a plăti comisioane? Asking whether there are commission fees when you withdraw money in a certain country
6.1 Reelle Indre Produkter
 SEKTION 6.1 REELLE INDRE PRODUKTER 6.1 Reelle Indre Produkter Definition 6.1.1 Et indre produkt på et reelt vektorrum V er en funktion, : V V R således at, for alle x, y V, I x, x 0 med lighed x = 0, II
SEKTION 6.1 REELLE INDRE PRODUKTER 6.1 Reelle Indre Produkter Definition 6.1.1 Et indre produkt på et reelt vektorrum V er en funktion, : V V R således at, for alle x, y V, I x, x 0 med lighed x = 0, II
Mat H 2 Øvelsesopgaver
 Mat H 2 Øvelsesopgaver 18. marts 1998 1) dx dt + 2t 1+t x = 1 2 1+t, fuldstændig løsning. 2 2) ẋ + t 2 x = t 2, fuldstændig løsning. 3) ẋ 2tx = t, x() = 1. 4) ẋ + 1 t x = 1 t 2, t >, undersøg løsningen
Mat H 2 Øvelsesopgaver 18. marts 1998 1) dx dt + 2t 1+t x = 1 2 1+t, fuldstændig løsning. 2 2) ẋ + t 2 x = t 2, fuldstændig løsning. 3) ẋ 2tx = t, x() = 1. 4) ẋ + 1 t x = 1 t 2, t >, undersøg løsningen
Oversigt Matematik Alfa 1, Januar 2003
 Oversigt [S], [LA] Nøgleord og begreber Egenvektorer, egenværdier og diagonalisering Dobbelt integral og polært koordinatskift Ortogonal projektion og mindste afstand Retningsafledt og gradient Maksimum/minimums
Oversigt [S], [LA] Nøgleord og begreber Egenvektorer, egenværdier og diagonalisering Dobbelt integral og polært koordinatskift Ortogonal projektion og mindste afstand Retningsafledt og gradient Maksimum/minimums
UGESEDDEL 10 LØSNINGER. = f
 UGESEDDEL 10 LØSNINGER Theorem 1. Algoritme for løsning af max f(x, y) når g(x, y) c. Dan Lagrange-funktionen: L (x, y) = f(x, y) λ(g(x, y) c). Beregn de partielle afledte af L og kræv at de begge er nul:
UGESEDDEL 10 LØSNINGER Theorem 1. Algoritme for løsning af max f(x, y) når g(x, y) c. Dan Lagrange-funktionen: L (x, y) = f(x, y) λ(g(x, y) c). Beregn de partielle afledte af L og kræv at de begge er nul:
GEOMETRI-TØ, UGE 6. . x 1 x 1. = x 1 x 2. x 2. k f
 GEOMETRI-TØ, UGE 6 Hvis I falder over tryk- eller regne-fejl i nedenstående, må I meget gerne sende rettelser til fuglede@imfaudk Opvarmningsopgave 1 Lad f : R 2 R være tre gange kontinuert differentierbar
GEOMETRI-TØ, UGE 6 Hvis I falder over tryk- eller regne-fejl i nedenstående, må I meget gerne sende rettelser til fuglede@imfaudk Opvarmningsopgave 1 Lad f : R 2 R være tre gange kontinuert differentierbar
Løsningsforslag til opgavesæt 5
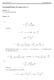 Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
Løb 1, 100m Frisvømning Damer # Nr. Navn Født Klub Licens Bassin Anmtid Status Gotthard Amalie Thirstrup Caroline Friis Elmquist Nicoline
 S i d e : 1D a t o : 0 6 d e c e m b e r 2 0 1 5Ti d : 1 5 : 11 : 3 5 Startliste Løb 1-35 Stævne navn : Julestævne 2015 Stævne by : Slagelse Arrangør : Slagelse Svømmeklub Løb 1, 100m Frisvømning Damer
S i d e : 1D a t o : 0 6 d e c e m b e r 2 0 1 5Ti d : 1 5 : 11 : 3 5 Startliste Løb 1-35 Stævne navn : Julestævne 2015 Stævne by : Slagelse Arrangør : Slagelse Svømmeklub Løb 1, 100m Frisvømning Damer
Løsningsforslag til opgavesæt 5
 Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
A B C D E Hjemmeværnmuseet's arkiv/depot Søgaard Distrikter - LMD. Reol/hylde Region/distrikt/m.m. Kasse nr. Indhold 2C3 Flyverhjemmeværne 1
 0 A B C D E Hjemmeværnmuseet's arkiv/depot Søgaard LMK Distrikter - LMD. Reol/hylde Region/distrikt/m.m. Kasse nr. Indhold C Flyverhjemmeværne Flyverhjemmeværnet LMD Odense Nyt fra stabseskadrillen -.
0 A B C D E Hjemmeværnmuseet's arkiv/depot Søgaard LMK Distrikter - LMD. Reol/hylde Region/distrikt/m.m. Kasse nr. Indhold C Flyverhjemmeværne Flyverhjemmeværnet LMD Odense Nyt fra stabseskadrillen -.
Huseftersynsordningen plus, minus ti år -
 Huseftersynsordningen plus, minus ti år - ! # # # % & # ( ( #! # ) # ( & # # # # +! #!# %, # # #! %.# / # # 0#( # # # # # # %, # # # 1 # # % 2 # & # # 0#( # # # # # 2 # #! 2 ( # # 3 ( & # # # (#! #, #
Huseftersynsordningen plus, minus ti år - ! # # # % & # ( ( #! # ) # ( & # # # # +! #!# %, # # #! %.# / # # 0#( # # # # # # %, # # # 1 # # % 2 # & # # 0#( # # # # # 2 # #! 2 ( # # 3 ( & # # # (#! #, #
Differentialregning i R k
 Differentialregning i R k Lad U R k være åben, og lad h : U R m være differentiabel. Den afledte i et punkt x U er Dh(x) = h 1 (x) x 1 h 2 (x) x 1. h m (x) x 1 h 1 (x) x 2... h 2 (x) x 2.... h m (x) x
Differentialregning i R k Lad U R k være åben, og lad h : U R m være differentiabel. Den afledte i et punkt x U er Dh(x) = h 1 (x) x 1 h 2 (x) x 1. h m (x) x 1 h 1 (x) x 2... h 2 (x) x 2.... h m (x) x
Antag at. 1) f : R k R m er differentiabel i x, 2) g : R m R p er differentiabel i y = f(x), . p.1/18
 Differentialregning i R k Kæderegel Lad U R k være åben, og lad h : U R m være differentiabel Antag at Den afledte i et punkt x U er Dh(x) = 1) f : R k R m er differentiabel i x, 2) g : R m R p er differentiabel
Differentialregning i R k Kæderegel Lad U R k være åben, og lad h : U R m være differentiabel Antag at Den afledte i et punkt x U er Dh(x) = 1) f : R k R m er differentiabel i x, 2) g : R m R p er differentiabel
MONOTONE POSITIVE SOLUTIONS FOR p-laplacian EQUATIONS WITH SIGN CHANGING COEFFICIENTS AND MULTI-POINT BOUNDARY CONDITIONS
 Electronic Journal of Differential Equations, Vol. 22, No. 22, pp. 2. ISSN: 72-669. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu ftp ejde.math.txstate.edu MONOTONE POSITIVE SOLUTIONS FOR
Electronic Journal of Differential Equations, Vol. 22, No. 22, pp. 2. ISSN: 72-669. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu ftp ejde.math.txstate.edu MONOTONE POSITIVE SOLUTIONS FOR
DOK DOK-facitliste 1. DOK-facitliste
 -facitliste 1 -facitliste Listens numre refererer til samlingen af supplerede -opgaver (de gamle eksamensopgaver. På listen står næsten kun facitter, og ikke tilstrækkelige svar på opgaverne. [Korrigeret
-facitliste 1 -facitliste Listens numre refererer til samlingen af supplerede -opgaver (de gamle eksamensopgaver. På listen står næsten kun facitter, og ikke tilstrækkelige svar på opgaverne. [Korrigeret
Giovanni Battista PERGOLESI ( ) Transcription pour orgue : R. LOPES
 Giovai Battista PERGOLESI (110-1) Stabat Mate Tascitio ou ogue : R. LOPES 1....... 8. 9. 10 11. 1. Stabat Mate doloosa Cuus aimam gemetem O quam tistis et alicta Quae moeebat et dolebat Quis est homo Vidit
Giovai Battista PERGOLESI (110-1) Stabat Mate Tascitio ou ogue : R. LOPES 1....... 8. 9. 10 11. 1. Stabat Mate doloosa Cuus aimam gemetem O quam tistis et alicta Quae moeebat et dolebat Quis est homo Vidit
Pontryagin Approximations for Optimal Design of Elastic Structures
 Pontryagin Approximations for Optimal Design of Elastic Structures Jesper Carlsson NADA, KTH jesperc@nada.kth.se Collaborators: Anders Szepessy, Mattias Sandberg October 5, 2005 A typical optimal design
Pontryagin Approximations for Optimal Design of Elastic Structures Jesper Carlsson NADA, KTH jesperc@nada.kth.se Collaborators: Anders Szepessy, Mattias Sandberg October 5, 2005 A typical optimal design
Kalkulus 2 - Grænseovergange, Kontinuitet og Følger
 Kalkulus - Grænseovergange, Kontinuitet og Følger Mads Friis 8. januar 05 Indhold Grundlæggende uligheder Grænseovergange 3 3 Kontinuitet 9 4 Følger 0 5 Perspektivering 4 Grundlæggende uligheder Sætning
Kalkulus - Grænseovergange, Kontinuitet og Følger Mads Friis 8. januar 05 Indhold Grundlæggende uligheder Grænseovergange 3 3 Kontinuitet 9 4 Følger 0 5 Perspektivering 4 Grundlæggende uligheder Sætning
S U R P R I N D E V I I T O R U L
 SURPRINDE VIITORUL *Captează mai mult. Creaza mai mult Vedeţi din perspective diferite Fiecare fotograf este unic. Indiferent ce idei, experienţă sau viziune creativă aveţi, există un obiectiv NIKKOR care
SURPRINDE VIITORUL *Captează mai mult. Creaza mai mult Vedeţi din perspective diferite Fiecare fotograf este unic. Indiferent ce idei, experienţă sau viziune creativă aveţi, există un obiectiv NIKKOR care
CONSILIUL UNIUNII EUROPENE. Bruxelles, 29 aprilie 2009 (19.05) (OR. en) 9241/09 PESC 545 COARM 25 NOTĂ
 CONSIIU UNIUNII EUPENE Bruxelles, 29 aprilie 2009 (19.05) (OR. en) 9241/09 PESC 545 COAR 25 NOTĂ Sursă: Destinatar: Subiect: Secretariatul Delegaţiile Ghidul de utilizare a Poziţiei comune 2008/944/PESC
CONSIIU UNIUNII EUPENE Bruxelles, 29 aprilie 2009 (19.05) (OR. en) 9241/09 PESC 545 COAR 25 NOTĂ Sursă: Destinatar: Subiect: Secretariatul Delegaţiile Ghidul de utilizare a Poziţiei comune 2008/944/PESC
Sandsynlighed og Statistik
 36 Sandsynlighed og Statistik 6.1 Indledning Denne note beskriver de statistiske begreber og formler som man med rimelig sandsynlighed kan komme ud for i eksperimentelle øvelser. Alt er yderst korfattet,
36 Sandsynlighed og Statistik 6.1 Indledning Denne note beskriver de statistiske begreber og formler som man med rimelig sandsynlighed kan komme ud for i eksperimentelle øvelser. Alt er yderst korfattet,
Nøgleord og begreber Analysens hovedsætning Stamfunktioner Itereret integral Test itereret integral Fubinis sætning Test Fubini Eksempler Test produkt
 Oversigt [S] 5.2, 5.3, 5.4, 2., 2.2 Nøgleord og begreber Analysens hovedsætning Stamfunktioner Itereret integral Test itereret integral Fubinis sætning Test Fubini Eksempler Test produkt Calculus - 26
Oversigt [S] 5.2, 5.3, 5.4, 2., 2.2 Nøgleord og begreber Analysens hovedsætning Stamfunktioner Itereret integral Test itereret integral Fubinis sætning Test Fubini Eksempler Test produkt Calculus - 26
Mr. Adam Smith Smith's Plastics 8 Crossfield Road Selly Oak Birmingham West Midlands B29 1WQ
 - Address Mr. J. Rhodes Rhodes & Rhodes Corp. 212 Silverback Drive California Springs CA 92926. American address format: Street number + street name Name of town + state abbreviation + zip code Mr. Adam
- Address Mr. J. Rhodes Rhodes & Rhodes Corp. 212 Silverback Drive California Springs CA 92926. American address format: Street number + street name Name of town + state abbreviation + zip code Mr. Adam
Noter til Lineær Algebra
 Noter til Lineær Algebra Eksamensnoter til LinAlg Martin Sparre, www.logx.dk, August 2007, Version π8 9450. INDHOLD 2 Indhold 0. Om disse noter.......................... 3 Abstrakte vektorrum 4. Definition
Noter til Lineær Algebra Eksamensnoter til LinAlg Martin Sparre, www.logx.dk, August 2007, Version π8 9450. INDHOLD 2 Indhold 0. Om disse noter.......................... 3 Abstrakte vektorrum 4. Definition
Nøgleord og begreber Analysens hovedsætning Stamfunktioner Itereret integral Test itereret integral Fubinis sætning Test Fubini Eksempler Test produkt
 Oversigt [S] 5., 5.3, 5.4,.,. Nøgleord og begreber Analysens hovedsætning Stamfunktioner Itereret integral Test itereret integral Fubinis sætning Test Fubini Eksempler Test produkt Calculus - 6 Uge 39.
Oversigt [S] 5., 5.3, 5.4,.,. Nøgleord og begreber Analysens hovedsætning Stamfunktioner Itereret integral Test itereret integral Fubinis sætning Test Fubini Eksempler Test produkt Calculus - 6 Uge 39.
Reeksamen 2014/2015 Mål- og integralteori
 Reeksamen 4/5 Mål- og integralteori Københavns Universitet Institut for Matematiske Fag Formalia Eksamensopgaven består af 4 opgaver med ialt spørgsmål. Ved bedømmelsen indgår de spørgsmål med samme vægt.
Reeksamen 4/5 Mål- og integralteori Københavns Universitet Institut for Matematiske Fag Formalia Eksamensopgaven består af 4 opgaver med ialt spørgsmål. Ved bedømmelsen indgår de spørgsmål med samme vægt.
Copiii sănătoși cu vârste cuprinse între 0-2 ani într-o tară nouă SUNDE BØRN I ET NYT LAND 0-2 ÅR RUMÆNSK
 Copiii sănătoși cu vârste cuprinse între 0-2 ani într-o tară nouă SUNDE BØRN I ET NYT LAND 0-2 ÅR RUMÆNSK 2017 Indhold Tillykke med jeres baby 1 At blive forældre i et fremmed land 2 Det danske sundhedsvæsen
Copiii sănătoși cu vârste cuprinse între 0-2 ani într-o tară nouă SUNDE BØRN I ET NYT LAND 0-2 ÅR RUMÆNSK 2017 Indhold Tillykke med jeres baby 1 At blive forældre i et fremmed land 2 Det danske sundhedsvæsen
INSTITUT FOR MATEMATIK OG DATALOGI. TIDLIGERE EKSAMENSOPGAVER MM501 Calculus I, MM502 Calculus II Januar 2006 juni 2010
 INSTITUT FOR MATEMATIK OG DATALOGI TIDLIGERE EKSAMENSOPGAVER MM501 Calculus I, MM502 Calculus II Januar 2006 juni 2010 Forord Denne opgavesamling indeholder samtlige eksamensopgaver, der har været stillet
INSTITUT FOR MATEMATIK OG DATALOGI TIDLIGERE EKSAMENSOPGAVER MM501 Calculus I, MM502 Calculus II Januar 2006 juni 2010 Forord Denne opgavesamling indeholder samtlige eksamensopgaver, der har været stillet
Formelsamling - MatF2. Therkel Zøllner og Amalie Christensen 27. juni 2009
 Formelsamling - MatF2 Therkel Zøllner og Amalie Christensen 27. juni 2009 1 Indhold 1 Kompleks variabel teori 3 1.1 Komplekse funktioner 825-830........................... 3 1.2 Powerserier af komplekse
Formelsamling - MatF2 Therkel Zøllner og Amalie Christensen 27. juni 2009 1 Indhold 1 Kompleks variabel teori 3 1.1 Komplekse funktioner 825-830........................... 3 1.2 Powerserier af komplekse
MASO Uge 8. Invers funktion sætning og Implicit given funktion sætning. Jesper Michael Møller. Department of Mathematics University of Copenhagen
 MASO Uge 8 Invers funktion sætning og Implicit given funktion sætning Jesper Michael Møller Department of Mathematics University of Copenhagen Uge 43 Formålet med MASO Oversigt Invertible og lokalt invertible
MASO Uge 8 Invers funktion sætning og Implicit given funktion sætning Jesper Michael Møller Department of Mathematics University of Copenhagen Uge 43 Formålet med MASO Oversigt Invertible og lokalt invertible
ANEXA I REZUMATUL CARACTERISTICILOR PRODUSULUI
 ANEXA I REZUMATUL CARACTERISTICILOR PRODUSULUI 1 1. DENUMIREA COMERCIALĂ A MEDICAMENTULUI Ranexa 375 mg comprimate cu eliberare prelungită 2. COMPOZIŢIA CALITATIVĂ ŞI CANTITATIVĂ Fiecare comprimat conţine
ANEXA I REZUMATUL CARACTERISTICILOR PRODUSULUI 1 1. DENUMIREA COMERCIALĂ A MEDICAMENTULUI Ranexa 375 mg comprimate cu eliberare prelungită 2. COMPOZIŢIA CALITATIVĂ ŞI CANTITATIVĂ Fiecare comprimat conţine
Rejse Almen. Almen - Essentielle. Almen - Samtale. At spørge efter hjælp. At spørge efter om en person snakker engelsk
 - Essentielle Können Sie mir bitte helfen? At spørge efter hjælp Sprechen Sie Englisch? At spørge efter om en person snakker engelsk Mă puteți ajuta, vă rog? Vorbiți în engleză? Sprechen Sie _[Sprache]_?
- Essentielle Können Sie mir bitte helfen? At spørge efter hjælp Sprechen Sie Englisch? At spørge efter om en person snakker engelsk Mă puteți ajuta, vă rog? Vorbiți în engleză? Sprechen Sie _[Sprache]_?
af koblede differentialligninger (se Apostol Bind II, s 229ff) 3. En n te ordens differentialligning
 EKSISTENS- OG ENTYDIGHEDSSÆTNINGEN Vi vil nu bevise eksistens- og entydighedssætningen for ordinære differentialligninger. For overskuelighedens skyld vil vi indskrænke os til at undersøge een 1. ordens
EKSISTENS- OG ENTYDIGHEDSSÆTNINGEN Vi vil nu bevise eksistens- og entydighedssætningen for ordinære differentialligninger. For overskuelighedens skyld vil vi indskrænke os til at undersøge een 1. ordens
= λ([ x, y)) + λ((y, x]) = ( y ( x)) + (x y) = 2(x y).
![= λ([ x, y)) + λ((y, x]) = ( y ( x)) + (x y) = 2(x y). = λ([ x, y)) + λ((y, x]) = ( y ( x)) + (x y) = 2(x y).](/thumbs/58/42581589.jpg) Analyse 2 Øvelser Rasmus Sylvester Bryder 17. og 20. september 2013 Supplerende opgave 1 Lad λ være Lebesgue-målet på R og lad A B(R). Definér en funktion f : [0, ) R ved f(x) = λ(a [ x, x]). Vis, at f(x)
Analyse 2 Øvelser Rasmus Sylvester Bryder 17. og 20. september 2013 Supplerende opgave 1 Lad λ være Lebesgue-målet på R og lad A B(R). Definér en funktion f : [0, ) R ved f(x) = λ(a [ x, x]). Vis, at f(x)
SUPPLERENDE OPGAVER TIL KOMPLEKS FUNKTIONSTEORI F2005
 SUPPLERENDE OPGAVER TIL KOMPLEKS FUNKTIONSTEORI F2005 0. maj, 2005 version nr. 8 JØRGEN VESTERSTRØM Indledende bemærkninger De foreliggende opgaver udgør et supplement til lærebogens opgaver. Afsnitsnummereringerne
SUPPLERENDE OPGAVER TIL KOMPLEKS FUNKTIONSTEORI F2005 0. maj, 2005 version nr. 8 JØRGEN VESTERSTRØM Indledende bemærkninger De foreliggende opgaver udgør et supplement til lærebogens opgaver. Afsnitsnummereringerne
DesignMat Den komplekse eksponentialfunktion og polynomier
 DesignMat Den komplekse eksponentialfunktion og polynomier Preben Alsholm Uge 8 Forår 010 1 Den komplekse eksponentialfunktion 1.1 Definitionen Definitionen Den velkendte eksponentialfunktion x e x vil
DesignMat Den komplekse eksponentialfunktion og polynomier Preben Alsholm Uge 8 Forår 010 1 Den komplekse eksponentialfunktion 1.1 Definitionen Definitionen Den velkendte eksponentialfunktion x e x vil
Sandsynlighedsteori
 Fordelingskatalog til Sandsynlighedsteori 1.1 + 1.2 Svend Erik Graversen August 2005 1 Dette katalog indeholder de vigtigste egenskaber ved de 6 mest almindelige diskrete fordelinger samt de 11 mest almindelige
Fordelingskatalog til Sandsynlighedsteori 1.1 + 1.2 Svend Erik Graversen August 2005 1 Dette katalog indeholder de vigtigste egenskaber ved de 6 mest almindelige diskrete fordelinger samt de 11 mest almindelige
MASO Uge 7. Differentiable funktioner. Jesper Michael Møller. Uge 7. Formålet med MASO. Department of Mathematics University of Copenhagen
 MASO Uge 7 Differentiable funktioner Jesper Michael Møller Department of Mathematics University of Copenhagen Uge 7 Formålet med MASO Oversigt Differentiable funktioner R n R m Differentiable funktioner
MASO Uge 7 Differentiable funktioner Jesper Michael Møller Department of Mathematics University of Copenhagen Uge 7 Formålet med MASO Oversigt Differentiable funktioner R n R m Differentiable funktioner
Trykfejlsliste - alle fejl Asymptotisk teori
 9. januar 2005 Stat 2A / EH Trykfejlsliste - alle fejl Asymptotisk teori Denne liste indeholder alle de regulære fejl, slåfejl og stavefejl der er fundet i 2A-noterne indtil nu. 9 1 Forkert: x C x ro alle
9. januar 2005 Stat 2A / EH Trykfejlsliste - alle fejl Asymptotisk teori Denne liste indeholder alle de regulære fejl, slåfejl og stavefejl der er fundet i 2A-noterne indtil nu. 9 1 Forkert: x C x ro alle
DIFFERENTIALLIGNINGER. Mogens Esrom Larsen
 DIERENTIALLIGNINGER Mogens Esrom Larsen København 21 Noter til indledning af kurset DL1, der er en indledning til teorien for partielle differentialligninger. Indhold 1. Kurver og flader. 1. 2. Differentialformer
DIERENTIALLIGNINGER Mogens Esrom Larsen København 21 Noter til indledning af kurset DL1, der er en indledning til teorien for partielle differentialligninger. Indhold 1. Kurver og flader. 1. 2. Differentialformer
Acest document reprezintă un instrument de documentare, iar instituţiile nu îşi asumă responsabilitatea pentru conţinutul său.
 1985R3821 RO 01.10.2011 015.001 1 Acest document reprezintă un instrument de documentare, iar instituţiile nu îşi asumă responsabilitatea pentru conţinutul său. B REGULAMENTUL (CEE) NR. 3821/85 AL CONSILIULUI
1985R3821 RO 01.10.2011 015.001 1 Acest document reprezintă un instrument de documentare, iar instituţiile nu îşi asumă responsabilitatea pentru conţinutul său. B REGULAMENTUL (CEE) NR. 3821/85 AL CONSILIULUI
Indhold. Litteratur 11
 Indhold Forord ii 00-sættet 1 Opgave 1....................................... 1 Spørgsmål (a).................................. 1 Spørgsmål (b).................................. 1 Spørgsmål (c)..................................
Indhold Forord ii 00-sættet 1 Opgave 1....................................... 1 Spørgsmål (a).................................. 1 Spørgsmål (b).................................. 1 Spørgsmål (c)..................................
 1 2 3 4 1 2 3 4 (p A ) (p B ) (p C ) 1 2, 3, 4 2, 3, 4 {2, 3, 4} 1 2 (p A ) (p B ) (p C ) d d {1, 2} (p A,p B )=0
1 2 3 4 1 2 3 4 (p A ) (p B ) (p C ) 1 2, 3, 4 2, 3, 4 {2, 3, 4} 1 2 (p A ) (p B ) (p C ) d d {1, 2} (p A,p B )=0
Den homogene ligning. Vi betragter den n te ordens, homogene, lineære differentialligning. d n y dt n. an 1 + any = 0 (1.2) dt. + a1 d n 1 y dt n 1
 1/7 Den homogene ligning Vi betragter den n te ordens, homogene, lineære differentialligning a 0 d n y dt n + a1 d n 1 y dt n 1 hvor a 0,..., a n R og a 0 0. Vi skriver ligningen på kort form som + + dy
1/7 Den homogene ligning Vi betragter den n te ordens, homogene, lineære differentialligning a 0 d n y dt n + a1 d n 1 y dt n 1 hvor a 0,..., a n R og a 0 0. Vi skriver ligningen på kort form som + + dy
Besvarelser til Calculus Ordinær Eksamen Juni 2018
 Besvarelser til Calculus Ordinær Eksamen - 5. Juni 08 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 5. Juni 08 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Wigner s semi-cirkel lov
 Wigner s semi-cirkel lov 12. december 2009 Eulers Venner Steen Thorbjørnsen Institut for Matematiske Fag Århus Universitet Diagonalisering af selvadjungeret matrix Lad H være en n n matrix med komplekse
Wigner s semi-cirkel lov 12. december 2009 Eulers Venner Steen Thorbjørnsen Institut for Matematiske Fag Århus Universitet Diagonalisering af selvadjungeret matrix Lad H være en n n matrix med komplekse
GEOMETRI-TØ, UGE 12. A σ (R) = A f σ (f(r))
 GEOMETRI-TØ, UGE 12 Hvis I falder over tryk- eller regne-fejl i nedenstående, må I meget gerne sende rettelser til fuglede@imfaudk Opvarmningsopgave 1, [P] 632 Vis at Ennepers flade σ(u, v) = ( u u 3 /3
GEOMETRI-TØ, UGE 12 Hvis I falder over tryk- eller regne-fejl i nedenstående, må I meget gerne sende rettelser til fuglede@imfaudk Opvarmningsopgave 1, [P] 632 Vis at Ennepers flade σ(u, v) = ( u u 3 /3
MATEMATIK 11 Eksamensopgaver Juni 1995 Juni 2001, 4. fjerdedel
 Juni 2000 MATEMATIK 11 Eksamensopgaver Juni 1995 Juni 2001, 4. fjerdedel Opgave 1. (a) Find den fuldstændige løsning til differentialligningen y 8y + 16y = 0. (b) Find den fuldstændige løsning til differentialligningen
Juni 2000 MATEMATIK 11 Eksamensopgaver Juni 1995 Juni 2001, 4. fjerdedel Opgave 1. (a) Find den fuldstændige løsning til differentialligningen y 8y + 16y = 0. (b) Find den fuldstændige løsning til differentialligningen
Matematik F Et bud på hvordan eksamenssæt løses
 Matematik F Et bud på hvordan eksamenssæt løses Jeppe Trøst Nielsen 11. april 21 Denne samling af ligninger og løsninger er udarbejdet efter det princip, at eksamenssættene ikke ændrer sig specielt meget
Matematik F Et bud på hvordan eksamenssæt løses Jeppe Trøst Nielsen 11. april 21 Denne samling af ligninger og løsninger er udarbejdet efter det princip, at eksamenssættene ikke ændrer sig specielt meget
Moderne acceleratorers fysik og anvendelse Forelæsning 2 Transverse motion, Lattices
 Moderne acceleratorers fysik og anvendelse Forelæsning 2 Transverse motion, Lattices Optiske elementer: Styring og fokusering. Bevægelsesligningen og dens løsning. Stabilitet. Typiske latticekonfigurationer.
Moderne acceleratorers fysik og anvendelse Forelæsning 2 Transverse motion, Lattices Optiske elementer: Styring og fokusering. Bevægelsesligningen og dens løsning. Stabilitet. Typiske latticekonfigurationer.
Calculus II Project. Calculus II Projekt. (26.3.2012 12.00 to 30.3.2012 12.00) (26.3.2012 12.00 til 30.3.2012 12.00)
 Calculus II Project Calculus II Projekt (26.3.212 12. to 3.3.212 12.) (26.3.212 12. til 3.3.212 12.) You have to solve the project questions on your own, i. e. you are not allowed to do it together in
Calculus II Project Calculus II Projekt (26.3.212 12. to 3.3.212 12.) (26.3.212 12. til 3.3.212 12.) You have to solve the project questions on your own, i. e. you are not allowed to do it together in
Cunoașteți-vă drepturile. destinat tuturor angajaților implicați în lucrările de construcție a metroului uşor în capitală
 Cunoașteți-vă drepturile destinat tuturor angajaților implicați în lucrările de construcție a metroului uşor în capitală 2018 Toți angajații care lucrează la construcția metroului şi a metroului uşor în
Cunoașteți-vă drepturile destinat tuturor angajaților implicați în lucrările de construcție a metroului uşor în capitală 2018 Toți angajații care lucrează la construcția metroului şi a metroului uşor în
UGESEDDEL 9 LØSNINGER. Sydsæter Theorem 1. Sætning om implicitte funktioner for ligningen f(x, y) = 0.
 UGESEDDEL 9 LØSNINGER Sydsæter 531 Theorem 1 Sætning om implicitte funktioner for ligningen f(x, y) = 0 Lad f(x, y) være C 1 i mængden A R n og lad (x 0, y 0 ) være et indre punkt i A hvor f(x 0, y 0 )
UGESEDDEL 9 LØSNINGER Sydsæter 531 Theorem 1 Sætning om implicitte funktioner for ligningen f(x, y) = 0 Lad f(x, y) være C 1 i mængden A R n og lad (x 0, y 0 ) være et indre punkt i A hvor f(x 0, y 0 )
Bemærkning Den dobbelte Riemannsum af en funktion f : R R er. 2 Sætning (Polært koordinatskift) For f kontinuert på det polære rektangel
 Oversigt [S].4,.5,.7 Pol og sigtelinje [S] Appendi H. Polr coordintes Nøgleord og egreer epetition: Polære koordinter Lgkgestkker Koordintskift Tpe II vrinten August, opgve Populære nvendelser Flv højere...
Oversigt [S].4,.5,.7 Pol og sigtelinje [S] Appendi H. Polr coordintes Nøgleord og egreer epetition: Polære koordinter Lgkgestkker Koordintskift Tpe II vrinten August, opgve Populære nvendelser Flv højere...
Aristoteles Camillo. To cite this version: HAL Id: hal
 An experimentally-based modeling study of the effect of anti-angiogenic therapies on primary tumor kinetics for data analysis of clinically relevant animal models of metastasis Aristoteles Camillo To cite
An experimentally-based modeling study of the effect of anti-angiogenic therapies on primary tumor kinetics for data analysis of clinically relevant animal models of metastasis Aristoteles Camillo To cite
Geschäftskorrespondenz Brief
 - Adresse Mr. J. Rhodes Rhodes & Rhodes Corp. 212 Silverback Drive California Springs CA 92926. Amerikanisches Adressenformat: Name der Stadt + Abkürzung des Staates + Postleitzahl Mr. J. Rhodes Rhodes
- Adresse Mr. J. Rhodes Rhodes & Rhodes Corp. 212 Silverback Drive California Springs CA 92926. Amerikanisches Adressenformat: Name der Stadt + Abkürzung des Staates + Postleitzahl Mr. J. Rhodes Rhodes
hvor a og b er konstanter. Ved middelværdidannelse fås videre
 Uge 3 Teoretisk Statistik. marts 004. Korrelation og uafhængighed, repetition. Eksempel fra sidste gang (uge ) 3. Middelværdivektor, kovarians- og korrelationsmatrix 4. Summer af stokastiske variable 5.Den
Uge 3 Teoretisk Statistik. marts 004. Korrelation og uafhængighed, repetition. Eksempel fra sidste gang (uge ) 3. Middelværdivektor, kovarians- og korrelationsmatrix 4. Summer af stokastiske variable 5.Den
Besvarelser til de to blokke opgaver på Ugeseddel 7
 Besvarelser til de to blokke opgaver på Ugeseddel 7 De anførte besvarelser er til dels mere summariske end en god eksamensbesvarelse bør være. Der kan godt være fejl i - jeg vil meget gerne informeres,
Besvarelser til de to blokke opgaver på Ugeseddel 7 De anførte besvarelser er til dels mere summariske end en god eksamensbesvarelse bør være. Der kan godt være fejl i - jeg vil meget gerne informeres,
Antag X 1, X 2,..., X n er n uafhængige stokastiske variable, hvor Var(X 1 )=σ 2 1,..., Var(X n )=σ 2 n.
 Simple fejlforplantningslov Landmålingens fejlteori Lektion 6 Den generelle fejlforplantningslov Antag X, X,, X n er n uafhængige stokastiske variable, hvor Var(X )σ,, Var(X n )σ n Lad Y g(x, X,, X n ),
Simple fejlforplantningslov Landmålingens fejlteori Lektion 6 Den generelle fejlforplantningslov Antag X, X,, X n er n uafhængige stokastiske variable, hvor Var(X )σ,, Var(X n )σ n Lad Y g(x, X,, X n ),
ANEXA I REZUMATUL CARACTERISTICILOR PRODUSULUI
 ANEXA I REZUMATUL CARACTERISTICILOR PRODUSULUI 1 1. DENUMIREA COMERCIALĂ A MEDICAMENTULUI Humalog 100 unități/ml, soluţie injectabilă în flacon 2. COMPOZIŢIA CALITATIVĂ ŞI CANTITATIVĂ 2.1 Descriere generală
ANEXA I REZUMATUL CARACTERISTICILOR PRODUSULUI 1 1. DENUMIREA COMERCIALĂ A MEDICAMENTULUI Humalog 100 unități/ml, soluţie injectabilă în flacon 2. COMPOZIŢIA CALITATIVĂ ŞI CANTITATIVĂ 2.1 Descriere generală
Sandsynlighedsregning
 Mogens Bladt www2.imm.dtu.dk/courses/02405 21. September, 2007 Lidt om binomialkoefficienter n størrelsen af en mængde/population. Vi ønsker at udtage en sub population af størrelse r. To sub populationer
Mogens Bladt www2.imm.dtu.dk/courses/02405 21. September, 2007 Lidt om binomialkoefficienter n størrelsen af en mængde/population. Vi ønsker at udtage en sub population af størrelse r. To sub populationer
Sandsynlighedsregning 9. forelæsning Bo Friis Nielsen
 Sandsynlighedsregning 9. forelæsning Bo Friis Nielsen Matematik og Computer Science Danmarks Tekniske Universitet 800 Kgs. Lyngby Danmark Email: bfni@dtu.dk Dagens emner afsnit 5.3 og 5.4 Simultane kontinuerte
Sandsynlighedsregning 9. forelæsning Bo Friis Nielsen Matematik og Computer Science Danmarks Tekniske Universitet 800 Kgs. Lyngby Danmark Email: bfni@dtu.dk Dagens emner afsnit 5.3 og 5.4 Simultane kontinuerte
Hamiltons princip. Et systems bane (i konfigurationsrummet) fra t 1 til t 2 er bestemt
 Hamtons prncp.1 Konfguratonsrum q 3 Et systems bane ( konfguratonsrummet) fra t t er bestemt af, at aktonsntegraet I = Lt har en statonær vær. t q 1 q () Systemet ska være monogensk, vs. ae kræfter (ekskusvt
Hamtons prncp.1 Konfguratonsrum q 3 Et systems bane ( konfguratonsrummet) fra t t er bestemt af, at aktonsntegraet I = Lt har en statonær vær. t q 1 q () Systemet ska være monogensk, vs. ae kræfter (ekskusvt
Bilag 2 - Spildevandsplan 2011-2021
 Bilag 2 - Spildevandsplan 2011-2021 Alle eksisterende ejendomme på følgende matrikler skal separatkloakeres Arninge 4c Ore By, Arninge 2016-2021 Arninge 4e Ore By, Arninge 2016-2021 Arninge 4f Ore By,
Bilag 2 - Spildevandsplan 2011-2021 Alle eksisterende ejendomme på følgende matrikler skal separatkloakeres Arninge 4c Ore By, Arninge 2016-2021 Arninge 4e Ore By, Arninge 2016-2021 Arninge 4f Ore By,
2 Separation af de variable. 4 Eksistens- og entydighed af løsninger. 5 Ligevægt og stabilitet. 6 En model for forrentning af kapital med udtræk
 Oversig Mes repeiion med fokus på de sværese emner Modul 3: Differenialligninger af. orden Maemaik og modeller 29 Thomas Vils Pedersen Insiu for Grundvidenskab og Miljø vils@life.ku.dk 3 simple yper differenialligninger
Oversig Mes repeiion med fokus på de sværese emner Modul 3: Differenialligninger af. orden Maemaik og modeller 29 Thomas Vils Pedersen Insiu for Grundvidenskab og Miljø vils@life.ku.dk 3 simple yper differenialligninger
