|
|
|
- Cecilie Mathiasen
- 4 år siden
- Visninger:
Transkript
1
2
3
4
5
6
7
8
9
10
11 (p A ) (p B ) (p C ) 1 2, 3, 4 2, 3, 4 {2, 3, 4} 1 2 (p A ) (p B ) (p C ) d d {1, 2} (p A,p B )=0<d {1,2,3,4} (p A,p B ) (p 1,...,p n ) (q 1,...,q n ) d(p, q) = n j=1 (p j q j ) 2, d(p, q) = 1 2 n j=1 p j q j
12 2 2, 3, 4 2, 3, 4 {1, 2, 3, 4} 0.13 {1, {2, 3, 4}} 0.14 d(p, q) = 1 i pi q i {1, 2} {3, 4} (p A ) (p B ) (p C ) (p A ) (p B ) (p C ) {1, 2, 3, 4} {1, 2} d(p, q) = ( ) i pi q i
13 8/9 8/10 9/10 p A p B p C d(p B,p A ) d(p B,p C ) 0 0 {1, 2} i
14
15
16
17 Θ={θ 1,...,θ n } (Θ) := {p R n + j p j =1,p j 0, j} Θ (Θ) = {p (Θ) p j > 0, j} p q (Θ) p i p(i) p i D Θ : (Θ) (Θ) R + {+ } Θ D Θ {+ } D Θ (Θ) (Θ) D Θ Θ p, q (Θ) D Θ (p, q) =0 p = q.
18 p, q D(p, q) =0 p = q Θ 1, Θ 2 γ :Θ 1 Θ 2 p, q (Θ 1 ) D Θ2 (p γ 1,q γ 1 )=D Θ1 (p, q), p γ 1 Θ 2 p γ 1 (θ 2 ):=p(γ 1 (θ 2 )) Θ n = Θ D n n n := {x R n i x i =1,x j 0} Θ Θ γ :Θ Θ D Θ R n p 1,p 2,q 1,q 2 n D n (λp 1 +(1 λ)p 2,λq 1 +(1 λ)q 2 ) {D n (p 1,q 1 ),D n (p 2,q 2 )}, λ [0, 1]
19 p 1,q 1,p 2,q 2 p 1 = p p 2 = q 1 = q 2 D n (λp +(1 λ)q, q) D n (p, q) p = p 1 = p 2 D n (p, λq 1 +(1 λ)q 2 ) {D n (p, q 1 ),D n (p, q 2 )} D n p, q n D n 1 ((p 1 + p 2,...,p n ), (q 1 + q 2,...,q n )) D n ((p 1,p 2,...,p n ), (q 1,q 2,...,q n )). n, m N p n q m p q nm nm p q p q =(p 1 q 1,...,p 1 q m,...,p j q 1,...,p j q m,...,p n q 1,...,p n q m ). n, m N p (1),p (2) n q (1),q (2) m D nm (p (1) q (1),p (2) q (2) )=D n (p (1),p (2) )+D m (q (1),q (2) ).
20 i =1,...n 1 p, q n i i +1 D n (p, (q 1,...,q i ϵ, q i+1 + ϵ,..., q n )) D n (p, q) i D n (p, q) :=. ϵ 0 ϵ i D n (p, q) q i +1 i i j id n(p,q) j D n(p,q) i, j {1,...,n 1} j D n (p, q) 0 i D n (p, q) j D n (p, q) = g(p i,p i+1,p j,p j+1 ; q i,q i+1,q j,q j+1 ), i, i +1,j,j+1
21 D Θ Θ p, q (Θ) D Θ (p, q) =a ( ) p(θ) p(θ) + b q(θ) θ Θ θ ( ) q(θ) q(θ), p(θ) a, b 0 ( D Θ (p, q) =a p(θ) z R \ { 0.5, 0.5} θ ( ) ) z 0.5 p(θ) q(θ) a>0 z > 0.5 a<0 z < 0.5 D(p, q) p, q n n p j = q j =0 0 α /0 β =0
22 0 (0/0) = 0 p j > 0=q j α, β > 0 p α j /0 = + 0/p β j =0 p j (p j /0) = + 0 (0/p j )=0 Supp(p) p Supp(p) ={θ Θ p θ > 0} p, q n j p j /q j D n (p, q) Θ n D(p, q) p q D(p, q) =D(q, p) p, q D(p, q) = j (p j q j ) ( pj q j ) = j p j ( pj q j ) + j ( ) qj q j ; p j ( ) D(p, q) = pj q j. j D(p, q) = j f j(p j,q j )
23 D(p, q) < + Supp(p) Supp(q) D KL (p q)+d KL (q p) D KL (p q) = j p j ( pj q j ) p q q p p q q Θ q p p LR q p(θ)q(θ ) p(θ )q(θ), θ θ. Θ f j :[0, 1] [0, 1] R
24 p LR q LR r Θ p i q j q i p j q i r j r i q j, i j. p, q, r n p< LR q< LR r, D(p, q) D(p, r). Θ p< FOSD q< FOSD r D(p, q) D(p, r) D αd α>0 q p j j q i p i, i=1 i=1 j, p FOSD q
25 ( D z j p j (p, q) := ( j p j ( pj q j ) z 0.5 ) ( pj q j ) z 0.5 ) z > 0.5, z < 0.5. z z D z D z p, q, r n D z (p, q) <D z (p, r) D z (p, q) >D z (p, r). D z j ( ) z 0.5 pj p j = ( ) qj p j φ z, φ z (x) =x 0.5 z. q j p j j p q (p 1 /q 1,...,p n /q n ) φ z p q z p j φ z (q j /p j )= j j ( ) z 0.5 pj p j = ( ) z 0.5 qj q j = q j φ z+1 (p j /q j ). q j p j j j φ z q j /p j p, q j p j qj p j =1 qj p j q j p j
26 z 0.5, 0.5 z > 0.5 φ z ( ) z < 0.5 φ z ( ) D z z q1 p 1! P q j p j j z p j z z q2 p 2 q3 p 3 q 1 /p 1 q 2 /p 2 q 3 /p 3 z>0.5 z(x) z(x) z(x) z < 0.5 φ z x z< 0.5 φ z x z>0.5 φ z x φ z z R \{0.5, 0.5} (D z ) z R\{ 0.5,0.5} p, q n z 0.5, 0.5 D z (p, q) =D z (q, p) z R z z 0.5 Dz (p, q) =( p(θ)/q(θ) p z 0.5),
27 w f : Θ R + f(θ) p w := ( i f(θ i) w p(θ i )) 1/w D z z =0.5 z = 0.5 D z (p, q) z 0.5 z 0.5 = j p j ( pj q j ) =: D 0.5 (p, q) z 0.5 D z (p, q) z 0.5 = j ( ) qj q j =: D 0.5 (p, q). p j z D z D z p q D z z f z p f z p z<z f D z R \ { 0.5, 0.5} D 0.5 D 0.5 (p, q) =D KL (p q) D 0.5 (p, q) =D KL (q p) p, q n D z n z < 0.5 D z (p, q) =+ Supp(p) Supp(q) =. z 0.5 z 0.5 D z (p, q) =+ Supp(p) \ Supp(q). z 0.5 D z (p, q) =+ Supp(q) \ Supp(p). n n \ n
28 D z n n n n n p D z (p, ) : n R q D z (p, q) z 0.5 D z (p, ) : n R p n D z θ Supp(p) ( D z j Supp(p) p j (p, q) = j Supp(p) p j ( pj ( pj q j ) z 0.5 ) q j ) z>0.5. z =0.5 D z (,q): n R q n z 0.5 D z (,q): n R q n D z θ Supp(q) ( D z j Supp(q) p j (p, q) = j Supp(q) p j ( pj ( pj q j ) z 0.5 ) q j ) z>0.5. z =0.5 D z (p, ) : n R p n z < 0.5 D z : n n R
29 D z (p, q) = j Supp(p) Supp(q) ( ) z 0.5 pj p j, q j j =0 n D z p, q n z 0.5 D z n z < 0.5 n x := j x j n z 0.5 ϵ, δ > 0 p, q,, n p q > x,y n x y δ, <ϵ, D z (, ) >D z ( p, q) z < 0.5 D z (p, q) ϵ δ p q δ D z (p, q) <ϵ D z z > 0.5 R n
30 z < 0.5 D z D z z > 0.5 p ϵ =(1 ϵ, ϵ) q ϵ =(1 ϵ 3,ϵ 3 ) ϵ 0 p ϵ,q ϵ (1, 0) p ϵ q ϵ 0 ( ) z 1 ϵ ( ϵ ) z D z (p ϵ,q ϵ )=(1 ϵ) + ϵ +, ϵ 0, 1 ϵ 3 ϵ 3 z>0.5 (1, 0) p ϵ q ϵ 1 θ 2 θ 2 D z z < 0.5 R n z > 0.5 D z (p, q) z>0.5 p
31 ( 1 α 1 j p j R α (p, q) = ( j p pj j q j ) ( pj q j ) α 1 ) α 1 α =1 C β (p, q) = j pβ j q1 β j,β (0, 1) D KL (p q) = ( ) j p pj j q j D S (p, q) = ( ) j (p pj j q j ) q j ( ) D B (p, q) = j pj q j D z 1 α 1 Dα 0.5 (p, q) α 0, 1 R α (p, q) = D 0.5 (p, q) α =1 C β (p, q) =( D β 0.5 (p, q)) D KL (p q) =D 0.5 (p, q) D S (p, q) =D 0.5 (p, q)+d 0.5 (p, q) D B (p, q) =D 0 (p, q)
32 p q α<0 D 0.5 (p, q) = ( j q pj j q j ) D 0.5 (p, q) D 0.5 (p, q)
33 g D(p, q) =g 1 ( j p j g(d(p i,q i )) ), D(p i,q i ) i Θ p, q (Θ) D Θ (p, q) =0 p = q. D D(p, q) > 0 p q
34 Θ 1, Θ 2 γ :Θ 1 Θ 2 p, q (Θ 1 ) D Θ2 (p γ 1,q γ 1 )=D Θ1 (p, q), p γ 1 Θ 2 p γ 1 (θ 2 ):=p(γ 1 (θ 2 )) D Θ n = Θ D Θ Θ
35 ( D n ) n 2,n N D n : (Θ) (Θ) R + {+ }, Dn (p, q) :=D Θ (p, q), Θ Θ = n (D n ) n 2 n D Θ Θ A Θ p(a) =q(a) p(a) (0, 1) p( A) A p( A c ) D n (p, q) D A (p( A),q( A)) D A c (p( A c ),q( A c )) D n (p, q) {D A (p( A),q( A)),D A c (p( A c ),q( A c ))}, A Θ p(a) =q(a) (0, 1) A A
36 p 1,p 2,q 1,q 2 p 1,p 2,q 1,q 2 n D n (λp 1 +(1 λ)p 2,λq 1 +(1 λ)q 2 ) {D n (p 1,q 1 ),D n (p 2,q 2 )}, λ [0, 1] D n : n n R {+ } D n p, q n λ [0, 1] D n (p, λp +(1 λ)q) D n (p, q). p, q, r n λ [0, 1] D n (λp +(1 λ)r, λq +(1 λ)r) D n (p, q). p, q 1,q 2 λ [0, 1] D n (p, λq 1 +(1 λ)q 2 ) {D n (p, q 1 ),D n (p, q 2 )}. A s p 1 = p( s), p 2 = p( s c ) q 1 = q( s), q 2 = q( s c ) λ = P p (s) = P p (s) D(p(s),q(s)) <D(p, q) D(p, q) D(p(s c ),q(s c )) P p (s) =P p (s)
37 B(p, ρ] :={q n D n (p, q) ρ} D n C n C C n D n (p, q) =D n ( p, q), p,q C p, q C p, q n D n (p, q) D n (e 1,e 2 ) (= D n (e j,e i ) i, j), e 1 =(1, 0, 0,...,0) e 2 =(0, 1, 0,...,0) n p, q n θ 1,θ 2 {θ 1,θ 2 } p,q n 1 p p =(p 1 + p 2,p 3,...,p n ) q (q 1 + q 2,q 3,...,q n ).
38 θ 1,θ 2 p, q n D n 1 ((p 1 + p 2,...,p n ), (q 1 + q 2,...,q n )) D n ((p 1,p 2,...,p n ), (q 1,q 2,...,q n )). A =(A j ) j Θ D A (p A,q A ) D n (p, q), p A (A) p A (A j ):= θ A j p(θ j ), A j A. n D n n Θ 1 Θ 2 n = Θ 1 m = Θ 2 n, m p (1) n q (1) m r (1) := p (1) q (1) (A j ) j Θ A j A i =, A j =Θ. j
39 (Θ 1 Θ 2 ) r (1) (θ 1,θ 2 ):=p (1) (θ 1 )q (1) (θ 2 ). r (1) p (1) q (1) Θ 1 Θ 2 n, m N p (1),p (2) n q (1),q (2) m D nm (p (1) q (1),p (2) q (2) )=D n (p (1),p (2) )+D m (q (1),q (2) ). p 1,q 1,p 2,q 2 n D nm (p 2 r, q 2 s) D nm (p 1 r, q 1 s) =D n (p 2,q 2 ) D n (p 1,q 1 ) r, s m. 1 2 p 1 p 2 q 1 q 2 P Q D(p 2,q 2 ) D(p 1,q 1 ) P Q r s p 1 r q 1 s p 2 r q 2 s r s 1
40 2 D, n p, q m D n (, ) D m ( p, q) D n n ( r, s) D m n ( p r, q s), r, s n p, q n r m D n (p, q) =D n m (p r, q r). D D
41 D D p, q n U q q U p p p U p q U q D(p,q) D(p, q) D(p, q ). D D φ : R + R + D := φ(d) D n p, q n D n (p, q) =D n+1 ((p 1,...,p n, 0), (q 1,...,q n, 0)).
42 p, q n Supp(p) Supp(q) = p j q j =0 j D D(p, q) =+. θ j p, q n p 1 q 1 = p 2 q 2. D n (p, q) =D n 1 ((p 1 + p 2,p 3,...,p n ), (q 1 + q 2,q 3,...,q n )). p n q 1 = (q 1 + q 2, 0,q 3,...,q n ) q 2 =(0,q 1 + q 2,q 3,...,q n ) [q 1,q 2 ]={r n r = λq 1 +(1 λ)q 2,λ [0, 1]}. p [q 1,q 2 ] q [q 1,q 2 ]
43 q1 q2 = p 1 p 2, r, r [q 1,q 2 ] r [r,q ] D n (p, r) D n (p, r ). p, q q [q 1,q 2 ] p r r 1 r 2 = p 1 p 2 q p D(p, q ) p [q 1,q 2 ] 3 p q 1 q 2 q q 1 2 n =3 D(p, q ) p q [q 1,q 2 ]
44 p, q n i D n (p, q) := ϵ 0 D n (p, (q 1,...,q i ϵ, q i+1 + ϵ,..., q n )) D n (p, q) ϵ i =1,...,n 1. i D n (p, q) D n q i i +1 (p, q) ( i D n (p, q)) n 1 i=1 D n (p, ) : n R + q D n (p, q) i, j D n (p, (q 1,...,q i ϵ,..., q j + ϵ,..., q n )) D n (p, q) ϵ 0 ϵ ( i D(p, q)) n 1 i=1 i, i +1,j,j+1 i, j {1,...,n 1} j D n (p, q) 0 i D n (p, q) j D n (p, q) = g(p i,p i+1,p j,p j+1 ; q i,q i+1,q j,q j+1 ),
45 i i +1 j j +1 n 1 j n 1 p, q D((p 1,...,p j, p j+1,..., p n ), (q 1,...,q j, q j+1,..., q n )) D((p 1,...,p j, p j+1,..., p n ), (q 1,...,q j, q j+1,..., q n )), D((p 1,...,p j, p j+1,..., p n ), (q 1,...,q j, q j+1,..., q n )) D((p 1,...,p j, p j+1,..., p n ), (q 1,...,q j, q j+1,..., q n )), p, q p, q n h D n (p, q) =D n (p, (...,q i + ϵ, q i ϵ,..., q j + h(ϵ),q j+1 h(ϵ))), h i, i+1,j,j+1
46 jd(p,q) i D(p,q) = h (0) i, i+1,j,j+1 1/z j (Π i ) i
47 D zj+0.5 (, ) p j D zj+0.5 (p j, Π) + D 0.5 z j (Π,p j ) D zj 0.5 (Π,p j ) π =(S, f(s θ)) S f( θ) (S) θ Θ f(s θ) s θ p(s) =(p 1 (s),...,p n (s)) p(θ j s) =p j (s) = f(s θ j)p j i f(s θ i)p i, s P p (s) := i f(s θ i)p i. p, q n p q D
48 π =(S, f(s θ)) s S D(p(s ),q(s )) <D(p, q). D p, q n π =(S, f(s θ)) s S D(p(s),q(s)) >D(p, q). p π E π p(d(p(s),q(s))) := s P p (s)d(p(s),q(s)). E π p(d(p(s),q(s))) D(p, q)
49 E π p[d(p(s),q(s))] E π p[d(p( s),q( s))], π π Θ π =(S, f(s θ)) π =( S,g( s θ)) π π π π g( s θ) = s λ s, s f(s θ), (λ s, s ) s, s s λ s, s =1 π π π π p θ q D p q n
50 π π E π p[d(p(s),q(s))] E π p[d(p( s),q( s))]. p p, q n E π p[d(p(s),q(s))] E π p[d(p( s),q( s))], D D p, q p q
51 D(p, q) =+ Supp(p) \ Supp(q). p, q D(p, q) = Supp(p) Supp(q) D(p, q) < + Supp(p) \ Supp(q) p, q 2 p =(p 1, 1 p 1 ) q =(0, 1) D(p, q) < q n = ( 1 n, 1 1 n) n D(p, q n ) <D(p, q) < q n [q, p] D(p, q n ) n s 0 p(s 0 ) (1, 0) q n (s 0 ) (0, 1) n ϵ q n D(p(s 0 ),q n (s 0 )) >D((1 ϵ, ϵ), (ϵ, 1 ϵ)). D((1 ϵ, ϵ), (ϵ, 1 ϵ)) ϵ 0 E π p(d(p(s),q n (s))) + D(p, q n ) D(p, q n ) < E π p(d(p(s),q n (s))). n ϵ
52 Supp(p) \ Supp(q) p q q(θ s) =0 θ Supp(p)\Supp(q) θ D(p, q) = D(p, q) < E π p[d(p(s),q(s))]. D D(p, q) =ad z (p, q) z 0.5 a>0 D D D(p, q) =ad z (p, q) z 0.5 a>0 π π p, q n E π p[d(p(s),q(s))] E π p[d(p( s),q( s))].
53 Θ Θ = n< + J J N x R + j J p j (Θ) u j : R + R j u j x 0 u (x) = x u (x) =0 j U j ( ) :=E p j(u j ):= i p j i u j(x j i ), x j i i = (x j 1,...,x j n) θ 1,...,θ n i I Θ 1 x i 0 i I I 2 I I =Θ (Π i ) i I i I Π i =1 (p j ) j p j (Θ)
54 Π i (Π i ) i I (x j i )j J i I j J (x j i ) i I R n p j i u j(x j i ) i i I Π i x i 1, i x j i = J. j J
55 j V j ( ) := i p j i (xj i 1), j G j ( ) :=U j ( ) U j ( ), =(1,...,1) x j i i p j i /Π i (p j 1/Π i,...,p j n/π n ) G j ( ) p Π G j ( ) D(p, Π) i j 1 i x j i i xj i 1
56 (u j ) j J 1 z j u j (x) = x1 1 1 z j > 0, x > 0. z j u j u j (x) u j (x) = z jx, z j (0, 1) z j (0, 1) z j > 1 p 1,...,p J n (u j ) j z j (0, 1) (Π i ) i 1 D zj+0.5 (q, p j ( I)), q (I) 1 z j j 1 1 xu (x) u (x) = 1 z j [0.07, 0.62]
57 V j ((x j i ) i)=(d z j+0.5 (p j ( I), Π) + D z j+0.5 (Π,p j ( I))) 1 j J; G j ((x j i ) i)= 1 ( ( )) 1 1 Dzj 0.5 (Π,p j ( I)), j J. z j 1 z j z j (0, 1) z j > 1 G j ((x j i ) i)= 1 ( 1 1 z j 1 ( D z j 0.5 (Π,p j ( I)) z j )), D z j 0.5 V j ((x j i ) i)=(d z j+0.5 (p j ( I), Π) D z j+0.5 (Π,p j ( I))) 1. z j
58 0 p j m N p j,(m) n m + j 1,j 2 J m 1,m 2 >m p j 1,(m 1 ) p j 2,(m 2 ) =0. ϵ m p j,(m)
59 ϵ j J m> m j (p j,(m) ) m n m + j n n (p j,(m) ) j J m N ε>0 pj,(m) i >ε>0 i =1,...,n j J m N m j u j 1 x j i 1 u j 1 u j(1) = 1 j z j = 1 u (1) 1 z j ũ j (x) := x1 1 1 z j u (1) = ũ j(1) u (1) = ũ j (1) I =Θ n
60 I Θ (u j ) j J 1 u j(1) = 1 1/u j (1) =: z j (0, 1) (p j,(m) ) j J m N m ((x j,(m) i ) j J i=1,...,n, (Πm i ) i ) m Π m q n j 1 1 z j D zj+0.5 (q, p j,(m) ). j m D z j +0.5 (p j,(m),π m ) D z j +0.5 (p j,(m), Π m ) =1 pj Π m Π m m i pj,(m) i (x j,(m) i 1) D z j+0.5 (p j,(m), Π m )+D z j+0.5 ( Π m,p j,(m) ) =1. m i pj,(m) i u i (x j,(m) i ) 1 1 z j D z j 0.5 ( Π m,p j,(m) ) =1.
61
62
63 H
64
65
66
67 Θ={θ 1,...,θ n } π =(S, (f(s θ)) s S,θ Θ ) S f( θ) (S) θ s θ f(s θ) > 0 f( θ) S(f( θ)) := {s S f(s θ) > 0}, S(f( θ)) < θ S Θ E Θ,S π =(S, (f(s θ)) s S,θ Θ ) S S(f( θ)) f( θ) θ π E Θ,S Θ A (A) A σ σ
68 π = ( f(s1 ) θ 1 )... f(s 1 θ n) f(s 2 θ 1 )... f(s 2 θ n) f(s m θ 1 )... f(s m θ n) f( θ) f(s θ) 0 s, θ s f(s θ) =1 θ Θ π π E Θ,S π s S f(s θ) =f(s θ ), θ, θ Θ. s f(s θ) =0 θ S(f( θ)) = S(f( θ )) θ, θ Θ, θ s θ S f(s θ θ) > 0
69 µ (Θ) µ(θ) > 0 θ Θ f(s θ) > 0 θ µ(θ s) = µ(θ)f(s θ) θ µ(θ )f(s θ ). µ(s) =µ s µ(θ) > 0 µ(θ s) > 0 s µ(θ s) Θ S c Θ,S : E Θ,S [0, + ] c Θ,S µ =(1, 0,...,0) (0, 1, 0,...,0) c Θ,S ((1 ϵ)π+ϵπ ) c Θ,S (π) π, π E Θ,S ϵ 0 + ϵ E Θ,S (1 ϵ)π + ϵπ E Θ,S
70 c Θ,S (π) =0 π π c Θ,S (π) < π 0 π c Θ,S (π) = + c Θ,S (π) c Θ,S Θ S f(s θ) c Θ,S
71 Θ, Θ S, S π =(S, (f(s θ)) s S,θ Θ ) π =(S, (g(s θ )) s S,θ Θ ) γ :Θ Θ λ : S S f(s θ) =g(λ(s) γ(θ)), s S, θ Θ. π π π π π =(S, (f(s θ)) s S,θ Θ ) π =(S, (g(s θ )) s S,θ Θ ) c Θ,S (π) =c Θ,S (π ) c Θ,S S c Θ Θ c Θ c Θ Θ = Θ Θ Θ c n π =(S, (f(s θ)) s S,θ Θ ) Θ n N E n n E n λπ +(1 λ)π E n π, π E n λ [0, 1]
72 π π n π, π E n c n (λπ +(1 λ)π ) {c n (π),c n (π )} λ [0, 1]. π π λπ +(1 λ)π c n (π) c c π = (S, (f(s θ)) s S,θ Θ ) A = (A i ) i S s S A i A s π =(A,f(A θ) A A,θ Θ ) π θ π π A j S A i A j = i j i A i = S
73 S S γ : S S π =(S, (f(s θ)) s S,θ Θ ) π := γ π =(S,g(s θ) s S,θ Θ) g(s θ) = s γ 1 (s ) f(s θ). γ π π γ π π γ π s 1 s 2 s 1 π = f(s 1 θ 1 )... f(s 1 θ n) f(s 2 θ 1 )... f(s 2 θ n) f(s 3 θ 1 )... f(s 3 θ n) f(s m θ 1 )... f(s m θ n) γ π ( = ) f(s 1 θ 1 )+f(s 2 θ 1 )... f(s 1 θ n)+f(s 2 θ n) f(s 3 θ 1 )... f(s 3 θ n) f(s m θ 1 )... f(s m θ n) π E n γ π E n γ : S S π = γ π π π S s γ π π γ : S S c n (γ π) c n (π). s 1,s 2 S f(s θ)/f(s θ ) θ, θ π s 1 s 2 {s 1,s 2 } γ 1 (s) s s S γ(s) =s
74 s 1,s 2 f(s 1 θ)f(s 2 θ )=f(s 1 θ )f(s 2 θ) θ, θ γ : S S γ(s 1 )=γ(s 2 ) γ(s) γ(s ) s s s, s s 1,s 2 c n (γ π) =c(π). π π = f(s 1 θ 1 )... f(s 1 θ n) f(s 2 θ 1 )... f(s 2 θ n) f(s m θ 1 )... f(s m θ n) kf(s m θ 1 )... kf(s m θ n) , k>0, π = ( f(s1 ) θ 1 )... f(s 1 θ n) f(s 2 θ 1 )... f(s 2 θ n) (1+k)f(s m θ 1 )... (1+k)f(s m θ n) c n ( π) c n (π) c n ( π) =c n (π) f(s θ) =0 θ
75 π π c(π) c( π) π = (S, (f(s θ)) s S,θ Θ ) π = (S, (g(s θ)) s S,θ Θ) g(s θ) = s λ s,s f(s θ), λ s,s 0 s S λ s,s =1 π π π π π π π π π π c n c n (π) c n ( π)
76 π =(S, (f(s θ)) s S,θ Θ ) S 1,S 2 S S 1 S 2 = S 1 S 2 = S π 1 =(S 1, (f(s θ)) s S1,θ Θ) π 2 =(S 2, (f(s θ)) s2 S,θ Θ) π = π 1 π 2 π 1 π 2 π 1 c n π c n π 1 π π 1, c n π c n π 2 π π 2, π 2 π 1 π 2 s S 1 f(s θ) 1 π ( ) π1 π = π θ Θ π 2 f(s 1 θ)+ f(s 2 θ) =1, s 1 S 1 s 2 S 2
77 ( ) c n (π) =h g(f(s θ 1 ),...,f(s θ n )), s S g :[0, 1] n [0, ] h :[0, + ] [0, + ] Θ Θ π E n f(s 1 θ 1 )... f(s 1 θ n ) π = f(s 2 θ 1 )... f(s 2 θ n ), π(θ 1,...,θ n 1 ) E n 1 f(s 1 θ 1 )... f(s 1 θ n 1 ) π(θ 1,...,θ n 1 )= f(s 2 θ 1 )... f(s 2 θ n 1 )
78 Θ = {θ 1,...,θ n 2, {θ n 1,θ n }} {θ n 1,θ n } θ n θ n 1 θ n 1 π π(θ 1,...,θ n 1 ) θ n θ 1,...,θ n 1 π π(θ 1,...,θ n 1 ) θ 1,θ n θ 2,θ n (θ n 1,θ n ) f(s 1 θ i ) f(s 1 θ j ) π(θ i,θ j ):= f(s 2 θ i ) f(s 2 θ j ), {θ i,θ j } π n>2 π E n c n (π) =c n 1 (π(θ 1,...,θ n 1 )) + h n 1 (c 2 (π(θ 1,θ n )),...,c 2 (π(θ n 1,θ n ))), h n :[0, ] n 1 [0, ] n h n h n
79 f( θ) c n n n 1 n th π 1 = (S 1, (f(s θ)) s S1,θ Θ) π 2 = (S 2, (f(s θ)) s S2,θ Θ) π := π 1 π 2 π =(S 1 S 2, (f(s 1 θ)f(s 2 θ)) (s1,s 2 ) S 1 S 2,θ Θ). π 1 π 2 π 1 π 2 π 1 π 2 π 1 π 2 π 1 π 2 S 1 S 2 S 1 S 2
80 c n (π π) =c n (π)+c n ( π). (c n ) n (c n ) n φ : E n R {+ } φ π φ(π) =0 φ(π) = (Θ) µ µ(θ) > 0 θ Θ δ j θ j δ j =(0,..., 1 j th,...,0) φ(π 1 π 2 )=φ(π 1 )+φ(π 2 ), π 1,π 2 E n.
81 H : (Θ) R H(µ) >H(δ j ) µ (Θ) j =1,..., Θ µ (Θ) φ µ : E n R φ µ (π) :=H(µ) P µ (s)h(µ(s)). s S φ µ (π) H H(µ) := θ µ(θ) (µ(θ)), φ µ H H(µ) > 0=H(δ j ) µ (Θ) φ µ H Θ Θ > 3 S c Θ,S ( ) f(s θi ) (f(s θ i ) f(s θ j )) = f(s θ s i,j j ) i,j D(f( θ i ),f( θ j )), P µ (s) θ µ(θ)f(s θ) µ s
82 D D(p, q) = ( ) i p i pi q i + ( i q i qi p i ) θ, θ Θ D(f( θ),f( θ )) s θ θ D(f( θ),f( θ )) D(p, q) = i p i ( pi q i ) + i q i ( qi p i ), p q q p ( ) c Θ,S
83 f(s θ) f(s θ ) θ θ c Θ,S (π) = π s S θ, θ Θ f(s θ) > 0=f(s θ ) Θ =2 Θ > 2 n = Θ Θ =2 Θ =2
84 c n c n 1 c 2 h n n =2 Θ =2 c 2 c KL 2 (π) = s [f(s θ 1) f(s θ 2 )][(f(s θ 1 )) (f(s θ 2 ))]; ( ) c B 2 (π) = s f(s θ1 )f(s θ 2 ). c B 2 (π) =+ π c KL 2 (π) =+ π 2 Θ =2 KL B π θ 1 s f(s θ 1 )=0<f(s θ 2 )
85 Ω D : (Ω) (Ω) [0, + ] Ω S (Ω) (S) f( θ) θ θ 1,θ 2 D(p, q) =D(q, p) p, q (Ω) θ 1 θ 2 θ 1 θ 2 2 <n< h n c n c 2 (π(θ 1,θ n )),...
86 c n f n f n (x 1,...,x n )= n x i, (x i ) i [0, ] n. i=1 c Θ,S = θ,θ c 2 (π(θ, θ )). Θ c Θ,S (π) = θ,θ c KL 2 (π(θ, θ )), c Θ,S (π) = θ,θ c B 2 (π(θ, θ )). c Θ,S Θ Θ > 2 c B 2 (π) π(θ, θ ) θ θ
87 n = Θ > 2 c Θ,S (π) = θ,θ c B 2 (π(θ, θ )). c(π) = s ( ) f(s θi ) (f(s θ i ) f(s θ j )) = f(s θ i,j j ) i,j D(f( θ i ),f( θ j )), c( ) c n ( ) c Θ,S ( ) c( ) π n E Θ,S f n (s θ) π E Θ,S f(s θ) π n c Θ =2 Θ > 2
88 π π n π f n (s θ) f(s θ) 0. s S,θ Θ π (π n ) n π n π c(π n ) (π n ) n c(π n ) 0 π n π c( ) f(s θ)/f(s θ ) 0 c 2 B (f(s θ)) s,θ µ
89 µ (Θ) P µ (s) := θ µ(θ)f(s θ) s µ(θ s) θ s µ (Θ) g(µ) := Θ µ(θ1 ) µ(θ n ) µ(θ 1 ),...,µ(θ n ) µ(θ) > 0 θ Θ µ (Θ) µ(θ) > 0 θ Θ π c(π) = s P µ (s) θ µ(θ s)n µ(θ) ((µ(θ s) [a(µ(s))])) =: s P µ (s)φ I (µ(s); µ), φ I (µ(s); µ) := θ µ(θ s)n µ(θ) ((µ(θ s) [a(µ(s))])) u : A Θ R V (µ) := a θ u(a, θ)µ(θ) µ π P µ (s)v (µ(s)) c(π), s c
90 P µ (s)(v (µ(s)) φ I (µ(s); µ)), (µ(s)) s s s P µ (s)µ(s) =µ, π c H (π; µ) := s P µ (s)(h(µ) H(µ(s))) =: s P µ (s)φ H (µ(s); µ), H(µ) = θ µ(θ) (µ(θ)) µ(s) φ I φ H µ (Θ) φ H (µ; µ) =φ I (µ; µ) =0 φ H ( ; µ) φ I ( ; µ) x (Θ) φ H (x; µ) < x (Θ) φ I (x; µ) = (Θ) (Θ) (Θ) = {µ (Θ) µ(θ), θ}
91 µ(s) =µ (Θ)
92
93
94
95
96
97
98 M = W =+ M = {m 0,m 1,m 2,...} W = {w 0,w 1,w 2,...} m j w n > mj W {m j } M {w n } W {m j } M {w n } w 1 > mj w 2 > mj m j > mj w 3 m j w 1 w 2 w 3 m j w n A W {m j } A M {w n } x A {m j } A {w n } x> mj y, y A \{x} > wn ).
99 m j A W {m j } W {m j } w 0 w j w j j>j j 0 w 0 {w 1,w 2,...,w n,...} A A A P (m j ):w j1,w j2,...,w jl,m j,w jl+1,...,w jm,...; m j w j1 w jk w jk k < k m j m j P (m j ):w j1,w j2,...,w jl,
100 P (m j ) m (M,W, ) M = {m 0,m 1,...} W = {w 0,w 1,...} =(P (x)) x M W x W x M P (x) W {x} M {x} P (x) µ µ : M W M W,
101 x M W µ(µ(x)) = x x µ(x) µ(x) M x W µ x µ (M,W, ) x x> x µ(x); (m, w) m> w µ(w) w> m µ(m). µ x y y x
102 (M,W, ) P (x) x (M,W, )
103 P (m 1 ):w 1 P (w 1 ):m 1,m 2 P (m 2 ):w 1,w 2 P (w 2 ):m 2,m 3 P (m 3 ):w 2,w 3 P (w 3 ):m 3,m P (m i ):w i 1,w i P (w i ):m i,m i w 1 m 1
104 m 2 m 2 m 2 w 2 m 3 m 2 m 3 i m i+1 w i w i+1 m i+2 µ M µ (j) ( ) j µ M j µ (j) (m) (µ (j) (m)) + j=1 µ M (m) := m µ M (m) =w m w µ M (w) =m µ M (w) =w j µ (j) (m) (µ (j) (m)) + j=1 W
105 µ M µ M µ W µ µ > M µ µ µ(m) m µ (m) m M; µ> M µ µ(m) > m µ (m) m M;
106 > W µ> M µ µ µ µ µ > M µ M µ M > M µ µ M M µ µ W W µ, µ. > M > W µ µ (M,W, ) µ> M µ µ > W µ. µ µ µ> M µ µ > M µ µ µ
107 µ µ M M µ M µ W, µ W (A, ) A A (A, )
108 a, b A c := a b c a c b c a c b c c a b a b a b c := a b c a c b c a c b c c x {µ(x),ν(x)} µ ν(x) := x {µ(x),ν(x)} x M x W x {µ(x),ν(x)} µ ν(x) := x {µ(x),ν(x)} x M x W. m µ ν(m) m µ ν(w) m (µ ν)(m) m µ(m),ν(m) m (µ ν)(m). µ ν µ ν µ ν (M,W, )
109 λ = µ ν λ := i I ν i µ ν µ ν λ := i I ν i λ i I ν i
110 µ M(µ) :={m M µ(m) m}, W (µ) :={w W µ(w) w}.
111 µ µ M(µ) =M(µ ), W (µ) =W (µ ), (M,W, ) µ µ M(µ) M(µ ) P (m 1 ):w 1 P (w 1 ):m 2,m 1 P (m 2 ):w 2,w 1 P (w 2 ):m 3,m 2 P (m 3 ):w 3,w 2 P (w 3 ):m 4,m P (m i ):w i,w i 1 P (w i ):m i+1,m i µ M µ W µ M (w i )=m i i N
112 µ W (w i )=m i+1 i N µ M (m 1 )=m 1 M(µ M ) M(µ W ), m 1 M(µ M ) \ M(µ W ). µ µ µ M µ M(µ) M(µ ). µ M(µ W ) M(µ) M(µ M );
113 W (µ M ) W (µ) W (µ W ). M(µ W ) M(µ) M(µ M ) ; W (µ M ) W (µ) W (µ W ). µ W (µ) = M(µ) M(µ) =M(µ ) µ µ A B A = B A = B A A B A B A = B
114 M = µ W µ M (M). M = µ W µ M (M) W = µ M µ W (W ). M µ W µ M (M) m M \ µ W µ M (M) µ M (m) W µ M (m) W \ µ M µ W (W ) µ M µ W m µ(m) W µ (m) =m µ, µ µ M (m) W f g x f(g(x)) A f(a) ={y y = f(x), x A}
115 µ W (m) =m µ M µ W µ M µ W µ M µ W µ M µ W µ M µ W M(µ) < + µ M = j M j W = j W j j M j, W j < + m M j m W j m> m w, m M j,w W \ W j. M W Z
116 P (m i ):w i,w i 1 P (w i ):m i+1,m i i Z µ M m i w i µ W m i w i 1 M(µ W )=M W (µ M )=W µ µ M(µ) W (µ) M(µ ) W (µ ). µ M µ W W M = {...,m i,...,m 1,m 0,m 1,...,m i,...}
117 P (m 1 ):w 3 P (w 1 ):m 3 P (m 2 ):w 4 P (w 2 ):m 4 P (m 3 ):w 5,w 1 P (w 3 ):m 5,m P (m i ):w i+2,w i 2 P (w i ):m i+2,m i µ M µ W {m 3,...,m i,...} = M(µ W ) M(µ M )={m 1,...,m i,...}, µ µ µ M,µ W P (m 1 ):w 3,w 1 P (w 1 ):m 3,m 1 P (m 2 ):w 4,w 2 P (w 2 ):m 4,m 2 P (m 3 ):w 5,w 3,w 1 P (w 3 ):m 5,m 3,m 1
118 P (m i ):w i+2,w i,w i 2 P (w i ):m i+2,m i,m i {m 3,...,m i,...} = M(µ W ) M(µ M )={m 1,...,m i,...}, µ µ(m i )=w i M W µ M(µ) M(µ ), µ
119 M t W t t M t W t µ ( t N M t, t N W t, )
120 t M t t W t t t t t t t t m M t t t m> m w, w W s,s<t,
121 m> m w w W s,s>t, (M,W, 1 ) (M,W, 2 )
122 (M,W, ) (M,W, ) µ M µ W
123
124
125
126
127
128 β
129
130
131
132
133 D(p, q) p q 0 i D(p, q) h i i +1 α p, q i i D(p, q) = h(p i,p i+1,q i,q i+1 ). α(p, q)
134 h n p(p i,p i+1,q i,q i+1 ) h(p 1,p 2,q 1,q 2 )=i(p 1,q 1 ) i(p 2,q 2 ), i :[0, 1] 2 R i(x, y) i(x, y) =G(x/y), G :(0, + ) R G G (x) =cx α α, c R. G (x) = 1 x ( a + b x) G (x) α(p, q)
135 p q j =1,...,n 1 j D(p, q) 0 n =2 p q 1 D(p, q) 0 1 D(p, q) =0 p, q q [p, q] γ(q, q ): 2 2 R D(p, q) =D(p, q )+D(p, p + ϵ(q, q )z), z =(1, 1) 1 D(p, q) =0 1 D(p, p + ϵ(q, q )z) = 1 D(p, p + ϵ(q, q )z) ϵ(q, q ) q =0, q [p, q] q q ϵ(q, q ) 0 y (0,δ) R 1 D(p, p + yz) 0 ϵ(q,q ) q =0 q q q q ϵ(q, q )=h(q ) q = q ϵ(q, q )=0 h(q )=0 q [p, q] q D(p, q) =D(p, q ) D(p, q) (p, q] 0=D(p, p) =D(p, q) D(p, q) (p, q] q (p, q) D(p, q ) < D(p, q) = D(p, q) q [p, q) 1 D(p, q) =0 D(p, ) [ q, q] p q 1 D(p, p + yz) =0 y (0,δ) D(p, p + yz) =D(p, p) =0
136 1 D(p, q) =0 q q [p, q] q D(p, q ) = D(p, q) q n =2 n j D(p, q) =0 j z i,j =(0,...,1, 0,..., 1, 0,...,0) D(p, q) q q [p, q] q [p, q] D(p, q) =D(p, q) D(p, q ) <D(p, q) q [p, q] D [p, q] D(p, ) q [ q, q] q p D(p, q) =0 n =2 [p, q] D(p, ) q D n (p, q) h :[0, 1] 4 R α(p, q) : n n R i D(p, q) = h(p i,p i+1,q i,q i+1 ), α(p, q) p, q n q p D(p, q) q p D(p, q + ϵ(q p)) D(p, q) q p D(p, q) =. ϵ 0 ϵ h x =(x 1,x 2,x 3,x 4 ) x 1 + x 2 1 x 3,x 4 1 h
137 (α, h) ( α, h) α(p, q) =k α(p, q) h(p i,p i+1,q i,q i+1 )=k h(p i,p i+1,q i,q i+1 ), k 0 p q n j j D(p, q) 0 h(p i,p i+1,q i,q i+1 ):=g(p i,p i+1,p j,p j+1,q i,q i+1,q j,q j+1 ), g h p j,p j+1,q j,q j+1 h(p i,p i+1,q i,q i+1 )=0 i D n (p, q) =0 i i D(p, q) i D(p, q) h(p i,p i+1,q i,q i+1 ) i, i D n (p, q) h(p i,p i+1,q i,q i+1 ) = jd n (p, p) = k D n (p, q) h(p k,p k+1,q k,q k+1 ) α(p, q) α(p, q) := h(p i,p i+1,q i,q i+1 ), i D(p, q) (α, h n p) ( α, h n p)
138 p, q h(i) := h(p i,p i+1,q i,q i+1 ) i D := i D(p, q) α := α(p, q) (α, h) ( α, h) h(j) j D = α α = h(i) i D, jd = h(j) i D h(i), α α = h(i) h(i). p i,q i,p i+1,q i+1 p, q α α = k = h(i) h(i), k p, q i :[0, 1] 2 R h(p 1,p 2,q 1,q 2 )=i(p 1,q 1 ) i(p 2,q 2 ), p 1,p 2,q 1,q 2 [0, 1] 4 i,j D(p, q) z ij = e i e j
139 i,i+1 D(p, q)+ i+1,i+2 D(p, q) = i,i+2 D(p, q), h h(p i,p i+1,q i,q i+1 ) α(p, q) + h(p i+1,p i+2,q i+1,q i+2 ) α(p, q) = h(p i,p i+2,q i,q i+2 ). α(p, q) h(p i,p i+1,q i,q i+1 )+h(p i+1,p i+2,q i+1,q i+2 )=h(p i,p i+2,q i,q i+2 ). h D p i h j j h 1 (p i,p i+1,q i,q i+1 )=h 1 (p i,p i+2,q i,q i+2 ), p i+1,q i+1,p i+2,q i+2 h 1 p i q i h 3 p i q i h i (1) i (2) h(p 1,p i+1,q i,q i+1 )=i (1) (p i,q i ) i (2) (p i+1,q i+1 ). h 1 (x, y, w, z) := h x h 2,h 3,h 4
140 i (1) i (2) x := p i = p i+1 = p i+2 y := q i = q i+1 = q i+2, 2h(x, x, y, y) =h(x, x, y, y) h(x, x, y, y) =0, x, y [0, 1] 2. i (1) i (2) i (1) (x, y) i (2) (x, y) =0, x, y [0, 1] 2, i (1) (x, y) =i (2) (x, y) i i(x, y) x/y i(x, y) =G(x/y), G : R + R p, q n q 1 =(q 1 + q 2, 0,q 3,...,q n ) q 2 =(0,q 1 + q 2,q 3,...,q n ) [q 1,q 2 ]={r n r = λq 1 +(1 λ)q 2,λ [0, 1]}.
141 r [q 1,q 2 ] D(p, r) r r 1 r 2 = p 1 p 2 D 1, D(p, r) = h(p 1,p 2,r 1,r 2 ) α(p, r) =0, i(p 1,r 1 ) i(p 2,r 2 ) α(p, q) =0, p 1 p 2 = r 1 r 2, i(p 1,r 1 )=i(p 2,r 2 ) p 1 r 1 = p 2 r 2, i i(p 1,r 1 )=G ( p1 r 1 ). G p =(p 1,...,p n ) n q =(q 1,...q n ) n λ := (λ, 1 λ)
142 2 γ =(γ,1 γ) 2 p λ =(λp 1, (1 λ)p 1,...,λp n, (1 λ)p n ), q γ =(γq 1, (1 γ)q 1,...,γq n, (1 γ)q n ), D(p λ, q γ) =D(p, q)+d(λ, γ), p ϵz i ( ( pi pi+1 )) G( ) G q i q i+1 α(p,q) RHS := ( ( ) ( )) p G i q i G pi+1 q i+1. α(p, q) LHS := ( ( ) ( )) ( ( ) ( )) λp λ G i γq i G λpi+1 γq i+1 +(1 λ) G (1 λ)pi (1 γ)q i G (1 λ)pi+1 (1 γ)q i+1 α(p λ, q γ) LHS = RHS α(p λ, q γ) α(p, q) = ( λ G ( ) ( λp i γq i G λpi+1 )) ( ( ) γq i+1 +(1 λ) G (1 λ)pi (1 γ)q i G ( ( ) ( )) p G i q i G pi+1 q i+1 ( )) (1 λ)pi+1 (1 γ)q i+1
143 r i = p i q i R 1 = λ R γ 2 = 1 λ 1 γ α(p λ, q γ) α(p, q) = λ (G (R 1r i ) G (R 1 r i+1 )) + (1 λ)(g (R 2 r i ) G (R 2 r i+1 )) (G (r i ) G (r i+1 )) α(p λ,q γ) α(p,q) r i r i+1 r i,r i+1 R + λ (G (R 1 r i ) G (R 1 r i+1 )) + (1 λ)(g (R 2 r i ) G (R 2 r i+1 )) (G (r i ) G (r i+1 )) = λ ( G (R 1 r i) G ( )) ( R 1 r i+1 +(1 λ) G (R2 r i) G ( R 2 r i+1)) ( G (r i ) G ( r i+1)) K(λ, γ) λ (G (R 1 x) G (R 1 y)) + (1 λ)(g (R 2 x) G (R 2 y)) (G (x) G (y)) = K(λ, γ), x, y [0, + ) R 1 := λ γ R 2 := 1 λ 1 γ G(x) G x 0 G(x) = x + G(x) = x 0 G(x) x + G(x) G G x, x G(x) = G(x ) G(y) =G(x) y [x, x ] [q 1,q ] [q,q 2 ]
144 G(x) 0 R >0 f(x) = f(rx), x + x + G G G(x) =+. x (0,+ ) G c 1 <G(x) <c 2 c 1,c 2 R x + I := x G(x) G λ (I G (R 1 y)) + (1 λ)(i G (R 2 y)) (I G (y)) = K(λ, γ). y 0 J := y 0 G(y) K(λ, γ) = λ (I J)+(1 λ)(i J) (I J) =1. K(λ, γ) =1 λ γ λ (G (R 1 x) G (R 1 y)) + (1 λ)(g (R 2 x) G (R 2 y)) = (G (x) G (y)).
145 λ 0 λ (G (R 1 x) G (R 1 y)) 0, (G (R 1 x) G (R 1 y)) R 2 1 G 1 γ (0, + ) ( ) ( ) x y G G = G(x) G(y). 1 γ 1 γ y + ( ) x>0 γ (0, 1) G = G(x), G x 1 γ G G (x) =cx α, α R c R G (x) = a x 2 + b x, a, b R G G p =0 G G (0, + ) x + x 0 x 0 G(x) = x 0 G(x) (, ) x + G(x) =±
146 λ (G (R 1 x) G (R 1 y)) + (1 λ)(g (R 2 x) G (R 2 y)) (G (x) G (y)) = K(λ, γ), x 0 λ (G (R 1 x) G (R 1 y)) + (1 λ)(g (R 2 x) G (R 2 y)) K(λ, γ) =, x 0 (G (x) G (y)) G(x) x 0 y R 1 R 2 λ (G (R 1 x) G (R 1 y)) + (1 λ)(g (R 2 x) G (R 2 y)) x 0 (G (x) G (y)) λg (R 1 x)+(1 λ)g (R 2 x) =, x 0 G (x) λ γ G(Rx) x 0 G(x) R. λg (R 1 x)+(1 λ)g (R 2 x) x 0 G (x) λg (R 1 x)+(1 λ)g (R 2 x) = G(Rx) x 0 G (Rx) G(x), x 0 λg(r 1 x)+(1 λ)g(r 2 x) G(Rx) R x 0 G(Rx) G(x)
147 L(R) := x 0 G(Rx) G(x), L(R) =R α α R G(Rx) L(R) = x 0 G(x) = G(Rx) G(R x) x + G(R x) G(x) ( ) R = L L(R ). R λ (G (R 1 x) G (R 1 y)) + (1 λ)(g (R 2 x) G (R 2 y)) x + (G (x) G (y)) = λ ( ) α λ +(1 λ) γ ( ) α 1 λ. 1 γ λ (G (R 1 x) G (R 1 y)) + (1 λ)(g (R 2 x) G (R 2 y)) (G (x) G (y)) x x (0, + ) λ (G (R 1 x) G (R 1 y)) + (1 λ)(g (R 2 x) G (R 2 y)) (G (x) G (y)) = λ ( ) α λ +(1 λ) γ ( ) α 1 λ, 1 γ x, y γ,λ
148 D x ( G (x) λ ( ) α λ +(1 λ) γ x [0, + ) λ, γ (0, 1) ( ) α ) 1 λ =(λr 1 G (R 1 x)+(1 λ)r 2 G (R 2 x)), 1 γ α =0, 1 α 0, 1 α =0 α = 1 λ (G (R 1 x) G (R 1 y)) + (1 λ)(g (R 2 x) G (R 2 y)) = (G (x) G (y)), x G (x) =(λr 1 G (R 1 x)+(1 λ)r 2 G (R 2 x)), x φ(x) :=xg (x) φ(x) =λφ(r 1 x)+(1 λ)φ(r 2 x), λ = 1 2 ( ) ( x 2φ(x) =φ + φ 2γ x 2(1 γ) ).
149 γ 0= 2x ( ) x (2γ) 2 φ + (2γ) ( 2x (2(1 γ)) 2 φ x (2(1 γ)) ). z = x 2γ ) φ (z γ = 1 γ ( ) 2 γ φ (z), 1 γ φ (z) = c z 2 c R γ (0, 1) γ/(1 γ) R + z φ(z) = a +b z φ (z) φ( ) G (x) = a x 2 + b x, α 0, 1 φ(x) :=xg (x) ( φ(x) λ ( ) α λ +(1 λ) γ ( ) α ) 1 λ = λφ(r 1 x)+(1 λ)φ(r 2 x). 1 γ λ [0, 1] γ G D D
150 λ 0 c(r) := λ 0 λφ (λr). c(r) = d r d R r r c(r )= λφ (λr )= r ) (λ λ 0 r λr 0 λr r φ r r r = r r c(r). α>0 λ 0 ( ) ( ) 1 x 1 φ(x) (1 γ) = c + φ α γ (1 γ) x, φ (0, + ) c c(r) =0 c(r) = d r d = xφ(x) γ 1 (1 γ) x α γ φ ( ) 1 (1 γ) x, x 0 xφ(x) d x γ φ ( d(1 γ), γ xφ(x) 1 d = x 0 γ (1 γ) x α γ φ ( ) 1 (1 γ) x = d γ(1 γ) d(1 γ), α γ ) 1 x (1 γ) γ α 1, 0
151 d =0 c(r) 0 c(x/r) =0 ( ) 1 φ (1 γ) x = 1 (1 γ) α φ(x). x γ φ(x) α φ(x) =cx α, G (x) =cx α 1, α R G (x) 1, 2 α 0, 1 a = 0 b = 0 G G(x) =ax α + b α 0, 1 G(x) =a (x)+ b x + c, a, b, c, z R
152 G (x) =ax α α R G (x) = a x + b x 2. G (x) α(p, q) G(x) =a (x)+ b + c α(p, q) =K x G(x) =ax z + b p, q n α(p, q) =K ( j ( ) ) z pj p j. q j λ, γ m m m =2 α(p λ, q γ) α(p, q) = m j=1 ( ) α λj λ j, γ j α =0, 1 α(p λ,q γ) α(p,q) =1 α(, ) p, q, λ, γ α 0, 1 α(p λ, q γ) =α(p, q) m j=1 ( ) α λj λ j. γ j D(p λ, q γ) =D(λ p, γ q) p, q λ, γ α(p λ, q γ) =α(λ, γ) j ( ) z pj p j, q j
153 α(p, q) j p j ( pj q j ) z = α(λ, γ) m j=1 λ j ( λj γ j ) z, α(p,q) ( ) z j p pj j q j p, q D Θ Θ p, q (Θ) D Θ (p, q) =a ( ) p(θ) p(θ) + b q(θ) θ Θ θ ( ) q(θ) q(θ), p(θ) a, b 0 ( D Θ (p, q) =a p(θ) z R \ { 0.5, 0.5} θ ( ) ) z 0.5 p(θ) q(θ) a>0 z > 0.5 a<0 z < 0.5 z 0
154 i D z (p, q) = h(p i,p i+1,q i,q i+1 ) α(p, q) = a ( p i ) z ( q i pi+1 j p j q i+1 ) z ( pj q j ) z, a, z R q + ϵz i,i+1 p D(p, q) =a ( j ( ) ) z pj p j + K, q j K D(q, q) =0 K =0 D(p, q) 0 p, q n z ( 1, 0) a<0 z ( 1, 0) x z j ( ) ( ) z z pj p j q j =1, q j j a ( j p j a<0 ( pj q j ) z ) 0 a 0 z (, 1) (0, + ) a>0 z (0, ) x z j ( ) ( ) z z pj p j q j =1, q j j D(p, q) 0 a 0 z (, 1)
155 a ( j ( ) ) ( z pj ( ) ) z 1 qj p j = a q j, q j p j j z 1 (0, + ) z +1 (, 0) j ( ) ( ) z 1 z+1 qj q j p j =1 p j j G(z) =a (x)+ b x α(p, q) ( i D(p, q) =a ( pi q i ) ( pi+1 q i+1 )) ( qi + b q ) i+1, p i p i+1 a, b R p a j ( ) qj q j + b p j j p j ( pj q j ) + K, a b D(p, p) =0 K =0 a b D(p, q) 0 a b a p =(ϵ, 1 ϵ, 0,...,0)
156 q =(0.5, 0.5, 0,...,0) ϵ 0 b j p j ( pj q j ) = ϵ 0 b(ϵ (2ϵ)+(1 ϵ) (2(1 ϵ))) = b (2), ϵ 0 a j ( ) qj q j =, a<0 p j ϵ D(p, q) = a, b p = q D(p, p) =0 x 1,x 2,y 1,y 2,λ [0, 1] ( ) (λx1 +(1 λ)x 2 ) (λx 1 +(1 λ)x 2 ) (λy 1 +(1 λ)y 2 ) λx 1 ( x1 y 1 ) +(1 λ)x 2 ( x2 y 2 ), x x (x) =0
157 ( λx 1 λx 1 +(1 λ)x 2 ( ) y1 (1 λ)x 2 + x 1 λx 1 +(1 λ)x 2 ( ) λx 1 y1 λx 1 +(1 λ)x 2 x 1 ( y2 x 2 )) (1 λ)x 2 λx 1 +(1 λ)x 2 ( y2 x 2 ), D Θ (λp 1 +(1 λ)p 2,λq 1 +(1 λ)q 2 ) λd(p 1,q 1 )+(1 λ)d(p 2,q 2 ), x z 0.5 z > 0.5 z < 0.5 p 1,p 2,q 1,q 2 z > 0.5 ( ) z 0.5 ( ) z 0.5 ( ) z 0.5 p1 + p 2 p1 p2 (p 1 + p 2 ) p 1 + p 2. q 1 + q 2 q 1 q 2 ( p1 q 1 + p ) 0.5 z 2 q 2 p 1 p 1 + p 2 p 1 p 1 + p 2 p 2 p 1 + p 2 ( q1 p 1 ) 0.5 z + p 2 p 1 + p 2 ( q2 p 2 ) 0.5 z,
158 z > 0.5 x 0.5 z z < 0.5 ( p1 p 1 + p 2 ( q1 p 1 ) + p 2 p 1 + p 2 ( )) 0.5 z q2 p 2 p 1 p 1 + p 2 ( q1 p 1 ) 0.5 z + p 2 p 1 + p 2 ( q2 p 2 ) 0.5 z, z < z (0, 1) x 0.5 z (ab) =(a) +(b) i,j (p ip j ) z = i pz i j pz j D(p, q) =D(q, p) p, q D(p, q) = j (p j q j ) ( pj q j ) = j p j ( pj q j ) + j ( ) qj q j ; p j
159 ( ) D(p, q) = pj q j. j D(p, q) < + Supp(p) Supp(q) p =(1, 0) q =(q 1, 1 q 1 ) q D(p, q) D(p, q) D(q, p) z =0 p =(0.5, 0.5) q =(q 1, 1 q 1 ) D(p, q) D(q, p) a b p, q, r n p< LR q< LR r, D(p, q) D(p, r). D D(p, q) = j f j(p j,q j ) f j :[0, 1] [0, 1] R
160 D(p, q) = ( i p i p, q, r p< LR q< LR r, ( p i q i ) z 0.5 ) z>0.5 i ( ) z 0.5 pi p i ( ) z 0.5 pi p i. q i r i i ϵ (0, 1) (D(p,ϵr+(1 ϵ)q)) ϵ 0 D(p, r) D(p, q) ( i p i ( ) ) z 0.5 p i ϵr i +(1 ϵ)q i ϵ ( 0 ( ) z+0.5 q i, i p i (1 ϵ)q i + ϵr i ) z+0.5 r i i p i (1 ϵ)q i + ϵr i ( p i (1 ϵ)q i +ϵr i ) z+0.5 p< LR ϵr +(1 ϵ)q q< LR r z < 0.5 z< 0.5 D(p, q) = i p i ( pi q i ) D(p, q) = i q i ( qi p i ) z 0.5, 0.5 z z D z D z
161 p, q, r n D z (p, q) <D z (p, r) D z (p, q) >D z (p, r). z 0.5, 0.5 i D z (p, q) j D z (p, q) = ( p i ) z+1 ( q i pi+1 ( ) z+1 ( ) z+1, pj pj+1 q j q j+1 q i+1 ) z+1 D(p, q) =K = D(p, (q 1,...,q i + ϵ, q i+1 ϵ,..., q j + g z (ϵ),q j+1 g z (ϵ),...,q n )), g z(0) = id z (p, q) j D z (p, q) = ( p i ) z+1 ( q i pi+1 ( ) z+1 ( ) z+1. pj pj+1 q j q j+1 q i+1 ) z+1 z z p, q n g z(0) g z(0). q D(p, q) p z i z j
162 3 p D z D z q D z (p, q) D z (p, q) z z p q r q D z (p, q) <D z (p, r) D z (p, r) <D z (p, q). p, q n z 0.5, 0.5 D z (p, q) =D z (q, p) z R z z 0.5 Dz (p, q) =( p(θ)/q(θ) p z 0.5), w f : Θ R + f(θ) p w := ( i f(θ i) w p(θ i )) 1/w
163 D z z =0.5 z = 0.5 D z (p, q) z 0.5 z 0.5 = j p j ( pj q j ) =: D 0.5 (p, q) z 0.5 D z (p, q) z 0.5 = j ( ) qj q j =: D 0.5 (p, q). p j D z f ( w 0 f p w = p j j ( pj q j ) ), p(θ)/q(θ) z 0.5 D z (p, q) z 0.5 = D z (q, p) z 0.5 z 0.5 w= z D w (q, p) = w 0.5 w 0.5, z < 0.5 D z (p, q) =+ Supp(p) Supp(q) =. z 0.5 z 0.5 D z (p, q) =+ Supp(p) \ Supp(q). z 0.5 D z (p, q) =+ Supp(q) \ Supp(p).
164 D z (p, q) z < 0.5 D z (p, q) = ( j p z+0.5 j q 0.5 z j ), z < z>0 < 0.5 z p, q n D z (p, q) =+ j pz+0.5 j q 0.5 z j =0 0 0 z>0.5 q j θ j Supp(p) \ Supp(q) D z j Supp(p) Supp(q) q j =0 p j D(p, q) < + z 0.5 D z (p, ) : n R p n D z θ Supp(p) ( D z j Supp(p) p j (p, q) = j Supp(p) p j ( pj ( pj q j ) z 0.5 ) q j ) z>0.5. z =0.5 D z (,q): n R q n z 0.5 D z (,q): n R q n D z
165 θ Supp(q) ( D z j Supp(q) p j (p, q) = j Supp(q) p j ( pj ( pj q j ) z 0.5 ) q j ) z>0.5. z =0.5 D z (p, ) : n R p n z < 0.5 D z : n n R D z (p, q) = j Supp(p) Supp(q) ( ) z 0.5 pj p j, q j j =0 z 0.5 z>0.5 D z (p, ) n D z n (q (n) ) n q (n) j 0 p j =0 D z (p, q (n) ) j p j > 0 ( D z (p, q (n) ) p z+0.5 j (q (n) j ) 0.5 z ) (0.5 z) (q (n) j ) +, q (n) j 0 (0.5 z) < 0 D z (p, q (n) ) + D(p, r) =+ p j > 0 r j =0 D z (p, )
166 n D z (p, q) = j Supp(p) ( ) z 0.5 pj p j. q j D z (,q): n R q n q n D z (,q) n q / n D z (,q) q q 1 =0 q j > 0 j =2,...,n z>0.5 D z (p, q) p p (m) p (m) j := 1 j =1 m (m 1) > 1 m(n 1) D w (p (m),q)=+ m Supp(p) \ Supp(q), p m p = ( ) 1 0, n 1,..., 1, n 1 D z (p,q) < + Supp(q) \ Supp(p) =. z =0.5 p q z < 0.5 z +0.5 z 0.5
167 D z (p, q) = j Supp(p) Supp(q) p z+0.5 j q z 0.5 j. z 0.5 ϵ, δ > 0 p, q,, n p q > x,y n x y δ, <ϵ, D z (, ) >D z ( p, q) z < 0.5 D z (p, q) ϵ δ p q δ D z (p, q) <ϵ z > 0.5 n =2 n (p, 1 p, 0,...,0) x,y 2 x y =1 ϵ δ p, q n p q > 1 δ p, q n D( p, q) < + (p m ) m, (q m ) n p m q m ϵ D(p m,q m ) + m + q m := (1/m, 1 1/m) p m =(1/m+ϵ, 1 1/m ϵ) p m q m ϵ z>0.5 D z (p, q) ( p m 1 ( p m 1 q 1 m ) z 0.5 ) = [ ( 1 m + ϵ )( 1 + ϵ ) z 0.5 ] m, 1 m
168 m + z =0.5 ( p m D 0.5 (p, q) p m 1 1 q1 m ) = ( ) 1 m + ϵ ( 1 + ϵ ) m, 1 m m + ϵ>0 z< 0.5 p q D z z < 0.5 n =2 n 2 p =(x, 1 x) q =(x + ϵ, 1 x ϵ) x [0, 1 ϵ] α := z +0.5 α (0, 1) z < 0.5 D z (p, q) = ( x α (x + ϵ) 1 α +(1 x) α (1 x ϵ) 1 α), x α (x+ϵ) 1 α (1 x) α (1 x ϵ) 1 α x α (x + ϵ) 1 α +(1 x) α (1 x ϵ) 1 α x =0 x =1 ϵ D z (p, q) { (ϵ α +(1 ϵ) 1 α ); ((1 ϵ) α + ϵ 1 α )}. ϵ 0 (ϵ α +(1 ϵ) 1 α ) ((1 ϵ) α +ϵ 1 α ) 0 δ := { (ϵ α +(1 ϵ) 1 α ); ((1 ϵ) α + ϵ 1 α )},
169 n =2 n p, q p j = 0 j p 1 = 0 D z (p, q) D z (p, (0,q 1 + q 2,...,q n )), n 1 p n q p q ϵ p j q j ϵ j p 1 <q 1 p =(0,p 1 + p 2,p 3,...,p n ), q =(q 1 p 1,q 2 + p 1,q 3,...,q n ). n =2 D z (p, q) D z (p,q ), p / n n 1 D Θ Θ ( D n ) n 2,n N D n : (Θ) (Θ) R + {+ }, Dn (p, q) :=D Θ (p, q), q 2 + p 1 < 1 j q j + p 1 < 1 j 2
170 Θ Θ = n D n p, q n λ [0, 1] D n (p, λp +(1 λ)q) D n (p, q). p, q, r n λ [0, 1] D n (λp +(1 λ)r, λq +(1 λ)r) D n (p, q). p, q 1,q 2 λ [0, 1] D n (p, λq 1 +(1 λ)q 2 ) {D n (p, q 1 ),D n (p, q 2 )}. B(p, ρ] :={q n D n (p, q) ρ} D n p 1 = p 2 = p q 1 = p p 1 = p p 2 = r = q 2
171 q 1 = q p 1 = p 2 = p D n C n D n (p, q) =D n ( p, q), p,q C p, q C p, q n D n (p, q) D n (e 1,e 2 ) (= D n (e j,e i ) i, j), e 1 =(1, 0, 0,...,0) e 2 =(0, 1, 0,...,0) s := p,q C D n (p, q) s R + {+ } (p m,q m ) C D n (p m,q m ) s ( p m, q m ) p m, q m C [p m,q m ] [ p m, q m ] D n ( p m, q m ) D n (p m,q m ) m D n ( p m, q m ) s, m D n ( p m, q m )=s s C C ( p m, q m ) C (p,q ) D n (p,q )=s D D D a, b n [a, b] [a, b] :={q n q = λa +(1 λ)b, λ [0, 1]}.
172 φ : R + R + D := φ(d) D n (e 1,e 2 ) D n (p, q) p, q n e 1 =(1, 0,...,0) e 2 =(0, 1, 0,...,0) p, q n D n (p, q) =D n+1 ((p 1,...,p n, 0), (q 1,...,q n, 0)), n =2 D 2 (e 1,e 2 ) >D 2 (e 1, (x, 1 x)) x (0, 1) D 2 (e 1,e 2 )=D 2 (e 1, (x, 1 x)) x (0, 1) p, q n x (0, 1) D n (p, q) =D 2 (e 1, (x, 1 x)), φ(x) =D 2 (e 1, (x, 1 x)). φ(1) = 0 φ(x) x 0 p, q n x D n (p, q) =D 2 (e 1, (x, 1 x)) D 2 x D n ψ ψ(d n (p q, r s)) =
173 ψ(d n (p, r)) + ψ(d n (q, s)). D n x, y, z D 4 (e 1 e 1, (x, 1 x) (y, 1 y)) = D 2 (e 1, (z,1 z)). ψ ψ(d 2 (e 1, (x, 1 x))) + ψ(d 2 (e 1, (y, 1 y))) = ψ(d 2 (e 1, (z,1 z))) x y D 4 (e 1 e 1, (x, 1 x) (y, 1 y)) = D 4 (e 1 e 1, (x, 1 x ) (y, 1 y )), ψ(φ(x))+ψ(φ(y)) = ψ(φ(x ))+ψ(φ(y )) φ(x ) >φ(x) w D 4 (e 1 e 1, (w, 1 w) (x, 1 x)) = D 2 (e 1, (x, 1 x )), D 8 (e 1 e 1 e 1, (w, 1 w) (x, 1 x) (y, 1 y)) = D 4 (e 1 e 1, (x, 1 x ) (y, 1 y)),
174 D 8 (e 1 e 1 e 1, (w, 1 w) (x, 1 x) (y, 1 y)) = D 8 (e 1 e 1 e 1, (w, 1 w) (x, 1 x ) (y, 1 y )), x D 4 (e 1 e 1, (w, 1 w) (y, 1 y )) = D 2 (e 1, (y, 1 y)). φ(x ) >φ(x) φ(y ) <φ(y) w D 4 (e 1 e 1, (w, 1 w ) (y, 1 y )) = D 2 (e 1, (y, 1 y)), w D 2 (e 1, (w, 1 w)) = D 2 (e 1, (w, 1 w )), ψ(φ(y )) ψ(φ(y)) = (ψ(φ(x )) ψ(φ(x))) ψ(φ(x)) + ψ(φ(y)) = ψ(φ(x )) + ψ(φ(y )) p, q, r, s ψ(d nm (p q, r s)) = ψ(d n (p, r)) + ψ(d m (q, s)).
175 x p,r (0, 1) x q,s D n (p, r) =D 2 (e 1, (x p,r, 1 x p,r )) D m (q, s) =D 2 (e 1, (x q,s, 1 x q,s )). x p,r x q,s D nm (p q, r s) =D nm (e 1 e 1, (x p,r, 1 x p,r ) (x q,s, 1 x q,s )). D n (p, r) D 2 (e 1, (x p,r, 1 x p,r )) D n (p, r) D 2 (e 1, (x p,r, 1 x p,r )) D nm (p q, r s) =D nm (e 1 q, (x p,r, 1 x p,r ) s), q, s (e 1 e 1, (x p,r, 1 x p,r ) (x q,s, 1 x q,s )) ψ(d 4 (e 1 e 1, (x p,r, 1 x p,r ) (x q,s, 1 x q,s ))) = ψ(d 2 (e 1, (x p,r, 1 x p,r ))) + ψ(d 2 (e 1, (x p,r, 1 x p,r ))). D 4 (e 1 e 1, (x p,r, 1 x p,r ) (x q,s, 1 x q,s )) = D nm (p q, r s),
176 D nm (p q, r s) =D n (p, r)+d m (q, s). D 2 (e 1,e 2 ) >D 2 (e 1, (x, 1 x)), x (0, 1). D 2 (e 1,e 2 )=D 2 (e 1, (x, 1 x)) x (0, 1) φ(z) :=D 2 ((z,1 z), (x, 1 x)) z (0, 1) ψ ψ(d(, )) p, q, r, s 2 n e 1 x D n p, q n D n (p, q) =D n+1 ((p 1,...,p n, 0), (q 1,...,q n, 0)). m n D m+1 ( p m+1, q m+1 ) D m ( p m, q m ), D m ( p m, q m ) m
177 p (1, 0) p (1, 0) := (p 1,...,p n, 0,...,0) = p 2n q (1, 0) = q 2n D 2n ( p 2n, q 2n )=D 2n (p (1, 0),q (1, 0)) = D n (p, q)+d 2 ((1, 0), (1, 0)), D 2 ((1, 0), (1, 0)) = 0 D 2n ( p 2n, q 2n )=D n (p, q), D mn ( p mn, q mn )=D n (p, q), m N D m ( p m, q m ) m p, q n Supp(p) Supp(q) = p j q j =0 j D D(p, q) =+. p, q n D(p, q) D((1, 0), (0, 1)), Θ A 1 := Supp(p) A 2 =Θ\ Supp(p) D((1, 0), (0, 1)) = +
178 D((1, 0), (0, 1)) < (1, 0) (1, 0) = (1, 0, 0, 0) (0, 1) (0, 1) = (0, 0, 0, 1). D((1, 0, 0, 0), (0, 0, 0, 1)) = D((1, 0), (0, 1)), D((1, 0) (1, 0), (0, 1) (0, 1)) = 2D((1, 0), (0, 1)) D((1, 0), (0, 1)) = 2D((1, 0), (0, 1)), D((1, 0), (0, 1)) < D((1, 0), (0, 1)) = 0 D(p, q) > 0 p q D((1, 0), (0, 1)) = p, q n p 1 q 1 = p 2 q 2. D n (p, q) =D n 1 ((p 1 + p 2,p 3,...,p n ), (q 1 + q 2,q 3,...,q n )). D n (p, q) D n 1 ((p 1 + p 2,p 3,...,p n ), (q 1 + q 2,q 3,...,q n )) D n (p, q) D n 1 ((p 1 + p 2,p 3,...,p n ), (q 1 + q 2,q 3,...,q n )) D(p, q) D((p 1 + p 2,p 3,...,p n ), (q 1 + q 2,q 3,...,q n )).
179 D((p 1 + p 2,p 3,...,p n ), (q 1 + q 2,q 3,...,q n )) = D((0,p 1 + p 2,p 3,...,p n ), (0,q 1 + q 2,q 3,...,q n )) D((p 1 + p 2,p 3,...,p n ), (q 1 + q 2,q 3,...,q n )) = D((p 1 + p 2, 0,p 3,...,p n ), (q 1 + q 2, 0,q 3,...,q n )). p = λ(p 1 + p 2, 0,p 3,...,p n )+(1 λ)(0,p 1 + p 2,p 3,...,p n ), λ = p 1 p 1 +p 2 q = λ (q 1 + q 2, 0,q 3,...,q n )+(1 λ )(0,q 1 + q 2,q 3,...,q n ), λ = q 1 q 1 +q 2. p 1 p 2 = q1 q 2 λ = λ D(p, q) {D((0,p 1 + p 2,p 3,...,p n ), (0,q 1 + q 2,q 3,...,q n )), D((p 1 + p 2, 0,p 3,...,p n ), (q 1 + q 2, 0,q 3,...,q n ))} = D((p 1 + p 2,p 3,...,p n ), (q 1 + q 2,q 3,...,q n )),
180 p n q 1 = (q 1 + q 2, 0,q 3,...,q n ) q 2 =(0,q 1 + q 2,q 3,...,q n ) [q 1,q 2 ]={r n r = λq 1 +(1 λ)q 2,λ [0, 1]}. p [q 1,q 2 ] q [q 1,q 2 ] q1 q2 = p 1 p 2, r, r [q 1,q 2 ] r [r,q ] D n (p, r) D n (p, r ). p 1 q 1 = p 2 q 2 D(p, q )=D((p 1 + p 2,...,p n ), (q 1 + q 2,...,q n )), r [q 1,q 2 ] D(p, r) D((p 1 + p 2,...,p n ), (q 1 + q 2,...,q n )),
181 r [q 1,q 2 ] D(p, r) D(p, q ), r [q 1,q 2 ]. f(q) :=D(p, q) r r r [r,q ], D(p, r) {D(p, r ),D(p, q )}, D(p, q ) D(p, r ) D(p, r) D(p, r ) p, q n p q D π =(S, f(s θ)) s S D(p(s ),q(s )) <D(p, q). D p, q n π =(S, f(s θ)) s S D(p(s),q(s)) >D(p, q). s θ 1 f(s θ 1 )=1 f(s θ j )=0 j =2,...,n p, q
182 p(s )=q(s )=(1, 0,...,0) D(p(s ),q(s )) = 0 <D(p, q), p q p q s D(p (s ),q(s )) <D(p,q ) s f(s θ) = k f(s θ), θ, k f(s θ) < 1 p := p (s ) q := q (s ) p(s) =p q(s) =q D(p, q) =D(p (s ),q(s )) <D(p,q )=D(p(s),q(s)), p q n π π E π p[d(p(s),q(s))] E π p[d(p( s),q( s))]. z 0.5
183 z 0.5 p =(1, 0,...,0) S π f(s θ 1 ) > 0 S π s S f(s θ j )=0 j 2 E π p[d(p(s),q(s))] = 0, s f(s θ j ) > 0 θ j 2 s S g( s θ j ) > 0 g( s θ j )= s λ s, s f(s θ j ), s λ s, s =1 s p q j ( s) > 0=p j ( s) D z (p( s),q( s)) = E π p[d(p( s),q( s))] =, z < 0.5 s S p 1 (s) = 1 D z (p(s),q(s)) = (q 1 (s) z+0.5 ) s (0.5 z) s f(s θ 1 ) (q 1 (s)) (0.5 z) s g( s θ 1 ) (q 1 ( s)),
184 (0.5 z) < 0 z < 0.5 g( s θ 1 ) (q 1 ( s)) s s f(s θ 1 ) (q 1 (s)) s s λ s, s =1 f(s θ 1 ) (q 1 (s)) = s s λ s, s f(s θ 1 ) (q 1 (s)) = s s λ s, s f(s θ 1 ) (q 1 (s)), s g( s θ 1 ) f(s θ 1 ) (q 1 (s)) = s s λ s, s f(s θ 1 ) (q 1 (s)) s = s g( s θ 1 ) s λ s, s f(s θ 1 ) g( s θ 1 ) (q 1 (s)), λ s, sf(s θ 1 ) g( s θ 1 ) s λ s, s f(s θ 1 ) g( s θ 1 ) =1 ( ) s λ s, s f(s θ 1 ) ( (q 1 (s) 1 )) g( s θ 1 ) ( s λ s, s f(s θ 1 ) g( s θ 1 ) ) f(s; q) q 1 f(s θ 1 ) ( = s λ s, sf(s; q) q 1 g( s θ 1 ) ), s λ s, sf(s; q) =f( s; q) ( s λ ) s, sf(s; q) = (q 1 ( s)), q 1 g( s θ 1 )
185 f(s θ 1 ) (q 1 (s)) s s g( s θ 1 ) (q 1 ( s)), D D(p, q) =ad z (p, q) z 0.5 a>0 z 0.5 D z z<0.5 p, q q j =0<p j D(p, q) < + q =(1, 0) p =(α, 1 α) D D D(p, q) =ad z (p, q) z 0.5 a>0 π π p, q n E π p[d(p(s),q(s))] E π p[d(p( s),q( s))].
186 p, q n q / n p / n Θ p p, q n π π φ : n R p n P p (s)φ(p(s)) s S s S P p ( s)φ(p( s)). D z (p(s),q(s)) p(s) z 0.5 q(s) p(s) p q q j (s) = q j i p j p j (s) q i p i p i (s) = r jp j (s) p(s) r, r j := q j p j
187 R n ( ( ) ) z 0.5 pj (s) D z (p(s),q(s)) = p j (s) q j j (s) ( ( ) ) z 0.5 p(s) r = p j (s) j r j =(z 0.5) (p(s) r)+(p(s) r z ), r z j := 1 r z 0.5 j z>0.5 D z (p(s),q(s)) p(s) r z (p(s) r z ) (z 0.5) (p(s) r) r 0 z 0.5 > 0 z =0.5 D 0.5 (p(s),q(s)) = j ( ) pj (s) p j (s) q j (s) = j p j (s)((p(s) r) (r j )) = p(s) (r)+(p(s) r), (r) :=((r 1 ),...,(r n )). D 0.5 (p(s),q(s)) p(s) p(s) z<0.5 p, q π E π p(d z (p(s),q(s))) >D(p, q);
188 p, q π E π p(ad 0.5 (p(s),q(s)) + bd 0.5 (p(s),q(s))) > ad 0.5 (p, q)+bd 0.5 (p, q)) z<0.5 p 2 q n =(1/n, 1 1/n) n D z (p, q) < D z (p, (0, 1)) < + π(ϵ) ϵ 0 E π(ϵ) p (D(p(s),q n (s))) + n π π(ϵ) f(s 0 θ 1 )=1 ϵ, f(s 1 θ 1 )=ϵ, f(s 1 θ 2 )=ϵ f(s 0 θ 2 )=1 ϵ. s 1 p 2 (s 0 )= ϵp 2 ϵp 2 +(1 ϵ)p 1 ; q 2 (s 0 )= ( 1 1 n) ϵ ( ) 1 1 n ϵ + 1 (1 ϵ). n ϵ = n 0.5 n + p 2 (s 0 ) 0 q 2 (s 0 ) 1 n E π(n 0.5 ) p (D(p(s),q(s))) P p (s 0 )D z ((1 δ, δ), (δ, 1 δ)),
189 δ (0, 1) n P p (s 0 ) > 0 D z (p, q n ) <D z (p, (0, 1)) < n E π(n 0.5 ) p (D z (p(s),q(s))) >D z (p, q n ), z D z ((1 δ, δ), (δ, 1 δ)) δ 0 D(p, q) =ad 0.5 (p, q) +bd 0.5 (p, q) p =(0.5 ϵ, ϵ, 0.5) q =(0.5 ϵ, δ, 0.5+ϵ δ) ( D(p, q) =a δ ( ) δ +(0.5+ϵ δ) ϵ ( + b ϵ ( )) 0.5+ϵ δ 0.5 ( ϵ ) ( +0.5 δ ϵ δ )). π =({s 1,s 2 },f(s θ)) f(s 1 θ 1 )=f(s 1 θ 2 )=1 f(s 2 θ 3 )=1 ϵ, δ π θ 3 p(s 2 )=q(s 2 )= (0, 0, 1) ϵ, δ p(s 1 )= ( ) 0.5 ϵ 0.5, ϵ 0.5, 0 q(s 1 )= ( ) 0.5 ϵ 0.5 ϵ + δ, δ 0.5 ϵ + δ, 0.
190 P p (s 1 )=0.5 ϵ, δ 0.5D(p(s 1 ),q(s 1 )) = 0.5aD 0.5 (p(s 1 ),q(s 1 )) + 0.5bD 0.5 (p(s 1 ),q(s 1 )). δ 0 ϵ 0.5 D 0.5 (p, q) 0.5D 0.5 (p(s 1 )q(s 1 )) D 0.5 (p, q) 0.5D 0.5 (p(s 1 )q(s 1 )) D 0.5 (p, q) 0.5D 0.5 (p(s 1 )q(s 1 )) ( ϵ ) ( ) 0.5+ϵ δ = ϵ +(0.5+ϵ δ) δ 0.5 ( ( ) 0.5 ϵ ϵ ( ( ϵ ) ( ))) 0.5 ϵ + δ ϵ + δ 0.5 δ δ ( ) ( ) 0.5+ϵ δ 0.5 ϵ + δ = δ ϵ. 0.5 δ δ = 0.5 ϵ ϵ 0.5 D 0.5 (p, q) 0.5D 0.5 (p(s 1 )q(s 1 ))
191 D 0.5 (p, q) 0.5D 0.5 (p(s 1 )q(s 1 )) D 0.5 (p, q) 0.5D 0.5 (p(s 1 )q(s 1 )) ( ) ( ) δ 0.5+ϵ δ = δ +(0.5+ϵ δ) ϵ 0.5 ( ( ) 0.5 ϵ 0.5 ϵ + δ ϵ + δ δ ( ( ) ( )) ) δ δ δ ϵ + δ ϵ 0.5 ϵ + δ ϵ 0.5 δ = 0.5 ϵ D 0.5 (p, q) =δ ( ) δ ϵ + (0.5+ϵ δ) ( ) 0.5+ϵ δ 0.5 δ = 0.5 ϵ 0.5D(p(s 1 ),q(s 1 )) p 1,...,p J n (u j ) j z j (0, 1) (Π i ) i 1 D zj+0.5 (q, p j ( I)), q (I) 1 z j j
192 V j ((x j i ) i)=(d z j+0.5 (p j ( I), Π) + D z j+0.5 (Π,p j ( I))) 1 j J; G j ((x j i ) i)= 1 ( ( )) 1 1 Dzj 0.5 (Π,p j ( I)), j J. z j 1 z j j (x j i ) i i p j i (x j i )1 1 z j 1 1 z j Π i x i 0, i x j i p j i (xj i ) 1/z j λπ i =0, λ x j i x j i = ( p j i λπ i ) zj, i Π ix j i =1 λ z j = i ( ) p j zj i Π i, Π i
193 x j i = ( p j i k Π k Π i ) zj ( Π k p j k ) zj, j 1= j x i,j = j ( p j i k Π k Π i ) zj ( Π k p j k ) zj, i i i +1 j ( p j i Π i ) zj ( k Π k ( ) zj p j i+1 Π i+1 Π k p j k ) zj =0, j 1 i ( ) 1 D zj+0.5 (Π,p j ( I)), 1 z j 1 i D D Π z i,i+1 D
194 V j ((x j i ) i)= i ( p j i xj i 1= i pj i ( k Π k ) zj Π i p j i Π k p j k ) zj 1 = (D z j+0.5 (p j ( I), Π) + D z j+0.5 (Π,p j ( I))) 1. u j (1) = z j u j (x j i )= z j i ( k Π k ) zj Π i p j i ( ) zj Π k p j k p j i u(xj i )= z j 1 1 z j ( i p j i ( Πi p j i ) ) ( ( 1 zj Π k k Π k p j k ) zj ) 1 z j 1, G j ((x j i ) i)= 1 ( ( )) 1 1 Dzj 0.5 (Π,p j ( I)), j J. z j 1 z j (u j ) j J 1 u j(1) = 1 1/u j (1) =: z j (0, 1) (p j,(m) ) j J m N m ((x j,(m) i ) j J i=1,...,n, (Πm i ) i ) m Π m q n j 1 1 z j D zj+0.5 (q, p j,(m) ).
195 j m D z j +0.5 (p j,(m),π m ) D z j +0.5 (p j,(m), Π m ) =1 pj Π m Π m m i pj,(m) i (x j,(m) i 1) D z j+0.5 (p j,(m), Π m )+D z j+0.5 ( Π m,p j,(m) ) =1. m i pj,(m) i u i (x j,(m) i ) 1 1 z j D z j 0.5 ( Π m,p j,(m) ) =1. m p j,(m) x j,(m) i 1 u j ũ j u j 1 1 z j ũ j (x) := x1 1 1, z j z j = 1 u (1)
196 J := ((p 1 i ) i,...,(p J i ) i ) ((x j i ( )) i,j, (Π i ( )) i, (λ j ( )) j ) u j x j i Π i λ j (( x j i ( )) i,j, ( Π i ( )) i, ( λ j ( )) j ) ũ j x j i ( ) j, i Π i ( ) i λ j ( ) j =(p,...,p ) x j i ( )= x j i ( ), v =(v 1,...,v J ) j J i vj i =0 pj + ϵv j n ϵ ((x j i ( )) i,j, (Π i ( )) i, (λ j ( )) j ) (( x j i ( )) i,j, ( Π i ( )) i, ( λ j ( )) j ) u j ũ j p j,(m) i u j(x j,(m) i ) λ m j Π m =0, p j,(m) i ũ j( x j,(m) i ) λ m j Π m =0,
197 Π i ( )= Πi ( ) λ j ( )= λj ( ). i, j x j i ( ) 1 =1, ( ) 1 x j i n n. x j i =(u ) 1 ( λj ( )Π i ( ) p i,j ) x j i ( ) = ( λj ( ) Π i ( ) p i,j ) zj ũj φ( ) := λ j ( )Π i ( ) p i,j φ( ) φ( )= φ( ),. 0/0 (x j i ( ) 1) ( x j =1, i ( ) 1) 1 u ((u ) 1 (φ( ))) φ( ), z j φ( ) φ( )
198 φ( ) 1 φ( ) 1 1 u ((u ) 1 (φ( ))) = z j φ( ), φ( ) φ( ) 0 p j i i xj i ( )pj i i xj i ( )pj i =1, D zj+0.5 (p j, Π( )) + D zj+0.5 ( Π( ),p j ) u j ũ j Π Π p j i Π j i ( ) = λ j( )u (x j i ( )) p j i Π j i ( ) = λ j ( )ũ ( x j i ( )), i, j p j i Π j i ( ) =1, p j i Π j i ( ) φ
199 (x i ) i x i 0, x i 1. i n G n G n n I(x y) x y n N x, y G n I(x, y) 0 x i y i i I(x y) 0 x i y i i I(1, 1/2) = 1 n, m N x 1,y 1 G n x 2,y 2 G m I(x 1 x 2 y 1 y 2 )= I(x 1 y 1 )+I(x 2 y 2 ) x G n y G m x y := (x 1,...,x n,y 1,...,y m ) G n+m g : R R x 1,x 2,y 1,y 2 x 1 x 2
200 y 1 y 2 I(x 1 x 2 y 1 y 2 )=g 1 ( i x1 i ) g(i(x 1 x 2 )) + ( ) j x2 j i x1 i + j x2 j g(i(y 1 y 2 )) (P 6) (P 7) x, y x i y i i x = y (P 7) I(p p) =0 P (8) (P 9) x 1,y 1,x 2,y 2 G 1 =[0, 1] I(x 1 x 2 y 1 y 2 )=I(x 1 y 1 )+I(x 2 y 2 ). I x, y [0, 1] I(x y) = β (x/y) β R (P 9) I 1 x, y [0, 1] (P 9) (P 10) I(x y) x G n y G m x y n m x i + y j 1. i=1 j=1
201 z,z [0, 1] I(z z )=β (z/z ) (P 10) x, y G n I(x y) =g 1 ( j x j i x g(α (x j /y j )) i ), g I (P 9) g(x) :=γe αx (P 8) I(x y) = 1 α 1 ( ) α 1 j x xj j y j j x j, R α (p, q) ( R α (p, q) = 1 ( ) ) α 1 α 1 pj p j. q j j (P 10) (p i /q i )
202 (P 10) x y (x, y) I(x y) (x, y) I(y x) (x, y) D(x, y) (x, y) D(y, x) D(p, q) = j q j ( qj p j ) n x 1,...,x n R ( M p φ (x 1,...,x n )=φ 1 j p ) jφ(x j ), n φ( ) p q p q
203 s 1,s 2 f(s 1 θ)f(s 2 θ )=f(s 1 θ )f(s 2 θ) θ, θ γ : S S γ(s 1 )=γ(s 2 ) γ(s) γ(s ) s s s, s s 1,s 2 c n (γ π) =c(π). c n (γ π) c n (π) c n (γ π) c n (π) k>0 kf(s 1 θ) =f(s 2 θ) θ Θ,
204 γ π = (( (1+k)f(s1 )) θ 1 )... (1+k)f(s 1 θ n) f(s 3 θ 1 )... f(s 3 θ n) f(s m θ 1 )... f(s m θ n) = ( 1+k k f(s 1+k 2 θ 1 )... k f(s 2 θ n) f(s 3 θ 1 )... f(s 3 θ n) f(s m θ 1 )... f(s m θ n) ), (1+k)f(s 1 θ 1 )... (1+k)f(s 1 θ n) c n (γ π) =c n f(s 3 θ 1 )... f(s 3 θ n) = c n f(s m θ 1 )... f(s m θ n) k k f(s 1+k 2 θ 1 )... k f(s 2 θ n) f(s 3 θ 1 )... f(s 3 θ n) f(s m θ 1 )... f(s m θ n) , π π = 1 k +1 (1+k)f(s 1 θ 1 )... (1+k)f(s 1 θ n) f(s 3 θ 1 )... f(s 3 θ n) + k f(s m θ 1 )... f(s m θ n) k k k f(s 1+k 2 θ 1 )... k f(s 2 θ n) f(s 3 θ 1 )... f(s 3 θ n) f(s m θ 1 )... f(s m θ n) c n (π) { c n (1+k)f(s 1 θ 1 )... (1+k)f(s 1 θ n) f(s 3 θ 1 )... f(s 3 θ n) f(s m θ 1 )... f(s m θ n) , c n k k f(s 1+k 2 θ 1 )... k f(s 2 θ n) f(s 3 θ 1 )... f(s 3 θ n) f(s m θ 1 )... f(s m θ n) }, c n (π) c n (γ π),
205 π π c n c n (π) c n (π ) π = (S, (f(s θ)) s S,θ Θ ) π = (S, (g(s θ)) s S,θ Θ) λ s,s 0 s S λ s,s =1 g(s θ) = s λ s,s f(s θ). s s f(s θ) > 0 θ s s g(s θ) > 0 π c n (π) =c n λ s1,s 1 f(s 1 θ 1 )... λ s1,s 1 f(s 1 θ n) λ s1,s 2 f(s 1 θ 1 )... λ s1,s 2 f(s 1 θ n) λ s1, sf(s 1 θ 1 )... λ s1, sf(s 1 θ n) f(s 2 θ 1 )... f(s 2 θ n) f(s m θ 1 )... f(s m θ n) , s s =1 λ s 1,s = 1 π c n (π) =c n λ s1,s 1 f(s 1 θ 1 )... λ s1,s 1 f(s 1 θ n) λ s1,s 2 f(s 1 θ 1 )... λ s1,s 2 f(s 1 θ n) λ s1, sf(s 1 θ 1 )... λ s1, sf(s 1 θ n) λ s2,s 1 f(s 2 θ 1 )... λ s2,s 1 f(s 2 θ n) λ s2, sf(s 2 θ 1 )... λ s2, sf(s 2 θ n) λ sm,s 1 f(s m θ 1 )... λ sm,s 1 f(s m θ n) λ sm, sf(s m θ 1 )... λ sm, sf(s m θ n) , s
206 c n λ s1,s 1 f(s 1 θ 1 )... λ s1,s 1 f(s 1 θ n) λ s1,s 2 f(s 1 θ 1 )... λ s1,s 2 f(s 1 θ n) λ s1, sf(s 1 θ 1 )... λ s1, sf(s 1 θ n) λ s2,s 1 f(s 2 θ 1 )... λ s2,s 1 f(s 2 θ n) λ s2, sf(s 2 θ 1 )... λ s2, sf(s 2 θ n) λ sm,s 1 f(s m θ 1 )... λ sm,s 1 f(s m θ n) λ sm, sf(s m θ 1 )... λ sm, sf(s m θ n) (( c n s λ s,s f(s θ 1)... s λ 1 s,s f(s θn) 1 s λ s,s f(s θ 1)... s λ 2 s,s f(s θn) s λ s, s f(s θ 1)... s λs, sf(s θn) )), π c n (π) c n (π ) φ : E n R {+ } φ π φ(π) =0 φ(π) = π π := π π c n (π) =c n ( π) =c n (π π) =c n (π)+c n (π), c n (π) =0 c n (π) = H : (Θ) R H(µ) >H(δ j ) µ (Θ) j =1,..., Θ µ (Θ) φ µ : E n R φ(π 1 π 2 )=φ(π 1 )+φ(π 2 ), π 1,π 2 E n.
207 φ µ (π) := H(µ) s S P µ (s)h(µ(s)). φ µ (π) π s s P µ (s) > 0 µ(s) =δ j j H(µ) > s S P µ(s)h(µ(s)) φ µ (π) > 0 π φ µ (π) = H Θ Θ > 3 S c Θ,S ( ) f(s θi ) (f(s θ i ) f(s θ j )) = f(s θ s i,j j ) i,j D(f( θ i ),f( θ j )), D D(p, q) = ( ) i p i pi q i + ( i q i qi p i ) c Θ,S = θ,θ c 2 (π(θ, θ )), c Θ,S (π) = θ,θ c KL 2 (π(θ, θ )), P µ (s) θ µ(θ)f(s θ) µ s
208 c Θ,S (π) = θ,θ c B 2 (π(θ, θ )), c Θ,S (π) = θ,θ c KL 2 (π(θ, θ )), c Θ,S (π) = π s S θ, θ Θ f(s θ) > 0=f(s θ ) c Θ,S (π) =0 D(f( θ),f( θ )) = θ, θ Θ D(f( θ),f( θ )) = s f(s θ) > 0=f(s θ ) f(s θ) =0<f(s θ ) c 2 c KL 2 (π) = s [f(s θ 1) f(s θ 2 )][(f(s θ 1 )) (f(s θ 2 ))]; ( ) c B 2 (π) = s f(s θ1 )f(s θ 2 ). 2 Θ =2 KL B
209 p, q f( θ),f( θ ) D(p, q) < p, q D D(p, q) = D(q, p) n =2 θ s c n f n f n (x 1,...,x n )= n x i, (x i ) i [0, ] n. i=1 Θ =3 c 3 (π) =c 2 (π(θ 1,θ 2 )) + f 2 (c 2 (π(θ 3,θ 2 )),c 2 (π(θ 1,θ 3 ))).
210 c 3 (π) =c 2 (π(θ 2,θ 3 )) + f 2 (c 2 (π(θ 1,θ 2 )),c 2 (π(θ 1,θ 3 ))), c 2 (π(θ 1,θ 2 )) + f 2 (c 2 (π(θ 3,θ 2 )),c 2 (π(θ 1,θ 3 ))) = c 2 (π(θ 2,θ 3 )) + f 2 (c 2 (π(θ 1,θ 2 )),c 2 (π(θ 1,θ 3 ))). c 2 f( θ 3 ) c 2 (π(θ 1,θ 3 )) (S) c 2 c 2 (π(θ 1,θ 3 )) 0 x f 2 (c 2 (π(θ 3,θ 2 )),c 2 (π(θ 1,θ 3 ))) c 2 (π(θ 1,θ 3 )) = c 2 (π(θ 1,θ 3 )). c 2 (π(θ 1,θ 3 )) 0 x f 2 (c 2 (π(θ 3,θ 2 )),c 2 (π(θ 1,θ 3 ))) = 1. c 2 (π(θ 1,θ 3 )) c 2 (π(θ 1,θ 3 )) x f 2 f 2
PC PSI PT JEAN-MARIE MONIER GUILLAUME HABERER CÉCILE LARDON MÉTHODES ET EXERCICES. Mathématiques. méthodes et exercices. 3 e.
 PC PSI PT MÉTHODES ET EXERCICES JEAN-MARIE MONIER GUILLAUME HABERER CÉCILE LARDON Mathématiques méthodes et exercices 3 e édition Conception et création de couverture : Atelier 3+ Dunod, 201 5 rue Laromiguière,
PC PSI PT MÉTHODES ET EXERCICES JEAN-MARIE MONIER GUILLAUME HABERER CÉCILE LARDON Mathématiques méthodes et exercices 3 e édition Conception et création de couverture : Atelier 3+ Dunod, 201 5 rue Laromiguière,
A B C D E Hjemmeværnmuseet's arkiv/depot Søgaard Distrikter - LMD. Reol/hylde Region/distrikt/m.m. Kasse nr. Indhold 2C3 Flyverhjemmeværne 1
 0 A B C D E Hjemmeværnmuseet's arkiv/depot Søgaard LMK Distrikter - LMD. Reol/hylde Region/distrikt/m.m. Kasse nr. Indhold C Flyverhjemmeværne Flyverhjemmeværnet LMD Odense Nyt fra stabseskadrillen -.
0 A B C D E Hjemmeværnmuseet's arkiv/depot Søgaard LMK Distrikter - LMD. Reol/hylde Region/distrikt/m.m. Kasse nr. Indhold C Flyverhjemmeværne Flyverhjemmeværnet LMD Odense Nyt fra stabseskadrillen -.
Områdeestimator. X x. P θ. ν θ. Θ C(x) En områdeestimator er en afbildning C : X P(Θ). . p.1/30
 Områdeestimator X (Ω, F) (X, E) x 01 01 P θ ν θ θ Θ 0000 1111 000000 111111 0000 1111 0000 1111 C(x) En områdeestimator er en afbildning C : X P(Θ).. p.1/30 Konfidensområde En områdestimator C : X P(Θ)
Områdeestimator X (Ω, F) (X, E) x 01 01 P θ ν θ θ Θ 0000 1111 000000 111111 0000 1111 0000 1111 C(x) En områdeestimator er en afbildning C : X P(Θ).. p.1/30 Konfidensområde En områdestimator C : X P(Θ)
Integration m.h.t. mål med tæthed
 Integration m.h.t. mål med tæthed Sætning (EH 11.7) Lad ν = f µ på (X, E). For alle g M + (X, E) gælder at gdν = g f dµ. Bevis: Standardbeviset: 1) indikatorfunktioner 2) simple funktioner 3) M + -funktioner.
Integration m.h.t. mål med tæthed Sætning (EH 11.7) Lad ν = f µ på (X, E). For alle g M + (X, E) gælder at gdν = g f dµ. Bevis: Standardbeviset: 1) indikatorfunktioner 2) simple funktioner 3) M + -funktioner.
StatDataN: Plot af data
 StatDataN: Plot af data JLJ StatDataN: Plot af data p. 1/39 Repetition binomial(n,p): P(X = k) = ( n) k p k (1 p) n k n uafhængige kast med en mønt, X= antal krone X binomial(n, p), Y binomial(m, p), uafhængige
StatDataN: Plot af data JLJ StatDataN: Plot af data p. 1/39 Repetition binomial(n,p): P(X = k) = ( n) k p k (1 p) n k n uafhængige kast med en mønt, X= antal krone X binomial(n, p), Y binomial(m, p), uafhængige
s", U u F F .xx r- \O Hd3 F:I rno H\O c.t F y(g \oo ett H I (l) ooo \oo cne rr') o NiE cne (.) c) b'6 P nh9a oq-o ts H" O.T!\ E trhnx 8. lxci va-.
 \.l \ \l \R cj U u \ < \) R " \ (\l l l!{ (J x ) ii 9/ & B U: >': :U S * i fl q!. > ' z 1 ( 8 :.xx \O 3 9 VY Y : ii 0) ) (!i! > l/. ( < l y( \O c. )< O c = O 1 O x 9 c ' c4 : l c. \ l.! (1) u f \ O 1 '
\.l \ \l \R cj U u \ < \) R " \ (\l l l!{ (J x ) ii 9/ & B U: >': :U S * i fl q!. > ' z 1 ( 8 :.xx \O 3 9 VY Y : ii 0) ) (!i! > l/. ( < l y( \O c. )< O c = O 1 O x 9 c ' c4 : l c. \ l.! (1) u f \ O 1 '
Tillæg til Lokalplan nr For boligbebyggelsen Røde Vejrmølle Parken. Miljø- og Teknikforvaltningen. Albertslund Kommune
 Miljø- og Teknikforvaltningen Albertslund Kommune Tillæg til Lokalplan nr. 18.5.1 www.albertslund.dk albertslund@albertslund.dk T 43 68 68 68 F 43 68 69 28 For boligbebyggelsen Røde Vejrmølle Parken Hvad
Miljø- og Teknikforvaltningen Albertslund Kommune Tillæg til Lokalplan nr. 18.5.1 www.albertslund.dk albertslund@albertslund.dk T 43 68 68 68 F 43 68 69 28 For boligbebyggelsen Røde Vejrmølle Parken Hvad
Formelsamling - MatF2. Therkel Zøllner og Amalie Christensen 27. juni 2009
 Formelsamling - MatF2 Therkel Zøllner og Amalie Christensen 27. juni 2009 1 Indhold 1 Kompleks variabel teori 3 1.1 Komplekse funktioner 825-830........................... 3 1.2 Powerserier af komplekse
Formelsamling - MatF2 Therkel Zøllner og Amalie Christensen 27. juni 2009 1 Indhold 1 Kompleks variabel teori 3 1.1 Komplekse funktioner 825-830........................... 3 1.2 Powerserier af komplekse
i9gx ov 9.5 ri= ()^ Y9 Fq -d E X< OHN ^ x- 3 b'< Liv []4 F SoO =+ ^, Xi* >; oxf t 5e tali> 9U< <sc) 3 3E F o': tox o ts>t co F: o)sn + ca
![i9gx ov 9.5 ri= ()^ Y9 Fq -d E X< OHN ^ x- 3 b'< Liv []4 F SoO =+ ^, Xi* >; oxf t 5e tali> 9U< <sc) 3 3E F o': tox o ts>t co F: o)sn + ca i9gx ov 9.5 ri= ()^ Y9 Fq -d E X< OHN ^ x- 3 b'< Liv []4 F SoO =+ ^, Xi* >; oxf t 5e tali> 9U< <sc) 3 3E F o': tox o ts>t co F: o)sn + ca](/thumbs/104/163744729.jpg) Li
Li
! "# "!# +,- ). "%/")" $" 0* '122 *3 14"5"""!! '16) "!! ":",3);/, 13":", <"))"/
 !! $%&'$( ))$*! +,- ). %/) $ 0* '122 *3 145!! '16)!! 1764)3)*83) 019313:,3);/, 13:,
!! $%&'$( ))$*! +,- ). %/) $ 0* '122 *3 145!! '16)!! 1764)3)*83) 019313:,3);/, 13:,
Nanostatistik: Konfidensinterval
 Nanostatistik: Konfidensinterval JLJ Nanostatistik: Konfidensinterval p. 1/37 Fraktilpåmindelse u p : Φ(u p ) = p, Φ( z ) = 1 Φ( z ) t p [f] : F t[f] (t p [f]) = p, F t[f] ( t ) = 1 F t[f] ( t ) F-fordeling:
Nanostatistik: Konfidensinterval JLJ Nanostatistik: Konfidensinterval p. 1/37 Fraktilpåmindelse u p : Φ(u p ) = p, Φ( z ) = 1 Φ( z ) t p [f] : F t[f] (t p [f]) = p, F t[f] ( t ) = 1 F t[f] ( t ) F-fordeling:
Løsningsforslag til opgavesæt 5
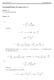 Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
Tillæg til Lokalplan nr For boligbebyggelsen Røde Vejrmølle Parken. Forslag. Miljø- og Teknikforvaltningen. Albertslund Kommune
 Miljø- og Teknikforvaltningen Albertslund Kommune Tillæg til Lokalplan nr. 18.5.1 www.albertslund.dk albertslund@albertslund.dk T 43 68 68 68 F 43 68 69 28 For boligbebyggelsen Røde Vejrmølle Parken Forslag
Miljø- og Teknikforvaltningen Albertslund Kommune Tillæg til Lokalplan nr. 18.5.1 www.albertslund.dk albertslund@albertslund.dk T 43 68 68 68 F 43 68 69 28 For boligbebyggelsen Røde Vejrmølle Parken Forslag
MÅLESTOKSFORHOLD HFB 2012 / 13. Målestoksforhold OP SL AG. Byggecentrum
 MÅLESTOKSFORHOLD Målestoksforhold 340 MÅLEENHEDER Måleenheder Omsætning: Gl. dansk mål metermål gl. engelsk mål (= amerikansk mål). Se også: Målesystemer og enheder. Gl. dansk mål Metermål Gl. engelsk
MÅLESTOKSFORHOLD Målestoksforhold 340 MÅLEENHEDER Måleenheder Omsætning: Gl. dansk mål metermål gl. engelsk mål (= amerikansk mål). Se også: Målesystemer og enheder. Gl. dansk mål Metermål Gl. engelsk
Integration m.h.t. mål med tæthed
 Integration m.h.t. mål med tæthed Sætning (EH 11.7) Lad ν = f µ på (X, E). For alle g M + (X, E) gælder at gdν = g f dµ. Bevis: Standardbeviset: 1) indikatorfunktioner 2) simple funktioner 3) M + -funktioner.
Integration m.h.t. mål med tæthed Sætning (EH 11.7) Lad ν = f µ på (X, E). For alle g M + (X, E) gælder at gdν = g f dµ. Bevis: Standardbeviset: 1) indikatorfunktioner 2) simple funktioner 3) M + -funktioner.
Differentialregning i R k
 Differentialregning i R k Lad U R k være åben, og lad h : U R m være differentiabel. Den afledte i et punkt x U er Dh(x) = h 1 (x) x 1 h 2 (x) x 1. h m (x) x 1 h 1 (x) x 2... h 2 (x) x 2.... h m (x) x
Differentialregning i R k Lad U R k være åben, og lad h : U R m være differentiabel. Den afledte i et punkt x U er Dh(x) = h 1 (x) x 1 h 2 (x) x 1. h m (x) x 1 h 1 (x) x 2... h 2 (x) x 2.... h m (x) x
Antag at. 1) f : R k R m er differentiabel i x, 2) g : R m R p er differentiabel i y = f(x), . p.1/18
 Differentialregning i R k Kæderegel Lad U R k være åben, og lad h : U R m være differentiabel Antag at Den afledte i et punkt x U er Dh(x) = 1) f : R k R m er differentiabel i x, 2) g : R m R p er differentiabel
Differentialregning i R k Kæderegel Lad U R k være åben, og lad h : U R m være differentiabel Antag at Den afledte i et punkt x U er Dh(x) = 1) f : R k R m er differentiabel i x, 2) g : R m R p er differentiabel
Tonelli light. Eksistensbeviset for µ ν gav målet. for G E K ved succesiv integration. Alternativ definition:
 Tonelli light Eksistensbeviset for µ ν gav målet ( ) λ(g) = G (x, y)dν(y) dµ(x) for G E K ved succesiv integration. Alternativ definition: ( ) λ(g) = G (x, y)dµ(x) dν(y). Som λ(a B) = µ(a)ν(b) gælder λ(a
Tonelli light Eksistensbeviset for µ ν gav målet ( ) λ(g) = G (x, y)dν(y) dµ(x) for G E K ved succesiv integration. Alternativ definition: ( ) λ(g) = G (x, y)dµ(x) dν(y). Som λ(a B) = µ(a)ν(b) gælder λ(a
Løsningsforslag til opgavesæt 5
 Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
hvor a og b er konstanter. Ved middelværdidannelse fås videre
 Uge 3 Teoretisk Statistik. marts 004. Korrelation og uafhængighed, repetition. Eksempel fra sidste gang (uge ) 3. Middelværdivektor, kovarians- og korrelationsmatrix 4. Summer af stokastiske variable 5.Den
Uge 3 Teoretisk Statistik. marts 004. Korrelation og uafhængighed, repetition. Eksempel fra sidste gang (uge ) 3. Middelværdivektor, kovarians- og korrelationsmatrix 4. Summer af stokastiske variable 5.Den
standard normalfordelingen på R 2.
 Standard normalfordelingen på R 2 Lad f (x, y) = 1 x 2 +y 2 2π e 2. Vi har så f (x, y) = 1 2π e x2 2 1 2π e y2 2, og ved Tonelli f dm 2 = 1. Ved µ(a) = A f dm 2 defineres et sandsynlighedsmål på R 2 målet
Standard normalfordelingen på R 2 Lad f (x, y) = 1 x 2 +y 2 2π e 2. Vi har så f (x, y) = 1 2π e x2 2 1 2π e y2 2, og ved Tonelli f dm 2 = 1. Ved µ(a) = A f dm 2 defineres et sandsynlighedsmål på R 2 målet
GEOMETRI-TØ, UGE 6. . x 1 x 1. = x 1 x 2. x 2. k f
 GEOMETRI-TØ, UGE 6 Hvis I falder over tryk- eller regne-fejl i nedenstående, må I meget gerne sende rettelser til fuglede@imfaudk Opvarmningsopgave 1 Lad f : R 2 R være tre gange kontinuert differentierbar
GEOMETRI-TØ, UGE 6 Hvis I falder over tryk- eller regne-fejl i nedenstående, må I meget gerne sende rettelser til fuglede@imfaudk Opvarmningsopgave 1 Lad f : R 2 R være tre gange kontinuert differentierbar
Sandsynlighedsteori
 Fordelingskatalog til Sandsynlighedsteori 1.1 + 1.2 Svend Erik Graversen August 2005 1 Dette katalog indeholder de vigtigste egenskaber ved de 6 mest almindelige diskrete fordelinger samt de 11 mest almindelige
Fordelingskatalog til Sandsynlighedsteori 1.1 + 1.2 Svend Erik Graversen August 2005 1 Dette katalog indeholder de vigtigste egenskaber ved de 6 mest almindelige diskrete fordelinger samt de 11 mest almindelige
Kortfattet svar til eksamen i Matematik F2 d. 21. juni 2017
 Kortfattet svar til eksamen i Matematik F2 d. 2. juni 27 Opgave Bestem for følgende tilfælde om en funktion f(z) af z = x + iy er analytisk i dele af den komplekse plan, hvis den har real del u(x, y) og
Kortfattet svar til eksamen i Matematik F2 d. 2. juni 27 Opgave Bestem for følgende tilfælde om en funktion f(z) af z = x + iy er analytisk i dele af den komplekse plan, hvis den har real del u(x, y) og
BYPLANVEDTÆGT nr. A 1 Avedøre Hvidovre kommune
 A l BYPLANVEDTÆGT nr. A 1 Avedøre Hvidovre kommune Byplanvedtægt for et område af Avedere by, Brendbyester sogn, Glostrup kommune, omfattende *Avederegård villaby«,»storegårdens villaby«og»vesterkær«.
A l BYPLANVEDTÆGT nr. A 1 Avedøre Hvidovre kommune Byplanvedtægt for et område af Avedere by, Brendbyester sogn, Glostrup kommune, omfattende *Avederegård villaby«,»storegårdens villaby«og»vesterkær«.
Huseftersynsordningen plus, minus ti år -
 Huseftersynsordningen plus, minus ti år - ! # # # % & # ( ( #! # ) # ( & # # # # +! #!# %, # # #! %.# / # # 0#( # # # # # # %, # # # 1 # # % 2 # & # # 0#( # # # # # 2 # #! 2 ( # # 3 ( & # # # (#! #, #
Huseftersynsordningen plus, minus ti år - ! # # # % & # ( ( #! # ) # ( & # # # # +! #!# %, # # #! %.# / # # 0#( # # # # # # %, # # # 1 # # % 2 # & # # 0#( # # # # # 2 # #! 2 ( # # 3 ( & # # # (#! #, #
Sandsynlighedsregning 9. forelæsning Bo Friis Nielsen
 Sandsynlighedsregning 9. forelæsning Bo Friis Nielsen Matematik og Computer Science Danmarks Tekniske Universitet 800 Kgs. Lyngby Danmark Email: bfni@dtu.dk Dagens emner afsnit 5.3 og 5.4 Simultane kontinuerte
Sandsynlighedsregning 9. forelæsning Bo Friis Nielsen Matematik og Computer Science Danmarks Tekniske Universitet 800 Kgs. Lyngby Danmark Email: bfni@dtu.dk Dagens emner afsnit 5.3 og 5.4 Simultane kontinuerte
LOKALPLAN 13.08A Tilbygninger i boligområdet Åsager
 LOKALPLAN 13.08A Tilbygninger i boligområdet Åsager Dokumentet har gennemgået en bearbejdning, for at komme på anvendelig digital form. Derfor kan afvigelser fra den tinglyste plan ikke udelukkes. GREVE
LOKALPLAN 13.08A Tilbygninger i boligområdet Åsager Dokumentet har gennemgået en bearbejdning, for at komme på anvendelig digital form. Derfor kan afvigelser fra den tinglyste plan ikke udelukkes. GREVE
! " # !" # $ % & ' ( ) * +, -. /
 !"#!# $%!"#$%&' ()*+,-./0' # ; >? FGHI J'# KLH MN KL!"#$%#&'()*+,-./ 0+ + 2 3456789:6;
!"#!# $%!"#$%&' ()*+,-./0' # ; >? FGHI J'# KLH MN KL!"#$%#&'()*+,-./ 0+ + 2 3456789:6;
Momenter som deskriptive størrelser. Hvad vi mangler fra onsdag. Momenter for sandsynlighedsmål
 Hvad vi mangler fra onsdag Momenter som deskriptive størrelser Sandsynlighedsmål er komplicerede objekter de tildeler numeriske værdier til alle hændelser i en σ-algebra. Vi har behov for simplere, deskriptive
Hvad vi mangler fra onsdag Momenter som deskriptive størrelser Sandsynlighedsmål er komplicerede objekter de tildeler numeriske værdier til alle hændelser i en σ-algebra. Vi har behov for simplere, deskriptive
Hvad vi mangler fra onsdag. Vi starter med at gennemgå slides fra onsdag.
 Hvad vi mangler fra onsdag Vi starter med at gennemgå slides 34-38 fra onsdag. Slide 1/17 Niels Richard Hansen MI forelæsninger 6. December, 2013 Momenter som deskriptive størrelser Sandsynlighedsmål er
Hvad vi mangler fra onsdag Vi starter med at gennemgå slides 34-38 fra onsdag. Slide 1/17 Niels Richard Hansen MI forelæsninger 6. December, 2013 Momenter som deskriptive størrelser Sandsynlighedsmål er
Nøgleord og begreber Lagranges metode i to variable Lagranges metode i tre variable Flere bindinger August 2000, opgave 7
 Oversigt [S] 11.8 Nøgleord og begreber Lagranges metode i to variable Lagranges metode i tre variable Flere bindinger August 2000, opgave 7 Calculus 2-2006 Uge 47.2-1 Skitse [S] 11.8 Niveaukurver y f(x,y)=1
Oversigt [S] 11.8 Nøgleord og begreber Lagranges metode i to variable Lagranges metode i tre variable Flere bindinger August 2000, opgave 7 Calculus 2-2006 Uge 47.2-1 Skitse [S] 11.8 Niveaukurver y f(x,y)=1
Eksamen i Mat F, april 2006
 Eksamen i Mat F, april 26 Opgave 1 Lad F være et vektorfelt, givet i retvinklede koordinater som: F x x F = F x i + F y j + F z k = F y = 2z F z y Udregn F og F: F = F x + F y + F z = 1 + +. F = F z F
Eksamen i Mat F, april 26 Opgave 1 Lad F være et vektorfelt, givet i retvinklede koordinater som: F x x F = F x i + F y j + F z k = F y = 2z F z y Udregn F og F: F = F x + F y + F z = 1 + +. F = F z F
Matthias Beck Gerald Marchesi Dennis Pixton Lucas Sabalka
 Matthias Beck Gerald Marchesi Dennis Pixton Lucas Sabalka Version.53 z 7! z 2 0 + i i x 2 + = 0. i i 2 + = 0 i 2 = i x 3 + px + q q q 2 4 + p3 27 p q C := {(x, y) : x, y 2 R}, (x, y)+(a, b) := (x
Matthias Beck Gerald Marchesi Dennis Pixton Lucas Sabalka Version.53 z 7! z 2 0 + i i x 2 + = 0. i i 2 + = 0 i 2 = i x 3 + px + q q q 2 4 + p3 27 p q C := {(x, y) : x, y 2 R}, (x, y)+(a, b) := (x
Sdr. Svenstrup By, Svenstrup. Signaturer: 9f. 7000f. 7000p. 7r 11y 11aa. 8l 7000b. 4gm Bonderup Gde., Ellidshøj 1p. 7000m 11q. Dalvej. 11z. 12e.
 2.000 o 47 2an 15b Banevej 15c 29d 30b 2a Sdr. By, 23s 23l 2ps 2h 4g 4ir 5bq 5o 3c holm Sdr. By, 7000aq 7do 15o 7000r 6l 7000q 10q 9ah 9ai 6dd 4h 5p 2b 9f 4c 10d 14g 1 5m 5r 8m 7000p 7p 6f 27d 4iø 4iz
2.000 o 47 2an 15b Banevej 15c 29d 30b 2a Sdr. By, 23s 23l 2ps 2h 4g 4ir 5bq 5o 3c holm Sdr. By, 7000aq 7do 15o 7000r 6l 7000q 10q 9ah 9ai 6dd 4h 5p 2b 9f 4c 10d 14g 1 5m 5r 8m 7000p 7p 6f 27d 4iø 4iz
Outline. Chapter 6: (cont d) Qijin Chen. November 21, 2013 NH = =6 CH = 15 4
 Chapter 6: Qjn Chen Department of Physcs, Zhejang Unversty November 1, 013 Copyrght c 013 by Qjn Chen; all rghts reserved. ω 3 4 1. (cont d) 1 3 n3n3n 3n (x 1, y 1, z 1 )(x, y, z ) (x 1 x ) + (y 1 y )
Chapter 6: Qjn Chen Department of Physcs, Zhejang Unversty November 1, 013 Copyrght c 013 by Qjn Chen; all rghts reserved. ω 3 4 1. (cont d) 1 3 n3n3n 3n (x 1, y 1, z 1 )(x, y, z ) (x 1 x ) + (y 1 y )
BYPLANVEDTÆGT FOR ÅLHOLMPARKEN. Byplanvedtægt nr. 53
 BYPLANVEDTÆGT FOR ÅLHOLMPARKEN Byplanvedtægt nr. 53 Byplanvedtægt nr. 53 for Ålholmparken I medfør af byplanloven (lovbekendtgørelse nr. 63 af 20. februar 1970) fastsættes følgende bestemmelser for det
BYPLANVEDTÆGT FOR ÅLHOLMPARKEN Byplanvedtægt nr. 53 Byplanvedtægt nr. 53 for Ålholmparken I medfør af byplanloven (lovbekendtgørelse nr. 63 af 20. februar 1970) fastsættes følgende bestemmelser for det
Tillæg til Lokalplan 65. For et villaområde kaldet Eventyrkvarteret
 Tillæg til Lokalplan 65 For et villaområde kaldet Eventyrkvarteret REDEGØRELSE... 3 Lokalplantillæg... 3 Formål... 3 Indhold... 3 Miljøvurdering... 4 VVM... 4 BESTEMMELSER... 5 1. Formål... 5 2. Lokalplanområdets
Tillæg til Lokalplan 65 For et villaområde kaldet Eventyrkvarteret REDEGØRELSE... 3 Lokalplantillæg... 3 Formål... 3 Indhold... 3 Miljøvurdering... 4 VVM... 4 BESTEMMELSER... 5 1. Formål... 5 2. Lokalplanområdets
Bachelorprojekt Banach-Tarski Paradokset
 Bachelorprojekt Banach-Tarski Paradokset Adam P. W. Sørensen (00885) Vejleder: Mikael Rørdam 3. maj 2007 Abstract The project is about paradoxical decompositions. First, free groups of rank two are shown
Bachelorprojekt Banach-Tarski Paradokset Adam P. W. Sørensen (00885) Vejleder: Mikael Rørdam 3. maj 2007 Abstract The project is about paradoxical decompositions. First, free groups of rank two are shown
Wigner s semi-cirkel lov
 Wigner s semi-cirkel lov 12. december 2009 Eulers Venner Steen Thorbjørnsen Institut for Matematiske Fag Århus Universitet Diagonalisering af selvadjungeret matrix Lad H være en n n matrix med komplekse
Wigner s semi-cirkel lov 12. december 2009 Eulers Venner Steen Thorbjørnsen Institut for Matematiske Fag Århus Universitet Diagonalisering af selvadjungeret matrix Lad H være en n n matrix med komplekse
LOKALPLAN 100. Del af Maglegård kvarter
 LOKALPLAN 100 Del af Maglegård kvarter GLADSAXE KOMMUNE 1997 HVORFOR LOKALPLAN? I Gladsaxe Kommune skal der normalt laves en lokalplan når dele af kommuneplanen skal realiseres, når der gennemføres større
LOKALPLAN 100 Del af Maglegård kvarter GLADSAXE KOMMUNE 1997 HVORFOR LOKALPLAN? I Gladsaxe Kommune skal der normalt laves en lokalplan når dele af kommuneplanen skal realiseres, når der gennemføres større
Gribskov kommune Tisvilde By, Tibirke
 Birkevænget 1 10 cx 2036 2 Birkevænget 2 10 cp 2836 2 Birkevænget 3 10 cz 2010 2 Birkevænget 5 10 cy 2085 2 Birkevænget 6 10 cr 2953 4 Samlet 10 cs 2940 ejendom Birkevænget 7 10 cn 2045 2 Birkevænget 9
Birkevænget 1 10 cx 2036 2 Birkevænget 2 10 cp 2836 2 Birkevænget 3 10 cz 2010 2 Birkevænget 5 10 cy 2085 2 Birkevænget 6 10 cr 2953 4 Samlet 10 cs 2940 ejendom Birkevænget 7 10 cn 2045 2 Birkevænget 9
Deskriptiv teori: den karakteristiske funktion
 Kapitel 15 Deskriptiv teori: den karakteristiske funktion Når man forsøger at karakterisere et sandsynlighedsmål ν på R ved hjælp af dets momenter, fortæller man essentielt hvordan man skal integrere polynomier
Kapitel 15 Deskriptiv teori: den karakteristiske funktion Når man forsøger at karakterisere et sandsynlighedsmål ν på R ved hjælp af dets momenter, fortæller man essentielt hvordan man skal integrere polynomier
Tillæg til Lokalplan nr For boligbebyggelsen Røde Vejrmølle Parken. Miljø- og Teknikforvaltningen. Albertslund Kommune
 Miljø- og Teknikforvaltningen Albertslund Kommune Tillæg til Lokalplan nr. 18.5.1 www.albertslund.dk albertslund@albertslund.dk T 43 68 68 68 F 43 68 69 28 For boligbebyggelsen Røde Vejrmølle Parken Hvad
Miljø- og Teknikforvaltningen Albertslund Kommune Tillæg til Lokalplan nr. 18.5.1 www.albertslund.dk albertslund@albertslund.dk T 43 68 68 68 F 43 68 69 28 For boligbebyggelsen Røde Vejrmølle Parken Hvad
Opgaver til f(z) = 1 z 4 1, g(z) = 1
 1.17 Opgaver til 1. 1 1.1. Vis, at f(z) = er vilkårligt ofte differentiabel i C \ {, 1}, og z(1 z) find et udtryk for f (n) (z) for alle n. (Vink. Skriv f(z) = 1 z + 1 1 z ). 1.2. Beskriv billedkurverne
1.17 Opgaver til 1. 1 1.1. Vis, at f(z) = er vilkårligt ofte differentiabel i C \ {, 1}, og z(1 z) find et udtryk for f (n) (z) for alle n. (Vink. Skriv f(z) = 1 z + 1 1 z ). 1.2. Beskriv billedkurverne
Eksamen 2014/2015 Mål- og integralteori
 Eksamen 4/5 Mål- og integralteori Københavns Universitet Institut for Matematiske Fag Formalia Eksamensopgaven består af 4 opgaver med ialt spørgsmål Ved bedømmelsen indgår de spørgsmål med samme vægt
Eksamen 4/5 Mål- og integralteori Københavns Universitet Institut for Matematiske Fag Formalia Eksamensopgaven består af 4 opgaver med ialt spørgsmål Ved bedømmelsen indgår de spørgsmål med samme vægt
Jazzens Stjerner Program
 Jzz S 2016-2017 Ih Jzz S 2016-2017 3 F 4 S 1: Tp 12. 2016 5 S 2: Txf 30. 2016 6 S 3: 15. c 2016 7 S 4: xf 11. 2017 8 S 5: 15. f 2017 9 S 6: 18. 2017 10 11 Sp M fh f. Jzz S, y p f, h 2014 2015 f- c- Jzz
Jzz S 2016-2017 Ih Jzz S 2016-2017 3 F 4 S 1: Tp 12. 2016 5 S 2: Txf 30. 2016 6 S 3: 15. c 2016 7 S 4: xf 11. 2017 8 S 5: 15. f 2017 9 S 6: 18. 2017 10 11 Sp M fh f. Jzz S, y p f, h 2014 2015 f- c- Jzz
ORDIIUER GENERALFORSAMLING
 Grundejerfrengen 18 Naesby Strand Til grundejerfrengens medlemmer; N^sby Strand, den 8. juli 2012. Hermed dkaldes til RIIUR GNRALFRSAMLING Lrdag den 28. juli 2012 kl. 16.00 i teltet a Grassgangen 11. Husk
Grundejerfrengen 18 Naesby Strand Til grundejerfrengens medlemmer; N^sby Strand, den 8. juli 2012. Hermed dkaldes til RIIUR GNRALFRSAMLING Lrdag den 28. juli 2012 kl. 16.00 i teltet a Grassgangen 11. Husk
Tillæg nr. 13 til Spildevandsplan Forslag til separering af Vesløs By August 2013
 Tillæg nr. 13 til Spildevandsplan 2009-2015 Forslag til separering af Vesløs By August 2013 1 Indholdsfortegnelse side 1. Indledning 3 2. Lovgrundlag 3 3. Forslag til Tillæg nr. 13 4 3.1. Området 4-7 3.2.
Tillæg nr. 13 til Spildevandsplan 2009-2015 Forslag til separering af Vesløs By August 2013 1 Indholdsfortegnelse side 1. Indledning 3 2. Lovgrundlag 3 3. Forslag til Tillæg nr. 13 4 3.1. Området 4-7 3.2.
Vej Nr. Matr.nr. Areal m² Heraf vej Parter Arresødalvej
 Samlet partsfortegnelse for Karsemosen Landvindingslag Gammel partsfordeling. Opstillet i adresseorden Erik B. Aksig 10. oktober 2013 Parter Parter Gribskov Halsnæs Arresødalvej 79 17 72540 357 357 Birkevænget
Samlet partsfortegnelse for Karsemosen Landvindingslag Gammel partsfordeling. Opstillet i adresseorden Erik B. Aksig 10. oktober 2013 Parter Parter Gribskov Halsnæs Arresødalvej 79 17 72540 357 357 Birkevænget
= λ([ x, y)) + λ((y, x]) = ( y ( x)) + (x y) = 2(x y).
![= λ([ x, y)) + λ((y, x]) = ( y ( x)) + (x y) = 2(x y). = λ([ x, y)) + λ((y, x]) = ( y ( x)) + (x y) = 2(x y).](/thumbs/58/42581589.jpg) Analyse 2 Øvelser Rasmus Sylvester Bryder 17. og 20. september 2013 Supplerende opgave 1 Lad λ være Lebesgue-målet på R og lad A B(R). Definér en funktion f : [0, ) R ved f(x) = λ(a [ x, x]). Vis, at f(x)
Analyse 2 Øvelser Rasmus Sylvester Bryder 17. og 20. september 2013 Supplerende opgave 1 Lad λ være Lebesgue-målet på R og lad A B(R). Definér en funktion f : [0, ) R ved f(x) = λ(a [ x, x]). Vis, at f(x)
6 Fleks-Time. 6 Fleks-Time
 KLASSE : 1a VHG, FORÅR 2013 CP 2x He 1a OC 1a GN 1a 1 fy/c 2.12 bi 2.15 Sa 1.1 DA 1.1 Kunst C WN 1a MN 1a JN 1a OC 1a JN 1a 2 id Id EN 1.1 ma 1.1 Sa 1.1 ma 1.1 CS 2x GN 1a JN 1a He 1a CS 2x 3 MA 2.3 DA
KLASSE : 1a VHG, FORÅR 2013 CP 2x He 1a OC 1a GN 1a 1 fy/c 2.12 bi 2.15 Sa 1.1 DA 1.1 Kunst C WN 1a MN 1a JN 1a OC 1a JN 1a 2 id Id EN 1.1 ma 1.1 Sa 1.1 ma 1.1 CS 2x GN 1a JN 1a He 1a CS 2x 3 MA 2.3 DA
MASO Uge 8. Invers funktion sætning og Implicit given funktion sætning. Jesper Michael Møller. Department of Mathematics University of Copenhagen
 MASO Uge 8 Invers funktion sætning og Implicit given funktion sætning Jesper Michael Møller Department of Mathematics University of Copenhagen Uge 43 Formålet med MASO Oversigt Invertible og lokalt invertible
MASO Uge 8 Invers funktion sætning og Implicit given funktion sætning Jesper Michael Møller Department of Mathematics University of Copenhagen Uge 43 Formålet med MASO Oversigt Invertible og lokalt invertible
Samlet partsfortegnelse for Karsemosen Landvindingslag Opstillet i adresseorden
 Samlet partsfortegnelse for Karsemosen Landvindingslag Opstillet i adresseorden Udarbejdet 21. august 2013. Revideret 31. jan. 2018. Revideret 8. februar. Revideret 31. januar 2018 af Stine Holm, Halsnæs
Samlet partsfortegnelse for Karsemosen Landvindingslag Opstillet i adresseorden Udarbejdet 21. august 2013. Revideret 31. jan. 2018. Revideret 8. februar. Revideret 31. januar 2018 af Stine Holm, Halsnæs
9 +: ;6$# < +,&# = '() 10, '! ##5
 !"#$%&' (') *+, ', ) - )., ' /01 /02-345, )6 /078 /09 /0:&,, '!"#$%& '() *#+,-.%& /01 2#%&% 345 $6 78$6 9 +: ;6$# < +,&# = '() 10, '!##5! ##5
!"#$%&' (') *+, ', ) - )., ' /01 /02-345, )6 /078 /09 /0:&,, '!"#$%& '() *#+,-.%& /01 2#%&% 345 $6 78$6 9 +: ;6$# < +,&# = '() 10, '!##5! ##5
SUPPLERENDE OPGAVER TIL KOMPLEKS FUNKTIONSTEORI F2005
 SUPPLERENDE OPGAVER TIL KOMPLEKS FUNKTIONSTEORI F2005 0. maj, 2005 version nr. 8 JØRGEN VESTERSTRØM Indledende bemærkninger De foreliggende opgaver udgør et supplement til lærebogens opgaver. Afsnitsnummereringerne
SUPPLERENDE OPGAVER TIL KOMPLEKS FUNKTIONSTEORI F2005 0. maj, 2005 version nr. 8 JØRGEN VESTERSTRØM Indledende bemærkninger De foreliggende opgaver udgør et supplement til lærebogens opgaver. Afsnitsnummereringerne
犖狌狋狉犻狋犻狅狀狅犳犛狆犲狀狋犕狌狊犺狉狅狅犿犛狌犫狊狋狉犪狋犲犪狀犱犻狋狊犃狆狆犾犻犮犪狋犻狅狀犻狀犔犻狏犲狊狋狅犮犽犉犲犲犱
 40 1 Vol.40No.1 20191 ActaEcolog iaeanimalisdomastici Jan.2019 欍欍欍欍欍欍欍欍欍欍!", ( @ABC DE C, 130118) [# $]!" #$%&'#& ( ) * +,-./0,.1 &' 2,3&'4256789,:; < [%&'] ; ;$% [ ] S811.5 [ ()*] A [ +, ] 1005 5228(2019)01
40 1 Vol.40No.1 20191 ActaEcolog iaeanimalisdomastici Jan.2019 欍欍欍欍欍欍欍欍欍欍!", ( @ABC DE C, 130118) [# $]!" #$%&'#& ( ) * +,-./0,.1 &' 2,3&'4256789,:; < [%&'] ; ;$% [ ] S811.5 [ ()*] A [ +, ] 1005 5228(2019)01
Institut for Matematiske Fag Aalborg Universitet Specielt: Var(aX) = a 2 VarX 1/40. Lad X α, X β og X γ være stokastiske variable (vinkelmålinger) med
 Repetition: Varians af linear kombination Landmålingens fejlteori Lektion 5 Fejlforplantning - rw@math.aau.dk Antag X 1, X,..., X n er uafhængige stokastiske variable, og Y er en linearkombination af X
Repetition: Varians af linear kombination Landmålingens fejlteori Lektion 5 Fejlforplantning - rw@math.aau.dk Antag X 1, X,..., X n er uafhængige stokastiske variable, og Y er en linearkombination af X
Byplanvedtægt 6. For dele af Rungsted og Vallerød by
 Byplanvedtægt 6 For dele af Rungsted og Vallerød by HØRSHOLM KOMMUNE Partiel byplan 6 for dele af Rungsted og Vallerød by I medfør af lov om byplaner, jfr. lovbekendtgørelse nr. 242 af 30. april 1949,
Byplanvedtægt 6 For dele af Rungsted og Vallerød by HØRSHOLM KOMMUNE Partiel byplan 6 for dele af Rungsted og Vallerød by I medfør af lov om byplaner, jfr. lovbekendtgørelse nr. 242 af 30. april 1949,
Matrikelnøgle 2002 for Grindsted Kommune i ejerlavsorden
 Side 1 af 137 Mølle Alle/Stadion Alle 001? (Sønder Omme) *** Ingen vurdering Loftvej 017?? Udgået ejendom Norden 001?? Undtaget vurdering Askjærvej 034 1a Askær Gårde Bebygget landbrug Frodeslundvej 073
Side 1 af 137 Mølle Alle/Stadion Alle 001? (Sønder Omme) *** Ingen vurdering Loftvej 017?? Udgået ejendom Norden 001?? Undtaget vurdering Askjærvej 034 1a Askær Gårde Bebygget landbrug Frodeslundvej 073
Moderne acceleratorers fysik og anvendelse Forelæsning 2 Transverse motion, Lattices
 Moderne acceleratorers fysik og anvendelse Forelæsning 2 Transverse motion, Lattices Optiske elementer: Styring og fokusering. Bevægelsesligningen og dens løsning. Stabilitet. Typiske latticekonfigurationer.
Moderne acceleratorers fysik og anvendelse Forelæsning 2 Transverse motion, Lattices Optiske elementer: Styring og fokusering. Bevægelsesligningen og dens løsning. Stabilitet. Typiske latticekonfigurationer.
Kompleks Funktionsteori
 Kompleks Funktionsteori Formelræs Holomorfe funktioner Sætning. (Caucy-Riemans ligninger). Funktionen f : G C, f = u+iv er holomorf i z 0 = x 0 + iy 0 hvis og kun hvis i punktet (x 0, y 0 ). du dx = dv
Kompleks Funktionsteori Formelræs Holomorfe funktioner Sætning. (Caucy-Riemans ligninger). Funktionen f : G C, f = u+iv er holomorf i z 0 = x 0 + iy 0 hvis og kun hvis i punktet (x 0, y 0 ). du dx = dv
Sandsynlighedsregning
 Mogens Bladt www2.imm.dtu.dk/courses/02405 21. September, 2007 Lidt om binomialkoefficienter n størrelsen af en mængde/population. Vi ønsker at udtage en sub population af størrelse r. To sub populationer
Mogens Bladt www2.imm.dtu.dk/courses/02405 21. September, 2007 Lidt om binomialkoefficienter n størrelsen af en mængde/population. Vi ønsker at udtage en sub population af størrelse r. To sub populationer
Dimensionsbegreber i Topologi. Mads Kjærulf Caspersen Henning Røigaard-Petersen 17. juni 2004
 Dimensionsbegreber i Topologi Mads Kjærulf Caspersen Henning Røigaard-Petersen 17. juni 2004 1 Indhold 1 Indledning 3 2 Topologisk Dimension 4 3 Hausdorff mål 10 4 Hausdorff dimension 15 4.1 Tæthederne
Dimensionsbegreber i Topologi Mads Kjærulf Caspersen Henning Røigaard-Petersen 17. juni 2004 1 Indhold 1 Indledning 3 2 Topologisk Dimension 4 3 Hausdorff mål 10 4 Hausdorff dimension 15 4.1 Tæthederne
Aristoteles Camillo. To cite this version: HAL Id: hal
 An experimentally-based modeling study of the effect of anti-angiogenic therapies on primary tumor kinetics for data analysis of clinically relevant animal models of metastasis Aristoteles Camillo To cite
An experimentally-based modeling study of the effect of anti-angiogenic therapies on primary tumor kinetics for data analysis of clinically relevant animal models of metastasis Aristoteles Camillo To cite
8 Regulære flader i R 3
 8 Regulære flader i R 3 Vi skal betragte særligt pæne delmængder S R 3 kaldet flader. I det følgende opfattes S som et topologisk rum i sportopologien, se Definition 5.9. En åben omegn U af p S er således
8 Regulære flader i R 3 Vi skal betragte særligt pæne delmængder S R 3 kaldet flader. I det følgende opfattes S som et topologisk rum i sportopologien, se Definition 5.9. En åben omegn U af p S er således
χ 2 -fordelte variable
 χ -fordelte varable Defnton af χ -fordelngen Kvadratsummen V n af n uafhængge standardserede normalfordelte stokastske varable sges at være χ -fordelt med n frhedsgrader. V n fremkommer altså som V n =
χ -fordelte varable Defnton af χ -fordelngen Kvadratsummen V n af n uafhængge standardserede normalfordelte stokastske varable sges at være χ -fordelt med n frhedsgrader. V n fremkommer altså som V n =
Fortolkning. Foldning af sandsynlighedsmål. Foldning af tætheder. Foldning af Γ-fordelinger Eksempel: Hvis X og Y er uafhængige og. Sætning (EH 20.
 Foldning af sandsnlighedsmål Lad µ og ν være to sandsnlighedsmål på (R, B). Fortolkning Lad φ : R R være φ(, ) = + for (, ) R. Lad X og Y være to reelle stokastiske variable defineret på (Ω, F, P). Definition
Foldning af sandsnlighedsmål Lad µ og ν være to sandsnlighedsmål på (R, B). Fortolkning Lad φ : R R være φ(, ) = + for (, ) R. Lad X og Y være to reelle stokastiske variable defineret på (Ω, F, P). Definition
PÅTEGNING PÅTEGNING DOKUMENT SOM PÅTEGNES: AREALANVENDELSE: Anvendelsesforhold
 PÅTEGNING DOKUMENT SOM PÅTEGNES: Dato/løbenummer: Dokument type: 04.04.1970-4607-04-S0001 Anden Servitut PÅTEGNING AREALANVENDELSE: Anvendelsesforhold SERVITUT TEKST: Påtegning Påtegningen indeholder følgende
PÅTEGNING DOKUMENT SOM PÅTEGNES: Dato/løbenummer: Dokument type: 04.04.1970-4607-04-S0001 Anden Servitut PÅTEGNING AREALANVENDELSE: Anvendelsesforhold SERVITUT TEKST: Påtegning Påtegningen indeholder følgende
Partiel byplan 11. For et kvarter vest for Mørkhøjvej og Hareskovvej. Gladsaxe Kommune
 Partiel byplan 11 For et kvarter vest for Mørkhøjvej og Hareskovvej Gladsaxe Kommune Byplanvedtægt for et kvarter vest for Mørkhøjvej og Hareskovvej bestående af den af boligministeriet den 24/2 1950 godkendte
Partiel byplan 11 For et kvarter vest for Mørkhøjvej og Hareskovvej Gladsaxe Kommune Byplanvedtægt for et kvarter vest for Mørkhøjvej og Hareskovvej bestående af den af boligministeriet den 24/2 1950 godkendte
Om hypoteseprøvning (1)
 E6 efterår 1999 Notat 16 Jørgen Larsen 11. november 1999 Om hypoteseprøvning 1) Det grundlæggende problem kan generelt formuleres sådan: Man har en statistisk model parametriseret med en parameter θ Ω;
E6 efterår 1999 Notat 16 Jørgen Larsen 11. november 1999 Om hypoteseprøvning 1) Det grundlæggende problem kan generelt formuleres sådan: Man har en statistisk model parametriseret med en parameter θ Ω;
Trykfejlsliste - alle fejl Asymptotisk teori
 9. januar 2005 Stat 2A / EH Trykfejlsliste - alle fejl Asymptotisk teori Denne liste indeholder alle de regulære fejl, slåfejl og stavefejl der er fundet i 2A-noterne indtil nu. 9 1 Forkert: x C x ro alle
9. januar 2005 Stat 2A / EH Trykfejlsliste - alle fejl Asymptotisk teori Denne liste indeholder alle de regulære fejl, slåfejl og stavefejl der er fundet i 2A-noterne indtil nu. 9 1 Forkert: x C x ro alle
MATEMATIK 11 Eksamensopgaver Juni 1995 Juni 2001, 3. fjerdedel
 MATEMATIK Eksamensopgaver Juni 995 Juni 200, 3. fjerdedel August 998 Opgave. Lad f : R \ {0} R betegne funktionen givet ved f(x) = ex x for x 0. (a) Find eventuelle lokale maksimums- og minimumspunkter
MATEMATIK Eksamensopgaver Juni 995 Juni 200, 3. fjerdedel August 998 Opgave. Lad f : R \ {0} R betegne funktionen givet ved f(x) = ex x for x 0. (a) Find eventuelle lokale maksimums- og minimumspunkter
GEOMETRI-TØ, UGE 3. og resultatet følger fra [P] Proposition 2.3.1, der siger, at
![GEOMETRI-TØ, UGE 3. og resultatet følger fra [P] Proposition 2.3.1, der siger, at GEOMETRI-TØ, UGE 3. og resultatet følger fra [P] Proposition 2.3.1, der siger, at](/thumbs/50/26870860.jpg) GEOMETRI-TØ, UGE 3 Hvis I falder over tryk- eller regne-fejl i nedenstående, må I meget gerne sende rettelser til fuglede@imf.au.dk. Opvarmningsopgave 1. Lad γ : (α, β) R 2 være en regulær kurve i planen.
GEOMETRI-TØ, UGE 3 Hvis I falder over tryk- eller regne-fejl i nedenstående, må I meget gerne sende rettelser til fuglede@imf.au.dk. Opvarmningsopgave 1. Lad γ : (α, β) R 2 være en regulær kurve i planen.
Integration og desintegration af mål
 Kapitel 20 Integration og desintegration af mål Lad som i kapitel 8 (X,E) og (Y,K) være to målbare rum. Vi vil i dette kapitel gå i detaljer med forholdet mellem mål på (X Y, E K) og mål på de to faktorrum
Kapitel 20 Integration og desintegration af mål Lad som i kapitel 8 (X,E) og (Y,K) være to målbare rum. Vi vil i dette kapitel gå i detaljer med forholdet mellem mål på (X Y, E K) og mål på de to faktorrum
Selv-absorberende C*-algebraer
 Selv-absorberende C*-algebraer Speciale af Randi Rohde 5. marts 006 Vejleder: Mikael Rørdam Indhold Indledning Tensorprodukter 3. Indledende resultater................................. 3. Fuldstændigt
Selv-absorberende C*-algebraer Speciale af Randi Rohde 5. marts 006 Vejleder: Mikael Rørdam Indhold Indledning Tensorprodukter 3. Indledende resultater................................. 3. Fuldstændigt
Antag X 1, X 2,..., X n er n uafhængige stokastiske variable, hvor Var(X 1 )=σ 2 1,..., Var(X n )=σ 2 n.
 Simple fejlforplantningslov Landmålingens fejlteori Lektion 6 Den generelle fejlforplantningslov Antag X, X,, X n er n uafhængige stokastiske variable, hvor Var(X )σ,, Var(X n )σ n Lad Y g(x, X,, X n ),
Simple fejlforplantningslov Landmålingens fejlteori Lektion 6 Den generelle fejlforplantningslov Antag X, X,, X n er n uafhængige stokastiske variable, hvor Var(X )σ,, Var(X n )σ n Lad Y g(x, X,, X n ),
Matematik F Et bud på hvordan eksamenssæt løses
 Matematik F Et bud på hvordan eksamenssæt løses Jeppe Trøst Nielsen 11. april 21 Denne samling af ligninger og løsninger er udarbejdet efter det princip, at eksamenssættene ikke ændrer sig specielt meget
Matematik F Et bud på hvordan eksamenssæt løses Jeppe Trøst Nielsen 11. april 21 Denne samling af ligninger og løsninger er udarbejdet efter det princip, at eksamenssættene ikke ændrer sig specielt meget
Aktuelt tinglyst dokument
 Aktuelt tinglyst dokument Dokument: Dato/løbenummer: 02.12.2011-1003152574 : Senest påtegnet: 02.12.2011 19:45:51 Ejendom: Adresse: Sct. Laurentii Vej 150 9990 Skagen 0092c 0090u 0095i 0090d 0110ac 0110ad
Aktuelt tinglyst dokument Dokument: Dato/løbenummer: 02.12.2011-1003152574 : Senest påtegnet: 02.12.2011 19:45:51 Ejendom: Adresse: Sct. Laurentii Vej 150 9990 Skagen 0092c 0090u 0095i 0090d 0110ac 0110ad
4. Differentialligninger i højere dimension, Dirichlet problemet
 4.1 4. Differentialligninger i højere dimension, Dirichlet problemet 4.1. Indledning, de forskellige typer. Der er tre hovedeksempler på partielle differentialligninger, som har særlig betydning i fysik:
4.1 4. Differentialligninger i højere dimension, Dirichlet problemet 4.1. Indledning, de forskellige typer. Der er tre hovedeksempler på partielle differentialligninger, som har særlig betydning i fysik:
Numerisk simulering af ikke-lineære fænomener inden for geoteknik
 Numerisk simulering af ikke-lineære fænomener inden for geoteknik Emil Smed Sørensen COWI, Aalborg Geoteknikerdagen - 9. juni 217 Page 1 of 25 Ph.d.-studie i perioden 212-216, AAU Titel: Numerical simulation
Numerisk simulering af ikke-lineære fænomener inden for geoteknik Emil Smed Sørensen COWI, Aalborg Geoteknikerdagen - 9. juni 217 Page 1 of 25 Ph.d.-studie i perioden 212-216, AAU Titel: Numerical simulation
Sylvain Meille. Étude du comportement mécanique du plâtre pris en relation avec sa microstructure.
 Étude du comportement mécanique du plâtre pris en relation avec sa microstructure Sylvain Meille To cite this version: Sylvain Meille. Étude du comportement mécanique du plâtre pris en relation avec sa
Étude du comportement mécanique du plâtre pris en relation avec sa microstructure Sylvain Meille To cite this version: Sylvain Meille. Étude du comportement mécanique du plâtre pris en relation avec sa
Eksamen i Mat F, april 2006
 Eksamen i Mat F, april 26 Opgave Lad F være et vektorfelt, givet i retvinklede koordinater som: Udregn F og F: F x F = F x i + F y j + F z k = F y = z 2 F z xz y 2 F = F x + F y + F z = + + x. F = F z
Eksamen i Mat F, april 26 Opgave Lad F være et vektorfelt, givet i retvinklede koordinater som: Udregn F og F: F x F = F x i + F y j + F z k = F y = z 2 F z xz y 2 F = F x + F y + F z = + + x. F = F z
M=3 kunde forbindelse. oprettet lokation Steinerkant
 M=3 åben facilitet kunde forbindelse lukket facilitet oprettet lokation Steinerkant v Connected facility location-problemet min i f i y i + d j c ij x ij + M c e z e (1) j i e hvorom gælder: x ij 1 j (2)
M=3 åben facilitet kunde forbindelse lukket facilitet oprettet lokation Steinerkant v Connected facility location-problemet min i f i y i + d j c ij x ij + M c e z e (1) j i e hvorom gælder: x ij 1 j (2)
Egentyngd (+Struc. dead load) Glas Nyttiglast balkong Egentyngd (+Struc. dead load) Glas Nyttiglast balkong
 Eurocode (NA: Swedih) Eurocode (NA: Swedih) Load combination No. Name ype Factor.35*Egentyngd +.35*Gla +.50*0.70*Nyttiglat balong Ultimate.350.350 3 Egentyngd + Gla + 0.30*Nyttiglat balong Ultimate Quaipermanent.050.0.0.500.000.000
Eurocode (NA: Swedih) Eurocode (NA: Swedih) Load combination No. Name ype Factor.35*Egentyngd +.35*Gla +.50*0.70*Nyttiglat balong Ultimate.350.350 3 Egentyngd + Gla + 0.30*Nyttiglat balong Ultimate Quaipermanent.050.0.0.500.000.000
since a p 1 1 (mod p). x = 0 1 ( 1) p 1 (p 1)! (mod p) (p 1)! 1 (mod p) for p odd and for p = 2, (2 1)! = 1! = 1 1 (mod 2).
 5 Sice φ = ϕ is multiplicative, if = m j= pα j j is the stadard factorisatio, m φ() = φ(p α j j ). j= Theorem so ( φ(p α ) = p α ) p φ() = ( ). p p Proof. Cosider the atural umbers i the iterval j p α.
5 Sice φ = ϕ is multiplicative, if = m j= pα j j is the stadard factorisatio, m φ() = φ(p α j j ). j= Theorem so ( φ(p α ) = p α ) p φ() = ( ). p p Proof. Cosider the atural umbers i the iterval j p α.
* I lr,3 I li=;ia. gltgetlneei. s I l.iel t cb,f. ? I lsa*l Is*iA. $ I l=r I leer'i. islel seelaliheia F I IFF I IFF*1. =:=l lh=;l lfre'si :=EU
 Y ci c+c\ > >> J 6B xr. t 0fJ) tt rj 6t (V 6g r cg A i! :.?6 [. _. 6> t\n t\\ Y '': t ib Y\At :U g i.j ct l l P ij li^ ri Y'+ (Yt r?3 '.0 ii r\ " \J/ iy ri 9 rt3.8 'n A! 6s X ct.:+. l*lq* Ui9 *..1 *.*.!i.i
Y ci c+c\ > >> J 6B xr. t 0fJ) tt rj 6t (V 6g r cg A i! :.?6 [. _. 6> t\n t\\ Y '': t ib Y\At :U g i.j ct l l P ij li^ ri Y'+ (Yt r?3 '.0 ii r\ " \J/ iy ri 9 rt3.8 'n A! 6s X ct.:+. l*lq* Ui9 *..1 *.*.!i.i
Vektoranalyse INDLEDNING. Indhold. 1 Integraltricks. Jens Kusk Block Jacobsen 21. januar 2008
 Vektoranalyse Jens Kusk Block Jacobsen 21. januar 2008 INLENING ette er en opsamling af ting, jeg synes er gode at have ifbm vektoranalyse som præsenteret i kurset VEKANAE07 ved IMF på AU. Noten er dels
Vektoranalyse Jens Kusk Block Jacobsen 21. januar 2008 INLENING ette er en opsamling af ting, jeg synes er gode at have ifbm vektoranalyse som præsenteret i kurset VEKANAE07 ved IMF på AU. Noten er dels
Statistiske Modeller 1: Notat 1
 Statistiske Modeller : Notat Jes Ledet Jese 9. august 005 Idhold Kast med k-sidet terig Betigig i multiomialfordelig 3 3 Fordelig af X + X - frembrigede fuktio 4 4 Maksimerig af log-likelihood 5 5 Afledede
Statistiske Modeller : Notat Jes Ledet Jese 9. august 005 Idhold Kast med k-sidet terig Betigig i multiomialfordelig 3 3 Fordelig af X + X - frembrigede fuktio 4 4 Maksimerig af log-likelihood 5 5 Afledede
! "#$ #% " (,-#,.#/,,0. urn:nbn:de:gbv: [http://nbn-resolving.de/urn/resolver.pl?urn=nbn%3ade%3agbv%3a ]
![! #$ #% (,-#,.#/,,0. urn:nbn:de:gbv: [http://nbn-resolving.de/urn/resolver.pl?urn=nbn%3ade%3agbv%3a ] ! #$ #% (,-#,.#/,,0. urn:nbn:de:gbv: [http://nbn-resolving.de/urn/resolver.pl?urn=nbn%3ade%3agbv%3a ]](/thumbs/76/73124791.jpg) ! "#$ #% "! & ###&'()*& ##%#+)! (,-#,.#/,,0 urn:nbn:de:gbv:3-000011215 [http://nbn-resolving.de/urn/resolver.pl?urn=nbn%3ade%3agbv%3a3-000011215] !" #$ % & "'% () ( $ * %"* +, -. ) # 01, 12 00 3, 14
! "#$ #% "! & ###&'()*& ##%#+)! (,-#,.#/,,0 urn:nbn:de:gbv:3-000011215 [http://nbn-resolving.de/urn/resolver.pl?urn=nbn%3ade%3agbv%3a3-000011215] !" #$ % & "'% () ( $ * %"* +, -. ) # 01, 12 00 3, 14
Trykfejlsliste - alle fejl Introduktion til Matematisk Statistik 2. udgave
 3. februar 2012 Stat 1TS / EH Trykfejlsliste - alle fejl Introduktion til Matematisk Statistik 2. udgave Denne liste indeholder alle de regulære fejl, slåfejl og stavefejl der er fundet i 2. udgave af
3. februar 2012 Stat 1TS / EH Trykfejlsliste - alle fejl Introduktion til Matematisk Statistik 2. udgave Denne liste indeholder alle de regulære fejl, slåfejl og stavefejl der er fundet i 2. udgave af
Deskriptiv teori i flere dimensioner
 Kapitel 17 Deskriptiv teori i flere dimensioner I kapitel 13 og 14 udviklede vi en række deskriptive værktøjer til at beskrive sandsynlighedsmål på (R, B). Vi vil i dette kapitel forsøge at udvikle varianter
Kapitel 17 Deskriptiv teori i flere dimensioner I kapitel 13 og 14 udviklede vi en række deskriptive værktøjer til at beskrive sandsynlighedsmål på (R, B). Vi vil i dette kapitel forsøge at udvikle varianter
Heisenbergs usikkerhedsrelationer. Abstrakt. Hvorfor? Funktionsrum. Nils Byrial Andersen Institut for Matematik. Matematiklærerdag 2013
 Heisenbergs usikkerhedsrelationer Nils Byrial Andersen Institut for Matematik Matematiklærerdag 013 1 / 17 Abstrakt Heisenbergs usikkerhedsrelationer udtrykker at man ikke på samme tid både kan bestemme
Heisenbergs usikkerhedsrelationer Nils Byrial Andersen Institut for Matematik Matematiklærerdag 013 1 / 17 Abstrakt Heisenbergs usikkerhedsrelationer udtrykker at man ikke på samme tid både kan bestemme
Kalkulus 2 - Grænseovergange, Kontinuitet og Følger
 Kalkulus - Grænseovergange, Kontinuitet og Følger Mads Friis 8. januar 05 Indhold Grundlæggende uligheder Grænseovergange 3 3 Kontinuitet 9 4 Følger 0 5 Perspektivering 4 Grundlæggende uligheder Sætning
Kalkulus - Grænseovergange, Kontinuitet og Følger Mads Friis 8. januar 05 Indhold Grundlæggende uligheder Grænseovergange 3 3 Kontinuitet 9 4 Følger 0 5 Perspektivering 4 Grundlæggende uligheder Sætning
檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪
 =>?@/0,J.AnhuiAgric.Sci.2019,47(2):34-37,79 29 0Z $ 1, 2, 2,0 2,0 3 (1. /W0S 1!, / 211200;2. / / &20, / 210095;3. 3 BC, 650000) "# [] -=., - HIJ [ 2] 29- =.*K, 8 11 ) *IJIC,EOPK52IJ, HIJ - =. [$>] 2- =.
=>?@/0,J.AnhuiAgric.Sci.2019,47(2):34-37,79 29 0Z $ 1, 2, 2,0 2,0 3 (1. /W0S 1!, / 211200;2. / / &20, / 210095;3. 3 BC, 650000) "# [] -=., - HIJ [ 2] 29- =.*K, 8 11 ) *IJIC,EOPK52IJ, HIJ - =. [$>] 2- =.
Helårsbeboelse i sommerhuse for pensionister
 Kortbilag 11A er rettet 19. sep. 2013, p.g.a. fejl i matrikelkortet. Nyt kortbilag 11A sidder bagerst i planen. Temalokalplan 360-50 og Kommuneplantillæg 13 Helårsbeboelse i sommerhuse for pensionister
Kortbilag 11A er rettet 19. sep. 2013, p.g.a. fejl i matrikelkortet. Nyt kortbilag 11A sidder bagerst i planen. Temalokalplan 360-50 og Kommuneplantillæg 13 Helårsbeboelse i sommerhuse for pensionister
Facitliste 1 MAT 2AL. 5. f (x) er irreducibel i Z 5 [X].
![Facitliste 1 MAT 2AL. 5. f (x) er irreducibel i Z 5 [X]. Facitliste 1 MAT 2AL. 5. f (x) er irreducibel i Z 5 [X].](/thumbs/92/109055649.jpg) Facitliste 1 Facitliste til eksamensopgaver Facit til de første 14 opgavesæt er blevet til paa basis af Jonas B. Rasmusssens facitliste. Han regnede størstedelen af opgaverne, medens han fulgte kurset,
Facitliste 1 Facitliste til eksamensopgaver Facit til de første 14 opgavesæt er blevet til paa basis af Jonas B. Rasmusssens facitliste. Han regnede størstedelen af opgaverne, medens han fulgte kurset,
6.1 Reelle Indre Produkter
 SEKTION 6.1 REELLE INDRE PRODUKTER 6.1 Reelle Indre Produkter Definition 6.1.1 Et indre produkt på et reelt vektorrum V er en funktion, : V V R således at, for alle x, y V, I x, x 0 med lighed x = 0, II
SEKTION 6.1 REELLE INDRE PRODUKTER 6.1 Reelle Indre Produkter Definition 6.1.1 Et indre produkt på et reelt vektorrum V er en funktion, : V V R således at, for alle x, y V, I x, x 0 med lighed x = 0, II
Ændring af rammeområde 3.BP.3 Østervang/ Bymarken
 Ændring af rammeområde 3.BP.3 Østervang/ Bymarken Tillæg 22 til Roskilde Kommuneplan 2013 Nord Vindingevej 4-6 3.BP.3 500 m Forord HVAD ER ET TILLÆG TIL KOMMUNEPLANEN? Den fysiske planlægning reguleres
Ændring af rammeområde 3.BP.3 Østervang/ Bymarken Tillæg 22 til Roskilde Kommuneplan 2013 Nord Vindingevej 4-6 3.BP.3 500 m Forord HVAD ER ET TILLÆG TIL KOMMUNEPLANEN? Den fysiske planlægning reguleres
Holdelementnavn XPRS fagbetegnelse (kort) Norm. elevtid (skoleår) Lektioner (antal) 1g ap Almen sprogfors 0 28 totalt 3g as Astronomi 44 1g bk
 Holdelementnavn XPRS fagbetegnelse (kort) Norm. elevtid (skoleår) Lektioner (antal) 1g ap Almen sprogfors 0 28 totalt 3g as Astronomi 44 1g bk Billedkunst 47 1g bi Biologi 10 41 2a BI Biologi 45 95 2c
Holdelementnavn XPRS fagbetegnelse (kort) Norm. elevtid (skoleår) Lektioner (antal) 1g ap Almen sprogfors 0 28 totalt 3g as Astronomi 44 1g bk Billedkunst 47 1g bi Biologi 10 41 2a BI Biologi 45 95 2c
