PC PSI PT JEAN-MARIE MONIER GUILLAUME HABERER CÉCILE LARDON MÉTHODES ET EXERCICES. Mathématiques. méthodes et exercices. 3 e.
|
|
|
- Bo Kronborg
- 6 år siden
- Visninger:
Transkript
1 PC PSI PT MÉTHODES ET EXERCICES JEAN-MARIE MONIER GUILLAUME HABERER CÉCILE LARDON Mathématiques méthodes et exercices 3 e édition
2 Conception et création de couverture : Atelier 3+ Dunod, rue Laromiguière, Paris ISBN
3
4 f : I C I R+ C. +, 0, a, a R x α f(x) x x x 1 f K E, A n(k) f(x) =λx λ K, x E {0}. f χf f E χf, ( ) 5 4 A = 2(R). 6 5 ( E ) f(p ) = λp P 0, P, P P. E f A χa A χa(λ) = 5 λ λ =(λ2 25)+24=λ 2 1=(λ + 1)(λ 1), A 1 1 R (A) ={ 1, 1} 1 ( x X = 2,1(R) y) X (A, 1) AX = X { 5x +4y = x x = y, 6x +5y = y ( 1 (A, 1) = ( ) (A, 1)=1, 1) X (A, 1) AX = X { 5x +4y = x 6x +4y =0, 6x +5y = y ( 2 (A, 1) = ( ) (A, 1)=1. 3) A 2(R)
5 I R (fn : I R)n N (Ak)k N I I k N Ak = I k N (fn)n Ak (fn)n (fn : I R)n N (Ak)k N I Ak = I k N (fn)n Ak (fn)n k N I (fn)n N f I n N fn f (fn)n N (gn)n N I (fngn)n N I I (fn)n N I g (fng)n N fn C.U. n f gn C.U. g fn + gn f + g n n (fn)n N f I n N fn C 1 I f C 1 I (fn)n N f I n N fn C 1 I (f n)n N I (Pn :[0;1] R)n1 R f f (fn : R R)n N C 1 (f n)n N R (fn)n N R y = f(x) Γ y = f(x), f(x) = 3 x 2 (x 6). { x(t) =t 2 1 Γ y(t) =2t 3 +3t 2 1. x(t) =t t Γ y(t) = t t. y = f(x) x Γ y = f(x), f(x) = x, f : R R, x f(x) = x. f C R f (n) (x) (n, x) N R. n N {0, 1} f (n) (x) =0, x R. C 1 (a, b) R 2 a b, f :[a; b] C C 1 [a; b]. b f(x) λx x a λ + 0. C 0 f :[0;+ [ R( C (xn)n N ]0 ; + [ xn n N, f(xn) =0 ). k N, f (k) (0) = 0. n 0 (x, y) R 2 x (1 + x) 0 <x<y < y (1 + y). 1 4 S = AA, n(r). S n +. λ R (S). V S λ. R (S) R+. XSX X n,1(r). L1,L2,L3 A L1 2 =1 L2 = ( a b c ) (L1 L2) = 0 L2 2 2 =1, L3 = L1 L2. Ω 3(R). (Ω). (Ω) =1 1. (Ω) =1 f f = E3 f f ΩX = X, X 3,1(R). θ f (Ω)=1+2 θ, θ [x, f(x), I] x E3 I I f (Ω) = 1 Ω f f f (M, N) ( n(r) ) 2 ( fa(m) fa(n) ) =(M N). S. ( A ) A = n ( A )=1, X n,1(r) {0} AX = λx. XSX C = AB BA. C n(r), C 2 n(r), C 4 + n. n(r). X X 3 = n. ( AA) = 2 (A) = 1. χ AA AA X (A). Y n,1(r), λ R, k N 1 1, k = t k 1 t XHnX X = x1 n,1(r). A A, A 1 + B. S = PDP 1, P n(r),d = (λ1,..., λn) n(r). P =(pij)ij. n i {1,..., n}, sii = λkp 2 ik. f λk p 2 ik, 1 i n. S ++ (X + λy )A(X + λy ) 0. k=1 0 xn f : x x. S + n S / ++ n n. S = A A S.
6 t R x 1 9 ( 6 x x I (a, b) R 2 x [a; b] I fn(x) n0 I =[0;1[ fn : I R, x x n I =[0;1[ fn : I R, x x n I =[ 1;1], fn : x x + 1 n +1 x + 1 n +2, + fn(x) = x +1 x n=0 n N 0 fn + gn fn + gn. I = R fn : I R, x 1 n 2 g : I R, x x fn I n1 fng n1 I n N 0 fng fn g. fn fn [1 ; + [ n1 1 (n +1) x 1 1, Rn n +1 n +1 ]1 ;+ [ =1 Rn n Rn(x) fn+1(x) = Rn 0 fn [1 ; + [ n n1 f : x 3 x 2 (x 6) R R {0, 6} x R {0, 6}, f x(x 4) (x) = ( 3 x 2 (x 6) ) 2 f x f (x) f(x) t x (t) x y y (t) f(x) =x x = x ( y ) 2 + o ( 1 x 2 )) = x 2 4 ( 1 ) x + o, x Γ D y = x 2, + Γ D y 1 O x Γ D 1 O 1 x A 1 x y C 1 R x (t) =2t, y (t) =6t 2 +6t =6t(t +1). x y +, x y 1 0, { x (t) =0 Γ t R, y (t) =0 t =0, Γ
7
8
9 K K R C n,p (K) K = R C
10 E K A, B, C E A +(B C) (A + B) (A + C). B C B, A +(B C) A + B, B C C, A +(B C) A + C A +(B C) (A + B) (A + C). x A +(B C) a A, y B C x = a + y a A y B x = a + y A + B a A y C x = a + y A + C x (A + B) (A + C) F, G E E F G = {0} F + G = E F F G G F G F G E F G = {0} F + G = E (E) = (F )+ (G), E n N n(r) n(r) n(r) n(r) n(r) n(r) n(r) n(r) n(r) n(r) n(r) n(r) 0 n(r) α R, A,B n(r) (αa + B) =α A + B = αa + B, αa + B n(r) n(r) n(r) n(r) n(r) 0 n(r) α R, A,B n(r) (αa + B) =α A + B = α( A)+( B) = (αa + B), αa + B n(r) n(r) n(r)
11 {0} n(r) n(r) A n(r) n(r) A = A A = A, 1 A = A, 2A =0 2A =0, A =0 2 n(r) n(r) {0} n(r) n(r) ={0} n(r)+ n(r) n(r) M n(r) S n(r), A n(r) M = S + A S n(r), A n(r) M = S + A M = (S + A) = S + A = S A. 1 2 S = 1 2 (M + M), A = 1 2 (M M). S = 1 2 (M + M), A = 1 2 (M M). S = 1 2 ( M + M) =S, S n(r) A = 1 2 ( M M) = A, A n(r) E = R 4 a =(1, 1, 1, 1), b =(1, 2, 3, 0), c =(1, 1, 1, 4), d =(1, 2, 3, 0), F = (a, b), G = (c, d). F G E S + A = 1 2 M + 1 M M 1 M = M, (S, A) 2 n(r)+ n(r) = n(r) n(r) n(r) n(r) n(r) (a, b) (c, d) F =(a, b) F G =(c, d) G F G =(a, b, c, d) E (F G)=4= (E), F G (α, β, γ, δ) R 4 α + β + γ + δ =0 α +2β γ +2δ =0 αa + βb + γc + δd =0 α +3β + γ 3δ =0 α +4γ =0 α = 4γ α = 4γ γ =0 β 3γ + δ =0 β = γ + δ δ =0 2β 5γ +2δ =0 2γ +2δ =0 α =0 3β 3γ 3δ =0 3γ +4δ =0 β =0. F G E F G E E
12 E K 5 F, G E F G = {0}, (F )=2, (G) =3. F G E (F +G) = (F )+ (G) (F G) =2+3 0 =5= (E), F + G = E F G = {0} F + G = E F G E E 1,..., E N E (x 1,..., x N ) E 1... E N N x i =0 = ( i {1,..., N}, x i =0 ) ( N ) N E i = (E i ) E 1,..., E N E R R R F 1 F 2 F 3 E ] ;1] ] ; 1] [1 ; + [ [ 1;+ [ F 1,F 2,F 3 E A R F = { f E ; x A, f(x) =0 } E F E 0 F α R, f,g F x A, (αf + g)(x) =αf(x) + g(x) =0, αf + g F }{{}}{{} =0 =0 F E F 1,F 2,F 3 E f 1 F 1,f 2 F 2,f 3 F 3 f 1 + f 2 + f 3 =0 x ] ; 1] F 1 F 2 f 1 (x) =0 f 2 (x) =0 f 3 (x) = ( f 1 (x)+f 2 (x) ) =0. x ] ; 1], f 3 (x) =0. F 3 x [ 1;+ [, f 3 (x) =0. x R, f 3 (x) =0, f 3 =0 f 1 =0 f 2 =0 F 1,F 2,F 3
13 (f a) a R a R { 0 x a f a : R R, x 1 x>a N N, a 1,..., a N R λ 1,..., λ N R N λ k f ak =0. k=1 i {1,..., N} λ i 0 f ai = 1 λ k f ak. λ i k i a R f a R {a} f a a 1 λ k f ak a i λ i k i f ai a i i {1,..., N}, λ i =0, (f ai ) 1iN (f a) a R (f a) a R (f a) a R a R f a : R R, x (x + a) a R x R, f a(x) =(x + a) = a x a x, f a =( a) +( a). f a f 0,f 1,f 2, (f 0,f 1,f 2 ) (f a) a R (f a) a R
14 H E E H E H 1 H H E (H) = (E) 1, E H 0 R E E R H E D E (1) 1 H D = {0} 0 0 u =(u n) n N E l u v = u (l) u = v +(l), v H, (l) D. H + D = E D H E H E { 1/2 } H = f E ; f =0 0 R E = C([0 ; 1], R). 1/2 ϕ : E R, f f 0 E 1/2 ϕ(1) = 1= H = (ϕ) E n N H = C n 1 [] E = C n[] E C H E (E) =n +1, (H) =n (H) = (E) 1 H E
15 0. N N, E K p 1,..., p N E N p i =0. i {1,..., N}, p i =0. i {1,..., N} E p i E (p i )= (p i ). ( N ) N N 0= p i = (p i )= (p i ). }{{} 0 i {1,..., N}, (p i )=0 i {1,..., N}, p i =0. A n,p (K) (A) =r P ( n (K), ) Q p (K) A = P n,p,r Q, r 0 n,p,r = 0 0 n,p (K). n, p, q, r N,A p,q(k), B n,r(k) (B) (A) (P, Q) n,p(k) q,r(k), B = PAQ. = (B) (A) a = (A), b = (B) R p(k), S q(k) A = R p,q,as T n(k), U r(k) B = T n,r,b U b a ( ) ( )( )( ) b 0 b 0 a 0 b 0 J n,r,b = = = n,p,b p,q,a q,r,b. B = T n,r,b U = T n,p,b p,q,a q,r,b U =(T n,p,b R 1 )(R p,q,as)(s 1 q,r,b U). P = T n,p,b R 1 n,p(k) Q = S 1 q,r,b U q,r(k), B = PAQ = (P, Q) n,p(k) q,r(k) B = PAQ (B) = ( (PA)Q ) (PA) (A).
16 n N A, B, C, D n(k) (α, β) K 2 α β ( ) ( ) α n 0 A B J =, M =. 0 β n C D M J B =0 C =0. ( )( ) ( )( ) α n 0 A B A B α n 0 JM = MJ = 0 β n C D C D 0 β n ( ) ( ) αa αb αa βb = βc βd αc βd { αb = βb βc = αc { (α β)b =0 (α β)c =0 { B =0 C =0. E K F E n = (E) p = (F ) L F (E) E F L(E) L F (E) L(E) G F E L F,G (E) E F G L(E) L F,G (E) L(E) L F (E) L(E) 0 L F (E) α E, f,g L F (E) x F, (αf + g)(x) =αf(x) + g(x) F, }{{}}{{} F F F αf + g αf + g L F (E) L F (E) L(E) E B = (e 1,..., e n) F (e 1,..., e p) F f L(E), M = B (f) F f M ( ) A B M =, 0 C A p(k), B p,n p (K), C n p (K) p(k) p,n p (K) n p (K) L F (E) (A, B, C) f E ( ) A B B (f) =, 0 C ( L F (E) ) = ( p(k) p,n p (K) n p (K) ) = ( ) p(k) + ( p,n p (K) ) + ( n p (K) ) = p 2 + p(n p)+(n p) 2 = n 2 np + p 2. L F (E) L(E) ( L F (E) ) = ( L(E) ) 1. ( )
17 ( ) n 2 np + p 2 = n 2 1 np p 2 =1 p (n p)=1 }{{}}{{} { p =1 n p =1 { n =2 p =1. N N L F (E) L(E) n =2 p =1 L F,G (E) L(E) L F,G (E) = L F (E) L G (E), L F,G (E) L(E) E B =(e 1,..., e n) E = F G (e 1,..., e p) F (e p+1,..., e q) G f L(E), M = B (f) F G f M ( ) A 0 M =, 0 C A p(k), C n p (K) p(k) n p (K) L F,G (E) (A, C) f E ( ) A 0 B (f) =, 0 C ( L F,G (E) ) = ( p(k) n p (K) ) = ( ) p(k) + ( n p (K) ) = p 2 +(n p) 2 ( L F,G (E) ) = ( L(E) ) 1 = n 2 2np +2p 2. n 2 2np +2p 2 = n 2 1 2(np p 2 )=1, L F,G (E) L(E)
18 E,F K n N E 1,..., E n E E 1,..., E n E ( x 1 E 1,..., x n E n, x1 + + x n =0 = x 1 =... = x n =0 ). E 1,..., E n E (i, j) {1,..., n} 2 (, i j = Ei E j = {0} ). E 1,E 2,E 3 E E 1 (E 2 + E 3 )=(E 1 E 2 )+(E 1 E 3 ). E 1,E 2,E 3 E E 1 +(E 2 E 3 )=(E 1 + E 2 ) (E 1 + E 3 ). R E = R R E 1 E 2 E E R 3 p, q, r 4p +5q +6r = R 3. f,g E (f) (f) g f g f,g E A, B n (K), (AB) = (BA) A, B n (K), (AB) = (A) (B)
19 E K A, B, C E. A + ( B (A + C) ) = A + ( C (A + B) ). ( f a :[0;+ [ R, x 1 ) x + a a ]0 ;+ [ ( f a : R R, x (x a) ) a R. A 3,2 (R) B 2,3 (R) AB = C, C C = , , ? n N,X= {x 1,..., x n } n F = K X i {1,..., n}, i : F K, f f(x i ), x i. ( i ) 1in F. n N (A, B) ( n (C) ) 2 AB BA = n ( ) A B n, p N M = A 0 C n (K), B n,p (K), C p (K). M A C A C M 1 ( f a : R R, x x a 3/2) a R RR. E K[]. E E
20 n N. A n (K) n (K) K, X (AX) n (K) θ : n (K) n (K) ( ) A n (K), X n (K), θ(a) (X) = (AX) K n N,A,B,C n (C) A 2 = A, B 2 = B, C 2 = C. M = A + 2 B + 3 C M 2 = M. B = C =0. n, p N,A n,p (K), r= (A). U n,r (K), V r,p (K), A = UV. M M =(U V ), (M) (U)+ (V ). ( ) R M M =, S (M) (R)+ (S). ( ) A B M M =, C D A D (M) (A)+ (B)+ (C)+ (D). ( ) A B m, n, p N m n p n, M = C 0 n (K), A m,p (K), B m,n p (K), C n m,p (K). M (A) m + p n.. 1. n, p N,A=(a ij ) ij n,p (K). ( n ) A l = a ij, A c = 1jp 1in X =(x j ) 1jp p,1 (K) X 1 = p ( p ) a ij, x j, X = 1jp x j. AX 1 AX A l =, A c =. X p,1(k) {0} X 1 X p,1(k) {0} X
21 E K F, G E E. G = { f L(E); (f) =F (f) =G }. G. E n = (E), p = (F ), B 1 =(e 1,..., e p ) F, B 2 =(e p+1,..., e n ) G, B =(e 1,..., e n ) E. θ : f B (f) (G, ) { ( ) } M 0 (H, ) H = 0 0 n (K); M p (K). n (K) n (K) n N {0, 1}. n (K) n (K). ( ) n, p N n B,B n,p (K), C p (K). = n + (C). 0 C n, p N,R n,p (K), S p,n (K). p + ( n + RS) =n + ( p + SR). ( ) A 0 n, p N,A n (K), B p (K). = (A)+ (B). 0 B ( ) ( ) A 0 B 0 n N,A,B n (K). 0 A 0 B A B n, ( p N,A,B ) ( n (K), ) U,V p (K). A B A 0 B 0 U V 0 U 0 V E K f L(E) F E (F ) (f) G F E (u, v) ( L(E) ) 2 (u f v) =F (u f v) =G. ( ) A B M =, A C D n (K), B n,p (K), C p,n (K), D p (K). M D CA 1 B M 1
22 X AXB =0 m, n, p, q N,A m,n (K), B p,q (K). E = { X n,p (K); AXB =0 }. E K n N,A n (K) B,C n (K) A = BC, B, C. ( ) A B n, p N M = C D A n (K) B n,p (K) C p,n (K) D p (K) (M) =n D = CA 1 B. K E K p N,F 1,..., F p E p F i = E. i {1,..., p} F i = E. GL(E) E K e = E, G GL(E) n = (G) p = 1 g. n g G h G, p h = p. p E. (g e) = (p). g G ( g G ) (g e) = 1 n (g). g G
23 (f a) a [0 ;+ [ (f a) a R (f 1,f 0,f 1 ) A, B (A, B) i {1,..., n} i F. ( i ) 1in j {1,..., n} f j : x i δ ij. ( ) X Y M = Z T a R, f a C 2 R {a} C 2 R. n = (E). (P 1,..., P n+1 ) (P 1 )... (P n+1 ), (Q 1,..., Q n+1 ) Q n+1 = P n+1 i {1,..., n}, (Q i ) < (P n+1 ), (P 1,..., P n) (P 1 ) <... < (P n) (S 1,..., S n) S n = P n i {1,..., n}, (S i )= (P n). A n(k), ϕ A : n(k) K, X (AX) n(k). θ (α, β, γ) Z 3 α + β 2+γ 3=0, α = β = γ =0. n,p,r. (M) =n. X p,1 (K), AX 1 A l X 1. j j n A l = a ij. X p,1 (K), AX A c X. 1 X = ε, ε p a i0 j a i0 j 0 ε j = a i0 j 1 a i0 j =0, p i 0 A c = a i0 j. G, G GL(E). F G, ( f ) G f M 0 B, M 0 0 p(k). ( ) M 0 A = H, M 0 0 p(k), f E, A B G. θ ϕ θ (G, ) (H, ).
24 H n(k). H n(k) =. H ( )( ) ( ) n B n B n 0 =. 0 C 0 p 0 C n + RS p + SR n + p... (u, v) ( L(E) ) 2 u f v = p, p F G.... ( ) X Y N =, MN = Z T n+p. ( )( )( n 0 A B n A 1 ) B CA 1 p C D 0 p ( ) A B = 0 D CA 1. B E K m,n,a p,q,b a = (A), b= (B) a b r = (A) < n ( ) M r r+1 (K) r Mr 0 N r = 0 0 n(k). ( )( )( n 0 A B n A 1 ) B CA 1 p C D 0 p ( ) A 0 = 0 CA 1. B D p. F 1,..., F p+1 E p+1 p F i = E, F p+1 E, F i E, p x, y E x / F p+1 y / F i, y x h G g g h G g h = g. g G g G p 2 x (g e), g G p(x) =x. x (p) g(x) = (g p)(x), g p = p.
25 n =2 n 3 (E 1 E 2 )+(E 1 E 3 ) E 1 (E 2 + E 3 ). E 1 +(E 2 E 3 ) (E 1 + E 2 ) (E 1 + E 3 ). E 1 E 2 E E 1 E 2 = {0} 0 f E f = g 1 + g 2 g 1 : x f(x)+f( x) f(x) f( x), g 2 : x, (g 1,g 2 ) E 1 E (p, q, r) 3= ( R 3)= (4p +5q +6r) =4 (p)+5 (q)+6 (r) =4 (p)+5 (q)+6 (r), (p), (q), (r) N ( E = ) R 2 f,g ( ) A =, B = n 2 A = B = n
26 x A + ( B (A + C) ). a A, b B (A + C) x = a + b. b B a A, c C b = a +c. x = a + b =(a + a )+c. a + a A. c C c =( a )+b A + B, c C (A + B). x A + ( C (A + B) ). A + ( B (A + C) ) A + ( C (A + B) ). (B, C) (C, B), A + ( B (A + C) ) = A + ( C (A + B) ). (A + B) (A + C). n N,a 1,..., a n ]0 ; + [ n λ 1,..., λ n R λ k f ak =0. k=1 x [0 ; + [, n λ k =0. x + a k=1 k [0 ; + [ R, λ k x R {a 1,...,a n}, =0. x + a k=1 k x a k k {1,..., n}, λ k =0. (f a) a ]0 ;+ [ a R x R, f a(x) = (x a) = a x a x, f a (f a) a R, 2 x R (f 1 + f 1 )(x) = (x +1)+ (x 1) =2 1 x =(2 1)f 0 (x), n f f 0 + f 1 =0, (f a) a R A = , B = 0 0 A = , B = (A, B) 3= (C) = (AB) (A) 2, (A, B) ( 1 0 ) ( 1 1 ) i {1,..., n}, i F i F K i α K, f, g F, i (αf + g) =(αf + g)(x i ) = αf(x i )+g(x i )=α i (f)+ i (g). n (α 1,..., α n) K n α i i =0. j {1,..., n} { f j : X K, x i 1 i = j 0 i j. n 0= α i f j (x i )=α j. ( 1,..., n) F. X n F = K X n F n ( 1,..., n) n F F. (A, B) ( ) 2 n(c) AB BA = n (AB BA) = ( n)=n. (AB BA) = (AB) (BA) =0, (A, B) ( ) 2 n(c) AB BA = n. ( ) A B (M) = = (A) (C) 0 C (M) 0 ( (A) 0 (C) 0 ) M A C
27 A C M ( M) 1 M M 1 X Y =. Z T ( )( ) ( ) MM 1 A B X Y n 0 = n+p = 0 C Z T 0 AX + BZ = n Z =0 AY + BT =0 T = C 1 CZ =0 C AX = n CT = p AY = BC 1 Z =0 A T = C 1 X = A 1 Y = A 1 BC 1. ( M 1 A 1 A = 1 BC 1 ) 0 C 1. n N a 1,..., a n R n λ 1,..., λ n R λ k f ak =0. k=1 i {1,..., n}. λ i 0. f ai = 1 λ k f ak. λ i 1kn, k i a R, f a C 2 R {a} C 2 R. f ai C 2 a i, f ai C 2 a i, i {1,..., n}, λ i =0. (f a) a R n = (E). n =1. n. E K[] n +1. E B =(P 1,..., P n+1 ). B, i {1,..., n +1}, (P i ) (P n+1 ). C = (Q 1,..., Q n+1 ) Q n+1 = P n+1 i {1,..., n} P i (P i ) < (P n+1 ) Q i = P i α i P n+1 (P i )= (P n+1 ), α i (P i α i P n+1 ) < (P n+1 ). α i P i P n+1 Q 1,..., Q n+1 P 1,..., P n+1. P n+1 = Q n+1 i {1,..., n} P i = Q i P i = Q i + α i Q n+1, P 1,..., P n+1 Q 1,..., Q n+1. (C) = (B) =E. (E) =n +1 C E n +1 C E. F = (Q 1,..., Q n), n R[]. F F =(R 1,..., R n) G =(R 1,..., R n,p n+1 ). E = F P n+1 K[] F F, G E. i {1,..., n}, R i (Q 1,..., Q n) (Q 1,..., Q n) < (P n+1 ) i {1,..., n}, (R i ) < (P n+1 ). G E n. n = (E). E E B =(P 1,..., P n) (P 1 ) <... < (P n). P i + P n i<n i {1,..., n} S i = P n i = n. i {1,..., n}, (S i )= (P n). S 1,..., S n P 1,..., P n. S i S n i<n i {1,..., n}, P i = S n i = n, P 1,..., P n S 1,..., S n. (E) =n C =(S 1,..., S n) n E, C E. E A n(k). ϕ A : n(k) K, X (AX) α K, X, Y n(k), ϕ A (αx + Y )= ( A(αX + Y ) ) = (αax + AY ) = α (AX)+ (AY )=αϕ A (X)+ϕ A (Y ). ϕ A n(k).
28 θ : n(k) n(k) A n(k), X n(k), θ(a)(x) = (AX). A n(k), θ(a) =ϕ A. θ α K, A, B n(k). X n(k) θ(αa + B)(X) = ( (αa + B)X ) = (αax + BX) =α (AX)+ (BX) = αθ(a)(x)+θ(b)(x) = ( αθ(a)+θ(b) ) (X), θ(αa + B) =αθ(a)+θ(b), θ. θ A (θ). θ(a) =0 X n(k), (AX) =0. A =(a ij ) ij. (i, j) {1,..., n}. a 1i 0= A ij )= (0) (0) = a ji, a ni i A j A =0. (θ) ={0}, θ θ : n(k) n(k) n(k) n(k) θ K A, B, C, M (M) = (A + 2 B + 3 C) = (A)+ 2 (B)+ 3 (C), ( ) (A) (M) + (B) 2+ (C) 3=0. } {{ } }{{} }{{} α β γ (α, β, γ) Z 3 α + β 2+γ 3=0. (α, β, γ) =(0, 0, 0). γ 3 α 2 +2β 2 +2αβ 2=3γ 2, 3γ 2 α 2 2β 2 αβ 0 2= Q, 2αβ 2 αβ =0. αγ =0 βγ =0. α 0, β =0 γ =0, α =0, α =0. βγ =0, β =0 γ =0 β =0 γ =0. α =0, β =0, γ =0. (B) =0 (C) =0, (B) = (B) =0 (C) = (C) =0, B =0 C =0. r = (A), P n(k), Q p(k) A = P n,p,rq, n,p,r = ( ) r 0 r,p r. 0 n r,r 0 n r,p r ( ) r (r ) n,p,r = 0 0 r,p r, n r,r A ( r A = P ) ( ) r 0 0 r,p r Q, n r,r }{{} V } {{ } U U n,r(k), V r,p(k). U 1,..., U p U V 1,..., V q V, (U 1,..., U p,v 1,..., V q) = (U 1,..., U p)+ (V 1,..., V q), (U 1,..., U p,v 1,..., V q) (U 1,..., U p)+ (V 1,..., V q), (M) (U)+ (V ). ( R ( ( (M) = = R ) = S) S) ( R S ) ( R)+ ( S)= (R)+ (S). ( ) ( ( A B A B (M) = + C D C) D) ( (A)+ (C) ) + ( (B)+ (D) ). M n = (M) (A)+ (B)+ (C). B m,n p (K) C n m,p (K), (B) n p (C) n m, n (A)+(n p)+(n m), (A) m + p n. x 1 X = p,1 (K) x p n p AX 1 = a ij x j n p a ij x j = p ( n ) a ij x j
29 p p A l x j = A l x j = A l X 1. X p,1 (K) {0}, A l = 1jp ( n j {1,..., p} A l = AX 1 X 1 A l. ) a ij, n a ij. X = j, j 1. a 1j X 1 =1 AX =, a nj p AX 1 = a ij = A l, AX 1 = A l. X 1 A l AX 1 = A l. X p,1 (K) {0} X 1 x 1 X = x p p,1 (K) n AX = a ij x j 1in p ( p ) a ij x j a ij X 1in 1in ( p ) = a ij X = A c X. 1in X p,1 (K) {0}, A c = 1in ( p i 0 {1,..., n} A c = 1 X = ε ε p j {1,..., p} ε j = AX X A c. ) a ij, p a i0 j. p,1 (K) a i0 j a i0 j a i0 j 0 1 a i0 j =0. X =1, X 1 X 0. AX = 1in ( p ) a ij ε j p a i0 jε j. j {1,..., p} a i0 jε j = a i0 j, a i0 j 0, a i0 j =0. p AX a i0 j = A c. AX X p,1 (K) A c. X AX = A c. X p,1 (K) {0} X G. f 1,f 2 G. (f 2 f 1 ) (f 2 )=F. z F. z F = (f 2 ), y E z = f 2 (y). E = F G, u F, v G y = u + v. z = f 2 (y) =f 2 (u + v) =f 2 (u)+f 2 (v). u F = (f 1 ), x E u = f 1 (x), v G = (f 2 ), f 2 (v) =0. ( z = f 2 f1 (x) ) = f 2 f 1 (x) (f 2 f 1 ). F (f 2 f 1 ). (f 2 f 1 )=F. (f 2 f 1 ) (f 1 )=G. ( x (f 2 f 1 ); f 2 f1 (x) ) =0, f 1 (x) (f 1 ) (f 2 )=F G = {0}, x (f 1 )=G. (f 2 f 1 ) G. (f 2 f 1 )=G. f 2 f 1 G. p F G. p L(E), (p) =F, (p) =G, p G. f G. x E, f(x) (f) =F, x E, p ( f(x) ) = f(x), p f = f. x E, x p(x) (p) =G = (f), x E, f ( x p(x) ) =0, x E, f(x) =f ( p(x) ), f = f p. p G.
30 f G. F G = (f) E, f : F (f) =F, x f(x) K g : E E, x f 1( p(x) ), p g (g) =f 1( p(e) ) = f 1 (F )=F. x E x (g) g(x) =0 f 1( p(x) ) =0 p(x) =0 x G, (g) =G. g G. x E (f g)(x) =f ( f 1( p(x) )) = f ( f 1( p(x) )) = p(x), f g = p. x E f(x) (f) =F, p ( f(x) ) = f(x), g ( f(x) ) = f 1( p ( f(x) )) = f 1( f(x) ). f = f p, f 1( f(x) ) = f 1( f ( p(x) )) = f 1( f ( p(x) )) = p(x). g f = p. g f = f g = p, f g (G, ). (G, ) f G, (f) ( =F ) (f) =G, M 0 f B, M 0 0 f f F. ( ) M 0 (M) = = (f) = (F )=p. 0 0 ( ) M 0 M p(k), H. 0 0 θ : G H, f B (f). ϕ A H, f E B (f) =A ( ) M 0 A = = 0 0 B (f) M p(k), (f) =F (f) =G, f G. θ ϕ ( )( ) M2 0 M1 0 f 1,f 2 G, θ(f 2 )θ(f 1 )= ( ) M2 M = 1 0 = θ(f f 1 ). θ (G, ) (H, ). (G, ) (H, ) θ : f B (f) (G, ) (H, ). H n(k). H n(k) =. H N n(k), N / H. N / H H n(k), n(k) =H KN. M H α K n = M + αn. M = n αn. N k N N k =0 ( k 1 ( n αn) (αn) p) = n α k N k = n p=0 ( k 1 (αn) p) ( n αn) = n α k N k = n, p=0 n αn n(k). M H n(k), H n(k) (0) (0) N 1 =,N 0 (0) 2 = (0) N 1 N 2 N 1 H N 2 H, H N 1 + N 2 H (0) N 1 + N 2 = 0, 0 (0) n(k) n(k).
 1 2 3 4 1 2 3 4 (p A ) (p B ) (p C ) 1 2, 3, 4 2, 3, 4 {2, 3, 4} 1 2 (p A ) (p B ) (p C ) d d {1, 2} (p A,p B )=0
1 2 3 4 1 2 3 4 (p A ) (p B ) (p C ) 1 2, 3, 4 2, 3, 4 {2, 3, 4} 1 2 (p A ) (p B ) (p C ) d d {1, 2} (p A,p B )=0
1.1 Legemer. Legemer er talsystemer udstyret med addition og multiplikation, hvor vi kan regner som vi plejer at gøre med de reelle tal.
 SEKTION 11 LEGEMER 11 Legemer Legemer er talsystemer udstyret med addition og multiplikation, hvor vi kan regner som vi plejer at gøre med de reelle tal Definition 111 Et legeme F er en mængde udstyret
SEKTION 11 LEGEMER 11 Legemer Legemer er talsystemer udstyret med addition og multiplikation, hvor vi kan regner som vi plejer at gøre med de reelle tal Definition 111 Et legeme F er en mængde udstyret
17 B 17 A 19 B 1 9 C A. Antal boliger: 37 Bolig størrelse: m2. 12 J 7000aa 31 J F 3 31 N 31 M. Tiltag:
 000p bb cg u F C D L z C ay ac bt 0af ae bi Nav: Tøreha resse: Søgae tal bolig: olig størrelse: - m 0ao s 0am bq 0p Nav: øgeha resse: Tøre -J tal bolig: 0 olig størrelse: m bl bx H y G br 000ak 0l bk bv
000p bb cg u F C D L z C ay ac bt 0af ae bi Nav: Tøreha resse: Søgae tal bolig: olig størrelse: - m 0ao s 0am bq 0p Nav: øgeha resse: Tøre -J tal bolig: 0 olig størrelse: m bl bx H y G br 000ak 0l bk bv
檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪
 =>?@/0,J.AnhuiAgric.Sci.2019,47(2):34-37,79 29 0Z $ 1, 2, 2,0 2,0 3 (1. /W0S 1!, / 211200;2. / / &20, / 210095;3. 3 BC, 650000) "# [] -=., - HIJ [ 2] 29- =.*K, 8 11 ) *IJIC,EOPK52IJ, HIJ - =. [$>] 2- =.
=>?@/0,J.AnhuiAgric.Sci.2019,47(2):34-37,79 29 0Z $ 1, 2, 2,0 2,0 3 (1. /W0S 1!, / 211200;2. / / &20, / 210095;3. 3 BC, 650000) "# [] -=., - HIJ [ 2] 29- =.*K, 8 11 ) *IJIC,EOPK52IJ, HIJ - =. [$>] 2- =.
:!!09 ;!' 09 % % (% %+ %1 164< 6 1 %- : #:%: %: : #: ):::::::::::::::::::::::!- : ::::::::::::::::::::::::::::::::"## 1 164< 6 1 % %12 %6!" #$%
 + 7 89 :!!09 ;!' 09 % % (% %+ %1 164< 6 1 %- : #:%: %: : #: ):::::::::::::::::::::::!- : ::::::::::::::::::::::::::::::::"## 1 164< 6 1 % %12 %6!" #$%&!"#$ %& ' ' ( ) * +, -. / 0 1 2 3 4 5 6 / 7 8 9 :
+ 7 89 :!!09 ;!' 09 % % (% %+ %1 164< 6 1 %- : #:%: %: : #: ):::::::::::::::::::::::!- : ::::::::::::::::::::::::::::::::"## 1 164< 6 1 % %12 %6!" #$%&!"#$ %& ' ' ( ) * +, -. / 0 1 2 3 4 5 6 / 7 8 9 :
Sandsynlighedsteori
 Fordelingskatalog til Sandsynlighedsteori 1.1 + 1.2 Svend Erik Graversen August 2005 1 Dette katalog indeholder de vigtigste egenskaber ved de 6 mest almindelige diskrete fordelinger samt de 11 mest almindelige
Fordelingskatalog til Sandsynlighedsteori 1.1 + 1.2 Svend Erik Graversen August 2005 1 Dette katalog indeholder de vigtigste egenskaber ved de 6 mest almindelige diskrete fordelinger samt de 11 mest almindelige
Bilag 2 - Spildevandsplan 2011-2021
 Bilag 2 - Spildevandsplan 2011-2021 Alle eksisterende ejendomme på følgende matrikler skal separatkloakeres Arninge 4c Ore By, Arninge 2016-2021 Arninge 4e Ore By, Arninge 2016-2021 Arninge 4f Ore By,
Bilag 2 - Spildevandsplan 2011-2021 Alle eksisterende ejendomme på følgende matrikler skal separatkloakeres Arninge 4c Ore By, Arninge 2016-2021 Arninge 4e Ore By, Arninge 2016-2021 Arninge 4f Ore By,
Konvekse mængder. Erik Christensen. 6. januar 2003
 Konvekse mængder Erik Christensen 6. januar 2003 Indholdsfortegnelse Afsnit 0 ELEMENTÆRE DEFINITIONER OG DET FUNDAMENTALE RESULTAT, 4 Afsnit 1 REPETITION, AFSTANDSMÅLET I Rn OG LINEÆRE AFBILDNINGER, 9
Konvekse mængder Erik Christensen 6. januar 2003 Indholdsfortegnelse Afsnit 0 ELEMENTÆRE DEFINITIONER OG DET FUNDAMENTALE RESULTAT, 4 Afsnit 1 REPETITION, AFSTANDSMÅLET I Rn OG LINEÆRE AFBILDNINGER, 9
A B C D E Hjemmeværnmuseet's arkiv/depot Søgaard Distrikter - LMD. Reol/hylde Region/distrikt/m.m. Kasse nr. Indhold 2C3 Flyverhjemmeværne 1
 0 A B C D E Hjemmeværnmuseet's arkiv/depot Søgaard LMK Distrikter - LMD. Reol/hylde Region/distrikt/m.m. Kasse nr. Indhold C Flyverhjemmeværne Flyverhjemmeværnet LMD Odense Nyt fra stabseskadrillen -.
0 A B C D E Hjemmeværnmuseet's arkiv/depot Søgaard LMK Distrikter - LMD. Reol/hylde Region/distrikt/m.m. Kasse nr. Indhold C Flyverhjemmeværne Flyverhjemmeværnet LMD Odense Nyt fra stabseskadrillen -.
Holdelementnavn XPRS fagbetegnelse (kort) Norm. elevtid (skoleår) Lektioner (antal) 1g ap Almen sprogfors 0 28 totalt 3g as Astronomi 44 1g bk
 Holdelementnavn XPRS fagbetegnelse (kort) Norm. elevtid (skoleår) Lektioner (antal) 1g ap Almen sprogfors 0 28 totalt 3g as Astronomi 44 1g bk Billedkunst 47 1g bi Biologi 10 41 2a BI Biologi 45 95 2c
Holdelementnavn XPRS fagbetegnelse (kort) Norm. elevtid (skoleår) Lektioner (antal) 1g ap Almen sprogfors 0 28 totalt 3g as Astronomi 44 1g bk Billedkunst 47 1g bi Biologi 10 41 2a BI Biologi 45 95 2c
GENTOFTE KOMMUNE B Y G NI NG S VÆ SE NET BYPLAN 16B
 GENTOFTE KOMMUNE B Y G NI NG S VÆ SE NET BYPLAN 16B Vedtægt for byplan 16B for en del af det mellem Strandvejen, Lille Strandvej, Kystlinien og Nordskel af ejendommene nord for Sundvænget beliggende område
GENTOFTE KOMMUNE B Y G NI NG S VÆ SE NET BYPLAN 16B Vedtægt for byplan 16B for en del af det mellem Strandvejen, Lille Strandvej, Kystlinien og Nordskel af ejendommene nord for Sundvænget beliggende område
Tidligere Eksamensopgaver MM505 Lineær Algebra
 Institut for Matematik og Datalogi Syddansk Universitet Tidligere Eksamensopgaver MM55 Lineær Algebra Indhold Typisk forside.................. 2 Juni 27.................... 3 Oktober 27..................
Institut for Matematik og Datalogi Syddansk Universitet Tidligere Eksamensopgaver MM55 Lineær Algebra Indhold Typisk forside.................. 2 Juni 27.................... 3 Oktober 27..................
Eric Nordenstam 1 Benjamin Young 2. FPSAC 12, Nagoya, Japan
 Eric 1 Benjamin 2 1 Fakultät für Matematik Universität Wien 2 Institutionen för Matematik Royal Institute of Technology (KTH) Stockholm FPSAC 12, Nagoya, Japan The Aztec Diamond Aztec diamonds of orders
Eric 1 Benjamin 2 1 Fakultät für Matematik Universität Wien 2 Institutionen för Matematik Royal Institute of Technology (KTH) Stockholm FPSAC 12, Nagoya, Japan The Aztec Diamond Aztec diamonds of orders
CIVILINGENIØREKSAMEN Side 1 af 18 sider. Skriftlig prøve, den: PQ. juli 200Z Kursus nr : (navn) (underskrift) (bord nr)
 CIVILINGENIØREKSAMEN Side 1 af 18 sider Skriftlig prøve, den: PQ. juli 200Z Kursus nr : 02405 Kursus navn: Sandsynlighedsregning Tilladte hjælpemidler: Alle Dette sæt er besvaret af: (navn) (underskrift)
CIVILINGENIØREKSAMEN Side 1 af 18 sider Skriftlig prøve, den: PQ. juli 200Z Kursus nr : 02405 Kursus navn: Sandsynlighedsregning Tilladte hjælpemidler: Alle Dette sæt er besvaret af: (navn) (underskrift)
Analyse 2. Gennemgå bevis for Sætning Supplerende opgave 1. Øvelser. Sætning 1. For alle mængder X gælder #X < #P(X).
 Analyse 2 Øvelser Rasmus Sylvester Bryder 3. og 6. september 2013 Gennemgå bevis for Sætning 2.10 Sætning 1. For alle mængder X gælder #X < #P(X). Bevis. Der findes en injektion X P(X), fx givet ved x
Analyse 2 Øvelser Rasmus Sylvester Bryder 3. og 6. september 2013 Gennemgå bevis for Sætning 2.10 Sætning 1. For alle mængder X gælder #X < #P(X). Bevis. Der findes en injektion X P(X), fx givet ved x
Oversigt [LA] 1, 2, 3, [S] 9.1-3
![Oversigt [LA] 1, 2, 3, [S] 9.1-3 Oversigt [LA] 1, 2, 3, [S] 9.1-3](/thumbs/70/62452762.jpg) Oversigt [LA] 1, 2, 3, [S] 9.1-3 Nøgleord og begreber Talpar, taltripler og n-tupler Linearkombination og span Test linearkombination Hvad er en matrix Matrix multiplikation Test matrix multiplikation
Oversigt [LA] 1, 2, 3, [S] 9.1-3 Nøgleord og begreber Talpar, taltripler og n-tupler Linearkombination og span Test linearkombination Hvad er en matrix Matrix multiplikation Test matrix multiplikation
Konvekse mængder. Erik Christensen
 Konvekse mængder Erik Christensen Indholdsfortegnelse Afsnit 0 ELEMENTÆRE DEFINITIONER OG DET FUNDAMENTALE RESULTAT, 4 Afsnit 1 REPETITION, AFSTANDSMÅLET I Rn OG LINEÆRE AFBILDNINGER, 9 Afsnit 2 AFFINE
Konvekse mængder Erik Christensen Indholdsfortegnelse Afsnit 0 ELEMENTÆRE DEFINITIONER OG DET FUNDAMENTALE RESULTAT, 4 Afsnit 1 REPETITION, AFSTANDSMÅLET I Rn OG LINEÆRE AFBILDNINGER, 9 Afsnit 2 AFFINE
DOKUMENT: Dato/løbenummer: TINGLYSNINGSDATO:
 side 1 ================================================================================ DOKUMENTAKTUELHENT ================================================================================ DOKUMENT: Dato/løbenummer:
side 1 ================================================================================ DOKUMENTAKTUELHENT ================================================================================ DOKUMENT: Dato/løbenummer:
! " # !" # $ % & ' ( ) * +, -. /
 !"#!# $%!"#$%&' ()*+,-./0' # ; >? FGHI J'# KLH MN KL!"#$%#&'()*+,-./ 0+ + 2 3456789:6;
!"#!# $%!"#$%&' ()*+,-./0' # ; >? FGHI J'# KLH MN KL!"#$%#&'()*+,-./ 0+ + 2 3456789:6;
INSTITUT FOR MATEMATISKE FAG c
 INSTITUT FOR MATEMATISKE FAG c AALBORG UNIVERSITET FREDRIK BAJERS VEJ 7 G 9220 AALBORG ØST Tlf.: 96 35 89 27 URL: www.math.aau.dk Fax: 98 15 81 29 E-mail: bjh@math.aau.dk Dataanalyse Sandsynlighed og stokastiske
INSTITUT FOR MATEMATISKE FAG c AALBORG UNIVERSITET FREDRIK BAJERS VEJ 7 G 9220 AALBORG ØST Tlf.: 96 35 89 27 URL: www.math.aau.dk Fax: 98 15 81 29 E-mail: bjh@math.aau.dk Dataanalyse Sandsynlighed og stokastiske
Lineær Algebra F08, MØ
 Lineær Algebra F08, MØ Vejledende besvarelser af udvalgte opgaver fra Ugeseddel 3 og 4 Ansvarsfraskrivelse: Den følgende vejledning er kun vejledende. Opgaverne kommer i vilkårlig rækkefølge. Visse steder
Lineær Algebra F08, MØ Vejledende besvarelser af udvalgte opgaver fra Ugeseddel 3 og 4 Ansvarsfraskrivelse: Den følgende vejledning er kun vejledende. Opgaverne kommer i vilkårlig rækkefølge. Visse steder
Oversigt [LA] 3, 4, 5
![Oversigt [LA] 3, 4, 5 Oversigt [LA] 3, 4, 5](/thumbs/55/37584246.jpg) Oversigt [LA] 3, 4, 5 Nøgleord og begreber Matrix multiplikation Identitetsmatricen Transponering Fra matrix til afbildning Fra afbildning til matrix Test matrix-afbildning Inverse matricer Test invers
Oversigt [LA] 3, 4, 5 Nøgleord og begreber Matrix multiplikation Identitetsmatricen Transponering Fra matrix til afbildning Fra afbildning til matrix Test matrix-afbildning Inverse matricer Test invers
Uge 10 Teoretisk Statistik 1. marts 2004
 1 Uge 10 Teoretisk Statistik 1. marts 004 1. u-fordelingen. Normalfordelingen 3. Middelværdi og varians 4. Mere normalfordelingsteori 5. Grafisk kontrol af normalfordelingsantagelse 6. Eksempler 7. Oversigt
1 Uge 10 Teoretisk Statistik 1. marts 004 1. u-fordelingen. Normalfordelingen 3. Middelværdi og varians 4. Mere normalfordelingsteori 5. Grafisk kontrol af normalfordelingsantagelse 6. Eksempler 7. Oversigt
Selv-absorberende C*-algebraer
 Selv-absorberende C*-algebraer Speciale af Randi Rohde 5. marts 006 Vejleder: Mikael Rørdam Indhold Indledning Tensorprodukter 3. Indledende resultater................................. 3. Fuldstændigt
Selv-absorberende C*-algebraer Speciale af Randi Rohde 5. marts 006 Vejleder: Mikael Rørdam Indhold Indledning Tensorprodukter 3. Indledende resultater................................. 3. Fuldstændigt
BYPLANVEDTÆGT nr. A 1 Avedøre Hvidovre kommune
 A l BYPLANVEDTÆGT nr. A 1 Avedøre Hvidovre kommune Byplanvedtægt for et område af Avedere by, Brendbyester sogn, Glostrup kommune, omfattende *Avederegård villaby«,»storegårdens villaby«og»vesterkær«.
A l BYPLANVEDTÆGT nr. A 1 Avedøre Hvidovre kommune Byplanvedtægt for et område af Avedere by, Brendbyester sogn, Glostrup kommune, omfattende *Avederegård villaby«,»storegårdens villaby«og»vesterkær«.
Sandsynlighedsregning
 Mogens Bladt www2.imm.dtu.dk/courses/02405 21. September, 2007 Lidt om binomialkoefficienter n størrelsen af en mængde/population. Vi ønsker at udtage en sub population af størrelse r. To sub populationer
Mogens Bladt www2.imm.dtu.dk/courses/02405 21. September, 2007 Lidt om binomialkoefficienter n størrelsen af en mængde/population. Vi ønsker at udtage en sub population af størrelse r. To sub populationer
Definition multiplikation En m n-matrix og en n p-matrix kan multipliceres (ganges sammen) til en m p-matrix.
 Oversigt [LA] 3, 4, 5 Nøgleord og begreber Matrix multiplikation Identitetsmatricen Transponering Fra matrix til afbildning Fra afbildning til matrix Test matrix-afbildning Inverse matricer Test invers
Oversigt [LA] 3, 4, 5 Nøgleord og begreber Matrix multiplikation Identitetsmatricen Transponering Fra matrix til afbildning Fra afbildning til matrix Test matrix-afbildning Inverse matricer Test invers
Nøgleord og begreber. Definition multiplikation En m n-matrix og en n p-matrix kan multipliceres (ganges sammen) til en m p-matrix.
 Oversigt [LA] 3, 4, 5 Matrix multiplikation Nøgleord og begreber Matrix multiplikation Identitetsmatricen Transponering Fra matrix til afbildning Fra afbildning til matrix Test matrix-afbildning Inverse
Oversigt [LA] 3, 4, 5 Matrix multiplikation Nøgleord og begreber Matrix multiplikation Identitetsmatricen Transponering Fra matrix til afbildning Fra afbildning til matrix Test matrix-afbildning Inverse
GEOMETRI-TØ, UGE 6. . x 1 x 1. = x 1 x 2. x 2. k f
 GEOMETRI-TØ, UGE 6 Hvis I falder over tryk- eller regne-fejl i nedenstående, må I meget gerne sende rettelser til fuglede@imfaudk Opvarmningsopgave 1 Lad f : R 2 R være tre gange kontinuert differentierbar
GEOMETRI-TØ, UGE 6 Hvis I falder over tryk- eller regne-fejl i nedenstående, må I meget gerne sende rettelser til fuglede@imfaudk Opvarmningsopgave 1 Lad f : R 2 R være tre gange kontinuert differentierbar
!" # $%&' ' '!! '('" %$'& )** +!"#$%&' *&'+,-. /0*& 1 -. *&'+ +-.)! '! &!!"# $%&' '& & '&!$ '!!"!'&!$! $ '&!$! '! 0! 2! #'! ' 3!!! "# $ %& ' "' #%& "#
 !" # $%&' ' '!! '('" %$'& )** +!"#$%&' *&'+,-. /0*& 1 -. *&'+ +-.)! '! &!!"# $%&' '& & '&!$ '!!"!'&!$! $ '&!$! '! 0! 2! #'! ' 3!!! "# $ %& ' "' #%& "#"! "# $ %& ) '"'4 & $%'!& 4 $'!" & #' &'!"$'$ 56! &
!" # $%&' ' '!! '('" %$'& )** +!"#$%&' *&'+,-. /0*& 1 -. *&'+ +-.)! '! &!!"# $%&' '& & '&!$ '!!"!'&!$! $ '&!$! '! 0! 2! #'! ' 3!!! "# $ %& ' "' #%& "#"! "# $ %& ) '"'4 & $%'!& 4 $'!" & #' &'!"$'$ 56! &
StatDataN: Plot af data
 StatDataN: Plot af data JLJ StatDataN: Plot af data p. 1/39 Repetition binomial(n,p): P(X = k) = ( n) k p k (1 p) n k n uafhængige kast med en mønt, X= antal krone X binomial(n, p), Y binomial(m, p), uafhængige
StatDataN: Plot af data JLJ StatDataN: Plot af data p. 1/39 Repetition binomial(n,p): P(X = k) = ( n) k p k (1 p) n k n uafhængige kast med en mønt, X= antal krone X binomial(n, p), Y binomial(m, p), uafhængige
Sandsynlighed og Statistik
 36 Sandsynlighed og Statistik 6.1 Indledning Denne note beskriver de statistiske begreber og formler som man med rimelig sandsynlighed kan komme ud for i eksperimentelle øvelser. Alt er yderst korfattet,
36 Sandsynlighed og Statistik 6.1 Indledning Denne note beskriver de statistiske begreber og formler som man med rimelig sandsynlighed kan komme ud for i eksperimentelle øvelser. Alt er yderst korfattet,
Normalfordelingen. Det centrale er gentagne målinger/observationer (en stikprøve), der kan beskrives ved den normale fordeling: 1 2πσ
 Normalfordelingen Det centrale er gentagne målinger/observationer (en stikprøve), der kan beskrives ved den normale fordeling: f(x) = ( ) 1 exp (x µ)2 2πσ 2 σ 2 Frekvensen af observationer i intervallet
Normalfordelingen Det centrale er gentagne målinger/observationer (en stikprøve), der kan beskrives ved den normale fordeling: f(x) = ( ) 1 exp (x µ)2 2πσ 2 σ 2 Frekvensen af observationer i intervallet
Områdeestimator. X x. P θ. ν θ. Θ C(x) En områdeestimator er en afbildning C : X P(Θ). . p.1/30
 Områdeestimator X (Ω, F) (X, E) x 01 01 P θ ν θ θ Θ 0000 1111 000000 111111 0000 1111 0000 1111 C(x) En områdeestimator er en afbildning C : X P(Θ).. p.1/30 Konfidensområde En områdestimator C : X P(Θ)
Områdeestimator X (Ω, F) (X, E) x 01 01 P θ ν θ θ Θ 0000 1111 000000 111111 0000 1111 0000 1111 C(x) En områdeestimator er en afbildning C : X P(Θ).. p.1/30 Konfidensområde En områdestimator C : X P(Θ)
LOKALPLAN NR. 8. Fanø Kommune. Klitarealer i sommerhusområderne Fanø Bad og Rindby Strand. Oktober 1979
 LOKALPLAN NR. 8 Fanø Kommune Klitarealer i sommerhusområderne Fanø Bad og Rindby Strand. Oktober 1979 2 Lokalplan 8 Fanø Kommune Anmelder: Advokat Chr. V. Thuesen Torvegade 28 6700 Esbjerg J.nr. 260 ct/aj
LOKALPLAN NR. 8 Fanø Kommune Klitarealer i sommerhusområderne Fanø Bad og Rindby Strand. Oktober 1979 2 Lokalplan 8 Fanø Kommune Anmelder: Advokat Chr. V. Thuesen Torvegade 28 6700 Esbjerg J.nr. 260 ct/aj
Koter i meter i henhold til DVR 90. Koordinatsystem er UTM32 1ga 1fa. Signaturer 1ig 1hz 1hl 1hp 1fh 1dø 1dx 1u. Matrikel 150aq cd 3bæ.
 Bilag Supplement til VVM Noter Mål: ad 36a 44a cd cs ee cr ed cq dz af ag af c db 35e d 7h 3cb 3bx ea gd fd go gq gu il gh ih Signaturer ig hz hl hp fh dø dx u Grundkort er udtegnet på baggrund af digitale
Bilag Supplement til VVM Noter Mål: ad 36a 44a cd cs ee cr ed cq dz af ag af c db 35e d 7h 3cb 3bx ea gd fd go gq gu il gh ih Signaturer ig hz hl hp fh dø dx u Grundkort er udtegnet på baggrund af digitale
Ændring af rammeområde 2.B.6 Østbyvej
 Ændring af rammeområde 2.B.6 Østbyvej Tillæg 12 til Roskilde Kommuneplan 2013 2.B.6 2.BT.4 0 500 m 500 Forord HVAD ER ET TILLÆG TIL KOMMUNEPLANEN? Den fysiske planlægning reguleres bl.a. gennem kommuneplanlægning.
Ændring af rammeområde 2.B.6 Østbyvej Tillæg 12 til Roskilde Kommuneplan 2013 2.B.6 2.BT.4 0 500 m 500 Forord HVAD ER ET TILLÆG TIL KOMMUNEPLANEN? Den fysiske planlægning reguleres bl.a. gennem kommuneplanlægning.
4.1 Lineære Transformationer
 SEKTION 41 LINEÆRE TRANSFORMATIONER 41 Lineære Transformationer Definition 411 ([L], s 175) Lad V, W være F-vektorrum En lineær transformation L : V W er en afbildning, som respekterer lineær struktur,
SEKTION 41 LINEÆRE TRANSFORMATIONER 41 Lineære Transformationer Definition 411 ([L], s 175) Lad V, W være F-vektorrum En lineær transformation L : V W er en afbildning, som respekterer lineær struktur,
Polynomium Et polynomium. Nulpolynomiet Nulpolynomiet er funktionen der er konstant nul, dvs. P(x) = 0, og dets grad sættes per definition til.
 Polynomier Polynomier Polynomium Et polynomium P(x) = a n x n + a n x n +... + a x + a 0 Disse noter giver en introduktion til polynomier, centrale sætninger om polynomiumsdivision, rødder og koefficienter
Polynomier Polynomier Polynomium Et polynomium P(x) = a n x n + a n x n +... + a x + a 0 Disse noter giver en introduktion til polynomier, centrale sætninger om polynomiumsdivision, rødder og koefficienter
χ 2 -fordelte variable
 χ -fordelte varable Defnton af χ -fordelngen Kvadratsummen V n af n uafhængge standardserede normalfordelte stokastske varable sges at være χ -fordelt med n frhedsgrader. V n fremkommer altså som V n =
χ -fordelte varable Defnton af χ -fordelngen Kvadratsummen V n af n uafhængge standardserede normalfordelte stokastske varable sges at være χ -fordelt med n frhedsgrader. V n fremkommer altså som V n =
Oversigt [S] 7.3, 7.4, 7.5, 7.6; [DL] 1, 2
![Oversigt [S] 7.3, 7.4, 7.5, 7.6; [DL] 1, 2 Oversigt [S] 7.3, 7.4, 7.5, 7.6; [DL] 1, 2](/thumbs/82/86922880.jpg) Oversigt [S] 7.3, 7.4, 7.5, 7.6; [DL] 1, 2 Her skal du lære om Separable ligninger Logistisk ligning og eksponentiel vækst 1. ordens lineær ligning August 2002, opgave 7 Rovdyr-Byttedyr system 1. ordens
Oversigt [S] 7.3, 7.4, 7.5, 7.6; [DL] 1, 2 Her skal du lære om Separable ligninger Logistisk ligning og eksponentiel vækst 1. ordens lineær ligning August 2002, opgave 7 Rovdyr-Byttedyr system 1. ordens
Statistik og Sandsynlighedsregning 2
 Statistik og Sandsynlighedsregning 2 Middelværdi og varians Helle Sørensen Uge 6, onsdag SaSt2 (Uge 6, onsdag) Middelværdi og varians 1 / 18 Program I formiddag: Tætheder og fordelingsfunktioner kort resume
Statistik og Sandsynlighedsregning 2 Middelværdi og varians Helle Sørensen Uge 6, onsdag SaSt2 (Uge 6, onsdag) Middelværdi og varians 1 / 18 Program I formiddag: Tætheder og fordelingsfunktioner kort resume
!"#$% &' & & ( &)*+,-./01 ' & :; 8 FGHIJK LMNO PQ R A S!"TUV WXY Y89 2 Z[\47] 4^_`abc 3 LMI( # V 7 %JK!" %JK LM&LM&A ab ( 89 \ TU
![!#$% &' & & ( &)*+,-./01 ' & :; 8 FGHIJK LMNO PQ R A S!TUV WXY Y89 2 Z[\47] 4^_`abc 3 LMI( # V 7 %JK! %JK LM&LM&A ab ( 89 \ TU !#$% &' & & ( &)*+,-./01 ' & :; 8 FGHIJK LMNO PQ R A S!TUV WXY Y89 2 Z[\47] 4^_`abc 3 LMI( # V 7 %JK! %JK LM&LM&A ab ( 89 \ TU](/thumbs/101/149254105.jpg) !"#$% &' & & ( &)*+,-./01 ' &2342564789:; 8 ? @ABCDE FGHIJK LMNO PQ R A S!"TUV WXY Y89 2 Z[\47] 4^_`abc 3 LMI( # V 7 %JK!" %JK LM&LM&A ab ( 89 \ TUY Y V Z Z[\4^ a c W X7Y J c N!"7 89 \!" EV ^ LMN c
!"#$% &' & & ( &)*+,-./01 ' &2342564789:; 8 ? @ABCDE FGHIJK LMNO PQ R A S!"TUV WXY Y89 2 Z[\47] 4^_`abc 3 LMI( # V 7 %JK!" %JK LM&LM&A ab ( 89 \ TUY Y V Z Z[\4^ a c W X7Y J c N!"7 89 \!" EV ^ LMN c
Module 1: Lineære modeller og lineær algebra
 Module : Lineære modeller og lineær algebra. Lineære normale modeller og lineær algebra......2 Lineær algebra...................... 6.2. Vektorer i R n................... 6.2.2 Regneregler for vektorrum...........
Module : Lineære modeller og lineær algebra. Lineære normale modeller og lineær algebra......2 Lineær algebra...................... 6.2. Vektorer i R n................... 6.2.2 Regneregler for vektorrum...........
Ortogonale Polynomier & Rodriguesformlen
 Ortogonale Polynomier & Rodriguesformlen MAT 10. SEMESTER SPECIALE MATEMATIK & STATISTIK AALBORG UNIVERSITET 8. JUNI 2017 Institut for Matematiske Fag Fredrik Bajers Vej 7G 9220 Aalborg Ø Telefon 99 40
Ortogonale Polynomier & Rodriguesformlen MAT 10. SEMESTER SPECIALE MATEMATIK & STATISTIK AALBORG UNIVERSITET 8. JUNI 2017 Institut for Matematiske Fag Fredrik Bajers Vej 7G 9220 Aalborg Ø Telefon 99 40
8 Regulære flader i R 3
 8 Regulære flader i R 3 Vi skal betragte særligt pæne delmængder S R 3 kaldet flader. I det følgende opfattes S som et topologisk rum i sportopologien, se Definition 5.9. En åben omegn U af p S er således
8 Regulære flader i R 3 Vi skal betragte særligt pæne delmængder S R 3 kaldet flader. I det følgende opfattes S som et topologisk rum i sportopologien, se Definition 5.9. En åben omegn U af p S er således
Hamiltons princip. Et systems bane (i konfigurationsrummet) fra t 1 til t 2 er bestemt
 Hamtons prncp.1 Konfguratonsrum q 3 Et systems bane ( konfguratonsrummet) fra t t er bestemt af, at aktonsntegraet I = Lt har en statonær vær. t q 1 q () Systemet ska være monogensk, vs. ae kræfter (ekskusvt
Hamtons prncp.1 Konfguratonsrum q 3 Et systems bane ( konfguratonsrummet) fra t t er bestemt af, at aktonsntegraet I = Lt har en statonær vær. t q 1 q () Systemet ska være monogensk, vs. ae kræfter (ekskusvt
Matrikelnøgle 2002 for Grindsted Kommune i ejerlavsorden
 Side 1 af 137 Mølle Alle/Stadion Alle 001? (Sønder Omme) *** Ingen vurdering Loftvej 017?? Udgået ejendom Norden 001?? Undtaget vurdering Askjærvej 034 1a Askær Gårde Bebygget landbrug Frodeslundvej 073
Side 1 af 137 Mølle Alle/Stadion Alle 001? (Sønder Omme) *** Ingen vurdering Loftvej 017?? Udgået ejendom Norden 001?? Undtaget vurdering Askjærvej 034 1a Askær Gårde Bebygget landbrug Frodeslundvej 073
Momenter som deskriptive størrelser. Hvad vi mangler fra onsdag. Momenter for sandsynlighedsmål
 Hvad vi mangler fra onsdag Momenter som deskriptive størrelser Sandsynlighedsmål er komplicerede objekter de tildeler numeriske værdier til alle hændelser i en σ-algebra. Vi har behov for simplere, deskriptive
Hvad vi mangler fra onsdag Momenter som deskriptive størrelser Sandsynlighedsmål er komplicerede objekter de tildeler numeriske værdier til alle hændelser i en σ-algebra. Vi har behov for simplere, deskriptive
Hvad vi mangler fra onsdag. Vi starter med at gennemgå slides fra onsdag.
 Hvad vi mangler fra onsdag Vi starter med at gennemgå slides 34-38 fra onsdag. Slide 1/17 Niels Richard Hansen MI forelæsninger 6. December, 2013 Momenter som deskriptive størrelser Sandsynlighedsmål er
Hvad vi mangler fra onsdag Vi starter med at gennemgå slides 34-38 fra onsdag. Slide 1/17 Niels Richard Hansen MI forelæsninger 6. December, 2013 Momenter som deskriptive størrelser Sandsynlighedsmål er
()&*&+&,-.%/ &$6 78)523)&%, 95%*.6%,0 :566.%$ ;1&,- <61(%,16 =>59236?6)4%$ @3)&B&)0
 !!"#$! "#$% &% $ $" ( $&"!!"##$%& ()!(%* &+*#,$-$*.+/!"#$%& ()*+,-./01234&5678!"# $ "! $%% $ "! &! $ "!!! ( $ " &! )*+ $ "!!,-. $ "!; WX)*Y,Z)!"JK,[\]^_ ab cde! $%##*# "; J"7IJKLMfghNijkl ab cde! $%##*#
!!"#$! "#$% &% $ $" ( $&"!!"##$%& ()!(%* &+*#,$-$*.+/!"#$%& ()*+,-./01234&5678!"# $ "! $%% $ "! &! $ "!!! ( $ " &! )*+ $ "!!,-. $ "!; WX)*Y,Z)!"JK,[\]^_ ab cde! $%##*# "; J"7IJKLMfghNijkl ab cde! $%##*#
8bu. 9g 1cø. Udarb./Tegn Kontrolleret Godkendt 1:5000. Odsherred Spildevand A/S Afskæring Tengslemark Rens Arealdisponeringsplan
 7 Strandvej 8 T 0 8 M M M M M Strandvej Strandvej 7 e f 7000k bu 8a 8bx a ah 8bu 8d 8bu a 8d 8m 8n 0da d 8bv 8c 8h t dy 0ft ag 9o 8g 8m 9g cø Servitutareal(89 m²) Forventet arbejdsareal(90 m²) :000 0-0-0
7 Strandvej 8 T 0 8 M M M M M Strandvej Strandvej 7 e f 7000k bu 8a 8bx a ah 8bu 8d 8bu a 8d 8m 8n 0da d 8bv 8c 8h t dy 0ft ag 9o 8g 8m 9g cø Servitutareal(89 m²) Forventet arbejdsareal(90 m²) :000 0-0-0
Course on Continuum Mechanics - academic year Màster en Enginyeria de Camins, Canals i Ports. Màster en Enginyeria Geològica i de Mines.
 Official Fom Chapte. Desciption of Motion (, t) (, t) + (, t) (, t) t t Chapte. Defomation an Stain s S X E X e i ij j i ij j F X X U F J E F F JJ J J T T T e F F jj j j T T T T s JJ T a JJ T E T t t ij
Official Fom Chapte. Desciption of Motion (, t) (, t) + (, t) (, t) t t Chapte. Defomation an Stain s S X E X e i ij j i ij j F X X U F J E F F JJ J J T T T e F F jj j j T T T T s JJ T a JJ T E T t t ij
MÅLESTOKSFORHOLD HFB 2012 / 13. Målestoksforhold OP SL AG. Byggecentrum
 MÅLESTOKSFORHOLD Målestoksforhold 340 MÅLEENHEDER Måleenheder Omsætning: Gl. dansk mål metermål gl. engelsk mål (= amerikansk mål). Se også: Målesystemer og enheder. Gl. dansk mål Metermål Gl. engelsk
MÅLESTOKSFORHOLD Målestoksforhold 340 MÅLEENHEDER Måleenheder Omsætning: Gl. dansk mål metermål gl. engelsk mål (= amerikansk mål). Se også: Målesystemer og enheder. Gl. dansk mål Metermål Gl. engelsk
DesignMat Uge 1 Repetition af forårets stof
 DesignMat Uge 1 Repetition af forårets stof Preben Alsholm Efterår 008 01 Lineært ligningssystem Lineært ligningssystem Et lineært ligningssystem: a 11 x 1 + a 1 x + + a 1n x n = b 1 a 1 x 1 + a x + +
DesignMat Uge 1 Repetition af forårets stof Preben Alsholm Efterår 008 01 Lineært ligningssystem Lineært ligningssystem Et lineært ligningssystem: a 11 x 1 + a 1 x + + a 1n x n = b 1 a 1 x 1 + a x + +
Noter til Lineær Algebra
 Noter til Lineær Algebra Eksamensnoter til LinAlg Martin Sparre, www.logx.dk, August 2007, Version π8 9450. INDHOLD 2 Indhold 0. Om disse noter.......................... 3 Abstrakte vektorrum 4. Definition
Noter til Lineær Algebra Eksamensnoter til LinAlg Martin Sparre, www.logx.dk, August 2007, Version π8 9450. INDHOLD 2 Indhold 0. Om disse noter.......................... 3 Abstrakte vektorrum 4. Definition
Integration m.h.t. mål med tæthed
 Integration m.h.t. mål med tæthed Sætning (EH 11.7) Lad ν = f µ på (X, E). For alle g M + (X, E) gælder at gdν = g f dµ. Bevis: Standardbeviset: 1) indikatorfunktioner 2) simple funktioner 3) M + -funktioner.
Integration m.h.t. mål med tæthed Sætning (EH 11.7) Lad ν = f µ på (X, E). For alle g M + (X, E) gælder at gdν = g f dµ. Bevis: Standardbeviset: 1) indikatorfunktioner 2) simple funktioner 3) M + -funktioner.
BYPLANVEDTÆGT FOR NØDEBO-OMRÅDET. Byplanvedtægt nr. 41
 BYPLANVEDTÆGT FOR NØDEBO-OMRÅDET Byplanvedtægt nr. 41 Byplanvedtægt nr. 41 - for Nødebo-området I medfør af byplanloven (lovbekendtgørelse nr. 63 af 20. februar 1970) fastsættes følgende bestemmelser for
BYPLANVEDTÆGT FOR NØDEBO-OMRÅDET Byplanvedtægt nr. 41 Byplanvedtægt nr. 41 - for Nødebo-området I medfør af byplanloven (lovbekendtgørelse nr. 63 af 20. februar 1970) fastsættes følgende bestemmelser for
Egentyngd (+Struc. dead load) Glas Nyttiglast balkong Egentyngd (+Struc. dead load) Glas Nyttiglast balkong
 Eurocode (NA: Swedih) Eurocode (NA: Swedih) Load combination No. Name ype Factor.35*Egentyngd +.35*Gla +.50*0.70*Nyttiglat balong Ultimate.350.350 3 Egentyngd + Gla + 0.30*Nyttiglat balong Ultimate Quaipermanent.050.0.0.500.000.000
Eurocode (NA: Swedih) Eurocode (NA: Swedih) Load combination No. Name ype Factor.35*Egentyngd +.35*Gla +.50*0.70*Nyttiglat balong Ultimate.350.350 3 Egentyngd + Gla + 0.30*Nyttiglat balong Ultimate Quaipermanent.050.0.0.500.000.000
On the Relations Between Fuzzy Topologies and α Cut Topologies
 S Ü Fen Ed Fak Fen Derg Sayı 23 (2004) 21-27, KONYA On the Relations Between Fuzzy Topologies and α Cut Topologies Zekeriya GÜNEY 1 Abstract: In this study, some relations have been generated between fuzzy
S Ü Fen Ed Fak Fen Derg Sayı 23 (2004) 21-27, KONYA On the Relations Between Fuzzy Topologies and α Cut Topologies Zekeriya GÜNEY 1 Abstract: In this study, some relations have been generated between fuzzy
STEMPELMÆRKE Roskilde herred ^ KUN GYLDIGT MED AFSTEMPLlMG AF DOMMERKCNTOBET5KASSKXONTKOUFPARAT GUNDSØ KOMMUNE u4 D ,161X
 STEMPELMÆRKE Roskilde herred ^ KUN GYLDIGT MED AFSTEMPLlMG AF DOMMERKCNTOBET5KASSKXONTKOUFPARAT GUNDSØ KOMMUNE u4 D 0 2 4 8,161X1871418000400.00 LOKALPLAN NR. 20.- Åben, lav boligbebyggelse i Jyllinge
STEMPELMÆRKE Roskilde herred ^ KUN GYLDIGT MED AFSTEMPLlMG AF DOMMERKCNTOBET5KASSKXONTKOUFPARAT GUNDSØ KOMMUNE u4 D 0 2 4 8,161X1871418000400.00 LOKALPLAN NR. 20.- Åben, lav boligbebyggelse i Jyllinge
Gamle eksamensopgaver (MASO)
 EO 1 Gamle eksamensopgaver (MASO) Opgave 1. (Vinteren 1990 91, opgave 1) a) Vis, at rækken er divergent. b) Vis, at rækken er konvergent. Opgave 2. (Vinteren 1990 91, opgave 2) Gør rede for at ligningssystemet
EO 1 Gamle eksamensopgaver (MASO) Opgave 1. (Vinteren 1990 91, opgave 1) a) Vis, at rækken er divergent. b) Vis, at rækken er konvergent. Opgave 2. (Vinteren 1990 91, opgave 2) Gør rede for at ligningssystemet
PerkinElmerhelpsprofesionalsaceleratesciencethrough innovativedetection,imaging,andinformaticssolutions.
 S h wp f p n p h wa yy u p p w d a y Su y ha bynd hn w Ema S a Mb Th g ba p a nwaab hu dwnf aud v ad ng pam andan v u u n La nm An n manuf a u ng v mpany h u h a byp ngaga n unwan dandma uma La nm Th NBA
S h wp f p n p h wa yy u p p w d a y Su y ha bynd hn w Ema S a Mb Th g ba p a nwaab hu dwnf aud v ad ng pam andan v u u n La nm An n manuf a u ng v mpany h u h a byp ngaga n unwan dandma uma La nm Th NBA
Der lader til at være en lille smule forvirring omkring funktionsbegrebet, og hvordan man, til en given talrække, kan finde dennes funktionsforskrift.
 Medudgangspunkti:Wikipedia:Funktion Derladertilatværeenlillesmuleforvirringomkringfunktionsbegrebet,og hvordanman,tilengiventalrække,kanfindedennesfunktionsforskrift. Jegkanafsløre,atdensammemetodeanvendesindenforkryptografiogtydning
Medudgangspunkti:Wikipedia:Funktion Derladertilatværeenlillesmuleforvirringomkringfunktionsbegrebet,og hvordanman,tilengiventalrække,kanfindedennesfunktionsforskrift. Jegkanafsløre,atdensammemetodeanvendesindenforkryptografiogtydning
A hybrid high-order locking-free method for linear elasticity on general meshes
 A hybri high-orer locking-free metho for linear elasticity on general meshes Daniele Antonio Di Pietro, Alexanre Ern o cite this version: Daniele Antonio Di Pietro, Alexanre Ern. A hybri high-orer locking-free
A hybri high-orer locking-free metho for linear elasticity on general meshes Daniele Antonio Di Pietro, Alexanre Ern o cite this version: Daniele Antonio Di Pietro, Alexanre Ern. A hybri high-orer locking-free
Matr. nr. 1aLungholm inddæmning, Olstrup
 Matr. nr. 1aLungholm inddæmning, Olstrup 1e 1a 1a 604024 m² 1r 1aa Tangvej 1n Tegningsnr. : LE34_ 100128-1016_ 2 Ret til at etablere natur (permanent indgreb), jf. 33, stk. 4 1: 3000 15 1q Matr. nr. 1rLungholm
Matr. nr. 1aLungholm inddæmning, Olstrup 1e 1a 1a 604024 m² 1r 1aa Tangvej 1n Tegningsnr. : LE34_ 100128-1016_ 2 Ret til at etablere natur (permanent indgreb), jf. 33, stk. 4 1: 3000 15 1q Matr. nr. 1rLungholm
Læsø Kommune. Lokalplan 0.1 for Læsøs sommerhusområder
 Anmelder: Læsø Kommune Doktorvejen 2 9940 Læsø Læsø Kommune Lokalplan 0.1 for Læsøs sommerhusområder Byrum By, Byrum: 4bn, 4bt, 4bu, 4bv, 4bx, 4by, 4bz, 4bæ, 4bø, 4ca, 4cb, 4cc, 4cd, 4ce, 4cf, 4cg, 4cy,
Anmelder: Læsø Kommune Doktorvejen 2 9940 Læsø Læsø Kommune Lokalplan 0.1 for Læsøs sommerhusområder Byrum By, Byrum: 4bn, 4bt, 4bu, 4bv, 4bx, 4by, 4bz, 4bæ, 4bø, 4ca, 4cb, 4cc, 4cd, 4ce, 4cf, 4cg, 4cy,
fhair 52.0"; ( ^ ^ as Z < ^ -» H S M 3
 fair 52.0"; (515 974 ^ ^ as ^ -» S M 3 > D Z (D Z Q LU LU > LU W CC LO CO > CD LJJ > LJJ O LL .. O ^ CO ^ ^ ui,"" 2.2 C d. ii "^ S Q ~ 2 & 2 ^ S i; 2 C O T3 Q _, - - ^ Z W O 1- ' O CM OOCMOOO'-'O'^'N
fair 52.0"; (515 974 ^ ^ as ^ -» S M 3 > D Z (D Z Q LU LU > LU W CC LO CO > CD LJJ > LJJ O LL .. O ^ CO ^ ^ ui,"" 2.2 C d. ii "^ S Q ~ 2 & 2 ^ S i; 2 C O T3 Q _, - - ^ Z W O 1- ' O CM OOCMOOO'-'O'^'N
Tillæg nr. 1 til lokalplan 01.32 For et sommerhusområde i Evetofte Januar 2012
 Tillæg nr. 1 til lokalplan 01.32 For et sommerhusområde i Evetofte Januar 2012 Natur og Udvikling Halsnæs Kommune Rådhuset Rådhuspladsen 1 3300 Frederiksværk Tlf. 47 78 40 00 Hvorfor laver vi en lokalplan?
Tillæg nr. 1 til lokalplan 01.32 For et sommerhusområde i Evetofte Januar 2012 Natur og Udvikling Halsnæs Kommune Rådhuset Rådhuspladsen 1 3300 Frederiksværk Tlf. 47 78 40 00 Hvorfor laver vi en lokalplan?
SMBJ5.0~SMBJ440CA. 600W Transient Voltage Suppressors. 1. 封裝 Package 封裝方式 Method: SMB/DO-214AA 封裝尺寸 Dimension: 如圖示. 2.
 1. 封裝 Package 封裝方式 Method: SMB/DO-214AA 封裝尺寸 Dimension: 如圖示 2. 產品特色 Features For surface mounted applications in order to optimize board space. Glass passivated junction Low inductance High temperature
1. 封裝 Package 封裝方式 Method: SMB/DO-214AA 封裝尺寸 Dimension: 如圖示 2. 產品特色 Features For surface mounted applications in order to optimize board space. Glass passivated junction Low inductance High temperature
Kommuneplantillæg. Tillæg nr. 10 til Kommuneplan Forsla
 Kommuneplantillæg Tillæg nr. 10 til Kommuneplan 2014 g Forsla Indledning Redegørelse Kommuneplanen revideres hvert fjerde år. Hvis der i den mellemliggende periode ønskes en ændringer i kommuneplanens
Kommuneplantillæg Tillæg nr. 10 til Kommuneplan 2014 g Forsla Indledning Redegørelse Kommuneplanen revideres hvert fjerde år. Hvis der i den mellemliggende periode ønskes en ændringer i kommuneplanens
Huseftersynsordningen plus, minus ti år -
 Huseftersynsordningen plus, minus ti år - ! # # # % & # ( ( #! # ) # ( & # # # # +! #!# %, # # #! %.# / # # 0#( # # # # # # %, # # # 1 # # % 2 # & # # 0#( # # # # # 2 # #! 2 ( # # 3 ( & # # # (#! #, #
Huseftersynsordningen plus, minus ti år - ! # # # % & # ( ( #! # ) # ( & # # # # +! #!# %, # # #! %.# / # # 0#( # # # # # # %, # # # 1 # # % 2 # & # # 0#( # # # # # 2 # #! 2 ( # # 3 ( & # # # (#! #, #
Elementær sandsynlighedsregning
 Elementær sandsynlighedsregning Sandsynlighedsbegrebet Et udfaldsrum S er mængden af alle de mulige udfald af et eksperiment. En hændelse A er en delmængde af udfaldsrummet S. Den hændelse, der ikke indeholder
Elementær sandsynlighedsregning Sandsynlighedsbegrebet Et udfaldsrum S er mængden af alle de mulige udfald af et eksperiment. En hændelse A er en delmængde af udfaldsrummet S. Den hændelse, der ikke indeholder
LOKALPLAN NR. 720.1. ANVENDELSE AF BOLIGER I TVERSTED Helårsstatus langs Tannisbugtvej og Bindslevvej samt sideveje m.v. til disse.
 LOKALPLAN NR. 720.1 ANVENDELSE AF BOLIGER I TVERSTED Helårsstatus langs Tannisbugtvej og Bindslevvej samt sideveje m.v. til disse. December 2007 HJØRRING KOMMUNE Side 3 LOKALPLAN NR. 720.1 FOR ANVENDELSEN
LOKALPLAN NR. 720.1 ANVENDELSE AF BOLIGER I TVERSTED Helårsstatus langs Tannisbugtvej og Bindslevvej samt sideveje m.v. til disse. December 2007 HJØRRING KOMMUNE Side 3 LOKALPLAN NR. 720.1 FOR ANVENDELSEN
Program. Statistik og Sandsynlighedsregning 2 Middelværdi og varians. Eksempler fra sidst. Sandsynlighedstæthed og sandsynlighedsmål
 Program Statistik og Sandsynlighedsregning 2 Middelværdi og varians Helle Sørensen Uge 6, onsdag I formiddag: Tætheder og fordelingsfunktioner kort resume fra i mandags og et par eksempler mere om sammenhængen
Program Statistik og Sandsynlighedsregning 2 Middelværdi og varians Helle Sørensen Uge 6, onsdag I formiddag: Tætheder og fordelingsfunktioner kort resume fra i mandags og et par eksempler mere om sammenhængen
Ny bevaringsliste 14. april 2011
 VEJNAVN HUSNR MATRIKELID EJENDOMSNR ABELIG Omr_bev Dronningvej 3 3v 0010164 Dronningvej 3 A Dronningvej 4A 3o 0010172 Dronningvej 4 A og B A Dronningvej 5 3x 0010180 Dronningvej 5 A Dronningvej 6 3p 0010199
VEJNAVN HUSNR MATRIKELID EJENDOMSNR ABELIG Omr_bev Dronningvej 3 3v 0010164 Dronningvej 3 A Dronningvej 4A 3o 0010172 Dronningvej 4 A og B A Dronningvej 5 3x 0010180 Dronningvej 5 A Dronningvej 6 3p 0010199
SUPPLERENDE OPGAVER TIL KOMPLEKS FUNKTIONSTEORI F2005
 SUPPLERENDE OPGAVER TIL KOMPLEKS FUNKTIONSTEORI F2005 0. maj, 2005 version nr. 8 JØRGEN VESTERSTRØM Indledende bemærkninger De foreliggende opgaver udgør et supplement til lærebogens opgaver. Afsnitsnummereringerne
SUPPLERENDE OPGAVER TIL KOMPLEKS FUNKTIONSTEORI F2005 0. maj, 2005 version nr. 8 JØRGEN VESTERSTRØM Indledende bemærkninger De foreliggende opgaver udgør et supplement til lærebogens opgaver. Afsnitsnummereringerne
LOKALPLAN GUG ERHVERV OG SPORTSANLÆG INDKILDEVEJ
 LOKALPLAN 07-021 ERHVERV OG SPORTSANLÆG INDKILDEVEJ GUG SEPTEMBER 1999 Matrikelkort: Bilag 1 Lokalplan 07-021 Erhverv og sportsanlæg, Indkildevej, Gug 9r "ak" Motorvej 9o "p" 9cx 9n 9cx 6dg
LOKALPLAN 07-021 ERHVERV OG SPORTSANLÆG INDKILDEVEJ GUG SEPTEMBER 1999 Matrikelkort: Bilag 1 Lokalplan 07-021 Erhverv og sportsanlæg, Indkildevej, Gug 9r "ak" Motorvej 9o "p" 9cx 9n 9cx 6dg
* I lr,3 I li=;ia. gltgetlneei. s I l.iel t cb,f. ? I lsa*l Is*iA. $ I l=r I leer'i. islel seelaliheia F I IFF I IFF*1. =:=l lh=;l lfre'si :=EU
 Y ci c+c\ > >> J 6B xr. t 0fJ) tt rj 6t (V 6g r cg A i! :.?6 [. _. 6> t\n t\\ Y '': t ib Y\At :U g i.j ct l l P ij li^ ri Y'+ (Yt r?3 '.0 ii r\ " \J/ iy ri 9 rt3.8 'n A! 6s X ct.:+. l*lq* Ui9 *..1 *.*.!i.i
Y ci c+c\ > >> J 6B xr. t 0fJ) tt rj 6t (V 6g r cg A i! :.?6 [. _. 6> t\n t\\ Y '': t ib Y\At :U g i.j ct l l P ij li^ ri Y'+ (Yt r?3 '.0 ii r\ " \J/ iy ri 9 rt3.8 'n A! 6s X ct.:+. l*lq* Ui9 *..1 *.*.!i.i
Svar på opgave 336 (Januar 2017)
 Svar på opgave 6 (Januar 07) Opgave: De komplekse tal a, b og c opfylder ligningssystemet Vis, at a, b og c er reelle. (a + b)(a + c) = b (b + c)(b + a) = c (c + a)(c + b) = a. Besvarelse:. metode Lad
Svar på opgave 6 (Januar 07) Opgave: De komplekse tal a, b og c opfylder ligningssystemet Vis, at a, b og c er reelle. (a + b)(a + c) = b (b + c)(b + a) = c (c + a)(c + b) = a. Besvarelse:. metode Lad
Liter 0 C. Liter sval - - - - - - - - - - - - - - - - - - - - - - - -
 Frederiksberg Forsyning /S Stæhr Johansens Vej 18 51 00 Email ff@frbforsyning.dk Web: www.frbforsyning.dk Markedsoversigt med EU's energimærkning: Køle/eskabe med 2 døre, Højde redde Dybde d() /år eg eg
Frederiksberg Forsyning /S Stæhr Johansens Vej 18 51 00 Email ff@frbforsyning.dk Web: www.frbforsyning.dk Markedsoversigt med EU's energimærkning: Køle/eskabe med 2 døre, Højde redde Dybde d() /år eg eg
Matr. nr. 271lRødby Markjorder
 Matr. nr. 271lRødby Markjorder 549a 271k 13a Finlandsvej 271i 629 m² 271l 2 m² 271n Sulkavavej 271m 271o 271q 271d 271p Sulkavavej 244ec Tegningsnr. : LE34_ 100128-1043_ 3 Ret til at udvide veje (midlertidigt
Matr. nr. 271lRødby Markjorder 549a 271k 13a Finlandsvej 271i 629 m² 271l 2 m² 271n Sulkavavej 271m 271o 271q 271d 271p Sulkavavej 244ec Tegningsnr. : LE34_ 100128-1043_ 3 Ret til at udvide veje (midlertidigt
STEMPELMÆRKE RINGKØBING KOMMUNE LOKALPLAN NR FOR ET BOLIGOMRÅDE ØST FOR SDR, RINGVEJ I RINGKØBING. (SUPPLEMENT TIL LOKALPLAN NR ).
 STEMPELMÆRKE KUN GYLDIGT MED AFSTEMPLING AF DOMMERKONTORETS KASSEKONTROLAPPARAT RINGKØBING KOMMUNE LOKALPLAN NR. 01.033 FOR ET BOLIGOMRÅDE ØST FOR SDR, RINGVEJ I RINGKØBING. (SUPPLEMENT TIL LOKALPLAN NR.
STEMPELMÆRKE KUN GYLDIGT MED AFSTEMPLING AF DOMMERKONTORETS KASSEKONTROLAPPARAT RINGKØBING KOMMUNE LOKALPLAN NR. 01.033 FOR ET BOLIGOMRÅDE ØST FOR SDR, RINGVEJ I RINGKØBING. (SUPPLEMENT TIL LOKALPLAN NR.
Byplanvedtægt 5. For den sydlige del af Furesøkvarteret. Lyngby-Taarbæk Kommune
 Byplanvedtægt 5 For den sydlige del af Furesøkvarteret Lyngby-Taarbæk Kommune BYPLANVEDTÆGT FOR DEN SYDLIGE DEL AF FURESØKVARTERET I LYNGBY-TAARBÆK KOMMUNE. 1. I medfør af lovbekendtgørelse nr. 242 af
Byplanvedtægt 5 For den sydlige del af Furesøkvarteret Lyngby-Taarbæk Kommune BYPLANVEDTÆGT FOR DEN SYDLIGE DEL AF FURESØKVARTERET I LYNGBY-TAARBÆK KOMMUNE. 1. I medfør af lovbekendtgørelse nr. 242 af
Taylorpolynomier og -rækker samt lokale ekstrema for funktioner af flere variable
 Taylorpolynomier og -rækker samt lokale ekstrema for funktioner af flere variable Morten Grud Rasmussen 1. marts 2016 1 Taylors Sætning for funktioner af én variabel Sætning 1.1 (Taylors Sætning med restled).
Taylorpolynomier og -rækker samt lokale ekstrema for funktioner af flere variable Morten Grud Rasmussen 1. marts 2016 1 Taylors Sætning for funktioner af én variabel Sætning 1.1 (Taylors Sætning med restled).
Aristoteles Camillo. To cite this version: HAL Id: hal
 An experimentally-based modeling study of the effect of anti-angiogenic therapies on primary tumor kinetics for data analysis of clinically relevant animal models of metastasis Aristoteles Camillo To cite
An experimentally-based modeling study of the effect of anti-angiogenic therapies on primary tumor kinetics for data analysis of clinically relevant animal models of metastasis Aristoteles Camillo To cite
DOK-facitliste DOK. DOK-facitliste 1
 -facitliste 1 -facitliste Listens numre refererer til samlingen af supplerede -opgaver (de gamle eksamensopgaver. På listen står næsten kun facitter, og ikke tilstrækkelige svar på opgaverne. [Korrigeret
-facitliste 1 -facitliste Listens numre refererer til samlingen af supplerede -opgaver (de gamle eksamensopgaver. På listen står næsten kun facitter, og ikke tilstrækkelige svar på opgaverne. [Korrigeret
Funktioner - Fase 2 Anvende ikke-lineære funktioner til beskrivelse
 Navn: Klasse: Funktioner - Fase 2 nvende ikke-lineære funktioner til beskrivelse Vurdering fra 1 til 5 (hvor 5 er højst) Læringsmål Selv Lærer Beviser og forslag til forbedring 1. Jeg kan løse problemer,
Navn: Klasse: Funktioner - Fase 2 nvende ikke-lineære funktioner til beskrivelse Vurdering fra 1 til 5 (hvor 5 er højst) Læringsmål Selv Lærer Beviser og forslag til forbedring 1. Jeg kan løse problemer,
Dynamiske Systemer. SIR-modellen. Matematik 3. semester 08 Gr. G2-104
 Dynamiske Systemer SIR-modellen Matematik 3. semester 08 Gr. G2-104 Titel: Dynamiske systemer -SIR-modellen Tema: Dynamiske systemer -iteration og approksimation Projektperiode: MAT1, 3. semester 2008
Dynamiske Systemer SIR-modellen Matematik 3. semester 08 Gr. G2-104 Titel: Dynamiske systemer -SIR-modellen Tema: Dynamiske systemer -iteration og approksimation Projektperiode: MAT1, 3. semester 2008
Bedste rette linje ved mindste kvadraters metode
 1/9 Bedste rette linje ved mindste kvadraters metode - fra www.borgeleo.dk Figur 1: Tre datapunkter og den bedste rette linje bestemt af A, B og C Målepunkter og bedste rette linje I ovenstående koordinatsystem
1/9 Bedste rette linje ved mindste kvadraters metode - fra www.borgeleo.dk Figur 1: Tre datapunkter og den bedste rette linje bestemt af A, B og C Målepunkter og bedste rette linje I ovenstående koordinatsystem
13 Markovprocesser med transitionssemigruppe
 13 Markovprocesser med transitionssemigruppe I nærværende kapitel vil vi antage at tilstandsrummet er polsk, hvilket sikrer, at der findes regulære betingede fordelinger. Vi skal se på eksistensen af Markovprocesser.
13 Markovprocesser med transitionssemigruppe I nærværende kapitel vil vi antage at tilstandsrummet er polsk, hvilket sikrer, at der findes regulære betingede fordelinger. Vi skal se på eksistensen af Markovprocesser.
264.. Cox, Daio Jang (23) Grandell (1976). 1.1 (Ω, F, {F, [, ]}, P). N λ, λ F, 1 2 u R, λ d < a... E{e iu(n 2 N 1 ) F λ 2 } = e {(eiu 1) 2 1 λ d}, F λ
![264.. Cox, Daio Jang (23) Grandell (1976). 1.1 (Ω, F, {F, [, ]}, P). N λ, λ F, 1 2 u R, λ d < a... E{e iu(n 2 N 1 ) F λ 2 } = e {(eiu 1) 2 1 λ d}, F λ 264.. Cox, Daio Jang (23) Grandell (1976). 1.1 (Ω, F, {F, [, ]}, P). N λ, λ F, 1 2 u R, λ d < a... E{e iu(n 2 N 1 ) F λ 2 } = e {(eiu 1) 2 1 λ d}, F λ](/thumbs/92/110314096.jpg) 212 6 Chinee Journal of Applied Probabiliy and Saiic Vol.28 No.3 Jun. 212 Lévy (,, 2156),, Lévy.., (Credi Defaul Swap). :,,,. : O211.6. 1.,.,.,,.,, O Kane urnbull (23), Jamhidian (24), Crepey, Jeanblanc
212 6 Chinee Journal of Applied Probabiliy and Saiic Vol.28 No.3 Jun. 212 Lévy (,, 2156),, Lévy.., (Credi Defaul Swap). :,,,. : O211.6. 1.,.,.,,.,, O Kane urnbull (23), Jamhidian (24), Crepey, Jeanblanc
Lokalplan nr. 59 (tidligere Holmsland Kommune)
 Lokalplan nr. 59 (tidligere Holmsland Kommune) er d. 03.06.2013 blevet delvis aflyst. Det aflyste område er i stedet omfattet af: Lokalplan nr. 274 For et område til sommerhusformål ved Klevevej, Lodbjerg
Lokalplan nr. 59 (tidligere Holmsland Kommune) er d. 03.06.2013 blevet delvis aflyst. Det aflyste område er i stedet omfattet af: Lokalplan nr. 274 For et område til sommerhusformål ved Klevevej, Lodbjerg
Vedtægter. for. Grundejerforeningen KILDEHOLM IV
 Vedtægter for Grundejerforeningen KILDEHOLM IV Vedtægter for "GRUNDEJERFORENINGEN KILDEHOLM IV" 1. Foreningens navn er "GRUNDEJERFORENINGEN KILDEHOLM IV". Foreningens hjemsted er Ølstykke. 2. Foreningens
Vedtægter for Grundejerforeningen KILDEHOLM IV Vedtægter for "GRUNDEJERFORENINGEN KILDEHOLM IV" 1. Foreningens navn er "GRUNDEJERFORENINGEN KILDEHOLM IV". Foreningens hjemsted er Ølstykke. 2. Foreningens
ODENSE KOMMUNE LOKALPLAN NR. 20-230
 ODENSE KOMMUNE LOKALPLAN NR. 20-230 FOR ET OMRÅDE MELLEM RISMARKSVEJ - TARUPVEJ - RUGVANG SAMT TILLÆG NR. 1 FOR LOKALPLANENS OMRÅDE B I N D H 0 L D S F 0 R T E G N E L S E AFSNIT 1. Lokalplanens formål
ODENSE KOMMUNE LOKALPLAN NR. 20-230 FOR ET OMRÅDE MELLEM RISMARKSVEJ - TARUPVEJ - RUGVANG SAMT TILLÆG NR. 1 FOR LOKALPLANENS OMRÅDE B I N D H 0 L D S F 0 R T E G N E L S E AFSNIT 1. Lokalplanens formål
Kommuneplantillæg Til æg nr. 10 til Kommuneplan 2014
 Kommuneplantillæg Tillæg nr. 10 til Kommuneplan 2014 Indledning Kommuneplanen revideres hvert fjerde år. Hvis der i den mellemliggende periode ønskes en ændringer i kommuneplanens indhold, skal der udarbejdes
Kommuneplantillæg Tillæg nr. 10 til Kommuneplan 2014 Indledning Kommuneplanen revideres hvert fjerde år. Hvis der i den mellemliggende periode ønskes en ændringer i kommuneplanens indhold, skal der udarbejdes
N o t e r t i l G e o m e t r i
 N o t e r t i l G e o m e t r i I b M a d s e n o g J o h a n D u p o n t J a n u a r 2 0 0 5 I n s t i t u t f o r M a t e m a t i s k e Fa g D e t N a t u rv i d e n s k a b e l i g e Fa k u l t e t
N o t e r t i l G e o m e t r i I b M a d s e n o g J o h a n D u p o n t J a n u a r 2 0 0 5 I n s t i t u t f o r M a t e m a t i s k e Fa g D e t N a t u rv i d e n s k a b e l i g e Fa k u l t e t
Jordforureningsattest
 Jordforureningsattest Denne jordforureningsattest er baseret på de informationer, der er registreret i den fællesoffentlige landsdækkende database på jordforureningsområdet, DKjord. Attesten er baseret
Jordforureningsattest Denne jordforureningsattest er baseret på de informationer, der er registreret i den fællesoffentlige landsdækkende database på jordforureningsområdet, DKjord. Attesten er baseret
Bjergbygade, Antvorskov Allé og Frederikshøjvej
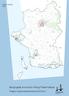 Teknik og Miljø 2015 Bjergbygade, Antvorskov Allé og Frederikshøjvej Tillæg 3 til digital spildevandsplan 2015-2018 Indhold Forord... 3 Baggrund... 3 Miljøvurdering... 4 Berørte ejendomme... 4 Liste over
Teknik og Miljø 2015 Bjergbygade, Antvorskov Allé og Frederikshøjvej Tillæg 3 til digital spildevandsplan 2015-2018 Indhold Forord... 3 Baggrund... 3 Miljøvurdering... 4 Berørte ejendomme... 4 Liste over
# (04&(0(+3++)0&)'50)+1 50*&') # < ; % #! <!! = #" < %! $! =
 " # " $ #$" & ' ( &'())&*))+,) ) ) " *+,+-. ) /*�. ) # *�. *+,+-. ) $ *+,+-. *�. ) *1/ +/. ) - *230. 4. 5 6 *7+ 3&80-. 4 / 4 4 " : " (0)1'0*)2)'. " : " 1 : "" 17;2+ " "# + "$ /; &*'()0)&))3)) / 6
" # " $ #$" & ' ( &'())&*))+,) ) ) " *+,+-. ) /*�. ) # *�. *+,+-. ) $ *+,+-. *�. ) *1/ +/. ) - *230. 4. 5 6 *7+ 3&80-. 4 / 4 4 " : " (0)1'0*)2)'. " : " 1 : "" 17;2+ " "# + "$ /; &*'()0)&))3)) / 6
