Matthias Beck Gerald Marchesi Dennis Pixton Lucas Sabalka
|
|
|
- Ingrid Jespersen
- 4 år siden
- Visninger:
Transkript
1 Matthias Beck Gerald Marchesi Dennis Pixton Lucas Sabalka Version.53
2
3 z 7! z i i
4
5
6
7
8 x 2 + = 0. i i 2 + = 0 i 2 = i x 3 + px + q q q p3 27
9 p q C := {(x, y) : x, y 2 R}, (x, y)+(a, b) := (x + a, y + b) (x, y) (a, b) := (xa yb, xb+ ya). C R (x,0) (x,0)+(y, 0) =(x + y, 0) (x,0) (y, 0) =(xy, 0).
10 C (C, +, ) (x, y), (a, b), (c, d ) 2 C (x, y)+(a, b) 2 C (x, y)+(a, b) +(c, d )=(x, y)+ (a, b)+(c, d ) (x, y)+(a, b)=(a, b)+(x, y) (x, y)+(0, 0)=(x, y) (x, y)+( x, y)=(0, 0) (x, y) (a, b)+(c, d ) =(x, y) (a, b)+(x, y) (c, d ) (x, y) (a, b) 2 C (x, y) (a, b) (c, d )=(x, y) (a, b) (c, d ) (x, y) (a, b)=(a, b) (x, y) (x, y) (, 0)=(x, y) (x, y) 2 C \{(0, 0)} : (x, y) Ä x x 2 +y, 2 y x 2 +y 2 ä =(, 0) (C, +) (0, 0) (C \{(0, 0)}, ) (, 0) R (x, y)+( x, y) =(x +( x), y +( y)) = (0, 0). (0, ) (0, ) =(, 0).
11 (a, 0) (x, y) =(ax, ay) (x, y) =(x,0)+(0, y) =(x,0) (, 0)+(y, 0) (0, ). R C (x,0) (y, 0) x y (x, y) (, 0) (0, ) x y (, 0) (0, ) i (x, y) x + y i x + iy. x y x + iy Re(x + iy)=x Im(x + iy)=y i 2 =. C d d C x + iy
12 k W D (x, y) R 2 x y R 2 z + z 2 z z 2 R 2 z = x + iy r = z := x 2 + y 2, z = x + iy φ 2 R x = r cosφ y = r sinφ. z = x +iy = + 0i 0 2π 4π 2π 2πk k 0 = 0 + 0i 0 φ
13 k D 0 z z 2π z = z, z 2 2 C R 2 d (z, z 2 ) R 2 d (z, z 2 )= z z 2 = z 2 z. z = x + iy z 2 = x 2 + iy 2 d (z, z 2 )= (x x 2 ) 2 +(y y 2 ) 2. z z 2 (x x 2 ) 2 =(x 2 x ) 2 (y y 2 ) 2 = (y 2 y ) 2 z 2 z z z 2 4z z 2 z z 2 = z 2 z z z 2 z 2 z x + iy r φ x 2 + iy 2 r 2
14 x f F... φ 2 x + iy =(r cosφ )+i(r sinφ ) x 2 + iy 2 = (r 2 cosφ 2 )+i(r 2 sinφ 2 ) (x + iy )(x 2 + iy 2 )=(r cosφ + ir sinφ )(r 2 cosφ 2 + ir 2 sinφ 2 ) =(r r 2 cosφ cosφ 2 r r 2 sinφ sinφ 2 )+i(r r 2 cosφ sinφ 2 + r r 2 sinφ cosφ 2 ) = r r 2 (cosφ cosφ 2 sinφ sinφ 2 )+i(cosφ sinφ 2 + sinφ cosφ 2 ) = r r 2 cos(φ + φ 2 )+i sin(φ + φ 2 ). r r 2 φ + φ 2 φ + φ 2 φ z z φ... z z 2 cosφ + i sinφ φ e iφ := cosφ + i sinφ. 2π
15 e 7πi 8 s s e πi 4 = p 2 + i p 2 e πi s 2 = i e iφ φ,φ,φ 2 2 R e iφ e iφ 2 = e i(φ +φ 2 ) e i0 = e i(φ+2π) = e iφ e iφ = e = e iφ iφ d dφ e iφ = ie iφ. e iφ d dφ e iφ = d dφ (cosφ + i sinφ) = sinφ+i cosφ = i (cosφ + i sinφ) = ieiφ. e 2πi = sin(2π)=0 cos(2π)= π i e
16 (e 2πi m n ) n = m n > 0 e 2πiq q 2 Q z n = e 2πi m n m n > 0 ζ ζ n = n ζ n th n ζ n = ζ n th 4 th ± ±i = e ± πi 2 4 th x + iy r φ x + iy = re iφ. p x 2 + y 2 apple p x 2 apple x apple p x 2 apple p x 2 + y 2 z applere(z) apple z z appleim(z) apple z. x + iy 2 = x 2 + y 2 =(x + iy)(x iy).
17 x + iy re i θ (x, y) z y x z r θ x + iy x iy x iy x + iy x + iy := x iy. z z z, z, z 2 2 C z ± z 2 = z ± z 2 z 2 = z z z z 2 = z z 2 Ä z z 2 ä = z z 2 z = z z = z Re(z)= 2 (z + z) Im(z)= 2i (z z) e iφ = e iφ. z = x + iy z 2 = x 2 + iy 2 z z 2 = (x x 2 y y 2 )+i(x y 2 + x 2 y )=(x x 2 y y 2 ) i(x y 2 + x 2 y ) =(x iy )(x 2 iy 2 )=z z 2.
18 z = z = z z 2. R n z, z 2 2 C z + z 2 apple z + z 2. z + z 2 2 = (z + z 2 ) (z + z 2 ) = (z + z 2 )(z + z 2 ) = z z + z z 2 + z 2 z + z 2 z 2 = z 2 + z z 2 + z z 2 + z 2 2 = z 2 + 2Re(z z 2 ) + z 2 2 apple z z z 2 + z 2 2 = z z z 2 + z 2 2 = z z z 2 + z 2 2 = ( z + z 2 ) 2, z, z 2,...,z n 2 C ±z ± z 2 apple z + z 2. ±z ± z 2 z z 2. nx z k k= apple nx z k. k= ±z = z
19 C R 2 y C [2 + i,2] D[ 2, 3 ] ~ x z w z w a r z 2 C z a = r r a a r C [a, r ] := {z 2 C : z a = r }. a r D[a, r ] := {z 2 C : z a < r }. D[a, r ] C [a, r ]
20 C G C a 2 G G a G b 2 C G b G G c 2 C G c G c d 2 G G d G d G G G G r > 0 a 2 C {z 2 C : z {z 2 C : z a > r } a < r } = D[a, r ] D[a, r ] := {z 2 C : z a appler } C? G G G G G G G [ G D[a, r ] D[a, r ] D[a, r ] C [a, r ] G G D[0, r ] r
21 R y x [0, ) (, 2] X, Y C A, B C X A Y B G C G A B X Y X =[0, ) Y =(, 2] A B A = D[0, ] B = D[2, ] X [Y =[0, 2]\{} C γ : [a, b]! C [a, b] R γ γ(t ), a apple t apple b
22 γ γ 0 γ : [a, b]! C t 0 2 [a, b] γ t 0 lim γ(t )=γ(t t!t 0 ), 0 γ 0 (t 0 )= lim t!t0 γ(t ) γ(t 0 ) t t 0. y 3 + i(t 2) 0 apple t apple 3 γ (t )= e it, π 2 apple t apple 2π γ 2 (t )= 6 t + i 2 (t ) 3 apple t apple 5 x γ γ 2 γ γ 3 (t )= e it, 0 apple t apple 3π 2, γ γ 3 γ γ 3 γ γ : [a, b]! C γ 0 (t ) a < t < b lim t!a + γ 0 (t ) lim t!b γ 0 (t )
23 [a, b] C R 2 x(t ) y(t ) γ(t )=x(t )+iy(t ) γ : [a, b]! C γ(t ) γ(a)=γ(b) γ : [a, b]! C γ(a)=γ(b) C [0, ] γ(t )=e it, 0 apple t apple 2π G C G G G C G G G G G z 0 z z n z k z k+ G k = 0,,...,n D[0, ] D[0, ] D[0, ] D[0, ] G = D[0, ] \ {0} D[0, ] G G
24 S C S z = + 2i w = 2 z + 3w i z 3 z 2 + z + i w z Re(w 2 + w) z a z+a 3+5i 7i+ a 2 R Ä +i p 3 2 ä 3 i n n i 3 i p 2+3i (2 + i)(4 + 3i) ( + i) 6 2i i p 5 i + i 3 + p 3 i (2 i) 2 3 4i Ä ä 4 p i 3 p 2 e i 3π 4 e i250π 34 e i π 2 2 e 4πi e ln(5) i d dφ e φ+iφ
25 a, b, c 2 R a 6= 0 az 2 + bz + c = 0 b ± p b 2 2a 4ac. p b 2 4ac = i p b 2 + 4ac b 2 4ac z = 0 2z 2 + 2z + 5 = 0 5z 2 + 4z + = 0 z 2 z = z 2 = 2z z 2 + 2z +( i)=0 a 2 C b 2 R z 2 + Re(az)+b = 0 a 2 4b z 6 = z 4 = 6 z 6 = 9 z 6 z 3 2 = 0 z = z = z z z = z z (z) 2 = z 2 z z 2 = 0 z = 0 z 2 = 0
26 n z n = z = e 2πi m n m 2 z n = z = e 2πi a n a 2 R a = m + b m 0 apple b < b z 5 = (z ) z 2 + 2z cos π 5 + z 2 2z cos 2π 5 + cos π 5 cos 2π 5 n w z n = w w cos(3φ)=cos 3 φ 3cosφ sin 2 φ sin(3φ)=3cos 2 φ sinφ sin 3 φ ñ x x, y 2 R M (x, y) := y ô y x M (x, y)+m (a, b) =M (x + a, y + b) M (x, y) M (a, b) =M (xa yb, xb+ ya). {M (x, y) : x, y 2 R} C = {(x, y) : x, y 2 R}
27 {z 2 C : z + i = 2} {z 2 C : z + i apple 2} {z 2 C : z = z + } {z 2 C : z = 2 z + } {z 2 C :Re(z + 2 2i)=3} z 2 C :Re(z 2 )= {z 2 C : z i + z + i = 3} z 2 C :Im(z 2 )= p p(z)= p (z) p(z)=0 p (z) = 0 z z 2 z z 2. z C [0, 2] z 2 apple 3 z + 3 < 2 Im(z) < z + z + = 2 z + z + < 3 0 < z < 2 z Re(z)+
28 G z 2 C z 2 < z < z < z = z = 2 G G G G G G A B B A B A B A A B C [ + i,] i 2i C [0, 34] ± ± 2i {z 2 C : z + z + = 4} G 2 < z < 3 G G
29 34 = i = π = 2 + 2i = 2 p 3 + i = 2 e i0 = 3 e πi 2 = 2 e i π = e 3πi 2 = 2 e 3πi 2 =
30 z + z + 2 2z z z 2 iz z z 2 Re(z) Im(z) i Im(z) z z i
31 f G C C f : G! C G f z 2 G z f (z) R m R n f (z) =z f (z)=2z + i f (z)=z 3 f (z)= z C z = 0 z f (x, y)=x 2iy f (x, y)=y 2 ix f (r,φ)=2r e i(φ+π)
32 f : G! C z 0 G w 0 ε > 0 δ > 0 z 2 G 0 < z z 0 < δ f (z) w 0 < ε w 0 f z z 0 lim z!z 0 f (z) =w 0. z 0 z z 0 0 < z z 0 z 0 f z 0 f f (z 0 ) lim z 2 = z!i ε > 0 δ > 0 0 < z i < δ z 2 + < ε z 2 + = z i z + i < δ z + i. δ z +i δ < min{ ε 3, } 0 < z i < δ z 2 + < 3δ < ε. ε > 0 0 < δ < min{ ε 3, } 0 < z z + i = z i + 2i apple z i + 2i < 3, i < δ z 2 ( ) = z 2 + = z i z + i < 3δ < ε. lim z!i z 2 =
33 w 0 z z 0 f : G! C lim z!z0 f (z)=w 0 G e G z 0 G e f e f G e lim e z!z0 f (z) w 0 z z z! 0 z! 0 z = x 2 R lim z!0 z z x = lim x!0 x = lim x x!0 x =. z = iy y 2 R lim z!0 z z iy = lim y!0 iy iy = lim y!0 iy =. z z z! 0 f g G z 0 G c 2 C lim z!z0 f (z) lim z!z0 g (z) lim z!z0 ( f (z)+cg(z)) = lim z!z0 f (z)+c lim z!z0 g (z) lim z!z0 ( f (z) g (z)) = lim z!z0 f (z) lim z!z0 g (z) lim z!z0 f (z) g (z) = lim z!z 0 f (z) lim z!z0 g (z) lim z!z0 g (z) 6= 0
34 c 6= 0 L = lim z!z0 f (z) M = lim z!z0 g (z) ε > 0 δ, δ 2 > 0 0 < z z 0 < δ f (z) L < ε 2 0 < z z 0 < δ 2 g (z) M < ε 2 c. δ = min{δ, δ 2 } 0 < z z 0 < δ ( f (z)+cg(z)) (L + cm) apple f (z) L + c g (z) M < ε. lim z!z0 ( f (z)+ cg(z)) = L + cm f : G! C z 0 2 G z 0 G lim z!z 0 f (z) = f (z 0 ) f z 0 f E G f z 2 E ε δ f : G! C z 0 2 G f z 0 ε δ f (z) f (z 0 ) < ε z 2 G z z 0 < δ. f : C! C f (z)=z 2 z = i C
35 g : C! C 8 < z z z 6= 0, g (z) := : z = 0. g z = 0 g : G! C { g (z) : z 2 G}. g f : H! C f g : G! C ( f g )(z) := f ( g (z)). g : G! C H f : H! C z 0 G lim z!z0 g (z) =w 0 2 H f w 0 lim z!z0 f ( g (z)) = f (w 0 ) lim f ( g (z)) = f z!z 0 Å ã lim g (z). z!z 0 ε > 0 η > 0 w w 0 < η f (w) f (w 0 ) < ε. η δ > 0 0 < z z 0 < δ g (z) w 0 < η. 0 < z z 0 < δ f ( g (z)) f (w 0 ) < ε. lim z!z0 f ( g (z)) = f (w 0 )
36 z z f (z) z! 0 z 0 0 f : G! C z 0 G f z 0 f 0 (z 0 ) := lim z!z0 f (z) f (z 0 ) z z 0, f z 0 f z 0 f z 0 f E G E C f : C! C f (z) =z 3 C z 0 2 C f (z) f (z lim 0 ) z 3 z0 3 (z 2 + zz = lim = lim 0 + z0 2)(z z 0 ) = 3z 2 z!z 0 z z z!z0 0 z z z!z0 0 0 z z. 0
37 f 0 f (z (z 0 )=lim 0 + h) f (z 0 ). h!0 h h f : C! C f (z)=(z) 2 0 f 0 z = z 0 + re iφ z 2 z z 0 2 = z 0 + reiφ = (z 0 + re iφ ) 2 z 0 z z 0 z 0 + re iφ z 0 re iφ = z z 0 re iφ + r 2 e 2iφ 2 z 0 re iφ = 2 z 0 e 2iφ + re 3iφ. 2 = 2 z 0 re iφ + r 2 e 2iφ re iφ z 0 6= 0 f (z) z! z 0 2 z 0 e 2iφ + re 3iφ r! 0 2 z 0 e 2iφ φ z z 0 z 0 = 0 re 3iφ = z e 3iφ lim z!0 z 2 z = lim z!0 z e 3iφ = lim z!0 z = 0, z 2 z lim 0 = lim z!z 0 z z 0 2 z z!0 z 2 = 0. f : C! C f (z)=z z z lim 0 z z = lim 0 z = lim z!z 0 z z z!z0 0 z z z!0 0 z,
38 f g z 2 C h g (z) f (z)+cg(z) 0 = f 0 (z)+cg 0 (z) c 2 C f (z) g (z) 0 = f 0 (z) g (z)+ f (z) g 0 (z) f (z) 0 = f 0 (z) g (z) f (z) g 0 (z) g (z) 2 6= 0 g (z) g (z) 2 z n 0 = nz n n g z h( g (z)) 0 = h 0 ( g (z)) g 0 (z). f (z)g (z) 0 f (z + h) g (z + h) f (z) g (z) = lim h!0 h f (z + h) ( g (z + h) g (z)) + ( f (z + h) f (z)) g (z) = lim h!0 h g (z + h) g (z) f (z + h) f (z) = lim f (z + h) + lim g (z) h!0 h h!0 h = f (z) g 0 (z)+ f 0 (z) g (z). f (z) γ(t ) f a 2 C f 0 (a) 6= 0 γ γ 2 a φ f γ γ 2 f (a) φ
39 γ (t ) γ 2 (t ) γ (0)= γ 2 (0)=a γ 0(0) γ a γ2 0(0) γ 2 a γ γ 2 f f (γ ) f (a) d dt f (γ (t )) = f 0 (γ (0)) γ 0 (0) = f 0 (a) γ 0 (0), t =0 f (γ 2 ) f (a) f 0 (a) γ2 0 (0) f γ 0(0) γ0 2 (0) f 0 (a) f 0 (a) f 0 (a) f : G! H w 2 H z 2 G f (z) =w w 2 H z 2 G z 2 G f (z) =w f : G! H g : H! G f f ( g (z)) = z z 2 H f g H G, H C f : G! H g : H! G f z 0 2 H f g (z 0 ) f 0 ( g (z 0 )) 6= 0 g z 0 g z 0 g 0 (z 0 )= f 0 ( g (z 0 )).
40 f ( g (z)) = z z 2 H g 0 (z 0 )= lim z!z0 g (z) g (z 0 ) z z 0 g (z) g (z = lim 0 ) z!z0 f ( g (z)) f ( g (z 0 )) = lim f ( g (z)) f ( g (z 0 )) g (z) g (z 0 ) z!z 0. w 0 = g (z 0 ) 8 f (w) f (w >< 0 ) w 6= w φ(w) := w w 0 0 >: f 0 (w 0 ) w = w 0. w 0 lim z!z0 g (z)=w 0 g g 0 (z 0 )= lim z!z0 φ ( g (z)) = Å φ lim g (z) z!z 0 ã = f 0 (w 0 ) = f 0 ( g (z 0 ). f : R 2! R f x (x 0, y f 0 ) y (x 0, y 0 ) (x 0, y 0 ) 2 R 2 f (z) f 0 (z 0 ) z 0 =(x 0, y 0 ) 2 C f 0 (z 0 ) f x (z 0 ) := lim x!x 0 f (x, y 0 ) f (x 0, y 0 ) x x 0
41 f y (z f (x 0 ) := lim 0, y) f (x 0, y 0 ) y!y 0 y y 0 f z 0 = x 0 + iy 0 f f x (z 0 )= i f y (z 0 ). f f x f y z 0 z 0 f z 0 f 0 f 0 (z 0 )= f x (z 0 ). f f (z)= f (x, y)=u(x, y)+iv(x, y) u f v f x = f x f y = f y f x = u x + iv x if y = i(u y + iv y )=v y iu y. u x (x 0, y 0 ) = v y (x 0, y 0 ) u y (x 0, y 0 ) = v x (x 0, y 0 ).
42 f z 0 = x 0 + iy 0 u v z 0 f = u + iv G u v G u v u xx (x 0, y 0 )=v yx (x 0, y 0 )=v xy (x 0, y 0 )= u yy (x 0, y 0 ), u xx (x 0, y 0 )+u yy (x 0, y 0 )=0 v G C G f G u v f : C! C f (z) =z 3 =(x + iy) 3 = x 3 3xy 2 + i 3x 2 y y 3. f x (z) =3x 2 3y 2 + 6ixy f y (z) = 6xy+ 3ix 2 3iy 2 C f x = if y f (z)=z 3 f : C! C f (z) =(z) 2 =(x iy) 2 = x 2 y 2 2ixy. f x (z) =2x 2iy f y (z) = 2y 2ix,
43 f x = if y z = 0 f (z)=(z) 2 C \{0} f z 0 =(x 0, y 0 ) f 0 (z 0 )= lim z!0 f (z 0 + z) f (z 0 ). z z z = x f 0 (z 0 )= lim x!0 f (z 0 + x) f (z 0 ) x = lim x!0 f (x 0 + x, y 0 ) f (x 0, y 0 ) x = f x (x 0, y 0 ). z = i y f 0 (z 0 )= lim i y!0 f (z 0 + i y) f (z 0 ) i y = lim y!0 i f (x 0, y 0 + y) f (x 0, y 0 ) y = i f y (x 0, y 0 ). f 0 (z 0 )= f x (z 0 )= if y (z 0 ) f x f y z 0 f 0 (z 0 )= f x (z 0 ) f x (z 0 )= x + i y z f x (z 0 )= x z f x (z 0 )+ y z if x (z x 0 )= z f x (z 0 )+ y z f y (z 0 ). f 0 (z 0 ) f (z 0 + z) f (z 0 ) z = f (z 0 + z) f (z 0 + x)+ f (z 0 + x) f (z 0 ) z = f (z 0 + x + i y) f (z 0 + x) + f (z 0 + x) f (z 0 ). z z
44 lim z!0 f (z 0 + z) f (z 0 ) f z x (z 0 ) y f (z0 + x + i y) = lim z!0 z y f (z 0 + x) f y (z 0 ) x f (z0 + x) f (z + lim 0 ) z!0 z x f x (z 0 ). 0 x y z z 0 0 f x (z 0 )= lim x!0 f (z 0 + x) f (z 0 ) x z! 0 x! 0 x y z! 0 u(z) v(z) f (z) 0 < a, b < u(x 0 + x, y 0 + y) u(x 0 + x, y 0 ) y v(x 0 + x, y 0 + y) v(x 0 + x, y 0 ) y = u y (x 0 + x, y 0 + a y) = v y (x 0 + x, y 0 + b y).
45 f (z 0 + x + i y) f (z 0 + x) f y y (z 0 ) u(x0 + x, y = 0 + y) u(x 0 + x, y 0 ) y v(x0 + x, y + i 0 + y) v(x 0 + x, y 0 ) y u y (z 0 ) v y (z 0 ) = u y (x 0 + x, y 0 + a y) u y (x 0, y 0 ) +i v y (x 0 + x, y 0 + b y) v y (x 0, y 0 ). u y v y (x 0, y 0 ) lim u z!0 y (x 0 + x, y 0 + a y) =u y (x 0, y 0 ) lim v z!0 y (x 0 + x, y 0 + b y) =v y (x 0, y 0 ), z! 0 0 I f : I! R f 0 (x) 0 x 2 I c 2 R f (x)=c x 2 I x, y 2 I f (y) f (x) = f 0 x + a(y x) (y x)
46 0 < a < f 0 (x + a(y x)) = 0 f (y)= f (x) x, y 2 I f I 0 f f f I f : {x + iy2 C : x 6= 0}!C 8 < Re z > 0, f (z) := : 2 Re z < 0, f 0 (z)=0 z f f C G C f : G! C f 0 (z) 0 z 2 G f f G H G y 0 2 R z 2 H Im(z)=y 0 u(z) f (z) z 2 H Im(z)=y 0 H u(z)=u(x, y 0 ) x z = x +iy 0 f 0 (z)=0 z 2 H u x (z)=re( f 0 (z)) = 0 u(z) H v(z) f (z) H v x (z)=im( f 0 (z)) = 0 H f (z) H f (z) H
47 f G x y G f (x)= f (y) f G z o 2 C lim z!z0 (az+b)=az 0 +b iz lim 3 z!i z+i lim (x + i(2x + y)) z! i f : G! C z 0 G f (z)=0 lim z!z0 f (z) = 0 lim z!z0 f (z)= x 2 y x 4 + y 2 z = x + iy6= 0. f 0 lim z!0 f (z) y = x 2
48 f : C! C f (z)=z 2 C g : C! C C \{0} 8 < z z z 6= 0, g (z)= : z = 0 f : C! C 8 < 0 z = 0 z f (z)= : q z = p q 2 Q \{0} 8 < 0 z = 0, f (z)= : sinφ z = re iφ 6= 0. z 0 G z 0 G f : C \{0}!C f (z) = z f 0 (z)= z 2 T (z) := az+b cz+d a, b, c, d 2 C ad bc 6= 0 T 0 (z)=0 f (z) z f f (z) x = Re z y = Im z
49 u v f (z) = u(x, y)+iv(x, y) u v f f (z)=e x e iy f (z)=2x + ixy 2 f (z)=x 2 + iy 2 f (z)=e x e iy f (z)=cos x cosh y f (z)=im z i sin x sinh y f (z)= z 2 = x 2 + y 2 f (z)=z Im z f (z)= ix+ y f (z)=4(re z)(im z) i(z) 2 f (z)=2xy i(x + y) 2 f (z)=z 2 z 2 f (z) =0 Re(z) Im(z) =0 f (z) = Re(z) Im(z) 6= 0 f z = 0 f z = 0 f G C f G f 0 = 0 f (z) f (z) G C f (z) G f f (z)=v(x)+iu(y) f x = Re(z) f y = Im(z) f (z)=az + b a 2 R b 2 C f u v u(z) v(z)= 3 z f
50 u = v u r r φ r = v φ r. u v u + iv u(x, y)=x 2 y 2 u(x, y)=cosh(y) sin(x) u(x, y)=2x 2 + x + 2y 2 u(x, y)= x x 2 +y 2 u(x, y)= x x 2 +y C u(x, y)= x 2 2 x 2 +y 2 u(x, y)=ax 2 + bxy+ cy 2, a b c u a = c u f (z)=az 2 A 2 C A a b c f 0 G C f : G! C f 00 (z) 0 z 2 G f (z)=az+ b a, b 2 C f 0 (z)=a f (z) az
51 f (z) = az + b cz+ d a, b, c, d 2 C ad bc 6= 0 f z f (z)= az+b cz+d C \{ d c } c = 0 f c 6= 0 az+b cz+d = a c ad bc = 0 f (z)= az+b cz+d a c
52 a, b, c, d 2 C c 6= 0 f : C \{ d c }!C\{a c } f (z)= az+b cz+d f : C \{ a c }!C\{ d c } f (z) = dz b cz+ a. f (z) c = 0 f C f (z)= z iz+i C \{ } z iz+ i = w () z = iw+ iw+, f (z)= iz+ iz+ C \{ i} f f (z )= f (z 2 ) az + b cz + d = az 2 + b cz 2 + d, (az + b)(cz 2 + d )=(az 2 + b)(cz + d ) (ad bc)(z z 2 )=0. ad bc 6= 0 z = z 2 f g (z)= dz b cz+a f g f : C \{ d c }!C\{a c } f (z)= az+b cz+d f 0 (z) = a(cz+ d ) c(az + b) (cz+ d ) 2 = ad bc (cz+ d ) 2
53 f (z) =z + b f (z) =az f (z) = z f (z) = az+b cz+d c = 0 c 6= 0 f (z) = a d z + b d, f (z) = bc ad c 2 z + d c + a c. f (z)= z iz+i φ 2 R f (e iφ )= e iφ ie iφ + i = (e iφ )(e iφ + ) i e iφ + 2 = e iφ e iφ i e iφ + 2 = 2Im(e iφ ) e iφ + 2 = 2 sinφ e iφ + 2, f f (z)= z x 0 +iy 0 r (x x 0 ) 2 +(y y 0 ) 2 = r 2 α(x 2 + y 2 )+βx + γ y + δ = 0
54 α β γ δ β 2 + γ 2 > 4 αδ α = 0 z = x + iy u + iv := z u + iv = x iy x 2 + y, 2 x 0 = α + β x 2 + y + y 2 γ x 2 + y + δ 2 x 2 + y 2 = α + βu γv + δ(u 2 + v 2 ). u + iv f f : G! C lim z!z0 f (z)= M > 0 δ > 0 z 2 G 0 < z z 0 < δ f (z) > M lim z! f (z)=l ε > 0 N > 0 z 2 G z > N f (z) L < ε lim z! f (z)= M > 0 N > 0 z 2 G z > N f (z) > M z 0 G G B > 0 z 2 G z > B
55 lim z!0 z 2 = M > 0 δ := p M 0 < z < δ f (z) = az+b cz+d lim z! f (z)= a c f (z) = z 2 > δ 2 = M. c 6= 0 L := ad bc ε > 0 N := L c + d 2 ε c z > N cz+ d c z d c z d > L c ε f (z) a c = c(az + b) a(cz+ d ) c(cz+ d ) = L c cz+ d < ε. C ± R C lim z!z0 f (z)= lim z!z0 g (z)=a lim z!z0 ( f (z)+ g (z)) = Ĉ := C [ {} a 2 C + a = a + = a 6= 0 a = a = a = 0 = a 6= 0 a 0 =. CP +
56 z +( z)=0 z! 0 z z f (z) = z z = 0 z = f (0) = f () =0 f (z) Ĉ f (z) =z + b z = f () = + b = f (z) =az a 6= 0 z = f () =a = Ĉ Ĉ ad bc 6= 0 c 6= 0 f : Ĉ! Ĉ 8 az+b d >< cz+d z 2 C \ c, f (z) := z = d c >:, a c z =. f c = 0 f ()= f (z)= z iz+i f ( )= f ()= f Ĉ! Ĉ i f (z)= z iz+i f C \{ } z = f Ĉ Ĉ z = f C Ĉ
57 Ĉ C z f : Ĉ! Ĉ f (z)= iz+i 7! 0, i 7!, 7!. i Ĉ f R Ĉ z z z 2 z 3 Ĉ z z 2 z 3 [z, z, z 2, z 3 ] := (z z )(z 2 z 3 ) (z z 3 )(z 2 z ). [z 3, z, z 2, z 3 ]= z z z 2 z 3 [z,, z 2, z 3 ]= z 2 z 3 z z 3 f (z) = z iz+i f (z) = [z,, i, ] f : Ĉ! Ĉ f (z) =[z, z, z 2, z 3 ] f (z )=0, f (z 2 )=, f (z 3 )=. g g (z )=0 g (z 2 )= g (z 3 )= f g f h := g f
58 h(0)= g ( f (0)) = g (z )=0 h()= h()= h(z)= az+b cz+d 0 = h(0) = b d = h() = a c = h() = a + b c + d = a d = a d =) b = 0 =) c = 0 =) a = d h(z) = az + b cz+ d = az d = a d z = z, h = g f f g Ĉ 0 z z 2 z 3 w w 2 w 3 z z 2 z 3 Ĉ w w 2 w 3 Ĉ h h(z )=w h(z 2 )=w 2 h(z 3 )=w 3 h = g f f (z) =[z, z, z 2, z 3 ] g (w) =[w, w, w 2, w 3 ] h z j w j h f (z j )=w j a b c d C R 3
59 C (x, y) R 3 C = {(x, y, 0) 2 R 3 } x +iy S 2 := (x, y, z) 2 R 3 : x 2 + y 2 + z 2 =. {(x, y, 0) : x 2 + y 2 = } N :=(0, 0, ) S 2 S :=(0, 0, ) S 2 Ĉ N φ: S2! Ĉ P 2 S 2 \{N } z P N P C Q φ(p ) := Q φ(n ) := φ 8 < x z φ(x, y, z)=, y z, 0 z 6=, : z =.
60 φ ( p, q, 0) = φ ()=(0, 0, ) 2 p p 2 + q 2 +, 2q p 2 + q 2 +, p2 + q 2 p 2 + q 2 + P =(x, y, z) 2 S 2 \{N } N P r (t )=N + t (P N )=(0, 0, )+t [(x, y, z) (0, 0, )] = (tx, ty, + t (z )) t 2 R r (t ) C 0 t = z t r φ φ Q =(p, q, 0) 2 C P =(x, y, z) 2 S 2 φ(p )=Q P x 2 + y 2 + z 2 x = φ(p )=Q z = p y z = q p 2 + q 2 = x 2 + y 2 ( z) 2 = z 2 ( z) 2 = + z z. p 2 + q 2 = +z z z x = p( z) y = q( z) φ φ φ φ φ S 2 Ĉ γ S2 2φ(γ) φ(γ) C N 2 γ S 2 S 2 H (x 0, y 0, z 0 ) H k H H = (x, y, z) 2 R 3 : (x, y, z) (x 0, y 0, z 0 )=k = (x, y, z) 2 R 3 : xx 0 + yy 0 + zz 0 = k.
61 k (x 0, y 0, z 0 ) 2 S 2 0 apple k apple k < 0 (x 0, y 0, z 0 ) ( x 0, y 0, z 0 ) k > H \ S 2 =? H \S 2 ( p, q, 0) φ φ ( p, q, 0) H φ ( p, q, 0) (z 0 k) p 2 +(2x 0 ) p +(z 0 k)q 2 +(2y 0 )q = z 0 + k. z 0 k = 0 ( p, q) ( p, q) z 0 = k N 2 H φ z 0 k 6= 0 p + x q + y 2 0 = k 2 z 0 k z 0 k (z 0 k). 2 ( p, q) k < k = k > S 2 ( p, q) R 3 f (z)=e i θ z φ S 2 f (z) =rz f (z) =z + b f (z)= z S 2 (x, y, z) 2 S 2
62 φ f S 2 φ φ(x, y, z)=( x z, y z, 0) p + iq = x z + i y z. p 2 + q 2 = +z z x 2 + y 2 = ( + z)( z) f Å ã x z + i y z = z x + iy = ( z)(x iy) x 2 + y 2 = x + z i y + z. φ φ(x, y, z)= ( x z, y z, 0) (x, y, z) f (z) = z S2 (x, y, z) (x, y, z) x f (z)= z C S 2 φ f (z) = z φ f (z)= z (0, 0, ) φ C S 2 x N φ C S 2 R 3 S 2 C z N Ĉ S 2 S 2 N
63 e it = cos t + i sin t exp : C! C z = x + iy exp(z) := e x (cos y + i sin y) = e x e iy. z, z, z 2 2 C exp (z ) exp (z 2 ) = exp (z + z 2 ) exp(z) = exp ( z) exp (z) = exp (Re z) exp(z) 6= 0 exp (z + 2πi) = exp (z) d dz exp (z) = exp (z). 2πi exp exp f (z)=exp(z) f x = e x (cos y + i sin y) f y = e x ( sin y + i cos y). e x = P k 0 k! x k
64 C f x (z) = i f y (z) z 2 C f (z)=exp(z) f 0 (z) = f (z) =exp(z). x z = x 2 R exp(x) =e x (cos 0 + i sin 0) = e x. sin z := 2i (exp(iz) exp( iz)) cos z := 2 (exp(iz)+exp( iz)), tan z := sin z cos z = i exp(2iz) exp(2iz)+ cot z := cos z sin z = i exp(2iz)+ exp(2iz), exp(z)exp( z)=exp(0)= exp sin cos
65 z = x 2 R sin z = 2i (exp(ix) exp( ix)) = 2i (cos x + i sin x cos( x) i sin( x)) = sin x. z, z, z 2 2 C sin( z)= sin z cos( z)=cos z sin(z + 2π)=sin z tan(z + π)=tan z cos(z + 2π)=cos z cot(z + π)=cot z sin(z + π 2 )=cos z cos(z + π 2 )= sin z sin (z + z 2 ) = sin z cos z 2 + cos z sin z 2 cos (z + z 2 ) = cos z cos z 2 sin z sin z 2 cos 2 z + sin 2 z = cos 2 z sin 2 z = cos(2z) d d sin z = cos z dz cos z = sin z. dz sin(iy) y!± sinh z = 2 (exp(z) exp( z)) cosh z = 2 (exp(z)+exp( z)) tanh z = sinh z cosh z = exp(2z) coth z = cosh z exp(2z)+ sinh z = exp(2z)+ exp(2z). d dz sinh z = cosh z d cosh z = sinh z. dz
66 sinh(iz)=i sin z cosh(iz)=cos z. exp((z)) = z = (exp z). exp f (z)=(z)+ 2πi exp exp G : G! C exp( z)=z G z = re iφ z = u(z)+iv(z) exp( z) =e u e iv = re iφ = z, e u = r e iv = e iφ v = φ + 2πk k 2 x ln(x) u = ln z z = ln z + i z z z Arg z z 6= 0 ( π, π] z Log :
67 C \{0}!C Log(z) := ln z + i Arg(z). Log Log(2) =ln(2)+i Arg(2) =ln(2) Log(i) =ln()+i Arg(i) = πi 2 Log( 3) =ln(3)+i Arg( 3) =ln(3)+πi Log( i) =ln( p 2)+i Arg( i) = 2 ln(2) πi 4. Log C\R apple0 G G \{0} z 0 Log(z 0 ) 2πi (exp z)=z z = x + iy Log(exp z) =ln e x e iy + i Arg(e x e iy )=ln e x + i Arg(e iy )=x + i Arg(e iy ). z = x + iy y 2 ( π, π] z (exp z) 6= z ln(xy)=ln(x)+ln(y) C Log(i)+Log(i ) =i π 2 + ln p 2 + 3πi 4 = 5πi 2 ln Log(i(i )) = Log( i) = 2 ln 2 3πi 4.
68 arg z := z log z := ln z + i arg z. arg log exp(log z)=z log G G d dz (z) = z. exp H := {(z) : z 2 G} f : H! G f (z)=exp(z) g : G! H g (z)=(z) g f g 0 (z) = exp 0 ( z) = exp( z) = z. a, b 2 C a 6= 0 a b a b := exp(b Log(a)). a b log a b
69 f (z)=e z e e = lim n! + n n f (x)=e x a z e Arg e = 0 e z = exp(z Log(e)) = exp (z (ln e + i Arg(e))) = exp (z ln(e)) = exp (z). a b a b e z 6= exp(z) f (z)= az+b cz+d f (z)= dz b cz+a c = 0 f : C! C f (z) = az+b d f (z) β 2 + γ 2 > 4 αδ x + iy u + iv f (z) = z iz+i f z f (z)=z e 2πi =
70 f (z)= +z z z = f G f (G) f a 2 C a < f a (z) := z a az. f a (z) f a (z)= f a (z) f a (z) D[0, ] ñ a A = c ô b d 2 2 ad bc Ĉ T az+b A (z) = cz+d T A T B = T A B Ĉ a 2 C lim z!z0 f (z)= lim z!z0 g (z)=a lim z!z0 ( f (z)+ g (z)) =. lim z!z0 f (z)= lim z!z0 g (z)=a 6= 0 lim z!z0 ( f (z) g (z)) =. lim z!z0 f (z)=lim z!z0 g (z)= lim z!z0 ( f (z) g (z)) =. lim z!z0 f (z)= lim z!z0 g (z)=a lim z!z0 g (z) f (z) = 0. lim z!z0 f (z)=0 lim z!z0 g (z)=a 6= 0 lim z!z0 g (z) f (z) =.
71 c 0, c,...,c d 2 C lim + c d + c d 2 z! z z + + c 0 =. 2 z d f (z)= 2z z+2 z w 0 ±2 i x y x = y 2 0 az+b cz+d! 0, 2!, 3!! 0, + i!, 2! 0! i,!,! i. z k C [ + i,] γ γ γ 0 2
72 z < w = iz i z+ x > 0, y > 0 w = z 0 < x < w = z z i z+i {x +iy2 C : x + y > 0} u = u(x, y) v = v(x, y) u x v x u y v y f = u + iv f 0 (z) 2 5. Ĉ f (z)= z 2 2z+ f f 0!!!0 f!! i i! f x y = x y y = x {x + iy 2 C : x + y = 0} {z 2 C : z < } {x + iy2 C : x + y > 0} {x + iy2 C : x + y < 0},
73 a 2 R \{0} y = a i 2a 2a z z 2 z 3 Ĉ z z z 2 z 3 [z, z, z 2, z 3 ] φ φ φ φ φ (0, 0, ), (0, 0, ), (, 0, 0), (0,, 0), (,, 0) H x + y z = 0 H H \ S 2 φ Ĉ S 2 φ S 2 NS N S N sin(z)=sin(z) cos(z)=cos(z) z = x + iy sin z = sin x cosh y + i cos x sinh y cos z = cos x cosh y i sin x sinh y sin z π
74 exp(z) z = iy, 0 apple y apple 2π z = + iy, 0 apple y apple 2π {z = x + iy2 C :0apple x apple, 0 apple y apple 2π}. z = x + iy sin z 2 = sin 2 x + sinh 2 y = cosh 2 y cos z 2 = cos 2 x + sinh 2 y = cosh 2 y cos 2 x sin 2 x cos x = 0 cot z 2 = cosh2 y cosh 2 y apple. y cot z 2 apple sinh2 y + sinh 2 y = + sinh 2 y apple + sinh 2 apple 2. tan(iz)=i tanh(z) π {z 2 C : 2 < Re z < π 2 } x = A sin t y = B cos t x = A cosh t y = B sinh t
75 Log(2i) ( ) i Log( + i). x + iy e i π e π i i e sin(i) exp(log(3 + 4i)) ( + i) 2 p 3 ( i) Ä i+ p 2 ä 4. arg(z) = arg(z) Arg(z)= Arg(z) log(z 2 ) 2 log z z z 2 sin z z 3 + (z 2i + ) (z)=ln z + i (z) 0 apple (z) < 2π exp(z) (z 3) i i z 3. Log(z)= πi 2 Log(z)= 3πi 2
76 exp(z)=πi sin(z)=cosh(4) cos(z)=0 sinh(z)=0 exp(iz)=exp(i z) z 2 = + i. < z < e Log C \ R apple0. G H := {(z) : z 2 G} : G! H f (z) : H! G f (z)=exp(z) f H a z = a Re z a c 2 C \{0} f (z)=z c exp(b log a) b z n b exp y = x x = t, y = t t! t! f (z)=z 2 f f
77 T i 2i 0 T f (T ) f (z)=z 2 Q i 2i f (Q ) i 2 + 2i 2i z(t )=2 + it u + iv = f (z(t )) (u, v)
78 / 0 2 5π 6 π 3 0 π 3 5π 6 exp
79 R b a f (x) dx a b a b a, b 2 R g : [a, b]! C b a g (t ) dt := b a Re g (t ) dt + i b a Im g (t ) dt. R 2 γ γ γ(t ), a apple t apple b f γ f γ b f = f (z) dz := f (γ(t ))γ 0 (t ) dt. γ γ a
80 γ γ(t ), a apple t apple b [a, c ] [c, c 2 ] [c n, c n ] [c n, b] f γ γ f := c a f (γ(t ))γ 0 (t ) dt + c2 b f (γ(t ))γ 0 (t ) dt + + f (γ(t ))γ 0 (t ) dt. c c n f : C! C f (z)=z 2 + i γ 0 + i γ(t )=t + it, 0 apple t apple γ 0 (t )= + i f (γ(t )) = (t it) 2 γ f = 0 (t it) 2 ( + i) dt =( + i) 0 = (t 2 2it 2 t 2 ) dt 2i( + i) 3 = 2 ( i). 3 γ y = x i γ(t )=t + it 2, 0 apple t apple γ 0 (t )= + 2it f (γ(t )) = (t it) 2 = t 2 t 4 2it 3, γ f = 0 (t 2 t 4 2it 3 ) ( + 2it) dt = 0 = (t 2 + 3t 4 2it 5 ) dt 2i 6 = 4 5 i 3. γ γ 0 γ 2 +i γ (t )=t, 0 apple t apple γ 2 (t )=+it, 0 apple t apple c i
81 γ f = γ γ 2 f + f = 0 t 2 dt + = 3 + i ( 2it t 2 ) dt = 3 + i Å 2i 2 0 ã 3 0 = i. ( it) 2 idt γ γ(t ), a apple t apple b σ(t ), c apple t apple d σ γ [c, d ] [a, b] γ σ σ = γ τ γ(t ), a apple t apple b σ(t ), c apple t apple d γ d c f (σ(t ))σ 0 (t ) dt = b a f (γ(t )) γ 0 (t ) dt. γ(t )=e it, 0 apple t apple 2π, σ(t )=e 2πi sin(t ), 0 apple t apple π 2, R γ f γ f = i 2π 0 f e it e it dt γ f = 2πi π 2 0 f Ä e 2πi sin(t )ä e 2πi sin(t ) cos(t ) dt.
82 γ length(γ) := b a γ 0 (t ) dt γ(t ) a apple t apple b γ 0 + i γ(t )=t + it 0 apple t apple γ 0 (t )= + i length(γ) = 0 + i dt = 0 p 2 dt = p 2. γ γ(t )=e it 0 apple t apple 2π γ 0 (t )=ie it length(γ) = 2π 0 i e it dt = 2π 0 dt = 2π. γ f g γ c 2 C ( f + cg)= f + c g. γ γ γ γ γ(t ), a apple t apple b γ γ(t ) := γ(a + b t ), a apple t apple b γ f = γ f.
83 γ γ 2 γ γ 2 γ γ 2 γ 2 γ γ γ 2 γ γ 2 f = f + f. γ f apple max f (z) length(γ). z2γ γ γ s = a + b t f = γ = = b a b a a b f (γ(a + b t ))(γ(a + b t )) 0 dt f (γ(a + b t )) γ 0 (a + b t ) dt f (γ(s)) γ 0 (s) ds = b a f (γ(s)) γ 0 (s) ds = γ f. γ(t ) γ γ 2 γ [a, b ] γ 2 [a 2, b 2 ] 8 < γ γ(t ) := (t ) a apple t apple b, : γ 2 (t b + a 2 ) b apple t apple b + b 2 a 2,
84 [a, b + b 2 a 2 ] γ γ 2 s = t b + a 2 γ γ 2 f = b +b 2 a 2 a b f (γ(t ))γ 0 (t ) dt = f (γ(t ))γ 0 (t ) dt + a = f + f. γ γ 2 b +b 2 a 2 b f (γ(t ))γ 0 (t ) dt γ [a, b ] γ γ [b, b + a 2 ] γ 2 b 2 φ = Ä Arg R γ f ä R γ f = R γ f e iφ R γ f 2 R γ f = e iφ b = apple a b a γ f b = Re e iφ a Re f (γ(t ))e iφ γ 0 (t ) dt f (γ(t ))e iφ γ 0 (t ) dt = apple max aapplet appleb f (γ(t )) b a γ 0 (t ) dt f (γ(t ))γ 0 (t ) dt b a f (γ(t )) γ 0 (t ) dt = max f (z) length(γ). z2γ γ dz z w = 2πi, γ w 2 C 2πi γ r 2π = γ dz z w apple max z2γ z w length(γ) = r 2πr.
85 C F G C F 0 (z) = f (z) z 2 G F f G f G F (z) =z 2 f (z)=2z F f G C F (z)=z 2 + c c 2 C Å d dz 2i (exp(iz) exp( iz)) ã = (exp(iz)+exp( iz)), 2 F (z)=sin z f (z)=cos z C F (z) =Log(z) f (z) = z C \ R apple0 f C \{0} f G C γ G γ(t ) a apple t apple b f G F f G γ f = F (γ(b)) F (γ(a)). d dt F (γ(t )) = f (γ(t )) γ0 (t ) γ f = b a f (γ(t )) γ 0 (t ) dt = F (γ(b)) F (γ(a)).
86 F (z)= 2 z 2 f (z)=z C γ f = 2 ( + i) = i γ γ(a)=γ(b) G C γ G f G G γ f = 0. f : C \{0}!C f (z)= z R γ f = 2πi γ C \{0} f C \{0} G C z 0 2 G f : G! C R f = 0 γ G γ F : G! C F (z) := γ z f, γ z G z 0 z f G F F z 0 z F 0 (z)= f (z) z 2 G G C z 0 2 G f : G! C R γ f = 0 γ G R σ f σ G z 0 z 2 G σ σ 2
87 σ σ 2 f f = f = 0. σ 2 σ σ 2 F (z) := f σ γ z F (z + h) F (z) = γ z+h f γ z f = γ f γ G z z + h z C R = h γ F (z + h) h F (z) f (z) = h γ f (w) dw f (z) h = h γ dw γ ( f (w) f (z)) dw. h λ z z + h G F (z + h) F (z) f (z) = f (w) f (z)) dw = h h γ( ( f (w) f (z)) dw. h λ h! 0 ε > 0 δ > 0 w z < δ =) f (w) f (z) < ε f z δ h < δ ( f (w) f (z)) dw apple h λ h max f (w) f (z) length(λ) w2λ = max f (w) f (z) < ε. w2λ
88 G C z 0 2 G f : G! C R f = 0 γ G γ F : G! C F (z) := γ z f, γ z G z 0 z f G R γ 0 γ G C γ 0 (t ), 0 apple t apple γ (t ), 0 apple t apple γ 0 G γ h : [0, ] 2! G s, t 2 [0, ] h(t, 0)=γ 0 (t ), h(t, )=γ (t ), h(0, s)=h(, s). γ G γ 2 γ G γ 2 h(t, s) s h(t, s) t s 0
89 γ 0 γ (C \{0}) ±3 ± 3i h(t, s) := ( 8 + 8it 0 apple t apple 8, 2 8t + i >< 8 apple t apple 3 8, s)e 2πit + 3s + 4i( 2t ) 3 8 apple t apple 5 8, 8t 6 i 5 8 >: apple t apple 7 8, + 8i(t ) 7 8 apple t apple h(t, s) 6= 0 0 apple t, s apple (C \ {0}) (C \{0}) G G G
90 G C f G γ 0 γ G γ 0 G γ γ 0 f = γ f. f γ dz z = 2πi γ f (z)= z G = C\{0} γ G f 2πi f 0 G h γ 0 γ
91 h 8 h (t, s) 0 apple t apple t, >< h 2 (t, s) t apple t apple t 2, h(t, s)= >: h n (t, s) t n apple t apple, h j (t, s) 0 apple s apple γ s h(t, s), 0 apple t apple I : [0, ]! C I (s) := γ s f, I (0)= R γ 0 f I ()= R γ f I I (0)=I () d ds I (s) = = = = d ds f (h(t, s)) h t dt = f 0 (h(t, s)) h s f 0 (h(t, s)) h t t f (h(t, s)) h s 0 s h t + f (h(t, s)) 2 h s t h s + f (h(t, s)) 2 h t s dt. f (h(t, s)) h t dt dt dt h f 0 h h t = t i
92 d ds I (s) = 0 t f (h(t, s)) h dt s = f (h(, s)) h (, s) s h f (h(0, s)) (0, s) =0, s h(0, s)=h(, s) s G C γ G γ G γ G 0 (C \ R) G C f G γ γ G 0 f = 0. γ
93 Log G = C\R apple0 γ G γ Log(z) dz = 0. C f γ γ f = 0. γ z 2 dz 2z γ γ dz z 2 2z = 2 γ dz z 2 dz 2 γ z. f (z)= z 2 f C\{2} γ (C\{2}) 2πi γ dz z 2 2z = πi.
94 C [a, r ]={z 2 C : z a = r } D[a, r ]={z 2 C : z a < r } D[a, r ]={z 2 C : z a apple r } a 2 C r > 0 C [a, r ] f D[w, R] f (w) = f (z) 2πi C [w,r] z w dz. f (z) z C [w, R] f (w) f = u + iv D[w, R] f (w) = 2π f w + Re it dt, 2π 0 u(w) = 2π u w + Re it dt v(w) = 2π v w + Re it dt. 2π 0 2π 0 f G D[w, R] f (z) z w H := G \{w} 0 < r < R C [w, r ] H C [w, R],
95 C [w,r] f (z) dz 2πi f(w) = z w = apple C [w,r ] C [w,r ] max z2c [w,r ] = max z2c [w,r ] f (z) dz dz f (w) z w C [w,r ] z w f (z) z f (w) dz w f (z) z f (z) f (w) r f (w) length (C [w, r ]) w 2πr = 2π max f (z) f (w). z2c [w,r ] ε > 0 f w δ > 0 z w < δ f (z) f (w) < ε 2π. z 2 C [w, δ 2 ] r = δ 2 C [w,r] f (z) dz 2πi f(w) < ε. z w ε f (w) = 2π 2πi 0 f (w + Re it ) w + Re it w ireit dt = 2π 2π 0 f w + Re it dt, u(w)+iv(w) = 2π 2π 0 u w + Re it dt + i 2π 2π 0 v w + Re it dt. C [i,] dz z 2 +.
96 f (z)= z+i C \{ i} D[i,] C [i,] dz z 2 + = C [i,] z+i z i dz = 2πi f(i) =2πi 2i = π. C [w, R] γ w f G γ R D[w, R] G f (z) z w H := G \{w} γ H C [w, R] f (w) = 2πi γ f (z) z w dz. γ γ γ γ f (w) f (w) γ γ γ D[w, R] γ γ C [w, R] γ D[w, R]
97 γ G γ G γ C [w, R] f G γ w γ γ G 0 f (w) = 2πi γ f (z) z w dz. γ G G γ γ G 0 G γ D[w, R] γ G γ C [w, R] C [w, R] G 0 γ G 0 G γ w γ G g (z) = z w z 6= w g G γ G 0 R g (z) dz = 0 γ R > 0 D[w, R] γ C\{ w } γ C [w, R] R g (z) dz = 2πi γ γ dz z 2 + = π
98 γ i (C \{ i}) C [0,3] exp(z) z 2 2z dz C [0,3] exp(z) z 2 2z dz = exp(z) 2 C [0,3] z 2 dz exp(z) dz. 2 C [0,3] z f (z)=exp(z) γ C [0,3] exp(z) z 2 2z dz = 2 2πi exp(2) 2 2πi exp(0) = πi e 2. γ(t )=3t + i apple t apple γ(t )=i sin(t ) π apple t apple π γ(t )=i + e i πt 0 apple t apple γ(t )=t ie it 0 apple t apple 2π C [ + i,] i 2i C [0, 34] ± ± 2i
99 f (z)=z dz z R γ γ w 2 C r > 0 C [w,r ] dz z w = 2πi. C [0, 2] f (z)=z + z f (z)=z 2 2z + 3 f (z)= z 4 f (z)=xy R xdz R ydz R zdz R zdz γ γ γ γ z z x ± iy γ 0 γ = C [0, ] γ = C [a, r ] a 2 C i R exp(3z) dz γ γ i γ = C [0, 3] γ y = x 2 x = 0 x = R f f γ γ f (z)=z 2 γ(t )=t + it 2 0 apple t apple f (z)=z γ i f (z)=exp(z) γ 0 z 0 f (z)= z 2 γ i
100 f (z)=z + z γ γ(t ) 0 apple t apple Im γ(t ) > 0 γ(0)= 4 + i γ()=6 + 2i f (z)=sin(z) γ i π γ γ σ τ R f σ = γ τ σ f g G γ G γ(a) γ(b) γ fg 0 = f (γ(b))g (γ(b)) f (γ(a))g (γ(a)) γ f 0 g. I (k) := R 2π e ikt dt 2π 0 I (0)= I (k)=0 k I ( 2 ) R C [0,2] z 2 dz. R z n dz = 0 γ γ n 6= n γ n = m γ R z dz = 2mπi γ
101 z 0 2 C γ z 0 γ n γ (z z 0 ) n dz = 8 < 2πi n =, : 0 R γ z exp(z 2 ) dz = 0 γ F (z)= i i 2 Log(z + i) Re(z) > 0 F (z) arctan z 2 Log(z i) +z 2 γ 4i z + dz z 2 dz γ z γ dz sin 2 (z) dz z 2 + z γ γ z i dz γ (t )=e it π, 2 apple t apple π 2 γ z i dz γ 2 (t )=e it, π 2 apple t apple 3π 2 γ 2 ±3 ± 3i a 2 C γ 0 γ a γ 0 C\{a} γ G
102 γ G γ(t ), t 2 [0, ] τ [0, ] [0, ] γ G γ τ τ s (t )= s τ(t )+( s)t 0 apple s apple C C G C f G f 0 γ γ G 0 γ f (z) dz = γ (u + iv)(dx + idy)= γ udx vdy + i γ vdx+ udy a 2 C I (r ) := C [0,r ] dz z a. r < a r > a γ r C \ {a} p(z) z γ C R γ p = 0. C [0,2] dz z 3 + = 0 C [0, 2] C [0, r ] r > R dz C [0,r ] z 3 + r!
103 2π 0 dφ 2 + sinφ z = e iφ 0 < r < 2π 2π 0 r 2 2r cos(φ)+r 2 dφ =. P r (φ) := r 2 2r cos(φ)+r 2 f g G γ G f (z)= g (z) z 2 γ f (z)= g (z) z γ r 6=, 3 I (r ) := C [ 2i,r ] dz z 2 + C [0,r ] dz z 2 2z 8 r = r = 3 r = 5 r = 3
104 z 2 C [,2] 4 z dz 2 sin z dz z C [0,] C [0,2] C [0,4] exp(z) z(z 3) dz exp(z) z(z 3) dz f (z) = z 2 γ = C [, ] σ = C [, ] R f = R f γ σ γ 6 G σ G = C \{±} f G z w G G f G f 0 γ w γ γ G 0 g : [0, ]! C g (t ) := γ f (w + t (z z w w)) dz. g 0 = 0 f t (z + t (w z)) g (0) g () G
105 f 0 f 00 f G γ G w γ f 00 (w) f 0 (w) = 2πi γ f (z) (z w) 2 dz. f 00 (w) = πi γ f (z) (z w) 3 dz.
106 f (w + w) w f (w) = w 2πi = 2πi γ γ f (z) z (w + w) dz 2πi γ f (z) (z w w)(z w) dz. f (z) z w dz w! 0 f (w + w) w f (w) = 2πi f (z) 2πi γ (z w) dz 2 f (z) γ (z w w)(z w) = w 2πi γ f (z) dz (z w) 2 f (z) dz. (z w w)(z w) 2 w! 0 w! 0 γ length(γ) M := max z2γ f (z) δ > 0 D[w, δ] \ γ =? z w δ z γ z 2 γ f (z) (z w w)(z w) 2 apple f (z) ( z w w ) z w 2 apple M (δ w )δ 2, w! 0 f 0 f 00 f f
107 C [0,] sin(z) z 2 dz = 2πi d dz sin(z) z=0 = 2πi cos(0) =2πi. i γ 2 / s ^ ] s γ j C [0,2] dz z 2 (z ), γ γ 2
108 C [0,2] dz z 2 (z ) = C [0,] cos(z) z 3 γ = 2πi = 0. dz z 2 (z ) + γ 2 d dz dz = πi z z=0 + 2πi d 2 dz 2 cos(z) z=0 dz z 2 (z ) = γ 2 = 2πi z z dz + 2 ( ) 2 = πi ( cos(0)) = πi. γ 2 + 2πi z 2 z dz f G f 00 f 0 G f 0 f 00 f 000 f (n) n f f (n) f G f G f x y f G γ f = 0 γ G f G
109 F f G F G f G γ G γ G G C γ G 0 γ G D[a, r ] C \ R apple0 C\R apple0 C \{0} (C \ {0}) f f G C G f : C! C f (z)=exp(z 2 ) F C F f (z)= z C \{0} C \{0} f (z) = z C \ R apple0 Log(z)
110 f G R γ f γ G γ(a) γ(b) z 2 {z 2 C : z < 2} z 2 z p(z) d z d p(z) d a d R 2 a d z d apple p(z) apple 2 a d z d z z R p(z) d a d a d z d p(z) = a d z d + a d z d + a d 2 z d a z + a 0 = a d z d + a d a d z + a d 2 a d z a a d z d + a 0 a d z d. z! 2 2 z C
111 p p(z) 6= 0 z 2 C p(z) p(0) = 2πi C [0,R] R > 0 d p(z) a d R p(z) z dz, p(0) = 2π C [0,R] dz zp(z) apple 2π max z2c [0,R] zp(z) 2πR apple 2 a d R. d R R p(0) = 0 p z a a p a p(z) z a C R p(x)=2x 4 + 5x R p C p(x) = x 2 + 2x = (x + i)(x i) Ä p 2 x + p 3 i ääp 2 x p 3 i ä
112 f (z) applem z 2 C w 2 C C [w, R] R > 0 f f 0 (w) = 2πi C [w,r] f (z) dz apple (z w) 2 2π max z2c [w,r] f (z) (z w) 2 2πR = max z2c [w,r] f (z) R apple M R. R f 0 = 0 f p p(z) 6= 0 z 2 C f (z)= p(z) f! 0 z! f f p dx x 2 + = π. σ R [ R, R] R R γ R R R R R >
113 γ R R s s R σ R σ R dz z 2 + = π. R > R! γ R dz z 2 + apple max z2γ R z R! π = lim R! σ R dz z 2 + = lim R! [ R,R] πr apple max z2γ R dz z lim R! γ R πr = z 2 dz z 2 + = πr R 2 dx x 2 +. É ±4 ± 4i exp(z 2 ) exp(3z) dz z 3 (z πi) dz 2 É É
114 É sin(2z) dz (z π) 2 É exp(z)cos(z) (z π) 3 dz f 00 f 0 (w) f 00 (w) f 0 (w) f (z) f 00 (w) C [0, 3] Log(z 4i) exp z z 3 z 2 z C [0,2] cos z z i z 3 2 sin z (z )2 (z + 4)(z 2 + ) exp(2z) (z ) 2 (z 2) exp z dz w w 6= (z w) 2 f : D[0, ]! C f (z) := [0,] dw wz f D[0, ]
115 f : R! R f (x) := 8 < x 2 sin( x ) x 6= 0, : 0 x = 0 R f 0 f (z)=z 2 exp(sin z) C f (z) =exp( z ) f (x)=e x f C lim z! f (z) f lim z! f (z) =L R > 0 f (z) L < z > R f (z) < L + z > R f (z) z apple R p n > 0 c, z, z 2,...,z k j,..., j k j + + j k = n p(z) =c (z z ) j (z z 2 ) j2 (z z k ) j k, f f (z) apple p z z 2 C f f M > 0 f (z) f M z 2 C
116 f f (z)=u(z)+iv(z) M > 0 u(z) applem z 2 C f exp( f (z)) f a b f (z) applea z +b z 2 C f f : D[0, ]! D[0, ] z < f 0 (z) apple z. dx x 4 +. f (z) = exp(iz) z 2 + R > R f = π σ R e σ R [ R, R] γ R R R R exp(iz) apple z f (z) apple 2 z z 2 R lim R! f = 0 lim γ R R! R[ R,R] f = π e cos(x) x 2 + dx = π e. cos(x) x 4 + dx.
117 G C f G γ G \{0} G γ(t ) a apple t apple b γ f (z) dz = σ Å ã f z z dz 2 σ(t ) := γ(t ) a apple t apple b lim z!0 f z z = L H := 2 z g : H [{0}!C g (z) := 8 < f z z 2 z 2 H, : L z = 0. g H [{0} γ f = σ g. : z 2 G \{0} R g R f σ γ R γ z n dz n 6= R γ z n dz = 0 n 6=
118 G C u : G! R G G u xx + u yy = 0. u(x, y)=xy C u xx +u yy = 0+0 = 0 u(x, y)=e x cos(y) C u xx + u yy = e x cos(y) e x cos(y) =0.
119 f = u + iv G u v G u v u v u x = v y u y = v x G u xx + u yy = (u x ) x + u y y = v y x + ( v x ) y = v yx v xy = 0. v v G G u(x, y)=xy C Im( f )=u f (z) = 2 z 2 = 2 x 2 y 2 + ixy u(x, y)=e x cos(y) C Re( f )=u f (z) =exp(z) =e x cos(y)+ie x sin(y) G G
120 u G v G f = u + iv G v u f v = Im f g := u x iu y. g g f g u Re g = u x Im g = u y u Re g Im g (Re g ) x = u xx = u yy = (Im g ) y (Re g ) y = u xy = u yx = (Im g ) x. g G h g G G h h = a + ib g = h 0 = a x + ib x = a x ia y. g u x u x = a x u(x, y)=a(x, y)+c(y) c y g h 0 u y = a y u(x, y)=a(x, y)+c(x) c x c u(x, y)=a(x, y)+c f (z) := h(z)+c G u g
121 f f = u + iv f 0 = u x + iv x = u x iu y. u G u x g = u x iu y G G u(x, y)=xy g := u x iu y = y ix = iz h(z) = i 2 z 2 = xy i 2 x 2 y 2 u u v(x, y) := 2 x 2 y 2 C u C y v(x, y) := 0 u (x, t ) dt x x 0 u (t, 0) dt y u
122 u + iv v y (x, y)= u(x, y), x u v y 2 u (x, y)= x 0 x u u = (x, y) y 2 (x, t ) dt u y (x,0)= y (x,0) y 0 u y (x,0)= 2 u u (x, t ) dt t2 u (x, y). y y (x,0) u G z 0 2 G u (n) (z 0 ) n r > 0 D[z 0, r ] G D[z 0, r ] f D[z 0, r ] u = Re f D[z 0, r ] f D[z 0, r ] u f G D[z 0, r ] f
123 u G D[w, r ] G u(w) = 2π u w + re it dt. 2π 0 R D[w, r ] D[w, R] G D[w, R] f D[w, R] u = Re f D[w, R] f f (w) = 2π f w + re it dt. 2π 0 G C u : G! R w 2 G D[w, r ] G u(z) apple u(w) z 2 D[w, r ] u(z 0 ) < u(w) z 0 2 D[w, r ] u G G w G w z 0 u(z 0 ) < u(w) r := z 0 w u(w) = 2π u w + re it dt. 2π 0 u(w) z 0 = w + re it 0 0 apple t0 < 2π u(z 0 ) < u(w) u [t 0, t ] [0, 2π] u(w + re it ) < u(w) t 0 apple t apple t
124 u(w) = 2π 2π = 2π 0 Ç t0 0 u w + re it dt t 2π å u w + re it dt + u w + re it dt + u w + re it dt t 0 t u(w) u(w) < Ç t0 t 2π å u(w) dt + u(w) dt + u(w) dt 2π 0 t 0 t = u(w), u u u f G f G ln f (z) G G f (z) ln u G w D[w, r ] G z 2 D[w, r ] u(z) apple u(w) f G G
125 u G sup u(z) =max u(z) inf u(z) =min u(z) z2g z2 G z2g z2 G G G u G u G u G u G u(z) apple sup u(z) =max u(z) =0 z2g z2 G u(z) inf u(z) =min u(z) =0, z2g z2 G u v G u(z) =v(z) z 2 G u(z) =v(z) z 2 G u v G G u v G u G G u G u G u u û e iφ := u e iφ û re iφ := 2π 2π 0 u e it P r (φ t ) dt r <,
126 P r (φ) û u u(x, y) v(x, y) G c 2 R u(x, y)+ cv(x, y) G u(x, y)=e x sin y u C f Re( f )=u u(x, y)=ln x 2 + y 2 u C \{0} u C \{0} f G ln f (x, y) G u(x, y) R 2! R x u
127 v(x, y) x 3 + y 3 + iv(x, y) f G C H := { f (z) : z 2 G} u H u( f (z)) G u(r,φ) R 2! R u(r,φ) r u r + u rr + r 2 u φφ = 0. u(r,φ)=r 2 cos(2φ) C u(r,φ) r u u(r,φ) φ u u C u u(x, y) x y u x y P r (φ) = r 2 2r cos(φ)+r 2, 0 < r < u D[0, ] r < u re iφ = 2π 2π 0 u e it P r (φ t ) dt. u D[0, ] R 0 > u D[0, R 0 ] f a (z) = z a az,
128 a 2 C a < u( f a (z)) D[0, R ] D[0, ] u( f a (z)) w = 0 u(a) = u( f a (z)) dz. 2πi C [0,] z f a (z) a = re iφ u(a) = 2π u e it a 2 2π 0 e it a 2 dt. G D[a, r ] G R > r D[a, r ] D[a, R] G G = C R = r + w 2 C \ G M = w a K = D[a, M ] \ G K z 0 2 K f (z)= z a K R = z 0 a
129 C [2,3] exp(z) sin(z) dz, s s π π
130 0 π a n a(n) (a n ) n= (a n ) n (a n ) n n (a n ) L 2 C ε > 0 N n N a n L < ε (a n ) L lim a n! n = L. L (a n ) lim n N i n 0 = i n n n n! i n n = 0 ε > 0 N > ε = i n n = n apple N < ε.
131 (a n ) L 2 C ε > 0 N n a n L ε (a n = i n ) L 2 C ε = 2 Re(L) 0 N n N a n = a 4k+2 = i 4k+2 = k 0 a n L = + L > 2. Re(L) < 0 N n N a n = a 4k = i 4k = k > 0 a n L = L > > 2. (a n = i n ) (a n ) (b n ) c 2 C lim a n! n + c lim b n! n = lim (a n! n + cb n ) lim a n! n lim b n! n = lim (a n! n b n ) lim n! a n lim n! b n an = lim n! b n lim a n! n = lim a n! n+ lim n! b n 6= 0 f : G! C L := lim n! a n a n 2 G lim f (a n! n )= f (L).
132 R (a n ) a n+ n a n+ apple a n n a n (a n ) a n := n!. a n apple 3 (a n ) e := + lim n! a n. 0 apple r < lim n! r n = 0 (a n = r n ) 0 L := lim n! r n L = lim n! r n = lim n! r n+ = r lim n! r n = rl. ( r )L = 0 r 6= 0 L = 0
133 x N x n p(n) c 2 C c > p(n) lim = 0. n! c n c 2 C c n lim n! n! = 0. (a n ) a n = P n k= b k a n = P n k=0 b k (b k ) a n = P n k= b k a n = P n k=0 b k R
134 L lim a n! n = lim n! nx b k = L. ε > 0 N n N k= nx b k L < ε. k= L = X b k k X b k L = k= z 2 C z < P k z k X z k z = z. k nx z k = z + z z n = z z n+, z k= n! z < X nx Å k k 2 + k = lim n! k= k Å = lim n! Å = lim n! n + ã k + ã = n ã n +
135 b k 2 R 0 X b k k b k = k! nx b k = k= nx k= k! X k k! = e R b k c k 0 k X b k X k c k. k P n k= b k nx c k k= apple nx b k. k= P k c k X k b k lim n! b n = 0. lim b n! n 6= 0 lim b n! n X b k k z P k z k lim n! z n
136 X k b k 0 = lim n! nx b k k= X n lim b n! k k= Ç X n = lim n! n b k k= k= å X b k = lim n! b n. P k k 0 L L = > = = L, f (x) f (x) f () f (2) f (3) f (4) f () f (2) f (3) f (4) f (5) x x
137 f : [, )! R 0 f (t ) dt apple X k f (k) apple f ()+ f (t ) dt. f [k, k + ] f (k) f (k + ) n n n + f : [, )! R 0 Pk f (k) R f (t ) dt R f (t ) dt = P n k= f (k) P k f (k) R f (t ) dt P n k= f (k) P k f (k) P k k p > p < p p = dx x p a p+ = lim a! p + + p p > X k b k X b k k
138 P k b k b k 8 8 < b + k := b k b k 0, < b b : k := k b k < 0, 0 : 0 0 apple b + k apple b k 0 apple b k apple b k k X X b + k k b k k X b k = X b + k + X b k. k k k b k 2 C b k = c k + id k 0 apple c k apple b k k P k c k P k d k P k c k P k d k X b k = X c k + i X d k. k k k ζ(z) := X k k z Re(z) > X k k z = X k k Re(z) z ζ(z) ζ(z) C\{}
139 P k ( ) k+ k X ( ) k+ k k = = Å ã + 2 Å ã Å 5 ã + 6 2k 2k = 2k(2k ) apple (2k ) apple 2 k, 2 P ( ) k+ k k P k ( ) k+ k G C f n : G! C n f : G! C z 2 G ( f n ) lim f n! n (z) = f (z). ( f n ) f : G! C ε > 0 N z 2 G n N f n (z) f (z) < ε. H G ( f n ) H 0 < Re(z) < Re(z)= 2
140 8 9 G 8 ε > 0 8 z 2 G 9 N 8 n N f n (z) f (z) < ε, G 8 ε > 0 9 N 8 z 2 G 8 n N f n (z) f (z) < ε. N z N z 2 G f n : D[0, ]! C f n (z)=z n f : D[0, ]! C f (z)=0 z = 0 ε > 0 0 < z < N > ln(ε) ln z n N f n (z) f (z) = z n 0 = z n apple z N < ε. f n : D[0, 2 ]! C f n (z)=zn f : D[0, 2 ]! C f (z)=0 ε > 0 z < 2 N > ln(2) ln(ε) n N f n (z) f (z) = z n apple z N < 2 N < ε.
141 ( f n ) G z 0 2 G lim lim f n! z!z n (z) = lim 0 z!z0 lim f n! n (z). G C f n : G! C n ( f n ) f : G! C f z 0 2 G f z 0 ε > 0 N z 2 G n N f n (z) f (z) < ε 3. f n ε > 0 δ > 0 z z 0 < δ f n (z) f n (z 0 ) < ε 3. f (z) f (z 0 ) = f (z) f n (z)+ f n (z) f n (z 0 )+ f n (z 0 ) f (z 0 ) apple f (z) f n (z) + f n (z) f n (z 0 ) + f n (z 0 ) f (z 0 ) < ε. f z 0 f n : [0, ]! R f n (x)=x n f : [0, ]! R 8 < 0 0 apple x <, f (x)= : x =.
142 f n : G! C n ( f n ) f : G! C γ G lim n! γ f n = γ ε > 0 N z 2 G n N γ f. f n (z) f (z) < ε length(γ). γ f n γ f = γ f n f apple max f z2γ n (z) f (z) length(γ) < ε. P k f k (z) G γ G X f k (z) dz = X k γ k γ f k (z) dz. M f k : G! C k f k (z) applem k z 2 G P k M k P k f k P k f k G P k f k
143 z P k f k (z) ε > 0 N n N X nx M k M k = X M k < ε. k k= k>n z 2 G n N X f k (z) k nx f k (z) = X k>n k= f k (z) apple X f k (z) apple X M k < ε, k>n k>n f k f k P k f k P k z k z z < X z k = k z z. f k (z) =z k 0 < r < M k = r k f k (z) = z k apple r k z appler, P k r k P k z k z appler P k z k z < z appler r < z 0 X c k (z k 0 z 0 ) k
144 c 0, c, c 2,...2 C X z k = k 0 z. z 0 = 0 c k = k 0 z < z appler r < P k 0 z k z P k 0 c k (z R 0 R = z 0 )k P k 0 c k (z z 0 )k z z 0 < R P k 0 c k (z z 0 )k z z 0 appler r < R P k 0 c k (z z 0 )k z z 0 > R P k 0 c k (z z 0 )k z z 0 = R R P k 0 c k (z z 0 )k D[z 0, R] R = C P k 0 c k (w z 0 )k P k 0 c k (z z 0 )k z z 0 < w z 0 r := w z 0 P k 0 c k (w z 0 )k lim k! c k (w z 0 ) k = 0 c k (w z 0 ) k = c k r k apple M.
145 z z 0 < w z 0 X k 0 c k (z z 0 ) k = X k 0 z c k r k z0 k r apple M X z z0 k. r k 0 z P k 0 c k (z z 0 )k z 0 < r S := x 2 R 0 : X c k x k. k S S P k 0 c k (z z 0 )k z z 0 appler r R = x 2 S x > r P k 0 c k r k c k (z z 0 ) k apple c k r k S R R = 0 P k 0 c k (z z 0 )k z = z 0 R > 0 z z 0 < R R S r 2 S z z 0 < r apple R. P k 0 c k (w z 0 )k w = z 0 + r P k 0 c k (z z 0 )k z z 0 appler r < R x 2 S r < x apple R P k 0 c k r k P k 0 c k (z z 0 )k z z 0 appler z z 0 > R r /2 S R apple r < z z 0. P k 0 c k r k P k 0 c k r k P k 0 c k (z z 0 )k
146 k lim k! ck P k 0 c k (z z 0 )k 8 < k lim k! ck = 0, R = : lim k! k c k R R = R P k 0 c k (z z 0 )k z z 0 < R z z 0 > R k r := z z 0 < R lim k! ck = R 2 R+r > R N k ck < 2 R+r k N k c k (z z 0 ) k = c k z z 0 k = Ä k ck r ä k Å ã 2r k < R + r P k=n c k (z z 0 ) k 2r R+r < P 2r k k 0 R+r Pk 0 c k (z z 0 )k k r = z z 0 > R lim k! ck = R 2 R+r < R N k ck > 2 R+r k N k c k (z z 0 ) k = Ä k ck r ä k Å ã 2r k > >, R + r c k (z z 0 ) k P k 0 c k (z z 0 )k X kz k k 0 lim k! k ck = lim k! kp k = lim k! e k ln(k) = e lim k! ln(k) k = e 0 =,
147 X k 0 k! z k. lim k! c k+ c k = lim k! k! (k + )! = lim k! k + = 0, P k 0 k! z k C P k 0 c k (z z 0 )k R > 0 D[z 0, R] w 2 D[z 0, R] r < R w 2 D[z 0, r ] R 6= r = w z 0 +R 2 P k 0 c k (z z 0 )k D[z 0, r ] D[z 0, r ] w P k 0 c k (z z 0 )k R > 0 γ D[z 0, R] γ γ X c k (z z 0 ) k dz = X c k (z z 0 ) k dz. k 0 k 0 γ γ X c k (z z 0 ) k dz = 0. k 0 r := max z2γ γ(z) z 0 γ D[z 0, r ] r < R P k 0 c k (z z 0 )k D[z 0, r ]
148 a n = e πin 4 a n = cos(n) a n = sin( n ) a n = ( )n n a n = 2 in 2 2n 2 + X + i n p X + 2i n p n 3 n 5 X Å ã n n n i X n n 3 + i n X n n 2 + 2n. lim a n! n = a =) lim a n! n = a lim a n! n = 0 () lim a n! n = 0 lim n! a n M a n applem n (a n ) a ε > 0 N 2 >0 n > N a n a < ε
149 k! apple 3 k(k+) k n n! apple 3. (c n ) (Re c n ) (Im c n ) Q a n apple b n apple c n n lim n! a n = lim n! c n = L lim n! b n = L Re e 2πit : t 2 Q \. (c n ) P n 0 c n P k 0 (c 2k +c 2k+ ) (c n ) 0 X b k lim k n! X k n b k = 0.
150 f n (x) := sin n (x) X k X k k k 2 + k k 3 + G C f n : G! C n (a n ) R lim n! a n = 0 n f n (z) applea n z 2 G. ( f n ) G G C f n : G! C n ( f n ) G (z n ) G lim f n! n (z n )=0. (z n = e n )
151 f n : [0, π]! R f n (x)=sin n (x) n ( f n ) f : [0, π]! R 8 < x = π 2 f (x)=, : 0 x 6= π 2, (nz n ) z n n +nz Re(z) 0 f n (x)=n 2 xe nx lim n! f n (x) =0 x 0 x = 0 x > 0 n x R lim n! 0 f n (x) dx 0 z 0 z 0 + 4z 3 z 2 z 2 (4 z) 2 cos z cos(z 2 ) z 2 sin z (sin z) 2
152 (c k ) P k 0 c k (z z 0 )k (c k ) 0 P k 0 c k (z z 0 )k f (z)= z f (z)=log(z) M X k X k 0 z k D[0, ] k 2 z k {z 2 C : z 2} z 2 C r > z X k 0 z k X k 0 z k + r < z w D[0, r ] 0 apple k w w r R = c lim k+ k! c P k k 0 c k (z z 0 )k 8 < c lim k+ k! c = 0, R = k : lim k! c k c k+ X a k 2 z k a 2 C X k n z k k 0 k 0 n 2
153 X k 0 z k! X k z k k k X k ( ) k k z k(k+) X cos(k) z k k 0 X 4 k (z 2) k k 0 X k 0 z 2k k! X k (z ) k X k(k k k 2 ) z k f : D[0, ]! C f dw f (z) := [0,] wz. f n : R 0! R f n (t )= n e t n n f n (t ) n f n (t ) R 0 R 0 f n (t ) dt 0 n!
154 C [2,3] exp(z) sin(z) dz. exp(z) sin(z) π exp(z) sin(z) π f (z)= P k 0 c k (z f D[z 0, R] z 0 )k R > 0 f D[z 0, R] γ D[z 0, R] R f = 0 γ
155 f (z)= P k 0 c k (z z 0 )k R > 0 f 0 (z) = X kc k (z z 0 ) k z 2 D[z 0, R], k R z 2 D[z 0, R] z z 0 < R R z z 0 < R < R γ := C [z 0, R ] D[z 0, R] z γ f D[z 0, R] f 0 f 0 (z) = 2πi γ = X k 0 c k 2πi f (w) (w z) dw = 2 2πi = X kc k (z z 0 ) k. k γ (w z 0 ) k (w z) dw = X c 2 k k 0 γ X c (w z) 2 k (w k 0 d dw (w z 0 )k w=z z 0 ) k dw (z z 0 ) k f 0 (z) R f 0 z z 0 < R R f (z) (z z 0 ) f 0 (z) f (z) f (z) = X k 0 z k k!.
156 f C f (z)=exp(z) f 0 (z) = d dz X k 0 z k k! = X k z k (k )! = X k 0 z k k! = f (z). d dz f (z) exp(z) = d dz ( f (z)exp( z)) = f 0 (z)exp( z) f (z)exp( z) =0, f (z) exp(z) z = 0 f (z)=exp(z) exp(z) sin z = 2i (exp(iz) exp( iz)) = Ç å X (iz) k X ( iz) k 2i k 0 k! k 0 k! = X Ä (iz) k ( ) k (iz) kä = X 2(iz) k 2i k 0 k! 2i k 0 k! = X (iz) 2 j + = X i 2 j z 2j+ = X ( ) j i j 0 (2j + )! j 0 (2 j + )! j 0 (2 j + )! z 2 j + = z z 3 3! + z 5 5! z 7 7! +. f 0 f 00 f (z)= P k 0 c k (z z 0 )k c k = f (k) (z 0 ). k!
157 f (z 0 )=c 0 f 0 (z 0 )=c f 0 f 00 (z) = X k(k ) c k (z z 0 ) k 2 k 2 f 00 (z 0 )=2 c 2 f 000 (z 0 )=6 c 3 f 0000 (z 0 )= 24 c 4 f D f D P k 0 c k (z z 0 )k P k 0 d k (z z 0 )k z 0 c k = d k k 0 f (z) =exp(z) z 0 = π f (k) (z 0 )=exp(z) z=π = e π, X k 0 e π k! (z π)k, z 2 C f D[z 0, R] f z 0 R f (z) = X k 0 c k (z z 0 ) k c k = 2πi γ f (w) dw, (w z 0 ) k+ γ D[z 0, R] z 0 γ
158 g (z) := f (z + z 0 ) g D[0, R] z 2 D[0, R] r := z +R 2 g (z) = g (w) 2πi C [0,r ] w z dw. w z w 2 C [0, r ] z w < w z = w z w = w X k 0 z w k w 2 C [0, r ] g (z) = 2πi C [0,r ] f (z)= g (z f (z) = X k 0 g (w) w z dw = g (w) X z 2πi C [0,r ] w k 0 w = X k 0 2πi C [0,r ] k dw g (w) dw w k+ z 0 ) Ç å f (w) dw (z z 2πi C [z 0,r ] (w z 0 ) k+ 0 ) k. z k. C [z 0,r ] f (w) dw = (w z 0 ) k+ γ f (w) dw. (w z 0 ) k+ f : G! C f z 0 2 G R
159 G G C z 0 2 G z 0 G G { z z 0 : z 2 G} z 0 G f : G! C z 0 2 G f z 0 z 0 G f : C \{±i}!c f (z) := z 2 + z 0 = 0 f ±i f f (z) = z 2 + = X k 0 z 2 k X = ( ) k z 2k, k 0 R f G γ w γ γ G 0 f (k) (w) = k! 2πi γ f (z) dz. (z w) k+ f D[w, R] f (z) applem z 2 D[w, R] f (k) (w) apple k! M. R k
160 r < R f (k) (w) = k! f (z) dz 2πi C [w,r ] (z w) k+ apple k! 2π apple k! 2π max z2c [w,r ] f (z) length(c [w, r ]) (z w) k+ M k! M 2πr =. r k+ r k r R G z 0 2 G G f : G! C z 0 2 G R > 0 c 0, c, c 2,...2 C X c k (z z 0 ) k k 0 D[z 0, R] f (z) D[z 0, R] f z 0 f G f G G G G p(z) d > 0 a p(a) =0 p(z) z a p(z)=(z a) q(z) q(z) d q(z) a (z a)
161 p(z) p(z) =(z a) m g (z) m apple d g (z) a m a p(z) f : G! C f a 2 G f D a f (z)=0 z 2 D m g : G! C g (a) 6= 0 f (z) =(z a) m g (z) z 2 G. a D[a, r ] f m f a a R > 0 f (z) = X c k (z a) k z 2 D[a, R], k 0 c 0 = f (a)=0 c k = 0 k 0 m c k = 0 k < m c m 6= 0 f (z)=0 z 2 D[a, R] z 2 D[a, R] f (z) =c m (z a) m + c m+ (z a) m+ + =(z a) m (c m + c m+ (z a)+ ) =(z a) m X c k+m (z a) k. k 0
162 g : G! C 8X c k+m (z a) >< k z 2 D[a, R], k 0 g (z) := f (z) >: z 2 G \ {a}. (z a) m z 2 D[a, R]\{a} g D[a, R] g G \ {a} g (a)=c m 6= 0 f (z) =(z a) m g (z) z 2 G. g (a) 6= 0 r > 0 g (z) 6= 0 z 2 D[a, r ] D[a, r ] f m f a G f : G! C f (a n )=0 (a n ) G f G f g G f (a k )= g (a k ) w 2 G a k 6= w k f (z)= g (z) z G G X := {a 2 G : r f (z)=0 z 2 D[a, r ]} Y := {a 2 G : r f (z) 6= 0 z 2 D[a, r ] \{a}}. f (a) 6= 0 f a f a 2 Y
163 f (a)=0 a 2 X a f a 2 Y G X Y X Y G X Y lim n! a n Y X G = X u : G! R w D[w, r ] G z 2 D[w, r ] u(z) apple u(w) f G f G f G sup f (z) = max f (z). z2g z2 G f f z 0 2 G max z2g f (z) = f (z 0 ) sup z2g f (z) applemax z2g f (z) z 0 G z 0 z 0 62 G z 0 G f G f a G f (a)=0 u G G
164 a 2 G R > 0 f (a) f (z) z 2 D[a, R] f f (a) =0 f (z) =0 z 2 D[a, R] f f (a) 6= 0 g : G! C g (z) := f (z) f (a) g (z) apple g (a) = z 2 D[a, R], g (a) = g r apple R Re( g (z)) > 0 z 2 D[a, r ] h : D[a, r ]! C h(z) := Log( g (z)) h(a) =Log( g (a)) = Log() =0 Re(h(z)) = Re(Log( g (z))) = ln( g (z) ) apple ln() =0. h D[a, r ] g (z)= exp(h(z)) exp(0)= z 2 D[a, r ] f (z)= f (a) g (z) f (a) z 2 D[a, r ] f G exp( z ) Å ã exp z = X k 0 Å ã k k! z = X k 0 k! z k,
165 X a k := X a k + X a k. k2 k 0 k a k 2 C z 0 X c k (z z 0 ) k. k2 exp( z ) 0 c k = 0 k < 0 z X c k (z z 0 ) k = X c k (z z 0 ) k + X c k (z z 0 ) k. k2 k 0 k R 2 {z 2 C : z z 0 < R 2 } {z 2 C : z z 0 appler 2 } r 2 < R 2 z z 0 < R R {z 2 C : z z 0 r } r > R A := {z 2 C : R < z z 0 < R 2 }
166 R < R 2 {z 2 C : r apple z z 0 appler 2 } R < r < r 2 < R 2. sin(z) z 0 = 0 g : D[0, π]! C 8 < sin(z) z z 6= 0, g (z) := : 0 z = 0. g lim z!0 sin(z) z z = 6. 8 < cos(z) g 0 sin (z)= 2 (z) + z z 6= 0, 2 : 6 z = 0, g D[0, π] g g (z) = 6 z z z 5 + z < π 0 < z < π sin(z) = z + 6 z z z 5 + g D[0, π] sin(z) z D[0, π] \{0} ζ(z)= P k k z C \{}
167 f A := {z 2 C : R < z z 0 < R 2 }. f A z 0 f (z) = X c k (z z 0 ) k c k = f (w) dw, k2 2πi C [z 0,r ] (w z 0 ) k+ R < r < R 2 C [z 0, r ] γ A C [z 0, r ] γ 2 γ γ g (z)= f (z + z 0 ) g {z 2 C : R < z < R 2 } R < r < z < r 2 < R 2 γ γ := C [0, r ]
Opgaver til f(z) = 1 z 4 1, g(z) = 1
 1.17 Opgaver til 1. 1 1.1. Vis, at f(z) = er vilkårligt ofte differentiabel i C \ {, 1}, og z(1 z) find et udtryk for f (n) (z) for alle n. (Vink. Skriv f(z) = 1 z + 1 1 z ). 1.2. Beskriv billedkurverne
1.17 Opgaver til 1. 1 1.1. Vis, at f(z) = er vilkårligt ofte differentiabel i C \ {, 1}, og z(1 z) find et udtryk for f (n) (z) for alle n. (Vink. Skriv f(z) = 1 z + 1 1 z ). 1.2. Beskriv billedkurverne
Komplekse Tal. 20. november 2009. UNF Odense. Steen Thorbjørnsen Institut for Matematiske Fag Århus Universitet
 Komplekse Tal 20. november 2009 UNF Odense Steen Thorbjørnsen Institut for Matematiske Fag Århus Universitet Fra de naturlige tal til de komplekse Optælling af størrelser i naturen De naturlige tal N (N
Komplekse Tal 20. november 2009 UNF Odense Steen Thorbjørnsen Institut for Matematiske Fag Århus Universitet Fra de naturlige tal til de komplekse Optælling af størrelser i naturen De naturlige tal N (N
MM501 forelæsningsslides
 MM501 forelæsningsslides uge 37, 2010 Produceret af Hans J. Munkholm 2009 bearbejdet af Jessica Carter 2010 1 Hvad er et komplekst tal? Hvordan regner man med komplekse tal? Man kan betragte udvidelsen
MM501 forelæsningsslides uge 37, 2010 Produceret af Hans J. Munkholm 2009 bearbejdet af Jessica Carter 2010 1 Hvad er et komplekst tal? Hvordan regner man med komplekse tal? Man kan betragte udvidelsen
SUPPLERENDE OPGAVER TIL KOMPLEKS FUNKTIONSTEORI F2005
 SUPPLERENDE OPGAVER TIL KOMPLEKS FUNKTIONSTEORI F2005 0. maj, 2005 version nr. 8 JØRGEN VESTERSTRØM Indledende bemærkninger De foreliggende opgaver udgør et supplement til lærebogens opgaver. Afsnitsnummereringerne
SUPPLERENDE OPGAVER TIL KOMPLEKS FUNKTIONSTEORI F2005 0. maj, 2005 version nr. 8 JØRGEN VESTERSTRØM Indledende bemærkninger De foreliggende opgaver udgør et supplement til lærebogens opgaver. Afsnitsnummereringerne
Kompleks Funktionsteori
 Kompleks Funktionsteori Formelræs Holomorfe funktioner Sætning. (Caucy-Riemans ligninger). Funktionen f : G C, f = u+iv er holomorf i z 0 = x 0 + iy 0 hvis og kun hvis i punktet (x 0, y 0 ). du dx = dv
Kompleks Funktionsteori Formelræs Holomorfe funktioner Sætning. (Caucy-Riemans ligninger). Funktionen f : G C, f = u+iv er holomorf i z 0 = x 0 + iy 0 hvis og kun hvis i punktet (x 0, y 0 ). du dx = dv
Kortfattet svar til eksamen i Matematik F2 d. 21. juni 2017
 Kortfattet svar til eksamen i Matematik F2 d. 2. juni 27 Opgave Bestem for følgende tilfælde om en funktion f(z) af z = x + iy er analytisk i dele af den komplekse plan, hvis den har real del u(x, y) og
Kortfattet svar til eksamen i Matematik F2 d. 2. juni 27 Opgave Bestem for følgende tilfælde om en funktion f(z) af z = x + iy er analytisk i dele af den komplekse plan, hvis den har real del u(x, y) og
Energy-saving Technology Adoption under Uncertainty in the Residential Sector
 Energy-saving Technology doption under Uncertainty in the esidential Sector Dorothée Charlier, lejandro Mosino, ude Pommeret To cite this version: Dorothée Charlier, lejandro Mosino, ude Pommeret. Energy-saving
Energy-saving Technology doption under Uncertainty in the esidential Sector Dorothée Charlier, lejandro Mosino, ude Pommeret To cite this version: Dorothée Charlier, lejandro Mosino, ude Pommeret. Energy-saving
PC PSI PT JEAN-MARIE MONIER GUILLAUME HABERER CÉCILE LARDON MÉTHODES ET EXERCICES. Mathématiques. méthodes et exercices. 3 e.
 PC PSI PT MÉTHODES ET EXERCICES JEAN-MARIE MONIER GUILLAUME HABERER CÉCILE LARDON Mathématiques méthodes et exercices 3 e édition Conception et création de couverture : Atelier 3+ Dunod, 201 5 rue Laromiguière,
PC PSI PT MÉTHODES ET EXERCICES JEAN-MARIE MONIER GUILLAUME HABERER CÉCILE LARDON Mathématiques méthodes et exercices 3 e édition Conception et création de couverture : Atelier 3+ Dunod, 201 5 rue Laromiguière,
Eksamen i Matematik F2 d. 19. juni Opgave 2. Svar. Korte svar (ikke fuldstændige)
 Eksamen i Matematik F2 d. 9. juni 28 Korte svar (ikke fuldstændige Opgave Find realdelen, Re z, og imaginærdelen, Im z, for følgende værdier af z, a z = 2 i b z = i i c z = ln( + i Find realdelen, Re z,
Eksamen i Matematik F2 d. 9. juni 28 Korte svar (ikke fuldstændige Opgave Find realdelen, Re z, og imaginærdelen, Im z, for følgende værdier af z, a z = 2 i b z = i i c z = ln( + i Find realdelen, Re z,
Komplekse tal. Mike Auerbach. Tornbjerg Gymnasium, Odense 2015
 Komplekse tal Mike Auerbach Tornbjerg Gymnasium, Odense 2015 Indhold 1 Vinkelmål og trigonometriske funktioner 2 1.1 Radianer................................................ 2 1.2 Cosinus og sinus som
Komplekse tal Mike Auerbach Tornbjerg Gymnasium, Odense 2015 Indhold 1 Vinkelmål og trigonometriske funktioner 2 1.1 Radianer................................................ 2 1.2 Cosinus og sinus som
Eksamen i Mat F, april 2006
 Eksamen i Mat F, april 26 Opgave 1 Lad F være et vektorfelt, givet i retvinklede koordinater som: F x x F = F x i + F y j + F z k = F y = 2z F z y Udregn F og F: F = F x + F y + F z = 1 + +. F = F z F
Eksamen i Mat F, april 26 Opgave 1 Lad F være et vektorfelt, givet i retvinklede koordinater som: F x x F = F x i + F y j + F z k = F y = 2z F z y Udregn F og F: F = F x + F y + F z = 1 + +. F = F z F
DesignMat Uge 1 Repetition af forårets stof
 DesignMat Uge 1 Repetition af forårets stof Preben Alsholm Efterår 008 01 Lineært ligningssystem Lineært ligningssystem Et lineært ligningssystem: a 11 x 1 + a 1 x + + a 1n x n = b 1 a 1 x 1 + a x + +
DesignMat Uge 1 Repetition af forårets stof Preben Alsholm Efterår 008 01 Lineært ligningssystem Lineært ligningssystem Et lineært ligningssystem: a 11 x 1 + a 1 x + + a 1n x n = b 1 a 1 x 1 + a x + +
Gribskov kommune Tisvilde By, Tibirke
 Birkevænget 1 10 cx 2036 2 Birkevænget 2 10 cp 2836 2 Birkevænget 3 10 cz 2010 2 Birkevænget 5 10 cy 2085 2 Birkevænget 6 10 cr 2953 4 Samlet 10 cs 2940 ejendom Birkevænget 7 10 cn 2045 2 Birkevænget 9
Birkevænget 1 10 cx 2036 2 Birkevænget 2 10 cp 2836 2 Birkevænget 3 10 cz 2010 2 Birkevænget 5 10 cy 2085 2 Birkevænget 6 10 cr 2953 4 Samlet 10 cs 2940 ejendom Birkevænget 7 10 cn 2045 2 Birkevænget 9
Inden der siges noget om komplekse tal, vil der i dette afsnit blive gennemgået en smule teori om trigonometriske funktioner.
 Komplekse tal Mike Auerbach Odense 2012 1 Vinkelmål og trigonometriske funktioner Inden der siges noget om komplekse tal, vil der i dette afsnit blive gennemgået en smule teori om trigonometriske funktioner.
Komplekse tal Mike Auerbach Odense 2012 1 Vinkelmål og trigonometriske funktioner Inden der siges noget om komplekse tal, vil der i dette afsnit blive gennemgået en smule teori om trigonometriske funktioner.
Nøgleord og begreber Komplekse tal Test komplekse tal Polære koordinater Kompleks polarform De Moivres sætning
 Oversigt [S] App. I, App. H.1 Nøgleord og begreber Komplekse tal Test komplekse tal Polære koordinater Kompleks polarform De Moivres sætning Test komplekse tal Komplekse rødder Kompleks eksponentialfunktion
Oversigt [S] App. I, App. H.1 Nøgleord og begreber Komplekse tal Test komplekse tal Polære koordinater Kompleks polarform De Moivres sætning Test komplekse tal Komplekse rødder Kompleks eksponentialfunktion
DOK-facitliste DOK. DOK-facitliste 1
 -facitliste 1 -facitliste Listens numre refererer til samlingen af supplerede -opgaver (de gamle eksamensopgaver. På listen står næsten kun facitter, og ikke tilstrækkelige svar på opgaverne. [Korrigeret
-facitliste 1 -facitliste Listens numre refererer til samlingen af supplerede -opgaver (de gamle eksamensopgaver. På listen står næsten kun facitter, og ikke tilstrækkelige svar på opgaverne. [Korrigeret
Svar til eksamen i Matematik F2 d. 23. juni 2016
 Svar til eksamen i Matematik F d. 3. juni 06 FORBEHOLD FOR FEJL! Bemærk, i modsætning til herunder, så skal det i besvarelsen fremgå tydeligt, hvordan polerne ndes og hvordan de enkelte residuer udregnes.
Svar til eksamen i Matematik F d. 3. juni 06 FORBEHOLD FOR FEJL! Bemærk, i modsætning til herunder, så skal det i besvarelsen fremgå tydeligt, hvordan polerne ndes og hvordan de enkelte residuer udregnes.
INSTITUT FOR MATEMATIK OG DATALOGI. TIDLIGERE EKSAMENSOPGAVER MM01 Juni 1993 marts 2006
 INSTITUT FOR MATEMATIK OG DATALOGI TIDLIGERE EKSAMENSOPGAVER MM01 Juni 1993 marts 2006 i Forord Denne opgavesamling skal bruges med den forståelse, at pensumbeskrivelsen for kurset har undergået en række
INSTITUT FOR MATEMATIK OG DATALOGI TIDLIGERE EKSAMENSOPGAVER MM01 Juni 1993 marts 2006 i Forord Denne opgavesamling skal bruges med den forståelse, at pensumbeskrivelsen for kurset har undergået en række
Idenne note giver vi et eksempel på, hvorledes det er vigtigt at holde sig
 Analyse : Eulers formel Sebastian rsted 9. maj 015 Idenne note giver vi et eksempel på, hvorledes det er vigtigt at holde sig for øje, hvor de matematiske resultater kommer fra, og hvad de baseres på;
Analyse : Eulers formel Sebastian rsted 9. maj 015 Idenne note giver vi et eksempel på, hvorledes det er vigtigt at holde sig for øje, hvor de matematiske resultater kommer fra, og hvad de baseres på;
GEOMETRI-TØ, UGE 3. og resultatet følger fra [P] Proposition 2.3.1, der siger, at
![GEOMETRI-TØ, UGE 3. og resultatet følger fra [P] Proposition 2.3.1, der siger, at GEOMETRI-TØ, UGE 3. og resultatet følger fra [P] Proposition 2.3.1, der siger, at](/thumbs/50/26870860.jpg) GEOMETRI-TØ, UGE 3 Hvis I falder over tryk- eller regne-fejl i nedenstående, må I meget gerne sende rettelser til fuglede@imf.au.dk. Opvarmningsopgave 1. Lad γ : (α, β) R 2 være en regulær kurve i planen.
GEOMETRI-TØ, UGE 3 Hvis I falder over tryk- eller regne-fejl i nedenstående, må I meget gerne sende rettelser til fuglede@imf.au.dk. Opvarmningsopgave 1. Lad γ : (α, β) R 2 være en regulær kurve i planen.
VIGTIG TRAFIKINFORMATION
 f pf p I é I I É é I y W w p y Æ f p I ü I y pp p II p f f f W p É y c I é É ü C ff f f f É y Æ p f é É Y Y y IX C f I y Y y p Y I I Æ Æ p p I y C p f p cp f y f f f y y w é p p p f@p f 35 26 69 00 f f,
f pf p I é I I É é I y W w p y Æ f p I ü I y pp p II p f f f W p É y c I é É ü C ff f f f É y Æ p f é É Y Y y IX C f I y Y y p Y I I Æ Æ p p I y C p f p cp f y f f f y y w é p p p f@p f 35 26 69 00 f f,
Matematik F2 Opgavesæt 2
 Opgaver uge 2 I denne uge kigger vi nærmere på Cauchy-Riemann betingelserne, potensrækker, konvergenskriterier og flertydige funktioner. Vi skal også se på integration langs en ve i den komplekse plan.
Opgaver uge 2 I denne uge kigger vi nærmere på Cauchy-Riemann betingelserne, potensrækker, konvergenskriterier og flertydige funktioner. Vi skal også se på integration langs en ve i den komplekse plan.
(c) Opskriv den reelle Fourierrække for funktionen y(t) fra (b), og afgør dernæst om y(t) er en lige eller ulige funktion eller ingen af delene.
 MATEMATIK 3 EN,MP 4. februar 2016 Eksamenopgaver fra 2011 2016 (jan. 2016) Givet at 0 for 0 < t < 1 mens e (t 1) cos(7(t 1)) for t 1, betragt da begyndelsesværdiproblemet for t > 0: y (t) + 2y (t) + 50y(t)
MATEMATIK 3 EN,MP 4. februar 2016 Eksamenopgaver fra 2011 2016 (jan. 2016) Givet at 0 for 0 < t < 1 mens e (t 1) cos(7(t 1)) for t 1, betragt da begyndelsesværdiproblemet for t > 0: y (t) + 2y (t) + 50y(t)
Oversigt [S] 7.3, 7.4, 7.5, 7.6; [DL] 1, 2
![Oversigt [S] 7.3, 7.4, 7.5, 7.6; [DL] 1, 2 Oversigt [S] 7.3, 7.4, 7.5, 7.6; [DL] 1, 2](/thumbs/82/86922880.jpg) Oversigt [S] 7.3, 7.4, 7.5, 7.6; [DL] 1, 2 Her skal du lære om Separable ligninger Logistisk ligning og eksponentiel vækst 1. ordens lineær ligning August 2002, opgave 7 Rovdyr-Byttedyr system 1. ordens
Oversigt [S] 7.3, 7.4, 7.5, 7.6; [DL] 1, 2 Her skal du lære om Separable ligninger Logistisk ligning og eksponentiel vækst 1. ordens lineær ligning August 2002, opgave 7 Rovdyr-Byttedyr system 1. ordens
Formelsamling - MatF2. Therkel Zøllner og Amalie Christensen 27. juni 2009
 Formelsamling - MatF2 Therkel Zøllner og Amalie Christensen 27. juni 2009 1 Indhold 1 Kompleks variabel teori 3 1.1 Komplekse funktioner 825-830........................... 3 1.2 Powerserier af komplekse
Formelsamling - MatF2 Therkel Zøllner og Amalie Christensen 27. juni 2009 1 Indhold 1 Kompleks variabel teori 3 1.1 Komplekse funktioner 825-830........................... 3 1.2 Powerserier af komplekse
Indhold. 4 Beretning Markedsføring i Kina 7 Lokalt samarbejde 8 1 ud af 3 gæster på 2 hjul 9 Møder og events 10 Fri adgang til natur
 Å I f f I f - f f f f f f f f f I f f f f f f f f f f f f f f f f f f f f f f I f f f f f f f f f f f f f f f f f f I f f V f f f f f f f f f f V f f C f f C V f f Ø f C I f C V f f f f f f - % f V V
Å I f f I f - f f f f f f f f f I f f f f f f f f f f f f f f f f f f f f f f I f f f f f f f f f f f f f f f f f f I f f V f f f f f f f f f f V f f C f f C V f f Ø f C I f C V f f f f f f - % f V V
MATEMATIK 3 EN,MP 17. september 2014 Oversigt nr. 1
 MATEMATIK 3 EN,MP 7. september 204 Oversigt nr. Her bringes en samling af de gamle eksamensopgaver: (jan. 204) Betragt begyndelsesværdiproblemet y (t) + 7y (t) + 2y(t) = e t sin(2t) for t > 0, y(0) = 2,
MATEMATIK 3 EN,MP 7. september 204 Oversigt nr. Her bringes en samling af de gamle eksamensopgaver: (jan. 204) Betragt begyndelsesværdiproblemet y (t) + 7y (t) + 2y(t) = e t sin(2t) for t > 0, y(0) = 2,
Indhold. Litteratur 11
 Indhold Forord ii 00-sættet 1 Opgave 1....................................... 1 Spørgsmål (a).................................. 1 Spørgsmål (b).................................. 1 Spørgsmål (c)..................................
Indhold Forord ii 00-sættet 1 Opgave 1....................................... 1 Spørgsmål (a).................................. 1 Spørgsmål (b).................................. 1 Spørgsmål (c)..................................
Nøgleord og begreber Analysens hovedsætning Stamfunktioner Itereret integral Test itereret integral Fubinis sætning Test Fubini Eksempler Test produkt
 Oversigt [S] 5., 5.3, 5.4,.,. Nøgleord og begreber Analysens hovedsætning Stamfunktioner Itereret integral Test itereret integral Fubinis sætning Test Fubini Eksempler Test produkt Calculus - 6 Uge 39.
Oversigt [S] 5., 5.3, 5.4,.,. Nøgleord og begreber Analysens hovedsætning Stamfunktioner Itereret integral Test itereret integral Fubinis sætning Test Fubini Eksempler Test produkt Calculus - 6 Uge 39.
A B C D E Hjemmeværnmuseet's arkiv/depot Søgaard Distrikter - LMD. Reol/hylde Region/distrikt/m.m. Kasse nr. Indhold 2C3 Flyverhjemmeværne 1
 0 A B C D E Hjemmeværnmuseet's arkiv/depot Søgaard LMK Distrikter - LMD. Reol/hylde Region/distrikt/m.m. Kasse nr. Indhold C Flyverhjemmeværne Flyverhjemmeværnet LMD Odense Nyt fra stabseskadrillen -.
0 A B C D E Hjemmeværnmuseet's arkiv/depot Søgaard LMK Distrikter - LMD. Reol/hylde Region/distrikt/m.m. Kasse nr. Indhold C Flyverhjemmeværne Flyverhjemmeværnet LMD Odense Nyt fra stabseskadrillen -.
Vej Nr. Matr.nr. Areal m² Heraf vej Parter Arresødalvej
 Samlet partsfortegnelse for Karsemosen Landvindingslag Gammel partsfordeling. Opstillet i adresseorden Erik B. Aksig 10. oktober 2013 Parter Parter Gribskov Halsnæs Arresødalvej 79 17 72540 357 357 Birkevænget
Samlet partsfortegnelse for Karsemosen Landvindingslag Gammel partsfordeling. Opstillet i adresseorden Erik B. Aksig 10. oktober 2013 Parter Parter Gribskov Halsnæs Arresødalvej 79 17 72540 357 357 Birkevænget
KOMPLEKS ANALYSE. noter til matematik beta H.A. NIELSEN
 KOMPLEKS ANALYSE noter til matematik beta H.A. NIELSEN institut for matematiske fag aarhus universitet 23 KOMPLEKS ANALYSE H.A. NIELSEN Indhold. Komplekse tal 2 2. Elementære funktioner 3. Holomorfe funktioner
KOMPLEKS ANALYSE noter til matematik beta H.A. NIELSEN institut for matematiske fag aarhus universitet 23 KOMPLEKS ANALYSE H.A. NIELSEN Indhold. Komplekse tal 2 2. Elementære funktioner 3. Holomorfe funktioner
Egentyngd (+Struc. dead load) Glas Nyttiglast balkong Egentyngd (+Struc. dead load) Glas Nyttiglast balkong
 Eurocode (NA: Swedih) Eurocode (NA: Swedih) Load combination No. Name ype Factor.35*Egentyngd +.35*Gla +.50*0.70*Nyttiglat balong Ultimate.350.350 3 Egentyngd + Gla + 0.30*Nyttiglat balong Ultimate Quaipermanent.050.0.0.500.000.000
Eurocode (NA: Swedih) Eurocode (NA: Swedih) Load combination No. Name ype Factor.35*Egentyngd +.35*Gla +.50*0.70*Nyttiglat balong Ultimate.350.350 3 Egentyngd + Gla + 0.30*Nyttiglat balong Ultimate Quaipermanent.050.0.0.500.000.000
Komplekse tal. x 2 = 1 (2) eller
 Komplekse tal En tilegnelse af stoffet i dette appendix kræver at man løser opgaverne Komplekse tal viser sig uhyre nyttige i fysikken, f.eks til løsning af lineære differentialligninger eller beskrivelse
Komplekse tal En tilegnelse af stoffet i dette appendix kræver at man løser opgaverne Komplekse tal viser sig uhyre nyttige i fysikken, f.eks til løsning af lineære differentialligninger eller beskrivelse
Løsningsforslag til opgavesæt 5
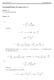 Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
!" # $% #&" &" '$"& %! (! "#$!" #!"#$% &' ( ()!*+(),- ()./&'01 2!3&'45 6 # 7 8()9:% ; %() AB;CD 5 E (- "#$ FG!HIJK9! AB LM NO(& &! 2PQR S9:T
 !"# $%#&"&"'$"&%! (! "#$!" #!"#$%& ()!*+(),-()./&'012!3&'45 6 #78()9:%%()=>?@56(!ABCD5E(-"#$!HIJ9! ABL(& &!2QRS9:TVWXY "#$&'!J8HIJ!Z( #$% "#$ HIJ ()* +,(,-./((( &' $) () *+ 01*1)10! "! #! $"%!&& '!"#$
!"# $%#&"&"'$"&%! (! "#$!" #!"#$%& ()!*+(),-()./&'012!3&'45 6 #78()9:%%()=>?@56(!ABCD5E(-"#$!HIJ9! ABL(& &!2QRS9:TVWXY "#$&'!J8HIJ!Z( #$% "#$ HIJ ()* +,(,-./((( &' $) () *+ 01*1)10! "! #! $"%!&& '!"#$
Gamle eksamensopgaver (MASO)
 EO 1 Gamle eksamensopgaver (MASO) Opgave 1. (Vinteren 1990 91, opgave 1) a) Vis, at rækken er divergent. b) Vis, at rækken er konvergent. Opgave 2. (Vinteren 1990 91, opgave 2) Gør rede for at ligningssystemet
EO 1 Gamle eksamensopgaver (MASO) Opgave 1. (Vinteren 1990 91, opgave 1) a) Vis, at rækken er divergent. b) Vis, at rækken er konvergent. Opgave 2. (Vinteren 1990 91, opgave 2) Gør rede for at ligningssystemet
Løsningsforslag til opgavesæt 5
 Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
Punktgrupper. Klaus Thomsen
 Punktgrupper Klaus Thomsen 1. Forord Disse noter er skrevet med henblik på et efteruddannelses-kursus for gymnasielærere i matematik og/eller kemi. Formålet er at give en introduktion til matematikken
Punktgrupper Klaus Thomsen 1. Forord Disse noter er skrevet med henblik på et efteruddannelses-kursus for gymnasielærere i matematik og/eller kemi. Formålet er at give en introduktion til matematikken
TÅRNBY KOMMUNE BILAG 1 ADMINSTRATIVE FORHOLD OG AREALAFGIVELSE
 TÅRNBY KOMMUNE BILAG 1 ADMINSTRATIVE FORHOLD OG AREALAFGIVELSE SERVITUTPÅLÆG I forbindelse med separatkloakering og klimatilpasning i eksisterende kloakoplande samt kloakering af ejendomme i det åbne land,
TÅRNBY KOMMUNE BILAG 1 ADMINSTRATIVE FORHOLD OG AREALAFGIVELSE SERVITUTPÅLÆG I forbindelse med separatkloakering og klimatilpasning i eksisterende kloakoplande samt kloakering af ejendomme i det åbne land,
Samlet partsfortegnelse for Karsemosen Landvindingslag Opstillet i adresseorden
 Samlet partsfortegnelse for Karsemosen Landvindingslag Opstillet i adresseorden Udarbejdet 21. august 2013. Revideret 31. jan. 2018. Revideret 8. februar. Revideret 31. januar 2018 af Stine Holm, Halsnæs
Samlet partsfortegnelse for Karsemosen Landvindingslag Opstillet i adresseorden Udarbejdet 21. august 2013. Revideret 31. jan. 2018. Revideret 8. februar. Revideret 31. januar 2018 af Stine Holm, Halsnæs
INSTITUT FOR MATEMATIK OG DATALOGI. TIDLIGERE EKSAMENSOPGAVER MM501 Calculus I, MM502 Calculus II Januar 2006 juni 2010
 INSTITUT FOR MATEMATIK OG DATALOGI TIDLIGERE EKSAMENSOPGAVER MM501 Calculus I, MM502 Calculus II Januar 2006 juni 2010 Forord Denne opgavesamling indeholder samtlige eksamensopgaver, der har været stillet
INSTITUT FOR MATEMATIK OG DATALOGI TIDLIGERE EKSAMENSOPGAVER MM501 Calculus I, MM502 Calculus II Januar 2006 juni 2010 Forord Denne opgavesamling indeholder samtlige eksamensopgaver, der har været stillet
Komplekse tal og rækker
 Komplekse tal og rækker John Olsen 1 Indledning Dette sæt noter er forelæsningsnoter til foredraget Komplekse tal og rækker. Noterne er beregnet til at blive brugt sammen med foredraget. I afsnit 2 bliver
Komplekse tal og rækker John Olsen 1 Indledning Dette sæt noter er forelæsningsnoter til foredraget Komplekse tal og rækker. Noterne er beregnet til at blive brugt sammen med foredraget. I afsnit 2 bliver
Eksamen i Mat F, april 2006
 Eksamen i Mat F, april 26 Opgave Lad F være et vektorfelt, givet i retvinklede koordinater som: Udregn F og F: F x F = F x i + F y j + F z k = F y = z 2 F z xz y 2 F = F x + F y + F z = + + x. F = F z
Eksamen i Mat F, april 26 Opgave Lad F være et vektorfelt, givet i retvinklede koordinater som: Udregn F og F: F x F = F x i + F y j + F z k = F y = z 2 F z xz y 2 F = F x + F y + F z = + + x. F = F z
! " # !" # $ % & ' ( ) * +, -. /
 !"#!# $%!"#$%&' ()*+,-./0' # ; >? FGHI J'# KLH MN KL!"#$%#&'()*+,-./ 0+ + 2 3456789:6;
!"#!# $%!"#$%&' ()*+,-./0' # ; >? FGHI J'# KLH MN KL!"#$%#&'()*+,-./ 0+ + 2 3456789:6;
DesignMat Den komplekse eksponentialfunktion og polynomier
 DesignMat Den komplekse eksponentialfunktion og polynomier Preben Alsholm Uge 8 Forår 010 1 Den komplekse eksponentialfunktion 1.1 Definitionen Definitionen Den velkendte eksponentialfunktion x e x vil
DesignMat Den komplekse eksponentialfunktion og polynomier Preben Alsholm Uge 8 Forår 010 1 Den komplekse eksponentialfunktion 1.1 Definitionen Definitionen Den velkendte eksponentialfunktion x e x vil
Besvarelser til Calculus Ordinær Eksamen Juni 2019
 Besvarelser til Calculus Ordinær Eksamen - 14. Juni 2019 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 14. Juni 2019 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
/AL-BANK. World Half Marathon Championships
 / W f Cpp 1 I å f f, f f å * å, *: C I x, c 2013 2 IF/ 2014 c, p IF5, yf F5 F, 7, p 7 IF/ 2014 9 1011 p1213 15 p p17 p19 21 Cp2014 #W2014 Ff: 3 P! w Y, U f, å f på p f p, p U f p på p, på å P Pz p pp,
/ W f Cpp 1 I å f f, f f å * å, *: C I x, c 2013 2 IF/ 2014 c, p IF5, yf F5 F, 7, p 7 IF/ 2014 9 1011 p1213 15 p p17 p19 21 Cp2014 #W2014 Ff: 3 P! w Y, U f, å f på p f p, p U f p på p, på å P Pz p pp,
Tillæg til Lokalplan nr For boligbebyggelsen Røde Vejrmølle Parken. Forslag. Miljø- og Teknikforvaltningen. Albertslund Kommune
 Miljø- og Teknikforvaltningen Albertslund Kommune Tillæg til Lokalplan nr. 18.5.1 www.albertslund.dk albertslund@albertslund.dk T 43 68 68 68 F 43 68 69 28 For boligbebyggelsen Røde Vejrmølle Parken Forslag
Miljø- og Teknikforvaltningen Albertslund Kommune Tillæg til Lokalplan nr. 18.5.1 www.albertslund.dk albertslund@albertslund.dk T 43 68 68 68 F 43 68 69 28 For boligbebyggelsen Røde Vejrmølle Parken Forslag
Wigner s semi-cirkel lov
 Wigner s semi-cirkel lov 12. december 2009 Eulers Venner Steen Thorbjørnsen Institut for Matematiske Fag Århus Universitet Diagonalisering af selvadjungeret matrix Lad H være en n n matrix med komplekse
Wigner s semi-cirkel lov 12. december 2009 Eulers Venner Steen Thorbjørnsen Institut for Matematiske Fag Århus Universitet Diagonalisering af selvadjungeret matrix Lad H være en n n matrix med komplekse
Besvarelser til Calculus Ordinær Eksamen Juni 2017
 Besvarelser til Calculus Ordinær Eksamen - 12. Juni 217 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 12. Juni 217 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Outline. Chapter 6: (cont d) Qijin Chen. November 21, 2013 NH = =6 CH = 15 4
 Chapter 6: Qjn Chen Department of Physcs, Zhejang Unversty November 1, 013 Copyrght c 013 by Qjn Chen; all rghts reserved. ω 3 4 1. (cont d) 1 3 n3n3n 3n (x 1, y 1, z 1 )(x, y, z ) (x 1 x ) + (y 1 y )
Chapter 6: Qjn Chen Department of Physcs, Zhejang Unversty November 1, 013 Copyrght c 013 by Qjn Chen; all rghts reserved. ω 3 4 1. (cont d) 1 3 n3n3n 3n (x 1, y 1, z 1 )(x, y, z ) (x 1 x ) + (y 1 y )
Mat 2KF Minilex. Henrik Dahl 2. januar Definitioner 2. 2 Sætninger 6. 3 Symboler Opskrifter og trix Gennemregnede eksempler 16
 Mat 2KF Minilex Henrik Dahl 2. januar 2004 Resumé ADVARSEL - dette er et total underground-dokument!. Det er livsfarligt at bruge ukritisk. Der er næsten sikkert graverende fejl. Jeg påtager mig intet
Mat 2KF Minilex Henrik Dahl 2. januar 2004 Resumé ADVARSEL - dette er et total underground-dokument!. Det er livsfarligt at bruge ukritisk. Der er næsten sikkert graverende fejl. Jeg påtager mig intet
Aristoteles Camillo. To cite this version: HAL Id: hal
 An experimentally-based modeling study of the effect of anti-angiogenic therapies on primary tumor kinetics for data analysis of clinically relevant animal models of metastasis Aristoteles Camillo To cite
An experimentally-based modeling study of the effect of anti-angiogenic therapies on primary tumor kinetics for data analysis of clinically relevant animal models of metastasis Aristoteles Camillo To cite
z j 2. Cauchy s formel er værd at tænke lidt nærmere over. Se på specialtilfældet 1 dz = 2πi z
 Matematik F2 - sæt 3 af 7 blok 4 f(z)dz = 0 Hovedemnet i denne uge er Cauchys sætning (den der står i denne sides hoved) og Cauchys formel. Desuden introduceres nulpunkter og singulariteter: simple poler,
Matematik F2 - sæt 3 af 7 blok 4 f(z)dz = 0 Hovedemnet i denne uge er Cauchys sætning (den der står i denne sides hoved) og Cauchys formel. Desuden introduceres nulpunkter og singulariteter: simple poler,
Matematik F2 Opgavesæt 1
 Opgaer uge 1 I denne uge er temaet komplekse tal og komplekse funktioner af en kompleks ariabel. De første opgaer skulle gerne øge jeres fortrolighed med komplekse tal. I kan med fordel repetere de basale
Opgaer uge 1 I denne uge er temaet komplekse tal og komplekse funktioner af en kompleks ariabel. De første opgaer skulle gerne øge jeres fortrolighed med komplekse tal. I kan med fordel repetere de basale
z + w z + w z w = z 2 w z w = z w z 2 = z z = a 2 + b 2 z w
 Komplekse tal Hvis z = a + ib og w = c + id gælder z + w = (a + c) + i(b + d) z w = (a c) + i(b d) z w = (ac bd) + i(ad bc) z w = a+ib c+id = ac+bd + i bc ad, w 0 c +d c +d z a b = i a +b a +b Konjugation
Komplekse tal Hvis z = a + ib og w = c + id gælder z + w = (a + c) + i(b + d) z w = (a c) + i(b d) z w = (ac bd) + i(ad bc) z w = a+ib c+id = ac+bd + i bc ad, w 0 c +d c +d z a b = i a +b a +b Konjugation
Benyttede bøger: Introduction to Cosmology, Barbara Ryden, 2003.
 Formelsamling Noter til Astronomi 1 You can know the name of a bird in all the languages of the world, but when you re finished, you ll know absolutely nothing whatever about the bird... So let s look
Formelsamling Noter til Astronomi 1 You can know the name of a bird in all the languages of the world, but when you re finished, you ll know absolutely nothing whatever about the bird... So let s look
Sandsynlighedsregning 9. forelæsning Bo Friis Nielsen
 Sandsynlighedsregning 9. forelæsning Bo Friis Nielsen Matematik og Computer Science Danmarks Tekniske Universitet 800 Kgs. Lyngby Danmark Email: bfni@dtu.dk Dagens emner afsnit 5.3 og 5.4 Simultane kontinuerte
Sandsynlighedsregning 9. forelæsning Bo Friis Nielsen Matematik og Computer Science Danmarks Tekniske Universitet 800 Kgs. Lyngby Danmark Email: bfni@dtu.dk Dagens emner afsnit 5.3 og 5.4 Simultane kontinuerte
MATEMATIK 11 Eksamensopgaver Juni 1995 Juni 2001, 4. fjerdedel
 Juni 2000 MATEMATIK 11 Eksamensopgaver Juni 1995 Juni 2001, 4. fjerdedel Opgave 1. (a) Find den fuldstændige løsning til differentialligningen y 8y + 16y = 0. (b) Find den fuldstændige løsning til differentialligningen
Juni 2000 MATEMATIK 11 Eksamensopgaver Juni 1995 Juni 2001, 4. fjerdedel Opgave 1. (a) Find den fuldstændige løsning til differentialligningen y 8y + 16y = 0. (b) Find den fuldstændige løsning til differentialligningen
Mat H 2 Øvelsesopgaver
 Mat H 2 Øvelsesopgaver 18. marts 1998 1) dx dt + 2t 1+t x = 1 2 1+t, fuldstændig løsning. 2 2) ẋ + t 2 x = t 2, fuldstændig løsning. 3) ẋ 2tx = t, x() = 1. 4) ẋ + 1 t x = 1 t 2, t >, undersøg løsningen
Mat H 2 Øvelsesopgaver 18. marts 1998 1) dx dt + 2t 1+t x = 1 2 1+t, fuldstændig løsning. 2 2) ẋ + t 2 x = t 2, fuldstændig løsning. 3) ẋ 2tx = t, x() = 1. 4) ẋ + 1 t x = 1 t 2, t >, undersøg løsningen
Kompleks funktionsteori. Christian Berg
 Kompleks funktionsteori Christian Berg 2004 Matematisk Afdeling Universitetsparken 5 2100 København Ø c Matematisk Afdeling 2004 Forord I 1990 udarbejdede jeg noter til kompleks funktionsteori. De indgik
Kompleks funktionsteori Christian Berg 2004 Matematisk Afdeling Universitetsparken 5 2100 København Ø c Matematisk Afdeling 2004 Forord I 1990 udarbejdede jeg noter til kompleks funktionsteori. De indgik
Kursusnoter til BasisMat
 Kursusnoter til BasisMat Peter Beelen Søren Thomsen Peter Nørtoft Morten Brøns Im z=re iα z =r arg(z)=α Re e iπ + 1 = 0 INSTITUT FOR MATEMATIK OG COMPUTER SCIENCE DANMARKS TEKNISKE UNIVERSITET 2016 Indhold
Kursusnoter til BasisMat Peter Beelen Søren Thomsen Peter Nørtoft Morten Brøns Im z=re iα z =r arg(z)=α Re e iπ + 1 = 0 INSTITUT FOR MATEMATIK OG COMPUTER SCIENCE DANMARKS TEKNISKE UNIVERSITET 2016 Indhold
VIGTIG TRAFIKINFORMATION
 f ø pf I pø ø ø é I I É é I ø ø I p I y W ø w p y Æ f y ü ø ø ø pp p f f f p W y II p É c I É ü C ø ff f f f Æ p ø É y Y ø Y f y f IX C É I yø Y y ø p ø Y I ø I Æø Æ p p ø C p f I y y ø ø f f ø f y ø y
f ø pf I pø ø ø é I I É é I ø ø I p I y W ø w p y Æ f y ü ø ø ø pp p f f f p W y II p É c I É ü C ø ff f f f Æ p ø É y Y ø Y f y f IX C É I yø Y y ø p ø Y I ø I Æø Æ p p ø C p f I y y ø ø f f ø f y ø y
Pontryagin Approximations for Optimal Design of Elastic Structures
 Pontryagin Approximations for Optimal Design of Elastic Structures Jesper Carlsson NADA, KTH jesperc@nada.kth.se Collaborators: Anders Szepessy, Mattias Sandberg October 5, 2005 A typical optimal design
Pontryagin Approximations for Optimal Design of Elastic Structures Jesper Carlsson NADA, KTH jesperc@nada.kth.se Collaborators: Anders Szepessy, Mattias Sandberg October 5, 2005 A typical optimal design
 1 2 3 4 1 2 3 4 (p A ) (p B ) (p C ) 1 2, 3, 4 2, 3, 4 {2, 3, 4} 1 2 (p A ) (p B ) (p C ) d d {1, 2} (p A,p B )=0
1 2 3 4 1 2 3 4 (p A ) (p B ) (p C ) 1 2, 3, 4 2, 3, 4 {2, 3, 4} 1 2 (p A ) (p B ) (p C ) d d {1, 2} (p A,p B )=0
Note om Laplace-transformationen
 Note om Laplace-transformationen Den harmoniske oscillator omskrevet til et ligningssystem I dette opgavesæt benyttes laplacetransformationen til at løse koblede differentialligninger. Fordelen ved at
Note om Laplace-transformationen Den harmoniske oscillator omskrevet til et ligningssystem I dette opgavesæt benyttes laplacetransformationen til at løse koblede differentialligninger. Fordelen ved at
Oversigt Matematik Alfa 1, August 2002
 Oversigt [S], [LA] Nøgleord og begreber Egenvektorer, egenværdier og diagonalisering Dobbelt integral og polært koordinatskift Ortogonal projektion og mindste afstand Retningsafledt og gradient Maksimum/minimums
Oversigt [S], [LA] Nøgleord og begreber Egenvektorer, egenværdier og diagonalisering Dobbelt integral og polært koordinatskift Ortogonal projektion og mindste afstand Retningsafledt og gradient Maksimum/minimums
Matematik F2 Opgavesæt 6
 Opgave 4: Udtryk funktionen f(θ) = sin θ ved hjælp af Legendre-polynomierne på formen P l (cos θ). Dvs. find koefficienterne a l i ekspansionen f(θ) = a l P l (cos θ) l= Svar: Bemærk, at funktionen er
Opgave 4: Udtryk funktionen f(θ) = sin θ ved hjælp af Legendre-polynomierne på formen P l (cos θ). Dvs. find koefficienterne a l i ekspansionen f(θ) = a l P l (cos θ) l= Svar: Bemærk, at funktionen er
Sandsynlighedsteori
 Fordelingskatalog til Sandsynlighedsteori 1.1 + 1.2 Svend Erik Graversen August 2005 1 Dette katalog indeholder de vigtigste egenskaber ved de 6 mest almindelige diskrete fordelinger samt de 11 mest almindelige
Fordelingskatalog til Sandsynlighedsteori 1.1 + 1.2 Svend Erik Graversen August 2005 1 Dette katalog indeholder de vigtigste egenskaber ved de 6 mest almindelige diskrete fordelinger samt de 11 mest almindelige
Besvarelser til Calculus Ordinær Eksamen Juni 2017
 Besvarelser til Calculus Ordinær Eksamen - 12. Juni 2017 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 12. Juni 2017 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Reeksamen i Calculus
 Reeksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design samt Det Ingeniør- og Naturvidenskabelige Fakultet. februar 08 Dette eksamenssæt består af 8 nummererede sider med afkrydsningsopgaver.
Reeksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design samt Det Ingeniør- og Naturvidenskabelige Fakultet. februar 08 Dette eksamenssæt består af 8 nummererede sider med afkrydsningsopgaver.
/AL-BANK. World Half Marathon Championships
 / W f Cpp 1 I å f f, f f å æ* å, *: C I x, c 2013 2 IF/ W F CPIIP 2014 Wc f IF P c5 Wc f C P 5 Wc f Cp Cy y F 7 Wc f C p 7 IF Cc IF Cp 9 IF/ W f Cpp 2014 pcp 1011 pc p1213 w 15 C p w 17 IF/ W f Cpp 2014
/ W f Cpp 1 I å f f, f f å æ* å, *: C I x, c 2013 2 IF/ W F CPIIP 2014 Wc f IF P c5 Wc f C P 5 Wc f Cp Cy y F 7 Wc f C p 7 IF Cc IF Cp 9 IF/ W f Cpp 2014 pcp 1011 pc p1213 w 15 C p w 17 IF/ W f Cpp 2014
DOK DOK-facitliste 1. DOK-facitliste
 -facitliste 1 -facitliste Listens numre refererer til samlingen af supplerede -opgaver (de gamle eksamensopgaver. På listen står næsten kun facitter, og ikke tilstrækkelige svar på opgaverne. [Korrigeret
-facitliste 1 -facitliste Listens numre refererer til samlingen af supplerede -opgaver (de gamle eksamensopgaver. På listen står næsten kun facitter, og ikke tilstrækkelige svar på opgaverne. [Korrigeret
Heisenbergs usikkerhedsrelationer. Abstrakt. Hvorfor? Funktionsrum. Nils Byrial Andersen Institut for Matematik. Matematiklærerdag 2013
 Heisenbergs usikkerhedsrelationer Nils Byrial Andersen Institut for Matematik Matematiklærerdag 013 1 / 17 Abstrakt Heisenbergs usikkerhedsrelationer udtrykker at man ikke på samme tid både kan bestemme
Heisenbergs usikkerhedsrelationer Nils Byrial Andersen Institut for Matematik Matematiklærerdag 013 1 / 17 Abstrakt Heisenbergs usikkerhedsrelationer udtrykker at man ikke på samme tid både kan bestemme
Calculus Uge
 Oversigt [S], [LA] Nøgleord og begreber Egenvektorer, egenværdier og diagonalisering Dobbelt integral og polært koordinatskift Ortogonal projektion og mindste afstand Retningsafledt og gradient Maksimum/minimums
Oversigt [S], [LA] Nøgleord og begreber Egenvektorer, egenværdier og diagonalisering Dobbelt integral og polært koordinatskift Ortogonal projektion og mindste afstand Retningsafledt og gradient Maksimum/minimums
Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 2016
 Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Matematik F2 Opgavesæt 1
 Opgaer uge 1 I denne uge er temaet komplekse tal og komplekse funktioner af en kompleks ariabel. De første opgaer skulle gerne øge jeres fortrolighed med komplekse tal. I kan med fordel repetere de basale
Opgaer uge 1 I denne uge er temaet komplekse tal og komplekse funktioner af en kompleks ariabel. De første opgaer skulle gerne øge jeres fortrolighed med komplekse tal. I kan med fordel repetere de basale
GENTOFTE KOMMUNE B Y G NI NG S VÆ SE NET BYPLAN 16B
 GENTOFTE KOMMUNE B Y G NI NG S VÆ SE NET BYPLAN 16B Vedtægt for byplan 16B for en del af det mellem Strandvejen, Lille Strandvej, Kystlinien og Nordskel af ejendommene nord for Sundvænget beliggende område
GENTOFTE KOMMUNE B Y G NI NG S VÆ SE NET BYPLAN 16B Vedtægt for byplan 16B for en del af det mellem Strandvejen, Lille Strandvej, Kystlinien og Nordskel af ejendommene nord for Sundvænget beliggende område
Komplekse tal. enote 29. 29.1 Indledning
 enote 29 1 enote 29 Komplekse tal I denne enote introduceres og undersøges talmængden C, de komplekse tal. Da C betragtes som en udvidelse af R forudsætter enoten almindeligt kendskab til de reelle tal,
enote 29 1 enote 29 Komplekse tal I denne enote introduceres og undersøges talmængden C, de komplekse tal. Da C betragtes som en udvidelse af R forudsætter enoten almindeligt kendskab til de reelle tal,
Tillæg til Lokalplan nr For boligbebyggelsen Røde Vejrmølle Parken. Miljø- og Teknikforvaltningen. Albertslund Kommune
 Miljø- og Teknikforvaltningen Albertslund Kommune Tillæg til Lokalplan nr. 18.5.1 www.albertslund.dk albertslund@albertslund.dk T 43 68 68 68 F 43 68 69 28 For boligbebyggelsen Røde Vejrmølle Parken Hvad
Miljø- og Teknikforvaltningen Albertslund Kommune Tillæg til Lokalplan nr. 18.5.1 www.albertslund.dk albertslund@albertslund.dk T 43 68 68 68 F 43 68 69 28 For boligbebyggelsen Røde Vejrmølle Parken Hvad
Foreningens navn er Grundejerforeningen Kærlodden nr. 5-161, Ballerup Kommune
 1 Navn og hjemsted Foreningens navn er Grundejerforeningen Kærlodden nr. 5-161, Ballerup Kommune 2 Område og medlemmer Foreningen omfatter ejere af følgende matr. nr. 3 ha, 3 hb, 3 hc, 3 hd, 3 he, 3 hf,
1 Navn og hjemsted Foreningens navn er Grundejerforeningen Kærlodden nr. 5-161, Ballerup Kommune 2 Område og medlemmer Foreningen omfatter ejere af følgende matr. nr. 3 ha, 3 hb, 3 hc, 3 hd, 3 he, 3 hf,
Nøgleord og begreber Separable ligninger 1. ordens lineær ligning August 2002, opgave 7 Rovdyr-Byttedyr system 1. ordens lineært system Opgave
 Oversigt [S] 7.3, 7.4, 7.5, 7.6; [LA] 14, 15 Nøgleord og begreber Separable ligninger 1. ordens lineær ligning August 2002, opgave 7 Rovdyr-Byttedyr system 1. ordens lineært system Opgave Calculus 2-2005
Oversigt [S] 7.3, 7.4, 7.5, 7.6; [LA] 14, 15 Nøgleord og begreber Separable ligninger 1. ordens lineær ligning August 2002, opgave 7 Rovdyr-Byttedyr system 1. ordens lineært system Opgave Calculus 2-2005
Besvarelse til eksamen i Matematik F2, 2012
 Besvarelse til eksamen i Matematik F2, 202 Partiel besvarelse - har ikke inkluderet alle detaljer! Med forbehold for tastefejl. Opgave Find og bestem typen af alle singulariteter for følgende funktioner:
Besvarelse til eksamen i Matematik F2, 202 Partiel besvarelse - har ikke inkluderet alle detaljer! Med forbehold for tastefejl. Opgave Find og bestem typen af alle singulariteter for følgende funktioner:
Prøveeksamen i Calculus
 Prøveeksamen i Calculus Første Studieår ved Det Teknisk-Naturvidenskabelige Fakultet og Det Sundhedsvidenskabelige Fakultet Marts 6 Dette eksamenssæt består af 9 nummererede sider med 4 afkrydsningsopgaver.
Prøveeksamen i Calculus Første Studieår ved Det Teknisk-Naturvidenskabelige Fakultet og Det Sundhedsvidenskabelige Fakultet Marts 6 Dette eksamenssæt består af 9 nummererede sider med 4 afkrydsningsopgaver.
Bilag 2 - Spildevandsplan 2011-2021
 Bilag 2 - Spildevandsplan 2011-2021 Alle eksisterende ejendomme på følgende matrikler skal separatkloakeres Arninge 4c Ore By, Arninge 2016-2021 Arninge 4e Ore By, Arninge 2016-2021 Arninge 4f Ore By,
Bilag 2 - Spildevandsplan 2011-2021 Alle eksisterende ejendomme på følgende matrikler skal separatkloakeres Arninge 4c Ore By, Arninge 2016-2021 Arninge 4e Ore By, Arninge 2016-2021 Arninge 4f Ore By,
Svar på opgave 336 (Januar 2017)
 Svar på opgave 6 (Januar 07) Opgave: De komplekse tal a, b og c opfylder ligningssystemet Vis, at a, b og c er reelle. (a + b)(a + c) = b (b + c)(b + a) = c (c + a)(c + b) = a. Besvarelse:. metode Lad
Svar på opgave 6 (Januar 07) Opgave: De komplekse tal a, b og c opfylder ligningssystemet Vis, at a, b og c er reelle. (a + b)(a + c) = b (b + c)(b + a) = c (c + a)(c + b) = a. Besvarelse:. metode Lad
Besvarelser til Calculus Ordinær eksamen - Efterår - 8. Januar 2016
 Besvarelser til Calculus Ordinær eksamen - Efterår - 8. Januar 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har
Besvarelser til Calculus Ordinær eksamen - Efterår - 8. Januar 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har
Eksamen i Calculus. 14. juni f (x, y, z) = 1 + x 2 + y 2. x 2 + y 2 1 Hele rummet uden z aksen
 Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 14. juni 019 Opgave 1 (6 point) En
Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 14. juni 019 Opgave 1 (6 point) En
Sandsynlighedsregning 9. forelæsning Bo Friis Nielsen
 Dages eer afsit 5.3 og 5.4 Siultae kotiuerte fordeliger P(X dx,y dy f(x,ydxdy Sadsylighedsregig 9. forelæsig Bo Friis Nielse Mateatik og Coputer Sciece Daarks Tekiske Uiversitet 8 Kgs. Lygby Daark Eail:
Dages eer afsit 5.3 og 5.4 Siultae kotiuerte fordeliger P(X dx,y dy f(x,ydxdy Sadsylighedsregig 9. forelæsig Bo Friis Nielse Mateatik og Coputer Sciece Daarks Tekiske Uiversitet 8 Kgs. Lygby Daark Eail:
DesignMat Komplekse tal
 DesignMat Komplekse tal Preben Alsholm Uge 7 Forår 010 1 Talmængder 1.1 Talmængder Talmængder N er mængden af naturlige tal, 1,, 3, 4, 5,... Z er mængden af hele tal... 5, 4, 3,, 1, 0, 1,, 3, 4, 5,....
DesignMat Komplekse tal Preben Alsholm Uge 7 Forår 010 1 Talmængder 1.1 Talmængder Talmængder N er mængden af naturlige tal, 1,, 3, 4, 5,... Z er mængden af hele tal... 5, 4, 3,, 1, 0, 1,, 3, 4, 5,....
Nøgleord og begreber Analysens hovedsætning Stamfunktioner Itereret integral Test itereret integral Fubinis sætning Test Fubini Eksempler Test produkt
 Oversigt [S] 5.2, 5.3, 5.4, 2., 2.2 Nøgleord og begreber Analysens hovedsætning Stamfunktioner Itereret integral Test itereret integral Fubinis sætning Test Fubini Eksempler Test produkt Calculus - 26
Oversigt [S] 5.2, 5.3, 5.4, 2., 2.2 Nøgleord og begreber Analysens hovedsætning Stamfunktioner Itereret integral Test itereret integral Fubinis sætning Test Fubini Eksempler Test produkt Calculus - 26
Eksamen i Calculus. 14. juni f (x, y, z) = 1 + x 2 + y 2. Hele rummet uden z aksen
 Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 14. juni 019 Opgave 1 (6 point) En
Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 14. juni 019 Opgave 1 (6 point) En
Eksamen i Calculus. 14. juni f (x, y, z) = 1 + x 2 + y 2. x 2 + y 2 1 Hele rummet uden z aksen
 Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 14. juni 19 Opgave 1 (6 point) En funktion
Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 14. juni 19 Opgave 1 (6 point) En funktion
BYPLANVEDTÆGT nr. A 1 Avedøre Hvidovre kommune
 A l BYPLANVEDTÆGT nr. A 1 Avedøre Hvidovre kommune Byplanvedtægt for et område af Avedere by, Brendbyester sogn, Glostrup kommune, omfattende *Avederegård villaby«,»storegårdens villaby«og»vesterkær«.
A l BYPLANVEDTÆGT nr. A 1 Avedøre Hvidovre kommune Byplanvedtægt for et område af Avedere by, Brendbyester sogn, Glostrup kommune, omfattende *Avederegård villaby«,»storegårdens villaby«og»vesterkær«.
Opgave 1 Opskriv følgende vinkler i radianer 180, 90, 135, 270, 60, 30.
 Opgaver Polære koordinater Opgave 1 Opskriv følgende vinkler i radianer 180, 90, 15, 70, 60, 0. Opgave Bestem sin π Opgave. Et punkt p i xy-planen er givet ved de kartesiske koordinater,. Bestem p s polære
Opgaver Polære koordinater Opgave 1 Opskriv følgende vinkler i radianer 180, 90, 15, 70, 60, 0. Opgave Bestem sin π Opgave. Et punkt p i xy-planen er givet ved de kartesiske koordinater,. Bestem p s polære
Differentialligninger. Ib Michelsen
 Differentialligninger Ib Michelsen Ikast 203 2 Indholdsfortegnelse Indholdsfortegnelse Indholdsfortegnelse...2 Ligninger og løsninger...3 Indledning...3 Lineære differentialligninger af første orden...3
Differentialligninger Ib Michelsen Ikast 203 2 Indholdsfortegnelse Indholdsfortegnelse Indholdsfortegnelse...2 Ligninger og løsninger...3 Indledning...3 Lineære differentialligninger af første orden...3
MÅLESTOKSFORHOLD HFB 2012 / 13. Målestoksforhold OP SL AG. Byggecentrum
 MÅLESTOKSFORHOLD Målestoksforhold 340 MÅLEENHEDER Måleenheder Omsætning: Gl. dansk mål metermål gl. engelsk mål (= amerikansk mål). Se også: Målesystemer og enheder. Gl. dansk mål Metermål Gl. engelsk
MÅLESTOKSFORHOLD Målestoksforhold 340 MÅLEENHEDER Måleenheder Omsætning: Gl. dansk mål metermål gl. engelsk mål (= amerikansk mål). Se også: Målesystemer og enheder. Gl. dansk mål Metermål Gl. engelsk
MATEMATIK 11 Eksamensopgaver Juni 1995 Juni 2001, 3. fjerdedel
 MATEMATIK Eksamensopgaver Juni 995 Juni 200, 3. fjerdedel August 998 Opgave. Lad f : R \ {0} R betegne funktionen givet ved f(x) = ex x for x 0. (a) Find eventuelle lokale maksimums- og minimumspunkter
MATEMATIK Eksamensopgaver Juni 995 Juni 200, 3. fjerdedel August 998 Opgave. Lad f : R \ {0} R betegne funktionen givet ved f(x) = ex x for x 0. (a) Find eventuelle lokale maksimums- og minimumspunkter
UGESEDDEL 9 LØSNINGER. Sydsæter Theorem 1. Sætning om implicitte funktioner for ligningen f(x, y) = 0.
 UGESEDDEL 9 LØSNINGER Sydsæter 531 Theorem 1 Sætning om implicitte funktioner for ligningen f(x, y) = 0 Lad f(x, y) være C 1 i mængden A R n og lad (x 0, y 0 ) være et indre punkt i A hvor f(x 0, y 0 )
UGESEDDEL 9 LØSNINGER Sydsæter 531 Theorem 1 Sætning om implicitte funktioner for ligningen f(x, y) = 0 Lad f(x, y) være C 1 i mængden A R n og lad (x 0, y 0 ) være et indre punkt i A hvor f(x 0, y 0 )
