Sådan bruges skydere til at undersøge funktioner, tangenter og integraler
|
|
|
- Frans Steffensen
- 9 år siden
- Visninger:
Transkript
1 Sådan bruges skydere til at undersøge funktioner, tangenter og integraler Freyja Hreinsdóttir University of Iceland 1 Indledning I mange lærebøger om differentiering er der øvelser af den slags, hvor den studerende bliver bedt om at finde ligningen for tangenten til grafen for en given funktion ved en given værdi, f.eks. x = 1. Disse opgaver løses sædvanligvis ved at differentiere funktionen, finde værdien af differentialkvotienten ved en given -værdi, f.eks., for at finde hældningen for tangenten og derefter finde ligningen for en linje gennem det givne punkt f.eks. Software som GeoGebra eller en grafregner er virkelig nyttige redskaber i sådanne situationer for at kontrollere, om det udregnede svar giver mening, og også for at forbinde de algebraiske beregninger, der lige er lavet, til det faktiske geometriske objekt, der er fundet frem til. Opgaven kan løses på to måder i GeoGebra: ved at udregne differentialkvotienten og dennes værdi eller ved at bruge tangentværktøjet. Differentialkvotienten kan udregnes ved at skrive Derivative eller i indtastningsfeltet og dens værdi ved en given -værdi ved at skrive f.eks. i indtastningsfeltet. Man kan også bruge tangentværktøjet for at få tangenten direkte på et bestemt punkt. Hvis det gøres på den måde, skal man først definere punktet på grafen for funktionen ved at skrive f.eks. i indtastningsfeltet eller bruge pegeværktøjet og klikke på grafen for funktionen. Fig. 1 Graf for en funktion med to af dens tangenter
2 GeoGebra kan give ekstremværdierne for polynomier og kan udregne numeriske yderpunkter for andre funktioner, hvis der opgives et interval (kommandoen er Extremum), og der er også en kommando, der giver punkterne for polynomiers vendepunkt (InflectionPoint). En anden opgavetype kan f.eks. være: Hældningen af tangenten til i punktet er. Find værdien af a. Denne type opgave kan kun løses med algebra, dvs. den studerende differentierer funktionen, erstatter værdien af x med og løser for få værdien af a: hvilket giver, så når opgaven er omdannet til en spørgsmål inden for algebra, viser det sig ofte, at det ikke er nødvendigt at lave en graf over funktionen eller kontrollere svaret. De fleste matematikbøger indeholder også mere komplicerede opgaver af samme type, der omfatter placering af relative minima og maksima, vendepunkter, integraler mv. Det antages i de fleste tilfælde, at udregningerne laves i hånden, og at opgaven konverteres til algebra, dvs. udregning af ligninger. Fokus er snarere på algebra fremfor den faktiske udformning af funktionen. Nedenfor er en beskrivelse af, hvor man kan bruge GeoGebra til at løse den slags opgaver med en mere grafisk tilgang. Mange af de opgaver, der er set på, stammer fra materiale fra et gymnasium i Island [3]. 2 Brug af skydere Det er ved at bruge GeoGebra meget nemt at undersøge, hvad der sker, når man ændrer værdien af et (eller flere) parametre, som optræder i definitionen af en funktion som den ovenfor. Et sådant parameter defineres ved at vælge skyderværktøjet Derefter åbnes et lille vindue: og klikke på visningen Graphics view. Fig. 2 Dette vindue bruges til at indstille værdien for intervallet af parametret mv. Eksemplet ovenfor løses ved at oprette en skyder a og derefter definere funktionen ovenfor ved at skrive i indtastningsfeltet. For at GeoGebra kan forstå, skal man enten skrive eller.
3 Fig. 3 Funktionen f(x) med den oprindelige værdi på [?] I figuren ovenfor blev først skyder a defineret og derefter funktionen. Derefter defineres punktet i indtastningsfeltet (det betegnes A), og tangentværktøjet bruges for at få tangenten til i det punkt. Nu bruges hældningsværktøjet for at markere tangentens hældning. Den ønskede værdi af findes ganske enkelt ved at flytte skyderen, til værdien af hældningen er. Fig. 4 Værdien giver den ønskede hældning Opgave: Grafen for funktionen har et minimum ved punktet og går gennem punktet. Find værdien af og ved at bruge skyder i GeoGebra (man skal ændre det interval, som er defineret udfra. Dette gøres ved at højreklikke på skyderen og vælge Object Egenskaber).
4 Opgave: Der er en given funktion. Tangenten til i punktet er vinkelret på linjen. Find værdien af og med skyderne i GeoGebra. Bemærk: Overvej, i hvilken rækkefølge skydernes værdi skal ændres. Fig. 5 Grafen for med en tangent gennem punktet. Linjen sammen med en vinkelret linje, der går gennem punktet [?] 3 3.-grads polynomium Opgaven nedenfor er fra et opgaveark, der blev udleveret til gymnasiestuderende [3]. Det antages, at de studerende løser det ved at bruge algebra efter differentiering. Formålet er at finde et 3.-grads polynomium, der opfylder følgende betingelser: Funktionen har et minimum ved. og dens graf har et vendepunkt ved. Nedenfor er en række trin, som man kan gennemgå for at løse denne opgave med skydere i GeoGebra. 1. Definer tre skyder, og. Definer 3.-grads polynomiet i indtastningsfeltet. Man kan gøre opgaven lidt nemmere ved at sikre sig, at skyderne kun omfatter hele tal. Dette gøres ved at højreklikke på skyderen og vælge Object egenskaber og under fanebladet Skyder sætte tilvæksten til Forsøg dig lidt frem med skyderne og prøv at finde værdier, så funktionen opfylder de givne betingelser. Læg især mærke til, hvilken virkning det har at ændre værdien af? 3. Skriv i indtastningsfeltet, højreklik på den viste graf, og vælg Properties. Skift farve på grafen for, så det er nemmere at skelne den fra grafen for. Skriv i indtastningsfeltet, og vælg en tredje farve til den fremkomne graf.
5 4. Udskift værdien af, og læg mærke til den virkning, det har på grafen for [?]. 5. Udskift værdien af, og læg mærke til den virkning, det har på grafen for. 6. Det er antaget, at f har et vendepunkt ved. Hvad siger det os om grafen for? Kan der findes en værdi på skyderen, der opfylder denne betingelse? 7. Det er antaget, at har et minimum ved. Hvad siger det om grafen for? Kan der findes en værdi på skyderen, der opfylder denne betingelse? Bemærk, at det måske er nødvendigt at ændre indstillingerne for skyderen. Det gøres ved at højreklikke på og vælge Properties. Grafen for f skulle nu have den ønskede facon, men værdien for d, der giver den rigtige placering af grafen, skal stadig findes. 8. Definer punktet i indtastningsfeltet. Udskift værdien af, til grafen for går gennem punktet. Hvis det er svært at se grafisk, kan man skrive i indtastningsfeltet for at få en nøjagtig værdi (i algebravinduet) og derefter flytte, til værdien er. 9. De rigtige værdier for b, c og d er nu fundet, og ligningen for funktionen skulle nu være i algebravinduet. Fig. 6 Løsningen på opgaven ovenfor Opgave: Hvis nu funktionen skal ændres, så vendepunktet er ved, hvilken skyder skal der så arbejdes med for at opnå det?
6 Opgave: Hvad nu, hvis vendepunktet ifølge de nye oplysninger er ved? Opgave: Kan værdierne på skyderne ændres, så f(x) ikke har nogen ekstrema? Hvordan? Opgave: Kan værdierne på skyderne ændres, så f(x) ikke har noget vendetangenpunkt? Hvordan? En traditionel måde at løse den oprindelige opgave på ville være at differentiere to gange og derefter bruge oplysningen om vendepunktet til at få ligningen, oplysningen om minimum til at få, og til sidst har man, eftersom er på grafen. Opgave: Definer en skyder mere, og redefiner polynomiet som. Opsæt ligningerne (med blyant og papir), som man får, hvis denne funktion skal opfylde ovenstående forudsætninger. Det skulle nu give ligninger med ubekendte, så der er en gruppe funktioner, der opfylder forudsætningerne. Kan parametrene og redefineres i forhold til for at få alle 3.-grads funktioner, der opfylder forudsætningerne? Opgave: Lav en tilsvarende opgave for et 4.-grads polynomium. Opgave: Lav tilsvarende opgaver med andre funktionstyper, f.eks. eksponentielle og logaritmiske funktioner, trigonometriske funktioner mv. 4 Opgaver med denne løsningsmetode Ikke alle opgaver af denne type er nemme at løse. Hvis man prøver løse en tilsvarende opgave: Find værdien af a, så opfylder, på samme måde, får man ikke løsningen så nemt som i de foregående eksempler. Når man begynder at gøre det, der blev gjort før, kan man se, at det ikke er så nemt at få en hældning med nøjagtigt værdien, dvs. hældningen hopper mellem store og små værdier. Det er derfor nemmere at klikke på punktet på skyderen og bruge piletasterne på tastaturet for at ændre værdien på skyderen. Når det gøres, ses det, at hældningen hopper mellem værdier, der er lidt større og mindre end. Det er derfor en god ide at indstille skyderen mere præcist. Højreklik på for at gøre det, og vælg Object properties, hvorefter stigningen sættes til. Nu skal det selvfølgelig sikres, at GeoGebra bruger nok decimaler. Det gøres under Options, og derefter vælges Rounding. Med denne stigning ses det, at giver hældningen, og giver hældningen. Den korrekte værdi af er derfor et sted mellem de to.
7 Fig. 7 Ændring af skyderens stigning Opgave: Prøv at forklare, hvad der sker. Tip: Løs opgaven med algebra. Opgave: Lav stigningen endnu mindre, og prøv at løse opgaven. Hvis man er tilstrækkeligt tålmodig til at arbejde med opgaven med endnu flere decimaler og mindre stigninger, skulle man til sidst få det resultat, at ser ud til at komme meget tæt på de ønskede værdier for hældningen. Tallet ser ud til at være tæt på en periodisk decimalbrøk, som kan konverteres til fraktionen, som er lige netop den løsning, man får ved at løse opgaven med algebra. 5 Newtons lov om køling Ifølge Newtons lov om køling er ændres temperaturen på en genstand sig proportionalt med forskellen i temperaturen på genstanden og det omgivende medium. Det giver differentialligningen, hvor T er temperaturen på genstanden, er temperaturen på det omgivende medium, og k er en konstant. Denne ligning har løsningen, hvor c er en konstant. Så hvis en kop kaffe med en temperatur på placeres i et rum ved ( ), og kaffen 5 minutter senere har temperaturen, kan man bruge de informationer til at finde værdierne for c og k og således få en model, der vil hjælpe en med at vurdere, hvornår kaffen kan drikkes (f.eks. ved ). Denne type opgaver løses i reglen med algebra, dvs. man sætter informationerne ind i en formel for at få ligninger, der skal løses: Man får derfor temperaturen Når t = 0, fås, så c = 75, og formlen er. Når t = 5, fås, hvilket giver [?] ( ), og det kan bruges til at finde ud af, hvornår kaffen har (i løbet af ca. 11 minutter). Det er nemt at tegne et billede af det i GeoGebra:
8 Fig. 8 Afkøling af kaffe I stedet for at beregne k ovenfor, kunne man have oprettet en skyder for k og derefter ændret dens værdi, til kurven ville gå igennem [?] Man kan gøre opgaven mere interessant ved at variere informationerne med skyderen. Der er i figuren ovenfor en skyder (selvom den ikke blev brugt), men det giver ikke rigtigt mening kun at ændre dens værdi, fordi informationen om kaffens temperatur efter 5 minutter så også skulle ændres samt værdien af k (hvis er mindre end, vil kaffens temperatur være mindre end i løbet af 5 minutter). Der skal bruges tre skydere mere, for temperaturen på genstanden i begyndelsen, for information om temperaturen efter m minutter og endelig en skyder m for minutter. Det er nemt at nedskrive en formel for k i forhold til de givne parametre og skrive den i indtastningsfeltet i GeoGebra: ( ) Opgave: Læg informationerne ovenfor ind i GeoGebra. Antag nu, at kaffekoppen sættes i vindueskarmen, hvor temperaturen er, og efter kun 3 minutter er temperaturen nede på. Hvornår kan kaffen drikkes? Opgave: Brug modellen ovenfor igen for afkøling af en dåsecola, der fra starten har rumtemperatur. Køleskabstemperaturen er, og den ideelle temperatur for en cola er (det er selvfølgelig en smagssag). Foretag nogle antagelser for værdierne for m og (man kan evt. eksperimentere med det og sammenligne med virkeligheden), og find ud af, hvor længe colaen skal blive i køleskabet. Prøv nu at udskifte køleskabet med fryseren ( ), og løs opgaven ud fra det. Læg begge grafer ind i samme grafiske visning for at kunne sammenligne. 5 Skydere og integration Enkle opgaver inden for integration kan løses direkte i GeoGebra, dvs. man kan definere en funktion og bruge kommandoen Integral[f(x)] for at få en primitiv funktion og kommandoen Integral[ f(x), a, b] for at få den bestemte integral fra a til b. Hvis man har to funktioner og, giver Integralmellem[f(x), g(x), a, b] integralen fra a til b.
9 I denne forbindelse bruges der typisk skydere til at vise, hvordan hhv. størsteværdien og mindsteværdien nærmer sig værdien af integralen, når antallet af intervaller øges. Fig. 9 Største- og mindsteværdier og integralen for en funktion Man kan også bruge skydere til at definere de dynamiske intervaller for integration. Fig. 10 Integrering Dette kan være nyttigt, når man skal studere visse problemer inden for integration. Der er f.eks. givet en funktion, og man skal besvare spørgsmålet, over hvilket interval er integralen af lig med et bestemt tal. En sådan opgave vil som regel blive løst ved at integrere, udskifte grænserne og og derefter løse opgaven. Med skyderne og kan man få GeoGebra til at beregne integralen og derefter ændre værdierne og, til man har den ønskede værdi. Nedenfor er en opgave fra en matematikbog af Greenwell, Ritchey og Lial [2]:
10 En sø begynder at blive forurenet på et tidspunkt er givet af formlen [?] med en hastighed på (i gallons pr. time), der hvor [?] er tiden i timer. Samtidigt begynder et rensefilter at fjerne forureningen med en hastighed på så længe, søen er forurenet. Opgaven er nu at a) finde mængden af forurening efter timer, b) bruge en grafisk regnemaskine til at finde tidspunkt, hvor den hastighed, som forureningen kommer til søen med, er lig med den hastighed, som forureningen fjernes med, c) finde mængden af forurening i søen på det tidspunkt, der blev fundet under punkt b, og d) finde det tidspunkt, hvor al forureningen er fjernet fra søen. Fig. 11 Del a og b af forureningsopgaven Del a løses ved at integrere f(x) g(x) fra 0 til 12 og del b ved at finde skæringspunktet for de to grafer. Del c løses ved at integrere fra 0 til 25, hvilket giver 105 gallon forurening. Efter t = 25 timer oprenses forureningen hurtigere, end den foregår, så forureningsmængden nedsættes. Der er f.eks. ved t = 30 timer en forurening på 100 gallon. For at finde ud af hvornår al forureningen er oprenset, skal man finde den øverste grænse L af integralen, således at [?] ( )
11 Dette kan selvfølgelig løses ved at integrere funktionen i hånden og løse den for L, men det er ganske praktisk at bruge en skyder her. Dvs. der defineres en skyder L, integralen fra 0 til L beregnes, og skyderen flyttes, til man kommer til et svar, der er tilstrækkeligt tæt på 0. Fig. 12 Efter 48 timer har oprensningen indhentet forureningen og oprenset den ophobede forurening Opgave: Løs opgaven ovenfor ud fra den antagelse, at forureningshastigheden er dobbelt så hurtig. Opgave: Hvis det antages, at oprensningshastigheden er lineær, hvad skal den så være, for at situationen kan komme under kontrol på mindre end 24 timer? (Tip: definer en skyder for koefficienten g(x).) Referencer [1] GeoGebra, kan downloades fra [2] Greenwell, R. N., Ritchey, N.P. og Lial, M.L. (2003), Calculus for the Life Sciences, USA: Pearson Education. [3] Stærðfræði 403, Menntaskólinn við Hamrahlíð (2010).
Sådan bruges skydere til at undersøge funktioner,
 Sådan bruges skydere til at undersøge funktioner, tangenter og integraler Freyja In optics Hreinsdóttir when it comes down to show the path of rays of light through glass, lenses or systems of University
Sådan bruges skydere til at undersøge funktioner, tangenter og integraler Freyja In optics Hreinsdóttir when it comes down to show the path of rays of light through glass, lenses or systems of University
Differentialregning. Ib Michelsen
 Differentialregning Ib Michelsen Ikast 2012 Forsidebilledet Tredjegradspolynomium i blåt med rød tangent Version: 0.02 (18-09-12) Denne side er (~ 2) Indholdsfortegnelse Introduktion...5 Definition af
Differentialregning Ib Michelsen Ikast 2012 Forsidebilledet Tredjegradspolynomium i blåt med rød tangent Version: 0.02 (18-09-12) Denne side er (~ 2) Indholdsfortegnelse Introduktion...5 Definition af
Når eleverne skal opdage betydningen af koefficienterne i udtrykket:
 Den rette linje og parablen GeoGebra er tænkt som et dynamisk geometriprogram, som både kan anvendes til euklidisk og analytisk geometri Eksempel Tegn linjen med ligningen: Indtast ligningen i Input-feltet.
Den rette linje og parablen GeoGebra er tænkt som et dynamisk geometriprogram, som både kan anvendes til euklidisk og analytisk geometri Eksempel Tegn linjen med ligningen: Indtast ligningen i Input-feltet.
Differential- ligninger
 Differential- ligninger Et oplæg 2007 Karsten Juul Dette hæfte er tænkt brugt som et oplæg der kan gennemgås før man går i gang med en lærebogs fremstilling af emnet differentialligninger Læreren skal
Differential- ligninger Et oplæg 2007 Karsten Juul Dette hæfte er tænkt brugt som et oplæg der kan gennemgås før man går i gang med en lærebogs fremstilling af emnet differentialligninger Læreren skal
Introduktion til Laplace transformen (Noter skrevet af Nikolaj Hess-Nielsen sidst revideret marts 2013)
 Introduktion til Laplace transformen (oter skrevet af ikolaj Hess-ielsen sidst revideret marts 23) Integration handler ikke kun om arealer. Tværtimod er integration basis for mange af de vigtigste værktøjer
Introduktion til Laplace transformen (oter skrevet af ikolaj Hess-ielsen sidst revideret marts 23) Integration handler ikke kun om arealer. Tværtimod er integration basis for mange af de vigtigste værktøjer
Newton-Raphsons metode
 Newton-Raphsons metode af John V. Petersen Indhold Indledning: Numerisk analyse og Newton-Raphsons metode... 2 Udlede Newtons iterations formel... 2 Sætning 1 Newtons metode... 4 Eksempel 1 konvergens...
Newton-Raphsons metode af John V. Petersen Indhold Indledning: Numerisk analyse og Newton-Raphsons metode... 2 Udlede Newtons iterations formel... 2 Sætning 1 Newtons metode... 4 Eksempel 1 konvergens...
Matematik B. Anders Jørgensen
 Matematik B Anders Jørgensen Løste opgaver: Juni 2015 Dette opgavesæt er givet til FriViden Dette opgavesæt blev lavet til en terminsprøve d. 7. april af Anders Jørgensen, VUC Vestsjælland Syd Karakteren
Matematik B Anders Jørgensen Løste opgaver: Juni 2015 Dette opgavesæt er givet til FriViden Dette opgavesæt blev lavet til en terminsprøve d. 7. april af Anders Jørgensen, VUC Vestsjælland Syd Karakteren
i x-aksens retning, så fås ). Forskriften for g fås altså ved i forskriften for f at udskifte alle forekomster af x med x x 0
 BAndengradspolynomier Et polynomium er en funktion på formen f ( ) = an + an + a+ a, hvor ai R kaldes polynomiets koefficienter. Graden af et polynomium er lig med den højeste potens af, for hvilket den
BAndengradspolynomier Et polynomium er en funktion på formen f ( ) = an + an + a+ a, hvor ai R kaldes polynomiets koefficienter. Graden af et polynomium er lig med den højeste potens af, for hvilket den
Integralregning med TI-Interactive! Stamfunktioner Integraler Arealer Jan Leffers (2005)
 Integralregning med TI-Interactive! Stamfunktioner Integraler Arealer Jan Leffers (005) Indholdsfortegnelse Indholdsfortegnelse... Stamfunktion og integralregning...3 Numerisk integration...3 Areal under
Integralregning med TI-Interactive! Stamfunktioner Integraler Arealer Jan Leffers (005) Indholdsfortegnelse Indholdsfortegnelse... Stamfunktion og integralregning...3 Numerisk integration...3 Areal under
Anvendelse af matematik til konkrete beregninger
 Anvendelse af matematik til konkrete beregninger ved J.B. Sand, Datalogisk Institut, KU Praktisk/teoretisk PROBLEM BEREGNINGSPROBLEM og INDDATA LØSNINGSMETODE EVT. LØSNING REGNEMASKINE Når man vil regne
Anvendelse af matematik til konkrete beregninger ved J.B. Sand, Datalogisk Institut, KU Praktisk/teoretisk PROBLEM BEREGNINGSPROBLEM og INDDATA LØSNINGSMETODE EVT. LØSNING REGNEMASKINE Når man vil regne
Opgave 1 10. Opgave 2 Andengradsligningen løses, idet. Opgave 3. 11 er en løsning til ligningen, da:
 7. marts 0 FVU AVU HF X FAG : Matematik B ark nr. antal ark 8 Opgave 0 a b 5 a b 5 = b 3 er en løsning til ligningen, da: = 9 = 3 Opgave Andengradsligningen løses, idet a = b = 3 c = 4 d (diskriminanten)
7. marts 0 FVU AVU HF X FAG : Matematik B ark nr. antal ark 8 Opgave 0 a b 5 a b 5 = b 3 er en løsning til ligningen, da: = 9 = 3 Opgave Andengradsligningen løses, idet a = b = 3 c = 4 d (diskriminanten)
Eksponentielle funktioner for C-niveau i hf
 Eksponentielle funktioner for C-niveau i hf 2017 Karsten Juul Procent 1. Procenter på en ny måde... 1 2. Bestem procentvis ændring... 2 3. Bestem begyndelsesværdi... 2 4. Bestem slutværdi... 3 5. Vækstrate...
Eksponentielle funktioner for C-niveau i hf 2017 Karsten Juul Procent 1. Procenter på en ny måde... 1 2. Bestem procentvis ændring... 2 3. Bestem begyndelsesværdi... 2 4. Bestem slutværdi... 3 5. Vækstrate...
Grafværktøjer til GeoMeter Grafværktøjer Hjælp Grafværktøjer.gsp Grafværktøjer
 Grafværktøjer til GeoMeter Bjørn Felsager, Haslev Gymnasium & HF, 2003 Når man installerer GeoMeter på sin maskine følger der en lang række specialværktøjer med. Men det er også muligt at skræddersy sine
Grafværktøjer til GeoMeter Bjørn Felsager, Haslev Gymnasium & HF, 2003 Når man installerer GeoMeter på sin maskine følger der en lang række specialværktøjer med. Men det er også muligt at skræddersy sine
Differentialregning. Et oplæg Karsten Juul L P
 Differentialregning Et oplæg L P A 2009 Karsten Juul Til eleven Dette hæfte kan I bruge inden I starter på differentialregningen i lærebogen Det meste af hæftet er små spørgsmål med korte svar Spørgsmålene
Differentialregning Et oplæg L P A 2009 Karsten Juul Til eleven Dette hæfte kan I bruge inden I starter på differentialregningen i lærebogen Det meste af hæftet er små spørgsmål med korte svar Spørgsmålene
Opstilling af model ved hjælp af differentialkvotient
 Opstilling af model ved hjælp af differentialkvotient N 0,35N 0, 76t 2010 Karsten Juul Til eleven Dette hæfte giver dig mulighed for at arbejde sådan med nogle begreber at der er god mulighed for at der
Opstilling af model ved hjælp af differentialkvotient N 0,35N 0, 76t 2010 Karsten Juul Til eleven Dette hæfte giver dig mulighed for at arbejde sådan med nogle begreber at der er god mulighed for at der
Differential- regning
 Differential- regning del f(5) () f f () f ( ) I 5 () 006 Karsten Juul Indhold 6 Kontinuert funktion 7 Monotoniforhold7 8 Lokale ekstrema44 9 Grænseværdi5 Differentialregning del udgave 006 006 Karsten
Differential- regning del f(5) () f f () f ( ) I 5 () 006 Karsten Juul Indhold 6 Kontinuert funktion 7 Monotoniforhold7 8 Lokale ekstrema44 9 Grænseværdi5 Differentialregning del udgave 006 006 Karsten
Løsningsforslag MatB December 2013
 Løsningsforslag MatB December 2013 Opgave 1 (5 %) a) En linje l går gennem punkterne: P( 2,3) og Q(2,1) a) Bestem en ligning for linjen l. Vi ved at linjen for en linje kan udtrykkes ved: y = αx + q hvor
Løsningsforslag MatB December 2013 Opgave 1 (5 %) a) En linje l går gennem punkterne: P( 2,3) og Q(2,1) a) Bestem en ligning for linjen l. Vi ved at linjen for en linje kan udtrykkes ved: y = αx + q hvor
Pointen med Differentiation
 Pointen med Differentiation Frank Nasser 20. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk:
Pointen med Differentiation Frank Nasser 20. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk:
Maple. Skærmbilledet. Vi starter med at se lidt nærmere på opstartsbilledet i Maple. Værktøjslinje til indtastningsområdet. Menulinje.
 Maple Dette kapitel giver en kort introduktion til hvordan Maple 12 kan benyttes til at løse mange af de opgaver, som man bliver mødt med i matematiktimerne på HHX. Skærmbilledet Vi starter med at se lidt
Maple Dette kapitel giver en kort introduktion til hvordan Maple 12 kan benyttes til at løse mange af de opgaver, som man bliver mødt med i matematiktimerne på HHX. Skærmbilledet Vi starter med at se lidt
Numeriske metoder - til løsning af differentialligninger - fra borgeleo.dk
 Numeriske metoder - til løsning af differentialligninger - fra borgeleo.dk Eksakte løsninger: fuldstændig løsning og partikulær løsning Mange differentialligninger kan løses eksakt. Fx kan differentialligningen
Numeriske metoder - til løsning af differentialligninger - fra borgeleo.dk Eksakte løsninger: fuldstændig løsning og partikulær løsning Mange differentialligninger kan løses eksakt. Fx kan differentialligningen
Matematik A-niveau - bestemmelse af monotoniforhold (EKSEMPEL 1): Side 94 opgave 11:
 Matematik A-niveau - bestemmelse af monotoniforhold (EKSEMPEL 1): Side 94 opgave 11: Opgave a) Ligningen for tangenten bestemmes. Dog defineres funktionen. Tangent-formlen er pr. definition. (1) Altså
Matematik A-niveau - bestemmelse af monotoniforhold (EKSEMPEL 1): Side 94 opgave 11: Opgave a) Ligningen for tangenten bestemmes. Dog defineres funktionen. Tangent-formlen er pr. definition. (1) Altså
Opgaver med hjælp Funktioner 2 - med Geogebra
 Opgaver med hjælp Funktioner 2 - med Geogebra Nulpunkter, monotoniforhold og ekstrema Formålet med denne note er at tegne os frem til nulpunkter, monotoniforhold og ekstrema for en funktion ved hjælp af
Opgaver med hjælp Funktioner 2 - med Geogebra Nulpunkter, monotoniforhold og ekstrema Formålet med denne note er at tegne os frem til nulpunkter, monotoniforhold og ekstrema for en funktion ved hjælp af
Opgave 1 - Lineær Funktioner. Opgave 2 - Funktioner. Opgave 3 - Tredjegradsligning
 Sh*maa03 1508 Matematik B->A, STX Anders Jørgensen, delprøve 1 - Uden hjælpemidler Følgende opgaver er regnet i hånden, hvorefter de er skrevet ind på PC. Opgave 1 - Lineær Funktioner Vi ved, at år 2001
Sh*maa03 1508 Matematik B->A, STX Anders Jørgensen, delprøve 1 - Uden hjælpemidler Følgende opgaver er regnet i hånden, hvorefter de er skrevet ind på PC. Opgave 1 - Lineær Funktioner Vi ved, at år 2001
Funktioner. 3. del Karsten Juul
 Funktioner 3. del 019 Karsten Juul Funktioner 3. del, 019 Karsten Juul 1/9-019 Nyeste version af dette hæfte kan downloades fra http://mat1.dk/noter.htm. Hæftet må benyttes i undervisningen hvis læreren
Funktioner 3. del 019 Karsten Juul Funktioner 3. del, 019 Karsten Juul 1/9-019 Nyeste version af dette hæfte kan downloades fra http://mat1.dk/noter.htm. Hæftet må benyttes i undervisningen hvis læreren
Integralregning Infinitesimalregning
 Udgave 2.1 Integralregning Infinitesimalregning Noterne gennemgår begreberne integral og stamfunktion, og anskuer dette som et redskab til bestemmelse af arealer under funktioner. Noterne er supplement
Udgave 2.1 Integralregning Infinitesimalregning Noterne gennemgår begreberne integral og stamfunktion, og anskuer dette som et redskab til bestemmelse af arealer under funktioner. Noterne er supplement
Opvarmningsopgaver. Gang parentesen ud: Forkort brøken: Gang parentesen ud: (1.5 + x) 2 (1 + x) 3. Forkort brøken. Gang parentesen ud: (x 0 + x) 3
 eks. Intro til differentialregning side 1 Opvarmningsopgaver 10. november 2012 12:58 Gang parentesen ud: Forkort brøken: Gang parentesen ud: (1.5 + x) 2 (1 + x) 3 Gang parentesen ud: Forkort brøken (x
eks. Intro til differentialregning side 1 Opvarmningsopgaver 10. november 2012 12:58 Gang parentesen ud: Forkort brøken: Gang parentesen ud: (1.5 + x) 2 (1 + x) 3 Gang parentesen ud: Forkort brøken (x
Løsninger til eksamensopgaver på A-niveau 2017
 Løsninger til eksamensopgaver på A-niveau 017 18. maj 017: Delprøven UDEN hjælpemidler Opgave 1: Alle funktionerne f, g og h er lineære funktioner (og ingen er mere lineære end andre) og kan skrives på
Løsninger til eksamensopgaver på A-niveau 017 18. maj 017: Delprøven UDEN hjælpemidler Opgave 1: Alle funktionerne f, g og h er lineære funktioner (og ingen er mere lineære end andre) og kan skrives på
APPENDIX A INTRODUKTION TIL DERIVE
 APPENDIX A INTRODUKTION TIL DERIVE z x y z=exp( x^2 0.5y^2) CAS er en fællesbetegnelse for matematikprogrammer, som foruden numeriske beregninger også kan regne med symboler og formler. Det betyder: Computer
APPENDIX A INTRODUKTION TIL DERIVE z x y z=exp( x^2 0.5y^2) CAS er en fællesbetegnelse for matematikprogrammer, som foruden numeriske beregninger også kan regne med symboler og formler. Det betyder: Computer
Grafregnerkravet på hf matematik tilvalg
 Grafregnerkravet på hf matematik tilvalg Dette dokument er en sammenskrivning af uddrag af følgende skrifter: Undervisningsvejledning nr. 21 for matematik i HF (september 1995); findes på adressen: http://us.uvm.dk/gymnasie/almen/vejledninger/undervishf/hfvej21.htm;
Grafregnerkravet på hf matematik tilvalg Dette dokument er en sammenskrivning af uddrag af følgende skrifter: Undervisningsvejledning nr. 21 for matematik i HF (september 1995); findes på adressen: http://us.uvm.dk/gymnasie/almen/vejledninger/undervishf/hfvej21.htm;
MATEMATIK B. Videooversigt
 MATEMATIK B Videooversigt 2. grads ligninger.... 2 CAS værktøj... 3 Differentialregning... 3 Eksamen... 5 Funktionsbegrebet... 5 Integralregning... 5 Statistik... 6 Vilkårlige trekanter... 7 71 videoer.
MATEMATIK B Videooversigt 2. grads ligninger.... 2 CAS værktøj... 3 Differentialregning... 3 Eksamen... 5 Funktionsbegrebet... 5 Integralregning... 5 Statistik... 6 Vilkårlige trekanter... 7 71 videoer.
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Jan 2016 - Juni 2019 Institution Hotel- og Restaurantskolen Uddannelse Fag og niveau Lærer(e) Hold EUX ernæringsassistent
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Jan 2016 - Juni 2019 Institution Hotel- og Restaurantskolen Uddannelse Fag og niveau Lærer(e) Hold EUX ernæringsassistent
Der er facit på side 7 i dokumentet. Til opgaver mærket med # er der vink eller kommentarer på side 6.
 Der er facit på side 7 i dokumentet. Til opgaver mærket med # er der vink eller kommentarer på side 6. 1. Figuren viser grafen for en funktion f. Aflæs definitionsmængde og værdimængde for f. # Aflæs f
Der er facit på side 7 i dokumentet. Til opgaver mærket med # er der vink eller kommentarer på side 6. 1. Figuren viser grafen for en funktion f. Aflæs definitionsmængde og værdimængde for f. # Aflæs f
Eksponentielle sammenhænge
 Eksponentielle sammenhænge Udgave 009 Karsten Juul Dette hæfte er en fortsættelse af hæftet "Lineære sammenhænge, udgave 009" Indhold 1 Eksponentielle sammenhænge, ligning og graf 1 Procent 7 3 Hvad fortæller
Eksponentielle sammenhænge Udgave 009 Karsten Juul Dette hæfte er en fortsættelse af hæftet "Lineære sammenhænge, udgave 009" Indhold 1 Eksponentielle sammenhænge, ligning og graf 1 Procent 7 3 Hvad fortæller
Introduktion til differentialregning 1. Jens Siegstad og Annegrethe Bak
 Introduktion til differentialregning 1 Jens Siegstad og Annegrete Bak 16. juli 2008 1 Indledning I denne note vil vi kort introduktion til differentilregning, idet vi skal bruge teorien i et emne, Matematisk
Introduktion til differentialregning 1 Jens Siegstad og Annegrete Bak 16. juli 2008 1 Indledning I denne note vil vi kort introduktion til differentilregning, idet vi skal bruge teorien i et emne, Matematisk
Kom i gang-opgaver til differentialregning
 Kom i gang-opgaver til differentialregning 00 Karsten Juul Det er kortsigtet at løse en opgave ved blot at udskifte tallene i en besvarelse af en tilsvarende opgave Dette skyldes at man så normalt ikke
Kom i gang-opgaver til differentialregning 00 Karsten Juul Det er kortsigtet at løse en opgave ved blot at udskifte tallene i en besvarelse af en tilsvarende opgave Dette skyldes at man så normalt ikke
Differentialligninger. Ib Michelsen
 Differentialligninger Ib Michelsen Ikast 203 2 Indholdsfortegnelse Indholdsfortegnelse Indholdsfortegnelse...2 Ligninger og løsninger...3 Indledning...3 Lineære differentialligninger af første orden...3
Differentialligninger Ib Michelsen Ikast 203 2 Indholdsfortegnelse Indholdsfortegnelse Indholdsfortegnelse...2 Ligninger og løsninger...3 Indledning...3 Lineære differentialligninger af første orden...3
Mujtaba og Farid Integralregning 06-08-2011
 Indholdsfortegnelse Integral regning:... 2 Ubestemt integral:... 2 Integrationsprøven:... 3 1) Integration af potensfunktioner:... 3 2) Integration af sum og Differens:... 3 3) Integration ved Multiplikation
Indholdsfortegnelse Integral regning:... 2 Ubestemt integral:... 2 Integrationsprøven:... 3 1) Integration af potensfunktioner:... 3 2) Integration af sum og Differens:... 3 3) Integration ved Multiplikation
Lineær Programmering i GeoGebra Side 1 af 8
 Lineær Programmering i GeoGebra Side 1 af 8 Grundlæggende find selv flere funktioner, fx i GG s indbyggede hjælpefunktion. Vær opmærksom på at grænsefladen i GeoGebra ændrer sig med tiden, da værktøjet
Lineær Programmering i GeoGebra Side 1 af 8 Grundlæggende find selv flere funktioner, fx i GG s indbyggede hjælpefunktion. Vær opmærksom på at grænsefladen i GeoGebra ændrer sig med tiden, da værktøjet
Matematik A STX 18. maj 2017 Vejledende løsning De første 6 opgaver løses uden hjælpemidler
 ADVARSEL! Før du anvender løsningerne, så husk at læs betingelserne for løsningerne, som du kan finde på hjemmesiden. Indeholder: Matematik A, STX 18 maj Matematik A, STX 23 maj Matematik A, STX 15 august
ADVARSEL! Før du anvender løsningerne, så husk at læs betingelserne for løsningerne, som du kan finde på hjemmesiden. Indeholder: Matematik A, STX 18 maj Matematik A, STX 23 maj Matematik A, STX 15 august
Spørgsmål Nr. 1. Spørgsmål Nr. 2
 Spørgsmål Nr. 1 TITEL: Statistik Definition af beskrivende statistik Opdeling af beskrivende statistik i grupperede observationer og ikke grupperede observationer Deskriptorerne typetal og middelværdi
Spørgsmål Nr. 1 TITEL: Statistik Definition af beskrivende statistik Opdeling af beskrivende statistik i grupperede observationer og ikke grupperede observationer Deskriptorerne typetal og middelværdi
Matematik A-niveau STX 1. juni 2010 Øvelse DELPRØVE 1 & DELPRØVE 2
 Matematik A-niveau STX 1. juni 2010 Øvelse DELPRØVE 1 & DELPRØVE 2 -----------------------------------------------------DELPRØVE 1------------------------------------------------------- Opgave 1 - Reduktion
Matematik A-niveau STX 1. juni 2010 Øvelse DELPRØVE 1 & DELPRØVE 2 -----------------------------------------------------DELPRØVE 1------------------------------------------------------- Opgave 1 - Reduktion
Fig. 1 En bue på en cirkel I Geogebra er der adskillige værktøjer til at konstruere cirkler og buer:
 Euclidean Eggs Freyja Hreinsdóttir, University of Iceland 1 Introduction Ved hjælp af et computerprogram som GeoGebra er det nemt at lave geometriske konstruktioner. Specielt er der gode værktøjer til
Euclidean Eggs Freyja Hreinsdóttir, University of Iceland 1 Introduction Ved hjælp af et computerprogram som GeoGebra er det nemt at lave geometriske konstruktioner. Specielt er der gode værktøjer til
Bedste rette linje ved mindste kvadraters metode
 1/9 Bedste rette linje ved mindste kvadraters metode - fra www.borgeleo.dk Figur 1: Tre datapunkter og den bedste rette linje bestemt af A, B og C Målepunkter og bedste rette linje I ovenstående koordinatsystem
1/9 Bedste rette linje ved mindste kvadraters metode - fra www.borgeleo.dk Figur 1: Tre datapunkter og den bedste rette linje bestemt af A, B og C Målepunkter og bedste rette linje I ovenstående koordinatsystem
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Skoleår 2019, eksamen maj / juni 2019 Institution Kolding HF og VUC Uddannelse Fag og niveau Lærer(e) Hold
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Skoleår 2019, eksamen maj / juni 2019 Institution Kolding HF og VUC Uddannelse Fag og niveau Lærer(e) Hold
Ligningsløsning som det at løse gåder
 Ligningsløsning som det at løse gåder Nedenstående er et skærmklip fra en TI-Nspirefil. Vi ser at tre kræmmerhuse og fem bolsjer balancerer med to kræmmerhuse og 10 bolsjer. Spørgsmålet er hvor mange bolsjer,
Ligningsløsning som det at løse gåder Nedenstående er et skærmklip fra en TI-Nspirefil. Vi ser at tre kræmmerhuse og fem bolsjer balancerer med to kræmmerhuse og 10 bolsjer. Spørgsmålet er hvor mange bolsjer,
χ 2 -test i GeoGebra Jens Sveistrup, Gammel Hellerup Gymnasium
 χ 2 -test i GeoGebra Jens Sveistrup, Gammel Hellerup Gymnasium Man kan nemt lave χ 2 -test i GeoGebra både goodness-of-fit-test og uafhængighedstest. Den følgende vejledning bygger på GeoGebra version
χ 2 -test i GeoGebra Jens Sveistrup, Gammel Hellerup Gymnasium Man kan nemt lave χ 2 -test i GeoGebra både goodness-of-fit-test og uafhængighedstest. Den følgende vejledning bygger på GeoGebra version
qwertyuiopåasdfghjklæøzxcvbnmqw ertyuiopåasdfghjklæøzxcvbnmqwert yuiopåasdfghjklæøzxcvbnmqwertyui Polynomier opåasdfghjklæøzxcvbnmqwertyuiopå
 qwertyuiopåasdfghjklæøzxcvbnmqw ertyuiopåasdfghjklæøzxcvbnmqwert yuiopåasdfghjklæøzxcvbnmqwertyui Polynomier opåasdfghjklæøzxcvbnmqwertyuiopå Kort gennemgang af polynomier og deres egenskaber. asdfghjklæøzxcvbnmqwertyuiopåasd
qwertyuiopåasdfghjklæøzxcvbnmqw ertyuiopåasdfghjklæøzxcvbnmqwert yuiopåasdfghjklæøzxcvbnmqwertyui Polynomier opåasdfghjklæøzxcvbnmqwertyuiopå Kort gennemgang af polynomier og deres egenskaber. asdfghjklæøzxcvbnmqwertyuiopåasd
Løsninger til eksamensopgaver på A-niveau 2019 ( ) ( )
 Løsninger til eksamensopgaver på A-niveau 019 1. maj 019: Delprøven UDEN hjælpemidler 1. maj 019 opgave 1: Man kan godt benytte substitutionsmetoden, lige store koefficienters metode eller determinantmetoden,
Løsninger til eksamensopgaver på A-niveau 019 1. maj 019: Delprøven UDEN hjælpemidler 1. maj 019 opgave 1: Man kan godt benytte substitutionsmetoden, lige store koefficienters metode eller determinantmetoden,
Graph brugermanual til matematik C
 Graph brugermanual til matematik C Forord Efterfølgende er en guide til programmet GRAPH. Programmet kan downloades gratis fra nettet og gemmes på computeren/et usb-stik. Det betyder, det også kan anvendes
Graph brugermanual til matematik C Forord Efterfølgende er en guide til programmet GRAPH. Programmet kan downloades gratis fra nettet og gemmes på computeren/et usb-stik. Det betyder, det også kan anvendes
Matematik A, STX. Vejledende eksamensopgaver
 Matematik A, STX EKSAMENSOPGAVER Vejledende eksamensopgaver 2015 Løsninger HF A-NIVEAU AF SAEID Af JAFARI Anders J., Mark Af K. & Saeid J. Anders J., Mark K. & Saeid J. Kun delprøver 2 Kun delprøve 2,
Matematik A, STX EKSAMENSOPGAVER Vejledende eksamensopgaver 2015 Løsninger HF A-NIVEAU AF SAEID Af JAFARI Anders J., Mark Af K. & Saeid J. Anders J., Mark K. & Saeid J. Kun delprøver 2 Kun delprøve 2,
PeterSørensen.dk : Differentiation
 PeterSørensen.dk : Differentiation Betydningen af ordet differentialkvotient...2 Sekant...2 Differentiable funktioner...3 Bestemmelse af differentialkvotient i praksis ved opgaveløsning...3 Regneregler:...3
PeterSørensen.dk : Differentiation Betydningen af ordet differentialkvotient...2 Sekant...2 Differentiable funktioner...3 Bestemmelse af differentialkvotient i praksis ved opgaveløsning...3 Regneregler:...3
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Institution Uddannelse Fag og niveau Lærer(e) Hold Maj-juni 2015 Skoleår 2014/2015 Thy-Mors HF & VUC Hfe Matematik,
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Institution Uddannelse Fag og niveau Lærer(e) Hold Maj-juni 2015 Skoleår 2014/2015 Thy-Mors HF & VUC Hfe Matematik,
Besvarelse af stx_081_matb 1. Opgave 2. Opgave 1 2. Ib Michelsen, 2z Side B_081. Reducer + + = + + = Værdien af
 Ib Michelsen, z Side 1 7-05-01 1 3 4 5 6 7 8 9 10 11 1 13 14 15 16 17 18 19 0 1 3 4 5 6 7 Besvarelse af stx_081_matb 1 Opgave 1 Reducer ( x + h) h( h + x) ( x h) h( h x) + + = x h xh h h x x + + = Værdien
Ib Michelsen, z Side 1 7-05-01 1 3 4 5 6 7 8 9 10 11 1 13 14 15 16 17 18 19 0 1 3 4 5 6 7 Besvarelse af stx_081_matb 1 Opgave 1 Reducer ( x + h) h( h + x) ( x h) h( h x) + + = x h xh h h x x + + = Værdien
Taylor-polynomier. John V Petersen
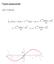 Taylor-polynomier John V Petersen Taylor-polynomier 2018 John V Petersen art-science-soul Indhold 1. Indledning... 4 2. Udledning af Sætning om Taylor polynomiet... 4 3. Sætning og Definition af Taylor
Taylor-polynomier John V Petersen Taylor-polynomier 2018 John V Petersen art-science-soul Indhold 1. Indledning... 4 2. Udledning af Sætning om Taylor polynomiet... 4 3. Sætning og Definition af Taylor
Matematik A-niveau 22. maj 2015 Delprøve 2. Løst af Anders Jørgensen og Saeid Jafari
 Matematik A-niveau 22. maj 2015 Delprøve 2 Løst af Anders Jørgensen og Saeid Jafari Opgave 7 - Analytisk Plangeometri Delopgave a) Vi starter ud med at undersøge afstanden fra punktet P(5,4) til linjen
Matematik A-niveau 22. maj 2015 Delprøve 2 Løst af Anders Jørgensen og Saeid Jafari Opgave 7 - Analytisk Plangeometri Delopgave a) Vi starter ud med at undersøge afstanden fra punktet P(5,4) til linjen
Afstande, skæringer og vinkler i rummet
 Afstande, skæringer og vinkler i rummet Frank Villa 2. maj 202 c 2008-20. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold
Afstande, skæringer og vinkler i rummet Frank Villa 2. maj 202 c 2008-20. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold
Et CAS program til Word.
 Et CAS program til Word. 1 WordMat WordMat er et CAS-program (computer algebra system) som man kan downloade gratis fra hjemmesiden www.eduap.com/wordmat/. Programmet fungerer kun i Word 2007 og 2010.
Et CAS program til Word. 1 WordMat WordMat er et CAS-program (computer algebra system) som man kan downloade gratis fra hjemmesiden www.eduap.com/wordmat/. Programmet fungerer kun i Word 2007 og 2010.
Matema10k. Matematik for hhx C-niveau. Arbejdsark til kapitlerne i bogen
 Matema10k Matematik for hhx C-niveau Arbejdsark til kapitlerne i bogen De følgende sider er arbejdsark og opgaver som kan bruges som introduktion til mange af bogens kapitler og underemner. De kan bruges
Matema10k Matematik for hhx C-niveau Arbejdsark til kapitlerne i bogen De følgende sider er arbejdsark og opgaver som kan bruges som introduktion til mange af bogens kapitler og underemner. De kan bruges
qwertyuiopåasdfghjklæøzxcvbnmqw ertyuiopåasdfghjklæøzxcvbnmqwert yuiopåasdfghjklæøzxcvbnmqwertyui opåasdfghjklæøzxcvbnmqwertyuiopå
 qwertyuiopåasdfghjklæøzxcvbnmqw ertyuiopåasdfghjklæøzxcvbnmqwert yuiopåasdfghjklæøzxcvbnmqwertyui opåasdfghjklæøzxcvbnmqwertyuiopå Polynomier Kort gennemgang af polynomier og deres asdfghjklæøzxcvbnmqwertyuiopåasd
qwertyuiopåasdfghjklæøzxcvbnmqw ertyuiopåasdfghjklæøzxcvbnmqwert yuiopåasdfghjklæøzxcvbnmqwertyui opåasdfghjklæøzxcvbnmqwertyuiopå Polynomier Kort gennemgang af polynomier og deres asdfghjklæøzxcvbnmqwertyuiopåasd
Løsninger til eksamensopgaver på A-niveau 2016
 Løsninger til eksamensopgaver på A-niveau 2016 24. maj 2016: Delprøven UDEN hjælpemidler Opgave 1: Da trekanterne er ensvinklede, er forholdene mellem korresponderende linjestykker i de to trekanter det
Løsninger til eksamensopgaver på A-niveau 2016 24. maj 2016: Delprøven UDEN hjælpemidler Opgave 1: Da trekanterne er ensvinklede, er forholdene mellem korresponderende linjestykker i de to trekanter det
Afstande, skæringer og vinkler i rummet
 Afstande, skæringer og vinkler i rummet Frank Nasser 9. april 20 c 2008-20. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her.
Afstande, skæringer og vinkler i rummet Frank Nasser 9. april 20 c 2008-20. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her.
Kapitel 3 Lineære sammenhænge
 Matematik C (må anvendes på Ørestad Gymnasium) Lineære sammenhænge Det sker tit, at man har flere variable, der beskriver en situation, og at der en sammenhæng mellem de variable. Enhver formel er faktisk
Matematik C (må anvendes på Ørestad Gymnasium) Lineære sammenhænge Det sker tit, at man har flere variable, der beskriver en situation, og at der en sammenhæng mellem de variable. Enhver formel er faktisk
Brug af TI-83. Løsning af uligheder: Andre ikke simple uligheder løses ved følgende metode - skitseret ved et eksempel : Løs uligheden
 Brug af TI-83 Løsning af andengradsligninger med TI-83 Indtast formlerne for d, og rødderne og gem dem i formellagrene u,v eller w. Gem værdierne for a, b og c i lagrene A, B og C Nedenstående display
Brug af TI-83 Løsning af andengradsligninger med TI-83 Indtast formlerne for d, og rødderne og gem dem i formellagrene u,v eller w. Gem værdierne for a, b og c i lagrene A, B og C Nedenstående display
Projektopgave 1. Navn: Jonas Pedersen Klasse: 3.4 Skole: Roskilde Tekniske Gymnasium Dato: 5/ Vejleder: Jørn Christian Bendtsen Fag: Matematik
 Projektopgave 1 Navn: Jonas Pedersen Klasse:.4 Skole: Roskilde Tekniske Gymnasium Dato: 5/9-011 Vejleder: Jørn Christian Bendtsen Fag: Matematik Indledning Jeg har i denne opgave fået følgende opstilling.
Projektopgave 1 Navn: Jonas Pedersen Klasse:.4 Skole: Roskilde Tekniske Gymnasium Dato: 5/9-011 Vejleder: Jørn Christian Bendtsen Fag: Matematik Indledning Jeg har i denne opgave fået følgende opstilling.
Løsninger til eksamensopgaver på B-niveau 2017
 Løsninger til eksamensopgaver på B-niveau 017 18. maj 017: Delprøven UDEN hjælpemidler Opgave 1: 4x 1 17 5x 4x 5x 17 1 9x 18 x Opgave : N betegner antallet af brugere af app en målt i tusinder. t angiver
Løsninger til eksamensopgaver på B-niveau 017 18. maj 017: Delprøven UDEN hjælpemidler Opgave 1: 4x 1 17 5x 4x 5x 17 1 9x 18 x Opgave : N betegner antallet af brugere af app en målt i tusinder. t angiver
11. Funktionsundersøgelse
 11. Funktionsundersøgelse Hayati Balo,AAMS Følgende fremstilling er baseret på 1. Nils Victor-Jensen,Matematik for adgangskursus, B-niveau 2, 2. udg. 11.1 Generelt om funktionsundersøgelse Formålet med
11. Funktionsundersøgelse Hayati Balo,AAMS Følgende fremstilling er baseret på 1. Nils Victor-Jensen,Matematik for adgangskursus, B-niveau 2, 2. udg. 11.1 Generelt om funktionsundersøgelse Formålet med
Differentialregning 2
 Differentialregning Hvis man ønsker mere udfordring, kan man springe de første 7 opgaver over. Opgave 1 Udregn monotoniintervallerne for funktionerne f 1 () = + 4, f () = 4 3 f 3 () = 3 6 + 9 +, f 4 ()
Differentialregning Hvis man ønsker mere udfordring, kan man springe de første 7 opgaver over. Opgave 1 Udregn monotoniintervallerne for funktionerne f 1 () = + 4, f () = 4 3 f 3 () = 3 6 + 9 +, f 4 ()
Side 1 af 10. Undervisningsbeskrivelse. Stamoplysninger til brug ved prøver til gymnasiale uddannelser. Termin Maj-juni 2009/10
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Maj-juni 2009/10 Institution Uddannelse Fag og niveau Lærer(e) Hold Handelsskolen Sjælland Syd, Vordingborg
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Maj-juni 2009/10 Institution Uddannelse Fag og niveau Lærer(e) Hold Handelsskolen Sjælland Syd, Vordingborg
Lineære sammenhænge. Udgave 2. 2009 Karsten Juul
 Lineære sammenhænge Udgave 2 y = 0,5x 2,5 2009 Karsten Juul Dette hæfte er en fortsættelse af hæftet "Variabelsammenhænge, 2. udgave 2009". Indhold 1. Lineære sammenhænge, ligning og graf... 1 2. Lineær
Lineære sammenhænge Udgave 2 y = 0,5x 2,5 2009 Karsten Juul Dette hæfte er en fortsættelse af hæftet "Variabelsammenhænge, 2. udgave 2009". Indhold 1. Lineære sammenhænge, ligning og graf... 1 2. Lineær
2 Erik Vestergaard www.matematikfysik.dk
 Erik Vestergaard www.matematikfysik.dk Erik Vestergaard www.matematikfysik.dk 3 Lineære funktioner En vigtig type funktioner at studere er de såkaldte lineære funktioner. Vi skal udlede en række egenskaber
Erik Vestergaard www.matematikfysik.dk Erik Vestergaard www.matematikfysik.dk 3 Lineære funktioner En vigtig type funktioner at studere er de såkaldte lineære funktioner. Vi skal udlede en række egenskaber
GeoGebra 3.0.0.0 Quickstart. det grundlæggende
 GeoGebra 3.0.0.0 Quickstart det grundlæggende Grete Ridder Ebbesen frit efter GeoGebra Quickstart af Markus Hohenwarter Virum, 28. februar 2009 Introduktion GeoGebra er et gratis og meget brugervenligt
GeoGebra 3.0.0.0 Quickstart det grundlæggende Grete Ridder Ebbesen frit efter GeoGebra Quickstart af Markus Hohenwarter Virum, 28. februar 2009 Introduktion GeoGebra er et gratis og meget brugervenligt
Chapter 3. Modulpakke 3: Egenværdier. 3.1 Indledning
 Chapter 3 Modulpakke 3: Egenværdier 3.1 Indledning En vektor v har som bekendt både størrelse og retning. Hvis man ganger vektoren fra højre på en kvadratisk matrix A bliver resultatet en ny vektor. Hvis
Chapter 3 Modulpakke 3: Egenværdier 3.1 Indledning En vektor v har som bekendt både størrelse og retning. Hvis man ganger vektoren fra højre på en kvadratisk matrix A bliver resultatet en ny vektor. Hvis
Matematik B-niveau 31. maj 2016 Delprøve 1
 Matematik B-niveau 31. maj 2016 Delprøve 1 Opgave 1 - Ligninger og reduktion (a + b) (a b) + b (a + b) = a 2 ab + ab b 2 + ab + b 2 = a 2 + ab Opgave 2 - Eksponentiel funktion 23 + 2x = 15 2x 2 = 8 x =
Matematik B-niveau 31. maj 2016 Delprøve 1 Opgave 1 - Ligninger og reduktion (a + b) (a b) + b (a + b) = a 2 ab + ab b 2 + ab + b 2 = a 2 + ab Opgave 2 - Eksponentiel funktion 23 + 2x = 15 2x 2 = 8 x =
Her er et spørgsmål, du måske aldrig har overvejet: kan man finde to trekanter med samme areal?
 Her er et spørgsmål, du måske aldrig har overvejet: kan man finde to trekanter med samme areal? Det er ret let at svare på: arealet af en trekant, husker vi fra vor kære folkeskole, findes ved at gange
Her er et spørgsmål, du måske aldrig har overvejet: kan man finde to trekanter med samme areal? Det er ret let at svare på: arealet af en trekant, husker vi fra vor kære folkeskole, findes ved at gange
Differential- regning
 Differential- regning del () f () m l () 6 Karsten Juul Indhold Tretrinsreglen 59 Formler for differentialkvotienter64 Regneregler for differentialkvotienter67 Differentialkvotient af sammensat funktion7
Differential- regning del () f () m l () 6 Karsten Juul Indhold Tretrinsreglen 59 Formler for differentialkvotienter64 Regneregler for differentialkvotienter67 Differentialkvotient af sammensat funktion7
Differentialregning Infinitesimalregning
 Udgave 2.1 Differentialregning Infinitesimalregning Noterne gennemgår begreberne differentialregning, og anskuer dette som et derligere redskab til vækst og funktioner. Noterne er supplement til kapitel
Udgave 2.1 Differentialregning Infinitesimalregning Noterne gennemgår begreberne differentialregning, og anskuer dette som et derligere redskab til vækst og funktioner. Noterne er supplement til kapitel
Løsningsforslag Mat B August 2012
 Løsningsforslag Mat B August 2012 Opgave 1 (5 %) a) Løs uligheden: 2x + 11 x 1 Løsning: 2x + 11 x 1 2x x + 1 0 3x + 12 0 3x 12 Divideres begge sider med -3 (og husk at vende ulighedstegnet!) x 4 Opgave
Løsningsforslag Mat B August 2012 Opgave 1 (5 %) a) Løs uligheden: 2x + 11 x 1 Løsning: 2x + 11 x 1 2x x + 1 0 3x + 12 0 3x 12 Divideres begge sider med -3 (og husk at vende ulighedstegnet!) x 4 Opgave
FUNKTIONER. Eks. hvis man sætter 3 ind på x s plads bliver værdien 2*3 + 5 = 11. Sætter man 4 ind på x s plads vil værdien blive 2*4 + 5 = 13
 En funktion beskriver, hvordan en afhængig variabel afhænger af en uafhængig variabel. Læringsmål Forstå koordinatsystemet Vide hvad 1. og 2. aksen er Vide at x er 1. akse og y er 2. akse Forståelsen for
En funktion beskriver, hvordan en afhængig variabel afhænger af en uafhængig variabel. Læringsmål Forstå koordinatsystemet Vide hvad 1. og 2. aksen er Vide at x er 1. akse og y er 2. akse Forståelsen for
Start-mat. for stx og hf Karsten Juul
 Start-mat for stx og hf 0,6 5, 9 2017 Karsten Juul Start-mat for stx og hf 2017 Karsten Juul 1/8-2017 (7/8-2017) Nyeste version af dette hæfte kan downloades fra http://mat1.dk/noter.htm. Hæftet må benyttes
Start-mat for stx og hf 0,6 5, 9 2017 Karsten Juul Start-mat for stx og hf 2017 Karsten Juul 1/8-2017 (7/8-2017) Nyeste version af dette hæfte kan downloades fra http://mat1.dk/noter.htm. Hæftet må benyttes
Projekt 2.2 Omvendt funktion og differentiation af omvendt funktion
 ISBN 978877664974 Projekter: Kapitel. Projekt. Omvendt funktion og differentiation af omvendt funktion Projekt. Omvendt funktion og differentiation af omvendt funktion Vi har i Bbogens kapitel 4 afsnit
ISBN 978877664974 Projekter: Kapitel. Projekt. Omvendt funktion og differentiation af omvendt funktion Projekt. Omvendt funktion og differentiation af omvendt funktion Vi har i Bbogens kapitel 4 afsnit
Øvelser til Eksamensopgaver i matematik
 Øvelser til Eksamensopgaver i matematik med TI-Nspire CAS ver. 2.0 Udarbejdet af: Brian M.V. Olesen Marts 2010 Indholdsfortegnelse TI-Nspire CAS version 2.0...2 Generelle TIPS & TRICKS (T&T)...3 Eksempel
Øvelser til Eksamensopgaver i matematik med TI-Nspire CAS ver. 2.0 Udarbejdet af: Brian M.V. Olesen Marts 2010 Indholdsfortegnelse TI-Nspire CAS version 2.0...2 Generelle TIPS & TRICKS (T&T)...3 Eksempel
Funktioner. 1. del Karsten Juul
 Funktioner 1. del 0,6 5, 9 2018 Karsten Juul 1. Koordinater 1.1 Koordinatsystem... 1 1.2 Kvadranter... 1 1.3 Koordinater... 2 1.4 Aflæs x-koordinat... 2 1.5 Aflæs y-koordinat... 2 1.6 Koordinatsæt... 2
Funktioner 1. del 0,6 5, 9 2018 Karsten Juul 1. Koordinater 1.1 Koordinatsystem... 1 1.2 Kvadranter... 1 1.3 Koordinater... 2 1.4 Aflæs x-koordinat... 2 1.5 Aflæs y-koordinat... 2 1.6 Koordinatsæt... 2
Polynomiumsbrøker og asymptoter
 Polynomiumsbrøker og asymptoter Frank Villa 9. marts 2012 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold
Polynomiumsbrøker og asymptoter Frank Villa 9. marts 2012 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold
Koblede differentialligninger.
 2. 3. 4. Koblede differentialligninger. En udvidelse af Newtons afkølingslov løst numerisk ved hjælp af integralkurver. Sidste gang så vi på, hvordan vi kunne opstille og løse en model for afkølingen af
2. 3. 4. Koblede differentialligninger. En udvidelse af Newtons afkølingslov løst numerisk ved hjælp af integralkurver. Sidste gang så vi på, hvordan vi kunne opstille og løse en model for afkølingen af
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Institution Uddannelse Fag og niveau Lærer(e) Termin hvori undervisningen afsluttes: maj-juni 2011 Uddannelsescenter
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Institution Uddannelse Fag og niveau Lærer(e) Termin hvori undervisningen afsluttes: maj-juni 2011 Uddannelsescenter
Studieplan. Stamoplysninger til brug ved prøver til gymnasiale uddannelser. Oversigt over gennemførte undervisningsforløb. Termin Aug. 14 jun.
 Studieplan Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Aug. 14 jun. 16 Institution Uddannelse Fag og niveau Lærer(e) Hold Vid Gymnasier HTX Matematik B Morten Käszner og Niels
Studieplan Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Aug. 14 jun. 16 Institution Uddannelse Fag og niveau Lærer(e) Hold Vid Gymnasier HTX Matematik B Morten Käszner og Niels
Formativ brug af folkeskolens prøver. Den skriftlige prøve i matematik i 10. klasse, FP10, maj 2018
 Formativ brug af folkeskolens prøver Den skriftlige prøve i matematik i 10. klasse, FP10, maj 2018 1 Til matematiklæreren i 10. klasse Dette er en rapport om den skriftlige prøve i matematik maj 2018.
Formativ brug af folkeskolens prøver Den skriftlige prøve i matematik i 10. klasse, FP10, maj 2018 1 Til matematiklæreren i 10. klasse Dette er en rapport om den skriftlige prøve i matematik maj 2018.
MATEMATIK A-NIVEAU. Kapitel 1
 MATEMATIK A-NIVEAU Vejledende eksempler på eksamensopgaver og eksamensopgaver i matematik, 01 Kapitel 1 016 MATEMATIK A-NIVEAU Vejledende eksempler på eksamensopgaver og eksamensopgaver i matematik 01
MATEMATIK A-NIVEAU Vejledende eksempler på eksamensopgaver og eksamensopgaver i matematik, 01 Kapitel 1 016 MATEMATIK A-NIVEAU Vejledende eksempler på eksamensopgaver og eksamensopgaver i matematik 01
Matematik A-niveau STX 24. maj 2016 Delprøve 2 VUC Vestsjælland Syd. www.matematikhjaelp.tk
 Matematik A-niveau STX 24. maj 2016 Delprøve 2 VUC Vestsjælland Syd www.matematikhjaelp.tk Opgave 7 - Eksponentielle funktioner I denne opgave, bliver der anvendt eksponentiel regression, men først defineres
Matematik A-niveau STX 24. maj 2016 Delprøve 2 VUC Vestsjælland Syd www.matematikhjaelp.tk Opgave 7 - Eksponentielle funktioner I denne opgave, bliver der anvendt eksponentiel regression, men først defineres
