Opstilling af model ved hjælp af differentialkvotient
|
|
|
- Merete Marcussen
- 10 år siden
- Visninger:
Transkript
1 Opstilling af model ved hjælp af differentialkvotient N 0,35N 0, 76t 2010 Karsten Juul
2 Til eleven Dette hæfte giver dig mulighed for at arbejde sådan med nogle begreber at der er god mulighed for at der går noget op for dig. Du skal selv skrive hæftet færdigt ved at udfylde de tomme pladser. Brug blyant og viskelæder. Indhold 1. Ligning for væksthastighed Udregne fremtidig størrelse ud fra væksthastighed Udføre udregningerne med Nspire Undersøge modeller...8 Opstilling af model ved hjælp af differentialkvotient 1. udgave Karsten Juul Dette hæfte kan downloades fra Hæftet må benyttes i undervisningen hvis læreren med det samme sender en til [email protected] som dels oplyser at dette hæfte benyttes, dels oplyser om hold, lærer og skole.
3 1. Ligning for væksthastighed Eksempel 1.1 På en skærm ser vi en stolpe der vokser. Vi kan hele tiden se tidspunkt, højde og højdens væksthastighed. Vi aflæser følgende: Tidspunkt i minutter Højde i cm 3,32 4,48 7,39 Væksthastighed i cm pr. minut 0,332 0,448 0,739 Det ser ud til at der gælder følgende regel: Når vi kender højden, kan vi udregne dens væksthastighed ved at. Vi vil skrive denne regel som en ligning. Derfor kalder vi højden h. Så kan vi skrive væksthastigheden sådan: h. Nu kan vi skrive reglen som følgende ligning: h. Eksempel 1.2 Nogle bakterier er et sted hvor der er rigelig plads og næring. Når der er 1000 bakterier, er væksthastigheden (tilvækst pr. minut) 8 bakterier. Når der er dobbelt så mange bakterier til at dele sig, dvs. når der er 2000 bakterier, er tilvæksten pr. minut bakterier. Når der er 4000 bakterier, er tilvæksten pr. minut bakterier. Når der er 1500 bakterier, er tilvæksten pr. minut bakterier. Når antal er 1000, fås tilvækst pr. minut ved at gange antal bakterier med. Når antal er 1500, fås tilvækst pr. minut ved at gange antal bakterier med. Når antal er 2000, fås tilvækst pr. minut ved at gange antal bakterier med. Når antal er 4000, fås tilvækst pr. minut ved at gange antal bakterier med. Antallet af bakterier kalder vi b. Så kan vi skrive væksthastigheden sådan:. Når vi kender antallet af bakterier, kan vi udregne væksthastigheden ved hjælp af ligningen:. Opstilling af model ved hjælp af differentialkvotient Side Karsten Juul
4 Eksempel 1.3 På en skærm er der en figur der vokser. Vi kan hele tiden se tidspunkt, diameter og diameterens væksthastighed. Vi har aflæst følgende: Tidspunkt i minutter 1,2 1,5 1,9 Diameter i cm 5,3 6,5 8,7 Væksthastighed i cm pr. minut 3,3 4,5 6,7 Det ser ud til at der gælder følgende regel: Når vi kender diameteren, kan vi udregne dens væksthastighed ved at. Vi vil skrive denne regel som en ligning. Derfor kalder vi diameteren d. Så kan vi skrive væksthastigheden sådan. Nu kan vi skrive reglen som følgende ligning:. Eksempel 1.4 Koncentrationen af et stof aftager: Tidspunkt (s) 0 2,5 7,5 Koncentration (mol/l) Væksthastighed (mol/l/s) 1,6 0,4 0,1 Ud fra disse tabelværdier kan vi gætte en regel for hvordan vi kan udregne væksthastigheden når vi kender koncentrationen. Når vi kalder koncentrationen for a, kan vi skrive reglen som følgende ligning: Eksempel 1.5 I et computerspil stiger prisen på en vare: Tidspunkt (timer) Pris (kr.) 0,72 4,39 49,6 Væksthastighed (kr. pr. time) 1,72 6,39 53,6 Ud fra disse tabelværdier kan vi gætte en regel for hvordan vi kan udregne væksthastigheden når vi kender tidspunkt og pris. Når vi kalder prisen p og tidspunktet t, kan vi skrive reglen som følgende ligning: Opstilling af model ved hjælp af differentialkvotient Side Karsten Juul
5 Eksempel 1.6 Grafen viser hvordan værdien af en vare falder. Grafen er tegnet tre gange. I hvert koordinatsystem er afsat ét punkt på grafen. Tangenten i dette punkt er tegnet. På det tidspunkt hvor værdien er 3 kr., er væksthastigheden 2 kr. pr. år. På det tidspunkt hvor værdien er kr., er væksthastigheden kr. pr. år. På det tidspunkt hvor værdien er kr., er væksthastigheden kr. pr. år. Ud fra disse tal kan vi gætte en regel for hvordan vi kan udregne væksthastigheden på et tidspunkt hvor vi kender varens værdi. Når vi kalder værdien v, kan vi skrive reglen som følgende ligning: Eksempel 1.7 I et kvadrat er sidens væksthastighed proportional med arealet. Der gælder altså følgende ligning hvor k er en konstant. Når sidens længde er 2, er sidens væksthastighed 12. Ud fra denne oplysning kan vi finde konstanten k sådan : s s Opstilling af model ved hjælp af differentialkvotient Side Karsten Juul
6 Eksempel 1.8 Der ledes salt ud i en sø med hastigheden 1,3 kg pr. dag. Saltet forlader søen med en hastighed på 8 % pr. dag (8 % af den mængde salt der er i søen på det pågældende tidspunkt). Når mængden af salt i søen er nået op på 5 kg, vokser mængden med hastigheden kg pr. dag. Når mængden af salt i søen er nået op på 16 kg, vokser mængden med hastigheden kg pr. dag. På et tidspunkt hvor mængden af salt i søen er kendt, kan væksthastigheden for mængden udregnes ved hjælp af ligningen hvor betegner mængden af salt i søen målt i kg. Som tiden går bliver mængden af salt i søen større og større, og væksthastigheden bliver og. 2. Udregne fremtidig størrelse ud fra væksthastighed Eksempel 2.1 Et kar fyldes med væske. Væskehøjdens væksthastighed er hele tiden 8,5 mm pr. time. I løbet af 7 timer bliver væskehøjden mm større. I løbet af 0,4 timer bliver væskehøjden mm større. På et tidspunkt er højden 42,51 mm. 0,02 timer senere er højden mm. Eksempel 2.2 Vægten af nogle bakterier vokser. t tidspunktet (målt i minutter) M vægten (målt i gram) Beskriv betydningen af symbolet M ' ligesom betydningen af M og t er beskrevet. M ' (målt i ) På ethvert tidspunkt kan væksthastigheden M ' udregnes ud fra vægten sådan: (1) M 0,012 M 1, 5. På det tidspunkt hvor vægten er 500 gram, vokser vægten med hastigheden På det tidspunkt hvor vægten er 600 gram, vokser vægten med hastigheden gram pr. minut. gram pr. minut. Væksthastigheden er ikke den samme hele tiden. Væksthastigheden bliver og. Vi går ud fra at væksthastigheden i løbet af 0,01 minut ændrer sig så lidt at vi kan regne som om den ikke ændrede sig. Eksemplet fortsætter på næste side. Opstilling af model ved hjælp af differentialkvotient Side Karsten Juul
7 På tidspunktet t 4 er vægten 500 gram. På tidspunktet t 4 er væksthastigheden gram pr. minut ifølge ligning (1). I det første 0,01 minut efter tidspunktet t 4 bliver vægten gram større. På tidspunktet t 4, 01 er vægten gram. Skriv alle 6 cifre! På tidspunktet t 4, 01 er væksthastigheden gram pr. minut ifølge ligning (1). På tidspunktet t 4, 02 er vægten gram. Skriv alle 10 cifre! I første skridt ovenfor udregnede vi vægten på tidspunktet t 4, 01. I andet skridt udregnede vi vægten på tidspunktet t 4, 02. Efter skridt mere har vi udregnet vægten på tidspunktet t 6. (Nspire er ca. et sekund om at gennemføre dette. I næste afsnit står hvad vi skal taste). Eksempel 2.3 En stolpes højde vokser. Højden h måles i cm, og tiden t måles i minutter. Følgende er oplyst: På tidspunktet t 16 er højden h 1, 40. På ethvert tidspunkt er væksthastigheden h 0, 025 h. På tidspunktet t 16 er væksthastigheden h. Husk at få alle lommeregnerens cifre frem. På Nspires regneside kan dette gøres ved at kopiere facit til ny linje. Væksthastigheden vokser hele tiden, men vi går ud fra at den næsten ikke når at ændre sig i løbet af 0, 01 minut. Så gælder: Når t 16, 01, er h + Når t 16, 01, er h Når t 16, 02, er h + Når t 16, 02, er h Når t 16, 03, er h + Hvis vi fortsætter på denne måde til t 20, finder vi ud af hvad h er når t 20. (Nspire er ca. et sekund om at gennemføre dette. I næste afsnit står hvad vi skal taste). Opstilling af model ved hjælp af differentialkvotient Side Karsten Juul
8 3. Udføre udregningerne med Nspire 1.7 Eksempel 3.1 I dette eksempel skal du få Nspire til at udføre de udregninger der er omtalt i eksempel 2.3. Start på et nyt dokument ( c 6:Nyt dokument ) og vælg regne-side ( 1:Tilføj Grafregner ). Hvis der er mere end én fane øverst, så er du ikke begyndt forfra. Vælg: b 9: Funktioner og programmer 1: Programeditor 1: Ny Giv programmet navnet md ( "m" for model, og "d" for differentialkvotient) og tast. Nu ser skærmen sådan ud: Mellem linjerne Prgm og EndPrgm skal vi skrive de kommandoer som Nspire skal udføre når vi i regnevinduet taster md( ). Du kan skifte mellem de to vinduer ved at taste / e. Skillelinjen mellem de to vinduer kan du flytte sådan: / c 5: Sidelayout 1: Brugerdefineret opdeling Tryk nogle gange på venstrepil eller højrepil og afslut med. Når du taster programmet der er vist på næste side, kan du bruge følgende oplysninger: Pilen er i øverste linje i symbolmenuen der fås frem ved at taste / k. Tast Local sådan: b 3: Definer variable 1: Local Tast Disp sådan: b 6: I/O 1: Disp Tast While... sådan: b 4: Kontrol 6: While...EndWhile (I stedet for at vælge Local, Disp og While...EndWhile i menuen kan du taste dem. I stedet for kan du taste : som laves om til når du gemmer programmet). Opstilling af model ved hjælp af differentialkvotient Side Karsten Juul
9 For at gøre programmet mere overskueligt er der lavet tomme linjer og indrykning ved hjælp af tasterne og _. En plads i Nspires lager giver vi navnet t. På denne plads anbringer vi tallet 16. Tallet på pladsen h ganger vi med 0,025. Resultatet anbringer vi på pladsen dh. Til tallet på pladsen h lægger vi 0,01 gange tallet på pladsen dh. Resultatet anbringer vi på pladsen h i stedet for det tal der stod i forvejen. Vi undersøger om tallet på pladsen t er mindre end 20. Hvis det er, udfører vi igen de tre kommandoer mellem While og EndWhile. Tallet på pladsen h skriver vi i regnevinduet. Afslut sådan: b 2: Kontroller syntaks og gem 1: Kontroller syntaks og gem. Skift til regnevinduet sådan: / e. Tast md() for at få programmet til at udregne resultatet (og skriv det i øvelse 2.3). Gem dokumentet (du skal senere ændre i det mange gange): / c 1: Filer 3: Gem Tast filnavnet model-diff-23 så du kan finde det igen, og tast. Luk ( c 6:Nyt dokument ) Afbryde kørende Nspire-program Hold tasten nede i noget tid: w eller d på lommeregner. F12 eller Pause på Windows. F5 på Mac. Eksempel 3.2 Vi vil nu løse problemet fra eksempel 2.2. Udfyld de tomme pladser på figuren til højre så programmet finder vægten til tiden t 6. I programmet står h og dh i stedet for M og M '. Hvis du vil skrive m og dm, så skal du rette det alle steder. Åbn dokumentet model-diff-23 og gem det under navnet model-diff-22 ( /c 1: Filer 4: Gem som ). Skriv rettelserne til programmet. Få Nspire til at kontrollere programmet og gemme det. Kør programmet. Hvis du har tastet rigtigt, skriver Nspire tallet 509,108, dvs. på tidspunktet 6 minutter er vægten 509 gram. Opstilling af model ved hjælp af differentialkvotient Side Karsten Juul
10 4. Undersøge modeller Husk at gemme programmet hver gang du har ændret det. Ellers får Eksempel 4.1 du det foregående resultat igen. Vi ser stadig på bakterierne fra eksemplerne 2.2 og 3.2. Ved hjælp af programmet i dokumentet model-diff-22 udfylder vi tabellen: t M t M Vi afsætter disse støttepunkter i koordinatsystemet til højre og tegner grafen for M. Eksempel 4.2 I eksempel 1.8 blev der ledt salt ud i en sø. Til tiden t 0 er der 5 kg salt i søen. Nedenfor til højre viser vi hvordan programmet md( ) skal ændres for at udregne mængden af salt i søen på tidspunktet t 15. Vi bruger programmet md( ) til at udfylde tabellen der viser hvordan saltmængden vokser: t Vi afsætter disse støttepunkter i koordinatsystemet og tegner grafen. Opstilling af model ved hjælp af differentialkvotient Side Karsten Juul
11 Eksempel 4.3 Vi måler tiden t i uger. I et bur er forholdene for en bestemt slags dyr sådan at deres antal N har væksthastigheden N 0,439 (620 N). Hvis der er 860 af disse dyr i buret, er væksthastigheden dyr pr. uge. Hvis væksthastigheden skal være positiv, skal antallet af dyr være. Tilfælde A: På tidspunktet t 0 er antallet N 860. Ved hjælp af programmet md( ) udregner vi at på tidspunktet t 2, 5 er antallet. På dette tidspunkt er væksthastigheden dyr pr. uge. Tilfælde B: På tidspunktet t 0 er antallet N 700. På tidspunktet t 0 er væksthastigheden dyr pr. uge. Tilfælde C: På tidspunktet t 0 er antallet N 620. På tidspunktet t 0 er væksthastigheden dyr pr. uge, så på tidspunktet t 0, 01 er antallet af dyr. På tidspunktet t 0, 01 er væksthastigheden dyr pr. uge. så på tidspunktet t 0, 02 er antallet af dyr. Tilfælde D: På tidspunktet t 0 er antallet N 260. På tidspunktet t 0 er væksthastigheden dyr pr. uge. På tidspunktet t 20 er antallet af dyr og væksthastigheden er dyr pr. uge. For hvert af tilfældene A, B, C og D tegner vi grafen i koordinatsystemet nedenfor ved først at bruge programmet md( ) til at udregne støttepunkter. Opstilling af model ved hjælp af differentialkvotient Side Karsten Juul
Differentialregning. Et oplæg Karsten Juul L P
 Differentialregning Et oplæg L P A 2009 Karsten Juul Til eleven Dette hæfte kan I bruge inden I starter på differentialregningen i lærebogen Det meste af hæftet er små spørgsmål med korte svar Spørgsmålene
Differentialregning Et oplæg L P A 2009 Karsten Juul Til eleven Dette hæfte kan I bruge inden I starter på differentialregningen i lærebogen Det meste af hæftet er små spørgsmål med korte svar Spørgsmålene
Variabel- sammenhænge
 Variabel- sammenhænge 2008 Karsten Juul Dette hæfte kan bruges som start på undervisningen i variabelsammenhænge for st og hf. Indhold 1. Hvordan viser en tabel sammenhængen mellem to variable?... 1 2.
Variabel- sammenhænge 2008 Karsten Juul Dette hæfte kan bruges som start på undervisningen i variabelsammenhænge for st og hf. Indhold 1. Hvordan viser en tabel sammenhængen mellem to variable?... 1 2.
Lineære sammenhænge. Udgave 2. 2009 Karsten Juul
 Lineære sammenhænge Udgave 2 y = 0,5x 2,5 2009 Karsten Juul Dette hæfte er en fortsættelse af hæftet "Variabelsammenhænge, 2. udgave 2009". Indhold 1. Lineære sammenhænge, ligning og graf... 1 2. Lineær
Lineære sammenhænge Udgave 2 y = 0,5x 2,5 2009 Karsten Juul Dette hæfte er en fortsættelse af hæftet "Variabelsammenhænge, 2. udgave 2009". Indhold 1. Lineære sammenhænge, ligning og graf... 1 2. Lineær
Eksponentielle sammenhænge
 Eksponentielle sammenhænge Udgave 009 Karsten Juul Dette hæfte er en fortsættelse af hæftet "Lineære sammenhænge, udgave 009" Indhold 1 Eksponentielle sammenhænge, ligning og graf 1 Procent 7 3 Hvad fortæller
Eksponentielle sammenhænge Udgave 009 Karsten Juul Dette hæfte er en fortsættelse af hæftet "Lineære sammenhænge, udgave 009" Indhold 1 Eksponentielle sammenhænge, ligning og graf 1 Procent 7 3 Hvad fortæller
Differential- ligninger
 Differential- ligninger Et oplæg 2007 Karsten Juul Dette hæfte er tænkt brugt som et oplæg der kan gennemgås før man går i gang med en lærebogs fremstilling af emnet differentialligninger Læreren skal
Differential- ligninger Et oplæg 2007 Karsten Juul Dette hæfte er tænkt brugt som et oplæg der kan gennemgås før man går i gang med en lærebogs fremstilling af emnet differentialligninger Læreren skal
Potensfunktioner samt proportional og omvent proportional. for hf Karsten Juul
 Potensfunktioner samt proportional og omvent proportional for hf 2018 Karsten Juul Potensfunktion 1. Oplæg til forskrift for potensfunktion...1 2. Forskrift for potensfunktion...2 3. Udregn x eller y i
Potensfunktioner samt proportional og omvent proportional for hf 2018 Karsten Juul Potensfunktion 1. Oplæg til forskrift for potensfunktion...1 2. Forskrift for potensfunktion...2 3. Udregn x eller y i
Differential- regning
 Differential- regning del () f () m l () 6 Karsten Juul Indhold Tretrinsreglen 59 Formler for differentialkvotienter64 Regneregler for differentialkvotienter67 Differentialkvotient af sammensat funktion7
Differential- regning del () f () m l () 6 Karsten Juul Indhold Tretrinsreglen 59 Formler for differentialkvotienter64 Regneregler for differentialkvotienter67 Differentialkvotient af sammensat funktion7
Start pä matematik. for gymnasiet og hf. 2010 (2012) Karsten Juul
 Start pä matematik for gymnasiet og hf 2010 (2012) Karsten Juul Til eleven Brug blyant og viskelåder när du skriver og tegner i håftet, sä du fär et håfte der er egnet til jåvnligt at slä op i under dit
Start pä matematik for gymnasiet og hf 2010 (2012) Karsten Juul Til eleven Brug blyant og viskelåder när du skriver og tegner i håftet, sä du fär et håfte der er egnet til jåvnligt at slä op i under dit
sammenhänge for C-niveau i stx 2013 Karsten Juul
 LineÄre sammenhänge for C-niveau i stx y 0,5x 2,5 203 Karsten Juul : OplÄg om lineäre sammenhänge 2 Ligning for lineär sammenhäng 2 3 Graf for lineär sammenhäng 2 4 Bestem y når vi kender x 3 5 Bestem
LineÄre sammenhänge for C-niveau i stx y 0,5x 2,5 203 Karsten Juul : OplÄg om lineäre sammenhänge 2 Ligning for lineär sammenhäng 2 3 Graf for lineär sammenhäng 2 4 Bestem y når vi kender x 3 5 Bestem
for matematik på C-niveau i stx og hf
 VariabelsammenhÄnge generelt for matematik på C-niveau i stx og hf NÅr x 2 er y 2,8. 2014 Karsten Juul 1. VariabelsammenhÄng og dens graf og ligning 1.1 Koordinatsystem I koordinatsystemer (se Figur 1):
VariabelsammenhÄnge generelt for matematik på C-niveau i stx og hf NÅr x 2 er y 2,8. 2014 Karsten Juul 1. VariabelsammenhÄng og dens graf og ligning 1.1 Koordinatsystem I koordinatsystemer (se Figur 1):
Differential- regning
 Differential- regning del f(5) () f f () f ( ) I 5 () 006 Karsten Juul Indhold 6 Kontinuert funktion 7 Monotoniforhold7 8 Lokale ekstrema44 9 Grænseværdi5 Differentialregning del udgave 006 006 Karsten
Differential- regning del f(5) () f f () f ( ) I 5 () 006 Karsten Juul Indhold 6 Kontinuert funktion 7 Monotoniforhold7 8 Lokale ekstrema44 9 Grænseværdi5 Differentialregning del udgave 006 006 Karsten
Kort om Eksponentielle Sammenhænge
 Øvelser til hæftet Kort om Eksponentielle Sammenhænge 2011 Karsten Juul Dette hæfte indeholder bl.a. mange småspørgsmål der gør det nemmere for elever at arbejde effektivt på at få kendskab til emnet.
Øvelser til hæftet Kort om Eksponentielle Sammenhænge 2011 Karsten Juul Dette hæfte indeholder bl.a. mange småspørgsmål der gør det nemmere for elever at arbejde effektivt på at få kendskab til emnet.
Undersøge funktion ved hjælp af graf. For hf-mat-c.
 Undersøge funktion ved hjælp af graf. For hf-mat-c. 2018 Karsten Juul Bestemme x og y 1. Bestemme x eller y...1 Andengradspolynomium 2. Forskrift for andengradspolynomium...2 3. Graf for andengradspolynomium...2
Undersøge funktion ved hjælp af graf. For hf-mat-c. 2018 Karsten Juul Bestemme x og y 1. Bestemme x eller y...1 Andengradspolynomium 2. Forskrift for andengradspolynomium...2 3. Graf for andengradspolynomium...2
Eksponentielle funktioner for C-niveau i hf
 Eksponentielle funktioner for C-niveau i hf 2017 Karsten Juul Procent 1. Procenter på en ny måde... 1 2. Bestem procentvis ændring... 2 3. Bestem begyndelsesværdi... 2 4. Bestem slutværdi... 3 5. Vækstrate...
Eksponentielle funktioner for C-niveau i hf 2017 Karsten Juul Procent 1. Procenter på en ny måde... 1 2. Bestem procentvis ændring... 2 3. Bestem begyndelsesværdi... 2 4. Bestem slutværdi... 3 5. Vækstrate...
GrundlÄggende variabelsammenhänge
 GrundlÄggende variabelsammenhänge for C-niveau i hf 2014 Karsten Juul LineÄr sammenhäng 1. OplÄg om lineäre sammenhänge... 1 2. Ligning for lineär sammenhäng... 1 3. Graf for lineär sammenhäng... 2 4.
GrundlÄggende variabelsammenhänge for C-niveau i hf 2014 Karsten Juul LineÄr sammenhäng 1. OplÄg om lineäre sammenhänge... 1 2. Ligning for lineär sammenhäng... 1 3. Graf for lineär sammenhäng... 2 4.
Vektorer i planen. Et oplæg Karsten Juul
 Vektorer i planen Et oplæg 3 4 4 2 2007 Karsten Juul Dette hæfte er tænkt brugt som et oplæg der skal gennemgås før man begynder på en lærebogs fremstilling af emnet vektorer. Formålet med øvelserne er
Vektorer i planen Et oplæg 3 4 4 2 2007 Karsten Juul Dette hæfte er tænkt brugt som et oplæg der skal gennemgås før man begynder på en lærebogs fremstilling af emnet vektorer. Formålet med øvelserne er
Simple udtryk og ligninger
 Simple udtryk og ligninger 009 Karsten Juul Til eleven Brug blyant og viskelæder når du skriver og tegner i hæftet, så du får et hæfte der er egenet til jævnligt at slå op i under dit videre arbejde med
Simple udtryk og ligninger 009 Karsten Juul Til eleven Brug blyant og viskelæder når du skriver og tegner i hæftet, så du får et hæfte der er egenet til jævnligt at slå op i under dit videre arbejde med
Variabel- sammenhænge
 Variabel- sammenhænge Udgave 2 2009 Karsten Juul Dette hæfte kan bruges som start på undervisningen i variabelsammenhænge for stx og hf. Hæftet er en introduktion til at kunne behandle to sammenhængende
Variabel- sammenhænge Udgave 2 2009 Karsten Juul Dette hæfte kan bruges som start på undervisningen i variabelsammenhænge for stx og hf. Hæftet er en introduktion til at kunne behandle to sammenhængende
Funktioner. 3. del Karsten Juul
 Funktioner 3. del 019 Karsten Juul Funktioner 3. del, 019 Karsten Juul 1/9-019 Nyeste version af dette hæfte kan downloades fra http://mat1.dk/noter.htm. Hæftet må benyttes i undervisningen hvis læreren
Funktioner 3. del 019 Karsten Juul Funktioner 3. del, 019 Karsten Juul 1/9-019 Nyeste version af dette hæfte kan downloades fra http://mat1.dk/noter.htm. Hæftet må benyttes i undervisningen hvis læreren
Funktioner. 2. del Karsten Juul
 Funktioner 2. del 2018 Karsten Juul 18. Eksponentiel funktion forskrift 18.1 Oplæg nr. 1 til forskrift for eksponentiel funktion... 52 18.2 Oplæg nr. 2 til forskrift for eksponentiel funktion... 53 18.3.
Funktioner 2. del 2018 Karsten Juul 18. Eksponentiel funktion forskrift 18.1 Oplæg nr. 1 til forskrift for eksponentiel funktion... 52 18.2 Oplæg nr. 2 til forskrift for eksponentiel funktion... 53 18.3.
Kom i gang-opgaver til differentialregning
 Kom i gang-opgaver til differentialregning 00 Karsten Juul Det er kortsigtet at løse en opgave ved blot at udskifte tallene i en besvarelse af en tilsvarende opgave Dette skyldes at man så normalt ikke
Kom i gang-opgaver til differentialregning 00 Karsten Juul Det er kortsigtet at løse en opgave ved blot at udskifte tallene i en besvarelse af en tilsvarende opgave Dette skyldes at man så normalt ikke
Funktioner. 1. del Karsten Juul
 Funktioner 1. del 0,6 5, 9 2018 Karsten Juul 1. Koordinater 1.1 Koordinatsystem... 1 1.2 Kvadranter... 1 1.3 Koordinater... 2 1.4 Aflæs x-koordinat... 2 1.5 Aflæs y-koordinat... 2 1.6 Koordinatsæt... 2
Funktioner 1. del 0,6 5, 9 2018 Karsten Juul 1. Koordinater 1.1 Koordinatsystem... 1 1.2 Kvadranter... 1 1.3 Koordinater... 2 1.4 Aflæs x-koordinat... 2 1.5 Aflæs y-koordinat... 2 1.6 Koordinatsæt... 2
Start-mat. for stx og hf Karsten Juul
 Start-mat for stx og hf 0,6 5, 9 2017 Karsten Juul Start-mat for stx og hf 2017 Karsten Juul 1/8-2017 (7/8-2017) Nyeste version af dette hæfte kan downloades fra http://mat1.dk/noter.htm. Hæftet må benyttes
Start-mat for stx og hf 0,6 5, 9 2017 Karsten Juul Start-mat for stx og hf 2017 Karsten Juul 1/8-2017 (7/8-2017) Nyeste version af dette hæfte kan downloades fra http://mat1.dk/noter.htm. Hæftet må benyttes
Differentialligninger
 Differentialligninger for A-niveau i st, udgave SkÄrmbillede fra TI-Nspire 015 Karsten Juul Differentialligninger for A-niveau i st, udgave 1 Hvad er en differentialligning? 1a OplÄg til differentialligninger1
Differentialligninger for A-niveau i st, udgave SkÄrmbillede fra TI-Nspire 015 Karsten Juul Differentialligninger for A-niveau i st, udgave 1 Hvad er en differentialligning? 1a OplÄg til differentialligninger1
Funktioner generelt. for matematik pä B- og A-niveau i stx og hf. 2014 Karsten Juul
 Funktioner generelt for matematik pä B- og A-niveau i st og hf f f ( ),8 014 Karsten Juul 1 Funktion og dens graf, forskrift og definitionsmängde 11 Koordinatsystem I koordinatsystemer (se Figur 1): -akse
Funktioner generelt for matematik pä B- og A-niveau i st og hf f f ( ),8 014 Karsten Juul 1 Funktion og dens graf, forskrift og definitionsmängde 11 Koordinatsystem I koordinatsystemer (se Figur 1): -akse
Integralregning. med Ävelser. for B-niveau i gymnasiet og hf. 2011 Karsten Juul
 Integralregning med Ävelser or B-niveau i gymnasiet og h 0 Karsten Juul Dette håte gennemgçr integralregningen or B-niveau uden at gäre det mere indviklet end kråvet Évelserne giver eleverne et kendskab
Integralregning med Ävelser or B-niveau i gymnasiet og h 0 Karsten Juul Dette håte gennemgçr integralregningen or B-niveau uden at gäre det mere indviklet end kråvet Évelserne giver eleverne et kendskab
Symbolsprog og Variabelsammenhænge
 Indledning til Symbolsprog og Variabelsammenhænge for Gymnasiet og Hf 1000 kr 500 0 0 5 10 15 timer 2005 Karsten Juul Brugsanvisning Du skal se i de fuldt optrukne rammer for at finde: Regler for løsning
Indledning til Symbolsprog og Variabelsammenhænge for Gymnasiet og Hf 1000 kr 500 0 0 5 10 15 timer 2005 Karsten Juul Brugsanvisning Du skal se i de fuldt optrukne rammer for at finde: Regler for løsning
Deskriptiv statistik for hf-matc
 Deskriptiv statistik for hf-matc 75 50 25 2018 Karsten Juul Deskriptiv statistik for hf-matc Hvad er deskriptiv statistik? 1.1 Hvad er deskriptiv statistik?... 1 1.2 Hvad er grupperede og ugrupperede data?...
Deskriptiv statistik for hf-matc 75 50 25 2018 Karsten Juul Deskriptiv statistik for hf-matc Hvad er deskriptiv statistik? 1.1 Hvad er deskriptiv statistik?... 1 1.2 Hvad er grupperede og ugrupperede data?...
Eksempler på problemløsning med differentialregning
 Eksempler på problemløsning med differentialregning 004 Karsten Juul Opgave 1: Monotoniforhold = 1+, x 3 3 x Bestem monotoniforholdene for f Besvarelse af opgave 1 Først differentierer vi f : (3 x) (3
Eksempler på problemløsning med differentialregning 004 Karsten Juul Opgave 1: Monotoniforhold = 1+, x 3 3 x Bestem monotoniforholdene for f Besvarelse af opgave 1 Først differentierer vi f : (3 x) (3
Deskriptiv statistik for matc i stx og hf
 Deskriptiv statistik for matc i stx og hf 75 50 25 2019 Karsten Juul Deskriptiv statistik for matc i stx og hf Hvad er deskriptiv statistik? 1.1 Hvad er deskriptiv statistik?... 1 1.2 Hvad er grupperede
Deskriptiv statistik for matc i stx og hf 75 50 25 2019 Karsten Juul Deskriptiv statistik for matc i stx og hf Hvad er deskriptiv statistik? 1.1 Hvad er deskriptiv statistik?... 1 1.2 Hvad er grupperede
Funktioner generelt. for matematik pä B-niveau i stx. 2013 Karsten Juul
 Funktioner generelt for matematik pä B-niveau i st f f ( ),8 0 Karsten Juul Funktioner generelt for matematik pä B-niveau i st Funktion, forskrift, definitionsmångde Find forskrift StÇrste og mindste vårdi
Funktioner generelt for matematik pä B-niveau i st f f ( ),8 0 Karsten Juul Funktioner generelt for matematik pä B-niveau i st Funktion, forskrift, definitionsmångde Find forskrift StÇrste og mindste vårdi
Der er facit på side 7 i dokumentet. Til opgaver mærket med # er der vink eller kommentarer på side 6.
 Der er facit på side 7 i dokumentet. Til opgaver mærket med # er der vink eller kommentarer på side 6. 1. Figuren viser grafen for en funktion f. Aflæs definitionsmængde og værdimængde for f. # Aflæs f
Der er facit på side 7 i dokumentet. Til opgaver mærket med # er der vink eller kommentarer på side 6. 1. Figuren viser grafen for en funktion f. Aflæs definitionsmængde og værdimængde for f. # Aflæs f
Tal, funktioner og grænseværdi
 Tal, funktioner og grænseværdi Skriv færdig-eksempler der kan udgøre en væsentlig del af et forløb der skal give indsigt vedrørende begrebet grænseværdi og nogle nødvendige forudsætninger om tal og funktioner
Tal, funktioner og grænseværdi Skriv færdig-eksempler der kan udgøre en væsentlig del af et forløb der skal give indsigt vedrørende begrebet grænseværdi og nogle nødvendige forudsætninger om tal og funktioner
Bogstavregning. En indledning for stx og hf. 2008 Karsten Juul
 Bogstavregning En indledning for stx og hf 2008 Karsten Juul Dette hæfte træner elever i den mest grundlæggende bogstavregning (som omtrent springes over i lærebøger for stx og hf). Når elever har lært
Bogstavregning En indledning for stx og hf 2008 Karsten Juul Dette hæfte træner elever i den mest grundlæggende bogstavregning (som omtrent springes over i lærebøger for stx og hf). Når elever har lært
Procent og rente Karsten Juul
 Procent og rente 2018 Karsten Juul 1. Procent 1.1 Oplæg til procent... 1 1.2 Udregn procent... 2 1.3. Udregn procent-ændring... 2 1.4 Udregn procent-fald... 3 1.5 Udregn procent-stigning... 3 1.6. Udregn
Procent og rente 2018 Karsten Juul 1. Procent 1.1 Oplæg til procent... 1 1.2 Udregn procent... 2 1.3. Udregn procent-ændring... 2 1.4 Udregn procent-fald... 3 1.5 Udregn procent-stigning... 3 1.6. Udregn
Nspire 4.2 kom godt i gang
 Nspire 4.2 kom godt i gang Disse 3 knapper åbner nyt dokument, henter eksisterende dokument og gemmer det åbne dokument Her kan dokumentet lukkes Indstillinger Indstillinger 1. Først skal vi have den rigtige
Nspire 4.2 kom godt i gang Disse 3 knapper åbner nyt dokument, henter eksisterende dokument og gemmer det åbne dokument Her kan dokumentet lukkes Indstillinger Indstillinger 1. Først skal vi have den rigtige
Integralregning med TI-Interactive! Stamfunktioner Integraler Arealer Jan Leffers (2005)
 Integralregning med TI-Interactive! Stamfunktioner Integraler Arealer Jan Leffers (005) Indholdsfortegnelse Indholdsfortegnelse... Stamfunktion og integralregning...3 Numerisk integration...3 Areal under
Integralregning med TI-Interactive! Stamfunktioner Integraler Arealer Jan Leffers (005) Indholdsfortegnelse Indholdsfortegnelse... Stamfunktion og integralregning...3 Numerisk integration...3 Areal under
sammenhänge for gymnasiet og hf 2010 Karsten Juul
 LineÄre sammenhänge for gymnasiet og hf y 0,5x 2,5 200 Karsten Juul I dette häfte har jeg gjort meget for at teksten er skrevet sçdan at du nemmere kan fç overblik over reglerne og den sammenhäng der er
LineÄre sammenhänge for gymnasiet og hf y 0,5x 2,5 200 Karsten Juul I dette häfte har jeg gjort meget for at teksten er skrevet sçdan at du nemmere kan fç overblik over reglerne og den sammenhäng der er
Differentialligninger
 Differentialligninger for A-niveau i st SkÄrmbillede fra TI-Nspire 013 Karsten Juul Differentialligninger for A-niveau i st 1 OplÄg til differentialligninger1 Hvad er en differentialligning?1 3 UndersÅg
Differentialligninger for A-niveau i st SkÄrmbillede fra TI-Nspire 013 Karsten Juul Differentialligninger for A-niveau i st 1 OplÄg til differentialligninger1 Hvad er en differentialligning?1 3 UndersÅg
for matematik pä B-niveau i hf
 for matematik pä B-niveau i hf 014 Karsten Juul TEST 1 StikprÅver... 1 1.1 Hvad er populationen?... 1 1. Hvad er stikpråven?... 1 1.3 Systematiske fejl ved valg af stikpråven.... 1 1.4 TilfÇldige fejl
for matematik pä B-niveau i hf 014 Karsten Juul TEST 1 StikprÅver... 1 1.1 Hvad er populationen?... 1 1. Hvad er stikpråven?... 1 1.3 Systematiske fejl ved valg af stikpråven.... 1 1.4 TilfÇldige fejl
Deskriptiv statistik. for C-niveau i hf. 2015 Karsten Juul
 Deskriptiv statistik for C-niveau i hf 75 50 25 2015 Karsten Juul DESKRIPTIV STATISTIK 1.1 Hvad er deskriptiv statistik?...1 1.2 Hvad er grupperede og ugrupperede data?...1 1.21 Eksempel pä ugrupperede
Deskriptiv statistik for C-niveau i hf 75 50 25 2015 Karsten Juul DESKRIPTIV STATISTIK 1.1 Hvad er deskriptiv statistik?...1 1.2 Hvad er grupperede og ugrupperede data?...1 1.21 Eksempel pä ugrupperede
En lille vejledning til lærere og elever i at bruge matematikprogrammet WordMat (begynderniveau)
 Matematik i WordMat En lille vejledning til lærere og elever i at bruge matematikprogrammet WordMat (begynderniveau) Indholdsfortegnelse 1. Introduktion... 3 2. Beregning... 4 3. Beregning med brøker...
Matematik i WordMat En lille vejledning til lærere og elever i at bruge matematikprogrammet WordMat (begynderniveau) Indholdsfortegnelse 1. Introduktion... 3 2. Beregning... 4 3. Beregning med brøker...
Introduktion til TI-Nspire 1. Dokumentformat
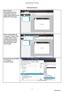 1 Dokumentformat Åbn TI-Nspire. Første gang man åbner programmet vises som regel et skærmbillede fra en håndholdt lommeregner. Denne visning skiftes til Computer i menuen eller ved ALT-Shift-C. Denne indstilling
1 Dokumentformat Åbn TI-Nspire. Første gang man åbner programmet vises som regel et skærmbillede fra en håndholdt lommeregner. Denne visning skiftes til Computer i menuen eller ved ALT-Shift-C. Denne indstilling
Trekants- beregning for hf
 Trekants- beregning for hf C C 5 l 5 A 34 8 B 018 Karsten Juul Indhold 1. Vinkler... 1 1.1 Regler for vinkler.... 1. Omkreds, areal, højde....1 Omkreds..... Rektangel....3 Kvadrat....4 Højde....5 Højde-grundlinje-formel
Trekants- beregning for hf C C 5 l 5 A 34 8 B 018 Karsten Juul Indhold 1. Vinkler... 1 1.1 Regler for vinkler.... 1. Omkreds, areal, højde....1 Omkreds..... Rektangel....3 Kvadrat....4 Højde....5 Højde-grundlinje-formel
Øvelser. Differentialregning for gymnasiet og hf Karsten Juul. til hæftet
 Øvelser til hæftet Differentialregning fr gymnasiet g hf f () t s f f () 00 Karsten Juul Øvelserne i dette hæfte får eleverne til at pdage hvad det er der fregår i differentialregningen Dette pnår man
Øvelser til hæftet Differentialregning fr gymnasiet g hf f () t s f f () 00 Karsten Juul Øvelserne i dette hæfte får eleverne til at pdage hvad det er der fregår i differentialregningen Dette pnår man
ØVEHÆFTE FOR MATEMATIK C FORMLER OG LIGNINGER
 ØVEHÆFTE FOR MATEMATIK C FORMLER OG LIGNINGER INDHOLDSFORTEGNELSE 0. FORMELSAMLING TIL FORMLER OG LIGNINGER... 2 Tal, regneoperationer og ligninger... 2 Ligning med + - / hvor x optræder 1 gang... 3 IT-programmer
ØVEHÆFTE FOR MATEMATIK C FORMLER OG LIGNINGER INDHOLDSFORTEGNELSE 0. FORMELSAMLING TIL FORMLER OG LIGNINGER... 2 Tal, regneoperationer og ligninger... 2 Ligning med + - / hvor x optræder 1 gang... 3 IT-programmer
Regneark Excel fortsat
 Regneark Excel fortsat Indhold SÅDAN TEGNES GRAFER I REGNEARK EXCEL... 1 i Excel 97-2003... 1 I Excel 2007... 1 ØVELSE... 2 I Excel 97-2003:... 2 I Excel 2007... 3 OM E-OPGAVER 12A... 4 Sådan tegnes grafer
Regneark Excel fortsat Indhold SÅDAN TEGNES GRAFER I REGNEARK EXCEL... 1 i Excel 97-2003... 1 I Excel 2007... 1 ØVELSE... 2 I Excel 97-2003:... 2 I Excel 2007... 3 OM E-OPGAVER 12A... 4 Sådan tegnes grafer
Sammenhæng mellem variable
 Sammenhæng mellem variable Indhold Variable... 1 Funktion... 2 Definitionsmængde... 2 Værdimængde... 2 Grafen for en funktion... 2 Koordinatsystem... 3 Koordinatsæt... 4 Intervaller... 5 Løsningsmængde...
Sammenhæng mellem variable Indhold Variable... 1 Funktion... 2 Definitionsmængde... 2 Værdimængde... 2 Grafen for en funktion... 2 Koordinatsystem... 3 Koordinatsæt... 4 Intervaller... 5 Løsningsmængde...
for gymnasiet og hf 2017 Karsten Juul
 for gymnasiet og hf 75 50 5 017 Karsten Juul Statistik for gymnasiet og hf 017 Karsten Juul 5/11-017 Nyeste version af dette hæfte kan downloades fra http://mat1.dk/noter.htm Hæftet må benyttes i undervisningen
for gymnasiet og hf 75 50 5 017 Karsten Juul Statistik for gymnasiet og hf 017 Karsten Juul 5/11-017 Nyeste version af dette hæfte kan downloades fra http://mat1.dk/noter.htm Hæftet må benyttes i undervisningen
Rumfang af væske i beholder
 Matematikprojekt Rumfang af væske i beholder Maila Walmod, 1.3 HTX Roskilde Afleveringsdato: Fredag d. 7. december 2007 1 Fru Hansen skal have en væskebeholder, hvor rumfanget af væsken skal kunne aflæses
Matematikprojekt Rumfang af væske i beholder Maila Walmod, 1.3 HTX Roskilde Afleveringsdato: Fredag d. 7. december 2007 1 Fru Hansen skal have en væskebeholder, hvor rumfanget af væsken skal kunne aflæses
sammenhänge 2008 Karsten Juul
 LineÄre sammenhänge y x 3 3 008 Karsten Juul Dette häfte er en fortsättelse af häftet "VariabelsammenhÄnge, 008". Indhold 8. Hvad er en lineär sammenhäng?... 3 9. Hvordan ser grafen ud for en lineär sammenhäng?...
LineÄre sammenhänge y x 3 3 008 Karsten Juul Dette häfte er en fortsättelse af häftet "VariabelsammenhÄnge, 008". Indhold 8. Hvad er en lineär sammenhäng?... 3 9. Hvordan ser grafen ud for en lineär sammenhäng?...
Potensfunktioner og dobbeltlogaritmisk papir
 1 Potensfunktioner og dobbeltlogaritmisk papir OBS: til skriftlig eksamen skal du kun kunne aflæse på en graf, der allerede er indtegnet på dobbeltlogaritmisk papir. Du kan ikke komme ud for at skulle
1 Potensfunktioner og dobbeltlogaritmisk papir OBS: til skriftlig eksamen skal du kun kunne aflæse på en graf, der allerede er indtegnet på dobbeltlogaritmisk papir. Du kan ikke komme ud for at skulle
Sandsynlighed. for matc i stx og hf Karsten Juul
 Sandsynlighed for matc i stx og hf 209 Karsten Juul . Udfald Vi drejer den gule skive om dens centrum og ser hvilket af de fem felter der standser ud for den røde pil. Da skiven sidst blev drejet, var
Sandsynlighed for matc i stx og hf 209 Karsten Juul . Udfald Vi drejer den gule skive om dens centrum og ser hvilket af de fem felter der standser ud for den røde pil. Da skiven sidst blev drejet, var
Lineære sammenhænge, residualplot og regression
 Lineære sammenhænge, residualplot og regression Opgave 1: Er der en bagvedliggende lineær sammenhæng? I mange sammenhænge indsamler man data som man ønsker at undersøge og afdække eventuelle sammenhænge
Lineære sammenhænge, residualplot og regression Opgave 1: Er der en bagvedliggende lineær sammenhæng? I mange sammenhænge indsamler man data som man ønsker at undersøge og afdække eventuelle sammenhænge
Integralregning. 1. del. 2006 Karsten Juul. M l
 Integralregning del () M l () 6 Karsten Juul Indhold Stamunktion OplÄg om stamunktion Deinition a stamunktion 6 Kontrol a stamunktion 9 SÄtning om stamunktionerne til en unktion Deinition a ubestemt integral
Integralregning del () M l () 6 Karsten Juul Indhold Stamunktion OplÄg om stamunktion Deinition a stamunktion 6 Kontrol a stamunktion 9 SÄtning om stamunktionerne til en unktion Deinition a ubestemt integral
ØVEHÆFTE FOR MATEMATIK C FORMLER OG LIGNINGER
 ØVEHÆFTE FOR MATEMATIK C FORMLER OG LIGNINGER INDHOLDSFORTEGNELSE 0. FORMELSAMLING TIL FORMLER OG LIGNINGER... 2 Tal, regneoperationer og ligninger... 2 Isolere en ubekendt... 3 Hvis x står i første brilleglas...
ØVEHÆFTE FOR MATEMATIK C FORMLER OG LIGNINGER INDHOLDSFORTEGNELSE 0. FORMELSAMLING TIL FORMLER OG LIGNINGER... 2 Tal, regneoperationer og ligninger... 2 Isolere en ubekendt... 3 Hvis x står i første brilleglas...
2HF091_MAC. Givet to ensvinklede trekanter som vist på figuren. De anførte mål er oplyst.
 Opgave 1 Givet to ensvinklede trekanter som vist på figuren. De anførte mål er oplyst. Da trekanterne er ensvinklede, har de proportionale sider; forstørrelsesfaktoren k findes som forholdet mellem c 1
Opgave 1 Givet to ensvinklede trekanter som vist på figuren. De anførte mål er oplyst. Da trekanterne er ensvinklede, har de proportionale sider; forstørrelsesfaktoren k findes som forholdet mellem c 1
for matematik pä B-niveau i hf
 for matematik pä B-niveau i hf 75 50 5 016 Karsten Juul GRUPPEREDE DATA 1.1 Hvad er deskriptiv statistik?...1 1. Hvad er grupperede og ugrupperede data?...1 1.1 Eksempel pä ugrupperede data...1 1. Eksempel
for matematik pä B-niveau i hf 75 50 5 016 Karsten Juul GRUPPEREDE DATA 1.1 Hvad er deskriptiv statistik?...1 1. Hvad er grupperede og ugrupperede data?...1 1.1 Eksempel pä ugrupperede data...1 1. Eksempel
Tegninger ved skriftlig prøve i fysik A, stx Om tegning på pdf-filer med Adobe Acrobat Reader og andre programmer
 Tegninger ved skriftlig prøve i fysik A, stx Om tegning på pdf-filer med Adobe Acrobat Reader og andre programmer Nils Kruse Fra sommeren 2018 bliver eksamensopgaverne i skriftlig fysik A udleveret digitalt.
Tegninger ved skriftlig prøve i fysik A, stx Om tegning på pdf-filer med Adobe Acrobat Reader og andre programmer Nils Kruse Fra sommeren 2018 bliver eksamensopgaverne i skriftlig fysik A udleveret digitalt.
Kapitel 3 Lineære sammenhænge
 Matematik C (må anvendes på Ørestad Gymnasium) Lineære sammenhænge Det sker tit, at man har flere variable, der beskriver en situation, og at der en sammenhæng mellem de variable. Enhver formel er faktisk
Matematik C (må anvendes på Ørestad Gymnasium) Lineære sammenhænge Det sker tit, at man har flere variable, der beskriver en situation, og at der en sammenhæng mellem de variable. Enhver formel er faktisk
Asymptoter. for standardforsøgene i matematik i gymnasiet. 2003 Karsten Juul
 Asymptoter for standardforsøgene i matematik i gymnasiet 2003 Karsten Juul Indledning om lodrette asymptoter Lad f være funktionen bestemt ved =, 2. 2 Vi udregner funktionsværdierne i nogle -værdier der
Asymptoter for standardforsøgene i matematik i gymnasiet 2003 Karsten Juul Indledning om lodrette asymptoter Lad f være funktionen bestemt ved =, 2. 2 Vi udregner funktionsværdierne i nogle -værdier der
Statistisk beskrivelse og test
 Statistisk beskrivelse og test 005 Karsten Juul Kapitel 1. Intervalhyppigheder Afsnit 1.1: Histogram En elevgruppe på et gymnasium har spurgt 100 tilfældigt valgte elever på gymnasiet om hvor lang tid
Statistisk beskrivelse og test 005 Karsten Juul Kapitel 1. Intervalhyppigheder Afsnit 1.1: Histogram En elevgruppe på et gymnasium har spurgt 100 tilfældigt valgte elever på gymnasiet om hvor lang tid
Indhold Grupperede observationer... 1 Ugrupperede observationer... 3 Analyse af normalfordelt observationssæt... 4
 BH Test for normalfordeling i WordMat Indhold Grupperede observationer... 1 Ugrupperede observationer... 3 Analyse af normalfordelt observationssæt... 4 Grupperede observationer Vi tager udgangspunkt i
BH Test for normalfordeling i WordMat Indhold Grupperede observationer... 1 Ugrupperede observationer... 3 Analyse af normalfordelt observationssæt... 4 Grupperede observationer Vi tager udgangspunkt i
Vejledning til WordMat på Mac
 Installation: WordMat på MAC Vejledning til WordMat på Mac Hent WordMat for MAC på www.eduap.com Installationen er først slut når du har gjort følgende 1. Åben Word 2. I menuen vælges: Word > Indstillinger
Installation: WordMat på MAC Vejledning til WordMat på Mac Hent WordMat for MAC på www.eduap.com Installationen er først slut når du har gjort følgende 1. Åben Word 2. I menuen vælges: Word > Indstillinger
Eksaminanderne på hf tilvalg forventes ikke at kunne udnytte grafregnerens muligheder for regression.
 Bilag 3: Uddrag af Matematik 1999. Skriftlig eksamen og større skriftlig opgave ved studentereksamen og hf. Kommentarer på baggrund af censorernes tilbagemeldinger HF-tilvalgsfag (opgavesæt HF 99-8-1)
Bilag 3: Uddrag af Matematik 1999. Skriftlig eksamen og større skriftlig opgave ved studentereksamen og hf. Kommentarer på baggrund af censorernes tilbagemeldinger HF-tilvalgsfag (opgavesæt HF 99-8-1)
Når eleverne skal opdage betydningen af koefficienterne i udtrykket:
 Den rette linje og parablen GeoGebra er tænkt som et dynamisk geometriprogram, som både kan anvendes til euklidisk og analytisk geometri Eksempel Tegn linjen med ligningen: Indtast ligningen i Input-feltet.
Den rette linje og parablen GeoGebra er tænkt som et dynamisk geometriprogram, som både kan anvendes til euklidisk og analytisk geometri Eksempel Tegn linjen med ligningen: Indtast ligningen i Input-feltet.
Variabelsammenhænge og grafer
 Variabelsammenhænge og grafer Indhold Variable... 1 Funktion... 1 Grafen for en funktion... 2 Proportionalitet... 4 Ligefrem proportional eller blot proportional... 4 Omvendt proportionalitet... 4 Intervaller...
Variabelsammenhænge og grafer Indhold Variable... 1 Funktion... 1 Grafen for en funktion... 2 Proportionalitet... 4 Ligefrem proportional eller blot proportional... 4 Omvendt proportionalitet... 4 Intervaller...
Sådan bruges skydere til at undersøge funktioner, tangenter og integraler
 Sådan bruges skydere til at undersøge funktioner, tangenter og integraler Freyja Hreinsdóttir University of Iceland 1 Indledning I mange lærebøger om differentiering er der øvelser af den slags, hvor den
Sådan bruges skydere til at undersøge funktioner, tangenter og integraler Freyja Hreinsdóttir University of Iceland 1 Indledning I mange lærebøger om differentiering er der øvelser af den slags, hvor den
Bedste rette linje ved mindste kvadraters metode
 1/9 Bedste rette linje ved mindste kvadraters metode - fra www.borgeleo.dk Figur 1: Tre datapunkter og den bedste rette linje bestemt af A, B og C Målepunkter og bedste rette linje I ovenstående koordinatsystem
1/9 Bedste rette linje ved mindste kvadraters metode - fra www.borgeleo.dk Figur 1: Tre datapunkter og den bedste rette linje bestemt af A, B og C Målepunkter og bedste rette linje I ovenstående koordinatsystem
Regning med funktioner - TAVLENOTER
 Sammensat funktion [Elevsamtaler] Jens Thostrup, GUX Nuuk 1 FACIT b) 1 og 3 er de eneste løsninger, der optræder i tabellen Jens Thostrup, GUX Nuuk 2 Regningsarter for funktioner Sumfunktion: (f+g)(x)
Sammensat funktion [Elevsamtaler] Jens Thostrup, GUX Nuuk 1 FACIT b) 1 og 3 er de eneste løsninger, der optræder i tabellen Jens Thostrup, GUX Nuuk 2 Regningsarter for funktioner Sumfunktion: (f+g)(x)
Kom godt i gang med Fable-robotten
 Kom godt i gang med Fable-robotten 1. Først skal du installere programmet på din computer. Gå ind på shaperobotics.com og under support vælger du download: Her vælger du, under PC App om du kører Windows
Kom godt i gang med Fable-robotten 1. Først skal du installere programmet på din computer. Gå ind på shaperobotics.com og under support vælger du download: Her vælger du, under PC App om du kører Windows
Uge / emne Indhold Materiale Mål Evaluering
 Årsplan for skoleåret 2016/2017 5. klasse matematik Uge / emne Indhold Materiale Mål Evaluering 33 36 Store tal og negative tal I gang med nyt bogsystem. Arbejde med store tal og med negative tal. Bruge
Årsplan for skoleåret 2016/2017 5. klasse matematik Uge / emne Indhold Materiale Mål Evaluering 33 36 Store tal og negative tal I gang med nyt bogsystem. Arbejde med store tal og med negative tal. Bruge
3D-grafik Karsten Juul
 3D-grafik 2005 Karsten Juul Når der i disse noter står at du skal få tegnet en figur, så er det meningen at du skal få tegnet den ved at taste tildelinger i Mathcad-dokumentet RumFig2 Det er selvfølgelig
3D-grafik 2005 Karsten Juul Når der i disse noter står at du skal få tegnet en figur, så er det meningen at du skal få tegnet den ved at taste tildelinger i Mathcad-dokumentet RumFig2 Det er selvfølgelig
matematik Demo excel trin 2 bernitt-matematik.dk 1 excel 2 2007 by bernitt-matematik.dk
 matematik excel trin 2 bernitt-matematik.dk 1 excel 2 2007 by bernitt-matematik.dk matematik excel 2 1. udgave som E-bog 2007 by bernitt-matematik.dk Kopiering af denne bog er kun tilladt efter aftale
matematik excel trin 2 bernitt-matematik.dk 1 excel 2 2007 by bernitt-matematik.dk matematik excel 2 1. udgave som E-bog 2007 by bernitt-matematik.dk Kopiering af denne bog er kun tilladt efter aftale
Talrækker. Aktivitet Emne Klassetrin Side
 VisiRegn ideer 3 Talrækker Inge B. Larsen [email protected] INFA juli 2001 Indhold: Aktivitet Emne Klassetrin Side Vejledning til Talrækker 2-4 Elevaktiviteter til Talrækker 3.1 Talrækker (1) M-Æ 5-9 3.2 Hanoi-spillet
VisiRegn ideer 3 Talrækker Inge B. Larsen [email protected] INFA juli 2001 Indhold: Aktivitet Emne Klassetrin Side Vejledning til Talrækker 2-4 Elevaktiviteter til Talrækker 3.1 Talrækker (1) M-Æ 5-9 3.2 Hanoi-spillet
Projekt 1.3 Brydningsloven
 Projekt 1.3 Brydningsloven Når en bølge, fx en lysbølge, rammer en grænseflade mellem to stoffer, vil bølgen normalt blive spaltet i to: Noget af bølgen kastes tilbage (spejling), hvor udfaldsvinklen u
Projekt 1.3 Brydningsloven Når en bølge, fx en lysbølge, rammer en grænseflade mellem to stoffer, vil bølgen normalt blive spaltet i to: Noget af bølgen kastes tilbage (spejling), hvor udfaldsvinklen u
Fable Kom godt i gang
 Fable Kom godt i gang Opdateret: 26-03-2018 Indholdsfortegnelse 1. Først skal du installere programmet på din computer 3 2. Når programmet er installeret er du klar til at pakke robotten ud 4 3. Nu er
Fable Kom godt i gang Opdateret: 26-03-2018 Indholdsfortegnelse 1. Først skal du installere programmet på din computer 3 2. Når programmet er installeret er du klar til at pakke robotten ud 4 3. Nu er
Nyt i Analyseportalen og Web Report Studio. Analyseportalen
 Nyt i Analyseportalen og Web Report Studio Analyseportalen Den nye Analyseportal er ikke meget anderledes end den gamle. Der er dog enkelte funktioner, der er blevet meget anderledes. De er omtalt i denne
Nyt i Analyseportalen og Web Report Studio Analyseportalen Den nye Analyseportal er ikke meget anderledes end den gamle. Der er dog enkelte funktioner, der er blevet meget anderledes. De er omtalt i denne
Erik Vestergaard 1. Opgaver. i Lineære. funktioner. og modeller
 Erik Vestergaard www.matematikfsik.dk Opgaver i Lineære funktioner og modeller Erik Vestergaard www.matematikfsik.dk Erik Vestergaard, Haderslev. www.matematikfsik.dk Teknik. Aflæse forskrift fra graf...
Erik Vestergaard www.matematikfsik.dk Opgaver i Lineære funktioner og modeller Erik Vestergaard www.matematikfsik.dk Erik Vestergaard, Haderslev. www.matematikfsik.dk Teknik. Aflæse forskrift fra graf...
Differentialregning med TI-Interactive! Indledende differentialregning Tangenter Monotoniforhold og ekstremum Optimering Jan Leffers (2009)
 Differentialregning med TI-Interactive! Indledende differentialregning Tangenter Monotoniforhold og ekstremum Optimering Jan Leffers (2009) Indholdsfortegnelse Indholdsfortegnelse...2 Indledende differentialregning...3
Differentialregning med TI-Interactive! Indledende differentialregning Tangenter Monotoniforhold og ekstremum Optimering Jan Leffers (2009) Indholdsfortegnelse Indholdsfortegnelse...2 Indledende differentialregning...3
Løsninger til eksamensopgaver på A-niveau 2019 ny ordning
 Løsninger til eksamensopgaver på A-niveau 2019 ny ordning Opgave 1: r ( t) Q( 7,8) 21. maj 2019: Delprøven UDEN hjælpemidler 2t + 1 = 2 t 1 a) Funktionsværdien bestemmes ved indsættelse af t-værdien: 2
Løsninger til eksamensopgaver på A-niveau 2019 ny ordning Opgave 1: r ( t) Q( 7,8) 21. maj 2019: Delprøven UDEN hjælpemidler 2t + 1 = 2 t 1 a) Funktionsværdien bestemmes ved indsættelse af t-værdien: 2
Lineær Programmering i GeoGebra Side 1 af 8
 Lineær Programmering i GeoGebra Side 1 af 8 Grundlæggende find selv flere funktioner, fx i GG s indbyggede hjælpefunktion. Vær opmærksom på at grænsefladen i GeoGebra ændrer sig med tiden, da værktøjet
Lineær Programmering i GeoGebra Side 1 af 8 Grundlæggende find selv flere funktioner, fx i GG s indbyggede hjælpefunktion. Vær opmærksom på at grænsefladen i GeoGebra ændrer sig med tiden, da værktøjet
Mathcad Survival Guide
 Mathcad Survival Guide Mathcad er en blanding mellem et tekstbehandlingsprogram (Word), et regneark (Ecel) og en grafisk CAS-lommeregner. Programmet er velegnet til matematikopgaver, fysikrapporter og
Mathcad Survival Guide Mathcad er en blanding mellem et tekstbehandlingsprogram (Word), et regneark (Ecel) og en grafisk CAS-lommeregner. Programmet er velegnet til matematikopgaver, fysikrapporter og
Fable Kom godt i gang
 Fable Kom godt i gang Vers. 1.3.1 Opdateret: 29-08-2018 Indholdsfortegnelse 1. Installer programmet 3 2. Pak robotten ud 5 3. I gang med at programmere 6 4. Programmér Fable til at køre fra 90 til -90
Fable Kom godt i gang Vers. 1.3.1 Opdateret: 29-08-2018 Indholdsfortegnelse 1. Installer programmet 3 2. Pak robotten ud 5 3. I gang med at programmere 6 4. Programmér Fable til at køre fra 90 til -90
Differentialregning. Supplerende opgaver til HTX Matematik 1 Nyt Teknisk Forlag. Opgaverne må frit benyttes i undervisningen.
 Differentialregning Side 1 0401 Figuren viser grafen for en funktion f. a) Find ud fra aflæsning på figuren f (3) og f (5) b) Find ud fra aflæsning på figuren fortegnet for hvert af tallene f (1,5), f
Differentialregning Side 1 0401 Figuren viser grafen for en funktion f. a) Find ud fra aflæsning på figuren f (3) og f (5) b) Find ud fra aflæsning på figuren fortegnet for hvert af tallene f (1,5), f
Klasse 1.4 Michael Jokil 03-05-2010
 HTX I ROSKILDE Afsluttende opgave Kommunikation og IT Klasse 1.4 Michael Jokil 03-05-2010 Indholdsfortegnelse Indledning... 3 Formål... 3 Planlægning... 4 Kommunikationsplan... 4 Kanylemodellen... 4 Teknisk
HTX I ROSKILDE Afsluttende opgave Kommunikation og IT Klasse 1.4 Michael Jokil 03-05-2010 Indholdsfortegnelse Indledning... 3 Formål... 3 Planlægning... 4 Kommunikationsplan... 4 Kanylemodellen... 4 Teknisk
QR15 Vejledning i at bestemme kvartilsæt og at tegne sumkurver med Nspire, Maple og Geogebra
 QR15 Vejledning i at bestemme kvartilsæt og at tegne sumkurver med Nspire, Maple og Geogebra Nspire: Vi har et datasæt. Der er overordnet to metoder til at tegne sumkurver i programmet, og vi beskriver
QR15 Vejledning i at bestemme kvartilsæt og at tegne sumkurver med Nspire, Maple og Geogebra Nspire: Vi har et datasæt. Der er overordnet to metoder til at tegne sumkurver i programmet, og vi beskriver
Formler & algebra - Fase 2 Omskriv & beregn med variable
 Navn: Klasse: Formler algebra - Fase Omskriv beregn med variable Vurdering fra til 5 (hvor 5 er højst) Læringsmål Selv Lærer Beviser og forslag til forbedring. Jeg kan opstille en linjes ligning, når jeg
Navn: Klasse: Formler algebra - Fase Omskriv beregn med variable Vurdering fra til 5 (hvor 5 er højst) Læringsmål Selv Lærer Beviser og forslag til forbedring. Jeg kan opstille en linjes ligning, når jeg
for gymnasiet og hf 2016 Karsten Juul
 for gymnasiet og hf 75 50 5 016 Karsten Juul Statistik for gymnasiet og hf Ä 016 Karsten Juul 4/1-016 Nyeste version af dette håfte kan downloades fra http://mat1.dk/noter.htm HÅftet mç benyttes i undervisningen
for gymnasiet og hf 75 50 5 016 Karsten Juul Statistik for gymnasiet og hf Ä 016 Karsten Juul 4/1-016 Nyeste version af dette håfte kan downloades fra http://mat1.dk/noter.htm HÅftet mç benyttes i undervisningen
Differentialkvotient bare en slags hældning
 Differentialkvotient bare en slags hældning Et kort eksperiment som indledning til differentialregning Forfatter: Behrndt Andersen, Texas Instruments, [email protected] Matematisk område+niveau: Differentialregning
Differentialkvotient bare en slags hældning Et kort eksperiment som indledning til differentialregning Forfatter: Behrndt Andersen, Texas Instruments, [email protected] Matematisk område+niveau: Differentialregning
Vejledning i brug af MiljøGIS.
 NOTAT Naturplanlægning, naturprojekter og skov J.nr. NST-3379-00005 Ref. MOBKI/TRDIP/KINIE Den 11. februar 2014 Vejledning i brug af MiljøGIS. Indholdsfortegnelse Introduktion... 3 1. Fremsøgning af lokalitet...
NOTAT Naturplanlægning, naturprojekter og skov J.nr. NST-3379-00005 Ref. MOBKI/TRDIP/KINIE Den 11. februar 2014 Vejledning i brug af MiljøGIS. Indholdsfortegnelse Introduktion... 3 1. Fremsøgning af lokalitet...
Arkiv i SIMU World. Arkivet ligger i SIMU World, og gør det muligt at arkivere jeres sager direkte i SIMU World.
 Indhold Hvad er Arkivet?... 2 Arkiv er elektronisk, og ligger nederst i hver menu... 3 Arkivgrupper... 3 Oprette hovedmapper under de enkelte faner... 5 Oprette sagsmapper under hovedmapper... 6 Arkivering
Indhold Hvad er Arkivet?... 2 Arkiv er elektronisk, og ligger nederst i hver menu... 3 Arkivgrupper... 3 Oprette hovedmapper under de enkelte faner... 5 Oprette sagsmapper under hovedmapper... 6 Arkivering
Et CAS program til Word.
 Et CAS program til Word. 1 WordMat WordMat er et CAS-program (computer algebra system) som man kan downloade gratis fra hjemmesiden www.eduap.com/wordmat/. Programmet fungerer kun i Word 2007 og 2010.
Et CAS program til Word. 1 WordMat WordMat er et CAS-program (computer algebra system) som man kan downloade gratis fra hjemmesiden www.eduap.com/wordmat/. Programmet fungerer kun i Word 2007 og 2010.
Differentialregning 2
 Differentialregning Hvis man ønsker mere udfordring, kan man springe de første 7 opgaver over. Opgave 1 Udregn monotoniintervallerne for funktionerne f 1 () = + 4, f () = 4 3 f 3 () = 3 6 + 9 +, f 4 ()
Differentialregning Hvis man ønsker mere udfordring, kan man springe de første 7 opgaver over. Opgave 1 Udregn monotoniintervallerne for funktionerne f 1 () = + 4, f () = 4 3 f 3 () = 3 6 + 9 +, f 4 ()
Velkommen til OnReg Agent.
 Velkommen til OnReg Agent. 2 OnReg Agent Velkommen til Onreg Agent Du er blevet tildelt brugernavn og kodeord til OnReg Agent. Denne guide beskriver hvordan du benytter systemet. Hvis arrangøren tillader
Velkommen til OnReg Agent. 2 OnReg Agent Velkommen til Onreg Agent Du er blevet tildelt brugernavn og kodeord til OnReg Agent. Denne guide beskriver hvordan du benytter systemet. Hvis arrangøren tillader
Maple. Skærmbilledet. Vi starter med at se lidt nærmere på opstartsbilledet i Maple. Værktøjslinje til indtastningsområdet. Menulinje.
 Maple Dette kapitel giver en kort introduktion til hvordan Maple 12 kan benyttes til at løse mange af de opgaver, som man bliver mødt med i matematiktimerne på HHX. Skærmbilledet Vi starter med at se lidt
Maple Dette kapitel giver en kort introduktion til hvordan Maple 12 kan benyttes til at løse mange af de opgaver, som man bliver mødt med i matematiktimerne på HHX. Skærmbilledet Vi starter med at se lidt
Brugervejledning til Graph
 Graph (brugervejledning) side 1/17 Steen Toft Jørgensen Brugervejledning til Graph Graph er et gratis program, som ikke fylder meget. Downloades på: www.padowan.dk/graph/. Programmet er lavet af Ivan Johansen,
Graph (brugervejledning) side 1/17 Steen Toft Jørgensen Brugervejledning til Graph Graph er et gratis program, som ikke fylder meget. Downloades på: www.padowan.dk/graph/. Programmet er lavet af Ivan Johansen,
Kort om Potenssammenhænge
 Øvelser til hæftet Kort om Potenssmmenhænge 2011 Krsten Juul Dette hæfte indeholder bl.. mnge småspørgsmål der gør det nemmere for elever t rbejde effektivt på t få kendskb til emnet. Indhold 1. Ligning
Øvelser til hæftet Kort om Potenssmmenhænge 2011 Krsten Juul Dette hæfte indeholder bl.. mnge småspørgsmål der gør det nemmere for elever t rbejde effektivt på t få kendskb til emnet. Indhold 1. Ligning
