Lineære 1. ordens differentialligningssystemer
|
|
|
- Kristen Sommer
- 10 år siden
- Visninger:
Transkript
1 enote enote Lineære ordens differentialligningssystemer Denne enote beskriver ordens differentialligningssystemer og viser, hvordan de kan løses enoten er i forlængelse af enote, der beskriver lineære differentialligninger generelt Det er derfor en god idé at have læst den først Desuden bruges egenværdier og -vektorer i løsningsproceduren, se enote 9 og enote 0 Version 3085 Differentialligningssystemer Vi vil i denne enote kigge på lineære koblede homogene differentialligninger af orden med konstante koefficienter (se forklaring nedenfor) En sådan samling af koblede differentialligninger kaldes et differentialligningssystem Et differentialligningssystem af orden med n ligninger ser principielt således ud: (t) = a (t) + a (t) + + a n n (t) (t) = a (t) + a (t) + + a n n (t) n(t) = a n (t) + a n (t) + + a nn n (t) (-) På venstresiden er differentialkvotienterne af de n ukendte funktioner (t), (t),, n (t) stillet op, mens hver højreside er en linearkombination af de n ukendte funktioner Koefficienterne (a erne) er reelle konstanter I matri-format kan systemet skrives således: (t) a a a n (t) (t) = a a a n (t) (-) n(t) a n a n a nn n (t)
2 enote DIFFERENTIALLIGNINGSSYSTEMER Endnu mere kompakt skrives det (t) = A(t) (-3) A kaldes systemmatricen Det er nu målet at løse et sådant differentialligningssystem, altså at bestemme (t) = ( (t), (t),, n (t)) Forklaring Hvad er et differentialligningssystem? Differentialligningssystemer er samlinger af differentialligninger Grunden til, at man ikke betragter differentialligningerne enkeltvis, er, at de ikke kan løses hver for sig, da de har for mange ubekendte Men da de samme ukendte funktioner optræder i flere ligninger, er ligningerne koblede En enkelt differentialligning fra et system kan for eksempel se således ud: (t) = 4 (t) (t) (-4) Det er ikke muligt at bestemme hverken (t) eller (t), da der er to ukendte funktioner men kun én differentialligning For at kunne løse et sådant system fuldt ud skal man have lige så mange ligninger, som man har ukendte funktioner (med deres tilhørende afledede) Den anden ligning i systemet kunne derfor være (t) = 6 (t) + (t) (-5) Vi har nu lige så mange ligninger (to), som vi har ukendte funktioner (to), og det er nu muligt at bestemme både (t) og (t) For overskuelighedens skyld skriver man differentialligningssystemer på matriform Systemet ovenfor ser således ud: [ (t) (t) = [ 4 6 [ (t) (t) (t) = [ 4 (t) = A (t) (-6) 6 Ser man bort fra, at det er vektorer og matricer, der opereres med, ligner ligningssystemet noget, vi har set før: (t) = A (t), som man allerede kunne løse i gymnasiet Løsningen til denne differentialligning er triviel: (t) = ce At, hvor c er en arbitrær konstant Nedenfor finder vi ud af, at løsningen til det tilsvarende system af differentialligninger er sammenlignelig med (t) = ce At Vi løser nu differentialligningssystemet i nedenstående sætning Sætningen indeholder
3 enote DIFFERENTIALLIGNINGSSYSTEMER 3 forudsætninger, der ikke altid er opfyldte De særtilfælde, hvor sætningen ikke gælder, undersøges senere Beviset for sætningen indeholder en meget kendt og brugt metode, kaldet diagonaliseringsmetoden Sætning Et lineært differentialligningssystem bestående af n ligninger med i alt n ukendte differentialble funktioner er givet ved (t) = A(t), t R (-7) Hvis A har n lineært uafhængige egenvektorer v, v,, v n tilhørende (ikke nødvendigvis forskellige) egenværdier λ, λ,, λ n, er systemets fuldstændige løsningsmængde bestemt ved (t) = c e λ t v + c e λ t v + + c n e λ nt v n, t R, (-8) hvor c, c,, c n er vilkårlige komplekse konstanter Læg mærke til, at det ikke altid er muligt at finde n lineært uafhængige egenvektorer Derfor kan man ikke altid bruge sætning til løsning af differentialligningssystemer af orden I sætningen er angivet den fuldstændige komplekse løsningsmængde for differentialligningssystemet Den fuldstændige reelle løsningsmængde kan derefter om nødvendigt findes som den reelle delmængde af den komplekse løsningsmængde Bevis Vi gætter på, at en løsning til differentialligningssystemet (t) = A(t) er en vektor v ganget på e λt, hvor λ er en konstant, så (t) = e λt v Vi har da den differentierede (t) = λe λt v (-9) Sættes dette udtryk for (t) ind i (-7) sammen med udtrykket for (t) fås λe λt v = Ae λt v λv = Av Av λv = 0 (A λe)v = 0 (-0) e λt er forskellig fra nul for ethvert t R, hvorfor det kan divideres ud Ligningen λv = Av genkendes som et egenværdiproblem, se enote 9 λ er derfor en egenværdi til A og v den tilhørende egenvektor De kan begge bestemmes Det er nu lykkedes os at finde ud af, at
4 enote DIFFERENTIALLIGNINGSSYSTEMER 4 e λt v er én løsning til differentialligningssystemet, når λ er en egenværdi og v den tilhørende egenvektor til A Til at bestemme den fuldstændige løsningsmængde bruges den såkaldte diagonaliseringsmetode: Vi antager, at A = A n n har n lineært uafhængige (reelle eller komplekse) egenvektorer v, v,, v n hørende til egenværdierne λ, λ,, λ n Vi indfører nu den regulære matri V, som indeholder alle egenvektorerne, V = [ v v v n (-) Endvidere indføres funktionen y, så y(t) = (y (t), y (t),, y n (t)), således, at (t) = Vy(t) (-) Vi har da, at (t) = Vy (t) Indsættes disse udtryk for (t) og (t) i (-7), fås Vy (t) = AVy(t) y (t) = V AVy(t) = Λy(t), (-3) hvor Λ = V AV = diag(λ, λ,, λ n ) er en diagonalmatri med egenværdierne tilhørende A Vi har nu ligningen y (t) = Λy(t), der kan skrives på følgende måde: y (t) = λ y (t) y (t) = λ y (t) y n(t) = λ n y n (t) (-4) da Λ kun har elementer forskellig fra nul i diagonalen Dette ligningssystem er ikke koblet I hver ligning optræder nemlig kun én funktion og dens afledede Derfor kan man løse dem enkeltvis, og den fuldstændige løsningsmængde til hver ligning er y(t) = ce λt for alle c C Samlet giver det den fuldstændige løsningsmængde bestående af følgende funktioner for alle c, c,, c n C: y(t) = y (t) y (t) y n (t) = c e λ t c e λ t c n e λ nt Da vi nu har løsningen y(t), kan vi også finde løsningen (t) = Vy(t), c e λ t (t) = Vy(t) = [ c e λ t v v v n c n e λ nt = c e λ t v + c e λ t v + + c n e λ nt v n (-5) (-6)
5 enote TO KOBLEDE DIFFERENTIALLIGNINGER 5 Vi har nu fundet den fuldstændige komplekse løsningsmængde til ligningssystemet i (-7), som består af funktionerne (t) for alle c, c,, c n C Eksempel 3 Et givet differentialligningssystem (t) = (t) + (t) (t) = 3 (t) (-7) skrives på matriform som (t) = [ (t) = A(t) (-8) 3 0 Det kan vises, at A har egenværdierne λ = 3 og λ = med de tilhørende egenvektorer v = (, ) og v = (, 3) (prøv selv!) Derfor er den fuldstændige reelle løsningsmængde til differentialligningssystemet givet ved nedenstående funktioner for alle c, c R: (t) = [ [ (t) = c (t) e 3t + c e t [ 3, t R (-9) Løsningen er fundet ved brug af sætning En anden måde at opskrive løsningsmængden på er ved at skille ligningssystemet ad, så udgør løsningsmængden, hvor t R, for alle c, c R (t) = c e 3t + c e t (t) = c e 3t 3c e t (-0) To koblede differentialligninger Givet et lineært homogent ordens differentialligningssystem med konstante koefficienter med n ligninger og n ukendte funktioner (t) = A(t), t R (-) Hvis systemmatricen A har n lineært uafhængige egenvektorer, kan systemets reelle løsningsmængde findes ved hjælp af sætning Hvis egenværdierne er reelle, kan den reelle løsningsmængde umiddelbart opskrives efter sætningens formel (-8), hvor de n tilhørende lineært uafhængige egenvektorer er reelle, og de arbitrære konstanter angives som reelle Hvis systemmatricen har egenværdier, som ikke er reelle, kan den
6 enote TO KOBLEDE DIFFERENTIALLIGNINGER 6 reelle løsningsmængde findes ved at uddrage den reelle delmængde af den komplekse løsningsmængde Også i dette tilfælde vil løsningsmængden kunne opskrives som en linearkombination af n lineært uafhængige reelle løsninger til differentialligningssystemet Tilbage har vi særtilfældet, hvor systemmatricen ikke har n lineært uafhængige egenvektorer Også her vil den reelle løsningsmængde være en linearkombination af n lineært uafhængige reelle løsninger til differentialligningssystemet Her kan diagonaliseringsmetoden af gode grunde ikke benyttes, og man må bruge andre metoder I dette afsnit gennemgår vi de nævnte tre tilfælde for systemer, der består af n = koblede differentialligninger med n = ukendte funktioner Dernæst i det efterfølgende afsnit generaliseres metoden til det generelle tilfælde for højere n end, se sætning 9 Metode 4 Den fuldstændige reelle løsningsmængde til differentialligningssystemet (t) = A(t), t R (-) bestående af n = ligninger med ukendte funktioner kan opskrives som (t) = c u (t) + c u (t), t R, (-3) hvor u og u er reelle lineært uafhængige partikulære løsninger, og c, c R Bestem først egenværdierne til A For rødderne i det karakteristiske polynomium A foreligger der tre muligheder: To reelle enkeltrødder I så fald har begge egenværdier λ og λ algebraisk multiplicitet og geometrisk multiplicitet, og vi kan sætte u (t) = e λ t v og u (t) = e λ t v, (-4) hvor v og v er egentlige egenvektorer tilhørende λ og λ respektivt To komplekse rødder De to egenværdier λ og λ er da hinandens konjugerede komplekse tal Vi bestemmer da u og u ved hjælp af metode 5 herunder En dobbeltrod Her har egenværdien λ algebraisk multiplicitet Hvis den geometriske multiplicitet af λ er, bestemmes u og u ved hjælp af metode 7
7 enote TO KOBLEDE DIFFERENTIALLIGNINGER 7 Ved den første mulighed i metode 4 med to forskellige reelle egenværdier, kan man udmiddelbart benytte sætning, idet de arbitrære konstanter vælges som reelle, se eksempel 3 Nu følger metoden, der tager sig af tilfældet med to komplekse egenværdier Metode 5 To lineært uafhængige reelle løsninger til differentialligningssystemet (t) = A(t), t R, (-5) hvor A har det komplekse egenværdipar λ = α + βi og λ = α βi med tilhørende egenvektorer v og v, er ( ) u (t) = Re e λt v = e αt (cos(βt)re(v) sin(βt)im(v)) ( ) (-6) u (t) = Im e λt v = e αt (sin(βt)re(v) + cos(βt)im(v)) Bevis Beviset medtages i næste version af denne enote Eksempel 6 To komplekse egenværdier Givet differentialligningssystemet (t) = Bestem den fuldstændige reelle løsningsmængde [ (t) = A(t) (-7) Egenværdierne bestemmes til λ = + i og λ = i med de tilhørende egenvektorer v = ( i, ) henholdsvis v = (i, ) Det ses, at der er to komplekse egenværdier og dertil to komplekse egenvektorer Derfor benytter vi det andet punkt i metode 5, og vi skal således bruge Re(v) og Im(v) fra en egenvektor samt α og β fra en egenværdi Med λ = + i aflæses α = og β =, og desuden haves v = [ [ i 0 = + i [ 0 = Re(v) + i Im(v), (-8)
8 enote TO KOBLEDE DIFFERENTIALLIGNINGER 8 så Re(v) = [ [ 0 og Im(v) = Ifølge metode 5 har vi da de to løsninger 0 [ u (t) = e (cos(t) t 0 [ u (t) = e (sin(t) t 0 sin(t) + cos(t) [ ) 0 [ ) 0 [ sin(t) = e t cos(t) (-9) [ cos(t) = e t (-30) sin(t) Den fuldstændige reelle løsningsmængde til differentialligningssystemet (-7) er da givet ved følgende funktioner for alle c, c R: ( [ sin(t) (t) = c u (t) + c u (t) = e t c cos(t) fundet ved hjælp af metode 4 + c [ cos(t) sin(t) ), t R, (-3) Bemærk i eksemplet, at kun den ene egenværdi samt dens tilhørende egenvektor blev benyttet Vi skal nemlig blot bruge reeldel og imaginærdel af egenværdi og egenvektor, og disse værdier er ens for både den konjugerede og den ikke-konjugerede Endelig beskrives metoden der kan bruges, hvis systemmatricen har egenværdien λ med am(λ) = og gm(λ) =, dvs hvor diagonalisering ikke mulig Metode 7 Hvis systemmatricen A til differentialligningssystemet (t) = A(t), t R (-3) har en egenværdi λ med algebraisk multiplicitet, men det tilhørende egenvektorrum kun har geometrisk multiplicitet, findes to lineært uafhængige løsninger til differentialligningssystemet af formen u (t) = e λt v u (t) = te λt v + e λt b, (-33) hvor v er egenvektoren tilhørende egenværdien λ, og b er løsning til det lineære ligningssystem (A λe)b = v (-34)
9 enote TO KOBLEDE DIFFERENTIALLIGNINGER 9 Bevis Det er åbenlyst, at den ene løsning til differentialligningssystemet er u (t) = e λt v Det svære er at finde endnu en løsning Vi gætter på en løsning af formen u (t) = te λt v + e λt b = e λt (tv + b), (-35) hvor v er en egenvektor tilhørende egenværdien λ, og b er en kompleks vektor Vi har da u (t) = λe λt (tv + b) + e λt v = (e λt + λte λt )v + λe λt b = e λt (( + λt)v + λb) (-36) Vi kontrollerer, om u (t) er en løsning ved at indsætte det i (t) = A(t), u (t) = Au (t) e λt (( + λt)v + λb) = Ae λt (tv + b) v + λtv + λb = Atv + Ab t(λv Av) + (v + λb Ab) = 0 λv Av = 0 v + λb Ab = 0 (-37) Den første ligning kan nemt omformes til Av = λv, og den ses at være sand, da v er en egenvektor tilhørende egenværdien λ Den anden ligning omformes: v + λb Ab = 0 Ab λb = v (A λe)b = v (-38) Hvis b opfylder det foreskrevne ligningssystem, vil u (t) i (-35) også være en løsning til differentialligningssystemet Vi har dermed fundet to løsninger, og vi skal nu blot finde ud af, om de er lineært uafhængige Dette gøres ved et normalt linearitetskriterium: Hvis ligningen k u + k u = 0 kun har løsningen k = k = 0, er u og u lineært uafhængige k u + k u = 0 k e λt v + k e λt (tv + b) = 0 t(k v) + (k v + k b) = 0 k v = 0 k v + k b = 0 (-39) Da v er en egenvektor, er den forskellig fra nulvektoren, og derfor er k = 0 ifølge den første ligning Den anden ligning er derved blevet reduceret til k v = 0, og med samme argument haves k = 0 Derfor er de to løsninger lineært uafhængige, og metoden er hermed bevist
10 enote TO KOBLEDE DIFFERENTIALLIGNINGER 0 Eksempel 8 En egenværdi med algebraisk multiplicitet Givet differentialligningssystemet (t) = [ 6 (t) = A(t) (-40) 4 Egenværdierne bestemmes for A: det(a λe) = 6 λ 4 λ = (6 λ)( λ) + 4 = λ 8λ + 96 = (λ 4) = 0 (-4) Der er altså kun én egenværdi, nemlig λ = 4, selvom det er et ( )-system, og den har am(λ) = Egenvektorerne bestemmes: [ [ [ 6 4 A 4E = = (-4) Man har da egenvektoren v = (, ) eller mere elegant v = (, ) Vi må altså konstatere, at egenværdien λ har algebraisk multiplicitet, men at det tilhørende vektorrum har geometrisk multiplicitet For at bestemme to uafhængige løsninger til differentialligningsystemet kan metode 7 bruges For at finde en vektor b løses følgende ligningssystem: Fra (A λe)b = v fås T = [ [ [ 4 b = [ så (-43) Dette giver b = (, ), hvis den frie variabel sættes til De to løsninger er da u (t) = e 4t [ u (t) = te 4t [ [ + e 4t (-44) Ved hjælp af metode 4 kan den fuldstændige løsningsmængde bestemmes til at være følgende funktioner for alle c, c R: (t) = c u (t) + c u (t) = c e 4t [ + c e 4t ( t [ + [ ) (-45)
11 enote 3 N-DIMENSIONALT LØSNINGSRUM 3 n-dimensionalt løsningsrum I det foregående afsnit har vi betragtet koblede systemer bestående af to lineære ligningssystemer med to ukendte funktioner Løsningsrummet er to-dimensionalt, idet det kan opskrives som en linearkombination af to lineært uafhængige løsninger Dette kan generaliseres til vilkårlige systemer med n koblede lineære differentialligninger med n ukendte funktioner Løsningsmængden er en linearkombination af netop n lineært uafhængige løsninger Dette formuleres i generel form i følgende sætning Sætning 9 Givet det lineære homogene ordens differentialligningssystem med konstante reelle koefficienter (t) = A(t), t R (-46) bestående af n ligninger og med i alt n ukendte differentiable funktioner Den fuldstændige reelle løsningsmængde til systemet er n-dimensional og kan opskrives ved (t) = c u (t) + c u (t) + + c n u n (t), (-47) hvor u (t), u (t),, u n (t) er lineært uafhængige reelle løsninger til differentialligningssystemet, og c, c,, c n R De forskellige løsninger u(t), der skal bruges i sætningen, kan findes ved at bruge de af metoderne 4, 5 og 7, der passer til de forskellige tilfælde af egenværdier og egenvektorer Herunder er et eksempel med et koblet system af tre differentiallinger, der eksemplificerer sætning 9 Eksempel 0 3 koblede differentialligninger Givet differentialligningssystemet (t) = 3 5 (t) = A(t) (-48) 4 6 Bestem systemets fuldstændige reelle løsningsmængde Egenværdierne og egenvektorene kan bestemmes og er som følger: λ = 4 med v = (0, 5, ) λ = med v = (5, 5, 3)
12 enote 3 N-DIMENSIONALT LØSNINGSRUM Desuden har λ algebraisk multiplicitet, men det tilhørende egenvektorrum har geometrisk multiplicitet Fordi n = 3 skal vi bruge 3 lineært uafhængige løsninger til at danne den fuldstændige løsningsmængde, som set i sætning 9 Egenværdierne betragtes hver for sig: ) Den første egenværdi, λ = 4, har både geometrisk og algebraisk multiplicitet lig Det giver netop følgende løsning ifølge metode 4: 0 u (t) = e λt v = e 4t 5 (-49) ) Den anden egenværdi, λ =, har algebraisk multiplicitet men geometrisk multiplicitet Derfor kan vi bruge metode 7 til at finde to løsninger Først bestemmes b: Fra (A λ E)b = v fås T = b = (-50) En partikulær løsning til dette ligningssystem er b = (0,, ) Med denne viden har vi yderligere to lineært uafhængige løsninger til differentialligningssystemet ifølge metode 7, nemlig 5 u (t) = e λt v = e t 5 3 (-5) 5 0 u 3 (t) = te λt v + e λt b = te t e t De tre løsninger viser sig desuden at være lineært uafhængige (vi lader det være op til læseren at vise) Ifølge metode 9 er den fuldstændige reelle løsningsmængde udgjort af følgende linearkombination for alle c, c, c 3 R: (t) = c u (t) + c u (t) + c 3 u 3 (t) (-5) Dette giver altså (t) = c e 4t 5 + c e t 5 + c 3 te t 5 + e t, (-53) 3 3 hvor t R, og alle c, c, c 3 R
13 enote 4 EKSISTENS OG ENTYDIGHED AF LØSNINGER 3 4 Eksistens og entydighed af løsninger Ifølge struktursætningen sætning 9 indeholder den fuldstændige løsningsmængde til et differentialligningssystem med n ligninger n arbitrære konstanter Hvis man har n begyndelsesværdibetingelser, kan konstanterne bestemmes, og vi får da en entydig løsning Dette formuleres i følgende eksistens- og entydighedssætning Sætning Eksistens og entydighed Et ordens differentialligningssystem bestående af n ligninger og n ukendte differentiable funktioner med konstante koefficienter er givet ved (t) = A(t), t I (-54) For ethvert t 0 I og ethvert talsæt y 0 = (y, y,, y n ) findes der netop én løsning (t) = ( (t), (t), n (t) ), der opfylder begyndelsesværdibetingelsen hvilket vil sige, at (t 0 ) = y 0, (-55) (t 0 ) = y, (t 0 ) = y,, n (t 0 ) = y n (-56) Beviset udelades Eksempel I eksempel 3 fandt vi den fuldstændige løsningsmængde til differentialligningssystemet [ (t) = (t), t R, (-57) 3 0 nemlig (t) = [ [ (t) = c (t) e 3t + c e t [ 3, t R (-58) Vi ønsker nu at bestemme den entydige løsning (t) = ( (t), (t)), som opfylder begyndelsesværdibetingelsen (0) = ( (0), (0)) = (6, 6) Dette giver ligningssystemet [ [ [ [ [ 6 = c 6 e 0 + c e 0 c = (-59) 3 3 Konstanterne c og c kan findes ved sædvanlig GaussJordan-elimination, [ [ [ (-60) c
14 enote 5 OMFORMNING AF LINEÆRE N TE ORDENS HOMOGENE DIFFERENTIALLIGNINGER TIL ET ORDENS DIFFERENTIALLIGNINGSSYSTEM 4 Man får altså løsningen (c, c ) = (6, 0), og den entydige og betingede løsning er derfor (t) = 6e 3t [ hvilket er det samme som, at + 0e t [ 3 I dette særtilfælde er de to funktioner altså identiske [ = 6e 3t, t R, (-6) (t) = 6e 3t (t) = 6e 3t (-6) 5 Omformning af lineære n te ordens homogene differentialligninger til et ordens differentialligningssystem Med lidt snilde er det muligt at omforme en vilkårlig homogen n te ordens differentialligning med konstante koefficienter til et differentialligningssystem, som kan løses ved hjælp af denne enote Metode 3 Fra differentialligning til differentialligningssystem En n te ordens lineær differentialligning (n) (t) + a n (n ) (t) + a n (n ) (t) + + a (t) + a 0 (t) = 0 (-63) for t R, kan omformes til et ordens differentialligningssystem, og systemet vil se således ud: og (t) = (t) (t) (t) n (t) n(t) = a 0 a a a n (t) (t) n (t) n (t) (-64) Notationen (n) (t) angiver ikke en opløftning med derimod et antal ganges differentiering! F er (3) (t) = (t) Beviset for denne omskrivning er simpelt og giver god forståelse for omformningen
15 enote 5 OMFORMNING AF LINEÆRE N TE ORDENS HOMOGENE DIFFERENTIALLIGNINGER TIL ET ORDENS DIFFERENTIALLIGNINGSSYSTEM 5 Bevis Lad der være givet en n te ordens differentialligning som i (-63) Vi indfører n funktioner på denne måde: (t) = (t) (t) = (t) = (t) 3 (t) = (t) = (t) 4 (t) = 3 (t) = (t) (-65) n (t) = n (t) = (n ) (t) n (t) = n (t) = (n ) (t) Disse nye udtryk indsættes i differentialligningen (-63), n(t) + a n n (t) + a n n (t) + + a (t) + a 0 (t) = 0 n(t) = a 0 (t) a (t) a n n (t) a n n (t) (-66) Denne ligning kan sammen med ligningerne (-65) skrives op på matriform: Metoden er nu bevist (t) (t) n (t) n(t) = a 0 a a a n (t) (t) n (t) n (t) (-67) Eksempel 4 Givet en lineær differentialligning af 3 orden med konstante koefficienter, (t) 4 (t) 7 (t) + 0(t) = 0, t R (-68) Bestem den fuldstændige løsningsmængde Vi ønsker at omforme ligningen til et ligningssystem på matriform, så vores metoder til løsning i denne enote kan benyttes Vi indfører funktionerne (t) = (t) (t) = (t) = (t) 3 (t) = (t) = (t) På denne måde kan vi omskrive differentialligningen til (-69) 3(t) 4 3 (t) 7 (t) + 0 (t) = 0, (-70)
16 enote 5 OMFORMNING AF LINEÆRE N TE ORDENS HOMOGENE DIFFERENTIALLIGNINGER TIL ET ORDENS DIFFERENTIALLIGNINGSSYSTEM 6 og vi kan da samle det i et ligningssystem, (t) = (t) (t) = 3(t) 3 (t) = 0 (t) + 7 (t) (t) (-7) Det skrives på matriform på denne måde: (t) = 0 0 (t) (-7) Egenværdierne bestemmes til at være λ =, λ = og λ 3 = 5 Den fuldstændige løsningsmængde til differentialligningssystemet er ifølge sætning givet ved følgende funktioner for alle de arbitrære konstanter c, c, c 3 R: hvor v, v og v 3 er de respektive egenvektorer (t) = c e t v + c e t v + c 3 e 5t v 3, t R, (-73) Vi skal imidlertid kun bruge løsningsmængden til (t) = (t), hvorfor den tages ud af systemet Desuden indfører vi nu tre nye arbitrære konstanter k, k, k 3 R, der skal gøre det ud for produkterne mellem c erne og egenvektorernes førstekoordinat Resultatet bliver således (t) = (t) = k e t + k e t + k 3 e 5t, t R (-74) Dette udgør den fuldstændige løsningsmængde til differentialligningen (-68) Hvis førstekoordinaten i v er 0 sættes k = 0, i modsat fald kan k være et vilkårligt reelt tal På samme måde med k og k 3
Lineære 1. ordens differentialligningssystemer
 enote enote Lineære ordens differentialligningssystemer Denne enote beskriver ordens differentialligningssystemer og viser, hvordan de kan løses enoten er i forlængelse af enote, der beskriver lineære
enote enote Lineære ordens differentialligningssystemer Denne enote beskriver ordens differentialligningssystemer og viser, hvordan de kan løses enoten er i forlængelse af enote, der beskriver lineære
Lineære 1. ordens differentialligningssystemer
 enote 7 enote 7 Lineære ordens differentialligningssystemer Denne enote beskriver ordens differentialligningssystemer og viser, hvordan de kan løses Der bruges egenværdier og egenvektorer i løsningsproceduren,
enote 7 enote 7 Lineære ordens differentialligningssystemer Denne enote beskriver ordens differentialligningssystemer og viser, hvordan de kan løses Der bruges egenværdier og egenvektorer i løsningsproceduren,
Lineære 2. ordens differentialligninger med konstante koefficienter
 enote 13 1 enote 13 Lineære 2. ordens differentialligninger med konstante koefficienter I forlængelse af enote 11 og enote 12 om differentialligninger, kommer nu denne enote omkring 2. ordens differentialligninger.
enote 13 1 enote 13 Lineære 2. ordens differentialligninger med konstante koefficienter I forlængelse af enote 11 og enote 12 om differentialligninger, kommer nu denne enote omkring 2. ordens differentialligninger.
Modulpakke 3: Lineære Ligningssystemer
 Chapter 4 Modulpakke 3: Lineære Ligningssystemer 4. Homogene systemer I teknikken møder man meget ofte modeller der leder til systemer af koblede differentialligninger. Et eksempel på et sådant system
Chapter 4 Modulpakke 3: Lineære Ligningssystemer 4. Homogene systemer I teknikken møder man meget ofte modeller der leder til systemer af koblede differentialligninger. Et eksempel på et sådant system
DesignMat Uge 4 Systemer af lineære differentialligninger I
 DesignMat Uge Systemer af lineære differentialligninger I Preben Alsholm Efterår 008 1 Lineære differentialligningssystemer 11 Lineært differentialligningssystem af første orden I Lineært differentialligningssystem
DesignMat Uge Systemer af lineære differentialligninger I Preben Alsholm Efterår 008 1 Lineære differentialligningssystemer 11 Lineært differentialligningssystem af første orden I Lineært differentialligningssystem
DesignMat Uge 1 Gensyn med forårets stof
 DesignMat Uge 1 Gensyn med forårets stof Preben Alsholm Efterår 2010 1 Hovedpunkter fra forårets pensum 11 Taylorpolynomium Taylorpolynomium Det n te Taylorpolynomium for f med udviklingspunkt x 0 : P
DesignMat Uge 1 Gensyn med forårets stof Preben Alsholm Efterår 2010 1 Hovedpunkter fra forårets pensum 11 Taylorpolynomium Taylorpolynomium Det n te Taylorpolynomium for f med udviklingspunkt x 0 : P
Lineære differentialligningers karakter og lineære 1. ordens differentialligninger
 enote 11 1 enote 11 Lineære differentialligningers karakter og lineære 1. ordens differentialligninger I denne note introduceres lineære differentialligninger, som er en speciel (og bekvem) form for differentialligninger.
enote 11 1 enote 11 Lineære differentialligningers karakter og lineære 1. ordens differentialligninger I denne note introduceres lineære differentialligninger, som er en speciel (og bekvem) form for differentialligninger.
Chapter 3. Modulpakke 3: Egenværdier. 3.1 Indledning
 Chapter 3 Modulpakke 3: Egenværdier 3.1 Indledning En vektor v har som bekendt både størrelse og retning. Hvis man ganger vektoren fra højre på en kvadratisk matrix A bliver resultatet en ny vektor. Hvis
Chapter 3 Modulpakke 3: Egenværdier 3.1 Indledning En vektor v har som bekendt både størrelse og retning. Hvis man ganger vektoren fra højre på en kvadratisk matrix A bliver resultatet en ny vektor. Hvis
DesignMat Uge 5 Systemer af lineære differentialligninger II
 DesignMat Uge 5 Systemer af lineære differentialligninger II Preben Alsholm Efterår 21 1 Lineære differentialligningssystemer 11 Lineært differentialligningssystem af første orden Lineært differentialligningssystem
DesignMat Uge 5 Systemer af lineære differentialligninger II Preben Alsholm Efterår 21 1 Lineære differentialligningssystemer 11 Lineært differentialligningssystem af første orden Lineært differentialligningssystem
Nøgleord og begreber. Definition 15.1 Den lineære 1. ordens differentialligning er
 Oversigt [S] 7.3, 7.4, 7.5, 7.6; [LA] 15, 16, 17 Nøgleord og begreber 1. ordens lineær ligning Løsningsmetode August 2002, opgave 7 1. ordens lineært system Løsning ved egenvektor Lille opgave Stor opgave
Oversigt [S] 7.3, 7.4, 7.5, 7.6; [LA] 15, 16, 17 Nøgleord og begreber 1. ordens lineær ligning Løsningsmetode August 2002, opgave 7 1. ordens lineært system Løsning ved egenvektor Lille opgave Stor opgave
Egenværdier og egenvektorer
 enote 9 enote 9 Egenværdier og egenvektorer Denne note indfører begreberne egenværdier og egenvektorer for lineære afbildninger i vilkårlige generelle vektorrum og går derefter i dybden med egenværdier
enote 9 enote 9 Egenværdier og egenvektorer Denne note indfører begreberne egenværdier og egenvektorer for lineære afbildninger i vilkårlige generelle vektorrum og går derefter i dybden med egenværdier
Oversigt [S] 7.3, 7.4, 7.5, 7.6; [LA] 15, 16, 17
![Oversigt [S] 7.3, 7.4, 7.5, 7.6; [LA] 15, 16, 17 Oversigt [S] 7.3, 7.4, 7.5, 7.6; [LA] 15, 16, 17](/thumbs/62/47131431.jpg) Oversigt [S] 7.3, 7.4, 7.5, 7.6; [LA] 15, 16, 17 Nøgleord og begreber 1. ordens lineær ligning Løsningsmetode August 2002, opgave 7 1. ordens lineært system Løsning ved egenvektor Lille opgave Stor opgave
Oversigt [S] 7.3, 7.4, 7.5, 7.6; [LA] 15, 16, 17 Nøgleord og begreber 1. ordens lineær ligning Løsningsmetode August 2002, opgave 7 1. ordens lineært system Løsning ved egenvektor Lille opgave Stor opgave
Noter om Komplekse Vektorrum, Funktionsrum og Differentialligninger LinAlg 2004/05-Version af 16. Dec.
 Noter om Komplekse Vektorrum, Funktionsrum og Differentialligninger LinAlg 2004/05-Version af 16. Dec. 1 Komplekse vektorrum I defininitionen af vektorrum i Afsnit 4.1 i Niels Vigand Pedersen Lineær Algebra
Noter om Komplekse Vektorrum, Funktionsrum og Differentialligninger LinAlg 2004/05-Version af 16. Dec. 1 Komplekse vektorrum I defininitionen af vektorrum i Afsnit 4.1 i Niels Vigand Pedersen Lineær Algebra
DesignMat Lineære differentialligninger I
 DesignMat Lineære differentialligninger I Preben Alsholm Uge 9 Forår 2010 1 Lineære differentialligninger af første orden 1.1 Normeret lineær differentialligning Normeret lineær differentialligning En
DesignMat Lineære differentialligninger I Preben Alsholm Uge 9 Forår 2010 1 Lineære differentialligninger af første orden 1.1 Normeret lineær differentialligning Normeret lineær differentialligning En
Førsteordens lineære differentialligninger
 enote 16 1 enote 16 Førsteordens lineære differentialligninger I denne enote gives først en kort introduktion til differentialligninger i almindelighed, hvorefter hovedemnet er en særlig type af differentialligninger,
enote 16 1 enote 16 Førsteordens lineære differentialligninger I denne enote gives først en kort introduktion til differentialligninger i almindelighed, hvorefter hovedemnet er en særlig type af differentialligninger,
Lineære ligningssystemer
 enote 6 1 enote 6 Lineære ligningssystemer Denne enote handler om lineære ligningssystemer, om metoder til at beskrive dem og løse dem, og om hvordan man kan få overblik over løsningsmængdernes struktur.
enote 6 1 enote 6 Lineære ligningssystemer Denne enote handler om lineære ligningssystemer, om metoder til at beskrive dem og løse dem, og om hvordan man kan få overblik over løsningsmængdernes struktur.
12.1 Cayley-Hamilton-Sætningen
 SEKTION 12.1 CAYLEY-HAMILTON-SÆTNINGEN 12.1 Cayley-Hamilton-Sætningen Sætning 12.1.1 (Cayley-Hamilton) Lad A Mat n,n (C). Så gælder p A (A) =. Sætningen gælder faktisk over et vilkårligt legeme, men vi
SEKTION 12.1 CAYLEY-HAMILTON-SÆTNINGEN 12.1 Cayley-Hamilton-Sætningen Sætning 12.1.1 (Cayley-Hamilton) Lad A Mat n,n (C). Så gælder p A (A) =. Sætningen gælder faktisk over et vilkårligt legeme, men vi
Affine rum. a 1 u 1 + a 2 u 2 + a 3 u 3 = a 1 u 1 + (1 a 1 )( u 2 + a 3. + a 3. u 3 ) 1 a 1. Da a 2
 Affine rum I denne note behandles kun rum over R. Alt kan imidlertid gennemføres på samme måde over C eller ethvert andet legeme. Et underrum U R n er karakteriseret ved at det er en delmængde som er lukket
Affine rum I denne note behandles kun rum over R. Alt kan imidlertid gennemføres på samme måde over C eller ethvert andet legeme. Et underrum U R n er karakteriseret ved at det er en delmængde som er lukket
Nøgleord og begreber Separable ligninger 1. ordens lineær ligning August 2002, opgave 7 Rovdyr-Byttedyr system 1. ordens lineært system Opgave
 Oversigt [S] 7.3, 7.4, 7.5, 7.6; [LA] 14, 15 Nøgleord og begreber Separable ligninger 1. ordens lineær ligning August 2002, opgave 7 Rovdyr-Byttedyr system 1. ordens lineært system Opgave Calculus 2-2005
Oversigt [S] 7.3, 7.4, 7.5, 7.6; [LA] 14, 15 Nøgleord og begreber Separable ligninger 1. ordens lineær ligning August 2002, opgave 7 Rovdyr-Byttedyr system 1. ordens lineært system Opgave Calculus 2-2005
Egenværdier og egenvektorer
 1 Egenværdier og egenvektorer 2 Definition Lad A være en n n matrix. En vektor v R n, v 0, kaldes en egenvektor for A, hvis der findes en skalar λ således Av = λv Skalaren λ kaldes en tilhørende egenværdi.
1 Egenværdier og egenvektorer 2 Definition Lad A være en n n matrix. En vektor v R n, v 0, kaldes en egenvektor for A, hvis der findes en skalar λ således Av = λv Skalaren λ kaldes en tilhørende egenværdi.
Lineære ligningssystemer
 enote 2 1 enote 2 Lineære ligningssystemer Denne enote handler om lineære ligningssystemer, om metoder til at beskrive dem og løse dem, og om hvordan man kan få overblik over løsningsmængdernes struktur.
enote 2 1 enote 2 Lineære ligningssystemer Denne enote handler om lineære ligningssystemer, om metoder til at beskrive dem og løse dem, og om hvordan man kan få overblik over løsningsmængdernes struktur.
DesignMat. Preben Alsholm. September Egenværdier og Egenvektorer. Preben Alsholm. Egenværdier og Egenvektorer
 DesignMat September 2008 fortsat Eksempel : et Eksempel 4 () af I II uden I Lad V være et vektorrum over L (enten R eller C). fortsat Eksempel : et Eksempel 4 () af I II uden I Lad V være et vektorrum
DesignMat September 2008 fortsat Eksempel : et Eksempel 4 () af I II uden I Lad V være et vektorrum over L (enten R eller C). fortsat Eksempel : et Eksempel 4 () af I II uden I Lad V være et vektorrum
Matematisk modellering og numeriske metoder. Lektion 5
 Matematisk modellering og numeriske metoder Lektion 5 Morten Grud Rasmussen 19. september, 2013 1 Euler-Cauchy-ligninger [Bogens afsnit 2.5, side 71] 1.1 De tre typer af Euler-Cauchy-ligninger Efter at
Matematisk modellering og numeriske metoder Lektion 5 Morten Grud Rasmussen 19. september, 2013 1 Euler-Cauchy-ligninger [Bogens afsnit 2.5, side 71] 1.1 De tre typer af Euler-Cauchy-ligninger Efter at
Komplekse tal. Mikkel Stouby Petersen 27. februar 2013
 Komplekse tal Mikkel Stouby Petersen 27. februar 2013 1 Motivationen Historien om de komplekse tal er i virkeligheden historien om at fjerne forhindringerne og gøre det umulige muligt. For at se det, vil
Komplekse tal Mikkel Stouby Petersen 27. februar 2013 1 Motivationen Historien om de komplekse tal er i virkeligheden historien om at fjerne forhindringerne og gøre det umulige muligt. For at se det, vil
Lineær algebra: Egenværdier, egenvektorer, diagonalisering
 Lineær algebra: Egenværdier, egenvektorer, diagonalisering Institut for Matematiske Fag Aalborg Universitet 2011 Egenvektorer og egenværdier Mål: Forståelse af afbildningen x Ax fra R n R n for en n n-matrix
Lineær algebra: Egenværdier, egenvektorer, diagonalisering Institut for Matematiske Fag Aalborg Universitet 2011 Egenvektorer og egenværdier Mål: Forståelse af afbildningen x Ax fra R n R n for en n n-matrix
Den homogene ligning. Vi betragter den n te ordens, homogene, lineære differentialligning. d n y dt n. an 1 + any = 0 (1.2) dt. + a1 d n 1 y dt n 1
 1/7 Den homogene ligning Vi betragter den n te ordens, homogene, lineære differentialligning a 0 d n y dt n + a1 d n 1 y dt n 1 hvor a 0,..., a n R og a 0 0. Vi skriver ligningen på kort form som + + dy
1/7 Den homogene ligning Vi betragter den n te ordens, homogene, lineære differentialligning a 0 d n y dt n + a1 d n 1 y dt n 1 hvor a 0,..., a n R og a 0 0. Vi skriver ligningen på kort form som + + dy
Besvarelser til Lineær Algebra Ordinær Eksamen Juni 2017
 Besvarelser til Lineær Algebra Ordinær Eksamen - 12. Juni 2017 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Lineær Algebra Ordinær Eksamen - 12. Juni 2017 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
9.1 Egenværdier og egenvektorer
 SEKTION 9.1 EGENVÆRDIER OG EGENVEKTORER 9.1 Egenværdier og egenvektorer Definition 9.1.1 1. Lad V være et F-vektorrum; og lad T : V V være en lineær transformation. λ F er en egenværdi for T, hvis der
SEKTION 9.1 EGENVÆRDIER OG EGENVEKTORER 9.1 Egenværdier og egenvektorer Definition 9.1.1 1. Lad V være et F-vektorrum; og lad T : V V være en lineær transformation. λ F er en egenværdi for T, hvis der
Differentialligninger Hvad beskriver en differentialligning? Hvordan noget ændrer sig (oftest over tid). Tangenthældninger langs en kurve.
 Differentialligninger Hvad beskriver en differentialligning? Hvordan noget ændrer sig (oftest over tid) Tangenthældninger langs en kurve x Retningsfelter x x(t) sin(π t) + x / π cos(π t) Jeppe Revall Frisvad
Differentialligninger Hvad beskriver en differentialligning? Hvordan noget ændrer sig (oftest over tid) Tangenthældninger langs en kurve x Retningsfelter x x(t) sin(π t) + x / π cos(π t) Jeppe Revall Frisvad
Noter til An0 DIFFERENTIALLIGNINGER MED KONSTANTE KOEFFICIENTER
 UDKAST 7122009 Noter til An0 Inst f Matematiske Fag Gerd Grubb December 2009 DIFFERENTIALLIGNINGER MED KONSTANTE KOEFFICIENTER 1 Generelle resultater 11 Introduktion I tidligere kurser er der gennemgået
UDKAST 7122009 Noter til An0 Inst f Matematiske Fag Gerd Grubb December 2009 DIFFERENTIALLIGNINGER MED KONSTANTE KOEFFICIENTER 1 Generelle resultater 11 Introduktion I tidligere kurser er der gennemgået
Symmetriske og ortogonale matricer Uge 7
 Symmetriske og ortogonale matricer Uge 7 Preben Alsholm Efterår 2009 1 Symmetriske og ortogonale matricer 1.1 Definitioner Definitioner En kvadratisk matrix A = [ a ij kaldes symmetrisk, hvis aij = a ji
Symmetriske og ortogonale matricer Uge 7 Preben Alsholm Efterår 2009 1 Symmetriske og ortogonale matricer 1.1 Definitioner Definitioner En kvadratisk matrix A = [ a ij kaldes symmetrisk, hvis aij = a ji
Matricer og lineære ligningssystemer
 Matricer og lineære ligningssystemer Grete Ridder Ebbesen Virum Gymnasium Indhold 1 Matricer 11 Grundlæggende begreber 1 Regning med matricer 3 13 Kvadratiske matricer og determinant 9 14 Invers matrix
Matricer og lineære ligningssystemer Grete Ridder Ebbesen Virum Gymnasium Indhold 1 Matricer 11 Grundlæggende begreber 1 Regning med matricer 3 13 Kvadratiske matricer og determinant 9 14 Invers matrix
Hans J. Munkholm: En besvarelse af
 Hans J. Munkholm: En besvarelse af Projekt for MM501, Lineære differentialligninger November-december 2009 Nummererede formler fra opgaveformuleringen Her samles alle opgavens differentialligninger og
Hans J. Munkholm: En besvarelse af Projekt for MM501, Lineære differentialligninger November-december 2009 Nummererede formler fra opgaveformuleringen Her samles alle opgavens differentialligninger og
Lotka-Volterra modellen
 Lotka-Volterra modellen G4-105 Matematik Aalborg Universitet 20. december 2016 School of Engineering and Science Fredrik Bajers Vej 7G 9220 Aalborg Øst www.ses.aau.dk Titel: Lotka-Volterra modellen Tema:
Lotka-Volterra modellen G4-105 Matematik Aalborg Universitet 20. december 2016 School of Engineering and Science Fredrik Bajers Vej 7G 9220 Aalborg Øst www.ses.aau.dk Titel: Lotka-Volterra modellen Tema:
Besvarelser til Lineær Algebra med Anvendelser Ordinær Eksamen 2016
 Besvarelser til Lineær Algebra med Anvendelser Ordinær Eksamen 206 Mikkel Findinge http://findinge.com/ Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan.
Besvarelser til Lineær Algebra med Anvendelser Ordinær Eksamen 206 Mikkel Findinge http://findinge.com/ Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan.
Algebra - Teori og problemløsning
 Algebra - Teori og problemløsning, januar 05, Kirsten Rosenkilde. Algebra - Teori og problemløsning Kapitel -3 giver en grundlæggende introduktion til at omskrive udtryk, faktorisere og løse ligningssystemer.
Algebra - Teori og problemløsning, januar 05, Kirsten Rosenkilde. Algebra - Teori og problemløsning Kapitel -3 giver en grundlæggende introduktion til at omskrive udtryk, faktorisere og løse ligningssystemer.
Kvadratiske matricer. enote Kvadratiske matricer
 enote enote Kvadratiske matricer I denne enote undersøges grundlæggende egenskaber ved mængden af kvadratiske matricer herunder indførelse af en invers matrix for visse kvadratiske matricer. Det forudsættes,
enote enote Kvadratiske matricer I denne enote undersøges grundlæggende egenskaber ved mængden af kvadratiske matricer herunder indførelse af en invers matrix for visse kvadratiske matricer. Det forudsættes,
Besvarelse af Eksamensopgaver Juni 2005 i Matematik H1
 Besvarelse af Eksamensopgaver Juni 5 i Matematik H Opgave De fire vektorer stilles op i en matrix som reduceres: 4 4 4 8 4 4 (a) Der er ledende et-taller så dim U =. Som basis kan f.eks. bruges a a jfr.
Besvarelse af Eksamensopgaver Juni 5 i Matematik H Opgave De fire vektorer stilles op i en matrix som reduceres: 4 4 4 8 4 4 (a) Der er ledende et-taller så dim U =. Som basis kan f.eks. bruges a a jfr.
Besvarelser til Lineær Algebra Ordinær Eksamen Juni 2018
 Besvarelser til Lineær Algebra Ordinær Eksamen - 5. Juni 28 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Lineær Algebra Ordinær Eksamen - 5. Juni 28 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Vektorrum. enote Generalisering af begrebet vektor
 enote 7 1 enote 7 Vektorrum I denne enote opstilles en generel teori for mængder, for hvilke der er defineret addition og multiplikation med skalar, og som opfylder de samme regneregler som geometriske
enote 7 1 enote 7 Vektorrum I denne enote opstilles en generel teori for mængder, for hvilke der er defineret addition og multiplikation med skalar, og som opfylder de samme regneregler som geometriske
Lineær Algebra eksamen, noter
 Lineær Algebra eksamen, noter Stig Døssing, 20094584 June 6, 2011 1 Emne 1: Løsninger og least squares - Løsning, ligningssystem RREF (ERO) løsninger Bevis at RREF matrix findes Løsninger til system (0,
Lineær Algebra eksamen, noter Stig Døssing, 20094584 June 6, 2011 1 Emne 1: Løsninger og least squares - Løsning, ligningssystem RREF (ERO) løsninger Bevis at RREF matrix findes Løsninger til system (0,
Modulpakke 3: Lineære Ligningssystemer
 Chapter 1 Modulpakke 3: Lineære Ligningssystemer 1.1 Indledning - typer af ligningesystemer og løsninger Den lineære ligning 2x=3 kan løses umiddelbart ved at dividere med 2 på begge sider, så vi får:
Chapter 1 Modulpakke 3: Lineære Ligningssystemer 1.1 Indledning - typer af ligningesystemer og løsninger Den lineære ligning 2x=3 kan løses umiddelbart ved at dividere med 2 på begge sider, så vi får:
EKSAMENSOPGAVELØSNINGER CALCULUS 2 (2005) JANUAR 2006 AARHUS UNIVERSITET.. Beregn den retningsafledede D u f(0, 0).
 EKSAMENSOPGAVELØSNINGER CALCULUS 2 (2005) JANUAR 2006 AARHUS UNIVERSITET H.A. NIELSEN & H.A. SALOMONSEN Opgave. Lad f betegne funktionen f(x, y) = x cos(y) + y sin(x). ) Angiv gradienten f. 2) Lad u betegne
EKSAMENSOPGAVELØSNINGER CALCULUS 2 (2005) JANUAR 2006 AARHUS UNIVERSITET H.A. NIELSEN & H.A. SALOMONSEN Opgave. Lad f betegne funktionen f(x, y) = x cos(y) + y sin(x). ) Angiv gradienten f. 2) Lad u betegne
Lineære ligningssystemer og Gauss-elimination
 Lineære ligningssystemer og Gauss-elimination Preben Alsholm 18 februar 008 1 Lineære ligningssystemer og Gauss-elimination 11 Et eksempel Et eksempel 100g mælk Komælk Fåremælk Gedemælk Protein g 6g 8g
Lineære ligningssystemer og Gauss-elimination Preben Alsholm 18 februar 008 1 Lineære ligningssystemer og Gauss-elimination 11 Et eksempel Et eksempel 100g mælk Komælk Fåremælk Gedemælk Protein g 6g 8g
Polynomier af én variabel
 enote 30 1 enote 30 Polynomier af én variabel I denne enote introduceres komplekse polynomier af én variabel. Der forudsættes elementært kendskab til komplekse tal, og kendskab til reelle polynomier af
enote 30 1 enote 30 Polynomier af én variabel I denne enote introduceres komplekse polynomier af én variabel. Der forudsættes elementært kendskab til komplekse tal, og kendskab til reelle polynomier af
DIFFERENTIALLIGNINGER NOTER TIL CALCULUS 2003 AARHUS UNIVERSITET
 DIFFERENTIALLIGNINGER NOTER TIL CALCULUS 2003 AARHUS UNIVERSITET H.A. NIELSEN INDHOLD. Lineær ligning 2 2. Lineært system 8 3. Generel ligning 6 4. Stabilitet 8 Litteratur 2 Noterne er til 4 timers forelæsninger
DIFFERENTIALLIGNINGER NOTER TIL CALCULUS 2003 AARHUS UNIVERSITET H.A. NIELSEN INDHOLD. Lineær ligning 2 2. Lineært system 8 3. Generel ligning 6 4. Stabilitet 8 Litteratur 2 Noterne er til 4 timers forelæsninger
Det teknisk-naturvidenskabelige basisår Matematik 1A, Efterår 2005, Hold 3 Prøveopgave C
 Det teknisk-naturvidenskabelige basisår Matematik 1A, Efterår 2005, Hold 3 Prøveopgave C Opgaven består af tre dele, hver med en række spørgsmål, efterfulgt af en liste af teorispørgsmål. I alle opgavespørgsmålene
Det teknisk-naturvidenskabelige basisår Matematik 1A, Efterår 2005, Hold 3 Prøveopgave C Opgaven består af tre dele, hver med en række spørgsmål, efterfulgt af en liste af teorispørgsmål. I alle opgavespørgsmålene
Oversigt [LA] 10, 11; [S] 9.3
![Oversigt [LA] 10, 11; [S] 9.3 Oversigt [LA] 10, 11; [S] 9.3](/thumbs/91/105982264.jpg) Oversigt [LA] 1, 11; [S] 9.3 Nøgleord og begreber Repetition: enhedsvektor og identitetsmatrix Diagonalmatricer Diagonalisering og egenvektorer Matrixpotens August 22, opgave 2 Skalarprodukt Længde Calculus
Oversigt [LA] 1, 11; [S] 9.3 Nøgleord og begreber Repetition: enhedsvektor og identitetsmatrix Diagonalmatricer Diagonalisering og egenvektorer Matrixpotens August 22, opgave 2 Skalarprodukt Længde Calculus
Ligningssystemer - nogle konklusioner efter miniprojektet
 Ligningssystemer - nogle konklusioner efter miniprojektet Ligningssystemet Ax = 0 har mere end en løsning (uendelig mange) hvis og kun hvis nullity(a) 0 Løsningerne til et konsistent ligningssystem Ax
Ligningssystemer - nogle konklusioner efter miniprojektet Ligningssystemet Ax = 0 har mere end en løsning (uendelig mange) hvis og kun hvis nullity(a) 0 Løsningerne til et konsistent ligningssystem Ax
Symmetriske matricer
 Symmetriske matricer Preben Alsholm 17. november 008 1 Symmetriske matricer 1.1 Definitioner Definitioner En kvadratisk matrix A = a ij kaldes symmetrisk, hvis aij = a ji for alle i og j. Altså hvis A
Symmetriske matricer Preben Alsholm 17. november 008 1 Symmetriske matricer 1.1 Definitioner Definitioner En kvadratisk matrix A = a ij kaldes symmetrisk, hvis aij = a ji for alle i og j. Altså hvis A
Besvarelser til de to blokke opgaver på Ugeseddel 7
 Besvarelser til de to blokke opgaver på Ugeseddel 7 De anførte besvarelser er til dels mere summariske end en god eksamensbesvarelse bør være. Der kan godt være fejl i - jeg vil meget gerne informeres,
Besvarelser til de to blokke opgaver på Ugeseddel 7 De anførte besvarelser er til dels mere summariske end en god eksamensbesvarelse bør være. Der kan godt være fejl i - jeg vil meget gerne informeres,
Lektion 13 Homogene lineære differentialligningssystemer
 Lektion 13 Lineære differentialligningssystemer Homogene lineære differentialligningssystemer med konstante koefficienter Inhomogene systemer To-kammer modeller Lotka Volterra (ikke lineært) 1 To-kammer
Lektion 13 Lineære differentialligningssystemer Homogene lineære differentialligningssystemer med konstante koefficienter Inhomogene systemer To-kammer modeller Lotka Volterra (ikke lineært) 1 To-kammer
Vejledende besvarelse på august 2009-sættet 2. december 2009
 Vejledende besvarelse på august 29-sættet 2. december 29 Det følgende er en vejledende besvarelse på eksamenssættet i kurset Calculus, som det så ud i august 29. Den tjener primært til illustration af,
Vejledende besvarelse på august 29-sættet 2. december 29 Det følgende er en vejledende besvarelse på eksamenssættet i kurset Calculus, som det så ud i august 29. Den tjener primært til illustration af,
Diagonalisering. Definition (diagonaliserbar)
 1 Diagonalisering 2 Definition (diagonaliserbar) Lad A være en n n-matrix. A siges at være diagonaliserbar hvis A er similær med en diagonal matrix, dvs. A = PDP 1, hvor D er en n n diagonal matrix og
1 Diagonalisering 2 Definition (diagonaliserbar) Lad A være en n n-matrix. A siges at være diagonaliserbar hvis A er similær med en diagonal matrix, dvs. A = PDP 1, hvor D er en n n diagonal matrix og
Definition multiplikation En m n-matrix og en n p-matrix kan multipliceres (ganges sammen) til en m p-matrix.
 Oversigt [LA] 3, 4, 5 Nøgleord og begreber Matrix multiplikation Identitetsmatricen Transponering Fra matrix til afbildning Fra afbildning til matrix Test matrix-afbildning Inverse matricer Test invers
Oversigt [LA] 3, 4, 5 Nøgleord og begreber Matrix multiplikation Identitetsmatricen Transponering Fra matrix til afbildning Fra afbildning til matrix Test matrix-afbildning Inverse matricer Test invers
Nøgleord og begreber. Definition multiplikation En m n-matrix og en n p-matrix kan multipliceres (ganges sammen) til en m p-matrix.
 Oversigt [LA] 3, 4, 5 Matrix multiplikation Nøgleord og begreber Matrix multiplikation Identitetsmatricen Transponering Fra matrix til afbildning Fra afbildning til matrix Test matrix-afbildning Inverse
Oversigt [LA] 3, 4, 5 Matrix multiplikation Nøgleord og begreber Matrix multiplikation Identitetsmatricen Transponering Fra matrix til afbildning Fra afbildning til matrix Test matrix-afbildning Inverse
Tidligere Eksamensopgaver MM505 Lineær Algebra
 Institut for Matematik og Datalogi Syddansk Universitet Tidligere Eksamensopgaver MM55 Lineær Algebra Indhold Typisk forside.................. 2 Juni 27.................... 3 Oktober 27..................
Institut for Matematik og Datalogi Syddansk Universitet Tidligere Eksamensopgaver MM55 Lineær Algebra Indhold Typisk forside.................. 2 Juni 27.................... 3 Oktober 27..................
Lektion 12. højere ordens lineære differentiallininger. homogene. inhomogene. eksempler
 Lektion 12 2. ordens lineære differentialligninger homogene inhomogene eksempler højere ordens lineære differentiallininger 1 Anden ordens lineære differentialligninger med konstante koefficienter A. Homogene
Lektion 12 2. ordens lineære differentialligninger homogene inhomogene eksempler højere ordens lineære differentiallininger 1 Anden ordens lineære differentialligninger med konstante koefficienter A. Homogene
Matematisk modellering og numeriske metoder. Lektion 6
 Matematisk modellering og numeriske metoder Lektion 6 Morten Grud Rasmussen 24. september, 2013 1 Forcerede oscillationer [Bogens afsnit 2.8, side 85] 1.1 Et forstyrret masse-fjeder-system I udledningen
Matematisk modellering og numeriske metoder Lektion 6 Morten Grud Rasmussen 24. september, 2013 1 Forcerede oscillationer [Bogens afsnit 2.8, side 85] 1.1 Et forstyrret masse-fjeder-system I udledningen
Komplekse Tal. 20. november 2009. UNF Odense. Steen Thorbjørnsen Institut for Matematiske Fag Århus Universitet
 Komplekse Tal 20. november 2009 UNF Odense Steen Thorbjørnsen Institut for Matematiske Fag Århus Universitet Fra de naturlige tal til de komplekse Optælling af størrelser i naturen De naturlige tal N (N
Komplekse Tal 20. november 2009 UNF Odense Steen Thorbjørnsen Institut for Matematiske Fag Århus Universitet Fra de naturlige tal til de komplekse Optælling af størrelser i naturen De naturlige tal N (N
2010 Matematik 2A hold 4 : Prøveeksamen juni 2010
 1 of 7 31-05-2010 13:18 2010 Matematik 2A hold 4 : Prøveeksamen juni 2010 Welcome Jens Mohr Mortensen [ My Profile ] View Details View Grade Help Quit & Save Feedback: Details Report [PRINT] 2010 Matematik
1 of 7 31-05-2010 13:18 2010 Matematik 2A hold 4 : Prøveeksamen juni 2010 Welcome Jens Mohr Mortensen [ My Profile ] View Details View Grade Help Quit & Save Feedback: Details Report [PRINT] 2010 Matematik
Matematisk modellering og numeriske metoder. Lektion 4
 Matematisk modellering og numeriske metoder Lektion 4 Morten Grud Rasmussen 17. september, 013 1 Homogene andenordens lineære ODE er [Bogens afsnit.1] 1.1 Linearitetsprincippet Vi så sidste gang, at førsteordens
Matematisk modellering og numeriske metoder Lektion 4 Morten Grud Rasmussen 17. september, 013 1 Homogene andenordens lineære ODE er [Bogens afsnit.1] 1.1 Linearitetsprincippet Vi så sidste gang, at førsteordens
Ligninger med reelle løsninger
 Ligninger med reelle løsninger Når man løser ligninger, er der nogle standardmetoder som er vigtige at kende. Her er der en kort introduktion til forskellige teknikker efterfulgt af opgaver hvor man kan
Ligninger med reelle løsninger Når man løser ligninger, er der nogle standardmetoder som er vigtige at kende. Her er der en kort introduktion til forskellige teknikker efterfulgt af opgaver hvor man kan
Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 2016
 Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Afstande, skæringer og vinkler i rummet
 Afstande, skæringer og vinkler i rummet Frank Villa 2. maj 202 c 2008-20. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold
Afstande, skæringer og vinkler i rummet Frank Villa 2. maj 202 c 2008-20. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold
Forelæsningsnoter til. Lineær Algebra. Niels Vigand Pedersen. Udgivet af. Asmus L. Schmidt. Københavns Universitet Matematisk Afdeling
 Forelæsningsnoter til Lineær Algebra Niels Vigand Pedersen Udgivet af Asmus L Schmidt Københavns Universitet Matematisk Afdeling August Revideret 9 ii udgave, oktober 9 Forord Gennem en særlig aftale varetages
Forelæsningsnoter til Lineær Algebra Niels Vigand Pedersen Udgivet af Asmus L Schmidt Københavns Universitet Matematisk Afdeling August Revideret 9 ii udgave, oktober 9 Forord Gennem en særlig aftale varetages
Matematik A. Højere teknisk eksamen. Forberedelsesmateriale. htx112-mat/a-26082011
 Matematik A Højere teknisk eksamen Forberedelsesmateriale htx112-mat/a-26082011 Fredag den 26. august 2011 Forord Forberedelsesmateriale til prøverne i matematik A Der er afsat 10 timer på 2 dage til
Matematik A Højere teknisk eksamen Forberedelsesmateriale htx112-mat/a-26082011 Fredag den 26. august 2011 Forord Forberedelsesmateriale til prøverne i matematik A Der er afsat 10 timer på 2 dage til
Besvarelser til Lineær Algebra Ordinær Eksamen - 5. Januar 2018
 Besvarelser til Lineær Algebra Ordinær Eksamen - 5. Januar 08 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Lineær Algebra Ordinær Eksamen - 5. Januar 08 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Ølopgaver i lineær algebra
 Ølopgaver i lineær algebra 30. maj, 2010 En stor del af de fænomener, vi observerer, er af lineær natur. De naturlige matematiske objekter i beskrivelsen heraf bliver vektorrum rum hvor man kan lægge elementer
Ølopgaver i lineær algebra 30. maj, 2010 En stor del af de fænomener, vi observerer, er af lineær natur. De naturlige matematiske objekter i beskrivelsen heraf bliver vektorrum rum hvor man kan lægge elementer
Oversigt [LA] 1, 2, 3, [S] 9.1-3
![Oversigt [LA] 1, 2, 3, [S] 9.1-3 Oversigt [LA] 1, 2, 3, [S] 9.1-3](/thumbs/74/70906933.jpg) Oversigt [LA], 2, 3, [S] 9.-3 Nøgleord og begreber Koordinatvektorer, talpar, taltripler og n-tupler Linearkombination Underrum og Span Test linearkombination Lineær uafhængighed Standard vektorer Basis
Oversigt [LA], 2, 3, [S] 9.-3 Nøgleord og begreber Koordinatvektorer, talpar, taltripler og n-tupler Linearkombination Underrum og Span Test linearkombination Lineær uafhængighed Standard vektorer Basis
Projekt 4.9 Bernouillis differentialligning
 Projekt 4.9 Bernouillis differentialligning (Dette projekt dækker læreplanens krav om supplerende stof vedr. differentialligningsmodeller. Projektet hænger godt sammen med projekt 4.0: Fiskerimodeller,
Projekt 4.9 Bernouillis differentialligning (Dette projekt dækker læreplanens krav om supplerende stof vedr. differentialligningsmodeller. Projektet hænger godt sammen med projekt 4.0: Fiskerimodeller,
Afstande, skæringer og vinkler i rummet
 Afstande, skæringer og vinkler i rummet Frank Nasser 9. april 20 c 2008-20. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her.
Afstande, skæringer og vinkler i rummet Frank Nasser 9. april 20 c 2008-20. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her.
Lineær Algebra. Lars Hesselholt og Nathalie Wahl
 Lineær Algebra Lars Hesselholt og Nathalie Wahl Oktober 2016 Forord Denne bog er beregnet til et første kursus i lineær algebra, men vi har lagt vægt på at fremstille dette materiale på en sådan måde,
Lineær Algebra Lars Hesselholt og Nathalie Wahl Oktober 2016 Forord Denne bog er beregnet til et første kursus i lineær algebra, men vi har lagt vægt på at fremstille dette materiale på en sådan måde,
Uge 6 Store Dag. Opgaver til OPGAVER 1. Opgave 1 Udregning af determinant. Håndregning Der er givet matricen A =
 OPGAVER Opgaver til Uge 6 Store Dag Opgave Udregning af determinant. Håndregning 0 Der er givet matricen A = 0 2 2 4 0 0. 2 0 a) Udregn det(a) ved opløsning efter en selvvalgt række eller søjle. b) Omform
OPGAVER Opgaver til Uge 6 Store Dag Opgave Udregning af determinant. Håndregning 0 Der er givet matricen A = 0 2 2 4 0 0. 2 0 a) Udregn det(a) ved opløsning efter en selvvalgt række eller søjle. b) Omform
Polynomier. Indhold. Georg Mohr-Konkurrencen. 1 Polynomier 2. 2 Polynomiumsdivision 4. 3 Algebraens fundamentalsætning og rødder 6
 Indhold 1 Polynomier 2 Polynomier 2 Polynomiumsdivision 4 3 Algebraens fundamentalsætning og rødder 6 4 Koefficienter 8 5 Polynomier med heltallige koefficienter 9 6 Mere om polynomier med heltallige koefficienter
Indhold 1 Polynomier 2 Polynomier 2 Polynomiumsdivision 4 3 Algebraens fundamentalsætning og rødder 6 4 Koefficienter 8 5 Polynomier med heltallige koefficienter 9 6 Mere om polynomier med heltallige koefficienter
Funktionalligninger. Anders Schack-Nielsen. 25. februar 2007
 Funktionalligninger Anders Schack-Nielsen 5. februar 007 Disse noter er en introduktion til funktionalligninger. En funktionalligning er en ligning (eller et ligningssystem) hvor den ubekendte er en funktion.
Funktionalligninger Anders Schack-Nielsen 5. februar 007 Disse noter er en introduktion til funktionalligninger. En funktionalligning er en ligning (eller et ligningssystem) hvor den ubekendte er en funktion.
Introduktion til Laplace transformen (Noter skrevet af Nikolaj Hess-Nielsen sidst revideret marts 2013)
 Introduktion til Laplace transformen (oter skrevet af ikolaj Hess-ielsen sidst revideret marts 23) Integration handler ikke kun om arealer. Tværtimod er integration basis for mange af de vigtigste værktøjer
Introduktion til Laplace transformen (oter skrevet af ikolaj Hess-ielsen sidst revideret marts 23) Integration handler ikke kun om arealer. Tværtimod er integration basis for mange af de vigtigste værktøjer
Besvarelser til Calculus og Lineær Algebra Globale Forretningssystemer Eksamen - 3. Juni 2014
 Besvarelser til Calculus og Lineær Algebra Globale Forretningssystemer Eksamen - 3. Juni 204 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over
Besvarelser til Calculus og Lineær Algebra Globale Forretningssystemer Eksamen - 3. Juni 204 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over
Komplekse tal. enote 29. 29.1 Indledning
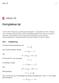 enote 29 1 enote 29 Komplekse tal I denne enote introduceres og undersøges talmængden C, de komplekse tal. Da C betragtes som en udvidelse af R forudsætter enoten almindeligt kendskab til de reelle tal,
enote 29 1 enote 29 Komplekse tal I denne enote introduceres og undersøges talmængden C, de komplekse tal. Da C betragtes som en udvidelse af R forudsætter enoten almindeligt kendskab til de reelle tal,
Projekt 4.6 Løsning af differentialligninger ved separation af de variable
 Projekt 4.6 Løsning af differentialligninger ved separation af de variable Differentialligninger af tpen d hx () hvor hx ()er en kontinuert funktion, er som nævnt blot et stamfunktionsproblem. De løses
Projekt 4.6 Løsning af differentialligninger ved separation af de variable Differentialligninger af tpen d hx () hvor hx ()er en kontinuert funktion, er som nævnt blot et stamfunktionsproblem. De løses
Matematisk modellering og numeriske metoder. Lektion 1
 Matematisk modellering og numeriske metoder Lektion 1 Morten Grud Rasmussen 4. september, 2013 1 Ordinære differentialligninger ODE er 1.1 ODE er helt grundlæggende Definition 1.1 (Ordinære differentialligninger).
Matematisk modellering og numeriske metoder Lektion 1 Morten Grud Rasmussen 4. september, 2013 1 Ordinære differentialligninger ODE er 1.1 ODE er helt grundlæggende Definition 1.1 (Ordinære differentialligninger).
Eksamen i Lineær Algebra. Første Studieår ved Det Tekniske Fakultet for IT og Design samt Det Ingeniør- og Naturvidenskabelige Fakultet
 Eksamen i Lineær Algebra Første Studieår ved Det Tekniske Fakultet for IT og Design samt Det Ingeniør- og Naturvidenskabelige Fakultet 4. januar 9 kl. 9:-: Dette eksamenssæt består af 8 nummererede sider
Eksamen i Lineær Algebra Første Studieår ved Det Tekniske Fakultet for IT og Design samt Det Ingeniør- og Naturvidenskabelige Fakultet 4. januar 9 kl. 9:-: Dette eksamenssæt består af 8 nummererede sider
Eulers equidimensionale differentialligning
 Eulers equidimensionale differentialligning Projektbesvarelse for MM501, udformet af Hans J. Munkholm Differentialligningen September-oktober 2009 For at kunne referere let og elegant gentages differentialligningen
Eulers equidimensionale differentialligning Projektbesvarelse for MM501, udformet af Hans J. Munkholm Differentialligningen September-oktober 2009 For at kunne referere let og elegant gentages differentialligningen
Kursusgang 3 Matrixalgebra Repetition
 Kursusgang 3 Repetition - froberg@mathaaudk http://peoplemathaaudk/ froberg/oecon3 Institut for Matematiske Fag Aalborg Universitet 12 september 2008 1/12 Lineære ligningssystemer Et lineært ligningssystem
Kursusgang 3 Repetition - froberg@mathaaudk http://peoplemathaaudk/ froberg/oecon3 Institut for Matematiske Fag Aalborg Universitet 12 september 2008 1/12 Lineære ligningssystemer Et lineært ligningssystem
Besvarelser til Calculus og Lineær Algebra Globale Forretningssystemer Eksamen - 8. Juni 2015
 Besvarelser til Calculus og Lineær Algebra Globale Forretningssystemer Eksamen - 8. Juni 05 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en
Besvarelser til Calculus og Lineær Algebra Globale Forretningssystemer Eksamen - 8. Juni 05 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en
Sylvesters kriterium. Nej, ikke mit kriterium. Sætning 9. Rasmus Sylvester Bryder
 Sætning 9 Sylvesters kriterium Nej, ikke mit kriterium Rasmus Sylvester Bryder Inspireret af en statistikers manglende råd om hvornår en kvadratisk matrix er positivt definit uden at skulle ud i at bestemme
Sætning 9 Sylvesters kriterium Nej, ikke mit kriterium Rasmus Sylvester Bryder Inspireret af en statistikers manglende råd om hvornår en kvadratisk matrix er positivt definit uden at skulle ud i at bestemme
Lokalt ekstremum DiploMat 01905
 Lokalt ekstremum DiploMat 0905 Preben Alsholm Institut for Matematik, DTU 6. oktober 00 De nition Et stationært punkt for en funktion af ere variable f vil i disse noter blive kaldt et egentligt saddelpunkt,
Lokalt ekstremum DiploMat 0905 Preben Alsholm Institut for Matematik, DTU 6. oktober 00 De nition Et stationært punkt for en funktion af ere variable f vil i disse noter blive kaldt et egentligt saddelpunkt,
Reaktionskinetik - 1 Baggrund. lineære og ikke-lineære differentialligninger. Køreplan
 Reaktionskinetik - lineære og ikke-lineære differentialligninger Køreplan 1 Baggrund På 2. eller 4. semester møder kemi/bioteknologi studerende faget Indledende Fysisk Kemi (26201/26202). Her behandles
Reaktionskinetik - lineære og ikke-lineære differentialligninger Køreplan 1 Baggrund På 2. eller 4. semester møder kemi/bioteknologi studerende faget Indledende Fysisk Kemi (26201/26202). Her behandles
Figur. To ligninger i to ubekendte. Definition Ved m lineære ligninger med n ubekendte forstås. Definition 6.4 Givet ligningssystemet
 Oversigt [LA] 6, 7, 8 Nøgleord og begreber Lineære ligningssystemer smængdens struktur Test løsningsmængde Rækkereduktion Reduceret matrix Test ligningssystem Rækkeoperationsmatricer Rangformlen Enten-eller
Oversigt [LA] 6, 7, 8 Nøgleord og begreber Lineære ligningssystemer smængdens struktur Test løsningsmængde Rækkereduktion Reduceret matrix Test ligningssystem Rækkeoperationsmatricer Rangformlen Enten-eller
