Teknisk Matematik FACITLISTE. Preben Madsen. Med kapitel af Thomas Bolander. 2. udgave. PRAXIS Nyt Teknisk Forlag
|
|
|
- Dorte Groth
- 5 år siden
- Visninger:
Transkript
1 3 Teknisk Matematik 2. udgave FACITLISTE Preben Madsen Med kapitel af Thomas Bolander PRAXIS Nyt Teknisk Forlag
2 Teknisk matematik 3 - Facitliste Indhold 1. Vektorregning i rummet 2. Trigonometriske funktioner 3. Mere differentialregning 4. Mere integralregning 5. Differentialligninger 6. Diskret matematik 7. Vektorfunktioner Vektorregning i rummet a) AAAA = ( 5) b) AAAA = 7, a) AAAA = 2,45, AAAA = 4,12, BBBB = 5,39 b) AA = 107,51 c) Areal = 4,81 d) MM BBBB = (3; 3; 1,5) e) mm BBBB = 2, a) TT(1; 1,5; 4), AA(2, 0, 0), BB(2, 3, 0), CC(0, 3, 0), DD(0, 0, 0) b) ss = 4, a) AA(3, 0, 0), BB(3; 2,5; 0), CC(3, 5, 0), DD(1,5; 1; 3), EE(1,5; 2,5; 3), FF(1,5; 4; 3) b) AAAA = 3,5 m, AAAA = 4,18 m, BBBB = 3,35 m, AAAA = CCCC = 4,18 m AAAA = CCCC = 3,5 m 1.05 a) - b) 1) aa xxxx = 3 2) aa yyyy = 4 3) aa xxxx = 2 4) aa xx = 3,61 5) aa yy = 5 6) aa zz = 4, a) Fremstiller en kugle med centrum (2, 6, 3) og radius rr = 7 b) Fremstiller en kugle med centrum (8, 5, 0) og radius rr = 11 2
3 c) Fremstiller en kugle med centrum ( 4, 7, 9) og radius rr = a) aa + bb = ( 8 ), aa + bb = 9,43 b) ( 2,11, 2) a) pp + qq + rr = ( 0 ), pp + qq + rr = 12, b) pp qq rr = ( 2 ), pp qq rr = 11, c) 2pp + 4qq 3rr = ( 16), 2pp + 4qq 3rr = 17,92 4 0, a) ee aa = ( 0,512 ) 0, a) vv = 134, a) tt = a) AA = 118,22, BB = 40,70, CC = 21, aa er parallel med bb, da 1,5aa = bb 1.14 a) tt = 12 b) tt = a) bb aa = 5,76 b) aa bb = 3,61 tt : x-aksen: ( 0), y-aksen: ( tt), z-aksen: ( 0) 0 0 tt xx 1 + 2tt xx 3 + 2tt 1.17 a) ( yy) = ( 2 4tt ) eller ( yy) = ( 2 4tt) zz 4 + 9tt zz 5 + 9tt b) Skæring med xy-plan: (1,89; 0,22; 0), skæring med xz-plan: (2; 0; 0,5), skæring med yz-plan: (0; 4; 8,5) 1.18 AA, BB oooo CC ligger på en ret linje, da AAAA = 3AAAA 1.19 a) Linjerne har ikke et skæringspunkt b) Linjerne er vindskæve 1.20 a) Linjerne har et skæringspunkt b) Skæringspunktet er (2,5,4) 1.21 a) Linjerne har ikke et skæringspunkt b) Linjerne er vindskæve 3
4 a) vv = 96,49 b) aa bb = ( 27) Areal = a) aa bb = ( 69 ) b) Areal = 106,19 60 xx a) ( yy) = ( 1) + ss ( 5 ) + tt ( 6) b) 10xx + yy 9zz + 15 = 0 zz xx , a) Punktet (5, 3, 4) ligger i planet b) ( yy) = ( 3) + ss ( 3 ) + tt ( 3 ) zz 4 0, a) 19xx + 7yy + 2zz 198 = a) zz = 0 b) AAAAAA: 3xx + zz 12 = 0, AAAAAA: 3yy + zz 12 = 0, CCCCCC: 3yy zz = 0, CCCCCC: 3xx zz = BBBBBBBBBB: yy = 0, AAAAAAAAAA: yy = 14, AAAAAAAA: xx = 8, CCCCCCCC: xx = 0, AAAAAAAA: zz = 0 EEEEEEEE: 3xx + 4zz 36 = 0, KKKKKKKK: 3xx + 4zz 12 = xx 2yy + 2zz 17 = 0 xx 0 + 1tt 1.31 a) ( yy) = ( tt) b) vv = 51,04 zz tt 1.32 a) vv = a) (xx, yy, zz) = (0, 8, 1) b) vv = 8,76 xx 1 + 4tt 1.34 a) ( yy) = ( 4 2tt) b) (xx, yy, zz) = ( 2,11; 5,56; 5,33) c) vv = 43 zz 3 3tt 1.35 a) vv = 33,40 b) vv = 85, ee = 5, ee = 4, ee = 5, ee = 9, a) Planerne er parallelle, da nn 2 = 3nn 1 b) ee = 0,43 4
5 1.41 a) ee = 11,84 b) 2xx + yy + zz 33 = 0 c) (16,5; 0; 0), (0, 33, 0), (0, 0, 33) 1.42 a) AA(6, 10, 2), BB(6, 0, 2), CC(0, 0, 2), DD(0, 10, 2), EE(3, 7, 4), FF(3, 3, 4) b) AAAA = 4,69 c) 2xx + 3zz 18 = 0 d) 2xx 3zz + 6 = 0 e) vv = 67, a) (1; 3,5; 0,5) b) (xx 4) 2 + (yy 1) 2 + (zz + 2) 2 = 5, Trigonometriske funktioner 2.01 a) 57,30 b) 134,46 c) 231,80 d) 342, a) 0,9460 b) 2,3702 c) 4,4803 d) 5, a) xx = 1,0759 eller xx = 2,0657 b) xx = 5,9575 eller xx = 3, a) xx = 0,4275 eller xx = 5,8557 b) xx = 1,8029 eller xx = 4, a) xx = 1,3819 eller xx = 4,5235 b) xx = 5,7727 eller xx = 2, a) LL = [0; 3,7360[ eller ]5,6888; 2ππ] b) LL = [0; 0,8038] eller [2,3378; 2ππ] c) LL = [0; 0,2014[ eller ]2,9402; 3,8492] eller [5,5756; 2ππ] 2.07 a) LL = [2,3746; 3,9086] bb) L = [0; 1,0701[ eeeeeeeeee ]5,2130; 2ππ] c) LL = ]1,3694; 2,1652] eller [4,1180; 4,9137[ 2.08 a) LL = [1,5222; 0,5ππ[ eller [4,6639; 1,5ππ[ b) LL = ]0,5ππ; 2,3562[ eeeeeeeeee ]1,5ππ; 5,4978[ c) LL = [0,1974; 0,9151[ eller [3,3390; 4,0567[ 2.09 a) xx = 0, ππ nn eller xx = 1,071 + ππ nn b) xx = 0, ππ nn eller xx = 0, ππ nn a) xx = 1, ππππ eller xx = 3, ππππ eller xx = 4, ππππ eller xx = 5, ππππ b) xx = ππππ eller xx = 0, ππππ eller xx = 5, ππππ 2.11 a) xx = 0, ππππ eller xx = 2, ππππ eller xx = 3, ππππ eller xx = 5, ππππ b) xx = 3, ππππ eller xx = 5, ππππ 2.12 a) xx = 2, ππππ b) xx = 1, ππππ 5
6 2.13 a) TT = 2 sek. b) tt = 0,5 sek. c) tt = 1,5 sek a) TT = 3,14 sek. b) tt = 1,29 sek. c) tt = 2,86 sek a) TT = 2,09 sek. b) tt = 1,57 sek. c) tt = 0,52 sek a) II(0) = 1,2 ampere b) II(3) = 2,38 ampere c) II mmmmmm = 4,4 ampere, II mmmmmm = 2 ampere d) tt = 12,5 sek. e) tt = 37,5 sek a) 33,55 liter b) h = 19,2 cm 2.18 a) - b) ff(tt) = 0,802 sin(0,502tt) + 2,5 c) 1,6 meter d) 6,26 timer 2.19 a) ff(xx) = 25 sin(0,04xx 0,5ππ) + 55 b) 3. Differentialregning II 3.01 a) ff (xx) = cos xx b) (1,57; 3), (4,71; 1), (7,85; 3), (11; 1) 3.02 a) ff (xx) = 2 sin xx b) (0, 1), (ππ; 3), (2ππ; 1), (3ππ; 3), (4ππ; 1) 3.03 a) ff (xx) = cos xx sin xx + 1 (cos xx) 2 b) yy = 2xx + 1 c) yy = 2xx + 0, a) ff (xx) = 30xx(7 + 3xx 2 ) 4 b) ff (xx) = 4(2 + 4xx 2 9xx 3 ) 3 (8xx 27xx 2 ) c) ff (xx) = 15(5xx 3) 4 d) ff (xx) = 2,5(3 xx) 1, a) ff (xx) = 3 cos(3xx) b) ff (xx) = 6 sin(3xx) cos(3xx) c) ff (xx) = 18xx cos(3xx) 2 d) ff (xx) = 3(sin(3xx)) 2 cos(3xx) 3.06 a ff (xx) = 8 cos(1 xx) sin(1 xx) b) ff (xx) = 18(sin(3xx)) 2 cos(3xx) c) ff (xx) = 1,5(2 xx+1)2 xx+1 d) ff (xx) = 15xx(1 xx 2 ) 1, a) vv(tt) = 10 9,82tt b) 1,018 sek. c) ss = 8,09 m d) aa(tt) = 9, a) DDDD(ff) = RR, skæringspunkter med x- og y-aksen: (1, 0), (0, 4). MMMMMM: (1, 0). Monotoniforhold: f er aftagende i ] ; 1] og voksende i [1; [. VVVV(ff) = [0; 3[ b) Skæringspunkter med x- og y-aksen: (0,6662; 0), (2,4754; 0), (0, 1). m sek 2 Lokalt mmmmmm: (1,57; 1) og (4,71; 1), Lokalt mmmmmm: (3,67; 1,25) og (5,80; 1,25). Monotoniforhold: ff er voksende i [0; 1,57], [3,67; 4,71] og [5,80; 2ππ]. 6
7 ff er aftagende i [1,57; 3,67] og [4,71; 5,80]. VVVV(ff) = [ 1,25; 1] c) DDDD(ff) = RR. Skæringspunkter med x- og y-aksen: ( 1,16; 0), (0, 0), (5,16; 0. ) Lokalt mmmmmm i ( 0,61; 0,97), lokalt mmmmmm i(3,28; 13,71). Monotoniforhold: ff er voksende i [ 0,61; 3,28] og ff er aftagende i ] ; 0,61] og [3,28; [ VVVV(ff) = RR d) DDDD(ff) = [ 3; 3]. Skæringspunkter med x- og y-aksen: ( 3, 0), (3, 0), (0, 3) Maksimum i (0, 3). Monotoniforhold: ff er voksende i [ 3, 0] og aftagende i [0, 3] VVVV(ff) = [0, 3] e) DDDD(ff) = RR. Skæringspunkter med x- og y-aksen: (0, 0), (1,59; 0). MMMMMM i (1; 0,75) Monotoniforhold: ff er aftagende i ] ; 1] oog voksende i [1; [. VVVV(ff) = [ 0,75; [ 3.09 a) Centrum (3, 4) og radius rr = 5 b) 3.10 a) xx 2 + (yy ) 2 = b) dyy dxx = 2xx 2yy c) aa AAAA = 0,18, aa CCCC = 0,18 d) AAAA: 1,8 %, CCCC: 1,8 % 4. Integralregning II 4.01 a) 1 2 xx2 cos xx + kk b) 1 3 xx3 ln cos xx + kk c) sin xx xx + kk d) cos xx sin xx + kk 4.02 a) 2 b) a) - b) AA = a) - b) AA = 0, AA = 0, AA = AA = 49, AA = 74, AA = a) ff(xx) = 0,08xx b) AA = 11,31 7
8 4.11 AA = 2, AA = 81, AA = 60, AA = 10, AA = 57, AA = 64, a) - b) (1,047; 0,866) c) AA = 2, a) - b) VV xx = 0, a) - b) VV xx = 944, VV xx = ππ rr 2 h 4.21 a) - b) VV xx = 113, a) - b) VV xx = 4 ππ rr a) yy = rr h xx + rr b) VV xx = 1 3 ππ rr2 h 4.24 a) yy = rr RR h xx + RR b) VV = 1 3 ππ h(rr2 + rr 2 + RR rr) 4.25 a) - b) AA = 4,5 c) VV xx = 19, a) - b) AA = 0,67 c) VV xx = 3, a) AA = 0,9389 b) VV xx = 14, a) VV xx = 127,76 b) VV yy = 301, a) VV xx = 25,13 cm 3 b) VV yy = 20,11 cm 3 c) h xx = 3,19 cm, h yy = 1,91 cm 4.30 a) VV xx = 8,46 b) VV yy = 7, LL = 4, LL = 6, a) - b) AA = 1,913 c) LL = 3, a) - b) AA = 4,701 c) LL = 3, a) VV = 690,3 mm a) VV = 44,18 cm 3 b) h = 4,068 cm c) VV = 16,14 cm 3 8
9 5. Differentialligninger 5.01 a) yy = 0,33xx 3 + 3xx + k b) yy = 0,33xx 3 + 3xx 5, a) yy = 0,5xx 4 + k b) yy = 0,5xx 4 + 1, a) vv = tt 2 6tt + 6 b) aa = 2tt 6 c) 5.04 a) vv = 2tt 3 3tt + 2 b) ss = 0,5tt 4 1,5tt 2 + 2tt 5.05 a) 0,0625xx 4 + 0,167xx 3 1,5xx 2 + 2xx + kk b) yy = xx 3 + 2xx 2 + kk c) yy = 3,33xx 3 + 6xx 2 14xx + kk d) yy = 2 (xx3 2) 3 + kk 5.06 a) yy = 0,5 ln(xx 2 + 4) + kk b) yy = 0,5 ln(xx 2 + 4) 0, a) yy = 2xx 3 + kk b) yy = 2xx a) yy = xx 2 + kk 1 xx + kk 2 b) yy = xx 2 2xx a) yy = 0,0833xx 4 + kk 1 xx + kk 2 b) yy = 0,0833xx 4 3xx + 3, a) yy = ±ccee 0,5xx2 b) yy = ee 0,5xx2, yy = 2ee 0,5xx2, yy = 0,6065ee 0,5xx2, yy = 1,2131ee 0.5xx a) yy = 10xx xx 2 + 2kk b) yy = 10xx xx a) yy = xx 2 + kk b) yy = xx 5.13 a) yy ± ccee 3xx b) yy = 0,4979ee 3xx c) yy = 30xx a) yy = ccee 0,5xx b) yy = 0,6065ee 0,5xx, yy = 1,2131ee 0,5xx 5.15 a) yy = ±ccee xx + 3 b) yy = 2ee xx a) yy = 0,25xx 2 + 1,5kk 2 + 0,5xxxx b) yy = 0,25xx 2 + 1,5xx + 2, a) yy = 0,5xx 2 + 0,25kk 2 + 0,5xxxx + 3 b) yy = 0,25xx a) yy = 1,5 1+kkee 3xx b) yy = 1,5 1+10,0428ee 3xx a) yy = 2 b) yy = 2 1+kkee 8xx 1+3ee 2 8xx, yy =, yy = 2 1+ee 8xx 1+933ee 8xx 5.20 yy = 0,167xx 3 + 0,5xx yy = ln ( 1 ee xx +kk ) 9
10 5.22 yy = (3 3 0,5xx 2) yy = 6,9988ee 0,05xx 5.24 a) yy = 1+399ee ,4715xx b) xx = 2, yy = 511, xx = 3, yy = 816, xx = 4, yy = 1300, xx = 5, yy = 2063 c) I uge nr. 13 vil halvdelen af befolkningen være smittet. 10
11 Diskret Matematik Kapitel til Teknisk Matematik, Bind 3 Løsninger Thomas Bolander 8. august 2018 Opgave 6.01 Rekursivt funktionsudtryk for det, man skylder, efter n år: { hvis n =0 f(n) = 1, 35 f(n) hvis n>0 Begyndelsesbetingelsen udtrykker, at når lånet optages skylder man kr. Rekursionsbetingelsen udtrykker at hver gang n stiger med én (der går et år), øges gælden med 35%. f(10) kan nu bestemmes ved gentagen substitution: f(10) = 1, 35 f(9) = 1, 35 1, 35 f(8) = 1, 35 2 f(8) = 1, , 35 f(7) =1, 35 3 f(7) = =1, f(0) = 1, = Det er med andre ord ret dyrt med den slags lån! Opgave 6.02 f(0) = 2, det aflæses direkte af begyndelsesbetingelsen. f(1) fås ved indsættelse i rekursionsbetingelsen: f(1) = 2 f(0) 1=2 2 1=3. f(2) kan så igen fås ved at indsætte ovenstående værdi for f(1) i rekursionsbetingelsen: f(2) = 2 f(1) 1=2 3 1=5. Opgave 6.03 Du løser den efter samme princip som Opgave Begyndelsesbetingelsen giver os direkte værdien af f(0) til at være 3. Det bruges så i rekursionsbetingelsen til at bestemme f(1): f(1) = f(0) 1= =7. Det kan vi så bruge til at bestemme f(2): f(2) = f(1) 1= =
12 Opgave 6.04 Som i de foregående to opgaver, pånær at n nu optræder to steder i rekursionsbetingelsen, og vi skal huske at indsætte værdien af n på begge pladser: f(0) = 1 f(1) = f(0) =1 2 +4=5 f(2) = f(1) =5 2 +8=33 f(3) = f(2) = = 1101 Opgave 6.05 Eftersom de 7 forretter, 8 hovedretter og 3 desserter kan kombineres uafhængigt af hinanden, er antallet af kombinationsmuligheder produktet af antallet af muligheder i hver af de tre retter. Det er altså = 168. Vi bruger gentagen substitution i den rekursive definition af fakultetsfunk- Opgave 6.06 tionen: 5! = 5 (5 1)! = 5 4! = 5 4 (4 1)! = 5 4 3!= ! = ! = ! = = I næstsidste omskrivning brugte vi begyndelsesbetingelsen 0! = 1. Opgave 6.07 Herunder er først n! i intervallet fra 0 til 5 markeret med sorte krydser og e n i samme interval vist ved den røde kurve Det kunne godt se ud som om fakultetsfunktionen vokser langsommere, men allerede hvis vi udvider intervallet til også at omfatte n = 6, kan vi se, at fakultetsfunktionen overhaler 2 12
13 eksponentialfunktionen: Og udvider vi med n = 7, n = 8 og n = 9, begynder eksponentialfunktionen at blive forsvindende lille i forhold til fakultetsfunktionen: Det samme mønster vil gentage sig, hvis vi i stedet sammenligner fakultetsfunktionen med 10 n eller 100 n, men der kræves selvfølgelig højere værdier af n inden fakultetsfunktionen overhaler. Fakultetsfunktionen overhaler 10 n for n = 25. Den overhaler 100 n omkring n = 450, men mange lommeregnere og CAS-værktøjer giver op ved så høje tal (450! er ca ). Opgave 6.08 De første to Fibonacci-tal fås direkte af begyndelsesbetingelserne: f(0) = 1 og f(1) = 1. De næste tal udregnes ved at bruge rekursionsbetingelsen: f(2) = f(1) + f(0) = = 2 f(3) = f(2) + f(1) = = 3 f(4) = f(3) + f(2) = = 5 f(5) = f(4) + f(3) = =
14 Opgave 6.09 I Eksempel 6.04 er værdierne af f(n) angivet op til n = 7. Vi kan bruge disse værdier til at udregne f(8), f(9) og f(10): Opgave 6.10 f(8) = f(7) + f(6) = = 34 f(9) = f(8) + f(7) = = 55 f(10) = f(9) + f(8) = = 89 a) Efter 0 måneder (altså i begyndelsen) er der netop ét kaninpar. Efter 1 måned har de ikke nået at reproducere sig, så derfor er der stadig kun ét kaninpar. Efter 2 måneder reproducerer de sig første gang, og der er derfor 2 kaninpar. Det første kaninpar reproducerer sig igen efter 3 måneder, så der bliver der tilføjet et nyt kaninpar, altså har vi nu 3 i alt. Endelig, efter 4 måneder, reproducerer både det første og det andet kaninpar, så vi i alt har = 5 kaninpar. Altså bliver tallene 1, 1, 2, 3 og 5, som var det vi skulle vise. b) Antallet af kaninpar efter n måneder er summen af to tal a og b givet ved: a = antallet af kaninpar som der var der i forvejen, dvs. antallet af kaninpar efter n 1 måneder. b = antallet af nye kaninpar som bliver født i den n te måned. Antallet b af nye kaninpar er lig med antallet af kaninpar som fandtes efter n 2 måneder, eftersom kaninerne begynder at reproducere efter 2 måneder. Altså får vi at antallet af kaninpar efter n måneder er summen af to tal a og b givet ved: a = antallet af kaninpar efter n 1 måneder. b = antallet af kaninpar efter n 2 måneder. Bruger vi nu f(n) til at betegne antallet af kaninpar efter n måneder fås således, at f(n) er summen af to tal a og b givet ved: a = f(n 1) b = f(n 2). Med andre ord fås f(n) =f(n 1) + f(n 2). Det er rekursionsbetingelsen for Fibonacci-tallene. Begyndelsesbetingelsen følger direkte af antallet af kaninpar efter 0 og 1 måned beregnet under a). Opgave 6.11 Se på definitionen af f(2). Den er givet ved rekursionsbetingelsen, som giver os f(2) = f(1) + f( 1). Problemet er her at definitionen ikke fortæller os hvad værdien af f( 1) er. Indtil videre har alle vores rekursive funktioner kun været defineret på de naturlige tal, og så giver udtrykket f( 1) slet ikke mening. Løsningen vil være at tilføje en begyndelsesbetingelse, som definerer f(2). Alternativt skulle selve rekursionsbetingelsen ændres, så f(n) ikke er defineret udfra f(n 3). 4 14
15 Opgave 6.12 a) En tom plade kan dækkes på netop én måde, så f(0) = 1. En plade af bredde 1 kan kun dækkes af en rød klods, så f(1) = 1. En plade af bredde 2 kan kun dækkes af 2 røde klodser, så f(2) = 1. En plade af bredde 3 kan enten dækkes af 3 røde klodser eller 1 blå, så f(3) = 2. En plade af bredde 4 kan dækkes af enten 1) 4 røde, 2) først en blå og så en rød eller 3) først en rød og så en blå. I alt fås så f(4) = 3. En plade af bredde 5 kan dækkes ved enten at starte med en rød, blå eller gul. Hvis vi starter med en rød, er der 4 knopper tilbage, som vi har set kan dækkes på f(4) = 3 måder. Hvis vi starter med en blå er der 2 knopper tilbage, som vi har set kan dækkes på f(2) = 1 måde. Hvis vi starter med en gul er der ingen knopper tilbage. Altså kan vi dække de 5 knopper på i alt = 5 måder. Vi kan lave et tilsvarende regnestykke for n = 6. Vi starter med rød, blå eller gul. Hvis vi starter med rød, er der 5 knopper tilbage, som kan dækkes på f(5) = 5 måder. Hvis vi starter med blå, er der 3 knopper tilbage, som kan dækkes på f(3) = 2 måder. Hvis vi starter med gul, er der 1 knop tilbage, som kan dækkes på f(1) = 1 måde. I alt fås altså f(6) = = 8. b) Allerede i svaret til spørgsmål a) antydede vi en rekursionsbetingelse. Når man skal finde ud af, hvor mange måder man kan dække n knopper på, gør man følgende. Først vælger man om man vil starte med rød, blå eller gul. Hvis man starter med rød, er der n 1 knopper tilbage. Hvis f(n) betegner antallet af måder, man kan dække n knopper på, vil man altså kunne dække resten af pladen på f(n 1) forskellige måder, hvis man starter med rød. Hvis man starter med blå, er der n 3 knopper tilbage, som kan dækkes på f(n 3) forskellige måder. Hvis man starter med gul, er der n 5 knopper tilbage, som kan dækkes på f(n 5) forskellige måder. Alt dette forudsætter selvfølgelig at n er stor nok, specifikt at n 5. Hvis ikke n 5, er det slet ikke sikkert vi kan lægge både røde, blå og gule klodser til at starte med. Vi har altså at der er f(n 1) måder som starter med rød, f(n 3) måder som starter med blå og f(n 5) måder som starter med gul. I alt fås så f(n) =f(n 1) + f(n 3) + f(n 5). Dette gælder som sagt dog kun når n 5. Så vi bliver nødt til at lave begyndelsesbetingelser for alle værdierne f(0),f(1),f(2),f(3) og f(4)! De relevante værdier af disse begyndelsebetingelser fandt vi under a). Den samlede definition af funktionen bliver så: 1 hvis n = 0, n = 1 eller n =2 2 hvis n =3 f(n) = 3 hvis n =4 f(n 1) + f(n 3) + f(n 5) hvis n
16 c) Vi kan nu bruge ovenstående funktionsudtryk til at beregne f(5) og f(6): f(5) = f(4) + f(2) + f(0)=3+1+1=5 f(6) = f(5) + f(3) + f(1)=5+2+1=8. Det passer med hvad vi fik under spørgsmål a). Opgave 6.13 Som i Eksempel 6.05 viser man begyndelsesbetingelsen og rekursionsbetingelsen ved at indsætte det lukkede udtryk for f(n) og omskrive: f(0) = 4 0 = 1 f(n) =4 n =4 4 n 1 =4 f(n 1) begyndelsebetingelse rekursionsbetingelse Opgave 6.14 Som i Opgave 6.14 skal vi bruge det lukkede udtryk til at vise at den rekursive definition holder. I dette tilfælde er det lukkede udtryk definitionen af f(n) som siger, at f(n) = 0, når n er ulige, og f(n) = 1, når n er lige. Eftersom 0 er et lige tal, fås f(0) = 1, og det viser begyndelsesbetingelsen af den rekursive definition. Vi skal nu vise rekursionsbetingelsen f(n) =1 f(n 1) for n>0. Udfra det lukkede udtryk har vi, at f(n) altid skifter mellem at være 0 eller 1. Mere præcist har vi, at f(n) = 0 hvis og kun hvis f(n 1) = 1; og omvendt, at f(n) = 1 hvis og kun hvis f(n 1) = 0. I alle tilfælde får vi således, at f(n) =1 f(n 1). Det viser rekursionsbetingelsen. Opgave 6.15 a) Første vers har 3 linjer, så f(0) = 3. Hvert vers i sangen har 1 linje mere end foregående vers. Derfor gælder f(n) = f(n 1) + 1 for n > 0. I alt bliver den rekursive definition så: { 3 hvis n =0 f(n) = n + 1 hvis n>0 b) Det passer på formen hvis vi vælger a = 3 og b = 1. c) Det eksplicitte udtryk bliver f(n) =a + nb =3+n. Det 11 te vers har f(10) linjer, som nu kan udregnes til f(10) = = 13. Det passer med den oprindelige version af sangen. Opgave 6.16 I løsningen til Opgave 6.01 fandt vi følgende rekursive udtryk for f(n): { hvis n =0 f(n) = 1, 35 f(n) hvis n>0 Det passer på formen angivet i formlen (7), hvis vi vælger a = og b =1, 35. Formlen (8) angiver da det tilsvarende eksplicitte udtryk: f(n) =a b n = , 35 n. Vi får så (igen) f(10) = , =
17 Opgave 6.17 a) Det første trekanttal har to 1 punkt i bunden, det næste har 2, det efterfølgende 3, osv. For at danne det næste trekanttal skal vi tilføje et ekstra punkt i bunden, og dernæst fylde punkter op så formen igen bliver en trekant. Hvis vi gør det på trekantfiguren, som svarer til tallet 21, får vi en trekantfigur med 7 nye punkter, altså = 28 kugler i alt. b) Som beskrevet i opgaven skal vi finde ud af hvor mange punkter der tilføjes når vi går fra den n 1 te til den n te trekant. Når vi går fra den første til den anden, tilføjer vi 2 punkter. Når vi går fra den anden til den tredje, tilføjer vi 3 punkter. Generelt kan vi se, at når vi går fra den n 1 te til den n te trekantfigur, så tilføjer vi altid n punkter. Vi får altså: f(n) =f(n 1) + antal ekstra punkter = f(n 1) + n Begyndelsesbetingelsen er blot f(0) = 0, fordi det første trekanttal er 0 (den tomme trekant). I alt bliver den rekursive definition således: { 0 hvis n =0 f(n) = f(n 1) + n hvis n>0 Her kan det være en god idé at tjekke at udtrykket passer med de tal vi allerede kender for f(n). Vi får f.eks. ved gentagen substitution at der gælder: f(6) = f(5) + 6 = f(4)+5+6=f(3)+4+5+6=f(2) = f(1) =f(0) = =21. Det passer heldigvis (den sjette trekantfigur har 21 punkter). c) Vi indsætter det eksplicitte udtryk for f(n) og viser at det opfylder begyndelsesbetingelsen og rekursionsbetingelsen fra spørgsmål b). Vi viser først begyndelsesbetingelsen: f(0) = 0 1 =0. 2 Det passer. Rekursionsbetingelsen er lidt sværere, og kræver at man laver nogle smarte omskrivninger: f(n) = n(n + 1) 2 = n2 + n 2 = n2 n +2n 2 = n2 n +n = 2 (n 1)n +n = f(n 1)+n. 2 d) Hvis der er 0 gæster, er der ingen at give hånd til. Så f(0) = 0, hvilket passer med begyndelsesbetingelsen af det rekursive udtryk ovenfor. Vi mangler så kun at vise, 7 17
18 at hvis der er n gæster for n>0, så bliver der givet netop f(n) håndtryk, hvor f(n) er givet ved det rekursive udtryk ovenfor: f(n) =f(n 1) + n. Vi skal altså vise, at med n gæster bliver der givet n flere håndtryk end hvis der kun er n 1 gæster. Men det er klart: hvis der i forvejen er n 1 gæster, og der så kommer en mere, så skal den nyankomne give hånd til værten og de n 1 andre gæster. Det er netop n ekstra håndtryk. Opgave 6.18 a) Vi benytter gentagen substitution: sfd(384, 162) = sfd(162, rest(384, 162)) = sfd(162, 60) = sfd(60, rest(162, 60)) = sfd(60, 42) = sfd(42, rest(60, 42)) = sfd(42, 18) = sfd(18, rest(42, 18)) = sfd(18, 6) = sfd(6, rest(18, 6)) = sfd(6, 0) = 6. b) Vi skal finde de størst mulige kvadratiske fliser, som præcist kan dække ef gulv at størrelse 384cm 162cm. Vi kan antage at 384cm er bredden og 162cm er højden af gulvet. For at fliserne kan dække gulvet præcist, skal der være et helt antal fliser i både bredden og højden. Hvis flisen har en siddelængde på x cm, skal x således gå op i både 384 og 162. Vi vil gerne have at x er så stor som muligt, så vi er altså på jagt efter det største tal x, som går op i både 384 og 162. Det er jo netop største fælles divisor af 384 og 162, som vi ovenfor beregnede til 6. Den maksimale kvadratiske flise, vi kan benytte, har altså en siddelængde på 6cm. Opgave 6.19 Opgave 6.20 Opgave 6.21 p q q q p p ( q p) S S F S S S F S S S F S F F S F F S S S p q q q p (q q) S S S S S F S S F S S F F F S F p q p q (p q) p ((p q) p) q S S S S S S F F S F F S S F S F F S F S 8 18
19 Opgave 6.22 a) Der er brug for to nye udsagnsvariable: m for at lave mad, og k for at købe ind. b) Kriterium 4 er, at hvis Selma skal lave mad (m), s å skal hun købe ind først (k). Det svarer således til formlen m k. Kriterium 5 er, at hvis Selma skal købe ind (k), s å kan hun ikke nå i biografen (b) og ikke lave afleveringsopgave (a). Altså, hvis k s å ikke b og ikke a. Det bliver til formlen k ( b a). c) Den samlede logiske formel for kriterierne 1 5 fås ved blot at tilføje de to nye kriterier fra b) som konjunkter til Selmas formel: (b h) (h b) ( h a) (m k) (k ( b a)). Hvis man skulle lave en sandhedstabel for denne formel, ville man have brug for 2 5 = 32 rækker, fordi der er i alt 5 udsagnsvariable i formlen: a, b, h, k og m. Opgave 6.23 a) p q. b) q r. c) r p. d) (p q) (p r) ( r p). e) p q r p q q r r p (p q) (p r) ( r p) S S S S S F F S S F S S S S S F S S S F F S F F S F S F F S S F S F F F S F F S S F F F S S S S S F F F S F S F Der er kun to løsninger, svarende til de to rækker hvor formlen fra d) er sand. I den første af disse rækker har vi p : S,q: S,r: F. Det svarer til, at vi inviterer Peru og Qatar, men afviser Rumænien. I den anden har vi p : F,q: F,r: S. Det svarer til at afvise Peru og Qatar, men invitere Rumænien. Begge muligheder kan ses at opfylde både kronprinsen, dronningen og kongens krav. 9 19
20 Opgave 6.24 a) b) Vi fortsætter talfølgen ved at tælle antal bier i de to nye generationer tilføjet ovenfor (de to øverste rækker af stamtræet): 1, 1, 2, 3, 5, 8. c) Værdierne af f(3), f(4) og f(5) kan vi direkte aflæse af talfølgen fra b). De er f(3) = 3, f(4) = 5 og f(5) = 8. For at bestemme f(6) skal vi gå endnu en generation tilbage. Det kan gøres ved at tilføje en ekstra generation til stamtræet ovenfor, eller blot at udregne hvor mange bier der vil være i en sådan ekstra generation. Hver af hunbierne i den ældste generation på stamtræet ovenfor har 2 forældre, og hver af hanbierne har 1 forældre. Der er 5 hunbier i den ældste generation, og 3 hanbier. Altså vil den ekstra generation have = 13 bier, og hermed fås f(6) = 13. d) Denne opgave løses ved blot at bruge stamtræet til at tjekke, at tallene passer. e) Grunden til der gælder f (n) =f(n 1) for alle n>0 er, at hver bi har én og kun én mor. Så det samlede antal af bier n 1 generationer tilbage, f(n 1), må være lige med antallet af mødre én generation længere tilbage, f (n). f) Denne opgave løses også ved blot at bruge stamtræet til at tjekke, at tallene passer. g) Grunden til at der gælder f (n) =f (n 1) for alle n>0 er, at hver hunbi har netop én far, mens ingen hanbier har en far. Så antallet af hunbier n 1 generationer tilbage, f (n 1), må dermed være lig med antallet af fædre én generation længere tilbage, f (n)
21 h) Det samlede antal bier n generationer tilbage er naturligvis summen af antal hanbier og antal hunbier n generationer tilbage. Altså f(n) =f (n)+f (n). Bruger vi resultaterne fra spørgsmål e) og g) fås så: f(n) =f (n)+f (n) =f(n 1) + f (n 1) = f(n 1) + f(n 2). Opgave 6.25 Bemærk først, at tallet i nederste højre hjørne af tabellen skulle have været et 1-tal: dødeligheden af rotter i alderen 2 3 er 100%. a) Vi bestemmer først antal rotter i aldersgruppen 0 1 efter 1 år. Det er de rotter, som bliver født i løbet af det første år. Ifølge tabellen vil der i gennemsnit blive født 0, 1 barn per rotte i alderen 0 1, 0, 7 barn per rotte i alderen 1 2 og 0, 1 barn per rotte i alderen 2 3. Der vil altså i gennemsnit i løbet af det første år blive født 0, 1 f [0;1] (0) + 0, 7 f [1;2] (0) + 0, 1 f [2;3] (0) = 0, , , 1 5=9 børn. Vi får således, at antallet af rotter i alderen 0 1 efter 1 år i gennemsnit er 9, altså f [0;1] (1) = 9. Vi bestemmer nu antal rotter i aldersgruppen 1 2 efter 1 år. Det er dem, af de oprindelige 15 rotter i aldersgruppen 0 1 år, som overlever det første år. Dødeligheden i denne gruppe er 20%, så i gennemsnit vil 0, 8 15 = 12 af dem overleve. Altså vil der i gennemsnit efter 1 år være 12 rotter i aldersgruppen 1 2 år, f [1;2] (1) = 12. Vi bestemmer nu antal rotter i aldersgruppen 2 3 efter 1 år. Det er dem, af de oprindelige 10 rotter i aldersgruppen 1 2 år, som overlever det første år. Vi får altså, i stil med ovenfor, f [2;3] (1) = 0, 8 10 = 8. b) Vi bestemmer først et rekursivt funktionsudtryk for f [0;1] (n). Begyndelsesbetingelsen er f [0;1] (0) = 15. Rekursionsbetingelsen fås ved at se på, hvor mange rotter der er i aldersgruppen 0 1 efter n år. Det er alle de rotter som er blevet født i løbet af det forløbende år, hvilket vi ligesom i a) udregner ved at se på hvor mange rotter der var i hver aldersgruppe det foregående år, og så gange det med fødselsraten. Vi får så: f [0;1] (n) =0, 1 f [0;1] (n 1)+0, 7 f [1;2] (n 1)+0, 1 f [2;3] (n 1) Sætter vi begyndelsesbetingelsen og rekursionsbetingelsen sammen, får vi følgende rekursive funktionsudtryk for f [0;1] (n): f [0;1] (n) = { 15 hvis n =0 0, 1 f [0;1] (n 1)+0, 7 f [1;2] (n 1)+0, 1 f [2;3] (n 1) hvis n>0 Vi bestemmer nu et rekursivt funktionsudtryk for f [1;2] (n). Begyndelsesbetingelsen er f [1;2] (0) = 10. Rekursionsbetingelsen fås ved at se på, hvor mange rotter der er i aldersgruppen 1 2 efter n år. Det er alle de rotter, som det foregående år var i 11 21
22 aldersgruppen 0 1 og er overlevet. Det udregnes på samme måde som i a), hvilket giver: f [1;2] (n) =0, 8 f [0;1] (n 1). Sætter vi begyndelsesbetingelsen og rekursionsbetingelsen sammen, får vi følgende rekursive funktionsudtryk for f [1;2] (n): { 10 hvis n =0 f [1;2] (n) = 0, 8 f [0;1] (n 1) hvis n>0 På tilsvarende vis får vi et rekursivt funktionsudtryk for f [2;3] (n): { 5 hvis n =0 f [2;3] (n) = 0, 8 f [1;2] (n 1) hvis n>0 c) Vi kan nu bestemme det samlede antal rotter efter 3 år ved at bruge gentagen substitution på ovenstående rekursive funktionsudtryk: f(3) = f [0;1] (3) + f [1;2] (3) + f [2;3] (3) =0, 1 f [0;1] (2) + 0, 7 f [1;2] (2) + 0, 1 f [2;3] (2) + 0, 8 f [0;1] (2) + 0, 8 f [1;2] (2) =0, 9 f [0;1] (2) + 1, 5 f [1;2] (2) + 0, 1 f [2;3] (2) =0, 9 (0, 1 f [0;1] (1) + 0, 7 f [1;2] (1) + 0, 1 f [2;3] (1)) + 1, 5 0, 8 f [0;1] (1) + 0, 1 0, 8 f [1;2] (1) =1, 29 f [0;1] (1) + 0, 71 f [1;2] (1) + 0, 09 f [2;3] (1) Vi kan nu indsætte værdierne af f [0;1] (1), f [1;2] (1) og f [2;3] (1) som vi fandt under a). Hermed fås: f(3) = 1, 29 f [0;1] (1) + 0, 71 f [1;2] (1) + 0, 09 f [2;3] (1) =1, , , 09 8 = 20, 85. I gennemsnit vil der altså være knapt 21 rotter efter 3 år. Opgave 6.26 a) Vi har brug for følgende udsagnsvariable: s: Simon kommer for sent til sit møde. u: Simon føler sig slået ud. j: Simon får jobbet
23 t: Simon tager en taxi hjem. b) Sætning 1 bliver til (s u) t. Sætning 2 bliver til j u. Sætning 3 bliver til (s t) j. c) Vi skal lave en sandhedstabel for den formel som siger, at sætning 1 og sætning 2 tilsammen medfører sætning 3. Det er følgende formel: ( ((s u) t) ( j u) ) ( (s t) j ) Her skal man holde tungen lige i munden med de mange paranteser. Sandhedstabellen får hele 2 4 = 16 rækker, fordi der er 4 udsagnsvariable. j s t u s u (s u) t j u s t (s t) j hele formlen S S S S S S S F S S S S S F F S S F S S S S F S S F S S S S S S F F F S S S S S S F S S F S S F S S S F S F F S S F S S S F F S F S S F S S S F F F F S S F S S F S S S S S S F S S F S S F F S F F S S F S F S S F S S F S F S F F F S F S F S F F S S F S S F S S F F S F F S F F S S F F F S F S S F S S F F F F F S F F S S Alle rækker i sandhedstabellen gør formlen sand (sidste søjle), så formlen er gyldig. Dermed er slutningen logisk korrekt. Det er altså rigtigt, at hvis de to præmisser er opfyldt for Simon, så er konklusionen også opfyldt. Man kan også prøve at kigge på de rent sproglige formuleringer af præmisser og konklusion, for at overbevise sig selv om at slutningen holder, men der går let kludder i argumentationen. Det vi i stedet har gjort ovenfor er at give et helt håndfast matematisk bevis for at slutnigen holder
24 7. Vektorfunktioner 7.01 a) b) (0,2) (0,5) c) t x 0 2,5 2-4,5 y 2 2,5 4 6,5 d) - e) Mindste afstand: 3, a) yy = xx + 2 b) yy = xx 2 + xx 5 c) yy = 5 sin(cos 1 (0,5xx)) 7.03 a) rr(tt) = ( tt2 + 4tt 2 ) tt b) rr(tt) = ( tt2 + 4tt 5 3tt 3 ) tt 7.04 a) ( xx + tt yy ) = ( tt ) b) ( xx + 13tt yy ) = ( tt ) eller (xx + 13tt yy ) = ( tt ) c) ( xx + tt cos 120 yy ) = ( tt sin 120 ) 7.05 a) ( xx + 3 cos tt yy ) = ( sin tt ) b) ( xx + 5 cos tt yy ) = ( sin tt ) 7.06 a) ( 2,1) b) Storakse: 8 Lilleakse: 6 c) Mindste afstand: 3,37 24
25 7.07 a) 7.08 a) 7.09 a) b) vv(tt) = ( 10tt + 15 ) c) (22,5; 51,25) d) (70,5; 0) e) 35,34 m/sec b) vv(tt) = ( 2tt 1 ) c) (xx, yy) = (4, 3) 2 b) vv(tt) = ( 10tt + 12 ) c) (0,4; 37,2) 7.10 a) rr(tt) = ( 0,2tt 0,08tt ) tt 0 b) (0,4; 016) c) 0,5tt + 2 cos(2tt) 7.11 a) rr(tt) = ( ) 2 sin(2tt) b) 7.12 a) 7.13 a) c) (0,394; 2) (1,177; 2) (1,963; 2) (2,750; 2) d) (2,016; 0,250) ( 1,230; 0,250) (3,586; 0,250) (0,341; 0,250) e) (1,177; 2) (2,750; 2) f) Højeste fart = 4,5 meter/sekund b) Omkreds = 26,73 b) (0, 0) (1,0) ( 1,0) c) (0,707; 1) (0,707; 1) ( 0,707; 1) ( 0,707; 1) d) (1,0) ( 1,0)
26 7.14 a) 7.15 a) b) (0,2) (0; 4,637) c) (ππ, 6) (2ππ, 2) (3ππ, 6) d) ( 0,685; 3) (6,968; 3) (5,598; 3) e) Fart = 2,89 meter/sekund b) (0,1) c) ( 0,58; 3,37) (0,58; 1,64) d) (0,39; 3,41) ( 0,13; 0,59) ( 0,57; 3,41) (0,36; 0,59) e) (0,377; 3,411) 3 cos(1tt) + 1 cos( 5tt) 7.16 a) rr(tt) = ( 3 sin(1tt) + 1 sin( 5tt) ) b) c) (0,2) (0, 2) (4,0) (2,71; 0) ( 2,71; 0) ( 4,0) d) (1,73; 1) (0,2) ( 1,73; 1) ( 1,73; 1) (0, 2) (1,73; 1) 26
Teknisk. Matematik FACITLISTE. Preben Madsen. 4. udgave
 Teknisk Preben Madsen Matematik 4. udgave FACITLISTE Indhold TAL OG ALGEBRA... LIGNINGER OG ULIGHEDER... GEOMETRI... 4 TRIGONOMETRI... 5 CIRKLEN... 5 6 OVERFLADER UDFOLDNINGER... 5 7 RUMFANG... 8 8 ANALYTISK
Teknisk Preben Madsen Matematik 4. udgave FACITLISTE Indhold TAL OG ALGEBRA... LIGNINGER OG ULIGHEDER... GEOMETRI... 4 TRIGONOMETRI... 5 CIRKLEN... 5 6 OVERFLADER UDFOLDNINGER... 5 7 RUMFANG... 8 8 ANALYTISK
Designmanual / Forskningens Døgn
 1/17 Designmanual / Forskningens Døgn Elementer 2 Logotype 2 Logotype på fotografi 3 Geometri 5 Forsk Geometri oversigt 6 Objekter 7 Forsk Objekt oversigt 8 Forhold mellem alle elementer 9 Farver 10 Font
1/17 Designmanual / Forskningens Døgn Elementer 2 Logotype 2 Logotype på fotografi 3 Geometri 5 Forsk Geometri oversigt 6 Objekter 7 Forsk Objekt oversigt 8 Forhold mellem alle elementer 9 Farver 10 Font
Bedste rette linje ved mindste kvadraters metode
 1/9 Bedste rette linje ved mindste kvadraters metode - fra www.borgeleo.dk Figur 1: Tre datapunkter og den bedste rette linje bestemt af A, B og C Målepunkter og bedste rette linje I ovenstående koordinatsystem
1/9 Bedste rette linje ved mindste kvadraters metode - fra www.borgeleo.dk Figur 1: Tre datapunkter og den bedste rette linje bestemt af A, B og C Målepunkter og bedste rette linje I ovenstående koordinatsystem
Kapitel 2. Differentialregning A
 Kapitel 2. Differentialregning A Indhold 2.2 Differentiabilitet og tangenter til grafer... 2 2.3 Sammensat funktion, eksponential-, logaritme- og potensfunktioner... 7 2.4 Regneregler for differentiation
Kapitel 2. Differentialregning A Indhold 2.2 Differentiabilitet og tangenter til grafer... 2 2.3 Sammensat funktion, eksponential-, logaritme- og potensfunktioner... 7 2.4 Regneregler for differentiation
Forslag til løsning af Opgaver til afsnittet om de naturlige tal (side 80)
 Forslag til løsning af Opgaver til afsnittet om de naturlige tal (side 80) Opgave 1 Vi skal tegne alle de linjestykker, der forbinder vilkårligt valgte punkter blandt de 4 punkter. Gennem forsøg finder
Forslag til løsning af Opgaver til afsnittet om de naturlige tal (side 80) Opgave 1 Vi skal tegne alle de linjestykker, der forbinder vilkårligt valgte punkter blandt de 4 punkter. Gennem forsøg finder
Matematik og samfundsfag Gini-koefficienten
 Erik Vestergaard www.matematikfysik.dk Matematik og samfundsfag Gini-koefficienten Den såkaldte Gini-koefficient, introduceret i 92 i en artikel af den italienske statistiker, demograf og sociolog Corrado
Erik Vestergaard www.matematikfysik.dk Matematik og samfundsfag Gini-koefficienten Den såkaldte Gini-koefficient, introduceret i 92 i en artikel af den italienske statistiker, demograf og sociolog Corrado
Nem grafik til websider
 Web design 101 Artiklen beskriver en nem måde, hvorpå du han lave ikon-lignende billeder til websider på basis af de symboltegnsæt, der er til rådighed på din computer. Metoden er særlig velegnet til små
Web design 101 Artiklen beskriver en nem måde, hvorpå du han lave ikon-lignende billeder til websider på basis af de symboltegnsæt, der er til rådighed på din computer. Metoden er særlig velegnet til små
Kriegers Flak Idefasen - Projektområde. Oversigt over detailkort
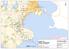 Kort nr. 1 Kort nr. 2 Kort nr. 3 Kort nr. 4 Kort nr. 5 Kort nr. 6 Kort nr. 7 Kort nr. 8 Kort nr. 9 Kort nr. 1 Kort nr. 11 i 1. offentlighedsfase (). Kort nr. 12 Kilometers 1 -. Oversigt over detailkort
Kort nr. 1 Kort nr. 2 Kort nr. 3 Kort nr. 4 Kort nr. 5 Kort nr. 6 Kort nr. 7 Kort nr. 8 Kort nr. 9 Kort nr. 1 Kort nr. 11 i 1. offentlighedsfase (). Kort nr. 12 Kilometers 1 -. Oversigt over detailkort
π er irrationel Frank Nasser 10. december 2011
 π er irrationel Frank Nasser 10. december 2011 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold 1 Introduktion
π er irrationel Frank Nasser 10. december 2011 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold 1 Introduktion
To find the English version of the exam, please read from the other end! Eksamen i Calculus
 To find the English version of the exam, please read from the other end! Se venligst bort fra den engelske version på bagsiden hvis du følger denne danske version af prøven. Eksamen i Calculus Første Studieår
To find the English version of the exam, please read from the other end! Se venligst bort fra den engelske version på bagsiden hvis du følger denne danske version af prøven. Eksamen i Calculus Første Studieår
AM Interactive (AMI) designguide
 AM Interactive (AMI) designguide AM Interactive designguide, Arild Garde Opdateret 3. september 2008 Identitet AMIs identitet sikres ved gennemført brug af logo, payoff, farver og typografi. Payoff time
AM Interactive (AMI) designguide AM Interactive designguide, Arild Garde Opdateret 3. september 2008 Identitet AMIs identitet sikres ved gennemført brug af logo, payoff, farver og typografi. Payoff time
AURA Energi A.m.b.a. Bilag til valgregulativ Bestyrelsen
 AURA Energi A.m.b.a. Bilag til valgregulativ Bestyrelsen Ved valg af medlemmer til AURA Energi A.m.b.a.s bestyrelse anvendes prioriteringsmetoden. Metoden indebærer, at der efter bestemmelserne i pkt.
AURA Energi A.m.b.a. Bilag til valgregulativ Bestyrelsen Ved valg af medlemmer til AURA Energi A.m.b.a.s bestyrelse anvendes prioriteringsmetoden. Metoden indebærer, at der efter bestemmelserne i pkt.
Variable. 1 a a + 2 3 a 5 2a 3a + 6 a + 5 3a a 2 a 2 a 2 5 7 15 5 21 5 25 0 2 0 6 9 0 9 4 0 1 3 3 3 9 3 1 0 0 2 0 5 6 5 0 0 2,5 1,5 4 7,5 4 0
 Variable 1 a a + 2 3 a 5 2a 3a + 6 a + 5 3a a 2 a 2 a 2 5 7 15 5 21 5 25 0 2 0 6 9 0 9 4 0 1 3 3 3 9 3 1 0 0 2 0 5 6 5 0 0 2,5 1,5 4 7,5 4 0 2 a x = 5 b x = 1 c x = 1 d y = 1 e z = 0 f Ingen løsning. 3
Variable 1 a a + 2 3 a 5 2a 3a + 6 a + 5 3a a 2 a 2 a 2 5 7 15 5 21 5 25 0 2 0 6 9 0 9 4 0 1 3 3 3 9 3 1 0 0 2 0 5 6 5 0 0 2,5 1,5 4 7,5 4 0 2 a x = 5 b x = 1 c x = 1 d y = 1 e z = 0 f Ingen løsning. 3
Afstande, skæringer og vinkler i rummet
 Afstande, skæringer og vinkler i rummet Frank Nasser 9. april 20 c 2008-20. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her.
Afstande, skæringer og vinkler i rummet Frank Nasser 9. april 20 c 2008-20. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her.
Projektopgave 1. Navn: Jonas Pedersen Klasse: 3.4 Skole: Roskilde Tekniske Gymnasium Dato: 5/ Vejleder: Jørn Christian Bendtsen Fag: Matematik
 Projektopgave 1 Navn: Jonas Pedersen Klasse:.4 Skole: Roskilde Tekniske Gymnasium Dato: 5/9-011 Vejleder: Jørn Christian Bendtsen Fag: Matematik Indledning Jeg har i denne opgave fået følgende opstilling.
Projektopgave 1 Navn: Jonas Pedersen Klasse:.4 Skole: Roskilde Tekniske Gymnasium Dato: 5/9-011 Vejleder: Jørn Christian Bendtsen Fag: Matematik Indledning Jeg har i denne opgave fået følgende opstilling.
Lokalt ekstremum DiploMat 01905
 Lokalt ekstremum DiploMat 0905 Preben Alsholm Institut for Matematik, DTU 6. oktober 00 De nition Et stationært punkt for en funktion af ere variable f vil i disse noter blive kaldt et egentligt saddelpunkt,
Lokalt ekstremum DiploMat 0905 Preben Alsholm Institut for Matematik, DTU 6. oktober 00 De nition Et stationært punkt for en funktion af ere variable f vil i disse noter blive kaldt et egentligt saddelpunkt,
FODMAPforum. Designmanual
 Designmanual Velkommen På de følgende sider finder du s designprogram. Med det ved hånden er du i stand til at designe løsninger til s grafiske flader. Her kan du slå op og finde ingredienserne til at
Designmanual Velkommen På de følgende sider finder du s designprogram. Med det ved hånden er du i stand til at designe løsninger til s grafiske flader. Her kan du slå op og finde ingredienserne til at
Afstande, skæringer og vinkler i rummet
 Afstande, skæringer og vinkler i rummet Frank Villa 2. maj 202 c 2008-20. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold
Afstande, skæringer og vinkler i rummet Frank Villa 2. maj 202 c 2008-20. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold
TREKANTER. Indledning. Typer af trekanter. Side 1 af 7. (Der har været tre kursister om at skrive denne projektrapport)
 Side 1 af 7 (Der har været tre kursister om at skrive denne projektrapport) TREKANTER Indledning Vi har valgt at bruge denne projektrapport til at udarbejde en oversigt over det mest grundlæggende materiale
Side 1 af 7 (Der har været tre kursister om at skrive denne projektrapport) TREKANTER Indledning Vi har valgt at bruge denne projektrapport til at udarbejde en oversigt over det mest grundlæggende materiale
MATEMATIK A-NIVEAU. Anders Jørgensen & Mark Kddafi. Vejledende eksempler på eksamensopgaver og eksamensopgaver i matematik, 2012
 MATEMATIK A-NIVEAU Vejledende eksempler på eksamensopgaver og eksamensopgaver i matematik, 01 Kapitel 3 Ligninger & formler 016 MATEMATIK A-NIVEAU Vejledende eksempler på eksamensopgaver og eksamensopgaver
MATEMATIK A-NIVEAU Vejledende eksempler på eksamensopgaver og eksamensopgaver i matematik, 01 Kapitel 3 Ligninger & formler 016 MATEMATIK A-NIVEAU Vejledende eksempler på eksamensopgaver og eksamensopgaver
Løsninger til eksamensopgaver på A-niveau 2017
 Løsninger til eksamensopgaver på A-niveau 017 18. maj 017: Delprøven UDEN hjælpemidler Opgave 1: Alle funktionerne f, g og h er lineære funktioner (og ingen er mere lineære end andre) og kan skrives på
Løsninger til eksamensopgaver på A-niveau 017 18. maj 017: Delprøven UDEN hjælpemidler Opgave 1: Alle funktionerne f, g og h er lineære funktioner (og ingen er mere lineære end andre) og kan skrives på
Algebra - Teori og problemløsning
 Algebra - Teori og problemløsning, januar 05, Kirsten Rosenkilde. Algebra - Teori og problemløsning Kapitel -3 giver en grundlæggende introduktion til at omskrive udtryk, faktorisere og løse ligningssystemer.
Algebra - Teori og problemløsning, januar 05, Kirsten Rosenkilde. Algebra - Teori og problemløsning Kapitel -3 giver en grundlæggende introduktion til at omskrive udtryk, faktorisere og løse ligningssystemer.
VEKTORGEOMETRI del 2 Skæringer Projektioner Vinkler Afstande
 VEKTORGEOMETRI del Skæringer Projektioner Vinkler Afstande x-klasserne Gammel Hellerup Gymnasium Februar 019 ; Michael Szymanski ; mz@ghg.dk 1 Indhold OVERSIGT... 3 SKÆRINGSPUNKTER OG RØRINGSPUNKTER...
VEKTORGEOMETRI del Skæringer Projektioner Vinkler Afstande x-klasserne Gammel Hellerup Gymnasium Februar 019 ; Michael Szymanski ; mz@ghg.dk 1 Indhold OVERSIGT... 3 SKÆRINGSPUNKTER OG RØRINGSPUNKTER...
Integralregning Infinitesimalregning
 Udgave 2.1 Integralregning Infinitesimalregning Noterne gennemgår begreberne integral og stamfunktion, og anskuer dette som et redskab til bestemmelse af arealer under funktioner. Noterne er supplement
Udgave 2.1 Integralregning Infinitesimalregning Noterne gennemgår begreberne integral og stamfunktion, og anskuer dette som et redskab til bestemmelse af arealer under funktioner. Noterne er supplement
Matematiske hjælpemidler. Koordinater. 2.1 De mange bredder.
 2. Matematiske hjælpemidler. Koordinater. 2.1 De mange bredder. 2.1 I Figur 1.1 i kapitel 1 er der vist et ideelt Kartesiske eller Euklidiske koordinatsystem, med koordinater ( X, Y, Z) = ( X 1, X 2, X
2. Matematiske hjælpemidler. Koordinater. 2.1 De mange bredder. 2.1 I Figur 1.1 i kapitel 1 er der vist et ideelt Kartesiske eller Euklidiske koordinatsystem, med koordinater ( X, Y, Z) = ( X 1, X 2, X
Tema: Kvadrattal og matematiske mønstre:
 2 Indholdsfortegnelse: Tema: Kvadrattal og matematiske mønstre: Side 4: Side 5: Side 9: Side 10: Side 12: Side 14: Side 15: Side 16: Side 19: Side 20: Side 21: Side 23: Problemformulering. En nem tilgang
2 Indholdsfortegnelse: Tema: Kvadrattal og matematiske mønstre: Side 4: Side 5: Side 9: Side 10: Side 12: Side 14: Side 15: Side 16: Side 19: Side 20: Side 21: Side 23: Problemformulering. En nem tilgang
Lineære sammenhænge. Udgave 2. 2009 Karsten Juul
 Lineære sammenhænge Udgave 2 y = 0,5x 2,5 2009 Karsten Juul Dette hæfte er en fortsættelse af hæftet "Variabelsammenhænge, 2. udgave 2009". Indhold 1. Lineære sammenhænge, ligning og graf... 1 2. Lineær
Lineære sammenhænge Udgave 2 y = 0,5x 2,5 2009 Karsten Juul Dette hæfte er en fortsættelse af hæftet "Variabelsammenhænge, 2. udgave 2009". Indhold 1. Lineære sammenhænge, ligning og graf... 1 2. Lineær
Matematik A-niveau 22. maj 2015 Delprøve 2. Løst af Anders Jørgensen og Saeid Jafari
 Matematik A-niveau 22. maj 2015 Delprøve 2 Løst af Anders Jørgensen og Saeid Jafari Opgave 7 - Analytisk Plangeometri Delopgave a) Vi starter ud med at undersøge afstanden fra punktet P(5,4) til linjen
Matematik A-niveau 22. maj 2015 Delprøve 2 Løst af Anders Jørgensen og Saeid Jafari Opgave 7 - Analytisk Plangeometri Delopgave a) Vi starter ud med at undersøge afstanden fra punktet P(5,4) til linjen
Hvis man ønsker mere udfordring, kan man springe den første opgave af hvert emne over.
 Opsamling Hvis man ønsker mere udfordring, kan man springe den første opgave af hvert emne over.. Brøkregning, parentesregneregler, kvadratsætningerne, potensregneregler og reduktion Udregn nedenstående
Opsamling Hvis man ønsker mere udfordring, kan man springe den første opgave af hvert emne over.. Brøkregning, parentesregneregler, kvadratsætningerne, potensregneregler og reduktion Udregn nedenstående
Grafik og billede MADS BACH SANDER
 Grafik og billede MADS BACH SANDER Indbydelse til konfirmation Mads der skal konfirmeres i 2018, havde bedt om min hjælp til at lave en sej indbydelse til sin fest. Mads ville ikke have noget alt for traditionelt
Grafik og billede MADS BACH SANDER Indbydelse til konfirmation Mads der skal konfirmeres i 2018, havde bedt om min hjælp til at lave en sej indbydelse til sin fest. Mads ville ikke have noget alt for traditionelt
Matematik. Formlen for en Kugle: 3 V = 4/3»r *n. Formlen for et Kugleafsnit: Formlen for en Keglestub: 2 2 V =n/3»h»(r + r + R*r)
 Matematik Vi har fået til opgave at bygge en ballon hvis volume mindst må være 1,2 Kubikmeter og max 1,5 kubikmeter. Så for at løse dette problem valgte vi at finde formlerne for en kugle, kugleafsnit
Matematik Vi har fået til opgave at bygge en ballon hvis volume mindst må være 1,2 Kubikmeter og max 1,5 kubikmeter. Så for at løse dette problem valgte vi at finde formlerne for en kugle, kugleafsnit
Vinkelrette linjer. Frank Villa. 4. november 2014
 Vinkelrette linjer Frank Villa 4. november 2014 Dette dokument er en del af MatBog.dk 2008-2012. IT Teaching Tools. ISBN-13: 978-87-92775-00-9. Se yderligere betingelser for brug her. Indhold 1 Introduktion
Vinkelrette linjer Frank Villa 4. november 2014 Dette dokument er en del af MatBog.dk 2008-2012. IT Teaching Tools. ISBN-13: 978-87-92775-00-9. Se yderligere betingelser for brug her. Indhold 1 Introduktion
NICHLAS STILLING HANSEN PORTFOLIO
 NICHLAS STILLING HANSEN PORTFOLIO OPGAVE At designe en ny hjemmeside til den lokale bilklub, American Style Car Club Hadsund. Den tidligere hjemmeside som klubben havde, levede ikke op til og indeholdte
NICHLAS STILLING HANSEN PORTFOLIO OPGAVE At designe en ny hjemmeside til den lokale bilklub, American Style Car Club Hadsund. Den tidligere hjemmeside som klubben havde, levede ikke op til og indeholdte
To find the English version of the exam, please read from the other end! Eksamen i Calculus
 To find the English version of the exam, please read from the other end! Se venligst bort fra den engelske version på bagsiden hvis du følger denne danske version af prøven. Eksamen i Calculus Første Studieår
To find the English version of the exam, please read from the other end! Se venligst bort fra den engelske version på bagsiden hvis du følger denne danske version af prøven. Eksamen i Calculus Første Studieår
Eksempel på den aksiomatisk deduktive metode
 Eksempel på den aksiomatisk deduktive metode Et rigtig godt eksempel på et aksiomatisk deduktivt system er Euklids Elementer. Euklid var græker og skrev Elemeterne omkring 300 f.kr. Værket består af 13
Eksempel på den aksiomatisk deduktive metode Et rigtig godt eksempel på et aksiomatisk deduktivt system er Euklids Elementer. Euklid var græker og skrev Elemeterne omkring 300 f.kr. Værket består af 13
MATEMATIK A-NIVEAU. Kapitel 1
 MATEMATIK A-NIVEAU Vejledende eksempler på eksamensopgaver og eksamensopgaver i matematik, 01 Kapitel 1 016 MATEMATIK A-NIVEAU Vejledende eksempler på eksamensopgaver og eksamensopgaver i matematik 01
MATEMATIK A-NIVEAU Vejledende eksempler på eksamensopgaver og eksamensopgaver i matematik, 01 Kapitel 1 016 MATEMATIK A-NIVEAU Vejledende eksempler på eksamensopgaver og eksamensopgaver i matematik 01
Opgave 1 - Lineær Funktioner. Opgave 2 - Funktioner. Opgave 3 - Tredjegradsligning
 Sh*maa03 1508 Matematik B->A, STX Anders Jørgensen, delprøve 1 - Uden hjælpemidler Følgende opgaver er regnet i hånden, hvorefter de er skrevet ind på PC. Opgave 1 - Lineær Funktioner Vi ved, at år 2001
Sh*maa03 1508 Matematik B->A, STX Anders Jørgensen, delprøve 1 - Uden hjælpemidler Følgende opgaver er regnet i hånden, hvorefter de er skrevet ind på PC. Opgave 1 - Lineær Funktioner Vi ved, at år 2001
Danmarks Tekniske Universitet
 Danmarks Tekniske Universitet Side 1 af 11 sider Skriftlig prøve, tirsdag den 24. maj, 2016 Kursus navn Fysik 1 Kursus nr. 10024 Varighed: 4 timer Tilladte hjælpemidler: Alle hjælpemidler tilladt "Vægtning":
Danmarks Tekniske Universitet Side 1 af 11 sider Skriftlig prøve, tirsdag den 24. maj, 2016 Kursus navn Fysik 1 Kursus nr. 10024 Varighed: 4 timer Tilladte hjælpemidler: Alle hjælpemidler tilladt "Vægtning":
Besvarelser til Calculus Ordinær Eksamen Juni 2017
 Besvarelser til Calculus Ordinær Eksamen - 12. Juni 2017 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 12. Juni 2017 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Matematik A STX 18. maj 2017 Vejledende løsning De første 6 opgaver løses uden hjælpemidler
 ADVARSEL! Før du anvender løsningerne, så husk at læs betingelserne for løsningerne, som du kan finde på hjemmesiden. Indeholder: Matematik A, STX 18 maj Matematik A, STX 23 maj Matematik A, STX 15 august
ADVARSEL! Før du anvender løsningerne, så husk at læs betingelserne for løsningerne, som du kan finde på hjemmesiden. Indeholder: Matematik A, STX 18 maj Matematik A, STX 23 maj Matematik A, STX 15 august
Differentiation af Trigonometriske Funktioner
 Differentiation af Trigonometriske Funktioner Frank Villa 15. oktober 01 Dette dokument er en del af MatBog.dk 008-01. IT Teaching Tools. ISBN-13: 978-87-9775-00-9. Se yderligere betingelser for brug her.
Differentiation af Trigonometriske Funktioner Frank Villa 15. oktober 01 Dette dokument er en del af MatBog.dk 008-01. IT Teaching Tools. ISBN-13: 978-87-9775-00-9. Se yderligere betingelser for brug her.
01017 Diskret Matematik E12 Alle bokse fra logikdelens slides
 01017 Diskret Matematik E12 Alle bokse fra logikdelens slides Thomas Bolander 1 Udsagnslogik 1.1 Formler og sandhedstildelinger symbol står for ikke eller og ( A And) hvis... så... hvis og kun hvis...
01017 Diskret Matematik E12 Alle bokse fra logikdelens slides Thomas Bolander 1 Udsagnslogik 1.1 Formler og sandhedstildelinger symbol står for ikke eller og ( A And) hvis... så... hvis og kun hvis...
Svar på opgave 336 (Januar 2017)
 Svar på opgave 6 (Januar 07) Opgave: De komplekse tal a, b og c opfylder ligningssystemet Vis, at a, b og c er reelle. (a + b)(a + c) = b (b + c)(b + a) = c (c + a)(c + b) = a. Besvarelse:. metode Lad
Svar på opgave 6 (Januar 07) Opgave: De komplekse tal a, b og c opfylder ligningssystemet Vis, at a, b og c er reelle. (a + b)(a + c) = b (b + c)(b + a) = c (c + a)(c + b) = a. Besvarelse:. metode Lad
ØVEHÆFTE FOR MATEMATIK C GEOMETRI
 ØVEHÆFTE FOR MATEMATIK C GEOMETRI Indhold Begreber i klassisk geometri + formelsamling... 2 Pythagoras Sætning... 8 Retvinklede trekanter. Beregn den ukendte side markeret med et bogstav.... 9 Øve vinkler
ØVEHÆFTE FOR MATEMATIK C GEOMETRI Indhold Begreber i klassisk geometri + formelsamling... 2 Pythagoras Sætning... 8 Retvinklede trekanter. Beregn den ukendte side markeret med et bogstav.... 9 Øve vinkler
Differentialregning med TI-Interactive! Indledende differentialregning Tangenter Monotoniforhold og ekstremum Optimering Jan Leffers (2009)
 Differentialregning med TI-Interactive! Indledende differentialregning Tangenter Monotoniforhold og ekstremum Optimering Jan Leffers (2009) Indholdsfortegnelse Indholdsfortegnelse...2 Indledende differentialregning...3
Differentialregning med TI-Interactive! Indledende differentialregning Tangenter Monotoniforhold og ekstremum Optimering Jan Leffers (2009) Indholdsfortegnelse Indholdsfortegnelse...2 Indledende differentialregning...3
Besvarelser til Calculus Ordinær Eksamen Juni 2019
 Besvarelser til Calculus Ordinær Eksamen - 14. Juni 2019 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 14. Juni 2019 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Matematik A STX december 2016 vejl. løsning Gratis anvendelse - læs betingelser!
 Matematik A STX december 2016 vejl. løsning www.matematikhfsvar.page.tl Gratis anvendelse - læs betingelser! Opgave 1 Lineær funktion. Oplysningerne findes i opgaven. Delprøve 1: Forskrift Opgave 2 Da
Matematik A STX december 2016 vejl. løsning www.matematikhfsvar.page.tl Gratis anvendelse - læs betingelser! Opgave 1 Lineær funktion. Oplysningerne findes i opgaven. Delprøve 1: Forskrift Opgave 2 Da
Excel regneark. I dette kapitel skal I arbejde med noget af det, Excel regneark kan bruges til. INTRO EXCEL REGNEARK
 Excel regneark Et regneark er et computerprogram, der bl.a. kan regne, tegne grafer og lave diagrammer. Regnearket kan bruges i mange forskellige sammenhænge, når I arbejder med matematik. Det kan gøre
Excel regneark Et regneark er et computerprogram, der bl.a. kan regne, tegne grafer og lave diagrammer. Regnearket kan bruges i mange forskellige sammenhænge, når I arbejder med matematik. Det kan gøre
Besvarelser til Calculus Ordinær Eksamen Juni 2018
 Besvarelser til Calculus Ordinær Eksamen - 5. Juni 08 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 5. Juni 08 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Pointen med Funktioner
 Pointen med Funktioner Frank Nasser 0. april 0 c 0080. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk: Dette er en
Pointen med Funktioner Frank Nasser 0. april 0 c 0080. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk: Dette er en
DET MÅ KUNNE GØRES BEDRE DESIGN EKSAMEN C
 DET MÅ KUNNE GØRES BEDRE DESIGN EKSAMEN C FORSIDE 1 IDÉ 1 EMBALLAGE TIL TYGGEGUMMI PROBLEM IDÉ 2 EMBALLAGE TIL PISTACHENØDDER Brugt tyggegummi sviner i gadebiledet og skader naturen, fordi folk bare spytter
DET MÅ KUNNE GØRES BEDRE DESIGN EKSAMEN C FORSIDE 1 IDÉ 1 EMBALLAGE TIL TYGGEGUMMI PROBLEM IDÉ 2 EMBALLAGE TIL PISTACHENØDDER Brugt tyggegummi sviner i gadebiledet og skader naturen, fordi folk bare spytter
fortsætte høj retning mellem mindre over større
 cirka (ca) omtrent overslag fortsætte stoppe gentage gentage det samme igen mønster glat ru kantet høj lav bakke lav høj regel formel lov retning højre nedad finde rundt rod orden nøjagtig præcis cirka
cirka (ca) omtrent overslag fortsætte stoppe gentage gentage det samme igen mønster glat ru kantet høj lav bakke lav høj regel formel lov retning højre nedad finde rundt rod orden nøjagtig præcis cirka
MATEMATIK 11 Eksamensopgaver Juni 1995 Juni 2001, 4. fjerdedel
 Juni 2000 MATEMATIK 11 Eksamensopgaver Juni 1995 Juni 2001, 4. fjerdedel Opgave 1. (a) Find den fuldstændige løsning til differentialligningen y 8y + 16y = 0. (b) Find den fuldstændige løsning til differentialligningen
Juni 2000 MATEMATIK 11 Eksamensopgaver Juni 1995 Juni 2001, 4. fjerdedel Opgave 1. (a) Find den fuldstændige løsning til differentialligningen y 8y + 16y = 0. (b) Find den fuldstændige løsning til differentialligningen
Ugesedler til sommerkursus
 Aalborg Universitet - Adgangskursus Ugesedler til sommerkursus Matematik B til A Jens Friis 12 Adgangskursus Strandvejen 12 14 9000 Aalborg tlf. 99 40 97 70 ak.aau.dk sommer Matematik A 1. Lektion : Mandag
Aalborg Universitet - Adgangskursus Ugesedler til sommerkursus Matematik B til A Jens Friis 12 Adgangskursus Strandvejen 12 14 9000 Aalborg tlf. 99 40 97 70 ak.aau.dk sommer Matematik A 1. Lektion : Mandag
Eksponentielle funktioner for C-niveau i hf
 Eksponentielle funktioner for C-niveau i hf 2017 Karsten Juul Procent 1. Procenter på en ny måde... 1 2. Bestem procentvis ændring... 2 3. Bestem begyndelsesværdi... 2 4. Bestem slutværdi... 3 5. Vækstrate...
Eksponentielle funktioner for C-niveau i hf 2017 Karsten Juul Procent 1. Procenter på en ny måde... 1 2. Bestem procentvis ændring... 2 3. Bestem begyndelsesværdi... 2 4. Bestem slutværdi... 3 5. Vækstrate...
MODUL 8. Differensligninger. Forfattere: Michael ELMEGÅRD & Øistein WIND-WILLASSEN. Modulet er baseret på noter af Peter BEELEN.
 MODUL 8 Differensligninger Forfattere: Michael ELMEGÅRD & Øistein WIND-WILLASSEN Modulet er baseret på noter af Peter BEELEN. 26. august 2014 2 Indhold 1 Introduktion 5 1.1 Rekursioner og differensligninger.........................
MODUL 8 Differensligninger Forfattere: Michael ELMEGÅRD & Øistein WIND-WILLASSEN Modulet er baseret på noter af Peter BEELEN. 26. august 2014 2 Indhold 1 Introduktion 5 1.1 Rekursioner og differensligninger.........................
Kalkulus 1 - Opgaver. Anne Ryelund, Anders Friis og Mads Friis. 20. januar 2015
 Kalkulus 1 - Opgaver Anne Ryelund, Anders Friis og Mads Friis 20. januar 2015 Mængder Opgave 1 Opskriv følgende mængder med korrekt mængdenotation. a) En mængde A indeholder alle hele tal fra og med 1
Kalkulus 1 - Opgaver Anne Ryelund, Anders Friis og Mads Friis 20. januar 2015 Mængder Opgave 1 Opskriv følgende mængder med korrekt mængdenotation. a) En mængde A indeholder alle hele tal fra og med 1
Eksponentielle sammenhænge
 Eksponentielle sammenhænge 0 1 2 3 4 5 6 7 8 9 10 11 12 13 Indholdsfortegnelse Variabel-sammenhænge... 1 1. Hvad er en eksponentiel sammenhæng?... 2 2. Forklaring med ord af eksponentiel vækst... 2, 6
Eksponentielle sammenhænge 0 1 2 3 4 5 6 7 8 9 10 11 12 13 Indholdsfortegnelse Variabel-sammenhænge... 1 1. Hvad er en eksponentiel sammenhæng?... 2 2. Forklaring med ord af eksponentiel vækst... 2, 6
Kapitel 3 Lineære sammenhænge
 Matematik C (må anvendes på Ørestad Gymnasium) Lineære sammenhænge Det sker tit, at man har flere variable, der beskriver en situation, og at der en sammenhæng mellem de variable. Enhver formel er faktisk
Matematik C (må anvendes på Ørestad Gymnasium) Lineære sammenhænge Det sker tit, at man har flere variable, der beskriver en situation, og at der en sammenhæng mellem de variable. Enhver formel er faktisk
Projekt 2.2 Omvendt funktion og differentiation af omvendt funktion
 ISBN 978877664974 Projekter: Kapitel. Projekt. Omvendt funktion og differentiation af omvendt funktion Projekt. Omvendt funktion og differentiation af omvendt funktion Vi har i Bbogens kapitel 4 afsnit
ISBN 978877664974 Projekter: Kapitel. Projekt. Omvendt funktion og differentiation af omvendt funktion Projekt. Omvendt funktion og differentiation af omvendt funktion Vi har i Bbogens kapitel 4 afsnit
Grafoplast opmærkningssystem
 Grafoplast Opmærkningssystem er et universelt system til nummerering/mærkning af alle typer ledninger, kabler, slanger, rør, kontaktorer m.m. Systemet består af forskellige tyller, som kan monteres på
Grafoplast Opmærkningssystem er et universelt system til nummerering/mærkning af alle typer ledninger, kabler, slanger, rør, kontaktorer m.m. Systemet består af forskellige tyller, som kan monteres på
20 = 2x + 2y. V (x, y) = 5xy. V (x) = 50x 5x 2.
 17 Optimering 17.1 Da omkræsen skal være 0cm har vi at 0 = x + y. Rumfanget V for kassen er en funktion der afhænger af både x og y givet ved V (x, y) = 5xy. Isolerer vi y i formlen for omkredsen og indsætter
17 Optimering 17.1 Da omkræsen skal være 0cm har vi at 0 = x + y. Rumfanget V for kassen er en funktion der afhænger af både x og y givet ved V (x, y) = 5xy. Isolerer vi y i formlen for omkredsen og indsætter
matx.dk Differentialregning Dennis Pipenbring
 mat.dk Differentialregning Dennis Pipenbring 0. december 00 Indold Differentialregning 3. Grænseværdi............................. 3. Kontinuitet.............................. 8 Differentialkvotienten
mat.dk Differentialregning Dennis Pipenbring 0. december 00 Indold Differentialregning 3. Grænseværdi............................. 3. Kontinuitet.............................. 8 Differentialkvotienten
Ting man gør med Vektorfunktioner
 Ting man gør med Vektorfunktioner Frank Nasser. april 11 c 8-11. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk: Dette
Ting man gør med Vektorfunktioner Frank Nasser. april 11 c 8-11. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk: Dette
Matematisk induktion
 Induktionsbeviser MT01.0.07 1 1 Induktionsbeviser Matematisk induktion Sætninger der udtaler sig om hvad der gælder for alle naturlige tal n N, kan undertiden bevises ved matematisk induktion. Idéen bag
Induktionsbeviser MT01.0.07 1 1 Induktionsbeviser Matematisk induktion Sætninger der udtaler sig om hvad der gælder for alle naturlige tal n N, kan undertiden bevises ved matematisk induktion. Idéen bag
Matematik A August 2016 Delprøve 1
 Anvendelse af løsningerne læses på hjemmesiden www.matematikhfsvar.page.tl Sættet løses med begrænset tekst og konklusion. Formålet er jo, at man kan se metoden, og ikke skrive af! Opgave 1 - Vektorer,
Anvendelse af løsningerne læses på hjemmesiden www.matematikhfsvar.page.tl Sættet løses med begrænset tekst og konklusion. Formålet er jo, at man kan se metoden, og ikke skrive af! Opgave 1 - Vektorer,
Matematiske metoder - Opgaver
 Matematiske metoder - Opgaver Anders Friis, Anne Ryelund 25. oktober 2014 Logik Opgave 1 Find selv på tre udtalelser (gerne sproglige). To af dem skal være udsagn, mens det tredje ikke må være et udsagn.
Matematiske metoder - Opgaver Anders Friis, Anne Ryelund 25. oktober 2014 Logik Opgave 1 Find selv på tre udtalelser (gerne sproglige). To af dem skal være udsagn, mens det tredje ikke må være et udsagn.
MATEMATIK A. Indhold. 92 videoer.
 MATEMATIK A Indhold Differentialligninger... 2 Differentialregning... 3 Eksamen... 3 Hvorfor Matematik?... 3 Integralregning... 3 Regression... 4 Statistik... 5 Trigonometriske funktioner... 5 Vektorer
MATEMATIK A Indhold Differentialligninger... 2 Differentialregning... 3 Eksamen... 3 Hvorfor Matematik?... 3 Integralregning... 3 Regression... 4 Statistik... 5 Trigonometriske funktioner... 5 Vektorer
Besvarelser til Calculus og Lineær Algebra Globale Forretningssystemer Eksamen - 3. Juni 2014
 Besvarelser til Calculus og Lineær Algebra Globale Forretningssystemer Eksamen - 3. Juni 204 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over
Besvarelser til Calculus og Lineær Algebra Globale Forretningssystemer Eksamen - 3. Juni 204 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over
Eksamen i Calculus. 14. juni f (x, y, z) = 1 + x 2 + y 2. Hele rummet uden z aksen
 Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 14. juni 019 Opgave 1 (6 point) En
Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 14. juni 019 Opgave 1 (6 point) En
Eksamen i Calculus. 14. juni f (x, y, z) = 1 + x 2 + y 2. x 2 + y 2 1 Hele rummet uden z aksen
 Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 14. juni 19 Opgave 1 (6 point) En funktion
Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 14. juni 19 Opgave 1 (6 point) En funktion
Pointen med Differentiation
 Pointen med Differentiation Frank Nasser 20. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk:
Pointen med Differentiation Frank Nasser 20. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk:
PROCESSUM DESIGNMANUAL 1.0 2013
 PROCESSUM DESIGNMANUAL 1.0 2013 1 INDHOLDSFORTEGNELSE INDHOLDSFORTEGNELSE FORORD RETNINGSLINJER LOGO PLACERING OG BRUG FRIZONE: PLACERING: TYPOGRAFI PRIMÆR TYPOGRAFI SEKUNDÆR TYPOGRAFI KOMMUNIKATION GRUNDPAPIR
PROCESSUM DESIGNMANUAL 1.0 2013 1 INDHOLDSFORTEGNELSE INDHOLDSFORTEGNELSE FORORD RETNINGSLINJER LOGO PLACERING OG BRUG FRIZONE: PLACERING: TYPOGRAFI PRIMÆR TYPOGRAFI SEKUNDÆR TYPOGRAFI KOMMUNIKATION GRUNDPAPIR
af koblede differentialligninger (se Apostol Bind II, s 229ff) 3. En n te ordens differentialligning
 EKSISTENS- OG ENTYDIGHEDSSÆTNINGEN Vi vil nu bevise eksistens- og entydighedssætningen for ordinære differentialligninger. For overskuelighedens skyld vil vi indskrænke os til at undersøge een 1. ordens
EKSISTENS- OG ENTYDIGHEDSSÆTNINGEN Vi vil nu bevise eksistens- og entydighedssætningen for ordinære differentialligninger. For overskuelighedens skyld vil vi indskrænke os til at undersøge een 1. ordens
Formler & algebra - Fase 2 Omskriv & beregn med variable
 Navn: Klasse: Formler algebra - Fase Omskriv beregn med variable Vurdering fra til 5 (hvor 5 er højst) Læringsmål Selv Lærer Beviser og forslag til forbedring. Jeg kan opstille en linjes ligning, når jeg
Navn: Klasse: Formler algebra - Fase Omskriv beregn med variable Vurdering fra til 5 (hvor 5 er højst) Læringsmål Selv Lærer Beviser og forslag til forbedring. Jeg kan opstille en linjes ligning, når jeg
Vektorer i 3D. 1. Grundbegreber. 1. Koordinater. Enhedsvektorerne. Vektor OP. De ortogonale enhedsvektorer kaldes for: Hvis punkt p har koordinaterne:
 Vektorer i 3D. Grundegreer. Koordinater z k P OP i 0 j x y Enhedsvektorerne De ortogonale enhedsvektorer kaldes for: i, j og k Vektor OP Hvis punkt p har koordinaterne: P ( a a a3 ) Så har vektor OP koordinaterne:
Vektorer i 3D. Grundegreer. Koordinater z k P OP i 0 j x y Enhedsvektorerne De ortogonale enhedsvektorer kaldes for: i, j og k Vektor OP Hvis punkt p har koordinaterne: P ( a a a3 ) Så har vektor OP koordinaterne:
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin aug 2014 - jun 2015 Institution Vid Gymnasier Uddannelse Fag og niveau Lærer(e) Hold HTX Matematik A Klavs
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin aug 2014 - jun 2015 Institution Vid Gymnasier Uddannelse Fag og niveau Lærer(e) Hold HTX Matematik A Klavs
Matematisk modellering og numeriske metoder
 Matematisk modellering og numeriske metoder Morten Grud Rasmussen 5. september 2016 1 Ordinære differentialligninger ODE er 1.1 ODE er helt grundlæggende Definition 1.1 (Ordinære differentialligninger).
Matematisk modellering og numeriske metoder Morten Grud Rasmussen 5. september 2016 1 Ordinære differentialligninger ODE er 1.1 ODE er helt grundlæggende Definition 1.1 (Ordinære differentialligninger).
LLZ DESIGN. Skabeloner og stencils
 DANSK DESIGN LLZ DESIGN Skabeloner og stencils Skabeloner og stencils til hobby. Brug kataloget 2015 til køb og kreativ inspiration. Til vægdekorationer, billedmageri, på tøj, møbler, papir, glas, postkort
DANSK DESIGN LLZ DESIGN Skabeloner og stencils Skabeloner og stencils til hobby. Brug kataloget 2015 til køb og kreativ inspiration. Til vægdekorationer, billedmageri, på tøj, møbler, papir, glas, postkort
Start pä matematik. for gymnasiet og hf. 2010 (2012) Karsten Juul
 Start pä matematik for gymnasiet og hf 2010 (2012) Karsten Juul Til eleven Brug blyant og viskelåder när du skriver og tegner i håftet, sä du fär et håfte der er egnet til jåvnligt at slä op i under dit
Start pä matematik for gymnasiet og hf 2010 (2012) Karsten Juul Til eleven Brug blyant og viskelåder när du skriver og tegner i håftet, sä du fär et håfte der er egnet til jåvnligt at slä op i under dit
Matematisk modellering og numeriske metoder. Lektion 5
 Matematisk modellering og numeriske metoder Lektion 5 Morten Grud Rasmussen 19. september, 2013 1 Euler-Cauchy-ligninger [Bogens afsnit 2.5, side 71] 1.1 De tre typer af Euler-Cauchy-ligninger Efter at
Matematisk modellering og numeriske metoder Lektion 5 Morten Grud Rasmussen 19. september, 2013 1 Euler-Cauchy-ligninger [Bogens afsnit 2.5, side 71] 1.1 De tre typer af Euler-Cauchy-ligninger Efter at
Differential- ligninger
 Differential- ligninger Et oplæg 2007 Karsten Juul Dette hæfte er tænkt brugt som et oplæg der kan gennemgås før man går i gang med en lærebogs fremstilling af emnet differentialligninger Læreren skal
Differential- ligninger Et oplæg 2007 Karsten Juul Dette hæfte er tænkt brugt som et oplæg der kan gennemgås før man går i gang med en lærebogs fremstilling af emnet differentialligninger Læreren skal
Emneopgave: Lineær- og kvadratisk programmering:
 Emneopgave: Lineær- og kvadratisk programmering: LINEÆR PROGRAMMERING I lineær programmering løser man problemer hvor man for en bestemt funktion ønsker at finde enten en maksimering eller en minimering
Emneopgave: Lineær- og kvadratisk programmering: LINEÆR PROGRAMMERING I lineær programmering løser man problemer hvor man for en bestemt funktion ønsker at finde enten en maksimering eller en minimering
Kommentarer til den ægyptiske beregning Kommentarer til den ægyptiske beregning... 5
 Hvad er matematik? C, i-bog ISBN 978 87 7066 499 8 Projekter: Kapitel - Projektet er delt i to små projekter, der kan laves uafhængigt af hinanden. Der afsættes fx - timer til vejledning med efterfølgende
Hvad er matematik? C, i-bog ISBN 978 87 7066 499 8 Projekter: Kapitel - Projektet er delt i to små projekter, der kan laves uafhængigt af hinanden. Der afsættes fx - timer til vejledning med efterfølgende
Funktionalligninger. Anders Schack-Nielsen. 25. februar 2007
 Funktionalligninger Anders Schack-Nielsen 5. februar 007 Disse noter er en introduktion til funktionalligninger. En funktionalligning er en ligning (eller et ligningssystem) hvor den ubekendte er en funktion.
Funktionalligninger Anders Schack-Nielsen 5. februar 007 Disse noter er en introduktion til funktionalligninger. En funktionalligning er en ligning (eller et ligningssystem) hvor den ubekendte er en funktion.
Ting man gør med Vektorfunktioner
 Ting man gør med Vektorfunktioner Frank Villa 3. august 13 Dette dokument er en del af MatBog.dk 8-1. IT Teaching Tools. ISBN-13: 978-87-9775--9. Se yderligere betingelser for brug her. Indhold 1 Introduktion
Ting man gør med Vektorfunktioner Frank Villa 3. august 13 Dette dokument er en del af MatBog.dk 8-1. IT Teaching Tools. ISBN-13: 978-87-9775--9. Se yderligere betingelser for brug her. Indhold 1 Introduktion
Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 2016
 Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Matematik A og Informationsteknologi B
 Matematik A og Informationsteknologi B Projektopgave 2 Eksponentielle modeller Benjamin Andreas Olander Christiansen Jens Werner Nielsen Klasse 2.4 6. december 2010 Vejledere: Jørn Christian Bendtsen og
Matematik A og Informationsteknologi B Projektopgave 2 Eksponentielle modeller Benjamin Andreas Olander Christiansen Jens Werner Nielsen Klasse 2.4 6. december 2010 Vejledere: Jørn Christian Bendtsen og
Projekt 1.4 De reelle tal og 2. hovedsætning om kontinuitet
 Projekt 1.4 De reelle tal og 2. hovedsætning om kontinuitet Mens den 1. hovedsætning om kontinuerte funktioner kom forholdsvis smertefrit ud af intervalrusebetragtninger, så er 2. hovedsætning betydeligt
Projekt 1.4 De reelle tal og 2. hovedsætning om kontinuitet Mens den 1. hovedsætning om kontinuerte funktioner kom forholdsvis smertefrit ud af intervalrusebetragtninger, så er 2. hovedsætning betydeligt
Løsninger til eksamensopgaver på A-niveau 2016
 Løsninger til eksamensopgaver på A-niveau 2016 24. maj 2016: Delprøven UDEN hjælpemidler Opgave 1: Da trekanterne er ensvinklede, er forholdene mellem korresponderende linjestykker i de to trekanter det
Løsninger til eksamensopgaver på A-niveau 2016 24. maj 2016: Delprøven UDEN hjælpemidler Opgave 1: Da trekanterne er ensvinklede, er forholdene mellem korresponderende linjestykker i de to trekanter det
Besvarelser til Calculus og Lineær Algebra Globale Forretningssystemer Eksamen - 8. Juni 2015
 Besvarelser til Calculus og Lineær Algebra Globale Forretningssystemer Eksamen - 8. Juni 05 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en
Besvarelser til Calculus og Lineær Algebra Globale Forretningssystemer Eksamen - 8. Juni 05 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en
Archimedes Princip. Frank Nasser. 12. april 2011
 Archimedes Princip Frank Nasser 12. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk: Dette er
Archimedes Princip Frank Nasser 12. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk: Dette er
Uendelige rækker og Taylor-rækker
 Uendelige rækker og Taylor-rækker Thomas Bolander, DTU Informatik Matematik: Videnskaben om det uendelige Folkeuniversitetet i København, efteråret 200 Thomas Bolander, FUKBH 0 s. /24 Forhold mellem endelighed
Uendelige rækker og Taylor-rækker Thomas Bolander, DTU Informatik Matematik: Videnskaben om det uendelige Folkeuniversitetet i København, efteråret 200 Thomas Bolander, FUKBH 0 s. /24 Forhold mellem endelighed
Differentialregning Infinitesimalregning
 Udgave 2.1 Differentialregning Infinitesimalregning Noterne gennemgår begreberne differentialregning, og anskuer dette som et derligere redskab til vækst og funktioner. Noterne er supplement til kapitel
Udgave 2.1 Differentialregning Infinitesimalregning Noterne gennemgår begreberne differentialregning, og anskuer dette som et derligere redskab til vækst og funktioner. Noterne er supplement til kapitel
Besvarelser til Calculus Ordinær eksamen - Efterår - 8. Januar 2016
 Besvarelser til Calculus Ordinær eksamen - Efterår - 8. Januar 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har
Besvarelser til Calculus Ordinær eksamen - Efterår - 8. Januar 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har
Elementær Matematik. Trigonometriske Funktioner
 Elementær Matematik Trigonometriske Funktioner Ole Witt-Hansen Indhold. Gradtal og radiantal.... sin x, cos x og tan x... 3. Trigonometriske ligninger...3 4. Trigonometriske uligheder...5 5. Harmoniske
Elementær Matematik Trigonometriske Funktioner Ole Witt-Hansen Indhold. Gradtal og radiantal.... sin x, cos x og tan x... 3. Trigonometriske ligninger...3 4. Trigonometriske uligheder...5 5. Harmoniske
Løsninger til eksamensopgaver på A-niveau 2019 ( ) ( )
 Løsninger til eksamensopgaver på A-niveau 019 1. maj 019: Delprøven UDEN hjælpemidler 1. maj 019 opgave 1: Man kan godt benytte substitutionsmetoden, lige store koefficienters metode eller determinantmetoden,
Løsninger til eksamensopgaver på A-niveau 019 1. maj 019: Delprøven UDEN hjælpemidler 1. maj 019 opgave 1: Man kan godt benytte substitutionsmetoden, lige store koefficienters metode eller determinantmetoden,
Differentialregning. Et oplæg Karsten Juul L P
 Differentialregning Et oplæg L P A 2009 Karsten Juul Til eleven Dette hæfte kan I bruge inden I starter på differentialregningen i lærebogen Det meste af hæftet er små spørgsmål med korte svar Spørgsmålene
Differentialregning Et oplæg L P A 2009 Karsten Juul Til eleven Dette hæfte kan I bruge inden I starter på differentialregningen i lærebogen Det meste af hæftet er små spørgsmål med korte svar Spørgsmålene
Løsningsforslag Mat B 10. februar 2012
 Løsningsforslag Mat B 10. februar 2012 Opgave 1 (5 %) En linje er givet ved: y = 3 4 x + 3 En trekant er afgrænset af linjen og koordinatakserne i første kvadrant. a) Beregn trekantens sider og areal.
Løsningsforslag Mat B 10. februar 2012 Opgave 1 (5 %) En linje er givet ved: y = 3 4 x + 3 En trekant er afgrænset af linjen og koordinatakserne i første kvadrant. a) Beregn trekantens sider og areal.
Matematik A, STX. Vejledende eksamensopgaver
 Matematik A, STX EKSAMENSOPGAVER Vejledende eksamensopgaver 2015 Løsninger HF A-NIVEAU AF SAEID Af JAFARI Anders J., Mark Af K. & Saeid J. Anders J., Mark K. & Saeid J. Kun delprøver 2 Kun delprøve 2,
Matematik A, STX EKSAMENSOPGAVER Vejledende eksamensopgaver 2015 Løsninger HF A-NIVEAU AF SAEID Af JAFARI Anders J., Mark Af K. & Saeid J. Anders J., Mark K. & Saeid J. Kun delprøver 2 Kun delprøve 2,
