Opgaveløsninger til Eksamensopgaver i Matematik F2 1. Den fjerde afledede regnes for konstant i intervallet [f (4) (t) =M 4 = 24] og dermed er:
|
|
|
- Ingelise Poulsen
- 5 år siden
- Visninger:
Transkript
1 Opgaveløsninger til Eksamensopgaver i Matematik F 1 Opgave 1 a) Simpsons algoritme med m =6ogh =.1: som medfører at s = f + f 6 =3.356 s 1 = f 1 + f 3 + f 5 = s = f + f 4 =.899 J = h 3 (s +4s 1 +s )= Den fjerde afledede regnes for konstant i intervallet [f (4) (t) =M 4 = 4] og dermed er: (b a) 5.65 ɛ s = M 4 = 4 = (m) [Tabelværdier og M 4 = 4 er resultater af antagelsen f(x) =1+x + x + x 3 + x 4, og i dette tilfælde er J = J + ɛ s =.89995]. b) Benyttes Kreyszigs betegnelser kan følgende tabel opstilles: x j f j f j f j 3 f j [opstilles næste linie i tabellen fås 4 f =.4 = M 4 h 4 ]. Benyttes ligning (14) (16) i 17.3 ( 18.3 i 7.ed.) med x =,x =.15 r = x x =1.5 fås h r(r 1) p 3 (.15)= f + r f + r(r 1)(r ) f + 3 f 3! = = hvor f(.15) p 3 (.15)med fejlen ɛ 3 = h4 4! r(r 1)(r )(r 3) f (4) (t) = (.5)( 1.5)4 = [Benyttes f(x) =1+x+x +x 3 +x 4 fås f(.15)= p 3 (.15)+ɛ 3 = ]. Ørsted Laboratoriet, September 3
2 Opgaveløsninger til Eksamensopgaver i Matematik F Opgave a) j t j f j =cos( π t j ) og dermed s = f + f 1 =1 s 1 = f 1 + f f 9 = s = f + f f 8 = C(1)= h (s +s 1 +s )=.7777 C(1)= h 3 (s +4s 1 +s )= (trapez) (Simpson) b) Benyttes f(t) =cos( π t )fås: f (t) = πt sin ( π t ) f ()=, f (1)= π f (t) = π sin ( π t ) (πt) cos ( π t ) f (t) = 3π t cos ( π t )+(πt) 3 sin ( π t ) f ()=, f (1)= π 3 og fejlene bliver ɛ = h 1 ɛ = h4 18 og dermed [ f (1) f () ] =.1 ( π) =.6 1 (trapez) [ f (1) f () ] = π3 = (Simpson) C(1) C(1)+ ɛ = (trapez og Simpson) Simpsons algoritme C(1)= med en fejl 1 5. Udnyttes dette ses, at C(1)+ ɛ forbedrer nøjagtigheden af trapez-resultatet med en faktor 1. Antages en lignende forbedring af Simpson-resultatet er C(1)= med en fejl svarende til at afrundingsfejlen dominerer [tabelværdien er C(1)= ].
3 Opgaveløsninger til Eksamensopgaver i Matematik F 3 Opgave 3 a) Benyttes (4a)side 851 (side 939 i 7.ed.)fås: (x 1)(x )(x 3) )(x )(x 3) p 3 (x) = +1(x ( 1)( )( 3) (1 )(1 )(1 3) (x )(x 1)(x 3) )(x 1)(x ) +( ) +3(x ( )( 1)( 3) (3 )(3 1)(3 ) = 1 ( x 3 6x +11x 6 ) + 1 ( x 3 5x +6x) 3 + ( x 3 4x +3x ) + 1 ( x 3 3x +x ) eller p 3 (x) = 5 3 x3 6x x + b) Newtons iterationsmetode er beskrevet i tabel 17.1 side 84 (tabel 18.1 side 93 i 7.ed.): x n+1 = x n p 3 (x n) p 3 (x n), p 3(x) =5x 1x fås n x n p 3 (x n ) p 3 (x n) og dermed x p =1.617 c) Vurdering af fejlen ved at tilnærme f(x)med p 3 (x)er givet ved (5)på side 851 (939): ɛ = ɛ 3 (x p ) = 1 (x 4! p )(x p 1)(x p )(x p 3)f (4) (t x p ) =.177 Vi har, at f(x) x f (x) p 3 (x) og dermed at fejlen ɛ svarer til en variation af x, somer ɛ x p 3 (x p ) = =.46 Dvs. at løsningen af f(x) =,når 1 <x<, må forventes at ligge i intervallet x p x <x<x p + x, eller 1.57 <x<1.67
4 Opgaveløsninger til Eksamensopgaver i Matematik F 4 Opgave 4 a) Ifølge Kreyszig 17.3 ( 18.3 i 7.ed.), ligning (6) (7), haves: hvor f(x) =p 4 (x) =p 3 (x)+a 4 (x x )(x x 1 )(x x )(x x 3 ) a 4 = og dermed f 4 p 3 (x 4 ) (x 4 x )(x 4 x 1 )(x 4 x )(x 4 x 3 ) = = 1 f(x) =x 3 4x +3x +1 1 x(x 1)(x )(x 3) = x 3 4x +3x +1 1 x4 +3x 3 11 x +3x = 1 x4 +4x 3 19 x +6x +1 Integreres funktionen fås 4 f(x)dx = [ 1 1 x5 + x x3 +3x + x ] 4 = =.9333 b) Benyttes Kreyszigs notation i Tabel 17.4 (18.4 i 7.ed.)om Simpsons algoritme fås: og idet h =1fås s = f + f 4 =; s 1 = f 1 + f 3 =; s = f = 1 J = h 3 (s +4s 1 +s )=1 3 ( + 8 )= 8 3 =.6667 Foratvurderefejlenɛ udregnes: og vi får: f (x) = 1x +4 ogdermed f ()= 4; f (4)= 4 ɛ h4 [ f (b) f (a) ] = ( 4 4)= 4 15 =.667 som er identisk med den korrekte størrelse af fejlen: ɛ = J J = = = (Vurderingen af fejlen udnytter en fjerdegrads-polynomium-tilnærmelse, som er eksakt i dette tilfælde).
5 Opgaveløsninger til Eksamensopgaver i Matematik F 5 Opgave 5 a) Anvendes Lagrange interpolations metode, (3a)og (3b)i 17.3 ( 18.3 i 7. udgave)fås: (x )(x 3) p (x) =f (1 )(1 3) + f (x 1)(x 3) 1 ( 1)( 3) + f (x 1)(x ) (3 1)(3 ) = f ( x 5x +6 ) ( f 1 x 4x +3 ) + f ( 3 x 3x + ) =.865x.675x Ligningen J (x) p (x) =for1<x<3 har løsningen x =.448. Benyttes ligning (5)i Kreyszig haves ɛ ( x) ( x x )( x x 1 )( x x 3 )J ( x)/3! =. b) Benyttes intervallængden h =.1π fås, idet g j = g( x, θ j ) j θ j π g j =cos(.448 sin θ) π.776.π π π π og trapez-metoden giver J ( x) =h [.5(g + g 5 )+(g 1 + g + g 3 + g 4 ) ] =.1π π [ ] =. Idet π g(.448,θ=.5π) =.1595 fås i tilfældet h =.5π J ( x) =.5π π [ ] =. Antages ɛ J h ved trapez-metoden er fejlen i første regning.5 gange mindre end i andet tilfælde og dermed 1/(.5 1)gange differensen mellem de to resultater, dvs. ɛ J [. (.)]/5.5 = Ved at udnytte J ( x) =. kan bestemmelsen af nulpunktets position x forbedres: x x J ( x)/j ( x) J ( x) p ( x) =.865 x.675 =.487 x =.44 [Det korrekte resultat er.448].
6 Opgaveløsninger til Eksamensopgaver i Matematik F 6 Opgave 6 a) Med h =.1π fås følgende værdier for x j og f j =1/ sin x j j x j f j g j = f j 1 x j.1π π π π π s = f + f 4 =4.367 ; s 1 = f 1 + f 3 =.7576 ; s = f =1.367 Simpsons algoritme med m = 4 eller h =.1π giver resultatet: J a = h 3 (s +4s 1 +s )= Den analytiske udtryk for integralet giver J = og dermed er fejlen: b) Fra søjlen med g j = f j 1 x j fås ɛ = J J a =.183 s = g + g 4 = ; s 1 = g 1 + g 3 = ; s = g =.1754 og dermed J b =.5π J 1 = h 3 (s +4s 1 +s )= π De afledede af f(x)og g(x) =f(x) 1 x er f (x) = cos x sin x f (x) = 5cosx sin x 6cos3 x sin 4 x Dermed fås følgende fejlvurderinger: 1 x dx + J 1 =ln = ; f (x) = 1 sin x + cos x sin 3 x ; g (x) =f (x)+ 6 x 4 ɛ a = h4 18 [f (b) f (a) ]= (.1π)4 ( )= ɛ b = h4 18 [g (b) g (a) ]= (.1π)4 ( )= Polynomium-beskrivelsen, som udnyttes i Simpsons algoritme, er ikke en god tilnærmelse til f(x)for x. Det betyder, at udregningen i a)giver en stor fejl og at fejlvurderingen ɛ a er næsten en faktor 3 forkert. Fremgangsmåden i b)giver et meget bedre resultat for J og en korrekt vurdering af fejlens størrelse (ɛ = ).
7 Opgaveløsninger til Eksamensopgaver i Matematik F 7 Opgave 7 a) Benyttes Kreyszigs betegnelser i afsnit 17.3 kan følgende tabel opstilles: x j f j f j f j 3 f j h =1 og r = x x ( ) 3 x = x og dermed f(x) p h 3 (x) = s f s= s eller x(x 1) x(x 1)(x ) f(x) 1.+x(.134)+ (.3) x(x 1)(x )(x 3) ɛ(x) =f(x) p 3 (x) f (4) (t); f (4) (t).5 4 Udtrykkene udledes fra Kreyszig 17.3, ligning (14)og (16), og giver følgende f(.5).9681 ; ɛ(.5)=. f(1.5).759 ; ɛ(1.5)=.1 f(.5).66 ; ɛ(.5)=. b) Trapez-metoden, 17.5 ligning (), giver resultatet (h = 1): J 1 = h(.5f + f 1 + f +.5f 3 )= = Benyttes f (t) 1 3 [f (3) f ()] f j 1 (.3.134).18 fås fra 17.5 ligning (3)eller Supplementets ligning (1.1): ɛ 1 h 1 (3 )f (t) h 1 [f (3) f ()].45 Simpsons algoritme, 17.5 Table 17.4, giver følgende resultat (h =.5): J =(h/3)[{f + f 3 } +{f 1 + f } +4{f(.5)+ f(1.5)+ f(.5)}] (.5/3)[ ] = I dette tilfælde er der to bidrag til fejlen, dels bidraget som skyldes Simpson tilnærmelsen ved udregning af J [ 17.5 ligning (8)eller Supplementet (1.)] og dels fejlen ved at benytte interpolationsværdierne for f(x): ɛ h4 18 (3 )f (4) (t)+ 4h [ɛ(.5)+ ɛ(1.5)+ ɛ(.5)] 3 = (.5) (.8)= =.19 Fejlen domineres af bidraget fra interpolationen, men er stadigvæk en faktor mindre end ved den simple udregning. Dvs. benyttes (højere ordens) interpolation kan fejlen ved udregning af et integral reduceres betydeligt. Bemærk, at trapez-metoden kun ville have reduceret fejlen med en faktor 4. Eksempel: f(x) =cos(πx/6) J =6/π =1.999.
8 Opgaveløsninger til Eksamensopgaver i Matematik F 8 Opgave 8 a) Idet Laplace-transformen af y betegnes Y = L{y} fås eller L{y } = sy y()= sy 1=L{x y} = 1 s Y (s +1)Y =1+ 1 s Y = 1 s s (s +1) = s s 1 s Den inverse Laplace-transformation af denne ligning giver resultatet: y = y(x) =e x + x 1 ; y(1)=.7358 b) Runge-Kutta algoritmen er beskrevet i tabel 19.4 side 948 (tabel.4 side 14 i 7.ed.). Her er h =1,x =,y =1,ogf(x, y) =x y: og dermed k 1 = hf(x,y )=hf(, 1)= 1 k = hf(x + 1 h, y + 1 k 1 )=hf(.5,.5)= k 3 = hf(x + 1 h, y + 1 k )=hf(.5, 1)=.5 k 4 = hf(x + h, y + k 3 )=hf(1,.5)=.5 y(1) y 1 = (k 1 +k +k 3 + k 4 )= ( )=.75 c) Funktionen y = y(x)går gennem (x, y) =(, 1)med hældningen y = 1 og gennem (x, y) =(1,.7358)med hældningen y = x y =.64. y skifter fortegn mellem de to punkter, og minimumspunktet bestemmes af y = x y = exp( x)+ 1 =, som har løsningen x =ln y =ln= Igrænsenx fås den asymptotiske opførsel y(x) y = x y 1 y = x x
9 Opgaveløsninger til Eksamensopgaver i Matematik F 9 Opgave 9 a) Den Laplace transformerede af foldningsintegralet t f(t) = τ sin(t τ)dτ = t sin t er og dermed F (s) =L{t}L{sin t} = 1 s 1 s +1 = 1 s 1 s +1 f(t) =L 1 {F (s)} = t sin t og idet sin(π/ τ) =cosτ fås for t = π/ f(π/)= π τ cos τdτ = π 1=.578 b) Funktionen g(τ) =τ cos τ med intervalopdelingen h =.1π, mellem a = og b = π/, er beskrevet ved følgende tabel [g j = g(τ j )]: Benyttes trapez-metoden fås: j τ j g j 1.1π.9878.π π π π f(π/)= h [ 1 g + g 1 + g + g 3 + g g 5] =.1π = Idet g (t) =cosτ τ sin τ, ogdermedg ()= 1 og g (π/)= π/, fås ɛ = h [ g (b) g (a) ] = (.1π) ( π 1 1 1) =.114 Den relative forskel mellem den tilnærmede værdi af integralet f(π/) f(π/)+ ɛ =.5773 og den korrekte værdi er af størrelsesordenen 1 4.
10 Opgaveløsninger til Eksamensopgaver i Matematik F 1 Opgave 1 a) Benyttes relationerne L{y } = sy y()og L x {x} =1/s transformeres differentialligningen over i L{y = y +x} sy 1=Y + s Y (s) = s + s (s 1) Omskrivning af brøken Y (s) = s + s (s 1) = a s 1 + b s + c s = as + bs b + cs cs s (s 1) giver resultatet: a + c =1,b c =, b = eller b = c = oga =3og dermed Y (s) = 3 s 1 s y(x) =L 1 {Y (s)} =3e x x s b) Algoritmen for Eulers forberede metode er opstillet i Table 19. (. i 7. udgave), og vi har følgende parameterværdier: h =. ; f(x n,y n )=y n +x n ; x =,y =1 Udnyttes ligningerne (7a)og (7b)i 19.1 [(5a)og (5b)i.1 i 7. udgave] fås: y n+1 = y n + 1 h[f(x n,y n )+f(x n+1,yn+1 = y n + hf(x n,y n ))] = y n + 1 h[y n +x n + {y n + h(y n +x n )+x n+1 }] =(1+h + 1 h )y n +(h + h )x n + h(x n + h) =1. y n +.44 x n +.4 = y n + 1 (k 1 + k ) I tabelform bliver resultatet, idet k 1 = hf(x n,y n ), k = hf(x n+1,y n + k 1 ), n x n y n y(x n ) y(x n ) y n y(x n ) k 1 k De resultater, der er bedt om, er: ỹ(1)= y 5 =4.18 og ɛ r = y(x 5 ) y 5 y(x 5 ) =.11
11 Opgaveløsninger til Eksamensopgaver i Matematik F 11 Opgave 11 a) Den Laplace transformerede differentialligning er L{y = y + x } sy y()= Y + s 3 Y (s) = s 3 (s 1) Omskrivning af brøken Y (s) = s 3 (s 1) = a s 1 + b s 3 + c s + d s = as3 +(s 1)(b + cs + ds ) s 3 (s 1) giver resultatet a + d =,c d =,b c =,og b =, eller a = b = c = d =ogdermed Y (s) = s 1 s 3 s y(x) =L 1 {Y (s)} =e x x x s b) Algoritmen for Eulers forberede metode er opstillet i tabel 19. og h =. ; f(x n,y n )=y n + x n ; x =,y = Udnyttes ligningerne (7a)og (7b)i 19.1 fås: y n+1 = y n + 1 h[f(x n,y n )+f(x n+1,yn+1) ] og yn+1 = y n + hf(x n,y n )=y n + h(y n + x n ) y n+1 = y n + 1 h[y n + x n + {y n + h(y n + x n)+(x n + h) }] =1. y n +. x n +.4 x n +.4 Benyttes tabel 19. direkte haves y n+1 = y n + 1 (k 1 + k ), hvor k 1 = hf(x n,y n )og k = hf(x n+1,y n + k 1 ) På tabelform bliver resultatet n x n y n k 1 k og dermed er svaret: ỹ(1)= y 5 = Den korrekte værdi er y(1)= og dermed bliver den relative fejl: ɛ r = y(1) ỹ(1) y(1) =4. 1 4
12 Opgaveløsninger til Eksamensopgaver i Matematik F 1 Opgave 1 a) Ifølge tabel 5.9 er L{ t/π} =1/s 3/ eller F (s) =L{ π t} = s 3/ G(s) =L{t 3/ } = L{tf(t)} = F (s) = 3 π 4s 5/ Benyttes foldningsintegral-sætningen ( 5.5 teorem 1)fås t 3π y(t) = g(τ)f(t τ)dτ Y (s) =F (s)g(s) = 8s 4 og dermed y(t) =L 1 {Y (s)} = π 16 t3 ; y(1)= π 16 = b) j x j f j Trapez metoden med h =.5 og f j = f(x j )=(x 3/ j 1) 1 x j J = h[ 1 (f + f 4 )+f 1 + f + f 3 ]=.4753 Idet f (x) = 3 x(1 x) x3/ 1 1 x og benyttes l Hôpitals regel [ x f 3/ ] 1 (1)= lim x 1 = lim 1 x x 1 fås følgende vurdering af fejlen Benyttes [ f ()= 1 3 ] x1/ (1 x) 1/ ɛ = h 1 [f (1) f ()] =.5 (.5)=.6 1 = 1 [ y(1)= J + 1 xdx= J + 3 (1 x) 3/] 1 = J + 3 giver de numeriske regninger at y(1) J + ɛ + 3 = = Den relative fejl er.%. En tilsvarende direkte beregning af y(1)vha. trapez metoden giver resultatet y(1)= ɛ, hvorfejlenɛ ikke kan vurderes ved udtrykket ovenfor, idet den afledede af x 3/ 1 x for x 1. Dette viser at polynomium tilnærmelsen til x 3/ 1 x, som udnyttes i trapez metoden, ikke er pålidelig når x er tæt ved 1.
13 Opgaveløsninger til Eksamensopgaver i Matematik F 13 Opgave 13 a) Laplace transformeres y +y +5y =5 ; y()= a ; y ()= b fås følgende sekulære ligning, hvor Y = Y (s) = L{y(t)}, s Y sa b +sy a +5Y = 5 s En omskrivning af sidste brøk giver og dermed hvoraf fås (s +s +5)Y (s +)a b = 5 s (s +)a + b Y (s) = s +s s(s +s +5) 5 s(s +s +5) = 1 s s + s +s +5 = 1 s s + (s +1) + Y = 1 s + (s +)(a 1)+ b (s +1) + = 1 s +(a 1) s +1 (s +1) (a + b 1) (s +1) + y(t) =L 1 {Y } =1+e t [(a 1)cos(t)+ 1 (a + b 1)sin(t)] b) y()= 1 + (a 1)= i) y( π 4 )=1+e π 4 1 (a + b 1)= 1 a = ; b =1 og dermed y(t) =1+e t cos(t) ii)indsættes begyndelsesbetingelserne, y ()= og y ()=, direkte i differentialligningen fortæller den, at 5y()= 5. Dermed er y()= a = 1 og y ()= b = og resultatet er y(t) =1
14 Opgaveløsninger til Eksamensopgaver i Matematik F 14 Opgave 14 a) Benyttes følgende relationer, se fx side 77 (side 9 i 7.ed.) L{ty } = d ds[ s Y (s) sy() y () ] = sy s Y + y() L{y } = sy y() L{ty} = d Y (s) = Y ds transformeres differentialligningen over i L{ty + y + ty} = (s +1)Y sy = (s>) og dermed bliver differentialligningen til bestemmelse af Y = Y (s): Løsningerne er: ln Y = eller Y = Y (s) = Y + s s +1 Y = s s +1 ds = 1 ln(s +1)+konstant A s +1 (A arbitrær konstant) b) Taylor-rækkeudvikling af Laplace-integralet: F (s) = e st f(t)dt = e st[ f()+ f ()t + 1! f ()t + ]dt = 1 s f()+ 1 s f ()+ 1!! s 3 f ()+ 1 3! 3! s 4 f ()+ eller [ 1 lim sf (s)= lim s s f()+ s f ()+ + 1 s n f (n) ()+ ] = f() som det skulle vises. Anvendes dette resultat på den generelle løsning fundet under punkt a)fås As lim sy (s)= lim s s s +1 = A og dermed, at valget A = 1 betyder at Y (s)er Laplace transformationen af funktionen y(t)med randbetingelsen y()= 1, eller L{J (t)} = 1 s +1
15 Opgaveløsninger til Eksamensopgaver i Matematik F 15 Opgave 15 a) Benyttes Heaviside funktionen, u(t a), kan v(t)skrives: t v(t) =V a [1 u(t a)]+v u(t a) = V [ ] t (t a)u(t a) a og benyttes t-forskydningsreglen, (3)side 67 [(4)side 79 i 7.ed.], fås V (s) =L{v(t)} = V as ( 1 e as ) b) Laplace transformationen af differentialligningen er: og dermed V = RI + L[sI i()] = RI + LsI V I = I(s) = Ls + R = V 1 ( 1 e as ) al s (s + R L ) = V ( 1 L L ) (1 ar s + R R e as ) s + R s L som ved invertering giver resultatet: i(t) = V ( t L ( 1 e R L t) [ u(t a) t a L ( 1 e R L (t a))]) ar R R c) For <t a er u(t a) =oge R L t 1 R L t + R L t, som indsat giver i(t) V [ t L ( R ar R L t R )] L t = V al t For t er u(t a) =1oge R L t, og dermed i(t) V (t L [ ar R t a L ]) = V R R
16 Opgaveløsninger til Eksamensopgaver i Matematik F 16 Opgave 16 a) j x j x j x (x j x) Fra tabellen fås, idet n =5, x = 1 n n j=1 x j = =3.9 s = 1 n 1 n (x j x) = j=1 4 s =.9 9% konfidensintervallet for µ er bestemt ud fra Student s t-fordelingen med n 1 = 4 frihedsgrader og γ =.9, dvs.: F (c) = 1 (1 + γ) =.95 c =.13 (tabel A9 i 8. og A1 i 7. udgave)og dermed k = sc/ n =.. Resultatet er, ifølge Table 3. i 8. udgave af Kreyszig (Table 4.6 i 7. udgave): CONF{x k<µ<x + k} =CONF{3.9 <µ<34.9} b) Det totale antal af mulige udfald er 6 6 = 36. Blandt disse udfald optælles mulighederne for en syver: 1 + 6, 6 + 1, + 5, 5 +, 3 + 4, 4 + 3, dvs. af de 36 muligheder er der 6 udfald med syv øjne: P (7 øjne)= p = 36 6 = 1 6. Sandsynligheden for at ( slå ) x syvere i 4 kast er bestemt af binomialfordelingen: n P (X = x) =f(x) = p x (1 p) 1 x med n =4ogp = 1 x 6,dvs. P (X )= P (X =)+P (X =3)+P (X =4) ( ) ( ) ( ) = (1 p) p + (1 p)p 3 + p =6 ( 5 6 ) ( 16 ) +4 ( 56 )( 16 ) 3 + ( 16 ) 4 =.1319 Ifølge Kreyszig, ligning (3)og (4)i.7 ( 3.6 i 7.ed.), er middelværdien af denne fordeling: µ = np =4 1 6 = 3 og variansen σ = np(1 p) = = 5 9 og dermed σ =.745.
17 Opgaveløsninger til Eksamensopgaver i Matematik F 17 Opgave 17 a) Normering af sandsynlighedstætheden giver: a f(x)dx = cdx= ac =1 c = 1 a a Middelværdien X =, dvs. at variansen bliver σ 1 = X X = X = a a x dx a =1 3 For den diskrete fordeling er X i = 1 b 1 b =og σ = 1 b + 1 ( b) =b og dermed at σ = σ 1 b = a 1. ( a ) 3 1 a = a 1 y(n) =±b ± b ± ±b (n tal)med sandsynligheden 1 de enkelte b er er +, eller ( ) n 1 P (i plustegn)= i n for at fortegnet foran (binomialfordeling med p = 1 ).Mediplusser bliver y = y i = ib (n i)b = (i n)b ( ) n 1 f n (y i )= i n, hvor y i =(i n)b og i =, 1,,...,n. b) I grænsen n 1 kan Y (n)tilnærmes med normalfordelingen, uanset valg af f(x),medµ =og σ = σn n = σ1 = n 1 a i=1 Dermed har Y (n)/σ n tilnærmelsesvis fordelingsfunktionen Φ(z = y(n)/σ n ), eller P ( 5a <Y(n) 5a) =P ( 5a/σ n <Z 5a/σ n ) =Φ(5a/σ n ) Φ( 5a/σ n )= 1 for n = n.opslagitabel8viseratz(d) =.674 og betyder at z(d) = 5a σ n = 5a a n /1 =.674 ( ) 5 n 1 = 66.4 eller n.674 = 661 (±1)
18 Opgaveløsninger til Eksamensopgaver i Matematik F 18 Opgave 18 a) Sandsynlighederne er bestemt ved Poisson fordelingen, som har frekvensfunktionen: f P (x) = µx x! e µ = x x! e hvor x er antallet af henfald i tidsintervallet t = /λ og µ = λt = er middelværdien. Dvs. P (X 3)= 1 F P ()= 1 f P () f P (1) f P ()= 1 1 e ( 1++)=.333 (se også tabel A6 side A88, side A1 i 7.ed.). b) Igrænsenµ 1er Dvs. P (µ µ X µ+ µ) = f P (x) 1 πσ e 1 ( x µ σ ), σ = µ µ+ µ µ µ f P (x)dx Φ( µ/σ) Φ( µ/σ) =.95 som medfører µ/σ =1.96 (tabel A8). Indsættes µ =.5µ og σ = µ fås.5µ µ =1.96 µ = 1537 c) I det generelle tilfælde er µ = λt og p(t) =f P ()= exp( λt),dvs. Med denne fordelingsfunktion fås: og F (t) =1 e λt, for t f(t) =F (t) = λe λt, for t [ ] G(u) = exp(ut ) = λe (u λ)t λ dt = u λ e (λ u)t = λ λ u idet det er forudsat at λ u>. Momenterne kan beregnes direkte, men udnyttes den moment-genererende funktion fås: T = G λ ()= (λ u) = λ 1 u= og dermed T = G λ ()= (λ u) 3 =λ u= σ = T T =λ λ = λ
19 Opgaveløsninger til Eksamensopgaver i Matematik F 19 Opgave 19 a) Sandsynligheden for at slå 1 sekser i første kast er P (X =1)=f(1)= 1 6. Sandsynligheden for først at slå 1 sekser i andet kast er lig sandsynligheden for seksere i første kast, = 5 6, gange sandsynligheden for en sekser i andet kast, eller P (X =)=f()= Generelt er f(x) = 1 6( 56 ) x 1 hvor x =1,, 3,... Fordelingsfunktionen er F (x) =f(1)+ f()+ + f(x) = 1 [ ( ) 5 x 1 ] 6 ( ) 56 n {( ) 56 x ( ) + 56 x+1 + }] = 1 [ 6 n= = 1 [ ( ) 56 n ( ) 6 56 x n= n= =1 ( 5 6 ) x ( 56 ) n ] = 1 6 [ 1 ( 56 ) x ] og det ses umiddelbart, at F (x) 1 =1for x. Desuden fås: P (3 <X 9)= F (9) F (3)= 1 ( 5 6 ) 9 1+ ( 56 ) 3 =.385 b) Den moment-genererende funktion er: De afledede er og dermed G(t) = x=1 ( ) 1 56 x 1 6 e xt = et 6 ( 56 e t) n n= = et = e t 6 et 6 5 e t (for 5e t < 6) G e t (t) = 6 5 e t et ( 5e t ) (6 5 e t ) = 6e t (6 5 e t ) G 6e t (t) = (6 5 e t ) 1et ( 5e t ) (6 5 e t ) 3 = (6 + 5et )6e t (6 5 e t ) 3 µ = X = G ()= 6 ; σ = X X = G () µ =66 36 = 3 Eksperimentet med at slå 4 seksere i højst tre kast med fire terninger, når man efter hvert kast beholder de seksere man har slået, kan ækvivaleres med et eksperiment, hvor man kaster hver af de fire terninger hver for sig. Sandsynligheden for at der er 1 sekser i højst tre kast er F(3)for hver af terningerne, dvs. den ønskede sandsynlighed er P (4 seksere i 3 kast)= [F (3)] 4 = [ 1 ( 5 ) 3 ] 4 ( ) 6 = =.315
20 Opgaveløsninger til Eksamensopgaver i Matematik F Opgave a) Der er 1 forskellige mulige udfald med lige stor sandsynlighed, dvs.: f(x) = 1 1 for x =, 1,,, 9 og for alle andre x. Middelværdien svarende til denne frekvensfunktion er 9 µ x = X = xf(x) =4.5 x= 9 og idet x = 85 fås x= σx = X X = =8.5 σ x =.87 Tælles antal udfald, hvor y(n) =,y(n) = 1,, y(n) = n og divideres med antallet af mulige udfald 1 n fås: P (Y (1) 1)= (1 + 1) 1 1 =. P (Y () )=(1++3) 1 =.6 P (Y (3) 3)=( ) 1 3 =. b) X i er statistisk uafhængige, og ifølge teorem 1 og 3 i.9 ( 3.8 i 7.ed.) gælder derfor generelt n n µ n = µ x = nµ x =4.5n ; σn = σx = nσx σ n =.87 n i=1 Når n 1 kan vi benytte The central limit theorem i 3.3 ( 4.6 i 7.ed.), og dermed at fordelingen er normal med middelværdi µ n og standardafvigelse σ n eller f n (y) = i=1 [ 1 exp 16.5nπ (y 4.5n) 16.5n At finde 95% konfidensintervallet svarer til at bestemme k således, at P (µ n k Y (n) µ n +k) =P ( k σ n Y (n) µ n σ n ] k σ n ) =Φ ( k σn ) 1=.95 og dermed, ifølge tabel A7 A8, at k =1.96σ n. Når n = 1 er µ n = 45 og k = = 178, og dermed bliver konfidensintervallet CONF{43 y(1) 4678}
21 Opgaveløsninger til Eksamensopgaver i Matematik F 1 Opgave 1 a) j x j x j x (x j x) Fra tabellen fås, idet n =5, s = 1 n 1 x = 1 n n j=1 n (x j x) = 8.8 j=1 4 x j = =1. s =1.48 9% konfidensintervallet for µ er bestemt ud fra Student s t-fordelingen med n 1 = 4 frihedsgrader og γ =.9, dvs.: F (c) = 1 (1 + γ) =.95 c =.13 (tabel A9 i 8. og A1 i 7. udgave)og dermed k = sc/ n =1.41. Resultatet er, ifølge Table 3. i 8. udgave af Kreyszig (Table 4.6 i 7. udgave): CONF{x k<µ<x + k} =CONF{8.79 <µ<11.61} b) x-interval b j z-interval e j (b j e j ) x< 7 7 <z< <x< <z< <x< <z< <x< 1.5 <z< <x< <z< <x< <z< <x< <z< <x <z< e j b j er antallet af målepunkter i de forskellige x-intervaller, b j = n = 1. Næste søjle viser de tilsvarende intervaller af z =(x µ)/σ, medµ =1. og σ =.. Fjerde søjle er de udregnede værdier af e j = n[φ(z ) Φ(z 1 )], hvor z 1 og z er intervalendepunkterne, og Φ(z)er den standardiserede normalfordeling opstillet i tabel A7. Antallet af intervaller er K = 8ogfrasidste søjle fås: χ K = (b j e j ) =.69 e j j=1 Dette resultat skal sammenlignes med χ -fordelingen med K r 1=5 frihedsgrader. To frihedsgrader, r =, er udnyttet ved at antage µ = x =1 og σ = s =. Ifølge Table 3.7 (4.1 i 7. udgave)kan hypotesen om at X er normalfordelt accepteres, hvis χ c, hvorc er løsningen til ligningen P (χ c) =1 α =.95. Fra tabel A1 (A11 i 7. udgave)fås, at c =11.7 >χ =.69, og dermed at hypotesen kan accepteres.
22 Opgaveløsninger til Eksamensopgaver i Matematik F Opgave a) De første fire søjler i følgende tabel opstilles: x y x xy y y y Benyttes ligning (7.4)i Supplement til Kreyszig fås fra tabellen, idet n =1 og D = n x i ( x i ) = 85, x k = i yi x i xi y i =.8 D k 1 = n x i y i x i yi =.486 D b) De to sidste søjler i tabellen er udfyldt ved at benytte y i = k + k 1 x i = x i, hvorefter (7.6) (7.8) i supplementet giver: s (y) = 1 (yi y n i ) =.3965 =.496 ; s(y) =.7 8 x s (k )= i D s (y) =.31 ; s(k )=.48 s (k 1 )= n D s (y) =.61 ; s(k 1 )=.78 95% konfidensintervallet for κ 1, og dermed også forκ og µ, er bestemt af Student s t-fordelingen med n = 8 frihedsgrader og γ =.95, dvs.: F (c) = 1 (1 + γ) =.975 c =.31 (tabel A9 i 8. og A1 i 7. udgave). Ifølge tabel 3.1 (4.13 i 7. udgave)og sidste paragraf i supplementet: CONF{ k cs(k ) <κ <k + cs(k )} =CONF{.1 <κ <.1} CONF{ k 1 cs(k 1 ) <κ 1 <k 1 + cs(k 1 )} =CONF{.468 <κ 1 <.54} CONF{ y cs( y ) < µ< y + cs( y )} =CONF{.63 < µ<.73} I sidste linie er y = y i /n =.683 med standardafvigelsen s( y ) = s(y)/ 1 =.. Ifølge hypotesen er κ =,κ 1 =.5, og µ = µ(x)/n =.5x i /1 =.75. Værdierne af κ og κ 1 tilhører 95% konfidensintervallerne, men µ =.75 ligger uden for 95% konfidensintervallet for µ. Benyttes det hertil svarende signifikans-niveau på 5% er svaret ja til at hypotesen kan afvises.
23 Opgaveløsninger til Eksamensopgaver i Matematik F 3 Opgave 3 a) Idet log a +logb =log(ab)og log 1 = 1 fås F (x) =f(1)+ f()+ + f(k)= [log log 1] + + [log(k +1) log k] 3 (k +1) =log =log(k +1) ; k x<k+1 1 k F (x) = for x<1 ; F (x) =F (9)= log 1 = 1 for x 9. Sandsynligheden for at første ciffer er lige er P (k lige)= f()+ f(4)+ f(6)+ f(8)= log 3 log + log 5 log 4 + =log =.3911 Middelværdien er, idet x log k =logk x, b) 9 µ = x = kf(k)= 1[log log 1] + [log 3 log ] + k=1 =log =log19 =3.44 9! k b k e k (b k e k ) b k er antallet af tal der har k som første ciffer, b k = n = 1. Næste søjle er de udregnede værdier forudsagt af Benford fordelingen: e k = nf(k) = 1 log[(k +1)/k]. Antallet af intervaller er K = 9 og fra sidste søjle fås: χ K = (b j e j ) =1.58 e j k=1 Dette resultat skal sammenlignes med χ -fordelingen med K r 1=8 frihedsgrader. r =, da Benford fordelingen er fastlagt på forhånd uden brug af stikprøven. Hypotesen er, at tallene i stikprøven har en fordeling som er i overensstemmelse med Benford fordelingen. Ifølge Table 3.7 (4.1 i 7. udgave)kan hypotesen accepteres, hvis χ c, hvorc er løsningen til ligningen P (χ c) =1 α =.95. Fra tabel A1 (A11 i 7. udgave)fås, at c =15.51 >χ =1.58, og dermed: hypotesen kan ikke afvises. e k
24 Opgaveløsninger til Eksamensopgaver i Matematik F 4 Opgave 4 a) Frekvensfunktionen for Poisson fordelingen er f(x) = µx x! e µ,hvorµ er middelværdien. Udnyttes det at X og Y er statistisk uafhængige fås 3 3 P (Z =3)= P (X = x Y =3 x) = P (X = x)p (Y =3 x) x= x= 3 x 3 3 x = x= x! e (3 x)! e 3 = e 5( ! + 1 3! +! ! 1) =.8333 e 5 =.144 For Poisson fordelingen er variansen lig med middelværdien, og benyttes teorem 1 og 3 i.9 fås: µ = Z = X + Y = X + Y = µ 1 + µ σ = Z Z = σ (x)+σ (y) = µ 1 + µ Z s fordeling tilnærmes med normalfordelingen med µ =5ogσ = 5og ( ) ( ) P (Z =3) Φ Φ 5 5 =Φ(.671) Φ( 1.118)= =.1193 ved brug af lineær interpolation i tabel A7. b) Ligningen xy = 3 har kun de (ikke-negative)heltallige løsningerne (x, y) = (1, 3)og (3,1). Det betyder, at nu er P (Z =3)=P (X =1)P (Y =3)+P (X =3)P (Y =1)=.876 I det generelle tilfælde fås (se også teoremi.9): µ = Z = XY = X Y = µ 1 µ Benyttes X = σ (x)+ X = µ 1 + µ 1 og tilsvarende for Y fås: σ = Z Z = X Y µ 1 µ = X Y µ 1 µ =(µ 1 + µ 1)(µ + µ ) µ 1µ = µ 1 µ (µ 1 + µ +1) Dvs., at i det betragtede tilfælde er µ =6ogσ = 3( )= 6 og ( ) ( ) P (Z =3) Φ Φ = = Alle resultater under a)er i overensstemmelse med at Z = X +Y har Poisson fordelingen med µ = µ 1 + µ,idetp(z =3)= 53 3! e 5. Dette forekommer intuitivt rigtigt og kan let eftervises generelt vha. moment-genererende funktioner. I tilfældet Z = XY er µ σ,ogz har ikke en Poisson fordeling. µ = 5erpå grænsen af hvor normalfordelingstilnærmelsen kan benyttes (især ude i halerne)og den relative fejl er 15% i a). µ er større i b)men den relative fejl er ca. to gange større i dette tilfælde (fordelingen er meget langt fra at være normal).
25 Opgaveløsninger til Eksamensopgaver i Matematik F 5 Opgave 5 a) I følge Supplementet (6.5)har Y en normalfordeling og Y = X 1 X = µ 1 µ (teorem 1 i.9). X 1 og X er uafhængige stokastiske variable med varianserne σ (x 1 )=σ /n 1 og σ (x )=σ /n, hvilket medfører ( 1 σ (y) =σ (x 1 )+σ (x )= σ + 1 ) n 1 n (teorem i.9). Ifølge teorem i 3.3 [tabel 3. eller Supplementet (5.6)] er konfidensintervallerne givet ved { CONF γ x α c α s α µ α x α + c α s } α nα nα og F t (c α )=(1+γ)/, hvor F t er Student s t-fordelingen med n α 1 frihedsgrader. Idet (1 + γ)/ =.975 er c 1 =.78 og c =.6 ifl. tabel A9 og dermed CONF γ {65.96 µ } ; CONF γ {63.38 µ 68.8} b) Idet P ( c T c) =F t (c) F t ( c) =F t (c) 1=γ =.95, hvor F t er Student s t-fordelingen med n 1 + n =13frihedsgraderfås fra tabel A9, at c =.16. Stikprøvens resultat for T er: t = x 1 x (µ 1 µ ) σ, og CONF γ { c t c} 1 σ n + 1 s y 1 n Benyttes s y =(4s 1 +9s )/13 = 18. og indsættes tallene i udtrykkene ovenfor fås, at 95% konfidensintervallet for Y = µ 1 µ bliver CONF γ {1.18 µ 1 µ 11.} Med et signifikans niveau α = 1 γ =.5 er µ 1 µ 1.18, hvilket betyder, at hypotesen µ 1 = µ kan afvises. Bemærk, at det ret store overlap mellem de to konfidensintervaller i a), fra til 68.8, kunne forlede til den modsatte konklusion. Ifølge definitionen i (3)er (n 1 + n )S y/σ =(n 1 1)S 1/σ +(n 1)S /σ De to led på højre side er stokastiske uafhængige størrelser, der har en χ fordeling med henholdsvis n 1 1ogn 1 frihedsgrader [teorem 3 i 3.3, Supplementet (5.13)]. Det betyder at (n 1 + n )S y /σ har en χ fordeling med n 1 1+n 1=n 1 + n frihedsgrader.
26 Opgaveløsninger til Eksamensopgaver i Matematik F 6 Opgave 6 a) De første fire søjler i følgende tabel opstilles: x y x xy y y y y y y Benyttes ligning (7.4)i Supplement til Kreyszig og indsættes tabelværdierne og n =6fås D = n x i ( x i ) = 15 og x k = i yi x i xi y i = D k 1 = n x i y i x i yi =3.9 eller y = x D Femte og sjette søjle i tabellen er udfyldt ved at benytte y i = k + k 1 x i = x i. Fra ligning (7.6)i supplementet fås s (y) = 1 n (yi y i ) = =3.15 ; s(y) =1.76 b) De to sidste søjler i tabellen er udfyldt ved at benytte resultatet af den kvadratiske regressionskurve: y i =(7 7 x +x )/35. Denne regressionskurve har 3 frie parametre og n i (7.6)erstattes af n 3og s (y) = 1 (yi y n 3 i ) =.8 =.761 ; s(y) = % konfidensintervallet for σ(y)bestemmes af χ -fordelingen med n frihedsgrader i det lineære og n 3 frihedsgrader i det kvadratiske tilfælde. Table A1 viser, at F (c 1 )=(1 γ)/ =.5 c 1 =.48 og F (c )= (1 + γ)/ =.975 c =11.14, med 4 frihedsgrader og γ =.95. Benyttes (5.15)i supplementet (med n 1 erstattet med n )fås i det lineære tilfælde: CONF { n γ s (y) <σ (y) < n s (y) } CONF c c γ {1.6 <σ(y) < 5.9} 1 Benyttes den kvadratiske regressionskurve er c 1 =. og c =9.35 (3 frihedsgrader)og dermed CONF { n 3 γ s (y) <σ (y) < n 3 s (y) } CONF c c γ {.16 <σ(y) < 1.} 1 De to konfidensintervaller overlapper ikke, dvs. de to hypoteser forudsiger signifikant forskellige værdier for σ(y) hypotesen, at regressionskurven er lineær, kan afvises. Hvis regressionskurven er lineær vil en antagelse om et ekstra kvadratisk led ikke resultere i en signifikant mindre værdi for σ(y). Omvendt, er regressionskurven kvadratisk, så vil antagelsen af en lineær kurve give et fejlbidrag til s(y)og dermed resultere i en større værdi for σ(y).
27 Opgaveløsninger til Eksamensopgaver i Matematik F 7 Opgave 7 a) De kovariante basisvektorer er givet ved, (19.5)eller (19.53): e i = r u i, dvs. e 1 = r θ =( sinθ, cos θ, ), e = r =(,, 1) z Heraf bestemmes den metriske tensors kovariante komponenter ( g ij = e i e j = 4sin θ +cos ) θ 1 b) Ifølge (19.63)er g ij g jk = δ i k (gij -matricen er den inverse til g ij -matricen): 1 g ij = 4sin θ +cos θ 1 De kontravariante komponenter g ij kan benyttes til at bestemme de kontravariante basisvektorer, e i = g ij e j (nederst side 77): e 1 = g 11 e 1 = ( sinθ, cos θ, ) 4sin θ +cos θ, e = g e =(,, 1) Christoffel symbolet af anden art er defineret, (19.74), Γ k ij = ek e i u j : Γ 1 11 = ( sinθ, cos θ, ) 4sin θ +cos θ og alle de andre 7 komponenter er. c) r s kontravariante komponenter er: ( cosθ, sin θ, )= 3sinθ cos θ 4sin θ +cos θ og dermed r 1 = r e 1 = 3sinθcos θ 4sin θ +cos θ, r = r e = z r 1 θ = 1 sin4 θ 3cos 4 θ +9sin θ cos θ (4 sin θ +cos θ), r z =1 Indsættes fås r i ;i = r1 θ + r z +Γ1 11r 1 =1+ 1 sin4 θ 3cos 4 θ (4 sin θ +cos θ) = 4 (3 sin θ +1)
28 Opgaveløsninger til Eksamensopgaver i Matematik F 8 Opgave 8 a) De kovariante basisvektorer er givet ved (19.5)eller (19.53): e i = r u i, dvs. e 1 = r α =( α, β, ) ; e = r β =(β,α,) ; e 3 = r =(,, 1) γ Heraf bestemmes den metriske tensors kovariante komponenter { } { } α + β gij = ei e j = α + β og g = α + β 1 Ifølge (19.63)er g ij g jk = δ i k (gij -matricen er den inverse til g ij -matricen): 1 { g ij } = { } 1 α + β g ij = 1 α + β 1 b) Indsættes x, y, z i funktionsudtrykket fås: f(α, β, γ) = 1 4 (α + β ) + γ, og dermed v 1 = f α = α(α + β ) ; v = f β = β(α + β ) ; v 3 = f γ =γ v 1 = g 1j v j = α ; v = g j v j = β ; v 3 = g 3j v j =γ Det indre produkt af v med sig selv er v v = v 1 v 1 + v v + v 3 v 3 =(α + β ) +4γ =4f(α, β, γ) og ifølge (19.95)er v = 1 g u i ( gv i ) = = [ 1 { (α α + β + β )α } + { (α + β )β } + { (α + β )γ }] α β γ 1 [ 3α α + β + β +3β + α +(α + β ) ] =6 Benyttes det kartesianske koordinatsystem fås: v = (r r) =(x, y, z), v v =4(x + y + z ), v = ++ = 6 som er de samme resultater som ovenfor. Dette er i overensstemmelse med at v er en 1. ordens tensor og dermed at kontraktionerne v v og v er skalare størrelser, der er uafhængige af koordinattransformationen.
29 Opgaveløsninger til Eksamensopgaver i Matematik F 9 Opgave 9 a) De kovariante basisvektorer er givet ved (19.5)eller (19.53), e i = r u i : e 1 = r α =(β,1) ; e = r β =(α, 1) Heraf bestemmes den metriske tensors kovariante komponenter ( ) { } { } 1+β 1+αβ gij = ei e j = 1+αβ 1+α Indføres e 1 =(c 1,c )giver ortogonalitetsbetingelserne de to ligninger: (1) βc 1 + c =1 og () αc 1 + c =. og benyttes samme fremgangsmåde for e fås løsningerne: e 1 = 1 α β ( 1,α) ; e = 1 (1, β) α β De eneste afledede af de kovariante basisvektorer, der ikke er, er: e 1 u = e 1 β =(1, ); e u 1 = e =(1, ) α Christoffel symbolet af anden art er defineret, (19.74), Γ k ij = e k e i u j,og Γ 1 1 =Γ1 1 = e1 (1, )= 1 α β ; Γ 1 =Γ 1 = e (1, )= 1 α β og de resterende fire: Γ 1 11 =Γ 11 =Γ1 =Γ =. b) De kontravariante komponenter af r = r 1 e 1 + r e er r 1 = r e 1 = 1 [ αβ + α(α + β) ]= α α β og dermed fås: r = α β ; r = r e = β α β ( α α β α ) ( β (α β) + α β β ) (α β) +Γ 1 1 r +Γ 1 r1 = α + β (α β) + β α β 1 α β + α α β 1 α β = Benyttes a = a 1 e 1 +a e fås a 1 =(1, 1) e 1 = α 1 α β og a =(1, 1) e = 1 β α β og T s kontravariante komponenter er givet ved: { T ij } ( = a 1 r 1 a 1 r ) 1 a r 1 a r = (α β) α (α 1) β (α 1) α (1 β) β (1 β)
30 Opgaveløsninger til Eksamensopgaver i Matematik F 3 Opgave 3 a) De kovariante basisvektorer er givet ved (19.5)eller (19.53)e i = r u i e 1 = r cos θ cos φ θ = a cos θ sin φ ; e = r sin θ sin φ sin θ φ = a sin θ cos φ Heraf bestemmes den metriske tensors kovariante komponenter ( ) { } { } a gij = ei e j = a sin θ Basisvektorerne skal opfylde ortonormeringsbetingelsen e i e j = δ j i og det ses uden videre at udtrykkene for e 1 og e medfører at e 1 e =oge e 1 =. Desuden gælder generelt at g = g ij =(e 1 e 1 )(e e ) (e 1 e ) og dermed at e 1 e 1 =1oge e = 1. Det vil sige at alle fire relationer er opfyldt. De kontravariante basisvektorer er e 1 = e 1 a = 1 cos θ cos φ cos θ sin φ ; e e = a sin θ a sin θ = 1 sin φ cos φ a sin θ b) De afledede af de kovariante basisvektorer er e 1 u 1 = a sin θ cos φ sin θ sin φ ; cos θ e 1 u = e cos θ sin φ u 1 = a e sin θ cos φ cos θ cos φ ; u = a sin θ sin φ { } Christoffel symbolerne af. art er defineret Γ k k ij = = e ij k e i u j og { } { } { 1 = sin θ cos θ ; = =cotθ 1 1} mens de resterende fem komponenter er. En direkte udregning viser at R 11 = { { }{ } + θ 1} 1 1 = cot θ θ +cot θ = 1 og idet g 11 =1/g 11 og g =1/g fås R = g ij R ij = 1 a R a sin θ R = a
31 Opgaveløsninger til Eksamensopgaver i Matematik F 31 Opgave 31 Ligningerne fremstiller overfladen af en torus (se figuren), hvis midterlinie er en cirkel med radius a liggende i xy-planet. Torus-rørets tværsnit er en cirkel med radius b, hvorb =.4a på figuren. a) De kovariante basisvektorer er givet ved (19.5)eller (19.53), e i = r u i : e 1 = r θ = b cos θ cos φ cos θ sin φ ; e = r =(a + b sin θ) sin φ cos φ sin θ φ Heraf bestemmes den metriske tensors kovariante komponenter, g ij = e i e j, {g ij } = ( ) b (a + b sin θ) og {g ij } = ( ) b (a + b sin θ) hvor de kontravariante komponenter er udregnet som den inverse matrix, g ik g kj = δ i j eller {gij } = {g ij } 1. De kontravariante basisvektorer er e 1 = g 1j e j = 1 cos θ cos φ cos θ sin φ ; e = g j e b j = sin θ 1 cos sin φ φ a + b sin θ b) En generalisering af (19.56)betyder at i to dimensioner er arealelementet da = gdu 1 du,hvorg er determinanten af {g ij } = b (a + b sin θ),og dermed da = b(a + b sin θ)dθdφ og det totale overfladeareal A = π π b(a + b sin θ)dθdφ = π πab dφ =4π ab De kovariante komponenter af T = r r er T ij = r i r j,hvorr i = r e i.idet r 1 = ab cos θ og r =fås T 11 = r 1 r 1 =(ab) cos θ og T 1 = T 1 = T = Ifølge øverst side 7 i noterne er komponenterne af den kovariante afledede: T ij;k = T ij,k Γ l ikt lj Γ l jkt il De to sidste led bidrager ikke når k =1,og hvorimod T 11;1 = T 11,1 = (ab) sin θ cos θ T 1; = T 1; = Γ 1 T 11 =(a + b sin θ)a b cos 3 θ De resterende 5 komponenter af den kovariante afledede er.
32 Opgaveløsninger til Eksamensopgaver i Matematik F 3 Opgave 3 a) De kovariante basisvektorer i u-koordinatsystemet er, ifølge (19.57): e 1 = r cos φ ρ = sin φ ; e = r ρ sin φ φ = ρ cos φ ; e 3 = r z = 1 De kovariante komponenter af S = r k er S ij = r i k j =(r e i )(k e j ),dvs. x 1 cos φ + x sin φ S = x 1 ρ sin φ + x ρ cos φ = ρ x 3 z Vedensimpelregningfås: ρ = r sin θ ; φ = ψ ; z = r cos θ og fra disse resultater: ρ ρ ρ r θ ψ φ φ φ U = r θ ψ = sin θ rcos θ 1 cos θ r sin θ z r z θ z ψ b) Benyttes ligning (1)i opgaveteksten fås: S = U t S U sin θ cosθ r sin θ sin θ rcos θ = r cos θ r sin θ 1 1 r cos θ cos θ r sin θ = r sin θ rcos θ 1 = r cos θ r sin θ cos θ r sin θ De to transformationsligninger for. ordens tensorer er: T ij = uk u l v i v j T kl ; T ij = vi v j u k u l T kl Den første ligning omsat til matrix notation lyder [T ] ij = kl [U] ki [U] lj [T ] kl = kl [U t ] ik [T ] kl [U] lj =[U t T U] ij i overensstemmelse med (1). Indføres [ V ] ij = vi u j fås i det anden tilfælde [T ] ij = kl [V ] ik [V ] jl [T] kl = kl [V ] ik [T] kl [V t ] lj =[V T V t ] ij igen i overensstemmelse med (1), hvor desuden [U V ] ij = k og dermed V = U 1. [U] ik [V ] kj = k u i v k v k u j = ui u j = δ ij
33 Opgaveløsninger til Eksamensopgaver i Matematik F 33 Opgave 33 a) De kovariante basisvektorer er givet ved (19.5)eller (19.53), e i = r u i : e 1 = r sin θ z cos θ θ = cos θ z sin θ ; e = r sin θ z = cos θ 1 Heraf bestemmes den metriske tensors kovariante komponenter, g ij = e i e j, ( ) {g ij } = 1+z 1 og g = g 1 ij =1+z De kontravariante komponenter er bestemt ved den inverse matrix, idet g ik g kj = δj i eller {gij } = {g ij } 1,dvs. {g ij } = 1 ( ) ( ) g 1 1+z = 1+z 1 1+z b) Relationen g ik g kj = δj i gik g ki = g ik g ik = δi i = (sporet af den todimensionale enhedsmatrix), hvormed fås R = R(z) =g ij R ij g ij = g ij g = g = (1 + z ) Fladens krumning afhænger kun af z, og K = R = 1 (1 + z for z ± ) Benyttes udtrykket øverst side 7 i noterne for de kovariante afledede af de kontravariante komponenter af en anden ordens tensor fås, at divergensen { } { } R ij i ;j = Rij,j + R lj lj j + R lj il = R ij,j + 1 ({ } { } ) i g g lj lj j + g lj il Den tilsvarende afledede af den metriske tensor g ij ;j =,ogdermeder R ij ;j = ( ) g ij u j g + 1g ( ) ( ) gij u j = g ij 1 u j g Idet g kun afhænger af u = z fås at: R 1j ;j = ( ) 1 g1 z g R j ;j = g z og dermed at: ( 1 g ) = 1 1+z z = 1+z 1+z z ( ) 1 (1 + z ) = ( ) 1 (1 + z ) 8z (1 + z ) 4 = 8z(1 + z ) (1 + z ) 4 g 1i R ij ;j =g 11 R1j ;j +g 8z 1 Rj ;j =(1+z ) (1 + z ) z(1 + z ) (1 + z ) 4 = g i R ij ;j = 1 8z (1 + z ) 4 + 8z(1 + z ) (1 + z ) 4 = 16z (1 + z ) 3 = R (z) og, idet R ;1 = R,1 = R/ θ =ogr ; = R, = R/ z = R (z),errelationen i opgaveteksten eftervist.
34 Opgaveløsninger til Eksamensopgaver i Matematik F 34 Opgave 34 a) De kovariante basisvektorer er givet ved (19.5)eller (19.53), e i = r u i : e 1 = r θ = a sin θ b cos θ ; e = r z = 1 Heraf bestemmes den metriske tensors kovariante komponenter, g ij = e i e j, ( {g ij } = a sin +b cos ) θ og dermed 1 (ds) = g ij du i du j =(a sin θ + b cos θ)(dθ) +(dz) Ifølge (1)er f (θ) =a sin θ+b cos θ og dz = z (θ)dθ = ci (θ)dθ = cf(θ)dθ og dermed (ds) = f (θ)(dθ) +[cf(θ)dθ] =(1+c )f (θ)(dθ) ds = ± 1+c f(θ)dθ s(θ) =± 1+c I(θ) s (θ) =(1+c )I (θ) [s(θ )=] b) Idet t θ du 1 /dt = dθ/dθ =1ogd u 1 /dt = bliver differentialligningerne for den geodætiske kurve: { 1 = 11} ṡ (i =1); s Ifølge regningerne under punkt a)er d z dθ = ṡ dz s dθ (i =) ṡ = ds dθ = ± 1+c f(θ) s = d s dθ = ± 1+c f (θ) og dermed (der gælder samme fortegn i de to ligninger), s ṡ = f { } (θ) f(θ) = 111 i overensstemmelse med differentialligningen i tilfældet i = 1. Ifølge(1)er z(θ) =z + ci(θ)som medfører at z (θ) =cf(θ)og z (θ) =cf (θ), hvormed den anden differentialligning også er opfyldt. I tilfældet a =,b=1er dvs. z 1 = z(θ 1 )=z + ci(π) =+ci(π) =1 c =1/I(π) s = s (θ 1 )=(1+c )I (π) =I (π)+1= s =4.946
35 Opgaveløsninger til Eksamensopgaver i Matematik F 35 Opgave 35 a) For en fastholdt værdi af ψ beskriver r overfladen af en tredimensional kugle med centrum i (,, )og radius A sin ψ i det tredimensionale rum udspændt af de tre første koordinater: x + y + z = A sin ψ. De kovariante basisvektorer er givet ved (19.5)eller (19.53), e i = r u i : e 1 = A( sin φ sin θ sin ψ, cos φ sin θ sin ψ,, ) e = A(cosφcos θ sin ψ, sin φ cos θ sin ψ, sin θ sin ψ, ) e 3 = A(cosφsin θ cos ψ, sin φ sin θ cos ψ, cos θ cos ψ, sin ψ) Heraf bestemmes den metriske tensors kovariante komponenter, g ij = e i e j, {g ij } = A sin θ sin ψ A sin ψ A b) Det differentielle volumenelement er dv = gdu 1 du du 3,hvorg er determinaten af g ij -matricen, dvs. g = A 6 sin θ sin 4 ψ og dermed dv = A 3 sin θ sin ψdφdθdψ Det totale volumen er π π π V = A 3 dφ sin θdθ sin ψdψ= A 3 π π =π A 3 Relationen R ij = (/A )g ij medfører at R = g ij R ij = A gij g ij = A δi i = 6 A Bemærk, at δi i betyder sporet af den tredimensionale enhedsmatrix. Resultatet kan også fås ved direkte indsættelse af g ij bestemt som den inverse matrix af {g ij }. Rummets krumning er i dette tilfælde givet ved R/6 som er konstant. En vilkårlig vektor v der tilhører overfladen kan skrives v = v i e i,hvorv i er vektorens kontravariante komponenter. Ved en direkte udregning fås r e 1 = A [ cos φ sin φ sin θ sin ψ +cosφsin φ sin θ sin ψ]= r e = A [(cos φ +sin φ)cos θ sin θ sin ψ cos θ sin θ sin ψ]= r e 3 = A [(cos φ +sin φ)sin θ sin ψ cos ψ +cos θ sin ψ cos ψ sin ψ cos ψ] = Resultatet r e i =betyder,atr v = v i (r e i )= og dermed at de to vektorer r og v er vinkelrette på hinanden.
36 Opgaveløsninger til Eksamensopgaver i Matematik F 36 Opgave 36 a) De kovariante basisvektorer er givet ved (19.5)eller (19.53), e i = r u i : e 1 = r t = cos θ sin θ ; e = r θ = t sin θ t cos θ k Heraf bestemmes den metriske tensors kovariante komponenter, g ij = e i e j, {g ij } = ( 1 ) t + k og {g ij } = ( 1 ) (t + k ) 1 hvor de kontravariante komponenter er udregnet som den inverse matrix, g ik g kj = δ i j eller {gij } = {g ij } 1. De kontravariante basisvektorer er e 1 = g 1j e j = cos θ sin θ ; e = g j e j = 1 t + k t sin θ t cos θ k b) De afledede af de kovariante basisvektorer er e 1 u 1 = e ; 1 u = e u 1 = sin θ e cos θ ; u = t { } Christoffel symbolerne af. art er defineret Γ k k ij = = e ij k e i u j { } 1 = t ; mens de resterende fem komponenter er. Ifølge øverst side 7 i Tensors er og dermed R ;1 = R t R ij;k = R ij,k { } { } 1 1 = = { } { } l l R ik lj R jk il { } { } l l R 1 l R 1 l = R t = k t (t + k ) t t + k k t t + k cos θ sin θ og { R 1} t + k = 4k t (t + k )
37 Opgaveløsninger til Eksamensopgaver i Matematik F 37 Opgave 37 a) De inverse elementer er: Q 1 = {1, 1, i, i, j, j, k, k}. Idet (±i) = 1 fås at (±i) 4 = 1 (og tilsvarende for j og k),dvs.atde6 elementer ±i, ±j, ±k har ordenen 4. 1 har ordenen (og 1 har ordenen 1). Konjugationsklasser: ±1 kommuterer med alle elementer, og dermed udgør 1 og 1 hver sin egen konjugationsklasse. Desuden er j 1 ij = jij = jk = i og kik = jk = i, som medfører, at i og i er i samme konjugationsklasse og, at de to elementer ikke er i klasse med andre (analogt for j og k). Der er alt i alt 5 konjugationsklasser: K(1)= {1}; K( 1)= { 1}; K(i) ={i, i}; K(j) ={j, j}; K(k) ={k, k} b) Undergruppernes orden er divisor i r =8 h = eller 4, og de er 1 undergruppe af orden : {1, 1}. 3 undergrupper af orden 4: {1,i, 1, i}, {1,j, 1, j} og {1,k, 1, k}. Alle 4 (egentlige)undergrupper er invariante, fordi hver af dem kun indeholder hele konjugationsklasser. [De tre 4. ordens undergrupper har index og må derfor være invariante]. Antallet af ikke-ækvivalente irreducible repræsentationer = antallet af konjugationsklasser = 5. Repræsentationernes grader, n 1 -n 5, bestemmes af n 1 + n + n 3 + n 4 + n 5 = r =8 som har løsningen n 1 = n = n 3 = n 4 =1, n 5 =. Karaktertavle: K(1) K( 1)K(i) K(j) K(k) A A A A E Kommentarer til karaktertavlen: 1) χ(1)= n i )Alle konjugationsklasser indeholder både et element og dets inverse alle karakterer er reelle, og i de éndimensionale tilfælde er χ A = ±1. 3)Ortogonalitet af rækker χ A ( 1)= χ A (1)= 1 er eneste løsning, og de resterende éndimensionale karakterer er derefter bestemt ved at benytte χ A = +1 eller 1. 4) χ E udfyldes (for eksempel)ved at udnytte ortogonalitet af søjler.
38 Opgaveløsninger til Eksamensopgaver i Matematik F 38 Opgave 38 a) G s Cayley-tavle (indgangssøjlen er venstre faktor i produkterne): E I A 1 A B 1 B C 1 C E E I A 1 A B 1 B C 1 C I I E A A 1 B B 1 C C 1 A 1 A 1 A I E C C 1 B 1 B A A A 1 E I C 1 C B B 1 B 1 B 1 B C 1 C E I A 1 A B B B 1 C C 1 I E A A 1 C 1 C 1 C B B 1 A A 1 E I C C C 1 B 1 B A 1 A I E b) Af tavlen fremgår det at elementerne {I, B 1,B,C 1,C } har ordenen og {A 1,A } har ordenen 4. Der er 3 undergrupper af 4. orden: H A = {E, A 1,I,A } C 4 H B = {E, I, B 1,B } C C H C = {E, I, C 1,C } C C c) A 1 og A tilhører samme konjugationsklasse, da fx B1 1 A 1B 1 = B 1 A 1 B 1 = A, og da de er de eneste elementer af 4. orden er der ikke andre elementer i denne klasse, sætning (4.4). Alle elementerne af. orden er beskrevet ved unitære matricer, idet der for disse elementer gælder at U = U 1 og at U = U,ogdermedatU 1 = U. For de to 4. ordens elementer gælder, at A 1 1 = A = A 1, og tilsvarende for A. ( ) Repræsentationen er irreducibel: Indføres en generel matrix T = t1 t t 3 t 4 som antages at kommuterer med alle matricerne i repræsentationen har vi: TC 1 = C 1 T t = t,t 3 = t 3 og dermed at t = t 3 =,hvorefter TA 1 = A 1 T t 1 = t 4. Dermed er den eneste matrix T der kommuterer med alle repræsentationens matricer lig med en konstant gange enhedsmatricen, hvilket er en tilstrækkelig betingelse [sætning (1.6) (1.8)] for at repræsentationen er irreducibel. Karakteren af de forskellige elementer er givet ved sporet af matricerne, dvs. χ(e) =, χ(i) = og χ(a 1 )=χ(a )=χ(b 1 )=χ(b )=χ(c 1 )=χ(c )=
39 Opgaveløsninger til Eksamensopgaver i Matematik F 39 Opgave 39 a) b i b i = a i+i = a = e, som betyder, at b 1 i = b i og at ordenen af de forskellige elementer er: 1. orden: e ;. orden: b 1,b,b 3,b 4,b 5 ; 5. orden: a, a,a 3,a 4. Udregning af de 4 konjugationer giver: a p a q a p = a q b 1 p a q b p = b p a q b p = b p b q+p = a p+4q+p = a 4q = a q a p b q a p = a p b q+3p = b p+q b 1 p b q b p = b p a q+p = b p 6q+6p = b p q Resultaterne viser at G s konjugationsklasser er K e = {e} ; K a = {a, a 4 } ; K a = {a,a 3 } ; K b = {b 1,b,b 3,b 4,b 5 } b) Antallet af ikke-ækvivalente irreducible repræsentationer = antallet af konjugationsklasser = 4. Repræsentationernes grader n 1 -n 4 bestemmes af n 1 + n + n 3 + n 4 = r =1, som har løsningen n 1 = n =1og n 3 = n 4 =. Karaktertavle: K e K a K a 5K b A A E 1 x 1 y 1 z 1 E x y z Kommentarer til karaktertavlen: 1) χ(1)= n i )Alle konjugationsklasser indeholder både et element og dets inverse alle karakterer er reelle, og i de éndimensionale tilfælde er χ A = ±1. 3)Ortogonalitet af de to første rækker χ A (K b )= 1 er eneste løsning. De resterende 6 ubekendte kan bestemmes på følgende måde: Normering af sidste søjle: 5[1 +( 1) + z1 + z ]=1 z 1 = z =. Ortogonalitet af 1. og. søjle: x 1 +x = x = 1 x 1 Normering af. søjle: [ x 1 + x ] = 1, som ved indsættelse af x giver x 1 + x 1 1= x 1 = α = 5 1 x = 1 α = 5+1 (andengradsligningen har rødderne α og 1 α og valget x 1 = 1 α vil kun betyde en ombytning af de to sidste rækker i karaktertavlen). y 1 og y bestemmes af de to samme ligninger. Benyttes fx at 1. og 3./4. række skal være ortogonale fås, at x 1 = α medfører: y 1 = 1 α = 5+1 og y = α = 5 1.
40 Opgaveløsninger til Eksamensopgaver i Matematik F 4 Opgave 4 a) G s Cayley-tavle: g 1 g g 3 g 4 g 5 g 6 g 1 g 1 g g 3 g 4 g 5 g 6 g g g 4 g 6 g 1 g 3 g 5 g 3 g 3 g 6 g g 5 g 1 g 4 g 4 g 4 g 1 g 5 g g 6 g 3 g 5 g 5 g 3 g 1 g 6 g 4 g g 6 g 6 g 5 g 4 g 3 g g 1 Det fremgår umiddelbart af tabellen, at e = g 1 = g1 1 ; g 1 = g 4 ; g3 1 = g 5 ; g4 1 = g ; g5 1 = g 3 ; g6 1 = g 6 g 1 har ordenen 1 ; g 6 har ordenen ; g og g 4 har ordenen 3 ;ogg 3 og g 5 har ordenen 6. G indeholder elementer, g 3 og g 5, som har samme orden som gruppen selv, og dermed er G cyklisk med ordenen r = 6 (og g 3 eller g 5 er gruppens frembringer). De ikke-trivielle undergrupper har ordenen h = eller 3 (h er divisor i r = 6). g 3 eller g 5 kan ikke være elementer i en undergruppe. Det betyder, at de eneste undergrupper er G = {g 1,g 6 } G 3 = {g 1,g,g 4 } og de er begge invariante, fordi gruppen G er kommutativ, g i g j = g j g i. De to undergrupper opfylder betingelserne i sætning (8.)i gruppeteorinoterne. G og G 3 er invariante undergrupper med fællesmængden {g 1 = e} og G G 3 = {g 1, g, g 4, g 6 g 1 = g 6, g 6 g = g 5, g 6 g 4 = g 3 } = G. Dermed er G G G 3. b) Idet G er en Abelsk gruppe danner alle elementer deres egen konjugationsklasse (gi 1 g j g i = g j ). Dvs. antallet af konjugationsklasser = r = 6. Antallet af ikke-ækvivalente irreducible repræsentationer = antallet af konjugationsklasser = 6. Repræsentationernes grader n 1 -n 6 bestemmes af n i = r = 6, som har løsningen n 1 = n = = n 6 =1. De 6 irreducible éndimensionale repræsentationer er: g 1 g g 3 g 4 g 5 g 6 f f 1 ω ω ω 4 ω 5 1 f 3 1 ω 4 ω ω ω 4 1 f f 5 1 ω ω 4 ω 4 ω 1 f 6 1 ω 4 ω 5 ω ω 1 hvor ω = e iπ/3 ;ogf og f 6 er tro repræsentationer.
Opgaveløsninger til Eksamensopgaver i Matematik F2 1. Den fjerde afledede regnes for konstant i intervallet [f (4) (t) =M 4 = 24] og dermed er:
![Opgaveløsninger til Eksamensopgaver i Matematik F2 1. Den fjerde afledede regnes for konstant i intervallet [f (4) (t) =M 4 = 24] og dermed er: Opgaveløsninger til Eksamensopgaver i Matematik F2 1. Den fjerde afledede regnes for konstant i intervallet [f (4) (t) =M 4 = 24] og dermed er:](/thumbs/99/142205454.jpg) Opgaveløsninger til Eksamensopgaver i Matematik F Opgave a) Simpsons algoritme med m =6ogh =.: som medfører at s = f + f 6 =3.356 s = f + f 3 + f 5 =4.4737 s = f + f 4 =.899 J = h 3 (s +4s +s )=.89996
Opgaveløsninger til Eksamensopgaver i Matematik F Opgave a) Simpsons algoritme med m =6ogh =.: som medfører at s = f + f 6 =3.356 s = f + f 3 + f 5 =4.4737 s = f + f 4 =.899 J = h 3 (s +4s +s )=.89996
Eksamensopgaver i Matematik F2
 Eksamensopgaver i Matematik F2 I. Numeriske metoder og Laplace transformation Opgave 1 (V 97/98) Funktionen f(x) er beskrevet ved følgende tabel [f j = f(x j )]: j x j f j 0 0 1.00000 1 0.1 1.11110 2 0.2
Eksamensopgaver i Matematik F2 I. Numeriske metoder og Laplace transformation Opgave 1 (V 97/98) Funktionen f(x) er beskrevet ved følgende tabel [f j = f(x j )]: j x j f j 0 0 1.00000 1 0.1 1.11110 2 0.2
Eksamensopgaver i Matematik F2
 Eksamensopgaver i Matematik F2 I. Numeriske metoder og Laplace transformation Opgave 1 (V 97/98) Funktionen f(x) er beskrevet ved følgende tabel [f j = f(x j )]: j x j f j 0 0 1.00000 1 0.1 1.11110 2 0.2
Eksamensopgaver i Matematik F2 I. Numeriske metoder og Laplace transformation Opgave 1 (V 97/98) Funktionen f(x) er beskrevet ved følgende tabel [f j = f(x j )]: j x j f j 0 0 1.00000 1 0.1 1.11110 2 0.2
Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 2016
 Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Landmålingens fejlteori - Lektion 2. Sandsynlighedsintervaller Estimation af µ Konfidensinterval for µ. Definition: Normalfordelingen
 Landmålingens fejlteori Lektion Sandsynlighedsintervaller Estimation af µ Konfidensinterval for µ - rw@math.aau.dk Institut for Matematiske Fag Aalborg Universitet En stokastisk variabel er en variabel,
Landmålingens fejlteori Lektion Sandsynlighedsintervaller Estimation af µ Konfidensinterval for µ - rw@math.aau.dk Institut for Matematiske Fag Aalborg Universitet En stokastisk variabel er en variabel,
Elementær sandsynlighedsregning
 Elementær sandsynlighedsregning Sandsynlighedsbegrebet Et udfaldsrum S er mængden af alle de mulige udfald af et eksperiment. En hændelse A er en delmængde af udfaldsrummet S. Den hændelse, der ikke indeholder
Elementær sandsynlighedsregning Sandsynlighedsbegrebet Et udfaldsrum S er mængden af alle de mulige udfald af et eksperiment. En hændelse A er en delmængde af udfaldsrummet S. Den hændelse, der ikke indeholder
Elementær sandsynlighedsregning
 Elementær sandsynlighedsregning Sandsynlighedsbegrebet Et udfaldsrum S er mængden af alle de mulige udfald af et eksperiment. En hændelse A er en delmængde af udfaldsrummet S. Et sandsynlighedsmål er en
Elementær sandsynlighedsregning Sandsynlighedsbegrebet Et udfaldsrum S er mængden af alle de mulige udfald af et eksperiment. En hændelse A er en delmængde af udfaldsrummet S. Et sandsynlighedsmål er en
Den todimensionale normalfordeling
 Den todimensionale normalfordeling Definition En todimensional stokastisk variabel X Y siges at være todimensional normalfordelt med parametrene µ µ og når den simultane tæthedsfunktion for X Y kan skrives
Den todimensionale normalfordeling Definition En todimensional stokastisk variabel X Y siges at være todimensional normalfordelt med parametrene µ µ og når den simultane tæthedsfunktion for X Y kan skrives
Teoretisk Statistik, 9 marts nb. Det forventes ikke, at alt materialet dækkes d. 9. marts.
 Teoretisk Statistik, 9 marts 2005 Empiriske analoger (Kap. 3.7) Normalfordelingen (Kap. 3.12) Opsamling på Kap. 3 nb. Det forventes ikke, at alt materialet dækkes d. 9. marts. 1 Empiriske analoger Betragt
Teoretisk Statistik, 9 marts 2005 Empiriske analoger (Kap. 3.7) Normalfordelingen (Kap. 3.12) Opsamling på Kap. 3 nb. Det forventes ikke, at alt materialet dækkes d. 9. marts. 1 Empiriske analoger Betragt
DesignMat Uge 1 Gensyn med forårets stof
 DesignMat Uge 1 Gensyn med forårets stof Preben Alsholm Efterår 2010 1 Hovedpunkter fra forårets pensum 11 Taylorpolynomium Taylorpolynomium Det n te Taylorpolynomium for f med udviklingspunkt x 0 : P
DesignMat Uge 1 Gensyn med forårets stof Preben Alsholm Efterår 2010 1 Hovedpunkter fra forårets pensum 11 Taylorpolynomium Taylorpolynomium Det n te Taylorpolynomium for f med udviklingspunkt x 0 : P
Besvarelser til Calculus Ordinær Eksamen Juni 2019
 Besvarelser til Calculus Ordinær Eksamen - 14. Juni 2019 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 14. Juni 2019 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Institut for Matematiske Fag Aalborg Universitet Specielt: Var(aX) = a 2 VarX 1/40. Lad X α, X β og X γ være stokastiske variable (vinkelmålinger) med
 Repetition: Varians af linear kombination Landmålingens fejlteori Lektion 5 Fejlforplantning - rw@math.aau.dk Antag X 1, X,..., X n er uafhængige stokastiske variable, og Y er en linearkombination af X
Repetition: Varians af linear kombination Landmålingens fejlteori Lektion 5 Fejlforplantning - rw@math.aau.dk Antag X 1, X,..., X n er uafhængige stokastiske variable, og Y er en linearkombination af X
Overheads til forelæsninger, mandag 5. uge På E har vi en mængde af mulige sandsynlighedsfordelinger for X, (P θ ) θ Θ.
 Statistiske modeller (Definitioner) Statistik og Sandsynlighedsregning 2 IH kapitel 0 og En observation er en vektor af tal x (x,..., x n ) E, der repræsenterer udfaldet af et (eller flere) eksperimenter.
Statistiske modeller (Definitioner) Statistik og Sandsynlighedsregning 2 IH kapitel 0 og En observation er en vektor af tal x (x,..., x n ) E, der repræsenterer udfaldet af et (eller flere) eksperimenter.
Definition: Normalfordelingen. siges at være normalfordelt med middelværdi µ og varians σ 2, hvor µ og σ er reelle tal og σ > 0.
 Landmålingens fejlteori Lektion 2 Transformation af stokastiske variable - kkb@math.aau.dk http://people.math.aau.dk/ kkb/undervisning/lf12 Institut for Matematiske Fag Aalborg Universitet Repetition:
Landmålingens fejlteori Lektion 2 Transformation af stokastiske variable - kkb@math.aau.dk http://people.math.aau.dk/ kkb/undervisning/lf12 Institut for Matematiske Fag Aalborg Universitet Repetition:
Eksamen i Mat F, april 2006
 Eksamen i Mat F, april 26 Opgave 1 Lad F være et vektorfelt, givet i retvinklede koordinater som: F x x F = F x i + F y j + F z k = F y = 2z F z y Udregn F og F: F = F x + F y + F z = 1 + +. F = F z F
Eksamen i Mat F, april 26 Opgave 1 Lad F være et vektorfelt, givet i retvinklede koordinater som: F x x F = F x i + F y j + F z k = F y = 2z F z y Udregn F og F: F = F x + F y + F z = 1 + +. F = F z F
Kvantitative Metoder 1 - Forår Dagens program
 Dagens program Afsnit 6.1 Den standardiserede normalfordeling Normalfordelingen Beskrivelse af normalfordelinger: - Tæthed og fordelingsfunktion - Middelværdi, varians og fraktiler Lineære transformationer
Dagens program Afsnit 6.1 Den standardiserede normalfordeling Normalfordelingen Beskrivelse af normalfordelinger: - Tæthed og fordelingsfunktion - Middelværdi, varians og fraktiler Lineære transformationer
Landmålingens fejlteori - Lektion 2 - Transformation af stokastiske variable
 Landmålingens fejlteori Lektion 2 Transformation af stokastiske variable - kkb@math.aau.dk http://people.math.aau.dk/ kkb/undervisning/lf12 Institut for Matematiske Fag Aalborg Universitet 1/31 Repetition:
Landmålingens fejlteori Lektion 2 Transformation af stokastiske variable - kkb@math.aau.dk http://people.math.aau.dk/ kkb/undervisning/lf12 Institut for Matematiske Fag Aalborg Universitet 1/31 Repetition:
Kvantitative Metoder 1 - Efterår Dagens program
 Dagens program Afsnit 6.1. Ligefordelinger, fra sidst Den standardiserede normalfordeling Normalfordelingen Beskrivelse af normalfordelinger: - Tæthed og fordelingsfunktion - Middelværdi, varians og fraktiler
Dagens program Afsnit 6.1. Ligefordelinger, fra sidst Den standardiserede normalfordeling Normalfordelingen Beskrivelse af normalfordelinger: - Tæthed og fordelingsfunktion - Middelværdi, varians og fraktiler
Produkt og marked - matematiske og statistiske metoder
 Produkt og marked - matematiske og statistiske metoder Rasmus Waagepetersen Institut for Matematiske Fag Aalborg Universitet February 19, 2016 1/26 Kursusindhold: Sandsynlighedsregning og lagerstyring
Produkt og marked - matematiske og statistiske metoder Rasmus Waagepetersen Institut for Matematiske Fag Aalborg Universitet February 19, 2016 1/26 Kursusindhold: Sandsynlighedsregning og lagerstyring
GEOMETRI-TØ, UGE 3. og resultatet følger fra [P] Proposition 2.3.1, der siger, at
![GEOMETRI-TØ, UGE 3. og resultatet følger fra [P] Proposition 2.3.1, der siger, at GEOMETRI-TØ, UGE 3. og resultatet følger fra [P] Proposition 2.3.1, der siger, at](/thumbs/50/26870860.jpg) GEOMETRI-TØ, UGE 3 Hvis I falder over tryk- eller regne-fejl i nedenstående, må I meget gerne sende rettelser til fuglede@imf.au.dk. Opvarmningsopgave 1. Lad γ : (α, β) R 2 være en regulær kurve i planen.
GEOMETRI-TØ, UGE 3 Hvis I falder over tryk- eller regne-fejl i nedenstående, må I meget gerne sende rettelser til fuglede@imf.au.dk. Opvarmningsopgave 1. Lad γ : (α, β) R 2 være en regulær kurve i planen.
Sandsynlighedsregning
 Mogens Bladt www2.imm.dtu.dk/courses/02405 21. September, 2007 Lidt om binomialkoefficienter n størrelsen af en mængde/population. Vi ønsker at udtage en sub population af størrelse r. To sub populationer
Mogens Bladt www2.imm.dtu.dk/courses/02405 21. September, 2007 Lidt om binomialkoefficienter n størrelsen af en mængde/population. Vi ønsker at udtage en sub population af størrelse r. To sub populationer
Wigner s semi-cirkel lov
 Wigner s semi-cirkel lov 12. december 2009 Eulers Venner Steen Thorbjørnsen Institut for Matematiske Fag Århus Universitet Diagonalisering af selvadjungeret matrix Lad H være en n n matrix med komplekse
Wigner s semi-cirkel lov 12. december 2009 Eulers Venner Steen Thorbjørnsen Institut for Matematiske Fag Århus Universitet Diagonalisering af selvadjungeret matrix Lad H være en n n matrix med komplekse
EKSAMENSOPGAVELØSNINGER CALCULUS 2 (2005) JANUAR 2006 AARHUS UNIVERSITET.. Beregn den retningsafledede D u f(0, 0).
 EKSAMENSOPGAVELØSNINGER CALCULUS 2 (2005) JANUAR 2006 AARHUS UNIVERSITET H.A. NIELSEN & H.A. SALOMONSEN Opgave. Lad f betegne funktionen f(x, y) = x cos(y) + y sin(x). ) Angiv gradienten f. 2) Lad u betegne
EKSAMENSOPGAVELØSNINGER CALCULUS 2 (2005) JANUAR 2006 AARHUS UNIVERSITET H.A. NIELSEN & H.A. SALOMONSEN Opgave. Lad f betegne funktionen f(x, y) = x cos(y) + y sin(x). ) Angiv gradienten f. 2) Lad u betegne
Eksamen i Calculus. 14. juni f (x, y, z) = 1 + x 2 + y 2. Hele rummet uden z aksen
 Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 14. juni 019 Opgave 1 (6 point) En
Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 14. juni 019 Opgave 1 (6 point) En
Eksamen i Calculus. 14. juni f (x, y, z) = 1 + x 2 + y 2. x 2 + y 2 1 Hele rummet uden z aksen
 Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 14. juni 19 Opgave 1 (6 point) En funktion
Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 14. juni 19 Opgave 1 (6 point) En funktion
Kursusindhold: Produkt og marked - matematiske og statistiske metoder. Monte Carlo
 Kursusindhold: Produkt og marked - matematiske og statistiske metoder Rasmus Waagepetersen Institut for Matematiske Fag Aalborg Universitet Sandsynlighedsregning og lagerstyring Normalfordelingen og Monte
Kursusindhold: Produkt og marked - matematiske og statistiske metoder Rasmus Waagepetersen Institut for Matematiske Fag Aalborg Universitet Sandsynlighedsregning og lagerstyring Normalfordelingen og Monte
Kortfattet svar til eksamen i Matematik F2 d. 21. juni 2017
 Kortfattet svar til eksamen i Matematik F2 d. 2. juni 27 Opgave Bestem for følgende tilfælde om en funktion f(z) af z = x + iy er analytisk i dele af den komplekse plan, hvis den har real del u(x, y) og
Kortfattet svar til eksamen i Matematik F2 d. 2. juni 27 Opgave Bestem for følgende tilfælde om en funktion f(z) af z = x + iy er analytisk i dele af den komplekse plan, hvis den har real del u(x, y) og
Sandsynlighed og Statistik
 36 Sandsynlighed og Statistik 6.1 Indledning Denne note beskriver de statistiske begreber og formler som man med rimelig sandsynlighed kan komme ud for i eksperimentelle øvelser. Alt er yderst korfattet,
36 Sandsynlighed og Statistik 6.1 Indledning Denne note beskriver de statistiske begreber og formler som man med rimelig sandsynlighed kan komme ud for i eksperimentelle øvelser. Alt er yderst korfattet,
Eksamen i Matematik F2 d. 19. juni Opgave 2. Svar. Korte svar (ikke fuldstændige)
 Eksamen i Matematik F2 d. 9. juni 28 Korte svar (ikke fuldstændige Opgave Find realdelen, Re z, og imaginærdelen, Im z, for følgende værdier af z, a z = 2 i b z = i i c z = ln( + i Find realdelen, Re z,
Eksamen i Matematik F2 d. 9. juni 28 Korte svar (ikke fuldstændige Opgave Find realdelen, Re z, og imaginærdelen, Im z, for følgende værdier af z, a z = 2 i b z = i i c z = ln( + i Find realdelen, Re z,
Besvarelser til Calculus Ordinær Eksamen - 5. Januar 2018
 Besvarelser til Calculus Ordinær Eksamen - 5. Januar 18 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 5. Januar 18 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Reeksamen 2014/2015 Mål- og integralteori
 Reeksamen 4/5 Mål- og integralteori Københavns Universitet Institut for Matematiske Fag Formalia Eksamensopgaven består af 4 opgaver med ialt spørgsmål. Ved bedømmelsen indgår de spørgsmål med samme vægt.
Reeksamen 4/5 Mål- og integralteori Københavns Universitet Institut for Matematiske Fag Formalia Eksamensopgaven består af 4 opgaver med ialt spørgsmål. Ved bedømmelsen indgår de spørgsmål med samme vægt.
Besvarelser til Calculus Ordinær Eksamen - 3. Januar 2017
 Besvarelser til Calculus Ordinær Eksamen - 3. Januar 17 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 3. Januar 17 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Landmålingens fejlteori Lektion 1 Det matematiske fundament Kontinuerte stokastiske variable
 Landmålingens fejlteori Lektion 1 Det matematiske fundament Kontinuerte stokastiske variable - rw@math.aau.dk Institut for Matematiske Fag Aalborg Universitet 1/41 Landmålingens fejlteori - lidt om kurset
Landmålingens fejlteori Lektion 1 Det matematiske fundament Kontinuerte stokastiske variable - rw@math.aau.dk Institut for Matematiske Fag Aalborg Universitet 1/41 Landmålingens fejlteori - lidt om kurset
Kursusindhold: Produkt og marked - matematiske og statistiske metoder. Monte Carlo
 Kursusindhold: Produkt og marked - matematiske og statistiske metoder Rasmus Waagepetersen Institut for Matematiske Fag Aalborg Universitet Sandsynlighedsregning og lagerstyring Normalfordelingen og Monte
Kursusindhold: Produkt og marked - matematiske og statistiske metoder Rasmus Waagepetersen Institut for Matematiske Fag Aalborg Universitet Sandsynlighedsregning og lagerstyring Normalfordelingen og Monte
Besvarelser til Calculus Ordinær Eksamen Juni 2018
 Besvarelser til Calculus Ordinær Eksamen - 5. Juni 08 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 5. Juni 08 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Kvantitative Metoder 1 - Forår 2007
 Dagens program Kapitel 8.7, 8.8 og 8.10 Momenter af gennemsnit og andele kap. 8.7 Eksempel med simulationer Den centrale grænseværdisætning (Central Limit Theorem) kap. 8.8 Simulationer Normalfordelte
Dagens program Kapitel 8.7, 8.8 og 8.10 Momenter af gennemsnit og andele kap. 8.7 Eksempel med simulationer Den centrale grænseværdisætning (Central Limit Theorem) kap. 8.8 Simulationer Normalfordelte
DESIGNMAT FORÅR 2012: UGESEDDEL Forberedelse Læs alle opgaverne fra tidligere ugesedler, og læg særlig mærke til dem du har spørgsmål til.
 DESIGNMAT FORÅR 2012: UGESEDDEL 13 INSTITUT FOR MATEMATIK 1. Forberedelse Læs alle opgaverne fra tidligere ugesedler, og læg særlig mærke til dem du har spørgsmål til. 2. Aktiviteter mandag 13 17 2.1.
DESIGNMAT FORÅR 2012: UGESEDDEL 13 INSTITUT FOR MATEMATIK 1. Forberedelse Læs alle opgaverne fra tidligere ugesedler, og læg særlig mærke til dem du har spørgsmål til. 2. Aktiviteter mandag 13 17 2.1.
CIVILINGENIØREKSAMEN Side 1 af 18 sider. Skriftlig prøve, den: PQ. juli 200Z Kursus nr : (navn) (underskrift) (bord nr)
 CIVILINGENIØREKSAMEN Side 1 af 18 sider Skriftlig prøve, den: PQ. juli 200Z Kursus nr : 02405 Kursus navn: Sandsynlighedsregning Tilladte hjælpemidler: Alle Dette sæt er besvaret af: (navn) (underskrift)
CIVILINGENIØREKSAMEN Side 1 af 18 sider Skriftlig prøve, den: PQ. juli 200Z Kursus nr : 02405 Kursus navn: Sandsynlighedsregning Tilladte hjælpemidler: Alle Dette sæt er besvaret af: (navn) (underskrift)
Uge 10 Teoretisk Statistik 1. marts 2004
 1 Uge 10 Teoretisk Statistik 1. marts 004 1. u-fordelingen. Normalfordelingen 3. Middelværdi og varians 4. Mere normalfordelingsteori 5. Grafisk kontrol af normalfordelingsantagelse 6. Eksempler 7. Oversigt
1 Uge 10 Teoretisk Statistik 1. marts 004 1. u-fordelingen. Normalfordelingen 3. Middelværdi og varians 4. Mere normalfordelingsteori 5. Grafisk kontrol af normalfordelingsantagelse 6. Eksempler 7. Oversigt
MLR antagelserne. Antagelse MLR.1:(Lineære parametre) Den statistiske model for populationen kan skrives som
 MLR antagelserne Antagelse MLR.1:(Lineære parametre) Den statistiske model for populationen kan skrives som y = β 0 + β 1 x 1 + β 2 x 2 + + β k x k + u, hvor β 0, β 1, β 2,...,β k er ukendte parametere,
MLR antagelserne Antagelse MLR.1:(Lineære parametre) Den statistiske model for populationen kan skrives som y = β 0 + β 1 x 1 + β 2 x 2 + + β k x k + u, hvor β 0, β 1, β 2,...,β k er ukendte parametere,
Landmålingens fejlteori - Repetition - Kontinuerte stokastiske variable - Lektion 3
 Landmålingens fejlteori Repetition - Kontinuerte stokastiske variable Lektion 4 - kkb@math.aau.dk http://people.math.aau.dk/ kkb/undervisning/lf10 Institut for Matematiske Fag Aalborg Universitet 29. april
Landmålingens fejlteori Repetition - Kontinuerte stokastiske variable Lektion 4 - kkb@math.aau.dk http://people.math.aau.dk/ kkb/undervisning/lf10 Institut for Matematiske Fag Aalborg Universitet 29. april
Fejlforplantning. Landmålingens fejlteori - Lektion 5 - Fejlforplantning. Repetition: Varians af linear kombination. Eksempel: Vinkelberegning
 Fejlforplantning Landmålingens fejlteori Lektion 5 Fejlforplantning - kkb@math.aau.dk http://people.math.aau.dk/ kkb/undervisning/lf13 Landmåling involverer ofte bestemmelse af størrelser som ikke kan
Fejlforplantning Landmålingens fejlteori Lektion 5 Fejlforplantning - kkb@math.aau.dk http://people.math.aau.dk/ kkb/undervisning/lf13 Landmåling involverer ofte bestemmelse af størrelser som ikke kan
Antag X 1, X 2,..., X n er n uafhængige stokastiske variable, hvor Var(X 1 )=σ 2 1,..., Var(X n )=σ 2 n.
 Simple fejlforplantningslov Landmålingens fejlteori Lektion 6 Den generelle fejlforplantningslov Antag X, X,, X n er n uafhængige stokastiske variable, hvor Var(X )σ,, Var(X n )σ n Lad Y g(x, X,, X n ),
Simple fejlforplantningslov Landmålingens fejlteori Lektion 6 Den generelle fejlforplantningslov Antag X, X,, X n er n uafhængige stokastiske variable, hvor Var(X )σ,, Var(X n )σ n Lad Y g(x, X,, X n ),
Et eksempel på en todimensional normalfordeling Anders Milhøj September 2006
 Et eksempel på en todimensional normalfordeling Anders Milhøj September 006 I dette notat gennemgås et eksempel, der illustrerer den todimensionale normalfordelings egenskaber. Notatet lægger sig op af
Et eksempel på en todimensional normalfordeling Anders Milhøj September 006 I dette notat gennemgås et eksempel, der illustrerer den todimensionale normalfordelings egenskaber. Notatet lægger sig op af
02402 Vejledende løsninger til Splus-opgaverne fra hele kurset
 02402 Vejledende løsninger til Splus-opgaverne fra hele kurset Vejledende løsning SPL3.3.1 Der er tale om en binomialfordeling med n =10ogp=0.6, og den angivne sandsynlighed er P (X =4) som i bogen også
02402 Vejledende løsninger til Splus-opgaverne fra hele kurset Vejledende løsning SPL3.3.1 Der er tale om en binomialfordeling med n =10ogp=0.6, og den angivne sandsynlighed er P (X =4) som i bogen også
1/41. 2/41 Landmålingens fejlteori - Lektion 1 - Kontinuerte stokastiske variable
 Landmålingens fejlteori - lidt om kurset Landmålingens fejlteori Lektion 1 Det matematiske fundament Kontinuerte stokastiske variable - rw@math.aau.dk Institut for Matematiske Fag Aalborg Universitet Kursusholder
Landmålingens fejlteori - lidt om kurset Landmålingens fejlteori Lektion 1 Det matematiske fundament Kontinuerte stokastiske variable - rw@math.aau.dk Institut for Matematiske Fag Aalborg Universitet Kursusholder
Sandsynlighedsregning 5. forelæsning Bo Friis Nielsen
 Sandsynlighedsregning 5. forelæsning Bo Friis Nielsen Matematik og Computer Science Danmarks Tekniske Universitet 2800 Kgs. Lyngby Danmark Email: bfni@dtu.dk Dagens emner afsnit 3.5 og 4.1 Poissonfordelingen
Sandsynlighedsregning 5. forelæsning Bo Friis Nielsen Matematik og Computer Science Danmarks Tekniske Universitet 2800 Kgs. Lyngby Danmark Email: bfni@dtu.dk Dagens emner afsnit 3.5 og 4.1 Poissonfordelingen
INSTITUT FOR MATEMATISKE FAG c
 INSTITUT FOR MATEMATISKE FAG c AALBORG UNIVERSITET FREDRIK BAJERS VEJ 7 G 9220 AALBORG ØST Tlf.: 96 35 89 27 URL: www.math.aau.dk Fax: 98 15 81 29 E-mail: bjh@math.aau.dk Dataanalyse Sandsynlighed og stokastiske
INSTITUT FOR MATEMATISKE FAG c AALBORG UNIVERSITET FREDRIK BAJERS VEJ 7 G 9220 AALBORG ØST Tlf.: 96 35 89 27 URL: www.math.aau.dk Fax: 98 15 81 29 E-mail: bjh@math.aau.dk Dataanalyse Sandsynlighed og stokastiske
Karakteristiske funktioner og Den Centrale Grænseværdisætning
 E6 efterår 1999 Notat 10 Jørgen Larsen 20. oktober 1999 Karakteristiske funktioner og Den Centrale Grænseværdisætning Karakteristiske funktioner som er nære slægtninge til Fourier-transformationen) er
E6 efterår 1999 Notat 10 Jørgen Larsen 20. oktober 1999 Karakteristiske funktioner og Den Centrale Grænseværdisætning Karakteristiske funktioner som er nære slægtninge til Fourier-transformationen) er
Løsninger til eksamensopgaver på A-niveau 2017
 Løsninger til eksamensopgaver på A-niveau 017 18. maj 017: Delprøven UDEN hjælpemidler Opgave 1: Alle funktionerne f, g og h er lineære funktioner (og ingen er mere lineære end andre) og kan skrives på
Løsninger til eksamensopgaver på A-niveau 017 18. maj 017: Delprøven UDEN hjælpemidler Opgave 1: Alle funktionerne f, g og h er lineære funktioner (og ingen er mere lineære end andre) og kan skrives på
Regneregler for middelværdier M(X+Y) = M X +M Y. Spredning varians og standardafvigelse. 1 n VAR(X) Y = a + bx VAR(Y) = VAR(a+bX) = b²var(x)
 Formelsamlingen 1 Regneregler for middelværdier M(a + bx) a + bm X M(X+Y) M X +M Y Spredning varians og standardafvigelse VAR(X) 1 n n i1 ( X i - M x ) 2 Y a + bx VAR(Y) VAR(a+bX) b²var(x) 2 Kovariansen
Formelsamlingen 1 Regneregler for middelværdier M(a + bx) a + bm X M(X+Y) M X +M Y Spredning varians og standardafvigelse VAR(X) 1 n n i1 ( X i - M x ) 2 Y a + bx VAR(Y) VAR(a+bX) b²var(x) 2 Kovariansen
Normalfordelingen. Det centrale er gentagne målinger/observationer (en stikprøve), der kan beskrives ved den normale fordeling: 1 2πσ
 Normalfordelingen Det centrale er gentagne målinger/observationer (en stikprøve), der kan beskrives ved den normale fordeling: f(x) = ( ) 1 exp (x µ)2 2πσ 2 σ 2 Frekvensen af observationer i intervallet
Normalfordelingen Det centrale er gentagne målinger/observationer (en stikprøve), der kan beskrives ved den normale fordeling: f(x) = ( ) 1 exp (x µ)2 2πσ 2 σ 2 Frekvensen af observationer i intervallet
8 Regulære flader i R 3
 8 Regulære flader i R 3 Vi skal betragte særligt pæne delmængder S R 3 kaldet flader. I det følgende opfattes S som et topologisk rum i sportopologien, se Definition 5.9. En åben omegn U af p S er således
8 Regulære flader i R 3 Vi skal betragte særligt pæne delmængder S R 3 kaldet flader. I det følgende opfattes S som et topologisk rum i sportopologien, se Definition 5.9. En åben omegn U af p S er således
Eksamen i Calculus. 14. juni f (x, y, z) = 1 + x 2 + y 2. x 2 + y 2 1 Hele rummet uden z aksen
 Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 14. juni 019 Opgave 1 (6 point) En
Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 14. juni 019 Opgave 1 (6 point) En
Oversigt over gruppeteori: definitioner og sætninger
 Oversigt over gruppeteori: definitioner og sætninger (G, ) kaldesengruppe, når følgende aksiomer er opfyldt: 0) (G, ) er en organiseret (stabil) mængde: a, b G a b G 1) Den associative lov gælder, dvs.
Oversigt over gruppeteori: definitioner og sætninger (G, ) kaldesengruppe, når følgende aksiomer er opfyldt: 0) (G, ) er en organiseret (stabil) mængde: a, b G a b G 1) Den associative lov gælder, dvs.
Lineære normale modeller (1) udkast. 1 Flerdimensionale stokastiske variable
 E6 efterår 999 Notat 8 Jørgen Larsen 22. november 999 Lineære normale modeller ) udkast Ved hjælp af lineær algebra kan man formulere og analysere de såkaldte lineære normale modeller meget overskueligt
E6 efterår 999 Notat 8 Jørgen Larsen 22. november 999 Lineære normale modeller ) udkast Ved hjælp af lineær algebra kan man formulere og analysere de såkaldte lineære normale modeller meget overskueligt
Kursusindhold: X i : tilfældig værdi af ite eksperiment. Antag X i kun antager værdierne 1, 2,..., M.
 Kursusindhold: Produkt og marked - matematiske og statistiske metoder Rasmus Waagepetersen Institut for Matematiske Fag Aalborg Universitet March 1, 2013 Sandsynlighedsregning og lagerstyring Normalfordelingen
Kursusindhold: Produkt og marked - matematiske og statistiske metoder Rasmus Waagepetersen Institut for Matematiske Fag Aalborg Universitet March 1, 2013 Sandsynlighedsregning og lagerstyring Normalfordelingen
Sandsynlighedsregning 9. forelæsning Bo Friis Nielsen
 Sandsynlighedsregning 9. forelæsning Bo Friis Nielsen Matematik og Computer Science Danmarks Tekniske Universitet 800 Kgs. Lyngby Danmark Email: bfni@dtu.dk Dagens emner afsnit 5.3 og 5.4 Simultane kontinuerte
Sandsynlighedsregning 9. forelæsning Bo Friis Nielsen Matematik og Computer Science Danmarks Tekniske Universitet 800 Kgs. Lyngby Danmark Email: bfni@dtu.dk Dagens emner afsnit 5.3 og 5.4 Simultane kontinuerte
Note om Laplace-transformationen
 Note om Laplace-transformationen Den harmoniske oscillator omskrevet til et ligningssystem I dette opgavesæt benyttes laplacetransformationen til at løse koblede differentialligninger. Fordelen ved at
Note om Laplace-transformationen Den harmoniske oscillator omskrevet til et ligningssystem I dette opgavesæt benyttes laplacetransformationen til at løse koblede differentialligninger. Fordelen ved at
Matematik F2 Opgavesæt 2
 Opgaver uge 2 I denne uge kigger vi nærmere på Cauchy-Riemann betingelserne, potensrækker, konvergenskriterier og flertydige funktioner. Vi skal også se på integration langs en ve i den komplekse plan.
Opgaver uge 2 I denne uge kigger vi nærmere på Cauchy-Riemann betingelserne, potensrækker, konvergenskriterier og flertydige funktioner. Vi skal også se på integration langs en ve i den komplekse plan.
Besvarelser til Calculus Ordinær Eksamen Juni 2017
 Besvarelser til Calculus Ordinær Eksamen - 12. Juni 2017 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 12. Juni 2017 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
MM501/MM503 forelæsningsslides
 MM501/MM503 forelæsningsslides uge 50, 2009 Produceret af Hans J. Munkholm 1 Separabel 1. ordens differentialligning En generel 1. ordens differentialligning har formen dx Eksempler = et udtryk, der indeholder
MM501/MM503 forelæsningsslides uge 50, 2009 Produceret af Hans J. Munkholm 1 Separabel 1. ordens differentialligning En generel 1. ordens differentialligning har formen dx Eksempler = et udtryk, der indeholder
02402 Vejledende løsninger til hjemmeopgaver og øvelser, Uge 4
 02402 Vejledende løsninger til hjemmeopgaver og øvelser, Uge 4 Vejledende løsning 5.46 P (0.010 < error < 0.015) = (0.015 0.010)/0.050 = 0.1 > punif(0.015,-0.025,0.025)-punif(0.01,-0.025,0.025) [1] 0.1
02402 Vejledende løsninger til hjemmeopgaver og øvelser, Uge 4 Vejledende løsning 5.46 P (0.010 < error < 0.015) = (0.015 0.010)/0.050 = 0.1 > punif(0.015,-0.025,0.025)-punif(0.01,-0.025,0.025) [1] 0.1
Forelæsning 3: Kapitel 5: Kontinuerte fordelinger
 Kursus 02402 Introduktion til Statistik Forelæsning 3: Kapitel 5: Kontinuerte fordelinger Per Bruun Brockhoff DTU Compute, Statistik og Dataanalyse Bygning 324, Rum 220 Danmarks Tekniske Universitet 2800
Kursus 02402 Introduktion til Statistik Forelæsning 3: Kapitel 5: Kontinuerte fordelinger Per Bruun Brockhoff DTU Compute, Statistik og Dataanalyse Bygning 324, Rum 220 Danmarks Tekniske Universitet 2800
MM501 forelæsningsslides
 MM501 forelæsningsslides uge 40, 2010 Produceret af Hans J. Munkholm bearbejdet af JC 1 Separabel 1. ordens differentialligning En generel 1. ordens differentialligning har formen s.445-8 dx Eksempler
MM501 forelæsningsslides uge 40, 2010 Produceret af Hans J. Munkholm bearbejdet af JC 1 Separabel 1. ordens differentialligning En generel 1. ordens differentialligning har formen s.445-8 dx Eksempler
Besvarelser til Calculus Ordinær Eksamen Januar 2019
 Besvarelser til Calculus Ordinær Eksamen - 14. Januar 19 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 14. Januar 19 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Statistik og Sandsynlighedsregning 2. Repetition og eksamen. Overheads til forelæsninger, mandag 7. uge
 Statistik og Sandsynlighedsregning 2 Repetition og eksamen Overheads til forelæsninger, mandag 7. uge 1 Normalfordelingen Erfaringsmæssigt er normalfordelingen velegnet til at beskrive variationen i mange
Statistik og Sandsynlighedsregning 2 Repetition og eksamen Overheads til forelæsninger, mandag 7. uge 1 Normalfordelingen Erfaringsmæssigt er normalfordelingen velegnet til at beskrive variationen i mange
Løsning til eksaminen d. 29. maj 2009
 DTU Informatik 02402 Introduktion til Statistik 20-2-01 LFF/lff Løsning til eksaminen d. 29. maj 2009 Referencer til Probability and Statistics for Engineers er angivet i rækkefølgen [8th edition, 7th
DTU Informatik 02402 Introduktion til Statistik 20-2-01 LFF/lff Løsning til eksaminen d. 29. maj 2009 Referencer til Probability and Statistics for Engineers er angivet i rækkefølgen [8th edition, 7th
Formelsamling - MatF2. Therkel Zøllner og Amalie Christensen 27. juni 2009
 Formelsamling - MatF2 Therkel Zøllner og Amalie Christensen 27. juni 2009 1 Indhold 1 Kompleks variabel teori 3 1.1 Komplekse funktioner 825-830........................... 3 1.2 Powerserier af komplekse
Formelsamling - MatF2 Therkel Zøllner og Amalie Christensen 27. juni 2009 1 Indhold 1 Kompleks variabel teori 3 1.1 Komplekse funktioner 825-830........................... 3 1.2 Powerserier af komplekse
Nanostatistik: Konfidensinterval
 Nanostatistik: Konfidensinterval JLJ Nanostatistik: Konfidensinterval p. 1/37 Fraktilpåmindelse u p : Φ(u p ) = p, Φ( z ) = 1 Φ( z ) t p [f] : F t[f] (t p [f]) = p, F t[f] ( t ) = 1 F t[f] ( t ) F-fordeling:
Nanostatistik: Konfidensinterval JLJ Nanostatistik: Konfidensinterval p. 1/37 Fraktilpåmindelse u p : Φ(u p ) = p, Φ( z ) = 1 Φ( z ) t p [f] : F t[f] (t p [f]) = p, F t[f] ( t ) = 1 F t[f] ( t ) F-fordeling:
DesignMat Uge 1 Repetition af forårets stof
 DesignMat Uge 1 Repetition af forårets stof Preben Alsholm Efterår 008 01 Lineært ligningssystem Lineært ligningssystem Et lineært ligningssystem: a 11 x 1 + a 1 x + + a 1n x n = b 1 a 1 x 1 + a x + +
DesignMat Uge 1 Repetition af forårets stof Preben Alsholm Efterår 008 01 Lineært ligningssystem Lineært ligningssystem Et lineært ligningssystem: a 11 x 1 + a 1 x + + a 1n x n = b 1 a 1 x 1 + a x + +
(c) Opskriv den reelle Fourierrække for funktionen y(t) fra (b), og afgør dernæst om y(t) er en lige eller ulige funktion eller ingen af delene.
 MATEMATIK 3 EN,MP 4. februar 2016 Eksamenopgaver fra 2011 2016 (jan. 2016) Givet at 0 for 0 < t < 1 mens e (t 1) cos(7(t 1)) for t 1, betragt da begyndelsesværdiproblemet for t > 0: y (t) + 2y (t) + 50y(t)
MATEMATIK 3 EN,MP 4. februar 2016 Eksamenopgaver fra 2011 2016 (jan. 2016) Givet at 0 for 0 < t < 1 mens e (t 1) cos(7(t 1)) for t 1, betragt da begyndelsesværdiproblemet for t > 0: y (t) + 2y (t) + 50y(t)
To find the English version of the exam, please read from the other end! Eksamen i Calculus
 To find the English version of the exam, please read from the other end! Se venligst bort fra den engelske version på bagsiden hvis du følger denne danske version af prøven. Eksamen i Calculus Første Studieår
To find the English version of the exam, please read from the other end! Se venligst bort fra den engelske version på bagsiden hvis du følger denne danske version af prøven. Eksamen i Calculus Første Studieår
Besvarelser til Calculus Ordinær eksamen - Efterår - 8. Januar 2016
 Besvarelser til Calculus Ordinær eksamen - Efterår - 8. Januar 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har
Besvarelser til Calculus Ordinær eksamen - Efterår - 8. Januar 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har
DANMARKS TEKNISKE UNIVERSITET Side 1 af 17 sider. Skriftlig prøve, den: 30. maj 2016 Kursus nr : (navn) (underskrift) (bord nr)
 DANMARKS TEKNISKE UNIVERSITET Side af 7 sider Skriftlig prøve, den: 0. maj 206 Kursus nr : 02405 Kursus navn: Sandsynlighedsregning Varighed : 4 timer Tilladte hjælpemidler: Alle Dette sæt er besvaret
DANMARKS TEKNISKE UNIVERSITET Side af 7 sider Skriftlig prøve, den: 0. maj 206 Kursus nr : 02405 Kursus navn: Sandsynlighedsregning Varighed : 4 timer Tilladte hjælpemidler: Alle Dette sæt er besvaret
Sandsynlighedsregning Oversigt over begreber og fordelinger
 Tue Tjur Marts 2007 Sandsynlighedsregning Oversigt over begreber og fordelinger Stat. MØK 2. år Kapitel : Sandsynlighedsfordelinger og stokastiske variable En sandsynlighedsfunktion på en mængde E (udfaldsrummet)
Tue Tjur Marts 2007 Sandsynlighedsregning Oversigt over begreber og fordelinger Stat. MØK 2. år Kapitel : Sandsynlighedsfordelinger og stokastiske variable En sandsynlighedsfunktion på en mængde E (udfaldsrummet)
GEOMETRI-TØ, UGE 6. . x 1 x 1. = x 1 x 2. x 2. k f
 GEOMETRI-TØ, UGE 6 Hvis I falder over tryk- eller regne-fejl i nedenstående, må I meget gerne sende rettelser til fuglede@imfaudk Opvarmningsopgave 1 Lad f : R 2 R være tre gange kontinuert differentierbar
GEOMETRI-TØ, UGE 6 Hvis I falder over tryk- eller regne-fejl i nedenstående, må I meget gerne sende rettelser til fuglede@imfaudk Opvarmningsopgave 1 Lad f : R 2 R være tre gange kontinuert differentierbar
hvor a og b er konstanter. Ved middelværdidannelse fås videre
 Uge 3 Teoretisk Statistik. marts 004. Korrelation og uafhængighed, repetition. Eksempel fra sidste gang (uge ) 3. Middelværdivektor, kovarians- og korrelationsmatrix 4. Summer af stokastiske variable 5.Den
Uge 3 Teoretisk Statistik. marts 004. Korrelation og uafhængighed, repetition. Eksempel fra sidste gang (uge ) 3. Middelværdivektor, kovarians- og korrelationsmatrix 4. Summer af stokastiske variable 5.Den
Modul 12: Regression og korrelation
 Forskningsenheden for Statistik ST01: Elementær Statistik Bent Jørgensen Modul 12: Regression og korrelation 12.1 Sammenligning af to regressionslinier........................ 1 12.1.1 Test for ens hældning............................
Forskningsenheden for Statistik ST01: Elementær Statistik Bent Jørgensen Modul 12: Regression og korrelation 12.1 Sammenligning af to regressionslinier........................ 1 12.1.1 Test for ens hældning............................
Introduktion til Statistik. Forelæsning 3: Kontinuerte fordelinger. Peder Bacher
 Introduktion til Statistik Forelæsning 3: Kontinuerte fordelinger Peder Bacher DTU Compute, Dynamiske Systemer Bygning 303B, Rum 009 Danmarks Tekniske Universitet 2800 Lyngby Danmark e-mail: pbac@dtu.dk
Introduktion til Statistik Forelæsning 3: Kontinuerte fordelinger Peder Bacher DTU Compute, Dynamiske Systemer Bygning 303B, Rum 009 Danmarks Tekniske Universitet 2800 Lyngby Danmark e-mail: pbac@dtu.dk
Løsning til eksaminen d. 14. december 2009
 DTU Informatik 02402 Introduktion til Statistik 200-2-0 LFF/lff Løsning til eksaminen d. 4. december 2009 Referencer til Probability and Statistics for Engineers er angivet i rækkefølgen [8th edition,
DTU Informatik 02402 Introduktion til Statistik 200-2-0 LFF/lff Løsning til eksaminen d. 4. december 2009 Referencer til Probability and Statistics for Engineers er angivet i rækkefølgen [8th edition,
Motivation. Konfidensintervaller og vurdering af usikkerhed på estimerede størrelser
 Motivation Konfidensintervaller og vurdering af usikkerhed på estimerede størrelser Rasmus Waagepetersen October 26, 2018 Eksempel: En landmåler får til opgave at måle længden λ fra A til B. Entreprenøren
Motivation Konfidensintervaller og vurdering af usikkerhed på estimerede størrelser Rasmus Waagepetersen October 26, 2018 Eksempel: En landmåler får til opgave at måle længden λ fra A til B. Entreprenøren
Poul Thyregod, introslide.tex Specialkursus vid.stat. foraar Lad θ = θ(β) R k for β B R m med m k
 Dagens program: Likelihoodfunktion, begreber : Mandag den 4. februar Den generelle lineære model score-funktion: første afledede af log-likelihood har middelværdien nul observeret information: anden afledede
Dagens program: Likelihoodfunktion, begreber : Mandag den 4. februar Den generelle lineære model score-funktion: første afledede af log-likelihood har middelværdien nul observeret information: anden afledede
Løsningsforslag til opgavesæt 5
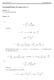 Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
z + w z + w z w = z 2 w z w = z w z 2 = z z = a 2 + b 2 z w
 Komplekse tal Hvis z = a + ib og w = c + id gælder z + w = (a + c) + i(b + d) z w = (a c) + i(b d) z w = (ac bd) + i(ad bc) z w = a+ib c+id = ac+bd + i bc ad, w 0 c +d c +d z a b = i a +b a +b Konjugation
Komplekse tal Hvis z = a + ib og w = c + id gælder z + w = (a + c) + i(b + d) z w = (a c) + i(b d) z w = (ac bd) + i(ad bc) z w = a+ib c+id = ac+bd + i bc ad, w 0 c +d c +d z a b = i a +b a +b Konjugation
Matematik og Form: Matrixmultiplikation. Regulære og singu
 Matematik og Form: Matrixmultiplikation. Regulære og singulære matricer Institut for Matematiske Fag Aalborg Universitet 2012 Matrixmultiplikation Definition Definition A = [a ij ], B = [b ij ]: AB = C
Matematik og Form: Matrixmultiplikation. Regulære og singulære matricer Institut for Matematiske Fag Aalborg Universitet 2012 Matrixmultiplikation Definition Definition A = [a ij ], B = [b ij ]: AB = C
Om hypoteseprøvning (1)
 E6 efterår 1999 Notat 16 Jørgen Larsen 11. november 1999 Om hypoteseprøvning 1) Det grundlæggende problem kan generelt formuleres sådan: Man har en statistisk model parametriseret med en parameter θ Ω;
E6 efterår 1999 Notat 16 Jørgen Larsen 11. november 1999 Om hypoteseprøvning 1) Det grundlæggende problem kan generelt formuleres sådan: Man har en statistisk model parametriseret med en parameter θ Ω;
Løsningsforslag til opgavesæt 5
 Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
MATEMATIK 11 Eksamensopgaver Juni 1995 Juni 2001, 4. fjerdedel
 Juni 2000 MATEMATIK 11 Eksamensopgaver Juni 1995 Juni 2001, 4. fjerdedel Opgave 1. (a) Find den fuldstændige løsning til differentialligningen y 8y + 16y = 0. (b) Find den fuldstændige løsning til differentialligningen
Juni 2000 MATEMATIK 11 Eksamensopgaver Juni 1995 Juni 2001, 4. fjerdedel Opgave 1. (a) Find den fuldstændige løsning til differentialligningen y 8y + 16y = 0. (b) Find den fuldstændige løsning til differentialligningen
Københavns Universitet, Det naturvidenskabelige Fakultet. Afleveringsopgave 1
 Københavns Universitet, Det naturvidenskabelige Fakultet 1 Lineær Algebra (LinAlg) Afleveringsopgave 1 Eventuelle besvarelser laves i grupper af - 3 personer og afleveres i to eksemplarer med 3 udfyldte
Københavns Universitet, Det naturvidenskabelige Fakultet 1 Lineær Algebra (LinAlg) Afleveringsopgave 1 Eventuelle besvarelser laves i grupper af - 3 personer og afleveres i to eksemplarer med 3 udfyldte
Statistiske modeller
 Statistiske modeller Statistisk model Datamatrice Variabelmatrice Hændelse Sandsynligheder Data Statistiske modeller indeholder: Variable Hændelser defineret ved mulige variabel værdier Sandsynligheder
Statistiske modeller Statistisk model Datamatrice Variabelmatrice Hændelse Sandsynligheder Data Statistiske modeller indeholder: Variable Hændelser defineret ved mulige variabel værdier Sandsynligheder
Landmålingens fejlteori - Lektion 3. Estimation af σ Dobbeltmålinger Geometrisk nivellement Linearisering
 Landmålingens fejlteori Lektion 3 Estimation af σ Dobbeltmålinger Geometrisk nivellement Linearisering - rw@math.aau.dk Institut for Matematiske Fag Aalborg Universitet 1/31 Repetition: Middelværdi og
Landmålingens fejlteori Lektion 3 Estimation af σ Dobbeltmålinger Geometrisk nivellement Linearisering - rw@math.aau.dk Institut for Matematiske Fag Aalborg Universitet 1/31 Repetition: Middelværdi og
Agenda Sandsynlighedsregning. Regneregler (kap. 3-4) Fordelinger og genkendelse af fordelinger (kap. 3-5) Simultane, marginale og betingede
 Agenda Sandsynlighedsregning. Regneregler (kap. 3-4) Fordelinger og genkendelse af fordelinger (kap. 3-5) Simultane, marginale og betingede fordelinger (kap. 4) Middelværdi og varians (kap. 3-4) Fordelingsresultater
Agenda Sandsynlighedsregning. Regneregler (kap. 3-4) Fordelinger og genkendelse af fordelinger (kap. 3-5) Simultane, marginale og betingede fordelinger (kap. 4) Middelværdi og varians (kap. 3-4) Fordelingsresultater
Landmålingens fejlteori - Lektion 5 - Fejlforplantning
 Landmålingens fejlteori Lektion 5 Fejlforplantning - kkb@math.aau.dk Institut for Matematiske Fag Aalborg Universitet 1/30 Fejlforplantning Landmåling involverer ofte bestemmelse af størrelser som ikke
Landmålingens fejlteori Lektion 5 Fejlforplantning - kkb@math.aau.dk Institut for Matematiske Fag Aalborg Universitet 1/30 Fejlforplantning Landmåling involverer ofte bestemmelse af størrelser som ikke
Opgave 1 Opskriv følgende vinkler i radianer 180, 90, 135, 270, 60, 30.
 Opgaver Polære koordinater Opgave 1 Opskriv følgende vinkler i radianer 180, 90, 15, 70, 60, 0. Opgave Bestem sin π Opgave. Et punkt p i xy-planen er givet ved de kartesiske koordinater,. Bestem p s polære
Opgaver Polære koordinater Opgave 1 Opskriv følgende vinkler i radianer 180, 90, 15, 70, 60, 0. Opgave Bestem sin π Opgave. Et punkt p i xy-planen er givet ved de kartesiske koordinater,. Bestem p s polære
Eksamen i Calculus. Første Studieår ved Det Teknisk-Naturvidenskabelige Fakultet og Det Sundhedsvidenskabelige Fakultet. 6.
 Eksamen i Calculus Første Studieår ved Det Teknisk-Naturvidenskabelige Fakultet og Det Sundhedsvidenskabelige Fakultet 6. juni 16 Dette eksamenssæt består af 1 nummererede sider med 14 afkrydsningsopgaver.
Eksamen i Calculus Første Studieår ved Det Teknisk-Naturvidenskabelige Fakultet og Det Sundhedsvidenskabelige Fakultet 6. juni 16 Dette eksamenssæt består af 1 nummererede sider med 14 afkrydsningsopgaver.
MATEMATIK A-NIVEAU. Kapitel 1
 MATEMATIK A-NIVEAU Vejledende eksempler på eksamensopgaver og eksamensopgaver i matematik, 01 Kapitel 1 016 MATEMATIK A-NIVEAU Vejledende eksempler på eksamensopgaver og eksamensopgaver i matematik 01
MATEMATIK A-NIVEAU Vejledende eksempler på eksamensopgaver og eksamensopgaver i matematik, 01 Kapitel 1 016 MATEMATIK A-NIVEAU Vejledende eksempler på eksamensopgaver og eksamensopgaver i matematik 01
Vejledende besvarelse på august 2009-sættet 2. december 2009
 Vejledende besvarelse på august 29-sættet 2. december 29 Det følgende er en vejledende besvarelse på eksamenssættet i kurset Calculus, som det så ud i august 29. Den tjener primært til illustration af,
Vejledende besvarelse på august 29-sættet 2. december 29 Det følgende er en vejledende besvarelse på eksamenssættet i kurset Calculus, som det så ud i august 29. Den tjener primært til illustration af,
Det Teknisk-Naturvidenskabelige Basisår Computerstøttet Beregning Naturvidenskab - Datalogi/Software/Matematik E-OPG 3
 Det Teknisk-Naturvidenskabelige Basisår 2003-2004 Computerstøttet Beregning Naturvidenskab - Datalogi/Software/Matematik 1 Introduktion E-OPG 3 Dette er den tredje store opgave, som skal danne grundlag
Det Teknisk-Naturvidenskabelige Basisår 2003-2004 Computerstøttet Beregning Naturvidenskab - Datalogi/Software/Matematik 1 Introduktion E-OPG 3 Dette er den tredje store opgave, som skal danne grundlag
Eksamen i Mat F, april 2006
 Eksamen i Mat F, april 26 Opgave Lad F være et vektorfelt, givet i retvinklede koordinater som: Udregn F og F: F x F = F x i + F y j + F z k = F y = z 2 F z xz y 2 F = F x + F y + F z = + + x. F = F z
Eksamen i Mat F, april 26 Opgave Lad F være et vektorfelt, givet i retvinklede koordinater som: Udregn F og F: F x F = F x i + F y j + F z k = F y = z 2 F z xz y 2 F = F x + F y + F z = + + x. F = F z
