2. Ved et roulettespil kan man vinde 0,10,100, 500 og 1000 kr. Sandsynligheden for gevinsterne ses af følgende skema:
|
|
|
- Christian Ulrik Henningsen
- 8 år siden
- Visninger:
Transkript
1 Der er hjælp til opgaver med # og facit på side 6 1. Et eksperiment kan beskrives med følgende skema: u P(u) 0,3 0,2 0,1 0,2 x Bestem x og sandsynligheden for at udfaldet er et lige tal.. 2. Ved et roulettespil kan man vinde 0,10,100, 500 og 1000 kr. Sandsynligheden for gevinsterne ses af følgende skema: Gevinst u P(u) 0,75 0,15 0,06 0,03 0,01 Bestem sandsynligheden for følgende hændelser: A: gevinsten er mindst 100 kr B: gevinsten er under 100 kr C: gevinsten er 100 kr eller 500 kr D: gevinsten er højst 100 kr Bestem den gennemsnitlige gevinst man kan forvente at få, hvis man spiller mange gange. 3. En sandsynlighedsfordeling er angivet i følgende stolpediagram: Bestem P(3), P(5) og middelværdien. 4. En sandsynlighedsfordeling er angivet i følgende skema u 1 4 x 10 P(u) 0,3 y 0,1 0,2 Middelværdien er 4,6. Bestem x og y. # Tegn et stolpediagram af fordelingen. 5. Et eksperiment består i at kaste to symmetriske terninger og aflæse det største øjental. Udfyld tabellen (brug en opstilling som figur 1 side 248 i noten Sandsynlighed ): u P(u) Bestem middelværdien og forklar betydningen af tallet. 1/6
2 6. Man kan bruge CAS til bestemmelse af fakultet [!] og kombinationer [K(n,r) = ncr]: K(n,r) kaldes ofte for Binomial-koefficient. Det vil her føre for vidt at beskrive for flere CAS-værktøjer, men da betegnelser og fremgangsmåde er ret ensartede i de forskellige CAS-værktøjer, så lad dig inspirere af forklaringen nedenfor og kig i vejledningen til dit eget CAS-værktøj. Her vises hvordan det gøres med TI-89. Tast 2nd 5, så kommer math-menuen frem, tast 7 for Probability. Vælg herefter 1 for! eller 3 for ncr (ell. Binomial-koefficient) Bestem: 5! 8! 12! Bestem: K(8,2) K(8,6) K(8,0) K(8,1) K(8,7) 7. I en klasse med 24 elever skal udvælges 5 elever. Hvor mange forskellige kombinationer er der? 8. I en binomialfordeling er antalsparameteren n = 6 og sandsynlighedsparameteren p = 0,8. Beregn P(0) K(6,0) 0,8 P(1) P(2) P(3) P(4) P(5) P(6) 0 0,2 6 Denne binomialfordeling betegnes også b(6, 0.8) [altså b(n, p) ] 9. I et spil er sandsynligheden for at få gevinst 0,25. Der spilles 3 gange. Bestem sandsynlighederne for at få gevinst hhv 0, 1, 2 og 3 gange. Tegn stolpediagram over fordelingen. Bestem middelværdien. 10. Et binomialforsøg hvor sandsynligheden for succes er 0,7 gentages 15 gange. X betegner antallet af succeser ved de 15 gentagelser. Bestem følgende sandsynligheder ved hjælp af CAS: a) P ( X 6) b) P ( X 6) c) P ( 2 X 10) d) P ( 2 X 10) e) P ( X 8) f) P ( X 8) 11. I et stort vareparti er 10% af enhederne defekte. Der udtages en stikprøve på 50 enheder. Bestem sandsynligheden for 2/6
3 A: Der er højst 5 defekte i stikprøven. B: Der er mindst 6 defekte i stikprøven. C Der er mellem 10 og 12 defekte i stikprøven Bestem middelværdien. 12. X betegner antal succeser i en binomialfordeling med antalsparameteren n og sandsynlighedsparameteren p = 0,4. Bestem P ( X 1), når n =10 Bestem P ( X 5), når n =13 Bestem P ( X 4), når n =13 Hvad skal n mindst være for at P ( X 4) bliver større end 0,95? 13. I en meningsmåling 10.november 2007 baseret på 980 vælgere foretaget af Epinion er fordelingen på politiske partier følgende: peger på Helle Thorning-Schmidt som statsminister Socialdemokraterne Radikale venstre SF Kristendemokraterne Enhedslisten (0,4% ved ikke) 26,2% 5,9 % 12,3% 1,2% 2,1% peger på Anders Fogh-Rasmussen som statsminister Konservative Dansk Folkeparti Venstre Ny alliance 9,3% 12,0% 27,2% 3,4% Bestem med 95% sikkerhed i hvilket interval den procentvise støtte til Helle Thorning-Schmidt er. Hvem grinede højest efter folketingsvalget d. 13. november 2007? 14. 3/6
4 Varighed i år Antal ialt I 2005 blev ægtepar skilt i Danmark. Tabellen til venstre viser hvor længe ægteskaberne havde varet. a) Udregn de kumulerede frekvenser, og tegn en sumkurve over fordelingen. b) Bestem kvartilsættet, og forklar hvad det fortæller om skilsmisserne i /6
5 Se tabellen side 300 i noten Statistik. Brug normalfordelingspapiret til at påvise at vægtene med god tilnærmelse er normalfordelte. Aflæs herefter på papiret middelværdi og spredning for fordelingen. 20. Løs først opgaven ved brug af normalfordelingspapir og herefter ved brug af CAS /6
6 23. Et kaffemærke leverer i 500grams pakninger. For en sikkerhedsskyld indstiller man påfyldningsmaskinen til at hælde 510gram kaffe i pakken. Det antages, at den påfyldte vægt er normalfordelt med middelværdi 510 og spredning 10. Bestem sandsynligheden for, at en tilfældig valgt pakke 1) vejer under 500gram. # 2) vejer mellem 500 og 520gram. # Vink til 4: Udnyt at summen af sandsynlighederne skal give 1 og bestem herved y # Vink til 23: 1) Udnyt at 500 netop er en spredning fra middelværdien. Så kan opgaven besvares ud fra kendskab til de særlige egenskaber ved en normalfordeling. 2) Samme princip kan bruges Facit: 1. x = 0,2 P(lige tal) = 0,4 2. P(A) = 0,10 P(B) = 0,90 P(C) = 0,09 P(D) = 0,96 32,5 3. P(3) = 0,20 P( 5) = 0,12 3,01 4. x = 7 y = 0,4 5. u P(u) = ~ 4, , ,0015 0,015 0, , , , , , , , =0, , , , , , , , , ,02353 = , , ,83142 n = mellem 44,5% og 50,9% 14. nedre kvartil: 6 median: 8 øvre kvartil: fordelingerne er nummereret i læseretningen og spredningen for den første fordeling betegnes s 1 osv. Så er s6 s1 s3 s2 s5 s4 og s 4 = middelværdien er 91,875 og s=34,5 18. Intervalfrekvenserne fås til interval Osv. intervalfrekvens 0,05 0,2-0,05=0,15 0,25-0.2=0,05 Herefter kan histogrammet tegnes og middelværdien udregnes som tidligere prøvet. 19. De kumulerede frekvenser afsættet i normalfordelingspapiret og den bedste rette linie tegnes. Da punkterne med god tilnærmelse ligger på linien er vægtene med god tilnærmelse normalfordelte. 70 kg og 10 kg. 20. a) 55,8 % (fundet ved TIStat.normCdf( 90, 110, 100, 13) ) b) 6,2 % 21. a) 0,21 % b) 34,6 % 22. a) 4,78 % (fundet ved TIStat.normCdf( -, 0.40, 0.50, 0.06) ) b) 20,23 % 23. a) 2,4%+13,6%=16,0% b) 34,1%+34,1%=68,2% 6/6
Statistik. Peter Sørensen: Statistik og sandsynlighed Side 1
 Statistik Formålet... 1 Mindsteværdi... 1 Størsteværdi... 1 Ikke grupperede observationer... 2 Median og kvartiler defineres ved ikke grupperede observationer således:... 2 Middeltal defineres ved ikke
Statistik Formålet... 1 Mindsteværdi... 1 Størsteværdi... 1 Ikke grupperede observationer... 2 Median og kvartiler defineres ved ikke grupperede observationer således:... 2 Middeltal defineres ved ikke
Statistik. Peter Sørensen: Statistik og sandsynlighed Side 1
 Statistik Formålet... 1 Mindsteværdi... 1 Størsteværdi... 1 Ikke grupperede observationer... 2 Median og kvartiler defineres ved ikke grupperede observationer således:... 2 Middeltal defineres ved ikke
Statistik Formålet... 1 Mindsteværdi... 1 Størsteværdi... 1 Ikke grupperede observationer... 2 Median og kvartiler defineres ved ikke grupperede observationer således:... 2 Middeltal defineres ved ikke
Definition. Definitioner
 Definition Landmålingens fejlteori Lektion Diskrete stokastiske variable En reel funktion defineret på et udfaldsrum (med sandsynlighedsfordeling) kaldes en stokastisk variabel. - kkb@math.aau.dk http://people.math.aau.dk/
Definition Landmålingens fejlteori Lektion Diskrete stokastiske variable En reel funktion defineret på et udfaldsrum (med sandsynlighedsfordeling) kaldes en stokastisk variabel. - kkb@math.aau.dk http://people.math.aau.dk/
Temaopgave i statistik for
 Temaopgave i statistik for matematik B og A Indhold Opgave 1. Kast med 12 terninger 20 gange i praksis... 3 Opgave 2. Kast med 12 terninger teoretisk... 4 Opgave 3. Kast med 12 terninger 20 gange simulering...
Temaopgave i statistik for matematik B og A Indhold Opgave 1. Kast med 12 terninger 20 gange i praksis... 3 Opgave 2. Kast med 12 terninger teoretisk... 4 Opgave 3. Kast med 12 terninger 20 gange simulering...
Kvantitative Metoder 1 - Forår 2007
 Dagens program Kapitel 4: Diskrete fordelinger Afsnit 4.1-4.2, 4.7: Bernoulli fordeling Binomial fordeling Store Tals Lov (Laws of Averages, Laws of Large Numbers) 1 Bernoulli fordeling Kvantitative Metoder
Dagens program Kapitel 4: Diskrete fordelinger Afsnit 4.1-4.2, 4.7: Bernoulli fordeling Binomial fordeling Store Tals Lov (Laws of Averages, Laws of Large Numbers) 1 Bernoulli fordeling Kvantitative Metoder
Deskriptiv statistik. Version 2.1. Noterne er et supplement til Vejen til matematik AB1. Henrik S. Hansen, Sct. Knuds Gymnasium
 Deskriptiv (beskrivende) statistik er den disciplin, der trækker de væsentligste oplysninger ud af et ofte uoverskueligt materiale. Det sker f.eks. ved at konstruere forskellige deskriptorer, d.v.s. regnestørrelser,
Deskriptiv (beskrivende) statistik er den disciplin, der trækker de væsentligste oplysninger ud af et ofte uoverskueligt materiale. Det sker f.eks. ved at konstruere forskellige deskriptorer, d.v.s. regnestørrelser,
Grupperede observationer et eksempel. (begreber fra MatC genopfriskes og varians og spredning indføres)
 Grupperede observationer et eksempel. (begreber fra MatC genopfriskes og varians og spredning indføres) Til Gribskovløbet 006 gennemførte 118 kvinder 1,4 km distancen. Fordelingen af kvindernes løbstider
Grupperede observationer et eksempel. (begreber fra MatC genopfriskes og varians og spredning indføres) Til Gribskovløbet 006 gennemførte 118 kvinder 1,4 km distancen. Fordelingen af kvindernes løbstider
Kvantitative Metoder 1 - Forår 2007
 Dagens program Kapitel 4: Diskrete fordelinger Hypergeometrisk fordeling, Afsnit 4.3 Multinomial fordeling, Afsnit 4.8 Geometrisk fordeling og Negativ binomialfordeling (Inverse Sampling), Afsnit 4.4 Approksimation
Dagens program Kapitel 4: Diskrete fordelinger Hypergeometrisk fordeling, Afsnit 4.3 Multinomial fordeling, Afsnit 4.8 Geometrisk fordeling og Negativ binomialfordeling (Inverse Sampling), Afsnit 4.4 Approksimation
Deskriptiv statistik for hf-matc
 Deskriptiv statistik for hf-matc 75 50 25 2018 Karsten Juul Deskriptiv statistik for hf-matc Hvad er deskriptiv statistik? 1.1 Hvad er deskriptiv statistik?... 1 1.2 Hvad er grupperede og ugrupperede data?...
Deskriptiv statistik for hf-matc 75 50 25 2018 Karsten Juul Deskriptiv statistik for hf-matc Hvad er deskriptiv statistik? 1.1 Hvad er deskriptiv statistik?... 1 1.2 Hvad er grupperede og ugrupperede data?...
Kursusindhold: X i : tilfældig værdi af ite eksperiment. Antag X i kun antager værdierne 1, 2,..., M.
 Kursusindhold: Produkt og marked - matematiske og statistiske metoder Rasmus Waagepetersen Institut for Matematiske Fag Aalborg Universitet March 1, 2013 Sandsynlighedsregning og lagerstyring Normalfordelingen
Kursusindhold: Produkt og marked - matematiske og statistiske metoder Rasmus Waagepetersen Institut for Matematiske Fag Aalborg Universitet March 1, 2013 Sandsynlighedsregning og lagerstyring Normalfordelingen
Kvantitative Metoder 1 - Efterår Dagens program
 Dagens program Approksimation af binomialsandsynligheder, Afsnit 4.5 Multinomial fordeling, Afsnit 4.8 Negativ binomialfordeling, Afsnit 4.4 Poisson fordeling og Poisson process, Afsnit 4.6 Kontinuerte
Dagens program Approksimation af binomialsandsynligheder, Afsnit 4.5 Multinomial fordeling, Afsnit 4.8 Negativ binomialfordeling, Afsnit 4.4 Poisson fordeling og Poisson process, Afsnit 4.6 Kontinuerte
Statistik er at behandle en stor mængde af tal, så de bliver lettere at overskue og forstå.
 Statistik er at behandle en stor mængde af tal, så de bliver lettere at overskue og forstå. Hvis man fx samler de karakterer, der er givet til en eksamen i én stor bunke (se herunder), kan det være svært
Statistik er at behandle en stor mængde af tal, så de bliver lettere at overskue og forstå. Hvis man fx samler de karakterer, der er givet til en eksamen i én stor bunke (se herunder), kan det være svært
for gymnasiet og hf 2017 Karsten Juul
 for gymnasiet og hf 75 50 5 017 Karsten Juul Statistik for gymnasiet og hf 017 Karsten Juul 5/11-017 Nyeste version af dette hæfte kan downloades fra http://mat1.dk/noter.htm Hæftet må benyttes i undervisningen
for gymnasiet og hf 75 50 5 017 Karsten Juul Statistik for gymnasiet og hf 017 Karsten Juul 5/11-017 Nyeste version af dette hæfte kan downloades fra http://mat1.dk/noter.htm Hæftet må benyttes i undervisningen
Statistik viden eller tilfældighed
 MATEMATIK i perspektiv Side 1 af 9 DNA-analyser 1 Sandsynligheden for at en uskyldig anklages Følgende histogram viser, hvordan fragmentlængden for et DNA-område varierer inden for befolkningen. Der indgår
MATEMATIK i perspektiv Side 1 af 9 DNA-analyser 1 Sandsynligheden for at en uskyldig anklages Følgende histogram viser, hvordan fragmentlængden for et DNA-område varierer inden for befolkningen. Der indgår
Antal timer 19 5 7 10 0 6 6 3 7 6 4 14 6 5 12 10 Køn k m k m m k m k m k k k m k k k
 Statistik 5 Statistik er en meget omfattende matematisk disciplin, og den anvendes i meget stor udstrækning i vores moderne samfund. Den handler om at analysere et (ofte meget stort) talmateriale. Det
Statistik 5 Statistik er en meget omfattende matematisk disciplin, og den anvendes i meget stor udstrækning i vores moderne samfund. Den handler om at analysere et (ofte meget stort) talmateriale. Det
5. Statistik. Hayati Balo,AAMS. 1. Carstensen, Frandsen og Studsgaard, stx mat B2, systime
 5. Statistik Hayati Balo,AAMS Følgende fremstilling er baseret på 1. Carstensen, Frandsen og Studsgaard, stx mat B2, systime 1. Ugrupperede Observationer Hvis der foreligger et antal målinger eller observationer
5. Statistik Hayati Balo,AAMS Følgende fremstilling er baseret på 1. Carstensen, Frandsen og Studsgaard, stx mat B2, systime 1. Ugrupperede Observationer Hvis der foreligger et antal målinger eller observationer
Statistik ved Bachelor-uddannelsen i folkesundhedsvidenskab. Statistisk Model
 Statistik ved Bachelor-uddannelsen i folkesundhedsvidenskab Statistisk Model Indhold Binomialfordeling Sandsynlighedsfunktion Middelværdi og spredning 1 Aalen: Innføring i statistik med medisinske eksempler
Statistik ved Bachelor-uddannelsen i folkesundhedsvidenskab Statistisk Model Indhold Binomialfordeling Sandsynlighedsfunktion Middelværdi og spredning 1 Aalen: Innføring i statistik med medisinske eksempler
Statistik. Statistik er analyse af indsamlet data. Det vil sige at man bearbejder et datamateriale som i matematik næsten altid er tal.
 Statistik Statistik er analyse af indsamlet data. Det vil sige at man bearbejder et datamateriale som i matematik næsten altid er tal. Derved får man et samlet overblik over talmaterialet, og man kan konkludere
Statistik Statistik er analyse af indsamlet data. Det vil sige at man bearbejder et datamateriale som i matematik næsten altid er tal. Derved får man et samlet overblik over talmaterialet, og man kan konkludere
Deskriptiv statistik for matc i stx og hf
 Deskriptiv statistik for matc i stx og hf 75 50 25 2019 Karsten Juul Deskriptiv statistik for matc i stx og hf Hvad er deskriptiv statistik? 1.1 Hvad er deskriptiv statistik?... 1 1.2 Hvad er grupperede
Deskriptiv statistik for matc i stx og hf 75 50 25 2019 Karsten Juul Deskriptiv statistik for matc i stx og hf Hvad er deskriptiv statistik? 1.1 Hvad er deskriptiv statistik?... 1 1.2 Hvad er grupperede
Supplement til kapitel 7: Approksimationen til normalfordelingen, s. 136
 Supplement til kapitel 7: Approksimationen til normalfordelingen, s. 36 Det er besværligt at regne med binomialfordelingen, og man vælger derfor ofte at bruge en approksimation med normalfordeling. Man
Supplement til kapitel 7: Approksimationen til normalfordelingen, s. 36 Det er besværligt at regne med binomialfordelingen, og man vælger derfor ofte at bruge en approksimation med normalfordeling. Man
Kursusindhold: X i : tilfældig værdi af ite eksperiment. Antag X i kun antager værdierne 1, 2,..., M.
 Kursusindhold: Produkt og marked - matematiske og statistiske metoder Rasmus Waagepetersen Institut for Matematiske Fag Aalborg Universitet February 9, 2015 Sandsynlighedsregning og lagerstyring Normalfordelingen
Kursusindhold: Produkt og marked - matematiske og statistiske metoder Rasmus Waagepetersen Institut for Matematiske Fag Aalborg Universitet February 9, 2015 Sandsynlighedsregning og lagerstyring Normalfordelingen
for gymnasiet og hf 2016 Karsten Juul
 for gymnasiet og hf 75 50 5 016 Karsten Juul Statistik for gymnasiet og hf Ä 016 Karsten Juul 4/1-016 Nyeste version af dette håfte kan downloades fra http://mat1.dk/noter.htm HÅftet mç benyttes i undervisningen
for gymnasiet og hf 75 50 5 016 Karsten Juul Statistik for gymnasiet og hf Ä 016 Karsten Juul 4/1-016 Nyeste version af dette håfte kan downloades fra http://mat1.dk/noter.htm HÅftet mç benyttes i undervisningen
J E T T E V E S T E R G A A R D
 BINOMIALT EST J E T T E V E S T E R G A A R D F I P B I O L O G I M A R S E L I S B O R G G Y M N A S I U M D. 1 3. M A R T S 2 0 1 9 K A L U N D B O R G G Y M N A S I U M D. 1 4. M A R T S 2 0 1 9 HVEM
BINOMIALT EST J E T T E V E S T E R G A A R D F I P B I O L O G I M A R S E L I S B O R G G Y M N A S I U M D. 1 3. M A R T S 2 0 1 9 K A L U N D B O R G G Y M N A S I U M D. 1 4. M A R T S 2 0 1 9 HVEM
Statistik (deskriptiv)
 Statistik (deskriptiv) Ikke-grupperede data For at behandle ikke-grupperede data i TI, skal data tastes ind i en liste. Dette kan gøres ved brug af List, hvis ikon er nr. 5 fra venstre på værktøjsbjælken
Statistik (deskriptiv) Ikke-grupperede data For at behandle ikke-grupperede data i TI, skal data tastes ind i en liste. Dette kan gøres ved brug af List, hvis ikon er nr. 5 fra venstre på værktøjsbjælken
Produkt og marked - matematiske og statistiske metoder
 Produkt og marked - matematiske og statistiske metoder Rasmus Waagepetersen Institut for Matematiske Fag Aalborg Universitet February 11, 2016 1/22 Kursusindhold: Sandsynlighedsregning og lagerstyring
Produkt og marked - matematiske og statistiske metoder Rasmus Waagepetersen Institut for Matematiske Fag Aalborg Universitet February 11, 2016 1/22 Kursusindhold: Sandsynlighedsregning og lagerstyring
Løsninger til kapitel 5
 1 Løsninger til kapitel 5 Opgave 51 Det nemmeste er her at omskrive alle sandsynlighederne til differenser mellem kumulerede sandsynligheder, dvs af sandsynligheder af formen, og derefter beregne disse
1 Løsninger til kapitel 5 Opgave 51 Det nemmeste er her at omskrive alle sandsynlighederne til differenser mellem kumulerede sandsynligheder, dvs af sandsynligheder af formen, og derefter beregne disse
Kombinatorik. Eksempel 2: En mand har 7 par bukser og 10 skjorter. Skal han både vælge en skjorte og et par bukser, så har han 10. 7=70 mulige valg.
 Noter til Biomat, 005. Kombinatorik. - eller kunsten at tælle. Alle tal i kombinatorik-afsnittet er hele og ikke-negative. Additionsprincippet enten - eller : Antag vi enten skal lave et valg med m muligheder
Noter til Biomat, 005. Kombinatorik. - eller kunsten at tælle. Alle tal i kombinatorik-afsnittet er hele og ikke-negative. Additionsprincippet enten - eller : Antag vi enten skal lave et valg med m muligheder
Kursusindhold: Produkt og marked - matematiske og statistiske metoder. Monte Carlo
 Kursusindhold: Produkt og marked - matematiske og statistiske metoder Rasmus Waagepetersen Institut for Matematiske Fag Aalborg Universitet Sandsynlighedsregning og lagerstyring Normalfordelingen og Monte
Kursusindhold: Produkt og marked - matematiske og statistiske metoder Rasmus Waagepetersen Institut for Matematiske Fag Aalborg Universitet Sandsynlighedsregning og lagerstyring Normalfordelingen og Monte
Vrede vestjyder afviser Løkkes stemmefiskeri
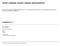 Vrede vestjyder afviser Løkkes stemmefiskeri På trods af VK-regeringens hjælpepakke til peger kun hver 11. vestjyde på Venstre som partiet, der vil løse udkantsdanmarks problemer. Kan koste venstre sejren
Vrede vestjyder afviser Løkkes stemmefiskeri På trods af VK-regeringens hjælpepakke til peger kun hver 11. vestjyde på Venstre som partiet, der vil løse udkantsdanmarks problemer. Kan koste venstre sejren
Sandsynlighed. for matc i stx og hf Karsten Juul
 Sandsynlighed for matc i stx og hf 209 Karsten Juul . Udfald Vi drejer den gule skive om dens centrum og ser hvilket af de fem felter der standser ud for den røde pil. Da skiven sidst blev drejet, var
Sandsynlighed for matc i stx og hf 209 Karsten Juul . Udfald Vi drejer den gule skive om dens centrum og ser hvilket af de fem felter der standser ud for den røde pil. Da skiven sidst blev drejet, var
Kursusindhold: Produkt og marked - matematiske og statistiske metoder. Monte Carlo
 Kursusindhold: Produkt og marked - matematiske og statistiske metoder Rasmus Waagepetersen Institut for Matematiske Fag Aalborg Universitet Sandsynlighedsregning og lagerstyring Normalfordelingen og Monte
Kursusindhold: Produkt og marked - matematiske og statistiske metoder Rasmus Waagepetersen Institut for Matematiske Fag Aalborg Universitet Sandsynlighedsregning og lagerstyring Normalfordelingen og Monte
Under 63 år : 92% Under 55 år : 55% Ved at trække den nederste fra den øverste af de to grupper fås: Melllem 55 og 63 år :
 1 501 Sumkurven viser aldersfordelingen for lærerne på et gymnasium. a) Hvor mange procent af lærerne er mellem 55 og 63 år? (Benyt gerne bilaget til at dokumentere svaret.) Løsning: Under 63 år : 92%
1 501 Sumkurven viser aldersfordelingen for lærerne på et gymnasium. a) Hvor mange procent af lærerne er mellem 55 og 63 år? (Benyt gerne bilaget til at dokumentere svaret.) Løsning: Under 63 år : 92%
Danskerne ønsker valg om sundhed
 Danskerne ønsker valg om sundhed Sundhedsvæsenet er det vigtigste tema for vælgerne, når de skal stemme ved det kommende folketingsvalg. Derefter følger skattepolitik og beskæftigelses- og arbejdsmarkedspolitik.
Danskerne ønsker valg om sundhed Sundhedsvæsenet er det vigtigste tema for vælgerne, når de skal stemme ved det kommende folketingsvalg. Derefter følger skattepolitik og beskæftigelses- og arbejdsmarkedspolitik.
Anvendt Statistik Lektion 2. Sandsynlighedsregning Sandsynlighedsfordelinger Normalfordelingen Stikprøvefordelinger
 Anvendt Statistik Lektion 2 Sandsynlighedsregning Sandsynlighedsfordelinger Normalfordelingen Stikprøvefordelinger Sandsynlighed: Opvarmning Udfald Resultatet af et eksperiment kaldes et udfald. Eksempler:
Anvendt Statistik Lektion 2 Sandsynlighedsregning Sandsynlighedsfordelinger Normalfordelingen Stikprøvefordelinger Sandsynlighed: Opvarmning Udfald Resultatet af et eksperiment kaldes et udfald. Eksempler:
Statistik. Deskriptiv statistik, normalfordeling og test. Karsten Juul
 Statistik Deskriptiv statistik, normalfordeling og test Karsten Juul Intervalhyppigheder En elevgruppe på et gymnasium har spurgt 100 tilfældigt valgte elever på gymnasiet om hvor lang tid det tager dem
Statistik Deskriptiv statistik, normalfordeling og test Karsten Juul Intervalhyppigheder En elevgruppe på et gymnasium har spurgt 100 tilfældigt valgte elever på gymnasiet om hvor lang tid det tager dem
Ved et folketingsvalg eller en folkeafstemning spørger man alle stemmeberettigede, og kun en del af dem stemmer.
 Matematik C (må anvendes på Ørestad Gymnasium) Statistik Statistik er bearbejdning af talmaterialer, der ofte indeholderstore mængder af tal. De indsamles og registreres i mange forskellige sammenhænge
Matematik C (må anvendes på Ørestad Gymnasium) Statistik Statistik er bearbejdning af talmaterialer, der ofte indeholderstore mængder af tal. De indsamles og registreres i mange forskellige sammenhænge
Oversigt over nyttige fordelinger
 Oversigt over nyttige fordelinger Helene Regitze Lund Wandsøe November 14, 2011 1 Bernoulli-fordelingen 1 Når et eksperiment har to mulige udfald: succes eller fiasko. X er en stokastisk variabel med følgende
Oversigt over nyttige fordelinger Helene Regitze Lund Wandsøe November 14, 2011 1 Bernoulli-fordelingen 1 Når et eksperiment har to mulige udfald: succes eller fiasko. X er en stokastisk variabel med følgende
Statistiske modeller
 Statistiske modeller Statistisk model Datamatrice Variabelmatrice Hændelse Sandsynligheder Data Statistiske modeller indeholder: Variable Hændelser defineret ved mulige variabel værdier Sandsynligheder
Statistiske modeller Statistisk model Datamatrice Variabelmatrice Hændelse Sandsynligheder Data Statistiske modeller indeholder: Variable Hændelser defineret ved mulige variabel værdier Sandsynligheder
Supplerende opgaver til TRIP s matematiske GRUNDBOG. Forlaget TRIP. Opgaverne må frit benyttes i undervisningen.
 48-50. Side 1 af 7 Statistik og sandsynlighedsregning ( 48-50) Opgaverne med svar starter på side 5, og deres numre har et s efter nummeret. Deres nummerering starter forfra. Svarene står fra side 6 med
48-50. Side 1 af 7 Statistik og sandsynlighedsregning ( 48-50) Opgaverne med svar starter på side 5, og deres numre har et s efter nummeret. Deres nummerering starter forfra. Svarene står fra side 6 med
Produkt og marked - matematiske og statistiske metoder
 Produkt og marked - matematiske og statistiske metoder Rasmus Waagepetersen Institut for Matematiske Fag Aalborg Universitet February 19, 2016 1/26 Kursusindhold: Sandsynlighedsregning og lagerstyring
Produkt og marked - matematiske og statistiske metoder Rasmus Waagepetersen Institut for Matematiske Fag Aalborg Universitet February 19, 2016 1/26 Kursusindhold: Sandsynlighedsregning og lagerstyring
Elementær sandsynlighedsregning
 Elementær sandsynlighedsregning Sandsynlighedsbegrebet Et udfaldsrum S er mængden af alle de mulige udfald af et eksperiment. En hændelse A er en delmængde af udfaldsrummet S. Et sandsynlighedsmål er en
Elementær sandsynlighedsregning Sandsynlighedsbegrebet Et udfaldsrum S er mængden af alle de mulige udfald af et eksperiment. En hændelse A er en delmængde af udfaldsrummet S. Et sandsynlighedsmål er en
Dansk Folkeparti står foran en krise
 Dansk Folkeparti står foran en krise To ud af tre vælgere - og over halvdelen af Venstres vælgere - ønsker mindre til Dansk Folkeparti. Kun inden for ældreplitik vurderer flertallet at DF har positiv.
Dansk Folkeparti står foran en krise To ud af tre vælgere - og over halvdelen af Venstres vælgere - ønsker mindre til Dansk Folkeparti. Kun inden for ældreplitik vurderer flertallet at DF har positiv.
for matematik pä B-niveau i hf
 for matematik pä B-niveau i hf 75 50 5 016 Karsten Juul GRUPPEREDE DATA 1.1 Hvad er deskriptiv statistik?...1 1. Hvad er grupperede og ugrupperede data?...1 1.1 Eksempel pä ugrupperede data...1 1. Eksempel
for matematik pä B-niveau i hf 75 50 5 016 Karsten Juul GRUPPEREDE DATA 1.1 Hvad er deskriptiv statistik?...1 1. Hvad er grupperede og ugrupperede data?...1 1.1 Eksempel pä ugrupperede data...1 1. Eksempel
Huskeliste Printark. U4 Tastetider U5 Hvor hurtigt regner du? E4 Begreber og fagord - Statistik. Materialer. Mobiltelefon Stopur
 Statistik - Lærervejledning Om kapitlet I dette kapitel om statistik skal eleverne arbejde med statistik og lære at indsamle, beskrive, bearbejde og præsentere store mængder af tal og data. I kapitlet
Statistik - Lærervejledning Om kapitlet I dette kapitel om statistik skal eleverne arbejde med statistik og lære at indsamle, beskrive, bearbejde og præsentere store mængder af tal og data. I kapitlet
Løsninger til kapitel 1
 Opgave. a) observation hyppighed frekvens kum. frekvens 2,25,25 3,875,325 2 3,875,5 3 3,875,6875 4,625,75 5,625,825 6,,825 7 2,25,9375 8,,9375 9,625, Frekvenser illustreres i et pindediagram,2,8,6,4,2,,8,6,4,2
Opgave. a) observation hyppighed frekvens kum. frekvens 2,25,25 3,875,325 2 3,875,5 3 3,875,6875 4,625,75 5,625,825 6,,825 7 2,25,9375 8,,9375 9,625, Frekvenser illustreres i et pindediagram,2,8,6,4,2,,8,6,4,2
Statistik. Kvartiler og middeltal defineres forskelligt ved grupperede observationer og ved ikke grupperede observationer.
 Statistik Formålet... 1 Mindsteværdi... 1 Størsteværdi... 1 Ikke grupperede observationer... 2 Median og kvartiler defineres ved ikke grupperede observationer således:... 2 Middeltal defineres ved ikke
Statistik Formålet... 1 Mindsteværdi... 1 Størsteværdi... 1 Ikke grupperede observationer... 2 Median og kvartiler defineres ved ikke grupperede observationer således:... 2 Middeltal defineres ved ikke
Nanostatistik: Opgavebesvarelser
 Nanostatistik: Opgavebesvarelser JLJ Nanostatistik: Opgavebesvarelser p. 1/16 Pakkemaskine En producent hævder at poserne indeholder i gennemsnit 16 ounces sukker. Data: 10 pakker sukker: 16.1, 15.8, 15.8,
Nanostatistik: Opgavebesvarelser JLJ Nanostatistik: Opgavebesvarelser p. 1/16 Pakkemaskine En producent hævder at poserne indeholder i gennemsnit 16 ounces sukker. Data: 10 pakker sukker: 16.1, 15.8, 15.8,
U L I G H E D I D A N M A R K
 D E N N I S P I P E N B R I N G U L I G H E D I D A N M A R K M AT X. D K Copyright 2013 Dennis Pipenbring offentliggjort på matx.dk layout af tufte-latex.googlecode.com Materialet er til fri afbenyttelse
D E N N I S P I P E N B R I N G U L I G H E D I D A N M A R K M AT X. D K Copyright 2013 Dennis Pipenbring offentliggjort på matx.dk layout af tufte-latex.googlecode.com Materialet er til fri afbenyttelse
Elementær sandsynlighedsregning
 Elementær sandsynlighedsregning Sandsynlighedsbegrebet Et udfaldsrum S er mængden af alle de mulige udfald af et eksperiment. En hændelse A er en delmængde af udfaldsrummet S. Den hændelse, der ikke indeholder
Elementær sandsynlighedsregning Sandsynlighedsbegrebet Et udfaldsrum S er mængden af alle de mulige udfald af et eksperiment. En hændelse A er en delmængde af udfaldsrummet S. Den hændelse, der ikke indeholder
Lyngallup profil af partier til BT Dato: 13. juni 2012
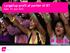 Lyngallup profil af partier til BT Dato: 13. juni 2012 Metode Feltperiode: 7. juni 13. juni 2012 Målgruppe: Repræsentativt udvalgte vælgere landet over på 18 eller derover Metode: GallupForum (webinterviews)
Lyngallup profil af partier til BT Dato: 13. juni 2012 Metode Feltperiode: 7. juni 13. juni 2012 Målgruppe: Repræsentativt udvalgte vælgere landet over på 18 eller derover Metode: GallupForum (webinterviews)
Løsning til eksamen d.27 Maj 2010
 DTU informatic 02402 Introduktion til Statistik Løsning til eksamen d.27 Maj 2010 Referencer til Probability and Statistics for Engineers er angivet i rækkefølgen [8th edition, 7th edition]. Opgave I.1
DTU informatic 02402 Introduktion til Statistik Løsning til eksamen d.27 Maj 2010 Referencer til Probability and Statistics for Engineers er angivet i rækkefølgen [8th edition, 7th edition]. Opgave I.1
SF er vælgernes reservehold
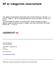 SF er vælgernes reservehold Hvis vælgerne skulle på et andet parti end deres foretrukne, ville flest 14 procent - vælge SF. Alle SF s potentielle r kommer fra partier i rød blok (R, S og EL). 12 procent
SF er vælgernes reservehold Hvis vælgerne skulle på et andet parti end deres foretrukne, ville flest 14 procent - vælge SF. Alle SF s potentielle r kommer fra partier i rød blok (R, S og EL). 12 procent
Danskerne kræver bogligt stærke børn
 Danskerne kræver bogligt stærke børn Hver anden dansker kræver at folkeskolen stiller større krav til eleverne i de boglige fag som dansk, matematik og sprog, mens kreativitet og fantasi er mindst vigtigt.
Danskerne kræver bogligt stærke børn Hver anden dansker kræver at folkeskolen stiller større krav til eleverne i de boglige fag som dansk, matematik og sprog, mens kreativitet og fantasi er mindst vigtigt.
Anvendt Statistik Lektion 2. Sandsynlighedsregning Sandsynlighedsfordelinger Normalfordelingen Stikprøvefordelinger
 Anvendt Statistik Lektion 2 Sandsynlighedsregning Sandsynlighedsfordelinger Normalfordelingen Stikprøvefordelinger Sandsynlighed: Opvarmning Udfald Resultatet af et eksperiment kaldes et udfald. Eksempler:
Anvendt Statistik Lektion 2 Sandsynlighedsregning Sandsynlighedsfordelinger Normalfordelingen Stikprøvefordelinger Sandsynlighed: Opvarmning Udfald Resultatet af et eksperiment kaldes et udfald. Eksempler:
Danskerne tror ikke på Løkke som statsminister
 Danskerne tror ikke på Løkke som statsminister Helle Thorning-Schmidt (S) er storfavorit til at vinde næste valg. 42 procent af vælgerne - og hver femte VKO vælger - tror mest på Thorning, mens kun 29
Danskerne tror ikke på Løkke som statsminister Helle Thorning-Schmidt (S) er storfavorit til at vinde næste valg. 42 procent af vælgerne - og hver femte VKO vælger - tror mest på Thorning, mens kun 29
Kapitel 4 Sandsynlighed og statistiske modeller
 Kapitel 4 Sandsynlighed og statistiske modeller Peter Tibert Stoltze stat@peterstoltze.dk Elementær statistik F2011 1 Indledning 2 Sandsynlighed i binomialfordelingen 3 Normalfordelingen 4 Modelkontrol
Kapitel 4 Sandsynlighed og statistiske modeller Peter Tibert Stoltze stat@peterstoltze.dk Elementær statistik F2011 1 Indledning 2 Sandsynlighed i binomialfordelingen 3 Normalfordelingen 4 Modelkontrol
1 Statistisk inferens: Hypotese og test Nulhypotese - alternativ Teststatistik P-værdi Signifikansniveau...
 Indhold 1 Statistisk inferens: Hypotese og test 2 1.1 Nulhypotese - alternativ.................................. 2 1.2 Teststatistik........................................ 3 1.3 P-værdi..........................................
Indhold 1 Statistisk inferens: Hypotese og test 2 1.1 Nulhypotese - alternativ.................................. 2 1.2 Teststatistik........................................ 3 1.3 P-værdi..........................................
for matematik pä B-niveau i hf
 for matematik pä B-niveau i hf 014 Karsten Juul TEST 1 StikprÅver... 1 1.1 Hvad er populationen?... 1 1. Hvad er stikpråven?... 1 1.3 Systematiske fejl ved valg af stikpråven.... 1 1.4 TilfÇldige fejl
for matematik pä B-niveau i hf 014 Karsten Juul TEST 1 StikprÅver... 1 1.1 Hvad er populationen?... 1 1. Hvad er stikpråven?... 1 1.3 Systematiske fejl ved valg af stikpråven.... 1 1.4 TilfÇldige fejl
[PJ] QuickGuide.dfw QuickGuide
![[PJ] QuickGuide.dfw QuickGuide [PJ] QuickGuide.dfw QuickGuide](/thumbs/62/47343789.jpg) [PJ] QuickGuide.dfw 07-04-003 QuickGuide Derives resultater Husk at Derive angiver decimalbrøker uden at forhøje sidste ciffer. Så når du udregner fx /3 får du 0.66666 og ikke 0.66667. Du kan altså ikke
[PJ] QuickGuide.dfw 07-04-003 QuickGuide Derives resultater Husk at Derive angiver decimalbrøker uden at forhøje sidste ciffer. Så når du udregner fx /3 får du 0.66666 og ikke 0.66667. Du kan altså ikke
Borgerlige vælgere sender blå blok på bænken
 Borgerlige vælgere sender blå blok på bænken 43 procent af de vælgere, der ved seneste valg stemte borgerligt, mener, at blå blok trænger til at komme i opposition. Det fremgår af en meningsmåling, som
Borgerlige vælgere sender blå blok på bænken 43 procent af de vælgere, der ved seneste valg stemte borgerligt, mener, at blå blok trænger til at komme i opposition. Det fremgår af en meningsmåling, som
Hvad er meningen? Et forløb om opinionsundersøgelser
 Hvad er meningen? Et forløb om opinionsundersøgelser Jette Rygaard Poulsen, Frederikshavn Gymnasium og HF-kursus Hans Vestergaard, Frederikshavn Gymnasium og HF-kursus Søren Lundbye-Christensen, AAU 17-10-2004
Hvad er meningen? Et forløb om opinionsundersøgelser Jette Rygaard Poulsen, Frederikshavn Gymnasium og HF-kursus Hans Vestergaard, Frederikshavn Gymnasium og HF-kursus Søren Lundbye-Christensen, AAU 17-10-2004
Færre vil give en hånd til Afrika
 Færre vil give en hånd til Afrika Næsten hver tredje synes Danmark giver for meget i ulandsbistand i 2005 var det kun hver sjette. Skepsissen skyldes mistillid til støttens virkning og hensynet til den
Færre vil give en hånd til Afrika Næsten hver tredje synes Danmark giver for meget i ulandsbistand i 2005 var det kun hver sjette. Skepsissen skyldes mistillid til støttens virkning og hensynet til den
Matematikkens mysterier - på et obligatorisk niveau. 9. Sandsynlighedsregning
 Matematikkens mysterier - på et obligatorisk niveau af Kenneth Hansen 9. Sandsynlighedsregning Hvad er den typiske størrelse af et nittehoved? 9. Statistik og sandsynlighedsregning Indhold 9.0 Indledning
Matematikkens mysterier - på et obligatorisk niveau af Kenneth Hansen 9. Sandsynlighedsregning Hvad er den typiske størrelse af et nittehoved? 9. Statistik og sandsynlighedsregning Indhold 9.0 Indledning
Under 63 år : 88% Under 55 år : 55% Ved at trække den nederste fra den øverste af de to grupper fås: Melllem 55 og 63 år :
 1 501 Sumkurven viser aldersfordelingen for lærerne på et gymnasium. a) Hvor mange procent af lærerne er mellem 55 og 63 år? (Benyt gerne bilaget til at dokumentere svaret.) Løsning: Under 63 år : 88%
1 501 Sumkurven viser aldersfordelingen for lærerne på et gymnasium. a) Hvor mange procent af lærerne er mellem 55 og 63 år? (Benyt gerne bilaget til at dokumentere svaret.) Løsning: Under 63 år : 88%
Danskerne må give op før pensionsalderen
 Danskerne må give op før pensionsalderen De fleste under 45 år regner ikke med at kunne arbejde så længe, som det bliver nødvendigt, hvis efterlønnen afskaffes. Det viser undersøgelse foretaget for Ugebrevet
Danskerne må give op før pensionsalderen De fleste under 45 år regner ikke med at kunne arbejde så længe, som det bliver nødvendigt, hvis efterlønnen afskaffes. Det viser undersøgelse foretaget for Ugebrevet
Nanostatistik: Opgaver
 Nanostatistik: Opgaver Jens Ledet Jensen, 19/01/05 Opgaver 1 Opgaver fra Indblik i Statistik 5 Eksamensopgaver fra tidligere år 11 i ii NANOSTATISTIK: OPGAVER Opgaver Opgave 1 God opgaveskik: Når I regner
Nanostatistik: Opgaver Jens Ledet Jensen, 19/01/05 Opgaver 1 Opgaver fra Indblik i Statistik 5 Eksamensopgaver fra tidligere år 11 i ii NANOSTATISTIK: OPGAVER Opgaver Opgave 1 God opgaveskik: Når I regner
Retsforbeholdet. Gallup for Berlingske. Retsforbeholdet. TNS Dato: 1. december 2015 Projekt: 62329
 Gallup for Berlingske Gallup om retsforbeholdet Feltperiode: Den 30. november 1. december 2015 Målgruppe: Repræsentativt udvalgte vælgere landet over på 18 eller derover Metode: GallupForum (webinterviews)
Gallup for Berlingske Gallup om retsforbeholdet Feltperiode: Den 30. november 1. december 2015 Målgruppe: Repræsentativt udvalgte vælgere landet over på 18 eller derover Metode: GallupForum (webinterviews)
Normalfordelingen og Stikprøvefordelinger
 Normalfordelingen og Stikprøvefordelinger Normalfordelingen Standard Normal Fordelingen Sandsynligheder for Normalfordelingen Transformation af Normalfordelte Stok.Var. Stikprøver og Stikprøvefordelinger
Normalfordelingen og Stikprøvefordelinger Normalfordelingen Standard Normal Fordelingen Sandsynligheder for Normalfordelingen Transformation af Normalfordelte Stok.Var. Stikprøver og Stikprøvefordelinger
I. Deskriptiv analyse af kroppens proportioner
 Projektet er delt i to, og man kan vælge kun at gennemføre den ene del. Man kan vælge selv at frembringe data, fx gennem et samarbejde med idræt eller biologi, eller man kan anvende de foreliggende data,
Projektet er delt i to, og man kan vælge kun at gennemføre den ene del. Man kan vælge selv at frembringe data, fx gennem et samarbejde med idræt eller biologi, eller man kan anvende de foreliggende data,
SANDSYNLIGHED FACIT SIDE 154-155
 SIDE 154-155 Opgave 1 A. Data (x) h(x) f(x) 2 1 0,042 3 3 0,125 4 6 0,25 5 3 0,125 6 4 0,16 7 1 0,042 8 2 0,0833 9 1 0,042 10 2 0,0833 11 1 0,042 B. C. Diagrammet (et søjlediagram) er lavet ud fra hyppigheden,
SIDE 154-155 Opgave 1 A. Data (x) h(x) f(x) 2 1 0,042 3 3 0,125 4 6 0,25 5 3 0,125 6 4 0,16 7 1 0,042 8 2 0,0833 9 1 0,042 10 2 0,0833 11 1 0,042 B. C. Diagrammet (et søjlediagram) er lavet ud fra hyppigheden,
Sandsynlighedsregning
 Sandsynlighedsregning En note om sandsynlighedsregning. Den er tænkt som supplement til Vejen til Matematik B2. Henrik S. Hansen, Sct. Knud Version 2.0 Indhold Indledning... 1 Sandsynlighedsregning...
Sandsynlighedsregning En note om sandsynlighedsregning. Den er tænkt som supplement til Vejen til Matematik B2. Henrik S. Hansen, Sct. Knud Version 2.0 Indhold Indledning... 1 Sandsynlighedsregning...
Oversigt. Kursus Introduktion til Statistik. Forelæsning 3: Kapitel 5: Kontinuerte fordelinger. Per Bruun Brockhoff.
 Kursus 242 Introduktion til Statistik Forelæsning 3: Kapitel 5: Kontinuerte fordelinger Per Bruun Brockhoff DTU Compute, Statistik Bygning 35/324 Danmarks Tekniske Universitet 28 Lyngby Danmark e-mail:
Kursus 242 Introduktion til Statistik Forelæsning 3: Kapitel 5: Kontinuerte fordelinger Per Bruun Brockhoff DTU Compute, Statistik Bygning 35/324 Danmarks Tekniske Universitet 28 Lyngby Danmark e-mail:
Hvad skal vi lave? Nulhypotese - alternativ. Teststatistik. Signifikansniveau
 Hvad skal vi lave? 1 Statistisk inferens: Hypotese og test Nulhypotese - alternativ. Teststatistik P-værdi Signifikansniveau 2 t-test for middelværdi Tosidet t-test for middelværdi Ensidet t-test for middelværdi
Hvad skal vi lave? 1 Statistisk inferens: Hypotese og test Nulhypotese - alternativ. Teststatistik P-værdi Signifikansniveau 2 t-test for middelværdi Tosidet t-test for middelværdi Ensidet t-test for middelværdi
statistik og sandsynlighed
 brikkerne til regning & matematik statistik og sandsynlighed trin 2 preben bernitt brikkerne statistik og sandsynlighed 2 1. udgave som E-bog ISBN: 978-87-92488-20-6 2004 by bernitt-matematik.dk Kopiering
brikkerne til regning & matematik statistik og sandsynlighed trin 2 preben bernitt brikkerne statistik og sandsynlighed 2 1. udgave som E-bog ISBN: 978-87-92488-20-6 2004 by bernitt-matematik.dk Kopiering
Deskriptiv statistik. for C-niveau i hf. 2015 Karsten Juul
 Deskriptiv statistik for C-niveau i hf 75 50 25 2015 Karsten Juul DESKRIPTIV STATISTIK 1.1 Hvad er deskriptiv statistik?...1 1.2 Hvad er grupperede og ugrupperede data?...1 1.21 Eksempel pä ugrupperede
Deskriptiv statistik for C-niveau i hf 75 50 25 2015 Karsten Juul DESKRIPTIV STATISTIK 1.1 Hvad er deskriptiv statistik?...1 1.2 Hvad er grupperede og ugrupperede data?...1 1.21 Eksempel pä ugrupperede
CIVILINGENIØREKSAMEN Side 1 af 18 sider. Skriftlig prøve, den: XY. december 200Z Kursus nr : (navn) (underskrift) (bord nr)
 CIVILINGENIØREKSAMEN Side 1 af 18 sider Skriftlig prøve, den: XY. december 200Z Kursus nr : 02405 Kursus navn: Sandsynlighedsregning Tilladte hjælpemidler: Alle Dette sæt er besvaret af: (navn) (underskrift)
CIVILINGENIØREKSAMEN Side 1 af 18 sider Skriftlig prøve, den: XY. december 200Z Kursus nr : 02405 Kursus navn: Sandsynlighedsregning Tilladte hjælpemidler: Alle Dette sæt er besvaret af: (navn) (underskrift)
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Institution Uddannelse Fag og niveau Lærer(e) Hold Termin hvori undervisningen afsluttes: maj-juni, 2014 IBC-Kolding
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Institution Uddannelse Fag og niveau Lærer(e) Hold Termin hvori undervisningen afsluttes: maj-juni, 2014 IBC-Kolding
Familiepolitik er usynlig for danskerne
 Familiepolitik er usynlig for danskerne Næsten hver anden dansker kan ikke få øje på noget parti, der specielt kæmper børnefamiliernes sag. Når danskerne skal pege på de partier, der bedst kæmper børnefamiliernes,
Familiepolitik er usynlig for danskerne Næsten hver anden dansker kan ikke få øje på noget parti, der specielt kæmper børnefamiliernes sag. Når danskerne skal pege på de partier, der bedst kæmper børnefamiliernes,
Forelæsning 3: Kapitel 5: Kontinuerte fordelinger
 Kursus 02402 Introduktion til Statistik Forelæsning 3: Kapitel 5: Kontinuerte fordelinger Per Bruun Brockhoff DTU Compute, Statistik og Dataanalyse Bygning 324, Rum 220 Danmarks Tekniske Universitet 2800
Kursus 02402 Introduktion til Statistik Forelæsning 3: Kapitel 5: Kontinuerte fordelinger Per Bruun Brockhoff DTU Compute, Statistik og Dataanalyse Bygning 324, Rum 220 Danmarks Tekniske Universitet 2800
9.1 I en klasse blev alle elevernes højde målt. Det gav følgende resultater:
 9. 9.1 I en klasse blev alle elevernes højde målt. Det gav følgende resultater: 1,70 1,56 1,61 1,75 1,69 1,70 1,84 1,72 1,79 1,67 1,63 1,69 1,83 1,73 1,52 1,61 1,86 1,64 1,72 1,81 Find mindsteværdi, størsteværdi,
9. 9.1 I en klasse blev alle elevernes højde målt. Det gav følgende resultater: 1,70 1,56 1,61 1,75 1,69 1,70 1,84 1,72 1,79 1,67 1,63 1,69 1,83 1,73 1,52 1,61 1,86 1,64 1,72 1,81 Find mindsteværdi, størsteværdi,
Kapitel 4 Sandsynlighed og statistiske modeller
 Kapitel 4 Sandsynlighed og statistiske modeller Peter Tibert Stoltze stat@peterstoltze.dk Elementær statistik F2011 1 / 22 Generalisering fra stikprøve til population Idé: Opstil en model for populationen
Kapitel 4 Sandsynlighed og statistiske modeller Peter Tibert Stoltze stat@peterstoltze.dk Elementær statistik F2011 1 / 22 Generalisering fra stikprøve til population Idé: Opstil en model for populationen
Løsning til eksaminen d. 14. december 2009
 DTU Informatik 02402 Introduktion til Statistik 200-2-0 LFF/lff Løsning til eksaminen d. 4. december 2009 Referencer til Probability and Statistics for Engineers er angivet i rækkefølgen [8th edition,
DTU Informatik 02402 Introduktion til Statistik 200-2-0 LFF/lff Løsning til eksaminen d. 4. december 2009 Referencer til Probability and Statistics for Engineers er angivet i rækkefølgen [8th edition,
Allan C. Malmberg. Terningkast
 Allan C. Malmberg Terningkast INFA 2008 Programmet Terning Terning er et INFA-program tilrettelagt med henblik på elever i 8. - 10. klasse som har særlig interesse i at arbejde med situationer af chancemæssig
Allan C. Malmberg Terningkast INFA 2008 Programmet Terning Terning er et INFA-program tilrettelagt med henblik på elever i 8. - 10. klasse som har særlig interesse i at arbejde med situationer af chancemæssig
Statistisk beskrivelse og test
 Statistisk beskrivelse og test 005 Karsten Juul Kapitel 1. Intervalhyppigheder Afsnit 1.1: Histogram En elevgruppe på et gymnasium har spurgt 100 tilfældigt valgte elever på gymnasiet om hvor lang tid
Statistisk beskrivelse og test 005 Karsten Juul Kapitel 1. Intervalhyppigheder Afsnit 1.1: Histogram En elevgruppe på et gymnasium har spurgt 100 tilfældigt valgte elever på gymnasiet om hvor lang tid
Matematik A. Studentereksamen
 Matematik A Studentereksamen stx122-mat/a-15082012 Onsdag den 15. august 2012 kl. 9.00-14.00 Opgavesættet er delt i to dele. Delprøven uden hjælpemidler består af opgave 1-6 med i alt 6 spørgsmål. Delprøven
Matematik A Studentereksamen stx122-mat/a-15082012 Onsdag den 15. august 2012 kl. 9.00-14.00 Opgavesættet er delt i to dele. Delprøven uden hjælpemidler består af opgave 1-6 med i alt 6 spørgsmål. Delprøven
Mrs. 11 procent ANALYSE-BUREAU I ANALYSE DANMARK PUBLICERET I UGEBREVET A4 I NR.: 18/2009 DATO: 18.05.2009 LINK TIL ARTIKEL I
 Mrs. 11 procent Effekten af Lene Espersen som formand for de konservative er begrænset udenfor V og K s egen vælgerskare. Og her er opbakningen til hende som eventuel ny statsminister halveret på 3 måneder.
Mrs. 11 procent Effekten af Lene Espersen som formand for de konservative er begrænset udenfor V og K s egen vælgerskare. Og her er opbakningen til hende som eventuel ny statsminister halveret på 3 måneder.
Lars Løkke kan halvere Venstre
 Lars Løkke kan halvere Venstre Kun hver fjerde vælger forventer, at Anders Fogh Rasmussen står i spidsen for Venstre ved næste Folketingsvalg. Hvis kronprins Lars Løkke Rasmussen overtager, vil kun hver
Lars Løkke kan halvere Venstre Kun hver fjerde vælger forventer, at Anders Fogh Rasmussen står i spidsen for Venstre ved næste Folketingsvalg. Hvis kronprins Lars Løkke Rasmussen overtager, vil kun hver
Sandsynlighedregning
 MOGENS ODDERSHEDE LARSEN Sandsynlighedregning + = - P(A B) P(A) P(B) P(A B). 1. udgave 2016 FORORD Dette notat giver en kort gennemgang af de grundlæggende begreber i sandsynlighedsregning. Det forudsættes,
MOGENS ODDERSHEDE LARSEN Sandsynlighedregning + = - P(A B) P(A) P(B) P(A B). 1. udgave 2016 FORORD Dette notat giver en kort gennemgang af de grundlæggende begreber i sandsynlighedsregning. Det forudsættes,
Repetition. Diskrete stokastiske variable. Kontinuerte stokastiske variable
 Normal fordelingen Normal fordelingen Egenskaber ved normalfordelingen Standard normal fordelingen Find sandsynligheder ud fra tabel Transformation af normal fordelte variable Invers transformation Repetition
Normal fordelingen Normal fordelingen Egenskaber ved normalfordelingen Standard normal fordelingen Find sandsynligheder ud fra tabel Transformation af normal fordelte variable Invers transformation Repetition
Bernoulli og binomial fordelingerne Kontinuerte stokastiske variable Normalfordelingen
 Bernoulli og binomial fordelingerne Kontinuerte stokastiske variable Normalfordelingen Repetition Lov om total sandsynlighed Bayes sætning P( B A) = P(A) = P(AI B) + P(AI P( A B) P( B) P( A B) P( B) +
Bernoulli og binomial fordelingerne Kontinuerte stokastiske variable Normalfordelingen Repetition Lov om total sandsynlighed Bayes sætning P( B A) = P(A) = P(AI B) + P(AI P( A B) P( B) P( A B) P( B) +
Online-appendiks til. Hvordan påvirkes vælgerne af meningsmålinger? Effekten af meningsmålinger på danskernes stemmeadfærd og sympati for partierne
 Online-appendiks til Hvordan påvirkes vælgerne af meningsmålinger? Effekten af meningsmålinger på danskernes stemmeadfærd og sympati for partierne Jens Olav Dahlgaard, Jonas H. Hansen, Kasper Møller Hansen
Online-appendiks til Hvordan påvirkes vælgerne af meningsmålinger? Effekten af meningsmålinger på danskernes stemmeadfærd og sympati for partierne Jens Olav Dahlgaard, Jonas H. Hansen, Kasper Møller Hansen
Matematik B. Højere handelseksamen. Fredag den 19. maj 2017 kl hhx171-mat/b
 Matematik B Højere handelseksamen hhx171-mat/b-19052017 Fredag den 19. maj 2017 kl. 9.00-13.00 Matematik B Prøven består af to delprøver. Delprøven uden hjælpemidler består af opgave 1 til 5 med i alt
Matematik B Højere handelseksamen hhx171-mat/b-19052017 Fredag den 19. maj 2017 kl. 9.00-13.00 Matematik B Prøven består af to delprøver. Delprøven uden hjælpemidler består af opgave 1 til 5 med i alt
TNS Gallup - Public Tema: SR udspil om asylpolitik FOLKETINGSVALG 13. NOVEMBER 2007. Public
 TNS Gallup - Public Tema: SR udspil om asylpolitik FOLKETINGSVALG 13. NOVEMBER 2007 Public Socialdemokraterne og De Radikale er netop blevet enige om, at alle asylansøgere også de afviste skal have mulighed
TNS Gallup - Public Tema: SR udspil om asylpolitik FOLKETINGSVALG 13. NOVEMBER 2007 Public Socialdemokraterne og De Radikale er netop blevet enige om, at alle asylansøgere også de afviste skal have mulighed
Normalfordelingen. Erik Vestergaard
 Normalfordelingen Erik Vestergaard Erik Vestergaard www.matematiksider.dk Erik Vestergaard, 008. Billeder: Forside: jakobkramer.dk/jakob Kramer Side 7: istock.com/elenathewise Side 8: istock.com/jaroon
Normalfordelingen Erik Vestergaard Erik Vestergaard www.matematiksider.dk Erik Vestergaard, 008. Billeder: Forside: jakobkramer.dk/jakob Kramer Side 7: istock.com/elenathewise Side 8: istock.com/jaroon
STUDENTEREKSAMEN MAJ-JUNI 2009 2009-8-2 MATEMATISK LINJE 2-ÅRIGT FORLØB TIL B-NIVEAU MATEMATIK DELPRØVEN UDEN HJÆLPEMIDLER
 STUDENTEREKSAMEN MAJ-JUNI 009 009-8- MATEMATISK LINJE -ÅRIGT FORLØB TIL B-NIVEAU MATEMATIK DELPRØVEN UDEN HJÆLPEMIDLER Mandag den 11. maj 009 kl. 9.00-10.00 BESVARELSEN AFLEVERES KL. 10.00 Der tildeles
STUDENTEREKSAMEN MAJ-JUNI 009 009-8- MATEMATISK LINJE -ÅRIGT FORLØB TIL B-NIVEAU MATEMATIK DELPRØVEN UDEN HJÆLPEMIDLER Mandag den 11. maj 009 kl. 9.00-10.00 BESVARELSEN AFLEVERES KL. 10.00 Der tildeles
Binomialfordelingen. Binomialfordelingen. Binomialfordelingen
 Statistik og Sandsynlighedsregning 1 MS kapitel 3 Susanne Ditlevsen Institut for Matematiske Fag Email: susanne@math.ku.dk http://math.ku.dk/ susanne Definition 3.2.1 Lad X 1, X 2,..., X n være uafhængige
Statistik og Sandsynlighedsregning 1 MS kapitel 3 Susanne Ditlevsen Institut for Matematiske Fag Email: susanne@math.ku.dk http://math.ku.dk/ susanne Definition 3.2.1 Lad X 1, X 2,..., X n være uafhængige
S og V er lige økonomisk ansvarlige
 S og V er lige økonomisk ansvarlige Venstre og Socialdemokraterne er i høj eller nogen grad økonomisk ansvarlige partier, der kan tage regeringsansvar for Danmarks økonomi. Det mener to ud af tre vælgere.
S og V er lige økonomisk ansvarlige Venstre og Socialdemokraterne er i høj eller nogen grad økonomisk ansvarlige partier, der kan tage regeringsansvar for Danmarks økonomi. Det mener to ud af tre vælgere.
Kvantitative Metoder 1 - Forår 2007
 Dagens program Kapitel 8.7, 8.8 og 8.10 Momenter af gennemsnit og andele kap. 8.7 Eksempel med simulationer Den centrale grænseværdisætning (Central Limit Theorem) kap. 8.8 Simulationer Normalfordelte
Dagens program Kapitel 8.7, 8.8 og 8.10 Momenter af gennemsnit og andele kap. 8.7 Eksempel med simulationer Den centrale grænseværdisætning (Central Limit Theorem) kap. 8.8 Simulationer Normalfordelte
S. 55 AFSNIT 3.2 Ø1 S. 55. Pindediagram
 AFSNIT 3.2 S. 55 Ø S. 55 a) Højden i cm Hyppighed Frekvens summeret frekvens Produkt x i h i f i F i x i f i 75 2,, 7,5 76,5,5 8,8 77 2,,25 7,7 78 3,5,4 26,7 79,5,45 8,95 8 2,,55 8 8,5,6 9,5 82,5,65 9,
AFSNIT 3.2 S. 55 Ø S. 55 a) Højden i cm Hyppighed Frekvens summeret frekvens Produkt x i h i f i F i x i f i 75 2,, 7,5 76,5,5 8,8 77 2,,25 7,7 78 3,5,4 26,7 79,5,45 8,95 8 2,,55 8 8,5,6 9,5 82,5,65 9,
Løsning til opgave 7, 9, 10 og 11C Matematik B Sommer 2014
 Vejledning til udvalgte opgave fra Matematik B, sommer 2014 Opgave 7 Størrelsen og udbudsprisen på 100 fritidshuse på Rømø er indsamlet via boligsiden.dk. a) Grafisk præsentation, der beskriver fordelingen
Vejledning til udvalgte opgave fra Matematik B, sommer 2014 Opgave 7 Størrelsen og udbudsprisen på 100 fritidshuse på Rømø er indsamlet via boligsiden.dk. a) Grafisk præsentation, der beskriver fordelingen
