Statistisk mekanik 1 Side 1 af 11 Introduktion. Indledning

Transkript

1 Statistis meani Side af Indledning Statisti er et uundværligt matematis redsab til besrivelsen af et system med uoversueligt mange bestanddele. F.es. er der så mange luftmoleyler i blot mm 3 luft, at det selv med mennesehedens samlede computerraft ie ville være muligt at besrive hver enelt moleyles bevægelse. Men vha. statisti an disse ubegribeligt mange moleyler besrives under ét, svarende til en besrivelse af moleylernes gennemsnitlige eller marosopise egensaber. Vha. statisti er det således muligt at sabe en forbindelse mellem de mirosopise egensaber af enelte (vante)partiler (f.es. atomer og moleyler) og de marosopise egensaber af store partielsystemer i form af gasser, væser eller faste stoffer. I det flg. introduceres en ræe centrale begreber inden for den statistise meani. Hvis luften antages at udgøre en ideal gas, an antallet af luftmoleyler beregnes ud fra idealgasligningen: PV = nrt 3 atm mm = n 8, 3 Kmol 20 C 5 atm, 0 0 Pa 3 ( ) ( 0 m) 3 n 8, 3 J atm K mol n = 4,5 0 5, 0 0 Pa 8 6 = 2, 50 0 mol = ( ) 0 m 9 3 6, 02 0 = n 8, 3 J 23 moleyler mol J mol 293 K

2 Statistis meani Side 2 af Energiniveauer og -tilstande Betragt flg. sematise repræsentation af et partielsystem 2, hvor der til hver hylde (energiniveau) svarer et antal æser (vantetilstande), som hver især indeholder et antal ugler (partiler): ε ε 3 ε 2 3 degenererede tilstande 3 : g 2 = 3, N 2 = 5. ε g : Ie-degenererede (grund)tilstand 4 : Degenerationsgraden af det te energiniveau. g =, N = 3. N : Besættelsestallet for det te energiniveau. Der må oplagt gælde N = N, (.) hvor N er det samlede antal partiler i systemet, samt hvor E er systemets (indre) energi. E = ε N, (.2) h F.es. partiel-i-en-asse, hvor ε = n, n = n + n + n, n, n, n, f. KM opg. E. 2 x y z x y z 8mL 3 4 n = 2, n = n = z x y. n = 2, n = n =, og x y z n = 2, n = n = y x z n = n = n =. x y z N.B.: I assen befinder der sig således (onret) 3 partiler, der (i overført betydning) befinder sig i grundtilstanden. Tilsvarende er der 5 partiler, som befinder sig i. exciterede tilstand osv.

3 Statistis meani Side 3 af En beregning af et systems marosopise egensaber (f.es. varmeapacitet) ræver viden om fordelingen af systemets partiler mellem de forsellige energiniveauer og (vante)tilstande. Studiet af de mulige sådanne fordelinger er således en helt central del af den statistise meani/termodynami 5. Assembly og ensemble Et system bestående af identise partiler aldes et assembly, og et system bestående af et antal identise replia af et sådant assembly aldes et ensemble. Marotilstande og mirotilstande N Kendsab til besættelsestallet for alle energiniveauer fastlægger marotilstanden for et assembly. Hvis partilerne er uselnelige, vil endsab til antallet af partiler i hver tilstand fastlægge mirotilstanden. Enhver marotilstand vil således bestå af et antal mirotilstande. Hvis partilerne er selnelige, ræver fastsættelsen af mirotilstanden endsab til hvile partiler, der befinder sig i hvile tilstande 6. Antallet af forsellige mirotilstande hørende til en given marotilstand er således væsentligt større for selnelige partiler end for uselnelige. 5 Statistis meani og statistis termodynami er således to ord for det samme. 6 Esempel: På en sole fastlægger antallet af elever på hvert lassetrin (energiniveau) marotilstanden. Hvis eleverne er uselnelige(!), fastlægger antallet i hver enelt lasse (tilstand) mirotilstanden. Hvis eleverne er selnelige, ræver fastlæggelse af mirotilstanden viden om hvile elever, der er i hvile lasser.

4 Statistis meani Side 4 af En marotilstand fastlægger således et systems målbare/marosopise egensaber såsom energi, massefylde, temperatur, try osv. 7, mens en mirotilstand fastlægger systemets mirosopise onfiguration såsom bevægelsesmønstret for gasmoleylerne i en beholder eller svingningsmønstret for atomerne i et metalgitter. At enhver marotilstand består af et antal mirotilstande, svarer således til at forsellige bevægelses- eller svingningsmønstre svarer til samme energi, massefylde, osv. Termodynamis sandsynlighed I prasis er der en begrænsning på det antal mirotilstande, som et givet assembly an befinde sig i. I et isoleret (og dermed luet) assembly er E og N f.es. onstante, hvilet sætter en begrænsning på de mulige miro- og marotilstande for det pågældende assembly. Som tiden går, vil et assembly løbende sifte mirotilstand, i tat med at partilerne veselvirer med hinanden eller med en evt. beholders vægge, idet de enelte partiler herved ændrer tilstand. 7 Men ie omvendt: To forsellige marotilstande an godt have samme marosopise egensaber.

5 Statistis meani Side 5 af Inden for den statistise meani herser flg. empiris baserede postulat: For et isoleret assembly er alle mulige mirotilstande lige sandsynlige. Altså: Inden for et langt tidsrum, hvor alle mulige mirotilstande når at optræde mange gange, optræder de mulige mirotilstande i sammenlagt lige lang tid. 8 I et ensemble bestående af så stort et antal assemblies, at hver mirotilstand foreommer mange gange, er der til et ethvert tidspunt lige mange assemblies endetegnet ved hver af de mulige mirotilstande. 9 I et isoleret assembly gennemløbes således med tiden alle mulige mirotilstande og dermed alle mulige marotilstande, og i henhold til ovenstående postulat er sandsynligheden for at finde et assembly i en given marotilstand udtryt ved antallet af mirotilstande hørende til den pågældende marotilstand. Antallet af mirotilstande hørende til den te marotilstand aldes derfor den termodynamise sandsynlighed W. Et assemblys termodynamise sandsynlighed er det totale antal mirotilstande: Ω = W. (.3) Den normerede sandsynlighed P, for at et assembly befinder sig i den te marotilstand, er givet ved andelen af mirotilstande hørende til den te marotilstand: P = W Ω. (.4) 8 Svarende til at man ved mange gentagne ast med en terning får lige mange ettere, toere, treere osv. 9 Svarende til at man ved slag med mange terninger får lige mange ettere, toere, treere osv.

6 Statistis meani Side 6 af Middelbesættelsestallet Som nævnt ovenfor vil et system til stadighed (og lynhurtigt) vesle mellem forsellige miro- og marotilstande, og systemets marosopise egensaber vil være resultatet af en midling over disse forsellige mirosopise tilstande. Et centralt begreb i forbindelse med besrivelsen af ovennævnte marosopise egensaber er middelbesættelsestallet N for det te energiniveau. Hvis besættelsestallet for det te energiniveau for et assembly i marotilstand betegnes N, fås ifølge udtry (.4) flg. udtry for middelbesættelsestallet: N = N Ω W. (.5) I raft af den ovenfor besrevne midling erstattes udtry (.2) f.es. med E = ε N. (.6) Evalueringen af udtry (.5) afhænger af, hvilen type partiler, der er tale om, og i den forbindelse selnes mellem flg. tre statistier : Bose-Einstein for uselnelige bosoner, der som beendt godt an befinde sig i samme tilstand. Fermi-Dirac for uselnelige fermioner, der som beendt overholder Paulis udeluelsesprincip og derfor ie an befinde sig i samme tilstand. Maxwell-Boltzmann for selnelige partiler, der godt an befinde sig i samme tilstand.

7 Statistis meani Side 7 af Bose-Einstein-statisti I det flg. udregnes den termodynamise sandsynlighed for en given marotilstand. Lad de tilstande hørende til energiniveau være nummereret,2,3,, og lad de g N partiler i energiniveau være navngivet abc,,,, sådan at én mulig fordeling af partilerne an srives () a ( 2) bc ( 3) 0 ()( )( ). (.7) Ovenstående sevens starter med et tal, hvilet der er g forsellige muligheder for. Herefter an de resterende g tal og bogstaver arrangeres på ( g + N) forsellige måder, svarende til alt i alt N! ( + ) g g N! forsellige sevenser. Den ræefølge, hvormed tilstandene opsrives, er imidlertid vilårlig, og da tilstandene an arrangeres på! g forsellige partielfordelinger med denne fator. forsellige måder 2, reduceres antallet af fysis Da partilerne er uselnelige, er det desuden un antallet af bogstaver inden for hver tilstand, der har betydning 3, og da de N bogstaver an ombyttes på! forsellige N måder, er der således w ( + )! ( + ) g! N! ( g! ) N! g g N g N = = fysis forsellige partielfordelinger i det te energiniveau 4.! (.8) 0 Partilerne er uselnelige, men som det også fremgi af KM3, giver det ie desto mindre mening at navngive dem, så længe alle målbare egensaber blot er uafhængige af denne navngivning. 2 bc 3 a repræsenterer f.es. samme partielfordeling som udtry (.7). [( ) ][( )][() ] 2 Der er g forsellige valgmuligheder på første plads, g på næste osv.

8 Statistis meani Side 8 af Da partielfordelingerne i de forsellige energiniveauer an optræde uafhængigt af hinanden, er den termodynamise sandsynlighed for den te marotilstand inden for Bose-Einstein-statistien således givet ved BE W = w : ( ) W BE g + N! =. (.9)! N! ( g ) 3 [() ][( 2) ][( 3) ] x pf repræsenterer f.es. samme partielfordeling som udtry (.7). Se i øvrigt note 0. 4 Udtry (.8) ses at overholde de oplagte betingelser = for g = eller = 0 samt w = g for N =. w N

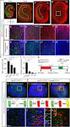
9 Statistis meani Side 9 af Esempel: Betragt et assembly bestående af N = 6 partiler, hvis tilladte energiniveauer ε = ε, = 0,,2, alle er trefold degenererede ( g = 3), og hvis samlede energi er E = 6ε : Ovenstående figur viser fordelingen af de 6 partiler i de mulige marotilstande, idet energisalaen er lodret med hvert vadrat repræsenterende tre degenererede tilstande. De termodynamise sandsynligheder beregnes vha. udtry (.9), og middelbesættelsestallene beregnes vha. udtry (.5).

10 Statistis meani Side 0 af Fermi-Dirac-statisti Med samme notation som før, men nu med den begrænsning, at der høest an være én partiel i hver tilstand, an én mulig fordeling srives () ( 2) ( 3) ( 4) idet ræefølgen af tilstande er ronologis fra ( ) a b c, (.0) g. til ( ) De N partiler an anbringes på 5 ( ) ( )( 2) ( ) g g g g N = g! ( g N ) forsellige måder, hvoraf der ligesom før i raft af partilernes uselnelighed er!! N identise permutationer af hver partielfordeling. Af ovenstående fås dermed 6 og endelig W w FD = g! ( ) g N! N! ( ) (.) g! =. (.2) g N! N! 5 Den første partiel har g muligheder, den næste har i raft af Paulis udeluelsesprincip 6 Bemær, at N g iht. udeluelsesprincippet. Udtry (.) ses i øvrigt at overholde de samme betingelser som i note 4. g muligheder osv.

11 Statistis meani Side af Maxwell-Boltzmann-statisti Da de selnelige partiler i det te energiniveau hver især an befinde sig i g forsellige tilstande, er der w N = g (.3) fysis forsellige partielfordelinger i det te energiniveau. Da partilerne er selnelige, vil en ombytning af to partiler fra to forsellige energiniveauer resultere i to forsellige mirotilstande, så den termodynamise sandsynlighed er givet ved an fordeles mellem de forsellige energiniveauer. w gange antallet af måder, hvorpå de i alt N partiler De N partiler an srives op i! forsellige sevenser, hvor de N første partiler hører til energiniveau osv. N De N partiler an srives op på N! forsellige måder, som alle svarer til samme fordeling af partiler til energiniveau, og tilsvarende for de øvrige energiniveauer. Dermed fås inden for Maxwell-Boltzmann-statistien flg. udtry for den termodynamise sandsynlighed for den te marotilstand: W MB N N! = g : N! W MB N g = N!. (.4) N!