Kvantisering af det elektromagnetiske felt
|
|
|
- Anita Andreasen
- 7 år siden
- Visninger:
Transkript
1 Kvantisering af det eletromagnetise felt Kristian Jerslev, 7494 Institut for Fysi og Astronomi, Aarhus Universitet Dated: 5. maj 9 Indhold I. INDLEDNING II. BØLGELIGNING FOR VEKTORPOTENTIALET UNDER COULOMBGAUGE A. Bølgeligningen for vetorpotentialet under coulombgauge B. Løsningerne til bølgeligningen C. Energien i en svingningsmode III. DET KVANTISEREDE ELEKTROMAGNETISKE FELT 4 A. Fotoner og feltenergi 4 B. Feltoperatorerne 5 C. Kohærente tilstande 5 IV. Veselvirning med et -niveau atom 6 Veselvirningsoperatoren 6 A. Absorbtion og stimuleret emission 7 B. Spontan emission 7 V. KONKLUSION 8 A. Tidsafhængig perturbationsteori 9 Litteratur 9 I. INDLEDNING Jeg vil i denne opgave indføre en vantemeanis besrivelse af det eletromagnetise felt, som jeg efterfølgende vil bruge til at besrive fysise fænomener, som ie an besrives tilfredsstillende med en lassis model. I det følgende følges Diracs vantiseringsprincip, hvoraf første sridt er at opsrive hamiltonfuntionen, H, for det eletromagnetise felt som en funtion af generaliserede oordinater og dertilhørende onjungerede impulser, q i og p i, se [4, apitel 7.] for besrivelse af generaliserede oordinater og generaliserede impulser. De to oordinater q i og p i siges at være anonise, hvis de opfylder differentialligningerne p i t = H q i og q i t = H p i. Kvantiseringsprincippet består nu i at omsrive systemets hamiltonfuntion til en hamiltonoperator, Ĥ, der er den lassise hamiltonfuntion, hvor q i og p i er erstattet af operatorerne ˆq i og ˆp i, der gives ommutatorrelationen [ ˆq i, ˆp j ] = i δ ij. Dette er den samme ommutatorrelation som gives de almindelige sted- og impulsoperatorer. Bemær, at det er et specialtilfælde af den mere generelle metode, hvor et lassis systems Poissonparanteser, {f, g}, erstattes med ommutatoren i [ ˆf, ĝ]; se [3, apitel 7.5] for detaljer om denne metode. Vores hensigt med det følgende er dermed at finde det eletromagnetise felts samlede energi, for derefter at forsøge at omsrive hamiltonfuntionen af variable, så er opfyldt. Herefter erstattes de anonise oordinater ved brug af. Fremgangsmåden er at betragte en volumen med dimensionerne L 3 i tomt rum. I dette volumen vil vi undersøge energien for samtlige muligheder for løbende eletromagnetise bølger. På baggrund af denne undersøgelse an vi overgå til en vantemeanis besrivelse af feltet og forlare fænomener, der ie lader sig gøre at forlare lassis. Til sidst i denne opgave er vedlagt et bilag, der ort præsenterer de dele af tidsafhængig perturbationsteori, der er nødvendig for visse dele af denne opgave. II. BØLGELIGNING FOR VEKTORPOTENTIALET UNDER COULOMBGAUGE A. Bølgeligningen for vetorpotentialet under coulombgauge Som nævnt ovenfor vil vi igge på et ubis område af rummet med dimensionerne L L L. Vores referencesystem lægges, så ubens ene hjørne befinder sig i origo, mens resten af uben lægges i første otant. Efterfølgende fyldes hele rummet ud med disse asser, hvorfor vi ræver, at bølgerne stemmer overens på ubens rand. Kuben benævnes vantiseringsaviteten. Vi betragter Maxwells ligninger for vauum: E =, 3 B =, 4 E = B t, 5 B = ɛ µ E t = c E t, 6 der alle er hentet fra []. Yderligere betragtes vetorpotentialet, A, der opfylder betingelsen, at A = B.
2 Under coulombgauge vælges A =. Ved at indsætte A = B i 5 fås da E = A t E + A =, t hvilet medfører, at E + A t = U, hvor U er en salar potentialfuntion. Vi vælger nu at igge på planbølgeløsninger, hvorfor U =, og ovenstående reduceres til E = A t. 7 Vi har dermed lavet en sammenhæng mellem det eletrise felt og vetorpotentialet. Ved at indsætte 7 i 6 fås da A = c A t A A A = c t A + c A t = A =, 8 hvor er D Alembert-operatoren. Undervejs udnyttede vi, at A = og vetoridentiteten v = v v. Ved at finde løsningerne til 8 an vi efterfølgende finde det eletrise og magnetise felt via E = A t og B = A. 9 B. Løsningerne til bølgeligningen De løsninger til 8 vi her er ude efter sal af fysise årsager ligge i L -rummet. Dermed an løsningen til differentialligningen opsrives som en fourierræe: A = = A C te i r + C te i r P, hvor P er en enhedsvetor i polariseringsretningen for bølgevetoren. r angiver retningsvetoren, mens C og C er fourieroefficienterne. Bemær, at stjernen angiver omplesonjungeret, da A sal være reel. Fra ravet om, at A = fås A = [C te i r C te i r i P ] =. Hvis dette sal være sandt for samtlige r og må det betyde, at salarprodutet P =, hvoraf det ses, som forventet, at polariseringen er vinelret på udbredelsesretningen. Dette resultat giver os egentlig to uafhængige polariseringsretninger, som burde blive inluderet i, men eftersom polariseringen ie spiller nogen større rolle i denne opgave, vil jeg undlade dette og tage det for underforstået og un bringe det frem, når det sal bruges. Jeg nævnte tidligere, at det er nødvendigt, at bølgerne stemmer overens på vantiseringsavitetens rand. Bølgevetoren er derfor begrænset til værdierne = L n xˆ x + n z ˆ z + nz ˆ z, hvor n x, n y, n z Z. Vi har nu onstrueret en fourierræe for vetorpotentialet, men vi mangler stadigvæ en esplicit tidsafhængighed. Indtil videre har vi ladet tidsafhængigheden ligge i fourieroefficienterne. For at finde den esplicitte tidsafhængighed for vetorpotentialet betragtes vetorpotentialet for én bølgevetor: A = C te i r + C te i r P. Indsættes dette i 8 fås da = [ C te i r + C te i r P ] + c A t = A + A c t = ω + A t, 3 hvor ω = c. Dette giver differentialligninger for C og C, der ser ud som C t = ω C og C t = ω C, 4 hvor vi vælger løsningerne til systemet 4 til at være C t = A e iω t og C t = A e iω t, hvor A og A blot er nye onstanter. Dette stemmer helt overens med, at den ene sal være den andens omplesonjungerede. Dermed an løsningen for vetorpotentialet for en svingningsmode opsrives som A = A e i r ω t + A e i r ω t P. 5 Den samlede løsning til det eletromagnetise felt er da blot en superposition af forsellige svingningsmodes. Her sal det ort nævnes, at på grund af de to uafhængige polariseringsretninger er der egentlig A for hver. Den fuldstændige løsning fås altså ved at sætte 5 ind i. Bemær endvidere, at metoden, der i dette afsnit er brugt til at finde løsningen til 8, er fuldstændig ævivalent til at løse 8 direte. Det har blot vist sig at være mere pratis at opsrive A som en fourierræe. C. Energien i en svingningsmode Næste sridt i vantiseringen består nu i at finde den samlede energi af det eletromagnetise felt. Vi finder
3 3 energien i en svingningsmode. Fra [, formel 9.53] fås den samlede energi i en svingningsmode, i det jeg integrerer op over vantiseringsaviteten, til H = ɛ E + µ B d 3 r. 6 V Det eletrise og magnetise felt findes ved at bruge 9 til E = A e i r ω t + A t e i r ω t P = iω A e i r ω t A e i r ω t P 7 B = [A e i r ω t + A e i ] r ω t P = P i A e i r ω t A e i r ω t = i E iω = ω E, 8 hvor vi undervejs benyttede vetoridentiteten f v = f v v f i beregningen af det magnetise felt. Da begge felter sal sættes i anden potens for at beregne H fås for det magnetise felt, at B µ = µ ω E = µ c E = ɛ E. 9 Ved brug af 9 reducerer 6 til H = ɛ E d 3 r. Umiddelbart ser det jo ie særlig ompliceret ud, men lad os srive integralet fuldt ud. Af notationsårsager er vi her gået tilbage til at bruge de tidsafhængige fourieroefficienter, hvilet vi vil bruge i størstedelen af den resterende del af opgaven. [ H = ɛ ω C t e i r + C t e i r V V ] C tc t d 3 r. Ved første øjeast ser det jo ie ligefrem indbydende ud. Her er det dog vigtigt, at vi ie mister modet, for netop de trælse led går ud under integrationen. Leddene e ±i r integrerer netop til, i det der er et helt antal svingninger henover hver dimension i vantiseringsaviteten. Da det resterende led, C tc t er uafhængigt af sted, vil integralet blot være volumenet af vores vantiseringsavitet. Det haves dermed, at H = ω ɛ C tc tv, hvor V er volumenet af vantiseringsaviteten. Det er nu simpelt at finde den samlede energi i aviteten. Under vadrering af det samlede felt opnås netop rydsled mellem forsellige modes af formen C tc tei r, der netop un giver bidrag, når =. Den samlede energi an da srives som en sum over energien for hver mode, og det haves, at H EM = H, 3 hvor H er energien i én svingningsmode. Vi er nu ved at være lar til at gå over til den vantiserede besrivelse af det eletromagnetise felt. Vi sal have fundet en måde at omsrive 3 til en form, der opfylder. Dette gøres ved at indføre nye variable, q i, p i R givet ved passende reelle- og imaginærdele af C t og C t, C t = ω q + ip 4 4ɛ ω V C t = ω q ip. 5 4ɛ ω V Ved at indsætte 4 og 5 i an energien i en svingningsmode nu srives ved de nye variable q og p som H = ω ɛ 4ɛ ω V ω q + ip ω q ip 4ɛ ω V = ω q + p, 6 som netop genendes som værende af samme form som energien i en harmonis oscillator med massen [, formel.46]. Bemær, at tidsafhængigheden bæres indirete af de nye oordinater, der så er funtioner af tiden. Selvfølgelig nytter denne omsrivning ie noget, hvis ie er opfyldt, så derfor isoleres q og p i ved brug af 4 og 5 til q = ɛ V C t + C t 7 p = ω ɛ V i C t C t. 8 Det er nu naturligvis interessant at se, om 7 og 8 er anonise; opfylder de? Ved indsættelse i fås q t = ɛ V Ċ t + Ċ t = p = H p p t = ɛ V Ċ i t Ċ t = ω q = H, q da det Ċ t = iω C t. De nye variabler opfylder altså, hvormed de er anonise, og an bruges til vantiseringen.
4 4 Lad os opsummere, hvad vi hidtil har lavet. Vi har altså omsrevet Maxwells ligninger under coulombgauge til en differentialligning for vetorpotentialet og ved at opsrive vetorpotentialet som en fourierræe har vi fundet løsningen til differentialligningen. Efterfølgende har vi indført nye variable, q og p, der viste sig at være anonise. Ved nu at bruge Diracs vantiseringsprincip og sende de anonise variable over i deres tilhørende operatorer samt benytte an vi dermed vantisere det eletromagnetise felt. III. DET KVANTISEREDE ELEKTROMAGNETISKE FELT Vi følger Diracs vantiseringsprincip og lader dermed de anonise variable gå over i operatorerne q ˆq og p ˆp, der har ommutatorrelationen [ ] q, p = i δ. 9 Ved denne overgang fås da en også en tilsvarende hamiltonoperator for energien for en svingningsmode. Hamiltonoperatoren for det eletromagnetise felt ser ud som Ĥ = ω ˆq + ˆp. 3 Sammenlign eventuelt med [, formel.46]. Hamiltonoperatoren for det samlede eletromagnetise felt fås som en sum over hamiltonoperatorer for hver svingningsmode jf. disussionen ovenfor: Ĥ EM = = Ĥ ω ˆq + ˆp. 3 Hamiltonoperatoren for det samlede eletromagnetise felt ligner til forvesling hamiltonoperatoren for den harmonise oscillator med en masse på. Denne lighed stier dog meget dybere end blot på udseendet, for de an fatis siges at være ens. En svingningsmode an altså betragtes som en selvstændig harmonis oscillator. Ved at følge metoden fra den harmonise oscillator definerer vi nu de samme stigeoperatorer â + = â = ω ω ˆq iˆp 3 ω ω ˆq + iˆp. 33 Her er det relevant at bemære, at disse operatorer er tidsafhængige netop fordi operatorerne for de anonise variable er tidsafhængige. Det viser sig, at man sagtens an lade tidsafhængigheden ligge i operatorerne frem for tilstandene - forsellen er blot hvilet billede man vælger at bruge. Når tidsafhængigheden ligger i tilstandene er man i Schrödingerbilledet, mens tidsafhængigheden ligger i operatorerne i Heisenbergbilledet. Ævivalent med fremgangsmåden for den harmonise oscillator er ommutatoren mellem 3 og 33 [â, â + ] =. 34 De to operatorer 3 og 33 har altså de helt samme algebraise egensaber som step-operatorerne for den harmonise oscillator. Ønser vi at finde tidsafhængigheden af en operator, ˆB, benyttes [5, formel 34] ˆB t = i [Ĥ, ˆB]. 35 Vi har nu ørt alt vores syts i stilling og er parat til at igge på onsevenser af vantiseringen og samtidig give en fysis fortolning af 3 og 33. A. Fotoner og feltenergi Som nævnt tidligere har stepoperatorerne for det eletromagnetise felt de helt samme algebraise egensaber som stepoperatorerne for den harmonise oscillator. Der gælder dermed ævivalent, at hamiltonoperatoren for det eletromagnetise felt an srives som Ĥ EM = â + â + ω. Deraf ses, at 3 og 33 henholdsvis tilføjer og fjerner energien ω fra det eletromagnetise felt. Denne energi genendes som energien for en foton med bølgetallet, hvorfor de to operatorer an toles som henholdsvis dannelsen og annihilationen af en foton i feltet. Det an vises, at impulsoperatoren for det eletromagnetise felt også giver et resultat, der styrer tolningen af stigeoperatorerne. Derfor aldes de også for sabelses- og annihilationsoperatorer. Det sal dog bemæres, at der ie er tale om en foton som de forstås i normal forstand - det er altså ie en rumlig loaliseret partiel. De to operatorer exciterer hele feltet og derfor er fotonen så at sige over hele feltet. Hvis vi ønser at onstruere en rumlig loaliseret bølgepae, sal vi derfor lave en superposition af forsellige bølgevetorer; nøjagtigt som vi normalt onstruerer loaliserede bølgepaer for eletroner. Af samme årsag an en rumlig loaliseret foton ie have nogen præcis energi. Tilstanden med ingen fotoner aldes derfor også vauumtilstanden og benævnes grundstilstanden for det eletromagnetise felt, vac >= >. Operatoren â + â = ˆn, der aldes tælleoperatoren, tæller netop antallet af fotoner med bølgetal og en tilhørende polarisering. En tilstand med et bestemt antal fotoner og bestemt, n >, aldes en Foc-tilstand. Disse tilstande er ortonormale, hvorfor < n n >= δ. Det ses nu, at â + n >= n + n + > 36 â n >= n n >, 37
5 5 hvor det direte ses, hvad de to operatorer gør ved en Foc-tilstand. Lad os prøve at finde forventningsenergien for det eletromagnetise felt i vauumtilstanden: E vac =< ĤEM > = ω = c, 38 hvor vi fra anden til tredje linje gangede summen med for at dæe de to forsellige polariseringer. Herfra går vi over til et integral, idet vi lader vantiseringsavitetens sider gå mod uendelig. Dermed bliver summen over siftet ud med et integral 3 L d = 3 L d π sin θdθ 39 hvor frontfatoren ommer fra sift af variabler fra at summere over n x, n y, n z til et integral over, hvor vi fra da har n x n y n z = 3 L x y z. Ved at indsætte integralet i 38 fås da 3 L π E vac = c d sin θdθ dφ 3 L = 4π c 3 d, 4 hvoraf det fremgår, at energien divergerer med 4. Energien af det eletromagnetise felt i vauumtilstanden er altså uendelig stor. Det virer naturligvis som et problem, at fysien tillader uendelig meget energi, men problemet løses i den fulde relativistise udgave af vanteeletrodynamien. B. Feltoperatorerne Fra 3 og 33 an de anonise operatorer isoleres, og disse an så igen indsættes i 7 og 8, hvormed der findes et udtry for fourieroefficienterne, der nu er operatorer, udtryt ved â og â +. Det haves dermed, at Ĉ t = ɛ ω V â og Ĉ t = ɛ ω V â+. Ved at indsætte disse oefficienter i og efterfølgende bruge 9 findes udtry for den eletrise feltoperator samt den dφ, magnetise feltoperator til ω ˆ E = i â e i r â + ɛ V e i r P 4 ˆ B = ɛ ω V i P â e i r â + e i r. 4 Tidsafhængigheden af felterne an esplicit findes ved at bruge 35 til at finde tidsafhængigheden af de to stepoperatorer. Lad os finde spredningen på det eletrise felt i en Foctilstand. På grund af Foc-tilstandenes indbyrdes ortogonalitet bliver forventningsværdien for det eletrise felt < n ˆ E n > = ω i â e i r â + ɛ V e i r P =. 43 Anderledes ser det dog ud, når spredningen på det vadrerede eletrise felt beregnes. Det udnyttes, at vi an vælge et vilårlig oordinatsystem, så vi evaluerer forventningsværdien i r =. Dermed haves, at < n ˆ E n >= ω n, 44 ɛ V der netop er forsellig fra nul på grund af rydsled imellem de to stigeoperatorer. Dermed har vi et udtry for spredningen på det eletrise felt i vauumtilstanden netop, hvor n =, der er forsellig fra nul. Dette er ofte omtalt som vauumflutuationer, og det er helt ævivalent med, at en harmonis oscillator ie an have en fast impuls og sted. Uendelig nulpuntsenergi samt vauumflutuationer giver anledning til effeter, der an måles esperimentelt. En af disse effeter er Casimireffeten. Denne effet er en raft, der opstår imellem to ledende parallelle plader, der ligger meget tæt ved hinanden. Det an vises, at raften pr. areal, der opstår imellem de to ledende plader, på grund af nulpuntsenergien, er givet ved df da = π c 4a 4, hvor a er afstanden imellem pladerne. Det sal bemæres, at raften er negativ - pladerne tiltræes altså. Det er dog ie altid tilfældet, og man an lave onfigurationer, hvor pladerne indbyrdes frastødes. C. Kohærente tilstande Hvis vi ønser at besrive en svingningsmode lassis, så sal vi have fat i de ohærente tilstande. Det an vises, at de ohærente tilstande minimerer usierheden for amplitude og fase, hvorfor de er gode bud på lassise svingningsmodes. For at finde disse tilstande sal vi
6 6 ort genoverveje, hvad annihilationsoperatoren gør ved en Foc-tilstand: der fjernes energien ω - altså fjernes en foton. Dette minder bestemt ie om en lassis monoromatis bølge med onstant intensitet, hvor vi vil unne forvente at unne detetere og dermed annihilere et bestemt antal fotoner uden at ændre væsentligt på bølgens intensitet. Derfor må det være ret nærliggende at finde de ohærente tilstande som egentilstande for annihilationsoperatoren: â ξ >= λ ξ >. 45 Hvis vi undersøger forventningsværdien for det eletrise felt i en ohærent tilstand fås da < ˆ E > = = i < ξ ˆ E ξ >=< ξ ˆ E ξ > ω ɛ V e i r < ξ â ξ > e i r < ξ â + ξ > P, 46 idet < ξ ˆ E ξ >= for. De indre produter evalueres til < ξ â ξ >= λ samt < ξ â + ξ >= λ. Da â hænger sammen med C t gennem Ĉ t = ɛ ω V â, vil C t = ɛ ω V λ være en egenværdi for Ĉ t, hvor det er λ, der bærer tidsafhængigheden. Benyttes denne sammenhæng ved at isolere for λ og herefter indsætte i 46 fås < ˆ E >= iω Cte i r C te i r P, 47 der netop ses at være 7. Den ohærente tilstand gensaber altså den lassis forventede svingningsmode. Vi an dermed gensabe hele den oprindelige bølge ved at lave en ohærent tilstand for hver svingningsmode. Srives de ohærente tilstande ved energi-egentilstande Foctilstande fås udvidelsen ξ >= λ n < ξ > n >, 48 n n! og ved at bruge normeringsbetingelsen, at < ξ ξ >= fås da, at ξ >= e λ n λ n n! n >. 49 Sandsynligheden for at måle n fotoner i en ohærent tilstand er da < n ξ >, der også an srives som P n = e λ λ n, 5 n! der også er en Poissonfordeling. Udføres et esperiment, hvor antallet af fotoner i en plan monoromatis bølge tælles i givne tidsrum, forventes altså en Poissonfordeling over antallet af fotoner. IV. VEKSELVIRKNING MED ET -NIVEAU ATOM Nu, hvor vi har fået stablet teorien på benene, vil vi prøve at anvende teorien til at besrive veselvirning imellem det eletromagnetise felt og atomer. Det viser sig nemlig, at fænomener som spontan emission helt naturligt falder ud af den indførte feltteori. Dette fænomen har ie unnet forlares tilfredsstillende ved en semi-lassis perturbationsteori se [], der dog godt an forlare absorbtion og stimuleret emission. Vi vil i det følgende igge ort på absorbtion og stimuleret emission, hvorefter vi går over til en mere detaljeret gennemgang af spontan emission. Vi betragter derfor et atom, hvor un to energiniveauer deltager i veselvirningen. De to niveauer aldes henholdsvis > og > med tilhørende energier ω og ω, hvor > er grundstilstanden. Frevensen, der svarer til overgangen fra det ene energiniveau til det andet aldes overgangsfresensen: ω = ω ω. Samtidig antages det, at energien i > er større end energien i >. Veselvirningsoperatoren For nu at unne behandle veselvirningen mellem lys og det eletromagnetise felt vil vi betragte atomet som en eletris dipol. Dermed antages det også, at den eletrise veselvirning er meget større end den magnetise. Yderligere vælger vi at antage, at bølgelængden for den stråling vi igger på er meget større end atomet selv. Dette har ie nogen betydning for optise frevenser, men hvis der arbejdes med røntgen- eller gammastråling an det have betydning. Atomet placeres i origo, hvormed r =. Det antages, at det eletrise felt an beregnes hen over hele atomet i r =. Klassis an veselvirningen imellem det eletrise felt og atomet den eletrise dipol besrives som p E se []. Kvantemeanis bliver dette til en veselvirningsoperator ˆ p ˆ E, hvor ˆ p er dipoloperatoren. Dipoloperatoren er givet ved eˆ r. Denne operator an omsrives ved at gange med på hver side, i det = >< + ><. Dermed fås eˆ r = i,j=, < i eˆ r j > i >< j. På grund af symmetri omring r vil diagonalledene < j eˆ r j >=. Sættes p = e < ˆ r >= e < ˆ r > an dipoloperatoren srives som eˆ r = p >< + p ><. 5 Det ses hermed, at dipoloperatoren ændrer atomets tilstand. Dette an også srives ved brug af stigeoperatorer, hvis ˆα = >< og ˆα + = ><. Dipoloperatoren tager da formen ˆ p = p ˆα + + pˆα. Ved brug af 4 an
7 7 veselvirningsoperatoren da udtryes som ˆV = i ω ɛ V p ˆα + + pˆα â â + P, 5 hvor det eletrise felt er evalueret i r =. Det bemæres nu, at 5 indeholder rydsled af stigeoperatorerne. Disse rydsled består af ledene ˆα + â, ˆα + â +, ˆα â og ˆα â +. Disse rydsled svarer henholdsvis til en absorbtion og esitation, emission og esitation, absorbtion og henfald samt emission og henfald, hvor ledene for emission og esitation samt absorbtion og henfald er ie energibevarende. I denne model vælger vi at se bort fra disse processer, der også un får betydning, når atomet ie længere an betragtes som en eletris dipol se [6]. For at vise, at vi med rimelighed an vælge at se bort fra disse processer vælger vi at se på tidsafhængigheden af rydsledene ved brug af 35. Tidsafhængigheden for de forsellige rydsled fås da til ˆα + â t = ˆα + â e iω ω ˆα â t = ˆα â e iω+ω ˆα + â + t = ˆα + â + e iω+ω ˆα â + t = ˆα â + e iω ω. I det optise område vil ledene med frevens ω +ω have en meget høj frevens. Dermed vil ω ω typis være meget lavere end ω + ω, hvorfor sidstnævnte midles ud i tid. Det er derfor også ledene med ω ω, der giver det største bidrag i veselvirningen. Denne approsimation aldes rotating wave approximation. Indføres nu betegnelsen γ = ω ɛ V p P, 53 an den samlede hamiltonoperator for systemet opsrives som Ĥ tot = Ĥatom + ĤEM + ˆV, 54 der også omtales som anden-vantiseringen af hamiltonoperatoren se [6, side 63-64], hvor ˆV an srives som ˆV = i γ ˆα + â γ ˆα â Vi vil nu benytte dette til at se ort på absorbtion og stimuleret emission, hvorefter vi vil igge mere detaljeret på spontan emission. Vi vil i det følgende derfor antage, at vi har et atom, der befinder sig i tilstanden > n >, hvor ω = ω - altså et atom, der befinder sig blandt en masse fotoner, hvis frevens svarer til overgangsfrevensen. A. Absorbtion og stimuleret emission Tilstanden > n > vil i princippet oble til tilstanden > n + > og alle tilstandene > > gennem 5. De sidstnævnte tilstande vil dog ie bidrage væsentligt til veselvirningen. Det an vises, at <, ˆV n, > giver en fator fra â +, mens der fra n + > > vil få en fator n +, der typis er meget større end. Det er af denne årsag, at det un er nødvendigt at igge på fotonerne med samme polarisering som Foctilstanden - præcis denne årsag, der giver mulighed for at få præcist polariseret lys og bølgelængde ud af en laser. Samme metode an bruges til at indse, at absorbtion fra tilstanden n > > un vedrører tilstanden n > >. De to væsentligste matrixelementer for absorbtion og emission i vores to-niveau atom bliver derfor <, n + ˆV, n > = i γ n + <, n ˆV, n > = i γ n, der ses gældende for henholdsvis emission og absorbtion. Man an indsætte disse matrixelementer i A3 og løse de fremomne differentialligninger, der vil resultere i oscillationer imellem de to tilstande. Disse oscillationer aldes Rabi-oscillationer, men vi vil dog ie løse differentialligningerne her. Dermed vil vores atom i dette tilfælde oscillere imellem de to tilstande med en bestemt frevens. Vi vil i dette tilfælde dog igge på problemstillingen mere valitativt. Som nævnt i bilaget vil matrixelementerne < j ˆV i > angive styren af veselvirningen imellem starttilstanden i > og sluttilstanden j >. Det er derfor bemærelsesværdigt, at i emissionstilfældet, hvor der ingen fotoner er til stede, fortsat er et matrixelement, der er forselligt fra nul netop på grund af n + -fatoren. Helt præcist vil dette medføre, at et atom i vauumtilstanden vil udføre Rabi-oscillationer - uden tilstedeværelsen af fotoner til at stimulere det! Her ses igen en obling til vauumfeltet, der giver anledning til at unne forlare spontan emission - et fænomen, der ie har unnet forlares i en semi-lassis model, hvor det eletromagnetise felt ie var vantiseret, og der derfor ie foreom nogen vauumtilstand. B. Spontan emission Som besrevet ovenfor vil et esiteret atom i vauum udføre Rabi-oscillationer - et fatum, der er meget tæt forbundet med spontan emission. Det er dog vigtigt at pointere, at atomet veselvirer med hele vauumtilstanden, hvormed oscillationerne med de enelte svingningsmodes bliver udvaset, så atomets esiterede energiniveauer vil henfalde esponentielt. For at behandle fænomenet med spontant emission vil vi starte med at betragte et atom i tilstanden > vac >. Denne tilstand repræsenterer altså et atom, der befinder sig i tilstanden > og samtidig befinder sig i vauum-tilstanden for det
8 8 eletromagnetise felt. Approsimationen, som vi ovenfor brugte, an i dette tilfælde ie genbruges, hvorfor vi er nød til at bruge den mere generelle tilstand φ >= c e iωt > vac > + c e iω ωt > >, 56 der netop angiver en superposition af en esiteret tilstand og ingen fotoner med en henfaldet tilstand med en foton. Hvis 56 indsættes i A3 fås differentialligningerne for oefficienterne c t og c t til ċ = c γ e iω ω t 57 ċ = c γ e iω ω t, 58 da ω + ω ω = ω ω og <, vac ˆV, >= i γ. Disse differentialligninger er desværre oblede, men frygt ie - vi an godt løse dem med enelte approsimationer, som vi ommer til lige om lidt. Vi starter med at integrere 58 fra til t, og ved at indsætte resultatet herfra i 57 fås da ċ t = t γ e iω ω t t c t dt, 59 i det vi har sat c =, da vi starter i tilstanden > vac >. Dette integral ser dog lettere besværligt ud, men vi an gøre nogle enelte approsimationer, der får det over i en lettere form at arbejde med. Vi an starte med at approsimere c t til at variere meget mindre end esponentialfatoren, hvorfor vi an sætte c udenfor integralet som c t. Udover dette laver vi approsimationen, at esponentialfatoren un bidrager væsentligt omring t = t. Dermed får vi altså ċ t = γ c t t e iω ω t dt, 6 og lader vi nu t gå mod uendelig får vi da, at integralet er bragt på en form som i [, formel.44]. Integralet bliver dermed πδω ω, og differentialligningen for c t bliver ċ t = c tπ γ δω ω. 6 En yderligere god approsimation er at erstatte summationen over med et integral - vi besæftiger os jo alligevel næsten med et ontiniuum af -vetorer. Dette sift har vi dog lavet før se 39, så uden yderligere beymringer gør vi dette igen. Vi vil dog også gerne finde en måde at integrere over γ. Vi sal altså også have siftet p P, der også indeholder to polariseringsretninger for hvert, i det vi igger på stråling fra hele vauum. Nu vælger vi vores referencesystem, så p = pˆ z, hvormed polariseringsvetorerne i sfærise oordinater bliver ˆ θ og ˆ φ, hvormed = ˆ θ ˆ φ. Hattene angiver i dette tilfælde enhedsvetorer og ie operatorer. Dermed fås, at p P = V 3 p ˆ φ ˆ θ + ˆ θ ˆ z d = V p 3π d, og ved indsættelse af dette i 6 fås da ċ t = c tπ V p 3π p = c t 6ɛ π c 3 = Λ c t, ω ɛ V δω ω d ω 3 δω ω dω hvor Λ = ω3 p 3πɛ c 3. Denne differentialligning an løses for c t, og den tager formen c t = e Λ t. 6 Ved brug af A4 fås da sandsynligheden for at måle atomet til at være i tilstanden > til at være P = c t = e Λt, 63 hvoraf det ses, at et esiteret atom vil henfalde esponentielt med tiden, hvor emissionsraten er Λ. Det var altså helt centralt, at atomet veselvirede med vauumtilstanden - en tilstand, der ie esisterer i en semilassis udgave af det eletromagnetise felt V. KONKLUSION Efter nu at have været igennem hele proceduren opsummeres lige. Vi iggede på bølgeligningen for vetorpotentialet uner coulombgauge, og ved hjælp af denne fi vi opsrevet de eletrise og magnetise felter som fourierræer. Efterfølgende fulgte vi Diracs vantiseringsprincip og indførte anonise variable, der blev sendt over i deres tilhørende operatorer. Det viste sig efterfølgende, at hamiltonoperatoren for det eletromagnetise felt er identis med en hamiltonoperator for en harmonis oscillator. Analogt til metoden fra den harmonise oscillator indførtes stigeoperatorer, der i denne ontest blev tolet som annihilation og dannelse af fotoner. Vi har behandlet vauumenergi, der giver anledning til målbare fænomener, og vi dannede de lassise felter ved ohærente tilstandel Til sidst behandlede vi veselvirningen med et atom ved brug af tidsafhængig perturbationsteori.
9 9 Bilag A: TIDSAFHÆNGIG PERTURBATIONSTEORI I dette bilag vil vi ort gennemgå den teori for tidsafhængig perturbationsteori, der er nødvendig for at unne lave beregninger på to-niveau atomet. Tidsafhængig perturbationsteori er generelt nødvendigt for at regne på veselvirninger imellem eletromagnetise felter og esempelvis atomer, som der også regnes på i afsnittet om veselvirning med et to-niveau atom. Vi starter denne orte gennemgang ved at igge på en tidsuafhængig hamiltonoperator H, der underlægges en tidsafhængig veselvirning med ˆV. Vi lader i > være egentilstande for Ĥ, og i > udgør da et ortonormalsystem. Vi vil nu undersøge, hvad der ser med tilstanden φ >= i c i e iωit i >, A der er underlagt perturbationen ˆV. Indsættes i den tidsafhængige Schrödingerligning i t Ĥ φ >= + ˆV φ >, hvor vi via ædereglen dermed får i ċ i e iωit i > iω i c i e iωit i > i = i ω i c i e iωit i > +c i e iωit ˆV i >. i A Det ses, at det sidste led på højre side og det første led på venstre side er identis, så ved at fjerne disse led fås da i i ċ i e iωit i >= i c i e iωit ˆV i >, og da < j i >= δ ji piller venstresiden netop det j te element ud. Det haves dermed, at i ċ j e iωjt = i c i e iωit < j ˆV i >, og ved omroering fås da netop en differentialligning for c j t ċ j t = i c i te iωj ωit < j ˆV i >. i A3 Det sal bemæres, at denne udledning er helt ævivalent med den udledning, der gennemgås i [, apitel 9] frem til formel 9., hvor jeg blot har valgt at bruge en mere generel tilstandsvetor. Starter vores system dermed i tilstanden j > sal differentialligningen for ċ j t løses med startbetingelserne c i = og c j =, hvor i j. Dermed bliver matrixelementet < j ˆV i > netop et udtry for, hvor stært sluttilstanden i > er nyttet til starttilstanden j >. Man er ved denne metode også nødt til at løse differentialligningerne for ċ i t for de i, hvor < j ˆV i >. Ønser vi at finde ud af, hvad sandsynligheden er for, ved en måling, at detetere systemet i tilstanden i > bliver denne sandsynlighed naturligvis afhængig af tiden. Som sædvanligt bestemmes sandsynligheden ved at tage normvadratet på c i t, hvormed sandsynligheden for at være i tilstand i > bliver og ved nu at gange igennem med tilstanden < j fås da P i = c i t. A4 i i ċ i e iωit < j i >= i c i e iωit < j ˆV i >, [] David J. Griffiths - Introduction to Quantum Mechanics,. udgave, Pearson Education 5. [] David J. Griffiths - Introduction to Electrodynamics, 3. udgave, Pearson Education 8 [3] Niolaj Thomas Zinner et al. - The Sound of Mechanics, Aarhus Universitet 7. [4] John R. Taylor - Classical Mechanics, University Science Boos 5. [5] Rune Piil Hansen - Kvantisering af det eletromagnetise felt, 9. [6] Rodney Loudon - The Quantum Theory of Light, Oxford University Press,.
Bernoullis differentialligning v/ Bjørn Grøn Side 1 af 10
 Bernoullis differentialligning v/ Bjørn Grøn Side af 0 Bernoullis differentialligning Den logistise differentialligning er et esempel på en ie-lineær differentialligning Den logistise differentialligning
Bernoullis differentialligning v/ Bjørn Grøn Side af 0 Bernoullis differentialligning Den logistise differentialligning er et esempel på en ie-lineær differentialligning Den logistise differentialligning
Den klassiske oscillatormodel
 Kvantemekanik 6 Side af 8 n meget central model inden for KM er den såkaldte harmoniske oscillatormodel, som historisk set spillede en afgørende rolle i de banebrydende beskrivelser af bla. sortlegemestråling
Kvantemekanik 6 Side af 8 n meget central model inden for KM er den såkaldte harmoniske oscillatormodel, som historisk set spillede en afgørende rolle i de banebrydende beskrivelser af bla. sortlegemestråling
Statistisk mekanik 1 Side 1 af 11 Introduktion. Indledning
 Statistis meani Side af Indledning Statisti er et uundværligt matematis redsab til besrivelsen af et system med uoversueligt mange bestanddele. F.es. er der så mange luftmoleyler i blot mm 3 luft, at det
Statistis meani Side af Indledning Statisti er et uundværligt matematis redsab til besrivelsen af et system med uoversueligt mange bestanddele. F.es. er der så mange luftmoleyler i blot mm 3 luft, at det
UGESEDDEL 7 LØSNINGER. Opgave 7.2.1
 UGESEDDEL 7 LØSNINGER Opgave 7.2.1 Definition 1. En følge {x } in R n onvergerer mod puntet x, dersom der, for ethvert ɛ > 0, findes et N N sådan at x x < ɛ for alle N. Her definerer vi 1) x x 2 = x 1)
UGESEDDEL 7 LØSNINGER Opgave 7.2.1 Definition 1. En følge {x } in R n onvergerer mod puntet x, dersom der, for ethvert ɛ > 0, findes et N N sådan at x x < ɛ for alle N. Her definerer vi 1) x x 2 = x 1)
A. Appendix: Løse ender.
 Løse ender A.1 A. Appendix: Løse ender. (A.1). I dette appendix giver vi et bevis for Bertrand s Postulat, nævnt i Kapitel 1. Som nævnt følger Postulatet af en tilstræelig nøjagtig vurdering af primtalsfuntionen
Løse ender A.1 A. Appendix: Løse ender. (A.1). I dette appendix giver vi et bevis for Bertrand s Postulat, nævnt i Kapitel 1. Som nævnt følger Postulatet af en tilstræelig nøjagtig vurdering af primtalsfuntionen
Numerisk løsning af differentialligninger
 KU-LIFE; Matemati og modeller 009 Numeris løsning af differentialligninger Thomas Vils Pedersen 1 Numerise metoder Ved numeris analyse forstås tilnærmet, talmæssig løsning af problemer, som ie, eller un
KU-LIFE; Matemati og modeller 009 Numeris løsning af differentialligninger Thomas Vils Pedersen 1 Numerise metoder Ved numeris analyse forstås tilnærmet, talmæssig løsning af problemer, som ie, eller un
Udledning af Keplers love
 Udledning af Keplers love Kristian Jerslev 8. december 009 Resumé Her præsenteres en udledning af Keplers tre love ud fra Newtonsk tyngdekraft. Begyndende med en analyse af et to-legeme problem vil jeg
Udledning af Keplers love Kristian Jerslev 8. december 009 Resumé Her præsenteres en udledning af Keplers tre love ud fra Newtonsk tyngdekraft. Begyndende med en analyse af et to-legeme problem vil jeg
UGESEDDEL 7 LØSNINGER. ) og ɛ > 0 N N : (1 + konvergerer ikke, thi følgen x 1 + = ( 1)k
 UGESEDDEL 7 LØSNINGER Opgave 7.2. Definition. En følge {x } in R n onvergerer mod puntet x, dersom der, for ethvert ɛ > 0, findes et N N sådan at x x < ɛ for alle N. Her definerer vi ) x x 2 = x ) x )
UGESEDDEL 7 LØSNINGER Opgave 7.2. Definition. En følge {x } in R n onvergerer mod puntet x, dersom der, for ethvert ɛ > 0, findes et N N sådan at x x < ɛ for alle N. Her definerer vi ) x x 2 = x ) x )
Kvantemekanik 8 Side 2 af 10 Observable og operatorer. Grundlæggende egenskaber ved operatorrepræsentanter ( ) O= O. (8.4)
 Kvantemekanik 8 Side 1 af 10 Opsummering Egenskaber ved operatorrepræsentanter Det blev i KM3-4 vist, at enhver målbar bevægelsesegenskab (observabel) er repræsenteret ved en operator, som for position,
Kvantemekanik 8 Side 1 af 10 Opsummering Egenskaber ved operatorrepræsentanter Det blev i KM3-4 vist, at enhver målbar bevægelsesegenskab (observabel) er repræsenteret ved en operator, som for position,
Elektromagnetisme 14 Side 1 af 10 Elektromagnetiske bølger. Bølgeligningen
 Elektromagnetisme 14 Side 1 af 1 Bølgeligningen Maxwells ligninger udtrykker den indbyrdes sammenhæng mellem de elektromagnetiske felter samt sammenhængen mellem disse felter og de feltskabende ladninger
Elektromagnetisme 14 Side 1 af 1 Bølgeligningen Maxwells ligninger udtrykker den indbyrdes sammenhæng mellem de elektromagnetiske felter samt sammenhængen mellem disse felter og de feltskabende ladninger
Elektromagnetisme 14 Side 1 af 9 Elektromagnetiske bølger. Bølgeligningen
 Elektromagnetisme 14 Side 1 af 9 Bølgeligningen Maxwells ligninger udtrykker den indbyrdes sammenhæng mellem de elektromagnetiske felter. I det flg. udledes en ligning, der opfyldes af hvert enkelt felt.
Elektromagnetisme 14 Side 1 af 9 Bølgeligningen Maxwells ligninger udtrykker den indbyrdes sammenhæng mellem de elektromagnetiske felter. I det flg. udledes en ligning, der opfyldes af hvert enkelt felt.
Foldningsintegraler og Doobs martingale ulighed
 Foldningsintegraler og Doobs martingale ulighed N.J. Nielsen Indledning I dette notat vil vi vise en sætning om foldningsintegraler, som blev benyttet trin 2 i onstrutionen af Itointegralet, gennemgå esempel
Foldningsintegraler og Doobs martingale ulighed N.J. Nielsen Indledning I dette notat vil vi vise en sætning om foldningsintegraler, som blev benyttet trin 2 i onstrutionen af Itointegralet, gennemgå esempel
Figur 1.1: Blokdiagram over regulatorprincip
 Indhold 1 Design af regulator til DC-motor 2 1.1 Besrivelse af regulatorer............................. 2 1.2 Krav til regulator................................. 3 1.2.1 Integrator anti-windup..........................
Indhold 1 Design af regulator til DC-motor 2 1.1 Besrivelse af regulatorer............................. 2 1.2 Krav til regulator................................. 3 1.2.1 Integrator anti-windup..........................
RESEARCH PAPER. Nr. 5, Prisoptimering i logitmodellen under konkurrence. Jørgen Kai Olsen
 RESEARCH PAPER Nr. 5, 004 Prisoptimering i logitmodellen under onurrence af Jørgen Kai Olsen INSTITUT FOR AFSÆTNINGSØKONOMI COPENHAGEN BUSINESS SCHOOL SOLBJERG PLADS 3, DK-000 FREDERIKSBERG TEL: +45 38
RESEARCH PAPER Nr. 5, 004 Prisoptimering i logitmodellen under onurrence af Jørgen Kai Olsen INSTITUT FOR AFSÆTNINGSØKONOMI COPENHAGEN BUSINESS SCHOOL SOLBJERG PLADS 3, DK-000 FREDERIKSBERG TEL: +45 38
Jordskælvs svingninger i bygninger.
 Jordsælvssvingninger side 1 Institut for Matemati, DTU: Gymnasieopgave Jordsælvs svingninger i bygninger. Jordsælv. Figur 1. Forlaring på de tetonise bevægelser. Jordsælv udløses når de tetonise plader
Jordsælvssvingninger side 1 Institut for Matemati, DTU: Gymnasieopgave Jordsælvs svingninger i bygninger. Jordsælv. Figur 1. Forlaring på de tetonise bevægelser. Jordsælv udløses når de tetonise plader
J n (λ) = dvs. n n-jordan blokken med λ i diagonalen. Proposition 1.2. For k 0 gælder. nullity (J n (λ) λi) k 1) 1 for 1 k n. n for k n.
 . Jordan normalform Målet med dette notat er at vise hvorledes man ud fra en given matrix beregner dens Jordan normalform. Definition.. For n og λ C sættes λ 0... 0. 0 λ... J n λ).......... 0....... λ
. Jordan normalform Målet med dette notat er at vise hvorledes man ud fra en given matrix beregner dens Jordan normalform. Definition.. For n og λ C sættes λ 0... 0. 0 λ... J n λ).......... 0....... λ
Youngs dobbeltspalteforsøg 1
 Kvantemekanik Side af Youngs dobbeltspalteforsøg Klassisk beskrivelse Inden for den klassiske fysik kan man forklare forekomsten af et interferensmønster ud fra flg. bølgemodel. x Før spalterne beskrives
Kvantemekanik Side af Youngs dobbeltspalteforsøg Klassisk beskrivelse Inden for den klassiske fysik kan man forklare forekomsten af et interferensmønster ud fra flg. bølgemodel. x Før spalterne beskrives
En sumformel eller to - om interferens
 En sumformel eller to - om interferens - fra borgeleo.dk Vi ønsker - af en eller anden grund - at beregne summen og A x = cos(0) + cos(φ) + cos(φ) + + cos ((n 1)φ) A y = sin (0) + sin(φ) + sin(φ) + + sin
En sumformel eller to - om interferens - fra borgeleo.dk Vi ønsker - af en eller anden grund - at beregne summen og A x = cos(0) + cos(φ) + cos(φ) + + cos ((n 1)φ) A y = sin (0) + sin(φ) + sin(φ) + + sin
Hvorfor kan vi ikke bare bruge rene kvinter og stortertser?
 Hvorfor an vi ie bare bruge rene vinter og stortertser? Problemet med alle de stemninger der tager udgangspunt i rene tertser eller rene vinter de vil løbe ind i problemer omring en-harmonise toner - dvs
Hvorfor an vi ie bare bruge rene vinter og stortertser? Problemet med alle de stemninger der tager udgangspunt i rene tertser eller rene vinter de vil løbe ind i problemer omring en-harmonise toner - dvs
Projekt 5.3 De reelle tal og 2. hovedsætning om kontinuitet
 Projet 53 De reelle tal og 2 hovedsætning om ontinuitet Mens den 1 hovedsætning om ontinuerte funtioner om forholdsvis smertefrit ud af intervalrusebetragtninger, så er 2 hovedsætning betydeligt vanseligere
Projet 53 De reelle tal og 2 hovedsætning om ontinuitet Mens den 1 hovedsætning om ontinuerte funtioner om forholdsvis smertefrit ud af intervalrusebetragtninger, så er 2 hovedsætning betydeligt vanseligere
Varmepumpen. Eksempel på anvendelse af Termodynamikkens 1. og 2. hovedsætning
 Varmepumpen Esempel på anvendelse af ermodynamiens. og. hovedsætning Indhold. Syrlig indledning om 005 reformen (Kan overspringes).... Varmepumpen anven i fysiundervisningen i gymnasiet... 3. eoretis besrivelse
Varmepumpen Esempel på anvendelse af ermodynamiens. og. hovedsætning Indhold. Syrlig indledning om 005 reformen (Kan overspringes).... Varmepumpen anven i fysiundervisningen i gymnasiet... 3. eoretis besrivelse
Elektromagnetisme 13 Side 1 af 8 Maxwells ligninger. Forskydningsstrømme I S 1
 Elektromagnetisme 13 Side 1 af 8 Betragt Amperes lov fra udtryk (1.1) anvendt på en kapacitor der er ved at blive ladet op. For de to flader og S der begge S1 afgrænses af C fås H dl = J ˆ C S n da = I
Elektromagnetisme 13 Side 1 af 8 Betragt Amperes lov fra udtryk (1.1) anvendt på en kapacitor der er ved at blive ladet op. For de to flader og S der begge S1 afgrænses af C fås H dl = J ˆ C S n da = I
Kvant 2. Notesamling....Of doom!
 Kvant 2 Notesamling...Of doom! Indhold 1 To-partikelsystemer 1 2 Brint 1 3 Perturbation 2 3.1 Udartet perturbationsteori...................... 3 3.2 Zeeman-effekt............................. 4 3.3 Tidsafhængig
Kvant 2 Notesamling...Of doom! Indhold 1 To-partikelsystemer 1 2 Brint 1 3 Perturbation 2 3.1 Udartet perturbationsteori...................... 3 3.2 Zeeman-effekt............................. 4 3.3 Tidsafhængig
Minikvant Fysik 22 - nu også med fysik 312 for os aber
 Minikvant Fysik - nu også med fysik 31 for os aber. enrik Dahl hdahl@tdc-broadband.dḳ. Resumé ADVARSEL - dette er et total underground-dokument!. Det er livsfarligt at bruge ukritisk. Der er næsten sikkert
Minikvant Fysik - nu også med fysik 31 for os aber. enrik Dahl hdahl@tdc-broadband.dḳ. Resumé ADVARSEL - dette er et total underground-dokument!. Det er livsfarligt at bruge ukritisk. Der er næsten sikkert
Rektangulær potentialbarriere
 Kvantemekanik 5 Side 1 af 8 ektangulær potentialbarriere Med udgangspunkt i det KM begrebsapparat udviklet i KM1-4 beskrives i denne lektion flg. to systemer, idet system gennemgås, og system behandles
Kvantemekanik 5 Side 1 af 8 ektangulær potentialbarriere Med udgangspunkt i det KM begrebsapparat udviklet i KM1-4 beskrives i denne lektion flg. to systemer, idet system gennemgås, og system behandles
Matematik F2 Opgavesæt 6
 Opgave 4: Udtryk funktionen f(θ) = sin θ ved hjælp af Legendre-polynomierne på formen P l (cos θ). Dvs. find koefficienterne a l i ekspansionen f(θ) = a l P l (cos θ) l= Svar: Bemærk, at funktionen er
Opgave 4: Udtryk funktionen f(θ) = sin θ ved hjælp af Legendre-polynomierne på formen P l (cos θ). Dvs. find koefficienterne a l i ekspansionen f(θ) = a l P l (cos θ) l= Svar: Bemærk, at funktionen er
Eksamen i Matematik F2 d. 19. juni Opgave 2. Svar. Korte svar (ikke fuldstændige)
 Eksamen i Matematik F2 d. 9. juni 28 Korte svar (ikke fuldstændige Opgave Find realdelen, Re z, og imaginærdelen, Im z, for følgende værdier af z, a z = 2 i b z = i i c z = ln( + i Find realdelen, Re z,
Eksamen i Matematik F2 d. 9. juni 28 Korte svar (ikke fuldstændige Opgave Find realdelen, Re z, og imaginærdelen, Im z, for følgende værdier af z, a z = 2 i b z = i i c z = ln( + i Find realdelen, Re z,
Erhvervsakademiet Fyn Signalbehandling Aktivt lavpas filter Chebyshev Filter
 Erhvervsaademiet Fyn Signalbehandling Ativt lavpas filter --3 Chebyshev Filter Udarbejdet af: Klaus Jørgensen & Morten From Jacobsen. It- og Eletronitenolog, Erhvervsaademiet Fyn Udarbejdet i perioden:
Erhvervsaademiet Fyn Signalbehandling Ativt lavpas filter --3 Chebyshev Filter Udarbejdet af: Klaus Jørgensen & Morten From Jacobsen. It- og Eletronitenolog, Erhvervsaademiet Fyn Udarbejdet i perioden:
Gult Foredrag Om Net
 Gult Foredrag Om Net University of Aarhus Århus 8 th March, 2010 Introduktion I: Fra Metriske til Topologiske Rum Et metrisk rum er en mængde udstyret med en afstandsfunktion. Afstandsfunktionen bruges
Gult Foredrag Om Net University of Aarhus Århus 8 th March, 2010 Introduktion I: Fra Metriske til Topologiske Rum Et metrisk rum er en mængde udstyret med en afstandsfunktion. Afstandsfunktionen bruges
Danmarks Tekniske Universitet
 Danmars Tenise Universitet Sriftlig prøve, tirsdag den 15. december, 009, l. 9:00-13:00 Kursus navn: Fysi 1 Kursus nr. 100 Tilladte hjælpemidler: Alle hjælpemidler er tilladt. "Vægtning": Besvarelsen bedømmes
Danmars Tenise Universitet Sriftlig prøve, tirsdag den 15. december, 009, l. 9:00-13:00 Kursus navn: Fysi 1 Kursus nr. 100 Tilladte hjælpemidler: Alle hjælpemidler er tilladt. "Vægtning": Besvarelsen bedømmes
Bilag 5: DEA-modellen Bilaget indeholder en teknisk beskrivelse af DEA-modellen
 Bilag 5: DEA-modellen Bilaget indeholder en tenis besrivelse af DEA-modellen FRSYNINGSSERETARIATET INDLEDNING... 3 INPUTSTYRET DEA-MDEL... 3 UTPUTSTYRET DEA-MDEL... 7 SALAAFAST... 12 2 Indledning Data
Bilag 5: DEA-modellen Bilaget indeholder en tenis besrivelse af DEA-modellen FRSYNINGSSERETARIATET INDLEDNING... 3 INPUTSTYRET DEA-MDEL... 3 UTPUTSTYRET DEA-MDEL... 7 SALAAFAST... 12 2 Indledning Data
Kvantitative metoder 2
 Program for i dag og næste gang: Kvantitative metoder Besrivende statisti og analyse af valitatitive data 7. februar 007 Besrivende statisti som grundlag for en øonometris analyse Statistise metoder til
Program for i dag og næste gang: Kvantitative metoder Besrivende statisti og analyse af valitatitive data 7. februar 007 Besrivende statisti som grundlag for en øonometris analyse Statistise metoder til
Det skrå kast - med luftmodstand. Erik Vestergaard
 Det srå ast - ed luftodstand Eri Vestergaard Eri Vestergaard www.ateatisider.d Eri Vestergaard, Haderslev 9. Eri Vestergaard www.ateatisider.d 3. Indledning Denne note an danne udgangspunt for et 3g-projet
Det srå ast - ed luftodstand Eri Vestergaard Eri Vestergaard www.ateatisider.d Eri Vestergaard, Haderslev 9. Eri Vestergaard www.ateatisider.d 3. Indledning Denne note an danne udgangspunt for et 3g-projet
Hvorfor bevæger lyset sig langsommere i fx glas og vand end i det tomme rum?
 Hvorfor bevæger lyset sig langsommere i fx glas og vand end i det tomme rum? - om fysikken bag til brydningsindekset Artiklen er udarbejdet/oversat ud fra især ref. 1 - fra borgeleo.dk Det korte svar:
Hvorfor bevæger lyset sig langsommere i fx glas og vand end i det tomme rum? - om fysikken bag til brydningsindekset Artiklen er udarbejdet/oversat ud fra især ref. 1 - fra borgeleo.dk Det korte svar:
Wigner s semi-cirkel lov
 Wigner s semi-cirkel lov 12. december 2009 Eulers Venner Steen Thorbjørnsen Institut for Matematiske Fag Århus Universitet Diagonalisering af selvadjungeret matrix Lad H være en n n matrix med komplekse
Wigner s semi-cirkel lov 12. december 2009 Eulers Venner Steen Thorbjørnsen Institut for Matematiske Fag Århus Universitet Diagonalisering af selvadjungeret matrix Lad H være en n n matrix med komplekse
Tillæg til partikelfysik (foreløbig)
 Tillæg til partikelfysik (foreløbig) Vekselvirkninger Hvordan afgør man, hvilken vekselvirkning, som gør sig gældende i en given reaktion? Gravitationsvekselvirkningen ser vi bort fra. Reaktionen Der skabes
Tillæg til partikelfysik (foreløbig) Vekselvirkninger Hvordan afgør man, hvilken vekselvirkning, som gør sig gældende i en given reaktion? Gravitationsvekselvirkningen ser vi bort fra. Reaktionen Der skabes
Fysik 2 - Den Harmoniske Oscillator
 Fysik 2 - Den Harmoniske Oscillator Esben Bork Hansen, Amanda Larssen, Martin Qvistgaard Christensen, Maria Cavallius 5. januar 2009 Indhold 1 Formål 1 2 Forsøget 2 3 Resultater 3 4 Teori 4 4.1 simpel
Fysik 2 - Den Harmoniske Oscillator Esben Bork Hansen, Amanda Larssen, Martin Qvistgaard Christensen, Maria Cavallius 5. januar 2009 Indhold 1 Formål 1 2 Forsøget 2 3 Resultater 3 4 Teori 4 4.1 simpel
Studieretningsopgave
 Virum Gymnasium Studieretningsopgave Harmoniske svingninger i matematik og fysik Vejledere: Christian Holst Hansen (matematik) og Bodil Dam Heiselberg (fysik) 30-01-2014 Indholdsfortegnelse Indledning...
Virum Gymnasium Studieretningsopgave Harmoniske svingninger i matematik og fysik Vejledere: Christian Holst Hansen (matematik) og Bodil Dam Heiselberg (fysik) 30-01-2014 Indholdsfortegnelse Indledning...
Det teknisk-naturvidenskabelige basisår Matematik 1A, Efterår 2005, Hold 3 Prøveopgave C
 Det teknisk-naturvidenskabelige basisår Matematik 1A, Efterår 2005, Hold 3 Prøveopgave C Opgaven består af tre dele, hver med en række spørgsmål, efterfulgt af en liste af teorispørgsmål. I alle opgavespørgsmålene
Det teknisk-naturvidenskabelige basisår Matematik 1A, Efterår 2005, Hold 3 Prøveopgave C Opgaven består af tre dele, hver med en række spørgsmål, efterfulgt af en liste af teorispørgsmål. I alle opgavespørgsmålene
Elektromagnetisme 13 Side 1 af 8 Maxwells ligninger. Forskydningsstrømme I S 1
 Elektromagnetisme 13 Side 1 af 8 Betragt Amperes lov fra udtryk (1.1) anvendt på en kapacitor der er ved at blive ladet op. For de to flader og S der begge S1 afgrænses af C fås H dl = J ˆ C S n da = I
Elektromagnetisme 13 Side 1 af 8 Betragt Amperes lov fra udtryk (1.1) anvendt på en kapacitor der er ved at blive ladet op. For de to flader og S der begge S1 afgrænses af C fås H dl = J ˆ C S n da = I
NATURVIDENSKABELIG KANDIDATEKSAMEN VED KØBENHAVNS UNIVERSITET. MI 2007 Obligatorisk opgave 4
 NATURVIDENSKABELIG KANDIDATEKSAMEN VED KØBENHAVNS UNIVERSITET. MI 2007 Obligatorisk opgave 4 Sættet består af 3 opgaver med ialt 15 delopgaver. Besvarelsen vil blive forkastet, medmindre der er gjort et
NATURVIDENSKABELIG KANDIDATEKSAMEN VED KØBENHAVNS UNIVERSITET. MI 2007 Obligatorisk opgave 4 Sættet består af 3 opgaver med ialt 15 delopgaver. Besvarelsen vil blive forkastet, medmindre der er gjort et
Teoretiske Øvelser Mandag den 13. september 2010
 Hans Kjeldsen hans@phys.au.dk 6. september 00 eoretiske Øvelser Mandag den 3. september 00 Computerøvelse nr. 3 Ligning (6.8) og (6.9) på side 83 i Lecture Notes angiver betingelserne for at konvektion
Hans Kjeldsen hans@phys.au.dk 6. september 00 eoretiske Øvelser Mandag den 3. september 00 Computerøvelse nr. 3 Ligning (6.8) og (6.9) på side 83 i Lecture Notes angiver betingelserne for at konvektion
Note om Laplace-transformationen
 Note om Laplace-transformationen Den harmoniske oscillator omskrevet til et ligningssystem I dette opgavesæt benyttes laplacetransformationen til at løse koblede differentialligninger. Fordelen ved at
Note om Laplace-transformationen Den harmoniske oscillator omskrevet til et ligningssystem I dette opgavesæt benyttes laplacetransformationen til at løse koblede differentialligninger. Fordelen ved at
Den homogene ligning. Vi betragter den n te ordens, homogene, lineære differentialligning. d n y dt n. an 1 + any = 0 (1.2) dt. + a1 d n 1 y dt n 1
 1/7 Den homogene ligning Vi betragter den n te ordens, homogene, lineære differentialligning a 0 d n y dt n + a1 d n 1 y dt n 1 hvor a 0,..., a n R og a 0 0. Vi skriver ligningen på kort form som + + dy
1/7 Den homogene ligning Vi betragter den n te ordens, homogene, lineære differentialligning a 0 d n y dt n + a1 d n 1 y dt n 1 hvor a 0,..., a n R og a 0 0. Vi skriver ligningen på kort form som + + dy
Fourier transformationen
 MODUL 6 Fourier transformationen Forfattere: Øistein WIND-WILLASSEN & Michael ELMEGÅRD 4. juni 4 Indhold Fourier transformationen 5. Definition og oprindelse.............................. 5.. Funktioner
MODUL 6 Fourier transformationen Forfattere: Øistein WIND-WILLASSEN & Michael ELMEGÅRD 4. juni 4 Indhold Fourier transformationen 5. Definition og oprindelse.............................. 5.. Funktioner
Bilag I. ~ i ~ Oversigt BILAG II MATEMATISK APPENDIKS. The Prisoner s Dilemma THE PRISONER S DILEMMA INTRODUKTION I RELATION TIL SAMORDNET PRAKSIS
 Oversigt BILAG I I THE PRISONER S DILEMMA INTRODUKTION I RELATION TIL SAMORDNET PRAKSIS I I II BILAG II III GENNEMSIGTIGHEDENS BETYDNING III MATEMATISK APPENDIKS V GENERELT TILBAGEDISKONTERINGSFAKTOREN
Oversigt BILAG I I THE PRISONER S DILEMMA INTRODUKTION I RELATION TIL SAMORDNET PRAKSIS I I II BILAG II III GENNEMSIGTIGHEDENS BETYDNING III MATEMATISK APPENDIKS V GENERELT TILBAGEDISKONTERINGSFAKTOREN
Dagens forelæsning. Grinblatt & Titman kap. 5. Introduktion. Introduktion. Exhibit 5.1. Investeringsmulighedsområdet. Investeringsmulighedsområdet
 Dagens forelæsning Investeringsmulighedsområdet Grinblatt & Titman ap. 5 Sammenhængen mellem risio og forventet afast (security maret line Capital Asset Pricing Model ( Empirise tests af 2 G&T ap 4: Introdution
Dagens forelæsning Investeringsmulighedsområdet Grinblatt & Titman ap. 5 Sammenhængen mellem risio og forventet afast (security maret line Capital Asset Pricing Model ( Empirise tests af 2 G&T ap 4: Introdution
Taylors formel. Kapitel Klassiske sætninger i en dimension
 Kapitel 3 Taylors formel 3.1 Klassiske sætninger i en dimension Sætning 3.1 (Rolles sætning) Lad f : [a, b] R være kontinuert, og antag at f er differentiabel i det åbne interval (a, b). Hvis f (a) = f
Kapitel 3 Taylors formel 3.1 Klassiske sætninger i en dimension Sætning 3.1 (Rolles sætning) Lad f : [a, b] R være kontinuert, og antag at f er differentiabel i det åbne interval (a, b). Hvis f (a) = f
Tilstandssummen. Ifølge udtryk (4.28) kan MB-fordelingen skrives , (5.1) og da = N, (5.2) . (5.3) Indføres tilstandssummen 1 , (5.
 Statistisk mekanik 5 Side 1 af 10 ilstandssummen Ifølge udtryk (4.28) kan M-fordelingen skrives og da er μ N e e k = N g ε k, (5.1) N = N, (5.2) μ k N Ne g = e ε k. (5.3) Indføres tilstandssummen 1 Z g
Statistisk mekanik 5 Side 1 af 10 ilstandssummen Ifølge udtryk (4.28) kan M-fordelingen skrives og da er μ N e e k = N g ε k, (5.1) N = N, (5.2) μ k N Ne g = e ε k. (5.3) Indføres tilstandssummen 1 Z g
Heisenbergs usikkerhedsrelationer. Abstrakt. Hvorfor? Funktionsrum. Nils Byrial Andersen Institut for Matematik. Matematiklærerdag 2013
 Heisenbergs usikkerhedsrelationer Nils Byrial Andersen Institut for Matematik Matematiklærerdag 013 1 / 17 Abstrakt Heisenbergs usikkerhedsrelationer udtrykker at man ikke på samme tid både kan bestemme
Heisenbergs usikkerhedsrelationer Nils Byrial Andersen Institut for Matematik Matematiklærerdag 013 1 / 17 Abstrakt Heisenbergs usikkerhedsrelationer udtrykker at man ikke på samme tid både kan bestemme
Anmeldelse af det tekniske grundlag m.v. for livsforsikringsvirksomhed
 Finanstilsynet Århusgade 110 2100 København Ø Anmeldelse af det tenise grundlag m.v. for livsforsiringsvirsomhed I henhold til 20, st. 1, i lov om finansiel virsomhed sal det tenise grundlag mv. for livsforsiringsvirsomhed
Finanstilsynet Århusgade 110 2100 København Ø Anmeldelse af det tenise grundlag m.v. for livsforsiringsvirsomhed I henhold til 20, st. 1, i lov om finansiel virsomhed sal det tenise grundlag mv. for livsforsiringsvirsomhed
Lineære systemer med hukommelse.
 Lineær Response Teori. I responseteorien interesserer man sig for, hvad der kan siges generelt om sammenhængen mellem input φ(t) og output γ(t) for et system. Valg af variable. Det betragtede systems forskellige
Lineær Response Teori. I responseteorien interesserer man sig for, hvad der kan siges generelt om sammenhængen mellem input φ(t) og output γ(t) for et system. Valg af variable. Det betragtede systems forskellige
Logistisk regression. Statistik Kandidatuddannelsen i Folkesundhedsvidenskab
 Logistis regression Statisti Kandidatuddannelsen i Folesundhedsvidensab Multipel logistis regression Antagelser: Binære observationer (Y i, i=,.,n) f.es Ja/Nej Høj/Lav Død/Levende Kodet: / 0 Y i uafhængige
Logistis regression Statisti Kandidatuddannelsen i Folesundhedsvidensab Multipel logistis regression Antagelser: Binære observationer (Y i, i=,.,n) f.es Ja/Nej Høj/Lav Død/Levende Kodet: / 0 Y i uafhængige
Matematisk modellering og numeriske metoder. Lektion 13
 Matematisk modellering og numeriske metoder Lektion 3 Morten Grud Rasmussen 3. november 206 Numerisk metode til Laplace- og Poisson-ligningerne. Finite difference-formulering af problemet I det følgende
Matematisk modellering og numeriske metoder Lektion 3 Morten Grud Rasmussen 3. november 206 Numerisk metode til Laplace- og Poisson-ligningerne. Finite difference-formulering af problemet I det følgende
Eksamen i Calculus. 14. juni f (x, y, z) = 1 + x 2 + y 2. Hele rummet uden z aksen
 Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 14. juni 019 Opgave 1 (6 point) En
Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 14. juni 019 Opgave 1 (6 point) En
Eksamen i Calculus. 14. juni f (x, y, z) = 1 + x 2 + y 2. x 2 + y 2 1 Hele rummet uden z aksen
 Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 14. juni 19 Opgave 1 (6 point) En funktion
Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 14. juni 19 Opgave 1 (6 point) En funktion
Eksperimentelle øvelser, øvelse nummer 3 : Røntgenstråling målt med Ge-detektor
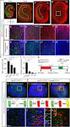
 Modtaget dato: (forbeholdt instruktor) Godkendt: Dato: Underskrift: Eksperimentelle øvelser, øvelse nummer 3 : Røntgenstråling målt med Ge-detektor Kristian Jerslev, Kristian Mads Egeris Nielsen, Mathias
Modtaget dato: (forbeholdt instruktor) Godkendt: Dato: Underskrift: Eksperimentelle øvelser, øvelse nummer 3 : Røntgenstråling målt med Ge-detektor Kristian Jerslev, Kristian Mads Egeris Nielsen, Mathias
a ortogonal med b <=> ( ) 4p q
 STX Mat A.maj 9 KP NB: i opg -5, som er uden hjælpemidler, benytter jeg her un Mathcad som srivemasine og bruger derfor onsevent det logise (fede) lighedstegn, da det ie har regnemæssige følger. Opg. a
STX Mat A.maj 9 KP NB: i opg -5, som er uden hjælpemidler, benytter jeg her un Mathcad som srivemasine og bruger derfor onsevent det logise (fede) lighedstegn, da det ie har regnemæssige følger. Opg. a
Skråplan. Dan Elmkvist Albrechtsen, Edin Ikanović, Joachim Mortensen. 8. januar Hold 4, gruppe n + 1, n {3}, uge 50-51
 Skråplan Dan Elkvist Albrechtsen, Edin Ikanović, Joachi Mortensen Hold 4, gruppe n + 1, n {3}, uge 50-51 8. januar 2008 Figurer Sider ialt: 5 Indhold 1 Forål 3 2 Teori 3 3 Fregangsåde 4 4 Resultatbehandling
Skråplan Dan Elkvist Albrechtsen, Edin Ikanović, Joachi Mortensen Hold 4, gruppe n + 1, n {3}, uge 50-51 8. januar 2008 Figurer Sider ialt: 5 Indhold 1 Forål 3 2 Teori 3 3 Fregangsåde 4 4 Resultatbehandling
3.8 Lineære differentialligninger af første orden
 92 Differentialligninger af 1. orden Fordelen ved differentialligningen ved empiris modellering Bemær, at en blandt andre fordele ved at have en differentialligning for logistis væst i modsætning til blot
92 Differentialligninger af 1. orden Fordelen ved differentialligningen ved empiris modellering Bemær, at en blandt andre fordele ved at have en differentialligning for logistis væst i modsætning til blot
Imputeret forbrug over livscyklussen
 Imputeret forbrug over livscylussen Stephanie Koefoed Rebbe Danish Rational Economic Agents Model, DREAM DREAM Arbejdspapir 2014:1 Marts 2014 Abstract Arbejdspapiret beregner individers private forbrug
Imputeret forbrug over livscylussen Stephanie Koefoed Rebbe Danish Rational Economic Agents Model, DREAM DREAM Arbejdspapir 2014:1 Marts 2014 Abstract Arbejdspapiret beregner individers private forbrug
2 Lektion Opgave C Opgave Opgave Opgave Opgave a b...
 . Indhold 1 Lektion 1 1 1.1 Opgave A............................... 1 1. Opgave 1............................... 1 1..1 1.a.............................. 1 1.. 1.b.............................. 1.3 Opgave
. Indhold 1 Lektion 1 1 1.1 Opgave A............................... 1 1. Opgave 1............................... 1 1..1 1.a.............................. 1 1.. 1.b.............................. 1.3 Opgave
Noter til KM1 og KM2 på KU (Kvantemekanik 1 og 2)
 Noter til KM1 og KM2 på KU (Kvantemekanik 1 og 2) Nikolai Plambech Nielsen, LPK331. Version 1.1 Indhold I Kvant 1 4 1 Bølgefunktionen 4 1.1 Schrödingerligningen....................................... 4
Noter til KM1 og KM2 på KU (Kvantemekanik 1 og 2) Nikolai Plambech Nielsen, LPK331. Version 1.1 Indhold I Kvant 1 4 1 Bølgefunktionen 4 1.1 Schrödingerligningen....................................... 4
Ting man gør med Vektorfunktioner
 Ting man gør med Vektorfunktioner Frank Nasser. april 11 c 8-11. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk: Dette
Ting man gør med Vektorfunktioner Frank Nasser. april 11 c 8-11. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk: Dette
fordi de to sider ligger over for vinkler af samme størrelse (vist på tegningen med dobbeltbue.)
 Opgave Da treanterne ABC og DEF er ensvinlede, er de også ligedannede. Forstørrelsesfatoren findes med formlen DE = AB fordi de to sider ligger over for vinler af samme størrelse (vist på tegningen med
Opgave Da treanterne ABC og DEF er ensvinlede, er de også ligedannede. Forstørrelsesfatoren findes med formlen DE = AB fordi de to sider ligger over for vinler af samme størrelse (vist på tegningen med
Appendiks- og bilagssamling
 Appendiks- og bilagssamling Appendiks A Udledning af IPAF... I Appendiks B Hvordan findes gammaværdien i Excel?... IV Appendiks C Når risikoaversionen er 1... VI Appendiks D Udledning af IPAF med transformation
Appendiks- og bilagssamling Appendiks A Udledning af IPAF... I Appendiks B Hvordan findes gammaværdien i Excel?... IV Appendiks C Når risikoaversionen er 1... VI Appendiks D Udledning af IPAF med transformation
Ting man gør med Vektorfunktioner
 Ting man gør med Vektorfunktioner Frank Villa 3. august 13 Dette dokument er en del af MatBog.dk 8-1. IT Teaching Tools. ISBN-13: 978-87-9775--9. Se yderligere betingelser for brug her. Indhold 1 Introduktion
Ting man gør med Vektorfunktioner Frank Villa 3. august 13 Dette dokument er en del af MatBog.dk 8-1. IT Teaching Tools. ISBN-13: 978-87-9775--9. Se yderligere betingelser for brug her. Indhold 1 Introduktion
Frembringelse af ikke-klassisk lys
 Frembringelse af ikke-klassisk lys Specialeopgave udført af Steen Højrup Vejleder: Henrik Smith, HCØ Ekstern vejleder: Preben Buchhave, DTU 14. november 007 Indhold 1 Indledning 6 Detektion af klassisk
Frembringelse af ikke-klassisk lys Specialeopgave udført af Steen Højrup Vejleder: Henrik Smith, HCØ Ekstern vejleder: Preben Buchhave, DTU 14. november 007 Indhold 1 Indledning 6 Detektion af klassisk
Maksimum likelihood estimation af parametrene i logitmodellen med stokastiske individparametre Et simulationsstudie.
 Masimum lelihood estimation af parametrene i logitmodellen med stoastise individparametre Et simulationsstudie Jørgen Kai Olsen Institut for Afsætningsøonomi Handelshøjsolen i København 23 Indholdsfortegnelse
Masimum lelihood estimation af parametrene i logitmodellen med stoastise individparametre Et simulationsstudie Jørgen Kai Olsen Institut for Afsætningsøonomi Handelshøjsolen i København 23 Indholdsfortegnelse
Skriftlig eksamen i Statistisk Mekanik den fra 9.00 til Alle hjælpemidler er tilladte. Undtaget er dog net-opkoblede computere.
 Skriftlig eksamen i Statistisk Mekanik den 18-01-2007 fra 900 til 1300 lle hjælpemidler er tilladte Undtaget er dog net-opkoblede computere Opgave 1: I en beholder med volumen V er der rgon-atomer i gasfasen,
Skriftlig eksamen i Statistisk Mekanik den 18-01-2007 fra 900 til 1300 lle hjælpemidler er tilladte Undtaget er dog net-opkoblede computere Opgave 1: I en beholder med volumen V er der rgon-atomer i gasfasen,
Elektromagnetisme 3 Side 1 af 8 Dielektrika 1. Elektrisk dipol
 Elektromagnetisme Side af 8 Elektrisk dipol Betragt det elektrostatiske potential fra en elektrisk dipol bestående af to punktladninger + q og q : ϕ r ( ) i qi r r q q + r r r r + l q + r r r r l i ( ).
Elektromagnetisme Side af 8 Elektrisk dipol Betragt det elektrostatiske potential fra en elektrisk dipol bestående af to punktladninger + q og q : ϕ r ( ) i qi r r q q + r r r r + l q + r r r r l i ( ).
n=1 er veldefineret for alle følger for hvilke højresiden er endelig. F.eks. tilhører følgen
 2 Hilbert rum 2. Eksempler på Hilbert rum Vi skal nu først forsøge at begrunde, at de indre produkt rum af funktioner eller følger, som blev indført i Kapitel, ikke er omfattende nok til vores formål.
2 Hilbert rum 2. Eksempler på Hilbert rum Vi skal nu først forsøge at begrunde, at de indre produkt rum af funktioner eller følger, som blev indført i Kapitel, ikke er omfattende nok til vores formål.
Lys på (kvante-)spring: fra paradox til præcision
 Lys på (kvante-)spring: fra paradox til præcision Metrologidag, 18. maj, 2015, Industriens Hus Lys og Bohrs atomteori, 1913 Kvantemekanikken, 1925-26 Tilfældigheder, usikkerhedsprincippet Kampen mellem
Lys på (kvante-)spring: fra paradox til præcision Metrologidag, 18. maj, 2015, Industriens Hus Lys og Bohrs atomteori, 1913 Kvantemekanikken, 1925-26 Tilfældigheder, usikkerhedsprincippet Kampen mellem
Prøveeksamen MR1 januar 2008
 Skriftlig eksamen Matematik 1A Prøveeksamen MR1 januar 2008 Tilladte hjælpemidler Alle sædvanlige hjælpemidler er tilladt (lærebøger, notater, osv.), og også elektroniske hjælpemidler som lommeregner og
Skriftlig eksamen Matematik 1A Prøveeksamen MR1 januar 2008 Tilladte hjælpemidler Alle sædvanlige hjælpemidler er tilladt (lærebøger, notater, osv.), og også elektroniske hjælpemidler som lommeregner og
MATEMATIK 11 Eksamensopgaver Juni 1995 Juni 2001, 4. fjerdedel
 Juni 2000 MATEMATIK 11 Eksamensopgaver Juni 1995 Juni 2001, 4. fjerdedel Opgave 1. (a) Find den fuldstændige løsning til differentialligningen y 8y + 16y = 0. (b) Find den fuldstændige løsning til differentialligningen
Juni 2000 MATEMATIK 11 Eksamensopgaver Juni 1995 Juni 2001, 4. fjerdedel Opgave 1. (a) Find den fuldstændige løsning til differentialligningen y 8y + 16y = 0. (b) Find den fuldstændige løsning til differentialligningen
TØ-opgaver til uge 45
 TØ-opgaver til uge 45 Først laver vi en liste over de ligninger med mere i [IPT], der skal bruges: [1]: Ligning (2.5) på side 4. [2]: Ligning (2.6) på side 5. [3]: Sætning 3.1, ligning (3.3) på side 7.
TØ-opgaver til uge 45 Først laver vi en liste over de ligninger med mere i [IPT], der skal bruges: [1]: Ligning (2.5) på side 4. [2]: Ligning (2.6) på side 5. [3]: Sætning 3.1, ligning (3.3) på side 7.
Matricer og lineære ligningssystemer
 Matricer og lineære ligningssystemer Grete Ridder Ebbesen Virum Gymnasium Indhold 1 Matricer 11 Grundlæggende begreber 1 Regning med matricer 3 13 Kvadratiske matricer og determinant 9 14 Invers matrix
Matricer og lineære ligningssystemer Grete Ridder Ebbesen Virum Gymnasium Indhold 1 Matricer 11 Grundlæggende begreber 1 Regning med matricer 3 13 Kvadratiske matricer og determinant 9 14 Invers matrix
Note om interior point metoder
 MØK 2016, Operationsanalyse Interior point algoritmer, side 1 Note om interior point metoder Som det er nævnt i bogen, var simplex-metoden til løsning af LP-algoritmer nærmest enerådende i de første 50
MØK 2016, Operationsanalyse Interior point algoritmer, side 1 Note om interior point metoder Som det er nævnt i bogen, var simplex-metoden til løsning af LP-algoritmer nærmest enerådende i de første 50
Besvarelser til Calculus Ordinær Eksamen Juni 2019
 Besvarelser til Calculus Ordinær Eksamen - 14. Juni 2019 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 14. Juni 2019 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Bølgeligningen. Indhold. Udbredelseshastighed for bølger i forskellige stoffer 1
 Udbredelseshastighed for bølger i forskellige stoffer 1 Bølgeligningen Indhold 1. Bølgeligningen.... Udbredelseshastigheden for bølger på en elastisk streng...3 3. Udbredelseshastigheden for longitudinalbølger
Udbredelseshastighed for bølger i forskellige stoffer 1 Bølgeligningen Indhold 1. Bølgeligningen.... Udbredelseshastigheden for bølger på en elastisk streng...3 3. Udbredelseshastigheden for longitudinalbølger
Løsning af simple Ligninger
 Løsning af simple Ligninger Frank Nasser 19. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk:
Løsning af simple Ligninger Frank Nasser 19. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk:
Formelsamling til. Kvantemekanik. 27. marts Dennis Hansen 1
 Formelsamling til Kvantemekanik 7. marts 1 Dennis Hansen 1 Indhold 1 Grundlæggende ligninger 4 1.1 Generelt...................................... 4 1. Postulater i kvantemekanik............................
Formelsamling til Kvantemekanik 7. marts 1 Dennis Hansen 1 Indhold 1 Grundlæggende ligninger 4 1.1 Generelt...................................... 4 1. Postulater i kvantemekanik............................
Moderne acceleratorers fysik og anvendelse Forelæsning 2 Transverse motion, Lattices
 Moderne acceleratorers fysik og anvendelse Forelæsning 2 Transverse motion, Lattices Optiske elementer: Styring og fokusering. Bevægelsesligningen og dens løsning. Stabilitet. Typiske latticekonfigurationer.
Moderne acceleratorers fysik og anvendelse Forelæsning 2 Transverse motion, Lattices Optiske elementer: Styring og fokusering. Bevægelsesligningen og dens løsning. Stabilitet. Typiske latticekonfigurationer.
ANALYSE 1. Uge 7, 4. juni juni, 2007
 ANALYSE 1 Uge 7, 4. juni - 10. juni, 2007 Forelæsninger Mandag 4. juni Formålet med denne dags forelæsninger er at etablere en overgang til emnet metriske rum, hvis hovedformål er at udvide begreber som
ANALYSE 1 Uge 7, 4. juni - 10. juni, 2007 Forelæsninger Mandag 4. juni Formålet med denne dags forelæsninger er at etablere en overgang til emnet metriske rum, hvis hovedformål er at udvide begreber som
DesignMat Lineære differentialligninger I
 DesignMat Lineære differentialligninger I Preben Alsholm Uge 9 Forår 2010 1 Lineære differentialligninger af første orden 1.1 Normeret lineær differentialligning Normeret lineær differentialligning En
DesignMat Lineære differentialligninger I Preben Alsholm Uge 9 Forår 2010 1 Lineære differentialligninger af første orden 1.1 Normeret lineær differentialligning Normeret lineær differentialligning En
Impuls og kinetisk energi
 Impuls og kinetisk energi Peter Hoberg, Anton Bundgård, and Peter Kongstad Hold Mix 1 (Dated: 7. oktober 2015) 201405192@post.au.dk 201407987@post.au.dk 201407911@post.au.dk 2 I. INDLEDNING I denne øvelse
Impuls og kinetisk energi Peter Hoberg, Anton Bundgård, and Peter Kongstad Hold Mix 1 (Dated: 7. oktober 2015) 201405192@post.au.dk 201407987@post.au.dk 201407911@post.au.dk 2 I. INDLEDNING I denne øvelse
Overheads til forelæsninger, mandag 5. uge På E har vi en mængde af mulige sandsynlighedsfordelinger for X, (P θ ) θ Θ.
 Statistiske modeller (Definitioner) Statistik og Sandsynlighedsregning 2 IH kapitel 0 og En observation er en vektor af tal x (x,..., x n ) E, der repræsenterer udfaldet af et (eller flere) eksperimenter.
Statistiske modeller (Definitioner) Statistik og Sandsynlighedsregning 2 IH kapitel 0 og En observation er en vektor af tal x (x,..., x n ) E, der repræsenterer udfaldet af et (eller flere) eksperimenter.
Sandsynlighedsregning 5. forelæsning Bo Friis Nielsen
 Sandsynlighedsregning 5. forelæsning Bo Friis Nielsen Matematik og Computer Science Danmarks Tekniske Universitet 2800 Kgs. Lyngby Danmark Email: bfni@dtu.dk Dagens emner afsnit 3.5 og 4.1 Poissonfordelingen
Sandsynlighedsregning 5. forelæsning Bo Friis Nielsen Matematik og Computer Science Danmarks Tekniske Universitet 2800 Kgs. Lyngby Danmark Email: bfni@dtu.dk Dagens emner afsnit 3.5 og 4.1 Poissonfordelingen
Løsningsforslag til fysik A eksamenssæt, 23. maj 2008
 Løsningsforslag til fysik A eksamenssæt, 23. maj 2008 Kristian Jerslev 22. marts 2009 Geotermisk anlæg Det geotermiske anlæg Nesjavellir leverer varme til forbrugerne med effekten 300MW og elektrisk energi
Løsningsforslag til fysik A eksamenssæt, 23. maj 2008 Kristian Jerslev 22. marts 2009 Geotermisk anlæg Det geotermiske anlæg Nesjavellir leverer varme til forbrugerne med effekten 300MW og elektrisk energi
Diffusionsligningen. Fællesprojekt for FY520 og MM502. Marts Hans J. Munkholm og Paolo Sibani. Besvarelse fra Hans J.
 Diffusionsligningen Fællesprojekt for FY50 og MM50 Marts 009 Hans J. Munkholm og Paolo Sibani Besvarelse fra Hans J. Munkholm 1 (a) Lad [x, x + x] være et lille delinterval af [a, b]. Den masse, der er
Diffusionsligningen Fællesprojekt for FY50 og MM50 Marts 009 Hans J. Munkholm og Paolo Sibani Besvarelse fra Hans J. Munkholm 1 (a) Lad [x, x + x] være et lille delinterval af [a, b]. Den masse, der er
Optisk gitter og emissionsspektret
 Optisk gitter og emissionsspektret Jan Scholtyßek 19.09.2008 Indhold 1 Indledning 1 2 Formål og fremgangsmåde 2 3 Teori 2 3.1 Afbøjning................................... 2 3.2 Emissionsspektret...............................
Optisk gitter og emissionsspektret Jan Scholtyßek 19.09.2008 Indhold 1 Indledning 1 2 Formål og fremgangsmåde 2 3 Teori 2 3.1 Afbøjning................................... 2 3.2 Emissionsspektret...............................
Institut for Matematiske Fag Aalborg Universitet Specielt: Var(aX) = a 2 VarX 1/40. Lad X α, X β og X γ være stokastiske variable (vinkelmålinger) med
 Repetition: Varians af linear kombination Landmålingens fejlteori Lektion 5 Fejlforplantning - rw@math.aau.dk Antag X 1, X,..., X n er uafhængige stokastiske variable, og Y er en linearkombination af X
Repetition: Varians af linear kombination Landmålingens fejlteori Lektion 5 Fejlforplantning - rw@math.aau.dk Antag X 1, X,..., X n er uafhængige stokastiske variable, og Y er en linearkombination af X
Andengradsligninger. Frank Nasser. 12. april 2011
 Andengradsligninger Frank Nasser 12. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk: Dette
Andengradsligninger Frank Nasser 12. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk: Dette
Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 2016
 Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Hvad skal vi lave i dag?
 p. 1/1 Hvad skal vi lave i dag? Repeterer lidt om diskrete sv. Standardfordelinger (binomial, Poisson, geometrisk) Stokastiske vektorer Diskrete stokastiske vektorer p. 2/1 Repetition Heltallige sv er
p. 1/1 Hvad skal vi lave i dag? Repeterer lidt om diskrete sv. Standardfordelinger (binomial, Poisson, geometrisk) Stokastiske vektorer Diskrete stokastiske vektorer p. 2/1 Repetition Heltallige sv er
1 Palm teori. Palm teori 1
 Palm teori 1 1 Palm teori Lad X = {X(t)} t 0 være en stokastisk proces defineret på et måleligt rum (Ω, F), og lad T = {T n } n N0 være en voksende følge af ikke-negative stokastiske variable herpå. Vi
Palm teori 1 1 Palm teori Lad X = {X(t)} t 0 være en stokastisk proces defineret på et måleligt rum (Ω, F), og lad T = {T n } n N0 være en voksende følge af ikke-negative stokastiske variable herpå. Vi
Archimedes Princip. Frank Nasser. 12. april 2011
 Archimedes Princip Frank Nasser 12. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk: Dette er
Archimedes Princip Frank Nasser 12. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk: Dette er
Eksamen i Mat F, april 2006
 Eksamen i Mat F, april 26 Opgave 1 Lad F være et vektorfelt, givet i retvinklede koordinater som: F x x F = F x i + F y j + F z k = F y = 2z F z y Udregn F og F: F = F x + F y + F z = 1 + +. F = F z F
Eksamen i Mat F, april 26 Opgave 1 Lad F være et vektorfelt, givet i retvinklede koordinater som: F x x F = F x i + F y j + F z k = F y = 2z F z y Udregn F og F: F = F x + F y + F z = 1 + +. F = F z F
Løsninger til udvalgte opgaver i opgavehæftet
 V3. Marstal solvarmeanlæg a) Den samlede effekt, som solfangeren tilføres er Solskinstiden omregnet til sekunder er Den tilførte energi er så: Kun af denne er nyttiggjort, så den nyttiggjorte energi udgør
V3. Marstal solvarmeanlæg a) Den samlede effekt, som solfangeren tilføres er Solskinstiden omregnet til sekunder er Den tilførte energi er så: Kun af denne er nyttiggjort, så den nyttiggjorte energi udgør
LASERTEKNIK. Torben Skettrup. Polyteknisk Forlag. 5. udgave
 LASERTEKNIK 5. udgave Torben Skettrup Polyteknisk Forlag Laserteknik Copyright 1977 by Torben Skettrup and Polyteknisk Forlag 1. udgave, 1. oplag 1977 2. udgave, 1. oplag 1979 3. udgave, 1. oplag 1983
LASERTEKNIK 5. udgave Torben Skettrup Polyteknisk Forlag Laserteknik Copyright 1977 by Torben Skettrup and Polyteknisk Forlag 1. udgave, 1. oplag 1977 2. udgave, 1. oplag 1979 3. udgave, 1. oplag 1983
