Regneregler. 1. Simple regler for regning med tal.
|
|
|
- Einar Dahl
- 8 år siden
- Visninger:
Transkript
1 Regneregler. Simple regler for regning med tl. Vi rejder l.. med følgende fire regningsrter: plus (), minus ( ), gnge () og dividere (: eller røkstreg, se senere), eller med fremmedord : ddition, sutrktion, multipliktion og division. Svrende til disse regningsrter tler vi om en sum, en differens, et produkt og en røk f/imellem to tl. Når vi opskriver en række tl med l.. disse regningsrters symoler ilndet, tler vi om et mtemtisk udtryk. Hvis et (mtemtisk) udtryk indeholder en multipliktion (et produkt, (gnge)) eller en division (en røk, (dividere)), så skl disse opertioner udføres før eventuelle dditioner (summer, (plus)) og sutrktioner (differenser, (minus)). Og hvis et udtryk indeholder prenteser, så skl disse regnes ud først. Dette er en del f regningsrternes hierrki, som omtles yderligere i det følgende. Eksempel.. ) ( giver ltså ikke, som mn måske kunne tro!!) ( 9) 0 0 d) 6, 8:,8 6,, 9, e) (6 :)8 (6 )8 8 6 f) (0 ) 9 (Bemærk, t dette er lig med: 0, så minusprentesen hæves ved t ændre fortegnene inde i prentesen!) Når mn skl udtrykke en division, så gøres det oftest ved hjælp f en røkstreg. Mn skriver f.eks. i stedet for : eller i stedet for : 9. 9 Det øverste tl i en røk (dvs. tllet over røkstregen) kldes tælleren, og det nederste tl (dvs. tllet under røkstregen) kldes nævneren. Bemærk desuden, t hvis der står en sum i tælleren eller nævneren f røken, så udregnes summen først, som om der stod en prentes omkring den (en skjult prentes), inden selve røken (divisionen) udregnes. Det smme er tilfældet, hvis der står en differens. Dette er også en del f regningsrternes hierrki. Eksempel.. ) 6 8, 6 0,8 8,,6
2 0 0 6 ( 6) ( ) , 0, ( ) ( ) ( ) 0 0 Hvis mn gnger et tl med sig selv, siger mn, t mn kvdrerer tllet, eller t mn tger tllet i nden. F.eks. er: 6, 0,6 0,60,6 0,6 og ( ) ( )( ) 9. På smme måde etyder f.eks., t mn gnger med sig selv tre gnge, ltså: Tllene, 0,6, ( ), kldes en potens f henholdsvis, 0,6, og. Når der optræder potenser i et udtryk, så skl disse udregnes før gnge og dividere, plus og minus. Men udtryk i prentes regnes stdigvæk først. Eksempel.. ) ( 6) ( 6) , 6, 0 6, ,0 0 d) (( ) ( 9) ): På ggrund f det ovenstående kn vi opstille følgende foreløige oversigt: Regningsrternes hierrki: Generelt regner mn fr venstre mod højre, når mn skl udregne værdien f et udtryk, men nogle regningsrter kommer før ndre (hr højere prioritet, ligger højere i hierrkiet):. Først eregnes udtryk i prenteser. Hvis der er prenteser inde i hinnden, egyndes med den inderste.. Herefter eregnes potenser.. Herefter foretges multipliktion (gnge) og division (røk).. Til sidst udføres ddition (plus, sum ) og sutrktion (minus).
3 Beregningen f udtryk inde i en prentes følger de smme regler/det smme hierrki og den derf givne rækkefølge (Jfr. Eksempel..d)). I denne forindelse minder vi om de skjulte prenteser i røker omtlt ovenfor. Øvelse.: Udregn hvert f følgende udtryk uden rug f regnemskine: ) 6 ( ) ( 8 ) ( ) : (6 ( ) ( 8) ( ) ) : ( ) (6 ) ( ) d) ( ) 6 : (9 ) 6 e) ( 0,) ( 6) (, ) 9 f) (6 9) 0 9 ( - ). Generelle regler for sum, differens og produkt I stedet for t regne med estemte værdier f tllene, kn vi regne med symolske værdier, idet vi lder tllene være repræsenteret ved ogstver. Hvis vi f.eks. vil skrive en sum f to tl uden t speifiere hvilke to tl det drejer sig om, så kn vi skrive:, hvor står for værdien f det ene tl og står for værdien f det ndet tl. Vi kunne også skrive p q eller α β, idet vi kn nvende de ogstver (l.. fr det ltinske eller græske lfet), som vi hr lyst til t nvende. Denne fremgngsmåde hr l.. den fordel, t vi kn ngive regneregler som gælder for lle tl unset de konkrete værdier. F.eks. kn vi skrive: ( for t fortælle, t reglen om t hæve/fjerne en prentes med et minus forn gælder for lle tl unset deres værdi. (Prentesen fjernes som omtlt ved t skifte fortegn på tllene inde i prentesen). Efter smme prinip kn vi nu opskrive følgende regler:
4 6 Sætning.. Den modstte værdi til den modstte værdi f et tl er lig med tllet selv: ( ). I en sum er rækkefølgen f de enkelte led uden etydning:. En plusprentes kn hæves og sættes uden videre: ) ( ) (. En minusprentes kn hæves og sættes, hvis mn inde i prentesen forndrer til og til : ) ( ) ( ) ( ) (. Fktorernes rækkefølge (orden) i et produkt er uden etydning: ) ) ( ( 6. En flerleddet størrelse gnges med et tl ved t gnge hvert led med tllet. ( y) y. Når en flerleddet størrelse hr en fælles fktor, kn denne sættes udenfor en prentes: y ( y ) 8. Mn gnger to flerleddede størrelser med hinnden ved t gnge hvert led i den ene med hvert led i den nden: ( ( d) d d 9. Kvdrtet på en toleddet størrelse er lig: Kvdrtet på første led plus kvdrtet på ndet led, eller det doelte produkt: ) ( ) ( ) ( 0. To tls sum gnge de smme to tls differens er lig kvdrtet på første led minus kvdrtet på ndet led: ( (. Mn kvdrerer et produkt ved t kvdrere hver fktor for sig. (
5 Bevis: Vi vil her kun evise regel 8. De øvrige forudsættes velkendte eller umiddelrt indlysende. Ad 8): ( ( d) ( ( d d d d d Ad 9): ( ( ( De øvrige regler i pkt. 9 evises på smme måde. Detljerne overldes til læseren. Ad 0): ( ( Ad ): ( (( Reduktion og omskrivning: Ved omskrivning f et mtemtisk udtryk forstås en eregningsmæssig ændring f udtrykket til ny form (f.eks. ved t prenteser regnes ud, multipliktioner udføres, led i nden regnes ud osv.). Ved reduktion f et mtemtisk udtryk forstås en omskrivning f udtrykket til en simplere form. Ved denne reduktion nvendes de gældende regneregler og regningsrternes hierrki, og værdien f udtrykket må ikke ændres. Med mindre ndet nævnes, så etyder reduér lmindeligvis: reduér mest muligt. Eksempel.. Vi vil reduére følgende udtryk mest muligt: ) ( ( ) ) ( ) ( ) ( ) Ad ): ( ( ) ) ( ) ( ) Ad : ( ) ( ) ( ) (6 ) (8 6) Eksempel.. Vi vil omskrive udtrykket 6 9 ved t skrive det som et produkt f to fktorer: Ved t se på regel 9. ) i sætning. får vi den idé, t 6 9 kn være kvdrtet på en toleddet størrelse, hvor først led er (idet der står ) og hvor ndet led er (idet der står 9 ). Hvis dette skl være tilfældet, skl det sidste led være det doelte produkt, og det ses netop, t 6, hvormed vi i lt hr: 6 9 ( ) ( )( )
6 8 En række f omskrivningens og reduktionens spekter, fkroge, fldgruer osv. vil live lotlgt ved t løse de følgende øvelser: Øvelse.. Omskriv: ) ( ) 9y 6y 9 6 Øvelse.: Reduer/omskriv: ) ( ) ( ) ( 8) d) ( ) e) ( ) f) 6 ( ) g) ( ( h) ( ) i) ( ( )) Øvelse.6. Reduér/omskriv: ) ( ( ( ) ) ) (d (y pq) (d (y pq) ( y z y z)( y z) d) ( ) ( (( ) ) ) Øvelse.. Omskriv til produkt f fktorer: ) 9 d) 6 69 e) 0 f) 9 g) 9 h) 6 i) 9 6 j) 0 k) 6 6 l) 6 m) 6 n) 6 o) Øvelse.8. Reduér: ) ( ( 8 ( ( ( d) ( y) ( 6y) ( y) e) ( ) ( ) ( ) f) ( (
7 9 g) ( y ) ( y) ( y) h) ( ( )) ( ( )) ( ( ) ) i) (( ( ( Øvelse.9. Reduér/omskriv: ) ( )( ) ( )( ) ( )( ) d) ( ) ( ) e) ( )(6 8) ( )( 6) f ) ( y)( 6y) g) ( ( 6 ) h) s)( s) ( Øvelse.0. Skriv følgende udtryk som kvdrtet på en toleddet størrelse: ) d) e) 6 f) p p g) h) z 6z 9 Øvelse.. Skriv følgende udtryk på formen ( : ) Øvelse.. Omskriv/Reduér følgende udtryk: ) ( ) ( ) ( 8)( 8) d) ( ) e) ( ) f) ( g) (8 y) h) ( )( ) i) ( j) ( )( ) k) ( y) l) ( y) ( y) Øvelse.. Reduér følgende udtryk: ) ( ( ( ( ( ( p) ( p) s( ) d) 9 ( ( 6 (
8 0. Simple regler for røker (division) med tl Ved en røk forstås et forhold mellem to tl, opskrevet ved hjælp f en røkstreg, hvor tllet over røkstregen kldes tælleren og tllet under røkstregen kldes nævneren. Værdien f røken findes ved t dividere nævneren op i tælleren. Eksempel.. er tælleren og nævneren, og røkens værdi er. I røken Tilsvrende hr vi, t i røkerne: 0,, 8 medens nævnerne er:,, 8 og. og er tællerne:,, 0 og, Og værdien f disse røker er giver ved: 0,, 0,, og 0,88. 8 Bemærk, t selv med 0 deimler (ifre efter kommet) er tllet 0,88 ikke så præis en værdi som selve røken Når der regnes med røker er der en række forhold t tge i etrgtning. Vi ser først på følgende: En røks fortegn estemmes f såvel tællers som nævners fortegn. Når der står en sum eller en differens i en røk, skl denne udregnes først (som om der stod en prentes omkring) inden selve røkens værdi udregnes. En røks værdi ændres ikke hvis tæller og nævner gnges eller divideres med smme tl (undtgen tllet 0). Eksempel ) Vedrørende fortegn hr vi f.eks., t:, og 8 6 Udtrykket: udregnes ved først t eregne og (som om 6 der stod en skjult prentes omkring disse led), og derefter udregne resten. 8 Vi får således: 0 6 6
9 Brøkerne og 0 Vi kn komme fr hr smme værdi, nemlig,, til 0. Vi siger d, t røken forlænges med. Og vi kn komme fr 0 til nemlig. Vi siger d, t røken forkortes med. 0 dvs.. 0 ved t gnge åde tæller og nævner med smme tl, nemlig ved t dividere åde tæller og nævner med smme tl, Smlet kn dette kort formuleres: 0 Når mn vil lægge røker smmen, skl de hve smme nævner (de skl være ensenævnte ). Hvis de hr den smme nævner (en fælles nævner), skl vi lot lægge tællerne smmen og eholde nævneren, hvorimod hvis de ikke hr en fælles nævner, må vi først forlænge eller forkorte røkerne på pssende måde, så de får en fællesnævner. Tilsvrende gøres ved en differens f røker. Eksempel.. ) 8 stykke lgkge plus 8 stykker lgkge, giver i lt 8 stykker lgkge, dvs. lgkge. 6 0,, For t udregne summen: må vi først give røkerne en fællesnævner. Det ses t 8 tllet kn ruges som fællesnævner, idet den første røk skl forlænges med medens den nden røk skl forlænges med for t få nævneren. Vi hr ltså: 8 8 d) For t udregne differensen: 0 9 må vi først finde en fællesnævner. Det ses, t tllet kn ruges. (Bemærk, t. Som fællesnævner kn ltid ruges produktet f nævnerne!). 9 9 Vi får hermed:
10 Med hensyn til t gnge og dividere i forindelse med røker gælder der følgende regler: Mn gnger en røk med et tl ved t gnge tælleren med tllet og eholde nævneren. Mn gnger to røker med hinnden ved t gnge tæller med tæller og nævner med nævner. Mn dividerer en røk med et tl ved t gnge røkens nævner med tllet og eholde tælleren. Mn dividerer med en røk ved t gnge med den omvendte røk, dvs. ved t gnge med den røk, hvor tæller og nævner hr yttet plds. Eksempel.. Indledningsvist konstterer vi, t f.eks. 6 gnge lgkge er 6 lgkge, dvs. ½ lgkge. Dernæst opfordres læseren til nøje t følge hver enkelt skridt i de følgende omskrivninger og overveje/konsttere, hvd der sker og hvilke regler der ruges: ) d) 8 e) g) h) i) 8 j) k) 8 l) n) p) r) t) : ( 6) m) ( 6) : 0 6 : o) 8 : 8 9 q) 9 6 : s) u)
11 Her følger en række øvelser til indøvning f regnereglerne for røker med tl: Øvelse.. Beregn uden rug f lommeregner: ) 6 ( )( 6 ) 8 ( ) 6 ( ) ( )( 0) ( 8) ( ) Øvelse.6. Forkort følgende røker mest muligt uden rug f lommeregner: ) d) e) f) g) 0 Øvelse.. Løs følgende uden rug f lommeregner: ) Forlæng, så nævneren liver 8 Forlæng 8, så nævneren liver 6 Forlæng, så nævneren liver delelig med 6 d) Skriv som en røk med nævneren e) Skriv som en røk med nævneren Øvelse.8. Løs følgende uden rug f lommeregner ) Forlæng røken med 6 Forlæng røken 9 med Øvelse.9. Reduér mest muligt uden rug f lommeregner og eregn værdien: 6 ) d) e) 8 6 6
12 Øvelse.0. Reduér mest muligt uden rug f lommeregner og eregn værdien: ) d) e) Øvelse.. Reduér mest muligt uden rug f lommeregner og eregn værdien: 6 ) 9 6 d) e) f) Øvelse.. Reduér mest muligt uden rug f lommeregner og eregn værdien: 8 ) 0 d) Øvelse.. Reduér mest muligt uden rug f lommeregner og eregn værdien: ) d) 9 Øvelse.. Reduér mest muligt uden rug f lommeregner og eregn værdien: 8 9 ) ( ) ( ) : 8 : : Øvelse.. Reduér mest muligt uden rug f lommeregner og eregn værdien: ) 6 d)
13 Øvelse.6. Reduér mest muligt uden rug f lommeregner og eregn værdien: ) : d) 6 9 Øvelse. Reduér mest muligt uden rug f lommeregner og eregn værdien: ) : : 6 : d) : e) 6: f) : 8 8 Skriv de smme opgver op v.hj.. røkstreger i stedet for divisionstegnet ( : ). Øvelse.8 Reduér mest muligt uden rug f lommeregner og eregn værdien: ) 9 6 d) Øvelse.9 Ved den reiprokke værdi f et tl forstås divideret med tllet (f.eks. er den reiprokke værdi f lig med ). Bestem uden rug f lommeregner den reiprokke værdi f tllene:,, og 6
14 6. Generelle regler for røker (division) Efter smme prinip som ved sum, differens og produkt kn generelle regler for regning med røker udtrykkes ved hjælp f symolske værdier, dvs. tl repræsenteret ved ogstver. I denne smmenhæng gælder følgende sætning (hvor vi som tidligere nævnt ruger røkstreger i stedet for divisionstegnet : i næsten lle situtioner). Sætning.. ) Fortegnet for en røk fstlægges f såvel tæller som nævner: ) ) En røk med flere led (sum eller differens) i tæller eller nævner indeholder skjulte prenteser, hvilket spiller en rolle når sådnne røker indgår i eregninger: ( d ( d) ) En røks værdi forndres ikke, hvis dens tæller og nævner gnges med smme tl ( 0) (Dette kldes forlængning): ) En røks værdi forndres ikke hvis dens tæller og nævner divideres med smme tl ( 0) (Dette kldes forkortning): y ) y ) Brøker med smme nævner lægges smmen (eller trækkes fr hinnden) ved t lægge tællerne smmen (eller trække tællerne fr hinnden) og eholde nævneren. ) 6) Mn dividerer en flerleddet størrelse med et tl ved t dividere hvert f leddene med tllet: )
15 ) Når røker skl lægges smmen eller trækkes fr hinnden, skl de hve smme nævner. Hvis dette ikke er tilfældet, må vi finde en fællesnævner for røkerne, og forkorte eller forlænge røkerne for t opnå denne fællesnævner. Som fællesnævner kn mn ltid enytte produktet f lle nævnerne: ) d d d d d d d d d d d d 8) Mn gnger en røk med et tl ved t gnge tælleren med tllet og eholde nævneren. 9) Mn gnger to røker med hinnden ved t gnge tæller med tæller og nævner med nævner. d d 0) Mn kvdrerer en røk ved t kvdrere tæller og nævner hver for sig. ) Mn dividerer en røk med et tl ved t gnge røkens nævner med tllet og eholde tælleren. : ) Mn dividerer med en røk ved t gnge med den omvendte røk. ) : d d d Bemærk desuden, t: Ved forkortning f en røk fortsætter mn lmindeligvis indtil røken er uforkortelig. Den reiprokke værdi f et tl defineres som: divideret med, dvs.
16 8 Eksempel.. ( ( ) ( ) ) 6 Først gnges -tllet op på den ene tæller og -tllet gnges op på den nden tæller. D røkerne llerede hr en fællesnævner (, sættes de på en fælles røkstreg og smtidig gnges og ind i de respektive prenteser. Bemærk minustegnet forn den sidste prentes, idet den sidste røk skulle trækkes fr. Endelig hæves minusprentesen og der redueres mest muligt. 8 d d Brøken forkortes med, med og med, hvilket er muligt, idet der åde i tæller og nævner står gnge imellem tllene/ogstverne. Vi kn kort sige, t røken forkortes med. y y y y( y) y ( y) y y y y y y y Først skffes en fællesnævner, nemlig y (Vi nvender ltså produktet f de to eksisterende nævnere). Den første røk skl derfor forlænges med y medens den nden røk skl forlænges med. D de to røker nu hr en fælles nævner, kn vi smle dem til én røk. Smtidig hermed hr vi gnget y og ind i de respektive prenteser. Endelig redueres mest muligt. (Bemærk, t denne sidste røk ikke kn forkortes med eller y, idet der står og ikke imellem og y i tælleren!!!) ( ( ( d) ( 0 ) ( Først udregnes tællerne, og herefter skffes en fællesnævner (igen ved lot t gnge de to eksisterende nævnere smmen). Den første røk forlænges derfor med, medens den nden røk forlænges med. Herefter smles de to røker på én fælles røkstreg, og smtidig hermed hr vi gnget tællerne ud. Endelig redueres mest muligt.
17 9 d ( d) ( ( d) e) : ( d) d d d ( d) d Først konstteres, t det udtryk vi skl reduere, estår f tre led. I det første led gnger vi tæller med tæller og nævner med nævner, og vi husker prentesen om d, idet dette er en flerleddet størrelse, som skl gnges med et tl. I det ndet led enytter vi reglen om, t en røk i nden er tælleren i nden divideret med nævneren i nden, og vi husker prentes omkring, idet det er hele tælleren, vi skl hve i nden. I det tredje led skulle vi dividere med en røk, hvilket hr ført til, t vi nu gnger med den omvendte røk. Herefter forkorter vi den første røk med og gnger ind i prentesen i tælleren, i den nden røk enytter vi, t (, og i det tredje led gnger vi røkerne smmen. D de tre røker, som vi herefter er nået frem til, lle hr smme nævner, hr vi llerede en fællesnævner, og vi kn derfor smle de tre røker til én røk. Vi husker her prentesen om d, idet den sidste røk skl trækkes fr de øvrige røker. Ved t hæve minusprentesen og reduére kommer vi endelig frem til resulttet. d Eksempel.. Ved reduktion f y yz 0y yz kn vi følge forskellige veje (fremgngsmåder): ) y yz 0y yz y ( z y) y z z y z y yz 0y yz y yz yz yz 0y yz z z z y z z y z y yz 0y yz y yz 0y y y y yz y z y z I den første omskrivning sætter vi et fælles led udenfor en prentes i tælleren, idet y indgår i lle tre led i tælleren. Smtidig fremhæver vi, t y også indgår i nævneren. Ved t forkorte røken med y, som nu er gnget på åde i tæller og nævner (jfr. sætning.. ) pkt. )), fremkommer resulttet. I den nden omskrivning enytter vi sætning.. 6), idet røken er udtryk for en flerleddet størrelse (tre led) delt med et tl. I hver f disse røker, hvor der ikke indgår eller, forkortes med y. (Egentlig kunne den første røk også forkortes med og den nden røk
18 0 med z, men dette undldes for t sikre en fælles nævner for de tre røker). D de tre røker hr en fælles nævner, smles de til én røk, hvormed resulttet fremkommer. I den tredje omskrivning forkorter vi røken direkte med y ved t dividere tæller og nævner med y. I denne smmenhæng husker vi på, t tælleren estår f flere led, hvorfor hvert led liver delt med y. Ved t forkorte hver f de fire små røker når vi frem til resulttet Her følger en række øvelser til indøvning f regnereglerne for røker: Øvelse.. Forkort følgende røker mest muligt: ) d) Øvelse.. ) Forlæng, så nævneren liver 0 Forlæng Forlæng, så nævneren liver, så nævneren liver delelig med d) Forlæng røken med Øvelse.6. Forkort røkerne: 8 ) 9 d) 6 9 e) 6 9 f) 6 9 g) 6 8
19 Øvelse.. Reduér/Omskriv følgende: ) 6 y y y 6 9 d) : e) Øvelse.8. Reduér: ) ( ) d) Øvelse.9. Reduer følgende: ) 6 d) e) Øvelse.0: Skriv tllet w som uforkortelig røk, når og y og w y y y y y Øvelse.. Reduér: ) y d) g) y ( y) 6 m m m 9 e) (y ) (y ) 0 f)
20 Øvelse.. Reduér: ) ) ( ) ( ) ( ) ( y y y y d) e) Øvelse.. Reduér mest muligt: ) q 8p : p q p : q p 6p pq q p d) y y y
21 . Kvdrtrod. Ved kvdrtroden f et ikke-negtivt tl forstås den ikke-negtive værdi, som opløftet i nden giver tllet. Til t eskrive kvdrtroden f et tl nvendes symolet. Hvis vi derfor vil ngive kvdrtroden f, så skriver vi:, og d er et ikke-negtivt tl, som opløftet i nden giver, (dvs. ) ser vi, t. Nu er det nturligvis således, t det kun er de færreste tl, der hr så pæne kvdrtrødder som vi netop så, t hr. Hvis vi f.eks. vil estemme værdien f, så findes der ikke noget pænt tl som opløftet i nden giver. På en regnemskine kn vi finde en tilnærmet værdi f. Med 6 deimler giver dette:,06, men denne værdi er ikke helt præis (emærk, t,06, , dvs. vi får ikke præis ). Unset hvor mnge deimler vi tger med (endeligt ntl), så vil vi stdigvæk kun hve en tilnærmet værdi f. Den mest præise ngivelse f det tl, som opløftet i nden giver, er derfor kvdrtroden f skrevet med kvdrtrodssymolet, ltså. I lmindelighed giver vi følgende definition: Definition.. Kvdrtroden f et ikke-negtivt tl etegnes. Værdien f er det ikke-negtive tl, som opløftet i nden giver. Dette kn også formuleres således: Hvis er et ikke-negtivt tl, dvs. hvis 0, så gælder der: ( ) ( 0 ) (Symolet læses: og, og det etyder, t egge udsgn omkring det skl være opfyldt. Symolet læses: ensetydende med, og det etyder, t hvis det ene udsgn ( ) gælder, så gælder det ndet udsgn ( 0 ) også og omvendt!). ( ) kldes ofte for rodprøven (dvs. en test f, t et udsgn om en kvdrtrod er korrekt) Bemærk l.., t vi ikke kn tge kvdrtroden f et negtivt tl, (hvorfor ikke??), og kvdrtroden f et tl ltid hr en positiv værdi eller evt. værdien 0, (idet 0 0 ).
22 Øvelse.. Udregn mest muligt inden lommeregneren tges i rug: ) 6 0, 6 8 ( ) 6 ( ) ( ) d) 9 : 9 98 : , Øvelse.. Bestem værdien f 6 6 og f 6 6. Kommentér resulttet. Bemærk den skjulte prentes i udtrykket 6 6 I lighed med sum, differens, produkt og røk gælder der også nogle regneregler for kvdrtrødder: Sætning.. ) For lle 0 er 0 ) For lle 0 er ( ) ) For lle 0 gælder ; og for lle < 0 gælder: ) For lle 0 gælder: ( ) (Tegnet læses eller og det etyder, t mindst et f udsgnene omkring det skl være opfyldt). ) For lle 0 og 0 gælder: 6) For lle 0 og > 0 gælder ) Kvdrtroden f en sum eller en differens kn ikke omskrives. Der gælder således lmindeligvis, t og (Tegnet etyder: er forskellig fr). Bevis: Ad ) og ): Dette følger direkte f definition.. Ad ): Hvis 0 så følger resulttet: direkte f rodprøven ( jfr. definition.) ( er et ikke-negtivt tl, som opløftet i nden giver ). Hvis < 0, så er > 0, og d ( ) ses værdien t psse i rodprøven, ltså: Hvis < 0, så er
23 Ad ): Vi skl evise, t der for et ikke-negtivt tl gælder: ( ), dvs. t udsgnet: er ensetydende med udsgnet:, og dette vil som nævnt tidligere sige, t vi skl rgumentere for, t hvis det ene udsgn gælder, så gælder det ndet også, og omvendt. Vi ntger først, t er opfyldt. Herf ses, t er et tl, som opløftet i nden giver tllet. Hvis er ikke-negtiv, så hr vi derfor ifølge definition., t. Hvis er negtiv, så hr vi dels, t er positiv, dels t ( ), hvormed vi ser, t opfylder rodprøven i definition.. Dette giver os, t: og dermed, t. Hermed er det ønskede evist. (Bemærkning til læseren: Ld dig ikke snyde f, t der står et minus forn og vi lligevel siger, t er positiv. Dette skyldes jo, t tllet selv er negtiv. Hvis f.eks., så er ( ), ltså et positivt tl). Vi ntger derefter omvendt, t udsgnet: er opfyldt. Hvis, så får vi ifølge regel ), t: ( ), og hvis, så ser vi tilsvrende, t ( ) ( ). Hermed er det ønskede evist. Ad ): Ifølge regel ) hr vi, t 0 og 0, hvorf vi ser, t 0. D vi desuden hr, t ( ( ) (, hvor regel ) er nvendt, får vi ifølge rodprøven det ønskede resultt. Ad 6): Bevises på helt smme måde som regel ). Detljerne overldes til læseren. Ad ): For t sikre, t de to størrelser ikke er ens, skl vi kunne finde et sæt f værdier, som giver forskellig værdi på venstresiden og på højresiden. I denne smmenhæng henvises til øvelse.. Eksempel.. ) (,),,, 0 ifølge regel ) og ) i sætning.. ifølge regel ) i sætning.. ifølge regel ) i sætning.. I denne og lignende situtioner tillder mn sig ofte t skrive følgende: ±, men det etyder det smme. Med deimlers nøjgtighed hr vi: ±, 60 d) Ifølge regel ) og 6) i sætning.. hr vi: og Regel ) og 6) kn imidlertid også nvendes fr højre mod venstre, f.eks. hvis vi vil omskrive 0 ( vi hr hér: ), eller hvis vi vil sætte et tl udenfor kvdrtrodstegnet f.eks. 60. Bemærk skrivemåden:, som ltså etyder: gnge med.
24 6 e) Ved nvendelse f regel ) i sætning. får vi: d d d, f) hvor vi også hr nvendt reglen om forkortning f røker. Hvis vi gerne vil undgå t hve et kvdrtrodstegn i nævneren, kn vi forlænge røken med d, hvormed vi får: d ( ( d) d d d kn ifølge regel ) i sætning. omskrives således: d, hvor regel ) igen er nvendt. ( g) Vi vil omskrive udtrykkene: og, så der ikke optræder kvdrtrødder 8 i nævnerne. Dette gøres ved t forlænge røkerne med et pssende smrt tl. Ved enyttelse f regel 0 i sætning. ses, t kvdrtrodstegnene kn forsvinde ved t forlænge den første røk med 8 og den sidste røk med. Dette giver følgende: ) 8 ( ( 8 8 ) ( ) 8 ) 8 ( 8) ( ) 8 8 og tilsvrende: ( ) 6 ( ) ( ) Her følger en række øvelser til indøvning f regnereglerne for kvdrtrødder: Øvelse.6. Udregn uden rug f lommeregner: ) 9 ( 9 ) ((8 ) ) ( ) 6 (9 ) Øvelse.. Bestem kvdrtroden f følgende tl v.hj.. lommeregneren:, 0, 000, 0, 0,, 0,0000, 0, og 6896
25 Øvelse.8 Reduér mest muligt: 8 Øvelse.9 Beregn følgende tl og kommentér resulttet. 6 00, 6 00,,, 69 8, 69 8 Øvelse.0. Bestem værdien f: ( ) og ( ) Øvelse.. Beregn uden rug f lommeregner: ) 00 6 d) 0 Øvelse.. Omskriv følgende røker, så der ikke optræder kvdrtrødder i nævneren, og reduér derefter mest muligt uden rug f lommeregner: ) d) 6 e) Øvelse.. Reduér mest muligt uden rug f lommeregner (Der optræder såkldte lndede tl i denne opgve, noget normlt ør undgås!!): ) d) e) 6 f) 0
26 8 Øvelse.. Reduér mest muligt (,,, y, p og q er lle positive tl): ) y y d) e) p p q q f) y g) y 6 9 Øvelse.. Argumenter for følgende regel: y y (Vejledning: Benyt sætning. pkt. ) og )) y
27 9 6. Potenser og rødder 6.. Potenser f tl og generelle regler for potenser. Ved en potens f et tl forstår vi lmindeligvis et tl opløftet i et helt tl. F.eks. er en potens f (tllet kldes eksponenten). Som det formodentlig er læseren ekendt hr vi, t: ( ), og vi ruger tlemåden: er gnget med sig selv gnge. Tilsvrende hr vi: (,) (,)(,)(,) (,6), og generelt hr vi, t hvis er et givet tl og n er et positivt helt tl, så er: n..., hvor der er n led i produktet. Dette potensegre vil vi nu udvide til t omftte ndre eksponenter end positive hele tl. I første omgng vil vi udvide det til t omftte lle heltllige eksponenter (ltså også 0 og negtive hele tl), og senere i kpitlet vil vi udvide det til t omftte eksponenter, som er en røk imellem to hele tl. Som motivtion for den første definition vil vi emærke, t hvis 0 er et givet tl, så gælder der for lle n, t n : n-, f.eks., t 9 : 8, : 0 og : (Hvorfor??). Denne potensregneregel vil vi nu enytte til t definere n, hvor n er 0 eller et negtivt helt tl. Vi hr: :, :, :. På smme måde fortsættes: :, 0 : :, 0 : :, osv. osv. : :, : : På ggrund f dette giver vi følgende definition: Definition 6.. For lle 0 og lle positive nturlige tl n sættes:, 0 n og n, Eksempel 6.. ) 8 0,6,6 0, 06 6 d) ( )
28 0 Ved omskrivninger f udtryk i forindelse med såvel det klssisk kendte som det udvidede potensegre (jfr. definition 6..) gælder der følgende regneregler, som nføres uden evis. (Beviset er ikke vnskeligt, men meget omstændeligt, idet der for hver del f sætningen skl tges hensyn til om n og m hver for sig er positive, nul eller negtive smt til deres indyrdes størrelsesforhold). Sætning 6.. For lle hele tl n og m, og for lle tl og, som ikke er 0, gælder der følgende regneregler: n n m n m n m nm nm ) ) ( ) ) m n ) n n n n ) ( ) n n 6) n og n n Eksempel 6.. ) Ifølge regel i sætning 6. hr vi:,6,6,6,6,6,6 (,6) Ifølge regel i sætning 6.. hr vi: 8 ( 8) ( ) ) (( ) ) ( ) ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) hvor vi i de sidste omskrivninger ruger regel ). Ifølge regel i sætning 6. hr vi: d) Ifølge regel i sætning 6. nvendt fr højre mod venstre hr vi: 8 0, ( 0,) (8 0,) ( 0,) ( 0,) ( ( 0,)) ( ) e) Ifølge diverse regler fr sætning 6. mm. hr vi: y ( y y ) 9 y ( ) y (y ) y 8 y y y 9 y Læseren opfordres krftigt til led for led t eskrive hvilke regler, der nvendes i dette sidste reduktionseksempel!
29 Øvelse 6.. Bevis regel ) i sætning 6. ved t gennemgå følgende skridt: ) Argumentér for, t reglen gælder, hvis n > 0 og m > 0 Argumentér for, t reglen gælder, hvis m 0 og n er vilkårligt vlgt. Argumentér for, t reglen gælder, hvis n > 0, m < 0 og n m > 0. Bemærk i denne smmenhæng, t d m < 0, så er m > 0, og t vi dermed hr: n m n..., m... hvor vi hr nvendt definition 6., og hvor der i den sidste røk står n er i tælleren og m er i nævneren. Omskriv videre herfr for t ende op med nm. d) Argumentér for, t reglen gælder, hvis n > 0, m < 0 og n < m. Anvend smme omskrivningsprinip som i e) Argumentér for, t reglen gælder, hvis n < 0 og m < 0. Anvend t n > 0 og m > 0, smt omskrivningsprinippet fr pkt.. f) Argumentér for, t d n og m optræder symmetrisk i regel, så er lle muligheder dækket i forindelse med de ovenstående tilfælde ) e), hvormed reglen er evist. Øvelse 6.6. Bevis regel 6) i sætning 6. (Vejledning: Opdel i tre tilfælde: n > 0, n 0 og n < 0 ) Her følger nogle øvelser til indøvning f potensregnereglerne: Øvelse 6.. Reduer følgende udtryk uden rug f lommeregner: ) e) (( i) ( ) ) ) ) ( f) j) ( 9 ( ) ) ) : ( g) k) ( ) ) ( (( ) ) d) 9 h) 8 l) (( ) ) Øvelse 6.8. Reduer følgende udtryk uden rug f lommeregner: ) ( ) 8 d) ( 8) ( ) e) ) ) (( f) ( ) ) ( ((( ) ) )
30 Øvelse 6.9. Udregn mest muligt inden lommeregneren tges i rug: ) ( )( ) 0, (9 9 6 ( ))( 6 ) 6 d) 9 : 8 8( 6) Øvelse 6.0. Reduér følgende udtryk: p (q 9 ) ) p q (pq) y ( y ) y y y 6.. Potenser f 0. Af en række årsger, der lle smmen knytter sig til, t vi nvender 0-tlsystemet til eskrivelse f størrelsen f forskellige værdier, er speielt reglerne for potenser f 0 f etydning. I forlængelse f definition 6. og sætning 6. ser vi, t der gælder følgende sætning: Sætning 6.. Regneregler for potenser f 0 For lle hele tl n og m gælder: n m n m n m ) ) 0 n 0 ) m 0 n n ) 0 og 0 n n 0 0 n m ( 0 ) 0 nm Eksempel 6.. ) d) 0 0 ( ) 0 0 e) 0 8 (0 (0 0 ) ) ( 0 ) 0 8
31 Potenser f 0 ruges speielt ved ngivelse f meget store eller meget små størrelser. Men inden vi kommer yderligere ind på dette, skl det først emærkes, t der er en nøje smmenhæng mellem potenser f 0 og ntl nuller forn eller gefter kommet i deimlrøker. Eksempel 6.. ) er det smme som 0 ( 0 ) 0,000 er det smme som 0 ( 0 ) 6,8 er det smme som,680 6 d) 0, er det smme som 8,60 Generelt gælder der, t kommet flyttes n pldser til højre ved t gnge med 0 n kommet flyttes n pldser til venstre ved t gnge med 0 n Eksempel 6.. Som netop omtlt ruges potenser f 0 l.. til t udtrykke meget store eller meget små størrelser. ) Hvis vi skl ngive Jordens msse, som er kg, så kn dette nemmere skrives og overskues på følgende måde:,980 kg Hvis vi skl ngive størrelsen f den elektriske ldning, der sidder på en elektron, så kn 9 vi skrive,600 C i stedet for: 0, C (C står for den fysiske enhed for elektrisk ldning: Coulom ) I forindelse med størrelser med en enhed (fysiske, kemiske, iologiske, geofysiske,... størrelser) nvendes potenser f 0 så ofte, t mn hr indført en forkortet etegnelse for visse potenser f 0. Disse går under nvnet: dekdiske præfikser (dekdisk kommer f deem, som etyder 0 på ltin, og et præfi er en størrelse, mn stiller forn (præ)). De dekdiske præfikser: T G M k h d d m µ n p f ter gig meg kilo hekto dek dei enti milli mikro nno pio femto tto Eksempel 6.. ) Hvis vi f.eks. tler om en elektrisk strømstyrke på,8 µa (læses: mikro-mpere), så etyder dette:,80-6 A Hvis vi tler om, t et givet krftværk kn levere en effekt på 60 MW (læses: megwtt), så etyder dette: W
Simple udtryk og ligninger
 Simple udtryk og ligninger for gymnsiet og hf 0 Krsten Juul Indhold Rækkefølge f + og... Smle led f smme type... Gnge ind i prentes. del... Rækkefølge f og smt f + og... Gnge ind i prentes. del... Hæve
Simple udtryk og ligninger for gymnsiet og hf 0 Krsten Juul Indhold Rækkefølge f + og... Smle led f smme type... Gnge ind i prentes. del... Rækkefølge f og smt f + og... Gnge ind i prentes. del... Hæve
Regneregler for brøker og potenser
 Regneregler for røker og potenser Roert Josen 4. ugust 009 Indhold Brøker. Eksempler......................................... Potenser 7. Eksempler......................................... 8 I de to fsnit
Regneregler for røker og potenser Roert Josen 4. ugust 009 Indhold Brøker. Eksempler......................................... Potenser 7. Eksempler......................................... 8 I de to fsnit
Bogstavregning. for gymnasiet og hf Karsten Juul. a a
 Bogstvregning for gymnsiet og hf 010 Krsten Juul Til eleven Brug lynt og viskelæder når du skriver og tegner i hæftet, så du får et hæfte der er egenet til jævnligt t slå op i under dit videre rejde med
Bogstvregning for gymnsiet og hf 010 Krsten Juul Til eleven Brug lynt og viskelæder når du skriver og tegner i hæftet, så du får et hæfte der er egenet til jævnligt t slå op i under dit videre rejde med
TAL OG BOGSTAVREGNING
 TAL OG BOGSTAVREGNING De elementære regnerter I mtemtik kn vi regne med tl, men vi kn også regne med bogstver, som gør det hele en smugle mere bstrkt. Først skl vi se lidt på de fire elementære regnerter,
TAL OG BOGSTAVREGNING De elementære regnerter I mtemtik kn vi regne med tl, men vi kn også regne med bogstver, som gør det hele en smugle mere bstrkt. Først skl vi se lidt på de fire elementære regnerter,
TAL OG REGNEREGLER. Vi ser nu på opbygningen af et legeme og noterer os samtidig, at de reelle tal velkendte regneoperationer + og er et legeme.
 TAL OG REGNEREGLER Inden for lgeren hr mn indført egreet legeme. Et legeme er en slgs konstruktion, hvor mn fstsætter to regneregler og nogle sætninger (ksiomer), der gælder for disse. Pointen med en sådn
TAL OG REGNEREGLER Inden for lgeren hr mn indført egreet legeme. Et legeme er en slgs konstruktion, hvor mn fstsætter to regneregler og nogle sætninger (ksiomer), der gælder for disse. Pointen med en sådn
Michel Mandix (2017) Derfor er der behov for en række værktøjer, som kan bruges også til de vilkårlige trekanter. a b c A B C
 Mihel Mndix (07) Sinusreltionen Nott Side f 9 Sinusreltionen Indtil videre, er der kun eskrevet, hvordn mn eregner på retvinklede treknter. Men desværre er det lngtfr lle treknter, som er retvinklede.
Mihel Mndix (07) Sinusreltionen Nott Side f 9 Sinusreltionen Indtil videre, er der kun eskrevet, hvordn mn eregner på retvinklede treknter. Men desværre er det lngtfr lle treknter, som er retvinklede.
Projekt 7.8 To ligninger med to ubekendte
 Projekt 78 To ligninger med to uekendte Den opgve t skulle løse to ligninger med to uekendte er vi stødt på i en række speciltilfælde under ehndlingen f vækstmodellerne: Funktionstype Ligningssystem Lineær
Projekt 78 To ligninger med to uekendte Den opgve t skulle løse to ligninger med to uekendte er vi stødt på i en række speciltilfælde under ehndlingen f vækstmodellerne: Funktionstype Ligningssystem Lineær
Projekt 5.7 Hovedsætninger om differentiable funktioner et opgaveforløb
 Hvd er mtemtik?, e-og Projekter: Kpitel 5 Projekt 57 Hovedsætninger om differentile funktioner Projekt 57 Hovedsætninger om differentile funktioner et opgveforlø Projektet er en udvidelse f fsnittet i
Hvd er mtemtik?, e-og Projekter: Kpitel 5 Projekt 57 Hovedsætninger om differentile funktioner Projekt 57 Hovedsætninger om differentile funktioner et opgveforlø Projektet er en udvidelse f fsnittet i
Elementær Matematik. Algebra Analytisk geometri Trigonometri Funktioner
 Elementær Mtemtik Alger Anlytisk geometri Trigonometri Funktioner Ole Witt-Hnsen Køge Gymnsium 0 Indhold Indhold... Kp. Tl og regning med tl.... De nturlige tl.... Regneregler for nturlige tl.... Kvdrtsætningerne.....
Elementær Mtemtik Alger Anlytisk geometri Trigonometri Funktioner Ole Witt-Hnsen Køge Gymnsium 0 Indhold Indhold... Kp. Tl og regning med tl.... De nturlige tl.... Regneregler for nturlige tl.... Kvdrtsætningerne.....
Integralregning. 2. del. 2006 Karsten Juul
 Integrlregning del ( ( 6 Krsten Juul Indhold 6 Uestemt integrl8 6 Sætning om eksistens stmunktioner 8 6 Oplæg til "regneregler or integrl"8 6 Regneregler or uestemt integrl 9 68 Foreredelse til "integrtion
Integrlregning del ( ( 6 Krsten Juul Indhold 6 Uestemt integrl8 6 Sætning om eksistens stmunktioner 8 6 Oplæg til "regneregler or integrl"8 6 Regneregler or uestemt integrl 9 68 Foreredelse til "integrtion
Lektion 7s Funktioner - supplerende eksempler
 Lektion 7s Funktioner - supplerende eksempler Oversigt over forskellige tper f funktioner Omvendt proportionlitet og hperler.grdsfunktioner og prler Eksponentilfunktioner Potensfunktioner Lektion 7s Side
Lektion 7s Funktioner - supplerende eksempler Oversigt over forskellige tper f funktioner Omvendt proportionlitet og hperler.grdsfunktioner og prler Eksponentilfunktioner Potensfunktioner Lektion 7s Side
Lektion 6 Bogstavregning
 Lektion Bogstvregning Formler... Reduktion... Ligninger... Lektion Side 1 Formler En formel er en slgs regne-opskrift, hvor mn med bogstver viser, hvorledes noget skl regnes ud. F.eks. formler til beregning
Lektion Bogstvregning Formler... Reduktion... Ligninger... Lektion Side 1 Formler En formel er en slgs regne-opskrift, hvor mn med bogstver viser, hvorledes noget skl regnes ud. F.eks. formler til beregning
ALGEBRA. symbolbehandling). Der arbejdes med hjælpemiddelkompetencen,
 INTRO Alger er lngt mere end ogstvregning. Alger kn være t omskrive ogstvtrk, men lger er f også t generlisere mønstre og smmenhænge, t eskrive smmenhænge mellem tlstørrelse f i forindelse med funktioner
INTRO Alger er lngt mere end ogstvregning. Alger kn være t omskrive ogstvtrk, men lger er f også t generlisere mønstre og smmenhænge, t eskrive smmenhænge mellem tlstørrelse f i forindelse med funktioner
Diverse. Ib Michelsen
 Diverse Ib Michelsen Ikst 2008 Forsidebilledet http://www.smtid.dk/visen/billede.php?billedenr69 Version: 0.02 (2-1-2009) Diverse (Denne side er A-2 f 32 sider) Indholdsfortegnelse Regning med procent
Diverse Ib Michelsen Ikst 2008 Forsidebilledet http://www.smtid.dk/visen/billede.php?billedenr69 Version: 0.02 (2-1-2009) Diverse (Denne side er A-2 f 32 sider) Indholdsfortegnelse Regning med procent
Eksponentielle Sammenhænge
 Kort om Eksponentielle Smmenhænge 011 Krsten Juul Dette hæfte indeholder pensum i eksponentielle smmenhænge for gymnsiet og hf. Indhold 1. Procenter på en ny måde... 1. Hvd er en eksponentiel smmenhæng?....
Kort om Eksponentielle Smmenhænge 011 Krsten Juul Dette hæfte indeholder pensum i eksponentielle smmenhænge for gymnsiet og hf. Indhold 1. Procenter på en ny måde... 1. Hvd er en eksponentiel smmenhæng?....
Potens- sammenhænge. inkl. proportionale og omvendt proportionale variable. 2010 Karsten Juul
 Potens- smmenhænge inkl. proportionle og omvendt proportionle vrible 010 Krsten Juul Dette hæfte er en fortsættelse f hæftet "Eksponentielle smmenhænge, udgve ". Indhold 1. Hvd er en potenssmmenhæng?...1.
Potens- smmenhænge inkl. proportionle og omvendt proportionle vrible 010 Krsten Juul Dette hæfte er en fortsættelse f hæftet "Eksponentielle smmenhænge, udgve ". Indhold 1. Hvd er en potenssmmenhæng?...1.
Matematikkens sprog INTRO
 Mtemtikkens sprog Mtemtik hr sit eget sprog, der består f tl og symboler fx regnetegn, brøkstreger bogstver og prenteser På mnge måder er det ret prktisk - det giver fx korte måder t skrive formler på.
Mtemtikkens sprog Mtemtik hr sit eget sprog, der består f tl og symboler fx regnetegn, brøkstreger bogstver og prenteser På mnge måder er det ret prktisk - det giver fx korte måder t skrive formler på.
Bogstavregning. En indledning for stx og hf 2. del. 2008 Karsten Juul
 Bogstvregning En indledning for st og f. del 008 Krsten Juul ) )( ( ) ( ) ( Indold 0. Gnge to prenteser....,, osv... 7. Kvdrtsætninger... 0. Brøer. del... Bogstvregning. En indledning for st og f.. del.
Bogstvregning En indledning for st og f. del 008 Krsten Juul ) )( ( ) ( ) ( Indold 0. Gnge to prenteser....,, osv... 7. Kvdrtsætninger... 0. Brøer. del... Bogstvregning. En indledning for st og f.. del.
Elementær Matematik. Analytisk geometri
 Elementær Mtemtik Anltisk geometri Ole Witt-Hnsen 0 Indhold. koordintsstemet.... Afstndsformlen.... Liniens ligning...4 4. Ortogonle linier...7 5. Liniers skæring. To ligninger med to uekendte....7 6.
Elementær Mtemtik Anltisk geometri Ole Witt-Hnsen 0 Indhold. koordintsstemet.... Afstndsformlen.... Liniens ligning...4 4. Ortogonle linier...7 5. Liniers skæring. To ligninger med to uekendte....7 6.
3. Vilkårlige trekanter
 3. Vilkårlige treknter 3. Vilkårlige treknter I dette fsnit vil vi beskæftige os med treknter, der ikke nødvendigvis er retvinklede. De formler, der er omtlt i fsnittet om retvinklede treknter, kn ikke
3. Vilkårlige treknter 3. Vilkårlige treknter I dette fsnit vil vi beskæftige os med treknter, der ikke nødvendigvis er retvinklede. De formler, der er omtlt i fsnittet om retvinklede treknter, kn ikke
Ny Sigma 9, s Andengradsfunktioner med regneforskrift af typen y = ax + bx + c, hvor a 0.
 Ny Sigm 9, s 110 Andengrdsfunktioner med regneforskrift f typen y = x + x + c, hvor 0 Lineære funktioner (førstegrdsfunktioner) med regneforskrift f typen y = αx + β Grfen for funktioner f disse typer
Ny Sigm 9, s 110 Andengrdsfunktioner med regneforskrift f typen y = x + x + c, hvor 0 Lineære funktioner (førstegrdsfunktioner) med regneforskrift f typen y = αx + β Grfen for funktioner f disse typer
Institut for Matematik, DTU: Gymnasieopgave. Integrationsprincippet og Keplers tønderegel
 Integrtionsprincippet og Keplers tønderegel. side Institut for Mtemtik, DTU: Gymnsieopgve Integrtionsprincippet og Keplers tønderegel Littertur: H. Elrønd Jensen, Mtemtisk nlyse, Institut for Mtemtik,
Integrtionsprincippet og Keplers tønderegel. side Institut for Mtemtik, DTU: Gymnsieopgve Integrtionsprincippet og Keplers tønderegel Littertur: H. Elrønd Jensen, Mtemtisk nlyse, Institut for Mtemtik,
Integralregning. Version juni Mike Vandal Auerbach
 Integrlregning Version.0 27. juni 209 y f x Mike Vndl Auerch www.mthemticus.dk Integrlregning Version.0, 209 Disse noter er skrevet til mtemtikundervisningen på stx A- og B-niveu efter gymnsiereformen
Integrlregning Version.0 27. juni 209 y f x Mike Vndl Auerch www.mthemticus.dk Integrlregning Version.0, 209 Disse noter er skrevet til mtemtikundervisningen på stx A- og B-niveu efter gymnsiereformen
Matematik. Kompendium i faget. Tømrerafdelingen. 1. Hovedforløb. a 2 = b 2 + c 2 2 b c cos A. cos A = b 2 + c 2 - a 2 2 b c
 Kompendium i fget Mtemtik Tømrerfdelingen 1. Hovedforlø. Trigonometri nvendes til eregning f snd længde og snd vinkel i profiler. Sinus Cosinus Tngens 2 2 + 2 2 os A os A 2 + 2-2 2 Svendorg Erhvervsskole
Kompendium i fget Mtemtik Tømrerfdelingen 1. Hovedforlø. Trigonometri nvendes til eregning f snd længde og snd vinkel i profiler. Sinus Cosinus Tngens 2 2 + 2 2 os A os A 2 + 2-2 2 Svendorg Erhvervsskole
gudmandsen.net y = b x a Illustration 1: potensfunktioner i 5 forskellige grupper
 gudmndsen.net Dette dokument er publiceret på http://www.gudmndsen.net/res/mt_vejl/. Ophvsret: Indholdet stilles til rådighed under Open Content License[http://opencontent.org/openpub/]. Kopiering, distribution
gudmndsen.net Dette dokument er publiceret på http://www.gudmndsen.net/res/mt_vejl/. Ophvsret: Indholdet stilles til rådighed under Open Content License[http://opencontent.org/openpub/]. Kopiering, distribution
Elementær Matematik. Vektorer i planen
 Elementær Mtemtik Vektorer i plnen Køge Gymnsium 0 Ole Witt-Hnsen Indhold. Prllelforskydninger i plnen. Vektorer.... Sum og differens f to vektorer... 3. Multipliktion f vektor med et tl...3 4. Opløsning
Elementær Mtemtik Vektorer i plnen Køge Gymnsium 0 Ole Witt-Hnsen Indhold. Prllelforskydninger i plnen. Vektorer.... Sum og differens f to vektorer... 3. Multipliktion f vektor med et tl...3 4. Opløsning
Spil- og beslutningsteori
 Spil- og eslutningsteori Peter Hrremoës Niels Brock 26. novemer 2 Beslutningsteori De økonomiske optimeringssitutioner, vi hr set på hidtil, hr været helt deterministiske. Det vil sige t vores gevinst
Spil- og eslutningsteori Peter Hrremoës Niels Brock 26. novemer 2 Beslutningsteori De økonomiske optimeringssitutioner, vi hr set på hidtil, hr været helt deterministiske. Det vil sige t vores gevinst
Trigonometri. Matematik A niveau
 Trigonometri Mtemtik A niveu Arhus Teh EUX Niels Junge Trigonometri Sinus Cosinus Tngens Her er definitionen for Cosinus Sinus og Tngens Mn kn sige t osinus er den projierede på x-ksen og sinus er den
Trigonometri Mtemtik A niveu Arhus Teh EUX Niels Junge Trigonometri Sinus Cosinus Tngens Her er definitionen for Cosinus Sinus og Tngens Mn kn sige t osinus er den projierede på x-ksen og sinus er den
Pointen med Integration
 Pointen med Integrtion Frnk Vill 3. oktober 2012 2008-2012. IT Teching Tools. ISBN-13: 978-87-92775-00-9. Dette dokument må kun nvendes til undervisning i klsser som bonnerer på MtBog.dk. Se yderligere
Pointen med Integrtion Frnk Vill 3. oktober 2012 2008-2012. IT Teching Tools. ISBN-13: 978-87-92775-00-9. Dette dokument må kun nvendes til undervisning i klsser som bonnerer på MtBog.dk. Se yderligere
MATEMATIK-KOMPENDIUM TIL KOMMENDE ELEVER PÅ DE GYMNASIALE UNGDOMSUDDANNELSER I SILKEBORG (HF, HHX, HTX & STX)
 Silkeorg -0- MATEMATIK-KOMPENDIUM TIL KOMMENDE ELEVER PÅ DE GYMNASIALE UNGDOMSUDDANNELSER I SILKEBORG (HF, HHX, HTX & STX) FACITLISTE Udrejdet f mtemtiklærere fr HF, HHX, HTX & STX. PS: Hvis du opdger
Silkeorg -0- MATEMATIK-KOMPENDIUM TIL KOMMENDE ELEVER PÅ DE GYMNASIALE UNGDOMSUDDANNELSER I SILKEBORG (HF, HHX, HTX & STX) FACITLISTE Udrejdet f mtemtiklærere fr HF, HHX, HTX & STX. PS: Hvis du opdger
Pointen med Integration
 Pointen med Integrtion Frnk Nsser 20. pril 2011 c 2008-2011. Dette dokument må kun nvendes til undervisning i klsser som bonnerer på MtBog.dk. Se yderligere betingelser for brug her. Bemærk: Dette er en
Pointen med Integrtion Frnk Nsser 20. pril 2011 c 2008-2011. Dette dokument må kun nvendes til undervisning i klsser som bonnerer på MtBog.dk. Se yderligere betingelser for brug her. Bemærk: Dette er en
Integration ved substitution og delvis (partiel) integration
 DEN TEKNISK-NATURVIDENSKABELIGE BASISUDDANNELSE MATEMATIK INTEGRATION EFTERÅRET Integrtion ved sustitution og delvis (prtiel) integrtion Differentil- og integrlregningens hovedsætning lyder: Hvis ƒ er
DEN TEKNISK-NATURVIDENSKABELIGE BASISUDDANNELSE MATEMATIK INTEGRATION EFTERÅRET Integrtion ved sustitution og delvis (prtiel) integrtion Differentil- og integrlregningens hovedsætning lyder: Hvis ƒ er
Analysens Fundamentalsætning
 Anlysens Fundmentlsætning Frnk Nsser 11. juli 2011 2008-2011. Dette dokument må kun nvendes til undervisning i klsser som bonnerer på MtBog.dk. Se yderligere betingelser for brug her. Indhold 1 Introduktion
Anlysens Fundmentlsætning Frnk Nsser 11. juli 2011 2008-2011. Dette dokument må kun nvendes til undervisning i klsser som bonnerer på MtBog.dk. Se yderligere betingelser for brug her. Indhold 1 Introduktion
2 Erik Vestergaard
 Erik Vestergrd www.mtemtikfysik.dk Erik Vestergrd www.mtemtikfysik.dk 3 Definition 1 En funktion på formen f ( x) = b x, x R +, hvor b R + og R er konstnter, kldes for en potensudvikling eller en potensiel
Erik Vestergrd www.mtemtikfysik.dk Erik Vestergrd www.mtemtikfysik.dk 3 Definition 1 En funktion på formen f ( x) = b x, x R +, hvor b R + og R er konstnter, kldes for en potensudvikling eller en potensiel
... ... ... ... ... ... ... b > 0 og x > 0, vil vi kalde en potensfunktion. 492 10. Potensfunktioner
 POTENSFUNKTIONER 0 49 0. Potensfunktioner POTENSFUNKTIONER DEFINITION En funktion med forskriften f( )= b hvor b > 0 og > 0 vil vi klde en potensfunktion. I MAT C kpitel så vi t hvis skl være et vilkårligt
POTENSFUNKTIONER 0 49 0. Potensfunktioner POTENSFUNKTIONER DEFINITION En funktion med forskriften f( )= b hvor b > 0 og > 0 vil vi klde en potensfunktion. I MAT C kpitel så vi t hvis skl være et vilkårligt
Matematik - introduktion. Martin Lauesen February 23, 2011
 Mtemtik - introduktion Mrtin Luesen Februry 23, 2011 1 Contents 1 Aritmetik og elementær lgebr 3 1.1 Symboler............................... 3 1.1.1 ligheder............................ 4 1.1.2 uligheder...........................
Mtemtik - introduktion Mrtin Luesen Februry 23, 2011 1 Contents 1 Aritmetik og elementær lgebr 3 1.1 Symboler............................... 3 1.1.1 ligheder............................ 4 1.1.2 uligheder...........................
INTEGRALREGNING. Opgaver til noterne kan findes her. PDF. Facit til opgaverne kan hentes her. PDF. Version: 5.0
 INTEGRALREGNING Version: 5.0 Noterne gennemgår egreerne: integrl og stmfunktion, og nskuer dette som et redsk til estemmelse f l.. reler under funktioner. Opgver til noterne kn findes her. PDF Fcit til
INTEGRALREGNING Version: 5.0 Noterne gennemgår egreerne: integrl og stmfunktion, og nskuer dette som et redsk til estemmelse f l.. reler under funktioner. Opgver til noterne kn findes her. PDF Fcit til
Matematisk modellering og numeriske metoder. Lektion 17
 Mtemtisk modellering og numeriske metoder Lektion 1 Morten Grud Rsmussen 8. november, 1 1 Numerisk integrtion og differentition [Bogens fsnit 19. side 84] 1.1 Grundlæggende om numerisk integrtion Vi vil
Mtemtisk modellering og numeriske metoder Lektion 1 Morten Grud Rsmussen 8. november, 1 1 Numerisk integrtion og differentition [Bogens fsnit 19. side 84] 1.1 Grundlæggende om numerisk integrtion Vi vil
UGESEDDEL 52. . Dette gøres nedenfor: > a LC
 UGESEDDE 52 Opgve 1 Denne opgve er et mtemtisk eksempel på Ricrdo s én-fktor model, der præsenteres i Krugmn & Obstfeld kpitel 2 side 12-19. Denne model beskriver hndel som et udslg f komprtive fordele
UGESEDDE 52 Opgve 1 Denne opgve er et mtemtisk eksempel på Ricrdo s én-fktor model, der præsenteres i Krugmn & Obstfeld kpitel 2 side 12-19. Denne model beskriver hndel som et udslg f komprtive fordele
Formelsamling Matematik C Indhold
 Formelsmling Mtemtik C Indhold Eksempler på esvrelser, lin, eksp, pot, geo... Tl, regneopertioner og ligninger... 6 Ligninger... 7 Geometri... 9 Funktioner og modeller... Lineær funktion... Procentregning...
Formelsmling Mtemtik C Indhold Eksempler på esvrelser, lin, eksp, pot, geo... Tl, regneopertioner og ligninger... 6 Ligninger... 7 Geometri... 9 Funktioner og modeller... Lineær funktion... Procentregning...
Trigonometri. Trigonometri. Sinus og cosinus... 2 Tangens... 6 Opgaver... 9. Side 1
 Trigonometri Sinus og osinus... 2 Tngens... 6 Opgver... 9 Side Sinus og osinus Til lle vinkler hører der to tl, som kldes osinus og sinus. Mn finder sinus og osinus til en vinkel ved t tegne vinklen midt
Trigonometri Sinus og osinus... 2 Tngens... 6 Opgver... 9 Side Sinus og osinus Til lle vinkler hører der to tl, som kldes osinus og sinus. Mn finder sinus og osinus til en vinkel ved t tegne vinklen midt
Opstakning og afstakning, fremadregning og tilbageregning
 1 Opstkning og fstkning, fremdregning og tilgeregning 1.1 Fremdregning og tilgeregning...2 1.2 Æskeregning...2 1.3 Høseringe-regning, indkodning og fkodning...3 1.4 Vndret tilgeregning, t dnse en ligning...3
1 Opstkning og fstkning, fremdregning og tilgeregning 1.1 Fremdregning og tilgeregning...2 1.2 Æskeregning...2 1.3 Høseringe-regning, indkodning og fkodning...3 1.4 Vndret tilgeregning, t dnse en ligning...3
Kort om Potenssammenhænge
 Øvelser til hæftet Kort om Potenssmmenhænge 2011 Krsten Juul Dette hæfte indeholder bl.. mnge småspørgsmål der gør det nemmere for elever t rbejde effektivt på t få kendskb til emnet. Indhold 1. Ligning
Øvelser til hæftet Kort om Potenssmmenhænge 2011 Krsten Juul Dette hæfte indeholder bl.. mnge småspørgsmål der gør det nemmere for elever t rbejde effektivt på t få kendskb til emnet. Indhold 1. Ligning
Projekt 8.4 Logaritmefunktionerne
 Hvd er mtemtik? Projekter: Kpitel 8. Projekt 8.4 Logritmefunktionerne Projekt 8.4 Logritmefunktionerne Indhold. log( ) og 0 som omvendte funktioner... 2 2. Den nturlige logritmefunktion, ln( ) og den nturlige
Hvd er mtemtik? Projekter: Kpitel 8. Projekt 8.4 Logritmefunktionerne Projekt 8.4 Logritmefunktionerne Indhold. log( ) og 0 som omvendte funktioner... 2 2. Den nturlige logritmefunktion, ln( ) og den nturlige
Bogstavregning. for gymnasiet og hf (2012) Karsten Juul
 Bogstvregning for gymnsiet og hf 010 (01) Krsten Juul Til eleven Brug lynt og viskeläder når du skriver og tegner i häftet, så du får et häfte der er egenet til jävnligt t slå op i under dit videre rejde
Bogstvregning for gymnsiet og hf 010 (01) Krsten Juul Til eleven Brug lynt og viskeläder når du skriver og tegner i häftet, så du får et häfte der er egenet til jävnligt t slå op i under dit videre rejde
Retningslinjer for bedømmelsen Georg Mohr-Konkurrencen runde
 Retningslinjer for bedømmelsen Georg Mohr-Konkurrencen 016. runde Besvrelser som flder uden for de løsninger som ligger til grund for pointskemerne, bedømmes ved nlogi så skridt med tilsvrende vægt i den
Retningslinjer for bedømmelsen Georg Mohr-Konkurrencen 016. runde Besvrelser som flder uden for de løsninger som ligger til grund for pointskemerne, bedømmes ved nlogi så skridt med tilsvrende vægt i den
ØVEHÆFTE FOR MATEMATIK C POTENS-SAMMENHÆNG
 ØVEHÆFTE FOR MATEMATIK C POTENS-SAMMENHÆNG INDHOLDSFORTEGNELSE 1 Formelsmling... side 2 Uddbning f visse formler... side 3 2 Grundlæggende færdigheder... side 5 2 Finde konstnterne og b i en formel...
ØVEHÆFTE FOR MATEMATIK C POTENS-SAMMENHÆNG INDHOLDSFORTEGNELSE 1 Formelsmling... side 2 Uddbning f visse formler... side 3 2 Grundlæggende færdigheder... side 5 2 Finde konstnterne og b i en formel...
Mere end blot lektiehjælp. Få topkarakter i din SRP. 12: Hovedafsnittene i din SRP (Redegørelse, analyse, diskussion)
 Mere end lot lektiehjælp Få topkrkter i din SRP 12: Hovedfsnittene i din SRP (Redegørelse, nlyse, diskussion) Hjælp til SRP-opgven Sidste år hjlp vi 3.600 gymnsieelever med en edre krkter i deres SRP-opgve.
Mere end lot lektiehjælp Få topkrkter i din SRP 12: Hovedfsnittene i din SRP (Redegørelse, nlyse, diskussion) Hjælp til SRP-opgven Sidste år hjlp vi 3.600 gymnsieelever med en edre krkter i deres SRP-opgve.
Elementær Matematik. Ligninger og uligheder
 Elementær Mtemtik Ligninger og uligheer Ole Witt-Hnsen 0 Inhol. Førstegrsligninger.... Nulreglen.... Uligheer og regning me uligheer.... Doeltuligheer.... Anengrsligningen... Ligninger og uligheer. Førstegrsligninger
Elementær Mtemtik Ligninger og uligheer Ole Witt-Hnsen 0 Inhol. Førstegrsligninger.... Nulreglen.... Uligheer og regning me uligheer.... Doeltuligheer.... Anengrsligningen... Ligninger og uligheer. Førstegrsligninger
Hvad ved du om mobning?
 TEST: Hvd ved du om moning? I testen her kn du fprøve, hvor meget du ved om moning på rejdspldsen. Testen estår f tre dele: Selve testen, hvor du skl sætte ét kryds for hvert f de ti spørgsmål. Et hurtigt
TEST: Hvd ved du om moning? I testen her kn du fprøve, hvor meget du ved om moning på rejdspldsen. Testen estår f tre dele: Selve testen, hvor du skl sætte ét kryds for hvert f de ti spørgsmål. Et hurtigt
INFINITESIMALREGNING del 2 Stamfunktioner og differentialkvotienter Regneregler Optimering Taylorrækker
 INFINITESIMALREGNING del Stmfunktioner og differentilkvotienter Regneregler Optimering Tylorrækker -klsserne Gmmel Hellerup Gymnsium Indholdsfortegnelse STAMFUNKTIONER... 3 REGNEREGLER... 9 AFLEDEDE FUNKTIONER...
INFINITESIMALREGNING del Stmfunktioner og differentilkvotienter Regneregler Optimering Tylorrækker -klsserne Gmmel Hellerup Gymnsium Indholdsfortegnelse STAMFUNKTIONER... 3 REGNEREGLER... 9 AFLEDEDE FUNKTIONER...
Elementær Matematik. Trigonometri
 Elementær Mtemtik Trigonometri Ole Witt-Hnsen 11 Indhold 1. Vinkler...1. Sinus, osinus og tngens...3.1 Overgngsformler...4 3. Den retvinklede treknt...6 4. Den lmindelige treknt. Sinus og osinus reltionerne...8
Elementær Mtemtik Trigonometri Ole Witt-Hnsen 11 Indhold 1. Vinkler...1. Sinus, osinus og tngens...3.1 Overgngsformler...4 3. Den retvinklede treknt...6 4. Den lmindelige treknt. Sinus og osinus reltionerne...8
Erik Vestergaard www.matematikfysik.dk. Erik Vestergaard, 2009.
 Erik Vestergrd www.mtemtikfysik.dk Erik Vestergrd, 009. Billeder: Forside: Collge f billeder: istock.com/titoslck istock.com/yuri Desuden egne fotos og illustrtioner Erik Vestergrd www.mtemtikfysik.dk
Erik Vestergrd www.mtemtikfysik.dk Erik Vestergrd, 009. Billeder: Forside: Collge f billeder: istock.com/titoslck istock.com/yuri Desuden egne fotos og illustrtioner Erik Vestergrd www.mtemtikfysik.dk
Formelsamling Mat. C & B
 Formelsmling Mt. C & B Indhold BRØER... PARENTESER...3 PROCENT...4 RENTE...5 INDES...6 GEOMETRI... Arel f treknt... Vinkelsum i en treknt... Ens- vinklede treknter... Vilkårlig treknt... Ret- vinklet treknt...8
Formelsmling Mt. C & B Indhold BRØER... PARENTESER...3 PROCENT...4 RENTE...5 INDES...6 GEOMETRI... Arel f treknt... Vinkelsum i en treknt... Ens- vinklede treknter... Vilkårlig treknt... Ret- vinklet treknt...8
Mattip om. Vinkler 2. Tilhørende kopier: Vinkler 2-3. Du skal lære om: Polygoner. Ligesidede trekanter. Gradtal og vinkelsum
 Mttip om Vinkler 2 Du skl lære om: Polygoner Kn ikke Kn næsten Kn Ligesidede treknter Grdtl og vinkelsum Ligeenede og retvinklede treknter At forlænge en linje i en treknt Tilhørende kopier: Vinkler 2-3
Mttip om Vinkler 2 Du skl lære om: Polygoner Kn ikke Kn næsten Kn Ligesidede treknter Grdtl og vinkelsum Ligeenede og retvinklede treknter At forlænge en linje i en treknt Tilhørende kopier: Vinkler 2-3
Projekt 6.5 Vektorers beskrivelseskraft
 Hvd er mtemtik? ISBN 978877066879 Projekt 65 Vektorers eskrivelseskrft Indhold Vektorer i gymnsiet Linjestykker og prllelogrmmer Bevis inden for den klssiske geometri Bevis med nvendelse f vektorer 3 Digonlerne
Hvd er mtemtik? ISBN 978877066879 Projekt 65 Vektorers eskrivelseskrft Indhold Vektorer i gymnsiet Linjestykker og prllelogrmmer Bevis inden for den klssiske geometri Bevis med nvendelse f vektorer 3 Digonlerne
Matematikkens mysterier - på et obligatorisk niveau. 2. Trigonometri
 Mtemtikkens mysterier - på et oligtorisk niveu f Kenneth Hnsen 2. Trigonometri T D Hvd er fstnden fr flodred til flodred? 2. Trigonometri og geometri Indhold.0 Indledning 2. Vinkler 3.2 Treknter og irkler
Mtemtikkens mysterier - på et oligtorisk niveu f Kenneth Hnsen 2. Trigonometri T D Hvd er fstnden fr flodred til flodred? 2. Trigonometri og geometri Indhold.0 Indledning 2. Vinkler 3.2 Treknter og irkler
MATEMATIK-KOMPENDIUM TIL KOMMENDE ELEVER PÅ DE GYMNASIALE UNGDOMSUDDANNELSER I SILKEBORG (HF, HHX, HTX & STX)
 Silkeborg 09-0-0 MATEMATIK-KOMPENDIUM TIL KOMMENDE ELEVER PÅ DE GYMNASIALE UNGDOMSUDDANNELSER I SILKEBORG (HF, HHX, HTX & STX) Udrbejdet f mtemtiklærere fr HF, HHX, HTX & STX. PS: Hvis du opdger fejl i
Silkeborg 09-0-0 MATEMATIK-KOMPENDIUM TIL KOMMENDE ELEVER PÅ DE GYMNASIALE UNGDOMSUDDANNELSER I SILKEBORG (HF, HHX, HTX & STX) Udrbejdet f mtemtiklærere fr HF, HHX, HTX & STX. PS: Hvis du opdger fejl i
ANALYSE 1, 2013, Uge 2
 ANALYSE 1, 2013, Uge 2 Forelæsninger Denne uges tem er uendelige rækker. Tirsdg: Tlrækker. En uendelig tlrække består ligesom en uendelig tlfølge f uendelig mnge tl. Forskellen mellem de to begreber består
ANALYSE 1, 2013, Uge 2 Forelæsninger Denne uges tem er uendelige rækker. Tirsdg: Tlrækker. En uendelig tlrække består ligesom en uendelig tlfølge f uendelig mnge tl. Forskellen mellem de to begreber består
Elementær Matematik. Vektorer i planen
 Elementær Mtemtik Vektorer i plnen Ole Witt-Hnsen 0 Indhold. Prllelforskydninger i plnen. Vektorer.... Sum og differens f to vektorer.... Multipliktion f vektor med et tl... 4. Opløsning f en vektor efter
Elementær Mtemtik Vektorer i plnen Ole Witt-Hnsen 0 Indhold. Prllelforskydninger i plnen. Vektorer.... Sum og differens f to vektorer.... Multipliktion f vektor med et tl... 4. Opløsning f en vektor efter
ANALYSE 1, 2014, Uge 3
 ANALYSE 1, 2014, Uge 3 Forelæsninger Tirsdg. Vi generliserer tlrækker til funktionsrækker ved t udskifte tllene med funktioner (TL Afsnit 12.5). Det svrer til forrige uges skridt fr tlfølger til funktionsfølger.
ANALYSE 1, 2014, Uge 3 Forelæsninger Tirsdg. Vi generliserer tlrækker til funktionsrækker ved t udskifte tllene med funktioner (TL Afsnit 12.5). Det svrer til forrige uges skridt fr tlfølger til funktionsfølger.
ANALYSE 1, 2015, Uge 2
 ANALYSE 1, 2015, Uge 2 Forelæsninger Denne uges tem er uendelige rækker. Tirsdg: Tlrækker. En uendelig tlrække består ligesom en uendelig tlfølge f uendelig mnge tl. Forskellen mellem de to begreber består
ANALYSE 1, 2015, Uge 2 Forelæsninger Denne uges tem er uendelige rækker. Tirsdg: Tlrækker. En uendelig tlrække består ligesom en uendelig tlfølge f uendelig mnge tl. Forskellen mellem de to begreber består
Analyse 30. januar 2015
 30. jnur 2015 Større dnsk indkomstulighed skyldes i høj grd stigende kpitlindkomster Af Kristin Thor Jkosen Udgivelsen f Thoms Pikettys Kpitlen i det 21. århundrede hr fstedkommet en del diskussion f de
30. jnur 2015 Større dnsk indkomstulighed skyldes i høj grd stigende kpitlindkomster Af Kristin Thor Jkosen Udgivelsen f Thoms Pikettys Kpitlen i det 21. århundrede hr fstedkommet en del diskussion f de
- 81 - , x I. kmx. Sætningen bevises ikke her. Interesserede læsere henvises til bogen: Differentialligninger og matematiske
 - 8 - Appendi : Logistisk vækst og integrlregning. I forbindelse med eksponentielle vækstfunktioner er der tle om en vækstform, hvor funktionens væksthstighed er proportionl med den ktuelle funktionsværdi,
- 8 - Appendi : Logistisk vækst og integrlregning. I forbindelse med eksponentielle vækstfunktioner er der tle om en vækstform, hvor funktionens væksthstighed er proportionl med den ktuelle funktionsværdi,
Lektion 6 Bogstavregning
 Mtemtik på Åbent VUC Lektion 6 Bogstvregning Formler... Udtryk... Ligninger... Ligninger som løsningsmetode i regneopgver... Simultion... Opsmlingsopgver... Lvet f Niels Jørgen Andresen, VUC Århus. Redigeret
Mtemtik på Åbent VUC Lektion 6 Bogstvregning Formler... Udtryk... Ligninger... Ligninger som løsningsmetode i regneopgver... Simultion... Opsmlingsopgver... Lvet f Niels Jørgen Andresen, VUC Århus. Redigeret
Mattip om. Vinkler 2. Tilhørende kopier: Vinkler 2 og 3. Du skal lære om: Polygoner. Ligesidede trekanter. Gradtal og vinkelsum
 Mttip om Vinkler 2 Du skl lære om: Polygoner Kn ikke Kn næsten Kn Ligesidede treknter Grdtl og vinkelsum Ligeenede og retvinklede treknter At forlænge en linje i en treknt Tilhørende kopier: Vinkler 2
Mttip om Vinkler 2 Du skl lære om: Polygoner Kn ikke Kn næsten Kn Ligesidede treknter Grdtl og vinkelsum Ligeenede og retvinklede treknter At forlænge en linje i en treknt Tilhørende kopier: Vinkler 2
Hvad ved du om mobning?
 TEST: Hvd ved du om moning? I testen her kn du fprøve, hvor meget du ved om moning på rejdspldsen. Testen estår f tre dele: Selve testen, hvor du skl sætte ét kryds for hvert f de ti spørgsmål. Et hurtigt
TEST: Hvd ved du om moning? I testen her kn du fprøve, hvor meget du ved om moning på rejdspldsen. Testen estår f tre dele: Selve testen, hvor du skl sætte ét kryds for hvert f de ti spørgsmål. Et hurtigt
Elementær Matematik. Lineære funktioner og Andengradspolynomiet
 Elementæ Mtemtik Lineæe funktione og Andengdspolynomiet Ole Witt-Hnsen Indhold. Den lineæe funktion.... Stykkevis lineæe funktione.... Andengdspolynomiet.... Pllelfoskydning f koodintsystemet.... Pllelfoskydning
Elementæ Mtemtik Lineæe funktione og Andengdspolynomiet Ole Witt-Hnsen Indhold. Den lineæe funktion.... Stykkevis lineæe funktione.... Andengdspolynomiet.... Pllelfoskydning f koodintsystemet.... Pllelfoskydning
Formelsamling Matematik C Indhold
 Formelsmling Mtemtik C Indhold Eksempler på besvrelser, lin, eksp, pot, geo... Tl, regneopertioner og ligninger... 6 Ligninger... 7 Geometri... 0 Funktioner og modeller... 3 Lineær funktion... 3 Procentregning...
Formelsmling Mtemtik C Indhold Eksempler på besvrelser, lin, eksp, pot, geo... Tl, regneopertioner og ligninger... 6 Ligninger... 7 Geometri... 0 Funktioner og modeller... 3 Lineær funktion... 3 Procentregning...
1 1 t 10 1. ( ) x 2 4. + k ================= sin( x) + 4 og har graf gennem (0,2), dvs F(0) = 2. + 4x + k
 0x-MA (0.0.08) _ opg (3:07) Integrtion ved substitution ( x + 7) 9 t x + 7 > t 9 t 0 + k 0 0 ( x + 7)0 + k b) x x + 4 t x + 4 > 3 x t t t x 3 t x x + k 3 t t + k ( ) x 4 3 x + 4 + + k c) cos( x)
0x-MA (0.0.08) _ opg (3:07) Integrtion ved substitution ( x + 7) 9 t x + 7 > t 9 t 0 + k 0 0 ( x + 7)0 + k b) x x + 4 t x + 4 > 3 x t t t x 3 t x x + k 3 t t + k ( ) x 4 3 x + 4 + + k c) cos( x)
Potens regression med TI-Nspire
 Potensvækst og modellering - Mt-B/A 2.b 2007-08 Potens regression med TI-Nspire Vi tger her udgngspunkt i et eksempel med tovværk, hvor mn får oplyst en tbel over smmenhængen mellem dimeteren (xdt) i millimeter
Potensvækst og modellering - Mt-B/A 2.b 2007-08 Potens regression med TI-Nspire Vi tger her udgngspunkt i et eksempel med tovværk, hvor mn får oplyst en tbel over smmenhængen mellem dimeteren (xdt) i millimeter
Regning. Mike Vandal Auerbach ( 7) 4x 2 y 2xy 5. 2x + 4 = 3. (x + 3)(2x 1) = 0. (a + b)(a b) a 2 + b 2 2ab.
 Mike Vandal Auerbach Regning + 6 ( 7) (x + )(x 1) = 0 x + = 7 + x y xy 5 7 + 5 (a + (a a + b ab www.mathematicus.dk Regning 1. udgave, 018 Disse noter er en opsamling på generelle regne- og algebraiske
Mike Vandal Auerbach Regning + 6 ( 7) (x + )(x 1) = 0 x + = 7 + x y xy 5 7 + 5 (a + (a a + b ab www.mathematicus.dk Regning 1. udgave, 018 Disse noter er en opsamling på generelle regne- og algebraiske
For så kan de to additionsformler samles i én formel, der kan ses som et specialtilfælde af den komplekse eksponentialfunktions funktionalligning,
 15.1. Komplekse integrler 293 læse, og hvordn gør mn det i prksis? Men den virkelige motivtion bg begrebet bliver udst til fsnit 18.5, hvor vi viser t foldning f sndsynlighedsmål lder sig udtrykke meget
15.1. Komplekse integrler 293 læse, og hvordn gør mn det i prksis? Men den virkelige motivtion bg begrebet bliver udst til fsnit 18.5, hvor vi viser t foldning f sndsynlighedsmål lder sig udtrykke meget
Projekt 10.3 Terningens fordobling
 Hvd er mtemtik? Projekter: Kpitel 0 Projekt 0.3 Terningens fordoling Elementerne indeholder, hvd mn kn deducere sig til og konstruere sig til ud fr de få givne ksiomer. Mn kn derfor i en vis forstnd sige,
Hvd er mtemtik? Projekter: Kpitel 0 Projekt 0.3 Terningens fordoling Elementerne indeholder, hvd mn kn deducere sig til og konstruere sig til ud fr de få givne ksiomer. Mn kn derfor i en vis forstnd sige,
ELEVER underviser elever En motiverende metode Drejebog med eksempler
 ELEVER underviser elever En motiverende metode Drejeog med eksempler Lyngy Tekniske Gymnsium Introduktion Lyngy Tekniske Gymnsium, HTX, hr i smrejde med Udviklingslortoriet for pædgogisk og didktisk prksis
ELEVER underviser elever En motiverende metode Drejeog med eksempler Lyngy Tekniske Gymnsium Introduktion Lyngy Tekniske Gymnsium, HTX, hr i smrejde med Udviklingslortoriet for pædgogisk og didktisk prksis
Grundlæggende funktioner
 Grundlæggende funktioner for A-niveu i st Udgve 5 018 Krsten Juul Grundlæggende funktioner for A-niveu i st Procent 1. Procenter på en ny måde... 1. Vækstrte... 3. Gennemsnitlig procent... Lineær vækst
Grundlæggende funktioner for A-niveu i st Udgve 5 018 Krsten Juul Grundlæggende funktioner for A-niveu i st Procent 1. Procenter på en ny måde... 1. Vækstrte... 3. Gennemsnitlig procent... Lineær vækst
Integralregning. Erik Vestergaard
 Integrlregning Erik Vestergrd Erik Vestergrd www.mtemtikfysik.dk Erik Vestergrd, Hderslev 4 Erik Vestergrd www.mtemtikfysik.dk Indholdsfortegnelse Indholdsfortegnelse. Indledning 4. Stmfunktioner 4. Smmenhængen
Integrlregning Erik Vestergrd Erik Vestergrd www.mtemtikfysik.dk Erik Vestergrd, Hderslev 4 Erik Vestergrd www.mtemtikfysik.dk Indholdsfortegnelse Indholdsfortegnelse. Indledning 4. Stmfunktioner 4. Smmenhængen
Michel Mandix (2010) INDHOLDSFORTEGNELSE:... 2 EN TREKANTS VINKELSUM... 3 PYTHAGORAS LÆRESÆTNING... 4 SINUSRELATIONERNE... 4 COSINUSRELATIONERNE...
 MATEMATIK NOTAT MATEMATISKE EVISER AF: CAND. POLYT. MICHEL MANDIX SIDSTE REVISION: FERUAR 04 Michel Mndi (00) Side f 35 Indholdsfortegnelse: INDHOLDSFORTEGNELSE:... EN TREKANTS VINKELSUM... 3 PYTHAGORAS
MATEMATIK NOTAT MATEMATISKE EVISER AF: CAND. POLYT. MICHEL MANDIX SIDSTE REVISION: FERUAR 04 Michel Mndi (00) Side f 35 Indholdsfortegnelse: INDHOLDSFORTEGNELSE:... EN TREKANTS VINKELSUM... 3 PYTHAGORAS
Eksempel 9.1. Areal = (a 1 + b 1 )(a 2 + b 2 ) a 1 a 2 b 1 b 2 2a 2 b 1 = a 1 b 2 a 2 b 1 a 1 a 2 = b 1 b 2. Eksempel = ( 1) = 10
 Oversigt [LA] 9 Nem vej til rel Nøgleord og begreber Helt simple determinnter Determinnt defineret Effektive regneregler Genkend determinnt nul determinnt nul Produktreglen Inversreglen inversregel og
Oversigt [LA] 9 Nem vej til rel Nøgleord og begreber Helt simple determinnter Determinnt defineret Effektive regneregler Genkend determinnt nul determinnt nul Produktreglen Inversreglen inversregel og
hvor A er de ydre kræfters arbejde på systemet og Q er varmen tilført fra omgivelserne til systemet.
 !#" $ "&% (')"&*,+.-&/102%435"&6,+879$ *1')*&: or et system, hvor kun den termiske energi ændres, vil tilvæksten E term i den termiske energi være: E term A + Q hvor A er de ydre kræfters rbejde på systemet
!#" $ "&% (')"&*,+.-&/102%435"&6,+879$ *1')*&: or et system, hvor kun den termiske energi ændres, vil tilvæksten E term i den termiske energi være: E term A + Q hvor A er de ydre kræfters rbejde på systemet
Oprids over grundforløbet i matematik
 Oprids over grundforløbet i matematik Dette oprids er tænkt som en meget kort gennemgang af de vigtigste hovedpointer vi har gennemgået i grundforløbet i matematik. Det er en kombination af at repetere
Oprids over grundforløbet i matematik Dette oprids er tænkt som en meget kort gennemgang af de vigtigste hovedpointer vi har gennemgået i grundforløbet i matematik. Det er en kombination af at repetere
Kompendium. Matematik HF C niveau. Frederiksberg HF Kursus. Lars Bronée 2014
 Kompendium Mtemtik HF C niveu π Frederiksberg HF Kursus Lrs Bronée 04 Mil: post@lrsbronee.dk Web: www.lrsbronee.dk Indholdsfortegnelse: Forord Det grundlæggende Ligningsløsning 8 Procentregning Rentesregning
Kompendium Mtemtik HF C niveu π Frederiksberg HF Kursus Lrs Bronée 04 Mil: post@lrsbronee.dk Web: www.lrsbronee.dk Indholdsfortegnelse: Forord Det grundlæggende Ligningsløsning 8 Procentregning Rentesregning
Taldiktat. Talhus. Tal. Format 5. Nr. 1. Enere 1. Tiere 10. Hundreder 100. Tusinder 1.000. Titusinder 10.000. Hundredetusinder 100.000 1.000.
 Tldiktt Nr. Timillioner 0.000.000 Millioner.000.000 Hundredetusinder.000 Tlhus Titusinder 0.000 Tusinder.000 Hundreder Tiere 0 Enere Prktivitet. Træk - kort i skjul fr et lmindeligt kortspil. Læg dem på
Tldiktt Nr. Timillioner 0.000.000 Millioner.000.000 Hundredetusinder.000 Tlhus Titusinder 0.000 Tusinder.000 Hundreder Tiere 0 Enere Prktivitet. Træk - kort i skjul fr et lmindeligt kortspil. Læg dem på
Undervisningsbeskrivelse
 Undervisningseskrivelse Stmoplysninger til rug ved prøver til gymnsile uddnnelser Termin Juni 2016 Institution Uddnnelse Fg og niveu Lærere Hold Fvrskov Gymnsium Stx Mtemtik A Peter Lundøer (Lu) 3k Mtemtik
Undervisningseskrivelse Stmoplysninger til rug ved prøver til gymnsile uddnnelser Termin Juni 2016 Institution Uddnnelse Fg og niveu Lærere Hold Fvrskov Gymnsium Stx Mtemtik A Peter Lundøer (Lu) 3k Mtemtik
Det dobbelttydige trekantstilfælde
 Det dobbelttydige trekntstilfælde Heine Strømdhl, Københvns Kommunes Ungdomsskoler Formålet med denne rtikel er t formulere en meget simpel grfisk løsningsmetode til det dobbelttydige trekntstilfælde med
Det dobbelttydige trekntstilfælde Heine Strømdhl, Københvns Kommunes Ungdomsskoler Formålet med denne rtikel er t formulere en meget simpel grfisk løsningsmetode til det dobbelttydige trekntstilfælde med
Matematik B-A. Trigonometri og Geometri. Niels Junge
 Mtemtik B-A Trigonometri og Geometri Niels Junge Indholdsfortegnelse Indledning...3 Trigonometri...3 Sinusreltionen:...6 Cosinusreltionen...7 Dobbeltydighed...7 Smmendrg...8 Retvinklede treknter...8 Ikke
Mtemtik B-A Trigonometri og Geometri Niels Junge Indholdsfortegnelse Indledning...3 Trigonometri...3 Sinusreltionen:...6 Cosinusreltionen...7 Dobbeltydighed...7 Smmendrg...8 Retvinklede treknter...8 Ikke
( ) Projekt 7.17 Simpsons formel A A A. Hvad er matematik? 3 ISBN
 Projekt 7.7 Simpsons formel Simpson vr søn f en selvlært væver, og skulle egentlig selv hve været en væver, men en solformørkelse vkte hns interesse for mtemtik og nturvidensk og mod lle odds lykkedes
Projekt 7.7 Simpsons formel Simpson vr søn f en selvlært væver, og skulle egentlig selv hve været en væver, men en solformørkelse vkte hns interesse for mtemtik og nturvidensk og mod lle odds lykkedes
MM501 forelæsningsslides
 MM501 forelæsningsslides uge 38, 010 Produceret f Hns J. Munkholm berbejdet f Jessic Crter 1 l Hopitls regler Afsnit 4.3 l Hopitls regel I omhndler beregning f grænseværdier f formen lim x f(x) g(x), hvor
MM501 forelæsningsslides uge 38, 010 Produceret f Hns J. Munkholm berbejdet f Jessic Crter 1 l Hopitls regler Afsnit 4.3 l Hopitls regel I omhndler beregning f grænseværdier f formen lim x f(x) g(x), hvor
Setup til kalibrering af Clamp on-flowmålere
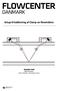 Setup til klirering f Clmp on-flowmålere Decemer 2018 Rpportforftter: Anders Niemnn, Teknologisk Institut Introduktion Ultrlyds-clmp-on flowmåling er en teknik, hvor mn ved hjælp f to trnsducere monteret
Setup til klirering f Clmp on-flowmålere Decemer 2018 Rpportforftter: Anders Niemnn, Teknologisk Institut Introduktion Ultrlyds-clmp-on flowmåling er en teknik, hvor mn ved hjælp f to trnsducere monteret
Algebra, ligninger og uligheder
 Alger, ligninger og uligheder I dette kpitel skl du rejde med lger, ligninger og uligheder. Et esøg på Bkken kn give nledning til mnge overvejelser over priser. Det kunne f være den smlede pris for turen
Alger, ligninger og uligheder I dette kpitel skl du rejde med lger, ligninger og uligheder. Et esøg på Bkken kn give nledning til mnge overvejelser over priser. Det kunne f være den smlede pris for turen
Geometrinoter 2. Brahmaguptas formel Arealet af en indskrivelig firkant ABCD kan tilsvarende beregnes ud fra firkantens sidelængder:
 Geometrinoter 2, jnur 2009, Kirsten Rosenkilde 1 Geometrinoter 2 Disse noter omhndler sætninger om treknter, trekntens ydre røringscirkler, to cirklers rdiklkse smt Simson- og Eulerlinjen i en treknt.
Geometrinoter 2, jnur 2009, Kirsten Rosenkilde 1 Geometrinoter 2 Disse noter omhndler sætninger om treknter, trekntens ydre røringscirkler, to cirklers rdiklkse smt Simson- og Eulerlinjen i en treknt.
Fælles for disse typer af funktioner er, at de som grundfunktion indeholder varianter af udtrykket x a.
 5. FORSKRIFT FOR EN POTENSFUNKTION Vi hr i vores gennemgng f de forskellige funktionstper llerede være inde på udtrk, som indeholder forskellige potenser f I dette kpitel skl vi se på forskellige tper
5. FORSKRIFT FOR EN POTENSFUNKTION Vi hr i vores gennemgng f de forskellige funktionstper llerede være inde på udtrk, som indeholder forskellige potenser f I dette kpitel skl vi se på forskellige tper
MM501 forelæsningsslides
 MM501 forelæsningsslides uge 39, 009 Produceret f Hns J. Munkholm 1 Linerisering s. 66-67 Lineriseringen f f omkring x =, er den lineære funktion, der hr tngenten som grf. Klder mn den L er forskriften
MM501 forelæsningsslides uge 39, 009 Produceret f Hns J. Munkholm 1 Linerisering s. 66-67 Lineriseringen f f omkring x =, er den lineære funktion, der hr tngenten som grf. Klder mn den L er forskriften
Algebra, ligninger og uligheder
 Alger, ligninger og uligheder I dette kpitel skl du rejde med ligninger og uligheder. Et esøg på Bkken kn give nledning til mnge overvejelser over priser. Det kunne fx være den smlede pris for turen og
Alger, ligninger og uligheder I dette kpitel skl du rejde med ligninger og uligheder. Et esøg på Bkken kn give nledning til mnge overvejelser over priser. Det kunne fx være den smlede pris for turen og
Krumningsradius & superellipsen
 Krumningsrdius & suerellisen Side /5 Steen Toft Jørgensen Krumningsrdius & suerellisen Formålet med dette mini-rojekt er t erhverve mtemtisk viden om krumningsrdius f en kurve og nvende denne viden å det
Krumningsrdius & suerellisen Side /5 Steen Toft Jørgensen Krumningsrdius & suerellisen Formålet med dette mini-rojekt er t erhverve mtemtisk viden om krumningsrdius f en kurve og nvende denne viden å det
SAMMEN ER BEBOERE I AFDELINGSBESTYRELSER I ORGANISATIONSBESTYRELSE I MEDARBEJDERE VI STÆRKE
 PGAVE- RUPPER 3B SAMMEN ER BEBOERE I AFDELINGSBESTYRELSER I ORGANISATIONSBESTYRELSE I MEDARBEJDERE VI STÆRKE I 1 I BAGGRUND 3B s orgnistionsestyrelse nedstte i efteråret 2016 en række opgvegrupper i forindelse
PGAVE- RUPPER 3B SAMMEN ER BEBOERE I AFDELINGSBESTYRELSER I ORGANISATIONSBESTYRELSE I MEDARBEJDERE VI STÆRKE I 1 I BAGGRUND 3B s orgnistionsestyrelse nedstte i efteråret 2016 en række opgvegrupper i forindelse
Matematisk modellering og numeriske metoder. Lektion 12
 Mtemtisk modellering numeriske metoder Lektion 12 Morten Grud Rsmussen 21. oktober, 213 1 Prtielle differentilligninger 1.1 Løsning f vrmeligningen vh. Fourierrækker [Bens sektion 12.6 på side 558] Vi
Mtemtisk modellering numeriske metoder Lektion 12 Morten Grud Rsmussen 21. oktober, 213 1 Prtielle differentilligninger 1.1 Løsning f vrmeligningen vh. Fourierrækker [Bens sektion 12.6 på side 558] Vi
Bogstavregning - supplerende eksempler. Reduktion... 54 b Ligninger... 54 d
 Mtetik på AVU Eksepler til iveu F, E og D Bogstvregig - supplerede eksepler Reduktio... Ligiger... d Bogstvregig Side Mtetik på AVU Eksepler til iveu F, E og D Reduktio M gger to preteser ed hide ved -
Mtetik på AVU Eksepler til iveu F, E og D Bogstvregig - supplerede eksepler Reduktio... Ligiger... d Bogstvregig Side Mtetik på AVU Eksepler til iveu F, E og D Reduktio M gger to preteser ed hide ved -
1. Eksperimenterende geometri og måling
 . Eksperimenterende geometri og måling Undersøgelse Undersøgelsen drejer sig om det såkldte Firfrveproblem. For mere end 00 år siden fndt mn ved sådnne undersøgelser frem til, t fire frver er nok til t
. Eksperimenterende geometri og måling Undersøgelse Undersøgelsen drejer sig om det såkldte Firfrveproblem. For mere end 00 år siden fndt mn ved sådnne undersøgelser frem til, t fire frver er nok til t
Grundlæggende matematiske begreber del 2 Algebraiske udtryk Ligninger Løsning af ligninger med én variabel
 Grundlæggende matematiske begreber del Algebraiske udtryk Ligninger Løsning af ligninger med én variabel x-klasserne Gammel Hellerup Gymnasium 1 Indholdsfortegnelse ALGEBRAISKE UDTRYK... 3 Regnearternes
Grundlæggende matematiske begreber del Algebraiske udtryk Ligninger Løsning af ligninger med én variabel x-klasserne Gammel Hellerup Gymnasium 1 Indholdsfortegnelse ALGEBRAISKE UDTRYK... 3 Regnearternes
