Prisdannelsen i det danske boligmarked diagnosticering af bobleelement
|
|
|
- Lærke Mortensen
- 10 år siden
- Visninger:
Transkript
1 Hovedopgave i finansiering, Insiu for Regnskab, Finansiering og Logisik Forfaer: Troels Lorenzen Vejleder: Tom Engsed Prisdannelsen i de danske boligmarked diagnosicering af bobleelemen Esimering af dynamisk prisdannelsesmodel og es af nuidsværdimodel med VAR meodikken Handelshøjskolen i Århus 26
2 Execuive Summery The markes for owner occupied homes in Denmark have experienced posiive excess reurn every year since 994. Excess reurn is defined as he housing marke reurn in excess of he inflaion in prices of oher consumpion. In he mos previous years he rise in prices has been exraordinary, and in some areas he excess reurn has been above 2 percen annually. Naurally, he debae is wheher or no prices are susained by fundamenals or by speculaion, which would indicae he exisence of a housing bubble. A housing bubble is he siuaion where homeowners pay a premium above fundamenal prices. Idenifying he cause of rapidly rising prices is crucial for sociey since housing wealh increase consumpion, aggregae demand and inflaes prices. The objecive of he hesis is herefore o analyze he prices in he Danish marke for owner occupied homes in order o idenify a poenial housing bubble. When analyzing prices in any marke, he presen value model is a useful ool. The model indicaes ha fundamenal prices are a funcion of fuure dividends. Tradiionally, expeced fuure dividends are discouned wih he reurn required by invenors. The dividend is easily recognized in financial markes such as markes for socks and bonds. However, i is quie difficul o idenify he dividend in he housing marke. In any good analysis of he housing marke he firs sep should be o idenify he facors deermining he economic value of he housing marke dividend. Since he value of he dividend is also a funcion of prices, he radiional presen value model as well as he radiional ess for marke efficiency does no apply. The soluion presened in he hesis is an error correcion model for he housing marke reurn. This is due he fac ha he prices of exising homes in he long run should be coinegraed wih he price of consrucing new homes. The analysis herefore follows he wo-sep procedure presened by Engle & Granger (987 and he economeric model proposed by Andersen e al. (993. This model is no a useful model for idenifying a poenial housing bubble. I is merely a model idenifying he significance of he economic facors ha explains he prices in he housing marke. The soluion o he problem is o esimae and es a radiional presen value model under he assumpion of no coine-
3 graion beween prices and consrucion cos. This secion follows he VAR mehod developed by Campbell and Shiller (987 and he presen value model of he housing marke developed by Black e al. (25. In an empirical analysis of he Danish housing marke annual daa from he period 955 o 23 is used. Since he exraordinary price increase in he mos recen years have no been embedded in hese daa, and since he daa are aggregaed daa on he Danish marke and no daa on specific markes, he analysis is sreched o quarerly observaions from early 992 o lae 25 from differen housing markes of Denmark. The conclusion on he prices in he Danish markes for owner occupied homes is ha prices indeed deviae from fundamenal prices. This conclusion is primarily based on he fac ha he case of coinegraion is no a very srong one and ha he differen models do no hold in he mos recen daase. The deviaion from fundamenal prices is no o be explained as a raional bubble, bu as irraional exuberance. The good news is ha he Danish housing marke is no dominaed by irraional exuberance o he same exen as some marke in he Unied Saes.
4 Indholdsforegnelse. Indledning.. Problemformulering 3.2. Afgrænsning 4 2. Fundamenalmodellen i e generel perspekiv Nuidsværdimodellen for dividenden 6 3. Teoreisk model for prisdannelsen på boligmarkede 3.. Fakorer, der påvirker eferspørgselen 3... Inflaion Indkoms Formueeffeker Ejers omkosninger Demografiske forhold Fakorer, der påvirker udbudde Privae boliginveseringer og Tobins Q-eori Boligmarkedes dynamik: Byggeomkosninger som prissanker Scenarioanalyse: Permanen renefald Scenarioanalyse: Øgede byggeomkosninger Boligmarkede som e sysem af inegrerede ligninger Beydningen af lejemarkede Udledning af dynamisk prisdannelsesmodel Markede for boligydelser Markede for boliger Tes specifikaion og økonomerisk eori Empiriske modeller Boligmarkede i en simpel regressionsmodel Blomgren-Hansen & Knøsgaards model for enfamiliehuse Danmarks Saisiks ADAM model Syrker og svagheder ved økonomerimodeller Udvidelse af grundmodellen Raionelle forvenninger og den efficiene markedshypoese Beydningen af imperfeke markedsforhold Raionelle bobler Naurlige bobler Irraional exuberance 47
5 6. Campbell & Shillers es af nuidsværdimodellen Nuidsværdimodel for boligmarkede Empirisk analyse af de danske boligmarked Daa og foreløbige resulaer Tes for koinegraion Esimering af dynamisk prisdannelsesmodel Tes af nuidsværdimodellen 7 8. Vurdering af boligmarkedes ilsand Tradiionelle forklaringer på de høje prisniveau Knaphed i byzoner Inernaionale sammenligninger Nye realkrediproduker Økonomiske forhold Efficienshypoesen og imperfeke markedsforhold Argumener for irraional exuberance Beydningen af likvidie: Moral hazard i krediinsiuioner Boligejernes forvenningsparadigme Psykologiske fakorer Konklusion 86. Perspekivering 9
6 . Indledning Siden 994 har prisudviklingen på ejerboliger i Danmark overgåe den generelle inflaion. Baggrunden for udviklingen i priserne på ejerboliger er bleve en sadig sørre del af den offenlige deba. Udgangspunke i debaen er en diskussion af, hvorvid prissigningerne kan forklares ud fra ændringer i fundamenale forhold, eller om der er ske en afkobling mellem fakiske og fundamenale priser. Selvom boligmarkede radiionel har nyd en særlig bevågenhed, er diskussionen herhjemme om spekulaiv adfærd og boligbobler e forholdsvis ny fænomen. I dagblade Børsen blev der i 25 brag 9 arikler med reference il en boligboble, mens der i 24 blev brag fem arikler og inden da blo en enkel i 22. En boligboble defineres som siuaionen hvor der er forskel mellem fakiske og fundamenale priser. Hvis prisdannelsen på boligmarkede ikke er en afspejling af udviklingen i de fundamenale forhold, eksiserer der e umiddelbar grundlag for inervenion. Huspriserne er nemlig en vigig deerminan af forbruge og dermed af økonomiens samlede eferspørgsel. Undersøgelser af Case e al. (2 og Shiller (24 af den amerikanske økonomi viser, a forbruge fakisk er mere følsom over for udviklingen på boligmarkede end overfor udviklingen på akie- og obligaionsmarkederne. En lignende konklusion kan findes i Heilbling & Torrones (23 med daa fra U.K. Herhjemme forklares forbruge som en funkion af boligmarkedes priser i de makroøkonomiske modeller. En boligboble vil derfor have sore samfundsøkonomiske konsekvenser, når den briser. Dee gælder både på de aggregerede niveau i form af økonomisk afmaning, og for den enkele huskøber, der med en høj gearing vil blive eknisk insolven eller i bedse ilfælde blo mise en del af sin egenkapial. Under en boligboble kan enkele samfundsgrupper også risikere a blive udelukke fra boligmarkede i de områder, hvor boblen forekommer, og de kan i sig selv have en samfundsmæssig konsekvens, såfrem de respekive grupper repræsenerer essenielle erhverv som sygeplejersker, lærer osv. Ejerboligmarkede vurderes ofe, med udgangspunk i nuidsværdimodellen, på forholde mellem husleje og huspriser, indkoms og huspriser m.fl. En markan afvigelse fra de hisoriske gennemsni idenificeres som en boble. Dee er pendanen il a vur- På baggrund af daa fra ADAMs daabank.
7 dere ilsanden i akiemarkederne på baggrund af dividende-pris (D/P forholde. I lierauren findes alrige eksempler på sådanne analyser. De amerikanske boligmarked er bl.a. undersøg af Case & Shiller (23 og i U.K. af Farlow (25a og Hawksworh (24. Herhjemme er en ilsvarende analyse lave af Madsen (25, der mener a kunne idenificere en boligboble, der kan forklares af leere adgang il finansiering og irraional exuberance. Modsa konkluderer Pedersen (24 på baggrund af e indeks for den reale husleje ved a bo i ejerbolig, a huslejen ligger æ på si hisoriske gennemsni og afviser derfor, a der er en boble i de danske boligmarked. Probleme med sådanne analyser er, a D/P forholde kun er konsan under forudsæning af, a dividenden forvenes a være konsan i alle fremidige perioder. En sådan forudsæning er undgåe i e sudie af Black e al. (25 af boligmarkede i U.K., der esimerer og eser fundamenalmodellen, med den disponible realindkoms som surroga for værdien af boligydelsen. boligydelsen er de udryk, som anvendes om boligmarkedes dividende. På den baggrund konkluderes de, a prisudvikling i U.K. ikke er præge af spekulaiv adfærd i samme grad, som prisudviklingen skyldes en overreakion på informaioner om fundamenale forhold. Refærdigvis skal de nævnes, a undersøgelserne af Farlow og af Case & Shiller er e led i e sørre arbejde med efficiens i boligmarkede, og a deres analyiske ilgange er alrige. I 25 udgaven af Shillers bog Irraional Exuberance er der endvidere ilføje e kapiel om irraional exuberance i boligmarkede. Prisdannelsen i boligmarkede er også bleve analysere i makroøkonomiske modeller. De makroøkonomiske modeller er modsa de eoreiske modeller indukive i den forsand, a de ager udgangspunk i empiriske erfaringer, dog med de krierium, a de esimerede modeller ikke må sride mod almen accepere økonomisk eori. De markoøkonomiske modeller har på den måde skab en eori om prisdannelsen i boligmarkede. Bl.a. har Andersen e al. (993 opsille en model for ejerboligmarkede, der ager udgangspunk i en ese, som er fremherskende i makromodellerne, nemlig a prisen på lang sig er forankre i byggeomkosningerne. En sådan eori har før være i sand il a forklare prisdannelsen i boligmarkede. Denne afhandling er e bidrag il debaen om udviklingen i priserne på de danske boligmarked. Afhandlingen beskæfiger sig med prisdannelsen på ejerboliger, og vil 2
8 dermed vurdere sandsynligheden for, a der eksiserer en boligboble. Problemerne med a diagnosicere prissigningerne som besem af fundamenale forhold eller som en decidere boligboble leder il følgende problemformulering... Problemformulering På kapialmarkederne er eorien om prisfassæelse forholdsvis enkel, der er bred enig om, a dividenden er fundamenal for prisen på en akie og renen for prisen på en obligaion. Afhandlingens udgangspunk er derfor en gennemgang af den fundamenale sammengæng mellem pris og dividende i e vilkårlig marked. Sammenhængen på boligmarkede er imidlerid noge uklar. Her eksiserer der ikke en sådan blåsemple prismodel. De er fordi dividenden er svær a idenificere som en enkel økonomisk fakor. Dividenden er nærmere en funkion af en række fakorer, herunder de fysiske udbud af boligydelser. Derfor ønskes følgende spørgsmål besvare: Hvilke økonomiske fakorer kan forvenes a have beydning for værdien af dividenden og dermed den fundamenale pris på en ejerbolig? Foruden vanskelighederne forbunde med a idenificere dividenden, lever boligmarkede si ege liv, der minder lid om måden, hvorpå priser dannes i de finansielle markeder. Med de menes, a priserne fassæes forskellig på kor og lang sig, fordi udbudde af boligydelser bland ande er en funkion af priserne. Der eksiserer derfor en dobbel kausalie, som er særlig for boligmarkede. Denne eori ønskes dokumenere ved besvarelse af følgende spørgsmål: Hvilken markedsilpasningsmekanisme nødvendiggør, a prisfassæelsen analyseres med en sondring mellem prisdannelsen på kor og lang sig? På baggrund af besvarelsen af ovensående spørgsmål opsilles der en eoreisk prismodel og på baggrund af den en dynamisk model for prisdannelsen, der kan håndere den særlige ilpasningsmekanisme. Denne del af afhandlingen relaerer sig il Engle & Grangers (987 fejlkorrekionsmodel og boligmodellen af Andersen e al. (993. Andersen e al. opsiller og eser en model for ilpasningsmekanismen i boligmarkede i perioden På baggrund af denne model ønskes der udvikle en model for prisen, hvilke fører il følgende del af den samlede problemformulering: 3
9 Udledning af en dynamisk prisdannelsesmodel il brug for en empirisk analyse af de danske boligmarked. Syrken ved ovensående model er, a den hånderer dynamikken i boligmarkede. De er dog ikke en decidere model for boligbobler. For a finde en bedre meode il a diagnosicere en evenuel boligboble, udvides grundanagelserne bag fundamenalmodellen med en eoreisk diskussion af markedsefficiens og af de forskellige bobleeorier i generel forsand. Dee gøres bl.a. med henblik på en senere vurdering af begrebernes anvendelighed som forklaring på den nuværende siuaion på boligmarkede, men førs og fremmes for a udvikle en konkre meode il a ese nuidsværdimodellen og dermed forekomsen af bobler. I den forbindelse specificeres en nuidsværdimodel for boligmarkede, der dog ignorerer ilpasningsmekanismen. Denne del relaerer sig specifik il Campbell & Shiller (987 og deres VAR meode il es af nuidsværdimodellen sam boligmodellen af Black e al. (25. Ovensående fører il følgende del af den samlede problemformulering: Udvikling af en meode il es af relevansen af den generelle nuidsværdimodel, sam opsilling af en nuidsværdimodel for boligmarkede. På baggrund af esimering af de eoreiske modeller på forskellige daasæ, og på baggrund af den eoreiske diskussion af markedsefficiens og boblebegreberne, analyseres prisdannelsen i boligmarkede, for a svare på afhandlingens hovedspørgsmål: Kan de senese års prissigninger forklares ud fra ændringer i fundamenale forhold, eller eksiserer der en indikaion på en boligboble?.2. Afgrænsning Som de fremgår af problemformuleringen, er der valg en analysemeode, hvor problemsillingen belyses ud fra e makroøkonomisk fundamen. Boligmarkede kunne også være analysere på baggrund af inveseringsbesluningen hos den enkele huskøber gennem en spørgeskemaundersøgelse af boligkøberens moivaioner og opfaelse af boligmarkede. Dee undlades, da udbye ikke sår mål med omkosningerne forbunde hermed. Alernaiv kunne nuidsværdimodellen være anvend i en analyse af 4
10 den inerne rene, der sæer nuidsværdien for e lejemål af en repræsenaiv bolig lig konanprisen på en ilsvarende ejerbolig, og dermed udrykker risikopræmien på ejerboligmarkede. Der eksiserer dog en del vanskeligheder forbunde med a få pålidelige daa il en sådan analyse. Boligejernes finansielle gearing kunne endvidere være vurdere på baggrund af en øvelse, hvor man finder rådighedsbeløbe efer boligomkosninger hos boligejere, der har valg afdragsfrie lån. Herefer findes den implicie indkomsforvenning, dvs. den signing i indkomsen, der er nødvendig for a kunne beale afdrag uden en redukion af rådighedsbeløbe. En lignende øvelse kan laves med flexlån og renekurven, hvor en sejl renekurve er ensbeydende med, a boligejere med flexlån forvener en ilsvarende sor signingen i indkomsen og omvend. Som nævn, er der valg en ilgang, hvor siuaionen på boligmarkede analyseres på baggrund af aggregerede økonomiske daa. Daasæe sammer fra flere kilder. De er skab på grundlag af daa fra ADAMs Daabank, Danmarks Saisik, Naionalbanken og Realkrediråde som årlige og kvaralsvise observaioner. Desværre er de ikke mulig a få daa, der både dækker de senese o års prissigninger, og som har en ilpas lang hisorik. Derfor anvendes daa med årlige observaioner fra ADAMs Daabank i perioden , som så suppleres med kvaralsvise observaioner fra perioden. kvaral 992 il 3. kvaral 25 fra de øvrige daakilder. Teorien bag den dynamiske prisdannelsesmodel sammer bl.a. fra prakiske erfaringer med forskellige økonomerimodeller. I forlængelse af udledningen af den dynamiske prisdannelsesmodel gennemgås de empiriske erfaringer med nogle af de mes beydningsfulde modeller. Dee gøres for a opnå e naurlig benchmark il en modelvalidering. I forbindelse med modelvalidering anages de, a de anvende OLS esimaorer er BLUE, og en egenlig es for fejlspecifikaioner undlades derfor eksplici. Der henvises i sede il relevane bilag og il daasæe. 5
11 2. Fundamenalmodellen i e generel perspekiv I dee afsni gennemgås forskellige variaioner af den velkende nuidsværdimodel. Gennemgangen skal danne grundlag for en eoreisk diskussion af de forskellige modelvariaioners forudsæninger og anvendelighed på boligmarkede. 2.. Nuidsværdimodellen for dividenden I dividendemodellen er de forvenede afkas konsan og definere som: E ( R E ( P Ω P E ( D Ω Ω = (2. P Hvor P og D er henholdsvis prisen og dividendebealingen på idspunk. Den maemaiske forvenning er her og i de eferfølgende beinge på de ilgængelige informaionssæ Ω, og der anvendes i de eferfølgende den mere enkle noaion E (. Noaionen vil igennem afhandlinger generel følge den, der er anvend i Cuhberson (996. De anages, a invesorerne, hvad enen de inveserer i finansielle akiver eller ejerboliger, kun er villig il a eje akive så længe, de giver de konsane afkas k, der neop kompenserer for den underliggende risiko: E ( R k, k > (2.2 = Ovensående er kend som e fair game for merafkase, der er differencen mellem de realiserede og de forvenede afkas. E fair game har en forvene værdi på nul, hvilke er en cenral anagelse med raionelle forvenninger. Ved a kombinere (2. og (2.2 fås Euler ligningen: P δ E ( P D (2.3 = Hvor δ = (k - er den konsane diskoneringsfakor. Som de fremgår af (2.3, er udrykke ikke endelig reducere, ide der på højresiden indgår e udryk for den frem- 6
12 idige pris P. Ved a fremføre (2.3 en periode og subsiuere opnås følgende udryk for prisen på idspunk : P = 2 δ E ( P 2 D 2 δe ( D Ovensående kan findes under forudsæningen om ieraive forvenninger, der gælder for maemaiske forvenninger, og ligesom fair game egenskaben er en cenral anagelse med raionelle forvenninger. Ieraive forvenninger kan formel skrives som: E E = E E 2... De ses, a der sadig indgår e udryk for den fremidige pris P 2 på højresiden, og ved genagende subsiuion n- gange vil relaionen sadig indeholde: δ n E n ( P D n For a afhjælpe dee problem pålægges ransversaliesbeingelsen: n limδ E ( P n n D n Beingelsen er holdbar, da diskoneringsfakoren som en konsekvens af (2.2 er mindre end, og såfrem den forvenede væks i dividenden ikke er eksplosiv. Transversaliesbeingelsen fremhæves som e pivopunk, da den udelukker raionelle bobler. Udrykke for den fundamenale pris bliver endelig: i= i P = δ E ( D (2.4 i Udover forudsæningerne om konsan afkaskrav, ieraive forvenninger og om a væksen i dividenden ikke må være eksplosiv, gælder de for dividendemodellen, a invesorerne skal have homogene forvenninger il D, og a de benyer den samme model il a besemme afkaskrave. 7
13 Priserne bør, i overenssemmelse med dividendemodellen, il enhver id afspejle nuidsværdien af forvenede fremidige dividender, når invesorerne er raionelle, der ikke eksiserer en raionel boble, og hvor diskoneringsfakoren er konsan. Modellen er generel, og andre forhold end dividenden kan ænkes a være fundamenale for prisen. Husleje eller indkoms kan eksempelvis være besemmende for den fundamenale pris på en ejerbolig. Hvorvid forudsæningen om konsan diskonering er empirisk holdbar er diskuabel, og der gives derfor eferfølgende en model, hvor diskoneringen er idsvarierende. Euler ligningen gælder både for nominelle og reale variable, og megen empiri søer konsan realafkas 2. Dermed vil dividendemodellen ofe være udryk i reale ermer. Inveseringshorisonen er uden beydning for fassæelsen af den fundamenale værdi. Selvom om enkele invesorer har en endelig inveseringshorison, vil invesorerne samle se benye formel (2.4, da de korsigede, men raionelle invesorer, ved indukion opnår samme udryk for P. Ofe vil man pålægge dividendemodellen en anagelse om den dividendegenererende proces. Hvis (real dividenden foruden e hvid søj led er en konsan, kan de være rimelig a anage a den forvenede dividende er en random walk uden drif 3. I e sådan ilfælde kan dividendemodellen med genagelse af ovensående redukionsprocedure reduceres il: P = D (2.5 k Resulae kan olkes, som a forholde mellem dividender og priser skal være konsan, nemlig svarende il k. Dee kan selvfølgelig eses empirisk, hvor de vil være naurlig a ese dividende-pris forholde udryk i reale ermer, neop fordi empirien søer konsan realafkas. E brud på hypoesen om e konsan dividendeafkas beyder ikke nødvendigvis, a der eksiserer en boble. De kan også skyldes e idsvarie- 2 Cuhberson (996, p d = g d - ε, hvor g = og ε ~ i.i.d.n(,σ 2. 8
14 rende afkaskrav, a andre forhold end D er fundamenal for prisen eller ændrede forvenninger. En implikaion af dividendemodellen er a ændringer i prisen udelukkende skyldes ændringer i dividenden. Med raionelle forvenninger skyldes ændringer i dividenden udelukkende ankomsen af ny informaion. Den beingede varians i priserne skal derfor afhænge af variansen i disse informaioner, der kan måles ved fejlledde, ε, i den random walk, der beskriver dividenden. De må derfor gælde 4 : ε var( P P = var( k (2.6 Såfrem de er mere rimelig a anage, a dividenden i sede har konsan væks, følger den en random walk med drif. Dividendemodellen kan herefer reduceres il: g P = D, k > g (2.7 k g Hvor g er den konsane væksrae i dividenden. Som nævn idligere kan der være ilfælde, hvor invesorerne kræver forskellig afkas i de enkele perioder. Relaionen i (2.2 vil i dee ilfælde være: E R i = k i (, k i > Dividendemodellen kan herefer og efer genagelse af ovensående redukionsprocedure reduceres il: j P = E δ i ( D j (2.8 j = i= Hvor δ i = (k i - er den idsvarierende diskoneringsfakor. Udrykke i (2.8 er mindre operaionel end dividendemodellen med konsan diskonering, ide højresiden 4 Cuhberson (996, p. 8. 9
15 i denne udvidelse også kræver en model for de ikke-observerede værdier af afkaskrave. Argumene for a benye en model med idsvarierende diskonering er, a de flese akivers risiko ikke er konsan, og invesorerne derfor kræver en idsvarierende risikopræmie. I forbindelse med esimering af den idsvarierende diskoneringsfakor benyes ofe en meode, der følger af Meron (973. Meron viser med udgangspunk i en ineremporal model, a merafkase på markedsporeføljen udover de risikofrie afkas er proporional med den forvenede varians på markedsporeføljen, hvorefer afkaskrave, såfrem dee besår af den risikofri rene og en risikopræmie, il idspunk i kan findes som 5 : k m, i f m, i 2 = R λ E ( σ (2.9 Hvor R f er den konsane risikofrie rene, λ er markedsprisen på risiko og proporionaliesfakoren, der afhænger af den konsane relaive risikoaversion, mens E (σ 2 m,i er den forvenede varians på idspunk i. Ligesom nuidsværdimodellen kræver en anagelse om den daagenererende proces for dividenden, eksempelvis en random walk, kræver modellen med idsvarierende diskonering som nævn også en model for den forvenede varians. Dee problem løses ofe i empiriske sammenhænge med en VAR model. Modellen for dividenden er e prakisk redskab, når man vil analysere priserne. Den maemaiske model er dog kun meningsfuld, når man kender og kan idenificere dividenden. I de eferfølgende afsni beskrives eorien i de radiionelle økonomeriske boligmodeller, der principiel er modeller for dividenden, ide der ages udgangspunk i de økonomiske fakorer, der kan forvenes a have fundamenal beydning for prisen på en ejerbolig. 5 Cuhberson (996, p. 82.
16 3. Teoreisk model for prisdannelsen på boligmarkede I dee afsni beskrives den eori, der er grundlag for arbejde med boligmarkede i de radiionelle økonomeriske modeller. Herhjemme blev fundamene il arbejde med boligmarkede i sådanne modeller lag af Groes & Møller (977 og især af Blomgren-Hansen & Knøsgaard (978. Forfaernes boligmodeller er med iden udvikle i de re sore makromodeller, der i dag udgør ADAM (Danmarks Saisik, MONA (Danmarks Naionalbank og SMEC (De Økonomiske Råd. Srukuren i de re modeller er re ens, og de ager alle udgangspunk i en ese om, a huspriserne er forankre i byggeomkosningerne på lang sig, og a den korsigede afvigelse skyldes forskellige sød il boligmarkede. Da srukuren i de re boligmodeller minder om hinanden, refereres der blo il ADAM modellen, da de er denne models daabank, der anvendes i afhandlingens empiriske afsni. På boligmarkede sondres mellem boligen som kapialgode og den boligydelse, som boligen producerer i hver periode. De er klar, a prisen på boligen må være en funkion af værdien af boligydelsen, som udrykker boligmarkedes dividende. En sådan fysisk opsplining af boligmarkede er dog sjælden observere, da boligejerne både ager rollen som producen og eferspørger af boligydelser. Dividenden er derfor svær a idenificere. I de radiionelle økonomerimodeller er en sådan sondring af samme grund ignorere på de eksplicie niveau. Inuiionen i modellerne er i sede, a prisen er en funkion af en række økonomiske fakorer, der påvirker udbudde og eferspørgslen efer boliger. Prisen er herefer den markedsclearende mekanisme. 3.. Fakorer, der påvirker eferspørgslen Den eferfølgende gennemgang vil beskæfige sig med komponenerne i funkionsudrykke for eferspørgslen Inflaion De er oplag, a eferspørgslen efer ejerboliger er en funkion af de generelle prisniveau eller inflaion. Man kan argumenere for, a huspriser er inflaionsneurale i den forsand, a priserne al ande lige følger udviklingen i de generelle forbrugerpriser, og således vil man ofe benye reale værdier i empiriske sammenhænge. Figur 3.. viser udviklingen i de nominelle huspriser og i prisen på ande forbrug end boligforbrug.
17 Figur 3.. Konanpriser og forbrugerpriser Nominel konanpris Pris på ande forbrug Periode: (955=, kilde: ADAMs daabank Figuren viser, a den nominelle prisudvikling på enfamiliehuse har være krafigere end udviklingen i priser på ande forbrug i perioden , og a den er eskalere siden begyndelsen af 99erne. Da enhver forbrugsbesluning er e fravalg af ande forbrug, bliver ejerboliger mere arakive, når priserne på øvrige forbrugsvarer siger. Er prisen på ejerboliger lav i relaiv forsand, øges eferspørgslen, hvilke lægger e opadgående pres på priserne, der vil sige indil forskellen il de generelle priser igen er eliminere. I empiriske modeller vil de derfor være naurlig a lade prisen på ande forbrug indgå som deflaor af de nominelle huspriser Indkoms Indkomsen fungerer som en naurlig afgrænsning for, hvor mege den enkele husholdning kan afse il boligforbrug, og de giver god mening, a væksen i indkomsen er besemmende for væksen i huspriserne. Spørgsmåle er, hvilke indkomsbegreb, der er de mes rigige a anvende i en model. De er naurligvis indkomsen efer skaer, der er ineressan. Endvidere bør indkomsen være i fase priser, så inflaionseffeken isoleres. Indkomsen anses for a være de dominerede argumen i eferspørgslen, og i lierauren findes også en lang række undersøgelser, hvor kun indkoms-pris forholde analyseres. Figur 3.2. viser udviklingen i husholdningernes disponible realindkoms, som den er definere i ADAMs daabank. 2
18 Figur 3.2. Disponibel realindkoms og real konanpris Disponibel realindkoms Real konanpris Periode: (955=, kilde: ADAMs daabank Figuren viser, a udvikling i den disponible realindkoms på lang sig har oversege udviklingen i de reale konanpriser, men a der samidig er sørre volailie i huspriserne. De er en rimelig anagelse, a indkomseffeken er mindre end, da husholdningerne ikke vil afse en sørre indkomsandel il boligforbrug ved sigende indkoms. Som de fremgår af figuren, er denne anagelse ikke nødvendigvis holdbar på kor sig Formueeffeker De kan virke uilsrækkelig a anvende indkomsbegrebe alene som deerminan for boligforbruge. I henhold il livsløbseorien 6 maksimerer de enkele agener i økonomien forbrugsnyen gennem deres liv under en budgeresrikion, hvor både livsidsindkomsen og formuen indgår. I den forsand skal boligforbruge, og dermed også eferspørgslen og i sidse ende prisen, afhænge både af fremidig indkoms og af formuen. Ved blo a anvende indkomsen eller nuidsværdien af forvenede fremidig indkomser (humankapialen ignorerer man således formueeffekerne på forbruge Ejers omkosninger Omkosningen ved a benye egen bolig, også kalde user cos, er elemenær for eferspørgslen efer ejerboliger. De er klar, a eferspørgslen må være en faldende funkion af denne omkosning. Nominelle user cos kan opdeles i fire grundelemener 7 : 6 Se eksempelvis kapiel 5 i Bodie e al. (2. 7 Pedersen (24, p. 3. 3
19 user cos = rene efer ska boligskaer i pc. afskrivningsrae forvenede kapialgevinser (3. De fire elemener er finansieringsomkosninger, boligskaer, afskrivninger og forvenede kapialgevinser. Afhandlingen vil age udgangspunk i denne definiion på ejers omkosninger ved boligbenyelse. For a få den reale user cos skal inflaionen rækkes fra den nominelle rene. Den reale user cos er selvfølgelig de mes korreke mål, da de er den reale finansieringsomkosning, der har beydning for huskøberen. Når der ales om e lav reneniveau, bør man indireke ale om e lav realreneniveau. I de eferfølgende ages der for overskuelighedens skyld udgangspunk i den nominelle rene. Der henvises il bilag for en eksak gennemgang af meoden il beregning af user cos. Finansieringsomkosninger: Den ypiske boliginvesering er præge af en mege høj gearing. 8 % af konanprisen kan realkredifinansieres, mens de reserende 2 % skal komme i form af egenkapial. Da de flese boligejere, især førsegangskøbere, ikke har den nødvendige egenkapial, vil sørsedelen af de 2 % også blive finansiere med fremmedkapial i form af e banklån. Udbealingen på en ejerbolig er ca. 5 %, mens de sidse 95 % alså vil have form af fremmedkapial. En boliginvesering kan derfor være geare op il 2 gange. Finansieringsomkosningen er den effekive finansieringsrene efer ska, ide renen er fradragsbereige. Den effekive rene beregnes som de vægede gennemsni af renen på banklåne (pålydende rene og den effekive obligaionsrene, dvs. den rene, der sæer de fremidige ydelser lig låneprovenue. I den siuaion hvor boliginveseringen ikke er geare, hvad i øvrig angår egenkapialen, må finansieringsomkosningen ænkes som en offeromkosning, dvs. som de afkas, der kunne være opnåe ved invesering i e subsiuerbar akiv (akiv med samme risiko. De kan være hensigsmæssig a anage, a de neop er afkase på en realkrediobligaion med samme varighed som de obligaioner, der anvendes il fremmedfinansieringen. Dermed anvendes der blo e udryk for finansieringsomkosningen, nemlig reneomkosningen efer ska. Figur 3.3. viser udviklingen i prisen på realkredifinansiering i perioden
20 Figur 3.3. Finansieringsomkosninger årig obligaionslån Byggerenen, kor Byggerenen, lang Periode: , kilde: Danmarks Naionalbank og Realkrediråde Figur 3.3. viser, a der i perioden har være fald i den effekive rene på realkrediobligaioner med 3 års løbeid. Dee reducerer user cos udrykke, hvilke naurligvis lægger e opadgående pres på boligpriserne. Siden 996 har der være mulighed for a benye en kor rene ved realkredifinansiering. De kore rener er, som figuren viser, lavere end de lange, og der kan således være ale om en dobbel renefaldseffek, ide renekurven for de førse er falde, og boligejerne samidig har fåe mulighed for a bevæge sig indad på kurven. Med korfrisede lån løbes en refinansieringsrisiko, hvilke hæmmer de opadgående prispres. De er vigig i forbindelse med modelovervejelser, a anvende en rene, der både indeholder muligheden for a finansiere huskøbe med en kor rene og med e radiionel realkredilån. Dee kunne være en gennemsnilig rene. Boligskaer Ejerboligen pålægges ejendomsska 8 og ejendomsværdiska 9. Disse skaer er en del af omkosningerne ved boligbenyelse og er således relevan for prisdannelsen. Ejendomsskaen, der også kaldes grundskyld, beregnes som en promille af ejendommens grundværdi. Den såkalde grundskyldspromille fassæes af de enkele kommuner. I 24 varierede grundskyldspromillen fra 6 il Ejendomsbeskaningsloven, se evenuel 9 Ejendomsværdiskaeloven. 5
21 Ejendomsværdiskaen opgøres progressiv. Ejendomsværdiskaen beregnes i 25 som % af den del af beregningsgrundlage, der ikke oversiger kr og som 3 % af resen. Ejendomsværdiskaen er afløser for den idligere lejeværdiska, hvor man beale indkomsska af ejendommes lejeværdi. Ska i forbindelse med ejendomssalg ignoreres i nærværende afhandling, ide reglerne er for komplekse il a modellere, og da gevinser ved frasalg af ejerbolig, der har være brug il egen benyelse, undagelsesvis er skaefrie. Skaesasen for skaepligig indkoms har naurligvis også beydning for prisdannelsen. De sker ved fassæelse af den disponible indkoms, hvor en lavere skaesas naurligvis vil øge den disponible indkoms og dermed lægge e opadgående pres på huspriserne. Omvend vil en lavere skaesas reducere skaefradrage ved fremmedfinansiering, hvilke lægger e nedadgående pres på huspriserne. Disse skaeforhold medages indireke, ide de frarækkes variablene for indkoms og rene. Afskrivninger En ejerbolig er naurligvis udsa for sliage, hvilke kommer il udryk i en løbende værdiforringelse. Afskrivninger kan også ses som e udryk for de løbende omkosninger, boligejeren har il isandsæelse. Derfor må afskrivninger indgå som en del af ejers omkosninger. Den nøjagige sliage er uhyre svær a esimere, og i empiriske undersøgelser afskrives boligbeholdningen derfor med en fas procensas på procen, m.a.o. anages de, a den årlige vedligeholdelsesomkosning er procen af huses værdi. Dee er imidlerid ikke hel problemfri, og som Andersen (992 har påpege i forbindelse med makromodellerne, er der risiko for, a e forker valg af afskrivningsprocen forplaner sig i modelesimaerne. Forvenede kapialgevinser Forvenede kapialgevinser på ejerboliger skal være en del af user cos udrykke, ide forvenninger om sigende konanpriser naurligvis holder omkosningen ved a benye egen bolig nede. Ud fra den beragning, a byggeomkosningerne på lang sig alene er besemmende for prisen på de eksiserende boliger, kan de være hensigs- Ejendomsavancebeskaningsloven. 6
22 mæssig a anvende e udryk for den forvenede inflaion i byggeomkosninger som udryk for den forvenede kapialgevins på ejerboliger. Pedersen (24 udvikler, i forbindelse med en analyse af prisudviklingen på ejerboliger, e udryk for den reale husleje ved a bo i ejerbolig, hvilke er user cos, som definere foroven gange med konanprisen deflaere med den generelle prisudvikling: Real husleje for ejere = user cos [konanpris/forbrugsdeflaor] (3.2 Udrykke i (2.2 skal ifølge Pedersen være konsan i fravær af en boligboble. Med indførelsen af reneilpasningslån og senere de afdragsfrie lån i 23, har boligejere, der har valg disse lån accepere en refinansieringsrisiko. De kan således diskueres, om denne risiko ikke er med il a holde omkosningerne ved a benye egen bolig oppe, i den forsand, a user cos udrykke burde indeholde e risikoillæg i ak med, a boligejerne vælger de mere risikobeonede lån. Senes har de være mulig a vælge en finansieringsform, hvor man kombinerer e reneilpasningslån med en reneopion. En såkald rene-cap. Reneopionen er naurligvis ikke grais, og den finansieres enen ved e fradrag i låneprovenue eller ved e illæg il den kore rene. E sådan illæg eller en højere effekiv rene som følge af e fradrag i låneprovenue, skal naurligvis være indehold i user cos udrykke som en hedgeomkosning i procen, og de er uanse, om den er eksplici eller ej Demografiske forhold Den absolue boligbeholdning er ikke e meningsfyld mål, men bør ses i forhold il analle af poenielle købere. Derfor ses de ofe i empiriske sammenhænge, a boligbeholdningen deflaeres med befolkningens sørrelse, eller a befolkningsalle indgår som separa variabel. Befolkningsalle kan dog være e uhensigsmæssig mål, da analle af poenielle købere bl.a. afhænger af andelen af enlige. Således kan analle af poenielle købere god sige, selvom befolkningsalle er konsan eller faldende. user cos = gennemsnilig rene efer ska boligskaer i pc. afskrivningsrae forvenede kapialgevinser risikopræmie, der er de gennemsnilige hedgeomkosninger i pc. 7
23 En hyppig anvend forklaring på de senese års prissigninger er, a den primær er dreve af udviklingen i Århus og København, og a den skyldes kombinaionen af neoilflyninger og knaphed på boliger (se eksempelvis Vismandsrapporen (FO25 eller Wagner (25. Dee afvises imidlerid af Madsen (25 som en fundamenal forklaring på de generelle prissigninger. Hvis neoindvandringen il København er sege, bør huspriserne i omegnskommunerne være falde, hvilke ikke er ilfælde. Figur 3.4. viser den geografisk fordele prisudviklingen mellem by- og landzoner Figur 3.4. Geografisk fordel prisudvikling Gns. pris pr. kvm i byzoner Gns. pris pr. kvm i landzoner Periode:. kvaral kvaral 25, kilde: Egen ilvirkning efer Realkrediråde De nominelle kvadrameerpriser, som fremgår af figuren, er funde på baggrund af konsruerede prisindeks (se bilag 2 for en gennemgang af beregningsmeoden. Af figuren fremgår de, a der eksiserer en beydelig divergens i prisudvikling mellem by- og landzoner. Tabel 3.. viser analle af neoilflyninger af hussande il byzoner, der er beregne som forskellen på il- og fraflyninger over kommunegrænserne og nye boligarealer, der er beregne som ændringen i den oale boligbesand mål i usinde kvadrameer (se bilag 3 for en gennemgang af beregningerne. Hvis de o serier summeres, og man herefer finder den værdi, der sæer analle af neoilflyninger lig de nye boligareal, får man værdien 42. Dee ækvivaleringspunk kan olkes som de boligareal, de ilflyende hussande i gennemsni skal eferspørge, hvis der i perioden skal være lige- 2 Byzoner er definere som København, Frederiksberg og Århus kommune. 8
24 væg mellem marginal udbud og eferspørgsel, dvs. hvis knaphedsargumene ikke skal være holdbar i byzonerne. Tabel 3..: Neoilflyning og nye boligarealer Neoilflyning il byzoner (hussande Nye boligarealer i byzoner (usinde kvm Kilde: Egen ilvirkning efer Danmarks Saisik Knaphedsargumen kan også finde søe i, a Hovedsadens Udviklingsråd, HUR, i deres Regionsplan 25 3, vurderer en mangel på ca.. boliger i Sorkøbenhavn Fakorer, der påvirker udbudde På hel kor sig ligger udbudde fas. Periodens udbud svarer il boligbeholdningen primo, dvs. boligbeholdningen primo den foregående periode plus denne periodes boliginveseringer minus afskrivninger. Da inveseringerne ager id, og ligesom afskrivningerne, er beskedne i forhold il den eksiserende boligbeholdning, vil priseffeken af nye inveseringer srække sig over id. På lang sig er inveseringsomfange, mål i forhold il boligbeholdningen i udgangssiuaionen, naurligvis beydelig. Generel findes o yper af inveseringer. Den førse er de profimoiverede privae inveseringer, og den anden er de offenlig søede inveseringer. Den adfærd, der ligger il grund for de privae inveseringer, kan beskrives ved Tobins Q-eori efer Tobin ( Privae boliginveseringer & Tobins Q-eori Tobins Q-eori beyder, a så længe den marginale pris er sørre (lavere end de marginale omkosninger, vil byggeindusrien ekspandere (konrahere, forudsa a der er ledige ressourcer i økonomien. Dee sker, når Q-værdien, der er forholde mellem den marginale pris og de marginale byggeomkosninger, er sørre end (mindre end. Byggeindusrien kan karakeriseres ved fuldkommen konkurrence, og dermed kan gennemsnilige priser og omkosninger benyes som empiriske modparer, forudsa a der hverken er skala- eller scope-økonomier. Endvidere er kapialkravene i byggeindusrien forholdsvis beskedne, adgangen il finansiering er uproblemaisk, og indusri
25 en har dermed en beydelig evne il a ilpasse sig ændringer i profimarginen, dog som nævn med en vis forsinkelse. På lang sig er udbudselasicieen mh. profimarginen derfor uendelig sor, forudsa a der er ledige ressourcer i økonomien og ikke knaphed på byggegrunde, mens den på kor sig er nul Boligmarkedes dynamik: Byggeomkosninger som prisanker Ovensående indikerer en særlig dynamik i prisdannelsen på boligmarkede. De kan siges, a kausalieen på boligmarkede på sig vil vende, så prisen går fra a være eferspørgsels- il udbudsbesem. De skyldes a udbudselasicieen er forskellig på kor og lang sig. På kor sig faslægges konanprisen på baggrund af primobeholdningen af boliger, den sidse periodes konanpris (pga. en vis ræghed i priserne 4, og simulan med eferspørgslen. Eferspørgslen besemmes af forskellige økonomiske fakorer som de generelle prisniveau, den disponible indkoms og user cos, indkoms. Herefer faslægges inveseringsbesluningen på baggrund af Q-værdien, hvilke efer afskrivninger giver ulimo beholdningen. Sådan genager boligmarkede sine funkioner i hver periode, indil ilpasningen er fuldsændig, dvs. indil Tobins Q er. Boliginveseringerne er dermed den mekanisme, der skubber boligmarkede ilbage i sin ligevæg. De siges derfor, a priserne på lang sig er forankre i byggeomkosningerne, og a afvigelser herfra kun er korsigede som konsekvens af sød il økonomien. Figur 3.5. illusrerer hvorledes byggeomkosningerne fungerer som e anker for prisudviklingen (Tobins Q. Den slangende adfærd omkring regressionsrenden indikerer, a der er en hvis ræghed i ilpasningen jf. Dam ( Dam (995, p. 6. 2
26 Figur 3.5: Byggeomkosninger som boligmarkedsanker 2..6 Konanpriser Byggeomkosninger Kilde: ADAMs daabank Boligmarkeds dynamik kan illusreres med en gennemgang af scenarier med forskellige eksogene sød. Gennemgangen ager udgangspunk i Dam ( Scenarioanalyse: Permanen renefald De senese års prissigninger argumeneres ofe som værende en konsekvens af e lav reneniveau. E permanen renefald vil påvirke boligmarkede via eferspørgslen igennem user cos udrykke. En lavere rene øger eferspørgslen pga. lavere finansieringsomkosninger, hvilke på kor sig hæver konanprisen. I overenssemmelse med Tobins Q-eori vil dee skabe inciamen il a øge boliginveseringerne. De sørre inveseringer beyder en sørre boligbeholdning ulimo. I den næse periode vil den sørre beholdning skabe e pres nedad på priserne, men samidig eksiserer der en vis ræghed i priserne. Den samlede effek vil være neoposiiv de førse år efer renefalde, men på e idspunk vil effeken af den sørre boligbeholdning forskubbe ræghedseffeken, og konanprisen vil begynde a falde mod si udgangspunk. På lang sig vil boligbeholdningen være øge så mege, a de neop modsvarer den posiive effek af de permanen lavere finansieringsomkosninger. En sådan cyklus er langrukken, og den fulde ilpasning sker over e par generaioner 5. Effeken af e renefald er således ransiorisk på prisen men permanen på boligbeholdningen. 5 Dam (995, p
27 Scenarioanalyse: Øgede byggeomkosninger En permanen forøgelse af byggeomkosningerne vil naurligvis gøre de mindre profiabel a invesere, og inveseringerne vil således begynde a falde. Falde i boliginveseringer vil reducere beholdningen, og give uændrede eferspørgselskomponener, vil dee presse konanpriserne opad. Denne proces forsæer, indil de mindre udbud har øge konanprisen ilsrækkelig il, a de igen bliver arakiv a invesere. Dee sker, når effeken har øge konanprisen i e omfang, der neop svarer il signingen i inveseringsprisen. På lang sig vil en permanen signing i inveseringsprisen give sig il udslag i en ilsvarende signing i konanpriserne, der i modsæning il scenarie med e renefald, forbliver permanen Boligmarkede som e sysem af inegrerede ligninger Af ovensående gennemgang fremgår de, a eferspørgslen, der er besemmende for prisen på kor sig, er en funkion en række økonomiske fakorer, hvilke generel kan skrives som: phk d = f (, fyd, uc,... (3.3 pc Hvor phk er konanpriserne, pc er de generelle forbrugerpriser, fyd er den disponibel realindkoms og uc er real user cos. Udbudde af boliger er periodens primobeholdning, der svarer il sidse periodes ulimobeholdning, k : s (3.4 = k Ulimo beholdningen defineres som: k = k ih a k, hvor ih = g,... ihx pi phk ( (3.5 Hvor ih er nye inveseringer i boliger, der er en funkion af profimoive og de offenlig søede projeker, ihx, mens a er afskrivningsraen. Konanprisen besemmes som: 22
28 phk h d s, phk (3.6 = ( I ligevæg macher eferspørgslen udbudde. Den reale værdi af boligbesanden er konsan, da nye inveseringer neop svarer il afskrivningerne. Den reale boligpris er også konsan svarende il byggeomkosningerne. I afsni 4 benyes ligningssyseme il a udvikle en dynamisk model for prisdannelsen 3.5. Beydningen af lejemarkede Lejemarkede er de enese marked, hvor man kan observere en fysisk opsplining mellem ejerboligen som kapialgode på den ene side og boligydelsen på den anden side. Man må forvene, a huslejen på lejeboliger er relevan i en analyse af boligpriserne, ide disse kan berages som en alernaivomkosning. Generel må de gælde, a huslejen ved a bo i egen bolig skal svare il huslejen ved a benye en lejebolig. Når dee ikke er ilfælde, må man forvene, a der sker subsiuering indil ligevægen igen er oprehold. Den eori, der indil videre er beskreve, foreager ikke en eksplici skildring mellem leje- og ejerboligmarkede. I sede anages de, a den omale effek indgår via prisen på andre forbrugsgoder. 23
29 4. Udledning af dynamisk prisdannelsesmodel Den dynamiske ilpasningsmodel, der er udvikle af Andersen e al. (993, ager udgangspunk i esen om byggeomkosninger som udgangspunk for prisdannelsen. Den eoreiske model bygger samidig på en eksplici sondring mellem markede for boliger og markede for boligydelser, dvs. mellem prisen og dividenden. Boligmarkede opdeles i e marked for boligydelser og e marked for boliger, og hovedesen er, a boliger vil blive eferspurg op il de punk, hvor nuidsværdien af de forvenede fremidige boligydelser svarer il konanprisen. Den eoreiske prismodel er således en variaion over fundamenalmodellen. Som de indireke fremgik af forrige afsni, er fundamenalmodellen kun anvendelig, hvis esen om ilpasningsmekanismen ikke er holdbar. I de ilfælde er de nemlig udelukkende eferspørgselskomponenerne, der besemmer prisen. Da de ikke kan anages a være ilfælde, skal dynamikken i udbudde indarbejdes i modellen 6. Eferfølgende gennemgås derfor en dynamisk model for prisdannelsen på boligmarkede, dvs. en model, der ager højde for de ineressane skif i prisdannelsen på kor og lang sig. For dealjer om udledningen henvises il bilag Markede for boligydelser Husholdningernes eferspørgsel i en given periode besemmes ved a afveje, hvor sor en andel af periodens disponible indkoms, der skal bruges på boligydelser, og hvor sor en andel, der skal bruges på ande forbrug. De kan som nævn diskueres, hvorvid indkomsen er den korreke forbrugsdeerminan, da periodens formueeffeker ignoreres. De anages dog eferfølgende, a eferspørgslen efer boligydelser i periode er en sigende funkion af periodens relaive pris og den disponible indkoms: pcxh d = f (, yd (4. pb Hvor pcxh er prisen på øvrige forbrugsvarer, pb er enhedsprisen på boligydelser, og yd er den disponible indkoms. Da boligydelser kun handles i forbindelse med udlejning, er pb ikke en pris i normal forsand, men afspejler derimod en subjekiv vurdering af værdi af boligydelsen. 6 Andersen e al. (993, p
30 Udbudde af boligydelser afhænger il enhver id af boligbeholdningen. Beholdningen af boliger ligger som nævn fas på kor sig. Udbude af boligydelser anages derfor a kunne beskrives som: s θ (4.2 = k Hvor k - er boligbeholdningen ved sluningen af forrige periode og således primo beholdningen i indeværende periode, og θ er en proporionaliesfakor. I ligevæg gælder: pcxh θ k = f (, yd (4.3 pb Hvilke omskrives il: pb pcxh h yd, k (4.4 = ( Prisen på en boligydelse er således sigende i pcxh og yd og faldende i k. Den subjekive værdi af boligydelser siger alså med den disponible indkoms og med de generelle prisniveau, mens værdien falder, når udbude siger Markede for boliger Andersen e al. definerer i e perfek kapialmarked uden ransakionsomkosninger og med risikoneurale invesorer følgende arbiragebeingelse: phk r ( dir = E ( pb d E ( phk ( a phk phkeje (4.5 Hvor phk er prisen på en bolig på idspunk, r er renen, der med anagelsen om risikoneuralie er den konsane risikofrie rene, og dir er skaesasen for kapialindkoms. Boligen producerer på idspunk den konsane ydelsesmængde d, der får den forvenede værdi E (pb d. Boligenheden kan efer afskrivninger sælges il den forvenede pris E (phk ( a. eje er sasen for boligskaer. 25
31 Arbiragebeingelsen i (4.5 svarer il definiionen på de forvenede afkas i dividendemodellen i (2.. Vensresiden angiver de neoafkas, der opnås ved a invesere phk på de finansielle markeder, mens højresiden angiver neoafkase ved en ilsvarende invesering i en ejerbolig, nemlig den forvenede værdi af boligydelsen, E (pb d, plus den forvenede salgspris, E (phk ( a, minus inveseringsprisen og skaeomkosningerne. Ved indsæelse af (4.4 i (4.5 og lid omrokering fås: phk pcxh h( yd, k d E ( phk ( a (4.6 ( r( dir eje E ( = Prisen på en boligenhed besemmes således af forvenningerne il forbrugerpriserne, den disponible indkoms, boligbeholdningen og den fremidige pris, der lægger en bund (lof for de akuelle priser, ide de forvenede fremidige prissigninger (fald allerede vil være indregne i priserne i dag. Derfor bør den viden, a boligpriserne på lang sig er forankre i byggeomkosningerne allerede påvirke den raionelle boligejers værdiansæelse i dag. Hvis man anager konsane rene- og skaesaser, og ikke forvener en eksplosion i prisen, kan (4.6 efer genagende subsiuioner omskrives il: d a phk = E ( pb i (4.7 ( r( dir eje i= ( r( dir eje i Hvor E (pb i er den forvenede værdi af boligydelsen på idspunke i. Prisrelaionen kan olkes som, a boliger eferspørges, indil prisen oversiger nuidsværdien af de fremidige boligydelser. Prisen på en ejerbolig er dermed en funkion af forvenningen il den fremidige disponible realindkoms og ikke mindse forvenningen il de fremidige udbud. Da boligbeholdningen ændres over id, kan (4.6 og dermed (4.7 ikke bruges direke i en dynamisk analyse. Den radiionelle nuidsværdimodel kan kun overføres il boligmarkede, når ilpasningsmekanismen er ude af drif af fundamenale årsager, dvs. når værdien af boligydelsen blo er en funkion af den disponible realindkoms. En 26
32 dynamisk analyse vil derimod kræve en indarbejdelse af de mekanismer, der skaber ændringerne i boligbeholdningen. Boligbeholdningen er i modellen af Andersen e al. besem akkura som i (3.5: k = k ih a k Bygherrens inciamen il a bygge e ny hus beskrives som sædvanlig i overenssemmelse med Tobins Q-eori, men i Andersen e al. er Q-værdien i ligevæg ubekend og udryk for kvaliesforskellen på nye og eksiserende boliger. Hvis der ikke er kapaciesbegrænsninger i byggeindusrien, vil der hele iden blive bygge, indil forfølgende er opfyld: phk = q (4.8 pi Byggeinveseringerne anages a være en sigende funkion af profimulighederne og inveseringerne i den foregående periode, ide høje byggeinveseringer implicerer høj kapacie: phk ih = g(, ih (4.9 pi Ligningen i (4.9 er naurligvis beinge af, a der er ledige ressourcer i økonomien, og da dee ikke alid er ilfælde, kan der på kor sig naurligvis være afvigelser fra ligevægsværdien af q uden a de fører il inveseringer. Hvis forbrugerpriserne, indkomsen, renen og de forskellige skaesaser anages a være eksogene, og hvis der samidig anages raionelle forvenninger, kan (3.5, (4.6 og (4.9 benyes il a foreage en dynamisk, pariel ligevægsanalyse af udviklingen i huspriserne, boligbeholdningen og byggeinveseringerne. Dee er den sædvanlige analyse af boligmarkede, der har være gennemgåe idligere i afsni
33 Som de har være nævn før, er realværdien af boligbeholdningen på lang sig konsan, inveseringerne svarer akkura il afskrivningerne, og byggeomkosningerne følger den generelle inflaion. På lang sig må derfor gælde, a phk = (πphk. Hvor π er den konsane inflaion. Anages de også, a den disponible realindkoms er konsan, får man fra (4.5: ( r ( dir eje a π q* = h( fyd*, k* d (4. Hvor q* er ligevægsforholde mellem phk og pcxh. Vensresiden angiver den reale husleje, mens højresiden angiver ligevægsværdien af boligydelsen. Den reale husleje er kun konsan, når boligmarkede er i ligevæg. Vensresiden er idenisk med de udryk, der er anvend af Pedersen (24, som argumenerer for, a en markan afvigelse fra de hisoriske gennemsni kan idenificeres som en boble. Ovensående viser imidlerid, a en afvigelse kan skyldes en uligevæg, der er skab af de korsigede eferspørgselspres. Teorien i Andersen e al. har o implikaioner for prisen, der begge skal være indehold i den samme empiriske model: Prisen på kor sig: phk = f pcxh, fyd, k, r( dir eje a π (4. ( Prisen på lang sig: phk = q pi De er selvfølgelig en mulighed a anvende en mere simpel model, der ignorerer boligmarkedes ilpasningsmekanisme. Dee vil nemlig gøre ligningen i (4.7 direke anvendelig. Dee er også kommenere i Andersen e al, men ignoreres foreløbig, da en sådan model anvendes i forbindelse med esimering og es af en nuidsværdimodel for boligmarkede. 28
34 4.3. Tes specifikaion og økonomerisk eori Inden der gives en konkre specifikaion il brug for den empiriske analyse, er de relevan a kommenere e par forhold ved økonomerisk analyse, da disse har beydningen for den anvende model. Granger & Newbold (974 påvise, a når o uafhængige ikke saionære processer regresseres op mod hinanden, vil man for ofe afvise nulhypoesen om ingen lineær sammenhæng il fordel for de ukorreke alernaiv 7. Er processerne derimod saionære vil problemerne med spuriøs regression kunne undgås. I empiriske sammenhænge aler man om kovarianssaionarie, hvilke er opfyld, når seriens middelværdi og varians er uafhængig af, og kovariansen mellem observaionerne x og x -s kun afhænger af afsanden -s. En serie er ikke saionær, hvis den besidder en enhedsrod. Dee er ilfælde for en random walk 8, hvor fejlledde er hvid søj, men hvor adfærden er mege persisen. En random walk siges a være saionær i førse differens, hvilke følger af hvid søj anagelsen. En differenssaionær serie (af førse orden går eferfølgende under beegnelsen I(. En serie, der allerede er saionær i niveau, beegnes derimod I(. De flese økonomiske variable besidder ikke saionære egenskaber i niveau og vil derfor være I(. Ved hjælp af de argumenerede Dickey-Fuller es 9 (ADF-es kan man ese for saionarie. Tessaisikken er dog hverken -fordel eller asympoisk normalfordel, da dee er beinge af saionarie. De kriiske værdier er i sede funde af Fuller og rapporeres sammen med oupue i de forskellige saisikprogrammer. For a opnå fuld syrke mod den alernaive proces, der kan indeholde både drifsled og en deerminisisk rend, bør ADF-ese gennemføres i de forskellige versioner. Som ovensående viser, er der overhængende risiko for spuriøse koefficiener, når o I( processer regresseres op mod hinanden, og generel vil ε = y θx være I(. 7 På e 95 % signifikansniveau kan de forvenes a nulhypoesen ukorrek afvises i 5 af regressioner. Granger & Newbold afvise nulhypoesen i op mod 85 % af sudies simulaioner. 8 x = m x - ε, hvor ε ~ i.i.d.n(,σ 2. 9 Δx = m m γx - β Δx - β k Δx -k ε. 29
35 Ovensående vise også, a en I( serie er differenssaionær, og derfor er de en løsning a regressere seriernes differenser op mod hinanden. Probleme er, a man herved miser den sammenhæng, der er posulere i seriernes niveau. Med andre ord miser modellen si raffinemen. Heldigvis er de mulig a finde værdier af θ, der gør fejlledde saionær i niveau. Når de er ilfælde siges x og y a være koinegrere. Inuiionen bag koinegraion er, a o variabler, som eksempelvis akiepriser og dividender, kore og lange rener eller huspriser og byggeomkosninger, kan besidde en synkroni, hvorved variablerne følges ad, i hver fald på lang sig. Når o variable er koinegrere, indgår de i en sabil langsigssammenhæng på rods af, a variablerne individuel ikke besidder sabile egenskaber. De beyder, a variablerne på lang sig ikke bevæger sig væk fra hinanden, men konvergerer mod en ligevæg. En speciel ype af dynamiske modeller er fejlkorrekionsmodeller. En fejlkorrekionsmodel er en model for den korsigede adfærd med en resrikion på langsigssammenhængen. En fejlkorrekionsmodel er derfor anvendelig, når en økonomisk eori posulerer en ligevægssammenhæng, der som minimum skal være opfyld på lang sig, eksempelvis konvergens mellem huspriser og byggeomkosninger. Der er o meoder il a esimere en fejlkorrekionsmodel. Den førs er a resringere langsigssammenhængen i overenssemmelse med en kend eoreisk ligevæg, og herefer konrollere de korsigede egenskaber. Den anden måde, som anvendes her, da Q-værdien er ubekend, er a esimere en fejlkorrekionsmodel med udgangspunk i en model for koinegraion. Når x og y er koinegrere med parameere θ, eksiserer endnu e I( variabel, der kan indgå i modellen: d ( y = α β ( L d( x γ ( L ε u (4.2 Hvor ε = y θx og u er hvid søj, og β(l og γ(l er lag polynomier i L lag. Dee er en fejlkorrekionsmodel med fejlkorrekionsparameere γ, hvor fejlkorrekionsledde er esimere, ide den eksake langsigsammenhæng ikke er kend på forhånd. Esimering af en sådan fejlkorrekionsmodel, hvilke er nødvendig i forbindelse med esimering af den dynamiske prisdannelsesmodel, kræver alså o rin, og kaldes derfor Engle & Grangers o-rinsprocedure efer Engle & Granger (987. Forolkningen af en 3
36 fejlkorrekionsmodel er, a fejlkorrekionsparameere udrykker periodens ilpasning mod ligevæg. Jo sørre parameer, jo sørre andel af ligevægsfejlen elimineres i hver periode. Hvis koefficienen il fejlkorrekionsledde i den dynamiske prisdannelsesmodel er sor, er de ensbeydende med, a boligmarkede hurig eliminerer præmien over byggeomkosningerne. Langsigssammenhængen mellem huspriser og byggeomkosninger i Andersens model er som bekend: phk = q pi Hvor q som nævn udrykker kvaliesforskellen på en eksiserende bolig og e nybyggeri i ligevæg. De må derfor anages, a q er mindre end. Inden de kan eses for koinegraion, må omkosningerne ved a bygge e hus faslægges. For a kunne ese hvorvid priserne på lang sig er forankre i byggeomkosningerne, anages de forenkle, a omkosningerne besår af selve byggeomkosningerne og prisen på byggegrunde: pi = f pibh, phgk (4.3 ( Hvor pibh og phgk er henholdsvis byggeomkosninger og priser på byggegrunde. Den konkree sammenhæng i (4.3 specificeres log-lineær: ln pi α α ln pibh α2 = ln phgk (4.4 Med anagelsen i (4.8 fås ln ln q ln pi z = β ln pibh β2 phk = β ln phgk z (4.5 Hvor β er lnq α, og z er e sokasisk fejlled, der skal være I( for, a huspriser og byggeomkosninger kan anages a være koinegrere. I Andersen e al. eses og anvendes fejlledde i en fejlkorrekionsmodel for prisilpasningen, som kaldes den dynamiske prisilpasningsmodel: 3
37 d ( ec = α β ( L d log f (. γ ( L ec u (4.6 Hvor f( er funkionsudrykke med de økonomiske fakorer, der i henhold il (4. forvenes a påvirke prisdannelse på kor sig, mens ec er de esimerede fejlkorrekionsled z. Modellen i Andersen e al. er en model for ilpasningen mod langsigsligevægen. Forolkningen af (4.6 er, a boligmarkede konsan er i en ilpasningsproces for a eliminere fejl, der er opsåe i foriden. Lag-specifikaionen er e udryk for, a ilpasningsprocessen ager id pga. en vis ræghed i boligmarkede. Da ilpasningen ikke foregår uforsyrre, er der medage forklarende variable på højresiden. I nærværende afhandling esimeres en variaion af den dynamiske ilpasningsmodel, hvilken kaldes den dynamiske prisdannelsesmodel: d log( phk = α β ( L d log f (. γ ( L ec u (4.7 Forolkningen af (4.7 er, a boligmarkedsafkase er en funkion af ændringer i de forhold, der har beydning for prisen på kor sig sam ligevægsfejlen Empiriske modeller I den danske lieraur har der være andre forsøg på a forklare prisdannelsen på ejerboliger i økonomeriske modeller. E par af modellerne har danne grundlag for den boligmarkedseori, der er beskreve foroven. Da meoden i de økonomeriske modeller er indukiv, er de relevan a gennemgå resulaerne af de forskellige modelesimaioner, ikke mindse for a have e naurlig benchmark il vurdering af den esimerede dynamiske prisdannelsesmodel. For en dealjere udledning af de enkele modeller henvises il originalkilderne eller oversigen i bilag 5. 32
38 4.4.. Boligmarkede i en simpel regressionsmodel De eoreiske grundlag er bl.a. lag af Groes & Møller (977, der med en simpel regressionsmodel undersøger i hvilke omfang, den generelle inflaion har påvirke prisdannelsen på parcelhuse og byggegrunde i perioden Efer en periode med prissigninger, der overgik den generelle prisudvikling, var der dengang, som der er i dag, en bred deba om, hvad der forårsagede prisudviklingen. Forfaerne konkluderede, a den primære forklaring var udviklingen i den disponible realindkoms, dlog(fyd, mens inflaionen, dlog(pc, ikke var slåe igennem i de omfang, de havde forvene. Endvidere fand forfaerne de anvendelig a definere en års-dummy for åre 96, der var e år med særlig sore prissigninger, og en dummy for den offenlige vurdering. Dummy variable ignoreres eferfølgende, da de ikke kan ilskrives nogen økonomisk mening udover a være e boblelignende led. Anagelsen i Groes & Møller er, a invesorerne i år afvejer nuidsværdien af de forvenede fremidige boligydelser med markedsprisen i år, og dermed benyer de modellen fra afsni 2. Den skønnede dividende dannes med udgangspunk i en række kende variable. Man anager, a eferspørgslen bl.a. er en funkion af priserne, de generelle prisniveau og den disponible realindkoms. Prisen er ikke den radiionelle konanpris, men derimod den priorierede pris, der er prisen med finansiering, herunder kursab, handelsomkosninger m.m. Da den priorierede pris ikke ækvivalerer en pengesum medages e korrekionsvariabel i modellen. De anages pga. variablenes eksponenielle karaker, a eferspørgslen er en muliplikaiv funkion af de nævne variable. De anages endvidere forsimple, a udbudde er en konsan plus en rend. De er selvfølgelig en grov forsimpling a anage, a udbudde på boligmarkede er dreve af en rend og ikke af e profimoiv. I forbindelse med esimering sæes eferspørgsel lig udbud, og der ages eferfølgende logarimiske differenser. Herved gøres modellen lineær, konsanerne elimineres og koefficienen il udbudsrenden vil pr. definiion så alene ilbage ide k k(- = k. Den endelig reducerede model for prisen er: d log php βd logkor β2d log pc β3 = β d log fyd ε 33
39 Hvor ε er hvid søj. Paramerene kan olkes som elasicieer, og sammer fra eferspørgslens elasicie overfor de enkele fakorer. Ved a bruge logarimiske differenser udrykker paramerene følsomheden overfor procenvise ændringer. En evenuel lagssrukur, der både giver eoreisk og empirisk mening, er ignorere, og således udrykker paramerene kun de korsigede effeker. Groes & Møllers model posulerer i sin enkelhed, a parcelhuspriserne er en log-lineær funkion af den samidige væks i den disponible realindkoms og den generelle inflaion. Esimaionsresulae fremgår af abel 4.. Tabel 4.. Esimaionsresula i Groes & Møller (977 Afhængig variabel: dlog(php Koefficien -saisik Konsan -,22 -,5 Korrekionsfakor dlog(kor -,39-3,65 Generel inflaion dlog(pc,76 4,55 Væks i disponibel realindkoms dlog(fyd,58 3,53 Periode: , R 2 :,83, DW: 2,49, kilde: Groes & Møller (977, p Resulaerne er med årsdummy for 96. Modellen vise sig signifikan og robus på empiriske daa. I modellen er indkomseffeken (,58 sørre end effeken fra inflaionen (,76. A inflaionselasicieen er forskellig fra er misænkelig, da realakiver som parcelhuse må forvenes a være inflaionsneurale. Den fundne indkomselasicie er desuden misænkelig sor. Groes & Møller forklarer den høje koefficien ud fra realisering af e behov om a blive boligejer. En anden forklaring kan være den simple anagelse om boligbeholdningen jf. kriikken af Andersen (992. Udover koefficienernes sørrelser er foregnene meningsfylde Blomgren-Hansen & Knøsgaards model for enfamiliehuse Boligmarkede spiller en cenral rolle i den pengepoliiske ransakionsmekanisme. De skyldes boligmarkedes inerakion med obligaionsmarkede og des rolle i opgørelsen af den privae formue og dermed i økonomiens samlede eferspørgsel. Blomgren-Hansen & Knøsgaard (978 opsiller en model for boligmarkedes inerakion med obligaionsmarkede og esimerer i den forbindelse effeken af inervenion, for a kunne vurdere muliplikaoreffeken af den føre pengepoliik. I forhold il nærværende afhandling er de blo den opsillede srukur for prisdannelsen på boligmarkede, der er ineressan. 34
40 Blomgren-Hansen & Knøsgaard undersøger markede for enfamiliehuse i perioden fra 2. halvår 96 il 2. halvår 977. I modsæning il Groes & Møller benyes konanprisen som prisbegreb, og på udbudssiden indføres nu en inveseringsrelaion, der esimeres simulan med konanprisen. Ud fra forsøg med en række variable finder forfaerne frem il en model, hvor den reale konanpris er forklare af boligbesanden pr. indbygger, u, den effekive obligaionsrene efer ska, i ( dir sam forvenede prissigninger E (π phk. Boligbesanden opgøres i sin moneære værdi og ikke som e fysisk anal. Indkomseffeken inddrages i modellen, ide konanprisen deflaeres med e imelønsindeks, w, hvorved boligens realværdi måles i imer. Eferspørgslen pr. indbygger kan, med underrykkelse af evenuel lag-srukur og med ignorering af dummyvariable, skrives log-lineær: d w = u log( phk i dir E u α log( phk log( ( log ( α α2 α3 π Hvor u er hvid søj. Ved a sæe eferspørgsel lig udbud findes konanprisrelaionen: phk k = β ε phk log( β log( β2 log( i ( dir β3 log E ( π w u Udbudde er i modsæning il Groes & Møller en sokasisk variabel, der er besem af inveseringsadfærden, der igen er besem af e profiargumen i overenssemmelse med Tobins Q-eori. Den effekive obligaionsrene er i modsæning il andre modeller endogen, ide formåle med sudie er a måle muliplikaoreffeken via boligmarkede af inervenion på obligaionsmarkede. De forvenede prissigninger modelleres med en AR model. Konanprisrelaionen er dermed en del af e sørre sysem af relaerede sokasiske ligninger og må derfor esimeres som sådan for a opnå unbiased og konsisene esimaorer. Resulae af sysemesimaionen er for konanprisrelaionen gengive i abel
41 Tabel 4.2. Esimaionsresula i Blomgren-Hansen & Knøsgaard (978 Afhængig variabel: log(phk /w Koefficien -saisik Konsan -3,73 27,47 Lagge boligbesand pr. indbygger log(k -2 /u -2 -,62 3, User cos log(i (-dir -,3 7,57 Forvene kapialgevins loge (π phk,25 9,4 Periode:. halvår halvår 977, R 2 :,99, DW:,7, kilde: Blomgren-Hansen & Knøsgaard (978, p Resulaerne er med dummyvariable. Med en forklaringsgrad på 99 % og signifikane paramere gav den esimerede model en god og robus forklaring på prisudviklingen i perioden. Konanprisrelaionen siger, a prisen er en funkion af boligbesanden pr. indbygger, den effekive obligaionsrene efer ska og forvenede kapialgevinser. Foregnene er meningsfylde, men koefficienen il den laggede boligbesand er sadig problemaisk. Den reciprokke værdi af koefficienen kan i Blomgren-Hansen og Knøsgaards model olkes som eferspørgslens elasicie mh. imeløn-pris forholde, da den sammer fra eferspørgselsfunkionen [α = -β - =,62]. Ifølge modellen forøges andelen af indkomsen, der bliver brug på ejerboligforbrug, når indkomsen siger, hvilke ikke virker inuiiv Danmarks Saisiks ADAM model Den senese version af Danmarks Saisiks makroøkonomiske model ADAM fra april 24 indeholder ca. 4. økonomiske variable og 2.25 relaioner, der beskriver den danske økonomi. ADAM følger som de andre makromodeller den keynesianske modelradiion og er således underlag Lucas-kriikken (se afsni 5... ADAMs daabank er den enese med al ilbage il 947 og er således anvendelig il analyser over en lang periode. Daabanken har danne grundlag for analysen af Andersen e al. (993, der benyede esimeringsperioden Ved esimering af den dynamiske prisdannelsesmodel er de derfor naurlig a forlænge med observaioner fra ADAMs daabank frem il 23. Den senese veldokumenerede boligmodel i ADAM er fra 995 (Dam (995, og den følger argumenaionen for oven, hvor de grundlæggende principper bygger på Blomgren-Hansen & Knøsgaard (978. Den senese version er dog fra 24, men den er kun sporadisk dokumenere i inerne arbejdspapirer. Der er imidlerid væsenlige forskelle på de o modeller, hvilke gennemgås eferfølgende. 36
42 Boligmodellen i ADAM ager udgangspunk i e sørre ligningssysem, der er gengive i (3.3, (3.4, (3.5 og (3.6 i en noge komprimere form. Funkionsudrykke i (3.3 operaionaliseres ved a skrive eferspørgslen som en log-lineær funkion: phk θ phk pcxh log d = α α θ log( log( α 2 log fyd α 3uc α 4π u pcxh θ pcxh Hvor u er hvid søj, og hvor en vis ræghed i priserne acceperes. Den generelle inflaion er udelukkende medage for a få user cos udryk i reale ermer. Ved a pålægge den sædvanlige ligevægsbeingelse fås konanprisrelaion i 995-modellen: phk log pcxh = k fyd phk pcxh β β log β2 log β3 β4π β5 log pcxh uc ε Paramerene i konanprisrelaionen relaerer sig naurligvis il eferspørgselsfunkionen. Erfaringen fra de idligere sudier viser, a eferspørgslens indkomselasicie bliver for sor, og de er derfor hensigsmæssig a resringere denne il (α 2 =, hvilke beyder, a udviklingen i boligbeholdning udvikler sig parallel med indkomsen i modellen. Denne resrikion forplaner sig i konanprisrelaionen da α 2 = -β 2 / β hvorved -β 2 = β. I abel 4.3. er esimaionsresulae vis. Tabel 4.3. Esimaionsresula i ADAM (995 Afhængig variabel: log(phk /pc Koefficien -saisik Konsan,6 2,95 Lagge boligbesand log(k - -,83 7,65 Disponibel realindkoms log(fyd,83 7,65 User cos uc -6,7-7,42 Generel inflaion π pcxh,66 4,62 Lagge real konanpris log(phk - /pc -,52,7 Periode: , R 2 :,96, DW:,44, kilde: Dam (995, p. 67. Modellen er både signifikan og robus. Ud fra en eoreisk beragning bør en øge nominel rene som konsekvens af en øge inflaion ikke påvirke konanprisen. De sore forskelle på koefficienerne il user cos [-6,7] og inflaion [,66] kan derfor 37
43 undre. Simuleringer med ADAM 2 viser, a såfrem den nominelle rene og inflaion begge siger %, falder huspriserne 2 %. Dee kan ikke umiddelbar forklares ud fra eorien, men de er en indikaion på, a boligejerne, ud fra en empirisk beragning, er følsom overfor den nominelle husleje og dermed den nominelle rene. På baggrund af den esimerede model forecases huspriserne frem il 994. I forecase opsår der e problem med negaive residualer, da de esimerede priser i alle år oversiger de observerede priser, hvilke indikerer, a modellen ikke er i sand il a forklarer prisfalde i den pågældende periode. ADAM modellen udvikles løbende, og i senese boligmodel fra 24 er der en del ændringer. Den eoreiske model for konanprisen er som følger: d phk d cxh pche = β β β ln( ln( 2 ln( 3 ln( * b pcxh phk pcxh k d k ε I den nye udgave af konanprisrelaionen er indkoms ersae med real makroforbrug pr. indbygger i overenssemmelse med livscykelhypoesen, da eferspørgselsfunkionen efer boligforbrug nu også indeholder e formueudryk. User cos udrykke beregnes anderledes, og endelig er boligbeholdningen medage i en fejlkorrekionsform, hvor k* udrykker den ønskede boligbeholdning. Konanprisrelaionen esimeres simulan med ADAMs forbrugsmodel og udrykke for ønske boligbeholdning. Esimaion af konanprisrelaionen giver følgende resulaer: Tabel 4.4. Esimaionsresula i ADAM (24 Afhængig variabel: dlog(phk Koefficien -saisik Makroforbrug dlog(cxh /u phk,5 N/A User cos dlog(pche /phk pcxh -,4 N/A Fejlkorrekionsled dlog(k - /k * - -,58 N/A Periode: 957-2, R 2 :,66, DW:,2, kilde: Junge (24, p. 3. Modellen har mise en del forklaringsevne. En esimaion med daa fra giver en forklaringsgrad på 66 % og en Durbin-Wason saisik på,2, hvilke signalerer, a der er e problem med posiiv auokorrelaion i residualerne. Modellens for- 2 Dam (995, p
44 casevne i perioden efer 2 har være ringe, da der sysemaisk har være negaive residualer. Forklaring på, a modellen sysemaisk har undervurdere de fakiske boligmarkedsafkas, er e dårlig udryk for renen, da den ikke fanger effeken af de nye låneyper ilsrækkelig Syrker og svagheder ved økonomerimodeller Økonomerimodellerne har en hisorisk god evne il a forklare prisdannelsen, og esimaerne er i bred udsrækning meningsfylde. Erfaringerne med økonomeriske boligmodeller har o implikaioner for en analyse af prisfassæelsen. Enen bruges modellen på hele perioden, hvorefer modellens robushed overfor forudsæninger, modellens forklaringsevne og paramere vurderes i en eoreisk koneks. En sådan meode giver dog ikke noge direke svar på spørgsmåle om en boligboble, men kan signalere om priserne er afkoble fra de fundamenale fakorer. Den anden implikaion er, a de er mulig a esimere en model på baggrund af en del af sikprøven og herefer forcase priserne i den sidse del af sikprøven. På baggrund af residualerne mellem de fakiske og forecasede priser foreages den egenlige analyse. Dee er dog problemaisk, ide man ignorerer modellens basale egenskaber. En sådan meode er også underlag Lucas-kriikken (jf. afsni 5... Syrken ved en dynamisk model er hensyne il de eoreiske fakum, a dividenden er en funkion af priserne. Probleme er alså, a den ikke er en decidere model for bobler. Efer en gennemgang af modeller for den fundamenale prisdannelse i boligmarkede, gennemgås i næse afsni udvidelser il den radiionelle fundamenalmodel. Disse udvidelser illader nemlig e bobleelemen og giver nogle grundlæggende meoder il a ese for markedseffciens og fundamenalmodellen i e vilkårlig marked. 2 Junge (24, p
45 5. Udvidelse af grundmodellen I den dynamiske prisdannelsesmodel analyseres prisdannelsen med den anagelse, a forvenningerne er raionelle, og a markedspriserne kan forklares ved en model for nuidsværdien af fremidige dividender. I dee afsni gennemgås de eoreiske og empiriske implikaioner af, a disse forudsæninger opblødes. De eoreiske diskussioner i dee afsni relaeres eksplici il boligmarkede i afsni Raionelle forvenninger og den efficiene markedshypoese I Cuhberson (996 er den raionelle forvenningshypoese ensbeydende med, a invesorerne danner deres forvenninger beinge på al ilgængelig og relevan informaion, og a invesorerne ikke begår sysemaiske fejl. Invesorernes forvenninger vil derfor i gennemsni være korreke, hvilke beyder, a forvenningsfejlen, der er forskellen på den realiserede og forvenede pris eller afkas, i gennemsni er nul. De raionelle forvenninger kan derfor siges a være unbiased. En anden konsekvens af den raionelle forvenningshypoese er, a ingen kan have komparaive fordele på baggrund af de ilgængelige informaionssæ. De raionelle invesorer vil nemlig akkumulere al ilgængelig og relevan informaion i priserne, og indregne ny relevan informaion umiddelbar efer denne er ilgængelig. Således kan kun nyheder påvirke prisen. Da nyheder pr. definiion er uforudsigelige, skal forvenningsfejlen under raionelle forvenninger være uforudsigelig på baggrund af de ilgængelige informaionssæ. Denne egenskab er kend som den orogonale egenskab. Den orogonale egenskab er ikke opfyld, når der er serielkorrelaion i forvenningsfejlen. En inuiiv forklaring på dee er, a forvenningsfejlen på idspunk, ε, er en del af de samidige informaionssæ Ω, og a afhængighed mellem ε og Ω, forekommer ved afhængighed mellem ε og ε, dvs. ved serielkorrelaion i fejlledde. Egenskaber som unbiased forvenninger, orogonalie og også ieraive forvenninger, der er nødvendig for a kunne udlede nuidsværdimodellen, holder for beingede maemaiske forvenninger. De er derfor hensigsmæssig a anage, a den raionelle invesor danner sine subjekive forvenninger som den beingede maemaiske forvenning på den ilgængelige informaion 22 : 22 Cuhberson (996, p.. 4
46 x ε, hvor E ( ε Ω = og E ( ε Ω Ω = (5. = E ( x Ω A forvenningsfejlen opfylder egenskaberne for beingede maemaiske forvenninger er beinge af, a invesorerne kender og anvender den sande sokasiske model for økonomien. De skal bemærkes, a den raionelle forvenningshypoese ikke siller krav il de højere momener af forvenningsfejlen. Eksempelvis er de ikke e krav, a variansen i fejlledde er konsan. Ovensående definiion på raionelle forvenninger er også kend som Muh-RE efer Muh (96. Indil Lucas & Sargen (978 var de mes almindelige anagelser om forvenningsdannelsen mere simpel. Man anog, a forvenningerne var animal spiri, hvor ændrede forvenninger var præge af auonomi. Alernaiv anog man, a forvenningerne var adapive, ide forvenninger il fremiden kunne findes ved eksrapolering af hisoriske daa. Eksempelvis afhænger variablene i de keynesianske modeller (makroøkonomiske modeller udelukkende af hisorik. Essensen i den såkalde Lucas-kriik af disse modeller er, a de ikke er i sand il a forklare ændrede forvenninger ved indførelsen af en ny poliik, da den nye poliik ikke kan findes i hisorikken. De ændrede forvenninger kan imidlerid begrundes ud fra Muh-RE, ide invesorerne med Muhs definiion har andre variable i informaionssæe end hisoriske observaioner. Makromodellerne hånderer derfor ikke nødvendigvis forvenningsdannelsen korrek i forbindelse med forecasing. Sammenhængen mellem adapive og raionelle forvenninger er nemlig, a raionelle forvenninger er adapive, mens adapive forvenninger ikke nødvendigvis er raionelle. Indil Samuelson (965 var den efficiene markedshypoese forbunde med random walk modellen, men ved a kræve saisisk uafhængighed mellem successive prisændringer, er random walk modellen simpelhen for resrikiv. Den kan derfor opfaes som e særilfælde af den mere accepable fair game model, der af Samuelson blev udled under en række resrikive forudsæninger, hvilke dog ikke skal berøres nærmere. Den efficiene markedshypoese forbindes førs og fremmes med fair game modellen og med definiionerne hos Fama (97, 99. Dog har Leroy (989 påpege en auologi hos Fama (97, og derfor er de Leroys definiion, der i dag er udgangspunke i eoreiske fremsillinger og empiriske undersøgelser af kapialmarke- 4
47 der. Da auologien i Famas arikel ikke har beydning for nærværende problemsilling argumeneres der på e generel og inuiiv niveau uden skelen il forskellen på de o fremsillinger. E efficien (kapial marked kan defineres som: A marke in which prices always fully reflec available informaion (Fama (97, p The cenral idea of efficien capial marke heory is ha securiies prices are deermined by he ineracion of self-ineresed raional agens (Leroy (989, p. 63. Som de fremgår af ovensående definiioner, er raionelle forvenninger en del af den efficiene markedshypoese. En implikaion af den efficiene markedshypoese er, a de ikke er mulig a opnå anormale afkas, dvs. sysemaiske afkas udover en fair kompensaion for den underliggende risiko. Den forvenede forskel på de realiserede og de forvenede afkas er som nævn nul, og de indikerer, a en es af den efficiene markedshypoese også er en es af modellen for de forvenede afkas. De følger af fair game modellen for merafkase sam definiion på logarimiske afkas, a logarimen il prisen skal følge en random walk med drifen k, svarende il de konsane afkaskrav 23. I forbindelse med empiriske es skal man naurligvis være opmærksom på, a random walk modellen som nævne er mere resrikiv end fair game modellen. Kan random walk modellen bekræfes med empiriske daa, er der indikaion på, a markede er efficien i den svage form, som de følger af Famas (97, 99 inddeling af de efficiene marked i følgende re niveauer: Den svage form: Priserne afspejler al hisorisk informaion. Den semi-særke form: Priserne afspejler al offenlig ilgængelig informaion, herunder hisorisk informaion. Den særke form: Priserne afspejler al informaion, dvs. udover hisorisk og anden offenlig informaion, er markede også en afspejling af insiderinformaion. 23 R k = ε => ln(p /P - = k ε => lnp = k lnp - ε. 42
48 I Cuhberson (996 gives der en formel definiion på den efficiene markedshypoese, der kan benyes i empiriske es på alle re niveauer. Hvis de relevane informaioner, der er nødvendige for a kunne esimere afkase il idspunke i er give ved informaionssæe Ω, mens invesorerne omkosningsfri har adgang il informaionssæe P Ω, er de en beingelse for, a den efficiene markedshypoese er opfyld, a 24 : f P ( P R i Ω = f ( R i Ω (5.2 Beingelsen i (5.2 siger, a invesorer benyer den sande sokasiske model for afkas. Den efficiene markedshypoese og raionelle forvenninger kan herefer eses ved a regressere de realiserede afkas på de forvenede afkas og på e eller flere elemener fra informaionssæe, som er definere i e af de re niveauer: = γ η (5.3 P P P R E ( R ' Ω Såfrem γ eller η p er seriel korrelere, er de e brud på forudsæningen om raionelle forvenninger og dermed også e brud på efficienshypoesen. Ved esimering af (5.3 vil E (η p være nul og dermed unbiased ved konsrukion. Om de reelle forvenninger også er unbiased, afhænger som nævn af, om invesorerne anvender den sande sokasiske model for økonomien. Ligningen i (5.3 er en es for informaionsmæssig efficiens. I afsni 6 gennemgås Campbell & Shillers VAR meode il es af nuidsværdimodeller efer Campbell & Shiller (987. De er denne meode, der anvendes i afhandlingens empiriske del, da den ilbyder en særkere es for informaionsmæssig efficiens end (5.3. En regression af ypen i (5.3 kan god søe den efficiene markedshypoese, dvs. a forvenningerne dannes raionel og anagelsen om orogonalie er rimelig, uden a de observerede priser dog svarer il de fundamenale priser. De er fordi (5.3 er forenelig med raionelle bobler, der beskrives i næse afsni. Campbell og Shillers VAR meode har i modsæning il (5.3 den syrke, a den kan bruges il a idenificere en evenuel raionel boble. Afsluningsvis konkluderes de, a en implikaion af den efficiene markedshypoese og raionelle forvenninger 24 Cuhberson (996, p
49 er, a de observerede priser skal svare il de fundamenale priser, med mindre der eksiserer en raionel boble Beydningen af imperfeke markedsforhold Ifølge Fama (97 er der re beingelser for informaionsmæssig efficiens: der må ikke være ransakionsomkosninger, alle relevane informaioner skal være ilgængelig uden omkosninger, og alle skal være enige om implikaionerne af de ilgængelige informaioner. Beingelserne er ilsrækkelige men ikke nødvendige. Med høje ransakionsomkosninger følger de af Fama, a e inerval af priser kan forenes med markedsefficiens. Loven om én pris er således ikke e sreng udryk, hvilke er relevan i en analyse af boligmarkede. A der eksiserer en vis ræghed i priserne er derfor ikke nødvendigvis i uoverenssemmelse med raionelle forvenninger, men kan være en konsekvens af imperfeke markedsforhold som høje ransakionsomkosninger. Med raionelle forvenninger og med e frikionsløs boligmarked bør priserne ilpasse sig ny informaion øjeblikkelig. Men de kan imidlerid argumeneres for, a informaioner er væsenlig længere om a blive afsløre på boligmarkede end på de finansielle markeder, neop pga. særlige markedsforhold. Boligmarkede er derfor sjælden efficien i den forsand, der er påpege i de forrige afsni. Denne diskussion forsæes i afsni Raionelle bobler De eoreiske fundamen il forklaring af, hvorfor de fakiske priser afviger fra de fundamenale priser, går i o reninger. Den ene forklaring er i overenssemmelse med anagelsen om raionelle forvenninger, nemlig eorien om raionelle bobler, mens den anden forklarer afvigelsen ud fra psykologiske fakorer. Den førse eori gennemgås eferfølgende. Muligheden for spekulaive bobler under raionelle forvenninger kan vises med udgangspunk i ligningen i (2.3. I ligningen ses, a prisen i dag afhænger af prisen i morgen. En arbirær boble opfylder Euler-ligningen, så længe den forvenede værdi af boblen på idspunk i er en eksponeniel fremskrivning af værdien af boblen på idspunk 25. Derfor kaldes raionelle bobler også eksplosive bobler, da boblen for- 25 Camerer (989, p
50 venes a vokse med en konsan rae i hver periode. Raionelle bobler forekommer således som en alernaiv løsning il Euler-ligningen, hvor ransversaliesbeingelsen ikke er opfyld: δ B (5.4 i P = E ( D i i= Teorien om raionelle bobler siger, a prisen er summen af fundamenalledde og bobleledde, der naurligvis kan være nul, men aldrig negaiv. Er bobleledde nul svarer de fakiske priser il akives fundamenalværdi. Teorien harmonerer med anagelsen om raionelle forvenninger, og dermed om a markede er informaionsmæssig efficien, fordi priserne afspejler den ilbagediskonerede værdi af den fremidige boble. Risikoen for a boblen kan springe, er ikke e brud med raionelle forvenninger så længe sandsynligheden ilbagediskoneres med bobleledde. Den økonomiske inuiion bag bobleledde i (5.4 er, a markede kan være præge af selvopfyldende forvenninger, dvs. forvenninger il prissigninger kan i sig selv medføre højere priser, der igen medfører nye prissigninger osv. Dee er naurligvis forudsa, a der er mulighed for a sælge akive. Diba & Grossman (988 har vis, a en boble kun kan eksisere hvis B >, dvs. a boblen skal sare på førse handelsdag. Diba & Grossman viser også, a når boblen førs springer, kan den ikke sare igen. Tirole (982 har vis, a en raionel boble også kan opså, selvom invesorerne har forskellig informaion. På rods af, a dee var en forudsæning i udledningen af fundamenalmodellen. Tirole (982, 985 opsiller re fakorer, der er nødvendige for, a en raionel boble kan opså. For de førse skal akive være holdbar, da man skal have forvenning il en genslagsværdi, der skal endvidere være knaphed på akive eller i de mindse e uelasisk udbud på kor sig, da akive ellers kan ersaes, og endelig skal der eksisere en konsensus om forsa væks i priserne. Der eksiserer en række argumener mod raionelle bobler. Som de fremgår af Camerer (989 kan bobler sjælden forekomme, når forvenningerne er adapive, og under visse markedsforhold kan bobler også udelukkes. Beingelsen for, a der kan opså en boble er, a akive har uendelig leveid, ellers kan bobler udelukkes ved baglæns in- 45
51 dukion. Derfor kan der ikke eksisere bobler på eksempelvis obligaionsmarkede, da invesorerne kender obligaionens erminalværdi. E lignende argumen finder anvendelse, hvis der er velfærdsbegrænsninger eller begrænsede lånemuligheder, da dee vil begrænse bobleleddes udviklingsmuligheder. Hvis der er e endelig anal invesorer, som ikke lever evig, kan der heller ikke eksisere en boble. Hvis en enkel invesor sælger under en boble (for a finansiere si eferlønsforbrug, vil de reserende være ilbage med en forvene gevins, der er negaiv. Med raionelle forvenninger og raionelle handelssraegier indser de øvrige invesorer dee, og ingen vil nogensinde købe il boblepriser. Tirole (985 viser imidlerid, a denne resrikion kan opløses med en anagelse om overlappende generaioner, dvs. med en anagelse om e uendelig anal invesorer. Hvis man på e marked, som eksempelvis boligmarkede, kan udelukke raionelle bobler med ovensående argumener, kan man overveje om de i en diskussion af prisdannelsen er ilsrækkelig, blo a ese for den orogonale egenskab. Kriikken har jo være, a neop raionelle bobler kan gemme sig i en es for informaionsmæssig efficiens. Dee er dog ikke hensigsmæssig hvis markedsforholdene er imperfeke, og derfor arbejdes der uafhængig af muligheden for raionelle bobler, på en konkre es for bobler. En konkurrerende eori il raionelle bobler er eorien om nær-raionelle bobler. De nær-raionelle bobler kan opså, selvom analle af invesorer er endelig. Med raionelle forvenninger har ingen invesorer en bedre sraegi end gennemsnie, og alle vil derfor have en lige andel i den negaive sum. Såfrem invesorerne har endens il a være overopimisiske mh. egne evner, er der mulighed for en boble 26. De opimisiske invesorer forvener nemlig ikke a få andel i den negaive sum, og de er således villige il a handle il boblepriser. De samme er ilfælde, hvis markedes afgrænsning ikke er almen kend, og der er vivl om, hvorvid andre kender begrænsningerne. I de ilfælde er invesorerne villige il a handle il boblepriser, da man forvener, a andre vil købe il boblepriser, fordi de ikke kender begrænsningerne. Dee er kend som greaer fool bubbles Camerer (989, p Camerer (989, p.. 46
52 5.3. Naurlige bobler Froo & Obsfeld (99 har definere såkalde naurlige bobler, der er kendeegnende ved, a de relaerer sig il fundamenale markedsforhold. Naurlige bobler er en ikkelineær funkion i dividenden, og udviklingen i boblen er ikke nødvendigvis eksplosiv. Modellens Bobleled vokser (falder med en signing (fald i dividenden. Froo & Obsfeld har funde en løsning på bobleledde, der opfylder Euler-ligningen: i P = δ E ( D i B( D, hvor = i B D = cd λ ( og c >, λ > (5.5 Med en anagelse om, a den reale dividende følger en random walk med drif, kan bobleløsning i (5.5 skrives som 28 : 2 μ σ / 2 P = αd cd, hvor α = ( e r e (5.6 λ Hvor μ er drifsledde, og σ 2 er den beingede varians. Med en lineær ransformaion af (5.6 eses forekomsen af naurlige bobler ved: P / D = c c D η (5.7 λ Hvor nulhypoesen for ingen boble er H : c = α og c =. Dermed skal P og D være koinegrere med koinegraionsparameere θ = c = α. Er koinegraionsparameere sørre end α er der egn på, a markede overreagerer ved ændrede dividender 29. Froo og Obsfeld påpeger, a der er problemer med OLS esimaionen af boblemodellen, ide esimaorerne både er biased og inefficiene 3, hvorved en forolkning er problemaisk Irraional exuberance Den anden eori, der forsøger a forklare afvigelsen mellem fakiske og fundamenale priser, er eorien om irraionelle bobler, dvs. a markederne er præge af psykologiske 28 Cuhberson (996, p Cuhberson (996, p Cuhberson (996, p
53 fakorer (fads og noise raders. Grundlæggende deler eorien invesorerne i o grupper: de raionelle og de irraionelle. Fadshypoesen siger, a de irraionelle invesorer handler ud fra en række sociale og psykologiske fakorer, der ikke har noge med den fundamenale værdi a gøre. Noise raders er mindre informerede invesorer, der handler ud fra søj i økonomien. De er en gængs opfaelse, a de irraionelle invesorer neo vil abe på deres inveseringer, og derfor vil blive presse ud af markede af de raionelle invesorer, og forekomsen af noise raders er derfor ikke nødvendigvis i uoverenssemmelse med den efficiene markedshypoese 3. De er dermed e brud på den efficiene markedshypoese, hvis de irraionelle invesorer er i sand il a overleve i markede (se eksempelvis De Long e al. (99. Dee kan være ilfælde, hvis der på markede er en koninuerlig ilgang af irraionelle invesorer. Den eferfølgende gennemgang vil primær age udgangspunk i fadskomponenerne og eksplici relaere sig il Shillers bog Irraional Exuberance fra 25, der bl.a. beskriver psykologiske fakorer i de amerikanske boligmarked. Da de er svær a foreage en empirisk es af fadshypoesen og noiserading, vil begreberne udelukkende blive relaere il boligmarkede på e kvaliaiv niveau. I Irraional exuberance defineres en boble: a siuaion in which emporarily high prices are susained largely by invesors enhusiasm raher han by consisen esimaion of real value (Shiller (25, p. xviii En er grundpillerne i eorien er, a flere gunsige forhold skal være il sede, for a en boble kan opså jf. analogien om, a Rom hverken blev bygge på en dag eller ødelag af en enkel begivenhed 32. Eksempelvis er en leere adgang il kredi kombinere med faldende rene og en posiiv udvikling i indkomsen gunsig for skabelsen af en boble i boligmarkede, da de kan skabe enusiasme bland invesorerne og dermed forvenninger il forsae prissigninger. Irraional exuberance kan ikke opså uden boligmarkedsdaa 33, dvs. der skal være en koninuerlig rapporering i medierne af niveaue af boligpriserne, før en begejsring kan opså bland invesorerne. Førs fra miden af 99erne har Realkrediråde sy- 3 Cuhberson (996, p Shiller (25, p Shiller (25, p
54 semaisk offenliggjor saisikker om kvadrameerpriser på forskellige boligyper og på forskellige geografiske markeder. Shiller inddeler endvidere de gunsige forhold i re fakorer: srukurelle, kulurelle og psykologiske. De srukurelle fakorer er fremskyndende for irraional exuberance. I al nævner Shiller 2 begivenheder i de amerikanske marked, der kan binde en irraionel boble sammen. Uden a gå i dealjer med disse, kan de nævnes, a signingen i de privae ejerskab og en højere grad af maerialisme i samfunde gør en ejerbolig mere arakiv i sin egenskab af inveseringsobjek. Dee skaber e eferspørgselspres, der ikke kan forklares af de fundamenale fakorer. Shiller nævner, a en lav inflaion hos invesorerne opfaes som egn på en sund økonomi, hvilke kan være grundlag for en ubegrunde opimisme. I de danske boligmarked kan de ænkes, a sørre konkurrence bland krediinsiuionerne leer adgangen il kredi og dermed fremmedfinansiering i boligkøbe, hvilke kan fremskynde en boligboble. De srukurelle fakorer har en selvopfyldende karaker, og effeken forsærkes af mekanismer som invesorernes forvenninger og ilro il markede. E eksempel på en forsærkende mekanisme er, når invesorerne ror, a markede på lang sig ikke kan falde. E beslæge koncep er feedback looping 34. Teorien siger, a invesorernes forvenninger dannes adapiv, dvs. a prissigninger i sig selv fører il forvenninger om yderligere prissigninger. Feedback looping beyder, a når de srukurelle fakorer har udløs prissigninger, vil der gå resonans i markede, og prissigningerne vil således forsæe. Disse prissigninger vedligeholdes af bluf og svindel ( naurally occurring Ponzi schemes 35, hvor soryelling er en vigig ingrediens. I boligmarkede har krediinsiuionerne og ejendomsmæglerne en ineresse i høje priser. Disse grupper vil således forsøge a raionalisere prissigningerne med mere eller mindre vivlsomme argumener (se eksempelvis Madsen (25. Shillers eori er konroversiel, da den srider med den gængse opfaelse af invesorerne som raionelle og fremadskuende. Teorien virker dog mere rimelig i boligmarkede end i de finansielle markeder, da invesorerne i boligmarkede er privae personer, der ikke nødvendigvis har kendskab il økonomisk eori. Da boligmarkede endvidere bevæger sig i lange cykler, eksiserer 34 Shiller (25, p Shiller (25, p
55 endnu en forudsæning for, a forvenningsdannelsen kan blive adapiv frem for raionel. De kulurelle fakorer beskriver mediernes rolle som formidler af den spekulaive boble, ide medierne dyrker den spekulaive adfærd i sin sræben på a skabe ineressane hisorier. En anden kulurel fakor er invesorernes generelle posiive opfaelse af fremiden. De psykologiske fakorer beskriver forhold, der beyder, a markedspriserne ikke nødvendigvis er i overenssemmelse med den efficiene markedshypoese. I relaion il afhandlingens problemsilling skal nævnes de psykologiske fakorer, som forbindes med flokadfærd (herd behavior. Mennesker er nemlig som sociale væsner modagelig overfor den dominerende holdning i flokken 36. Dee perspekiv er e alernaiv il feedback looping eorien, da invesorernes forvenninger ager udgangspunk i andres forvenninger. Holdninger spredes i denne eori epidemisk bland invesorerne 37, der adaperer andres holdninger og ilsidesæer en subjekiv og raionel vurdering af prisen på e akiv. I de mes eksreme ilfælde siges de populær, a den blinde leder den blinde 38. E ande psykologisk begreb, der er relevan for nærværende afhandling er misundelse. Misundelse skal forsås i den forsand, a hisorier om sore gevinser i medierne eller hos bekende påvirker inveseringsbesluningen. 36 Shiller (25, p. 59, jf. Asch og Milgram sudierne. 37 Shiller (25, p Shiller (25, p
56 6. Campbell & Shillers es af nuidsværdimodellen I de eferfølgende gennemgås elemener fra Campbell & Shillers eori, som vil blive anvend i forbindelse med den empiriske analyse. Gennemgangen må således ikke opfaes som udømmende. Campbell & Shiller (987 ager udgangspunk i en radiionel nuidsværdimodel for o økonomiske variable, som siger, a Y er en lineær funkion af den ilbagediskonerede værdi af forvenede fremidige y, hvilke de skriver: Y i= i = θ ( δ δ E ( y c (6. i Hvor θ er proporionaliesfakoren mellem Y og y, δ er diskoneringsfakoren, og c er en konsan. Nuidsværdimodellen kan med raionelle forvenninger anvendes på renesrukuren 39, hvor Y og y repræsenerer henholdsvis lange og kore rener. Modellen kan anvendes på akiekurser, hvor Y er kursen og y er dividenden, og endelig kan nuidsværdimodellen anvendes på boligmarkede. E eksempel herpå er Black e al. (25, der eser en model, hvor den reale huspris er en funkion af den disponible realindkoms, ide de anages, a indkomsen er de bedse udryk for ilgængeligheden på boligmarkede. På rods af, a nuidsværdimodellen er forholdsvis simpel, eksiserer der en del konroverser i forbindelse med empiriske es af dens validie. For de førse er en saisisk afvisning af modellen ikke nødvendigvis de samme, som a modellen har dårlig forklaringsevne og således bør forkases ud fra e økonomisk perspekiv. For de ande eksiserer der e sor udbud af es i lierauren, og de er ikke klar, hvorledes disse es indbyrdes er relaere 4. Endelig er de ofe påkræve, a variablene er saionære, hvilke (formenlig førs opnås med differenser, hvorved modellen miser si raffinemen, da modellen neop er posulere i niveau. Modellen i (6. kan eses med en specifikaion svarende il ligningen i (5.3. Variablene skal imidlerid være saionære i niveau for a undgå problemer med spuriøsie 39 På renemarkederne anvendes VAR meoden il a ese pure expecaions hypohesis og derfor ikke om der forekommer en boble, men derimod om anagelsen om raionelle forvenninger er rimelig. 4 Campbell & Shiller (987, p
57 og dermed en ukorrek afvisning af raionelle forvenninger og nuidsværdimodellen. Endvidere er (5.3, som nævn idligere, forenelig med en udvidelse af (6., der indeholder en raionel boble, og derfor kan specifikaionen, selv med saionære variable, ikke bruges il a foreage en diagnosicering af boligmarkede i e fundamenal elemen og en boble. Med andre ord vil en model svarende il (5.3 ikke sige noge om, i hvilke omfang boligmarkede afviger fra sin fundamenale værdi. Campbell & Shiller løser probleme med ikke-saionære variable ved a definere en ny variabel: S Y θy S kan udrykke spredningen mellem kore og lange rener eller dividende-pris forholde på akie- og boligmarkeder. Så længe man har e surroga for boligmarkedes dividende, er der således ingen forskel på a anvende Campbell & Shillers meode på akie- og boligmarkeder. Ved a frarække θy på begge sider af (6. findes e alernaiv udryk af nuidsværdimodellen: S = E ( S * * c, hvor i S = θ δ Δy i (6.2 = i Ifølge (6.2 er S en konsan plus de opimale forecas, og S * er e væge gennemsni af fremidige ændringer i y. Da de kan forvenes, a y er differenssaionær, kan de også forvenes, a S er saionær i niveau. Herved er der funde e alernaiv udryk af nuidsværdimodellen, der kun indeholder saionære variable. De skal bemærkes, a de er ilsrækkelig a arbejde med variablene S og Δy for a analysere sammenhængen mellem Y og y 4. I de ilfælde hvor der eksiserer en raionel boble, vil højresiden af (6. indeholde e bobleled. Bobleledde vil være genage i (6.2, og da boblen er eksplosiv pr. kon- 4 Campbell & Shiller (987, p
58 srukion, vil der være eksplosiv adfærd i S. Denne adfærd vil også være overfør il ΔY. Dermed kan der eses for raionelle bobler ved a ese sabilieen i S og ΔY. Campbell & Shiller opsiller en VAR model for a kunne generere forvenede værdier af fremidige dividender eller for a være mere korrek ændringerne heri. I overenssemmelse med (6.2 kan man på den baggrund finde e eoreisk udryk for S. Udgangspunke for forvenningsgenereringen er e 2-variable VAR-sysem for S og Δy (frarukke deres middelværdier: Δy a( L = S c( L b( L Δy d( L S u u 2 (6.3 Eller: z = A z v (6.4 Hvor a(l, b(l, c(l og d(l er lag polynomier i p lag. Fejlledde u i er naurligvis e hvid søj led. VAR modellen kan bruges il a esimere forvenede fremidige værdier af Δy, ide de gælder a: E = i ( z i A z (6.5 Denne forvenning er dog beinge på e forholdsvis begrænse informaionssæ, der besår af nuværende og laggede værdier af Y og y. Den raionelle forvenningsdannelse er dermed begrænse il a være adapiv, dvs. der foreages eksrapolering på informaionssæe. En implikaion af dee er, a der skal være lineær Granger kausalie gående fra S mod Δy 42. Er dee ikke ilfælde, er de økonomeriske informaionssæ, der er indehold i VAR modellen ikke ilsrækkelig. 42 Campbell & Shiller (987, p
59 Ved subsiuering af (6.5 i (6.2 og ved hjælp af o selekionsvekorer g og h, der begge er rækkevekorer med 2p elemener, der alle er nul undagen de p. elemen i g og de førse elemen i h, der begge er, fås: S * i= i = i i i = θ δ Δy g z θ δ h A z (6.6 i= Hvilke yderligere kan reduceres il: g z = θ h δa( I δa (6.7 z Hvor de er udnye, a den uendelige sum konvergerer, da variablene er saionære 43. Højresiden af ligningen i (6.6 kan olkes som e udryk for den eoreiske værdi af S. Den eoreiske S er proporionaliesfakoren gange på forvenede fremidige ændringer i y. Konsanledde er fjerne, da variablene i modellen er afvigelser fra deres ubeingede middelværdier. I forhold il akie- og boligmarkeder udrykker højresiden af (6.6 alså de eoreiske dividende-pris forhold. Hvorvid de eoreiske dividende-pris forhold svarer il de fakisk observerede, som de jo er posulere i (6.6, kan vurderes på re måder 44. For de førse ved en grafisk vurdering af S mod S *, for de ande ved a undersøge om volailieen i de o serier er idenisk og for de redje vha. en Wald-es for de resrikioner (6.6 pålægger modellen. Selvom Wald esen er arakiv i sin egenskab af essaisik, er de en smule problemaisk a anvende esen i neop boligmarkede. Waldesen giver svar på spørgsmåle, om forskellen mellem S og S * skyldes ande end søj, dvs. sysemaiske forhold. Som de vil blive argumenere for i afsni 8.2., er der grund il a forvene en sysemaisk afvigelse alene pga. markedsforholdene i boligmarkede. Syrken ved Campbell & Shillers VAR meodik er, a nuidsværdimodellen kan esimeres og eses med e forholdsvis begrænse daasæ. Man har således kun behov for 43 i a =, hvis a <. i= a 44 Cuhberson (996, p
60 hisoriske observaioner af priser og dividender. Endelig giver VAR meoden ikke kun svar på nuidsværdimodellens validie i en saisisk henseende, i den forsand a nuidsværdimodellen enen fasholdes eller afvises. VAR meoden kan også bruges il a beregne den konkree præmie over fundamenalværdien (S S *, der i dee ilfælde svarer il boligboblen. 6.. Nuidsværdimodel for boligmarkede Som de har være nævn idligere, argumeneres der ofe for, a sammenhængen mellem e huslejeindeks eller indkomsen og boligpriserne, svarer il sammenhængen mellem dividender og akiekurser. Under visse forudsæning skal dee forhold være konsan. Kan de ikke forvenes, a dividenden er konsan eller har konsan væks, end ikke i reale ermer, holder en sådan analyse af dividende-pris forholde ikke. Dee problem kan løses ved a ese nuidsværdimodellen med VAR meoden. I dee afsni udvikles en nuidsværdimodel for boligmarkede og en ilhørende es specifikaion. Nuidsværdimodellen bygger på den mege vigige anagelse, a ilpasningsmekanismen, som er beskreve i forbindelse med de økonomeriske modeller, ikke fungerer af fundamenale årsager, hvilke eksempelvis er ilfælde, hvis der er knaphed i byggesekoren. Black e al. (25 formulerer i en analyse af ejerboligmarkede i U.K. en nuidsværdimodel med idsvarierende diskonering (se bilag 6 for dealjer om udledningen. Som surroga for boligmarkedes dividende anvendes den disponible realindkoms, og der anages idsvarierende diskonering. Anagelsen hos Black e al. er den sædvanlige anagelsen om, a markedsprisen svarer il den fundamenale pris på boligmarkede, når følgende beingelse opfyld: j P = i] Y j j = i= [ δ (6.8 P er den reale konanpris, δ er den idsvarierende diskonering, og Y er boligmarkedes dividende, der er angive ved den disponible realindkoms. Boligmarkedsafkas på idspunk defineres på radiionel vis som: 55
61 r ln( R (6.9 Definiionen i (6.9 gøres lineær med en førse ordens Taylor ekspansion omkring de geomeriske middelværdier af P og Y, og skrives derefer: r = k μ p ( μ y p, hvor P μ = (6. P Y Hvor p og y er logarimen il henholdsvis pris og dividende, og μ er en konsan i inervalle ];[, dog æ på. Ligningen for boligmarkedsafkase er ikke særlig inuiiv og kan ikke ilskrives nogen særlig økonomisk mening. Desuden indeholder ligningen variable, der ikke kan forvenes a være saionære, og er dermed ikke særlig anvendelig i en empirisk analyse. Ved a definere (log pris-indkoms forholde, S = p y, kan (6. reduceres il 45 : S μ (6. = k S Δy r Herved er der opnåe e udryk med saionære variable. Efer genagende subsiuion, med pålægning af ransversaliesbeingelsen og under anagelse af konsan afkaskrav fremkommer følgende ex ane udryk for den fundamenale sammenhæng i boligmarkede: * i S = μ EΔy i = i c, hvor k r c = (6.2 μ Ligningen i (6.2 svarer il modellen hos Campbell & Shiller (987 med en proporionaliesfakor på θ =. Ligningen kan olkes som, a pris-indkoms forholde er posiiv (negaiv relaere il posiive (negaive ændringer i den fremidige disponible realindkoms og afhænger derudover af en konsan, der igen afhænger af invesorernes konsane afkaskrav. En implikaion af (6.2 er, a pris-indkoms forholde god kan variere over id, uden a de er ensbeydende med, a der eksiserer en boble. Hvis pris-indkoms forholde afviger fra sin hisoriske middelværdi, kan de være for- 45 Bemærk a S-sørrelsen er vend om i forhold il de radiionelle dividende-pris forhold. 56
62 klare i modellen som ændrede forvenninger. Anagelsen om konsan afkaskrav gør modellen nemmere a esimere, men ud fra e eoreisk synspunk er anagelsen kriisk, da der kan argumeneres for, a indførelsen af nye realkrediproduker har beyde e sørre afkaskrav pga. den indføre refinansieringsrisiko, mens finansieringomkosningerne på den anden side er falde. Ligningen i (6.2 kan operaionaliseres med VAR meoden og de o selekionsvekorer, der er beskreve i foregående afsni. Således kan der findes e udryk for boligmarkedes eoreiske pris-indkoms forhold, S * : S * = g z = h A( I μ A z (6.3 Herfra følger den eoreiske boligpris: p * S y (6.4 = * Med en radiionel Wald es kan de eses, hvorvid S * = S er opfyld i saisisk forsand. Dee gøres ved a ese den implicie resrikion i (6.3: g ( I μ A = h A (6.4 Ligningen i (6.4 pålægger paramerene i A maricen en række resrikioner. For en gennemgang af disse resrikioner og af selve Wald esen henvises il bilag 7. 57
63 7. Empirisk analyse af de danske boligmarked Den empiriske analyse af de danske boligmarked ager udgangspunk i en esimering af o forskellige modeller. Den ene model er den dynamiske prisdannelsesmodel, som er gennemgåe i afsni 4. Teorien bag modellen er bl.a. udvikle af Andersen e al. (993 og ese i empiriske daa for perioden I den eferfølgende analyse reesimeres en variaion af den originale model med nye daa. En sådan ilgang virker uproblemaisk, men der er desværre en del problemer forbunde med a anvende daa fra ADAMs daabank. Disse problemer diskueres inden den egenlige esimering. Den anden model er en nuidsværdimodel for boligmarkede, der kan opfaes som e særilfælde af den dynamiske prisdannelsesmodel, hvor ilpasningsmekanismen er ude af drif. Nuidsværdimodellen for boligmarkede er udled i afsni Daa og foreløbige resulaer For en komple oversig over de anvende daasæ henvises il bilag 8. ADAMs daabank er opdaere frem il 23 og er udgangspunk for analysen. Herudover suppleres med daa fra Danmarks Saisiks, Danmarks Naionalbank og Realkrediråde. Daaene fra ADAM er årlige observaioner i perioden , mens de øvrige daa er kvaralsvise observaioner i perioden fra. kvaral 992 il 3. kvaral 25, der er sammensa af flere kilder. Daaene fra ADAMs daabank giver mulighed for a foreage en analyse i e mege lang perspekiv, men lider under e vis akualiesproblem. Derfor suppleres med nyere daa. I bilage er daaene gengive i niveau, mens de i analysen indgår under forskellige ransformaioner. Eferfølgende ages der udgangspunk i daaene fra ADAMs Daabank, medmindre ande er nævn. Konanprisen på enfamiliehuse (landsgennemsni er ilgængelig i indeksform i ADAMs Daabank og hos Danmarks Saisik, hvor der også findes daa for priser på ejerlejligheder (landsgennemsni. Hos Realkrediråde kan man finde kvadrameerpriser fordel på boligyper (parcel- og rækkehuse, ejerlejligheder og friidshuse og på områder (kommuner, hvilke gør de mulig a analysere prisdannelsen geografisk og på de forskellige boligyper. I lyse af den divergerende prisudvikling mellem Købehavn og resen af lande er sådanne saisikker selvfølgelig ineressane. Der er derfor på baggrund af daa fra Realkrediråde konsruere prisindeks for by- og landzoner (se evenuel bilag 2 for dealjer om konsrukionen af disse indeks. 58
64 A konanprisen, ligesom sørsedelen af de øvrige økonomiske fakorer, kun er ilgængelig i indeksform i ADAMs Daabank og hos Danmarks Saisik i almindelighed, er uproblemaisk i forhold il de økonomeriske modeller, da variablene ransformeres il logarimiske differenser for a undgå problemerne med spuriøsie. Tabel 7.. og abel 7.2. viser deskripive saisikker og resulae af en es for enhedsrødder i de forskellige prisbegreber. Tabel 7.. Deskripive saisikker for reale konanpriser (al i procen fphk fphk fphk2 fphk3 fphk4 fphk5 Realafkas p.a., hele perioden,89 4,97 7,2,49 6,78,39 Realafkas p.a., perioden efer 23 N/A,72 6,47 2,74,69 2,23 Sandardafvigelse p.a. 7,8 3,5 4,57 3,93 3,48 4,72 Kilder og perioder: ADAMs daabank: (fphk = pris på enfamiliehuse, Danmarks Saisik: 992k2-25k2 (fphk = pris på enfamiliehuse, fphk2 = pris på ejerlejligheder og Realkrediråde: 995k2-25k3 (fphk3 = gns. kvm. pris i byzoner, fphk4 = gns. kvm. pris i landzoner, fphk5 gns. kvm. pris på friidshuse. Anvend konvereringsmeode: r / = ( r /4 4, σ(r / = σ(r /4 4. Af ovensående abel ses, a prisudviklingen har være mes dramaisk i årene efer 23. Denne prisudvikling er desværre ikke indehold i de daa, der henes i ADAMs daabank, hvilke naurligvis må erindres i analysen. Prisudviklingen har være mes krafig i byzonerne (fphk3, på friidshuse (fphk5 og på ejerlejligheder (fphk2. De senese år har prissigningerne være sabile, hvilke kommer il udryk i en lavere sandardafvigelse. Tabel 7.2. Tes for enhedsrødder i reale konanpriser fphk fphk fphk2 fphk3 fphk4 fphk5 i niveau Med konsan -2,7,75,86 2,,2 3,75 Med konsan & rend -2,73-2,,49 5,92 -,4 2,4 Uden konsan & rend,93 2,78,75,23 2,32 7,27 i førse differens Med konsan -5,4 *** -3,64 *** -,26 3,25-2,5-3,45 *** Med konsan & rend -5,8 *** -2,37-2,22 2,34-2,26-4,36 *** Uden konsan & rend -4,92 *** -,54,5,26 -,77-2,7 ** Kilder og perioder: se noe under abel 7.. *** signifikan på 99 % niveau, ** signifikan på 95 % niveau, * signifikan på 99 % niveau. Vurdere på baggrund af Fullers kriiske værdier. Anvend laglængde: 5 år 59
65 Ikke overraskende må hypoesen om en enhedsrod i priserne acceperes, og de ses, a konanpriser il dels er saionære i førse differens, i hver fald med daa fra ADAMs daabank. De er imidlerid svær a afvise en enhedsrod i de mes akuelle og højfrekvene prisserier fra Danmarks Saisik og Realkrediråde. Resulaerne viser, a der er en høj grad af persisens i prisændringerne på især ejerlejligheder og i byzonerne (fphk2 og fphk3. I bilag 9 er vis resulaerne af es for saionarie i de øvrige variable, der indgår i daasæe. De ses, a daa for boligbeholdning (k i begge daasæ og inflaion i den lange serie (pcxh ikke har saionære egenskaber i førse differens, hvilke kan skabe spuriøsie i den dynamiske prisdannelsesmodel. For andre deskripive saisikker henvises il daasæe. Den generelle inflaion er i daasæe med årsdaa udryk ved e indeks for prisen på ande forbrug end boligforbrug (pcxh, mens der er brug e generel forbrugerprisindeks fra Danmarks Saisik (pc i de ande daasæ. I perioden har udviklingen i den nominelle konsanpris på enfamiliehuse oversege prisudviklingen på andre forbrugsgoder jf. figur 3.. I figur 7.. er vis udviklingen i den reale konanpris, hvor byggeomkosninger (pibh er anvend som deflaor. 2. Figur 7.. Real konanpris Periode: (955=, kilde: ADAMs daabank. Seriens middelværdi er,52, sandardafvigelsen er,24 og Jarque-Bara saisikken er,25. Figur 7. viser, a væksen i konanpriser generel oversiger udviklingen i byggeomkosninger (bemærk, a prisen på byggegrunde ignoreres. I 23 var realprisen på e niveau, der ligger knap 2 sandardafvigelser over de hisoriske gennemsni. Som de fremgår af idsserien, bevæger boligmarkede sig i cykler: efer en periode med real- 6
66 væks kommer en periode med fald. Dee var sids ilfælde omkring 98 og 99 og harmonerer i øvrig ganske god med boligmarkedseorien, hvor realprissigninger på sig korrigeres af e sørre boligudbud. En forsigig forolkning af prisernes anaomi er, a cyklerne er bleve korere og spænde mellem op og bund sørre. Siden 23 har de årlige realafkas på enfamiliehuse være knap 2 % (fphk. De høje realprisniveau i figur 7.. er således forøge yderligere, hvilke kan skyldes en boligboble. En høj realpris er ikke problemaisk på kor sig, hvis de fundamenale forhold illader de. Den disponible realindkoms anses for a være de dominerende argumen i boligprisen. I figur 7.2. er vis den hisoriske udvikling i indkoms-pris forholde. Dee forhold svarer som bekend il dividende-pris forholde på akier: e lav dividendepris forhold anses som en indikaion på en boble. Af figuren ses krafige udsving i begyndelsen af 98erne og 99erne, hvilke falder sammen med de sore fald i den reale konanpris. I 23 var pris-indkoms forholde æ på si hisoriske gennemsni. Med viden om prisudviklingen siden 23 er de plausibel, a dividende-prisforholde eferfølgende er falde e god sykke under si hisoriske gennemsni. Falde i indkoms-pris forholde siden miden af 99erne er e udryk for, a væksen i de reale huspriser oversiger den samidig væks i den disponible realindkoms Figur 7.2. Indkoms-pris forholde Periode: (955 =, kilde: ADAMs Daabank (fydk/fphk. Seriens middelværdi er,7, sandardafvigelsen er,2 og Jarque-Bara saisikken er 6,7. I ADAM modellen anvendes forskellige indkomsbegreber (yd, ydk, ydl og w. I forbindelse med esimaionen af den dynamiske prismodel er der prøve med de forskellige variable. yd-variablen dækker over den disponible indkoms i husholdningerne, der udover lønsummen også indeholder formueeffeker som resindkomsen i erhver- 6
67 vene, neorener og neoudbealinger fra pensioner. ydk-variablen er den korsigede indkoms, der er yd frarukke neoudbealingerne fra pensionsselskaber. ydlvariablen er den langsigede indkoms, der er definere som indkomsen i de privae erhverv frarukke afkas på pensionsopsparinger. w er lønsummen 46. I daasæe med kvaralsdaa er funde e lønindeks over indusrien hos Danmarks Saisik, som anvendes som udryk for husholdningernes indkoms. De, der er vigig, er a variablen fanger de marginale effeker, dvs. effeken af væksen i indkomsen, ikke a variablen er e god surroga i niveau. En redje fakor, der har beydning for prisen på kor sig, er ejers omkosninger, der er definere som finansieringsomkosninger plus boligskaer plus vedligeholdelsesomkosninger eller afskrivninger minus den forvenede inflaion i boligpriserne. På baggrund af denne user cos udvikler Pedersen (24 e mål for den reale husleje ved a benye egen bolig jf. (2.2. Den reale husleje er beregne på baggrund af daa fra ADAMs Daabank som: Husleje ] phk ejere, = [ i ( dir eje a E ( π (7. pcxh phk Hvor den forvenede inflaion i huspriser er,5 gange den forvenede inflaion i byggeomkosninger i overenssemmelse med hovedesen i boligmarkedseorien. Koefficienen er valg arbirær pga. en vis ræghed i prisdannelsen jf. abel 7.2 (se evenuel diskussionen i afsni Den forvenede inflaion i byggeomkosninger findes ved eksrapolering i overenssemmelse med ADAM modellen som: phk pibh pibh E ( π =,5[,75E ( π,25( ] (7.2 pibh På baggrund af ligningerne i (7. og (7.2 er den reale husleje ved a benye egen bolig beregne, og den hisoriske udvikling er vis i figur Se evenuel bilag 8 eller variabelbrowseren il ADAM modellen på 62
68 Figur 7.3. Real husleje ved a benye egen bolig Periode: (956=, kilde: ADAMs daabank. Seriens middelværdi er,48, sandardafvigelsen er,26 og Jarque-Bara saisikken er,73. De kan konkluderes, a den reale husleje ved a benye egen bolig ligger æ på de hisoriske gennemsni i 23, hvilke er i overenssemmelse med Pedersen (24. Konklusion er dog mege følsom overfor anagelsen om forvenede kapialgevinser, og billede er en del anderledes, hvis man lader inflaionsforvenningen slå fuld igennem (se bilag. I forbindelse med esimaionen af den dynamiske prismodel er anvend e nominel udryk for user cos (uc, da den generelle inflaion indgår som en separa variabel i modellen. Således er forvenede kapialgevinser ikke indehold i user cos variablen. Renevariablen, der er hene i ADAMs Daabank, har idligere være kriisere for ikke a fange effeken af de nye låneyper ilsrækkelig (Junge (24. I daasæe med kvaralsvise daa er user cos beregne på baggrund af reneindeks fra Naionalbanken (effekive rene på realkredi obligaioner med 3 års løbeid og Realkrediråde (kore og lange byggerener, og de er arbirær valg a lade de o rener indgå med samme væg. Boligbeholdningen (k er funde som den reale kapialværdi af den samlede boligbesand, dvs. både leje- og ejerboliger. Da der ikke kan findes ilsvarende saisikker med kvaralsvise observaioner, er daaene fra ADAM daabank inrapolere i de supplerende daasæ frem il 23, hvorefer boligbeholdningen er fremskreve med den gennemsnilige væks. 63
69 Inveseringsprisen indgår som en funkion af selve byggeomkosningerne (pibh og priser på byggegrunde (phgk. Hos Danmarks Saisik er der funde e byggeomkosningsindeks med kvaralvise observaioner Tes for koinegraion Den grundlæggende anagelse er, a huspriserne på lang sig er udbudsbesem af byggeomkosningerne, og der er derfor god grund il a forvene, a huspriserne og byggeomkosninger er koinegrere. Langsigssammenhængen mellem huspriser og byggeomkosninger er idligere i (4.5 funde il a være: log β β log pibh β2 phk = log phgk z Hvor z er fejlkorrekionsledde, der skal være I(, for a huspriser og byggeomkosninger kan anages a være koinegrere 47. For kvaralsvise daa findes kun al for pibh. Tesen gennemføres som e ADF-es for I( mod I(, hvilke er en illempning, da Fullers kriiske værdier ikke er hel velegne il koinegraionses 48. Tabel 7.3. Tes for koinegraion Afhængig variabel: log(phk Esimaionsperiode Koefficien -saisik Koefficien -saisik Konsan, 3,35 -,2 -,73 Byggeomkosninger log(pibh,69,7,53 9,24 Grundpriser log(phgk,26 5,44,34 9,43 Forklaringsgrad,99,99 ADF-es - med konsan -2,3-3,9 *** - med konsan & rend -,78-3,83 ** - uden konsan & rend -2, ** -3,97 *** *** signifikan på 99 % niveau, ** signifikan på 95 % niveau, * signifikan på 99 % niveau. Vurdere på baggrund af Fullers kriiske værdier. Anvend lag-længde: 5 år 47 Bemærk, a de implici er anage, a byggeomkosningerne er inegrere af samme orden som huspriserne, dvs. byggeomkosninger er saionære i førse differens. 48 Gujarai (995, P
70 Resulaerne i abel 7.3. bekræfer, med daa fra ADAM, a huspriser og byggeomkosninger (sadig er koinegrere, og resulaerne semmer i sore ræk overens med Andersen e al for perioden A der er mindre afvigelser mellem koefficienerne og de ilhørende sandardfejl, skal formenlig forklares ved, a variablene i ADAM i dag opgøres anderledes, men sadig udrykker de samme økonomiske fænomen. Syrken af esen er dog en del mindre i den længere daaserie, hvilke fremgår af figur 7.4, hvor der ses en afkobling mellem konanpriser og byggeomkosninger. Figur 7.4. Udvikling i huspriser, byggeomkosninger og priser på byggegrunde Konanpriser Byggeomkosninger Grundpriser Kilde: ADAMs daabank I bilag er vis resulae af es for koinegraion mellem byggeomkosninger og de øvrige konanprisbegreber. Anagelsen om koinegraion er noge sværere a accepere i de nyere daa. Dog kan de på baggrund af daa fra Realkrediråde ikke afvises, a der er koinegraion mellem priser i landzonerne og byggeomkosninger, jf. en p- værdi på,2. De er naurligvis problemaisk, a der ikke eksiserer daa for grundpriser Esimering af dynamisk prisdannelsesmodel På baggrund af modellen for langsigssammenhængen kan den dynamiske prisdannelsesmodel i (4.7 esimeres. Af hensyn il analle af frihedsgrader esimeres modellen i op il 2 lag 49. Den generelle model for boligmarkedsafkase har følgende udseende: 49 Andersen e al. (993, p
71 d log( phk = α β d log( k β d log( uc β d log( uc 3 β d log( pcxh β d log( pcxh β d log( k γ ec 2 β d log( fw β d log( fw 5 2 γ ec ε (7.3 Hvor k som bekend er kapialmængden af alle boligyper, uc er den nominelle user cos eksklusiv forvene kapialgevins, der er beregne efer formel (3., fw er lønsummen i reale ermer, da den disponible realindkoms i ADAM viser sig mindre signifikan, pcxh er prisen på ande forbrug end boligforbrug, og endelig er ec de esimerede fejlkorrekionsled (z. Resulae af esimaionen er præsenere i abel 7.4. Tabel 7.4. Esimaion af generel dynamisk prismodel Afhængig variabel: dlog(fphk Esimaionsperiode Koefficien -saisik Koefficien -saisik Konsan α -,4 -,82 -,4 -,2 Boligbeholdning dlog(k - 3,84,74 6,7 2,3 dlog(k -2 -,66 -,73-3,58 -,4 User cos dlog(uc -,6-5, -,65-4,42 dlog(uc -,2,7 -,9 -,6 Realløn dlog(fw,3,34,2,5 dlog(fw -,75,88,6,7 Inflaion dlog(pcxh -,25-2,6 -,3-2,9 dlog(pcxh -,7,47,49,79 Fejlkorrekionsled ec -,3 2,25,7,36 ec -2 -,42-2,86 -,38-2,2 Forklaringsgrad,67,75 DW,54,53 Inflaionen indgår som e selvsændig led, da den både påvirker den real user cos via realrene og værdien af boligydelser 5. Som nævn idligere er de ikke hel uproblemaisk a anvende daa fra ADAMs daabank. Siden Andersen e al. er der ske ændringer i ADAM modellen, og de beyder, a enkele variable i dag opgøres anderledes. Dee er årsagen il, a den reale lønsum har bedre performance i modellen end variablen for disponibel realindkoms, som den er definere i ADAM, og derfor anvendes lønsummen som udryk for indkomsfænomene. 5 Andersen e al. (993, p
72 Den generelle model i abel 7.4. reduceres efer Hendrys meode (generel-o-specific, hvor variable, der ikke er signifikane på e 95 % signifikansniveau, successiv udelades af modellen. Den specifikke model er herefer: Tabel 7.5. Esimaion af specifik dynamisk prismodel Afhængig variabel: dlog(fphk Esimaionsperiode Koefficien -saisik Koefficien -saisik Konsan α -,4-2,4 - - Boligbeholdning dlog(k - 2,7 2,23 4,54 6,8 dlog(k User cos dlog(uc -,58-5,76 -,56-5,79 dlog(uc Realløn dlog(fw dlog(fw -,85 2, Inflaion dlog(pcxh -,52-6, -,58-6,58 dlog(pcxh -,8 2, Fejlkorrekionsled ec -,3 2,8 - - ec -2 -,45-4,2 -,47-4,36 Forklaringsgrad,68,72 DW,6,42 På baggrund af den specifikke model konkluderes de, a ilpasningsdynamikken ikke fungerer som idligere. Uligevægen i boligmarkede bliver gradvis eliminere med en vis ræghed, men for den længere esimaionsperiode ses, a der også findes e signifikan korrekionsvariabel med posiiv foregn. Dee kan ikke forklares ud fra eorien, men den empiriske forolkning er, a en opsåe uligevæg har en endens il a udvide sig i den eferfølgende periode, og alså ikke blive korrigere som eorien foreskriver. A konsanen er signifikan, kan heller ikke forklares ud fra eorien, da de reale boligmarkedsafkas i ligevæg bør være nul. Den posiive effek af ændringer i boligbeholdningen srider også mod de eoreiske grundlag. De er dog ikke noge ny fænomen, a boligbeholdningen ikke passer 67
73 ind 5. Andersen e al. forklarer dee med forekomsen af mulikollinarie, da ændringer i boligbeholdningen i eorien forklares af fejlkorrekionsledde som indikaor på profiabilieen ved a invesere i boligmarkede. En anden forklaring kan være opgørelsesmeodikken hos ADAM, hvor boligbeholdningen opgøres som kapialværdien af boligmarkede, og dermed er en funkion af priserne. Denne gensidige afhængighed er e poeniel problem med OLS. Esimaorerne er nemlig ikke BLUE, hvis boligbeholdningen korrelerer med residualerne (se eksempelvis Gujarai (995. Desuden vise en ADF-es, a variablen ikke er saionær i førse differens, hvilke forklarer signifikansniveaue. For a afhjælpe probleme har de være forsøg med beholdningen af ejerboliger alene, sam en boligbeholdning, der er deflaere med befolkningsalle, jf. Blomgren-Hansen & Knøsgaard (978. Dee har dog ikke kunne forbedre modellen. ADAM modellen (995 har som nævn være esimere med en resrikion på paramerene, der sæer koefficienen il boligbeholdningen lig koefficienen il indkomsen. Dee er undlad, da resrikionen sammer fra en specifik eferspørgselsfunkion, der ikke er udvikle her. Den nominelle user cos er signifikan og med korrek foregn. Konanprisens afhængighed af ejers omkosninger har ikke ændre sig med nye daa. Endvidere er reallønnen signifikan på nye daa og med de korreke foregn. Inflaionsvariablen viser modsridende effeker på nye daa. Den negaive effek er sørs og mes signifikan. Dee problem forklaredes i Andersen e al. med, a der er komplemenarie mellem boligforbrug og ande forbrug. En anden forklaring er, a variablen ikke er saionær i førse differens. Figur 7.5. viser de fakiske boligmarkedsafkas og de ændringer, der kan forklares ved hjælp af den specifikke model. 5 Andersen e al. (993, p
74 Figur 7.5. Fakiske og esimerede boligmarkedsafkas Residual Acual Fied Esimaionsperiode På rods af ovennævne problemer er modellen ikke forringe væsenlig i forhold il den i Andersen e al. Durbin-Wason saisikken viser, a der er problemer med posiiv korrelaion, men a probleme ikke er signifikan. Der er også forsøg alernaive specifikaioner af modellen med den nominelle konanpris og med laggede konanpriser på højresiden. Dee giver dog ikke anledning il forbedringer. Da de kan konsaeres a k og pcxh variablene ikke har saionære egenskaber, er der i bilag 2 esimere en model uden disse variable. Denne esimaion viser en pænere model i hver fald for den korere periode. De ses her, a koefficienen il indkomsvariablen oversiger værdien. Dermed er prisens korsigede indkomselasicie misænkelig høj. Modellen er ikke ilfredssillende, da variablene for boligbeholdningen og inflaionen på forhånd er fravalg. Udover dee er der foreage en decidere modelvalidering. De er undersøg, hvorvid de er rimelig a anage, a residualerne er hvid søj, og dermed opfylder Gauss-Markov krierierne. Der er anvend en anden es for serielkorrelaion, da Durbin-Wason saisikken er forbunde med en række svagheder i idsserier 52. Der er ingen grund il a ro, a der er problemer med evenuelle forudsæningsbrud. I bilag 3 er vis resulae af en esimaion af den dynamiske prismodel i de mes akuelle daa (kvaralsvise observaioner fra 992k-25k3 og forskellige prisbegreber. De fremgår, a den dynamiske model kollapser, og der i de specifikke modeller 52 Greene (2, p
75 kun eferlades variable, der ikke er saionære. I enkele modeller er realindkomsen og inflaionen dog signifikan. De kan diskueres, om der ikke skulle være valg en længere lag-srukur, da modellen er esimerere på baggrund af højfrekvene daa. Desuden er de forklarende variable ikke lige velegnede på alle segmener. Frem il 23 kan den dynamiske prismodel forklare prisdannelsen i de danske boligmarked nogenlunde. Huspriser er sadig koinegrere med byggeomkosninger, der er en funkion af selve konsrukionsomkosningerne og priserne på byggegrunde. Syrken af esen for koinegraion er dog forringe siden 99, hvilke er problemaisk. Den dynamiske prismodel har sine mangler, men de er ikke noge ny fænomen. Dee skal formenlig ilskrives kvalieen af daasæe, der indeholder variable, der afhænger af andre variable, og som ikke har de ønskede differenssaionære egenskaber. Anvendes nyere daa og daa fra forskellige delmarkeder (enfamiliehuse, ejerlejligheder, byzoner, landzoner og friidshuse er huspriser, med undagelse af landzonerne, ikke længere koinegrere med byggeomkosninger. De kan ses i lyse af knaphedsargumene og manglende daa for byggegrunde, i særdeles for boligmarkede i byzonerne og for friidshuse. Modellerne er insignifikane, hvilke også kan skyldes den forholdsvis kore esimaionsperiode eller kvalieen af daaene. Boligmarkedseorien har en vis validie frem il 23, men kan alså ikke bekræfes på hel nye daa. En anden måde a vurdere boligmarkedseoriens validie på empiriske daa kunne være a benye esimaerne fra den kore periode ( og forecase de eferfølgende afkas og herefer vurdere modellen på residualernes sørrelse og foregn. En sådan ilgang er dog undlad, da meoden ignorerer modellens fundamenale egenskaber og effeken af nye poliikker Tes af nuidsværdimodellen I forbindelse med esimaion og es af nuidsværdimodellen på boligmarkede ages udgangspunk i den specifikaion, der er give i afsni 6, og som er inspirere af Black e al. (25. Black e al. bruger daa for huspriser i U.K. i perioden 4. kvaral 974 il 3. kvaral 23. Endvidere benyer Black e al. e hedonisk boligmarkedsindeks, mens nærværende afhandling benyer konanprisindeks. E hedonisk indeks har den 7
76 syrke, a værdien af boligens aribuer er fassa individuel i hver periode, hvorefer værdien af en repræsenaiv bolig findes ved aggregering. Dee indeks er således udryk for en bolig med konsan kvalie, hvorimod konanprisindekse kan have en kvaliesbias. Kvaliesbias er også e ema hos Case & Shiller (987, 989. Case & Shiller har konsruere e såkald gensalgsindeks 53, som er udgangspunk for deres analyser. Gensalgsindekse er basere på salgspriser på ejendomme, der har være solg mere end én gang, og dermed er de sikre, a der er konsan kvalie i daaene. I den eferfølgende fremsilling er analysen basere på konanprisindekse fra ADAMs Daabank sam ADAMs variabel for husholdningernes disponible indkoms på kor sig. I figur 7.6. er vis udviklingen i de reale boligmarkedsafkas og væksen i den disponible realindkoms. Figur 7.6. Væks i realløn og reale boligemarkedsafkas Væks i realløn Real boligmarkedsafkas Kilde: ADAMs Daabank Figur 7.6. viser, a realafkase på boligmarkede har en endens il a svinge omkring væksen i reallønnen og bevæge sig i cykler, hvilke svarer il observaionerne i Black e al. (25. Forneden viser abel 7.6. en række deskripive saisikker for realafkase på enfamiliehuse (dlog(fphk = Δp, væksen i reallønninger (dlog(fydk = Δy sam pris-indkoms forholde (log(fphk log(fydk = S. 53 Weighed Repeaed Sales Index (WRS. 7
77 Tabel 7.6. Deskripive saisikker Δp Δy S Middelværdi,89 % 2,9 % -2,7 Sandardafvigelse 7,8 % 3,79 %,7 ADF-es - Med konsan -5,42 *** -7,79 *** -2,5 - Med konsan & rend -5,43 *** -8,77 *** -2,76 - Uden konsan & rend -5,4 *** -,62 *,2 Periode: , kilde: ADAMs Daabank. *** signifikan på 99 % niveau, ** signifikan på 95 % niveau, * signifikan på 99 % niveau. Vurdere på baggrund af Fullers kriiske værdier. Anvend laglængde: 5 år Af abellen fremgår, a de gennemsnilige realafkas på enfamiliehuse i perioden er,89 %, a sandardafvigelse er 7,8 %, og a afkasvariablen er saionær. Dee er naurligvis en genagelse af resulaerne fra abel 7.. og abel 7.2. Den gennemsnilige væks i den disponible realindkoms har i perioden være 2,9 % om åre med en sandardafvigelse på 3,79 %. Væksen i den disponible realindkoms har også saionære egenskaber. De empiriske pris-indkoms forhold har en middelværdi på -2,7, en sandardafvigelse på,7 og en enhedsrod kan ikke afvises med en ilpas sor sikkerhed, hvilke formenlig skyldes de lange cykler i boligmarkede. De skal nævnes, a i overenssemmelse med Black e al. er de anage, a koinegraionsparameere mellem pris og indkoms er. Dee er ikke er nødvendigvis i henhold il Campbell & Shillers meodik jf. proporionaliesfakoren i (6.. S kan således opnå saionære egenskaber med θ. I Andersen e al. er dividenden da også en funkion af indkoms og ikke indkomsen alene. Pris-indkoms forholde er ikke særlig inuiiv, da den reale konanpris sammer fra e indeks med 995=, og den disponible realindkoms er opgjor i millioner kroner for samlige hussande. I VAR modellen indgår Δy og S variablene som afvigelser fra deres ubeingede middelværdier. Dermed er de uden beydning, a variablene er opgjor i forskellig niveau, da modellen kun beskæfiger sig med de dynamiske effeker. Endvidere kan de ved en ADF-es konsaeres, a variablene som afvigelser fra deres middelværdier, har saionære egenskaber, hvorved den manglende afvisning af en enhedsrod i S herefer forekommer uproblemaisk. 72
78 E ande problem, der opsår som konsekvens af daaenes forskellige formaer, er, a den beregnede diskoneringsfakor, μ, ilnærmelsesvis er. Da dee ikke kan ilskrives en økonomisk mening, er i sede valg en μ, der ilnærmelsesvis er i forbindelse med esimering af ( Den anvende VAR model il forecasing er: Δy Δy S S a = c a 2 c 2 b d b2 Δy Δ y d 2 S S 2 2 u u 2 (5.4 Resulae af esimaionen af ovensående 2-variabel VAR model i 2 lags, besem ud fra Akaike og Schwarz informaionskrierierne, med daa fra ADAMs Daabank er vis i abel 7.7. Tabel 7.7. Esimaion af VAR model z Δy middel(δy S middel(s Δy - middel(δy -,8,68 (-,6 (2,27 Δy -2 middel(δy,6,27 (,38 (,95 S - middel(s,6,9 (,83 (8,54 S -2 middel(s, -,38 (,8 (-2,67 Forklaringsgrad,3,85 Akaike informaionskrierium -5,98 Schwarz informaionskrierium -5,66 Wald-saisik 34,6 *** Periode: , kilde: ADAMs Daabank. -saisikker i parenes. *** signifikan på 99 % niveau, ** signifikan på 95 % niveau, * signifikan på 99 % niveau. Vurdere på baggrund af Fullers kriiske værdier. Anvend lag-længde: 5 år Som de fremgår af abellen, er forklaringsgraden i ligningen for væks i disponibel realindkoms forholdsvis lav, hvilke hænger sammen med de lave -saisikker. Modellen for pris-indkoms forhold har en noge bedre forklaringsevne, hvilke hænger sammen med den høje signifikans af laggede værdier af variablen selv. På baggrund 54 Konkre er valg en diskonering svarende il ( Δp Δy - = (,89 % 2,9 % - =,96. 73
79 af VAR oupue beregnes e udryk for den eoreiske værdi af S * i overenssemmelse med (6.3. De eoreiske og de fakiske pris-indkoms forhold er illusrere i figur 7.7. Figur 7.7. Teoreisk vs. fakisk pris-indkoms forhold S* S Periode: , kilde: ADAMs Daabank. Pris-indkoms forholdene er frarukke deres beingede middelværdier. De o serier er ydeligvis ikke sammenfaldende, hvilke indikerer, a priserne på boligmarkede i e hisorisk perspekiv ikke afspejler den fundamenale værdi, som er angive af den disponible indkoms. Dee bekræfes også af den mege signifikane Wald saisik (se evenuel bilag 7 for dealjer. Analysen semmer overens med de resulaer, Black e al. finder på boligmarkede i U.K. Der kan være flere ekniske forklaringer på, a de o serier ikke er sammenfaldende. Udover dem, der nævnes senere i afsni 8.2., kan nævnes forudsæningen om konsan diskonering og den lave signifikans i modellen for forvene væks i disponibel realindkoms. Af figuren fremgår e sammenfald mellem de eoreiske og fakiske pris-indhold forhold i sluningen af perioden, hvilke kan opfaes om en indikaion på, a markedspriserne ikke indeholder en boble. De er selvfølgelig ineressan a se, om denne konklusion holder på nyere daa. Som de fremgår af bilag 4 er de svær a finde pæne modeller for nyere daa, og generel oversiger de fakiske prisindkoms forhold de eoreiske ved udgangen af 25. Den primære forklaring på afvigelserne mellem eoreiske og fakiske priser er i Black e al., a boligejeren overforolker beydningen af ændringer i indkomsen. En sådan boblemodel minder om modellen for de naurlige bobler (Froo & Obsfeld (99. 74
80 Af figur 7.6. fremgår e forløb, der kan søe en sådan ese. De var være forsøg a esimere en model svarende il Froo & Obsfeld, men resulaerne er ikke meningsfylde, da dividendeafkase oversiger afkase på priser, og resulaerne rapporeres derfor ikke. 75
81 8. Vurdering af boligmarkedes ilsand På baggrund af en dynamisk model for prisen og årlige observaioner fra perioden , har de økonomiske fakorer sadig forklaringsevne over for prisen på ejerboliger. Denne analyse finder søe i en esimaion af de eoreiske pris-indkoms forhold, der viser, a de fakiske pris-indkoms forhold i 23 falder sammen med de eoreiske. Der er dog e par forhold, der er værd a nævne. For de førse signalerer analysen af koinegraion en (begyndende afkobling fra byggeomkosninger. I lyse af knapheden i byzonerne, er dee ikke nødvendigvis problemaisk. De er problemaisk, fordi daaene er landsgennemsni, og argumene således ikke holder, da kun hver iende handel er i byzoner 55. For de ande er user cos effeken sabil, hvilke kan undre i lyse af, a de nye realkrediproduker er mere risikable. Man kunne således have forvene e fald i koefficienen, da den dobbele renefaldseffek ikke bør slå hel igennem. For de redje er de økonomeriske modeller problemaiske i lyse af boblediskussionen, ide en overreakion på beydningen af ændringer i fundamenale forhold, som eksempelvis en lavere nominel rene, kan gemme sig i esimaerne. De skal også nævnes, a ligningen i VAR modellen, der bruges il a forecase ændringer i dividende har emmelig lav forklaringsevne. I 23 bør den fremadreede og ikke minds raionelle vurdering af boligmarkede være, a priserne på sig vil falde, da priserne oversiger byggeomkosningerne i e ikke uvæsenlig omfang. De sker imidlerid ikke, og de forskellige modeller kollapser i de mes akuelle daa. Spørgsmåle er da, om afkoblingen er e udryk for spekulaion. Bekymring om boligmarkedes ilsand opsår for alvor med den viden, a priserne siden 23 er forsa med a sige, og endda mege krafig med op il 22 % om åre i reale ermer i byzonerne! Spørgsmåle er, hvad der foregår i boligmarkede. Raionelle bobler, som er gennemgåe i afsni 5.2. kan udelukkes af forskellige årsager. Som Diba & Grossman (988 har vis, skal en raionel boble opså på førse handelsdag, og hisoriske se aldrig være sprunge. Den førse handelsdag er svær a idenificere på boligmarkede, men må være forbunde med den privae ejendomsre, hvis hisorie er minds lige så lang som realkrediens. Derudover viser de lange cykler i boligmarkede, a bobler opsår og 55 Vurdere på baggrund af de daa fra Realkrediråde, der indgår i konsrukionen af prisindeks. 76
82 springer. Camerer (989 nævner, a raionelle bobler ikke harmonerer med adapive forvenninger, hvilke kan være ilfælde på boligmarkede. Derudover sæer likvidiesbegrænsninger e naurlig lof for prisudviklingen, hvorved bobler, under raionelle forvenninger, kan udelukkes ved baglæns indukion. Konklusionen må være, a raionelle bobler ikke kan opså på boligmarkede. Teorien om nær-raionelle bobler som greaer fool bubbles og naurlige bobler, kan give en bedre indsig i boligmarkedes ilsand. Hvis eorien om likvidiesbegrænsningerne ikke anses for a være almen kend, er invesorerne villige il a handle boliger med en præmie udover den fundamenale værdi, da de forvener, a andre er villig il a gøre de samme. Analysen i afsni 7.4. yder på, a eorien om naurlige bobler, hvor markede overreagerer på ændrede forvenninger, kan have en vis relevans på boligmarkede. Den forerukne forklaring på siuaionen i boligmarkede er imidlerid irraional exuberance. Eferfølgende gives en række argumener, der sandsynliggør, a der er irraional exuberance i de danske boligmarked. 8.. Tradiionelle forklaringer på de høje prisniveau I dee afsni gennemgås nogle de mes forekommende forklaringer på de høje prisniveau. Disse forklaringer kan også opfaes som en del af irraional exuberance, såfrem der er vivl om forklaringernes validie. I de ilfælde er forklaringerne nemlig en del af naurally occurring Ponzi schemes. Der findes også en række naurlige argumener for prisernes anaomi, dvs. hvorfor man kan forvene en afvigelse mellem fundamenale og fakiske priser, ræghed og dermed manglende efficiens i boligmarkede. Disse argumener, der hænger sammen med boligmarkedes særlige markedsforhold, gennemgås i de eferfølgende afsni Knaphed i byzoner Bland de mes almindelige forklaringer på de høje prisniveau, især i byzonerne, er knaphedsargumene. Der er grund il a ro, a argumene er holdbar i en vis udrækning jf. afsni og se evenuel Vismandsrapporen (FO25 og Wagner (25. Knapheden i byzoner forklarer imidlerid ikke prissigninger i de øvrige Danmark, hvor der også beales en pæn præmie over byggeomkosningerne. 77
83 8..2. Inernaionale sammenligninger E ande argumen er, a boligmarkede i København er inde i en fase, hvor de konvergerer mod højere inernaionale niveauer som i eksempelvis London. De usande ved dee argumen er, a de økonomiske forhold er vid forskellige i de o byer (se evenuel Madsen (25. Argumene kan heller ikke bruges i en diskussion af boligbobler, da der ikke eksiserer nogen garani for, a boligpriserne i London ikke indeholder e bobleelemen Nye realkrediproduker Som de har være nævn idligere, har de siden 996 være mulig a finansiere huskøbe med en kor rene ved e reneilpasningslån. Senere har de være mulig med afdragsfrie lån og renegaranilån. Der har således være ale om en dobbele renefaldseffek over de senese åri, som har presse priserne op. For de førse fordi boligejernes finansieringsomkosninger er falde pga. de lavere reneniveau, og for de ande pga. muligheden for a placere sig i de kore segmen på renekurven. De nye realkrediproduker reducerer naurligvis user cos, men samidig løbes en genfinansieringsrisiko. Krediinsiuionerne udaler selv, a de ikke yder de risikable lån, hvis boligejerne ikke har luf i økonomien il renesigninger, afdrag eller omlægninger il de radiionelle låneyper. Hvis man ser bor fra de lavere reneniveau, og kun fokuserer på muligheden for en kor rene, er de korrek, a user cos er falde med de nye låneyper. Dee skaber grundlag for en sørre eferspørgsel, ide boligejeren ud fra en (korsige ydelsesberagning kan klare en sørre gæld. Men hvis krediinsiuionerne ikke illader en sådan budgeering, er de svær a se, hvor eferspørgselspresse skal komme fra. Hvis adgangen il fremmedfinansiering derimod ikke er begrænse i de nævne omfang, vil nye produkyper selvfølgelig påvirke prisen, men de er en hel anden diskussion (jf. afsni Økonomiske forhold De påpeges ofe a de økonomiske forhold er særlig gunsige for boligmarkede. Udover de lave reneniveau og inflaion, er der god væks i økonomien, og dermed også en høj velfærd, der naurligvis afspejler sig i høje priser på boligmarkede. Argumene har en vis relevans, da indkomsen er en vigig deerminan af huspriserne. Reneargumene er imidlerid lid mere konroversiel. De, der er relevan, er nemlig real- 78
84 renen, da inflaionen reducerer realværdien af gælden. Realrenen er ikke falde i samme omfang som den nominelle rene, men analysen viser alligevel, a den nominelle user cos har forklaringsevne overfor prisen. Dee er dog ikke noge ny fænomen Efficienshypoesen og imperfeke markedsforhold I modsæning il de finansielle markeder er boligmarkede fragmenere og uigennemsigig, og mens akier giver en konsan residualre er bolignyen subjekiv. Ejerboliger er ikke e sandardisere produk, men en pakke af særlige karakerisika, der ikke kan handles isolere og dermed prissæes enydig. Dee vanskeliggør en egenlig prissammenligning og enhver ale om en rigig pris. For de ande er omkosninger i forbindelse med e samidig køb og salg af ejerboliger beydelige i forhold il konanprisen. Ud over høje handelsomkosninger er der også beydelige beholdningsomkosninger i form af ejendomsskaer og afskrivninger forbunde med a besidde en ejerbolig. Endvidere beyder skaereglerne, a de er vanskelig a profiere på ejendomshandel udover egen bolig. Dee begrænser inciamene il a udnye priva informaion om boligmarkede og lave arbirage. For de redje løber poenielle boligkøbere ind i likvidiesbegrænsninger, da personer med lav eller negaiv egenkapial kan have begrænse adgang il den nødvendige fremmedkapial. Likvidiesbegrænsningerne bevirker også, a priva informaion om boligmarkede ikke bliver spred i samme omfang, som hvis der havde være en leere adgang il kapialen. For de fjerde er der ikke mulighed for a gå kor i boligmarkede, og der eksiserer ingen hedge insrumener, hvilke hindrer arbirage yderligere. Den, der har priva informaion, og som mener, der eksiserer en fejlprissæning, har svær ved a kommunikere dee ved sin adfærd jf. ovensående. Hvis en andel af poenielle og fakiske boligejere besidder informaion om, a priserne bør falde, har de poenielle købere som nævn ikke mulighed for a gå kor, og de, der ejer en bolig, afholdes i e vis omfang fra a sælge pga. de høje ransakionsomkosninger. Informaionens eksklusivie fasholdes umiddelbar ved den manglende adfærd, men spredes 79
85 over id, fordi de poenielle købere udskyder købe, mens de, der planlægger a flye i lejebolig fremskynder salge. Igennem imingen af køb og salg spredes informaionen med en vis forsinkelse 56. A der eksiserer en ræghed i prisdannelsen på boligmarkede, er også resulae af e sudie af Case & Shiller (989, 99, der konkluderer, a der er serielkorrelaion i prisændringer. A de også er ilfælde i Danmark, kommer il udryk i vanskelighederne ved a afvise en enhedsrod i konanprisændringer jf. abel 7.2. Manglende informaionsmæssig efficiens kan med ovensående il dels forklares ved e imperfek marked, og ikke nødvendigvis ved manglende raionalie bland invesorerne. I øvrig er de vanskelig a ese den orogonale egenskab i boligmarkede, da fair game modellen for afkas er inklusiv dividender, dvs. boligydelser, der ikke er indehold i afkase på priserne. E ande forhold er, a boligmarkedseorien fakisk acceperer ræghed i priserne. Prisilpasningen foregår jo over flere år, da udbudde er uelasisk på kor sig. Med raionelle forvenninger og med perfeke markedsforhold, vil priserne i boligmarkede øjeblikkelig ilpasse sig ny informaion om fundamenale forhold og gradvis bevæge sig mod ligevægen q, der er besem af byggeomkosningerne og kvaliesforskellen på nye og eksiserende boliger. Dee svarer il A i figur 8.. Pga. de ovennævne markedsforhold er der grund il a forvene e forløb, der i sede svarer il B. E sådan slangende forløb fremgår også af figur 3.5. Figur 8.: Prisilpasning på boligmarkede 56 Andersen e al. (993, p
86 Spørgsmåle om efficiens i boligmarkede kan således ikke afgøres ved a ese for, om der er afhængighed mellem eferfølgende prisændringer, da en vis ræghed fakisk harmonerer med raionelle forvenninger (A og B. Der er også derfor, a den dynamiske prismodel er definere med en lag-specifikaion. Spørgsmåle om markedsefficiens og boligbobler bør i sede være e spørgsmål om, hvorvid de korsigede udsving er for krafige Argumener for irraional exuberance En mulig forklaring på de krafige udsving på boligmarkede er irraional exuberance. I den eoreiske fremsilling blev nævn, a prissigninger under irraional exuberance vedligeholdes af hisorier som naurally occuring Ponzi schemes. Spørgsmåle er om før nævne forklaringer, der ofe ses anvend af krediinsiuioner og ejendomsmæglere, kan kædes sammen med irraional exuberance som udbred naurally occurring Ponzi schemes. Eferfølgende gennemgås en række argumener mod raionelle forvenninger og dermed for irraional exuberance i boligmarkede, som forklaring på prisudviklingen siden miden af 99erne og i særdeleshed efer Beydningen af likvidie: Moral hazard i krediinsiuioner Likvidiesbegrænsninger har være nævn som e argumen mod en raionel boligboble. En mindre resrikiv krediraioneringspoliik er dog en fremskyndende fakor for irraional exuberance. Den finansielle sekor har være præge af en række liberaliseringer, og med nye produker og sørre konkurrence om kunderne er der risiko for moral hazard. Krediinsiuionerne er mere villige il a låne penge ud, når prisen siger. Samidig indager bankrådgiveren rollen som sælger, da der skal skabes omsæningen i virksomheden. Selvom krediinsiuionerne i forbindelse med deres rådgivning kun yder korfrisede eller afdragsfrie lån, hvis der er plads i kundens økonomi il renesigninger og afdrag, viser en undersøgelse af Andersen & Juul (25, a 4 % af familier med o børn ikke har de månedlige rådighedsbeløb, som krediinsiuionerne selv anbefaler. En undersøgelse af Lunde (25 viser, a gældsandelen er sege med 58 % fra 987 il 22. Dee er en indikaion på, a likvidiesbegrænsningerne ikke er så væsenlige, som de 8
87 har være idligere, og a boligejerne måske ikke forsår beydningen af den finansielle gearing. Når den finansielle gearing vurderes i en virksomhed, måles den, afhængig af akivernes karaker, enen i forhold il egenkapialen eller i forhold il indjeningen. På samme måde bør boligejerne måle fremmedkapialen i boligen i forhold il friværdien, eller måske endnu bedre i forhold il årsindkomsen. Såfrem enkele boligejere, måske fordi krediinsiuionerne giver dem lov, i sede vurderer deres finansielle gearing på forholde mellem førse års ydelsen og indkomsen, er der risiko for, a gælden øges uhensigsmæssig. I ilfælde, hvor den korsigede ydelse falder pga. muligheden for afdragsfrihed eller en kor placering på renekurven, vil disse boligejere ikke forbinde en sørre gældsandel med en sørre solvensrisiko, fordi den korsigede ydelse er konsan i forhold il indkomsen. En sådan korsige adfærd hos den enkele er med il a presse priserne over de niveau, der kan forklares af en fundamenalmodel. Hvis boligejerne samidig opfaer deres bolig som e inveseringsobjek og ror på forsae prissigninger, eksiserer der måske samidig en villighed il a øge indkomsandelen il boligforbrug, for a få andel i gevinserne. I månedsmagasine Penge & Privaøkonomi fra april 25 er der vis e eksempel på, hvorledes effeken af renegaranilån, efer journalisens overbevisning, bør påvirke boligmarkede. Journalisen argumenerer for, a boliger skal handles på den månedlige ydelse, og a boligejeren således bør opage mere gæld med de nye låneyper. En sådan ankegang, kan måske nok forklare høje priser, men spørgsmåle er, om de er forsvarlig ud fra e fundamenal perspekiv Boligejernes forvenningsparadigme Da boligmarkede bevæger sig i lange cykler, kan der opså en form for selekiv hukommelse bland invesorerne. Efer en id med prissigninger kan forvenningerne blive adapive i den forsand, a man glemmer, a huspriserne kan falde jf. eorien om feedback looping. Dee skaber naurligvis begejsring og roen på, a priserne vil forsæe med a sige. Siuaionen kan illusreres med en økonom fra Realkredi Danmark, der il DR Nyhederne udaler, a boligejerne opfaer boliger som skaeki- 82
88 ser fyld med mursen 57. E af de førse og forsærkende elemener i irraional exuberance er invesorernes forvenninger i de, der kan beegnes som e bedse invesering paradigme. Dee paradigme indeholder en selekiv hukommelse og en opfaelse af boliger som e inveseringsobjek, der har e god afkaspoenielle og ingen eller ubeydelig risiko. A forvenningsdannelsen er selekiv på de amerikanske boligmarked, viser en undersøgelse af Case & Shiller (988, 23. Case & Shiller foreager en spørgeskemaundersøgelse i fire amerikanske byer 58, der repræsenerer forskellige ilsande i boligmarkede. I 23 ilkendegav mere end 75 % af huskøberne i Los Angeles, a der havde være en krafig signing i huspriserne siden 988. Priserne var ren fakisk falde fra 99 il 996 med ca. 3 %. I de mindre glamourøse Milwaukee var blo 3 % af de adspurge af denne opfaelse, og de er på rods af, a den gennemsnilige signing i perioden fakisk var idenisk for de o byer. I 23 svarede 46 % af de adspurge 59, a de il dels opfaede boligkøbe som en invesering. Samidige forvenede 9 % af amerikanerne yderligere prissigninger, og a huspriserne i gennemsni ville sige med 4 % om åre over de næse år. Dee er endda med en yders begrænse risiko, ide 36 % af de adspurge forband inveseringen med ingen eller ubeydelig risiko. Spørgsmåle er, i hvilke omfang Case & Shillers undersøgelser kan overføres il danske forhold. E lignende, men knap så veldokumenere resula for de danske boligmarked kan findes i en måling fra Greens Analyseinsiu 6 fra okober 25, der viser, a 92 % af boligejerne i København forvener yderligere prissigninger. En undersøgelse foreage af Økonomi- og Erhvervsminiserie 6 i juli 25 viser, a 8 % af boligejerne i byzonerne forvener, a huspriserne i gennemsni vil sige med over % over de næse 5 år. E resula, der rods al er mindre end de i Case & Shillers undersøgelser. 57 DR Nyhederne online, Økonomer advarer om muligheden for prisboble, 24. okober Los Angeles, San Francisco, Boson og Milwaukee. 59 Simpel gennemsni af de fire byer. 6 Målingen er på Inernee omal hos DR Nyheder og hos Dansk Ejendomsmæglerforening, under de forskellige overskrifer: Boligejerne er farlig opimisiske og Forsigig opimisme hos boligejere! 6 Økonomisk Tema Nr.. augus 25, Økonomi- og Erhvervsminiserie. 83
89 Psykologiske fakorer Case & Shillers undersøgelser (988, 23 viser også andre egn på irraional exuberance. De er egn på herd behavior, hvor følelser og word of mouh er vigige deerminaner i købsbesluningen. I 23 svarede 46 %, a såfrem de ikke købe en ejerbolig nu, ville de ikke have råd senere, og 64 % mene, a køb over den udbude pris er e egn på panik bland køberne. Disse svar er forunderlige, fordi der i e marked med fundamenale priser ikke eksiserer sådanne afgrænsninger. Med fundamenale priser har de poenielle boligkøber nu som i fremiden råd il a komme inde på markede. En indikaion på, a sådanne fakorer også er il sede i de hjemlige boligmarked, finder man i en TV2 dokumenarudsendelse 62 fra april 25. Her udaler e par førsegangskøbere, a de har fåe a vide af deres ejendomsmægler, a de er med a komme ind på boligmarkede (København, inden de er for sen. A følelser er en del af købsbesluningen, er også en del af Case & Shillers sudier. I 23 svarer mere end en redjedel af de adspurge, a deres huskøb er påvirke af den begejsring, der eksiserer på boligmarkede og af samaler med venner og bekende. Poenielle boligkøbere bliver nemlig misundelige, når de læser eller hører om andre, der er bleve friværdi-millionærer på ganske få år. Effeken forsærkes kun af, a friværdien kan belånes il en lav rene og bruges på ande forbrug måske købe af bolig nummer o. Case & Shillers o spørgeskemaundersøgelser viser egn på irraional exuberance. Hovedkonklusionen er, a boligkøbe er dreve af spekulaion, og a der eksiserer særke forvenninger il høje afkas og begrænse risiko. Irraional exuberance som forklaring på de høje priser på ejerboliger ager afsæ i gunsige økonomiske forhold, som en lav nominel rene kombinere med økonomisk væks. Liberalisering af den finansielle sekor har medfør nye realkrediproduker og sørre konkurrence mellem krediinsiuionerne, hvilke leer adgangen il fremmedfinansieringen i boligen og i former, der kan reducere den korsigede ydelse. Disse fakorer leder il prissigninger i boligmarkede, hvor der opsår feedback looping. Feedback looping opsår nem 62 TV2 dok., Panik på boligmarkede, send førse gang 2. april
90 på boligmarkede, da boligmarkedes hisorisk lange cykler skaber en form for adapive forvenninger, hvor boligejerne forrænger, a priserne kan falde. Visse ineressegrupper holder liv i prissigningerne med mere eller mindre vivlsomme hisorier, der refærdiggør e høj prisniveau. Fakisk viser Case & Shillers undersøgelse, a 87 % af boligkøberne finder disse hisorier mere roværdig en forklaringerne om psykologiske fakorer. 85
91 9. konklusion Baggrunden for de senese års prissigninger på ejerboliger er bleve en sadig sørre del af den offenlige deba. Siden 994 er de reale huspriser i Danmark sege hver år. Prissigningerne er eskalere, og siden 23 er priserne i enkele områder sege med op il 22 % om åre. Udgangspunke for afhandlingen er derfor, a vurdere hvorvid denne prisdannelse kan forklares ud fra ændringer i de økonomiske forhold, der må anages a være fundamenale for prisen, eller om boligpriserne indeholder e bobleelemen. Boligmarkedes ilsand vurderes ofe på baggrund af forskellige nøgleal, der fungerer som indikaor på en boligboble. Disse mål minder om dividende-pris forholde, der er kende fra analyser af akiemarkede. Bland de populære mål er forholde mellem konanpriser og byggeomkosninger, der er e alernaiv udryk for den reale konanpris, forholde mellem den disponible indkoms og den reale konanpris og endelig huslejen ved a benye egen bolig. Målene er illokkende i sin enkelhed, men i forhold il nærværende afhandling anvendes de kun i en præliminær analyse, da de er udled under den resrikive forudsæning, a den dividendegenerende proces er en random walk. I sede er valg en analysemeode, der er basere på nuidsværdimodellen i en mere fleksibel form. A analysere prisdannelsen i boligmarkede er dog ikke uden problemer. Nuidsværdimodellen, der angiver prisen som en lineær funkion af den forvenede fremidige dividende, kan ikke uden videre overføres il boligmarkede. Værdien af dividenden er i boligmarkede svær a idenificere og den har endvidere endogene egenskaber, hvor værdien af boligydelsen bl.a. er en funkion af boligbeholdningen. Da boligbeholdningen er en funkion af priserne, eksiserer en dobbelkausalie, der problemaiserer de a finde en fornufig model for prisen. Andersen e al. (993 opsiller en eoreisk nuidsværdimodel, hvor dividendevariablen bl.a. er en funkion af boligbeholdningen. Probleme er a finde en empirisk model, der kan håndere dividendens særlige egenskab. Løsningen er, da boligbeholdningen ikke er en funkion af priserne alene, men af priserne i forhold il byggeomkosningerne, og dermed en funkion af profimulighederne, a udnye eorien om koinegraion. Hvis priserne er en funkion af boligbeholdningen, der igen er en funkion 86
92 af profimulighederne, vil boligbeholdningen udvide sig indil profien er eliminere. Sag med andre ord, må boligpriser og byggeomkosningerne være ideniske på lang sig (med en mindre forskel, der udrykker kvaliesforskellen på eksiserende og ny byggeri. Der eses derfor for koinegraion mellem konanpriser og e funkionsudryk for omkosningerne ved a bygge ny. Disse omkosninger er en log-lineær funkion af maerialeomkosninger og priser på byggegrunde. På baggrund af modellen for koinegraion, er der opnåe e udryk for ligevægsfejlen i boligmarkede. I overenssemmelse med Engle & Granger (987 o-rinsprocedure benyes den fundne serie af ligevægsfejl herefer i en fejlkorrekionsmodel for prisdannelsen, hvor prisen, eller mere korrek boligmarkedes afkas, specificeres som en funkion af fejlkorrekionsledde og de fakorer, der har beydning for prisen på kor sig. Disse fakorer er væksen i den disponible realindkoms, inflaionen, ændringer i udbudde og ejers omkosninger, som i nuidsværdimodellen af Andersen e al. udgør diskoneringen. Nuidsværdimodellen er udled under forudsæning af, a invesorernes forvenninger dannes raionel, dvs. deres forvenninger dannes som den maemaiske forvenning beinge på de ilgængelige informaionssæ, og a priserne svarer il de fundamenale priser. E led i analysen af boligmarkedes ilsand er a vurdere de eoreiske og ikke minds empiriske implikaioner af, a disse forudsæninger opøs. Raionelle forvenninger og den efficiene markedshypoese kan eses ved a vurdere, hvorvid fremidige prisændringer kan forudsiges på baggrund af de eksiserende informaionssæ. En sådan es siger imidlerid ine om, hvorvid markedspriserne afviger fra de fundamenale priser, da esen ikke srider mod forekomsen af en raionel boble. Der er dog en mere væsenlig grund il, a eorien er knap så anvendelig på boligmarkede. For de førse reducerer en række markedsforhold inciamene il a udnye priva informaion, hvilke gør markede mindre efficien. For de ande ager ilpasningen il markedsligevægen id, da de ager id a opføre nye boliger. Tilpasningen srækker sig over flere år, hvorved man må forvene i en vis ræghed i priserne, der ikke srider mod raionelle forvenninger. Den dynamiske prisdannelsesmodel er ikke e god værkøj il a afsløre bobler, især fordi bobler, der en er funkion af de fundamenale fakorer, dvs. hvor markede overreagerer på beydningen af ændringer i de fundamenale forhold, kan skjule sig i modellen. Derudover medager den dynamiske model ikke eksplici forvenningerne il 87
93 fremidige dividender. På den baggrund er en nuidsværdimodel for indkomsen ineressan. Svagheden ved en sådan model er dog, a den ignorerer boligmarkedes ilpasningsmekanisme, og således kun er holdbar, når der er reel knaphed i byggesekoren. Syrken ved meoden er, a den kan bruges il a vurdere om afvigelser fra fundamenale priser kan beegnes som en boligboble. Den empiriske analyse gennemføres på baggrund af de o modeller og med daa fra ADAMs daabank for perioden Den dynamiske prisdannelsesmodel kan sammenlignes med modellen i Andersen e al. og andre empiriske økonomerimodeller som naurlige benchmark. Da daaene i ADAMs Daabank ikke nødvendigvis er eksogene og har ændre sig over id, og modellen i Andersen e al. i øvrig er en model for ilpasningen, esimeres den dynamiske prisdannelsesmodel illige for samme periode, som er anvend i Andersen e al. På baggrund af den specifikke model for den fulde periode kan de konkluderes, a ilpasningsmekanismen ikke fungerer som idligere. Dee kommer også il udryk i den lavere signifikans af esen for koinegraion. Den disponible realindkoms, der i den dynamiske ilpasningsmodel er repræsenere ved en lønsumsvariabel, og user cos, har begge god performance. De kan imidlerid undre, a koefficienen il user cos ikke er falde i den fulde periode, da de nominelle renefald, der alene kan ilskrives muligheden for finansiering med en kor rene, ikke bør have samme effek som e fald i den lange rene. De er fordi, de korfrisede lån er mere risikable, og konsekvensen af den lavere rene således bør være en nedsæelse af boligforbruge frem for opagelse af mere gæld. Noge lignende er gældende for de afdragsfrie lån. Den reducerede ydelse bør normal ikke føre il, a (den raionelle boligejer opager mere gæld, da den fremidige ydelse således bliver sørre end ved radiionel realkredifinansiering. Der kan dog være ilfælde, hvor sørre gæld fakisk harmonerer med raionelle forvenninger. De er ilfælde, hvor den forvenede væks i indkomsen er sor, hvilke ypisk er ilfælde for førsegangskøbere. Probleme for førsegangskøberne er imidlerid, a de ikke har nogen egenkapial, og derfor allerede løber en sørre solvensrisiko, der kun forøges, når de fravælger afdragene. For de ande ligger i udrykke den forvenede væks i indkomsen er sor yderligere e risikoelemen. Konklusion på effeken af de nye realkrediproduker er, a den har være sørre, end hvad der kan begrundes med den økonomiske eori. 88
94 På baggrund af variablen for inflaion, kan der ales om en nominel reneeffek på prisen, da inflaionen ikke har den effek, som kan forvenes i overenssemmelse med eorien. Den nominelle reneeffek er dog ikke noge ny fænomen. A der i modellen er e signifikan inflaionsvariabel med negaiv foregn, kan forklares ved variablens manglende saionære egenskaber. De samme er gældende for variablen for boligbeholdningen. På baggrund af den præliminære analyse og den specifikke model for den dynamiske prisdannelse fra 955 il 23, er hovedkonklusionen, a indkomsen og omkosningen ved a bo il leje i egen bolig (sadig har ilfredssillende forklaringsevne overfor prisen. De er imidlerid problemaisk, a ilpasningsmekanismen ikke fungerer som idligere. Knaphedsargumene kan med en vis rimelighed anages for byzoner, men ikke på de daa, der bruges i analysen, der som bekend er al for hele lande. Der er derfor grund il a ro, a prisudvikling op igennem 99erne er præge af spekulaiv adfærd, og a der dermed eksiserer en boligboble. Denne opfaelse syrkes med den viden, a priserne er sege endog mege krafige efer 23, og a den dynamiske prisdannelsesmodel ikke er signifikan i hel nye daa, hvor analysen gennemføres i forskellige boligsegmener med kvaralsdaa fra. kvaral 992 il 3. kvaral 25. Analysen er også udvide med en nuidsværdimodel for boligmarkede. Nuidsværdimodellen og meoden il a ese dens validie er udvikle i overenssemmelse med Campbell & Shiller (987 og Black e al. (25. Teses modellen i de samme daa, der har være anvend il a esimere den dynamiske prismodel, kan de konkluderes, a de fakiske pris-indkoms forhold i e hisorisk perspekiv varierer omkring de eoreiske forhold, og a de o indeks er sammenfaldende i 23. De ses, a den del af VAR modellen, der bruges il a forecase ændringerne i dividenden, har mege ringe forklaringsevne, hvorved modellerne ikke ilfører analysen megen værdi, udover de saiske dividende-forhold, der blev anvend i den præliminære analyse. Teses nuidsværdimodellen i nyere daa opnås ikke meningsfylde resulaer, og generel ses de, a de fakiske pris-indkoms forhold oversiger de eoreiske ved udgangen af
95 På baggrund af erfaringerne med de o modeller, er der grund il a ro, a der i boligmarkede beales en præmie ud over den fundamenale pris. En sådan præmie beales fra id il anden pga. rægheden i markede. Men med den viden, a priserne er sege krafig de senese par år, og ikke, som de kunne være forvene, er konvergere mod byggeomkosningerne, er der grund il a ale om en boligboble. Da raionelle bobler ikke kan eksisere i boligmarkede, er de oplag a beegne boblen som den nærraionelle siuaion, hvor markede overreagerer på informaioner om de fundamenale forhold (Black e al. (25. En anden og måske bedre forklaring er, a der er irraional exuberance i boligmarkede, som Shiller (25 argumenerer for, a de er ilfælde i de amerikanske boligmarked. Da boligmarkede bevæger sig i lange cykler, er der grundlag for, a forvenningerne kan blive selekive i den forsand, a boligejerne forrænger, a priserne kan falde. En række gunsige forhold som lav nominel reneniveau, økonomisk væks sam nye realkrediproduker og sørre villighed il udlåning i krediinsiuionerne, har udløs prissigningerne i boligmarkede, hvilke er nok il a danne e forvenningsparadigme, hvor boligejerne ror på flere prissigninger, hvilke så opfyldes, og gør a boligmarkede får en eikee som den bedse invesering. Prissigningerne vedligeholdes med soryelling og psykologiske forhold som misundelse over, a andre har fåe del i gevinsen på boligmarkede. En kvaliaiv analyse af boligmarkede viser egn på irraional exuberance. Irraional exuberance er en konroversiel eori, fordi de økonomiske modeller bygger på raionelle forvenninger, men irraionalie er måske mere sandsynlig i neop boligmarkede end andre markeder, fordi invesorer er privae personer og ikke professionelle økonomer. Om irraional exuberance er en god eori eller ej, er i princippe underordne, for en ing er sikker, priserne er for høje de er billigere a bygge ny, i hver fald i områder uden knaphed på byggegrunde. 9
96 . Perspekivering Afhandlingens perspekivering går i o reninger. Den ene handler om en bedre boligmodel, og den anden handler om de løsninger, der findes på probleme med boligbobler. De sore problem ved a finde en fornufig model for prisdannelsen er, a man på den ene side ønsker en model, der forklarer prisernes ilpasning il byggeomkosninger, og på den side er en model for bobler. De er derfor e oplag udviklingsområde a finde en fundamenalmodel, der opdeler dividenden eller værdien af boligydelsen i e indkomsrelaere og e udbudsrelaere elemen. Herefer skal man benye en 3-varibel VAR model eller en 4-variabel model, hvis man ønsker idsvariende diskonering, og vil finde den eoreiske pris under forudsæning af, a den viden, a priserne på lang sig er forankre i byggeomkosningerne, lægger e naurlig lof på priserne på kor sig. Når de dominerende argumen i boligkøbe ikke længere er behove for en bolig men e spekulaiv moiv, er der ilsrækkelige forudsæninger for, a der kan opså en boble i boligmarkede. De korsigede problem med boligbobler er, a en sor gruppe udelukkes for markede, mens en anden gruppe ager en uhensigsmæssig sor solvensrisiko. Da bobler har de med a sprænge, er der risiko for, a boligejerne miser en del af deres egenkapial eller i værse fald bliver eknisk insolvene. Dee kan medføre ubealelig gæld og personlige konkurser. Der har være foreslåe forskellige løsningsmodeller. Fra poliisk side har der være forslag om, a saen skal hjælpe de boligejere, der risikerer a få økonomiske problemer, hvis boligmarkede begynder a falde. Dee forslag blev heldigvis forkase, da en sådan implici garani kun forværrer ilsanden på boligmarkede. E ande forslag har være, a begynde a beskae kapialgevinser på boligmarkede. E bedre forslag er, a boligejerne selv bealer for en sådan garani. Inden for de senese åri har produkudvikling på realkredimarkede være beydelig. Hvor man idligere finansierede huskøbe med salg af realkrediobligaioner med 3 års løbeid, er de nu mulig a vælge bland flere produker, der er srukurere på forskellig vis. I 996 blev de mulig a finansiere huskøbe med kombinaionen af korfrisede obligaionslån og løbende refinansiering. I 23 blev de mulig med afdrags- 9
97 frie lån, hvor e sående lån kombineres med en annuie, og i 24 blev de mulig a kombinere de korfrisede lån med en reneopion. Denne udvikling vidner om en branche med sor kreaivie inden for, hvad der er mulig for huskøberen. Med en reneopion sikrer huskøberen sig imod, a ydelsen siger. Der er således ale om a hedge den renerisiko, der er forbunde med de korfrisede lån. Man kan i forlængelse heraf foreslå, a man kombinerer en af de re grundlæggende låneyper med en puopion på e prisindeks for ejerboliger (se eksempelvis Case e al. (995. På den måde er boligejerne selv med il a beale for en garani mod a blive insolven, ide man med puopionen hedger solvensrisikoen. Dee vil naurligvis kræve, a krediinsiuionerne har inciamen il a skabe e likvid marked for e prisindeks for boligmarkede og de produker, der skal udledes herpå. 92
98 Lieraurlise Andersen, E. (992: En bedre boligmodel. Naionaløkonomisk Tidsskrif bind 3, pp Andersen, L.L. & H. Juul (25: Hvor går lånene hen? Gjellerup. Andersen, T.M., H.J. Jørgensen, C. Koch, H.O. Larsen & P.B. Sørensen (993: Skaepoliikken og ejerboligmarkede eori og empiri. Naionaløkonomisk Tidsskrif, bind 3, pp Black, A., P. Fraser & M. Hoesli (25: House Prices, Fundamenals and Inflaion. Inernaional Cener for Financial Asse Managemen and Engineering (FAME research paper 29. Blomgren-Hansen, N. & J.E. Knøsgaard (978: Boligmarkede i den pengepoliiske ransmissionsmekanisme. Naionaløkonomisk Tidsskrif, bind 6, pp Bodie, Z. & R.C. Meron (2: Finance. Prenice Hall. Camerer, C. (989: Bubbles and Fads in Asse Prices. Journal of Ecomomic Surveys, vol. 3, pp Campbell, J.Y. & R.J. Shiller (987: Coinegreion and Tess of Presen Value Models. Journal of Poliical Economy, vol. 95, pp Case, K E., J.M. Quigley & R.J. Shiller (2: Comparing Wealh Effecs: he Sock Marke versus he Housing Marke. Naional Bureau of Economic Research (NBER Working Paper no Case, K E. & R.J. Shiller (987: Prices of Single-Family Homes since 97: New Indexes for Four Ciies. New England Economic Review, (Sepember/Ocober, pp Case, K E. & R.J. Shiller (988: The Behaviour of Home Buyers in Boom and Pos-Boom Markes. New England Economic Review, (November/December, pp Case, K E. & R.J. Shiller (989: The Efficiency of he Marke for Single- Family Homes. American Economic Review, Vol. 79, No., pp Case, K E. & R.J. Shiller (99: Forecasing Prices and Excess Reurns in he Housing Marke. American Real Esae and Urban Economics Associaion Journal, Vol. 8, No. 3, pp
99 Case, K.E. & R.J. Shiller & A. Weiss (995: Morgage Defaul Risk and Real Esae Prices: The Use of Index-based Fuures and Opions in Real Esae. Naional Bureau of Economic Research (NBER working paper 578. Case, K.E. & R.J. Shiller (23: Is There a Bubble in he Housing Marke? Broking Papers on Economic Aciviy, Vol. 23, No. 2, pp Cuhberson (996: Quaniaive Financial Economics Sock, Bonds and Foreign Exchange. Wiley. Dam, P.U. (995: ADAM En model af dansk økonomi. Danmarks Naionalbank (24: Mona en kvaralsmodel af dansk økonomi. De Long, J.B., A. Schleifer, L.H. Summers & R.J. Waldmann (99: Noise Traders Risk in Financial Markes. Journal of Poliical Economy, vol. 98, no. 4, pp Diba & Grossman (988. The Theory of Raional Bubbles in Sock Prices. Economic Journal, vol. 98, pp Engle, R F. & C.W.J. Granger (987. Co-Inegraion and Error Correcion: Represenaion, Esimaion, and Tesing. Economerica, vol. 55, 2, pp Fama, E.F. (97: Efficien Capial Markes: A Review of Theory and Empirical Work. The Journal of Finance, Vol. 25, 2, pp Fama, E.F. (97: Efficien Capial Markes: II. The Journal of Finance, Vol. 25, 2, pp Farlow, A. (24a: The UK House Prices: A Criical Assessmen. Working Paper, Credi Suisse Firs Boson and Universiy of Oxford. Farlow, A. (24b: The UK Housing Marke: Bubbles and Buyers. Working Paper, Credi Suisse Firs Boson and Universiy of Oxford. Froo, K.A. & M. Obsfeld (99: Inrinsic Bubbles: The Case of Sock Prices. American Economic Review, vol. 8, no. 5, pp Granger, C.W.J. & P. Newbold (974: Spurious Regression in Economerics. Journal of Economerics, vol. 2, pp. -2. Greene, W.H. (2: Economeric Analysis. 4rd Ediion, Prenice-Hall Groes, N. & M. Møller (977: Priser på huse og grunde. Naionaløkonomisk Tidsskrif, bind 5, pp Gujerai, D.N. (995: Basic Economerics. 3rd Ediion, McGraw-Hill. 94
100 Hawksworh, J. (24. Oulook for UK House Prices. Price Waerhouse Coopers UK Economic Oulook 24, pp Heilbling, M. & T. Torrones (23: When Bubbles Burs. Inernaional Moneary Fond (IMF World Economic Oulook 23, pp Junge, M. (24: Forbrugs- og boligrelaioner, okober 24. Inern arbejdspapir, Danmarks Saisik, Modelgruppen. Junge, M. (24: Forbrugs- og boligrelaioner, okober 24. Inern arbejdspapir, Danmarks Saisik, Modelgruppen. Leroy, S.F. (989. Efficien Capial Markes and Maringales. Journal of Economics Lieraure, vol. 27, pp Lucas, R. & T.J. Sargen (978: Afer Keynesian Economics. Federal Reserve Bank of Boson Afer he Phillips Curve. Lunde, J. (25: The owner-occupiers capial srucure during a house price boom Does negaive equiy exis as a permanen feaure in he Danish housing marke? Copenhagen Business School working paper Madsen, J.B. (25: Hvornår Briser Husboblen? Fagblade Huse. Meron, R.C. (973: An Ineremporal Capial Asse Pricing Model. Economerica, vol. 4, pp Muh, J.F. (96: Raional Expecaions amd he Theory of Price Movemens. Economerica, vol. 29, 3, pp Pedersen, E.H. (24: Udviklingen i konanpriser på ejerboliger. Danmarks Naionalbanks kvaralsoversig,. kvaral 24, pp Samuelson, P. (965: Proof ha Properly Anicipaed Prices Flucuae Randomly. Indusrial Managemen Review, Vol. 6, pp Shiller, R.J. (24: Household Reacion o Changes in Housing Wealh. Cowles Foundaion Discussion Paper 459. Shiller, R.J. (25: Irraional Exuberance. 2nd Ediion, Princeon Universiy Press. Tirole, J. (982. On he Possibiliy of Speculaion under Raional Expecaions. Economerica, vol. 5, pp Tirole, J. (985. Asse Bubbles and overlapping Generaions. Economerica, vol. 53, 6, pp Tobin, J. (969: A general Equilibrium Approach o Moneary Theory. Journal of Money, Credi, and Banking,, pp
101 Wagner, R. (25: En model for de danske ejerboligpriser. Økonomi- og Erhvervsminiserie arbejdspapir nr.. Økonomiske Råd (99: SMEC Modelbeskrivelse og -egenskaber. Økonomiske Råd (25: Vismandsrapporen. Vismandsrapporen foråre 25. Økonomi- og Erhvervsminiserie (25: Prissigninger på boligmarkede. Økonomisk Tema nr.. 96
102 Oversig over bilag Bilag : Beregning af ejers omkosninger (user cos Bilag 2: Konsruerede prisindeks for by- og landzoner Bilag 3: Demografisk analyse af knaphedsargumene Bilag 4: Udledning af dynamisk prisdannelsesmodel Bilag 5: Udledning i empiriske modeller Bilag 6: Udledning af nuidsværdimodel for boligmarkede Bilag 7: Resrikioner på nuidsværdimodellen Bilag 8: Daasæ Bilag 9: Tes for saionarie Bilag : Real husleje ved a benye egen bolig under fuld efficiens Bilag : Tes for koinegraion i nyere daa Bilag 2: Validering af dynamiske prisdannelsesmodel Bilag 3: Esimaion af dynamisk prisdannelsesmodel i nyere daa Bilag 4: Esimering af eoreiske pris-indkoms forhold i nyere daa
103 Bilag : Beregning af ejers omkosninger (user cos Ejers omkosninger ved a benye egen bolig defineres: user cos = rene efer ska boligskaer i pc. afskrivningsrae forvenede kapialgevinser Ejers omkosninger kan konkreiseres il: phk uc = i ( dir lv dir e ev a E ( π Hvor i er den gennemsnilige finansieringsrene, dir er den direke skaesas, lv er den nu afskaffede lejeværdiskaesas, e er ejendomsskaesasen, ev er ejendomsværdiskaesasen, a er afskrivningsraen og E (π phk er de forvenede kapialgevinser på ejerboliger. De forvenede kapialgevinser findes i henhold il ADAM modellen med udgangspunk i den forvenede inflaion i byggeomkosninger (pibh: phk ( π =,5E ( π pibh E Hvor pibh pibh pibh E ( π =,75E ( π,25( pibh I user cos udrykke indgår inflaionen kun med halv væg som udryk for en hvis ræghed i prisdannelsen. På baggrund af de nominel user cos kan man finde den reale husleje ved a bo i ejerbolig, hvilke beregnes som: uc ( phk / pcxh Hvor pcxh er prisen på ande forbrug end boligforbrug. Bilag
104 Bilag 2: Konsruerede prisindeks for by- og landzoner Hos Realkrediråde kan der findes al for kvadrameerpriser og anal handler fordel på boligyper (parcel- og rækkehuse, ejerlejligheder og friidshuse og fordel geografisk på kommuner. Kommunerne inddeles i følgende zoner: Byzoner = Københavns kommune, Frederiksberg kommune og Århus kommune Landzoner = øvrige Danmark På baggrund af ovensående, er der konsruere prisindeks for ejerboliger (parcel- og rækkehuse plus ejerlejligheder for de o zoner (se evenuel regnearke boligmarkedsdaa.xls/rkr. Meoden er som følger: Prisindeks for parcel- og rækkehuse: H par ræk par ræk par ræk par ræk Kbh Fre par ræk Århus P by = PKbh Fre P par ræk par ræk Århus par ræk par ræk H Kbh Fre H H Århus Kbh Fre H Århus og H P par ræk land = i= P par ræk område: i H i= par ræk område: i H par ræk område: i - samme princip for ejerlejligheder. Herefer fusioneres de o indeks il e indeks for ejerboliger: P ejerbolig by H par ræk par ræk by = Pby par ræk par ræk Hby Hby P ejerlejl Århus H H ejerlejl by ejerlejl ejerlejl by Hby - samme princip for landzoner. Bilag 2
105 Bilag 3: Demografisk analyse af knaphedsargumene Hos Danmarks saisik er hene følgende saisikker over hussandsflyninger over kommunegrænser (hel og delvis: Tilflyede Par med/uden børn København Frederiksberg Århus Øvrige familier med/uden børn København Frederiksberg Århus Enlige med/uden børn København Frederiksberg Århus Fraflyede Par med/uden børn København Frederiksberg Århus Øvrige familier med/uden børn København Frederiksberg Århus Enlige med/uden børn København Frederiksberg Århus Tilflyede Par med/uden børn København Frederiksberg Århus Øvrige familier med/uden børn København Frederiksberg Århus Enlige med/uden børn København Frederiksberg Århus Fraflyede Par med/uden børn København Frederiksberg Århus Øvrige familier med/uden børn København Frederiksberg Århus Enlige med/uden børn København Frederiksberg Århus På baggrund af disse saisikker er neoilflyningerne il byzoner beregne (se evenuel regnearke boligmarkedsdaa.xls/dst Demo: Toale ilflyninger Toale fraflyninger Hussandsflyninger, neo, i København, Frederiksberg og Århus Bilag 3
106 Herefer er der funde al for boligbeholdningen i byzoner, mål i usinde kvadrameer: København og Frederiksberg Suehuse il landbrugsejendomme Parcelhuse Række-,kæde- og dobbelhuse Eageboligbebyggelse Kollegier Anden helårsbeboelse Århus Suehuse il landbrugsejendomme Parcelhuse Række-,kæde- og dobbelhuse Eageboligbebyggelse Kollegier Anden helårsbeboelse Toale eageareal Ændring Herefer findes nye boligarealer som summen af ændringerne, og følgende ligning løses for x: Neoilflyninger = c = x c x = ΔBoligbeholdning x Hvor x er de ækvivaleringspunk, der sæer den marginale ændring i hussande lig de nye boligareal i perioden Dermed kan knaphedsargumene afvises, hvis de er rimelig a de ilflyende hussande ikke eferspørger mere end 42 kvadrameer bolig i gennemsni. Bilag 3
107 Bilag 4 Bilag 4: Udledning af dynamisk prisdannelsesmodel Hvis værdien af boligydelsen er:, ( = k yd pcxh h pb (a Og følgende arbiragebeingelsen holder: phk eje phk a phk E d pb E dir r phk = ( ( ( ( (a2 Kan prisen på en ejerbolig skrives: ( ( ( (, ( ( ( ( ( ( ( ( ( ( ( ( ( ( ( eje dir r a phk E d k yd h pcxh E phk a phk E d pb E eje dir r phk a phk E d pb E phk eje phk dir r phk phk eje phk a phk E d pb E dir r phk = = = = c c c (a3 Indsæes for phk fås: ( ( ( ( ( ( ( ( ( ( ( ( ( ] ( ( ( ( ( ( ( [ ( ( ( ( ( ( ( ( ( ( ( a phk E eje dir r a d pb E eje dir r d pb E eje dir r phk eje dir r a phk E a d pb E d pb E eje dir r phk eje dir r a eje dir r a phk E d pb E d pb E phk = = = c c
108 Bilag 4 Genages processen n- gange fås: n n n n i i i i n n n n n n a phk E eje dir r a d pb E eje dir r eje dir r phk a pkh E eje dir r a d pb E eje dir r a d pb E eje dir r d pb E eje dir r phk ( ( ( ( ( ( ( ( ( ( ( ( ( ( ( ( ( ( ( ( ( (... ( ( ( ( ( ( ( ( 2 2 = = = c Hvilke efer pålægning af ransversaliesbeingelsen: ( ( ( ( ( lim = n n n n a phk E eje dir r Og med lid omrokering, giver: = = ( ( ( ( ( i i i pb E eje dir r a eje dir r d phk (a4
109 Udrykke i (a3 kan i ligevæg, hvor realværdien af boligbeholdning og den disponible realindkoms er konsan, og hvor huspriserne følger den generelle inflaion, skrives: E ( pcxh phk = c h( yd, k d E ( phk ( r( dir eje phk ( r( dir eje = pcxh ( π h( yd c phk ( r( dir eje = pcxh h( yd c phk ( r( dir eje phk aphk πphk aπphk = pcxh h( fyd*, k* d c ( r( dir eje a π q* = h( fyd*, k* d ( a, k d phk ( π ( a, k d πh( yd, k d phk aphk πphk aπphk Hvor π er den konsane inflaion i ligevæg og de er udnye a aπ ~. q* er ligevægsforholde mellem phk og pcxh. Bilag 4
110 Bilag 5 Bilag 5: Udledning i empiriske modeller Model af Groes & Møller: fyd d pc d kor d php d u fyd d pc d kor d k php d u fyd d pc d kor d k php d u fyd d pc d kor d php d k u fyd pc kor php k k u fyd pc kor php d fyd pc kor php d ε β β β β α α α α α α α α α α α α α α α α α α α α α α α α α α ν α α α α α = = = = = = = log log log log log log log log log log log log log log log log log log log log log log log log log log log log log c c c c c c Model af Blomgren-Hansen & Knøsgaard: phk phk phk phk phk phk E dir i u k w phk u E dir i u k w phk u E dir i u k w phk u E dir i u k phk w u E dir r phk w u k E dir i phk w u d ε π β β β β α π α α α α α α α π α α α α π α α α α π α α α α ν π α α α α = = = = = = ( log ( log log( log( ( log ( log log( log log( ( log ( log log( log log( ( log ( log log( log log( ( log ( log log( log log( ( ( ( c c c c c
111 Model i ADAM: phk * log( d = π u α α log( α2 log( fyd α3uc α4 pcxh pc De anages a den ligevægsskabende pris, phk*, kan beskrives ved følgende ligning: phk phk * phk log( = θ log( ( θ log( pcxh pcxh pcxh c phk * log( = θ pcxh phk log( θ pcxh phk ( θ log( pcxh Hvorefer de med ligevægsbeingelsen følger: log( d = α α [ θ c α θα uc phk phk log( θ ( θ log( pcxh pcxh pc α θu phk phk log( = α θα α θ log( k α θθ ( θ log( pcxh pcxh α θα π phk phk αθ log( = α log( k αθ ( θ log( pcxh pcxh c c 3 4 phk log( = β β log( k β2 log( fyd β3uc β4π pcxh ] α log( fyd α uc pc 2 α log( fyd α uc 2 phk β5 log( pcxh α θα log( fyd ε α π 4 pc α π 4 u pc u ADAMs boligmodel esimeres under resrikionen α 2 =, hvilke beyder: β2 β = α θ, β2 = α θα2 = β2 = β β Hvilke skrives ind i modellen, der herefer bliver: Bilag 5
112 Bilag 5 pc pcxh phk uc fyd k pcxh phk ε β π β β β β = log( ] log( [log( log( 5 4 3
113 Bilag 6: Udledning af nuidsværdimodel for boligmarkede Såfrem priserne på ejerboliger er give ved deres fundamenalværdi, gælder med idsvarierende afkaskrav: j P = i Y j j = i= δ (b De logarimiske afkas defineres: r ln( R (b2 Og dermed følger: r P Y = ln( = ln( P Y ln( P = ln[exp( p exp( y ] p (b3 P Hvor ln(p = p og ln(y = y. Ligningen (b3 kan gøres lineær med en førse orden Taylor ekspansion omkring de geomeriske middelværdier P og Y: r = k μ p ( μ y p, hvor P μ = og < μ < (b4 P D Da hverken p og y er saionære, defineres e ny variabel: S p y (b5 S er (log pris-indkoms forholde. Frarækkes y på begge sider af (b4, kan ligningen omskrives il: Bilag 6
114 Bilag 6 ( ( Δ = = = r y S k S r y y y p k y p y p y y p k y r μ μ μ c c (b6 Efer genagende subsiuion og med pålægning af ransversaliesbeingelsen fås: = = = = = Δ = Δ = Δ Δ = ] [ i i i i i i i i i i i i i i r y k S r y S k S r y r y S k k S μ μ μ μ μ μ μ μ μ c c c (b7 Ved a anage konsan afkaskrav og age den maemaiske forvenning fås en forenkle udgave af Blacks model for boligmarkede: c y E S i i i Δ = = μ, hvor μ = r k c (b8
115 Bilag 7 Bilag 7: Resrikioner på nuidsværdimodellen Af (6.3 følger: z A I A h z g S * ( = = μ Heri ligger implici resrikioner på A maricen: A h A I g z A I A h z g S ( ( * = = = μ μ c Hvilke på marixform (for en 2-variabel VAR model i 2 lags er: [ ] [ ] [ ] [ ] [ ] [ ] b b a a d d c c d d c c b b a a d d c c b b a a d d c c b b a a d d c c b b a a = = = μ μ μ μ μ μ μ μ μ μ μ μ μ μ μ c c
116 Med udgangspunk i ovensående resrikionsvekor gennemføres Wald-ese i daasæe med årlige observaioner: A maricen er funde som: a c a 2 c 2 b d b2,878 = d 2,67642,5589,26582,678,955,3674,38243 Og μ er: ( Δp Δy = (,89% 2,9% =,96758 Hvilke giver følgende resrikioner: [ μc μc μd μd ] = [ a a b b ] c [,64969,25468,43797,367397] = [,878,5589,678,3674] Disse resrikioner ese i EViews, hvilke giver følgende resula: Wald Tes: Equaion: WALD Tes Saisic Value df Probabiliy F-saisic (4, 42. Chi-square Null Hypohesis Summary: Normalized Resricion (= Value Sd. Err C( C( C( C( Bilag 7
117 Bilag 8: Daasæ Årlige observaioner fra ADAMs Daabank Variabel Navn Periode Kommenar Konanprisen på enfamiliehuse Prisindeks for byggesekoren Konanprisen på byggegrunde Kapialmængden af boliger (alle yper phk pibh phgk k =, originalkilden er ejendomssalg, Sasskaedirekorae 995=, beregne i ADAM 995=, originalkilden er ejendomssalg, Sasskaedirekorae Mio. kr. (995, beregne i ADAM, ADAM-navn: fkbh Ejers omkosninger uc Disponibel indkoms i yd 955- husholdningerne 23 Disponibel indkoms i ydk 955- husholdningerne på kor 23 sig Disponibel indkoms i ydl 955- husholdningerne på lang 23 sig Lønsum i al w Egne beregninger (se bilag Mio. kr., beregne i ADAM, ADAM-navn: ydph. Variabelen er summen af lønninger, neorener, overskud i erhvervene sam neooverførelser fra pensioner minus skaer Mio. kr., beregne i ADAM, ADAM-navn: ydphk2. Variabel er den disponible indkoms i husholdningerne uden neoudbealinger fra pensioner og formueafkas på pensionsopsparinger Mio. kr., beregne i ADAM, ADAM-navn: ydpl. Variabel er den disponible indkoms i den privae sekor frarukke formueafkas på pensionsopsparinger plus værdiilvæksen i boligsekoren Mio. kr., beregne i ADAM, ADAM-navn: yw Prisen på forbrug af andre forbrugsgoder end boligforbrug pcxh Prisudryk for privaforbrug, ADAM-navn: pcp4xhv ADAMs Daabank er gengive i Excel-arke: boligmarkedsdaa.xls, hvor der også findes e link il ADAMs variabelbrowser. EViews filen: aarsdaa.wf, indeholder daasæe i nominel og deflaere form. Variable med e f indikerer a de ilsvarende nominelle variabel er deflaere prisen på andre forbrugsgoder, pcxh. EViews filen: blackaarsdaa.wf, indeholder ransformerede variable, som indgår i VAR modellen. Bilag 8
118 Kvaralsvise observaioner fra øvrige daakilder Variabel Navn Periode Kommenar Konanprisen på enfamiliehuse Konanprisen på ejerlejligheder phk 992k- 25k2 phk2 992k- 25k2 Danmarks Saisik, 995=, Danmarks Saisik, 995=, Gennemsnilig kvadrameerpris på boliger i byzoner phk3 995k- 25k3 Gennemsnilig phk4 995k- kvadrameerpris på 25k3 boliger i landzoner Gennemsnilig phk5 995k- kvadrameerpris på 25k3 friidshuse Byggeomkosninger pibh 992k- 25k3 Realkrediråde/Egne beregninger (se bilag 2 Realkrediråde/Egne beregninger (se bilag 2 Realkrediråde/Egne beregninger (se bilag 2 Danmarks Saisik, 23k= Kapialmængden af boliger (alle yper k 992k- 25k3 ADAMs Daabank. Fra 23 er kapialmængden fremskreve med den gennemsnilige væks Ejers omkosninger uc 992k- 25k3 Løn w 992k- 25k3 Egne beregninger. Renen er frem il 997k3 e indeks for realkrediobligaioner med 3 års løbeid fra Naionalbanken, hvorefer der anvendes e simpel gennemsni af den kore- og lange byggerene fra Realkrediråde. Øvrige daa er hene i ADAMs daabank Danmarks Saisik, 98= Generelle forbrugerpriser pc 992k- 25k3 Danmarks Saisik, 2= I daasæe indgår daa, der er ransformere fra højfrekvene il lavfrekvene observaioner (fra måned il kvaral vha. simpel gennemsni, sam daa, der er ransformere fra lavfrekvene il højfrekvene observaioner (fra år il kvaral vha. inrapolering. For dealjer henvises il Excel-arke: boligmarkedsdaa.xls. EViews filen: kvaralsdaa.wf, indeholder daasæe i nominel og deflaere form. Variable med e f indikerer a de ilsvarende nominelle variabel er deflaere med de generelle forbrugerpriser, pc. EViews filen: blackkvaralsdaa.wf, indeholder ransformerede variable, som indgår i VAR modellen. Bilag 8
119 obs PHK PIBH PHGK K UC YD NA
120 YDK YDL W PCXH
121 obs PHK PHK2 PHK3 PHK4 PHK5 PIBH 992: NA NA NA : NA NA NA : NA NA NA : NA NA NA : NA NA NA : NA NA NA : NA NA NA : NA NA NA : NA NA NA : NA NA NA : NA NA NA : NA NA NA : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : :3 NA NA
122 K UC W PC
123 Bilag 9: Tes for saionarie Årlige observaioner fra ADAMs Daabank Null Hypohesis: K has a uni roo Exogenous: Consan Lag Lengh: (Auomaic based on SIC, MAXLAG=5 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: K has a uni roo Exogenous: Consan, Linear Trend Lag Lengh: (Auomaic based on SIC, MAXLAG=5 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: K has a uni roo Exogenous: None Lag Lengh: (Auomaic based on SIC, MAXLAG=5 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: D(K has a uni roo Exogenous: Consan Lag Lengh: (Auomaic based on SIC, MAXLAG=5 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: D(K has a uni roo Exogenous: Consan, Linear Trend Lag Lengh: (Auomaic based on SIC, MAXLAG=5 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: D(K has a uni roo Exogenous: None Lag Lengh: (Auomaic based on SIC, MAXLAG=5 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Bilag 9
124 Null Hypohesis: UC has a uni roo Exogenous: Consan Lag Lengh: (Auomaic based on SIC, MAXLAG=5 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: UC has a uni roo Exogenous: Consan, Linear Trend Lag Lengh: (Auomaic based on SIC, MAXLAG=5 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: UC has a uni roo Exogenous: None Lag Lengh: (Auomaic based on SIC, MAXLAG=5 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: D(UC has a uni roo Exogenous: Consan Lag Lengh: (Auomaic based on SIC, MAXLAG=5 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: D(UC has a uni roo Exogenous: Consan, Linear Trend Lag Lengh: (Auomaic based on SIC, MAXLAG=5 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: D(UC has a uni roo Exogenous: None Lag Lengh: (Auomaic based on SIC, MAXLAG=5 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Bilag 9
125 Null Hypohesis: FYD has a uni roo Exogenous: Consan Lag Lengh: (Auomaic based on SIC, MAXLAG=5 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: FYD has a uni roo Exogenous: Consan, Linear Trend Lag Lengh: (Auomaic based on SIC, MAXLAG=5 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: FYD has a uni roo Exogenous: None Lag Lengh: (Auomaic based on SIC, MAXLAG=5 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: D(FYD has a uni roo Exogenous: Consan Lag Lengh: (Auomaic based on SIC, MAXLAG=5 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: D(FYD has a uni roo Exogenous: Consan, Linear Trend Lag Lengh: (Auomaic based on SIC, MAXLAG=5 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: D(FYD has a uni roo Exogenous: None Lag Lengh: 3 (Auomaic based on SIC, MAXLAG=5 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Bilag 9
126 Null Hypohesis: FYDK has a uni roo Exogenous: Consan Lag Lengh: (Auomaic based on SIC, MAXLAG=5 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: FYDK has a uni roo Exogenous: Consan, Linear Trend Lag Lengh: (Auomaic based on SIC, MAXLAG=5 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: FYDK has a uni roo Exogenous: None Lag Lengh: (Auomaic based on SIC, MAXLAG=5 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: D(FYDK has a uni roo Exogenous: Consan Lag Lengh: (Auomaic based on SIC, MAXLAG=5 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: D(FYDK has a uni roo Exogenous: Consan, Linear Trend Lag Lengh: (Auomaic based on SIC, MAXLAG=5 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: D(FYDK has a uni roo Exogenous: None Lag Lengh: 3 (Auomaic based on SIC, MAXLAG=5 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Bilag 9
127 Null Hypohesis: FYDL has a uni roo Exogenous: Consan Lag Lengh: (Auomaic based on SIC, MAXLAG=5 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: FYDL has a uni roo Exogenous: Consan, Linear Trend Lag Lengh: (Auomaic based on SIC, MAXLAG=5 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: FYDL has a uni roo Exogenous: None Lag Lengh: (Auomaic based on SIC, MAXLAG=5 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: D(FYDL has a uni roo Exogenous: Consan Lag Lengh: (Auomaic based on SIC, MAXLAG=5 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: D(FYDL has a uni roo Exogenous: Consan, Linear Trend Lag Lengh: (Auomaic based on SIC, MAXLAG=5 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: D(FYDL has a uni roo Exogenous: None Lag Lengh: (Auomaic based on SIC, MAXLAG=5 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Bilag 9
128 Null Hypohesis: FW has a uni roo Exogenous: Consan Lag Lengh: (Auomaic based on SIC, MAXLAG=5 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: FW has a uni roo Exogenous: Consan, Linear Trend Lag Lengh: (Auomaic based on SIC, MAXLAG=5 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: FW has a uni roo Exogenous: None Lag Lengh: (Auomaic based on SIC, MAXLAG=5 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: D(FW has a uni roo Exogenous: Consan Lag Lengh: (Auomaic based on SIC, MAXLAG=5 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: D(FW has a uni roo Exogenous: Consan, Linear Trend Lag Lengh: (Auomaic based on SIC, MAXLAG=5 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: D(FW has a uni roo Exogenous: None Lag Lengh: 2 (Auomaic based on SIC, MAXLAG=5 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Bilag 9
129 Null Hypohesis: PCXH has a uni roo Exogenous: Consan Lag Lengh: 2 (Auomaic based on SIC, MAXLAG=5 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: PCXH has a uni roo Exogenous: Consan, Linear Trend Lag Lengh: 2 (Auomaic based on SIC, MAXLAG=5 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: PCXH has a uni roo Exogenous: None Lag Lengh: 2 (Auomaic based on SIC, MAXLAG=5 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: D(PCXH has a uni roo Exogenous: Consan Lag Lengh: (Auomaic based on SIC, MAXLAG=5 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: D(PCXH has a uni roo Exogenous: Consan, Linear Trend Lag Lengh: (Auomaic based on SIC, MAXLAG=5 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: D(PCXH has a uni roo Exogenous: None Lag Lengh: (Auomaic based on SIC, MAXLAG=5 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Bilag 9
130 Kvaralsdaa Null Hypohesis: K has a uni roo Exogenous: Consan Lag Lengh: (Auomaic based on SIC, MAXLAG=2 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: K has a uni roo Exogenous: Consan, Linear Trend Lag Lengh: (Auomaic based on SIC, MAXLAG=2 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: K has a uni roo Exogenous: None Lag Lengh: (Auomaic based on SIC, MAXLAG=2 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: D(K has a uni roo Exogenous: Consan Lag Lengh: (Auomaic based on SIC, MAXLAG=2 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: D(K has a uni roo Exogenous: Consan, Linear Trend Lag Lengh: (Auomaic based on SIC, MAXLAG=2 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: D(K has a uni roo Exogenous: None Lag Lengh: (Auomaic based on SIC, MAXLAG=2 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Bilag 9
131 Null Hypohesis: UC has a uni roo Exogenous: Consan Lag Lengh: (Auomaic based on SIC, MAXLAG=2 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: UC has a uni roo Exogenous: Consan, Linear Trend Lag Lengh: (Auomaic based on SIC, MAXLAG=2 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: UC has a uni roo Exogenous: None Lag Lengh: (Auomaic based on SIC, MAXLAG=2 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: D(UC has a uni roo Exogenous: Consan Lag Lengh: (Auomaic based on SIC, MAXLAG=2 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: D(UC has a uni roo Exogenous: Consan, Linear Trend Lag Lengh: (Auomaic based on SIC, MAXLAG=2 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: D(UC has a uni roo Exogenous: None Lag Lengh: (Auomaic based on SIC, MAXLAG=2 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Bilag 9
132 Null Hypohesis: FW has a uni roo Exogenous: Consan Lag Lengh: 7 (Auomaic based on SIC, MAXLAG=2 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: FW has a uni roo Exogenous: Consan, Linear Trend Lag Lengh: 4 (Auomaic based on SIC, MAXLAG=2 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: FW has a uni roo Exogenous: None Lag Lengh: 7 (Auomaic based on SIC, MAXLAG=2 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: D(FW has a uni roo Exogenous: Consan Lag Lengh: 6 (Auomaic based on SIC, MAXLAG=2 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: D(FW has a uni roo Exogenous: Consan, Linear Trend Lag Lengh: 6 (Auomaic based on SIC, MAXLAG=2 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: D(FW has a uni roo Exogenous: None Lag Lengh: 3 (Auomaic based on SIC, MAXLAG=2 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Bilag 9
133 Null Hypohesis: PC has a uni roo Exogenous: Consan Lag Lengh: 5 (Auomaic based on SIC, MAXLAG=2 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: PC has a uni roo Exogenous: Consan, Linear Trend Lag Lengh: 4 (Auomaic based on SIC, MAXLAG=2 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: PC has a uni roo Exogenous: None Lag Lengh: 4 (Auomaic based on SIC, MAXLAG=2 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: D(PC has a uni roo Exogenous: Consan Lag Lengh: 4 (Auomaic based on SIC, MAXLAG=2 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: D(PC has a uni roo Exogenous: Consan, Linear Trend Lag Lengh: 4 (Auomaic based on SIC, MAXLAG=2 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: D(PC has a uni roo Exogenous: None Lag Lengh: 3 (Auomaic based on SIC, MAXLAG=2 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Bilag 9
134 Bilag : Real husleje ved a benye egen bolig under fuld efficiens Periode: (956=, kilde: ADAMs Daabank. Seriens middelværdi er,, sandardafvigelsen er,47 og Jarque-Bara saisikken er,82. Bilag
135 Bilag : Tes for koinegraion i nyere daa Dependen Variable: LOG(PHK Mehod: Leas Squares Sample(adjused: 992: 25:2 Included observaions: 54 afer adjusing endpoins Variable Coefficien Sd. Error -Saisic Prob. LOG(PIBH C R-squared.9846 Mean dependen var Adjused R-squared S.D. dependen var S.E. of regression Akaike info crierion Sum squared resid.7239 Schwarz crierion Log likelihood F-saisic Durbin-Wason sa Prob(F-saisic. Null Hypohesis: EC has a uni roo Exogenous: Consan Lag Lengh: (Auomaic based on SIC, MAXLAG=2 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: EC has a uni roo Exogenous: Consan, Linear Trend Lag Lengh: (Auomaic based on SIC, MAXLAG=2 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: EC has a uni roo Exogenous: None Lag Lengh: (Auomaic based on SIC, MAXLAG=2 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Bilag
136 Dependen Variable: LOG(PHK2 Mehod: Leas Squares Sample(adjused: 992: 25:2 Included observaions: 54 afer adjusing endpoins Variable Coefficien Sd. Error -Saisic Prob. LOG(PIBH C R-squared Mean dependen var Adjused R-squared S.D. dependen var S.E. of regression.5347 Akaike info crierion Sum squared resid Schwarz crierion Log likelihood F-saisic Durbin-Wason sa Prob(F-saisic. Null Hypohesis: EC2 has a uni roo Exogenous: Consan Lag Lengh: (Auomaic based on SIC, MAXLAG=2 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: EC2 has a uni roo Exogenous: Consan, Linear Trend Lag Lengh: (Auomaic based on SIC, MAXLAG=2 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: EC2 has a uni roo Exogenous: None Lag Lengh: (Auomaic based on SIC, MAXLAG=2 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Bilag
137 Dependen Variable: LOG(PHK3 Mehod: Leas Squares Sample(adjused: 995: 25:3 Included observaions: 43 afer adjusing endpoins Variable Coefficien Sd. Error -Saisic Prob. LOG(PIBH C R-squared Mean dependen var Adjused R-squared S.D. dependen var S.E. of regression.4769 Akaike info crierion Sum squared resid.6847 Schwarz crierion Log likelihood F-saisic Durbin-Wason sa.4893 Prob(F-saisic. Null Hypohesis: EC3 has a uni roo Exogenous: Consan Lag Lengh: (Auomaic based on SIC, MAXLAG=6 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: EC3 has a uni roo Exogenous: Consan, Linear Trend Lag Lengh: (Auomaic based on SIC, MAXLAG=6 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: EC3 has a uni roo Exogenous: None Lag Lengh: (Auomaic based on SIC, MAXLAG=6 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Bilag
138 Dependen Variable: LOG(PHK4 Mehod: Leas Squares Sample(adjused: 995: 25:3 Included observaions: 43 afer adjusing endpoins Variable Coefficien Sd. Error -Saisic Prob. LOG(PIBH C R-squared Mean dependen var Adjused R-squared.9854 S.D. dependen var S.E. of regression.343 Akaike info crierion Sum squared resid Schwarz crierion Log likelihood F-saisic Durbin-Wason sa Prob(F-saisic. Null Hypohesis: EC4 has a uni roo Exogenous: Consan Lag Lengh: (Auomaic based on SIC, MAXLAG=6 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: EC4 has a uni roo Exogenous: Consan, Linear Trend Lag Lengh: (Auomaic based on SIC, MAXLAG=6 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: EC4 has a uni roo Exogenous: None Lag Lengh: (Auomaic based on SIC, MAXLAG=6 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Bilag
139 Dependen Variable: LOG(PHK5 Mehod: Leas Squares Sample(adjused: 995: 25:3 Included observaions: 43 afer adjusing endpoins Variable Coefficien Sd. Error -Saisic Prob. LOG(PIBH C R-squared Mean dependen var 9.53 Adjused R-squared S.D. dependen var.3268 S.E. of regression Akaike info crierion Sum squared resid.9464 Schwarz crierion Log likelihood F-saisic Durbin-Wason sa.2693 Prob(F-saisic. Null Hypohesis: EC5 has a uni roo Exogenous: Consan Lag Lengh: (Auomaic based on SIC, MAXLAG=6 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: EC5 has a uni roo Exogenous: Consan, Linear Trend Lag Lengh: (Auomaic based on SIC, MAXLAG=6 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Null Hypohesis: EC5 has a uni roo Exogenous: None Lag Lengh: (Auomaic based on SIC, MAXLAG=6 -Saisic Prob.* Augmened Dickey-Fuller es saisic Tes criical values: % level % level % level Bilag
140 Bilag 2: Validering af dynamisk prisdannelsesmodel Model uden k og pcxh Dependen Variable: DLOG(FPHK Mehod: Leas Squares Sample(adjused: Included observaions: 46 afer adjusing endpoins Variable Coefficien Sd. Error -Saisic Prob. C EC3( EC3( DLOG(UC DLOG(UC( DLOG(FW DLOG(FW( R-squared Mean dependen var.8454 Adjused R-squared S.D. dependen var S.E. of regression.5368 Akaike info crierion Sum squared resid.9834 Schwarz crierion Log likelihood F-saisic Durbin-Wason sa Prob(F-saisic.6 Dependen Variable: DLOG(FPHK Mehod: Leas Squares Sample(adjused: Included observaions: 47 afer adjusing endpoins Variable Coefficien Sd. Error -Saisic Prob. C EC3( EC3( DLOG(UC DLOG(FW R-squared.5543 Mean dependen var.234 Adjused R-squared.5538 S.D. dependen var.7756 S.E. of regression Akaike info crierion Sum squared resid.283 Schwarz crierion Log likelihood F-saisic Durbin-Wason sa Prob(F-saisic Residual Acual Fied Bilag 2
141 Dependen Variable: DLOG(FPHK Mehod: Leas Squares Sample(adjused: Included observaions: 34 afer adjusing endpoins Variable Coefficien Sd. Error -Saisic Prob. C EC9( EC9( DLOG(UC DLOG(UC( DLOG(FW DLOG(FW( R-squared.6336 Mean dependen var.992 Adjused R-squared S.D. dependen var.837 S.E. of regression Akaike info crierion Sum squared resid.8464 Schwarz crierion Log likelihood F-saisic Durbin-Wason sa Prob(F-saisic.69 Dependen Variable: DLOG(FPHK Mehod: Leas Squares Sample(adjused: Included observaions: 35 afer adjusing endpoins Variable Coefficien Sd. Error -Saisic Prob. C EC9( DLOG(UC DLOG(FW DLOG(FW( R-squared Mean dependen var.582 Adjused R-squared S.D. dependen var S.E. of regression.5473 Akaike info crierion Sum squared resid.884 Schwarz crierion Log likelihood F-saisic Durbin-Wason sa.7858 Prob(F-saisic Residual Acual Fied Bilag 2
142 Validering af dynamisk prismodel (residualer Series: Residuals Sample Observaions 47 Mean.63E-7 Median Maximum.625 Minimum Sd. Dev Skewness.3386 Kurosis Jarque-Bera.543 Probabiliy ARCH Tes: F-saisic Probabiliy.2637 Obs*R-squared Probabiliy Tes Equaion: Dependen Variable: RESID^2 Mehod: Leas Squares Sample(adjused: Included observaions: 42 afer adjusing endpoins Variable Coefficien Sd. Error -Saisic Prob. C RESID^2( RESID^2( RESID^2( RESID^2( RESID^2( R-squared Mean dependen var.74 Adjused R-squared.4778 S.D. dependen var.233 S.E. of regression.99 Akaike info crierion Sum squared resid.43 Schwarz crierion Log likelihood F-saisic Durbin-Wason sa Prob(F-saisic.2637 Bilag 2
143 Breusch-Godfrey Serial Correlaion LM Tes: F-saisic Probabiliy Obs*R-squared Probabiliy.647 Tes Equaion: Dependen Variable: RESID Mehod: Leas Squares Presample missing value lagged residuals se o zero. Variable Coefficien Sd. Error -Saisic Prob. C EC3( EC3( DLOG(K( DLOG(UC DLOG(FW( DLOG(PCXH DLOG(PCXH( RESID( RESID( RESID( RESID( RESID( R-squared.7798 Mean dependen var.63e-7 Adjused R-squared S.D. dependen var S.E. of regression Akaike info crierion Sum squared resid.8295 Schwarz crierion Log likelihood F-saisic Durbin-Wason sa Prob(F-saisic Bilag 2
144 Bilag 3: Esimering af dynamisk prisdannelsesmodel i nyere daa Dependen Variable: DLOG(FPHK Mehod: Leas Squares Sample(adjused: 992:4 25:2 Included observaions: 5 afer adjusing endpoins Variable Coefficien Sd. Error -Saisic Prob. C EC( EC( DLOG(K( DLOG(K( DLOG(UC DLOG(UC( DLOG(FW DLOG(FW( DLOG(PC DLOG(PC( R-squared.4793 Mean dependen var.328 Adjused R-squared S.D. dependen var.6876 S.E. of regression.4528 Akaike info crierion Sum squared resid.8443 Schwarz crierion Log likelihood F-saisic Durbin-Wason sa Prob(F-saisic.27 Dependen Variable: DLOG(FPHK Mehod: Leas Squares Sample(adjused: 992:4 25:2 Included observaions: 5 afer adjusing endpoins Variable Coefficien Sd. Error -Saisic Prob. EC( EC( DLOG(K( R-squared Mean dependen var.328 Adjused R-squared S.D. dependen var.6876 S.E. of regression.4474 Akaike info crierion Sum squared resid.56 Schwarz crierion Log likelihood Durbin-Wason sa Bilag 3
145 Dependen Variable: DLOG(FPHK2 Sample(adjused: 992:4 25:2 Included observaions: 5 afer adjusing endpoins Variable Coefficien Sd. Error -Saisic Prob. C EC2( EC2( DLOG(K( DLOG(K( DLOG(UC DLOG(UC( DLOG(FW DLOG(FW( DLOG(PC DLOG(PC( R-squared.4989 Mean dependen var.947 Adjused R-squared S.D. dependen var.267 S.E. of regression.877 Akaike info crierion Sum squared resid.37 Schwarz crierion Log likelihood F-saisic Durbin-Wason sa.6785 Prob(F-saisic.22 Dependen Variable: DLOG(FPHK2 Mehod: Leas Squares Sample(adjused: 992:4 25:2 Included observaions: 5 afer adjusing endpoins Variable Coefficien Sd. Error -Saisic Prob. EC2( DLOG(K( DLOG(FW R-squared Mean dependen var.947 Adjused R-squared S.D. dependen var.267 S.E. of regression.842 Akaike info crierion Sum squared resid.5799 Schwarz crierion Log likelihood Durbin-Wason sa Bilag 3
146 Dependen Variable: DLOG(FPHK3 Mehod: Leas Squares Sample(adjused: 995:3 25:3 Included observaions: 4 afer adjusing endpoins Variable Coefficien Sd. Error -Saisic Prob. C EC3( EC3( DLOG(K( DLOG(K( DLOG(UC DLOG(UC( DLOG(FW DLOG(FW( DLOG(PC DLOG(PC( R-squared Mean dependen var.2885 Adjused R-squared S.D. dependen var.9456 S.E. of regression.88 Akaike info crierion Sum squared resid.65 Schwarz crierion Log likelihood.335 F-saisic Durbin-Wason sa Prob(F-saisic Dependen Variable: DLOG(FPHK3 Mehod: Leas Squares Sample(adjused: 995:2 25:3 Included observaions: 42 afer adjusing endpoins Variable Coefficien Sd. Error -Saisic Prob. C EC3( DLOG(PC R-squared Mean dependen var Adjused R-squared S.D. dependen var.964 S.E. of regression.837 Akaike info crierion Sum squared resid.2829 Schwarz crierion Log likelihood.3734 F-saisic Durbin-Wason sa Prob(F-saisic.6874 Bilag 3
147 Dependen Variable: DLOG(FPHK4 Mehod: Leas Squares Sample(adjused: 995:3 25:3 Included observaions: 4 afer adjusing endpoins Variable Coefficien Sd. Error -Saisic Prob. C EC4( EC4( DLOG(K( DLOG(K( DLOG(UC DLOG(UC( DLOG(FW DLOG(FW( DLOG(PC DLOG(PC( R-squared Mean dependen var.6376 Adjused R-squared -.28 S.D. dependen var.759 S.E. of regression.7679 Akaike info crierion Sum squared resid.9377 Schwarz crierion Log likelihood F-saisic Durbin-Wason sa.9343 Prob(F-saisic Dependen Variable: DLOG(FPHK4 Mehod: Leas Squares Sample(adjused: 995:2 25:3 Included observaions: 42 afer adjusing endpoins Variable Coefficien Sd. Error -Saisic Prob. C DLOG(FW( R-squared.7 Mean dependen var.6539 Adjused R-squared S.D. dependen var.746 S.E. of regression.654 Akaike info crierion Sum squared resid.39 Schwarz crierion Log likelihood F-saisic Durbin-Wason sa Prob(F-saisic.6644 Bilag 3
148 Dependen Variable: DLOG(FPHK5 Mehod: Leas Squares Sample(adjused: 995:3 25:3 Included observaions: 4 afer adjusing endpoins Variable Coefficien Sd. Error -Saisic Prob. C EC5( EC5( DLOG(K( DLOG(K( DLOG(UC DLOG(UC( DLOG(FW DLOG(FW( DLOG(PC DLOG(PC( R-squared Mean dependen var Adjused R-squared S.D. dependen var.2257 S.E. of regression.2399 Akaike info crierion Sum squared resid.7265 Schwarz crierion Log likelihood.626 F-saisic.5432 Durbin-Wason sa Prob(F-saisic.847 Dependen Variable: DLOG(FPHK5 Mehod: Leas Squares Sample(adjused: 995:2 25:3 Included observaions: 42 afer adjusing endpoins Variable Coefficien Sd. Error -Saisic Prob. C R-squared. Mean dependen var.2522 Adjused R-squared. S.D. dependen var.2362 S.E. of regression.2362 Akaike info crierion Sum squared resid.2284 Schwarz crierion Log likelihood Durbin-Wason sa Bilag 3
149 Bilag 4: Esimering af eoreiske pris-indkoms forhold i nyere daa Vecor Auoregression Esimaes Sample(adjused: 992:4 25:2 Included observaions: 5 afer adjusing endpoins Sandard errors in ( & -saisics in [ ] DYMEAN SMEAN DYMEAN( (.679 (.5483 [ ] [ ] DYMEAN( (.4376 ( [.295] [.95753] SMEAN( (.3986 (.2864 [-.4825] [ ] SMEAN( (.45 (.2958 [.2344] [-5.728] R-squared Adj. R-squared Sum sq. resids S.E. equaion F-saisic Log likelihood Akaike AIC Schwarz SC Mean dependen -7.2E S.D. dependen Deerminan Residual 6.56E-9 Covariance Log Likelihood (d.f. adjused Akaike Informaion Crieria Schwarz Crieria S* S Bilag 4
150 Vecor Auoregression Esimaes Sample(adjused: 992:4 25:2 Included observaions: 5 afer adjusing endpoins Sandard errors in ( & -saisics in [ ] DYMEAN2 SMEAN2 DYMEAN2( (.66 ( [-2.578] [ ] DYMEAN2( (.4276 ( [.566] [.2659] SMEAN2( (.333 (.2457 [-.6846] [ 3.435] SMEAN2( (.394 (.274 [.7678] [-5.372] R-squared Adj. R-squared Sum sq. resids S.E. equaion F-saisic Log likelihood Akaike AIC Schwarz SC Mean dependen -7.2E S.D. dependen Deerminan Residual.2E-8 Covariance Log Likelihood (d.f. adjused Akaike Informaion Crieria Schwarz Crieria S* S Bilag 4
151 Vecor Auoregression Esimaes Sample(adjused: 995:4 25:3 Included observaions: 4 afer adjusing endpoins Sandard errors in ( & -saisics in [ ] DYMEAN3 SMEAN3 DYMEAN3( (.6545 ( [-.895] [-.477] DYMEAN3( (.825 (.6435 [ ] [.4536] SMEAN3( (.32 (.3 [-.465] [ 7.79] SMEAN3( (.33 (.64 [-.2474] [ ] R-squared Adj. R-squared Sum sq. resids S.E. equaion F-saisic Log likelihood Akaike AIC Schwarz SC Mean dependen S.D. dependen Deerminan Residual 9.36E-9 Covariance Log Likelihood (d.f. adjused Akaike Informaion Crieria Schwarz Crieria S* S Bilag 4
152 Vecor Auoregression Esimaes Sample(adjused: 995:4 25:3 Included observaions: 4 afer adjusing endpoins Sandard errors in ( & -saisics in [ ] DYMEAN4 SMEAN4 DYMEAN4( (.6323 ( [ ] [-.88] DYMEAN4( (.898 (.6653 [-.3748] [ ] SMEAN4( (.439 (.649 [-.4446] [ 8.699] SMEAN4( (.429 (.5683 [.32348] [ ] R-squared Adj. R-squared Sum sq. resids S.E. equaion F-saisic Log likelihood Akaike AIC Schwarz SC Mean dependen S.D. dependen Deerminan Residual 9.63E-9 Covariance Log Likelihood (d.f. adjused Akaike Informaion Crieria Schwarz Crieria S* S Bilag 4
153 Vecor Auoregression Esimaes Sample(adjused: 995:4 25:3 Included observaions: 4 afer adjusing endpoins Sandard errors in ( & -saisics in [ ] DYMEAN5 SMEAN5 DYMEAN5( (.79 ( [-.7437] [.8999] DYMEAN5( (.895 ( [ ] [.82467] SMEAN5( (.2928 (.5 [.3754] [.28] SMEAN5( (.2977 (.5355 [ ] [ ] R-squared Adj. R-squared Sum sq. resids S.E. equaion F-saisic Log likelihood Akaike AIC Schwarz SC Mean dependen S.D. dependen Deerminan Residual.82E-8 Covariance Log Likelihood (d.f. adjused Akaike Informaion Crieria Schwarz Crieria Bilag 4
Bankernes renter forklares af andet end Nationalbankens udlånsrente
 N O T A T Bankernes rener forklares af ande end Naionalbankens udlånsrene 20. maj 2009 Kor resumé I forbindelse med de senese renesænkninger fra Naionalbanken er bankerne bleve beskyld for ikke a sænke
N O T A T Bankernes rener forklares af ande end Naionalbankens udlånsrene 20. maj 2009 Kor resumé I forbindelse med de senese renesænkninger fra Naionalbanken er bankerne bleve beskyld for ikke a sænke
Dagens forelæsning. Claus Munk. kap. 4. Arbitrage. Obligationsprisfastsættelse. Ingen-Arbitrage princippet. Nulkuponobligationer
 Dagens forelæsning Ingen-Arbirage princippe Claus Munk kap. 4 Nulkuponobligaioner Simpel og generel boosrapping Nulkuponrenesrukuren Forwardrener 2 Obligaionsprisfassæelse Arbirage Værdien af en obligaion
Dagens forelæsning Ingen-Arbirage princippe Claus Munk kap. 4 Nulkuponobligaioner Simpel og generel boosrapping Nulkuponrenesrukuren Forwardrener 2 Obligaionsprisfassæelse Arbirage Værdien af en obligaion
Udlånsvækst drives af efterspørgslen
 N O T A T Udlånsvæks drives af eferspørgslen 12. januar 211 Kor resumé Der har den senese id være megen fokus på bankers og realkrediinsiuers udlån il virksomheder og husholdninger. Især er bankerne fra
N O T A T Udlånsvæks drives af eferspørgslen 12. januar 211 Kor resumé Der har den senese id være megen fokus på bankers og realkrediinsiuers udlån il virksomheder og husholdninger. Især er bankerne fra
Vækst på kort og langt sigt
 12 SAMFUNDSØKONOMEN NR. 1 MARTS 2014 VÆKST PÅ KORT OG LANG SIGT Væks på kor og lang sig Efer re års silsand i dansk økonomi er de naurlig, a ineressen for a skabe økonomisk væks er beydelig. Ariklen gennemgår
12 SAMFUNDSØKONOMEN NR. 1 MARTS 2014 VÆKST PÅ KORT OG LANG SIGT Væks på kor og lang sig Efer re års silsand i dansk økonomi er de naurlig, a ineressen for a skabe økonomisk væks er beydelig. Ariklen gennemgår
EPIDEMIERS DYNAMIK. Kasper Larsen, Bjarke Vilster Hansen. Henriette Elgaard Nissen, Louise Legaard og
 EPDEMER DYAMK AF Kasper Larsen, Bjarke Vilser Hansen Henriee Elgaard issen, Louise Legaard og Charloe Plesher-Frankild 1. Miniprojek idefagssupplering, RUC Deember 2007 DLEDG Maemaisk modellering kan anvendes
EPDEMER DYAMK AF Kasper Larsen, Bjarke Vilser Hansen Henriee Elgaard issen, Louise Legaard og Charloe Plesher-Frankild 1. Miniprojek idefagssupplering, RUC Deember 2007 DLEDG Maemaisk modellering kan anvendes
MAKRO 2 ENDOGEN VÆKST
 ENDOGEN VÆKST MAKRO 2 2. årsprøve Forelæsning 7 Kapiel 8 Hans Jørgen Whia-Jacobsen econ.ku.dk/okojacob/makro-2-f09/makro I modeller med endogen væks er den langsigede væksrae i oupu pr. mand endogen besem.
ENDOGEN VÆKST MAKRO 2 2. årsprøve Forelæsning 7 Kapiel 8 Hans Jørgen Whia-Jacobsen econ.ku.dk/okojacob/makro-2-f09/makro I modeller med endogen væks er den langsigede væksrae i oupu pr. mand endogen besem.
Udviklingen i boligomkostninger, efficiensanalyse samt udbuds- og priselasticitet på det Københavnske boligmarked
 Specialeafhandling for Cand. Merc sudie Erhvervsøkonomisk insiu Forfaere: Anne Kvis Nielsen Jan Furbo Fuglsang Pedersen Vejleder: Tom Engsed Udviklingen i boligomkosninger, efficiensanalyse sam udbuds-
Specialeafhandling for Cand. Merc sudie Erhvervsøkonomisk insiu Forfaere: Anne Kvis Nielsen Jan Furbo Fuglsang Pedersen Vejleder: Tom Engsed Udviklingen i boligomkosninger, efficiensanalyse sam udbuds-
Matematik A. Studentereksamen. Forberedelsesmateriale til de digitale eksamensopgaver med adgang til internettet. stx141-matn/a-05052014
 Maemaik A Sudenereksamen Forberedelsesmaeriale il de digiale eksamensopgaver med adgang il inernee sx141-matn/a-0505014 Mandag den 5. maj 014 Forberedelsesmaeriale il sx A ne MATEMATIK Der skal afsæes
Maemaik A Sudenereksamen Forberedelsesmaeriale il de digiale eksamensopgaver med adgang il inernee sx141-matn/a-0505014 Mandag den 5. maj 014 Forberedelsesmaeriale il sx A ne MATEMATIK Der skal afsæes
Danmarks Nationalbank
 Danmarks Naionalbank Kvar al so ver sig 3. kvaral Del 2 202 D A N M A R K S N A T I O N A L B A N K 2 0 2 3 KVARTALSOVERSIGT, 3. KVARTAL 202, Del 2 De lille billede på forsiden viser Arne Jacobsens ur,
Danmarks Naionalbank Kvar al so ver sig 3. kvaral Del 2 202 D A N M A R K S N A T I O N A L B A N K 2 0 2 3 KVARTALSOVERSIGT, 3. KVARTAL 202, Del 2 De lille billede på forsiden viser Arne Jacobsens ur,
Finansministeriets beregning af gab og strukturelle niveauer
 Noa. november (revidere. maj ) Finansminiseries beregning af gab og srukurelle niveauer Vurdering af oupugabe (forskellen mellem fakisk og poeniel produkion) og de srukurelle niveauer for ledighed og arbejdssyrke
Noa. november (revidere. maj ) Finansminiseries beregning af gab og srukurelle niveauer Vurdering af oupugabe (forskellen mellem fakisk og poeniel produkion) og de srukurelle niveauer for ledighed og arbejdssyrke
I dette appendiks uddybes kemien bag enzymkinetikken i Bioteknologi 2, side 60-72.
 Bioeknologi 2, Tema 4 5 Kineik Kineik er sudier af reakionshasigheden hvor man eksperimenel undersøger de fakorer, der påvirker reakionshasigheden, og hvor resulaerne afslører reakionens mekanisme og ransiion
Bioeknologi 2, Tema 4 5 Kineik Kineik er sudier af reakionshasigheden hvor man eksperimenel undersøger de fakorer, der påvirker reakionshasigheden, og hvor resulaerne afslører reakionens mekanisme og ransiion
RETTEVEJLEDNING TIL Tag-Med-Hjem-Eksamen Makroøkonomi, 2. Årsprøve Efterårssemestret 2003
 RETTEVEJLEDNING TIL Tag-Med-Hjem-Eksamen Makroøkonomi, 2. Årsprøve Eferårssemesre 2003 Generelle bemærkninger Opgaven er den redje i en ny ordning, hvorefer eksamen efer førse semeser af makro på 2.år
RETTEVEJLEDNING TIL Tag-Med-Hjem-Eksamen Makroøkonomi, 2. Årsprøve Eferårssemesre 2003 Generelle bemærkninger Opgaven er den redje i en ny ordning, hvorefer eksamen efer førse semeser af makro på 2.år
Multivariate kointegrationsanalyser - En analyse af risikopræmien på det danske aktiemarked
 Cand.merc.(ma)-sudie Økonomisk nsiu Kandidaafhandling Mulivariae koinegraionsanalyser - En analyse af risikopræmien på de danske akiemarked Suderende: Louise Wellner Bech flevere: 9. april 9 Vejleder:
Cand.merc.(ma)-sudie Økonomisk nsiu Kandidaafhandling Mulivariae koinegraionsanalyser - En analyse af risikopræmien på de danske akiemarked Suderende: Louise Wellner Bech flevere: 9. april 9 Vejleder:
Hvordan ville en rendyrket dual indkomstskattemodel. Arbejdspapir II
 Hvordan ville en rendyrke dual indkomsskaemodel virke i Danmark? Simulering af en ensare ska på al kapialindkoms Arbejdspapir II Ændre opsparingsadfærd Skaeminiserie 2007 2007.II Arbejdspapir II - Ændre
Hvordan ville en rendyrke dual indkomsskaemodel virke i Danmark? Simulering af en ensare ska på al kapialindkoms Arbejdspapir II Ændre opsparingsadfærd Skaeminiserie 2007 2007.II Arbejdspapir II - Ændre
Øger Transparens Konkurrencen? - Teoretisk modellering og anvendelse på markedet for mobiltelefoni
 DET SAMFUNDSVIDENSKABELIGE FAKULTET KØBENHAVNS UNIVERSITET Øger Transarens Konkurrencen? - Teoreisk modellering og anvendelse å markede for mobilelefoni Bjørn Kyed Olsen Nr. 97/004 Projek- & Karrierevejledningen
DET SAMFUNDSVIDENSKABELIGE FAKULTET KØBENHAVNS UNIVERSITET Øger Transarens Konkurrencen? - Teoreisk modellering og anvendelse å markede for mobilelefoni Bjørn Kyed Olsen Nr. 97/004 Projek- & Karrierevejledningen
PENGEPOLITIKKENS INDFLYDELSE PÅ AKTIEMARKEDET
 HANDELSHØJSKOLEN I ÅRHUS INSTITUT FOR FINANSIERING CAND.MERC. FINANSIERING KANDIDATAFHANDLING VEJLEDER: MICHAEL CHRISTENSEN UDARBEJDET AF: JULIE LINDBJERG NIELSEN PENGEPOLITIKKENS INDFLYDELSE PÅ AKTIEMARKEDET
HANDELSHØJSKOLEN I ÅRHUS INSTITUT FOR FINANSIERING CAND.MERC. FINANSIERING KANDIDATAFHANDLING VEJLEDER: MICHAEL CHRISTENSEN UDARBEJDET AF: JULIE LINDBJERG NIELSEN PENGEPOLITIKKENS INDFLYDELSE PÅ AKTIEMARKEDET
Porteføljeteori: Investeringsejendomme i investeringsporteføljen. - Med særligt fokus på investering gennem et kommanditselskab
 Poreføljeeori: Inveseringsejendomme i inveseringsporeføljen - Med særlig fokus på invesering gennem e kommandiselskab Jonas Frøslev (300041) MSc in Finance Aarhus Universie, Business and Social Sciences
Poreføljeeori: Inveseringsejendomme i inveseringsporeføljen - Med særlig fokus på invesering gennem e kommandiselskab Jonas Frøslev (300041) MSc in Finance Aarhus Universie, Business and Social Sciences
 8.14 Teknisk grundlag for PFA Plus: Bilag 9-15 Indholdsforegnelse 9 Bilag: Indbealingssikring... 3 1 Bilag: Udbealingssikring... 4 1.1 Gradvis ilknyning af udbealingssikring... 4 11 Bilag: Omkosninger...
8.14 Teknisk grundlag for PFA Plus: Bilag 9-15 Indholdsforegnelse 9 Bilag: Indbealingssikring... 3 1 Bilag: Udbealingssikring... 4 1.1 Gradvis ilknyning af udbealingssikring... 4 11 Bilag: Omkosninger...
Ejendomsinvestering og finansiering
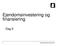 Ejendomsinvesering og finansiering Dag 5 1 Ejendomsinvesering og finansiering Undervisningsplan Inrodukion Inveseringsejendomsmarkede Teori- og meodegrundlag Inrodukion il måling af ejendomsafkas Renesregning
Ejendomsinvesering og finansiering Dag 5 1 Ejendomsinvesering og finansiering Undervisningsplan Inrodukion Inveseringsejendomsmarkede Teori- og meodegrundlag Inrodukion il måling af ejendomsafkas Renesregning
Dynamiske identiteter med kædeindeks
 Danmarks Saisik MODELGRUPPEN Arbejdspapir* Grane Høegh 2. mars 2007 Dynamiske idenieer med kædeindeks Resumé: den nye modelversion er vi gåe fra fasbase over il kædeprissørrelser. De beyder a de gamle
Danmarks Saisik MODELGRUPPEN Arbejdspapir* Grane Høegh 2. mars 2007 Dynamiske idenieer med kædeindeks Resumé: den nye modelversion er vi gåe fra fasbase over il kædeprissørrelser. De beyder a de gamle
Optimalt porteføljevalg i en model med intern habit nyttefunktion og stokastiske investeringsmuligheder
 Opimal poreføljevalg i en model med inern habi nyefunkion og sokasiske inveseringsmuligheder Thomas Hemming Larsen cand.merc.(ma.) sudie Insiu for Finansiering Copenhagen Business School Vejleder: Carsen
Opimal poreføljevalg i en model med inern habi nyefunkion og sokasiske inveseringsmuligheder Thomas Hemming Larsen cand.merc.(ma.) sudie Insiu for Finansiering Copenhagen Business School Vejleder: Carsen
Makroøkonomiprojekt Kartoffelkuren - Hensigter og konsekvenser Efterår 2004 HA 3. semester Gruppe 13
 Side 1 af 34 Tielblad Dao: 16. december 2004 Forelæser: Ben Dalum og Björn Johnson Vejleder: Ger Villumsen Berglind Thorseinsdoir Charloa Rosenquis Daniel Skogemann Lise Pedersen Maria Rasmussen Susanne
Side 1 af 34 Tielblad Dao: 16. december 2004 Forelæser: Ben Dalum og Björn Johnson Vejleder: Ger Villumsen Berglind Thorseinsdoir Charloa Rosenquis Daniel Skogemann Lise Pedersen Maria Rasmussen Susanne
Finanspolitik i makroøkonomiske modeller
 33 Finanspoliik i makroøkonomiske modeller Jesper Pedersen, Økonomisk Afdeling 1 1. INDLEDNING OG SAMMENFATNING Finanspoliik og pengepoliik er radiionel se de o vigigse økonomiske insrumener il sabilisering
33 Finanspoliik i makroøkonomiske modeller Jesper Pedersen, Økonomisk Afdeling 1 1. INDLEDNING OG SAMMENFATNING Finanspoliik og pengepoliik er radiionel se de o vigigse økonomiske insrumener il sabilisering
Skriftlig prøve Kredsløbsteori Onsdag 3. Juni 2009 kl (2 timer) Løsningsforslag
 Skriflig prøve Kredsløbseori Onsdag 3. Juni 29 kl. 2.3 4.3 (2 imer) øsningsforslag Opgave : (35 poin) En overføringsfunkion, H(s), har formen: Besem hvilke poler og nulpunker der er indehold i H(s) Tegn
Skriflig prøve Kredsløbseori Onsdag 3. Juni 29 kl. 2.3 4.3 (2 imer) øsningsforslag Opgave : (35 poin) En overføringsfunkion, H(s), har formen: Besem hvilke poler og nulpunker der er indehold i H(s) Tegn
Danmarks fremtidige befolkning Befolkningsfremskrivning 2009. Marianne Frank Hansen og Mathilde Louise Barington
 Danmarks fremidige befolkning Befolkningsfremskrivning 29 Marianne Frank Hansen og Mahilde Louise Baringon Augus 29 Indholdsforegnelse Danmarks fremidige befolkning... 1 Befolkningsfremskrivning 29...
Danmarks fremidige befolkning Befolkningsfremskrivning 29 Marianne Frank Hansen og Mahilde Louise Baringon Augus 29 Indholdsforegnelse Danmarks fremidige befolkning... 1 Befolkningsfremskrivning 29...
Appendisk 1. Formel beskrivelse af modellen
 Appendisk. Formel beskrivelse af modellen I dee appendiks foreages en mere formel opsilning af den model, der er beskreve i ariklen. Generel: Renen og alle produenpriser - eksklusiv lønnen - er give fra
Appendisk. Formel beskrivelse af modellen I dee appendiks foreages en mere formel opsilning af den model, der er beskreve i ariklen. Generel: Renen og alle produenpriser - eksklusiv lønnen - er give fra
Fysikrapport: Vejr og klima. Maila Walmod, 1.3 HTX, Rosklide. I gruppe med Ann-Sofie N. Schou og Camilla Jensen
 Fysikrappor: Vejr og klima Maila Walmod, 13 HTX, Rosklide I gruppe med Ann-Sofie N Schou og Camilla Jensen Afleveringsdao: 30 november 2007 1 I dagens deba høres orde global opvarmning ofe Men hvad vil
Fysikrappor: Vejr og klima Maila Walmod, 13 HTX, Rosklide I gruppe med Ann-Sofie N Schou og Camilla Jensen Afleveringsdao: 30 november 2007 1 I dagens deba høres orde global opvarmning ofe Men hvad vil
PROSPEKT FOR. Hedgeforeningen Jyske Invest
 Prospek PROSPEKT FOR Hedgeforeningen Jyske Inves Ansvar for prospek Hedgeforeningen Jyske Inves er ansvarlig for prospekes indhold. Vi erklærer herved, a oplysningerne i prospeke os bekend er rigige og
Prospek PROSPEKT FOR Hedgeforeningen Jyske Inves Ansvar for prospek Hedgeforeningen Jyske Inves er ansvarlig for prospekes indhold. Vi erklærer herved, a oplysningerne i prospeke os bekend er rigige og
Prisfastsættelse af fastforrentede konverterbare realkreditobligationer
 Copenhagen Business School 2010 Kandidaspeciale Cand.merc.ma Prisfassæelse af fasforrenede konvererbare realkrediobligaioner Vejleder: Niels Rom Aflevering: 28. juli 2010 Forfaere: Mille Lykke Helverskov
Copenhagen Business School 2010 Kandidaspeciale Cand.merc.ma Prisfassæelse af fasforrenede konvererbare realkrediobligaioner Vejleder: Niels Rom Aflevering: 28. juli 2010 Forfaere: Mille Lykke Helverskov
Prisfastsættelse og hedging af optioner under stokastisk volatilitet
 Erhvervsøkonomisk insiu Afhandling Vejleder: Peer Løche Jørgensen Forfaere: Kasper Korgaard Anders Weihrauch Prisfassæelse og hedging af opioner under sokasisk volailie Suppose we use he sandard deviaion
Erhvervsøkonomisk insiu Afhandling Vejleder: Peer Løche Jørgensen Forfaere: Kasper Korgaard Anders Weihrauch Prisfassæelse og hedging af opioner under sokasisk volailie Suppose we use he sandard deviaion
Dagens forelæsning. Claus Munk. kap. 4. Arbitrage. Obligationsprisfastsættelse. Ingen-Arbitrage princippet. Illustration af arbitrage
 Dages forelæsig Ige-Arbirage pricippe Claus Muk kap. 4 Nulkupoobligaioer Simpel og geerel boosrappig Forwardreer Obligaiosprisfassæelse Arbirage Værdie af e obligaio Nuidsværdie af obligaioes fremidige
Dages forelæsig Ige-Arbirage pricippe Claus Muk kap. 4 Nulkupoobligaioer Simpel og geerel boosrappig Forwardreer Obligaiosprisfassæelse Arbirage Værdie af e obligaio Nuidsværdie af obligaioes fremidige
FARVEAVL myter og facts Eller: Sådan får man en blomstret collie!
 FARVEAVL myer og facs Eller: Sådan får man en blomsre collie! Da en opdræer for nylig parrede en blue merle æve med en zobel han, blev der en del snak bland colliefolk. De gør man bare ikke man ved aldrig
FARVEAVL myer og facs Eller: Sådan får man en blomsre collie! Da en opdræer for nylig parrede en blue merle æve med en zobel han, blev der en del snak bland colliefolk. De gør man bare ikke man ved aldrig
2 Separation af de variable. 4 Eksistens- og entydighed af løsninger. 5 Ligevægt og stabilitet. 6 En model for forrentning af kapital med udtræk
 Oversig Mes repeiion med fokus på de sværese emner Modul 3: Differenialligninger af. orden Maemaik og modeller 29 Thomas Vils Pedersen Insiu for Grundvidenskab og Miljø [email protected] 3 simple yper differenialligninger
Oversig Mes repeiion med fokus på de sværese emner Modul 3: Differenialligninger af. orden Maemaik og modeller 29 Thomas Vils Pedersen Insiu for Grundvidenskab og Miljø [email protected] 3 simple yper differenialligninger
Undervisningsmaterialie
 The ScienceMah-projec: Idea: Claus Michelsen & Jan Alexis ielsen, Syddansk Universie Odense, Denmark Undervisningsmaerialie Ark il suderende og opgaver The ScienceMah-projec: Idea: Claus Michelsen & Jan
The ScienceMah-projec: Idea: Claus Michelsen & Jan Alexis ielsen, Syddansk Universie Odense, Denmark Undervisningsmaerialie Ark il suderende og opgaver The ScienceMah-projec: Idea: Claus Michelsen & Jan
Projekt 6.3 Løsning af differentialligningen y
 Projek 6.3 Løsning af differenialligningen + c y 0 Ved a ygge videre på de løsningsmeoder, vi havde succes med ved løsning af ligningerne uden ledde y med den enkelafledede, er vi nu i sand il a løse den
Projek 6.3 Løsning af differenialligningen + c y 0 Ved a ygge videre på de løsningsmeoder, vi havde succes med ved løsning af ligningerne uden ledde y med den enkelafledede, er vi nu i sand il a løse den
Modellering af den Nordiske spotpris på elektricitet
 Modellering af den Nordiske spopris på elekricie Speciale Udarbejde af: Randi Krisiansen Oecon. 10. semeser Samfundsøkonomi, Aalborg Universie 2 RANDI KRISTIANSEN STUDIENUMMER 20062862 Tielblad Uddannelse:
Modellering af den Nordiske spopris på elekricie Speciale Udarbejde af: Randi Krisiansen Oecon. 10. semeser Samfundsøkonomi, Aalborg Universie 2 RANDI KRISTIANSEN STUDIENUMMER 20062862 Tielblad Uddannelse:
Newtons afkølingslov løst ved hjælp af linjeelementer og integralkurver
 Newons afkølingslov løs ved hjælp af linjeelemener og inegralkurver Vi så idligere på e eksempel, hvor en kop kakao med emperauren sar afkøles i e lokale med emperauren slu. Vi fik, a emperaurfalde var
Newons afkølingslov løs ved hjælp af linjeelemener og inegralkurver Vi så idligere på e eksempel, hvor en kop kakao med emperauren sar afkøles i e lokale med emperauren slu. Vi fik, a emperaurfalde var
Afrapportering om danske undertekster på nabolandskanalerne
 1 Noa Afrapporering om danske underekser på nabolandskanalerne Sepember 2011 2 Dee noa indeholder: 1. Indledning 2. Baggrund 3. Rammer 4. Berening 2010 5. Økonomi Bilag 1. Saisik over anal eksede programmer
1 Noa Afrapporering om danske underekser på nabolandskanalerne Sepember 2011 2 Dee noa indeholder: 1. Indledning 2. Baggrund 3. Rammer 4. Berening 2010 5. Økonomi Bilag 1. Saisik over anal eksede programmer
Lindab Comdif. Fleksibilitet ved fortrængning. fortrængningsarmaturer. Comdif er en serie af luftfordelingsarmaturer til fortrængningsventilation.
 comfor forrængningsarmaurer Lindab Comdif 0 Lindab Comdif Ved forrængningsvenilaion ilføres lufen direke i opholds-zonen ved gulvniveau - med lav hasighed og underemperaur. Lufen udbreder sig over hele
comfor forrængningsarmaurer Lindab Comdif 0 Lindab Comdif Ved forrængningsvenilaion ilføres lufen direke i opholds-zonen ved gulvniveau - med lav hasighed og underemperaur. Lufen udbreder sig over hele
i(t) = 1 L v( τ)dτ + i(0)
 EE Basis - 2010 2/22/10/JHM PE-Kursus: Kredsløbseori (KRT): ECTS: 5 TID: Mandag d. 22/2 LØSNINGSFORSLAG: Opgave 1: Vi ser sraks, a der er ale om en enkel spole, hvor vi direke pårykker en kend spænding.
EE Basis - 2010 2/22/10/JHM PE-Kursus: Kredsløbseori (KRT): ECTS: 5 TID: Mandag d. 22/2 LØSNINGSFORSLAG: Opgave 1: Vi ser sraks, a der er ale om en enkel spole, hvor vi direke pårykker en kend spænding.
DiploMat Løsninger til 4-timersprøven 4/6 2004
 DiploMa Løsninger il -imersprøven / Preben Alsholm / Opgave Polynomie p er give ved p (z) = z 8 z + z + z 8z + De oplyses, a polynomie også kan skrives således p (z) = z + z z + Vi skal nde polynomies
DiploMa Løsninger il -imersprøven / Preben Alsholm / Opgave Polynomie p er give ved p (z) = z 8 z + z + z 8z + De oplyses, a polynomie også kan skrives således p (z) = z + z z + Vi skal nde polynomies
Beregning af prisindeks for ejendomssalg
 Damarks Saisik, Priser og Forbrug 2. april 203 Ejedomssalg JHO/- Beregig af prisideks for ejedomssalg Baggrud: e radiioel prisideks, fx forbrugerprisidekse, ka ma ofe følge e ideisk produk over id og sammelige
Damarks Saisik, Priser og Forbrug 2. april 203 Ejedomssalg JHO/- Beregig af prisideks for ejedomssalg Baggrud: e radiioel prisideks, fx forbrugerprisidekse, ka ma ofe følge e ideisk produk over id og sammelige
Den forbrugsbaserede prisfastsættelsesmodel:
 Insiu for Regnskab, Finansiering og Logisik Cand.merc.finansiering Kandidaafhandling Vejleder: Tom Engsed Forfaere: Sig Vinher Møller Minh Tuong Den forbrugsbaserede prisfassæelsesmodel: En empirisk sammenligning
Insiu for Regnskab, Finansiering og Logisik Cand.merc.finansiering Kandidaafhandling Vejleder: Tom Engsed Forfaere: Sig Vinher Møller Minh Tuong Den forbrugsbaserede prisfassæelsesmodel: En empirisk sammenligning
BAT Nr. 6 oktober 2006. Skatteminister Kristian Jensen vil erstatte 2.700 medarbejdere med postkort!
 B A T k a r e l l e BAT Nr. 6 okober 2006 I BAT har vi med ineresse bemærke de 13 nye iniiaiver, som Beskæfigelsesminiseren har iværksa med de formål a gøre de leere for danske virksomheder a få udenlandsk
B A T k a r e l l e BAT Nr. 6 okober 2006 I BAT har vi med ineresse bemærke de 13 nye iniiaiver, som Beskæfigelsesminiseren har iværksa med de formål a gøre de leere for danske virksomheder a få udenlandsk
Logaritme-, eksponential- og potensfunktioner
 Logarime-, eksponenial- og poensfunkioner John Napier (550-67. Peer Haremoës Niels Brock April 7, 200 Indledning Eksponenial- og logarimefunkioner blev indfør på Ma C niveau, men dengang havde vi ikke
Logarime-, eksponenial- og poensfunkioner John Napier (550-67. Peer Haremoës Niels Brock April 7, 200 Indledning Eksponenial- og logarimefunkioner blev indfør på Ma C niveau, men dengang havde vi ikke
tegnsprog Kursuskatalog 2015
 egnsprog Kursuskaalog 2015 Hvordan finder du di niveau? Hvor holdes kurserne? Hvordan ilmelder du dig? 5 Hvad koser e kursus? 6 Tegnsprog for begyndere 8 Tegnsprog på mellemniveau 10 Tegnsprog for øvede
egnsprog Kursuskaalog 2015 Hvordan finder du di niveau? Hvor holdes kurserne? Hvordan ilmelder du dig? 5 Hvad koser e kursus? 6 Tegnsprog for begyndere 8 Tegnsprog på mellemniveau 10 Tegnsprog for øvede
Hvor meget er det værd at kunne udskyde sine afdrag, som man vil?
 Hvor mege er de værd a kunne udskyde sine afdrag, som man vil? Bjarke Jensen Rolf Poulsen 1 Indledning For den almindelig fordrukne og forgældede danske boligejer var 1. okober 2003 en god dag: Billigere
Hvor mege er de værd a kunne udskyde sine afdrag, som man vil? Bjarke Jensen Rolf Poulsen 1 Indledning For den almindelig fordrukne og forgældede danske boligejer var 1. okober 2003 en god dag: Billigere
Newton, Einstein og Universets ekspansion
 Newon, Einsein og Universes ekspansion Bernhard Lind Shisad, Viborg Tekniske ymnasium Friedmann ligningerne beskriver sammenhængen mellem idsudviklingen af Universes udvidelse og densieen af sof og energi.
Newon, Einsein og Universes ekspansion Bernhard Lind Shisad, Viborg Tekniske ymnasium Friedmann ligningerne beskriver sammenhængen mellem idsudviklingen af Universes udvidelse og densieen af sof og energi.
FitzHugh Nagumo modellen
 FizHugh Nagumo modellen maemaisk modellering af signaler i nerve- og muskelceller Torsen Tranum Rømer, Frederikserg Gymnasium Fagene maemaik og idræ supplerer hinanden god inden for en lang række emner.
FizHugh Nagumo modellen maemaisk modellering af signaler i nerve- og muskelceller Torsen Tranum Rømer, Frederikserg Gymnasium Fagene maemaik og idræ supplerer hinanden god inden for en lang række emner.
Badevandet 2010 Teknik & Miljø - -Maj 2011
 Badevande 2010 Teknik & Miljø - Maj 2011 Udgiver: Bornholms Regionskommune, Teknik & Miljø, Naur Skovløkken 4, Tejn 3770 Allinge Udgivelsesår: 2011 Tiel: Badevande, 2010 Teks og layou: Forside: Journalnummer:
Badevande 2010 Teknik & Miljø - Maj 2011 Udgiver: Bornholms Regionskommune, Teknik & Miljø, Naur Skovløkken 4, Tejn 3770 Allinge Udgivelsesår: 2011 Tiel: Badevande, 2010 Teks og layou: Forside: Journalnummer:
MAKRO 2 KAPITEL 7: GRÆNSER FOR VÆKST? SOLOW-MODELLEN MED NATURRESSOURCER. - uundværlig i frembringelsen af aggregeret output og. 2.
 KAPITEL 7: GRÆNSER FOR VÆKST? SOLOW-MODELLEN MED NATURRESSOURCER MAKRO 2 2. årsprøve Klassisk syn: JORDEN/NATUREN er en produkionsfakor, som er - uundværlig i frembringelsen af aggregere oupu og Forelæsning
KAPITEL 7: GRÆNSER FOR VÆKST? SOLOW-MODELLEN MED NATURRESSOURCER MAKRO 2 2. årsprøve Klassisk syn: JORDEN/NATUREN er en produkionsfakor, som er - uundværlig i frembringelsen af aggregere oupu og Forelæsning
Værdien af den traditionelle pensionskontrakt
 Handelshøjskolen i Århus Erhvervsøkonomisk Insiu Kandidaafhandling cand.merc. finansiering Værdien af den radiionelle pensionskonrak En opionsbasere synsvinkel Februar 2007 Opgaven er udarbejde af: Carsen
Handelshøjskolen i Århus Erhvervsøkonomisk Insiu Kandidaafhandling cand.merc. finansiering Værdien af den radiionelle pensionskonrak En opionsbasere synsvinkel Februar 2007 Opgaven er udarbejde af: Carsen
Logaritme-, eksponential- og potensfunktioner
 Logarime-, eksponenial- og poensfunkioner John Napier (550-67. Peer Haremoës Niels Brock July 27, 200 Indledning Eksponenial- og logarimefunkioner blev indfør på Ma C nivea uden en præcis definiion. Funkionerne
Logarime-, eksponenial- og poensfunkioner John Napier (550-67. Peer Haremoës Niels Brock July 27, 200 Indledning Eksponenial- og logarimefunkioner blev indfør på Ma C nivea uden en præcis definiion. Funkionerne
1. Aftalen... 2. 1.A. Elektronisk kommunikation meddelelser mellem parterne... 2 1.B. Fortrydelsesret for forbrugere... 2 2. Aftalens parter...
 Gener el l ebe i ngel s erf orl ever i ngogdr i f af L ok al Tel ef onens j enes er Ver s i on1. 0-Febr uar2013 L ok al Tel ef onena/ S-Pos bok s201-8310tr anbj er gj-k on ak @l ok al el ef onen. dk www.
Gener el l ebe i ngel s erf orl ever i ngogdr i f af L ok al Tel ef onens j enes er Ver s i on1. 0-Febr uar2013 L ok al Tel ef onena/ S-Pos bok s201-8310tr anbj er gj-k on ak @l ok al el ef onen. dk www.
5 Lønindeks for den private sektor
 57 5 Lønindeks for den privae sekor 5.1 Grundlæggende informaion om indekse 5.2 Navn Lønindeks for den privae sekor. Der offenliggøres e ilsvarende lønindeks for den offenlige sekor, der i princippe beregnes
57 5 Lønindeks for den privae sekor 5.1 Grundlæggende informaion om indekse 5.2 Navn Lønindeks for den privae sekor. Der offenliggøres e ilsvarende lønindeks for den offenlige sekor, der i princippe beregnes
Fremadrettede overenskomster i byggeriet
 B A T k a r e l l e Nr. 2 april 2007 Mange unge i dag ved ikke, hvad fagforeningen sår for, og de er fagforeningens forpligigelse a videregive arven il de kommende generaioner. Side 4 Ny forskning fra
B A T k a r e l l e Nr. 2 april 2007 Mange unge i dag ved ikke, hvad fagforeningen sår for, og de er fagforeningens forpligigelse a videregive arven il de kommende generaioner. Side 4 Ny forskning fra
En-dimensionel model af Spruce Budworm udbrud
 En-dimensionel model af Sprce dworm dbrd Kenneh Hagde Mandr p Niel sen o g K asper j er ing Søby Jensen, ph.d-sderende ved oskilde Universie i hhv. maemaisk modellering og maemaikkens didakik. Maemaisk
En-dimensionel model af Sprce dworm dbrd Kenneh Hagde Mandr p Niel sen o g K asper j er ing Søby Jensen, ph.d-sderende ved oskilde Universie i hhv. maemaisk modellering og maemaikkens didakik. Maemaisk
Pensions- og hensættelsesgrundlag for ATP gældende pr. 30. juni 2014
 Pensions- og hensæelsesgrundlag for ATP gældende pr. 30. juni 2014 Indhold 1 Indledning 6 1.1 Lovgrundlag.............................. 6 1.2 Ordningerne.............................. 6 2 Risikofakorer
Pensions- og hensæelsesgrundlag for ATP gældende pr. 30. juni 2014 Indhold 1 Indledning 6 1.1 Lovgrundlag.............................. 6 1.2 Ordningerne.............................. 6 2 Risikofakorer
