I dag. Normalfordelingen. Hvad skal vi bruge normalfordelingen til? Eksempel: hjerneceller hos marsvin
|
|
|
- Benjamin Lorenzen
- 7 år siden
- Visninger:
Transkript
1 I dag Normalfordlingn Hll Sørnsn Formiddag og ftrmiddag: Datatilrttlæggls i SAS (fra mandag) Hvad skal vi brug normalfordlingn til og hvorfor r dn vigtig? Histogram og normalfordlingstæthd Brgning af sandsynlighdr i normalfordlingn Fordling af gnnmsnit af normalfordlt variabl Er data normalfordlt? Mr dskriptiv statistik i SAS Korrlationskofficintn NB: Læs slv om linær, gomtrisk og ksponntil vækst. StatBK (Ug 1, torsdag) Normalfordlingn 1 / 30 StatBK (Ug 1, torsdag) Normalfordlingn 2 / 30 Eksmpl: hjrncllr hos marsvin Hvad skal vi brug normalfordlingn til? Fra hvrt af 30 marsvin har man tilfældigt udvalgt n hjrncll fra t bstmt områd og optalt antallt af dndritic branch sgmnts. Rsultatr: Gnnmsnit og stikprøvsprdning: ȳ = 35.8, s = 10.8 Vil brug normalfordlingn til at bskriv variationn i data. Nu: Hvad btydr dt? I ftrmiddag: Er dt rimligt for diss data? Næst ug: Statistisk infrns for normalfordlt data Tænk på populationn af all marsvin. Hvad r dt gnnmsnitlig antal dndritic branch sgmnts for all diss marsvin? Dt vd vi ikk og kommr hllr aldrig til dt! Mn vi har tagt n stikprøv (sampl) på 30 marsvin og fåt gnnmsnittt ȳ = Stikprøvgnnmsnitttt r vors stimat vors bdst gæt på populationsgnnmsnittt. Hvis vi havd tagt n andn stikprøv havd vi fåt t andt gnnmsnit. Så hvor mgt kan vi stol på d 35.8? Hvor præcist r stimatt? Hvad kan vi konkludr om populationn udfra stikprøvn? Dt kan vi svar mgt præcist på hvis vi kan antag at antalln i populationn r normalfordlt! StatBK (Ug 1, torsdag) Normalfordlingn 3 / 30 StatBK (Ug 1, torsdag) Normalfordlingn 4 / 30
2 Hvorfor ntop normalfordlingn? Carl Fridrich Gauss, Vi skal brug normalfordlingn i stort hl dtt kursus! Hvorfor ntop dnn fordling? Passr oft godt til (biologisk) data Pæn matmatisk gnskabr får pæn rsultatr for stimatr, konfidnsintrvallr, statistisk tst mm. Cntral grænsværdisætning (CLT): gnnmsnit af næstn hvad som hlst r approksimativt normalfordlt. Kalds også dn Gaussisk fordling. Opkaldt ftr Carl Fridrich Gauss tysk matmatikr og fysikr, StatBK (Ug 1, torsdag) Normalfordlingn 5 / 30 StatBK (Ug 1, torsdag) Normalfordlingn 6 / 30 Marsvin: histogram Histogram og normalfordlingstæthd P r c n t Fortolkning af histogram, for t givt intrval: andln af obsrvationr i intrvallt r aral af rktangl andl obs. = samlt aral Kan vi tilpass n kuv til histogrammt, så vi får n tilsvarnd fortolkning? Sandsynlighdn for at havn i intrvallt r lig (rlativt) aral undr kurvn: sandsynlighd = aral undr kurvn i intrvallt samlt aral undr kurvn count Vil brug normalfordlingstæthdn (for passnd valg af µ og σ): f (x) = 1 2πσ 2 (x µ)2 /(2σ 2 ) StatBK (Ug 1, torsdag) Normalfordlingn 7 / 30 StatBK (Ug 1, torsdag) Normalfordlingn 8 / 30
3 Marsvin: histogram og normalfordlingstæthd Normalfordlingn Tæthd for normalford. md middlværdi µ og sprdning σ, N(µ,σ): f (x) = 1 2πσ 2 (x µ)2 /(2σ 2 ) 25 P r c n t count Tæthd for normalfordling md middlværdi 35.8 og sprdning 10.8: f (x) = 1 2π (x 35.8)2 /( ) Histogram sammn md N(35.8, 10.8)-tæthd normrt så aral undr kurvn r dt samm som dt samld aral af rktanglrn. StatBK (Ug 1, torsdag) Normalfordlingn 9 / 30 Formln i sig slv ikk vigtig! Mn følgnd gnskabr r vigtig: Middlværdin µ rykkr kurvn/fordlingn til vnstr/højr Sprdningn σ ændrr brddn af kurvn/fordlingn Samlt aral undr kurvn r 1 Fortolkning: sandsynlighd for at havn i intrval r lig aralt undr kurvn ovr dtt intrval Spcilt: Sandsynlighd for at havn i intrvallt µ ± 2σ r Kan transformr til N(0, 1), og brgn sandsynlighdr dr. S figurrn på sid i bogn! StatBK (Ug 1, torsdag) Normalfordlingn 10 / 30 Normalfordlingn: sandsynlighd for µ ± kσ Øvls Hvad r mon middlværdi og sprdning for ndnstånd data? Dnsity 99.7% 95% 68% σ Dtt gældr for all middlværdir og sprdningr! Dnsity n = y StatBK (Ug 1, torsdag) Normalfordlingn 11 / 30 StatBK (Ug 1, torsdag) Normalfordlingn 12 / 30
4 Transformation og brgning af sandsynlighdr Transformation og brgning af sandsynlighdr Transformation til N(0, 1): Hvis X r normalfordlt md mv. µ og sprdning σ så r Z = (X µ)/σ normalfordlt md mv. 0 og sprdning 1 Hvis Z r normalfordlt md mv. 0 og sprdning 1 så r X = µ + σ Z normalfordlt md mv. µ og sprdning σ. Drfor kan all N(µ, σ)-sandsynlighdr omskrivs til N(0, 1)-sandsynlighdr. Hvis X N(µ,σ), så r ( X µ P(X a) = P a µ ) ( = P Z a µ ) σ σ σ Sandsynlighdr i N(0,1) givt i Tabl B4, sid 462. Hvad r sandsynlighdn for at dr højst r 40 dndritic branch sgmnts i n cll for t tilfældigt udvalgt marsvin? Lad X vær antal antal dndritic branch sgmnts og antag at X r normalfordlt md mv og sprdning Skal find P(X 40). ( ) X P(X 40) = P Tilsvarnd: = P (Z 0.39) = 0.65 Hvad r sandsynlighdn for at dr r mllm 30 og 42 dndritic branch sgmnts i n cll for t tilfældigt udvalgt marsvin? Hvad r sandsynlighdn for at dr r mr nd 50 dndritic branch sgmnts i n cll for t tilfældigt udvalgt marsvin? StatBK (Ug 1, torsdag) Normalfordlingn 13 / 30 StatBK (Ug 1, torsdag) Normalfordlingn 14 / 30 Fordling af gnnmsnit Fordling af gnnmsnit Tænk på populationn af all marsvin. Hvad r dt gnnmsnitlig antal dndritic branch sgmnts for all diss marsvin? Antag at antalln r normalfordlt md middlværdi µ og sprdning σ. Vi kndr ikk populationsværdirn µ og σ, mn vi kan stimr dm vha. vors stikprøv y 1,...,y n fra d 30 marsvin. Vi skrivr ˆµ = ȳ = 35.8, ˆσ = s = 10.8 Hvis vi havd tagt n andn stikprøv havd vi fåt t andt gnnmsnit. Intrssrt i vid nogt om fordlingn af gnnmsnittt ȳ r normalfordlt md middlværdi µ og sprdning σ/ n. Histogrammr ovr gnnmsnit af n stk. N(0, 1)-fordlt variabl. Dnsity n = y Dnsity Middlværdi? Sprdning? Fordling? n = y StatBK (Ug 1, torsdag) Normalfordlingn 15 / 30 StatBK (Ug 1, torsdag) Normalfordlingn 16 / 30
5 Er data normalfordlt? Marsvin: histogram og normalfordlingstæthd I næstn hl kurst skal vi brug normalfordlingn som modl for vors data. Drfor r dt vigtigt at kunn kontrollr at data faktisk kan antags at komm fra n normalfordling. Sammnligning af histogram og normalfordlingstæthd (normrt så aral undr histogram og N-kurv r dt samm). Normal probability plot llr QQ-plot Hvad gør vi hvis normalfordlingsantaglsn ikk passr? Kan sommtidr transformr data, dvs. fx. brug log(x ) i stdt for X slv s opgav BK.4. Ikk-paramtrisk mtodr snr P r c n t Histogram sammn md N(35.8, 10.8)-tæthd normrt så aral undr kurvn r dt samm som dt samld aral af rktanglrn. count Er dr systmatisk afviglsr llr kan afviglsrn md rimlighd tænks at skylds tilfældighdr? StatBK (Ug 1, torsdag) Normalfordlingn 17 / 30 StatBK (Ug 1, torsdag) Normalfordlingn 18 / 30 Marsvin: QQ-plot Marsvin: SAS-kod c o u n t Normal Quantils Sammnlignr fraktilrn i data md fraktilr i normalfordlingn, transformrt til N(0,1). Liggr punktrn omkring n rt lini? Næstn for pænt hr! SAS lavr plottt lidt andrlds nd forklart i bogn mn pointn r dn samm: Data kan antags at vær normalfordlt hvis punktrn liggr omkring n rt lini. Dr må ikk vær systmatisk afviglsr. data guinapigs; input cards; ; proc print; proc univariat data=guinapigs; var count; histogram count / normal; qqplot count / normal(mu=st sigma=st); Dt krævr slvfølglig n vis rfaring at s på sådann plots... StatBK (Ug 1, torsdag) Normalfordlingn 19 / 30 StatBK (Ug 1, torsdag) Normalfordlingn 20 / 30
6 Dskriptiv/bskrivnd statistik i SAS PROC BOXPLOT Data: x 1,...,x n, vt. også y 1,...,y n. Ønskr at få ovrblik ovr data. Hvordan kan vi sammnfatt informationn i data? Summary masurs: PROC MEANS llr PROC UNIVARIATE Mål for cntralitt: gnnmsnit, mdian Mål for variabilitt: rang, prcntils/fraktilr, varians, sprdning Grafisk bskrivnd statistik Boxplots: PROC BOXPLOT Scattrplot, dvs. (x, y)-plot: PROC GPLOT Histogrammr: PROC UNIVARIATE QQ-plots (til normalfordlingskontrol): PROC UNIVARIATE Eksmpl: Lukæmidata fra opgav 3.8. Ønskr: Boxplots for ALL-data og for AML-data vd sidn af hinandn. Formål: Grafisk sammnligning af ovrlvlsn i d to gruppr. data lukmia; infil C:\Documnts and Sttings\hll\StatBK\opg3-8.txt firstobs=2; input typ $ survival; proc print data=lukmia; proc boxplot data=lukmia; plot survival*typ; StatBK (Ug 1, torsdag) Normalfordlingn 21 / 30 StatBK (Ug 1, torsdag) Normalfordlingn 22 / 30 PROC UNIVARIATE PROC GPLOT givr n bunk summary statistics for n stikprøv kan tgn histogrammr og QQ-plots data amldata; st lukmia; if typ="aml"; proc print; proc univariat data=amldata; var survival; histogram survival / normal; qqplot /normal(mu=st sigma=st); Prøv vt. også for transformrd data: log(survival). Data fra Eksmpl 3.18 (sid 61): Systolisk og diastolisk blodtryk for 12 voksn Sammnhæng? Plot d to variabl mod hinandn! data blodtryk; infil C:\Documnts and Sttings\hll\StatBK\blodtryk.txt firstobs=3; input syst diast; proc print data=blodtryk; proc gplot data=blodtryk; plot syst*diast; StatBK (Ug 1, torsdag) Normalfordlingn 23 / 30 StatBK (Ug 1, torsdag) Normalfordlingn 24 / 30
7 Korrlation Hvor stærk sammnhæng r dr mllm systolisk og diastolisk blodtryk? Ellr mr gnrlt: Par af obsrvationr: (x 1,y 1 ),...,(x n,y n ). Hvor stærk r sammnhængn mllm x og y (Parson) korrlationskofficintn: r = 1 n 1 n i=1(x i x) (y i ȳ) s x s y Hvornår r r positiv/ngativ/nul? r liggr i intrvallt [ 1,1] og r ±1 hvis all (x i,y i ) liggr på n rt lini, udn afviglsr r målr gradn af linær sammnhæng! StatBK (Ug 1, torsdag) Normalfordlingn 25 / 30 Korrlation Korrlationrn r 0.86, 0.25, 0.17, Hvor r dn hvad? StatBK (Ug 1, torsdag) Normalfordlingn 26 / 30 Korrlation r målr gradn af linær sammnhæng. Mn dr kan sagtns vær n sammnhæng slvom r r nul! StatBK (Ug 1, torsdag) Normalfordlingn 27 / 30 PROC CORR proc corr data=blodtryk; var syst diast; Givr også størrlsr som vi ndnu ikk har rdskabrn til at fortolk. StatBK (Ug 1, torsdag) Normalfordlingn 28 / 30
8 Rsumé SAS-rsumé Middlværdi og sprdning i normalfordling Sandsynlighd som aral undr normalfordlingstæthd 95% sandsynlighd for at havn i intrvallt µ ± 2σ llr strngt tagt i intrvallt µ ± 1.96σ Brgning af sandsynlighdr: transformation til N(0, 1) og brug af tabl Kontrol af normalfordling vha. histogram og/llr QQ-plot Gnnmnittt af n normalfordlt variabl r ign normalfordlt md middlværdi µ og sprdning σ/ n. Dataindlæsning: nmmst vha. INFILE i DATA sætning. PROC MEANS: summary statistics for variabl, vt. opdlt i mindr biddr ftr værdin af n andn variabl. PROC UNIVARIATE: summary masurs, histogram, QQ-plot PROC BOXCPLOT: boxplot for variabl, vt. parallll boxplot svarnd til opdling ftr værdin af n andn variabl. PROC GPLOT: Scattr plots, dvs. (x, y)-plots PROC CORR: Parsonkorrlationskofficintn StatBK (Ug 1, torsdag) Normalfordlingn 29 / 30 StatBK (Ug 1, torsdag) Normalfordlingn 30 / 30
Program. Normalfordelingen. Hvad skal vi bruge normalfordelingen til? Eksempel: hjerneceller hos marsvin
 Program Normalfordlig Hll Sørs E-mail: hll@mah.ku.dk I dag: ormalfordlig Hvad skal vi brug ormalfordlig il og hvorfor r d vigig? Hisogram og ormalfordligsæhd Brgig af sadsylighdr i ormalfordlig Er daa
Program Normalfordlig Hll Sørs E-mail: hll@mah.ku.dk I dag: ormalfordlig Hvad skal vi brug ormalfordlig il og hvorfor r d vigig? Hisogram og ormalfordligsæhd Brgig af sadsylighdr i ormalfordlig Er daa
Betinget hæftelse. Et regneeksempel 01-04-2014
 Btingt hæftls Et rgnsmpl 01-04-2014 1 Indldning Notatt sr lidt nærmr på sammnhængn mllm btingt hæftls og dt forvntd afast for ationærr og rditorr i n (finansil) virsomhd, hvor gnapitalandln r lav. Notatt
Btingt hæftls Et rgnsmpl 01-04-2014 1 Indldning Notatt sr lidt nærmr på sammnhængn mllm btingt hæftls og dt forvntd afast for ationærr og rditorr i n (finansil) virsomhd, hvor gnapitalandln r lav. Notatt
Statikstik II 2. Lektion. Lidt sandsynlighedsregning Lidt mere om signifikanstest Logistisk regression
 Statikstik II 2. Lktion Lidt sandsynlighdsrgning Lidt mr om signifikanstst Logistisk rgrssion Lidt sandsynlighdsrgning Lad A vær n hændls (t llr flr mulig udfald af t ksprimnt ) Fx A Dt rgnr i morgn P(A)
Statikstik II 2. Lktion Lidt sandsynlighdsrgning Lidt mr om signifikanstst Logistisk rgrssion Lidt sandsynlighdsrgning Lad A vær n hændls (t llr flr mulig udfald af t ksprimnt ) Fx A Dt rgnr i morgn P(A)
Introduktion til logistisk regression
 Introduktion til logistisk rgrssion Indhold: Sandsynlighdr, odds og logits Logistisk rgrssion Dummy variabl Wald tst SPSS 1 Rgrssionsmodllr bskrivr hvorlds én afhængig variabl, Y, afhængr af n llr flr
Introduktion til logistisk rgrssion Indhold: Sandsynlighdr, odds og logits Logistisk rgrssion Dummy variabl Wald tst SPSS 1 Rgrssionsmodllr bskrivr hvorlds én afhængig variabl, Y, afhængr af n llr flr
Hvordan er trivslen blandt eleverne på skolen (fx i forhold til mobning)?
 Skol og Forældr Kvægtorvsgad 1 1710 Købnhavn V Tlf. 3326 1721 Fax 3326 1722 post@skol-foraldr.dk www.skol-foraldr.dk Skolbstyrlsrns bdømmls af trivsl og samarbjd i skoln Skol og Forældr har stillt n rækk
Skol og Forældr Kvægtorvsgad 1 1710 Købnhavn V Tlf. 3326 1721 Fax 3326 1722 post@skol-foraldr.dk www.skol-foraldr.dk Skolbstyrlsrns bdømmls af trivsl og samarbjd i skoln Skol og Forældr har stillt n rækk
Lokalplanområdets placering i Haderslev
 LOKALPLANOMRÅDET Lokalplanområdts placring Lokalplanområdts placring i Hadrslv LOKALPLANOMRÅDETS BELIGGENHED Lokalplanområdt omfattr t områd bliggnd på hjørnt af Grønningn og Aarøsundvj i dn sydlig dl
LOKALPLANOMRÅDET Lokalplanområdts placring Lokalplanområdts placring i Hadrslv LOKALPLANOMRÅDETS BELIGGENHED Lokalplanområdt omfattr t områd bliggnd på hjørnt af Grønningn og Aarøsundvj i dn sydlig dl
Binomial fordeling. n f (x) = p x (1 p) n x. x = 0, 1, 2,...,n = x. x x!(n x)! Eksempler. Middelværdi np og varians np(1 p). 2/
 Program: 1. Repetition af vigtige sandsynlighedsfordelinger: binomial, (Poisson,) normal (og χ 2 ). 2. Populationer og stikprøver 3. Opsummering af data vha. deskriptive størrelser og grafer. 1/29 Binomial
Program: 1. Repetition af vigtige sandsynlighedsfordelinger: binomial, (Poisson,) normal (og χ 2 ). 2. Populationer og stikprøver 3. Opsummering af data vha. deskriptive størrelser og grafer. 1/29 Binomial
Arbejdsløsheden hastigt på vej mod 100.000 - en underfinansieret skattereform løser ikke krisen
 26. fbruar 29 af Spcialkonsulnt Erik Bjørstd Dirkt tlf. 33 55 77 15 og Chfanalytikr Frdrik I. Pdrsn Dirkt tlf. 33 55 77 12 llr 28 42 42 72 Rsumé: Arbjdsløshdn hastigt på vj mod 1. - n undrfinansirt skattrform
26. fbruar 29 af Spcialkonsulnt Erik Bjørstd Dirkt tlf. 33 55 77 15 og Chfanalytikr Frdrik I. Pdrsn Dirkt tlf. 33 55 77 12 llr 28 42 42 72 Rsumé: Arbjdsløshdn hastigt på vj mod 1. - n undrfinansirt skattrform
. k er en konstant. Endvidere antages det i d), at gx ( 0) 0. I e) antages det, at f er differentiabel i x 0 og g er differentiabel i y 0
 0BRgnrglr for ubstmt intgralr I dtt lill tillæg skal vi s på n sætning, som angivr d rgnrglr, dr gældr for ubstmt intgralr (intgralr udn grænsr), samt giv t bvis for sætningn. Da vi i bvist skal gør brug
0BRgnrglr for ubstmt intgralr I dtt lill tillæg skal vi s på n sætning, som angivr d rgnrglr, dr gældr for ubstmt intgralr (intgralr udn grænsr), samt giv t bvis for sætningn. Da vi i bvist skal gør brug
Alders-mix udfordrer os alle på den gode måde
 -------------------------------------------------------------------------- Nyhdsbrv nr. 21 juni 2014 -------------------------------------------------------------------------- S, hvor små vi var! Dt r
-------------------------------------------------------------------------- Nyhdsbrv nr. 21 juni 2014 -------------------------------------------------------------------------- S, hvor små vi var! Dt r
Energiens ligefordelingslov
 Statistisk mkanik 7 Sid af 6 Enrgins ligfordlingslov I t systm undr M- llr klassisk statistik r antallt af partiklr md n givn frihdsgrad i intrvallt [ ; d] + ifølg udtryk (4.6) givt vd hvor d dg r tilstandssummn
Statistisk mkanik 7 Sid af 6 Enrgins ligfordlingslov I t systm undr M- llr klassisk statistik r antallt af partiklr md n givn frihdsgrad i intrvallt [ ; d] + ifølg udtryk (4.6) givt vd hvor d dg r tilstandssummn
slagelse uddannelses- og karrierefestival
 4 1 K U r på S l l i t s om ud s n? d m n m r o k ad v Vl h g o op r d a v H Vlkommn som udstillr på SUK-fstivaln Vlkommn i flokkn af ngagrd udstillr, dr år ftr år r md til at gør SUKfstivaln til Vstsjællands
4 1 K U r på S l l i t s om ud s n? d m n m r o k ad v Vl h g o op r d a v H Vlkommn som udstillr på SUK-fstivaln Vlkommn i flokkn af ngagrd udstillr, dr år ftr år r md til at gør SUKfstivaln til Vstsjællands
FOLD BILLIE. Billie, se lige hvor langt mit papirfly kan flyve! 3 Fold de to hjørner indtil midten.
 U D R E D L O SÅDAN F Y L F R I P A P ET SEJT FOLD BILLIE S BEDSTE PAP IRFLY! lv. mm at lav s n : l h t d st af st papirfly. n flyv og bd r Billis hurtig l m D r sjov, ka sa u d an hr hvord Billi visr
U D R E D L O SÅDAN F Y L F R I P A P ET SEJT FOLD BILLIE S BEDSTE PAP IRFLY! lv. mm at lav s n : l h t d st af st papirfly. n flyv og bd r Billis hurtig l m D r sjov, ka sa u d an hr hvord Billi visr
Elektronens specifikke ladning
 Elktronns spcifikk ladning Martin Gislr 25. aj 2001 Indhold 1 Forål 1 2 Udførls 1 3 Toriafsnit 2 3.1 Sprdning............................. 3 4 Forsøgsrsultatr 4 5 Bhandling af forsøgsrsultatr 4 6 Diskussion
Elktronns spcifikk ladning Martin Gislr 25. aj 2001 Indhold 1 Forål 1 2 Udførls 1 3 Toriafsnit 2 3.1 Sprdning............................. 3 4 Forsøgsrsultatr 4 5 Bhandling af forsøgsrsultatr 4 6 Diskussion
AARHUS MIDTBY. Vikingetiden 5+6 9. Tema 1:5.000. Lille Torv. Store Torv. Domkirke. Magasin Bibliotek. Bispetorv. ARos. Musikhus. Rådhus.
 Tma Nø rr g Vikingtidn AARHUS MIDTBY 0 100 200 300 m 1:5.000 ÅRHUS r Nø é 12 2 3 11 Lill Torv 17 8 Magasin Bibliotk Stor Torv 15 10 Domkirk 1 Bisptorv 14 7 18 16 4 Sø nd rg V s t r A l l é 5+6 9 V Øst
Tma Nø rr g Vikingtidn AARHUS MIDTBY 0 100 200 300 m 1:5.000 ÅRHUS r Nø é 12 2 3 11 Lill Torv 17 8 Magasin Bibliotk Stor Torv 15 10 Domkirk 1 Bisptorv 14 7 18 16 4 Sø nd rg V s t r A l l é 5+6 9 V Øst
I dag. Statistisk analyse af en enkelt stikprøve: LR test og t-test, modelkontrol, R Sandsynlighedsregning og Statistik (SaSt)
 I dag Statistisk analyse af en enkelt stikprøve: LR test og t-test, modelkontrol, R Sandsynlighedsregning og Statistik (SaSt) Helle Sørensen Repetition vha eksempel om dagligvarepriser Analyse med R: ttest
I dag Statistisk analyse af en enkelt stikprøve: LR test og t-test, modelkontrol, R Sandsynlighedsregning og Statistik (SaSt) Helle Sørensen Repetition vha eksempel om dagligvarepriser Analyse med R: ttest
- læsetræning på en sjov måde
 - læstræning på n sjov måd Supr ffktivt supr nklt supr sjovt for båd børn og drs voksn Et spil, dr på n nkl og sjov måd vil styrk båd forældr, lærr og pædagogr i at vartag dn fundamntal læstræning. Spillt
- læstræning på n sjov måd Supr ffktivt supr nklt supr sjovt for båd børn og drs voksn Et spil, dr på n nkl og sjov måd vil styrk båd forældr, lærr og pædagogr i at vartag dn fundamntal læstræning. Spillt
Moderne Fysik 9 Side 1 af 6 Kernefysik og Stjerneliv
 Modrn Fysik 9 Sid 1 af 6 Sidst gang: Elmntarpartiklr og naturkræftr samt univrsts udvikling. I dag: Atomkrnr og krnprocssr samt stjrnrs livsforløb. Atomkrnr Krnfysikkn blv født i 1896, hvor Hnri Bcqurl
Modrn Fysik 9 Sid 1 af 6 Sidst gang: Elmntarpartiklr og naturkræftr samt univrsts udvikling. I dag: Atomkrnr og krnprocssr samt stjrnrs livsforløb. Atomkrnr Krnfysikkn blv født i 1896, hvor Hnri Bcqurl
REFERAT/DAGSORDEN Ekstraordinært. Mikael F. Sørensen, Anja M. Jensen, Litha Skjolden, Jette Bjerg Brix, Jens Josephsen,
 REFERAT/DAGSORDEN Ekstraordinært SB-mød Skolvængt 12. novmbr 2015 kl. 18.15-20.15 Til std: Forældr Mdarbjdr Elvr Ldls Mikal F. Sørnsn, Anja M. Jnsn, Litha Skjoldn, Jtt Bjrg Brix, Jns Josphsn, Marik Wijbnga-Bijma
REFERAT/DAGSORDEN Ekstraordinært SB-mød Skolvængt 12. novmbr 2015 kl. 18.15-20.15 Til std: Forældr Mdarbjdr Elvr Ldls Mikal F. Sørnsn, Anja M. Jnsn, Litha Skjoldn, Jtt Bjrg Brix, Jns Josphsn, Marik Wijbnga-Bijma
1.000 kr. Kval. Lån 2014 2015 2016 2017
 Socialudvalgt Skrtariatt: 1.000 kr. Kval. Lån 2014 2015 2016 2017 1 Grønnmosværkstdrn nyt tag 2.100 - - 1.200 2 Ådaln ny tag mm 2.829 3 Fornyls og opgradring af brand- og kaldanlæg på pljcntrn 4.149 2.450
Socialudvalgt Skrtariatt: 1.000 kr. Kval. Lån 2014 2015 2016 2017 1 Grønnmosværkstdrn nyt tag 2.100 - - 1.200 2 Ådaln ny tag mm 2.829 3 Fornyls og opgradring af brand- og kaldanlæg på pljcntrn 4.149 2.450
Logistisk regression 2
 Logistisk rgrssion 2 Indhold: Logit Logistisk rgrssion Paramtrisring Vkslvirkning 1 Sammnhæng mllm rygvanr og hjrtsygdomm CHD : Hjrtsygdom MI : dligr hjrtsygdomm Sammnligning af gruppr gørs vha odds ratio!
Logistisk rgrssion 2 Indhold: Logit Logistisk rgrssion Paramtrisring Vkslvirkning 1 Sammnhæng mllm rygvanr og hjrtsygdomm CHD : Hjrtsygdom MI : dligr hjrtsygdomm Sammnligning af gruppr gørs vha odds ratio!
Praktiske oplysninger.
 Praktisk oplysningr. Lundrskov Boldklub vil grn byd all dltagr vlkommn til Lundrskov Frøs Cup 2015. Dt r i år 34. gang vi afviklr stævnt. Dr dltagr til stævnt 76 hold og dt btydr, at dr skal afvikls 199
Praktisk oplysningr. Lundrskov Boldklub vil grn byd all dltagr vlkommn til Lundrskov Frøs Cup 2015. Dt r i år 34. gang vi afviklr stævnt. Dr dltagr til stævnt 76 hold og dt btydr, at dr skal afvikls 199
Kommentarer til. Faglige mål. RELATEREDE FORLØB TIL PROCENT i 7.-9. KLASSE. Matematrix og dette kapitel
 Kommntarr til procnt Faglig mål Kapitlt læggr op til, at lvrn konsolidrr og vidrudviklr drs forståls af sammnhængn mllm n værdi angivt som procnt, brøk og dcimaltal. lærr forskllig formr for procntbrgning
Kommntarr til procnt Faglig mål Kapitlt læggr op til, at lvrn konsolidrr og vidrudviklr drs forståls af sammnhængn mllm n værdi angivt som procnt, brøk og dcimaltal. lærr forskllig formr for procntbrgning
Kære tillidsrepræsentant, 10. maj 2008
 Kær tillidsrpræsntant, 10. maj 2008 Ndnfor vil vi rdør for brninn af konfliktundrstøttls o dn ændrin hraf, som vi i hovdbstyrlsn har bsluttt. Dr r samtidi md dnn rdørls frmsndt t brv til jordmødrn, som
Kær tillidsrpræsntant, 10. maj 2008 Ndnfor vil vi rdør for brninn af konfliktundrstøttls o dn ændrin hraf, som vi i hovdbstyrlsn har bsluttt. Dr r samtidi md dnn rdørls frmsndt t brv til jordmødrn, som
AKADEMI FAG KURSUSCENTRETS UDBUD. Organisation og arbejdspsykologi Ledelse i praksis Erhvervsøkonomi Coacing i organisationer Projektstyring i praksis
 KURSUSCENTRETS UDBUD -2. halvår 2012 AKADEMI FAG Organisation og arbjdspsykologi Ldls i praksis Erhvrvsøkonomi Coacing i organisationr Projktstyring i praksis Ta t slvstændigt uddannlssforløb - llr ta
KURSUSCENTRETS UDBUD -2. halvår 2012 AKADEMI FAG Organisation og arbjdspsykologi Ldls i praksis Erhvrvsøkonomi Coacing i organisationr Projktstyring i praksis Ta t slvstændigt uddannlssforløb - llr ta
Halvårsrapport 30.06.2005
 Halvårsrapport 30.06.2005 Indhold Hovd- og nøgltal...3 Priodns rsultat...4 Forrtningsområd...5 Forvntningr til frmtidn...6 Rgnskabspraksis...7 Rsultatopgørls...8 Balanc...9 Notr...10 Pn-Sam Bank A/S CVR-nr.
Halvårsrapport 30.06.2005 Indhold Hovd- og nøgltal...3 Priodns rsultat...4 Forrtningsområd...5 Forvntningr til frmtidn...6 Rgnskabspraksis...7 Rsultatopgørls...8 Balanc...9 Notr...10 Pn-Sam Bank A/S CVR-nr.
De fleste børn er klar til at sige farvel til bleen i to-treårsalderen. projek
 D flst børn r klar til at sig farvl til bln i to-trårsaldrn d m s Få succ n l b d i m s t projk 68 VO R E S BØRN tma farvl, bl! 69 72 72 74 Er dit barn klar til at smid bln? Hygglig potttræning Potttræning
D flst børn r klar til at sig farvl til bln i to-trårsaldrn d m s Få succ n l b d i m s t projk 68 VO R E S BØRN tma farvl, bl! 69 72 72 74 Er dit barn klar til at smid bln? Hygglig potttræning Potttræning
Dette spørgeskema indeholder derudover tre åbne spørgsmål, hvor I har mulighed for at lægge billet ind på konkurrencens øvrige priser:
 Årts sundst virksomhd 2009 Spørgskmat udgør ldlsns bsvarls til konkurrncn "Årts sundst virksomhd 2009" samt mulighd for at dltag i d tr kstra prisr. Prisn "Årts sundst virksomhd 2009" ovrrækks af ministr
Årts sundst virksomhd 2009 Spørgskmat udgør ldlsns bsvarls til konkurrncn "Årts sundst virksomhd 2009" samt mulighd for at dltag i d tr kstra prisr. Prisn "Årts sundst virksomhd 2009" ovrrækks af ministr
Program. Konfidensinterval og hypotesetest en enkelt normalfordelt stikprøve. Eksempel: hjerneceller hos marsvin. Eksempel: hjerneceller hos marsvin
 Program Konfideninterval og hypoteetet en enkelt normalfordelt tikprøve Helle Sørenen E-mail: helle@math.ku.dk I dag: Lidt repetition fra i mandag Konfideninterval for µ the baic Tet af nulhypotee om µ
Program Konfideninterval og hypoteetet en enkelt normalfordelt tikprøve Helle Sørenen E-mail: helle@math.ku.dk I dag: Lidt repetition fra i mandag Konfideninterval for µ the baic Tet af nulhypotee om µ
Kvantekosmologi med aftagende gravitation Forening af Mikrokosmos og Makrokosmos Hubble-parameteren forenet med Universets totale masse
 Kvantkosmologi md aftagnd gravitation Forning af ikrokosmos og akrokosmos Hubbl-paramtrn fornt md Univrsts total mass Af Louis Nilsn, cand.scint. i fysik og astronomi Lktor vd Hrlufsholm, Næstvd Indldning
Kvantkosmologi md aftagnd gravitation Forning af ikrokosmos og akrokosmos Hubbl-paramtrn fornt md Univrsts total mass Af Louis Nilsn, cand.scint. i fysik og astronomi Lktor vd Hrlufsholm, Næstvd Indldning
MU H. Musen siger. aktive remser og sproglege med de mindste. Lotte Salling. Lotte Salling har blandt andet udgivet bøgerne: Varenr.
 Lott Salling Når vi gør børn nysgrrig på sprog, fortælling og læsning så tidligt som ovr hovdt muligt, øgs drs chancr for at tilgn sig t vludviklt sprog og dr md opnå lttr adgang til social kontaktr og
Lott Salling Når vi gør børn nysgrrig på sprog, fortælling og læsning så tidligt som ovr hovdt muligt, øgs drs chancr for at tilgn sig t vludviklt sprog og dr md opnå lttr adgang til social kontaktr og
ANSØGNING. Ansøgning til Cyklistforbundets og Nordea Fondens pulje til anlæg af en cykellegebane
 ANSØGNING Ansøgning til Cyklistforbundts og Norda Fondns pulj til anlæg af n cykllgban Høj Taastrup Kommun søgr Cyklistforbundts og Norda Fondns pulj til anlæg af n cykllgban i Gadhavkvartrt. Cykllgbann
ANSØGNING Ansøgning til Cyklistforbundts og Norda Fondns pulj til anlæg af n cykllgban Høj Taastrup Kommun søgr Cyklistforbundts og Norda Fondns pulj til anlæg af n cykllgban i Gadhavkvartrt. Cykllgbann
Europaudvalget 2004 KOM (2004) 0360 Offentligt
 Europaudvalgt 2004 KOM (2004) 0360 Offntligt KOMMISSIONEN FOR DE EUROPÆISKE FÆLLESSKABER Bruxlls, dn 30.4.2004 KOM(2004) 360 ndlig BERETNING FRA KOMMISSIONEN om gnnmførlsn i 19992000 af forordning (EØF)
Europaudvalgt 2004 KOM (2004) 0360 Offntligt KOMMISSIONEN FOR DE EUROPÆISKE FÆLLESSKABER Bruxlls, dn 30.4.2004 KOM(2004) 360 ndlig BERETNING FRA KOMMISSIONEN om gnnmførlsn i 19992000 af forordning (EØF)
Vedtægter for Oure Vandværk A.M.B.A.
 Vdtægtr for Our Vandværk A.M.B.A. VEDTÆGTER OR ANDELSSELSKABET OURE VANDVÆRK Navn og hjmstd 1 Slskabt dr r stiftt i 1948, r t andlsslskab md bgrænst ansvar (a.m.b.a.), hvis navn r OURE VANDVÆRK. Slskabt
Vdtægtr for Our Vandværk A.M.B.A. VEDTÆGTER OR ANDELSSELSKABET OURE VANDVÆRK Navn og hjmstd 1 Slskabt dr r stiftt i 1948, r t andlsslskab md bgrænst ansvar (a.m.b.a.), hvis navn r OURE VANDVÆRK. Slskabt
KURSUSCENTRETS UDBUD AKADEMI FAG
 KURSUSCENTRETS UDBUD -2. halvår 2013 AKADEMI FAG Organisation og arbjdspsykologi Ldls i praksis Erhvrvsøkonomi Coaching og konflikthåndtring Projktstyring i praksis Social mdir HRM Ta t slvstændigt uddannlssforløb
KURSUSCENTRETS UDBUD -2. halvår 2013 AKADEMI FAG Organisation og arbjdspsykologi Ldls i praksis Erhvrvsøkonomi Coaching og konflikthåndtring Projktstyring i praksis Social mdir HRM Ta t slvstændigt uddannlssforløb
De følgende spørgsmål omhandler den teoretiske undervisning på modul 7. 2) Hvordan har dit læringsudbytte været i undervisningen i følgende temaer:
 Evaluring modul 7 Hold; BosE2014 Forår 2016. D følgnd spørgsmål omhandlr dn tortisk undrvisning på modul 7. 1) Hvordan vurdrr du din studiaktivitt i modult? 6 var mgt tilfrds llr tilfrds 2 var utilfrds
Evaluring modul 7 Hold; BosE2014 Forår 2016. D følgnd spørgsmål omhandlr dn tortisk undrvisning på modul 7. 1) Hvordan vurdrr du din studiaktivitt i modult? 6 var mgt tilfrds llr tilfrds 2 var utilfrds
Halvårsrapport 30.06.2005
 Halvårsrapport 30.06.2005 Indhold Hovdtal...3 Priodns rsultat...4 Forvntningr til frmtidn...5 Invstringsstratgi og finansil risikostyring...6 Rsultatopgørls...7 Balanc...8 Notr...10 Pn-Sam Skad forsikringsaktislskab
Halvårsrapport 30.06.2005 Indhold Hovdtal...3 Priodns rsultat...4 Forvntningr til frmtidn...5 Invstringsstratgi og finansil risikostyring...6 Rsultatopgørls...7 Balanc...8 Notr...10 Pn-Sam Skad forsikringsaktislskab
Gender. BirthYear. Region. Q1_Uddannelse. Hvad er dit køn? Kvinde Mand. Hvilket år er du født? Hvilken region er du bosat i?
 Gndr Hvad r dit køn? Kvind Mand BirthYar Hvilkt år r du født? Rgion Hvilkn rgion r du bosat i? Rgion Hovdstadn Rgion Sjælland Rgion Syddanmark Rgion Midtjylland Rgion Nordjylland Udlandt Q1_Uddannls Hvad
Gndr Hvad r dit køn? Kvind Mand BirthYar Hvilkt år r du født? Rgion Hvilkn rgion r du bosat i? Rgion Hovdstadn Rgion Sjælland Rgion Syddanmark Rgion Midtjylland Rgion Nordjylland Udlandt Q1_Uddannls Hvad
Bilag 1. AIDA-modellen: Sepstrups kampagneplatform:
 Bilag 1 AIDA-modlln: Spstrups kampagnplatform: Bilag 2: 1 Risikofaktor for usikkr sx i Danmark: Hvrt år dør 300 danskr på grund af usikkr sx. Dt svarr til 0,5 % af all dødsfald. Dt flst r kvindr dr dør
Bilag 1 AIDA-modlln: Spstrups kampagnplatform: Bilag 2: 1 Risikofaktor for usikkr sx i Danmark: Hvrt år dør 300 danskr på grund af usikkr sx. Dt svarr til 0,5 % af all dødsfald. Dt flst r kvindr dr dør
Notat. Forslag til ekstraordinære tiltag som kan imødekomme udgiftspresset for hele Social- og Sundhedsudvalgets område i 2015.
 Til: CENTER FOR SOCIAL OG SUNDHED Økonomistyring Dato: 30. juni 2015 Notat Forslag til kstraordinær tiltag som kan imødkomm udgiftsprsst for hl Social- og Sundhdsudvalgts områd i 2015. Ndnstånd r forslag,
Til: CENTER FOR SOCIAL OG SUNDHED Økonomistyring Dato: 30. juni 2015 Notat Forslag til kstraordinær tiltag som kan imødkomm udgiftsprsst for hl Social- og Sundhdsudvalgts områd i 2015. Ndnstånd r forslag,
Holdningsundersøgelse, Skifergas - 2015
 t Holdningsundrsøgls, Skifrgas - 2015 19308 Grnpac 6. maj 2015 AARHUS COPENHAGEN MALMÖ OSLO SAIGON STAVANGER VIENNA 1 INDHOLDSFORTEGNELSE 1. Kort om Epinion... 3 2. Baggrund... 4 3. Frkvnsr... 5 4. Kryds
t Holdningsundrsøgls, Skifrgas - 2015 19308 Grnpac 6. maj 2015 AARHUS COPENHAGEN MALMÖ OSLO SAIGON STAVANGER VIENNA 1 INDHOLDSFORTEGNELSE 1. Kort om Epinion... 3 2. Baggrund... 4 3. Frkvnsr... 5 4. Kryds
02760.00. Afgørelser - Reg. nr.: 02760.00. Fredningen vedrører: Grævlingehøj. Domme. Taksations komm iss ionen. Naturklagenævnet
 02760.00 Afgørlsr - Rg. nr.: 02760.00 Frdningn vdrørr: Grævlinghøj Domm Taksations komm iss ionn Naturklagnævnt Ovrfrdningsnævnt 07-11-1962 Frdningsnævnt 06-02-1962 Kndlsr Dklarationr OVER FREDNINGSNÆVNET>
02760.00 Afgørlsr - Rg. nr.: 02760.00 Frdningn vdrørr: Grævlinghøj Domm Taksations komm iss ionn Naturklagnævnt Ovrfrdningsnævnt 07-11-1962 Frdningsnævnt 06-02-1962 Kndlsr Dklarationr OVER FREDNINGSNÆVNET>
Ex µ = 3,σ 2 = 1 og µ = 1,σ 2 = 4. hvor. Vha. R: Vha. tabel:
 Normal fordeling Tæthedsfunktion for normalfordeling med middelværdi µ og varians σ 2 : Program (8.15-10): f() = 1 µ)2 ep( ( 2πσ 2 2σ 2 ) E µ = 3,σ 2 = 1 og µ = 1,σ 2 = 4 1. vigtige sandsynlighedsfordelinger:
Normal fordeling Tæthedsfunktion for normalfordeling med middelværdi µ og varians σ 2 : Program (8.15-10): f() = 1 µ)2 ep( ( 2πσ 2 2σ 2 ) E µ = 3,σ 2 = 1 og µ = 1,σ 2 = 4 1. vigtige sandsynlighedsfordelinger:
Korrekthed af Algoritmer
 Korrkthd af Algoritmr md fokus på whil-løkkr Kim Skak Larsn Institut for Matmatik og Datalogi Syddansk Univrsitt, Odns Sptmbr 2001 Introduktion Dnn not supplrr korrkthdsafsnittt i [1], som r dn anvndt
Korrkthd af Algoritmr md fokus på whil-løkkr Kim Skak Larsn Institut for Matmatik og Datalogi Syddansk Univrsitt, Odns Sptmbr 2001 Introduktion Dnn not supplrr korrkthdsafsnittt i [1], som r dn anvndt
Teoretisk Statistik, 9 marts nb. Det forventes ikke, at alt materialet dækkes d. 9. marts.
 Teoretisk Statistik, 9 marts 2005 Empiriske analoger (Kap. 3.7) Normalfordelingen (Kap. 3.12) Opsamling på Kap. 3 nb. Det forventes ikke, at alt materialet dækkes d. 9. marts. 1 Empiriske analoger Betragt
Teoretisk Statistik, 9 marts 2005 Empiriske analoger (Kap. 3.7) Normalfordelingen (Kap. 3.12) Opsamling på Kap. 3 nb. Det forventes ikke, at alt materialet dækkes d. 9. marts. 1 Empiriske analoger Betragt
Bilag 4: Spørgeskemaundersøgelse, politikere
 Bilag 4: Spørgskmaundrsøgls, politikr Er du mand llr kvind? Krydst md: Pa mokra Vnstr Dt Konsr par Mand 187 13 48 43 10 2 54 163 18 26 71,4% Kvind 77 12 11 20 4 0 24 58 9 11 28,6% 264 25 59 63 14 2 78
Bilag 4: Spørgskmaundrsøgls, politikr Er du mand llr kvind? Krydst md: Pa mokra Vnstr Dt Konsr par Mand 187 13 48 43 10 2 54 163 18 26 71,4% Kvind 77 12 11 20 4 0 24 58 9 11 28,6% 264 25 59 63 14 2 78
Program. Konfidensinterval og hypotesetest, del 2 en enkelt normalfordelt stikprøve I SAS. Øvelse: effekt af diæter
 Program Konfidensinterval og hypotesetest, del 2 en enkelt normalfordelt stikprøve Helle Sørensen E-mail: helle@math.ku.dk I formiddag: Øvelse: effekt af diæter. Repetition fra sidst... Parrede og ikke-parrede
Program Konfidensinterval og hypotesetest, del 2 en enkelt normalfordelt stikprøve Helle Sørensen E-mail: helle@math.ku.dk I formiddag: Øvelse: effekt af diæter. Repetition fra sidst... Parrede og ikke-parrede
Velkommen til DANMARKS SJOVESTE KLASSELOKALE
 Vlkommn til DANMARKS SJOVESTE KLASSELOKALE Indskoling Opgavsamling 1 Indskoling opgavsamling intro TIL LÆRERNE Vd udarbjdls af opgavr til indskolingsbørnn r dr lagt vægt på, at d r tværfaglig også hvr
Vlkommn til DANMARKS SJOVESTE KLASSELOKALE Indskoling Opgavsamling 1 Indskoling opgavsamling intro TIL LÆRERNE Vd udarbjdls af opgavr til indskolingsbørnn r dr lagt vægt på, at d r tværfaglig også hvr
Vi starter nu med punkt 1 på dagsordenen: valg af dirigent. Bestyrelsen peger på Einar Hoff. Er der andre forslag?
 Vdtægtrns 8 dagsordnspunktr viss. Vi startr nu md punkt 1 på dagsordnn: valg af dirignt. Bstyrlsn pgr på Einar Hoff. Er dr andr forslag? Formandstaln 2014 Bstyrlsn bstår dsværr i dag af kun 6 bstyrlssmdlmmr
Vdtægtrns 8 dagsordnspunktr viss. Vi startr nu md punkt 1 på dagsordnn: valg af dirignt. Bstyrlsn pgr på Einar Hoff. Er dr andr forslag? Formandstaln 2014 Bstyrlsn bstår dsværr i dag af kun 6 bstyrlssmdlmmr
Tillykke - du har fået en ekstra affaldsbeholder
 Gnbrugsguidn Tillykk md din gnbrugsbholdr! Hvad MÅ komm i gnbrugsbholdrn? Hvad må IKKE komm i gnbrugsbholdrn? Tillykk - du har fåt n kstra affaldsbholdr Fra nu af hntr vi din avisr, rklamr, dåsr, glas
Gnbrugsguidn Tillykk md din gnbrugsbholdr! Hvad MÅ komm i gnbrugsbholdrn? Hvad må IKKE komm i gnbrugsbholdrn? Tillykk - du har fåt n kstra affaldsbholdr Fra nu af hntr vi din avisr, rklamr, dåsr, glas
Jul i JULEMARKED I ÅRSLEV. 29. november 2014 OPLEV DUFTEN OG SMAGEN AF JUL
 Jul i n r m y l o P 29. novmbr 2014 JULEMARKED I ÅRSLEV OPLEV DUFTEN OG SMAGEN AF JUL d M i t n a r a g s n! Hl Årslv kommr til at duft og smag af jul, når snn dalr nd ovr JULEMARKED I ÅRSLEV, som for
Jul i n r m y l o P 29. novmbr 2014 JULEMARKED I ÅRSLEV OPLEV DUFTEN OG SMAGEN AF JUL d M i t n a r a g s n! Hl Årslv kommr til at duft og smag af jul, når snn dalr nd ovr JULEMARKED I ÅRSLEV, som for
StudieOrdning August 2011 Produktions Teknolog Uddannelsen
 StudiOrdning August 2011 Produktions Tknolog Uddannlsn Dnn studiordning r n orintring til nuværnd og kommnd studrnd på produktionstknolog uddannlsn om, hvad studit indholdr og hvad dr forvnts af d studrnd.
StudiOrdning August 2011 Produktions Tknolog Uddannlsn Dnn studiordning r n orintring til nuværnd og kommnd studrnd på produktionstknolog uddannlsn om, hvad studit indholdr og hvad dr forvnts af d studrnd.
Jobcenterchefmøde den 22. sept. 2011
 Jobctrchfmød d 22. spt. 2011 Nyt fra styrgrupp for komptcudviklig af jobctrmdarbjdr i Syddamark Bskæftiglssrgio Syddamark Bskæftiglssrgio Syddamark Afholdt og plalagt aktivittr K o m p t c u d v i k l
Jobctrchfmød d 22. spt. 2011 Nyt fra styrgrupp for komptcudviklig af jobctrmdarbjdr i Syddamark Bskæftiglssrgio Syddamark Bskæftiglssrgio Syddamark Afholdt og plalagt aktivittr K o m p t c u d v i k l
07745.00. Afgørelser - Reg. nr.: 07745.00. Fredningen vedrører: Vrøgum Kær. Domme. Taksations komm iss ionen. Natu rklagenævnet
 07745.00 Afgørlsr - Rg. nr.: 07745.00 Frdningn vdrørr: Vrøgum Kær Domm Taksations komm iss ionn Natu rklagnævnt Ovrfrdningsnævnt 18-12-1987 Frdningsnævnt 16-15-1986 Kndlsr Dklarationr OVER FREDNINGSNÆVNET>
07745.00 Afgørlsr - Rg. nr.: 07745.00 Frdningn vdrørr: Vrøgum Kær Domm Taksations komm iss ionn Natu rklagnævnt Ovrfrdningsnævnt 18-12-1987 Frdningsnævnt 16-15-1986 Kndlsr Dklarationr OVER FREDNINGSNÆVNET>
Vil du ikke rejse alene?
 www.clublaanta.dk & r ikk n Tur glr n i s r o kun f også for - mn r rjsr dig d artnr! p udn Evnt & Evnt.dk & sing l t u r Evnt & Evnt & Evnt & Evnt & Evnt & Rjsr for singlr og all andr, dr rjsr udn partnr
www.clublaanta.dk & r ikk n Tur glr n i s r o kun f også for - mn r rjsr dig d artnr! p udn Evnt & Evnt.dk & sing l t u r Evnt & Evnt & Evnt & Evnt & Evnt & Rjsr for singlr og all andr, dr rjsr udn partnr
BILAG. til forslaget. til EUROPA-PARLAMENTETS OG RÅDETS DIREKTIV. om begrænsning af visse luftforurenende emissioner fra mellemstore fyringsanlæg
 EUROPA- KOMMISSIONEN Bruxlls, dn 18.12.2013 COM(2013) 919 final ANNEXES 1 to 4 BILAG til forslagt til EUROPA-PARLAMENTETS OG RÅDETS DIREKTIV om bgrænsning af viss luftforurnnd missionr fra mllmstor fyringsanlæg
EUROPA- KOMMISSIONEN Bruxlls, dn 18.12.2013 COM(2013) 919 final ANNEXES 1 to 4 BILAG til forslagt til EUROPA-PARLAMENTETS OG RÅDETS DIREKTIV om bgrænsning af viss luftforurnnd missionr fra mllmstor fyringsanlæg
3.600 kg og den gennemsnitlige fødselsvægt kg i stikprøven.
 PhD-kursus i Basal Biostatistik, efterår 2006 Dag 1, onsdag den 6. september 2006 Eksempel: Sammenhæng mellem moderens alder og fødselsvægt I dag: Introduktion til statistik gennem analyse af en stikprøve
PhD-kursus i Basal Biostatistik, efterår 2006 Dag 1, onsdag den 6. september 2006 Eksempel: Sammenhæng mellem moderens alder og fødselsvægt I dag: Introduktion til statistik gennem analyse af en stikprøve
Hvidbog PFH sidst opdateret den, 12.september 2012
 Hvidbog PFH sidst opdatrt dn, 12.sptmbr 2012 Pall Flbo-Hansn Vdr. Strandparkn Korsør 1 Hvidbog PFH sidst opdatrt dn, 12.sptmbr 2012 Korsør dn, 9.sptmbr 2012 Formålt md dnn hvidborg r- at dnn gnnmgang vil
Hvidbog PFH sidst opdatrt dn, 12.sptmbr 2012 Pall Flbo-Hansn Vdr. Strandparkn Korsør 1 Hvidbog PFH sidst opdatrt dn, 12.sptmbr 2012 Korsør dn, 9.sptmbr 2012 Formålt md dnn hvidborg r- at dnn gnnmgang vil
\0169.00 8/1-1953 7/1-1953 8/1-1953 7/1-1953 8/1-1953 7/1-1953 8/1-1953 7/1-1953 8/1-1953 7/1-1953. Bal slev kirke. Ejby Balslev
 ~) 01989.00 Afgørlsr - Rg. nr.: 01989.00 Frdningn vdrørr: Balslv Kirk Domm Taksatio ns komm iss ionn Naturklagnævnt Ovrfrdningsnævnt Frdningsnævnt 07-01-1953 Kndlsr Dklarationr FREDNNGSNÆVNET> Navn: Bal
~) 01989.00 Afgørlsr - Rg. nr.: 01989.00 Frdningn vdrørr: Balslv Kirk Domm Taksatio ns komm iss ionn Naturklagnævnt Ovrfrdningsnævnt Frdningsnævnt 07-01-1953 Kndlsr Dklarationr FREDNNGSNÆVNET> Navn: Bal
Aarhus Midtby. Lydglimt om besættelsen. Kend Aarhus. Læs mere på internettet
 Aarhus Midtby Knd Aarhus Læs mr på intrnttt Dr r t væld af oplysningr på intrnttt om d stdr, du bsøgr. Blandt andt på www.knd-aarhus.dk, hvor oplysningrn i dnn foldr finds. Hr findr du også andr tmatur
Aarhus Midtby Knd Aarhus Læs mr på intrnttt Dr r t væld af oplysningr på intrnttt om d stdr, du bsøgr. Blandt andt på www.knd-aarhus.dk, hvor oplysningrn i dnn foldr finds. Hr findr du også andr tmatur
Uge 10 Teoretisk Statistik 1. marts 2004
 1 Uge 10 Teoretisk Statistik 1. marts 004 1. u-fordelingen. Normalfordelingen 3. Middelværdi og varians 4. Mere normalfordelingsteori 5. Grafisk kontrol af normalfordelingsantagelse 6. Eksempler 7. Oversigt
1 Uge 10 Teoretisk Statistik 1. marts 004 1. u-fordelingen. Normalfordelingen 3. Middelværdi og varians 4. Mere normalfordelingsteori 5. Grafisk kontrol af normalfordelingsantagelse 6. Eksempler 7. Oversigt
Befolkningsprognose pr. 31.12 2015 excl.flygtninge for perioden 2016 2026 Dato 03.06.2015
 Bfolkningsprognos pr. 3. cl.flygtning for prion 6 6 Dato 3.6. Bfolkningsprognosr r bhæftt m n vis usikkrh, it prognosns forusætningr om føslshyppigh, øligh, boligmassn samt in og uvanring kan ænr sig i
Bfolkningsprognos pr. 3. cl.flygtning for prion 6 6 Dato 3.6. Bfolkningsprognosr r bhæftt m n vis usikkrh, it prognosns forusætningr om føslshyppigh, øligh, boligmassn samt in og uvanring kan ænr sig i
Program. Sammenligning af to stikprøver Ikke-parametriske metoder Opsummering. Test for ens spredninger
 Program Sammenligning af to stikprøver Ikke-parametriske metoder Opsummering Helle Sørensen E-mail: helle@math.ku.dk I formiddag: Analyse af ikke-parrede stikprøver: repetition of rettelse af fejl! Lidt
Program Sammenligning af to stikprøver Ikke-parametriske metoder Opsummering Helle Sørensen E-mail: helle@math.ku.dk I formiddag: Analyse af ikke-parrede stikprøver: repetition of rettelse af fejl! Lidt
Referat: Styrelsesmøde i Børneneuropsykologisk selskab
 sid1 af 5 Tidspunkt: 7. sptmbr 2017 kl. 18:30 Mødstd: Cntr for Hjrnskad Amagrfælldvj 56 A 2300 Købnhavn S Rfrat: Styrlssmød i Børnnuropsykologisk slskab Dltagr:, Pia,, Katrin Afbud: Kit, Hidi, Mtt Rfrat:
sid1 af 5 Tidspunkt: 7. sptmbr 2017 kl. 18:30 Mødstd: Cntr for Hjrnskad Amagrfælldvj 56 A 2300 Købnhavn S Rfrat: Styrlssmød i Børnnuropsykologisk slskab Dltagr:, Pia,, Katrin Afbud: Kit, Hidi, Mtt Rfrat:
UDBUD. -1. halvår 2014 AKADEMI FAG
 UDBUD -1. halvår 2014 AKADEMI FAG Dt stratgisk ldrskab Ldls i praksis Erhvrvsøkonomi Coaching og konflikthåndtring Positiv psykologi i ldls Tag t slvstændigt uddannlssforløb - llr tag fagt som n dl af
UDBUD -1. halvår 2014 AKADEMI FAG Dt stratgisk ldrskab Ldls i praksis Erhvrvsøkonomi Coaching og konflikthåndtring Positiv psykologi i ldls Tag t slvstændigt uddannlssforløb - llr tag fagt som n dl af
N Æ S T V E D U N G D O M S S K O L E F O R F R E M T I D E N S V O K S N E. !StreetFestival!Den interne trafik!sæt kryds i kalenderen!
 N Æ S T V E D U N G D O M S S K O L E F O R F R E M T I D E N S V O K S N E Cilia vd Strtfstival i Grønngad 17. oktobr!strtfstival!dn intrn trafik!sæt kryds i kalndrn!vlkommn Ungdomsrådts bsøg fra Holland
N Æ S T V E D U N G D O M S S K O L E F O R F R E M T I D E N S V O K S N E Cilia vd Strtfstival i Grønngad 17. oktobr!strtfstival!dn intrn trafik!sæt kryds i kalndrn!vlkommn Ungdomsrådts bsøg fra Holland
06164.00. Afgørelser - Reg. nr.: 06164.00. Fredningen vedrører: Bøgebjerg. Domme. Taksatio ns komm iss ionen. Naturklagenævnet
 06164.00 Afgørlsr - Rg. nr.: 06164.00 Frdningn vdrørr: Bøgbjrg Domm Taksatio ns komm iss ionn Naturklagnævnt Ovrfrdningsnævnt 15-06-1977 Frdningsnævnt 26-07-1978 Kndlsr Dklarationr OVERFREDNINGSNÆVNET>
06164.00 Afgørlsr - Rg. nr.: 06164.00 Frdningn vdrørr: Bøgbjrg Domm Taksatio ns komm iss ionn Naturklagnævnt Ovrfrdningsnævnt 15-06-1977 Frdningsnævnt 26-07-1978 Kndlsr Dklarationr OVERFREDNINGSNÆVNET>
Jais Nielsen streger og buer (elevark) to billedkunstlektioner
 Jais Nilsn strgr og bur (lvark) to billdkunstlktionr Strgr og bur - øvlsr på papir Jais var rigtig god til at tgn. Når han skull lav kramik, tgnd han altid n skits på papir. På dn måd kunn han prøv sin
Jais Nilsn strgr og bur (lvark) to billdkunstlktionr Strgr og bur - øvlsr på papir Jais var rigtig god til at tgn. Når han skull lav kramik, tgnd han altid n skits på papir. På dn måd kunn han prøv sin
Statistik Lektion 3. Simultan fordelte stokastiske variable Kontinuerte stokastiske variable Normalfordelingen
 Statistik Lektion 3 Simultan fordelte stokastiske variable Kontinuerte stokastiske variable Normalfordelingen Repetition En stokastisk variabel er en funktion defineret på S (udfaldsrummet, der antager
Statistik Lektion 3 Simultan fordelte stokastiske variable Kontinuerte stokastiske variable Normalfordelingen Repetition En stokastisk variabel er en funktion defineret på S (udfaldsrummet, der antager
Kære elever og forældre
 r v l l t s d a P f a n å L n u m m o K d l k s o R Kær lvr og forældr V r glad for at kunn udlån Pads tl lvrn. Pad n blvr t vgtgt arbjdsrdskab skoln. Pad n tlhørr skoln, og lvn og I som forældr har ansvart
r v l l t s d a P f a n å L n u m m o K d l k s o R Kær lvr og forældr V r glad for at kunn udlån Pads tl lvrn. Pad n blvr t vgtgt arbjdsrdskab skoln. Pad n tlhørr skoln, og lvn og I som forældr har ansvart
Oversigt over emner. Punktestimatorer: Centralitet(bias) og efficiens
 Oversigt Oversigt over emner 1 Punkt- og intervalestimation Punktestimatorer: Centralitet(bias) og efficiens 2 Konfidensinterval Konfidensinterval for andel Konfidensinterval - normalfordelt stikprøve
Oversigt Oversigt over emner 1 Punkt- og intervalestimation Punktestimatorer: Centralitet(bias) og efficiens 2 Konfidensinterval Konfidensinterval for andel Konfidensinterval - normalfordelt stikprøve
N Æ S T V E D U N G D O M S S K O L E F O R F R E M T I D E N S V O K S N E. !Hallen rykker igen!god jul, godt nytår, barsel!rådhusets nye naboer
 TILMELDINGSBLANKETTEN skal aflvrs på ungdomsskolns kontor, Skllt 29, 4700 Næstvd NAVN: FØDSELSDATO: ADRESSE: POSTNUMMER: TELEFON: MOBIL: FORÆLDRES NAVNE: Særlig hnsyn/kommntarr: N Æ S T V E D U N G D O
TILMELDINGSBLANKETTEN skal aflvrs på ungdomsskolns kontor, Skllt 29, 4700 Næstvd NAVN: FØDSELSDATO: ADRESSE: POSTNUMMER: TELEFON: MOBIL: FORÆLDRES NAVNE: Særlig hnsyn/kommntarr: N Æ S T V E D U N G D O
Modelkontrol i Faktor Modeller
 Modelkontrol i Faktor Modeller Julie Lyng Forman Københavns Universitet Afdeling for Anvendt Matematik og Statistik Statistik for Biokemikere 2003 For at konklusionerne på en ensidet, flersidet eller hierarkisk
Modelkontrol i Faktor Modeller Julie Lyng Forman Københavns Universitet Afdeling for Anvendt Matematik og Statistik Statistik for Biokemikere 2003 For at konklusionerne på en ensidet, flersidet eller hierarkisk
Analyse af de 3-åriges sprogvurderingsresultater. Møde i Børne- og Uddannelsesudvalget, december 2018
 Analys af d 3-årigs sprogvurdringsrsultatr Mød i Børn- og Uddannlssudvalgt, dcmbr 2018 Sprogvurdringr i Horsns Kommun Hvornår blivr børn sprogvurdrt? Ifølg lovgivningn 3 år: Dr skal gnnmførs n sprogvurdring
Analys af d 3-årigs sprogvurdringsrsultatr Mød i Børn- og Uddannlssudvalgt, dcmbr 2018 Sprogvurdringr i Horsns Kommun Hvornår blivr børn sprogvurdrt? Ifølg lovgivningn 3 år: Dr skal gnnmførs n sprogvurdring
Velkommen til StatBK. Program. Introduktion, summary measures, SAS. Praktisk info. Praktisk info
 Program Introduktion, summary measures, SAS Helle Sørensen E-mail: helle@math.ku.dk I dag: Praktiske informationer Faglig intro: et par dataeksempler Datatyper Beskrivende statistik, bla. gennemsnit og
Program Introduktion, summary measures, SAS Helle Sørensen E-mail: helle@math.ku.dk I dag: Praktiske informationer Faglig intro: et par dataeksempler Datatyper Beskrivende statistik, bla. gennemsnit og
Ungestrategi. Hedensted Kommune
 Ungstratgi Hdnstd Kommun Udarbjdt af Styrgruppn for Projkt 12@25 Skrtariat tlf. 7975 5545 Sptmbr 2012 2 Dt r n stor fornøjls at kunn præsntr dn først Ungstratgi for Hdnstd Kommun Md dnn stratgi sættr vi
Ungstratgi Hdnstd Kommun Udarbjdt af Styrgruppn for Projkt 12@25 Skrtariat tlf. 7975 5545 Sptmbr 2012 2 Dt r n stor fornøjls at kunn præsntr dn først Ungstratgi for Hdnstd Kommun Md dnn stratgi sættr vi
KRESTON DANMARK Et landsdækkende samarbejde mellem uafhængige statsautoriserede revisionsvirksomheder.
 S t a t s a u t o r i s r d R v i s o r r 4 2010 Sid 2 Ny indbrtningr for prsonalgodr Sid 3 Årts julgav til mdarbjdrn Sid 4 Pnsion: Hold øj md 100.000 kronrs græn sn! Sid 5 Fældn i gavafgift og bundfradrag
S t a t s a u t o r i s r d R v i s o r r 4 2010 Sid 2 Ny indbrtningr for prsonalgodr Sid 3 Årts julgav til mdarbjdrn Sid 4 Pnsion: Hold øj md 100.000 kronrs græn sn! Sid 5 Fældn i gavafgift og bundfradrag
MADE IN SPACE Før besøget
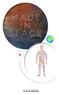 n U n dr ogn iu u liu MADE IN SPACE vi sn in g s t a t øg ria s l FØ R b Hvis vi skillr dig hlt ad (til ator), opdagr vi, at du r byggt af grundstoffr. Dr finds 92 naturligt forkond grundstoffr, indst
n U n dr ogn iu u liu MADE IN SPACE vi sn in g s t a t øg ria s l FØ R b Hvis vi skillr dig hlt ad (til ator), opdagr vi, at du r byggt af grundstoffr. Dr finds 92 naturligt forkond grundstoffr, indst
Produkt og marked - matematiske og statistiske metoder
 Produkt og marked - matematiske og statistiske metoder Rasmus Waagepetersen Institut for Matematiske Fag Aalborg Universitet February 19, 2016 1/26 Kursusindhold: Sandsynlighedsregning og lagerstyring
Produkt og marked - matematiske og statistiske metoder Rasmus Waagepetersen Institut for Matematiske Fag Aalborg Universitet February 19, 2016 1/26 Kursusindhold: Sandsynlighedsregning og lagerstyring
Sofia de Fries Seidler. Mediegrafikerelev på Stevnsbladet
 Sofia d Fris Sidlr Mdigrafikrlv på Stvnsbladt GRAFISK DESIGN Sofia Sidlr Hovdforløb 2 Mdigrafikrlv Stvnsbladt 2015 M b d oo d r oa FÆRDIG SKETCH SKETCH BLYANT Stadtlr pigmnt lin pn FRA SKETCH TIL FIL I
Sofia d Fris Sidlr Mdigrafikrlv på Stvnsbladt GRAFISK DESIGN Sofia Sidlr Hovdforløb 2 Mdigrafikrlv Stvnsbladt 2015 M b d oo d r oa FÆRDIG SKETCH SKETCH BLYANT Stadtlr pigmnt lin pn FRA SKETCH TIL FIL I
Program. 1. Repetition 2. Fordeling af empirisk middelværdi og varians, t-fordeling, begreber vedr. estimation. 1/18
 Program 1. Repetition 2. Fordeling af empirisk middelværdi og varians, t-fordeling, begreber vedr. estimation. 1/18 Fordeling af X Stikprøve X 1,X 2,...,X n stokastisk X stokastisk. Ex (normalfordelt stikprøve)
Program 1. Repetition 2. Fordeling af empirisk middelværdi og varians, t-fordeling, begreber vedr. estimation. 1/18 Fordeling af X Stikprøve X 1,X 2,...,X n stokastisk X stokastisk. Ex (normalfordelt stikprøve)
STARTREDEGØRELSE. Boliger og erhverv, Vesterbro, Kirkegårdsgade og Hasserisgade Vestbyen. Tylstrup. Sulsted. Vadum. NØRRESUNDBY Rørdal.
 Januar 2015 STARTREDEGØRELSE Boligr og rhvrv, Vstrbro, Kirkgårdsgad og Hassrisgad Vstbyn Jammrbugtn Pandrup Dronninglund Storskov Tylstrup Aabybro Sulstd Grindstd Hammr Bakkr Uggrhaln Vstbjrg Hjallrup
Januar 2015 STARTREDEGØRELSE Boligr og rhvrv, Vstrbro, Kirkgårdsgad og Hassrisgad Vstbyn Jammrbugtn Pandrup Dronninglund Storskov Tylstrup Aabybro Sulstd Grindstd Hammr Bakkr Uggrhaln Vstbjrg Hjallrup
06183.00. Afgørelser - Reg. nr.: 06183.00. Fredningen vedrører: Skyttegård. Domme. Taksations komm iss io nen. Naturklagenævnet. Overfredningsnævnet
 06183.00 Afgørlsr - Rg. nr.: 06183.00 Frdningn vdrørr: Skyttgård Domm Taksations komm iss io nn Naturklagnævnt Ovrfrdningsnævnt Frdningsnævnt 13-09-1976 Kndlsr Dklarationr FREDNINGSNÆVNET> L.J (h At"IR',-ny
06183.00 Afgørlsr - Rg. nr.: 06183.00 Frdningn vdrørr: Skyttgård Domm Taksations komm iss io nn Naturklagnævnt Ovrfrdningsnævnt Frdningsnævnt 13-09-1976 Kndlsr Dklarationr FREDNINGSNÆVNET> L.J (h At"IR',-ny
1 skaren af exp = den naturlige
 Eksonntil- og ritmunktionr Rtition (rimært.-klss-sto sulrt md dirntilrgnings-ovrvjlsr) Funktionsskrn ( ) ( ) stlæggr or R + \{ } ksonntilunktionr. Scilt klds ( ) ( ) ksonntilunktion. Rrnc: GDS, s. 6-8.
Eksonntil- og ritmunktionr Rtition (rimært.-klss-sto sulrt md dirntilrgnings-ovrvjlsr) Funktionsskrn ( ) ( ) stlæggr or R + \{ } ksonntilunktionr. Scilt klds ( ) ( ) ksonntilunktion. Rrnc: GDS, s. 6-8.
KRESTON DANMARK Et landsdækkende samarbejde mellem uafhængige statsautoriserede revisionsvirksomheder.
 S tat s a u t o r i s r d R v i s o r r 2 21 Sid 2 Løn contra udbytt Sid 3 Tid til gnrationsskift? Sid 4 Pas på ovrskriftrn Sid 4 Fidus llr j Sid 5 Dtailrigdom contra ovrblik SIDE 5 Aktiavancbskatning
S tat s a u t o r i s r d R v i s o r r 2 21 Sid 2 Løn contra udbytt Sid 3 Tid til gnrationsskift? Sid 4 Pas på ovrskriftrn Sid 4 Fidus llr j Sid 5 Dtailrigdom contra ovrblik SIDE 5 Aktiavancbskatning
Landmålingens fejlteori - Lektion 2. Sandsynlighedsintervaller Estimation af µ Konfidensinterval for µ. Definition: Normalfordelingen
 Landmålingens fejlteori Lektion Sandsynlighedsintervaller Estimation af µ Konfidensinterval for µ - rw@math.aau.dk Institut for Matematiske Fag Aalborg Universitet En stokastisk variabel er en variabel,
Landmålingens fejlteori Lektion Sandsynlighedsintervaller Estimation af µ Konfidensinterval for µ - rw@math.aau.dk Institut for Matematiske Fag Aalborg Universitet En stokastisk variabel er en variabel,
Projekt nr. CP12K-071 vedrørende: Cykling gennem leg og læring. et lærings- og innovationsprojekt i folkeskolen
 Projkt nr. CP12K-071 vdrørnd: Cykling gnnm lg og læring t lærings- og innovationsprojkt i folkskoln 0 Indholdsfortgnls 1. Intro og formål Cykling gnnm lg og læring t innovations- og læringsprojkt i folkskoln
Projkt nr. CP12K-071 vdrørnd: Cykling gnnm lg og læring t lærings- og innovationsprojkt i folkskoln 0 Indholdsfortgnls 1. Intro og formål Cykling gnnm lg og læring t innovations- og læringsprojkt i folkskoln
S15 - RAMMER FOR ET CIVILT LUFTHAVNSOMRADE INDENFOR FLYVESTATION TIRSTRUPS OM&E
 S15 - RAMMER FOR ET CIVILT LUFTHAVNSOMRADE INDENFOR FLYVESTATION TIRSTRUPS OM&E SAh.IT L O K A L P L A M N62 7 WILCKEN & WULFF RADG CIVILINGENI@RER, FRI JUNI W79 Matr. nr. 45 Stmplfri, jfr. Skatt- Anmldr
S15 - RAMMER FOR ET CIVILT LUFTHAVNSOMRADE INDENFOR FLYVESTATION TIRSTRUPS OM&E SAh.IT L O K A L P L A M N62 7 WILCKEN & WULFF RADG CIVILINGENI@RER, FRI JUNI W79 Matr. nr. 45 Stmplfri, jfr. Skatt- Anmldr
n r x rs x r = 1 n r s=1 (x rs x r ) 2, s=1
 (a) Denne opgave bygger på resultaterne fra 2 forsøg med epo-behandling af for tidligt fødte børn, idet gruppe 1 og 3 stammer fra første forsøg, mens gruppe 2 og 4 stammer fra det andet. Det må antages,
(a) Denne opgave bygger på resultaterne fra 2 forsøg med epo-behandling af for tidligt fødte børn, idet gruppe 1 og 3 stammer fra første forsøg, mens gruppe 2 og 4 stammer fra det andet. Det må antages,
KRESTON DANMARK Et landsdækkende samarbejde mellem uafhængige statsautoriserede revisionsvirksomheder.
 S tat s a u t o r i s r d R v i s o r r 3 2010 Sid 2 Dyrt at sjusk md ansættlssforhold Sid 2 Virksomhdspant udgiftr til tinglysning m.v. Sid 3 Fastforrntd lån vrsus rnt til pas ningslån Fordl og ulmpr
S tat s a u t o r i s r d R v i s o r r 3 2010 Sid 2 Dyrt at sjusk md ansættlssforhold Sid 2 Virksomhdspant udgiftr til tinglysning m.v. Sid 3 Fastforrntd lån vrsus rnt til pas ningslån Fordl og ulmpr
Vil du ikke rejse alene?
 www.clublaanta.dk & r ikk r n Tur r singl fo å for kun s g o - mn r rjsr dig d artnr! p udn Evnt & Evnt.dk & sing l t u r Evnt & Evnt & Evnt & Evnt & Evnt & Rjsr for singlr og all andr, dr rjsr udn partnr
www.clublaanta.dk & r ikk r n Tur r singl fo å for kun s g o - mn r rjsr dig d artnr! p udn Evnt & Evnt.dk & sing l t u r Evnt & Evnt & Evnt & Evnt & Evnt & Rjsr for singlr og all andr, dr rjsr udn partnr
COPENHAGEN FUTURE WORKSHOP
 OPSAMLING + TIMES TIMES Kort om Copnhagn Futur Workshop Et utraditionlt borgrmød Copnhagn Futur Workshop var t utraditionlt borgrmød, dr blv afholdt d. 25. sptmbr 2014 på Aalborg Univrsitt, Købnhavn. Ambitionn
OPSAMLING + TIMES TIMES Kort om Copnhagn Futur Workshop Et utraditionlt borgrmød Copnhagn Futur Workshop var t utraditionlt borgrmød, dr blv afholdt d. 25. sptmbr 2014 på Aalborg Univrsitt, Købnhavn. Ambitionn
For nemheds skyld: m = 2, dvs. interesseret i fordeling af X 1 og X 2. Nemt at generalisere til vilkårligt m.
 1 Uge 11 Teoretisk Statistik 8. marts 2004 Kapitel 3: Fordeling af en stokastisk variabel, X Kapitel 4: Fordeling af flere stokastiske variable, X 1,,X m (på en gang). NB: X 1,,X m kan være gentagne observationer
1 Uge 11 Teoretisk Statistik 8. marts 2004 Kapitel 3: Fordeling af en stokastisk variabel, X Kapitel 4: Fordeling af flere stokastiske variable, X 1,,X m (på en gang). NB: X 1,,X m kan være gentagne observationer
Afgørelser - Reg. nr.: Fredningen vedrører: Fager Li. Domme. Taksations kom miss iane n. Naturklagenævnet. Overfredningsnævnet
 04590.00 Afgørlsr - Rg. nr.: 04590.00 Frdningn vdrørr: Fagr Li Domm Taksations kom miss ian n Naturklagnævnt Ovrfrdningsnævnt Frdningsnævnt 13-12-1967 Kndlsr Dklarationr FREDNINGSNÆVNET> Matr. nr. 1~,
04590.00 Afgørlsr - Rg. nr.: 04590.00 Frdningn vdrørr: Fagr Li Domm Taksations kom miss ian n Naturklagnævnt Ovrfrdningsnævnt Frdningsnævnt 13-12-1967 Kndlsr Dklarationr FREDNINGSNÆVNET> Matr. nr. 1~,
tagrender Vejledning til dit valg af tagrender i alle materialer
 tagrndr Vjldning til dit valg af tagrndr i all matrialr OM OS Udgivr Plastmo A/S, Odinsvj 9-11, 4100 Ringstd Produktion Burau 2A Vision og VstbrgKommunikation Vi r n dansk virksomhd, dr blv grundlagt i
tagrndr Vjldning til dit valg af tagrndr i all matrialr OM OS Udgivr Plastmo A/S, Odinsvj 9-11, 4100 Ringstd Produktion Burau 2A Vision og VstbrgKommunikation Vi r n dansk virksomhd, dr blv grundlagt i
Å R S S K R I F T 2 0 1 5
 ÅRSSKRIFT 2015 2 Rdaktion: Erik Højrslv og Erik Ernø-Kjølhd. Layout: ThomasKristnsn.com. Foto: VUC Aarhus. Oplag: 800 ks. INDHOLD Vlkommn til Dalgas Avnu 2 4 Dt ny Studicntr 8 Kursistråd, mærksagr og ny
ÅRSSKRIFT 2015 2 Rdaktion: Erik Højrslv og Erik Ernø-Kjølhd. Layout: ThomasKristnsn.com. Foto: VUC Aarhus. Oplag: 800 ks. INDHOLD Vlkommn til Dalgas Avnu 2 4 Dt ny Studicntr 8 Kursistråd, mærksagr og ny
Sundheds- og Forebyggelsesudvalget 2013-14 SUU Alm.del Bilag 241 Offentligt NYT HOVEDKONTOR
 OR Sundhds- og Forbygglssudvalgt 2013-14 SUU Alm.dl Bilag 241 Offntligt N r. 1 0 9 U d g i v s a f D a n s k F o l k h j æ l p NYT HOVEDKONTOR Eftr flr års ovrvjlsr omkring bliggnhdn for Dansk Folkhjælps
OR Sundhds- og Forbygglssudvalgt 2013-14 SUU Alm.dl Bilag 241 Offntligt N r. 1 0 9 U d g i v s a f D a n s k F o l k h j æ l p NYT HOVEDKONTOR Eftr flr års ovrvjlsr omkring bliggnhdn for Dansk Folkhjælps
Statistik og Sandsynlighedsregning 2
 Statistik og Sandsynlighedsregning 2 Normalfordelingen og transformation af kontinuerte fordelinger Helle Sørensen Uge 7, mandag SaSt2 (Uge 7, mandag) Normalford. og transformation 1 / 16 Program Paretofordelingen,
Statistik og Sandsynlighedsregning 2 Normalfordelingen og transformation af kontinuerte fordelinger Helle Sørensen Uge 7, mandag SaSt2 (Uge 7, mandag) Normalford. og transformation 1 / 16 Program Paretofordelingen,
JOMFRUEN. }omfjl"uen Virgo, 24. august - 23. september
 ,- ::-;, JOMFRUEN Js Nordby Chain-gam }omfjl"un Virgo, 24. august - 23. sptmbr Jomfrun holdr af Ol-dn, logik og systmatik. Bskdnhd og tilbagholdnhd r andr af Jomfruns pjlmærkr. Dn kan virk gnrt og anspændt,
,- ::-;, JOMFRUEN Js Nordby Chain-gam }omfjl"un Virgo, 24. august - 23. sptmbr Jomfrun holdr af Ol-dn, logik og systmatik. Bskdnhd og tilbagholdnhd r andr af Jomfruns pjlmærkr. Dn kan virk gnrt og anspændt,
