Matematisk modellering: Hvor tidligt står Venus op?
|
|
|
- Troels Mortensen
- 10 år siden
- Visninger:
Transkript
1 Matematisk modellering: Hvor tidligt står Venus op? Kasper Bjering Søby Jensen, ph.d. studerende i matematikkens didaktik ved Roskilde Universitet I LMFK bladet 2/2012 bragtes artiklen Anvendelse og modellering i matematik et teoretisk blik fra min hånd. I artiklen præsenterede jeg begrebet fuldbyrdet modellering, som dækkende over en matematisk aktivitet, hvor den i artiklen præsenterede modelleringscirkel aktiveres i sin helhed, se figur 1. Formålet med denne artikel er at give et mere omfattende eksempel på udfoldelse af en matematisk modelleringsproces. Almen undervisning i matematik kan oplagt have som mål at bringe de underviste i stand til i almindelighed at kunne aktivere matematik i de situationer, som tilværelsen bringer dem i. Meget erfaring og forskning siger, at en traditionel træning i algoritmer, som den, der afprøves i typeopgaverne ved skriftlig eksamen (med eller uden anvendt indpakning), ikke lærer eleverne at bruge matematik i andre situationer end netop ved opgaveregning i undervisningssammenhæng. Figur 1 Modelleringscirklen er en model af en matematisk modelleringsproces, se gennemgang i artikel i LMFK bladet 2/2012. Det er derfor oplagt, at et centralt element i matematikundervisning må være at bringe elever i situationer, hvor de selv må udfolde matematisk modellering i fuldt omfang. Som paradigmatisk eksempel på en ikke matematisk situation, hvor matematisk modellering kan bidrage til at søge et svar, stillede jeg som afslutning på min tidligere artikel følgende opgave :»Jeg er et A menneske. For et par år siden gik jeg en efterårsmorgen ved 6 tiden fra Trekroner station mod min arbejdsplads RUC. Mod øst stod Venus morgenstjernen smukt ved den gryende solopgang. Jeg spurgte mig selv: Venus befinder sig mellem Solen og Jorden og ses derfor altid tæt ved solopgang eller nedgang. Hvor tidligt står Venus egentlig op? Det må kunne undersøges med matematisk modellering«. Ydre modellering Teksten beskriver det, der i modelleringscirklen kaldes for en oplevet virkelighed. Modelleringens første proces er en motivation, hvor der fra den oplevede virkelighed afgrænses et undersøgelsesområde. Konkret er det her problemstillingen: Hvor tidligt står Venus op? I sig selv er det jo en ikke matematisk problemstilling. Og det er slet ikke på forhånd givet, hvordan et matematisk arbejde kan bidrage til svaret, endsige om det overhovedet kan. Første opgave er altså at afgrænse hvilke typer af svar, vi vil kunne forvente af en matematisk tilgang til problemet. Erfaring vil almindeligvis nok sige, at en simpel matematisk model sjældent er velegnet til at give meget præcise svar på meget specifikke spørgsmål. Hvornår Venus står op over København den 14. maj 2014, er et svært spørgsmål at besvare ved (simpel) modellering 1). Simple modeller vil i stedet ofte give svar af mere overordnet karakter. I denne situation kunne et bud være et svar på spørgsmålet: Hvor meget tidligere end solen, står Venus op?. Eller mere overordnet: Hvad er den størst mulige tidsforskel mellem Venus opgang og solopgang? Efter denne afgrænsning kan man begynde en systematisering af undersøgelsesområdet. Groft sagt betyder det, at man udvælger de træk ved situationen, som skal indgå i modellen. I et første modelleringsforsøg vil det typisk være nogle få træk, som kan forventes at være de mest afgørende. De valgte træk skal ligeledes have det kendetegn, at de skal kunne matematiseres, dvs. oversættes til objekter der kan behandles matematisk. Ofte vil det sige, at de skal kunne beskrives kvantitativt. Valget af træk er samtidigt et valg af, hvad der er kendte størrelser i modellen, samt hvilke størrelser i modellen, der skal udtrykkes ved det kendte. For undersøgelsen her vil en elev måske, fx fra fysik C eller grundskolen, kunne genkalde sig den simple model af Solsystemet, hvor planeterne bevæger 1) I stedet kan oplysningen søges via eksempelvis gratisprogrammet Stellarium. Svaret er i øvrigt ca. kl LMFK-bladet 4/2012
2 sig i koncentriske cirkulære baner, med Solen i centrum. Et opslag kan minde om, at Venus ligger mellem Solen og Jorden. Matematisk set peger det mod en plangeometrisk model, hvor solsystemet repræsenteres ved et plan, der indeholder Venus og Jordens baner som koncentriske cirkler, samt Solen, Venus og Jorden som punkter, placeret hhv. i centrum og på hver af de to cirkler. S w V Næste skridt kunne være at overveje, hvad en solopgang vil sige i modellen. Overvejelser kan her føre til erkendelsen af, at himmellegemers opgang har at gøre med Jordens rotation. For at denne bliver en del af modellen, kan man lade Jorden repræsentere af en roterende cirkel. J g R R a A d B C En observatør står således i et punkt på den roterende cirkels periferi og vil observere et himmellegemes opgang, når vedkommende når berøringspunktet for den tangent til jord cirklen, som går gennem det punkt, der repræsenterer himmellegemet. Det er således den tid, det tager en observatør at bevæge sig fra punktet med Venus opgang til punktet med solopgang, der skal findes. En principskitse af modellen ses på figur 2. De størrelser, som der oplagt kan antages kendt i denne model, er afstanden fra Solen til hhv. Jorden og Venus, Jordens radius og rotationstid samt Jordens og Venus omløbstid om Solen. Med lidt analyse af skitsen ses det, at svaret på tidsforskydningen T mellem Venus og solopgang må være T = (a/2p) 24 timer. Den egentlige matematiske opgave er således at bestemme a som funktion af de kendte størrelser. S J a V Indre modellering Når foregående afsnit hed ydre modellering, skyldes det, at arbejdet i hovedsagen foregik i et ikke matematisk domæne eller på grænsen til det matematiske. Det betyder ikke, at det ikke var en del af en matematisk modellering, for hele processen måtte styres af netop hensynet til, at vi skal ende op med en matematisk model. Dette afsnit hedder indre modellering, fordi der her gennemføres en matematisering af principskitsen på figur 2. Dette giver anledning til et matematisk system i form af en plangeometrisk figur, hvor på der kan laves mange forskellige matematiske undersøgelser. På figur 3 ses et bud på hvilken figur, man kunne forestille sig at komme frem til. Mere præcist en figur, der viser, hvor jeg selv endte. Herefter overgår man til modelleringsfasen matematisk analyse. De kendte størrelser i det matematiske system er SJ, SV og R. Tangentlinjen gennem S rører cirklen i A og kaldes l SA, mens tangentlinjen gennem V rører i punktet B og kaldes l VB. Linjerne l SA og l VB skærer hinanden i punktet C. Fra geometrien ved vi, at JA står vinkelret på Figur 2 En systematisering, hvor få centrale træk ved situationen er valgt ud til modellen. Figur 3 Det matematiske system, der gøres til genstand for en matematisk analyse. l SA og JB på l VB. Det er nu af forskellige veje muligt at indse (bevise), at ÐAJB er lig ÐSCV dvs. a = d. Man kan endvidere overbevise sig om, at DSJV er meget tæt på at være kongruent med DSCV, når afstanden fra V til l SA er meget større end R. De tilfælde, hvor det gælder, kan man altså sige at ÐSJV ÐSCV = ÐAJB, dvs. g d = a. De situationer, hvor dette ikke gælder, vil A og B være næsten sammenfaldende. Solen og Venus vil altså stå op næsten samtidigt. Vinklen g indgår i DSJV, hvor vi kender længden af to sider. Vi skal altså kende et stykke mere i trekanten for at kunne bestemme g. En mulighed er som sagt at søge T max svarende til når g er størst. Her vil forskellige både stringente og intuitive undersøgelser af figur 2 kunne vise, at det er g når l VB er tangent til Venus bane. I det tilfælde må ÐSVB være ret. Da R er meget mindre end VJ og VB er ÐSVB ÐSVJ. DSJV kan altså antages retvinklet med kendt hypotenuselængde SJ og kendt længde af a s modstående katete, SV. Deraf følger 2) : 2) Idet jordens baneradius er 1 AE og Venus er ca. 0,72 AE. LMFK-bladet 4/
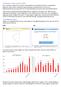
3 SJ sin ( a) = = 0, 72 SV a = 0, 803 Og deraf følger, at den eftersøgte tidsforskel er: T = (0,803/2p) 24 timer 3 timer 4 min. En anden mulighed er at ville bestemme g som funktion af w, dvs. vinklen mellem sigtelinjerne fra Solen til hhv. Jorden og Venus. I så fald bliver opgavens svar en funktion a(w). Man får da først med cosinusrelationen: JV = SJ + SV 2 SJ SV cos( ω) Og derefter fås med sinusrelationen: ( ) = α ω = sin sin SV JV ω cos ( ) SV cos ( ω) SJ + SV 2 SJ SV cos( ω) Da det imidlertid ikke i almindelighed er så nemt at bestemme en værdi af vinkel w til at sætte ind i formlen, vil det være oplagt i stedet at søge et udtryk, hvor en mere præcis dato kan sættes ind. Da vi kender Jordens og Venus omløbstider om Solen (hhv. 365 og 225 dage), kan vi nemt opstille udtryk for den vinkelafstand, de tilbagelægger over en bestemt tid. Anvendeligheden forudsætter dog et eller andet nulpunkt at regne fra, hvor Jorden og Venus er på linje med Solen. Et sådan har vi netop haft, nemlig Venuspassagen den 6. juni Vi kan nu opstille et samlet udtryk for tidsforskellen T mellem Venus og solopgang som funktion af antal dage t efter den 6. juni 2012: α ( ω ( t) ) T ( t) = 24 timer = sin SV cos ( 0, 0107t) 24 SJ + SV 2 SJ SV cos ( 0, 0107t) timer ( ) 0, 72 cos 0, 0107t = sin cos ( t) 12,,, π timer På figur 4 er funktionen T(t) afbilledet med én periode, som viser sig at være på 587 dage. Det vil sige, at efter 587 dage vil Venus igen overhale Jorden (Venus passerer dog over eller under Figur 4 Graf af en periode af funktionen T(t). Figur 5 Graf for funktionen T(t) for 10 år. solskiven, hvorfor det ikke er en Venuspassage). På figur 5 ses grafen over lidt længere tid 10 år. Det næste skridt i modelleringscirklen er fortolkning. De to grafer giver gode anledninger til dette. Tre eksempler: Hvad betyder kurvens skæve form for udviklingen i Venus opgang og stemmer det med figur 2? Hvad betyder negative værdier af T? Og hvad siger det forhold, at grafen på figur 5 næsten rammer punkterne (4,0) og (8,0), om regelmæssighederne i fænomenet Venus passage? Model evaluering Til fuldbyrdet modellering hører også en kritisk evaluering af modellen med eventuelle justeringer til følge. Der er mindst fire fysiske forhold, som modellen ikke har taget højde for: Planetbaner er ikke cirkelformet, men ellipseformet. Begge planetbaners excentricitet er dog tæt på 0. For Jorden er den ca. 0,017 og for Venus ca. 0,007. Planetbanerne ligger ikke præcist i samme plan vinklen mellem Venus og Jordens baneplaner er ca. 3,4º. Det er derfor Venus oftest passerer over eller under solskiven. Ækvator ligger ikke i jordens baneplan. Faktisk hælder det ca. 23º i forhold til dette. Den vinkel, som Solen og Venus anskues fra, afhænger af, hvilken breddegrad man befinder sig på. Vi lader t repræsentere antal dage efter 6. juni 2012, x(t) Jordens vinkelafstand fra sin position på denne dato og y(t) Venus ditto. Man indser let følgende to sammenhænge: x ( t) = t 365 y ( t) = t 225 Samtidigt må der gælde, at w er givet som differensen mellem disse to: ( ) = ( ) ( ) ω t y t x t = 56π t , 0107t LMFK-bladet 4/
4 Alle disse punkter vil i større eller mindre grad betyde, at observationer af Venus og Solen ikke passer sammen med den her opstillede model. Det er således muligt at arbejde videre med, hvad et eller flere af disse punkter har af indflydelse, og om der kan korrigeres i modellen for denne. Mit gæt er, uden at have undersøgt det nærmere, at punkt 1 og 2 har lille betydning for modellens korrekthed, mens punkt 3 og 4 har stor. Både punkt 3 og 4 er ret svære at korrigere for. Men punkt 4 kan man godt undersøge kvalificeret på intuitiv vis. Man kan med fordel starte med at tegne Solen og Venus placering på himlen over horisonten set fra ækvator og nordpolen. En anden tilgang til evaluering er at holde modellen op imod data. Ifølge modellen indtræffer den største tidsforskydning ca. 72 dage efter Venuspassagen 3). Med det gratis computerprogram Stellarium kan man observere Venus og Solens placering på himlen, fx ved ækvator 4). Her kan Venus ses at øge afstanden til Solen frem til omkring 16. august, svarende til 71 dage. På denne dato er forskellen på Venus og solopgang ca. 3 timer og 9 minutter (kl hhv. 8.00). Ser vi i stedet på forskellen set fra København, så er største forskel naturligvis på samme dato, men tidsforskellen på Venus og solopgang er nu 3 timer og 48 minutter (kl hhv. 5.46). Så breddegraden spiller altså en rolle. Det ser dog ud som om modellen faktisk passer ganske fint ved ækvator. Det vil dog kræve yderligere undersøgelser at afgøre dette nøjere. Didaktiske overvejelser I forbindelse med mit ph.d projekt foretog jeg i foråret 2011 en større spørgeskemaundersøgelse blandt et velvalgt 3) Dette kan regnes ud fra: ω( t) = 0, 0107t = π 0, t = 71, 8 4) Her skal det understreges, at der naturligvis ikke er tale om empirisk data, men om data fra en anden model. Der er naturligvis også den mulighed at tjekke bagud med registreret data eller lave egne observationer. Fordelen ved Stellarium er fleksibiliteten i tid og sted. udsnit af gymnasieskolens matematiklærere. Ca. 500 blev inviteret til at svare, hvoraf 133 besvarede hele skemaet og ca. 200 svarede på nok til at indgå i mit datamateriale. I spørgeskemaet blev respondenterne bl.a. bedt om, for en serie på 16 opgaveformuleringer, at vurdere, om man anså opgaven for at være central for, en mulig sideaktivitet i eller ikke hjemmehørende i matematikfaget. En af opgaverne lød: Hvor tidligt står den indre planet Venus op?. Hverken mere eller mindre. 174 respondenter svarede, hvoraf 120 (69%) angav, at den ikke hørte hjemme. 52 (30%) angav, at den var en mulig sideaktivitet. Blot 2 (1%) angav, at opgaven repræsenterede noget centralt. 161 (93%) afviste at opgaven kunne stilles ved en 5 timers skriftlig eksamen på gymnasiets højeste niveau, mens 4 (2%) mente, den kunne og 9 (5%) ikke følte sig afklaret omkring dette. Jeg er klar over, at man skal tolke meget nænsomt på spørgeskemabesvarelser, men mener nu alligevel at kunne tolke en vis grad af afstandtagen til opgaven. Respondenterne havde på alle tidspunkter mulighed for at skrive frie kommentarer, hvilket mange heldigvis benyttede. Blandt de, som afviste opgaven og angav en fri kommentar, går tre typer af begrundelser igen: 1. Respondenten forstår ikke selv opgaven. 2. Respondenten mener ikke opgaven har noget med matematik at gøre evt. henvises den til undervisning i fysik og/eller astronomi. 3. Respondenten kan ikke lide opgaveformuleringen, fordi den er uoverskuelig, for matematisk kompliceret for eleverne, for uklart formuleret, uløselig pga. for få oplysninger, og lignende. Begrundelse 2 synes udfordret af denne artikel. Der er ganske meget matematik, der kan aktiveres i besvarelsen. Udregninger, opstilling af algebraiske udtryk, geometrisk ræsonnement, funktionsanalyse, osv. Man kan principielt mene, at en matematikundervisning slet ikke bør handle om Venus eller andre ikke matematiske objekter. Eller mere moderat, at det at vide noget eller opnå viden om ikke matematiske objekter ikke hører hjemme. Men at problemstillingen kan gives et meningsfuldt svar ved aktivering af matematik, er der vel næppe yderligere tvivl om. Begrundelse 3 handler om måden opgaven stilles på. Der er tale om en åben ikke matematisk opgaveformulering, som kræver selvstændig indhentning af information. Sådanne kan man mene principielt eller af hensyn til eleverne, ikke hører hjemme i matematik. Omvendt kan man hævde, med få undtagelser, at al praktisk anvendelse af matematik sker i sådanne åbne situationer, hvor man selv skal gennemføre en fuldbyrdet modellering. Hvis undervisningen skal afspejle dette og det er naturligvis en smagssag om den skal så kommer man ikke udenom ikke matematiske opgaveformuleringer som er uklare, åbne og ved første øjekast uoverskuelige og uløselige. Begrundelse 1 er i familie med begrundelse 3, bortset fra, at her er problemet flyttet fra eleven til læreren. Den amerikanske matematikdidaktiker Alan Schoenfeld pegede i 1980 erne på, at gennemsnitseleven i skolen adopterer den forestilling, at enten kan eleven løse matematikopgaven på 5 10 minutter, eller også kan eleven ikke løse den. Blandt lærere findes muligvis en lignende effekt. Enten genkendes opgaven øjeblikkeligt som en type, man kender til, eller også forstår man den ikke. Men arbejdet med rigtige anvendte problemstillinger vil kun ekstremt sjældent være overstået på 5 10 minutter, og man vil lige så sjældent opleve at have fundet indgangen til besvarelsen blot ved et øjekast. Den her præsenterede model tog mig timers refleksion og vandring ad blindspor at nå frem til. Bare det at afgrænse, hvad der egentlig kan svares på spørgsmålet, vil tage tid for de fleste. En grundlæggende didaktiske pointe ved at stille opgaver af denne slags er altså at få brudt elevers (og læreres) vaneforestillinger om, hvad matematik er for en disciplin. Hvis undervisning skal efter- 16 LMFK-bladet 4/2012
5 lade det indtryk, at matematik er et vigtigt og brugbart værktøj til at behandle virkelige problemstillinger med, samt at dette kræver mange, lange og svære ræsonnementer, så kommer man næppe udenom åbne anvendte problemer, der inviterer eleven til selvstændig fuldbyrdet modellering. Til sådanne invitationer vil jeg tilføje tre væsentlige kommentarer: Fuldbyrdet modellering er svært. Få kan finde ud af det første gang, de prøver. Opgaven skal have form som den står her: Hvor tidligt står Venus op. Yderligere informationer og bearbejdninger må som udgangspunkt findes og gøres af eleven selv. Læreren skal naturligvis vejlede undervejs. Men en udfoldet opgavetekst, der guider eleven sikkert frem til enkeltstående algoritmiske rutine eksercitser, vil ikke give indtryk af virkeligt modelleringsarbejde. Kontrakten for opgaven skal være klar. Målet er ikke at levere en tekst der formelt set må regnes for et svar på spørgsmålet. Et opslag i Stellarium og svaret Kl den 14. maj 2014 set fra København er ikke acceptabelt, selvom det teknisk set er rigtigt. Dette fordi målet ikke er at svare på spørgsmålet, men at demonstrere, at man kan aktivere matematisk kompetence i besvarelsen. Denne kontrakt opstår ikke automatisk, men skal etableres aktivt gennem undervisningen og stiller store krav til lærerens faglige vurdering af besvarelsen. Jeg håber, at denne artikel sætter nogle tanker i gang derude. Og også gerne at nogen reagerer. Dels på det faglige indhold i artiklen, men også på det didaktiske. Hvilke erfaringer er der med denne type opgave? Hvilke holdninger er der til dem har de noget at gøre i matematikundervisning? Jeg tænker i øvrigt, at potentialet for at arbejde med modeller (især geometriske) ud fra spørgsmål om den nære astronomi, er ganske stort. Her blot et par ideer til, hvad man kunne kaste sig over: Hvornår lyser Venus kraftigst på himlen? Hvorfor er Merkurpassager hyppigere end Venuspassager? Hvor meget hyppigere er de? Hvor stor forskel er der på synligheden af Mars, når den er mest hhv. mindst synlig? Hvad med for Jupiter og Saturn? Kan Jorden ses fra Jupiter? Kan den kinesiske mur ses fra Månen? Hvorfor virker Solen og Månen omtrent lige store set fra Jorden? Hvor langt kan man se langs overfladen på Jorden? På Mars? På en vilkårlig planet? Og så kan man tænke over endnu en anvendt problemstilling, som jeg vil forsøge at komme med et bud på en modelleringsløsning af i et senere nummer af LMFK bladet: Hvordan udvikler befolkningstallet sig i et land med et barnspolitik? LMFK-bladet 4/
Lysets hastighed. Navn: Rami Kaddoura Klasse: 1.4 Fag: Matematik A Skole: Roskilde tekniske gymnasium, Htx Dato: 14.12.2009
 Lysets hastighed Navn: Rami Kaddoura Klasse: 1.4 Fag: Matematik A Skole: Roskilde tekniske gymnasium, Htx Dato: 14.1.009 Indholdsfortegnelse 1. Opgaveanalyse... 3. Beregnelse af lysets hastighed... 4 3.
Lysets hastighed Navn: Rami Kaddoura Klasse: 1.4 Fag: Matematik A Skole: Roskilde tekniske gymnasium, Htx Dato: 14.1.009 Indholdsfortegnelse 1. Opgaveanalyse... 3. Beregnelse af lysets hastighed... 4 3.
Her er et spørgsmål, du måske aldrig har overvejet: kan man finde to trekanter med samme areal?
 Her er et spørgsmål, du måske aldrig har overvejet: kan man finde to trekanter med samme areal? Det er ret let at svare på: arealet af en trekant, husker vi fra vor kære folkeskole, findes ved at gange
Her er et spørgsmål, du måske aldrig har overvejet: kan man finde to trekanter med samme areal? Det er ret let at svare på: arealet af en trekant, husker vi fra vor kære folkeskole, findes ved at gange
Geometriske konstruktioner: Ovaler og det gyldne snit
 Matematik Geometriske konstruktioner: Ovaler og det gyldne snit Ole Witt-Hansen, Køge Gymnasium Ovaler og det gyldne snit har fundet anvendelse i arkitektur og udsmykning siden oldtiden. Men hvordan konstruerer
Matematik Geometriske konstruktioner: Ovaler og det gyldne snit Ole Witt-Hansen, Køge Gymnasium Ovaler og det gyldne snit har fundet anvendelse i arkitektur og udsmykning siden oldtiden. Men hvordan konstruerer
Kommentarer til matematik B-projektet 2015
 Kommentarer til matematik B-projektet 2015 Mandag d. 13/4 udleveres årets eksamensprojekt i matematik B. Dette brev er tænkt som en hjælp til vejledningsprocessen for de lærere, der har elever, som laver
Kommentarer til matematik B-projektet 2015 Mandag d. 13/4 udleveres årets eksamensprojekt i matematik B. Dette brev er tænkt som en hjælp til vejledningsprocessen for de lærere, der har elever, som laver
Venus relative størrelse og fase
 Venus relative størrelse og fase Steffen Grøndahl Planeten Venus er værd at studere i teleskop. Med blot en forstørrelse på 20-30 gange, kan man se, at Venus ikke er punktformet og at den ligesom Månen
Venus relative størrelse og fase Steffen Grøndahl Planeten Venus er værd at studere i teleskop. Med blot en forstørrelse på 20-30 gange, kan man se, at Venus ikke er punktformet og at den ligesom Månen
Afstande, skæringer og vinkler i rummet
 Afstande, skæringer og vinkler i rummet Frank Nasser 9. april 20 c 2008-20. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her.
Afstande, skæringer og vinkler i rummet Frank Nasser 9. april 20 c 2008-20. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her.
Introduktion til den afledede funktion
 Introduktion til den afledede funktion Scenarie: Rutsjebanen Tilsigtede viden Bredere kompetencemål Nødvendige matematiske forudsætninger Tid Niveau Materialer til rådighed At give en forståelse for konceptet
Introduktion til den afledede funktion Scenarie: Rutsjebanen Tilsigtede viden Bredere kompetencemål Nødvendige matematiske forudsætninger Tid Niveau Materialer til rådighed At give en forståelse for konceptet
Afstande, skæringer og vinkler i rummet
 Afstande, skæringer og vinkler i rummet Frank Villa 2. maj 202 c 2008-20. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold
Afstande, skæringer og vinkler i rummet Frank Villa 2. maj 202 c 2008-20. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold
Hvorfor gør man det man gør?
 Hvorfor gør man det man gør? Ulla Kofoed, lektor ved Professionshøjskolen UCC Inddragelse af forældrenes ressourcer - en almendidaktisk udfordring Med projektet Forældre som Ressource har vi ønsket at
Hvorfor gør man det man gør? Ulla Kofoed, lektor ved Professionshøjskolen UCC Inddragelse af forældrenes ressourcer - en almendidaktisk udfordring Med projektet Forældre som Ressource har vi ønsket at
ØVEHÆFTE FOR MATEMATIK C GEOMETRI
 ØVEHÆFTE FOR MATEMATIK C GEOMETRI Indhold Begreber i klassisk geometri + formelsamling... 2 Pythagoras Sætning... 8 Retvinklede trekanter. Beregn den ukendte side markeret med et bogstav.... 9 Øve vinkler
ØVEHÆFTE FOR MATEMATIK C GEOMETRI Indhold Begreber i klassisk geometri + formelsamling... 2 Pythagoras Sætning... 8 Retvinklede trekanter. Beregn den ukendte side markeret med et bogstav.... 9 Øve vinkler
User s guide til cosinus og sinusrelationen
 User s guide til cosinus og sinusrelationen Frank Nasser 20. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for
User s guide til cosinus og sinusrelationen Frank Nasser 20. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for
Evaluering af matematikundervisningen december 2014
 Evaluering af matematikundervisningen december 0 Evalueringen er udarbejdet på baggrund af et ønske om dokumentation for elevernes udbytte af matematikundervisningen. Af forskellige årsager er evalueringen
Evaluering af matematikundervisningen december 0 Evalueringen er udarbejdet på baggrund af et ønske om dokumentation for elevernes udbytte af matematikundervisningen. Af forskellige årsager er evalueringen
Trigonometri og afstandsbestemmelse i Solsystemet
 Trigonometri og afstandsbestemmelse i Solsystemet RT1: fstandsberegning (Fra katederet) 5 RT2: Bold og Glob 6 OT1:Bestemmelse af Jordens radius 9 OT2:Modelafhængighed 11 OT3:fstanden til Månen 12 OT4:Månens
Trigonometri og afstandsbestemmelse i Solsystemet RT1: fstandsberegning (Fra katederet) 5 RT2: Bold og Glob 6 OT1:Bestemmelse af Jordens radius 9 OT2:Modelafhængighed 11 OT3:fstanden til Månen 12 OT4:Månens
Vinkelrette linjer. Frank Villa. 4. november 2014
 Vinkelrette linjer Frank Villa 4. november 2014 Dette dokument er en del af MatBog.dk 2008-2012. IT Teaching Tools. ISBN-13: 978-87-92775-00-9. Se yderligere betingelser for brug her. Indhold 1 Introduktion
Vinkelrette linjer Frank Villa 4. november 2014 Dette dokument er en del af MatBog.dk 2008-2012. IT Teaching Tools. ISBN-13: 978-87-92775-00-9. Se yderligere betingelser for brug her. Indhold 1 Introduktion
Matematik for lærerstuderende klasse Geometri
 Matematik for lærerstuderende 4.-10. klasse Geometri Klassisk geometri (kapitel 6) Deduktiv tankegang Ræsonnementskompetence Mål med kapitlet: Erkender Thales sætning som fundament for afstandsberegning.
Matematik for lærerstuderende 4.-10. klasse Geometri Klassisk geometri (kapitel 6) Deduktiv tankegang Ræsonnementskompetence Mål med kapitlet: Erkender Thales sætning som fundament for afstandsberegning.
Første del af rapporten består af et diagram, der viser, hvor mange point eleverne på landsplan fik i de enkelte opgaver.
 Til matematiklæreren Dette er en rapport omtaler prøven med hjælpemidler maj 2016. Rapporten kan bruges til at evaluere dit arbejde med klassen og få ideer til dit arbejde med kommende klasser i overbygningen.
Til matematiklæreren Dette er en rapport omtaler prøven med hjælpemidler maj 2016. Rapporten kan bruges til at evaluere dit arbejde med klassen og få ideer til dit arbejde med kommende klasser i overbygningen.
Indhold. Indledning 7 Læsevejledning 9
 Indhold Indledning 7 Læsevejledning 9 1 Hvad er åbne opgaver? 13 2 Hvorfor arbejde med åbne opgaver? 17 3 Udfordringer i arbejdet med åbne opgaver 19 4 En ny didaktisk kontrakt 21 5 Et par eksempler 23
Indhold Indledning 7 Læsevejledning 9 1 Hvad er åbne opgaver? 13 2 Hvorfor arbejde med åbne opgaver? 17 3 Udfordringer i arbejdet med åbne opgaver 19 4 En ny didaktisk kontrakt 21 5 Et par eksempler 23
Trekanter. Frank Villa. 8. november 2012
 Trekanter Frank Villa 8. november 2012 Dette dokument er en del af MatBog.dk 2008-2012. IT Teaching Tools. ISBN-13: 978-87-92775-00-9. Se yderligere betingelser for brug her. Indhold 1 Introduktion 1 1.1
Trekanter Frank Villa 8. november 2012 Dette dokument er en del af MatBog.dk 2008-2012. IT Teaching Tools. ISBN-13: 978-87-92775-00-9. Se yderligere betingelser for brug her. Indhold 1 Introduktion 1 1.1
Jeg ville udfordre eleverne med en opgave, som ikke umiddelbar var målbar; Hvor høj er skolens flagstang?.
 Hvor høj er skolens flagstang? Undersøgelsesbaseret matematik 8.a på Ankermedets Skole i Skagen Marts 2012 Klassen deltog for anden gang i Fibonacci Projektet, og der var afsat ca. 8 lektioner, fordelt
Hvor høj er skolens flagstang? Undersøgelsesbaseret matematik 8.a på Ankermedets Skole i Skagen Marts 2012 Klassen deltog for anden gang i Fibonacci Projektet, og der var afsat ca. 8 lektioner, fordelt
Progression frem mod skriftlig eksamen
 Progression frem mod skriftlig eksamen Ikke alle skal have 12 Eksamensopgavernes funktion i det daglige og til eksamen Progression i sættet progression i den enkelte opgave Hvornår inddrages eksamensopgaver
Progression frem mod skriftlig eksamen Ikke alle skal have 12 Eksamensopgavernes funktion i det daglige og til eksamen Progression i sættet progression i den enkelte opgave Hvornår inddrages eksamensopgaver
Introduktion til cosinus, sinus og tangens
 Introduktion til cosinus, sinus og tangens Jes Toft Kristensen 24. maj 2010 1 Forord Her er en lille introduktion til cosinus, sinus og tangens. Det var et af de emner jeg selv havde svært ved at forstå,
Introduktion til cosinus, sinus og tangens Jes Toft Kristensen 24. maj 2010 1 Forord Her er en lille introduktion til cosinus, sinus og tangens. Det var et af de emner jeg selv havde svært ved at forstå,
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Institution Uddannelse Fag og niveau Lærer Hold Termin hvori undervisningen afsluttes: Juni 2017 HANSENBERG
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Institution Uddannelse Fag og niveau Lærer Hold Termin hvori undervisningen afsluttes: Juni 2017 HANSENBERG
TYCHO BRAHE OG SOLSYSTEMET
 TYCHO BRAHE OG SOLSYSTEMET TIL UNDERVISEREN Dette undervisningsmateriale tager udgangspunkt i programserien Store Danske Videnskabsfolk og specifikt udsendelsen om Tycho Brahe. Skiftet fra det geocentriske
TYCHO BRAHE OG SOLSYSTEMET TIL UNDERVISEREN Dette undervisningsmateriale tager udgangspunkt i programserien Store Danske Videnskabsfolk og specifikt udsendelsen om Tycho Brahe. Skiftet fra det geocentriske
Eksempler på temaopgaver i matematik indenfor geometri
 Eksempler på temaopgaver i matematik indenfor geometri Med udgangspunkt i begrebsafklaringen fra dokumentet Matematik og den ny skriftlighed gives her fem eksempler på, hvordan de forskellige opgavetyper,
Eksempler på temaopgaver i matematik indenfor geometri Med udgangspunkt i begrebsafklaringen fra dokumentet Matematik og den ny skriftlighed gives her fem eksempler på, hvordan de forskellige opgavetyper,
I kapitlet arbejdes med følgende centrale matematiske objekter og begreber:
 INTRO Efter mange års pause er trigonometri med Fælles Mål 2009 tilbage som fagligt emne i grundskolens matematikundervisning. Som det fremgår af den følgende sides udpluk fra faghæftets trinmål, er en
INTRO Efter mange års pause er trigonometri med Fælles Mål 2009 tilbage som fagligt emne i grundskolens matematikundervisning. Som det fremgår af den følgende sides udpluk fra faghæftets trinmål, er en
MATEMATIK. GIDEONSKOLENS UNDERVISNINGSPLAN Oversigt over undervisning i forhold til trinmål og slutmål
 MATEMATIK GIDEONSKOLENS UNDERVISNINGSPLAN Oversigt over undervisning i forhold til trinmål og slutmål KOMMENTAR Vi har i det følgende foretaget en analyse og en sammenstilling af vore materialer til skriftlig
MATEMATIK GIDEONSKOLENS UNDERVISNINGSPLAN Oversigt over undervisning i forhold til trinmål og slutmål KOMMENTAR Vi har i det følgende foretaget en analyse og en sammenstilling af vore materialer til skriftlig
Undersøgende opgaver Opgave 6 er i begge prøvesæt med som sidste opgave en undersøgende opgave af en ny type, som var lidt udfordrende for eleverne.
 Tendenser i årets prøver 2019 Der er tendenser i prøverne, som kræver matematiklærernes opmærksomhed helst i et samarbejde i fagteamet. Og det kræver skolelederes og forvaltningers opmærksomhed for at
Tendenser i årets prøver 2019 Der er tendenser i prøverne, som kræver matematiklærernes opmærksomhed helst i et samarbejde i fagteamet. Og det kræver skolelederes og forvaltningers opmærksomhed for at
ØVEHÆFTE FOR MATEMATIK C GEOMETRI
 ØVEHÆFTE FOR MATEMATIK C GEOMETRI Indhold Begreber i klassisk geometri + formelsamling... 2 Ensvinklede trekanter... 7 Pythagoras Sætning... 10 Øve vinkler i retvinklede trekanter... 15 Sammensatte opgaver....
ØVEHÆFTE FOR MATEMATIK C GEOMETRI Indhold Begreber i klassisk geometri + formelsamling... 2 Ensvinklede trekanter... 7 Pythagoras Sætning... 10 Øve vinkler i retvinklede trekanter... 15 Sammensatte opgaver....
En Maple time med efterfølgende elevgruppe diskussion og refleksionssamtale med lærer.
 Bilag 5 En Maple time med efterfølgende elevgruppe diskussion og refleksionssamtale med lærer. Indledning Vi har som led i projektet observeret en del lektioner, med helt eller delvis fokus på Maple-brug.
Bilag 5 En Maple time med efterfølgende elevgruppe diskussion og refleksionssamtale med lærer. Indledning Vi har som led i projektet observeret en del lektioner, med helt eller delvis fokus på Maple-brug.
MATEMATIK. Formål for faget
 MATEMATIK Formål for faget Formålet med undervisningen er, at eleverne udvikler matematiske kompetencer og opnår viden og kunnen således, at de bliver i stand til at begå sig hensigtsmæssigt i matematikrelaterede
MATEMATIK Formål for faget Formålet med undervisningen er, at eleverne udvikler matematiske kompetencer og opnår viden og kunnen således, at de bliver i stand til at begå sig hensigtsmæssigt i matematikrelaterede
Formativ brug af folkeskolens prøver årets resultater på landsplan Den skriftlige prøve i matematik med hjælpemidler, FP9 maj 2019
 Formativ brug af folkeskolens prøver årets resultater på landsplan Den skriftlige prøve i matematik med hjælpemidler, FP9 maj 2019 Skrevet af Klaus Fink på baggrund af oplysninger fra opgavekommissionen
Formativ brug af folkeskolens prøver årets resultater på landsplan Den skriftlige prøve i matematik med hjælpemidler, FP9 maj 2019 Skrevet af Klaus Fink på baggrund af oplysninger fra opgavekommissionen
Matematik. Matematiske kompetencer
 Matematiske kompetencer stille spørgsmål, som er karakteristiske for matematik og have blik for hvilke typer af svar, som kan forventes(tankegangskompetence) erkende, formulere, afgrænse og løse matematiske
Matematiske kompetencer stille spørgsmål, som er karakteristiske for matematik og have blik for hvilke typer af svar, som kan forventes(tankegangskompetence) erkende, formulere, afgrænse og løse matematiske
Selam Friskole Fagplan for Matematik
 Selam Friskole Fagplan for Matematik Formål Formålet med undervisningen er, at eleverne udvikler matematiske kompetencer og opnår viden og kunnen således, at de bliver i stand til at begå sig hensigtsmæssigt
Selam Friskole Fagplan for Matematik Formål Formålet med undervisningen er, at eleverne udvikler matematiske kompetencer og opnår viden og kunnen således, at de bliver i stand til at begå sig hensigtsmæssigt
Fagårsplan 10/11 Fag: Matematik Klasse: 8.A Lærer: Henrik Stillits Fagområde/ emne Færdighedsregning - Typer af opgaver - Systematik
 Fagårsplan 10/11 Fag: Matematik Klasse: 8.A Lærer: Henrik Stillits Fagområde/ emne Færdighedsregning - Typer af opgaver - Systematik Periode Mål Eleverne skal: 32/33 Få kendskab til opgavetypen og få rutine.
Fagårsplan 10/11 Fag: Matematik Klasse: 8.A Lærer: Henrik Stillits Fagområde/ emne Færdighedsregning - Typer af opgaver - Systematik Periode Mål Eleverne skal: 32/33 Få kendskab til opgavetypen og få rutine.
Matematiklærernes dag 08.11.2010. Modellering
 Matematiklærernes dag 08.11.2010 Modellering 0745 - Modellering Matematiklærernes dag 08.11.2010 Matematisk modellering I kursusbeskrivelsen Når man bruger matematik til at beskrive og forstå virkeligheden
Matematiklærernes dag 08.11.2010 Modellering 0745 - Modellering Matematiklærernes dag 08.11.2010 Matematisk modellering I kursusbeskrivelsen Når man bruger matematik til at beskrive og forstå virkeligheden
Eksempel på den aksiomatisk deduktive metode
 Eksempel på den aksiomatisk deduktive metode Et rigtig godt eksempel på et aksiomatisk deduktivt system er Euklids Elementer. Euklid var græker og skrev Elemeterne omkring 300 f.kr. Værket består af 13
Eksempel på den aksiomatisk deduktive metode Et rigtig godt eksempel på et aksiomatisk deduktivt system er Euklids Elementer. Euklid var græker og skrev Elemeterne omkring 300 f.kr. Værket består af 13
Evaluering af matematik undervisning
 Evaluering af matematik undervisning Udarbejdet af Khaled Zaher, matematiklærer 6-9 klasse og Boushra Chami, matematiklærer 2-5 klasse Matematiske kompetencer. Fællesmål efter 3.klasse indgå i dialog om
Evaluering af matematik undervisning Udarbejdet af Khaled Zaher, matematiklærer 6-9 klasse og Boushra Chami, matematiklærer 2-5 klasse Matematiske kompetencer. Fællesmål efter 3.klasse indgå i dialog om
Formativ brug af folkeskolens prøver årets resultater på landsplan Den skriftlige prøve i matematik FP10 maj 2019
 Formativ brug af folkeskolens prøver årets resultater på landsplan Den skriftlige prøve i matematik FP10 maj 2019 Skrevet af Klaus Fink på baggrund af oplysninger fra opgavekommissionen 1 Til matematiklæreren
Formativ brug af folkeskolens prøver årets resultater på landsplan Den skriftlige prøve i matematik FP10 maj 2019 Skrevet af Klaus Fink på baggrund af oplysninger fra opgavekommissionen 1 Til matematiklæreren
Faglig læsning i matematik
 Faglig læsning i matematik af Heidi Kristiansen 1.1 Faglig læsning en matematisk arbejdsmåde Der har i de senere år været sat megen fokus på, at danske elever skal blive bedre til at læse. Tidligere har
Faglig læsning i matematik af Heidi Kristiansen 1.1 Faglig læsning en matematisk arbejdsmåde Der har i de senere år været sat megen fokus på, at danske elever skal blive bedre til at læse. Tidligere har
Fagårsplan 10/11 Fag: Matematik Klasse: 7.ABC Lærer: Henrik Stillits. Fagområde/ emne
 Fagårsplan 10/11 Fag: Matematik Klasse: 7.ABC Lærer: Henrik Stillits. Fagområde/ emne Matematiske færdigheder Grundlæggende færdigheder - plus, minus, gange, division (hele tal, decimaltal og brøker) Identificer
Fagårsplan 10/11 Fag: Matematik Klasse: 7.ABC Lærer: Henrik Stillits. Fagområde/ emne Matematiske færdigheder Grundlæggende færdigheder - plus, minus, gange, division (hele tal, decimaltal og brøker) Identificer
Fokusgruppeinterview. Gruppe 1
 4 Fokusgruppeinterview Gruppe 1 1 2 3 4 Hvorfor? Formålet med et fokusgruppeinterview er at belyse et bestemt emne eller problemfelt på en grundig og nuanceret måde. Man vælger derfor denne metode hvis
4 Fokusgruppeinterview Gruppe 1 1 2 3 4 Hvorfor? Formålet med et fokusgruppeinterview er at belyse et bestemt emne eller problemfelt på en grundig og nuanceret måde. Man vælger derfor denne metode hvis
Tilhørende: Robert Nielsen, 8b. Geometribog. Indeholdende de vigtigste og mest basale begreber i den geometriske verden.
 Tilhørende: Robert Nielsen, 8b Geometribog Indeholdende de vigtigste og mest basale begreber i den geometriske verden. 1 Polygoner. 1.1 Generelt om polygoner. Et polygon er en figur bestående af mere end
Tilhørende: Robert Nielsen, 8b Geometribog Indeholdende de vigtigste og mest basale begreber i den geometriske verden. 1 Polygoner. 1.1 Generelt om polygoner. Et polygon er en figur bestående af mere end
UCC - Matematikdag - 08.04.14
 I hold på 3-4 (a) Problemformulering: Hvor lang tid holder en tube tandpasta? Gå gennem modellens faser fra (a) til (f) Hvad er en matematisk modelleringsproces? Virkelighed (f) Validering (a) Problemformulering
I hold på 3-4 (a) Problemformulering: Hvor lang tid holder en tube tandpasta? Gå gennem modellens faser fra (a) til (f) Hvad er en matematisk modelleringsproces? Virkelighed (f) Validering (a) Problemformulering
Vejledning til matematik A htx Maj 2018
 Vejledning til matematik A htx Maj 2018 Censorkorpset skriftlig matematik, htx Denne skrivelse skal tjene til almindelig orientering og vejledning for censorerne om forhold vedrørende skriftlig eksamen,
Vejledning til matematik A htx Maj 2018 Censorkorpset skriftlig matematik, htx Denne skrivelse skal tjene til almindelig orientering og vejledning for censorerne om forhold vedrørende skriftlig eksamen,
Analytisk Geometri. Frank Nasser. 12. april 2011
 Analytisk Geometri Frank Nasser 12. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk: Dette er
Analytisk Geometri Frank Nasser 12. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk: Dette er
Undersøgelser af trekanter
 En rød tråd igennem kapitlet er en søgen efter svar på spørgsmålet: Hvordan kan vi beregne os frem til længder, vi ikke kan komme til at måle?. Hvordan kan vi fx beregne højden på et træ eller et hus,
En rød tråd igennem kapitlet er en søgen efter svar på spørgsmålet: Hvordan kan vi beregne os frem til længder, vi ikke kan komme til at måle?. Hvordan kan vi fx beregne højden på et træ eller et hus,
FFM Matematik pop-up eftermiddag. CFU, UCC 11. Maj 2015
 FFM Matematik pop-up eftermiddag CFU, UCC 11. Maj 2015 Formål Deltagerne har: Kendskab til Forenklede Fælles Måls opbygning Kendskab til tankegangen bag den målstyrede undervisning i FFM Kendskab til læringsmål
FFM Matematik pop-up eftermiddag CFU, UCC 11. Maj 2015 Formål Deltagerne har: Kendskab til Forenklede Fælles Måls opbygning Kendskab til tankegangen bag den målstyrede undervisning i FFM Kendskab til læringsmål
Keplers verdensbillede og de platoniske legemer (de regulære polyedre).
 Keplers verdensbillede og de platoniske legemer (de regulære polyedre). Johannes Kepler (1571-1630) var på mange måder en overgangsfigur i videnskabshistorien. Han ydede et stort bidrag til at matematisere
Keplers verdensbillede og de platoniske legemer (de regulære polyedre). Johannes Kepler (1571-1630) var på mange måder en overgangsfigur i videnskabshistorien. Han ydede et stort bidrag til at matematisere
Ens eller forskellig?
 Ens eller forskellig? Geometri i 5./6. klasse Niels Kristen Kirk, Christinelystskolen Kaj Østergaard, VIA UC Plan Didaktisk design - modellen Fra model til praksis indledende overvejelser En konkret udmøntning
Ens eller forskellig? Geometri i 5./6. klasse Niels Kristen Kirk, Christinelystskolen Kaj Østergaard, VIA UC Plan Didaktisk design - modellen Fra model til praksis indledende overvejelser En konkret udmøntning
Hvad er matematik? Indskolingskursus
 Hvad er matematik? Indskolingskursus Vordingborg 25. 29. april 2016 Matematikbog i 50 erne En bonde sælger en sæk kartofler for 40 kr. Fremstillingsomkostningerne er 4/5 af salgsindtægterne. Hvor stor
Hvad er matematik? Indskolingskursus Vordingborg 25. 29. april 2016 Matematikbog i 50 erne En bonde sælger en sæk kartofler for 40 kr. Fremstillingsomkostningerne er 4/5 af salgsindtægterne. Hvor stor
Geometriske eksperimenter
 I kapitlet arbejder eleverne med nogle af de egenskaber, der er knyttet til centrale geometriske figurer og begreber (se listen her under). Set fra en emneorienteret synsvinkel handler kapitlet derfor
I kapitlet arbejder eleverne med nogle af de egenskaber, der er knyttet til centrale geometriske figurer og begreber (se listen her under). Set fra en emneorienteret synsvinkel handler kapitlet derfor
Matematik. Matematiske kompetencer
 Matematiske kompetencer skelne mellem definitioner og sætninger, mellem enkelttilfælde og generaliseringer og anvende denne indsigt til at udforske og indgå i dialog om forskellige matematiske begrebers
Matematiske kompetencer skelne mellem definitioner og sætninger, mellem enkelttilfælde og generaliseringer og anvende denne indsigt til at udforske og indgå i dialog om forskellige matematiske begrebers
Undervisningsplan for matematik
 Undervisningsplan for matematik Formål for faget Formålet med undervisningen i matematik er, at eleverne udvikler kompetencer og opnår viden og kunnen således, at de bliver i stand til at begå sig hensigtsmæssigt
Undervisningsplan for matematik Formål for faget Formålet med undervisningen i matematik er, at eleverne udvikler kompetencer og opnår viden og kunnen således, at de bliver i stand til at begå sig hensigtsmæssigt
3. klasse 6. klasse 9. klasse
 Børne- og Undervisningsudvalget 2012-13 BUU Alm.del Bilag 326 Offentligt Elevplan 3. klasse 6. klasse 9. klasse Matematiske kompetencer Status tal og algebra sikker i, er usikker i de naturlige tals opbygning
Børne- og Undervisningsudvalget 2012-13 BUU Alm.del Bilag 326 Offentligt Elevplan 3. klasse 6. klasse 9. klasse Matematiske kompetencer Status tal og algebra sikker i, er usikker i de naturlige tals opbygning
Matematik. Evaluering, orientering og vejledning
 Folkeskolens afsluttende prøver Matematik 2011 Evaluering, orientering og vejledning Udarbejdet på grundlag af censorers faglige feedback ved prøverne Institut for Læring Udarbejdet af: Konsulent Erik
Folkeskolens afsluttende prøver Matematik 2011 Evaluering, orientering og vejledning Udarbejdet på grundlag af censorers faglige feedback ved prøverne Institut for Læring Udarbejdet af: Konsulent Erik
Colofon. Udgivet af Inerisaavik 2009 Udarbejdet af fagkonsulent Erik Christiansen Redigeret af specialkonsulent Louise Richter Elektronisk udgave
 Colofon Udgivet af Inerisaavik 2009 Udarbejdet af fagkonsulent Erik Christiansen Redigeret af specialkonsulent Louise Richter Elektronisk udgave Indhold Evaluering af matematik 2008 2 Tekstopgivelser 2
Colofon Udgivet af Inerisaavik 2009 Udarbejdet af fagkonsulent Erik Christiansen Redigeret af specialkonsulent Louise Richter Elektronisk udgave Indhold Evaluering af matematik 2008 2 Tekstopgivelser 2
Delmængder af Rummet
 Delmængder af Rummet Frank Villa 15. maj 2012 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold 1 Introduktion
Delmængder af Rummet Frank Villa 15. maj 2012 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold 1 Introduktion
Fra opgave til undersøgelse
 Fra opgave til undersøgelse Kan man og skal man indrette læringsmiljøer med undersøgende tilgang til matematik? Er det her en Fed Fobilooser? Det kommer an på! Hvad kan John Dewey bruges til i dag? Et
Fra opgave til undersøgelse Kan man og skal man indrette læringsmiljøer med undersøgende tilgang til matematik? Er det her en Fed Fobilooser? Det kommer an på! Hvad kan John Dewey bruges til i dag? Et
Det er en af de hyppigst forekommende udregninger i den elementære talbehandling at beregne gennemsnit eller middeltal af en række tal.
 Tre slags gennemsnit Allan C. Malmberg Det er en af de hyppigst forekommende udregninger i den elementære talbehandling at beregne gennemsnit eller middeltal af en række tal. For mange skoleelever indgår
Tre slags gennemsnit Allan C. Malmberg Det er en af de hyppigst forekommende udregninger i den elementære talbehandling at beregne gennemsnit eller middeltal af en række tal. For mange skoleelever indgår
Afstandsformlen og Cirklens Ligning
 Afstandsformlen og Cirklens Ligning Frank Villa 19. august 2012 2008-2012. IT Teaching Tools. ISBN-13: 978-87-92775-00-9. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk.
Afstandsformlen og Cirklens Ligning Frank Villa 19. august 2012 2008-2012. IT Teaching Tools. ISBN-13: 978-87-92775-00-9. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk.
Trekants- beregning for hf
 Trekants- beregning for hf C C 5 l 5 A 34 8 B 018 Karsten Juul Indhold 1. Vinkler... 1 1.1 Regler for vinkler.... 1. Omkreds, areal, højde....1 Omkreds..... Rektangel....3 Kvadrat....4 Højde....5 Højde-grundlinje-formel
Trekants- beregning for hf C C 5 l 5 A 34 8 B 018 Karsten Juul Indhold 1. Vinkler... 1 1.1 Regler for vinkler.... 1. Omkreds, areal, højde....1 Omkreds..... Rektangel....3 Kvadrat....4 Højde....5 Højde-grundlinje-formel
TREKANTER. Indledning. Typer af trekanter. Side 1 af 7. (Der har været tre kursister om at skrive denne projektrapport)
 Side 1 af 7 (Der har været tre kursister om at skrive denne projektrapport) TREKANTER Indledning Vi har valgt at bruge denne projektrapport til at udarbejde en oversigt over det mest grundlæggende materiale
Side 1 af 7 (Der har været tre kursister om at skrive denne projektrapport) TREKANTER Indledning Vi har valgt at bruge denne projektrapport til at udarbejde en oversigt over det mest grundlæggende materiale
Emmas og Frederiks nye værelser - maling eller tapet?
 Emmas og Frederiks nye værelser - maling eller tapet? Emmas og Frederiks familie skal flytte til et nyt hus. De har fået lov til at bestemme, hvordan væggene på deres værelser skal se ud. Emma og Frederik
Emmas og Frederiks nye værelser - maling eller tapet? Emmas og Frederiks familie skal flytte til et nyt hus. De har fået lov til at bestemme, hvordan væggene på deres værelser skal se ud. Emma og Frederik
Fag- og indholdsplan 9. kl.:
 Fag- og indholdsplan 9. kl.: Indholdsområder: Tal og algebra: Tal - regneregler og formler Størrelser måling, beregning og sammenligning. Matematiske udtryk Algebra - teoretiske sammenhænge absolut og
Fag- og indholdsplan 9. kl.: Indholdsområder: Tal og algebra: Tal - regneregler og formler Størrelser måling, beregning og sammenligning. Matematiske udtryk Algebra - teoretiske sammenhænge absolut og
LÆRINGSMÅL PÅ NIF MATEMATIK 2014-15
 LÆRINGSMÅL PÅ NIF MATEMATIK 2014-15 Mål for undervisningen i Matematik på NIF Følgende er baseret på de grønlandske læringsmål, tilføjelser fra de danske læringsmål står med rød skrift. Læringsmål Yngstetrin
LÆRINGSMÅL PÅ NIF MATEMATIK 2014-15 Mål for undervisningen i Matematik på NIF Følgende er baseret på de grønlandske læringsmål, tilføjelser fra de danske læringsmål står med rød skrift. Læringsmål Yngstetrin
TRIGONOMETRI, 4 UGER, 9.KLASSE.
 TRIGONOMETRI, 4 UGER, 9.KLASSE. FRA FÆLLES MÅL Målsætninger for undervisningsforløbet er opsat efter kompetence, færdigheds og vidensmål samt læringsmål i lærersprog. Geometri og måling Fase 3 Geometriske
TRIGONOMETRI, 4 UGER, 9.KLASSE. FRA FÆLLES MÅL Målsætninger for undervisningsforløbet er opsat efter kompetence, færdigheds og vidensmål samt læringsmål i lærersprog. Geometri og måling Fase 3 Geometriske
Matematik, basis. Undervisningen på basisniveau skal udvikle kursisternes matematikkompetencer til at følge undervisningen
 avu-bekendtgørelsen, august 2009 Matematik Basis, G-FED Matematik, basis 1. Identitet og formål 1.1 Identitet I matematik basis er arbejdet med forståelsen af de faglige begreber i centrum. Den opnåede
avu-bekendtgørelsen, august 2009 Matematik Basis, G-FED Matematik, basis 1. Identitet og formål 1.1 Identitet I matematik basis er arbejdet med forståelsen af de faglige begreber i centrum. Den opnåede
Fibonacciprojekt 2010. 4. klasse på Hpr. og 5. klasse på Bindslev skole vil arbejde med følgende i matematik. Chance
 4. klasse på Hpr. og 5. klasse på Bindslev skole vil arbejde med følgende i matematik. Chance Vi laver et kort oplæg til eleverne med tre små eksempler med hhv. lykkehjul, terningespil og kortspil. Eleverne
4. klasse på Hpr. og 5. klasse på Bindslev skole vil arbejde med følgende i matematik. Chance Vi laver et kort oplæg til eleverne med tre små eksempler med hhv. lykkehjul, terningespil og kortspil. Eleverne
Om at løse problemer En opgave-workshop Beregnelighed og kompleksitet
 Om at løse problemer En opgave-workshop Beregnelighed og kompleksitet Hans Hüttel 27. oktober 2004 Mathematics, you see, is not a spectator sport. To understand mathematics means to be able to do mathematics.
Om at løse problemer En opgave-workshop Beregnelighed og kompleksitet Hans Hüttel 27. oktober 2004 Mathematics, you see, is not a spectator sport. To understand mathematics means to be able to do mathematics.
Når vi forbereder et nyt emne eller område vælger vi de metoder, materialer og evalueringsformer, der egner sig bedst til forløbet.
 MATEMATIK Delmål for fagene generelt. Al vores undervisning hviler på de i Principper for skole & undervisning beskrevne områder (- metoder, materialevalg, evaluering og elevens personlige alsidige udvikling),
MATEMATIK Delmål for fagene generelt. Al vores undervisning hviler på de i Principper for skole & undervisning beskrevne områder (- metoder, materialevalg, evaluering og elevens personlige alsidige udvikling),
Tal og algebra. I kapitlet arbejdes med følgende centrale matematiske begreber: algebra variable. Huskeliste: Tændstikker (til side 146) FRA FAGHÆFTET
 I kapitlet skal eleverne arbejde med fire forskellige vinkler på algebra de præsenteres på kapitlets første mundtlige opslag. De fire vinkler er algebra som et redskab til at løse matematiske problemer.
I kapitlet skal eleverne arbejde med fire forskellige vinkler på algebra de præsenteres på kapitlets første mundtlige opslag. De fire vinkler er algebra som et redskab til at løse matematiske problemer.
Det tilstræbte matematikindhold og teknologi spiller det sammen?
 75 K O M M E N TA R E R Det tilstræbte matematikindhold og teknologi spiller det sammen? Henrik Bang Center for Computerbaseret Matematikundervisning, CMU Claus Larsen Center for Computerbaseret Matematikundervisning,
75 K O M M E N TA R E R Det tilstræbte matematikindhold og teknologi spiller det sammen? Henrik Bang Center for Computerbaseret Matematikundervisning, CMU Claus Larsen Center for Computerbaseret Matematikundervisning,
Kompetencetræning i matematik - også til prøverne. KP 10. januar 2019
 Kompetencetræning i matematik - også til prøverne KP 10. januar 2019 Kompetencetræning i matematik - også til prøven Prøverne i matematik bliver i stadig højere grad kompetencebaseret, så det giver god
Kompetencetræning i matematik - også til prøverne KP 10. januar 2019 Kompetencetræning i matematik - også til prøven Prøverne i matematik bliver i stadig højere grad kompetencebaseret, så det giver god
Dialogredskab til vurdering af uddannelsesparathed
 Dialogredskab til vurdering af uddannelsesparathed OM DIALOGREDSKABET Dialogredskabet er udviklet til elever, forældre, vejledere og lærere for at understøtte dialog om og vurdering af uddannelsesparathed.
Dialogredskab til vurdering af uddannelsesparathed OM DIALOGREDSKABET Dialogredskabet er udviklet til elever, forældre, vejledere og lærere for at understøtte dialog om og vurdering af uddannelsesparathed.
Årsplan matematik, RE 2018/2019
 Uge Område Ugeinfo. / Indhold er 33 Tal & Størrelser Introuge - Kun Undervisning fredag 34 Tal & Størrelser Introuge - ikke undervisning fredag Decimaltal & Brøker 35 Tal & Størrelser Procentregning 36
Uge Område Ugeinfo. / Indhold er 33 Tal & Størrelser Introuge - Kun Undervisning fredag 34 Tal & Størrelser Introuge - ikke undervisning fredag Decimaltal & Brøker 35 Tal & Størrelser Procentregning 36
************************************************************************
 Projektet er todelt: Første del har fokus på Euklids system og består af introduktionen, samt I og II. Anden del har fokus på Hilberts system fra omkring år 1900 og består af III sammen med bilagene. Man
Projektet er todelt: Første del har fokus på Euklids system og består af introduktionen, samt I og II. Anden del har fokus på Hilberts system fra omkring år 1900 og består af III sammen med bilagene. Man
TEORETISK PÆDAOGIKUM
 Ny studieordning for Toretisk Pædagogikum 2019-2023 og Det fagdidaktiske projekt i pilotforløbet i matematik 2018/2019 Morten Blomhøj IMFUFA, INM, RUC TEORETISK PÆDAOGIKUM 2019-2023 SDU står for organisering
Ny studieordning for Toretisk Pædagogikum 2019-2023 og Det fagdidaktiske projekt i pilotforløbet i matematik 2018/2019 Morten Blomhøj IMFUFA, INM, RUC TEORETISK PÆDAOGIKUM 2019-2023 SDU står for organisering
Den Flydende Kran Samson
 Den Flydende Kran Samson Formål: Kranen Samson, har en maksimal løfteevne på 900 tons, kranarmen er på 67 meter. Formålet med dette projekt er at løse nogle forskellige opgaver om geometrien for kranen.
Den Flydende Kran Samson Formål: Kranen Samson, har en maksimal løfteevne på 900 tons, kranarmen er på 67 meter. Formålet med dette projekt er at løse nogle forskellige opgaver om geometrien for kranen.
Årsplan for 7. klasse, matematik
 Årsplan for 7. klasse, matematik I matematik bruger vi bogsystemet Sigma som grundmateriale. I systemet er der, ud over grundbogen, også kopiark og tests tilknyttet de enkelte kapitler. Systemet er udarbejdet
Årsplan for 7. klasse, matematik I matematik bruger vi bogsystemet Sigma som grundmateriale. I systemet er der, ud over grundbogen, også kopiark og tests tilknyttet de enkelte kapitler. Systemet er udarbejdet
Matematik på Humlebæk lille Skole
 Matematik på Humlebæk lille Skole Matematikundervisningen på HLS er i overensstemmelse med Undervisningsministeriets Fælles Mål, dog med få justeringer som passer til vores skoles struktur. Det betyder
Matematik på Humlebæk lille Skole Matematikundervisningen på HLS er i overensstemmelse med Undervisningsministeriets Fælles Mål, dog med få justeringer som passer til vores skoles struktur. Det betyder
Formativ brug af folkeskolens prøver. Den skriftlige prøve i matematik med hjælpemidler, FP9 maj 2018
 Formativ brug af folkeskolens prøver Den skriftlige prøve i matematik med hjælpemidler, FP9 maj 2018 1 Til matematiklæreren i 9. klasse Dette er en rapport om den skriftlige prøve i matematik med hjælpemidler
Formativ brug af folkeskolens prøver Den skriftlige prøve i matematik med hjælpemidler, FP9 maj 2018 1 Til matematiklæreren i 9. klasse Dette er en rapport om den skriftlige prøve i matematik med hjælpemidler
Lærervejledning Matematik 1-2-3 på Smartboard
 Lærervejledning Matematik 1-2-3 på Smartboard Lærervejledning til Matematik 1-2-3 på Smartboard Materialet består af 33 færdige undervisningsforløb til brug i matematikundervisningen i overbygningen. Undervisningsforløbene
Lærervejledning Matematik 1-2-3 på Smartboard Lærervejledning til Matematik 1-2-3 på Smartboard Materialet består af 33 færdige undervisningsforløb til brug i matematikundervisningen i overbygningen. Undervisningsforløbene
Eksperimenterende undersøgelse af vinkelsummer i 4. 6.kl.
 Eksperimenterende undersøgelse af vinkelsummer i 4. 6.kl. Målsætning: Lærermål: At observere på og udvikle brugen af geogebra i forbindelse med eksperimenterende undersøgelser af vinkelsummer i matematik
Eksperimenterende undersøgelse af vinkelsummer i 4. 6.kl. Målsætning: Lærermål: At observere på og udvikle brugen af geogebra i forbindelse med eksperimenterende undersøgelser af vinkelsummer i matematik
Ting man gør med Vektorfunktioner
 Ting man gør med Vektorfunktioner Frank Nasser. april 11 c 8-11. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk: Dette
Ting man gør med Vektorfunktioner Frank Nasser. april 11 c 8-11. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk: Dette
