Begrebsafklaring og struktur som metode
|
|
|
- Max Holm
- 5 år siden
- Visninger:
Transkript
1 Begrebsafklaring og struktur som metode Marianne Bie, Borupgaard Gymnasium & Hans Bolvinkel, Nørre Gymnasium Indledning I gymnasiet møder man ikke sjældent formuleringer som:» så ryger 2x over på den anden side«,» funktionen f til x«,»ligmedstegnet«,» det gør man bare, jeg kan ikke forklare hvorfor«og lignende. Det er formuleringer, som udtrykker en sproglig usikkerhed, som, ifølge vores undersøgelser, afspejler og afspejles i en matematisk usikkerhed. Sproget hænger sammen med den måde, vi opfatter verden på, og hvis de matematiske begreber står upræcist defineret for eleverne, så bliver deres arbejde med begreberne tilsvarende upræcist. Som eksempel har vi undersøgt ligningsløsning, hvor alene begrebet ligning for de fleste elever var svært at definere. Eleverne har et billede af, hvad en ligning er, et billede, der er skabt i folkeskolen, men som sjældent harmonerer 100 % med definitionen på en ligning. Dvs. at der opstår en diskrepans mellem elevernes begrebsbillede og begrebsdefinitionen (Tall & Vinner 1981), som får afgørende indflydelse på elevernes valg af løsningsmetode. Hvis eleverne ikke opfatter et udtryk som en ligning, når det rent faktisk er en ligning, så ved de heller ikke, hvilke løsningsværktøjer de skal gribe til i mødet med dette udtryk. Hvad det vil sige at løse en ligning, fremstår også tåget for eleverne. De er med på, at det handler om at få x til at stå alene, men formålet med at isolere x, og hvad det egentlig betyder og medfører, at x f.eks. er lig 2, er ikke klart for dem. Hermed bliver ligningsløsning til en esoterisk og formålsløs øvelse. Denne gruppe af elever kan, viste det sig, hjælpes af en indledende begrebsafklaring efterfulgt af en fastlagt procedure hæftet op på de præcist veldefinerede matematiske begreber. Lignende problemer har vi set i elevernes arbejde med bevisførelse. For nogle elever i gymnasiet opfattes bevisførelse som et meningsløst ritual, som skal memoreres, snarere end den række af logiske argumenter, der fører til rigtigheden af et påstået udsagn. Disse elever kan hjælpes ved først at italesætte bevisets rolle i faget matematik og dernæst, i lighed med den førnævnte gruppe af elever, knytte en række faste begreber og procedurer til bevisførelsen. Alt i alt peger vores undersøgelser altså på, at en indledende begrebsafklaring, en generel præcision i sproget og en fast struktureret metode er afgørende i matematikundervisningen. Dette leder til en styrkelse af både kommunikationskompetencen og symbol og formalismekompetencen, som er to af de otte matematiske kompetencer beskrevet i Uddannelsesstyrelsens kompetenceprojekt (Niss & Jensen Herefter KOMrapporten). I de kommende afsnit vil vi uddybe disse elementer fra de tre projektrapporter, som vi har skrevet i forbindelse med matematik vejlederuddannelsen på RUC fra september 2013 til januar Projektrapporternes titler er Sprog og ligninger, Argumentationssystematik i bevisførelse og Struktur og modellering. Hvert af de tre forløb bestod af tre faser, som beskrevet af Uffe Thomas Jankvist & Mogens Niss (2015). Eleverne blev bedt om at tage en detektionstest, og på baggrund af denne blev to fire elever udvalgt per klasse med henblik på diagnosticering. Diagnosticeringen havde et omfang af ca. 20 minutter og havde som formål at identificere de snublesten, der sætter en begrænsning for elevens læring. Under diagnosticeringen forsøgte vi så vidt muligt at tie stille. Vi ville høre, hvad eleven tænkte, samt vedkommendes argumenter herfor, og en af pointerne med diagnosticeringen er netop at høre en eventuel fejlagtig argumentation for på den måde at kunne identificere fejlopfattelser. Interventionen bestod af tre til fire sessioner af 20 minutters varighed i de første to projekter om ligningsløsning og bevisførelse og tre sessioner af længere varighed i det sidste projekt om modellering. Dette skyldes, at vi i de to første projekter kun vejledte én elev ad gangen, mens vi i modelleringsprojektet arbejdede med gruppeintervention. Vi arbejdede i samtlige forløb med stx elever fra 1. g eller 2. g, der havde matematik på B niveau. En gruppe af tre elever var med i alle tre forløb, idet de startede i 1. g i august 2013 og dermed var midt i 2. g ved uddannelsens afslutning i januar Vigtigheden af begrebsafklaring David Tall og Shlomo Vinner (1981) skelner mellem begrebsbillede og begrebsdefinition. Her er essensen, at eleverne kan have et billede af, hvad eksempelvis en ligning, et bevis eller en model er, som ikke stemmer overens med den korrekte og præcise definition af begrebet. Efter vores arbejde med de tre projekter står det klart, at en succesfuld intervention må starte med, at elev og vejleder bliver enige om, hvad der overhovedet tales om. Elevernes billede af et begreb kan være fragmentarisk og situa tionsafhængigt, og de kan have problemer med præcist at definere begrebet. Elevernes sprog afspejler således deres viden om et emne, og vores tese var, at det at træne et præcist sprog således også ville hjælpe eleverne til at få et bedre greb om emnet. Vokabulariet skulle gerne hjælpe på to måder. For det første med præcist at vide, hvad der ligger i et begreb. For det andet ønskede vi ved hjælp af sproget at skabe en vis struktur, sådan at eleverne både lærte ord som f.eks. faktor og led, men også lærte at sætte dem i relation til processen, hvad enten det drejede sig om ligningsløsning, bevisførelse eller modellering. I vores første projekt om sprog og ligninger (Fuglsang Damgaard, Bie & Bolvinkel 2014a) indledte vi interventionen med at vise eleverne en række udtryk og bede dem om at udpege de udtryk, der ikke var ligninger. Her viste det sig, at flere elever havde et mangelfuldt 22 LMFK-bladet 1/2018
2 begreb om, hvad en ligning er. Således blev ligninger som (x 3)(x 7) = 0 og 3x 2 + 5x 2 = 0 af en elev afvist, fordi»de ser underlige ud«, mens en anden elev afviste 9 = m 5 som værende en ligning, fordi den ikke indeholdt noget x. Noget så simpelt som at læse en kort definition på en ligning op, nemlig at»en ligning er et udsagn, hvori der indgår et lighedstegn og en eller flere ubekendte«, fik dem til at rette deres fejl. Ligeså var flere elever ikke klar over, hvad det egentlig vil sige at løse en ligning eller de var i hvert fald ikke i stand til præcist at formulere det, hvilket udsagn som»at finde«og»det vil sige at finde den ubekendte; altså finde ud af, hvad den er; i forhold til lighedstegnet«vidner om. Udsagnene er som sådan ikke forkerte, men de er upræcise og mangelfulde og vidner om et ufuldstændigt begrebsbillede. Det er ikke så sært, at eleverne har problemer med at løse ligninger, når de ikke ved, hvad de gør. Vi forsøgte at hjælpe eleverne med at sætte de korrekte ord på processen, hvilket uddybes i næste afsnit, og baseret på elevernes præstation i den sidste session sammenlignet med deres præstation til diagnosticeringssamtalen har det hjulpet dem gevaldigt. Således bevægede en af eleverne sig fra at beskrive det at dividere i en ligning ved» så skal man et eller andet sådan her«(tegner en vandret streg) til»jeg dividerer med koefficienten«. I vores andet projekt om argumentationsteknik i bevisførelse (Fugsang Damgaard, Bie & Bolvinkel 2014b) blev eleverne i diagnosticeringen spurgt, hvad et bevis er. Også her tegnede der sig et forskel- *) Stephen Toulmins argumentationsmodel skildrer argumenters opbygning med seks elementer, hvoraf de tre er faste (påstand, belæg, hjemmel), og de tre er frie (styrkemarligartet billede af besvarelser, der alle havde noget rigtigt i sig, men som ikke var fuldstændig udtømmende. Vi indledte interventionen med at tale om matematikkens natur og bevisets rolle, herunder hvorfor vi i det hele taget har beviser. Betydningen af ord som beviser og sandhed er besværlige at forstå for eleverne og er i øvrigt et spørgsmål, der har optaget filosoffer i tusindvis af år, så der er ikke noget at sige til, at en elev, uden en diskussion af emnet, har et uklart billede af begrebet. De to begreber blev diskuteret med eleverne, idet matematikken blev sammenlignet med de naturvidenskabelige fag. Næste skridt var som i første projekt at introducere en struktur i beviset. Vi brugte Stephen Toulmins argumentationsmodel *) (Jørgensen & Onsberg 1987) og ord som belæg og påstand og forsøgte på den måde at vise eleverne, at et matematisk bevis er en argumentationskæde og ikke en arbitrær opremsning af matematiske udsagn. Derfor er det altså muligt at lære og huske et bevis ved hjælp af et par holdepunkter samt at huske på de grundlæggende matematiske regler. Som i første projekt tog eleverne ordene til sig, hvilket udsagn som»vores belæg er, at vi kender denne formel fra folkeskolen«og»det er vores påstand, at...«bevidner. I det tredje og sidste projekt om struktur og modellering (Fugl- sang Damgaard, Bie & Bolvinkel 2014c) arbejdede vi med modeller. Igen stod det uklart for nogle elever, hvad en model og en sammenhæng mellem variable egentlig er. Eksempelvis udspillede følgende dialog sig med en elev, der blev bedt om at opskrive sammenhængen mellem antallet af lærere og elever på en skole (Niss & Jankvist 2013b), idet han fik at vide, at kør, gendrivelse, rygdækning). Vi har alene arbejdet med grundmodellen, som består af argumenter med de tre faste elementer. der var seks gange så mange elever som lærere på skolen: Michael: y = e 6 + l, hvor e er eleverne, l er lærerne, og y er formlen, ligesom y = ax + b. Hvad betyder det, når der står, at noget skal udtrykke en sammenhæng? Michael: Øh det ved jeg ikke er det så forkert at lave en model? Ligesom i de foregående projekter arbejdede vi her med at strukturere processen for eleverne, sådan at de kunne få nogle værktøjer til at finde et sted at starte. Vi valgte at lave gruppeintervention denne gang, og oplevelsen var den samme som i de foregående to projekter, nemlig at eleverne ved hjælp af en simpel procedure og en sikrere brug af begreber kom meget længere i processen end tidligere. Samlet kan altså siges, at en begrebsafklaring og en struktur afledt af et præcist sprogbrug har vist sig at være en uundværlig del af interventionen. Eleverne udtrykte selv stor begejstring i samtlige projekter over deres udbytte af så relativt kort tidsforbrug ( minutter). Deres øgede selvsikkerhed har været tydelig at spore, ligesom en generel tro på egne evner inden for matematikken er blevet styrket. Det gælder både henover de tre til fire gange, det enkelte forløb varede, og i de almindelige matematikmoduler, efter at forløbet var afsluttet. Vores vurdering er dog, at hvis effekterne også skal være holdbare på endnu længere sigt, så bør man fortsætte arbejdet med disse elever kontinuerligt. Her kunne man f.eks. tilbyde dem korte brush up kurser efter hvert forløb eller repetitionsgange af tidligere gennemgået stof. LMFK-bladet 1/
3 Struktur Når den indledende begrebsafklaring er klaret, hvordan kan man så støtte sine elever i den videre læringsproces, så udbyttet bliver størst? Vi vil her uddybe, hvordan man kan strukturere strategiske testspørgsmål og procedurer i undervisningen. Sproglig struktur i ligningsløsning I forløbet om ligningsløsning var første skridt at afdække, hvad en ligning overhovedet er. Dernæst afsøgte vi, om eleverne kunne italesætte, hvad det vil sige at løse en ligning, og hvad det vil sige, at noget er en løsning til en ligning. Her spørges Helle om, hvad det vil sige at løse en ligning: Helle: Man skal finde x eller b eller c. Hvad gælder der om det tal, du finder? Helle: Det ved jeg ikke. Herefter løser Helle ligningen 2x + 5 = 17 og får x = 6. Hun spørges: Hvad betyder det, at x = 6? Helle: Det ved jeg faktisk ikke. Hun bliver bedt om at sætte x = 6 ind i den oprindelige ligning, og hun får 13 = 17, idet hun regner venstresiden ud som Helle: Er det rigtigt? Nej eller jo. Er det en ligning, når der ikke er noget x? Sekvensen viser, at selv om Helle måske nok kan udføre de matematiske operationer, der skal til for at løse denne ligning, så har hun ikke rigtigt nogen idé om, hvad løsningen er et udtryk for. Derfor er man som lærer nødt til at sikre sig, at det står klart for eleverne, hvad løsningen betyder i både en matematisk og virkelighedsnær kontekst. Ikke alle elever behersker ved indgangen til gymnasiet at løse simple førstegradsligninger. Her følger et par eksempler på de udfordringer, eleverne kan møde. En elev blev præsenteret for ligningen 4b = 4 + b, som er taget fra detektionstest 1 (Niss & Jankvist 2013a): Lene: Det irriterer mig, at der ikke står x. Skal vi se på den, hvor der står x? Lene: Ja, er det ikke det, vi plejer? Ligningen lyder 4 x = 4 + x. Lene: Man skal ligesom minusse noget herovre, for at det bliver isoleret. Lene trækker x fra på begge sider, så der står 4 x x = 4. Lene: Det er vel bare 4 x? Lene hjælpes og får udtrykket 3 x = 4. Lene: Så skal man et eller andet sådan her. Lene tegner en vandret streg under 3x og under 4. Lene: Lene: Hvorfor det? Det ved jeg ikke. Det skal man bare Hvorfor vil du dividere? Det skal man bare. Sekvensen viser, dels at Lene har et snævert begrebsbillede af en ligning, og dels at hun opfatter ligningsløsning operationelt og ikke strukturelt (Sfard 1991). Dvs. at ligningsløsning for Lene bliver en proces, der indeholder en række handlinger og fremgangsmåder, som hun har svært ved at begrunde, men som hun i nogen grad er i stand til at foretage. Det peger derfor også på, at hun har en instrumentel tilgang til ligningsløsning fremfor en relationel, da dette ville kræve, at hun udover at kunne foretage de konkrete operationer også skulle vide, hvorfor hun foretog dem (Skemp 1979) (den relationelle tilgang). Dette er hukommelsesmæssigt en omfattende proces, og kun med den strukturelle opfattelse (som er knyttet til det matematiske objekt) kan eleverne genkende objektet og manipulere det i andre sammenhænge. Det peger på mangler inden for både symbol og formalismekompetencen og kommunikationskompetencen (Niss & Jensen 2002). Fordi Lene ikke forstår spillereglerne i ligningsløsning, kan hun heller ikke sætte ord på sin metode, som bliver en svær og måske meningsløs procedure for hende. Men vi kan hjælpe Lene og andre i hendes situation ved at lære hende fagvokabulariet (led, faktor, koefficient m.m.) og reglerne, der knytter sig til elementerne i ligningsløsning, samt insistere på, at hun anvender de rigtige ord og betegnelser. Mere konkret giver vi Lene en ordliste, der består af to søjler en begrebssøjle og en eksempelsøjle, hvorefter vejlederen gennemgår et begreb ved at forklare, hvad det betyder, og hvornår det bruges. Derefter anvendes det på et eksempel, så eleven kan høre, hvordan begrebet bruges i en sætning. Slutteligt prøver eleven selv ved at gennemgå et par eksempler, som vist på modstående side. Regler formuleret i ord Reglerne introduceres gennem eksempler. Man må lægge det samme tal til på begge sider af lighedstegnet. Man må trække det samme tal fra på begge sider af lighedstegnet. Man må gange med det samme tal i alle led på begge sider af lighedstegnet (dog ikke 0). Man må dividere med det samme tal i alle led på begge sider aflighedstegnet (dog ikke 0). Efter så lille en intervention oplevede vi til vores overraskelse, at de forholdsvis svage elever, vi havde arbejdet med, nu havde en reel løsningsstrategi baseret på handlinger, der rent sprogligt var indlært. 24 LMFK-bladet 1/2018
4 Begreb F.eks. kommer Lenes løsning af ligningen nu til at starte med en konstatering af:»der er to led på højre side og et led på venstre side«,»jeg samler led med den ubekendte på højre side«,»jeg trækker 4 fra på begge sider«og»jeg dividerer med koefficienten til den ubekendte på begge sider«. Det korrekte matematiske sprog giver et stillads for mønstergenkendelse og øger dermed elevernes forståelse af ligningen og dens elementer. Hermed har eleverne fået styrket to kompetencer fra KOM rapporten, nemlig kommunikationskompetencen og symbol og formalismekompetencen, en styrkelse, der hviler på den faste procedure ved konsekvent at bruge begreberne fra ord og regellisten. Eksempel Lighedstegn = Regneoperationer Led adskilles af + og Led, der lægges sammen, giver en sum Led, der trækkes fra hinanden, giver en differens Man ganger faktorer med hinanden, og man får et produkt Den ubekendte Koefficient er den faktor, der står foran den ubekendte Lægge til Trække fra Gange Dividere 8x + 4 3y 5y + 3y = 8y, hvor 5y og 3y er led, og 8y er summen (og et led) 3x +14x + x = 18x = 17 3a a = 2a, hvor 3a og a er led, og 2a er differensen (og et led) p 8p = 7p 5 6 = 30, hvor 5 og 6 er faktorer, og 30 produktet 3z 8 = 24z I en ligning angives den ubekendte med et symbol, eksempelvis x, m eller t, og det er værdien af den ubekendte, der skal findes 4 y, hvor 4 og y er faktorer, 4 er koefficient, og y er ubekendt Sproglig struktur i bevisførelse Bevisførelse er en væsentlig del af matematikundervisningen og en obligatorisk del af den mundtlige eksamen på B og A niveau, men hvordan sikrer man sig, at det ikke bliver en gang rituel udenadslære? Vi mødte hos vores elever forestillinger om bevisførelse som henholdsvis»lange og indviklede«,»med en høj forklaringsgrad«eller bare»mærkelige«(fuglsang Damgaard, Bie & Bolvinkel 2014b), hvilket er meget naturligt, set i lyset af, at bevisførelse som disciplin er helt ny for dem. Som tidligere nævnt er det vigtigt at begrebsafklare, så eleverne fra begyndelsen har en fornemmelse af, hvilken status bevisførelse har i matematik, nemlig en status, som er fundamentalt anderledes end i alle andre fag. Dernæst kan man, ligesom med ligninger, stilladsere elevernes forståelse ved hjælp af en række strategiske holdepunkter. Vi tog udgangspunkt i Toulmins argumentationsmodel og måden, den anvendes på hos Christine Knipping (2008), ved at vise eleverne, at der altid er nogle faste mønstre og strukturer, som kan kobles på Toulmins begreber. Vi startede med at lægge vægt på, at ordet sætning henviser til to forskellige ting, alt efter om man bruger det i dansk eller i matematik. Det er vigtigt, fordi eleven ofte kun har den danskfaglige reference (eller den almenkendte definition af ordet), og for at forstå, hvad indholdet af en matematisk sætning er, skal man altså se ud over denne. En matematisk sætning er mere at opfatte som en påstand, og for at argumentere for dens rigtighed kan man gøre brug af argumentationsanalyse og spørge:»hvorfor gælder denne sætning?«i matematik vil der så følge en række begrundelser eller belæg, der slutteligt vil ende i hovedpåstanden. Vi ville forsøge at hjælpe eleven til en mere sikker bevisstrategi gennem altid at starte med at skrive hovedpåstanden op, tegne en eventuel skitse samt huske et til to holdepunkter gennem beviset. Hvis eleven følte sig sikker på, hvordan beviset er skruet sammen, håbede vi, at eleven kunne gennemgå et bevis uden at føle sig nødsaget til at lære det udenad eller læse op fra et papir (Fuglsang Damgaard, Bie & Bolvinkel 2014b). Vokabulariet, der skal læres og trænes, er påstand, belæg, definition, sætning, argumentationskæde, forudsætning, kendt viden og holdepunkter, og på illustrationen nedenfor er vist, hvordan eleverne kan støttes gennem brug af termerne. Her er der tale om beviset for en af formlerne for arealet af en trekant, og meningen er, at eleverne ud fra disse punkter skal kunne gennemføre beviset. LMFK-bladet 1/
5 Sætning: (Hovedpåstand) I en vilkårlig trekant ABC gælder, at arealet er T = 1/2 a b sin(c). Bevis: (Argumentationskæde) Holdepunkter: Kendt viden Skitse Kendt viden: Arealet af en trekant er T = 1/2 h a a Sinusformel i retvinklet trekant sin(v) = mod/hyp Hvordan lyder det så, når en elev skal bruge begreberne efter at være præsenteret for dem? Her møder vi Mette, der netop skal gennemgå beviset for arealformlen uden noter: Uden?! Ja, uden at du kigger i dine noter. Så jeg må slet ikke kigge i dem?! Mette mindes nu om begreberne hovedpåstand, påstand, belæg, argumentationskæde og holdepunkt, hvorefter hun straks går i gang ned at opskrive hovedpåstanden og tegner en skitse, som fungerer som holdepunkt. C b A h a a Så har jeg en påstand, der hedder sin(c) er lig med højden fra A divideret med b. Mit belæg for det, det er så denne her påstand [Mette peger på sin(v) = modstående/hypotenusen]. Og jeg ved jo så, at den modstående katete... det fandt jeg ud af, at det var h a, fordi at hvis jeg tog denne her retvinklede trekant heroppe i mit holdepunkt, så hedder den modstående katete h, højden fra A. Og jeg ved, at hypotenusen hedder lille b. Ja. c B Og så har jeg en ny påstand, der hedder T = 1/2 a sin(c) b. Og belægget for det er så både denne her påstand (Mette peger på arealformlen for en retvinklet trekant) og denne her påstand (peger på sin(c) = h a /b). I den her (peger igen på sin(c) = h a /b) skal h a isoleres. Det gør jeg ved at gange med b på begge sider. Da Mette har gennemført beviset, konfronteres hun med, at hun har gennemført beviset uden at kigge på sit papir. Ja. Jeg prøvede at huske, hvad der stod på papiret, men det kunne jeg ikke helt, og så tænkte jeg, ok, det er bare påstand, belæg, påstand, belæg. Har denne her metode hjulpet dig til at gennemgå et bevis? [Tænkepause] Det synes jeg fordi at da jeg skulle øve det derhjemme i går, så kiggede jeg heller ikke på de her papirer, og så tænkte jeg bare, at jeg skal huske, at jeg skal have hovedpåstand, påstand og belæg og holdepunkt. Og så kiggede jeg også andre beviser igennem, og så tænkte jeg, at nu giver det faktisk mening. Nu ved jeg, hvad der er hvad og sådan noget. Sekvensen antyder, at Mette har fået et redskab til at kunne læse beviser, så hun bedre kan forstå og overskue de forskellige trin, der er i et matematisk bevis og ikke mindst hvorfor de forskellige trin optræder i beviset. Vi skal dog påpege, at ikke alle vores elever klarede det helt så godt. Dette skyldes imidlertid ikke brugen af begreber og holdepunkter, som var en stor hjælp for alle. Snarere viste det sig, at problemerne opstod i udførelsen af de algebraiske manipulationer. Det er ærgerligt, at det er disse, der skal bremse for en mere flydende gennemgang, når nu eleverne faktisk både ved, hvad et bevis er, og kender og kan bruge argumentationsterminologien. Men det peger også på, at ligningsløsning og algebraisk sikkerhed er funda- mentale egenskaber i mange af gymnasiematematikkens grene. Sproglig struktur i modellering Arbejdet med matematiske modeller i gymnasiet kan tage flere former. Eleverne kan eksempelvis manipulere med en kendt model for at finde værdien af en ukendt variabel, de kan få til opgave at forklare betydningen af konstanter og variable i en model, eller de kan blive bedt om at opstille en matematisk model på baggrund af en sproglig beskrivelse. I vores tredje projekt koncentrerede vi os om denne sidstnævnte matematisering, dvs. den helt konkrete oversættelse fra sprog til matematik. Som i de tidligere projekter ønskede vi via sproget at strukturere elevernes arbejde med matematiseringen. Endvidere ønskede vi at undersøge, hvorvidt opgaver stillet i et letgenkendeligt ekstra matematisk domæne var lettere at arbejde med for eleverne end opgaver stillet i et mindre genkendeligt ekstramatematisk domæne. Sagt på en anden måde ville vi undersøge, om elever har lettere ved modelleringsopgaver omhandlende computerspil, tøjindkøb og lignende end ved opgaver, der omhandler, hvor meget en hundestejle forbrænder i timen afhængigt af dens alder. Vores arbejde med eleverne afslørede, at sproget endnu en gang var en snublesten. For det første var eleverne usikre på betydningen af matematiske begreber som sammenhæng og model, hvilket kan ses i Michaels tidligere udsagn, hvor han troede, at en sammenhæng skal være på en for ham velkendt form, og dermed griber han den lineære model uden at overveje, hvad opgaven egentlig går ud på. Dette illustreres også i følgende samtale, hvor Rikke (2. g) bliver bedt om at opskrive en sammenhæng, der illustrerer, at der er seks gange så mange elever som lærere på en skole: Rikke: [skriver x + 6x] Jeg tænker, at antallet af lærere må være x, og så må antallet af elever være 6x. Hvad tænker du, når der står, at 26 LMFK-bladet 1/2018
6 du skal opskrive en sammenhæng mellem antallet af lærere og elever? Hvad er det egentlig, der bliver spurgt om? Rikke: Det ved jeg ikke... Endvidere forstyrrede flere ikke matematiske ord eleverne i deres arbejde. Dette var både ord som normalt forbindes med andre fag, men også dagligdagsord som træterning og omkostninger. Som i de tidligere forløb var vores første indsatspunkt derfor at hjælpe eleverne med at skabe orden i opgaven, og til dette formål udarbejdede vi med udgangspunkt i Cardalle Elawar (1995) en række hjælpespørgsmål: 1. Forståelse. Forstår jeg betydningen af ordene? Forstår jeg meningen med opgaven? 2. Visualisering. Kan jeg tegne en model af problemstillingen? Kan jeg visualisere den? 3. Sortering. Har jeg alle nødvendige informationer? Hvilke informationer er vigtige, og hvilke er ikke vigtige? 4. Symboler og eksempel. Navngiv de variable og konstante størrelser. Prøv at lave et eksempel, hvor du indsætter talværdier. 5. Formel. Opskriv sammenhængen mellem de variable og konstante størrelser som en formel. 6. Beregning. Hvordan skal jeg beregne løsningen? Hvilke matematikoperationer har jeg problemer med? Vi valgte at arbejde med grupper á tre fire elever i dette forløb, fordi vi mente, at eleverne ville have glæde af at diskutere med hinanden i stedet for at tænke højt foran læreren. Det tredje hjælpespørgsmål har som formål at få eleverne til at indse, at en matematisk model ikke kan inkorporere samtlige variable. I den første udgave af vores hjælpespørgsmål var beregningseksemplet i spørgsmål fire udeladt. Arbejdet med eleverne viste dog, at de var meget glade for at arbejde med helt konkrete værdier, og at et konkret eksempel hjalp dem med at opstille den generelle sammenhæng. Eleverne blev nu udsat for en række opgaver, som de diskuterede, mens læreren observerede og hjalp på vej, når og hvis det var nødvendigt. Opgaverne så ved første øjekast meget forskellige ud. Nogle havde en letgenkendelig kontekst, mens andre var mere tekniske og skrevet i et sprog med et stort antal fremmedord. De underliggende matematiske modeller adskilte sig ikke nævneværdigt i sværhedsgrad; det var alene indpakningerne, der var forskellige. Dette var helt bevidst, idet vi ønskede at undersøge, om konteksten havde en betydning for elevernes evne til at løse opgaverne på modstående side: Hvor lang tid holder en flaske shampoo? Prisen på en taxatur kan beskrives ved y = 5x + 25, hvor x angiver antallet af kørte kilometer, og y angiver den samlede pris. Er det en god model? Et vandkraftværk er et anlæg til produktion af elektricitet, hvor man udnytter en faldhøjde (potentiel energi) af en vandmasse til at drive en vandturbine, som er koblet til en generator. Hvor meget skal en kilowatttime koste for at dække omkostningerne ved at have et vandkraftværk? Giv et forslag til et betalingssystem i et parkeringshus ved siden af et varehus, der hverken skræmmer kunderne væk eller resulterer i, at de holder der 24 timer i døgnet. Opstil en matematisk model, der kan afgøre, hvilken kø man skal vælge i et supermarked. Efter den indledende begrebsafklaring af begreber som sammenhæng, model, variable og konstanter kastede eleverne sig over opgaverne. Allerede fra første samtale observerede vi, at eleverne var gode til at indse, at en model ikke kan tage højde for samtlige variable, og at nogle variable derfor må frasorteres. I starten kneb det gevaldigt med matematiseringsdelen, men inklusionen af arbejdsspørgsmål fire, der kalder på et konkret eksempel, viste sig at give eleverne det sidste skub på vejen. Følgende samtale udspillede sig i en 1.g gruppe, der arbejdede med sidste opgave, hvor de skulle opstille en matematisk model, der kunne afgøre, hvilken kø man skulle stille sig ved i et supermarked. Henriette: Man kunne vælge at sige, hvor lang tid det i gennemsnit tog en kunde at komme igennem med x antal varer. Men så skal man beslutte sig for et eller andet. Mark: Men du skal også have et starttal, for det tager jo, hvad, 20 sekunder at betjene hver kunde? Så det kunne hedde y = x , hvor x et er antal varer. Amanda: Men tager det 20 sekunder for hver vare? Mark: Skal vi sige 3 sekunder? Eleverne får herefter opstillet sammenhængen y = 3x + 20p, hvor x er antallet af varer i køen, og p er antallet af personer. Denne formaliserer de yderligere, så de får, at y = q x + z p, hvor q er antal sekunder pr. vare, og z er antal sekunder pr. personlig betjening. Begrebet om en matematisk model er således ikke længere fremmed for eleverne, og det at introducere variable i en matematisk model er blevet noget, de bare gør. Begrebsafklaringen har gjort dem i stand til at samtale om en model ved brug af korrekte matematiske begreber, og brugen af et konkret taleksempel har fungeret som katalysator for arbejdet hen mod en færdig model. Forløbet viste også, at man gør eleverne en bjørnetjeneste ved at stille dem foran modeller, der beskriver indviklede videnskabelige sammenhænge. Det er meget muligt, at sådanne modeller har en baggrund i den virkelige verden, men det virker forstyrrende for eleverne. Snarere bør introduktionen til modellering foregå ved brug af simple, letgenkendelige modeller skrevet i et hverdagsagtigt sprog og omhandlende genkendelige kontekster. I opgaven om vandkraftværket sagde en elev eksempelvis:»jeg skal læse den [teksten] en milliard gange og bruger for lang tid på det. Selv om jeg læser og forstår ordene, kan jeg ikke holde fokus«, og en hel gruppe vidste simpelthen ikke, hvad en kilowatttime er. LMFK-bladet 1/
7 Lighedstegnet og dets betydning I samtlige projekter var en mangelfuld symbol og formalismekompetence et evigt problem. Det var ikke så overraskende i første projekt, hvor problemer med at forstå lighedstegnets betydning naturligt nok vil resultere i problemer med at løse en ligning. En elev havde som beskrevet tidligere problemer med at svare på, om 13 = 17 er korrekt. Eksemplet viser, at lighedstegnet ikke nødvendigvis udtrykker ækvivalens for eleven og derved heller ikke opfattes som et relationelt eller operationelt tegn. I tredje projekt om matematisk modellering ses nogle af de samme problemer med lighedstegnet som i første projekt. Matias skriver relationen»1= 6«, som skal betyde, at for hver gang der er en lærer, er der seks elever. Ligesom for Helle betyder det ikke, at begge sider er ens, ej heller er det en opfordring til at udføre en regneoperation. Man kunne få den mistanke, at Matias ikke har forstået, hvad opgaven går ud på, men det viser en senere forklaring, at han har. Faktisk udtrykker han meget præcist den lineære relation, der er imellem antal lærere og antal elever:»formlen skal på en eller anden måde være: For hver gang der er én lærer, det vil sige vokser med 1, så skal den gå 6 op«. Men han pointerer faktisk i en sætning lige før også, hvad problemet er. Han mestrer simpelthen ikke det sprog, som skal bruges til at udtrykke den matematiske relation:»problemet er, at jeg ikke umiddelbart ved, hvordan jeg skal formulere det«. Så kommunikationskompetencen er stækket, fordi han mangler de matematiske byggesten i form af symbolsproget, han skal udtrykke sig med. Men hvordan får så Helle og Matias idéen om at godtage åbenlyst forkerte udtryk? Der er noget forskelligt på spil hos dem, selv om eksemplerne kan se ens ud. For Matias vedkommende tror vi, at hans problemer skyldes, at hverdagssproget har overtaget i modelleringskonteksten. Ser man på, hvordan man i dagligdags sprog anvender formuleringer som»der sættes lighedstegn mellem«, kan en hur- tig Googlesøgning afsløre et hav af forskelligartede udtryk. Fra en RUC opgave om sundhedsfremme (Hasanbegovic 2013) fås citatet:»dette i så høj grad, at der er tendenser til, at der sættes lighedstegn mellem at være tynd og at være sund«. Og fra en artikel i Ugeskrift for Læger (Eika & Malling 2013) ses:»et andet forslag har været at sætte lighedstegn mellem professionalisme i udøvelsen af lægegerningen og evnen til at kunne argumentere for (reflektere over) de valg, man træffer«. Dette er blot to eksempler på, hvordan»at sætte lighedstegn mellem«bliver brugt i videnskabelige sammenhænge i en ikkematematisk kontekst. Men i en matematisk forstand ville disse lighedstegn være lige så lidt gyldige som dem, Matias arbejder med, fordi det synes klart, at der ikke er ækvivalens mellem at være tynd og være sund eller mellem at være professionel og at kunne argumentere for sine valg. Vi mener derfor, at brugen af lighedstegnet knytter sig til en sproglig opfattelse af det, hvor der gemt i symbolet ligger en forkortelse af en række sproglige elementer. Tegnet kan skifte karakter efter sammenhængen, det bruges i, og udtrykker ikke ækvivalens. Men det kan udtrykke essensen af opgavens logiske forbindelsesord (for hver lærer er der seks elever) eller årsagssammenhæng (hvis der er én lærer, så er der seks elever). Og det kan indeholde småord, der i en matematisk kontekst er afgørende, men som i hverdagssproget ikke har den store betydning. Et eksempel herpå ses i en opgave om en terning, hvor Matias skriver»6 = sider«. På højre side burde der stå»antal sider«, hvis lighedstegnet skulle udtrykke ækvivalens. Konklusion I vores tre projekter forsøgte vi at hjælpe eleverne ved at sætte ind på to fronter. For det første arbejdede vi med at begrebsafklare, så der blev skabt enighed om, hvorom der samtaltes, og begrebet blev afmystificeret. For det andet skabte vi struktur inden for de forskellige matematiske områder ved at anvende begreberne på en systematisk måde. Resultatet var overvejende positivt. Eleverne tog begreberne til sig og viste store fremskridt, hvad enten det var inden for ligningsløsning, bevisførelse eller modellering. Derudover øgedes deres selvtillid og glæden ved faget, om end effekten af at blive set og have tid alene med læreren ikke må undervurderes. Vi er samtidig blevet meget bevidste om, at visse mangler inden for symbol og formalismekompetencen spænder ben for eleverne inden for alle matematiske områder. Dette understreger vigtigheden af at have fokus på den algebraiske manipulation. Langtidseffekterne af matematikvejledningen for vores elever er sværere at sige noget entydigt om. En enkelt elev har valgt matematik på A niveau og klarer sig over gennemsnittet. Til den skriftlige eksamen i sommeren 2015 har de elever, der har været oppe, alle bestået med middelkarakterer eller derover. Træerne vokser dog ikke ind i himlen. To elever, der både deltog i matematikvejledningen i 1. g og igen i 2. g, har i deres terminsprøver begge fået 00. Dette viser os, at det kræver en målrettet indsats fra både elever og lærere, også efter at vejledningsforløbet er tilendebragt, at fastholde de positive effekter af forløbet. I vejledningen har vi haft fokus på begrebsafklaring og struktur som en metode til at afhjælpe matematikvanskeligheder hos svage elever. Men det er ikke en metode, der udelukkende er forbeholdt vejledningssituationen. Vi har begge kunnet overføre den til klasseundervisningen, hvor resten af klassens elever har lige så meget brug for præcision i sproget og klare strukturer, som de svage elever har. Referencer Cardelle Elawar, Maria (1995): Effects of metacognitive instruction on low achievers in mathematics problems. Teaching and Teacher Education, vol. 11, s Eika, Berit & Bente Vigh Malling (2013): Speciallægeuddannelsens rolle som professional er kompleks og bør 28 LMFK-bladet 1/2018
8 omdefineres. Ugeskrift for Læger, vol. 175(24), s Fuglsang Damgaard, Anne Calina, Marianne Bie & Hans Bolvinkel (2014a): Sprog og ligninger, projektopgave 1, matematikvejlederuddannelsen. Roskilde Universitet. Fuglsang Damgaard, Anne Calina, Marianne Bie & Hans Bolvinkel (2014b): Argumentationsteknik i bevisførelse, projektopgave 2, matematikvejlederuddannelsen. Roskilde Universitet. Fuglsang Damgaard, Anne Calina, Marianne Bie & Hans Bolvinkel (2014c): Struktur og modellering, projektopgave 3, matematikvejlederuddannelsen. Roskilde Universitet. Hasanbegovic, Azra, Marlene Højmark, Pia Laursen, Ulla Uldahl & Christina Olofsson Sørensen (2013): Når sundheden skal frem & vægten skal ned! Hvad er der på spil i en sundhedsfremmende kommunal intervention? Master i sundhedsfremme. Roskilde Universitet. Jørgensen, Charlotte & Merete Onsberg (1987): Praktisk argumentation. Teknisk Forlag, Viby. Knipping, Christine (2008). A method revealing structures of argumentations in classroom proving processes. ZDM The international Journal on Mathematics Education, vol 40, s Niss, Mogens & Uffe Thomas Jankvist (2013a): 57 Spørgsmål fra Professoren (detektionstest 1). Materiale udleveret til matematikvejlederuddannelsen, Roskilde Universitet. Niss, Mogens & Uffe Thomas Jankvist (2013b): 13 Spørgsmål fra Professoren (detektionstest 3). Materiale udleveret til matematikvejlederuddannelsen, Roskilde Universitet. Niss, Mogens & Tomas Højgaard Jensen (2002): Kompetencer og matematik læring ideer og inspiration til udvikling af matematikundervisning i Danmark. Uddannelsesstyrelsens temahæfteserie nr. 18. Undervisningsministeriet, København. Sfard, Anna (1991): On the dual nature of mathematical conceptions: reflections on processes and objects as different sides of the same coin. Educational Studies in Mathematics, vol. 22, s Skemp, Richard R. (1979): Goals of learning and qualities of understanding. Mathematics Teaching, vol. 88, s Tall, David & Shlomo Vinner (1981): Concept image and concept definition in mathematics with particular reference to limits and continuity. Educational Studies in Mathematics, vol. 12, s Foreningen af eksaminerede matematikvejledere Foreningen af eksaminerede matematikvejledere ved de gymnasiale uddannelser har tidligere i LMFK bladet givet et indblik i, hvordan man på et grundlag af matematikdidaktisk forskning kan arbejde med elever, der udviser særlige læringsvanskeligheder i matematik. Det vil vi gerne gøre igen ved at præsentere endnu en artikel skrevet af to kolleger, der på det andet hold gennemførte uddannelsesprogrammet til matematikvejleder ved Roskilde Universitet. Artiklen, som er et gentryk af kapitel 1 i bogen Læringsvanskeligheder i matematik hvordan kan de forstås og afhjælpes, Forlaget Frydenlund, viser noget af den matematikdidaktik, vi benytter i vores arbejder som vejledere, men også i høj grad som undervisere. Bogen indeholder fem yderligere kapitler, skrevet af andre matematikvejledere, samt en indledning. En tidligere bog skrevet af matematikvejledere, Fra snublesten til byggesten, udkom i 2016 ligeledes på Forlaget Frydenlund. Artiklen er ikke mindst tænkt som en invitation til, at vi matematiklærere som faggruppe bliver bedre til at udveksle solidt funderede didaktiske overvejelser og tiltag, meget gerne her i bladet. Fra foreningen vil vi gerne takke LMFK, Forlaget Frydenlund, bogens to redaktører samt kapitlets to forfattere for at gøre det muligt. Nærmere oplysninger om Foreningen af eksaminerede matematikvejledere kan fås hos formanden, Morten Stoklund Larsen, matematikvejleder.dk For yderligere information kan følgende link benyttes: vejleder RUC, ruc.dk/matematikvejleder Under forudsætning af tilstrækkelig deltagelse optages endnu et hold matematikvejledere i efteråret Opnås ikke fornøden deltagelse til dette hold, vil uddannelsen blive nedlagt. Fra snublesten til byggesten: frydenlund.dk/varebeskrivelse/3773 Læringsvanskeligheder i matematik: frydenlund.dk/varebeskrivelse/ LMFK-bladet 1/2018
Matematikvejledning i praksis. Marianne Bie, Rysensteen Hans Bolvinkel, Nørre G
 Matematikvejledning i praksis Marianne Bie, Rysensteen Hans Bolvinkel, Nørre G 1 De tre projekter Projekt 1 Projekt 2 Projekt 3 Tema: Begreber og begrebsdannelse Sprog og ligninger Tema: Argumentation
Matematikvejledning i praksis Marianne Bie, Rysensteen Hans Bolvinkel, Nørre G 1 De tre projekter Projekt 1 Projekt 2 Projekt 3 Tema: Begreber og begrebsdannelse Sprog og ligninger Tema: Argumentation
Artiklen om Begreber og funktioner er et særtryk af kapitel 3 i den viste udgivelse.
 Begreb om funktioner Klaus Bruun Pedersen & Anders Torp 1 Indledning I dette kapitel vil vi beskrive en proces, hvorigennem vi har afdækket en række elevers funktionsforståelse, og vi vil give eksempler
Begreb om funktioner Klaus Bruun Pedersen & Anders Torp 1 Indledning I dette kapitel vil vi beskrive en proces, hvorigennem vi har afdækket en række elevers funktionsforståelse, og vi vil give eksempler
Matematiske kompetencer - hvad og hvorfor? DLF-Kursus Frederikshavn 24.-25.9 2015 Eva Rønn UCC
 Matematiske kompetencer - hvad og hvorfor? DLF-Kursus Frederikshavn 24.-25.9 2015 Eva Rønn UCC Komrapporten Kompetencer og matematiklæring. Ideer og inspiration til udvikling af matematikundervisningen
Matematiske kompetencer - hvad og hvorfor? DLF-Kursus Frederikshavn 24.-25.9 2015 Eva Rønn UCC Komrapporten Kompetencer og matematiklæring. Ideer og inspiration til udvikling af matematikundervisningen
Hvem skal samle handsken op?
 85 Hvem skal samle handsken op? Henrik Peter Bang, Christianshavns Gymnasium, Niels Grønbæk, Institut, Claus Richard Larsen, Christianshavns Gymnasium, Kommentar til Udfordringer ved undervisning i enzymer,
85 Hvem skal samle handsken op? Henrik Peter Bang, Christianshavns Gymnasium, Niels Grønbæk, Institut, Claus Richard Larsen, Christianshavns Gymnasium, Kommentar til Udfordringer ved undervisning i enzymer,
IT i forhold til overgangen mellem grundskolen og gymnasiet. Uffe Thomas Jankvist, DPU, AU
 IT i forhold til overgangen mellem grundskolen og gymnasiet Uffe Thomas Jankvist, DPU, AU Disposition Kort om overgangsproblemer mellem folkeskole og gymnasium (2 rapporter og lidt fra PISA-2012) 405 1.g
IT i forhold til overgangen mellem grundskolen og gymnasiet Uffe Thomas Jankvist, DPU, AU Disposition Kort om overgangsproblemer mellem folkeskole og gymnasium (2 rapporter og lidt fra PISA-2012) 405 1.g
Løsning af simple Ligninger
 Løsning af simple Ligninger Frank Nasser 19. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk:
Løsning af simple Ligninger Frank Nasser 19. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk:
Kommentarer til matematik B-projektet 2015
 Kommentarer til matematik B-projektet 2015 Mandag d. 13/4 udleveres årets eksamensprojekt i matematik B. Dette brev er tænkt som en hjælp til vejledningsprocessen for de lærere, der har elever, som laver
Kommentarer til matematik B-projektet 2015 Mandag d. 13/4 udleveres årets eksamensprojekt i matematik B. Dette brev er tænkt som en hjælp til vejledningsprocessen for de lærere, der har elever, som laver
Omskrivningsregler. Frank Nasser. 10. december 2011
 Omskrivningsregler Frank Nasser 10. december 2011 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold 1 Introduktion
Omskrivningsregler Frank Nasser 10. december 2011 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold 1 Introduktion
Matematikkens metoder illustreret med eksempler fra ligningernes historie. Jessica Carter Institut for Matematik og Datalogi, SDU 12.
 illustreret med eksempler fra ligningernes historie Institut for Matematik og Datalogi, SDU 12. april 2019 Matematiklærerdag, Aarhus Universitet I læreplanen for Studieretningsprojektet står: I studieretningsprojektet
illustreret med eksempler fra ligningernes historie Institut for Matematik og Datalogi, SDU 12. april 2019 Matematiklærerdag, Aarhus Universitet I læreplanen for Studieretningsprojektet står: I studieretningsprojektet
I kapitlet arbejdes med følgende centrale matematiske objekter og begreber:
 INTRO Efter mange års pause er trigonometri med Fælles Mål 2009 tilbage som fagligt emne i grundskolens matematikundervisning. Som det fremgår af den følgende sides udpluk fra faghæftets trinmål, er en
INTRO Efter mange års pause er trigonometri med Fælles Mål 2009 tilbage som fagligt emne i grundskolens matematikundervisning. Som det fremgår af den følgende sides udpluk fra faghæftets trinmål, er en
Andengradsligninger. Frank Nasser. 12. april 2011
 Andengradsligninger Frank Nasser 12. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk: Dette
Andengradsligninger Frank Nasser 12. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk: Dette
Formativ brug af folkeskolens prøver årets resultater på landsplan Den skriftlige prøve i matematik FP10 maj 2019
 Formativ brug af folkeskolens prøver årets resultater på landsplan Den skriftlige prøve i matematik FP10 maj 2019 Skrevet af Klaus Fink på baggrund af oplysninger fra opgavekommissionen 1 Til matematiklæreren
Formativ brug af folkeskolens prøver årets resultater på landsplan Den skriftlige prøve i matematik FP10 maj 2019 Skrevet af Klaus Fink på baggrund af oplysninger fra opgavekommissionen 1 Til matematiklæreren
2 Udfoldning af kompetencebegrebet
 Elevplan 2 Udfoldning af kompetencebegrebet Kompetencebegrebet anvendes i dag i mange forskellige sammenhænge og med forskellig betydning. I denne publikation som i bekendtgørelse og vejledning til matematik
Elevplan 2 Udfoldning af kompetencebegrebet Kompetencebegrebet anvendes i dag i mange forskellige sammenhænge og med forskellig betydning. I denne publikation som i bekendtgørelse og vejledning til matematik
Regneoperationerne plus og minus er hinandens omvendte regneoperation og at gange og dividere er hinandens omvendte regneoperation.
 Ligninger Eksempel 1. Et eksempel på en ligning er 2x 4 = 10 En ligning er et matematisk udtryk hvor der indgår et lighedstegn. I en ligning indgår der et bogstav, en ukendt størrelse/variabel. Dette bogstav
Ligninger Eksempel 1. Et eksempel på en ligning er 2x 4 = 10 En ligning er et matematisk udtryk hvor der indgår et lighedstegn. I en ligning indgår der et bogstav, en ukendt størrelse/variabel. Dette bogstav
ØVEHÆFTE FOR MATEMATIK C FORMLER OG LIGNINGER
 ØVEHÆFTE FOR MATEMATIK C FORMLER OG LIGNINGER INDHOLDSFORTEGNELSE 0. FORMELSAMLING TIL FORMLER OG LIGNINGER... 2 Tal, regneoperationer og ligninger... 2 Isolere en ubekendt... 3 Hvis x står i første brilleglas...
ØVEHÆFTE FOR MATEMATIK C FORMLER OG LIGNINGER INDHOLDSFORTEGNELSE 0. FORMELSAMLING TIL FORMLER OG LIGNINGER... 2 Tal, regneoperationer og ligninger... 2 Isolere en ubekendt... 3 Hvis x står i første brilleglas...
Elementær Matematik. Mængder og udsagn
 Elementær Matematik Mængder og udsagn Ole Witt-Hansen 2011 Indhold 1. Mængder...1 1.1 Intervaller...4 2. Matematisk Logik. Udsagnslogik...5 3. Åbne udsagn...9 Mængder og Udsagn 1 1. Mængder En mængde er
Elementær Matematik Mængder og udsagn Ole Witt-Hansen 2011 Indhold 1. Mængder...1 1.1 Intervaller...4 2. Matematisk Logik. Udsagnslogik...5 3. Åbne udsagn...9 Mængder og Udsagn 1 1. Mængder En mængde er
Andengradsligninger. Frank Nasser. 11. juli 2011
 Andengradsligninger Frank Nasser 11. juli 2011 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold 1 Introduktion
Andengradsligninger Frank Nasser 11. juli 2011 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold 1 Introduktion
Funktioner og ligninger
 Eleverne har både i Kolorit på mellemtrinnet og i Kolorit 7 matematik grundbog arbejdet med funktioner. I 7. klasse blev funktionsbegrebet defineret, og eleverne arbejdede med forskellige måder at beskrive
Eleverne har både i Kolorit på mellemtrinnet og i Kolorit 7 matematik grundbog arbejdet med funktioner. I 7. klasse blev funktionsbegrebet defineret, og eleverne arbejdede med forskellige måder at beskrive
Nogle didaktiske overvejelser vedrørende indledende undervisning i funktionsbegrebet i gymnasiet og nærværende hæftes nytte i så henseende.
 Nogle didaktiske overvejelser vedrørende indledende undervisning i funktionsbegrebet i gymnasiet og nærværende hæftes nytte i så henseende. af Dinna Balling og Jørn Schmidt. Hæftet Lige og ulige sætter
Nogle didaktiske overvejelser vedrørende indledende undervisning i funktionsbegrebet i gymnasiet og nærværende hæftes nytte i så henseende. af Dinna Balling og Jørn Schmidt. Hæftet Lige og ulige sætter
Formalia AT 2 på Svendborg Gymnasium og HF
 Formalia AT 2 på Svendborg Gymnasium og HF AT 2 ligger lige i foråret i 1.g. AT 2 er det første AT-forløb, hvor du arbejder med et skriftligt produkt. Formål Omfang Produktkrav Produktbedømmelse Opgavens
Formalia AT 2 på Svendborg Gymnasium og HF AT 2 ligger lige i foråret i 1.g. AT 2 er det første AT-forløb, hvor du arbejder med et skriftligt produkt. Formål Omfang Produktkrav Produktbedømmelse Opgavens
Problemløsning i retvinklede trekanter
 Problemløsning i retvinklede trekanter Frank Villa 14. februar 2012 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug
Problemløsning i retvinklede trekanter Frank Villa 14. februar 2012 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug
Formativ brug af folkeskolens prøver årets resultater på landsplan Den skriftlige prøve i matematik med hjælpemidler, FP9 maj 2019
 Formativ brug af folkeskolens prøver årets resultater på landsplan Den skriftlige prøve i matematik med hjælpemidler, FP9 maj 2019 Skrevet af Klaus Fink på baggrund af oplysninger fra opgavekommissionen
Formativ brug af folkeskolens prøver årets resultater på landsplan Den skriftlige prøve i matematik med hjælpemidler, FP9 maj 2019 Skrevet af Klaus Fink på baggrund af oplysninger fra opgavekommissionen
Progression frem mod skriftlig eksamen
 Progression frem mod skriftlig eksamen Ikke alle skal have 12 Eksamensopgavernes funktion i det daglige og til eksamen Progression i sættet progression i den enkelte opgave Hvornår inddrages eksamensopgaver
Progression frem mod skriftlig eksamen Ikke alle skal have 12 Eksamensopgavernes funktion i det daglige og til eksamen Progression i sættet progression i den enkelte opgave Hvornår inddrages eksamensopgaver
VUC Vestsjælland Syd, Slagelse Nr. 2 Institution: Projekt Vejanlæg. Matematik B-niveau Differentialregning
 VUC Vestsjælland Syd, Slagelse Nr. 2 Institution: 333247 2015 Projekt Matematik B-niveau Differentialregning Anders Jørgensen, Kirstine Irming, Mark Kddafi, Zehra Köse og Tobias Winberg Indledning I dette
VUC Vestsjælland Syd, Slagelse Nr. 2 Institution: 333247 2015 Projekt Matematik B-niveau Differentialregning Anders Jørgensen, Kirstine Irming, Mark Kddafi, Zehra Köse og Tobias Winberg Indledning I dette
De rigtige reelle tal
 De rigtige reelle tal Frank Villa 17. januar 2014 Dette dokument er en del af MatBog.dk 2008-2012. IT Teaching Tools. ISBN-13: 978-87-92775-00-9. Se yderligere betingelser for brug her. Indhold 1 Introduktion
De rigtige reelle tal Frank Villa 17. januar 2014 Dette dokument er en del af MatBog.dk 2008-2012. IT Teaching Tools. ISBN-13: 978-87-92775-00-9. Se yderligere betingelser for brug her. Indhold 1 Introduktion
Årsplan matematik 8. klasse
 Årsplan matematik 8. klasse 2019-2020 Eleverne arbejder med grundbogen Matematrix 8. I undervisningen inddrages digitale undervisningsredskaber såsom Geogebra, Wordmat, MatematikFessor, emat, excel og
Årsplan matematik 8. klasse 2019-2020 Eleverne arbejder med grundbogen Matematrix 8. I undervisningen inddrages digitale undervisningsredskaber såsom Geogebra, Wordmat, MatematikFessor, emat, excel og
Elev-til-elev læring med opgaveeksempler. uden hjælpemidler
 Program for løft af de fagligt svageste elever Intensivt læringsforløb Lærervejledning Elev-til-elev læring med opgaveeksempler fra prøven uden hjælpemidler Dato December 2017 Udviklet for Undervisningsministeriet
Program for løft af de fagligt svageste elever Intensivt læringsforløb Lærervejledning Elev-til-elev læring med opgaveeksempler fra prøven uden hjælpemidler Dato December 2017 Udviklet for Undervisningsministeriet
Vejledning til forløb om regnestrategier med multiplikation og division
 Vejledning til forløb om regnestrategier med multiplikation og division Denne lærervejledning beskriver i detaljer forløbets gennemførelse med fokus på lærerstilladsering og modellering. Beskrivelserne
Vejledning til forløb om regnestrategier med multiplikation og division Denne lærervejledning beskriver i detaljer forløbets gennemførelse med fokus på lærerstilladsering og modellering. Beskrivelserne
DMUK forår Ama El-Nazzal 10. Maj 2016
 DMUK forår 2016 { Ama El-Nazzal 10. Maj 2016 Lidt om mig selv: Ama El-Nazzal, Cand.scient 2007 Gymnasielærer i matematik og kemi, 2007- Preventing Dropout 2011-2014 Matematikvejlederuddannelsen på RUC,
DMUK forår 2016 { Ama El-Nazzal 10. Maj 2016 Lidt om mig selv: Ama El-Nazzal, Cand.scient 2007 Gymnasielærer i matematik og kemi, 2007- Preventing Dropout 2011-2014 Matematikvejlederuddannelsen på RUC,
Pointen med Differentiation
 Pointen med Differentiation Frank Nasser 20. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk:
Pointen med Differentiation Frank Nasser 20. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk:
Her er et spørgsmål, du måske aldrig har overvejet: kan man finde to trekanter med samme areal?
 Her er et spørgsmål, du måske aldrig har overvejet: kan man finde to trekanter med samme areal? Det er ret let at svare på: arealet af en trekant, husker vi fra vor kære folkeskole, findes ved at gange
Her er et spørgsmål, du måske aldrig har overvejet: kan man finde to trekanter med samme areal? Det er ret let at svare på: arealet af en trekant, husker vi fra vor kære folkeskole, findes ved at gange
Vinkelrette linjer. Frank Villa. 4. november 2014
 Vinkelrette linjer Frank Villa 4. november 2014 Dette dokument er en del af MatBog.dk 2008-2012. IT Teaching Tools. ISBN-13: 978-87-92775-00-9. Se yderligere betingelser for brug her. Indhold 1 Introduktion
Vinkelrette linjer Frank Villa 4. november 2014 Dette dokument er en del af MatBog.dk 2008-2012. IT Teaching Tools. ISBN-13: 978-87-92775-00-9. Se yderligere betingelser for brug her. Indhold 1 Introduktion
UNDERVISNING I PROBLEMLØSNING
 UNDERVISNING I PROBLEMLØSNING Fra Pernille Pinds hjemmeside: www.pindogbjerre.dk Kapitel 1 af min bog "Gode grublere og sikre strategier" Bogen kan købes i min online-butik, i boghandlere og kan lånes
UNDERVISNING I PROBLEMLØSNING Fra Pernille Pinds hjemmeside: www.pindogbjerre.dk Kapitel 1 af min bog "Gode grublere og sikre strategier" Bogen kan købes i min online-butik, i boghandlere og kan lånes
Matematiske metoder - Opgavesæt
 Matematiske metoder - Opgavesæt Anders Friis, Anne Ryelund, Mads Friis, Signe Baggesen 24. maj 208 Beskrivelse af opgavesættet I dette opgavesæt vil du støde på opgaver, der er markeret med enten 0, eller
Matematiske metoder - Opgavesæt Anders Friis, Anne Ryelund, Mads Friis, Signe Baggesen 24. maj 208 Beskrivelse af opgavesættet I dette opgavesæt vil du støde på opgaver, der er markeret med enten 0, eller
Evaluering af matematik undervisning
 Evaluering af matematik undervisning Udarbejdet af Khaled Zaher, matematiklærer 6-9 klasse og Boushra Chami, matematiklærer 2-5 klasse Matematiske kompetencer. Fællesmål efter 3.klasse indgå i dialog om
Evaluering af matematik undervisning Udarbejdet af Khaled Zaher, matematiklærer 6-9 klasse og Boushra Chami, matematiklærer 2-5 klasse Matematiske kompetencer. Fællesmål efter 3.klasse indgå i dialog om
Matematik for stx C-niveau
 Thomas Jensen og Morten Overgård Nielsen Matematik for stx C-niveau Frydenlund Nu 2. reviderede, udvidede og ajourførte udgave Nu 2. reviderede, udvidede og ajourførte udgave Matema10k Matematik for stx
Thomas Jensen og Morten Overgård Nielsen Matematik for stx C-niveau Frydenlund Nu 2. reviderede, udvidede og ajourførte udgave Nu 2. reviderede, udvidede og ajourførte udgave Matema10k Matematik for stx
SÆRE SYMBOLER OG FORVIRRENDE FORMLER
 SÆRE SYMBOLER OG FORVIRRENDE FORMLER Et oplæg om brugen af symboler og formler i undervisningen og om nogle af de problemer, de er skyld i. Marit Hvalsøe Schou IN D H O L D Præsentation Symboler i overgangen
SÆRE SYMBOLER OG FORVIRRENDE FORMLER Et oplæg om brugen af symboler og formler i undervisningen og om nogle af de problemer, de er skyld i. Marit Hvalsøe Schou IN D H O L D Præsentation Symboler i overgangen
Lineære differentialligningers karakter og lineære 1. ordens differentialligninger
 enote 11 1 enote 11 Lineære differentialligningers karakter og lineære 1. ordens differentialligninger I denne note introduceres lineære differentialligninger, som er en speciel (og bekvem) form for differentialligninger.
enote 11 1 enote 11 Lineære differentialligningers karakter og lineære 1. ordens differentialligninger I denne note introduceres lineære differentialligninger, som er en speciel (og bekvem) form for differentialligninger.
Den mundtlige prøve i matematik og forenklede Fælles Mål Odense 20. April 2015
 Den mundtlige prøve i matematik og forenklede Fælles Mål Odense 20. April 2015 153 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 + 13 + 14+ 15 + 16 + 17 153 = 1! + 2! + 3! + 4! + 5! 153 = 1 3 + 5
Den mundtlige prøve i matematik og forenklede Fælles Mål Odense 20. April 2015 153 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 + 13 + 14+ 15 + 16 + 17 153 = 1! + 2! + 3! + 4! + 5! 153 = 1 3 + 5
Matematisk argumentation
 Kapitlets omdrejningspunkt er matematisk argumentation, der især bruges i forbindelse med bevisførelse altså, når det drejer sig om at overbevise andre om, at matematiske påstande er sande eller falske.
Kapitlets omdrejningspunkt er matematisk argumentation, der især bruges i forbindelse med bevisførelse altså, når det drejer sig om at overbevise andre om, at matematiske påstande er sande eller falske.
Modellering. Matematisk undersøgelse af omverdenen. Matematisk modellering kan opfattes som en matematisk undersøgelse af vores omverden.
 Modellering Matematisk undersøgelse af omverdenen. 1 Modellering hvad? Matematisk modellering kan opfattes som en matematisk undersøgelse af vores omverden. Matematisk modellering omfatter noget udenfor
Modellering Matematisk undersøgelse af omverdenen. 1 Modellering hvad? Matematisk modellering kan opfattes som en matematisk undersøgelse af vores omverden. Matematisk modellering omfatter noget udenfor
Kapitel 3 Lineære sammenhænge
 Matematik C (må anvendes på Ørestad Gymnasium) Lineære sammenhænge Det sker tit, at man har flere variable, der beskriver en situation, og at der en sammenhæng mellem de variable. Enhver formel er faktisk
Matematik C (må anvendes på Ørestad Gymnasium) Lineære sammenhænge Det sker tit, at man har flere variable, der beskriver en situation, og at der en sammenhæng mellem de variable. Enhver formel er faktisk
8:30-14:30 Sproglig udvikling Kort aktivitet Planlægning af undervisningsforløb Fremlæggelse af undervisningsforløb
 8:30-14:30 Sproglig udvikling Kort aktivitet Planlægning af undervisningsforløb Fremlæggelse af undervisningsforløb Kaffepause 10:00-10:15 Frokost 12:15-13:00 Kaffepause 13:45-14:00 SPROGLIG UDVIKLING
8:30-14:30 Sproglig udvikling Kort aktivitet Planlægning af undervisningsforløb Fremlæggelse af undervisningsforløb Kaffepause 10:00-10:15 Frokost 12:15-13:00 Kaffepause 13:45-14:00 SPROGLIG UDVIKLING
TREKANTER. Indledning. Typer af trekanter. Side 1 af 7. (Der har været tre kursister om at skrive denne projektrapport)
 Side 1 af 7 (Der har været tre kursister om at skrive denne projektrapport) TREKANTER Indledning Vi har valgt at bruge denne projektrapport til at udarbejde en oversigt over det mest grundlæggende materiale
Side 1 af 7 (Der har været tre kursister om at skrive denne projektrapport) TREKANTER Indledning Vi har valgt at bruge denne projektrapport til at udarbejde en oversigt over det mest grundlæggende materiale
CAS som grundvilkår. Matematik på hf. Marts 2015 Bodil Bruun, fagkonsulent i matematik stx/hf
 CAS som grundvilkår Matematik på hf Marts 2015 Bodil Bruun, fagkonsulent i matematik stx/hf At spørge og svare i, med, om matematik At omgås sprog og redskaber i matematik De 8 kompetencer = 2 + 6 kompetencer
CAS som grundvilkår Matematik på hf Marts 2015 Bodil Bruun, fagkonsulent i matematik stx/hf At spørge og svare i, med, om matematik At omgås sprog og redskaber i matematik De 8 kompetencer = 2 + 6 kompetencer
Undersøgende opgaver Opgave 6 er i begge prøvesæt med som sidste opgave en undersøgende opgave af en ny type, som var lidt udfordrende for eleverne.
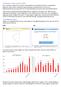 Tendenser i årets prøver 2019 Der er tendenser i prøverne, som kræver matematiklærernes opmærksomhed helst i et samarbejde i fagteamet. Og det kræver skolelederes og forvaltningers opmærksomhed for at
Tendenser i årets prøver 2019 Der er tendenser i prøverne, som kræver matematiklærernes opmærksomhed helst i et samarbejde i fagteamet. Og det kræver skolelederes og forvaltningers opmærksomhed for at
Infokløft. Beskrivelse. Faglige mål (i dette eksempel) Sproglige mål(i dette eksempel)
 Infokløft Beskrivelse Eleverne sidder 2 og 2 med skærm imellem sig De får forskellig information som de skiftes til at diktere til hinanden. Fx en tegning eller ord /begreber. Der er fokus på præcis formulering
Infokløft Beskrivelse Eleverne sidder 2 og 2 med skærm imellem sig De får forskellig information som de skiftes til at diktere til hinanden. Fx en tegning eller ord /begreber. Der er fokus på præcis formulering
Studieretningsopgave
 Virum Gymnasium Studieretningsopgave Harmoniske svingninger i matematik og fysik Vejledere: Christian Holst Hansen (matematik) og Bodil Dam Heiselberg (fysik) 30-01-2014 Indholdsfortegnelse Indledning...
Virum Gymnasium Studieretningsopgave Harmoniske svingninger i matematik og fysik Vejledere: Christian Holst Hansen (matematik) og Bodil Dam Heiselberg (fysik) 30-01-2014 Indholdsfortegnelse Indledning...
Formativ brug af folkeskolens prøver. Den skriftlige prøve i matematik med hjælpemidler, FP9 maj 2018
 Formativ brug af folkeskolens prøver Den skriftlige prøve i matematik med hjælpemidler, FP9 maj 2018 1 Til matematiklæreren i 9. klasse Dette er en rapport om den skriftlige prøve i matematik med hjælpemidler
Formativ brug af folkeskolens prøver Den skriftlige prøve i matematik med hjælpemidler, FP9 maj 2018 1 Til matematiklæreren i 9. klasse Dette er en rapport om den skriftlige prøve i matematik med hjælpemidler
Eksempel på den aksiomatisk deduktive metode
 Eksempel på den aksiomatisk deduktive metode Et rigtig godt eksempel på et aksiomatisk deduktivt system er Euklids Elementer. Euklid var græker og skrev Elemeterne omkring 300 f.kr. Værket består af 13
Eksempel på den aksiomatisk deduktive metode Et rigtig godt eksempel på et aksiomatisk deduktivt system er Euklids Elementer. Euklid var græker og skrev Elemeterne omkring 300 f.kr. Værket består af 13
Studieplan Stamoplysninger Periode Institution Uddannelse Fag og niveau Lærer(e) Hold Oversigt over planlagte undervisningsforløb Titel 1
 Studieplan Stamoplysninger Periode August - November 2018 Institution Vejen Business College Uddannelse Fag og niveau Lærer(e) Hold HHX Matematik B (Grundforløb) Søren Andresen 18-HH11, 18-HH12, 18-HH13
Studieplan Stamoplysninger Periode August - November 2018 Institution Vejen Business College Uddannelse Fag og niveau Lærer(e) Hold HHX Matematik B (Grundforløb) Søren Andresen 18-HH11, 18-HH12, 18-HH13
THOMAS KAAS (UCC & AU, DPU), WEBINAR, 31. JANUAR, 2018
 THOMAS KAAS (UCC & AU, DPU), WEBINAR, 31. JANUAR, 2018 Hvad er algebra i grundskolen, og hvorfor er det svært? Hvad er tidlig algebra, og hvorfor skulle det hjælpe? Undervisning med tidlig algebra hvad
THOMAS KAAS (UCC & AU, DPU), WEBINAR, 31. JANUAR, 2018 Hvad er algebra i grundskolen, og hvorfor er det svært? Hvad er tidlig algebra, og hvorfor skulle det hjælpe? Undervisning med tidlig algebra hvad
Grundfagsbekendtgørelsen Fagbilag juni 2004 MATEMATIK. Formål
 Grundfagsbekendtgørelsen Fagbilag juni 2004 MATEMATIK Formål Formålet med faget er, at eleverne bliver i stand til at identificere matematiske problemstillinger i både erhvervsfaglig og almen sammenhæng,
Grundfagsbekendtgørelsen Fagbilag juni 2004 MATEMATIK Formål Formålet med faget er, at eleverne bliver i stand til at identificere matematiske problemstillinger i både erhvervsfaglig og almen sammenhæng,
Indholdsfortegnelse. DUEK vejledning og vejleder Vejledning af unge på efterskole
 Indholdsfortegnelse Indledning... 2 Problemstilling... 2 Problemformulering... 2 Socialkognitiv karriereteori - SCCT... 3 Nøglebegreb 1 - Tro på egen formåen... 3 Nøglebegreb 2 - Forventninger til udbyttet...
Indholdsfortegnelse Indledning... 2 Problemstilling... 2 Problemformulering... 2 Socialkognitiv karriereteori - SCCT... 3 Nøglebegreb 1 - Tro på egen formåen... 3 Nøglebegreb 2 - Forventninger til udbyttet...
Ideer til sproglige aktiviteter.
 Matematikundervisning har gennem de senere år fokuseret på refleksion, problemløsning og kommunikation som både et mål og et middel i forhold til elevernes matematiske forståelse og begrebsudvikling. I
Matematikundervisning har gennem de senere år fokuseret på refleksion, problemløsning og kommunikation som både et mål og et middel i forhold til elevernes matematiske forståelse og begrebsudvikling. I
3. klasse 6. klasse 9. klasse
 Børne- og Undervisningsudvalget 2012-13 BUU Alm.del Bilag 326 Offentligt Elevplan 3. klasse 6. klasse 9. klasse Matematiske kompetencer Status tal og algebra sikker i, er usikker i de naturlige tals opbygning
Børne- og Undervisningsudvalget 2012-13 BUU Alm.del Bilag 326 Offentligt Elevplan 3. klasse 6. klasse 9. klasse Matematiske kompetencer Status tal og algebra sikker i, er usikker i de naturlige tals opbygning
Guide til lektielæsning
 Guide til lektielæsning Gefions lærere har udarbejdet denne guide om lektielæsning. Den henvender sig til alle Gefions elever og er relevant for alle fag. Faglig læsning (=lektielæsning) 5- trinsmodellen
Guide til lektielæsning Gefions lærere har udarbejdet denne guide om lektielæsning. Den henvender sig til alle Gefions elever og er relevant for alle fag. Faglig læsning (=lektielæsning) 5- trinsmodellen
User s guide til cosinus og sinusrelationen
 User s guide til cosinus og sinusrelationen Frank Nasser 20. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for
User s guide til cosinus og sinusrelationen Frank Nasser 20. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for
Eksponentielle sammenhænge
 Eksponentielle sammenhænge 0 1 2 3 4 5 6 7 8 9 10 11 12 13 Indholdsfortegnelse Variabel-sammenhænge... 1 1. Hvad er en eksponentiel sammenhæng?... 2 2. Forklaring med ord af eksponentiel vækst... 2, 6
Eksponentielle sammenhænge 0 1 2 3 4 5 6 7 8 9 10 11 12 13 Indholdsfortegnelse Variabel-sammenhænge... 1 1. Hvad er en eksponentiel sammenhæng?... 2 2. Forklaring med ord af eksponentiel vækst... 2, 6
Matematik projekt. Klasse: Sh-mab05. Fag: Matematik B. Projekt: Trigonometri
 Matematik projekt Klasse: Sh-mab05 Fag: Matematik B Projekt: Trigonometri Kursister: Anders Jørgensen, Kirstine Irming, Mark Petersen, Tobias Winberg & Zehra Köse Underviser: Vibeke Wulff Side 1 af 11
Matematik projekt Klasse: Sh-mab05 Fag: Matematik B Projekt: Trigonometri Kursister: Anders Jørgensen, Kirstine Irming, Mark Petersen, Tobias Winberg & Zehra Köse Underviser: Vibeke Wulff Side 1 af 11
Vejledning til forløbet: Hvad er chancen?
 Vejledning til forløbet: Hvad er chancen? Denne lærervejledning beskriver i detaljer forløbets gennemførelse med fokus på lærerstilladsering og modellering. Beskrivelserne er blevet til på baggrund af
Vejledning til forløbet: Hvad er chancen? Denne lærervejledning beskriver i detaljer forløbets gennemførelse med fokus på lærerstilladsering og modellering. Beskrivelserne er blevet til på baggrund af
1: Hvilket studium er du optaget på: 2: Hvilke af nedenstående forelæsninger har du deltaget i?
 1: Hvilket studium er du optaget på: 2: Hvilke af nedenstående forelæsninger har du deltaget i? 3: Hvis du har deltaget i mindre end halvdelen af kursusgangene bedes du venligst begrunde hvorfor har deltaget
1: Hvilket studium er du optaget på: 2: Hvilke af nedenstående forelæsninger har du deltaget i? 3: Hvis du har deltaget i mindre end halvdelen af kursusgangene bedes du venligst begrunde hvorfor har deltaget
Flere ligninger med flere ukendte
 Flere ligninger med flere ukendte Frank Villa 14. februar 2012 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her.
Flere ligninger med flere ukendte Frank Villa 14. februar 2012 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her.
Vejledende karakterbeskrivelse Erhvervsuddannelserne Matematik Undervisningsministeriet, marts 2007
 Vejledende karakterbeskrivelse Erhvervsuddannelserne Matematik Undervisningsministeriet, marts 2007 Fra 1. august 2007 skal al bedømmelse i matematik i erhvervsuddannelserne foregå efter 7-skalaen. I herværende
Vejledende karakterbeskrivelse Erhvervsuddannelserne Matematik Undervisningsministeriet, marts 2007 Fra 1. august 2007 skal al bedømmelse i matematik i erhvervsuddannelserne foregå efter 7-skalaen. I herværende
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Termin Maj 2015 Institution Skive Tekniske Gymnasium Uddannelse Fag og niveau Lærer(e) Hold HTX Matematik A Niveau A Emil Hartvig emh@skivets.dk 1bhtx13 Oversigt over gennemførte
Undervisningsbeskrivelse Termin Maj 2015 Institution Skive Tekniske Gymnasium Uddannelse Fag og niveau Lærer(e) Hold HTX Matematik A Niveau A Emil Hartvig emh@skivets.dk 1bhtx13 Oversigt over gennemførte
Indhold. Indledning 7 Læsevejledning 9
 Indhold Indledning 7 Læsevejledning 9 1 Hvad er åbne opgaver? 13 2 Hvorfor arbejde med åbne opgaver? 17 3 Udfordringer i arbejdet med åbne opgaver 19 4 En ny didaktisk kontrakt 21 5 Et par eksempler 23
Indhold Indledning 7 Læsevejledning 9 1 Hvad er åbne opgaver? 13 2 Hvorfor arbejde med åbne opgaver? 17 3 Udfordringer i arbejdet med åbne opgaver 19 4 En ny didaktisk kontrakt 21 5 Et par eksempler 23
Tal og algebra. I kapitlet arbejdes med følgende centrale matematiske begreber: algebra variable. Huskeliste: Tændstikker (til side 146) FRA FAGHÆFTET
 I kapitlet skal eleverne arbejde med fire forskellige vinkler på algebra de præsenteres på kapitlets første mundtlige opslag. De fire vinkler er algebra som et redskab til at løse matematiske problemer.
I kapitlet skal eleverne arbejde med fire forskellige vinkler på algebra de præsenteres på kapitlets første mundtlige opslag. De fire vinkler er algebra som et redskab til at løse matematiske problemer.
Fag- og indholdsplan 9. kl.:
 Fag- og indholdsplan 9. kl.: Indholdsområder: Tal og algebra: Tal - regneregler og formler Størrelser måling, beregning og sammenligning. Matematiske udtryk Algebra - teoretiske sammenhænge absolut og
Fag- og indholdsplan 9. kl.: Indholdsområder: Tal og algebra: Tal - regneregler og formler Størrelser måling, beregning og sammenligning. Matematiske udtryk Algebra - teoretiske sammenhænge absolut og
Matematisk modellering og numeriske metoder. Lektion 8
 Matematisk modellering og numeriske metoder Lektion 8 Morten Grud Rasmussen 18. oktober 216 1 Fourierrækker 1.1 Periodiske funktioner Definition 1.1 (Periodiske funktioner). En periodisk funktion f er
Matematisk modellering og numeriske metoder Lektion 8 Morten Grud Rasmussen 18. oktober 216 1 Fourierrækker 1.1 Periodiske funktioner Definition 1.1 (Periodiske funktioner). En periodisk funktion f er
Noter til Perspektiver i Matematikken
 Noter til Perspektiver i Matematikken Henrik Stetkær 25. august 2003 1 Indledning I dette kursus (Perspektiver i Matematikken) skal vi studere de hele tal og deres egenskaber. Vi lader Z betegne mængden
Noter til Perspektiver i Matematikken Henrik Stetkær 25. august 2003 1 Indledning I dette kursus (Perspektiver i Matematikken) skal vi studere de hele tal og deres egenskaber. Vi lader Z betegne mængden
UCC - Matematikdag - 08.04.14
 UCSJ Målstyret + 21 PD - UCC - 25.02.14 www.mikaelskaanstroem.dk Der var engang. Skovshoved Skole Hvad svarer du på elevspørgsmålet: Hvad skal jeg gøre for at få en højere karakter i mundtlig matematik?
UCSJ Målstyret + 21 PD - UCC - 25.02.14 www.mikaelskaanstroem.dk Der var engang. Skovshoved Skole Hvad svarer du på elevspørgsmålet: Hvad skal jeg gøre for at få en højere karakter i mundtlig matematik?
UNDERVISNINGS DIFFERENTIERING I GYMNASIET
 UNDERVISNINGS DIFFERENTIERING Udviklingsredskab Dette udviklingsredskab henvender sig til gymnasielærere. Udviklingsredskabet guider jer igennem et selvevalueringsforløb. Når I anvender redskabet sammen
UNDERVISNINGS DIFFERENTIERING Udviklingsredskab Dette udviklingsredskab henvender sig til gymnasielærere. Udviklingsredskabet guider jer igennem et selvevalueringsforløb. Når I anvender redskabet sammen
ØVEHÆFTE FOR MATEMATIK C GEOMETRI
 ØVEHÆFTE FOR MATEMATIK C GEOMETRI Indhold Begreber i klassisk geometri + formelsamling... 2 Pythagoras Sætning... 8 Retvinklede trekanter. Beregn den ukendte side markeret med et bogstav.... 9 Øve vinkler
ØVEHÆFTE FOR MATEMATIK C GEOMETRI Indhold Begreber i klassisk geometri + formelsamling... 2 Pythagoras Sætning... 8 Retvinklede trekanter. Beregn den ukendte side markeret med et bogstav.... 9 Øve vinkler
Mundtlig prøve i Matematik
 Mundtlig prøve i Matematik Mandag d. 9. september 2013 CFU Sjælland Mikael Scheby Dagens indhold Velkomst, præsentation, formål med dagen Vekselvirkning mellem formalia, oplæg og arbejde med eksempler
Mundtlig prøve i Matematik Mandag d. 9. september 2013 CFU Sjælland Mikael Scheby Dagens indhold Velkomst, præsentation, formål med dagen Vekselvirkning mellem formalia, oplæg og arbejde med eksempler
Oprids over grundforløbet i matematik
 Oprids over grundforløbet i matematik Dette oprids er tænkt som en meget kort gennemgang af de vigtigste hovedpointer vi har gennemgået i grundforløbet i matematik. Det er en kombination af at repetere
Oprids over grundforløbet i matematik Dette oprids er tænkt som en meget kort gennemgang af de vigtigste hovedpointer vi har gennemgået i grundforløbet i matematik. Det er en kombination af at repetere
Lærervejledning Matematik 1-2-3 på Smartboard
 Lærervejledning Matematik 1-2-3 på Smartboard Lærervejledning til Matematik 1-2-3 på Smartboard Materialet består af 33 færdige undervisningsforløb til brug i matematikundervisningen i overbygningen. Undervisningsforløbene
Lærervejledning Matematik 1-2-3 på Smartboard Lærervejledning til Matematik 1-2-3 på Smartboard Materialet består af 33 færdige undervisningsforløb til brug i matematikundervisningen i overbygningen. Undervisningsforløbene
Space Challenge og Undervisningsminsteriets Fælles Mål for folkeskolen
 Space Challenge og Undervisningsminsteriets Fælles Mål for folkeskolen I dette kapitel beskrives det, hvilke Fælles Mål man kan nå inden for udvalgte fag, når man i skolen laver aktiviteter med Space Challenge.
Space Challenge og Undervisningsminsteriets Fælles Mål for folkeskolen I dette kapitel beskrives det, hvilke Fælles Mål man kan nå inden for udvalgte fag, når man i skolen laver aktiviteter med Space Challenge.
Mundtlig prøve i Matematik
 Mundtlig prøve i Matematik Tirsdag d. 9. september 2014 CFU Sjælland Mikael Scheby NTS-Center Øst Dagens indhold Prøvebekendtgørelse highlights Vekselvirkning mellem formalia, oplæg og arbejde med eksempler
Mundtlig prøve i Matematik Tirsdag d. 9. september 2014 CFU Sjælland Mikael Scheby NTS-Center Øst Dagens indhold Prøvebekendtgørelse highlights Vekselvirkning mellem formalia, oplæg og arbejde med eksempler
Euklids algoritme og kædebrøker
 Euklids algoritme og kædebrøker Michael Knudsen I denne note vil vi med Z, Q og R betegne mængden af henholdsvis de hele, de rationale og de reelle tal. Altså er { m } Z = {..., 2,, 0,, 2,...} og Q = n
Euklids algoritme og kædebrøker Michael Knudsen I denne note vil vi med Z, Q og R betegne mængden af henholdsvis de hele, de rationale og de reelle tal. Altså er { m } Z = {..., 2,, 0,, 2,...} og Q = n
Opgaver hørende til undervisningsmateriale om Herons formel
 Opgaver hørende til undervisningsmateriale om Herons formel 20. juni 2016 I Herons formel (Danielsen og Sørensen, 2016) er stillet en række opgaver, som her gengives. Referencer Danielsen, Kristian og
Opgaver hørende til undervisningsmateriale om Herons formel 20. juni 2016 I Herons formel (Danielsen og Sørensen, 2016) er stillet en række opgaver, som her gengives. Referencer Danielsen, Kristian og
resultaterne og sammenholde dem med hinanden.
 ! "#$%!& ' ( ( ' Hvordan har du fattet interesse for at undervise dine kollegaer i dansk som 2. sprog? Det er meget tilfældighedernes spil. Det startede med, at Lise Thorn bad mig om at tage på et kursus,
! "#$%!& ' ( ( ' Hvordan har du fattet interesse for at undervise dine kollegaer i dansk som 2. sprog? Det er meget tilfældighedernes spil. Det startede med, at Lise Thorn bad mig om at tage på et kursus,
Elevens data: Fornavn: Efternavn: Skole/Gymnasium: Klasse: Dreng: Pige:
 Interviewskema Unge matematiksvage Elevens data: Fornavn: Efternavn: Skole/Gymnasium: Klasse: Dreng: Pige: Læreren skal huske: Hvis det kan lade sig gøre er det en god ide at elevens egen matematik lærer
Interviewskema Unge matematiksvage Elevens data: Fornavn: Efternavn: Skole/Gymnasium: Klasse: Dreng: Pige: Læreren skal huske: Hvis det kan lade sig gøre er det en god ide at elevens egen matematik lærer
Anvendt litteratur : Mat C v. Bregendal, Nitschky Schmidt og Vestergård, Systime 2005
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin juni 2011 Institution Campus Bornholm Uddannelse Fag og niveau Lærer Hold Hhx Matematik C Peter Seide 1AB
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin juni 2011 Institution Campus Bornholm Uddannelse Fag og niveau Lærer Hold Hhx Matematik C Peter Seide 1AB
Ny skriftlighed - Matematik
 Ny skriftlighed - Matematik Indhold Andres tanker og ideer:... 2 Andre nyttige links:... 2 Kompetencer:... 2 Eksempler på opgaver der træner forskellige kompetencer... 3 Eksempel 1: Opgaveløsning med forskellige
Ny skriftlighed - Matematik Indhold Andres tanker og ideer:... 2 Andre nyttige links:... 2 Kompetencer:... 2 Eksempler på opgaver der træner forskellige kompetencer... 3 Eksempel 1: Opgaveløsning med forskellige
Ræsonnement og tankegang. DLF-Kursus Ringsted 17.-18.9 2015 Eva Rønn UCC
 Ræsonnement og tankegang DLF-Kursus Ringsted 17.-18.9 2015 Eva Rønn UCC Vivianis sætning - optakt Vicenzo Viviani (1622-1703) var en italiensk matematiker. Han var elev af Galilei. Denne opgave handler
Ræsonnement og tankegang DLF-Kursus Ringsted 17.-18.9 2015 Eva Rønn UCC Vivianis sætning - optakt Vicenzo Viviani (1622-1703) var en italiensk matematiker. Han var elev af Galilei. Denne opgave handler
Trekanter. Frank Villa. 8. november 2012
 Trekanter Frank Villa 8. november 2012 Dette dokument er en del af MatBog.dk 2008-2012. IT Teaching Tools. ISBN-13: 978-87-92775-00-9. Se yderligere betingelser for brug her. Indhold 1 Introduktion 1 1.1
Trekanter Frank Villa 8. november 2012 Dette dokument er en del af MatBog.dk 2008-2012. IT Teaching Tools. ISBN-13: 978-87-92775-00-9. Se yderligere betingelser for brug her. Indhold 1 Introduktion 1 1.1
Anden del af prøven er en individuel prøve med fokus på (simple) matematisk ræsonnementer og (simpel) bevisførelse.
 Nye Mundtlige Prøver Gruppedelprøver i matematik på C- og B-niveau Læreplanernes formulering om de mundtlige prøver Der afholdes en todelt mundtlig prøve. Første del af prøven er en problemorienteret prøve
Nye Mundtlige Prøver Gruppedelprøver i matematik på C- og B-niveau Læreplanernes formulering om de mundtlige prøver Der afholdes en todelt mundtlig prøve. Første del af prøven er en problemorienteret prøve
VIL KAN SKAL -MODELLEN
 en VILLA VENIRE artikel VIL KAN SKAL -MODELLEN ET PAR METODER af CHRISTOFFER RUDE 2 VIL-KAN-SKAL MODELLEN en VILLA VENIRE artikel Gennem flere år har Villa Venire arbejdet med VIL-KAN-SKAL-modellen til
en VILLA VENIRE artikel VIL KAN SKAL -MODELLEN ET PAR METODER af CHRISTOFFER RUDE 2 VIL-KAN-SKAL MODELLEN en VILLA VENIRE artikel Gennem flere år har Villa Venire arbejdet med VIL-KAN-SKAL-modellen til
ALMINDELIGT ANVENDTE FUNKTIONER
 ALMINDELIGT ANVENDTE FUNKTIONER I dette kapitel gennemgås de almindelige regnefunktioner, samt en række af de mest nødvendige redigerings- og formateringsfunktioner. De øvrige redigerings- og formateringsfunktioner
ALMINDELIGT ANVENDTE FUNKTIONER I dette kapitel gennemgås de almindelige regnefunktioner, samt en række af de mest nødvendige redigerings- og formateringsfunktioner. De øvrige redigerings- og formateringsfunktioner
Fagårsplan 10/11 Fag: Matematik Klasse: 7.ABC Lærer: Henrik Stillits. Fagområde/ emne
 Fagårsplan 10/11 Fag: Matematik Klasse: 7.ABC Lærer: Henrik Stillits. Fagområde/ emne Matematiske færdigheder Grundlæggende færdigheder - plus, minus, gange, division (hele tal, decimaltal og brøker) Identificer
Fagårsplan 10/11 Fag: Matematik Klasse: 7.ABC Lærer: Henrik Stillits. Fagområde/ emne Matematiske færdigheder Grundlæggende færdigheder - plus, minus, gange, division (hele tal, decimaltal og brøker) Identificer
MATEMATIKUNDERVISNING OG NEGATIV SOCIAL ARV
 1 MATEMATIKUNDERVISNING OG NEGATIV SOCIAL ARV Arbejdsgruppen for matematik stx om problemer for elever med gymnasiefremmed baggrund: Marianne Kesselhahn, Egedal Gymnasium og HF, Niels Hjølund Pedersen,
1 MATEMATIKUNDERVISNING OG NEGATIV SOCIAL ARV Arbejdsgruppen for matematik stx om problemer for elever med gymnasiefremmed baggrund: Marianne Kesselhahn, Egedal Gymnasium og HF, Niels Hjølund Pedersen,
Miss Markmans hemmeligheder. 10 sikre tips til succes på telefonen
 Miss Markmans hemmeligheder 10 sikre tips til succes på telefonen Guldkorn fra tusindvis af timer på telefonen Vi gør det hver eneste dag. Igen og igen. Tager telefonen og ringer til beslutningstagere,
Miss Markmans hemmeligheder 10 sikre tips til succes på telefonen Guldkorn fra tusindvis af timer på telefonen Vi gør det hver eneste dag. Igen og igen. Tager telefonen og ringer til beslutningstagere,
Årsplan for 7. klasse, matematik
 Årsplan for 7. klasse, matematik I matematik bruger vi bogsystemet Sigma som grundmateriale. I systemet er der, ud over grundbogen, også kopiark og tests tilknyttet de enkelte kapitler. Systemet er udarbejdet
Årsplan for 7. klasse, matematik I matematik bruger vi bogsystemet Sigma som grundmateriale. I systemet er der, ud over grundbogen, også kopiark og tests tilknyttet de enkelte kapitler. Systemet er udarbejdet
Læseplan for faget matematik. 1. 9. klassetrin
 Læseplan for faget matematik 1. 9. klassetrin Matematikundervisningen bygger på elevernes mange forudsætninger, som de har med når de starter i skolen. Der bygges videre på elevernes forskellige faglige
Læseplan for faget matematik 1. 9. klassetrin Matematikundervisningen bygger på elevernes mange forudsætninger, som de har med når de starter i skolen. Der bygges videre på elevernes forskellige faglige
Første del af rapporten består af et diagram, der viser, hvor mange point eleverne på landsplan fik i de enkelte opgaver.
 Til matematiklæreren Dette er en rapport omtaler prøven med hjælpemidler maj 2016. Rapporten kan bruges til at evaluere dit arbejde med klassen og få ideer til dit arbejde med kommende klasser i overbygningen.
Til matematiklæreren Dette er en rapport omtaler prøven med hjælpemidler maj 2016. Rapporten kan bruges til at evaluere dit arbejde med klassen og få ideer til dit arbejde med kommende klasser i overbygningen.
Danske elevers udfordringer i matematik. Uffe Thomas Jankvist AU (DPU) & RUC
 Danske elevers udfordringer i matematik Uffe Thomas Jankvist AU (DPU) & RUC Disposition for de næste 30 min. Matematikspecifikke udfordringer matematikvanskeligheder Hvad ved vi fra PISA set fra et fagdidaktisk
Danske elevers udfordringer i matematik Uffe Thomas Jankvist AU (DPU) & RUC Disposition for de næste 30 min. Matematikspecifikke udfordringer matematikvanskeligheder Hvad ved vi fra PISA set fra et fagdidaktisk
LÆRINGSSTILSTEST TEST TESTVÆRKTØJ TIL VEJLEDERE / Et screeningsværktøj så du sikrer en god læring hos dine elever og mindsker frafald.
 TEST TESTVÆRKTØJ TIL VEJLEDERE / LÆRINGSSTILSTEST Et screeningsværktøj så du sikrer en god læring hos dine elever og mindsker frafald. 1 LÆRINGSSTILSTEST / Når du kender dine elevers måde at lære på, kan
TEST TESTVÆRKTØJ TIL VEJLEDERE / LÆRINGSSTILSTEST Et screeningsværktøj så du sikrer en god læring hos dine elever og mindsker frafald. 1 LÆRINGSSTILSTEST / Når du kender dine elevers måde at lære på, kan
FFM Matematik pop-up eftermiddag. CFU, UCC 11. Maj 2015
 FFM Matematik pop-up eftermiddag CFU, UCC 11. Maj 2015 Formål Deltagerne har: Kendskab til Forenklede Fælles Måls opbygning Kendskab til tankegangen bag den målstyrede undervisning i FFM Kendskab til læringsmål
FFM Matematik pop-up eftermiddag CFU, UCC 11. Maj 2015 Formål Deltagerne har: Kendskab til Forenklede Fælles Måls opbygning Kendskab til tankegangen bag den målstyrede undervisning i FFM Kendskab til læringsmål
Formativ brug af folkeskolens prøver. Den skriftlige prøve i matematik i 10. klasse, FP10, maj 2018
 Formativ brug af folkeskolens prøver Den skriftlige prøve i matematik i 10. klasse, FP10, maj 2018 1 Til matematiklæreren i 10. klasse Dette er en rapport om den skriftlige prøve i matematik maj 2018.
Formativ brug af folkeskolens prøver Den skriftlige prøve i matematik i 10. klasse, FP10, maj 2018 1 Til matematiklæreren i 10. klasse Dette er en rapport om den skriftlige prøve i matematik maj 2018.
Kompetencemål for Matematik, 4.-10. klassetrin
 Kompetencemål for Matematik, 4.-10. klassetrin Matematik omhandler samspil mellem matematiske emner, matematiske arbejds- og tænkemåder, matematikdidaktisk teori samt matematiklærerens praksis i folkeskolen
Kompetencemål for Matematik, 4.-10. klassetrin Matematik omhandler samspil mellem matematiske emner, matematiske arbejds- og tænkemåder, matematikdidaktisk teori samt matematiklærerens praksis i folkeskolen
