STÅLSØJLER Mads Bech Olesen
|
|
|
- Thorvald Bertelsen
- 8 år siden
- Visninger:
Transkript
1 STÅLSØJLER Mads Bech Olesen Centralt belastede søjler Ved aksial trykbelastning af et slankt konstruktionselement er der en tendens til at elementet slår ud til siden. Denne form for instabilitet kaldes i daglig tale søjlevirkning (eng: flexural buckling). Bæreevnen afhænger både af søjlens statik (søjlelængde), stivheder (elasticitetsmodul og inertimoment) samt materialets styrke (flydestyrke). De forøgede bøjningsnormalspændinger som opstår pga. deformationen, når søjlen slår ud til siden, er afgørende for beregningen af trykkapaciteten. Det ideelle tilfælde: Centralt belastet søjle uden imperfektioner Der betragtes en stålsøjle uden imperfektioner såsom forhåndskrumninger, egenspændinger m.m. Søjlen belastes med en centralt virkende trykkraft N c i aksialretningen. I dette tilfælde benyttes Eulers formel til bestemmelse af den kritiske normalkraft N cr. N c N cr = π E I l s () Figur : Centralt belastet søjle Hvis den centrale tryklast N c øges udover den kritiske normalkraft N cr vil søjlen teoretisk set knække ud til siden. Dette fænomen kaldes for søjleinstabilitet. Udbøjningen kombineret med den aksiale trykkraft N c giver et moment i søjlen og normalspændingerne fra dertil hørende tryk og bøjning vil overskride materialestyrken. Dermed kollapser søjlen. For den centralt belastede søjle uden imperfektioner afhænger selve bæreevneudtrykket for N cr alene af søjlens stivhed (E og I) og søjlelængde (l s ) selvom det faktisk er en overskridelse af kapaciteten for normalspændingerne som får søjlen til at kollapse. Eulers formel gælder udelukkende for ideelle trykpåvirkede elementer som er meget slanke. Såfremt trykpåvirkede elementer er meget kompakte, og dermed har en lille slankhed, er det alene materialets flydestyrke som begrænser trykbæreevnen. Dette tydeliggøres i et tænkt tilfælde hvor en søjle har uendelig lille søjlelængde l s. Teoretisk set ville der forekomme uendelig stor værdi af N cr ved brug af Eulers formel.
2 Dette kan imidlertid ikke lade sig gøre idet tryknormalspændingen σ c i en søjle aldrig kan blive større end selve flydestyrken f y. For den centralt belastede søjle uden imperfektioner er Eulers formel dermed kun gældende, når den tilhørende kritiske spænding σ cr er mindre end den karakteristiske flydestyrke. σ cr = π E I l s A () Formlen kan ved division med omskrives til: σ cr = π E I l = χ Euler = (3) s A Ovenstående udtrykker ratio mellem den kritiske spænding for tryk og den karakteristiske flydestyrke. Dette kan også benævnes Euler-søjlereduktionsfaktoren χ Euler,idet denne ved multiplikation med flydestyrken netop giver bæreevnen, som den kritiske spænding σ cr. σ cr = σ cr (4) Der indføres det geometriske slankhedsforhold: λ = l s i slankhedsforhold: og inertiradius: i = I A og der indføres det relative λ rel = = l s A σ cr π = ( l s E I i ) π E = λ π E (5) Det bemærkes at det geometriske slankhedsforhold λ er forskelligt fra det relative slankhedsforhold λ rel. Der gælder følgende: = σ cr = χ Euler (6) λ rel Ovenstående udtrykker dermed søjlereduktionsfaktoren for en centralt belastet søjle uden imperfektioner og er afbilledet på grafen i figur. Bemærk at udtrykket kun er gældende for værdier af λ rel større end. For værdier af λ rel mindre end eller lig med svarer bæreevnen blot til trykstyrken.
3 Figur : χ Euler som funktion af λ rel 3
4 Det virkelige tilfælde : Centralt belastet søjle med imperfektioner Den ideelle søjle uden imperfektioner findes imidlertid ikke i virkeligheden og det er derfor nødvendigt med et udvidet bæreevneudtryk som tager hensyn hertil. Der betragtes en stålsøjle med imperfektioner i form af en initialudbøjning u 0. Elementet har altså en krumning (forhåndsudbøjning) inden trykbelastningen forekommer (Figur 3). Søjlen belastes med en centralt virkende trykkraft N c i aksialretningen. Lasten giver en udbøjningsforøgelse u N og summen af udbøjningerne u total er initialudbøjnigen plus udbøjningsforøgelsen (Figur 4). Figur 3: u 0 Figur 4: u total Søjlens deformation antages i den ubelastede situation at følge initialudbøjningsfunktionen: u 0 (x) = u 0 sin (π x l ) (7) Ved central trykpåvirkning N c opstår der tilsvarende udbøjningsforøgelsesfunktionen: u N (x) = u N sin (π x l ) (8) Den totale udbøjningsfunktion er summen af initialudbøjningen og udbøjningsforøgelsen: u total (x) = u 0 (x) + u N (x) = u total sin (π x l ) (9) Hvor u 0, u N og u total er udbøjningerne midt på søjlen, l er søjlens længde og x er aksen i søjlens aksialretning. 4
5 Ved central trykpåvirkning N c opstår der tilsvarende en momentfunktion for initialudbøjningen: M 0 (x) = N c u 0 sin (π x l ) (0) Og en momentfunktion for udbøjningsforøgelsen: M N (x) = N c u N sin (π x l ) () Den totale momentfunktion kan udtrykkes som M total (x) = M 0 (x) + M N (x) = N c u total sin (π x l ) () Figur 5: M total 5
6 For bestemmelse af den totale udbøjning u total som funktion af initialudbøjningen u 0 tages der udgangspunkt i bjælkens differentialligning: d u dx = M E I (3) Ligningen kan omskrives til: M = d u E I (4) dx Funktionsudtrykkene fra søjlen indsættes: M total (x) = d u N (x) dx E I (5) Da momentet i søjlen udelukkende optræder når udbøjningsforøgelsen u N forekommer, er det også kun denne del af udbøjningen som indgår i ovenstående differentialligning. Der gælder at hvis der ikke er nogen søjlelast N c så er udbøjningen alene u 0 og der forekommer dermed ingen momentpåvirkning. Initialudbøjningen u 0, alene, forekommer altså udelukkende i en situation hvor der ikke er spændinger i søjlen. Udtrykket omskrives ved brug af forudsætningerne for søjlen: N c u total (x) = d (u total (x) u 0 (x)) dx E I (6) N c u total sin (π x l ) = d (u total sin (π x l ) u 0 sin (π x l )) dx E I (7) N c u total sin (π x l ) = π E I l (u total u 0 ) sin (π x l ) (8) Eulers formel benyttes og udtrykket forkortes yderligere: N cr = π E I l () N c u total = N cr (u total u 0 ) (9) u total (N cr N c ) = u 0 N cr (0) u total = u 0 N cr N cr N c () 6
7 Den totale udbøjning u total kan dermed udtrykkes som en funktion af initilaludbøjningen u 0 og en forøgelsesfaktor. Det ses af () at når tryklasten N c er nul bliver den totale udbøjning lig initialudbøjningen. Tilsvarende gælder at når N c nærmer sig N cr bliver den totale udbøjning uendelig stor. Forøgelsesfaktoren udtrykkes som: N cr N cr N c = N c N cr () Forøgelsesfaktoren, som også kaldes andenordenseffekten eller momentforøgelsesfaktoren, kan grafisk vise at der i et trykpåvirket element ikke er ligefrem proportionalitet mellem last og bæreevne. Figur 6: Forøgelsesfaktoren N c Ncr som funktion af N c N cr 7
8 For bestemmelse af bæreevnen tages der udgangspunkt i brudbetingelsen: σ c + σ m = (3) Hvor σ c er tryknormalspændingen i aksialretningen fra normalkraften, σ m er normalspændingen fra momentet, er den karakteristiske flydestyrke. Spændingerne erstattes af følgende udtryk: σ c = N c A (4) σ m = M W (5) M = N c u total (6) N c A + N c u total W = (7) Fra tidligere haves: u total = u 0 N cr N cr N c () Udtrykkene sammensættes og der mulitipliceres med brøken A A : N c + A A A N c u 0 N cr = (8) W N cr N c Udtrykket reduceres: σ c + σ c A W u 0 σ cr σ cr σ c = (9) Der multipliceres med (σ cr - σ c ): σ c (σ cr σ c ) + σ c σ cr A W u 0 = σ cr σ c (30) Der indføres søjlereduktionsfaktoren χ som er forholdet mellem tryknormalspændingen og trykstyrken: Udtrykket (3) indsættes i (30): χ = σ c (3) χ σ cr χ σ c + χ σ cr A W u 0 = σ cr σ c (3) Der divideres med flydestyrken : χ σ cr σ c χ + χ σ cr A W u 0 = σ cr σ c (33) 8
9 Fra tidligere haves: λ = σ cr (6) rel Udtrykket (6) indsættes sammen med udtrykket for χ (3) i (33): χ χ + χ A W u 0 = χ (34) Der multipliceres med λ rel: λ rel λ rel λ rel χ χ λ rel + χ ( A W u 0 ) = χ λ rel (35) Der indføres faktoren ή som ud fra søjlens initialudbøjningen, geometri og styrker udtrykker søjlens rethed: ή = A W u 0 (36) Initialbøjningen kan som udgangspunkt sættes til /00 af søjlelængden: Bæreevneudtrykket reduceres nu yderligere: Søjlereduktionsfaktoren kan nu udtrykkes som: u 0 = l s 000 (37) χ λ rel χ (λ rel + ή + ) + = 0 (38) χ = 4 λ rel + ή + λ rel + λ rel (ή ) + (ή + ) λ rel (39) Dette kan på nemmere vis opstilles som to kombinerede udtryk: φ = 0,5 ( + ή + λ rel ) (40) χ = φ+ φ λ rel (4) Bæreevne (karakteristisk) ved trykpåvirkning: N c χ A (4) I specialtilfældet hvor u 0 er nul bliver ή ligeledes nul og dermed bliver søjlereduktionsfaktoren χ = σ cr svarende til den ideele søjle uden forhåndskrumninger. 9
10 Bæreevne (karakteristisk) ved kombineret trykpåvirkning og momentpåvirkning om én akse: Når et element er påvirket af både aksialt tryk og bøjning om én akse kan bæreevnen eftervises ved brug af følgende udtryk: N c χ A + M N cr (43) W el N cr N c Hvor trykbæreevnen er reduceret med søjlereduktionsfaktoren χ og hvor momentbelastningen er forøget med forøgelsesfaktoren andenordenseffekterne. N cr N cr N c () således at både tryknormalkraft og momentpåvirkning tager højde for 0
11 Beregning efter DS/EN 993 I DS/EN 993 er faktoren ή erstattet af et udtryk som dækker imperfektioner såsom forhåndkrumninger, egenspændinger, skævheder m.m. og hvor et reelt kendskab til initialudbøjningen u 0 ikke er nødvendigt. λ rel benævnes i DS/EN 993 som λ ή = α (λ rel,y 0,) (44) Svarende til: u 0 = α (λ rel,y 0,) W A (45) idet ή = A W u 0 (36) Hvor α er en variabel imperfektionsfaktor som afhænger af ståltværsnittes udformning, den betragtede udbøjningsakse, fremstillingsmetode m.m. Imperfektionsfaktoren α varierer i intervallet 0,3 0,76. λ rel,y skal mindst have værdien 0,. Ved værdier mindre end 0, er der ingen søjlevirkning og flydestyrken f y er alene begrænsende for bæreevnen. I DS/EN 993 er formeludtrykkene for bestemmelse af bæreevne i forhold til y og z-aksen: χ = φ + φ λ rel (46) Hvor: Bæreevne ved trykpåvirkning (tværsnitsklasse -3): φ = 0,5 ( + α (λ rel 0,) + λ rel ) (47) N b,rd = χ A N Ed (48) Hvor N b,rd er den regningsmæssige bæreevne mht. stabilitetssvigt af et trykpåvirket element og N Ed er den regningsmæssige værdi af trykkraften. Ovenstående udtryk for søjlereduktionsfaktoren er afbilledet i nedenstående figur hvor λ rel er x-aksen og χ er y-aksen. Den røde kurve viser den imperfekte søjle som kun gælder for værdier af λ rel større end 0,. Imperfektionsfaktoren α er sat til værdien 0, svarende til søjlekurve a. Den grå kurve viser den ideelle Euler søjle, som kun gælder for værdier af λ rel større end.
12 Figur 7: Søjlereduktionsfaktorer χ som funktion af λ rel Bæreevne ved kombineret trykpåvirkning og momentpåvirkning (tværsnitsklasse -3): Når et element er påvirket af både aksialt tryk og bøjning kan bærevenen eftervises ved brug af følgende udtryk udtryk: N Ed χ y N + k yy Rk M y,ed χ LT M y,rk + k yz M z,ed M z,rk (49) Hvor: χ LT er kipningsreduktionsfaktoren N Ed + k χ z N zy Rk k yy, k yz, k zy og k zz er interaktionsfaktorer M y,ed χ LT M y,rk + k zz M z,ed M z,rk (50) For yderligere information henvises til Stålkonstruktioner efter DS/EN 993 af Bjarne Chr. Jensen og DS/EN 993.
Løsning, Bygningskonstruktion og Arkitektur, opgave 6
 Løsning, Bygningskonstruktion og Arkitektur, opgave 6 For en excentrisk og tværbelastet søjle skal det vises, at normalkraften i søjlen er under den kritiske værdi mht. søjlevirkning og at momentet i søjlen
Løsning, Bygningskonstruktion og Arkitektur, opgave 6 For en excentrisk og tværbelastet søjle skal det vises, at normalkraften i søjlen er under den kritiske værdi mht. søjlevirkning og at momentet i søjlen
Bygningskonstruktion og arkitektur
 Bygningskonstruktion og arkitektur Program lektion 9 8.30-9.15 Bæreevnebestemmelse af centralt, ekscentrisk og tværbelastet stålsøjle. 9.15 9.30 Pause 9.30 10.15 Bæreevnebestemmelse af centralt, ekscentrisk
Bygningskonstruktion og arkitektur Program lektion 9 8.30-9.15 Bæreevnebestemmelse af centralt, ekscentrisk og tværbelastet stålsøjle. 9.15 9.30 Pause 9.30 10.15 Bæreevnebestemmelse af centralt, ekscentrisk
Kipning, momentpåvirket søjle og rammehjørne
 Kipning, momentpåvirket søjle og rammehjørne april 05, LC Den viste halbygning er opbygget af en række stålrammer med en koorogeret stålplade som tegdækning. Stålpladen fungerer som stiv skive i tagkonstruktionen.
Kipning, momentpåvirket søjle og rammehjørne april 05, LC Den viste halbygning er opbygget af en række stålrammer med en koorogeret stålplade som tegdækning. Stålpladen fungerer som stiv skive i tagkonstruktionen.
Betonkonstruktioner, 4 (Deformationsberegninger og søjler)
 Christian Frier Aalborg Universitet 006 Betonkonstruktioner, 4 (Deformationsberegninger og søjler) Deformationsberegning af bjælker - Urevnet tværsnit - Revnet tværsnit - Deformationsberegninger i praksis
Christian Frier Aalborg Universitet 006 Betonkonstruktioner, 4 (Deformationsberegninger og søjler) Deformationsberegning af bjælker - Urevnet tværsnit - Revnet tværsnit - Deformationsberegninger i praksis
DS/EN 1993-1-1 DK NA:2010
 Nationalt Anneks til Eurocode 3: Stålkonstruktioner Del 1-1: Generelle regler samt regler for bygningskonstruktioner Forord Dette nationale anneks (NA) er en sammenskrivning af EN 1993-1-1 DK NA:2007 og
Nationalt Anneks til Eurocode 3: Stålkonstruktioner Del 1-1: Generelle regler samt regler for bygningskonstruktioner Forord Dette nationale anneks (NA) er en sammenskrivning af EN 1993-1-1 DK NA:2007 og
Centralt belastede søjler med konstant tværsnit
 Centralt belastede søjler med konstant tværsnit Af Jimmy Lauridsen Indhold 1 Den kritiske bærevene... 1 1.1 Elasticitetsmodulet... 2 1.2 Inertimomentet... 4 1.3 Søjlelængde... 8 1 Den kritiske bæreevne
Centralt belastede søjler med konstant tværsnit Af Jimmy Lauridsen Indhold 1 Den kritiske bærevene... 1 1.1 Elasticitetsmodulet... 2 1.2 Inertimomentet... 4 1.3 Søjlelængde... 8 1 Den kritiske bæreevne
NOTAT BEREGNING AF JORDTRYK VHA EC6DESIGN.COM. ÆKVIVALENT ENSFORDELT LAST
 pdc/sol NOTAT BEREGNING AF JORDTRYK VHA EC6DESIGN.COM. ÆKVIVALENT ENSFORDELT LAST Teknologiparken Kongsvang Allé 29 8000 Aarhus C 72 20 20 00 [email protected] www.teknologisk.dk Indledning I dette notat
pdc/sol NOTAT BEREGNING AF JORDTRYK VHA EC6DESIGN.COM. ÆKVIVALENT ENSFORDELT LAST Teknologiparken Kongsvang Allé 29 8000 Aarhus C 72 20 20 00 [email protected] www.teknologisk.dk Indledning I dette notat
Brøns Maskinforretning Nyt domicil på Hovedvejen i Brøns Projektering af en ny maskinhal i Brøns Statiske beregninger
 Brøns Maskinforretning Nyt domicil på Hovedvejen i Brøns Projektering af en ny maskinhal i Brøns Statiske beregninger Aalborg Universitet Esbjerg Shahyan Haji - Diplomingeniørprojekt Den 7. januar 2016
Brøns Maskinforretning Nyt domicil på Hovedvejen i Brøns Projektering af en ny maskinhal i Brøns Statiske beregninger Aalborg Universitet Esbjerg Shahyan Haji - Diplomingeniørprojekt Den 7. januar 2016
DS/EN DK NA:2014 v2
 DS/EN 1993-1-1 DK NA:2014 Nationalt anneks til Eurocode 3: Stålkonstruktioner Del 1-1: Generelle regler samt regler for bygningskonstruktioner Forord Dette nationale anneks (NA) er en revision af DS/EN
DS/EN 1993-1-1 DK NA:2014 Nationalt anneks til Eurocode 3: Stålkonstruktioner Del 1-1: Generelle regler samt regler for bygningskonstruktioner Forord Dette nationale anneks (NA) er en revision af DS/EN
Konstruktionsmæssige forhold med 3D betonprint
 Konstruktionsmæssige forhold med 3D betonprint Eksisterende printprincipper og deres statiske muligheder og begrænsninger v. Kåre Flindt Jørgensen, NCC Danmark A/S 1 Vægprincipper Kantvægge V-gitret væg
Konstruktionsmæssige forhold med 3D betonprint Eksisterende printprincipper og deres statiske muligheder og begrænsninger v. Kåre Flindt Jørgensen, NCC Danmark A/S 1 Vægprincipper Kantvægge V-gitret væg
Søjler og vægge Centralt og excentrisk belastede. Per Goltermann
 Søjler og vægge Centralt og excentrisk belastede Per Goltermann Søjler: De små og ret almindelige Søjler i kontorbyggeri (bygning 101). Præfab vægelementer i boligblok Søjler under bro (Skovdiget). Betonkonstruktioner
Søjler og vægge Centralt og excentrisk belastede Per Goltermann Søjler: De små og ret almindelige Søjler i kontorbyggeri (bygning 101). Præfab vægelementer i boligblok Søjler under bro (Skovdiget). Betonkonstruktioner
Bærende konstruktion Vejledning i beregning af søjle i træ. Fremgangsmåde efter gennemført undervisning med PowerPoint.
 Bærende konstruktion Fremgangsmåde efter gennemført undervisning med PowerPoint. Jens Sørensen 21-05-2010 Indholdsfortegnelse INDHOLDSFORTEGNELSE... 2 FORORD... 3 BAGGRUND... 4 DET GENNEMGÅENDE EKSEMPEL...
Bærende konstruktion Fremgangsmåde efter gennemført undervisning med PowerPoint. Jens Sørensen 21-05-2010 Indholdsfortegnelse INDHOLDSFORTEGNELSE... 2 FORORD... 3 BAGGRUND... 4 DET GENNEMGÅENDE EKSEMPEL...
Program lektion Indre kræfter i plane konstruktioner Snitkræfter
 Tektonik Program lektion 4 12.30-13.15 Indre kræfter i plane konstruktioner 13.15 13.30 Pause 13.30 14.15 Tøjninger og spændinger Spændinger i plan bjælke Deformationer i plan bjælke Kursusholder Poul
Tektonik Program lektion 4 12.30-13.15 Indre kræfter i plane konstruktioner 13.15 13.30 Pause 13.30 14.15 Tøjninger og spændinger Spændinger i plan bjælke Deformationer i plan bjælke Kursusholder Poul
BEREGNING AF U-TVÆRSNIT SOM ET KOMPLEKST TVÆRSNIT
 Indledning BEREGNING AF U-TVÆRSNIT SOM ET KOMPLEKST TVÆRSNIT Teknologiparken Kongsvang Allé 29 8000 Aarhus C 72 20 20 00 [email protected] www.teknologisk.dk I dette notat gennemregnes som eksempel et
Indledning BEREGNING AF U-TVÆRSNIT SOM ET KOMPLEKST TVÆRSNIT Teknologiparken Kongsvang Allé 29 8000 Aarhus C 72 20 20 00 [email protected] www.teknologisk.dk I dette notat gennemregnes som eksempel et
Lodret belastet muret væg efter EC6
 Notat Lodret belastet muret væg efter EC6 EC6 er den europæiske murværksnorm også benævnt DS/EN 1996-1-1:006 Programmodulet "Lodret belastet muret væg efter EC6" kan beregne en bærende væg som enten kan
Notat Lodret belastet muret væg efter EC6 EC6 er den europæiske murværksnorm også benævnt DS/EN 1996-1-1:006 Programmodulet "Lodret belastet muret væg efter EC6" kan beregne en bærende væg som enten kan
Indhold. B Skitseforslag A 13 B.1 Dimensionering af ramme i forslag A C Skitseforslag B 15 C.1 Dimensionering af søjle...
 Indhold A Laster og lastkombinationer 1 A.1 Karakteristiske laster................................ 1 A.1.1 Karakteristisk egenlast........................... 1 A.1.2 Karakteristisk nyttelast..........................
Indhold A Laster og lastkombinationer 1 A.1 Karakteristiske laster................................ 1 A.1.1 Karakteristisk egenlast........................... 1 A.1.2 Karakteristisk nyttelast..........................
Eftervisning af bygningens stabilitet
 Bilag A Eftervisning af bygningens stabilitet I det følgende afsnit eftervises, hvorvidt bygningens bærende konstruktioner har tilstrækkelig stabilitet til at optage de laster, der påvirker bygningen.
Bilag A Eftervisning af bygningens stabilitet I det følgende afsnit eftervises, hvorvidt bygningens bærende konstruktioner har tilstrækkelig stabilitet til at optage de laster, der påvirker bygningen.
Redegørelse for den statiske dokumentation
 Redegørelse for den statiske dokumentation Udvidelse af 3stk. dørhuller - Frederiksberg Allé Byggepladsens adresse: Frederiksberg Allé 1820 Matrikelnr.: 25ed AB Clausen A/S side 2 af 15 INDHOLD side A1
Redegørelse for den statiske dokumentation Udvidelse af 3stk. dørhuller - Frederiksberg Allé Byggepladsens adresse: Frederiksberg Allé 1820 Matrikelnr.: 25ed AB Clausen A/S side 2 af 15 INDHOLD side A1
VEJDIREKTORATET FLYTBAR MAST TIL MONTAGE AF KAMERA
 VEJDIREKTORATET FLYTBAR MAST TIL MONTAGE AF KAMERA TL-Engineering oktober 2009 Indholdsfortegnelse 1. Generelt... 3 2. Grundlag... 3 2.1. Standarder... 3 3. Vindlast... 3 4. Flytbar mast... 4 5. Fodplade...
VEJDIREKTORATET FLYTBAR MAST TIL MONTAGE AF KAMERA TL-Engineering oktober 2009 Indholdsfortegnelse 1. Generelt... 3 2. Grundlag... 3 2.1. Standarder... 3 3. Vindlast... 3 4. Flytbar mast... 4 5. Fodplade...
Bærende konstruktion Vejledning i beregning af søjle i stål. Fremgangsmåde efter gennemført undervisning med PowerPoint.
 Bærende konstruktion Fremgangsmåde efter gennemført undervisning med PowerPoint. Jens Sørensen 28-05-2010 Indholdsfortegnelse INDHOLDSFORTEGNELSE... 2 FORORD... 3 BAGGRUND... 4 DET GENNEMGÅENDE EKSEMPEL...
Bærende konstruktion Fremgangsmåde efter gennemført undervisning med PowerPoint. Jens Sørensen 28-05-2010 Indholdsfortegnelse INDHOLDSFORTEGNELSE... 2 FORORD... 3 BAGGRUND... 4 DET GENNEMGÅENDE EKSEMPEL...
11/3/2002. Statik og bygningskonstruktion Program lektion Tøjninger og spændinger. Introduktion. Tøjninger og spændinger
 Statik og bygningskonstruktion rogram lektion 9 8.30-9.15 Tøjninger og spændinger 9.15 9.30 ause 9.30 10.15 Spændinger i plan bjælke Deformationer i plan bjælke 10.15 10.45 ause 10.45 1.00 Opgaveregning
Statik og bygningskonstruktion rogram lektion 9 8.30-9.15 Tøjninger og spændinger 9.15 9.30 ause 9.30 10.15 Spændinger i plan bjælke Deformationer i plan bjælke 10.15 10.45 ause 10.45 1.00 Opgaveregning
A. Konstruktionsdokumentation
 A. Konstruktionsdokumentation A.. Statiske Beregninger-konstruktionsafsnit, Betonelementer Juni 018 : 01.06.016 A.. Statiske Beregninger-konstruktionsafsnit, Betonelementer Rev. : 0.06.018 Side /13 SBi
A. Konstruktionsdokumentation A.. Statiske Beregninger-konstruktionsafsnit, Betonelementer Juni 018 : 01.06.016 A.. Statiske Beregninger-konstruktionsafsnit, Betonelementer Rev. : 0.06.018 Side /13 SBi
I den gældende udgave af EN (6.17) angives det, at søjlevirkning kan optræde
 Lodret belastet muret væg Indledning Modulet anvender beregningsmodellen angivet i EN 1996-1-1, anneks G. Modulet anvendes, når der i et vægfelt er mulighed for (risiko for) 2. ordens effekter (dvs. søjlevirkning).
Lodret belastet muret væg Indledning Modulet anvender beregningsmodellen angivet i EN 1996-1-1, anneks G. Modulet anvendes, når der i et vægfelt er mulighed for (risiko for) 2. ordens effekter (dvs. søjlevirkning).
Program lektion Indre kræfter i plane konstruktioner Snitkræfter Indre kræfter i plane konstruktioner Snitkræfter.
 Tektonik Program lektion 4 8.15-9.00 Indre kræfter i plane konstruktioner 9.00 9.15 Pause 9.15 10.00 Indre kræfter i plane konstruktioner. Opgaver 10.00 10.15 Pause 10.15 12.00 Tøjninger og spændinger
Tektonik Program lektion 4 8.15-9.00 Indre kræfter i plane konstruktioner 9.00 9.15 Pause 9.15 10.00 Indre kræfter i plane konstruktioner. Opgaver 10.00 10.15 Pause 10.15 12.00 Tøjninger og spændinger
Betonkonstruktioner Lektion 1
 Betonkonstruktioner Lektion 1 Hans Ole Lund Christiansen [email protected] Det Tekniske Fakultet 1 Materialeegenskaber Det Tekniske Fakultet 2 Beton Beton Består af: - Vand - Cement - Sand/grus -Sten Det
Betonkonstruktioner Lektion 1 Hans Ole Lund Christiansen [email protected] Det Tekniske Fakultet 1 Materialeegenskaber Det Tekniske Fakultet 2 Beton Beton Består af: - Vand - Cement - Sand/grus -Sten Det
En sædvanlig hulmur som angivet i figur 1 betragtes. Kun bagmuren gennemregnes.
 Tværbelastet rektangulær væg En sædvanlig hulmur som angivet i figur 1 betragtes. Kun bagmuren gennemregnes. Den samlede vindlast er 1,20 kn/m 2. Formuren regnes udnyttet 100 % og optager 0,3 kn/m 2. Bagmuren
Tværbelastet rektangulær væg En sædvanlig hulmur som angivet i figur 1 betragtes. Kun bagmuren gennemregnes. Den samlede vindlast er 1,20 kn/m 2. Formuren regnes udnyttet 100 % og optager 0,3 kn/m 2. Bagmuren
Deformation af stålbjælker
 Deformation af stålbjælker Af Jimmy Lauridsen Indhold 1 Nedbøjning af bjælker... 1 1.1 Elasticitetsmodulet... 2 1.2 Inertimomentet... 4 2 Formelsamling for typiske systemer... 8 1 Nedbøjning af bjælker
Deformation af stålbjælker Af Jimmy Lauridsen Indhold 1 Nedbøjning af bjælker... 1 1.1 Elasticitetsmodulet... 2 1.2 Inertimomentet... 4 2 Formelsamling for typiske systemer... 8 1 Nedbøjning af bjælker
DS/EN 15512 DK NA:2011
 DS/EN 15512 DK NA:2011 Nationalt anneks til Stationære opbevaringssystemer af stål Justerbare pallereolsystemer Principper for dimensionering. Forord Dette nationale anneks (NA) er det første danske NA
DS/EN 15512 DK NA:2011 Nationalt anneks til Stationære opbevaringssystemer af stål Justerbare pallereolsystemer Principper for dimensionering. Forord Dette nationale anneks (NA) er det første danske NA
Mujtaba og Farid Integralregning 06-08-2011
 Indholdsfortegnelse Integral regning:... 2 Ubestemt integral:... 2 Integrationsprøven:... 3 1) Integration af potensfunktioner:... 3 2) Integration af sum og Differens:... 3 3) Integration ved Multiplikation
Indholdsfortegnelse Integral regning:... 2 Ubestemt integral:... 2 Integrationsprøven:... 3 1) Integration af potensfunktioner:... 3 2) Integration af sum og Differens:... 3 3) Integration ved Multiplikation
Dimensionering af samling
 Bilag A Dimensionering af samling I det efterfølgende afsnit redegøres for dimensioneringen af en lodret støbeskelssamling mellem to betonelementer i tværvæggen. På nedenstående gur ses, hvorledes tværvæggene
Bilag A Dimensionering af samling I det efterfølgende afsnit redegøres for dimensioneringen af en lodret støbeskelssamling mellem to betonelementer i tværvæggen. På nedenstående gur ses, hvorledes tværvæggene
Modulet beregner en trådbinders tryk- og trækbæreevne under hensyntagen til:
 Binder Modulet beregner en trådbinders tryk- og trækbæreevne under hensyntagen til: Differensbevægelse (0,21 mm/m målt fra estimeret tyngdepunkt ved sokkel til fjerneste binder) Forhåndskrumning (Sættes
Binder Modulet beregner en trådbinders tryk- og trækbæreevne under hensyntagen til: Differensbevægelse (0,21 mm/m målt fra estimeret tyngdepunkt ved sokkel til fjerneste binder) Forhåndskrumning (Sættes
Formler & algebra - Fase 2 Omskriv & beregn med variable
 Navn: Klasse: Formler algebra - Fase Omskriv beregn med variable Vurdering fra til 5 (hvor 5 er højst) Læringsmål Selv Lærer Beviser og forslag til forbedring. Jeg kan opstille en linjes ligning, når jeg
Navn: Klasse: Formler algebra - Fase Omskriv beregn med variable Vurdering fra til 5 (hvor 5 er højst) Læringsmål Selv Lærer Beviser og forslag til forbedring. Jeg kan opstille en linjes ligning, når jeg
Betonkonstruktioner Lektion 3
 Betonkonstruktioner Lektion 3 Hans Ole Lund Christiansen [email protected] 1 Teori fra 1. og. lektion Hvad er et stift plastisk materiale? Hvad er forskellen på en elastisk og plastisk spændingsfordeling?
Betonkonstruktioner Lektion 3 Hans Ole Lund Christiansen [email protected] 1 Teori fra 1. og. lektion Hvad er et stift plastisk materiale? Hvad er forskellen på en elastisk og plastisk spændingsfordeling?
BEREGNING AF O-TVÆRSNIT SOM ET KOMPLEKST TVÆRSNIT
 Indledning BEREGNING AF O-TVÆRSNIT SOM ET KOMPLEKST TVÆRSNIT Teknologiparken Kongsvang Allé 29 8000 Aarhus C 72 20 20 00 [email protected] www.teknologisk.dk I dette notat gennemregnes som eksempel et
Indledning BEREGNING AF O-TVÆRSNIT SOM ET KOMPLEKST TVÆRSNIT Teknologiparken Kongsvang Allé 29 8000 Aarhus C 72 20 20 00 [email protected] www.teknologisk.dk I dette notat gennemregnes som eksempel et
Stabilitet af rammer - Deformationsmetoden
 Stabilitet af rammer - Deformationsmetoden Lars Damkilde Institut for Bærende Konstruktioner og Materialer Danmarks Tekniske Universitet DK-2800 Lyngby September 1998 Resumé Rapporten omhandler beregning
Stabilitet af rammer - Deformationsmetoden Lars Damkilde Institut for Bærende Konstruktioner og Materialer Danmarks Tekniske Universitet DK-2800 Lyngby September 1998 Resumé Rapporten omhandler beregning
Statiske beregninger for mastetelt type D=28m
 Statiske beregninger for mastetelt type D=28m Beregningsanalyse Studsgaard A/S Projekt nr. 2005040101 Version 1 Udarbejdet af HL, MP & MAX Kontrolleret af JS Godkendt af JS 1 Indholdsfortegnelse: Side
Statiske beregninger for mastetelt type D=28m Beregningsanalyse Studsgaard A/S Projekt nr. 2005040101 Version 1 Udarbejdet af HL, MP & MAX Kontrolleret af JS Godkendt af JS 1 Indholdsfortegnelse: Side
Betonkonstruktioner Lektion 4
 Betonkonstruktioner Lektion 4 Hans Ole Lund Christiansen [email protected] Fault of Engineering 1 Bøjning med forskdning -Brudtilstand Fault of Engineering 2 Introduktion til Diagonaltrkmetoden I forbindelse
Betonkonstruktioner Lektion 4 Hans Ole Lund Christiansen [email protected] Fault of Engineering 1 Bøjning med forskdning -Brudtilstand Fault of Engineering 2 Introduktion til Diagonaltrkmetoden I forbindelse
Bedste rette linje ved mindste kvadraters metode
 1/9 Bedste rette linje ved mindste kvadraters metode - fra www.borgeleo.dk Figur 1: Tre datapunkter og den bedste rette linje bestemt af A, B og C Målepunkter og bedste rette linje I ovenstående koordinatsystem
1/9 Bedste rette linje ved mindste kvadraters metode - fra www.borgeleo.dk Figur 1: Tre datapunkter og den bedste rette linje bestemt af A, B og C Målepunkter og bedste rette linje I ovenstående koordinatsystem
Beton- konstruktioner. Beton- konstruktioner. efter DS/EN 1992-1-1. efter DS/EN 1992-1-1. Bjarne Chr. Jensen. 2. udgave. Nyt Teknisk Forlag
 2. UDGAVE ISBN 978-87-571-2766-9 9 788757 127669 varenr. 84016-1 konstruktioner efter DS/EN 1992-1-1 Betonkonstruktioner efter DS/EN 1992-1-1 behandler beregninger af betonkonstruktioner efter den nye
2. UDGAVE ISBN 978-87-571-2766-9 9 788757 127669 varenr. 84016-1 konstruktioner efter DS/EN 1992-1-1 Betonkonstruktioner efter DS/EN 1992-1-1 behandler beregninger af betonkonstruktioner efter den nye
Kursusgang 9: Introduktion til elementmetodeprogrammet Abaqus første del
 1 elementmetodeprogrammet Abaqus første del Kursus: Statik IV Uddannelse: 5. semester, bachelor/diplomingeniøruddannelsen i konstruktion Forelæser: Johan Clausen Institut for Byggeri og Anlæg Efterår,
1 elementmetodeprogrammet Abaqus første del Kursus: Statik IV Uddannelse: 5. semester, bachelor/diplomingeniøruddannelsen i konstruktion Forelæser: Johan Clausen Institut for Byggeri og Anlæg Efterår,
STATISKE BEREGNINGER vedrørende stålbjælker
 Willemoesgade 2 5610 Assens Mobil 22 13 06 44 E-mail [email protected] STATISKE BEREGNINGER vedrørende stålbjælker Stefansgade 65 3 TV, 2200 København N Sag Nr.: 15.342 Dato: 17-11-2015 Rev.: 04-12-2015
Willemoesgade 2 5610 Assens Mobil 22 13 06 44 E-mail [email protected] STATISKE BEREGNINGER vedrørende stålbjælker Stefansgade 65 3 TV, 2200 København N Sag Nr.: 15.342 Dato: 17-11-2015 Rev.: 04-12-2015
Om- og tilbygning af Forum Faaborg i Faaborg-Midtfyn kommune
 Om- og tilbygning af Forum Faaborg i Faaborg-Midtfyn kommune Projektgrundlag Anders Malund Dammark Jensen 10-01-2017 2 Titel: Om- og tilbygning af Forum Faaborg i Faaborg-Midtfyn kommune Semester: 7. semester
Om- og tilbygning af Forum Faaborg i Faaborg-Midtfyn kommune Projektgrundlag Anders Malund Dammark Jensen 10-01-2017 2 Titel: Om- og tilbygning af Forum Faaborg i Faaborg-Midtfyn kommune Semester: 7. semester
DS/EN DK NA:2015
 Nationalt anneks til Eurocode 3: Stålkonstruktioner Del 1-1: Generelle regler samt regler for bygningskonstruktioner Forord Dette nationale anneks (NA) er en revision af DS/EN 1993-1-1 DK NA:2014 og erstatter
Nationalt anneks til Eurocode 3: Stålkonstruktioner Del 1-1: Generelle regler samt regler for bygningskonstruktioner Forord Dette nationale anneks (NA) er en revision af DS/EN 1993-1-1 DK NA:2014 og erstatter
Profil dimension, valgt: Valgt profil: HEB 120 Ændres med pilene
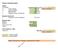 Simpelt undertsøttet bjælke Indtast: Anvendelse: Konsekvensklasse, CC2 F y Lodret nyttelast 600 [kg] Ændres med pilene F z Vandret nyttelast 200 [kg] L Bjælkelængde 5.500 [mm] a Længde fra ende 1 til lastpunkt
Simpelt undertsøttet bjælke Indtast: Anvendelse: Konsekvensklasse, CC2 F y Lodret nyttelast 600 [kg] Ændres med pilene F z Vandret nyttelast 200 [kg] L Bjælkelængde 5.500 [mm] a Længde fra ende 1 til lastpunkt
TUNGE SKILLEVÆGGE PÅ FLERE LAG TRYKFAST ISOLERING. Input Betondæk Her angives tykkelsen på dækket samt den aktuelle karakteristiske trykstyrke.
 pdc/jnk/sol TUNGE SKILLEVÆGGE PÅ FLERE LAG TRYKFAST ISOLERING Indledning Teknologisk Institut, byggeri har for Plastindustrien i Danmark udført dette projekt vedrørende bestemmelse af bæreevne for tunge
pdc/jnk/sol TUNGE SKILLEVÆGGE PÅ FLERE LAG TRYKFAST ISOLERING Indledning Teknologisk Institut, byggeri har for Plastindustrien i Danmark udført dette projekt vedrørende bestemmelse af bæreevne for tunge
A. Konstruktionsdokumentation Initialer : MOHI A2.1 Statiske beregninger - Konstruktionsafsnit Fag : BÆR. KONST. Dato : 08-06-2012 Side : 1 af 141
 Side : 1 af 141 Indhold A2.2 Statiske beregninger Konstruktionsafsnit 2 1. Dimensionering af bjælke-forbindelsesgangen. 2 1.1 Dimensionering af bjælke i modulline G3 i Tagkonstruktionen. 2 1.2 Dimensionering
Side : 1 af 141 Indhold A2.2 Statiske beregninger Konstruktionsafsnit 2 1. Dimensionering af bjælke-forbindelsesgangen. 2 1.1 Dimensionering af bjælke i modulline G3 i Tagkonstruktionen. 2 1.2 Dimensionering
Bøjning i brudgrænsetilstanden. Per Goltermann
 Bøjning i brudgrænsetilstanden Per Goltermann Lektionens indhold 1. De grundlæggende antagelser/regler 2. Materialernes arbejdskurver 3. Bøjning: De forskellige stadier 4. Ren bøjning i simpelt tværsnit
Bøjning i brudgrænsetilstanden Per Goltermann Lektionens indhold 1. De grundlæggende antagelser/regler 2. Materialernes arbejdskurver 3. Bøjning: De forskellige stadier 4. Ren bøjning i simpelt tværsnit
DS/EN 1520 DK NA:2011
 Nationalt anneks til DS/EN 1520:2011 Præfabrikerede armerede elementer af letbeton med lette tilslag og åben struktur med bærende eller ikke bærende armering Forord Dette nationale anneks (NA) knytter
Nationalt anneks til DS/EN 1520:2011 Præfabrikerede armerede elementer af letbeton med lette tilslag og åben struktur med bærende eller ikke bærende armering Forord Dette nationale anneks (NA) knytter
Løsning til prøveeksamen 1
 IMM - DTU 020 Probability 2006-2-8 BFN/bfn Løsning til prøveeksamen Spørgsmål ) For en indikatorvariabel I A for hændelsen A gælder E(I A ) = P(A) (se for eksemepl side 68). Således er E(X) = P(N ) = =
IMM - DTU 020 Probability 2006-2-8 BFN/bfn Løsning til prøveeksamen Spørgsmål ) For en indikatorvariabel I A for hændelsen A gælder E(I A ) = P(A) (se for eksemepl side 68). Således er E(X) = P(N ) = =
Eksempel Boltet bjælke-søjlesamling
 Eksempel Boltet bjælke-søjlesamling Dette eksemplet bygger på beregningsvejledningerne i afsnit 6 om bærende samlinger i H- eller I-profiler. En momentpåvirket samling mellem en HEB-søjle og en IPE-bjælke
Eksempel Boltet bjælke-søjlesamling Dette eksemplet bygger på beregningsvejledningerne i afsnit 6 om bærende samlinger i H- eller I-profiler. En momentpåvirket samling mellem en HEB-søjle og en IPE-bjælke
Dimensionering af statisk belastede svejste samlinger efter EUROCODE No. 9
 Dokument: SASAK-RAP-DE-AKS-FI-0003-01 Dimensionering af statisk belastede svejste samlinger efter EUROCODE No. 9 SASAK Projekt 1 - Designregler Lars Tofte Johansen FORCE Instituttet, september 2001 Dimensionering
Dokument: SASAK-RAP-DE-AKS-FI-0003-01 Dimensionering af statisk belastede svejste samlinger efter EUROCODE No. 9 SASAK Projekt 1 - Designregler Lars Tofte Johansen FORCE Instituttet, september 2001 Dimensionering
Diffusionsligningen. Fællesprojekt for FY520 og MM502. Marts Hans J. Munkholm og Paolo Sibani. Besvarelse fra Hans J.
 Diffusionsligningen Fællesprojekt for FY50 og MM50 Marts 009 Hans J. Munkholm og Paolo Sibani Besvarelse fra Hans J. Munkholm 1 (a) Lad [x, x + x] være et lille delinterval af [a, b]. Den masse, der er
Diffusionsligningen Fællesprojekt for FY50 og MM50 Marts 009 Hans J. Munkholm og Paolo Sibani Besvarelse fra Hans J. Munkholm 1 (a) Lad [x, x + x] være et lille delinterval af [a, b]. Den masse, der er
Projektering af en ny fabrikationshal i Kjersing
 Projektering af en ny fabrikationshal i Kjersing Dokumentationsrapport Stålkonstruktioner B4-2-F12-H130 Christian Rompf, Mikkel Schmidt, Sonni Drangå og Maria Larsen Aalborg Universitet Esbjerg B4-2-F12-H130
Projektering af en ny fabrikationshal i Kjersing Dokumentationsrapport Stålkonstruktioner B4-2-F12-H130 Christian Rompf, Mikkel Schmidt, Sonni Drangå og Maria Larsen Aalborg Universitet Esbjerg B4-2-F12-H130
DS/EN DK NA:2013
 COPYRIGHT Danish Standards Foundation. NOT FOR COMMERCIAL USE OR REPRODUCTION. Nationalt anneks til Stationære opbevaringssystemer af stål Justerbare pallereolsystemer Principper for dimensionering Forord
COPYRIGHT Danish Standards Foundation. NOT FOR COMMERCIAL USE OR REPRODUCTION. Nationalt anneks til Stationære opbevaringssystemer af stål Justerbare pallereolsystemer Principper for dimensionering Forord
PRAKTISK PROJEKTERING EKSEMPEL
 PRAKTISK PROJEKTERING EKSEMPEL FORUDSÆTNINGER Dette eksempel er tilrettet fra et kursus afholdt i 2014: Fra arkitekten fås: Plantegning, opstalt, snit (og detaljer). Tegninger fra HusCompagniet anvendes
PRAKTISK PROJEKTERING EKSEMPEL FORUDSÆTNINGER Dette eksempel er tilrettet fra et kursus afholdt i 2014: Fra arkitekten fås: Plantegning, opstalt, snit (og detaljer). Tegninger fra HusCompagniet anvendes
Analytisk geometri. Et simpelt eksempel på dette er en ret linje. Som bekendt kan en ret linje skrives på formen
 Analtisk geometri Mike Auerbach Odense 2015 Den klassiske geometri beskæftiger sig med alle mulige former for figurer: Linjer, trekanter, cirkler, parabler, ellipser osv. I den analtiske geometri lægger
Analtisk geometri Mike Auerbach Odense 2015 Den klassiske geometri beskæftiger sig med alle mulige former for figurer: Linjer, trekanter, cirkler, parabler, ellipser osv. I den analtiske geometri lægger
Redegørelse for den statiske dokumentation Nedrivning af bærende væg - Lysbrovej 13
 Redegørelse for den statiske dokumentation Nedrivning af bærende væg - Lysbrovej 13 Dato: 22. Januar 2015 Byggepladsens adresse: Lysbrovej 13 Matr. nr. 6af AB Clausen A/S STATISK DUMENTATION Adresse: Lysbrovej
Redegørelse for den statiske dokumentation Nedrivning af bærende væg - Lysbrovej 13 Dato: 22. Januar 2015 Byggepladsens adresse: Lysbrovej 13 Matr. nr. 6af AB Clausen A/S STATISK DUMENTATION Adresse: Lysbrovej
Opgave 1. Spørgsmål 4. Bestem reaktionerne i A og B. Bestem bøjningsmomentet i B og C. Bestem hvor forskydningskraften i bjælken er 0.
 alborg Universitet Esbjerg Side 1 af 4 sider Skriftlig røve den 6. juni 2011 Kursus navn: Grundlæggende Statik og Styrkelære, 2. semester Tilladte hjælemidler: lle Vægtning : lle ogaver vægter som udgangsunkt
alborg Universitet Esbjerg Side 1 af 4 sider Skriftlig røve den 6. juni 2011 Kursus navn: Grundlæggende Statik og Styrkelære, 2. semester Tilladte hjælemidler: lle Vægtning : lle ogaver vægter som udgangsunkt
Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 2016
 Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
11/3/2002. Statik og bygningskonstruktion Program lektion Søjlen. Søjlen. Søjlen Pause
 Statik og bygningskonstruktion Program lektion 10 8.30-9.15 9.15 9.30 Pause 9.30 10.15 af bygningskonstruktioner 10.15 10.45 Pause 10.45 1.00 Opgaveregning Kursusholder Poul Henning Kirkegaard, institut
Statik og bygningskonstruktion Program lektion 10 8.30-9.15 9.15 9.30 Pause 9.30 10.15 af bygningskonstruktioner 10.15 10.45 Pause 10.45 1.00 Opgaveregning Kursusholder Poul Henning Kirkegaard, institut
MURVÆRKSPROJEKTERING VER. 4.0 SBI - MUC DOKUMENTATION Side 1
 DOKUMENTATION Side 1 Modulet Kombinationsvægge Indledning Modulet arbejder på et vægfelt uden åbninger, og modulets opgave er At fordele vandret last samt topmomenter mellem bagvæg og formur At bestemme
DOKUMENTATION Side 1 Modulet Kombinationsvægge Indledning Modulet arbejder på et vægfelt uden åbninger, og modulets opgave er At fordele vandret last samt topmomenter mellem bagvæg og formur At bestemme
Algebra - Teori og problemløsning
 Algebra - Teori og problemløsning, januar 05, Kirsten Rosenkilde. Algebra - Teori og problemløsning Kapitel -3 giver en grundlæggende introduktion til at omskrive udtryk, faktorisere og løse ligningssystemer.
Algebra - Teori og problemløsning, januar 05, Kirsten Rosenkilde. Algebra - Teori og problemløsning Kapitel -3 giver en grundlæggende introduktion til at omskrive udtryk, faktorisere og løse ligningssystemer.
TUNGE SKILLEVÆGGE PÅ TRYKFAST ISOLERING BEREGNINGSMODELLER
 pdc/sol TUNGE SKILLEVÆGGE PÅ TRYKFAST ISOLERING BEREGNINGSMODELLER Indledning Teknologisk Institut, byggeri har for EPS sektionen under Plastindustrien udført dette projekt vedrørende anvendelse af trykfast
pdc/sol TUNGE SKILLEVÆGGE PÅ TRYKFAST ISOLERING BEREGNINGSMODELLER Indledning Teknologisk Institut, byggeri har for EPS sektionen under Plastindustrien udført dette projekt vedrørende anvendelse af trykfast
STATISK DOKUMENTATION
 STATISK DOKUMENTATION for Ombygning Cæciliavej 22, 2500 Valby Matrikelnummer: 1766 Beregninger udført af Lars Holm Regnestuen Rådgivende Ingeniører Oversigt Nærværende statiske dokumentation indeholder:
STATISK DOKUMENTATION for Ombygning Cæciliavej 22, 2500 Valby Matrikelnummer: 1766 Beregninger udført af Lars Holm Regnestuen Rådgivende Ingeniører Oversigt Nærværende statiske dokumentation indeholder:
Projektering af en ny fabrikationshal i Kjersing
 Projektering af en ny fabrikationshal i Kjersing Dokumentationsrapport Trækonstruktioner B4-2-F12-H130 Christian Rompf, Mikkel Schmidt, Sonni Drangå og Maria Larsen Aalborg Universitet Esbjerg B4-2-F12-H130
Projektering af en ny fabrikationshal i Kjersing Dokumentationsrapport Trækonstruktioner B4-2-F12-H130 Christian Rompf, Mikkel Schmidt, Sonni Drangå og Maria Larsen Aalborg Universitet Esbjerg B4-2-F12-H130
Kursusgang 10: Introduktion til elementmetodeprogrammet Abaqus anden del
 1 elementmetodeprogrammet Abaqus anden del Kursus: Statik IV Uddannelse: 5. semester, bachelor/diplomingeniøruddannelsen i konstruktion Forelæser: Johan Clausen Institut for Byggeri og Anlæg Efterår, 2010
1 elementmetodeprogrammet Abaqus anden del Kursus: Statik IV Uddannelse: 5. semester, bachelor/diplomingeniøruddannelsen i konstruktion Forelæser: Johan Clausen Institut for Byggeri og Anlæg Efterår, 2010
Besvarelser til Calculus Ordinær Eksamen Juni 2019
 Besvarelser til Calculus Ordinær Eksamen - 14. Juni 2019 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 14. Juni 2019 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
INGENIØRHØJSKOLEN I ÅRHUS Bygningsteknik Bygningsdesign. Stålkonstruktioner BK301
 INGENIØRHØJSKOLEN I ÅRHUS Bygningsteknik Bygningsdesign Stålkonstruktioner Januar 2009 BK301 Peter Ehlers Indhold Indhold side 1. Materialer: Stål 3 Certifikater 5 Svejseelektroder 9 Svejsetråd 11 2. Plastisk
INGENIØRHØJSKOLEN I ÅRHUS Bygningsteknik Bygningsdesign Stålkonstruktioner Januar 2009 BK301 Peter Ehlers Indhold Indhold side 1. Materialer: Stål 3 Certifikater 5 Svejseelektroder 9 Svejsetråd 11 2. Plastisk
Differentialligninger. Ib Michelsen
 Differentialligninger Ib Michelsen Ikast 203 2 Indholdsfortegnelse Indholdsfortegnelse Indholdsfortegnelse...2 Ligninger og løsninger...3 Indledning...3 Lineære differentialligninger af første orden...3
Differentialligninger Ib Michelsen Ikast 203 2 Indholdsfortegnelse Indholdsfortegnelse Indholdsfortegnelse...2 Ligninger og løsninger...3 Indledning...3 Lineære differentialligninger af første orden...3
Stabilitet - Programdokumentation
 Make IT simple 1 Stabilitet - Programdokumentation Anvendte betegnelser Vægskive Et rektangulært vægstykke/vægelement i den enkelte etage, som indgår i det lodret bærende og stabiliserende system af vægge
Make IT simple 1 Stabilitet - Programdokumentation Anvendte betegnelser Vægskive Et rektangulært vægstykke/vægelement i den enkelte etage, som indgår i det lodret bærende og stabiliserende system af vægge
Matematisk modellering og numeriske metoder
 Matematisk modellering og numeriske metoder Morten Grud Rasmussen 5. september 2016 1 Ordinære differentialligninger ODE er 1.1 ODE er helt grundlæggende Definition 1.1 (Ordinære differentialligninger).
Matematisk modellering og numeriske metoder Morten Grud Rasmussen 5. september 2016 1 Ordinære differentialligninger ODE er 1.1 ODE er helt grundlæggende Definition 1.1 (Ordinære differentialligninger).
Aalborg Universitet Esbjerg 18. december 2009 Spændings- og deformationsanalyse af perforeret RHS stålprofil Appendiks K Analytiske
 18. december 2009 Spændings- og deformationsanalyse af perforeret RHS stålprofil Appendiks K Analytiske overslagsberegninger Appendiks K Analytiske overslagsberegninger... 3 K-1. Airy s spændingsfunktion
18. december 2009 Spændings- og deformationsanalyse af perforeret RHS stålprofil Appendiks K Analytiske overslagsberegninger Appendiks K Analytiske overslagsberegninger... 3 K-1. Airy s spændingsfunktion
Kapitel 2 Tal og variable
 Tal og variable Uden tal ingen matematik - matematik handler om tal og anvendelse af tal. Matematik beskæftiger sig ikke udelukkende med konkrete problemer fra andre fag, og de konkrete tal fra andre fagområder
Tal og variable Uden tal ingen matematik - matematik handler om tal og anvendelse af tal. Matematik beskæftiger sig ikke udelukkende med konkrete problemer fra andre fag, og de konkrete tal fra andre fagområder
DesignMat Uge 1 Gensyn med forårets stof
 DesignMat Uge 1 Gensyn med forårets stof Preben Alsholm Efterår 2010 1 Hovedpunkter fra forårets pensum 11 Taylorpolynomium Taylorpolynomium Det n te Taylorpolynomium for f med udviklingspunkt x 0 : P
DesignMat Uge 1 Gensyn med forårets stof Preben Alsholm Efterår 2010 1 Hovedpunkter fra forårets pensum 11 Taylorpolynomium Taylorpolynomium Det n te Taylorpolynomium for f med udviklingspunkt x 0 : P
DS/EN DK NA:2013
 Nationalt anneks til Præfabrikerede armerede komponenter af autoklaveret porebeton Forord Dette nationale anneks (NA) er en revision af EN 12602 DK NA:2008 og erstatter dette fra 2013-09-01. Der er foretaget
Nationalt anneks til Præfabrikerede armerede komponenter af autoklaveret porebeton Forord Dette nationale anneks (NA) er en revision af EN 12602 DK NA:2008 og erstatter dette fra 2013-09-01. Der er foretaget
Tillæg 1 til SBI-anvisning 194, 3. udgave: Trækonstruktioner. Forbindelser. 1. udgave, 2005
 Tillæg 1 til SBI-anvisning 194, 3. udgave: Trækonstruktioner Forbindelser 1. udgave, 2005 Tillæg 1 til SBI-anvisning 194, 3. udgave: Trækonstruktioner Forbindelser H. J. Larsen SBi Statens Byggeforskningsinstitut
Tillæg 1 til SBI-anvisning 194, 3. udgave: Trækonstruktioner Forbindelser 1. udgave, 2005 Tillæg 1 til SBI-anvisning 194, 3. udgave: Trækonstruktioner Forbindelser H. J. Larsen SBi Statens Byggeforskningsinstitut
Statik og styrkelære
 Bukserobot Statik og styrkelære Refleksioner over hvilke styrkemæssige udfordringer en given last har på den valgte konstruktion. Hvilke ydre kræfter påvirker konstruktionen og hvor er de placeret Materialer
Bukserobot Statik og styrkelære Refleksioner over hvilke styrkemæssige udfordringer en given last har på den valgte konstruktion. Hvilke ydre kræfter påvirker konstruktionen og hvor er de placeret Materialer
10.3 E-modul. Af Jens Ole Frederiksen og Gitte Normann Munch-Petersen. Betonhåndbogen, 10 Hærdnende og hærdnet beton
 10.3 E-modul Af Jens Ole Frederiksen og Gitte Normann Munch-Petersen Forskellige materialer har forskellige E-moduler. Hvis man fx placerer 15 ton (svarende til 10 typiske mellemklassebiler) oven på en
10.3 E-modul Af Jens Ole Frederiksen og Gitte Normann Munch-Petersen Forskellige materialer har forskellige E-moduler. Hvis man fx placerer 15 ton (svarende til 10 typiske mellemklassebiler) oven på en
Armeringsstål Klasse A eller klasse B? Bjarne Chr. Jensen Side 1. Armeringsstål Klasse A eller klasse B?
 Bjarne Chr. Jensen Side 1 Armeringsstål Klasse A eller klasse B? Bjarne Chr. Jensen 13. august 2007 Bjarne Chr. Jensen Side 2 Introduktion Nærværende lille notat er blevet til på initiativ af direktør
Bjarne Chr. Jensen Side 1 Armeringsstål Klasse A eller klasse B? Bjarne Chr. Jensen 13. august 2007 Bjarne Chr. Jensen Side 2 Introduktion Nærværende lille notat er blevet til på initiativ af direktør
Projektering af Letbanebro over Djurslandmotorvejen. Statiske beregninger
 Projektering af Letbanebro over Djurslandmotorvejen Statiske beregninger Bachelorprojekt Diana Mogensen Aalborg Universitet Esbjerg Den 7. januar 2016 Titelblad Titel: Tema: Bachelorprojekt Uddannelse:
Projektering af Letbanebro over Djurslandmotorvejen Statiske beregninger Bachelorprojekt Diana Mogensen Aalborg Universitet Esbjerg Den 7. januar 2016 Titelblad Titel: Tema: Bachelorprojekt Uddannelse:
DS/EN 1993 FU:2009 Forkortet udgave af Eurocode 3 Stålkonstruktioner
 Forkortet udgave af Eurocode 3 Stålkonstruktioner Forkortet udgave af Eurocode 3 Stålkonstruktioner DANSK STANDARD 2009 Projektnummer M236168 Grafisk tilrettelæggelse: Dansk Standard Omslag: Dansk Standard
Forkortet udgave af Eurocode 3 Stålkonstruktioner Forkortet udgave af Eurocode 3 Stålkonstruktioner DANSK STANDARD 2009 Projektnummer M236168 Grafisk tilrettelæggelse: Dansk Standard Omslag: Dansk Standard
Redegørelse for den statiske dokumentation Nedrivning af bærende væg -Bianco Lunos Allé 8B st tv
 J Redegørelse for den statiske dokumentation Nedrivning af bærende væg -Bianco Lunos Allé 8B st tv Rev. 12-07-2016 Sags nr.: 16-0239 Byggepladsens adresse: Bianco Lunos Allé 8B st tv 1868 Frederiksberg
J Redegørelse for den statiske dokumentation Nedrivning af bærende væg -Bianco Lunos Allé 8B st tv Rev. 12-07-2016 Sags nr.: 16-0239 Byggepladsens adresse: Bianco Lunos Allé 8B st tv 1868 Frederiksberg
Betonkonstruktioner - Lektion 3 - opgave 1
 Betonkonstruktioner - Lektion 3 - opgave Data: bredde flange b 50mm Højde 400mm Rumvægt ρ 4 kn m 3 Længde L 4m q 0 kn R 0kN m q egen ρb.44 kn m M Ed 8 q egen q L 4 RL 4.88 kn m Linjelast for egen vægten
Betonkonstruktioner - Lektion 3 - opgave Data: bredde flange b 50mm Højde 400mm Rumvægt ρ 4 kn m 3 Længde L 4m q 0 kn R 0kN m q egen ρb.44 kn m M Ed 8 q egen q L 4 RL 4.88 kn m Linjelast for egen vægten
Om sikkerheden af højhuse i Rødovre
 Om sikkerheden af højhuse i Rødovre Jørgen Munch-Andersen og Jørgen Nielsen SBi, Aalborg Universitet Sammenfatning 1 Revurdering af tidligere prøvning af betonstyrken i de primære konstruktioner viser
Om sikkerheden af højhuse i Rødovre Jørgen Munch-Andersen og Jørgen Nielsen SBi, Aalborg Universitet Sammenfatning 1 Revurdering af tidligere prøvning af betonstyrken i de primære konstruktioner viser
Programdokumentation - Skivemodel
 Make IT simple 1 Programdokumentation - Skivemodel Anvendte betegnelser Vægskive Et rektangulært vægstykke/vægelement i den enkelte etage, som indgår i det lodret bærende og stabiliserende system af vægge
Make IT simple 1 Programdokumentation - Skivemodel Anvendte betegnelser Vægskive Et rektangulært vægstykke/vægelement i den enkelte etage, som indgår i det lodret bærende og stabiliserende system af vægge
appendiks a konstruktion
 appendiks a konstruktion Disposition I dette appendiks behandles det konstruktive system dvs. opstilling af strukturelle systemer samt dimensionering. Appendikset disponeres som følgende. NB! Beregningen
appendiks a konstruktion Disposition I dette appendiks behandles det konstruktive system dvs. opstilling af strukturelle systemer samt dimensionering. Appendikset disponeres som følgende. NB! Beregningen
Vridning, hvælving og kipning
 Vridning, vælving og kipning april 17/LC Vridning vælving og kipning 1 Vridning, vælving og kipning april 17/LC Indold 1 Hvælvingsinertimoment. 1.1 Teoretisk udledning for et U-profil. 1. Taelværdier 1.3
Vridning, vælving og kipning april 17/LC Vridning vælving og kipning 1 Vridning, vælving og kipning april 17/LC Indold 1 Hvælvingsinertimoment. 1.1 Teoretisk udledning for et U-profil. 1. Taelværdier 1.3
Decimaltal, brøker og procent Negative tal Potens, rødder og pi Reelle og irrationale tal
 Navn: Nr.: Klasse: Prøvedato: mat7 Noter: Kompetencemål efter 9. klassetrin Eleven kan anvende reelle tal og algebraiske udtryk i matematiske undersøgelser Tal og algebra Tal Titalssystem Decimaltal, brøker
Navn: Nr.: Klasse: Prøvedato: mat7 Noter: Kompetencemål efter 9. klassetrin Eleven kan anvende reelle tal og algebraiske udtryk i matematiske undersøgelser Tal og algebra Tal Titalssystem Decimaltal, brøker
TALTEORI Wilsons sætning og Euler-Fermats sætning.
 Wilsons sætning og Euler-Fermats sætning, oktober 2008, Kirsten Rosenkilde 1 TALTEORI Wilsons sætning og Euler-Fermats sætning. Disse noter forudsætter et grundlæggende kendskab til talteori som man kan
Wilsons sætning og Euler-Fermats sætning, oktober 2008, Kirsten Rosenkilde 1 TALTEORI Wilsons sætning og Euler-Fermats sætning. Disse noter forudsætter et grundlæggende kendskab til talteori som man kan
MATEMATIK A-NIVEAU. Anders Jørgensen & Mark Kddafi. Vejledende eksempler på eksamensopgaver og eksamensopgaver i matematik, 2012
 MATEMATIK A-NIVEAU Vejledende eksempler på eksamensopgaver og eksamensopgaver i matematik, 01 Kapitel 3 Ligninger & formler 016 MATEMATIK A-NIVEAU Vejledende eksempler på eksamensopgaver og eksamensopgaver
MATEMATIK A-NIVEAU Vejledende eksempler på eksamensopgaver og eksamensopgaver i matematik, 01 Kapitel 3 Ligninger & formler 016 MATEMATIK A-NIVEAU Vejledende eksempler på eksamensopgaver og eksamensopgaver
NemStatik. Stabilitet - Programdokumentation. Anvendte betegnelser. Beregningsmodel. Make IT simple
 Stabilitet - Programdokumentation Anvendte betegnelser Vægskive Et rektangulært vægstykke/vægelement i den enkelte etage, som indgår i det lodret bærende og stabiliserende system af vægge N Ed M Ed e l
Stabilitet - Programdokumentation Anvendte betegnelser Vægskive Et rektangulært vægstykke/vægelement i den enkelte etage, som indgår i det lodret bærende og stabiliserende system af vægge N Ed M Ed e l
Beregningsopgave 2 om bærende konstruktioner
 OPGAVEEKSEMPEL Beregningsopgave 2 om bærende konstruktioner Indledning: Familien Jensen har netop købt nyt hus. Huset skal moderniseres, og familien ønsker i den forbindelse at ændre på nogle af de bærende
OPGAVEEKSEMPEL Beregningsopgave 2 om bærende konstruktioner Indledning: Familien Jensen har netop købt nyt hus. Huset skal moderniseres, og familien ønsker i den forbindelse at ændre på nogle af de bærende
En sumformel eller to - om interferens
 En sumformel eller to - om interferens - fra borgeleo.dk Vi ønsker - af en eller anden grund - at beregne summen og A x = cos(0) + cos(φ) + cos(φ) + + cos ((n 1)φ) A y = sin (0) + sin(φ) + sin(φ) + + sin
En sumformel eller to - om interferens - fra borgeleo.dk Vi ønsker - af en eller anden grund - at beregne summen og A x = cos(0) + cos(φ) + cos(φ) + + cos ((n 1)φ) A y = sin (0) + sin(φ) + sin(φ) + + sin
Dansk Konstruktions- og Beton Institut. Udformning og beregning af samlinger mellem betonelementer. 3 Beregning og udformning af støbeskel
 Udformning og beregning af samlinger mellem betonelementer 3 Beregning og udformning af støbeskel Kursusmateriale Januar 2010 Indholdsfortegnelse 3 Beregning og udformning af støbeskel 1 31 Indledning
Udformning og beregning af samlinger mellem betonelementer 3 Beregning og udformning af støbeskel Kursusmateriale Januar 2010 Indholdsfortegnelse 3 Beregning og udformning af støbeskel 1 31 Indledning
Beregning af angrebspunktet for luftens kræfter for henholdsvis en konisk, parabolsk, elliptisk og tangent ogive spids
 Beregning af angrebspunktet for luftens kræfter for henholdsvis en konisk, parabolsk, elliptisk og tangent ogive spids Jørgen Franck Til beregning af angrebspunktet for luftens kræfter på raketspidser
Beregning af angrebspunktet for luftens kræfter for henholdsvis en konisk, parabolsk, elliptisk og tangent ogive spids Jørgen Franck Til beregning af angrebspunktet for luftens kræfter på raketspidser
VEJLEDNING DIMENSIONERING AF STØJSKÆRME OG TILHØRENDE FUNDAMENTER
 DATO DOKUMENT SAGSBEHANDLER MAIL TELEFON 28. maj 2015 14/10726-2 Charlotte Sejr [email protected] 7244 2340 VEJLEDNING DIMENSIONERING AF STØJSKÆRME OG TILHØRENDE FUNDAMENTER Thomas Helsteds Vej 11 8660 Skanderborg
DATO DOKUMENT SAGSBEHANDLER MAIL TELEFON 28. maj 2015 14/10726-2 Charlotte Sejr [email protected] 7244 2340 VEJLEDNING DIMENSIONERING AF STØJSKÆRME OG TILHØRENDE FUNDAMENTER Thomas Helsteds Vej 11 8660 Skanderborg
Sustainable Analysis of BuildingsKrydstogtsterminal Nordhavn
 Sustainable Analysis of BuildingsKrydstogtsterminal Nordhavn By Daniel Refer Appendix Aalborg University M.Sc. 3. semester Fall 2011 Title: Sustainable Analysis of Buildings - Krydstogtsterminal Nordhavn
Sustainable Analysis of BuildingsKrydstogtsterminal Nordhavn By Daniel Refer Appendix Aalborg University M.Sc. 3. semester Fall 2011 Title: Sustainable Analysis of Buildings - Krydstogtsterminal Nordhavn
