Mat 2KF Minilex. Henrik Dahl 2. januar Definitioner 2. 2 Sætninger 6. 3 Symboler Opskrifter og trix Gennemregnede eksempler 16
|
|
|
- Marianne Henriksen
- 5 år siden
- Visninger:
Transkript
1 Mat 2KF Minilex Henrik Dahl 2. januar 2004 Resumé ADVARSEL - dette er et total underground-dokument!. Det er livsfarligt at bruge ukritisk. Der er næsten sikkert graverende fejl. Jeg påtager mig intet ansvar overhovedet for noget som helst. Faktisk vil jeg for en sikkerheds skyld fraråde brug af det følgende... Ved referencer til lærebøgerne bruges (B) for Berg (Kompleks funktionsteori), og (S) for Solovej (Supplement). Check altid referencen for at være sikker, og lav kun henvisninger til de officielle lærebøger - absolut ikke til dette dokument. Indhold 1 Definitioner 2 2 Sætninger 6 3 Symboler 15 4 Opskrifter og trix 15 5 Gennemregnede eksempler 16 Nogle nyttige formler med i i 2 = 1 i 3 = i i 4 = 1 1/i = i i = ( 1) 4 1/ i = ( 1) 3/4 e iπ = 1 e iπ/2 = i e iπ/2 = i Log (i) = iπ/2 Log ( i) = iπ/2 Log ( 1) = iπ sinh(iz) = i sin z sin(iz) = i sinh(z) cosh(iz) = cos(z) cos(iz) = cosh(z) 1
2 1 DEFINITIONER 2 1 Definitioner Afstand arg Arg Afstand mellem to komplekse tal z, w er z w. (B.p.5) For z C\{0} betegner arg z mængden af argumenter for z, dvs. {θ R z = z e iθ } (B.p.79) For z C\{0} betegner Arg z det entydigt bestemte argument, der tilhører ] π, π], dvs. Arg z arg z ] π, π], arg z = Arg z + 2πZ. Hovedargumentet er en kontinuert argumentfunktion for den opskårne plan C π = C \ {z R z 0}. Vi har idet z = x+iy Arg z = Arccos x y (y > 0) = Arctan y x x (x > 0) = Arccos z (y < 0), så Arg C på den opskårne plan. (B.p.79) Kan for hvert α R bestemme Arg α for den opskårne plan C α = C \ {re iα r 0} ved Arg α (z) arg z ]α 2π, α[. Da Arg α z = Arg ( e i(π α) z ) + α π for z C α er Arg α C på den opskårne plan. (B.p.79) Argumentfunktion Argumentvariation Begrænset mængde Cirkelskive Differentiabel funktion Diskret mængde Fortætnings-punkt Gren Harmonisk funktion Ved en argumentfunktion for A C \ {0} forstås en funktion θ : A R så θ(z) arg z for z A, dvs. z = z e iθ(z) (B.p.79) Lad : [a, b] C \ {0} være kontinuert kurve, der ikke passerer 0. Ved argumentvariationen langs forstås tallet argvar() = θ(b) θ(a) hvor θ er en vilkårlig kontinuert argumentfunktion langs (B.D.5.12 (p.82)) M er begrænset hvis der findes K så z K for z M (B.p.57) Cirkelskive : K(a, r) = {z C a z < r} er den åbne cirkelskive med centrum a og radius r. Den udprikkede cirkelskive er K (a, r) = K(a, r) \ {a} = {z C 0 < a z < r} (B.p.5) G C åben, f : G C. f er differentiabel i z 0 G hvis f(z0+h) f(z0) h, h K (0, r) har grænseværdi for h 0. Grænseværdien kaldes differentialkvotienten og betegnes f (z 0 ) (B.D.1.1 (p.5)) Lad G C åben. A G kaldes diskret i G, hvis A ikke har nogen fortætningspunkter i G (B.D.5.5 (p.77)) Lad A C være givet. Et punkt a C kaldes et fortætningspunkt for A hvis r > 0 : K (a, r) A. Ækvivalent hermed: der findes en følge x n A \ {a} så x n a for n. (B.D.5.4 (p.77)) Se f.eks. på z 1/n. En gren heraf er en funktion f : A C defineret på delmængde A C så f(z) = z 1/n for alle z A. Hvis f : A C er en gren, så er z f(z)e 2πik/n også en gren for k N 0. 0 er et forgreningspunkt for z 1/n (B. p.83)) φ : G R, G R 2, G åben, φ C 2 kaldes harmonisk hvis 2 φ = 0 i G. Så Ref og Imf, f H(G) er harmoniske (B.p.63) Hel funktion En holomorf funktion f : C C kaldes hel. (ex. polynomier, exp, sin, cos, sinh,
3 1 DEFINITIONER 3 cosh, modex. 1/z) (B.p.66) Holomorf funktion Hovedlogaritme G C åben, f : G C. f er holomorf i G hvis f er differentiabel i alle punkter i G. Mængden af holomorfe funktioner på G kaldes H(G) (B.D.1.1 (p.5)) Den værdi af log, der svarer til hovedargumentet af z kaldes hovedlogaritmen og betegnes Log z, dvs. Log z = log z + iarg z, og er den omvendte funktion til restriktionen af exp til strimlen {z C π < Imz π} (B.p.84)) Integrale f : [a, b] C kontinuert. gælder. (B.p.29) b a f(t)dt = b a Ref(t)dt + b Imf(t)dt. Sædvanlige regler a Isoleret punkt Kompleks funktion Komplekst tal Et punkt a A der ikke er fortætningspunkt for A kaldes et isoleret punkt i A. Der gælder r > 0 : K(a, r) A = {a}. (B.D.5.4 (p.77)) f : A C, A C (B.p.5). f(z) = Ref(z) + iimf(z) (B.p.6) f(x + iy) = u(x, y) + iv(x, y) (B.p.14) Komplekst tal z = x + iy = r(cos θ + i sin θ). x = Re(z) kaldes realdel, y = Im(z) imaginærdel, r = z = x 2 + y 2 modulus, og arg(z) er mængden af θ R hvor z = r(cos θ + i sin θ) for z 0 (B.p.5) Rez og z er ikke differentiable nogetsteds i C (B.O. 1.5 (p.25)) Kontinuert funktion f : A C, A C hvor der gælder (B.p.5) ε > 0 δ > 0 z A : z z 0 < δ f(z) f(z 0 ) < ε Konveks mængde Konvergens, punktvis Konvergens, uniform G C er konveks hvis for alle a, b G : (1 t)a + tb G for t [0, 1] (B.p.41) En følge af funktioner f n : M C konvergerer punktvis mod f : M C hvis (B.p.55) x M ε > 0 N N n N : f(x) f n (x) < ε En følge af funktioner f n : M C konvergerer uniformt mod f : M C hvis (B.D.4.1 (p.56)) ε > 0 N N x M n N : f(x) f n (x) < ε (Alternativt sup{ f(x) f n (x) x M} 0). Konvergens, lokalt uniform Konvergens, af række Kurveintegrale Lad G C være åben. En følge af funktioner f n : G C siges at konvergere lokalt uniformt mod f : G C hvis a G r > 0 : K(a, r) G f n f uniformt for z K(a, r) (B.D.4.14 (p.65)) En uendelig række 0 f n(x) af funktioner f n : M C er uniformt konvergent med sumfunktion s : M C hviss s n (x) = n 0 f k(x), x M konvergerer uniformt mod s (B.D.4.3 (p.58)) : [a, b] C orienteret og C 1 -kurve. Lad = ([a, b]), og lad f : C være kontinuert. Ved kurveintegralet af f langs forstås det komplekse tal f = f(z)dz = b a f((t)) (t)dt (B.D.2.2 (p.31)). Bemærk: f = f
4 1 DEFINITIONER 4 Kurveintegrale langs vej Kurve-sammenhæng Laplace-operator Laurent-række : [a, b] C orienteret og stykkevist C 1 (vej).. Ved kurveintegralet af f langs vejen forstås det komplekse tal f = 1 n f = n 1 j f = n tj 1 t j 1 f((t)) (t)dt (B.D.2.5 (p.33)). A C er kurvesammenhængende, hvis to vilkårlige punkter fra A kan forbindes med en kontinuert kurve, der forløber helt i A. P, Q A kontinuert : [0, 1] C t [0, 1] : (0) = P, (1) = Q, (t) A. Område er kurvesammenhængende (B.D.5.1 (p.75)) 2 = = 2 x y 2 (B.p.63) Ved en Laurentrække forstås en dobbelt uendelig række af formen c nz n hvor (c n ) n Z er givne komplekse tal og z C \ {0} (B.D.6.16 (p.110)) Den skal forstås som summen af to uendelige rækker: 1 c nz n + 0 c nz n hvor de forlanges, at begge rækker er konvergente. Hvis konvergensradier er hhv. ρ 1, ρ 2 er rækken absolut konvergent i ringområdet G = {z C 1/ρ 1 < z < ρ 2 } mellem de to koncentriske cirkler med centrum i 0 og radier 1/ρ 1, ρ 2. Den ved Laurentrækken definerede funktion er holomorf i G (B.p ) Kan også tages i centrum a: c n(z a) n på ringområdet {z C R 1 < z a < R 2 } (B.p.111) Logaritme-funktion Længde af vej Ved en logaritmefunktion for A C \ {0} forstås en funktion l : A C, så l(z) log z for z A, altså så exp(l(z)) = z. Hvis α er en argumentfunktion for A så er l(z) = log z + iα(z) en logaritmefunktion for A og hvis l er en logaritmefunktion for A, så er α = Iml en argumentfunktion for A. Dermed ses, at A C \ {0} har en kontinuert argumentfunktion netop hvis den har en kontinuert logaritmefunktion. Log α er en holomorf gren af logaritmen i den opskårne plan C α og er der en stamfunktion til 1/z. Log π = Log på C π (B.p.84-85) : [a, b] C en vej, (t) = x(t) + iy(t). Længden er L() = b a (t) dt = x (t) 2 + y (t) 2 dt (idet (t) stykvist kontinuert så integrabel). (B.D.2.7 (p.34)) b a Meromorf funktion Funktion, der ikke har væsentlige singulariteter. Mængden heraf betegnes M(G) (B.p.99) Ved en meromorf funktion i et område G C forstås en afbildning h : G C med egenskaberne (B.D.6.15 (p.108)) P = {z G h(z) = } er diskret i G Restriktionen f = h G\P er holomorf i den åbne mængde G \ P Ethvert punkt a P er en pol for f. En holomorf funktion i G er meromorf med P =. (B.p.109) Funktionen h(z) = f(z)/g(z) er meromorf med polmængde består af de a Z(g) hvor ordenen som nævnernulpunkt er større end ordenen som tællernulpunkt. Man kan på naturlig måde addere og multiplicere to meromorfe funktioner idet sum og produkt er holomorfe uden for den samlede polmængde, men visse af polerne kan være hævelige singulariteter for resultatet. Hvis h er meromorf og 0 er også 1/h meromorf. Nulpunkter for h af orden n er også nulpunkter af orden n for 1/h, og
5 1 DEFINITIONER 5 det samme gælder for polerne. (B.p.109) En rational funktion er meromorf i C med kun endeligt mange poler (B.p.109) Omløbstal Område Område, enkeltsammenhængende Område, stjerneformet Pol Potensfunktion For en lukket kontinuert kurve : [a, b] C \ {0} kaldes ω(, 0) = 1 2π argvar() Z kurvens omløbstal om 0 (B.D.5.12 (p.82)). Bem. omløbstallet skifter fortegn hvis gennemløbsretningen ændres. G C åben kaldes et område hvis alle P, Q G kan forbindes med trappelinje i G (B.D.1.8 p.16) G C område. For to vilkårlige kurver med samme start- og slutpunkt gælder, at den ene kan deformeres kontinuert over i den anden (område uden huller ). Formelt: Der findes kontinuert homotopi H : [0, 1] [0, 1] G med H(t, 0) = 0 (t), H(t, 1) = 1 (t), H(t, s) = s (t) hvor t [0, 1] og s (0) = H(0, s) = a, s (1) = H(1, s) = b. (B.p. 41) Bem: enkeltsammenhængende konveks stjerneformet. G C område. G er stjerneformet om a G hvis der for alle z G gælder, at linjestykket [a, z] G (B.p.41) En isoleret singularitet a kaldes en pol af orden m N for f hvis (z a) m f(z) har en grænseværdi for z a og lim z a (z a) m f(z) 0. En pol af orden 1 kaldes en simpel pol (B.D.6.10 (p.104)) Potenser z α, (z, α C) defineres for z 0 ved z α = exp(α log z) og er dermed en uendelig mængde. (B.p.86) Hvis l er en holomorf gren af logaritmen for et område G C\{0}, så er exp(αl(z)) en holomorf gren af z α med afledet α exp((α 1)l(z)) (B.p.87) Principal del Rational funktion Residuum Singularitet Stamfunktion Trappelinje Den til f H(G \ {a}) hørende funktion f e (z) = 1 c n(z a) n - altså summen af leddene hørende til negative potenser i Laurentrækken kaldes den principale del af f. f(z) f e (z) er holomorf i G \ {a}, og har en hævelig singularitet for z = a. f i = f f e fastlægger den holomorfe udvidelse til a (B.D.6.20, p.115)) Ved en rational funktion forstås et udtryk af formen p(z)/q(z) hvor p, q C(z), q 0. Funktionen f(z) = p(z)/q(z) er dermed holomorf i C \ Z(q) og Z(f) = Z(p) (B.p.105) Lad f H(G \ {a}) have en isoleret singularitet for z = a G med Laurentrækken f(z) = c n(z a) n. Koefficienten c 1 kaldes residuet af f i a og betegnes Res(f, a), så Res(f, a) = c 1 = 1 2πi f(z)dz, 0 < r < ρ, hvor K(a, ρ) er den K(a,r) største cirkelskive i G med centrum i a (B.p.125) Lad G C område og a G. Hvis f H(G \ {a}) kaldes a en isoleret singularitet for f. Hvis f kan tillægges en kompleks værdi i a så f bliver holomorf i G siges singulariteten at være hævelig. Den værdi f skal tillægges i a er lim z a f(z). Ellers kaldes singulariteten essentiel (B.D.6.8 (p.103)) f : G C, G C område. En funktion F : G C kaldes en stamfunktion til f, hvis F er holomorf i G og F = f (B.D.2.10 (p.35) Kurve bestående af vandrette og lodrette linjestykker (B.D.1.8 (p. 16))
6 2 SÆTNINGER 6 Vej En vej (contour) er en parameterfremstilling : [a, b] C, som er stykkevist C 1. (B.D.2.5 (p.33)) 2 Sætninger Arcsin Argumentfunktion du 1 u 2 Funktionen Arcsin z =, z G(= C \ {x R x 1}) der fås ved at [0,z] integrere langs linjestykket fra 0 til z (eller via vej) er holomorf i G og stamfunktion til 1/ 1 z 2 (B.p.89) Lad θ : A R være kontinuert argumentfunktion for en kurvesammenhængende A C \ {0}. Så er for hvert p Z også θ + 2πp en kontinuert argumentfunktion for A, og der er ikke andre. (B.L.5.8 (p.80)) Lad : [a, b] C være kontinuert kurve, der forløber helt i en cirkelskive K(z 0, r) C \ {0}. Så findes en kontinuert argumentfunktion langs kurven (B.L.5.9 (p.80)) Lad : [a, b] C være kontinuert kurve, der ikke passerer gennem 0. Så findes en kontinuert argumentfunktion θ : [a, b] R langs og enhver kontinuert argumentfunktion langs er givet som θ(t) + 2pπ for passende fast p Z (B.S.5.10 (p.81)) (Bemærk - billedet har ikke nødvendigvis kontinuert argumentfunktion). Ethvert enkeltsammenhængende område G C \ {0} har en kontinuert argumentfunktion (B.S.5.14 (p.85)) Differentiabilitet Lad K være en afsluttet og begrænset mængde i C (eller generelt R k ). Til enhver familie (G i ) i I af åbne mængder i R k som overdækker K, dvs. K i I G i findes endeligt mange indices i 1,..., i n så K G 1 G n (B.S.4.13 (p.64)) Cauchy-Riemann: f(z) = f(x + iy) = u(x, u) + iv(x, y) komplekst differentiabel i z 0 = x 0 + iy 0 1) u, v begge differentiable i (x 0, y 0 ) og 2) Cauchy-Riemann differentialligningerne opfyldt: u x = v y, u y = v x i z 0 - f er holomorf i G, hvis disse betingelser gælder i G. (B.S.1.6 (p.14)) Lad f H(G), G åben. Så er f vilkårligt ofte differentiabel. (PB.S.4.8 (p.60)) Diskret mængde Borels overdækningssætning Eksponentialfunktionen Lad G C åben. En diskret mængde A G er tællelig og G \ A er åben (B.S.5.6 (p.77)) Potensrække: exp(z) = 0 zn n! med ρ = og exp (z) = exp(z) (B.F.(1),(2) (p.19)) Funktionalligning: exp(z 1 + z 2 ) = exp(z 1 ) exp(z 2 ) (B.S.1.15 (p.20)). Eulers formel: exp(iz) = cos z+i sin z = exp(x)(cos y+i sin y)(z = x+iy), exp(iθ) = cos θ + i sin θ (B.S.1.16 (p.21)) e z = e x, e 2πi = 1, e iπ = 1 (B.S.1.16 (p.22))
7 2 SÆTNINGER 7 Eksponentialfunktionen er periodisk med periode 2πi (B.p.22) Ligningen exp(z) = 1 har løsningerne z = 2πip, p Z (B.S.1.18 (p.23)) Estimationslemma Faktorisering Lad : [a, b] C være parameterfremstilling for en vej. For kontinuert funktion f : C gælder f maxz f(z) L() = max t [a,b] f((t)) L() (B.L.2.8 (p.34) Ofte findes vurdering f(z) K z, så max f K. Da fås f KL(). (B.p.34). Lad f H(G) og antag, at f ikke er identisk 0. Hvis a G er et nulpunkt for f (dvs. f(a) = 0), så findes entydigt n N og en entydig g H(G), g(a) 0 så f(z) = (z a) n g(z), z G. Tallet n kaldes nulpunktets multiplicitet eller orden (B.S.6.1 (p.99)) Ordenen af nulpunktet a for f betegnes ord(f, a). Et nulpunkt af orden 1 kaldes et simpelt nulpunkt (B.p.100) Lad G være et område i C og antag, at f H(G) kun har endeligt mange nulpunkter i G. Da findes et polynomium p(z) og en nulpunktsfri funktion ϕ H(G), så f(z) = p(z)ϕ(z), z G. (Opg. 6.1 (p.120)) Fliselemma Harmonisk funktion Hel funktion, billede Holomorfi Lad G C åben og : [a, b] C kontinuert kurve, der forløber helt i G. Der findes endeligt mange delepunkter a = t 0 < t 1 < < t n = b i [a, b] og en radius r > 0, så n 0 K((t i ), r) G og så ([t i, t i+1 ]) K((t i ), t), i = 0, 1,, n 1 (B.L.5.2 (p.76) Lad u være reel C 2 funktion, der er harmonisk i et enkeltsammenhængende område G R 2 C. Så findes en holomorf funktion f : G C med Ref = u, og f er fastlagt på nær addition af en rent imaginær konstant. (Begge veje gælder) (B.S.4.10 (p.63)) Picards sætning: For en ikke-konstant hel funktion f : C C er enten f(c) = C eller f(c) = C\{a} for passende a C. Hvis f ikke er et polynomium, er f 1 ({w}) en uendelig mængde for alle w C på nær højst et enkelt. (B.S.4.19 (p.67)) Moreras sætning: Lad f : G C (G åben) være kontinuert i område G C. Hvis f = 0 for enhver lukket vej i G eller blot f = 0 for enhver massiv trekant G, så er f holomorf i G (B.S.4.12 (p.64)) Hvis f(z) er kontinuert i et enkeltsammenhængende område G og f(z)dz = 0 for enhver lukket vej G, så er f analytisk på hele G (WA p.347). Hyperbolske funktioner sinh z = ez e z 2, cosh z = ez +e z 2 (B.p.23) Potensrækker sinh z = 0 z 2n+1 (2n+1)!, cosh z = 0 z 2n (2n)! med ρ = (B.p.23). Differentialkvotienter sinh (z) = cosh(z), cosh (z) = sinh(z). (B.p.24) Sammenhæng med trigonometriske sinh(iz) = i sin z, sin(iz) = i sinh z, cosh(iz) = cos z, cos(iz) = cosh z.(b.p.24). Desuden sin(x + iy) = sin x cosh y + i cos x sinh y (B.O.1.12 (p.26)) Idoitformlen cosh 2 z sinh 2 z = 1 (B.p.24)
8 2 SÆTNINGER 8 Tan mv. tanh z = sinh z/ cosh z, coth z = cosh z/ sinh z. Holomorfe i C\{iπ/2+iπZ} hhv. C \ iπz (B.p.24) Identitetssætning for holomorfe funktioner Integration Hvis to holomorfe funktioner f, g i et område G stemmer overens i en delmængde A G som har et fortætningspunkt i G, da er f(z) = g(z) for alle z G (B.S.6.5 (p.101)) f : [a, b] C kontinuert. Trekantsuligheden b a f(t)dt b f(t) dt gælder a (B.S.2.1 (p.29)) (idet Rew Rew w Hvis f : G C kontinuert, G C område, og F : G C stamfunktion for f, gælder f(z)dz = F (z 2) F (z 1 ) = F ((b)) F ((a)) for enhver vej fra z 1 til z 2. Specielt gælder f = 0 for enhver lukket vej (B.S.2.11 (p.35)) Cauchys integralsætning : f : G C holomorf i enkeltsammenhængende område G C. Lad være en lukket vej i G. Da gælder f(z)dz = 0 (B.S.3.1 (p.42)) (brug evt. lukkede trappelinjer) Cauchys integralsætning for stjerneformet område: Lad G C være stjerneformet område og f H(G). For enhver lukket vej i G gælder f(z)dz = 0 (B.S.3.3 (p.45)) Cauchys integralformel: Lad f : G C være holomorf i åben mængde G og antag, at K(a, r) G (plads til en lidt større cirkelskive). For alle z 0 K(a, r) gælder (idet cirklen gennemløbes en gang mod uret) f(z 0 ) = 1 f(z) dz 2πi K(a,r) z z 0 (B.S.3.8 (p.48)). Desuden gælder (ved differentiation under integraltegnet) (B.S.4.8 (p.60)) f (n) (z 0 ) = n! f(z) 2πi K(a,r) (z z 0 ) n+1 dz, n N 0 Udvidet version: Lad f H(G), G enkeltsammenhængende område. Lad være en lukket vej i G. Da er ω(, z 0 )f(z 0 ) = 1 f(z) 2πi z z 0 dz, z 0 G\ (Opg. 6.8 (p.121)) Middelværdikorollar: Lad f : G C holomorf i åben mængde G med K(a, r) G. Da gælder f(a) = 1 2π 2π f(a+re iθ )dθ, dvs. værdien i centrum er lig middelværdien 0 af værdierne på periferien. (B.K.3.9 (p.49)) Stamfunktion: Enhver holomorf funktion i et enkeltsammenhængende område har en stamfunktion (B.S.3.5 (p.46)). Goursats lemma: G C åben, f H(G). Da er f(z)dz = 0 for enhver massiv trekant G (B.L.3.2 (p.43)) Cauchys residuesætning: Lad G være enkeltsammenhængende område og lad P = {a 1,..., a n } G. Lad være en simpel lukket vej i G som omslutter a 1,..., a n og som gennemløbes en gang med positiv orientering. For f H(G \ P ) gælder
9 2 SÆTNINGER 9 (B.S.7.1 (p.125)) (Bemærk, polernes orden er uden betydning) f(z)dz = 2πi Lad f være en rational funktion f(z) = p(z) q(z) n Res(f, a j ) 1 = a0+a1z+ +amzm b 0+b 1z+ +b nz n, a m 0, b n 0 og antag, at n m + 2 og at f ikke har nogen poler på den reelle akse. Så er f(x)dx = 2πi k 1 Res(f, z j) hvor z j er polerne i den øvre halvplan (B.S.7.8 (p.133)). (I nedre halvplan ændres fortegn (B.p.134)) Lad f være en meromorf funktion i C uden poler på den reelle akse og med kun endeligt mange poler z j i den øvre halvplan. Hvis max 0 t π f(re it ) 0, R så R vil lim R R f(x)eiλx dx = 2πi k 1 Res(f(z)eiλz, z j ), λ > 0 (B.S.7.10 (p.134))(i nedre halvplan ændres fortegn og λ < 0) (B.p.135)) Lad h : G C { } være meromorf i et enkeltsammenhængdende område G og lad være en positivt orienteret simpel lukket ved i G, der ikke går igennem nogen af h s nulpunkter og poler. Så er 1 2πi h (z) h(z) dz = N P lig med antallet N af nulpunkter minus antallet P af poler for h i det delområde af G som omslutter. Ved udregningen tælles et nulpunkt eller en pol af orden m som tallet m (B.S.7.3 (p.128)) Jacobi-determinant f(z) = f(x + iy) = u(x, y) + iv(x, y). Jacobi-determinanten er (B.p.16) det J = ( ) 2 u + x ( ) 2 v = x ( ) 2 u + y ( ) 2 v = f 2 y Konstante funktioner f H(G), G C område. Hvis f (z) = 0 i alle z G, så er f konstant (B.S.1.9 (p. 16)). Hvis f kun har reelle værdier er f konstant (B.K.1.10 (p.16)) Hvis f er konstant er f konstant (B.O.1.7 (p.25)) En begrænset hel funktion er konstant (Liouvilles sætning) (B.S.4.20 (p.67)) (ditto for f(z) analytisk og begrænset (WA. p.348)) Lad f : A C være kontinuert på kurvesammenhængende A C. Hvis f(a) er diskret i C er f konstant (B.S.5.7 (p.78)) Se også identitetssætningen Kontinuitet f kontinuert ensbetydende med, at Ref og Imf begge kontinuerte (B.p.6) For f H(G), G åben er f kontinuert (P.Bem. 4.9 (p.62)). Lad M C og f n : M C uniformt konvergent mod f : M C. Hvis alle f n er kontinuerte i z 0 M, så er f også kontinuert i z 0 (B.S.4.2 (p.57)) Konvergens, kompakt uniform Lad G C åben. En følge af funktioner f n : G C konvergerer lokalt uniformt
10 2 SÆTNINGER 10 mod f : G C hviss: For hver afsluttet og begrænset delmængde K G vil f n (z) f(z) uniformt for z K (B.S.4.15 (p.65)) Konvergens, lokal uniform Lad G C åben. Hvis en følge af funktioner f n : G C, f n H(G) konvergerer lokalt uniformt på G mod f : G C, da er f H(G) Følgen af afledede f n konvergerer lokalt uniformt mod f på G (B.S.4.17 (p.66)) (Det gælder også for n te afledede (B.p.66)) Konvergens, rangorden Punktvis konvergens svagere uniform konvergens (B.p.65) end lokal/kompakt uniform konvergens svagere end Konvergensradius Laurentrække L Hospitals regel Logaritme Lad f H(C\P ), P C diskret i C og antag, at ingen af f s singulariteter a P er hævelige. For hvert z 0 C \ P fremstilles f ved en potensrække f(z) = 0 a n(z z 0 ) n i den største åbne cirkelskive K(z 0, ρ) C \ P, og ρ = inf{ z 0 a a P } er konvergensradius. (B.S.6.24,p ) Antag, at f er holomorf i ringområdet G = {z C R 1 < z a < R 2 hvor 0 R 1 < R 2. Så fremstilles f i G som sum af en entydigt bestemt Laurentrække f(z) = c n(z a) n, z G, og koefficienterne i rækken er givet ved c n = 1 f(z) 2πi (z a) dz, n Z, hvor r ]R n+1 1, R 2 [ er vilkårlig. (B.S.6.17 (p.111)) K(a,r) Antag, at f, g H(G) ikke er identisk 0 i en omegn af a G. Grænseværdien f(z) lim z a g(z) eksisterer hviss ord(f, a) ord(g, a), og så gælder lim z a f(z) g(z) = f (q) (a) g (q) (a) hvor q = ord(g, a) og dermed g (q) (a) 0 (B.S.6.7 (p.102)) Lad G C \ {0} område. Hvis der findes en kontinuert argumentfunktion α for G, så er l(z) = log z + iα(z), z G en holomorf gren af logaritmen, og den er stamfunktion til 1/z, dvs. l (z) = 1/z. (B.S.5.14 (p.85)). Også l(z) + 2πip, p Z er holomorf gren af logaritmen på G, og der er ikke andre (P.Bem (p.86)) For z < 1 gælder potensrækkeudviklingen Log(1 + z) = z z2 1 ( 1) n 1 n z n med konvergensradius 1 (B.S.5.16, (p.86)) 2 + z3 Lad : [a, b] C \ {0} være en vej, der ikke passerer 0. Så er iargvar(). Hvis er lukket er omløbstallet om 0 givet ved ω(, 0) = 1 2πi et helt tal! (B.S.5.23 (p.90)) dz z 3 + = = log (b) (a) + - altså Der gælder tilsvarende for lukket vej, at ω(, z 0 ) = 1 dz 2πi z z 0, z 0 C\ (B.p.94) dz z n te rødder Nulpunkt, isoleret Lad n N være givet. Funktionen z n afbilder vinkelrummet {z C\{0} Arg z < π/n} bijektivt på C π. Den omvendt funktion ρ n (z) = ( z 1/n )e iarg z/n er en holomorf gren af z 1/n på C π (B.S.5.13 (p.83)). Der gælder d dz z1/n = z1/n 1 n Lad f H(G) og antag, at f ikke er identisk 0. Ethvert nulpunkt a for f er isoleret i den forstand, at der findes r > 0 så f(z) 0 for z K (a, r). Mængden Z(f) af nulpunkter for f er diskret i G, specielt er Z(f) tællelig (B.S.6.3 (p. 101)) Der gælder også, at hvis P G er diskret i G, så findes f H(G) så Z(f) = P (B.p.101)
11 2 SÆTNINGER 11 Exp er nulpunktsfri i C, sin z har numerable nulpunkter z = pπ, p Z, sin(1/z) på C \ {0} har nulpunkter (pπ) 1, p Z (B.p.101) Nulpunkt, orden Lad f H(G) og antag, at f ikke er identisk 0. For et nulpunkt a G er ordenen n karakteriseret ved f(a) = f (a) = = f (n 1) (a) = 0, f (n) (a) 0 (B.K.6.2 (p.101) Lad f, g H(G) hvor G er et enkeltsammenhængende område. Lad være en simpel lukket vej i G og antag at f(z) g(z) < f(z), z. Så har f og g samme antal nulpunkter talt med multiplicitet i det begrænsede område, som omslutter (Rouches sætning) (B.S.7.5 (p.130)) Nulpunkter og poler, argumentprincippet Lad h : G C { } være meromorf i et enkeltsammenhængdende område G og lad være en positivt orienteret simpel lukket ved i G, der ikke går igennem nogen af h s nulpunkter og poler. Så er 1 h (z) 2πi h(z) dz = N P lig med antallet N af nulpunkter minus antallet P af poler for h i det delområde af G som omslutter. Ved udregningen tælles et nulpunkt eller en pol af orden m som tallet m (B.S.7.3 (p.128)) argvar(γ) = 2π(N P ) - da 1 b 2πi a h ((t)) (t) h((t)) dt = ω(γ, 0) (B.7.4, s.129) Ombytning af grænseovergange Lad : [a, b] C vej i C og lad f n : C være følge af kontinuerte funktioner. (B.S.4.6 (p.59)) Hvis f n f uniformt på gælder lim n f n = f = lim n f n Hvis 0 f n konvergerer uniformt mod s : C på gælder 0 f n = s = 0 f n. Omløbstal om 0 Omløbstal om z Omløbstallet omkring 0 er givet som ω(, 0) = n 1 0 sign(a k ) altså antallet af gange krydser L i positiv omløbsretning minus antallet af gange krydser L i negativ omløbsretning (B.S.5.24 (p.91-92)) Omløbstallet omkring z G er givet som ω(, z) = ω( z, 0) idet z : [a, b] C er kurven t (t) z som ikke passerer 0, (B.p.93) Lad : [a, b] C være lukket kontinuert kurve. Omløbstallet ω(, ) : C \ Z er konstant i hvert af komponenterne af C \ (B.S.5.25 (p.94)) Område En åben kurvesammenhængende mængde G C er et område i den forstand at to vilkårlige punkter i G kan forbindes med en trappelinje (B.S.5.3 (p.76)) Om et område G C er følgende betingelser ensbetydende (B.S.5.18 (p.88)) G er enkeltsammenhængende Alle f H(G) har en stamfunktion For alle f H(G) og enhver lukket vej i G gælder f(z)dz = 0 Alle nulpunktsfri f H(G) har en holomorf logaritme, dvs. l H(G) så exp(l) = f
12 2 SÆTNINGER 12 Alle nulpunktsfri f H(G) har en holomorf kvadratrod, dvs. g H(G) : g 2 = f Enhver nulpunktsfri f H(G) findes en holomorf gren af f α = exp(αl) hvor α C og l er en holomorf gren af logaritmen til f Riemanns afbildningssætning: Lad G være et enkeltsammenhængende område, G C. Så findes en bijektiv holomorf funktion ϕ : G K(0, 1). (B.S.5.19 (p.88)). Den omvendte funktion ϕ 1 er også holomorf. Pol Polynomiers division Polynomiers rødder Potensfunktion Potensrækker a m k (z a) k Antag f{ H(G \ {a}) har en pol af orden m i a. Funktionen (z a) g(z) = m f(z), z G \ {a} lim z a (z a) m f(z), z = a er da holomorf i G og har potensrække g(z) = 0 a n(z a) n i den største åbne cirkelskive K(a, ρ) G. Der gælder for z K (a, ρ), at f(z) = a0 a (z a) + 1 m (z a) + + am 1 m 1 z a + 0 a m+k(z a) k. Funktionen p(1/(z a)) = m 1 hvor p(z) = m 1 a m kz k kaldes den principale del af f i a. Når man trækker den principale del fra f får man en holomorf funktion med en hævelig singularitet i a, så singulariteten er koncentreret i den principale del af f. (B.p. 104) Lad d C[z] (dvs. polynomium) være forskellig fra nulpolynomiet. Til p C[z] findes entydigt bestemte polynomier q, r C[z] så p = qd + r, grad(r) <grad(d). Polynomierne d, q, r kaldes heholdsvis divisor, kvotient og rest. Hvis d, p har reelle koefficienter, så gælder det også for q, r. (B.S.4.22 (p.68)) Et polynomium p(z) af grad n 1 har netop n rødder i C, regnet med multiplicitet (B.K.4.25 (p.69)) Binomialrækken: ( ) Lad α C. For z < 1 gælder (1 + z) α = exp(αlog (1 + z)) = α 0 z n n (B.S.5.17 (p.87)) En potensrække, 0 a nz n og dens ledvist differentierede a nnz n 1 = 0 a n+1(n + 1)z n har samme konvergensradius (B.L.1.11 (p.17)) 1 Den ved potensrækken 0 a nz n fremstillede funktion f er holomorf i konvergenscirkelskiven K(0, ρ) og f (z) = n=1 na nz n 1 for z < ρ (B.S.1.12 (p.17)) Desuden er f vilkårligt ofte differentiabel i K(0, ρ) og a k = f (k) (0) k!, k = 0, 1,.... Dermed er potensrækken sin egen Taylorrække omkring 0, f(z) = f (n) (0) n=0 n! z n, z < ρ. (B.K.1.13 (p.19)) Lad potensrækkerne f(z) = 0 a nz n, g(z) = 0 b nz n have konvergensradier ρ 1, ρ 2. Hvis der findes 0 < ρ min(ρ 1, ρ 2 ) så f(z) = g(z) for z < ρ, så er a n = b n for alle n. (B.S.1.14 (p.19)) En potensrække 0 a nz n med konvergensradius ρ og sumfunktion f(z) = 0 a nz n, z K(0, ρ) konvergerer uniformt mod f på enhver lukket cirkelskive K(0, r) med r < ρ (Men ikke nødvendigvis på K(0, ρ)). (B.S.4.5 (p.58)) Potensrække, kriterier for konvergensradius Givet en potensrække n=0 a n(z b) n, a n, b C, hvor der findes et N N, så
13 2 SÆTNINGER 13 a n 0 for n N. a 1. Hvis grænseværdien R = lim n n a n+1 for potensrækken. (Kvotientkriteriet) eksisterer, da er R konvergensradius 2. Hvis grænseværdien R = lim n a n 1/n eksisterer, da er R konvergensradius for potensrækken (Rodkriteriet). Bemærk i begge tilfælde kan R godt være. (S.S.5.2.3) Rational funktion Regneregler bevarer holomorfi Residuer, beregning Dekomponering: Lad r, q C[z] være uden fælles nulpunkter, 0 grad(r) < grad(q), og lad a 1,..., a k være nulpunkterne for q med multipliciteter m 1,..., m k. Der findes entydigt bestemte konstanter c j,l C så r(z) q(z) = k mj c j,l j=1 l=1 (z a j). l Formlen udtrykker, at den rationale funktion er sum af sine principale dele. (B.S.6.12 (p.106)) Mængden H(G) i en åben G C er stabil ved addition, subtraktion, multiplikation, og (såfremt nævneren aldrig=0) division. (B.S.1.3 (s.1.2)). Sædvanlige regneregler for differentiation gælder, herunder sammensatte funktioner og inverse: Lad f H(G) være injektiv. Så er f(g) åben i C og f 1 (f(z)) = 1 f (z) (B.S.1.4 (p.12)) Antag, at h har en simpel pol i a. Så er Res(h, a) = lim z a (z a)h(z). (B.p.126) Antag, at h = f/g er meromorf med en simpel pol i a og at f(a) 0, g(a) = 0, g (a) 0. Så er Res(h, a) = f(a)/g (a) (B.p.127) Antag, at h har en pol af orden m 1 i a. Idet vi definerer ϕ ved ϕ(z) = (z a) m h(z) så ϕ har en hævelig singularitet i a er Res(h, a) = ϕ(m 1) (a) (m 1)! (B.p.127) Rouches sætning Lad f, g H(G) hvor G er et enkeltsammenhængende område. Lad være en simpel lukket vej i G og antag at f(z) g(z) < f(z), z. Så har f og g samme antal nulpunkter talt med multiplicitet i det begrænsede område, som omslutter (Rouches sætning) (B.S.7.5 (p.130)) Singularitet, Hvis f H(G \ {a}) har en essentiel singularitet i a, så er f(k (a, r)) overalt tæt Carosati-Weierstrass i C for ethvert r > 0 hvor K(a, r) G (bem. A C overalt tæt hvis A = C) (B.S.6.11 (p.105)) Singularitet, hævelig Singularitet, afgørelse af type Antag f H(G \ {a}), f ikke identisk 0, og at f er begrænset i K (a, r) for r > 0. Så har f en hævelig singularitet i a. (B.S.6.9 (p.103)) Den isolerede singularitet a for f H(G\{a}) med Laurentrækken f(z) = c n(z a) n, z K (a, ρ) er (B.S.6.21 (p.116)) hævelig hviss c n = 0 for n < 0 pol hviss c n = 0 for alle n < 0 på nær endeligt mange. Polens orden er det største m > 0 så c m 0 essentiel hviss c n 0 for uendeligt mange n < 0 Spejlings-princippet Lad G C åben og f H(G). Den i x-aksen spejlede mængde og funktion defineres ved G = {z C z G}, f : G C, f (z) = f(z), z G. Der gælder, at f H(G ) og (f ) = (f ) (Opg (p.120))
14 2 SÆTNINGER 14 Hvis G er spejlingsinvariant, dvs. G = G er G R. f H(G) er reel på G R hviss f er spejlingsinvariant (f = f eller f(z)f(z)) (Opg (p.120)) En hel funktion f(z) = 0 a nz n er spejlingsinvariant hviss a n R, n N 0 (Opg (p.120)) Stamfunktion Lad f : G C kontinuert, G C område, og antag f = 0 for enhver lukket trappelinje i G. Da har f en stamfunktion (givet ved F = f med z z trappelinje fra z 0 til z) (B.L.2.12 (p.36)) For kontinuert f : G C på område G C er følgende ensbetydende f har stamfunktion For vilkårlige z 1, z 2 G har f samme værdi for enhver vej i G fra z 1 til z 2 f = 0 for enhver lukket vej i G. Når betingelserne er opfyldt finder man en stamfunktion F til f ved at vælge z 0 G og sætte F (z) = f hvor er vilkårlig vej (f.eks. trappelinje) i G fra z 0 til z (B.S.2.13 (p.38)) Hvis f : G C i område G C har en stamfunktion, da er den (f) holomorf (B.S.4.11 (p.64)) Taylorrække Lad f H(G), G åben. Så er for alle a G Taylorrækken med centrum a konvergent med sum f i den største åbne cirkelskive K(a, ρ) G: f(z) = f (n) (a) 0 n! (z a) n, z K(a, ρ) (B.S.4.8 (p.60)) f er altså analytisk, faktisk C (B.p.62), Trigonometriske funktioner Potensrækker sin z = 0 (p.21)) ( 1) n z 2n+1 (2n+1)!,, cos z = ( 1) n z 2n 0 (2n)! med ρ = (B.(7)-(8) Euler: sin z = eiz e iz 2i, cos z = eiz +e iz 2 Additionsformler: sin(θ 1 +θ 2 ) = sin θ 1 cos θ2+cos θ 1 sin θ2, cos(θ 1 +θ 2 ) = cos θ 1 cos θ 2 sin θ 1 sin θ 2 (B (10)-(11) (p.22)). De Moivre: (cos θ + i sin θ) n = cos nθ + i sin nθ (B p.22) tan z = sin z/ cos z og cot z = cos z/ sin z er holomorfe i C \ {π/2 + πz} og C \ πz (B.p.23) tan (n) z = n+1 0 a n,k tan k z med a n,k 0, a n,k Z og a n,k = 0 når sign(n) = sign(k). (B.O.1.17 (p.27)) Weierstrass Majorantrækkesætning Lad 0 f n(x) være uendelig række af f n : M C og antag, at der findes en konvergent majorantrække, dvs. en konvergent række 0 a n med positive led, så n N 0 x M : f n (x) a n. Så er rækken 0 f n(x) uniformt konvergent på M (B.S.4.4 (p.58))
15 3 SYMBOLER 15 Åbne mængder Lad G C være åben og antag at K(a, r) G. Da findes R > r med K(a, R) G (altid plads til en lidt større cirkelskive) (B.L. 3.6 (p.47)) 3 Symboler arg(z) C α H(G) Im(z) K(a, r) K (a, r) K(a, r) K(a, r) L() l(z) Log z M(G) ω(, 0) ord(f, a) Re(z) Res(f, a) z Z(f) Argument Opskåret plan Parameterfremstilling for vej Billedet af Mængden af holomorfe funktioner på G Imaginærdel Åben cirkelskive Udprikket cirkelskive Afsluttet cirkelskive Rand af cirkelskive Længden af vejen Logaritmefunktion Hovedlogaritme Mængden af meromorfe funktioner på G Omløbstal for omkring 0 Ordenen af nulpunkt a for f Realdel Residuum for f i a Modulus Nulpunktsmængde for f 4 Opskrifter og trix 1 z(1 z) = 1 z z (B.O.1.1 (p.25)) Singularitet, afgørelse af type Den isolerede singularitet a for f H(G\{a}) med Laurentrækken f(z) = c n(z a) n, z K (a, ρ) er (B.S.6.21 (p.116)) hævelig hviss c n = 0 for n < 0
16 5 GENNEMREGNEDE EKSEMPLER 16 pol hviss c n = 0 for alle n < 0 på nær endeligt mange. Polens orden er det største m > 0 så c m 0 essentiel hviss c n 0 for uendeligt mange n < 0 Residuer, beregning Antag, at h har en simpel pol i a. Så er Res(h, a) = lim z a (z a)h(z). (B.p.126) Antag, at h = f/g er meromorf med en simpel pol i a og at f(a) 0, g(a) = 0, g (a) 0. Så er Res(h, a) = f(a)/g (a) (B.p.127) Antag, at h har en pol af orden m 1 i a. Idet vi definerer ϕ ved ϕ(z) = (z a) m h(z) så ϕ har en hævelig singularitet i a er Res(h, a) = ϕ(m 1) (a) (m 1)! (B.p.127) Nulpunkter og poler Potensrække, kriterier for konvergensradius Lad h : G C { } være meromorf i et enkeltsammenhængdende område G og lad være en positivt orienteret simpel lukket ved i G, der ikke går igennem nogen 1 h af h s nulpunkter og poler. Så er (z) 2πi h(z) dz lig med antallet N af nulpunkter minus antallet P af poler for h i det delområde af G som omslutter. Ved udregningen tælles et nulpunkt eller en pol af orden m som tallet m (B.S.7.3 (p.128)) Givet en potensrække n=0 a n(z b) n, a n, b C, hvor der findes et N N, så a n 0 for n N. a 1. Hvis grænseværdien R = lim n n a n+1 for potensrækken. (Kvotientkriteriet) eksisterer, da er R konvergensradius 2. Hvis grænseværdien R = lim n a n 1/n eksisterer, da er R konvergensradius for potensrækken (Rodkriteriet). Bemærk i begge tilfælde kan R godt være. (S.S.5.2.3) 5 Gennemregnede eksempler { dz 0, n 1 C r z = (Ex. 2.14, p.38). C n 2πi, n = 1 r : z = r (enkelt positivt cirkelgennemløb), n Z. Konklusion: n 1 stamfunktion z 1 n /(1 n), z 1 ingen stamfunktion i C \ {0}. 1 2i z (z 2 +1) 2 dz = 0 (Opg. 2.3(p.39)) for lukket vej i C \ {±i} P (z)dz = 0 (Opg. 2.4(p.39)) for lukket vej i C og P (z) polynomium. zdz R (Opg. 2.5 (p.39)) for lukket vej i C f (z)g(z)dz = f(z)g (z)dz (Opg. 2.6 (p.39)) for f, g H(G), lukket vej i området G. K(0,2) sin z 1+z 2 dz = πi(e 1/e) (Ex (p. 49)) 1 2π e 1 2 t2 e itb dt = e 1 2 b2, b R (Ex (p.50)) Log z = dt [1,z] t, z G Stamfunktion til 1/z i G = C\], 0] (stjerneformet om 1). (Opg. 3.5, 3.6 (p.52-53))
17 5 GENNEMREGNEDE EKSEMPLER 17 Log (re iθ ) = log r + iθ for z = re iθ, θ ] π, π[, r > 0. (Opg. 3.6 (p.53)) Arctan z = 1 0 zdt 1+t 2 z 2 på G = C \ {iy y 1} (Opg. 3.8 (p.53)) Arctan z H(G), d dt Arctan z = 1 1+z 2 (Opg. 3.8 (p.53)) Arctan z = z z3 3 + z5 5 +, z < 1 (Opg. 3.8 (p.53)) 0 sin(x 2 )dx = cos(x 2 )dx = π 0 2 (Opg. 3.9 (p.53)) 2 u(a) = 1 2π 2π u(a + re iθ )dθ for u : G R harmonisk i åben G C og K(a, r) G 0 (Opg. 4.5 (p.70)) f(c) = C for f ikke-konstant hel funktion (Opg (p.71)) arg(z 1 z 2 ) = arg z 1 + arg a 2 log(z 1 z 2 ) = log z 1 + log z 2 for z 1, z 2 C \ {0} (Opg.5.2 (p.95)) Arg (z 1 z 2 ) = Arg z 1 + Arg a 2 Log (z 1 z 2 ) = Log z 1 + Log z 2 for Rez 1 > 0 og Rez 2 > 0 (men ikke generelt for z 1, z 2 C \ {0}) (Opg.5.2 (p.95)) {z C z = 1} har ingen kontinuert argumentfunktion (Opg. 5.4 (p.95)) Arg (z α ) = αarg (z), z α = z α, z C π (Opg. 5.8 (p.96)) G åben, f H(G) nulpunktsfri. log f er harmonisk i G argvar( δ) = argvar()+argvar(δ) for : [a, b] C\{0}, δ : [b, c] C\{0}, (b) = δ(b) (Opg.5,5 (p.96)) ( 0 a nz n ) ( 0 b nz n ) = 0 c nz n, c n = n 0 a kb n k Cauchy-multiplikation (Opg.5.12 (p.97))
18 Indeks K(0, 1) og område, 12, 3, 3 Åben mængde Cirkelskive, 15 Afstand, 2 Analytisk funktion, 14 Arcsin, 6 Arg z, 2 arg z, 2, 3 Argument, 3 Argumentfunktion, 2, 6 og logaritmefunktion, 4 Argumentprincippet, 9, 11 Argumentvariation, 2 argvar, 2 Begrænset mængde, 2 Beregning af residuum, 13, 16 Billede af hel funktion, 7 Binomialrække, 12 Borels overdækningssætning, 6 Carosati-Weierstrass sætning, 13 Cauchy-multiplikation af potensrækker, 17 Cauchy-Riemann, 6 Jacobi-determinant, 9 Cauchys integralformel, 8 Udvidet, 8 Cauchys integralsætning, 8 For stjerneformet område, 8 Cauchys residuesætning, 8 Cirkelskive Åben, 2 Udprikket, 2 De Moivre, 14 Dekomponering Rational funktion, 13 Differentiabel funktion, 2 Differentiabilitet, 6 Holomorf funktion, 6 Uendelig, 6 Diskret mængde, 2, 6 Division af polynomier, 12 Eksponentialfunktionen Euler, 6 exp(z)=1, 7 Periode, 7 Potensrække, 6 Enkeltsammenhængende område, 5, 11 Essentiel singularitet, 5, 13 Estimationslemma, 7 Euler Cos, 14 Eksponentialfunktion, 6 Sin, 14 Faktorisering, 7 Fliselemma, 7 Forgreningspunkt, 2 Fortætningspunkt, 2 Funktion Analytisk, 14 Harmonisk, 2 Hel, 2 Hel, billede, 7 Meromorf, 4 Rational, 5 Goursats lemma, 8 Grænseovergange Ombytning af, 11 Gren, 2 Hævelig singularitet, 5, 13 Harmonisk funktion, 2 Holomorfi, 7 Hel funktion, 2 Billede, 7 Holomorf funktion, 3 Harmonisk funktion, 7 Hel, 2 Hel, billede, 7 Moreras sætning, 7 Regneregler, 13 Stamfunktion, 14 Holomorf funktion Identitetssætningen, 8 Holomorf udvidelse, 5 Homotopi, 5 Hovedlogaritme, 3 Hyperbolske funktioner, 7 Differentialkvotienter, 7 Idiotformlen, 7 og trigonometriske, 7 Potensrækker, 7 Tangens hyperbolsk, 8 Identitetssætningen for holomorfe funktioner, 8 18
19 INDEKS 19 Identitetssætningen for potensrækker, 12 Imaginærdel, 3 Integrale, 3 Estimationslemma, 7 Kurveintegrale, 3 Kurveintegrale langs vej, 4 Integration Cauchy for stjerneformet område, 8 Cauchys integralformel, 8 Cauchys residuesætning, 8 Cauchys sætning, 8 Goursats lemma, 8 Meromorf funktion, 9 Middelværdikorollar, 8 Poler og nulpunkter, 9, 11 Rational funktion, 9 Stamfunktion, 8 Trekantsulighed, 8 Udvidet Cauchys integralformel, 8 Isoleret nulpunkt, 10 Isoleret punkt, 3 Isoleret singularitet, 5 Jacobi-determinant, 9 Kompleks funktion, 3 Differentiabilitet, 2, 6 Hel, 2 Holomorf, 3 Kontinuitet, 3, 9 Komplekst tal, 3 Argument, 3 Imaginærdel, 3 Modulus, 3 Polære koordinater, 3 Realdel, 3 Konstante funktioner, 9 Kontinuert funktion, 3 Kontinuitet, 9 og uniform konvergens, 9 Konveks mængde, 3 Konvergens Af række, 3 Kompakt uniform, 9 Lokal uniform, 3, 10 Potensrækker, 12 Punktvis, 3 Rangorden, 10 Uniform, 3 Uniform og kontinuitet, 9 uniform og Weierstrass, 14 Konvergensradius, 10 Kriterier, 12, 16 Kriterier For konvergensradius, 12, 16 Kurveintegrale, 3 Langs vej, 4 Kurvesammenhæng, 4 Kvadratrod og område, 12 Kvotientkriteriet For konvergensradius, 13, 16 L Hospitals regel, 10 Længde Af vej, 4 Laplace-operator, 4 Laurentrække, 4, 10 Liouvilles sætning, 9 Logaritme, 10 Hovedlogaritme, 3 og omløbstal, 10 og område, 11 Logaritmefunktion, 4 og argumentfunktion, 4 Lokal uniform konvergens, 3, 10 Meromorf funktion, 4 Integration, 9 Middelværdikorollar, 8 Modulus, 3 Moreras sætning, 7 Multiplicitet, 7 Nulpunkt Isoleret, 10 Multiplicitet, 7 Orden, 7, 11 Simpelt, 7 Nulpunkter Antal, 11 Nulpunkter og poler, 11, 16 Nulpunkter, antal, 11 Nulpunktsmængde Diskret, 10 Ombytning af grænseovergange, 11 Omløbstal, 5 Konstant i komponenter, 11 og logaritme, 10 om 0, 11 om z, 11 Område, 5 Ækvivalenser, 11 Enkeltsammenhængende, 5, 11
20 INDEKS 20 Logaritme, 11 og bijektion på K(0, 1), 12 og kurvesammenhæng, 11 og kvadratrod, 12 og lukket integral, 11 og potensfunktion, 12 og stamfunktion, 11 Stjerneformet, 5 Opskåret plan, 2 Orden, 7 Nulpunkt, 11 Pol, 5 Parametrisering, 3 Picards sætning, 7 Pol, 5, 12 Orden, 5 Simpel, 5 Polære koordinater, 3 Poler og nulpunkter, 16 Antal, 11 og integral, 11 Polynomium Division, 12 Rødder, 12 Potensfunktion, 5 Binomialrække, 12 og område, 12 Potensrække Cauchy-multiplikation, 17 Konvergensradius kriterier, 12, 16 Potensrækker, 12 Holomorfi, 12 Identitetssætningen, 12 Taylorrække, 12 Uendeligt differentiable, 12 Uniform konvergens, 12 Principal del, 5, 12 Punktvis konvergens, 3 Rødder i polynomier, 12 Rational funktion, 5, 13 Integration, 9 Realdel, 3 regneregler Holomorf funktion, 13 Residuum, 5 Beregning, 13, 16 og integration, 8 Riemanns afbildningssætning, 12 Ringområde, 4 Rodfunktion, 10 Rodkriteriet For konvergensradius, 13, 16 Rouches sætning, 11, 13 Simpel pol, 5 Simpelt nulpunkt, 7 Singularitet, 5 Afgørelse af type, 13, 15 Essentiel, 5, 13 Hævelig, 5, 13 Isoleret, 5 Spejlingsprincippet, 13 Stamfunktion, 5 Ækvivalenser, 14 Eksistens, 8, 14 Holomorfi, 14 og område, 11 Stjerneformet område, 5 Taylorrække Holomorf funktion, 14 Trappelinje, 5 Trigonometriske funktioner Additionsformler, 14 De Moivre, 14 Euler, 14 Holomorfi, 14 Potensrække, 14 Udvidelse Holomorf, 5 Uniform konvergens, 3 Af række, 3 Kompakt, 9 Kontinuitetsbevarelse, 9 Ombytning af grænseovergange, 11 Potensrækker, 12 Weierstrass, 14 Vej, 6 Længde, 4 Weierstrass majorantrækkesætning, 14
Kompleks Funktionsteori
 Kompleks Funktionsteori Formelræs Holomorfe funktioner Sætning. (Caucy-Riemans ligninger). Funktionen f : G C, f = u+iv er holomorf i z 0 = x 0 + iy 0 hvis og kun hvis i punktet (x 0, y 0 ). du dx = dv
Kompleks Funktionsteori Formelræs Holomorfe funktioner Sætning. (Caucy-Riemans ligninger). Funktionen f : G C, f = u+iv er holomorf i z 0 = x 0 + iy 0 hvis og kun hvis i punktet (x 0, y 0 ). du dx = dv
Opgaver til f(z) = 1 z 4 1, g(z) = 1
 1.17 Opgaver til 1. 1 1.1. Vis, at f(z) = er vilkårligt ofte differentiabel i C \ {, 1}, og z(1 z) find et udtryk for f (n) (z) for alle n. (Vink. Skriv f(z) = 1 z + 1 1 z ). 1.2. Beskriv billedkurverne
1.17 Opgaver til 1. 1 1.1. Vis, at f(z) = er vilkårligt ofte differentiabel i C \ {, 1}, og z(1 z) find et udtryk for f (n) (z) for alle n. (Vink. Skriv f(z) = 1 z + 1 1 z ). 1.2. Beskriv billedkurverne
SUPPLERENDE OPGAVER TIL KOMPLEKS FUNKTIONSTEORI F2005
 SUPPLERENDE OPGAVER TIL KOMPLEKS FUNKTIONSTEORI F2005 0. maj, 2005 version nr. 8 JØRGEN VESTERSTRØM Indledende bemærkninger De foreliggende opgaver udgør et supplement til lærebogens opgaver. Afsnitsnummereringerne
SUPPLERENDE OPGAVER TIL KOMPLEKS FUNKTIONSTEORI F2005 0. maj, 2005 version nr. 8 JØRGEN VESTERSTRØM Indledende bemærkninger De foreliggende opgaver udgør et supplement til lærebogens opgaver. Afsnitsnummereringerne
Nøgleord og begreber Komplekse tal Test komplekse tal Polære koordinater Kompleks polarform De Moivres sætning
 Oversigt [S] App. I, App. H.1 Nøgleord og begreber Komplekse tal Test komplekse tal Polære koordinater Kompleks polarform De Moivres sætning Test komplekse tal Komplekse rødder Kompleks eksponentialfunktion
Oversigt [S] App. I, App. H.1 Nøgleord og begreber Komplekse tal Test komplekse tal Polære koordinater Kompleks polarform De Moivres sætning Test komplekse tal Komplekse rødder Kompleks eksponentialfunktion
(c) Opskriv den reelle Fourierrække for funktionen y(t) fra (b), og afgør dernæst om y(t) er en lige eller ulige funktion eller ingen af delene.
 MATEMATIK 3 EN,MP 4. februar 2016 Eksamenopgaver fra 2011 2016 (jan. 2016) Givet at 0 for 0 < t < 1 mens e (t 1) cos(7(t 1)) for t 1, betragt da begyndelsesværdiproblemet for t > 0: y (t) + 2y (t) + 50y(t)
MATEMATIK 3 EN,MP 4. februar 2016 Eksamenopgaver fra 2011 2016 (jan. 2016) Givet at 0 for 0 < t < 1 mens e (t 1) cos(7(t 1)) for t 1, betragt da begyndelsesværdiproblemet for t > 0: y (t) + 2y (t) + 50y(t)
DesignMat Uge 1 Repetition af forårets stof
 DesignMat Uge 1 Repetition af forårets stof Preben Alsholm Efterår 008 01 Lineært ligningssystem Lineært ligningssystem Et lineært ligningssystem: a 11 x 1 + a 1 x + + a 1n x n = b 1 a 1 x 1 + a x + +
DesignMat Uge 1 Repetition af forårets stof Preben Alsholm Efterår 008 01 Lineært ligningssystem Lineært ligningssystem Et lineært ligningssystem: a 11 x 1 + a 1 x + + a 1n x n = b 1 a 1 x 1 + a x + +
z j 2. Cauchy s formel er værd at tænke lidt nærmere over. Se på specialtilfældet 1 dz = 2πi z
 Matematik F2 - sæt 3 af 7 blok 4 f(z)dz = 0 Hovedemnet i denne uge er Cauchys sætning (den der står i denne sides hoved) og Cauchys formel. Desuden introduceres nulpunkter og singulariteter: simple poler,
Matematik F2 - sæt 3 af 7 blok 4 f(z)dz = 0 Hovedemnet i denne uge er Cauchys sætning (den der står i denne sides hoved) og Cauchys formel. Desuden introduceres nulpunkter og singulariteter: simple poler,
Eksamen i Matematik F2 d. 19. juni Opgave 2. Svar. Korte svar (ikke fuldstændige)
 Eksamen i Matematik F2 d. 9. juni 28 Korte svar (ikke fuldstændige Opgave Find realdelen, Re z, og imaginærdelen, Im z, for følgende værdier af z, a z = 2 i b z = i i c z = ln( + i Find realdelen, Re z,
Eksamen i Matematik F2 d. 9. juni 28 Korte svar (ikke fuldstændige Opgave Find realdelen, Re z, og imaginærdelen, Im z, for følgende værdier af z, a z = 2 i b z = i i c z = ln( + i Find realdelen, Re z,
DesignMat Den komplekse eksponentialfunktion og polynomier
 DesignMat Den komplekse eksponentialfunktion og polynomier Preben Alsholm Uge 8 Forår 010 1 Den komplekse eksponentialfunktion 1.1 Definitionen Definitionen Den velkendte eksponentialfunktion x e x vil
DesignMat Den komplekse eksponentialfunktion og polynomier Preben Alsholm Uge 8 Forår 010 1 Den komplekse eksponentialfunktion 1.1 Definitionen Definitionen Den velkendte eksponentialfunktion x e x vil
MATEMATIK 3 EN,MP 17. september 2014 Oversigt nr. 1
 MATEMATIK 3 EN,MP 7. september 204 Oversigt nr. Her bringes en samling af de gamle eksamensopgaver: (jan. 204) Betragt begyndelsesværdiproblemet y (t) + 7y (t) + 2y(t) = e t sin(2t) for t > 0, y(0) = 2,
MATEMATIK 3 EN,MP 7. september 204 Oversigt nr. Her bringes en samling af de gamle eksamensopgaver: (jan. 204) Betragt begyndelsesværdiproblemet y (t) + 7y (t) + 2y(t) = e t sin(2t) for t > 0, y(0) = 2,
Besvarelse til eksamen i Matematik F2, 2012
 Besvarelse til eksamen i Matematik F2, 202 Partiel besvarelse - har ikke inkluderet alle detaljer! Med forbehold for tastefejl. Opgave Find og bestem typen af alle singulariteter for følgende funktioner:
Besvarelse til eksamen i Matematik F2, 202 Partiel besvarelse - har ikke inkluderet alle detaljer! Med forbehold for tastefejl. Opgave Find og bestem typen af alle singulariteter for følgende funktioner:
Kortfattet svar til eksamen i Matematik F2 d. 21. juni 2017
 Kortfattet svar til eksamen i Matematik F2 d. 2. juni 27 Opgave Bestem for følgende tilfælde om en funktion f(z) af z = x + iy er analytisk i dele af den komplekse plan, hvis den har real del u(x, y) og
Kortfattet svar til eksamen i Matematik F2 d. 2. juni 27 Opgave Bestem for følgende tilfælde om en funktion f(z) af z = x + iy er analytisk i dele af den komplekse plan, hvis den har real del u(x, y) og
Formelsamling - MatF2. Therkel Zøllner og Amalie Christensen 27. juni 2009
 Formelsamling - MatF2 Therkel Zøllner og Amalie Christensen 27. juni 2009 1 Indhold 1 Kompleks variabel teori 3 1.1 Komplekse funktioner 825-830........................... 3 1.2 Powerserier af komplekse
Formelsamling - MatF2 Therkel Zøllner og Amalie Christensen 27. juni 2009 1 Indhold 1 Kompleks variabel teori 3 1.1 Komplekse funktioner 825-830........................... 3 1.2 Powerserier af komplekse
KOMPLEKS ANALYSE. noter til matematik beta H.A. NIELSEN
 KOMPLEKS ANALYSE noter til matematik beta H.A. NIELSEN institut for matematiske fag aarhus universitet 23 KOMPLEKS ANALYSE H.A. NIELSEN Indhold. Komplekse tal 2 2. Elementære funktioner 3. Holomorfe funktioner
KOMPLEKS ANALYSE noter til matematik beta H.A. NIELSEN institut for matematiske fag aarhus universitet 23 KOMPLEKS ANALYSE H.A. NIELSEN Indhold. Komplekse tal 2 2. Elementære funktioner 3. Holomorfe funktioner
Ordliste MM511 Kompleks Analyse
 Ordliste MM511 Kompleks Analyse Jens Siegstad jesie04@student.sdu.dk A Absolute convergence = absolut konvergens Analytic = analytisk Antiderivative = stamfunktion Annulus = annulus, ringområde Argument
Ordliste MM511 Kompleks Analyse Jens Siegstad jesie04@student.sdu.dk A Absolute convergence = absolut konvergens Analytic = analytisk Antiderivative = stamfunktion Annulus = annulus, ringområde Argument
Svar til eksamen i Matematik F2 d. 23. juni 2016
 Svar til eksamen i Matematik F d. 3. juni 06 FORBEHOLD FOR FEJL! Bemærk, i modsætning til herunder, så skal det i besvarelsen fremgå tydeligt, hvordan polerne ndes og hvordan de enkelte residuer udregnes.
Svar til eksamen i Matematik F d. 3. juni 06 FORBEHOLD FOR FEJL! Bemærk, i modsætning til herunder, så skal det i besvarelsen fremgå tydeligt, hvordan polerne ndes og hvordan de enkelte residuer udregnes.
MATEMATIK 11 Eksamensopgaver Juni 1995 Juni 2001, 4. fjerdedel
 Juni 2000 MATEMATIK 11 Eksamensopgaver Juni 1995 Juni 2001, 4. fjerdedel Opgave 1. (a) Find den fuldstændige løsning til differentialligningen y 8y + 16y = 0. (b) Find den fuldstændige løsning til differentialligningen
Juni 2000 MATEMATIK 11 Eksamensopgaver Juni 1995 Juni 2001, 4. fjerdedel Opgave 1. (a) Find den fuldstændige løsning til differentialligningen y 8y + 16y = 0. (b) Find den fuldstændige løsning til differentialligningen
Kompleks funktionsteori. Christian Berg
 Kompleks funktionsteori Christian Berg 2004 Matematisk Afdeling Universitetsparken 5 2100 København Ø c Matematisk Afdeling 2004 Forord I 1990 udarbejdede jeg noter til kompleks funktionsteori. De indgik
Kompleks funktionsteori Christian Berg 2004 Matematisk Afdeling Universitetsparken 5 2100 København Ø c Matematisk Afdeling 2004 Forord I 1990 udarbejdede jeg noter til kompleks funktionsteori. De indgik
Komplekse Tal. 20. november 2009. UNF Odense. Steen Thorbjørnsen Institut for Matematiske Fag Århus Universitet
 Komplekse Tal 20. november 2009 UNF Odense Steen Thorbjørnsen Institut for Matematiske Fag Århus Universitet Fra de naturlige tal til de komplekse Optælling af størrelser i naturen De naturlige tal N (N
Komplekse Tal 20. november 2009 UNF Odense Steen Thorbjørnsen Institut for Matematiske Fag Århus Universitet Fra de naturlige tal til de komplekse Optælling af størrelser i naturen De naturlige tal N (N
MM502+4 forelæsningsslides
 MM502+4 forelæsningsslides uge 11+12 1, 2009 Produceret af Hans J. Munkholm, delvis på baggrund af lignende materiale udarbejdet af Mikael Rørdam 1 I nærværende forbindelse er 11 + 12 23 1 Egenskaber for
MM502+4 forelæsningsslides uge 11+12 1, 2009 Produceret af Hans J. Munkholm, delvis på baggrund af lignende materiale udarbejdet af Mikael Rørdam 1 I nærværende forbindelse er 11 + 12 23 1 Egenskaber for
DesignMat Komplekse tal
 DesignMat Komplekse tal Preben Alsholm Uge 7 Forår 010 1 Talmængder 1.1 Talmængder Talmængder N er mængden af naturlige tal, 1,, 3, 4, 5,... Z er mængden af hele tal... 5, 4, 3,, 1, 0, 1,, 3, 4, 5,....
DesignMat Komplekse tal Preben Alsholm Uge 7 Forår 010 1 Talmængder 1.1 Talmængder Talmængder N er mængden af naturlige tal, 1,, 3, 4, 5,... Z er mængden af hele tal... 5, 4, 3,, 1, 0, 1,, 3, 4, 5,....
Analyse 1, Prøve 4 Besvarelse
 Københavns Universitet Prøve ved Det naturvidenskabelige Fakultet juni 2011 1 Analyse 1, Prøve 4 Besvarelse Lad Opgave 1 (50%) M = {T R 2 T er en åben trekant} og lad A : M R være arealfunktionen, dvs.
Københavns Universitet Prøve ved Det naturvidenskabelige Fakultet juni 2011 1 Analyse 1, Prøve 4 Besvarelse Lad Opgave 1 (50%) M = {T R 2 T er en åben trekant} og lad A : M R være arealfunktionen, dvs.
Komplekse tal og rækker
 Komplekse tal og rækker John Olsen 1 Indledning Dette sæt noter er forelæsningsnoter til foredraget Komplekse tal og rækker. Noterne er beregnet til at blive brugt sammen med foredraget. I afsnit 2 bliver
Komplekse tal og rækker John Olsen 1 Indledning Dette sæt noter er forelæsningsnoter til foredraget Komplekse tal og rækker. Noterne er beregnet til at blive brugt sammen med foredraget. I afsnit 2 bliver
MM501 forelæsningsslides
 MM501 forelæsningsslides uge 37, 2010 Produceret af Hans J. Munkholm 2009 bearbejdet af Jessica Carter 2010 1 Hvad er et komplekst tal? Hvordan regner man med komplekse tal? Man kan betragte udvidelsen
MM501 forelæsningsslides uge 37, 2010 Produceret af Hans J. Munkholm 2009 bearbejdet af Jessica Carter 2010 1 Hvad er et komplekst tal? Hvordan regner man med komplekse tal? Man kan betragte udvidelsen
Matematik F2 Opgavesæt 2
 Opgaver uge 2 I denne uge kigger vi nærmere på Cauchy-Riemann betingelserne, potensrækker, konvergenskriterier og flertydige funktioner. Vi skal også se på integration langs en ve i den komplekse plan.
Opgaver uge 2 I denne uge kigger vi nærmere på Cauchy-Riemann betingelserne, potensrækker, konvergenskriterier og flertydige funktioner. Vi skal også se på integration langs en ve i den komplekse plan.
Supplerende opgaver. S1.3.1 Lad A, B og C være delmængder af X. Vis at
 Supplerende opgaver Analyse Jørgen Vesterstrøm Forår 2004 S.3. Lad A, B og C være delmængder af X. Vis at (A B C) (A B C) (A B) C og find en nødvendig og tilstrækkelig betingelse for at der gælder lighedstegn
Supplerende opgaver Analyse Jørgen Vesterstrøm Forår 2004 S.3. Lad A, B og C være delmængder af X. Vis at (A B C) (A B C) (A B) C og find en nødvendig og tilstrækkelig betingelse for at der gælder lighedstegn
MATEMATIK 3 EN,MP 30. august 2013 Oversigt nr. 1
 EN,MP 30. august 2013 Oversigt nr. 1 Litteratur: I Matematik 3 bruger vi (igen) i efteråret 2013 E. Kreyzig: Advanced engineering mathematics, 10. udg., Wiley, 2011. Beskrivelse: Kurset vil handle om matematiske
EN,MP 30. august 2013 Oversigt nr. 1 Litteratur: I Matematik 3 bruger vi (igen) i efteråret 2013 E. Kreyzig: Advanced engineering mathematics, 10. udg., Wiley, 2011. Beskrivelse: Kurset vil handle om matematiske
2. Fourierrækker i en variabel
 .1. Fourierrækker i en variabel I Kapitel II 7 blev der indført, dels funktionsrummene L p (X, µ) (mere udførligt skrevet L p (X, E, µ)), dels rummene L p (X, µ), der fås af L p (X, µ) ved at funktioner
.1. Fourierrækker i en variabel I Kapitel II 7 blev der indført, dels funktionsrummene L p (X, µ) (mere udførligt skrevet L p (X, E, µ)), dels rummene L p (X, µ), der fås af L p (X, µ) ved at funktioner
MATEMATIK 3 ET,MP, FYS, NANO 29. august 2012 Oversigt nr. 1
 ET,MP, FYS, NANO 29. august 202 Oversigt nr. Litteratur: I Matematik 3 bruger vi i efteråret 202 følgende bog: E. Kreyzig: Advanced engineering mathematics, 0. udg., Wiley, 20. Beskrivelse: Kurset vil
ET,MP, FYS, NANO 29. august 202 Oversigt nr. Litteratur: I Matematik 3 bruger vi i efteråret 202 følgende bog: E. Kreyzig: Advanced engineering mathematics, 0. udg., Wiley, 20. Beskrivelse: Kurset vil
Oversigt [S] 8.7, 8.8, 8.9
![Oversigt [S] 8.7, 8.8, 8.9 Oversigt [S] 8.7, 8.8, 8.9](/thumbs/62/47922248.jpg) Oversigt [S] 8.7, 8.8, 8.9 Nøgleord og begreber Potensrækker og opgaver Binomialformlen Binomialkoefficienter Binomialrækken Taylor polynomier Vurdering af Taylor s restled Eksponentialrækken konvereger
Oversigt [S] 8.7, 8.8, 8.9 Nøgleord og begreber Potensrækker og opgaver Binomialformlen Binomialkoefficienter Binomialrækken Taylor polynomier Vurdering af Taylor s restled Eksponentialrækken konvereger
Inden der siges noget om komplekse tal, vil der i dette afsnit blive gennemgået en smule teori om trigonometriske funktioner.
 Komplekse tal Mike Auerbach Odense 2012 1 Vinkelmål og trigonometriske funktioner Inden der siges noget om komplekse tal, vil der i dette afsnit blive gennemgået en smule teori om trigonometriske funktioner.
Komplekse tal Mike Auerbach Odense 2012 1 Vinkelmål og trigonometriske funktioner Inden der siges noget om komplekse tal, vil der i dette afsnit blive gennemgået en smule teori om trigonometriske funktioner.
Noter om komplekse tal
 Noter om komplekse tal Preben Alsholm Januar 008 1 Den komplekse eksponentialfunktion Vi erindrer først om den sædvanlige og velkendte reelle eksponentialfunktion. Vi skal undertiden nde det nyttigt, at
Noter om komplekse tal Preben Alsholm Januar 008 1 Den komplekse eksponentialfunktion Vi erindrer først om den sædvanlige og velkendte reelle eksponentialfunktion. Vi skal undertiden nde det nyttigt, at
Afgør for hver af følgende rækker om den er divergent, betinget konvergent eller absolut konvergent. 2 n. n=1 2n (n + 1)2 1 = 2(n + n+1
 Analyse Reeksamen 00 Rasmus Sylvester Bryder 5. august 0 Opgave Afgør for hver af følgende rækker om den er divergent, betinget konvergent eller absolut konvergent. ( ) n n +3n+7 n= n + For alle n N vil
Analyse Reeksamen 00 Rasmus Sylvester Bryder 5. august 0 Opgave Afgør for hver af følgende rækker om den er divergent, betinget konvergent eller absolut konvergent. ( ) n n +3n+7 n= n + For alle n N vil
DesignMat Uge 1 Gensyn med forårets stof
 DesignMat Uge 1 Gensyn med forårets stof Preben Alsholm Efterår 2010 1 Hovedpunkter fra forårets pensum 11 Taylorpolynomium Taylorpolynomium Det n te Taylorpolynomium for f med udviklingspunkt x 0 : P
DesignMat Uge 1 Gensyn med forårets stof Preben Alsholm Efterår 2010 1 Hovedpunkter fra forårets pensum 11 Taylorpolynomium Taylorpolynomium Det n te Taylorpolynomium for f med udviklingspunkt x 0 : P
MATEMATIK 11 Eksamensopgaver Juni 1995 Juni 2001, 3. fjerdedel
 MATEMATIK Eksamensopgaver Juni 995 Juni 200, 3. fjerdedel August 998 Opgave. Lad f : R \ {0} R betegne funktionen givet ved f(x) = ex x for x 0. (a) Find eventuelle lokale maksimums- og minimumspunkter
MATEMATIK Eksamensopgaver Juni 995 Juni 200, 3. fjerdedel August 998 Opgave. Lad f : R \ {0} R betegne funktionen givet ved f(x) = ex x for x 0. (a) Find eventuelle lokale maksimums- og minimumspunkter
Besvarelses forslag til Tag-hjemeksamen Vinteren 02 03
 IMFUFA Carsten Lunde Petersen Besvarelses forslag til Tag-hjemeksamen Vinteren 02 0 Hvor ikke andet er angivet er henvisninger til W.R.Wade An Introduction to analysis. Opgave a) Idet udtrykket e x2 cos
IMFUFA Carsten Lunde Petersen Besvarelses forslag til Tag-hjemeksamen Vinteren 02 0 Hvor ikke andet er angivet er henvisninger til W.R.Wade An Introduction to analysis. Opgave a) Idet udtrykket e x2 cos
Fundamentale begreber fra Analysen. Introduktion. De reelle tal. Carsten Lunde Petersen
 IMFUFA Carsten Lunde Petersen Fundamentale begreber fra Analysen Introduktion Disse noter udgør et meget ltreret udkik over de grundlæggende begreber i reel analyse. Noten indeholder meget lidt om det
IMFUFA Carsten Lunde Petersen Fundamentale begreber fra Analysen Introduktion Disse noter udgør et meget ltreret udkik over de grundlæggende begreber i reel analyse. Noten indeholder meget lidt om det
Komplekse tal. Preben Alsholm Juli 2006
 Komplekse tal Preben Alsholm Juli 006 Talmængder og regneregler for tal. Talmængder Indenfor matematikken optræder der forskellige klasser af tal: Naturlige tal. N er mængden af naturlige tal, ; ; 3; 4;
Komplekse tal Preben Alsholm Juli 006 Talmængder og regneregler for tal. Talmængder Indenfor matematikken optræder der forskellige klasser af tal: Naturlige tal. N er mængden af naturlige tal, ; ; 3; 4;
Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 2016
 Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Komplekse tal. Mike Auerbach. Tornbjerg Gymnasium, Odense 2015
 Komplekse tal Mike Auerbach Tornbjerg Gymnasium, Odense 2015 Indhold 1 Vinkelmål og trigonometriske funktioner 2 1.1 Radianer................................................ 2 1.2 Cosinus og sinus som
Komplekse tal Mike Auerbach Tornbjerg Gymnasium, Odense 2015 Indhold 1 Vinkelmål og trigonometriske funktioner 2 1.1 Radianer................................................ 2 1.2 Cosinus og sinus som
Besvarelse, Eksamen Analyse 1, 2013
 Københavns Universitet Prøve ved Det naturvidenskabelige Fakultet juni 23 Besvarelse, Eksamen Analyse, 23 Opgave Lad, for n N, funktionen f n : [, ) R være givet ved NB. Trykfejl. Burde være x. f n (x)
Københavns Universitet Prøve ved Det naturvidenskabelige Fakultet juni 23 Besvarelse, Eksamen Analyse, 23 Opgave Lad, for n N, funktionen f n : [, ) R være givet ved NB. Trykfejl. Burde være x. f n (x)
MATEMATIK 3 EN3,MP3 28. august 2015 Oversigt nr. 1
 EN3,MP3 28. august 205 Oversigt nr. Litteratur: I Matematik 3 bruger vi (igen) i efteråret 205 [K] E. Kreyzig: Advanced engineering mathematics, 0. udg., Wiley, 20. Beskrivelse: Kurset vil handle om matematiske
EN3,MP3 28. august 205 Oversigt nr. Litteratur: I Matematik 3 bruger vi (igen) i efteråret 205 [K] E. Kreyzig: Advanced engineering mathematics, 0. udg., Wiley, 20. Beskrivelse: Kurset vil handle om matematiske
Den homogene ligning. Vi betragter den n te ordens, homogene, lineære differentialligning. d n y dt n. an 1 + any = 0 (1.2) dt. + a1 d n 1 y dt n 1
 1/7 Den homogene ligning Vi betragter den n te ordens, homogene, lineære differentialligning a 0 d n y dt n + a1 d n 1 y dt n 1 hvor a 0,..., a n R og a 0 0. Vi skriver ligningen på kort form som + + dy
1/7 Den homogene ligning Vi betragter den n te ordens, homogene, lineære differentialligning a 0 d n y dt n + a1 d n 1 y dt n 1 hvor a 0,..., a n R og a 0 0. Vi skriver ligningen på kort form som + + dy
Lektion 1. Tal. Ligninger og uligheder. Funktioner. Trigonometriske funktioner. Grænseværdi for en funktion. Kontinuerte funktioner.
 Lektion Tal Ligninger og uligheder Funktioner Trigonometriske funktioner Grænseværdi for en funktion Kontinuerte funktioner Opgaver Tal Man tænker ofte på de reelle tal, R, som en tallinje (uden huller).
Lektion Tal Ligninger og uligheder Funktioner Trigonometriske funktioner Grænseværdi for en funktion Kontinuerte funktioner Opgaver Tal Man tænker ofte på de reelle tal, R, som en tallinje (uden huller).
Mere om differentiabilitet
 Mere om differentiabilitet En uddybning af side 57 i Spor - Komplekse tal Kompleks funktionsteori er et af de vigtigste emner i matematikken og samtidig et af de smukkeste I bogen har vi primært beskæftiget
Mere om differentiabilitet En uddybning af side 57 i Spor - Komplekse tal Kompleks funktionsteori er et af de vigtigste emner i matematikken og samtidig et af de smukkeste I bogen har vi primært beskæftiget
Idenne note giver vi et eksempel på, hvorledes det er vigtigt at holde sig
 Analyse : Eulers formel Sebastian rsted 9. maj 015 Idenne note giver vi et eksempel på, hvorledes det er vigtigt at holde sig for øje, hvor de matematiske resultater kommer fra, og hvad de baseres på;
Analyse : Eulers formel Sebastian rsted 9. maj 015 Idenne note giver vi et eksempel på, hvorledes det er vigtigt at holde sig for øje, hvor de matematiske resultater kommer fra, og hvad de baseres på;
Komplekse tal. enote 29. 29.1 Indledning
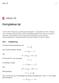 enote 29 1 enote 29 Komplekse tal I denne enote introduceres og undersøges talmængden C, de komplekse tal. Da C betragtes som en udvidelse af R forudsætter enoten almindeligt kendskab til de reelle tal,
enote 29 1 enote 29 Komplekse tal I denne enote introduceres og undersøges talmængden C, de komplekse tal. Da C betragtes som en udvidelse af R forudsætter enoten almindeligt kendskab til de reelle tal,
Komplekse tal. x 2 = 1 (2) eller
 Komplekse tal En tilegnelse af stoffet i dette appendix kræver at man løser opgaverne Komplekse tal viser sig uhyre nyttige i fysikken, f.eks til løsning af lineære differentialligninger eller beskrivelse
Komplekse tal En tilegnelse af stoffet i dette appendix kræver at man løser opgaverne Komplekse tal viser sig uhyre nyttige i fysikken, f.eks til løsning af lineære differentialligninger eller beskrivelse
Indhold. Litteratur 11
 Indhold Forord ii 00-sættet 1 Opgave 1....................................... 1 Spørgsmål (a).................................. 1 Spørgsmål (b).................................. 1 Spørgsmål (c)..................................
Indhold Forord ii 00-sættet 1 Opgave 1....................................... 1 Spørgsmål (a).................................. 1 Spørgsmål (b).................................. 1 Spørgsmål (c)..................................
Matematik 1 Semesteruge 5 6 (30. september oktober 2002) side 1. Komplekse tal Arbejdsplan
 Matematik Semesteruge 5 6 (30. september -. oktober 2002) side Komplekse tal Arbejdsplan I semesterugerne 5 og 6 erstattes den regulære undervisning (forelæsninger og fællestimer) af selvstudium med opgaveregning
Matematik Semesteruge 5 6 (30. september -. oktober 2002) side Komplekse tal Arbejdsplan I semesterugerne 5 og 6 erstattes den regulære undervisning (forelæsninger og fællestimer) af selvstudium med opgaveregning
Besvarelser til Calculus Ordinær Eksamen Juni 2019
 Besvarelser til Calculus Ordinær Eksamen - 14. Juni 2019 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 14. Juni 2019 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Hilbert rum. Chapter 3. 3.1 Indre produkt rum
 Chapter 3 Hilbert rum 3.1 Indre produkt rum I det følgende skal vi gøre brug af komplekse såvel som reelle vektorrum. Idet L betegner enten R eller C minder vi om, at et vektorrum over L er en mængde E
Chapter 3 Hilbert rum 3.1 Indre produkt rum I det følgende skal vi gøre brug af komplekse såvel som reelle vektorrum. Idet L betegner enten R eller C minder vi om, at et vektorrum over L er en mængde E
Kalkulus 2 - Grænseovergange, Kontinuitet og Følger
 Kalkulus - Grænseovergange, Kontinuitet og Følger Mads Friis 8. januar 05 Indhold Grundlæggende uligheder Grænseovergange 3 3 Kontinuitet 9 4 Følger 0 5 Perspektivering 4 Grundlæggende uligheder Sætning
Kalkulus - Grænseovergange, Kontinuitet og Følger Mads Friis 8. januar 05 Indhold Grundlæggende uligheder Grænseovergange 3 3 Kontinuitet 9 4 Følger 0 5 Perspektivering 4 Grundlæggende uligheder Sætning
Matematik 1 Semesteruge 5 6 (1. oktober oktober 2001) side 1 Komplekse tal Arbejdsplan
 Matematik 1 Semesteruge 5 6 (1. oktober - 12. oktober 2001) side 1 Komplekse tal Arbejdsplan I semesterugerne 5 og 6 erstattes den regulære undervisning (forelæsninger og fællestimer) af selvstudium med
Matematik 1 Semesteruge 5 6 (1. oktober - 12. oktober 2001) side 1 Komplekse tal Arbejdsplan I semesterugerne 5 og 6 erstattes den regulære undervisning (forelæsninger og fællestimer) af selvstudium med
Komplekse tal og algebraens fundamentalsætning.
 Komplekse tal og algebraens fundamentalsætning. Michael Knudsen 10. oktober 2005 1 Ligningsløsning Lad N = {0,1,2,...} betegne mængden af de naturlige tal og betragt ligningen ax + b = 0, a,b N,a 0. Findes
Komplekse tal og algebraens fundamentalsætning. Michael Knudsen 10. oktober 2005 1 Ligningsløsning Lad N = {0,1,2,...} betegne mængden af de naturlige tal og betragt ligningen ax + b = 0, a,b N,a 0. Findes
DesignMat Uge 8 Integration og elementære funktioner
 DesignMat Uge 8 Integration og elementære funktioner Preben Alsholm Forår 008 Hyperbolske funktioner. sinh og cosh sinh og cosh Sinus hyperbolsk efineres sålees for alle x R sinh x = ex e x Cosinus hyperbolsk
DesignMat Uge 8 Integration og elementære funktioner Preben Alsholm Forår 008 Hyperbolske funktioner. sinh og cosh sinh og cosh Sinus hyperbolsk efineres sålees for alle x R sinh x = ex e x Cosinus hyperbolsk
MASO-Eksempler. x n. + 1 = 1 y n
 3. oktober EXPL 1 Eksempel 1. Et par talfølger: (1 ( (3 (4 (5 (6 (7 (8 MASO-Eksempler,,,,,,..., n =, 1, 1, 1, 1, 1, 1,..., n = 1 1,, 1,, 1,, 1,..., n = (1 + ( 1 n /,, 1,,,, 3,..., n = n(1 + ( 1 n /4, 1,
3. oktober EXPL 1 Eksempel 1. Et par talfølger: (1 ( (3 (4 (5 (6 (7 (8 MASO-Eksempler,,,,,,..., n =, 1, 1, 1, 1, 1, 1,..., n = 1 1,, 1,, 1,, 1,..., n = (1 + ( 1 n /,, 1,,,, 3,..., n = n(1 + ( 1 n /4, 1,
Matematik F2 Opgavesæt 1
 Opgaer uge 1 I denne uge er temaet komplekse tal og komplekse funktioner af en kompleks ariabel. De første opgaer skulle gerne øge jeres fortrolighed med komplekse tal. I kan med fordel repetere de basale
Opgaer uge 1 I denne uge er temaet komplekse tal og komplekse funktioner af en kompleks ariabel. De første opgaer skulle gerne øge jeres fortrolighed med komplekse tal. I kan med fordel repetere de basale
Projekt 2.2 Omvendt funktion og differentiation af omvendt funktion
 ISBN 978877664974 Projekter: Kapitel. Projekt. Omvendt funktion og differentiation af omvendt funktion Projekt. Omvendt funktion og differentiation af omvendt funktion Vi har i Bbogens kapitel 4 afsnit
ISBN 978877664974 Projekter: Kapitel. Projekt. Omvendt funktion og differentiation af omvendt funktion Projekt. Omvendt funktion og differentiation af omvendt funktion Vi har i Bbogens kapitel 4 afsnit
MATEMATIK 3 EN,MP 28. august 2014 Oversigt nr. 1
 EN,MP 28. august 2014 Oversigt nr. 1 Litteratur: I Matematik 3 bruger vi (igen) i efteråret 2014 [K] E. Kreyzig: Advanced engineering mathematics, 10. udg., Wiley, 2011. Beskrivelse: Kurset vil handle
EN,MP 28. august 2014 Oversigt nr. 1 Litteratur: I Matematik 3 bruger vi (igen) i efteråret 2014 [K] E. Kreyzig: Advanced engineering mathematics, 10. udg., Wiley, 2011. Beskrivelse: Kurset vil handle
Komplekse tal. enote Indledning
 enote 1 1 enote 1 Komplekse tal I denne enote introduceres og undersøges talmængden C, de komplekse tal. Da C betragtes som en udvidelse af R, forudsætter enoten almindeligt kendskab til de reelle tal,
enote 1 1 enote 1 Komplekse tal I denne enote introduceres og undersøges talmængden C, de komplekse tal. Da C betragtes som en udvidelse af R, forudsætter enoten almindeligt kendskab til de reelle tal,
Analyse 1. Mads Friis Anders Friis Anne Ryelund. 25. maj 2018
 Analyse 1 Mads Friis Anders Friis Anne Ryelund 25. maj 2018 Indhold Introduktion Aksiomer og den matematiske metode Formalistisk struktur Mængder Introduktion Definitioner Delmængder Fællesmængde og foreningsmængde
Analyse 1 Mads Friis Anders Friis Anne Ryelund 25. maj 2018 Indhold Introduktion Aksiomer og den matematiske metode Formalistisk struktur Mængder Introduktion Definitioner Delmængder Fællesmængde og foreningsmængde
Noter til MatF2 på KU (Matematik for Fysikere 2)
 Noter til MatF2 på KU (Matematik for Fysikere 2) af Nikolai Plambech Nielsen, LPK33, Version.0 8. juni 206 Resumé Dette notesæt er udarbejdet til kurset Matematik for Fysikere 2 (Forkortet MatF2). Bogen,
Noter til MatF2 på KU (Matematik for Fysikere 2) af Nikolai Plambech Nielsen, LPK33, Version.0 8. juni 206 Resumé Dette notesæt er udarbejdet til kurset Matematik for Fysikere 2 (Forkortet MatF2). Bogen,
Pseudospektrer og normvurderinger
 master 2009/6/3 0:27 page I # Pseudospektrer og normvurderinger af Lars V. Iversen Dan V. Jensen Ove L. Sandau AALBORG UNIVERSITET d Institut for Matematiske Fag Gruppe G3-09 MAT6. februar 5. juni 2009
master 2009/6/3 0:27 page I # Pseudospektrer og normvurderinger af Lars V. Iversen Dan V. Jensen Ove L. Sandau AALBORG UNIVERSITET d Institut for Matematiske Fag Gruppe G3-09 MAT6. februar 5. juni 2009
Matematik F2 Opgavesæt 1
 Opgaer uge 1 I denne uge er temaet komplekse tal og komplekse funktioner af en kompleks ariabel. De første opgaer skulle gerne øge jeres fortrolighed med komplekse tal. I kan med fordel repetere de basale
Opgaer uge 1 I denne uge er temaet komplekse tal og komplekse funktioner af en kompleks ariabel. De første opgaer skulle gerne øge jeres fortrolighed med komplekse tal. I kan med fordel repetere de basale
z + w z + w z w = z 2 w z w = z w z 2 = z z = a 2 + b 2 z w
 Komplekse tal Hvis z = a + ib og w = c + id gælder z + w = (a + c) + i(b + d) z w = (a c) + i(b d) z w = (ac bd) + i(ad bc) z w = a+ib c+id = ac+bd + i bc ad, w 0 c +d c +d z a b = i a +b a +b Konjugation
Komplekse tal Hvis z = a + ib og w = c + id gælder z + w = (a + c) + i(b + d) z w = (a c) + i(b d) z w = (ac bd) + i(ad bc) z w = a+ib c+id = ac+bd + i bc ad, w 0 c +d c +d z a b = i a +b a +b Konjugation
ANALYSE 1, 2014, Uge 5
 ANALYSE, 204, Uge 5 Afleveringsfrist for Prøve 2 er Tirsdag den 20/5 kl 0:5. Forelæsninger Tirsdag Vi går videre med Afsnit 4 om uniform konvergens af Fourierrækker, hvor hovedsætningen er Sætning 4.3.
ANALYSE, 204, Uge 5 Afleveringsfrist for Prøve 2 er Tirsdag den 20/5 kl 0:5. Forelæsninger Tirsdag Vi går videre med Afsnit 4 om uniform konvergens af Fourierrækker, hvor hovedsætningen er Sætning 4.3.
8 Regulære flader i R 3
 8 Regulære flader i R 3 Vi skal betragte særligt pæne delmængder S R 3 kaldet flader. I det følgende opfattes S som et topologisk rum i sportopologien, se Definition 5.9. En åben omegn U af p S er således
8 Regulære flader i R 3 Vi skal betragte særligt pæne delmængder S R 3 kaldet flader. I det følgende opfattes S som et topologisk rum i sportopologien, se Definition 5.9. En åben omegn U af p S er således
Noter om Komplekse Vektorrum, Funktionsrum og Differentialligninger LinAlg 2004/05-Version af 16. Dec.
 Noter om Komplekse Vektorrum, Funktionsrum og Differentialligninger LinAlg 2004/05-Version af 16. Dec. 1 Komplekse vektorrum I defininitionen af vektorrum i Afsnit 4.1 i Niels Vigand Pedersen Lineær Algebra
Noter om Komplekse Vektorrum, Funktionsrum og Differentialligninger LinAlg 2004/05-Version af 16. Dec. 1 Komplekse vektorrum I defininitionen af vektorrum i Afsnit 4.1 i Niels Vigand Pedersen Lineær Algebra
Løsningsforslag til opgavesæt 5
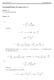 Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
Besvarelser til Calculus Ordinær Eksamen Januar 2019
 Besvarelser til Calculus Ordinær Eksamen - 14. Januar 19 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 14. Januar 19 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Eksamen i Calculus. 14. juni f (x, y, z) = 1 + x 2 + y 2. Hele rummet uden z aksen
 Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 14. juni 019 Opgave 1 (6 point) En
Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 14. juni 019 Opgave 1 (6 point) En
Eksamen i Calculus. 14. juni f (x, y, z) = 1 + x 2 + y 2. x 2 + y 2 1 Hele rummet uden z aksen
 Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 14. juni 19 Opgave 1 (6 point) En funktion
Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 14. juni 19 Opgave 1 (6 point) En funktion
01141 COMPLEX ANALYSIS 2005 Short Dictionary Translation from English to Danish
 01141 COMPLEX ANALYSIS 2005 Short Dictionary Translation from English to Danish A B C Absolute value = absolut værdi, 8 Absolute convergence = absolut konvergens, 237 Accumulation point = akkumulations-punkt,
01141 COMPLEX ANALYSIS 2005 Short Dictionary Translation from English to Danish A B C Absolute value = absolut værdi, 8 Absolute convergence = absolut konvergens, 237 Accumulation point = akkumulations-punkt,
Besvarelser til Calculus Ordinær Eksamen Juni 2018
 Besvarelser til Calculus Ordinær Eksamen - 5. Juni 08 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 5. Juni 08 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
t a l e n t c a m p d k Kalkulus 1 Mads Friis Anders Friis Anne Ryelund Signe Baggesen 10. januar 2015 Slide 1/54
 Slide 1/54 Indhold 1 2 3 4 5 Slide 2/54 Indhold 1 2 3 4 5 Slide 3/54 1) Hvad er et aksiom? Slide 4/54 1) Hvad er et aksiom? 2) Hvorfor har vi brug for aksiomer? The Monty Hall Problem Slide 4/54 1) Hvad
Slide 1/54 Indhold 1 2 3 4 5 Slide 2/54 Indhold 1 2 3 4 5 Slide 3/54 1) Hvad er et aksiom? Slide 4/54 1) Hvad er et aksiom? 2) Hvorfor har vi brug for aksiomer? The Monty Hall Problem Slide 4/54 1) Hvad
Fordybelsesprojekt Matematik 2, forår 2005 Potensrækker
 Fordybelsesprojekt Matematik 2, forår 2005 Potensrækker Arne Jensen 7. 11. marts 2005 1 Indledning I forbindelse med kurset i Reelle og Komplekse Funktioner afholdes et fordybelsesprojekt med et omfang
Fordybelsesprojekt Matematik 2, forår 2005 Potensrækker Arne Jensen 7. 11. marts 2005 1 Indledning I forbindelse med kurset i Reelle og Komplekse Funktioner afholdes et fordybelsesprojekt med et omfang
Mat H /05 Note 2 10/11-04 Gerd Grubb
 Mat H 1 2004/05 Note 2 10/11-04 Gerd Grubb Nødvendige og tilstrækkelige betingelser for ekstremum, konkave og konvekse funktioner. Fremstillingen i Kapitel 13.1 2 af Sydsæters bog [MA1] suppleres her med
Mat H 1 2004/05 Note 2 10/11-04 Gerd Grubb Nødvendige og tilstrækkelige betingelser for ekstremum, konkave og konvekse funktioner. Fremstillingen i Kapitel 13.1 2 af Sydsæters bog [MA1] suppleres her med
To find the English version of the exam, please read from the other end! Eksamen i Calculus
 To find the English version of the exam, please read from the other end! Se venligst bort fra den engelske version på bagsiden hvis du følger denne danske version af prøven. Eksamen i Calculus Første Studieår
To find the English version of the exam, please read from the other end! Se venligst bort fra den engelske version på bagsiden hvis du følger denne danske version af prøven. Eksamen i Calculus Første Studieår
Analyse 2. Gennemgå bevis for Sætning Supplerende opgave 1. Øvelser. Sætning 1. For alle mængder X gælder #X < #P(X).
 Analyse 2 Øvelser Rasmus Sylvester Bryder 3. og 6. september 2013 Gennemgå bevis for Sætning 2.10 Sætning 1. For alle mængder X gælder #X < #P(X). Bevis. Der findes en injektion X P(X), fx givet ved x
Analyse 2 Øvelser Rasmus Sylvester Bryder 3. og 6. september 2013 Gennemgå bevis for Sætning 2.10 Sætning 1. For alle mængder X gælder #X < #P(X). Bevis. Der findes en injektion X P(X), fx givet ved x
Eksamen i Mat F, april 2006
 Eksamen i Mat F, april 26 Opgave 1 Lad F være et vektorfelt, givet i retvinklede koordinater som: F x x F = F x i + F y j + F z k = F y = 2z F z y Udregn F og F: F = F x + F y + F z = 1 + +. F = F z F
Eksamen i Mat F, april 26 Opgave 1 Lad F være et vektorfelt, givet i retvinklede koordinater som: F x x F = F x i + F y j + F z k = F y = 2z F z y Udregn F og F: F = F x + F y + F z = 1 + +. F = F z F
Indledning. 1 Martingalerepræsentationssætningen
 Indledning I disse noter vil uddybe nogle af Øksendals resultater i afsnittene 4 og 7 samt give andre beviser for dem. Disse resultater er gennemgået til forelæsningerne. 1 Martingalerepræsentationssætningen
Indledning I disse noter vil uddybe nogle af Øksendals resultater i afsnittene 4 og 7 samt give andre beviser for dem. Disse resultater er gennemgået til forelæsningerne. 1 Martingalerepræsentationssætningen
Oversigt [S] 9.6, 11.1, 11.2, App. H.1
![Oversigt [S] 9.6, 11.1, 11.2, App. H.1 Oversigt [S] 9.6, 11.1, 11.2, App. H.1](/thumbs/62/47252518.jpg) Oversigt [S] 9.6, 11.1, 11.2, App. H.1 Her skal du lære om 1. Funktioner i flere variable 2. Grafen og niveaukurver 3. Grænseovergange og grænseværdier 4. Kontinuitet i flere variable 5. Polære koordinater
Oversigt [S] 9.6, 11.1, 11.2, App. H.1 Her skal du lære om 1. Funktioner i flere variable 2. Grafen og niveaukurver 3. Grænseovergange og grænseværdier 4. Kontinuitet i flere variable 5. Polære koordinater
Analyse 1. Matthias Christandl
 Analyse 1 Matthias Christandl Marts 2019 ii Forord Følger af tal kan opføre sig på mange forskellige måder, bare tænk på talfølgerne som går mod uendelig, som konvergerer mod nul, og 1, 2, 3, 4, 5,...,
Analyse 1 Matthias Christandl Marts 2019 ii Forord Følger af tal kan opføre sig på mange forskellige måder, bare tænk på talfølgerne som går mod uendelig, som konvergerer mod nul, og 1, 2, 3, 4, 5,...,
Eksamen i Calculus Mandag den 4. juni 2012
 Eksamen i Calculus Mandag den 4. juni 212 Første Studieår ved Det Teknisk-Naturvidenskabelige Fakultet og Det Sundhedsvidenskabelige Fakultet Nærværende eksamenssæt består af 7 nummererede sider med ialt
Eksamen i Calculus Mandag den 4. juni 212 Første Studieår ved Det Teknisk-Naturvidenskabelige Fakultet og Det Sundhedsvidenskabelige Fakultet Nærværende eksamenssæt består af 7 nummererede sider med ialt
Løsningsforslag til opgavesæt 5
 Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
Eksamen i Calculus. Onsdag den 1. juni Første Studieår ved Det Teknisk-Naturvidenskabelige Fakultet og Det Sundhedsvidenskabelige Fakultet
 Eksamen i Calculus Onsdag den 1. juni 211 Første Studieår ved Det Teknisk-Naturvidenskabelige Fakultet og Det Sundhedsvidenskabelige Fakultet Nærværende eksamenssæt består af 7 nummererede sider med ialt
Eksamen i Calculus Onsdag den 1. juni 211 Første Studieår ved Det Teknisk-Naturvidenskabelige Fakultet og Det Sundhedsvidenskabelige Fakultet Nærværende eksamenssæt består af 7 nummererede sider med ialt
Besvarelser til Calculus Ordinær Eksamen - 3. Januar 2017
 Besvarelser til Calculus Ordinær Eksamen - 3. Januar 17 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 3. Januar 17 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Kursusnoter til BasisMat
 Kursusnoter til BasisMat Peter Beelen Søren Thomsen Peter Nørtoft Morten Brøns Im z=re iα z =r arg(z)=α Re e iπ + 1 = 0 INSTITUT FOR MATEMATIK OG COMPUTER SCIENCE DANMARKS TEKNISKE UNIVERSITET 2016 Indhold
Kursusnoter til BasisMat Peter Beelen Søren Thomsen Peter Nørtoft Morten Brøns Im z=re iα z =r arg(z)=α Re e iπ + 1 = 0 INSTITUT FOR MATEMATIK OG COMPUTER SCIENCE DANMARKS TEKNISKE UNIVERSITET 2016 Indhold
Analyse 1, Prøve 2 Besvarelse
 Københavns Universitet Prøve ved Det naturvidenskabelige Fakultet maj Analyse, Prøve Besvarelse Opgave (3%) (a) (%) Bestem mængden af x R for hvilke rækken ( + (x) n ) er konvergent og angiv sumfunktionen
Københavns Universitet Prøve ved Det naturvidenskabelige Fakultet maj Analyse, Prøve Besvarelse Opgave (3%) (a) (%) Bestem mængden af x R for hvilke rækken ( + (x) n ) er konvergent og angiv sumfunktionen
MASO Uge 1. Relle tal Følger. Jesper Michael Møller. 10. september Department of Mathematics University of Copenhagen
 MASO Uge 1 Relle tal Jesper Michael Møller Department of Mathematics University of Copenhagen 10. september 2018 Oversigt Relle tal Notation Tal Største og mindste element, mindste overtal og største undertal
MASO Uge 1 Relle tal Jesper Michael Møller Department of Mathematics University of Copenhagen 10. september 2018 Oversigt Relle tal Notation Tal Største og mindste element, mindste overtal og største undertal
matx.dk Differentialregning Dennis Pipenbring
 mat.dk Differentialregning Dennis Pipenbring 0. december 00 Indold Differentialregning 3. Grænseværdi............................. 3. Kontinuitet.............................. 8 Differentialkvotienten
mat.dk Differentialregning Dennis Pipenbring 0. december 00 Indold Differentialregning 3. Grænseværdi............................. 3. Kontinuitet.............................. 8 Differentialkvotienten
MASO Uge 7. Differentiable funktioner. Jesper Michael Møller. Uge 7. Formålet med MASO. Department of Mathematics University of Copenhagen
 MASO Uge 7 Differentiable funktioner Jesper Michael Møller Department of Mathematics University of Copenhagen Uge 7 Formålet med MASO Oversigt Differentiable funktioner R n R m Differentiable funktioner
MASO Uge 7 Differentiable funktioner Jesper Michael Møller Department of Mathematics University of Copenhagen Uge 7 Formålet med MASO Oversigt Differentiable funktioner R n R m Differentiable funktioner
Matematik F2 Opgavesæt 6
 Opgave 4: Udtryk funktionen f(θ) = sin θ ved hjælp af Legendre-polynomierne på formen P l (cos θ). Dvs. find koefficienterne a l i ekspansionen f(θ) = a l P l (cos θ) l= Svar: Bemærk, at funktionen er
Opgave 4: Udtryk funktionen f(θ) = sin θ ved hjælp af Legendre-polynomierne på formen P l (cos θ). Dvs. find koefficienterne a l i ekspansionen f(θ) = a l P l (cos θ) l= Svar: Bemærk, at funktionen er
Komplekse tal. Mikkel Stouby Petersen 27. februar 2013
 Komplekse tal Mikkel Stouby Petersen 27. februar 2013 1 Motivationen Historien om de komplekse tal er i virkeligheden historien om at fjerne forhindringerne og gøre det umulige muligt. For at se det, vil
Komplekse tal Mikkel Stouby Petersen 27. februar 2013 1 Motivationen Historien om de komplekse tal er i virkeligheden historien om at fjerne forhindringerne og gøre det umulige muligt. For at se det, vil
INSTITUT FOR MATEMATIK OG DATALOGI. TIDLIGERE EKSAMENSOPGAVER MM01 Juni 1993 marts 2006
 INSTITUT FOR MATEMATIK OG DATALOGI TIDLIGERE EKSAMENSOPGAVER MM01 Juni 1993 marts 2006 i Forord Denne opgavesamling skal bruges med den forståelse, at pensumbeskrivelsen for kurset har undergået en række
INSTITUT FOR MATEMATIK OG DATALOGI TIDLIGERE EKSAMENSOPGAVER MM01 Juni 1993 marts 2006 i Forord Denne opgavesamling skal bruges med den forståelse, at pensumbeskrivelsen for kurset har undergået en række
Potensrækker. Morten Grud Rasmussen 1 10. november 2015. Definition 1 (Potensrække). En potensrække er en uendelig række på formen
 Potensrækker Morten Grud Rasmussen 1 10 november 2015 Definition og konvergens af potensrækker Definition 1 Potensrække) En potensrække er en uendelig række på formen a n pz aq n, 1) hvor afsnittene er
Potensrækker Morten Grud Rasmussen 1 10 november 2015 Definition og konvergens af potensrækker Definition 1 Potensrække) En potensrække er en uendelig række på formen a n pz aq n, 1) hvor afsnittene er
4. Differentialligninger i højere dimension, Dirichlet problemet
 4.1 4. Differentialligninger i højere dimension, Dirichlet problemet 4.1. Indledning, de forskellige typer. Der er tre hovedeksempler på partielle differentialligninger, som har særlig betydning i fysik:
4.1 4. Differentialligninger i højere dimension, Dirichlet problemet 4.1. Indledning, de forskellige typer. Der er tre hovedeksempler på partielle differentialligninger, som har særlig betydning i fysik:
= λ([ x, y)) + λ((y, x]) = ( y ( x)) + (x y) = 2(x y).
![= λ([ x, y)) + λ((y, x]) = ( y ( x)) + (x y) = 2(x y). = λ([ x, y)) + λ((y, x]) = ( y ( x)) + (x y) = 2(x y).](/thumbs/58/42581589.jpg) Analyse 2 Øvelser Rasmus Sylvester Bryder 17. og 20. september 2013 Supplerende opgave 1 Lad λ være Lebesgue-målet på R og lad A B(R). Definér en funktion f : [0, ) R ved f(x) = λ(a [ x, x]). Vis, at f(x)
Analyse 2 Øvelser Rasmus Sylvester Bryder 17. og 20. september 2013 Supplerende opgave 1 Lad λ være Lebesgue-målet på R og lad A B(R). Definér en funktion f : [0, ) R ved f(x) = λ(a [ x, x]). Vis, at f(x)
Funktioner af to variable
 enote 15 1 enote 15 Funktioner af to variable I denne og i de efterfølgende enoter vil vi udvide funktionsbegrebet til at omfatte reelle funktioner af flere variable; vi starter udvidelsen med 2 variable,
enote 15 1 enote 15 Funktioner af to variable I denne og i de efterfølgende enoter vil vi udvide funktionsbegrebet til at omfatte reelle funktioner af flere variable; vi starter udvidelsen med 2 variable,
