Formelsamling. Noter til Fysik 4 Elektromagnetisme
|
|
|
- Helle Rasmussen
- 8 år siden
- Visninger:
Transkript
1 Formelsamling Noter til Fysik 4 Elektromagnetisme You can know the name of a bird in all the languages of the world, but when you re finished, you ll know absolutely nothing whatever about the bird... So let s look at the bird and see what it s doing that s what counts. I learned very early the difference between knowing the name of something and knowing something. Richard P. Feynman Benyttede bøger: Introduction to Electrodynamics, David J. Griffiths, De overordnede kapitelnumre i denne formelsamling svarer til de behandlede kapitler i bogen Introduction to Electrodynamics. Sammensat af Kristoffer Stensbo-Smidt 28. juni 2007
2 INDHOLD Indhold 1 Vector Analysis Vektoralgebra Integralregning Dirac-delta-funktionen Vektorfelter Electrostatics Coulombs lov Elektriske felter Kontinuerte distributioner Divergens og curl af elektrostatiske felter Gauss lov i funktion Curlet af E Elektrisk potentiale Hurtig oversigt Overfladeladning Arbejde og energi Ledere Overfladeladning og kraft på en leder Kapacitorer Special Techniques Laplace s ligning I én dimension I to dimensioner I tre dimensioner Entydighedssætninger Billedmetoden Multipoler Electric Fields in Matter Bundne ladninger Elektrisk forskydning Grænsebetingelser Lineære dielektrika Grænseværdiproblemer Energi og kræfter Magnetostatik Divergens og curl af B Magnetisk vektorpotential Hurtig oversigt Grænsebetingelser Multipolekspansion Magnetic Fields in Matter Kraft og kraftmoment Felter fra et magnetiseret objekt H-feltet Grænsebetingelser Lineært og ikke-lineært materiale Side 2 af 21
3 INDHOLD 7 Elektrodynamik Elektromotorisk kraft Elektromagnetisk induktion Induktans Energi i magnetiske felter Udvalgte formler Bennys tavle E-felter Potentialer B-felter Indeks 21 Side 3 af 21
4 1 Vector Analysis 1 Vector Analysis 1.1 Vektoralgebra S. 3ff. Små, hyggelige formler: A B = 0 A B det(a, B) = 0 A B (I to dimensioner) A B = 0 A B (I tre dimensioner) A B = AB cos θ (B A) = (A B) A (B C) = B(A C) C(A C) A (B C) = B (C A) = C (A B) A x A y A z A (B C) = B x B y B z C x C y C z 1.2 Integralregning S. 31. Divergensteoremet: (også kaldet Gauss teorem eller Greens teorem) ( v) dτ = v da V S S. 34. Stokes teorem: ( v) da = v dl S. 37. Partiel integration: b S P b f(x) g(x) dx = [F (x) g(x)] b a F (x) g (x) dx a a 1.3 Dirac-delta-funktionen S For Dirac-delta-funktionen centreret om x = a og funktionen f(x): f(x)δ(x a) dx = f(a) hele R 3 f(r)δ 3 (r a) dτ = f(a) (En dimension) (Tre dimensioner) 1.4 Vektorfelter Teorem 1.1 (S. 53. Irrotational fields ) Følgende punkter er ækvivalente: 1. F = 0 overalt. 2. b F dl afhænger kun af endepunkterne, ikke af vejen. a 3. F dl = 0 for ethvert lukket loop. 4. F er gradienten af en skalar, F = V. Teorem 1.2 (S. 54. Solenoidal fields ) Følgende punkter er ækvivalente: Side 4 af 21
5 2 Electrostatics 1. F = 0 overalt. 2. F da afhænger kun af randen, ikke af overfladen. 3. F da = 0 for enhver lukket overflade. 4. F er rotationen af en vektor, F = A. 2 Electrostatics 2.1 Coulombs lov S. 59. Coulombs lov: F = 1 qq r r 3 (r r ) hvor r er positionen af testladningen Q, mens r er positionen af punktladningen q. 2.2 Elektriske felter S. 60. Punktladninger q 1, q 2,..., q n med afstande r r 1, r r 2,..., r r n fra Q: Kontinuerte distributioner S. 62. Kontinuerte elektriske felter: F = QE, E(r) = 1 Linjeladning: λ er ladning pr. linjeelement dl : E(r) = 1 P n i=1 q i r r i 3 (r r i ) λ(r ) r r 3 (r r ) dl Overfladeladning: σ er ladning pr. overfladeelement da : E(r) = 1 σ(r ) r r 3 (r r ) da Volumenladning: ρ er ladning pr. volumenelement dτ : E(r) = 1 ρ(r ) r r 3 (r r ) dτ S V 2.3 Divergens og curl af elektrostatiske felter S. 67. Fluxen af et felt E er givet som: Φ E E da S. 68. For enhver lukket overflade gælder Gauss lov: E da = 1 Q enc ε 0 S S E = 1 ε 0 ρ(r) (Integralform) (Differentialform) hvor Q enc er den totale ladning indenfor overfladen. Side 5 af 21
6 2.4 Elektrisk potentiale Gauss lov i funktion S. 71. Det elektriske felt i afstanden r fra en uniformt ladet sfærisk kilde med ladningen q: E = 1 q r 2 ˆr S. 73. Det elektriske felt inde i en lang cylinder hvor ladningsdensiteten afhænger af afstanden s fra aksen og en konstant k, dvs. ρ = ks: E = 1 3ε 0 ks 2 ŝ S. 74. Det elektriske felt i en hvilken som helst afstand fra en uendeligt plan med uniform overfladeladning σ: hvor ˆn er enhedsvektoren, der peger væk fra planen. E = σ 2ε 0 ˆn Curlet af E S. 77. For enhver statisk ladningsdistribution gælder: E dl = Elektrisk potentiale S. 78. Det elektriske potentiale er defineret som hvor O er et referencepunkt. Differentialversion: Forskellen mellem to punkter er: E = 0 V (r) r O E = V V (b) V (a) = E dl b a E dl Bemærk: Forskellen ændres ikke, hvis der skiftes referencepunkt O. S. 81. Superpositionsprincippet gælder: S. 83. Poissons ligning: F = F 1 + F E = E 1 + E V = V 1 + V V = ρ ε 0 Side 6 af 21
7 2.4 Elektrisk potentiale Hvis ρ = 0 får man Laplace s ligning: 2 V = 0 S. 84. Potentialet af punktladninger q n er: V (r) = 1 n i=1 q i r r i For forskellige ladninger: V (r) = 1 V (r) = 1 V (r) = 1 λ(r ) r r dl (Linjeladning) σ(r ) r r da (Overfladeladning) ρ(r ) r r dτ (Volumenladning) Hurtig oversigt S. 87. Nyttig figur: ρ ρ r r dτ E = 1 E = ρ ε 0 ; E = 0 r r r r 3 ρ dτ V = 1 2 V = ρ ε 0 E = V V V = E dl E Overfladeladning S. 89. Det elektriske felt er diskontinuert, når man krydser en overfladespænding. Forskellen fra den ene til den anden side er: E over E under = σ ε 0 ˆn hvor ˆn er enhedsvektoren vinkelret på overfladen, pegende fra under til over. Dette gælder kun for overfladen selv et eksternt felt er kontinuert gennem overfladen! Side 7 af 21
8 2.5 Arbejde og energi Potentialet er kontinuert, mens gradienten af potentialet ikke er: V over = V under V over ˆn V under ˆn = 1 ε 0 ρ 2.5 Arbejde og energi S. 91. Arbejde, der kræves for at flytte en ladning Q fra a til b: W = Q(V (b) V (a)) Hvis ladningen flyttes fra til r bliver arbejdet blot W = QV (r). S. 92. Arbejde, der kræves, for at samle n ladninger q i : W = 1 2 n q i V (r i ) i=1 Dette svarer også til den energi, man får, hvis man fjerner ladningerne helt fra hinanden. Energien, der kræves for at danne ladningerne, er ikke talt med her. S. 93. For en volumenladning: W = 1 2 ρv dτ = ε 0 2 Hele R 3 E 2 dτ Dette er den totale energi i samlingen af ladninger, dvs. inkl. energien, der kræves for at danne ladningerne! For en linjeladning og en overfladeladning fås: W = 1 λv dl (Linjeladning) 2 W = 1 σv da (Overfladeladning) 2 S. 96. Vigtigt! Superpositionsprincippet kan ikke bruges på arbejdet! 2.6 Ledere S. 97. Egenskaber ved perfekte ledere: E = 0 inden i en leder. Hvis lederen placeres i et elektrisk felt, vil der inden i lederen dannes et andet i modsat retning, som får det totale felt indeni til at blive 0. ρ = 0 inden i en leder. Der er ladning, bare ligeså meget positivt som negativt. Summen inden i bliver 0. Er der en ladning, vil denne ligge på overfladen. En leder har samme potentiale overalt, sålænge det er indeni eller på overfladen af en leder. Her gælder: V (a) = V (b). E står vinkelret på overfladen lige udenfor lederen Overfladeladning og kraft på en leder S Lige udenfor en leder er feltet E = σ ε 0 ˆn Side 8 af 21
9 3 Special Techniques Kraften pr. areal er givet ved: f = σe gennemsnit = 1 2 σ(e over + E under ) = 1 2ε 0 σ 2ˆn P = ε 0 2 E Kapacitorer S Kapacitansen er givet som C Q V hvor V = V + V er forskellen i potentialet mellem de to ledere. Q er den positive leders ladning. S Arbejdet det kræver at oplade en kapacitor: W = 1 2 CV 2 3 Special Techniques 3.1 Laplace s ligning S Laplace s ligning: I én dimension S Laplace s ligning bliver: 2 V = 2 V x V y V z 2 = 0 Løsningen bliver: 2 V x 2 = 0 V (x) = mx + b S Bemærk: 1. V (x) er et gennemsnit: V (x) = 1 [V (x + a) + V (x a)] 2 2. Der findes ingen lokale ekstrema disse kan kun findes i endepunkterne I to dimensioner S Laplace s ligning bliver: Her findes ingen generel løsning! S Bemærk: 2 V x V y 2 = 0 Side 9 af 21
10 3.2 Billedmetoden 1. V (x, y) er et gennemsnit af punkterne omkring det: V (x, y) = 1 2πR cirkel V dl 2. Der findes ingen lokale ekstrema disse kan kun findes på randen I tre dimensioner S Laplace s ligning bliver: S Bemærk: 2 V x V y V z 2 = 0 1. V (r) er et gennemsnit af punkterne i en kugle omkring det: V (r) = 1 4πR 2 V da kugle 2. Der findes ingen lokale ekstrema disse kan kun findes på randen Entydighedssætninger S Første entydighedssætning: Løsningen til Laplace s ligning i et volumen V er unikt bestemt, hvis V er bestemt på overfladen S. S Anden entydighedssætning: I et volumen V omkranset af ledere og som indeholder en bestemt ladningsdensitet ρ er det elektriske felt unikt bestemt, hvis den totale ladning på hver leder er givet. (Regionen som helhed kan være omkranset af en anden leder eller slet ikke være omkranset af noget). S Alternativ første entydighedssætning: Potentialet V i et volumen V er unikt bestemt hvis (a) ladningsdensiteten i regionen og (b) værdien af V på hele randen er bestemt. 3.2 Billedmetoden S Betragt en punktladning q i punktet (0, 0, d) og et ledende plan i xy-planen. For at finde bl.a. potentialet i området over planet betragtes i stedet to modsatte ladninger i (0, 0, d) og (0, 0, d). S Potentialet bliver: V (x, y, z) = 1 [ q x2 + y 2 + (z d) 2 S Overfladeladningen induceret på det ledende plan er: σ(x, y) = Den totale ladning induceret på planet er Q = q. Kraften bliver: S Energien bliver: qd 2π(x 2 + y 2 + d 2 ) 3/2 F = 1 q 2 (2d) 2 ẑ W = 1 q 2 4d Dette er også arbejdet, der skal bruges, for at bringe ladningen ind fra. ] q x2 + y 2 + (z + d) 2 Side 10 af 21
11 3.3 Multipoler Bemærkning 3.1 (S Regler for billeder) 1. Man må ikke indsætte billedladninger i den region, man finder potentialet i. 2. Billedladningerne skal summere til den korrekte totale ladning i hver region. 3.3 Multipoler S Dipolmomentet er defineret som p r ρ(r ) dτ Dipol-potentialet er: Fra Bennys note E3.4.2: Potentialet bliver da: V dip (r) = 1 p r r 3 V (r) = 1 Q r + 1 p r r 3 S Dipolmomentet for en samling punktladninger: n p = q i r i Dipolmomentet for den fysiske dipol: i=1 p = qd hvor d går fra den negative ladning til den positive. S Flyttes koordinatsystemet et stykke a, ændres dipolmomentet: S Den elektriske dipol: E dip (r, θ) = 4 Electric Fields in Matter S Dipolmomentet er proportional til E: p = p Qa p (2 cos θˆr + sin θ ˆθ) r3 p = αe hvor α er atomar polarisabilitet. S Kraftmomentet om dipolens center er givet som: N = p E S om et hvilket som helst andet punkt er givet som: hvor F er givet som N = (p E) + (r F) S Polarisationen er defineret som dipolmomentet per volumen: i V P p i V hvor V er et lille volumen. F = (p )E F = (p E) (Side 258) Side 11 af 21
12 4.1 Bundne ladninger 4.1 Bundne ladninger S Bundet overfladeladning: S Bundet volumenladning: σ b = P ˆn ρ b = P 4.2 Elektrisk forskydning S Den elektriske forskydning er defineret som D ε 0 E + P Gauss lov bliver da: D = ρ f D da = Q fenc (Differentialform) (Integralform) Metode 4.1 (S Beregning af forskydning) Hvis der er symmetri, benyt Gauss lov på sammen måde som til at beregne det elektriske felt. Hvis der ikke er symmetri, find en anden måde! Men antag aldrig at D er bestemt udelukkende ved den frie ladning! Grænsebetingelser S Forskydningen er diskontinuert over en overflade: Dover Dunder = σ f og D over D under = P over P under S For E-feltet: 4.3 Lineære dielektrika E over E under = σ ε 0 E over E under = 0 S For lineære dielektrika kan polarisationen kan også skrives som: hvor χ e er den elektriske susceptibilitet. S Der vil altid gælde, at hvor ε = ε 0 (1 + χ e ) kaldes permittiviteten. Den relative permittivitet er givet ved P = ε 0 χ e E D = εe ε r 1 + χ e = ε ε 0 Side 12 af 21
13 5 Magnetostatik Grænseværdiproblemer S For volumenladningerne gælder der: Energi og kræfter ( ) χe ρ b = ρ f 1 + χ e S Energien i en kapacitor fyldt med et dielektrisk materiale bliver W = 1 D E dτ 2 S Kraften, en kapacitor vil udøve på det mellemliggende materiale for at holde det inde, kan beregnes som F = ε 0χ e a 2d V 2 hvor a er arealet af kapacitoren og d er afstanden mellem de to plader. 5 Magnetostatik S Lorentz-kraftloven: F = Q[E + (v B)] S Magnetiske kræfter udfører intet arbejde! S Den magnetiske kraft kan også udtrykkes ved strømstyrken: F mag = I (dl B) hvor dl er i strømmens retning. S Fladestrømsdensiteten defineres som: K di dl = σv hvor σ er fladeladningsdensiteten. Den magnetiske kraft kan da bestemmes som: F mag = (v B)σ da = (K B) da S Volumenstrømsdensiteten defineres som: J di da = ρv hvor ρ er volumenladningsdensiteten. Den magnetiske kraf kan da bestemmes som: F mag = (v B)ρ dτ = (J B) dτ S Kontinuitetsligningen: J = ρ t Side 13 af 21
14 5.1 Divergens og curl af B S Biot-Savarts lov: B(r) = µ 0 I (r r ) 4π r r 3 dl = µ 0 dl 4π I (r r ) r r 3 S Biot-Savarts lov for flade- og volumenstrømme: B(r) = µ 0 4π 5.1 Divergens og curl af B S Divergensen er altid 0: S Ampères lov: K(r ) (r r ) r r 3 da og B(r) = µ 0 4π B = 0 J(r ) (r r ) r r 3 dτ B = µ 0 J B dl = µ 0 I enc (Differentialform) (Integralform) For forskellige B-felter, se afsnit 8.4 side 20 i denne formelsamling. 5.2 Magnetisk vektorpotential S Sammenhæng mellem B og vektorpotentialet A: Divergensen er 0: S Ampères lov kan skrives: B = A A = 0 2 A = µ 0 J S Hvis strømmen går mod 0 for r kan A bestemmes ved A(r) = µ 0 I(r ) 4π r r dl = µ 0I 1 4π r r dl (Linjestrømme) A(r) = µ 0 K(r ) 4π r r da (Fladestrømme) A(r) = µ 0 J(r ) 4π r r dτ (Volumenstrømme) S I lighed med Ampères lov fås: A dl = Φ hvor Φ er fluxen af B gennem det pågældende loop. Side 14 af 21
15 5.2 Magnetisk vektorpotential Hurtig oversigt S Nyttig figur: J A = µ 0 J 4π r r dτ 2 A = µ 0 J B = µ 0 4π J (r r ) r r 3 dτ B = µ 0 J; B = 0 B = A; A = 0 A B Grænsebetingelser S For B-feltet: Altså: hvor ˆn er normalvektoren til overfladen. S A er kontinuert: Men det er den afledede ikke: B over = B under B over B under = µ 0K B over B under = µ 0 (K ˆn) A over n A over = A under A under n = µ 0 K Multipolekspansion S Vektorpotentialets dipol: A dip (r) = µ 0 m (r r ) 4π r r 3 hvor m I da = Ia er det magnetiske dipolmoment og a er vektorarealet af loopet. S Den magnetiske dipol: B dip (r) = µ 0m 4πr 3 (2 cos θˆr + sin θ ˆθ) Side 15 af 21
16 6 Magnetic Fields in Matter 6 Magnetic Fields in Matter 6.1 Kraft og kraftmoment S Kraftmomentet på enhver ladningsdistribution i et magnetisk felt: N = m B hvor m er det magnetiske dipolmoment. I et uniformt magnetfelt er den resulterende kraft på et ladningsloop 0. S For et infinitesimalt loop med dipolmoment m i et felt B er kraften: 6.2 Felter fra et magnetiseret objekt S Bundet volumenstrøm: Bundet fladestrøm: hvor ˆn er normalvektoren. 6.3 H-feltet S H er givet som: Ampères lov bliver da: F = (m B) J b = M K b = M ˆn H 1 µ 0 B M H = J f H dl = I fenc (Differentialform) (Integralform) S Divergensen af H er normalt ikke (som B) lig 0: H = M Grænsebetingelser S For H: Hover H under = (M over M under ) H over H under = K f ˆn S For B: Bover B under = 0 B over B under = µ 0(K ˆn) Side 16 af 21
17 6.4 Lineært og ikke-lineært materiale 6.4 Lineært og ikke-lineært materiale S Lineære materialer opfylder følgende relation: M = χ m H hvor χ m kaldes den magnetiske susceptibilitet (skema s. 275). S Relationen melllem B og H: B = µh hvor µ µ 0 (1 + χ m ) kaldes permeabiliteten. Den relative permeabilitet er givet som µ r 1 + χ m = µ/µ 0. S I et homogent lineært materiale: 7 Elektrodynamik S Ohms lov: J b = χ m J f J = σ(e + v B) σe da v oftest er ubetydelig. σ kaldes for konduktiviteten. Nogle gange oplyses resistiviteten ρ = 1/σ (skema s. 286). S Ohms lov er også kendt som: V = IR hvor V er potentialforskellen mellem to elektroder, I er strømstyrken mellem dem og R er resistansen, der afhænger af geometrien. S Joules opvarmningslov: P = V I = I 2 R hvor P er effekten, V er potentialforskellen, I er strømstyrken og R er resistansen. 7.1 Elektromotorisk kraft S Den elektromotoriske kraft (emf) er givet som E f dl = f s dl hvor f = f s + E er den elektrostatiske kraft og f s er kraften, der får elektronerne til at flytte sig (som bæltet i en Van de Graaff-generator). Idéelt gælder der: V = E og dermed også E = IR (Ohms lov, s. 298). S For en ledningsloop, der trækkes gennem et magnetfelt gælder der (Lenz lov): hvor Φ B da er fluxen af B gennem loopet. E = dφ dt Side 17 af 21
18 7.2 Elektromagnetisk induktion 7.2 Elektromagnetisk induktion S Ændres den magnetiske flux gennem et loop dannes en emf: E = dφ dt For det inducerede elektriske felt gælder Faradays lov: B B dl = t da E = B t (Integralform) (Differentialform) Hvis symmetrien tillader det, kan Faradays lov i integralform benyttes på samme måde som Ampères lov for B-felter. S En anden version af Faradays lov i integralform: E dl = dφ dt Induktans S Hvis en strøm I 1 løber gennem loop 1, bliver fluxen gennem loop 2: hvor M er den gensidige induktans. S Ændres strømmen induceres der en emf: Φ 2 = MI 1 Φ 1 = MI 2 E 2 = M di 1 dt S Der induceres også en emf i loopet, hvor strømmen ændres: E = L di dt hvor L kaldes selv-induktansen eller bare induktansen Energi i magnetiske felter S Forøges strømstyrken i en ledning fra 0 til I, er der udført et arbejde: W = 1 2 LI2 S Arbejdet mere generelt: W = 1 2 (A J) dτ = 1 2µ 0 B 2 dτ Side 18 af 21
19 8 Udvalgte formler 8 Udvalgte formler 8.1 Bennys tavle Elektrostatik F = qe Magnetostatik E = ρ ε 0 B = 0 E = 0 E = V F = qv B B = µ 0 J B = A 2 V = ρ 2 A = µ 0 J ( A = 0) ε 0 V (r) = 1 ρ(r ) r r dτ A(r) = µ 0 J(r ) 4π r r dτ D = ε 0 E + P H = B µ 0 M 8.2 E-felter S. 65. Punktladning: S. 63. Uendelig lang linje: D = ρ f H = J f W = D E dτ W = B H dτ W = ε 0 E 2 dτ W = B H dτ N = p E N = m B ρ b = P σ b = P ˆn i V P = p i V E = 1 q r 2 ˆr E = 1 2λ s ŝ S. 63. Afstanden z over midtpunktet af en endelig linje med længden 2L: E = 1 2λL z z 2 + L ẑ 2 S. 64. I afstanden z på aksen af en ring med radius r: (opgave) E = λ rz 2ε 0 (r 2 + z 2 ) ẑ 3/2 S. 64. I afstanden z på aksen af en cirkelskrive med radius R: (opgave) E = σ ( ) z 1 ẑ 2ε 0 R2 + z 2 J b = M K b = M ˆn i V M = m i V Side 19 af 21
20 8.3 Potentialer S. 72. En uendelig plan: S. 71. Kugle: Altså det samme som en punktladning! E = σ 2ε 0 ˆn E = 1 q r 2 ˆr 8.3 Potentialer S. 84. Punktladning: V (r) = 1 q r S. 82. Kugleskal med radius R, overfladeladning σ og total ladning q: V (r) = { 1 q 1 S. 82. Kugle med radius R og total ladning q: (opgave) r = R2 σ ε 0r q R = Rσ ε 0 for r > R for r < R S For en enkelt dipol: V (r) = { 1 q 1 r ε 0r ( 3 r2 q 2R R 2 ) V (r) = 1 (r r ) p r r 3 for r > R for r < R 8.4 B-felter S Uendelig lang wire: B = µ 0I 2πs ˆϕ S Uendelig, uniform fladestrøm K = Kˆx over xy-planen: { +(µ 0 /2)Kŷ for z < 0, B = (µ 0 /2)Kŷ for z > 0. S B-feltet i afstanden z på aksen af en cirkulær ring med radius R og strøm I: B = µ 0I 2 R 2 (R 2 + z 2 ) 3/2 S Uendelig lang cylinder (spole) med radius R, n vindinger pr. enhedslængde: { µ 0 niẑ indeni cylinderen, B = 0 udenfor cylinderen. S Torus (spole) med ialt N vindinger: B = { µ0ni 2πs ˆϕ indeni spolen, 0 udenfor spolen. Side 20 af 21
21 Indeks A, 14 Ampères lov, 14, 16 arbejde, 8 linjeladning, 8 overfladeladning, 8 volumenladning, 8 B-felter, 20 Biot-Savarts lov, 14 bundne ladninger, 12 Coulombs lov, 5 dipolmoment, 11 fysisk dipol, 11 Dirac-δ-funktion, 4 divergensteoremet, 4 elektrisk dipol, 11 elektrisk felt, 5 linjeladning, 5 overfladeladning, 5 volumenladning, 5 elektrisk potentiale, 6 elektromotorisk kraft, 17 emf, 17 entydighedssætninger, 10 Faradays lov, 18 fladestrømsdensitet, 13 flux, 5 forskydning, 12 Gauss lov, 5 Gauss teorem, 4 gensidig induktans, 18 Greens teorem, 4 kraftmoment elektrisk felt, 11 magnetisk felt, 16 Laplace s ligning, 7, 9 leder, 8 Lenz lov, 17 Lorentz-kraftlov, 13 magnetisk dipol, 15 magnetisk dipolmoment, 15 magnetisk susceptibilitet, 17 magnetisk vektorpotential, 14 Ohms lov, 17 partiel integration, 4 permeabilitet, 17 Poissons ligning, 6 polarisation, 11, 12 potentiale linjeladning, 7 overfladeladning, 7 punktladning, 7 volumenladning, 7 potentialer, 20 resistivitet, 17 solenoidal fields, 4 Stokes teorem, 4 superposition, 6 volumenstrømsdensitet, 13 H, 16 hurtig oversigt elektrostatik, 7 magnetostatic, 15 irrotational fields, 4 Joules lov, 17 kapacitor, 9 konduktivitet, 17 kontinuitetsligningen, 13 kraft elektrisk felt, 11 magnetisk felt, 16 21
Noter til elektromagnetisme
 Noter til elektromagnetisme Martin Sparre www.logx.dk 20-06-2007 1 Elektrostatik Coloumbs lov F Q = 1 qq r r 4πε 0 r r 2 r r Det elektriske felt: F Q (r) = QE(r), E(r) = 1 q i r r i 4πε 0 r r i i 2 r r
Noter til elektromagnetisme Martin Sparre www.logx.dk 20-06-2007 1 Elektrostatik Coloumbs lov F Q = 1 qq r r 4πε 0 r r 2 r r Det elektriske felt: F Q (r) = QE(r), E(r) = 1 q i r r i 4πε 0 r r i i 2 r r
KØBENHAVNS UNIVERSITET NATURVIDENSKABELIG BACHELORUDDANNELSE Skriftlig prøve i Fysik 4 (Elektromagnetisme) 27. juni 2008
 KØBENHAVNS UNIVERSITET NATURVIDENSKABELIG BACHELORUDDANNELSE Skriftlig prøve i Fysik 4 (Elektromagnetisme) 27. juni 2008 Tilladte hjælpemidler: Medbragt litteratur, noter og lommeregner. Der må besvares
KØBENHAVNS UNIVERSITET NATURVIDENSKABELIG BACHELORUDDANNELSE Skriftlig prøve i Fysik 4 (Elektromagnetisme) 27. juni 2008 Tilladte hjælpemidler: Medbragt litteratur, noter og lommeregner. Der må besvares
Fysik 21 Elektromagnetisme Formelsamling til eksamen
 Fysik 21 Elektromagnetisme Formelsamling til eksamen Sebastian B. Simonsen 31. januar 2005 Indhold 1 Kapitel 2 - Electrostatics 3 2 Kapitel 3 - Special Techniques 5 2.1 Separation af variable.......................
Fysik 21 Elektromagnetisme Formelsamling til eksamen Sebastian B. Simonsen 31. januar 2005 Indhold 1 Kapitel 2 - Electrostatics 3 2 Kapitel 3 - Special Techniques 5 2.1 Separation af variable.......................
Fysik 21 Formeloversigt
 Fysik 21 Formeloversigt Henrik Dahl 18. januar 2004 Indhold 1 Betegnelser og enheder 2 2 Formler 4 2.1 Elektrostatik............................. 4 2.1.1 Generelt............................ 4 2.1.2 Kraft,
Fysik 21 Formeloversigt Henrik Dahl 18. januar 2004 Indhold 1 Betegnelser og enheder 2 2 Formler 4 2.1 Elektrostatik............................. 4 2.1.1 Generelt............................ 4 2.1.2 Kraft,
Noter til EM1 på KU (Elektromagnetisme 1)
 Noter til EM1 på KU (Elektromagnetisme 1) af Nikolai Plambech Nielsen, LPK331. Version 1.0 13. juni 2016 Introduktion Dette er min samling af noter til kurset EM1 (Normalt bare kaldt EL). I kurset bruges
Noter til EM1 på KU (Elektromagnetisme 1) af Nikolai Plambech Nielsen, LPK331. Version 1.0 13. juni 2016 Introduktion Dette er min samling af noter til kurset EM1 (Normalt bare kaldt EL). I kurset bruges
Benyttede bøger: Statistisk fysik 1, uredigerede noter, Per Hedegård, 2007.
 Formelsamling Noter til Fysik 3 You can know the name of a bird in all the languages of the world, but when you re finished, you ll know absolutely nothing whatever about the bird... So let s look at the
Formelsamling Noter til Fysik 3 You can know the name of a bird in all the languages of the world, but when you re finished, you ll know absolutely nothing whatever about the bird... So let s look at the
Ordliste. Teknisk håndbog om magnetfelter og elektriske felter
 Ordliste Teknisk håndbog om magnetfelter og elektriske felter Afladning Atom B-felt Dielektrika Dipol Dosimeter E-felt Eksponering Elektricitetsmængde Elektrisk elementarladning Elektrisk felt Elektrisk
Ordliste Teknisk håndbog om magnetfelter og elektriske felter Afladning Atom B-felt Dielektrika Dipol Dosimeter E-felt Eksponering Elektricitetsmængde Elektrisk elementarladning Elektrisk felt Elektrisk
Elektromagnetisme 13 Side 1 af 8 Maxwells ligninger. Forskydningsstrømme I S 1
 Elektromagnetisme 13 Side 1 af 8 Betragt Amperes lov fra udtryk (1.1) anvendt på en kapacitor der er ved at blive ladet op. For de to flader og S der begge S1 afgrænses af C fås H dl = J ˆ C S n da = I
Elektromagnetisme 13 Side 1 af 8 Betragt Amperes lov fra udtryk (1.1) anvendt på en kapacitor der er ved at blive ladet op. For de to flader og S der begge S1 afgrænses af C fås H dl = J ˆ C S n da = I
Opgave 1. (a) Bestem de to kapacitorers kapacitanser C 1 og C 2.
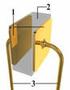 2 Opgave 1 I første del af denne opgave skal kapacitansen af to kapacitorer bestemmes. Den ene kapacitor er konstrueret af to tynde koaksiale cylinderskaller af metal. Den inderste skal har radius r a
2 Opgave 1 I første del af denne opgave skal kapacitansen af to kapacitorer bestemmes. Den ene kapacitor er konstrueret af to tynde koaksiale cylinderskaller af metal. Den inderste skal har radius r a
Elektromagnetisme 7 Side 1 af 12 Elektrisk strøm. Elektrisk strøm
 Elektromagnetisme 7 Side 1 af 1 Med dette emne overgås fra elektrostatikken, som beskriver stationære ladninger, til elektrodynamikken, som beskriver ladninger i bevægelse (elektriske strømme, magnetfelter,
Elektromagnetisme 7 Side 1 af 1 Med dette emne overgås fra elektrostatikken, som beskriver stationære ladninger, til elektrodynamikken, som beskriver ladninger i bevægelse (elektriske strømme, magnetfelter,
AARHUS UNIVERSITET. Det naturvidenskabelige fakultet 3. kvarter forår OPGAVESTILLER: Allan H. Sørensen
 AARHUS UNIVERSITET Det naturvidenskabelige fakultet 3. kvarter forår 2006 FAG: Elektromagnetisme OPGAVESTILLER: Allan H. Sørensen Antal sider i opgavesættet (inkl. forsiden): 5 Eksamensdag: fredag dato:
AARHUS UNIVERSITET Det naturvidenskabelige fakultet 3. kvarter forår 2006 FAG: Elektromagnetisme OPGAVESTILLER: Allan H. Sørensen Antal sider i opgavesættet (inkl. forsiden): 5 Eksamensdag: fredag dato:
Elektromagnetisme 10 Side 1 af 12 Magnetisme. Magnetisering
 Elektroagnetise 10 Side 1 af 12 Magnetisering Magnetfelter skabes af ladninger i bevægelse, altså af elektriske strøe. I den forbindelse skelnes elle to typer af agnetfeltskabende strøe: Frie strøe, der
Elektroagnetise 10 Side 1 af 12 Magnetisering Magnetfelter skabes af ladninger i bevægelse, altså af elektriske strøe. I den forbindelse skelnes elle to typer af agnetfeltskabende strøe: Frie strøe, der
Formelsamling og noter. Elektrodynamik og bølger
 Formelsamling og noter. Elektrodynamik og bølger 26. oktober 212 Dennis Hansen E = ρ ɛ B = E = B B = µ J + µ ɛ E E da = Q enc ɛ E dl = Φ B Ei = L i di i dt + Q i C i + R i Ẽ i = iωl i Ĩ i + i ωc i Ĩ i
Formelsamling og noter. Elektrodynamik og bølger 26. oktober 212 Dennis Hansen E = ρ ɛ B = E = B B = µ J + µ ɛ E E da = Q enc ɛ E dl = Φ B Ei = L i di i dt + Q i C i + R i Ẽ i = iωl i Ĩ i + i ωc i Ĩ i
Elektromagnetisme 13 Side 1 af 8 Maxwells ligninger. Forskydningsstrømme I S 1
 Elektromagnetisme 13 Side 1 af 8 Betragt Amperes lov fra udtryk (1.1) anvendt på en kapacitor der er ved at blive ladet op. For de to flader og S der begge S1 afgrænses af C fås H dl = J ˆ C S n da = I
Elektromagnetisme 13 Side 1 af 8 Betragt Amperes lov fra udtryk (1.1) anvendt på en kapacitor der er ved at blive ladet op. For de to flader og S der begge S1 afgrænses af C fås H dl = J ˆ C S n da = I
DETTE OPGAVESÆT INDEHOLDER 6 OPGAVER MED IALT 11 SPØRGSMÅL. VED BEDØMMELSEN VÆGTES DE ENKELTE
 DETTE OPGAVESÆT INDEHOLDER 6 OPGAVER MED IALT 11 SPØRGSMÅL. VED BEDØMMELSEN VÆGTES DE ENKELTE SPØRGSMÅL ENS. SPØRGSMÅLENE I DE ENKELTE OPGAVER KAN LØSES UAFHÆNGIGT AF HINANDEN. 1 Opgave 1 En cylinderkapacitor
DETTE OPGAVESÆT INDEHOLDER 6 OPGAVER MED IALT 11 SPØRGSMÅL. VED BEDØMMELSEN VÆGTES DE ENKELTE SPØRGSMÅL ENS. SPØRGSMÅLENE I DE ENKELTE OPGAVER KAN LØSES UAFHÆNGIGT AF HINANDEN. 1 Opgave 1 En cylinderkapacitor
SPOLER (DC) Princippet (magnetiske felter) Induktion og selvinduktion Induktans (selvinduktionskoefficient)
 SPOLER (DC) Princippet (magnetiske felter) Induktion og selvinduktion Induktans (selvinduktionskoefficient) Princippet Hvis vi betragter kredsskemaet her til højre, og fokuserer på delen med sort stregfarve,
SPOLER (DC) Princippet (magnetiske felter) Induktion og selvinduktion Induktans (selvinduktionskoefficient) Princippet Hvis vi betragter kredsskemaet her til højre, og fokuserer på delen med sort stregfarve,
DETTE OPGAVESÆT INDEHOLDER 5 OPGAVER MED IALT 11 SPØRGSMÅL. VED BEDØMMELSEN VÆGTES DE ENKELTE
 DETTE OPGAVESÆT INDEHOLDER 5 OPGAVER MED IALT 11 SPØRGSMÅL. VED BEDØMMELSEN VÆGTES DE ENKELTE SPØRGSMÅL ENS. SPØRGSMÅLENE I DE ENKELTE OPGAVER KAN LØSES UAFHÆNGIGT AF HINANDEN. 1 Opgave 1 En massiv metalkugle
DETTE OPGAVESÆT INDEHOLDER 5 OPGAVER MED IALT 11 SPØRGSMÅL. VED BEDØMMELSEN VÆGTES DE ENKELTE SPØRGSMÅL ENS. SPØRGSMÅLENE I DE ENKELTE OPGAVER KAN LØSES UAFHÆNGIGT AF HINANDEN. 1 Opgave 1 En massiv metalkugle
Elektromagnetisme 7 Side 1 af 12 Elektrisk strøm. Elektrisk strøm
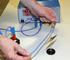 Elektromagnetisme 7 Side 1 af 12 Med dette emne overgås fra elektrostatikken, som beskriver stationære ladninger, til elektrodynamikken, som beskriver ladninger i bevægelse (elektriske strømme, magnetfelter,
Elektromagnetisme 7 Side 1 af 12 Med dette emne overgås fra elektrostatikken, som beskriver stationære ladninger, til elektrodynamikken, som beskriver ladninger i bevægelse (elektriske strømme, magnetfelter,
Noter til EM2 på KU (Elektrodynamik og Bølger)
 Noter til EM2 på KU (Elektrodynamik og Bølger) af Nikolai Plambech Nielsen, LPK331. Version 1.0 Indhold I Kredsløbsregning 6 1 Grundlæggende elektronik (Noter kapitel 2) 7 1.1 Passive komponenter.......................................
Noter til EM2 på KU (Elektrodynamik og Bølger) af Nikolai Plambech Nielsen, LPK331. Version 1.0 Indhold I Kredsløbsregning 6 1 Grundlæggende elektronik (Noter kapitel 2) 7 1.1 Passive komponenter.......................................
13 cm. Tværsnit af kernens ben: 30 mm 30 mm
 Opgaver: Opgave 6.1 På figuren er vist en transformator, der skal anvendes i en strømforsyning. Den relative permeabilitet for kernen er 2500, og kernen kan regnes for at være lineær. 13 cm µ r = 2500
Opgaver: Opgave 6.1 På figuren er vist en transformator, der skal anvendes i en strømforsyning. Den relative permeabilitet for kernen er 2500, og kernen kan regnes for at være lineær. 13 cm µ r = 2500
U = φ. R = ρ l A. Figur 1 Sammenhængen mellem potential, φ og spændingsfald, U: U = φ = φ 1 φ 2.
 Ohms lov Vi vil samle os en række byggestene, som kan bruges i modelleringen af fysiske systemer. De første to var hhv. en spændingskilde og en strømkilde. Disse elementer (sources) er aktive og kan tilføre
Ohms lov Vi vil samle os en række byggestene, som kan bruges i modelleringen af fysiske systemer. De første to var hhv. en spændingskilde og en strømkilde. Disse elementer (sources) er aktive og kan tilføre
Elektromagnetisme 3 Side 1 af 8 Dielektrika 1. Elektrisk dipol
 Elektromagnetisme Side af 8 Elektrisk dipol Betragt det elektrostatiske potential fra en elektrisk dipol bestående af to punktladninger + q og q : ϕ r ( ) i qi r r q q + r r r r + l q + r r r r l i ( ).
Elektromagnetisme Side af 8 Elektrisk dipol Betragt det elektrostatiske potential fra en elektrisk dipol bestående af to punktladninger + q og q : ϕ r ( ) i qi r r q q + r r r r + l q + r r r r l i ( ).
Danmarks Tekniske Universitet
 Danmarks Tekniske Universitet Side 1 af 11 sider Skriftlig prøve, lørdag den 12. december, 2015 Kursus navn Fysik 1 Kursus nr. 10916 Varighed: 4 timer Tilladte hjælpemidler: Alle hjælpemidler tilladt "Vægtning":
Danmarks Tekniske Universitet Side 1 af 11 sider Skriftlig prøve, lørdag den 12. december, 2015 Kursus navn Fysik 1 Kursus nr. 10916 Varighed: 4 timer Tilladte hjælpemidler: Alle hjælpemidler tilladt "Vægtning":
AARHUS UNIVERSITET. Det Naturvidenskabelige Fakultet Augusteksamen OPGAVESTILLER: Allan H. Sørensen
 AARHUS UNIVERSITET Det Naturvidenskabelige Fakultet Augusteksamen 2006 FAG: Elektromagnetisme OPGAVESTILLER: Allan H. Sørensen Antal sider i opgavesættet (inkl. forsiden): 6 Eksamensdag: fredag dato: 11.
AARHUS UNIVERSITET Det Naturvidenskabelige Fakultet Augusteksamen 2006 FAG: Elektromagnetisme OPGAVESTILLER: Allan H. Sørensen Antal sider i opgavesættet (inkl. forsiden): 6 Eksamensdag: fredag dato: 11.
KØBENHAVNS UNIVERSITET NATURVIDENSKABELIG BACHELORUDDANNELSE Skriftlig prøve i Fysik 4 (Elektromagnetisme) 26. juni 2009
 KØBENHAVNS UNIVERSITET NATURVIDENSKABELIG BACHELORUDDANNELSE Skriftlig prøve i Fyik 4 (Elektromagnetime) 26. juni 2009 Tilladte hjælpemidler: Medbragt litteratur, noter og lommeregner. Der må bevare med
KØBENHAVNS UNIVERSITET NATURVIDENSKABELIG BACHELORUDDANNELSE Skriftlig prøve i Fyik 4 (Elektromagnetime) 26. juni 2009 Tilladte hjælpemidler: Medbragt litteratur, noter og lommeregner. Der må bevare med
3.3 Andre spørgsmål... 12
 e k s ame nso p g av e r Contents Første spørgsmål. Opgave 4.3........................................ E-feltet udenfor et dielektrikum......................... E-feltet indeni et dielektrikum.......................
e k s ame nso p g av e r Contents Første spørgsmål. Opgave 4.3........................................ E-feltet udenfor et dielektrikum......................... E-feltet indeni et dielektrikum.......................
Matematisk modellering og numeriske metoder. Lektion 13
 Matematisk modellering og numeriske metoder Lektion 3 Morten Grud Rasmussen 9. november 25 Divergens af et vektorfelt [Sektion 9.8 og.7 i bogen, s. 43]. Definition af og og egenskaber for divergens Lad
Matematisk modellering og numeriske metoder Lektion 3 Morten Grud Rasmussen 9. november 25 Divergens af et vektorfelt [Sektion 9.8 og.7 i bogen, s. 43]. Definition af og og egenskaber for divergens Lad
Elektromagnetisme 10 Side 1 af 11 Magnetisme. Magnetisering
 Elektroagnetise 10 Side 1 af 11 Magnetisering Magnetfelter skabes af ladninger i bevægelse, altså af elektriske strøe. I den forbindelse skelnes elle to typer af agnetfeltskabende strøe: Frie strøe, der
Elektroagnetise 10 Side 1 af 11 Magnetisering Magnetfelter skabes af ladninger i bevægelse, altså af elektriske strøe. I den forbindelse skelnes elle to typer af agnetfeltskabende strøe: Frie strøe, der
Formelsamling og noter. Elektromagnetisme
 Formelsamling og noter. Elektromagnetisme 3. august 2 Dennis Hansen Generelt E = ρ ɛ E = B t B = B = µ J + µ ɛ E t I stof E da = Q enc ɛ D = ɛ E + P D = ɛe E dl = Φ B H = B M H = µ µ B B da = D = ρ free
Formelsamling og noter. Elektromagnetisme 3. august 2 Dennis Hansen Generelt E = ρ ɛ E = B t B = B = µ J + µ ɛ E t I stof E da = Q enc ɛ D = ɛ E + P D = ɛe E dl = Φ B H = B M H = µ µ B B da = D = ρ free
Niels Jonassen ELEKTRO MAGNETISME. Polyteknisk Forlag
 Niels Jonassen ELEKTRO MAGNETISME Polyteknisk Forlag FORORD Denne bog er en stærkt revideret og omarbejdet udgave af noter og kompendier, der siden 1984 har været anvendt ved kurser i elektromagnetisme
Niels Jonassen ELEKTRO MAGNETISME Polyteknisk Forlag FORORD Denne bog er en stærkt revideret og omarbejdet udgave af noter og kompendier, der siden 1984 har været anvendt ved kurser i elektromagnetisme
ELEKTROMAGNETISME. "Quasistatiske elektriske og magnetiske felter", side Notem kaldes herefter QEMF.
 Institut for elektroniske systemer EIT3/18 180917HEb ELEKTROMAGNETISME www.kom.aau.dk/~heb/kurser/elektro-18 MM 1: Fredag d. 28. september 2018 kl. 8.15 i B2-104 Emner: Læsning: Indledning til kurset Emner
Institut for elektroniske systemer EIT3/18 180917HEb ELEKTROMAGNETISME www.kom.aau.dk/~heb/kurser/elektro-18 MM 1: Fredag d. 28. september 2018 kl. 8.15 i B2-104 Emner: Læsning: Indledning til kurset Emner
Antennens udstrålingsmodstand hvad er det for en størrelse?
 Antennens udstrålingsmodstand hvad er det for en størrelse? Det faktum, at lyset har en endelig hastighed er en forudsætning for at en antenne udstråler, og at den har en ohmsk udstrålingsmodstand. Den
Antennens udstrålingsmodstand hvad er det for en størrelse? Det faktum, at lyset har en endelig hastighed er en forudsætning for at en antenne udstråler, og at den har en ohmsk udstrålingsmodstand. Den
FREMSTILLING AF VEKSELSPÆNDING. Induktion Generatorprincippet
 AC FREMSTILLING AF VEKSELSPÆNDING Induktion Generatorprincippet Induktion: Som vi tidligere har gennemgået, så induceres der en elektromotorisk kraft i en ledersløjfe, hvis denne udsættes for et varierende
AC FREMSTILLING AF VEKSELSPÆNDING Induktion Generatorprincippet Induktion: Som vi tidligere har gennemgået, så induceres der en elektromotorisk kraft i en ledersløjfe, hvis denne udsættes for et varierende
KONDENSATORER (DC) Princip og kapacitans Serie og parallel kobling Op- og afladning
 KONDENSATORER (DC) Princip og kapacitans Serie og parallel kobling Op- og afladning Side 1 Side 2 Princippet: Coulombs lov: = k Q 1 Q 2 r 2 Side 3 Princippet: Coulombs lov: = k Q 1 Q 2 r 2 Ladningerne
KONDENSATORER (DC) Princip og kapacitans Serie og parallel kobling Op- og afladning Side 1 Side 2 Princippet: Coulombs lov: = k Q 1 Q 2 r 2 Side 3 Princippet: Coulombs lov: = k Q 1 Q 2 r 2 Ladningerne
Stern og Gerlachs Eksperiment
 Stern og Gerlachs Eksperiment Spin, rumkvantisering og Københavnerfortolkning Jacob Nielsen 1 Eksperimentelle resultater, der viser energiens kvantisering forelå, da Bohr opstillede sin Planetmodel. Her
Stern og Gerlachs Eksperiment Spin, rumkvantisering og Københavnerfortolkning Jacob Nielsen 1 Eksperimentelle resultater, der viser energiens kvantisering forelå, da Bohr opstillede sin Planetmodel. Her
Elektrodynamik. Christian Andersen. 15. juni 2010. Indhold 1. 1 Indledning 3
 Elektodynamik Chistian Andesen 15. juni 010 Indhold Indhold 1 1 Indledning 3 Elektostatik 3.1 Det elektiske felt............................. 3. Divegens og Cul af E-felte...................... 3.3 Elektisk
Elektodynamik Chistian Andesen 15. juni 010 Indhold Indhold 1 1 Indledning 3 Elektostatik 3.1 Det elektiske felt............................. 3. Divegens og Cul af E-felte...................... 3.3 Elektisk
Når strømstyrken ikke er for stor, kan batteriet holde spændingsforskellen konstant på 12 V.
 For at svare på nogle af spørgsmålene i dette opgavesæt kan det sagtens være, at du bliver nødt til at hente informationer på internettet. Til den ende kan oplyses, at der er anbragt relevante link på
For at svare på nogle af spørgsmålene i dette opgavesæt kan det sagtens være, at du bliver nødt til at hente informationer på internettet. Til den ende kan oplyses, at der er anbragt relevante link på
MATEMATIK A-NIVEAU. Kapitel 1
 MATEMATIK A-NIVEAU Vejledende eksempler på eksamensopgaver og eksamensopgaver i matematik, 01 Kapitel 1 016 MATEMATIK A-NIVEAU Vejledende eksempler på eksamensopgaver og eksamensopgaver i matematik 01
MATEMATIK A-NIVEAU Vejledende eksempler på eksamensopgaver og eksamensopgaver i matematik, 01 Kapitel 1 016 MATEMATIK A-NIVEAU Vejledende eksempler på eksamensopgaver og eksamensopgaver i matematik 01
Danmarks Tekniske Universitet
 Danmarks Tekniske Universitet Side 1 af 14 sider Skriftlig prøve, lørdag den 12. december, 2015 Kursus navn Fysik 1 Kursus nr. 10916 Varighed: 4 timer Tilladte hjælpemidler: Alle hjælpemidler tilladt "Vægtning":
Danmarks Tekniske Universitet Side 1 af 14 sider Skriftlig prøve, lørdag den 12. december, 2015 Kursus navn Fysik 1 Kursus nr. 10916 Varighed: 4 timer Tilladte hjælpemidler: Alle hjælpemidler tilladt "Vægtning":
MODUL 5 ELLÆRE: INTRONOTE. 1 Basisbegreber
 1 Basisbegreber ellæren er de mest grundlæggende størrelser strøm, spænding og resistans Strøm er ladningsbevægelse, og som det fremgår af bogen, er strømmens retning modsat de bevægende elektroners retning
1 Basisbegreber ellæren er de mest grundlæggende størrelser strøm, spænding og resistans Strøm er ladningsbevægelse, og som det fremgår af bogen, er strømmens retning modsat de bevægende elektroners retning
Epistel E2 Partiel differentiation
 Epistel E2 Partiel differentiation Benny Lautrup 19 februar 24 Funktioner af flere variable kan differentieres efter hver enkelt, med de øvrige variable fasthol Definitionen er f(x, y) x f(x, y) f(x +
Epistel E2 Partiel differentiation Benny Lautrup 19 februar 24 Funktioner af flere variable kan differentieres efter hver enkelt, med de øvrige variable fasthol Definitionen er f(x, y) x f(x, y) f(x +
ELLÆRENS KERNE- BEGREBER (DC) Hvad er elektrisk: Ladning Strømstyrke Spændingsforskel Resistans Energi og effekt
 ELLÆRENS KERNE- BEGREBER (DC) Hvad er elektrisk: Ladning Strømstyrke Spændingsforskel Resistans Energi og effekt Atomets partikler: Elektrisk ladning Lad os se på et fysisk stof som kobber: Side 1 Atomets
ELLÆRENS KERNE- BEGREBER (DC) Hvad er elektrisk: Ladning Strømstyrke Spændingsforskel Resistans Energi og effekt Atomets partikler: Elektrisk ladning Lad os se på et fysisk stof som kobber: Side 1 Atomets
E JLEJKTROMAGNJETKSME
 Bent Elbek E JLEJKTROMAGNJETKSME Klassisk elektromagnetisk feltteori med grundlag og anvendelser Niels Bohr Institutet 1993 ELEKTROMAGNETISME Manuskriptet er skrevet i L\.TEX og direkte reproduceret fra
Bent Elbek E JLEJKTROMAGNJETKSME Klassisk elektromagnetisk feltteori med grundlag og anvendelser Niels Bohr Institutet 1993 ELEKTROMAGNETISME Manuskriptet er skrevet i L\.TEX og direkte reproduceret fra
Kære selvstuderende i: Fysik A. Herunder ser du det materiale, der udgør dit eksaminationsgrundlag.
 Kære selvstuderende i: Fysik A Herunder ser du det materiale, der udgør dit eksaminationsgrundlag. Bøgerne er Vejen til fysik AB1 og Vejen til fysik A2 2. udgave, som kan købes hos http://www.hax.dk/ og
Kære selvstuderende i: Fysik A Herunder ser du det materiale, der udgør dit eksaminationsgrundlag. Bøgerne er Vejen til fysik AB1 og Vejen til fysik A2 2. udgave, som kan købes hos http://www.hax.dk/ og
Fysikkens store teorier fra Newton til nu
 Fysikkens store teorier fra Newton til nu Elektromagnetisme og lidt QED 20. marts 2014 Jesper Mygind Emeritus Institut for Fysik Danmarks Tekniske Universitet E-mail: myg@fysik.dtu.dk URL: http://dcwww.fys.dtu.dk/~myg/
Fysikkens store teorier fra Newton til nu Elektromagnetisme og lidt QED 20. marts 2014 Jesper Mygind Emeritus Institut for Fysik Danmarks Tekniske Universitet E-mail: myg@fysik.dtu.dk URL: http://dcwww.fys.dtu.dk/~myg/
Torben Laubst. Grundlæggende. Polyteknisk Forlag
 Torben Laubst Grundlæggende Polyteknisk Forlag Torben Laubst Grundlæggende Polyteknisk Forlag DIA- EP 1990 3. udgave INDHOLDSFORTEGNELSE 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. Indledning Transformeres principielle
Torben Laubst Grundlæggende Polyteknisk Forlag Torben Laubst Grundlæggende Polyteknisk Forlag DIA- EP 1990 3. udgave INDHOLDSFORTEGNELSE 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. Indledning Transformeres principielle
Maj 2015 (alle opgaver og alle spørgsmål)
 Maj 2015 (alle opgaver og alle spørgsmål) Alternativ besvarelse (med brug af Maple til beregninger, incl. pakker til VektorAnalyse2 og Integrator8). Ved eksamen er der ikke tid til f.eks. at lave illustrationer,
Maj 2015 (alle opgaver og alle spørgsmål) Alternativ besvarelse (med brug af Maple til beregninger, incl. pakker til VektorAnalyse2 og Integrator8). Ved eksamen er der ikke tid til f.eks. at lave illustrationer,
a og b Den magnetiske kraftlov Og måling af B ved hjælp af Tangensboussole
 3.1.2. a og b Den magnetiske kraftlov Og måling af B ved hjælp af Tangensboussole Udført d. 15.04.08 Deltagere Kåre Stokvad Hansen Max Berg Michael Ole Olsen 1 Formål: Formålet med øvelsen er at måle/beregne
3.1.2. a og b Den magnetiske kraftlov Og måling af B ved hjælp af Tangensboussole Udført d. 15.04.08 Deltagere Kåre Stokvad Hansen Max Berg Michael Ole Olsen 1 Formål: Formålet med øvelsen er at måle/beregne
Danmarks Tekniske Universitet
 Danmarks Tekniske Universitet Side 1 af 9 sider Skriftlig prøve, lørdag den 13. december, 2014 Kursus navn Fysik 1 Kursus nr. 10916 Varighed: 4 timer Tilladte hjælpemidler: Alle tilladte hjælpemidler på
Danmarks Tekniske Universitet Side 1 af 9 sider Skriftlig prøve, lørdag den 13. december, 2014 Kursus navn Fysik 1 Kursus nr. 10916 Varighed: 4 timer Tilladte hjælpemidler: Alle tilladte hjælpemidler på
Undervisningsbeskrivelse for: 3g FY
 Undervisningsbeskrivelse for: 3g FY Fag: Fysik B->A, STX Niveau: A Institution: Grindsted Gymnasium & HF (565013) Hold: 2g FY Termin: Juni 2018 Uddannelse: STX Lærer(e): Forløbsoversigt (10): 1 14.08.17
Undervisningsbeskrivelse for: 3g FY Fag: Fysik B->A, STX Niveau: A Institution: Grindsted Gymnasium & HF (565013) Hold: 2g FY Termin: Juni 2018 Uddannelse: STX Lærer(e): Forløbsoversigt (10): 1 14.08.17
Danmarks Tekniske Universitet
 Danmarks Tekniske Universitet Side 1 af 10 sider Skriftlig prøve, lørdag den 23. maj, 2015 Kursus navn Fysik 1 Kursus nr. 10916 Varighed: 4 timer Tilladte hjælpemidler: Alle hjælpemidler tilladt "Vægtning":
Danmarks Tekniske Universitet Side 1 af 10 sider Skriftlig prøve, lørdag den 23. maj, 2015 Kursus navn Fysik 1 Kursus nr. 10916 Varighed: 4 timer Tilladte hjælpemidler: Alle hjælpemidler tilladt "Vægtning":
Eksamen maj 2018, Matematik 1, DTU
 Eksamen maj 2018, Matematik 1, DTU NB: Nedenstående udregninger viser flere steder mere end én metode. Det er der IKKE tid til eksamen! Ligeledes er der ikke krav om eller tid til at illustrere med plots!
Eksamen maj 2018, Matematik 1, DTU NB: Nedenstående udregninger viser flere steder mere end én metode. Det er der IKKE tid til eksamen! Ligeledes er der ikke krav om eller tid til at illustrere med plots!
Kapitel 10. B-felt fra en enkelt leder. B (t) = hvor: B(t) = Magnetfeltet (µt) I(t) = Strømmen i lederen (A) d = Afstanden mellem leder og punkt (m)
 Kapitel 10 Beregning af magnetiske felter For at beregne det magnetiske felt fra højspændingsledninger/kabler, skal strømmene i alle ledere (fase-, jord- og eventuelle skærmledere) kendes. Den inducerede
Kapitel 10 Beregning af magnetiske felter For at beregne det magnetiske felt fra højspændingsledninger/kabler, skal strømmene i alle ledere (fase-, jord- og eventuelle skærmledere) kendes. Den inducerede
Undervisningsbeskrivelse. Fysik A - 2.A
 Undervisningsbeskrivelse. Fysik A - 2.A Termin August 2014 Juni 2017 Institution Uddannelse Fag og niveau Lærer Rybners HTX HTX Fysik A Jesper Pedersen (JEPE) Hold 2.A Oversigt over planlagte undervisningsforløb
Undervisningsbeskrivelse. Fysik A - 2.A Termin August 2014 Juni 2017 Institution Uddannelse Fag og niveau Lærer Rybners HTX HTX Fysik A Jesper Pedersen (JEPE) Hold 2.A Oversigt over planlagte undervisningsforløb
Elektromagnetisme 8 Side 1 af 8 Magnetfelter 1. Magnetisk induktion. To punktladninger og q påvirker (i vakuum) som bekendt hinanden med en. qq C.
 Elektroagnetise 8 Side 1 af 8 Magnetisk induktion To punktladninger og q påvirker (i vakuu) so bekendt hinanden ed en q1 elektrisk kraft (oulobkraft) F 1 qq 1 1 = 4πε 1 0 r1 r ˆ. (8.1) Hvis de to ladninger
Elektroagnetise 8 Side 1 af 8 Magnetisk induktion To punktladninger og q påvirker (i vakuu) so bekendt hinanden ed en q1 elektrisk kraft (oulobkraft) F 1 qq 1 1 = 4πε 1 0 r1 r ˆ. (8.1) Hvis de to ladninger
Optimale konstruktioner - når naturen former. Opgaver. Opgaver og links, der knytter sig til artiklen om topologioptimering
 Opgaver Opgaver og links, der knytter sig til artiklen om solsikke Opgave 1 Opgave 2 Opgaver og links, der knytter sig til artiklen om bobler Opgave 3 Opgave 4 Opgaver og links, der knytter sig til artiklen
Opgaver Opgaver og links, der knytter sig til artiklen om solsikke Opgave 1 Opgave 2 Opgaver og links, der knytter sig til artiklen om bobler Opgave 3 Opgave 4 Opgaver og links, der knytter sig til artiklen
8 Regulære flader i R 3
 8 Regulære flader i R 3 Vi skal betragte særligt pæne delmængder S R 3 kaldet flader. I det følgende opfattes S som et topologisk rum i sportopologien, se Definition 5.9. En åben omegn U af p S er således
8 Regulære flader i R 3 Vi skal betragte særligt pæne delmængder S R 3 kaldet flader. I det følgende opfattes S som et topologisk rum i sportopologien, se Definition 5.9. En åben omegn U af p S er således
Protoner med magnetfelter i alle mulige retninger.
 Magnetisk resonansspektroskopi Protoners magnetfelt I 1820 lavede HC Ørsted et eksperiment, der senere skulle gå over i historiebøgerne. Han placerede en magnet i nærheden af en ledning og så, at når der
Magnetisk resonansspektroskopi Protoners magnetfelt I 1820 lavede HC Ørsted et eksperiment, der senere skulle gå over i historiebøgerne. Han placerede en magnet i nærheden af en ledning og så, at når der
Magnetisme og harddisk-teknologi
 Magnetisme og harddisk-teknologi 10030 Fysik og Nanoteknologi Februar 010 af Claus Schelde Jacobsen (DTU Fysik) csj@fysik.dtu.dk Mikkel Fougt Hansen (DTU Nanotech) mikkel.hansen@nanotech.dtu.dk 010 Version:
Magnetisme og harddisk-teknologi 10030 Fysik og Nanoteknologi Februar 010 af Claus Schelde Jacobsen (DTU Fysik) csj@fysik.dtu.dk Mikkel Fougt Hansen (DTU Nanotech) mikkel.hansen@nanotech.dtu.dk 010 Version:
INERTIMOMENT for stive legemer
 Projekt: INERTIMOMENT for stive legemer Formålet med projektet er at træne integralregning og samtidig se en ikke-triviel anvendelse i fysik. 0. Definition af inertimoment Inertimomentet angives med bogstavet
Projekt: INERTIMOMENT for stive legemer Formålet med projektet er at træne integralregning og samtidig se en ikke-triviel anvendelse i fysik. 0. Definition af inertimoment Inertimomentet angives med bogstavet
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Maj-juni 2018 Institution Marie Kruses Skole Uddannelse Fag og niveau Lærer(e) Hold STX Fysik B A Mads Hoy
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Maj-juni 2018 Institution Marie Kruses Skole Uddannelse Fag og niveau Lærer(e) Hold STX Fysik B A Mads Hoy
Vejledende besvarelse på august 2009-sættet 2. december 2009
 Vejledende besvarelse på august 29-sættet 2. december 29 Det følgende er en vejledende besvarelse på eksamenssættet i kurset Calculus, som det så ud i august 29. Den tjener primært til illustration af,
Vejledende besvarelse på august 29-sættet 2. december 29 Det følgende er en vejledende besvarelse på eksamenssættet i kurset Calculus, som det så ud i august 29. Den tjener primært til illustration af,
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Skoleår forår 2019, eksamen maj-juni 2019 Institution Kolding HF & VUC Uddannelse STX Fag og niveau Matematik
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Skoleår forår 2019, eksamen maj-juni 2019 Institution Kolding HF & VUC Uddannelse STX Fag og niveau Matematik
Dansk Fysikolympiade 2015 Udtagelsesprøve søndag den 19. april 2015. Teoretisk prøve. Prøvetid: 3 timer
 Dansk Fysikolympiade 2015 Udtagelsesprøve søndag den 19. april 2015 Teoretisk prøve Prøvetid: 3 timer Opgavesættet består af 15 spørgsmål fordelt på 5 opgaver. Bemærk, at de enkelte spørgsmål ikke tæller
Dansk Fysikolympiade 2015 Udtagelsesprøve søndag den 19. april 2015 Teoretisk prøve Prøvetid: 3 timer Opgavesættet består af 15 spørgsmål fordelt på 5 opgaver. Bemærk, at de enkelte spørgsmål ikke tæller
Vektorer i 3D. 1. Grundbegreber. 1. Koordinater. Enhedsvektorerne. Vektor OP. De ortogonale enhedsvektorer kaldes for: Hvis punkt p har koordinaterne:
 Vektorer i 3D. Grundegreer. Koordinater z k P OP i 0 j x y Enhedsvektorerne De ortogonale enhedsvektorer kaldes for: i, j og k Vektor OP Hvis punkt p har koordinaterne: P ( a a a3 ) Så har vektor OP koordinaterne:
Vektorer i 3D. Grundegreer. Koordinater z k P OP i 0 j x y Enhedsvektorerne De ortogonale enhedsvektorer kaldes for: i, j og k Vektor OP Hvis punkt p har koordinaterne: P ( a a a3 ) Så har vektor OP koordinaterne:
Elektromagnetisme 15 Side 1 af 5 Molekylært elektrisk felt. Molekylært E-felt i et dielektrikum. mol
 lektromagnetisme 15 Side 1 af 5 Molekylært -felt i et dielektrikum Det ekylære elektriske felt, som et enkelt ekyle i et dielektrikum oplever, er ikke det samme som det makroskopiske -felt defineret i
lektromagnetisme 15 Side 1 af 5 Molekylært -felt i et dielektrikum Det ekylære elektriske felt, som et enkelt ekyle i et dielektrikum oplever, er ikke det samme som det makroskopiske -felt defineret i
MM01 (Mat A) Ugeseddel 1
 Institut for Matematik og Datalogi 2. august 200 Syddansk Universitet, Odense HJM/LL MM0 (Mat A) Ugeseddel Velkommen til kurset MM0 (Matematik A). Forelæsninger: afholdes i to ugentlige timer, onsdag kl.
Institut for Matematik og Datalogi 2. august 200 Syddansk Universitet, Odense HJM/LL MM0 (Mat A) Ugeseddel Velkommen til kurset MM0 (Matematik A). Forelæsninger: afholdes i to ugentlige timer, onsdag kl.
Formelsamling Noter til MatF 1
 Formelsamling Noter til MatF 1 You can know the name of a bird in all the languages of the world, but when you re finished, you ll know absolutely nothing whatever about the bird...o let s look at the
Formelsamling Noter til MatF 1 You can know the name of a bird in all the languages of the world, but when you re finished, you ll know absolutely nothing whatever about the bird...o let s look at the
Undervisningsbeskrivelse Mat A 2007-2010
 Undervisningsbeskrivelse Mat A 2007-2010 Termin Maj 2010 Institution HTX-Sukkertoppen Uddannelse HTX Fag og Niveau Matematik A Lærer Reza Farzin Hold HTX 3.L / science Titel 1 Titel 2 Titel 4 Titel 5 Titel
Undervisningsbeskrivelse Mat A 2007-2010 Termin Maj 2010 Institution HTX-Sukkertoppen Uddannelse HTX Fag og Niveau Matematik A Lærer Reza Farzin Hold HTX 3.L / science Titel 1 Titel 2 Titel 4 Titel 5 Titel
Teknologi & kommunikation
 Grundlæggende Side af NV Elektrotekniske grundbegreber Version.0 Spænding, strøm og modstand Elektricitet: dannet af det græske ord elektron, hvilket betyder rav, idet man tidligere iagttog gnidningselektricitet
Grundlæggende Side af NV Elektrotekniske grundbegreber Version.0 Spænding, strøm og modstand Elektricitet: dannet af det græske ord elektron, hvilket betyder rav, idet man tidligere iagttog gnidningselektricitet
Vektoranalyse INDLEDNING. Indhold. 1 Integraltricks. Jens Kusk Block Jacobsen 21. januar 2008
 Vektoranalyse Jens Kusk Block Jacobsen 21. januar 2008 INLENING ette er en opsamling af ting, jeg synes er gode at have ifbm vektoranalyse som præsenteret i kurset VEKANAE07 ved IMF på AU. Noten er dels
Vektoranalyse Jens Kusk Block Jacobsen 21. januar 2008 INLENING ette er en opsamling af ting, jeg synes er gode at have ifbm vektoranalyse som præsenteret i kurset VEKANAE07 ved IMF på AU. Noten er dels
Strøm til hjernen Elektromagnetisme
 Strøm til hjernen Forkortelser F = Forsøg (som vi udfører) FB = Forsøg med børn (forsøg som vi udfører, men som børnene deltager aktivt i) H = Hands-on forsøg (børnene får selv lov til at prøve det hele)
Strøm til hjernen Forkortelser F = Forsøg (som vi udfører) FB = Forsøg med børn (forsøg som vi udfører, men som børnene deltager aktivt i) H = Hands-on forsøg (børnene får selv lov til at prøve det hele)
Hvorfor bevæger lyset sig langsommere i fx glas og vand end i det tomme rum?
 Hvorfor bevæger lyset sig langsommere i fx glas og vand end i det tomme rum? - om fysikken bag til brydningsindekset Artiklen er udarbejdet/oversat ud fra især ref. 1 - fra borgeleo.dk Det korte svar:
Hvorfor bevæger lyset sig langsommere i fx glas og vand end i det tomme rum? - om fysikken bag til brydningsindekset Artiklen er udarbejdet/oversat ud fra især ref. 1 - fra borgeleo.dk Det korte svar:
Indre modstand og energiindhold i et batteri
 Indre modstand og energiindhold i et batteri Side 1 af 10 Indre modstand og energiindhold i et batteri... 1 Formål... 3 Teori... 3 Ohms lov... 3 Forsøgsopstilling... 5 Batteriets indre modstand... 5 Afladning
Indre modstand og energiindhold i et batteri Side 1 af 10 Indre modstand og energiindhold i et batteri... 1 Formål... 3 Teori... 3 Ohms lov... 3 Forsøgsopstilling... 5 Batteriets indre modstand... 5 Afladning
Mere om differentiabilitet
 Mere om differentiabilitet En uddybning af side 57 i Spor - Komplekse tal Kompleks funktionsteori er et af de vigtigste emner i matematikken og samtidig et af de smukkeste I bogen har vi primært beskæftiget
Mere om differentiabilitet En uddybning af side 57 i Spor - Komplekse tal Kompleks funktionsteori er et af de vigtigste emner i matematikken og samtidig et af de smukkeste I bogen har vi primært beskæftiget
a og b. Den magnetiske kraftlov Og måling af B ved hjælp af Tangensboussole
 3.1.2. a og b Den magnetiske kraftlov Og måling af B ved hjælp af Tangensboussole Udført d. 15.04.08 Deltagere Kåre Stokvad Hansen Max Berg Michael Ole Olsen 1 Formål: Formålet med øvelsen er at måle/beregne
3.1.2. a og b Den magnetiske kraftlov Og måling af B ved hjælp af Tangensboussole Udført d. 15.04.08 Deltagere Kåre Stokvad Hansen Max Berg Michael Ole Olsen 1 Formål: Formålet med øvelsen er at måle/beregne
Vejledende opgaver i kernestofområdet i fysik-a Elektriske og magnetiske felter
 Oktober 2012 Vejledende opgaver i kernestofområdet i fysik-a Elektriske og magnetiske felter Da læreplanen for fysik på A-niveau i stx blev revideret i 2010, blev kernestoffet udvidet med emnet Elektriske
Oktober 2012 Vejledende opgaver i kernestofområdet i fysik-a Elektriske og magnetiske felter Da læreplanen for fysik på A-niveau i stx blev revideret i 2010, blev kernestoffet udvidet med emnet Elektriske
Hvis man ønsker mere udfordring, kan man springe de første 10 opgaver over. , og et punkt er givet ved: P (2, 1).
 Plangeometri Hvis man ønsker mere udfordring, kan man springe de første 10 opgaver over Opgave 1 To linjer er givet ved ligningerne: x y 0 og x b y 4 0, hvor b er en konstant a) Beregn konstanten b således,
Plangeometri Hvis man ønsker mere udfordring, kan man springe de første 10 opgaver over Opgave 1 To linjer er givet ved ligningerne: x y 0 og x b y 4 0, hvor b er en konstant a) Beregn konstanten b således,
Vektorfelter. enote Vektorfelter
 enote 24 1 enote 24 Vektorfelter I enote 6 indføres og studeres vektorer i plan og rum. I enote 16 ser vi på gradienterne for funktioner f (x, y) af to variable. Et gradientvektorfelt for en funktion af
enote 24 1 enote 24 Vektorfelter I enote 6 indføres og studeres vektorer i plan og rum. I enote 16 ser vi på gradienterne for funktioner f (x, y) af to variable. Et gradientvektorfelt for en funktion af
Benyttede bøger: Introduction to Cosmology, Barbara Ryden, 2003.
 Formelsamling Noter til Astronomi 1 You can know the name of a bird in all the languages of the world, but when you re finished, you ll know absolutely nothing whatever about the bird... So let s look
Formelsamling Noter til Astronomi 1 You can know the name of a bird in all the languages of the world, but when you re finished, you ll know absolutely nothing whatever about the bird... So let s look
Integralregning Infinitesimalregning
 Udgave 2.1 Integralregning Infinitesimalregning Noterne gennemgår begreberne integral og stamfunktion, og anskuer dette som et redskab til bestemmelse af arealer under funktioner. Noterne er supplement
Udgave 2.1 Integralregning Infinitesimalregning Noterne gennemgår begreberne integral og stamfunktion, og anskuer dette som et redskab til bestemmelse af arealer under funktioner. Noterne er supplement
Elektromagnetisme 14 Side 1 af 10 Elektromagnetiske bølger. Bølgeligningen
 Elektromagnetisme 14 Side 1 af 1 Bølgeligningen Maxwells ligninger udtrykker den indbyrdes sammenhæng mellem de elektromagnetiske felter samt sammenhængen mellem disse felter og de feltskabende ladninger
Elektromagnetisme 14 Side 1 af 1 Bølgeligningen Maxwells ligninger udtrykker den indbyrdes sammenhæng mellem de elektromagnetiske felter samt sammenhængen mellem disse felter og de feltskabende ladninger
Gradienter og tangentplaner
 enote 16 1 enote 16 Gradienter og tangentplaner I denne enote vil vi fokusere lidt nærmere på den geometriske analyse og inspektion af funktioner af to variable. Vi vil især studere sammenhængen mellem
enote 16 1 enote 16 Gradienter og tangentplaner I denne enote vil vi fokusere lidt nærmere på den geometriske analyse og inspektion af funktioner af to variable. Vi vil især studere sammenhængen mellem
Noter om Komplekse Vektorrum, Funktionsrum og Differentialligninger LinAlg 2004/05-Version af 16. Dec.
 Noter om Komplekse Vektorrum, Funktionsrum og Differentialligninger LinAlg 2004/05-Version af 16. Dec. 1 Komplekse vektorrum I defininitionen af vektorrum i Afsnit 4.1 i Niels Vigand Pedersen Lineær Algebra
Noter om Komplekse Vektorrum, Funktionsrum og Differentialligninger LinAlg 2004/05-Version af 16. Dec. 1 Komplekse vektorrum I defininitionen af vektorrum i Afsnit 4.1 i Niels Vigand Pedersen Lineær Algebra
Undervisningsbeskrivelse for: gsfya403 S13/14 Fysik B->A, STX
 Undervisningsbeskrivelse for: gsfya403 S13/14 Fysik B->A, STX Fag: Fysik B->A, STX Niveau: A Institution: Københavns VUC - Sankt Petri Passage 1 (280103) Hold: Fysik B-A 4 uger Termin: August 2013 Uddannelse:
Undervisningsbeskrivelse for: gsfya403 S13/14 Fysik B->A, STX Fag: Fysik B->A, STX Niveau: A Institution: Københavns VUC - Sankt Petri Passage 1 (280103) Hold: Fysik B-A 4 uger Termin: August 2013 Uddannelse:
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Institution Uddannelse Fag og niveau Lærer(e) Hold Termin hvori undervisningen afsluttes: maj-juni 2015 Københavns
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Institution Uddannelse Fag og niveau Lærer(e) Hold Termin hvori undervisningen afsluttes: maj-juni 2015 Københavns
Hvis man ønsker mere udfordring, kan man springe de første 10 opgaver over. 1, og et punkt er givet ved: (2, 1)
 Plangeometri Hvis man ønsker mere udfordring, kan man springe de første 10 opgaver over. Opgave 1 To linjer er givet ved ligningerne: x y 0 og x b y 4 0, hvor b er en konstant. a) Beregn konstanten b således,
Plangeometri Hvis man ønsker mere udfordring, kan man springe de første 10 opgaver over. Opgave 1 To linjer er givet ved ligningerne: x y 0 og x b y 4 0, hvor b er en konstant. a) Beregn konstanten b således,
Eksamen i fysik 2016
 Eksamen i fysik 2016 NB: Jeg gør brug af DATABOG fysik kemi, 11. udgave, 4. oplag & Fysik i overblik, 1. oplag. Opgave 1 Proptrækker Vi kender vinens volumen og masse. Enheden liter omregnes til kubikmeter.
Eksamen i fysik 2016 NB: Jeg gør brug af DATABOG fysik kemi, 11. udgave, 4. oplag & Fysik i overblik, 1. oplag. Opgave 1 Proptrækker Vi kender vinens volumen og masse. Enheden liter omregnes til kubikmeter.
Til at beregne varmelegemets resistans. Kan ohms lov bruges. Hvor R er modstanden/resistansen, U er spændingsfaldet og I er strømstyrken.
 I alle opgaver er der afrundet til det antal betydende cifre, som oplysningen med mindst mulige cifre i opgaven har. Opgave 1 Færdig Spændingsfaldet over varmelegemet er 3.2 V, og varmelegemet omsætter
I alle opgaver er der afrundet til det antal betydende cifre, som oplysningen med mindst mulige cifre i opgaven har. Opgave 1 Færdig Spændingsfaldet over varmelegemet er 3.2 V, og varmelegemet omsætter
MATEMATIK ( 5 h ) DATO: 8. juni 2009
 EUROPÆISK STUDENTEREKSAMEN 2009 MATEMATIK ( 5 h ) DATO: 8. juni 2009 PRØVENS VARIGHED: 4 timer (240 minutter) TILLADTE HJÆLPEMIDLER Europaskolernes formelsamling Ikke-grafisk, ikke-programmerbar lommeregner
EUROPÆISK STUDENTEREKSAMEN 2009 MATEMATIK ( 5 h ) DATO: 8. juni 2009 PRØVENS VARIGHED: 4 timer (240 minutter) TILLADTE HJÆLPEMIDLER Europaskolernes formelsamling Ikke-grafisk, ikke-programmerbar lommeregner
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin december 09 Institution Teknisk Gymnasium Grenaa, Viden Djurs Uddannelse Fag og niveau Lærer(e) Hold htx Fysik
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin december 09 Institution Teknisk Gymnasium Grenaa, Viden Djurs Uddannelse Fag og niveau Lærer(e) Hold htx Fysik
MM502+4 forelæsningsslides. uge 6, 2009
 MM502+4 forelæsningsslides uge 6, 2009 1 Definition partielle afledede: De (første) partielle afledede af en funktion f(x, y) af to variable er f(x + h, y) f(x, y) f 1 (x, y) := lim h 0 h f(x, y + k) f(x,
MM502+4 forelæsningsslides uge 6, 2009 1 Definition partielle afledede: De (første) partielle afledede af en funktion f(x, y) af to variable er f(x + h, y) f(x, y) f 1 (x, y) := lim h 0 h f(x, y + k) f(x,
Hvis man ønsker mere udfordring, kan man springe de første 7 opgaver over. Skitser det omdrejningslegeme, der fremkommer, når grafen for f ( x)
 Integralregning 3 Hvis man ønsker mere udfordring, kan man springe de første 7 opgaver over. Opgave Skitser det omdrejningslegeme, der fremkommer, når grafen for f ( x) x i [,] drejes 36 om x-aksen. Vis,
Integralregning 3 Hvis man ønsker mere udfordring, kan man springe de første 7 opgaver over. Opgave Skitser det omdrejningslegeme, der fremkommer, når grafen for f ( x) x i [,] drejes 36 om x-aksen. Vis,
Eksamen maj 2019, Matematik 1, DTU
 Eksamen maj 2019, Matematik 1, DTU NB: Nedenstående udregninger viser flere steder mere end én metode. Det er der IKKE tid til eksamen! Ligeledes er der ikke krav om eller tid til at illustrere med plots.
Eksamen maj 2019, Matematik 1, DTU NB: Nedenstående udregninger viser flere steder mere end én metode. Det er der IKKE tid til eksamen! Ligeledes er der ikke krav om eller tid til at illustrere med plots.
Elektromagnetisme 14 Side 1 af 9 Elektromagnetiske bølger. Bølgeligningen
 Elektromagnetisme 14 Side 1 af 9 Bølgeligningen Maxwells ligninger udtrykker den indbyrdes sammenhæng mellem de elektromagnetiske felter. I det flg. udledes en ligning, der opfyldes af hvert enkelt felt.
Elektromagnetisme 14 Side 1 af 9 Bølgeligningen Maxwells ligninger udtrykker den indbyrdes sammenhæng mellem de elektromagnetiske felter. I det flg. udledes en ligning, der opfyldes af hvert enkelt felt.
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Maj / Juni 2016 Institution Den Jyske Håndværkerskole Uddannelse Fag og niveau Lærer Hold EUX - Tømre Matematik
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Maj / Juni 2016 Institution Den Jyske Håndværkerskole Uddannelse Fag og niveau Lærer Hold EUX - Tømre Matematik
Teknisk. Matematik FACITLISTE. Preben Madsen. 4. udgave
 Teknisk Preben Madsen Matematik 4. udgave FACITLISTE Indhold TAL OG ALGEBRA... LIGNINGER OG ULIGHEDER... GEOMETRI... 4 TRIGONOMETRI... 5 CIRKLEN... 5 6 OVERFLADER UDFOLDNINGER... 5 7 RUMFANG... 8 8 ANALYTISK
Teknisk Preben Madsen Matematik 4. udgave FACITLISTE Indhold TAL OG ALGEBRA... LIGNINGER OG ULIGHEDER... GEOMETRI... 4 TRIGONOMETRI... 5 CIRKLEN... 5 6 OVERFLADER UDFOLDNINGER... 5 7 RUMFANG... 8 8 ANALYTISK
Danmarks Tekniske Universitet
 Danmarks Tekniske Universitet Side 1 af 11 sider Skriftlig prøve, lørdag den 22. august, 2015 Kursus navn Fysik 1 Kursus nr. 10916 Varighed: 4 timer Tilladte hjælpemidler: Alle hjælpemidler tilladt "Vægtning":
Danmarks Tekniske Universitet Side 1 af 11 sider Skriftlig prøve, lørdag den 22. august, 2015 Kursus navn Fysik 1 Kursus nr. 10916 Varighed: 4 timer Tilladte hjælpemidler: Alle hjælpemidler tilladt "Vægtning":
Lineær beamoptik 1. Koordinatsystem
 Lineær beamoptik 1 1 Wille kapitel 3.1 til og med 3.6 (undtagen 3.3) Koordinatsystem Indledning / overblik Rækkeudvikling af feltet Bevægelsesligningen Løsning af bevægelsesligningen Transfermatricer og
Lineær beamoptik 1 1 Wille kapitel 3.1 til og med 3.6 (undtagen 3.3) Koordinatsystem Indledning / overblik Rækkeudvikling af feltet Bevægelsesligningen Løsning af bevægelsesligningen Transfermatricer og
6 Plasmadiagnostik 6.1 Tætheds- og temperaturmålinger ved Thomsonspredning
 49 6 Plasmadiagnostik Plasmadiagnostik er en fællesbetegnelse for de forskellige typer måleudstyr, der benyttes til måling af plasmaers parametre og egenskaber. I fusionseksperimenter er der behov for
49 6 Plasmadiagnostik Plasmadiagnostik er en fællesbetegnelse for de forskellige typer måleudstyr, der benyttes til måling af plasmaers parametre og egenskaber. I fusionseksperimenter er der behov for
