Vismandsspillet og makroøkonomi
|
|
|
- Klaus Skaarup
- 8 år siden
- Visninger:
Transkript
1 Vismandsspillet og makroøkonomi Dette notat om makroøkonomi er skrevet af Henrik Adrian, Helge Gram Christensen, Morten Gjeddebæk og Ernst Jensen på et udviklingsseminar mellem matematik og samfundsfag den april Vi skylder stor tak til Nikolaj Malchow-Møller for grundig gennemlæsning og en række forbedringer i teksten. Det er hensigten med notatet, at det skal kunne bruges på efteruddannelseskurser for de nævnte fag i forbindelse med gymnasiereformen. Men vi har også søgt at udforme det, så det kan bruges som udgangspunkt for undervisningsmateriale til eleverne. Der er ingen copyright, så enhver har lov at bearbejde materialet efter ønske. Forløbet om makroøkonomi starter med, at en række økonomiske begreber og metoder præsenteres i samfundsfag, bl.a. gennem brug af "Vismandsspillet". Dette forløb er beskrevet nærmere andetsteds. Nærværende notat henvender sig primært til matematiklæreren og begynder på det sted i forløbet, hvor eleverne i samfundsfag har fået præsenteret nedenstående model af økonomiske sammenhænge. Vi tager udgangspunkt i følgende to ligninger: (1) Y d = C+G+I+X M (2) Y p = Y d De bogstaver, der indgår i de to ligninger, står for: Y d (Yield) er den samlede indenlandske efterspørgsel (demand), dvs. den samlede efterspørgsel efter indenlandsk producerede varer. Denne kaldes også den aggregerede efterspørgsel. Y p er den samlede indenlandske produktion, også kaldet BNP (Bruttonationalproduktet). Denne er også lig med den samlede indkomst i samfundet. C (Consumption) er det private forbrug. I det følgende antages den at være en funktion af indkomsten i samfundet. G (Government) er summen af G 1 (= offentligt forbrug) og G 2 (=offentlige investeringer). I (Investeringer) er de private investeringer. X (export) er den samlede eksport. M (import) er den samlede import. Ligning (1) siger, at den samlede indenlandske efterspørgsel er givet ved summen af det private forbrug (C), offentligt forbrug og investeringer (G), private investeringer (I) og export (X) fratrukket import (M). Ligning (2) siger, at den samlede produktion er bestemt af den samlede efterspørgsel i samfundet. Dvs. modellen antager, at udbuddet (produktionen, Y p ) tilpasser sig efterspørgslen (Y d ). side 1 af 7
2 Uanset om det forholder sig således, at udbuddet (Y p ) tilpasser sig efterspørgslen (Y d ) eller omvendt så gælder det dog, at den samlede produktion (Y p ) er lig med C + G + I + X M. Dette kaldes også forsyningsbalancen. Øvelse. Find i Vismandsspillet oplysningerne for 2002 om forsyningsbalancen og tjek, at Y=1184 (mia kr.). Man kan også finde tallene i en statistisk oversigt. Når modellen antager, at udbuddet (Y p ) tilpasser sig efterspørgslen (Y d ), så betyder det, at når der fx vedtages en stigning i de offentlige udgifter (G), så påvirker det den samlede efterspørgsel (Y d ), som igen påvirker den samlede produktion (Y p ) og indkomst. Det er imidlertid ikke de eneste effekter, vi får. Dette illustreres i den følgende figur. Vi ser nu på, hvilken betydning det får, hvis det offentlige øger G med!g = 10 (mia kr.) G Y d = G Y d Y p = Y d Y p Skat = t Yp Y d = C C C=c(1-t) Y p Opsparing = (1-c)(1-t) Y p Der sker det, at når det offentlige forbrug (G) stiger, så stiger den samlede efterspørgsel (Y d ), og dermed den samlede produktion (Y p ). Dette får indkomsten til at stige. En del af indkomststigningen går til øgede skattebetalinger, en del går til øget opsparing, og en del går til øget efterspørgsel efter forbrug. Den øgede efterspørgsel efter forbrug øger den samlede efterspørgsel (Y d ), som øger produktionen og indkomsten osv. Dette kan vi også formalisere ved at anvende en specifik model for, hvorledes C afhænger af Y: C = C 0 + c*(1 t)*y side 2 af 7
3 Her er: c t forbrugskvoten (den marginale forbrugstilbøjelighed = marginal propensity to consume), der her sættes til 0,8. marginalskatten, som vi sætter til 0,5. Det er realistiske tal, men valgt, så vi får bekvemme udregninger i det følgende. (Her kan man overveje hvor realistisk modellen er). Hvis vi sætter C 0 = 85,3 fås: C = 85,3 + 0,4*Y som med Y = 1184 giver C = 558,9 svarende til værdien fra vismandsspillet. Med disse værdier stemmer ligningen (1). Her følger en rekursiv beskrivelse af, hvad der sker, ud fra ligningerne: (3) Y d = 0,4*Y p +C 0 + G + I + X M (4) Y p = Y d Når staten fx øger G med!g =10 mia kr. til (indenlandske) materialer og løn til at bygge en bro, så stiger Y d umiddelbart med 10 mia. i henhold til ligningen!y d = 10. Og umiddelbart stiger produktionen Y p også med 10. I første runde er Y (fællesbetegnelse for både Y d og Y p ) således øget med 10. Men en stigning i Y p (produktion og dermed indkomst) på 10 giver ved indsættelse i (3), at højresiden vokser med 0,4*10 = 4 og dermed vokser Y d med yderligere 4. Af de ekstra 10 mia som arbejdere og ejere af produktionsanlæg fik, brugte de altså igen de 4 til øget forbrug. I anden runde er Y derfor yderligere steget med 4. Når vi indsætter en værdi af Y p på højre side i (3), der er øget med disse 4, fås dermed: I tredje runde er Y yderligere steget med 0,4*4= 1,6. Og i fjerde med 0,4*1,6 = 0,64. Og i femte med 0,4*1,6 = 0,256. Og i sjette med 0,4*0,256 = 0,1024. Ændringerne er nu så små, at vi slutter. I alt er Y steget med ,6+0,64+0, ,1024= 16,6. side 3 af 7
4 Når staten pumper 10 mia kr. ud, vokser Y samlet med 16,6 mia kr. Virkningen er altså en vækst i Y på 1,66 gange. Man kalder derfor dette tal for multiplikatoren for G, idet det var G, vi øgede. I vismandsmodellen benyttes sådanne multiplikatorer. Figuren kaldes det Keynesianske kryds. På 1.aksen er Y p og på 2.aksen Y d. Linjen Y d = k 0 + 0,4*Y p er indtegnet. k 0 = C 0 + G + I + X M er alle konstanterne i ligningen (3). Endvidere er vinkelhalveringslinjen, hvor Y d = Y p, indtegnet. Skæringspunktet giver den værdi af Y = 1184, vi fandt ovenfor. Men i øvrigt skal figuren illustrere principperne, så de fleste afstande er overdrevet for at kunne ses. Når staten øger G med!g = 10, bliver konstanten k 0 altså 10 større. Linjen løftes!g=10. De tilsvarende punkter på diagonalen er markeret: først den umiddelbare stigning i Y d i første runde på 10. Så stigningen i anden runde på 4. De følgende er for små til at kunne ses på figuren. Tilsammen adderer stigningerne op til en ændring i Y på!y = 16,6. side 4 af 7
5 Hvis man søger på nettet efter "keynesian cross", kan man være heldig at finde en lille animation som fx denne I (3) og (4) står Y p og Y d for samme Y (der produceres lige så meget som der efterspørges). Sammenhængen mellem Y, G og de øvrige konstante størrelser er altså: (5) Y = c*(1 t)*y + G + I + X M + C 0 (med et fint ord, siges Y at være implicit bestemt af ligningen). Når ligningen ikke er sværere, kan vi isolere Y 1 (6) Y= (G + konst) 1 c(1 t) Y er altså en lineær funktion af G. Med vores taleksempel får vi: Y = 1 G + k = 1,6667G + k 1 0,4 Dette betyder, at hvis eksempelvis G øges med 10, øges Y med 1,6667*10. Y-ændringen multipliceres altså med 1,6667. I runderne ovenfor fandt vi netop denne værdi af multiplikatoren for G, dog kun med to decimaler til 1,66, fordi vi stoppede efter 6 runder. Dette notat skifter nu stil. Ovenfor har vi forsøgt at give en så udførlig omtale af emnet, at den kan bruges til elever. I det følgende antydes nogle temaer og øvelser, der tager afsæt i det foregående. De skal af læreren kasseres eller udbygges og tilpasses elevernes forudsætninger. Med brug af differentialregning kan ovenstående også skrives som: dg = 1,6667 side 5 af 7
6 Øvelse. Undersøg betydningen for konvergensen af størrelsen af c, t og/eller selve hældningen. Omtale af kvotientrækker. Fx et induktivt forløb, hvor eleverne gætter summen, når faktoren er et pænt helt tal.. Bevis for sumsætningen. Induktivt forløb om andre rækker, fx differensrække, sum af kvadrattal, trekanttal og pyramidetal. En hjælp hertil er i TI-83 at sætte L 1 til n og L 2 til s n for en række værdier af n og derefter bruge polynomiel regression. Måske sluttes med induktionsbevis. Med brug af differentiation af sammensat funktion: Ligningen (1) skrives lidt simplere, idet vi udelader størrelser, vi ikke vil ændre. Så fås og Y = C + I C = g(y) g var ovenfor en lineær funktion. Vi vil se, hvor langt vi kan komme blot ved at antage, at g er voksende. (Eksemplet kan findes i Sydsæter, example 7.1.3). Når vi indsætter, fås Y = g(y) + I Vi vil finde multiplikatoren for I, altså se, hvor meget en forøgelse af investeringerne på 1 mia påvirker Y. Vi finder dc dc = + 1 = + 1 = g'( Y ) + 1 (1 g'( Y )) = 1 1 = 1 g'( Y ) side 6 af 7
7 Øvelse: sammenlign med den lineære ovenfor. Øvelse: g'(y) kaldes den marginale forbrugstilbøjelighed (marginal propensity to consume). Hvad kan man slutte, blot man antager, at g (Y) er positiv? Er dette realistisk? Kan man forestille sig g (Y)>1? g (Y) antages ofte at være aftagende i Y. Det vil sige, at g (Y) er negativ. Hvilken betydning får det for multiplikatoren? Kilder: Adrian, Henrik & Jesper Jespersen m.fl. Europaøkonomi, Gyldendal Undervisning 1995, side Finansrådet, 2003 Vismandsspillet Malchow-Møller, Nikolaj og Jens Jakob Nordvig-Rasmussen: Traditionelle Makromodeller, notat, der vil være at finde på EMUen Sydsæter, Knut & Peter Hammond: Essential Mathematics for Economic Analysis, Pearson Education 2002 Forslag til videre læsning: Begg, David, Fischer, Stanley and Dornbusch, Rudiger (2003): Economics. 7th Ed. McGraw-Hill. London 2003 Jespersen, Jesper (2004): Introduktion til Makroøkonomisk teori. 2.Udgave. Jurist- og økonomforbundets Forlag 2004 Keiding, Hans og Lund, Lars ( 1988): Nationaløkonomi I-II. Nyt Nordisk Forlag 1988 (2 rev.udg 1991) side 7 af 7
Opgavebesvarelse - Øvelse 3
 Opgavebesvarelse - Øvelse 3 Opgave 3.2 Lad økonomien være karakteriseret ved følgende adfærdsligninger: a) Løs for ligevægts BNP: derved at vi bruger ligningen. b) Løs for den disponible indkomst: c) Løs
Opgavebesvarelse - Øvelse 3 Opgave 3.2 Lad økonomien være karakteriseret ved følgende adfærdsligninger: a) Løs for ligevægts BNP: derved at vi bruger ligningen. b) Løs for den disponible indkomst: c) Løs
Matematik - samfundsfag Marianne Kesselhahn og Bent Fischer-Nielsen
 Matematik - samfundsfag Marianne Kesselhahn og Bent Fischer-Nielsen Læreplan, vejledning og kurser Statistik og vælgeradfærd Økonomisk politik og makroøkonomiske modeller Velfærdssamfundet og mikroøkonomiske
Matematik - samfundsfag Marianne Kesselhahn og Bent Fischer-Nielsen Læreplan, vejledning og kurser Statistik og vælgeradfærd Økonomisk politik og makroøkonomiske modeller Velfærdssamfundet og mikroøkonomiske
Analyse. Effekten af en fordobling i eksportefterspørgslen. 16. marts Af Sebastian Skovgaard Naur
 Analyse 16. marts 2017 Effekten af en fordobling i eksportefterspørgslen efter energiteknologi Af Sebastian Skovgaard Naur I notatet analyseres makroøkonomiske effekter af en lineær stigning i efterspørgslen
Analyse 16. marts 2017 Effekten af en fordobling i eksportefterspørgslen efter energiteknologi Af Sebastian Skovgaard Naur I notatet analyseres makroøkonomiske effekter af en lineær stigning i efterspørgslen
Forslag til løsning af Opgaver til afsnittet om de naturlige tal (side 80)
 Forslag til løsning af Opgaver til afsnittet om de naturlige tal (side 80) Opgave 1 Vi skal tegne alle de linjestykker, der forbinder vilkårligt valgte punkter blandt de 4 punkter. Gennem forsøg finder
Forslag til løsning af Opgaver til afsnittet om de naturlige tal (side 80) Opgave 1 Vi skal tegne alle de linjestykker, der forbinder vilkårligt valgte punkter blandt de 4 punkter. Gennem forsøg finder
Udledning af multiplikatoreffekten
 Udledning af multiplikatoreffekten Af Thomas Schausen Et tværfagligt undervisningsmateriale i matematik og samfundsfag fra Materialet er udarbejdet med støtte fra Undervisningsministeriet, og kan frit
Udledning af multiplikatoreffekten Af Thomas Schausen Et tværfagligt undervisningsmateriale i matematik og samfundsfag fra Materialet er udarbejdet med støtte fra Undervisningsministeriet, og kan frit
Jesper Jespersen Henrik R. Jensen. Introduktion til. Makro. økonomi 2. UDGAVE. Jurist- og Økonomforbundets Forlag
 Jesper Jespersen Henrik R. Jensen Introduktion til Makro økonomi 2. UDGAVE Jurist- og Økonomforbundets Forlag Introduktion til Makroøkonomi Jesper Jespersen Henrik R. Jensen Introduktion til Makroøkonomi
Jesper Jespersen Henrik R. Jensen Introduktion til Makro økonomi 2. UDGAVE Jurist- og Økonomforbundets Forlag Introduktion til Makroøkonomi Jesper Jespersen Henrik R. Jensen Introduktion til Makroøkonomi
MAKROøkonomi. Kapitel 9 - Varemarkedet og finanspolitikken. Opgaver. Opgave 1. Forklar følgende figurer fra bogen:
 MAKROøkonomi Kapitel 9 - Varemarkedet og finanspolitikken Opgaver Opgave 1 Forklar følgende figurer fra bogen: 1 Opgave 2 1. Forklar begreberne den marginale forbrugskvote og den gennemsnitlige forbrugskvote
MAKROøkonomi Kapitel 9 - Varemarkedet og finanspolitikken Opgaver Opgave 1 Forklar følgende figurer fra bogen: 1 Opgave 2 1. Forklar begreberne den marginale forbrugskvote og den gennemsnitlige forbrugskvote
MAKROøkonomi. Kapitel 3 - Nationalregnskabet. Vejledende besvarelse
 MAKROøkonomi Kapitel 3 - Nationalregnskabet Vejledende besvarelse Opgave 1 I et land, der ikke har samhandel eller andre transaktioner med udlandet (altså en lukket økonomi) produceres der 4 varer, vare
MAKROøkonomi Kapitel 3 - Nationalregnskabet Vejledende besvarelse Opgave 1 I et land, der ikke har samhandel eller andre transaktioner med udlandet (altså en lukket økonomi) produceres der 4 varer, vare
ØKONOMISKE PRINCIPPER B
 ØKONOMISKE PRINCIPPER B Forelæsning til studiepraktik baseret på Mankiw kap. 3: National Income: Where It Comes From and Where It Goes Jesper Linaa De Økonomiske Råd / Københavns Universitet Oktober 2016
ØKONOMISKE PRINCIPPER B Forelæsning til studiepraktik baseret på Mankiw kap. 3: National Income: Where It Comes From and Where It Goes Jesper Linaa De Økonomiske Råd / Københavns Universitet Oktober 2016
Øvelse 11 - Opsummering af den lukkede økonomi
 Øvelse 11 - Opsummering af den lukkede økonomi Tobias Markeprand 18. november 2008 X3 Opgave 1 C = 275 + 0, 75(Y T ) (Privat forbrug) I = 75 6, 25i (Investeringer) G = 350 (Offentligt forbrug) T = 387,
Øvelse 11 - Opsummering af den lukkede økonomi Tobias Markeprand 18. november 2008 X3 Opgave 1 C = 275 + 0, 75(Y T ) (Privat forbrug) I = 75 6, 25i (Investeringer) G = 350 (Offentligt forbrug) T = 387,
I dette kapitel beskrives varemarkedet, som er baggrunden for IS-kurven. Først ses der på, hvad BNP består af:
 Del 2 På kort sigt I de næste tre kapitler vil de værktøjer, du skal bruge for at kunne analysere en økonomi på kort sigt, blive gennemgået. Til at gøre dette er det vigtigste værktøj IS-LM-modellen, som
Del 2 På kort sigt I de næste tre kapitler vil de værktøjer, du skal bruge for at kunne analysere en økonomi på kort sigt, blive gennemgået. Til at gøre dette er det vigtigste værktøj IS-LM-modellen, som
Emneopgave: Lineær- og kvadratisk programmering:
 Emneopgave: Lineær- og kvadratisk programmering: LINEÆR PROGRAMMERING I lineær programmering løser man problemer hvor man for en bestemt funktion ønsker at finde enten en maksimering eller en minimering
Emneopgave: Lineær- og kvadratisk programmering: LINEÆR PROGRAMMERING I lineær programmering løser man problemer hvor man for en bestemt funktion ønsker at finde enten en maksimering eller en minimering
Øvelsessæt til Makroøkonomi
 Øvelsessæt til Makroøkonomi 1 2009 Oversigt over øvelsesgange: 24. april 2009: Introduktion til faget Opgaverne 2.3, 2.4 og 2.5 på side 38 i 4. Udgave og 59 i 5. udgave af Macroeconomics 15. maj 2009:
Øvelsessæt til Makroøkonomi 1 2009 Oversigt over øvelsesgange: 24. april 2009: Introduktion til faget Opgaverne 2.3, 2.4 og 2.5 på side 38 i 4. Udgave og 59 i 5. udgave af Macroeconomics 15. maj 2009:
Kvalitativ Introduktion til Matematik-Økonomi
 Kvalitativ Introduktion til Matematik-Økonomi matematik-økonomi studiet 1. basissemester Esben Høg I17 Aalborg Universitet 7. og 9. december 2009 Institut for Matematiske Fag Aalborg Universitet Esben
Kvalitativ Introduktion til Matematik-Økonomi matematik-økonomi studiet 1. basissemester Esben Høg I17 Aalborg Universitet 7. og 9. december 2009 Institut for Matematiske Fag Aalborg Universitet Esben
Introduktion til Modelanalyse Note til Økonomiske Principper B
 Introduktion til Modelanalyse Note til Økonomiske Principper B ved Claus Thustrup Kreiner Gitte Yding Michaelsen Hans Jørgen Whitta-Jacobsen Introduktion til modelanalyse Claus Thustrup Kreiner Gitte Yding
Introduktion til Modelanalyse Note til Økonomiske Principper B ved Claus Thustrup Kreiner Gitte Yding Michaelsen Hans Jørgen Whitta-Jacobsen Introduktion til modelanalyse Claus Thustrup Kreiner Gitte Yding
ØKONOMISKE PRINCIPPER B
 ØKONOMISKE PRINCIPPER B 1. årsprøve, 2. semester Mankiw kap. 11: Aggregate Demand I: Building the IS-LM Model Jesper Linaa Fra kapitel 10: Lang sigt vs. kort sigt P LRAS SRAS AD Side 2 Lang sigt vs. kort
ØKONOMISKE PRINCIPPER B 1. årsprøve, 2. semester Mankiw kap. 11: Aggregate Demand I: Building the IS-LM Model Jesper Linaa Fra kapitel 10: Lang sigt vs. kort sigt P LRAS SRAS AD Side 2 Lang sigt vs. kort
Øvelse 17 - Åbne økonomier
 Øvelse 17 - Åbne økonomier Tobias Markeprand 20. januar 2009 Opgave 21.2 Betragt et land, der opererer under faste valutakurser, med den samlede efterspørgsel og udbud givet ved ligninger (21.1) og (21.2)
Øvelse 17 - Åbne økonomier Tobias Markeprand 20. januar 2009 Opgave 21.2 Betragt et land, der opererer under faste valutakurser, med den samlede efterspørgsel og udbud givet ved ligninger (21.1) og (21.2)
Integralregning Infinitesimalregning
 Udgave 2.1 Integralregning Infinitesimalregning Noterne gennemgår begreberne integral og stamfunktion, og anskuer dette som et redskab til bestemmelse af arealer under funktioner. Noterne er supplement
Udgave 2.1 Integralregning Infinitesimalregning Noterne gennemgår begreberne integral og stamfunktion, og anskuer dette som et redskab til bestemmelse af arealer under funktioner. Noterne er supplement
Lineære sammenhænge. Udgave 2. 2009 Karsten Juul
 Lineære sammenhænge Udgave 2 y = 0,5x 2,5 2009 Karsten Juul Dette hæfte er en fortsættelse af hæftet "Variabelsammenhænge, 2. udgave 2009". Indhold 1. Lineære sammenhænge, ligning og graf... 1 2. Lineær
Lineære sammenhænge Udgave 2 y = 0,5x 2,5 2009 Karsten Juul Dette hæfte er en fortsættelse af hæftet "Variabelsammenhænge, 2. udgave 2009". Indhold 1. Lineære sammenhænge, ligning og graf... 1 2. Lineær
IS-relationen (varemarkedet) i en åben økonomi.
 IS-relationen (varemarkedet) i en åben økonomi. Det har ikke været nødvendigt at skelne mellem 1) Indenlandsk efterspørgsel efter varer 2) Efterspørgsel efter indenlandske varer For den åbne økonomi er
IS-relationen (varemarkedet) i en åben økonomi. Det har ikke været nødvendigt at skelne mellem 1) Indenlandsk efterspørgsel efter varer 2) Efterspørgsel efter indenlandske varer For den åbne økonomi er
Eksponentielle sammenhænge
 Eksponentielle sammenhænge 0 1 2 3 4 5 6 7 8 9 10 11 12 13 Indholdsfortegnelse Variabel-sammenhænge... 1 1. Hvad er en eksponentiel sammenhæng?... 2 2. Forklaring med ord af eksponentiel vækst... 2, 6
Eksponentielle sammenhænge 0 1 2 3 4 5 6 7 8 9 10 11 12 13 Indholdsfortegnelse Variabel-sammenhænge... 1 1. Hvad er en eksponentiel sammenhæng?... 2 2. Forklaring med ord af eksponentiel vækst... 2, 6
ØKONOMISKE PRINCIPPER II
 ØKONOMISKE PRINCIPPER II 1. årsprøve, 2. semester Forelæsning 13 Pensum: Mankiw & Taylor kapitel 34 Claus Thustrup Kreiner www.econ.ku.dk/ctk/principperii Fra kapitel 33 AD-AS-diagrammet AD: Negativ hældning
ØKONOMISKE PRINCIPPER II 1. årsprøve, 2. semester Forelæsning 13 Pensum: Mankiw & Taylor kapitel 34 Claus Thustrup Kreiner www.econ.ku.dk/ctk/principperii Fra kapitel 33 AD-AS-diagrammet AD: Negativ hældning
De økonomiske konsekvenser af højt uddannet merindvandring til den offentlige sektor 1.
 De økonomiske konsekvenser af højt uddannet merindvandring til den offentlige sektor 1. November 4, 2015 Indledning. Notatet opsummerer resultaterne af et marginaleksperiment udført til DREAM modellen.
De økonomiske konsekvenser af højt uddannet merindvandring til den offentlige sektor 1. November 4, 2015 Indledning. Notatet opsummerer resultaterne af et marginaleksperiment udført til DREAM modellen.
Indledning. Tekniske forudsætninger for beregningerne. 23. januar 2014
 Vurdering af krav til arbejdsstyrke og arbejdstid, hvis Danmark hhv. skal være lige så rigt som Sverige eller blot være blandt de 10 rigeste lande i OECD 1 i 2030 23. januar 2014 Indledning Nærværende
Vurdering af krav til arbejdsstyrke og arbejdstid, hvis Danmark hhv. skal være lige så rigt som Sverige eller blot være blandt de 10 rigeste lande i OECD 1 i 2030 23. januar 2014 Indledning Nærværende
Øvelse 15. Tobias Markeprand. 16. december 2008
 Øvelse 15 Tobias Markeprand 16. december 2008 1 Opgave 19.8 Politik koordinering og verdensøkonomien Betragt en åben økonomi hvor den reale valutakurs er fast og lig 1. Forbrug, investeringer og offentligt
Øvelse 15 Tobias Markeprand 16. december 2008 1 Opgave 19.8 Politik koordinering og verdensøkonomien Betragt en åben økonomi hvor den reale valutakurs er fast og lig 1. Forbrug, investeringer og offentligt
Grafmanipulation. Frank Nasser. 14. april 2011
 Grafmanipulation Frank Nasser 14. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk: Dette er
Grafmanipulation Frank Nasser 14. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk: Dette er
Rettevejledning til eksamensopgave i Makroøkonomi, 2. årsprøve: Økonomien på kort sigt Eksamenstermin 2005 II
 Rettevejledning til eksamensopgave i Makroøkonomi, 2. årsprøve: Økonomien på kort sigt ksamenstermin 25 II Ad spørgsmål 1: n permanent finanspolitisk lempelse i euroland vil i modellen (1) til (3) manifestere
Rettevejledning til eksamensopgave i Makroøkonomi, 2. årsprøve: Økonomien på kort sigt ksamenstermin 25 II Ad spørgsmål 1: n permanent finanspolitisk lempelse i euroland vil i modellen (1) til (3) manifestere
Derfor medfører øget arbejdsudbud Øget beskæftigelse. Af Mads Lundby Hansen
 Derfor medfører øget arbejdsudbud Øget beskæftigelse Af Mads Lundby Hansen 1 Velkommen til CEPOS TANK&TÆNK Denne publikation er en del af CEPOS TANK&TÆNK. CEPOS TANK&TÆNK henvender sig til elever og lærere
Derfor medfører øget arbejdsudbud Øget beskæftigelse Af Mads Lundby Hansen 1 Velkommen til CEPOS TANK&TÆNK Denne publikation er en del af CEPOS TANK&TÆNK. CEPOS TANK&TÆNK henvender sig til elever og lærere
Øvelse 5. Tobias Markeprand. October 8, 2008
 Øvelse 5 Tobias arkeprand October 8, 2008 Opgave 3.7 Formålet med denne øvelse er at analysere ændringen i indkomstdannelsesmodellen med investeringer der afhænger af indkomst/produktionen. Den positive
Øvelse 5 Tobias arkeprand October 8, 2008 Opgave 3.7 Formålet med denne øvelse er at analysere ændringen i indkomstdannelsesmodellen med investeringer der afhænger af indkomst/produktionen. Den positive
Konkludere nuanceret ud fra tabeller. Foretage relevante beregninger ud fra absolutte tal, indsætte i tabel og diagram. Brug af lommeregner og Excel.
 Emne Samfundsfag Matematik Procentregning (vækst, andel) og indekstal Diagrammer ud fra Excel Vækstrate og logaritmisk skala Renten Ricardos tese om komparative fordele Efterspørgsel, udbud og prisdannelse
Emne Samfundsfag Matematik Procentregning (vækst, andel) og indekstal Diagrammer ud fra Excel Vækstrate og logaritmisk skala Renten Ricardos tese om komparative fordele Efterspørgsel, udbud og prisdannelse
MAKROøkonomi. Kapitel 12 - Stabiliseringspolitik på langt sigt. Vejledende besvarelse. Opgave 1
 MAKROøkonomi Kapitel 12 - Stabiliseringspolitik på langt sigt Vejledende besvarelse Opgave 1 Antag en lille åben økonomi med faste valutakurser og frie kapitalbevægelser. Landet har oparbejdet et pænt
MAKROøkonomi Kapitel 12 - Stabiliseringspolitik på langt sigt Vejledende besvarelse Opgave 1 Antag en lille åben økonomi med faste valutakurser og frie kapitalbevægelser. Landet har oparbejdet et pænt
Elementær Matematik. Funktioner og deres grafer
 Elementær Matematik Funktioner og deres grafer Ole Witt-Hansen 0 Indhold. Funktioner.... Grafen for en funktion...3. grafers skæring med koordinat akser...4. To grafers skæringspunkter...4 3. Egenskaber
Elementær Matematik Funktioner og deres grafer Ole Witt-Hansen 0 Indhold. Funktioner.... Grafen for en funktion...3. grafers skæring med koordinat akser...4. To grafers skæringspunkter...4 3. Egenskaber
Bedste rette linje ved mindste kvadraters metode
 1/9 Bedste rette linje ved mindste kvadraters metode - fra www.borgeleo.dk Figur 1: Tre datapunkter og den bedste rette linje bestemt af A, B og C Målepunkter og bedste rette linje I ovenstående koordinatsystem
1/9 Bedste rette linje ved mindste kvadraters metode - fra www.borgeleo.dk Figur 1: Tre datapunkter og den bedste rette linje bestemt af A, B og C Målepunkter og bedste rette linje I ovenstående koordinatsystem
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin maj-juni 11/12 Institution VUC Holstebro-Lemvig-Struer Uddannelse Fag og niveau Lærer(e) Hold Hf/hfe Matematik
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin maj-juni 11/12 Institution VUC Holstebro-Lemvig-Struer Uddannelse Fag og niveau Lærer(e) Hold Hf/hfe Matematik
ØKONOMISKE PRINCIPPER B
 ØKONOMISKE PRINCIPPER B Forelæsning til studiepraktik baseret på Mankiw kap. 3: National Income: Where It Comes From and Where It Goes Kamilla Holmgaard, Jesper Linaa De Økonomiske Råd / Københavns Universitet
ØKONOMISKE PRINCIPPER B Forelæsning til studiepraktik baseret på Mankiw kap. 3: National Income: Where It Comes From and Where It Goes Kamilla Holmgaard, Jesper Linaa De Økonomiske Råd / Københavns Universitet
Hjemmeopgavesæt 1, løsningsskitse
 Hjemmeopgavesæt 1, løsningsskitse Teacher 26. oktober 2008 OPGAVE 1 1. Den samlede efterspørgsel, Z findes ved: Z = C + I + G = 40 + 0.8(Y 150 0.25Y ) + 80 + 400 = 0.6Y + 400 Ligevægtsindkomsten bliver:
Hjemmeopgavesæt 1, løsningsskitse Teacher 26. oktober 2008 OPGAVE 1 1. Den samlede efterspørgsel, Z findes ved: Z = C + I + G = 40 + 0.8(Y 150 0.25Y ) + 80 + 400 = 0.6Y + 400 Ligevægtsindkomsten bliver:
Differential- regning
 Differential- regning del () f () m l () 6 Karsten Juul Indhold Tretrinsreglen 59 Formler for differentialkvotienter64 Regneregler for differentialkvotienter67 Differentialkvotient af sammensat funktion7
Differential- regning del () f () m l () 6 Karsten Juul Indhold Tretrinsreglen 59 Formler for differentialkvotienter64 Regneregler for differentialkvotienter67 Differentialkvotient af sammensat funktion7
Projektopgaver om nationalregnskabsligningen og multiplikatoreffekten
 Projektopgaver om nationalregnskabsligningen og multiplikatoreffekten Indledning Som afslutning på vores studieretningsforløb i samfundsfag og matematik skal I gruppevis udarbejde forskellige projektopgaver.
Projektopgaver om nationalregnskabsligningen og multiplikatoreffekten Indledning Som afslutning på vores studieretningsforløb i samfundsfag og matematik skal I gruppevis udarbejde forskellige projektopgaver.
Opgave X4. Tobias Markeprand. January 13, Vi betragter en økonomi med adfærdsligninger
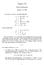 Opgave X4 Tobias Markeprand January 13, 2009 Vi betragter en økonomi med adfærdsligninger og ligevægtsligninger C = 60 + 0:8 (Y T ) I = 250 10i G = 150 N X = 400 0:1Y 500E T = 50 + 0:25Y M d = 0:25Y 10i
Opgave X4 Tobias Markeprand January 13, 2009 Vi betragter en økonomi med adfærdsligninger og ligevægtsligninger C = 60 + 0:8 (Y T ) I = 250 10i G = 150 N X = 400 0:1Y 500E T = 50 + 0:25Y M d = 0:25Y 10i
Nationalregnskab Marts-version
 Nationalregnskab 216. Marts-version April 217 Danmark Statistik Sejrøgade 11 21 København Ø Nationalregnskab 216. Marts-version Danmarks Statistik April 217 Udarbejdet af: Bo Siemsen, bsm@dst.dk 2/1 Nationalregnskab
Nationalregnskab 216. Marts-version April 217 Danmark Statistik Sejrøgade 11 21 København Ø Nationalregnskab 216. Marts-version Danmarks Statistik April 217 Udarbejdet af: Bo Siemsen, bsm@dst.dk 2/1 Nationalregnskab
Indkomstdannelsesteori. Tema 7
 Indkomstdannelsesteori Tema 7 Udgangspunktet Nationalregnskabet er regnskabsmæssige identiteter; Nu kobles adfærd og adfærds betydning for det økonomiske forløb på; Tankerne om udbudsøkonomi negligeres,
Indkomstdannelsesteori Tema 7 Udgangspunktet Nationalregnskabet er regnskabsmæssige identiteter; Nu kobles adfærd og adfærds betydning for det økonomiske forløb på; Tankerne om udbudsøkonomi negligeres,
Lynprøve. Makroøkonomi, 1. årsprøve, foråret Nogle svar
 Opgave 1. Lynprøve Makroøkonomi, 1. årsprøve, foråret 2005 Nogle svar 1.1 Korrekt. Dette er jo Fisher-effekten baseret på Fisher-ligningen, i = r + π eller "more precisely written" i = r + π e. Realrenten
Opgave 1. Lynprøve Makroøkonomi, 1. årsprøve, foråret 2005 Nogle svar 1.1 Korrekt. Dette er jo Fisher-effekten baseret på Fisher-ligningen, i = r + π eller "more precisely written" i = r + π e. Realrenten
VisiRegn: En e-bro mellem regning og algebra
 Artikel i Matematik nr. 2 marts 2001 VisiRegn: En e-bro mellem regning og algebra Inge B. Larsen Siden midten af 80 erne har vi i INFA-projektet arbejdet med at udvikle regne(arks)programmer til skolens
Artikel i Matematik nr. 2 marts 2001 VisiRegn: En e-bro mellem regning og algebra Inge B. Larsen Siden midten af 80 erne har vi i INFA-projektet arbejdet med at udvikle regne(arks)programmer til skolens
Finansøkonom 2010/12 Globaløkonomi
 Finansøkonom 2010/12 Globaløkonomi Opgaver om handelsteorier og handelsrestriktioner Opgave 1 I nedenstående tabel er vist arbejdsproduktiviteten for to varer i to lande. Produktion per mand per dag Sko
Finansøkonom 2010/12 Globaløkonomi Opgaver om handelsteorier og handelsrestriktioner Opgave 1 I nedenstående tabel er vist arbejdsproduktiviteten for to varer i to lande. Produktion per mand per dag Sko
Projekt 2.9 Sumkurver som funktionsudtryk anvendt til Lorenzkurver og Ginikoefficienter (især for B- og A-niveau)
 Projekt 2.9 Sumkurver som funktionsudtryk anvendt til Lorenzkurver og Ginikoefficienter En sumkurve fremkommer ifølge definitionen, ved at vi forbinder en række punkter afsat i et koordinatsystem med rette
Projekt 2.9 Sumkurver som funktionsudtryk anvendt til Lorenzkurver og Ginikoefficienter En sumkurve fremkommer ifølge definitionen, ved at vi forbinder en række punkter afsat i et koordinatsystem med rette
Eksponentielle sammenhænge
 Eksponentielle sammenhænge Udgave 009 Karsten Juul Dette hæfte er en fortsættelse af hæftet "Lineære sammenhænge, udgave 009" Indhold 1 Eksponentielle sammenhænge, ligning og graf 1 Procent 7 3 Hvad fortæller
Eksponentielle sammenhænge Udgave 009 Karsten Juul Dette hæfte er en fortsættelse af hæftet "Lineære sammenhænge, udgave 009" Indhold 1 Eksponentielle sammenhænge, ligning og graf 1 Procent 7 3 Hvad fortæller
Matematik A. Studentereksamen. Forberedelsesmateriale til de digitale eksamensopgaver med adgang til internettet
 Matematik A Studentereksamen Forberedelsesmateriale til de digitale eksamensopgaver med adgang til internettet st131-matn/a-6513 Mandag den 6 maj 13 Forberedelsesmateriale til st A Net MATEMATIK Der skal
Matematik A Studentereksamen Forberedelsesmateriale til de digitale eksamensopgaver med adgang til internettet st131-matn/a-6513 Mandag den 6 maj 13 Forberedelsesmateriale til st A Net MATEMATIK Der skal
Matematik A. Højere handelseksamen. Gammel ordning. Mandag den 17. december 2018 kl gl-hhx183-mat/a
 Matematik A Højere handelseksamen Gammel ordning gl-hhx183-mat/a-17122018 Mandag den 17. december 2018 kl. 9.00-14.00 Matematik A Prøven består af to delprøver. Delprøven uden hjælpemidler består af opgave
Matematik A Højere handelseksamen Gammel ordning gl-hhx183-mat/a-17122018 Mandag den 17. december 2018 kl. 9.00-14.00 Matematik A Prøven består af to delprøver. Delprøven uden hjælpemidler består af opgave
Det er en af de hyppigst forekommende udregninger i den elementære talbehandling at beregne gennemsnit eller middeltal af en række tal.
 Tre slags gennemsnit Allan C. Malmberg Det er en af de hyppigst forekommende udregninger i den elementære talbehandling at beregne gennemsnit eller middeltal af en række tal. For mange skoleelever indgår
Tre slags gennemsnit Allan C. Malmberg Det er en af de hyppigst forekommende udregninger i den elementære talbehandling at beregne gennemsnit eller middeltal af en række tal. For mange skoleelever indgår
Differentialregning med TI-Interactive! Indledende differentialregning Tangenter Monotoniforhold og ekstremum Optimering Jan Leffers (2009)
 Differentialregning med TI-Interactive! Indledende differentialregning Tangenter Monotoniforhold og ekstremum Optimering Jan Leffers (2009) Indholdsfortegnelse Indholdsfortegnelse...2 Indledende differentialregning...3
Differentialregning med TI-Interactive! Indledende differentialregning Tangenter Monotoniforhold og ekstremum Optimering Jan Leffers (2009) Indholdsfortegnelse Indholdsfortegnelse...2 Indledende differentialregning...3
Afstande, skæringer og vinkler i rummet
 Afstande, skæringer og vinkler i rummet Frank Nasser 9. april 20 c 2008-20. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her.
Afstande, skæringer og vinkler i rummet Frank Nasser 9. april 20 c 2008-20. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her.
MATEMATIK A-NIVEAU-Net Forberedelsesmateriale
 STUDENTEREKSAMEN SOMMERTERMIN 13 MATEMATIK A-NIVEAU-Net Forberedelsesmateriale 6 timer med vejledning Forberedelsesmateriale til de skriftlige prøver sommertermin 13 st131-matn/a-6513 Forberedelsesmateriale
STUDENTEREKSAMEN SOMMERTERMIN 13 MATEMATIK A-NIVEAU-Net Forberedelsesmateriale 6 timer med vejledning Forberedelsesmateriale til de skriftlige prøver sommertermin 13 st131-matn/a-6513 Forberedelsesmateriale
MAKROØKONOMI FRAKAPITEL9:LANGTSIGTVSKORTSIGT. Forskel i antagelser? Implikation for AS-AD diagram? 1. årsprøve, 2. semester.
 FRAKAPITEL9:LANGTSIGTVSKORTSIGT MAKROØKONOMI Forskel i antagelser? Implikation for AS-AD diagram? 1. årsprøve, 2. semester Forelæsning 8 Aggregeret efterspørgsel I Pensum: Mankiw kapitel 10 Claus Thustrup
FRAKAPITEL9:LANGTSIGTVSKORTSIGT MAKROØKONOMI Forskel i antagelser? Implikation for AS-AD diagram? 1. årsprøve, 2. semester Forelæsning 8 Aggregeret efterspørgsel I Pensum: Mankiw kapitel 10 Claus Thustrup
Nationalregnskab og betalingsbalance
 Dansk økonomi til Økonomisk vækst i Bruttonationalproduktet steg med, pct. i. Efter fire år med høje vækstrater i -7, økonomisk nedgang i 8 og den historiske tilbagegang på, pct. i 9 genvandt dansk økonomi
Dansk økonomi til Økonomisk vækst i Bruttonationalproduktet steg med, pct. i. Efter fire år med høje vækstrater i -7, økonomisk nedgang i 8 og den historiske tilbagegang på, pct. i 9 genvandt dansk økonomi
Introduktion til differentialregning 1. Jens Siegstad og Annegrethe Bak
 Introduktion til differentialregning 1 Jens Siegstad og Annegrete Bak 16. juli 2008 1 Indledning I denne note vil vi kort introduktion til differentilregning, idet vi skal bruge teorien i et emne, Matematisk
Introduktion til differentialregning 1 Jens Siegstad og Annegrete Bak 16. juli 2008 1 Indledning I denne note vil vi kort introduktion til differentilregning, idet vi skal bruge teorien i et emne, Matematisk
Start pä matematik. for gymnasiet og hf. 2010 (2012) Karsten Juul
 Start pä matematik for gymnasiet og hf 2010 (2012) Karsten Juul Til eleven Brug blyant og viskelåder när du skriver og tegner i håftet, sä du fär et håfte der er egnet til jåvnligt at slä op i under dit
Start pä matematik for gymnasiet og hf 2010 (2012) Karsten Juul Til eleven Brug blyant og viskelåder när du skriver og tegner i håftet, sä du fär et håfte der er egnet til jåvnligt at slä op i under dit
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Sommer 2015 Institution Campus vejle Uddannelse Fag og niveau Lærer(e) Hold HHX Matematik B (Valghold) PEJE
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Sommer 2015 Institution Campus vejle Uddannelse Fag og niveau Lærer(e) Hold HHX Matematik B (Valghold) PEJE
Studieretningsopgave
 Virum Gymnasium Studieretningsopgave Harmoniske svingninger i matematik og fysik Vejledere: Christian Holst Hansen (matematik) og Bodil Dam Heiselberg (fysik) 30-01-2014 Indholdsfortegnelse Indledning...
Virum Gymnasium Studieretningsopgave Harmoniske svingninger i matematik og fysik Vejledere: Christian Holst Hansen (matematik) og Bodil Dam Heiselberg (fysik) 30-01-2014 Indholdsfortegnelse Indledning...
ØVEHÆFTE FOR MATEMATIK C FORMLER OG LIGNINGER
 ØVEHÆFTE FOR MATEMATIK C FORMLER OG LIGNINGER INDHOLDSFORTEGNELSE 0. FORMELSAMLING TIL FORMLER OG LIGNINGER... 2 Tal, regneoperationer og ligninger... 2 Isolere en ubekendt... 3 Hvis x står i første brilleglas...
ØVEHÆFTE FOR MATEMATIK C FORMLER OG LIGNINGER INDHOLDSFORTEGNELSE 0. FORMELSAMLING TIL FORMLER OG LIGNINGER... 2 Tal, regneoperationer og ligninger... 2 Isolere en ubekendt... 3 Hvis x står i første brilleglas...
Vejledende opgavebesvarelse Økonomisk kandidateksamen 2004II 1. årsprøve, Makroøkonomi
 Vejledende opgavebesvarelse Økonomisk kandidateksamen 2004II 1. årsprøve, Makroøkonomi Claus Thustrup Kreiner Juni 2004 OPGAVE 1 1.1 Forkert. Møntningsgevinst beskriver en gevinst centralbanken/staten
Vejledende opgavebesvarelse Økonomisk kandidateksamen 2004II 1. årsprøve, Makroøkonomi Claus Thustrup Kreiner Juni 2004 OPGAVE 1 1.1 Forkert. Møntningsgevinst beskriver en gevinst centralbanken/staten
Besvarelse af stx_081_matb 1. Opgave 2. Opgave 1 2. Ib Michelsen, 2z Side B_081. Reducer + + = + + = Værdien af
 Ib Michelsen, z Side 1 7-05-01 1 3 4 5 6 7 8 9 10 11 1 13 14 15 16 17 18 19 0 1 3 4 5 6 7 Besvarelse af stx_081_matb 1 Opgave 1 Reducer ( x + h) h( h + x) ( x h) h( h x) + + = x h xh h h x x + + = Værdien
Ib Michelsen, z Side 1 7-05-01 1 3 4 5 6 7 8 9 10 11 1 13 14 15 16 17 18 19 0 1 3 4 5 6 7 Besvarelse af stx_081_matb 1 Opgave 1 Reducer ( x + h) h( h + x) ( x h) h( h x) + + = x h xh h h x x + + = Værdien
Differentialregning. Ib Michelsen
 Differentialregning Ib Michelsen Ikast 2012 Forsidebilledet Tredjegradspolynomium i blåt med rød tangent Version: 0.02 (18-09-12) Denne side er (~ 2) Indholdsfortegnelse Introduktion...5 Definition af
Differentialregning Ib Michelsen Ikast 2012 Forsidebilledet Tredjegradspolynomium i blåt med rød tangent Version: 0.02 (18-09-12) Denne side er (~ 2) Indholdsfortegnelse Introduktion...5 Definition af
Hjemmeopgave 3. Makro 1, 2. årsprøve, efteråret 2007 Hans Jørgen Whitta-Jacobsen
 Hjemmeopgave 3 Makro 1, 2. årsprøve, efteråret 2007 Hans Jørgen Whitta-Jacobsen Opgavebesvarelse afleveres til holdlærer i uge 46. Opgave 1. Empirisk opgave I det vedlagte figurbilag gælder Figur 1 og
Hjemmeopgave 3 Makro 1, 2. årsprøve, efteråret 2007 Hans Jørgen Whitta-Jacobsen Opgavebesvarelse afleveres til holdlærer i uge 46. Opgave 1. Empirisk opgave I det vedlagte figurbilag gælder Figur 1 og
Modellering af elektroniske komponenter
 Modellering af elektroniske komponenter Formålet er at give studerende indblik i hvordan matematik som fag kan bruges i forbindelse med at modellere fysiske fænomener. Herunder anvendelse af Grafregner(TI-89)
Modellering af elektroniske komponenter Formålet er at give studerende indblik i hvordan matematik som fag kan bruges i forbindelse med at modellere fysiske fænomener. Herunder anvendelse af Grafregner(TI-89)
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Maj juni 2012 Institution Campus Vejle Uddannelse Fag og niveau Lærer(e) Hold HHX Matematik B Ejner Husum
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Maj juni 2012 Institution Campus Vejle Uddannelse Fag og niveau Lærer(e) Hold HHX Matematik B Ejner Husum
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Sommer 2015 Institution 414 Københavns VUC Uddannelse Fag og niveau Lærer(e) Hold hfe Matematik B Henrik Sandler
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Sommer 2015 Institution 414 Københavns VUC Uddannelse Fag og niveau Lærer(e) Hold hfe Matematik B Henrik Sandler
VUC Vestsjælland Syd, Slagelse Nr. 1 Institution: Projekt Trigonometri
 VUC Vestsjælland Syd, Slagelse Nr. 1 Institution: 333247 2015 Anders Jørgensen, Mark Kddafi, David Jensen, Kourosh Abady og Nikolaj Eriksen 1. Indledning I dette projekt, vil man kunne se definitioner
VUC Vestsjælland Syd, Slagelse Nr. 1 Institution: 333247 2015 Anders Jørgensen, Mark Kddafi, David Jensen, Kourosh Abady og Nikolaj Eriksen 1. Indledning I dette projekt, vil man kunne se definitioner
Matematik for stx C-niveau
 Thomas Jensen og Morten Overgård Nielsen Matematik for stx C-niveau Frydenlund Nu 2. reviderede, udvidede og ajourførte udgave Nu 2. reviderede, udvidede og ajourførte udgave Matema10k Matematik for stx
Thomas Jensen og Morten Overgård Nielsen Matematik for stx C-niveau Frydenlund Nu 2. reviderede, udvidede og ajourførte udgave Nu 2. reviderede, udvidede og ajourførte udgave Matema10k Matematik for stx
Notat. Notat om produktivitet og lange videregående uddannelser. Martin Junge. Oktober
 Notat Oktober Notat om produktivitet og lange videregående uddannelser Martin Junge Oktober 21 Notat om produktivitet og lange videregående uddannelser Notat om produktivitet og lange videregående uddannelser
Notat Oktober Notat om produktivitet og lange videregående uddannelser Martin Junge Oktober 21 Notat om produktivitet og lange videregående uddannelser Notat om produktivitet og lange videregående uddannelser
Eksaminationsgrundlag for selvstuderende
 Eksaminationsgrundlag for selvstuderende Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Institution Uddannelse Fag og niveau Hold Vinter 2016/17 Thy-Mors HF & VUC Hfe Matematik,
Eksaminationsgrundlag for selvstuderende Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Institution Uddannelse Fag og niveau Hold Vinter 2016/17 Thy-Mors HF & VUC Hfe Matematik,
Variabel- sammenhænge
 Variabel- sammenhænge 2008 Karsten Juul Dette hæfte kan bruges som start på undervisningen i variabelsammenhænge for st og hf. Indhold 1. Hvordan viser en tabel sammenhængen mellem to variable?... 1 2.
Variabel- sammenhænge 2008 Karsten Juul Dette hæfte kan bruges som start på undervisningen i variabelsammenhænge for st og hf. Indhold 1. Hvordan viser en tabel sammenhængen mellem to variable?... 1 2.
Pointen med Differentiation
 Pointen med Differentiation Frank Nasser 20. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk:
Pointen med Differentiation Frank Nasser 20. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk:
Potensfunktioner samt proportional og omvent proportional. for hf Karsten Juul
 Potensfunktioner samt proportional og omvent proportional for hf 2018 Karsten Juul Potensfunktion 1. Oplæg til forskrift for potensfunktion...1 2. Forskrift for potensfunktion...2 3. Udregn x eller y i
Potensfunktioner samt proportional og omvent proportional for hf 2018 Karsten Juul Potensfunktion 1. Oplæg til forskrift for potensfunktion...1 2. Forskrift for potensfunktion...2 3. Udregn x eller y i
Matema10k. Matematik for gymnasiet. Bind 3 A-niveau. af Thomas Jensen, Claus Jessen og Morten Overgård Nielsen
 Matema10k Matematik for gymnasiet Bind 3 A-niveau af Thomas Jensen, Claus Jessen og Morten Overgård Nielsen 4 Thomas Jensen, Claus Jessen og Morten Overgård Nielsen Matema10k Matematik for stx. Bind 3.
Matema10k Matematik for gymnasiet Bind 3 A-niveau af Thomas Jensen, Claus Jessen og Morten Overgård Nielsen 4 Thomas Jensen, Claus Jessen og Morten Overgård Nielsen Matema10k Matematik for stx. Bind 3.
Lineære sammenhænge, residualplot og regression
 Lineære sammenhænge, residualplot og regression Opgave 1: Er der en bagvedliggende lineær sammenhæng? I mange sammenhænge indsamler man data som man ønsker at undersøge og afdække eventuelle sammenhænge
Lineære sammenhænge, residualplot og regression Opgave 1: Er der en bagvedliggende lineær sammenhæng? I mange sammenhænge indsamler man data som man ønsker at undersøge og afdække eventuelle sammenhænge
Eksempel på den aksiomatisk deduktive metode
 Eksempel på den aksiomatisk deduktive metode Et rigtig godt eksempel på et aksiomatisk deduktivt system er Euklids Elementer. Euklid var græker og skrev Elemeterne omkring 300 f.kr. Værket består af 13
Eksempel på den aksiomatisk deduktive metode Et rigtig godt eksempel på et aksiomatisk deduktivt system er Euklids Elementer. Euklid var græker og skrev Elemeterne omkring 300 f.kr. Værket består af 13
Projekt 2.2 Omvendt funktion og differentiation af omvendt funktion
 ISBN 978877664974 Projekter: Kapitel. Projekt. Omvendt funktion og differentiation af omvendt funktion Projekt. Omvendt funktion og differentiation af omvendt funktion Vi har i Bbogens kapitel 4 afsnit
ISBN 978877664974 Projekter: Kapitel. Projekt. Omvendt funktion og differentiation af omvendt funktion Projekt. Omvendt funktion og differentiation af omvendt funktion Vi har i Bbogens kapitel 4 afsnit
Makroøkonomi. Olivier Blanchard ch. 3: The Goods Market
 Syddansk Universitet HD 1. del, Samfundsøkonomi Kapitel- og noteoversigt: 1. Den økonomiske model 2. Indkomstdannelsesmodellen Makroøkonomi Olivier Blanchard ch. 3: The Goods Market 3. Nærmere om samspillet
Syddansk Universitet HD 1. del, Samfundsøkonomi Kapitel- og noteoversigt: 1. Den økonomiske model 2. Indkomstdannelsesmodellen Makroøkonomi Olivier Blanchard ch. 3: The Goods Market 3. Nærmere om samspillet
Kapital- og rentesregning
 Rentesregning Rettet den 28-12-11 Kapital- og rentesregning Kapital- og rentesregning Navngivning ved rentesregning I eksempler som Niels Oles, hvor man indskyder en kapital i en bank (én gang), og banken
Rentesregning Rettet den 28-12-11 Kapital- og rentesregning Kapital- og rentesregning Navngivning ved rentesregning I eksempler som Niels Oles, hvor man indskyder en kapital i en bank (én gang), og banken
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Maj / Juni 2017 Institution Den Jyske Håndværkerskole Uddannelse Fag og niveau Lærer Hold EUX - Tømre Matematik
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Maj / Juni 2017 Institution Den Jyske Håndværkerskole Uddannelse Fag og niveau Lærer Hold EUX - Tømre Matematik
Uafhængig og afhængig variabel
 Uddrag fra http://www.emu.dk/gym/fag/ma/undervisningsforloeb/hf-mat-c/introduktion.doc ved Hans Vestergaard, Morten Overgaard Nielsen, Peter Trautner Brander Variable og sammenhænge... 1 Uafhængig og afhængig
Uddrag fra http://www.emu.dk/gym/fag/ma/undervisningsforloeb/hf-mat-c/introduktion.doc ved Hans Vestergaard, Morten Overgaard Nielsen, Peter Trautner Brander Variable og sammenhænge... 1 Uafhængig og afhængig
tjek.me Forårskatalog 2018 Matematik By Knowmio
 tjek.me Forårskatalog 2018 Matematik Velkommen til tjek.me forårskatalog for matematik 1. til 9. klasse tjek.me er et online, spilbaseret evalueringsværktøj, som giver indsigt i elevernes progression.
tjek.me Forårskatalog 2018 Matematik Velkommen til tjek.me forårskatalog for matematik 1. til 9. klasse tjek.me er et online, spilbaseret evalueringsværktøj, som giver indsigt i elevernes progression.
Funktioner. 1. del Karsten Juul
 Funktioner 1. del 0,6 5, 9 2018 Karsten Juul 1. Koordinater 1.1 Koordinatsystem... 1 1.2 Kvadranter... 1 1.3 Koordinater... 2 1.4 Aflæs x-koordinat... 2 1.5 Aflæs y-koordinat... 2 1.6 Koordinatsæt... 2
Funktioner 1. del 0,6 5, 9 2018 Karsten Juul 1. Koordinater 1.1 Koordinatsystem... 1 1.2 Kvadranter... 1 1.3 Koordinater... 2 1.4 Aflæs x-koordinat... 2 1.5 Aflæs y-koordinat... 2 1.6 Koordinatsæt... 2
Eksperimenter med simple log-lineære funktioner og brugen af justeringsled i fremskrivninger II (Kontantpris og justeringsled II)
 Danmarks Statistik MODELGRUPPEN Arbejdspapir* Tony Maarsleth Kristensen..9 Henrik C. Olesen Eksperimenter med simple log-lineære funktioner og brugen af justeringsled i fremskrivninger II (Kontantpris
Danmarks Statistik MODELGRUPPEN Arbejdspapir* Tony Maarsleth Kristensen..9 Henrik C. Olesen Eksperimenter med simple log-lineære funktioner og brugen af justeringsled i fremskrivninger II (Kontantpris
Matematik A. Højere handelseksamen. Tirsdag den 15. december 2015 kl hhx153-mat/a
 Matematik A Højere handelseksamen hh153-mat/a-15122015 Tirsdag den 15. december 2015 kl. 9.00-14.00 Matematik A Prøven består af to delprøver. Delprøven uden hjælpemidler består af opgave 1 til 5 med i
Matematik A Højere handelseksamen hh153-mat/a-15122015 Tirsdag den 15. december 2015 kl. 9.00-14.00 Matematik A Prøven består af to delprøver. Delprøven uden hjælpemidler består af opgave 1 til 5 med i
I et år er der følgende transaktioner mellem Danmark og udlandet (i mia. kr.)
 MAKROøkonomi Kapitel 4 - Betalingsbalancen Vejledende Besvarelse Opgave 1 I et år er der følgende transaktioner mellem Danmark og udlandet (i mia. kr.) Eksport af varer (fob) 450 Import af varer (fob)
MAKROøkonomi Kapitel 4 - Betalingsbalancen Vejledende Besvarelse Opgave 1 I et år er der følgende transaktioner mellem Danmark og udlandet (i mia. kr.) Eksport af varer (fob) 450 Import af varer (fob)
Afstande, skæringer og vinkler i rummet
 Afstande, skæringer og vinkler i rummet Frank Villa 2. maj 202 c 2008-20. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold
Afstande, skæringer og vinkler i rummet Frank Villa 2. maj 202 c 2008-20. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold
Matematikrapport for skoleåret , Egedal Kommune
 1 af 14 Indhold Indledning...3 Resultater for hele Egedal Kommune...4 1.klasserne 15/16...6 2.klasserne 15/16...8 4. klasserne 15/16...10 7. klasserne 15/16...12 Anbefalinger...14 2 af 14 Indledning I
1 af 14 Indhold Indledning...3 Resultater for hele Egedal Kommune...4 1.klasserne 15/16...6 2.klasserne 15/16...8 4. klasserne 15/16...10 7. klasserne 15/16...12 Anbefalinger...14 2 af 14 Indledning I
MAKRO 1. 2. årsprøve, forår 2007. Forelæsning 2. Mankiw kapitel 3. Peter Birch Sørensen. www.econ.ku.dk/okopbs/courses.htm
 MAKRO 1 2. årsprøve, forår 2007 Forelæsning 2 Mankiw kapitel 3 Peter Birch Sørensen www.econ.ku.dk/okopbs/courses.htm DEN GRUNDLÆGGENDE KLASSISKE MODEL: REPETITION Langsigtsmodel for en lukket økonomi.
MAKRO 1 2. årsprøve, forår 2007 Forelæsning 2 Mankiw kapitel 3 Peter Birch Sørensen www.econ.ku.dk/okopbs/courses.htm DEN GRUNDLÆGGENDE KLASSISKE MODEL: REPETITION Langsigtsmodel for en lukket økonomi.
Computerundervisning
 Frederiksberg Seminarium Computerundervisning Koordinatsystemer og funktioner Elevmateriale 30-01-2009 Udarbejdet af: Pernille Suhr Poulsen Christina Klitlyng Julie Nielsen Opgaver GeoGebra Om at genkende
Frederiksberg Seminarium Computerundervisning Koordinatsystemer og funktioner Elevmateriale 30-01-2009 Udarbejdet af: Pernille Suhr Poulsen Christina Klitlyng Julie Nielsen Opgaver GeoGebra Om at genkende
Residualer i grundforløbet
 Erik Vestergaard www.matematikfysik.dk 1 Residualer i grundforløbet I dette lille tillæg til grundforløbet, skal vi kigge på begreberne residualer, residualplot samt residualspredning. Vi vil se, hvad
Erik Vestergaard www.matematikfysik.dk 1 Residualer i grundforløbet I dette lille tillæg til grundforløbet, skal vi kigge på begreberne residualer, residualplot samt residualspredning. Vi vil se, hvad
Skriftlig eksamen i samfundsfag
 OpenSamf Skriftlig eksamen i samfundsfag Indholdsfortegnelse 1. Introduktion 2. Præcise nedslag 3. Beregninger 3.1. Hvad kan absolutte tal være? 3.2. Procentvis ændring (vækst) 3.2.1 Tolkning af egne beregninger
OpenSamf Skriftlig eksamen i samfundsfag Indholdsfortegnelse 1. Introduktion 2. Præcise nedslag 3. Beregninger 3.1. Hvad kan absolutte tal være? 3.2. Procentvis ændring (vækst) 3.2.1 Tolkning af egne beregninger
Beregninger til Arbejdsmarkedsrapport 2013. - Analyse af mervækst i de individuelle offentlige udgifter til sundhed og ældrepleje 1
 Beregninger til Arbejdsmarkedsrapport 2013. - Analyse af mervækst i de individuelle offentlige udgifter til sundhed og ældrepleje 1 31. oktober 2013 Indledning I DREAMs grundforløb er de offentlige udgifter
Beregninger til Arbejdsmarkedsrapport 2013. - Analyse af mervækst i de individuelle offentlige udgifter til sundhed og ældrepleje 1 31. oktober 2013 Indledning I DREAMs grundforløb er de offentlige udgifter
Substitutions- og indkomsteffekt ved prisændringer
 Substitutions- og indkomsteffekt ved prisændringer Erik Bennike 14. november 2009 Denne note giver en beskrivelse af de relevante begreber omkring substitutions- og indkomsteffekter i mikroøkonomi. 1 Introduktion
Substitutions- og indkomsteffekt ved prisændringer Erik Bennike 14. november 2009 Denne note giver en beskrivelse af de relevante begreber omkring substitutions- og indkomsteffekter i mikroøkonomi. 1 Introduktion
MODELSÆT 2; MATEMATIK TIL LÆREREKSAMEN
 MODELSÆT ; MATEMATIK TIL LÆREREKSAMEN Forberedende materiale Den individuelle skriftlige røve i matematik vil tage udgangsunkt i følgende materiale:. En diskette med to regnearks-filer og en MathCad-fil..
MODELSÆT ; MATEMATIK TIL LÆREREKSAMEN Forberedende materiale Den individuelle skriftlige røve i matematik vil tage udgangsunkt i følgende materiale:. En diskette med to regnearks-filer og en MathCad-fil..
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Sommer 2015 Institution Campus vejle Uddannelse Fag og niveau Lærer(e) Hold HHX Matematik C PEJE (Pernille
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Sommer 2015 Institution Campus vejle Uddannelse Fag og niveau Lærer(e) Hold HHX Matematik C PEJE (Pernille
Differentialregning. Et oplæg Karsten Juul L P
 Differentialregning Et oplæg L P A 2009 Karsten Juul Til eleven Dette hæfte kan I bruge inden I starter på differentialregningen i lærebogen Det meste af hæftet er små spørgsmål med korte svar Spørgsmålene
Differentialregning Et oplæg L P A 2009 Karsten Juul Til eleven Dette hæfte kan I bruge inden I starter på differentialregningen i lærebogen Det meste af hæftet er små spørgsmål med korte svar Spørgsmålene
[FUNKTIONER] Hvornår kan vi kalde en sammenhæng en funktion, og hvilke egenskaber har disse i givet fald. Vers. 2.0
![[FUNKTIONER] Hvornår kan vi kalde en sammenhæng en funktion, og hvilke egenskaber har disse i givet fald. Vers. 2.0 [FUNKTIONER] Hvornår kan vi kalde en sammenhæng en funktion, og hvilke egenskaber har disse i givet fald. Vers. 2.0](/thumbs/48/24857099.jpg) MaB Sct. Knud Gymnasium, Henrik S. Hansen % [FUNKTIONER] Hvornår kan vi kalde en sammenhæng en funktion, og hvilke egenskaber har disse i givet fald. Vers..0 Indhold Funktioner... Entydighed... Injektiv...
MaB Sct. Knud Gymnasium, Henrik S. Hansen % [FUNKTIONER] Hvornår kan vi kalde en sammenhæng en funktion, og hvilke egenskaber har disse i givet fald. Vers..0 Indhold Funktioner... Entydighed... Injektiv...
Algebra - Teori og problemløsning
 Algebra - Teori og problemløsning, januar 05, Kirsten Rosenkilde. Algebra - Teori og problemløsning Kapitel -3 giver en grundlæggende introduktion til at omskrive udtryk, faktorisere og løse ligningssystemer.
Algebra - Teori og problemløsning, januar 05, Kirsten Rosenkilde. Algebra - Teori og problemløsning Kapitel -3 giver en grundlæggende introduktion til at omskrive udtryk, faktorisere og løse ligningssystemer.
Trekants- beregning for hf
 Trekants- beregning for hf C C 5 l 5 A 34 8 B 018 Karsten Juul Indhold 1. Vinkler... 1 1.1 Regler for vinkler.... 1. Omkreds, areal, højde....1 Omkreds..... Rektangel....3 Kvadrat....4 Højde....5 Højde-grundlinje-formel
Trekants- beregning for hf C C 5 l 5 A 34 8 B 018 Karsten Juul Indhold 1. Vinkler... 1 1.1 Regler for vinkler.... 1. Omkreds, areal, højde....1 Omkreds..... Rektangel....3 Kvadrat....4 Højde....5 Højde-grundlinje-formel
