(UKYHUYV NRQRPL)RUnU &KU+MRUWK$QGHUVHQ
|
|
|
- Kirsten Dalgaard
- 8 år siden
- Visninger:
Transkript
1 (UKYHUYV NRQRPL)RUnU &KU+MRUWK$QGHUVHQ (QQRWHRPOLQH USURJUDPPHULQJ Lineær programmering, eller LP-modeller, som de ofte kaldes, var en metode, der blev udviklet i 50'erne og 60'erne. I Danmark var især Sven Danø, professor i driftsøkonomi ved Københavns Universitet, medvirkende til udbredelsen af metoden. Som et blandt mange eksempler kan man forestille sig følgende situation: En virksomhed har en produktion af to forskellige produkter A og B, som begge skal undergå behandling på to 3 forskellige maskiner, M1, M2 og M3. 0DVNLQH 0DVNLQH 0DVNLQH: Vare A kræver 1 times maskintid og vare B kræver 2 timers maskintid Der er ialt maskintimer til rådighed vare A kræver 1 times maskintid, og vare B kræver 1 times maskintid, ' NQLQJVELGUDJ Vare A: 6 kr. Vare B. 5 kr. Der er ialt maskintimer til rådighed Vare A kræver 3 times maskintid vare B kræver 2 timers maskintid Der er ialt maskintimer til rådighed. %HVWHPGHQRSWLPDOHSURGXNWLRQDIGHWRSURGXNWHU Det økonomiske problem består i, at vare A giver det højeste dækningsbidrag, men beslaglægger også mere maskintid per enhed, især på maskine 3. Uden systematik er det svært at overskue problemets løsning. Lad os derfor stille det formelt op. Vi vil maksimere en målfunktion, der består af summen af dækningsbidragene fra de to produktioner, altså summen af dækningsbidraget fra A, d.v.s. 6*A, hvor A er det faktiske antal producerede enheder, og dækningsbidraget fra B, altså 5*B, hvor B er det faktiske antal enheder. Formelt skrives dette som MAKS: 6*A + 5*B under nogle bibetingelser. Den første maskine giver ELEHWLQJHOVHQ eller UHVWULNWLRQHQ, at A + 2*B Vi regner i timer, og har ikke mere end timer til rådighed. Det er vigtigt at notere sig ulighedstegnet, for vi kan godt lade en maskine stå ledig (selv om det alt andet lige er uøkonomisk), men vi kan ikke bruge flere maskintimer, end vi har. Bemærk, at
2 sådanne tekniske koefficienter, der mere eller mindre eksplicit bliver antaget konstante, bevirker, at restriktionen bliver lineæ r. Tilsvarende udtryk får vi for de to andre maskiner. Formelt skriver vi, at vi vil maksimere målfunktionen under bibetingelserne, som SUB: 1*A + 2*B (svarende til maskine 1) 1*A + 1*B (svarende til maskine 2) 3*A + 2*B (svarende til maskine 3) A 0 (Produktionen af A kan ikke blive negativ) B 0 (Produktionen af B kan ikke blive negativ) I den generelle udformning kan der væ re m restriktioner (maskiner) og n varer, hvor vare i giver dæ kningsbidraget d i.d.v.s. at vi får MAX: G * [ = 1 SUB: a 11 x a 1n x n b a 1m x a mn x m b m Eller i mere kompakt matrixnotation 0$;G[ 68%$[ E, hvor d er en n'dimensional ræ kkevektor, x er en n'dimensional søjlevektor, A er en (m,n) matrix og b er en m'dimensional søjlevektor. Her angiver a ij den mæ ngde (maskin)timer, der er nødvendig for vare i ved maskine j; de kaldes ofte GHWHNQLVNHNRHIILFLHQWHU. Der er intet i vejen for, at nogle af dem kan væ re nul, men de kan selvfølgelig ikke blive negative. b j angiver maskinkapaciteten for maskine j, = 1,,,m. Lineæ r programmering består således i at maksimere en lineæ r funktion, målfunktionen, som også kan have andre navne såsom kriteriefunktionen eller mere konkret f.eks. dæ kningsbidragsfunktionen, under et sæ t af lineæ re uligheder. I nogle situationer er der tale om et minimeringsproblem, men principperne er de samme. 7RYDUHLOOXVWUDWLRQHvis der kun er 2 varer A og B, kan LP problemet gives en meget oplysende grafisk illustration. 2
3 Vi tegner en figur med A og B ud af akserne. $ % )LJXU Restriktionerne afgræ nser en polygon. På figuren er der indtegnet 3 restriktioner. Vi kan højst producere inden for hver restriktion, så vi må ligge på eller nedenfor alle 3 linier. Det betyder, at vores PXOLJKHGVRPUnGH for produktionen blive afgræ nset af markerede polygon ORSTU, som består af en ræ kke endepunkter, hvor to restriktioner skæ rer hinanden, forbundet med rette linier. Spørgsmålet er så, hvilket punkt vi skal væ lge, når vi skal væ lge os et punkt enten inden for eller på randen af denne polygon. Da målfunktionen er lineæ r i A og B, vil en k pct. forøgelse af både A og B give en k pct. forøgelse af dæ kningsbidraget. Det vil derfor aldrig kunne betale sig at producere inden for randen af mulighedsområdet. I eksemplet ovenfor med 2 varer havde vi, at det samlede dæ kningsbidrag D var D = 6*A + 5*B eller A = D/6-5/6*B Vores målsæ tningsfunktion er altså en linie med hæ ldningen -5/6, der skal forskubbes så langt ud mod højre som muligt, hvorved D/6 og dermed D bliver så stor som mulig. På figuren er denne ligning illustreret med 3 stiplede linier, som skal forskydes ud mod randen så langt som muligt i pilens retning (vinkelret på de 3 stiplede linier). Der er nu to muligheder: 3
4 Enten er denne linie parallel med en af linierne (fig 2a), eller også vil den komme til at ligge og vippe på et endepunkt (fig. 2b). Figur 2a Figur 2b På figur 2a og 2b er kun vist et udsnit af mulighedsområdet. Den afgørende pointe er, at på figur 2b er der ingen tvivl, endepunktet er det punkt, vi læ ngst kan forskyde dæ kningsbidragslinien til, og dermed det optimale punkt. Men på figur 2a vil godt nok alle punkter, der sammenfalder med dæ kningsbidragslinien, i princippet væ re lige gode, men også endepunktet vil væ re lige så godt. 9LEHK YHUDOWVnLNNHXQGHUV JHDOOHSXQNWHUSnUDQGHQDI ILJXUHQPHQNDQQ MHVPHGXQGHUV JHHQGHSXQNWHUQH. På figur 1 svarer det til, at den optimale løsning må væ re et af punkterne R, S, T, U. Der kan i hvert fald ikke findes nogen bedre løsning. Denne egenskab ved LP var baggrunden for en ofte anvendt DOJRULWPH eller beregningsmetode, som blev kaldt SIMPLEX-metoden, og som løst sagt bestod i at undersøge endepunkterne efter en næ rmere bestemt fremgangsmåde. Udviklingen inden for EDB har imidlertid bevirket, at der ikke læ ngere er det samme behov for at beskæ ftige sig med detaljerne i den algoritme, da der findes en lang ræ kke programmer til at løse LP problemer med, så vi vil her mere koncentrere os om at vise, hvordan man i praksis kan løse LP problemer. I næ ste afsnit skal vi konkret vise, hvordan LP problemer kan formuleres RJ O VHV i Excel, selv om mere professionelle anvendelser utvivlsomt vil anvende et egentligt LP-program. Men forinden er der grund til at fremhæ ve nogle sæ rlige egenskaber ved løsningen. 4
5 %LQGHQGHRJLNNHELQGHQGHUHVWULNWLRQHUBetragt figuren nedenfor $ Der er indtegnet 4 restriktioner. Hvis det optimale punkt er A, fremkommet ved en skæ ring mellem restriktion 1 og restriktion 2, ses det klart af figuren, at restriktion 3 konkret ikke har nogen betydning for den optimale løsning; vi siger, at den er LNNHELQGHQGH. Omvendt er restriktion 1 og 2 bindende. For en ELQGHQGH restriktion gæ lder, at lighedstegnet i optimum er opfyldt, medens det strenge ulighedstegn < gæ lder for den ikke-bindende restriktion. Restriktion 4 er aldrig bindende - den er tegnet parallelt med restriktion 1 og kunne svare til en restriktion A+2B ; en sådan restriktion ligger helt uden for restriktion 1. Det vil imidlertid ofte væ re sådan, at om en restriktion er bindende eller ej, vil afhæ nge ikke kun af restriktionen selv, men af såvel koefficientmatricen af tekniske koefficienter som af de koefficienter - "de relative priser" - der indgår i målfunktionen. Hvis man æ ndrede de relative priser, kunne restriktion 3 blive bindende, medens f.eks. restriktion 1 ikke ville blive bindende. En bindende restriktion j læ gger pr. definition bånd på vores handlinger, så hvis vi løsner bindingen, d.v.s. forøger b j, vil vi også forøge vores dæ kningsbidrag D. Som en illustration kan tages eksemplet ovenfor med 2 varer, hvor den optimale produktionsomfang viser sig at blive bestemt af de to bindende restriktioner 2 og 3, se nedenfor, medens restriktion 1 er ikke-bindende. Vi kan altså opfatte situationen således, at vi finder optimum ved hjæ lp af at maksimere dæ kningsbidraget under bibetingelserne 2 og 3, idet der anvendes lighedstegn. Vi danner på sæ dvanlig facon Lagrangefunktionen L med de tilhørende multiplikatorer 8 og ( og differentierer. L = 6 A + 5 B - 8 (A+B ) - ((3A + 2B ) 5
6 L/ A = ( = 0 L/ B = ( = 0 L/ 8 = A + B = 0 L/ ( = 3A + 2B = 0 Vi får 8 = 3 og ( = 1 og iøvrigt også A = og B = Med andre ord: Hvis vi forøger kapaciten for restriktion 2 med 1 enhed, vil dæ kningsbidraget stige med 3 enheder. For restriktion 3 er det tilsvarende tal 1. Tallene 8 og ( kaldes VN\JJHSULVHU De viser, hvad en marginal forøgelse på 1 enhed af kapaciteten på en restriktion vil give i bidrag i målfunktionen. Det følger intuitivt heraf, selv om det ikke er bevist, at: VN\JJHSULVHQSnLNNHELQGHQGHUHVWULNWLRQHUHU Der sker jo ikke nogen påvirkning af det samlede dæ kningsbidrag, hvis vi marginalt forøger kapaciteten. Dette er et vigtigt resultat, som har talrige økonomiske anvendelser. Da maskine 1 ikke giver nogen bindende restriktion, er skyggeprisen for dens anvendelse 0. Det vil sige, at indtil restriktionen for maskine 1 bliver bindende, er det gratis at anvende den. Lad os f.eks. antage, at virksomheden får en lille ny ordre, som den skal give et tilbud på, som involverer de 3 maskiner med et forbrug på 10 timer hver. Hvordan skal man så indregne væ rdien af tidsforbruget ved brug af de tre maskiner? Svaret er umiddelbart givet ved anvendelse af skyggepriser: Maskine 1 er gratis, så det koster ikke virksomheden noget at anvende den (marginalt) mere. Ved brug af maskine 2 i 10 timer går vi derimod glip af en indtjening af 3*10 kroner og ved brug af maskine 3 i 10 timer går vi ligeledes glip af 1*10 kroner, så opportunity costs ved den nye ordre er (for så vidt angår dette maskintidsforbrug) = = 40 kroner. Lad os resumere resultaterne Restriktionen er bindende Skyggeprisen er positiv Restriktionen er marginalt ikkebindende Skyggeprisen er nul ved marginale æ ndringer Restriktionen er aldrig bindende Skyggeprisen er altid nul 6
7 (NVHPSHOSnO VQLQJDI/3SUREOHPYHGKM OSDI(;&(/VHPDSSHQ/3 SURJUDPPHULQJPHG(;&(/ Det anbefales at printe denne vejledning ud eller have den liggende, medens regnearket gennemgås. Lad os have ovenstående problem MAKS: 6A + 5B SUB: (1) A+2B (2) A+ B (3) 3A+2B (4) A 0 (5) B 0 Da der kun er to variable A og B, kan der findes en grafisk løsning. Denne er givet i arket Grafisk Illustration. De 3 restriktioner er indtegnet tillige med isoprofitlinien, som er den røde kurve og markerer hæ ldningen på dæ kningsbidraget D = 6A+5B. Det er denne linie, som vi skal parallelforskyde så langt som muligt opad til højre. Det kan væ re lidt svæ rt at se helt klart, hvilken løsning, der er optimal, men der er to kandidater, nemlig (A,B) = ( , ) og (A,B) = ( ,50.000) de præ cise væ rdier for disse to punkter kan findes ved simpelthen at løse de tilhørende ligninger. En direkte indsæ ttelse i målfunktionen giver hhv og , så den optimale løsning bliver A = og B = , altså den løsning, vi fandt fra før. I EXCEL løses det eksakt på følgende måde. Se Excel-regnearket LPprogrammering med EXCEL med følgende ark 1. Problemformulering 2. Grafisk løsning 3. Svarrapport 1 4. Sensitititetsrapport 1 5. Svarrapport 2 Vi foretager nu følgende skridt: 1) Definer to celler svarende til de to væ rdier A og B. Her er sat A = a1 og B = b1. 2) Sæ t helt foreløbigt a1=1 og b1=1. 3) Indsæ t målfunktionen i f.eks. som her cellen a3, idet der skrives = 6*A1+5*B1. Der vises nu (selvfølgelig) tallet 11. (Gangetallene * er her overflødige, men anbefales i praksis.) 4) Skriv de 3 lineæ re restriktioner og de to ikke-negativitetsbetingelser som vist, f.eks. den første som =A1+2*B1. Da vi foreløbigt har sat A1=1 og B1=1, fås tallet 3.Læ g mæ rke til, at vi skriver venstresiden af uligheden i èn celle, og højresiden i en anden. 7
8 5) Tryk på funktioner i menulinien og find Problemløser (eng. solver ). 1 Vi skal nu udfylde 4 felter. a) Målcellen, nemlig den størrelse, som vi ønsker at maksimere. b) Rubrikken maks, min eller lig med. Vi væ lger maks. c) Ved redigering af cellerne: A1 og B1. For det er jo netop disse væ rdier, som vi kan æ ndre på. Hvis de ikke står ved siden af hinanden, skal du anvende et semikolon efter hver henvisning. d) Underlagt betingelserne. Tryk på Tilføj og indlæ g den første betingelse. Tryk på tilføj igen og indlæ g den næ ste o.s.v. Når alle 5 betingelser er indføjet, tryk på Løs, og EXCEL giver en meddelelse om, at den har fundet en løsning. 6) Sæ t kryds i rubrikken Behold problemløsning og tryk på svarrapport. Denne fremkommer på et sæ rligt ark kaldet Svarrapport 1, som typisk bliver sat ind i starten af projektmappen. Det har et udseende som vist på Excel-arket. Læ s dette. Noter, at slutvæ rdien for målvariablen er , altså den løsning, vi fandt ovenfor. Noter, at restriktion (1) ikke er bindende, jfr. ovenfor, og at restriktion (2) og (3) er bindende. Noter også, at vi direkte får udskrevet, hvor meget der er af ledig kapacitet ved den optimale løsning for restriktion 1. Løs problemet igen og bed om en sensitivitetsrapport. Konstater, at Lagrangemultiplikatoren = skyggeprisen for restriktion 2 er på 3 og for restriktion 3 er skyggeprisen på 1. Altså de løsninger, vi fandt ovenfor. Hermed er vi for så vidt fæ rdige, som vi har løst vores problem, men for illustrationens skyld fortsæ tter vi med. 7) Vi ser, hvad der sker, hvis vi antager, at kapaciteten for (den bindende) restriktion 2 ikke var , men , men problemet (1)-(5) i øvrigt er uæ ndret. MAKS: 6A + 5B SUB: (1) A+2B (2) A+ B (3) 3A+2B (4) A 0 (5) B 0 Vi indtaster problemet igen, blot med i stedet for og løser. 8) På arket svarrapport 2 er vist, at målfunktionen, slutvæ rdien æ ndrer sig til , hvor den før var , altså en stigning på 3. Men det var jo netop definitionen af skyggeprisen på restriktionen, som vi netop har fundet til at blive 3. 1 Hvis problemløser (solver) ikke er tilgæ ngelig, kan du gå ind på funktioner i menuen og se under "tilføjelsesprogrammer", om den er tilgæ ngelig der. Hvis den er tilgæ ngelig som tilføjelsesprogram, må du installere den. Alternativt må du sørge for at få den installeret. 8
9 (W DGYDUHQGH VOXWRUG LP-modeller har væ ret ganske populæ re, såvel i økonomisk teori som i praksis, og de anvendes stadigt, men nok ikke i samme omfang. Det skyldes nok to forskellige forhold. For det første, at de har en tilbøjelighed til at give for drastiske resultater. De giver ikke anledning til marginale æ ndringer i de optimale væ rdier som følge af marginale æ ndringer i parametrene. Enten giver de slet ingen æ ndringer - den optimale løsning er den samme i et vist parameterinterval - eller også de giver de anledning til ganske store æ ndringer. I sidste tilfæ lde kan en lille æ ndring i en teknisk koefficient forårsage en drastisk æ ndring i den optimale løsning. Det kan for så vidt også væ re rigtigt, men som en beskrivelse af virkeligheden er det typisk ikke tilfæ ldet. For det andet var LP en lang overgang i praksis den eneste modeltype, der teknisk og beregningsmæ ssigt kunne håndteres. Dette medførte en vis tilbøjelighed til at antage linearitet, også hvor der kræ vedes en del god vilje for at acceptere denne forudsæ tning. Med moderne hjæ lpemidler er det ikke på samme måde læ ngere nødvendigt af beregningstekniske hensyn at kræ ve linearitet. Og det er det faktisk heller ikke i Excel. %UXJDISUREOHPO VHUWLOPHUHJHQHUHOOHPDNVLPHULQJVSUREOHPHU Funktionen "Problemløser" i Excel er ikke begræ nset til blot LP-problemer eller overhovedet indrettet specielt til disse. Der er intet i vejen for, at der i målfunktionen indgår et ikke-linæ rt udtryk, f.eks. at prisen er en faldende funktion af den solgte mæ ngde. Hvis f.eks. på vare A er 15-0,3 A og prisen på vare B er 10-0,4 B, fås målfunktionen MAKS: -0,3*A *A -0,4*B *B, som så kan maksimeres under de relevante bibetingelser. Men hvis såvel målfunktion som bibetingelser er af speciel karakter, er der ingen garanti for hverken eksistens eller entydighed af en løsning. Ikke desto mindre er problemløserfunktionen et ganske kraftigt væ rktøj til "mindre" problemer, så derfor 7LOO\NNH 'X HU QX L VWDQG WLO NRQNUHW DW O VH IOHUH HUKYHUYV NRQRPLVNH SUREOHPHU HQG GH IOHVWH LNNHEORWLWHRULHQPHQRJVnLSUDNVLV 9
/LQH UHIWHUVS UJVHOVIXQNWLRQRJ0DUJLQDOUHYHQXH
 /LQH UHIWHUVS UJVHOVIXQNWLRQRJ0DUJLQDOUHYHQXH Efterspørgselsfunktionen beskriver sammenhængen mellem den pris man tager for sit produkt, og den mængde man kan forvente at afsætte. Det gælder typisk, at
/LQH UHIWHUVS UJVHOVIXQNWLRQRJ0DUJLQDOUHYHQXH Efterspørgselsfunktionen beskriver sammenhængen mellem den pris man tager for sit produkt, og den mængde man kan forvente at afsætte. Det gælder typisk, at
Start Excel Du skal starte med at åbne Excel. I Excel åbner du herefter en tom projektmappe.
 Lineær programmering i Excel Version for PC I lærebogens kapitel 29 afsnit 4 er det med 2 eksempler blevet vist, hvordan kapacitetsstyringen kan optimeres, når der er 2 produktionsmuligheder og flere knappe
Lineær programmering i Excel Version for PC I lærebogens kapitel 29 afsnit 4 er det med 2 eksempler blevet vist, hvordan kapacitetsstyringen kan optimeres, når der er 2 produktionsmuligheder og flere knappe
Emneopgave: Lineær- og kvadratisk programmering:
 Emneopgave: Lineær- og kvadratisk programmering: LINEÆR PROGRAMMERING I lineær programmering løser man problemer hvor man for en bestemt funktion ønsker at finde enten en maksimering eller en minimering
Emneopgave: Lineær- og kvadratisk programmering: LINEÆR PROGRAMMERING I lineær programmering løser man problemer hvor man for en bestemt funktion ønsker at finde enten en maksimering eller en minimering
Prøveanalyse: Varicella-Zoster virus-antistof
 1 Søg prøven frem. Indsætningspunktet (cursoren) stiller sig ved Analysen, fordi denne undersøgelse, i denne opsætning, ikke kræver en tolkning. 2 Analyseresultatet indtastes. Resultatvæ rdier er de tilladte
1 Søg prøven frem. Indsætningspunktet (cursoren) stiller sig ved Analysen, fordi denne undersøgelse, i denne opsætning, ikke kræver en tolkning. 2 Analyseresultatet indtastes. Resultatvæ rdier er de tilladte
LINEÆR PROGRAMMERING I EXCEL
 LINEÆR PROGRAMMERING I EXCEL K A P P E N D I X I lærebogens kapitel 29 afsnit 3 er det med 2 eksempler blevet vist, hvordan kapacitetsstyringen kan optimeres, når der er 2 produktionsmuligheder og flere
LINEÆR PROGRAMMERING I EXCEL K A P P E N D I X I lærebogens kapitel 29 afsnit 3 er det med 2 eksempler blevet vist, hvordan kapacitetsstyringen kan optimeres, når der er 2 produktionsmuligheder og flere
Lineær programmering. med Derive. Børge Jørgensen
 Lineær programmering med Derive Børge Jørgensen 1 Indholdsfortegnelse. Forord ---------------------------------------------------------------------------------- 2 Introduktion til lineær programmering
Lineær programmering med Derive Børge Jørgensen 1 Indholdsfortegnelse. Forord ---------------------------------------------------------------------------------- 2 Introduktion til lineær programmering
Kap.værdi / nutidsværdi: Værdien af en betalingsstrøm (ind & udbetalinger) opgjort i NUTIDSKRONER. ( L) QAntal perioder L Kalkulationsrenten
 ,QYHVWHULQJ %HJUHEHU Kalkulationsrente: Virksomhedens subjektive tidspræferencerate. Typisk er dette alternativrenten, fx kassekreditrenten. Det er den rente virksomheden PLQGVW skal have i afkast ved
,QYHVWHULQJ %HJUHEHU Kalkulationsrente: Virksomhedens subjektive tidspræferencerate. Typisk er dette alternativrenten, fx kassekreditrenten. Det er den rente virksomheden PLQGVW skal have i afkast ved
Kapitel 9. Optimering i Microsoft Excel 97/2000
 Kapitel 9 Optimering i Microsoft Excel 97/2000 9.1 Indledning... 164 9.2 Numerisk løsning af ligninger... 164 9.3 Optimering under bibetingelser... 164 9.4 Modelformulering... 165 9.5 Gode råd ommodellering...
Kapitel 9 Optimering i Microsoft Excel 97/2000 9.1 Indledning... 164 9.2 Numerisk løsning af ligninger... 164 9.3 Optimering under bibetingelser... 164 9.4 Modelformulering... 165 9.5 Gode råd ommodellering...
Frederiksværk Kommune
 Tillæg I til Lokalplan 04.5 For Frederiksværk Amtsgymnasium Marts 2006 Frederiksværk Kommune Tillæg 1 til lokalplan 04.5 Frederiksværk Kommune Rådhuset Rådhuspladsen 1 3300 Frederiksværk Tlf. 47 78 40
Tillæg I til Lokalplan 04.5 For Frederiksværk Amtsgymnasium Marts 2006 Frederiksværk Kommune Tillæg 1 til lokalplan 04.5 Frederiksværk Kommune Rådhuset Rådhuspladsen 1 3300 Frederiksværk Tlf. 47 78 40
Begræ nset garanti for Samsung SSD For alle Samsung SSD'er
 Begræ nset garanti for Samsung SSD For alle Samsung SSD'er Version 1.0. Gæ ldende fra: [dato]. Tak, fordi du har købt et SAMSUNG Solid State Drive ("Produktet"). SAMSUNG væ rdsæ tter dit køb og tilstræ
Begræ nset garanti for Samsung SSD For alle Samsung SSD'er Version 1.0. Gæ ldende fra: [dato]. Tak, fordi du har købt et SAMSUNG Solid State Drive ("Produktet"). SAMSUNG væ rdsæ tter dit køb og tilstræ
Operationsanalyse Eksamensnoter Frederik Silbye
 OPERATIONSANALYSE - EK SAMENSNOTER Konvertering til standard-form...2 Løsning af LP-problemer via simplex...2 Tilføjelser til simplex...3 Sensitivitetsanalyser...3 Dualitet...5.DSLWDO Transportproblemer...6
OPERATIONSANALYSE - EK SAMENSNOTER Konvertering til standard-form...2 Løsning af LP-problemer via simplex...2 Tilføjelser til simplex...3 Sensitivitetsanalyser...3 Dualitet...5.DSLWDO Transportproblemer...6
BRUGER-VEJLEDNING (TRAMPOLIN)
 BRUGER-VEJLEDNING (TRAMPOLIN) 1 I TILFÆ LDE AF MANGLENDE ELLER BESKADIGEDE DELE SKAL DU KONTAKTE FORHANDLEREN FOR HJÆ LP. Advarsel: Forhandleren er ikke ansvarlig for personskader i forbindelse med brug
BRUGER-VEJLEDNING (TRAMPOLIN) 1 I TILFÆ LDE AF MANGLENDE ELLER BESKADIGEDE DELE SKAL DU KONTAKTE FORHANDLEREN FOR HJÆ LP. Advarsel: Forhandleren er ikke ansvarlig for personskader i forbindelse med brug
Forord... 2. Indledning... 4. Undersøgelsens design og metode... 4. Danske virksomheders arbejde med APV... 5
 Indholdsfortegnelse Forord... 2 Indledning... 4 Undersøgelsens design og metode... 4 Danske virksomheders arbejde med APV... 5 Danske virksomheders ressourceforbrug ved APV... 8 Danske virksomhedernes
Indholdsfortegnelse Forord... 2 Indledning... 4 Undersøgelsens design og metode... 4 Danske virksomheders arbejde med APV... 5 Danske virksomheders ressourceforbrug ved APV... 8 Danske virksomhedernes
/DQGVVNDWWHUHWWHQV %UXJHUWLOIUHGVKHGVXQGHUV JHOVH 1RYHPEHU
 /DQGVVNDWWHUHWWHQV %UXJHUWLOIUHGVKHGVXQGHUV JHOVH 1RYHPEHU,QGKROGVIRUWHJQHOVH 1. Baggrunden for undersøgelsen 2. Hovedindtrykket af undersøgelsen 3. Tidligere undersøgelser 4. Deltagerne i undersøgelsen
/DQGVVNDWWHUHWWHQV %UXJHUWLOIUHGVKHGVXQGHUV JHOVH 1RYHPEHU,QGKROGVIRUWHJQHOVH 1. Baggrunden for undersøgelsen 2. Hovedindtrykket af undersøgelsen 3. Tidligere undersøgelser 4. Deltagerne i undersøgelsen
Frederiksværk Kommune
 Lokalplan 02.9 For Asserbo Golfbane Januar 2005 Frederiksværk Kommune Frederiksværk Kommune Rådhuset Rådhuspladsen 1 3300 Frederiksværk Tlf. 47 78 40 00 Kopi: Frederiksværk Kommune. Oplag: 150 stk. Lokalplanen
Lokalplan 02.9 For Asserbo Golfbane Januar 2005 Frederiksværk Kommune Frederiksværk Kommune Rådhuset Rådhuspladsen 1 3300 Frederiksværk Tlf. 47 78 40 00 Kopi: Frederiksværk Kommune. Oplag: 150 stk. Lokalplanen
Indholdsfortegnelse...1. Køn og ungdomsuddannelserne...2 Problemer med statistikken på området...2 Hovedpointerne...3
 Den.11.juni 2003. QRJXQJGRPVXGGDQQHOVHUQH,QGKROGVIRUWHJQHOVH Indholdsfortegnelse...1 Køn og ungdomsuddannelserne...2 Problemer med statistikken på området...2 Hovedpointerne...3 Generelt om uddannelsesniveauet...4
Den.11.juni 2003. QRJXQJGRPVXGGDQQHOVHUQH,QGKROGVIRUWHJQHOVH Indholdsfortegnelse...1 Køn og ungdomsuddannelserne...2 Problemer med statistikken på området...2 Hovedpointerne...3 Generelt om uddannelsesniveauet...4
Stan s Notubes paksalve til dæ k Schwalbe Doc Blue Pro. Følg fabrikantens anvisninger for korrekt anvendelse af paksalven.
 ø ø 1 Tillykke med købet af dette GIANT Slangeløs fæ lgbånd kit. Denne teknologi forbedrer den generelle kørselskvalitet af dit GIANT WheelSystem ved at forbedre dæ kkets ydeevne. Du kan cykle med lavere
ø ø 1 Tillykke med købet af dette GIANT Slangeløs fæ lgbånd kit. Denne teknologi forbedrer den generelle kørselskvalitet af dit GIANT WheelSystem ved at forbedre dæ kkets ydeevne. Du kan cykle med lavere
Frederiksværk Kommune
 Lokalplan 04.61 For tæt lav boligbebyggelse ved Hanehovedvej og Havnevej Forslag November 2006 Frederiksværk Kommune Frederiksværk Kommune Rådhuset Rådhuspladsen 1 3300 Frederiksværk Tlf. 47 78 40 00 Kopi:
Lokalplan 04.61 For tæt lav boligbebyggelse ved Hanehovedvej og Havnevej Forslag November 2006 Frederiksværk Kommune Frederiksværk Kommune Rådhuset Rådhuspladsen 1 3300 Frederiksværk Tlf. 47 78 40 00 Kopi:
Note om interior point metoder
 MØK 2016, Operationsanalyse Interior point algoritmer, side 1 Note om interior point metoder Som det er nævnt i bogen, var simplex-metoden til løsning af LP-algoritmer nærmest enerådende i de første 50
MØK 2016, Operationsanalyse Interior point algoritmer, side 1 Note om interior point metoder Som det er nævnt i bogen, var simplex-metoden til løsning af LP-algoritmer nærmest enerådende i de første 50
-9-8 -7-6 -5-4 -3-2 -1 1 2 3 4 5 6 7 8 9. f(x)=2x-1 Serie 1
 En funktion beskriver en sammenhæng mellem elementer fra to mængder - en definitionsmængde = Dm(f) består af -værdier og en værdimængde = Vm(f) består af -værdier. Til hvert element i Dm(f) knttes netop
En funktion beskriver en sammenhæng mellem elementer fra to mængder - en definitionsmængde = Dm(f) består af -værdier og en værdimængde = Vm(f) består af -værdier. Til hvert element i Dm(f) knttes netop
Forbrug hos Danmarks befolkning. Forbrug hos Danmarks befolkning
 DEL 8 BILAG 8. BILAG Bilag 1: Årstal 2006 2007 2008 2009 2010 2011 2012 2013 2014 Digitalt Tv 27 38 53 60 74 3D-tv 4 14 17 17 Smart-tv 24 34 Bærbar computer, lap-top 72 78 81 81 86 Tablet pc, mini computer
DEL 8 BILAG 8. BILAG Bilag 1: Årstal 2006 2007 2008 2009 2010 2011 2012 2013 2014 Digitalt Tv 27 38 53 60 74 3D-tv 4 14 17 17 Smart-tv 24 34 Bærbar computer, lap-top 72 78 81 81 86 Tablet pc, mini computer
Opgaver til Kapitel 6 MatB
 Opgave 1 En funktion i to variable er givet ved f (, ) = + 5 + 0 Indtegn niveauliner svarende til N(0), N(200) og N(400) og illustrér ved hjælp af en pil på niveaulinjerne den retning, hvori niveauet bliver
Opgave 1 En funktion i to variable er givet ved f (, ) = + 5 + 0 Indtegn niveauliner svarende til N(0), N(200) og N(400) og illustrér ved hjælp af en pil på niveaulinjerne den retning, hvori niveauet bliver
Sikkerhedsorganisation og arbejdsmiljø på små virksomheder
 Sikkerhedsorganisation og arbejdsmiljø på små virksomheder Øje på arbejdsmiljøet, maj 2002 Udgivet af Landsorganisationen i Danmark Rosenørns Allè 12 1634 København V E-mail: lo@lo.dk Tlf.: 3524 6000 Fax:
Sikkerhedsorganisation og arbejdsmiljø på små virksomheder Øje på arbejdsmiljøet, maj 2002 Udgivet af Landsorganisationen i Danmark Rosenørns Allè 12 1634 København V E-mail: lo@lo.dk Tlf.: 3524 6000 Fax:
0 OGUXS.RPPXQH V *U QQH,QGN EVSROLWLN
 0 OGUXS.RPPXQH V *U QQH,QGN EVSROLWLN %LODJ$ *U Q+DQGOLQJVSODQ IRUSHULRGHQ MDQXDUWLOGHFHPEHU Møldrup Kommunes første Grønne Handlingsplan har to overordnede mål : $WVLNUHDWGHQ*U QQH,QGN EVSROLWLNEOLYHUNHQGWKHU
0 OGUXS.RPPXQH V *U QQH,QGN EVSROLWLN %LODJ$ *U Q+DQGOLQJVSODQ IRUSHULRGHQ MDQXDUWLOGHFHPEHU Møldrup Kommunes første Grønne Handlingsplan har to overordnede mål : $WVLNUHDWGHQ*U QQH,QGN EVSROLWLNEOLYHUNHQGWKHU
MOGENS ODDERSHEDE LARSEN. Lineær Planlægning (programmering) med Excel
 MOGENS ODDERSHEDE LARSEN Lineær Planlægning (programmering) med Excel 2. udgave 2007 1 Indhold FORORD Denne bog forklarer ved anvendelse af nogle typiske eksempler, hvad der er karakteristisk ved LP -
MOGENS ODDERSHEDE LARSEN Lineær Planlægning (programmering) med Excel 2. udgave 2007 1 Indhold FORORD Denne bog forklarer ved anvendelse af nogle typiske eksempler, hvad der er karakteristisk ved LP -
fordi 45 sekunder = 3/4 minut = 0,750 minut
 +YDGHU*36" GPS = Global Position System. Det består af 24 satellitter som cirkulerer ca. 20.000 km. over jorden. Disse sender kontinuerligt et tidssignal, og det er det signals forsinkelse som gør at positionen
+YDGHU*36" GPS = Global Position System. Det består af 24 satellitter som cirkulerer ca. 20.000 km. over jorden. Disse sender kontinuerligt et tidssignal, og det er det signals forsinkelse som gør at positionen
Projekt Lineær programmering i to variable
 Projekt 5.5 - Lineær programmering i to variable. Den grundlæggende ide i lineær programmering Håndtering af optimeringsproblemer er et af de store anvendelsesområder inden for differentialregningen. Det
Projekt 5.5 - Lineær programmering i to variable. Den grundlæggende ide i lineær programmering Håndtering af optimeringsproblemer er et af de store anvendelsesområder inden for differentialregningen. Det
Tillæg I til Lokalplan For boligområdet Bjørnebakken. Oktober Frederiksværk Kommune
 Tillæg I til Lokalplan 05.10 For boligområdet Bjørnebakken Oktober 2004 Frederiksværk Kommune Tillæg I til lokalplan 05.10 Frederiksværk Kommune Rådhuset Rådhuspladsen 1 3300 Frederiksværk Tlf. 47 78 40
Tillæg I til Lokalplan 05.10 For boligområdet Bjørnebakken Oktober 2004 Frederiksværk Kommune Tillæg I til lokalplan 05.10 Frederiksværk Kommune Rådhuset Rådhuspladsen 1 3300 Frederiksværk Tlf. 47 78 40
Ugeseddel 12(10.12 14.12)
 Ugeseddel (..) Matematisk Programmering Niels Lauritzen..7 FORELÆSNINGER I ugen. 7. gennemgik vi algoritmer til løsning af heltalsprogrammer ved hjælp af simplex algoritmen. Dette er heltalsprogrammeringsugesedlen
Ugeseddel (..) Matematisk Programmering Niels Lauritzen..7 FORELÆSNINGER I ugen. 7. gennemgik vi algoritmer til løsning af heltalsprogrammer ved hjælp af simplex algoritmen. Dette er heltalsprogrammeringsugesedlen
UGESEDDEL 10 LØSNINGER. = f
 UGESEDDEL 10 LØSNINGER Theorem 1. Algoritme for løsning af max f(x, y) når g(x, y) c. Dan Lagrange-funktionen: L (x, y) = f(x, y) λ(g(x, y) c). Beregn de partielle afledte af L og kræv at de begge er nul:
UGESEDDEL 10 LØSNINGER Theorem 1. Algoritme for løsning af max f(x, y) når g(x, y) c. Dan Lagrange-funktionen: L (x, y) = f(x, y) λ(g(x, y) c). Beregn de partielle afledte af L og kræv at de begge er nul:
%HP UNQLQJHUWLOORYIRUVODJHW $OPLQGHOLJHEHP UNQLQJHU
 %HP UNQLQJHUWLOORYIRUVODJHW $OPLQGHOLJHEHP UNQLQJHU /RYIRUVODJHWVLQGKROG Formålet med den foreslåede lovændring er at overføre dele af Kirkeministeriets kompetence inden for lov om begravelse og ligbrænding
%HP UNQLQJHUWLOORYIRUVODJHW $OPLQGHOLJHEHP UNQLQJHU /RYIRUVODJHWVLQGKROG Formålet med den foreslåede lovændring er at overføre dele af Kirkeministeriets kompetence inden for lov om begravelse og ligbrænding
Prøveeksamen december 2010 matematik studiet med svar
 Første studieår Introduktion til matematiske metoder Prøveeksamen december 2010 matematik studiet med svar Varighed: 4 timer Tilladte hjælpemidler: Lærebøger, notater mv. må medbringes. Ikke tilladte hjælpemidler:
Første studieår Introduktion til matematiske metoder Prøveeksamen december 2010 matematik studiet med svar Varighed: 4 timer Tilladte hjælpemidler: Lærebøger, notater mv. må medbringes. Ikke tilladte hjælpemidler:
Projekt 4.6 Løsning af differentialligninger ved separation af de variable
 Projekt 4.6 Løsning af differentialligninger ved separation af de variable Differentialligninger af tpen d hx () hvor hx ()er en kontinuert funktion, er som nævnt blot et stamfunktionsproblem. De løses
Projekt 4.6 Løsning af differentialligninger ved separation af de variable Differentialligninger af tpen d hx () hvor hx ()er en kontinuert funktion, er som nævnt blot et stamfunktionsproblem. De løses
Mandags Chancen. En optimal spilstrategi. Erik Vestergaard
 Mandags Chancen En optimal spilstrategi Erik Vestergaard Spilleregler denne note skal vi studere en optimal spilstrategi i det spil, som i fjernsynet går under navnet Mandags Chancen. Spillets regler er
Mandags Chancen En optimal spilstrategi Erik Vestergaard Spilleregler denne note skal vi studere en optimal spilstrategi i det spil, som i fjernsynet går under navnet Mandags Chancen. Spillets regler er
Kursusgang 3 Matrixalgebra Repetition
 Kursusgang 3 Repetition - froberg@mathaaudk http://peoplemathaaudk/ froberg/oecon3 Institut for Matematiske Fag Aalborg Universitet 12 september 2008 1/12 Lineære ligningssystemer Et lineært ligningssystem
Kursusgang 3 Repetition - froberg@mathaaudk http://peoplemathaaudk/ froberg/oecon3 Institut for Matematiske Fag Aalborg Universitet 12 september 2008 1/12 Lineære ligningssystemer Et lineært ligningssystem
Bruger- og pårørendeundersøgelser - Bøgehusene Jon H adsund Jon.H stab.rm.dk Karen N ørskov Jensen stab.rm.dk Folkesundhed og Kv
 Bruger- og pårørendeundersøgelser - Bøgehusene Marts 2012 Bruger- og pårørendeundersøgelser - Bøgehusene Jon H adsund Jon.H adsund@ stab.rm.dk Karen N ørskov Jensen Karen.Jensen@ stab.rm.dk Folkesundhed
Bruger- og pårørendeundersøgelser - Bøgehusene Marts 2012 Bruger- og pårørendeundersøgelser - Bøgehusene Jon H adsund Jon.H adsund@ stab.rm.dk Karen N ørskov Jensen Karen.Jensen@ stab.rm.dk Folkesundhed
Frederiksværk Kommune
 For ældre- og plejecenter i Arresøparken Maj 2005 Frederiksværk Kommune Frederiksværk Kommune Rådhuset Rådhuspladsen 1 3300 Frederiksværk Tlf. 47 78 40 00 Kopi: Frederiksværk Kommune. Oplag: 120 stk. Lokalplanen
For ældre- og plejecenter i Arresøparken Maj 2005 Frederiksværk Kommune Frederiksværk Kommune Rådhuset Rådhuspladsen 1 3300 Frederiksværk Tlf. 47 78 40 00 Kopi: Frederiksværk Kommune. Oplag: 120 stk. Lokalplanen
6WUDWHJLIRU HIIHNWLYRSJDYHYDUHWDJHOVH Sn.LUNHPLQLVWHULHWVPLQLVWHURPUnGH
 .LUNHPLQLVWHULHW Frederiksholms Kanal 21, Postboks 2123, DK 1015 København K Tlf.: 33 92 33 90 Fax: 33 92 39 13 e-post: km@km.dk 6WUDWHJLIRU HIIHNWLYRSJDYHYDUHWDJHOVH Sn.LUNHPLQLVWHULHWVPLQLVWHURPUnGH
.LUNHPLQLVWHULHW Frederiksholms Kanal 21, Postboks 2123, DK 1015 København K Tlf.: 33 92 33 90 Fax: 33 92 39 13 e-post: km@km.dk 6WUDWHJLIRU HIIHNWLYRSJDYHYDUHWDJHOVH Sn.LUNHPLQLVWHULHWVPLQLVWHURPUnGH
SP-1101W/SP-2101W Quick Installation Guide
 SP-1101W/SP-2101W Quick Installation Guide 05-2014 / v1.0 1 I. Produktinformation I-1. Pakkens indhold Smart stikkontakt Lyninstallationsguide CD med hurtig installationsvejledning I-2. Frontpanel Strømlysdioder
SP-1101W/SP-2101W Quick Installation Guide 05-2014 / v1.0 1 I. Produktinformation I-1. Pakkens indhold Smart stikkontakt Lyninstallationsguide CD med hurtig installationsvejledning I-2. Frontpanel Strømlysdioder
Matematik A. Højere handelseksamen. 1. Delprøve, uden hjælpemidler. kl. 9.00-14.00
 Matematik A Højere handelseksamen 1. Delprøve, uden hjælpemidler kl. 9.00-10.00 hh101-mat/a-27052010 Torsdag den 27. maj 2010 kl. 9.00-14.00 Matematik A Prøven uden hjælpemidler Prøvens varighed er 1 time.
Matematik A Højere handelseksamen 1. Delprøve, uden hjælpemidler kl. 9.00-10.00 hh101-mat/a-27052010 Torsdag den 27. maj 2010 kl. 9.00-14.00 Matematik A Prøven uden hjælpemidler Prøvens varighed er 1 time.
i x-aksens retning, så fås ). Forskriften for g fås altså ved i forskriften for f at udskifte alle forekomster af x med x x 0
 BAndengradspolynomier Et polynomium er en funktion på formen f ( ) = an + an + a+ a, hvor ai R kaldes polynomiets koefficienter. Graden af et polynomium er lig med den højeste potens af, for hvilket den
BAndengradspolynomier Et polynomium er en funktion på formen f ( ) = an + an + a+ a, hvor ai R kaldes polynomiets koefficienter. Graden af et polynomium er lig med den højeste potens af, for hvilket den
Introduktion til EXCEL med øvelser
 Side 1 af 10 Introduktion til EXCEL med øvelser Du kender en almindelig regnemaskine, som kan være til stort hjælp, når man skal beregne resultater med store tal. Et regneark er en anden form for regnemaskine,
Side 1 af 10 Introduktion til EXCEL med øvelser Du kender en almindelig regnemaskine, som kan være til stort hjælp, når man skal beregne resultater med store tal. Et regneark er en anden form for regnemaskine,
FRA OMSORG TIL RESSOURCER
 FRA OMSORG TIL RESSOURCER JANNE HEDEGAARD HANSEN LEKTOR, PH.D. DPU, ÅRHUS FORHOLDET MELLEM POLITIK OG PÆDAGOGIK Socialpæ dagogisk arbejde er underlagt politisk formulerede mål - lovgivning Socia lpæ da
FRA OMSORG TIL RESSOURCER JANNE HEDEGAARD HANSEN LEKTOR, PH.D. DPU, ÅRHUS FORHOLDET MELLEM POLITIK OG PÆDAGOGIK Socialpæ dagogisk arbejde er underlagt politisk formulerede mål - lovgivning Socia lpæ da
Substitutions- og indkomsteffekt ved prisændringer
 Substitutions- og indkomsteffekt ved prisændringer Erik Bennike 14. november 2009 Denne note giver en beskrivelse af de relevante begreber omkring substitutions- og indkomsteffekter i mikroøkonomi. 1 Introduktion
Substitutions- og indkomsteffekt ved prisændringer Erik Bennike 14. november 2009 Denne note giver en beskrivelse af de relevante begreber omkring substitutions- og indkomsteffekter i mikroøkonomi. 1 Introduktion
Overfø rsel af LP-Bå nd-minidisk til CD
 1 Overfø rsel af LP-Bå nd-minidisk til CD (Kort vejledning i overfø rsel af analog lyd til CD) Version 1.1 20. januarr 2002 Sø ren Rich. Christensen Indledning... 2 Oversigt over processen... 3 Indspilning...
1 Overfø rsel af LP-Bå nd-minidisk til CD (Kort vejledning i overfø rsel af analog lyd til CD) Version 1.1 20. januarr 2002 Sø ren Rich. Christensen Indledning... 2 Oversigt over processen... 3 Indspilning...
0LQLVWHULHWIRU) GHYDUHU/DQGEUXJRJ)LVNHUL
 0LQLVWHULHWIRU) GHYDUHU/DQGEUXJRJ)LVNHUL Internationalt Fiskerikontor Sagsnr.: 10360/325926 Den 29. november 2007 UFSV/MOIM/BRRA Bilag 133 127$77,/ 8'9$/*(7),6.(5, RPIRUVODJWLO5nGHWVIRURUGQLQJRPIDVWV WWHOVHIRUDIILVNHULPXOLJKHGHURJGHUWLO
0LQLVWHULHWIRU) GHYDUHU/DQGEUXJRJ)LVNHUL Internationalt Fiskerikontor Sagsnr.: 10360/325926 Den 29. november 2007 UFSV/MOIM/BRRA Bilag 133 127$77,/ 8'9$/*(7),6.(5, RPIRUVODJWLO5nGHWVIRURUGQLQJRPIDVWV WWHOVHIRUDIILVNHULPXOLJKHGHURJGHUWLO
Affine rum. a 1 u 1 + a 2 u 2 + a 3 u 3 = a 1 u 1 + (1 a 1 )( u 2 + a 3. + a 3. u 3 ) 1 a 1. Da a 2
 Affine rum I denne note behandles kun rum over R. Alt kan imidlertid gennemføres på samme måde over C eller ethvert andet legeme. Et underrum U R n er karakteriseret ved at det er en delmængde som er lukket
Affine rum I denne note behandles kun rum over R. Alt kan imidlertid gennemføres på samme måde over C eller ethvert andet legeme. Et underrum U R n er karakteriseret ved at det er en delmængde som er lukket
Matricer og lineære ligningssystemer
 Matricer og lineære ligningssystemer Grete Ridder Ebbesen Virum Gymnasium Indhold 1 Matricer 11 Grundlæggende begreber 1 Regning med matricer 3 13 Kvadratiske matricer og determinant 9 14 Invers matrix
Matricer og lineære ligningssystemer Grete Ridder Ebbesen Virum Gymnasium Indhold 1 Matricer 11 Grundlæggende begreber 1 Regning med matricer 3 13 Kvadratiske matricer og determinant 9 14 Invers matrix
Kort til Husdyrgodkendelse / Excel data og Næsgaard Markkort
 Kort til og Næsgaard Markkort Kun i ADVICER Dette afsnit er kun relevant hvis du arbejder med AD- VICER udgaven af Næsgaard Markkort (rådgiverudgaven). Funktionen findes IKKE i PLUS og OPTI udgaven af
Kort til og Næsgaard Markkort Kun i ADVICER Dette afsnit er kun relevant hvis du arbejder med AD- VICER udgaven af Næsgaard Markkort (rådgiverudgaven). Funktionen findes IKKE i PLUS og OPTI udgaven af
Lineære ligningssystemer
 enote 2 1 enote 2 Lineære ligningssystemer Denne enote handler om lineære ligningssystemer, om metoder til at beskrive dem og løse dem, og om hvordan man kan få overblik over løsningsmængdernes struktur.
enote 2 1 enote 2 Lineære ligningssystemer Denne enote handler om lineære ligningssystemer, om metoder til at beskrive dem og løse dem, og om hvordan man kan få overblik over løsningsmængdernes struktur.
Matematik og samfundsfag Gini-koefficienten
 Erik Vestergaard www.matematikfysik.dk Matematik og samfundsfag Gini-koefficienten Den såkaldte Gini-koefficient, introduceret i 92 i en artikel af den italienske statistiker, demograf og sociolog Corrado
Erik Vestergaard www.matematikfysik.dk Matematik og samfundsfag Gini-koefficienten Den såkaldte Gini-koefficient, introduceret i 92 i en artikel af den italienske statistiker, demograf og sociolog Corrado
Form let med dette notat er at danne grundlag for denne beslutning. Notatet best r af fłlgende 5 afsnit:
 Notat Forvaltning: konomiafdelingen Dato: J.nr.: Br.nr.: 18. september 2009 Udf rdiget af: Brian Hansen Vedrłrende: Valg mellem statsgaranti og selvbudgettering i 2010 Notatet sendes/sendt til: konomiudvalg
Notat Forvaltning: konomiafdelingen Dato: J.nr.: Br.nr.: 18. september 2009 Udf rdiget af: Brian Hansen Vedrłrende: Valg mellem statsgaranti og selvbudgettering i 2010 Notatet sendes/sendt til: konomiudvalg
Brugervejledning. ADVARSEL: Voksensamling nødvendig.
 Brugervejledning X580 EN14619 Class A Læ s og forstå denne vejledning, før du lader dit barn bruge dette produkt! Hvis du har brug for hjæ lp, skal du kontakte din forhandler. ADVARSEL: Voksensamling nødvendig.
Brugervejledning X580 EN14619 Class A Læ s og forstå denne vejledning, før du lader dit barn bruge dette produkt! Hvis du har brug for hjæ lp, skal du kontakte din forhandler. ADVARSEL: Voksensamling nødvendig.
qwertyuiopåasdfghjklæøzxcvbnmqw ertyuiopåasdfghjklæøzxcvbnmqwert yuiopåasdfghjklæøzxcvbnmqwertyui Polynomier opåasdfghjklæøzxcvbnmqwertyuiopå
 qwertyuiopåasdfghjklæøzxcvbnmqw ertyuiopåasdfghjklæøzxcvbnmqwert yuiopåasdfghjklæøzxcvbnmqwertyui Polynomier opåasdfghjklæøzxcvbnmqwertyuiopå Kort gennemgang af polynomier og deres egenskaber. asdfghjklæøzxcvbnmqwertyuiopåasd
qwertyuiopåasdfghjklæøzxcvbnmqw ertyuiopåasdfghjklæøzxcvbnmqwert yuiopåasdfghjklæøzxcvbnmqwertyui Polynomier opåasdfghjklæøzxcvbnmqwertyuiopå Kort gennemgang af polynomier og deres egenskaber. asdfghjklæøzxcvbnmqwertyuiopåasd
Kommunale stordriftsfordele. - myte eller realitet?
 Kommunale stordriftsfordele - myte eller realitet? Af Kurt Houlberg, direktør for ECO-Analyse A/S Publiceret i Nordisk Administrativt Tidsskrift 1/1995, 76. årgang 1995 Nordisk Administrativt Forbund og
Kommunale stordriftsfordele - myte eller realitet? Af Kurt Houlberg, direktør for ECO-Analyse A/S Publiceret i Nordisk Administrativt Tidsskrift 1/1995, 76. årgang 1995 Nordisk Administrativt Forbund og
IBM PureApplication Service Infrastructure
 IBM Vilkår for brug SaaS-specifikke produktvilkår IBM PureApplication Service Infrastructure Vilkår for brug består af disse IBM Vilkår for brug SaaS-specifikke produktvilkår (kaldet SaaS-specifikke produktvilkår)
IBM Vilkår for brug SaaS-specifikke produktvilkår IBM PureApplication Service Infrastructure Vilkår for brug består af disse IBM Vilkår for brug SaaS-specifikke produktvilkår (kaldet SaaS-specifikke produktvilkår)
Lineær og kvadratisk programmering med TI NSpire CAS version 3.2
 Lineær og kvadratisk programmering med TI NSpire CAS version 3.2 Indhold 1. Lineær programmering i 2 variable: x og y... 1 Eksempel 1: Elementær grafisk løsning i 2d... 1 Eksempel 1: Grafisk løsning i
Lineær og kvadratisk programmering med TI NSpire CAS version 3.2 Indhold 1. Lineær programmering i 2 variable: x og y... 1 Eksempel 1: Elementær grafisk løsning i 2d... 1 Eksempel 1: Grafisk løsning i
2. Funktioner af to variable
 . Funktioner af to variable Opgave 1 Grafisk udformning af de to funktioner,, Opgave f (, y) = z = 5 y N(0) = z = 0 0 = 5 y + y = 5 C = ( ; y) = (0;0) r = 5 Dette medfører som vist en cirkel, med centrum
. Funktioner af to variable Opgave 1 Grafisk udformning af de to funktioner,, Opgave f (, y) = z = 5 y N(0) = z = 0 0 = 5 y + y = 5 C = ( ; y) = (0;0) r = 5 Dette medfører som vist en cirkel, med centrum
Privatlivspolitik for Foreningen FISKEN
 Privatlivspolitik for Foreningen FISKEN Juni 2018 FISKEN behandler personoplysninger og skal overholde lovgivningen og principperne for god databehandlingsskik. Derfor har vi vedtaget denne privatlivspolitik,
Privatlivspolitik for Foreningen FISKEN Juni 2018 FISKEN behandler personoplysninger og skal overholde lovgivningen og principperne for god databehandlingsskik. Derfor har vi vedtaget denne privatlivspolitik,
DiskStation DS211j, DS211
 DiskStation DS211j, DS211 Hurtig installationsvejledning Dokument-id: Synology_QIG_2bayCL_20101028 SIKKERHEDSINSTRUKTIONER Læ s disse sikkerhedsinstruktioner nøje før brugen, og opbevar denne vejledning
DiskStation DS211j, DS211 Hurtig installationsvejledning Dokument-id: Synology_QIG_2bayCL_20101028 SIKKERHEDSINSTRUKTIONER Læ s disse sikkerhedsinstruktioner nøje før brugen, og opbevar denne vejledning
1 Kapitel 5: Forbrugervalg
 1 Kapitel 5: Forbrugervalg Vi har set på: 1. Budgetbegrænsninger. 2. Præferencer og nyttefunktioner. Nu stykker vi det hele sammen og studerer forbrugerens valg. 1 2 Optimalt forbrug - gra sk fremstilling
1 Kapitel 5: Forbrugervalg Vi har set på: 1. Budgetbegrænsninger. 2. Præferencer og nyttefunktioner. Nu stykker vi det hele sammen og studerer forbrugerens valg. 1 2 Optimalt forbrug - gra sk fremstilling
Frederiksværk Kommune
 For Møllevang Juni 2005 Frederiksværk Kommune Frederiksværk Kommune Rådhuset Rådhuspladsen 1 3300 Frederiksværk Tlf. 47 78 40 00 Kopi: Frederiksværk Kommune. Oplag: 200 stk. Lokalplanen er udarbejdet af
For Møllevang Juni 2005 Frederiksværk Kommune Frederiksværk Kommune Rådhuset Rådhuspladsen 1 3300 Frederiksværk Tlf. 47 78 40 00 Kopi: Frederiksværk Kommune. Oplag: 200 stk. Lokalplanen er udarbejdet af
Fejlkorligerende køder Fejlkorrigerende koder
 Fejlkorligerende køder Fejlkorrigerende koder Olav Geil Skal man sende en fødselsdagsgave til fætter Børge, så pakker man den godt ind i håb om, at kun indpakningen er beskadiget ved modtagelsen. Noget
Fejlkorligerende køder Fejlkorrigerende koder Olav Geil Skal man sende en fødselsdagsgave til fætter Børge, så pakker man den godt ind i håb om, at kun indpakningen er beskadiget ved modtagelsen. Noget
Gennemsnit og normalfordeling illustreret med terningkast, simulering og SLUMP()
 Gennemsnit og normalfordeling illustreret med terningkast, simulering og SLUMP() John Andersen, Læreruddannelsen i Aarhus, VIA Et kast med 10 terninger gav følgende udfald Fig. 1 Result of rolling 10 dices
Gennemsnit og normalfordeling illustreret med terningkast, simulering og SLUMP() John Andersen, Læreruddannelsen i Aarhus, VIA Et kast med 10 terninger gav følgende udfald Fig. 1 Result of rolling 10 dices
IKKE-LINEÆR OPTIMERING
 IKKE-LINEÆR OPTIMERING JESPER MICHAEL MØLLER Indhold 1 Konvekse funktioner 1 2 Optimering uden bibetingelser 1 3 Optimering under bibetingelser givet ved ligheder 2 4 Optimering under bibetingelser givet
IKKE-LINEÆR OPTIMERING JESPER MICHAEL MØLLER Indhold 1 Konvekse funktioner 1 2 Optimering uden bibetingelser 1 3 Optimering under bibetingelser givet ved ligheder 2 4 Optimering under bibetingelser givet
Statistik. Peter Sørensen: Statistik og sandsynlighed Side 1
 Statistik Formålet... 1 Mindsteværdi... 1 Størsteværdi... 1 Ikke grupperede observationer... 2 Median og kvartiler defineres ved ikke grupperede observationer således:... 2 Middeltal defineres ved ikke
Statistik Formålet... 1 Mindsteværdi... 1 Størsteværdi... 1 Ikke grupperede observationer... 2 Median og kvartiler defineres ved ikke grupperede observationer således:... 2 Middeltal defineres ved ikke
Når eleverne skal opdage betydningen af koefficienterne i udtrykket:
 Den rette linje og parablen GeoGebra er tænkt som et dynamisk geometriprogram, som både kan anvendes til euklidisk og analytisk geometri Eksempel Tegn linjen med ligningen: Indtast ligningen i Input-feltet.
Den rette linje og parablen GeoGebra er tænkt som et dynamisk geometriprogram, som både kan anvendes til euklidisk og analytisk geometri Eksempel Tegn linjen med ligningen: Indtast ligningen i Input-feltet.
Medlemmernes forhold til foreningen
 VEDTÆ GTER FOR Navn, hjemsted og formål Foreningens navn er Grundejerforeningen Møgelkæ r, og hjemstedet er Viborg Kommune under Retten i Viborg, der er foreningens væ rneting. Foreningens formål er at
VEDTÆ GTER FOR Navn, hjemsted og formål Foreningens navn er Grundejerforeningen Møgelkæ r, og hjemstedet er Viborg Kommune under Retten i Viborg, der er foreningens væ rneting. Foreningens formål er at
DREAMs disaggregerede. befolkningsfremskrivning til år 2100
 DREAMs disaggregerede befolkningsfremskrivning til år 2100 Metode og resultater Peter Stephensen og Lars Haagen Pedersen 2002 Forord DREAM har siden 1999 årligt udarbejdet befolkningsprognoser. Med virkning
DREAMs disaggregerede befolkningsfremskrivning til år 2100 Metode og resultater Peter Stephensen og Lars Haagen Pedersen 2002 Forord DREAM har siden 1999 årligt udarbejdet befolkningsprognoser. Med virkning
Afstande, skæringer og vinkler i rummet
 Afstande, skæringer og vinkler i rummet Frank Villa 2. maj 202 c 2008-20. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold
Afstande, skæringer og vinkler i rummet Frank Villa 2. maj 202 c 2008-20. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold
Øvelse 17 - Åbne økonomier
 Øvelse 17 - Åbne økonomier Tobias Markeprand 20. januar 2009 Opgave 21.2 Betragt et land, der opererer under faste valutakurser, med den samlede efterspørgsel og udbud givet ved ligninger (21.1) og (21.2)
Øvelse 17 - Åbne økonomier Tobias Markeprand 20. januar 2009 Opgave 21.2 Betragt et land, der opererer under faste valutakurser, med den samlede efterspørgsel og udbud givet ved ligninger (21.1) og (21.2)
Debat oplæg: Udpegning af indvindingsoplande t il almene vandforsyninger uden f or områder med særlige drikkevandsint eresser,qgkrog
 Side 1 af 6 Debat oplæg: Udpegning af indvindingsoplande t il almene vandforsyninger uden f or områder med særlige drikkevandsint eresser,qgkrog )RUPnO %DJJUXQG +YRUIRUHUXGSHJQLQJHQYLJWLJ.RQVHNYHQVHU 'HWYLGHUHIRUO
Side 1 af 6 Debat oplæg: Udpegning af indvindingsoplande t il almene vandforsyninger uden f or områder med særlige drikkevandsint eresser,qgkrog )RUPnO %DJJUXQG +YRUIRUHUXGSHJQLQJHQYLJWLJ.RQVHNYHQVHU 'HWYLGHUHIRUO
matematik-økonomi-studerende
 matematik-økonomi-studerende Første studieår Introduktion til matematiske metoder i økonomi Skriftlig prøveeksamen december 2012 med korte svar Dato: selvvalgt Tidspunkt: varighed 4 timer Tilladte hjælpemidler:
matematik-økonomi-studerende Første studieår Introduktion til matematiske metoder i økonomi Skriftlig prøveeksamen december 2012 med korte svar Dato: selvvalgt Tidspunkt: varighed 4 timer Tilladte hjælpemidler:
6WDQGDUGLVHUHWIDQJVWDI\QJOHIXJOHL'\EHQGDO6DOWHQ/DQJV 6NRYGLVWULNW
 6WDQGDUGLVHUHWIDQJVWDI\QJOHIXJOHL'\EHQGDO6DOWHQ/DQJV 6NRYGLVWULNW Af Jan Drachmann )RURUG Denne rapport præsenterer resultaterne fra årets standardiserede fangst af ynglefugle i Dybendal beliggende i Salten
6WDQGDUGLVHUHWIDQJVWDI\QJOHIXJOHL'\EHQGDO6DOWHQ/DQJV 6NRYGLVWULNW Af Jan Drachmann )RURUG Denne rapport præsenterer resultaterne fra årets standardiserede fangst af ynglefugle i Dybendal beliggende i Salten
Omstilling og arbejdsmiljø i den offentlige sektor. En caseanalyse
 Omstilling og arbejdsmiljø i den offentlige sektor. En caseanalyse Øje på arbejdsmiljøet, maj 2002 Udgivet af Landsorganisationen i Danmark Rosenørns Alle 12 1634 København V E-mail: lo@lo.dk Tlf.: 3524
Omstilling og arbejdsmiljø i den offentlige sektor. En caseanalyse Øje på arbejdsmiljøet, maj 2002 Udgivet af Landsorganisationen i Danmark Rosenørns Alle 12 1634 København V E-mail: lo@lo.dk Tlf.: 3524
Algebra - Teori og problemløsning
 Algebra - Teori og problemløsning, januar 05, Kirsten Rosenkilde. Algebra - Teori og problemløsning Kapitel -3 giver en grundlæggende introduktion til at omskrive udtryk, faktorisere og løse ligningssystemer.
Algebra - Teori og problemløsning, januar 05, Kirsten Rosenkilde. Algebra - Teori og problemløsning Kapitel -3 giver en grundlæggende introduktion til at omskrive udtryk, faktorisere og løse ligningssystemer.
Disposition for kursus i Excel2007
 Disposition for kursus i Excel2007 Analyse af data (1) Demo Øvelser Målsøgning o evt. opgave 11 Scenariestyring o evt. opgave 12 Datatabel o evt. opgave 13 Evt. Graf og tendens o evt. opgave 10 Subtotaler
Disposition for kursus i Excel2007 Analyse af data (1) Demo Øvelser Målsøgning o evt. opgave 11 Scenariestyring o evt. opgave 12 Datatabel o evt. opgave 13 Evt. Graf og tendens o evt. opgave 10 Subtotaler
Afstande, skæringer og vinkler i rummet
 Afstande, skæringer og vinkler i rummet Frank Nasser 9. april 20 c 2008-20. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her.
Afstande, skæringer og vinkler i rummet Frank Nasser 9. april 20 c 2008-20. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her.
Værdier for samarbejdet med pårørende - Sundhed og Omsorg
 Værdier for samarbejdet med pårørende - Sundhed og Omsorg Indledning Et godt socialt netværk kan både give støtte, omsorg og bidrage med praktisk hjælp i hverdagen. Derfor spiller pårørende ofte en betydningsfuld
Værdier for samarbejdet med pårørende - Sundhed og Omsorg Indledning Et godt socialt netværk kan både give støtte, omsorg og bidrage med praktisk hjælp i hverdagen. Derfor spiller pårørende ofte en betydningsfuld
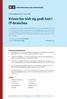 ATP-beskæftigelsestal 3. kvartal 2009 Krisen har bidt sig godt fast i IT -branchen D en økonom iske krise har gjort endnu et solidt indhug i IT-branchens beskæ ftigelse. Branchen har nu i de tre første
ATP-beskæftigelsestal 3. kvartal 2009 Krisen har bidt sig godt fast i IT -branchen D en økonom iske krise har gjort endnu et solidt indhug i IT-branchens beskæ ftigelse. Branchen har nu i de tre første
For at få tegnet en graf trykkes på knappen for graftegning. Knap for graftegning
 Graftegning på regneark. Ved hjælp af Excel regneark kan man nemt tegne grafer. Man åbner for regnearket ligger under Microsoft Office. Så indtaster man tallene fra tabellen i regnearkets celler i en vandret
Graftegning på regneark. Ved hjælp af Excel regneark kan man nemt tegne grafer. Man åbner for regnearket ligger under Microsoft Office. Så indtaster man tallene fra tabellen i regnearkets celler i en vandret
Differentialregning Infinitesimalregning
 Udgave 2.1 Differentialregning Infinitesimalregning Noterne gennemgår begreberne differentialregning, og anskuer dette som et derligere redskab til vækst og funktioner. Noterne er supplement til kapitel
Udgave 2.1 Differentialregning Infinitesimalregning Noterne gennemgår begreberne differentialregning, og anskuer dette som et derligere redskab til vækst og funktioner. Noterne er supplement til kapitel
Opgave 6. Opgave 7. Peter Harremoës Matematik A med hjælpemidler 26 maj 2015. a) Se Bilag 2! b) Variablen n isoleres. L = 2 z 1 α. L = 2 z 1 α L = n =
 Opgave 6 a) Se Bilag 2! b) Variablen n isoleres ( L = 2 z 1 α 2 ) 2 L = 2 z 1 α 2 L = 2 z 1 α 2 n = ( ˆp (1 ˆp) n ˆp (1 ˆp) n ˆp (1 ˆp) ( n ( ˆp (1 ˆp) ) 1/2 ) 2 L 2 z 1 α 2 n ) 1/2 Opgave 7 n = 4ˆp (1
Opgave 6 a) Se Bilag 2! b) Variablen n isoleres ( L = 2 z 1 α 2 ) 2 L = 2 z 1 α 2 L = 2 z 1 α 2 n = ( ˆp (1 ˆp) n ˆp (1 ˆp) n ˆp (1 ˆp) ( n ( ˆp (1 ˆp) ) 1/2 ) 2 L 2 z 1 α 2 n ) 1/2 Opgave 7 n = 4ˆp (1
Statistik. Peter Sørensen: Statistik og sandsynlighed Side 1
 Statistik Formålet... 1 Mindsteværdi... 1 Størsteværdi... 1 Ikke grupperede observationer... 2 Median og kvartiler defineres ved ikke grupperede observationer således:... 2 Middeltal defineres ved ikke
Statistik Formålet... 1 Mindsteværdi... 1 Størsteværdi... 1 Ikke grupperede observationer... 2 Median og kvartiler defineres ved ikke grupperede observationer således:... 2 Middeltal defineres ved ikke
Rådet for Den Europæiske Union Bruxelles, den 23. oktober 2017 (OR. en)
 Rådet for Den Europæiske Union Bruxelles, den 23. oktober 2017 (OR. en) Interinstitutionel sag: 2017/0267 (NLE) 13535/17 UD 238 CID 5 TRANS 425 FORSLAG fra: modtaget: 20. oktober 2017 til: Komm. dok. nr.:
Rådet for Den Europæiske Union Bruxelles, den 23. oktober 2017 (OR. en) Interinstitutionel sag: 2017/0267 (NLE) 13535/17 UD 238 CID 5 TRANS 425 FORSLAG fra: modtaget: 20. oktober 2017 til: Komm. dok. nr.:
Funktionsterminologi
 Funktionsterminologi Frank Villa 17. januar 2014 Dette dokument er en del af MatBog.dk 2008-2012. IT Teaching Tools. ISBN-13: 978-87-92775-00-9. Se yderligere betingelser for brug her. Indhold 1 Introduktion
Funktionsterminologi Frank Villa 17. januar 2014 Dette dokument er en del af MatBog.dk 2008-2012. IT Teaching Tools. ISBN-13: 978-87-92775-00-9. Se yderligere betingelser for brug her. Indhold 1 Introduktion
Bilag til Statistik i løb : Statistik og Microsoft Excel tastevejledning / af Lars Bo Kristensen
 Bilag til Statistik i løb : Statistik og Microsoft Excel tastevejledning / af Lars Bo Kristensen Microsoft Excel har en del standard anvendelsesmuligheder i forhold til den beskrivende statistik og statistisk
Bilag til Statistik i løb : Statistik og Microsoft Excel tastevejledning / af Lars Bo Kristensen Microsoft Excel har en del standard anvendelsesmuligheder i forhold til den beskrivende statistik og statistisk
 ATP-beskæftigelsestal 3. kvartal 2009 Fra 2. til3. kvartal20 0 9 faldt beskæ ftigelsen m ed 4,6 pct. ivikarbranchen og fortsæ tter derm ed den nedadgående tendens fra 20 0 8 og 20 0 9. Faldet har dog ikke
ATP-beskæftigelsestal 3. kvartal 2009 Fra 2. til3. kvartal20 0 9 faldt beskæ ftigelsen m ed 4,6 pct. ivikarbranchen og fortsæ tter derm ed den nedadgående tendens fra 20 0 8 og 20 0 9. Faldet har dog ikke
Stadsarkitektens kontor Byplanafdelingen Rådhuset Postboks 32 Århus d. 26-4-2003 8100 Århus C
 Jan Larsen Kornmodsbakken 176 8210 Århus V Tlf. 8675 0319 E-mail: info@udvandrerne.dk Stadsarkitektens kontor Byplanafdelingen Rådhuset Postboks 32 Århus d. 26-4-2003 8100 Århus C,QGVLJHOVHPRGIRUVODJWLOORNDOSODQ%ROLJRJHUKYHUYVRPUnGHYHG6RPPHUYHMRJ9LERUJYHML
Jan Larsen Kornmodsbakken 176 8210 Århus V Tlf. 8675 0319 E-mail: info@udvandrerne.dk Stadsarkitektens kontor Byplanafdelingen Rådhuset Postboks 32 Århus d. 26-4-2003 8100 Århus C,QGVLJHOVHPRGIRUVODJWLOORNDOSODQ%ROLJRJHUKYHUYVRPUnGHYHG6RPPHUYHMRJ9LERUJYHML
Frederiksværk Kommune
 For Hanehoved Nordøst Oktober 2004 Frederiksværk Kommune Frederiksværk Kommune Rådhuset Rådhuspladsen 1 3300 Frederiksværk Tlf. 47 78 40 00 Amtskode 020 Kommunekode 211 Oplag: 200 stk. Lokalplanen er udarbejdet
For Hanehoved Nordøst Oktober 2004 Frederiksværk Kommune Frederiksværk Kommune Rådhuset Rådhuspladsen 1 3300 Frederiksværk Tlf. 47 78 40 00 Amtskode 020 Kommunekode 211 Oplag: 200 stk. Lokalplanen er udarbejdet
Opgaverne, der er afleveret er rettet med den udsendte rettevejlednings vejledende vægtning af de enkelte spørgsmål.
 Dette opgavesæt indeholder løsningsforslag til opgavesættet: Stedprøve 5. maj 200 Det skal her understreges, at der er tale om et løsningsforslag. Nogle af opgaverne er rene beregningsopgaver, hvor der
Dette opgavesæt indeholder løsningsforslag til opgavesættet: Stedprøve 5. maj 200 Det skal her understreges, at der er tale om et løsningsforslag. Nogle af opgaverne er rene beregningsopgaver, hvor der
Projekt 1.4 Tagrendeproblemet en instruktiv øvelse i modellering med IT.
 Projekt 1.4 Tagrendeproblemet en instruktiv øvelse i modellering med IT. Projektet kan bl.a. anvendes til et forløb, hvor en af målsætningerne er at lære om samspillet mellem værktøjsprogrammernes geometriske
Projekt 1.4 Tagrendeproblemet en instruktiv øvelse i modellering med IT. Projektet kan bl.a. anvendes til et forløb, hvor en af målsætningerne er at lære om samspillet mellem værktøjsprogrammernes geometriske
ABBYY FineReader 14. Brugervejledning ABBYY Production LLC. Alle rettigheder forbeholdes.
 ABBYY FineReader 14 Brugervejledning 2017 ABBYY Production LLC. Alle rettigheder forbeholdes. Oplysningerne i dette dokument kan uden videre æ ndres, og ABBYY har intet ansvar for dokumentets indhold.
ABBYY FineReader 14 Brugervejledning 2017 ABBYY Production LLC. Alle rettigheder forbeholdes. Oplysningerne i dette dokument kan uden videre æ ndres, og ABBYY har intet ansvar for dokumentets indhold.
Lineære differentialligningers karakter og lineære 1. ordens differentialligninger
 enote 11 1 enote 11 Lineære differentialligningers karakter og lineære 1. ordens differentialligninger I denne note introduceres lineære differentialligninger, som er en speciel (og bekvem) form for differentialligninger.
enote 11 1 enote 11 Lineære differentialligningers karakter og lineære 1. ordens differentialligninger I denne note introduceres lineære differentialligninger, som er en speciel (og bekvem) form for differentialligninger.
LO s formand Hans Jensen. Tale ved LO s konference om globalisering. Odense d. 31. jan. 2005
 LO s formand Hans Jensen Tale ved LO s konference om globalisering Odense d. 31. jan. 2005 --------------------------------------------------------------------- I valgkampe går det alt for ofte sådan,
LO s formand Hans Jensen Tale ved LO s konference om globalisering Odense d. 31. jan. 2005 --------------------------------------------------------------------- I valgkampe går det alt for ofte sådan,
Pointen med Funktioner
 Pointen med Funktioner Frank Nasser 0. april 0 c 0080. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk: Dette er en
Pointen med Funktioner Frank Nasser 0. april 0 c 0080. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk: Dette er en
R esultatdokum entation for M øllebæ kken 2012 Center for Børn, Unge og Specialrådgivning, Region M idtjylland Yderligere inform ation: Konsulent Ande
 R esultatdokum entation for M øllebæ kken 2012 Center for Børn, Unge og Specialrådgivning, Region M idtjylland Folkesundhed og Kvalitetsudvikling O lof Palm es Allé 15 8200 Århus N 1 R esultatdokum entation
R esultatdokum entation for M øllebæ kken 2012 Center for Børn, Unge og Specialrådgivning, Region M idtjylland Folkesundhed og Kvalitetsudvikling O lof Palm es Allé 15 8200 Århus N 1 R esultatdokum entation
