Har PISA tabt pusten?
|
|
|
- Thorvald Petersen
- 8 år siden
- Visninger:
Transkript
1 86 KOMMENTARER Har PISA tabt pusten? Inge Henningsen, exbus, DPU, Aarhus Universitet Abstract. For at kunne levere de rangordninger af lande som tydeligvis efterspørges hos beslutningstagere og i offentligheden, har PISA valgt at basere sine analyser på et sæt af oversimplificerede modeller. I artiklen diskuteres nogle af de konsekvenser det får når de statistiske og datatekniske krav får forrang frem for de faglige samtidig med at der hos mange af deltagerne i de nationale PISA-konsortier synes at være en svigtende forståelse for de metodiske begrænsninger som de valgte analysemodeller medfører. Som eksempler ses der på undersøgelser af hvordan drenge og piger klarer forskellige opgavetyper, og på (mis)brug af kompetenceniveauerne til på papiret at identificere grupper af elever der ikke læser godt nok til at gennemføre en ungdomsuddannelse. I kølvandet på offentliggørelsen af resultaterne fra PISA 2009 har resultaterne ikke givet de sædvanlige store overskrifter. Årsagerne kan være mange. S og SF har altid haft et ambivalent forhold til PISA. Efter ti år med regeringsmagten har de borgerlige svært ved at udnytte dårlige eller halvsløje resultater politisk. Samtidig sker der ikke rigtig noget nyt i PISA. Ranglisterne med lande, det primære formål med PISA, har vist sig alt for stationære til at de fortsat rigtig er interessante. At Danmark går fra en naturfagsscore på 496 i 2006 til 499 i 2009, eller at man flytter sig fra 15.- til 18.-pladsen i matematik, sætter ikke længere sindene i kog. Trods dette spiller internationale læse/regneundersøgelser en væsentlig rolle i skoledebatten og har betydelig indflydelse på indretningen af de nationale skolesystemer. Det er derfor vigtigt at data fra sådanne undersøgelser bliver analyseret og fortolket professionelt og retvisende. I forhold til PISA er der rejst mange spørgsmål vedrørende sammenligneligheden af testresultater på tværs af landegrænser og særligt om det er muligt at lave opgaver der er kuturelt og sprogligt neutrale, se fx Goldstein (2004) og Hopmann, Brinek & Retzl (2007). Der er imidlertid også problemer i meget af den nationale følgeforskning der udføres af PISA-konsortierne. I takt med at interessen for de internationale rangeringer falder, rettes opmærksomheden andre steder hen. I Danmark i stigende grad mod udviklingen over tid i de
2 KOMMENTARER Har PISA tabt pusten? 87 nationale scorer og undersøgelser af danske elevers præstationer ved forskellige opgavetyper. Men disse sammenligninger indeholder væsentlige metodologiske problemer som stammer direkte fra de greb som PISA har benyttet for at kunne retfærdiggøre udarbejdelsen af de nationale ranglister. Raschmodellen Problemet med at sikre sammenlignelighed på tværs af kulturer og uddannelsessystemer søges i PISA løst ved at udvælge opgavesæt inden for hvert af de faglige domæner matematik, læsning og naturvidenskab der på et empirisk grundlag (pilottestning) er valgt så de alle tester de samme færdigheder. Dette formaliseres ved at opgavebesvarelserne for hvert fagligt domæne skal kunne beskrives ved en endimensional item respons model (Raschmodel). Herved sikrer man entydigt bestemte nationale ranglister fordi PISA-scoren på meningsfyldt måde kan baseres på summen af rigtige besvarelser. Dette stiller imidlertid nogle helt særlige krav til de anvendte opgavesæt. Her skal alle opgaver nemlig måle det samme. Det kan formaliseres i en række krav til opgaverne i sættet (se fx Kreiner, 2007): De målte færdigheder skal kunne repræsenteres ved en enkelt latent intervalskala. Ingen differentiel item-funktion, dvs. at items (opgaver) skal fungere på samme måde for alle respondenter. Der må fx hverken være pigeopgaver eller drengeopgaver i sættet, og items skal fungere på samme måde i forskellige lande. Sammenligninger mellem respondenter skal være principielt uafhængige af hvilke delsæt af opgaverne der inkluderes i prøven. Vi skal se på hvad dette betyder for opgaverne. I PISA beskrives matematikdomænet eksempelvis ved matematiske situationer, kontekster, idéområder, discipliner og kompetencer (se Lindenskov & Weng, 2010, s. 85). Men uanset hvilke idéområder (rum og form, forandringer og sammenhænge, størrelser, usikkerhed) eller matematiske discipliner (tal, algebra, geometri, sandsynlighed, statistik) en opgave i PISA kommer fra, så skal den måle dette samme og fx være lige svær for to elever der er lige dygtige. Bemærk at dette naturligvis ikke gælder for alle matematikopgaver, men det er et krav til den samling af opgaver der sammen kan indgå i et prøvesæt hvis det skal analyseres med en Raschmodel. I PISA forsøger man at opnå den homogenitet som Raschmodellen kræver, ved at lave en eller flere pilottest hvor man lader et antal elever regne opgaverne, og så fjerne de opgaver der ikke passer sammen med de andre. Hvis der er nogle opgaver som elever i de nordiske lande er særlig gode til at besvare, så kan de ikke være med
3 88 Inge Henningsen KOMMENTARER i sættet. Tilsvarende kan man hverken have drenge- eller pigeopgaver med i et opgavesæt. Man kan dog godt have opgaver der favoriserer elever fra et bestemt land. Men hvis man har det, så skal alle opgaverne favorisere elever fra dette land (oven i købet i samme grad alle sammen). Ikke mange er i tvivl om at matematik og matematikkundskaber har mange forskellige dimensioner. Et forsøg på at beskrive dette er fx KOM-rapportens otte kompetencer (Undervisningsministeriet, 2002). De fleste vil også medgive at forskellige elever har deres styrke på forskellige områder, ligesom matematikundervisningen ikke lægger vægt på de samme ting i alle lande. Man kan også sige at eksistensen af alle de mange opgaver som ikke passer ind i PISA s Raschmodeller, er et empirisk bevis på at matematikkundskaber ikke kan beskrives med en endimensionel latent variabel. Raschanalysen benægter ikke dette. Den kræver bare at alle opgaver i et prøvesæt undersøger den samme latente dimension mens de lader alle de andre dimensioner ligge. Som det fremgår af det foregående, så lægger brug af Raschmodeller nogle betydelige begrænsninger på hvilke opgaver man kan inkludere i et prøvesæt. Brug af disse modeller har imidlertid også meget indsnævrende konsekvenser for hvilke forskningsspørgsmål man kan stille til data fra PISA-undersøgelserne. Ikke-spørgsmål Det følger af diskussionen i det foregående afsnit at visse forskningsspørgsmål ikke kan besvares når man analyserer data fra PISA, idet disse spørgsmål refererer til dimensioner som bevidst er forsøgt fjernet ved testkonstruktionen. Eksempler på ikke-spørgsmål fra domænet matematik kunne være: Hvad karakteriserer items hvor piger scorer (relativt) højt? Hvad karakteriserer opgaver som er specielt vanskelige for de svage elever? Er der faglige områder hvor de danske elever er specielt stærke/svage? Disse spørgsmål forudsætter nemlig implicit at matematik har flere dimensioner, og at det reflekteres i det anvendte prøvesæt. I modsætning hertil står konstruktionen af PISA-opgaverne hvor man gennem omfattende pilottestning forsøger at udelukke opgaver hvis de fungerer forskelligt fra land til land eller forskelligt mellem de to køn eller på anden vis er differentielle. Tilbage bliver et ensartet sæt af opgaver der tester en bestemt, men uspecificeret dimension i matematikkunnen. 1 1 Resultatet fremstilles imidlertid som et universelt gyldigt mål for matematikkunnen der kan bruges til rangordning af lande og forskellige grupper af elever. PISA fokuserer på matematik-kompetencer, som kan siges at være relevante for ethvert voksent menneske i et højteknologisk demokratisk samfund. (Lindenskov & Weng, 2004, s. 38)
4 KOMMENTARER Har PISA tabt pusten? 89 Lykkes det for PISA? Allerup (2005) har ved undersøgelse af læseresultater fra 2000 og 2003 vist at de brugte skalaer er skæve i forhold til køn. For nylig har Kreiner (2011) i en omfattende afprøvning af PISA s læseopgaver fra 2003 påvist eksistensen af differentiel itemfunktion mellem lande. Han viser konkret at man kan finde to delsæt af de anvendte læseopgaver der placerer Danmark som henholdsvis nr. 3 og nr. 42 blandt alle lande, altså at landenes placering på PISA s rangliste er en funktion af hvilke opgaver der tages med i opgavesættet. Når PISA alligevel viser relativt konstante resultater fra år til år, kan det skyldes at opgavesættene i høj grad er de samme og at nye opgaver vælges sådan at de passer med de gamle men Kreiners resultater viser at et andet grundlæggende sæt af opgaver kunne have ført til en anden rangering. Påvisningen af differentiel item-funktion i PISA s opgaver var egentlig ikke mit formål med at diskutere Raschmodellen. Derimod vil jeg beskrive min forundring over at PISA s forskere i mange af deres artikler forholder sig så afslappet til de grundlæggende modelkrav i PISA at de bygger deres forskning på at de ikke er opfyldt. Jeg har udvalgt nogle eksempler fra rapporten om PISA I afsnittet om naturvidenskab diskuterer Sørensen & Davidsson forskelle mellem piger og drenge i PISA. Vores analyser i 2009 af de opgaver, som eleverne har løst, viser samme mønster som i 2006 i forhold til danske elevers præstationer. Piger og drenge klarer opgaver inden for Biologiske systemer på samme niveau, mens drenge er bedre inden for Teknologiske systemer, Fysiske systemer og Jordens og universets systemer. Piger klarer opgaver inden for Naturvidenskabelige undersøgelser bedre end drenge, men drenge er bedre til Naturvidenskabelige forklaringer. Dette sætter sig igennem i kompetenceområderne. Piger er bedre til området Anvende naturvidenskabelig evidens, men drenge er bedre til Identificere naturvidenskabelige spørgsmål og Forklare fænomener ud fra naturvidenskab. (Sørensen & Davidsson, 2010, s. 121) I dette citat giver forfatterne helt klart udtryk for at PISA-opgaverne i forhold til køn udviser differentiel item-funktion. Der er nogle opgaver der er lettere for piger, og nogle der er lettere for drenge. Hvis det er rigtigt, så holder Raschmodellen ikke, og så er det meningsløst at sammenligne pigers og drenges samlede scorer i naturvidenskab fordi den fundne forskel i drengenes favør udelukkende kan ses som et resultat af sammensætningen af prøvesættet. Hvis man havde valgt flere opgaver omhandlende pigeområderne Naturvidenskabelige undersøgelser og Anvende naturvidenskabelig evidens, så ville pigerne have klaret sig bedre, og vi havde fået et andet resultat i PISA Har man først konstateret at opgaverne fungerer forskelligt for piger og drenge, giver det ikke længere mening at sammenligne drenges og pigers totalscorer. Man genfinder problemstillingen i undersøgelsen af matematik i PISA. Her skriver Lindenskov & Weng:
5 90 Inge Henningsen KOMMENTARER Man kan her spørge, om der er særlige faglige områder, der motiverer og understøtter drengene, det være sig særlige kontekster eller opgaveformater. I PISA 2003 sås interessante variationer i præstationsforskellene mellem drenge og piger i Danmark. Præstationerne var svagest på området forandringer og sammenhænge, hvor der også var stor forskel på pigers og drenges præstationer. På området størrelser sås den mindste forskel på 9 scorepoint mellem piger og drenge, mens der på usikkerhed er en stor forskel på 22. Undersøgelser i danske klasserum vil sammen med nærmere analyser af datamateriale i PISA gennem årene være nødvendige for at forstå præstationsforskellene og deres variationer. (Lindenskov & Weng, 2010, s. 100) I de to ovenfor omtalte situationer antages analyserne at svare på forskningsspørgsmål inden for henholdsvis naturvidenskab og matematik. Men det er kun meningsfyldt at spørge sådan på basis af PISA s materiale hvis man på forhånd går ud fra at opgaverne i PISA ikke opfylder det grundlæggende krav om fravær af differentiel item-funktion. Til det kan man sige at Allerups og Kreiners undersøgelser tyder på at der er differentiel item-funktion i PISA. Alligevel kan man undre sig over at centrale forskere i det danske PISA-projekt i deres forskning går ud fra at Raschmodellen ikke holder uden at komme med nogen kommentarer til dette. Yderligere må man tage i betragtning at PISA-opgaverne ikke skal være repræsentative for problemerne i de forskellige sfærer, men tværtimod skal være tilpasset således at de trods forskellighed i testede områder, discipliner og kompetencer skal måle det samme. Derfor er PISA s opgaver på mange måder det dårligst mulige udgangspunkt for at undersøge forskelle fx mellem drenge og piger i matematik eller naturfag. Opsummerende kan man sige at det at undersøge forskelle på piger og drenge på grundlag af PISA-opgaverne er at stille forskningsspørgsmål der er inkompatible med den grundmodel som PISA analyseres inden for, samtidig med at opgaverne i PISA næppe kan antages at være karakteristiske for forskellene mellem piger og drenge. Kompetenceniveauer i PISA Ud over testscorerne opererer PISA for hvert af domænerne med en række kompetenceniveauer. De angives at være beskrevet i form af de færdigheder som elever på det pågældende niveau antages at have. I det følgende beskrives niveau 5 i matematik. Elever, der præsterede på næsthøjeste niveau, 5, er karakteriserede ved at kunne arbejde med opstilling af modellering i komplekse matematikholdige situationer, for eksempel ved at kunne identificere muligheder og begrænsninger ved en model ud fra givne antagelser for opstillingen af modellen. Således kan eleven udvælge, sammenligne og vurdere,
6 KOMMENTARER Har PISA tabt pusten? 91 hvilke strategier der er bedst egnede til at behandle et problem i relation til en eller flere mulige modeller. Elever på dette niveau udviser også indikationer på god forståelse og fortolkning af repræsentationer i problembehandling af de matematikholdige situationer. (Lindenskov & Weng, 2010, s. 91) Ovenstående beskrivelse forudsætter principielt en nøje sammenhæng mellem de krav opgaverne stiller, og de færdigheder eleverne har når de kan løse dem. Men i praksis er det sådan at opgaverne i PISA indplaceres på kompetenceniveauer alene ud fra elevscorerne, ikke ud fra deres indhold. Peter Allerup har vist hvordan nogle opgaver skifter sværhedsgrad fra PISA 2000 til PISA 2003 (Allerup, 2005). Et eksempel er læseopgaven R067Q05. I PISA 2000 havde en gennemsnitlig OECD-elev en sandsynlighed på 38 % for at svare rigtigt på denne opgave. I PISA 2003 havde den tilsvarende elev 76 % chance for at svare rigtigt. Uanset at det er den samme opgave, så ligger den på to forskellige kompetenceniveauer de to år. Det er derfor svært at se hvordan det kan forenes med udsagn af typen placering på mathematical literacy skalaen er foregået på baggrund af omhyggelige overvejelser af, hvilke typer af kompetencer der kan relateres til disse. (Lindenskov & Weng, 2004, s. 48). Funktionelle analfabeter I Danmark har andelen af elever på det laveste PISA-niveau i læsning fået sit eget liv i uddannelsesdebatten. Her lyder det ofte at 17 % af de unge forlader folkeskolen uden at kunne læse og skrive, til tider formuleret lidt mere forsigtigt som at 17 % ikke læser godt nok til at gennemføre en ungdomsuddannelse, og i debatten er de blevet benævnt funktionelle analfabeter. Se mere i Henningsen (2008). Udsagnet om funktionelle analfabeter stammer fra debatten om PISA 2003 hvor 17 % af de danske elever i læsning blev placeret på (eller under) det man betegner som laveste PISA-niveau. Disse elever fik den karakteristik at deres læsekundskaber ikke var gode nok til at de kunne gennemføre en ungdomsuddannelse. Problemet var bare at placeringen ikke sagde noget veldefineret om hvor godt eller dårligt eleverne læste. Sagen er nemlig at grænsen for niveau 1 i PISA fastlægges på grundlag af alle besvarelser fra OECD-landene, sådan at der altid skal være 18 % der ligger på eller under niveau 1. Om en elev falder over eller under niveau 1, siger altså kun noget om hvordan vedkommende læser i forhold til andre elever i OECD-landene, men ikke noget om hvordan eleven læser eksempelvis i forhold til kravene på en ungdomsuddannelse, der jo heller ikke er nogen entydigt bestemt størrelse på tværs af lande og på tværs af uddannelser. Der foreligger heller ikke i dag så vidt vides systematiske danske eller internationale evidensbaserede undersøgelser af i hvilket omfang elever på de
7 92 Inge Henningsen KOMMENTARER forskellige PISA-niveauer faktisk kommer igennem ungdomsuddannelserne, eller hvilke konkrete krav disse egentlig stiller. Det er fx betegnende at et af resultaterne fra PISA 2009 blev slået stort op: 50 % af alle elever med anden etnisk baggrund end dansk skulle have så dårlige skolekundskaber at de ikke kunne gennemføre en ungdomsuddannelse. Samtidig antages det i Undervisningsministeriets egne prognoser baseret på gennemførelsestal fra tidligere år at 77 % af disse unge i løbet af deres karriere vil gennemføre mindst en ungdomsuddannelse. Det er svært at se hvordan dette hænger sammen og det gør det da heller ikke. I tekstboksen er de omtalte tal og argumenter vist i form af en fiktiv PISA-opgave. En fiktiv PISA-opgave Lykke og Asger diskuterer uddannelse. Lykke siger at der er en stigende tendens til at flere og flere drenge falder ud af uddannelsessystemet. Asger siger at han er uenig, og henviser til følgende tabel, der er udarbejdet for undervisningsministeriet af UNI-C Statistik og Analyse. a) Hvem mener du har ret ud fra tabellen? b) Hvad kunne Asger sige som belæg for sin påstand? Sufian har hørt på deres diskussion. Han siger at det har stået i avisen at ifølge den nye PISA-undersøgelse forlader 50 % af de tosprogede elever folkeskolen uden at
8 KOMMENTARER Har PISA tabt pusten? 93 beherske de basale færdigheder til at kunne fortsætte på en ungdomsuddannelse. Ud fra figuren mener han ikke at det kan passe. c) Hvad kunne Sufian sige for at underbygge sit synspunkt? Svar på fiktiv PISA-opgave a) Asger har ret. b) Figuren viser at andelen af drenge der har gennemført en ungdomsuddannelse, har ligget næsten konstant siden 2001, og at svingningerne ligger inden for hvad man ville forvente i en fremskrivningsmodel. c) Figuren viser at i perioden efter 2000 forventes over 70 % af en årgang elever af anden etnisk herkomst at få mindst en ungdomsuddannelse. Dette modsiger PISA s påstand om de tosprogede elever. Referencer: Information. (marts 2011). Tosprogede elever halter stadig bagefter. telegram/ Lange, T. Hvor stor en andel af en årgang forventes at få en uddannelse?. service/statistik/tvaergaaende/andel %20der %20faar %20uddannelse.aspx. Perspektiver PISA er primært et politisk projekt der skal forsyne uddannelsespolitikere, uddannelsesadministratorer og praktikere med en omfattende vurdering af læringsresultater (Egelund, 2007, s. 6). For at kunne levere de rangordninger af lande som så åbenbart efterspørges både hos beslutningstagere og i offentligheden, har PISA valgt at basere sine analyser på et sæt af oversimplificerede modeller. Men det har sin pris. Jeg har i artiklen forsøgt at diskutere nogle af de konsekvenser det får når man lader de statistiske og datatekniske krav få forrang frem for det faglige samtidig med at der hos mange af deltagerne i de nationale PISA-konsortier synes at være en svigtende forståelse for de metodiske begrænsninger som de valgte analysemodeller medfører. Referencer Allerup, P. (2005). PISA præstationer målinger med skæve målestokke? Dansk Pædagogisk Tidsskrift, 53(1), s Egelund, N. (2007). PISA 2006 undersøgelsen en sammenfatning. København: Danmarks Pædagogiske Universitetsforlag.
9 94 Inge Henningsen KOMMENTARER Goldstein, H. (2004). International Comparisons of Student Attainment: Some Issues Arising from the PISA Study. Assessment in Education, 11(3), s Henningsen, I. (2008). Holder PISA, hvad PISA lover? Pædagogisk Psykologisk Tidsskrift, 48(5-6), s Hopmann, S.T., Brinek, G. & Retzl, M. (red.). (2007). PISA zufolge PISA PISA According to PISA. Berlin: LIT Verlag. Kreiner, S. (2007). Itemanalyse af matematikprøven. I: M. Hermansen (red.), Skolens gode og onde cirkler, s Frederiksberg: Samfundslitteratur. Kreiner, S. (2011). Is the Foundation under PISA Solid? A Critical Look at the Scaling Model Underlying International Comparisons of Student Attainment. (under udgivelse). Lange, T. (2011). Hvor stor en andel af en årgang forventes at få en uddannelse?. Lokaliseret på: %20der %20faar %20uddannelse.aspx. Lindenskov, L. & Weng, P. (2004). Matematisk kompetence. I: J. Meiding (red.), PISA 2003 Danske unge i en international sammenligning (s ). København: Danmarks Pædagogiske Universitets Forlag. Lindenskov, L. & Weng, P. (2010). Matematik. I: N. Egelund (red.), PISA Danske unge i international sammenligning. Bind 1 Resultatrapport (s ). København: DPU, AKF, SFI. Sørensen, H. & Davidsson, E. (2010). Naturvidenskab. I: N. Egelund (red.), PISA Danske unge i international sammenligning. Bind 1 Resultatrapport (s ). København: DPU, AKF, SFI. Undervisningsministeriet. (2002). Kompetencer og matematiklæring. København.
Nationale test. v. Marie Teglhus Møller. Slides er desværre uden eksempelopgaver, da disse ikke må udleveres. marie@eystein.dk
 Nationale test v. Marie Teglhus Møller Slides er desværre uden eksempelopgaver, da disse ikke må udleveres. marie@eystein.dk Oplæg for dagen Hvad er en pædagogisk test? Hvilke krav stilles der til opgaverne
Nationale test v. Marie Teglhus Møller Slides er desværre uden eksempelopgaver, da disse ikke må udleveres. marie@eystein.dk Oplæg for dagen Hvad er en pædagogisk test? Hvilke krav stilles der til opgaverne
De danske PISA-rapporters håndtering af PISAundersøgelserne
 Kommentarer 79 De danske PISA-rapporters håndtering af PISAundersøgelserne Hans Bay, UCC I december 2010 udkom den 4. danske PISA-rapport (PISA, 2009). Rapporten er omtalt i MONA i Egelund (2011), i Davidsson
Kommentarer 79 De danske PISA-rapporters håndtering af PISAundersøgelserne Hans Bay, UCC I december 2010 udkom den 4. danske PISA-rapport (PISA, 2009). Rapporten er omtalt i MONA i Egelund (2011), i Davidsson
Hvordan er det vi tester?
 Hvordan er det vi tester? Inge Henningsen Dansma 5. oktober 2018 Når man kvantificerer mennesker Internationale og nationale læse/regneundersøgelser spiller en væsentlig rolle i den offentlige debat om
Hvordan er det vi tester? Inge Henningsen Dansma 5. oktober 2018 Når man kvantificerer mennesker Internationale og nationale læse/regneundersøgelser spiller en væsentlig rolle i den offentlige debat om
Et kritisk blik på PISA. Inge Henningsen
 Et kritisk blik på PISA Inge Henningsen Presseklip 1. april 2014 PISA-rapport: Hver femte danske skoleelev kan ikke passe et job 20 procent af de danske skoleelever er så dårlige til at løse dagligdags
Et kritisk blik på PISA Inge Henningsen Presseklip 1. april 2014 PISA-rapport: Hver femte danske skoleelev kan ikke passe et job 20 procent af de danske skoleelever er så dårlige til at løse dagligdags
Analyse af PISA data fra 2006.
 Analyse af PISA data fra 2006. Svend Kreiner Indledning PISA undersøgelsernes gennemføres for OECD og de har det primære formål er at undersøge, herunder rangordne, en voksende række af lande med hensyn
Analyse af PISA data fra 2006. Svend Kreiner Indledning PISA undersøgelsernes gennemføres for OECD og de har det primære formål er at undersøge, herunder rangordne, en voksende række af lande med hensyn
Kan unge med dårlige læsefærdigheder. ungdomsuddannelse? Arbejdspapir Socialforskningsinstituttet The Danish National Institute of Social Research
 Kan unge med dårlige læsefærdigheder gennemføre en ungdomsuddannelse? Dines Andersen Børn, integration og ligestilling Arbejdspapir 1:2005 Arbejdspapir Socialforskningsinstituttet The Danish National Institute
Kan unge med dårlige læsefærdigheder gennemføre en ungdomsuddannelse? Dines Andersen Børn, integration og ligestilling Arbejdspapir 1:2005 Arbejdspapir Socialforskningsinstituttet The Danish National Institute
Pisa 2003 +2006. Læseundersøgelser & debat
 Pisa 2003 +2006 Læseundersøgelser & debat 1. Den danske regering indvilgede i at lade OECD gennemføre et review af grundskolen folkeskolen efter hvad regeringen betragtede som skuffende resultater, der
Pisa 2003 +2006 Læseundersøgelser & debat 1. Den danske regering indvilgede i at lade OECD gennemføre et review af grundskolen folkeskolen efter hvad regeringen betragtede som skuffende resultater, der
Skolekundskaber og integration1
 Skolekundskaber og integration1 Skolekundskaberne og især matematikkundskaberne målt ved karakteren i folkeskolens afgangsprøve har stor betydning for, om indvandrere og efterkommere får en ungdomsuddannelse.
Skolekundskaber og integration1 Skolekundskaberne og især matematikkundskaberne målt ved karakteren i folkeskolens afgangsprøve har stor betydning for, om indvandrere og efterkommere får en ungdomsuddannelse.
Tillæg til LEKS-Longitudinal
 1 Tillæg til LEKS-Longitudinal En undersøgelse af uddannelsesforløb for unge, der i 2007 gik ud af 9. klasse i de københavnske folkeskoler Vibeke Hetmar, Peter Allerup og André Torre Institut for Uddannelse
1 Tillæg til LEKS-Longitudinal En undersøgelse af uddannelsesforløb for unge, der i 2007 gik ud af 9. klasse i de københavnske folkeskoler Vibeke Hetmar, Peter Allerup og André Torre Institut for Uddannelse
Bilag om folkeskolens resultater 1
 DANMARK I DEN GLOBALE ØKONOMI SEKRETARIATET FOR MINISTERUDVALGET Prins Jørgens Gård 11, 1218 København K Telefon 33 92 33 00 - Fax 33 11 16 65 Bilag om folkeskolens resultater 1 I. Oversigt over danske
DANMARK I DEN GLOBALE ØKONOMI SEKRETARIATET FOR MINISTERUDVALGET Prins Jørgens Gård 11, 1218 København K Telefon 33 92 33 00 - Fax 33 11 16 65 Bilag om folkeskolens resultater 1 I. Oversigt over danske
PISA-informationsmøde
 PISA-informationsmøde PISA set med den danske folkeskoles briller Klaus Fink, læringskonsulent UVM Side 1 Fagformål forenklede Fælles Mål Eleverne skal i faget matematik udvikle matematiske kompetencer
PISA-informationsmøde PISA set med den danske folkeskoles briller Klaus Fink, læringskonsulent UVM Side 1 Fagformål forenklede Fælles Mål Eleverne skal i faget matematik udvikle matematiske kompetencer
Sammenhængen mellem folkeskolens faglige niveau og sandsynligheden for at gennemføre en ungdomsuddannelse
 NOTAT 18. MARTS 2011 Sammenhængen mellem folkeskolens faglige niveau og sandsynligheden for at gennemføre en ungdomsuddannelse Jørgen Søndergaard, SFI Danmark er fortsat langt fra målet om, at 95 pct.
NOTAT 18. MARTS 2011 Sammenhængen mellem folkeskolens faglige niveau og sandsynligheden for at gennemføre en ungdomsuddannelse Jørgen Søndergaard, SFI Danmark er fortsat langt fra målet om, at 95 pct.
Udviklingen i matematik målt i de danske PISA rapporter
 Nationaløkonomisk Tidsskrift 149 (2011): 126-135 Udviklingen i matematik målt i de danske PISA rapporter Hans Bay Professionshøjskolen UCC, E-mail: HAB@UCC.dk Siden den første PISA rapport udkom i december
Nationaløkonomisk Tidsskrift 149 (2011): 126-135 Udviklingen i matematik målt i de danske PISA rapporter Hans Bay Professionshøjskolen UCC, E-mail: HAB@UCC.dk Siden den første PISA rapport udkom i december
Fagårsplan 10/11 Fag: Matematik Klasse: 7.ABC Lærer: Henrik Stillits. Fagområde/ emne
 Fagårsplan 10/11 Fag: Matematik Klasse: 7.ABC Lærer: Henrik Stillits. Fagområde/ emne Matematiske færdigheder Grundlæggende færdigheder - plus, minus, gange, division (hele tal, decimaltal og brøker) Identificer
Fagårsplan 10/11 Fag: Matematik Klasse: 7.ABC Lærer: Henrik Stillits. Fagområde/ emne Matematiske færdigheder Grundlæggende færdigheder - plus, minus, gange, division (hele tal, decimaltal og brøker) Identificer
Hovedresultater fra PISA Etnisk 2015
 Hovedresultater fra PISA Etnisk 2015 Baggrund I PISA-undersøgelserne fra 2009, 2012 og 2015 er der i forbindelse med den ordinære PISA-undersøgelse foretaget en oversampling af elever med anden etnisk
Hovedresultater fra PISA Etnisk 2015 Baggrund I PISA-undersøgelserne fra 2009, 2012 og 2015 er der i forbindelse med den ordinære PISA-undersøgelse foretaget en oversampling af elever med anden etnisk
Nationale test i Danmark - fra et fagdidaktisk perspektiv
 Eksamen og prøver i norsk og nordisk skole Nationale test i Danmark - fra et fagdidaktisk perspektiv Mit arbejde med tests... Innovative testredskaber Hvad er Nationale Test? 10 obligatoriske test i 2.-8.
Eksamen og prøver i norsk og nordisk skole Nationale test i Danmark - fra et fagdidaktisk perspektiv Mit arbejde med tests... Innovative testredskaber Hvad er Nationale Test? 10 obligatoriske test i 2.-8.
Fagsyn i folkeskolens naturfag og i PISA
 Fagsyn i folkeskolens naturfag og i PISA Hvad er forholdet mellem Naturfaghæfternes fagsyn og PISA s fagsyn? Hvad er det, der testes i PISA s naturfagsprøver? Følgeforskning til PISA-København 2008 (LEKS
Fagsyn i folkeskolens naturfag og i PISA Hvad er forholdet mellem Naturfaghæfternes fagsyn og PISA s fagsyn? Hvad er det, der testes i PISA s naturfagsprøver? Følgeforskning til PISA-København 2008 (LEKS
PISA NATURVIDENSKAB AARHUS UNIVERSITET HELENE SØRENSEN LEKTOR EMERITA PISA ORIENTERINGSMØDE 16. JANUAR 2015
 PISA NATURVIDENSKAB 1. Scientific literacy 2. Rammerne for opgaverne 3. Eksempel på gammel opgave 4. Hvad kan man få ud af PISA 5. Hvad har jeg lært af PISA 6. Opsamling FORMÅL FOR NATURFAG 2014 Naturvidenskabelig
PISA NATURVIDENSKAB 1. Scientific literacy 2. Rammerne for opgaverne 3. Eksempel på gammel opgave 4. Hvad kan man få ud af PISA 5. Hvad har jeg lært af PISA 6. Opsamling FORMÅL FOR NATURFAG 2014 Naturvidenskabelig
Resultatet af den kommunale test i matematik
 Resultatet af den kommunale test i matematik Egedal Kommune 2012 Udarbejdet af Merete Hersløv Brodersen Pædagogisk medarbejder i matematik Indholdsfortegnelse: Indledning... 3 Resultaterne for hele Egedal
Resultatet af den kommunale test i matematik Egedal Kommune 2012 Udarbejdet af Merete Hersløv Brodersen Pædagogisk medarbejder i matematik Indholdsfortegnelse: Indledning... 3 Resultaterne for hele Egedal
Kompetencemål for Matematik, 1.-6. klassetrin
 Kompetencemål for Matematik, 1.-6. klassetrin Matematik omhandler samspil mellem matematiske emner, matematiske kompetencer, matematikdidaktik samt matematiklærerens praksis i folkeskolen og bidrager herved
Kompetencemål for Matematik, 1.-6. klassetrin Matematik omhandler samspil mellem matematiske emner, matematiske kompetencer, matematikdidaktik samt matematiklærerens praksis i folkeskolen og bidrager herved
Dette notat indeholder en oversigt over hovedresultater fra PISA Etnisk 2012. Notatet består af følgende
 PISA Etnisk 2012: Kort opsummering af de væsentligste resultater Dette notat indeholder en oversigt over hovedresultater fra PISA Etnisk 2012. Notatet består af følgende afsnit: Fem hovedresultater Overordnede
PISA Etnisk 2012: Kort opsummering af de væsentligste resultater Dette notat indeholder en oversigt over hovedresultater fra PISA Etnisk 2012. Notatet består af følgende afsnit: Fem hovedresultater Overordnede
Appendiks 3 Beregneren - progression i de nationale matematiktest - Vejledning til brug af beregner af progression i matematik
 Appendiks 3: Analyse af en elevs testforløb i 3. og 6. klasse I de nationale test er resultaterne baseret på et forholdsvist begrænset antal opgaver. Et vigtigt hensyn ved designet af testene har været,
Appendiks 3: Analyse af en elevs testforløb i 3. og 6. klasse I de nationale test er resultaterne baseret på et forholdsvist begrænset antal opgaver. Et vigtigt hensyn ved designet af testene har været,
Emmas og Frederiks nye værelser - maling eller tapet?
 Emmas og Frederiks nye værelser - maling eller tapet? Emmas og Frederiks familie skal flytte til et nyt hus. De har fået lov til at bestemme, hvordan væggene på deres værelser skal se ud. Emma og Frederik
Emmas og Frederiks nye værelser - maling eller tapet? Emmas og Frederiks familie skal flytte til et nyt hus. De har fået lov til at bestemme, hvordan væggene på deres værelser skal se ud. Emma og Frederik
Undersøgende opgaver Opgave 6 er i begge prøvesæt med som sidste opgave en undersøgende opgave af en ny type, som var lidt udfordrende for eleverne.
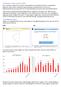 Tendenser i årets prøver 2019 Der er tendenser i prøverne, som kræver matematiklærernes opmærksomhed helst i et samarbejde i fagteamet. Og det kræver skolelederes og forvaltningers opmærksomhed for at
Tendenser i årets prøver 2019 Der er tendenser i prøverne, som kræver matematiklærernes opmærksomhed helst i et samarbejde i fagteamet. Og det kræver skolelederes og forvaltningers opmærksomhed for at
Formativ brug af folkeskolens prøver. Den skriftlige prøve i matematik i 10. klasse, FP10, maj 2018
 Formativ brug af folkeskolens prøver Den skriftlige prøve i matematik i 10. klasse, FP10, maj 2018 1 Til matematiklæreren i 10. klasse Dette er en rapport om den skriftlige prøve i matematik maj 2018.
Formativ brug af folkeskolens prøver Den skriftlige prøve i matematik i 10. klasse, FP10, maj 2018 1 Til matematiklæreren i 10. klasse Dette er en rapport om den skriftlige prøve i matematik maj 2018.
Indhold. Abstracts... 473
 Indhold Mindord om Arne Søgaard 1912-2008..................................... 379 Inge Henningsen: Holder PISA, hvad PISA lover........................... 380 Lise Render Nielsen: Problematisk eller anerkendt?
Indhold Mindord om Arne Søgaard 1912-2008..................................... 379 Inge Henningsen: Holder PISA, hvad PISA lover........................... 380 Lise Render Nielsen: Problematisk eller anerkendt?
Pigernes og drengenes forhold til matematik i Danmark
 Peter Weng Pigernes og drengenes forhold til matematik i Danmark på grundlag af informationerne fra TIMSS 26 Forskellen mellem pigerne og drengenes præstationer i TIMSS-undersøgelsen blev et fokuspunkt
Peter Weng Pigernes og drengenes forhold til matematik i Danmark på grundlag af informationerne fra TIMSS 26 Forskellen mellem pigerne og drengenes præstationer i TIMSS-undersøgelsen blev et fokuspunkt
Matematiske kompetencer - hvad og hvorfor? DLF-Kursus Frederikshavn 24.-25.9 2015 Eva Rønn UCC
 Matematiske kompetencer - hvad og hvorfor? DLF-Kursus Frederikshavn 24.-25.9 2015 Eva Rønn UCC Komrapporten Kompetencer og matematiklæring. Ideer og inspiration til udvikling af matematikundervisningen
Matematiske kompetencer - hvad og hvorfor? DLF-Kursus Frederikshavn 24.-25.9 2015 Eva Rønn UCC Komrapporten Kompetencer og matematiklæring. Ideer og inspiration til udvikling af matematikundervisningen
Faglig læsning i matematik
 Faglig læsning i matematik af Heidi Kristiansen 1.1 Faglig læsning en matematisk arbejdsmåde Der har i de senere år været sat megen fokus på, at danske elever skal blive bedre til at læse. Tidligere har
Faglig læsning i matematik af Heidi Kristiansen 1.1 Faglig læsning en matematisk arbejdsmåde Der har i de senere år været sat megen fokus på, at danske elever skal blive bedre til at læse. Tidligere har
Kompetencemål for Matematik, 4.-10. klassetrin
 Kompetencemål for Matematik, 4.-10. klassetrin Matematik omhandler samspil mellem matematiske emner, matematiske arbejds- og tænkemåder, matematikdidaktisk teori samt matematiklærerens praksis i folkeskolen
Kompetencemål for Matematik, 4.-10. klassetrin Matematik omhandler samspil mellem matematiske emner, matematiske arbejds- og tænkemåder, matematikdidaktisk teori samt matematiklærerens praksis i folkeskolen
Bilag 2: Undersøgelse af de nationale tests reliabilitet. Sammenfatning
 Bilag 2: Undersøgelse af de nationale tests reliabilitet Sammenfatning I efteråret 2014 blev der i alt gennemført ca. 485.000 frivillige nationale tests. 296.000 deltog i de frivillige test, heraf deltog
Bilag 2: Undersøgelse af de nationale tests reliabilitet Sammenfatning I efteråret 2014 blev der i alt gennemført ca. 485.000 frivillige nationale tests. 296.000 deltog i de frivillige test, heraf deltog
Evalueringsrapport klasselæseprøver 8. klasse november 2008
 Evalueringsrapport klasselæseprøver 8. klasse november 2008 Pædagogisk Psykologisk Rådgivning Idrætsvej 1 6580 Vamdrup v. læsekonsulenterne Lotte Koefoed Jensen og Majbrit Jensen 1 Indhold 1. Indledning
Evalueringsrapport klasselæseprøver 8. klasse november 2008 Pædagogisk Psykologisk Rådgivning Idrætsvej 1 6580 Vamdrup v. læsekonsulenterne Lotte Koefoed Jensen og Majbrit Jensen 1 Indhold 1. Indledning
Fokusområde Matematik: Erfaringer fra PISA 2012
 Fokusområde Matematik: Erfaringer fra PISA 2012 Lena Lindenskov & Uffe Thomas Jankvist Institut for Uddannelse og Pædagogik (DPU), Aarhus Universitet, Campus Emdrup 15 16 januar 2015 Hvad vi bl.a. vil
Fokusområde Matematik: Erfaringer fra PISA 2012 Lena Lindenskov & Uffe Thomas Jankvist Institut for Uddannelse og Pædagogik (DPU), Aarhus Universitet, Campus Emdrup 15 16 januar 2015 Hvad vi bl.a. vil
Appendiks 1: Om baggrund og teori bag valg af skala
 Appendiks 1: Om baggrund og teori bag valg af skala De nationale test gav i 2010 for første gang danske lærere mulighed for at foretage en egentlig måling på en skala af deres elevers præstationer på grundlag
Appendiks 1: Om baggrund og teori bag valg af skala De nationale test gav i 2010 for første gang danske lærere mulighed for at foretage en egentlig måling på en skala af deres elevers præstationer på grundlag
TOSPROGEDE UNGES LÆSNING BELYST MED PISA
 TOSPROGEDE UNGES LÆSNING BELYST MED PISA NIELS EGELUND, PROFESSOR, DR.PÆD., DANMARKS INSTITUT FOR PÆDAGOGIK OG UDDANNELSE, AARHUS UNIVERSITET I slutningen af 1990 erne begyndte der at komme forskningsmæssig
TOSPROGEDE UNGES LÆSNING BELYST MED PISA NIELS EGELUND, PROFESSOR, DR.PÆD., DANMARKS INSTITUT FOR PÆDAGOGIK OG UDDANNELSE, AARHUS UNIVERSITET I slutningen af 1990 erne begyndte der at komme forskningsmæssig
Statusredegørelsen for folkeskolens udvikling
 Statusredegørelsen for folkeskolens udvikling For skoleåret 2016/2017 Statusredegørelsen for folkeskolens udvikling For skoleåret 2016/2017 Layout: Presse- og Kommunikationssekretariatet, Undervisningsministeriet
Statusredegørelsen for folkeskolens udvikling For skoleåret 2016/2017 Statusredegørelsen for folkeskolens udvikling For skoleåret 2016/2017 Layout: Presse- og Kommunikationssekretariatet, Undervisningsministeriet
Formativ brug af folkeskolens prøver årets resultater på landsplan Den skriftlige prøve i matematik med hjælpemidler, FP9 maj 2019
 Formativ brug af folkeskolens prøver årets resultater på landsplan Den skriftlige prøve i matematik med hjælpemidler, FP9 maj 2019 Skrevet af Klaus Fink på baggrund af oplysninger fra opgavekommissionen
Formativ brug af folkeskolens prøver årets resultater på landsplan Den skriftlige prøve i matematik med hjælpemidler, FP9 maj 2019 Skrevet af Klaus Fink på baggrund af oplysninger fra opgavekommissionen
Den Sociale Kapitalfond Analyse Voksende karaktergab mellem drenge og piger i grundskolen
 Den Sociale Kapitalfond Analyse Voksende karaktergab mellem drenge og piger i grundskolen April 27 Kontakt: Analysechef Kristian Thor Jakobsen Tlf.: 322 6792 Den Sociale Kapitalfond Management ApS HOVEDKONKLUSIONER
Den Sociale Kapitalfond Analyse Voksende karaktergab mellem drenge og piger i grundskolen April 27 Kontakt: Analysechef Kristian Thor Jakobsen Tlf.: 322 6792 Den Sociale Kapitalfond Management ApS HOVEDKONKLUSIONER
National reference for de nationale test
 National reference for de nationale test Der er tre principielt forskellige repræsentative kvantitative opgørelse af læring i grundskolen i Danmark: De internationale undersøgelser (ILSA 1 ), Folkeskolens
National reference for de nationale test Der er tre principielt forskellige repræsentative kvantitative opgørelse af læring i grundskolen i Danmark: De internationale undersøgelser (ILSA 1 ), Folkeskolens
Nationale test et eksperiment til mere end 50 millioner
 69 Nationale test et eksperiment til mere end 50 millioner Sebastian Horst, Institut for Naturfagenes Didaktik, Københavns Universitet Abstract De nationale test i folkeskolen er nu snart klar til brug.
69 Nationale test et eksperiment til mere end 50 millioner Sebastian Horst, Institut for Naturfagenes Didaktik, Københavns Universitet Abstract De nationale test i folkeskolen er nu snart klar til brug.
Hvem sagde variabelkontrol?
 73 Hvem sagde variabelkontrol? Peter Limkilde, Odsherreds Gymnasium Kommentar til Niels Bonderup Doh n: Naturfagsmaraton: et (interesseskabende?) forløb i natur/ teknik MONA, 2014(2) Indledning Jeg læste
73 Hvem sagde variabelkontrol? Peter Limkilde, Odsherreds Gymnasium Kommentar til Niels Bonderup Doh n: Naturfagsmaraton: et (interesseskabende?) forløb i natur/ teknik MONA, 2014(2) Indledning Jeg læste
Forside. Nationale test. information til forældre. Januar Titel 1
 Forside Nationale test information til forældre Januar 2017 Titel 1 Nationale test information til forældre Tekst: Fokus Kommunikation og Undervisningsministeriet Produktion: Fokus Kommunikation Grafisk
Forside Nationale test information til forældre Januar 2017 Titel 1 Nationale test information til forældre Tekst: Fokus Kommunikation og Undervisningsministeriet Produktion: Fokus Kommunikation Grafisk
Det fælles i det faglige. Ph.d. Bodil Nielsen
 Det fælles i det faglige Ph.d. Bodil Nielsen bodilnsti@gmail.com Det fælles i det faglige kompetencer på tværs Undersøgelse og dialog Eleverne skal lære at - forholde sig undersøgende til omverdenen -
Det fælles i det faglige Ph.d. Bodil Nielsen bodilnsti@gmail.com Det fælles i det faglige kompetencer på tværs Undersøgelse og dialog Eleverne skal lære at - forholde sig undersøgende til omverdenen -
Sammenhængen mellem elevernes trivsel og elevernes nationale testresultater.
 Sammenhængen mellem elevernes trivsel og elevernes nationale testresultater. 1 Sammenfatning Der er en statistisk signifikant positiv sammenhæng mellem opnåelse af et godt testresultat og elevernes oplevede
Sammenhængen mellem elevernes trivsel og elevernes nationale testresultater. 1 Sammenfatning Der er en statistisk signifikant positiv sammenhæng mellem opnåelse af et godt testresultat og elevernes oplevede
Uddybning om naturfag. Ved Helene Sørensen, lektor emerita på DPU
 Uddybning om naturfag Ved Helene Sørensen, lektor emerita på DPU DEN TEORETISKE RAMME FOR NATURFAGLIG KOMPETENCE som udfordrer elever til at bruge Kontekst Personlige, lokale/nationale eller globale forhold,
Uddybning om naturfag Ved Helene Sørensen, lektor emerita på DPU DEN TEORETISKE RAMME FOR NATURFAGLIG KOMPETENCE som udfordrer elever til at bruge Kontekst Personlige, lokale/nationale eller globale forhold,
Faglige resultater for folkeskolen i København og øvrige resultater i tilknytning hertil skoleåret 2017/18
 KØBENHAVNS KOMMUNE Børne- og Ungdomsforvaltningen Center for Policy NOTAT 1. november 2018 Faglige resultater for folkeskolen i København og øvrige resultater i tilknytning hertil skoleåret 2017/18 BUU
KØBENHAVNS KOMMUNE Børne- og Ungdomsforvaltningen Center for Policy NOTAT 1. november 2018 Faglige resultater for folkeskolen i København og øvrige resultater i tilknytning hertil skoleåret 2017/18 BUU
Statistik viden eller tilfældighed
 MATEMATIK i perspektiv Side 1 af 9 DNA-analyser 1 Sandsynligheden for at en uskyldig anklages Følgende histogram viser, hvordan fragmentlængden for et DNA-område varierer inden for befolkningen. Der indgår
MATEMATIK i perspektiv Side 1 af 9 DNA-analyser 1 Sandsynligheden for at en uskyldig anklages Følgende histogram viser, hvordan fragmentlængden for et DNA-område varierer inden for befolkningen. Der indgår
Tryghed og holdning til politi og retssystem
 JUSTITSMINISTERIETS FORSKNINGSKONTOR JANUAR Tryghed og holdning til politi og retssystem Danmark i forhold til andre europæiske lande. UNDERSØGELSENS MATERIALE I etableredes European Social Survey (ESS),
JUSTITSMINISTERIETS FORSKNINGSKONTOR JANUAR Tryghed og holdning til politi og retssystem Danmark i forhold til andre europæiske lande. UNDERSØGELSENS MATERIALE I etableredes European Social Survey (ESS),
Analyse: God stemning i klasseværelset er afgørende for børns læring
 Analyse: God stemning i klasseværelset er afgørende for børns læring Jeg lærer mere, hvis der er en god stemning i klassen Ni ud af ti elever i folkeskolens udskoling er enige i, at de lærer mere, hvis
Analyse: God stemning i klasseværelset er afgørende for børns læring Jeg lærer mere, hvis der er en god stemning i klassen Ni ud af ti elever i folkeskolens udskoling er enige i, at de lærer mere, hvis
05/09/14. PISA-relatering af de kriteriebaserede. Delrapport 2 teknisk rapport og dokumentation
 05/09/14 PISA-relatering af de kriteriebaserede nationale test Delrapport 2 teknisk rapport og dokumentation For information on obtaining additional copies, permission to reprint or translate this work,
05/09/14 PISA-relatering af de kriteriebaserede nationale test Delrapport 2 teknisk rapport og dokumentation For information on obtaining additional copies, permission to reprint or translate this work,
Udvikling af faglærerteam
 80 KOMMENTARER Udvikling af faglærerteam Ole Goldbech, Professionshøjskolen UCC Kommentar til artiklen MaTeam-projektet om matematiklærerfagteam, matematiklærerkompetencer og didaktisk modellering i MONA,
80 KOMMENTARER Udvikling af faglærerteam Ole Goldbech, Professionshøjskolen UCC Kommentar til artiklen MaTeam-projektet om matematiklærerfagteam, matematiklærerkompetencer og didaktisk modellering i MONA,
Dansk-historieopgaven (DHO) skrivevejledning
 Dansk-historieopgaven (DHO) skrivevejledning Indhold Formalia, opsætning og indhold... Faser i opgaveskrivningen... Første fase: Idéfasen... Anden fase: Indsamlingsfasen... Tredje fase: Læse- og bearbejdningsfasen...
Dansk-historieopgaven (DHO) skrivevejledning Indhold Formalia, opsætning og indhold... Faser i opgaveskrivningen... Første fase: Idéfasen... Anden fase: Indsamlingsfasen... Tredje fase: Læse- og bearbejdningsfasen...
Kompetencemål i undervisningsfaget Matematik yngste klassetrin
 Kompetencemål i undervisningsfaget Matematik yngste klassetrin Kort bestemmelse af faget Faget matematik er i læreruddannelsen karakteriseret ved et samspil mellem matematiske emner, matematiske arbejds-
Kompetencemål i undervisningsfaget Matematik yngste klassetrin Kort bestemmelse af faget Faget matematik er i læreruddannelsen karakteriseret ved et samspil mellem matematiske emner, matematiske arbejds-
Læring af test. Rapport for. Aarhus Analyse Skoleåret
 Læring af test Rapport for Skoleåret 2016 2017 Aarhus Analyse www.aarhus-analyse.dk Introduktion Skoleledere har adgang til masser af data på deres elever. Udfordringen er derfor ikke at skaffe adgang
Læring af test Rapport for Skoleåret 2016 2017 Aarhus Analyse www.aarhus-analyse.dk Introduktion Skoleledere har adgang til masser af data på deres elever. Udfordringen er derfor ikke at skaffe adgang
Formativ brug af folkeskolens prøver årets resultater på landsplan Den skriftlige prøve i matematik FP10 maj 2019
 Formativ brug af folkeskolens prøver årets resultater på landsplan Den skriftlige prøve i matematik FP10 maj 2019 Skrevet af Klaus Fink på baggrund af oplysninger fra opgavekommissionen 1 Til matematiklæreren
Formativ brug af folkeskolens prøver årets resultater på landsplan Den skriftlige prøve i matematik FP10 maj 2019 Skrevet af Klaus Fink på baggrund af oplysninger fra opgavekommissionen 1 Til matematiklæreren
En prøveform for piger?
 1 En prøveform for piger? Over de seneste ti år er karaktergabet mellem drenge og piger i folkeskolen vokset, når vi ser på resultaterne af folkeskolens afgangsprøve. I samme periode er karaktergabet mellem
1 En prøveform for piger? Over de seneste ti år er karaktergabet mellem drenge og piger i folkeskolen vokset, når vi ser på resultaterne af folkeskolens afgangsprøve. I samme periode er karaktergabet mellem
DEFF Projekt evaluering
 DEFF Projekt evaluering I projektet stilles kvalitetssikrede, internationale biblioteksressourcer til rådighed for gymnasieelever, så de kan benyttes i den daglige undervisning og især i forbindelse med
DEFF Projekt evaluering I projektet stilles kvalitetssikrede, internationale biblioteksressourcer til rådighed for gymnasieelever, så de kan benyttes i den daglige undervisning og især i forbindelse med
PISA (Programme for International Student Assessment) 2009
 58 AKTUEL ANALYSE PISA (Programme for International Student Assessment) 2009 Niels Egelund Redaktionen: Vi har bedt to eksperter, nemlig Niels Egelund, professor og direktør for Center for Strategisk Uddannelsesforskning,
58 AKTUEL ANALYSE PISA (Programme for International Student Assessment) 2009 Niels Egelund Redaktionen: Vi har bedt to eksperter, nemlig Niels Egelund, professor og direktør for Center for Strategisk Uddannelsesforskning,
Faglige resultater for folkeskolen i København og øvrige resultater i tilknytning hertil
 KØBENHAVNS KOMMUNE Børne- og Ungdomsforvaltningen Center for Policy NOTAT Til Børne- og Ungdomsudvalget 20. november 2017 Sagsnr. 2017-0351770 Faglige resultater for folkeskolen i København og øvrige resultater
KØBENHAVNS KOMMUNE Børne- og Ungdomsforvaltningen Center for Policy NOTAT Til Børne- og Ungdomsudvalget 20. november 2017 Sagsnr. 2017-0351770 Faglige resultater for folkeskolen i København og øvrige resultater
En prøveform for piger?
 1 En prøveform for piger? Over de seneste ti år er karaktergabet mellem drenge og piger i folkeskolen vokset, når vi ser på resultaterne af folkeskolens afgangsprøve. En stigning på 6 procentpoint i perioden
1 En prøveform for piger? Over de seneste ti år er karaktergabet mellem drenge og piger i folkeskolen vokset, når vi ser på resultaterne af folkeskolens afgangsprøve. En stigning på 6 procentpoint i perioden
Analyse 20. januar 2015
 20. januar 2015 Stigende karakterforskelle mellem drenge og piger ved grundskolens 9. kl. afgangsprøver Af Kristian Thor Jakobsen Generelt klarer kvinder sig bedre end mænd i det danske uddannelsessystem.
20. januar 2015 Stigende karakterforskelle mellem drenge og piger ved grundskolens 9. kl. afgangsprøver Af Kristian Thor Jakobsen Generelt klarer kvinder sig bedre end mænd i det danske uddannelsessystem.
Matematik. Evaluering, orientering og vejledning
 Folkeskolens afsluttende prøver Matematik 2014 Evaluering, orientering og vejledning Institut for Læring Evaluering af årets matematikprøver Følgende rapport er udformet således, at resultater fra karakterdatabasen
Folkeskolens afsluttende prøver Matematik 2014 Evaluering, orientering og vejledning Institut for Læring Evaluering af årets matematikprøver Følgende rapport er udformet således, at resultater fra karakterdatabasen
LEKS-Longitudinal. En undersøgelse af uddannelsesforløb for unge, der i 2007 gik ud af 9. klasse i de københavnske folkeskoler
 LEKS-Longitudinal En undersøgelse af uddannelsesforløb for unge, der i 2007 gik ud af 9. klasse i de københavnske folkeskoler Peter Allerup, André Torre og Vibeke Hetmar Institut for Uddannelse og Pædagogik
LEKS-Longitudinal En undersøgelse af uddannelsesforløb for unge, der i 2007 gik ud af 9. klasse i de københavnske folkeskoler Peter Allerup, André Torre og Vibeke Hetmar Institut for Uddannelse og Pædagogik
Første del af rapporten består af et diagram, der viser, hvor mange point eleverne på landsplan fik i de enkelte opgaver.
 Til matematiklæreren Dette er en rapport omtaler prøven med hjælpemidler maj 2016. Rapporten kan bruges til at evaluere dit arbejde med klassen og få ideer til dit arbejde med kommende klasser i overbygningen.
Til matematiklæreren Dette er en rapport omtaler prøven med hjælpemidler maj 2016. Rapporten kan bruges til at evaluere dit arbejde med klassen og få ideer til dit arbejde med kommende klasser i overbygningen.
TIMSS Trends in International Mathematics and Science Study
 TIMSS 2019 Trends in International Mathematics and Science Study TIMSS 2019 er en international undersøgelse, der kortlægger 4. klasseelevers færdigheder og kompetencer i matematik og natur/teknologi.
TIMSS 2019 Trends in International Mathematics and Science Study TIMSS 2019 er en international undersøgelse, der kortlægger 4. klasseelevers færdigheder og kompetencer i matematik og natur/teknologi.
Kompetencemål for Matematik, klassetrin
 Kompetencemål for Matematik, 1.-6. klassetrin Matematik omhandler samspil mellem matematiske emner, matematiske arbejds- og tænkemåder, matematikdidaktik samt matematiklærerens praksis i folkeskolen og
Kompetencemål for Matematik, 1.-6. klassetrin Matematik omhandler samspil mellem matematiske emner, matematiske arbejds- og tænkemåder, matematikdidaktik samt matematiklærerens praksis i folkeskolen og
PISA Problemløsning 2012: Kort opsummering af de væsentligste resultater
 PISA Problemløsning 2012: Kort opsummering af de væsentligste resultater Dette notat indeholder en oversigt over hovedresultaterne fra PISA Problemløsning 2012. Notatet består af følgende afsnit: Fire
PISA Problemløsning 2012: Kort opsummering af de væsentligste resultater Dette notat indeholder en oversigt over hovedresultaterne fra PISA Problemløsning 2012. Notatet består af følgende afsnit: Fire
Generelt er korrelationen mellem elevens samlede vurdering i forsøg 1 og forsøg 2 på 0,79.
 Olof Palmes Allé 38 8200 Aarhus N Tlf.nr.: 35 87 88 89 E-mail: stil@stil.dk www.stil.dk CVR-nr.: 13223459 Undersøgelse af de nationale tests reliabilitet 26.02.2016 Sammenfatning I efteråret 2014 blev
Olof Palmes Allé 38 8200 Aarhus N Tlf.nr.: 35 87 88 89 E-mail: stil@stil.dk www.stil.dk CVR-nr.: 13223459 Undersøgelse af de nationale tests reliabilitet 26.02.2016 Sammenfatning I efteråret 2014 blev
Fælles forenklede mål - folkeskolen
 Fælles forenklede mål - folkeskolen Dansk [ Færdigheds- og vidensmål efter 2. klasse ] Kompetencemål: Eleven kan kommunikere med opmærksomhed på sprog og relationer i nære hverdagssituationer Eleven kan
Fælles forenklede mål - folkeskolen Dansk [ Færdigheds- og vidensmål efter 2. klasse ] Kompetencemål: Eleven kan kommunikere med opmærksomhed på sprog og relationer i nære hverdagssituationer Eleven kan
Formativ brug af folkeskolens prøver. Den skriftlige prøve i matematik med hjælpemidler, FP9 maj 2018
 Formativ brug af folkeskolens prøver Den skriftlige prøve i matematik med hjælpemidler, FP9 maj 2018 1 Til matematiklæreren i 9. klasse Dette er en rapport om den skriftlige prøve i matematik med hjælpemidler
Formativ brug af folkeskolens prøver Den skriftlige prøve i matematik med hjælpemidler, FP9 maj 2018 1 Til matematiklæreren i 9. klasse Dette er en rapport om den skriftlige prøve i matematik med hjælpemidler
HB Cafe TR tema 2016
 HB Cafe TR tema 2016 Velkommen til cafeen: Et ulighedsskabende og sorterende uddannelsessystem. Cafeen vil lægge op til diskussion om flg: Antallet af unge uden uddannelse og job er stigende. De mange
HB Cafe TR tema 2016 Velkommen til cafeen: Et ulighedsskabende og sorterende uddannelsessystem. Cafeen vil lægge op til diskussion om flg: Antallet af unge uden uddannelse og job er stigende. De mange
Guide til lektielæsning
 Guide til lektielæsning Gefions lærere har udarbejdet denne guide om lektielæsning. Den henvender sig til alle Gefions elever og er relevant for alle fag. Faglig læsning (=lektielæsning) 5- trinsmodellen
Guide til lektielæsning Gefions lærere har udarbejdet denne guide om lektielæsning. Den henvender sig til alle Gefions elever og er relevant for alle fag. Faglig læsning (=lektielæsning) 5- trinsmodellen
Brevet følges af en til skolens officielle adresse med emnet: TIMSS2015 deltagelse
 Oktober 2014 Kære Vi vil gerne Invitere dig og din skole til at deltage i den internationale undersøgelse TIMSS 2015 Ved at deltage i TIMSS får I og én af jeres 4. klasser muligheden for at bidrage til
Oktober 2014 Kære Vi vil gerne Invitere dig og din skole til at deltage i den internationale undersøgelse TIMSS 2015 Ved at deltage i TIMSS får I og én af jeres 4. klasser muligheden for at bidrage til
Drengene klarer sig dårligere end pigerne i 4 ud af 5 fag
 Kan folkeskolen favne drengene godt nok? Drengene klarer sig dårligere end pigerne i 4 ud af 5 fag I fire ud af fem fag ved afgangsprøverne i 9. klasse klarer pigerne sig bedre end drengene. En gennemgang
Kan folkeskolen favne drengene godt nok? Drengene klarer sig dårligere end pigerne i 4 ud af 5 fag I fire ud af fem fag ved afgangsprøverne i 9. klasse klarer pigerne sig bedre end drengene. En gennemgang
Internationale læseundersøgelser og PIRLS. Programme for International Student Assessment
 Internationale læseundersøgelser og PIRLS 1991 2000 2000 2003 2006 2006 2009 2010 2011 Programme for g International Student Assessment 1 Hvad undersøges: 2000 / 2009 2003 / 2012 2006 / 2015 Læsning Matematik
Internationale læseundersøgelser og PIRLS 1991 2000 2000 2003 2006 2006 2009 2010 2011 Programme for g International Student Assessment 1 Hvad undersøges: 2000 / 2009 2003 / 2012 2006 / 2015 Læsning Matematik
UDDANNELSESPARATHEDSVURDERING også kåldet en UPV
 UDDANNELSESPARATHEDSVURDERING også kåldet en UPV Ikke alle unge har lige gode forudsætninger for at gennemføre den ungdomsuddannelse, de vælger efter grundskolen. Undersøgelser har vist, at nogle unge
UDDANNELSESPARATHEDSVURDERING også kåldet en UPV Ikke alle unge har lige gode forudsætninger for at gennemføre den ungdomsuddannelse, de vælger efter grundskolen. Undersøgelser har vist, at nogle unge
Forudsigeligt frafald svækker erhvervsuddannelserne
 Forudsigeligt frafald svækker erhvervsuddannelserne Elever og lærere er enige: Tusindvis af unge optages på erhvervsuddannelserne med meget lille udsigt til at kunne gennemføre. Synspunktet understøttes
Forudsigeligt frafald svækker erhvervsuddannelserne Elever og lærere er enige: Tusindvis af unge optages på erhvervsuddannelserne med meget lille udsigt til at kunne gennemføre. Synspunktet understøttes
KVALITETSRAPPORT FOR. Torstorp Skole 2016/17
 KVALITETSRAPPORT FOR Torstorp Skole 2016/17 INDHOLDSFORTEGNELSE Indhold INDHOLDSFORTEGNELSE... 2 FORORD... Fejl! Bogmærke er ikke defineret. PRÆSENTATION AF SKOLEN... 4 SAMMENFATTENDE HELHEDSVURDERING...
KVALITETSRAPPORT FOR Torstorp Skole 2016/17 INDHOLDSFORTEGNELSE Indhold INDHOLDSFORTEGNELSE... 2 FORORD... Fejl! Bogmærke er ikke defineret. PRÆSENTATION AF SKOLEN... 4 SAMMENFATTENDE HELHEDSVURDERING...
PISA naturfag 2009 PISA Hvad måler PISA naturfag?
 66 AKTUEL ANALYSE PISA naturfag 2009 Eva Davidsson PISA 2009 Vi skal nu se lidt nærmere på hvad PISA-undersøgelserne egentlig kan fortælle om elevers kundskaber i naturfag. Jeg vil først i korthed redegøre
66 AKTUEL ANALYSE PISA naturfag 2009 Eva Davidsson PISA 2009 Vi skal nu se lidt nærmere på hvad PISA-undersøgelserne egentlig kan fortælle om elevers kundskaber i naturfag. Jeg vil først i korthed redegøre
Baggrundsnotat om 10. klasse: Søgemønstre, elevsammensætning og effekt
 Baggrundsnotat om 10. klasse: Søgemønstre, elevsammensætning og effekt Side 1 af 11 I dette baggrundsnotat præsenteres et uddrag af analyser og fakta for 10. klasse i Aarhus Kommune: Udviklingen i søgningen
Baggrundsnotat om 10. klasse: Søgemønstre, elevsammensætning og effekt Side 1 af 11 I dette baggrundsnotat præsenteres et uddrag af analyser og fakta for 10. klasse i Aarhus Kommune: Udviklingen i søgningen
Fagårsplan 10/11 Fag: Matematik Klasse: 8.A Lærer: Henrik Stillits Fagområde/ emne Færdighedsregning - Typer af opgaver - Systematik
 Fagårsplan 10/11 Fag: Matematik Klasse: 8.A Lærer: Henrik Stillits Fagområde/ emne Færdighedsregning - Typer af opgaver - Systematik Periode Mål Eleverne skal: 32/33 Få kendskab til opgavetypen og få rutine.
Fagårsplan 10/11 Fag: Matematik Klasse: 8.A Lærer: Henrik Stillits Fagområde/ emne Færdighedsregning - Typer af opgaver - Systematik Periode Mål Eleverne skal: 32/33 Få kendskab til opgavetypen og få rutine.
Lyngallup om folkeskolen Dato: 27. marts 2012
 Lyngallup om folkeskolen Dato: 27. marts 2012 Metode Feltperiode: 22. 27. marts 2012 Målgruppe: Repræsentativt udvalgte vælgere landet over på 18 eller derover Metode: GallupForum (webinterviews) Stikprøvestørrelse:
Lyngallup om folkeskolen Dato: 27. marts 2012 Metode Feltperiode: 22. 27. marts 2012 Målgruppe: Repræsentativt udvalgte vælgere landet over på 18 eller derover Metode: GallupForum (webinterviews) Stikprøvestørrelse:
Fagplan og mål for matematik 7-9 klasse
 Fagplan og mål for matematik 7-9 klasse På Slotsparkens Friskole følger vi Undervisningsministeriets mål for de fag. Kompetencemål se link : http://ffm.emu.dk Fagets kompetenceområder: Matematiske kompetencer
Fagplan og mål for matematik 7-9 klasse På Slotsparkens Friskole følger vi Undervisningsministeriets mål for de fag. Kompetencemål se link : http://ffm.emu.dk Fagets kompetenceområder: Matematiske kompetencer
Pigerne er bedst til matematik i gymnasiet
 ANALYSE Pigerne er bedst til matematik i gymnasiet I den offentlige debat fremstilles det ofte som om, at sprog er noget for piger, mens matematik er noget for drenge. Denne analyse viser, at det langt
ANALYSE Pigerne er bedst til matematik i gymnasiet I den offentlige debat fremstilles det ofte som om, at sprog er noget for piger, mens matematik er noget for drenge. Denne analyse viser, at det langt
Survey om brug af og tilfredshed med resultatvisning i nationale test
 Survey om brug af og tilfredshed med i nationale test Notat MBUL: Styrelsen for Undervisning og Kvalitet Oktober 2016 Indholdsfortegnelse 1. Resume 2. Data og besvarelser 3. Lærernes tilfredshed 4. Lærernes
Survey om brug af og tilfredshed med i nationale test Notat MBUL: Styrelsen for Undervisning og Kvalitet Oktober 2016 Indholdsfortegnelse 1. Resume 2. Data og besvarelser 3. Lærernes tilfredshed 4. Lærernes
PISA 2006. Danske unge i en international sammenligning
 PISA 2006 Danske unge i en international sammenligning PISA 2006 Danske unge i en international sammenligning Niels Egelund (red.) Danmarks Pædagogiske Universitetsforlag Danmarks Pædagogiske Universitetsskole
PISA 2006 Danske unge i en international sammenligning PISA 2006 Danske unge i en international sammenligning Niels Egelund (red.) Danmarks Pædagogiske Universitetsforlag Danmarks Pædagogiske Universitetsskole
Undersøgende matematik i prøverne. Odense 26. april 2019
 Undersøgende matematik i prøverne Odense 26. april 2019 Programmet En del af opgaverne i Folkeskolens Prøver handler om, at eleverne skal undersøge et eller andet. Det er ofte opgaver, eleverne har svært
Undersøgende matematik i prøverne Odense 26. april 2019 Programmet En del af opgaverne i Folkeskolens Prøver handler om, at eleverne skal undersøge et eller andet. Det er ofte opgaver, eleverne har svært
SUPPLEMENT TIL EVALUERING AF DE NATIONALE TEST RAPPORT
 Til Undervisningsministeriet (Kvalitets- og Tilsynsstyrelsen) Dokumenttype Rapport Dato August 2014 SUPPLEMENT TIL EVALUERING AF DE NATIONALE TEST RAPPORT NATIONALE TEST RAPPORT INDHOLD 1. Indledning og
Til Undervisningsministeriet (Kvalitets- og Tilsynsstyrelsen) Dokumenttype Rapport Dato August 2014 SUPPLEMENT TIL EVALUERING AF DE NATIONALE TEST RAPPORT NATIONALE TEST RAPPORT INDHOLD 1. Indledning og
Colofon. Udgivet af Inerisaavik 2009 Udarbejdet af fagkonsulent Erik Christiansen Redigeret af specialkonsulent Louise Richter Elektronisk udgave
 Colofon Udgivet af Inerisaavik 2009 Udarbejdet af fagkonsulent Erik Christiansen Redigeret af specialkonsulent Louise Richter Elektronisk udgave Indhold Evaluering af matematik 2008 2 Tekstopgivelser 2
Colofon Udgivet af Inerisaavik 2009 Udarbejdet af fagkonsulent Erik Christiansen Redigeret af specialkonsulent Louise Richter Elektronisk udgave Indhold Evaluering af matematik 2008 2 Tekstopgivelser 2
De gymnasiale eksamensresultater og karakterer 2012
 De gymnasiale eksamensresultater og karakterer 2012 UNI C Statistik & Analyse har opgjort årets eksamensresultater for de gymnasiale uddannelser i dette notat. Eksamensresultatgennemsnittene er desuden
De gymnasiale eksamensresultater og karakterer 2012 UNI C Statistik & Analyse har opgjort årets eksamensresultater for de gymnasiale uddannelser i dette notat. Eksamensresultatgennemsnittene er desuden
Elev-til-elev læring med opgaveeksempler. uden hjælpemidler
 Program for løft af de fagligt svageste elever Intensivt læringsforløb Lærervejledning Elev-til-elev læring med opgaveeksempler fra prøven uden hjælpemidler Dato December 2017 Udviklet for Undervisningsministeriet
Program for løft af de fagligt svageste elever Intensivt læringsforløb Lærervejledning Elev-til-elev læring med opgaveeksempler fra prøven uden hjælpemidler Dato December 2017 Udviklet for Undervisningsministeriet
Danske elevers oplevelser af og syn på udeskole
 Danske elevers oplevelser af og syn på udeskole Lærke Mygind, Steno Diabetes Center, Niels Ejbye-Ernst, VIAUC & Peter Bentsen, Steno Diabetes Center (2016) Udarbejdet i forbindelse med projekt Udvikling
Danske elevers oplevelser af og syn på udeskole Lærke Mygind, Steno Diabetes Center, Niels Ejbye-Ernst, VIAUC & Peter Bentsen, Steno Diabetes Center (2016) Udarbejdet i forbindelse med projekt Udvikling
Meningsmålinger - hvad kan vi sige med sikkerhed?
 Meningsmålinger - hvad kan vi sige med sikkerhed? af Kenneth Madsen - søndag, oktober 28, 2012 http://www.opensamf.dk/2012/10/meningsmalinger-hvad-kan-vi-sige-med-sikkerhed/ Jeg vil i dette indlæg præsentere
Meningsmålinger - hvad kan vi sige med sikkerhed? af Kenneth Madsen - søndag, oktober 28, 2012 http://www.opensamf.dk/2012/10/meningsmalinger-hvad-kan-vi-sige-med-sikkerhed/ Jeg vil i dette indlæg præsentere
Konference om mundtlige prøver PRØV! Et program til de mundtlige prøver (og det daglige arbejde?)
 Konference om mundtlige prøver PRØV! Et program til de mundtlige prøver (og det daglige arbejde?) En tydelig problemstilling, som Mundtlig prøve? giver mulighed for at vise matematiske kompetencer, viden
Konference om mundtlige prøver PRØV! Et program til de mundtlige prøver (og det daglige arbejde?) En tydelig problemstilling, som Mundtlig prøve? giver mulighed for at vise matematiske kompetencer, viden
Matematikken i PISA i didaktisk perspektiv
 56 Aktuel analyse Matematikken i PISA i didaktisk perspektiv Lena Lindenskov, DPU- Aarhus Universitet Peter Weng, DPU- Aarhus Universitet Abstract. Denne artikel fokuserer på matematik i PISA. Den præsenterer
56 Aktuel analyse Matematikken i PISA i didaktisk perspektiv Lena Lindenskov, DPU- Aarhus Universitet Peter Weng, DPU- Aarhus Universitet Abstract. Denne artikel fokuserer på matematik i PISA. Den præsenterer
Dansk Clearinghouse for Uddannelsesforskning
 DANSK CLEARINGHOUSE FOR UDDANNELSESFORSKNING ARTS AARHUS UNIVERSITET Dansk Clearinghouse for Uddannelsesforskning Institut for Uddannelse og Pædagogik (DPU) Arts Aarhus Universitet Notat om forskningskvalitet,
DANSK CLEARINGHOUSE FOR UDDANNELSESFORSKNING ARTS AARHUS UNIVERSITET Dansk Clearinghouse for Uddannelsesforskning Institut for Uddannelse og Pædagogik (DPU) Arts Aarhus Universitet Notat om forskningskvalitet,
Frederikssund Kommune. Matematikstrategi
 Frederikssund Kommune Matematikstrategi 2016-2020 Matematikstrategi Forord Matematik er et redskab til at forstå verden omkring os og en del af børn og unges dannelse. For at kunne tage aktiv del i livet
Frederikssund Kommune Matematikstrategi 2016-2020 Matematikstrategi Forord Matematik er et redskab til at forstå verden omkring os og en del af børn og unges dannelse. For at kunne tage aktiv del i livet
Matematik - undervisningsplan Årsplan 2015 & 2016 Klassetrin: 9-10.
 Form Undervisningen vil veksle mellem individuelt arbejde, gruppearbejde og tavleundervisning. Materialer Undervisningen tager udgangspunkt i følgende grundbøger og digitale lærings- og undervisningsplatforme.
Form Undervisningen vil veksle mellem individuelt arbejde, gruppearbejde og tavleundervisning. Materialer Undervisningen tager udgangspunkt i følgende grundbøger og digitale lærings- og undervisningsplatforme.
Fremstillingsformer i historie
 Fremstillingsformer i historie DET BESKRIVENDE NIVEAU Et referat er en kortfattet, neutral og loyal gengivelse af tekstens væsentligste indhold. Du skal vise, at du kan skelne væsentligt fra uvæsentligt
Fremstillingsformer i historie DET BESKRIVENDE NIVEAU Et referat er en kortfattet, neutral og loyal gengivelse af tekstens væsentligste indhold. Du skal vise, at du kan skelne væsentligt fra uvæsentligt
2 Udfoldning af kompetencebegrebet
 Elevplan 2 Udfoldning af kompetencebegrebet Kompetencebegrebet anvendes i dag i mange forskellige sammenhænge og med forskellig betydning. I denne publikation som i bekendtgørelse og vejledning til matematik
Elevplan 2 Udfoldning af kompetencebegrebet Kompetencebegrebet anvendes i dag i mange forskellige sammenhænge og med forskellig betydning. I denne publikation som i bekendtgørelse og vejledning til matematik
