05/09/14. PISA-relatering af de kriteriebaserede. Delrapport 2 teknisk rapport og dokumentation
|
|
|
- Else Beck
- 8 år siden
- Visninger:
Transkript
1 05/09/14 PISA-relatering af de kriteriebaserede nationale test Delrapport 2 teknisk rapport og dokumentation
2 For information on obtaining additional copies, permission to reprint or translate this work, and all other correspondence, please contact: DAMVAD damvad.com Copyright PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM
3 Contents 1 Indledning Arbejdet med rapporten Notation og terminologi 6 2 Sammenfatning af analyseresultater Indledning Læsning Matematik Forventede PISA-resultater i forhold til de enkelte profilområder i DNT 11 3 Deskriptive analyser Sammenhæng mellem testresultater i de nationale test og senere resultater i PISA Kriteriebaserede scores og kategoriseringer Kriteriebaserede scores og senere PISA-resultater Effekt af sen skolestart og undervisning i 9. klasse Effekt af køn og etnicitet på testresultater i dansk og matematik Socioøkonomisk niveau 38 4 Analyse af data vedrørende læsning Den prædiktive model Tolkning af effektparametrene Prædiktioner på gruppeniveau Formidling af resultater Effekt af alder og et ekstra skoleår Analyse med DNT-resultater i læsning i 6. klasse 52 5 Analyse af data vedrørende matematik Plan for analysen Analyse af effekten af DNT-resultater på PISA-logits for elever med sen skolestart Estimation af effekten af undervisningen i 9. klasse Den prædiktive model Tolkning af effekt-parametrene 57 6 Diskussion Analysens forudsætninger Kriteriebaserede scores og kategorier Prædiktion af PISA-resultater ved 15 års alderen eller ved udgangen af 9. klasse 58 7 Appendiks A Rasch modellen og logit værdier 60 8 Appendiks B estimation af dygtigheden 70 9 Appendiks C: Estimation af færdigheder i matematik ud fra PISAs data Appendiks D: Omregning af PISA-logits til PISA-scores og PISA-kategorier 85 PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM 3
4 1 Indledning Undervisningsministeriet har for at styrke opfølgningen af de faglige mål i aftalen om den seneste folkeskolereform, Et fagligt løft af folkeskolen, igangsat et arbejde med at kriteriebasere de nationale test. Da de nationale test første gang blev indført i 2010, var tilbagemeldingerne af testresultaterne normbaserede og derfor uden faste kriterier for, hvornår en elevs resultater i et givent fag på et givent klassetrin var tilfredsstillende. I stedet blev resultaterne for den enkelte elev sammenlignet med andre elevers resultater, opgjort som landsgennemsnittet i I Et fagligt løft af folkeskolen er der formuleret en række konkrete faglige mål for folkeskolen. Målene er bl.a., at mindst 80 pct. af eleverne skal være gode til at læse og regne i de nationale test, og at andelen af de allerdygtigste elever i dansk og matematik skal stige år for år. Derudover skal andelen af elever med dårlige resultater i de nationale test for læsning og matematik reduceres år for år. For at der kan følges op på disse nationale mål, kriteriebaseres de nationale test, så der fremover også er en fast skala, der indikerer om en elevs resultater er gode eller dårlige på baggrund af fagligt fastsatte kriterier. Arbejdsgrupper af personer med faglig indsigt i de enkelte testfag (opgavekommissionerne) har i første halvdel af 2014 formuleret en række foreløbige kriterier for at vurdere den enkelte elevs resultater i de nationale test. På baggrund af kriterierne inddeles elevernes testresultater i en række kategorier, der spænder fra utilstrækkelig til fremragende. På tidspunktet for afrapporteringen er de foreløbige kriterier ved at blive pilotafprøvet. Den nærværende undersøgelse skal ses i sammenhæng med, at der ud over de nationale test samtidig gennemføres PISA-undersøgelser i Danmark, der også indeholder kategoriseringer af elevernes faglige niveau. I forbindelse med dette projekt er der derfor blevet lagt vægt på at undersøge sammenhængen mellem de foreløbige kriteriebaserede kategorier og PISAs kategorier. Det overordnede formål med projektet er at opstille en sandsynlighedsbaseret model for at relatere resultaterne i de nationale test til resultaterne i PISAundersøgelsen fra Undersøgelsens formål er nærmere beskrevet i boks 1.1 nedenfor. Undersøgelsen tager dermed sit udgangspunkt i de foreløbige kriterier for vurdering af elevers præstationer i de nationale test og sammenholder dem med resultaterne i PISA-undersøgelsen fra Boks 1.1 Formålet med opgaven Formålet med opgaven er at klarlægge, hvorvidt resultater i de nationale test kan relateres til PISA-resultater. Målsætningen med afdækningen er således at udarbejde: En sandsynlighedsbaseret model for relateringen af resultater i de nationale test på test- og profilområdeniveau til PISA. Testniveauer, som skal inddrages, er: o o matematik (herunder profilområderne: (1) tal og algebra, (2) geometri og (3) matematik i anvendelse) læsning (herunder profilområderne: (1) sprogforståelse, (2) afkodning og (3) tekstforståelse) Relatering af de kriteriebaserede kategorier i de nationale test med kategorier i PISA Derudover ønskes det afdækket: o o hvor stort et sammenfald, der er blandt elever, der ikke har deltaget i de nationale test og PISA. eventuelt hvorvidt de socioøkonomiske effekter er ens i de nationale test og PISA. Kilde: Kvalitets- og Tilsynsstyrelsen 2014 Grundet undersøgelsens tekniske natur afrapporteres den i to delrapporter: Delrapport 1 formidling af resultater og Delrapport 2 teknisk rapport og dokumentation. Hvor den første delrapport afrapporterer projektets overordnede konklusioner og herigennem formidler analysens resultater, vil nærværende rapport i stedet fokusere på opstillingen af den statistiske model samt de metodiske og datamæssige udfordringer i forlængelse heraf. 4 PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM
5 1.1 Arbejdet med rapporten Delrapport 2 giver svaret på det overordnede spørgsmål, der blev stillet til undersøgelsen af relationerne mellem resultater fra de nationale test og PISA-målingerne: Er det muligt at opstille en sandsynlighedsbaseret (dvs. statistisk) model, der beskriver disse relationer? Da resultaterne fra de nationale test typisk vil foreligge før (og ofte flere år før) resultaterne i PISA, er dette spørgsmål blevet tolket som et spørgsmål om det er muligt at opstille en statistisk model, der kan bruges til at forudsige resultater i PISA ud fra tidligere resultater i de nationale test. Rapporten beskriver og dokumenterer de statistiske analyser, som har ført frem til disse modeller. Arbejdet har primært været fokuseret på resultater fra de nationale test i læsning i 8. klasse i 2011 og 2012, hvor datagrundlaget er stærkest, og på resultater fra de nationale test i matematik i 6. klasse i Det datagrundlag, der benyttes til at beskrive sammenhængen mellem resultaterne i matematik er svagere end datagrundlaget bag analyserne af færdigheder i læsning, idet der kun foreligger testresultater i matematik fra de nationale test for elever, der gik i 6. klasse i Da flertallet af de elever, som deltog i PISA i 2012, gik i 6. klasse i 2009, betyder det både, at der mangler resultater fra de nationale test for flertallet af eleverne, og at der er en risiko for systematiske fejl, fordi de elever, der gik i 6. klasse i 2010 endnu ikke havde modtaget undervisning i 9. klasse, da de blev testet af PISA 1. sig gøre at justere for den manglende undervisning i 9. klasse, således at der også kunne opstilles en prædiktiv model for elever, der går i 6. klasse tre år før, de testes af PISA. Løsningen på dette problem er beskrevet i kapitel 4 og 5. De data, der er stillet til rådighed for analyserne, omfatter også resultater i læsning fra 6. klasse i Dette materiale lider af de samme svagheder som datamaterialet vedrørende matematik i 6. klasse, men der er alligevel udført supplerende analyser af sammenhængen mellem læseresultater fra de nationale test i 6. klasse og de senere PISA-resultater i læsning. Både PISA og de nationale test benytter såkaldte Rasch-modeller til at beskrive den effekt, som elevernes dygtighed har på svarene på opgaverne i de pædagogiske test. I disse modeller måles færdighederne på skalaer, der omtales som logit-skalaer. Da logit-skalaer har egenskaber, som gør dem særlig velegnede for statistiske analyser, er det disse skalaværdier, der er blevet anvendt i forbindelse med udviklingen af de statistiske modeller. Logit-værdier opfattes på den anden side som vanskeligt forståelige. De nationale test og PISA omregner derfor logit-værdierne til værdier på skalaer, der opfattes som lettere at tolke på. For at gøre resultaterne fra anvendelse af modellerne mere tilgængelige, giver denne rapport også svar på, hvordan man kan omkode modellernes logit-værdier til værdier på de skalaer, som de nationale test og PISA normalt benytter sig af. Af denne grund har det været en central opgave for undersøgelsen, at finde ud af, om det kunne lade 1 Projektet har desuden haft adgang til resultater fra såkaldte frivillige nationale test. Dette materiale er imidlertid så begrænset og, som følge af frivilligheden, så usystematisk, at det ikke har kunnet bidrage til at forbedre sikkerheden i de statistiske analyser. Dette materiale er derfor ikke analyseret i forbindelse med dette arbejde. PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM 5
6 1.2 Notation og terminologi Rapporten beskæftiger sig med statistisk tekniske forhold. Af denne grund er fremstillingen også teknisk og bruger statistisk teknisk terminologi på helt samme måde, som det f.eks. er tilfældet med PISAs tekniske rapporter. For at spare læseren for besværet med at finde frem til udtryk og terminologi, der er defineret andre steder i sådanne rapporter, er det som regel en hjælp til læseren, hvis rapporterne starter med en oversigt over den notation og terminologi, som vil blive defineret og brugt i rapporterne. Det vil vi derfor også gøre her. Forkortelsen DNT refererer til de nationale test. Forkortelsen DIF ( Differentiel item funktion ) refererer til situationer, hvor testopgaver fungerer forskelligt i forskellige sammenhænge. Lokal afhængighed refererer til situationer, hvor sammenhængen mellem svarene på forskellige testopgaver ikke kan forklares 100 pct. af den bagvedliggende færdighed, som opgaverne skal måle. Egenskaber som DIF og lokal afhængighed er fænomener, som man rutinemæssigt forsøger at undgå, når man konstruerer pædagogiske test generelt. Fænomenerne forekommer alligevel i både DNT og PISA, men der er metoder, som kan håndtere disse problemer uden at det ødelægger målingerne af elevernes færdigheder. Disse metoder er blevet anvendt i forbindelse med analyserne. En logit-værdi er det mål for elevernes færdigheder, som både benyttes af Rasch-modellen og af andre psykometriske skala-modeller. Logit-værdierne antages at være de grundlæggende repræsentationer af elevernes færdigheder, som alle andre mål for færdighederne kan føres tilbage til. En DNT-logit er en logit-værdi beregnet for et af profilområderne i de nationale test. Disse logit-værdier er inkluderet i de data, som UNI-C har stillet til rådighed for analyserne. En PISA-logit er en logit-værdi knyttet til et testresultat fra PISA. Disse logit-værdier er blevet beregnet i forbindelse med projektet, fordi PISA ikke selv leverer sådanne mål. Da skalamodellen, som benyttes af PISA, afviger fra skalamodellen, der benyttes i denne undersøgelse, vil der være en vis grad af forskel på de logit-værdier, som PISA kunne have beregnet og dem, som vi har beregnet. Det der er vigtigt at huske, er derfor, at en PISA-logit i denne rapport er beregnet ud fra en skalamodel, der er specielt tilpasset til danske elever. En PISA-score er en værdi på en skala fra 0 til 1000, som PISA benytter sig af. PISA-scoren er en lineær transformation af de logit værdier, som PISA ville rapportere, hvis de ønskede at rapportere testresultater på elevniveau. Sådanne PISA-scores beregnes også i forbindelse med dette projekt, men relationen mellem PISA-logits i denne rapport og de såkaldte PISA-scores er en ikke-lineær relation pga. forskellene mellem den danske skalamodel og den skalamodel, som PISA bruger. DNT-percentiler er normbaserede scores, der angiver hvor eleven er placeret i forhold til den elevpopulation, som de nationale test betragter som standardpopulationen. DNT-kategorier og PISA-kategorier opdeler testresultaterne i et relativt lille antal kategorier, der definerer forskellige færdighedsniveauer. DNT-kategorierne er normbaserede og fastlagt ud fra skæringspunkter på percentil-skalaen. Med hensyn til den nærmere definition af PISAs kategorier henvises til dokumentationen for PISA. I forhold til dette arbejde 6 PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM
7 er det ikke afgørende, hvorledes kategorierne er defineret, men kun, at det er muligt at kategorisere de forskellige PISA-logits på en måde, der stemmer overens med kategorierne. I stedet for egentlige PISA-scores rapporterer PISA såkaldte plausible værdier knyttet til de enkelte elever. Disse værdier er ikke egentlige testscores, men derimod tilfældigt udtrukne tal fra PISAs skalamodel, der kan bruges til at kortlægge fordelingen af PISA-scores i større grupper (eller hele lande). Denne undersøgelse har brugt de plausible værdier, som leveres sammen med data fra PISA, til at fastlægge relationen mellem PISA-logits og PISAscores, men ellers har de ikke haft nogen betydning for de analyser, som denne rapport beskriver. Der foretages en række statistiske tests i forbindelse med analyserne. Hvis signifikans-sandsynlighederne (p-værdierne) er mindre end 0,00005 omtales resultaterne som højsignifikante. PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM 7
8 2 Sammenfatning af analyseresultater 2.1 Indledning Resultaterne af det arbejde, som omtales i denne rapport, kan sammenfattes i følgende punkter: Resultat nr. 1 Det vigtigste resultat er, at det har været muligt at udvikle statistiske modeller, som kan bruges til at forudsige testresultater i læsning og matematik i PISA ud fra oplysninger om testresultater i de samme fag fra den nationale test. Disse resultater er beskrevet i kapitlerne 4 og 5. For at komme frem til disse resultater har det været nødvendigt først at løse en række underordnede problemer, som i flere tilfælde forventes at have interesse i sig selv. Resultat nr. 2 De prædiktive modeller forudsætter, at der kan påvises en klar statistisk sammenhæng mellem DNTresultater og PISA-resultater. At dette er tilfældet kan man se i Delrapport 1 - formidling af resultater og kapitel 3 i denne rapport. Resultaterne har interesse i sig selv, fordi resultaterne kan tages som et udtryk for, at både DNT og PISA-målingerne er kriterievalide. 2 Resultat nr. 3 De prædiktive modeller forudsætter, at det har været muligt at måle elevernes færdigheder på Raschmodellens logit-skala. I forbindelse med DNT har dette ikke været et problem, fordi de data, der er stillet til rådighed for undersøgelsen, indeholder logit-værdier for alle profilområder. I forbindelse med PISA har det imidlertid været nødvendigt først at undersøge, om det overhovedet kan lade sig gøre at beregne logit-værdier ud fra svarene på de enkelte 2 Kriterievaliditet er et krav om, at en pædagogisk test skal korrelere med de forhold, som man på forhånd ved, at det fænomen, som testen forsøger at måle, hænger sammen med. For ikke at blive misforstået, skal det understreges, at validitet kræver andet og meget mere end kriterievaliditet, læse- og matematikopgaver i PISA, og derefter at foretage beregningerne. Appendiks A beskriver en række af de forhold omkring Rasch-modellen, der har spillet en rolle for de analyser, som har ført frem til logit-værdierne for både læsning og matematik, mens Appendiks B og C beskriver analyserne mere detaljeret. Appendiks A giver desuden retningslinjer for, hvorledes man kan tolke forskelle på logit-skalaerne, som kan hjælpe til at gøre parametrene i de statistiske prædiktionsmodeller mere forståelige. Resultat nr. 4 Den skalamodel, som PISA anvender, er ikke rettet specifikt mod danske elever. PISAs skalamodel afviger derfor fra de skalamodeller, der er anvendt i denne rapport. Årsagen til dette har været at undgå systematiske fejl, som kunne vanskeliggøre udviklingen af de prædiktive modeller. Det er på den anden side ønskværdigt at kunne fremlægge resultater fra anvendelsen af modellerne på en måde, der er genkendelig for personer, som er vant til at se PISA-resultater i form af PISA-scores og PISA-kategorier. Appendiks A forklarer, hvorfor dette kan lade sig gøre, 3 mens Appendiks D viser, hvordan det skal gøres. Resten af dette kapitel giver et resume af, hvad de prædiktive modeller kan fortælle om henholdsvis læsning og matematik. 2.2 Læsning Hovedresultatet af analyserne er, at PISA-logits kan prædikteres ud fra tidligere DNT-logits, og at præmen kravet om kriterievaliditet er et uomgængeligt krav, som disse test altså lever op til. 3 Forklaringen kan findes i afsnittet med overskriften Estimation af logitværdier med forkerte Rasch-modeller 8 PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM
9 diktionen forbedres, hvis der tages højde for elevens køn, herkomst og om der er tale om en elev med normal eller sen skolestart 4. De prædikterede PISA-logits kan beregnes ud fra følgende relativt simple lineære funktion: PISA logit = 0, ,119 S + 0,099 A +0,438 T 0,180 D 0,282 E + 0,350 N Forskellen på drenge og piger er på logit-skalaen lig med 0,180. Sammenholdes dette estimat med estimatet for normal skolegang ses, at effekten af køn er svagere end effekten af skolestarten. Forholdet mellem sandsynlighederne for korrekt svar for piger og drenge viser da også, at piger alt andet lige - kun har 9 pct. større chance for at løse en relevant opgave korrekt end en dreng har. I denne formel er: - S lig med DNT-logit for sprogforståelse, - A lig med DNT-logit for afkodning, - T lig med DNT-logit for tekstforståelse, - D er lig 1, hvis der er tale om en dreng og 0, hvis der er tale om en pige, - E er lig med 1, hvis der er tale om en elev med anden etnisk herkomst end dansk og 0, hvis eleven er etnisk dansk af herkomst, - N er 1, hvis eleven er startet normalt og 0, hvis eleven er en sen skolestarter. Alle tallene i formlen refererer til forskelle målt på Rasch-modellens logit-skala. Appendiks A beskriver, hvorledes disse logit-forskelle skal tolkes. Ifølge modellen er spørgsmålet om normal eller sen skolestart (N) den stærkest virkende baggrundsfaktor. Parameteren på 0,35 kan omregnes til, at forholdet mellem sandsynligheden for, at en elev med normal skolestart vil svare rigtigt på en relevant 5 opgave og sandsynligheden for, at en elev med sen skolestart svarer rigtigt på den samme opgave, vil være 1,19. Alt andet lige 6 vil eleven med normal skolestart, der blev testet i 9. klasse, altså have 19 pct. større chance for at svare rigtigt på opgaven end eleven med sen skolestart, som gik i 8. klasse, da han eller hun blev testet af PISA. Resultaterne af analyserne viser, at tekstforståelsen er den afgørende faktor i prædiktionen af PISA-resultatet i læsning, og at der ikke mistes meget forklaringskraft, hvis man undlader at inddrage sprogforståelse og afkodning, når man forsøger at forudsige PISA-resultatet. Dette resultat understøttes af analyser, hvor inklusion af testresultater i læsning fra 6. klasse betyder, at der ikke længere kan påvises en effekt af sprogforståelse, og at det kun er afkodningen i 6. klasse, som i et begrænset omfang bidrager til prædiktionen af det senere PISA-resultat i læsning. Det, som PISAs læsetest måler, svarer med andre ord til det ene af de tre profilområder i DNT, mens DNT sigter bredere end PISA fordi DNT også måler sprogforståelse og afkodning. Relationen mellem de PISA-logits, som benyttes i denne undersøgelse, og de PISA-scores, som PISA benytter sig af, er ikke lineær. Følgende formel kan imidlertid bruges, hvis man ønsker at beregne en PISA-score ud fra en PISA-logit: PISA score = 515, ,185 PISA logit 2,155 (PISA logit ) 2 Af de øvrige resultater, som analyserne har afkastet, er det især betydningen af spørgsmålet om 4 PISA 2012 testede elever, der var født i De fleste af disse elever gik i 9. klasse i 2012, men der var en ikke ubetydelig andel af elever fra 8. klasse på grund af sen skolestart, et forhold der har væsentlig betydning for forståelsen af fordelingen af PISA-resultaterne. 5 En relevant opgave er en opgave, der hverken er for svær eller for let for eleven 6 Samme testresultater i DNT, samme køn og samme etniske baggrund. PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM 9
10 normal eller sen skolestart, der har interesse. Grundet en sen skolestart har enkelte elever haft et års mindre undervisning i den periode, der er gået fra de blev testet i DNT til de blev testet i PISA som 15- årige. Dette må selvfølgelig forventes at have betydning for de senere testresultater i PISA. Ud over dette problem, er der også det forhold, at det er velkendt, at der blandt eleverne med sen skolestart findes elever, der er startet sent pga. udviklingsmæssige eller indlæringsmæssige problemer. De relativt dårligere PISA-resultater for elever med sen skolestart kan derfor skyldes to ting: at de har haft et års mindre skolegang, og/eller at de som udgangspunkt er svagere funderet end eleverne med normal skolestart. Vi har i analysen forsøgt at fokusere på dette spørgsmål, for at forbedre prædiktionen af PISA-resultaterne og har i den sammenhæng været i stand til at skille effekten af det manglende år fra effekten af det svagere udgangspunkt. For overhovedet at gennemføre analyserne, har det været nødvendigt at foretage en række antagelser om effekten af et ekstra år med matematik, før man bliver testet af PISA. Antagelser, som det i sagens natur ikke er muligt at afprøve. Antagelserne er beskrevet i Kapitel 5. Vi betragter antagelserne som forholdsvis forsigtige og realistiske. Vi har derfor også været i stand til at konstruere en model, der kan prædiktere PISA-resultater i matematik for både elever med normal og sen skolestart. Prædiktionsmodellen definerer den forventede PISA-logit ved følgende lineære funktion af de tre logit-værdier, som de nationale test beregner i forbindelse med afprøvningen i matematik: PISA logit = 0, ,200 T + 0,310 G + 0,380 A + 0,130 D 0,455 E + 0,406 N Ud over at dette er med til at forbedre prædiktionen af PISA-resultaterne, indebærer disse resultater også den sidegevinst, at det er muligt at forudsige, hvorledes PISA-resultaterne ville se ud for de sene skolestartere, hvis de først blev testet af PISA umiddelbart før det obligatoriske skoleforløb slutter i 9. klasse. 2.3 Matematik På samme måde som for læsningen, kan resultaterne for matematik tages som udtryk for gensidig kriterie-evaluering af DNT og PISA-målingerne. Tilstedeværelsen af korrelationer mellem testresultaterne fra DNT og PISA er takket være deres høje signifikans indiskutable. Korrelationerne er svagere end i modellen for læsning. Dette er dog forventeligt, idet der er en tidsmæssig forskel på to år mellem resultaterne i de nationale test og resultaterne i PISA. I denne formel er - T lig med DNT-logit for tal og algebra, - G lig med DNT-logit for geometri, - A lig med DNT-logit for matematik i anvendelse, - D er lig 1, hvis der er tale om en dreng og 0, hvis der er tale om en pige, E er lig med 1, hvis der er tale om en elev med anden etnisk herkomst end dansk og 0, hvis eleven er etnisk dansk af herkomst, - N er 1, hvis eleven er startet normalt og 0, hvis eleven er en sen skolestarter. I modsætning til læsningen, er der ikke et enkelt dominerende profilområde, som har betydning for det senere PISA-resultat i matematik. Anvendt matematik synes at have den stærkeste effekt, men både tal og algebra og (især) geometri skal medtages, hvis prædiktionen af PISA-resultatet skal optimeres. 10 PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM
11 På samme måde som med læsningen, kan den beregnede PISA-logit omregnes til en PISA-score mellem på den skala, som PISA normalt benytter. Den funktion, der skal benyttes er givet ved: PISA score = 471, ,663 PISA logit 5,719 (PISA logit ) 2 Effekten af normal skolestart er lidt større i modellen for matematik end for læsning. Elever med normal skolestart har (alt andet lige) næsten 25 pct. større chance for at svare korrekt på en relevant opgave end eleverne med sen skolestart, som endnu ikke har haft undervisningen i matematik i 9. klasse før de testes af PISA. Forskellen på effekten af undervisning i 9. klasse i henholdsvis matematik og dansk er næppe nogen overraskelse, da der undervises målrettet i matematik i 9. klasse, men ikke i læsning. Analysen viser i øvrigt, at undervisningen i 9. klasse i matematik ville forbedre PISA-scoren for elever med sen skolestart med ca. 30 point (svarende til et trin på PISAs kategorisystem), hvis PISA ventede med at teste dem i 9. klasse umiddelbart før afgangen fra den lovpligtige del af folkeskolen. 2.4 Forventede PISA-resultater i forhold til de enkelte profilområder i DNT Tabellerne i dette afsnit kan benyttes til at give et første slag på tasken med hensyn til de forventede resultater i PISA ud fra de enkelte profilområder i henholdsvis dansk og matematik. Tabellerne kan benyttes til prædiktion, men det skal understreges, at en markant bedre prædiktion af PISA-resultater opnås ved at inddrage alle fagets profilområder sammen med oplysningerne om elevens køn, herkomst og tidspunkt for skolestart. 7 TABEL 2.1 Forventede PISA-resultater ift. sprogforståelse i 8. klasse målt i logits Interval Forventet PISA-logit Forventet PISA-score (-4,-3) -2, (-3,-2) -1, (-2,-1) -0, (-1,0 ) -0, ( 0,1 ) 0, ( 1,2 ) 0, ( 2,3 ) 0, ( 3,4 ) 0, Note: Interval for logit for sprogforståelse. Middelværdien for intervallet. TABEL 2.2 Forventede PISA resultater i læsning ift. testresultater i afkodning i 8. klasse målt i logits Interval Forventet PISA logit Forventet PISA score (-4,-3) -2, (-3,-2) -1, (-2,-1) -1, (-1,0 ) -1, ( 0,1 ) -0, ( 1,2 ) -0, ( 2,3 ) -0, ( 3,4 ) -0, ( 4,5 ) 0, ( 5,6 ) 0, ( 6,7 ) 1, , Note: Interval for logit for afkodning. Middelværdien for intervallet. 7 Hvis man nøjes med at prædiktere de senere PISA-resultater ved et enkelt profilområde samtidig med at man kategoriserer testresultaterne i en række kategorier i stedet at bruge de præcise målinger, bliver forklaringsværdien væsentligt reduceret med R 2 -værdier helt ned til 0,22. PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM 11
12 Bemærk, at testresultaterne fra de nationale test er angivet ved niveauer på den logit-skala, som de nationale test benytter sig af, mens de forventede PISA-resultater angives både på logit-skalaen og på den skala fra , som PISA benytter sig af. Tabellerne indeholder kun resultater for de logit-niveauer i de nationale test, som er observeret i de data, der har været stillet til rådighed for analysen. TABEL 2.3 Forventede PISA resultater i forhold til testresultatet på tekstforståelse i 8. klasse målt i logits Interval Forventet PISA logit Forventet PISA score (-4,-3) -2, (-3,-2) -1, (-2,-1) -1, (-1,0 ) -0, ( 0,1 ) 0, ( 1,2 ) 0, ( 2,3 ) 1, ( 3,4 ) 1, ( 4,5 ) 2, ( 5,6 ) - - ( 6,7 ) , Note: Interval for logit for tekstforståelse. Middelværdien for intervallet. Da der kun foreligger resultater i matematik i 6. klasse fra elever, der gik i 8. klasse, da de blev testet af PISA, har det været nødvendigt at foretage specielle beregninger for at prædiktere, hvorledes testresultaterne ville se ud, hvis eleverne var blevet testet i 9. klasse (ligesom det var tilfældet med flertallet af eleverne). Tabel 4 vise derfor både, hvorledes de forventede PISA-resultater ser ud for elever, der bliver testet af PISA i 8. klasse, og de forventede værdier for elever, som testes af PISA i 9. klasse. TABEL 2.4 Forventede PISA resultater i matematik ift. testresultater i tal og algebra i 6. klasse målt i logits Interval Forventet PISA logit Forventet PISA score i 8. klasse i 9.klasse i 8. klasse i 9.klasse (-3,-2) -2,50-2, (-2,-1) -1,94-1, (-1,0 ) -1,27-0, ( 0,1 ) -0,74-0, ( 1,2 ) -0,11 0, ( 2,3 ) 0,33 0, ( 3,4 ) 0,86 1, Note: Interval for logit for tal og algebra. Middelværdien for intervallet. TABEL 2.5 Forventede PISA resultater i forhold til testresultatet på geometri i 8. klasse målt i logits Interval Forventet PISA logit Forventet PISA score i 8. klasse i 9.klasse i 8. klasse i 9.klasse (-3,-2) -1,57-1, (-2,-1) -1,83-1, (-1,0 ) -1,10-0, ( 0,1 ) -0,41-0, ( 1,2 ) 0,20 0, ( 2,3 ) 1,41 1, ( 3,4 ) Note: Interval for logit for geometri. Middelværdien for intervallet. 12 PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM
13 TABEL 2.6 Forventede PISA resultater i forhold til testresultatet på matematik i anvendelse i 8. klasse målt i logits Interval Forventet PISA logit Forventet PISA score i 8. klasse i 9.klasse i 8. klasse i 9.klasse (-3,-2) -2,18-1, (-2,-1) -1,57-1, (-1,0 ) -0,94-0, ( 0,1 ) -0,32 0, ( 1,2 ) 0,39 0, ( 2,3 ) 1,16 1, ( 3,4 ) 1,82 2, Note: Interval for logit for matematik i anvendelse. Middelværdien for intervallet. PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM 13
14 3 Deskriptive analyser Dette kapitel præsenterer resultater fra de deskriptive analyser, der blev foretaget som optakt til de regressionsanalyser, der er beskrevet i kapitel 4. Det datagrundlag, der er benyttet til analyserne i denne rapport, omfatter dels testresultater fra de nationale test for de elever, der blev udtrukket til PISA 2012 og som også deltog i de obligatoriske nationale test, og dels testresultater og baggrundsvariable fra PISA 2012: 1) estimater af elevernes færdigheder på Rasch modellens logit-skala for hvert profilområde for sig, 2) percentil-scores, der angiver elevernes placering i forhold til den standardpopulation, som de nationale test anvender, 3) normbaserede klassifikationer ud fra de nævnte percentil-scores, 4) De (foreløbige 9 ) kriteriebaserede scores, 5) De kriteriebaserede kategoriseringer. 1) Matematik i 6. klasse i elever har et resultat fra denne test og PISA ) Læsning i 6. klasse i elever har et resultat fra denne test og PISA ) Læsning i 8. klasse i 2011 og elever har et resultat fra disse test og PISA Testresultaterne fra PISA 2012 omfattede resultater i læsning og matematik. Baggrundsoplysningerne omfattede oplysninger om elevens køn, alder, herkomst og socioøkonomisk og kulturel status. Ud over de nævnte baggrundsvariable fra PISA 2012 blev oplysningerne om det tidspunkt (2011 eller 2012), hvor eleverne deltog i de obligatoriske test i læsning i 8. klasse brugt til at definere en baggrundsvariabel, der skelner mellem elever med normal skolestart (8. klasse testresultat i 2011) og elever med sen skolestart (8. klasse testresultat i 2012) 8. Testresultaterne fra de nationale test (DNT) består dels af Testresultaterne fra PISA består af svarene på de enkelte opgaver i læsning og matematik, men egentlige estimater af elevernes færdigheder findes ikke. Det har derfor været nødvendigt først at beregne disse estimater som optakt til analyserne af sammenhængen mellem DNT og PISA resultater, og derefter at konvertere disse estimater til skalaværdier og kategoriseringer, der svarer til dem, som PISA benytter sig af. Rasch modellen og den logitskala, som Rasch modellen bruger til at måle færdighederne på, er beskrevet i Appendiks A. De analyser, der førte frem til estimaterne af elevernes færdigheder ud fra svarene på PISA opgaverne er beskrevet i Appendiks B og C. Omregningen fra Rasch modellens logit-værdier til PISAs skalaer og kategoriseringer er beskrevet i Appendiks D. Det egentlige formål med de deskriptive analyser, der beskrives i dette kapitel, var at undersøge om sammenhængen mellem DNT- og PISA-resultater var så tydelig, at det var realistisk at tro på, at det kunne lade sig gøre at opstille en egentlig statistisk model, som kunne bruges til at forudsige PISA-resultaterne. 8 Aldersfordelingen i 6. og 8. klasse beskrives i kapitlerne 4 og 5. 9 Arbejdet med at kriteriebasere de nationale test er ikke endegyldigt. Der er derfor taget udgangspunkt i de foreløbige kriterier i hele rapporten. 14 PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM
15 De kriteriebaserede scores og kategorier er opgørelser af testresultater på en sådan måde, at fagkyndige har været i stand til at vurdere kvaliteten af præstationerne i de pædagogiske test ud fra faglige kriterier. Da det er første gang, der fremlægges resultater om de kriteriebaserede opgørelser, vil databeskrivelsen i dette kapitel i højere grad fokusere på disse opgørelser end på percentil-værdier og normbaserede kategoriseringer. 3.1 Sammenhæng mellem testresultater i de nationale test og senere resultater i PISA DNT- og PISA-resultaterne gensidigt kriterievaliderer hinanden. De efterfølgende figurer og tabellerne med korrelationer mellem testresultaterne underbygger denne konklusion for både læsning og matematik. For så vidt angår læsefærdigheden viser analyserne desuden, at PISAs læsescore er meget stærkere relateret til profilområdet tekstforståelse i de nationale test end til de to andre profilområder. Set ud fra den synsvinkel repræsenterer PISA testen en snævrere operationalisering af læsning end de nationale test, som ud over tekstforståelse også måler sprogforståelse og afkodning. På trods af den tidsmæssige forskel mellem DNT og PISA er der en klar sammenhæng mellem testresultaterne. Dette måske knap så overraskende resultat er naturligvis en forudsætning for at forudsige PISA resultater ud fra DNT, men det er også vigtigt for diskussionen af validiteten af de nationale test og PISAs test. Et af aspekterne i denne diskussion handler om et begreb, der omtales som kriterievaliditet. Kravet om kriterievaliditet er et krav om, at resultaterne fra en test, der måler en bestemt færdighed, skal være statistisk korreleret med fænomener, som man allerede på forhånd ved er relateret til den færdighed, man forsøger at måle. Da DNT og PISA måler profilområder knyttet til den samme færdighed, er det derfor et uomgængeligt krav, at DNT- og PISA-resultater skal være indbyrdes korrelerede, hvis man vil påstå, at målingen ved de to testsystemer er kriterievalide. Der er intet krav om at korrelationen skal være meget stærk, da det drejer sig om forskellige profilområder og fordi der er en tidsmæssig forskel mellem DNT- og PISA-resultaterne, men sammenhængen skal være tydelig og statistisk højsignifikant. Da det er tilfældet her, kan vi konkludere, at Figur 1 viser sammenhængen mellem DNT-resultater i tekstforståelse og senere PISA resultater i læsning målt på logit niveau, mens Figur 2 viser den samme sammenhæng mellem DNT-resultater målt på percentil-skalaen og PISA-resultater i form af PISA-scores. De to figurer illustrerer den samme tendens, men tendensen fremtræder forskelligt i figurerne. I figur 1, hvor der bruges logit-værdier, ses en lineær sammenhæng mellem testresultaterne. I denne figur er det også muligt at se, at sammenhængen er lidt svagere blandt elever med sen skolestart end blandt elever med normal skolestart. I figur 2 er sammenhængen også tydeligt monotont voksende, men tendensen er ikke lineær, og det er vanskeligere at se, at der skulle være forskel på tendenserne blandt elever med normal og sen skolestart. Det er denne forskel på tendenserne, der er grunden til, at den modeludvikling, der har været det egentlige formål med dette arbejde, er foregået på logit-niveau og ikke med udgangspunkt i en af de andre skalaer. Med hensyn til formidlingen af resultaterne er det derimod åbenlyst, at resultaterne vil være lettere tilgængelige, hvis de rapporteres ved hjælp af de skalaer, som man traditionelt benytter PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM 15
16 sig af. Det vil derfor være de skalaer, der benyttes i resten af dette kapitel. FIGUR 3.1 Sammenhæng mellem tekstforståelse i de nationale test og PISA resultater i læsning FIGUR 3.2 Sammenhæng mellem tekstforståelse i de nationale test og resultater i læsning i PISA Note: Begge testresultater måles på Rasch modellens logit-skala. Resultater svarende til Figur 3.1 og 3.2 kan findes for samtlige profilområder i DNT og for både læsning og matematik i PISA. I stedet for at vise alle disse tabeller, viser de efterfølgende tabeller korrelationerne mellem profilområder og PISA for hvert fag for sig. Note: DNT-resultatet på percentil-skalaen og PISA-resultater målt PISAskalaen. Tabel 3.3 og 3.4 viser korrelationskoefficienterne for elever med henholdsvis normal og sen skolegang (svarende til at eleven er henholdsvis 14 og 15 år i 8. klasse) i forhold til deres resultater i læsning. Tabel 3.5 viser de tilsvarende resultater for matematik for elever med sen skolestart (svarende til en alder på ca. 13 år). Da der ikke foreligger DNT-resultater for matematik i 6. klasse for elever med normal skolestart, kan disse naturligvis ikke vises. 16 PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM
17 Korrelationerne i tabellerne dokumenterer kriterievaliditeten 10 for samtlige profilområder i de nationale test i læsning i 8. klasse og i matematik i 6. klasse. Bemærk, at sprogforståelse og afkodning også korrelerer med PISAs læsetest, men at korrelationen mellem tekstforståelse og PISAs læseresultater er stærkere. Dette resultat bekræftes af de analyser, der beskrives i Kapitel 4, hvor det vises, at sprogforståelse og afkodning bidrager så lidt til forudsigelsen af senere PISA resultater i læsning, at der tabes meget lidt, hvis de ikke inddrages i en samlet model. TABEL 3.3 Korrelation mellem testresultater i læsning for elever med normal skolestart Sprogforståelse Sprog- Forståelse Afkodning Tekstforståelse PISA læsning 1 0,55 0,61 0,46 Afkodning 1 0,62 0,49 Tekstforståelse PISA læsning 1 0,62 Note: Logit-værdiers lineære korrelation. Alle korrelationer er statistisk signifikante på et 1 pct. niveau elever har resultater for DNT, for PISA. Af disse har resultater for begge tests. 1 TABEL 3.4 Korrelation mellem testresultater i læsning for elever med sen skolestart Sprog- Forståelse Sprogforståelse Afkodning Tekstforståelse PISA læsning 1 0,56 0,61 0,42 Afkodning 1 0,64 0,48 Tekstforståelse PISA læsning 1 0,59 Note: Logit-værdiers lineære korrelation. Alle korrelationer er statistisk signifikante på et 1 pct. niveau elever har resultater for DNT, 964 for PISA. Af disse har 781 resultater for begge tests. TABEL 3.5 Korrelation mellem testresultater i matematik for elever med sen skolestart Tal og Algebra Tal og Algebra Geometri Anvendt matematik 1 PISA matematik 1 0,58 0,67 0,48 Geometri 1 0,62 0,51 Anvendt matematik PISA matematik 1 0,55 1 Note: Logit-værdiers lineære korrelation. Alle korrelationer er statistisk signifikante på et 1 pct. niveau elever har resultater for DNT, for PISA. Af disse har resultater for begge tests. Den store forskel skyldes, at kun sene skolestartere har DNT data i matematik. I matematik forholder det sig anderledes. Matematik i anvendelse korrelerer en smule stærkere til PISAs matematik test end de to andre, men både Tal og Algebra og Geometri bidrager med så meget, at de 10 For ikke at blive misforstået er det nødvendigt at understrege, at kriterievaliditet kun er et af flere krav, der skal tilgodeses, hvis man vil argumentere at en pædagogisk test giver valide målinger af færdigheder. Disse krav omfatter både indholdsmæssige og statistiske krav. Da det ligger uden for rammerne af dette arbejde at undersøge og dokumentere validiteten af DNT og PISA, vil vi derfor nøjes med at konkludere, at kravene om kriterie-validitet er opfyldt. PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM 17
18 ikke kan undværes i forbindelse med en forudsigelse af senere PISA resultater. PISAs matematik test måler alle tre matematik-aspekter. En sammenligning af tabel 3.3 og 3.4 viser, at korrelationerne er svagest blandt elever med sen skolestart som testes nogenlunde samtidigt i DNT og PISA, men forskellen er meget begrænset. Analyserne i Kapitel 4 viser, at effekten af DNT-resultaterne på PISA-resultatet vil være den samme for elever med normal og sen skolestart, efter at der er taget højde for den effekt, som undervisningen i 9. klasse har haft for eleverne med normal skolestart. Da der mangler DNT-oplysninger om matematik i 6. klasse fra 2009, kan vi ikke undersøge, om det samme er tilfældet i matematik. Det er imidlertid en rimelig antagelse at gå ud fra, at det samme er tilfældet her. Hvis det derfor er muligt at estimere effekten af undervisningen i matematik i 9. klasse, vil det også være muligt at opstille en statistisk model for matematik, der både kan bruges for elever med sen skolestart og elever med normal skolestart. 3.2 Kriteriebaserede scores og kategoriseringer Den kriteriebaserede score repræsenterer en ny udvikling i de nationale test, som ikke findes beskrevet og dokumenteret andetsteds. Vi forventer derfor, at der vil være interesse for, hvorledes de kriteriebaserede resultater ser ud i forhold til de opgørelser af testresultater, som man ellers præsenteres for i forbindelse med de nationale test. I forbindelse med adaptive test besvarer eleverne ofte helt forskellige opgaver, og der vil være meget få elever, der svarer på præcis de samme opgaver. På trods af dette kan man hvis nogle bestemte forudsætninger er opfyldt beregne tal for hvor dygtige eleverne er, som kan sammenlignes, selvom eleverne har svaret på forskellige opgaver. I forbindelse med de nationale test er disse tal enten tal på Rasch modellens logit-skala eller tal på en percentilskala, der placerer eleverne i forhold til en bestemt standardpopulation. Problemet med disse tal er, at de kun kan bruges til at afgøre om visse elever er dygtigere end andre elever, men at de ikke i sig selv fortæller noget om hvilke elever, der er dygtige, og hvilke der ikke er dygtige nok. Kriteriebaserede scores og kategoriseringer er et forsøg på at løse op for dette problem. En kriteriebaseret score er den forventede score på et bestemt antal opgaver ud fra oplysninger om, hvor eleven ligger på logit-skalaen. De opgaver, som den kriteriebaserede score refererer til skal være opgaver, der er udvalgt af fagkyndige på en sådan måde, at de fagkyndige efterfølgende er i stand til at konkludere, at et vist antal point er udtryk for en god eller dårlig besvarelse. Om der, med andre ord, ser ud til at være tale om en dygtig eller mindre dygtig elev. Kvalitets- og Tilsynsstyrelsen har bedt en række fagkyndige stå for et sådant udvalg af opgaver, og for en klassifikation af de kriteriebaserede scores i et mindre antal kategorier fra ikke tilfredsstillende til fremragende 11. Da der er tale om et igangværende udviklingsprojekt er de tal, der fremlægges i denne rapport formodentlig de første tal, der dokumenterer hvorledes kriteriebaseret scoring fungerer 11 På samme måde som i forbindelse med alle pædagogiske test, er validiteten af den kriteriebaserede scoring et spørgsmål om indholdsmæssige og statistiske kriterier. En af forfatterne til denne rapport har bistået Kvalitets- og tilsynsstyrelsen med definitionen af, hvad en kriteriebaseret score er, og med de statistiske redskaber, der skal til, for at regne fra logit værdier til kriteriebaserede scores. Vi kan derfor stå inde for de metodiske aspekter af de kriteriebaserede resultater. De indholdsmæssige sider valget af opgaver og definitionen af kategorierne er de fagkyndiges ansvar. Da der er tale om igangværende udviklingsarbejde er vi desværre ikke i stand til at referere til en egentlig publikation, hvor disse aspekter er dokumenteret. 18 PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM
19 i praksis, og hvorledes kriteriebaserede resultater fra de nationale test relaterer sig til PISA. Figur 3.6 viser sammenhængen mellem den kriteriebaserede score i tekstforståelse i 8. klasse og den tilsvarende percentil med farvekoder, der viser, hvorledes de fagkyndige har klassificeret de kriteriebaserede scores. Tilsvarende figurer kan vises for samtlige profilområder for både læsning og matematik. Figur 3.6 viser, at de svageste 10 pct. af læserne er karakteriseret ved enten ikke tilstrækkelige eller mangelfulde præstationer. I den næstsvageste gruppe karakteriseres præstationen i de fleste tilfælde som jævn, men i de bedste tilfælde som god. I midtergruppen med percentil-værdier fra pct. er der altid tale om en god præstation, mens FIGUR 3.6 Sammenhæng mellem kriteriebaserede scores og normbaserede (percentil-)værdier Note: De kriteriebaserede kategorier er angivet ved farvekoder, mens de vandrette linjer definerer de normbaserede kategorier. PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM 19
20 den næstbedste normative gruppe har præstationer, der enten er gode eller rigtig gode. De fremragende præstationer findes i alle tilfælde blandt de 10 pct. bedste elever. Udover at dokumentere, hvor stor en del af eleverne, der er karakteriseret ved god eller bedre tekstforståelse, er den væsentligste forskel på de normbaserede og kriteriebaserede kategoriseringer, at de kriteriebaserede kategorier differentierer væsentligt bedre blandt de svageste og de stærkeste læsere, og at de derfor giver læreren et bedre og mere nuanceret grundlag for planlægningen af undervisningen for disse elever. Tabellerne viser sammenhængen mellem de normbaserede DNT-kategorier og de kriteriebaserede kategorier for de seks forskellige profilområder. Tabellerne er baseret på testresultater fra de elever, der deltog i PISA 2012 og som har deltaget i de nationale tests. Tabeller baseret på alle elever med et testresultat fra de nationale test kan således afvige. Samtlige tabeller bekræfter det indtryk, som figur 3.6 gav. De kriteriebaserede kategoriseringer differentierer klart bedre blandt både svage som stærke elever. Dette resultat må være særdeles formålstjenligt, fordi det i givet fald kan give læreren oplysninger, som kan være nyttige i forbindelse med planlægning af undervisningen for elever, der på forskellig vis svage som stærke afviger fra det store flertal i klassen. 20 PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM
21 TABEL 3.7 Sprogforståelse 8. klasse. Sammenhæng mellem normative og kriteriebaserede kategorier Kriteriebaseret skala Ikke tilstrækkelig Mangelfuld Jævn God Rigtig god Fremragende Total Antal i rækken Interval, normbaseret Op til 10 pct. 14,6 85, pct. - 4,1 90,9 5, pct , pct ,6 5, pct. og derover ,8 14, Samlet fordeling 2,3 14,4 22,3 49,3 10,3 1, TABEL 3.8 Afkodning 8. klasse. Sammenhæng mellem normative og kriteriebaserede kategorier Kriteriebaseret skala Ikke tilstrækkelig Mangelfuld Jævn God Rigtig god Fremragende Total Antal i rækken Interval, normbaseret Op til 10 pct. 19,8 52,2 28, pct ,9 92, pct , pct , pct.og derover , Samlet fordeling 2,5 6,7 5,1 85, TABEL 3.9 Tekstforståelse, 8. klasse. Sammenhæng mellem normative og kriteriebaserede kategorier Kriteriebaseret skala Ikke tilstrækkelig Mangelfuld Jævn God Rigtig god Fremragende Total Antal i rækken Interval, normbaseret op til 10 pct. 14,3 61,9 23, pct ,0 27, pct , pct ,1 50, pct. og derover ,3 21, Samlet fordeling 1,6 6,7 21,7 46,3 21,4 2, Note: Pct. af rækkerne er angivet. Tabellerne er baseret på testresultater fra elever, der har deltaget i både DNT og PISA PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM 21
22 TABEL 3.10 Tal og algebra, 6. klasse. Sammenhæng mellem normative og kriteriebaserede kategorier. Kriteriebaseret skala Ikke tilstrækkelig Mangelfuld Jævn God Rigtig god Fremragende Total Antal i rækken Interval, normbaseret op til 10 pct. 24,1 75, pct. - 54,2 45, pct ,4 68, pct ,7 34, pct. og derover ,4 32, Samlet fordeling 3,9 28,0 23,1 32,5 10,4 2, TABEL 3.11 Geometri, 6. klasse. Sammenhæng mellem normative og kriteriebaserede kategorier Kriteriebaseret skala Ikke tilstrækkelig Mangelfuld Jævn God Rigtig god Fremragende Total Antal i rækken Interval, normbaseret op til 10 pct. 11,6 88, pct. - 18,5 81, pct ,0 55, pct ,0 51, pct. og derover ,3 32, Samlet fordeling 1,9 21,2 40,0 20,9 13,7 2, TABEL 3.12 Matematik i anvendelse, 6. klasse. Sammenhæng mellem normative og kriteriebaserede kategorier Kriteriebaseret skala Ikke tilstrækkelig Mangelfuld Jævn God Rigtig god Fremragende Total Antal i rækken Interval, normbaseret op til 10 pct. 34,5 65, pct. - 63,9 36, pct ,8 71, pct ,7 2, pct. og derover ,2 13, Samlet fordeling 5,6 32,5 19,5 35,4 6,1 0, Note: Sene skolestartere. Tabellerne er baseret på testresultater fra elever, der har deltaget i både DNT og PISA 22 PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM
23 3.3 Kriteriebaserede scores og senere PISAresultater Dette afsnit beskriver sammenhængen mellem de kriteriebaserede DNT-resultater og resultaterne i PISA. læseprøve målt på PISAs skala er vist i figur 3.13 (beregningen af værdierne på PISAs skala er beskrevet i appendiks D). Sammenhængen er monotont voksende jo bedre kriteriebaseret score i tekstforståelse, jo bedre resultat på PISAs skala. Sammenhængen mellem den kriteriebaserede score i tekstforståelse og det senere resultat i PISAs FIGUR 3.13 Sammenhæng mellem kriteriebaserede scores i tekstforståelse og læsefærdigheder målt på PISAs skala Kilde: [Text] Note: Tekstforståelse i De Nationale Test i 8. klasse. PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM 23
24 Tabel 3.14 viser den gennemsnitlige score på PI- SAs skala i de seks kriteriebaserede kategorier for tekstforståelse og tabel 3.15 viser fordelingen over de syv kategorier, som PISA ofte benytter, når de præsenterer deres resultater. TABEL 3.14 Gennemsnitlige PISA-resultater i læsning Kriteriebaseret skala (tekstforståelse) Gennemsnit N Standardafvigelse Ikke tilstrækkelig Mangelfuld Jævn God Rigtig god Fremragende Samlet fordeling Note: PISA-resultaterne er opdelt på de seks kriteriebaserede kategorier for tekstforståelse i 8. klasse. Tabellerne er baseret på testresultater fra elever, der har deltaget i både DNT og PISA Figur 3.13 og de to tabeller fortæller en og samme historie. Relationen mellem de to testresultater er monotont voksende, jo bedre resultat i de nationale test, jo bedre resultat i PISA. Hvorvidt man foretrækker den ene eller anden måde at illustrere sammenhængen afhænger af det formål, man har med illustrationen. Figur 3.13 illustrerer tingene på det niveau, som den statistiske model fungerer på. Tabel 3.14 illustrerer den bedste måde at håndtere PISAs testresultater på, hvis resultaterne skal bruges til statistiske sammenligninger af testresultater i forskellige grupper eller under forskellige betingelser. Hvis hensigten f.eks. er, at sammenligne kriteriebaserede testresultater før og efter implementeringen af folkeskolereformen, vil det være mere hensigtsmæssigt at basere konklusioner på sammenligninger af de gennemsnitlige kriteriebaserede scores før og efter skolereformen, end på fordelingen henover de seks kriteriebaserede kategorier. TABEL 3.15 Sammenhæng mellem kriteriebaserede scores i tekstforståelse i 8. klasse og kategorisering af læsefærdigheden ifølge PISA 2012 PISA-kategori Antal i <1b 1b 1a Total rækken Kriteriebaseret skala, DNT Utilstrækkelig 10,5 26,3 26,3 28,9 5,3 2, Mangelfuld 4,5 17,9 35,0 34,6 6,9 1, Jævn 2,4 6,2 25,4 39,9 23,2 2,6 0, God 0,3 1,4 8,5 32,5 37,8 14,6 4,7 0, Rigtig god 0,1 0,2 1,5 12,1 36,1 38,2 10,3 1, Fremragende - - 1,0 3,1 15,6 47,9 31,3 1, Samlet fordeling 1,0 3,3 11,9 28,9 31,8 17,3 5,3 0, Note: Pct. af rækkerne angivet. Således ses fordelingen af læseresultater på PISAs kategorier inden for hver af de seks kriteriebaserede kategorier. Tabellerne er kun baseret på testresultater fra elever, der har deltaget i både DNT og PISA 24 PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM
25 Tabel 3.15 beskriver til gengæld substansen i testene på en måde, der vil være langt mere relevant for lærere og andre, der skal tolke og bruge testresultaterne. Elever med præstationer, der karakteriseres som ikke tilstrækkelige ender typisk i PISA kategorierne fra under 1b til 2. Hvis 3præstationen er mangelfuld, vil PISA resultatet typisk ligge i kategorierne 1b 2. En jævn præstation efterfølges af kategorierne 1a- 3 i PISA. Elever med en god præstation placerer sig efterfølgende i kategorierne 2-4 i PISA og så fremdeles. TABEL 3.16 Sammenhæng mellem kriteriebaserede scores i sprogforståelse i 8. klasse og kategorisering af læsefærdigheden ifølge PISA 2012 PISA-kategori Antal i <1b 1b 1a Total rækken Kriteriebaseret skala, DNT Utilstrækkelig 8,4 19,3 38,6 27,7 4,8 1, Mangelfuld 2,8 11,0 27,4 40,1 17,3 1, Jævn 1,0 4,2 16,8 39,0 31,7 6,8 0, God 0,3 0,9 6,6 25,0 38,6 23,3 4,9 0, Rigtig god 0,9 1,1 4,2 17,9 28,8 33,9 11,8 1, Fremragende 2,9 1,5 14,7 25,0 22,1 26,5 5,9 1, Samlet fordeling 1,1 3,3 12,1 29,3 32,3 17,5 3,9 0, TABEL 3.17 Sammenhæng mellem kriteriebaserede scores i afkodning i 8. klasse og kategorisering af læsefærdigheden ifølge PISA 2012 PISA-kategori <1b 1b 1a Total Kriteriebaseret skala, DNT Antal i rækken Utilstrækkelig 4,1 30,1 31,5 24,7 6,8 2, Mangelfuld 5,7 10,2 26,5 39,6 13,9 3,7 0, Jævn 1,0 9,6 29,4 36,0 20,8 3, God 0,7 2,0 9,8 28,3 34,6 19,6 4,5 0, Rigtig god Fremragende Samlet fordeling 1,1 3,4 12,1 29,3 32,3 17,6 4,0 0, Note: Pct. af rækkerne angivet. Tabellerne er baseret på testresultater fra elever, der har deltaget i både DNT og PISA PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM 25
26 Det er bemærkelsesværdigt, at der er nogle ganske få elever med gode eller endda fremragende præstationer i de nationale test, der slutter i PISA niveauer under 2 og at der også er elever med utilstrækkelige, mangelfulde eller jævne resultater i de nationale test, der slutter på niveau 4-5 i PISA. De inkonsistente resultater afspejler det ikke ukendte fænomen, at forløbene af pædagogiske test en gang i mellem kører af sporet for eleverne og fører til testresultater, der ikke afspejler elevernes egentlige niveau. Det er formodentlig det, der har været tilfældet for den ene elev, der havde en fremragende præstation i de nationale test, men som endte på niveau 1a i PISA (tabel 3.15). Den eneste fornuftige konklusion er her, at forløbet af PISA testen må være kørt skævt. Det er i den sammenhæng betryggende, at der er så få elever med inkonsistente resultater. Et resultat, der også kan tages som en gensidig validering af de nationale test og PISA. Selvom testresultaterne i sagens natur er usikre, er resultaterne konsistente for det meget store flertal af eleverne. FIGUR 3.18 Sammenhæng mellem kriteriebaserede scores i tal og algebra i 6. klasse og kategorisering af færdigheder i matematik ifølge PISA PISA-kategori Antal i Total Kriteriebaseret skala, rækken DNT Utilstrækkelig 82,8 13,8 3, Mangelfuld 57,1 28,4 10,8 3, Jævn 38,8 33,7 20,2 7, God 25,1 35,3 27,3 11,0 1, Rigtig god 10,6 20,3 26,8 30,1 12, Fremragende 4,5 18,2 18,2 22,7 31,8 4, Samlet fordeling 35,9 30,5 20,5 10,4 2,5 0, Note: Tabellen indeholder kun elever med sen skolestart. Pct. af rækkerne angivet. Således ses fordelingen af resultater i tal og algebra på PISAs kategorier inden for hver af de seks kriteriebaserede kategorier. 26 PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM
27 Tabel 3.15 er den indholdsmæssigt mest interessante måde at beskrive sammenhængen mellem de nationale test og PISA, selvom figur 3.13 og tabel 3.14 hver for sig er bedre, hvis det drejer sig om rene statistiske anvendelser af testresultaterne. I resten af dette afsnit vil det derfor være den form for tabeller, der vil blive anvendt til at beskrive sammenhængen mellem profilområder i de nationale test og testresultater fra PISA. Tabellerne vil stort set blive præsenteret uden kommentarer, idet vi forventer at læseren selv kan læse tabellerne og tolke indholdet. Tabel beskriver sammenhængen mellem DNT-resultater i tal og algebra, geometri og matematik i anvendelse og resultatet af PISAs matematiktest. Når man læser tabellerne, skal man være opmærksom på, at materialet kun omfatter elever, der deltog i de nationale test i 6. klasse i 2010 og TABEL 3.19 Sammenhæng mellem kriteriebaserede scores i geometri i 6. klasse og kategorisering af færdigheder i matematik ifølge PISA PISA-kategori Antal i Total Kriteriebaseret skala, rækken DNT Utilstrækkelig 85,7-14, Mangelfuld 58,7 32,2 6,7 2, Jævn 41,2 33,3 18,5 6,1 0, God 20,1 32,5 33,3 12,0 2, Rigtig god 15,5 25,2 25,2 26,5 7,1 0, Fremragende 4,0-24,0 44,0 28, Samlet fordeling 35,9 30,5 20,5 10,4 2,5 0, TABEL 3.20 Sammenhæng mellem kriteriebaserede scores i matematik i anvendelse i 6. klasse og kategorisering af færdigheder i matematik ifølge PISA PISA-kategori Antal i Total Kriteriebaseret skala, rækken DNT Utilstrækkelig 85,4 7,3 2,4 4, Mangelfuld 56,4 31,8 9,4 2, Jævn 35,8 32,8 25,9 5, God 20,2 34,1 27,7 16,0 2, Rigtig god 7,9 14,5 28,9 28,9 19, Fremragende 10,0 10,0-30,0 40,0 10, Samlet fordeling 35,9 30,5 20,5 10,4 2,5 0, Note: Sene skolestartere i begge tabeller. PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM 27
28 som derfor blev testet af PISA i 8. klasse. Dette forhold, og det, som det betyder for tolkningen af resultaterne, diskuteres i næste afsnit. Resultaterne i tabel udviser en høj grad af konsistens. Bemærk, at der ikke er nogen elever med utilstrækkelige eller mangelfulde præstationer i de nationale test, som to år senere dukker op i kategorierne 5 og 6 i PISA. I den anden ende, dvs. blandt elever med rigtig gode eller fremragende præstationer i 2010, kan konsistensen diskuteres, idet der er flere af disse elever, der to år senere findes i kategorierne 1 og 2 i PISA. Dette kunne i første omgang tages som udtryk for problemer med PISAs klassifikation af eleverne, men før man drager den konklusion, er der to forhold, der skal tages i betragtning. Det ene er den tidsmæssige forskel mellem resultaterne fra de nationale test og PISA. For de elever, der optræder i tabel , er denne forskel to år. I lyset af denne forskel er det næppe urealistisk at forestille sig, at der er en del af de dygtige elever i 2010, der er stået af matematikken i løbet af de to år der gik, inden de blev testet af PISA. Tallene i tabellerne er i hvert fald konsistente med en sådan konklusion. Den anden faktor har at gøre med, at de elever, der optræder i tabellerne er testet af PISA i 8. klasse, mens det store flertal af elever, som PISA testede i 2012 var elever i 9. klasse. Hvis PISAs test passer til elevpopulationen med opgaver, der er tilstrækkelig udfordrende for flertallet af eleverne, indebærer det, at PISAs test først og fremmest retter sig mod elever fra 9. klasse. Hvis dette er tilfældet, er det åbenlyst, at de elever, der blev testet i 8. klasse må komme til kort i forbindelse med opgaver, der dækker det pensum, som dækkes i 9. klasse. Dette forhold kan i sig selv forklare, at elever med gode resultater i de nationale test i 6. klasse har væsentligt dårligere resultater i PISA i Det er ikke muligt ud fra de foreliggende data at tage stilling til, om det er den ene eller måske begge faktorer, der er på spil, når dygtige elever fra 2010 præsterer dårligt i Det eneste, vi kan konkludere her, er, at de inkonsistente resultater ikke nødvendigvis er udtryk for problemer med PISAs matematiktest. 3.4 Effekt af sen skolestart og undervisning i 9. klasse Formålet med dette afsnit er at vise den effekt, som sen skolestart og undervisning i 9. klasse har på testresultaterne i læsning, og derefter at knytte nogle kommentarer til, hvorledes der vil blive taget højde for disse faktorer i forbindelse med analyserne af resultater i matematik. Det er velkendt, at der blandt elever med sen skolestart er elever, der starter sent pga. udviklingsmæssige eller indlæringsmæssige problemer. Selvom dette selvsagt ikke gælder alle elever med sen skolestart, forventer vi, at gruppen af elever med sen skolestart som gruppe betragtet klarer sig dårligere end elever med normal skolestart. Dette bekræftes af tabel 3.21, der viser de gennemsnitlige kriteriescores i de tre profilområder i læsning blandt elever med normal og sen skolestart. Alle forskellene er højsignifikante. 28 PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM
29 TABEL 3.21 Gennemsnitlige testresultater i læsning for elever med normal og sen skolestart Profilområde Sprog- forståelse Afkodning Tekst- forståelse Skolestart N Gns. Std. afvigelse Std. fejl Normal ,0 5,0 0,1 Sen ,6 5,8 0,2 Normal ,9 5,7 0,1 Sen ,1 7,4 0,2 Normal ,3 8,1 0,1 Sen ,2 9,0 0,2 Note: De gennemsnitlige testresultater er udtryk for scoren på de kriteriebaserede kategorier. Alle forskelle er højsignifikante. Tabellen er baseret på testresultater fra elever, der har deltaget i både DNT og PISA. Tabel viser fordelingerne i forhold til de kriteriebaserede kategorier for de tre profilområder. I forhold til forskellen på elever med normal og sen skolestart fortæller disse tabeller intet, som ikke kan læses i tabel 3.21, men tabellerne indeholder informationer om fordelingen af eleverne, som er af interesse i sig selv. Med hensyn til tekstforståelsen, der i forhold til læsning i PISA er det mest interessante af de tre profilområder, ses det bl.a. at 73 pct. af eleverne har præstationer, som de fagkyndige karakteriserer som gode eller bedre. Blandt eleverne med sen skolestart er det samme tal kun 58,2 pct. Udover at være statistisk højsignifikant er dette et udtryk for en særdeles markant forskel på læsefærdigheder blandt elever med normal og sen skolestart. TABEL 3.22 Sammenhæng mellem skolestart og de kriteriebaserede kategorier for sprogforståelse i 8. klasse Utilstrækkelig Mangelfuld Jævn God Rigtig god Fremragende Total Antal i rækken Normal skolestart 1,6 12,7 22,1 51,7 10,4 1, Sen skolestart 4,7 20,7 22,8 40,5 9,8 1, Alle elever 2,3 14,4 22,3 49,3 10,3 1, TABEL 3.23 Sammenhæng mellem skolestart og de kriteriebaserede kategorier for afkodning i 8. klasse Utilstrækkelig Mangelfuld Jævn God Rigtig god Fremragende Total Antal i rækken Normal skolestart 1,9 5,7 5,0 87, Sen skolestart 4,9 10,3 5,6 79, Alle elever 2,5 6,7 5,1 85, Note: Pct. af rækker angivet. PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM 29
30 Tendensen i tabel 3.25 er den samme som tendenserne i tabel , men beregninger af korrelationskoefficienter viser, at tendensen er stærkere i denne tabel end i tabellerne for profilområderne. Grunden til dette er det ekstra års undervisning i 9. klasse, som elever med normal skolestart har haft før de blev testet af PISA, ud over det faglige forspring, som de havde, da de blev DNT-testet i 8. klasse. I de analyser, der omtales i Kapitel 4, beregnes der et kvantitativt mål for denne effekt. Effekten skal først og fremmest bruges til senere forudsigelser af PISA-resultater, men den kan også bruges til at opjustere tabel 3.25 s tal for elever med sen skolestart til det, som man ville forvente, hvis de var blevet testet af PISA i 9. klasse. De justerede tal, der gennemsnitligt betyder et løft på 28 point på PISAskalaen, er vist i tabel Forskellen på elever med normal og sen skolestart er stadig tydelig, men svagere end i tabel TABEL 3.24 Sammenhæng mellem skolestart og de kriteriebaserede kategorier for tekstforståelse i 8. klasse Utilstrækkelig Mangelfuld Jævn God Rigtig god Fremragende Total Antal i rækken Normal skolestart 1,1 5,7 19,9 47,7 23,0 2,5 100, Sen skolestart 3,1 10,5 28,2 41,3 15,5 1,4 100, Alle elever 1,6 6,7 21,7 46,3 21,4 2,3 100, TABEL 3.25 Fordeling af elever med normal og sen skolestart mht. PISA kategorier i 2012 <1b 1b 1a Total Antal i rækken Normal skolestart 0,9 2,4 10,0 26,8 34,3 20,3 4,9 0, Sen skolestart 2,7 7,2 21,7 34,9 25,2 7,2 0,9 0, Alle elever 1,2 3,3 12,2 28,3 32,6 17,9 4,1 0, TABEL 3.26 Fordeling af elever med normal og sen skolestart mht. PISA kategorier i 2012 korrigeret for manglende undervisning <1b 1b 1a Total Antal i rækken Normal skolestart 0,9 2,4 10,0 26,8 34,3 20,3 4,9 0, Sen skolestart 2,1 3,8 14,0 30,2 36,4 11,2 1,8 0, Alle elever 1,1 2,7 10,7 27,5 34,7 18,6 4,3 0, Note: Pct. af rækker angivet. Forskellen på observationer i tabel 3.24, og de i tabel 3.25 og 3.26 skyldes, at matematik var i fokus i 2012, og det derfor ikke er alle, som har et resultat i læsning fra PISA. I tabel 3.26 er resultaterne for eleverne med sen skolestart korrigeret til det niveau, man ville forvente, hvis de havde modtaget samme mængde undervisning som elever, der har haft en normal skolestart. Beregningerne der ligger til grund for korrektionen, præsenteres i kapitel PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM
31 Kapitel 4 beregner effekten af undervisningen i 9. klasse på to forskellige måder, der giver stort set samme resultat. I forbindelse med resultaterne i matematik, kan effekten kun beregnes på den ene måde, fordi der mangler matematikresultater for de nationale test i 6. klasse for elever med normal skolestart. Dette resultat, der først og fremmest har en rolle at spille i den statistiske model, kan også bruges til at beregne skønsmæssige tal for hvorledes PISA-resultaterne vil fordele sig i forhold til resultaterne i matematik i 6. klasse, for elever der testes af PISA i 9. klasse. Dvs. hvorledes resultaterne kan forventes at fordele sig, hvis der er tale om elever med normal skolestart, eller hvis eleverne med sen skolestart var blevet testet af PISA i 9. klasse i stedet for 8. klasse. Disse fordelinger vises i tabel Tallene i disse tabeller skal sammenlignes med tallene i tabel , der viser de samme tendenser for elever med sen skolestart uden undervisning i 9. klasse før PISA. FIGUR 3.27 Sammenhæng mellem kriteriebaserede scores i tal og algebra i 6. klasse og kategorisering af færdigheder i matematik ifølge PISA 2012 efter justering for undervisning i 9. klasse PISA kategori i 9. klasse kriteriebaseret kategori, tal og algebra Total Utilstrækkelig 75,9 13,8 10, Mangelfuld 39,9 36,9 17,2 4,9 1,1-100 Jævn 24,4 33,7 28,7 11,2 1,9-100 God 16,0 29,5 31,7 19,6 3,3-100 Rigtig god 7,3 12,2 25,2 35,8 18,7 0,8 100 Fremragende 4,5 9,1 22,7 27,3 27,3 9,1 100 Samlet fordeling 24,5 29,5 25,8 15,3 4,6 0,3 100 Note: Pct. af rækker angivet. PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM 31
32 TABEL 3.28 Sammenhæng mellem kriteriebaserede scores i geometri i 6. klasse og kategorisering af færdigheder i matematik ifølge PISA 2012 efter justering for undervisning i 9. klasse. PISA kategori i 9. klasse Kriteriebaseret kategori, Geometri Total Utilstrækkelig 57,1 28,6 7,1 7,1-100 Mangelfuld 46,6 33,7 15,4 3,8 0,5 100 Jævn 26,7 37,2 23,7 10,1 2,3 100 God 11,1 23,2 41,9 18,8 4,7 100 Rigtig god 9,0 16,8 25,2 36,1 11,6 1,3 100 Fremragende 4,0-12,0 44,0 36,0 4,0 100 Samlet fordeling 24,5 29,5 25,8 15,3 4,6 0,3 100 TABEL 3.29 Sammenhæng mellem kriteriebaserede scores i matematik i anvendelse i 6. klasse og kategorisering af færdigheder i matematik ifølge PISA 2012 efter justering for undervisning i 9. klasse. PISA kategori i 9. klasse Kriteriebaseret kategori, Matematik i anvendelse Total Utilstrækkelig 75,6 12,2 7,3 4, Mangelfuld 38,8 37,9 19,1 3,6 0,6-100 Jævn 22,9 32,3 35,3 8,5 1,0-100 God 12,8 27,2 29,9 24,4 5,7-100 Rigtig god 3,9 10,5 19,7 39,5 25,0 1,3 100 Fremragende - 10,0 10,0 30,0 30,0 20,0 100 Samlet fordeling 24,5 29,5 25,8 15,3 4,6 0,3 100 Note: Pct. af rækker angivet. 32 PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM
33 3.5 Effekt af køn og etnicitet på testresultater i dansk og matematik Tabellerne i dette afsnit viser fordelingen af resultater for drenge og piger, og for elever med dansk og ikke-dansk baggrund i forhold til de nationale test kriteriebaserede kategorier samt PISAs kategoriseringer. Det er velkendt, at både køn og herkomst har betydning for testresultater i dansk og matematik. Det er derfor ingen overraskelse at dette også ses i DNT- og PISA-data. Kønsforskellene er mindre markante. Piger læser ikke overraskende bedre end drengene, men forskellen drejer sig først og fremmest om forskelle i tekstforståelse. I forbindelse med matematik er det ikke muligt ud fra det foreliggende materiale at sige noget om, hvorledes elevpopulationen som helhed er fordelt, og derfor heller ikke om danske elever er tæt på eller langt fra skolereformens mål. For så vidt angår matematikken, bekræfter tabellerne i øvrigt, at drenge er bedre til matematik end piger. Forskellen på danske elever og elever med en anden baggrund er markant. I forbindelse med PISA 2012 blev elever med en ikke-dansk baggrund oversamplet. Af denne grund vil tabeller, der ikke skelner mellem danske elever og elever med en anden etnisk baggrund, tegne et skævt bilede af fordelingen af danske folkeskoleelevers færdigheder. Hvis eleverne stratificeres med hensyn til etnisk baggrund kan man under forudsætning af at udvalget af elever til PISA består af et repræsentativt udvalg af danske elever udtale os om fordelingen af læsefærdigheder blandt danske elever i 8. klasse. Tabel 3.30 til 3.33 viser, at de danske elever halter lidt bagud i sprogforståelse med hensyn til skolereformens mål, der sigter mod at 80 pct. af eleverne skal være gode læsere, når der anvendes den foreløbige kriteriebaserede kategorisering. De danske elever er til gengæld langt over dette mål med hensyn til afkodning, og de er der næsten med hensyn til tekstforståelsen, hvor 78.5 pct. er gode læsere. Elever med en ikke-dansk baggrund, er der også med hensyn til afkodning i 8. klasse, men de hænger langt bagud i forhold til både sprog- og tekstforståelse. PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM 33
34 TABEL 3.30 Fordeling af testresultater i sprogforståelse i 8. klasse i forhold til køn og etnisk baggrund Utilstrækkelig Mangelfuld Jævn God Rigtig god Fremragende Total Dreng Pige Total Ikke-etnisk dansker 4,7 23,2 29,2 32,4 7,8 2,7 100 Etnisk dansker 0,8 8,1 20,1 56,5 13,3 1,3 100 Total 1,7 11,8 22,3 50,5 11,9 1,6 100 Ikke-etnisk dansker 6,6 26,8 27,1 29,9 7,8 1,9 100 Etnisk dansker 0,6 9,5 19,6 58,5 10,3 1,5 100 Total 2,2 14,3 21,7 50,6 9,6 1,6 100 Ikke-etnisk dansker 5,7 25,1 28,1 31,0 7,8 2,3 100 Etnisk dansker 0,7 8,8 19,8 57,5 11,8 1,4 100 TABEL 3.31 Fordeling af testresultater i afkodning i 8. klasse i forhold til køn og etnisk baggrund Utilstrækkelig Mangelfuld Jævn God Rigtig god Fremragende Total Dreng Pige Total Ikke-etnisk dansker 2,7 10,5 8,2 78, Etnisk dansker 2,0 4,9 3,7 89, Total 2,2 6,3 4,8 86, Ikke-etnisk dansker 3,1 10,2 6,4 80, Etnisk dansker 0,7 3,7 4,0 91, Total 1,3 5,5 4,7 88, Ikke-etnisk dansker 2,9 10,3 7,2 79, Etnisk dansker 1,3 4,3 3,8 90, Note: Pct. af rækker angivet. Sene skolestartere N= 34 PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM
35 TABEL 3.32 Procentvis fordeling af testresultater i tekstforståelse i 8. klasse i forhold til køn og etnisk baggrund Utilstrækkelig Mangelfuld Jævn God Rigtig god Fremragende Total Dreng Pige Total Ikke-etnisk dansker 2,3 12,3 33,1 42,9 9,4 100 Etnisk dansker 1,3 4,6 17,2 48,1 26,6 2,3 100 Total 1,5 6,5 21,1 46,8 22,3 1,7 100 Ikke-etnisk dansker 0,5 10,7 31,4 44,7 12,1 0,5 100 Etnisk dansker 0,2 3,2 16,6 48,4 27,6 3,9 100 Total 0,3 5,3 20,7 47,4 23,3 3,0 100 Ikke-etnisk dansker 1,4 11,5 32,2 43,9 10,8 0,3 100 Etnisk dansker 0,7 3,9 16,9 48,3 27,1 3,1 100 TABEL 3.33 Procentvis fordeling af læsefærdighed ifølge PISA 2012 <1b 1b 1a Total Dreng Pige Total Ikke-etnisk dansker 4,9 6,6 24,6 37,0 20,7 5,7 0,5 100 Etnisk dansker 0,7 2,9 11,4 29,4 34,9 17,1 3,0 0,7 100 Total 1,7 3,8 14,6 31,3 31,5 14,3 2,4 0,5 100 Ikke-etnisk dansker 2,1 6,3 18,3 34,0 27,4 9,8 2,2 100 Etnisk dansker 0,2 1,5 6,5 22,2 36,1 25,8 7,3 0,4 100 Total 0,7 2,8 9,8 25,5 33,7 21,3 5,9 0,3 100 Ikke-etnisk dansker 3,3 6,5 21,2 35,3 24,3 7,9 1,4 100 Etnisk dansker 0,4 2,2 9,0 25,9 35,5 21,4 5,1 0,5 100 Note: Pct. af rækker angivet. Sene skolestartere. PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM 35
36 TABEL 3.34 Procentvis fordeling af testresultater i tal og algebra i 6. klasse for elever med sen skolestart Utilstrækkelig Mangelfuld Jævn God Rigtig god Fremragende Total Dreng Pige Total Ikke-etnisk dansker 3,3 26,3 25,8 33 9,1 2,4 100 Etnisk dansker 0,7 22,6 23,4 36,7 13,9 2,8 100 Total 1,5 23,7 24,2 35,5 12,4 2,7 100 Ikke-etnisk dansker 7,5 32,9 21,4 31,2 5,8 1,2 100 Etnisk dansker 2,7 23,5 26,5 32,3 13,7 1,3 100 Total 4,8 27,6 24,3 31,8 10,3 1,3 100 Ikke-etnisk dansker 5,2 29,3 23,8 32,2 7,6 1,8 100 Etnisk dansker 1,3 22,9 24,5 35,2 13,8 2,3 100 TABEL 3.35 Procentvis fordeling af testresultater i geometri i 6. klasse for elever med sen skolestart Utilstrækkelig Mangelfuld Jævn God Rigtig god Fremragende Total Dreng Pige Total Ikke-etnisk dansker 2,4 27,3 44,5 13,4 11,0 1,4 100 Etnisk dansker 0,9 12,6 38,6 25,4 18,7 3,9 100 Total 1,3 17,2 40,4 21,6 16,3 3,1 100 Ikke-etnisk dansker 1,7 36,4 38,2 16,2 6,9 0,6 100 Etnisk dansker 1,3 13,7 39,8 27,9 15,5 1,8 100 Total 1,5 23,6 39,1 22,8 11,8 1,3 100 Ikke-etnisk dansker 2,1 31,4 41,6 14,7 9,2 1,0 100 Etnisk dansker 1,0 13,0 39,0 26,2 17,6 3,2 100 Note: Pct. af rækker angivet. Sene skolestartere. 36 PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM
37 TABEL 3.36 Procentvis fordeling af testresultater i matematik i anvendelse i 6. klasse for elever med sen skolestart Dreng Pige Total Utilstrækkelig Mangelfuld Jævn God Rigtig god Fremragende Total Ikke-etnisk dansker 3,3 37,3 19,1 34,4 5,7 100 Etnisk dansker 3,5 23,2 17,6 43,2 10,4 2,2 100 Total 3,4 27,6 18,1 40,4 9 1,5 100 Ikke-etnisk dansker 7,5 43,4 20,8 25,4 2,9 100 Etnisk dansker 2,7 31,4 19,9 40,7 5,3 100 Total 4,8 36,6 20,3 34,1 4,3 100 Ikke-etnisk dansker 5,2 40,1 19,9 30,4 4,5 100 Etnisk dansker 3,2 25,9 18,3 42,4 8,7 1,5 100 TABEL 3.37 Procentvis fordeling af testresultater i matematik i PISA Total Ikke-etnisk dansker 34,4 35,8 19,6 7,7 2,4 0,2 100 Dreng Etnisk dansker 12,4 22,9 31,3 22,1 9,6 1,7 100 Total 18 26,2 28,3 18,5 7,7 1,3 100 Ikke-etnisk dansker 43,3 30,1 16,8 7,7 2 0,2 100 Pige Etnisk dansker 14,9 25, ,3 9,3 1,2 100 Total 22,6 26,6 26,4 16,2 7, Total Ikke-etnisk dansker 39 32,8 18,1 7,7 2,1 0,2 100 Etnisk dansker 13,6 24,1 30,7 20,7 9,4 1,5 100 Note: Sene skolestartere. PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM 37
38 3.6 Socioøkonomisk niveau Figur 3.38 og 3.40 viser sammenhængen mellem elevernes socioøkonomiske baggrund og resultater i tekstforståelse i de nationale test og læsning i PISA. Tendenserne er svage, men tydelige og bemærkelsesværdigt ens. Dette bekræftes af de korrelationskoefficienter, som kan ses i tabel 3.39, som også viser, at effekten af det socioøkonomiske niveau er en anelse stærkere relateret til matematikresultater fra PISA end til profilområderne i matematik i de nationale test. FIGUR 3.38 Sammenhæng mellem socioøkonomisk niveau og kriteriebaseret score i tekstforståelse i 8. klasse 38 PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM
39 FIGUR 3.39 Oversigt over korrelationen mellem socioøkonomisk status og testresultater i de nationale test og PISA. Profilområde Korrelation Sprogforståelse 8. klasse 0,30 Afkodning 8. klasse 0,25 Tekstforståelse 8. klasse 0,33 PISA læsning 0,34 Tal og algebra 6. klasse elever med sen skolestart Geometri 6. klasse elever med sen skolestart Matematik i anvendelse 6. klasse elever med sen skolestart 0,23 0,28 0,25 Det socioøkonomiske niveau har rutinemæssigt været inddraget i de analyser, der har ført til den statistiske model, der beskrives i Kapitel 4. Disse analyser bekræfter at socioøkonomisk niveau har en effekt på PISA-resultaterne, selvom der tages højde for den effekt, som det socioøkonomiske niveau har haft på resultaterne i de nationale test. Analyserne viser imidlertid også at den statistiske forklaringskraft af det socioøkonomiske indeks er særdeles beskeden, og at man derfor kan undlade at inddrage socioøkonomisk status i beregningerne uden at det forringer resultaterne nævneværdigt. PISA 2012 læsning elever med sen skolestart 0,33 Note: Alle testresultater er målt på logit-skalaen. Bemærk, at det såkaldte ESCS indeks, der beskriver det socioøkonomiske niveau, er defineret af PISA i Da resultaterne i matematik i 6. klasse stammer fra 2010, dvs. to år før PISA, må man forvente, at korrelationerne mellem profilområderne i matematik og indekset vil være en smule svagere end korrelationen mellem PISAs test i matematik og indekset. Ud fra denne betragtning kan der ikke formuleres nogen konklusioner, der antyder, at socioøkonomisk niveau er stærkere relateret til resultater fra den ene af de to test. Socioøkonomisk niveau er tydeligt, men svagt korreleret med begge former for test. 12 Jf. Egelund (red) (2013). PISA 2012 danske unge i en international sammenligning. KORA, København. Publikationen, der kan hentes fra hjemmesiden indeholder dokumentation for den danske del af PISA samt referencer til andre publikationer med oplysninger om PISA. PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM 39
40 FIGUR 3.40 Figur 3.6. Sammenhæng mellem socioøkonomisk niveau og PISA score i læsning i PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM
41 4 Analyse af data vedrørende læsning 4.1 Den prædiktive model Dette kapitel beskriver de analyser, der er foretaget for at undersøge om, og i givet fald på hvilken måde, DNT-resultaterne i læsning kan prædiktere senere PISA resultater i de samme fag. Analyserne er baseret på lineære regressionsanalyser, hvor PISAresultatet optræder som den afhængige variabel, og hvor DNT-resultater og forskellige baggrundsvariable inddrages som uafhængige variable. I samtlige analyser er testresultaterne fra både PISA og DNT målt på Rasch modellens logit-skala 13. Analyserne kunne ikke påvise nogen effekt af elevernes alder på PISA-resultatet, når der tages højde for den betydning, som alderen allerede har haft for DNT-resultaterne. For alle andre baggrundsvariable køn, herkomst, normal eller sen skolegang og socioøkonomisk status kunne der derimod påvises en direkte effekt på PISA-resultatet. Disse variable har naturligvis også betydning for DNT-resultaterne, men denne effekt kan altså ikke fuldstændig forklare den effekt, som disse variable har på PISA resultatet. Analysen kunne heller ikke påvise nogen interaktion mellem effekterne af de uafhængige variable. Effekten af DNT-resultaterne er med andre ord den samme for drenge og piger, for elever med normal eller sen skolestart, for elever med dansk eller ikkedansk etnisk baggrund og for elever fra familier med høj eller lav socioøkonomisk status. Slutresultatet er derfor, at PISA-resultatet kan forudsiges ved hjælp af en relativt enkel lineær regressionsmodel. både hver for sig og samlet. De tre første modeller inddrager kun et enkelt profilområde. Af disse, har tekstforståelsen en klart bedre forklaringsgrad end de to andre profilområder. Model 4 inddrager alle tre profilområder. Det forbedrer forklaringsgraden, men det er værd at bemærke, at forklaringsgraden ikke er væsentligt forbedret i forhold til Model 3, hvor der kun tages højde for tekstforståelsen. Model 5 tilføjer socioøkonomisk status. Effekten af denne variabel er højsignifikant, men variablen bidrager ikke til at forbedre forklaringsgraden. Af de tre baggrundsvariable er det spørgsmålene om elevens herkomst og skolestarten (normal eller sen), som har den væsentligste betydning, mens effekten af køn er svagere. Det er dog bemærkelsesværdigt, at effekten af den etniske baggrund reduceres væsentligt, når den socioøkonomiske status inddrages sammen med de øvrige variable. Dette forklarer to ting: For det første, at en stor del af forskellen på danske elever og elever med anden etnisk baggrund skyldes socioøkonomisk status. Og for det andet, at årsagen til, at den socioøkonomiske status ikke bidrager væsentligt til forklaringsgraden, er, at der allerede er taget højde for en del af den socioøkonomiske faktor i model 4 i og med at denne model tager højde for elevernes etniske baggrund. Endelig er ESCS-variablen et udtryk for den socioøkonomiske og kulturelle status på det tidspunkt, hvor eleverne deltager i PISA undersøgelsen, og således ikke noget der findes data for på tidspunktet for DNT. Tabel 4.1 viser parametrene for fem regressionsmodeller, hvor der ud over de nævnte baggrundsvariable tages højde for de enkelte profilområder 13 Jf. Appendiks A-C. PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM 41
42 I lyset af disse resultater er det Model 4, der er det naturlige valg, hvis man ønsker at prædiktere PISAresultater i læsning ud fra tidligere DNT-resultater i læsning i 8. klasse. Ifølge denne model skal det forventede PISA-resultat beregnes som PISA logit = 0, ,119 S + 0,099 A + 0,438 T 0,180 D 0,282 E + 0,350 N Den forventede PISA-logit kan betragtes som et estimat af den samme PISA-logit, som ellers estimeres ud fra svarene på opgaverne i PISAs test. Set ud fra denne synsvinkel er standardfejlen på målingen (dvs. SEM) lig med 0,84. I forbindelse med målinger af elevers færdigheder på Rasch modellens logit-skala er en standardfejl af denne størrelse større end hvad der er tilfredsstillende. Prædiktionerne kan altså ikke erstatte egentlige test. For at sætte denne usikkerhed i perspektiv bemærkes det, at standardfejlene på de målinger, som man kan beregne ud fra svarene på PISAs opgaver, i gennemsnit er lig med 0,64 (jf. Appendiks B). 4.2 Tolkning af effektparametrene Det er erfaringsmæssigt vanskeligt at tolke betydningen af effekt-parametrene i prædiktionsmodellen, fordi de refererer til forskelle på den abstrakte logit-skala. Det er således naturligt at spørge om TABEL 4.1 Fem forskellige regressionsmodeller for resultatet i PISA læsning Uafhængig variabel Model 1 Model 2 Model 3 Model 4 Model 5 Konstant -0,105-1,192-0,400-0,745-0,762 Sprogforståelse (S) Afkodning (A) Tekstforståelse (T) Køn (dreng) (D) Anden herkomst (E) Normal skolestart (N) ESCS 0,449 (0,015) -0,273 (0,030) -0,449 (0,035) 0,422 (0,039) 0,328 (0,010) -0,210 (0,029) -0,452 (0,034) 0,427 (0,038) 0,583 (0,013) -0,161 (0,027) -0,329 (0,032) 0,357 (0,035) 0,119 (0,016) 0,099 (0,012) 0,438 (0,017) -0,180 (0,027) -0,282 (0,031) 0,350 (0,034) 0,114 (0,017) 0,103 (0,012) 0,413 (0,017) -0,182 (0,027) -0,180 (0,033) 0,333 (0,035) 0,109 (0,016) R 2 0,289 0,304 0,419 0,442 0,442 SEM 0,953 0,943 0,861 0,845 0,834 Note: Standardfejl på parameterestimaterne l i parentes. SEM er modellens standardafvigelsen omkring det forventede PISA resultat på logit-skalaen. 42 PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM
43 herkomsten har en stærk eller svag effekt på de senere PISA-resultater, men vanskeligt at svare på ud fra tallet på -0,282, hvis man ikke har nogen erfaringer med tal på logit-skalaen. At det er vanskeligt betyder dog ikke, at det er umuligt. For at se hvordan, skal man forestille sig to elever med forskellig herkomst, men med det samme køn, den samme skolestart, og de samme DNT-resultater. Under disse forudsætninger, forventes eleven med dansk herkomst at ligge 0,282 logit-point over eleven med fremmed herkomst, når de testes af PISA. Denne logit-forskel kan omregnes til en forskel på PISA-skalaen på ca. 19 point 14. Hvis man har en fornemmelse for værdierne på PISAs skala vil man derfor også have en fornemmelse for, hvad det er modellen siger om betydningen af herkomsten. Hvis man ikke har en fornemmelse for PISA-værdier hjælper det naturligvis heller ikke. I sådanne tilfælde kan man i stedet forsøge at fortolke effekten i form af et mål for relativ effekt, der angiver forholdet mellem to elevers sandsynligheder for at svare korrekt på opgaverne i pædagogiske test. Det, som man skal huske er, at der aldrig er 100 pct. garanti for at en meget dygtig elev svarer rigtigt på en let opgave. Der vil selvfølgelig være en meget stor sandsynlighed for et korrekt svar, men noget kan jo gå galt. Tilsvarende betragtninger gælder for alle elever og opgaver, fordi Rasch modellen kun postulerer, at der er en vis sandsynlighed for et korrekt svar, og at denne sandsynlighed afhænger af hvor dygtig eleven er samt hvor vanskelig opgaven er. Betragt igen de to elever fra før, hvor alt er lige bortset fra herkomsten. Da de to elever er forskellige, har de hver deres sandsynligheder for at svare korrekt på PISA-opgaverne, men forholdet mellem sandsynlighederne kan kun have noget at gøre med herkomsten, fordi alt andet ellers er lige. Som konsekvens af det, kan man definere den relative effekt af herkomsten som forholdet mellem sandsynligheden for, at den dygtigste elev svarer korrekt på en passende valgt opgave og sandsynligheden for, at den mindre dygtige elev svarer korrekt på opgaven. Hvis dette forhold er stort er der en stærk effekt, hvis det er lille er effekten beskeden. Målet for de relative effekter er nærmere beskrevet i Appendiks A, som også indeholder tabeller, som man kan bruge, hvis man vil omsætte logit forskelle til disse effekter. I denne tabel kan man aflæse, at en logit-forskel på 0,28 svarer til en relativ effekt på 1,15. En dansk elev har altså 15 pct. større chance for at svare rigtigt på en testopgave end en elev med en anden familiemæssig baggrund (svarende til ca. 4 flere korrekte svar i en test med 25 opgaver), selvom denne elev har det samme køn, den samme skolestart, og præcis de samme testresultater i DNT. De samme tolkninger kan lægges ned over effektparametrene for køn og skolestart. Effekten af køn svarer til at piger alt andet lige forventes at score 12 PISA-point højere end drenge og at den relative effekt er lig med 1,09. Effekten af skolestarten betyder at en elev med normal skolestart og derfor undervisning i 9. klasse alt andet lige forventes at ligge 24 PISA-point over eleven med sen skolestart, som testes af PISA i 8. klasse. Den relative effekt er i dette tilfælde lig med 1,19 svarende til fem ekstra korrekte svar på 25 opgaver. 14 Jf. afsnit 4.4 og Appendiks D. PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM 43
44 Effekten af de kontinuerte DNT-resultater kan ikke umiddelbart vurderes på denne måde. For at gøre effekten af disse variable sammenlignelige med effekter af de andre variable, starter man derfor med at undersøge, hvor stor forskel, der kan forventes at være på DNT-logit værdierne fra to tilfældigt udvalgte elever, hvorefter man beregne PISA-forskelle og relative effekter for sådanne typiske forskelle på eleverne. Disse beregninger afslører, at tekstforståelsen er den helt dominerende faktor i forbindelse med prædiktionen af læsefærdigheder i PISA. Alt andet lige dvs. hvis der kun er forskelle på DNTresultatet for tekstforståelse og hvis DNT-resultatet ikke afhang af de andre faktorer, forventes den elev, der har det bedste resultat i tekstforståelse at komme til at ligge 71 PISA point over eleven med det dårligste resultat i tekstforståelse. Det svarer til en relativ effekt på 1,68. De tilsvarende relative effekter for sprogforståelse og afkodning er henholdsvis 1,06 og 1,08, der angiver forskellen mellem de forventede og observerede PISA-logits. Hvis modellens antagelser om normalfordelingen er realistisk skal residualerne også være normalfordelte. Figur 4.2 viser fordelingen af residualerne for model 4. Det fremgår tydeligt, at der er næsten perfekt tilpasning mellem regressionsmodellens antagelser og de observerede data. Prædiktionsmodellen kan derfor bruges til beregning af forventede resultater på både individ- og gruppeniveau. FIGUR 4.2 Fordeling af residualer for model 4 (tabel 7) 4.3 Prædiktioner på gruppeniveau Den lineære regressionsmodel forudsætter at fordelingen af PISA-resultatet er betinget normal givet værdierne af de uafhængige variable. Den forventede PISA-logit er det bedste bud på, hvor de enkelte elever vil placere sig i PISA ud fra DNT-resultaterne og værdierne af baggrundsvariablene. Hvis man, udover at forudsige PISA resultater for enkelte elever, har i sinde at benytte modellen til at forudsige fordelingen af PISA resultater for en større gruppe af elever, er man nødt til at tage højde for hvordan resultaterne kan variere omkring de forventede værdier. Denne fordeling kan også estimeres ud fra modellen, men det forudsætter, at antagelsen om normalfordelingen er realistisk og mere end en bekvemmelighedsantagelse. For at kontrollere at dette er tilfældet, skal man se på fordelingen af de såkaldte residualer Note: Hver søjle dækker over et interval på 0,25 på logit-skalaen. Da formlen for de forventede logit-værdier er beregnet til forudsigelser på individ-niveau vil fordelingen af de forventede værdier for alle elever tegne et billede af en fordeling med en alt for lille spredning i forhold til den sande fordeling i gruppen. Dette er illustreret i figur 4.3 og figur 4.4. Figur 4.3 viser fordelingen af de observerede PISA-logits for alle de elever, der både deltog i DNT og PISA. Figur 4.4 viser fordelingen af de logit-værdier, som modellen forventer ud fra oplysningerne om DNT-resultaterne og værdierne af de forskellige baggrundsvariable. 44 PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM
45 De to fordelinger ligner hinanden og har den samme middelværdi på 0,28, men spredningen af de observerede værdier (standard afvigelse = 1,13) er åbenlyst større end spredningen af de forventede værdier (standard afvigelse = 0,75). Det er vigtigt at holde fast på, at forskellen på fordelingerne i figur 4.3 og 4.4 ikke er et udtryk for, at der er noget galt med prædiktionsfordelingen. Det er et udtryk for, at forudsigelser på individniveau og gruppeniveau er to forskellige ting. På individniveau giver modellen det bedst mulige bud på, hvor man kan forvente at elevens PISA-resultater vil ligge. Hvis man ønsker at sige noget om en større gruppe af FIGUR 4.3 Fordeling af observerede logit-værdier for læsning FIGUR 4.4 Fordeling af forventede PISA-logits for læsning Note: Note: Hver søjle dækker over et interval på 0,25 på logit-skalaen. PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM 45
46 elever, er man imidlertid nødt til at tage højde for, at der er en høj grad af tilfældighed, som også vil spille ind. En elev der har en forventet PISA-logit på 0,6 vil f.eks. med 5 pct. risiko ende med en logit-værdi, der er mindre end 0,6-1,96 0,845 = -1,06 eller større end 0,6-1,96 0,845 = 2,26, fordi afvigelsen fra den forventede værdi vil følge en normalfordeling med middelværdi 0 og standardafvigelse 0,845. Selvom disse afvigelser er relativt usandsynlige, så vil de iflg. sandsynlighedsregningens love forekomme, når der er tale om større grupper af elever. Og disse afvigelser skal naturligvis regnes med, når det er fordelingen af logit-værdierne og ikke de enkelte logit-værdier, man er interesserede i. FIGUR 4.5 Den forventede fordeling af PISA-logits for læsning derefter kortlægge fordelingen af de tal 15, som man er kommet frem til. Figur 4.5 viser resultatet. Man kan stadig se forskelle på den observerede fordeling og fordelingen af de tilfældige logit-værdier, hvilket også er at forvente, fordi der er tilfældighed på spil i både de observerede og de beregnede tal, men fordelingen i figur 4.5 har en middelværdi på 0,29 og en standard afvigelse på 1,03 og passer væsentlig bedre til fordelingen i figur Formidling af resultater Præsentationen af resultaterne må afhænge af formålet. Det er modellens forudsætning, at alle modelberegningerne foregår på logit-niveau, men man kan efterfølgende omregne både DNT- og PISA-logits til værdier på de skalaer, som man foretrækker. Omregning af DNT-resultater til percentil-værdier og normbaserede kategorier eller kriteriebaserede scores eller kategorier ligger allerede implementeret i de nationale test. Omregningen fra PISA-logits til PISA-scores er beskrevet i Appendiks D. Den forventede PISA-score svarende til en bestemt PISAlogit er lig med PISA score = 515, ,185 Pisa logit 2,155 (Pisa logit ) 2 Note: Hver søjle dækker over et interval på 0,25 på logit-skalaen. Dette kan gøres på flere forskellige måder. En enkel metode, som vil fungere fint, hvis der er tale om større grupper, vil være at lægge et tilfældigt tal fra den nævnte normalfordeling med middelværdi 0 og standardafvigelse 0,845 til den forventede værdi, og 15 PISA ville formodentlig kalde sådanne tal for plausible værdier, men terminologien er misvisende, fordi disse tal netop ikke er specielt plausible på individniveau. Men uanset, hvad man har lyst til at kalde dem, så fungere tingene på gruppeniveau, hvor man får et plausibelt billede af fordelingen. 46 PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM
47 FIGUR 4.6 Sammenhæng mellem DNT-resultater i tekstforståelse og forventede resultater af PISAs læsetest (model 4) beskrevet på seks forskellige måder Note: De forventede PISA-værdier måles som logit-værdier i søjlen til venstre og som værdier på PISAs skala i søjlen til højre. I den øverste række vises testresultater i tekstforståelse i form af logits, i den midterste i form af percentil-værdier og i den nederste i form af kriteriebaserede scores. PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM 47
48 Da DNT- og PISA-resultater kan måles på henholdsvis tre og to forskellige skalaer kan man plotte PISA-resultater i forhold til DNT-resultater på mange forskellige måder. Dette er for eksemplets skyld illustreret for DNT-resultaterne i tekstforståelse og de forventede PISA-resultater (baseret på den foretrukne model 4) i læsning i figur 4.6 og tabel 4.7 og 4.8, hvor en og samme sammenhæng vises på otte forskellige måder. Valget af tekstforståelse skyldes, at det er tekstforståelsen, der fortæller mest om det forventede PISA-resultat. Bemærk, at der til hvert resultat af tekstforståelsen findes flere forskellige forventede PISA-resultater. Det skyldes effekten af baggrundsvariablene og de andre profilområder. Det er dog tydeligt på trods af effekten af de andre variable at relationen på logit-niveau er lineær og at brugen af de andre skalaer fører til ikke-lineære sammenhænge. Figur 4.5 og tabellerne 4.7 og 4.8 blev vist for at illustrere, hvor mange forskellige måder resultaterne af modelberegningerne kan præsenteres på. Hvad man til syvende og sidst beslutter sig til at bruge, må afhænge af formålet. Der er næppe en måde, der vil være formålstjenlig til samtlige formål. Som afslutning på dette afsnit viser tabel 4.9, hvorledes sammenhængen mellem tekstforståelsen og TABEL 4.7 Sammenhæng mellem kriteriebaserede resultater i tekstforståelse og forventede PISA-resultater i læsning PISA-kategori Antal i <1b 1b 1a Total rækken Kriteriebaseret skala, DNT Utilstrækkelig 28,9 55,3 15, Mangelfuld 0,8 17,5 69,9 11, Jævn - 0,2 22,1 76,0 1, God - - 1,0 41,7 57,2 0, Rigtig god ,6 72,5 25, Fremragende ,1 92,8 5, Samlet fordeling 0,3 1,6 9,4 36,6 43,9 8,1 0, TABEL 4.8 Sammenhæng mellem normbaserede resultater i tekstforståelse og forventede PISA-resultater i læsning PISA-kategori Antal i <1b 1b 1a Total rækken Normbaseret skala, DNT op til 10 pct. 3,4 17,2 60,6 18, pct. - 0,1 14,6 81,0 4, pct ,5 45,6 53,8 0, pct ,2 89,3 3, pct. og derover ,8 64,1 1, Samlet fordeling 0,3 1,6 9,4 36,6 43,9 8,1 0, PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM
49 de forventede PISA-resultater i læsning ville se ud, hvis eleverne med sen skolestart var blevet testet af PISA i 9. i stedet for 8. klasse. Tabellen skal sammenlignes med tabel 4.7. Forskydningerne i forhold til det, som tabel 4.7 forventer, er tydelige i begge ender af læse-skalaen. Hvor meget forskydningerne betyder, er et læsefagligt spørgsmål, som denne beregning ikke kan besvare. TABEL 4.9 Sammenhæng mellem kriteriebaserede resultater i tekstforståelse og de forventede PISA-resultater i læsning, hvis elever med sen skolestart var blevet testet af PISA i 9. i stedet for 8. klasse. PISA-kategori Antal i <1b 1b 1a Total rækken Kriteriebaseret skala, DNT Utilstrækkelig 7,9 71,1 21, Mangelfuld - 11,4 70,3 18, Jævn ,4 84,5 2, God - - 0,1 37,0 62,7 0, Rigtig god ,6 69,8 29, Fremragende ,8 6, Samlet fordeling 0,1 1,3 7,2 36,3 45,9 9,0 0, PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM 49
50 4.5 Effekt af alder og et ekstra skoleår PISA tester elever på et bestemt alderstrin, men på forskellige klassetrin. De fleste af de elever, der deltager i PISA-undersøgelser vil gå i 9. klasse på det tidspunkt, de bliver testet af PISA. Derudover er der imidlertid en ikke ubetydelig gruppe af elever, der er karakteriseret ved to forhold: Det er elever, der er startet relativt sent i skolen og det er elever, der har modtaget et års mindre undervisning, på det tidspunkt de bliver testet af PISA, sammenlignet med de andre elever. Disse forhold ville i sig selv være tilstrækkelig grund til at se nærmere på både den betydning, som alderen og det ekstra års undervisning har for testresultaterne i PISA, og specielt at undersøge, om det er muligt at skille alderseffekten fra effekten af et års undervisning i 9. klasse. Ud over denne almene interesse i problemet, er det imidlertid nødvendigt at belyse denne problematik i forhold til læsefærdigheden, fordi erfaringerne med en sådan analyse vil være nyttige i forbindelse med analysen mellem resultater i matematik i DNT og PISA, idet der kun foreligger DNT-resultater i matematik for elever med sen skolegang. FIGUR 4.10 Fordeling af alder i 8. klasse for elever med normal eller sen skolestart 50 PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM
51 Figur 4.10 viser aldersfordelingen i 8. klasse 16 blandt elever med normal og sen skolestart. Alderen for elever med normal skolestart ligger i intervallet fra 13,8 til 15,3 år med et gennemsnit på 14,8 år. Alderen for elever med sen skolestart ligger i intervallet fra 15,3 til 17,2 år med et gennemsnit på 15,6 år. Det forhold, at der er et veldefineret skæringspunkt på 15,3 år mellem aldersfordelingerne i de to grupper, vil have en væsentlig betydning for de efterfølgende analyser af effekten af det ekstra skoleår. 1) At alderseffekten er forskellig i de to grupper og at alderseffekten er meget stærkere blandt elever med sen skolestart end blandt elever med normal skolestart. 2) At der som udgangspunkt ikke er nogen indlæringsmæssige forskelle på 15,4-årige elever med sen skolestart og 15,2-årige med normal skolestart. Tabel 4.11 viser estimaterne af alderseffekten i to forskellige modeller. I forbindelse med udviklingen af den prædiktive model, blev alderen rutinemæssigt inkluderet som en af de forklarende variable. Analyserne viste imidlertid, at alderen ikke havde nogen direkte effekt på PISA-resultatet, når der samtidig blev korrigeret for DNT-resultaterne. Det betyder to ting: For det første, at alderens betydning for PISA-resultaterne er indirekte, og går gennem den effekt, som alderen har haft på DNT-resultaterne. Og for det andet, at den effekt på 0,357 på PISA-logit resultatet, som modellen tilskriver skolestarten, er en effekt af den ekstra undervisning, som eleverne med normal skolestart har modtaget i 9. klasse. Dette resultat vil imidlertid ikke være til nogen gavn i sig selv i forbindelse med modeludviklingen for matematik, fordi de analyser, som tabel 4.1 fortæller om, ikke er mulige når det drejer sig om matematik. Der er imidlertid en anden mulighed. Tabel 4.11 viser to modeller, hvor der er kontrolleret for alder i stedet for DNT-resultater fra 8. klasse. Disse modeller giver et andet bud på effekten af undervisningen i 9. klasse. Analysen bygger på to forudsætninger 17 : TABEL 4.11 Regressionsparametre med alder i stedet for DNTresultater Uafhængig variabel Model 6 Model 7 Konstant 7,555 7,552 Køn (Dreng) -0,236 < 0,0005 Sen skolestart -5,540 < 0,0005 Herkomst -0,676 < 0,0005 Alder for elever med -0,091 normal skolestart 0.15 Alder for elever med sen skolestart < 0,0005-0,240 < 0,0005-6,878 < 0,0005-0,676 < 0,0005-0,474 < 0,0005 Note: I to modeller for PISA-logit-værdier i læsning. Tal i kursiv under estimat angiver signifikansniveuaet. Skolestartsvariablen (sen) har omvendt definition ift. tabel 4.1 (normal), og derfor også omvendt fortegn. Hvis disse to forudsætninger holder må forskellen på en 15,3-årig elev med normal skolestart og en 15,3-årig elev med sen skolestart være et udtryk for det ekstra år i 9. klasse, som den første elev har gået i skole. Den første af de to forudsætninger kan afprøves empirisk. Den anden kan ikke afprøves, men troværdigheden af beregningerne kan afprøves ved at sammenligne resultatet med effekten af 16 Alderen i 8. klasse er beregnet ud fra PISA registrering af alderen, idet der er trukket et år fra alderen blandt de elever, der er blevet PISA testet i 9. klasse. 17 Forudsætningerne bygger på en antagelse om at det især er eleverne med meget sen skolestart, der har indlæringsmæssige problemer, mens der til gengæld ikke er systematiske forskelle på elever, der ligger tæt på det aldersmæssige skæringspunkt mellem de to elevgrupper. PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM 51
52 skolestarten ifølge model 4 i tabel 4.1. Hvis resultaterne ligger tæt på hinanden, vil vi tage det som udtryk for, at analysen med alderen i stedet for testresultaterne giver et anvendeligt bud på effekten af undervisningen i 9. klasse, og vil derfor bruge den samme metode i forbindelse med udviklingen af modellen for matematik. Alderseffekten blandt elever med normal skolestart er insignifikant. Vi beregner derfor de forventede logit-værdier under både model 6 og model 7. Konstantleddene i model 6 og 7 er lig med henholdsvis 7,555 og 7,552. De forventede PISA-logitværdier blandt elever med og uden normal skolestart er givet ved Model 6: Normal skolestart: 7,555 0,236 D 5,540 SS 0,091 Alder Sen skolestart: 7,555 0,236 D 0,474 Alder Model 7: Normal skolestart: 7,552 0,240 D 6,878 SS Sen skolestart: 7,552 0,240 D 0,474 Alder Man skal ikke lade sig forvirre af, at effekten af en normal skolegang ser ud til at være stærkt negativ, fordi denne tilsyneladende effekt mere end modregnes af den stærkere effekt af alderen blandt elever med sen skolestart. For at beregne et realistisk bud på effekten af en normal eller sen skolestart antager vi, at elever der er 15,3 år gamle i 8. klasse har de samme forudsætninger på skolestarttidspunktet og at beslutningen om at starte sent eller tidligere er et udtryk for beslutninger, der intet har at gøre med deres indlæringsmæssige forudsætninger. I det omfang denne antagelse er realistisk vil forskellen på de forventede PISA-logit-værdier være et udtryk for effekten af den undervisning, som eleverne med normal skolegang i modsætning til eleverne med sen skolegang har modtaget i 0. klasse. Denne effekt viser sig at være 0,32 under model 6 og 0,37 under model 7. Da disse tal ligger tæt på den værdi på 0,35, som effekten af det ekstra år i skolen havde iflg. model 4 med DNT-resultaterne som forklarende variable, kan det ikke umiddelbart afvises, at metoden kan bruges til at estimere effekten af det ekstra skoleår, selvom man ikke har fuldstændig adgang til testresultater fra tidligere år. Det er denne situation, som analyserne af matematikresultaterne er nødt til at forholde sig til. 4.6 Analyse med DNT-resultater i læsning i 6. klasse Udover DNT-resultaterne i læsning i 8. klasse foreligger der også testresultater i læsning i 6. klasse for elever med sen skolegang. Tabel 4.12 viser tre modeller for prædiktion af PISAresultater i læsning, hvor disse oplysninger også benyttes. I den første model inddrages kun DNT-resultater fra 6. klasse. Alle de uafhængige variable har betydning for PISA-resultatet i læsning to år senere. Det er bemærkelsesværdigt, at der ikke er den samme forskel på effekterne af de tre profilområder, som i forbindelse med læsning i 8. klasse. I den anden model inkluderes både DNT-resultater fra 6. og 8. klasse. Denne analyse kan derfor fortælle noget om, i hvor høj grad inklusion af resultater fra 6. klasse kan forbedre prædiktionen af PISAresultaterne ud fra DNT-oplysninger om læsning i 8. klasse. Det viser sig ikke at være tilfældet. Resultaterne er imidlertid interessante, fordi de afslører, at oplysninger om afkodning og tekstforståelse i PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM
53 klasse har en større betydning end oplysningerne om sprogforståelse i 8. klasse samt at sprogforståelse i 6. klasse heller ikke bidrager til prædiktionen. ud fra DNT-resultater i læsning i 6. klasse, men prædiktionen er ikke overraskende svagere end prædiktionen baseret på DNT-oplysninger fra 8. klasse. TABEL 4.12 Regressionskoefficienter og andre parametre for PISA læsning Model 8 Model 9 Model 10 Konstant -0,404-0,607-0,631 Sprogforståelse 6. kl 0,187 (0,041) Afkodning 6.kl. 0,165 Tekstforståelse 6. kl Sprogforståelse 8. kl. (0,034) 0,254 (0,254) 0,069 (0,044) 0,122 (0,038) 0,120 (0,050) 0,037 (0,036) Afkodning 8.kl. 0,026 Tekstforståelse 8.kl Køn (dreng) (D) -0,209 Anden herkomst (E) (0,064) -0,202 (0,070) (0,028) 0,273 (0,045) -0,220 (0,066) -0,195 (0,071) 0,156 (0,035) 0,143 (0,049) 0,315 (0,041) -0,198 (0,065) -0,240 (0,068) R 2 0,372 0,412 0,406 SEM 0,829 0,792 0,794 Resultaterne viser også, at det ikke forbedrer prædiktionen, hvis oplysninger om læsning i 6. klasse tilføjes oplysningerne fra 8. klasse. Til gengæld fremkommer nogle oplysninger, som kunne være af interesse for læseforskere. Et af disse resultater er, at profilområdet sprogforståelse ikke bidrager til prædiktionen af PISAs læseresultater, hvis der både er oplysninger om tekstforståelse fra 6. og 8. klasse, og at afkodning i 6. klasse har større effekt end afkodning i 8. klasse. Det peger altså med andre ord på, at PISAs test ikke måler sprogforståelse, men alene tekstforståelse. Da disse umiddelbart interessante fund ikke har direkte betydning for denne analyse, vil de ikke blive yderligere diskuteret i denne rapport. Note: Tallene i parentes angiver standardfejlene. R2 angiver modellens forklaringsgrad, mens SEM er lig med standardafvigelsen omkring det forventede PISA resultat i læsning. I den tredje og sidste model er de tre variable, der ikke havde signifikant effekt på PISA-resultatet, udeladt. Det svækker prædiktionen en anelse, men resultaterne bekræfter, at disse variable i givet fald kan undværes. Resultatet af de analyser, der er beskrevet i tabel 4.12, bekræfter at PISA-resultater kan prædikteres PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM 53
54 5 Analyse af data vedrørende matematik 5.1 Plan for analysen Da der kun foreligger DNT-resultater i matematik for elever, der fik testet deres færdigheder i 6. klasse i 2010 for de elever, der betegnes som elever med sen skolestart, er det nødvendigt at dele denne analyse op i to dele. Den første del ser på relationen mellem resultater i PISA og DNT for eleverne med sen skolestart. Disse analyser svarer fuldstændig til de analyser af læseresultaterne, der blev præsenteret i kapitel 4, med den ene forskel, at oplysningen om normal og sen skolestart ikke indgår. På grundlag af disse analyser udvælges den model, der efterfølgende skal danne grundlaget for en model, hvor der også tages højde for effekten af undervisning i matematik i 9. klasse, og som derfor kan bruges til at prædiktere PISA resultater i matematik ud fra DNT-resultater i matematik i 6. klasse. Den anden del ser på den effekt, som alder, køn og herkomst har på PISA-resultaterne. I disse analyser inddrages DNT-resultaterne i matematik ikke. Det betyder, at denne analyse kan anvende data for elever med både en normal og en sen skolegang, og at resultaterne kan bruges til at estimere effekten af matematikundervisningen i 9. klasse. Resultaterne af disse to analyser vil til sidst blive kombineret i en samlet model, der kan bruges til at prædiktere PISA-resultater i matematik i 15 års alderen ud fra DNT-resultater i matematik i 6. klasse. Konstruktionen af denne model bygger på nogle forudsætninger, som var opfyldt i forbindelse med modellen for læsefærdighederne. Disse forudsætninger vil blive beskrevet i det afsnit, hvor den samlede model præsenteres. 5.2 Analyse af effekten af DNT-resultater på PISA-logits for elever med sen skolestart Tabel 5.1 viser regressionsparametrene for den model, hvor der udover DNT resultater også kontrolleres for køn og socioøkonomisk status. Alle faktorer på nær køn er højsignifikante. I modsætning til resultaterne i læsning, viser resultaterne i tabel 5.1, at alle tre profilområder bidrager til prædiktionen af resultater i matematik. Anvendt matematik har en anelse bedre forklaringsgrad end de to andre profilområder, men alle tre profilområder skal inkluderes, for at optimere prædiktionen. Effekten af køn understøttes af en p-værdi på Evidensen for en kønsforskel er med andre ord begrænset, men vi har alligevel holdt den inde i modellen, fordi den tendens, som den er et udtryk for, er den tendens, som vi ville forvente. En del af den samlede effekt af køn på resultaterne i PISA er naturligvis fanget af de kønsmæssige forskelle på DNT-resultaterne. Det forhold, at køn har en effekt på PISA-resultaterne efter at der er taget højde for DNT-resultaterne indikerer enten, at køn har en effekt på den fortsatte udvikling af færdigheder i matematik fra 6. klasse frem til PISA-testene i 15 års alderen eller at PISAs matematik-test måler sider af færdighederne i matematik, som ikke dækkes af DNTs profilområder. Effekten af herkomst er til gengæld markant og højsignifikant. Ikke-danske elever ligger gennemsnitligt 0,46 logit-point efter de danske elever. 54 PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM
55 Socioøkonomisk status bidrager ikke i nævneværdig grad til prædiktionen af PISA-resultaterne, selvom effekten isoleret set er højsignifikant, men den socioøkonomiske status reducerer effekten af både herkomsten og (i meget begrænset omfang) af de andre variable. Årsagen til, at inklusion af den socioøkonomiske status bidrager så lidt til selve prædiktionen i model 5 i forhold til model 4, er formodentlig den samme som for læsning: at der allerede er taget højde for en del af den socioøkonomiske effekt ved inklusion af herkomst og testresultater i model Estimation af effekten af undervisningen i 9. klasse Gevinsten ved at gå i 9. klasse før man testes af PISA estimeres på samme måde som for læsefærdigheden. Tabel 5.2 viser resultatet af en regressionsanalyse, hvor PISA-resultatet prædikteres af køn, herkomst, alder og skolestart, og hvor det på samme måde som i de tilsvarende analyser for læsning antages, at alderseffekten er forskellig (mindre) for elever med normal skolestart og elever med sen skolestart. TABEL 5.1 Fem forskellige regressionsmodeller for PISA-resultat i matematik Model 1 Model 2 Model 3 Model 4 Model 5 Konstant -0,918-0,746-0,513-0,658-0,675 Tal og algebra (T) Geometri (G) Anvendt matematik (G) Køn (dreng) (D) Anden herkomst (E) ESCS 0,567 (0,035) 0,171 (0,059) -0,608 (0,060) 0,683 (0,041) 0,205 (0,059) -0,487 (0,061) 0,653 (0,033) 0,143 (0,057) -0,541 (0,058) 0,200 (0,042) 0,310 (0,047) 0,380 (0,044) 0,130 (0,055) - 0,455 (0,057) 0,194 (0,0043) 0,291 (0,049) 0,375 (0,045) 0,119 (0,056) - 0,341 R 2 0,308 0,313 0,365 0,412 0,413 SEM 0,920 0,917 0,881 0,849 0,845 Note: Analysen omfatter udelukkende elever med sen skolestart. Standardfejl på parameterestimaterne l i parentes. SEM er modellens standardafvigelsen omkring det forventede PISA resultat på logit-skalaen. (0,062) 0,129 (0,032) PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM 55
56 TABEL 5.2 Regressionsparametre med alder i 6. klasse i stedet for testresultater fra DNT Uafhængig variabel Model 6 Model 7 Køn (Dreng) <0,0005 Sen skolestart -2,347 <0,0005 Anden herkomst -0,839 Alder for elever med normal skolestart Alder for elever med sen skolestart <0, <0,0005 Note: To modeller for PISA-resultater i matematik -0,240 <0,0005-6,878 <0,0005-0,676 <0,0005-0,474 <0,0005 I modsætning til situationen med læsning, kan der også påvises en signifikant effekt af alderen blandt elever med normal skolestart, men effekten er som forventet meget svagere for elever med normal skolestart end for elever med sen skolestart. Hvis der ikke var tale om en effekt af det ekstra år i skolen ville man forvente, at den funktion, der beskrev det forventede PISA-resultat var en kontinuert funktion af alderen med en svagere hældning blandt eleverne med normal skolestart og alder i 6. klasse lig med 13,3. For at vurdere effekten af at have gået i 9. klasse skal man derfor beregne hvor langt regressionslinjerne for elever med normal og sen skolestart ligger fra hinanden i punktet 13,3. Denne effekt viser sig at være lig med 0.406, dvs. tæt på, men lidt større end den effekt som undervisningen i 9. klasse havde på læsefærdigheden. skolestart er korrekt, kan resultaterne af de to analyser kombineres til følgende formel til beregning af de forventede PISA-resultater i matematik: PISA logit = 0, ,200 T + 0,310 G + 0,380 A + 0,130 D 0,455 E + 0,406 N Hvor T er DNT-logit for Tal og Algebra, G er DNTlogit for Geometri, A er DNT-logit for Anvendt matematik, D er lig med 1, hvis det er en dreng og 0 hvis det er en pige, E er lig med 1, hvis det ikke er en etnisk dansk elev og 0, hvis elever er dansk, og endelig N = 1 hvis der er tale om en elev med normal skolestart og lig med 0, hvis skolestarten er sen. Denne model bygger på forudsætninger, som datagrundlaget ikke giver mulighed for at kontrollere. For det første, at effekten af DNT-resultater,køn samt herkomst er den samme for elever med normal og sen skolestart og for det andet, at estimatet af effekten af skolegangen i 9. klasse, som blev beregnet i afsnit 5.3, er (tæt på) det samme, som en analyse af elever med både normal og sen skolegang ville komme frem til. Begge disse forudsætninger var opfyldt i forbindelse med læsningen. Vi er derfor nogenlunde trygge ved også at antage, at det er tilfældet i forbindelse med matematik. På samme måde, som det var tilfældet i forbindelse med læsningen, afhænger kvaliteten af eventuelle prædiktioner på gruppeniveau af, om de residualer, der beregnes i forbindelse med regressionsanalyserne har tilnærmelsesvist normale fordelinger. Det var tilfældet for modellen for læsning, og det er også tilfældet for matematik, som vist i figur Den prædiktive model Hvis antagelsen om at effekten af DNT-resultater og køn er den samme for elever med normal og sen 56 PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM
57 FIGUR 5.3 Residualer fra model 4 i tabel 5.1. Effekten af DNT-resultater i matematik er svagere end effekten af herkomst og skolestart. For tal og algebra er den relative effekt på 1,09 og en forventet PISA-forskel på 14 point. For geometri er de samme tal 1,11 og 18. Matematik i anvendelse har en stærkere effekt end de to andre profilområder, men effekten er svagere end for herkomst og skolestart. Den relative effekt er 1,17 med en forventet PISA forskel på 25. Omkodningen fra PISA-logits til PISA-scores er beskrevet i appendiks D. På samme måde som for læsning, skal der bruges en relativt enkel, kvadratisk formel, for at komme fra logit-værdierne til de scores, som PISA foretrækker: PISA score = 471, ,663 PISA logit (PISA logit ) Tolkning af effekt-parametrene Forskellen på effekten af DNTs prøver i læsning og matematik er ikke overraskende. DNT-prøverne i læsning i 8. klasse ligger kun op til et år før PISAs test, mens der til gengæld vil være 2-3 års forskel på tidspunktet for matematikprøverne i 6. klasse og PISAs prøver. Effekten af de tidligere testresultater skal derfor i sagens natur være svagere for matematik end for læsning. Herkomst har til gengæld haft længere tid til at påvirke niveauet på det tidspunkt PISA sætter ind, og må derfor forventes at have en lidt stærkere effekt end for læsning. Præcis, som resultaterne viste. Effekten af skolestarten er i realiteten en effekt af undervisningen i 9. klasse, og er derfor den samme faktor for læsning og matematik. Effekten af denne faktor skal derfor være nogenlunde den samme for de to fag. Effekt-parametrene i modellen kan tolkes på samme måde, som det blev gjort for læse-modellen, men resultatet er bemærkelsesværdigt forskelligt fra det, som blev fundet for læsningen. Herkomst og skolestart er de to dominerende faktorer med relative effekter på henholdsvis 1,25 og 1,22 og logit-forskelle som alt andet lige svarer til forskelle i PISA-scores på 36 og 32 point. Effekten af køn er til gengæld begrænset med en relativ effekt på 1,07 og en forventet PISA forskel på ca. 10 point. PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM 57
58 6 Diskussion 6.1 Analysens forudsætninger De analyser, som denne rapport omtaler, bygger på en række forudsætninger, som ikke alle er afprøvede af os. verne. Man kan naturligvis godt forestille sig, at skolestarten påvirker den effekt, som køn og herkomst har på DNT-resultater i 6. eller 8. klasse, men det behøver ikke at betyde, at det samme er tilfældet i de sidste skoleår fra DNT til PISA. De tre væsentligste forudsætninger er, at logit-værdierne for de enkelte profilområder i DNT giver valide målinger uden systematiske fejl, Vi har i Appendiks B og C argumenteret for hvorfor vi mener, at den tredje forudsætning holder. Det eneste problem, der kunne rykke ved denne vurdering er en enkelt ud af et relativt stort antal matematikopgaver. at skolestarten ikke påvirker den effekt, som testresultater fra DNT, køn og herkomst har på de senere PISA-resultater i matematik, at de afvigelser fra Rasch modellen, som påvises i Appendiks B og C ikke medfører nogen væsentlige systematiske fejl i målingerne af færdigheder i læsning og matematik ved hjælp af svarene på PISAs opgaver. Vi betragter de tre forudsætninger som relativt realistiske. Den første er realistisk, fordi vi ved, at DNT-opgaverne oprindelig blev accepteret af de samme metoder, som vi har brugt til at afprøve Rasch modellen i forhold til PISA i Appendiks B og C. Man kan ikke afvise, at sværhedsgraderne kan have ændret sig siden da, men indtil der foreligger håndfast bevis for, at det er tilfældet, har vi ingen grund til at tro, at der skulle være væsentlige problemer med denne antagelse. Den anden er realistisk, fordi denne antagelse holdt for læsning. Det er i den sammenhæng vigtigt at holde fast i, at det, som analysen handler om, er den fortsatte udvikling af færdigheder fra DNT-resultaterne forelå til det tidspunkt, hvor PISA testede ele- 6.2 Kriteriebaserede scores og kategorier De kriteriebaserede scores og kategorier ser ud til at fungere efter hensigten. Det er til syvende og sidst op til fagfolkene at forsvare definitionen af de kriteriebaserede kategorier, men analyserne viser, at der ikke er problemer med at håndtere dem i forbindelse med modelberegningerne, så længe de foretages på logit-niveau, hvorefter logit-værdierne omregnes til kriteriebaserede scores. Sammenligning mellem de kriteriebaserede kategorier på den ene side og de normbaserede kategorier på den anden forekom umiddelbart at falde ud til de kriteriebaserede kategoriers fordel. Om det samme kan siges om PISAs kategorier kan diskuteres. Her er konklusionen snarere, at de kriteriebaserede scores og kategorier kan bidrage til at kaste lidt lys over indholdet af PISAs kategorier, men at det modsatte næppe kan siges at være tilfældet på grund af den tidsmæssige forskydning mellem DNT og PISA. 6.3 Prædiktion af PISA-resultater ved 15 års alderen eller ved udgangen af 9. klasse Effekten af forhold som køn og herkomst er naturligvis vigtige faktorer i forbindelse med analyse af testdata, og der er ingen tvivl om, at de bør medtages i modeller, der forsøger at forudsige senere 58 PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM
59 PISA resultater. Hvorvidt analyserne har afkastet ny viden om disse variable er mere tvivlsomt. Ingen af tendenserne knyttet til disse variable fortæller noget, man ikke allerede ved i forvejen. Spørgsmålet om den sene skolestart og effekten af undervisningen i 9. klasse er derimod mere interessant og et vigtigt bidrag for at nå frem til en model for prædiktion af kommende PISA resultater, og fordi det ikke er noget, der tidligere har været diskuteret i forbindelse med PISA. Ud over, at det har været nødvendigt at estimere effekten af undervisning i 9. klasse for at nå frem til en model for prædiktion af PISA-resultater i matematik, kan resultaterne også bruges til beregne skøn over, hvor de sene skolestartere ville placere sig, hvis de blev testet af PISA i 9. klasse resultater, som i givet fald ville give et mere kvalificeret bud på forventningerne til disse elever efter folkeskolen. PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM 59
60 7 Appendiks A Rasch modellen og logit værdier De nationale test og PISA anvender såkaldte Rasch modeller som grundlaget for beregninger af elevernes færdigheder. Da det er umuligt at forstå og i givet fald at værdsætte den måde testresultaterne håndteres på af DNT og PISA, indeholder dette appendiks en kort beskrivelse af Rasch modellerne og af de forhold, der måske gør anvendelse af Rasch modellerne i DNT og PISA lidt usædvanlige i forhold til gængse anvendelser af modellerne. Da der er tale om matematiske modeller, vil dette appendiks gøre brug af et vist minimum af matematisk notation og terminologi. Vi har dog forsøgt at holde dette på et niveau, der ikke overskrider det, man kan risikere at komme ud for i undervisningen i matematik i gymnasiet. Rasch modellerne beskriver, hvorledes sandsynligheden for at en elev svarer rigtigt på en opgave, afhænger af en ukendt parameter, der angiver elevens niveau og af en eller flere parametre, der angiver opgavens sværhedsgrad. Parametrene i statistiske modeller angives som regel ved hjælp af græske bogstaver. Det vil også være tilfældet her, hvor dygtigheden angives ved hjælp af (theta), mens sværhedsgraderne angives ved hjælp af er (beta). Rasch modeller for dikotome opgaver Dikotome opgaver er opgaver, hvor svarene på opgaverne kodes som enten 1 for rigtigt eller 0 for forkert, og hvor den samlede score for alle opgaver derfor fortæller, hvor mange opgaver, der er blevet besvaret korrekt. Rasch modellen for sådanne opgaver antager, at hver elev er karakteriseret ved en dygtighedsparameter ( ), og at hver opgave har en tilsvarende sværhedsgrad ( ). Ud fra værdierne af disse parametre beregner Rasch modellen sandsynligheden for at elev nr. v svarer korrekt på opgave nr. i ved hjælp af nedenstående formel (1). exp( ) v 1 exp( ) v i i (1) Det forhold, at sandsynligheden for et korrekt svar er en funktion af forskellen på dygtighed og sværhedsgraden, tages som regel som et udtryk for to ting. For det første, at dygtigheden og sværhedsgraden måles på en og samme skala. Og for det andet, at skalaen er en såkaldt intervalskala 18 med et arbitrært nulpunkt, fordi forskellen på forskellige elever vil være den samme, selvom man flytter nulpunktet for skalaen ved at lægge den samme konstant til både dygtigheden og sværhedsgraden. Den skala, som dygtigheden i Rasch modellen måles på, omtales som en logit-skala. Forståelsen af logit-skalaen som en intervalskala har været afgørende for de analyser, der ligger bag resultaterne i denne rapport, fordi de statistiske modeller 19, som har været anvendt, forudsætter data på dette skalaniveau. Logit-skalaen opfattes med rette som en abstrakt og vanskeligt tilgængelig skala. Det betyder dog ikke, at det er helt umuligt, at tolke noget som helst ud fra logit-værdierne. Hvordan man kan gøre det beskrives i et efterfølgende afsnit i dette appendiks, som også beskriver, hvorledes man kan tolke forskelle på de skalaer, som PISA benytter sig af. Partiel credit modeller for polytome opgaver. Opgaver, hvor man kan score fra nul og op til en bestemt maksimumværdi, omtales ofte som polytome opgaver. Rasch modeller for sådanne opgaver omtales som partiel credit modeller (PCM), fordi 18 En intervalskala er en skala, hvor man kan flytte nulpunktet og ændre måleenheden ved en lineær transformation af de oprindelige skalaværdier. Kalendertid er et oplagt eksempel på en intervalskala. Temperatur er en anden. 19 Generelle lineære modeller. 60 PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM
61 modellen beskriver, hvorledes eleven kan få delvis kredit svarende til kvaliteten af løsningen, selvom denne ikke skulle være fuldstændig korrekt. Ifølge PCM modellen for opgaver, hvor man kan score fra 0 til 2 point, afhænger sandsynlighederne for 0, 1 eller 2 point af den samme dygtighedsparameter ( v), som modellen for dikotome items samt af to opgaveparametre ( i1 og i2), der tilsammen giver et (komplekst) billede af opgavens sværhedsgrad. Sandsynlighederne for henholdsvis 0 (helt forkert), 1 (delvist korrekt) og 2 point (helt korrekt) er ifølge PCM modellen givet ved formlerne (2a)-(2c): S sandsynligheden for 0 point: 1 e v i1 1 v e i1 v i1 Sandsynligheden for 1 point: e v i1 i 2 v i1 v i1 v i1 i 2 1 e e Sandsynligheden for 2 point: e v i1 i1 i 2 v i1 v i1 v i1 i 2 1 e e v (2a) (2b) (2c) -parametrene i PCM modellen omtales som tærskelværdier, mens summen af tærskelværdierne ofte tages som et samlet udtryk for opgavens sværhedsgrad. Bemærk, at sandsynlighederne afhænger af forskellen mellem elevernes dygtighed og opgaveparametrene. Tærskelværdierne og sværhedsgraden i PCM modellen opfattes derfor også som værdier på en intervalskala på præcis samme måde, som det var tilfældet med Rasch modellen for dikotome opgaver. Polytome opgaver i de nationale test og PISA. PISA-testene indeholder flere opgaver, hvor der kan gives partiel kredit, hvis besvarelsen af opgaven ikke er fuldstændig korrekt. Det er derfor klart, at PISA-testene ikke kan nøjes med Rasch modeller for dikotome opgaver, men er nødt til at anvende PCM modellen for en del af opgaverne. De nationale test indeholdt i starten kun dikotome opgaver, hvor besvarelserne enten kodes som forkerte eller korrekte. Dette lagde i første omgang op til en Rasch model for dikotome opgaver. Da det viste sig, at mange opgaver i de nationale test var konstrueret på en sådan måde, at man kunne forudse, at besvarelserne fra de nationale test ikke kunne leve op til et af de fundamentale krav, som Rasch modellen og de fleste andre psykometriske skalamodeller forudsætter, blev det også besluttet at anvende PCM modellen til analysen af resultaterne fra de nationale test. Det krav, som opgaverne i de nationale test ikke kunne leve op til, omtales i psykometrisk jargon som et krav om lokal uafhængighed. Lokal uafhængighed forudsætter, at besvarelsen af en opgave kun afhænger af hvor dygtig eleven er og hvor vanskelig opgaven er, og at besvarelsen af en opgave hverken påvirkes af eller påvirker svarene på andre opgaver. Dette krav kunne DNT-opgaverne ikke leve op til, fordi opgaverne i DNT omfatter flere delspørgsmål, der dels fremlægges samlet til den samme kontekst og som i mange tilfælde er formuleret på en sådan måde, at valget af svar til et underspørgsmål udelukker, at det samme svar bruges til andre underspørgsmål. I stedet for at behandle hvert enkelt underspørgsmål som enkelte dikotome opgaver, blev det derfor besluttet at definere opgaverne som polytome opgaver, hvor man fik point (dvs. partiel kredit) svarende til antallet af korrekte underspørgsmål, og at bruge PCM modellen til at beskrive, hvorledes antallet af point på de enkelte opgaver afhænger af elevens dygtighed. PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM 61
62 Baggrunden for dette valg er to resultater fra teorien for Rasch modeller, som måske ikke er alment kendte, og som det derfor er hensigtsmæssigt at minde om, hvis man vil forklare valget af PCM modellen til de nationale test. Det første resultat siger, at summen af to opgaver, der passer til en Rasch model for dikotome eller polytome opgaver, og som tilfredsstiller kravet om lokal uafhængighed, vil opføre sig som en polytom opgave fra PCM modellen. Det andet resultat siger, at summen af to opgaver, der ikke lever op til kravet om lokal uafhængighed under visse betingelser vil opføre sig som en polytom opgave fra PCM modellen 20. For at gardere sig mod risikoen for lokal afhængighed blev det derfor fra starten besluttet at behandle samtlige DNT-opgaver som polytome opgaver med scores, der angav, hvor mange af de enkelte underspørgsmål, der var korrekt besvaret. I de tilfælde, hvor underspørgsmålene i virkeligheden var lokalt uafhængige Rasch-opgaver, garanterer det første resultat, at det samlede antal point vil opføre sig som en polytom Rasch-opgave. I de tilfælde, hvor underspørgsmålene er afhængige fortæller det andet resultat, at det ikke er umuligt, at det samlede antal point alligevel opfører sig som en polytomt Rasch-opgave 21. En gennemgang af opgaverne i PISAs test viser, at disse opgaver i mange tilfælde også er konstrueret som opgaver med flere underspøgsmål. PISA håndterer disse underspørgsmål som enkeltstående dikotome opgaver. Dette rejser en mistanke om, at der kan være tale om lokal afhængighed, en mistanke, der blev bekræftet af de indledende analyser af de danske PISA-data. Af den grund blev det derfor besluttet at analysere besvarelserne af opgaverne i PISA på den samme måde som i DNT. Dvs. ved først at optælle antallet af point på de underspørgsmålene inden for en samlet opgave, og derefter at analysere den samlede opgavescore ved hjælp af PCM modellen. I de tilfælde, hvor der i virkeligheden er tale om uafhængige delopgaver, kan vi igen referere til det første resultat og argumentere for, at der ikke er sket nogle fejl. I de tilfælde, hvor der er lokal afhængighed, kan denne måde at analysere resultaterne på være med til at korrigere for en unøjagtighed i den model, som PISA har benyttet. Om estimation af dygtigheden ved hjælp af forkerte Rasch modeller Den overordnede opgave, som denne rapport forsøger at løse, er, at relatere testresultater fra DNT til testresultater fra PISA. Da PISA ikke beregner egentlige estimater af dygtigheden 22 for de enkelte elever har det været nødvendigt at beregne dygtigheden for de enkelte elever ud fra svarene på de enkelte PISA-opgaver, for at løse denne opgave. For at beregne estimater af hvor dygtige eleverne er, skal der først beregnes estimater af opgavernes sværhedsgrader ud fra de danske PISA-data. Da det dels er kendt, at opgavernes sværhedsgrader er forskellige fra land til land 23 og da der, som nævnt i 20 Interesserede læsere kan bl.a. læse om disse resultater i Christensen, K.B., Kreiner, S. & Mesbah, M. (2013). Rasch models in Health. ISTE Ltd. & John Wiley & Sons, Inc., London og I Kreiner, S. & Christensen, K.B. (2007). Validity and objectivity in health related summated scales: analysis by graphical loglinear Rasch models. I Von Davier, M. & Carstensen C. (eds). Multivariate and Mixture Distribution Rasch models Extensions and Applications Springer Verlag, New York, side Uden garanti, naturligvis. Hvorvidt det samlede antal point rent faktisk passer til Rasch modellen må afprøves empirisk. Den eneste ulempe ved denne fremgangsmåde er, at det kan være vanskeligt at afgøre, hvor fejlen ligger, hvis en af disse polytome opgaver forkastes. Er det alle underspørgsmål, et af underspørgsmålene eller den måde, underspøgsmålene hænger sammen på, der er synderen. 22 PISA beregner såkaldte plausible værdier, som ikke er egentlige estimater af dygtigheden, men som under nogle bestemte forudsætninger kan benyttes til at estimere fordelingen af dygtigheden i forskellige gruppe. 23 Brev fra Andreas Schleicher til Times Educational Supplement PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM
63 det foregående afsnit, tages højde for eventuel lokal afhængighed mellem PISA-opgaverne er det klart, at de estimater af dygtigheden, som beregnes i forbindelse med dette arbejde, i et vist omfang vil afvige fra de estimater, som PISA i givet fald ville kunne beregne. Der er derfor behov for et svar på spørgsmålet om, hvordan resultater fra en korrekt Rasch model vil relatere sig til resultater fra en Rasch model med antagelser om opgavernes sværhedsgrader, der ikke passer helt til virkeligheden. Svaret på dette spørgsmål er relativt enkelt: Antag, at ( 1,.., n) er estimater af dygtigheden for n elever baseret på en korrekt Rasch model og at ( 1,.., n) er estimater for de samme elever baseret på en Rasch model med forkerte sværhedsgrader. Under disse forudsætninger kan det vises, at relationen mellem de to estimater er monotont, men ikke lineært voksende, og i øvrigt at afvigelserne fra lineariteten formodentlig kun vil være bemærkelsesværdige blandt henholdsvis svage og stærke elever. Da dette resultatet ikke er almindelig kendt, vil beviset blive skitseret her for situationer, hvor alle elever har svaret på alle opgaver 24. Bemærk først, at estimatet af dygtigheden i en Rasch model er en voksende funktion af antallet af korrekte opgaver. Hvis S er lig med den samlede score på alle opgaver har vi derfor to voksende funktioner, der definerer de to forskellige estimater af dygtigheden f1 der bruger de rigtige sværhedsgrader og f2 der bruger de forkerte: = f1(s) og = f2(s). De to funktioner er monotont voksende og i øvrigt kontinuerte, hvis vi tillader S at tage en hvilken som helst reel værdi mellem 0 og det maksimale antal point, man kan få på testen. Der eksisterer derfor inverse (monotont voksende) 1 funktioner, s f 1 1 ( ) og s f 2 ( ), som kan bruges til at regne tilbage fra estimaterne af dygtigheden til den samlede score. Det betyder, at estimatet af dygtigheden baseret på en Rasch model med forkerte sværhedsgrader er givet ved en monotont voksende funktion af estimatet af dygtigheden baseret på korrekte sværhedsgrader, f f Relationen mellem de to estimater kan ikke forventes at være lineær. Da den sande værdi,, måler dygtigheden på en intervalskala følger det, at målingen ved hjælp af ikke er en intervalskalamåling, og at man derfor taber fordelene ved intervalskalaerne, hvis man bruger de forkerte målinger i stedet. Ordningsegenskaberne er derimod bevaret. Hvis det væsentligste formål f.eks. er at definere normbaserede kategorier, vil placeringen af de enkelte elever være de samme med de to målinger og vil f.eks. være helt enige om hvilke elever, der er de 10 pct. dygtigste og de 10 pct. mindst dygtige og man kan ækvivalere de skæringspunkter på de to skalaer, der definerer disse normative kategorier ud fra fordelingerne af de to forskellige estimater af dygtigheden. Denne sidste egenskab har spillet en afgørende rolle for ækvivaleringen af PI- SAs scores til de estimater af dygtigheden, som denne rapport benytter Beviset kan uden problemer generaliseres til situationer, hvor eleverne ikke svarer på alle opgaver, sådan som det er tilfældet i både PISA og DNT. Man skal blot erstatte den observerede score med den forventede score på alle eller en delmængde af opgaverne (f.eks. DNTs kriteriebaserede score) 25 For ikke at blive misforstået skal det understreges, at disse resultater hverken lægger til eller trækker fra i den igangværende diskussion om sammenligninger på tværs af forskellige lande, fordi funktionen, f1, der definerer de sande målinger af elevernes færdigheder er forskellige fra land til land. PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM 63
64 Om logit-værdier og PISA-scores Det hævdes ofte, at logit-værdier er for abstrakte til at være forståelige for personer uden statistiske og psykometriske forudsætninger. Dette er ikke helt forkert, men det er på den anden side heller ikke helt rigtigt. Da logit-værdier, og især forskelle på logitværdier, spiller en central rolle i de statistiske modeller, som denne rapport handler om, indeholder dette afsnit en forklaring på, hvad logit-værdier er, og hvordan forskelle på logit-værdierne kan tolkes. Da den skala, som PISA benytter sig af, er en transformeret logit-skala, med et nulpunkt og en måleenhed, som PISA har valgt, kan retningslinjerne for, hvorledes forskelle på logit-skalaen skal tolkes udvides til tolkningsregler for forskelle på PISA-skalaen. For det første: En logit er et kvantitativt mål for chancerne for at et eller andet sker, f.eks. at der svares forkert på en DNT-opgave. Normalt måler man chancer ved hjælp af sandsynligheder. I visse situationer typisk i forbindelse med spil foretrækker man at bruge odds i stedet for sandsynligheder. I princippet er sandsynligheder og odds lige gode eller lige dårlige som mål for chancer, fordi der til hver sandsynlighed, p, findes en bestemt odds-værdi, odds=p/(1-p). En sandsynlighed på 1/3 svarer derfor til odds på 1:2 eller mere præcist til odds = 0,5. Logit-værdien er defineret som den naturlige logaritme af odds-værdien, logit = ln(odds) svarende til at odds er lig med eksponentialfunktionen af logit værdien, odds=e logit. Logit-værdier er derfor blot et andet mål for chancerne, for at noget forekommer, og man kan regne tilbage til sandsynlighederne ved formlen p = e logit /(1+ e logit ). Man kan argumentere for, at logit-værdier teknisk set er bedre mål for chancer end sandsynligheder og det er derfor, at Rasch modellen og mange andre statistiske modeller reformulerer sandsynligheder til noget, der har med logits at gøre 26. Prisen for de tekniske fordele ved logit-værdierne er blot, at man bruger et mål for chancer, hvor fornemmelsen for tallene vil være fuldstændigt fordampet for langt de fleste brugere. I forbindelse med anvendelser af logistiske regressionsmodeller omregner man derfor som regel resultaterne så de i stedet for at handle om forskelle på logit-værdier handler om såkaldte odds-ratio værdier eller om mål for relativ risiko, der defineres som forholdet mellem to sandsynligheder. Det er det samme, som vi vil forsøge at gøre i resten af dette afsnit. Vi vil ikke benytte risikoterminologien, fordi det lyder fjollet at tale om risikoen for at svare korrekt på en opgave, men ideen vil være den samme. For at se på den effekt, som en forskel på logit-værdierne i to forskellige situationer betyder for svarene på opgaverne (f.eks. to elevers svar på den samme opgave eller en elevs svar på to forskellige opgaver), vil vi omregne logit-forskellen til et mål for relativ effekt defineret som forholdet mellem sandsynligheden for et korrekt svar i den ene situation, og sandsynligheden for et korrekt svar i den anden situation. Den logit-værdi, der angiver hvor dygtig en elev er, siger ikke noget i sig selv om hvor dygtig eleven er, men logit-værdier for to elever kan bruges til at vise mere om, hvor disse elever ligger i forhold til hinanden, ud over det ene, at eleven med den største logit-værdi er den dygtigste. Det, der har interesse, hvis man vil sammenligne to elever, er forskellen mellem elevernes logit-værdier, fordi denne forskel kan fortælle hvor meget større chancer den dygtig- 26 Logistisk regression er det bedste eksempel på sådanne modeller. 64 PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM
65 ste elev har for at svare korrekt på opgaverne i forhold til den mindre dygtige. Chancerne i sig selv afhænger af, om der er tale om lette eller vanskelige opgaver. Hvis der er tale om meget vanskelige opgaver med ringe sandsynlighed for et korrekt svar fra de to elever, har logit forskellen relativt stor betydning. Hvis opgaverne er meget lette med tæt på 100 pct. sandsynlighed for et korrekt svar, betyder logit-forskellen relativt lidt, fordi en sandsynlighed tæt ved 100 pct. ikke kan hæves ret meget. Som illustration af det, som vi vil omtale som den relative effekt af forskelle på logit-skalaen, vil vi se på en situation med en opgave med stort set samme chance for at svare forkert eller rigtigt og en logitforskel på elevernes færdigheder på 0,30. Dvs. en situation, hvor opgavens sværhedsgrad er lig med 0,00 og logit-værdierne for eleverne er lig med -0,15 og +0,15. Ved at indsætte disse tal i formel (1) vil man se, at den mindst dygtige elev har 46.3 pct. chance for at svare rigtigt, mens sandsynligheden for at den dygtigste elev svarer korrekt er lig med 53,7 pct.. Det, som vi i det efterfølgende vil beskrive som den relative effekt af forskellen på de to elever, er lig med forholdet mellem de to sandsynligheder, dvs. 0,537/0,463 = 1,162. Den dygtigste elev har altså 16 pct. større sandsynlighed for at svare rigtigt på en udfordrende opgave, hvis sværhedsgraden modsvarer elevernes færdigheder. Tabel A.1 illustrerer dette for fem forskellige forskelle på logit-skalaen og fem forskellige sværhedsgrader 27 af opgaverne fra meget vanskelige opgaver, hvor eleverne kun har ca. 5 pct. chance for at finde den rigtige løsning, over vanskelige opgaver med 25 pct. chance for en korrekt løsning, udfordrende opgaver med 50 pct., lette opgaver med 75 pct. og til sidst meget lette opgaver, hvor der er 95 pct. sandsynlighed for en korrekt besvarelse. TABEL A.1 Relativ effekt af logit-forskelle på chancerne for rigtigt svar for forskellige sværhedsgrader Logit m. svær Svær Udfordr. Let m. let 0,1 1,100 1,078 1,051 1,025 1,005 0,5 1,608 1,454 1,284 1,134 1,026 1,0 2,581 2,109 1,649 1,289 1,053 1,5 4,133 3,041 2,117 1,474 1,084 2,0 6,589 4,352 2,718 1,698 1,121 Effekten af forskellen på logit-værdier for to forskellige elever afhænger af, om der er tale om lette eller vanskelige opgaver, fordi der er grænser for, hvor meget bedre chancerne kan blive, hvis der allerede er ca. 95 pct. chance for et rigtigt svar. I epidemiologiske situationer, hvor forekomsten af hændelserne (sygdom eller død) er meget små, definerer man den relative risiko som forholdet mellem to situationer med lille sandsynlighed for at forekomme. En tilsvarende definition vil være meningsløs i forbindelse med opgaver i pædagogiske test, hvor der kun vil være meget få meget vanskelige opgaver med små sandsynligheder for korrekte svar. I sådanne situationer er det bedre at definere den relative effekt i forhold til det, der i tabel A1 omtales som udfordrende opgaver, fordi en pædagogisk test fungerer bedst, hvis opgaverne er udfordrende, men hverken for lette eller for vanskelige for eleverne 28. Ud fra denne synsvinkel svarer en logit-forskel på 0,1 til en relativ effekt på 1,051, svarende til at den dygtigste elev har 5 pct. større chancer for at ramme rigtigt på en udfordrende opgave end den mindre dygtige elev. 27 Udsagnene om sværhedsgrader er relative til hvor dygtige eleverne er. En let opgave for en dygtig elev kan være en meget vanskelig opgave for en mindre dygtig elev. 28 Det er præcis det, som er baggrunden for såkaldte adaptive tests. Adaptive test forsøger efter bedste evne, at udvælge opgaver, der er udfordrende, men hverken for lette eller for svære for eleverne. PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM 65
66 Boks: Beregningerne af PISA-scores Tabel A.2 viser de relative effekter for logit forskelle fra 0 til 2, når det antages at opgaverne er udfordrende, dvs med 50 pct. chance for korrekt svar. Værdierne i disse tabeller er blevet anvendt til at tolke de logit-forskelle, som optræder i analyserne i kapitel 3. PISA benytter sig af en skala med værdier mellem 0 og 1000, som i realiteten er en lineær transformation af logit-værdier. Boksen viser, hvorledes PISA beregnede skalaværdierne for læsning i 2000 og Det følgende beskriver med PISAs egne ord deres metode til beregning af PISA score ud fra logit-værdier: The reading plausible values were equated to the PISA 2000 scale. Since the same items were used in PISA 2003 as in PISA 2006, and in each case the mean of the item parameter estimates is set at zero, the transformation was exactly the same as in PISA For female students: PISA 2000 scale score = (( * Logit ) / ) * For male students: PISA 2000 scale score = (( * Logit ) / ) * For students with missing gender code: PISA 2000 scale score = (( * Logit ) / ) * For details about equating procedures in 2003, the reader is referred to the PISA 2003 Technical Report (OECD, 2005) Kilde: PISA 2006 technical report, side Det har ikke været muligt at finde nogen forklaring på de forskellige beregninger for drenge og piger. Det er imidlertid et godt gæt at antage, at det er udtryk for et forsøg på at kontrollere den form for differentiel item funktion, som påvises i Appendiks B og C. Det, der er vigtigst her, er at dokumentere påstanden om at PISA-skalaen ikke er andet og mere end en logit-skala med et andet nulpunkt og en anden måleenhed, end den logit-skalaen ellers benytter sig af. 66 PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM
67 Da PISA-skalaen i realiteten er en logit-skala, kan tolkningerne af logit-forskelle som udtryk for relativ effekt uden problemer overføres til tolkninger af forskelle på PISA-skalaen. Formlerne i boksen er unødigt kryptiske, men man kan ved at rykke lidt rundt på de enkelte led overbevise sig om, at PISA-scores ifølge PISA i 2006 er givet ved PISA-score drenge = 87,21 logit+459,03 PISA-score piger = 88,05 logit+451,38 PISA-score uoplyst køn = 88,12 logit+454,38 Enheden på PISAs skala svarer med andre ord til en logit forskel på ca. 1/88 = 0,0114. For at bestemme den relative effekt af forskelle på PISA-skalaen, skal man derfor først omregne til logit-forskellen ved at gange med 0,014, hvorefter man kan finde den relative effekt i tabel A.1. Det kan f.eks. vises, at enheden i PISA-skalaen for læsning er ca. 1/80 af enheden på den originale logit-skala. En forskel på et enkelt PISA point svarer altså til en logit-forskel på 0,0125 logit. TABEL A.2 Oversigt over relative effekter for logit-forskelle fra 0 til 2,09 Logit-forskel 0,00 0,01 0,02 0,03 0,04 0,05 0,06 0,07 0,08 0,09 0,0 1,000 1,005 1,010 1,015 1,020 1,025 1,030 1,036 1,041 1,046 0,1 1,051 1,057 1,062 1,067 1,073 1,078 1,083 1,089 1,094 1,100 0,2 1,105 1,111 1,116 1,122 1,127 1,133 1,139 1,145 1,150 1,156 0,3 1,162 1,168 1,174 1,179 1,185 1,191 1,197 1,203 1,209 1,215 0,4 1,221 1,228 1,234 1,240 1,246 1,252 1,259 1,265 1,271 1,278 0,5 1,284 1,290 1,297 1,303 1,310 1,317 1,323 1,330 1,336 1,343 0,6 1,350 1,357 1,363 1,370 1,377 1,384 1,391 1,398 1,405 1,412 0,7 1,419 1,426 1,433 1,441 1,448 1,455 1,462 1,470 1,477 1,484 0,8 1,492 1,499 1,507 1,514 1,522 1,530 1,537 1,545 1,553 1,560 0,9 1,568 1,576 1,584 1,592 1,600 1,608 1,616 1,624 1,632 1,640 1,0 1,649 1,657 1,665 1,674 1,682 1,690 1,699 1,707 1,716 1,725 1,1 1,733 1,742 1,751 1,759 1,768 1,777 1,786 1,795 1,804 1,813 1,2 1,822 1,831 1,840 1,850 1,859 1,868 1,878 1,887 1,896 1,906 1,3 1,916 1,925 1,935 1,944 1,954 1,964 1,974 1,984 1,994 2,004 1,4 2,014 2,024 2,034 2,044 2,054 2,065 2,075 2,085 2,096 2,106 1,5 2,117 2,128 2,138 2,149 2,160 2,171 2,181 2,192 2,203 2,214 1,6 2,226 2,237 2,248 2,259 2,270 2,282 2,293 2,305 2,316 2,328 1,7 2,340 2,351 2,363 2,375 2,387 2,399 2,411 2,423 2,435 2,447 1,8 2,460 2,472 2,484 2,497 2,509 2,522 2,535 2,547 2,560 2,573 1,9 2,586 2,599 2,612 2,625 2,638 2,651 2,664 2,678 2,691 2,705 2,0 2,718 2,732 2,746 2,759 2,773 2,787 2,801 2,815 2,829 2,843 PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM 67
68 TABEL A.3 Relativ effekt af forskelle på PISA-skalaen for læsning Forskel målt på PISA-skalaen Logit-forskel Effekt på chancen for korrekt svar 1 0,011 1, ,057 1, ,114 1, ,284 1,150 Note: Effekt på udfordrende, men ikke vanskelige opgaver. Tabel A.3 viser effekten af en række forskellige forskelle på PISA-skalaen. En forskel på 1 point har en meget begrænset effekt som næppe vil kunne aflæses med almindelige test med opgaver. En forskel på 10 PISA point svarer til at den dygtigste elev vil have ca. 6 pct. bedre chancer for korrekte svar på de udfordrende opgaver svarende til ca. en ekstra korrekt besvaret opgave 30 i en almindelig test. En PISA-forskel på 25 point forøger chancerne for en korrekt opgave med 15 pct. svarende til at den dygtigste elev vil have ca. 4 flere korrekte svar på opgaverne end den mindst dygtige Afprøvning af Rasch modellen Validiteten og kvaliteten af målinger ved hjælp af Rasch modellen og andre psykometriske skalamodeller afhænger af tilpasningen mellem data og model. Hvis tilpasningen er god, vil målingerne af elevernes færdigheder kun være præget af en form for usystematisk usikkerhed, der kun afhænger af antallet af opgaver og af, hvor godt opgaverne passer til eleven. Men der vil ikke være nogen systematiske fejl. Hvis tilpasningen er dårlig er der en risiko for systematiske og i værste tilfælde vildledende testresultater. Da chancerne for at etablere en forholdsvis enkel model, der kan relatere DNT-resultater til PISA-resultater, afhænger af, at der ikke er nogen systematiske fejl i målingerne af elevernes færdigheder, er tilpasningen mellem Rasch modellen og PISAs data blevet afprøvet på fuldstændig samme måde og ved hjælp af det samme program 31, som blev benyttet i forbindelse med udviklingen af de nationale test, som tilpasningen mellem Rasch modellen og DNTresultaterne blev afprøvet. Resultaterne af analyserne fremlægges i Appendiks B og C. Analyserne har især haft fokus på tre problemer: 1) hvor godt de enkelte opgaver passer til Rasch modellen, 2) om der er forskel på opgavernes sværhedsgrader for drenge og piger, og 3) om opgavernes sværhedsgrader afhænger af det prøvehefte, som opgaverne optræder i. I de tilfælde, hvor sværhedsgraderne afhænger af køn eller prøvehæfter er der i psykometrisk jargon tale om differentiel item funktion (DIF). I de tilfælde, hvor der blev fundet DIF i forhold til køn i de nationale test blev opgaverne fjernet for at undgå systematiske målefejl for drenge og piger. Da vores analyser af PISA-data ikke drejer sig om test-udvikling, har vi i stedet justeret for DIF ved at betragte opgaver med DIF som to forskellige opgaver med hver deres sværhedsgrader. En opgave, som drengene skal svare på og en anden (med samme indhold), som pigerne skal svare på. Efter korrektionen for DIF er der enkelte opgaver, med dårlig tilpasning til Rasch modellen. Der kan være flere forskellige årsager til den dårlige tilpasning: fra indholdsmæssige og substantielt vigtige problemer, til problemer med den måde opgaverne 30 Mindre, hvis testen indeholder mange opgaver, der er for lette eller for svære for eleverne. 31 Programmet hedder RUMM2030. Dokumentationen for programmet og de teststørrelser, der beregnes, kan findes i Andrich, D, Sheridan, B. & Luo, G. (2010). RUMM2030. Computer software and manual. RUMM laboratory, Perth, Australia. 68 PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM
69 er konstrueret på. I de tilfælde, hvor den samlede score på en opgave er lig med antallet af rigtigt bevarede underspørgsmål, kan fejlen skyldes en banal fejl i et enkelt af disse underspørgsmål. Da vi ikke har haft adgang til selve opgaverne, har vi ikke haft mulighed for at grave dybere i problemerne her. Opgaverne er derfor bevaret og beregningerne gennemført, som om tilpasningen mellem Rasch modellerne og besvarelserne af PISAs opgaver har været tilfredsstillende efter den justering for lokal afhængighed, som anvendelse af de samlede opgave scores er udtryk for, og efter justering for DIF i forhold til køn og prøvehæfte. Oplysningerne om hvilke opgaver, som mistanken især retter sig mod pga. manglende tilpasning til Rasch modellen, kan findes i Appendiks B og C. PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM 69
70 8 Appendiks B estimation af dygtigheden Da det datagrundlag, der er stillet til rådighed for analyserne, ikke indeholder mål for elevernes dygtigheder, har det været nødvendigt, at beregne disse tal ud fra elevernes svar på PISAs opgaver. Vi har til dette formål benyttet den samme form for Rasch model, som PISA og DNT benytter sig af, og som er beskrevet i Appendiks A. Det er kendt, at PISAs skalamodel ikke svarer perfekt til danske elever (Jf. Kreiner, S. & Christensen, K.B. (2014): Analysis of model fit an robustness. A new look at a scaling model underlying ranking of countries according to reading literacy. Psychometrika, Vol. 79, ). Da formålet har været at udføre en så nøjagtig analyse som muligt på de danske data, er der blevet korrigeret for en del af disse unøjagtigheder i estimationen af elevernes dygtigheder. Dette appendiks dokumenterer disse beregninger for PISAs læsetest. Som nævnt i Appendiks A er antallet af korrekte svar på de enkelte underspørgsmål i PISAs opgaver talt sammen til en samlet score for opgaven som helhed for at tage højde for eventuel lokal afhængighed mellem delopgaverne inden for den samlede opgave. Disse opgavescores betragtes herefter som polytome opgaver. Formålet med den analyse, som beskrives i dette appendiks, har været at undersøge, om disse polytome opgaver passer til en Rasch model og efter korrektion af eventuelle fejl - at beregne estimater af dygtigheden for de enkelte elever. Analysen omfatter altså følgende fire trin. En afprøvning af Rasch modellen. I denne del af analysen vil der bl.a. blive fokuseret på eventuelle tegn på, at opgaverne fungerer forskelligt for drenge og piger, fordi det kan være med til at skævvride eventuelle forskelle på disse elever og de efterfølgende analyser, der relaterer DNT-resultater til PISA resultater. Test af en generaliseret Rasch model, hvor visse opgaver antages at have forskellige sværhedsgrader for drenge og piger. TABEL B.1 Sværhedsgrader og tærskelværdier (Thr1-5) for læseopgaver uden DIF i forhold til køn Opgave Sværhedsgrad Thr1 Thr2 Thr3 Thr4 Thr5 R456-1,56-1,76-1,78-1,15.. R446-1,39-2,28-0,50... R453-0,58-1,12-0,84-0,51 0,13. R420-0,49-1,29-0,84-0,70-0,35 0,70 R412 0,02-1,56-0,70 0,55 1,81. R406 0,20-0,57-0,73 1,91.. R455 0,40-0,98-0,47 0,87 2,16. R432 0,42-1,23-1,00 3,49.. R437 0,91-0,66 0,68 2,71.. Note: Opgaverne præsenteres sorteret efter sværhedsgrad. 70 PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM
71 Estimation af logit-værdier for de enkelte elever. Opgaverne optræder på forskellig måde i forskellige såkaldte prøvehæfter. PISA antager, at placeringen af opgaverne kan have en vis betydning for, om opgaverne opfattes som lettere eller sværere. Opgaver, der optræder tidligt forventes at være relativt lettere end de tilsvarende opgaver, når de optræder sent. På grund af disse antagelser korrigerer PISA elevernes logit-værdier, således at slutresultaterne bliver sammenlignelige fra prøvehæfte til prøvehæfte. Sådanne korrektioner vil også blive taget i anvendelse her. Da det til syvende og sidst er slutresultatet, der har interesse, vil dette appendiks kun beskrive den endelige Rasch model, hvor der er taget højde for at visse opgaver fungerer forskelligt for drenge og piger. relativt begrænset. Der kan derfor forventes en forholdsvis stor usikkerhed på PISAs målinger af elevernes færdigheder. Antallet af elever, der har taget testen og som kan bruges til at afprøve tilpasningen til Rasch modellen, er til gengæld af en sådan størrelsesorden at man kan forvente at finde selv begrænsede afvigelser fra Rasch modellen. Analyserne afslørede stærk evidens for differentiel item funktion i forhold til køn for tre opgaver. Tabel B.1 viser estimaterne af sværhedsgrader og tærskelværdier for de opgaver, hvor der ikke var DIF i forhold til køn, mens tabel 8.2 viser sværhedsgrader og tærskelværdier for drenge og piger hver for sig for de tre opgaver, hvor sværhedsgraderne var forskellige for drenge og piger. I begge tabeller er opgaverne sorteret, således at de letteste opgaver kommer først og de vanskeligste sidst. PISA indsamler data ved hjælp af prøvehæfter, der indeholder nogle, men ikke alle de opgaver, som PISA benytter. PISA 2012 havde fokus på matematik og ikke læsning. Af den grund foreligger der kun svar på læseopgaver for 5156 elever, der i gennemsnit svarede på 5,3 opgaver med et gennemsnitligt antal delopgaver på tilsammen 18,4. I forhold til gængse pædagogiske test er dette antal af opgaver Tabel B.2 viser, at opgaverne R424 og R220 er væsentligt lettere for drenge end piger, mens opgave R404 er lettere for piger end for drenge. R220 er i øvrigt lettere end R404 for drengene, mens R404 er lettere end R220 for pigerne. En overordnet test for tilpasningen til modellen beskrevet i tabel B.1 og B.2 forkaster modellen (X 2 = TABEL B.2 Sværhedsgrader og tærskelværdier (Thr1-5) for læseopgaver med DIF i forhold til køn Opgave - køn Sværhedsgrad Thr1 Thr2 Thr3 Thr4 Thr5 R424 - drenge -0,34-1,47-0,40 0,83.. R424 - piger -0,14-1,09-0,25 0,93.. R220 - drenge 0,51-0,17 0,50 1,19.. R220 - piger 0,80-0,08 0,85 1,63.. R404 - piger 0,60-1,01 0,10 0,64 1,14 2,12 R404 - drenge 0,65-0,82 0,27 0,61 0,99 2,18 Note: Opgaverne præsenteres sorteret efter sværhedsgrad. PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM 71
72 353,4, df = 135, p <0.0005). Tabel B.3 og B.4 viser tests for tilpasning til Rasch modellen for de enkelte læseopgaver hver for sig. Fire opgaver, R406, R453, R432 og R420, passer relativt dårligt til Rasch modellen. R406 diskriminerer for svagt, mens de tre andre diskriminerer for godt. Tabel B.4 viser tests for tilpasning til Rasch modellen for alle opgaver uden DIF i forhold til køn 32. Tabellen indeholder to test. Et 2 -test der afprøver om sammenhængen mellem dygtigheden og chancerne for korrekte svar på opgaven svarer til det, som Rasch modellen forventer og en F-test for DIF i forhold til køn. 2 -testet fortæller i givet fald kun, om der ser ud til at være noget galt. For at få en fornemmelse af, hvad der i givet fald er galt skal man set på det såkaldte Fit-residual. Hvis det er positivt, er sammenhængen mellem dygtigheden og chancerne for et korrekt svar for svag. Hvis det er negativt er sammenhængen for stærk. Opgaven er set fra Rasch modellens synsvinkel for god til at være sand. Tabel B.4 indeholder fejl af begge typer. Da det er kendt, at inklusion af opgaver, der ikke hænger godt nok sammen med den færdighed man ønsker at måle har den konsekvens, at der er andre opgaver, hvor det vil komme til at se ud, som om sammenhængen er for stærk, samler mistanken om dårlig tilpasning sig først og fremmest omkring opgave R406. TABEL B.3 Test for tilpasning til Rasch modellen for opgaver med DIF i forhold til køn. Opgave - køn Sværhedsgrad Fit- Residual R404 - piger 0,60-2,98 15,6 0,0752 R404 - drenge 0,65-1,53 27,7 0,0011 R220 - drenge 0,51-0,67 14,4 0,1098 R220 - piger 0,80-0,26 11,8 0,2223 R424 - piger -0,14 0,73 22,0 0,0089 R424 - drenge -0,34 2,25 9,2 0,4183 Kilde: [Text] Note: Antallet af frihedsgrader for χ2 testet er lig med 9. Opgaverne præsenteres sorteret mht. fit-residualet. χ 2 p Tabel B.3 viser testene for tilpasning til Rasch modellen for de opgaver, hvor der er påvist DIF i forhold til køn. Da der allerede er påvist DIF er disse test ikke inkluderet. 32 Det er velkendt, at der er en ikke uvæsentlig risiko for at komme ud for falske signifikante resultater, når man foretager en lang række statistiske test. Vi har taget højde for dette problem ved såkaldte Bonferroni metoder før vores konklusioner. P-værdier mellem 1 og 5 pct. kan kun betragtes som relativt svag evidens mod de hypoteser, som testene afprøver. Da svag empirisk evidens efter vores mening kræver indholdsmæssige substantielle argumenter før der drages for firkantede konklusioner, og da vi ikke har adgang til PISAs opgaver og derfor ikke kan have sådanne argumenter, har vi været meget tilbageholdende med konklusioner i sådanne tilfælde. 72 PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM
73 For at give en fornemmelse af, hvad det er, der gør, at tilpasningen mellem opgave R406 og Rasch modellen er for dårlig viser Figur B.7 den såkaldte itemkarakteristiske kurve for denne opgave, som viser det forventede antal point på opgaven i forhold til elevens dygtighed. Den kontinuerte kurve viser, hvad Rasch modellen forventer. Punkterne viser, det gennemsnitlige antal point i 10 forskellige grupper i forhold til det gennemsnitlige dygtighed i grupperne. Hvis der er god tilpasning til modellen, skal disse punkter ligge tæt på kurven. Figur B.7 viser at punkterne fordeler sig lidt for fladt i forhold til kurven for de dygtigste elever, men som helhed forekommer tilpasningen acceptabel selvom det statistisk er stærkt nok til at påvise, at der er systematisk forskel på svarene på opgaven og det, Rasch modellen forventer. Næste skridt er at estimere elevernes dygtighed ud fra oplysningerne om sværhedsgrader og tærskelværdier i Tabel B.1. Figur B.5 viser fordelingen af disse estimater, og Figur B.6 viser fordelingen af standardfejlene på estimaterne. Fordelingen af dygtigheden er pænt symmetrisk, men lidt for spids til at passe til en normalfordeling. Standardfejlen er i gennemsnit lig med 0,62, dvs. dårligere end standardfejlene i de nationale test. I lyset af det forholdsvist beskedne antal læseopgaver, som eleverne har haft mulighed for at svare på, er dette resultat ikke overraskende. I lyset af dette konkluderer vi, at tilpasningen mellem data og en Rasch model, hvor der er taget højde for DIF i forhold til køn og lokal afhængigheder mellem de forskellige underspørgsmål inden for opgaven, er tilstrækkelig godt til at man kan stole på resultaterne. TABEL B.4 Test for tilpasning til Rasch modellen for opgaver uden DIF i forhold til køn Opgave Sværhedsgrad Fit-Residual χ 2 p F-test for DIF p R453-0,58-3,94 63,5 0,0000 5,9 0,015 R432 0,42-3,42 41,2 0,0000 1,2 0,274 R420-0,49-2,18 34,2 0,0001 0,1 0,722 R412 0,02-0,76 25,3 0,0027 0,1 0,804 R455 0,40 0,03 15,2 0,0855 2,2 0,141 R446-1,39 0,35 13,1 0,1578 0,8 0,366 R456-1,56 1,55 24,2 0,0040 0,9 0,331 R406 0,20 2,24 33,3 0,0001 3,9 0,049 R437 0,91 3,73 2,6 0,9794 3,4 0,066 Note: Antallet af frihedsgrader for χ2 testet er lig med 9. Opgaverne præsenteres sorteret mht. fit-residualet. PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM 73
74 FIGUR B.5 FORDELING AF ESTIMATER AF DYGTIGHEDEN I LÆSNING FIGUR B.6 FORDELING AF STANDARDFEJLENE PÅ PER- SONESTIMATERNE FIGUR B.7 ITEM-KARAKTERISTISK KURVE FOR OPGAVE R PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM
75 Placeringen af opgaverne i de forskellige prøvehæfter forventes af PISA at have betydning for hvor vanskelige eleverne opfatter opgaverne. Dette forhold korrigerer PISA for ved at antage, at der lægges en hæfte-specifik konstant til alle sværhedsgraderne i de opgaver, der indgår i et prøvehæfte. Hvis der ikke korrigeres herfor i beregningerne af dygtigheden, vil analysen lægge denne konstant til estimaterne af dygtigheden i stedet for sværhedsgraderne, således at forskellen på sværhedsgraderne kommer til at optræde som forskelle i dygtigheden blandt elever, der er blevet testet med forskellige prøvehæfter. TABEL B.8 Logit gennemsnit blandt elever der har været testet ved hjælp af forskellige prøvehæfte Logit-gennemsnit Prøvehæfte Antal elever Standardfejl ,103 0, ,477 0, ,339 0, ,150 0, ,231 0, ,295 0, ,368 0, ,293 0, ,353 0, ,687 0,108 Note: Hæfte 20 er et særligt hæfte, der anvendes til svagere elever. på 0,48 må opfattes som relativt lettere. I de øvrige hæfter ligger logit-gennemsnittene omkring 0.31 uden signifikante afvigelser. Som konsekvens heraf, justeres logit-værdierne fra hæfte 2, 3 og 6, således at gennemsnittet blandt disse elever svarer til gennemsnittet af logit-værdierne (lig med 0,31) for de elever, der er blevet testet med andre prøvehæfter. Sammenfatning Tilpasningen til en generaliseret Rasch model, hvor der tages højde for 1) lokal afhængighed mellem delopgaver inden for den samlede hovedopgave, 2) DIF i forhold til køn og 3) DIF i forhold til prøvehæfte er tilstrækkelig god til at man kan stole på resultaterne. Der var en enkelt opgave med for dårlig tilpasning til modellen, men afvigelserne mellem det forventede og det observerede var så begrænsede, at det vil have meget lille effekt på estimaterne af elevernes færdigheder. Andre opgaver så ud til at passe for godt. Dette kan skyldes den nævnte opgave, men det kan også skyldes lokal afhængighed mellem opgaverne og eventuelt at PISAs test måler mere end en læsedimension. Uden adgang til indholdet af PISA-opgaverne er det ikke muligt at komme nærmere på en forklaring. Da antallet af opgaver, der diskriminerede for godt, var begrænset og da en grafisk vurdering af de item-karakteristiske kurver for disse opgaver tendenserne også fortalte, at afvigelserne var begrænsede, ændrer dette ikke ved konklusionen vedrørende estimatet af læsefærdigheden. Tabel B.8 viser den gennemsnitlige dygtighed i forhold til det anvendte prøvehæfte. Forskellene er højsignifikante. En parvis sammenligning af niveauerne i de forskellige hæfter viser imidlertid, at læseopgaverne i hæfte 2 og 6 opfattes som relativt vanskelige, idet logit-gennemsnittet blandt elever, der har svaret på opgaver i disse hæfter er lig med 0,13, mens opgaverne i hæfte 3 med et logit-gennemsnit PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM 75
76 9 Appendiks C: Estimation af færdigheder i matematik ud fra PI- SAs data Dette appendiks beskriver item-analysen af svarene på PISAs matematik test. Analysen er foretaget på samme måde, som for læseresultaterne. Datagrundlaget er bedre mht. til antallet af opgaver og antallet af elever, der har besvaret opgaverne, fordi matematik var i fokus i Tilpasningen til Rasch modellen er dårligere for matematikopgaverne end for læseopgaverne selvom der korrigeres for DIF i forhold til køn (X 2 = 1542,2, df = 414, p < ). Tabel C.1 og C.2 viser de estimerede sværhedsgrader og tærskelværdier på samme måde som i tabel B.1 og B.2, mens Tabellerne C.3 og C.4 viser testene for tilpasningen til Rasch modellen. Målingerne af elevernes færdigheder i matematik er af nogenlunde samme kvalitet som målingerne af læsefærdigheden. Det gennemsnitlige antal opgaver per elev er 11.8 svarende til 19,9 delopgaver. Den gennemsnitlige standardfejl på personestimatet er lig med 0,64 dvs. noget ringere end DNT. Korrektionen for effekten af prøvehæfterne på opgavernes sværhedsgrader foregik på samme måde som for læseprøven (jf. tabel C.11). Matematik opgaverne opleves som lettere i hæfterne 2, 4, 9 og 13, hvor logit-gennemsnittet er lig med -0,17, end i de øvrige hæfter, hvor det gennemsnitlige logit niveau er på -0,32. Logit-værdierne i de fire nævnte hæfter justeres derfor nedad, så det kommer til at svare til niveauet i de andre hæfter, før resultaterne overføres til analyserne af sammenhængen mellem DNT- og PISA resultater. i forbindelse med estimationen af færdighederne i matematik er den polytome opgave M564, der opsummerer resultaterne af to delspørgsmål. Uden adgang til PISAs opgaver, vil ethvert forsøg på at forklare, hvad problemet med M564 er, være udtryk for spekulation. Det eneste, vi kan gøre her, er at notere, at denne opgave kan have påvirket testresultaterne for de elever, der er blevet præsenteret for denne opgave. I betragtning af det samlede antal matematikopgaver i PISA 2012, forventer vi ikke at det er sket i væsentlig grad, men problemet er der. De fire opgaver med dårlig tilpasning til Rasch modellen vil føre til at visse opgaver ser ud til at fungere for godt, med negative fit-residuals og signifikante test-størrelser. Sådanne opgaver findes, men heller ikke her er der muligheder for at afgøre om problemerne udelukkende skyldes de fire mindre end gode opgaver. Figur C.5 C.8 viser de item-karakteristiske kurver for disse opgaver, således at læseren selv kan vurdere graden af manglende tilpasning til Rasch modellen. Figurerne C.9 og C.10 viser fordelingen af færdighederne i matematik og standardfejlen på estimaterne af færdigheden. På samme måde som for vurderingerne af læsefærdigheden er usikkerheden noget større i PISA end i DNT. Analyserne afslørede dårlig tilpasning til Rasch modellen med positive fit-residuals og højsignifikante 2 test for fire opgaver. Tre af disse (M423, M474 og M800) er lette dikotome opgaver, som næppe påvirker testresultatet i væsentlig grad. Den eneste opgave, som kunne give anledning til systematiske fejl 76 PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM
77 TABEL C.1 Sværhedsgrader og tærskelværdier for matematikopgaver uden DIF i forhold til køn Opgave Sværhedsgrad Thr1 Thr2 Thr3 Thr4 [Head M800-2,345-2, M423-2,233-2, M033-1,566-1, M474-1,396-1, M305-1,367-1, M909-1,202-3,059-0,596 0,050. M447-1,050-1, M559-1,044-1, M919-0,989-1,992 0,015.. M420-0,649-0, M915-0,547-1,385 0,291.. M905-0,493-1,460 0,473.. M273-0,345-0, M906-0,310-1,012 0,843-0,760. M571-0,228-0, M411-0,095-0,710 0,519.. M603-0,005-0, M034 0,078 0, M155 0,090-1,130-1,024-0,511 0,249 M564 0,140-0,549 0,829.. M408 0,248 0, M828 0,793-0,616 0,551 2,444. M446 0,901-1,259 3,060.. M442 1,024 1, M903 1,428 1,623 0,590 2,069. M464 1,769 1, M00K 1,848 1, M462 2,157 2,613 1,701.. M943 2,396-0,123 4,916.. M00G 2,440 2, PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM 77
78 TABEL C.2 Sværhedsgrader og tærskelværdier for matematikopgaver med DIF i forhold til køn (sorteret efter location) Opgave køn Location Thr1 Thr2 Thr3 M918 piger -1,817-2,570-1,679-1,201 M918 - drenge -1,484-1,766-1,793-0,895 M408 - drenge -1,131-1,131.. M496 - drenge -0,743-0,921-0,564. M408 - piger -0,694-0,694.. M496 - piger -0,403-0,573-0,234. M192 - drenge -0,010-0,010.. M00F - piger 0,047 0,047.. M923 - drenge 0,202-1,387 0,082 1,910 M00F - drenge 0,505 0,505.. M923 - piger 0,528-1,028 0,281 2,332 M192 - piger 0,564 0,564.. M803 - drenge 0,974 0,974.. M406 - drenge 1,143 1,184 1,102. M406 - piger 1,402 1,632 1,171. M803 - piger 1,467 1, PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM
79 TABEL C.3 Test for tilpasning til Rasch modellen. Opgaver uden DIF I forhold til køn (sorteret efter Fit-Residual) Opgave Sværhedsgrad Fit-Residual χ 2 p F-test for DIF p M905-0,493-7,318 81,3 0,0000 0,86 0,3534 M442 1,024-4,888 72,3 0,0000 6,60 0,0102 M906-0,310-4,792 37,1 0,0000 6,09 0,0137 M464 1,769-4,218 73,1 0,0000 0,02 0,9036 M00G 2,440-3,745 32,9 0,0001 9,03 0,0027 M155 0,090-3,318 43,2 0,0000 0,10 0,7543 M909-1,202-3,317 13,1 0, ,55 0,0011 M446 0,901-3,219 96,2 0,0000 0,28 0,5954 M447-1,050-2,528 39,7 0,0000 0,04 0,8341 M903 1,428-2,426 16,1 0,0639 0,13 0,7167 M462 2,157-2,291 13,5 0,1418 0,37 0,5447 M571-0,228-1,937 42,9 0,0000 0,97 0,3260 M828 0,793-1,172 16,6 0,0550 5,35 0,0208 M411-0,095-0,826 21,0 0,0128 2,09 0,1489 M559-1,044-0,421 16,3 0,0610 0,00 0,9630 M915-0,547 0,014 11,7 0,2291 1,55 0,2128 M034 0,078 0,209 17,1 0,0474 1,20 0,2729 M00K 1,848 0,281 10,9 0,2811 0,96 0,3280 M919-0,989 0,671 37,6 0,0000 7,34 0,0068 M408 0,248 1,591 22,7 0,0068 0,77 0,3818 M305-1,367 1,628 14,4 0,1092 0,39 0,5332 M033-1,566 2,767 6,8 0,6622 0,86 0,3535 M603-0,005 2,857 17,3 0,0447 0,80 0,3728 M420-0,649 3,657 17,8 0,0380 2,07 0,1509 M943 2,396 3,807 24,2 0,0040 1,56 0,2117 M423-2,233 4,530 57,5 0,0000 0,04 0,8347 M800-2,345 4, ,4 0,0000 0,07 0,7964 M474-1,396 5,616 38,7 0,0000 0,01 0,9164 M273-0,345 5,776 25,2 0,0028 1,28 0,2578 M564 0,140 6,363 68,4 0,0000 0,26 0,6077 PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM 79
80 TABEL C.4 Test for tilpasning til Rasch modellen for opgaver med DIF i forhold til køn (sorteret efter Fit-Residual) Opgave Sværhedsgrad Fit-Residual χ 2 p M803 - drenge 0,974-4,408 53,4 0,0000 M406 - piger 1,402-3,473 37,6 0,0000 M803 - piger 1,467-3,372 42,7 0,0000 M406 - drenge 1,143-3,121 27,7 0,0011 M192 - drenge -0,010-3,089 41,4 0,0000 M192 - piger 0,564-1,889 22,1 0,0086 M00F - piger 0,047-1,746 19,5 0,0215 M408 - piger -0,694-1,197 17,4 0,0422 M923 - drenge 0,202-1,195 21,5 0,0107 M408 - drenge -1,131-1,107 30,4 0,0004 M00F - drenge 0,505 0,161 11,1 0,2720 M918 - piger -1,817 0,363 23,7 0,0048 M923 - piger 0,528 0,499 13,0 0,1624 M496 - piger -0,403 2,129 13,2 0,1540 M496 - drenge -0,743 2,398 9,2 0,4174 M918 - drenge -1,484 4,469 39,6 0, PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM
81 FIGUR C.5 Item karakteristisk kurve for opgave M423 FIGUR C.6 Item karakteristisk kurve for opgave M474 PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM 81
82 FIGUR C.7 Item karakteristisk kurve for opgave M564 FIGUR C.8 Item karakteristisk kurve for opgave M PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM
83 FIGUR C.9 Fordeling af matematikfærdigheder FIGUR C.10 Fordeling af standardfejl PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM 83
84 TABEL C.11 Gennemsnitlige logit niveauer i forskellige booklets Prøvehæfte Antal elever Logit-gennemsnit Standard afvigelse , , , , , , , , , , , , , ,121 med information om de svageste elever. Opgave M564 er mere problematisk. Det er en polytom opgave, hvor man kan få fra 0 til 2 point, som vil være udfordrende og derfor informativ for en stor del af eleverne. Da denne opgave korrelerer for svagt med færdighederne i matematik, vil den kunne være med til at udviske forskellene på de dygtige og de mindre dygtige elever. Da der på den anden side kun er tale om en ud af 38 opgaver med dette problem, forventes denne opgave kun at resultere i meget begrænsede systematiske fejl i forbindelse med målingerne af færdighederne. Sammenfatning Tilpasningen af matematikopgaverne til Rasch modellen er ikke så god for matematik som for læsning, selvom der er blevet korrigeret for lokal afhængighed mellem delopgaver fra samme hovedopgave samt DIF i forhold til køn og prøvehæfte. Dette er ikke nødvendigvis overraskende. Dels inkluderede PISA2012 væsentligt flere matematikopgaver end læseopgaver og dels var der mange nye matematikopgaver, som måske ikke har været så omhyggeligt afprøvede som de opgaver, der havde været med i flere PISA-runder. I forbindelse med den form for testudvikling, som fandt sted i forbindelse med de nationale test, ville opgaver som M423, M474, M564 og M800 være blevet taget ud og enten omskrevet eller erstattet af andre. Denne mulighed foreligger ikke i forbindelse med dette arbejde. Af de fire problematiske opgaver er der tre lette dikotome, der ikke ville kunne forstyrre det samlede billede i væsentlig grad, fordi disse tre opgaver kun bidrager 84 PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM
85 10 Appendiks D: Omregning af PISA-logits til PISA-scores og PISA-kategorier PISA rapporterer resultater i form af PISA-scores med værdier mellem 0 og 1000 eller PISA-kategorier, der opdeler elevernes færdigheder i en række niveauer. PISA beregner deres PISA-score som en lineær funktion af logit-værdier. På grund af afvigelsen mellem den måde PISA beregner sine logitværdier på og den måde, det er sket her, vil relationen mellem vores logit-værdier og PISA-scores, sådan som PISA definerer dem, være ikke-lineær. Det betyder ikke, at det er umuligt at beregne PISA-lignende scores og PISA-kategorier ud fra de logitværdier, der bruges i denne rapport, men kun at det er en lille smule vanskeligere. Dette appendiks beskriver, hvorledes det skal gøres. TABEL D.1 Fordeling mht. PISA-kategorier i læsning blandt etnisk danske elever Niveau Interval Andel plausible værdier (pct.) Øvre skæringspunkt (logit) <1b ,5-2,24 1b ,2-1,54 1a ,3-0, , ,9 1, ,5 2, ,2 4, ,4 Note: Logit-skæringspunkter er beregnet ud fra de danske resultater. PISA definerer PISA-kategorierne ved hjælp af skæringspunkter på PISAs skala. Definitionerne af kategorierne og de dertil hørende skæringspunkter på PISAs skala er vist i tabel D.1 og D.2 for henholdsvis læsning og matematik sammen med et estimat af fordelingen af de etnisk danske elever 33 baseret på de plausible værdier som PISA har beregnet. TABEL D.2 Fordeling mht. PISA-kategorier i matematik blandt etnisk danske elever Niveau Interval Andel plausible værdier (pct.) Øvre skæringspunkt (logit) < ,3-2, ,7-1, ,2-0, ,7 0, ,2 1, ,2 2, ,6 Note: Logit-skæringspunkter er beregnet ud fra de danske resultater. PISAs plausible værdier kan benyttes til at estimere fordelingen af elever mht. de forskellige niveauer ud fra de skæringspunkter, der adskiller kategorierne. Disse fordelinger er vist som den tredje søjle i tabel D.1 og D.2 for de etnisk danske elever. Da der vil være en monotont voksende relation mellem værdierne på PISA skalaen på den ene side og værdierne på logit-skalaen på den anden side, er det muligt at definere de værdier på logit-skalaen, der svarer til de niveauer, som PISA-kategorierne definerer. Da 0,5 pct. af eleverne har en logit-værdi i læsning, der er mindre end eller lig -2,24 følger det f.eks., at en logit-værdi på -2,24 svare til en værdi på 261 på PISA skala. Figur D.3 og D.4 viser relationen mellem skæringspunkterne ifølge PISAs skala og skæringspunkterne på logit-skalaerne for henholdsvis læsning og matematik. I begge tilfælde ses en nydelig tilpasning til 33 PISA rapporterer fordelingen af elever over de forskellige niveauer for både etnisk danske og etnisk ikke danske elever. Da de etnisk danske elever er overrepræsenteret i materialet fra PISA 2012 er vi nødt til at skille disse to grupper ad, i forbindelse med disse beregninger, og da datamaterialet med etnisk danske er det klart største er det det, vi har benyttet til beregningerne. PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM 85
86 en kvadratisk relation 34. Disse relationer definerer de funktioner, der skal bruges for at omregne de logit-værdier, der er estimeret på de danske data under forudsætninger, der passer til Danmark til værdier på en skala, der svarer til den, som PISA benytter sig af. Disse funktioner er Læsning PISA score = 515, ,185 Pisa logit 2,155 (Pisa logit ) 2 Matematik PISA score = 471, ,663 PISA logit (PISA logit ) 2 PISAs retorik omkring den niveaudeling, som kategoriseringen af resultaterne i tabel 10.1 og 10.2 er udtryk for antyder, at kategorierne skal opfattes som kriteriebaserede kategorier. For ikke at blive misforstået skal det understreges, at de beregninger, der er foretaget her, ikke kan tages til indtægt for eller imod en sådan tolkning. På samme måde, som i tilfældet med de kriteriebaserede kategorier i de nationale test, skal sådanne argumenter motiveres og dokumenteres indholdsmæssigt og ikke statistisk. Læsere, der er interesserede i sådanne forhold, må derfor søge denne dokumentation i de tekniske rapporter fra PISA. Det eneste, som vi har påvist her, er, at testresultaterne kan kategoriseres på samme måde ud fra værdier på logit-skalaen og på PISAs egen skala, og at dette kan bruges til at bestemme, hvordan man regner fra værdier på logit-skalaen til værdier på PISAs skala. 34 Nydeligere for læsning end for matematik, hvor datamaterialet er spinklere og usikkerheden derfor større. 86 PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM
87 FIGUR D.3 Relation mellem PISA-logit og PISA-score for læsning FIGUR D.4 Relation mellem PISA-logit og PISA-score for matematik PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM 87
88 88 PISA-RELATERING AF DE KRITERIEBASEREDE NATIONALE TEST DAMVAD.COM
89 Sørkedalsveien 10A N-0369 Oslo Frederik Langes Gate 20 N-9008 Tromsø Badstuestræde 20 DK-1209 Copenhagen K
05/09/14. PISA-relatering af de kriteriebaserede. Delrapport 1 formidling af resultater
 05/09/14 PISA-relatering af de kriteriebaserede nationale test Delrapport 1 formidling af resultater For information on obtaining additional copies, permission to reprint or translate this work, and all
05/09/14 PISA-relatering af de kriteriebaserede nationale test Delrapport 1 formidling af resultater For information on obtaining additional copies, permission to reprint or translate this work, and all
Bilagsnotat til: De nationale tests måleegenskaber
 Bilagsnotat til: De nationale tests måleegenskaber Baggrund Der er ti obligatoriske test á 45 minutters varighed i løbet af elevernes skoletid. Disse er fordelt på seks forskellige fag og seks forskellige
Bilagsnotat til: De nationale tests måleegenskaber Baggrund Der er ti obligatoriske test á 45 minutters varighed i løbet af elevernes skoletid. Disse er fordelt på seks forskellige fag og seks forskellige
Bilag 2: Undersøgelse af de nationale tests reliabilitet. Sammenfatning
 Bilag 2: Undersøgelse af de nationale tests reliabilitet Sammenfatning I efteråret 2014 blev der i alt gennemført ca. 485.000 frivillige nationale tests. 296.000 deltog i de frivillige test, heraf deltog
Bilag 2: Undersøgelse af de nationale tests reliabilitet Sammenfatning I efteråret 2014 blev der i alt gennemført ca. 485.000 frivillige nationale tests. 296.000 deltog i de frivillige test, heraf deltog
Sammenhængen mellem elevernes trivsel og elevernes nationale testresultater.
 Sammenhængen mellem elevernes trivsel og elevernes nationale testresultater. 1 Sammenfatning Der er en statistisk signifikant positiv sammenhæng mellem opnåelse af et godt testresultat og elevernes oplevede
Sammenhængen mellem elevernes trivsel og elevernes nationale testresultater. 1 Sammenfatning Der er en statistisk signifikant positiv sammenhæng mellem opnåelse af et godt testresultat og elevernes oplevede
De nationale tests måleegenskaber
 De nationale tests måleegenskaber September 2016 De nationale tests måleegenskaber BAGGRUND De nationale test blev indført i 2010 for at forbedre evalueringskulturen i folkeskolen. Hensigten var bl.a.
De nationale tests måleegenskaber September 2016 De nationale tests måleegenskaber BAGGRUND De nationale test blev indført i 2010 for at forbedre evalueringskulturen i folkeskolen. Hensigten var bl.a.
Generelt er korrelationen mellem elevens samlede vurdering i forsøg 1 og forsøg 2 på 0,79.
 Olof Palmes Allé 38 8200 Aarhus N Tlf.nr.: 35 87 88 89 E-mail: stil@stil.dk www.stil.dk CVR-nr.: 13223459 Undersøgelse af de nationale tests reliabilitet 26.02.2016 Sammenfatning I efteråret 2014 blev
Olof Palmes Allé 38 8200 Aarhus N Tlf.nr.: 35 87 88 89 E-mail: stil@stil.dk www.stil.dk CVR-nr.: 13223459 Undersøgelse af de nationale tests reliabilitet 26.02.2016 Sammenfatning I efteråret 2014 blev
De nationale test foråret National præstationsprofil
 De nationale test foråret 2016 National præstationsprofil De nationale test foråret 2016 National præstationsprofil Styrelsen for It og Læring Styrelsen for It og Læring, oktober 2016 Indhold Sammenfatning...
De nationale test foråret 2016 National præstationsprofil De nationale test foråret 2016 National præstationsprofil Styrelsen for It og Læring Styrelsen for It og Læring, oktober 2016 Indhold Sammenfatning...
Appendiks 2: Progression i de nationale test og Beregneren
 : Progression i de nationale test og Beregneren Følgende appendiks indeholder en sammenligning af testsystemets og Beregnerens progression-visninger. Formålet er at give et indblik i de forskellige måder,
: Progression i de nationale test og Beregneren Følgende appendiks indeholder en sammenligning af testsystemets og Beregnerens progression-visninger. Formålet er at give et indblik i de forskellige måder,
Statusredegørelsen for folkeskolens udvikling
 Statusredegørelsen for folkeskolens udvikling For skoleåret 2016/2017 Statusredegørelsen for folkeskolens udvikling For skoleåret 2016/2017 Layout: Presse- og Kommunikationssekretariatet, Undervisningsministeriet
Statusredegørelsen for folkeskolens udvikling For skoleåret 2016/2017 Statusredegørelsen for folkeskolens udvikling For skoleåret 2016/2017 Layout: Presse- og Kommunikationssekretariatet, Undervisningsministeriet
Læring af test. Rapport for. Aarhus Analyse Skoleåret
 Læring af test Rapport for Skoleåret 2016 2017 Aarhus Analyse www.aarhus-analyse.dk Introduktion Skoleledere har adgang til masser af data på deres elever. Udfordringen er derfor ikke at skaffe adgang
Læring af test Rapport for Skoleåret 2016 2017 Aarhus Analyse www.aarhus-analyse.dk Introduktion Skoleledere har adgang til masser af data på deres elever. Udfordringen er derfor ikke at skaffe adgang
Elever med ikke-vestlig herkomst halter bagefter i de nationale test
 Elever med ikke-vestlig herkomst halter bagefter i de nationale test Af Center for Data og Analyse Følgende notat belyser forskellen i faglige præstationer mellem elever med dansk herkomst og elever med
Elever med ikke-vestlig herkomst halter bagefter i de nationale test Af Center for Data og Analyse Følgende notat belyser forskellen i faglige præstationer mellem elever med dansk herkomst og elever med
Appendiks 1: Om baggrund og teori bag valg af skala
 Appendiks 1: Om baggrund og teori bag valg af skala De nationale test gav i 2010 for første gang danske lærere mulighed for at foretage en egentlig måling på en skala af deres elevers præstationer på grundlag
Appendiks 1: Om baggrund og teori bag valg af skala De nationale test gav i 2010 for første gang danske lærere mulighed for at foretage en egentlig måling på en skala af deres elevers præstationer på grundlag
Forside. Nationale test. information til forældre. Januar Titel 1
 Forside Nationale test information til forældre Januar 2017 Titel 1 Nationale test information til forældre Tekst: Fokus Kommunikation og Undervisningsministeriet Produktion: Fokus Kommunikation Grafisk
Forside Nationale test information til forældre Januar 2017 Titel 1 Nationale test information til forældre Tekst: Fokus Kommunikation og Undervisningsministeriet Produktion: Fokus Kommunikation Grafisk
Nationale test. v. Marie Teglhus Møller. Slides er desværre uden eksempelopgaver, da disse ikke må udleveres. marie@eystein.dk
 Nationale test v. Marie Teglhus Møller Slides er desværre uden eksempelopgaver, da disse ikke må udleveres. marie@eystein.dk Oplæg for dagen Hvad er en pædagogisk test? Hvilke krav stilles der til opgaverne
Nationale test v. Marie Teglhus Møller Slides er desværre uden eksempelopgaver, da disse ikke må udleveres. marie@eystein.dk Oplæg for dagen Hvad er en pædagogisk test? Hvilke krav stilles der til opgaverne
Nationale test i Danmark - fra et fagdidaktisk perspektiv
 Eksamen og prøver i norsk og nordisk skole Nationale test i Danmark - fra et fagdidaktisk perspektiv Mit arbejde med tests... Innovative testredskaber Hvad er Nationale Test? 10 obligatoriske test i 2.-8.
Eksamen og prøver i norsk og nordisk skole Nationale test i Danmark - fra et fagdidaktisk perspektiv Mit arbejde med tests... Innovative testredskaber Hvad er Nationale Test? 10 obligatoriske test i 2.-8.
September 2012. Resume: Efterskolerne og uddannelsesmobilitet. Udarbejdet af DAMVAD for Efterskoleforeningen
 September 2012 Resume: Efterskolerne og uddannelsesmobilitet Udarbejdet af DAMVAD for Efterskoleforeningen For information on obtaining additional copies, permission to reprint or translate this work,
September 2012 Resume: Efterskolerne og uddannelsesmobilitet Udarbejdet af DAMVAD for Efterskoleforeningen For information on obtaining additional copies, permission to reprint or translate this work,
Sammenhængen mellem folkeskolens faglige niveau og sandsynligheden for at gennemføre en ungdomsuddannelse
 NOTAT 18. MARTS 2011 Sammenhængen mellem folkeskolens faglige niveau og sandsynligheden for at gennemføre en ungdomsuddannelse Jørgen Søndergaard, SFI Danmark er fortsat langt fra målet om, at 95 pct.
NOTAT 18. MARTS 2011 Sammenhængen mellem folkeskolens faglige niveau og sandsynligheden for at gennemføre en ungdomsuddannelse Jørgen Søndergaard, SFI Danmark er fortsat langt fra målet om, at 95 pct.
SUPPLEMENT TIL EVALUERING AF DE NATIONALE TEST RAPPORT
 Til Undervisningsministeriet (Kvalitets- og Tilsynsstyrelsen) Dokumenttype Rapport Dato August 2014 SUPPLEMENT TIL EVALUERING AF DE NATIONALE TEST RAPPORT NATIONALE TEST RAPPORT INDHOLD 1. Indledning og
Til Undervisningsministeriet (Kvalitets- og Tilsynsstyrelsen) Dokumenttype Rapport Dato August 2014 SUPPLEMENT TIL EVALUERING AF DE NATIONALE TEST RAPPORT NATIONALE TEST RAPPORT INDHOLD 1. Indledning og
Resultaterne fra de obligatoriske nationale test 2017
 Resultaterne fra de obligatoriske nationale test 2017 Resultaterne fra de obligatoriske nationale test i skoleåret 2016/2017 viser meget små udsving i forhold til resultaterne fra 2015/2016. Andelen af
Resultaterne fra de obligatoriske nationale test 2017 Resultaterne fra de obligatoriske nationale test i skoleåret 2016/2017 viser meget små udsving i forhold til resultaterne fra 2015/2016. Andelen af
Kvalitetsrapport Holmegårdskolen De nationale test 2015/16 og 2016/17
 Kvalitetsrapport Holmegårdskolen De nationale test 2015/16 og 2016/17 Holmegårdsskolen - Fortroligt materiale - Indholdsfortegnelse FORMÅL MED KVALITETSRAPPORTER... 4 INDLEDNING... 4 DE NATIONALE MÅL FOR
Kvalitetsrapport Holmegårdskolen De nationale test 2015/16 og 2016/17 Holmegårdsskolen - Fortroligt materiale - Indholdsfortegnelse FORMÅL MED KVALITETSRAPPORTER... 4 INDLEDNING... 4 DE NATIONALE MÅL FOR
Appendiks 3 Beregneren - progression i de nationale matematiktest - Vejledning til brug af beregner af progression i matematik
 Appendiks 3: Analyse af en elevs testforløb i 3. og 6. klasse I de nationale test er resultaterne baseret på et forholdsvist begrænset antal opgaver. Et vigtigt hensyn ved designet af testene har været,
Appendiks 3: Analyse af en elevs testforløb i 3. og 6. klasse I de nationale test er resultaterne baseret på et forholdsvist begrænset antal opgaver. Et vigtigt hensyn ved designet af testene har været,
National præstationsprofil dansk, læsning
 National præstationsprofil dansk, læsning sammenklip af National præstationsprofil 2012/13 fra Undervisningsministeriets hjemmeside Den nationale præstationsprofil viser, hvordan alle elever i folkeskolen
National præstationsprofil dansk, læsning sammenklip af National præstationsprofil 2012/13 fra Undervisningsministeriets hjemmeside Den nationale præstationsprofil viser, hvordan alle elever i folkeskolen
De socioøkonomiske referencer for gymnasiekarakterer 2014
 De socioøkonomiske referencer for gymnasiekarakterer 2014 Indhold Sammenfatning... 5 Indledning... 7 Datagrundlag... 9 Elever... 9 Fag, prøveform og niveau... 9 Socioøkonomiske baggrundsvariable... 10
De socioøkonomiske referencer for gymnasiekarakterer 2014 Indhold Sammenfatning... 5 Indledning... 7 Datagrundlag... 9 Elever... 9 Fag, prøveform og niveau... 9 Socioøkonomiske baggrundsvariable... 10
Notat. Den adaptive algoritme i De Nationale Test. Opbygning af test og testforløb. januar 2015
 Notat Vedrørende: Den adaptive algoritme i De Nationale Test Olof Palmes Allé 38 8200 Aarhus N Tlf.nr.: 35 87 88 89 E-mail: stil@stil.dk www.stil.dk CVR-nr.: 13223459 Den adaptive algoritme i De Nationale
Notat Vedrørende: Den adaptive algoritme i De Nationale Test Olof Palmes Allé 38 8200 Aarhus N Tlf.nr.: 35 87 88 89 E-mail: stil@stil.dk www.stil.dk CVR-nr.: 13223459 Den adaptive algoritme i De Nationale
Hovedresultater fra PISA Etnisk 2015
 Hovedresultater fra PISA Etnisk 2015 Baggrund I PISA-undersøgelserne fra 2009, 2012 og 2015 er der i forbindelse med den ordinære PISA-undersøgelse foretaget en oversampling af elever med anden etnisk
Hovedresultater fra PISA Etnisk 2015 Baggrund I PISA-undersøgelserne fra 2009, 2012 og 2015 er der i forbindelse med den ordinære PISA-undersøgelse foretaget en oversampling af elever med anden etnisk
Kvalitetsrapport. Center for Børn og Læring. Skoleåret 2016/17. Lokalrapport for: Kibæk skole
 Kvalitetsrapport Center for Børn og Læring Skoleåret 2016/17 Lokalrapport for: Kibæk skole 1 Indholdsfortegnelse Indledning...3 Skolebestyrelsens udtalelse...4 Skoleledelsens udtalelse...4 Resultat bemærkninger...5
Kvalitetsrapport Center for Børn og Læring Skoleåret 2016/17 Lokalrapport for: Kibæk skole 1 Indholdsfortegnelse Indledning...3 Skolebestyrelsens udtalelse...4 Skoleledelsens udtalelse...4 Resultat bemærkninger...5
De socioøkonomiske referencer for gymnasiekarakterer 2016
 De socioøkonomiske referencer for gymnasiekarakterer 2016 Indhold Sammenfatning... 5 Indledning... 7 Datagrundlag... 9 Elever... 9 Fag, prøveform og niveau... 9 Socioøkonomiske baggrundsvariable... 10
De socioøkonomiske referencer for gymnasiekarakterer 2016 Indhold Sammenfatning... 5 Indledning... 7 Datagrundlag... 9 Elever... 9 Fag, prøveform og niveau... 9 Socioøkonomiske baggrundsvariable... 10
KVALITETSRAPPORT FOR. Torstorp Skole 2016/17
 KVALITETSRAPPORT FOR Torstorp Skole 2016/17 INDHOLDSFORTEGNELSE Indhold INDHOLDSFORTEGNELSE... 2 FORORD... Fejl! Bogmærke er ikke defineret. PRÆSENTATION AF SKOLEN... 4 SAMMENFATTENDE HELHEDSVURDERING...
KVALITETSRAPPORT FOR Torstorp Skole 2016/17 INDHOLDSFORTEGNELSE Indhold INDHOLDSFORTEGNELSE... 2 FORORD... Fejl! Bogmærke er ikke defineret. PRÆSENTATION AF SKOLEN... 4 SAMMENFATTENDE HELHEDSVURDERING...
Forcensur ved folkeskolens 9. Klasses afgangsprøver 2015
 8. april 2016 Forcensur ved folkeskolens 9. Klasses afgangsprøver 2015 Udarbejdet af DAMVAD Analytics i samarbejde med Svend Kreiner for Styrelsen for Undervisning og Kvalitet, Ministeriet for Børn, Undervisning
8. april 2016 Forcensur ved folkeskolens 9. Klasses afgangsprøver 2015 Udarbejdet af DAMVAD Analytics i samarbejde med Svend Kreiner for Styrelsen for Undervisning og Kvalitet, Ministeriet for Børn, Undervisning
Indhold SOLRØD KOMMUNE SKOLE OG DAGTILBUD NOTAT. Emne: Solrød Folkeskoler i tal. Til: Orientering. Dato: 17. november 2014
 SOLRØD KOMMUNE SKOLE OG DAGTILBUD NOTAT Emne: Til: Solrød Folkeskoler i tal Orientering Dato: 17. november 2014 Sagsbeh.: Thomas Petersen Sagsnr.: Indhold Karaktergennemsnit... 2 Folkeskolens afgangsprøver
SOLRØD KOMMUNE SKOLE OG DAGTILBUD NOTAT Emne: Til: Solrød Folkeskoler i tal Orientering Dato: 17. november 2014 Sagsbeh.: Thomas Petersen Sagsnr.: Indhold Karaktergennemsnit... 2 Folkeskolens afgangsprøver
Bilag til. Kvalitetsrapport 2013-2014
 Bilag til Kvalitetsrapport 2013-2014 Udarbejdet marts 2015 Ifølge Bekendtgørelse om kvalitetsrapporter i folkeskolen skal der fremover udarbejdes en kvalitetsrapport hvert andet år. I skoleåret 2014/2015
Bilag til Kvalitetsrapport 2013-2014 Udarbejdet marts 2015 Ifølge Bekendtgørelse om kvalitetsrapporter i folkeskolen skal der fremover udarbejdes en kvalitetsrapport hvert andet år. I skoleåret 2014/2015
Dette notat indeholder en oversigt over hovedresultater fra PISA Etnisk 2012. Notatet består af følgende
 PISA Etnisk 2012: Kort opsummering af de væsentligste resultater Dette notat indeholder en oversigt over hovedresultater fra PISA Etnisk 2012. Notatet består af følgende afsnit: Fem hovedresultater Overordnede
PISA Etnisk 2012: Kort opsummering af de væsentligste resultater Dette notat indeholder en oversigt over hovedresultater fra PISA Etnisk 2012. Notatet består af følgende afsnit: Fem hovedresultater Overordnede
Kvalitetsrapport. Center for Børn og Læring. Skoleåret 2016/17. Lokalrapport for: Gullestrup skole
 Kvalitetsrapport Center for Børn og Læring Skoleåret 2016/17 Lokalrapport for: Gullestrup skole 1 Indholdsfortegnelse Indledning...3 Skolebestyrelsens udtalelse...4 Skoleledelsens udtalelse...4 Resultat
Kvalitetsrapport Center for Børn og Læring Skoleåret 2016/17 Lokalrapport for: Gullestrup skole 1 Indholdsfortegnelse Indledning...3 Skolebestyrelsens udtalelse...4 Skoleledelsens udtalelse...4 Resultat
UNDERVISNINGSEFFEKT-MODELLEN 2006 METODE OG RESULTATER
 UNDERVISNINGSEFFEKT-MODELLEN 2006 METODE OG RESULTATER Undervisningseffekten udregnes som forskellen mellem den forventede og den faktiske karakter i 9. klasses afgangsprøve. Undervisningseffekten udregnes
UNDERVISNINGSEFFEKT-MODELLEN 2006 METODE OG RESULTATER Undervisningseffekten udregnes som forskellen mellem den forventede og den faktiske karakter i 9. klasses afgangsprøve. Undervisningseffekten udregnes
Kvalitetsrapport. Center for Børn og Læring. Skoleåret 2016/17. Lokalrapport for: Aulum-Hodsager skole
 Kvalitetsrapport Center for Børn og Læring Skoleåret 2016/17 Lokalrapport for: Aulum-Hodsager skole 1 Indholdsfortegnelse Indledning...3 Skolebestyrelsens udtalelse...4 Skoleledelsens udtalelse...5 Resultat
Kvalitetsrapport Center for Børn og Læring Skoleåret 2016/17 Lokalrapport for: Aulum-Hodsager skole 1 Indholdsfortegnelse Indledning...3 Skolebestyrelsens udtalelse...4 Skoleledelsens udtalelse...5 Resultat
ØVELSE: ANVENDELSE AF DATA PÅ SKOLEOMRÅDET ET TÆNKT EKSEMPEL
 ØVELSE: ANVENDELSE AF DATA PÅ SKOLEOMRÅDET ET TÆNKT EKSEMPEL I Varde Kommune ønsker man, som drøftet i går, at fokusere på det strategiske tema øget chancelighed/bryde den negative sociale arv. Konkrete
ØVELSE: ANVENDELSE AF DATA PÅ SKOLEOMRÅDET ET TÆNKT EKSEMPEL I Varde Kommune ønsker man, som drøftet i går, at fokusere på det strategiske tema øget chancelighed/bryde den negative sociale arv. Konkrete
De socioøkonomiske referencer for gymnasiekarakterer Metodenotat
 De socioøkonomiske referencer for gymnasiekarakterer 2017 Metodenotat Indhold Sammenfatning... 5 Baggrund... 7 Datagrundlag... 9 Elever... 9 Fag, prøveform og niveau... 9 Socioøkonomiske baggrundsvariable...
De socioøkonomiske referencer for gymnasiekarakterer 2017 Metodenotat Indhold Sammenfatning... 5 Baggrund... 7 Datagrundlag... 9 Elever... 9 Fag, prøveform og niveau... 9 Socioøkonomiske baggrundsvariable...
STATUSRAPPORT 2015/16. Strandskolen Greve Kommune
 STATUSRAPPORT 2015/16 Strandskolen Greve Kommune INDHOLDSFORTEGNELSE 1 RESULTATER 3 1.1 Bliver alle så dygtige, som de kan? 3 1.2 Elevernes faglige niveau når de forlader folkeskolen 9 1.3 Overgang til
STATUSRAPPORT 2015/16 Strandskolen Greve Kommune INDHOLDSFORTEGNELSE 1 RESULTATER 3 1.1 Bliver alle så dygtige, som de kan? 3 1.2 Elevernes faglige niveau når de forlader folkeskolen 9 1.3 Overgang til
Brug testresultaterne. - inspiration til brug af de nye kriteriebaserede testresultater i matematik. Titel 1
 Brug testresultaterne - inspiration til brug af de nye kriteriebaserede testresultater i matematik Titel 1 Brug testresultaterne - inspiration til brug af de nye kriteriebaserede testresultater Matematik
Brug testresultaterne - inspiration til brug af de nye kriteriebaserede testresultater i matematik Titel 1 Brug testresultaterne - inspiration til brug af de nye kriteriebaserede testresultater Matematik
Pisa 2003 +2006. Læseundersøgelser & debat
 Pisa 2003 +2006 Læseundersøgelser & debat 1. Den danske regering indvilgede i at lade OECD gennemføre et review af grundskolen folkeskolen efter hvad regeringen betragtede som skuffende resultater, der
Pisa 2003 +2006 Læseundersøgelser & debat 1. Den danske regering indvilgede i at lade OECD gennemføre et review af grundskolen folkeskolen efter hvad regeringen betragtede som skuffende resultater, der
Introduktion til Beregneren og arbejde med progression i DNT Vejen kommune, Brørup, 24.-25.marts 2015. Jakob Wandall, NordicMetrics ApS
 Introduktion til Beregneren og arbejde med progression i DNT Vejen kommune, Brørup, 24.-25.marts 2015 Jakob Wandall, NordicMetrics ApS Baggrund Samfundsvidenskab (Cand. Polit) 1984-1994 Forskning, statistik
Introduktion til Beregneren og arbejde med progression i DNT Vejen kommune, Brørup, 24.-25.marts 2015 Jakob Wandall, NordicMetrics ApS Baggrund Samfundsvidenskab (Cand. Polit) 1984-1994 Forskning, statistik
Resultatet af den kommunale test i matematik
 Resultatet af den kommunale test i matematik Egedal Kommune 2012 Udarbejdet af Merete Hersløv Brodersen Pædagogisk medarbejder i matematik Indholdsfortegnelse: Indledning... 3 Resultaterne for hele Egedal
Resultatet af den kommunale test i matematik Egedal Kommune 2012 Udarbejdet af Merete Hersløv Brodersen Pædagogisk medarbejder i matematik Indholdsfortegnelse: Indledning... 3 Resultaterne for hele Egedal
BILAG 3: DETALJERET REDEGØ- RELSE FOR REGISTER- ANALYSER
 Til Undervisningsministeriet (Kvalitets- og Tilsynsstyrelsen) Dokumenttype Bilag til Evaluering af de nationale test i folkeskolen Dato September 2013 BILAG 3: DETALJERET REDEGØ- RELSE FOR REGISTER- ANALYSER
Til Undervisningsministeriet (Kvalitets- og Tilsynsstyrelsen) Dokumenttype Bilag til Evaluering af de nationale test i folkeskolen Dato September 2013 BILAG 3: DETALJERET REDEGØ- RELSE FOR REGISTER- ANALYSER
Beregneren Skole-Hjem-udgaven - Tillæg til vejledning til brug af Beregneren med kriteriescorer
 Beregneren Skole-Hjem-udgaven - Tillæg til vejledning til brug af Beregneren med kriteriescorer Introduktion Denne vejledning skal ses som et tillæg til i Vejledningen til Beregneren i standardudgaven.
Beregneren Skole-Hjem-udgaven - Tillæg til vejledning til brug af Beregneren med kriteriescorer Introduktion Denne vejledning skal ses som et tillæg til i Vejledningen til Beregneren i standardudgaven.
Om opgavetyper og usikkerhed i de nationale test
 Om opgavetyper og usikkerhed i de nationale test Af Svend Kreiner, juni 2017 1 Indholdsfortegnelse side 1. Indledning 3 2. Baggrunden 3 3. Udfordringer 4 4. Datagrundlaget 7 5. Om fejl i pædagogiske test
Om opgavetyper og usikkerhed i de nationale test Af Svend Kreiner, juni 2017 1 Indholdsfortegnelse side 1. Indledning 3 2. Baggrunden 3 3. Udfordringer 4 4. Datagrundlaget 7 5. Om fejl i pædagogiske test
KVALITETSRAPPORT SKOLEOMRÅDET 2012/2013 KVALITETSRAPPORT 2013/14. Langeland Kommune. Hjernen&Hjertet
 KVALITETSRAPPORT SKOLEOMRÅDET 2012/2013 RAMBØLL KOMMUNE KVALITETSRAPPORT 2013/14 Langeland Kommune Hjernen&Hjertet 1 Indholdsfortegnelse 1 FORORD 3 2 LÆSEVEJLEDNING 4 2.1 Formål med kvalitetsrapporten
KVALITETSRAPPORT SKOLEOMRÅDET 2012/2013 RAMBØLL KOMMUNE KVALITETSRAPPORT 2013/14 Langeland Kommune Hjernen&Hjertet 1 Indholdsfortegnelse 1 FORORD 3 2 LÆSEVEJLEDNING 4 2.1 Formål med kvalitetsrapporten
Kvalitetsrapport. Center for Børn og Læring. Skoleåret 2016/17. Lokalrapport for: Vildbjerg Skole
 Kvalitetsrapport Center for Børn og Læring Skoleåret 2016/17 Lokalrapport for: Vildbjerg Skole 1 Indholdsfortegnelse Indledning...3 Skolebestyrelsens udtalelse...4 Skoleledelsens udtalelse...5 Resultat
Kvalitetsrapport Center for Børn og Læring Skoleåret 2016/17 Lokalrapport for: Vildbjerg Skole 1 Indholdsfortegnelse Indledning...3 Skolebestyrelsens udtalelse...4 Skoleledelsens udtalelse...5 Resultat
Forside. Vejledning om de nationale test. til kommuner. Januar Titel 1
 Forside Vejledning om de nationale test til kommuner Januar 2017 Titel 1 Indhold Læsevejledning 5 Bag om de nationale test 6 De nationale test er et supplement 6 Fag og klassetrin for obligatoriske test
Forside Vejledning om de nationale test til kommuner Januar 2017 Titel 1 Indhold Læsevejledning 5 Bag om de nationale test 6 De nationale test er et supplement 6 Fag og klassetrin for obligatoriske test
- Vejledning til brug af beregner af læseudvikling
 Beregneren - progression i de nationale læsetest - Vejledning til brug af beregner af læseudvikling Læsevejledning og praktiske spørgsmål Vejledning indeholder 3 dele: 1. En indledning, som overordnet
Beregneren - progression i de nationale læsetest - Vejledning til brug af beregner af læseudvikling Læsevejledning og praktiske spørgsmål Vejledning indeholder 3 dele: 1. En indledning, som overordnet
KVALITETSRAPPORT FOR Hedehusene Skole 2016/17
 KVALITETSRAPPORT FOR Hedehusene Skole 2016/17 HØJE TAASTRUP KOMMUNE Indholdsfortegnelse FORORD... 2 PRÆSENTATION AF SKOLEN... 3 SAMMENFATTENDE HELHEDSVURDERING... 4 RESULTATER... 5 Bliver alle så dygtige,
KVALITETSRAPPORT FOR Hedehusene Skole 2016/17 HØJE TAASTRUP KOMMUNE Indholdsfortegnelse FORORD... 2 PRÆSENTATION AF SKOLEN... 3 SAMMENFATTENDE HELHEDSVURDERING... 4 RESULTATER... 5 Bliver alle så dygtige,
Introduktion til kompetenceudvikling: Beregneren og Lærings- progression i DNT Aalborg, Gigantium, 4.-5.marts 2015
 Introduktion til kompetenceudvikling: Beregneren og Lærings- progression i DNT Aalborg, Gigantium, 4.-5.marts 2015 Jakob Wandall & Søren Munkedal, NordicMetrics ApS Vores baggrund Samfundsvidenskab Arbejdet
Introduktion til kompetenceudvikling: Beregneren og Lærings- progression i DNT Aalborg, Gigantium, 4.-5.marts 2015 Jakob Wandall & Søren Munkedal, NordicMetrics ApS Vores baggrund Samfundsvidenskab Arbejdet
Fordeling af midler til specialundervisning
 NOTAT Fordeling af midler til specialundervisning Model for Norddjurs Kommune Søren Teglgaard Jakobsen December 2012 Købmagergade 22. 1150 København K. tlf. 444 555 00. kora@kora.dk. www.kora.dk Indholdsfortegnelse
NOTAT Fordeling af midler til specialundervisning Model for Norddjurs Kommune Søren Teglgaard Jakobsen December 2012 Købmagergade 22. 1150 København K. tlf. 444 555 00. kora@kora.dk. www.kora.dk Indholdsfortegnelse
Analyse af nystartende elever og omgængere i grundskolens børnehaveklasse. Baseret på data for skoleåret 2010/11
 Analyse af nystartende elever og omgængere i grundskolens børnehaveklasse Baseret på data for skoleåret 2010/11 Analyse af nystartende elever og omgængere i grundskolens børnehaveklasse Baseret på data
Analyse af nystartende elever og omgængere i grundskolens børnehaveklasse Baseret på data for skoleåret 2010/11 Analyse af nystartende elever og omgængere i grundskolens børnehaveklasse Baseret på data
Kvalitetsrapport. Center for Børn og Læring. Skoleåret 2016/17. Lokalrapport for: Tjørring skole
 Kvalitetsrapport Center for Børn og Læring Skoleåret 2016/17 Lokalrapport for: Tjørring skole 1 Indholdsfortegnelse Indledning...3 Skolebestyrelsens udtalelse...4 Skoleledelsens udtalelse...4 Resultat
Kvalitetsrapport Center for Børn og Læring Skoleåret 2016/17 Lokalrapport for: Tjørring skole 1 Indholdsfortegnelse Indledning...3 Skolebestyrelsens udtalelse...4 Skoleledelsens udtalelse...4 Resultat
Kvalitetsrapport. Center for Børn og Læring. Skoleåret 2016/17. Lokalrapport for: Gjellerupskolen
 Kvalitetsrapport Center for Børn og Læring Skoleåret 2016/17 Lokalrapport for: Gjellerupskolen 1 Indholdsfortegnelse Indledning...3 Skolebestyrelsens udtalelse...4 Skoleledelsens udtalelse...4 Resultat
Kvalitetsrapport Center for Børn og Læring Skoleåret 2016/17 Lokalrapport for: Gjellerupskolen 1 Indholdsfortegnelse Indledning...3 Skolebestyrelsens udtalelse...4 Skoleledelsens udtalelse...4 Resultat
Hvad er den socioøkonomiske reference? Hvordan læses den socioøkonomiske reference?... 2
 Indhold Hvad er den socioøkonomiske reference?... 2 Hvordan læses den socioøkonomiske reference?... 2 Hvordan kan man bruge den socioøkonomiske reference?... 3 Statistisk usikkerhed... 5 Bag om den socioøkonomiske
Indhold Hvad er den socioøkonomiske reference?... 2 Hvordan læses den socioøkonomiske reference?... 2 Hvordan kan man bruge den socioøkonomiske reference?... 3 Statistisk usikkerhed... 5 Bag om den socioøkonomiske
Forside. Vejledning om de nationale test. til skoleledere. Januar Titel 1
 Forside Vejledning om de nationale test til skoleledere Januar 2017 Titel 1 Indhold Læsevejledning 5 Bag om de nationale test 6 Formålet med de nationale test 6 Disse områder tester de nationale test 6
Forside Vejledning om de nationale test til skoleledere Januar 2017 Titel 1 Indhold Læsevejledning 5 Bag om de nationale test 6 Formålet med de nationale test 6 Disse områder tester de nationale test 6
Notat Vedrørende: Sagsnavn: Sagsnummer: Skrevet af: Forvaltning: Dato: Sendes til: Børn og Skoleudvalget 1. Indledning
 Notat Vedrørende: Supplerende notat til kvalitetsrapporten 2014 Oversigt over resultaterne af de nationale tests for Randers kommune og fraværstal Sagsnavn: Kvalitetsrapport 2014 Sagsnummer: 17.01.10-P05-2-15
Notat Vedrørende: Supplerende notat til kvalitetsrapporten 2014 Oversigt over resultaterne af de nationale tests for Randers kommune og fraværstal Sagsnavn: Kvalitetsrapport 2014 Sagsnummer: 17.01.10-P05-2-15
En prøveform for piger?
 1 En prøveform for piger? Over de seneste ti år er karaktergabet mellem drenge og piger i folkeskolen vokset, når vi ser på resultaterne af folkeskolens afgangsprøve. I samme periode er karaktergabet mellem
1 En prøveform for piger? Over de seneste ti år er karaktergabet mellem drenge og piger i folkeskolen vokset, når vi ser på resultaterne af folkeskolens afgangsprøve. I samme periode er karaktergabet mellem
Anvendelse af testresultater fra de nationale test for skoleledere og kommuner
 Anvendelse af testresultater fra de nationale test for skoleledere og kommuner Anvendelse af testresultater fra de nationale test for skoleledere og kommuner Redaktion: Anne Ebdrup Foto: Ulrik Jantzen/
Anvendelse af testresultater fra de nationale test for skoleledere og kommuner Anvendelse af testresultater fra de nationale test for skoleledere og kommuner Redaktion: Anne Ebdrup Foto: Ulrik Jantzen/
Frafaldet på erhvervsuddannelserne er mindsket efter reformen
 14. november 218 218:23 Rettet 3. december 218 Figur 1 var fejlbehæftet (y-akse var forkert). Figur er udskriftet. Frafaldet på erhvervsuddannelserne er mindsket efter reformen Af Anne Nissen Bonde, Charlotte
14. november 218 218:23 Rettet 3. december 218 Figur 1 var fejlbehæftet (y-akse var forkert). Figur er udskriftet. Frafaldet på erhvervsuddannelserne er mindsket efter reformen Af Anne Nissen Bonde, Charlotte
Anvendelse af testresultater fra de nationale test for skoleledere og kommuner
 Anvendelse af testresultater fra de nationale test for skoleledere og kommuner Indhold Om vejledningen... 4 Kort om testene... 5 Anvendelse af testresultater fra de nationale test for skoleledere og kommuner
Anvendelse af testresultater fra de nationale test for skoleledere og kommuner Indhold Om vejledningen... 4 Kort om testene... 5 Anvendelse af testresultater fra de nationale test for skoleledere og kommuner
En prøveform for piger?
 1 En prøveform for piger? Over de seneste ti år er karaktergabet mellem drenge og piger i folkeskolen vokset, når vi ser på resultaterne af folkeskolens afgangsprøve. En stigning på 6 procentpoint i perioden
1 En prøveform for piger? Over de seneste ti år er karaktergabet mellem drenge og piger i folkeskolen vokset, når vi ser på resultaterne af folkeskolens afgangsprøve. En stigning på 6 procentpoint i perioden
STATUSRAPPORT 2015/16. Selsmoseskolen Høje-Taastrup Kommune
 STATUSRAPPORT 2015/16 Selsmoseskolen Høje-Taastrup Kommune INDHOLDSFORTEGNELSE 1 PRÆSENTATION AF SKOLEN 3 2 SAMMENFATTENDE HELHEDSVURDERING 4 3 RESULTATER 5 3.1 Bliver alle så dygtige, som de kan? 5 3.2
STATUSRAPPORT 2015/16 Selsmoseskolen Høje-Taastrup Kommune INDHOLDSFORTEGNELSE 1 PRÆSENTATION AF SKOLEN 3 2 SAMMENFATTENDE HELHEDSVURDERING 4 3 RESULTATER 5 3.1 Bliver alle så dygtige, som de kan? 5 3.2
De socioøkonomiske referencer for grundskolekarakterer 2016
 De socioøkonomiske referencer for grundskolekarakterer 2016 1 Indhold Sammenfatning.. 4 Elevgrundlag... 8 Skoleåret 2015/2016... 8 3-års perioden 2013/2014-2015/2016... 10 Skoletype... 11 December 2016
De socioøkonomiske referencer for grundskolekarakterer 2016 1 Indhold Sammenfatning.. 4 Elevgrundlag... 8 Skoleåret 2015/2016... 8 3-års perioden 2013/2014-2015/2016... 10 Skoletype... 11 December 2016
Læseundersøgelse blandt unge i målgruppe for forberedende grunduddannelse (FGU)
 Læseundersøgelse blandt unge i målgruppe for forberedende grunduddannelse (FGU) Anna Steenberg Gellert og Carsten Elbro, Center for Læseforskning, Københavns Universitet Baggrund På den nyligt oprettede
Læseundersøgelse blandt unge i målgruppe for forberedende grunduddannelse (FGU) Anna Steenberg Gellert og Carsten Elbro, Center for Læseforskning, Københavns Universitet Baggrund På den nyligt oprettede
Socioøkonomisk reference: I hvilke prøver og på hvilke skoletyper klarer eleverne sig bedre end forventet i 9. klasse i 2016/2017?
 Socioøkonomisk reference: I hvilke prøver og på hvilke skoletyper klarer eleverne sig bedre end forventet i 9. klasse i 2016/2017? Mange undersøgelser viser, at elevernes karakterer hænger sammen med deres
Socioøkonomisk reference: I hvilke prøver og på hvilke skoletyper klarer eleverne sig bedre end forventet i 9. klasse i 2016/2017? Mange undersøgelser viser, at elevernes karakterer hænger sammen med deres
De socioøkonomiske referencer for gymnasiekarakterer 2013
 De socioøkonomiske referencer for gymnasiekarakterer 2013 Indhold Sammenfatning... 5 Indledning... 7 Datagrundlag... 9 Elever... 9 Fag, prøveform og niveau... 9 Socioøkonomiske baggrundsvariable... 9
De socioøkonomiske referencer for gymnasiekarakterer 2013 Indhold Sammenfatning... 5 Indledning... 7 Datagrundlag... 9 Elever... 9 Fag, prøveform og niveau... 9 Socioøkonomiske baggrundsvariable... 9
Kvalitetsrapport. Center for Børn og Læring. Skoleåret 2016/17. Lokalrapport for: Herningsholmskolen
 Kvalitetsrapport Center for Børn og Læring Skoleåret 2016/17 Lokalrapport for: Herningsholmskolen 1 Indholdsfortegnelse Indledning...3 Skolebestyrelsens udtalelse...4 Skoleledelsens udtalelse...4 Resultat
Kvalitetsrapport Center for Børn og Læring Skoleåret 2016/17 Lokalrapport for: Herningsholmskolen 1 Indholdsfortegnelse Indledning...3 Skolebestyrelsens udtalelse...4 Skoleledelsens udtalelse...4 Resultat
Fokuspunkter i oplæg
 Data i folkeskolen Fokuspunkter i oplæg Sammenhængen til kick-off konferencen Dataforståelser Nationale test Progressionsmåling Nye visninger og funktionalitet Anbefalinger fra forskning Læringskonsulenternes
Data i folkeskolen Fokuspunkter i oplæg Sammenhængen til kick-off konferencen Dataforståelser Nationale test Progressionsmåling Nye visninger og funktionalitet Anbefalinger fra forskning Læringskonsulenternes
KVALITETSRAPPORT 2014/15. Virum Skole Lyngby-Taarbæk Kommune
 KVALITETSRAPPORT 2014/15 Virum Skole Lyngby-Taarbæk Kommune Indholdsfortegnelse 1 PRÆSENTATION AF SKOLEN 3 2 SAMMENFATTENDE HELHEDSVURDERING 4 3 RESULTATER 5 3.1 Bliver alle så dygtige, som de kan? 5 3.2
KVALITETSRAPPORT 2014/15 Virum Skole Lyngby-Taarbæk Kommune Indholdsfortegnelse 1 PRÆSENTATION AF SKOLEN 3 2 SAMMENFATTENDE HELHEDSVURDERING 4 3 RESULTATER 5 3.1 Bliver alle så dygtige, som de kan? 5 3.2
Statusnotat. for skoleåret 2017/2018. Allerød Kommune Skole og Dagtilbud
 28-02-2019 Statusnotat for skoleåret /2018 Allerød Kommune Skole og Dagtilbud 1 Indhold Statusnotat /2018...2 Indledning...2 Mål og resultatmål...2 Trivsel...3 Elevernes trivsel skal øges...3 Trivsel i
28-02-2019 Statusnotat for skoleåret /2018 Allerød Kommune Skole og Dagtilbud 1 Indhold Statusnotat /2018...2 Indledning...2 Mål og resultatmål...2 Trivsel...3 Elevernes trivsel skal øges...3 Trivsel i
Vejledning for anvendelse af Beregneren til Matematik. Måling af progression i de nationale til i matematik
 Vejledning for anvendelse af Beregneren til Matematik Læsevejledning og praktiske spørgsmål Vejledningen indeholder 3 dele: 1. En indledning, som overordnet beskriver baggrunden for projektet Øget pædagogisk
Vejledning for anvendelse af Beregneren til Matematik Læsevejledning og praktiske spørgsmål Vejledningen indeholder 3 dele: 1. En indledning, som overordnet beskriver baggrunden for projektet Øget pædagogisk
Analyse af sociale baggrundsfaktorer for elever, der opnår bonus A
 Analyse af sociale baggrundsfaktorer for elever, der opnår bonus A Analyse af sociale baggrundsfaktorer for elever, der opnår Bonus A Forfattere: Jeppe Christiansen og Lone Juul Hune UNI C UNI C, juni
Analyse af sociale baggrundsfaktorer for elever, der opnår bonus A Analyse af sociale baggrundsfaktorer for elever, der opnår Bonus A Forfattere: Jeppe Christiansen og Lone Juul Hune UNI C UNI C, juni
Elever i børnehaveklasse, skoleåret 2014/2015
 Elever i børnehaveklasse, skoleåret 2014/2015 Elevtallene for børnehaveklasse i grundskolen for skoleåret 2014/15 viser, at: I skoleåret 2014/2015 startede knap 67.600 elever i børnehaveklasse i grundskolen.
Elever i børnehaveklasse, skoleåret 2014/2015 Elevtallene for børnehaveklasse i grundskolen for skoleåret 2014/15 viser, at: I skoleåret 2014/2015 startede knap 67.600 elever i børnehaveklasse i grundskolen.
Sammenhængsanalyser. Et eksempel: Sammenhæng mellem rygevaner som 45-årig og selvvurderet helbred som 51 blandt mænd fra Københavns amt.
 Sammenhængsanalyser Et eksempel: Sammenhæng mellem rygevaner som 45-årig og selvvurderet helbred som 51 blandt mænd fra Københavns amt. rygevaner som 45 årig * helbred som 51 årig Crosstabulation rygevaner
Sammenhængsanalyser Et eksempel: Sammenhæng mellem rygevaner som 45-årig og selvvurderet helbred som 51 blandt mænd fra Københavns amt. rygevaner som 45 årig * helbred som 51 årig Crosstabulation rygevaner
KVALITETSRAPPORT. Skoleåret 2017/18. Skanderborg Kommune
 KVALITETSRAPPORT Skoleåret 20 Skanderborg Kommune INDHOLD 1. LÆSEVEJLEDNING... 2 1.1. Kvalitetsrapportens datagrundlag... 2 1.2. Rapportens opbygning... 3 2. RESULTATER... 4 2.1. Karakterer ved afslutningen
KVALITETSRAPPORT Skoleåret 20 Skanderborg Kommune INDHOLD 1. LÆSEVEJLEDNING... 2 1.1. Kvalitetsrapportens datagrundlag... 2 1.2. Rapportens opbygning... 3 2. RESULTATER... 4 2.1. Karakterer ved afslutningen
STATUSRAPPORT 2015/16. Sølystskolen Silkeborg Kommune
 STATUSRAPPORT 2015/16 Sølystskolen Silkeborg Kommune INDHOLDSFORTEGNELSE 1 RESULTATER 3 1.1 Bliver alle så dygtige, som de kan? 3 1.2 Elevernes faglige niveau når de forlader folkeskolen 9 1.3 Overgang
STATUSRAPPORT 2015/16 Sølystskolen Silkeborg Kommune INDHOLDSFORTEGNELSE 1 RESULTATER 3 1.1 Bliver alle så dygtige, som de kan? 3 1.2 Elevernes faglige niveau når de forlader folkeskolen 9 1.3 Overgang
KVALITETSRAPPORT 2014/15. Issø-skolen Svendborg Kommune
 KVALITETSRAPPORT 2014/15 Issø-skolen Svendborg Kommune Indholdsfortegnelse 1 FORORD 3 2 PRÆSENTATION AF SKOLEN 4 3 SAMMENFATTENDE HELHEDSVURDERING 5 4 RESULTATER 6 4.1 Bliver alle så dygtige, som de kan?
KVALITETSRAPPORT 2014/15 Issø-skolen Svendborg Kommune Indholdsfortegnelse 1 FORORD 3 2 PRÆSENTATION AF SKOLEN 4 3 SAMMENFATTENDE HELHEDSVURDERING 5 4 RESULTATER 6 4.1 Bliver alle så dygtige, som de kan?
Kvalitetsrapport. Center for Børn og Læring. Skoleåret 2016/17. Lokalrapport for: Timring skole
 Kvalitetsrapport Center for Børn og Læring Skoleåret 2016/17 Lokalrapport for: Timring skole 1 Indholdsfortegnelse Indledning...3 Skolebestyrelsens udtalelse...4 Skoleledelsens udtalelse...5 Resultat bemærkninger...5
Kvalitetsrapport Center for Børn og Læring Skoleåret 2016/17 Lokalrapport for: Timring skole 1 Indholdsfortegnelse Indledning...3 Skolebestyrelsens udtalelse...4 Skoleledelsens udtalelse...5 Resultat bemærkninger...5
Indvandrere og efterkommere i foreninger er frivillige i samme grad som danskere
 1 Indvandrere og efterkommere i foreninger er frivillige i samme grad som danskere Færre med ikke-vestlige oprindelse end dansk oprindelse er medlem af en forening. Men ikke-vestlige indvandrere og efterkommere
1 Indvandrere og efterkommere i foreninger er frivillige i samme grad som danskere Færre med ikke-vestlige oprindelse end dansk oprindelse er medlem af en forening. Men ikke-vestlige indvandrere og efterkommere
De danske PISA-rapporters håndtering af PISAundersøgelserne
 Kommentarer 79 De danske PISA-rapporters håndtering af PISAundersøgelserne Hans Bay, UCC I december 2010 udkom den 4. danske PISA-rapport (PISA, 2009). Rapporten er omtalt i MONA i Egelund (2011), i Davidsson
Kommentarer 79 De danske PISA-rapporters håndtering af PISAundersøgelserne Hans Bay, UCC I december 2010 udkom den 4. danske PISA-rapport (PISA, 2009). Rapporten er omtalt i MONA i Egelund (2011), i Davidsson
KVALITETSRAPPORT FOR ØRSTEDSKOLEN 2016/17
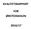 KVALITETSRAPPORT FOR ØRSTEDSKOLEN 2016/17 INDHOLDSFORTEGNELSE 1. FORORD 2. PRÆSENTATION AF SKOLEN 3. SAMMENFATTENDE HELHEDSVURDERING 4. RESULTATER 4.1. Bliver alle så dygtige, som de kan? 4.2. Elevernes
KVALITETSRAPPORT FOR ØRSTEDSKOLEN 2016/17 INDHOLDSFORTEGNELSE 1. FORORD 2. PRÆSENTATION AF SKOLEN 3. SAMMENFATTENDE HELHEDSVURDERING 4. RESULTATER 4.1. Bliver alle så dygtige, som de kan? 4.2. Elevernes
Notat til Statsrevisorerne om beretning om udviklingen af de nationale test. April 2014
 Notat til Statsrevisorerne om beretning om udviklingen af de nationale test April 2014 FORTSAT NOTAT TIL STATSREVISORERNE 1 Opfølgning i sagen om beretning om udviklingen af de nationale test (beretning
Notat til Statsrevisorerne om beretning om udviklingen af de nationale test April 2014 FORTSAT NOTAT TIL STATSREVISORERNE 1 Opfølgning i sagen om beretning om udviklingen af de nationale test (beretning
Forslag fra arbejdsgruppe 7:
 Forslag fra arbejdsgruppe 7: - En målstyret skole Marts 2015 Billeder: Colourbox.dk Læs om folkeskolereformen og de øvrige arbejdsgrupper på www.norddjurs.dk/folkeskolereformen 2 Forord Der er 3 nationale
Forslag fra arbejdsgruppe 7: - En målstyret skole Marts 2015 Billeder: Colourbox.dk Læs om folkeskolereformen og de øvrige arbejdsgrupper på www.norddjurs.dk/folkeskolereformen 2 Forord Der er 3 nationale
Analyse 17. marts 2015
 17. marts 2015 Indvandrerpiger fra ghettoer klarer sig særligt dårligt i grundskolen Af Kristian Thor Jakobsen Børn med ikke-vestlig baggrund klarer sig dårligst ved grundskolens afgangsprøver i dansk
17. marts 2015 Indvandrerpiger fra ghettoer klarer sig særligt dårligt i grundskolen Af Kristian Thor Jakobsen Børn med ikke-vestlig baggrund klarer sig dårligst ved grundskolens afgangsprøver i dansk
Kapitel 2: Evaluering af elevernes udbytte af undervisningen
 Kapitel 2: Evaluering af elevernes udbytte af undervisningen På Hindholm Privatskole er evaluering en naturlig del af undervisningen. Den foregår dels løbende og i forskellig form - dels på fastlagte tidspunkter
Kapitel 2: Evaluering af elevernes udbytte af undervisningen På Hindholm Privatskole er evaluering en naturlig del af undervisningen. Den foregår dels løbende og i forskellig form - dels på fastlagte tidspunkter
Status / evaluering på arbejdet med folkeskolereformen i Rebild kommune
 Status / evaluering på arbejdet med folkeskolereformen i Rebild kommune Center Børn og Unge Journalnr: 17.01.00-A00-3-16 Ref.: Helle Grynderup Dato: 03-11-2016 Baggrund Børne- og Ungdomsudvalget godkendte
Status / evaluering på arbejdet med folkeskolereformen i Rebild kommune Center Børn og Unge Journalnr: 17.01.00-A00-3-16 Ref.: Helle Grynderup Dato: 03-11-2016 Baggrund Børne- og Ungdomsudvalget godkendte
Elever i børnehaveklasse, skoleåret 2016/2017
 Elever i børnehaveklasse, skoleåret 2016/2017 Elevtallene for børnehaveklasse i grundskolen for skoleåret 2016/17 viser, at: I skoleåret 2016/2017 startede ca. 66.300 elever i børnehaveklasse i grundskolen.
Elever i børnehaveklasse, skoleåret 2016/2017 Elevtallene for børnehaveklasse i grundskolen for skoleåret 2016/17 viser, at: I skoleåret 2016/2017 startede ca. 66.300 elever i børnehaveklasse i grundskolen.
Notat 5.1.: Elevers karaktergennemsnit og fordeling på almene efterskoler
 Notat 5..: Elevers karaktergennemsnit og fordeling på almene efterskoler Af Konsulent Mette Hjort-Madsen og Konsulent Ole Bjerring, Efterskoleforeningen Udarbejdet for Arbejdsgruppe om tilskudsrevision,
Notat 5..: Elevers karaktergennemsnit og fordeling på almene efterskoler Af Konsulent Mette Hjort-Madsen og Konsulent Ole Bjerring, Efterskoleforeningen Udarbejdet for Arbejdsgruppe om tilskudsrevision,
NY CHANCE TIL ALLE HALTER
 16. april 2008 af Jes Vilhelmsen direkte tlf. 33557721 Resumé: NY CHANCE TIL ALLE HALTER Vurderet ud fra regeringens egne målsætninger halter NY CHANCE TIL ALLE, og værst ser det ud med hensyn til målet
16. april 2008 af Jes Vilhelmsen direkte tlf. 33557721 Resumé: NY CHANCE TIL ALLE HALTER Vurderet ud fra regeringens egne målsætninger halter NY CHANCE TIL ALLE, og værst ser det ud med hensyn til målet
HVAD ER UNDERVISNINGSEFFEKTEN
 HVAD ER UNDERVISNINGSEFFEKTEN Undervisningseffekten viser, hvordan eleverne på en given skole klarer sig sammenlignet med, hvordan man skulle forvente, at de ville klare sig ud fra forældrenes baggrund.
HVAD ER UNDERVISNINGSEFFEKTEN Undervisningseffekten viser, hvordan eleverne på en given skole klarer sig sammenlignet med, hvordan man skulle forvente, at de ville klare sig ud fra forældrenes baggrund.
Betydning af elevernes sociale baggrund. Undervisningsministeriet
 Betydning af elevernes sociale baggrund Undervisningsministeriet Betydning af elevernes sociale baggrund Pointe 1: Der er flest fagligt svage elever på hf...... 4 Pointe 2: Et fagligt svagt elevgrundlag
Betydning af elevernes sociale baggrund Undervisningsministeriet Betydning af elevernes sociale baggrund Pointe 1: Der er flest fagligt svage elever på hf...... 4 Pointe 2: Et fagligt svagt elevgrundlag
KVALITETSRAPPORT 2014/15 Mølleskolen Skanderborg Kommune
 FOTOGRAF: JENS PETER ENGEDAL KVALITETSRAPPORT 2014/15 Mølleskolen Skanderborg Kommune Indholdsfortegnelse 1 RESULTATER 3 1.1 Bliver alle så dygtige, som de kan? 3 1.2 Elevernes faglige niveau når de forlader
FOTOGRAF: JENS PETER ENGEDAL KVALITETSRAPPORT 2014/15 Mølleskolen Skanderborg Kommune Indholdsfortegnelse 1 RESULTATER 3 1.1 Bliver alle så dygtige, som de kan? 3 1.2 Elevernes faglige niveau når de forlader
Nye resultatmål. Inspirationsmøde om skolereform og Aarhusaftale Den 21. januar 2015
 Nye resultatmål Inspirationsmøde om skolereform og Aarhusaftale Den 21. januar 2015 Tre overordnede mål for folkeskolen 1. Folkeskolen skal udfordre alle elever, så de bliver så dygtige, de kan 2. Folkeskolen
Nye resultatmål Inspirationsmøde om skolereform og Aarhusaftale Den 21. januar 2015 Tre overordnede mål for folkeskolen 1. Folkeskolen skal udfordre alle elever, så de bliver så dygtige, de kan 2. Folkeskolen
STATUSRAPPORT 2015/16. Torstorp Skole Høje-Taastrup Kommune
 STATUSRAPPORT 2015/16 Torstorp Skole Høje-Taastrup Kommune INDHOLDSFORTEGNELSE 1 FORORD 3 2 PRÆSENTATION AF SKOLEN 4 3 SAMMENFATTENDE HELHEDSVURDERING 5 4 RESULTATER 6 4.1 Bliver alle så dygtige, som de
STATUSRAPPORT 2015/16 Torstorp Skole Høje-Taastrup Kommune INDHOLDSFORTEGNELSE 1 FORORD 3 2 PRÆSENTATION AF SKOLEN 4 3 SAMMENFATTENDE HELHEDSVURDERING 5 4 RESULTATER 6 4.1 Bliver alle så dygtige, som de
National reference for de nationale test
 National reference for de nationale test Der er tre principielt forskellige repræsentative kvantitative opgørelse af læring i grundskolen i Danmark: De internationale undersøgelser (ILSA 1 ), Folkeskolens
National reference for de nationale test Der er tre principielt forskellige repræsentative kvantitative opgørelse af læring i grundskolen i Danmark: De internationale undersøgelser (ILSA 1 ), Folkeskolens
Psykisk arbejdsmiljø og stress
 Psykisk arbejdsmiljø og stress - Hvilke faktorer har indflydelse på det psykiske arbejdsmiljø og medarbejdernes stress Marts 2018 Konklusion Denne analyse forsøger at afklare, hvilke faktorer der påvirker
Psykisk arbejdsmiljø og stress - Hvilke faktorer har indflydelse på det psykiske arbejdsmiljø og medarbejdernes stress Marts 2018 Konklusion Denne analyse forsøger at afklare, hvilke faktorer der påvirker
Notat vedr. læseresultater for skoleårene 2012/2013, 2013/2014 og 2014/2015
 Notat Center for Dagtilbud og Skoler Dagtilbud og Skoler Birkedalsvej 27 3000 Helsingør Tlf. 49282782 ltp08@helsingor.dk Dato 09.01.2015 Sagsbeh. Lene Tetzlaff-Petersen Notat vedr. læseresultater for skoleårene
Notat Center for Dagtilbud og Skoler Dagtilbud og Skoler Birkedalsvej 27 3000 Helsingør Tlf. 49282782 ltp08@helsingor.dk Dato 09.01.2015 Sagsbeh. Lene Tetzlaff-Petersen Notat vedr. læseresultater for skoleårene
FORÆLDRETILFREDSHED 2016 DAGTILBUD GLADSAXE KOMMUNE
 FORÆLDRETILFREDSHED 2016 DAGTILBUD GLADSAXE KOMMUNE 1 INDHOLD 01 Introduktion 02 Læsevejledning 03 Samlede resultater 04 Resultater på tværs 05 Prioriteringskort 06 Metode 2 01. INTRODUKTION Forældretilfredsheden
FORÆLDRETILFREDSHED 2016 DAGTILBUD GLADSAXE KOMMUNE 1 INDHOLD 01 Introduktion 02 Læsevejledning 03 Samlede resultater 04 Resultater på tværs 05 Prioriteringskort 06 Metode 2 01. INTRODUKTION Forældretilfredsheden
