Vektorfelter langs kurver
|
|
|
- Bent Dahl
- 6 år siden
- Visninger:
Transkript
1 enote 25 1 enote 25 Vektorfelter langs kurver I enote 24 dyrkes de indledende overvejelser om vektorfelter. I denne enote vil vi se på vektorfelternes værdier langs kurver og benytte metoder fra enote 22 om kurveintegration til at opstille de såkaldte tangentielle kurveintegraler og bruge dem til at undersøge om et givet vektorfelt er et gradientvektorfelt eller ej. Hvis et vektorfelt er et gradientvektorfelt for en funktion f (x, y, z) så kan vi konstruere alle sådanne stamfunktioner ved hjælp af tangentiel kurveintegration af vektorfeltet. Og som vi skal se, gælder det også omvendt, at hvis det tangentielle kurveintegral af et givet vektorfeltet over enhver lukket kurve er, så er vektorfeltet et gradientvektorfelt. Det tangentielle kurveintegral af et vektorfelt over en lukket kurve kaldes cirkulationen af vektorfeltet over kurven. Alene ud fra navnet er det ikke overraskende, at en sådan generel cirkulation er ækvivalent med, at vektorfeltet selv har rotationsvektorfeltet Det tangentielle kurveintegral Lad V(x, y, z) være et glat vektorfelt i rummet, se enote 24 og lad K r betegne en glat parametriseret kurve: K r : r(u) (x(u), y(u), z(u)), u [a, b]. (25-1) Langs med kurven K r har vi så i ethvert punkt r(u) på kurven to vektorer, dels vektorfeltets værdi i punktet, V(r(u)), og dels tangentvektoren r (u) til kurven i punktet. Ved hjælp af disse to vektorer kan vi konstruere en glat funktion på kurven, som derefter kan integreres over kurven: Det tangentielle kurveintegral af V(x, y, z) langs en given parametriseret kurve K r er kurveintegralet af længden af projektionen (med fortegn) af V(r(u)) på kurvens tangent der er repræsenteret ved r (u). Det ønskede integral er altså defineret således:
2 enote DET TANGENTIELLE KURVEINTEGRAL 2 Definition 25.1 Det tangentielle kurveintegral af V(x, y, z) langs K r er defineret ved: Tan(V, K r ) V e dµ. (25-2) K r Integranden er altså i dette tilfælde givet ved skalarproduktet: f (r(u)) V(r(u)) e(u), (25-3) hvor e(u) er defineret ved e(u) { r (u)/ r (u) hvis r (u) hvis r (u). (25-4) Bemærk, at så har vi for alle u: e(u) r (u) r (u). (25-5) Det tangentielle kurveintegral Tan(V, K r ) af V langs K r er derfor relativt simpelt at udregne - vi behøver faktisk ikke først at finde Jacobi-funktionen Jacobi r (u), altså længden af r (u) : Tan(V, K r ) V e dµ K r b a b a b a (V(r(u)) e(u)) Jacobi r (u) du V(r(u)) (e(u) r (u) ) du V(r(u)) r (u) du. Vi har altså følgende simple udtryk for tangentielle kurveintegraler: (25-6) Sætning 25.2 Det tangentielle kurveintegral af V(x, y, z) langs K r kan beregnes således: b Tan(V, K r ) V e dµ K r a V(r(u)) r (u) du. (25-7)
3 enote DET TANGENTIELLE KURVEINTEGRAL 3 Læg mærke til, at den sidste integrand i (25-6) er kontinuert når V(x, y, z) og r (u) er kontinuerte selv om det ikke umiddelbart fremgår af definitionen (vektorfeltet e(u) er jo ikke nødvendigvis kontinuert - medmindre r(u) er en regulær parameterfremstilling). Hvis kurven gennemløbes baglæns, så skifter Tan(V, K r ) fortegn. Lad nemlig K r : r(u) r(b + a u), u [a, b]. (25-8) Så er r (u) r (u) og e(u) e(u) sådan at Tan(V, K r ) Tan(V, K r ). (25-9) Definition 25.3 I analogi med det tangentielle kurveintegral definerer vi det ortogonale kurveintegral Ort(V, K r ) af V langs K r ved at projicere V(r(u)) vinkelret ind på den plan i rummet, som selv står vinkelret på r (u) og dernæst finde kurveintegralet af længden af den projektion (som funktion af u). Eksempel 25.4 Lad V(x, y, z) (, z, y). Vi ønsker at bestemme det tangentielle kurveintegral af V langs følgende parametriserede stykke af en skruelinje [ K r : r(u) (cos(u), sin(u), u), u, π ]. (25-1) 2 Ved at indsætte i (25-6) fås Tan(V, K r ) π/2 π/2 π/2 V(r(u)) r (u) du (, u, sin(u)) ( sin(u), cos(u), 1) du (u cos(u) + sin(u)) du [u sin(u)] π/2 π 2. (25-11)
4 enote DET TANGENTIELLE KURVEINTEGRAL 4 Figur 25.1: Skruelinjen r(u) ( cos(u), sin(u), 1 1 u), u [ 2π, 2π], og vektorfeltet V(x, y, z) (x, (x + y), 2z) er her antydet dels i rummet og dels langs skruelinjen. Opgave 25.5 Lad V(x, y, z) (, x, z). Bestem både det tangentielle og det ortogonale kurveintegral af V langs følgende parametriserede stykke af en cirkel [ K r : r(u) (cos(u), sin(u), ), u, π ]. (25-12) 2
5 enote DET TANGENTIELLE KURVEINTEGRAL 5 Metode 25.6 Tangentielle linjeintegraler til variabel punkt Lad V(x, y, z) være et givet vektorfelt i rummet. Vi vil nu konstruere en funktion F (x, y, z) i rummet som i punktet (x, y, z ) er defineret til at være kurveintegralet af V(x, y, z) langs det rette linjestykke fra (,, ) til punktet (x, y, z ), dvs. F defineres således: F (x, y, z ) Tan(V, K r ), (25-13) hvor kurven er givet ved den simplest mulige kurve fra (,, ) til (x, y, z ): K r : r(u) (u x, u y, u z ) u (x, y, z ), u [, 1]. (25-14) Så har vi dermed følgende funktionsværdier for (stjerne-)funktionen hørende til V(x, y, z): F (x, y, z ) Tan(V, K r ) V(r(u)) r (u) du (x, y, z ) V(u x, u y, u z ) du. (25-15) Det sidste integral i (25-15) skal forstås som et integral af hver af de tre koordinatfunktioner af V(u x, u y, u z ). Integralet giver dermed en vektor med tre komposanter sådan at skalarproduktet med stedvektoren (x, y, z ) derefter giver en talværdi, som altså er værdien af -funktionen F (x, y, z) i (x, y, z ). Eksempel 25.7 Konstruktion af tangentiel linjeintegral til variable punkt Lad V(x, y, z) betegne følgende vektorfelt i rummet: V(x, y, z) (x, 2y, 3z). (25-16) Så er den tilhørende -funktion: F (x, y, z ) (x, y, z ) (x, y, z ) V(u x, u y, u z ) du (u x, 2u y, 3u z ) du 1 2 (x, y, z ) (x, 2 y, 3 z ) 1 2 (x y z 2 ) (25-17) 1 2 x2 + y z2.
6 enote STAMFUNKTION TIL ET GRADIENTVEKTORFELT 6 Bemærk, at (stjerne-)funktionen F (x, y, z) 1 2 x2 + y x2 som er konstrueret i eksempel 25.7 har følgende gradient, som netop er det vektorfelt vi begyndte med: F (x, y, z) (x, 2y, 3z) V(x, y, z). (25-18) Det er ikke nogen tilfældighed! Vektorfeltet har rotationsvektorfelt Rot, og er derfor et gradientvektorfelt, som vi skal se i sætning nedenfor Stamfunktion til et gradientvektorfelt Definition 25.8 Stamfunktion for et gradientvektorfelt Lad V(x, y, z) være et glat vektorfelt i rummet. Hvis der findes en glat funktion f (x, y, z) således at f (x, y, z) V(x, y, z), (25-19) så siges f (x, y, z) at være en stamfunktion til vektorfeltet V(x, y, z). Hvis vi kender én stamfunktion, så kender vi enhver af dem pånær en arbitrær konstant! Som vi skal se giver metode 25.6 en konstruktion af alle stamfunktioner til et givet vektorfelt. Hvis der ikke findes nogen stamfunktion til vektorfeltet, så får vi ikke desto mindre alligevel med den metode konstrueret en -funktion i rummet den funktion er imidlertid i så fald ikke nogen stamfunktion. Det kan og bør selvfølgelig afgøres ved at gøre prøve, altså ved direkte at beregne gradienten af -funktionen og sammenligne med det givne vektorfelt. Opgave 25.9 Lad V(x, y, z) betegne vektorfeltet: V(x, y, z) (x, 2y, 3z). (25-2) bestem funktionsværdierne for (stjerne-)funktionen F p (x, y, z) ud fra det generelle punkt p (a, b, c) hørende til V(x, y, z).
7 enote STAMFUNKTION TIL ET GRADIENTVEKTORFELT 7 Vink: Det rette linjestykke fra punktet (a, b, c) til (x, y, z ) kan parametriseres således: K r : r(u) (a + u (x a), b + u (y b), c + u (z c)), u [, 1]. (25-21) således at Gælder det stadig, at r (u) (x a), y b, z c). (25-22) F p (x, y, z) V(x, y, z)? (25-23) Sætning 25.1 Tangentielt kurveintegral af et gradientvektorfelt Lad f (x, y, z) betegne en glat funktion af de tre variable i rummet, og lad V(x, y, z) f (x, y, z) betegne gradientvektorfeltet for f (x, y, z). Lad K r være en glat parametriseret kurve fra et punkt p til et punkt q i rummet. Kurven behøver ikke nødvendigvis at være retlinjet. Så gælder følgende: Det tangentielle kurveintegral af f (x, y, z) langs K r afhænger kun af p og q og er uafhængig af kurven: Tan(V, K r ) f (q) f (p). (25-24) Bevis Vi bruger kædereglen fra enote 16 på den sammensatte funktion h(u) f (r(u)) hvor r(u), u ]u, u 1 [, er en vilkårlig differentiabel kurve fra p (x, y, z ) r(u ) til q (x 1, y 1, z 1 ) r(u 1 ) og får derved: h (u) r (u) f (r(u)). (25-25) Heraf følger, at h(u) er en stamfunktion til funktionen på højresiden af ovenstående ligning: Men da får vi dermed og det var det vi skulle vise. h(u 1 ) h(u ) u1 u r (u) f (r(u)) du. (25-26) h(u ) f (r(u )) f (p), h(u 1 ) f (r(u 1 )) f (q), u1 f (q) f (p) + r (u) f (r(u)) du u f (p) + Tan(V, K r ), (25-27) (25-28)
8 enote STAMFUNKTION TIL ET GRADIENTVEKTORFELT 8 Figur 25.2: Den lukkede kurve r(u) (cos(t), sin(t), cos(2 t)), u [ π, π] og gradientvektorfeltet V(x, y, z) (x, y, z) f (x, y, z) for f (x, y, z) (x 2 + y 2 + z 2 )/2 er her antydet dels i rummet og dels langs kurven. Hvis kurven er lukket gerne sammensat af et endeligt antal glatte kurver som f.eks i en polygon med retlinede kanter får vi at det tangentielle kurveintegral af et gradientvektorfelt over den lukkede kurve er. Definition Cirkulationen af et vektorfelt langs en lukket kurve Lad K r betegne en lukket kurve i rummet (som gerne kan være sammensat af et endeligt antal glatte kurver). Lad V(x, y, z) være et glat vektorfelt i rummet. Så kalder vi det tangentielle kurveintegral af V(x, y, z) over K r cirkulationen af V(x, y, z) over K r og skriver: Cirk(V, K r ) Tan(V, K r ). (25-29) Betegnelsen cirkulation er helt rimelig. Hvis vektorfeltet er et gradientvektorfelt ved vi, at rotationen er overalt, se enote 24, og det stemmer med, at cirkulationen i disse tilfælde også er for enhver lukket kurve. Vi har allerede nu indset den ene halvdel af følgende sætning den anden (lidt vanskeligere) halvdel er bevist nedenfor:
9 enote STAMFUNKTION TIL ET GRADIENTVEKTORFELT 9 Sætning Cirkulationssætningen Et glat vektorfelt V(x, y, z) i rummet er et gradientvektorfelt hvis og kun hvis der gælder: Cirk(V, K r ) (25-3) for alle lukkede kurver K r. En stamfunktion kan konstrueres ved linjeintegralmetoden Bevis Som nævnt ved vi allerede, at hvis V(x, y, z) er et gradientvektorfelt, så er cirkulationen for enhver lukket kurve. Den anden vej handler altså om at antage, at alle lukkede kurver giver cirkulation og derudfra slutte, at så er det pågældende vektorfelt et gradientvektorfelt. Vi vil derfor konstruere en funktion F(x, y, z) hvis gradientvektorfelt er det givne vektorfelt. Der er i ovenstående fremstilling stort set kun én kandidat, der eventuelt ville kunne bruges som en sådan funktion, nemlig -funktionen F (x, y, z) hørende til V(x, y, z): F (x, y, z) (x, y, z) V(u x, u y, u z) du. (25-31) Da cirkulationen er langs enhver lukket kurve ved vi, at denne funktion ikke afhænger af integrationsvejen: Det tangentielle kurveintegral af V(x, y, z) langs enhver anden kurve fra (,, ) til (x, y, z) vil give samme værdi som F (x, y, z). Vi vil vise, at gradienten af F (x, y, z) i punktet (x, y, x ) er V(x, y, z ), så vi ser på F (x, y, z) F (x, y, z ) + Tan(V, K r ), (25-32) hvor K r er en vilkårlig glat kurve fra (udviklings-)punktet (x, y, z ) til et vilkårligt andet punkt (x, y, z). Vi vælger igen det rette linjestykke mellem de to punkter: K r : r(u) (x, y, z ) + u ((x, y, z) (x, y, z )), u [, 1], (25-33) og får så: Tan(V, K r ) (x x, y y, z z ) V(r(u)) du (25-34) Det første bidrag til dette skalarprodukt er (x x ) V 1 (r(u)) du. (25-35) Vi vil nu benytte den observation (se opgave 25.13), at der for enhver glat funktion g(u) på [, 1] gælder, at der findes en værdi ξ imellem og 1 således at g(u) du g(ξ). (25-36)
10 enote STAMFUNKTION TIL ET GRADIENTVEKTORFELT 1 Ved at bruge den integral-middelværdisætning får vi til indsættelse i (25-35): (x x ) V 1 (r(u)) du (x x )V 1 (r(ξ 1 )) (x x ) (V 1 (x, y, z ) + ε 1 (x x, y y, z z )), (25-37) idet V 1 (x, y, z) V 1 (x, y, z ) for (x, y, z) (x, y, z ). Tilsvarende fås for de to andre bidrag til skalarproduktet i (25-34), således at vi samlet har: Tan(V, K r ) (x x, y y, z z ) (V(x, y, z ) + ε(x x, y y, z z )) (x x, y y, z z ) V(x, y, z ) + ρ (x,y,z )(x, y, z) ε(x x, y y, z z ) (25-38) Vi indsætter til sidst i (25-32) og får følgende ligning F (x, y, z) F (x, y, z ) + Tan(V, K r ) F (x, y, z ) + (x x, y y, z z ) V(x, y, z ) + ρ (x,y,z )(x, y, z) ε(x x, y y, z z ). (25-39) Gradienten af (stjerne-)funktionen F (x, y, z) i (x, y, z ) kan derefter aflæses ved direkte inspektion det er jo faktoren på (x x, y y, z z ) før epsilon-leddet: F (x, y, z ) V(x, y, z ), (25-4) hvilket netop betyder, at V(x, y, z) er et gradientvektorfelt (med F (x, y, z) som stamfunktion), og det var det vi skulle vise. Opgave Overvej og indse den påstand vi har brugt i beviset for sætning 25.12: For enhver glat funktion g(u) på [, 1] gælder, at der findes en værdi ξ imellem og 1 således at g(u) du g(ξ). (25-41) I analogi med cirkulationssætningen har vi ligeledes en to-vejs kobling mellem gradientvektorfelt-egenskaben og rotation :
11 enote STAMFUNKTION TIL ET GRADIENTVEKTORFELT 11 Sætning Stamfunktions-sætningen Et glat vektorfelt V(x, y, z) i rummet er et gradientvektorfelt hvis og kun hvis der gælder: Rot(V)(x, y, z) (,, ). (25-42) En stamfunktion til vektorfeltet V(x, y, z) kan konstrueres ved linjeintegralmetoden Bevis Vi nøjes med at se på den ene (lette) vej rotationen af et gradientvektorfelt er. Se også den påstand i sætning i enote 24. Lad altså f (x, y, z) være en glat funktion i rummet. Så er ( ) f (x, y, z) f x(x, y, z), f y(x, y, z), f z(x, y, z). (25-43) Idet vi nøjes med at fokusere på første koordinat i rotationsvektoren får vi heraf: ( Rot( f )(x, y, z) y f z(x, y, z) ) z f y(x, y, z),, ( ) f zy(x, y, z) f yz(x, y, z),, (,, ), (25-44) og tilsvarende for de to andre koordinater. Eksempel Tangentielt kurveintegral af et ikke-gradientvektorfelt Lad V(x, y, z) ( y, x, ). Så er V(x, y, z) ikke et gradientvektorfelt idet Rot(V)(x, y, z) (,, 2) (,, ), se også eksempel 24.3 i enote 24. Hvis vi vælger den lukkede kurve: K r : r(u) (cos(u), sin(u), ), u [ π, π], (25-45) får vi i overensstemmelse med cirkulationssætningen en cirkulation, der ikke er : Tan(V, K r ) π π π π π π ( sin(u), cos(u), ) ( sin(u), cos(u), ) du ( sin 2 (u) + cos 2 (u) ) du 1 du 2 π. (25-46)
12 enote STAMFUNKTION TIL ET GRADIENTVEKTORFELT 12 Hvis vi konstruerer -funktionen hørende til V(x, y, z) ( y, x, ) får vi en veldefineret funktion i rummet: F (x, y, z) (x, y, z) (x, y, z) V(u x, u y, u z) du ( u y, u x, ) du 1 ((x, y, z) ( y, x, )) 2 (25-47), og det er klart ikke en stamfunktion til V(x, y, z), hvilket er i fuld overensstemmelse med stamfunktionssætningen.
13 enote OPSUMMERING Opsummering Vi har defineret det tangentielle kurveintegral for glatte vektorfelter langs glatte parametriserede kurver og vist, hvordan de tangentielle kurveintegraler kan benyttes til at konstruere stamfunktioner til et vektorfelt V(x, y, z) hvis ellers vektorfeltet er et gradientvektorfelt. Det tangentielle kurveintegral af V(x, y, z) langs den parametriserede kurve K r kan beregnes således: Tan(V, K r ) b a V(r(u)) r (u) du. (25-48) Hvis kurven K r er lukket, så betegnes kurven med K r, det tangentielle kurveintegral kaldes i så fald cirkulationen af vektorfeltet langs den lukkede kurve, og vi skriver Cirk(V, K r ) Tan(V, K r ). (25-49) Stamfunktionssætningen giver en nødvendig og tilstrækkelig betingelse for at et givet vektorfelt er et gradientvektorfelt: V(x, y, z) er et gradientvektorfelt hvis og kun hvis Rot(V)(x, y, z) (,, ). Cirkulationssætningen udtrykker en tilsvarende nødvendig og tilstrækkelig betingelse for gradientfelt-egenskaben udtrykt ved cirkluationen af vektorfeltet langs lukkede kurver: V(x, y, z) er et gradientvektorfelt hvis og kun hvis Cirk(V, K r ) for alle lukkede kurver K r. Stjerne-funktionen F (x, y, z) hørende til et gradientvektorfelt V(x, y, z) er en stamfunktion til V(x, y, z). Funktionen beregnes som det tangentielle linjeintegral fra (,, ) til punktet (x, y, z) således: F (x, y, z) Tan(V, K r ) (x, y, z) V(r(u)) r (u) du V(u x, u y, u z) du. (25-5)
Gradienter og tangentplaner
 enote 16 1 enote 16 Gradienter og tangentplaner I denne enote vil vi fokusere lidt nærmere på den geometriske analyse og inspektion af funktioner af to variable. Vi vil især studere sammenhængen mellem
enote 16 1 enote 16 Gradienter og tangentplaner I denne enote vil vi fokusere lidt nærmere på den geometriske analyse og inspektion af funktioner af to variable. Vi vil især studere sammenhængen mellem
Kurve- og plan-integraler
 enote 22 1 enote 22 Kurve- og plan-integraler Vi vil her med udgangspunkt i de metoder og resultater der er opstillet i enote 21 vise, hvordan Riemann-integralerne derfra kan benyttes til blandt andet
enote 22 1 enote 22 Kurve- og plan-integraler Vi vil her med udgangspunkt i de metoder og resultater der er opstillet i enote 21 vise, hvordan Riemann-integralerne derfra kan benyttes til blandt andet
Vektorfelter. enote Vektorfelter
 enote 24 1 enote 24 Vektorfelter I enote 6 indføres og studeres vektorer i plan og rum. I enote 16 ser vi på gradienterne for funktioner f (x, y) af to variable. Et gradientvektorfelt for en funktion af
enote 24 1 enote 24 Vektorfelter I enote 6 indføres og studeres vektorer i plan og rum. I enote 16 ser vi på gradienterne for funktioner f (x, y) af to variable. Et gradientvektorfelt for en funktion af
Funktioner af to variable
 enote 15 1 enote 15 Funktioner af to variable I denne og i de efterfølgende enoter vil vi udvide funktionsbegrebet til at omfatte reelle funktioner af flere variable; vi starter udvidelsen med 2 variable,
enote 15 1 enote 15 Funktioner af to variable I denne og i de efterfølgende enoter vil vi udvide funktionsbegrebet til at omfatte reelle funktioner af flere variable; vi starter udvidelsen med 2 variable,
Andengradsligninger i to og tre variable
 enote 0 enote 0 Andengradsligninger i to og tre variable I denne enote vil vi igen beskæftige os med andengradspolynomierne i to og tre variable som også er behandlet og undersøgt med forskellige teknikker
enote 0 enote 0 Andengradsligninger i to og tre variable I denne enote vil vi igen beskæftige os med andengradspolynomierne i to og tre variable som også er behandlet og undersøgt med forskellige teknikker
Maj 2013 (alle opgaver og alle spørgsmål)
 Maj 2013 (alle opgaver og alle spørgsmål) Alternativ besvarelse (med brug af Maple til beregninger, incl. pakker til VektorAnalyse2 og Integrator8). Jeg gider ikke håndregne i de simple spørgsmål! Her
Maj 2013 (alle opgaver og alle spørgsmål) Alternativ besvarelse (med brug af Maple til beregninger, incl. pakker til VektorAnalyse2 og Integrator8). Jeg gider ikke håndregne i de simple spørgsmål! Her
Stokes rotationssætning
 enote 27 1 enote 27 Stokes rotationssætning I denne enote vil vi benytte Gauss divergenssætning fra enote 26 til at motivere, bevise, og illustrere Stokes sætning, som udtrykker en præcis sammenhæng mellem
enote 27 1 enote 27 Stokes rotationssætning I denne enote vil vi benytte Gauss divergenssætning fra enote 26 til at motivere, bevise, og illustrere Stokes sætning, som udtrykker en præcis sammenhæng mellem
8 Regulære flader i R 3
 8 Regulære flader i R 3 Vi skal betragte særligt pæne delmængder S R 3 kaldet flader. I det følgende opfattes S som et topologisk rum i sportopologien, se Definition 5.9. En åben omegn U af p S er således
8 Regulære flader i R 3 Vi skal betragte særligt pæne delmængder S R 3 kaldet flader. I det følgende opfattes S som et topologisk rum i sportopologien, se Definition 5.9. En åben omegn U af p S er således
Taylor s approksimationsformler for funktioner af én variabel
 enote 4 1 enote 4 Taylor s approksimationsformler for funktioner af én variabel I enote 19 og enote 21 er det vist hvordan funktioner af én og to variable kan approksimeres med førstegradspolynomier i
enote 4 1 enote 4 Taylor s approksimationsformler for funktioner af én variabel I enote 19 og enote 21 er det vist hvordan funktioner af én og to variable kan approksimeres med førstegradspolynomier i
Eksamen maj 2019, Matematik 1, DTU
 Eksamen maj 2019, Matematik 1, DTU NB: Nedenstående udregninger viser flere steder mere end én metode. Det er der IKKE tid til eksamen! Ligeledes er der ikke krav om eller tid til at illustrere med plots.
Eksamen maj 2019, Matematik 1, DTU NB: Nedenstående udregninger viser flere steder mere end én metode. Det er der IKKE tid til eksamen! Ligeledes er der ikke krav om eller tid til at illustrere med plots.
OPGAVE 1 Det nedenstående klip er fra et Maple-ark hvor en reel funktion f (x, y) med definitionsmængden (x,y) x 2 + y 2 < 1 } bliver undersøgt:
 DANMARKS TEKNISKE UNIVERSITET Skriftlig prøve den 7. maj 00. Kursus Navn: Matematik (-timers prøve for forårssemesteret). Kursus nr. 0005 Tilladte hjælpemidler: Alle af DTU tilladte hjælpemidler må medbringes
DANMARKS TEKNISKE UNIVERSITET Skriftlig prøve den 7. maj 00. Kursus Navn: Matematik (-timers prøve for forårssemesteret). Kursus nr. 0005 Tilladte hjælpemidler: Alle af DTU tilladte hjælpemidler må medbringes
Taylor s approksimationsformler for funktioner af én variabel
 enote 17 1 enote 17 Taylor s approksimationsformler for funktioner af én variabel I enote 14 og enote 16 er det vist hvordan funktioner af én og to variable kan approksimeres med førstegradspolynomier
enote 17 1 enote 17 Taylor s approksimationsformler for funktioner af én variabel I enote 14 og enote 16 er det vist hvordan funktioner af én og to variable kan approksimeres med førstegradspolynomier
Flade- og rum-integraler
 enote 25 1 enote 25 Flade- og rum-integraler Flade og rumintegraler opstilles her på stort set samme måde som kurve- og planintegralerne i enote 22, som derved sammen med den grundlæggende generelle indførelse
enote 25 1 enote 25 Flade- og rum-integraler Flade og rumintegraler opstilles her på stort set samme måde som kurve- og planintegralerne i enote 22, som derved sammen med den grundlæggende generelle indførelse
Mat 1. 2-timersprøve den 13. maj 2017.
 Mat. -timersprøve den. maj 7. JE.5.7 Opgave restart:with(plots): En funktion f af to reelle variable er for x, y s, givet ved f:=(x,y)-y/(x^+y^); f d x, y / y x Cy f(x,y); y x Cy Spørgsmål I x, y Kplanen
Mat. -timersprøve den. maj 7. JE.5.7 Opgave restart:with(plots): En funktion f af to reelle variable er for x, y s, givet ved f:=(x,y)-y/(x^+y^); f d x, y / y x Cy f(x,y); y x Cy Spørgsmål I x, y Kplanen
MASO Uge 7. Differentiable funktioner. Jesper Michael Møller. Uge 7. Formålet med MASO. Department of Mathematics University of Copenhagen
 MASO Uge 7 Differentiable funktioner Jesper Michael Møller Department of Mathematics University of Copenhagen Uge 7 Formålet med MASO Oversigt Differentiable funktioner R n R m Differentiable funktioner
MASO Uge 7 Differentiable funktioner Jesper Michael Møller Department of Mathematics University of Copenhagen Uge 7 Formålet med MASO Oversigt Differentiable funktioner R n R m Differentiable funktioner
Partielle afledede og retningsafledede
 Partielle afledede og retningsafledede 1 Partielle afledede, definitioner og notationer Bertragt en funktion af to reelle variable f : D R, hvor D R 2 er et åbent område Med benyttelse af tilvækstfunktionen
Partielle afledede og retningsafledede 1 Partielle afledede, definitioner og notationer Bertragt en funktion af to reelle variable f : D R, hvor D R 2 er et åbent område Med benyttelse af tilvækstfunktionen
MASO Uge 8. Invers funktion sætning og Implicit given funktion sætning. Jesper Michael Møller. Department of Mathematics University of Copenhagen
 MASO Uge 8 Invers funktion sætning og Implicit given funktion sætning Jesper Michael Møller Department of Mathematics University of Copenhagen Uge 43 Formålet med MASO Oversigt Invertible og lokalt invertible
MASO Uge 8 Invers funktion sætning og Implicit given funktion sætning Jesper Michael Møller Department of Mathematics University of Copenhagen Uge 43 Formålet med MASO Oversigt Invertible og lokalt invertible
Geometriske grundbegreber 8. lektion
 1 / 14 Geometriske grundbegreber 8. lektion Martin Raussen Institut for matematiske fag Aalborg Universitet 1.4.2008 2 / 14 (Regulære) parameterfremstillinger for en flade Eksempler Kurver på flader og
1 / 14 Geometriske grundbegreber 8. lektion Martin Raussen Institut for matematiske fag Aalborg Universitet 1.4.2008 2 / 14 (Regulære) parameterfremstillinger for en flade Eksempler Kurver på flader og
GEOMETRI-TØ, UGE 12. A σ (R) = A f σ (f(r))
 GEOMETRI-TØ, UGE 12 Hvis I falder over tryk- eller regne-fejl i nedenstående, må I meget gerne sende rettelser til fuglede@imfaudk Opvarmningsopgave 1, [P] 632 Vis at Ennepers flade σ(u, v) = ( u u 3 /3
GEOMETRI-TØ, UGE 12 Hvis I falder over tryk- eller regne-fejl i nedenstående, må I meget gerne sende rettelser til fuglede@imfaudk Opvarmningsopgave 1, [P] 632 Vis at Ennepers flade σ(u, v) = ( u u 3 /3
Vejledende besvarelse på august 2009-sættet 2. december 2009
 Vejledende besvarelse på august 29-sættet 2. december 29 Det følgende er en vejledende besvarelse på eksamenssættet i kurset Calculus, som det så ud i august 29. Den tjener primært til illustration af,
Vejledende besvarelse på august 29-sættet 2. december 29 Det følgende er en vejledende besvarelse på eksamenssættet i kurset Calculus, som det så ud i august 29. Den tjener primært til illustration af,
GEOMETRI-TØ, UGE 11. Opvarmningsopgave 2, [P] 6.1.1 (i,ii,iv). Udregn første fundamentalform af følgende flader
![GEOMETRI-TØ, UGE 11. Opvarmningsopgave 2, [P] 6.1.1 (i,ii,iv). Udregn første fundamentalform af følgende flader GEOMETRI-TØ, UGE 11. Opvarmningsopgave 2, [P] 6.1.1 (i,ii,iv). Udregn første fundamentalform af følgende flader](/thumbs/33/15809111.jpg) GEOMETRI-TØ, UGE Hvis I falder over tryk- eller regne-fejl i nedenstående, må I meget gerne sende rettelser til fuglede@imf.au.dk. Opvarmningsopgave, [P] 5... Find parametriseringer af de kvadratiske flader
GEOMETRI-TØ, UGE Hvis I falder over tryk- eller regne-fejl i nedenstående, må I meget gerne sende rettelser til fuglede@imf.au.dk. Opvarmningsopgave, [P] 5... Find parametriseringer af de kvadratiske flader
STEEN MARKVORSEN DTU COMPUTE 2016
 STEEN MARKVORSEN DTU COMPUTE 2016 2 Indhold 1 Regulære flader i rummet 5 1.1 Det sædvanlige koordinatsystem i rummet..................... 5 1.2 Graf-flader for funktioner af to variable......................
STEEN MARKVORSEN DTU COMPUTE 2016 2 Indhold 1 Regulære flader i rummet 5 1.1 Det sædvanlige koordinatsystem i rummet..................... 5 1.2 Graf-flader for funktioner af to variable......................
Grafisk bestemmelse - fortsat Støttepunkter. Grafisk bestemmelse y. giver grafen. Niveaukurver og retning u = ( 1
 Oversigt [S]. Nøgleord og begreber Retningsafledt Gradientvektor Gradient i flere variable Fortolkning af gradientvektoren Agst, opgave 5 Delvis afledt [S]. Directional derivatives and te... Definition
Oversigt [S]. Nøgleord og begreber Retningsafledt Gradientvektor Gradient i flere variable Fortolkning af gradientvektoren Agst, opgave 5 Delvis afledt [S]. Directional derivatives and te... Definition
GEOMETRI-TØ, UGE 3. og resultatet følger fra [P] Proposition 2.3.1, der siger, at
![GEOMETRI-TØ, UGE 3. og resultatet følger fra [P] Proposition 2.3.1, der siger, at GEOMETRI-TØ, UGE 3. og resultatet følger fra [P] Proposition 2.3.1, der siger, at](/thumbs/50/26870860.jpg) GEOMETRI-TØ, UGE 3 Hvis I falder over tryk- eller regne-fejl i nedenstående, må I meget gerne sende rettelser til fuglede@imf.au.dk. Opvarmningsopgave 1. Lad γ : (α, β) R 2 være en regulær kurve i planen.
GEOMETRI-TØ, UGE 3 Hvis I falder over tryk- eller regne-fejl i nedenstående, må I meget gerne sende rettelser til fuglede@imf.au.dk. Opvarmningsopgave 1. Lad γ : (α, β) R 2 være en regulær kurve i planen.
Matematisk modellering og numeriske metoder. Lektion 13
 Matematisk modellering og numeriske metoder Lektion 3 Morten Grud Rasmussen 9. november 25 Divergens af et vektorfelt [Sektion 9.8 og.7 i bogen, s. 43]. Definition af og og egenskaber for divergens Lad
Matematisk modellering og numeriske metoder Lektion 3 Morten Grud Rasmussen 9. november 25 Divergens af et vektorfelt [Sektion 9.8 og.7 i bogen, s. 43]. Definition af og og egenskaber for divergens Lad
MASO Uge 7. Differentiable funktioner. Jesper Michael Møller. Uge 7. Formålet med MASO. Department of Mathematics University of Copenhagen
 MASO Uge 7 Differentiable funktioner Jesper Michael Møller Department of Mathematics University of Copenhagen Uge 7 Formålet med MASO Oversigt Differentiable funktioner f : R R En funktion f : R R er differentiabel
MASO Uge 7 Differentiable funktioner Jesper Michael Møller Department of Mathematics University of Copenhagen Uge 7 Formålet med MASO Oversigt Differentiable funktioner f : R R En funktion f : R R er differentiabel
MATEMATIK 11 Eksamensopgaver Juni 1995 Juni 2001, 4. fjerdedel
 Juni 2000 MATEMATIK 11 Eksamensopgaver Juni 1995 Juni 2001, 4. fjerdedel Opgave 1. (a) Find den fuldstændige løsning til differentialligningen y 8y + 16y = 0. (b) Find den fuldstændige løsning til differentialligningen
Juni 2000 MATEMATIK 11 Eksamensopgaver Juni 1995 Juni 2001, 4. fjerdedel Opgave 1. (a) Find den fuldstændige løsning til differentialligningen y 8y + 16y = 0. (b) Find den fuldstændige løsning til differentialligningen
Vektorer og lineær regression
 Vektorer og lineær regression Peter Harremoës Niels Brock April 03 Planproduktet Vi har set, at man kan gange en vektor med et tal Et oplagt spørgsmål er, om man også kan gange to vektorer med hinanden
Vektorer og lineær regression Peter Harremoës Niels Brock April 03 Planproduktet Vi har set, at man kan gange en vektor med et tal Et oplagt spørgsmål er, om man også kan gange to vektorer med hinanden
Projekt 4.6 Løsning af differentialligninger ved separation af de variable
 Projekt 4.6 Løsning af differentialligninger ved separation af de variable Differentialligninger af tpen d hx () hvor hx ()er en kontinuert funktion, er som nævnt blot et stamfunktionsproblem. De løses
Projekt 4.6 Løsning af differentialligninger ved separation af de variable Differentialligninger af tpen d hx () hvor hx ()er en kontinuert funktion, er som nævnt blot et stamfunktionsproblem. De løses
Vektorer og lineær regression. Peter Harremoës Niels Brock
 Vektorer og lineær regression Peter Harremoës Niels Brock April 2013 1 Planproduktet Vi har set, at man kan gange en vektor med et tal. Et oplagt spørgsmål er, om man også kan gange to vektorer med hinanden.
Vektorer og lineær regression Peter Harremoës Niels Brock April 2013 1 Planproduktet Vi har set, at man kan gange en vektor med et tal. Et oplagt spørgsmål er, om man også kan gange to vektorer med hinanden.
STEEN MARKVORSEN DTU MATEMATIK
 STEEN MARKVORSEN DTU MATEMATIK 2 Indhold 1 Introduktion 5 1.1 Hvad handler det om?................................ 6 1.1.1 Rumfang-problemet............................ 6 1.2 Approksimerende summer og
STEEN MARKVORSEN DTU MATEMATIK 2 Indhold 1 Introduktion 5 1.1 Hvad handler det om?................................ 6 1.1.1 Rumfang-problemet............................ 6 1.2 Approksimerende summer og
Integration i flere Variable. Steen Markvorsen Institut for Matematik, DTU
 Integration i flere Variable Steen Markvorsen Institut for Matematik, DTU 20. februar 2008 2 Indhold 1 Introduktion 5 1.1 Hvad handler det om?................................ 6 1.2 Approksimerende summer
Integration i flere Variable Steen Markvorsen Institut for Matematik, DTU 20. februar 2008 2 Indhold 1 Introduktion 5 1.1 Hvad handler det om?................................ 6 1.2 Approksimerende summer
Mat 1. 2-timersprøve den 17. maj 2016.
 Mat -timersprøve den 7 maj 6 JE 6 Opgave restart; Givet funktionen f:=x-sqrt(*x-); Spørgsmål f := x/ x K Funktionen er defineret for x K R x R Dvs Dm f er intervallet [ ;N[ Spørgsmål Med udviklingspunktet
Mat -timersprøve den 7 maj 6 JE 6 Opgave restart; Givet funktionen f:=x-sqrt(*x-); Spørgsmål f := x/ x K Funktionen er defineret for x K R x R Dvs Dm f er intervallet [ ;N[ Spørgsmål Med udviklingspunktet
Vektoranalyse INDLEDNING. Indhold. 1 Integraltricks. Jens Kusk Block Jacobsen 21. januar 2008
 Vektoranalyse Jens Kusk Block Jacobsen 21. januar 2008 INLENING ette er en opsamling af ting, jeg synes er gode at have ifbm vektoranalyse som præsenteret i kurset VEKANAE07 ved IMF på AU. Noten er dels
Vektoranalyse Jens Kusk Block Jacobsen 21. januar 2008 INLENING ette er en opsamling af ting, jeg synes er gode at have ifbm vektoranalyse som præsenteret i kurset VEKANAE07 ved IMF på AU. Noten er dels
MATEMATIK A-NIVEAU-Net Forberedelsesmateriale
 STUDENTEREKSAMEN SOMMERTERMIN 13 MATEMATIK A-NIVEAU-Net Forberedelsesmateriale 6 timer med vejledning Forberedelsesmateriale til de skriftlige prøver sommertermin 13 st131-matn/a-6513 Forberedelsesmateriale
STUDENTEREKSAMEN SOMMERTERMIN 13 MATEMATIK A-NIVEAU-Net Forberedelsesmateriale 6 timer med vejledning Forberedelsesmateriale til de skriftlige prøver sommertermin 13 st131-matn/a-6513 Forberedelsesmateriale
Integralregning Infinitesimalregning
 Udgave 2.1 Integralregning Infinitesimalregning Noterne gennemgår begreberne integral og stamfunktion, og anskuer dette som et redskab til bestemmelse af arealer under funktioner. Noterne er supplement
Udgave 2.1 Integralregning Infinitesimalregning Noterne gennemgår begreberne integral og stamfunktion, og anskuer dette som et redskab til bestemmelse af arealer under funktioner. Noterne er supplement
EKSAMENSOPGAVELØSNINGER CALCULUS 2 (2005) AUGUST 2006 AARHUS UNIVERSITET
 EKSAMENSOPGAVELØSNINGER CALCULUS 2 (2005) AUGUST 2006 AARHUS UNIVERSITET H.A. NIELSEN & H.A. SALOMONSEN Opgave. Lad f betegne funktionen f(x,y) = x 3 + x 2 y + xy 2 + y 3. ) Angiv gradienten f. 2) Angiv
EKSAMENSOPGAVELØSNINGER CALCULUS 2 (2005) AUGUST 2006 AARHUS UNIVERSITET H.A. NIELSEN & H.A. SALOMONSEN Opgave. Lad f betegne funktionen f(x,y) = x 3 + x 2 y + xy 2 + y 3. ) Angiv gradienten f. 2) Angiv
Flade- og rum-integraler
 enote 23 1 enote 23 Flade- og rum-integraler Flade og rumintegraler opstilles her på stort set samme måde som kurve- og planintegralerne i enote 22, som derved sammen med den grundlæggende generelle indførelse
enote 23 1 enote 23 Flade- og rum-integraler Flade og rumintegraler opstilles her på stort set samme måde som kurve- og planintegralerne i enote 22, som derved sammen med den grundlæggende generelle indførelse
Matematik A. Studentereksamen. Forberedelsesmateriale til de digitale eksamensopgaver med adgang til internettet
 Matematik A Studentereksamen Forberedelsesmateriale til de digitale eksamensopgaver med adgang til internettet st131-matn/a-6513 Mandag den 6 maj 13 Forberedelsesmateriale til st A Net MATEMATIK Der skal
Matematik A Studentereksamen Forberedelsesmateriale til de digitale eksamensopgaver med adgang til internettet st131-matn/a-6513 Mandag den 6 maj 13 Forberedelsesmateriale til st A Net MATEMATIK Der skal
Maj 2015 (alle opgaver og alle spørgsmål)
 Maj 2015 (alle opgaver og alle spørgsmål) Alternativ besvarelse (med brug af Maple til beregninger, incl. pakker til VektorAnalyse2 og Integrator8). Ved eksamen er der ikke tid til f.eks. at lave illustrationer,
Maj 2015 (alle opgaver og alle spørgsmål) Alternativ besvarelse (med brug af Maple til beregninger, incl. pakker til VektorAnalyse2 og Integrator8). Ved eksamen er der ikke tid til f.eks. at lave illustrationer,
EKSAMENSOPGAVELØSNINGER CALCULUS 2 (2005) JANUAR 2006 AARHUS UNIVERSITET.. Beregn den retningsafledede D u f(0, 0).
 EKSAMENSOPGAVELØSNINGER CALCULUS 2 (2005) JANUAR 2006 AARHUS UNIVERSITET H.A. NIELSEN & H.A. SALOMONSEN Opgave. Lad f betegne funktionen f(x, y) = x cos(y) + y sin(x). ) Angiv gradienten f. 2) Lad u betegne
EKSAMENSOPGAVELØSNINGER CALCULUS 2 (2005) JANUAR 2006 AARHUS UNIVERSITET H.A. NIELSEN & H.A. SALOMONSEN Opgave. Lad f betegne funktionen f(x, y) = x cos(y) + y sin(x). ) Angiv gradienten f. 2) Lad u betegne
Besvarelser til Calculus Ordinær Eksamen - 3. Januar 2017
 Besvarelser til Calculus Ordinær Eksamen - 3. Januar 17 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 3. Januar 17 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Mat H /05 Note 2 10/11-04 Gerd Grubb
 Mat H 1 2004/05 Note 2 10/11-04 Gerd Grubb Nødvendige og tilstrækkelige betingelser for ekstremum, konkave og konvekse funktioner. Fremstillingen i Kapitel 13.1 2 af Sydsæters bog [MA1] suppleres her med
Mat H 1 2004/05 Note 2 10/11-04 Gerd Grubb Nødvendige og tilstrækkelige betingelser for ekstremum, konkave og konvekse funktioner. Fremstillingen i Kapitel 13.1 2 af Sydsæters bog [MA1] suppleres her med
Om første og anden fundamentalform
 Geometri, foråret 2005 Jørgen Larsen 9. marts 2005 Om første og anden fundamentalform 1 Tangentrummet; første fundamentalform Vi betragter en flade S parametriseret med σ. Lad P = σu 0, v 0 være et punkt
Geometri, foråret 2005 Jørgen Larsen 9. marts 2005 Om første og anden fundamentalform 1 Tangentrummet; første fundamentalform Vi betragter en flade S parametriseret med σ. Lad P = σu 0, v 0 være et punkt
Bevægelsens Geometri
 Bevægelsens Geometri Vi vil betragte bevægelsen af et punkt. Dette punkt kan f.eks. være tyngdepunktet af en flue, et menneske, et molekyle, en galakse eller hvad man nu ellers har lyst til at beskrive.
Bevægelsens Geometri Vi vil betragte bevægelsen af et punkt. Dette punkt kan f.eks. være tyngdepunktet af en flue, et menneske, et molekyle, en galakse eller hvad man nu ellers har lyst til at beskrive.
Kræfter og Arbejde. Frank Nasser. 21. april 2011
 Kræfter og Arbejde Frank Nasser 21. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk: Dette er
Kræfter og Arbejde Frank Nasser 21. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk: Dette er
Differentialkvotient af cosinus og sinus
 Differentialkvotient af cosinus og sinus Overgangsformler cos( + p ) = cos sin( + p ) = sin cos( -) = cos sin( -) = -sin cos( p - ) = - cos sin( p - ) = sin cos( p + ) = -cos sin( p + ) = -sin (bevises
Differentialkvotient af cosinus og sinus Overgangsformler cos( + p ) = cos sin( + p ) = sin cos( -) = cos sin( -) = -sin cos( p - ) = - cos sin( p - ) = sin cos( p + ) = -cos sin( p + ) = -sin (bevises
Eksamen i Mat F, april 2006
 Eksamen i Mat F, april 26 Opgave Lad F være et vektorfelt, givet i retvinklede koordinater som: Udregn F og F: F x F = F x i + F y j + F z k = F y = z 2 F z xz y 2 F = F x + F y + F z = + + x. F = F z
Eksamen i Mat F, april 26 Opgave Lad F være et vektorfelt, givet i retvinklede koordinater som: Udregn F og F: F x F = F x i + F y j + F z k = F y = z 2 F z xz y 2 F = F x + F y + F z = + + x. F = F z
Matematik F2 Opgavesæt 2
 Opgaver uge 2 I denne uge kigger vi nærmere på Cauchy-Riemann betingelserne, potensrækker, konvergenskriterier og flertydige funktioner. Vi skal også se på integration langs en ve i den komplekse plan.
Opgaver uge 2 I denne uge kigger vi nærmere på Cauchy-Riemann betingelserne, potensrækker, konvergenskriterier og flertydige funktioner. Vi skal også se på integration langs en ve i den komplekse plan.
Eksamen maj 2018, Matematik 1, DTU
 Eksamen maj 2018, Matematik 1, DTU NB: Nedenstående udregninger viser flere steder mere end én metode. Det er der IKKE tid til eksamen! Ligeledes er der ikke krav om eller tid til at illustrere med plots!
Eksamen maj 2018, Matematik 1, DTU NB: Nedenstående udregninger viser flere steder mere end én metode. Det er der IKKE tid til eksamen! Ligeledes er der ikke krav om eller tid til at illustrere med plots!
Supplement til Matematik 1GB. Jan Philip Solovej
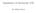 Supplement til Matematik 1GB Jan Philip Solovej ii c 2001 Jan Philip Solovej, Institut for Matematiske Fag, Københavns Universitet. Alle har tilladelse til at reproducere hele eller dele af dette materiale
Supplement til Matematik 1GB Jan Philip Solovej ii c 2001 Jan Philip Solovej, Institut for Matematiske Fag, Københavns Universitet. Alle har tilladelse til at reproducere hele eller dele af dette materiale
Lidt om plane kurver og geometrisk kontinuitet
 Lidt om plane kurver og geometrisk kontinuitet Jesper Møller og Rasmus P. Waagepetersen, Institut for Matematiske Fag, Aalborg Universitet September 3, 2003 1 Indledning Dette notesæt giver en oversigt
Lidt om plane kurver og geometrisk kontinuitet Jesper Møller og Rasmus P. Waagepetersen, Institut for Matematiske Fag, Aalborg Universitet September 3, 2003 1 Indledning Dette notesæt giver en oversigt
MATEMATIK 3 EN,MP 17. september 2014 Oversigt nr. 1
 MATEMATIK 3 EN,MP 7. september 204 Oversigt nr. Her bringes en samling af de gamle eksamensopgaver: (jan. 204) Betragt begyndelsesværdiproblemet y (t) + 7y (t) + 2y(t) = e t sin(2t) for t > 0, y(0) = 2,
MATEMATIK 3 EN,MP 7. september 204 Oversigt nr. Her bringes en samling af de gamle eksamensopgaver: (jan. 204) Betragt begyndelsesværdiproblemet y (t) + 7y (t) + 2y(t) = e t sin(2t) for t > 0, y(0) = 2,
π er irrationel Frank Nasser 10. december 2011
 π er irrationel Frank Nasser 10. december 2011 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold 1 Introduktion
π er irrationel Frank Nasser 10. december 2011 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold 1 Introduktion
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Institution Uddannelse Fag og niveau Lærer(e) Termin hvori undervisningen afsluttes: maj-juni 2018 Rybners
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Institution Uddannelse Fag og niveau Lærer(e) Termin hvori undervisningen afsluttes: maj-juni 2018 Rybners
Integration i flere Variable. Steen Markvorsen DTU Matematik
 Integration i flere Variable Steen Markvorsen DTU Matematik 20. februar 2009 2 Indhold 1 Introduktion 5 1.1 Hvad handler det om?................................ 6 1.1.1 Rumfang-problemet............................
Integration i flere Variable Steen Markvorsen DTU Matematik 20. februar 2009 2 Indhold 1 Introduktion 5 1.1 Hvad handler det om?................................ 6 1.1.1 Rumfang-problemet............................
Lineære differentialligningers karakter og lineære 1. ordens differentialligninger
 enote 11 1 enote 11 Lineære differentialligningers karakter og lineære 1. ordens differentialligninger I denne note introduceres lineære differentialligninger, som er en speciel (og bekvem) form for differentialligninger.
enote 11 1 enote 11 Lineære differentialligningers karakter og lineære 1. ordens differentialligninger I denne note introduceres lineære differentialligninger, som er en speciel (og bekvem) form for differentialligninger.
Affine rum. a 1 u 1 + a 2 u 2 + a 3 u 3 = a 1 u 1 + (1 a 1 )( u 2 + a 3. + a 3. u 3 ) 1 a 1. Da a 2
 Affine rum I denne note behandles kun rum over R. Alt kan imidlertid gennemføres på samme måde over C eller ethvert andet legeme. Et underrum U R n er karakteriseret ved at det er en delmængde som er lukket
Affine rum I denne note behandles kun rum over R. Alt kan imidlertid gennemføres på samme måde over C eller ethvert andet legeme. Et underrum U R n er karakteriseret ved at det er en delmængde som er lukket
Additionsformlerne. Frank Villa. 19. august 2012
 Additionsformlerne Frank Villa 19. august 2012 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold 1 Introduktion
Additionsformlerne Frank Villa 19. august 2012 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold 1 Introduktion
Førsteordens lineære differentialligninger
 enote 16 1 enote 16 Førsteordens lineære differentialligninger I denne enote gives først en kort introduktion til differentialligninger i almindelighed, hvorefter hovedemnet er en særlig type af differentialligninger,
enote 16 1 enote 16 Førsteordens lineære differentialligninger I denne enote gives først en kort introduktion til differentialligninger i almindelighed, hvorefter hovedemnet er en særlig type af differentialligninger,
Højere Teknisk Eksamen maj 2008. Matematik A. Forberedelsesmateriale til 5 timers skriftlig prøve NY ORDNING. Undervisningsministeriet
 Højere Teknisk Eksamen maj 2008 HTX081-MAA Matematik A Forberedelsesmateriale til 5 timers skriftlig prøve NY ORDNING Undervisningsministeriet Fra onsdag den 28. maj til torsdag den 29. maj 2008 Forord
Højere Teknisk Eksamen maj 2008 HTX081-MAA Matematik A Forberedelsesmateriale til 5 timers skriftlig prøve NY ORDNING Undervisningsministeriet Fra onsdag den 28. maj til torsdag den 29. maj 2008 Forord
Eksamen i Matematik F2 d. 19. juni Opgave 2. Svar. Korte svar (ikke fuldstændige)
 Eksamen i Matematik F2 d. 9. juni 28 Korte svar (ikke fuldstændige Opgave Find realdelen, Re z, og imaginærdelen, Im z, for følgende værdier af z, a z = 2 i b z = i i c z = ln( + i Find realdelen, Re z,
Eksamen i Matematik F2 d. 9. juni 28 Korte svar (ikke fuldstændige Opgave Find realdelen, Re z, og imaginærdelen, Im z, for følgende værdier af z, a z = 2 i b z = i i c z = ln( + i Find realdelen, Re z,
z j 2. Cauchy s formel er værd at tænke lidt nærmere over. Se på specialtilfældet 1 dz = 2πi z
 Matematik F2 - sæt 3 af 7 blok 4 f(z)dz = 0 Hovedemnet i denne uge er Cauchys sætning (den der står i denne sides hoved) og Cauchys formel. Desuden introduceres nulpunkter og singulariteter: simple poler,
Matematik F2 - sæt 3 af 7 blok 4 f(z)dz = 0 Hovedemnet i denne uge er Cauchys sætning (den der står i denne sides hoved) og Cauchys formel. Desuden introduceres nulpunkter og singulariteter: simple poler,
Nedenfor er tegnet svingningsmønsteret for to sinus-toner med frekvensen 440 og 443 Hz:
 Appendiks 1: Om svævning: Hvis to toner ligger meget tæt på hinanden opstår et interessant akustisk og matematisk fænomen, der kaldes svævning. Det er dette fænomen, der ligger bag alle de steder, hvor
Appendiks 1: Om svævning: Hvis to toner ligger meget tæt på hinanden opstår et interessant akustisk og matematisk fænomen, der kaldes svævning. Det er dette fænomen, der ligger bag alle de steder, hvor
(c) Opskriv den reelle Fourierrække for funktionen y(t) fra (b), og afgør dernæst om y(t) er en lige eller ulige funktion eller ingen af delene.
 MATEMATIK 3 EN,MP 4. februar 2016 Eksamenopgaver fra 2011 2016 (jan. 2016) Givet at 0 for 0 < t < 1 mens e (t 1) cos(7(t 1)) for t 1, betragt da begyndelsesværdiproblemet for t > 0: y (t) + 2y (t) + 50y(t)
MATEMATIK 3 EN,MP 4. februar 2016 Eksamenopgaver fra 2011 2016 (jan. 2016) Givet at 0 for 0 < t < 1 mens e (t 1) cos(7(t 1)) for t 1, betragt da begyndelsesværdiproblemet for t > 0: y (t) + 2y (t) + 50y(t)
Løsning til øvelse 7.8, side 272: Københavns Politigård
 website: link fra, kapitel 7, afsnit 2 Løsning til øvelse 7.8, side 272: Københavns Politigård Bemærk: Benyt fx formelsamlingen til stxa side 10-14 til at finde de relevante formler. (Geogebra starter
website: link fra, kapitel 7, afsnit 2 Løsning til øvelse 7.8, side 272: Københavns Politigård Bemærk: Benyt fx formelsamlingen til stxa side 10-14 til at finde de relevante formler. (Geogebra starter
Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 2016
 Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Elementær Matematik. Funktioner og deres grafer
 Elementær Matematik Funktioner og deres grafer Ole Witt-Hansen 0 Indhold. Funktioner.... Grafen for en funktion...3. grafers skæring med koordinat akser...4. To grafers skæringspunkter...4 3. Egenskaber
Elementær Matematik Funktioner og deres grafer Ole Witt-Hansen 0 Indhold. Funktioner.... Grafen for en funktion...3. grafers skæring med koordinat akser...4. To grafers skæringspunkter...4 3. Egenskaber
Integration i flere Variable. Steen Markvorsen Institut for Matematik, DTU
 Integration i flere Variable Steen Markvorsen Institut for Matematik, DTU 14. februar 2006 2 Indhold 1 Introduktion 5 1.1 Hvad er et punkt og hvordan ser vi det?...................... 6 1.2 Summer og integraler................................
Integration i flere Variable Steen Markvorsen Institut for Matematik, DTU 14. februar 2006 2 Indhold 1 Introduktion 5 1.1 Hvad er et punkt og hvordan ser vi det?...................... 6 1.2 Summer og integraler................................
En differentiabel funktion hvis afledte ikke er kontinuert Søren Knudby
 24 En differentiabel funktion hvis afledte ikke er kontinuert Søren Knudby Det er velkendt for de fleste, at differentiabilitet af en reel funktion f medfører kontinuitet af f, mens det modsatte ikke gælder
24 En differentiabel funktion hvis afledte ikke er kontinuert Søren Knudby Det er velkendt for de fleste, at differentiabilitet af en reel funktion f medfører kontinuitet af f, mens det modsatte ikke gælder
LiA 2 Side 0. Lineær algebra 3. kursusgang
 LiA 2 Side 0 Lineær algebra 3. kursusgang LiA 2 Side 1 Højdeforskelle. D C 0.7 0.7 0.8 E LiA 2 Side 2 Vi har tre punkter C, D og E. Højderne er h C, h D, h E. (I det følgende benævnes disse også x, y,
LiA 2 Side 0 Lineær algebra 3. kursusgang LiA 2 Side 1 Højdeforskelle. D C 0.7 0.7 0.8 E LiA 2 Side 2 Vi har tre punkter C, D og E. Højderne er h C, h D, h E. (I det følgende benævnes disse også x, y,
Funktion af flere variable
 Funktion af flere variable Preben Alsholm 6. oktober 2008 1 Funktion af flere variable 1.1 Punktmængder i R k : Definitioner Punktmængder i flerdimensionale rum: Definitioner q Normen af x 2 R k er kxk
Funktion af flere variable Preben Alsholm 6. oktober 2008 1 Funktion af flere variable 1.1 Punktmængder i R k : Definitioner Punktmængder i flerdimensionale rum: Definitioner q Normen af x 2 R k er kxk
Besvarelser til Calculus Ordinær Eksamen - 5. Januar 2018
 Besvarelser til Calculus Ordinær Eksamen - 5. Januar 18 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 5. Januar 18 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Matematisk modellering og numeriske metoder. Lektion 8
 Matematisk modellering og numeriske metoder Lektion 8 Morten Grud Rasmussen 18. oktober 216 1 Fourierrækker 1.1 Periodiske funktioner Definition 1.1 (Periodiske funktioner). En periodisk funktion f er
Matematisk modellering og numeriske metoder Lektion 8 Morten Grud Rasmussen 18. oktober 216 1 Fourierrækker 1.1 Periodiske funktioner Definition 1.1 (Periodiske funktioner). En periodisk funktion f er
Værktøjskasse til analytisk Geometri
 Værktøjskasse til analytisk Geometri Frank Villa. september 04 Dette dokument er en del af MatBog.dk 008-0. IT Teaching Tools. ISBN-3: 978-87-9775-00-9. Se yderligere betingelser for brug her. Indhold
Værktøjskasse til analytisk Geometri Frank Villa. september 04 Dette dokument er en del af MatBog.dk 008-0. IT Teaching Tools. ISBN-3: 978-87-9775-00-9. Se yderligere betingelser for brug her. Indhold
11. Funktionsundersøgelse
 11. Funktionsundersøgelse Hayati Balo,AAMS Følgende fremstilling er baseret på 1. Nils Victor-Jensen,Matematik for adgangskursus, B-niveau 2, 2. udg. 11.1 Generelt om funktionsundersøgelse Formålet med
11. Funktionsundersøgelse Hayati Balo,AAMS Følgende fremstilling er baseret på 1. Nils Victor-Jensen,Matematik for adgangskursus, B-niveau 2, 2. udg. 11.1 Generelt om funktionsundersøgelse Formålet med
Funktion af flere variable
 Funktion af flere variable Preben Alsolm 24. april 2008 1 Funktion af flere variable 1.1 Differentiabilitet for funktion af én variabel Differentiabilitet for funktion af én variabel f kaldes differentiabel
Funktion af flere variable Preben Alsolm 24. april 2008 1 Funktion af flere variable 1.1 Differentiabilitet for funktion af én variabel Differentiabilitet for funktion af én variabel f kaldes differentiabel
Epistel E2 Partiel differentiation
 Epistel E2 Partiel differentiation Benny Lautrup 19 februar 24 Funktioner af flere variable kan differentieres efter hver enkelt, med de øvrige variable fasthol Definitionen er f(x, y) x f(x, y) f(x +
Epistel E2 Partiel differentiation Benny Lautrup 19 februar 24 Funktioner af flere variable kan differentieres efter hver enkelt, med de øvrige variable fasthol Definitionen er f(x, y) x f(x, y) f(x +
Sætning (Kædereglen) For f(u), u = g(x) differentiable er den sammensatte funktion F = f g differentiabel med
 Oversigt [S] 3.5, 11.5 Nøgleord og begreber Kædereglen i en variabel Kædereglen to variable Test kædereglen Kædereglen i tre eller flere variable Jacobimatricen Kædereglen på matrixform Test matrixform
Oversigt [S] 3.5, 11.5 Nøgleord og begreber Kædereglen i en variabel Kædereglen to variable Test kædereglen Kædereglen i tre eller flere variable Jacobimatricen Kædereglen på matrixform Test matrixform
Værktøjskasse til analytisk Geometri
 Værktøjskasse til analytisk Geometri Frank Nasser 0. april 0 c 008-0. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk:
Værktøjskasse til analytisk Geometri Frank Nasser 0. april 0 c 008-0. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk:
Differentiation af sammensatte funktioner
 1/7 Differentiation af sammensatte funktioner - Fra www.borgeleo.dk En sammensat funktion af den variable x er en funktion, vor x først indsættes i den såkaldte indre funktion. Resultatet fra den indre
1/7 Differentiation af sammensatte funktioner - Fra www.borgeleo.dk En sammensat funktion af den variable x er en funktion, vor x først indsættes i den såkaldte indre funktion. Resultatet fra den indre
Vektorfunktioner. (Parameterkurver) x-klasserne Gammel Hellerup Gymnasium
 Vektorfunktioner (Parameterkurver) x-klasserne Gammel Hellerup Gymnasium Indholdsfortegnelse VEKTORFUNKTIONER... Centrale begreber... Cirkler... 5 Epicykler... 7 Snurretoppen... 9 Ellipser... 1 Parabler...
Vektorfunktioner (Parameterkurver) x-klasserne Gammel Hellerup Gymnasium Indholdsfortegnelse VEKTORFUNKTIONER... Centrale begreber... Cirkler... 5 Epicykler... 7 Snurretoppen... 9 Ellipser... 1 Parabler...
MATEMATIK 11 Eksamensopgaver Juni 1995 Juni 2001, 3. fjerdedel
 MATEMATIK Eksamensopgaver Juni 995 Juni 200, 3. fjerdedel August 998 Opgave. Lad f : R \ {0} R betegne funktionen givet ved f(x) = ex x for x 0. (a) Find eventuelle lokale maksimums- og minimumspunkter
MATEMATIK Eksamensopgaver Juni 995 Juni 200, 3. fjerdedel August 998 Opgave. Lad f : R \ {0} R betegne funktionen givet ved f(x) = ex x for x 0. (a) Find eventuelle lokale maksimums- og minimumspunkter
Hvis man ønsker mere udfordring, kan man springe den første opgave af hvert emne over.
 Opsamling Hvis man ønsker mere udfordring, kan man springe den første opgave af hvert emne over.. Brøkregning, parentesregneregler, kvadratsætningerne, potensregneregler og reduktion Udregn nedenstående
Opsamling Hvis man ønsker mere udfordring, kan man springe den første opgave af hvert emne over.. Brøkregning, parentesregneregler, kvadratsætningerne, potensregneregler og reduktion Udregn nedenstående
Matematisk modellering og numeriske metoder
 Matematisk modellering og numeriske metoder Morten Grud Rasmussen 5. september 2016 1 Ordinære differentialligninger ODE er 1.1 ODE er helt grundlæggende Definition 1.1 (Ordinære differentialligninger).
Matematisk modellering og numeriske metoder Morten Grud Rasmussen 5. september 2016 1 Ordinære differentialligninger ODE er 1.1 ODE er helt grundlæggende Definition 1.1 (Ordinære differentialligninger).
Uge 11 Lille Dag. Opgaver til OPGAVER 1. Det ortogonale komplement
 OPGAVER 1 Opgaver til Uge 11 Lille Dag Opgave 1 Det ortogonale komplement a) I R 2 er der givet vektoren (3, 7). Angiv en basis for det ortogonale komplement. b) Find i R 3 en basis for det ortogonale
OPGAVER 1 Opgaver til Uge 11 Lille Dag Opgave 1 Det ortogonale komplement a) I R 2 er der givet vektoren (3, 7). Angiv en basis for det ortogonale komplement. b) Find i R 3 en basis for det ortogonale
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin December/januar 14/15 Institution VUC Vestegnen Uddannelse Fag og niveau Lærer(e) Hold stx Mat A Karin Hansen
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin December/januar 14/15 Institution VUC Vestegnen Uddannelse Fag og niveau Lærer(e) Hold stx Mat A Karin Hansen
Integration i flere Variable
 Integration i flere Variable Steen Markvorsen Institut for Matematik og Learning Lab DTU 28. januar 2005 2 Indhold Introduktion 5. Hvad er et punkt og hvordan ser vi det?...................... 6.2 Summer
Integration i flere Variable Steen Markvorsen Institut for Matematik og Learning Lab DTU 28. januar 2005 2 Indhold Introduktion 5. Hvad er et punkt og hvordan ser vi det?...................... 6.2 Summer
Besvarelser til Calculus Ordinær Eksamen Juni 2018
 Besvarelser til Calculus Ordinær Eksamen - 5. Juni 08 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 5. Juni 08 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus og Lineær Algebra Globale Forretningssystemer Eksamen - 3. Juni 2014
 Besvarelser til Calculus og Lineær Algebra Globale Forretningssystemer Eksamen - 3. Juni 204 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over
Besvarelser til Calculus og Lineær Algebra Globale Forretningssystemer Eksamen - 3. Juni 204 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over
Ting man gør med Vektorfunktioner
 Ting man gør med Vektorfunktioner Frank Villa 3. august 13 Dette dokument er en del af MatBog.dk 8-1. IT Teaching Tools. ISBN-13: 978-87-9775--9. Se yderligere betingelser for brug her. Indhold 1 Introduktion
Ting man gør med Vektorfunktioner Frank Villa 3. august 13 Dette dokument er en del af MatBog.dk 8-1. IT Teaching Tools. ISBN-13: 978-87-9775--9. Se yderligere betingelser for brug her. Indhold 1 Introduktion
Gauss divergenssætning
 enote 26 1 enote 26 Gauss divergenssætning I denne enote vil vi bruge flowkurver for vektorfelter til at undersøge hvordan overfladen af et rumligt område deformeres ved flowet og dermed afspejler en tilsvarende
enote 26 1 enote 26 Gauss divergenssætning I denne enote vil vi bruge flowkurver for vektorfelter til at undersøge hvordan overfladen af et rumligt område deformeres ved flowet og dermed afspejler en tilsvarende
Matematisk modellering og numeriske metoder. Lektion 1
 Matematisk modellering og numeriske metoder Lektion 1 Morten Grud Rasmussen 4. september, 2013 1 Ordinære differentialligninger ODE er 1.1 ODE er helt grundlæggende Definition 1.1 (Ordinære differentialligninger).
Matematisk modellering og numeriske metoder Lektion 1 Morten Grud Rasmussen 4. september, 2013 1 Ordinære differentialligninger ODE er 1.1 ODE er helt grundlæggende Definition 1.1 (Ordinære differentialligninger).
Eksamen i Mat F, april 2006
 Eksamen i Mat F, april 26 Opgave 1 Lad F være et vektorfelt, givet i retvinklede koordinater som: F x x F = F x i + F y j + F z k = F y = 2z F z y Udregn F og F: F = F x + F y + F z = 1 + +. F = F z F
Eksamen i Mat F, april 26 Opgave 1 Lad F være et vektorfelt, givet i retvinklede koordinater som: F x x F = F x i + F y j + F z k = F y = 2z F z y Udregn F og F: F = F x + F y + F z = 1 + +. F = F z F
Undervisningsbeskrivelse
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Institution Uddannelse Fag og niveau Lærer(e) Hold December 2015 vinter VUC Vestegnen stx Mat A Gert Friis
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Institution Uddannelse Fag og niveau Lærer(e) Hold December 2015 vinter VUC Vestegnen stx Mat A Gert Friis
Indhold. Litteratur 11
 Indhold Forord ii 00-sættet 1 Opgave 1....................................... 1 Spørgsmål (a).................................. 1 Spørgsmål (b).................................. 1 Spørgsmål (c)..................................
Indhold Forord ii 00-sættet 1 Opgave 1....................................... 1 Spørgsmål (a).................................. 1 Spørgsmål (b).................................. 1 Spørgsmål (c)..................................
Integralregning ( 23-27)
 Integralregning ( -7) -7 Side Bestem ved håndkraft samtlige stamfunktioner til hver af funktionerne a) f() =, + 7 ) f() = 7 + 7 c) f() = ep() + ln() d) f() = e ep() + Bestem ved håndkraft samtlige stamfunktioner
Integralregning ( -7) -7 Side Bestem ved håndkraft samtlige stamfunktioner til hver af funktionerne a) f() =, + 7 ) f() = 7 + 7 c) f() = ep() + ln() d) f() = e ep() + Bestem ved håndkraft samtlige stamfunktioner
Opgave 1 Opskriv følgende vinkler i radianer 180, 90, 135, 270, 60, 30.
 Opgaver Polære koordinater Opgave 1 Opskriv følgende vinkler i radianer 180, 90, 15, 70, 60, 0. Opgave Bestem sin π Opgave. Et punkt p i xy-planen er givet ved de kartesiske koordinater,. Bestem p s polære
Opgaver Polære koordinater Opgave 1 Opskriv følgende vinkler i radianer 180, 90, 15, 70, 60, 0. Opgave Bestem sin π Opgave. Et punkt p i xy-planen er givet ved de kartesiske koordinater,. Bestem p s polære
Lokalt ekstremum DiploMat 01905
 Lokalt ekstremum DiploMat 0905 Preben Alsholm Institut for Matematik, DTU 6. oktober 00 De nition Et stationært punkt for en funktion af ere variable f vil i disse noter blive kaldt et egentligt saddelpunkt,
Lokalt ekstremum DiploMat 0905 Preben Alsholm Institut for Matematik, DTU 6. oktober 00 De nition Et stationært punkt for en funktion af ere variable f vil i disse noter blive kaldt et egentligt saddelpunkt,
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Maj-juni 2019 Institution
 Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Maj-juni 2019 Institution Kruses Gymnasium Uddannelse Fag og niveau Lærer(e) Hold Stx Matematik A Angela N.
Undervisningsbeskrivelse Stamoplysninger til brug ved prøver til gymnasiale uddannelser Termin Maj-juni 2019 Institution Kruses Gymnasium Uddannelse Fag og niveau Lærer(e) Hold Stx Matematik A Angela N.
